Графическое решение квадратных уравнений. Видеоурок. Алгебра 8 Класс

На этом уроке мы рассмотрим тему «Графическое решение квадратных уравнений»

Уравнение вида 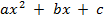 = 0, где а ≠ 0 называется квадратным. Если же а = 0, то у нас будет линейное уравнение, а на данном уроке мы их не рассматриваем.

Функция 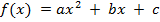, где а ≠ 0 называется квадратичной функцией. Графиком этой функции является парабола. Если a > 0, то ветви данной параболы направлены вверх. Если же a < 0, то ветви параболы направлены вниз. Шаблоном для данной параболы является парабола .

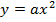Координаты вершины:

 =

  = —

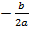
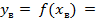
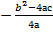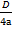
Единственный метод, которым сейчас можем решить квадратное уравнение, – это графический метод, который и рассмотрим в следующем примере.

Решить уравнение  = 0

Решение:

Построим график функции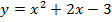

Шаблоном является график функции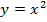

Получаем график :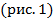

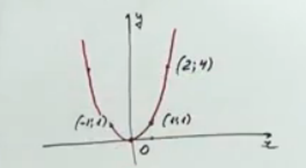
Рис. 1. Иллюстрация к примеру

Итак, мы построили график функции у = x². Для того чтобы построить график функции 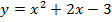, надо сдвинуть вершину графика. Чтобы понять, куда ее сдвинуть, есть 2 способа:

1^й способ. Вычислим

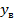, а потом  (а = 1; b = 2; c = -3)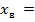

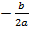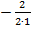   =  = -1

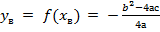 = (-1)

2 + 2 ∙ (-1) – 3 = -4

Так как мы знаем теперь координаты вершины параболы (-1; -4), то теперь помещаем вершину туда и получаем график искомой параболы (которая будет пересекаться с осью Охв точках (-3; 0) и (1; 0) .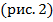

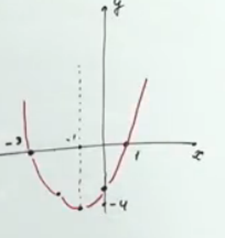
Рис. 2. Иллюстрация к примеру, второй способ

Корнями же уравнения будет точки пересечения с осью О_х.

Проверим:

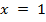 тогда 1² +2 ∙1 -3 = 0                          0 = 0 (1 – корень данного уравнения)

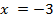 тогда (-3)² + 2 ∙ (-3) – 3 = 0             0 = 0 (-3 – корень данного уравнения)

Ответ: 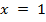 и  

И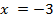звестно, что любая прямая (включая и ось Ох) рассекает параболу в 2^х точках. Эти точки мы и предъявили, значит, задача решена правильно.

2^й способ. Он заключается в выделении полного квадрата.

 

 

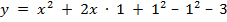
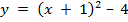
Чтобы учесть 1, нужно сдвинуть исходную параболу на 1 единицу влево, а для учета 4 нам надо сдвинуть параболу на 4 единицы вниз. И мы получим график исходной функции. Далее мы выполняем действия, упомянутые в 1^м способе. Ответ также будет 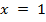 и .

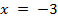Рассмотрим иной способ решения того же уравнения:

Решить уравнение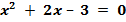

 

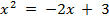
Строим графики функци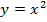й  и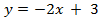

Как построить график функции 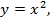 уже известно (его шаблоном будет парабола).

А график функции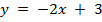

 строим с помощью таблицы:

х	0
у	3	0

      

            
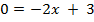
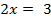
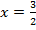
Тогда рисуем графики :

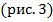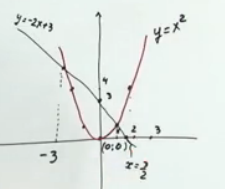
Рис. 3. Иллюстрация к примеру

Аккуратный чертеж показывает, что графики функций пересекаются в точках с абсциссами 1 и -3. При проверке мы подтверждаем, что решением являются 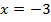 и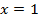

.

Ответ: х = -3 и х = 1.

Преимущество данного способа в том, мы строили самую простую из всех возможных парабол. Однако нам пришлось также строить график линейной функции, но он строится несложно. Затем получили 2 точки пересечения, определили абсциссы, которые надо проверить.

Рассмотрим уравнение в общем виде 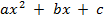 = 0, где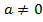

Для решения данного уравнения необходимо:

1-й способ (построить график всей функции)

а) Надо построить параболу функции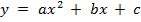

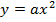, используя шаблон .

б) Найти точки пересечения с осью Ох и взять их абсциссы .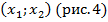

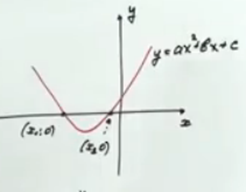
Рис. 4. Иллюстрация к примеру б)

в) Осуществить проверку взятых абсцисс методом подставления их в уравнение и выписать ответ.

2-й способ (уединить член с )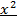

а) Видоизменить уравнение за счет уединения : .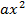

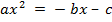б) Построить параболу 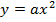 и прямую .

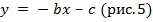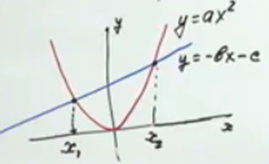
Рис. 5. Иллюстрация к примеру б)

в) Найти абсциссы точек пересечения графиков .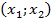

г) Осуществить проверку взятых абсцисс методом подставления их в уравнение и выписать ответ .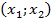

Замечания:

а) 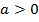, так как уравнение можно умножить на -1 почленно;

б) прямая пересекает параболу не более чем в 2-х точках.

Из положительных моментов стоит отметить, что графический метод позволяет решить такие уравнения, которые мы не можем решить аналитически.

Среди недостатков выделяют то, что надо считывать, почти угадывать абсциссы (приближенность метода – его минус).

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5 издание. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Домашнее задание

1. № 23.4, 23.7, 23.8 стр. 145. Мордкович А.Г. Алгебра 8 класс. Задачник для учащихся общеобразовательных школ.– 12-е изд. – М.: Мнемозина, 2010. – 273 стр.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал Fxyz.ru  (Источник).
2. Интернет-портал Festival.1september.ru  (Источник).
3. Интернет-портал Unimath.ru  (Источник).

interneturok.ru

Графическое решение квадратных уравнений

На уроке учащиеся продемонстрировали знания и умения программы:

– распознавать виды функции, строить их графики;
– отрабатывали навыки построения квадратичной функции;
– отрабатывали графические способы решения квадратных уравнений, используя метод выделения полного квадрата.

Мне захотелось уделить особое внимание решению задач с параметром, так как ЕГЭ по математике предлагает очень много заданий такого типа.

Возможность применить на уроке такой вид работы дали мне сами ученики, так как они имеют достаточную базу знаний, которые можно углубить и расширить.

Заранее подготовленные учащимися шаблоны позволили экономить время урока. В ходе урока мне удалось реализовать поставленные задачи в начале урока и получить ожидаемый результат.

Использование физкультминутки помогло избежать переутомления учащихся, сохранить продуктивную мотивацию получения знаний.

В целом результатом урока я довольна, но думаю, что есть еще резервные возможности: современные инновационные технологические средства, которыми мы, к сожалению, не имеем возможности пользоваться.

Тип урока: закрепление изученного материала.

Цели урока:

• Общеобразовательные и дидактические:
  • развивать разнообразные способы мыслительной деятельности учащихся;
  • формировать способности самостоятельного решения задач;
  • воспитывать математическую культуру учащихся;
  • развивать интуицию учащихся и умение пользоваться    полученными знаниями.
• Учебные цели:
  • обобщить ранее изученные сведения по теме «Графическое  решение квадратных уравнений»;
  • повторить построение графиков квадратичной функции;
  • сформировать навыки использования алгоритмов решения квадратичных уравнений графическим методом.
• Воспитательные:
  • привитие интереса к учебной деятельности, к  предмету математики;
  • формирование толерантности (терпимости), умения работать в коллективе.

ХОД УРОКА

I. Организационный момент

– Сегодня на уроке мы обобщим и закрепим графическое решение квадратных уравнений различными способами.
В дальнейшем эти навыки нам будут нужны в старших классах на уроках математики при решении тригонометрических и логарифмических  уравнений, нахождения площади криволинейной трапеции, а также на уроках физики.

II. Проверка домашней работы

Разберем на доске № 23.5(г).

Решить это уравнение с помощью параболы и прямой.

Решение:

х² + х – 6 = 0
Преобразуем уравнение:  х² = 6 – х
Введем функции:

у = х²;   квадратичная функция                                         у = 6 – х    линейная,
графиком  явл. парабола,                                                   графиком  явл. прямая,

Строем в одной системе координат графики функций (по шаблону)

Получили две точки пересечения.

Решением квадратного уравнения являются абсциссы этих точек х₁ = – 3, х₂ = 2.

Ответ:  – 3; 2.

III. Фронтальный опрос

• Что является графиком квадратичной функции?
• Скажите алгоритм построения графика квадратичной функции?
• Что называется квадратичным уравнением?
• Приведите примеры квадратичных уравнений?
• Запишите на доске свой пример квадратичного уравнения, Назовите,  чему равны коэффициенты?
• Что значит решить уравнение?
• Сколько способов вы знаете графического решения квадратных уравнений?
• В чем заключается графические способы решение квадратных уравнений:

IV. Закрепление материала

№ 23.6 (а)

На доске решают учащиеся первым, вторым, третьим  способами.

Класс решает четвертым

– х² + 6х – 5 = 0

Преобразую квадратное уравнение, выделяя полный квадрат двучлена:

– х² + 6х – 5 = – (х² – 6х + 5) = – (х² – 6х + 32 – 9 + 5) = – ((х – 3)² – 4) = – (х – 3)² + 4

Получили квадратное уравнение:

– (х – 3)² + 4 = 0

Введем функцию:

у = – (х² – 3)² + 4

Квадратичная функция вида у = а (х + L)² + m

Графиком явл. парабола, ветви направлены вниз, сдвиг основной параболы по оси Ох в право на 3 ед., по оси Оу вверх на 4 ед., вершина (3; 4). 

Строим по шаблону.

Нашли точки пересечения  параболы с осью Ох. Абсциссы этих точек явл. решением данного уравнения.  х = 1, х = 5.

Давайте посмотрим другие графические решение у доски. Прокомментируйте свой способ решения квадратных уравнений.

1 ученик

Решение:

– х² + 6х – 5 = 0

Введем функцию у = – х + 6х – 5, квадратичная функция, графиком является парабола, ветви направлены вниз, вершина

х₀ = – в/2а
х₀ = – 6/– 2 = 3
у₀ = – 3² + 18 = 9;  точка (3; 9)
ось симметрии х = 3

Строим по шаблону

Получили точки пересечения с осью Ох, абсциссы этих точек являются решением квадратного уравнения. Два корня х₁ = 1, х₂ = 5

2 ученик

Решение:

– х² + 6х – 5 = 0

Преобразуем:  – х² + 6х = 5

Введем функции: у1 = – х² + 6х, у2 = 5, линейная функция, квадратичная функция, графиком  графиком явл. прямая у || Ох явл. парабола, ветви направлены   вниз, вершина  х₀ = – в/2а
х₀ = – 6/– 2 = 3
у₀ = – 3² + 18 = 9;
(3; 9).
ось симметрии х = 3
Строим по шаблону
Получили точки пересечения
параболы и прямой, их абсциссы являются решением квадратного уравнения. Два корня х₁ = 1, х₂ = 5
Итак, одно и тоже уравнение можно решать различными способами, а ответ получаться должен один и тот же.

V. Физкультминутка

VI. Решение задачи с параметром

№ 23.19

При каких значениях р уравнение х² + 6х + 8 = р:
– Не имеет корней?
– Имеет один корень?
– Имеет два  корня?
Чем отличается это уравнение от предыдущего?
Правильно, буквой!
Эту букву в дальнейшем мы будем называть параметром, Р.
Пока она вам ни о чем не говорит. Но мы будем  в дальнейшем решать различные задачи с параметром.
Сегодня решим квадратное уравнение с параметром графическим методом, используя третий способ с помощью параболы и прямой параллельной оси абсцисс.
Ученик помогает учителю решать у доски.
С чего начнем решать?

Зададим функции:

у₁ = х² + 6х + 8                                        у₂ = р линейная функция,
квадратичная функция,                          графиком является прямая
графиком явл. парабола,
ветви направлены вниз, вершина 

х₀ = – в/2а,
х₀ = – 6/2 = – 3
у₀ = (– 3)² + 6(– 3) + 8 = – 1
(– 3; – 1)

Ось симметрии х = 3, таблицу строить не буду, а возьму шаблон у = х² и приложу к вершине параболы.
Парабола построена! Теперь надо провести прямую у = р.
– Где надо начертить прямую р, чтобы получить два корня?
– Где надо начертить прямую р, чтобы получить один корень?
– Где надо начертить прямую р, чтобы не было корней?
– Итак, сколько наше уравнение может иметь корней?
– Понравилась задача? Спасибо за помощь! Оценка 5.

VII. Самостоятельная работа по вариантам (5 мин.)

I В.                                         II В.

у = х² – 5х + 6                       у = – х² + х – 6

Решить квадратное уравнение графическим способом, выбирая для вас удобный способ. Если кто-то справится с заданием раньше, проверьте свое решение другим способом. За это будет выставляться дополнительная оценка.

VIII. Итог урока

– Чему научились вы на сегодняшнем уроке?
– Сегодня на уроке мы с вами квадратные уравнения решали графическим методом, используя различные способы решения, и рассмотрели графический способ решения квадратного уравнения с параметром!
– Переходим к домашнему заданию.

IХ.  Домашнее задание

1. Домашняя контрольная работа на стр. 147, из задачника Мордковича по вариантам I и II.
2. На кружке, в среду, будем решать V-м способом, (гипербола и прямая).

Х. Литература:

1.  А.Г. Мордкович. Алгебра-8. Часть 1. Учебник для учащихся образовательных учреждений. М.: Мнемозина, 2008 г.
2.  А.Г. Мордкович, Л.А.Александрова, Т.Н. Мишустина, Е.Е. Тульчинская. Алгебра – 8. Часть 2. Задачник для учащихся образовательных учреждений. М.: Мнемозина, 2008 г.
3.  А.Г. Мордкович. Алгебра 7-9. Методическое пособие для учителя.М.: Мнемозина, 2004 г.
4.  Л.А. Александрова. Алгебра-8. Самостоятельные работы для учащихся образовательных учреждений./Под ред. А.Г. Мордковича. М.: Мнемозина, 2009 г.

urok.1sept.ru

Как решить квадратное уравнение графически

Пусть имеется полное квадратное уравнение: A*x2+B*x+C=0, где A, B и C — любые числа, причем A не равно нулю. Это общий случай квадратного уравнения. Существует также приведенный вид, в котором A=1. Чтобы решить графически любое уравнение, нужно перенести в другую часть слагаемое с наибольшей степенью и приравнять обе части к какой-либо переменной.

После этого в левой части уравнения останется A*x2, а в правой — B*x-C (можно предположить, что B — отрицательное число, сути это не меняет). Получится уравнение A*x2=B*x-C=y. Для наглядности в этом случае обе части приравнены к переменной y.

Теперь можно записать два уравнения: y=A*x2 и y=B*x-C. Далее необходимо построить график каждой из этих функций. График y=A*x2 представляет собой параболу с вершиной в начале координат, ветви которой направлены вверх или вниз, в зависимости от знака числа A. Если оно отрицательно, ветви направлены вниз, если положительно — вверх.

График y=B*x-C представляет собой обычную прямую линию. Если C=0, прямая проходит через начало координат. В общем случае она отсекает от оси ординат отрезок, равный С. Угол наклона этой прямой относительно оси абсцисс определяется коэффициентом B. Он равен тангенсу наклона этого угла.

После того как графики построены, будет видно, что они пересекутся в двух точках. Координаты этих точек по оси абсцисс определяют корни квадратного уравнения. Для их точного определения нужно четко строить графики и правильно выбрать масштаб.

Существует еще один способ графического решения квадратного уравнения. Необязательно переносить B*x+C в другую часть уравнения. Можно сразу построить график функции y=A*x2+B*x+C. Такой график представляет собой параболу с вершиной в произвольной точке. Этот способ сложнее предыдущего, зато можно построить только один график, чтобы решить уравнение.

Сначала нужно определить вершину параболы с координатами x0 и y0. Ее абсцисса вычисляется по формуле x0=-B/2*a. Для определения ординаты нужно подставить полученное значение абсциссы в исходную функцию. Математически это утверждение записывается так: y0=y(x0).

Затем требуется найти две точки, симметричные оси параболы. В них исходная функция должна обращаться в ноль. После этого можно строить параболу. Точки ее пересечения с осью Х дадут два корня квадратного уравнения.

www.kakprosto.ru

Онлайн урок графический метод решения квадратных уравнений.

Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.

 

 

 

 

 

 

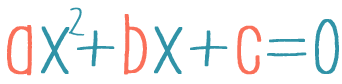
Квадратное уравнение — это уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа, причем a ≠ 0.

 

 

 

 

 

 

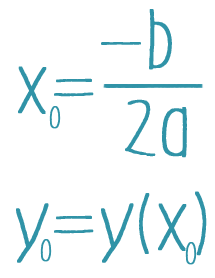
Координаты вершины параболы A(x₀; y₀), задаваемой функцией y = ax² + bx + c.

 

 

 

 

 

 

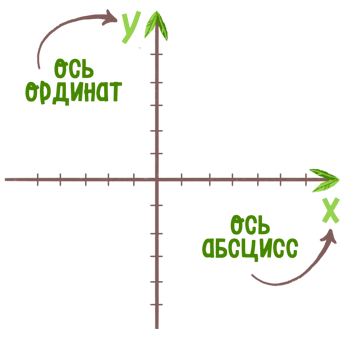
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями абсцисс и ординат на плоскости.

 

 

 

 

Теперь выбери соответствия между картинками и определениями, которые мы только что повторили.

 

 

 

 

 

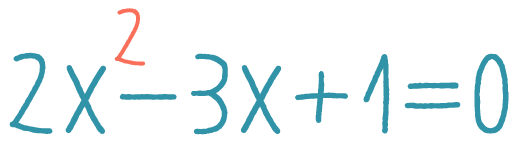
a = 2; b = 3; c = 1a = 2; b = -3; c = 1a = -3; b = 2; c = 1a = 2; b = -3; c = -1

 

 

 

 

 

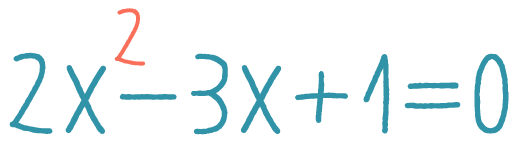
x₀ = -2/3 = -2/3x₀ = -2/2 · 3 = -1/3x₀ = 3/2 · 2 = 3/4x₀ = -1/2 · 3 = -1/6

 

 

 

 

 

ось абсциссось ординаткоординатный луч

 

 

 

 

Прежде чем мы начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:

1. Графический метод.

2. Решение квадратных уравнений с помощью графика.

myalfaschool.ru

Графическое решение квадратных уравнений

Тема урока: Графическое решение квадратных уравнений.

Цели урока:

Каждый учащийся:

• Систематизирует свои знания по теме «Построение графика квадратичной функции»,

• Распознает квадратные уравнения,

• Решает квадратные уравнения графическим способом,

• Правильно определяет методы решения конкретного уравнения в знакомой ситуации.

Повторяем:

• Построение параболы по алгоритму и с помощью метода выделения полного квадрата из квадратного трехчлена,

• Преобразование графиков функций с помощью параллельного переноса вдоль осей координат.

Знания и навыки:

Каждый учащийся:

• Знает определение квадратичной функции,

• Знает алгоритм построения графика квадратичной функции,

• Знает шаблоны графиков изученных функций,

• Умеет строить графики изученных функций с помощью параллельного переноса вдоль осей координат,

• Умеет решать квадратные уравнения графическим способом.

Наглядные пособия и раздаточный материал:

• Презентация,

• Демонстрационный материал (рисунки с графиками функций),

• Интерактивная доска,

• Раздаточный материал: шаблоны системы координат, кружки трех цветов.

Ход урока.

Этапы урока

Деятельность учителя

Деятельность учащихся

1. Оргмомент.

Мотивация учебной деятельности.

Учитель настраивает учащихся на исследовательскую работу на уроке.

Здравствуйте, ребята. Наш сегодняшний урок я хотела бы начать словами великого мыслителя и философа Конфуция (551-479гг до н.э.)

Три пути ведут к знаниям:

Путь размышления самый благородный,

Путь подражания самый легкий,

Путь опыта самый горький.

-Как вы понимаете смысл этого высказывания?

Значит лучший способ изучить что-либо – это открыть самому. Сегодня мы с вами постараемся выполнить наставления этого великого человека и с помощью размышлений открыть что – то новое для себя.

Учащиеся, прослушав высказывание, дают объяснения

2. Актуализация опорных знаний учащихся, проверка домашнего задания

Учитель с помощью интерактивной доски проводит проверку домашнего задания

Одновременно с этим учитель проводит устную работу, выполнение которой дает возможность повторения знаний по построению графиков функций, необходимых для изучения нового материала.

Ученик выполняет построение графика функции у=2х²+8х+6 на макете системы координат и указывает свойства: ось параболы, промежутки возрастания, убывания, нули функции, промежутки знакопостоянства. После завершения отвечает на вопросы сверстников:

• Какая функция называется квадратичной?

• Что является осью параболы и как ее найти?

• Что такое нули функции и как их найти?

Учащиеся работают с дидактическим материалом (приложение 1), отвечая устно, аргументируя правильность рассуждений по мере необходимости, повторяя теоретический материал.

3. Объяснение нового материала.

Учитель с помощью задания на интерактивной доске подводит учащихся к формулировке темы и целей урока.

— Так что же называют нулями функции?

-Подставьте в формулу данной функции значение переменной у=0 и скажите, что за равенство получилось? Почему?

— Что значит решить уравнение?

— Что называют корнем уравнения?

-Будут ли значения х=-3 и х=-1 корнями данного уравнения?

-Что это значит?

— Что бы вы хотели узнать об уравнениях такого вида? Мы ведь уже знакомы с линейными уравнениями и по вашему опыту работы с ними поставьте перед собой задачи.

— Вспомним определение квадратичной функции.

— Линейная функция – линейные уравнения, квадратичная функция -…

— Попробуйте сформулировать определение квадратных уравнений.

-Давайте рассмотрим это определение и попытаемся выделить существенные признаки, по которым мы будем распознавать квадратные уравнения.

-Что стоит в левой части уравнения? Правой части?

-Какую степень он имеет?

-Как можно переформулировать определение?

-Почему поставлено условие а≠0 и почему это условие накладывается только на а?

-Какие из уравнений будут квадратными:

2х²+5х-3=0

5х-х²=0

х-4=0

5х³-х²+4=0

х²-7+3х³=0 ?

-Что такое квадратное уравнение мы уже знаем. Перейдем к следующей цели: как решаются квадратные уравнения. Но мы ведь нашли корни данного уравнения, значит, мы его решили. Как?

-Что значит решить уравнение графически?

— А мы ведь строили только график левой части уравнения и назвали корни уравнения. Почему?

— Как бы вы сформулировали тему урока?

— Мы договорили следовать словам великого философа Конфуция и в данной ситуации мы не будем отступать от этого правила. Решать неравенства по шаблону мы не будем. Лучше решить одну задачу разными способами, чем несколько задач одним и тем же способом. Давайте применим правила, изученные еще в 6 классе: перенос слагаемых из одной части уравнения в другую, изменив при этом знак и умножение, деление обеих частей уравнения на число отличное от нуля.

— Какой из способов вам понравился больше всего?

— Перейдем к последней из задач, которые мы поставили перед собой: «Сколько корней может иметь квадратное уравнение?». Какое свойство функции нам поможет ответить на вопрос?

-Сейчас мы обратимся к учебнику. Изучая тему квадратичной функции, мы с вами работали с графиками парабол. Откройте страницу учебника 116, 126, 135. Проанализируйте, сколько точек пересечения с осью Ох может иметь парабола?

-Как тогда мы ответим на вопрос: «Сколько корней может иметь квадратное уравнение?»

Учащиеся формулируют тему и цели урока, отвечая на вопросы учителя.

— Нулями функции называют значения переменной х, при которых у=0

— 2х²+8х+6=0. Это уравнение, так как

равенство, содержащее переменную, называют уравнением.

— Решить уравнении – значит найти все его корни или доказать, что их нет.

— Корнем уравнения называют значение переменной, при подстановке которого в уравнение получается верное числовое равенство.

Да, так как точки (-3;0) и (-1;0) принадлежат графику функции. Мы в формулу подставили значение координаты у точки, значит, если подставим значение координаты х точки, то получим верное числовое равенство.

Нули квадратичной функции являются корнями соответствующего уравнения.

— Как эти уравнения называются?

-Сколько решений имеют?

— Как решаются?

Функцию вида у=ах²+вх+с , где а, в, с –произвольные числа, причем а≠0, называют квадратичной функцией.

-Квадратные уравнения.

Уравнения вида ах²+вх+с=0 , где а, в, с –произвольные числа, причем а≠0, называют квадратными уравнениями.

-Слева стоит многочлен, справа ноль.

— Вторую

— Квадратное уравнение это уравнение, в левой части которого многочлен второй степени, а в правой ноль.

— Если а=0, то слева получим многочлен первой степени, а если в=0 или с=0 или в=0 и с=0, то многочлен будет второй степени.

-2х²+5х-3=0

5х-х²=0

— Графически.

— В одной системе координат построить графики левой и правой частей уравнения и найти их точки пересечения, если они есть. Координата х почки пересечения графиков и будет ответом уравнения.

-Потому, что график правой части уравнения у=0 совпадает с осью Ох и ее можно было не строить, а лишь назвать точки пересечения графика с осью ОХ.

— Графическое решение квадратных уравнений.

Учащиеся выполняют перенос слагаемых и с помощью графического метода решения уравнений находят корни уравнения.

2х²+8х=-6. Слева парабола, которую нужно построить по алгоритму. Мы такой случай уже рассмотрели.

2х²+6= -8х

2х²= -8х-6

2х+8= —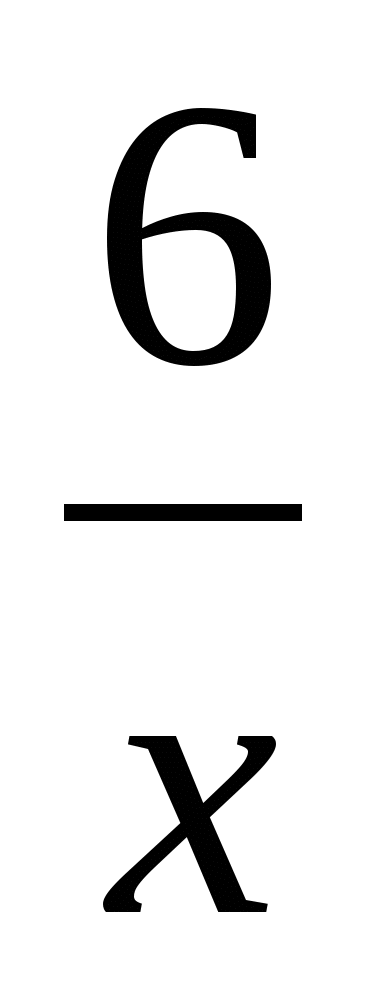

Учащиеся называют способы, показавшиеся им более легкими и удобными.

-Свойство нулей функции.

-Две точки, одну точку пересечения и не иметь точек пересечения.

-Один корень, два корня и не иметь корней.

4. Закрепление изученного материала.

-А сейчас я вам предлагаю решить уравнение удобным для вас способом.

3х²+6х+1=0

-Выбран не совсем удобный способ? Давайте попробуем другим способом. А в чем проблема? Как вы думаете?

— Да, ребята графический способ решения уравнений иногда красив и удобен, но не дает стопроцентной гарантии решения. Значит это не единственный способ решения и существуют другие способы, с которыми нам еще предстоит познакомиться.

Один учащийся работает у доски, а остальные в тетрадях.

-Корни уравнения не являются целыми числами.

5. Итог урока.

Итак, что нового вы узнали на уроке?

-Что называют квадратным уравнением.

-Сколько оно может иметь корней.

— Корнями квадратного уравнения являются нули соответствующей квадратичной функции.

— Графически квадратное уравнение можно решить разными способами.

6.Домашнее задание.

Стр. 145 № 23.4(а,в), 23.6(б,в), 23.8(а)

Учащиеся записывают в дневники

7. Рефлексия.

Ребята, вам понравился урок? Для того, чтобы я это поняла, поднимите кружок с соответствующим цветом:

Красный – ничего не понял

Желтый – понял, но не до конца

Зеленый – мне все понятно.

Урок окончен. Спасибо за внимание.

infourok.ru

Решение квадратных уравнений графическим способом

I V. Физминутка.

Отвели свой взгляд направо,

Отвели свой взгляд налево,

Оглядели потолок,

Посмотрели все вперёд.

Раз – согнулись – разогнулись,

Два ─ согнулись – потянулись,

Три – в ладоши три хлопка,

Головою три кивка.

Пять и шесть тихо сесть.

V. Практическая работа.

Раздаются учащимся дифференцированные задания на карточках. 6 уравнений

-х² — 6х – 8 = 0, х² – 4х + 5 = 0, х² — 5х + 6 = 0, 2х² – 11х + 5 = 0, -2х² + 9х – 9 =0, 1\2х² — 5х + 12 = 0

С помощью правильных ответов вы разгадаете первое слово фразы номеру уравнения правильному ответу соответствует буква из этого слова.

Ответы учащихся: М О С К В А

Москва столица нашей Родины. Несколько фактов о Москве. Москва самый населенный город России и Европы, в Москве проживает свыше 12млн жителей. Если сложить все улицы города, то их протяженность составит около 4350 км. Пешеходу, идущему со скоростью 5км\ч без остановок, понадобиться больше месяца, чтобы преодолеть это расстояние. Московский Кремль считается одним из крупнейшим музеем мира. 7 сентября Москве исполнилось 870 лет со дня образования города Героя – Москва.

Учитель: Прочитайте пожалуйста фразу А.С. Пушкина из романа «Евгений Онегин», которая у нас получилась «Москва … как много в этом звуке для сердца русского слилось».

(Как часто в горестной разлуке,

В моей блуждающей судьбе,

Москва, я думал о тебе!

Москва … как много в этом звуке

Для сердца русского слилось!

Как много в нём отозвалось.)

VII. Подведение итогов урока.

Вы замечательно поработали на уроке. Проверив ваши работы и учитывая ваши ответы за устную работу, я поставила вам оценки в индивидуальную таблицу.

Каждый ученик класса принимал участие в уроке. Во время урока заполняется индивидуальная таблица, в которой виден результат его работы на уроке.

работа

Общая

оценка

Надеюсь, этот материал вы не забудете. Помните слова французского инженера-физика Лауэ: «Образование есть то, что остается, когда все выученное уже забыто». Думаю, что образование, которое вы получите, будет соответствовать времени, в котором мы живем. А чтобы это случилось на самом деле, предлагаю вам выполнить следующую творческую домашнюю работу.

VIII. Домашнее задание. Из параграфа выбрать любых 5 уравнений и решить разными способами

Творческое задание: составить рекламу параболе или гиперболе;

сочинить сказку или рассказ на тему «Замечательные

кривые».

IX. Рефлексия.

Ребята, а как вы думаете всегда ли целесообразно использовать графический способ для решения квадратных уравнений (Нет)

Почему нет ( могут быть большие значения и дробные числа) Все правильно поэтому на следующих уроках мы научимся решать квадратные уравнения аналитическим способом с помощью формулы дискриминанта и теоремы Виетта.

На практике из обилия способов выбирают тот, который больше нравится или более понятен. Графические способы решения уравнений понятны, но как вы уже сказали они не дают стопроцентной гарантии решения любого уравнения. Это нужно учитывать. — Возможен вариант, что корень уравнения – это дробное или иррациональное число, т.е. мы сможем найти только приближенное значение корня. — Либо уравнение таково, что ограниченные размеры листа не позволяют построить графики х² – 22х – 103 = 0

Сегодня я узнал…

Было интересно…

Было трудно…

Я понял, что…

Теперь я могу…

Я научился…

У меня получилось…

Я попробую…

Меня заинтересовало…

Мне захотелось…

Я не забуду …

infourok.ru

План-конспект урока по алгебре (8 класс) по теме: Графическое решение квадратных уравнений

Открытый урок по математике

8 класс.

Тема:

«Графическое решение квадратных уравнений».

Учитель: Паламарчук Н.К.

МОУ гимназия № 2

г. Железнодорожный

Тема: «Графическое решение квадратных уравнений».

Цели:

Образовательные:

1. Закрепить умение строить  графики  различных  функции;
2. Формировать умение решать квадратные уравнения графическим  способом.

 Развивающие:

1. Развить творческие способности у учащихся в ходе выполнения  заданий;
2. Развивать умение обосновывать свое решение;
3. Развить умение находить свои ошибки.

Воспитательные:

1. Развивать умение вести индивидуальную дискуссию, самостоятельного поиска решения, нахождения разных способов решения новой задачи;
2. Формирование ответственности каждого за поведения при обсуждении, ораторского мастерства, самооценки качества своего труда.

Формы проведения урока: демонстрация слайдов, устный опрос, самостоятельная работа в тетрадях, работа у доски.

Материалы и оборудование:

 Компьютер, мультимедийный проектор, задачник, мел, доска.

Ход урока:

1. Организационный момент.

(отметить отсутствующих, записать тему, определить цели урока).

Сегодня на уроке мы вспомним: какие функции Вам знакомы; как выглядят их графики, а так же научимся решать графическим способом квадратные уравнения.

2. Актуализация знаний.

1. Какая функция называется квадратичной; линейной?
2. Что является их графиками?
3. Обратно пропорциональная зависимость? Ее график?
4. Что значит решить уравнение?
5.  Что значит решить уравнение  графически?
6. Как построить прямую, параболу, гиперболу?

3. Изучение нового материала.

С квадратными уравнениями вы уже встречались в курсе алгебры 7-го класса. Вспомним, что  квадратным  уравнением называют уравнение вида  aх2 +bх+c = 0, где a,b,c – любые числа, причем а≠0.

Используя   знания о некоторых функциях и их графиках, мы можем решать некоторые квадратные уравнения, причем Слайд 1.

различными способами; мы рассмотрим эти способы на примере одного квадратного уравнения.  

Слайд 2.

Рассмотрим уравнение    x2 – 2x – 3 = 0.

Первый способ: построить график функции y = x2 – 2x –3 Клик по алгоритму Клик и Клик найти точки его пресечения с осью х.

Корни уравнения равны абсциссам точек пересечения параболы с осью ОХ

Слайд 4.

Второй способ: преобразовать уравнение, оставив в левой части только слагаемое, содержащее квадрат переменной. 

Строим параболу y = x2 и прямую y = 2x + 3, находим точки их пересечения.

Корни уравнения – абсциссы точек пересечения параболы с прямой.

Слайд 6.

 Третий способ: преобразовать уравнение, оставив в левой части слагаемое, содержащее квадрат переменной и свободный член. 

Строим параболу y = x2 – 3 и прямую y = 2x, находим точки их пересечения.

Корни уравнения – абсциссы точек пересечения параболы с прямой.

Слайд 8.

Четвертый способ: преобразуем уравнение, используя метод выделения полного квадрата. 

Строим параболу y = (x – 1)2 и прямую y = 4, находим точки их пересечения.

Корни уравнения – абсциссы точек пересечения параболы с прямой.

Слайд 10.

Пятый способ: преобразуем уравнение, разделив почленно обе части уравнения на х. 

Строим  гиперболу  у = 3/x и прямую y = х – 2, находим точки их пересечения.

Корни уравнения – абсциссы точек пересечения гиперболы с прямой.

Слайд 12.

Мы рассмотрели все способы графического решения квадратных уравнений. Следует отметить, что первые четыре способа применимы к любым квадратным уравнениям, а пятый только к тем, у которых с ≠ 0.

Вы можете для решения выбирать наиболее удобный для вас способ.

Слайд 13. Решите уравнение x2 – 4x + 3 = 0 (один ученик у доски)

Проверим: Слайд 14.

4. Закрепление.

Решите графически уравнения: (по одному ученику у доски)

№ 23. 5 а) x2 – x – 2 = 0 (ответ: 2; — 1)

№ 23. 6 а) – x2 + 6x – 5 = 0 (ответ: 1; 5)

При наличии времени выполнить задания:

№ 23. 8 в) x2 + 2x + 4 = 0

Докажите, что уравнение не имеет корней. (парабола с вершиной в точке (-1; 3), ветви направлены вверх).

№ 23.9. Решить задачу:

Найдите стороны прямоугольника, если известно, что его площадь равна 8 см2, а длина на 2 см больше ширины.

Решение:

1 этап: составление математической модели.

Пусть х см – длина прямоугольника, тогда (х – 2) см – ширина. Площадь прямоугольника можно вычислить х (х – 2). Зная, что S = 8 см2, составим уравнение:  х (х – 2) = 8.

2 этап: работа с составленной моделью.

х (х – 2) = 8;

х2 – 2х – 8 = 0;

хв = — (-2)/2 = 1, ув = — 9.

х1 = — 2; х2 = 4.

3этап: ответ на вопрос задачи.

х – это длина, значит х > 0, значит х = — 2 не подходит по смыслу задачи.

Длина прямоугольника – 4 см, тогда ширина прямоугольника 2 см.

ОТВЕТ: длина прямоугольника 4 см, ширина – 2 см.

5. Подведение итогов.

65535. Чему вы сегодня научились?
65536. Каким способом предпочтительнее выполнять задание?
65537. Оценивание. Выставление оценок в дневники.

6. Домашнее задание.

§ 23. №№ 23.3 а), 23. 5 г), 23. 6 г)

Литература:

1. Программы. Математика. 5 – 6 классы. Алгебра 7 – 9 классы. Алгебра и начала анализа. 10 – 11 классы /авт.-сост. И. И. Зубарева, А. Г. Мордкович. – 2 издание, исправленное и дополненное. – М.: Мнемозина, 2009.
2. Мордкович А. Г.

Алгебра. 8 кл.: Учебник для общеобразовательных учреждений./ Мордкович А. Г. — М.: Мнемозина, 2009. – 215с.

3. Мордкович А. Г. и др.

Алгебра. 8 кл.: Задачник для общеобразовательных учреждений. / Мордкович А. Г.- 10-е издание, стереотипное. -М.: Мнемозина, 2009.

nsportal.ru