Отношение площадей подобных треугольников. Видеоурок. Геометрия 8 Класс
Тема: Подобные треугольники
Урок: Отношение площадей подобных треугольников
Начнем с того, что введем определение подобных треугольников.
Определение. Два треугольника называются подобными, еслиих углы попарно равны, а стороны, лежащие напротив соответственных углов, пропорциональны (см. Рис. 1).
 . Отношение длин сторон треугольников называют коэффициентом подобия (
. Отношение длин сторон треугольников называют коэффициентом подобия ( ).
).

Рис. 1
Замечание. Пропорциональные стороны подобных треугольников называют еще сходственными сторонами
Важно понимать, что в подобных треугольниках пропорциональны не только стороны, но и другие соответственные линейные элементы: высоты, медианы, биссектрисы, проведенные к соответственным сторонам, периметры и т.п. Т.е. все эти величины относятся, как коэффициент подобия. Вопрос заключается в том, верно ли аналогичное утверждение и для площадей треугольников. Для того чтобы ответить на этот вопрос, сформулируем теорему.
Теорема 1. Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Доказательство. Изобразим подобные треугольники  на Рис. 2.
на Рис. 2.

Рис. 2
Из подобия треугольников по определению следует, что 
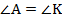 ), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем этот факт в виде формулы:
), то их площади относятся, как произведение сторон, заключающих данные углы. Запишем этот факт в виде формулы: , что и требовалось доказать.
, что и требовалось доказать.
Доказано.
Замечание. Возможно доказательство этой теоремы не единственным указанным способом, а и с использованием различных формул для вычисления площади треугольника, но мы их указывать не будем.
Рассмотрим ряд примеров, в которых применяется рассмотренная теорема.
Пример 1. Если два треугольника подобны с коэффициентом подобия 
Решение. Задача устная и не требует выполнения чертежа. Воспользуемся изученной теоремой:  .
.
Ответ. 2.
Пример 2. Треугольники
interneturok.ru
Урок «Определение подобных треугольников»
Урок геометрии в 8 классе
Тема. Определение подобных треугольников.
Учитель математики МБОУ СОШ №49 г.Шахты
Гладкая Н.В.
Цель:
-
Ввести новые понятия: отношение отрезков, пропорциональные отрезки, сходственные стороны, подобные треугольники, коэффициент подобия.
Учить использовать новые понятия, а также известные определения и теоремы для решения задач.
Развивать логическое мышление.
Ход урока.
①Повторение ранее изученных понятий.
Что называют отношением чисел? (Это частное от деления двух чисел, которое показывает, во сколько раз одно число больше другого, или, какую часть одно число составляет от другого)
Что называют пропорцией? (Равенство двух отношений)
В чем заключается основное свойство пропорции? (Произведение крайних членов пропорции равно произведению ее средних членов)
② Проверка решения задач, подготавливающих введение новых понятий. (Домашнее задание)
Задача №1.
Длина прямой тропинки на дачном участке, ведущей от дома к сараю, составляет 12 м, а тропинки, ведущей к колодцу, составляет 15 м.
Найти отношение первой длины ко второй.
 . Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй).
. Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй).Найти отношение второй длины к первой.
 . Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой).
. Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой).Выразить величины в сантиметрах и снова найти отношения. (
 .
.Выразить величины в километрах и найти отношения.
.
Сделать вывод о том, зависит ли отношение длин отрезков от того, в каких единицах они выражены. (Не зависит).
Задача №2.

Найти отношение отрезков:
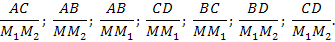
Выбрать равные отношения и записать их равенство.
Решение:
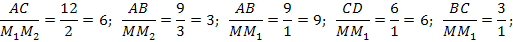

③ Самостоятельная работа с текстом и закрепление новых знаний.
Работа с текстом пункта 56 «Пропорциональные отрезки» из §1 ( учебник Л. С. Атанасяна). Прочесть текст, выбрать, сформулировать и записать определения следующих понятий.
Отношение отрезков. (Отношением отрезков АВ и СD называется отношение их длин, то есть
 .
.Пропорциональные отрезки. (Отрезки АВ и СD пропорциональны отрезкам
. , если
, если  . Отрезки
. Отрезки  , если справедливо равенство
, если справедливо равенство 
Закрепление новых знаний.
№533 (устно). Найти отношение отрезков ABи CD, если их длины равны соответственно 15 см и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах? (Отношение равно
 ; при изменении единиц длины оно не меняется)
; при изменении единиц длины оно не меняется)№534 (устно, использовать результаты решения домашней задачи №2). Пропорциональны ли изображенные на рисунке отрезки: а)
 ; б)
; б) ; в)
; в)
④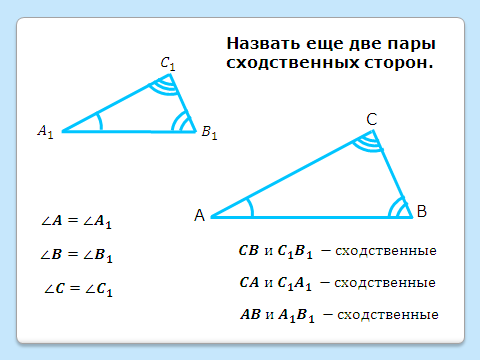 Определение подобных треугольников.
Определение подобных треугольников.
Демонстрация двух треугольников, у которых углы соответственно равны.
Первоначально на рисунке изображены два треугольника.
Выделить цветным мелом пару равных углов: 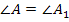 , а за тем пару сторон, лежащих против этих углов:
, а за тем пару сторон, лежащих против этих углов: 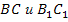 ; вводится их название – сходственные стороны.
; вводится их название – сходственные стороны.
Для закрепления понимания предлагается назвать еще две пары сходственных сторон, после чего появляется соответствующая запись: 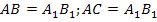
Демонстрация двух треугольников: 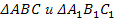 , у которых о
, у которых о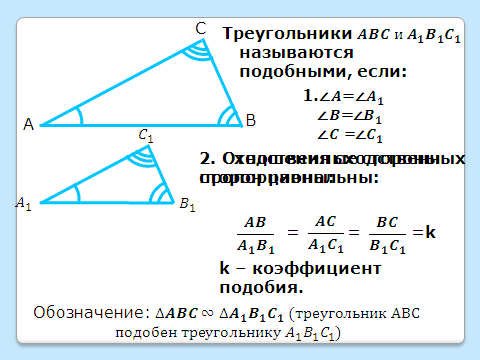 тмечены соответственно равные углы, а рядом – запись «Треугольники
тмечены соответственно равные углы, а рядом – запись «Треугольники 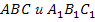 называются подобными, если…»
называются подобными, если…»
«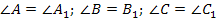 .»
.»
«Отношения сходственных сторон…»
Задание ученикам: Назвать отношения сходственных сторон.
Сделать запись на доске, выражающая отношения сходственных сторон: 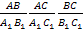 .
.
-Какой знак можно поставить между этими отношениями?
-Что означает равенство отношений для отрезков 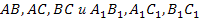 ?
?
Вывод: «Сходственные стороны пропорциональны»
Затем вводится число k для обозначения равных отношений, его название – коэффициент подобия, появляются соответствующие записи на слайде.
Последним шагом вводится обозначение подобных треугольников: 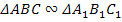 .
.
⑤Решение задач.
№541.Подобны ли треугольники 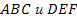 , если
, если 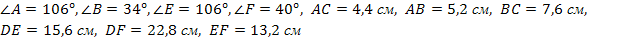 ?
?
ΔABC
ΔDEF
∠A=106ᵒ
∠B=34ᵒ
∠E=106ᵒ
∠F=40ᵒ
AC=4,4 см
AB=5,2 см
BC=7,6 см
DE=15,6 см
DF=22,8 см
EF=13,2 см
Найти
ΔABC∾ΔDEF?
Решение:
ΔABC: ∠A=106ᵒ; ∠B=34ᵒ; ∠C=180ᵒ — (106ᵒ+34ᵒ)=40ᵒ (из теоремы Пифагора)
ΔDEF: ∠E=106ᵒ; ∠F=40ᵒ; ∠D=180ᵒ — (106ᵒ+40ᵒ)=34ᵒ (из теоремы Пифагора)
П

олучили: ∠A=∠E; ∠B=∠D; ∠C=∠FСходственные стороны (лежат против равных углов): ABи ED; ACи EF; BCи DF.



Так как ∠A=∠E; ∠B=∠D; ∠C=∠F;
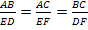 , то ΔABC∾ΔEDF (по определению)
, то ΔABC∾ΔEDF (по определению)
Вывод: ΔABC∾ΔEDF.
⑥Домашнее задание.
§1(п. 56, п. 57) – знать смысл понятий
Отношение отрезков.
Пропорциональные отрезки.
Сходственные стороны у треугольников.
Подобные треугольники.
Коэффициент подобия.
№542 (решить)
№535 (разобрать и записать доказательство, разбив его на пункты)
Решение задач.
№542.
Дано:ΔABC∾ΔKMN;
ABи KM– сходственные;
BCи MN – сходственные;
АВ=4 см;
ВС=5 см;
СА=7 см;
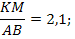
Найти:
KM; MN; KN.
Решение:
Сходственные стороны в подобных треугольниках лежат против равных углов.
АВ и КМ – сходственные, значит ∠С=∠N.
ВС и МN – сходственные, значит∠А=∠К.
2)Получаем следующий чертеж
3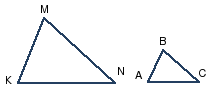
)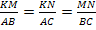 (так как ΔMNK∾ΔBCA) и
(так как ΔMNK∾ΔBCA) и 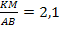 . Тогда
. Тогда
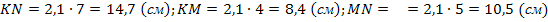 .
.
Ответ:KN=14,7 см; KM=8,4 см; MN=10,5 см.
№535.
Дано:ΔАВС;
AD – биссектриса
Доказать:

Ч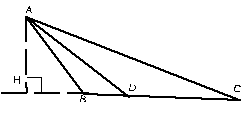
ертеж:
Доказательство:
 ;
;  .
.Так как∠BAD=∠DAC, то по теореме об отношении площадей треугольников, имеющих соответственно равные углы
 .
.Учитывая пункты 1 и 2, получаем
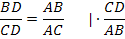

Вывод. Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
infourok.ru
Определение подобных треугольников
Пропорциональные отрезки
Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.
Определение 1
Отношением двух отрезков называется отношение их длин.
Понятие пропорциональности отрезков имеет место и для большего числа отрезков. Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
То есть отрезки $AB$, $A_1B_1$, $\ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.
Подобные треугольники
Вспомним для начала, что вообще представляет себе понятие подобия.
Определение 3
Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.

Рисунок 1. Два треугольника
Пусть у этих треугольников $\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1$. Введем следующее определение:
Определение 4
Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.
На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.
Определение 5
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]На рисунке 1 изображены подобные треугольники.
Обозначение: $ABC\sim A_1B_1C_1$
Для понятия подобия существует также понятие коэффициента подобия.
Определение 6
Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.
Площади подобных треугольников
Рассмотрим теперь теорему об отношении площадей подобных треугольников.
Теорема 1
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\]Доказательство.
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).

Рисунок 2.
Для доказательства этой теоремы вспомним следующую теорему:
Теорема 2
Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$\angle A=\angle A_1$. Тогда, по теореме 2, получим, что
Так как $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$, получим
Теорема доказана.
Задачи, связанные с понятием подобия треугольника
Пример 1
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2,\ BC=5,\ AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.
Решение.
Данная задача имеет два возможных решения.
Пусть $k=\frac{A_1B_1}{AB}=\frac{{B_1C}_1}{BC}=\frac{A_1C_1}{AC}$.
Тогда $A_1B_1=kAB,\ {B_1C}_1=kBC,\ A_1C_1=kAC$.
Следовательно, $A_1B_1=4,\ {B_1C}_1=10,\ A_1C_1=12$
Пусть $k=\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$
Тогда $A_1B_1=\frac{AB}{k},\ {B_1C}_1=\frac{BC}{k},\ A_1C_1=\frac{AC}{k}$.
Следовательно, $A_1B_1=1,\ {B_1C}_1=2,5,\ \ A_1C_1=3$.
Пример 2
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Сторона первого треугольника $AB=2$, соответствующая сторона второго треугольника $A_1B_1=6$. Высота первого треугольника $CH=4$. Найти площадь второго треугольника.
Решение.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то $k=\frac{AB}{A_1B_1}=\frac{1}{3}$.
Найдем площадь первого треугольника.
\[S=\frac{1}{2}AB\cdot CH=\frac{1}{2}\cdot 2\cdot 4=4\]По теореме 1, имеем:
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \[S_{A_1B_1C_1}=36\]Ответ: $36$.
spravochnick.ru
Как найти коэффициент подобия?
Здравствуйте! Ой, я так Вас понимаю, так как эта тема не самая лёгкая для быстрого усвоения. Но я уверена, что смогу Вам хоть немного приблизиться к пониманию того, как найти коэффициент подобия и усвоение того, что это такое вообще.Начать следует нам с того, что нужно понять, какие же треугольники являются подобными.
Итак, подобными считаются те треугольники, чьи углы равны, а соответствующие стороны пропорциональны. Подобие на письме, в задачах, как и все значения имеет своё символ, которым зачастую и записывается — . И в виде записей, это всё выглядит так:
А теперь попробуем решить задачу, которую Вы предоставили. Итак, нам известно, что треугольники — подобны, а отношение их сторон: . Исходя из этого делаем вывод, что коэффициент подобия этих треугольников:
теперь мы можем вывести значения сторон.
- Сторона :
- Сторона :
- Сторона :
Ответ: см
ru.solverbook.com
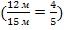 . Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй).
. Что показывает данная величина? ( Показывает, какую часть составляет первая величина от второй).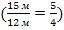 . Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой).
. Что показывает данная величина? ( Показывает, во сколько раз вторая величина больше первой). .
.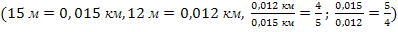
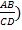 .
.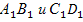 , если
, если 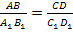 . Отрезки
. Отрезки 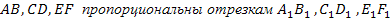 , если справедливо равенство
, если справедливо равенство 
 ; при изменении единиц длины оно не меняется)
; при изменении единиц длины оно не меняется)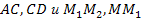 ; б)
; б)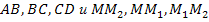 ; в)
; в)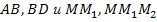
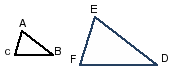
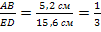
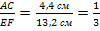
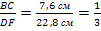
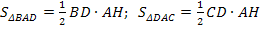 ;
; 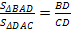 .
.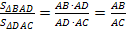 .
.