Подобные треугольники. Пропорциональные отрезки — методическая рекомендация. Геометрия, 8 класс.
| 1. | Отношение сторон подобных треугольников | 1 вид — рецептивный | лёгкое | 1 Б. | Написание отношения сторон подобных треугольников. |
| 2. | Отношение отрезков | лёгкое |
1 Б.
|
Вычисление длины отрезка, если известна длина другого отрезка и их отношение. | |
| 3. | Отношение отрезков, длина отрезка | 2 вид — интерпретация | лёгкое | 1 Б. | Вычисление длины отрезка по данному отношению и длине другого отрезка. |
4.
|
Пропорциональные отрезки | 2 вид — интерпретация | лёгкое | 2 Б. | Пропорциональные отрезки. Вычисление неизвестного члена пропорции, который находится в числителе. |
| 5. | Подобные треугольники, отношение площадей | 2 вид — интерпретация | среднее |
1 Б.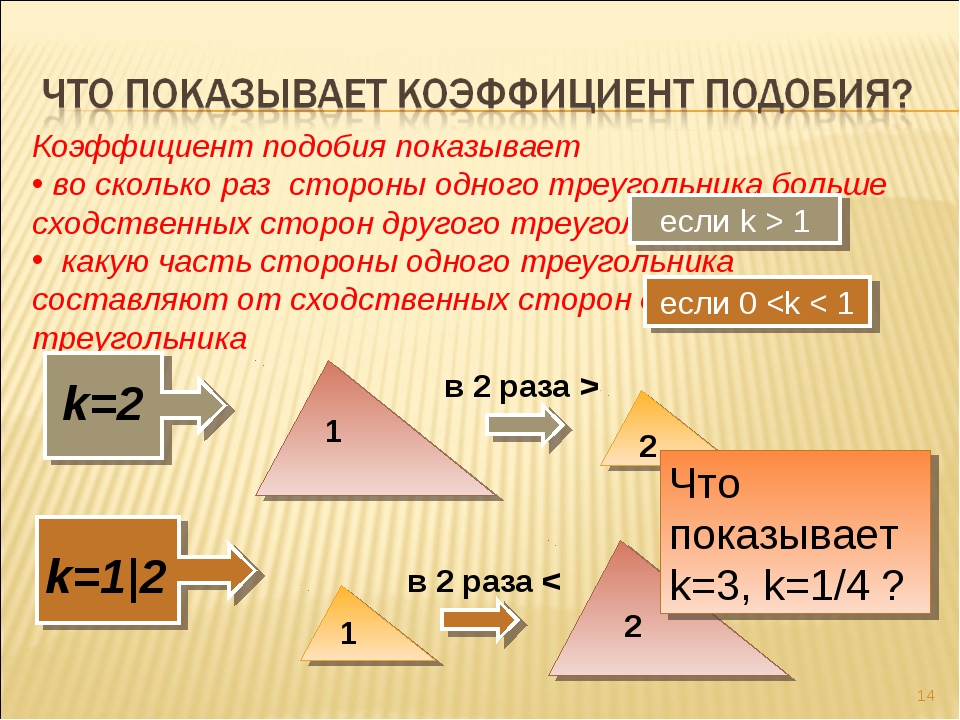
|
Нахождение отношений периметров или площадей подобных треугольников. |
| 6. | Длины частей отрезка | 2 вид — интерпретация | среднее | 3 Б. | Вычисление длин частей отрезка, если известна длина всего отрезка и отношение его частей. |
7.
|
Периметры и площади подобных треугольников | 2 вид — интерпретация | среднее | 3 Б. | Вычисление периметра и площади одного из данных подобных треугольников. |
| 8. | Площади подобных треугольников | 2 вид — интерпретация | среднее |
4 Б.
|
Вычисление площадей подобных треугольников. |
| 9. | Периметр равнобедренной трапеции | 2 вид — интерпретация | среднее | 3 Б. | Вычисление периметра равнобедренной трапеции, подобные треугольники. |
10.
|
Подобные прямоугольные треугольники | 2 вид — интерпретация | среднее | 3 Б. | Вычисление стороны одного из подобных прямоугольных треугольников. |
| 11. | Подобные треугольники | 2 вид — интерпретация | среднее |
3 Б.
|
Вычисление стороны одного из данных подобных треугольников. |
| 12. | Подобные треугольники, коэффициент подобия (1) | 2 вид — интерпретация | среднее | 4 Б. | Вычисление стороны одного из данных подобных треугольников, коэффициент подобия k < 1. |
13.
|
Подобные треугольники, коэффициент подобия (2) | 2 вид — интерпретация | среднее | 4 Б. | Вычисление стороны одного из данных подобных треугольников, коэффициент подобия k > 1. |
| 14. | Площади подобных треугольников | 3 вид — анализ | сложное |
4 Б.
|
Использование соотношения площадей подобных треугольников для определения сторон. |
Подобие треугольников, отношение площадей, сторон. Коэффициент подобия. Тест
Всего вопросов: 10
Вопрос 1. Найдите отношение отрезков АВ и CD, если их длины равны соответственно 15 см и 20 см.
Вопрос 2. Отрезок ВD является биссектрисой треугольника ABC. Найдите AB, если ВС=9см, AD=7,5см, DC=4,5см.
Вопрос 3. Отрезок AD является биссектрисой треугольника ABC. Найдите BD, если АВ=14 см, ВС=20 см, АС=21 см.
Вопрос 4. Биссектриса AD треугольника АВС делит сторону BC на отрезки CD и BD, равные соответственно 4,5 см и 13,5 см. Найдите АВ, если периметр треугольника АВС равен 42 см.
Вопрос 5. В подобных треугольниках АВС и KМN стороны АВ и КМ, BC и MN являются сходственными. Найдите наименьшую сторону треугольника KMN, если АВ=4 см, ВС=5 см, СА=7 см, КМ/АВ=2,1
Вопрос 6. Площади двух подобных треугольников равны 75 м2 и 300 м2. Одна из сторон второго треугольника равна 9 м. Найдите сходственную ей сторону первого треугольника.
Вопрос 7. Треугольники АВС и A1B1C1 подобны, и их сходственные стороны относятся как 6:5. Площадь треугольника АВС больше площади треугольника A1B1C1 на 77 см2. Найдите площадь меньшего треугольника.
Вопрос 8. Треугольники АВС и A1B1C1 подобны. Сходственные стороны ВС и B1C1 соответственно равны 1,4 м и 56 см. Найдите отношение периметров треугольников АВС и A1B1C1 .
Вопрос 9. Стороны данного треугольника равны 15 см, 20 см и 30 см. Найдите наибольшую сторону треугольника, подобного данному, если его периметр 26 см.
Вопрос 10. Через точку М, взятую на медиане АD треугольника ABC, и вершину В проведена прямая, пересекающая сторону АС в точке К. Найдите отношение АК/КС, если M — середина отрезка AD.
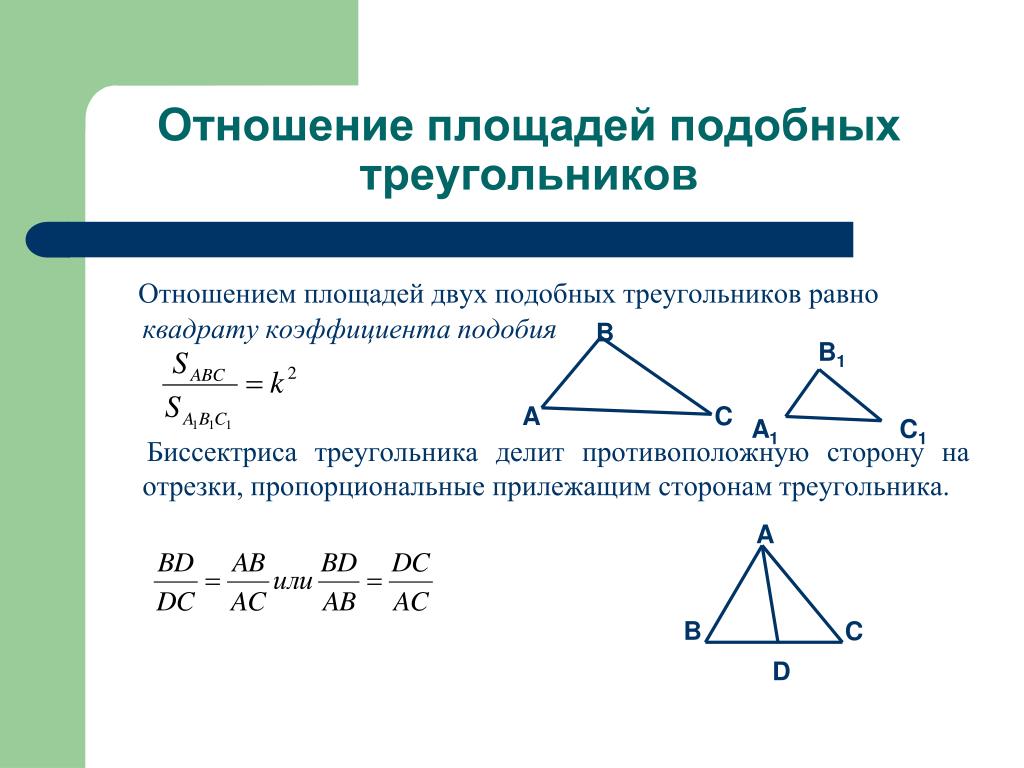
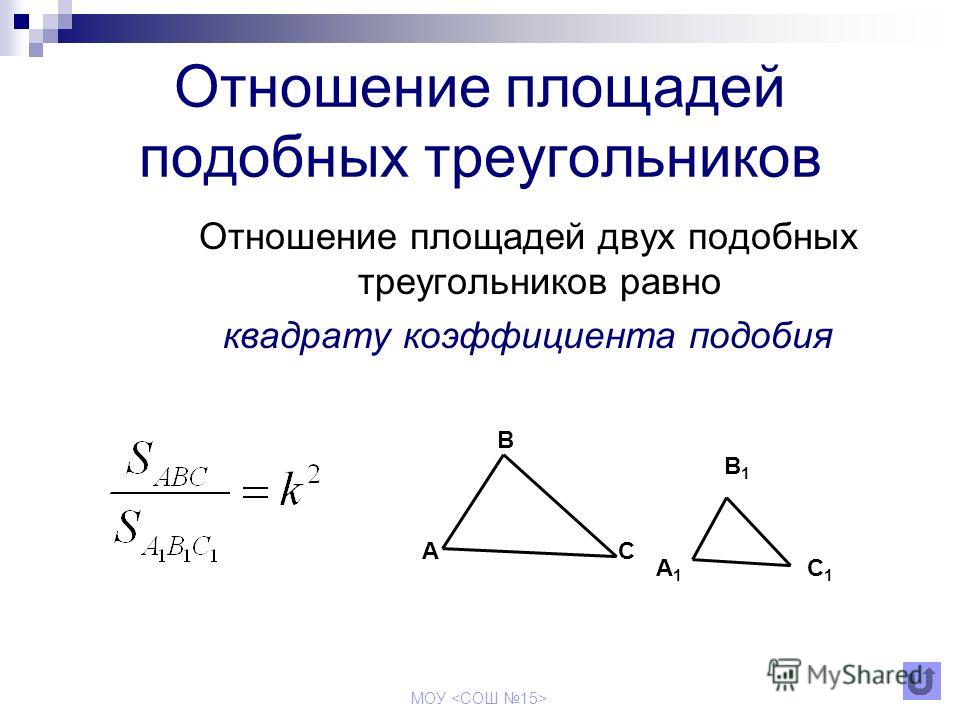
Отношение площадей равно квадрату коэффициента подобия. «отношение площадей подобных треугольников»
Определение и свойства подобных треугольников
Числа a 1 , a 2 , a 3 , …, a n называются пропорциональными числам b 1 , b 2 , b 3 , …, b n , если выполняется равенство: a 1 /b 1 = а 2 /b 2 = a 3 /b 3 = … = a n /b n = k, где k – некоторое число, которое называют коэффициентом пропорциональности.
Пример. Числа 6; 7,5 и 15 пропорциональны числам ‑4; 5 и 10. Коэффициентом пропорциональности является число ‑1,5, поскольку
6/-4 = -7,5/5 = 15/-10 = -1,5.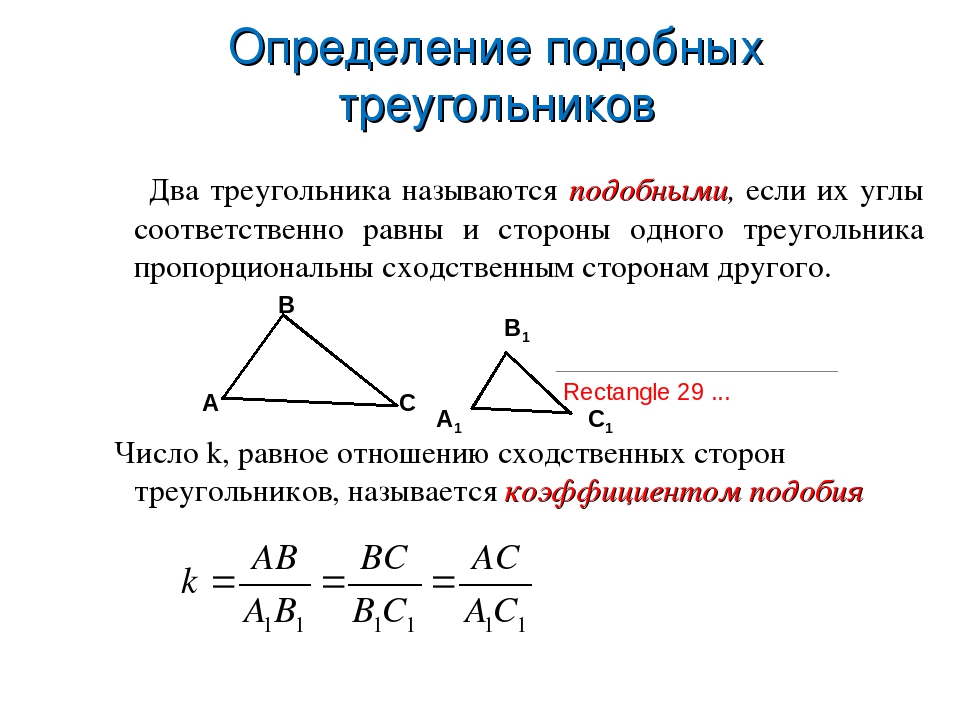
Пропорциональность чисел имеет место быть, если эти числа связаны пропорцией.
Известно, что пропорцию можно составить не менее чем из четырех чисел, поэтому понятие пропорциональности применимо как минимум к четырем числам (одна пара чисел пропорциональна другой паре, или одна тройка чисел пропорциональна другой тройке, и т.д.).
Рассмотрим на рис. 1 два треугольника АВС и А 1 В 1 С 1 с равными попарно углами: A = A 1 , B = B 1 , C = C 1 .
Стороны, которые противолежат равным парам углов обоих треугольников, называются сходственными . Так, на рис. 1 стороны AB и A 1 B 1 , AC и A 1 C 1 , BC и B 1 C 1 , сходственные, поскольку лежат напротив соответственно равных углов треугольников ABC и A 1 B 1 C 1 .
Дадим определение подобных треугольников:
Два треугольника называются подобными , если их углы попарно равны, а сходственные стороны пропорциональны.
Отношение сходственных сторон подобных треугольников называется коэффициентом подобия .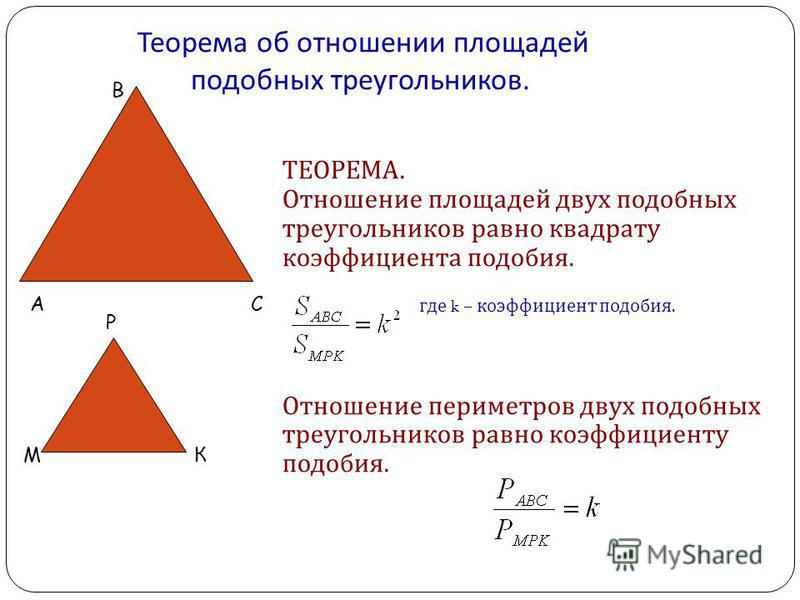
Подобные треугольники обозначаются следующим образом: Δ ABC ~ Δ A 1 B 1 C 1 .
Итак, на рис. 2 имеем: Δ ABC ~ Δ A 1 B 1 C 1
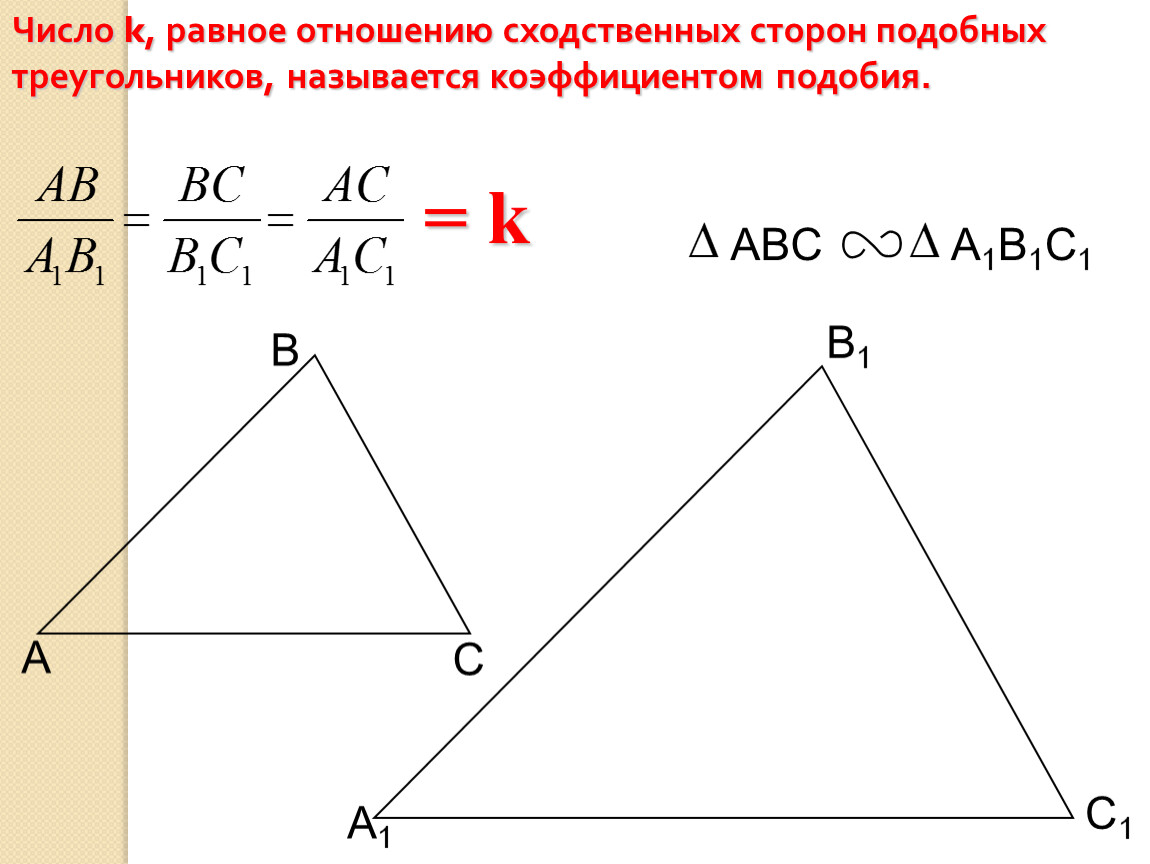
углы A = A 1 , B = B 1 , C = C 1 и AB/A 1 B 1 = ВC/В 1 C 1 = АС/А 1 С 1 = k, где k – коэффициент подобия. Из рис. 2 видно, что у подобных треугольников одинаковые пропорции, и отличаются они лишь масштабом.
Замечание 1: Равные треугольники подобны с коэффициентом 1.
Замечание 2:
При обозначении подобных треугольников следует упорядочить их вершины таким образом, чтобы углы при них были попарно равны. Например, для треугольников, изображенных на рисунке 2 говорить, что Δ ABC ~ Δ B 1 C 1 A 1 некорректно. Соблюдая правильный порядок вершин, удобно выписывать пропорцию, связывающую сходственные стороны треугольников, не обращаясь к чертежу: в числителе и знаменателе соответствующих отношений должны стоять пары вершин, занимающих одинаковые позиции в обозначении подобных треугольников. К примеру, из записи «Δ ABC ~ Δ KNL» следует, что углы A = K, B = N, C = L, и АВ/KN = BC/NL = AC/KL.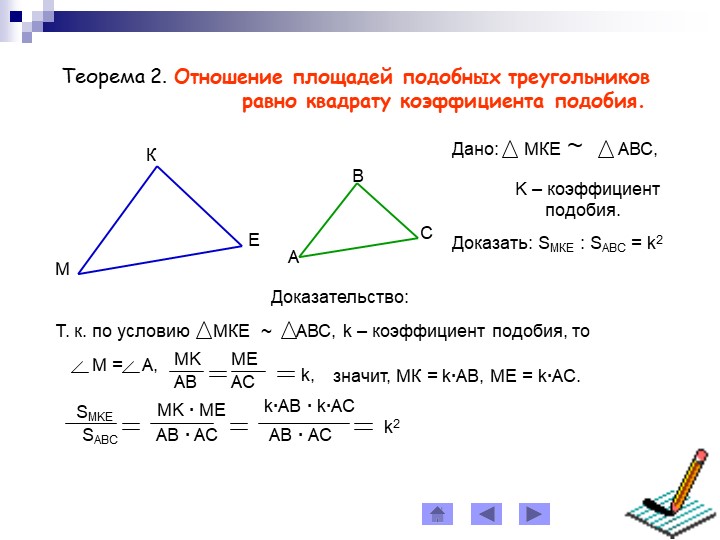
Замечание 3: Те требования, которые перечислены в определении подобных треугольников, являются избыточными. Признаки подобия треугольников, которые содержат меньше требований к подобным треугольникам докажем чуть позже.
Сформулируем свойства подобных треугольников:
- Отношение соответственных линейных элементов подобных треугольников равно коэффициенту их подобия. К таким элементам подобных треугольников относятся те, которые измеряются в единицах длины. Это, например, сторона треугольника, периметр, медиана. Угол или площадь к таким элементам не относятся.
- Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Пусть треугольники ABC и A 1 B 1 C 1 подобны с коэффициентом k (рис. 2).
Докажем, что S ABC /S A1 B1 C1 = k 2 .
Поскольку углы подобных треугольников попарно равны, т.е A = A 1 , и по теореме об отношении площадей треугольников, имеющих по равному углу, имеем:
S ABC /S A1 B1 C1 = (AB · AC) / (A 1 B 1 · A 1 C 1) = AB/A 1 B 1 · AC/A 1 C 1 .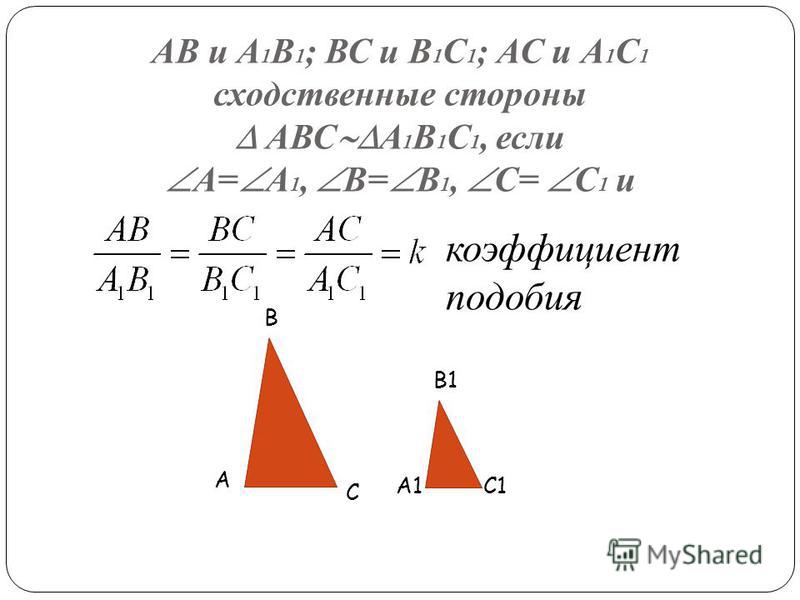
В силу подобия треугольников AB/A 1 B 1 = k и AC/A 1 C 1 = k,
поэтому S ABC /S A1 B1 C1 = AB/A 1 B 1 · AC/A 1 C 1 = k · k = k 2 .
Замечание: Сформулированные выше свойства подобных треугольников справедливы и для произвольных фигур.
Признаки подобия треугольников
Требования, которые предъявляются к подобным треугольникам определением (это равенство углов и пропорциональность сторон) являются избыточными. Устанавливать подобие треугольников можно и по меньшему количеству элементов.
Так, при решении задач чаще всего используется первый признак подобия треугольников, утверждающий, что для подобия двух треугольников достаточно равенства их углов:
Первый признак подобия треугольников (по двум углам): Если два угла одного треугольника соответственно равны двум углам второго треугольника, то эти треугольники подобны (рис. 3) .
Пусть даны треугольники Δ ABC, Δ A 1 B 1 C 1 , в которых углы A = A 1 , B = B 1 . Необходимо доказать, что Δ ABC ~ Δ A 1 B 1 C 1 .
Необходимо доказать, что Δ ABC ~ Δ A 1 B 1 C 1 .
Доказательство.
1) По теореме о сумме углов треугольника имеем:
угол C = 180 ° (угол A + угол B) = 180° (угол A 1 + угол B 1) = угол C 1 .
2) По теореме об отношении площадей треугольников, имеющих по равному углу,
S ABC /S A1 B1 C1 = (AB · AC) / (A 1 B 1 · A 1 C 1) = (AB · ВC) / (A 1 B 1 · В 1 C 1) = (AС · ВC) / (A 1 С 1 · В 1 C 1).
3) Из равенства (AB · AC) / (A 1 B 1 · A 1 C 1) = (AB · ВC) / (A 1 B 1 · В 1 C 1) следует, что AC/A 1 C 1 = BС/В 1 С 1 .
4) Из равенства (AB · ВC) / (A 1 B 1 · В 1 C 1) = (AС · ВC) / (A 1 С 1 · В 1 C 1) следует, что AВ/A 1 В 1 = АС/А 1 С 1 .
Таким образом, у треугольников ABCи A 1 B 1 C 1 DA = DA 1 , DB = DB 1 , DC = DC 1 , и AB/A 1 B 1 = АС/А 1 С 1 .
5) AB/A 1 B 1 = АС/А 1 С 1 = ВC/В 1 C 1 , то есть сходственные стороны пропорциональны. А значит, Δ ABC ~ Δ A 1 B 1 C 1 по определению.
Теорема о пропорциональных отрезках.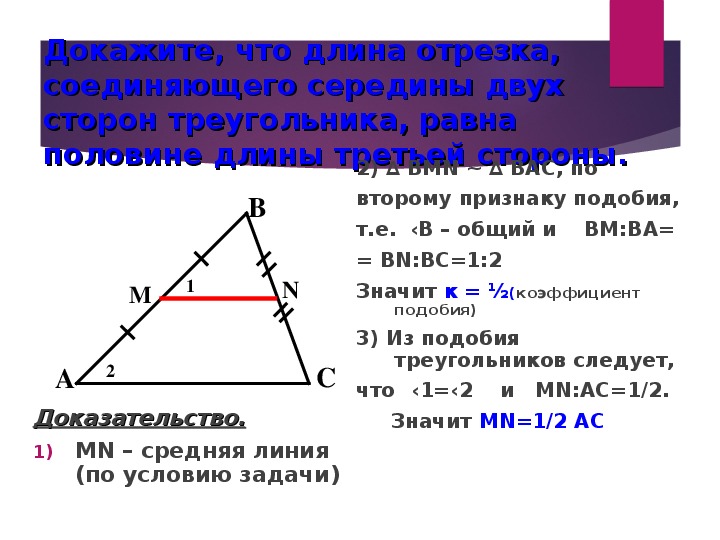 Деление отрезка в заданном отношении
Деление отрезка в заданном отношении
Теорема о пропорциональных отрезках является обобщением теоремы Фалеса.
Для использования теоремы Фалеса необходимо, чтобы параллельные прямые, пересекающие две данные прямые, отсекали на одной из них равные отрезки. Обобщенная же теорема Фалеса утверждает, что если параллельные прямые пересекают две данные прямые, то отрезки, отсекаемые ими на одной прямой, пропорциональны отрезкам, отсекаемым на второй прямой.
Теорема о пропорциональных отрезках доказывается аналогично теореме Фалеса (только вместо равенства треугольников здесь используется их подобие).
Теорема о пропорциональных отрезках (обобщенная теорема Фалеса): Параллельные прямые, пересекающие две данные прямые, отсекают на них пропорциональные отрезки.
Свойство медиан треугольника
Первый признак подобия треугольников позволяет доказать свойство медиан треугольника:
Свойство медиан треугольника:
Медианы треугольника пересекаются в одной точке, и делятся этой точкой в отношении 2: 1, считая от вершины (рис. 4) .
4) .
Точка пересечения медиан называется центроидом треугольника.
Пусть дан Δ ABC, у которого AA 1 , BB 1 , CC 1 – медианы, кроме того, AA 1 ∩CC 1 = O. Необходимо доказать, что BB 1 ∩ CC 1 = O и АО/ОА 1 = ВО/ОВ 1 = СО/ОС 1 = 2.
Доказательство.
1) Проведем среднюю линию A 1 C 1 . По теореме о средней линии треугольника A 1 C 1 || AC, и A 1 C 1 = AC/2.
2) Треугольники AOC и A 1 OC 1 подобны по двум углам (угол AOC = углу A 1 OC 1 как вертикальные, угол OAC = углу OA 1 C 1 как внутренние накрест лежащие при A 1 C 1 || AC и секущей AA 1), следовательно, по определению подобных треугольников АО/А 1 О = ОС/ОС 1 = АС/А 1 С 1 = 2.
3) Пусть BB 1 ∩CC 1 = O 1 . Аналогично пунктам 1 и 2 можно доказать, что ВО/О 1 В 1 = СО 1 /О 1 С = 2. Но поскольку на отрезке СС 1 существует единственная точка О, делящая его в отношении СО: ОС 1 = 2: 1, то точки О и О 1 совпадают. Значит, все медианы треугольника пересекаются в одной точке, делящей каждую из них в отношении 2: 1, считая от вершины.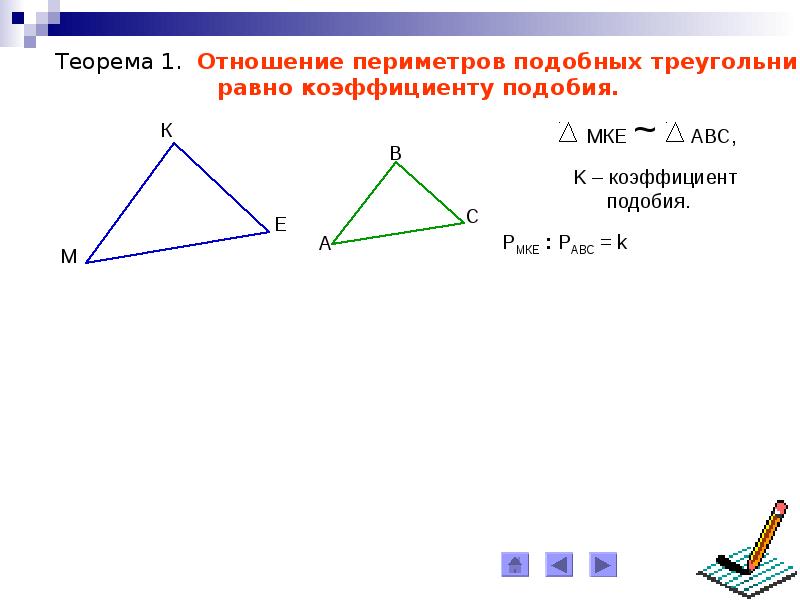
В курсе геометрии в теме «площади многоугольников» доказывается тот факт, что медиана разбивает произвольный треугольник на две равновеликие части. Кроме того, при пересечении трех медиан треугольника образуется шесть равновеликих треугольников.
Остались вопросы? Не знаете, как решать задачи на подобие треугольников?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Пропорциональные отрезки
Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.
Определение 1
Отношением двух отрезков называется отношение их длин.
Понятие пропорциональности отрезков имеет место и для большего числа отрезков. Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
То есть отрезки $AB$, $A_1B_1$, $\ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.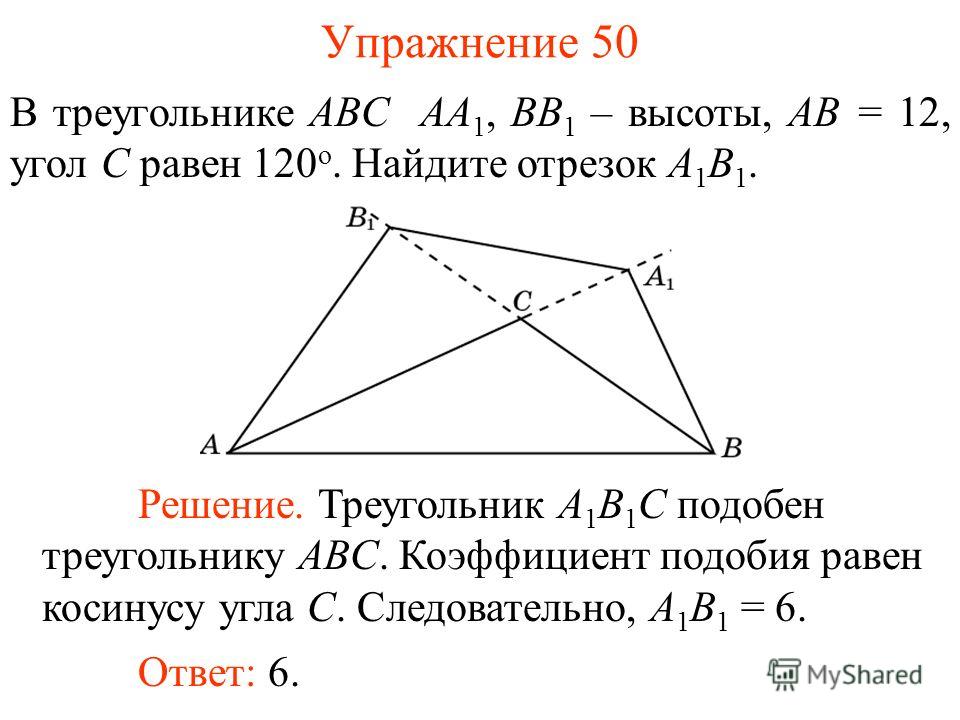
Подобные треугольники
Вспомним для начала, что вообще представляет себе понятие подобия.
Определение 3
Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.
Рисунок 1. Два треугольника
Пусть у этих треугольников $\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1$. Введем следующее определение:
Определение 4
Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.
На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.
Определение 5
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]
На рисунке 1 изображены подобные треугольники. 2\]
2\]
Доказательство.
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).
Рисунок 2.
Для доказательства этой теоремы вспомним следующую теорему:
Теорема 2
Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$\angle A=\angle A_1$. Тогда, по теореме 2, получим, что
Так как $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$, получим
Теорема доказана.
Задачи, связанные с понятием подобия треугольника
Пример 1
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2,\ BC=5,\ AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.
Решение.
Данная задача имеет два возможных решения.
- Учитель: Что называется отношением двух отрезков?
- Учитель: В каком случае отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1
- Учитель: Дайте определение подобных треугольников? Обратитесь к вашему опорному конспекту. У Вас три варианта ответа на этот вопрос. Выберите правильный. Обведите его.
- Учитель: Чему равно отношение площадей двух треугольников, имеющих по равному углу?
- выделение красным цветом главных понятий;
- анимированное построение графической части для уточнения определения, наглядности при объяснении материала;
- заключение в рамку основных алгебраических выражений по теме;
- использование рисунков для понимания практического смысла изучаемого понятия.
Слайд 8
Пропорциональные отрезки. Определение подобных треугольников Отношение площадей подобных треугольников Первый признак подобия треугольников (Доказательство) Второй признак подобия треугольников (Доказательство) Третий признак подобия треугольников (Доказательство) Практическое приложение
Слайд 9
Продолжение
Основные сведенья Измерительные работы на местности Определения высоты предмета Определение расстояния до недоступной точки Определения расстояния построением подобных треугольников (1) (2) (5) (4) (3)
Слайд 10
Пропорциональные отрезки
Отношением отрезков АВ и СD называется отношение их длин т.е АВ/СD .Говорят что отрезки АВ и CD пропорциональны отрезкам A1 B1 и C1 D1,если AB/А1В1=CD/C1D1.
 Понятие пропорциональности вводится и для большого числа отрезков
Понятие пропорциональности вводится и для большого числа отрезковСлайд 11
Определение подобных треугольников.
Два треугольника называются подобными, Если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
Слайд 12
Отношение площадей подобных треугольников
Теорема Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия
Слайд 13
Доказательство.
Пусть треугольники АВС иА1В1С1 подобны и причем коэффициент подобия равен r. Обозначим буквами S и S1 площади этих треугольников. Так как угол А=углуА1, то S/S1=AB*AC/A1B1*A1C1(по теореме об отношение площадей отношения подобия треугольников, имеющих по равному углу). По формулам(2) имеем: АВ/А1В1=R, АС/А1С1=R, поэтому S/S=R 2
Слайд 14
Первый признак подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники равны А В С
Слайд 15
Второй признак подобия треугольников
Если две стороны другого треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

Слайд 16
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны. А В С
Слайд 17
Доказательство.(1)
Дано:АВС и А1В1С1-два треугольника, у которых угол А =углуА1, угол В= углу В1 Докажем,что треугольник АВС треугольник А!В1С1
Слайд 18
Доказательство.
По теореме о сумме углов треугольника угол С=180градусов-угол А-угол В, угол С=180градусов-уголА – угол В, и, значит, угол С= углу С. Таким образом, углы треугольника АВС соответственно равны углам треугольника А В С 1 1 1 1 1 1 1
Слайд 19
Докажем,что стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С.Так как угол А= углу А и угол С= углу С,то S авс /Sa в c =АВ*АС/А В * А С S авс /Sа в с = СА*СВ/С А *С В. 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Слайд 20
Из этих равенств следует, что АВ/А В =ВС/В С Аналогично используя равенства угол А= углу А Угол В = углу В,получаем,ВС/В С = СА/С А.
 Итак стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С
Теорема доказана.
1
1
1
1
1
1
1
1
Итак стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С
Теорема доказана.
1
1
1
1
1
1
1
1Слайд 21
Доказательство (2)
Дано: два треугольника АВС и А В С,у которых АВ/А В=АС/А С, угол А= углу А Доказать что треугольник АВС треугольнику А В С.Для этого, учитывая первый признак подобия треугольников, достаточно доказать, что угол В = углу В 1 1 1 1 1 1 1 1 1 1
Слайд 22
Рассмотрим треугольник АВС, у которого угол1=углуА, угол2 = углу В.Треугольники АВС А В С подобны по первому признаку подобия треугольников, поэтому АВ/А В = АС /А С. С другой стороны, по условию АВ/А В =АС /А С.Из этих двух равенств получаем АС=АС. 2 1 1 2 1 1 1 1 1 2 1 1 1 1 1 1 2
Слайд 23
Треугольники АВС и АВС равны по двум сторонам между ними (АВ — общая сторона, АС=АС и угол А = углу 1 ,поскольку угол А= углу А и угол 1=углу А). Отсюда следует,что угол В = углу 2 ,а так как угол 2 = углу В,то угол В = углу В. Теорема доказана.
 2
2
1
1
1
1
2
2
1
1
1
1Слайд 24
Доказательство (3)
Дано: стороны треугольников АВС и А В С пропорциональны. Докажем,что треугольник АВС треугольнику А В С 1 1 1
Слайд 25
Доказательство
Для этого,учитывая второй признак подобия треугольников достаточно доказать что угол А= углу А. Рассмотрим треугольник АВС, у которого угол 1=углу А, угол 2= углу В. Треугольники АВС и А В С подобны по первому признаку подобия треугольников,поэтому АВ/А В = ВС / В С = С А/С А.
Слайд 26
Сравнивая эти равенства с равенствами (1) получаем: ВС=ВС, СА= С А. Треугольники АВС и АВС равны по трем сторонам. Отсюда следует,что угол А = углу 1 а так как угол1 = углу А, то угол А = углу А. Теорема доказана. 2 2 2 1 1
Слайд 27
Практические приложения подобия треугольников
При решение многих задач на построение треугольников применяют так называемый метод подобия. Он состоит в том, что сначала на основании некоторых данных стоят треугольник, подобный искомому, а затем, используя остальные данные,строят искомый треугольник
Слайд 28
Задача №1
Построить треугольник по данным двум углам и биссектрисе при вершине третьего угла
Слайд 29
Решение
Сначала построим какой — нибудь треугольник,подобный искомому.
 Для этого начертим произвольный отрезок А В и постоим треугольник А В С, у которого углы А и В соответственно равны данным углам
Для этого начертим произвольный отрезок А В и постоим треугольник А В С, у которого углы А и В соответственно равны данным угламСлайд 30
Продолжение
Далее построим биссектрису угла С и отложим на ней отрезок СD ,равны данному отрезку. Через точку D проведём прямую, параллельную А В. Она пересекает стороны угла С в некоторых точках А и В.треугольник АВС искомый
Слайд 31
В само деле,так как АВ параллельна А В,то угол А = углу А,угол В = углу В, и, следовательно,два угла треугольника АВС соответственно равны данным углам. По построению биссектриса CD треугольника АВС равна данному отрезку.Итак, треугольник АВС удовлетворяет всем условиям задачи.
Слайд 32
Основное сведенья(1)
1.Треугольник АВС подобен треугольнику А В С тогда и только тогда,когда выполнено одно из следующих эквивалентных условий. 1 1 1
Слайд 33
Условия
А)АВ:ВС:СА = А В: В С: С А; В)АВ:ВС=А В:В С и угол АВС= углу А В С; В)угол АВС= углу А В С и угол ВАС = углу В А С.
 1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1Слайд 34
Основное сведенья(2)
2) если параллельные прямые отсекают от угла с вершиной А треугольники АВ С и АВ С, то эти треугольники подобны и АВ:АВ = АС: АС (точки В и В лежат на одной стороне угла, С и С – на другой). 1 1 2 2 1 2 1 2 1 2 1 2
Слайд 35
Основное сведенья(3)
3) средней линией треугольника называют отрезок,соединяющий середины боковых сторон. Этот отрезок параллелен третьей стороне и равен половине её длины. Средней линией трапеции называют отрезок,соединяющий середины боковых сторон трапеции. Этот отрезок параллелен основаниям и равен полусумме их длин
Слайд 36
Основное сведенья (4)
4) отношение площадей подобных треугольников равно квадрату коэффициента подобия, т.е.квадрату отношения длин соответствующих сторон. Это следует,например,из формулы Sавс=0,5*АВ*АСsinА.
Слайд 37
Основное сведенье (5)
Многоугольники А А …А и В В …В называют подобными, если А А:А А:…:А А =В В:В В:…В В и углы при вершинах А …,А.
 Равны соответственно углам при вершинах А,….,А равны
Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия
1
2
n
1
2
n
1
2
2
3
n
1
1
2
2
3
n
1
1
n
1
n
Равны соответственно углам при вершинах А,….,А равны
Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия
1
2
n
1
2
n
1
2
2
3
n
1
1
2
2
3
n
1
1
n
1
nСлайд 38
Измерительные работы на местности
Свойства подобных треугольников могут быть использованы для проведения различных измерительных работ на местности. Мы рассмотрим две задачи: определение высоты предмета на местности и расстояние до недоступной точки.
Слайд 39
Задача №1
Определение высоты предмета
Слайд 40
Продолжение
Предположим что нам нужно определить высоту какого-нибудь предмета,например высоту телеграфного столба А С, для этого поставим на некотором расстоянии от столба шест АС с вращающейся планкой и направим планку на верхнюю точку А столба.отметим на поверхности земли точку В, в которой прямая А А пересекается с поверхностью земли.
 1
1
1
1
1
1
1
1Слайд 41
Прямоугольные треугольники А С В и АСВ подобны по первому признаку треугольников (угол С = углу С = 90градусов, угол В – общий). Из подобия треугольников следует А С /АС= ВС /ВС, откуда А С =АС*ВС /ВС измерив расстояние ВС и ВС и зная длину АС шеста по полученной формуле определяем высоту А С телеграфного столба 1 1 1 1 1 1 1 1 1 1
Слайд 42
Задача (2)
Определения расстояния до недоступной точки
Слайд 43
Продолжение
Предположим,что нам нужно найти расстояние от пункта А до недоступного пункта В.для этого на местности выбираем точку С, провешиваем отрезок АС и измеряем его. Затем с помощью астролябия измеряем углы А и С. На листе бумаги строим какой-нибудь треугольник А В С,у которого угол А = углу А, угол С = углу С,и измеряем длины сторон А В и А С этого треугольника. 1 1 1 1 1 1 1 1 1
Слайд 44
Так как треугольник АВС и А В С подобны (по первому признаку подобия треугольников), то АВ/А В =АС А С,откуда получаем АВ= АС*А В /А С.
 Эта формула позволяет по известным расстояниям АС, А С и А В,найти расстояние АВ.
1
1
1
1
1
1
1
1
1
1
1
1
1
Эта формула позволяет по известным расстояниям АС, А С и А В,найти расстояние АВ.
1
1
1
1
1
1
1
1
1
1
1
1
1Слайд 45
Для упрощения вычислений удобно построить треугольник А В С таким образом,чтобы А С: АС =1:1000. например если АС=130м,то расстояние А С возьмём равным 130мм. В этом случае АВ=АС/А С * А В =1000*А В,поэтому,измерив расстояние А В в миллиметрах,мы сразу получаем расстояние АВ в метрах 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
Слайд 46
Пример
Пусть АС=130м, угол А=73градусов,угол С=58градусов.на бумаге строим треугольник А В С так, чтобы угол А =73градуса,угол С =58градусов, А С =130мм,и измеряем отрезок А В. Он равен 153мм, поэтому искомое расстояние рано153м. 1 1 1 1 1
Слайд 47
Определение расстояние построением подобных треугольников
При определении расстояния до отдалённых или недоступных предметов, можно использовать следующий приём. На обычную спичку надо нанести чернилами или карандашом двухмиллиметровые деления.
 Также нужно знать примерную высоту предмета, до которого определяется расстояние. Так рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник-2,2м,телеграфический столб-6м,одноэтажный дом без крыши -2,5-4м.
Также нужно знать примерную высоту предмета, до которого определяется расстояние. Так рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник-2,2м,телеграфический столб-6м,одноэтажный дом без крыши -2,5-4м.Слайд 48
Продолжение
Допустим, надо определить расстояние до столба. Направляем на него спичку на вытянутой руке, длина которой приблизительно равна 60 см.предположим, высота столба выглядит равной двум делениям спички, т.е. 4 мм. Имея такие данные составим пропорцию:0.6/х=0.004/6.0;х=(0,6*6)/0ю004=900.Таким образом до столба 900м.
Посмотреть все слайды
- View 1 выдержка, фон ссылок
- Посмотреть 2 выдержки, справочная информация
- Посмотреть 1 отрывок, справочная информация
- Просмотр 3 выдержек, методы ссылок
- Просмотр 1 выдержки, справочная информация
Пусть $k=\frac{A_1B_1}{AB}=\frac{{B_1C}_1}{BC}=\frac{A_1C_1}{AC}$. 2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \
2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \
Пропорциональные отрезки
Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.
Определение 1
Отношением двух отрезков называется отношение их длин.
Понятие пропорциональности отрезков имеет место и для большего числа отрезков. Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
То есть отрезки $AB$, $A_1B_1$, $\ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.
Подобные треугольники
Вспомним для начала, что вообще представляет себе понятие подобия.
Определение 3
Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.
Рисунок 1. Два треугольника
Пусть у этих треугольников $\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1$. Введем следующее определение:
Введем следующее определение:
Определение 4
Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.
На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.
Определение 5
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]
На рисунке 1 изображены подобные треугольники.
Обозначение: $ABC\sim A_1B_1C_1$
Для понятия подобия существует также понятие коэффициента подобия.
Определение 6
Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.
Площади подобных треугольников
Рассмотрим теперь теорему об отношении площадей подобных треугольников.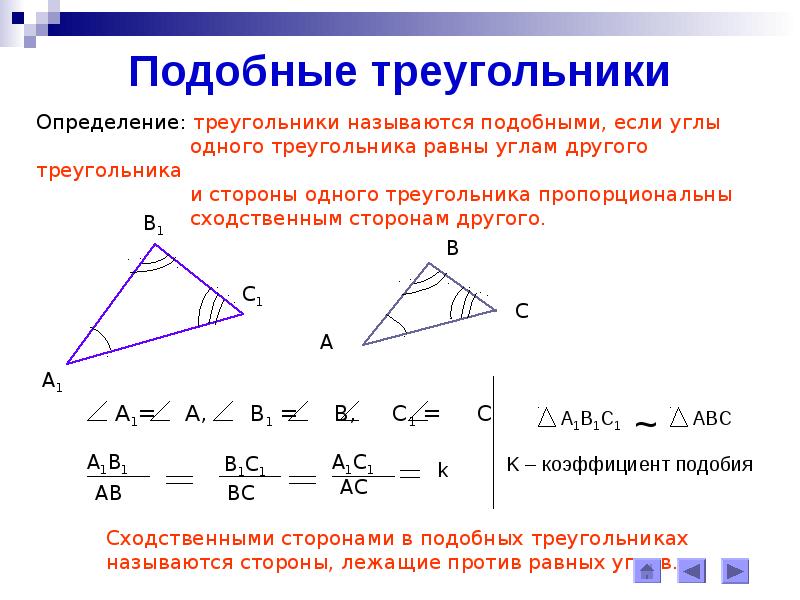 2\]
2\]
Доказательство.
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).
Рисунок 2.
Для доказательства этой теоремы вспомним следующую теорему:
Теорема 2
Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$\angle A=\angle A_1$. Тогда, по теореме 2, получим, что
Так как $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$, получим
Теорема доказана.
Задачи, связанные с понятием подобия треугольника
Пример 1
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2,\ BC=5,\ AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.
Решение.
Данная задача имеет два возможных решения.
Пусть $k=\frac{A_1B_1}{AB}=\frac{{B_1C}_1}{BC}=\frac{A_1C_1}{AC}$. 2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \
2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \
Цель урока:Доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач.
Задачи урока:
обучающие – доказать свойство площадей подобных треугольников и показать его практическую значимость при решении задач;
развивающие – развивать умение анализировать и подбирать аргументацию при решении задачи, способ решения которой неизвестен;
воспитательные – воспитывать интерес к предмету через содержание учебного процесса и создание ситуации успеха, воспитывать умение работать в группе.
Учащийся владеет следующими знаниями:
Единица деятельностного содержания, которое нужно усвоить учащимся:
Ход урока.
1. Организационный момент.
2. Актуализация знаний.
3. Работа с проблемной ситуацией.
4. Подведение итогов урока и запись домашнего задания, рефлексия.
Методы обучения: словесные, наглядные, проблемно-поисковые.
Формы обучения:фронтальная работа, работа в мини-группы, индивидуальная и самостоятельная работа.
Технологии: задачно-целевая, информационные технологии, компетентностный подход.
Оборудование:
компьютер, проектор для демонстрации презентации, интерактивная доска, документ камера;
компьютерная презентация в MicrosoftPowerPoint;
опорный конспект;
Сегодня на уроке мы будем работать не в тетрадях, а в опорных конспектах, которые будете заполнять на продолжение всего урока. Подпишите его. Оценка за урок будет состоять из двух составляющих: за опорный конспект и за активную работу на уроке.
2. Актуализация знаний учащихся. Подготовка к активной учебно-познавательной деятельности на основном этапе урока.
Мы продолжаем с вами изучать тему «подобие треугольников». Поэтому давайте вспомним то, что изучали на прошлом уроке.
 Теоретическая разминка. Тест. В ваших опорных конспектах первое задание имеет тестовый характер. Ответьте на вопросы, выбирая один из предложенных вариантов ответа, где необходимо впишите свой ответ.
Теоретическая разминка. Тест. В ваших опорных конспектах первое задание имеет тестовый характер. Ответьте на вопросы, выбирая один из предложенных вариантов ответа, где необходимо впишите свой ответ.Ответ: Отношением двух отрезков двух отрезков называется отношение их длин.
Ответ: отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1 , если
Ваши варианты. Хорошо. Не забудьте исправить у кого не так.
Так, пожалуйста, какой вариант выбрал ты_______
Ответ: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сторонам другого треугольника.

Молодцы! Исправьте у кого не так.
Ответ: Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
Решение задач по готовым чертежам. Далее наша разминка будет происходить в ходе решения задач по готовым чертежам. Эти задачи так же вы видите в ваших опорных конспектах.
Рефлексия. Давайте уточним, какие знания и умения позволили нам решить эти задачи. Какими методами решения мы пользовались (фиксация ответов на доске).
Возможные ответы:
Определение подобных треугольников;
Применение определения подобных треугольников при решении задач;
Теорема об отношении площадей треугольников имеющих по равному углу;
А сейчас я предлагаю к решению несколько задач способ решения, которых перекликается с темой урок, но связаны они больше с географией.
Ситуация успеха.
Первая задача перед Вами. Над этой задачей работаем самостоятельно. Первый справившийся покажет свое решение у доски, и кто-то продемонстрирует свое решение через документ камеру, поэтому пишем красиво и аккуратно.
Ответ: стороны бермудского треугольника 2000 км, 1840 км, 2220 км. Длина границы 6060 км.
Рефлексия.
Возможный ответ: у подобных треугольников сходственные стороны пропорциональны.
Ситуация успеха.
С размерами Бермудского треугольника мы разобрались. Ну а теперь выясним измерения цветочной клумбы. Переворачиваем опорные конспекты. Вторая задача. Эту задачу решаем, работая в парах. Проверяем аналогичным способом, но только результат будет представлять уже пара первая справившаяся с заданием.
Ответ: стороны треугольной клумбы 10м и 11м 20 см.
Итак, сверяемся. Все ли согласны? Кто решал другим способом?
Рефлексия.
Каким способом действия вы пользовались при решении этой задачи? Запишите в свой опорный конспект.
Возможный ответ:
у подобных треугольников соответственные углы равны;
площади треугольников имеющих по равному углу относятся как произведения сторон заключающих равные углы.
Ситуация сбоя.
При решениитретьей задачи учащиеся сталкиваются с проблемой. У них не получается решить задачу, так как по их мнению недостаточно полное условие задачи или получают необоснованный ответ.
С таким типом задач учащиеся не встречались ранее, поэтому произошел сбой при решении задачи.
Рефлексия.
Каким методом пытались решить?
Почему не получилось решить последнее уравнение?
Ученики: Мы не можем найти площадь треугольника, если известны только площадь подобного треугольника и коэффициент подобия.
Таким образом, цель нашего урока найти площадь треугольника, если известны только площадь подобного треугольника и коэффициент подобия.
Давайте переформулируем задачу на геометрический язык. Решим ее, а затем вернемся к этой задаче.
Вывод: Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Ну а теперь давайте вернемся к задаче №3 и решим ее, опираясь на доказанный факт.
7. Итог урока
Что сегодня вы научились делать нового?
Решать задачи, в которых известны коэффициент подобия и площадь одного из подобных треугольников.
Какое геометрическое свойство нам в этом помогло?
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Домашнее задание.
П. 58 стр.139 №546, 548
Творческое задание.
Найдите чему равно отношение периметров двух подобных треугольников (№547)
До свидания.
Средняя линия треугольника, теория в ЕГЭ по математике
\[{\Large{\text{Подобие треугольников}}}\]
Определения
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого
(стороны называются сходственными, если они лежат напротив равных углов).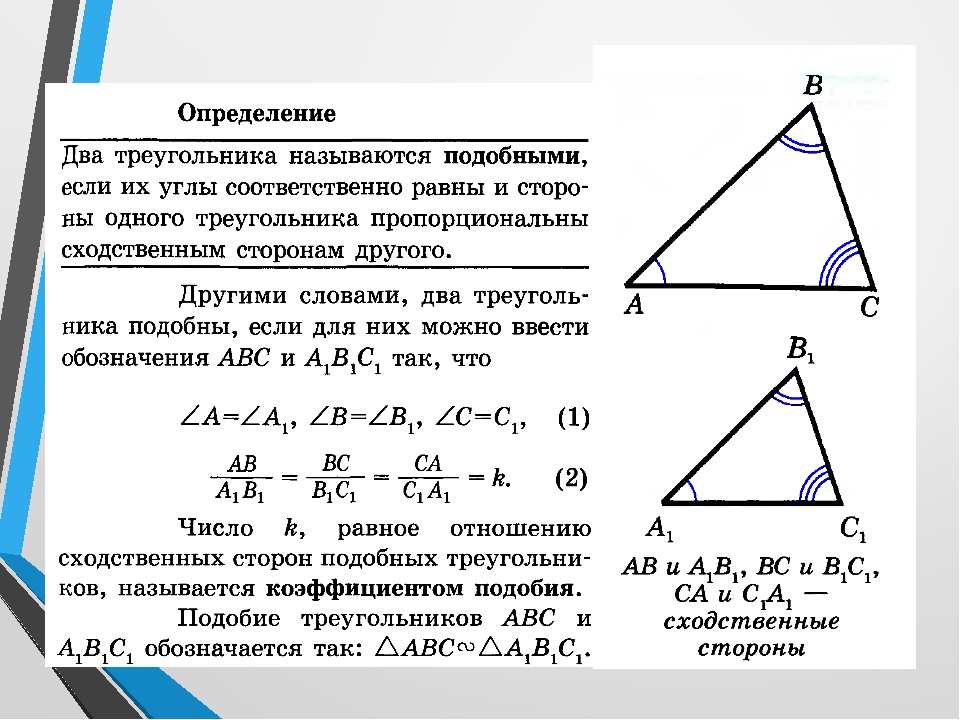
Коэффициент подобия (подобных) треугольников – это число, равное отношению сходственных сторон этих треугольников.
Определение
Периметр треугольника – это сумма длин всех его сторон.
Теорема
Отношение периметров двух подобных треугольников равно коэффициенту подобия.
Доказательство
Рассмотрим треугольники \(ABC\) и \(A_1B_1C_1\) со сторонами \(a,b,c\) и \(a_1, b_1, c_1\) соответственно (см. рисунок выше).
Тогда \(P_{ABC}=a+b+c=ka_1+kb_1+kc_1=k(a_1+b_1+c_1)=k\cdot P_{A_1B_1C_1}\)
Теорема
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Доказательство
Пусть треугольники \(ABC\) и \(A_1B_1C_1\) подобны, причём \(\dfrac{AB}{A_1B_1} = \dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1} = k\). Обозначим буквами \(S\) и \(S_1\) площади этих треугольников соответственно. \circ
— \angle A_1 — \angle B_1 = \angle C_1\), то есть углы треугольника \(ABC\) соответственно равны углам треугольника \(A_1B_1C_1\).
\circ
— \angle A_1 — \angle B_1 = \angle C_1\), то есть углы треугольника \(ABC\) соответственно равны углам треугольника \(A_1B_1C_1\).
Так как \(\angle A = \angle A_1\) и \(\angle B = \angle B_1\), то \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot AC}{A_1B_1\cdot A_1C_1}\) и \(\dfrac{S_{ABC}}{S_{A_1B_1C_1}} = \dfrac{AB\cdot BC}{A_1B_1\cdot B_1C_1}\).
Из этих равенств следует, что \(\dfrac{AC}{A_1C_1} = \dfrac{BC}{B_1C_1}\).
Аналогично доказывается, что \(\dfrac{AC}{A_1C_1} = \dfrac{AB}{A_1B_1}\) (используя равенства \(\angle B = \angle B_1\), \(\angle C = \angle C_1\)).
В итоге, стороны треугольника \(ABC\) пропорциональны сходственным сторонам треугольника \(A_1B_1C_1\), что и требовалось доказать.
Теорема (второй признак подобия треугольников)
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Доказательство
Рассмотрим два треугольника \(ABC\) и \(A’B’C’\), таких что \(\dfrac{AB}{A’B’}=\dfrac{AC}{A’C’}\), \(\angle BAC = \angle A’\). Докажем, что треугольники \(ABC\) и \(A’B’C’\) – подобны. Учитывая первый признак подобия треугольников, достаточно показать, что \(\angle B = \angle B’\).
Рассмотрим треугольник \(ABC»\), у которого \(\angle 1 = \angle A’\), \(\angle 2 = \angle B’\). Треугольники \(ABC»\) и \(A’B’C’\) подобны по первому признаку подобия треугольников, тогда \(\dfrac{AB}{A’B’} = \dfrac{AC»}{A’C’}\).
С другой стороны, по условию \(\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’}\). Из последних двух равенств следует, что \(AC = AC»\).
Треугольники \(ABC\) и \(ABC»\) равны по двум сторонам и углу между ними, следовательно, \(\angle B = \angle 2 = \angle B’\).
Теорема (третий признак подобия треугольников)
Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Доказательство
Пусть стороны треугольников \(ABC\) и \(A’B’C’\) пропорциональны: \(\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’} = \dfrac{BC}{B’C’}\). Докажем, что треугольники \(ABC\) и \(A’B’C’\) подобны.
Для этого, учитывая второй признак подобия треугольников, достаточно доказать, что \(\angle BAC = \angle A’\).
Рассмотрим треугольник \(ABC»\), у которого \(\angle 1 = \angle A’\), \(\angle 2 = \angle B’\).
Треугольники \(ABC»\) и \(A’B’C’\) подобны по первому признаку подобия треугольников, следовательно, \(\dfrac{AB}{A’B’} = \dfrac{BC»}{B’C’} = \dfrac{C»A}{C’A’}\).
Из последней цепочки равенств и условия \(\dfrac{AB}{A’B’} = \dfrac{AC}{A’C’} = \dfrac{BC}{B’C’}\) вытекает, что \(BC = BC»\), \(CA = C»A\).
Треугольники \(ABC\) и \(ABC»\) равны по трем сторонам, следовательно, \(\angle BAC = \angle 1 = \angle A’\).
\[{\Large{\text{Теорема Фалеса}}}\]
Теорема
Если на одной из сторон угла отметить равные между собой отрезки и через их концы провести параллельные прямые, то эти прямые отсекут на второй стороне также равные между собой отрезки.
Доказательство
Докажем сначала лемму: Если в \(\triangle OBB_1\) через середину \(A\) стороны \(OB\) проведена прямая \(a\parallel BB_1\), то она пересечет сторону \(OB_1\) также в середине.
Через точку \(B_1\) проведем \(l\parallel OB\). Пусть \(l\cap a=K\). Тогда \(ABB_1K\) — параллелограмм, следовательно, \(B_1K=AB=OA\) и \(\angle A_1KB_1=\angle ABB_1=\angle OAA_1\); \(\angle AA_1O=\angle KA_1B_1\) как вертикальные. Значит, по второму признаку \(\triangle OAA_1=\triangle B_1KA_1 \Rightarrow OA_1=A_1B_1\). Лемма доказана.
Перейдем к доказательству теоремы. Пусть \(OA=AB=BC\), \(a\parallel b\parallel c\) и нужно доказать, что \(OA_1=A_1B_1=B_1C_1\).
Таким образом, по данной лемме \(OA_1=A_1B_1\). Докажем, что \(A_1B_1=B_1C_1\). Проведем через точку \(B_1\) прямую \(d\parallel OC\), причем пусть \(d\cap a=D_1, d\cap c=D_2\). Тогда \(ABB_1D_1, BCD_2B_1\) — параллелограммы, следовательно, \(D_1B_1=AB=BC=B_1D_2\). Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\) как вертикальные, \(\angle
A_1D_1B_1=\angle C_1D_2B_1\) как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2
\Rightarrow A_1B_1=B_1C_1\).
Таким образом, \(\angle A_1B_1D_1=\angle C_1B_1D_2\) как вертикальные, \(\angle
A_1D_1B_1=\angle C_1D_2B_1\) как накрест лежащие, и, значит, по второму признаку \(\triangle A_1B_1D_1=\triangle C_1B_1D_2
\Rightarrow A_1B_1=B_1C_1\).
Теорема Фалеса
Параллельные прямые отсекают на сторонах угла пропорциональные отрезки.
Доказательство
Пусть параллельные прямые \(p\parallel q\parallel r\parallel s\) разбили одну из прямых на отрезки \(a, b, c, d\). Тогда вторую прямую эти прямые должны разбить на отрезки \(ka, kb, kc, kd\) соответственно, где \(k\) – некоторое число, тот самый коэффициент пропорциональности отрезков.
Проведем через точку \(A_1\) прямую \(p\parallel OD\) (\(ABB_2A_1\) — параллелограмм, следовательно, \(AB=A_1B_2\)). Тогда \(\triangle OAA_1 \sim \triangle A_1B_1B_2\) по двум углам. Следовательно, \(\dfrac{OA}{A_1B_2}=\dfrac{OA_1}{A_1B_1} \Rightarrow A_1B_1=kb\).
Аналогично проведем через \(B_1\) прямую \(q\parallel OD \Rightarrow
\triangle OBB_1\sim \triangle B_1C_1C_2 \Rightarrow B_1C_1=kc\) и т. д.
д.
\[{\Large{\text{Средняя линия треугольника}}}\]
Определение
Средняя линия треугольника – это отрезок, соединяющий середины любых двух сторон треугольника.
Теорема
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Доказательство
1) Параллельность средней линию основанию следует из доказанной выше леммы.
2) Докажем, что \(MN=\dfrac12 AC\).
Через точку \(N\) проведем прямую параллельно \(AB\). Пусть эта прямая пересекла сторону \(AC\) в точке \(K\). Тогда \(AMNK\) — параллелограмм (\(AM\parallel NK, MN\parallel AK\) по предыдущему пункту). Значит, \(MN=AK\).
Т.к. \(NK\parallel AB\) и \(N\) – середина \(BC\), то по теореме Фалеса \(K\) – середина \(AC\). Следовательно, \(MN=AK=KC=\dfrac12 AC\).
Следствие
Средняя линия треугольника отсекает от него треугольник, подобный данному с коэффициентом \(\frac12\).
Преобразование подобия — Геометрия — Мастер-класс
Подобие фигур
Преобразования подобия
Еще в Древней Греции возникло учение о подобные фигуры. В частности, в книге «Начала» Евклид пишет о преобразовании подобия.
Преобразованием подобия, или сходством называется такое преобразование одной фигуры в другую, при котором расстояния между точками изменяются в одно и то же число раз. Это число называется коэффициентом сходства. Коэффициент подобия обозначается латинской буквой k и является положительным числом.
Если коэффициент подобия равен единице, то преобразование является движением;
если коэффициент подобия меньше единицы, то
расстояние между точками уменьшается; если коэффициент сходства больше
единицы, то расстояние между точками увеличивается.
Преобразование подобия имеет такие свойства:
— преобразования подобия переводит прямые в прямые, півпрямі — в півпрямі, отрезки — в отрезки;
— преобразования подобия сохраняет углы между півпрямими;
— преобразования подобия переводит параллельные прямые в параллельные прямые.
Две фигуры называются подобными, если одну из них можно получить из второй с помощью преобразования подобия. Подобие фигур означает, что независимо от размеров и положения на плоскости эти фигуры имеют одинаковую форму.
Все круги являются подобными фигурами, все квадраты есть подобными фигурами.
Если первая фигура подобна второй фигуре с коэффициентом k, то вторая фигура тоже подобная первой фигуре, но с
коэффициентом, обратным числу k, — 1/k . Одним из преобразований подобия является гомотетія.
Одним из преобразований подобия является гомотетія.
Если две подобные фигуры размещены так, что все півпрямі, проведенные с некоторой точки через точки одной фигуры, проходят через соответствующие точки второй фигуры, то это гомотетія.
Гомотетією с центром в точке О и коэффициентом k называется такое преобразование одной фигуры в другую, при котором каждая точка Х первой фигуры переходит в точку Х’ второй фигуры так, что точка Х’ лежит на луче, выходящем из точки О и проходит через точку Х, а расстояние между точкой О и точкой Х‘ равна расстоянию между точкой А и точкой Х, умноженной на коэффициент гомотетії k.
Практические советы.
Чтобы построить отрезок, гомотетичний данном отрезке
с заданным центром гомотетії и заданным коэффициентом гомотетії, проведите
півпрямі с началом в центре гомотетії, которые проходят через концы отрезка. На
півпрямих от их начала отложите отрезки, длины которых равны
соответственно длинам отрезков, соединяющих центр гомотетії с концами заданного
отрезка, умноженных на коэффициент гомотетії, и соединяют точки, полученные на
півпрямих.
На
півпрямих от их начала отложите отрезки, длины которых равны
соответственно длинам отрезков, соединяющих центр гомотетії с концами заданного
отрезка, умноженных на коэффициент гомотетії, и соединяют точки, полученные на
півпрямих.
Коэффициент подобия геометрического — Энциклопедия по машиностроению XXL
Механическое или вообще физическое подобие можно рассматривать как обобщение геометрического подобия. Две геометрические фигуры подобны, если отношения всех соответственных длин одинаковы. Если известен коэффициент подобия— масштаб, то простым умножением на величину масштаба размеров одной геометрической фигуры получаются размеры другой, ей подобной геометрической фигуры. [c.58]При теоретическом анализе используют модели дефектов в виде отражателей правильной геометрической формы (сфера, диск, цилиндр). В экспериментах точно воспроизвести расчетные модели в натуральном образце удается далеко не всегда.
 Например, практически невозможно выполнить модель дефекта в виде гонкого диска в толще образца. Поэтому при измерениях используют искусственные дефекты в виде полостей правильной геометрической формы с выходом на поверхность образца. Широко применяют также жидкостное моделирование, основанное на подобии процессов распространения продольных звуковых волн в твердом теле и в жидкости (коэффициент подобия где , Сда — скорости ультразвука в металле и жидкости). Основное преимущество этого способа анализа в том, что исследование можно проводить на искусственных дефектах, идентичных расчетной модели.
[c.104]
Например, практически невозможно выполнить модель дефекта в виде гонкого диска в толще образца. Поэтому при измерениях используют искусственные дефекты в виде полостей правильной геометрической формы с выходом на поверхность образца. Широко применяют также жидкостное моделирование, основанное на подобии процессов распространения продольных звуковых волн в твердом теле и в жидкости (коэффициент подобия где , Сда — скорости ультразвука в металле и жидкости). Основное преимущество этого способа анализа в том, что исследование можно проводить на искусственных дефектах, идентичных расчетной модели.
[c.104]Физические параметры течения и соответствующие коэффициенты подобия (преобразования) представлены в табл. 1-16, Индексом I обозначены параметры натурного потока, а индексом И — модельного, В качестве независимых приняты геометрический масштаб модели Kl и масштаб температур Кт- Значение Kl лимитировано источником питания, а Кт — условиями простоты и надежности эксперимента. Остальные коэффициенты (масштаб ы) могут быть выражены через Кц и Кт (см. табл. 1-16).
[c.60]
Остальные коэффициенты (масштаб ы) могут быть выражены через Кц и Кт (см. табл. 1-16).
[c.60]
Общий случай конструкции конечной толщины. Рассмотрим любую могущую деформироваться конструкцию при действии нагрузки. Изготовим модель такой конструкции с соблюдением масштаба, но из другого материала. Исследуем теперь условия, которые должны быть удовлетворены для упругих постоянных и действующих нагрузок, чтобы деформации основной системы и модели были геометрически подобны. Пусть k будет коэффициент подобия между моделью и оригиналом, так что если I—какая-либо длина в оригинале, то kl будет соответствующей ей длиной в модели. [c.540]
Для того чтобы коэффициенты сопротивления геометрически подобных тел были одинаковы, необходимо, как установлено в 2, чтобы обтекающие их потоки были динамически подобны. Выясним, какие именно условия динамического подобия являются в аэродинамике основными и каким путем можно осуществить эти условия в эксперименте. [c.581]
[c.581]
Если сравнить уравнения периодической упругой кривой (3.1) — (3.7) с уравнениями упругой линии изогнутого стержня (см. 2.2) и с выражениями для коэффициентов подобия упругих линий (см. 2.3), то легко увидеть, что в задачах основного класса при любой схеме нагружения прямого или криволинейного стержня всегда можно найти на периодической упругой кривой такой участок, который будет геометрически подобен исследуемой упругой линии стержня при сколь угодно больших перемещениях при изгибе. Будем называть такой участок периодической упругой кривой эквивалентным участком. Концевые точки этого участка будем обозначать теми же знаками О п 1, как и концы упругой линии стержня. [c.58]
Уточненное определение р иногда выполняют на плоских образцах с помощью двух геометрически подобных ячеек в каждой имеется система из четырех электродов — два измерительных и два высоковольтных, соединенных попарно в параллель (рис.
 25-8). Если толщины образцов t к f, то под коэффициентом подобия понимают отношение k = ttt. Значения диаметров электродов должны удовлетворять условию
[c.493]
25-8). Если толщины образцов t к f, то под коэффициентом подобия понимают отношение k = ttt. Значения диаметров электродов должны удовлетворять условию
[c.493]Течения двух газов с геометрически подобными и подобно расположенными границами называются динамически подобными течениями, если параметры одного течения могут быть получены из соответствующих параметров другого течения в соответственных точках в соответственные моменты времени путем умножения на одинаковые для всех точек множители, которые называются коэффициентами подобия. Из этого определения следует, что линии тока в обоих течениях будут подобными. В установившихся течениях вопрос о времени отпадает. [c.136]
В большинстве случаев моделирование основано на рассмотрении физически подобных явлений. Изучение интересующего нас натурного явления мы заменяем изучением физически подобного явления, которое удобнее и выгоднее осуществить. Механическое или вообще физическое подобие можно рассматривать как обобщение геометрического подобия. Две геометрические фигуры подобны, если отношения всех соответственных длин одинаковы. Если известен коэффициент подобия — масштаб, то простым умножением размеров одной геометрической фигуры на величину масштаба получаются размеры другой, ей подобной геометрической фигуры.
[c.426]
Две геометрические фигуры подобны, если отношения всех соответственных длин одинаковы. Если известен коэффициент подобия — масштаб, то простым умножением размеров одной геометрической фигуры на величину масштаба получаются размеры другой, ей подобной геометрической фигуры.
[c.426]
Имеются две геометрически подобные колебательные системы в виде грузиков на пружинах, изготовленные из одного материала. Во сколько раз отличаются периоды колебаний Коэффициент подобия п. [c.8]
Значения I и s неудобны для расчетов. Используя геометрическое подобие зубьев различного модуля, эти величины выражают через безразмерные коэффициенты [c.120]
По результатам экспериментов коэффициент к можно определить с помощью формулы (6.23), если измерить среднюю скорость V и падение напора h . В п. 6.4 даны указания о рациональном, теоретически обоснованном способе обработки таких опытных данных. Согласно выражению (6.25) следует найти эмпирическую зависимость к от числа Re и какого-либо безразмерного параметра, определяющего геометрическое подобие потоков.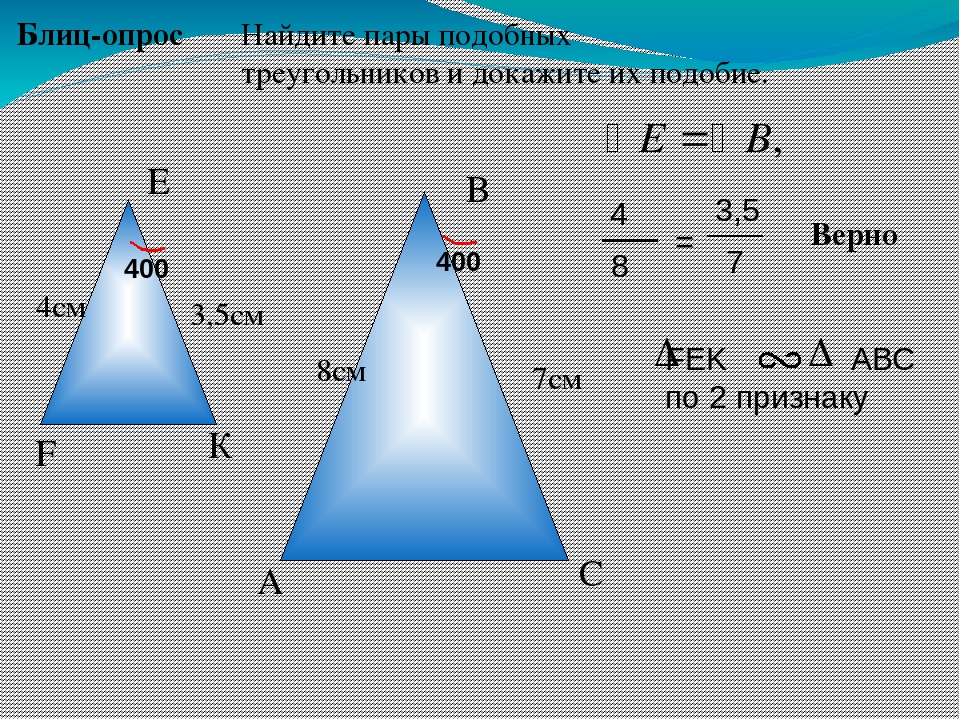 [c.148]
[c.148]
Следует иметь в виду, что динамическое или вообще физическое подобие является обобщением геометрического подобия. Как известно из геометрии, две фигуры подобны в том случае, когда отношения всех соответственных размеров этих фигур одинаковы, т. е. когда размеры одной фигуры могут быть получены простым умножением размеров другой фигуры на некоторый масштабный коэффициент. Точно так же динамически или физически подобными явлениями называют такие явления, когда по заданным характеристикам одного явления можно получить соответствующие характеристики другого явления также путем простого умножения этих характеристик на соответствующие переходные масштабные коэффициенты. [c.110]
Потоки жидкости, удовлетворяющие одновременно условиям геометрического, кинематического и динамического подобия, называются гидродинамически подобными потоками, а коэффициенты пропорциональности М1, Мр М , Мр и т. д.— масштабными множителями.
[c. 301]
301]
Геометрическое подобие означает пропорциональность характерных линейных размеров рассматриваемых потоков. В дальнейшем будем использовать термины натурный поток н поток на модели не вводя никаких ограничений на коэффициенты пропорциональности параметры первого потока будем записывать с индексом н , второго — с индексом м . [c.380]
Правильная картина движения жидкости и соответствующие закономерности гидравлического сопротивления и теплообмена могут быть получены только в моделях, рассчитанных по правилам моделирования, обеспечивающих подобие явлений в образце и модели. При этом необходимыми и достаточными условиями теплового подобия являются следующие 1) геометрическое подобие 2) подобие условий движения жидкости при входе 3) подобие физических свойств в сходственных точках модели и образца (постоянство отношения плотностей, коэффициентов вязкости и др.) 4) подобие температурных полей на границах 5) одинаковость значений определяющих критериев Re и Рг при вынужденном и Gr и Рг при свободном движении жидкости. При этом одинаковость определяющих критериев подобия достаточно установить в каком-либо одном сходственном сечении.
[c.257]
При этом одинаковость определяющих критериев подобия достаточно установить в каком-либо одном сходственном сечении.
[c.257]
Правильная картина движения жидкости и соответствующие закономерности гидравлического сопротивления и теплообмена могут быть получены только в моделях, рассчитанных по правилам моделирования, обеспечивающих подобие явлений в образце и модели. При этом необходимыми и достаточными условиями теплового подобия являются следующие 1) геометрическое подобие 2) подобие условий движения жидкости при входе 3) подобие физических свойств в сходственных точках модели и образца (постоянство отношения плотностей, коэффициентов вязкости и др.) 4) п6- [c.275]
Принцип геометрического подобия в конструктивно-унифицированных рядах металлорежущих станков, а также установившиеся во всем мире более или менее близкие одна другой общие конструктивные схемы аналогичных типов станков позволяют на основе выбранного закона изменения веса основных нагруженных деталей в зависимости от изменения исходных параметров распространить этот закон на изменение веса станка в целом.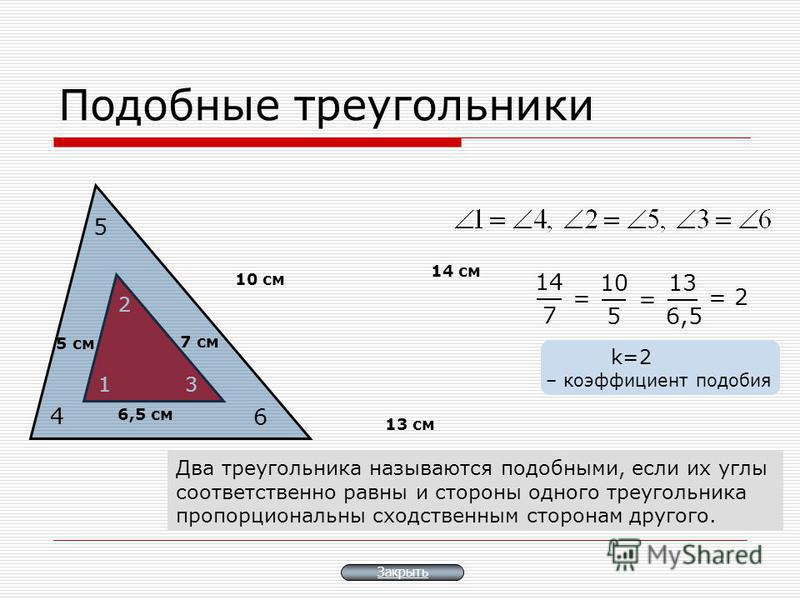 Статистический анализ весов достаточно большого количества моделей станков ведущих фирм различных стран мира дает возможность установить коэффициенты или другие показатели экономичного веса и принять их в качестве стандартных. Эта методика, основанная на статистическом анализе, применима для металлорежущих станков любых типов.
[c.67]
Статистический анализ весов достаточно большого количества моделей станков ведущих фирм различных стран мира дает возможность установить коэффициенты или другие показатели экономичного веса и принять их в качестве стандартных. Эта методика, основанная на статистическом анализе, применима для металлорежущих станков любых типов.
[c.67]
При испытаниях на пальчиковой машине воспроизводятся реальные значения только удельного давления и скорости скольжения в плоскости трения пары. Но при этом не осуществляется тепловое моделирование. Объемная температура и отвод тепла от плоскости трения значительно отличаются от натуры. Это происходит потому, что на пальчиковой машине ни в какой мере не соблюдается принцип геометрического подобия с натурным тормозом и прежде всего отношение площадей трения элементов пары, характеризуемое коэффициентом взаимного перекрытия Квз- [c.132]
При продувке моделей мазутных горелок на этом стенде работает один тракт стенда. Масштаб моделей горелок выбирается в зависимости от располагаемого расхода и давления вентилятора стенда. При холодном моделировании горелок, кроме геометрического подобия, необходимо достичь режима автомодельности, когда наблюдается постоянство значений коэффициентов аэродинамического сопротивления для различных значений числа Рейнольдса Ке.
[c.140]
Масштаб моделей горелок выбирается в зависимости от располагаемого расхода и давления вентилятора стенда. При холодном моделировании горелок, кроме геометрического подобия, необходимо достичь режима автомодельности, когда наблюдается постоянство значений коэффициентов аэродинамического сопротивления для различных значений числа Рейнольдса Ке.
[c.140]
Геометрические преобразования, выполняемые над фигурами, можно оценить параметрически аналогично геометрическим условиям. Пусть фигура AB DEF (см. рис. 14) задана параметрами формы. Необходимо построить фигуру A B D E-i F-i , подобную фигуре AB DEF. Для определения параметров формы новой фигуры необходимо указать один параметр > О, называемый коэффициентом подобия. Этот параметр характеризует преобразование подобия. [c.38]
Выполняя условия деформационного подобия при исследовании плоского напряженного состояния составных плоских тел оптическим методом [56], сохраняем равенство коэффициентов подобия для натуры и модели. Р1апример, во взятом натурном литом чугунном образце с орнаментом модуль упругости поверхностного слоя, имеющего мелкокристаллическую структуру, i H=l,55-10 кгс/мм , а нилотношения модулей упругости слоев из оптически активного материала при выполнении геометрического и силового подобия (рис. 21).
[c.32]
Р1апример, во взятом натурном литом чугунном образце с орнаментом модуль упругости поверхностного слоя, имеющего мелкокристаллическую структуру, i H=l,55-10 кгс/мм , а нилотношения модулей упругости слоев из оптически активного материала при выполнении геометрического и силового подобия (рис. 21).
[c.32]
Повреждаемость 2—i03 3 —107 Пов горпые наг])узки, влияние на механич. Boii-ства 2 — 192 Поглощения коэффициент 2—404 Податливость 1—301 Подобие геометрическое 2—404 [c.514]
Физическое подобие определяется аналогично геометрическому подобию. При геометрическом подобии отношения всех соответствующих длин рассматриваемых фигур одинаковы, т. е. если известен масштаб, то путем умножения размеров одной фигуры на масштаб (коэффициент подобия) можно получить размеры другой (геометрически подобной) фигуры. Аналогично этому два физических явления подобны, если по числедаым значениям характеристик одного явления можно получить численные значения характеристик другого явления аналогичным переходом от одной системы измерения к другой с использованием переходных масштабов [29]. [c.42]
[c.42]
Полученный комплекс является искомым критерием подобия, который называется критерием Фурье и обозначается через Ро, а при выборе констант подобия в этом случае должно выполняться условие кцкх1к 1 1. Коэффициент подобия представляет собой отношение отрезков, соединяющих в первой и второй системах две сходственные точки. Поэтому под размером в критерии подобия можно понимать любой геометрический размер нужно только, чтобы для всех систем критерий вычислялся по этому размеру. Характерный размер, вводимый в критерий подобия, называется определяющим размером системы, Обычно для труб определяющим размером является диаметр, для плит — их толщина и т, д. [c.237]
Так как условие Re idem при наличии геометрического подобия определяет кинематическое подобие напорных потоков, безразмерные характеристики последних (коэффициенты сопротивления, расхода и т. д.) являются фуикция.ми Re Это же относится и к процессам истечения через малые отверстия и насадки, на которЕ.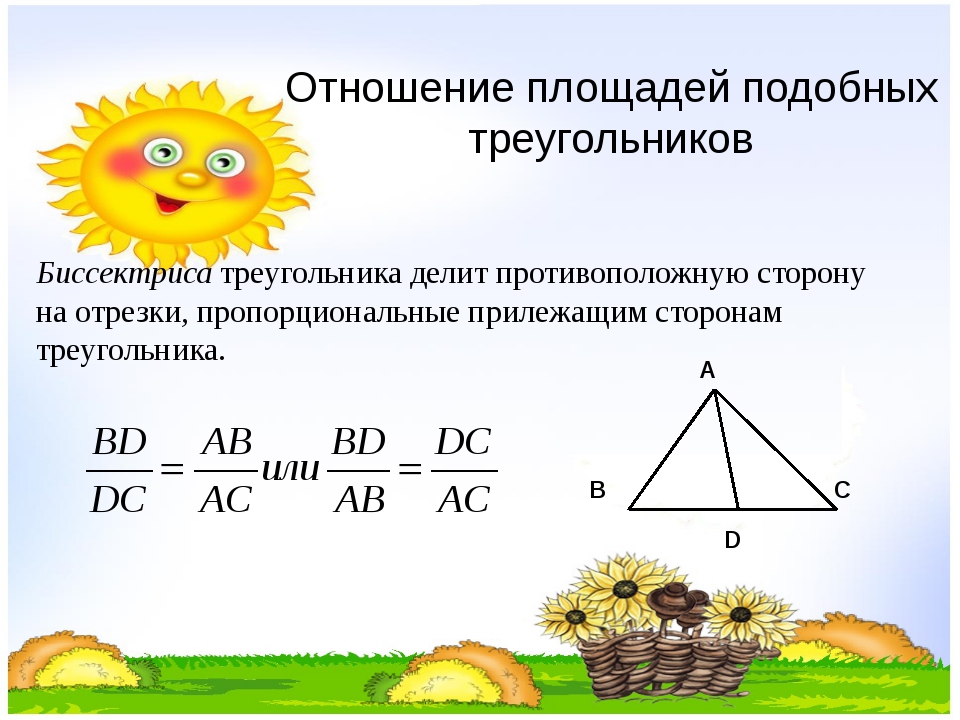 1е весомость жидкости практически не влияет.
[c.108]
1е весомость жидкости практически не влияет.
[c.108]
Третья теорема исходит из предположения, -что явления протекают в геометрпчески подобных системах (поэтому геометрическое подобие систем есть первое необходимое условие для существования подобия), что для рассматриваемого явления можно составить дифференциальные уравнения, что установлено существование и единственность решения уравнения при заданных граничных условиях, что известны численные значения коэффициентов и физических параметров, входящих в дифференциальное уравнение. [c.417]
Нели по расчету значение коэффициента К,. > 2.,, 3, то нужно принять конструктивные меры по улучшению работы передачи. Приводные цепи проектируют на основе геометрического подобия, поэтому площадь проекции опорной поверхности шар пира для каждого размерно1 о ряда цепей можно представить п виде А =сР , где с -коэф( )ициент пропорциональности, однорядных цепей, кроме цепей, не входящих в закономерный размерный ряд ПР-Н-460 ПР-12,7-400-1 и ПР-12,7-900-2 (см, табл, 12.
 1),
[c.257]
1),
[c.257]С помощью уравнения подобия можно определить число Нуссель-та и, следовательно, соответствующие значения коэффициента теплоотдачи. При решении уравнений подобия важную роль играют понятия определяющей температуры и определяющего геометрического размера. Определяющей температурой называется температура, которой соответствуют значения физических параметров сэеды, входящих в числа подобия определянщим размером — характерный линейный размер /, определяющий развитие процесса. Например, для труб круглого сечения определяющим линейным размером является диаметр для каналов некруглого сечения — эквивалентный диаметр = 4Г/Р, где Р — площадь поперечного сечения канала, а Р — смоченный периметр сечения. [c.161]
При осуществлении масштабных коэффициентов (табл. 16) на модельных лабораторных образцах можно получить идентичные натуре температурные поля. Интерес в этом случае представляет не только применение переходных коэффициентов к конкретной соударяющейся паре, геометрически подобной натурной, но и проверка возможности моделирования при афинном подобии натуры и модели, т. е, когда модельные и натурные образцы геометрически не подобны.
[c.156]
е, когда модельные и натурные образцы геометрически не подобны.
[c.156]
Рассмотрим задачу моделирования для однородного упругого тела. Вместо натурного тела (натуры) для изучения наиряжений, деформаций и неремещений воспользуемся моделью, геометрически подобной натуре, с ко эффвцИ0нтом геометрического подобия k — = LJL , La и — характерные размеры натуры и модели. Натурное тело нагружено поверхностными ра спределенными нагрузками Ри, объемными силами на части его поверхности заданы пере-меш.ония Uoi н. Модуль упругости и коэффициент Пуассона материала, натуры соответственно ц и Цн- Величины, характеризующие м,одель и натуру, связаны соотношениями [c.9]
Отсюда видно, что при неизменном давлении р и коэффициенте трения р и при сохранении геометрического подобия а = onst) тормозной момент многодискового тормоза пропорционален величине zRI. Таким образом, один и тот же тормозной момент может быть осуществлен различными тормозами при условии, чтобы zR = onst. [c.228]
[c.228]
В многономенклатурных и мелкосерийных производствах с частой сменяемостью изделий применяется метод типовых коэффициентов использования материалов. За основу подразделения изделий на группы принимают и кгнструктивное и технологическое подобия. Вся номенклатура производимой продукции подразделяется на группы с учетом того, что подобная геометрическая форма и технология изготовления деталей в изделиях обеспечивают примерное равенство технологических отходов и коэффициенты использования материалов являются примерно одинаковыми. [c.173]
Презентация «определение подобных треугольников». Презентация на тему «определение подобных треугольников» Практические приложения подобия треугольников
1.1. Пропорциональные отрезки Определение подобных треугольников 1.2. Определение подобных треугольников 1.3. Отношение площадей подобных треугольников Отношение площадей подобных треугольников Свойства подобия.
1.1 Пропорциональные отрезки. Отношением отрезков AB и CD называется отношение их длин, т. е. Говорят, что отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1, если ПРИМЕР 1. Отрезки AB и CD, длины которых равны 2 см и 1см, пропорциональны отрезкам A 1 B 1 и C 1 D 1,отрезки которых равны 3см и 1,5см. В самом деле,
Отношением отрезков AB и CD называется отношение их длин, т. е. Говорят, что отрезки AB и CD пропорциональны отрезкам A 1 B 1 и C 1 D 1, если ПРИМЕР 1. Отрезки AB и CD, длины которых равны 2 см и 1см, пропорциональны отрезкам A 1 B 1 и C 1 D 1,отрезки которых равны 3см и 1,5см. В самом деле,
1.2. Определение подобных треугольников. В повседневной жизни встречаются предметы одинаковой формы, но разных размеров, например футбольный и теннисный мячи, круглая тарелка и большое круглое блюдо. В геометрии фигуры одинаковой формы принято называть подобными. Так, подобными являются любые два квадрата, любые два круга. Введем понятие подобных треугольников.
1.2. Определение подобных треугольников. ПОДОБИЕ, геометрическое понятие, характеризующее наличие одинаковой формы у геометрических фигур, независимо от их размеров. Две фигуры F1 и F2 называются подобными, если между их точками можно установить взаимно однозначное соответствие, при котором отношение расстояний между любыми парами соответствующих точек фигур F1 и F2 равно одной и той же постоянной k, называемой коэффициентом подобия. Углы между соответствующими линиями подобных фигур равны. Подобные фигуры F1 и F2.
Углы между соответствующими линиями подобных фигур равны. Подобные фигуры F1 и F2.
Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. Другими словами, два треугольника подобны, если их можно обозначить буквами ABC и A 1 B 1 C 1 так, что A= A 1, B= B 1, C= C 1, Число k, равное отношению сходственных сторон треугольников, называется коэффициентом подобия.
1.3. Отношение площадей подобных треугольников. Теорема. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия. Доказательство. Пусть треугольники ABC и A1B1C1 подобны и коэффициент подобия равен k. Обозначим буквами S и S1 площади этих треугольников. Так как A= A1, то
Свойства подобия. Задача 2. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника Решение. Пусть AD – биссектриса треугольника ABC. Докажем, что Треугольники ABD и ACD имеют общую высоту AH, поэтому 12 A H B D C
Пусть AD – биссектриса треугольника ABC. Докажем, что Треугольники ABD и ACD имеют общую высоту AH, поэтому 12 A H B D C
Доказательство: По теореме о сумме углов: С = А — В, а С 1 = А 1 — В 1,значит С= С 1. Так как А= А 1 и С= С 1, то и От этого следует: Получается, что сходственные стороны пропорциональны. Дано: АВС и А 1 В 1 С 1 А= А 1 В= В 1 Доказать: АВС А 1 В 1 С 1 А С В А1А1 В1В1 С1С1
АВС 2 А 1 В 1 С 1 (по первому признаку),значит, с другой стороны,из этих равенств получается АС= =АС 2. АВС= АВС 2 -по двум сторонам и углу между ними (АВ-общая сторона, АС=АС 2 и,т.к. и).Значит и, то АВС А1В1С1 Дано: АВС и А 1 В 1 С 1 Д-ть: Доказательство: Рассмотрим АВС 2, у которого и
Доказательство: А 1 В 1 – средняя линия, и А 1 В 1 //АВ, поэтому и Значит АОВ А 1 ОВ 1 (по двум углам),то Но АВ=А 1 В 1, поэтому АО=2А 1 О и ВО=2В 1 О. Значит точка О- пересечение медиан АА 1 и ВВ 1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка О – пересечение медиан ВВ 1 и СС 1 делит каждую из них в отношении 2:1, считая от вершины. Значит точка О – пересечения медиан АА 1, ВВ 1 и СС 1 делит их в отношении 2:1, считая от вершины.
Значит точка О- пересечение медиан АА 1 и ВВ 1 делит каждую из них в отношении 2:1, считая от вершины. Аналогично доказывается, что точка О – пересечение медиан ВВ 1 и СС 1 делит каждую из них в отношении 2:1, считая от вершины. Значит точка О – пересечения медиан АА 1, ВВ 1 и СС 1 делит их в отношении 2:1, считая от вершины.
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Подобные треугольники
Подобные фигуры Фигуры принято называть подобными, если они имеют одинаковую форму (похожи по виду).
Подобие в жизни(карты местности)
Пропорциональные отрезки Определение: отрезки называются пропорциональными, если пропорциональны их длины. 12 6 8 4 А 1 В 1 АВ С 1 К 1 СК Говорят, что отрезки А 1 В 1 и С 1 К 1 пропорциональны отрезкам АВ и СК. Пропорциональны ли отрезки АВ и СК отрезкам ЕР и НТ, если: а) АВ = 15 см, СК = 2,5 см, ЕР = 3 см, НТ = 0,5 см? б) АВ = 12 см, СК = 2,5 см, ЕР = 36 см, НТ = 5 см? в) АВ = 24см, СК = 2,5 см, ЕР = 12 см, НТ = 5 см? да нет нет А В 6 см С К 4 см А 1 В 1 12 см С 1 8 см К 1
б Пропорциональные отрезки Тест 1.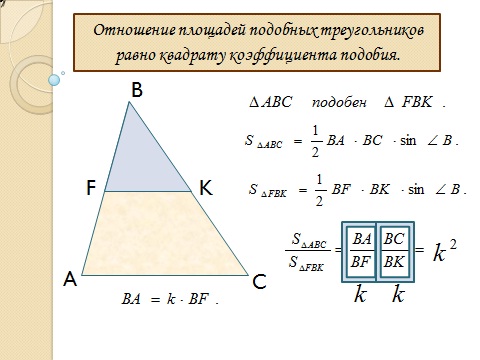 Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ; МЕ РН АВ СК; АВ СК МЕ РН.
Указать верное утверждение: а) отрезки АВ и РН пропорциональны отрезкам СК и МЕ; б) отрезки МЕ и АВ пропорциональны отрезкам РН и СК; в) отрезки АВ и МЕ пропорциональны отрезкам РН и СК. А В 3 см С К 2см М Е 9 см Р Н 6 см Приложение: равенство МЕ АВ РН СК можно записать ещё тремя равенствами: РН СК МЕ АВ; МЕ РН АВ СК; АВ СК МЕ РН.
Пропорциональные отрезки 2 . Тест F Y Z R L S N 1 c м 2 см 4 см 2 см 3 см Какой отрезок нужно вписать, чтобы было верным утверждение: отрезки FY и YZ пропорциональны отрезкам LS и ……. а) RL ; б) RS ; в) SN а) RL
Пропорциональные отрезки (нужное свойство) Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника. Н Дано: АВС, АК – биссектриса. Доказательство: 1 А В К С 2 Т. к. АК – биссектриса, то 1 = 2, значит, АВК и АСК имеют по равному углу, поэтому Доказать: ВК АВ КС АС S АВК S АСК АВ ∙ АК АС ∙ АК AB AC АВК и АСК имеют общую высоту АН, значит, S АВК S АСК ВК К C AB А C BK K С ВК АВ КС АС Следовательно, Проведём АН ВС.
Подобные треугольники Определение: треугольники называются подобными, если углы одного треугольника равны углам другого треугольника и стороны одного треугольника пропорциональны сходственным сторонам другого. А 1 В 1 С 1 А В С Сходственными сторонами в подобных треугольниках называются стороны, лежащие против равных углов. А 1 = А, В 1 = В, С 1 = С А 1 В 1 В 1 С 1 А 1 С 1 АВ ВС АС k A 1 B 1 C 1 ABC K – коэффициент подобия ~
Подобные треугольники А 1 В 1 С 1 А В С Нужное свойство: А 1 = А, В 1 = В, С 1 = С, АВ ВС АС А 1 В 1 В 1 С 1 А 1 С 1 1 k ABC ~ A 1 B 1 C 1 , – коэффициент подобия 1 k A 1 B 1 C 1 ABC , K – коэффициент подобия ~
Реши задачи 3. По данным на чертеже найти стороны АВ и В 1 С 1 подобных треугольников АВС и А 1 В 1 С 1: А В С А 1 С 1 В 1 6 3 4 2,5 ? ? Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 3 . 2. Найти стороны А 1 В 1 С 1 , подобного АВС, если АВ = 6, ВС= 12. АС = 9 и k = 1/3.
Теорема 1. Отношение периметров подобных треугольников равно коэффициенту подобия.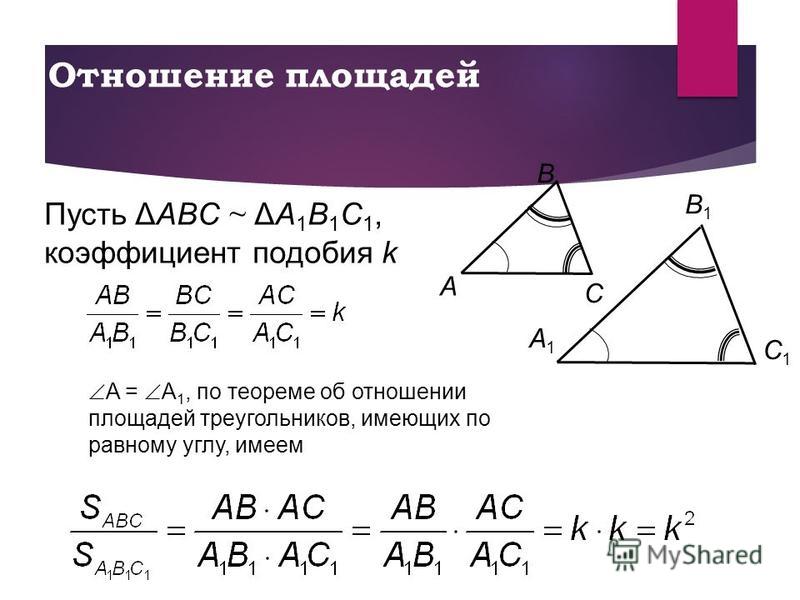 М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ: Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС. Значит, Р МКЕ: Р АВС = k .
М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: Р МКЕ: Р АВС = k Доказательство: K , МК АВ КЕ ВС МЕ АС Значит, МК = k ∙ АВ, КЕ = k ∙ ВС, МЕ = k ∙ АС. Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то Р МКЕ = МК + КЕ + МЕ = k ∙ АВ + k ∙ ВС + k ∙ АС = k ∙ (АВ + ВС + АС) = k ∙ Р АВС. Значит, Р МКЕ: Р АВС = k .
Теорема 2. Отношение площадей подобных треугольников равно квадрату коэффициент a подобия. М К Е A B C Дано: МКЕ ~ АВС, K – коэффициент подобия. Доказать: S МКЕ: S АВС = k 2 Доказательство: Т. к. по условию МКЕ ~ АВС, k – коэффициент подобия, то M = A, k, MK AB ME AC значит, МК = k ∙ АВ, МЕ = k ∙ АС. S MKE S ABC MK ∙ ME AB ∙ AC k ∙ АВ ∙ k ∙ АС АВ ∙ АС k 2
Реши задачи Две сходственные стороны подобных треугольников равны 8 см и 4 см. Периметр второго треугольника равен 12 см. Чему равен периметр первого треугольника? 24 см 2. Две сходственные стороны подобных треугольников равны 9 см и 3 см. Площадь второго треугольника равна 9 см 2 . Чему равна площадь первого треугольника? 81 см 2 3. Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника? 8 см
Две сходственные стороны подобных треугольников равны 5 см и 10 см. Площадь второго треугольника равна 32 см 2 . Чему равна площадь первого треугольника? 8 см 2 4. Площади двух подобных треугольников равны 12 см 2 и 48 см 2 . Одна из сторон первого треугольника равна 4 см. Чему равна сходственная сторона второго треугольника? 8 см
Решение задачи Площади двух подобных треугольников равны 50 дм 2 и 32 дм 2 , сумма их периметров равна 117 дм. Найдите периметр каждого треугольника. Найти: Р АВС, Р РЕК Решение: Т. к. по условию треугольники АВС и РЕК подобны, то: Дано: АВС, РЕК подобны, S АВС = 50 дм 2 , S РЕК = 32 дм 2 , Р АВС + Р РЕК = 117дм. S АВС S РЕК 50 32 25 16 K 2 . Значит, k = 5 4 K , Р АВС Р РЕК Р АВС Р РЕК 5 4 1,25 Значит, Р АВС = 1,25 Р РЕК Пусть Р РЕК = х дм, тогда Р АВС = 1,25 х дм Т. к. по условию Р АВС + Р РЕК = 117дм, то 1,25 х + х = 117, х = 52. Значит, Р РЕК = 52 дм, Р АВС = 117 – 52 = 65 (дм). Ответ: 65 дм, 52 дм.
« Математику уже затем учить следует, что она ум в порядок приводит» М.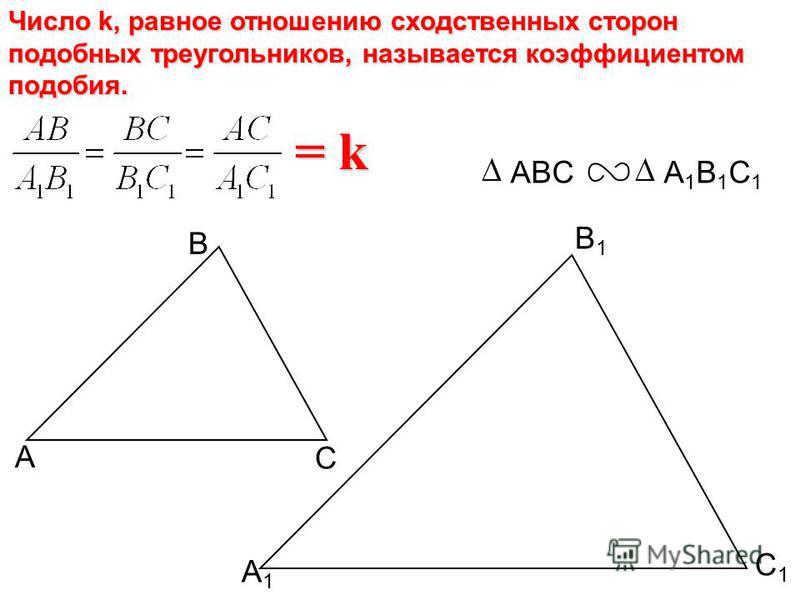 В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.
В. Ломоносов Желаю успехов в учёбе! Михайлова Л. П. ГОУ ЦО № 173.
краткое содержание других презентаций
«Геометрия «Подобные треугольники»» — Основное тригонометрическое тождество. Второй признак подобия треугольников. Синус, косинус и тангенс. Значения синуса, косинуса и тангенса для углов 30°, 45°, 60°. Подобные треугольники. Подобие прямоугольных треугольников. Продолжение боковых сторон. Пропорциональные отрезки. Теорема об отношении площадей подобных треугольников. Значения синуса, косинуса и тангенса. Две стороны треугольника соединили отрезком, непараллельным третьей.
«Нахождение площади трапеции» — Результаты. Свойства прямоугольного треугольника. Найдите площадь трапеции. Сравните площади. Обозначь основания. Задания для самоконтроля. Площадь трапеции. Повторение пройденного материала. Ловушка. Запиши формулы. Сформировать умение применять формулу. Найдите площадь. Площадь клетки. Решение поставленной задачи. Подведём итоги. Площадь.
«Четырёхугольники, их признаки и свойства» — Ромб. Четырёхугольники, их признаки и свойства. Познакомить с видами четырёхугольников. Прямоугольник. Свойства параллелограмма. Прямоугольник, у которого все стороны равны. Четырехугольник, вершины которого находятся в серединах сторон. Диагонали. Виды четырёхугольников. Тесты. Из каких двух равных треугольников можно сложить квадрат. Виды трапеций. Углы ромба. Квадрат. Признаки параллелограмма. Четырехугольники.
Четырёхугольники, их признаки и свойства. Познакомить с видами четырёхугольников. Прямоугольник. Свойства параллелограмма. Прямоугольник, у которого все стороны равны. Четырехугольник, вершины которого находятся в серединах сторон. Диагонали. Виды четырёхугольников. Тесты. Из каких двух равных треугольников можно сложить квадрат. Виды трапеций. Углы ромба. Квадрат. Признаки параллелограмма. Четырехугольники.
«Теорема о вписанном угле» — Радиус окружности равен 4 см. Ответ. Острый угол. Закрепление изученного материала. Актуализация знаний учащихся. Актуализация знаний. Изучение нового материала. Радиус окружности. Как называется угол с вершиной в центре окружности. Найти угол между хордами. Понятие вписанного угла. Треугольник. Найти угол между ними. Решение. Проверь себя. Правильный ответ. Окружности пересекаются. Теорема о вписанном угле.
«Теорема Пифагора для прямоугольного треугольника» — Прямоугольный треугольник. Имя Пифагора. Сочетание двух противоречивых начал. Геродот. Формулировки теоремы. Античные авторы. Пифагор Самосский. Монета с изображением Пифагора. Теорема Пифагора. Учение Пифагора.
Формулировки теоремы. Античные авторы. Пифагор Самосский. Монета с изображением Пифагора. Теорема Пифагора. Учение Пифагора.
«Понятие площади многоугольника» — Смежные стороны параллелограмма. Площадь треугольника. Математический диктант. Параллелограмм. Площадь ромба. Понятие площади многоугольника. Площадь прямоугольника. Площадь трапеции. Высоты. Площадь многоугольников. Площадь прямоугольного треугольника. Теорема. Острый угол. Площадь параллелограмма. Вычислите площадь ромба. Найти площадь прямоугольного треугольника. Треугольники. Единицы измерения площади.
Презентация «Определение подобных треугольников» охватывает этап введения нового понятия на уроке геометрии в 8 классе — подобия треугольников. После уточнения понятия пропорциональности отрезков, на основе которого строится понятие подобия, ученики переходят к рассмотрению достаточно сложного для них материала — подобия. При помощи презентации учитель во время объяснения формирует четкое представление учеников об изучаемом предмете — подобии треугольников, продолжает формировать навыки использования математической речи, формирует навыки применения изученного понятия для решения практических задач.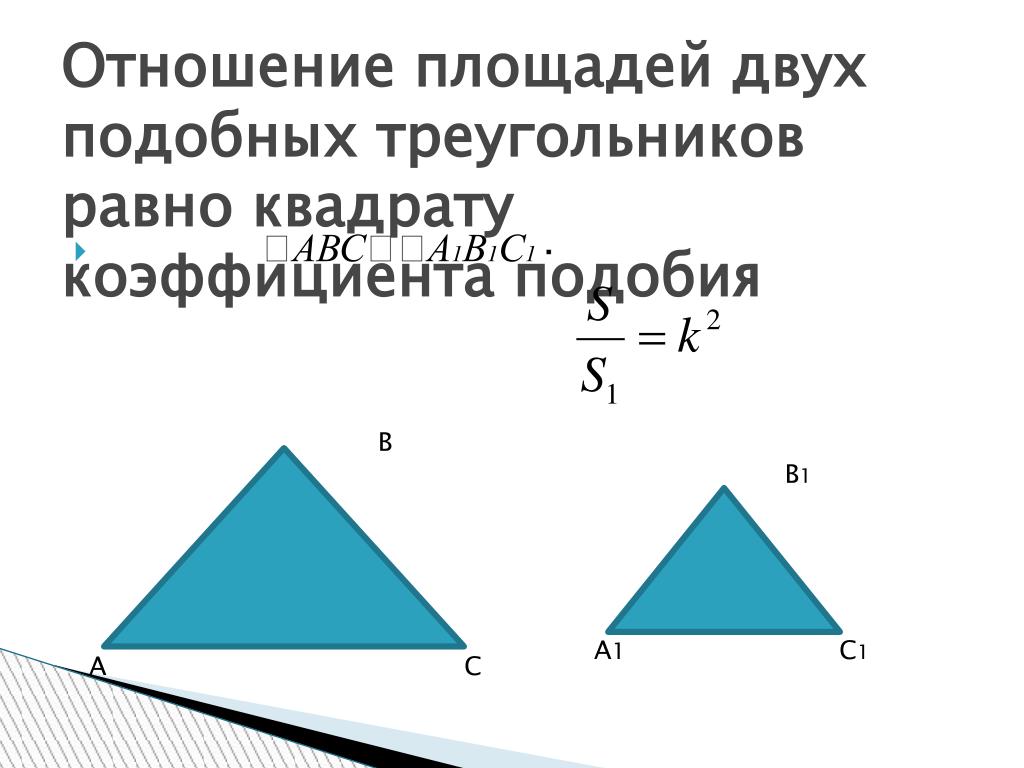
слайды 1-2 (Тема презентации «Определение подобных треугольников», примерs)
Для объяснения свойства подобия треугольников в презентации используются следующие инструменты:
Такая демонстрация позволяет углубить понимание материала, облегчить его запоминание.
Начинается презентация с демонстрации предметов, на очертаниях которых строятся подобные геометрические фигуры. В качестве примеров приводятся футбольный и гандбольный мячи, узорчатые тарелки разных размеров. Справа от предметов изображаются очертания фигур, которые подобны между собой — большой и маленький квадрат, большой и маленький круг.
слайды 3-4 (определение подобных треугольников)
Такая демонстрация, вводящая ученика в изучение данного понятия через практическое применение, очень эффективна и помогает решить одну из важных целей урока — закрепить представление ученика об изучаемом предмете.
На следующем слайде понятие подобия раскладывается на составляющие при помощи двух построенных треугольников АВС и А1В1С1. Используя анимацию, постепенно соответствующие углы отмечаются как равные. Соответствующие углы обозначаются одинаково — А и А1 одним полукругом, В и В1 — двумя, С и С1 — тремя. При том, что данные треугольники имеют равные углы, их соответствующие стороны называют сходственными. Данное выражение в дальнейшем необходимо употреблять при решении геометрических задач, поэтому выражение выделено зеленым цветом, означая необходимость запомнить его и употреблять в дальнейшем.
слайд 5 (сайт)
Теперь можно сформулировать определение подобия треугольников при соответствующем равенстве углов и пропорциональности сходственных сторон. Далее демонстрируется алгебраическая запись условий подобия треугольников — равенство углов и пропорциональность всех трех сторон. Условие пропорциональности сторон заключено в рамку для запоминания. Результат отношения каждой пары — одно и то же число. Оно обозначается k и определяется как коэффициент подобия треугольников.
Оно обозначается k и определяется как коэффициент подобия треугольников.
На основе изученного понятия следует изучение следующих тем курса геометрии — отношения площадей подобных треугольников, признаки подобия треугольников.
Данная презентация «Определение подобных треугольников» может быть рекомендована не только в качестве демонстрационного материала на уроке геометрии, сопровождающая объяснение учителя. Она может помочь ученику в самостоятельном изучении материала, а также поможет объяснить понятие подобия на уроке при дистанционном обучении.
Слайд 2
Немного о себе
Привет всем меня зовут Алеся мне 15 лет учусь в №11 школе в 8 «Г» классе. Я занимаюсь в клубе самодеятельной песни. Мой клуб называется КСП «Вдохновение». Люблю делать проекты. Один из которых вы видите сейчас.
Слайд 3
Цели проекта
Сделать всё возможное для ребят чтобы они поняли где использовались подобные треугольники в древности и для чего они нужны
Слайд 4
Мотивационный материал
Я считаю подобные треугольники нужны для определения расстояния до недоступной нам точки и высоты предмета
Слайд 5
Использования в жизни.

Ну я думаю что подобные треугольники пригодились бы для определения расстояния до недоступной точки и в строительстве здания.
Слайд 6
Тема
Подобные треугольники
Слайд 7
Определение подобных треугольников
метрик для оценки вашей модели семантической сегментации | by Ekin Tiu
Давайте сначала рассчитаем IoU корабля. Мы предполагаем, что общая площадь изображения равна 100 (100 пикселей). Во-первых, давайте подумаем о перекрытии кораблей. Мы можем представить, что мы перемещаем прогнозируемую сегментацию (слева) прямо над истинной поверхностью (справа) и смотрим, есть ли перекрывающиеся пиксели корабля. Поскольку пиксели, классифицируемые моделью как корабли, отсутствуют, имеется 0 перекрывающихся пикселей кораблей.
Поскольку пиксели, классифицируемые моделью как корабли, отсутствуют, имеется 0 перекрывающихся пикселей кораблей.
Объединение состоит из всех пикселей, классифицированных как корабли из обоих изображений , за вычетом перекрытия/пересечения.В этом случае есть 5 пикселей (это произвольный выбор числа), которые классифицируются как общее количество кораблей. Вычтите перекрытие/пересечение, равное 0, чтобы получить 5 в качестве площади объединения. Проведя расчеты, мы узнаем, что IoU составляет всего 47,5%! См. расчет ниже.
Вот подробный расчет:
Корабли: Площадь перекрытия = 0, Площадь соединения = (5+0)-0 = 5
Площадь перекрытия/Площадь соединения = 0% черный фон, делаем то же самое.
Фон: Площадь перекрытия = 95, Площадь объединения = (95+100)–95 = 100
Площадь перекрытия/площадь объединения = 95%
Среднее значение IoU = (Корабли + Фон)/2 = (0%+95%)/2 = 47,5%
Ничего себе. Это намного ниже рассчитанной нами точности пикселей 95%. Очевидно, что 47,5 — гораздо лучший показатель успеха нашей сегментации или, точнее, ее отсутствия.
Это намного ниже рассчитанной нами точности пикселей 95%. Очевидно, что 47,5 — гораздо лучший показатель успеха нашей сегментации или, точнее, ее отсутствия.
Вот отличная реализация Keras, которую я использовал в своих проектах:
из keras import backend как Kdef iou_coef(y_true, y_pred, smooth=1):
пересечение = K.сумма (K.abs (y_true * y_pred), ось = [1,2,3])
union = K.sum (y_true, [1,2,3]) + K.sum (y_pred, [1,2, 3])-intersection
iou = K.mean((intersection + smooth) / (union + smooth), axis=0)
return iou
И y_true, и y_pred равны м x r x c x n где m — количество изображений, r — количество строк, c — количество столбцов и n — количество классов.
Проще говоря, коэффициент кости равен 2 * площадь перекрытия, деленная на общее количество пикселей в обоих изображениях. (см. объяснение области соединения в разделе 2).
Иллюстрация коэффициента игры в кости.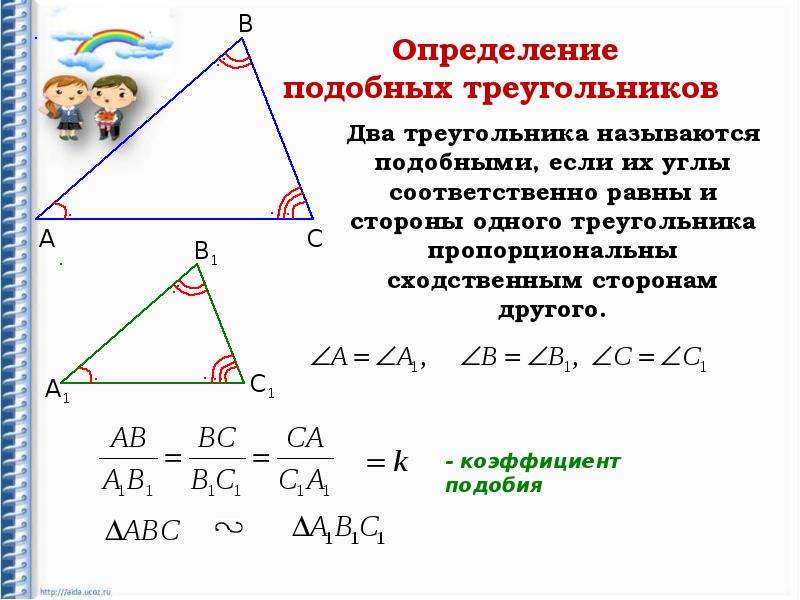 2xOverlap/Общее количество пикселей
2xOverlap/Общее количество пикселейТаким образом, для того же сценария, что и в 1 и 2, мы должны выполнить следующие вычисления:
Общее количество пикселей для обоих объединенных изображений = 200
Корабли: Площадь перекрытия = 0
( 2 * Площадь перекрытия)/(общее количество пикселей) = 0/200 = 0
Фон: Площадь перекрытия = 95
(2 * Площадь перекрытия)/(общее количество пикселей) = 95*2/200 = 0.95
Кубики = (Корабли + Фон)/2 = (0%+95%)/2 = 47,5%
В этом случае мы получили то же значение, что и IoU, но это не всегда будет быть дело.
Коэффициент Dice очень похож на IoU. Они положительно коррелированы, то есть если один говорит, что модель А лучше модели Б при сегментации изображения, то другой скажет то же самое. Как и IoU, они оба варьируются от 0 до 1, где 1 означает наибольшее сходство между предсказанным и истинным.
Чтобы лучше понять различия между ними, я рекомендую прочитать следующий ответ Stack Exchange:
Вот реализация коэффициента игры в кости с теми же условиями ввода, которые указаны в разделе 2:
def dice_coef(y_true, y_pred, smooth=1 ):
пересечение = K.sum(y_true * y_pred, ось=[1,2,3])
union = K.sum(y_true, ось=[1,2,3]) + K.sum(y_pred, ось =[1,2,3])
кубиков = K.mean((2. * пересечение + сглаживание)/(объединение + сглаживание), ось = 0)
возврат кубиков
В заключение, наиболее часто используемые метрики для семантической сегментация — это IoU и коэффициент Dice.Я включил реализации кода в Keras и объясню их более подробно в следующей статье.
Как некоторые из вас, возможно, заметили, я намеренно исключил обсуждения и объяснения относительно истинно положительных, истинно отрицательных, ложноположительных и ложноотрицательных результатов. Хотя они важны, я считаю, что они запутывают четкое концептуальное понимание этих показателей, которое я пытался подчеркнуть в этой статье.
Я надеюсь, что эта статья поможет лучше понять каждую метрику, чтобы у вас было более глубокое понимание во время реализации или при чтении литературы.
Набор инструментов для обработки изображений Документация
Страница, которую вы искали, не существует.
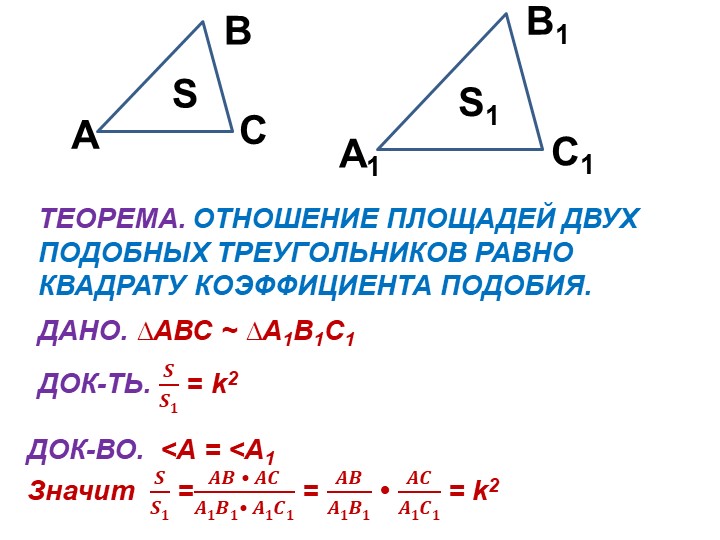 Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.
Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.Выполнение обработки, визуализации и анализа изображений
Image Processing Toolbox™ предоставляет исчерпывающий набор эталонных стандартных алгоритмов и рабочих процессов. приложения для обработки изображений, анализа, визуализации и разработки алгоритмов.Ты сможешь выполнять сегментацию изображения, улучшение изображения, шумоподавление, геометрические преобразования, и регистрация изображений с использованием глубокого обучения и традиционных методов обработки изображений. То toolbox поддерживает обработку 2D, 3D и произвольно больших изображений.
Приложения Image Processing Toolbox позволяют автоматизировать стандартные рабочие процессы обработки изображений. Вы можете интерактивно
сегментировать данные изображений, сравнивать методы регистрации изображений и выполнять пакетную обработку больших наборов данных.Функции и приложения визуализации позволяют просматривать изображения, трехмерные объемы и видео; регулировать
контраст; создавать гистограммы; и управлять областями интереса (ROI).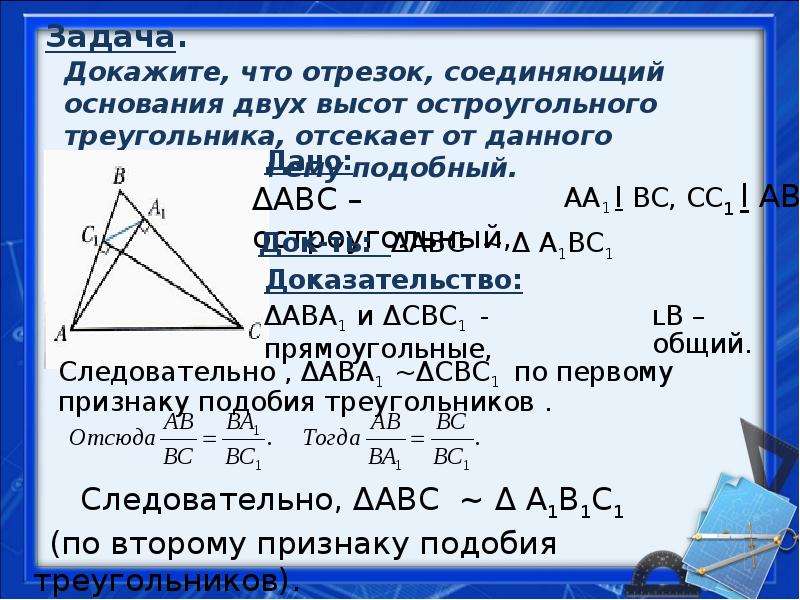
Вы можете ускорить свои алгоритмы, запустив их на многоядерных процессорах и графических процессорах. Многие функции панели инструментов поддерживают генерацию кода C/C++ для прототипирования настольных компьютеров и встроенного машинного зрения развертывание системы.
Изучите основы Image Processing Toolbox
Импорт и экспорт данных изображений, преобразование типов и классов изображений
Интерактивные инструменты для отображения и исследования изображений
Масштабирование, поворот, выполнение других преобразований N-D и выравнивание изображений с помощью корреляция интенсивности, сопоставление признаков или отображение контрольных точек
Регулировка контраста, морфологическая фильтрация, устранение размытия, на основе области интереса обработка
Анализ областей, анализ текстуры, статистика пикселей и изображений
Выполнение задач по обработке изображений, таких как удаление шума и выполнение преобразования изображения в изображение с использованием глубоких нейронных сетей (требуется Deep Learning Toolbox™)
Фильтрация, сегментация и выполнение других операций обработки изображений в 3D объемные данные
Импорт, экспорт, обработка и визуализация гиперспектральных данных
Генерация C-кода, HDL-кода и функций MEX, а также запуск обработки изображений код на графическом процессоре (GPU)
Image Processing Toolbox Документация
Страница, которую вы искали, не существует.
 Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.
Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.Выполнение обработки, визуализации и анализа изображений
Image Processing Toolbox™ предоставляет исчерпывающий набор эталонных стандартных алгоритмов и рабочих процессов. приложения для обработки изображений, анализа, визуализации и разработки алгоритмов. Ты сможешь выполнять сегментацию изображения, улучшение изображения, шумоподавление, геометрические преобразования, и регистрация изображений с использованием глубокого обучения и традиционных методов обработки изображений.То toolbox поддерживает обработку 2D, 3D и произвольно больших изображений.
Приложения Image Processing Toolbox позволяют автоматизировать стандартные рабочие процессы обработки изображений. Вы можете интерактивно
сегментировать данные изображений, сравнивать методы регистрации изображений и выполнять пакетную обработку больших наборов данных.
Функции и приложения визуализации позволяют просматривать изображения, трехмерные объемы и видео; регулировать
контраст; создавать гистограммы; и управлять областями интереса (ROI).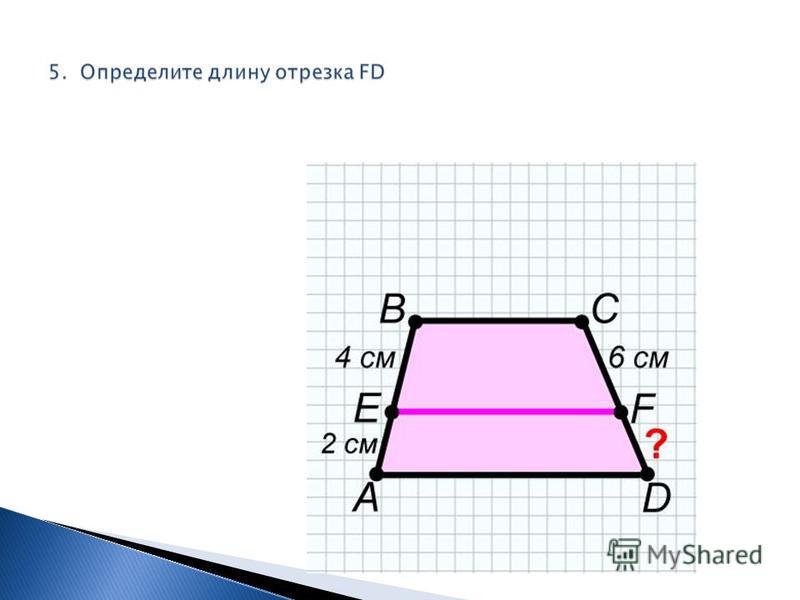
Вы можете ускорить свои алгоритмы, запустив их на многоядерных процессорах и графических процессорах.Многие функции панели инструментов поддерживают генерацию кода C/C++ для прототипирования настольных компьютеров и встроенного машинного зрения развертывание системы.
Изучите основы Image Processing Toolbox
Импорт и экспорт данных изображений, преобразование типов и классов изображений
Интерактивные инструменты для отображения и исследования изображений
Масштабирование, поворот, выполнение других преобразований N-D и выравнивание изображений с помощью корреляция интенсивности, сопоставление признаков или отображение контрольных точек
Регулировка контраста, морфологическая фильтрация, устранение размытия, на основе области интереса обработка
Анализ областей, анализ текстуры, статистика пикселей и изображений
Выполнение задач по обработке изображений, таких как удаление шума и выполнение преобразования изображения в изображение с использованием глубоких нейронных сетей (требуется Deep Learning Toolbox™)
Фильтрация, сегментация и выполнение других операций обработки изображений в 3D объемные данные
Импорт, экспорт, обработка и визуализация гиперспектральных данных
Генерация C-кода, HDL-кода и функций MEX, а также запуск обработки изображений код на графическом процессоре (GPU)
Image Processing Toolbox Документация
Страница, которую вы искали, не существует.
 Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.
Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.Выполнение обработки, визуализации и анализа изображений
Image Processing Toolbox™ предоставляет исчерпывающий набор эталонных стандартных алгоритмов и рабочих процессов. приложения для обработки изображений, анализа, визуализации и разработки алгоритмов. Ты сможешь выполнять сегментацию изображения, улучшение изображения, шумоподавление, геометрические преобразования, и регистрация изображений с использованием глубокого обучения и традиционных методов обработки изображений.То toolbox поддерживает обработку 2D, 3D и произвольно больших изображений.
Приложения Image Processing Toolbox позволяют автоматизировать стандартные рабочие процессы обработки изображений. Вы можете интерактивно
сегментировать данные изображений, сравнивать методы регистрации изображений и выполнять пакетную обработку больших наборов данных.
Функции и приложения визуализации позволяют просматривать изображения, трехмерные объемы и видео; регулировать
контраст; создавать гистограммы; и управлять областями интереса (ROI).
Вы можете ускорить свои алгоритмы, запустив их на многоядерных процессорах и графических процессорах.Многие функции панели инструментов поддерживают генерацию кода C/C++ для прототипирования настольных компьютеров и встроенного машинного зрения развертывание системы.
Изучите основы Image Processing Toolbox
Импорт и экспорт данных изображений, преобразование типов и классов изображений
Интерактивные инструменты для отображения и исследования изображений
Масштабирование, поворот, выполнение других преобразований N-D и выравнивание изображений с помощью корреляция интенсивности, сопоставление признаков или отображение контрольных точек
Регулировка контраста, морфологическая фильтрация, устранение размытия, на основе области интереса обработка
Анализ областей, анализ текстуры, статистика пикселей и изображений
Выполнение задач по обработке изображений, таких как удаление шума и выполнение преобразования изображения в изображение с использованием глубоких нейронных сетей (требуется Deep Learning Toolbox™)
Фильтрация, сегментация и выполнение других операций обработки изображений в 3D объемные данные
Импорт, экспорт, обработка и визуализация гиперспектральных данных
Генерация C-кода, HDL-кода и функций MEX, а также запуск обработки изображений код на графическом процессоре (GPU)
Image Processing Toolbox Документация
Страница, которую вы искали, не существует.
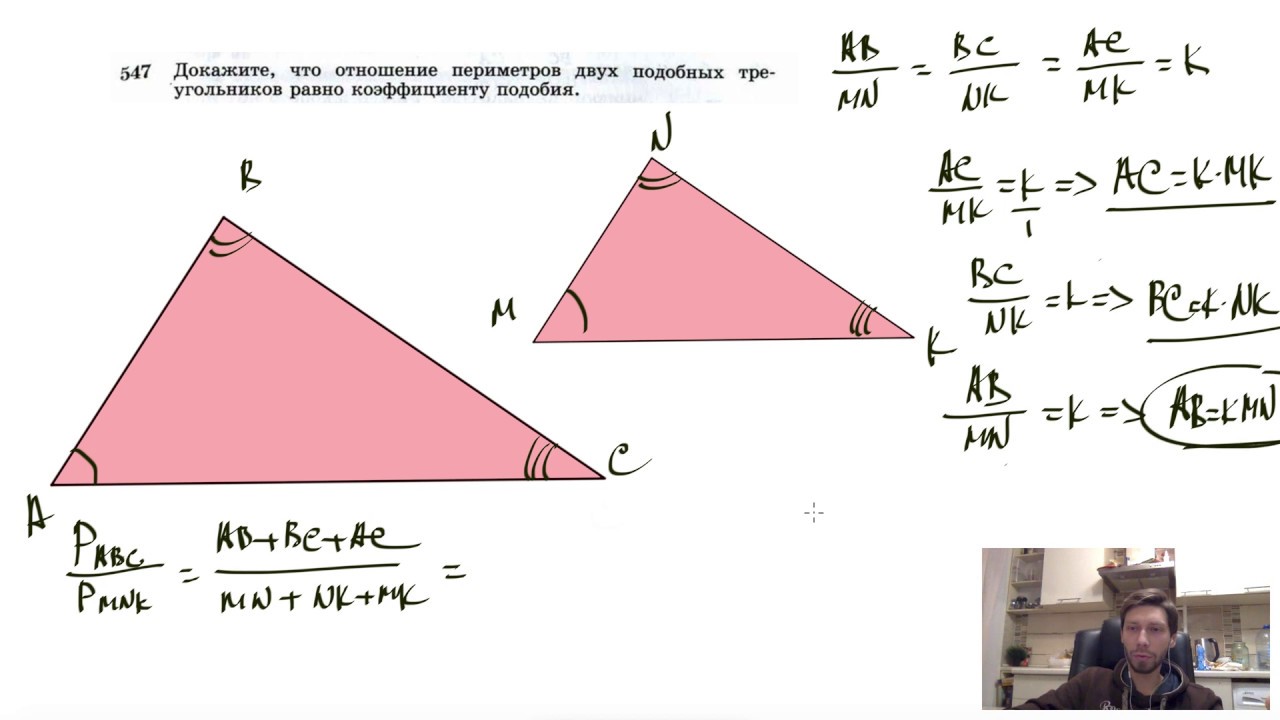 Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.
Используйте окно поиска или просмотрите темы ниже, чтобы найти нужную страницу.Выполнение обработки, визуализации и анализа изображений
Image Processing Toolbox™ предоставляет исчерпывающий набор эталонных стандартных алгоритмов и рабочих процессов. приложения для обработки изображений, анализа, визуализации и разработки алгоритмов. Ты сможешь выполнять сегментацию изображения, улучшение изображения, шумоподавление, геометрические преобразования, и регистрация изображений с использованием глубокого обучения и традиционных методов обработки изображений.То toolbox поддерживает обработку 2D, 3D и произвольно больших изображений.
Приложения Image Processing Toolbox позволяют автоматизировать стандартные рабочие процессы обработки изображений. Вы можете интерактивно
сегментировать данные изображений, сравнивать методы регистрации изображений и выполнять пакетную обработку больших наборов данных.
Функции и приложения визуализации позволяют просматривать изображения, трехмерные объемы и видео; регулировать
контраст; создавать гистограммы; и управлять областями интереса (ROI).
Вы можете ускорить свои алгоритмы, запустив их на многоядерных процессорах и графических процессорах.Многие функции панели инструментов поддерживают генерацию кода C/C++ для прототипирования настольных компьютеров и встроенного машинного зрения развертывание системы.
Изучите основы Image Processing Toolbox
Импорт и экспорт данных изображений, преобразование типов и классов изображений
Интерактивные инструменты для отображения и исследования изображений
Масштабирование, поворот, выполнение других преобразований N-D и выравнивание изображений с помощью корреляция интенсивности, сопоставление признаков или отображение контрольных точек
Регулировка контраста, морфологическая фильтрация, устранение размытия, на основе области интереса обработка
Анализ областей, анализ текстуры, статистика пикселей и изображений
Выполнение задач по обработке изображений, таких как удаление шума и выполнение преобразования изображения в изображение с использованием глубоких нейронных сетей (требуется Deep Learning Toolbox™)
Фильтрация, сегментация и выполнение других операций обработки изображений в 3D объемные данные
Импорт, экспорт, обработка и визуализация гиперспектральных данных
Генерация C-кода, HDL-кода и функций MEX, а также запуск обработки изображений код на графическом процессоре (GPU)
[PDF] Сходство и соответствие сегментации
ПОКАЗЫВАЕТСЯ 1-10 ИЗ 27 ССЫЛОК
СОРТИРОВАТЬ ПОRelevanceMost Influenced PapersRecency
Критика и улучшение метрики оценки для сегментации текста
к метрике Pk, называемой Window Diff, которая перемещает окно фиксированного размера по тексту и наказывает алгоритм всякий раз, когда количество границ в окне не соответствует истинному количеству границ для этого окна текста. Expand
Expand
О методологиях оценки для алгоритмов сегментации текста
Создание сегментации ссылки является довольно сложной задачей, в этом документе описывается новая метрика оценки, которая опирается на стабильность сегментации лицом к лицу. преобразования текста и две предложенные метрики обеспечивают действительно лучшие показатели точности сегментации текста, чем существующие меры. ExpandСтатистические модели для сегментации текста
Оценка подхода на количественной и качественной основе демонстрирует его эффективность в двух очень разных областях: новостных статьях Wall Street Journal и расшифровках новостных сюжетов телевизионных передач, с использованием новая вероятностно-мотивированная метрика ошибок.ExpandСегментация текста с использованием экспоненциальных моделей
В этой работе используются языковые модели ближнего и дальнего действия, которые помогают выявлять вероятные места изменения тем в тексте, и предлагается новая вероятностно-мотивированная метрика ошибок для использования при обработке естественного языка и информационно-поисковые сообщества.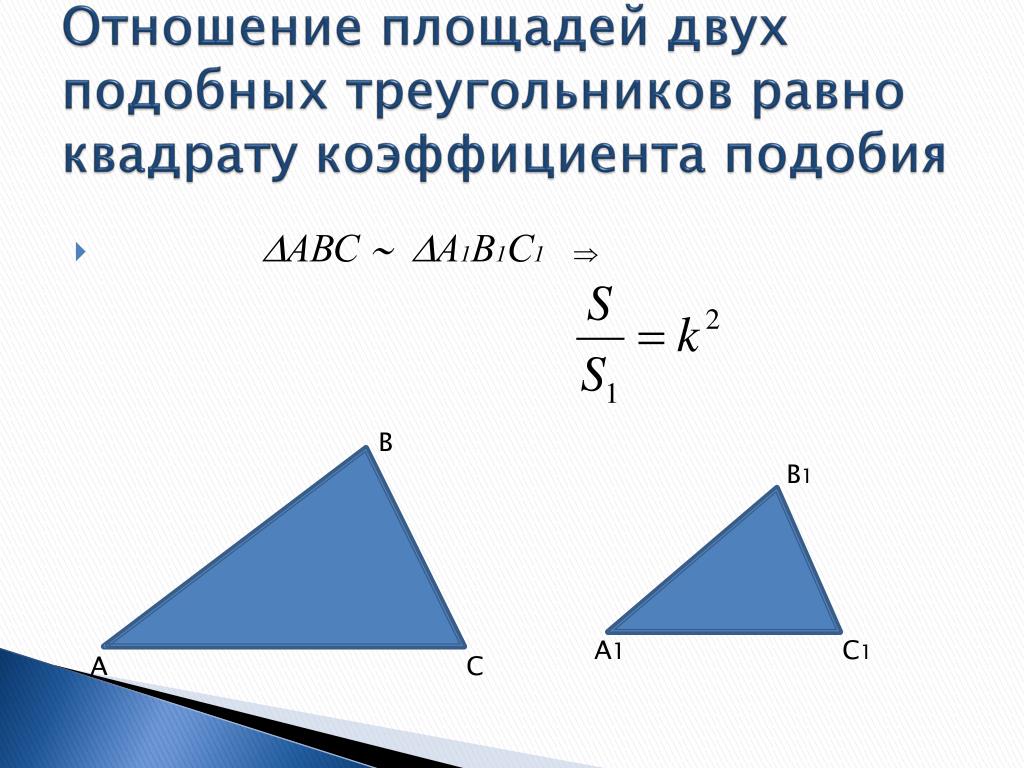 Expand
ExpandОбзорная статья: Inter-Coder Agreement for Computational Linguistics
Утверждается, что взвешенные, альфа-подобные коэффициенты, традиционно менее используемые, чем каппа-подобные меры в компьютерной лингвистике, могут быть более подходящими для многих задач по аннотации корпуса, но их использование делает интерпретацию значения коэффициента еще более сложной.ExpandМозаика текста: сегментация текста на многоабзацные отрывки подтем
Алгоритм полностью реализован, и показано, что он производит сегментацию, которая хорошо соответствует человеческим суждениям о границах подтем 12 текстов, которые должен быть полезен для многих задач анализа текста, включая поиск и обобщение информации. ExpandТегирование, конкурирующее с людьми, с использованием автоматического извлечения ключевой фразы
В этом документе показано, как документы могут быть автоматически помечены тегами с помощью современного алгоритма извлечения ключевой фразы, и улучшена производительность в этой новой области используя новый алгоритм «Мауи», который использует семантическую информацию, извлеченную из Википедии. Expand
ExpandGale Apps — Технические трудности
Технические трудности
Приложение, к которому вы пытаетесь получить доступ, в настоящее время недоступно. Приносим свои извинения за доставленные неудобства. Повторите попытку через несколько секунд.
Если проблемы с доступом сохраняются, обратитесь за помощью в наш отдел технической поддержки по телефону 1-800-877-4253. Еще раз спасибо, что выбрали Gale, обучающую компанию Cengage.
org.springframework.remoting.RemoteAccessException: невозможно получить доступ к удаленной службе [authorizationService@theBLISAuthorizationService]; вложенным исключением является Ice.UnknownException
unknown = «java.lang.IndexOutOfBoundsException: индекс 0 выходит за границы для длины 0
в java.base/jdk.internal. util.Preconditions.outOfBounds(Preconditions.ява: 64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
на com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.ява: 60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
на com.
util.Preconditions.outOfBounds(Preconditions.ява: 64)
в java.base/jdk.internal.util.Preconditions.outOfBoundsCheckIndex(Preconditions.java:70)
в java.base/jdk.internal.util.Preconditions.checkIndex(Preconditions.java:248)
в java.base/java.util.Objects.checkIndex(Objects.java:372)
в java.base/java.util.ArrayList.get(ArrayList.java:458)
на com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.populateSessionProperties(LazyUserSessionDataLoaderStoredProcedure.ява: 60)
в com.gale.blis.data.subscription.dao.LazyUserSessionDataLoaderStoredProcedure.reQuery(LazyUserSessionDataLoaderStoredProcedure.java:53)
в com.gale.blis.data.model.session.UserGroupEntitlementsManager.reinitializeUserGroupEntitlements(UserGroupEntitlementsManager.java:30)
в com.gale.blis.data.model.session.UserGroupSessionManager.getUserGroupEntitlements(UserGroupSessionManager.java:17)
на com.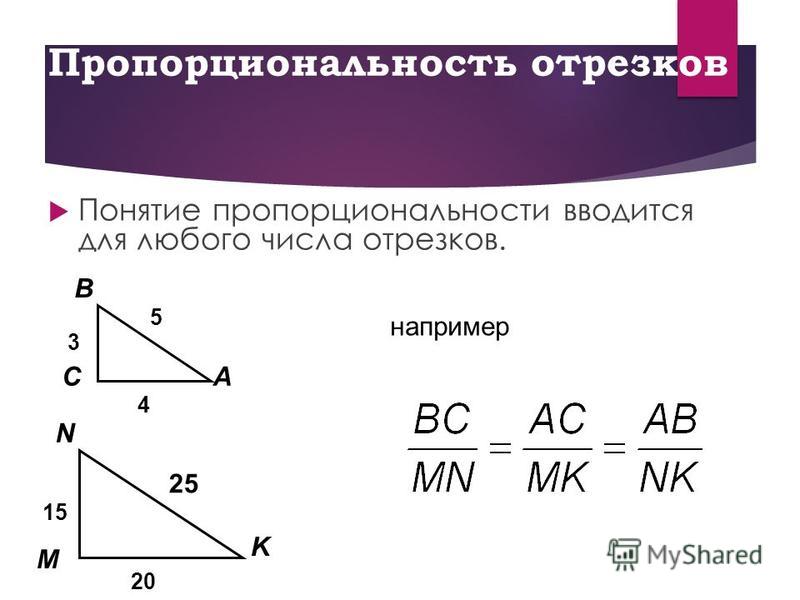 gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
в ком.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer.
gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getProductSubscriptionCriteria(CrossSearchProductContentModuleFetcher.java:244)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getSubscribedCrossSearchProductsForUser(CrossSearchProductContentModuleFetcher.java:71)
на com.gale.blis.api.authorize.contentmodulefetchers.CrossSearchProductContentModuleFetcher.getAvailableContentModulesForProduct(CrossSearchProductContentModuleFetcher.java:52)
в ком.gale.blis.api.authorize.strategy.productentry.strategy.AbstractProductEntryAuthorizer.getContentModules(AbstractProductEntryAuthorizer.java:130)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.isAuthorized(CrossSearchProductEntryAuthorizer.java:82)
на com.gale.blis.api.authorize.strategy.productentry.strategy.CrossSearchProductEntryAuthorizer.authorizeProductEntry(CrossSearchProductEntryAuthorizer. java:44)
в ком.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
на com.gale.blis.auth._AuthorizationServiceDisp._iceD_authorize(_AuthorizationServiceDisp.java:141)
в com.gale.blis.auth._AuthorizationServiceDisp._iceDispatch(_AuthorizationServiceDisp.java:359)
в IceInternal.Incoming.invoke(Incoming.java:209)
в Ice.ConnectionI.invokeAll(ConnectionI.java:2800)
в Ice.ConnectionI.dispatch(ConnectionI.java:1385)
в Ice.ConnectionI.message(ConnectionI.java:1296)
в IceInternal.
java:44)
в ком.gale.blis.api.authorize.strategy.ProductEntryAuthorizer.authorize(ProductEntryAuthorizer.java:31)
в com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody0(BLISAuthorizationServiceImpl.java:57)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize_aroundBody1$advice(BLISAuthorizationServiceImpl.java:61)
на com.gale.blis.api.BLISAuthorizationServiceImpl.authorize(BLISAuthorizationServiceImpl.java:1)
на com.gale.blis.auth._AuthorizationServiceDisp._iceD_authorize(_AuthorizationServiceDisp.java:141)
в com.gale.blis.auth._AuthorizationServiceDisp._iceDispatch(_AuthorizationServiceDisp.java:359)
в IceInternal.Incoming.invoke(Incoming.java:209)
в Ice.ConnectionI.invokeAll(ConnectionI.java:2800)
в Ice.ConnectionI.dispatch(ConnectionI.java:1385)
в Ice.ConnectionI.message(ConnectionI.java:1296)
в IceInternal.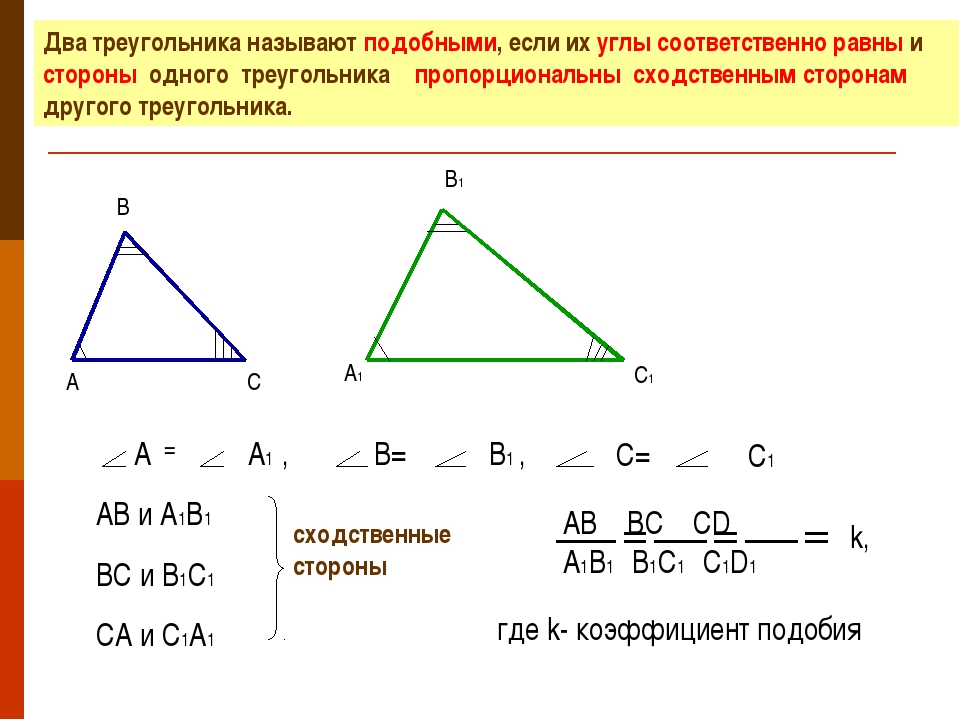 ThreadPool.запустить (ThreadPool.java: 396)
в IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:765)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:365) org.springframework.remoting.ice.IceClientInterceptor.вызывать (IceClientInterceptor.java:327) org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71) org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186) org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:212) com.sun.proxy.$Proxy130.authorize(Неизвестный источник) ком.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61) com.gale.apps.service.impl.MetadataResolverService.
ThreadPool.запустить (ThreadPool.java: 396)
в IceInternal.ThreadPool.access$500(ThreadPool.java:7)
в IceInternal.ThreadPool$EventHandlerThread.run(ThreadPool.java:765)
в java.base/java.lang.Thread.run(Thread.java:834)
»
org.springframework.remoting.ice.IceClientInterceptor.convertIceAccessException(IceClientInterceptor.java:365) org.springframework.remoting.ice.IceClientInterceptor.вызывать (IceClientInterceptor.java:327) org.springframework.remoting.ice.MonitoringIceProxyFactoryBean.invoke(MonitoringIceProxyFactoryBean.java:71) org.springframework.aop.framework.ReflectiveMethodInvocation.proceed(ReflectiveMethodInvocation.java:186) org.springframework.aop.framework.JdkDynamicAopProxy.invoke(JdkDynamicAopProxy.java:212) com.sun.proxy.$Proxy130.authorize(Неизвестный источник) ком.gale.auth.service.BlisService.getAuthorizationResponse(BlisService.java:61) com.gale.apps.service.impl.MetadataResolverService. resolveMetadata(MetadataResolverService.java:65) com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57) com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22) jdk.internal.reflect.GeneratedMethodAccessor252.invoke (неизвестный источник) Ява.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43) java.base/java.lang.reflect.Method.invoke(Method.java:566) org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:215) org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:142) org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:102) org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895) org.springframework.
resolveMetadata(MetadataResolverService.java:65) com.gale.apps.controllers.DiscoveryController.resolveDocument(DiscoveryController.java:57) com.gale.apps.controllers.DocumentController.redirectToDocument(DocumentController.java:22) jdk.internal.reflect.GeneratedMethodAccessor252.invoke (неизвестный источник) Ява.base/jdk.internal.reflect.DelegatingMethodAccessorImpl.invoke(DelegatingMethodAccessorImpl.java:43) java.base/java.lang.reflect.Method.invoke(Method.java:566) org.springframework.web.method.support.InvocableHandlerMethod.doInvoke(InvocableHandlerMethod.java:215) org.springframework.web.method.support.InvocableHandlerMethod.invokeForRequest(InvocableHandlerMethod.java:142) org.springframework.web.servlet.mvc.method.annotation.ServletInvocableHandlerMethod.invokeAndHandle(ServletInvocableHandlerMethod.java:102) org.springframework.web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.invokeHandlerMethod (RequestMappingHandlerAdapter.java:895) org.springframework. web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:800) org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.дескриптор (AbstractHandlerMethodAdapter.java:87) org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1038) org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:942) org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:998) org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:890) javax.servlet.http.HttpServlet.service(HttpServlet.java:626) org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:875) javax.servlet.http.HttpServlet.service(HttpServlet.java:733) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) орг.apache.
web.servlet.mvc.method.annotation.RequestMappingHandlerAdapter.handleInternal (RequestMappingHandlerAdapter.java:800) org.springframework.web.servlet.mvc.method.AbstractHandlerMethodAdapter.дескриптор (AbstractHandlerMethodAdapter.java:87) org.springframework.web.servlet.DispatcherServlet.doDispatch(DispatcherServlet.java:1038) org.springframework.web.servlet.DispatcherServlet.doService(DispatcherServlet.java:942) org.springframework.web.servlet.FrameworkServlet.processRequest(FrameworkServlet.java:998) org.springframework.web.servlet.FrameworkServlet.doGet(FrameworkServlet.java:890) javax.servlet.http.HttpServlet.service(HttpServlet.java:626) org.springframework.web.servlet.FrameworkServlet.service(FrameworkServlet.java:875) javax.servlet.http.HttpServlet.service(HttpServlet.java:733) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:227) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) орг.apache.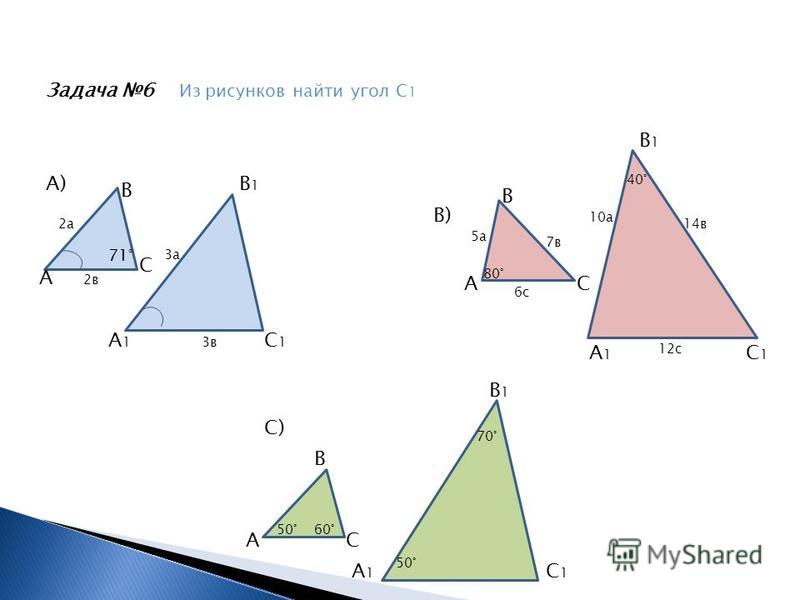 tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.ява: 189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:63) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) орг.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.
tomcat.websocket.server.WsFilter.doFilter(WsFilter.java:53) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.catalina.filters.HttpHeaderSecurityFilter.doFilter(HttpHeaderSecurityFilter.java:126) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.ява: 189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.servlet.resource.ResourceUrlEncodingFilter.doFilter(ResourceUrlEncodingFilter.java:63) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) орг.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain. java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.внутреннийDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.ява: 162) org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:130) org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:66) org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:105) org.springframework.web.filter.
java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.внутреннийDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:101) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.ява: 162) org.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:130) org.springframework.boot.web.servlet.support.ErrorPageFilter.access$000(ErrorPageFilter.java:66) org.springframework.boot.web.servlet.support.ErrorPageFilter$1.doFilterInternal(ErrorPageFilter.java:105) org.springframework.web.filter. OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) орг.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:123) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.actuate.web.trace.servlet.HttpTraceFilter.doFilterInternal(HttpTraceFilter.java:90) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java: 99) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.
OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) орг.springframework.boot.web.servlet.support.ErrorPageFilter.doFilter(ErrorPageFilter.java:123) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.actuate.web.trace.servlet.HttpTraceFilter.doFilterInternal(HttpTraceFilter.java:90) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.RequestContextFilter.doFilterInternal (RequestContextFilter.java: 99) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain. java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:92) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) орг.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.HiddenHttpMethodFilter.doFilterInternal (HiddenHttpMethodFilter.java:93) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.внутреннийDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:154) org.
java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.FormContentFilter.doFilterInternal (FormContentFilter.java:92) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) орг.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.HiddenHttpMethodFilter.doFilterInternal (HiddenHttpMethodFilter.java:93) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.внутреннийDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:154) org. springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:122) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal(WebMvcMetricsFilter.java:107) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:200) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.ява: 202) org.
springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.filterAndRecordMetrics(WebMvcMetricsFilter.java:122) org.springframework.boot.actuate.metrics.web.servlet.WebMvcMetricsFilter.doFilterInternal(WebMvcMetricsFilter.java:107) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.springframework.web.filter.CharacterEncodingFilter.doFilterInternal (CharacterEncodingFilter.java:200) org.springframework.web.filter.OncePerRequestFilter.doFilter(OncePerRequestFilter.java:107) org.apache.catalina.core.ApplicationFilterChain.internalDoFilter(ApplicationFilterChain.java:189) org.apache.catalina.core.ApplicationFilterChain.doFilter(ApplicationFilterChain.java:162) org.apache.catalina.core.StandardWrapperValve.invoke(StandardWrapperValve.ява: 202) org. apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97) org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542) org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143) org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92) org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.ява: 687) org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78) org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357) org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374) org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65) org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.ява: 893) org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707) org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49) java.base/java.
apache.catalina.core.StandardContextValve.invoke(StandardContextValve.java:97) org.apache.catalina.authenticator.AuthenticatorBase.invoke(AuthenticatorBase.java:542) org.apache.catalina.core.StandardHostValve.invoke(StandardHostValve.java:143) org.apache.catalina.valves.ErrorReportValve.invoke(ErrorReportValve.java:92) org.apache.catalina.valves.AbstractAccessLogValve.invoke(AbstractAccessLogValve.ява: 687) org.apache.catalina.core.StandardEngineValve.invoke(StandardEngineValve.java:78) org.apache.catalina.connector.CoyoteAdapter.service(CoyoteAdapter.java:357) org.apache.coyote.http11.Http11Processor.service(Http11Processor.java:374) org.apache.coyote.AbstractProcessorLight.process(AbstractProcessorLight.java:65) org.apache.coyote.AbstractProtocol$ConnectionHandler.process(AbstractProtocol.ява: 893) org.apache.tomcat.util.net.NioEndpoint$SocketProcessor.doRun(NioEndpoint.java:1707) org.apache.tomcat.util.net.SocketProcessorBase.run(SocketProcessorBase.java:49) java.base/java.
 Понятие пропорциональности вводится и для большого числа отрезков
Понятие пропорциональности вводится и для большого числа отрезков
 Итак стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С
Теорема доказана.
1
1
1
1
1
1
1
1
Итак стороны треугольника АВС пропорциональны сходственным сторонам треугольника А В С
Теорема доказана.
1
1
1
1
1
1
1
1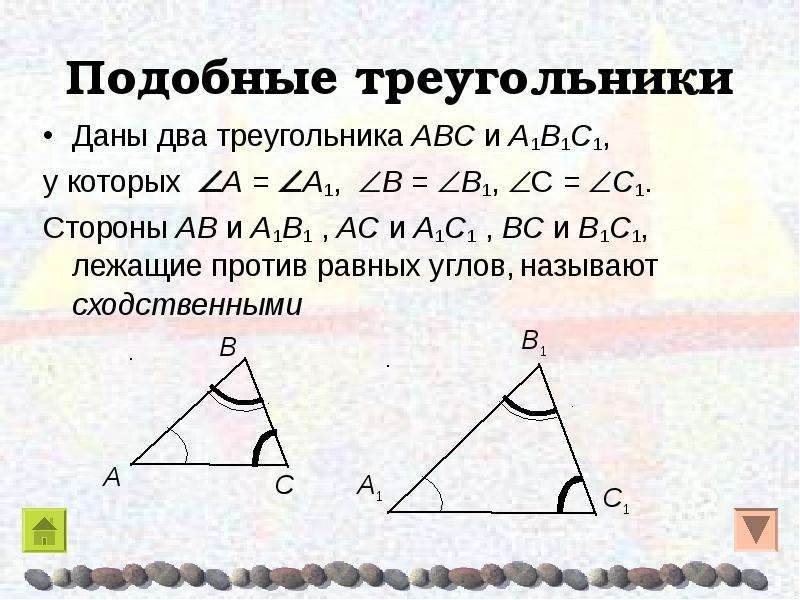 2
2
1
1
1
1
2
2
1
1
1
1 Для этого начертим произвольный отрезок А В и постоим треугольник А В С, у которого углы А и В соответственно равны данным углам
Для этого начертим произвольный отрезок А В и постоим треугольник А В С, у которого углы А и В соответственно равны данным углам 1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1 Равны соответственно углам при вершинах А,….,А равны
Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия
1
2
n
1
2
n
1
2
2
3
n
1
1
2
2
3
n
1
1
n
1
n
Равны соответственно углам при вершинах А,….,А равны
Отношение соответственных диагоналей подобных многоугольников равно коэффициенту подобия; для описанных подобных многоугольников отношение радиусов вписанных окружностей также равно коэффициенту подобия
1
2
n
1
2
n
1
2
2
3
n
1
1
2
2
3
n
1
1
n
1
n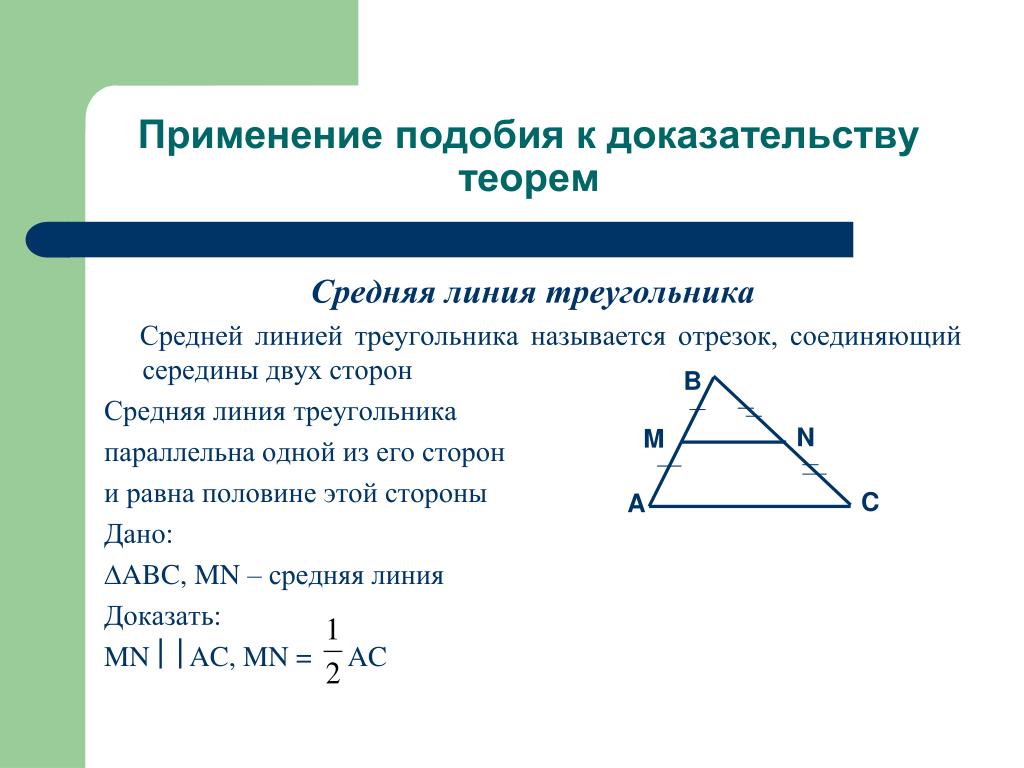 1
1
1
1
1
1
1
1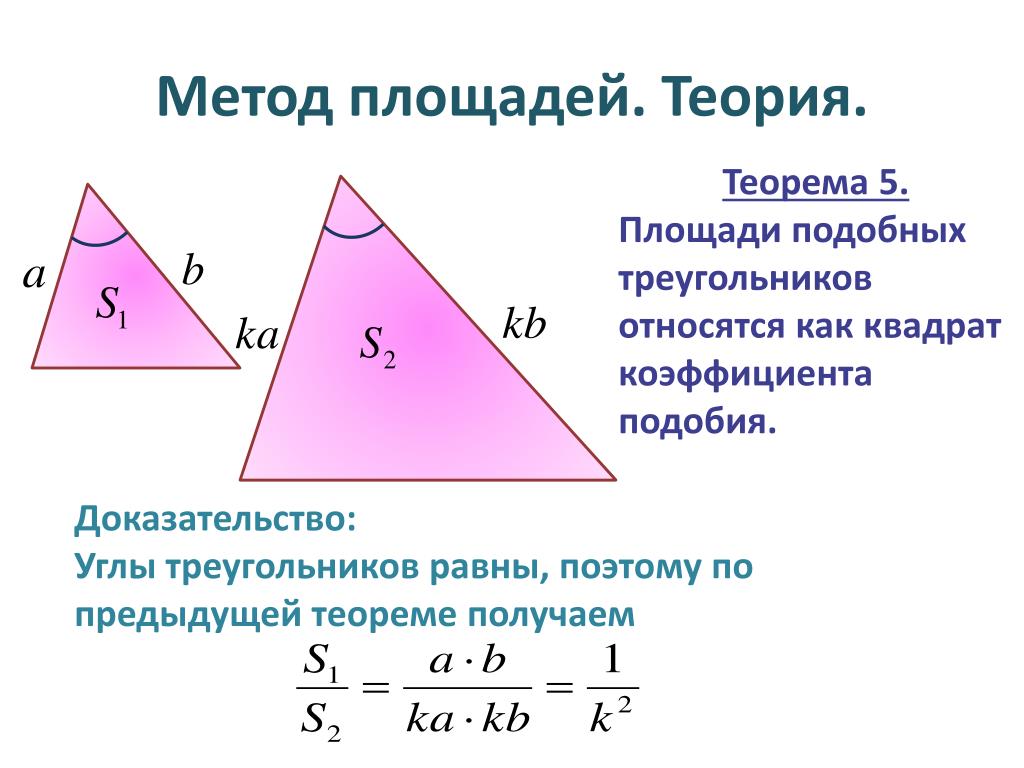 Эта формула позволяет по известным расстояниям АС, А С и А В,найти расстояние АВ.
1
1
1
1
1
1
1
1
1
1
1
1
1
Эта формула позволяет по известным расстояниям АС, А С и А В,найти расстояние АВ.
1
1
1
1
1
1
1
1
1
1
1
1
1 Также нужно знать примерную высоту предмета, до которого определяется расстояние. Так рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник-2,2м,телеграфический столб-6м,одноэтажный дом без крыши -2,5-4м.
Также нужно знать примерную высоту предмета, до которого определяется расстояние. Так рост человека равен 1,7-1,8 м, колесо автомобиля 0,5 м, всадник-2,2м,телеграфический столб-6м,одноэтажный дом без крыши -2,5-4м. sum(y_true * y_pred, ось=[1,2,3])
sum(y_true * y_pred, ось=[1,2,3])