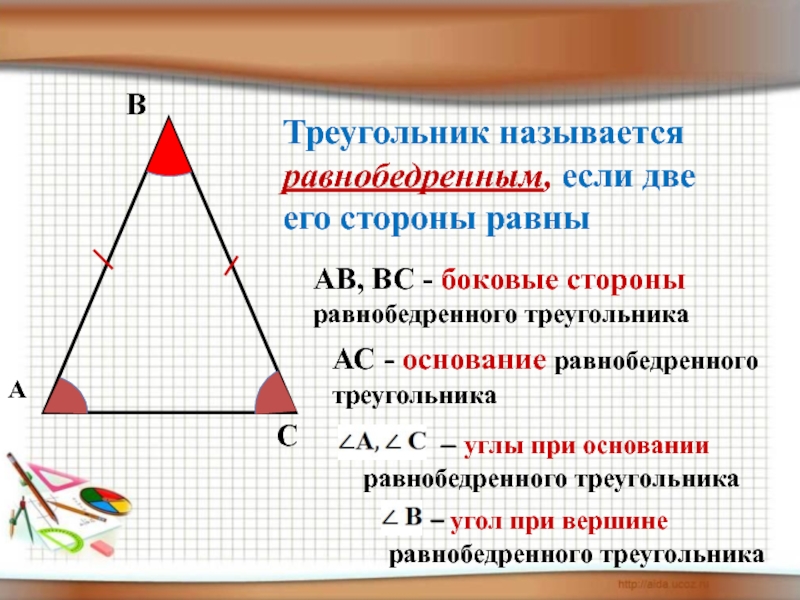
\(\bullet\) Внешний угол \(\angle BCD\) треугольника \(ABC\) равен сумме двух углов треугольника, не смежных с ним.
Факт 4.
\(\bullet\) Биссектрисы смежных углов взаимно перпендикулярны.
\(\bullet\) Биссектрисы односторонних углов при параллельных прямых взаимно перпендикулярны.
Факт 5.
\(\bullet\) Прямая теорема: каждая точка биссектрисы угла равноудалена от сторон угла.
\(\bullet\) Обратная теорема: если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Факт 6.
\(\bullet\) Равнобедренный треугольник – треугольник, у которого две стороны равны. Третья сторона треугольника называется основанием.
Первое свойство равнобедренного треугольника:
Второе свойство равнобедренного треугольника: углы при основании равны.
Первый признак равнобедренного треугольника: если у треугольника два угла равны, то он равнобедренный.
Второй признак равнобедренного треугольника: если у треугольника совпадают высота и медиана (высота и биссектриса или медиана и биссектриса), проведенные к одной и той же стороне, то этот треугольник является равнобедренным.
Факт 7.
\(\bullet\) Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Факт 8.
\(\bullet\) Медианы в треугольнике точкой пересечения делятся в отношении \(2:1\), считая от вершины.
Факт 9.
\(\bullet\) Медиана треугольника, проведенная из вершины прямого угла, равна половине гипотенузы.
Факт 10.
\(\bullet\) Высота, проведенная из вершины прямого угла треугольника, делит его на два треугольника, подобных исходному.
Факт 11.
\(\bullet\) Средняя линия треугольника – отрезок, соединяющий середины двух его сторон.
\(\bullet\) 1. Средняя линия треугольника параллельна третьей стороне.
\(\bullet\) 2. Средняя линия треугольника равна половине третьей стороны.
\(\bullet\) 3. Средняя линия отсекает от треугольника подобный ему треугольник.
Равнобедренный и равносторонний треугольник.
- Свадьба
- Праздники
- Дети
- Фитнес
- 8 Марта
- Мода
- Отношения
Поиск
- Свадьба
- Праздники
- Дети
- Фитнес
- 8 Марта
Урок 10.
Равнобедренный треугольник (1) Треугольник
называется равнобедренным, если у него две стороны равны.Равные стороны равнобедренного треугольника называются
У равнобедренного треугольника углы при основании равны
(∠ B = ∠ C),
а биссектриса, проведённая к основанию, будет медианою и высотою (отрезок АL). – если в треугольнике два угла равны (∠ B = ∠ C), то он равнобедренный.
В равнобедренном треугольнике сумма внутренних углов с одним из внешних составляет
4/3 π.
Определите углы треугольника. Пусть в ∆ АВС, где АВ – основание, АС = ВС, углы при основании равны х, угол при вершине у, а внешний угол при вершине равен z. Тогда 2x + y + z = 4/3 π,
y + z = π; x = π/6,
y = π – π/3 = 2/3 π.
В ∆ АВС сторона АС продолжена за точку А на длину АD = АВ и за точку С на длину СЕ = ВС. Точки Е и D соединены с точкой В. Определите углы ∆ DВЕ, если известны углы ∆ АВС.
РЕШЕНИЕ: Обозначим
∠ ВАС = α, ∠ ВСА
= γ,
тогда
∠ ВАD = π – α,
∠ ВСЕ = π – γ.
Поскольку
∆ АВD и ∆ ВСЕ
равнобедренные, то
Равносторонний
треугольник – это отдельный вид равнобедренного треугольника. У равностороннего
треугольника центры вписанной и описанной окружности, центр тяжести и ортоцентр
совпадают.
Задания к уроку 10
Как найти углы равнобедренного треугольника
Что такое равнобедренный треугольник?
Равнобедренный треугольник — это треугольник, у которого две равные стороны и два равных угла. Две равные стороны отмечены линиями, а два равных угла лежат напротив этих сторон.
Мы можем распознать равнобедренный треугольник, потому что две его стороны отмечены линиями.
Ниже приведен пример равнобедренного треугольника.
У него две равные стороны, отмеченные маленькой синей линией.
Он имеет два равных угла, отмеченных красным.
Мы видим, что в этом равнобедренном треугольнике два угла при основании имеют одинаковую величину.
Все равнобедренные треугольники имеют линию симметрии между двумя равными сторонами.
Стороны одинаковой длины отмечены короткой линией.
Два равных угла лежат напротив двух равных сторон.
Угол, под которым встречаются эти две отмеченные стороны, является нечетным и, следовательно, отличается от двух других углов.
Если нам говорят, что один из отмеченных углов равен 70°, то и другой отмеченный угол также должен быть равен 70°.
Как найти недостающий угол в равнобедренном треугольнике
Чтобы найти недостающий угол в равнобедренном треугольнике, выполните следующие действия:
- Если недостающий угол лежит напротив отмеченной стороны, то недостающий угол равен углу, лежащему напротив другой отмеченной стороны.
- Если отсутствующий угол не лежит напротив отмеченной стороны, то сложите два угла напротив отмеченных сторон вместе и вычтите этот результат из 180.
Дело в том, что сумма всех трех углов равнобедренного треугольника должна составлять 180°.
Например, в равнобедренном треугольнике ниже нам нужно найти недостающий угол при вершине треугольника.
Два угла при основании лежат напротив отмеченных линий и, следовательно, равны друг другу.
Оба угла при основании равны 70 градусов.
Недостающий угол не находится напротив двух отмеченных сторон, поэтому мы складываем два основных угла вместе, а затем вычитаем этот результат из 180, чтобы получить ответ.
70° + 70° = 140°
Два угла при основании в сумме дают 140°.
Углы равнобедренного треугольника в сумме дают 180°.
Мы вычитаем 140° из 180°, чтобы увидеть размер оставшегося угла.
180° – 140° = 40°
Недостающий угол при вершине этого равнобедренного треугольника равен 40°.
Мы также можем подумать: «Какой угол нам нужно прибавить к 70° и 70°, чтобы получить 180°?»
Ответ: 40°.
Как найти недостающие углы в равнобедренном треугольнике только из одного угла
Если в равнобедренном треугольнике известен только один угол, то мы можем найти два других недостающих угла, используя следующие шаги:
- Если известный угол лежит против отмеченной стороны, то угол против другой отмеченной стороны такой же. Сложите эти два угла вместе и вычтите результат из 180°, чтобы найти оставшийся третий угол.
- Если известный угол не лежит напротив отмеченной стороны, то вычтите этот угол из 180° и разделите результат на два, чтобы получить размер обоих недостающих углов.
Вот пример нахождения двух недостающих углов в равнобедренном треугольнике по одному известному углу.
Мы знаем, что один угол равен 50°. Этот угол лежит против одной из отмеченных сторон.
Это означает, что он имеет тот же размер, что и угол, который находится напротив другой отмеченной стороны. Это угол «а».
Следовательно, угол «а» тоже равен 50°.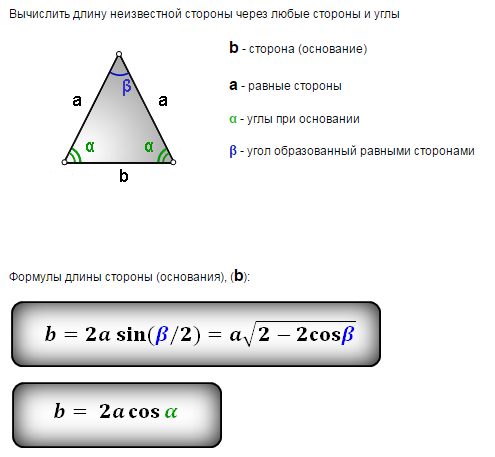
Теперь, чтобы найти угол «b», мы используем тот факт, что все три угла в сумме составляют 180 °.
Чтобы найти угол «b», мы вычитаем оба угла по 50° из 180°.Сначала мы складываем два угла 50 ° вместе.
50° + 50° = 100°
и 180° – 100° = 80°
Угол b равен 80°, потому что сумма всех углов треугольника равна 180°.
Вот еще один пример нахождения недостающих углов в равнобедренных треугольниках, когда известен один угол.
На этот раз мы знаем угол, который не лежит против отмеченной стороны. У нас 30°.
Мы можем вычесть 30° из 180°, чтобы увидеть, сколько в сумме составляют углы «a» и «b».
180° – 30° = 150°
Итак, углы «а» и «b» в сумме дают 150°.
Поскольку углы «а» и «b» лежат напротив отмеченных сторон, они равны друг другу.
Величина этих двух углов одинакова.
Разделим 150° на две равные части, чтобы посмотреть, чему равны углы «а» и «b».
150° ÷ 2 = 75°
Это потому, что 75° + 75° = 150°.
Углы «а» и «b» равны 75°.
Мы видим, что три угла равнобедренного треугольника в сумме дают 180°.
75° + 75° + 30 = 180°.
Как найти длину стороны остроугольного/тупоугольного равнобедренного треугольника
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
равнобедренных треугольников — Бесплатная помощь по математике
В мире геометрии существует множество типов треугольников.
Существует особый треугольник, называемый равнобедренным треугольником .В равнобедренном треугольнике углы при основании имеют одинаковую градусную меру и, следовательно, равны (конгруэнтны). Точно так же, если два угла треугольника имеют одинаковую меру, то стороны , противоположные этим углам, имеют одинаковую длину. Самый простой способ определить равнобедренный треугольник состоит в том, что у него две равные стороны .
В равнобедренном треугольнике две стороны называются катетами, а третья сторона называется основанием. Угол, расположенный против основания, называется вершиной.
Образец А:
Угол при вершине B равнобедренного треугольника ABC равен 120 градусам. Найдите градусную меру каждого угла при основании.
Решение:
(1) Пусть x = мера каждого угла при основании.
(2) Составьте уравнение и найдите x.
угол основания + угол основания + 120 градусов = 180 градусов
х + х + 120 градусов = 180 градусов
2х + 120 = 180
2х = 180 — 120
2х = 60
х = 60/2
х = 30
Каждый угол при основании треугольника ABC равен 30 градусам.
Образец Б:
В равнобедренном треугольнике RST угол S является углом при вершине. Углы при основании R и T равны 64 градусам. Найдите градусную меру угла при вершине S.
Решение:
(1) Пусть x = мера угла при вершине S.
(2) Составьте уравнение и найдите x.
угол основания + угол основания + угол при вершине S = 180 градусов
64 градуса + 64 градуса + х = 180 градусов
128 + х = 180
х = 180 — 128
х = 52
Угол при вершине S в треугольнике RST равен 52 градусам.
Образец С:
Градусная мера угла при основании равнобедренного треугольника XYZ в три раза превышает градусную меру вершины Y на 60. Найдите градусную меру угла при вершине Y. Обратите внимание, что трудно нарисовать рисунок, не зная, какие углы самые большие.
Нам нужно составить уравнение из этой задачи, поэтому давайте выясним, что оно пытается нам сказать. Сначала мы читаем «Градусная мера угла при основании», поэтому начнем с X =
.
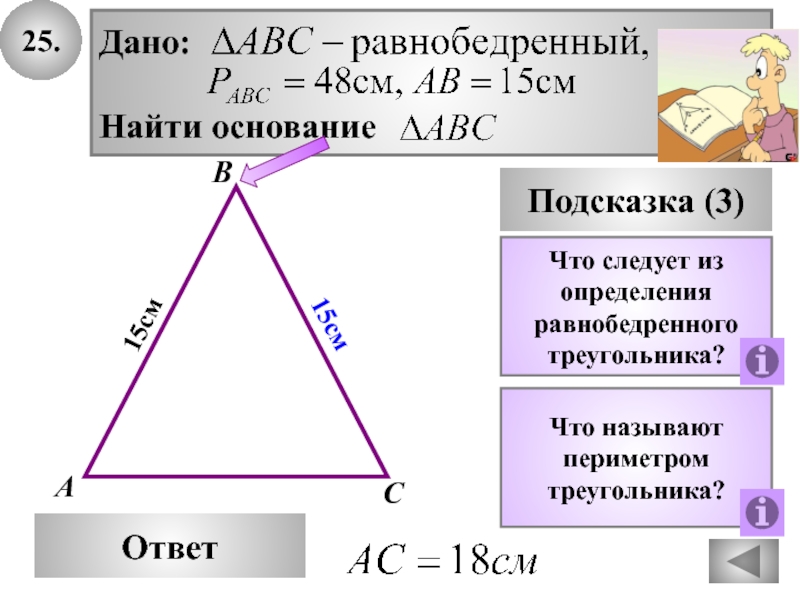
Наше уравнение на данный момент: X=
Теперь мы видим «превышает в три раза… Y… на 60», что означает 3Y + 60.
Теперь наше уравнение: X = 3Y + 60
Поскольку мы знаем, что X = Z, потому что это равнобедренный треугольник, мы можем найти меры всех углов.
угол основания + угол основания + вершина = 180
Х + Y + Z = 180
(3Г + 60) + Г+ (3Г + 60) = 180
7Г + 120 = 180
7Г = 60
Y = 60/7
Y = 8,57 градусов
Угол при вершине Y треугольника XYZ равен 8.57 градусов.
Урок, проведенный мистером Фелизом
Что такое равнобедренный треугольник? — [Определение, факты и примеры]
Что такое равнобедренный треугольник?
Треугольник с двумя сторонами равной длины является равнобедренным треугольником. Две равные стороны равнобедренного треугольника известны как «ноги», тогда как третья или неравная сторона известна как «основание».
Углы, противолежащие равным сторонам равнобедренного треугольника, всегда равны.В данном равнобедренном треугольнике, если AB = AC, то ∠B = ∠C
Вот несколько примеров равнобедренного треугольника:
Примеры из жизни
Многие вещи в мире имеют форму равнобедренного треугольника. Некоторые популярные примеры равнобедренного треугольника в реальной жизни — это кусок пиццы, пара сережек.
Непримеры
Общие свойства
Равные стороны равнобедренного треугольника называются катетами.
Третья и неравная сторона равнобедренного треугольника называется «основанием».
Угол между двумя равными сторонами равнобедренного треугольника известен как «угол при вершине».
Углы, образующие основание равнобедренного треугольника, называются углами при основании.
Углы, лежащие напротив равных сторон равнобедренного треугольника, всегда равны.
Все три угла, расположенные внутри равнобедренного треугольника, острые, что означает, что углы меньше 90°.
Сумма трех углов равнобедренного треугольника всегда равна 180°, а это значит, что мы можем узнать третий угол треугольника, если известны два угла равнобедренного треугольника.
Интересные факты
|
Иллюстративная математика
Задача
Миссис Лу попросила учеников своего класса найти равнобедренные треугольники, вершины которых лежат на координатной сетке.
Для каждого приведенного ниже примера объясните, почему треугольник равнобедренный.
- Джессика рисует следующий треугольник:
- Фото Брюса здесь:
- Ян рисует эту картину:
Комментарий IM
В этой задаче рассматриваются некоторые треугольники в координатной плоскости и как сделать вывод, что эти треугольники равнобедренные.Один из способов сделать это — вычислить длины сторон по теореме Пифагора. Однако этот метод не всегда является наиболее эффективным. Для треугольников, приведенных в пунктах (а) и (б), два
ветвей получается перемещением по линиям сетки, из одной вершины, на одинаковое количество квадратов по вертикали и горизонтали. Кроме того, в частях (а) и (б) нетрудно идентифицировать линию отражающей симметрии. Таким образом, в этих двух случаях есть альтернативные объяснения, и учитель может захотеть подчеркнуть это.Для части (c) нелегко увидеть, что этот треугольник равнобедренный без теоремы Пифагора.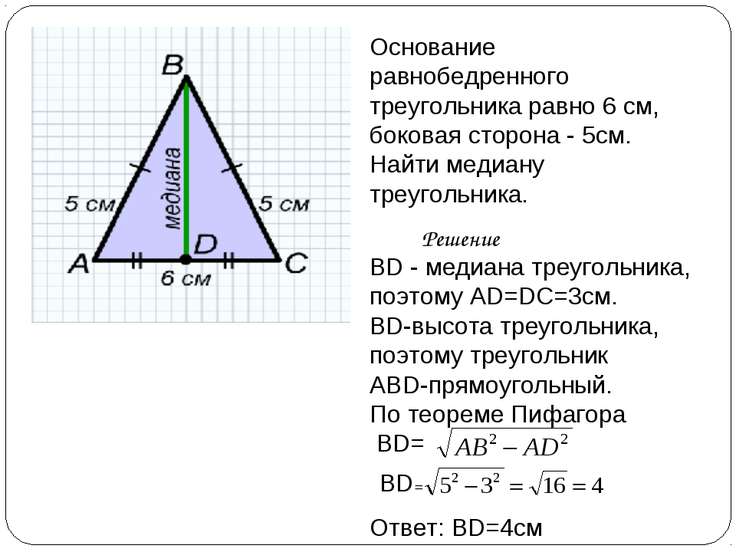
Учитель может попросить учащихся объяснить, почему треугольники в (a) и (b) являются равнобедренными без , используя теорему Пифагора, если это не встречается в работе учащихся.
В качестве расширения (или введения) представленного здесь задания учитель может предложить каждому учащемуся нарисовать равнобедренный треугольник, вершины которого находятся в точках координатной сетки.Затем они могут обменяться примерами и проверить, что треугольники равнобедренные. Если ни один учащийся не придумает пример, подобный приведенному в частях (b) и (c), учитель может представить их. Один из типов равнобедренного треугольника, который, скорее всего, составят учащиеся, — это прямоугольный равнобедренный треугольник, как показано ниже:
В этом случае $\overline{AC}$ и $\overline{AB}$ имеют длину 4 единицы: поскольку они лежат вдоль линий сетки, это можно увидеть, сосчитав прямоугольники.
Это задание дает учащимся возможность участвовать в MP3, конструировать жизнеспособные аргументы и критиковать рассуждения других.
Им нужно объяснить, почему каждый из данных треугольников является равнобедренным, и в этих трех случаях, вероятно, применимы разные рассуждения. Более того, если учащимся предлагается составить свои собственные равнобедренные треугольники, а затем обменяться ими друг с другом, это дает им дополнительную возможность проанализировать рассуждения своих одноклассников.
Эта задача тесно связана с www.illustrativemathematics.org/illustrations/1245, где прямоугольник размещается в координатной сетке под углом.2. \end{выравнивание}
Связь этого примера с текущей задачей заключается в том, что можно создать равнобедренный треугольник, начав, например, с точки (0,0), а затем пройдя вправо 11 и вверх 2 до (11,2), а затем пройдя вправо 10 и вверх 5 до (10,5). Эти три вершины составляют равнобедренный треугольник, как мы можем видеть, используя теорему Пифагора и вычисления выше, которые показывают, что две стороны имеют длину $\sqrt{125}$.
Как найти площадь равнобедренного треугольника — видео и расшифровка урока
Формула
Хорошо, теперь, когда мы разобрались с частями, давайте сосредоточимся на целом.
Чтобы найти площадь равнобедренного треугольника, мы используем следующую формулу:
где A площадь:
A = (1/2) b h
- b 21 база
- h высота треугольника
Например, если бы у нас был равнобедренный треугольник с основанием 8 сантиметров и высотой 10 сантиметров, мы подставили бы b = 8 и h = 10 в формулу, чтобы найти площадь, например:
A = (1/2) B H H
A = (1/2) ⋅ 8 ⋅ 10
A = 40
Мы видим, что область inoSceles треугольник с основание 8 см и высота 10 см это 40 квадратных сантиметров.
Нахождение высоты
Теперь мы знаем, что нахождение площади равнобедренного треугольника аналогично нахождению площади любого треугольника — мы используем формулу площади треугольника A = (1/2) б з . Однако нам часто не дают высоту равнобедренного треугольника, и она нам определенно нужна, чтобы использовать формулу.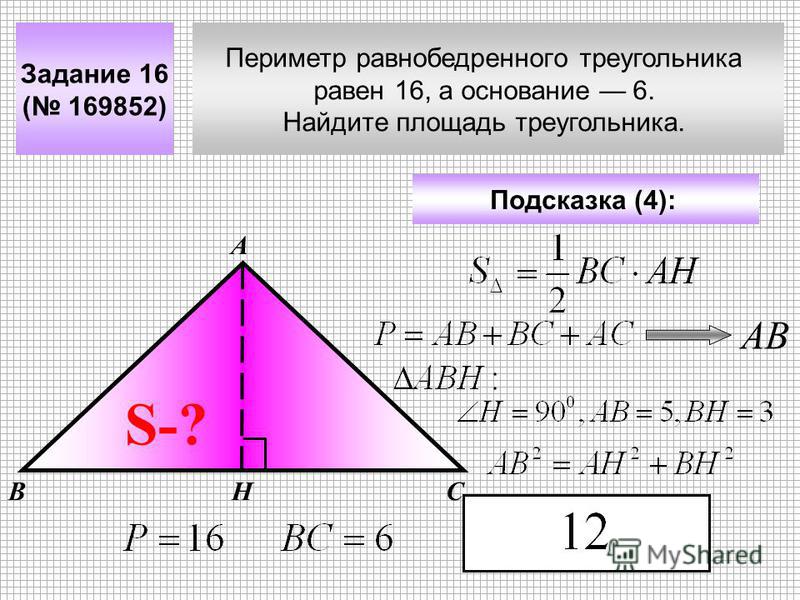
Гораздо чаще у нас будут длины катетов и основания равнобедренного треугольника, чем высота.
Например, предположим, что вы покупаете наклейку государственного парка на лобовое стекло вашего автомобиля в форме равнобедренного треугольника. На наклейке указаны длины сторон 8см, 8см и 6см. Он не дает ни высоты, ни площади наклейки, и вам нужно найти площадь, чтобы узнать, сколько места она займет на вашем лобовом стекле. У вас есть длина основания 6 сантиметров, но чтобы найти площадь, вы должны найти высоту наклейки, поэтому давайте посмотрим, как это сделать.
В общем, линия, представляющая высоту равнобедренного треугольника, пересекает основание таким образом, что оно делит основание пополам. Это разделит треугольник на два прямоугольных треугольника, как на нашей наклейке:
| . |
Исходя из этого, мы можем использовать теорему Пифагора , которая утверждает, что если a и b — катеты прямоугольного треугольника, а c — гипотенуза (или самая длинная сторона), то a 2 + б 2 = с 2.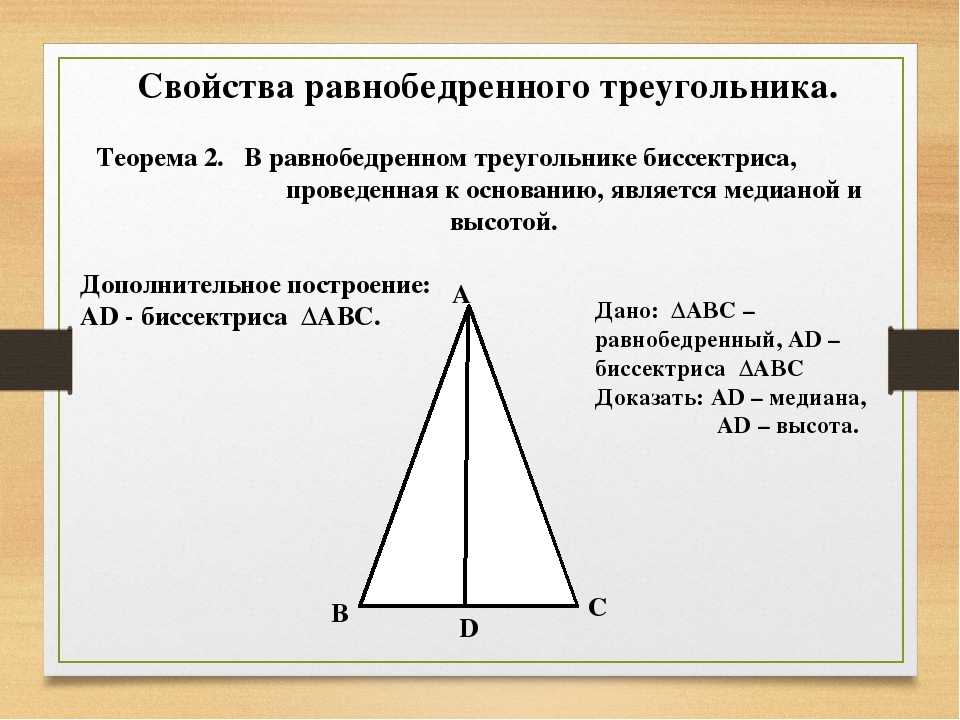
Мы можем использовать это, чтобы найти высоту.
Теперь взгляните на любой из прямоугольных треугольников на нашей наклейке. Мы видим, что у него есть ножки длиной 3см. и ч см., а гипотенуза длиной 8см. Следовательно, мы можем подставить это в теорему Пифагора, чтобы получить следующее уравнение:
32 + ч 2 = 82
Отлично, теперь мы можем найти ч в этом уравнении, и у нас есть высота!
h равно квадратному корню из 55, но это очень длинное число, которое постоянно повторяется.В данном случае мы округляем квадратный корень из 55, поэтому будем говорить, что высота примерно равна 7,4, что и означает волнистый знак равенства.
Благодаря этому процессу мы получаем, что ч ≈ 7,4 сантиметра. Видишь, это не так уж и плохо! В общем, чтобы найти высоту равнобедренного треугольника, мы просто делим треугольник на два прямоугольных треугольника линией, представляющей высоту, а затем используем теорему Пифагора, чтобы найти высоту.
Easy peasy, и теперь мы можем найти площадь вашей наклейки! Просто подставляем b = 6 и h = 7.4 в формулу площади, например:
A = (1/2) ⋅ 6 ⋅ 7,4
A = 22,2
Получаем, что площадь вашей наклейки составляет 22,2 квадратных сантиметра, и теперь вы знаете сколько места он займет на лобовом стекле. Здорово!
Краткое содержание урока
Когда дело доходит до нахождения площади равнобедренного треугольника, это так же просто, как подставить значения в формулу площади и решить. Хорошо, что мы теперь знакомы с этой формулой. Что еще лучше, так это то, что мы также знаем, как найти высоту равнобедренного треугольника, используя теорему Пифагора , если у нас нет ее для нахождения площади.Просто разделите основание пополам и используйте его как одно из значений в теореме. Подставьте полученное значение в формулу, как обычно, и все готово!
Прямоугольный равнобедренный треугольник. Темы по тригонометрии
Темы | Дом
5
РАВНОБЕРЕЖНЫЙ ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК — один из двух особых треугольников.
(Другой — треугольник 30°-60°-90°.) Учащийся должен знать отношения сторон.
(У равнобедренного треугольника две стороны равны.См. определение 8 в книге «Некоторые теоремы плоской геометрии». Теоремы, цитируемые ниже, будут найдены там.)
Теорема. В равнобедренном прямоугольном треугольнике стороны относятся как 1:1:.
Доказательство . В равнобедренном прямоугольном треугольнике равные стороны составляют прямой угол. Они имеют отношение равенства, 1 : 1.
Чтобы найти отношение числа гипотенузы ч , по теореме Пифагора имеем
ч 2 = 1 2 + 1 2 = 2.
Следовательно,
ч = .
(Урок 26 алгебры.) Следовательно, три стороны находятся в отношении
.1 : 1 : .
Обратите внимание, что поскольку прямоугольный треугольник равнобедренный, то и углы при его основании равны. (Теорема 3.) Следовательно, каждый из этих острых углов равен 45°.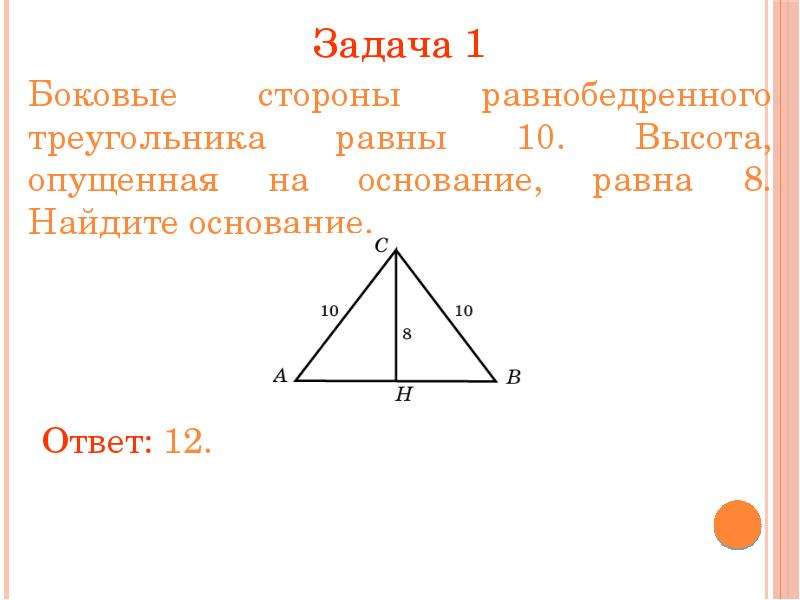
(Определение измерения углов в «градусах» см. в Теме 12.)
Пример 1.Оцените sin 45° и tan 45°.
Ответ . Для любой задачи, связанной с углом 45°, учащийся не должен обращаться к Таблице. Скорее нарисуйте треугольник и поместите числа отношений.
Видим:
| sin 45° | = | 1 | = ½, |
по рационализации знаменателя. (Урок 26 алгебры.)
Проблема.Оцените cos 45° и csc 45°.
| cos 45° = | 1 | = ½. |
Таким образом, cos 45° равен sin 45°; они являются дополнениями.
| csc 45° = | 1 | = . |
Пример 2. Решите равнобедренный прямоугольный треугольник со стороной 6.5 см.
Ответ . Чтобы решить треугольник, нужно знать все три стороны и все три угла.
Поскольку это равнобедренный прямоугольный треугольник, единственная проблема состоит в том, чтобы найти неизвестную гипотенузу.
Но в любом равнобедренном прямоугольном треугольнике стороны относятся как 1 : 1 : , как показано справа. В треугольнике слева сторона, соответствующая 1, умножена на 6,5. Следовательно, каждая сторона будет умножена на 6,5. гипотенуза будет 6.5. (Теорема о том же кратном.)
Всякий раз, когда мы знаем отношение чисел, мы используем этот метод подобных фигур для решения треугольника, а не тригонометрическую таблицу.
(В теме 6 мы будем решать прямоугольные треугольники, отношения сторон которых нам неизвестны.)
Пример 3. В равнобедренном прямоугольном треугольнике гипотенуза равна дюймам. Какой длины стороны?
Ответ . Учащийся должен начертить треугольники и разместить числа отношений.
Как была умножена сторона, соответствующая ?
Согласно правилу умножения радикалов, он был умножен на .