Презентация к уроку по математике (5 класс) на тему: Презентация «Комбинаторные задачи»
Слайд 1
Решите задачу: Прямоугольник состоит из трех квадратов. Сколькими способами можно раскрасить эти квадраты тремя красками: красной, зеленой и синей? 6Слайд 2
Комбинаторные задачи
Слайд 3
Классная работа 18.01 . Комбинаторные задачи
Слайд 4
Комбинаторика раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов
Слайд 5
КОМБИНАТОРНАЯ ЗАДАЧА – это задача, требующая осуществления перебора всех возможных вариантов или подсчета их числа.
Слайд 6
Решить комбинаторную задачу — это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.
Слайд 7
ОРГАНИЗОВАННЫЙ ПЕРЕБОР – строгий порядок разбора всех случаев, возможных решений .
Слайд 8
Решение задачи методом полного перебора всех возможных вариантов Задача 1: Прямоугольник состоит из трех квадратов. Сколькими способами можно раскрасить эти квадраты тремя красками: красной, зеленой и синей?
Слайд 9
Решение задачи: 6 способов
Слайд 10
Решение задачи методом полного перебора всех возможных вариантов Задача 2 Сколько двузначных чисел можно составить, используя цифры 1; 4; 7? ( цифры могут повторяться ) Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания: 11;14;17;(начали с 1) 41;44;47;(начали с 4) 71;74;77;(начали с 7) Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел. Ответ: 9 чисел.
Слайд 11
Решение задач с помощью дерева возможных вариантов Существует более общий подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название — дерево возможных вариантов . При правильном построении дерева ни один из возможных вариантов решения не будет потерян.
Слайд 12
Задача . Рассмотрим задачу о составлении трехзначных чисел из цифр 1;4;7 ( цифры в записи числа не повторяются ). Для её решения построим схему-дерево возможных вариантов. число 1 4 7 4 7 7 4 1 7 7 1 4 1 4 1 Ответ: числа 147; 417 ; 471; 714 ; 741 174 ;
Слайд 13
Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, булочки, печенья и вафель?
Слайд 14
Решение задачи: Ответ: 6 способов
Слайд 15
С. 163, №645, 647 (самостоятельно) Работа по учебнику:
Слайд 16
№645. Запишите все двузначные числа, в записи которых используются только цифры 1; 2 и 3 (цифры могут повторятся) Решение . Двузначное число Первая цифра 1 2 3 Вторая цифра 1 2 3 1 2 3 1 2 3 Варианты числа: 11; 12; 13; 21; 22; 23; 31; 32; 33 Ответ: 9 чисел
Слайд 17
№647. У ослика Иа-Иа есть 3 надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько есть вариантов у Иа-Иа ? Решение. друзья шарики Винни-Пух Пятачок Кролик Ответ: 6 вариантов
Слайд 18
Правило умножения в комбинаторных задачах. Для комбинаторной задачи с умножением можно построить дерево вариантов, но такое дерево строить станет намного сложнее, именно поэтому используется метод умножения, чтобы запись была короче. Рассмотрим этот метод на примере одной задачи: На обед в школьной столовой предлагается 2 вида супа , 3 вторых блюда и 4 разных сока . Сколько различных обедов можно составить по предложенному меню? Рассуждение: Первое блюдо можно выбрать 2 способами , для каждого вида супа можно выбрать второе блюдо из 3 предложенных , уже получается 6 вариантов , осталось выбрать напиток: для каждого из 6 полученных наборов существует 4 способа выбора напитка. Ответ: 24 способа.
Слайд 19
Оформление: Суп — 2 способа Вторые блюда — 3 способа Сок — 4 способа Решение: 2 x 3 x 4 = 24 Ответ: Можно составить 24 варианта различных обедов
Слайд 20
С. 165, № 663, 664 (самостоятельно) Работа по учебнику:
Слайд 21
Перестановки в комбинаторных задачах. В комбинаторике часто приходиться решать задачу о том, сколькими способами можно расположить в ряд или, как говорят математики, упорядочить все элементы некоторого множества. Каждое из таких расположений называют перестановкой.
Слайд 22
Миша решил в воскресенье навестить дедушку , своего друга Петю и старшего брата Володю . В каком порядке он может организовать визиты? Сколько вариантов получилось ?
Слайд 23
Решение задачи: 6 способов
Слайд 24
Здесь речь идет о числе перестановок, т.е. о выполнении трех визитов в разной последовательности. Сначала Миша выбирает, к кому отправится в первую очередь – 3 способа, затем он идет в гости к кому – то из 2 оставшихся, ну а затем – к последнему. 3•2•1= 6 способов
Слайд 25
Задача. В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними? Решение. Первое место может занять любой из 4 участников. При этом второе место может занять любой из трёх оставшихся, третье – любой из двух оставшихся, а на четвёртом месте остаётся последний участник. Значит, места между участниками могут быть распределены следующим образом 4 •3•2•1= 24 . Ответ: 24 способами.
Слайд 26
Андрей, Боря, Витя и Дима решили покататься на карусели. На ней было 4 сиденья с изображением льва , слона , тигра и медведя . Ребята заспорили, кому где сидеть, поэтому решили перепробовать все способы. Сколько раз нужно в таком случае прокатиться на карусели? Решение: Здесь речь идет о числе перестановок, т.е. о размещении 4 мальчиков по 4 местам разными способами: 4! = 24
Слайд 27
С. 166, №672 (самостоятельно) Работа по учебнику:
Слайд 28
§24, вопросы № 1-2, №652, 665, 669(1) Домашнее задание Что такое факториал ?
nsportal.ru
Сценарий урока по математике в 5 классе по теме Комбинаторные задачи
Сценарий урока по математике в 5 классе
по теме «Комбинаторные задачи»
Цели урока:
Показать учащимся на примерах практическое применение комбинаторики в повседневной жизни;
Рассмотреть методы решения простейших комбинаторных задач (метод перебора, дерево возможных вариантов)
Научить применять и решать простейшие комбинаторные задачи практического содержания.
Задачи урока:
Образовательные (формирование познавательных УУД):
— сформировать у учащихся основы элементарных знаний по комбинаторике;
— определить содержание знаний и умений учащихся по данной теме;
— использование знаково-символических средств, общих схем решения;
— выполнение логических операций сравнения, анализа, обобщения, классификации;
— выделять и формулировать познавательные цели, осознанно и произвольно строить
свои высказывания.
Развивающие (формирование регулятивных УУД):
— планировать свою деятельность в зависимости от конкретных условий;
— выбирать способы решения задач в зависимости от конкретных условий;
— развитие приемов умственной деятельности, внимания, памяти, творческой
активности;
— развивать логическое мышление, интерес к изучению математики;
— умение обрабатывать информацию и ранжировать ее по указанным основаниям;
— контроль и оценка процесса и результатов действия.
Воспитательные (формирование коммуникативных и личностных УУД):
— умение слушать и вступать в диалог;
— участвовать в коллективном обсуждении проблем;
— воспитывать ответственность и аккуратность;
— выработка уверенности в собственных силах;
— формирование умения проверять результаты деятельности;
— развивать умение дискуссионной и групповой работы.
Тип урока: урок открытия нового знания
Форма работы учащихся: фронтальная, групповая, парная, индивидуальная.
Необходимое оборудование: компьютер, доска, учебник, проектор, наглядные материалы, презентация к уроку.
Урок №№155-156
Время: 80 мин
Ход урока.
Урок №1
Создание внешней мотивации изучения темы урока. Данный прием позволяет привлечь интерес учащихся к изучению новой темы, не блокируя восприятия непонятными терминами. Полная готовность класса и оборудования, быстрое включение учащихся в деловой ритм.
Учитель:
Прозвенел сейчас звонок.
Начинаем мы урок.
Посмотрите, всё ли в порядке:
Книжка, ручка и тетрадка.
Все ли правильно сидят?
Все ли внимательно глядят?
Каждый хочет получать
только лишь оценку «5”?
Учитель. Здравствуйте, ребята! Я рада вас видеть в хорошем настроении. Откройте тетради, запишите число, классная работа, тему урока (я записываю на доске слово «Тема», выдерживаю паузу до тех пор, пока все не обратят внимания на мою руку, которая не хочет выводить саму тему).
Ребята, извините, но моя рука отказалась написать тему урока, и, кажется, неслучайно! Вот вам еще одна загадка, которую вы разгадаете уже в середине урока: почему рука отказалась записать тему урока? (данный вопрос записываю в уголке классной доски). Тему урока мы запишем позже.
Но начинать урок нам все равно надо, и начнем с хорошо знакомого материала.
II. Мотивирование (самоопределение) к учебной деятельности (7 мин)
Учитель: Что нового вы узнали на предыдущих уроках?
Дети: Событие может быть достоверным, невозможным или случайным.
На слайде читаем определение этих событий.
слайд 1


Учитель: Ребята! Давайте вспомним, как решаются такие задачи.
На экране появляется слайд с условием задач. Начинаем обсуждение заданий. Учащиеся дают ответы, объясняют свою точку зрения, ссылаясь на определения этих событий. Учимся ясно, точно, грамотно излагать свои мысли в устной речи.
(Слайд 2)

Учитель: Все молодцы, с заданием справились. Приведите свои примеры событий? Приходилось ли вам сталкиваться с этими понятиями в жизни? (ответы детей)
Дети: После воскресенья всегда будет понедельник, вода замерзла при температуре +25 градусов.
III. Подготовка учащихся к объяснению нового знания, выполнение ими пробного учебного действия и фиксация индивидуального затруднения. Погружение в проблему (12 мин)
На данном этапе организуется подготовка и мотивация учащихся к надлежащему самостоятельному выполнению пробного учебного действия, его осуществление и фиксация индивидуального затруднения.
Учитель: Мы сейчас будем решать интересные задачи. Я класс разделю на 4 группы. Каждой группе дам задание и набор раздаточного материала. Время вам на обсуждение в группе 4 минуты, а на представление решения задачи отводится 2 минуты.
Все расселись по группам и приступили к работе. В это время учитель выступает в роли консультанта.
Задания:
Группа 1. Решить задачу, разыграв сценку.
Группа 2. Решить задачу, составив таблицу.
Группа 3. Решить задачу, изготовив вымпела.
Группа 4. Решить задачу, расставив фигуры.
Во время обсуждения учитель является консультантом.
Учитель: Время прошло. Слово предоставляется поочередно каждой группе. Остальные внимательно слушают.
(Приложение 1) (Слайды 3,5,7,9)

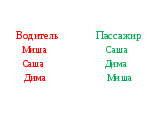


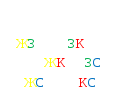

Молодцы! А теперь немного отдохнем.
IV. Физкультминутка. (2 мин)
Учитель: Давайте здороваться, т.е. все встанем и пожмем друг другу руки (все дети встали и начали подходить к друг другу здороваться). Теперь сядьте все на свои места и подумайте, как ответить на такой вопрос: «В классе нас сколько? (22 человека) «Сколько было всего рукопожатий?» Дети начинают рассуждать, но быстро запутываются.
У детей возникла проблема. На данном этапе учитель организует выявление учащимися места и причины затруднения (большое число).
Учитель: Давайте немного упростим задачу и посчитаем рукопожатия между группами, в которых вы работали. Сколько групп? (3 мин)
Итак, какие будут ответы? Учащиеся начинают рассуждать, обсуждать, показывать решение задачи. Обсуждается, как оформить запись в тетрадь. Ответ записывают на доске. (6) Ребята, скажите, проблема решена?
Дети: Мы не знаем, как решать, если числа большие. Вот этим и займемся, когда выясним что это за задачи.
V. Построение проекта выхода из затруднения (цель и тема, способ, план, средство).
(6 мин)
На данном этапе учащиеся в коммуникативной форме обдумывают будущие свои действия (формулируют тему, цель, задачи, строят план достижения цели) и определяют средства (алгоритмы, модели, учебник). Этим процессом руководит учитель (подводящий диалог, побуждающий диалог).
Учитель: Ребята! Какие действия вы делали при решении задач?
Дети: перебирали варианты, составляли комбинации, комбинировали, делали перебор.
Учитель: Как можно назвать такие задачи из ваших предложений? Дети начинают составлять названия.
Дети: комбинаторные
Учитель: А как, тогда будет называться раздел математики, где живут такие задачи?
Дети: комбинаторика.


 слайд 11
слайд 11


Учитель: Молодцы! Все правильно. Запомните! Особая примета комбинаторных задач – это вопрос, который можно сформулировать таким образом, что он начинался бы словами: Сколькими способами…?, сколько вариантов…?
Теперь мы можем записать тему урока?
Дети: да.
Учитель: как называется тема урока?
Дети: решение комбинаторных задач.
Учитель: Можете теперь сказать: почему рука отказалась записать тему урока?
Дети: слово комбинаторика было бы нам непонятно.
Учитель:
Откройте тетради и запишите теперь тему урока. Запишите понятия «комбинаторика», «комбинаторные задачи».
Как говорят «Без знания прошлого нет настоящего, нет будущего».
Посмотрите презентацию, которую подготовил ваш одноклассник
Презентация «Истоки комбинаторики» (5 мин)
VI. Рефлексия 1 урока. (3мин) прием «Телеграмма»
Учитель: Кратко напишите пожелание себе с точки зрения изученного на уроке, оцените себя и отправьте мне.
Всем спасибо! Сейчас вы идете на перемену, а на втором уроке продолжим узнавать много интересного о комбинаторике и ее задачах.
Урок №2
VII. Построение проекта выхода из затруднения (продолжение) (2 мин)
Учитель:
Будь внимательней, дружок.
Нам урок пора начать.
Пришло время вычислять.
И на трудные вопросы
Вы ответ сумейте дать.
Каждый из вас сегодня постарается ответить на… проблемный вопрос
(Слайд 13)
Из этой проблемы вытекает цель урока. Сформулируйте цель урока?
Дети: продолжить знакомство с наукой комбинаторика.
Учитель: Какие перед нами ставятся задачи?
Дети: научиться решать комбинаторные задачи, узнать способы решения задач.
Учитель: А чтобы у вас была путеводная звезда, к которой бы вы шли, я выдвинула следующую гипотезу: решение комбинаторных задач развивает творческие способности, логическое мышление, помогает при решении олимпиадных задач на ГИА, ЕГЭ.
(слайд 14)

В конце урока вам предстоит подтвердить или опровергнуть ее.
VIII. Изучение нового материала. Решение задач (доказательство гипотезы). Работа с учебником.
1.Откройте учебник на странице 252, записываем задачу №967. В задаче решение уже готово. Ваша задача разобрать образец решения и выяснить схему решения таких заданий. Дети начинают читать текст задачи (3 мин)
К доске выходит ученик и записывает решение (проговаривание и обязательное пояснение решения задачи).
Б Б С С К К
С ; К ; Б ; К ; Б ; С
К С К Б С Б.
Дети делают вывод, что получили 6 комбинаций. Значит, указанную символику при выборе государственного флага могут использовать 6 стран.
Учитель: Какой флаг является Государственным флагом России?
Дети отвечают. (Слайд 16)
На флаге России:
Три горизонтальные полосы одинаковой ширины.
Цвета полос: белый, синий, красный.
2. Задача № 969. Читаем задачу. Выделяем, что дано в задаче, что требуется найти, как это делать. Какие способы? Как можно записать решение? (на столах у учащихся лежат цветные карандаши зеленый, черный, желтый). Кто какой способ взял? (6 мин) Устанавливаем логику перебора (не случайным образом, а установив некоторый порядок)

Учитель. Решая комбинаторные задачи, мы ищем способ перебора всех возможных переборов. Часто процесс перебора удобно осуществлять путем построения специальной схемы (прошу учащихся найти в тексте параграфа, как называется такая схема). Дети находят и называют «дерево возможных вариантов». Почему так назвали? Внешне такая схема напоминает дерево, отсюда название.

(Слайд 18)
VIII. Физкультминутка (2 мин)
Поработали, ребятки!
А теперь – все на зарядку!
Влево, вправо повернитесь,
Наклонитесь, поднимитесь.
Руки вверх и руки вбок,
И на месте прыг да скок!
А теперь бежим вприпрыжку,
Молодцы вы, ребятишки!
Замедляем, дети, шаг
И на месте стой! Вот так!
А теперь мы сядем дружно,
Нам ещё работать нужно!
Разбор задач по слайдам. Дерево возможных вариантов (10 мин)
(Слайды 19, 20, 21)
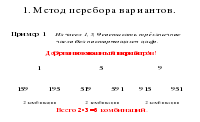
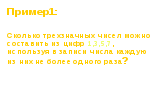


VIII. Самостоятельная работа с самопроверкой по эталону ( 10 мин)..
Задача № 970 из учебника.
Ответ:24

Проверка идет по парам (ученики обмениваются тетрадями и проверяют работу соседа). Оценивают работу друг друга. Листы передают учителю на стол.
IX. Итог урока ( 4 мин)
На примере решенных задач мы увидели практическое применение «Комбинаторики» в различных сферах деятельности человека, т.е. выяснили, где в реальной жизни мы встречаемся с комбинаторикой.
(Слайд 22, 23)


В ближайшем будущем мы научимся решать более сложные задачи комбинаторики, а ваши знания будут востребованы при решении задач олимпиадного типа, ГИА и ЕГЭ. Комбинаторика играет большую роль в практической деятельности человека.
Вывод

Запишите домашнее задание №977, №975, 979, 971. Вы должны выбрать сами и решить не менее 2 задач. Вы можете посмотреть видео урок по данной теме.
http://interneturok.ru/ru/school/matematika/5-klass/instrumenty-dlja-vychislenij-i-izmerenij/kombinatorika-logika-perebora
X. Рефлексия. (3 мин)
Подводим итоги урока. Каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность, эффективность работы класса, увлекательность и полезность выбранных форм работы. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске:

Урок закончен, спасибо.
infourok.ru
Научно-исследовательская работа по математике на тему «Комбинаторные задачи» (5 класс)
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «КОЛЫВАНСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №2» МБОУ «Колыванская СОШ № 2» 633160 РФ, Новосибирская обл.р.п. Колывань, пр-кт Революционный. 21[email protected] тел/факс 8-38352-51-283 |
Комбинаторика.
Задачи.
Авторы работы:
Горлова Анастасия Владимировна, 5 Б класс,
Адрес: Колывань, ул. Некрасова, 2а кв.12
Кудряшова Анастасия Дмитриевна, 5 Б класс,
Адрес: Б. Оеш, ул. Озерная, 50 кв 1
Руководитель:
Клоненгер Светлана Викторовна,
учитель математики первой
квалификационной категории
р.п. Колывань, 2019 г.
Содержание
страница
Введение 3
Цели и задачи работы 4
История возникновения и развития комбинаторики 4
Комбинаторные задачи. Особенность решения комбинаторных задач. 5
Способы решения комбинаторных задач 6
Области применения комбинаторики 8
Заключение 9
Литература 10
Приложение 1. 11
Введение
С комбинаторными задачами мы познакомились задолго до изучения этой темы на уроках математики. В интернете мы читали разные задачи, искали интересную информацию. И нашли такую задачу: У Маши было 3 юбочки и 4 кофточки. Сколько возможных комплектов одежды есть у Маши, чтобы каждый день ходить в новом наряде, с условием, что все вещи сочетаются друг с другом? Оказалось, что 12. Почти на две недели. Мы стали рассуждать, если добавить еще кофту, юбку и две пары туфель. Сначала предположили, что ответ будет около 18-20 нарядов. Стали изучать способы решения комбинаторных задач. Когда эта задача была решена, то оказалось, что таких нарядов будет 40. Это было невероятно. Потом мы узнали, что для блокировки телефона пин-кодом из 4 цифр имеется 10000 вариантов. Оказалось, что без решения угадать ответ, даже примерно, невозможно. Но и сами ответы поражали воображение. 
Нам стало интересно, какие еще задачи бывают, кто первым их придумал.
Мы решили изучить историю комбинаторики и некоторые способы решения задач и поделиться своими знаниями с одноклассниками на уроке «Математика вокруг нас», где мы представили свой небольшой проект. Позже на уроках математики мы опять встретили задачи из комбинаторики. Мы уже знали, как их решать, тем более, способов решения мы освоили больше, чем изучается в 5 классе. Мы быстро решили все задачи и тогда начали сочинять свои. Это оказалось трудным, но увлекательным занятием. Нам помогали одноклассники, они предлагали идеи для задач. Так у нас получился небольшой сборник интересных задач по комбинаторике, который, мы надеемся, пригодится нам в дальнейшей учебе и при сдаче экзаменов.
А мы задались вопросом, только ли для уроков математики нужна комбинаторика? Насколько эти знания важны для жизни? И какую сферу своей будущей работы надо выбрать, чтобы снова встретится с комбинаторикой?
Цели и задачи работы
Цель: Научиться понимать и составлять комбинаторные задачи. Исследовать в каких сферах деятельности человека комбинаторика нашла широкое применение
Задачи:
— Изучить историю возникновения и развития комбинаторики,
— Изучить некоторые способы решения комбинаторных задач,
— Научиться понимать и составлять задачи на применение различных способов решений.
— Исследовать области применения комбинаторики, связанные с практической деятельностью человека.
История возникновения и развития комбинаторики
Еще в 5 веке до нашей эры в китайской «Книге перемен» написано, что всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. В 4 веке до нашей эры в Древней Греции подсчитывали число комбинаций слогов в стихотворных размерах, изучали фигуры, которые можно составить из частей особым образом разрезанного квадрата. В 12 веке индийский математик Бхаскара исследовал задачи, связанные с перестановками и сочетаниями. Стремительно развиваться комбинаторика начала в 16 веке. Первоначально она применялась для расчета шансов на выигрыш в различных азартных играх: рулетке, игре в кости, а также в карточных играх. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Ясно, что первоначально комбинаторные задачи касались в основном азартных игр. Исследования вопросов комбинаторики предпринимали итальянские математики Тарталья и Кардано, французы Паскаль и Ферма.
Сам термин «комбинаторика» придумал Лейбниц, который в 1666 году (ему было 20 лет) опубликовал книгу «Рассуждение о комбинаторном искусстве». Правда термин «комбинаторика» Лейбниц понимал чрезмерно широко, включая в него даже логику.
Комбинаторные задачи. Особенность решения комбинаторных задач.
Слово «комбинаторика» происходит от латинского слова combinare, которое означает соединять, сочетать. Она включает в себя задачи, решая которые приходиться составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций. Такие задачи называются комбинаторными задачами. Особая примета комбинаторных задач – вопрос, который можно сформулировать таким образом, что он начинался бы словами: Сколькими способами…? Сколько вариантов…? Для того, чтобы решить задачу по комбинаторике, необходимо сначала понять её смысл, то есть, представить мысленно процесс или действие, описанное в задаче. Нужно чётко определить тип соединений в задаче, а для этого надо, составив несколько различных комбинаций, проверить, повторяются ли элементы, меняется ли их состав, важен ли порядок элементов. Если же комбинаторная задача содержит ряд ограничений, то нужно понять, как влияют или не влияют эти ограничения на соединения. В том случае, если трудно сразу определить какие-либо важные моменты задачи, то неплохо было бы попытаться разобраться в более лёгкой задаче. Например, в той, в которой не учитываются ограничения, если они есть в исходной задаче, или же в задаче, в которой рассматривается меньшее количество элементов, тогда проще будет понять принцип образования выборок. Когда комбинаторная задача состоит из различных комбинаций элементарных задач, то нужно просто разбить задачу на подзадачи. Далее мы изучили три способа решения задач. В процессе исследования мы пришли к выводу, что каждый из способов имеет свои достоинства и свои недостатки.
Способы решения комбинаторных задач
Способ перебора.
Задача №1. У мамы в саду растут розы, астры, гладиолусы, пионы и георгины. Мне на урок биологии нужно принести три разных цветка. Сколько способов у меня есть для того, чтобы выбрать три цветка из маминого сада?
Решение. Зашифруем название цветов: астра (А), роза (Р), пион (П), гладиолус (Гл), георгин (Гр). Возьмем первым цветком розу. Посчитаем все варианты, когда в «букете» будет роза. 
Р А П; Р А Гл; Р А Гр;
Р П Гл; Р П Гр;
Р Гл Гр.
Дальше считаем, когда розы нет:
А П Гл; А П Гр;
А Гл Гр; П Гл Гр.
Итого, 10 способов.
(Перебор всех вариантов можно вести иначе, например, берём 2 цветка и перебираем варианты третьего).
Дерево возможных вариантов.
Задача №2. Сколько двузначных чисел можно составить, используя цифры 1, 4 и 7?
Решение. 
Действительно, если перевернуть рисунок, он будет похож на дерево с пушистой кроной.
Правило Умножения.
Задача №3. На каникулах город Кемерово посетят школьники из Колывани. Они могут приехать поездом или автобусом. В Кемерово им предложено на выбор посетить областной краеведческий музей, музей — заповедник угледобычи под открытым небом «Красная сопка» или совершить экскурсию в кемеровский ботанический сад. Сколько возможных экскурсионных маршрутов предложили учащимся? (Эта задача составлена нами).


Решение. Если школьники поедут поездом, то у них есть три выбора экскурсий. Если поедут автобусом, тоже 3 экскурсии. Значит, 2*3=6 (экскурсионных маршрутов).
Мы рассмотрели три основных способа решения комбинаторных задач. Однако, многие задачи имеют ограничения и их нужно учитывать при решении. На базе этих задач мы самостоятельно составили сборник задач, причем, некоторые из них, на первый взгляд, кажутся очень похожими. На самом деле это не так. Накладывая определенные ограничения, мы получили «похожие» задачи с разными решениями.
Области применения комбинаторики
В процессе составления задач мы обращались к дополнительным источникам. Биология, там мы искали название насекомых, цветов, животных. География – название городов и их достопримечательности. Конечно же, история с её историческими событиями и именами великих людей. Даже поинтересовались музыкой, как располагаются музыканты в квартете. Большую помощь нам оказала Википедия. 
Нас заинтересовало, в каких сферах деятельности людей мы можем встретиться с комбинаторикой. Оказалось, что далеко ходить не надо и с этим мы встречаемся каждый день в школе, кроме каникул: наше расписание уроков. Значит, и в любом другом учебном заведении, чтобы составить расписание занятий;
— в нашей и любой другой столовой, чтобы составить меню;
— у мамы в магазине, чтобы оформить витрину с товарами;
— у врача, чтобы попасть к пациентам и как можно скорее оказать помощь;
А также:
— в экономике, чтобы анализировать варианты купли-продажи акций;
— в криптографии, чтобы разработать методы шифрования или взломать шифр;
— на почте, чтобы распределить варианты пересылки;
— в агротехнике, размещать посевы на нескольких полях;
— в лингвистике, для рассмотрения вариантов комбинаций букв;
— в биологии, для расшифровки кода ДНК;
— в военном деле, для расположения подразделений;
— в астрологии, анализировать расположения планет и созвездий;
— в спорте, для расчета количества игр между участниками;
— география, для раскрашивания карт;
— на производствах, для распределения нескольких видов работ между рабочими;
-в азартных играх, лотереях, для подсчёта частоты выигрыша;
— в химии, для анализа возможных связей между химическими элементами;
и во многих других сферах деятельности человека, все их перечислить оказалось невозможно, потому что, как только мы начинали изучать, чем занимается выбранная сфера, выяснялось, что комбинаторика и здесь работает.
Заключение
Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.
В ближайшем будущем мы научимся решать более сложные задачи комбинаторики, а наши знания по теме будут востребованы при решении задач олимпиадного типа, задач из ЕГЭ.
Мы выяснили, что комбинаторика играет большую роль в практической деятельности человека.
Комбинаторные задачи могут дать ответ на многие вопросы, связанные с практической деятельностью людей, а решение задач помогает развивать умственные способности, логическое мышление, вычислительные навыки.
Мы выяснили, что знание комбинаторики необходимо представителям самых разных специальностей. Всё это необходимо для всестороннего развития личности. Современный человек должен обладать хорошей математической подготовкой, уметь применить свои знания и навыки на практике.
А мы, как оказалось, очень давно, даже не замечая этого, каждый день применяем комбинаторику в своей жизни. Вся жизнь, с самого её начала, это выбор. Каждый день мы выбираем варианты: что поесть, во что одеться, куда пойти, чем заняться, как учиться, где учиться и так далее. И от правильности выбора зависит наше будущее.
А люди, которые умеют рассуждать, перебирать различные варианты решений, быстрее находят выход даже из самых безвыходных ситуаций.
Литература
https://ru.wikipedia.org/wiki/Лейбниц,_Готфрид_Вильгельм
https://ru.wikipedia.org/wiki/История_комбинаторики
https://dic.academic.ru/dic.nsf/ruwiki/1509070
https://4brain.ru/blog/комбинаторное-мышление/
https://www.google.ru/search?newwindow=1&rlz=1C1PRFI_enRU809RU812&q=%D0%BA%D0%BE%D0%BC%D0%B1%D0%B8%D0%BD%D0%B0%D1%82%D0%BE%D1%80%D0%B8%D0%BA%D0%B0+%D0%B2+%D1%80%D0%B5%D0%B0%D0%BB%D1%8C%D0%BD%D0%BE%D0%B9+%D0%B6%D0%B8%D0%B7%D0%BD%D0%B8&sa=X&ved=2ahUKEwiB3LzIm4PfAhUGjCwKHQiOA_oQ1QIoAHoECAYQAQ&biw=1366&bih=657
https://eduherald.ru/ru/article/view?id=11943
http://xn--i1abbnckbmcl9fb.xn--p1ai/%D1%81%D1%82%D0%B0%D1%82%D1%8C%D0%B8/596798/
http://rutrip.net/sibir/kemerovskaya-oblast/kemerovo/dostoprimechatelnosti-kemerova
Приложение
Задача 1. Из группы учащихся, которые входят в редколлегию 5Б класса, классный руководитель выделяет двоих для оформления стенгазеты для школы. Сколько существует вариантов такой пары, если группа состоит из 6 человек?
Решение: Зашифруем учеников 1,2,3,4,5,6. Тогда пары могут быть такие 1и 2; 1 и 3; 1 и 4; 1 и 5; 1и 6; 2 и 3; 2 и 4; 2 и 5; 2 и 6; 3 и 4; 3 и 5; 3 и 6; 4 и 5; 4и 6; 5 и 6. Ответ: 15 пар.
Задача 2. У Насти пять подруг: Катя, Таня, Лиза, Кристина и Аня. Она решила пригласить двух из них в кино. Укажите все возможные варианты выбора подруг. Сколько таких вариантов? 
Решение: С Катей 4 пары, с Таней 3 пары, с Лизой 2 пары, с Кристиной 1 пара. Ответ: 10 вариантов.
Задача 3. Мы с подругой спекли пирожки, из них 2 с картошкой, 2 с вишней и 1 с яблоком. Мы решили угостить двумя пирожками Светлану Викторовну. Сколько способов выбора угощения из двух пирожков для этого существует?
Решение: Перечислим все возможные варианты. 2 с картошкой, 2 с вишней, картошка и вишня, картошка и яблоко, вишня и яблоко. Ответ: 5 способов.
Задача 4. У Насти 4 юбочки, 5 кофточек и 2 пары новых туфелек. Все вещи в гардеробе сочетаются. Сколько дней Настя может выходить в разных нарядах, не повторяя комплект?
Решение: 4*5*2=40. Ответ: 40 дней.
Задача 5. Моей маленькой сестре дали кубики: 2 красных, 1 зелёный, 3 желтых: из них надо собрать светофор. Сколько есть способов собрать светофор, если все кубики одинакового размера?
Решение: 1 способ.
Задача 6. Моей маленькой сестре дали кубики: 2 красных, 1 зелёный, 3 желтых: из них надо собрать светофор. Сколько есть способов собрать светофор, при условии, что все кубики пронумерованы?
Решение: 2*1*3=6. Ответ: 6 светофоров.
Задача 7. В моей комнате веселились: 1 маленькая муха, 1 большая муха , 1 комар, случайно залетевшие 1 стрекоза и 1 пчела. Мой отважный кот Тимка прогнал 3 насекомых. Сколько есть вариантов из 3насекомых, которых прогнал Тимка?
Решение: Перечислим: м – маленькая муха, М — большая муха, к — комар, с — стрекоза, п – пчела. мМк, мМс, мМп, мкс, мкп, мсп. Теперь без м : Мкс, Мкп, Мсп, ксп. Ответ: 10 вариантов.
Задача 8. У Тани есть фрукты: яблоко, груша и банан и апельсин. На столе стоят две одинаковых вазы. Сколько существует способов разложить фрукты в вазы? Учтите вариант, когда ваза остается пустой.
Решение: Я и Г,Б,А; Г и Я,Б,А; Б и Я,Г,А; А и Я,Б,Г; Я,Г и Б,А;
Я,Б и Г,А; Я,А и Г,Б; и все фрукты в одной вазе. Ответ: 8 способов.
Задача 9. Настя Горлова идет от дома до магазина 2 дорогами, а от магазина до школы 3 дорогами. Сколько вариантов маршрутов от дома до школы есть у Насти?
Решение: 2*3+6 . Ответ: 6 маршрутов.
Задача 10. Четыре лучших подруги встретились в школе после каникул и решили обняться – каждая пара по одному разу. Сколько получилось обнимашек?
Решение: 1 2 Ответ: 6 обнимашек.
3 4
Задача 11. В областных соревнованиях по футболу участвовало 8 команд из разных районов Новосибирской области: Колыванского, Коченевского, Тогучинского, Ордынского, Купинского, Искитимского, Карасукского, Мошковского. В первый день каждая команда провела с каждой из остальных по одной игре. Сколько всего игр было в первый день?
Решение: 7+6+5+4+3+2+1=28. Ответ: 28 игр.
Задача 12. Мама утром мне предложила на выбор чай, сок или какао. А на столе в вазе лежали ватрушка, круассан, кекс и пончик. Сколько вариантов завтрака у меня есть, если я возьму один напиток и одну вкусняшку?
Решение: 3*4=12. Ответ: 12 завтраков.
Задача 13. Принцесса собирается на бал. У неё есть 5 новых бальных платьев и 4 пары замечательных туфель, которые подойдут к каждому платью. Сколько возможных комплектов может составить принцесса, чтобы блистать на балу?
Решение: 5*4=20. Ответ: 20 комплектов для бала.

Задача 14. Составить трехзначное число из цифр 1, 4, 8, 9. Сколько таких чисел существует?
Решение: 4*4*4=64. Ответ: 64 чисел.
Задача 15. Составить трехзначное число из цифр 1, 4, 8, 9. Сколько таких чисел существует, при условии, что все цифры различны?
Решение: 4*3*2=24. Ответ: 24 числа.
Задача 16. Составить трехзначное число из цифр 1, 4, 8, 9. Сколько таких чисел существует, при условии, что число делится на 2?
Решение: 4*4*2=32. Ответ: 32 числа.
Задача 17. Составить трехзначное число из цифр 1, 4, 8, 9. Сколько таких чисел существует, при условии, что число не делится на 2?
Решение: 64-32=32. Ответ: 32.
Задача 18. Составить трехзначное число из цифр 1, 4, 8, 0. Сколько таких чисел существует?
Решение: 3*4*4=48. Ответ: 48 чисел.
Задача 19. Составить трехзначное число из цифр 1, 4, 8, 0. Сколько таких чисел существует, при условии, что цифры не повторяются и число не делится на 2?
Решение: 401, 481, 801, 841. Ответ: 4 числа.

Задача 20. В понедельник у нас по расписанию музыка, информатика, физкультура, математика и русский язык. Сколько вариантов расписания из 5 уроков можно составить на этот день?
Решение: 5*4*3*2*1=120. Ответ: 120 вариантов.
Задача 21. В понедельник у нас по расписанию музыка, информатика, физкультура, математика и русский язык. Сколько вариантов расписания можно составить на этот день, если первым уроком стоит информатика?
Решение: 1*4*3*2*1=24. Ответ: 24 варианта.
Задача 22. В понедельник у нас по расписанию музыка, информатика, физкультура, математика и русский язык. Сколько вариантов расписания можно составить на этот день, если первым уроком стоит информатика, а последним не математика?
Решение: Когда первый урок информатика, то вариантов 24. Каждый из оставшихся предметов может быть последним одинаковое число раз. Значит, 24/4=6 раз. То есть математика не была последней 24-6=18. Ответ: 18 вариантов
Задача 23.
Проказница-Мартышка,
Осел,
Козел,
Да косолапый Мишка,
Затеяли сыграть Квартет.
Достали нот, баса, альта, две скрипки,
И сели на лужок под липки,—
Пленять своим искусством свет.
Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой!» кричит Мартышка: «погодите!
Как музыке идти? Ведь вы не так сидите.
Сколько есть вариантов рассадить музыкантов?
Решение: При условии правильного расположения инструментов, осталось рассадить зверей. За первым инструментом может сидеть любой из 4 зверей, за вторым только один из троих, так как первый уже на месте и т.д. 4*3*2*1=24 . Ответ: 24 варианта
Задача 24. Посадил дед репку, выросла репка большая пребольшая. И вот тянут они репку впятером: дед, бабка, внучка, жучка и кошка. И так встанут друг за другом, и сяк, а вытянуть не могут. А мышка из окошка поглядывает, да записывает все варианты их расстановки. Сколько всего было таких расстановок? Сколько времени потрачено на расстановки, пока догадливая кошка не сообразила позвать мышку? (На каждую расстановку потрачено 2 минуты).
Решение: На первое место может встать любой из 5, на второе — любой из 4, потом из 3..то есть 5*4*3*2*1=120 вариантов. На каждую расстановку потрачено 2 минуты, то есть 120*2=240минут= 240/60=4 часа. Ответ: 4 часа тянули репку незадачливые дачники.
infourok.ru
№ | Этап урока | Деятельность учителя | Речь учителя. Задания для учащихся. | Деятельность ученика | Формируемые УУД | |||
Познаватель- ные | Регулятивные | Коммуникатив- ные | Личност- ные | |||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
1 | Организацион-ный момент. Мотивация к учебной деятельности. | Приветствие учащихся; проверка готовности класса к уроку; организация внимания. Устанавливает тематические рамки. Организует уточнение типа урока и называние шагов деятельности. | (слайд 1). Здравствуйте, ребята. Сегодня урок мне хотелось бы начать со слов Владимира Мономаха “Что умеете хорошего, то не забывайте, а чего не умеете, тому учитесь…” А знаете ли вы, кто такой Владимир Мономах? Владимир Всеволодович Мономах (1053–1125) – полководец и государственный деятель Древней Руси, писатель, мыслитель. (слайд 2)В некоторых русских народных сказках добрый молодец оказавшись на распутье, читает на камне: «вперед поедешь- голову сложишь, направо поедешь- коня потеряешь, налево поедешь- меча лишишься». С какой проблемой сталкивается богатырь? А в нашей жизни встречаются похожие проблемы? Встречаются ли в математике задачи с похожей проблемой? Задачи, содержащие вопросы типа: “Сколькими способами?”, “Сколько всего существует вариантов, комбинаций” , называются комбинаторными. Раздел математики, занимающийся комбинаторными задачами, называется комбинаторика. Комбинаторные задачи – это задачи, требующие осуществления перебора всех возможных вариантов или подсчета их числа. Как вы думаете, какая тема сегодняшнего урока? Чем мы будем сегодня заниматься? Запишите тему урока. (Слайд 3) | Слушают учителя, Определяют тему урока и намечают шаги учебной деятельности. | Осознанное и произвольное построение речевого высказывания | Прогнозирование своей деятельности | Умение слушать и вступать в диалог | Умение выделять нравственный аспект поведения |
2 | Актуализация и фиксирование индивидуального затруднения в пробном действии, выявление причин затруднения. | Учащимся раздает цветные полоски (белая, синяя, красная). Организует фиксирование индивидуального затруднения. Объясняет значения цветов флага России. | А теперь, ребята, давайте вместе с вами попробуем решить комбинаторную задачу. Несколько стран в качестве символа своего государства решили использовать флаг в виде 3-х горизонтальных полос одинаковых по ширине и цвету: синий, красный и белый. Сколько стран могут использовать такую символику при условии, что у каждой страны свой отличный от других флаг? Попробуйте составить из полосок эти флаги. Есть ли среди них вам известный флаг? (слайд 4) А что же означают цвета на Российском флаге? Белый- мир, чистота, совершенство,синий- веру и верность, красный- силу, энергию. А знаете ли вы, какие государства имеют флаги с теми же цветами?(слайд 5) Россия, Сербия, Нидерланды | Слушают учителя. Участвуют в работе по выходу из проблемной ситуации, отвечают на поставленные вопросы, приводят примеры. | Уметь ориентироваться в своей системе знаний | Уметь проговаривать последовательность действий, высказывать свое предположение
| Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог | Учебное сотрудни-чество со сверстниками и учителем |
3 | Построение проекта выхода из затруднения | Вместе с учениками определяет цель урока- научиться более рациональным способам решения задачи. Составляют совместный план действий. Знакомит учащихся с способами решения задачи. Слайды 3-4 Комментирует, направляет работу учащихся. | Метод поребора всех вариантов без какого- либо правила- не самый рациональный. Как вы думаете, в математике есть другие способы решения подобных задач? Какую же цель мы поставим сегодня на уроке? (слайд 6)Есть несколько способов решения комбинаторных задач. Сейчас мы их рассмотрим. Существует общий подход к решению самых разных комбинаторных задач с помощью составления таблицы вариантов. (слайд 7). Во многих случаях оказывается полезным еще один прием – построение картинки- схемы перебора вариантов. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян. (слайд 8) Но способ перебора возможных вариантов далеко не всегда применим, ведь количество комбинаций может исчисляться миллионами. Здесь на помощь приходят несколько замечательных комбинаторных правил, которые позволяют подсчитать количество комбинаций без их прямого перечисления. Мы с вами рассмотрим одно из таких правил – правило умножения. (слайд 9) Есть еще один способ решения (слайд 10) комбинаторных задач – с помощью графов. Задача. Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий? Для начала необходимо выяснить с учащимися, как можно обозначить каждого человека (быстрее и удобнее изображать людей точками, которые располагаются примерно по кругу, чтобы записи были понятными и наглядными). Рукопожатия удобно обозначить черточками. Сначала составить рукопожатия одного человека (точку соединить со всеми остальными), потом перейти к другому человеку. Проведенные линии помогут увидеть, с кем он уже поздоровался, а с кем нет. Составить недостающие рукопожатия. Так действовали до тех пор, пока все не поздоровались друг с другом. Сосчитать количество черточек. | Учащиеся определяют цель урока. Слушают, отвечают на вопросы учителя и решают задачу методом составления таблицы вариантов Слушают, составляют дерево вариантов Решают задачу по правилу произведения Решают задачу с помощью графов | Структурирование знаний. | Уметь формулировать учебную задачу, определять последовательность промежуточных действий с учетом конечного результата. | Умение слушать и вступать в диалог Коллективное обсуждение проблем (при необходимости) | Проявление терпения и аккуратности при поиске решения
|
4 | Физминутка | Сменить деятельность, обеспечить эмоциональную разгрузку учащихся. | (слайд 11) Вижу, что вы немного устали, так давайте немного разомнемся.
. | Учащиеся сменили вид деятельности (отдохнули) и готовы продолжать работу | Планирование своей деятельности | Умение слушать | Осознание ценности здоровья | |
5 | Реализация построенного проекта и первичное закрепление. | Организует реализацию построенного проекта в соответствии с планом, фиксирование нового знания в речи и знаках. Учитель в процессе работы учащихся – консультант. Выслушивает ответы , задает наводящие вопросы. Хвалит детей. Отмечает степень вовлеченности учащихся в работу | А теперь посмотрим, как вы усвоили тему. (Слайды 12-21)
Работа в паре
Самостоятельная работа
| Решение с комментированием.Под руководством учителя фиксируют новое знание в речи и знаках. 3 • 3 = 9 способами, т.е. получится 9 чисел. 14,17,41,47,71,74. 4 • 3 • 2 • 1= 24 (варианта) 4 • 2 = 8 (маршрутов) КЧ, КЗ, КС, ЧЗ, ЧС, ЗС 3 • 4 • 2 = 24 (варианта костюма.) 11 • 10 = 110 (способами.) | Уметь добывать новые знания, использовать знаково- символические средства для решения задач | Планирование своей деятельности для решения поставленной задачи | Уметь работать в группе, формулировать свои мысли, слушать и понимать других. | Проявление доброжелательности в дискуссии. Проявление доверия к собеседнику |
6 | Рефлексия учебной деятельности | Подводит итоги работы. Организует фиксирование нового содержания, рефлексию, самооценку. Вносит корректировку в ответы учащихся Задает домашнее задание. | Вот и подходит к концу наш урок. (слайд 22) Ребята, вы сегодня сделали шаг в большой раздел математики- «элементы статистики и теория вероятностей».Комбинаторика- это начало этого раздела. В заданиях ГИА и ЕГЭ встречаются задачи из этого раздела. А в ВУЗах этот раздел математики изучается отдельным предметом. Вот почему важно уметь решать подобные задачи. Как вы считаете, мы сегодня достигли нашей цели, почему? Ученикам предлагается ответить на 3 блиц — вопроса: (слайд 24)
Домашнее задание:
| Отвечают на вопросы учителя, рассказывают, что узнали, что получилось. Осуществляют самооценку. Самостоятельно выполняют домашнее задание | Осознанное и произвольное построение речевого высказывания | Выделение и осознание изученного | Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог | Ориентация в межличностных отношениях |
nsportal.ru
Решение комбинаторных задач в 5 классе
Технологическая карта урока математики по теме «Решение комбинаторных задач» 5 класс
Алешихина Ирина Алексеевна, учитель математики МОУ «сош №9»,г. Сыктывкар
Разделы: Преподавание математики
________________________________________
Класс: 5.
Авторы УМК:
Тема урока: решение комбинаторных задач
Тип урока: урок открытия нового знания.
Цель урока: Организовать деятельность учащихся по планированию совместно с учителем изучения новой темы. Обеспечить применение учащимися новых знаний и способов действий в разнообразных ситуациях.
Задачи урока:
Личностные: анализировать свои действия и действия одноклассников, сотрудничать со сверстниками и учителем, осознание собственных мотивов учебной деятельности и личностного смысла учения; стремиться открывать новое знание, новые способы действия
Предметные: научиться применять новые знания к решению задач базового уровня, учиться видеть возможность применения этих знаний.
Метапредметные: умение грамотно и логично излагать свои мысли; осмысление поставленной учебной задачи; решение задачи; умение применять правила работы в парах; контроль своих действий при решении познавательной задачи.
Ресурсы урока: мультимедийный проектор, экран, презентация «решение комбинаторных задач», смайлики для рефлексии, карточки для работы в парах.
Ход урока представлен в Таблице.
Приложения к уроку: Презентация.
Используемая литература:
1.Учебник «Математика 5», авторы: Виленкин Н.Я, Жохов В.И., Чесноков А.С., Шварцбурд С.И.
2. «Элементы статистики и теории вероятности»,авторы Макарычев Ю.Н.,Миндюк Н.Г.
Формы работы на уроке: фронтальная, индивидуальная, работа в парах.
Применяемые технологии: проблемное обучение; дифференцированное обучение; традиционное обучение;
Используемые методы обучения: устный фронтальный опрос; создание проблемной ситуации; практикум; письменный опрос.
План урока:
- Организационный момент
- Проверка домашнего задания
- Постановка учебных задач
- Совместное исследование проблемы
- Конструирование нового способа действия
- Переход к этапу решения частных задач
- Рефлексия
Перед уроком группе учащихся дается задание инсценировать басню Крылова «Квартет».
Проказница-Мартышка, Осел, Козел,
Да косолапый Мишка
Затеяли сыграть Квартет.
Достали нот, баса, альта, две скрипки
И сели на лужок под липки, —
Пленять своим искусством свет.
Ударили в смычки, дерут, а толку нет.
«Стой, братцы, стой! — кричит Мартышка. — Погодите!
Как музыке идти? Ведь вы не так сидите.
Ты с басом, Мишенька, садись против альта,
Я, прима, сяду против вторы;
Тогда пойдет уж музыка не та:
У нас запляшут лес и горы!»
Расселись, начали Квартет;
Он все-таки на лад нейдет.
«Постойте ж, я сыскал секрет? —
Кричит Осел, — мы, верно, уж поладим,
Коль рядом сядем».
Послушались Осла: уселись чинно в ряд;
А все-таки Квартет нейдет на лад.
Вот пуще прежнего пошли у них разборы
И споры, кому и как сидеть.
Случилось Соловью на шум их прилететь.
Тут с просьбой все к нему, чтоб их решить сомненье.
«Пожалуй, — говорят, — возьми на час терпенье,
Чтобы Квартет в порядок наш привесть:
И ноты есть у нас, и инструменты есть,
Скажи лишь, как нам сесть!» —
«Чтоб музыкантом быть, так надобно уменье
И уши ваших понежней, —
Им отвечает Соловей, —
А вы, друзья, как ни садитесь;
Всё в музыканты не годитесь».
Всем учащимся задается д/з:
1. Если использовать для символики флага 3 горизонтальные полосы и цвета синий, красный и белый, то сколько флагов может получиться?
2. Сколько четырехзначных чисел можно составить из цифр 2,0,1,5, если цифры не повторяются?
Ход урока:
Деятельность учителя
Деятельность учащихся
УУД
1. Учитель проверяет готовность класса к уроку. Отмечает отсутствующих.
Выполняют рекомендации учителя
Р
2. Опрос желающих учащихся по результатам д/з, один из них комментирует ход решения, оформляет задачу 2 на доске.
Слайд1,2
Работа в парах по проверке домашнего задания.
Р;
П
3. Как вы справились с заданием? С помощью чего вы решили задачи?
С какими типами задач вы уже знакомы?
Эти задачи вы уже встречали? Как вы думаете, как их можно назвать?
В тетрадях запишем тему урока:
«Решение комбинаторных задач»
Слайд 3
Отвечают на вопросы учителя:
Решение задач происходит с помощью перебора.
Л
Р
К
4. Организует погружение в проблему: попробуйте решить задачу способом, подобным тому, что вы применили в решении дз.
Слайд 4
Рациональным способом решения подобных задач является правило умножения. Объясняет правило умножения.
Решение задач слайда 5,6
Решение задач слайда 7,8
Пытаются решить задачу известным способом, понимают, что нужен более рациональный способ решения.
Решают задачу новым способом.
Решают задачу, 1 ученик оформляет решение у доски.
Решают задачи в парах, проверяют ответы.
П
К
Р
5. Оказывается в жизни множество ситуаций, где применяются комбинаторные задачи.
Слайд 9
Учащиеся инсценируют басню Крылова «Квартет». Отвечают на поставленный вопрос.
П
Р
Вводит понятие «Факториал», приводит примеры решения заданий.
Слайды 10,11,12,13
Учащиеся записывают, проговаривают.
П
К
Р
Задача с шахматами (слайд 14). Задает наводящие вопросы, показывает способ решения с помощью графов.
Записывают решение.
П
К
Р
6.Закрепление материала.
Задачи слайда 15,16,17
Решают в парах, выбирают для каждой задачи один из алгоритмов решения, проверяют.
Л
П
К
7.Рефлексия.
Что нового мы узнали на уроке? С какими понятиями познакомились? Пригодится ли это в повседневной жизни? Было интересно?
Слайд 18
Вспоминают, отвечают на вопросы.
Р
Объясняет домашнее задание.
Слайд 19
Записывают домашнее задание
Р
С помощью смайликов оцените свою работу на уроке.
Красный- замечательно
Желтый- хорошо
Синий- удовлетворительно.
Слайд 20
Оценивают свою деятельность на уроке
Л
Применяемые обозначения: УУД – универсальные учебные действия;
Л-личностные
Р- регулятивные
К- коммутативные
П- познавательные
Просмотр содержимого документа
«решение комбинаторных задач в 5 классе »


Флаг России Белый, синий и красный цвета с древних времен на Руси означали: белый цвет — благородство и откровенность; синий цвет — верность, честность, безупречность и целомудрие; красный цвет — мужество, смелость, великодушие и любовь.

Решение комбинаторных задач
Учитель математики МОУ «сош№9» Алешихина И.А.

Сколько существует шестизначных телефонных номеров, начинающихся с цифр 23?
1млн
20000
23000
500
1000
200
10000

Вы забыли код на входной двери. Сколько времени вы потратите на разгадывание кода?
Если код четырехзначный
Если цифры набираются последовательно
10*10*10*10=10000 вариантов, если на каждый вариант потратить 1 минуту, то 10000 минут займет примерно 167 часов

Вы забыли код на входной двери. Сколько времени вы потратите на разгадывание кода?
Если код четырехзначный
Если цифры набираются одновременно
10*9*8*7*=5040 вариантов, если тратить на каждый 1 минуту, то вы затратите 84 часа.

Сколько существует четных трехзначных чисел? Сколько существует нечетных трехзначных чисел?
10*10*5=500

Сколько существует трехзначных чисел, которые делятся на 5?
10*10*2=200

Сколько существует способов рассадить зверей ?
5*4*3*2*1=120 вариантов


ЧТОБЫ ВЫЧИСЛИТЬ 9!=1*2*3*4*5*6*7*8*9

10 человек обедают в ресторане. Официант предложил им каждый день приходить обедать и рассаживаться по новому. Когда же все перестановки закончатся, он обещал подавать обеды за счет заведения. Предложение понравилось. Когда настанет этот долгожданный день?

В классе 25 человек. Сколькими способами можно рассадить их по партам?
25!=25*24*23*22*21*20*19*18*17*16*15*14*13*12*11*10*9*8*7*6*5*4*3*2*1=
15 551 210 043 330 985 984 000 000
способов

Машенька решила провести шашечный турнир с тремя друзьями. Сколько партий состоится?

На завтрак медведь может выпить морс, чай или молоко и съесть плюшку, бутерброд, пряник или кекс. Сколько вариантов завтрака у медведя?
3*4=12 вариантов

Маша хочет обменяться фотографиями с 4 подружками. Сколько фотографий будет всего?
10*2=20 фотографий

В семье три человека, на кухне три стула. Сколько дней члены семьи могут рассаживаться на стульях без повторений?
3!=3*2*1=6 дней

Давай-ка, повторим

Домашнее задание:
Придумать такие задачи, для решения которых понадобятся знания нашего урока.

замечательно
хорошо
удовлетворительно

Веселые стишки
2 15 42
42 15
37 08 5
20 20 20!
7 14 106
2 06 13
37 08 5
20 20 20!
kopilkaurokov.ru
Методическая разработка по алгебре (5 класс) по теме: Знакомьтесь, комбинаторика!
«Знакомьтесь, комбинаторика!»
(5 класс)
В последние годы все больше внимания уделяется проблемам развивающего обучения. Небывалый рост объема информации требует от современного человека таких качеств, как инициативность, изобретательность, предприимчивость, способность быстро и безошибочно принимать решения. А это невозможно без умения работать творчески, самостоятельно. Если в недавнем прошлом основной задачей, стоящей перед учителем, была передача ученикам определенной суммы знаний, то в настоящее время на первый план выдвигается задача развития учащихся в процессе обучения. Обучение математике должно быть ориентировано не столько на собственно математическое образование, в узком смысле этого слова, сколько на образование с помощью математики.
Развитие математического мышления и творческих способностей осуществляется в ходе размышлений учащихся над задачами. Самостоятельная деятельность учащихся по решению задач занимает главное место в обучении математике. Умение решать задачи – критерий успешности в учебе. Очень важно показать, как обычную жизненную ситуацию можно описать математической моделью.
Материалы разработки могут быть использованы как в рамках урока (5 – 7 класс), так и на занятиях математического кружка или факультатива.
Целью разработки является повышение математической культуры учащихся, пробуждение и развитие устойчивого интереса к математике, расширение и углубление знаний.
Основные задачи, решаемые внедрением разработки – это знакомство на популярном уровне с комбинаторикой – разделом дискретной математики, который приобрел сегодня серьезное значение в связи с развитием теории вероятностей, математической логики, информационных технологий. Учащиеся должны получить представление о том, что такое комбинаторная задача, познакомиться с методами и правилами ее решения.
На этом богатом материале повышается уровень математического и логического мышления учащихся, развиваются навыки исследовательской деятельности.
Пояснительная записка
Занятия по программе Е.В.Смыкаловой «Развивающее обучение на уроках математики» проводятся мною систематически в рамках учебного времени. Такие уроки я провожу в начале и в конце четверти, чтобы активизировать деятельность учащихся, пробудить и развить интерес к математике. Кроме этого, одну – две нестандартные задачи стараюсь рассмотреть на каждом уроке, наряду с программным материалом, развивая тем самым в учениках «вкус» к познанию. При подготовке к подобным занятиям использую материалы пособия Е.В.Смыкаловой «Математика: дополнительные главы – 5 класс», а также задания из УМК Л.Г.Петерсон и Н.Я.Виленкина.
План урока
- Организационный момент
- Актуализация знаний учащихся
- Исторический экскурс (сообщение ученика)
- Теоретический материал
- Решение задач (с элементами самопроверки)
- Постановка домашнего задания, повторение теории
- Самостоятельная работа (взаимопроверка)
- Подведение итогов урока
(раздаточный материал) ПРИЛОЖЕНИЕ 1
К а р т а у р о к а
«Считай несчастным тот день или тот час, в который ты не усвоил ничего нового и ничего не прибавил к своему образованию»,
«Учиться нелегко, но интересно». Ян Амос Коменский (1592-1670),
чешский педагог, писатель
тема урока __________________________________________________________________
Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения заданных элементов по заданным правилам.
Правило суммы
(выбор одного элемента)
А – m способов
В – n способов
А В – (m+n) способов
Например: 5 яблок, 4 груши.
Выбор яблока или груши:
5 + 4 = 9 способов
Правило произведения
(выбор пары,
нескольких элементов)
А – m способов
В – n способов
А В – (m·n) способов
Например: 2 конверта, 3 открытки.
Выбор конверта с открыткой:
2 · 3 = 6 способов
(обратная сторона) ПРИЛОЖЕНИЕ 1
Решение задач
№1. П Л А Т О К
согласных букв ____________
гласных букв ______________
выбор пары ________________ способов
№ 2. 3 шляпы, 4 плаща, 2 пары сапог
выбор костюма ____________ способов
№ 3. 11 человек
капитан ___________ вариантов
заместитель ________ вариантов
выбор пары _____________ вариантов
№ 4. 1, 4, 7
__________________
__________________________________
№ 5. 1, 2, 3, 4, 5
__________________
__________________________________
№ 6. 0, 1, 2, 3
а)
__________________
__________________________________
б)
__________________
___________________________________
№ 7. 1, 3, 5, 7, 9; меньше 400
__________________
__________________________________
№ 8. ________________________________________________________________________________________________________________________________________________________
______________________________________
№ 9. ____________________________________________________________________________________________________________________________________________________________________
_________________________________________
_________________________________________
№ 10.
_____________________________________________________________________________________________________________________________________________________________________________________________________________
№ 11.
_____________________________________________________________________________________________________________________________________________________________________________________________________________
_________________________________________
(раздаточный материал)
Задачи к уроку «Знакомьтесь, комбинаторика!»
- Сколькими способами можно выбрать гласную и согласную буквы в слове «платок»?
- У одного знаменитого мушкетера в гардеробе имеются 3 элегантных шляпы, 4 чудных плаща и 2 пары отличных сапог. Сколько вариантов костюма ему можно составить?
- В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами можно это сделать?
- Сколько различных двузначных чисел можно составить, используя цифры 1, 4, 7, если допустить повторение цифр?
- Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется?
- Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3, если цифры: а) могут повторяться; б) не могут повторяться?
- Сколько различных трехзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая цифра может быть использована только один раз?
- Шифр для сейфа состоит из пяти различных цифр. Сколько различных вариантов составления шифра?
——————————————-
ПРИЛОЖЕНИЕ 2
- Сколькими способами можно разместить 6 человек за столом, на котором поставлено 6 приборов?
- В пятом классе изучаются 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 уроков и все уроки – разные?
- Сколько вариантов семизначных телефонных номеров можно составить, если исключить из них номера, начинающиеся с 0 и 9?
- Сколько различных чисел, меньших миллиона, можно записать с помощью цифр 8 и 9?
«Переменка»
Найдите закономерность построения
последовательности 111, 213, 141,
516, 171, 819, 202, 122…
Домашнее задание
- В 5 «б» классе 26 учеников. Сколькими способами можно выбрать старосту класса и его заместителя? старосту, заместителя и ответственного за дежурство?
- В магазине купили 9 красных, 10 зеленых и 7 желтых воздушных шаров. Сколькими способами можно взять один любой шар? зеленый и желтый шар? красный или желтый?
3 шара разного цвета?
2 шара разного цвета? (рассмотреть
все возможные варианты)
Актуализация знаний.
Повторение пройденного (решение задач методом перебора).
«Счет и внимание – основы порядка в голове»
(И.Г.Песталоцци)
- Сколько различных двузначных чисел можно составить из цифр 5 и 0
(без повтора)? 1 число (50)
- Сколько различных двузначных чисел можно составить из цифр 3 и 5
(повтор допускается)? 4 числа (33, 55, 53, 35)
- Сколько различных трехзначных чисел можно составить из цифр 3 и 5
(повтор допускается)? 8 чисел (333, 555, 355, 533, 335, 553, 353, 535)
- Сколько различных трехзначных чисел можно составить из цифр 3, 8, 7
(без повтора)? 6 чисел (387, 378, 837, 873, 738, 783)
Используя количество полученных в каждом задании чисел, составить название темы сегодняшнего урока и вписать ее в карту урока: «Знакомьтесь, ___________________ !»
1 число – «комби»
2 числа – «вичи»
3 числа – «рум»
4 числа – «нато»
5 чисел – «тема»
6 чисел – «ка»
7 чисел – «аза»
8 чисел – «ри»
9 чисел – «немо»
10 чисел – «хор»
Ответ: «комбинаторика»
В математике существует немало задач, в которых требуется из имеющихся элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, образованных по определенному правилу. Решая подобные задачи, приходится перебирать различные варианты, переставлять заданные элементы, комбинировать их. Такие задачи называются комбинаторными, а раздел математики, занимающийся решением этих задач, называется комбинаторикой.
Исторический экскурс (сообщение учащегося)
С комбинаторными задачами люди имели дело еще в глубокой древности, когда, например, выбирали наилучшее расположение воинов во время охоты, придумывали узоры на одежде или посуде. В дальнейшем появились игры, требовавшие умения планировать, рассчитывать свои действия, продумывать возможные комбинации. Приспособления для таких игр археологи находили в древних захоронениях, например, в пирамиде египетского фараона Тутанхамона (II век до н.э.). А позже появились нарды, шашки, шахматы.
Долгие века комбинаторика развивалась внутри арифметики, алгебры и геометрии. Так, древнегреческие ученые большое внимание уделяли и комбинаторике чисел – составление и изучение магических квадратов, и геометрической комбинаторике – разрезанию фигур.
Как ветвь математики комбинаторика возникла только в XVII веке. Гражданин Франции Шевалье Де Марэ любил изобретать различные игры, играя в которые, получал очень интересные результаты. Например, однажды он придумал такую игру: бросает 4 кости, выигрывает тот, у кого на одной есть шестерка. Но с ним очень быстро перестали играть, так как он слишком часто выигрывал. В другой раз Шевалье придумал такую игру: бросает две кости несколько раз, выигрывает, если хотя бы раз выпало две шестерки. Однако вскоре он сам бросил играть, так как стал часто проигрывать. Такой исход дела очень удивил Шевалье де Марэ, и он обратился к двум крупнейшим математикам Франции того времени – Блезу Паскалю и Пьеру Ферма с вопросом, как можно объяснить эти удачи и проигрыши в игре, а также, как правильно делать ставки в таких и в аналогичных играх.
Решая эту задачу, Блез Паскаль и Пьер Ферма разработали начало двух ветвей математики: комбинаторики и теории вероятности. Впоследствии этими науками занимались многие великие математики тех времен: Готфрид Вильгельм Лейбниц, Якоб Бернулли, Леонард Эйлер и др.
Использование комбинаторики в настоящее время очень разнообразно. Одно из них – кодирование и расшифровка текстов (шифр появился еще в средние века). В биологии комбинаторика служит для подсчета клеточных структур ДНК и РНК, в физике – для описания свойств кристаллов. Также комбинаторика широко используется и в химии.
Теоретический материал.
Комбинаторика – это раздел математики, посвященный решению задач выбора и расположения заданных элементов по заданным правилам (см. карту урока).
Обычный вопрос в комбинаторных задачах – это «Сколькими способами…?» или
«Сколько вариантов…?»
Комбинаторные задачи можно решать несколькими способами: методом перебора, перестановок (с ним мы уже знакомы), использование определенных правил комбинаторики (с ними мы познакомимся сегодня на уроке) и с помощью построения так называемого «дерева вариантов» (о нем мы поговорим позже).
Итак, начнем знакомиться с правилами комбинаторики – это правила суммы и произведения.
Правило суммы:
если некоторый элемент А можно выбрать m способами, а элемент В можно выбрать n способами, то выбор «либо А, либо В» можно сделать (m + n) способами. Например, если вам предлагают 5 яблок и 4 груши, то выбрать один плод можно 5 + 4 = 9 способами (см. карту урока).
Устно решите следующие задачи:
а) В вазе 6 яблок, 5 груш и 4 сливы. Сколько вариантов выбора одного плода?
(15 вариантов)
б) В магазине продаются 3 алые, 2 белые и 4 желтые розы. Сколькими способами можно купить один цветок? (9 способов)
Еще раз обращаем внимание на то, что мы выбираем лишь один из предложенных элементов.
Правило произведения:
если некоторый элемент А можно выбрать m способами, а элемент В можно выбрать n способами, то выбор «А и В» можно сделать (m · n) способами. Например, если вам предлагают 2 конверта и 3 открытки, то составить пару (конверт и открытка) можно 3 · 2 = 6 способами (см. карту урока).
Устно решите следующие задачи:
а) Сколько танцевальных пар можно составить из 8 юношей и 6 девушек? (48 пар)
б) В столовой имеются в продаже 4 первых блюда и 7 вторых. Сколько различных вариантов обеда из двух блюд можно заказать? (28 вариантов)
Обращаем внимание на то, что мы выбираем пару элементов из предложенных множеств.
Решение задач
Учащиеся работают на бланках карты урока в соответствующем разделе, тексты задач на отдельных листах у каждого ученика. Список задач можно изменять, добавляя или убирая некоторые вопросы в зависимости от уровня подготовки класса. Можно разбить задачи по уровню сложности, некоторые оставить для самостоятельного решения. В некоторых задачах полезно подчеркнуть, что они уже ранее решались методом перебора, а сегодня – второй способ их решения. Осуществить на этом этапе дифференцированный подход. Ввести элементы самостоятельной работы с последующей самопроверкой.
- Сколькими способами можно выбрать гласную и согласную буквы в слове «платок»? (Согласных букв в слове – 4, гласных букв – 2, значит, по правилу умножения, вариантов выбора пары — 4 · 2 = 8.)
- У одного довольно знаменитого мушкетера в гардеробе имеются 3 элегантных шляпы,
4 чудных плаща и 2 пары отличных сапог. Сколько вариантов костюма ему можно со-
ставить? (Выбираем по одному элементу из трех множеств, то есть, составляем
«тройку», значит, по правилу умножения получаем 3 · 4 · 2 = 24 варианта костюма.)
- В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами можно это сделать? (Всего 11 человек, значит, капитана можно выбрать 11-ю способами, осталось 10 футболистов, из которых можно выбрать заместителя капитана. Итак, пару, капитана и его заместителя, можно выбрать 11 · 10 = 110 способами.)
- Сколько различных двузначных чисел можно составить, используя цифры 1, 4, 7, если допустить повторение цифр? (Должно получиться двузначное число – всего две позиции. На первую позицию можно поставить любую из предложенных цифр – 3 варианта выбора, на вторую позицию, с учетом возможности повтора цифры, тоже 3 варианта выбора. Значит, пару цифр мы составляем 3 · 3 = 9 способами, т.е. получится 9 чисел.
Запись решения:
3 ∙ 3 = 9 чисел.
Такая запись решения используется во всех подобных задачах при работе на бланках карты урока.)
- Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра не повторяется? (Трехзначное число: первая позиция – 5 вариантов цифр, вторая позиция, с учетом исключения повторов цифр, — 4 варианта, третья позиция – 3 варианта. Получаем 5 · 4 · 3 = 60 чисел.)
- Сколько различных двузначных чисел можно составить из цифр 0, 1, 2, 3, если цифры:
а) могут повторяться; б) не могут повторяться? ( а) Двузначное число, как и любое мно-
гозначное, не может начинаться с 0, поэтому на первую позицию можно поставить
лишь 3 из имеющихся 4-х цифр, 3 варианта выбора, на вторую позицию, с учетом по-
втора, можно поставить любую из цифр – 4 варианта выбора. Поэтому получается
3 · 4 = 12 чисел; б) Первая позиция – 3 варианта, вторая позиция – 3 варианта, т.к.
повтор исключается. Получаем 3 · 3 = 9 чисел.)
- Сколько различных трехзначных чисел, меньших 400, можно составить из цифр 1, 3, 5, 7, 9, если любая цифра может быть использована только один раз? (Трехзначное число < 400, значит, на первую позицию можно поставить лишь 1 или 3 – 2 варианта выбора, на вторую, исключая повтор, – 4 варианта цифр из 5-ти, на третью позицию – 3 варианта. Получается 2 · 4 · 3 = 24 числа.)
- Шифр для сейфа состоит из пяти различных цифр. Сколько различных вариантов составления шифра? (5 · 4 · 3 · 2 · 1 = 120 вариантов.)
- Сколькими способами можно разместить 6 человек за столом, на котором поставлено
6 приборов? (6 · 5 · 4 · 3 · 2 · 1 = 720 способов.)
- В пятом классе изучаются 8 предметов. Сколько различных вариантов расписания можно составить на понедельник, если в этот день должно быть 5 уроков и все уроки – разные? (8 · 7 · 6 · 5 · 4 = 6720 вариантов.)
- Сколько вариантов семизначных телефонных номеров можно составить, если исключить из них номера, начинающиеся с 0 и 9? (Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – всего 10 цифр, исключая по условию 0 и 9 в начале номера, с учетом возможности повтора, получаем 8 · 10 · 10 · 10 · 10 · 10 · 10 = 8 000 000 номеров.)
- Сколько различных чисел, меньших миллиона, можно записать с помощью цифр
8 и 9? (Однозначных чисел – 2, двузначных чисел — 2 · 2 = 4, трехзначных чисел –
2 · 2 · 2 = 8, четырехзначных чисел – 16, пятизначных чисел – 32, шестизначных
чисел – 64. А всего — 2 + 4 + 8 + 16 + 32 + 64 = 126 чисел.)
«Переменка»
Найдите закономерность построения последовательности 111, 213, 141, 516, 171, 819, 202, 122… (В данной последовательности надо иначе расставить запятые, и получим 11, 12, 13, 14, 15…)
Постановка домашнего задания ( см. приложение 2), повторение теоретического материала (правила сложения и умножения, условия выбора элементов).
Самостоятельная работа (с последующей взаимопроверкой в парах)
- Выбор одного любого элемента из предложенных множеств выполняется по правилу ______________________. Выбор пары и более элементов из множеств происходит по правилу ______________________.
- В вазе стоят 5 красных, 3 белых и 3 желтых тюльпана. Один цветок из вазы можно выбрать _______ способами, три цветка разного цвета ________ способами.
- Сколько различных трехзначных чисел можно составить, используя цифры 3 и 5, если их повтор допускается? ____________________________________________________________
- В четверг в первом классе должно быть 4 урока: письмо, чтение, математика, физкультура. Сколько различных вариантов расписания на этот день можно предложить?
_________________________________________________________________________________
Ответы: сложения, умножения, 11, 45, 2 · 2 · 2 =8, 4 · 3 · 2 · 1 = 24.
Взаимопроверка, выставление оценок, обсуждение результатов.
Подведение итогов урока
На этом этапе урока, помимо традиционной беседы о том, какие задачи ставились, насколько успешно с ними справились, следует вернуться к эпиграфу урока (см. бланк карты урока) и поразмышлять о словах Я.А.Коменского.
Кроме того, ученикам предлагается ответить на 3 блиц — вопроса:
- На сегодняшнем уроке мне было … (легко, обычно, трудно)
- Новый материал я … (усвоил и могу применить, усвоил и затрудняюсь применить, не усвоил)
- Моя самооценка за урок …
Ответы на приведенные вопросы можно не подписывать, т.к. их основная функция помочь учителю проанализировать урок и его результаты.
П о с л е с л о в и е
На следующем уроке предполагается отработка пройденного материала на этапе устной работы, введения понятия «дерево возможных вариантов» как еще одного способа решения комбинаторных задач, систематизация изученных методов решения задач, практикум по решению задач различными способами, решение задач повышенного уровня, контроль знаний.
или
и
nsportal.ru
Комбинаторика 5 класс — математика, презентации

Комбинаторика
5 класс

Contents
- Click to add Text
- Click to add Text
- Click to add Text
- Click to add Text
- Click to add Text
- Click to add Text
- Click to add Text
Content
Content
Вперед поедешь – голову сложишь, направо поедешь – коня потеряешь, налево поедешь – меча лишишься.
«Витязь на распутье» 1882 г. Васнецов Виктор Михайлович

Комбинаторика — ветвь математики, изучающая комбинации и перестановки предметов.
Термин « комбинаторика » происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».
Комбинаторика — раздел математики, посвящённый решению задач выбора и расположения элементов в соответствии с данными условиями.

В доисторическую эпоху люди сталкивались с комбинаторными задачами.
Выбирать и расположить предметы в определенном порядке, отыскивать среди разных расположений наилучшее – вот задачи, решаемые в быту, на охоте или в сражениях.
Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э.

В Древней Греции
подсчитывали число различных комбинаций длинных и коротких слогов в стихотворных размерах, занимались теорией фигурных чисел, изучали фигуры, которые можно составить из частей особым образом, разрезанного квадрата, и т.д.

Со временем появились различные игры ( нарды, карты, шашки, шахматы и т. д.).
В каждой из этих игр приходилось рассматривать различные сочетания фигур, и выигрывал тот, кто их лучше изучал, знал выигрышные комбинации и умел избегать проигрышных.

Задача о семи старухах
Старухи идут в Рим, каждая имеет 7 мулов, каждый мул несет 7 мешков, в каждом мешке лежит 7 хлебов, у каждого хлеба лежит 7 ножей, каждый нож нарежет 7 кусков хлеба. Чему равно общее число всего перечисленного?
В историческом отношении эта задача интересна тем, что она тождественна с задачей о кошках, которая встречалась в папирусе Ринда (Египет), то есть через три тысячи лет после египетских школьников задачу предлагалось решить итальянским школьникам.

При тайных переписках дипломаты стали применять шифры, которые были основаны на различных перестановках букв, чисел, заменах букв с использованием ключевых слов и т. д.

Готфрид Вильгельм Лейбниц (1.07.1646 — 14.11.1716)
Комбинаторику, как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г. Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666г. Он также впервые ввел термин «Комбинаторика».

Задача Эйлера о мостах
Река образует острова, и через два речных рукава перекинуто 7 мостов. Спрашивается, можно ли пройти все 7 мостов так, чтобы каждый был пройден по одному лишь разу.
Эйлер показал, что это невозможно, и рассмотрел более общую задачу, в которой речь идет о любом числе местностей, как-либо разделенных рукавами рек и соединенных мостами.

Леонард Эйлер
(1707-1783)

Комбинаторная задача – задача, в которой идет речь о тех или иных комбинациях предметов

Способы решения комбинаторных задач
Таблица вариантов
Дерево вариантов
Правило умножения

1. Таблица вариантов
КБС
БСК
КСБ
СБК
БКС
СКБ

2. Дерево вариантов

3. Правило умножения
1 полоса — 3 способа
2 полоса — 2 способа
3 полоса — 1 способ
3 ∙ 2 ∙ 1 = 6
Ответ: 6 способов

Нидерланды
Сербия
Россия

Решение задач

Задача 1
Сколько можно составить двузначных чисел, в записи которых используются только цифры:
а) 1 и 2;
б) 3 и 0?

Задача 2
Какие двузначные числа можно составить из цифр 1, 2 и 3, если:
а) цифры в записи числа не повторяются;
б) цифры в записи числа могут повторяться?

Задача 3
Какие трехзначные числа можно составить из цифр 4, 5 и 0, если:
а) цифры в записи числа не повторяются;
б) цифры в записи числа могут повторяться?

Задание 4
Виталик, Дима и Сергей решили вместе сфотографироваться. Сколькими различными способами они могут сесть рядом?

Способ решения
Плюсы
Дерево вариантов
Минусы
Наглядность, возможность увидеть все варианты
Табличный
Очень громоздкий и длительный, если много различных вариантов
Наглядность, компактность, возможность увидеть все варианты
Правило умножения
Невозможность решать задачи, в которых более двух составляющих одного события
Компактность,
быстрота решения
«Не видно» самих вариантов, можно только просчитать их количество.

Картинки:
http://server-life.ru/845-tf2-roll-the-dice-brosit-kosti.html
http://vivatcasino.com/istoria_igry_v_kosti.aspx
http://only-most.ru/?p=2098
http://photo.sibnet.ru/alb48804/ft1162009/
necessity
kopilkaurokov.ru