Урок по математике на тему: «Комбинаторные задачи», 6 класс
Тема урока «Комбинаторные задачи», 6 класс
Цели урока:
— обобщить и систематизировать знания о комбинаторных задачах;
— повторить способы решения комбинаторных задач;
— совершенствовать навыки решения данных задач;
— развивать умение дискуссионной и групповой работы;
— развитие коммуникативных компетенций;
— формирование умений мыслить системно, находить творческий подход в своей работе;
— умение создать и защитить минипроект по теме «Комбинаторные задачи».
Выставка творческих работ по теме «Комбинаторные задачи»
Презентация. Приложение №1.
Класс разбит на 5 групп.
Ход занятия
Организационный момент.
Учитель. В вашем, 6 а классе, много ребят творческих, участвующих во всевозможных олимпиадах, конкурсах, проектах. Недавно были подведены результаты заочной российской олимпиады «Авангард», где участвовали ребята. Сегодня они получают дипломы призёров данной олимпиады. ( 5 человек).
Мы закончили изучать интересную тему, учились решать задачи по данной теме, выполняли творческое задание. Как эта тема называлась и чему мы научились, изучая данную тему?
Актуализация знаний.
Кто вспомнит, что это за раздел математики, комбинаторные задачи?
(ответы учащихся)
Сообщение ученицы. Слайд №3.
Комбинаторика – раздел математики, в котором изучают вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям можно составить из данных объёктов. Выбором объектов и расположением их в том или ином порядке приходиться заниматься чуть ли не во всех областях человеческой деятельности. Например, конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему сельхозкультуры на нескольких полях, химику, изучающему строение молекул.
С аналогичными задачами, получившими название комбинаторных, люди столкнулись в глубокой древности. В Китае увлекались составлением магических квадратов, в Древней Греции подсчитывали число различных комбинаций длинных и коротких слогов стихотворных размеров. Комбинаторные задачи возникли в связи с такими играми, как шашки, шахматы, карты, кости и др.Чтобы их решить, нужно было уметь подсчитывать число различных комбинаций, подчинённых тем или иным условиям.Кто напомнит, какими способами мы научились решать комбинаторные задачи? Слайд №4.
Перебор возможных вариантов.
Таблицей.
Дерево возможных вариантов.
Правило умножения.
Правило треугольника.
С помощью графов.
Презентация способов решения задач. (Выступает с презентацией ученица, слайды с №5 по №10). Учащиеся работают в группах.
А сейчас мы вспомним отдельно каждый способ. Я вам буду предлагать задачу, вы в группах решите ёё и скажете правильный ответ. Затем проверим решение с помощью презентации.
1.Перебор возможных вариантов.
Сколько существует двухзначных чисел, составленных из цифр: 0, 5, 8 ?
Решение. 58, 50, 80, 85.
Ответ: 4 числа.
2. Таблицей.
Алла, Бэла, Валентина и Галина во время майского праздника подарили друг другу по одному цветку. Причём каждая девочка подарила каждой по одному цветку. Сколько всего цветков было подарено?
Решение.
Ответ: 12 цветков.
А
Б
В
Г
А
——
+
+
+
Б
+
___
+
+
В
+
+
—-
+
Г
+
+
+
—-
3.Дерево возможных вариантов.
Никита, Борис, Виктор, и Григорий играли в шахматы. Каждый сыграл по 1 партии. Сколько сыграно партий?
Решение.
 Никита
Никита
Б
 орис Виктор Григорий
орис Виктор Григорий
Виктор Григорий Григорий
Ответ. 6 партий.
Правило умножения.
В меню в столовой предложены на выбор 3 первых блюда, 5 вторых и 4 третьих блюд. Сколько различных вариантов обедов, состоящих из 1 первого, 1 второго и 1 третьего блюда, можно составить из предложенного меню?
Решение. 3*5*4=60
Ответ: 60 блюд.
5.Правило треугольника.
Встретились 5 приятелей и обменялись рукопожатиями. Сколько всего сделано рукопожатий?
Решение.
1 2 3 4 5
1 — + + + +
2 — — + + +
3 — — — + +
4 — — — — +
— — — — — Ответ: 10 рукопожатий.
6.С помощью графа.
По окончанию деловой встречи 4 специалиста обменялись визитными карточками (каждый вручил свою карточку каждому). Сколько визитных карточек было роздано?
Решение.
Ответ. 12 визиток



4.Работа в группах. Слайд №11.
Сейчас я предлагаю каждой группе решить задачу одну и ту же, но разными способами. Каждая группа оформляет своё решение на листе фломастерами.
Задача. Андрей, Борис, Виктор и Григорий после возвращения из спортивного лагеря подарили друг другу на память свои фотографии. Причём каждый мальчик подарил каждому по 1 фотографии. Сколько всего фотографий было подарено?
Решение задач вывешивается на доске. Выполняется анализ решения задач каждой группы.
Защита минипроектов. Слайд № 12.
Каждый из вас дома выполнил творческую работу. Кто–то сам составил и решил задачи несколькими способами, другие нашли задачи в интернете и тоже их представили. Послушаем наиболее удачные и интересные работы.
(Выступление 5 учащихся)
Итог урока. Домашнее задание.
Слайд № 13. Знаешь ли ты?
Как прочитать и решить такой пример?
10!
6!
8!
Поищите в справочной литературе, в интернете ответ на этот вопрос.
Учитель. Рефлексия. Итак, мы закончили изучать тему из раздела Комбинаторики. Интересно ли было решать комбинаторные задачи? Понравился ли урок? (Учащиеся показывают рисунки рожицы с улыбкой или грустные).
Нам ещё предстоит познакомиться с другим разделом математики: теорией вероятности. Это тоже интересная тема. Но о ней мы поговорим позже.
«Решение комбинаторных задач методом перебора» (математика, 6 класс)
Решение задачи методом полного перебора всех возможных вариантов.
1) Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11; 14; 17; (начали с 1)
41; 44; 47; (начали с 4)
71; 74; 77; (начали с 7)
Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.
Ответ: 9 чисел.
Решение задач методом полного перебора на доске и в тетрадях.
Сколько трёхзначных чисел можно составить, используя цифры 3 и 5?
В школе проводятся соревнования по хоккею. В качестве призов решили использовать мячи, ракетки, клюшки и шайбы. Сколько различных призов можно составить из этих предметов, если каждому победителю решено давать по 2 разных предмета?
В четверг в первом классе должно быть 3 урока: русский язык, математика и физкультура. Сколько различных вариантов расписания можно составить на этот день?
Решение задач с помощью дерева возможных вариантов на доске и в тетрадях. Существует общий подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян. 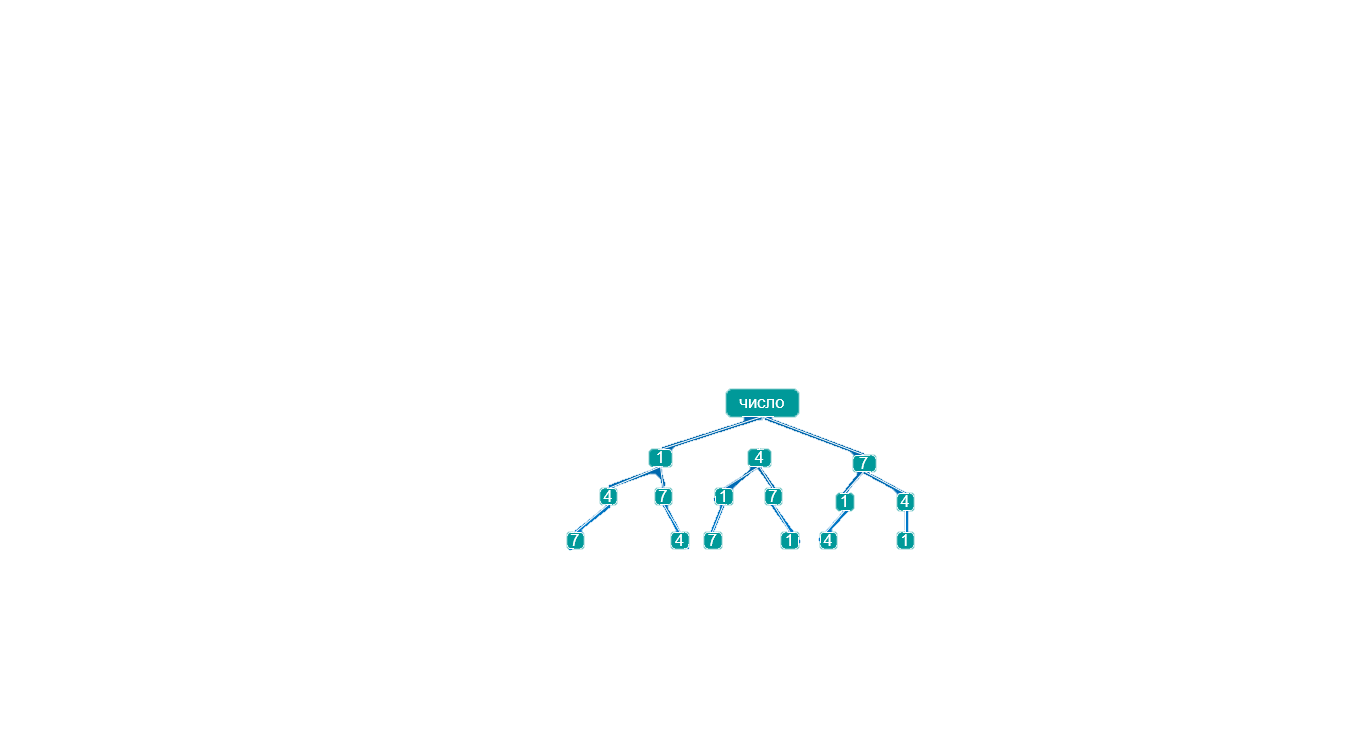
Задача. Рассмотрим задачу о составлении трехзначных чисел из цифр 1; 4; 7. Для её решения построим схему-дерево возможных вариантов, которое наглядно показывает решение задачи.
Решение задач с использованием дерева возможных вариантов на доске и в тетрадях.
В костюмерной танцевального кружка имеются жёлтые и зелёные кофты, а также синие и чёрные юбки. Сколько можно из них составить различных костюмов.
Сколькими способами три друга могут разделить между собой 2 банана, 2 груши и 2 персика так, чтобы каждый получил по два каких-нибудь плода?
Служитель зоопарка должен дать зайцу два различных овоща. Запишите все такие пары, если имеются морковь, свекла и капуста.
Из 4 ребят надо выделить двоих для дежурства по классу. Сколькими способами это можно сделать?
Наташа хочет сделать аппликацию на платье из двух цветных вертикальных полос. Из скольких вариантов придётся выбирать Наташе, если у неё есть материя жёлтого, красного и синего цвета?
Правило умножения в комбинаторных задачах. Для комбинаторной задачи с умножением можно построить дерево вариантов, но такое дерево строить станет намного сложнее, именно поэтому используется метод умножения, чтобы запись была короче.
Рассмотрим этот метод на примере одной задачи: На обед в школьной столовой предлагается 2 супа, 3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню?
Суп 2 Вторые блюда 3 Сок 4
Решение: 2 x 3 x 4 = 24
Ответ: Можно составить 24 варианта различных обедов.
Имеется 3 вида конвертов и 4 вида марок. Сколько существует вариантов выбора конверта с маркой?
Решение:Так как у нас существует 3 видов конвертов, то мы можем выбрать любой и наклеить на него одну их 4 марок, следовательно, если мы берем 1 конверт, то у нас есть 4 варианта марок на выбор. Если же у нас имеется 3 конвертов, то количество вариантов для выбора становится: 3 *4 = 12 вариантов.
Ответ: 12 способов, которыми можно выбрать конверт и марку для посылки письма
В кружке 6 учеников. Сколькими способами можно выбрать старосту кружка и его заместителя?
Решение: Первый может быть староста, а второй заместитель. Второй может быть заместитель, а первый староста. Порядок важен. Используем правило умножения. Выбор старосты — 6 вариантов. Выбор заместителя – 6-1 =5 вариантов. По правилу умножения: 6·5=30 способов.
Ответ: 30.
В буфете есть 4 сорта пирожков. Сколькими способами ученик может купить себе 2 пирожка?
Сколько существует пятизначных чисел, на конце которых стоит четная цифра?
Цифр в числе 10 Вариантов выбора первой цифры – 9 ( 0 на первом месте стоять не может) Вариантов выбора второй цифры – 10 Вариантов выбора третий цифры — 10 Вариантов выбора четвертой цифры — 10 Вариантов выбора пятой цифры – 5 (существует только пять четных цифр) По правилу умножения: 9·10·10·10·5 = 45000 вариантов
Ответ: 4500.
9. Перестановки в комбинаторных задачах. В комбинаторике часто приходиться решать задачу о том, сколькими способами можно расположить в ряд или, как говорят математики, упорядочить все элементы некоторого множества. Каждое из таких расположений называют перестановкой.
Задача. В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними?
Решение: первое место может занять любой из 4 участников. При этом второе место может занять любой из трёх оставшихся, третье – любой из двух оставшихся, а на четвёртом месте остаётся последний участник.
Значит, места между участниками могут быть распределены следующим образом
4 • 3 • 2 • 1 = 24.
Ответ: 24 способами.
10. Решите задачу на перестановки.
Задача. Андрей, Борис и Василий входят в комнату по одному. Сколько у них есть способов это сделать?
Решение. Пусть первым войдёт Андрей, но тогда вторым может войти Борис или Василий, то есть имеются две возможности. Аналогично есть две возможности, если первым войдёт Борис и если первым войдёт Василий. Таким образом 6 возможностей.
Ответ: 6 способов.
Задача 2. Буратино пришел в школу и встретил своих друзей Арлекин, Пьеро, Мальвину. Они все обменялись рукопожатиями. Сколько всего рукопожатий было?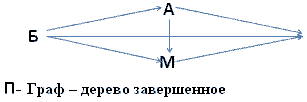
Метод перебора.
БА; БП; БМ; АП; АМ; ПМ.
Если Буратино пожал руки троим друзья, то Арлекин и Буратино обменялись рукопожатиями, значит, Арлекин еще пожмет руки Пьеро и Мальвине, а Мальвина еще пожмет Пьеро руку.
3 + 2 + 1 = 6
Ответ: 6
План-конспект занятия (6 класс) на тему: Задачи на перебор
Тема: Задачи на перебор
Цели: создать организационные и содержательные условия для формирования умений решения комбинаторных задач
Задачи:
образовательные: научить учащихся находить возможные комбинации, составленные из чисел, слов, предметов, отвечающие условию задачи;
воспитательные: владение интеллектуальными умениями и мыслительными операциями;
развивающие: развитие познавательного интереса учащихся.
Планируемые результаты изучения темы:
Личностные: Ученик получит возможность для формирования устойчивых эстетических предпочтений, способности к эмоциональному восприятию материала, положительного отношения к учению, к предмету; получит возможность для формирования коммуникативной компетентности в общении.
Предметные: Ученик научиться: анализировать объекты, сравнивать, сопоставлять, устанавливать взаимосвязь объектов, делать выводы, составлять логическую цепочку рассуждений, создавать схемы и модели задачи.
Ученик получит возможность: научиться организовывать учебное сотрудничество со сверстниками.
Метапредметные: Ученик научиться: отбирать метод решения комбинаторной задачи по её содержанию; решать простейшие комбинаторные задачи. Ученик получит возможность: углубить и развить представления о комбинаторных задачах.
Ход занятия
- Актуализация знаний
1) Определить арифметическое действие, с помощью которого из двух крайних чисел получено среднее, и вместо знака «?» вставить пропущенное число.
42(47)5 6(66)11 36(25)11 48(4)12
31(?)8 5(?)12 48(?)12 100(?)5
Ответ: 39, 60, 36, 20.
- Требуется распилить бревно на 6 частей. Каждый распил занимает 2 минуты. Сколько времени потребуется на эту работу?
Ответ: 10 минут.
3) Сколькими способами можно уплатить без сдачи 28 копеек, имея только монеты 1-и 5- копеечного достоинства?
- Изучение нового материала
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
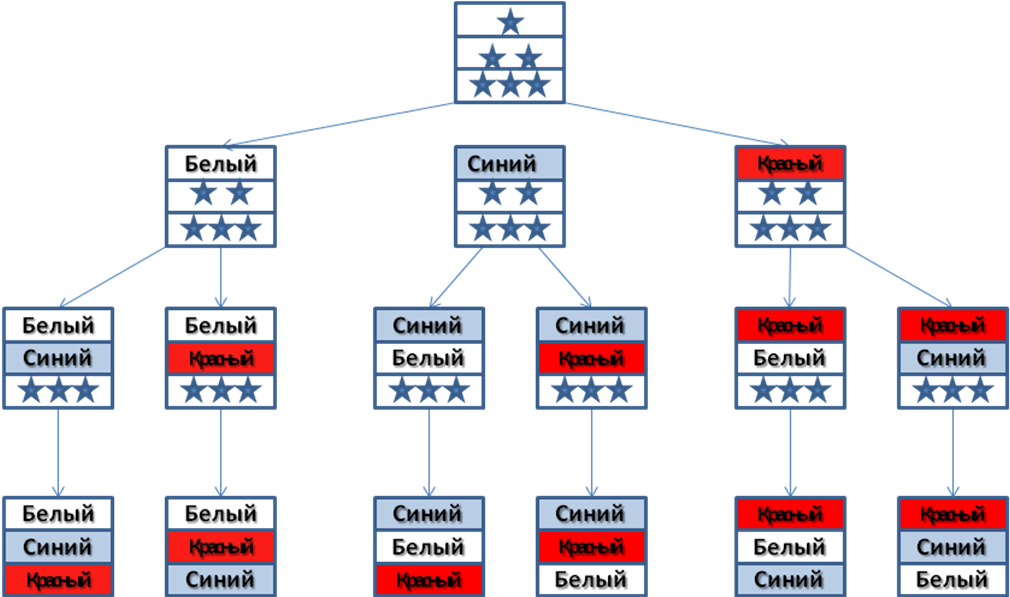
Задача 1. Государственные флаги многих стран состоят из горизонтальных или вертикальных полос разных цветов. Сколько существует различных флагов, состоящих из двух горизонтальных полос одинаковой ширины и разного цвета, при этом используются цвета — белый, красный и синий.
Решение. Пусть верхняя полоска флага белая (Б). Тогда нижняя полоса может быть красной (К) или синей (С). Получили две комбинации — два варианта флага. Если верхняя полоса флага — красная, то нижняя может быть белой или синей. Получим еще два варианта флага. Пусть, наконец, верхняя полоса — синяя, тогда нижняя может быть белой или красной. Это еще два варианта флага. Всего получили 3∙2 = 6 комбинаций — шесть вариантов флагов.
Задача 2. Сколько трехзначных цифр можно составить из цифр «1», «3», «5», «7», используя в записи числа каждую цифру не более одного раза?
Решение. Способ I. Чтобы ответить на этот вопрос, выпишем все такие числа. Пусть на первом месте стоит «1». На втором месте может быть записана любая из цифр «3», «5», «7». Запишем, например, на втором месте цифру «3». Тогда в качестве третьей цифры можно взять «5» или «7». Получим два числа 135 и 137. Если на втором месте написать цифру «5», то в качестве третьей цифры можно взять цифру «3» или «7». В этом случае получим числа 153 и 157. Если же, наконец, на втором месте записать цифру «7», то получим числа 173 и 175. Итак, мы составили все числа, которые начинаются с «1». Таких чисел шесть: 135, 137, 153, 157, 173, 175. Аналогичным способом можно составить числа, которые начинаются с цифры «3», с цифры «5», с цифры «7». Полученные результаты запишем в четыре строки, в каждой из которых шесть чисел:
Таким образом, из цифр «1», «3», «5», «7» (без повторения цифр) можно составить 24 трехзначных числа.
3) В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Назовите возможные варианты распределения призовых мест.
Ответ:
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.
Самые разные комбинаторные задачи решаются с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда и название метода — дерево возможных вариантов.
Проиллюстрируем проведенный перебор вариантов на так называемом дереве возможных вариантов
Проиллюстрируем проведенный перебор вариантов на так называемом дереве возможных вариантов .
Задача. Из города A в город B ведут две дороги, из города B в город C — три дороги, из города C до пристани — две дороги. Туристы хотят проехать из города A через города B и C к пристани. Сколькими способами они могут выбрать маршрут?
Решение. Путь из A в B туристы могут выбрать двумя способами. Далее, в каждом случае они могут проехать из B в C тремя способами. Значит, имеются 2∙3 вариантов маршрута из A в C. Так как из города C на пристань можно попасть двумя способами, то всего существует 2∙3∙2, то есть 12 способов выбора туристами маршрута из города A к пристани.
Решить комбинаторную задачу – это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.
В разделе представлены комбинаторные задачи на размещение, сочетание, перестановки с повторением и без повторения элементов. Используется естественный, доступный детям всех возрастов метод решения комбинаторных задач с помощью непосредственного перебора возможных вариантов (комбинаций).
- Формирование умений и навыков
Решение задач методом полного перебора всех возможных вариантов:
- Какие трехзначные числа можно составить из цифр 0, 2, 4?
Ответ: 200, 202, 204, 220, 222, 224, 240, 242, 244, 400, 402, 404, 420, 422, 424, 440, 442, 444.
- Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
Решение: Для того чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11; 14; 17; (начали с 1)
41; 44; 47; (начали с 4)
71; 74; 77; (начали с 7)
Ответ: 9 чисел.
- На обед в школьной столовой предлагается 2 супа,3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню?
Суп х2, вторые блюда х3, сок х4
Решение: 2 x 3 x 4 = 24
Ответ: Можно составить 24 варианта различных обедов.
- Андрей, Борис и Василий входят в комнату по одному. Сколько у них есть способов это сделать?
Решение. Пусть первым войдёт Андрей, но тогда вторым может войти Борис или Василий, то есть имеются две возможности. Аналогично есть две возможности, если первым войдёт Борис и если первым войдёт Василий.
2 x 3 =6. Таким образом, 6 возможностей.
Ответ: 6 способов.
4. Решение задач самостоятельно.
1) На завтрак в школьной столовой любой ученик может выбрать булочку, ватрушку, кекс или сочник, а запить их он может соком, чаем или компотом. Сколько вариантов завтрака предлагается в школьной столовой?
2) Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
- Итог урока
- Какие задачи называются комбинаторными?
- Что означает слово «комбинаторика»?
- Как формулируется комбинаторное правило умножения?
- Задание на дом
Придумать задачу на комбинаторное правило умножения. Решить ее и оформить решение на альбомном листе.
«Правило умножения для комбинаторных задач»
Математика 6кл. Урок 59.
Тема: «Правило умножения для комбинаторных задач»
Цели: ввести правило умножения для комбинаторных задач; закрепить знания учащихся по отдельным темам комбинаторики; тренировать способности практического использования дерева возможных вариантов; развивать внимание, исследовательские умения, речь.
Задачи:
Образовательные: развитие умения решать комбинаторные задачи методом полного перебора вариантов; выработка умения применять математическую теорию в конкретных ситуациях; знакомство учащихся с элементами гуманитарного знания, связанного с математикой.
Развивающие: развитие умения делать выбор рационального способа кодирования; развитие умения самостоятельно выбирать способ решения и умение обосновывать выбор; развитие умения решать задачи путем логических рассуждений.
Воспитательные: воспитывать чувство ответственности за качество и результат выполняемой работы; прививать сознательное отношение к труду; формировать ответственность за конечный результат; воспитать культуру учебного труда, повысить мотивацию обучения.
Ход урока
1. Организационный момент
Здравствуйте, ребята!
Собрать тетради с домашним заданием ответить на вопросы. Очень часто в жизни приходится делать выбор, принимать решения. Это сделать очень трудно не потому, что его нет, или оно одно и поэтому его трудно его найти, а приходится выбирать из множества возможных вариантов, различных способов, комбинаций, и нам всегда хочется, чтобы этот выбор был оптимальным.
Озвучить цели.
2. Объяснение и закрепление нового материала.
Задачи, которые мы будем сегодня решать помогут вам творить, думать необычно, оригинально, видеть то, мимо чего вы часто проходили не замечая, любить неизвестное, новое, преодолевать трудности и идти через неизвестное вперед. Стр.112-113.
Комбинаторика – раздел математики, в которой изучается, сколько различных комбинаций, подчиненных тем или иным условиям можно составить из заданных объектов.
И еще сегодня в очередной раз убедимся, что наш мир полон математики и продолжим исследование на предмет выявления математики вокруг нас.
Начнем с самой математики.
Задача №1
Сколько четных двузначных чисел можно составить из цифр 0, 1, 2, 4, 5, 9?
Составим дерево возможных вариантов.
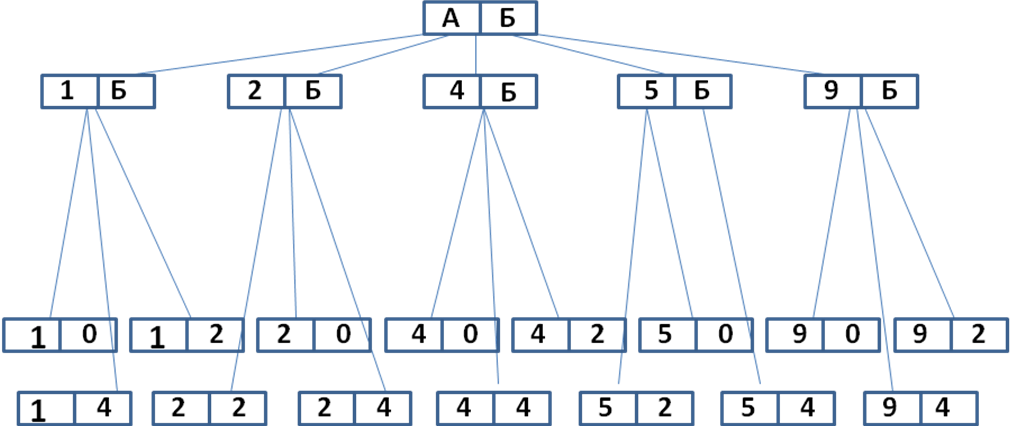
Какие из предложенных цифр могут стоять на первом месте? (Ответ: 1, 2, 4, 5, 9)
Какие на втором месте? Почему? (Ответ: 2, 0, 4)
Сколькими способами мы выбираем первую цифру? (Ответ: пятью)
Сколькими способами мы выбираем вторую цифру? (Ответ: тремя)
5*3=15 четных двухзначных чисел.
Правило умножения
Для того, чтобы найти число всех возможных исходов независимого проведения двух испытаний А и В, следует перемножить число всех исходов испытания А на число всех исходов испытания В.
Что подразумевается в этой задаче под словами «исход» и «испытание»?
Откроем учебники на стр.116 № 501 (закрепление)
Решение
а) 5*5=25
б) 5*4=20 Ответ: а) 25, б) 20.
Ребята, представьте на миг, чтобы стало в школе, если бы не было расписания. Трудно пришлось бы и детям и учителям. Даже в одном классе трудно решить проблему.
Давайте, в помощь тому, кто составляет школьное расписание, решим задачу.
Задача №2
В 6 классе в субботу 5 уроков:
История
Математика
Иностранный язык
Физкультура
ИЗО
Сколько можно составить вариантов расписания, зная точно, что изо последний урок.
Решение
Закодируем:
И – история, М – математика, Я — иностранный язык, Ф – физкультура.
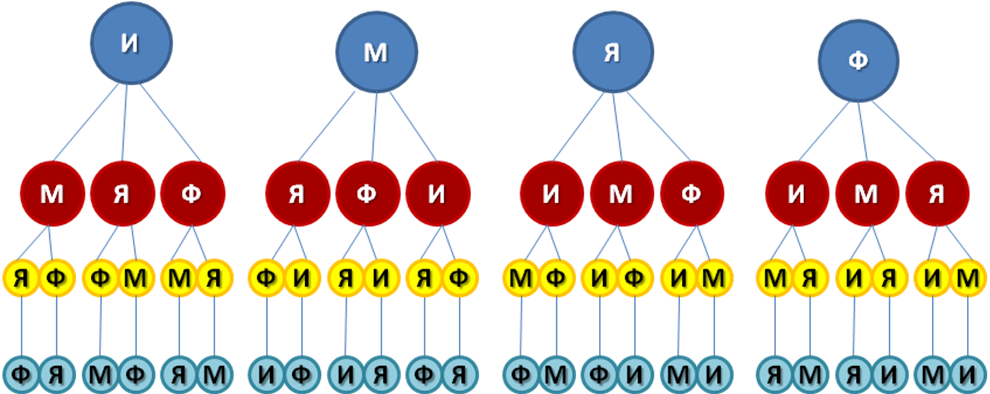
Давайте сосчитаем, сколько вариантов у нас получилось, если первый урок будет история?
(Ответ: 6 вариантов х 4 =24)
4х3х2х1=24
Да, трудно придется тому, кто забудет порядок уроков, и, не посмотрит в расписание, захочет заполнить дневник.
Задача №3 (№ 495 из учебника стр. 115)
Прочитать задачу вслух.
Решим задачу, используя правило умножения.
3*2*1=6 вариантов. Дерево возможных вариантов
Какие еще государства используют для своего государственного флага такую символику?
(Ответ: Люксембург, Нидерланды, Югославия)
IV. Самостоятельная работа.
I вариант №502, II вариант №503.
V. Подведение итогов
Мы буквально на несколько минут заглянули на уроки из расписания и действительно встретились с математикой.
Математика — повсюду. Глазом только поведешь и примеров сразу уйму ты вокруг себя найдешь.
VI. Домашнее задание
§ 16 № 496, 504, 511.
Оценки за урок
Методическая разработка по алгебре (6 класс) по теме: проект по комбинаторике
Проект
«Заряжай мозги!»
по теме:
«Элементы комбинаторики».
( задачи на перебор возможных вариантов и правило умножения).
Участники проекта:
учитель математики Устинкина С. А.
и учащиеся 6 класса
Время работы над проектом 3 урока
Март 2012
Цели проекта:
- Формирование грамотности в сфере элементарной комбинаторики.
- Приобретение навыков самостоятельной работы с информационными ресурсами.
- Формирование навыков коллективной работы.
- Развитие творческих способностей.
- Создание методички по комбинаторике в 6 классе «Заряжай мозги!»
Гипотеза исследования заключается в недостаточном количестве материала для изучения учащимися 6 класса раздела под названием «Комбинаторика»
Для подтверждения выдвинутой гипотезы были поставлены следующие задачи:
- Изучить историю комбинаторики.
- Разобрать методы решения комбинаторных задач с использованием некоторых правил комбинаторики.
- Выбрать задачи с помощью описанных правил.
- Решить отобранные задачи.
- Составление своих задач.
- Создание методички «Заряжай мозги!».
Самостоятельные исследования учащихся в рамках учебного проекта
- История комбинаторики.
- Просмотр различных задач по комбинаторике в различной литературе уровня 6 класса.
- Составление своих задач с различными способами решения.
- Обсуждение содержания и дизайна оформления методички «Заряжай мозги!»
Практическая значимость проекта
состоит в том, что составленная методичка может успешно применяться при изучении темы, для проверки знаний по комбинаторике учащихся 6 класса и развитию логического мышления детей,
как дополнение к материалу учебника 6 класса.
Краткая аннотация проекта.
Проект реализуется в рамках изучения темы «Комбинаторика» в 6 классе. Материал направлен на активизацию исследовательской деятельности учащихся.
Возможность выбора индивидуальных заданий позволяет поддерживать интерес к решению задач учащимися с разными способностями. Работа над проектом способствует развитию навыков самостоятельной экспериментальной деятельности и навыков коллективной работы. Проект предполагает творческое освоение ребятами ряда учебных тем, а именно: применение комбинаторики.
В рамках проекта один урок отводится под обсуждение в классе основных теоретических положений по теме, затем идет практическое применение знаний: решение готовых задач из учебника и составление своих комбинаторных задач из повседневной жизни и различных жизненных ситуаций. Ожидается, что самостоятельная работа по проектному методу позволит заинтересовать ребят, в результате чего они лучше овладеют основными теоретическими положениями учебной темы «комбинаторика» и разовьют в себе исследовательские навыки.
Продукт проекта – методичка «Заряжай мозги!»
« ЗАРЯЖАЙ МОЗГИ!»
Элементы комбинаторики: задачи на перебор возможных вариантов и правило умножения
авторы: учащиеся 6 класса
Под руководством учителя математики
Устинкиной С. А.
Март 2012
Содержание.
- От авторов.
- Из истории комбинаторики. Подготовили Изранцев Артем и Ситникова Алла.
- Немного от учителя:
1)Введение новых знаний.
Перестановки. Факториал.
2)задачи от учителя
- Задачи. Составила Целыковская Надя.
- Задачи от Колдина Дениса.
- «Попробуйте решить!».
Подготовила Потапова Александра.
- Задачи от Ситниковой Аллы.
- Решите задачу. Составил Веселов Саша.
- От авторов.
Мы, учащиеся 6 класса, хотим внести свой вклад в изучение комбинаторики, так как эта тема нас заинтересовала и увлекла. Мы составили свои задачи на комбинаторику. Сюжеты задач взяты из практических ситуаций, которые часто встречаются в нашей жизни. И хотим, чтобы эти задачи научились решать и ребята последующих шестых классов. И чтобы они тоже придумали свои задачи на комбинаторику и это стало бы традицией. И может быть когда- нибудь выйдет в свет книга с нашими задачами…
2.Из истории комбинаторики.
Первые научные исследования по комбинаторике принадлежат итальянским ученым Дж.Кардано, Н.Тарталье (ок.1499-1557), Г.Галилею (1564-1642) и французским ученым Б.Паскалю (1623-1662) и П.Ферма. Комбинаторику как самостоятельный раздел математики первым стал рассматривать немецкий ученый Г.Лейбниц в своей работе «Об искусстве комбинаторики», опубликованной в 1666 году. Он также впервые ввел термин «комбинаторика». Значительный вклад в развитие комбинаторики внес Л.Эйлер.Изучением размещений впервые занимался Я. Бернулли во второй части своей книги «Искусство предугадывания» в 1713 г. Современная символика сочетаний была предложена разными авторами учебных руководств только в 19 веке. Все разнообразие комбинаторных формул может быть выведено из двух основных утверждений, касающихся конечных множеств – правило суммы и правило произведения.
- 1) Введение новых знаний.
Перестановки . Факториал.
Пример1. Пусть имеются три книги. Обозначим их буквами a, b, c. Эти книги можно расставить на полке по-разному: abc, acb, bac, bca, cab, cba.
Каждое из этих расположений называют перестановкой из трех элементов.
Перестановкой из n элементов называется каждое расположение этих элементов в определенном порядке.
Число перестановок из n элементов обозначается символом Pn (читается «Р из n»).
Мы установили, что Р = 6. Для того, чтобы найти число перестановок из трех элементов, можно не выписывать эти перестановки, а воспользоваться правилом умножения.
Будем рассуждать так. На первое место можно поставить любой из трех элементов. Для каждого выбора первого элемента есть две возможности выбора второго из оставшихся двух элементов. Наконец, для каждого выбора первых двух элементов остается единственная возможность выбора третьего элемента. Значит, число перестановок из трех элементов равно 3•2•1, т.е. 6.
Выведем теперь формулу для числа перестановок из п элементов.
Пусть мы имеем n элементов. На первое место можно поставить любой из них. Для каждого выбора первого элемента на второе место можно поставить один из оставшихся n-1 элементов. Для каждого выбора первых двух элементов на третье место можно поставить один из оставшихся n-2 элементов и т.д. в результате получим, что
Pn = n(n-1)(n-2) •…•3•2•1.
Расположив множители в порядке возрастания, получим
Pn = 1•2•3•…•(n-2)(n-1)n.
Для произведения первых n натуральных чисел используется специальное обозначение: n! (читается «n факториал»).
Таким образом, число всевозможных перестановок из n элементов вычисляется по формуле Pn = n!
Например, 2!=1•2=2; 5!=1•2•3•4•5=120.
По определению считают, что 1!=1.
Пример2. В расписании на понедельник шесть уроков: алгебра, геометрия, биология, история, физкультура, химия. Сколькими способами можно составить расписание на этот день так, чтобы два урока математики (алгебра и геометрия) стояли рядом?
Решение: Рассмотрим алгебру и геометрию как один урок. Тогда расписание надо составить не из 6, а из 5 уроков – Р5 способов. В каждой из полученных комбинаций можно выполнить Р2 перестановки алгебры и геометрии. Значит, искомое число способов составления расписания:
Р5∙Р2=1∙2∙3∙4∙5∙1∙2= 120∙2=240
Ответ: 240 способов.
Пример3 Из группы теннисистов, в которую входят четыре человека – Антонов, Григорьев, Сергеев и Федоров, тренер выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
Решение: Составим сначала все пары, в которые входит Антонов (для краткости будем писать первые буквы фамилий). Получим три пары: АГ, АС, АФ.
Выпишем теперь пары, в которые входит Григорьев, но не входит Антонов. Таких пар две: ГС, ГФ.
Далее составим пары, в которые входит Сергеев, но не входят Антонов и Григорьев. Такая пара только одна: СФ.
Других вариантов составления пар нет, так как все пары, в которые входит Федоров уже составлены. Итак, мы получили 6 пар: АГ, АС, АФ
ГС, ГФ
СФ,
т.е. 3•2•1=6. значит, существует всего шесть вариантов выбора тренером пары теннисистов из данной группы.
Способ рассуждений, которым мы воспользовались при решении задачи, называют перебором возможных вариантов.
2) Задачи от учителя.
Реши сам
№1. Имеется белый хлеб, черный хлеб, сыр, колбаса и
варенье. Сколько видов бутербродов можно
приготовить?
№2.На тарелке лежат 5 яблок и 4 апельсина. Сколькими
способами можно выбрать один плод?
№3.На тарелке лежат 5 яблок и 4 апельсина. Сколькими
способами можно выбрать пару плодов, состоящую из
яблока и апельсина?
№4.Учащиеся 6 класса решили обменяться фотографиями. Сколько фотографий для этого потребуется, если в классе 8 человек?
4. Задачи. Составила Целыковская Надя.
№1 Перечислите все возможные варианты разложения по двум вазам одного яблока и одной груши.
№2. В каждую из 3-х ваз: хрустальную, керамическую и стеклянную — пробуют поставить по одному из двух букетов цветов: роз и гвоздик. Перечислите все возможные варианты установки каждого букета в вазу.
№3.У Ани есть любимый костюм, в котором она ходит в школу. Она надевает к нему белую0 голубую, розовую или красную блузку, а в качестве «сменки» берет босоножки или туфли. Кроме того у Ани есть три разных бантика, подходящих ко всем блузкам.
а) Нарисуйте дерево возможных вариантов Аниной одежды.
б) Сколько дней Аня может выглядеть по-новому в этом костюме?
в) Сколько дней она будет ходить в туфлях?
5. Задачи от Колдина Дениса.
- У мамы есть 3 платья и 2 ожерелья. Сколько существует у неё вариантов выбора платья и ожерелья чтобы пойти в театр.
- В туристическом бюро мне предложили «горящий» тур по странам Европы: Польша Германия и Франция. Сколько может мне предложить тур- агентство выбора маршрутов посещения стран Европы.
- В нашем классе 8 человек. Нам нужно выбрать старосту класса и его заместителя. Сколько возможно вариантов выбора старосты и его заместителя.
- У солдата сверхсрочника есть 3 пары обуви, 2-е брюк и одна рубашка. Сколько у него вариантов одеться по-разному?
6.«Попробуйте решить!».
Подготовила Потапова Александра.
№1.У Дениса дама есть три поручения: помыть посуду,
вынести мусор и пропылесосить. Сколько дней он может
выполнять эти поручения в разном порядке?
№2. Алла решила купить подруге на день рождения блузку. В магазине были блузки четырех цветов: розовая, голубая, белая и фиолетовая. Ей очень понравились блузки и она решила купить и себе. Сколько вариантов покупки двух блузок разного цвета есть у Аллы?
№3. У тебя есть цифры: 3 , 6, 7,9. Сколько можно составить из этих цифр двузначных чисел, чтобы в записи числа цифра не повторялась?
7. Задачи от Ситниковой Аллы.
1. Алла, Саша и Надя купили красивую шкатулку и решили рассмотреть её по очереди. Выпишите все варианты такой очереди, в которой Алла на первом месте? Выпишите варианты очереди, в которой Саша не на последнем месте.
2. Составьте все множества, равные данному множеству
( 1, 2, 9).
3. Каждый из 4-х друзей может получить за контрольную по математике любую отметку от 2 до 5. Сколько существует вариантов получения ими отметок? Выпишите все эти варианты.
8.Решите задачу. Составил Веселов Саша.
№1. Дима, Саша и Вова накопили денег и купили интересный фильм. Задумались, в какой очереди они будут его смотреть. Саша вспомнил, что недавно на уроке математике они решали такие комбинаторные задачи и предложил посчитать все варианты такой очереди. Так сколько таких вариантов?
- Ответы и решения к задачам.
3. 2) Задачи от учителя. Реши сам.
№1.
№2.
№3.
№4.
4. Задачи. Составила Целыковская Надя.
№1
№ способа | Первая ваза | Вторая ваза |
1 | Яблоко и груша | пусто |
2 | яблоко | груша |
3 | груша | Яблоко |
4 | пусто | Яблоко и груша |
Ответ: 4 варианта.
№2. 6 вариантов.
№3. б) 24 дня.
в) 12 дней ( половина вариантов)
5. Задачи от Колдина Дениса.
№1.
№2.
№3
№4.
6.«Попробуйте решить!».
Подготовила Потапова Александра.
№1.
№2.
№3.
7. Задачи от Ситниковой Аллы.
№1.
№2.
№3.
8.Решите задачу. Составил Веселов Саша.
№1.
План-конспект занятия по алгебре (6 класс) на тему: Комбинаторика для всех
Открытый урок по теме «Комбинаторика для всех»
Разработала и провела учитель математики МБОУ «ООШ с. Мордово» Ивлева Мария Владимировна
Класс: 6.
Предмет: математика.
Тип урока: повторение и систематизация знаний.
Цель: повторить и систематизировать знания и умения учащихся решать комбинаторные задачи различными методами.
Задачи:
- Совершенствовать навыки нахождения возможных комбинаций, составленных из чисел, слов, предметов.
- Учить отбирать метод решения комбинаторной задачи по её содержанию.
- Совершенствовать операции умственной деятельности: анализ, синтез, классификация, способность наблюдать и делать вывод, выделять существенные признаки.
- Способствовать формированию познавательного интереса к предмету, ответственность за качество и результат выполняемой работы.
Оборудование урока:
- Раздаточный материал (карта ученика).
- Мультимедиа для презентации.
- Материал для задачи (5 карточек, цветные нитки).
Пояснения:
Элементы комбинаторики в учебниках Виленкина Н.Я. и др. изучаются в 5 классе разрозненно. Авторы предлагают учащимся комбинаторные задачи с разбором решения и с пояснениями, тут же вводятся необходимые математические понятия. Данный урок направлен на повторение и систематизацию всего материала по комбинаторике за 5 класс, который вписывается в рамки одного урока.
Ход урока.
— Наш сегодняшний урок не совсем обычный «Комбинаторика для всех». Как вы думаете, чем мы будем заниматься? Как можно по-другому сформулировать тему урока? (ответы и рассуждения учащихся)
Один из предложенных вариантов записывается на доску и в рабочие карты учащихся, например, «Решение комбинаторных задач» или «Методы решения комбинаторных задач».
— С названием определились. Раз есть тема урока, то можно поговорить, что за этот урок мы должны сделать.
Дети предлагают варианты. Наиболее правильные учитель записывает на доску, а учащиеся в графу «НАДО» в своих рабочих картах.
— Это цель урока для всего класса. Мне хочется, чтобы вы подумали и записали на листочках (рабочая карта), что конкретно ВЫ хотите получить от этого урока. Отнеситесь серьёзно к выполнению этого задания. И может кто-нибудь захочет озвучить своё желание?
Учащиеся в течении 1-2 минут записывают свои мысли в рабочую карту в графе «ХОЧУ».
— Посмотрите внимательно на ваши листы, что осталось незаполненным? (графа «МОГУ») К ней мы вернёмся в конце урока.
В начале урока прозвучали два понятия: «комбинаторика» и «комбинаторная задача». Вспомним из 5 класса, что означают эти понятия. Если возникли трудности, то на ваших листах есть подсказки. Вам необходимо вставить пропуски, дописав пропущенные слова. Мной были подобраны самые простые толкования этих математических терминов.
«Комбинаторика – это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из объектов задачи»
«Комбинаторная задача – это задача на перебор и подсчёт количества составленных комбинаций».
Обсуждение идёт сообща, учащиеся результат записывают в рабочую карту.
— Все молодцы. А сейчас мы переходим к решению комбинаторных задач. Для начала вспомним примеры этих задач, которые вы решали в 5 классе (учащиеся называют по несколько предметов). Решим следующую задачу (работа в тетрадях):
сколько двузначных чисел можно составить из цифр 1, 5, 9 при условии, что цифры не повторяются (задача есть в картах и презентации). На решение вам отводится только 2 минуты. Потом ответы сверим.
Учащиеся на местах (индивидуальная работа) решают предложенную задачу методом перебора (большинство). После того, как время закончилось, проверяются ответы и выписываются полученные комбинации.
— Как вы решали данную задачу? Как можно назвать этот метод решения комбинаторных задач?
Учащиеся объясняют суть решения, предлагают названия метода. После обсуждения идёт работа с картой: постепенное заполнение 1 столбца таблицы «Методы решения комбинаторных задач» (аналогичная таблица в презентации).
Название метода | Достоинства метода | Недостатки метода |
Метод перебора | ||
— Усложним немного задачу: сколько трёхзначных чисел можно составить из цифр 2, 5, 7, 9 при условии, что цифры не повторяются? (работа в тетрадях) Подумайте, применим ли здесь метод перебора, да или нет, почему? (обсуждение) Вспомните из 5 класса, какие интересные фигуры мы рисовали при решении таких задач? (показать пример из учебника Виленкина Н.Я. «Математика. 5 класс»). Как они называются? Может кто-нибудь попробует изобразить дерево вариантов для этой задачи и подсчитать количество чисел?
Разбор задачи у доски. Работа с картами (заполняем 1 столбец).
Название метода | Достоинства метода | Недостатки метода |
Метод перебора | ||
Дерево вариантов | ||
— Все молодцы! Разомнёмся перед более сложной задачей (физкультминутка).
Мы хлопаем в ладоши, хлоп, хлоп
хлопки над головой
Мы топаем ногами, топ, топ
высоко поднимаем колени
Качаем головой
головой вперед назад подвигать
Мы руки поднимаем, мы руки опускаем
руки поднять, опустить
Мы низко приседаем и прямо мы встаем
присесть и подпрыгнуть
Руки вниз, на бочок.
Разжимаем- в кулачок
Руки вверх и в кулачок
Разжимаем на бочок
На носочки поднимайся
Приседай и выпрямляйся
Ноги вместе. ноги врозь.
— Но, есть еще один способ, и мы сейчас его вспомним. Для этого решим задачу: сколько можно составить четырёхзначных чисел из цифр 0, 1, 3, 4, 6, 8 при условии, что цифры не повторяются. Возможно ли здесь перебрать все вариант? Правильно, можно, но долго и всё равно можно что-нибудь пропустить. Можно ли здесь составить граф? Попробуйте (работа в тетрадях). Слишком громоздким получается дерево. Тогда подумайте, как можно решить эту задачу без перебора и деревьев. Посмотрите, когда мы решали первую задачу, у нас было 3 цифры и двузначное число, всего вариантов 6. Дальше 4 цифры и трёхзначное число, всего вариантов 24. Не догадались? Посмотрите внимательно тогда на дерево в предыдущей задаче, оно должно вам помочь. Молодцы. Ведь для первой цифры в числе существует 5 вариантов (без 0), для второй – 5 вариантов (цифры не повторяются + 0), для третьей – 4 варианта, для четвёртой – 3 варианта. Перемножаем и получаем 300 различных чисел. Поэтому в нашу таблицу можно записать еще один метод решения – правило умножения.
Работа с картами (заполняем 1 столбец).
Название метода | Достоинства метода | Недостатки метода |
Метод перебора | ||
Дерево вариантов | ||
Правило умножения |
— Все правила из 5 класса мы повторили, осталось посмотреть, как вы умеете решать комбинаторные задачи разными методами. Я вам предлагаю 3 задачи (раздаточный материал + презентация). Решать их вы можете любым способом. Первую задачу мы разберем вместе. Вторую вы уже попробуете сами, а один человек на закрытой доске. А вот третью задачу мы перенесем в реальность.
- Сколькими способами можно выбрать 5 различных красок из имеющихся 11 красок?
- В вазе лежат 3 яблок и 6 груш. Лена выбирает либо яблоко, либо грушу, после чего Петя выбирает из оставшихся фруктов и яблоко и грушу. Сколько возможно таких выборов для Пети? При каком выборе Лены у Пети больше возможностей?
- При встрече 5 товарищей обменялись рукопожатиями. Сколько всего было рукопожатий?
Перед решением третьей задачи надо из класса выбрать 5 человек, определить каждому номер от1 до 5 и каждому раздать по 5 ниток различных цветов. Учащиеся вызываются к доске и с помощью разноцветных ниток обмениваются рукопожатиями. Остальные фиксируют результаты.
— Каким методом мы решали эту задачу? На дом вам нужно будет подумать над решение этой задачи оставшимися двумя методами. А теперь мы обратим своё внимание на ту таблицу, которую мы весь урок постепенно заполняли. Сейчас вы поработаете в группах: 1 группа – метод перебора, 2 группа – дерево вариантов, 3 группа – правило умножения. Ваша задача: из рассмотренных задач и из всего сказанного выделить достоинства и недостатки каждого метода.
Учащиеся заполняют таблицу (групповая работа). Всего минуты 2-3, потом проверка. Если время позволяет, учащиеся могут перенести таблицу с слайда (готовую) в свою карту.
Название метода | Достоинства метода | Недостатки метода |
Метод перебора | Наглядность, возможность увидеть все варианты. «Теоретически» можно решить любую комбинаторную задачу | Очень длительный, можно пропустить варианты |
Дерево вариантов | Наглядность, возможность увидеть все варианты | Очень громоздкий и длительный. Не все задачи могут быть решены с его помощью |
Правило умножения | Компактность, быстрота решения. | «Не видно» самих вариантов, можно посчитать только их количество. Не все задачи могут быть решены с его помощью. |
— Все молодцы! Отлично поработали на уроке. Осталось до конца заполнить ваши листы. Это графа «МОГУ». Перечислите и кратко запишите, что вы уже можете или знаете, связанное с комбинаторикой и комбинаторными задачами. Молодцы! Вы уже многое знаете и многое еще узнаете в старших класса по комбинаторике. В заключении урока я хотела, чтобы вы ответили, а точнее дописали, на 3 вопроса:
- На уроке мне понравилось…
- На уроке не понравилось…
- Свою работу на уроке я оцениваю на …
Листки мне ваши сдайте, я их верну. Спасибо за урок! До свидания!
Если останется время, можно предложить дополнительные задачи:
- В соревнованиях участвуют 15 футбольных команд. Сколькими способами между ними могут распределиться золотая и серебряная медали?
- Сколько двузначных чисел, у которых обе цифры четные?
- Сколько пятизначных чисел, которые делятся на 5?
- Сколькими способами из 30 шестиклассников можно выбрать делегацию, состоящую из трех человек?
- В вазе лежат 10 яблок, 5 груш и 6 бананов. Сколькими способами можно взять один банан или одно яблоко?
- В отряде 5 разведчиков, 3 связиста и 2 сапера. Сколькими способами можно выбрать одного бойца, чтобы он был разведчиком или связистом? Сколькими способами можно составить отряд из трех человек, чтобы в него вошли разведчик, связист и сапер?
- Сколько осмысленных слов можно составить из букв слова «пирог»?
- 3 мальчика купили три билета на хоккей на 9, 10, 11 места. Сколькими способами они могут занять эти места?
А теперь, давайте проведем самоанализ урока.
- На уроке мне понравилось__________________________________________________________
_________________________________________________________________________________
- На уроке не понравилось___________________________________________________________
_________________________________________________________________________________
- Свою работу на уроке я оцениваю на_________________________________________________
Учебно-методический материал по математике (6 класс) на тему: Правило умножения при решении комбинаторных задач
Решение комбинаторных задач.
I.
Задача 1. Несколько стран решили использовать для своего государственного флага символику в виде трех горизонтальных полос одинаковой ширины разных цветов – белого, синего, красного. Сколько стран могут использовать такую символику при условии, что у каждой страны – свой флаг?
В 5-м классе для решения такой задачи использовали построение «дерева» возможных вариантов.
Построим «дерево» вариантов и ответим на вопрос задачи.
Используя дерево возможных вариантов, мы можем подсчитать, сколько стран могут использовать такую символику.
Таким образом, получилось 6 комбинаций. Значит, указанную символику при выборе государственного флага могут использовать 6 стран.
Вопрос на который вы должны знать ответ: какой из представленных на рисунке флагов является Государственным флагом России?
Белый цвет означает мир, чистоту, совершенство; синий – цвет веры и верности; красный – энергию, силу, кровь, пролитую за Отечество.
II.
- Задача 2: Сколько двузначных чисел можно составить из цифр 0, 1, 2, 3, 4?
«Дерево» вариантов имеет много «веток». Так как вариантов много, то можно легко допустить ошибку в подсчете всевозможных способов.
Подсчитаем количество данных двузначных чисел, используя логические рассуждения и здравый смысл.
- У интересующих нас двузначных чисел на первом месте (цифра десятков) может находиться любая из заданных цифр кроме цифры 0. Не существует двузначного числа, начинающегося с цифры 0.
Значит, цифрой десятков может служить одна из цифр 1, 2, 3 или 4. Поэтому в первой группе только 4 «ветви».
- Для цифры единиц для каждого из этих случаев возможны пять вариантов – 0, 1, 2, 3, 4.
Всего получаем 4•5 = 20 вариантов.
Про такой способ рассуждений обычно говорят так: мы использовали правило умножения.
- Правило умножения.
Если первый элемент в комбинации можно выбрать a способами, после чего второй элемент – b способами, то общее число комбинаций из двух элементов можно будет выбрать a •b способами.
Устные задачи на применение правила умножения.
- У Насти 3 брюк и 5 блузок, удачно сочетающихся по цвету. Сколько различных комбинаций одежды она может составить? (3∙5=15)
- В 6-м классе в пятницу 6 уроков: математика, русский язык, информатика, физкультура, биология и музыка. Сколько можно составить вариантов расписания в субботу? (6∙5∙4∙3∙2∙1=720).
3. Выполнение заданий.
Задача 3.
В списке учеников 6-го класса 15 девочек и 13 мальчиков. Нужно выбрать двух дежурных по классу. Сколькими способами это можно сделать: а) при условии, что пару дежурных обязательно должны составить мальчик и девочка, б) без указанного условия?
Решение:
А) Для выбора девочки в качестве дежурного есть 15 вариантов. Если девочка дежурной назначена, то имеется 13 вариантов выбора мальчика в качестве второго дежурного.
Всего: 15*13= 195 способов.
Ответ: 195 способов.
Б) Для выбора первого дежурного имеется 28 способов. Для каждого из них существует 27 способов выбора второго дежурного.
Всего 28*27 = 756 способов.
Но среди этих 756 пар есть одинаковые пары. Для простоты рассуждений перенумеруем учеников (в списке каждому ученику присваивается номер). Тогда ясно, что например, пара «ученик №1, ученик №2» и пара «ученик №2 , ученик №1» это одна и та же пара. Таким образом, мы каждую пару посчитали дважды. Значит, полученный результат надо уменьшить вдвое: 756:2= 378
Ответ: 378 способов.
В данной задаче использовали правило деления: если при подсчете искомых комбинаций каждую из них подсчитали т раз, то нужно поделить найденное количество комбинаций на m.
Сравнение способов решения комбинаторных задач.
Способ решения | «Плюсы» | «Минусы» |
«Дерево» возможных вариантов | Можно увидеть все варианты | Громоздкий способ, если много вариантов |
Правило умножения, правило деления | Быстрота решения, компактность | Невозможно увидеть все варианты, можно только подсчитать их количество |
Для каждой конкретной задачи выбираете удобный способ решения!
Задача 4.
В списке учеников 6-го класса 15 девочек и 13 мальчиков. Нужно выделить группу из трех человек для посещения заболевшего ученика этого класса. Сколькими способами это можно сделать, если
а) все члены этой группы – девочки
б) все члены этой группы – мальчики;
в) в группе 1 девочка и 2 мальчика;
г) в группе 2 девочки и 1 мальчик?
а) 455 способов;
б) 220 способов;
в) 990 способов;
г) 1260 способов.
Задача 5.
В списке 6-го класса 15 девочек и 13 мальчиков. Нужно выделить группу из трех человек для посещения заболевшей ученицы этого класса. Сколькими способами это можно сделать, если:
а) все члены группы – девочки;
б) все члены группы – мальчики;
в) в группе 1 девочка и 2 мальчика;
г) в группе 2 девочки и 1 мальчик?
Решение:
а) 14∙13∙12=2184, 2184 : 6=364.
Ответ: 364 способа.
б) 13∙12∙11=1716, 1716:6=286.
Ответ: 286 способов.
в) (13∙12):2=78, 78∙14=1092.
Ответ: 1092способа.
г) ((14∙13):2) ∙13=1183.
Ответ: 1183 способа.
Задача 6.
В двух урнах имеется по семь шаров, в каждой – семи различных цветов: красного, оранжевого, желтого, зеленого, голубого, синего, фиолетового. Из каждой урны одновременно вынимается по одному шару.
а) Сколько существует комбинаций, при которых вынутые шары одного цвета?
Ответ: 7.
б) Сколько возможно комбинаций, при которых вытянутые шары разных цветов?
Ответ: 21 комбинация.
в) Сколько всего существует различных комбинаций вынутых шаров (комбинации типа «белый – красный» и «красный – белый» считаются одинаковыми?
Ответ: 28 комбинаций.