Конвекция в природе и в технике
Само слово на латыни означает «перенос». А процесс конвекции характеризуется переносом тепла в газообразных, жидких и даже твердых сыпучих средах веществами. В природе законы конвекции мы наблюдаем вокруг себя ежедневно. Именно природное явление называют естественной конвекцией, при которой нижние уровни вещества при нагревании самопроизвольно начинают движение вверх, а более холодные уровни опускаются на их место.
Увидеть это можно, если повесить над пламенем листик из бумаги, который станет двигаться от поднимающегося вверх теплого воздуха. В жидкости этот процесс происходит благодаря нагреванию нижних слоев, которые постепенно передают тепло к верхним. Так, к примеру, закипает вода. Интересно, что если пытаться нагреть воду сверху, то конвекции не произойдет, потому что физическое движение теплого вещества вниз, а холодного вверх просто невозможно. Вынужденной конвекцией называется усиленное перемешивание газа или жидкости с помощью мешалок или вентиляторов.
Обогреватели с разной конвекцией
Любой из обогревателей прогревает помещение по законам конвекции. Но одни из них создают вынужденное перемещение нагретых слоев воздуха, а другие работают на основе естественных движений тепла. К примеру, тепловентиляторы, нагревая воздух, еще и раздувают его по всему помещению. А вот масляные радиаторы или отопительные конвекторы действуют по естественным законам природы. Если говорить о масляных устройствах, то перемешивание теплого воздуха с холодным при их работе происходит быстрее, благодаря высокой температуре нагрева, но при этом воздух сильно сушится. А вот конвекторы электрические отзывы получают всегда самые положительные, ведь принцип естественного передвижения теплых масс позволил создать батарею, которая не вредит здоровью и безопасна в эксплуатации бесконечно долго. Воздух в комнате при этом не пересушивается, температура поддерживается все время, опасности ожогов нет совершенно.
Конвекционные печи
Применение конвекционного принципа в микроволновках, духовках и печах позволило ускорить и улучшить выпечку и приготовление разных блюд.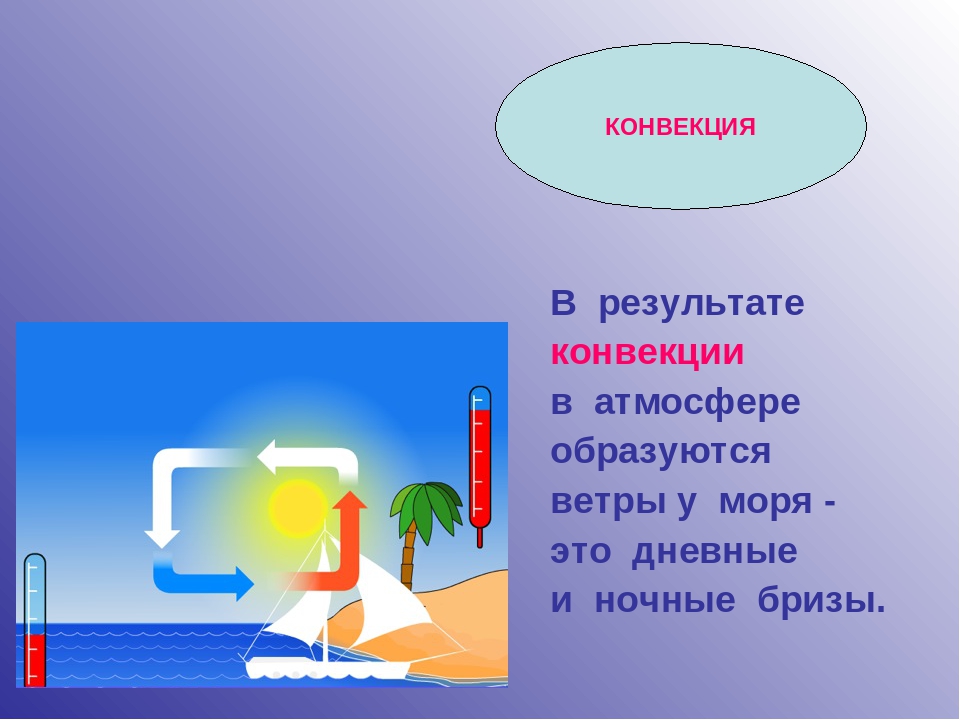 Суть работы конвекционных печей состоит в том, что благодаря вмонтированному в заднюю стенку нагревательному элементу и вентилятору, при включении происходит принудительная циркуляция горячего воздуха. Под воздействием этой циркуляции внутреннее пространство разогревается намного быстрее и равномернее, а, значит, и воздействие на продукты будет одновременным со всех сторон. Выпечка в таких печах всегда будет идеальной. Именно поэтому конвекционные печи относят к профессиональной технике и используют их в хлебопекарнях, фаст-фудах, ресторанах и кафе и т.п. В современных кухонных духовках для домашнего быта тоже начали уже встраивать конвекционную систему, и это очень понравилось всем хозяйкам и любителям вкусно покушать.
Суть работы конвекционных печей состоит в том, что благодаря вмонтированному в заднюю стенку нагревательному элементу и вентилятору, при включении происходит принудительная циркуляция горячего воздуха. Под воздействием этой циркуляции внутреннее пространство разогревается намного быстрее и равномернее, а, значит, и воздействие на продукты будет одновременным со всех сторон. Выпечка в таких печах всегда будет идеальной. Именно поэтому конвекционные печи относят к профессиональной технике и используют их в хлебопекарнях, фаст-фудах, ресторанах и кафе и т.п. В современных кухонных духовках для домашнего быта тоже начали уже встраивать конвекционную систему, и это очень понравилось всем хозяйкам и любителям вкусно покушать.
Циркуляция воздуха в холодильниках
В холодильных устройствах также работает принцип конвекции, только в этом случае требуется заполнение внутренних отделений не теплым воздухом, а холодным. К примеру, наш холодильник Snaige без устали вырабатывает холод с помощью циркулирующего по трубам фреона, который охлаждает верхние слои в холодильной камере. Охлажденный воздух опускается вниз и вытесняет теплый вверх, где тот также охлаждается. Так вся камера заполняется холодом, что и нужно в холодильных устройствах. Чтобы циркуляция холодных потоков была эффективней, не нужно загружать внутреннее пространство холодильника до отказа, оставьте проемы для свободного движения.
Охлажденный воздух опускается вниз и вытесняет теплый вверх, где тот также охлаждается. Так вся камера заполняется холодом, что и нужно в холодильных устройствах. Чтобы циркуляция холодных потоков была эффективней, не нужно загружать внутреннее пространство холодильника до отказа, оставьте проемы для свободного движения.
Конвекция в природе и технике
«Конвекцияв природе и технике»
Если бы я захотел читать не зная букв, это было бы бессмыслицей. Точно так же, если бы я захотел судить о явлениях природы, не имея представления о началах вещей, это было бы такой же бессмыслицей…
М.В. Ломоносов
Что такое конвекция?
Конвекция (от лат. convectio — доставка) – это вид теплообмена, при котором тепло переносится самими струями газа или жидкости.
Объяснение конвекции
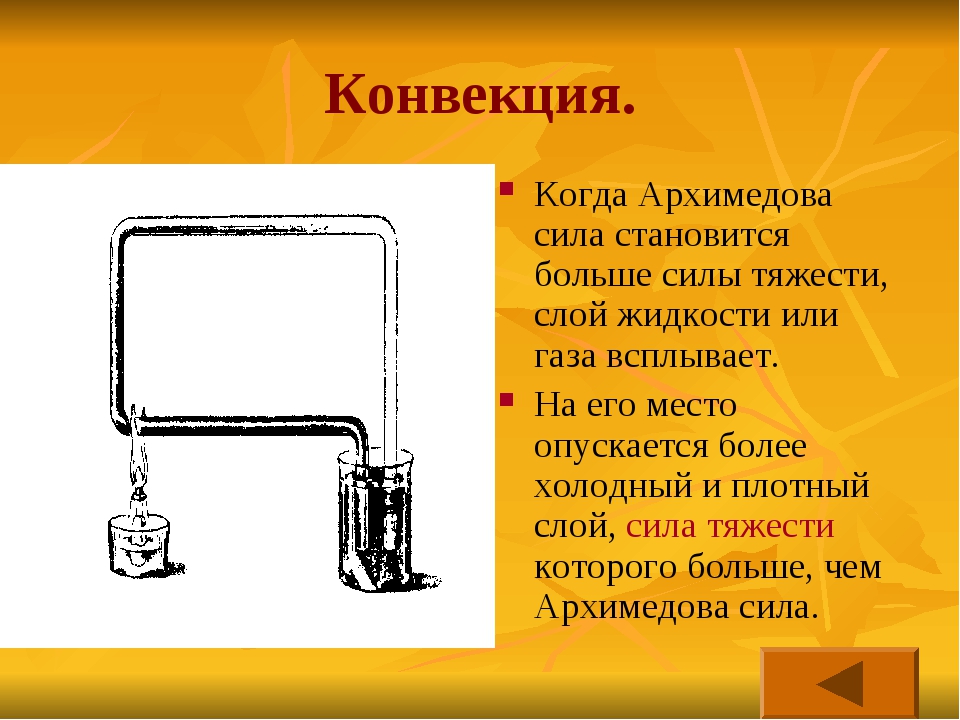
Явление конвекции можно объяснить законом Архимеда и явлением теплового расширения тел.
При повышении температуры объем жидкости возрастает, а плотность уменьшается. Под действием архимедовых сил менее плотная нагретая жидкость поднимается вверх, а более плотная холодная жидкость опускается вниз. Если же жидкость нагревать сверх, то менее плотная теплая жидкость там и останется и конвекция не возникнет. Так устанавливается круговорот жидкости, сопровождающийся переносом энергии от нагретых участков к более холодным. Совершенно аналогичным образом возникает конвекция в газах.
Механизм конвекции:
Виды конвекции
естественная
вынужденная
Особенности конвекции
- возникает в жидкостях и газах, невозможна в твердых телах и вакууме;
- само вещество переносится;
- нагревать вещества нужно снизу.
в жидкостях
в газах
Естественная конвекция
Для возникновения естественной конвекции требуется подогрев жидкости снизу (или охлаждение сверху), причем нагрев в разных участках должен быть неравномерным.
Вынужденная конвекция
При вынужденной конвекции потоки нагретой (или охлажденной) жидкости или газа переносятся под действием насосов или вентиляторов. Такая конвекция используется в тех случаях, когда естественная конвекция оказывается недостаточно эффективной, а также в состоянии невесомости, когда естественная конвекция невозможна.
Конвекция в природе и технике
работа обычной батареи отопления;
тяга в печи;
отопление дома;
образование облаков;
образование ветра, бриза и муссонов;
движение тектонических плит;
процессы горообразования;
процесс дымообразования из труб и кратеров вулканов;
процесс охлаждения продуктов в холодильнике;
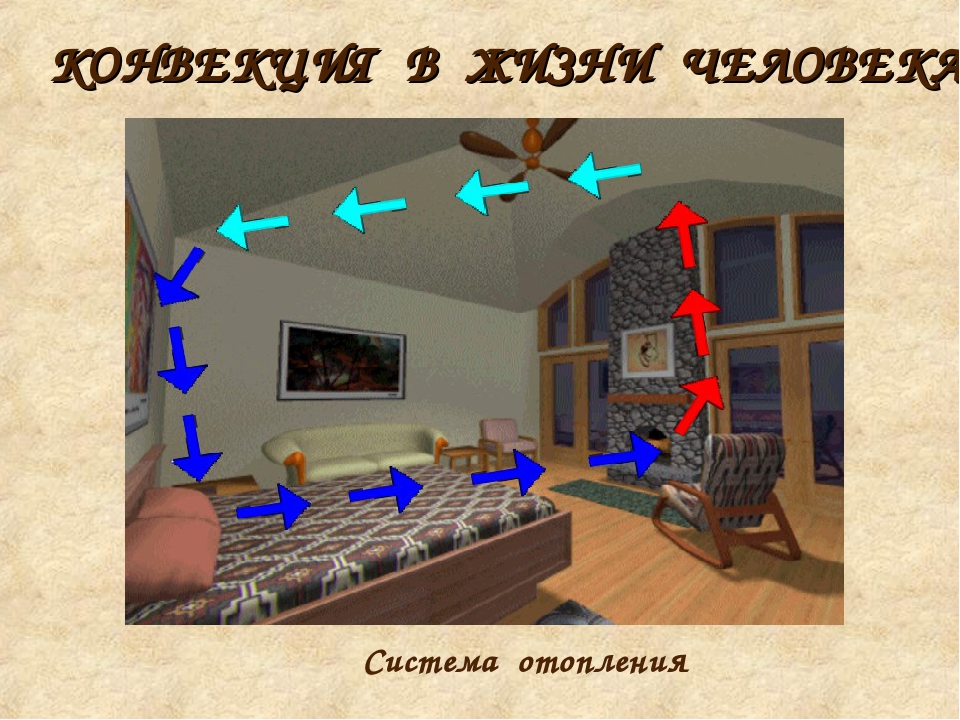
КОНВЕКЦИЯ В ЖИЗНИ ЧЕЛОВЕКА
ОБЪЯСНИ ЗАДАЧУ
: Пришёл купец к другому купцу в гости. Тот гостю обрадовался, и самовар растапливать стал. Наложил щепок в самоварную трубу, поджёг их сверху.
Почему алюминиевая кружка с чаем обжигает губы, а фарфоровая чашка с чаем нет?
Ветры бризы, возникающие на берегах морей. В каком направлении дуют они в летние дни днем и ночью и почему? Где надо расположить лед: снизу или сверху, чтобы охладить продукты?
Литература.
1.Алейникова Л.А. Теплообмен в природе и технике. Физика. Издательский дом «Первое сентября» №22, 2006 г.
2. Атаманченко А.К. Физика за малые деньги. Издательство «Школа – Пресс», «Физика в школе», 1998, №2.
3.Галин Н. М., Кириллов П. Л. Тепломассообмен. — М.: Энергоатомиздат, 1987.
4.Григорьев Б. А., Цветков Ф. Ф. Тепломассообмен: Учеб. пособие — 2-е изд. — М: МЭИ, 2005.
5.Касьянов В.А. Физика. 10 кл.: Учебн. для общеобразоват. учеб. заведений. – М.: Дрофа, 2005.
6. Крюков С.Н. Физика: третий вопрос в экзаменационных билетах: итоговая аттестация. 11 класс. – М.: Чистые пруды, 2007.
Крюков С.Н. Физика: третий вопрос в экзаменационных билетах: итоговая аттестация. 11 класс. – М.: Чистые пруды, 2007.
7.Материал из Википедии — свободной энциклопедии.
8. Мир физики в художественной литературе/ Ред.-сост. С.А.Тихомирова. – М.: Школа – Пресс, 1997.
9.Перышкин А.В. Физика. 8 кл.: Учеб. для общеобразоват.учреждений. – М.: Дрофа, 2004.
10.Семке А.И. Практические работы по физике с экологическим содержанием: Естественнонаучный профиль. 9-11 классы. – М.: Чистые пруды, 2008.
11. Семке А.И. Физика и живая природа: Занимательный материал к уроку. 7-9 классы. – М.: Чистые пруды, 2008.
12. Физика: Молекулярная физика и термодинамика с основами общей астрономии: Учеб.для 7 кл. общеобразоват.учреждений / Под редакцией А.А.Фадеевой. – М.: Просвещение, 2000.
13. http://images.yandex.ru
Реферат Конвекция В Природе – Telegraph
➡➡➡ ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ!
Реферат Конвекция В Природе
(c) 2019 — 2020. Информационный Центр НПИ.
Информационный Центр НПИ.
Работает на WordPress
|
Education Hub автор: WEN Themes
Конспект по физике для 8 класса «Конвекция». ВЫ УЗНАЕТЕ: Что такое конвекция. Какие виды конвекции существуют.
Если жидкости и газы обладают низкой теплопроводностью, то как же тогда нам удаётся достаточно быстро прогреть воздух в помещении и вскипятить воду?
Находясь рядом с горячей плитой, можно почувствовать тёплые струи воздуха, поднимающиеся над ней. Этот же эффект хорошо ощущается, если сверху поднести руку к горящей свече или горящей электрической лампочке.
Это физическое явления используется в игрушке «музыкальная ёлочка». Когда зажигаются свечки, под действием возникающих струй тёплого воздуха, направленных вверх, вертушка начинает вращаться, а колокольчики — звенеть.
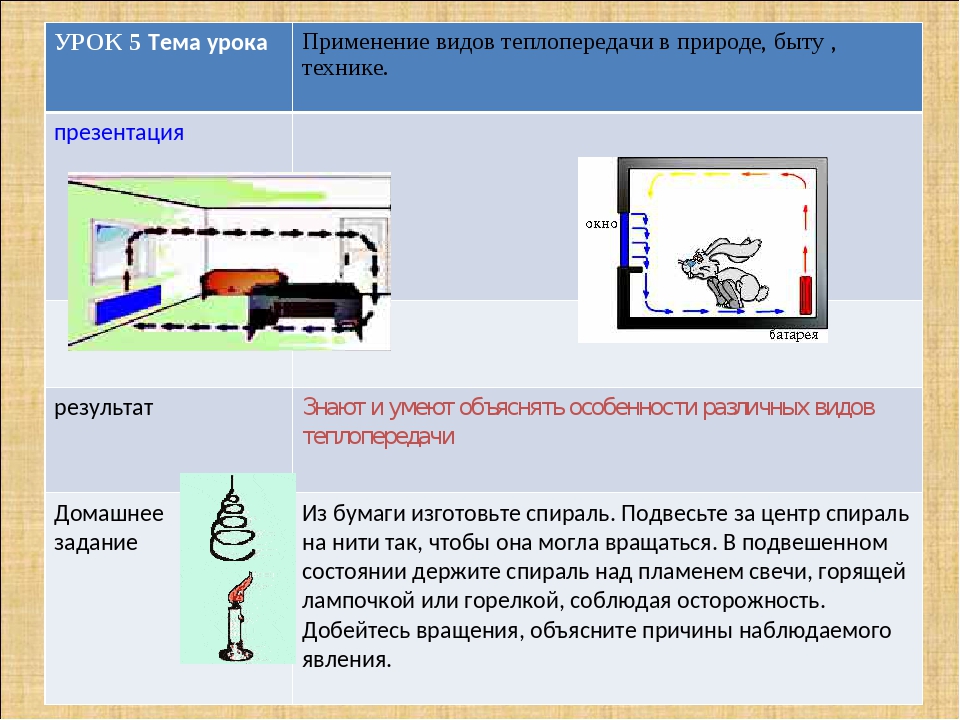
Если сделать из бумаги спираль и поместить её над включённой электрической лампочкой, как показано на рисунке, под действием поднимающегося нагретого воздуха спираль начнёт вращаться.
В этом опыте, так же как и в игрушке «музыкальная ёлочка», происходит нагревание воздуха, находящегося вблизи горящей лампочки или свечи. При этом он расширяется, и его плотность становится меньше плотности окружающего холодного воздуха. Под действием выталкивающей (архимедовой) силы со стороны холодного воздуха тёплый воздух вытесняется вверх. Образовавшийся воздушный поток и вращает спираль.
Аналогичные явления происходят и при нагревании жидкости, если источник тепла находится снизу.
Нагретые слои жидкости имеют меньшую плотность. Поэтому сила тяжести, действующая на них, становится меньше архимедовой силы, действующей на эти слои со стороны окружающей жидкости. Вследствие этого нагретые слои воды начинают подниматься вверх, а на их место опускаются более холодные слои жидкости. Этот процесс продолжается до тех пор, пока вся жидкость не прогреется одинаково по всему объёму.
Рассмотрим следующий опыт. На дно колбы с водой аккуратно опустим несколько кристалликов любого красителя (например, марганцовокислого калия). Начнём нагревать колбу снизу. Сразу станет хорошо видно, как со дна колбы поднимаются окрашенные струйки воды.
Начнём нагревать колбу снизу. Сразу станет хорошо видно, как со дна колбы поднимаются окрашенные струйки воды.
При нагревании воздуха или воды снизу происходит теплопередача, обусловленная переносом вещества и отличающаяся от теплопроводности. Этот процесс называют конвекцией (от лат. convectio — перенесение).
Конвекция — это вид теплопередачи, при котором энергия передаётся потоками (или струями) жидкости или газа.
В 7 классе мы говорили о том, что строение твёрдых тел отличается от строения жидкостей и газов. В твёрдых телах перенос вещества невозможен, поэтому конвекция наблюдается только в жидкостях и газах. В твёрдых телах она не происходит.
В закрытом помещении при работе отопительных приборов всегда возникает явление конвекции. Поэтому разница температур воздуха у пола и вблизи потолка может достигать нескольких градусов.
Различают два вида конвекции: естественную и вынужденную. Рассмотренные выше процессы нагревания воздуха и жидкости являются примерами естественной конвекции. Для её возникновения требуется либо подогрев жидкости или газа снизу, либо охлаждение сверху.
Для её возникновения требуется либо подогрев жидкости или газа снизу, либо охлаждение сверху.
Вынужденная конвекция наблюдается в случае, когда потоки нагретой или охлаждённой жидкости или газа переносятся под действием насосов или вентиляторов.
Конвекция является очень распространённым явлением в природе. Она выполняет основную роль в образовании в атмосфере потоков воздуха — ветров. Нагреваясь над одними участками земли и охлаждаясь над другими, воздух начинает циркулировать, перенося с собой энергию и влагу.
Эти же причины порождают дневные и ночные бризы — ветры, попеременно дующие от моря к суше днём и от суши к морю ночью. В течение дня температура земли становится заметно выше, чем температура моря. Соответственно и воздух, соприкасающийся с землёй, теплеет, расширяется и его плотность уменьшается. За счёт явления конвекции возникает циркулирующее течение воздушных масс. Ночью происходит обратный процесс, так как земля охлаждается до температуры, которая ниже, чем температура моря.
Благодаря конвекции птицы способны подолгу парить в воздухе. Разные участки земли прогреваются по-разному, и из-за этого возни кают восходящие воздушные потоки. Эти же потоки используются при полётах на дельтапланах.
Из-за конвекции нагретый пар из труб котельных и дым из печных труб при отсутствии ветра поднимаются вверх, так как имеют более низкую плотность, чем окружающий воздух.
В быту мы привыкли к тому, что при нагреве воды источник тепла располагается снизу. Нагревательные приборы в комнате также всегда расположены внизу.
Опыты показывают, что при нагревании сверху как жидкостей, так и газов конвекции не происходит. В этом случае просто не возникает выталкивающая сила, так как нагретые слои с меньшей плотностью располагаются сверху.
Естественная и вынужденная конвекция лежат в основе действия отопительной системы зданий. Нагревание воды может производиться либо непосредственно в здании при помощи специального котла, либо за пределами отапливаемого помещения при наличии системы центрального отопления. Горячая вода, поступающая в дом или нагретая в котле, поднимается вверх, а затем спускается по трубам и распределяется по помещениям, отдавая тепло в радиаторах.
Горячая вода, поступающая в дом или нагретая в котле, поднимается вверх, а затем спускается по трубам и распределяется по помещениям, отдавая тепло в радиаторах.
Вы смотрели Конспект по физике для 8 класса «Конвекция» .
Сохранить моё имя, email и адрес сайта в этом браузере для последующих моих комментариев.
Конвекция в природе
Конвекция | реферат [14,5 K], добавлен 26.01.2012
Конвекция в природе и в технике — Мир хоккея
Реферат на тему » Конвекция дома»
Конвекция в природе и технике
Курсовая Работа По Ветеринарной Патологической Анатомии
Темы Сочинений По Литературе Отцы И Дети
Сочинение На Тему Почему Интересна Этимология
Жаһанданудың Пайдасы Мен Зияны Аргументативті Эссе
Как Написать Практическая Значимость Курсовой Работы
Конвекция. Примеры конвекции в природе и технике
Цели урока: |
|
Форма урока: |
Поисковая беседа. |
Оборудование: |
Вертушка, электроплитка, экран, проектор, горелка, сухое горючее, колба с водой, кристаллики краски, две пробирки, заполненные водой и воздухом, изображение схемы водяного отопления здания. |
Ход урока
I. Организация класса.
II. Фронтальное повторение с целью подготовки учащихся к восприятию нового материала и выявления качества усвоения ими материала по теплопроводности.
Опрос
- Что такое плотность вещества? В каких единицах она измеряется?
- Как расположатся в закрытом сосуде следующие вещества: вода, воздух, спирт, ртуть? Почему?
- Что называют силой тяжести? В каких единицах ее измеряют?
- Что такое архимедова сила? Где она возникает? От чего зависит ее величина?
- Чем отличаются движения молекул в твердом теле, жидкости и газе?
- Какую энергию называют внутренней?
- Какими способами можно изменить внутреннюю энергию тела?
- Что понимают под теплопередачей?
- С каким видом теплопередачи мы познакомились на прошлом уроке?
Один из учеников с места рассказывает о теплопроводности.
Дополнительные вопросы.
- Почему в строительной технике широко используют пористый материал?
- Что называют тепловым движением?
Второй ученик с места рассказывает о теплопроводности различных веществ.
Дополнительные вопросы.
- Для чего зимой на радиаторы автомобилей надевают утеплительные чехлы?
- Что называют внутренней энергией тела?
Третий ученик отвечает по карточке.
- Почему старое зимнее пальто со сбившейся в комки ватой плохо греет?
- Быстродвижущийся автомобиль остановлен тормозами. Куда девалась при этом его кинетическая энергия?
- Зависит внутренняя энергия тела от движения тела или от положения этого тела?
Четвертый ученик (по карточке)
- Почему алюминиевая кружка с чаем обжигает губы, а фарфоровая чашка с чаем нет?
- Почему наружные части сверхзвуковых самолетов приходится охлаждать при помощи специальных аппаратов?
- Что называют теплопередачей?
Пятый ученик (по карточке)
- Почему можно небольшую стеклянную палочку, накаленную с одного конца, держать за другой конец, не обжигая пальцев, а железный прут нельзя?
- Как надо поступить (отпустить нить или растянуть сильнее) с слегка растянутой резиновой нитью, чтобы ее внутренняя энергия увеличилась? Что называется теплопроводностью?
Шестой ученик (по карточке)
- Расскажите, основываясь на своих жизненных наблюдениях, чтоб служить защитой от зимних морозов различным животным и птицам.
 Какую роль при этом играет теплопроводность меха, перьевого покрова, подкожного жира и т.п.?
Какую роль при этом играет теплопроводность меха, перьевого покрова, подкожного жира и т.п.? - Если к точильному камню прижать кусок стали, то сыплются искры. Каково их происхождение?
- Какую энергию называют внутренней энергией тела?
Седьмой ученик (по карточке)
- Какие их перечисленных веществ: бумага, солома, серебро, воздух, опилки- хорошие проводники тепла и плохие проводники тепла?
- Молоток будет нагреваться, когда им отбивают косу и когда он лежит на солнце в жаркий летний день. Назовите способы изменения внутренней энергии молотка в обоих случаях.
- Что называется тепловым движением?
Ответы учащихся должны быть полными, с объяснением.
Ответы комментируются и оцениваются. Оценки выставляются в дневники.
III. Изучение нового материала.
Пронаблюдаем интересное явление. Вертушка, помещенная над пламенем горелки, вращается.
Вертушка, помещенная над пламенем горелки, вращается.
Почему?
Учащиеся пытаются отвечать. Воздух нагрелся и расширился.
Может ли здесь тепло передаваться теплопроводностью?
Нет, так как воздух плохой проводник тепла.
Здесь мы наблюдаем иной вид теплопередачи, который называется конвекцией.
Конвекцией называется перенос энергии самими струями жидкости или газа.
Наблюдаем струи воздуха от той же горелки в проекции на экран.
Объяснение учителя (дважды).
Воздух, соприкасающийся с горелкой, нагревается и расширяется. Плотность расширившегося воздуха меньше, чем плотность холодного. Поэтому слой теплого воздуха всплывает в холодном воздухе. Ведь архимедова сила, действующая на теплый воздух со стороны холодного снизу вверх, больше, чем сила тяжести, действующая на теплый воздух, направленная вниз. Затем прогревается и начинает двигаться вверх следующий слой холодного воздуха и т.д. Перемещается само вещество.
А в каких веществах, кроме газа, может наблюдаться конвекция? Может ли она наблюдаться в твердых телах и жидкостях?
Почему?
Наблюдаем конвекцию в жидкостях на примере воды в колбе с опущенными в нее кристалликами краски и нагреваемой на электрической плитке.
Учащиеся повторяют объяснения учителя.
Итак, конвекцией называется перенос энергии самими струями жидкости или газа (записываем определение в тетрадях).
Затем уточняем понятия естественной или свободной и вынужденной конвекции.
А теперь думаем над вопросом:
Где надо расположить горелку, чтобы нагреть жидкость или газ?
Почему?
Посмотрим, что будет, если горелка располагается сверху. Наблюдаем опыт с пробирками, заполненными водой и воздухом нагреваемым сверху.
Нижние слои воздуха и воды холодные. Нет циркуляции. Нет конвекции.
Теплопроводность воздуха и воды мала. Поэтому придется долго ждать, пока воздух и вода прогреются.
Рассмотрим примеры конвекции в природе и технике.
- Ветры бризы, возникающие на берегах морей. В каком направлении дуют они в летние дни днем и ночью и почему?
Отвечают учащиеся, так как они это изучали на уроках географии в 5 классе. Бриз — это движение холодного воздуха.
- Тяга. Что такое горение? Без чего не может быть горение?
Отвечают учащиеся.
Учитель рассказывает о предположении в 15 столетии Леонардо да Винчи использовать трубу (металлическую) для создания тяги. «Где появляется огонь, — говорил Леонардо да Винчи — там вокруг него образуется воздушное течение, оно его поддерживает и усиливает».
Через 300 лет металлические трубы заменили в керосиновой лампе стеклянной, а на заводах — кирпичной.
Как же создается тяга?
Объясняет учитель. Чему выше труба, сооруженная над топкой, тем больше разница давлений наружного воздуха и воздуха в трубе. Поэтому тяга усиливается при увеличении высоты трубы. - Центральное водяное отопление — примеры использования свободной или вынужденной конвекции. Рассматривается его устройство, рассказывается о ТЭЦ.
IV. Презентация «Конвекция»
Приложение 1
V. Закрепление.
Закрепление.
- Что такое конвекция?
- В каких веществах ее можно наблюдать? В каких веществах она возможна?
- Как осуществляется конвекция в наших жилых комнатах?
- Где надо расположить лед: снизу или сверху, чтобы охладить продукты?
VI. Проверочный тест.
Ребята, вам предлагается ряд утверждений, среди которых как правильные, так и неверные. Прослушав высказывание, вы должны или согласиться с ним, или не согласиться. Если утверждение верное, то ставите знак «+» ,если утверждение неверное-ставите знак «-».
- При нагревании объем тела уменьшается, а при охлаждении увеличивается(-).
- Газ не имеет собственной формы и постоянного объема. Он полностью занимает весь предоставленный ему объем(+).
- Диффузия может происходить только в жидкостях или газах(-).
- Молекулы движутся только в жидкостях или газах, а в твердых телах покоятся(-).

- Теплопередача-это один из способов изменения внутренней энергии тела(+).
- Жидкость легко меняет свою форму(+).
- Конвекция возможна только в твердых телах и в газах(-).
- Конвекция играет основную роль в передаче тепла при нагревании воды в кастрюле, стоящей на плите(+).
- Нагревание и охлаждение воздуха в помещениях основано на конвекции(+).
- При увеличении температуры молекулы вещества увеличиваются в размере(-).
На дом: § 5, упр.2, В.И.Лукашик №971-974,979.
Домашнее задание комментируется. Обращается внимание на рисунок 12 и особенный интересный вопрос, стоящий в №979.
Межпредметные связи – с зоологией (см. вопрос шестому ученику), географией (6 класс, ветры бризы) и химией (8класс, горение).
Список использованной литературы
- А.В. Перышкин, Физика 8 кл.: Учебник для общеобразовательных учебных заведений – 3-е издание
- В.
 И. Лукашик, Е.В. Иванова, Сборник задач по физике для 7-9 классов общеобразовательных учреждений — 20-е издание
И. Лукашик, Е.В. Иванова, Сборник задач по физике для 7-9 классов общеобразовательных учреждений — 20-е издание - Ю.В. Щербакова, Занимательная физика на уроках и внеклассных мероприятиях. 7-9 классы – 2-е издание
- Н.А. Якушевская, Повторение и контроль знаний по физике на уроках и внеклассных мероприятиях, 7-9 классы: диктанты, тесты, кроссворды, внеклассные мероприятия – 2-е издание
- Л.А. Кирик, Физика-8, Методические материалы
Изучение нового вида теплопередачи — презентация онлайн
1. Разработка урока по теме: Изучение нового вида теплопередачи (конвекции). (8 класс)
Учитель физикиМОУ«Лицей №124» г.Барнаула
Новиков Алексей Владимирович
2007год.
2. Комментарий к уроку.
Урок разработан по технологии деятельностного метода(Петерсон Л.Г. программа «Школа 2000…») и соответствующей ей
системе дидактических принципов, которые синтезируют идеи
современной дидактики (А.
 Н. Леонтьев, П.Я. Гальперин, Л.В.
Н. Леонтьев, П.Я. Гальперин, Л.В.Занков, В.В. Давыдов и др.)
Тип урока – урок изучения нового материала. Данный урок –
четвёртый урок в теме «Тепловые явления» (программа и учебник
«Физика-8» Пёрышкина А.В.).Обучение организовано учителем на
деятельностной основе. Учащиеся, сами приходят к выводу о том,
что есть другой вид теплопередачи, кроме теплопроводности.
Формулируют сами цель урока: изучить новый вид теплопередачи
(учитель только вводит термин «конвекция»), сами делают и
формулируют выводы, сами оценивают результаты своей
деятельности на уроке.
Урок разбит на три этапа:
1. Ориентировочно — мотивационный этап.
2. Операционально-исполнительский этап.
3. Рефлексивно — оценочный этап.
Данный урок представлен на конкурс в связи с
появлением в школах компьютерного измерительного
комплекса лаборатории L-микро. В настоящее время
наблюдается дефицит методических разработок по
использованию данной измерительной системы.

Применение лаборатории L-микро позволяет совместить
преимущества живого эксперимента и компьютерной
обработки результатов, позволяет наглядно увидеть на
экране зависимость одной физической величины от
другой непосредственно в процессе измерений (в данном
уроке зависимость температуры от времени). Важно то,
что компьютером обрабатываются не какие-то
виртуальные, а реальные физические процессы
наблюдаемые здесь же.
Современное общество ожидает от образования
подготовленных, коммуникабельных людей с высоким
уровнем развития, с умениями одновременно работать в
группе и принимать самостоятельные решения. В рамках
данного урока, через групповую работу учащихся
развивается способность критически анализировать
полученную информацию, защищать обоснованно свою
точку зрения, находить верное решение.
На основе наблюдений и экспериментов учащиеся
могут сформировать знания о конвекции, ее механизме,
ее особенностях, учатся работать с графиками.

В опыте №3 показываются одновременно конвекция
в жидкости и газе, такое сочетание приборов ранее не
встречалось, конвекционная вертушка изготовлена
учащимися (видеоролик, на котором показан данный
опыт, создан автором, может быть использован в качестве
видеодемонстрации конвекции).
5. Урок: Изучение нового вида теплопередачи (конвекции).(8 класс)
Цели урока:• Познакомить учащихся с конвекцией,
выяснить причины её возникновения;
изучить примеры проявления в природе.
• Развитие коммуникативных навыков
учащихся через организацию групповой
работы.
• Развитие творческого мышления учащихся.
6. I.Ориентировочно-мотивационный этап:
I.Ориентировочномотивационный этап:1. Актуализация знаний о теплопередаче,
выравнивание стартовых позиций.
2. Создание ситуации успеха. Задание 1.
3. Проблемная ситуация, постановка учебной
задачи. Задание 2. Опыт №1.
7. II.Операционально-исполнительский этап:
II. Операциональноисполнительский этап:
Операциональноисполнительский этап:1.
2.
3.
4.
Задание 2. Опыт №3.
Задание 2. Опыт №4.
Задание 3.
Задание 4.
8. III. Рефлексивно-оценочный этап:
1. Обобщение темы урока. Задание 5.2. Итоговая самооценка.
3. Домашнее задание.
9. Оборудование и материалы:
Компьютерный измерительный блок.Мультимедийный проектор (телевизор), датчик
температуры (0-1200С) – 2 шт., рабочее поле со
стержнями, плата с зажимами — 2 шт., стакан из
термостойкого стекла, теплоизоляционная
перегородка. Штативы, алюминиевый стакан от
калориметра, прибор для демонстрации конвекции
в жидкости, спиртовка, вертушка для демонстрации
конвекции в газе, ложка, раздаточный материал.
10. Источники информации:
Тепловые явления. Руководство по выполнению
экспериментов. – М.: МГИУ, 2006.-36с
Тульчинский М.Е. качественные задачи по
физике в 6 –7 классах. Пособие для учителей. М.,
«Просвещение», 1976.

http://l-micro.ru
Петерсон Л.Г. Технология деятельностного
метода как средство реализации современных
целей образования. – М.: УМЦ «Школа 2000 …»,
2004.
11. Содержание урока
I.Ориентировочно-мотивационный этап:1. Актуализация знаний о теплопередаче,
выравнивание стартовых позиций.
2. Создание ситуации успеха.
Учитель организует работу в группах, выдаёт
раздаточный материал, предлагает выполнить
задание №1.
Учащиеся обращают внимание на то, что воздух
плохой проводник тепла. Вопросы простые, по
прошлой теме. Ситуация успеха.
Задание
№1
Заполните пропуски в тексте:
1.Двойные рамы предохраняют от холода, потому что
воздух, находящийся между ними, обладает …
теплопроводностью.
2. Медь, свинец, сталь, обладают … теплопроводностью.
3.Чтобы плодовые деревья не вымерзли, их
приствольные круги на зиму покрывают опилками.
Опилки обладают … теплопроводностью.
4.
 Чтобы ручка утюга не нагревалась, её делают из
Чтобы ручка утюга не нагревалась, её делают изпластмассы. Пластмасса обладает …
теплопроводностью.
5.В строительной технике широко применяют пористый
строительный материал (газобетон, пенопласт и т.д.),
потому что он обладает … теплопроводностью.
6.Вывод – у газов (воздуха) … теплопроводность.
Слова для вставки: плохой, хорошей.
3. Проблемная ситуация, постановка
учебной задачи.
Учитель показывает опыт №1
«Наблюдение конвекции в газе». Датчик
температуры нагревается когда он над
рукой и не нагревается когда он под ней.
14. Задание №2
Пронаблюдайте опыты и графики к ним,ответьте на вопросы.
Опыт №1.
1. Воздух плохой проводник, но тепло
проводит. Почему?
2. Когда рука сверху воздух не проводит
тепло, когда снизу – проводит. Почему?
3. Как изменилась температура датчика от
18,6 с до 35 с?
16. Ситуация успеха переходит в ситуацию всеобщего неуспеха
В конце первого этапа происходит формированиепроблемы и цели урока, не учителем, а самими
учащимися, на основе нехватки знаний для решения
данной проблемы.

Учащиеся отвечают на вопросы задания №2 к опыту №1
и приходят сами к выводу о том, что есть другой вид
теплопередачи, кроме теплопроводности.
Формулируют сами цель урока: изучить новый вид
теплопередачи.
После обсуждения учитель говорит название нового
вида теплопередачи, т. к. учащиеся не знают его, и
записывает на доске тему урока: «Конвекция».
17. II.Операционально-исполнительский этап:
Учитель показывает опыт №2 «Наблюдениеконвекции в газе». Над нагретым цилиндром и
под ним находятся датчики температуры.
Верхний датчик нагревается, нижний – нет.
18. Вопросы к опыту №2
1. Почемуверхний
термометр
нагревается
до
более
высокой
температуры, чем нижний?
2. Какова разность температур верхнего и
нижнего
термометра?
Сравните
разность температур в опыте №1 и
опыте №2.
Учитель демонстрирует опыт №3 «Наблюдение
естественной конвекции в жидкости и газе».

Учащиеся наблюдают одновременное
движение жидкости в трубке и вращение
вертушки и отвечают на вопросы.
1. Чем вызвано движение окрашенной
жидкости в сосуде?
2. Чем вызвано вращение вертушки?
Из обсуждения результатов опытов №2-3
учащиеся делают вывод:
энергия переносится струями вещества
(газа и жидкости).
21. Учитель демонстрирует опыт №4
«Наблюдениеконвекции при
смешивании горячей
и холодной воды,
разделённой до этого
перегородкой».
22. 1. Почему, при смешивании жидкости наблюдаются затухающие температурные кривые в виде пульсаций?
23. 2. Сравните температуру смеси с расчётной (среднее арифметическое между горячей и холодной водой).
24. 3. Почему на разной глубине датчики показывают разную температуру?
25. 4. Чему равна температура воды после перемешивания её ложкой?
5. Чем переносится энергия во всех опытах?6. Как могли бы измениться результаты опытов,
если вместо воды взять другую жидкость?
7.
 Что произошло бы в опыте №4, если сразу
Что произошло бы в опыте №4, если сразупосле удаления перегородки воду перемешать?
Учащиеся обращают внимание на то, что
естественная конвекция происходит из-за
различия температур в разных местах среды и
вызванного этим различия плотностей. При
вынужденной конвекции энергия нагретой
жидкости или газа переносится, главным образом,
с помощью насоса, мешалок и других устройств.
Учитель предлагает выполнить, а учащиеся
выполняют 3-е и 4-е задание.
Задание
№3
1. Продолжите и запишите в тетрадь определение.
Конвекция – это вид теплопередачи, при котором
энергия … .
2. Запишите виды конвекции.
Задание
№4
Ответьте на вопросы:
1.Почему жидкости и газы нагревают снизу?
2.Почему батареи отопления помещают обычно внизу
под окнами, кондиционеры – наверху?
3.Почему невозможна передача энергии конвекцией в
твёрдых телах?
4.Почему при нагревании жидкости сверху конвекция
не возникает?
29.
 III. Рефлексивно-оценочный этап: 1. Обобщение темы урока.
III. Рефлексивно-оценочный этап: 1. Обобщение темы урока.2. Итоговая самооценка.
3. Домашнее задание
Учитель предлагает выполнить задание №5,
ответить на вопросы анкеты.
Знаю, и могу Знаю, но надо Не знаю.
объяснить
подучить.
другому.
Что такое конвекция?
В
чём
различие
конвекцией
теплопроводностью?
между
и
Как происходит естественная
конвекция?
Как происходит вынужденная
конвекция?
Напишите коротко ответ на
вопрос: « В чём на ваш взгляд
преимущества
применения
компьютерного
блока
на
уроке?»
Учащиеся отвечают на обобщенные
вопросы по теме, соотносят свои
полученные знания с поставленной
целью. Удалось ли им достигнуть цели?
Рассматривают вопросы на проверку
понимания темы. Делают для себя
вывод, насколько они были успешны на
уроке, что необходимо предпринять,
чтобы лучше усвоить понятие
конвекции.
 Сдают анкету.
Сдают анкету.32. Домашнее задание:
1 уровень. §5, задачи №759-762,767.По желанию:
2 уровень. 1. Изготовить прибор для
демонстрации конвекции.
2. Подготовить доклад о
проявлении конвекции в природе и технике.
Учитель благодарит учащихся за работу на
уроке.
33. Спасибо за внимание!
• Автор:• Новиков Алексей
Владимирович,
• учитель физики высшей
категории МОУ «Лицей №124»
г. Барнаула
• Электронная почта:
[email protected]
34. конец
Конвекция — Физическая энциклопедия
КОНВЕКЦИЯ (от лат.
convectio — доставка) — перенос массы в результате перемещения сплошной среды
(газа, жидкости). Существуют различные виды К. в зависимости от причин, её порождающих;
наиболее распространённые — свободная, вынужденная и капиллярная К.
Свободная (естеств.) К.
возникает под действием архимедовых сил в поле силы тяжести, если имеют место
неоднородности плотности в отд. местах среды, к-рые возникают в результате наличия
в жидкости или газе разницы темп-р или концентраций примеси. Примером свободной
К. является движение воздуха в помещении при наличии отопительного прибора (радиатора
или печи). При увеличении темп-ры плотность газов уменьшается и нагретый воздух
всплывает наверх, а его место занимает более холодный воздух, опускающийся вниз
в др. части помещения. В результате в помещении развивается вихревое движение
воздуха. Свободная К. играет важную роль как в технике, так и в природе, она
определяет вертикальные перемещения воздушных масс в атмосфере и водяных масс
в морях и океанах. См. также Конвективный теплообмен.
местах среды, к-рые возникают в результате наличия
в жидкости или газе разницы темп-р или концентраций примеси. Примером свободной
К. является движение воздуха в помещении при наличии отопительного прибора (радиатора
или печи). При увеличении темп-ры плотность газов уменьшается и нагретый воздух
всплывает наверх, а его место занимает более холодный воздух, опускающийся вниз
в др. части помещения. В результате в помещении развивается вихревое движение
воздуха. Свободная К. играет важную роль как в технике, так и в природе, она
определяет вертикальные перемещения воздушных масс в атмосфере и водяных масс
в морях и океанах. См. также Конвективный теплообмен.
Вынужденная К. вызывается
внеш. механич. воздействием на среду. Примерами вынужденной К. являются движение
воздуха в помещении под действием вентилятора, течение жидкости в трубе под
действием гидронасоса и др. При движении тела в покоящейся среде относительное
движение среды в системе координат, связанной с телом, также представляет собой
частный случай вынужденной К. Физ. процессы, происходящие при вынужденной К.,
связанной с движением тел с большими скоростями в атмосфере, моделируются в аэродинамических трубах, где воспроизводится обтекание неподвижных моделей
потоком воздуха.
Физ. процессы, происходящие при вынужденной К.,
связанной с движением тел с большими скоростями в атмосфере, моделируются в аэродинамических трубах, где воспроизводится обтекание неподвижных моделей
потоком воздуха.
Капиллярная К. возникает
в объёмах жидкости со свободной поверхностью при существовании вдоль такой поверхности
перепадов поверхностного натяжения. Наиб. распространённой причиной появления
таких перепадов является изменение темп-ры вдоль свободной поверхности (термокапиллярная
К.), другая возможная причина — присутствие в жидкости поверхностно-активной
примеси с изменяющейся концентрацией. Интенсивность капиллярной К. довольно
мала. В обычных условиях она, как правило, не является существенной на фоне
вынужденной или свободной К. Однако в космич. технике, в условиях свободного
полёта за пределами атмосферы, когда интенсивность свободной К. становится весьма
незначительной из-за невесомости, именно благодаря капиллярной К. в сосудах
с жидкостью могут возникать слабые конвек-тивные движения, к-рые (как и свободноконвективные
движения, порождаемые микрогравитацией) существенно затрудняют практич. реализацию
условий невесомости. Н. А. Анфимов.
в сосудах
с жидкостью могут возникать слабые конвек-тивные движения, к-рые (как и свободноконвективные
движения, порождаемые микрогравитацией) существенно затрудняют практич. реализацию
условий невесомости. Н. А. Анфимов.
Предметный указатель >>
Естественная конвекция — обзор
6.1 Введение
Естественная конвекция — это форма конвективной теплопередачи, при которой движущей силой объемного движения или адвекции являются силы самоиндуцированной энергии. Эти силы могут быть вызваны градиентами температуры или концентрации. В этой книге мы фокусируем наше внимание на естественном конвекционном потоке и теплопередаче за счет температурных градиентов. В свете вышеприведенного утверждения интуитивно очевидно, что поток и теплопередача будут тесно связаны в естественной конвекции.Из-за объемного движения передача тепла естественной конвекцией будет в несколько раз больше, чем при молекулярной проводимости. Даже в этом случае, поскольку в естественной конвекции не участвуют никакие внешние факторы, такие как насос или воздуходувка, скорости будут небольшими, обычно порядка см / с или десятков см / с, в отличие от нескольких м / с, которые обычно наблюдается при принудительной конвекции. Как следствие этого, скорость теплопередачи при естественной конвекции будет ниже, чем при принудительной конвекции в конкретной ситуации, если все другие управляющие переменные, такие как разность температур, геометрия и среда, одинаковы.Напомним, что традиционно конвекция, вызванная внешним воздействием, таким как насос, вентилятор или воздуходувка, получила название «принудительной» конвекции. В связи с этим естественная конвекция, в которой нет «принуждения», так сказать, внешнего воздействия, также известна как свободная конвекция.
Как следствие этого, скорость теплопередачи при естественной конвекции будет ниже, чем при принудительной конвекции в конкретной ситуации, если все другие управляющие переменные, такие как разность температур, геометрия и среда, одинаковы.Напомним, что традиционно конвекция, вызванная внешним воздействием, таким как насос, вентилятор или воздуходувка, получила название «принудительной» конвекции. В связи с этим естественная конвекция, в которой нет «принуждения», так сказать, внешнего воздействия, также известна как свободная конвекция.
Рассмотрим две бесконечно широкие горизонтальные параллельные пластины при температурах T 1 и T 2 соответственно. Пусть пространство между двумя пластинами занято такой средой, как воздух. Существуют две возможности, как показано на рис.6.1.
Рисунок 6.1. Среда заключена между двумя параллельными пластинами с температурами T 1 и T 2 . (A) T 1 & gt; T 2 (B) T 1 & lt; Т 2 .
В ситуации (A) верхняя пластина горячее, чем нижняя пластина. Ввиду этого, когда воздух (или любая другая среда в этом отношении) нагревается от верхней пластины, он остается наверху, поскольку нагретый воздух менее плотный. Таким образом, это представляет собой устойчивое устройство с точки зрения конвекции, а это означает, что в этом случае естественная конвекция не возникает.Даже в этом случае теплопередача будет происходить между T 1 и T 2 через воздух через путь теплопроводности или молекулярной диффузии. Также может происходить излучение, но это зависит от разницы между T 1 и T 2 , радиационных свойств поверхностей и так далее. Радиационному теплообмену посвящена восьмая глава этой книги.
Пока достаточно сказать, что на рис. 6.1A представлена ситуация «нет потока», «нет естественной конвекции». Ситуация на рис.6.1B, тем не менее, интересно. Нагреваемая пластина находится внизу, поэтому воздух, контактирующий с ней, нагревается и поднимается вверх. Как только воздух попадает на верхнюю пластину, он охлаждается, становится более плотным и возвращается к нижней пластине, чтобы снова нагреться и продолжить цикл. Это типичная естественная конвекция.
Как только воздух попадает на верхнюю пластину, он охлаждается, становится более плотным и возвращается к нижней пластине, чтобы снова нагреться и продолжить цикл. Это типичная естественная конвекция.
Применения этого легиона, например, для охлаждения электронного оборудования, такого как трансформаторы, теплопередачи в окнах с двойным стеклопакетом, солнечных коллекторов, теплогидравлики в ядерных реакторах и так далее.Список бесконечен. Чтобы подчеркнуть, что приведенный выше не является банальным и забитым списком применений естественной конвекции, мы хотели бы обратить ваше внимание на ядерную катастрофу на Фукусима-дайити, которая произошла 11 марта 2011 года. Катастрофа впервые началась при землетрясении, и как только землетрясение было обнаружено, ядерные реакторы остановились. Однако из-за проблем с сетью электроснабжение прекратилось, и аварийные дизель-генераторные установки начали обеспечивать циркуляцию теплоносителя через активные зоны ядерных реакторов для отвода остаточного тепла (которое не прекращается немедленно и соответствует типичному q = ae − bt вид распределения, где a и b — известные константы, t — время, а q — тепловыделение). Однако землетрясение вызвало цунами высотой почти 50 футов, затопившее подвал завода, парализовав аварийный генератор. Это привело к так называемой аварии с потерей теплоносителя (LOCA), расплавлению реактора и выбросу радиации в атмосферу. Основная проблема здесь заключалась в том, что система отвода остаточного тепла была разработана только для случая принудительной конвекции, и система не могла предотвратить LOCA, если аварийные генераторы вышли из строя. Система отвода остаточного тепла, которая работала бы даже при естественной конвекции, потребовала бы значительных инженерных усилий, включения дымоходов и т. Д., Но спасла бы положение.Даже в обычном ноутбуке тепловая трубка отводит тепло, выделяемое процессором, но конденсация пара на самой тепловой трубке должна происходить за счет естественной конвекции и излучения со всех поверхностей ноутбука. Стоит помнить, что в конечном итоге любое выделяемое тепло должно выделяться в окружающий воздух или в близлежащее озеро, пруд, море или космическое пространство.
Однако землетрясение вызвало цунами высотой почти 50 футов, затопившее подвал завода, парализовав аварийный генератор. Это привело к так называемой аварии с потерей теплоносителя (LOCA), расплавлению реактора и выбросу радиации в атмосферу. Основная проблема здесь заключалась в том, что система отвода остаточного тепла была разработана только для случая принудительной конвекции, и система не могла предотвратить LOCA, если аварийные генераторы вышли из строя. Система отвода остаточного тепла, которая работала бы даже при естественной конвекции, потребовала бы значительных инженерных усилий, включения дымоходов и т. Д., Но спасла бы положение.Даже в обычном ноутбуке тепловая трубка отводит тепло, выделяемое процессором, но конденсация пара на самой тепловой трубке должна происходить за счет естественной конвекции и излучения со всех поверхностей ноутбука. Стоит помнить, что в конечном итоге любое выделяемое тепло должно выделяться в окружающий воздух или в близлежащее озеро, пруд, море или космическое пространство. Задача специалиста по теплопередаче состоит в том, чтобы обеспечить и спроектировать этот путь, который был бы надежным, безопасным, экономичным, экологически чистым и соответствовал всем руководящим принципам и законам.
Задача специалиста по теплопередаче состоит в том, чтобы обеспечить и спроектировать этот путь, который был бы надежным, безопасным, экономичным, экологически чистым и соответствовал всем руководящим принципам и законам.
Коэффициент конвективной теплопередачи — обзор
Оцените температуру воздуха на выходе и эффективность коллектора, показанного на рисунке 3.30, для следующих характеристик коллектора:
Ширина коллектора, Вт = 1,2 м.
Длина коллектора, L = 4 м.
Глубина воздушного канала, с = 15 мм.
Полная инсоляция, G т = 890 Вт / м 2
Температура окружающей среды, T a = 15 ° C = 288 K.
Эффективное (τα) = 0,90.
Коэффициент теплопотери, U L = 6,5 Вт / м 2 -K.
Коэффициент излучения пластины поглотителя, ε p = 0,92.
Коэффициент излучения задней пластины, ε b = 0,92.
Массовый расход воздуха = 0,06 кг / с.
Температура воздуха на входе, T i = 50 ° C = 323 K.
Решение
Здесь нам нужно начать с принятия значений для T p и T b . Для экономии времени подобраны правильные значения; но в реальной ситуации решение нужно искать путем итераций. Предполагаемые значения: T p = 340 K и T b = 334 K (они должны быть в пределах 10 K). По этим двум температурам можно определить среднюю температуру воздуха по формуле
4 (Tm, воздух) 3 = (Tp + Tb) (Tp2 + Tb2)
, откуда
Tm, воздух = (Tp + Tb) (Tp2 + Tb2) 43 = (340 + 334) (3402 + 3342) 43 = 337 K
Коэффициент теплопередачи излучения от поглотителя к задней пластине равен
час, p-g2 = σ ( Tp + Tb) (Tp2 + Tb2) (1 / ɛp) + (1 / ɛb) -1 = (5. 67 × 10-8) (340 + 334) (3402 + 3342) (1 / 0,92) + (1 / 0,92) -1 = 7,395 Вт / м2-К
67 × 10-8) (340 + 334) (3402 + 3342) (1 / 0,92) + (1 / 0,92) -1 = 7,395 Вт / м2-К
От T м , воздух , следующие свойства воздуха можно получить из Приложения 5:
μ = 2,051 × 10-5 кг / м-ск = 0,029 Вт / м-Kcp = 1008 Дж / кг-K
Из гидродинамики гидравлический диаметр воздушный канал равен
D = 4 (Площадь поперечного сечения потока, увлажняемый периметр) = 4 (Ws2W) = 2s = 2 × 0,015 = 0,03
Число Рейнольдса равно
Re = ρVDμ = m˙DAμ = 0.06 × 0,03 (1,2 × 0,015) × 2,051 × 10-5 = 4875,5
Следовательно, поток является турбулентным, для которого применимо следующее уравнение: Nu = 0,0158 (Re) 0,8 . Так как Nu = ( h c D ) / k , коэффициент конвективной теплопередачи определяется как
hc, pa = hc, ba = (kD) 0,0158 (Re) 0,8 = (0,0290,03) 0,0158 (4875,5) 0,8 = 13,625 Вт / м2-К
Из уравнения. (3,69),
h = hc, p-a + 1 (1 / hc, ba) + (1 / hr, pb) = 13,625 + 1 (1 / 13,625) + (1 / 7,395) = 18,4 Вт / м2-К
Из уравнения. (3,72),
(3,72),
F ′ = hh + UL = 18,418,4 + 6,5 = 0,739
Поглощенное солнечное излучение составляет
S = Gt (τα) = 890 × 0,9 = 801 Вт / м2
Из уравнения. (3,74),
To = Ti + 1UL [S-UL (Ti-Ta)] [1-exp (-AcULF′m˙cp)] = 323+ (16,5) [801-6,5 (323-288)] [1-exp (- (1,2 × 4) × 6,5 × 0,7390,06 × 1007)] = 351 K
Следовательно, средняя температура воздуха составляет ½ (351 + 323) = 337 K, что равно значению предполагалось раньше. Если есть разница в двух средних значениях, требуется итерация. Для такого рода задач требуется всего одна итерация, чтобы найти правильное решение с использованием предполагаемых значений, которые дают новую среднюю температуру.
Из уравнения. (3,58),
FR = m˙cpAcUL {1-exp [-ULF’Acm˙cp]} = 0,06 × 1008 (1,2 × 4) × 6,5 {1-exp [-6,5 × 0,739 × (1,2 × 4) 0,06 × 1008]} = 0,614
Из уравнения. (3,76),
Qu = AcFR [S-UL (Ti-Ta)] = (1,2 × 4) × 0,614 [801-6,5 (323-288)] = 1690 Вт
Наконец, эффективность коллектора составляет
η = QuAcGt = 1690 (1,2 × 4) × 890 = 0,396
Комплексные исследования смешанной конвекции Fe-этиленгликоль-наножидкости внутри корпуса с различными препятствиями с использованием решеточного метода Больцмана
Исходя из предположений и геометрии, массы, импульса, а уравнения энергии записываются следующим образом: 8 :
$$ \ frac {\ partial u} {{\ partial x}} + \ frac {\ partial v} {{\ partial y}} = 0 $$
(1)
$$ \ rho_ {nf} \ left ({\ frac {\ partial u} {{\ partial t}} + u \ frac {\ partial u} {{\ partial x}} + v \ frac {\ partial u} {{\ partial y}}} \ right) = — \ frac {\ partial p} {{\ partial x}} + \ mu_ {nf} \ left ({\ frac {{\ partial ^ {2} u }} {{\ partial x ^ {2}}} + \ frac {{\ partial ^ {2} u}} {{\ partial y ^ {2}}}} \ right) $$
(2)
$$ \ rho_ {nf} \ left ({u \ frac {\ partial v} {{\ partial x}} + v \ frac {\ partial v} {{\ partial y}}} \ right) = — \ frac {\ partial p} {{\ partial y}} + \ mu_ {nf} \ left ({\ frac {{\ partial ^ {2} v}} {{\ partial x ^ {2}}} + \ frac {{\ partial ^ {2} v}} {{\ partial y ^ {2}}}} \ right) + F_ {y} $$
(3)
$$ u \ frac {\ partial T} {{\ partial x}} + v \ frac {\ partial T} {{\ partial y}} = \ alpha_ {nf} \ left ({\ frac {{\ partial ^ {2} T}} {{\ partial x ^ {2}}} + \ frac {{\ partial ^ {2} T}} {{\ partial y ^ {2}}}} \ right) + \ гидроразрыв {{Q_ {O}}} {{\ left ({\ rho C_ {p}} \ right) _ {nf}}} \ left ({T — T_ {c}} \ right) $$
(4)
где в уравнении. (3), \ ({F} _ {y} \) — полная объемная сила в направлении y.
(3), \ ({F} _ {y} \) — полная объемная сила в направлении y.
$$ F_ {y} = \ left ({\ rho \ beta} \ right) _ {nf} g_ {y} \ left ({T — T_ {m}} \ right) $$
(5)
Обзор LBM
В этом исследовании использованная LBM аналогична применяемой модели ссылок 2,3,4 . Тепловая модель LBM включает две функции распределения f и g для областей расхода и температуры соответственно. В данной презентации реализована модель D2Q9, которая указана на рис.{eq} \ left ({{\ varvec {x}}, t} \ right) — f_ {i} \ left ({{\ varvec {x}}, t} \ right)} \ right] + {\ Delta } t {\ varvec {c}} _ {{\ varvec {i}}} {\ varvec {F}} $$
(6)
$$ g_ {i} \ left ({{\ varvec {x}} + {\ varvec {c}} _ {{\ varvec {i}}} {\ Delta} t, t + {\ Delta} t } \ right) = g_ {i} \ left ({{\ varvec {x}}, t} \ right) + \ frac {{{\ Delta} t}} {{\ tau_ {D}}} \ left [ {g_ {i} \ left ({{\ varvec {x}}, t} \ right) — g_ {i} \ left ({{\ varvec {x}}, t} \ right)} \ right] $$
(7)
где Δt, c i , F, \ ({\ tau} _ {\ upsilon} \) и \ ({\ tau} _ {D} \) — время релаксации LBM, прерывистой скорости сети в направлении i, внешняя сила в направлении скорости сети, время покоя для потока и температурная область, соответственно. {2} = 1/3 \) для модели D2Q2, а C s — скорость звука, равная \ (c / \ sqrt 3 \), \ (c = {\ Delta} x / {\ Delta} t = {\ Delta} y / {\ Delta} t \) 34 .
{2} = 1/3 \) для модели D2Q2, а C s — скорость звука, равная \ (c / \ sqrt 3 \), \ (c = {\ Delta} x / {\ Delta} t = {\ Delta} y / {\ Delta} t \) 34 .
$$ c_ {i} = \ left \ {{\ begin {array} {* {20} l} 0 \ hfill & {i = 0} \ hfill \\ {c \ left ({\ cos \ left [ {\ left ({i — 1} \ right) \ frac {\ pi} {2}} \ right], \ sin \ left [{\ left ({i — 1} \ right) \ frac {\ pi} { 2}} \ right]} \ right)} \ hfill & {i = 1 — 4} \ hfill \\ {c \ left ({\ cos \ left [{\ left ({i — 5} \ right) \ frac {\ pi} {2} + \ frac {\ pi} {4}} \ right], \ sin \ left [{\ left ({i — 5} \ right) \ frac {\ pi} {2} + \ frac {\ pi} {4}} \ right]} \ right)} \ hfill & {i = 5-8} \ hfill \\ \ end {array}} \ right \} $$
(10)
Рисунок 2Чтобы учесть эффекты выталкивающей силы в модели, силовой член в формуле.(5) определяется с использованием следующего уравнения 35 .
$$ F = 3w_ {i} g_ {y} \ beta \ Delta \ Theta $$
(11)
где \ (g_ {y} = {\ varvec {g}} \ cos \ theta \) и \ ({\ Theta} \) — безразмерная температура, которая определяется как:
$$ {\ Theta} = \ frac {{T — T_ {c}}} {{T — T_ {H}}} $$
(12)
Теплофизические свойства наножидкости
Следующие уравнения используются для определения теплофизических свойств наножидкости 36,37 . {2}} {137750} — \ frac {3020039T} {330600} + \ frac {338555} {2204} \)
{2}} {137750} — \ frac {3020039T} {330600} + \ frac {338555} {2204} \)
Другие свойства наножидкости рассчитываются с использованием вязкости и теплопроводности наножидкости 36 .
$$ \ nu_ {nf} = \ frac {{\ mu_ {nf}}} {{\ rho_ {nf}}} $$
(18)
$$ \ alpha_ {nf} = k_ {nf} / \ left ({\ rho c_ {pnf}} \ right) $$
(19)
Используя приведенные выше утверждения, можно определить время релаксации для областей расхода и температуры 36 .
$$ {\ uptau} _ {{\ upnu}} = 3 \ nu_ {nf} \ left ({lbm} \ right) + 0,5 $$
(20)
$$ \ tau_ {D} = 3 \ alpha_ {nf} \ left ({lbm} \ right) + 0.5 $$
(21)
Наконец, микроскопические переменные рассчитываются с помощью следующих уравнений.
$$ {\ uprho} _ {{{\ text {nf}}}} = \ mathop \ sum \ limits_ {i} f_ {i} $$
(22)
$$ {\ uprho} {\ varvec {u}} = \ mathop \ sum \ limits _ {{\ varvec {i}}} f_ {i} {\ varvec {c}} _ {{\ varvec {i} }} $$
(23)
$$ {\ Theta} = \ mathop \ sum \ limits_ {i} g_ {i} $$
(24)
Также в таблице 1 представлены теплофизические свойства наночастиц Fe и этиленгликолевой жидкости.Среднее число Нуссельта (\ ({\ mathrm {Nu}} _ {\ mathrm {avg}}) \) является наиболее важным безразмерным параметром для отчета о теплопередаче, которое может быть получено в следующей форме путем интегрирования из местного числа Нуссельта на правая стенка 30 .
$$ {\ text {Nu}} _ {y} = — \ frac {{k_ {nf}}} {{k_ {f}}} \ frac {H} {{{\ Delta} T}} \ гидроразрыв {\ partial T} {{\ partial x}} | _ {x = L} $$
(25)
$$ {\ text {Nu}} _ {{{\ text {avg}}}} = \ frac {1} {{\ text {H}}} \ smallint Nu_ {y} dy $$
(26)
Таблица 1 Теплофизические свойства базовой жидкости и НЧ. {- 5} $$
{- 5} $$(27)
где \ (nn \) — количество раздражений.
Граничные условия
На неподвижных стенках применяется граничное условие возврата. Для восточной, западной и южной стен представлены следующие уравнения соответственно 35 :
$$ f_ {3} = f_ {1}, f_ {6} = f_ {8}, f_ {7} = f_ { 5} $$
(28)
$$ f_ {1} = f_ {3}, f_ {8} = f_ {6}, f_ {5} = f_ {7} $$
(29)
$$ f_ {2} = f_ {4}, f_ {5} = f_ {7}, f_ {6} = f_ {8} $$
(30)
Для северной стены, двигаясь слева направо, уравнения граничных условий:
$$ \ begin {align} \ rho_ {N} & = \ frac {1} {{1 + v_ {N}}} \ left [{f_ {0} + f_ {2} + f_ {3} + 2 \ left ({f_ {2} + f_ {6} + f_ {5}} \ right)} \ right] \\ f_ {7} & = f_ {5} + 0.5 \ left ({f_ {1} — f_ {3}} \ right) — \ frac {1} {6} \ rho_ {N} v_ {N} — 0,5 \ rho_ {N} u_ {N} \\ f_ {8} & = f_ {6} + 0,5 \ left ({f_ {3} — f_ {1}} \ right) — \ frac {1} {6} \ rho_ {N} v_ {N} + 0,5 \ rho_ {N} u_ {N} \\ f_ {4} & = f_ {2} — \ frac {2} {3} \ rho_ {N} v_ {N} \\ \ end {align} $$
(31)
Для источников тепла температура известна \ (\ left ({{\ varvec {T}} _ {{\ varvec {H}}} = 1} \ right) \). Таким образом, для источника тепла на правой стене:
Таким образом, для источника тепла на правой стене:
$$ g_ {3} = T_ {H} \ left ({w \ left (3 \ right) + w \ left (1 \ right)} \ right) — g_ {1} $$
(32)
$$ g_ {7} = T_ {H} \ left ({w \ left (7 \ right) + w \ left (5 \ right)} \ right) — g_ {5} $$
(33)
$$ g_ {6} = T_ {H} \ left ({w \ left (6 \ right) + w \ left (8 \ right)} \ right) — g_ {8} $$
(34)
и для южной стены:
$$ g_ {2} = T_ {H} \ left ({w \ left (2 \ right) + w \ left (4 \ right)} \ right) — g_ {4 } $$
(35)
$$ g_ {5} = T_ {H} \ left ({w \ left (5 \ right) + w \ left (7 \ right)} \ right) — g_ {7} $$
(36)
$$ g_ {6} = T_ {H} \ left ({w \ left (6 \ right) + w \ left (8 \ right)} \ right) — g_ {8} $$
(37)
Безразмерные числа, которые используются в этой работе для определения характеристики потока, — это Ri, Ra и Pr, которые определяются как:
$$ Ra = \ frac {g \ beta} {{\ nu \ alpha}} {\ Delta} TL ^ {3} $$
(38)
$$ pr = \ nu / \ alpha $$
(39)
$$ Ri = \ frac {Ra} {{pr \ cdot Re ^ {2}}} $$
(40)
Как видно из приведенных выше уравнений, когда Ri> 1, влияние естественной конвекции более важно, а когда Ri <1, им можно пренебречь.
Визуализация теплопередачи МГД естественной конвекцией теплопередачи наножидкости в призматическом корпусе
Abstract
Тепловая передача за счет естественной конвекции для визуализации характеристик теплопередачи методом теплопроводов в призматической полости, заполненной наножидкостью Cu-H 2 O учет двух различных температурных граничных условий выполняется численно. Две верхние наклонные стенки нагреваются при низкой температуре, в то время как нижняя стенка нагревается в двух различных условиях нагрева, таких как однородный температурный режим и линейный температурный режим.Две вертикальные стены утеплены. Для решения нелинейных уравнений с частными производными для численных расчетов применяется метод конечных элементов с взвешенной остаточной формой Галеркина. Тепловые линии, контуры изотермы, контуры линий тока и число Нуссельта используются для отображения результатов численного моделирования для параметров модели, названных объемной долей наночастиц, числом Гартмана и числом Рэлея. Результаты показывают, что скорость теплопередачи оказывает значительное влияние на тепловые граничные условия и форму наночастиц.Значение переноса температуры значительно увеличивается с увеличением числа Рэлея, а также с увеличением объемной доли наночастиц. Число Гартмана положительно влияет на поток жидкости и перенос температуры. Характеристики переноса тепла с использованием метода тепловых линий также выполняются для прогнозирования лучшего преобразования энергии по сравнению с контурами изотермы. Кроме того, для исследования наилучших характеристик теплопередачи также используются различные типы наножидкостей.
Результаты показывают, что скорость теплопередачи оказывает значительное влияние на тепловые граничные условия и форму наночастиц.Значение переноса температуры значительно увеличивается с увеличением числа Рэлея, а также с увеличением объемной доли наночастиц. Число Гартмана положительно влияет на поток жидкости и перенос температуры. Характеристики переноса тепла с использованием метода тепловых линий также выполняются для прогнозирования лучшего преобразования энергии по сравнению с контурами изотермы. Кроме того, для исследования наилучших характеристик теплопередачи также используются различные типы наножидкостей.
Условия темы: Прикладная математика, Машиностроение
Введение
Наножидкости состоят из наночастиц, таких как Co, Zn, Ag, Cu, Al 2 O 3 , TiO 2 и Fe 3 O 4 и т. Д.и обычные жидкости, называемые водой, моторным маслом, керосином и т. д. Эти наножидкости широко используются в качестве благородных жидкостей во многих инженерных и промышленных приложениях. Основными задачами исследования наножидкостей является поиск высотных возможных решений при низких затратах. В последние несколько лет междисциплинарные исследования наножидкостей расширились для прекрасного использования в реальной жизни в промышленности и машиностроении. Например, солнечное водонагревание, теплообменники, топливные элементы, дизельное сгорание, двигатели транспортных средств, ядерные системы, бытовые холодильники и смазочные материалы.Чой 1 исследовал технологию наножидкостей для ее настоящего и будущего включения. Buongiorno 2 выполнял конвективный перенос температуры в наножидкостях. Jou et al. 3 численно исследовали свободное обычное увеличение температуры в полости прямоугольной формы с использованием наножидкостей. Ece et al. 4 выполнено о влиянии магнитного поля на свободноконвективный поток с использованием прогрева и холодных прилегающих стен внутри прямоугольного ограждения.
Основными задачами исследования наножидкостей является поиск высотных возможных решений при низких затратах. В последние несколько лет междисциплинарные исследования наножидкостей расширились для прекрасного использования в реальной жизни в промышленности и машиностроении. Например, солнечное водонагревание, теплообменники, топливные элементы, дизельное сгорание, двигатели транспортных средств, ядерные системы, бытовые холодильники и смазочные материалы.Чой 1 исследовал технологию наножидкостей для ее настоящего и будущего включения. Buongiorno 2 выполнял конвективный перенос температуры в наножидкостях. Jou et al. 3 численно исследовали свободное обычное увеличение температуры в полости прямоугольной формы с использованием наножидкостей. Ece et al. 4 выполнено о влиянии магнитного поля на свободноконвективный поток с использованием прогрева и холодных прилегающих стен внутри прямоугольного ограждения. Das et al. 5 исследовали нежидкости и их применение в науке и технике. Озтоп и др. 6 исследовали конвективное течение в частично подогретой полости прямоугольной формы с использованием наножидкостей.
Das et al. 5 исследовали нежидкости и их применение в науке и технике. Озтоп и др. 6 исследовали конвективное течение в частично подогретой полости прямоугольной формы с использованием наножидкостей.
Перенос температуры за счет плавучести, вызванный течением, в наши дни становится монументальным инженером-чудом. Системы теплопередачи и охлаждения с естественной конвекцией в закрытых помещениях представляют собой серьезное чудо в геофизике, геотермальных резервуарах, конструкции теплообменников, механической и электронной промышленности.Многие ученые и исследователи очень заинтересованы в изучении распределения переноса температуры, теплового потока и структуры потока. Например, Ghasemi et al. 7 , выполненное относительно свободно конвективного температурного потока с использованием наножидкостей CuO-вода внутри висящей полости. Рахмам и др. 8 исследовали комбинированный конвективный поток в прямоугольном корпусе. Wong et al. 9 исследовали как настоящее, так и будущее зачисление наножидкостей.Seleh et al. 10 исследовали свободно-конвекционный температурный поток с использованием наножидкостей в полости трапециевидной формы. Арани и др. 11 исследовали в отношении естественного конвекционного потока в наножидкостях внутри квадратного корпуса с использованием нагретого лезвия. Basak et al. 12 исследованы в отношении анализа тепловых линий при свободноконвекционном потоке с использованием наножидкостей в квадратном корпусе для нескольких нагретых граничных систем.Cheikh et al. 13 исследовано на предмет конвективного потока наножидкостей в квадратной полости в условиях неравномерного нагрева. Свободный конвекционный температурный поток в наножидкости с использованием постоянного теплового потока был исследован Seyyedi et al. 14 . Salma et al. 15 исследовали свободноконвекционный поток наножидкостей внутри призматической оболочки.
Wong et al. 9 исследовали как настоящее, так и будущее зачисление наножидкостей.Seleh et al. 10 исследовали свободно-конвекционный температурный поток с использованием наножидкостей в полости трапециевидной формы. Арани и др. 11 исследовали в отношении естественного конвекционного потока в наножидкостях внутри квадратного корпуса с использованием нагретого лезвия. Basak et al. 12 исследованы в отношении анализа тепловых линий при свободноконвекционном потоке с использованием наножидкостей в квадратном корпусе для нескольких нагретых граничных систем.Cheikh et al. 13 исследовано на предмет конвективного потока наножидкостей в квадратной полости в условиях неравномерного нагрева. Свободный конвекционный температурный поток в наножидкости с использованием постоянного теплового потока был исследован Seyyedi et al. 14 . Salma et al. 15 исследовали свободноконвекционный поток наножидкостей внутри призматической оболочки.
В процессе двумерной конвективной теплопередачи тепловая линия является лучшим методом понимания и анализа теплового потока.Реальный путь конвективной теплопередачи или системы рекуперации тепла визуализируется методом тепловых линий. Линии тока полностью иллюстрируют течение жидкости, тогда как контуры изотермы описывают просто распределения температуры, которые не подходят для визуализации переноса температуры. Метод тепловых линий аналогичен линиям тока, что важно для анализа движения жидкости. Методы теплопроводов — лучшие меры для поиска систем восстановления температуры, а также фактического пути передачи температуры за счет конвекции.Тепловые линии обычно иллюстрируют температурные функции, которые удовлетворяют уравнению энергии, в то время как функция тока удовлетворяет уравнениям сохранения массы. Линия тепла связана с числом Нуссельта, которое зависит от безразмерной формы преобразования. Линии теплового потока представлены линиями тепла, которые иллюстрируют траекторию теплового потока, перпендикулярную изотермическим линиям при конвективном переносе температуры.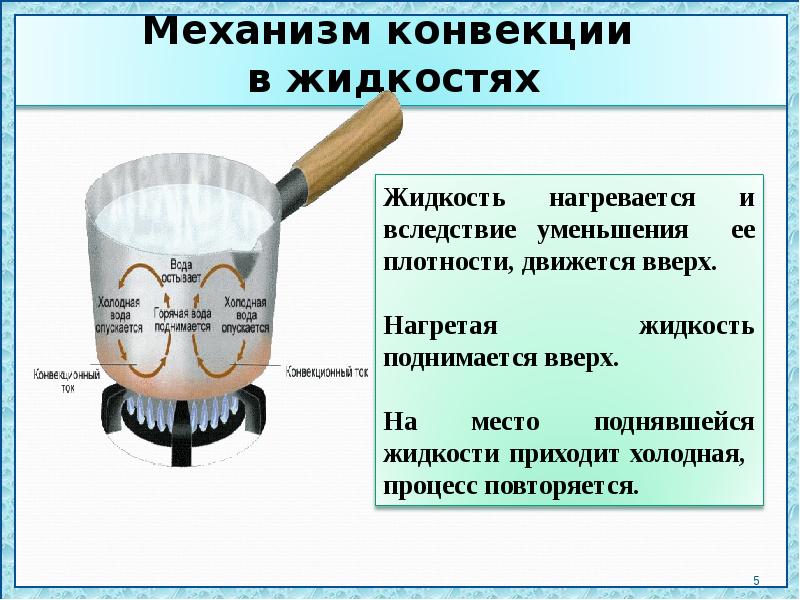 Тепловые линии математически представлены тепловой функцией, и каждая тепловая функция соответствует постоянной функции.Кимура и Беджан 16 впервые представили концепцию тепловой линии. Salma et al. 17 дополнительно изучили визуализацию тепловых линий на магнитно-гидродинамическом комбинированном конвективном потоке, включая нагретый блок. Уддин и др. 18 исследовал основные концепции, а также области применения наножидкостей. Alam et al. 19 исследованы в отношении исследования тепловых линий при свободном конвективном течении, а также передачи температуры в призматической полости с использованием МКЭ.Alsabery et al. 20 исследовал эксперимент по анализу тепловых линий над конвекционным потоком в квадратном корпусе с использованием синусоидальных температурных мутаций. Шейха и др. 21 исследовали конвективный температурный поток наножидкостей внутри трапециевидной полости.
Тепловые линии математически представлены тепловой функцией, и каждая тепловая функция соответствует постоянной функции.Кимура и Беджан 16 впервые представили концепцию тепловой линии. Salma et al. 17 дополнительно изучили визуализацию тепловых линий на магнитно-гидродинамическом комбинированном конвективном потоке, включая нагретый блок. Уддин и др. 18 исследовал основные концепции, а также области применения наножидкостей. Alam et al. 19 исследованы в отношении исследования тепловых линий при свободном конвективном течении, а также передачи температуры в призматической полости с использованием МКЭ.Alsabery et al. 20 исследовал эксперимент по анализу тепловых линий над конвекционным потоком в квадратном корпусе с использованием синусоидальных температурных мутаций. Шейха и др. 21 исследовали конвективный температурный поток наножидкостей внутри трапециевидной полости.
Влияние магнитогидродинамики (МГД) на потоки естественной конвекции, а также теплопередачу наножидкостей в последние годы привлекло к себе пристальное внимание в связи с их широким разнообразием приложений в области науки, промышленности и техники.По этой причине многие ученые и исследователи были заинтересованы в проведении численного моделирования для изучения потока жидкости, переноса тепла и температурного потока. Kalbani et al. 22 исследовал конвективный температурный поток в наножидкостях внутри квадратной полости на предмет существования магнитогидродинамики. Латифа и др. 23 исследовали конвективный температурный поток внутри квадратной полости с использованием магнитогидродинамики. Шеремет и др. 24 , 25 исследовали естественную конвекцию наножидкости в различных полостях, используя математическую модель Буонджорно. Они обнаружили, что дополнительные наночастицы усиливают конвекционный поток. Другое исследование 26 — 28 также исследовало естественную конвекцию наножидкостей внутри полостей. Основная цель этого исследования — проанализировать конвекционный поток в призматической полости с использованием наножидкости медь-вода для визуализации температурного потока, а также нахождения правильного пути изменения температуры.Влияние объемной доли наночастиц, числа Гартмана и числа Рэлея на распределение температуры, а также поток жидкости в призматической полости производятся численно и наблюдаются в физической точке зрения.
Другое исследование 26 — 28 также исследовало естественную конвекцию наножидкостей внутри полостей. Основная цель этого исследования — проанализировать конвекционный поток в призматической полости с использованием наножидкости медь-вода для визуализации температурного потока, а также нахождения правильного пути изменения температуры.Влияние объемной доли наночастиц, числа Гартмана и числа Рэлея на распределение температуры, а также поток жидкости в призматической полости производятся численно и наблюдаются в физической точке зрения.
Постановка задачи
Физическая модель
Физическая модель, учитывающая двухмерный ламинарный поток несжимаемой свободной конвекции в полости призматической формы, равномерно заряженной наножидкостью Cu-H 2 O. Мы взяли воду (H 2 O) в качестве базовой жидкости и медь (Cu) в качестве наночастиц.L представляет собой высоту и длину базовой стены шкафа. Естественная конвекция возникла из-за разницы температур между нагретыми и холодными стенами. Нижняя стенка нагревается при T = Tc + (Th-Tc) (1-x / L) (линейно) и T = Th (равномерно), в то время как верхние наклонные стенки нагреваются при низкой температуре T = Tc. Вертикальные стены сохраняются при утеплении. Нижняя стенка представляет координату x, а левая вертикальная стенка представляет координату y. Ускорение свободного падения действует в отрицательном направлении оси y.Считается, что наночастицы однородно диспергированы в базовой жидкости, и между базовой жидкостью и наночастицами не происходит динамического и теплового скольжения. Отсутствие скользящих стенок учитывается для всех твердых границ. Для исследования используются различные типы базовой жидкости, такие как керосин и этиленгликоль (EG), и различные типы наночастиц, такие как кобальт (Co), оксид алюминия (Al 2 O 3 ) и оксиды титана (TiO 2 ). среднее число Нуссельта у обогреваемой стены Рис.показали схематическое зрелище геометрии, привязанной к системе координат, а теплофизические свойства наночастиц, включая базовые жидкости, представлены в таблице.
Нижняя стенка нагревается при T = Tc + (Th-Tc) (1-x / L) (линейно) и T = Th (равномерно), в то время как верхние наклонные стенки нагреваются при низкой температуре T = Tc. Вертикальные стены сохраняются при утеплении. Нижняя стенка представляет координату x, а левая вертикальная стенка представляет координату y. Ускорение свободного падения действует в отрицательном направлении оси y.Считается, что наночастицы однородно диспергированы в базовой жидкости, и между базовой жидкостью и наночастицами не происходит динамического и теплового скольжения. Отсутствие скользящих стенок учитывается для всех твердых границ. Для исследования используются различные типы базовой жидкости, такие как керосин и этиленгликоль (EG), и различные типы наночастиц, такие как кобальт (Co), оксид алюминия (Al 2 O 3 ) и оксиды титана (TiO 2 ). среднее число Нуссельта у обогреваемой стены Рис.показали схематическое зрелище геометрии, привязанной к системе координат, а теплофизические свойства наночастиц, включая базовые жидкости, представлены в таблице.
Схематический вид призматической оболочки.
Таблица 1
Теплофизические характеристики твердых частиц и базовой жидкости (см. 33 ).
| Базовая жидкость / наночастицы | c p [JKg −1 K −1 ] | ρ [км −3 ] | k [Wm −1 K −1 ] | μ [кгм −1 с −1 ] | β × 10 –5 [K −1 ] | σ [Sm −1 ] | Pr |
|---|---|---|---|---|---|---|---|
| Вода (H 2 O) | 4179 | 997. 1 1 | 0,613 | 0,001003 | 21 | 5,5 × 10 –6 | 6,8377 |
| Керосин | 2090 | 780 | 0,149164 | 6,0 | 23,004 | ||
| Этиленгликоль (EG) | 2382,1 | 1117,48 | 0,2492 | 0,022 | 57 | 1,07 × 10 –8 210350 | . 3 3 |
| Cu | 385 | 8933 | 400 | — | 1,67 | 5.96 × 10 7 | — |
| Co | 1003420890 | 9034208 | 1,3 | 1,602 × 10 7 | — | ||
| Al 2 O 3 | 765 | 3970 | 40 | — | 835 1035 | 3,5 —||
| TiO 2 | 686. 2 2 | 4250 | 8,9538 | — | 0,90 | 2,6 × 10 7 | — |
Математическая модель
Управляющие уравнения для вышеупомянутого x + v∂u∂y = -∂p∂x + μnf∂2u∂2x + ∂2u∂2y
2
ρnfu∂v∂x + v∂v∂y = -∂p∂y + μnf∂2v∂ 2x + ∂2v∂2y + ρβnfg (T-Tc) -σnfB02v
3
u∂T∂x + v∂T∂y = αnf∂2T∂2x + ∂2T∂2y
4
Граничные условия
Вкл. нижняя стенка:
случай II: u = v = 0, T = Tc + (Th-Tc) 1-xL
5b
На вершине наклонной стены: u = v = 0, T = Tc
5c
на перпендикулярной стене: u = 0, v = 0, ∂T∂x = 0
5d
Физические и термические свойства наножидкостей
Для улучшения тепловых характеристик наножидкостей важны тепловые и физические свойства наножидкостей. Следующие физические и термические характеристики наножидкостей приняты во внимание и перечислены как вязкость, плотность, температуропроводность, теплоемкость, теплопроводность, коэффициент теплового расширения и электропроводность, соответственно (см. Kalbani et al. 29 ):
Следующие физические и термические характеристики наножидкостей приняты во внимание и перечислены как вязкость, плотность, температуропроводность, теплоемкость, теплопроводность, коэффициент теплового расширения и электропроводность, соответственно (см. Kalbani et al. 29 ):
(ρcp) nf = (1-ϕ) (ρcp) bf + ϕ (ρcp) sp
9
knfkbf = ksp + (n-1) kbf- (n-1) (kbf-ksp) ϕksp + (n- 1) kbf + (kbf-ksp) ϕ
10
(ρβ) nf = (1-ϕ) (ρβ) bf + ϕ (ρβ) sp
11
σnf = σsp + 2σbf-2 (σbf-σsp ) ϕσsp + 2σbf + (σbf-σsp) ϕσbf
12
Анализ размеров
Мы вводим следующие безразмерные переменные для сокращения уравнений.( 1 ) — ( 4 ) в безразмерную форму, включая граничные условия ( 5a ) — ( 5d ):
X = xL, Y = yL, U = uLαbf, V = vLαbf, θ = T-TcTh-Tc, P = pL2ρnfαbf2
13
Основные уравнения в безразмерной форме выражаются как:
U∂U∂X + V∂U∂Y = -ρbfρnf∂P∂X + Prρbfρnf∂2U∂ 2X + ∂2U∂2Y
15
U∂V∂X + V∂V∂Y = -ρbfρnf∂P∂Y + Prρbfρnf∂2V∂2X + ∂2V∂2Y + ρβnfρnfβbfRaPrθ-ρbfρnf ∂X + V∂θ∂Y = αnfαbf∂2θ∂2X + ∂2θ∂2Y
17
В приведенных выше основных безразмерных уравнениях Ra = gβbfTh-TcL3υbfαbf — число Рэлея, Pr = υbfαbf — число Прандтля, а Ha = BoLσbf / μbf — число Гартмана.
Безразмерные формы граничных условий
На нижней стенке:
Случай II: U = 0, V = 0, θ = 1-X
18b
Наклонные стены на вершине: U = 0, V = 0, θ = 0
18c
На левой и правой вертикальных стенах: u = 0, v = 0, ∂θ∂X = 0
18d
Расчет числа Нуссельта
Выражается местное и среднее число Нуссельта на нижней прогретой стене соответственно как:
NuL = LqwkbfTh-Tc, где qw = -knf∂T∂yy = 0
19
Nuav = -knfkbf∫01∂θ∂YdX
20
Вычислительный процесс
Управляющее безразмерное уравнение .( 14 ) — ( 17 ), включая граничные условия ( 18a ) — ( 18d ), выполняются с применением анализа методом конечных элементов взвешенной остаточной формы Галеркина. Zienkiewicz et al. 30 подробно описал численный метод. Во-первых, неоднородный треугольный элемент формируется путем дискретизации области решения на ограниченное количество сеток. Шесть узловых треугольных элементов используются для развития этого метода. Затем интегральные уравнения формируются из основных уравнений в частных производных с использованием метода взвешенных невязок Галеркина.Квадратурная техника Гаусса также используется во всех частях интегральных уравнений. Эти уравнения также модифицируются с использованием граничных условий. В эти алгебраические уравнения применяется итерационная техника Ньютона – Рафсона для решения этих алгебраических уравнений в матричной форме. Критерий сходимости этого метода задается как Mn + 1-Mn≤10-5, где M представляет U, V, θ как зависимые переменные, а n — номер итерации.
Шесть узловых треугольных элементов используются для развития этого метода. Затем интегральные уравнения формируются из основных уравнений в частных производных с использованием метода взвешенных невязок Галеркина.Квадратурная техника Гаусса также используется во всех частях интегральных уравнений. Эти уравнения также модифицируются с использованием граничных условий. В эти алгебраические уравнения применяется итерационная техника Ньютона – Рафсона для решения этих алгебраических уравнений в матричной форме. Критерий сходимости этого метода задается как Mn + 1-Mn≤10-5, где M представляет U, V, θ как зависимые переменные, а n — номер итерации.
Тест независимости от сетки
Комплексный эксперимент с независимостью от сетки используется для обеспечения независимого от сетки решения существующей проблемы призматической оболочки, когда Ra = 105, ϕ = 0.04 и n = 3 (сферическая форма наночастиц). Используются пять различных систем неоднородной сетки в пределах разрешения: нормальное, точное, более мелкое, сверхтонкое и чрезвычайно точное, включая элементы 1365, 2116, 5699, 14 514 и 20 584. Для вышеупомянутых элементов рассчитывается среднее число Нуссельта (Nuav) для понимания тонкости сетки, которая показана на рис. Элементы 14 514 немного отличаются от результатов, полученных для элементов 20 584. Следовательно, элементы размером 14 514 используются для численных расчетов, чтобы получить требуемое сеточно-независимое решение.
Для вышеупомянутых элементов рассчитывается среднее число Нуссельта (Nuav) для понимания тонкости сетки, которая показана на рис. Элементы 14 514 немного отличаются от результатов, полученных для элементов 20 584. Следовательно, элементы размером 14 514 используются для численных расчетов, чтобы получить требуемое сеточно-независимое решение.
Среднее число Нуссельта различных элементов с Ra = 105, Pr = 6,8377, n = 3, ϕ = 0,04.
Проверка кода
Настоящие результаты сравниваются с данными Ghasemi et al. 24 для проверки точности с использованием контуров линий тока (левый столбец) и контуров изотермы (правый столбец), когда ϕ = 0,02,
Ra = 105 и Ha = 30, что показано на рис. Настоящий числовой код также подтверждается числовыми данными Ghasemi et al. 31 для различных чисел Рэлея и объемной доли наночастиц с учетом двумерного естественного конвекционного потока Al 2 O 3 -водная наножидкость при наличии магнитного эффекта (Ha = 30). Настоящий числовой код также сравнивается с Wan et al. 32 с учетом Pr = 0,07 и квадратной полости, заполненной воздухом. Текущий код перенесен для квадратной полости, заполненной воздухом, для сравнения. Результаты представляют собой хорошее соответствие при использовании текущего числового кода в таблице.
Настоящий числовой код также сравнивается с Wan et al. 32 с учетом Pr = 0,07 и квадратной полости, заполненной воздухом. Текущий код перенесен для квадратной полости, заполненной воздухом, для сравнения. Результаты представляют собой хорошее соответствие при использовании текущего числового кода в таблице.
Сравните текущие результаты (нижний ряд) и Ghasemi et al. 31 (верхний ряд) при ϕ = 0,03, Ra = 105 и Ha = 30.
Таблица 2
Сравнение численных данных среднего числа Нуссельта (Nuav) с Ghasemi et al. 31 и Wan et al. 32 для различных чисел Рэлея и объемной доли наночастиц.
| ϕ = 0 | ϕ = 0,02 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Ra | Ghasemi et al. 24 | Ван и др. 25 25 | Настоящее исследование | Ghasemi et al. 24 | Настоящее исследование | ||||
| 10 3 | 1.002 | 1.117 | 1.002 | 1.060 | 1.060 | ||||
| 10 4 | 1.183 | 2.254 | 1.182 | 1.212 | 1.20358 | 1. 2035 2035 | 3,138 | 3,138 | 3,097 |
| 10 6 | 7,907 | 8,976 | 7,820 | 7,979 | 7,796 | ||||
результаты обсуждения
, контуры изотермы и тепловые линии для анализа температурного потока свободной конвекции, а также потока жидкости в призматическом корпусе.Наночастицы меди сферической формы (n = 3) обрабатываются жидкостью на водной основе. Численные результаты обсуждались для различных параметров, называемых объемной долей наночастиц (ϕ), числом Гартмана (Ha) и числом Рэлея (Ra) при потоке жидкости, теплопередаче, а также характеристиками переноса температуры с учетом изотермических линий, линий тока, тепловых линий, локальных и локальных среднее число Нуссельта с использованием двух различных температурных граничных условий вдоль горизонтальной стенки.
На рисунке показано влияние числа Рэлея Ra (= 103-106) при ϕ = 0.04 и Ha = 10 на линиях тока, контурах изотермы, а также на линиях тепла в условиях равномерного прогрева на горизонтальной стенке. На рисунке (а) показано, что два симметричных ролика, вращающихся в противоположных направлениях относительно центральной вертикальной линии, сформированы внутри полости с каждым Ra. Также вихревые проушины расположены по соседству с центром половины поперечного сечения каверны, хотя дно имеет равномерно нагретый. Левая камера циркулирует против часовой стрелки, тогда как правая камера циркулирует по часовой стрелке внутри корпуса.Физический смысл этого заключается в том, что плотность холодной жидкости у верхних наклонных стенок выше, чем у нагретой жидкости у нижней стенки внутри корпуса. Тяжелая жидкость движется вниз, в то время как относительно редко частая жидкость движется вверх. Затем объемная жидкость вталкивается в термический пограничный слой, расположенный рядом с нижней горячей стенкой, и совершает вращающийся узор. Для увеличения Ra две рециркуляционные клетки растут. Это означает, что нагретая жидкость сильнее ускоряется за счет эффекта плавучести.
Для увеличения Ra две рециркуляционные клетки растут. Это означает, что нагретая жидкость сильнее ускоряется за счет эффекта плавучести.
Результаты числа Рэлея Ra на ( a ) Контуры обтекания, ( b ) Контуры изотермы ( c ) Тепловые линии для однородных тепловых граничных условий на нижней стенке при ϕ = 0,04 и Ha = 10.
Режим передачи температуры (теплопроводность или конвекция), а также полезность температуры определяются по контурам изотермы. На рисунке (b) показано, что при низком числе Рэлея Ra (= 103,104) контуры изотермы почти параллельны у нижней горячей стенки, что указывает на то, что конвекция в полости слабее.Электропроводность — это основной режим температурного потока внутри корпуса из-за однородного прогрева на нижней стенке. Небольшая компактность контуров изотермы наблюдается также в центре каверны, что представляет собой плохо конвективный температурный поток. При увеличении Ra контуры изотермы оказываются излишне искаженными, а также исчезают в центре полости, образуя форму гриба. Для Ra = 105,106 конкретный рисунок изотерм, подобный грибу, указывает на то, что температурная энергия течет внутри жидкости полости с нижней нагретой стороны за счет потенциальных эффектов плавучести.Рисунок (c) демонстрирует, что теплопроводы чистые и примерно параллельны перпендикулярным стенкам, что приводит к изменению температуры в результате теплопроводности. Плотность тепловых линий рядом с нагретой стенкой усиливает, а также препятствует более высокому параметру Ra, обусловленному плавучестью. Компактность теплопроводов увеличивается в середине шкафа из-за сильной конвекции. Кроме того, при более высоком Ra внутри корпуса создаются два симметричных небольших вихря относительно центральной вертикальной линии, что согласуется с структурой функции тока.Следовательно, конвекция является доминирующей формой температурного потока при верхнем параметре плавучести.
Для Ra = 105,106 конкретный рисунок изотерм, подобный грибу, указывает на то, что температурная энергия течет внутри жидкости полости с нижней нагретой стороны за счет потенциальных эффектов плавучести.Рисунок (c) демонстрирует, что теплопроводы чистые и примерно параллельны перпендикулярным стенкам, что приводит к изменению температуры в результате теплопроводности. Плотность тепловых линий рядом с нагретой стенкой усиливает, а также препятствует более высокому параметру Ra, обусловленному плавучестью. Компактность теплопроводов увеличивается в середине шкафа из-за сильной конвекции. Кроме того, при более высоком Ra внутри корпуса создаются два симметричных небольших вихря относительно центральной вертикальной линии, что согласуется с структурой функции тока.Следовательно, конвекция является доминирующей формой температурного потока при верхнем параметре плавучести.
Влияние числа Рэлея (Ra = 103-106) на контуры линий тока, изотермы и тепловые линии при ϕ = 0,04 и Ha = 10 для условий линейного обогрева на нижней стенке показаны на рис. Соответственно. Рисунок (а) показывает, что на контуры обтекаемой формы полностью не влияют частицы наножидкости внутри корпуса. Температура горизонтальной стороны выше по сравнению с болтающимися сторонами, поэтому соседняя жидкость нижней стенки получает температуру, и после этого эта жидкость выходит вверх в более холодную жидкость, в результате создается циркуляционная ячейка, в результате чего значение передачи температуры увеличивается на более холодных стенках.Физический смысл этого заключается в том, что при достаточной разнице температур между нагретыми и охлажденными стенками внутри корпуса создается потенциальная подъемная сила. При низком Ra воздействие конвекции мало заметно из-за незначительного действия силы инерции в механизмах температурного потока. Для верхних значений Ra (= 105,106) контуры линий тока разлагаются, и появляется одно потенциальное распространение в жидкость внутри полости для увеличения интенсивности конвективного потока температуры, в результате чего возникает вторичная циркуляция в верхних углах, соседних с наклонной.
Соответственно. Рисунок (а) показывает, что на контуры обтекаемой формы полностью не влияют частицы наножидкости внутри корпуса. Температура горизонтальной стороны выше по сравнению с болтающимися сторонами, поэтому соседняя жидкость нижней стенки получает температуру, и после этого эта жидкость выходит вверх в более холодную жидкость, в результате создается циркуляционная ячейка, в результате чего значение передачи температуры увеличивается на более холодных стенках.Физический смысл этого заключается в том, что при достаточной разнице температур между нагретыми и охлажденными стенками внутри корпуса создается потенциальная подъемная сила. При низком Ra воздействие конвекции мало заметно из-за незначительного действия силы инерции в механизмах температурного потока. Для верхних значений Ra (= 105,106) контуры линий тока разлагаются, и появляется одно потенциальное распространение в жидкость внутри полости для увеличения интенсивности конвективного потока температуры, в результате чего возникает вторичная циркуляция в верхних углах, соседних с наклонной. стены.На рисунке (б) показано, что для меньшего Ra (= 103,104) наблюдаются параллельные контуры изотермы соседней прогретой стенки из-за потенциальной проводимости формы температурных распределений. Для верхнего числа Рэлея также наблюдается превышение искаженных контуров изотермы в центре полости из-за увеличения конвекции внутри корпуса. Для Ra = 106 компактность и высокая плотность изотермического рисунка отмечаются рядом с горизонтальными нагретыми и свисающими холодными стенками крыши, что представляет собой высокий температурный градиент в этих областях.
стены.На рисунке (б) показано, что для меньшего Ra (= 103,104) наблюдаются параллельные контуры изотермы соседней прогретой стенки из-за потенциальной проводимости формы температурных распределений. Для верхнего числа Рэлея также наблюдается превышение искаженных контуров изотермы в центре полости из-за увеличения конвекции внутри корпуса. Для Ra = 106 компактность и высокая плотность изотермического рисунка отмечаются рядом с горизонтальными нагретыми и свисающими холодными стенками крыши, что представляет собой высокий температурный градиент в этих областях.
Влияние числа Рэлея (Ra) на ( a ) Линии тока ( b ) Изотермы ( c ) Тепловые линии для линейно теплового граничного условия на нижней стенке, когда ϕ = 0,04 и Ha = 10.
To представляет температурный поток внутри корпуса, теплопроводный температурный поток -∂θ∂X, ∂θ∂Y используется для тепловой функции, тогда как конвективный температурный поток Uθ, Vθ используется для отображения температурного потока. Тепловые линии представляют собой способ изменения температуры, возникающий в прогретом режиме, а финиш в холодном режиме.На рисунке (c) показано, что тепловые линии распределены почти без разбора в соответствии с циркуляцией по часовой стрелке и против часовой стрелки для меньшего Ra (= 103) от горизонтальной нагретой стороны к верхним наклонным холодным сторонам из-за низкой силы потока жидкости, а также температуры, протекающей в основном за счет теплопроводности. .
Тепловые линии представляют собой способ изменения температуры, возникающий в прогретом режиме, а финиш в холодном режиме.На рисунке (c) показано, что тепловые линии распределены почти без разбора в соответствии с циркуляцией по часовой стрелке и против часовой стрелки для меньшего Ra (= 103) от горизонтальной нагретой стороны к верхним наклонным холодным сторонам из-за низкой силы потока жидкости, а также температуры, протекающей в основном за счет теплопроводности. .
По мере увеличения Ra интенсивность потока значительно увеличивается, рисунок тепловых линий постепенно разрушается, и в верхнем углу внутри ограждения создается дополнительная крошечная прокатная камера.Интенсивность температурного потока у нижней утепленной стенки выше, чем у верхней холодной стенки. Следовательно, для определения температурного потока, а также анализа теплопередачи, тепловые линии являются достаточными механизмами. Кроме того, тепловые линии выглядят как обтекаемые контуры для более высоких значений Ra.
Рисунок, соответственно, демонстрирует результаты объемной доли наночастиц (ϕ = 0,0.025,0.05,0.1) при Ra = 105 на контурах обтекания, контурах изотермы и тепловых линиях для однородной нижней прогретой стенки.На рисунке (а) показано, что две противоположно симметричные камеры встречного вращения относительно центральной вертикальной линии сформированы внутри полости для равномерного нагрева стенки. Левая циркуляция внутри корпуса осуществляется по часовой стрелке, а другая ячейка — по часовой стрелке. Эта конкретная форма является результатом однородного подогрева граничного условия на горизонтальной стороне. Физическая причина этой конкретной формы обтекаемых контуров уже рассказана. При увеличении ϕ характер линий тока почти аналогичен чистому типу проводимости.Кроме того, при добавлении наночастиц в базовую жидкость внутри полости наблюдается очень незначительное влияние наножидкостей на конвекцию.
Влияние объемной доли наночастиц (ϕ) на ( a ) Линии тока ( b ) Изотермы ( c ) Тепловые линии для однородного теплового граничного условия на нижней стенке при Ra = 105 и Ha = 10.
На рисунке (b) показаны изотермические контуры, расставленные в центральной плоскости внутри полости, образуя особую форму гриба.Это показывает, что энергия течет внутри жидкости с горизонтальной нагретой стороны. На этом же рисунке видно, что контуры изотермы практически параллельны соседним разогретым и холодным стенкам. Соседняя с жидкостью горизонтальная нагретая стенка принимает температуру и движется вверх в более холодную жидкость. Следовательно, на холодной стене увеличивается температурный поток. На этом рисунке показано, что имеется плотный узор изотермы возле нагретых и охлажденных стенок, который указывает на высокий градиент температуры в этих областях.Это обстоятельство остается неизменным при добавлении наночастиц в корпус. На рисунке (c) показано, что тепловые линии идентичны для всех значений наночастиц, и внутри корпуса создаются два симметричных небольших вихря относительно центральной вертикальной линии, что согласуется с моделью функции тока. При ϕ = 0,1 компактность теплопроводов увеличивается в середине шкафа из-за сильной конвекции.
Рисунок, соответственно, иллюстрирует влияние объемной доли наночастиц (ϕ = 0,0.025,0.05,0.1) с фиксированным Ra = 105 на контурах линий тока, контурах изотермы и тепловых линиях для стенки с линейно-нижним обогревом. Рисунок (а) демонстрирует, что линии тока параллельны друг другу соседней нагретой стенке из-за проводимости, а также вторичного вихря, развивающегося на верхних углах, соседних с наклонной стенкой внутри полости. При более высоком значении наночастиц изотермы искажаются, и в середине корпуса замечается один массивный вихрь. Рисунок (б) показывает, что параллельные изотермы соседствуют с прогретыми и остывшими стенками.Мы уже наблюдали эту подобную особую форму. На рисунке (c) показаны компактные тепловые линии посередине внутри полости, что указывает на область высокотемпературного потока. Линии тока также почти параллельны у нижней прогретой стенки и похожи на изотермы, которые мы уже наблюдали. При увеличении количества наночастиц плотность тепловых линий увеличивается в центре корпуса.
Влияние объемной доли наночастиц (ϕ) на ( a ) Линии тока ( b ) Изотермы ( c ) Тепловые линии для линейно теплового граничного условия на нижней стенке при Ra = 105 и Ha = 10.
Влияние числа Гартмана (Ha) с использованием линий тока, изотерм и тепловых линий показано на рис. и для равномерного температурного режима и линейных тепловых граничных условий, соответственно, когда Ra = 105 и ϕ = 0,04. Эти цифры показывают, что число Гартмана оказывает значительное влияние на температурную область. На рисунке (а) показаны линии тока для различных чисел Гартмана. На этих рисунках показана аналогичная симметричная картина линий тока для всех рассмотренных значений числа Гартмана. Две симметричные вращающиеся ячейки сформированы внутри полости, где левая ячейка вращается против часовой стрелки, а правая ячейки вращаются по часовой стрелке.Сила вращения уменьшается с увеличением числа Гартмана, то есть сила потока уменьшается с сильным магнитным полем. При приложении внешнего магнитного поля более сильное поле воздействует на движущуюся жидкость, которая обладает магнитной восприимчивостью, что ослабляет циркуляцию потока внутри корпуса. Кроме того, сила Лоренца, возникающая при приложении магнитного поля, по своей природе препятствует изменению его генерации в случае движения жидкости, и, следовательно, это силовое поле ослабляет потоки внутри корпуса.На рисунке (б) видно, что изотермические линии все более искажаются внутри каверны и плотнее у нижней нагретой стенки при отсутствии числа Гартмана. При низком числе Гартмана (Ha = 0) более высокий градиент температуры наблюдается у донной прогретой стенки. Плотность линий тока уменьшается под действием более сильного магнитного поля. Кроме того, изотермические линии смещаются вверх ближе к средней части нижней нагретой стенки, что указывает на область более высокого теплопереноса.
При приложении внешнего магнитного поля более сильное поле воздействует на движущуюся жидкость, которая обладает магнитной восприимчивостью, что ослабляет циркуляцию потока внутри корпуса. Кроме того, сила Лоренца, возникающая при приложении магнитного поля, по своей природе препятствует изменению его генерации в случае движения жидкости, и, следовательно, это силовое поле ослабляет потоки внутри корпуса.На рисунке (б) видно, что изотермические линии все более искажаются внутри каверны и плотнее у нижней нагретой стенки при отсутствии числа Гартмана. При низком числе Гартмана (Ha = 0) более высокий градиент температуры наблюдается у донной прогретой стенки. Плотность линий тока уменьшается под действием более сильного магнитного поля. Кроме того, изотермические линии смещаются вверх ближе к средней части нижней нагретой стенки, что указывает на область более высокого теплопереноса.
Результаты числа Гартмана (Ha) на ( a ) Контуры линии тока, ( b ) Контуры изотермы ( c ) Тепловые линии для однородных тепловых граничных условий на нижней стенке при ϕ = 0. 04 и Ra = 105.
04 и Ra = 105.
Результаты числа Гартмана (Ha) на ( a ) контурах линии тока, ( b ) контурах изотермы (c) Тепловые линии для линейных тепловых граничных условий на нижней стенке, когда ϕ = 0,04 и Ra = 105.
Большая циркуляционная ячейка с маленькой трубкой в верхней части корпуса показана на рис. (А) для условий линейной температуры. Эта вращающаяся ячейка становится меньше по мере увеличения влияния числа Гартмана, которое указывает скорость декокции за счет эффекта числа Гартмана.Это происходит из-за действия магнитного поля, которое замедляет течение жидкости. На рисунке (c) показаны характеристики теплопередачи метода тепловых линий для воздействия числа Гартмана. Эти цифры показывают прохождение теплопровода от нижней нагретой стены к верхней холодной стене. Две симметричные вращающиеся ячейки наблюдаются при отсутствии числа Гартмана и меньшего числа Гартмана. Тепловые линии более плотные вблизи центральной вертикальной линии полости. Теплоперенос уменьшается с увеличением интенсивности числа Гартмана.Для более высокого числа Гартмана (Ha = 50) теплопроводы идут к верхним наклонным стенкам от нижней нагреваемой стенки. Теплота потока уменьшается из-за более низкой скорости при более высокой напряженности магнитного поля. Аналогичная картина тепловых линий с большим центральным кругом наблюдается для линейных тепловых условий на рис. (C) для всех значений числа Гартмана.
Теплоперенос уменьшается с увеличением интенсивности числа Гартмана.Для более высокого числа Гартмана (Ha = 50) теплопроводы идут к верхним наклонным стенкам от нижней нагреваемой стенки. Теплота потока уменьшается из-за более низкой скорости при более высокой напряженности магнитного поля. Аналогичная картина тепловых линий с большим центральным кругом наблюдается для линейных тепловых условий на рис. (C) для всех значений числа Гартмана.
На рисунках и, соответственно, представлены эффекты локального числа Нуссельта (NuL) для объемных долей Ra и наночастиц на нижней горячей стенке для однородных тепловых граничных условий и линейных температурных граничных условий.Эти цифры показывают увеличение средней скорости переноса температуры для увеличения как числа Рэлея, так и объемных долей наночастиц как для однородно теплового граничного условия, так и для линейно теплового граничного условия. При низком Ra (= 103,104) (NuL) остается почти постоянным, в то время как местное число Нуссельта увеличивается для преобладающей области естественной конвекции (Ra> 104) внутри ограждения. На рисунке представлены локальные распределения числа Нуссельта вдоль нагретой стенки для числа Гартмана как для однородных, так и для линейных температурных граничных условий.Эти рисунки показывают, что местное число Нуссельта быстро убывает при увеличении числа Гартмана для системы с однородной температурой, чем для системы с линейной температурой. Кроме того, изменение значения объемной доли наночастиц существенно влияет на Местное число Нуссельта.
На рисунке представлены локальные распределения числа Нуссельта вдоль нагретой стенки для числа Гартмана как для однородных, так и для линейных температурных граничных условий.Эти рисунки показывают, что местное число Нуссельта быстро убывает при увеличении числа Гартмана для системы с однородной температурой, чем для системы с линейной температурой. Кроме того, изменение значения объемной доли наночастиц существенно влияет на Местное число Нуссельта.
Локальное число Нуссельта числа Рэлея для ( a ) стенки с равномерным нагревом снизу ( b ) линейно нагревает нижнюю стенку при ϕ = 0,04 и Ha = 10.
Локальное число Нуссельта объемной доли наночастиц для ( a ) равномерно нагретой снизу стенки ( b ) линейно нагревает нижнюю стенку при Ra = 105 и Ha = 10.
Локальное число Нуссельта объемной доли наночастиц для ( a ) равномерно нагретой снизу стенки ( b ) линейно нагревает нижнюю стенку при Ra = 105 и ϕ = 0,04.
На рисунке показано, что среднее число Нуссельта монотонно увеличивается с увеличением Ra. Интересно отметить, что однородный нагретый режим на нижней стенке обеспечивает самый высокий температурный поток внутри камеры, чем линейный температурный режим. На рисунках и показано, что среднее число Нуссельта увеличивается с увеличением числа Рэлея и добавления наночастиц в базовую жидкость, тогда как уменьшается с увеличением числа Гартмана.Скорость переноса тепла значительно увеличивается с увеличением объемной доли наночастиц. Это связано с более высокой теплопроводностью наножидкостей по сравнению с базовой жидкостью. Кроме того, при низких значениях Ra влияние объемной доли наночастиц на теплоотдачу более выражено. На рисунке показано, что скорость теплопередачи значительно выше для формы лезвия наночастиц, чем для сферической формы наночастиц. Это связано с тем, что меньше сферичность формы лезвия наночастиц.Более того, среднее число Нуссельта более очевидно для более высокой объемной доли наночастиц. Более того, среднее число Нуссельта выше для наночастиц лысой формы по сравнению с другими наночастицами любой формы, такими как сферические, кирпичные, цилиндрические и пластинчатые.
Более того, среднее число Нуссельта выше для наночастиц лысой формы по сравнению с другими наночастицами любой формы, такими как сферические, кирпичные, цилиндрические и пластинчатые.
Среднее число Нуссельта числа Рэлея для двух различных граничных условий с подогревом на нижней стенке.
Среднее число Нуссельта объемной доли наночастиц и число Хартмана для наножидкости Cu-H 2 O.
Среднее число Нуссельта объемной доли наночастиц и число Рэлея для наножидкости Cu-H 2 O.
Среднее число Нуссельта объемной доли наночастиц и различная форма наночастиц для наножидкости Cu-H 2 O.
Параметр «Объемная доля наночастиц» является ключевым фактором при изучении того, как наночастицы влияют на поток жидкости, а также на температурный перенос наножидкостей. Типы наночастиц также являются ключевым фактором для улучшения теплопередачи.В таблице показано среднее число Нуссельта (Nu av ) вдоль нижней нагретой стенки полости для различных значений объемных долей наночастиц и различных типов наночастиц базовых жидкостей, таких как вода (H 2 O), керосин и этиленгликоль (EG ) с четырьмя различными типами наночастиц, такими как Cu, Co, Al 2 O 3 и TiO 2 , когда Ra = 10 5 , Ha = 15 и n = 3. Наблюдается, что средний Число Нуссельта увеличивается с увеличением объемной доли наночастиц для всех типов наножидкостей.Это связано с более высокой теплопроводностью наночастиц. В таблице показана самая высокая теплопередача для наножидкостей на основе керосина по сравнению с наножидкостями на водной основе и на основе этиленгликоля. Хотя наночастицы Cu имеют более высокую теплопроводность, чем Co, Al 2 O 3 и TiO 2 , керосиновые наножидкости показывают более высокую скорость теплопередачи. Самая низкая теплопередача наблюдается для наножидкостей на водной основе из-за более низкой теплопроводности и более высокой динамической вязкости жидкости на основе.
Наблюдается, что средний Число Нуссельта увеличивается с увеличением объемной доли наночастиц для всех типов наножидкостей.Это связано с более высокой теплопроводностью наночастиц. В таблице показана самая высокая теплопередача для наножидкостей на основе керосина по сравнению с наножидкостями на водной основе и на основе этиленгликоля. Хотя наночастицы Cu имеют более высокую теплопроводность, чем Co, Al 2 O 3 и TiO 2 , керосиновые наножидкости показывают более высокую скорость теплопередачи. Самая низкая теплопередача наблюдается для наножидкостей на водной основе из-за более низкой теплопроводности и более высокой динамической вязкости жидкости на основе.
Таблица 3
Среднее число Нуссельта вдоль нижней нагретой стенки для различных типов наножидкостей и разного размера наночастиц при Ra = 105 и Ha = 10.
Нанофлюиды ϕ Nu av Увеличение (%) Наножидкости ϕ Nu av Вода 0,00 5,0869043 — Cu-керосин 0. 00
00 5,1108449 — 0,01 5,1279040 0,81 0,01 5,33 4,46 0,03 0,03 0,10 5,4715713 7,56 0,10 5,7623863 12,75 Попутная вода 0,00 5. 0869043
0869043 — Кокеросин 0,00 5,1108449 — 0,01 5,1255934 0,76 0,01 5,405 9045 9045 903 903 903 903 905 5,405 9045 903 903 903 903 5,405 0,05 5,77 13,08 0,10 5,4451034 7,04 0,10 5,9494259 16,41 5,0869043 — Al 2 O 3 -керосин 0,00 5,1108449 — 0,01 5,149845 5,149845 0,05 5,4261935 6,67 0,05 5,5797743 9,18 0,10 5. 7008267
7008267 12,07 0.10 5,8481775 14,43 TiO 2 -водный 0,00 5,0869043 — TiO 2 -керосин 3 0,0050 9045 9045 0,0850 9045 5,1394618 1,04 0,01 5,1601554 0,96 0,05 5,3977902 6,11 0,05 5,4457005 55 0,10 5,6101714 10,29 0,10 5,7818382 13,13 Cu-EG 0,00 5,1015819 2 0,00 5,1015913 — 0,01 5,13 0,73 0,01 5,1662068 1,27 0,05 0,053897890 5,649 0,05 5,4683156 7,19 0,10 5,5339510 8,47 0,10 5,82 9015 9015 950 945 TiO 2 -EG 0,00 5,1015913 — 0,01 5,13 0,74 0,01 5. 1564652
1564652 1,08 0,05 5,3895143 5,64 0,05 5,4205563 6,25 0,10 0,10 % PDF-1.6
%
1 0 объект
>
эндобдж
6 0 объект
>
эндобдж
2 0 obj
>
/ Шрифт>
>>
/ Поля []
>>
эндобдж
3 0 obj
>
ручей
2015-11-18T12: 49: 13 + 01: 00Canon iR-ADV C7270 2015-11-18T18: 29: 52 + 01: 002015-11-18T18: 29: 52 + 01: 00Adobe Acrobat Pro DC 15 Заглушка захвата бумаги- inapplication / pdfuuid: 4d664c56-0000-8887-177e-c32600000000uuid:
e41-0fda-4231-bd05-a6e6eb5e8ddd конечный поток
эндобдж
4 0 объект
>
эндобдж
5 0 объект
>
эндобдж
7 0 объект
>
эндобдж
8 0 объект
>
эндобдж
9 0 объект
>
эндобдж
10 0 объект
>
ручей
HyTSw oɞc
[5laQIBHADED2mtFOE. c} 08 8 GNg9w ߽
c} 08 8 GNg9w ߽ Комбинированное ламинарное течение естественной и принудительной конвекции и теплопередача жидкостей с источниками тепла и без них в каналах с линейно изменяющейся температурой стенок
Версия PDF также доступна для скачивания.
ВОЗ
Люди и организации, связанные либо с созданием этого отчета, либо с его содержанием.
Что
Описательная информация, помогающая идентифицировать этот отчет.Перейдите по ссылкам ниже, чтобы найти похожие предметы в Электронной библиотеке.
Когда
Даты и периоды времени, связанные с этим отчетом.
Статистика использования
Когда последний раз использовался этот отчет?
Взаимодействовать с этим отчетом
Вот несколько советов, что делать дальше.
Версия PDF также доступна для скачивания.
Ссылки, права, повторное использование
Международная структура взаимодействия изображений
Распечатать / Поделиться
Печать
Электронная почта
Твиттер
Facebook
Tumblr
Reddit
Ссылки для роботов
Полезные ссылки в машиночитаемом формате.
Ключ архивных ресурсов (ARK)
Международная структура взаимодействия изображений (IIIF)
Форматы метаданных
Картинки
URL
Статистика
Острах, Симон. Комбинированное ламинарное течение естественной и принудительной конвекции и теплопередача жидкостей с источниками тепла и без них в каналах с линейно изменяющейся температурой стенок.
отчет,
Апрель 1954 г .;
(https://digital.library.unt.edu/ark:/67531/metadc56936/:
по состоянию на 1 января 2022 г.), Библиотеки Университета Северного Техаса, Цифровая библиотека UNT, https://digital.library.unt.edu; кредитование Департамента государственных документов библиотек ЕНТ.
Комбинированное ламинарное течение естественной и принудительной конвекции и теплопередача жидкостей с источниками тепла и без них в каналах с линейно изменяющейся температурой стенок.
отчет,
Апрель 1954 г .;
(https://digital.library.unt.edu/ark:/67531/metadc56936/:
по состоянию на 1 января 2022 г.), Библиотеки Университета Северного Техаса, Цифровая библиотека UNT, https://digital.library.unt.edu; кредитование Департамента государственных документов библиотек ЕНТ.
Исследование теплопередачи естественной конвекции наножидкости в открытых L-образных полостях с использованием LBM
[1] Ханафер, Х.М. и Чамха А.Дж., Гидромагнитная естественная конвекция от наклонного пористого квадратного корпуса с выделением тепла, Численный перенос тепла, Часть A: Приложения , 33 (8), 1998, 891-910.
[2] Ким, Б.С., Ли, Б.И., Ли, Н., Чой, Г., Гемминг, Т., Чо, Х.Х., Интеллектуальные интерфейсы в нано-стиле: гибкая интерактивность и ее влияние на теплопередачу, Scientific Reports , 7, 2017, 45323.
[3] Хан И. и Шах Н.А., Научный отчет по анализу теплопередачи в смешанном конвекционном потоке жидкости Максвелла над колеблющейся вертикальной пластиной, Scientific Reports , 7, 2017, 40147.
[4] Thippeswamy, L.R. и Ядав А.К., Увеличение теплопередачи с использованием в контуре естественной циркуляции, Scientific Reports , 10, 2020, 1507.
[5] Фаттахи, Э., Фархади, М., Седиги, К., Моделирование теплопередачи естественной конвекции в эксцентрическом кольцевом пространстве на решетке Больцмана, International Journal of Thermal Sciences , 49, 2010, 2353-2362.
[6] Немати, Х., Фархади, М., Седиги, К., Фаттахи, Э., Рабиенатай, А.А., Моделирование наножидкости через решетку Больцмана в полости, управляемой крышкой , International Communications in Heat and Mass Transfer , 37, 2010, 1528-1534.
[7] Кефаяти, Г.Х.Р., Хоссейнизаде, С.Ф., Горджи, М., Саджади, Х., Моделирование естественной конвекции в высоких помещениях с использованием решеток Больцмана с использованием наножидкости вода / Si, International Communications in Heat and Mass Transfer , 38, 2011, 798-805.
[8] Немати, Х., Фархади, М., Седиги, К., Ашоринеджад, Х.Р., Фаттахи, Э., Влияние магнитного поля на естественный конвекционный тепловой поток наножидкости в прямоугольной полости с использованием решетчатой модели Больцмана, Scientia Iranica , 19 (2), 2012, 303–310.
[9] Джурабиан, М., Фархади, М., Рабиенатай Дарзи, А.А., Моделирование естественного конвекционного плавления в наклонной полости с использованием решеточного метода Больцмана, Scientia Iranica , 19 (4), 2012, 1066–1073.
[10] Джин, Л., Чжан, X., Ниу, X., Моделирование решеточного Больцмана для термочувствительных магнитных жидкостей в пористой квадратной полости, Journal of Magnetism and Magnetic Materials , 324, 2012, 44- 51.
[11] Назари М., Кайхани М. Х., Сравнительное решение естественной конвекции в открытой полости с использованием различных граничных условий с помощью метода Больцмана на решетке, Journal of Heat and Mass Transfer Research , 3, 2016, 115- 129.
[12] Ахмед М., Эсламиан, М., Естественная конвекция в квадратном корпусе с дифференциальным обогревом, заполненном нанофлюидом: значение силы термофореза и скорости скольжения / дрейфа, International Communications in Heat and Mass Transfer , 58, 2014, 1–11.
[13] Саджади, Х., Салманзаде, М., Ахмади, Г., Джафари, С., Исследование осаждения и рассеивания частиц с использованием гибридной модели LES / RANS на основе метода решетчатого Больцмана, Scientia Iranica , 25, 2018, 3173-3182.
[14] Джалали, А., Делуэи, А.А., Хорашадизаде, М., Голмохаммади, А.М., Каримнеджад, С., мезоскопическое моделирование принудительной конвективной теплопередачи потока жидкости Карроу-Ясуда по наклонному квадрату: вязкость, зависящая от температуры , Журнал прикладной и вычислительной механики , 6 (2), 2020, 307-319.
[15] Чой, У.С., Повышение теплопроводности жидкостей с помощью наночастиц, разработка и применение неньютоновских потоков, ASME , 66, 1995, 99-105.
[16] Хашим, Хафиз, А., Альшомрани, А.С., Хан, М., Множественные физические аспекты во время анализа потока и теплопередачи жидкости Карро с наночастицами, Scientific Reports , 8, 2018, 17402.
[17] Каррильо-Бердуго, И., Зоррилла, Д., Санчес-Маркес, Дж., Агилар, Т., Галлардо, Дж. Дж., Гомес-Вилларехо, Р., Алькантара, Р., Фернандес-Лоренцо, К., Навас, Дж., Формулировка на основе интерфейса и перспективы на молекулярном уровне теплопроводности и накопления энергии в наножидкостях, Scientific Reports , 9, 2019, 7595.
[18] Шейхолеслами, М., Саджади, Х., Делуэи, А.А., Аташафруз, М., Ли, Ж., Магнитная сила и влияние излучения на транспортировку наножидкости через проницаемую среду с учетом наночастиц, Журнал термического анализа и калориметрии , 136, 2019, 2477–2485.
[19] Чамха, А.Дж., Молана, М., Рахнама, А., Гадами Ф., О применении наножидкостей в микроканалах: всесторонний обзор, Powder Technology , 332, 2018, 287-322.
[20] Чамха, А.Дж., Рашад, А.М., Мансур, М.А., Армагани, Т., Галамбаз, М., Влияние теплоотвода и источника и генерации энтропии на смешанную МГД конвекцию наножидкости Cu-вода в крышке. ведомый квадратный пористый корпус с частичным скольжением, Physics of Fluids , 29, 2017, 052001-22.
[21] Рашад, А.М., Армагани, Т., Чамха, А.Дж., Мансур, М.А., Генерация энтропии и естественная МГД конвекция наножидкости в наклонной квадратной пористой полости: влияние радиатора, размера и расположения источника, Китайский журнал физики , 56 (1), 2018, 193-211.
[22] Ханафер, К., Вафай, К., Лайтстоун, М., Повышение теплопередачи за счет плавучести в двумерном корпусе с использованием наножидкости, International Journal of Heat and Mass Transfer , 46, 2003, 3639- 3653.
[23] Лай, Ф. Х., Янг, Ю.Т., Моделирование решеточно-Больцмана естественной конвекции теплопередачи наножидкостей / воды в квадратном корпусе, International Journal of Thermal Sciences , 50, 2011, 1930-1941.
Х., Янг, Ю.Т., Моделирование решеточно-Больцмана естественной конвекции теплопередачи наножидкостей / воды в квадратном корпусе, International Journal of Thermal Sciences , 50, 2011, 1930-1941.
[24] Фаттахи, Э., Фархади, М., Седиги, К., Немати, Х., Решеточно-Больцмановское моделирование естественной конвективной теплопередачи в нанофлюидах, International Journal of Thermal Sciences , 52, 2012, 137-144.
[25] Кефаяти, GH.R., Влияние магнитного поля на естественную конвекцию в открытой полости, подчиненной наножидкости вода / оксид алюминия, с использованием метода решетки Больцмана, International Communications in Heat and Mass Transfer , 40, 2013, 67 –77.
[26] Озтоп, Х.Ф., Абу-Нада, Э., Численное исследование естественной конвекции в частично нагретых прямоугольных корпусах, заполненных наножидкостями, International Journal of Heat and Fluid Flow , 29, 2008, 1326-1336.
[27] Джаханшахи, М., Хоссейнизаде, С.Ф. , Алипанах М., Дехгани А., Вакилинеджад Г.Р., Численное моделирование свободной конвекции на основе экспериментально измеренной проводимости в квадратной полости с использованием наножидкости вода / Si, International Communications in Heat and Mass Transfer , 37, 2010, 687-694.
, Алипанах М., Дехгани А., Вакилинеджад Г.Р., Численное моделирование свободной конвекции на основе экспериментально измеренной проводимости в квадратной полости с использованием наножидкости вода / Si, International Communications in Heat and Mass Transfer , 37, 2010, 687-694.
[28] Махмуди, А.Х., Шахи, М., Шахедин, А.М., Хемати, Н., Численное моделирование естественной конвекции в открытом корпусе с двумя вертикальными тонкими источниками тепла, подвергающимися воздействию наножидкости, International Communications in Heat and Mass Перевод , 38, 2011, 110-118.
[29] Кефаяти, GHR, Хоссейнизаде, С.Ф., Горджи, М., Саджади, Х., Моделирование естественной конвекции на решетке Больцмана в открытом корпусе, подчиненном наножидкости вода / медь , International Journal of Thermal Sciences , 52, 2012, 91-101.
[30] Шахриари А.Р., Джафари, С., Рахнама, М., Бехзадмехр, А., Влияние переменных свойств наножидкости на естественную конвекцию в квадратной полости с использованием метода решетки Больцмана, Международный обзор машиностроения , , 7, 2013 г. , 442–452 .
, 442–452 .
[31] Ху, Й., Хе, Й., Ци, К., Цзян, Б., Шлаберг, Х.И., Экспериментальное и численное исследование естественной конвекции в квадратном корпусе, заполненном наножидкостью, International Journal of Heat and Массообмен , 78, 2014, 380-392.
[32] Чжоу, В.Н., Ян, Ю.Ю., Сюй, Дж. Л., Больцмановское моделирование на решетке улучшенной теплопередачи наножидкостей, International Communications in Heat and Mass Transfer , 55, 2014, 113-120.
[33] Хоссейни, М., Мустафа, М.Т., Джафарьяр, М., Мохаммадиан, Э., Наножидкость в наклонной полости с частично нагретыми стенками, журнал Journal of Molecular Liquids , 199, 2014, 545-551.
[34] Джафари, М., Фархади, М., Акбарзаде, С., Эбрахими, М., Моделирование решеточно-Больцмана естественной конвекции теплопередачи SWCNT-наножидкости в открытом корпусе, Ain Shams Engineering Journal , 6 (3), 2015, 913-927.
[35] Шейхолеслами, М., Ашоринеджад, Х.Р., Рана, П., Моделирование на решетке Больцмана увеличения теплопередачи наножидкостей и генерации энтропии, Журнал молекулярных жидкостей , , 214, 2016, 86-95.
[36] Саджади, Х., Делуэи, А.А., Изади, М., Мохебби, Р., Исследование естественной МГД конвекции в пористой среде методом Больцмана с двойной решеткой МРТ с использованием гибридной наножидкости MWCNT– / вода, International Journal тепломассообмена , 132, 2019, 1087-1104.
[37] Саджади, Х., Амири Делуэи, А., Аташафруз, М., Шейхолеслами, М., Двойное МРТ-решеточное моделирование Больцмана трехмерной МГД естественной конвекции в кубической полости с синусоидальным распределением температуры с использованием наножидкости, Международный журнал тепломассообмена , 126, 2018, 489–503.
[38] Рахими, А., Kasaeipoor, A., Malekshah, EH, kolsi, L., Анализ естественной конвекции путем генерации энтропии и визуализации тепловых линий с использованием метода Больцмана на решетке в заполненной наножидкостью полости, включенной с внутренними нагревателями — Эмпирические теплофизические свойства, Журнал молекулярных жидкостей , 133, 2017, 199-216.
[39] Рахими, А. , Касаейпур, А., Малекшах, Э. Х., Моделирование на решетке Больцмана естественной конвекции и генерации энтропии в полостях, заполненных наножидкостью при наличии внутренних твердых тел. Экспериментальные теплофизические свойства, Journal of Molecular Жидкости , 242, 2017, 580-593.
, Касаейпур, А., Малекшах, Э. Х., Моделирование на решетке Больцмана естественной конвекции и генерации энтропии в полостях, заполненных наножидкостью при наличии внутренних твердых тел. Экспериментальные теплофизические свойства, Journal of Molecular Жидкости , 242, 2017, 580-593.
[40] Мехризи, А., Фархади, М., Шаямер, С., Естественный конвекционный поток наножидкости Cu – Вода в горизонтальных цилиндрических кольцах с внутренним треугольным цилиндром с использованием решеточного метода Больцмана, International Communications in Heat and Mass Transfer , 44, 2013, 147-156.
[41] Абдаллауи, М.Эл., Хаснауи, М., Амахмид, А., Численное моделирование естественной конвекции между децентрированным треугольным нагревательным цилиндром и квадратным внешним цилиндром, заполненным чистой жидкостью или наножидкостью, с использованием решеточного метода Больцмана, Powder Technology , 277, 2015, 193–205.
[42] Хатами, М., Численное исследование естественной конвекции наножидкостей в прямоугольной полости, включая нагретые ребра, Journal of Molecular Liquids , 233, 2017, 1-8.
[43] Тораби, М., Кейхани, А.Р., Петерсон, Г.П., Комплексное исследование естественной конвекции внутри частично дифференциально нагретой полости с тонким ребром с использованием двух решеточных функций распределения Больцмана, International Journal of Heat and Mass Перевод , 115, 2017, 264-277.
[44] Чамха, А.Дж., Доостанидезфули, А., Изадпанахи, Э., Галамбаз, М., Теплопередача с фазовым переходом материалов с фазовым переходом с единичными / гибридными наночастицами над нагретым горизонтальным цилиндром, заключенным в квадратную полость, Advanced Powder Technology , 28 (2), 2017, 385-397.
[45] Порданджани, А.Х., Джаханбахши, А., Надушан, А.А., Афранд, М., Влияние двух изотермических препятствий на естественную конвекцию наножидкости в присутствии магнитного поля внутри корпуса с синусоидальным распределением температуры стенок, Международный журнал тепло- и массообмена , 121, 2018, 565–578.
[46] Сиаваши М., Юсофванд Р. , Резанежад С., Влияние наножидкости и пористых ребер на естественную конвекцию и генерацию энтропии потока внутри полости, Advanced Powder Technology , 29, 2018, 142-156 .
, Резанежад С., Влияние наножидкости и пористых ребер на естественную конвекцию и генерацию энтропии потока внутри полости, Advanced Powder Technology , 29, 2018, 142-156 .
[47] Виджайбабу, Т.Р., Дхинакаран, С., MHD Естественная конвекция вокруг проницаемого треугольного цилиндра внутри квадратного корпуса, заполненного наножидкостью — O: исследование LBM, International Journal of Mechanical Sciences , 153–154, 2019, 500-516.
[48] Хашим, И., Альсабери, А.И., Шеремет, М.А., Чамха, А.Дж., Численное исследование естественной конвекции водной наножидкости в волнистой полости с проводящим внутренним блоком с использованием двухфазной модели Буонджорно, Advanced Powder Technology , 30, 2019, 399-414.
[49] Диндарло, М. Р., Пайан, С., Влияние толщины ребер, глубины канавок и угла их крепления к горячей стенке на максимальное снижение теплопередачи в квадратном корпусе, International Journal of Thermal Sciences , 136, 2019, 473–490.
[50] Коджа, А., Озтоп, Х.Ф., Варол, Ю., Численный анализ естественной конвекции в односкатных крышах с карнизами зданий для холодного климата, Компьютеры и математика с приложениями , 56, 2008, 3165-3174.
[51] Дехнави, Р., Резвани, А., Численное исследование естественной конвекции теплопередачи наножидкостей в Γ-образной полости, Сверхрешетки и микроструктуры , 52, 2012, 312–325.
[52] Калтех, М., Хасани, Х., Моделирование на решетке Больцмана свободной конвекции тепла с помощью наножидкостей в L-образном корпусе, Сверхрешетки и микроструктуры , 66, 2014, 112-128.
[53] Парвин, С., Насрин, Р., Алима, М.А., Хоссейн, Н.Ф., Чамха А.Дж., Изменение теплопроводности естественного конвекционного потока воды и наножидкости оксида алюминия в затрубном пространстве, International Journal of Heat and Mass Transfer , 55, 2012, 5268–5274.
[54] Гальегос, А.Д., Малага, К., Естественная конвекция в эксцентрических сферических кольцах, European Journal of Mechanics — B / Fluids , 65, 2017, 464-471.
[55] Парвин, С., Насрин, Р., Алим, М.А., Хоссейн, Н.Ф., Чамха, А.Дж., Изменение теплопроводности при естественной конвекции потока наножидкости вода-оксид алюминия в кольцевом пространстве, International Journal of Heat and Mass Transfer , 55, 2012, 5268– 5274.
[56] Шейхолеслами М., Горджи-Бандпи М., Сейеди С.М., Ганджи Д.Д., Рокни, Х.Б., Сулеймани, С., Применение LBM для моделирования естественной конвекции в заполненной нанофлюидом квадратной полости с кривой границы, Powder Technology , 247, 2013, 87–94.
[57] Гади, Аризона, Хагиги Асл, А., Валипур, М.С., Численное моделирование двойной диффузионной естественной конвекции внутри дугообразного корпуса, заполненного пористой средой, Journal of Heat and Mass Transfer Research , 1 , 2014, 83-91.
[58] Jayhooni, S.М.Х., Джафарпур, К., Численное моделирование теплообмена ламинарной свободной конвекции вокруг изотермических вогнутых и выпуклых форм тела, Журнал исследований тепломассопереноса , 2, 2015, 37-44.
[59] Резвани А., Валипур М.С., Биглари М., Численное исследование генерации энтропии для естественной конвекции в цилиндрических полостях, Журнал исследований тепломассопереноса , 3 (2016) 89-99.
[60] Гасеми Б., Аминосадати С.М., Броуновское движение наночастиц в треугольном корпусе с естественной конвекцией, International Journal of Thermal Sciences , 49, 2010, 931-940.
[61] Салех, Х., Рослан, Р., Хашим, И., Естественная конвекция теплопередачи в заполненном наножидкостью трапециевидном корпусе, International Journal of Heat and Mass Transfer , 54, 2011, 194-201.
[62] Меджри, И., Махмуди, А., Аббасси, М.А., Омри, А., LBM-моделирование естественной конвекции в наклонной треугольной полости, заполненной водой, Alexandria Engineering Journal , 55 (2), 2016 , 1385–1394.
[63] Чамха, А.Дж., Исмаил, М., Kasaeipoor, A., Armaghani, T., Генерация энтропии и естественная конвекция наножидкости CuO-вода в C-образной полости под действием магнитного поля, Энтропия , 18 (2), 2016, 50.
[64] Мохебби, Р., Изади, М., Чамха, А.Дж., Расположение источника тепла и естественная конвекция в С-образном корпусе, насыщенном наножидкостью, Physics of Fluids , 29, 2017, 122009-13.
[65] Бондарева, Н.С., Шеремет, М.А., Озтоп, Х.Ф., Абу-Хамде, Н., Генерация энтропии за счет естественной конвекции наножидкости в частично открытой треугольной полости, Advanced Powder Technology , 28 (1) , 2017, 244-255.
[66] Махмуди, М., Хашеми, С.М., Численное исследование естественной конвекции наножидкости в C-образных корпусах, International Journal of Thermal Sciences , 55, 2012, 76-89.
[67] Мансур, М.А., Бакьер, А.Й., Бакер, Май, Естественная конвекция локализованных источников тепла Т-образных корпусов, заполненных наножидкостью, Американский журнал инженерных исследований , 2 (7), 2013, 49-61 .
[68] Бакьер, М.А.Й., Поток в открытых С-образных полостях: насколько изменение границ влияет на нанофлюид?, Технические науки и технологии, Международный журнал , 17, 2014, 116-130.
[69] Эсфеа, М.Х., Аббасиан Арани, А.А., Янк, В. М., Агаи, А., Естественная конвекция в Т-образных полостях, заполненных суспензиями на водной основе многостенных углеродных нанотрубок, функционализированных с помощью COOH, International Journal of Mechanical Sciences , 121, 2017, 21–32.
[70] Махмуд С., Свободная конвекция внутри L-образного корпуса, International Communications in Heat and Mass Transfer , 29, 2002, 1005-1013.
[71] Тасним, С.Х., Махмуд, С., Ламинарная свободная конвекция внутри наклонного L-образного корпуса, International Communications in Heat and Mass Transfer , 33, 2006, 936-942.
[72] Махмуди М., Численное моделирование свободной конвекции наножидкости в L-образных полостях, International Journal of Thermal Sciences , 50, 2011, 1731-1740.
[73] Шейхолеслами М., Горджи-Бандпи М., Ганджи Д.Д., Сулеймани С. Теплопередача естественной конвекцией в наклонном L-образном корпусе, заполненном наножидкостью, Иранский журнал науки и технологий, Транзакции Машиностроение , 38, 2014, 217-226.
[74] Млики, Б., Аббасси, М.А., Гедри, К., Омри, А., Моделирование естественной конвекции на решетке Больцмана в L-образном корпусе в присутствии наножидкости, Engineering Science and Technology an International Journal , 18, 2015, 503-511 .
[75] Мохебби, Р., Рашиди, М.М., Численное моделирование естественной конвекционной теплопередачи наножидкости в L-образном корпусе с препятствием для нагрева, Журнал Тайваньского института инженеров-химиков , 72, 2017, 70-84.
[76] Рахими, А., Касаэйпур, А., Малекшах, Э.Х., Амири, А., Анализ естественной конвекции с использованием генерации энтропии и визуализации тепловых линий в полой L-образной полости, заполненной наножидкостью, с использованием решеточного метода Больцмана. -физические свойства, Physica E: Низкоразмерные системы и наноструктуры , 97, 2018, 82-97.
[77] Чжан Р., Агахани, С., Хаджатзаде Порданджани, А. и др., Исследование генерации энтропии при естественной конвекции ньютоновских и неньютоновских жидкостей внутри L-образной полости под действием магнитного поля: применение решеточного метода Больцмана, The European Физический журнал плюс , 135, 2020, 184.
[78] Изади, М., Мохебби, Р., Делуэи, А.А., Саджади, Х., Естественная конвекция намагничивающейся гибридной наножидкости внутри пористой оболочки под действием двух переменных магнитных полей, International Journal of Mechanical Sciences , 151, 2019, 154-169.
[79] Аббасси, М.А., Сафаи, М.Р., Джебали, Р., Гедри, К., Зегмати, Б., Альрашедг, AAAA, LBM-моделирование свободной конвекции в печи для сжигания с нанофлюидом, содержащей горячий блок, International Journal наук , 148, 2018, 393-408.
[80] Ма, Й., Мохебби, Р., Рашиди, М.М., Янг, Ж., Моделирование естественной конвекции наножидкости в U-образной полости, снабженной препятствием для нагрева: Эффект соотношения сторон полости, Journal of Тайваньский институт инженеров-химиков , 93, 2018, 263-276.
[81] Ю.М. Со, М. Йонг Ха, Ю. Гэп Парк, Численное исследование трехмерной естественной конвекции с цилиндром в длинном прямоугольном корпусе. Часть I. Размерный эффект круглого или эллиптического цилиндра, International Journal of Heat and Mass Transfer , 134, 2019, 420-436.
[82] Датта, С., Госвами, Н., Бисвас, А.К., Пати, С., Численное исследование магнитогидродинамической теплопередачи естественной конвекции и генерации энтропии в ромбической оболочке, заполненной наножидкостью Cu-вода, International Journal of Тепло- и массообмен , 136, 2019, 777–798.
[83] Пурусотаман А., Малекшах Э. Х., Моделирование МГД свободной конвекции наножидкости в V-образном микроэлектронном модуле на решетке Больцмана, Thermal Science and Engineering Progress , 10, 2019, 186-197.
[84] Яхиауи, А., Джеззар, М., Наджи, Х., Моделирование улучшения теплопередачи с помощью наножидкости на водной основе в корпусах с изогнутыми боковыми стенками, International Communications in Heat and Mass Transfer , 100, 2019, 118–132.
[85] Альмешаал, М.А., Маатки, К., Колси, Л., Гачем, К., Чамха, А.Дж., Естественная конвекция 3D-типа Рэлея-Бенара в L-образных оболочках, заполненных наножидкостью MWCNT, с учетом агрегации эффект, Математические методы в прикладных науках , 2020, 1–17.
[86] Догончи, А.С., Чамха, А.Дж., Сейеди, С.М., Хашеми-Тилехнои, М., Ганджи, Д.Д., Влияние вязкой диссипации на свободноконвекционный поток наножидкости Cu-вода в круглом корпусе с пористостью с учетом внутреннего источника тепла , Журнал прикладной и вычислительной механики , 5 (4), 2019, 717-726.
[87] Бежан, А., Convection Heat Transfer , John Wiley & Sons, Inc., Хобокен, Нью-Джерси, США, 2004.
[88] Мохамад, А.А., Кузьмин, А., Критическая оценка силового члена в решеточном методе Больцмана, проблема естественной конвекции, International Journal of Heat and Mass Transfer , 53, 2010, 990-996.
[89] Мохамад, А.А., Эль-Ганауи, М., Беннасер, Р., Моделирование естественной конвекции решеткой Больцмана в открытом корпусе, International Journal of Thermal Sciences , 48, 2009, 1870-1875.
[90] Ван, X.Q., Муджумдар, А.С., Характеристики теплопередачи наножидкостей: обзор, International Journal of Thermal Sciences , 46 (1), 2007, 1-19.
 Для увеличения Ra две рециркуляционные клетки растут. Это означает, что нагретая жидкость сильнее ускоряется за счет эффекта плавучести.
Для увеличения Ra две рециркуляционные клетки растут. Это означает, что нагретая жидкость сильнее ускоряется за счет эффекта плавучести. Для Ra = 105,106 конкретный рисунок изотерм, подобный грибу, указывает на то, что температурная энергия течет внутри жидкости полости с нижней нагретой стороны за счет потенциальных эффектов плавучести.Рисунок (c) демонстрирует, что теплопроводы чистые и примерно параллельны перпендикулярным стенкам, что приводит к изменению температуры в результате теплопроводности. Плотность тепловых линий рядом с нагретой стенкой усиливает, а также препятствует более высокому параметру Ra, обусловленному плавучестью. Компактность теплопроводов увеличивается в середине шкафа из-за сильной конвекции. Кроме того, при более высоком Ra внутри корпуса создаются два симметричных небольших вихря относительно центральной вертикальной линии, что согласуется с структурой функции тока.Следовательно, конвекция является доминирующей формой температурного потока при верхнем параметре плавучести.
Для Ra = 105,106 конкретный рисунок изотерм, подобный грибу, указывает на то, что температурная энергия течет внутри жидкости полости с нижней нагретой стороны за счет потенциальных эффектов плавучести.Рисунок (c) демонстрирует, что теплопроводы чистые и примерно параллельны перпендикулярным стенкам, что приводит к изменению температуры в результате теплопроводности. Плотность тепловых линий рядом с нагретой стенкой усиливает, а также препятствует более высокому параметру Ra, обусловленному плавучестью. Компактность теплопроводов увеличивается в середине шкафа из-за сильной конвекции. Кроме того, при более высоком Ra внутри корпуса создаются два симметричных небольших вихря относительно центральной вертикальной линии, что согласуется с структурой функции тока.Следовательно, конвекция является доминирующей формой температурного потока при верхнем параметре плавучести. Соответственно. Рисунок (а) показывает, что на контуры обтекаемой формы полностью не влияют частицы наножидкости внутри корпуса. Температура горизонтальной стороны выше по сравнению с болтающимися сторонами, поэтому соседняя жидкость нижней стенки получает температуру, и после этого эта жидкость выходит вверх в более холодную жидкость, в результате создается циркуляционная ячейка, в результате чего значение передачи температуры увеличивается на более холодных стенках.Физический смысл этого заключается в том, что при достаточной разнице температур между нагретыми и охлажденными стенками внутри корпуса создается потенциальная подъемная сила. При низком Ra воздействие конвекции мало заметно из-за незначительного действия силы инерции в механизмах температурного потока. Для верхних значений Ra (= 105,106) контуры линий тока разлагаются, и появляется одно потенциальное распространение в жидкость внутри полости для увеличения интенсивности конвективного потока температуры, в результате чего возникает вторичная циркуляция в верхних углах, соседних с наклонной.
Соответственно. Рисунок (а) показывает, что на контуры обтекаемой формы полностью не влияют частицы наножидкости внутри корпуса. Температура горизонтальной стороны выше по сравнению с болтающимися сторонами, поэтому соседняя жидкость нижней стенки получает температуру, и после этого эта жидкость выходит вверх в более холодную жидкость, в результате создается циркуляционная ячейка, в результате чего значение передачи температуры увеличивается на более холодных стенках.Физический смысл этого заключается в том, что при достаточной разнице температур между нагретыми и охлажденными стенками внутри корпуса создается потенциальная подъемная сила. При низком Ra воздействие конвекции мало заметно из-за незначительного действия силы инерции в механизмах температурного потока. Для верхних значений Ra (= 105,106) контуры линий тока разлагаются, и появляется одно потенциальное распространение в жидкость внутри полости для увеличения интенсивности конвективного потока температуры, в результате чего возникает вторичная циркуляция в верхних углах, соседних с наклонной. стены.На рисунке (б) показано, что для меньшего Ra (= 103,104) наблюдаются параллельные контуры изотермы соседней прогретой стенки из-за потенциальной проводимости формы температурных распределений. Для верхнего числа Рэлея также наблюдается превышение искаженных контуров изотермы в центре полости из-за увеличения конвекции внутри корпуса. Для Ra = 106 компактность и высокая плотность изотермического рисунка отмечаются рядом с горизонтальными нагретыми и свисающими холодными стенками крыши, что представляет собой высокий температурный градиент в этих областях.
стены.На рисунке (б) показано, что для меньшего Ra (= 103,104) наблюдаются параллельные контуры изотермы соседней прогретой стенки из-за потенциальной проводимости формы температурных распределений. Для верхнего числа Рэлея также наблюдается превышение искаженных контуров изотермы в центре полости из-за увеличения конвекции внутри корпуса. Для Ra = 106 компактность и высокая плотность изотермического рисунка отмечаются рядом с горизонтальными нагретыми и свисающими холодными стенками крыши, что представляет собой высокий температурный градиент в этих областях. Тепловые линии представляют собой способ изменения температуры, возникающий в прогретом режиме, а финиш в холодном режиме.На рисунке (c) показано, что тепловые линии распределены почти без разбора в соответствии с циркуляцией по часовой стрелке и против часовой стрелки для меньшего Ra (= 103) от горизонтальной нагретой стороны к верхним наклонным холодным сторонам из-за низкой силы потока жидкости, а также температуры, протекающей в основном за счет теплопроводности. .
Тепловые линии представляют собой способ изменения температуры, возникающий в прогретом режиме, а финиш в холодном режиме.На рисунке (c) показано, что тепловые линии распределены почти без разбора в соответствии с циркуляцией по часовой стрелке и против часовой стрелки для меньшего Ra (= 103) от горизонтальной нагретой стороны к верхним наклонным холодным сторонам из-за низкой силы потока жидкости, а также температуры, протекающей в основном за счет теплопроводности. .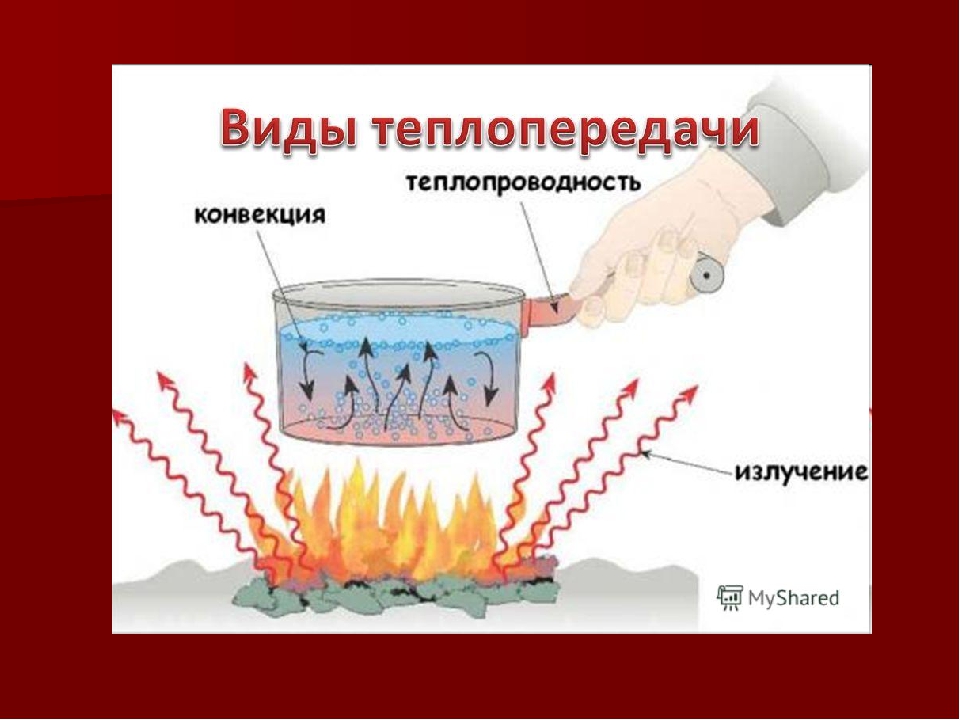


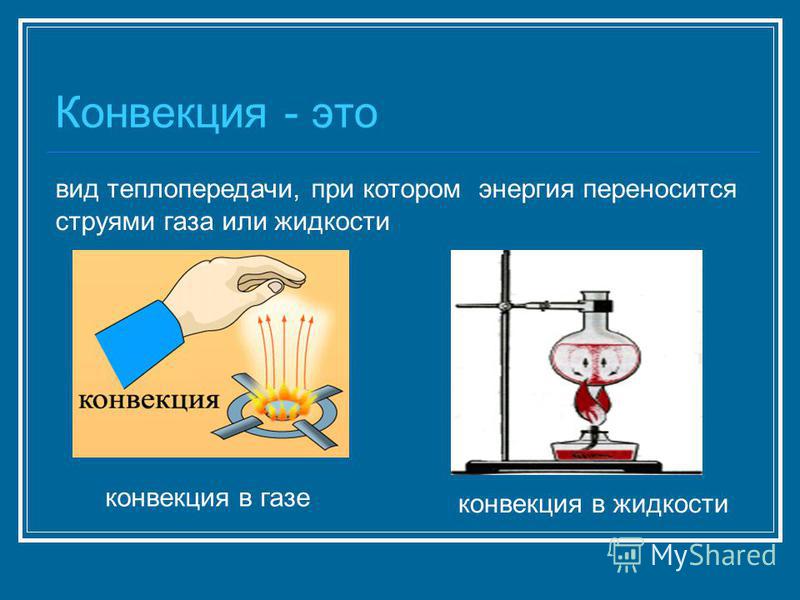
 При приложении внешнего магнитного поля более сильное поле воздействует на движущуюся жидкость, которая обладает магнитной восприимчивостью, что ослабляет циркуляцию потока внутри корпуса. Кроме того, сила Лоренца, возникающая при приложении магнитного поля, по своей природе препятствует изменению его генерации в случае движения жидкости, и, следовательно, это силовое поле ослабляет потоки внутри корпуса.На рисунке (б) видно, что изотермические линии все более искажаются внутри каверны и плотнее у нижней нагретой стенки при отсутствии числа Гартмана. При низком числе Гартмана (Ha = 0) более высокий градиент температуры наблюдается у донной прогретой стенки. Плотность линий тока уменьшается под действием более сильного магнитного поля. Кроме того, изотермические линии смещаются вверх ближе к средней части нижней нагретой стенки, что указывает на область более высокого теплопереноса.
При приложении внешнего магнитного поля более сильное поле воздействует на движущуюся жидкость, которая обладает магнитной восприимчивостью, что ослабляет циркуляцию потока внутри корпуса. Кроме того, сила Лоренца, возникающая при приложении магнитного поля, по своей природе препятствует изменению его генерации в случае движения жидкости, и, следовательно, это силовое поле ослабляет потоки внутри корпуса.На рисунке (б) видно, что изотермические линии все более искажаются внутри каверны и плотнее у нижней нагретой стенки при отсутствии числа Гартмана. При низком числе Гартмана (Ha = 0) более высокий градиент температуры наблюдается у донной прогретой стенки. Плотность линий тока уменьшается под действием более сильного магнитного поля. Кроме того, изотермические линии смещаются вверх ближе к средней части нижней нагретой стенки, что указывает на область более высокого теплопереноса.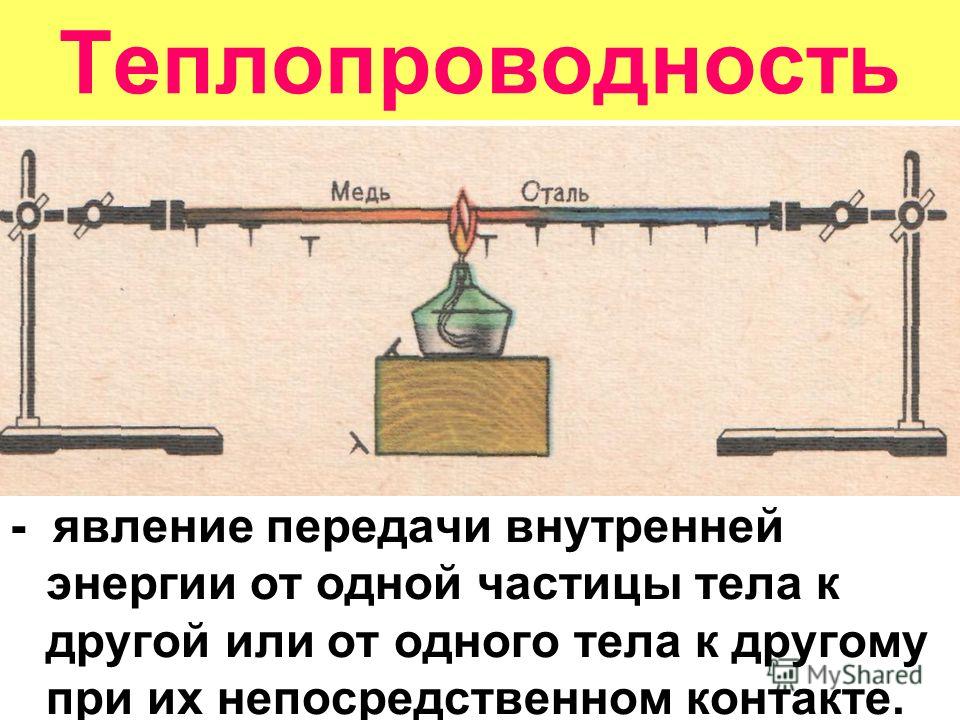 04 и Ra = 105.
04 и Ra = 105. Теплоперенос уменьшается с увеличением интенсивности числа Гартмана.Для более высокого числа Гартмана (Ha = 50) теплопроводы идут к верхним наклонным стенкам от нижней нагреваемой стенки. Теплота потока уменьшается из-за более низкой скорости при более высокой напряженности магнитного поля. Аналогичная картина тепловых линий с большим центральным кругом наблюдается для линейных тепловых условий на рис. (C) для всех значений числа Гартмана.
Теплоперенос уменьшается с увеличением интенсивности числа Гартмана.Для более высокого числа Гартмана (Ha = 50) теплопроводы идут к верхним наклонным стенкам от нижней нагреваемой стенки. Теплота потока уменьшается из-за более низкой скорости при более высокой напряженности магнитного поля. Аналогичная картина тепловых линий с большим центральным кругом наблюдается для линейных тепловых условий на рис. (C) для всех значений числа Гартмана. На рисунке представлены локальные распределения числа Нуссельта вдоль нагретой стенки для числа Гартмана как для однородных, так и для линейных температурных граничных условий.Эти рисунки показывают, что местное число Нуссельта быстро убывает при увеличении числа Гартмана для системы с однородной температурой, чем для системы с линейной температурой. Кроме того, изменение значения объемной доли наночастиц существенно влияет на Местное число Нуссельта.
На рисунке представлены локальные распределения числа Нуссельта вдоль нагретой стенки для числа Гартмана как для однородных, так и для линейных температурных граничных условий.Эти рисунки показывают, что местное число Нуссельта быстро убывает при увеличении числа Гартмана для системы с однородной температурой, чем для системы с линейной температурой. Кроме того, изменение значения объемной доли наночастиц существенно влияет на Местное число Нуссельта.
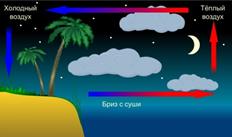 Более того, среднее число Нуссельта выше для наночастиц лысой формы по сравнению с другими наночастицами любой формы, такими как сферические, кирпичные, цилиндрические и пластинчатые.
Более того, среднее число Нуссельта выше для наночастиц лысой формы по сравнению с другими наночастицами любой формы, такими как сферические, кирпичные, цилиндрические и пластинчатые. Наблюдается, что средний Число Нуссельта увеличивается с увеличением объемной доли наночастиц для всех типов наножидкостей.Это связано с более высокой теплопроводностью наночастиц. В таблице показана самая высокая теплопередача для наножидкостей на основе керосина по сравнению с наножидкостями на водной основе и на основе этиленгликоля. Хотя наночастицы Cu имеют более высокую теплопроводность, чем Co, Al 2 O 3 и TiO 2 , керосиновые наножидкости показывают более высокую скорость теплопередачи. Самая низкая теплопередача наблюдается для наножидкостей на водной основе из-за более низкой теплопроводности и более высокой динамической вязкости жидкости на основе.
Наблюдается, что средний Число Нуссельта увеличивается с увеличением объемной доли наночастиц для всех типов наножидкостей.Это связано с более высокой теплопроводностью наночастиц. В таблице показана самая высокая теплопередача для наножидкостей на основе керосина по сравнению с наножидкостями на водной основе и на основе этиленгликоля. Хотя наночастицы Cu имеют более высокую теплопроводность, чем Co, Al 2 O 3 и TiO 2 , керосиновые наножидкости показывают более высокую скорость теплопередачи. Самая низкая теплопередача наблюдается для наножидкостей на водной основе из-за более низкой теплопроводности и более высокой динамической вязкости жидкости на основе.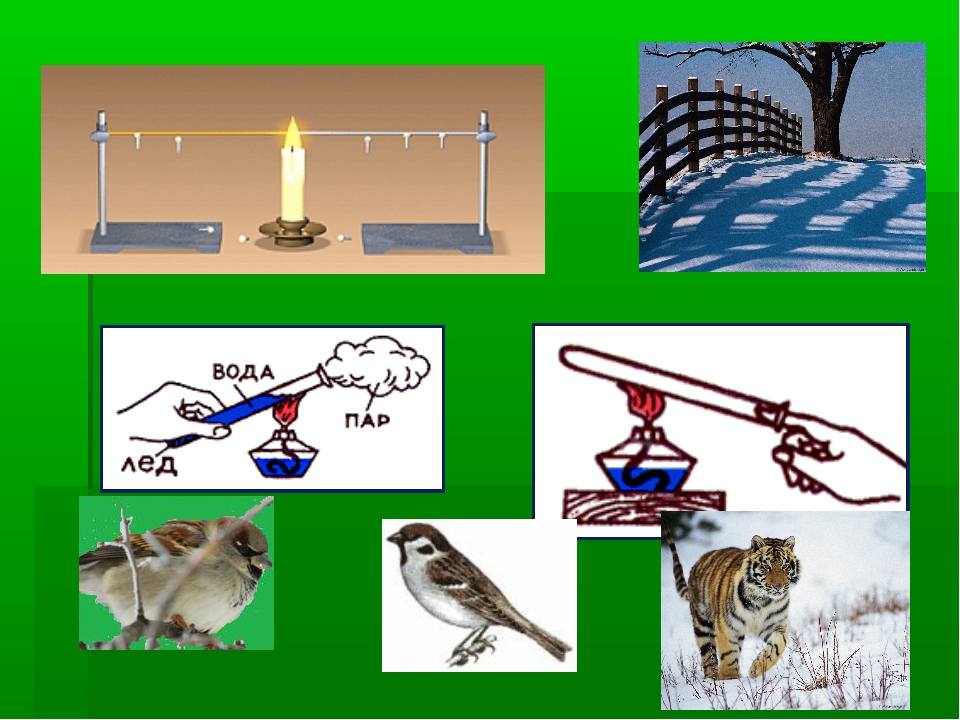 00
00 0869043
0869043 7008267
7008267 1564652
1564652% PDF-1.6 % 1 0 объект > эндобдж 6 0 объект > эндобдж 2 0 obj > / Шрифт> >> / Поля [] >> эндобдж 3 0 obj > ручей 2015-11-18T12: 49: 13 + 01: 00Canon iR-ADV C7270 2015-11-18T18: 29: 52 + 01: 002015-11-18T18: 29: 52 + 01: 00Adobe Acrobat Pro DC 15 Заглушка захвата бумаги- inapplication / pdfuuid: 4d664c56-0000-8887-177e-c32600000000uuid:
e41-0fda-4231-bd05-a6e6eb5e8ddd конечный поток эндобдж 4 0 объект > эндобдж 5 0 объект > эндобдж 7 0 объект > эндобдж 8 0 объект > эндобдж 9 0 объект > эндобдж 10 0 объект > ручей HyTSw oɞc [5laQIBHADED2mtFOE. c} 08 8 GNg9w ߽
c} 08 8 GNg9w ߽Комбинированное ламинарное течение естественной и принудительной конвекции и теплопередача жидкостей с источниками тепла и без них в каналах с линейно изменяющейся температурой стенок
Версия PDF также доступна для скачивания.
ВОЗ
Люди и организации, связанные либо с созданием этого отчета, либо с его содержанием.
Что
Описательная информация, помогающая идентифицировать этот отчет.Перейдите по ссылкам ниже, чтобы найти похожие предметы в Электронной библиотеке.
Когда
Даты и периоды времени, связанные с этим отчетом.
Статистика использования
Когда последний раз использовался этот отчет?
Взаимодействовать с этим отчетом
Вот несколько советов, что делать дальше.
Версия PDF также доступна для скачивания.
Ссылки, права, повторное использование
Международная структура взаимодействия изображений
Распечатать / Поделиться
Печать
Электронная почта
Твиттер
Facebook
Tumblr
Reddit
Ссылки для роботов
Полезные ссылки в машиночитаемом формате.
Ключ архивных ресурсов (ARK)
Международная структура взаимодействия изображений (IIIF)
Форматы метаданных
Картинки
URL
Статистика
Острах, Симон. Комбинированное ламинарное течение естественной и принудительной конвекции и теплопередача жидкостей с источниками тепла и без них в каналах с линейно изменяющейся температурой стенок.
отчет,
Апрель 1954 г .;
(https://digital.library.unt.edu/ark:/67531/metadc56936/:
по состоянию на 1 января 2022 г.), Библиотеки Университета Северного Техаса, Цифровая библиотека UNT, https://digital.library.unt.edu; кредитование Департамента государственных документов библиотек ЕНТ.
Комбинированное ламинарное течение естественной и принудительной конвекции и теплопередача жидкостей с источниками тепла и без них в каналах с линейно изменяющейся температурой стенок.
отчет,
Апрель 1954 г .;
(https://digital.library.unt.edu/ark:/67531/metadc56936/:
по состоянию на 1 января 2022 г.), Библиотеки Университета Северного Техаса, Цифровая библиотека UNT, https://digital.library.unt.edu; кредитование Департамента государственных документов библиотек ЕНТ.
Исследование теплопередачи естественной конвекции наножидкости в открытых L-образных полостях с использованием LBM
[1] Ханафер, Х.М. и Чамха А.Дж., Гидромагнитная естественная конвекция от наклонного пористого квадратного корпуса с выделением тепла, Численный перенос тепла, Часть A: Приложения , 33 (8), 1998, 891-910.
[2] Ким, Б.С., Ли, Б.И., Ли, Н., Чой, Г., Гемминг, Т., Чо, Х.Х., Интеллектуальные интерфейсы в нано-стиле: гибкая интерактивность и ее влияние на теплопередачу, Scientific Reports , 7, 2017, 45323.
[3] Хан И. и Шах Н.А., Научный отчет по анализу теплопередачи в смешанном конвекционном потоке жидкости Максвелла над колеблющейся вертикальной пластиной, Scientific Reports , 7, 2017, 40147.
[4] Thippeswamy, L.R. и Ядав А.К., Увеличение теплопередачи с использованием в контуре естественной циркуляции, Scientific Reports , 10, 2020, 1507.
[5] Фаттахи, Э., Фархади, М., Седиги, К., Моделирование теплопередачи естественной конвекции в эксцентрическом кольцевом пространстве на решетке Больцмана, International Journal of Thermal Sciences , 49, 2010, 2353-2362.
[6] Немати, Х., Фархади, М., Седиги, К., Фаттахи, Э., Рабиенатай, А.А., Моделирование наножидкости через решетку Больцмана в полости, управляемой крышкой , International Communications in Heat and Mass Transfer , 37, 2010, 1528-1534.
[7] Кефаяти, Г.Х.Р., Хоссейнизаде, С.Ф., Горджи, М., Саджади, Х., Моделирование естественной конвекции в высоких помещениях с использованием решеток Больцмана с использованием наножидкости вода / Si, International Communications in Heat and Mass Transfer , 38, 2011, 798-805.
[8] Немати, Х., Фархади, М., Седиги, К., Ашоринеджад, Х.Р., Фаттахи, Э., Влияние магнитного поля на естественный конвекционный тепловой поток наножидкости в прямоугольной полости с использованием решетчатой модели Больцмана, Scientia Iranica , 19 (2), 2012, 303–310.
[9] Джурабиан, М., Фархади, М., Рабиенатай Дарзи, А.А., Моделирование естественного конвекционного плавления в наклонной полости с использованием решеточного метода Больцмана, Scientia Iranica , 19 (4), 2012, 1066–1073.
[10] Джин, Л., Чжан, X., Ниу, X., Моделирование решеточного Больцмана для термочувствительных магнитных жидкостей в пористой квадратной полости, Journal of Magnetism and Magnetic Materials , 324, 2012, 44- 51.
[11] Назари М., Кайхани М. Х., Сравнительное решение естественной конвекции в открытой полости с использованием различных граничных условий с помощью метода Больцмана на решетке, Journal of Heat and Mass Transfer Research , 3, 2016, 115- 129.
[12] Ахмед М., Эсламиан, М., Естественная конвекция в квадратном корпусе с дифференциальным обогревом, заполненном нанофлюидом: значение силы термофореза и скорости скольжения / дрейфа, International Communications in Heat and Mass Transfer , 58, 2014, 1–11.
[13] Саджади, Х., Салманзаде, М., Ахмади, Г., Джафари, С., Исследование осаждения и рассеивания частиц с использованием гибридной модели LES / RANS на основе метода решетчатого Больцмана, Scientia Iranica , 25, 2018, 3173-3182.
[14] Джалали, А., Делуэи, А.А., Хорашадизаде, М., Голмохаммади, А.М., Каримнеджад, С., мезоскопическое моделирование принудительной конвективной теплопередачи потока жидкости Карроу-Ясуда по наклонному квадрату: вязкость, зависящая от температуры , Журнал прикладной и вычислительной механики , 6 (2), 2020, 307-319.
[15] Чой, У.С., Повышение теплопроводности жидкостей с помощью наночастиц, разработка и применение неньютоновских потоков, ASME , 66, 1995, 99-105.
[16] Хашим, Хафиз, А., Альшомрани, А.С., Хан, М., Множественные физические аспекты во время анализа потока и теплопередачи жидкости Карро с наночастицами, Scientific Reports , 8, 2018, 17402.
[17] Каррильо-Бердуго, И., Зоррилла, Д., Санчес-Маркес, Дж., Агилар, Т., Галлардо, Дж. Дж., Гомес-Вилларехо, Р., Алькантара, Р., Фернандес-Лоренцо, К., Навас, Дж., Формулировка на основе интерфейса и перспективы на молекулярном уровне теплопроводности и накопления энергии в наножидкостях, Scientific Reports , 9, 2019, 7595.
[18] Шейхолеслами, М., Саджади, Х., Делуэи, А.А., Аташафруз, М., Ли, Ж., Магнитная сила и влияние излучения на транспортировку наножидкости через проницаемую среду с учетом наночастиц, Журнал термического анализа и калориметрии , 136, 2019, 2477–2485.
[19] Чамха, А.Дж., Молана, М., Рахнама, А., Гадами Ф., О применении наножидкостей в микроканалах: всесторонний обзор, Powder Technology , 332, 2018, 287-322.
[20] Чамха, А.Дж., Рашад, А.М., Мансур, М.А., Армагани, Т., Галамбаз, М., Влияние теплоотвода и источника и генерации энтропии на смешанную МГД конвекцию наножидкости Cu-вода в крышке. ведомый квадратный пористый корпус с частичным скольжением, Physics of Fluids , 29, 2017, 052001-22.
[21] Рашад, А.М., Армагани, Т., Чамха, А.Дж., Мансур, М.А., Генерация энтропии и естественная МГД конвекция наножидкости в наклонной квадратной пористой полости: влияние радиатора, размера и расположения источника, Китайский журнал физики , 56 (1), 2018, 193-211.
[22] Ханафер, К., Вафай, К., Лайтстоун, М., Повышение теплопередачи за счет плавучести в двумерном корпусе с использованием наножидкости, International Journal of Heat and Mass Transfer , 46, 2003, 3639- 3653.
[23] Лай, Ф. Х., Янг, Ю.Т., Моделирование решеточно-Больцмана естественной конвекции теплопередачи наножидкостей / воды в квадратном корпусе, International Journal of Thermal Sciences , 50, 2011, 1930-1941.
Х., Янг, Ю.Т., Моделирование решеточно-Больцмана естественной конвекции теплопередачи наножидкостей / воды в квадратном корпусе, International Journal of Thermal Sciences , 50, 2011, 1930-1941.
[24] Фаттахи, Э., Фархади, М., Седиги, К., Немати, Х., Решеточно-Больцмановское моделирование естественной конвективной теплопередачи в нанофлюидах, International Journal of Thermal Sciences , 52, 2012, 137-144.
[25] Кефаяти, GH.R., Влияние магнитного поля на естественную конвекцию в открытой полости, подчиненной наножидкости вода / оксид алюминия, с использованием метода решетки Больцмана, International Communications in Heat and Mass Transfer , 40, 2013, 67 –77.
[26] Озтоп, Х.Ф., Абу-Нада, Э., Численное исследование естественной конвекции в частично нагретых прямоугольных корпусах, заполненных наножидкостями, International Journal of Heat and Fluid Flow , 29, 2008, 1326-1336.
[27] Джаханшахи, М., Хоссейнизаде, С.Ф. , Алипанах М., Дехгани А., Вакилинеджад Г.Р., Численное моделирование свободной конвекции на основе экспериментально измеренной проводимости в квадратной полости с использованием наножидкости вода / Si, International Communications in Heat and Mass Transfer , 37, 2010, 687-694.
, Алипанах М., Дехгани А., Вакилинеджад Г.Р., Численное моделирование свободной конвекции на основе экспериментально измеренной проводимости в квадратной полости с использованием наножидкости вода / Si, International Communications in Heat and Mass Transfer , 37, 2010, 687-694.
[28] Махмуди, А.Х., Шахи, М., Шахедин, А.М., Хемати, Н., Численное моделирование естественной конвекции в открытом корпусе с двумя вертикальными тонкими источниками тепла, подвергающимися воздействию наножидкости, International Communications in Heat and Mass Перевод , 38, 2011, 110-118.
[29] Кефаяти, GHR, Хоссейнизаде, С.Ф., Горджи, М., Саджади, Х., Моделирование естественной конвекции на решетке Больцмана в открытом корпусе, подчиненном наножидкости вода / медь , International Journal of Thermal Sciences , 52, 2012, 91-101.
[30] Шахриари А.Р., Джафари, С., Рахнама, М., Бехзадмехр, А., Влияние переменных свойств наножидкости на естественную конвекцию в квадратной полости с использованием метода решетки Больцмана, Международный обзор машиностроения , , 7, 2013 г. , 442–452 .
, 442–452 .
[31] Ху, Й., Хе, Й., Ци, К., Цзян, Б., Шлаберг, Х.И., Экспериментальное и численное исследование естественной конвекции в квадратном корпусе, заполненном наножидкостью, International Journal of Heat and Массообмен , 78, 2014, 380-392.
[32] Чжоу, В.Н., Ян, Ю.Ю., Сюй, Дж. Л., Больцмановское моделирование на решетке улучшенной теплопередачи наножидкостей, International Communications in Heat and Mass Transfer , 55, 2014, 113-120.
[33] Хоссейни, М., Мустафа, М.Т., Джафарьяр, М., Мохаммадиан, Э., Наножидкость в наклонной полости с частично нагретыми стенками, журнал Journal of Molecular Liquids , 199, 2014, 545-551.
[34] Джафари, М., Фархади, М., Акбарзаде, С., Эбрахими, М., Моделирование решеточно-Больцмана естественной конвекции теплопередачи SWCNT-наножидкости в открытом корпусе, Ain Shams Engineering Journal , 6 (3), 2015, 913-927.
[35] Шейхолеслами, М., Ашоринеджад, Х.Р., Рана, П., Моделирование на решетке Больцмана увеличения теплопередачи наножидкостей и генерации энтропии, Журнал молекулярных жидкостей , , 214, 2016, 86-95.
[36] Саджади, Х., Делуэи, А.А., Изади, М., Мохебби, Р., Исследование естественной МГД конвекции в пористой среде методом Больцмана с двойной решеткой МРТ с использованием гибридной наножидкости MWCNT– / вода, International Journal тепломассообмена , 132, 2019, 1087-1104.
[37] Саджади, Х., Амири Делуэи, А., Аташафруз, М., Шейхолеслами, М., Двойное МРТ-решеточное моделирование Больцмана трехмерной МГД естественной конвекции в кубической полости с синусоидальным распределением температуры с использованием наножидкости, Международный журнал тепломассообмена , 126, 2018, 489–503.
[38] Рахими, А., Kasaeipoor, A., Malekshah, EH, kolsi, L., Анализ естественной конвекции путем генерации энтропии и визуализации тепловых линий с использованием метода Больцмана на решетке в заполненной наножидкостью полости, включенной с внутренними нагревателями — Эмпирические теплофизические свойства, Журнал молекулярных жидкостей , 133, 2017, 199-216.
[39] Рахими, А. , Касаейпур, А., Малекшах, Э. Х., Моделирование на решетке Больцмана естественной конвекции и генерации энтропии в полостях, заполненных наножидкостью при наличии внутренних твердых тел. Экспериментальные теплофизические свойства, Journal of Molecular Жидкости , 242, 2017, 580-593.
, Касаейпур, А., Малекшах, Э. Х., Моделирование на решетке Больцмана естественной конвекции и генерации энтропии в полостях, заполненных наножидкостью при наличии внутренних твердых тел. Экспериментальные теплофизические свойства, Journal of Molecular Жидкости , 242, 2017, 580-593.
[40] Мехризи, А., Фархади, М., Шаямер, С., Естественный конвекционный поток наножидкости Cu – Вода в горизонтальных цилиндрических кольцах с внутренним треугольным цилиндром с использованием решеточного метода Больцмана, International Communications in Heat and Mass Transfer , 44, 2013, 147-156.
[41] Абдаллауи, М.Эл., Хаснауи, М., Амахмид, А., Численное моделирование естественной конвекции между децентрированным треугольным нагревательным цилиндром и квадратным внешним цилиндром, заполненным чистой жидкостью или наножидкостью, с использованием решеточного метода Больцмана, Powder Technology , 277, 2015, 193–205.
[42] Хатами, М., Численное исследование естественной конвекции наножидкостей в прямоугольной полости, включая нагретые ребра, Journal of Molecular Liquids , 233, 2017, 1-8.
[43] Тораби, М., Кейхани, А.Р., Петерсон, Г.П., Комплексное исследование естественной конвекции внутри частично дифференциально нагретой полости с тонким ребром с использованием двух решеточных функций распределения Больцмана, International Journal of Heat and Mass Перевод , 115, 2017, 264-277.
[44] Чамха, А.Дж., Доостанидезфули, А., Изадпанахи, Э., Галамбаз, М., Теплопередача с фазовым переходом материалов с фазовым переходом с единичными / гибридными наночастицами над нагретым горизонтальным цилиндром, заключенным в квадратную полость, Advanced Powder Technology , 28 (2), 2017, 385-397.
[45] Порданджани, А.Х., Джаханбахши, А., Надушан, А.А., Афранд, М., Влияние двух изотермических препятствий на естественную конвекцию наножидкости в присутствии магнитного поля внутри корпуса с синусоидальным распределением температуры стенок, Международный журнал тепло- и массообмена , 121, 2018, 565–578.
[46] Сиаваши М., Юсофванд Р. , Резанежад С., Влияние наножидкости и пористых ребер на естественную конвекцию и генерацию энтропии потока внутри полости, Advanced Powder Technology , 29, 2018, 142-156 .
, Резанежад С., Влияние наножидкости и пористых ребер на естественную конвекцию и генерацию энтропии потока внутри полости, Advanced Powder Technology , 29, 2018, 142-156 .
[47] Виджайбабу, Т.Р., Дхинакаран, С., MHD Естественная конвекция вокруг проницаемого треугольного цилиндра внутри квадратного корпуса, заполненного наножидкостью — O: исследование LBM, International Journal of Mechanical Sciences , 153–154, 2019, 500-516.
[48] Хашим, И., Альсабери, А.И., Шеремет, М.А., Чамха, А.Дж., Численное исследование естественной конвекции водной наножидкости в волнистой полости с проводящим внутренним блоком с использованием двухфазной модели Буонджорно, Advanced Powder Technology , 30, 2019, 399-414.
[49] Диндарло, М. Р., Пайан, С., Влияние толщины ребер, глубины канавок и угла их крепления к горячей стенке на максимальное снижение теплопередачи в квадратном корпусе, International Journal of Thermal Sciences , 136, 2019, 473–490.
[50] Коджа, А., Озтоп, Х.Ф., Варол, Ю., Численный анализ естественной конвекции в односкатных крышах с карнизами зданий для холодного климата, Компьютеры и математика с приложениями , 56, 2008, 3165-3174.
[51] Дехнави, Р., Резвани, А., Численное исследование естественной конвекции теплопередачи наножидкостей в Γ-образной полости, Сверхрешетки и микроструктуры , 52, 2012, 312–325.
[52] Калтех, М., Хасани, Х., Моделирование на решетке Больцмана свободной конвекции тепла с помощью наножидкостей в L-образном корпусе, Сверхрешетки и микроструктуры , 66, 2014, 112-128.
[53] Парвин, С., Насрин, Р., Алима, М.А., Хоссейн, Н.Ф., Чамха А.Дж., Изменение теплопроводности естественного конвекционного потока воды и наножидкости оксида алюминия в затрубном пространстве, International Journal of Heat and Mass Transfer , 55, 2012, 5268–5274.
[54] Гальегос, А.Д., Малага, К., Естественная конвекция в эксцентрических сферических кольцах, European Journal of Mechanics — B / Fluids , 65, 2017, 464-471.
[55] Парвин, С., Насрин, Р., Алим, М.А., Хоссейн, Н.Ф., Чамха, А.Дж., Изменение теплопроводности при естественной конвекции потока наножидкости вода-оксид алюминия в кольцевом пространстве, International Journal of Heat and Mass Transfer , 55, 2012, 5268– 5274.
[56] Шейхолеслами М., Горджи-Бандпи М., Сейеди С.М., Ганджи Д.Д., Рокни, Х.Б., Сулеймани, С., Применение LBM для моделирования естественной конвекции в заполненной нанофлюидом квадратной полости с кривой границы, Powder Technology , 247, 2013, 87–94.
[57] Гади, Аризона, Хагиги Асл, А., Валипур, М.С., Численное моделирование двойной диффузионной естественной конвекции внутри дугообразного корпуса, заполненного пористой средой, Journal of Heat and Mass Transfer Research , 1 , 2014, 83-91.
[58] Jayhooni, S.М.Х., Джафарпур, К., Численное моделирование теплообмена ламинарной свободной конвекции вокруг изотермических вогнутых и выпуклых форм тела, Журнал исследований тепломассопереноса , 2, 2015, 37-44.
[59] Резвани А., Валипур М.С., Биглари М., Численное исследование генерации энтропии для естественной конвекции в цилиндрических полостях, Журнал исследований тепломассопереноса , 3 (2016) 89-99.
[60] Гасеми Б., Аминосадати С.М., Броуновское движение наночастиц в треугольном корпусе с естественной конвекцией, International Journal of Thermal Sciences , 49, 2010, 931-940.
[61] Салех, Х., Рослан, Р., Хашим, И., Естественная конвекция теплопередачи в заполненном наножидкостью трапециевидном корпусе, International Journal of Heat and Mass Transfer , 54, 2011, 194-201.
[62] Меджри, И., Махмуди, А., Аббасси, М.А., Омри, А., LBM-моделирование естественной конвекции в наклонной треугольной полости, заполненной водой, Alexandria Engineering Journal , 55 (2), 2016 , 1385–1394.
[63] Чамха, А.Дж., Исмаил, М., Kasaeipoor, A., Armaghani, T., Генерация энтропии и естественная конвекция наножидкости CuO-вода в C-образной полости под действием магнитного поля, Энтропия , 18 (2), 2016, 50.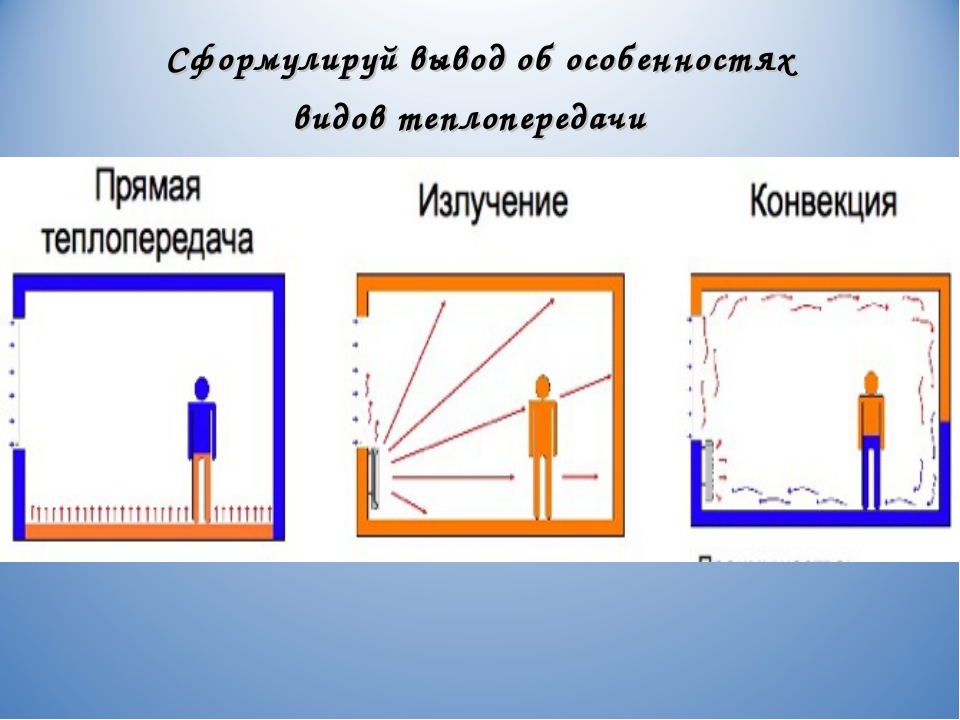
[64] Мохебби, Р., Изади, М., Чамха, А.Дж., Расположение источника тепла и естественная конвекция в С-образном корпусе, насыщенном наножидкостью, Physics of Fluids , 29, 2017, 122009-13.
[65] Бондарева, Н.С., Шеремет, М.А., Озтоп, Х.Ф., Абу-Хамде, Н., Генерация энтропии за счет естественной конвекции наножидкости в частично открытой треугольной полости, Advanced Powder Technology , 28 (1) , 2017, 244-255.
[66] Махмуди, М., Хашеми, С.М., Численное исследование естественной конвекции наножидкости в C-образных корпусах, International Journal of Thermal Sciences , 55, 2012, 76-89.
[67] Мансур, М.А., Бакьер, А.Й., Бакер, Май, Естественная конвекция локализованных источников тепла Т-образных корпусов, заполненных наножидкостью, Американский журнал инженерных исследований , 2 (7), 2013, 49-61 .
[68] Бакьер, М.А.Й., Поток в открытых С-образных полостях: насколько изменение границ влияет на нанофлюид?, Технические науки и технологии, Международный журнал , 17, 2014, 116-130.
[69] Эсфеа, М.Х., Аббасиан Арани, А.А., Янк, В. М., Агаи, А., Естественная конвекция в Т-образных полостях, заполненных суспензиями на водной основе многостенных углеродных нанотрубок, функционализированных с помощью COOH, International Journal of Mechanical Sciences , 121, 2017, 21–32.
[70] Махмуд С., Свободная конвекция внутри L-образного корпуса, International Communications in Heat and Mass Transfer , 29, 2002, 1005-1013.
[71] Тасним, С.Х., Махмуд, С., Ламинарная свободная конвекция внутри наклонного L-образного корпуса, International Communications in Heat and Mass Transfer , 33, 2006, 936-942.
[72] Махмуди М., Численное моделирование свободной конвекции наножидкости в L-образных полостях, International Journal of Thermal Sciences , 50, 2011, 1731-1740.
[73] Шейхолеслами М., Горджи-Бандпи М., Ганджи Д.Д., Сулеймани С. Теплопередача естественной конвекцией в наклонном L-образном корпусе, заполненном наножидкостью, Иранский журнал науки и технологий, Транзакции Машиностроение , 38, 2014, 217-226.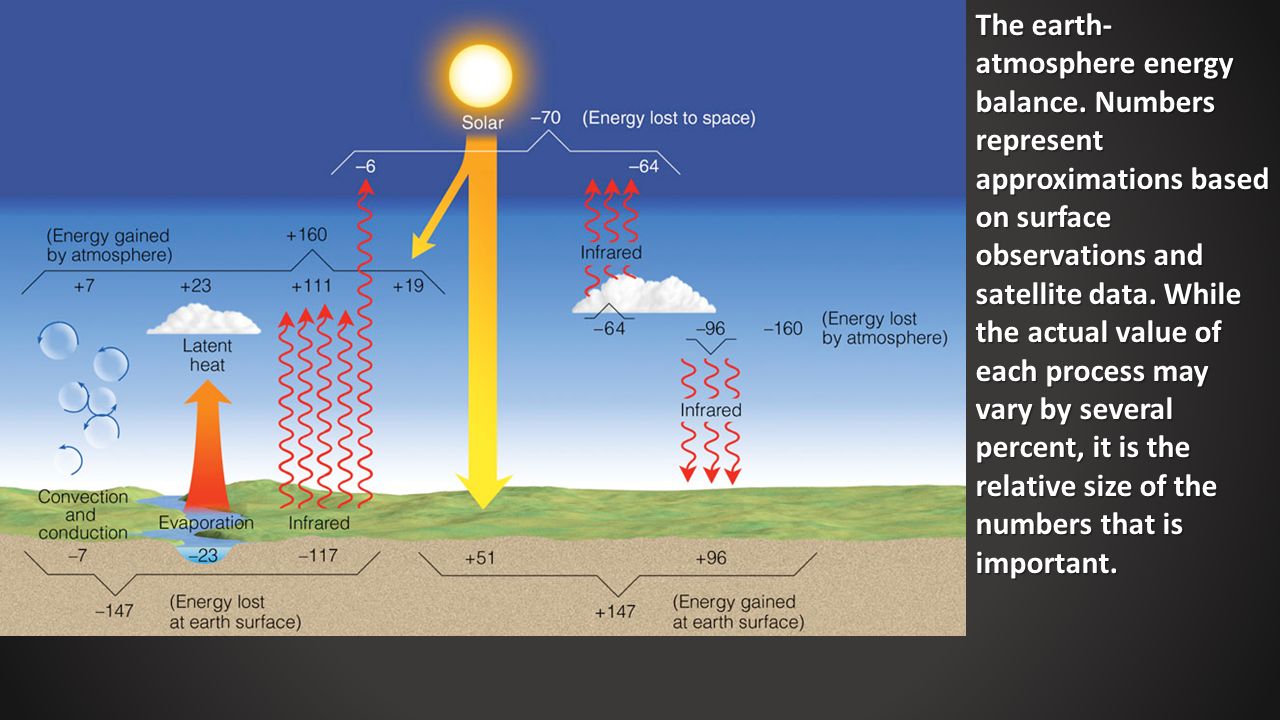
[74] Млики, Б., Аббасси, М.А., Гедри, К., Омри, А., Моделирование естественной конвекции на решетке Больцмана в L-образном корпусе в присутствии наножидкости, Engineering Science and Technology an International Journal , 18, 2015, 503-511 .
[75] Мохебби, Р., Рашиди, М.М., Численное моделирование естественной конвекционной теплопередачи наножидкости в L-образном корпусе с препятствием для нагрева, Журнал Тайваньского института инженеров-химиков , 72, 2017, 70-84.
[76] Рахими, А., Касаэйпур, А., Малекшах, Э.Х., Амири, А., Анализ естественной конвекции с использованием генерации энтропии и визуализации тепловых линий в полой L-образной полости, заполненной наножидкостью, с использованием решеточного метода Больцмана. -физические свойства, Physica E: Низкоразмерные системы и наноструктуры , 97, 2018, 82-97.
[77] Чжан Р., Агахани, С., Хаджатзаде Порданджани, А. и др., Исследование генерации энтропии при естественной конвекции ньютоновских и неньютоновских жидкостей внутри L-образной полости под действием магнитного поля: применение решеточного метода Больцмана, The European Физический журнал плюс , 135, 2020, 184.
[78] Изади, М., Мохебби, Р., Делуэи, А.А., Саджади, Х., Естественная конвекция намагничивающейся гибридной наножидкости внутри пористой оболочки под действием двух переменных магнитных полей, International Journal of Mechanical Sciences , 151, 2019, 154-169.
[79] Аббасси, М.А., Сафаи, М.Р., Джебали, Р., Гедри, К., Зегмати, Б., Альрашедг, AAAA, LBM-моделирование свободной конвекции в печи для сжигания с нанофлюидом, содержащей горячий блок, International Journal наук , 148, 2018, 393-408.
[80] Ма, Й., Мохебби, Р., Рашиди, М.М., Янг, Ж., Моделирование естественной конвекции наножидкости в U-образной полости, снабженной препятствием для нагрева: Эффект соотношения сторон полости, Journal of Тайваньский институт инженеров-химиков , 93, 2018, 263-276.
[81] Ю.М. Со, М. Йонг Ха, Ю. Гэп Парк, Численное исследование трехмерной естественной конвекции с цилиндром в длинном прямоугольном корпусе. Часть I. Размерный эффект круглого или эллиптического цилиндра, International Journal of Heat and Mass Transfer , 134, 2019, 420-436.
[82] Датта, С., Госвами, Н., Бисвас, А.К., Пати, С., Численное исследование магнитогидродинамической теплопередачи естественной конвекции и генерации энтропии в ромбической оболочке, заполненной наножидкостью Cu-вода, International Journal of Тепло- и массообмен , 136, 2019, 777–798.
[83] Пурусотаман А., Малекшах Э. Х., Моделирование МГД свободной конвекции наножидкости в V-образном микроэлектронном модуле на решетке Больцмана, Thermal Science and Engineering Progress , 10, 2019, 186-197.
[84] Яхиауи, А., Джеззар, М., Наджи, Х., Моделирование улучшения теплопередачи с помощью наножидкости на водной основе в корпусах с изогнутыми боковыми стенками, International Communications in Heat and Mass Transfer , 100, 2019, 118–132.
[85] Альмешаал, М.А., Маатки, К., Колси, Л., Гачем, К., Чамха, А.Дж., Естественная конвекция 3D-типа Рэлея-Бенара в L-образных оболочках, заполненных наножидкостью MWCNT, с учетом агрегации эффект, Математические методы в прикладных науках , 2020, 1–17.
[86] Догончи, А.С., Чамха, А.Дж., Сейеди, С.М., Хашеми-Тилехнои, М., Ганджи, Д.Д., Влияние вязкой диссипации на свободноконвекционный поток наножидкости Cu-вода в круглом корпусе с пористостью с учетом внутреннего источника тепла , Журнал прикладной и вычислительной механики , 5 (4), 2019, 717-726.
[87] Бежан, А., Convection Heat Transfer , John Wiley & Sons, Inc., Хобокен, Нью-Джерси, США, 2004.
[88] Мохамад, А.А., Кузьмин, А., Критическая оценка силового члена в решеточном методе Больцмана, проблема естественной конвекции, International Journal of Heat and Mass Transfer , 53, 2010, 990-996.
[89] Мохамад, А.А., Эль-Ганауи, М., Беннасер, Р., Моделирование естественной конвекции решеткой Больцмана в открытом корпусе, International Journal of Thermal Sciences , 48, 2009, 1870-1875.
[90] Ван, X.Q., Муджумдар, А.С., Характеристики теплопередачи наножидкостей: обзор, International Journal of Thermal Sciences , 46 (1), 2007, 1-19.

 Какую роль при этом играет теплопроводность меха, перьевого покрова, подкожного жира и т.п.?
Какую роль при этом играет теплопроводность меха, перьевого покрова, подкожного жира и т.п.?
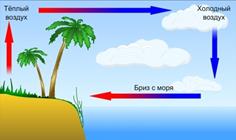
 И. Лукашик, Е.В. Иванова, Сборник задач по физике для 7-9 классов общеобразовательных учреждений — 20-е издание
И. Лукашик, Е.В. Иванова, Сборник задач по физике для 7-9 классов общеобразовательных учреждений — 20-е издание