Вектор в системе координат — урок. Геометрия, 9 класс.
Вспомним, что при умножении вектора на число k≠0 мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если k>0, или противоположно направлены, если k<0. Длины векторов различаются \(k\) раз.

Справедливо и обратное суждение.
Если ненулевые векторы коллинеарны, то обязательно можно найти число k≠0 так, что b→=k⋅a→.
Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде c→=k⋅a→+m⋅b→. Говорят, что вектор c→ разложен по векторам a→ и b→, а числа \(k\) и \(m\) называют коэффициентами разложения.
Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.
Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают i→ и j→.

Если от начала координат отложить вектор a→, то его можно разложить по векторам i→ и j→ следующим образом: a→=3⋅i→+2⋅j→.
В этом разложении коэффициенты координатных векторов называют координатами вектора a→.
Это записывают как a→3;2.
Любой вектор, который равен с вектором a→, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.
Равные векторы имеют равные координаты.
Но в то же время в координатной системе можно переместить векторы i→ и j→, таким образом определить координаты векторов независимо от их места расположения в координатной системе.
Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.
Связь между координатами противоположных векторов следует из того, что, если умножить вектор на \(-1\), результатом будет противоположный вектор.
У противоположных векторов противоположные координаты.
Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.

www.yaklass.ru
Координаты вектора / Метод координат / Справочник по геометрии 7-9 класс
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
На рисунке выше оси 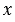 и
и  перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор — это вектор, длина которого равна 1.
перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор — это вектор, длина которого равна 1.
Отложим от начала координат О единичные векторы и 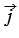
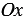 и
и 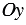 соответственно.
соответственно.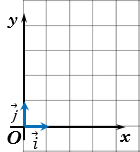
Векторы и 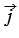 называют координатными векторами.
называют координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор 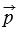 можно разложить по координатным векторам, т.е. представить в виде
можно разложить по координатным векторам, т.е. представить в виде  , причем коэффициенты разложения
, причем коэффициенты разложения  и
и 
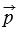 по координатным векторам называются координатами вектора
по координатным векторам называются координатами вектора 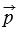 в данной системе координат.
в данной системе координат.Координаты вектора записывают в фигурных скобках после обозначения вектора:  .
.
На рисунке выше .
Нулевой вектор можно представить в виде , следовательно, его координаты равны нулю: 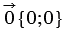 .
.
Если векторы и равны, то и 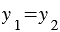 . Значит, координаты равных векторов соответственно равны.
. Значит, координаты равных векторов соответственно равны.
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:
| 10 |
Доказательство
Дано: ,  ,
,  .
.
Доказать: 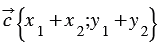 .
.
Доказательство:
По условию и  , тогда и
, тогда и 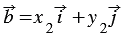 .
.
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим:  , следовательно, координаты вектора
, следовательно, координаты вектора 
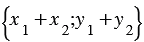 , т.е.
, т.е. 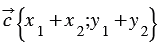 . Что и требовалось доказать.
. Что и требовалось доказать.| 20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. |
Доказательство
Дано: ,  ,
, 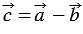 .
.
Доказать: 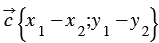 .
.
Доказательство:
По условию и  , тогда (1) и
, тогда (1) и 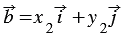 . (2)
. (2)
Вычтем из равенства
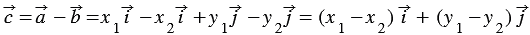 , следовательно, координаты вектора
, следовательно, координаты вектора 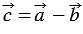 равны
равны 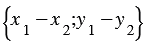 , т.е.
, т.е. 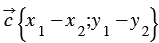 . Что и требовалось доказать.
. Что и требовалось доказать.| 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. |
Доказательство
Дано: 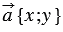 ,
, 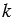 — число,
— число, 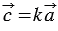
Доказать: 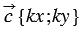 .
.
Доказательство:
По условию 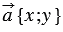 , значит, .
, значит, .
Умножим последнее равенство на число 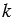 и используя свойства умножения вектора на число, получим:
и используя свойства умножения вектора на число, получим: 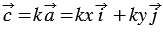 , следовательно, координаты вектора
, следовательно, координаты вектора 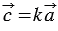 равны
равны 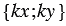 , т.е.
, т.е. 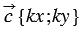 . Что и требовалось доказать.
. Что и требовалось доказать.
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример
Найти координаты вектора 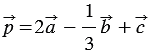 , если известно, что .
, если известно, что .
Решение:
По правилу 30 вектор  будет иметь координаты
будет иметь координаты 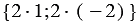 , т.е.
, т.е.  , вектор
, вектор 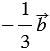 координаты , т.е.
координаты , т.е.  .
.
Так как , то координаты вектора 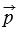 можно найти по правилу 10:
можно найти по правилу 10:  , т.е. .
, т.е. .
Ответ:
.budu5.com
§3. Координаты вектора
До сих пор считалось, что векторы
рассматриваются в пространстве. Начиная
с этого момента будим считать, что все
векторы рассматриваются на плоскости.
Будем также полагать, что на плоскости
задана Декартова система координат
(даже если об этом не говорится),
представляющая две взаимно перпендикулярные
числовые оси – горизонтальная ось  и
вертикальная ось
и
вертикальная ось .
Тогда каждой точке
.
Тогда каждой точке на
плоскости ставится в соответствие пара
чисел
на
плоскости ставится в соответствие пара
чисел
 соответствует точка плоскости такая,
что пара чисел
соответствует точка плоскости такая,
что пара чисел являются ее координатами.
являются ее координатами. 
Рис. 19.
Из элементарной геометрии известно,
что если на плоскости имеются две точки 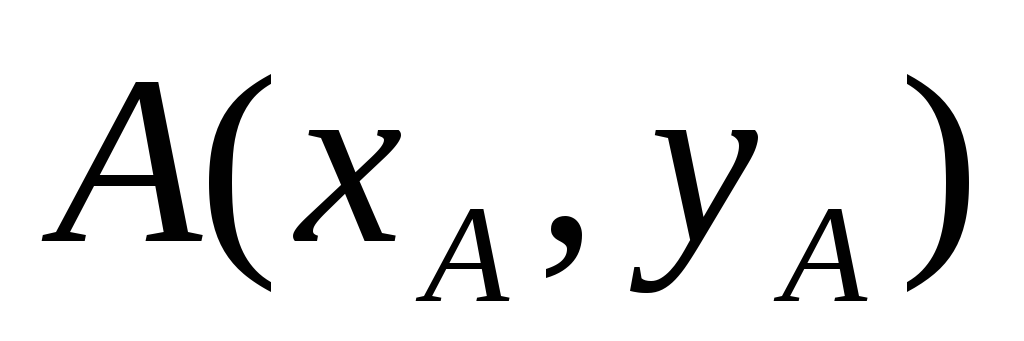 и
и ,
то расстояние
,
то расстояние между
этими точками выражается через их
координаты по формуле
между
этими точками выражается через их
координаты по формуле
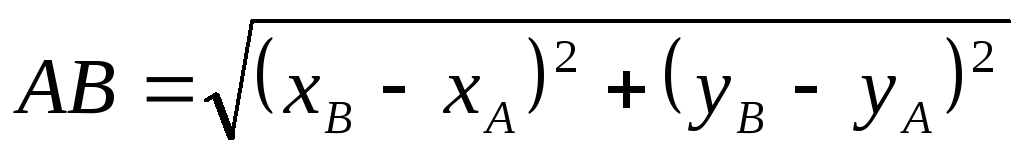 .
. Пусть на плоскости задана Декартова
система координат. Орт оси  будем обозначать символом
будем обозначать символом ,
а орт оси
,
а орт оси символом
символом .
Проекцию произвольного
.
Проекцию произвольного вектора
вектора на ось
на ось будем обозначать символом
будем обозначать символом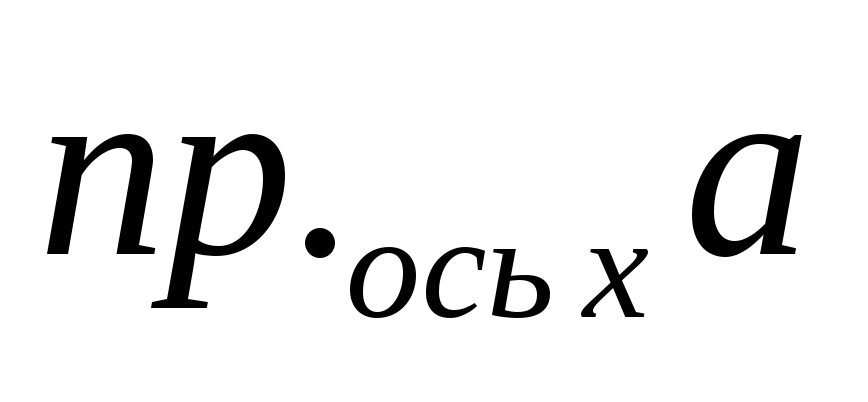
 символом
символом .
. 
Рис. 20.
Пусть  — произвольный вектор на плоскости.
Имеет место следующая теорема.
— произвольный вектор на плоскости.
Имеет место следующая теорема.
Теорема 22.
Для любого вектора  на плоскости существует пара чисел
на плоскости существует пара чисел таких, что справедливо равенство
таких, что справедливо равенство
 .
.
При этом  ,
, .
.
Доказательство.

Рис. 21.
Пусть дан вектор .
Отложим вектор
.
Отложим вектор от начала координат. Обозначим через
от начала координат. Обозначим через вектор-проекцию вектора
вектор-проекцию вектора на ось
на ось ,
а через
,
а через вектор-проекцию вектора
вектор-проекцию вектора на ось
на ось .
Тогда, как видно из рисунка 21, имеет
место равенство
.
Тогда, как видно из рисунка 21, имеет
место равенство
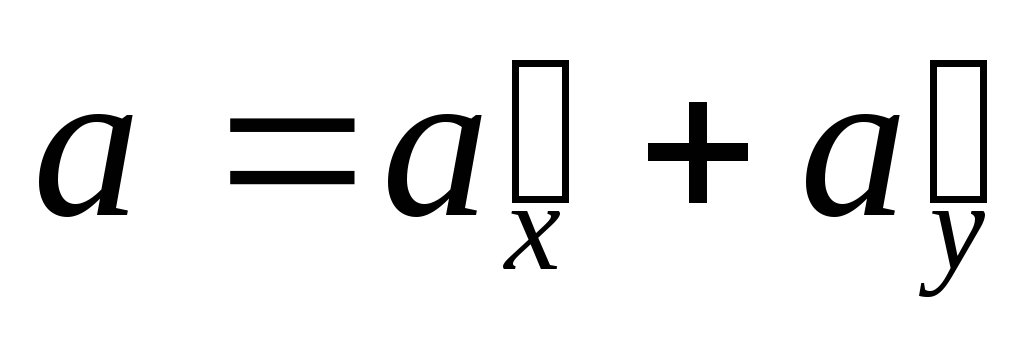 .
.
 Согласно
теореме 9,
Согласно
теореме 9,
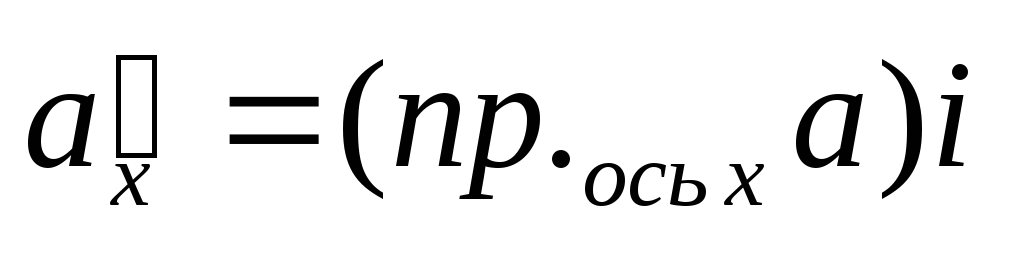 ,
,
 .
.
Обозначим  ,
,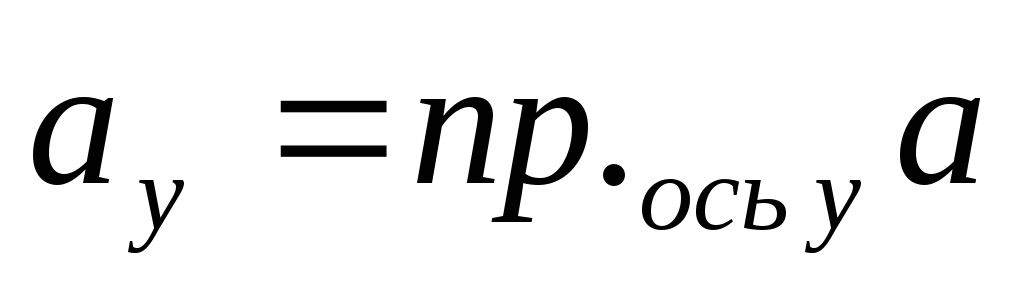 .
Тогда получаем
.
Тогда получаем
 .
.
Итак, доказано, что для любого вектора  существует пара чисел
существует пара чисел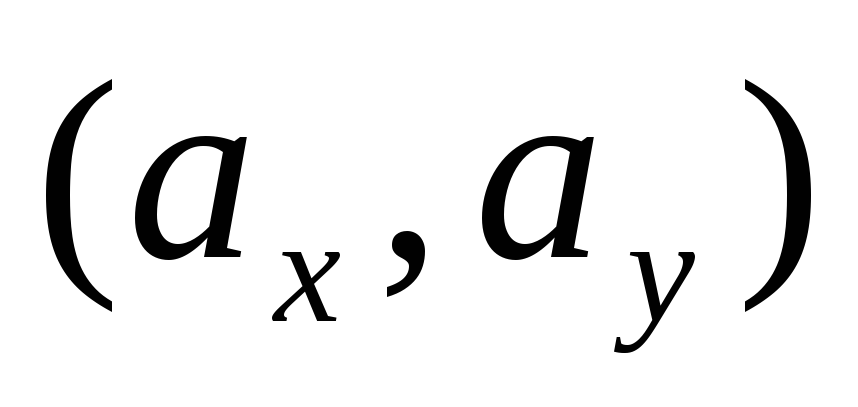 таких, что справедливо равенство
таких, что справедливо равенство
 ,
,
Причем,
 ,
,
 .
.
При другом расположении вектора  относительно осей доказательство
аналогично.
относительно осей доказательство
аналогично.
Определение.
Пара чисел  и
и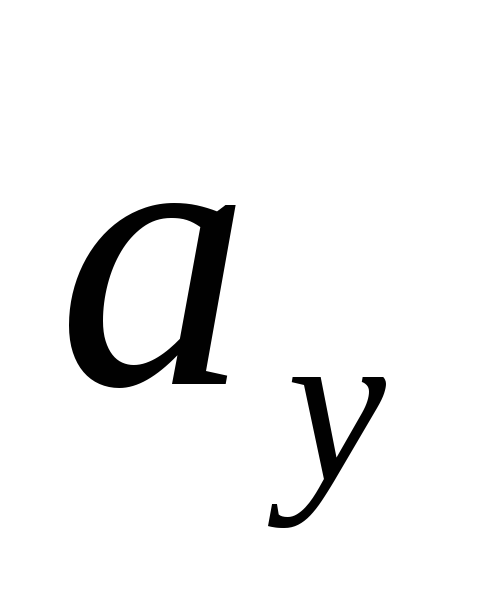 таких, что
таких, что ,
называются координатами вектора
,
называются координатами вектора .
Число
.
Число называется иксовой координатой, а число
называется иксовой координатой, а число игрековой координатой.
игрековой координатой.
Определение.
Пара ортов осей координат  называется ортонормированным базисом
на плоскости. Представление любого
вектора
называется ортонормированным базисом
на плоскости. Представление любого
вектора в виде
в виде называется разложением вектора
называется разложением вектора по базису
по базису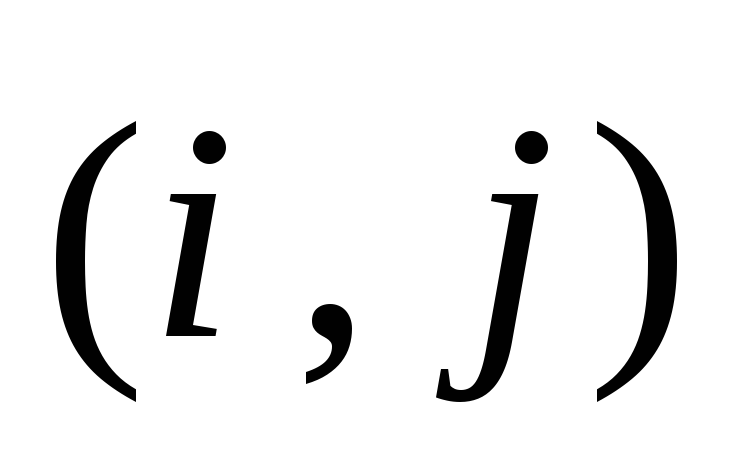 .
.
Непосредственно из определения координат вектора следует, что если координаты векторов равны, то равны и сами векторы. Справедливо также и обратное утверждение.
Теорема.
Равные векторы имеют равные координаты.
Доказательство.
Пусть
 ,
,
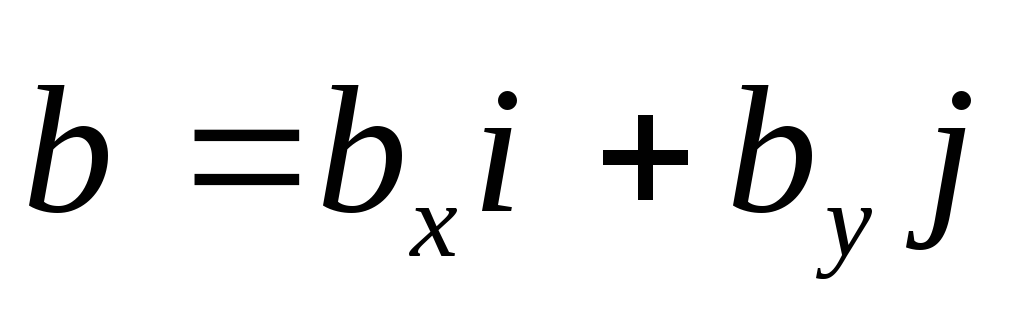
и  .
Докажем, что
.
Докажем, что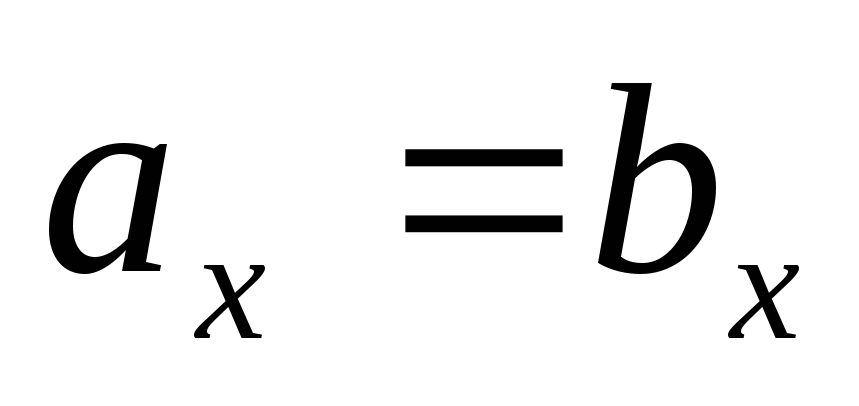 ,
, .
.
Из равенства векторов следует, что
 .
.
Отсюда
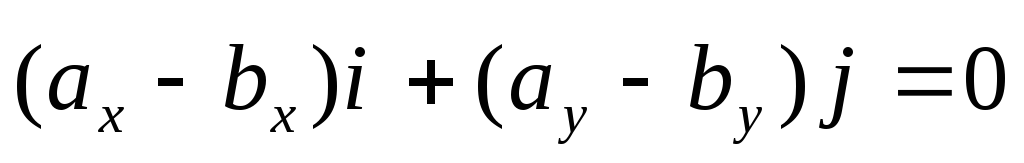 .
.
Допустим, что 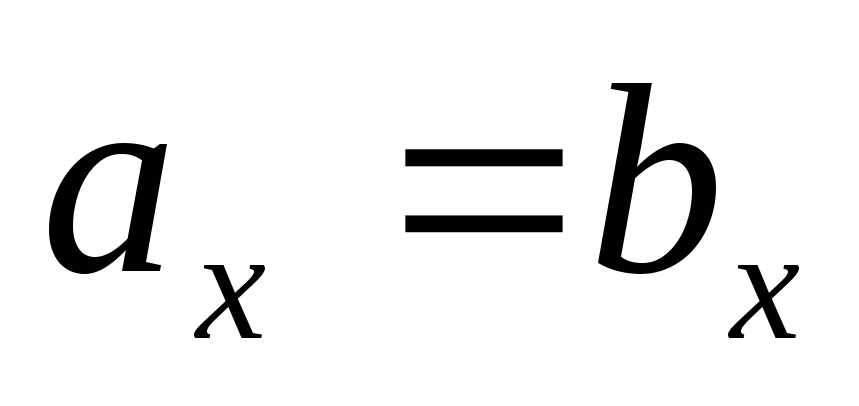 ,
а
,
а .
.
Тогда
и значит ,
что не верно. Аналогично, если
,
что не верно. Аналогично, если ,
но
,
но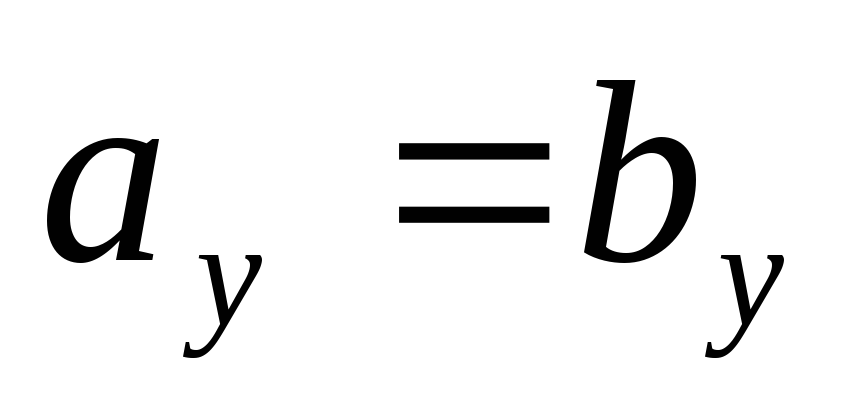 ,
то
,
то .
Отсюда
.
Отсюда ,
что не верно. Наконец, если допустить,
что
,
что не верно. Наконец, если допустить,
что и
и ,
то получаем, что
,
то получаем, что
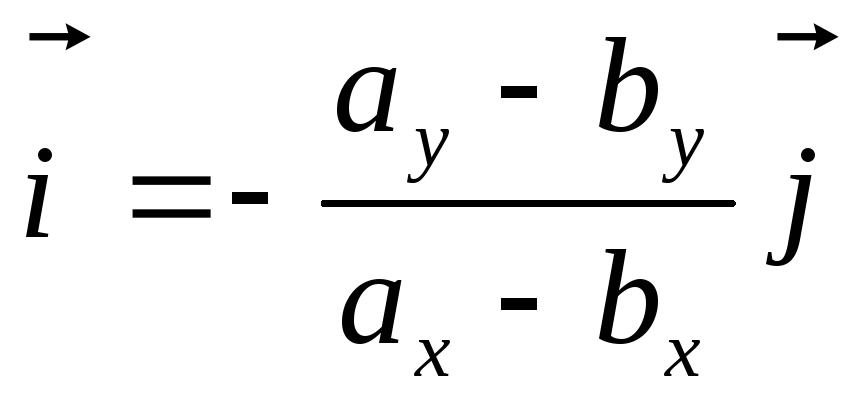 .
.
Это означает, что векторы  и
и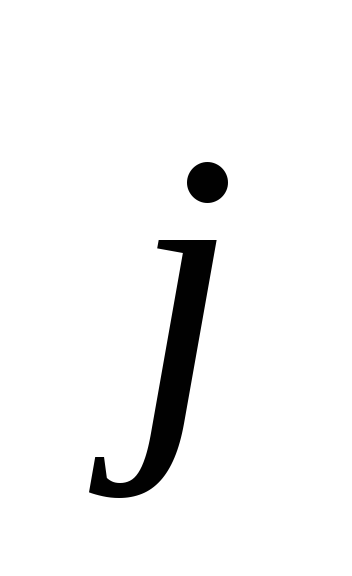 коллинеареы. Но это не верно, так как
они перпендикулярны. Следовательно,
остается, что
коллинеареы. Но это не верно, так как
они перпендикулярны. Следовательно,
остается, что ,
, ,
что и требовалось доказать.
,
что и требовалось доказать.
Таким образом, координаты вектора
полностью определяют сам вектор. Зная
координаты  и
и вектора
вектора можно построить сам вектор
можно построить сам вектор , построив векторы
, построив векторы и
и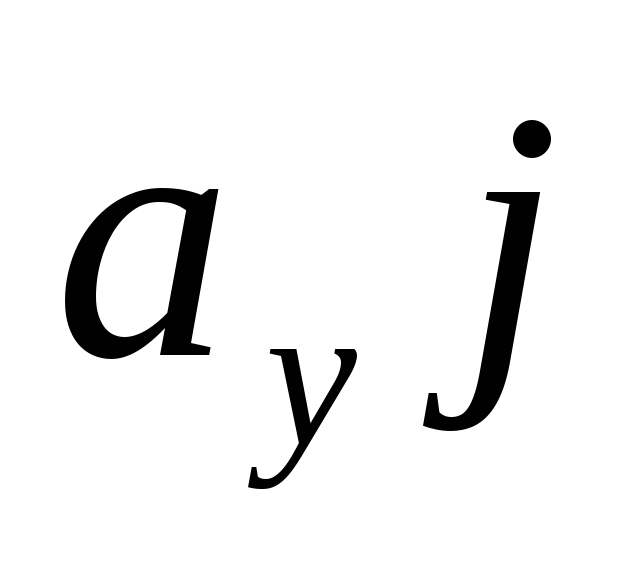 и сложив их. Поэтому часто сам вектор
и сложив их. Поэтому часто сам вектор обозначают в виде пары его координат и
пишут
обозначают в виде пары его координат и
пишут .
Такая запись означает, что.
.
Такая запись означает, что.
Непосредственно из определения координат вектора следует следующая теорема.
Теорема.
При сложении векторов их координаты складываются а при умножении вектора на число его координаты умножаются на это число. Записываются эти утверждения в виде
 ,
,
 .
.
Доказательство.
 ,
,
 .
.
Далее установим как связаны координаты вектора с координатами его концов.
Теорема.
Пусть  ,
причем начало вектора точка
,
причем начало вектора точка имеет координаты
имеет координаты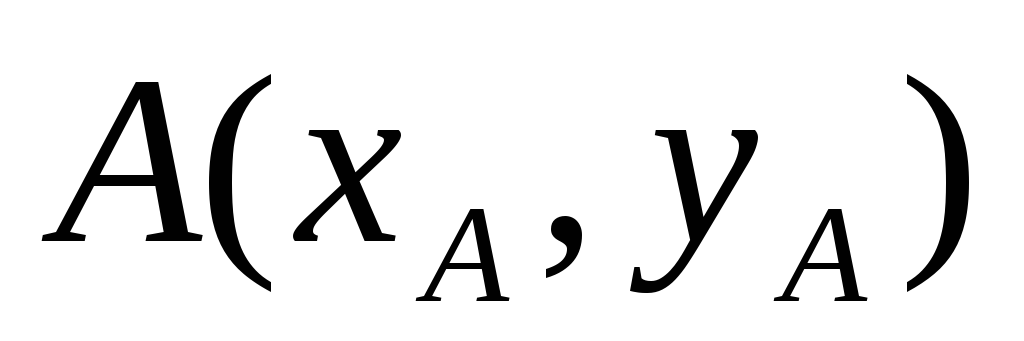 ,
а конец вектора есть точка
,
а конец вектора есть точка .
Тогда координаты вектора связаны с
координатами его концов следующими
соотношениями
.
Тогда координаты вектора связаны с
координатами его концов следующими
соотношениями
 ,
,
 .
.
Доказательство.
Пусть  и пусть вектор-проекция вектора
и пусть вектор-проекция вектора на ось
на ось
 сонаправлен с осью
сонаправлен с осью (см. рис. 22). Тогда
(см. рис. 22). Тогда
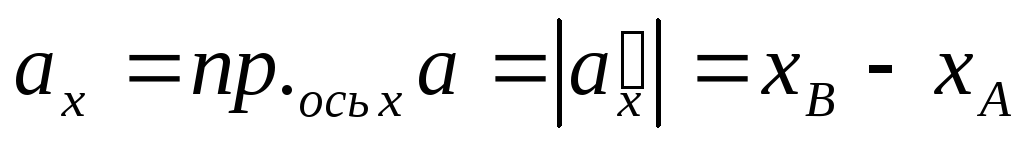 ,
,
т ак
как длина отрезка на числовой оси
ак
как длина отрезка на числовой оси равна координате правого конца минус
координата левого конца. Если вектор
равна координате правого конца минус
координата левого конца. Если вектор

Рис. 22.
 противонаправлен оси
противонаправлен оси (как
на Рис. 23), то
(как
на Рис. 23), то
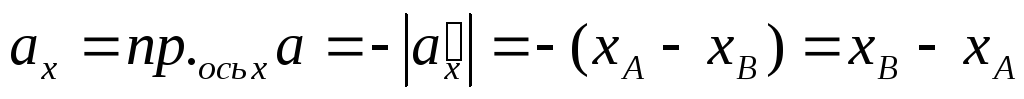 .
.
 Рис. 23.
Рис. 23.
Если  ,
то в этом случае
,
то в этом случае и тогда получаем
и тогда получаем
 .
.
Таким образом, при любом расположении
вектора  относительно
осей координат его координата
относительно
осей координат его координата равна
равна
 .
.
Аналогично доказывается, что
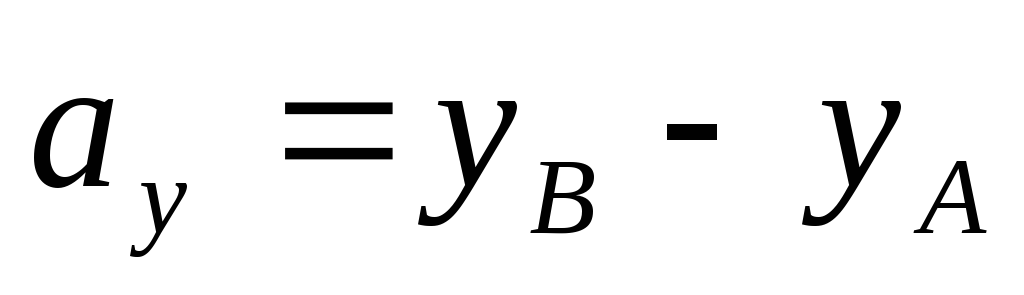 .
.
Пример.
Даны координаты концов вектора  :
: .
Найти координаты вектора
.
Найти координаты вектора .
.
Решение.
 .
.
В следующей теореме приводится выражение длины вектора через его координаты.
Теорема 15.
Пусть  .Тогда
.Тогда
 .
.
Доказательство.
Пусть 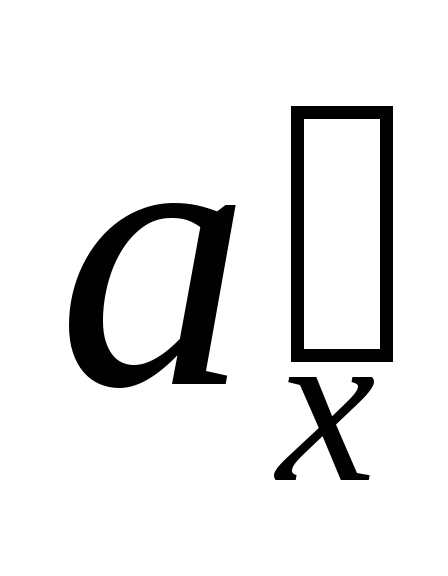 и
и — вектор-проекции вектора
— вектор-проекции вектора на оси
на оси и
и ,
соответственно. Тогда, как показано при
доказательстве теоремы 9, имеет место
равенство
,
соответственно. Тогда, как показано при
доказательстве теоремы 9, имеет место
равенство
 .
.
При этом, векторы 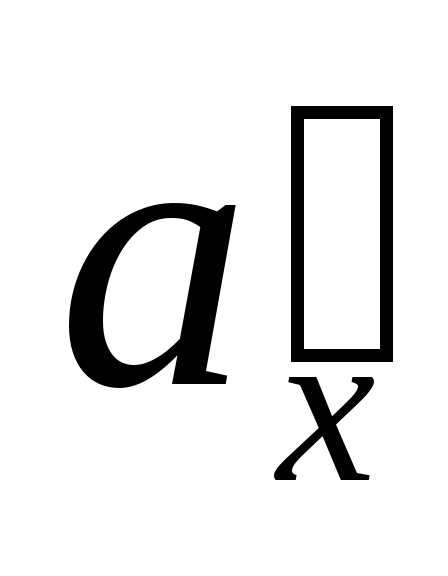 и
и взаимно перпендикулярны. При сложении
этих векторов по правилу треугольника
получаем прямоугольный треугольник
(см. Рис. 24).
взаимно перпендикулярны. При сложении
этих векторов по правилу треугольника
получаем прямоугольный треугольник
(см. Рис. 24).

Рис. 24.
По теореме Пифагора имеем
 .
.
Но
 ,
,
 .
.
Следовательно
 ,
,
 .
.
Отсюда
 .
.
Или
 .
.
Пример.
 .Найти
.Найти .
.
Решение.
 .
.
Введем понятие направляющих косинусов вектора .
Определение.
Пусть вектор  составляет с осью
составляет с осью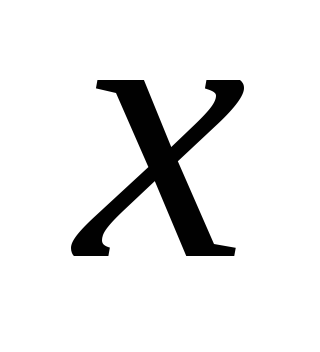 угол
угол ,
а с осью
,
а с осью угол(см. Рис. 25).
угол(см. Рис. 25).

Рис. 25.
Тогда
 ,
,
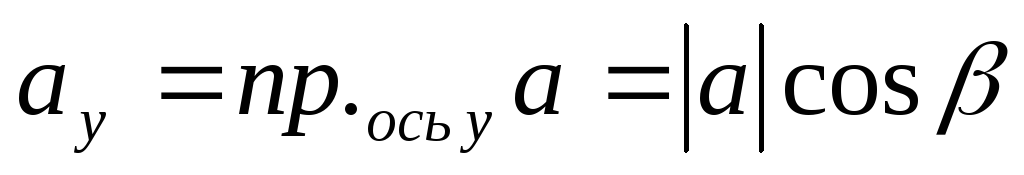 .
.
Следовательно,

Так как для любого вектора  имеет место равенство
имеет место равенство
 ,
,
Где  — орт вектора
— орт вектора ,
то есть вектор единичной длины,
сонаправленный с вектором
,
то есть вектор единичной длины,
сонаправленный с вектором ,
то
,
то
 .
.
Вектор  определяет направление вектора
определяет направление вектора .
Его координаты
.
Его координаты и
и называются направляющими косинусами
вектора
называются направляющими косинусами
вектора .
Направляющие косинусы вектора можно
выразить через его координаты по формулам
.
Направляющие косинусы вектора можно
выразить через его координаты по формулам
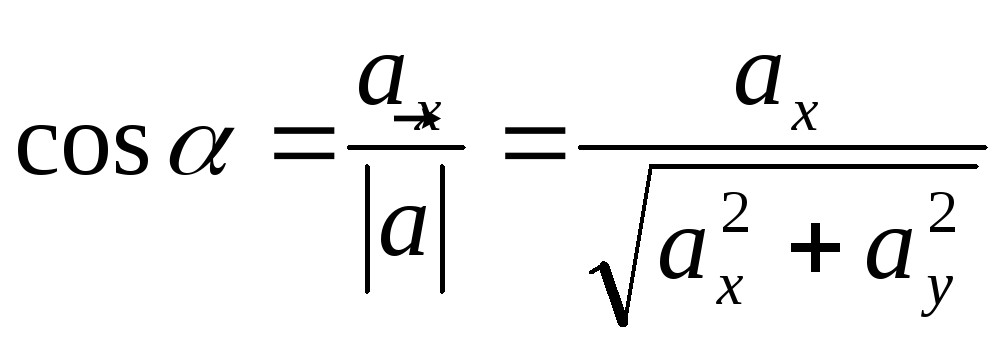 ,
,
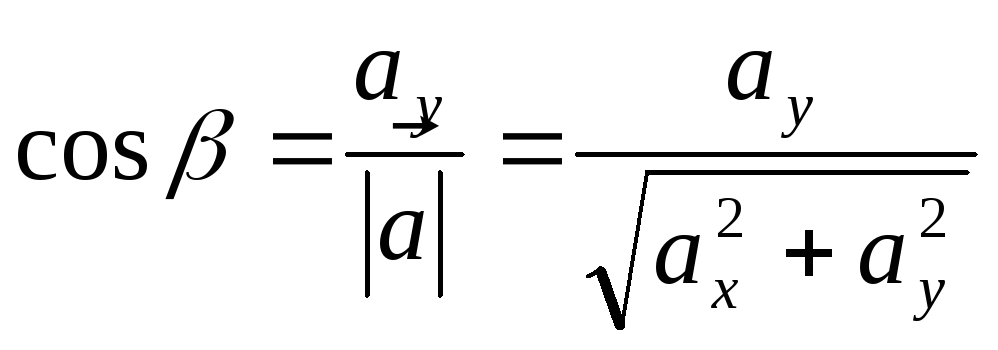 .
.
Имеет место соотношение

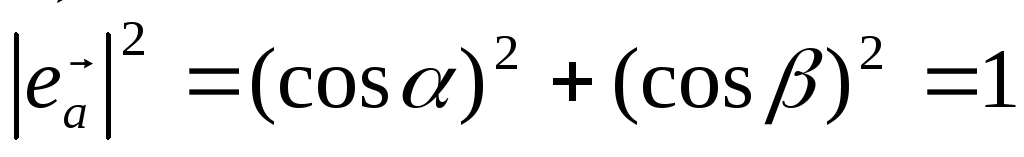 .
.
До настоящего момента в этом параграфе считалось, что все векторы располагаются в одной и той же плоскости. Теперь сделаем обобщение для векторов в пространстве.
Будем считать, что в пространстве
задана Декартова система координат с
осями  ,
, и
и .
.
Орты осей  ,
, и
и будем обозначать символами
будем обозначать символами ,
, и
и ,
соответственно (Рис. 26).
,
соответственно (Рис. 26).
Можно показать, что все понятия и формулы, которые были получены для векторов на плоскости, обобщаются для
 Рис. 26.
Рис. 26.
векторов в пространстве. Тройка векторов  называется ортонормированным базисом
в пространстве.
называется ортонормированным базисом
в пространстве.
Пусть  ,
, и
и — вектор-проекции векторана
оси
— вектор-проекции векторана
оси ,
, и
и ,
соответственно. Тогда
,
соответственно. Тогда
 .
.
В свою очередь
 ,
,
 ,
,
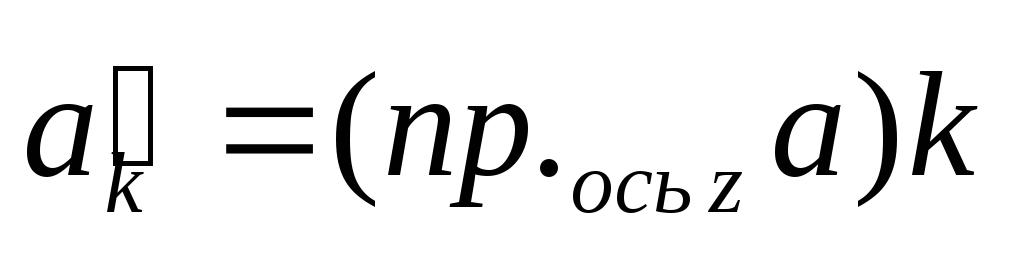 .
.
Если обозначить
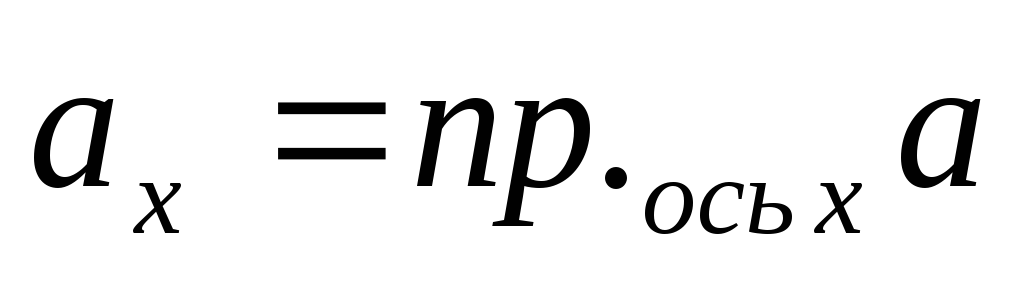 ,
,
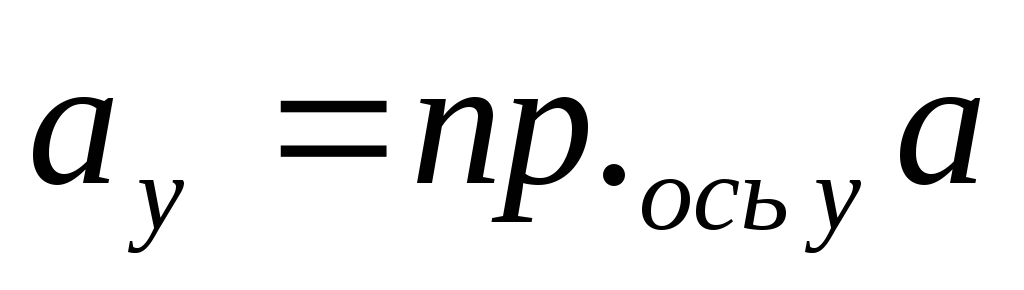 ,
,
 ,
,
То получаем равенство
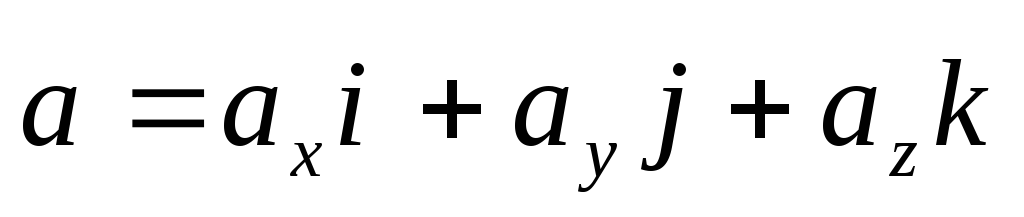 .
.
Коэффициенты перед базисными векторами 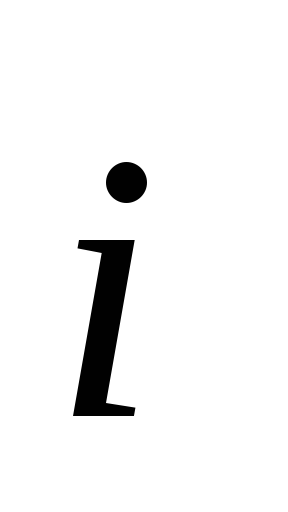 ,
,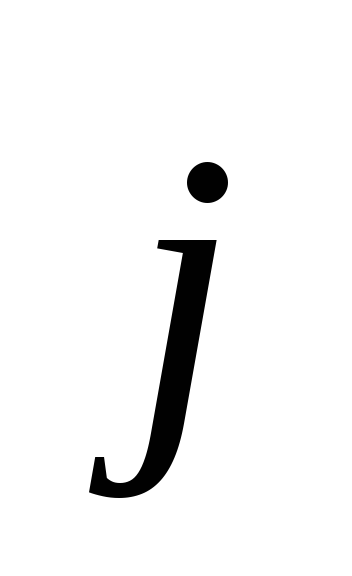 и
и называются координатами вектора
называются координатами вектора .
Таким образом, для любого вектора
.
Таким образом, для любого вектора в пространстве существует тройка чисел
в пространстве существует тройка чисел ,
, ,
, ,
называемых координатами вектора
,
называемых координатами вектора таких,
что для этого вектора справедливо
представление
таких,
что для этого вектора справедливо
представление
 .
.
Вектор  в этом случае также обозначают в виде
в этом случае также обозначают в виде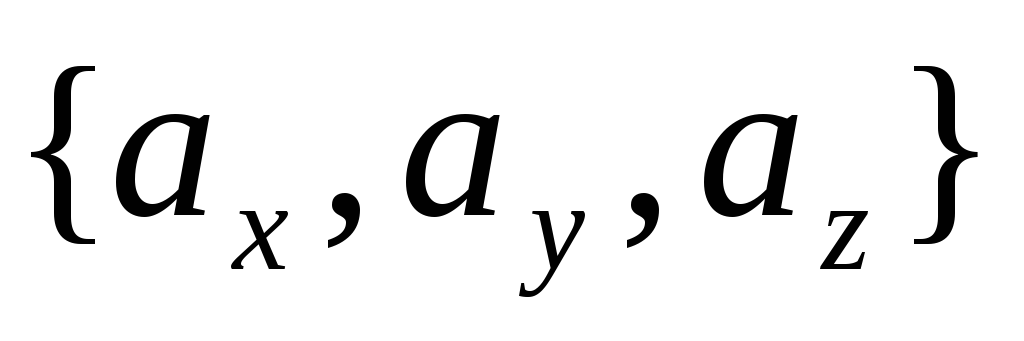 .
При этом, координаты вектора равны
проекциям этого вектора на координатные
оси
.
При этом, координаты вектора равны
проекциям этого вектора на координатные
оси
 ,
,
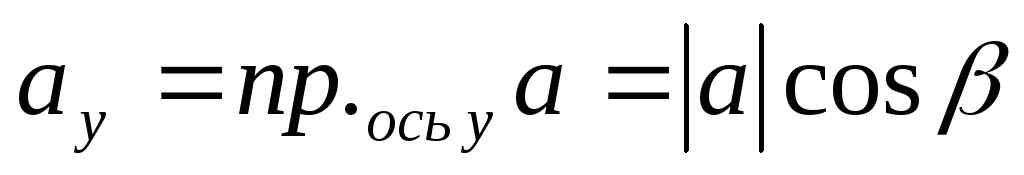 ,
,
 ,
,
где  —
угол между вектором
—
угол между вектором и осью
и осью ,
, —
угол между вектором
—
угол между вектором и осью
и осью ,
, — угол между вектором
— угол между вектором и осью
и осью .
.
Длина вектора  выражается через его координаты по
формуле
выражается через его координаты по
формуле
 .
.
Справедливы утверждения о том, что
равные векторы имеют равные координаты,
при сложении векторов их координаты
складываются, а при умножении вектора
на число его координаты умножаются на
это число.  ,
, и
и называются
направляющими косинусами вектора
называются
направляющими косинусами вектора .
Они связаны с координатами вектора
формулами
.
Они связаны с координатами вектора
формулами
 ,
, ,
, .
.
Отсюда следует соотношение
 .
.
Если концы вектора  имеют
координаты
имеют
координаты ,
, ,
то координаты вектора
,
то координаты вектора связаны с координатами концов вектора
соотношениями
связаны с координатами концов вектора
соотношениями
 ,
,
 ,
,
 .
.
Пример.
Даны точки  и
и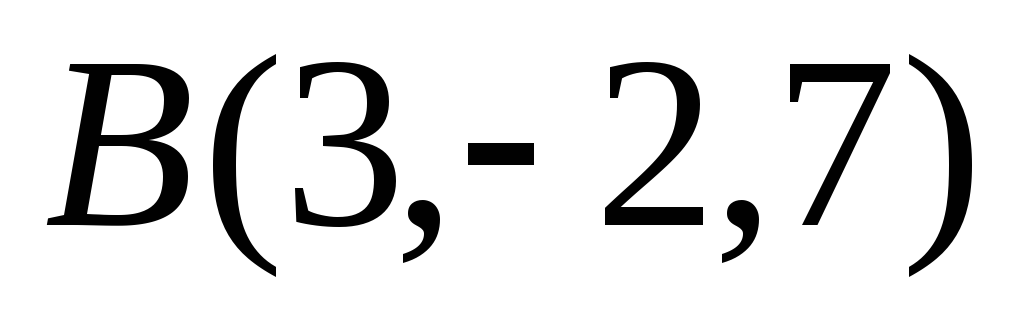 .
Найти координаты вектора
.
Найти координаты вектора .
.
Решение.
 .
.
studfile.net
Координаты вектора. Видеоурок. Геометрия 9 Класс
Существуют такие величины, для которых важным является не только размер, но и направление. Например, сила или скорость. Такие величины называются векторными, и к их изучению мы и приступаем. Мы вспомним основные сведения о векторах, введем понятие координат вектора и решим несколько типовых задач на координаты.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»
Вектором (от лат. vector – «переносчик») называется направленный отрезок, имеющий длину и определенное направление. Графически векторы изображаются в виде направленных отрезков прямой определенной длины (см. Рис. 1).
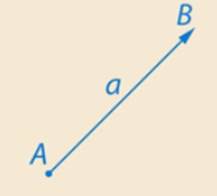
Рис. 1. Вектор
Вектор, начало которого есть точка  , а конец – точка
, а конец – точка  , обозначается
, обозначается  (см. Рис. 1). Также векторы обозначают одной маленькой буквой, например
(см. Рис. 1). Также векторы обозначают одной маленькой буквой, например  .
.
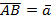
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых:  (см. Рис. 2).
(см. Рис. 2).

Рис. 2. Коллинеарные векторы
Два коллинеарных вектора  и
и  называются сонаправленными векторами, если их направления совпадают:
называются сонаправленными векторами, если их направления совпадают: 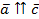 (см. Рис. 2).
(см. Рис. 2).
Два коллинеарных вектора  и
и  называются противоположно направленнымивекторами, если их направления противоположны:
называются противоположно направленнымивекторами, если их направления противоположны: 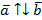 (см. Рис. 2).
(см. Рис. 2).
Векторы  и
и  называются равными, если они сонаправлены и их абсолютные величины равны (см. Рис. 3).
называются равными, если они сонаправлены и их абсолютные величины равны (см. Рис. 3).
 , если: 1.
, если: 1. 
2. 

Рис. 3. Равные векторы
Произведение ненулевого вектора начисло – это вектор, коллинеарный данному (сонаправленный данному, если число положительное, имеющий противоположное направление, если число отрицательное), а его модуль равен модулю данного вектора, умноженному на модуль числа (см. Рис. 4).

Рис. 4. Произведение вектора на число
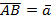

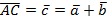 (см. Рис. 5)
(см. Рис. 5)
Рис. 5. Сложение векторов
Даны два коллинеарных вектора  и
и  (см. Рис. 6), причем
(см. Рис. 6), причем 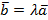 .
.

Рис. 6. Коллинеарные векторы
 – это коэффициент пропорциональности (число), для нахождения этого числа необходимо:
– это коэффициент пропорциональности (число), для нахождения этого числа необходимо:
1. Если  и
и  – это сонаправленные векторы:
– это сонаправленные векторы:


2. Если  и
и  – это противоположно направленные векторы:
– это противоположно направленные векторы:


На плоскости для задания произвольного вектора необходимы две координаты и пара неколлинеарных векторов.
Теорема
Любой вектор можно разложить по двум данным неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом, то есть для любых неколлинеарных  ,
,  и для любого
и для любого  найдется единственная пара действительных чисел
найдется единственная пара действительных чисел 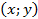 таких, что
таких, что  .
.
Доказательство теоремы
Дано: 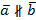 ,
,  (см. Рис. 7)
(см. Рис. 7)
Доказать:
1.  ,
,
2. равенство  верно для единственной пары чисел
верно для единственной пары чисел 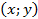 .
.
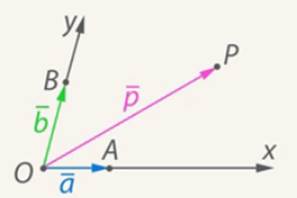
Рис. 7. Иллюстрация к доказательству
Доказательство
1. Из точки проведем прямую (параллельно
проведем прямую (параллельно  ), на пересечении с осью
), на пересечении с осью  получим точку
получим точку 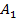 (см. Рис. 8). Вектор
(см. Рис. 8). Вектор  будет равен:
будет равен:

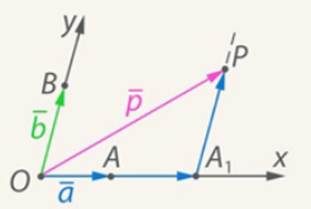
Рис. 8. Иллюстрация к доказательству
Вектор  коллинеарен вектору
коллинеарен вектору  , следовательно, найдется такое число
, следовательно, найдется такое число  , которое при умножении на вектор
, которое при умножении на вектор  даст нам вектор
даст нам вектор  .
.
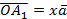
Вектор 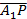 коллинеарен вектору
коллинеарен вектору  , следовательно, найдется такое число
, следовательно, найдется такое число  , которое при умножении на вектор
, которое при умножении на вектор  даст нам вектор
даст нам вектор 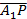 .
.

Следовательно:
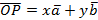
То есть существует такая пара чисел 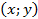 , что:
, что:  .
.
2. Методом от противного докажем, что пара чисел 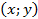 единственна.
единственна.
Имеем:  для
для 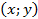
Предположим, что существует другая пара чисел  такая, что
такая, что  . Вычтем из первого равенства второе:
. Вычтем из первого равенства второе:


Пусть  , то есть
, то есть 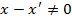 . Тогда:
. Тогда:


Получили, что векторы
interneturok.ru
координатный вектор — это… Что такое координатный вектор?
- координатный адрес
- координатный вычислительный
Смотреть что такое «координатный вектор» в других словарях:
Уравнения Максвелла — Классическая электродинамика … Википедия
Амплитуда рассеяния — Квантовая механика … Википедия
ПОКООРДИНАТНОГО СПУСКА МЕТОД — один из методов минимизации функций многих переменных, использующий лишь значения минимизируемой функции. П. с. м. применяется в тех случаях, когда минимизируемая функция недифференцируема или вычисление ее производных требует большого объема… … Математическая энциклопедия
Прямоугольная система координат — Прямоугольная система координат прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для… … Википедия
Векторное исчисление — математическая дисциплина, в которой изучают свойства операций над Векторами евклидова пространства. При этом понятие вектора представляет собой математическую абстракцию величин, характеризующихся не только численным значением, но и… … Большая советская энциклопедия
ОСНОВАНИЯ ГЕОМЕТРИИ — раздел геометрии, в к ром исследуются основные понятия геометрии, соотношения между ними и связанные с ними вопросы. Важная роль основных понятий и соотношений между ними, на базе к рых строятся определения фигур и доказываются геометрич.… … Математическая энциклопедия
Момент импульса — У этого термина существуют и другие значения, см. Момент. Момент импульса Размерность L2MT−1 Единицы измерения … Википедия
Кинетический момент — Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси… … Википедия
Момент количества движения — Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси… … Википедия
Момент орбитальный — Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси… … Википедия
Орбитальный момент — Момент импульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси… … Википедия
dic.academic.ru
что такое координаты вектора? Мне нужно только определение.
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору. На плоскости координаты вектора v относительно данного базиса (a, b) – это такая пара чисел (x; y), что v = xa + yb. Любой вектор имеет однозначно определенные координаты относительно любого базиса. При сложении векторов складываются их соответственные координаты; при умножении вектора на число каждая координата умножается на это число. Скалярное произведение векторов с координатами (x; y) и (x’; y’) равно сумме произведений соответственных координат: xx’ + yy’. Чтобы вычислить координаты вектора, зная координаты (x1; y1) его начала A и координаты (x2; y2) его конца B, нужно из координат конца вычесть координаты начала: (x2 – x1; y2 – y1). Все сказанное справедливо и для случая пространства с той разницей, что базис в пространстве состоит из трех векторов, а наборы координат векторов и точек – из трех чисел.
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
Координа́ты ве́ктора ― коэффициенты единственно возможной линейной комбинации базисных векторов в выбранной системе координат, равной данному вектору.
touch.otvet.mail.ru
Координаты вектора
Предварительные сведения
Здесь мы ограничимся двумерным случаем. Введение понятия для трехмерного случая проводится аналогично. Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.
Лемма 1: Если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны, и вектор $\overrightarrow{a}$ не является нулевым, то существует действительное число $k$, такое что выполняется равенство$\overrightarrow{b}=k\overrightarrow{a}$
Доказательство.
Возможны два случая:
$\overrightarrow{a}\uparrow \uparrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены, а $k\ge 0$, то векторы $k\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены. Далее, имеем, что
\[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
$\overrightarrow{a}\uparrow \downarrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=-\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ противоположно направленные, а $k \[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]
Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
Лемма доказана.
Теорема 1
Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом:
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]Доказательство.
Существование: Докажем, что такое разложение имеет место. Здесь возможны два случая:
Вектор $\overrightarrow{c}$ коллинеарен (к примеру) вектору $\overrightarrow{b}$.
По лемме 1, будем иметь
\[\overrightarrow{c}=n\overrightarrow{b}\]Значит, если число $m=0$, то получим
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]Вектор $\overrightarrow{c}$ не коллинеарен векторам $\overrightarrow{a}$ и $\overrightarrow{b}$.
Возьмем произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OB}=\overrightarrow{b},\ \overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OC}=\overrightarrow{c}$. Пусть Проведем прямую $CD||OB$ (рис. 1)

Рисунок 1. Иллюстрация теоремы 1
По правилу треугольника для сложения векторов, получим
\[\overrightarrow{c}=\overrightarrow{OD}+\overrightarrow{DC}\]По построению, получаем что векторы $\overrightarrow{OD}||\overrightarrow{a}$ и $\overrightarrow{DC}||\overrightarrow{b}$, следовательно, по лемме 1, имеем
\[\overrightarrow{OD}=m\overrightarrow{a},\ \overrightarrow{DC}=n\overrightarrow{b}\]Значит
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]
Единственность: Предположим противное, что помимо разложения$\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}$ существует разложение $\overrightarrow{c}=m’\overrightarrow{a}+n’\overrightarrow{b}$. Вычтем эти два равенства из друг друга:
Получаем систему:

Рисунок 2.
Следовательно, разложение единственно.
Теорема доказана.
Координаты вектора
Рассмотрим далее систему координат. От начала координат $O$ в направлении оси $Ox$ отложим вектор $\overrightarrow{i}$, а в направлении оси $Oy$ отложим вектор $\overrightarrow{j}$, длины которых равны единице.
Определение 1
Векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ называются координатными векторами.
Так как векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ не коллинеарны то, по теореме 1, любой вектор можно разложить в виде $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$.
Определение 2
Коэффициенты разложения вектора $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$ называются координатами данного вектора в данной системе координат, то есть
\[\overrightarrow{c}=\{m,\ n\}\]Линейные операции над векторами
Теорема 2
Теорема о сумме векторов: Координаты суммы векторов равны сумме соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема 3
Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема 4
Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.
Доказательство.
Пусть $\overrightarrow{a}=\left\{x,\ y\right\}$, тогда $\overrightarrow{a}=x\overrightarrow{i}+\ y\overrightarrow{j}.$
Следовательно
Теорема доказана.
Пример задачи на нахождение координат вектора
Пример 1
Пусть $\overrightarrow{a}=\left\{3,\ 4\right\}$, $\overrightarrow{b}=\{2,\ -1\}$. Найти $\overrightarrow{a}+\overrightarrow{b}$, $\overrightarrow{a}-\overrightarrow{b}$ и $3\overrightarrow{a}$.
Решение.
\[\overrightarrow{a}+\overrightarrow{b}=\left\{3+2,\ 4-1\right\}=\{5,\ 3\}\] \[\overrightarrow{a}-\overrightarrow{b}=\left\{3-2,\ 4+1\right\}=\{1,\ 5\}\] \[3\overrightarrow{a}=\left\{3\cdot 3,3\cdot 4\right\}=\{9,12\}\]spravochnick.ru
