Квадратный корень
Предварительные навыкиОсновные сведения
Чтобы найти площадь квадрата, нужно длину его стороны возвести во вторую степень.
Найдём площадь квадрата, длина стороны которого 3 см
S = 32 = 9 см2
Теперь решим обратную задачу. А именно, зная площадь квадрата определим длину его стороны. Для этого воспользуемся таким инструментом как кóрень. Корень бывает квадратный, кубический, а также n-й степени.
Сейчас наш интерес вызывает квадратный корень. По другому его называют кóрнем второй степени.
Для нахождения длины стороны нашего квадрата, нужно найти число, вторая степень которого равна 9. Таковым является число 3. Это число и является кóрнем.
Введём для работы с корнями новые обозначения.
Символ кóрня выглядит как . Это по причине того, что слово корень в математике употребляется как радикал
 А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня .
А слово радикал происходит от латинского radix (что в переводе означает корень). Первая буква слова radix это r впоследствии преобразилась в символ корня .Под корнем располагáют подкореннóе выражение. В нашем случае подкоренным выражением будет число 9 (площадь квадрата)
Нас интересовал квадратный корень (он же корень второй степени), поэтому слева над корнем указываем число 2. Это число называют показателем корня (или степенью корня)
Получили выражение, которое читается так: «квадратный корень из числа 9». С этого момента возникает новая задача по поиску самогó корня.
Если число 3 возвести во вторую степень, то получится число 9. Поэтому число 3 и будет ответом:
Значит квадрат площадью 9 см2 имеет сторону, длина которой 3 см. Приведённое действие называют
извлечéнием квадрáтного кóрня.Нетрудно догадаться, что квадратным корнем из числа 9 также является отрицательное число −3. При его возведении во вторую степень тоже получается число 9
При его возведении во вторую степень тоже получается число 9
Получается, что выражение имеет два значения: 3 и −3. Но длина стороны квадрата не может быть отрицательным числом, поэтому для нашей задачи ответ будет только один, а именно 3.
Вообще, квадратный корень имеет два противоположных значения: положительное и отрицательное.
Например, извлечём квадратный корень из числа 4
Это выражение имеет два значения: 2 и −2, поскольку при возведении этих чисел во вторую степень, получится один и тот же результат 4
Поэтому ответ к выражению вида записывают с плюсом и минусом. Плюс с минусом означает, что квадратный корень имеет два противоположных значения.
Запишем ответ к выражению с плюсом и минусом:
Определения
Дадим определение квадратному корню.
Квадратным корнем из числа a называют такое число b, вторая степень которого равна a.
То есть число b должно быть таким, чтобы выполнялось равенство b2 = a. Число b (оно же корень) обозначается через радикал так, что . На практике левая и правая часть поменяны местами и мы видим привычное выражение
Число b (оно же корень) обозначается через радикал так, что . На практике левая и правая часть поменяны местами и мы видим привычное выражение
Например, квадратным корнем из числá 16 есть число 4, поскольку число 4 во второй степени равно 16
42 = 16
Корень 4 можно обозначить через радикал так, что .
Также квадратным корнем из числá 16 есть число −4, поскольку число −4 во второй степени равно 16
(−4)2 = 16
Если при решении задачи интересует только положительное значение, то корень называют не просто квадратным, а
арифметическим квадратным.Арифметический квадратный корень из числá a — это неотрицательное число b (b ≥ 0), при котором выполняется равенство b2 = a.
В нашем примере квадратными корнями из числá 16 являются корни 4 и −4, но арифметическим из них является только корень 4.
В разговорном языке можно использовать сокращение. К примеру, выражение полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
К примеру, выражение полностью читается так: «квадратный корень из числá шестнадцать», а в сокращённом варианте можно прочитать так: «корень из шестнадцати».
Не следует путать понятия корень и квадрат. Квадрат это число, которое получилось в результате возведения какого-нибудь числá во вторую степень. Например, числа 25, 36, 49 являются квадратами, потому что они получились в результате возведения во вторую степень чисел 5, 6 и 7 соответственно.
Корнями же являются числа 5, 6 и 7. Они являются теми числами, которые во второй степени равны 25, 36 и 49 соответственно.
Чаще всего в квадратных корнях показатель кóрня вообще не указывается. Так, вместо записи можно использовать запись. Если в учебнике по математике встретится корень без показателя, то нужно понимать, что это квадратный корень.
Квадратный корень из единицы равен единице. То есть справедливо следующее равенство:
Это по причине того, что единица во второй степени равна единице:
12 = 1
и квадрат, состоящий из одной квадратной единицы, имеет сторону, равную единице:
Квадратный корень из нуля равен нулю. То есть справедливо равенство , поскольку 02 = 0.
То есть справедливо равенство , поскольку 02 = 0.
Выражение вида смысла не имеет. Например, не имеет смысла выражение , поскольку вторая степень любого числа есть число положительное. Невозможно найти число, вторая степень которого будет равна −4.
Если выражение вида возвести во вторую степень, то есть если записать , то это выражение будет равно подкореннóму выражению a
Например, выражение равно 4
Это потому что выражение равно значению 2. Но это значение сразу возвóдится во вторую степень и получается результат 4.
Еще примеры:
Корень из квадрата числá равен модулю этого числá:
Например, корень из числá 5, возведённого во вторую степень, равен модулю числá 5
Если во вторую степень возвóдится отрицательное число, ответ опять же будет положительным. Например, корень из числá −5, возведённого во вторую степень, равен модулю числá −5. А модуль числа −5 равен 5
Действительно, если не пользуясь правилом , вычислять выражение обычным методом — сначала возвести число −5 во вторую степень, затем извлечь полученный результат, то полýчим ответ 5
Не следует путать правило с правилом . Правило верно при любом a, тогда как правило верно в том случае, если выражение имеет смысл.
Правило верно при любом a, тогда как правило верно в том случае, если выражение имеет смысл.
В некоторых учебниках знак корня может выглядеть без верхней линии. Выглядит это так:
Примеры: √4, √9, √16.
Мéньшему числу соответствует мéньший корень, а бóльшему числу соответствует бóльший корень.
Например, рассмотрим числа 49 и 64. Число 49 меньше, чем число 64.
49 < 64
Если извлечь квадратные корни из этих чисел, то числу 49 будет соответствовать меньший корень, а числу 64 — бóльший. Действительно, √49 = 7, а √64 = 8,
√49 < √64
Отсюда:
7 < 8
Примеры извлечения квадратных корней
Рассмотрим несколько простых примеров на извлечение квадратных корней.
Пример 1. Извлечь квадратный корень √36
Данный квадратный корень равен числу, квадрат которого равен 36. Таковым является число 6, поскольку 62 = 36
√36 = 6
Пример 2. Извлечь квадратный корень √49
Извлечь квадратный корень √49
Данный квадратный корень равен числу, квадрат которого равен 49. Таковым является число 7, поскольку 72 = 49
√49 = 7
В таких простых примерах достаточно знать таблицу умножения. Так, мы помним, что число 49 входит в таблицу умножения на семь. То есть:
7 × 7 = 49
Но 7 × 7 это 72
72 = 49
Отсюда, √49 = 7.
Пример 3. Извлечь квадратный корень √100
Данный квадратный корень равен числу, квадрат которого равен 100. Таковым является число 10, поскольку 102 = 100
√100 = 10
Число 100 это последнее число, корень которого можно извлечь с помощью таблицы умножения. Для чисел, бóльших 100, квадратные корни можно находить с помощью таблицы квадратов.
Пример 3. Извлечь квадратный корень √256
Данный квадратный корень равен числу, квадрат которого равен 256. Чтобы найти это число, воспользуемся таблицей квадратов.
Нахóдим в таблице квадратов число 256 и двигаясь от него влево и вверх определяем цифры, которые образуют число, квадрат которого равен 256.
Видим, что это число 16. Значит √256 = 16.
Пример 4. Найти значение выражения 2√16
В данном примере число 2 умножается на выражение с корнем. Сначала вычислим корень √16, затем перемнóжим его с числом 2
Пример 7. Решить уравнение
В данном примере нужно найти значение переменной x, при котором левая часть будет равна 4.
Значение переменной
x равно 16, поскольку . Значит корень уравнения равен 16.Примечание. Не следует путать корень уравнения и квадратный корень. Корень уравнения это значение переменной, при котором уравнение обращается в верное числовое равенство. А квадратный корень это число, вторая степень которого равна выражению, находящемуся под радикалом .
Подобные примеры решают, пользуясь определением квадратного корня. Давайте и мы поступим так же.
Давайте и мы поступим так же.
Из определения мы знаем, что квадратный корень равен числу b, при котором выполняется равенство b2 = a.
Применим равенство b2 = a к нашему примеру . Роль переменной b у нас играет число 4, а роль переменной a — выражение, находящееся под корнем , а именно переменная x
В выражении 42 = x вычислим левую часть, полýчим 16 = x. Поменяем левую и правую часть местами, полýчим x = 16. В результате приходим к тому, что нашлось значение переменной x.
Пример 8. Решить уравнение
Перенесем −8 в правую часть, изменив знак:
Возведем правую часть во вторую степень и приравняем её к переменной x
Вычислим правую часть, полýчим 64 = x. Поменяем левую и правую часть местами, полýчим x = 64. Значит корень уравнения равен 64
Пример 9. Решить уравнение
Решить уравнение
Воспользуемся определением квадратного корня:
Роль переменной b играет число 7, а роль переменной a — подкореннóе выражение 3 + 5x. Возведем число 7 во вторую степень и приравняем его к 3 + 5x
В выражении 72 = 3 + 5x вычислим левую часть полýчим 49 = 3 + 5x. Получилось обычное линейное уравнение. Решим его:
Корень уравнения равен . Выполним проверку, подставив его в исходное уравнение:
Пример 10. Найти значение выражения
В этом выражении число 2 умножается на квадратный корень из числа 49.
Сначала нужно извлечь квадратный корень и перемножить его с числом 2
Приближённое значение квадратного корня
Не каждый квадратный корень можно извлечь. Извлечь квадратный корень можно только в том случае, если удаётся найти число, вторая степень которого равна подкореннóму выражению.
Например, извлечь квадратный корень можно, потому что удаётся найти число, вторая степень которого равна подкореннóму выражению. Таковым является число 8, поскольку 82 = 64. То есть
Таковым является число 8, поскольку 82 = 64. То есть
А извлечь квадратный корень нельзя, потому что невозможно найти число, вторая степень которого равна 3. В таком случае говорят, что квадратный корень из числа 3 не извлекается.
Зато можно извлечь квадратный корень из числа 3 приближённо. Извлечь квадратный корень приближённо означает найти значение, которое при возведении во вторую степень будет максимально близко к подкореннóму выражению.
Приближённое значение ищут с определенной точностью: с точностью до целых, с точностью до десятых, с точностью до сотых и так далее.
Найдём значение корня приближённо с точностью до десятых. Словосочетание «с точностью до десятых» говорит о том, что приближённое значение корня будет представлять собой десятичную дробь, у которой после запятой одна цифра.
Для начала найдём ближайшее меньшее число, корень которого можно извлечь. Таковым является число 1. Корень из этого числа равен самому этому числу:
√1 = 1
Аналогично находим ближайшее бóльшее число, корень которого можно извлечь. Таковым является число 4. Корень из этого числа равен 2
Таковым является число 4. Корень из этого числа равен 2
√4 = 2
√1 меньше, чем √4
√1 < √4
А √3 больше, чем √1 но меньше, чем √4. Запишем это в виде двойного неравенства:
√1 < √3 < √4
Точные значения корней √1 и √4 известны. Это числа 1 и 2
1 < √3 < 2
Тогда очевидно, что значение корня √3 будет представлять собой десятичную дробь, потому что между числами 1 и 2 нет целых чисел.
Для нахождения приближённого значения квадратного корня √3 будем проверять десятичные дроби, располагающиеся в интервале от 1 до 2, возводя их в квадрат. Делать это будем до тех пор пока не полýчим значение, максимально близкое к 3. Проверим к примеру дробь 1,1
1,12 = 1,21
Получился результат 1,21, который не очень близок к подкореннóму выражению 3. Значит 1,1 не годится в качестве приближённого значения квадратного корня √3, потому что оно малó.
Проверим тогда дробь 1,8
1,82 = 3,24
Получился результат 3,24, который близок к подкореннóму выражению, но превосходит его на 0,24. Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.
Значит 1,8 не годится в качестве приближенного значения корня √3, потому что оно великó.
Проверим тогда дробь 1,7
1,72 = 2,89
Получился результат 2,89, который уже близок к подкореннóму выражению. Значит 1,7 и будет приближённым значением квадратного корня √3. Напомним, что знак приближенного значения выглядит как ≈
√3 ≈ 1,7
Значение 1,6 проверять не нужно, потому что в результате получится число 2,56, которое дальше от трёх, чем значение 2,89. А значение 1,8, как было показано ранее, является уже большим.
В данном случае мы нашли приближенное значение корня √3 с точностью до десятых. Значение можно получить ещё более точно. Для этого его следует находить с точностью до сотых.
Чтобы найти значение с точностью до сотых проверим десятичные дроби в интервале от 1,7 до 1,8
1,7 < √3 < 1,8
Проверим дробь 1,74
1,742 = 3,0276
Получился результат 3,0276, который близок к подкореннóму выражению, но превосходит его на 0,0276. Значит значение 1,74 великó для корня √3.
Значит значение 1,74 великó для корня √3.
Проверим тогда дробь 1,73
1,732 = 2,9929
Получился результат 2,9929, который близок к подкореннóму выражению √3. Значит 1,73 будет приближённым значением квадратного корня √3 с точностью до сотых.
Процесс нахождения приближённого значения квадратного корня продолжается бесконечно. Так, корень √3 можно находить с точностью до тысячных, десятитысячных и так далее:
√3 = 1,732 (вычислено с точностью до тысячных)
√3 = 1,7320 (вычислено с точностью до десятитысячных)
√3 = 1,73205 (вычислено с точностью до ста тысячных).
Ещё квадратный корень можно извлечь с точностью до целых. Приближённое значение квадратного корня √3 с точностью до целых равно единице:
√3 ≈ 1
Значение 2 будет слишком большим, поскольку при возведении этого числа во вторую степень получается число 4, которое больше подкоренного выражения. Нас же интересуют значения, которые при возведении во вторую степень равны подкореннóму выражению или максимально близки к нему, но не превосходят его.
В зависимости от решаемой задачи допускается находить значение, вторая степень которого больше подкоренного выражения. Это значение называют приближённым значением квадратного корня с избытком. Поговорим об этом подробнее.
Приближенное значение квадратного корня с недостатком или избытком
Иногда можно встретить задание, в котором требуется найти приближённое значение корня с недостатком или избытком.
В предыдущей теме мы нашли приближённое значение корня √3 с точностью до десятых с недостатком. Недостаток понимается в том смысле, что до значения 3 нам недоставало ещё некоторых частей. Так, найдя приближённое значение √3 с точностью до десятых, мы получили 1,7. Это значение является значением с недостатком, поскольку при возведении этого числа во вторую степень полýчим результат 2,89. Этому результату недостаёт ещё 0,11 чтобы получить число 3. То есть, 2,89 + 0,11 = 3.
С избытком же называют приближённые значения, которые при возведении во вторую степень дают результат, который превосходит подкореннóе выражение. Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.
Так, вычисляя корень √3 приближённо, мы проверили значение 1,8. Это значение является приближённым значением корня √3 с точностью до десятых с избытком, поскольку при возведении 1,8 во вторую степень, получаем число 3,24. Этот результат превосходит подкореннóе выражение на 0,24. То есть 3,24 − 3 = 0,24.
Приближённое значение квадратного корня √3 с точностью до целых тоже был найден с недостатком:
√3 ≈ 1
Это потому что при возведении единицы в квадрат получаем единицу. То есть до числа 3 недостаёт ещё 2.
Приближённое значение квадратного корня √3 с точностью до целых можно найти и с избытком. Тогда этот корень приближённо будет равен 2
√3 ≈ 2
Это потому что при возведении числа 2 в квадрат получаем 4. Число 4 превосходит подкореннóе выражение 3 на единицу. Извлекая приближённо квадратный корень с избытком желательно уточнять, что корень извлечен именно с избытком:
√3 ≈ 2 (с избытком)
Потому что приближённое значение чаще всего ищется с недостатком, чем с избытком.
Дополнительно следует упомянуть, что в некоторых учебниках словосочетания «с точностью до целых», «с точностью до десятых», с «точностью до сотых», заменяют на словосочетания «с точностью до 1», «с точностью до 0,1», «с точностью до 0,01» соответственно.
Так, если в задании сказано извлечь квадратный корень из числа 5 с точностью до 0,01, то это значит что корень следует извлекать приближённо с точностью до сотых:
√5 ≈ 2,23
Пример 2. Извлечь квадратный корень из числа 51 с точностью до 1
√51 ≈ 7
Пример 3. Извлечь квадратный корень из числа 51 с точностью до 0,1
√51 ≈ 7,1
Пример 4. Извлечь квадратный корень из числа 51 с точностью до 0,01
√51 ≈ 7,14
Границы, в пределах которых располагаются корни
Если исходное число принадлежит промежутку [1; 100], то квадратный корень из этого исходного числа будет принадлежать промежутку [1; 10].
Например, пусть исходным числом будет 64. Данное число принадлежит промежутку [1; 100]. Сразу делаем вывод, что квадратный корень из числа 64 будет принадлежать промежутку [1; 10]. Теперь вспоминаем таблицу умножения. Какое перемножение двух одинаковых сомножителей даёт в результате 64? Ясно, что перемножение 8 × 8, а это есть 82 = 64. Значит квадратный корень из числа 64 есть 8
Пример 2. Извлечь квадратный корень из числа 49
Число 49 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 7, поскольку 72 = 49
√49 = 7
Пример 2. Извлечь квадратный корень из числа 1
Число 1 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 1, поскольку 12 = 1
√1 = 1
Пример 3. Извлечь квадратный корень из числа 100
Число 100 принадлежит промежутку [1; 100]. Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 102 = 100
Значит квадратный корень будет принадлежать промежутку [1; 10]. Этим корнем будет число 10, поскольку 102 = 100
√100 = 10
Понятно, что промежуток [1; 100] содержит ещё и числа, квадратные корни из которых не извлекаются. Для таких чисел корень нужно извлекать приближённо. Тем не менее, приближённый корень тоже будет располагаться в пределах промежутка [1; 10].
Например, извлечём квадратный корень из числа 37. Нет целого числа, вторая степень которого была бы равна 37. Поэтому извлекать квадратный корень следует приближённо. Извлечём его к примеру с точностью до сотых:
√37 ≈ 6,08
Для облегчения можно находить ближайшее меньшее число, корень из которого извлекается. Таковым в данном примере было число 36. Квадратный корень из него равен 6. И далее отталкиваясь от числа 6, можно находить приближённое значение корня √37, проверяя различные десятичные дроби, целая часть которых равна 6.
Квадраты чисел от 1 до 10 обязательно нужно знать наизусть. Ниже представлены эти квадраты:
Ниже представлены эти квадраты:
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
И обратно, следует знать значения квадратных корней этих квадратов:
Если к любому числу от 1 до 10 в конце дописать ноль (или несколько нулей), и затем возвести это число во вторую степень, то в полученном числе будет в два раза больше нулей.
Например, 62 = 36. Допишем к числу 6 один ноль, полýчим 60. Возведём число 60 во вторую степень, полýчим 3600
602 = 3600
А если к числу 6 дописать два нуля, и возвести это число во вторую степень, то полýчим число, в котором четыре нуля. То есть в два раза больше нулей:
6002 = 360000
Тогда можно сделать следующий вывод:
Если исходное число содержит знакомый нам квадрат и чётное количество нулей, то можно извлечь квадратный корень из этого числа. Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Для этого следует извлечь корень из знакомого нам квадрата и затем записать половину количества нулей из исходного числа.
Например, извлечём квадратный корень из числа 900. Видим, что в данном числе есть знакомый нам квадрат 9. Извлекаем из него корень, получаем 3
Теперь из исходного числа записываем половину от количества нулей. В исходном числе 900 содержится два нуля. Половина этого количества нулей есть один ноль. Записываем его в ответе после цифры 3
Пример 2. Извлечём квадратный корень из числа 90000
Здесь опять же имеется знакомый нам квадрат 9 и чётное количество нулей. Извлекаем корень из числа 9 и записываем половину от количества нулей. В исходном числе содержится четыре нуля. Половиной же этого количества нулей будет два нуля:
Пример 3. Извлечем квадратный корень из числа 36000000
Здесь имеется знакомый нам квадрат 36 и чётное количество нулей. Извлекаем корень из числа 36 и записываем половину от количества нулей. В исходном числе шесть нулей. Половиной же будет три нуля:
В исходном числе шесть нулей. Половиной же будет три нуля:
Пример 4. Извлечем квадратный корень из числа 2500
Здесь имеется знакомый нам квадрат 25 и чётное количество нулей. Извлекаем корень из числа 25 и записываем половину от количества нулей. В исходном числе два нуля. Половиной же будет один ноль:
Если подкореннóе число увеличить (или уменьшить) в 100, 10000 то корень увеличится (или уменьшится) в 10, 100 раз соответственно.
Например, . Если увеличим подкореннóе число в 100 раз, то квадратный корень увеличится в 10 раз:
И наоборот, если в равенстве уменьшим подкореннóе число в 100 раз, то квадратный корень уменьшится в 10 раз:
Пример 2. Увеличим в равенстве подкореннóе число в 10000, тогда квадратный корень 70 увеличиться в 100 раз
Пример 3. Уменьшим в равенстве подкореннóе число в 100 раз, тогда квадратный корень 70 уменьшится в 10 раз
Эта закономерность позволяет извлечь квадратный корень из десятичной дроби, если в данной дроби после запятой содéржатся две цифры, и эти две цифры образуют знакомый нам квадрат. В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
В таких случаях данную десятичную дробь следует умножить на 100. Затем извлечь квадратный корень из получившегося числа и уменьшить подкореннóе число в сто раз.
Например, извлечём квадратный корень из числа 0,25. В данной десятичной дроби после запятой содержатся две цифры и эти две цифры образуют знакомый нам квадрат 25.
Умнóжим десятичную дробь 0,25 на 100, полýчим 25. А из числа 25 квадратный корень извлекается легко:
Но нам изначально нужно было извлечь корень из 0,25, а не из 25. Чтобы исправить ситуацию, вернём нашу десятичную дробь. Если в равенстве подкореннóе число уменьшить в 100 раз, то полýчим под корнем 0,25 и соответственно ответ уменьшится в 10 раз:
Обычно в таких случаях достаточно уметь передвигáть запятую. Потому что сдвинуть в числе запятую вправо на две цифры это всё равно что умножить это число на 100.
В предыдущем примере в подкоренном числе 0,25 можно было сдвинуть запятую вправо на две цифры, а в полученном ответе сдвинуть её влево на одну цифру.
Например, извлечем корень из числа 0,81. Мысленно передвинем запятую вправо на две цифры, полýчим 81. Теперь извлечём квадратный корень из числа 81, полýчим ответ 9. В ответе 9 передвинем запятую влево на одну цифру, полýчим 0,9. Значит, .
Это правило работает и в ситуации, когда после запятой содержатся четыре цифры и эти цифры образуют знакомый нам квадрат.
Например, десятичная дробь 0,1225 содержит после запятой четыре цифры. Эти четыре цифры образуют число 1225, квадратный корень из которого равен 35.
Тогда можно извлечь квадратный корень и из 0,1225. Умнóжим данную десятичную дробь на 10000, полýчим 1225. Из числа 1225 квадратный корень можно извлечь с помощью таблицы квадратов:
Но нам изначально нужно было извлечь корень из 0,1225, а не из 1225. Чтобы исправить ситуацию, в равенстве подкореннóе число уменьшим в 10000 раз. В результате под корнем образуется десятичная дробь 0,1225, а правая часть уменьшится в 100 раз
Эта же закономерность будет работать и при извлечении корней из дробей вида 12,25. Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Если цифры из которых состоит десятичная дробь образуют знакомый нам квадрат, при этом после запятой содержится чётное количество цифр, то можно извлечь корень из этой десятичной дроби.
Умнóжим десятичную дробь 12,25 на 100, полýчим 1225. Извлечём корень из числа 1225
Теперь в равенстве уменьшим подкореннóе число в 100 раз. В результате под корнем образуется число 12,25, и соответственно ответ уменьшится в 10 раз
Если исходное число принадлежит промежутку [100; 10000], то квадратный корень из этого исходного числа будет принадлежать промежутку [10; 100].
В этом случае применяется таблица квадратов:
Например, пусть исходным числом будет 576. Данное число принадлежит промежутку [100; 10000]. Сразу делаем вывод, что квадратный корень из числа 576 будет принадлежать промежутку [10; 100]. Теперь открываем таблицу квадратов и смотрим какое число во второй степени равно 576
Видим, что это число 24. Значит .
Значит .
Пример 2. Извлечь квадратный корень из числа 432.
Число 432 принадлежит промежутку [100; 10000]. Значит квадратный корень следует искать в промежутке [10; 100]. Открываем таблицу квадратов и смотрим какое число во второй степени равно 432. Обнаруживаем, что число 432 в таблице квадратов отсутствует. В этом случае квадратный корень следует искать приближённо.
Извлечем квадратный корень из числа 432 с точностью до десятых.
В таблице квадратов ближайшее меньшее число к 432 это число 400. Квадратный корень из него равен 20. Отталкиваясь от числа 20, будем проверять различные десятичные дроби, целая часть которых равна 20.
Проверим, например, число 20,8. Для этого возведём его в квадрат:
20,82 = 432,64
Получилось число 432,64 которое превосходит исходное число 432 на 0,64. Видим, что значение 20,8 великó для корня √432. Проверим тогда значение 20,7
20,72 = 428,49
Значение 20,7 годится в качестве корня, поскольку в результате возведения этого числа в квадрат получается число 428,49, которое меньше исходного числа 432, но близко к нему. Значит √432 ≈ 20,7.
Значит √432 ≈ 20,7.
Необязательно запоминать промежутки чтобы узнать в каких границах располагается корень. Можно воспользоваться методом нахождения ближайших квадратов с чётным количеством нулей на конце.
Например, извлечём корень из числа 4225. Нам известен ближайший меньший квадрат 3600, и ближайший больший квадрат 4900
3600 < 4225 < 4900
Извлечём квадратные корни из чисел 3600 и 4900. Это числа 60 и 70 соответственно:
Тогда можно понять, что квадратный корень из числа 4225 располагается между числами 60 и 70. Можно даже найти его методом подбора. Корни 60 и 70 исключаем сразу, поскольку это корни чисел 3600 и 4900. Затем можно проверить, например, корень 64. Возведём его в квадрат (или умнóжим данное число само на себя)
Корень 64 не годится. Проверим корень 65
Получается 4225. Значит 65 является корнем числа 4225
Тождественные преобразования с квадратными корнями
Над квадратными корнями можно выполнять различные тождественные преобразования, тем самым облегчая их вычисление. Рассмотрим некоторые из этих преобразований.
Рассмотрим некоторые из этих преобразований.
Квадратный корень из произведения
Квадратный корень из произведения это выражение вида , где a и b некоторые числа.
Например, выражение является квадратным корнем из произведения чисел 4 и 9.
Чтобы извлечь такой квадратный корень, нужно по отдельности извлечь квадратные корни из множителей 4 и 9, представив выражение в виде произведения корней . Вычислив по отдельности эти корни полýчим произведение 2 × 3, которое равно 6
Конечно, можно не прибегать к таким манипуляциям, а вычислить сначала подкореннóе выражение 4 × 9, которое равно 36. Затем извлечь квадратный корень из числа 36
Но при извлечении квадратных корней из больших чисел это правило может оказаться весьма полезным.
Допустим, потребовалось извлечь квадратный корень из числа 144. Этот корень легко определяется с помощью таблицы квадратов — он равен 12
Но предстáвим, что таблицы квадратов под рукой не оказалось. В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
В этом случае число 144 можно разложить на простые множители. Затем из этих простых множителей составить числа, квадратные корни из которых извлекаются.
Итак, разлóжим число 144 на простые множители:
Получили следующее разложение:
В разложéнии содержатся четыре двойки и две тройки. При этом все числа, входящие в разложение, перемнóжены. Это позволяет предстáвить произведения одинаковых сомножителей в виде степени с показателем 2.
Тогда четыре двойки можно заменить на запись 22 × 22, а две тройки заменить на 32
В результате будем иметь следующее разложение:
Теперь можно извлекáть квадратный корень из разложения числа 144
Применим правило извлечения квадратного корня из произведения:
Ранее было сказано, что если подкореннóе выражение возведенó во вторую степень, то такой квадратный корень равен модулю из подкореннóго выражения.
Тогда получится произведение 2 × 2 × 3, которое равно 12
Простые множители представляют в виде степени для удобства и короткой записи. Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Допускается также записывать их под кóрнем как есть, чтобы впоследствии перемнóжив их, получить новые сомножители.
Так, разложив число 144 на простые множители, мы получили разложение 2 × 2 × 2 × 2 × 3 × 3. Это разложение можно записать под кóрнем как есть:
затем перемнóжить некоторые сомножители так, чтобы получились числа, квадратные корни из которых извлекаются. В данном случае можно дважды перемнóжить две двойки и один раз перемнóжить две тройки:
Затем применить правило извлечения квадратного корня из произведения и получить окончательный ответ:
С помощью правила извлечения квадратного корня из произведения можно извлекать корень и из других больших чисел. В том числе, из тех чисел, которых нет в таблице квадратов.
Например, извлечём квадратный корень из числа 13456. Этого числа нет в таблице квадратов, поэтому воспользуемся правилом извлечения квадратного корня из произведения, предварительно разложив число 13456 на простые множители.
Итак, разложим число 13456 на простые множители:
В разложении имеются четыре двойки и два числа 29. Двойки дважды предстáвим как 22. А два числа 29 предстáвим как 292. В результате полýчим следующее разложение числа 13456
Теперь будем извлекать квадратный корень из разложения числа 13456
Итак, если a ≥ 0 и b ≥ 0, то . То есть корень из произведения неотрицательных множителей равен произведению корней из этих множителей.
Докажем равенство . Для этого воспользуемся определением квадратного корня.
Согласно определению, квадратным корня из числа a есть число b, при котором выполняется равенство b2 = a.
В нашем случае нужно удостовериться, что правая часть равенства при возведении во вторую степень даст в результате подкореннóе выражение левой части, то есть выражение ab.
Итак, выпишем правую часть равенства и возведём ее во вторую степень:
Теперь воспользуемся правилом возведения в степень произведения. Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
Согласно этому правилу, каждый множитель данного произведения нужно возвести в указанную степень:
Ранее было сказано, что если выражение вида возвести во вторую степень, то получится подкореннóе выражение. Применим это правило. Тогда полýчим ab. А это есть подкореннóе выражение квадратного корня
Значит равенство справедливо, поскольку при возведéнии правой части во вторую степень, получается подкореннóе выражение левой части.
Правило извлечения квадратного корня из произведения работает и в случае, если под кóрнем располагается более двух множителей. То есть справедливым будет следующее равенство:
, при a ≥ 0 и b ≥ 0, c ≥ 0.
Пример 1. Найти значение квадратного корня
Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
Пример 2. Найти значение квадратного корня
Предстáвим число 250 в виде произведения чисел 25 и 10.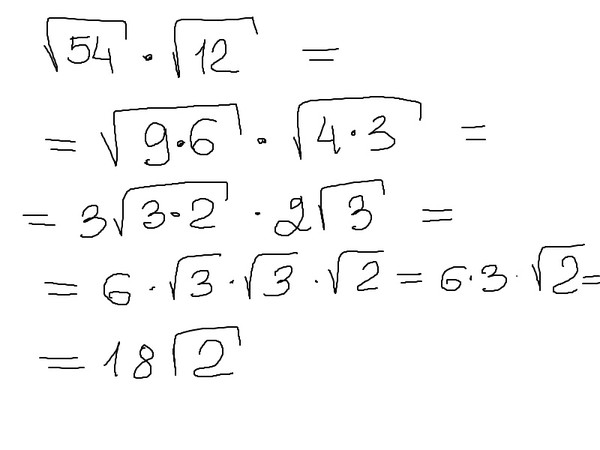 Делать это будем под знáком корня:
Делать это будем под знáком корня:
Теперь под кóрнем образовалось два одинаковых множителя 10 и 10. Перемнóжим их, полýчим 100
Далее применяем правило извлечения квадратного кóрня из произведения и получáем окончательный ответ:
Пример 3. Найти значение квадратного корня
Воспользуемся правилом возведения степени в степень. Степень 114 предстáвим как (112)2.
Теперь воспользуемся правилом извлечения квадратного кóрня из квадрата числа:
В нашем случае квадратный корень из числа (112)2 будет равен 112. Говоря простым языком, внешний показатель степени 2 исчезнет, а внутренний останется:
Далее возводим число 11 во вторую степень и получаем окончательный ответ:
Этот пример также можно решить, воспользовавшись правилом извлечения квадратного корня из произведения. Для этого подкореннóе выражение 114 нужно записать в виде произведения 112 × 112. Затем извлечь квадратный корень из этого произведения:
Затем извлечь квадратный корень из этого произведения:
Пример 4. Найти значение квадратного корня
Перепишем степень 34 в виде (32)2, а степень 56 в виде (53)2
Далее используем правило извлечения квадратного кóрня из произведения:
Далее используем правило извлечения квадратного кóрня из квадрата числа:
Вычислим произведение получившихся степеней и полýчим окончательный ответ:
Сомножители, находящиеся под корнем, могут быть десятичными дробями. Например, извлечём квадратный корень из произведения
Запишем корень в виде произведения корней, извлечём их, затем найдём значение полученного произведения:
Пример 6. Найти значение квадратного корня
Пример 7. Найти значение квадратного корня
Если первый сомножитель умножить на число n, а второй сомножитель разделить на это число n, то произведение не изменится.
Например, произведение 8 × 4 равно 32
8 × 4 = 32
Умнóжим сомножитель 8 скажем на число 2, а сомножитель 4 раздéлим на это же число 2. Тогда получится произведение 16 × 2, которое тоже равно 32.
(8 × 2) × (4 : 2) = 32
Это свойство полезно при решении некоторых задач на извлечение квадратных корней. Сомножители подкореннóго выражения можно умнóжить и разделить так, чтобы корни из них извлекались.
Например, извлечём квадратный корень из произведения . Если сразу воспользоваться правилом извлечения квадратного корня из произведения, то не полýчится извлечь корни √1,6 и √90, потому что они не извлекаются.
Проанализировав подкореннóе выражение 1,6 × 90, можно заметить, что если первый сомножитель 1,6 умножить на 10, а второй сомножитель 90 разделить на 10, то полýчится произведение 16 × 9. Из такого произведения квадратный корень можно извлечь, пользуясь правилом извлечения квадратного корня из произведения.
Запишем полное решение данного примера:
Процесс умножения и деления можно выполнять в уме. Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
Также можно пропустить подробную запись извлечения квадратного корня из каждого сомножителя. Тогда решение станóвится короче:
Пример 9. Найти значение квадратного корня
Умнóжим первый сомножитель на 10, а второй раздéлим на 10. Тогда под кóрнем образуется произведение 36 × 0,04, квадратный корень из которого извлекается:
Если в равенстве поменять местами левую и правую часть, то полýчим равенство . Это преобразовáние позволяет упрощáть вычисление некоторых корней.
Например, узнáем чему равно значение выражения .
Квадратные корни из чисел 10 и 40 не извлекаются. Воспользуемся правилом , то есть заменим выражение из двух корней на выражение с одним корнем, под которым будет произведение из чисел 10 и 40
Теперь найдём значение произведения, находящегося под корнем:
А квадратный корень из числа 400 извлекается. Он равен 20
Сомножители, располагáющиеся под корнем, можно расклáдывать на множители, группировáть, представлять в виде степени, а также перемножáть для получения новых сомножителей, корни из которых извлекаются.
Например, найдём значение выражения .
Воспользуемся правилом
Сомножитель 32 это 25. Предстáвим этот сомножитель как 2 × 24
Перемнóжим сомножители 2 и 2, полýчим 4. А сомножитель 24 предстáвим в виде степени с показателем 2
Теперь воспóльзуемся правилом и вычислим окончательный ответ:
Пример 12. Найти значение выражения
Воспользуемся правилом
Сомножитель 8 это 2 × 2 × 2, а сомножитель 98 это 2 × 7 × 7
Теперь под кóрнем имеются четыре двойки и две семёрки. Четыре двойки можно записать как 22 × 22, а две семёрки как 72
Теперь воспользуемся правилом и вычислим окончательный ответ:
Квадратный корень из дроби
Квадратный корень вида равен дроби, в числителе которой квадратный корень из числа a, а в знаменателе — квадратный корень из числа b
Например, квадратный корень из дроби равен дроби, в числителе которой квадратный корень из числа 4, а в знаменателе — квадратный корень из числа 9
Вычислим квадратные корни в числителе и знаменателе:
Значит, квадратный корень из дроби равен .
Докáжем, что равенство является верным.
Возведём правую часть во вторую степень. Если в результате полýчим дробь , то это будет означать, что равенство верно:
Пример 1. Извлечь квадратный корень
Воспользуемся правилом извлечения квадратного корня из дроби:
Пример 2. Извлечь квадратный корень
Переведём подкореннóе выражение в неправильную дробь, затем воспользуемся правилом извлечения квадратного корня из дроби:
Пример 3. Извлечь квадратный корень
Квадратным корнем из числа 0,09 является 0,3. Но можно извлечь этот корень, воспользовавшись правилом извлечения квадратного корня из дроби.
Предстáвим подкоренное выражение в виде обыкновенной дроби. 0,09 это девять сотых:
Теперь можно воспользоваться правилом извлечения квадратного корня из дроби:
Пример 4. Найти значение выражения
Извлечём корни из 0,09 и 0,25, затем сложим полученные результаты:
Также можно воспользоваться правилом извлечения квадратного корня из дроби:
В данном примере первый способ оказался проще и удобнее.
Пример 5. Найти значение выражения
Сначала вычислим квадратный корень, затем перемнóжим его с 10. Получившийся результат вычтем из 4
Пример 6. Найти значение выражения
Сначала найдём значение квадратного корня . Он равен 0,6 поскольку 0,62 = 0,36
Теперь вычислим получившееся выражение. Согласно порядку действий, сначала надо выполнить умножение, затем сложение:
Вынесение множителя из-под знака корня
В некоторых задачах может быть полезным вынесение множителя из-под знака корня.
Рассмотрим квадратный корень из произведения . Согласно правилу извлечения квадратного корня из произведения, нужно извлечь квадратный корень из каждого множителя данного произведения:
В нашем примере квадратный корень извлекается только из множителя 4. Его мы извлечём, а выражение оставим без изменений:
Это и есть вынесение множителя из-под знака корня.
На практике подкореннóе выражение чаще всего требуется разложить на множители.
Пример 2. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 9 и 2. Тогда полýчим:
Теперь воспользуемся правило извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 9. Множитель 2 остáвим под кóрнем:
Пример 3. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 121 и 3. Тогда полýчим:
Теперь воспользуемся правилом извлечения квадратного корня из произведения. Извлечь можно только корень из множителя 121. Выражение √3 остáвим под корнем:
Пример 4. Вынести множитель из-под знака корня в выражении
Воспользуемся правилом извлечения квадратного корня из произведения:
Квадратный корень извлекается только из числа 121. Извлечём его, а выражение √15 оставим без изменений:
Получается, что множитель 11 вынесен из-под знака корня. Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:
Вынесенный множитель принято записывать до выражения с корнем. Поменяем выражения √15 и 11 местами:
Пример 5. Вынести множитель из-под знака корня в выражении
Разлóжим подкореннóе выражение на множители 4 и 3
Воспользуемся правилом извлечения квадратного корня из произведения:
Извлечём корень из числа 4, а выражение √3 остáвим без изменений:
Пример 6. Упростить выражение
Предстáвим второе слагаемое в виде . А третье слагаемое предстáвим в виде
Теперь в выражениях и вынесем множитель из-под знака корня:
Во втором слагаемом перемнóжим числа −4 и 4. Остальное перепишем без изменений:
Замечáем, что получившемся выражении квадратный корень √3 является общим множителем. Вынесем его за скобки:
Вычислим содержимое скобок, полýчим −1
Если множителем является −1, то записывают только минус. Единица опускается. Тогда полýчим окончательный ответ −√3
Тогда полýчим окончательный ответ −√3
Внесение множителя под знак корня
Рассмотрим следующее выражение:
В этом выражении число 5 умнóжено на квадратный корень из числа 9. Найдём значение этого выражения.
Сначала извлечём квадратный корень, затем перемнóжим его с числом 5.
Квадратный корень из 9 равен 3. Перемнóжим его с числом 5. Тогда полýчим 15
Число 5 в данном случае было множителем. Внесём этот множитель под знак корня. Но сделать это нужно таким образом, чтобы в результате наших действий значение исходного выражения не изменилось. Проще говоря, после внесения множителя 5 под знак корня, получившееся выражение по-прежнему должно быть равно 15.
Значение выражения не изменится, если число 5 возвести во вторую степень и только тогда внести его под корень:
Итак, если данó выражение , и нужно внести множитель a под знак корня, то надо возвести во вторую степень множитель a и внести его под корень:
Пример 1. Внести множитель под знак корня в выражении
Внести множитель под знак корня в выражении
Возведём число 7 во вторую степень и внесём его под знак корня:
Пример 2. Внести множитель под знак корня в выражении
Возведём число 10 во вторую степень и внесем его под знак корня:
Пример 3. Внести множитель под знак корня в выражении
Вносить под знак корня можно только положительный множитель. Ранее было сказано, что выражение вида не имеет смысла.
Однако, если перед знаком кóрня располагается отрицательный множитель, то минус можно оставить за знáком корня, а самó число внести под знак корня.
Пример 4. Внести множитель по знак корня в выражении
В этом примере под знак корня внóсится только 3. Минус остаётся за знáком корня:
Пример 5. Выполнить возведéние в степень в следующем выражении:
Воспользуемся формулой квадрата суммы двух выражений:
(a + b)2 = a2 + 2ab + b2
Роль переменной a в данном случае играет выражение √3, роль переменной b — выражение √2. Тогда полýчим:
Тогда полýчим:
Теперь необходимо упростить получившееся выражение.
Для выражений и применим правило . Ранее мы говорили, что если выражение вида возвести во вторую степень, то это выражение будет равно подкореннóму выражению a.
А в выражении для множителей и применим правило . То есть заменим произведение корней на один общий корень:
Приведём подобные слагаемые. В данном случае можно сложить слагаемые 3 и 2. А в слагаемом вычислить произведение, которое под кóрнем:
Задания для самостоятельного решения
Задание 1. Найдите значение квадратного корня:
Решение:
Задание 2. Найдите значение квадратного корня:
Решение:
Задание 3. Найдите значение квадратного корня:
Решение:
Задание 4. Найдите значение выражения:
Решение:
Задание 5. Найдите значение квадратного корня:
Решение:
Задание 6. Найдите значение квадратного корня:
Решение:
Задание 7. Найдите значение квадратного корня:
Найдите значение квадратного корня:
Решение:
Задание 8. Найдите значения следующих выражений:
Решение:
Задание 9. Извлеките квадратный корень из числа 4624
Решение:
Задание 10. Извлеките квадратный корень из числа 11025
Решение:
Задание 11. Найдите значение квадратного корня:
Решение:
Задание 12. Найдите значение квадратного корня:
Решение:
Задание 13. Найдите значение квадратного корня:
Решение:
Задание 14. Найдите значение квадратного корня:
Решение:
Задание 15. Найдите значение квадратного корня:
Решение:
Задание 16. Найдите значение выражения:
Решение:
Задание 17. Найдите значение выражения:
Решение:
Задание 18. Найдите значение выражения:
Решение:
Задание 19. Найдите значение выражения:
Решение:
Задание 20. Найдите значение выражения:
Решение:
Задание 21. Найдите значение выражения:
Найдите значение выражения:
Решение:
Задание 22. Найдите значение выражения:
Решение:
Задание 23. Найдите значение выражения:
Решение:
Задание 24. Найдите значение выражения:
Решение:
Задание 25. Найдите значение выражения:
Решение:
Задание 26. Найдите значение выражения:
Решение:
Задание 27. Найдите значение выражения:
Решение:
Задание 28. Найдите значение выражения:
Решение:
Задание 29. Найдите значение выражения:
Решение:
Задание 30. Найдите значение выражения:
Решение:
Задание 31. Найдите значение выражения:
Решение:
Задание 32. Найдите значение выражения:
Решение:
Задание 33. Найдите значение выражения:
Решение:
Задание 34. Вынести множитель из-под знака корня:
Решение:
Задание 35. Вынести множитель из-под знака корня:
Решение:
Задание 36. Вынести множитель из-под знака корня:
Вынести множитель из-под знака корня:
Решение:
Задание 37. Вынести множитель из-под знака корня:
Решение:
Задание 38. Вынести множитель из-под знака корня:
Решение:
Задание 39. Вынести множитель из-под знака корня:
Решение:
Задание 40. Вынести множитель из-под знака корня:
Решение:
Задание 41. Вынести множитель из-под знака корня:
Решение:
Задание 42. Вынести множитель из-под знака корня:
Решение:
Задание 43. Вынести множитель из-под знака корня:
Решение:
Задание 44. Вынести множитель из-под знака корня в следующих выражениях:
Решение:
Задание 45. Внести множитель под знак корня:
Решение:
Задание 46. Внести множитель под знак корня:
Решение:
Задание 47. Внести множитель под знак корня:
Решение:
Задание 48. Внести множитель под знак корня:
Внести множитель под знак корня:
Решение:
Задание 49. Внести множитель под знак корня:
Решение:
Задание 50. Внести множитель под знак корня в следующих выражениях:
Решение:
Задание 51. Упростить выражение:
Решение:
Задание 52. Упростить выражение:
Решение:
Задание 53. Упростить выражение:
Решение:
Задание 54. Упростить выражение:
Решение:
Задание 55. Упростить выражение:
Решение:
Задание 56. Упростить выражение:
Решение:
Задание 57. Упростить выражение:
Решение:
Задание 58. Упростить выражение:
Решение:
Задание 59. Упростить выражение:
Решение:
Задание 60. Упростить выражение:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Преобразование выражений,содержащих операцию извлечения квадратного корня
здравствуйте тема данного видеоурока преобразование выражений содержащих операцию извлечения квадратного корня то есть пользуясь известными свойствами мы будем преобразовывать различные выражения для начала напомню эти свойства если у вас есть выражение корень из а в квадрате это выражение равняется а если у вас есть корень из произведения то мы можем применить корень отдельно каждому множителю аналогично если у вас есть деление или / то мы можем применить корень отдельно числителю отдельных к знаменателю и у вас если есть корень извлекающий ся из а некоторые четной степени то это равняется а в степени n то есть степень делим показатель степени делим на 2 здесь будем подразумевать что выражение а и б у нас не отрицательны а в этом случае естественно b не равно нулю давайте рассмотрим примеры попробуем извлечь корень из вот этой алгебраической дроби как мы знаем мы можем отдельно применить корни числителю и к знаменателю а в числителе мы можем отдельно применить корень каждому множителю так и сделай корень из 16 это 4 корень из х в четвертой степени мы знаем что тогда нужно степень разделить будет а в квадрате корень из b в восьмой степени 8 делим на 2 будет b в четвертой степени теперь со знаменателю конь и 49 это 7 корень из c в шестой степени это у нас c в кубе и корень из b в квадрате это у нас д второй пример 32x корней 7 как мы можем посчитать чтобы вычислить корень давайте сначала преобразуем 32 мы запишем как 16 умноженная на 2 x 7 степени мы можем записать как x 6 степени умноженное на x знаменателе 75 мы можем представить как 25 умноженное на 3y кубе мы представим как y квадрат на y азат 6 так и оставим для чего мы это делали чтобы получить четные степени теперь давайте извлекать корень корни 16 это 4 корень из x 6 степени это x в кубе корень из 2 и корень из x у нас не излечиться поэтому выражение корень из 2 x у нас останется теперь знаменателе корня из 25 это 5 корень из x y квадрате это y корень из s 6 степени это z в кубе но тройка и y у нас останется дальше мы уже упростить не сможем то есть мы вынесли максимальное выражение из-под знака корня в этих же примерах нам нужно наоборот внести внутри знака корня как мы можем это сделать то есть нам нужно это записать в виде одного корня однако 4 внесет а под знак корня как 1 16 действительно 1 16 извлекаем корень как раз выйдет 1 4 здесь еще есть 32 32 на 16 это будет два значит это корень из 2 дальше уже не упростится минус две третьих корень из 15 знак минус внутрь корнем и внести не можем поэтому он останется снаружи а вот две третьих несется в корень как 4 9 я просто возвела в квадрат корень из 4 девятых это две третьих и умножаем на 15 15 и 9 сокращает смотри здесь будет 5 здесь будет 3 и того будет минус корень сверху у нас 20 снизу 3 минус корень из 20 третьих рассмотрим следующие примеры корень из а плюс корень из b умножить на корень из минус корень из b давайте попробуем это упростить мы видим что это не что иное как формула разности квадратов тогда мы это можно записать как корень из а в квадрате минус корень из b в квадрате но мы знаем что корень из а в квадрате это просто а корень из b в квадрате это просто b и того а минус b попробуем преобразовать вот это выражение 4х минус 4 корня b плюс b 4 а мы можем записать как 2 корень из а в квадрате действительно 2 в квадрате 4 корни за в квадрате у минус вот это выражение можно следующим образом как два умноженное на 2 корень из а и умножить на корень из b дважды два это четыре корень и за и корень из b и b мы можем записать как корень из b в квадрате и того вы обратили внимание что у нас получилось формула квадрат разности а квадрат минус 2b плюс б квадрат то есть это будет равняется 2 кори а минус корень b и все это в квадрате давайте попробуем найти разности вот этих двух дробей находим общий знаменатель общий знаменатель будет корень x минус 2 умножить на корень x дополнительный множитель здесь у нас будет корень из x здесь заполнители множитель будет корень из x минус 2 теперь посчитаем корень из x умножаем на корень из x + 1 корень из x на корень из x это x корень из x на 1 это корень из x теперь здесь корень из x умножаем на корень из x и не забываем про знак минус впереди это будет минус x корень из x на 3 my с минусом -3 корень из x теперь минус 2 на корень из x и минус впереди это два корень из x минус 2 на 3 и еще минус это плюс 6 теперь преобразуем числитель у нас x минус экзамен уничтожится корни из x плюс 2 корень из x минус 3 корень из x также взаимно уничтожаются останется просто 6 и того у нас будет шесть давайте снизу раскроем корень из x на корень языка будет x минус 2 корень из x рассмотрим следующий пример и если у вас знаменателе дроби содержится корень то тогда говорят что знаменателе присутствует иррациональность и рациональность знаменателе очень часто нам приходится от этой иррациональности избавляться то есть нужно переписать эту дробь в таком виде чтобы в знаменателе уже не было корней для того чтобы избавиться и от иррациональности поступает следующим образом если у нас один только корень в знаменателе то мы просто и числитель и знаменатель этой дроби домножаем на этот корень здесь у нас корень из 7 значит числитель и знаменатель дроби домножаем на корень из 7 тогда у нас сверху получится один на корень из 7 это корень из 7 а снизу корень из 7 на core i7 это 7 то есть мы эту дробь переписали в таком виде здесь знаменателе уже корней нет говорят что мы избавились от иррациональности давайте попробуем избавиться от иррациональности в других примерах если у вас знаменатель дроби содержит не просто корень а сумма или разность выражений среди которых есть хотя бы один корень то тогда чтобы избавиться от иррациональности поступает следующим образом говорят что нужно давно жить на сопряженное выражение сопряженным выражением является такое же выражение как знаменателей которая отличается только знаком то есть чтобы избавиться от иррациональности мы числитель и знаменатель дроби там ножа им на выражение корни 7 если здесь плюс 110 соответственно минус корень из 7 минус коль не 6 и смотрим что получится сверху у нас 1 умножить на корень из 7 минус корень из 6 так и оставляем а снизу получится 7 plus корни 6 умножить на 7 корень из 7 минус корни 6 это есть ни что иное как разность квадратов то есть мы должны привести выражение к разности квадратов это у нас будет корень из 7 в квадрате минус корень из 6 в квадрате или 7 минус шесть на семь минус 6 это один значит у нас будет корни 7 минус корень из 6 попробуем решить 3 3 пример также домножаем на сопряженное данном случае сопряженное будет являться выражение корни с 15 если здесь минус тот день будет плюс корень из двенадцати до умножаем числитель домножаем знаменатель тогда сверху у нас будет шесть корень из 15 плюс корень из 12 а снизу будет разность квадратов корень из 15 квадрате минус корень из 12 квадрате или 15 минус 12 15 минус 12 это 36 делить на 3 это два и того будет два корень из 15 плюс корень из 12 и рассмотрим последний пример чтобы упростить это выражение в каждом слагаемом нам нужно избавиться от иррациональности начнем с первого чтобы избавиться от иррациональности здесь у нас просто один корень мы домножаем на этот корень во втором случае мы будем дам нажать на корень из 7 плюс корень из 5 и числитель и знаменатель здесь мы домножаем на корень из 5 минус корень из трех теперь преобразуем каждую дробь 7 умножить на корень из 7 это будет 7 корней 7 а снизу будет корень из 7 на корня семьи это семь это вот эта семерка с эта семерка сократится останется просто корень из 7 то есть мы сократили это выражение и это выражение теперь здесь корня из 7 минус корень из 5 на корень из 7 плюс корень из 5 опять же это будет разность квадратов это будет 7 минус 5 просто 220 вот эта двойка сократится останется корень из 7 плюс корень из 5 не забываем что перед ним стоит знак минус значит будет корни 7 минус корень из 5 и аналогично здесь корень из 5 плюс корень из 3 умножаем на корень из 5 минус корень из трех это будет пять минус три или просто 2 здесь у нас 4 сокращается с этой двойкой остается 2 + 2 умножаем на корень из 5 минус 2 на корень из 3 останется просто посчитать корень из 7 займа уничтожается минус корень из 5 + 2 корень из 5 это просто корень из 5 и минус 2 корень из 3 таким образом избавившись от иррациональности мы преобразовали это выражение а на этом данный видео урок окончен [музыка]
Возведение в степень и извлечение корня из числа онлайн.

Корень из числа
Корень нечётной степени из положительного числа
В результате вычисления корня нечётной степени из положительного числа будет положительное число: .
Пример Вычислим корни нечётной степени из 8, 27, 125, 243
Корни 3 степени также называют кубическими корнями.
В результате вычисления корней 5-ой степени из положительных чисел, получили также положительные числа.
Корень нечётной степени из отрицательного числа
В результате вычисления корня нечётной степени из отрицательного числа будет отрицательное число: .
Пример Найдем корни 3 и 5 степеней из отрицательных чисел.
Корень четной степени из положительного числа
Корень чётной степени из положительного числа имеет два значения, положительное и отрицательное: .
Пример Вычислим корни 2 и 4 степени.
Корень 2-й степени называют квадратный корнем.
Корень четной степени из отрицательного числа
Корень четной степени из отрицательного числа не существует для вещественных чисел.
Корень любой степени из нуля
Числа в степени -1, 0, 1
Число в -1 степени
Число 3 в -1 степени можно представить в виде дроби . Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Обратная операция также верна ,
любую дробь можно представить как число в -1 степени, для этого нужно поменять числить и знаменатель местами.
Число является обратным числом 5, т.е. их произведение равно единице , такое равенство выполнено для любого числа
Пример Представить дробь в степени -1
Число в 1 степени
Число в первой степени является самим числом a1=a
Число в 0 степени
Любое число в степени ноль равно единице a0=1
Как с помощью циркуля и линейки находить корни, квадраты и обратные величины чисел
Представьте, что у вас нет под рукой калькулятора (но есть циркуль и линейка или угольник) и вам нужно посчитать результат в виде отрезка. Задача решается за менее чем 5 простых шагов.
Задача решается за менее чем 5 простых шагов.
Базовая формула вычисления
Для начала докажем одну формулу, которая нам будет помогать с дальнейшим решением.
В прямоугольном треугольнике ABC проведем высоту h на сторону C. По теореме Пифагора выводим:
Подставляем всё в первую формулу:
И если раскрыть скобки:
После сокращения получаем:
Вот с помощью этой формулы и будем выводить наши решения.
Единичная мера длины
Так как мы вычисления проводим на плоскости с отрезками, нам необходимо определиться с мерой единичной длины равной 1. Если мы отложим отрезок 1 дециметр, то он так же будет равен 10 сантиметрам, 100 миллиметрам или 4 дюймам. Один отрезок и 4 разных чисел разной меры длины его определяют. Что бы выбрать одну систему счисления длин отрезков, примем за единицу длины какой-то отрезок. Какой — определим по ходу расчетов, и он зафиксирует нужную меру длины.
Циркуль как универсальный инструмент
Циркуль удобно использовать как средство:
отмерить отрезок определенной длины, при этом знать величину этой длины совершенно нет надобности.
прочертить дугу на одинаковом расстоянии от определённой точки.
отложить перпендикуляр к линии через определённую точку. Для этой цели удобнее использовать угольник с прямым углом, чем циркулем чертить 4 дуги.
Вычисление квадрата длины
Для вычисления квадрата величины X используем нашу формулу в виде:
Чертим прямую линию достаточной длины.
Откладываем на ней отрезок единичной длины.
От правого конца единичного отрезка 1 откладываем вверх перпендикуляр длиной X.
Проводим линию от левого конца единичного отрезка 1 до верхнего конца отрезка X.
От этого отрезка откладываем перпендикуляр на линию продолжения единичного отрезка 1. Их пересечение и есть правый край квадрата длины. Левый край начинается от точки, где отложена высота.
Их пересечение и есть правый край квадрата длины. Левый край начинается от точки, где отложена высота.
Пример. У вас есть какой-то квадрат, со стороной X, начерченный на плоскости или на земле. Нужно узнать его площадь в попугаях. Одна сторона квадрата длиной X у нас уже есть. На соседней стороне откладываем длину одного попугая (там где 1 находится). Соединяем концы линией, откладываем перпендикуляр, продлеваем отрезок с попугаями до перпендикуляра и получаем решение в квадратных попугаях.
Вычисление квадратного корня длины
Для вычисления квадратного корня величины используем нашу формулу в виде:
Чертим прямую линию достаточной длины.
Откладываем на ней единичный отрезок длины 1.
На продолжении единичного отрезка откладываем отрезок длины X.
Полученный отрезок 1+X делим пополам с помощью циркуля и получаем точку O. Как это сделать, приводить здесь не буду, это задачка из школьного курса. Обозначим длину найденной половины как
Обозначим длину найденной половины как R.
Вокруг центра O, циркулем нарисуем дугу радиусом R.
От правого конца отрезка 1 отложим вверх перпендикуляр до пересечения с дугой окружности. Длина этого перпендикуляра и будет равна корню квадратному из длины X.
Вычисление обратной величины длины
Для вычисления обратной величины длины используем нашу формулу в виде:
Решение очень похоже на нахождение квадрата величины, только a и h меняются местами.
Чертим прямую линию достаточной длины.
Откладываем на ней отрезок длины X.
От правого края отрезка X откладываем вверх перпендикуляр единичной длины 1.
Соединяем концы отрезков линией.
От верхнего конца отрезка X откладываем перпендикуляр к линии продолжения отрезка 1. Полученный отрезок и есть решение.
Выводы
Приведенные выкладки удобны, когда не хочется возиться с цифрами и их арифметическими вычислениями, которые всё равно будут обратно приложены к длинам отрезков.
Если величина X сильно отличается от единичного отрезка 1, ошибка вычисления может быть значительной. Но если применить масштабирование, то ошибку можно значительно уменьшить. Например, при захождении корня длины 20, его можно поделить на 16 (4 раза поделить пополам), а потом ответ умножить на 4 (4 раза отложить полученный отрезок).
как сделать и 20 фото окрашивания
Универсальность омбре несомненна, но когда речь заходит о длине волос, обнаруживаются некоторые тонкости.
Завсегдатаи салонов красоты знают, что волосы ниже плеч уже считаются длинными и обычно требуют свыше 150 мл красителя. Для классического омбре с растяжкой одного оттенка хватит и одного тюбика, а если вы планируете начинать градиент в 3-5 сантиметрах от корней, то запаситесь тремя тюбиками. Если краска останется – не беда, но и наносить излишки на волосы не стоит, поскольку на оттенок это никак не повлияет, а вот кончики длинных прядей могут пострадать совершенно незаслуженно.
Средние волосы опускаются ниже подбородка, но не доходят до плеч, и, как правило, самостоятельно сделать на них омбре не составляет труда. При переходе от натурального оттенка одного тюбика краски будет достаточно. Единственный – и очень условный – минус градиента на прядях средней длины заключается в том, что оттенок на нижней части длины будет непосредственно у лица, поэтому цвет нужно подбирать очень тщательно, учитывая подтон и состояние кожи, цвет глаз. К примеру, пепельный блонд предательски подчеркнет каждую морщинку и любые неровности на коже.
Предпочитаете классический боб, стрижку гарсон или пикси? На такой длине омбре проводить сложно, но возможно. Ограничьтесь одним тюбиком краски при одноцветном градиенте, а на сложное колорирование с переходом трех-четырех цветов берите по одной упаковке каждого тона. На коротких прядях колористы сначала обесцвечивают пряди ниже линии будущего перехода, а затем наносят цветную краску от корней до кончиков – так проще получить сглаженную градацию.
Бесспорно модное и интересное окрашивание уже хочется повторить своими руками. Рискнем? С нашей пошаговой инструкцией вы получите представление об исполнении классического градиента с ценными подсказками от экспертов Garnier. Так что в будущем вам будет проще покрасить волосы с эффектом омбре в домашних условиях себе или подругам, на длинные, средние или короткие, светлые или темные волосы, в прямой или обратной технике – или даже сделать цветной мультиколор, как настоящий стилист. Все получится!
Эти «мелочи» – все, что нужно для омбре, но от них успех первого эксперимента, особенно в домашних, а не салонных условиях, зависит чуть ли не на 100%.
- Расческа-гребень.
- Старая одежда или профессиональная пелерина.
- Краска в нужном количестве, осветлитель и оксид.
- Тонкие перчатки.
- Две плоские кисти (или одна, но тогда ее придется мыть).
- Керамическая или стеклянная миска.
- Маленькие эластичные резинки для волос или заколки.

Перед окрашиванием не мойте волосы – естественный липидный слой обеспечит защиту при осветлении не хуже, чем салонные добавки для щадящего обесцвечивания.
- Тщательно расчешитесь и разделите волосы резинками или заколками на 6-12 частей, в зависимости от густоты шевелюры. Они должны фиксировать пряди чуть выше той линии, которую вы определили как желаемую для градиента.
- Подготовьте смесь оксида с осветляющим порошком и нанесите ее на волосы от линии будущего перехода вниз, причем чем ближе к кончикам – тем гуще.
- Дайте составу время подействовать согласно рекомендациям производителя.
- Промойте волосы водой с мягким шампунем и высушите их феном.
- Тщательно смешайте в миске краситель с проявителем (обычно идет в комплекте с краской) по инструкции, указанной на упаковке.
- Нанесите краситель на обесцвеченные пряди по направлению роста волос слегка размашистыми движениями, заходя выше линии обесцвечивания, чтобы избежать резкого перехода цвета.
 Помните, что стойкий краситель требует сухих волос, а безаммиачный наносится на чуть влажную шевелюру.
Помните, что стойкий краситель требует сухих волос, а безаммиачный наносится на чуть влажную шевелюру. - Посидите с книгой или смартфоном, пока краситель действует. Обычно на это нужно не более 20 минут, но у производителя вашей краски могут быть другие указания на этот счет.
- Промойте волосы сначала только водой, а потом мягким шампунем. Нанесите на две минуты любой подходящий кондиционер для сглаживания кутикулы и закрепления цвета. Эксперты Garnier рекомендуют бальзам-ополаскиватель «Аргановое масло и клюква» для окрашенных волос.
- Высушите волосы естественным путем или феном и наслаждайтесь своим собственным авторским омбре.
Специально для визуалов представляем графическую пошаговую инструкцию – это фото доказывает, что омбре в домашних условиях ничуть не головоломнее, чем обычное окрашивание.
Правда ли, что плавного перехода в технике омбре можно добиться дома простой расческой? Евгений Седой делится профессиональной хитростью.
«Для этого нужно разделить волосы на пряди и начесать их с помощью гребня. Движение расчески следует начинать как можно ближе к концам, двигаясь в направлении корней. Начес не должен быть плотным, чтобы потом его можно было расчесать. Таким образом, часть кончиков волос сместится к корнями, и когда вы нанесёте краску для перехода, четкой границы уже не будет».
Движение расчески следует начинать как можно ближе к концам, двигаясь в направлении корней. Начес не должен быть плотным, чтобы потом его можно было расчесать. Таким образом, часть кончиков волос сместится к корнями, и когда вы нанесёте краску для перехода, четкой границы уже не будет».
Выбирайте красители только проверенных известных брендов, заинтересованных в собственной репутации. И непременно замените привычный уход на специальные средства для окрашенных волос с антиоксидантами и без сульфатов. Поддержать яркость платинового омбре помогут средства с фиолетовыми пигментами для борьбы с желтизной.
Эксперты Garnier предлагают следовать правилу трех «не» в домашнем уходе за омбре:
- не мойте волосы горячей водой;
- не используйте питательные маски в первые 3-4 недели после окрашивания;
- не выходите из дома, не нанеся на пряди несмываемое средство с UV-фильтрами и антиоксидантами.

Когда омбре заметно отрастет – то есть не ранее, чем через полгода, – повторите процедуру с легким начесом и осветлением. Но на этот раз не затрагивайте кончики волос, которые уже были осветлены при первом окрашивании. А затем проведите тонирование длины, нанося краску чуть выше линии перехода и до самых корней.
Готово! Омбре снова выглядит великолепно, причем в этом только ваша заслуга.
Кутья на Рождество — три проверенных рецепта кутьи с пшеницей, рисом и булгуром
В традиционном рецепте для приготовления кутьи используют пшеницу, но можно взять и другие крупы
Уже совсем скоро христиане будут праздновать великий праздник Рождества Христова, с которым связано множество традиций и запретов. Одной из важнейших традиций является приготовление традиционного кутьи — сладкой каши с орешками, изюмом и маком.
Рецептов этого блюда множество, однако «Телеграф» собрал три наиболее удачных и проверенных варианта. Один из них, к слову, предложил известный украинский повар Евгений Клопотенко.
Один из них, к слову, предложил известный украинский повар Евгений Клопотенко.
Кутья из пшеницы по рецепту Евгения Клопотенко
Ингредиенты
- Пшеница — 1 стакан
- Вода — 4 стакана
- Сливочное масло — 50 гр. на щедрую кутью (или 2 ст. л. подсолнечного масла, если на постную)
- Мед — 2-3 ст. л.
- Мак — 2 ст. л.
- Грецкие орехи — 1 горсть
- Курага — 100 г
- Изюм — 1 горсть
- Лимон – 1 шт. (цедра и сок)
- Корень имбиря — 1 см
Приготовление
- Пшеницу залейте водой на ночь, чтобы у нее было время набухнуть. Перед приготовлением воду сливаем, а затем снова заливаем чистой. Ставим кашу на маленький огонь и варим 30-60 минут до готовности.
- В теплую кашу добавляем 50 г масла.
- Курагу нарезаем небольшими кубиками. Если попалась очень жесткая, то запарьте ее в кипятке на 5 минут.
- В кашу добавляем курагу, изюм, мак и 1 см корня имбиря, который нужно натереть на мелкой терке.

- Туда же отправляем горсть нарубленных грецких орехов, цедру одного лимона.
- Добавляем в кутью 2-3 столовых ложки меда и 1-2 ложки лимонного сока.
- Чтобы кутья настоялась, оставьте ее минимум на 2 часа в холодильнике, а затем подавайте на стол.
Рисовая кутья с медом и черносливом
Ингредиенты
- Рис — 1 ст.
- Мак (маковая начинка с сахаром – 100 г, чистый мак – 20 г) — 100 г
- Сухофрукты (курага – 50 г; чернослив – 50 г) — 100 г
- Изюм — 50 г
- Орехи грецкие — 200 г
- Мед — 100 мл
- Цукаты — 100 г
Приготовление
- В небольшие отдельные емкости необходимо сложить сухофрукты – изюм, чернослив, курагу – и залить их кипяченой водой на 20 минут.
- Маковую начинку заливаем кипятком таким образом – на 100 грамм даем 50 мл воды, если чистый мак – то на 20 грамм даем 40 мл воды. Оставляем тоже на 20 минут.
- Часть грецких орехов рубим грубо, другую часть мелко натираем на терке.

- Готовим рис – сначала крупу промываем, а затем заливаем водой в соотношении 1:2 и ставим на огонь. В среднем на приготовление риса уходит 20-30 минут, после чего выключаем и даем ему настояться. Затем рис необходимо промыть холодной водой и добавить в него 2 столовые ложки сахара.
- Сладкий рис кладем в посудину, добавляем туда маковую начинку и изюм. Высыпаем натертый грецкий орех.
- Сливаем из сухофруктов воду, режем кубиками и добавляем в кашу с маком и орехами. Туда же выливаем мед.
- Перед подачей можно украсить блюдо сухофруктами и орехами.
Кутья из булгура
Ингредиенты
- Булгур — 1 стакан
- Растительное масло — 40 граммов
- Мед — по вкусу
- Орехи — по вкусу
Приготовление
- Булгур тщательно промыть и дать время на то, чтобы из него стекла лишняя вода.
- За это время подготовьте орехи, мед и фрукты, чтобы украсить кутью.

- Варим булгур – заливаем в кастрюлю несколько столовых ложек растительного масла и добавляем булгур без воды. Жарим в кастрюле в течение 5 минут, после чего заливаем водой и варим до готовности.
- Солим кашу только после того, как булгур поварился в течение 5 минут. Затем накрываем крышкой и держим так, пока не сварится.
- Готовую кашу отставляем и даем ей полностью охладиться, тем временем рубим мелко орехи.
- Растапливаем мед так, чтобы им можно было полить нашу кутью.
- Поливаем кутью растопленным медом, а сверху украшаем фруктами, орехами или изюмом.
Ранее Телеграф сообщал, как правильно приготовить традиционную кутью на Рождество.
Поделиться с друзьямиПоделитесь с друзьями в соцсетях
Не понравилось 0
чел. Понравилось 1
чел.
Понравилось 1
чел.
Что такое RMS | Алексей Данилов
Если у вас приличный опыт звукорежиссуры и с аудиоредакторами вы на «ты», скорее всего, эта небольшая статья ничего нового для вас не откроет. В ней речь пойдет о технических характеристиках звука, таких как пиковая амплитуда и различные виды RMS.
Впрочем, иногда бывает весьма полезно уложить в голове уже знакомую информацию словами другого человека.
Пиковая амплитуда
Главный абсолютный показатель громкости в звуковой дорожке – это пики. Открывая файл в любом редакторе, вы видите прорисовку волны, которая в громких местах подскакивает вверх. Эти «подскоки» как раз и называются пиками, или пиковой амплитудой (Peak Amplitude).
Нужно помнить, что звук – не математическая, а физическая величина, значение его громкости не может быть отрицательным. Соответственно, горизонтальная линия, изображающая ось Х, не означает, что волна ниже нее имеет отрицательную громкость. Самый тихий звук находится не в самой нижней точке рабочего окна, а на уровне оси Х. Любые отклонения вверх или вниз – некоторая неотрицательная громкость. Всплеск вниз будет таким же заметным, как и всплеск вверх на ту же амплитуду.
Соответственно, горизонтальная линия, изображающая ось Х, не означает, что волна ниже нее имеет отрицательную громкость. Самый тихий звук находится не в самой нижней точке рабочего окна, а на уровне оси Х. Любые отклонения вверх или вниз – некоторая неотрицательная громкость. Всплеск вниз будет таким же заметным, как и всплеск вверх на ту же амплитуду.
Условно принято, что в цифровой среде максимальная громкость не может быть выше 0 дБ, а отсчеты громкости ведутся от максимума вниз: -2 дБ громче, чем -4 дБ.
Но не путайте значение 0 дБ с осью Х, которую скорее можно назвать «минус бесконечностью». 0 дБ – это ограничительные линии, которые можно найти в аудиоредакторе с двух сторон от волны – сверху и снизу (см. рисунок). Выход за пределы этого уровня приведет к клипам, то есть к искажениям сигнала. Клипы можно получить двумя способами – ошибками во время записи (слишком сильно разогнанная чувствительность микрофона или инструмента) или ошибками при обработке уже записанных фрагментов.
Обычные методы увеличения громкости на первых порах приобщения к сфере звукорежиссуры – это повышение чувствительности (Gain) или нормализация (Normalize). Эти два приема – по сути одно и то же, только первый позволяет изменить громкость на заданное значение, а во второй – привести к заданному уровню.
Например, если в треке максимальный пик находится на -3 дБ, то можно увеличить чувствительность всей дорожки на 3 дБ или нормализовать до 0 дБ, в обоих случаях произойдет одно и то же – звук станет громче на 3 дБ, а пик окажется на значении 0.
Но и здесь нужно быть внимательным. Если пиковое значение исходного сигнала -3 дБ, а вы пытаетесь увеличить чувствительность на 4 дБ, то в результате громкость пика превысит 0 дБ и приведет к клипу. Нет, значения +1 дБ на графике не появится, вы просто увидите обрезанную верхушку волны ровно по уровню 0 дБ, а при воспроизведении услышите треск. Более гуманным способом повышения громкости является нормализация до 0 дБ, которая автоматически вычислит максимальный уровень и предотвратит клипы.
Более гуманным способом повышения громкости является нормализация до 0 дБ, которая автоматически вычислит максимальный уровень и предотвратит клипы.
Зачем же тогда нужна функция изменения чувствительности? Во-первых, с ее помощью можно не только увеличить громкость, но и уменьшить. А во-вторых – опытный звукорежиссер использует манипуляции с чувствительностью для выравнивания громкости звучания дорожки в ручном режиме, учитывая необходимый запас в децибелах для будущей обработки (хедрум).
К примеру, бывает, что бочка, бас-гитара или голос записаны динамически неровно, а использовать компрессор нецелесообразно. Тогда проваливающиеся участки можно аккуратно поднять, а слишком громкие – слегка убавить. Такая процедура наносит звуку намного меньше вреда, чем топтание дорожки компрессией, но она требует опыта.
Однако наведение порядка с пиковыми значениями через нормализацию или гейн практически никогда не дает ощутимого эффекта по увеличению громкости песни. Чтобы заставить композицию звучать громче, необходимы более глубокие вмешательства, связанные с уменьшением ее динамического диапазона.
Чтобы заставить композицию звучать громче, необходимы более глубокие вмешательства, связанные с уменьшением ее динамического диапазона.
RMS и его разновидности
Для условной градации песен по громкости и анализа динамического диапазона звукорежиссеры используют характеристику RMS в различных видах.
RMS – параметр, показывающий среднюю громкость звучания трека или какой-либо его части. С математической точки зрения RMS (Root Mean Square) – это среднеквадратическое значение громкостей всех семплов дорожки.
По сути, звуковой файл – это многократное чередование амплитудных пиков и провалов волны. Даже в очень громкой музыке невозможна ситуация, когда волна непрерывно находится на максимуме своей амплитуды, ей обязательно надо проходить через центральную ось, ведь звук – это колебания.
В любой записи есть определенное количество громких и тихих участков, а также участки с промежуточными значениями громкости. Минимальный дискретный участок звукового файла – это семпл. Каждый семпл в звуковой дорожке имеет свою амплитуду, то есть воспроизводится на определенной громкости.
Каждый семпл в звуковой дорожке имеет свою амплитуду, то есть воспроизводится на определенной громкости.
При работе на частоте дискретизации 44,1 кГц в 1 секунде записи содержится 44100 семплов. Если композиция длится 1 минуту, то всего в ней 2,646 млн. семплов. Чтобы вычислить RMS, нужно громкость (амплитуду) каждого семпла возвести в квадрат, суммировать все получившиеся значения, потом это число разделить на количество семплов, и из результата вычислить квадратный корень. Как будто бы сложно, но на деле все элементарно:
Где a – это каждый отдельный семпл, n – количество семплов.
Среднеквадратическое – это почти то же самое, что знакомое всем из школы среднее арифметическое, только каждое слагаемое возводится в квадрат, а из общего результата дроби вычисляется квадратный корень.
Разные аудиоредакторы немного по-разному подходят к анализу RMS, но в целом концепция схожая. Очень удобен для этих целей Adobe Audition. При сборе статистических данных по файлу программа учитывает следующие показатели:
При сборе статистических данных по файлу программа учитывает следующие показатели:
- Minimum Sample Value (минимальное значение семпла) – самая нижняя точка графика. Не путайте с самым тихим значением, наоборот – это громкая амплитуда в отрицательном от оси Х направлении.
- Maximum Sample Value (максимальное значение семпла) – самая верхняя точка графика.
- Peak Amplitude (пиковая амплитуда) – значение самого громкого пика во всем треке в децибелах.
- Possibly Clipped Samples (семплы с возможными клипами) – показывает семпл с подозрением на появление клипа.
- DC Offset (Direct current offset) – «смещение по постоянному току». Отображается, если в графике (а соответственно и в самом звуке) присутствует общее смещение по амплитуде. Офсет возникает в результате некачественной записи, когда в звук добавляются некоторые постоянные значения. На слух DC Offset чаще всего незаметен, но при обработке может привести к определенным проблемам, в том числе и к ограничению по громкости звука.

- Total RMS (общий RMS) – среднеквадратическое значение громкости по всему треку.
- Average RMS (средний RMS) – среднеквадратическое значение громкости по всему треку с учетом особенностей восприятия звука человеком.
- Maximum RMS (максимальный RMS) – участок записи с наибольшей громкостью.
- Minimum RMS (минимальный RMS) – участок записи с наименьшей громкостью.
- Actual Bit Depth (актуальная разрядность) – показывает действительную разрядность (битность) сигнала.
Нажав в каждом случае на кнопку со стрелочкой, можно переместиться к тому участку файла, который учитывается в данной графе статистики, причем эта функция доступна для каждого канала в отдельности.
Важно понять, что максимальный RMS – это не то же самое, что пиковое значение. Пик – это обычно один семпл с наибольшей амплитудой, а максимальный RMS – это участок, где плотность громких всплесков наибольшая. В зависимости от продолжительности анализируемых участков, эти области могут даже и не совпадать. По умолчанию Adobe Audition берет за основу расчета участки в 50 миллисекунд.
В зависимости от продолжительности анализируемых участков, эти области могут даже и не совпадать. По умолчанию Adobe Audition берет за основу расчета участки в 50 миллисекунд.
Нужно также внести уточнение по Total и Average RMS. Не все аудиоредакторы показывают оба эти параметра, кроме того, некоторые программы обозначают «средним» то, что Adobe Audition называет «общим». Если нужно разобраться в этом глубже следует обращаться к инструкциям конкретного приложения, но на практике их значения чаще всего довольно близки.
Также нужно учитывать, что при расчете общего и среднего RMS программа будет учитывать тишину в начале и в конце файла. Чтобы полученные данные были ближе к реальности, лишние секунды имеет смысл удалять или оставлять за пределами выделенной для анализа области.
В ближайшее время в моем блоге будут опубликованы две больших статьи, затрагивающих вопросы громкостей, мастеринга и динамической обработки сигнала. Некоторые материалы из этих статей уже доступны читателям моей книги «Академия Мюзикмейкера», но будет и значительная часть новой информации.
Если вам интересно, как добиться от своей записи плотного звучания и громкости, сопоставимой с фирменными записями, следите за обновлениями. Чтобы не пропустить статьи, можно подписаться на блог, и тогда они будут отправлены вам прямо на электронный адрес.
Ну и конечно, любые дополнения и уточнения всегда приветствуются. А если у вас возникли какие-либо вопросы – задавайте их в комментариях, по возможности постараюсь на них ответить максимально подробно.
UPD Обещанные статьи уже опубликованы: Мастеринг и громкость звука и Компрессия звука
© Алексей ДаниловИллюстрации: А. Рублевский При перепечатывании ссылка на источник обязательна
Хотите получать новые статьи
прямо на почту?
Подпишитесь на обновления блога А. Данилова
Интересное:
Упрощение квадратного корня
Чтобы упростить извлечение квадратного корня: сделайте число внутри квадратного корня как можно меньшим (но все же целым числом):
Пример: √12 проще как 2√3
Возьмите калькулятор и проверьте, хотите ли вы: они оба имеют одинаковое значение!
Вот правило: когда a и b не отрицательны
А вот как им пользоваться:
Пример: упрощение √12
12 равно 4 умножить на 3:
√12 = √ (4 × 3)
Используйте правило:
√ (4 × 3) = √4 × √3
И квадратный корень из 4 равен 2:
.
√4 × √3 = 2√3
Итак, √12 проще, чем 2√3
Другой пример:
Пример: упрощение √8
√8 = √ (4 × 2) = √4 × √2 = 2√2
(поскольку квадратный корень из 4 равен 2)
И еще:
Пример: упрощение √18
√18 = √ (9 × 2) = √9 × √2 = 3√2
Часто помогает разложить числа (лучше всего на простые числа):
Пример: упрощение √6 × √15
Сначала мы можем объединить два числа:
√6 × √15 = √ (6 × 15)
Затем мы множим их:
√ (6 × 15) = √ (2 × 3 × 3 × 5)
Дальше видим две тройки и решаем «вытащить их»:
√ (2 × 3 × 3 × 5) = √ (3 × 3) × √ (2 × 5) = 3√10
Фракции
Аналогичное правило для дробей:
Пример: упрощение √30 / √10
Сначала мы можем объединить два числа:
√30 / √10 = √ (30/10)
Затем упростите:
√ (30/10) = √3
Примеры посложнее
Пример: упрощение
√20 × √5 √2Посмотрите, сможете ли вы выполнить следующие шаги:
√20 × √5 √2
√ (2 × 2 × 5) × √5 √2
√2 × √2 × √5 × √5 √2
√2 × √5 × √5
√2 × 5
5√2
Пример: упрощение 2√12 + 9√3
Первое упрощение 2√12:
2√12 = 2 × 2√3 = 4√3
Теперь оба члена имеют √3, мы можем их сложить:
4√3 + 9√3 = (4 + 9) √3 = 13√3
Surds
Примечание: корень, который мы не можем упростить , называется Surd. Итак, √3 — сюрд. Но √4 = 2 — это не сюрд.
Итак, √3 — сюрд. Но √4 = 2 — это не сюрд.
квадратный корень из 20 — Как найти квадратный корень из 20?
Квадратный корень из 20 выражается как √20 в радикальной форме и как (20) ½ или (20) 0,5 в экспоненциальной форме. Квадратный корень из 20, округленный до 8 знаков после запятой, составляет 4,47213595. Это положительное решение уравнения x 2 = 20. Мы можем выразить квадратный корень из 20 в его низшей радикальной форме как 2 √5.
- Квадратный корень из 20: 4,472135958
- Квадратный корень из 20 в экспоненциальной форме: (20) ½ или (20) 0,5
- Квадратный корень из 20 в радикальной форме: √20 или 2 √5
Что такое квадратный корень из 20?
Квадратный корень из 20 может быть получен из числа, квадрат которого дает исходное число. Какое это могло быть число? Видно, что не существует целых чисел, квадрат которых дает 20.
Какое это могло быть число? Видно, что не существует целых чисел, квадрат которых дает 20.
√ 20 = 4,472
Чтобы проверить этот ответ, мы можем найти (4.472) 2 и увидеть, что мы получаем число 19.998784 … которое очень близко к 20, когда оно округляется до ближайшего значения.
Является ли квадратный корень из 20 рациональным или иррациональным?
Рациональное число является завершающим или не завершающим и имеет повторяющийся образец в своей десятичной части. Мы видели, что √ 20 = 4,4721359549. Это не завершение, и десятичная часть не имеет повторяющегося шаблона.Так что это НЕ рациональное число. Следовательно, √ 20 — иррациональное число.
Как найти квадратный корень из 20?
Существуют разные способы найти квадратный корень из любого числа. Щелкните здесь, чтобы узнать об этом больше.
Упрощенная радикальная форма квадратного корня из 20
20 не является простым числом. Таким образом, у него более двух множителей: 1, 2, 4, 5, 10 и 20. Чтобы найти квадратный корень из любого числа, мы берем одно число из каждой пары одинаковых чисел из его разложения на простые числа и умножаем их.Факторизация 20 составляет 2 × 2 × 5, что дает 1 пару одинаковых чисел. Таким образом, простейшая радикальная форма √ 20 — это сама 2 √ 5.
Квадратный корень из 20 методом длинного деления
Квадратный корень из 20 можно найти следующим образом.
- Шаг 1 : Пара цифр заданного числа, начинающаяся с цифры на своем месте. Поставьте горизонтальную полосу, чтобы обозначить сопряжение.
- Шаг 2 : Теперь нам нужно найти число, которое при умножении на само себя дает произведение, меньшее или равное 20.
 Как мы знаем, 4 × 4 = 16 <20. Следовательно, делитель равен 4, а частное равно 4.
Как мы знаем, 4 × 4 = 16 <20. Следовательно, делитель равен 4, а частное равно 4. - Шаг 3 : Теперь нам нужно уменьшить 00 и умножить частное на 2. Это дает нам 8. Следовательно, 8 — это начальная цифра нового делителя.
- Шаг 4 : 4 помещается на место нового делителя, потому что, когда 84 умножается на 4, мы получаем 336. Полученный ответ теперь равен 64, и мы опускаем 00.
- Шаг 5 : Теперь частное становится 44 и умножается на 2.Это дает 88, которое затем станет начальной цифрой нового делителя.
- Шаг 6 : 7 помещается на место нового делителя, потому что при умножении 887 на 7 мы получаем 6209. Это дает ответ 191, и мы опускаем 00 вниз.
- Шаг 7 : Теперь частное 447 при умножении на 2 дает 894, что будет начальной цифрой нового делителя.
- Шаг 8 : 2 — новый делитель, потому что, умножив 8942 на 2, мы получим 17884.
 Итак, теперь ответ — 1216, а следующая цифра частного — 2.
Итак, теперь ответ — 1216, а следующая цифра частного — 2.
Итак, мы получили √ 20 = 4,472. Повторяя этот процесс дальше, получаем, что √ 20 = 4,4721359549 …
Изучите квадратные корни с помощью иллюстраций и интерактивных примеров
Важные примечания:
- 20 лежит между 16 и 25. Таким образом, √ 20 лежит между √ 16 и √ 25, т.е. √ 20 лежит между 16 и 25
- Метод разложения на простые множители записывается как квадратный корень из неполного квадратного числа в простейшей радикальной форме.Например: 20 = 2 × 2 × 5. Итак, √ 20 = √ 2 × 2 × 5 = 2 √ 5.
Аналитический центр:
- Может ли квадратный корень быть отрицательным?
- Является ли √ -20 действительным числом?
Пример 1 : У Джуди есть квадратная комната площадью 20 квадратных футов.
 Какой будет длина пола в комнате? Округлите ответ до ближайшей десятой.
Какой будет длина пола в комнате? Округлите ответ до ближайшей десятой.Решение
Предположим, что длина комнаты составляет x футов. Тогда площадь этажа комнаты составит x 2 квадратных фута. По предоставленной информации:
х 2 = 20
x = √ 20 = 4,5 футаОкончательный ответ округляется до ближайшей десятой. Следовательно, длина комнаты составляет 4,5 фута.
Пример 2 : Если площадь круга составляет 20π квадратных дюймов.Каков его радиус?
Решение
Тогда площадь определяется по формуле площади круга πr 2 квадратных дюймов. По предоставленной информации,
πr 2 = 20π
г 2 = 20Взяв квадратный корень с обеих сторон, получим √ r 2 = √ 20. Мы знаем, что квадратный корень из r 2 равен r.

При вычислении квадратного корня из 20 получается 4,47 дюйма.Пример: Если площадь круга равна 20π в 2 .Найдите радиус круга.
Решение:
Пусть ‘r’ будет радиусом круга.
⇒ Площадь круга = πr 2 = 20π дюйм 2
⇒ r = ± √20 из
Поскольку радиус не может быть отрицательным,
⇒ г = √20
Корень квадратный из 20 равен 4,472.
⇒ r = 4,472 дюйм
перейти к слайду перейти к слайду
Хотите заложить прочный фундамент в математике?
Выйдите за рамки запоминания формул и поймите «почему» за ними.Испытайте Cuemath и приступайте к работе.
Забронируйте бесплатную пробную версию Класс
часто задаваемых вопросов о квадратном корне из 20
Что такое квадратный корень из 20?
Квадратный корень из 20 равен 4,47213.
Почему квадратный корень из 20 — иррациональное число?
После разложения на простые множители 20, т. Е. 2 2 × 5 1 , 5 находится в нечетной степени. Следовательно, квадратный корень из 20 иррационален.
Е. 2 2 × 5 1 , 5 находится в нечетной степени. Следовательно, квадратный корень из 20 иррационален.
Что такое квадратный корень из 20 в простейшей радикальной форме?
Нам нужно выразить 20 как произведение его простых множителей i.е. 20 = 2 × 2 × 5. Следовательно, √20 = √2 × 2 × 5 = 2 √5. Таким образом, квадратный корень из 20 в младшей радикальной форме равен 2 √5.
Число 20 — это идеальный квадрат?
Разложение на простые множители числа 20 = 2 2 × 5 1 . Здесь простого множителя 5 нет в паре. Следовательно, 20 — не идеальный квадрат.
Вычислить 4 плюс 12 квадратный корень 20
Данное выражение равно 4 + 12 √20. Мы знаем, что квадратный корень из 20 равен 4,472. Следовательно, 4 + 12 √20 = 4 + 12 × 4.472 = 4 + 53,666 = 57,666
Что такое квадратный корень 2 из 20?
Корень квадратный из 20 равен 4,472. Следовательно, 2 √20 = 2 × 4,472 = 8,944.
Калькулятор квадратного корняКалькулятор квадратного корня
О калькуляторе квадратного корня
Калькулятор квадратного корня используется для нахождения квадратного корня из введенного числа.
Квадратный корень
В математике квадратный корень из числа x — это такое число r, что r 2 = x.
Например:
1. Квадратный корень из 25 равен 5, потому что 5 2 = 25.
3. Квадратный корень из 2 приблизительно равен 1,41421356237.
3. Квадратный корень числа пи (π) приблизительно равен 1,77245385102.
Таблица квадратного корня
Ниже приводится таблица квадратного корня от 1 до 1000 с округлением до 5 цифр:
9045 128451 11.26943| x | √x | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||||||
| 2 | 1.41421 | |||||||||||||
| 3 | 1.73205 | |||||||||||||
| 4 | 2 | |||||||||||||
| 5 | 2.23607 | |||||||||||||
| 6 | 2.44949 | |||||||||||||
| 9 | 3 | |||||||||||||
| 10 | 3,16228 | |||||||||||||
| 11 | 3,31662 | |||||||||||||
| 12 | 3,4641 | |||||||||||||
| 60555 | ||||||||||||||
| 14 | 3,74166 | |||||||||||||
| 15 | 3,87298 | |||||||||||||
| 16 | 4 | |||||||||||||
| 17 | 4,12311 | |||||||||||||
| 20 | 4. 47214 47214 | |||||||||||||
| 21 | 4.58258 | |||||||||||||
| 22 | 4.69042 | |||||||||||||
| 23 | 4.79583 | |||||||||||||
| 24 | 4,89898 | |||||||||||||
| 25 | 5 | |||||||||||||
| 26 | 5,09902 | |||||||||||||
| 27 5,3 | 5,19615 | 27 5,3 | 5,19615 | |||||||||||
| 30 | 5,47723 | |||||||||||||
| 31 | 5,56776 | |||||||||||||
| 32 | 5,65685 | |||||||||||||
| 33 | 5.74456 | |||||||||||||
| 34 | 5,83095 | |||||||||||||
| 35 | 5, | |||||||||||||
| 36 | 6 | 6 | ||||||||||||
| 37 | 6.08276 | 6.08276 | 6.08276 | 6.08276 | 6.08276 | |||||||||
| 40 | 6.32456 | |||||||||||||
| 41 | 6.40312 | |||||||||||||
| 42 | 6.48074 | |||||||||||||
| 43 | 6. 55744 55744 | |||||||||||||
| 44 | 6.63325 | |||||||||||||
| 45 | 6.7082 | |||||||||||||
| 46 | 6.78233 | |||||||||||||
| 7.855659 | ||||||||||||||
| 50 | 7.07107 | |||||||||||||
| 51 | 7.14143 | |||||||||||||
| 52 | 7.2111 | |||||||||||||
| 53 | 7.28011 | |||||||||||||
| 54 | 7,34847 | |||||||||||||
| 55 | 7,4162 | |||||||||||||
| 56 | 7,48331 | |||||||||||||
| 57 | 7,54983 | 7,54983 | 57 | 7,54983 | ||||||||||
| 60 | 7.74597 | |||||||||||||
| 61 | 7.81025 | |||||||||||||
| 62 | 7.87401 | |||||||||||||
| 63 | 7. | |||||||||||||
| 64 | 8 | |||||||||||||
| 65 | 8.06226 | |||||||||||||
| 66 | 8. 12404 12404 | |||||||||||||
| 67 | 8,18535 | 8,18535 | 8,18535 | 8,18535 | ||||||||||
| 70 | 8.3666 | |||||||||||||
| 71 | 8.42615 | |||||||||||||
| 72 | 8.48528 | |||||||||||||
| 73 | 8.544 | |||||||||||||
| 74 | 8.60233 | |||||||||||||
| 75 | 8.66025 | |||||||||||||
| 76 | 8.7178 | |||||||||||||
| 77 | 8.77496 | 8.7178 | 8.77496 | 77 | 8.77496 | 77 | 8.77496 9045 | |||||||
| 80 | 8. | |||||||||||||
| 81 | 9 | |||||||||||||
| 82 | 9.05539 | |||||||||||||
| 83 | 9.11043 | |||||||||||||
| 84 | 9.16515 | |||||||||||||
| 85 | 9.21954 | |||||||||||||
| 86 | 9.27362 | |||||||||||||
| 9.27362 | ||||||||||||||
| 87 | 9.32738 | |||||||||||||
| 90 | 9,48683 | |||||||||||||
| 91 | 9,53939 | |||||||||||||
| 92 | 9,59166 | |||||||||||||
| 93 | 9. 64365 64365 | |||||||||||||
| 94 | 9.69536 | |||||||||||||
| 95 | 9.74679 | |||||||||||||
| 96 | 9.79796 | |||||||||||||
| 100 | 10 | |||||||||||||
| 101 | 10.04988 | |||||||||||||
| 102 | 10.0995 | |||||||||||||
| 103 | 10.14889 | |||||||||||||
| 104 | 10.19804 | |||||||||||||
| 105 | 10.24695 | |||||||||||||
| 106 | 10.29563 | |||||||||||||
| 107 | 10.34409 9045 | 10.34409 | 107 | 10.34409 9045 | ||||||||||
| 110 | 10.48809 | |||||||||||||
| 111 | 10.53565 | |||||||||||||
| 112 | 10.58301 | |||||||||||||
| 113 | 10.63015 | |||||||||||||
| 114 | 10.67708 | |||||||||||||
| 115 | 10.72381 | |||||||||||||
| 116 | 10. 77033 77033 | |||||||||||||
| 117 | ||||||||||||||
| 117 | 10.81665 | 10.81665 | 117 | 10.81665 | 10.81665 | |||||||||
| 120 | 10. | |||||||||||||
| 121 | 11 | |||||||||||||
| 122 | 11.04536 | |||||||||||||
| 123 | 11.09054 | |||||||||||||
| 124 | 11.13553 | |||||||||||||
| 125 | 11.18034 | |||||||||||||
| 126 | 11.22497 | |||||||||||||
| 11.22497 | ||||||||||||||
| 127 | 11.26943 | 127 | 11.26943 9045 | |||||||||||
| 130 | 11.40175 | |||||||||||||
| 131 | 11.44552 | |||||||||||||
| 132 | 11.48913 | |||||||||||||
| 133 | 11.53256 | |||||||||||||
| 134 | 11,57584 | |||||||||||||
| 135 | 11,61895 | |||||||||||||
| 136 | 11,6619 | |||||||||||||
| 11,6619 | ||||||||||||||
| 137 | 11,7047 | 11,7047 | 137 | 11,7047 | 11,7047 | |||||||||
| 140 | 11. 83216 83216 | |||||||||||||
| 141 | 11.87434 | |||||||||||||
| 142 | 11. | |||||||||||||
| 143 | 11. | |||||||||||||
| 144 | 12 | |||||||||||||
| 145 | 12.04159 | |||||||||||||
| 146 | 12.08305 | |||||||||||||
| 147 | 12.12436 | 147 | 12.12436 | |||||||||||
| 150 | 12.24745 | |||||||||||||
| 151 | 12.28821 | |||||||||||||
| 152 | 12.32883 | |||||||||||||
| 153 | 12.36932 | |||||||||||||
| 154 | 12,40967 | |||||||||||||
| 155 | 12,4499 | |||||||||||||
| 156 | 12,49 | |||||||||||||
| 157 | 12,52996 | |||||||||||||
| 158 | 12,56981 | |||||||||||||
| 159 | 12,60952 | |||||||||||||
| 160 | 12.64911 | |||||||||||||
| 161 | 12.68858 | |||||||||||||
| 162 | 12.72792 | |||||||||||||
| 163 | 12.76715 | |||||||||||||
| 164 | 12. 80625 80625 | |||||||||||||
| 165 | 12.84523 | |||||||||||||
| 166 | 12.8841 | |||||||||||||
| 167 5 | ||||||||||||||
| 170 | 13.0384 | |||||||||||||
| 171 | 13.0767 | |||||||||||||
| 172 | 13.11488 | |||||||||||||
| 173 | 13.15295 | |||||||||||||
| 174 | 13,19091 | |||||||||||||
| 175 | 13,22876 | |||||||||||||
| 176 | 13,2665 | |||||||||||||
| 177 | 13,30413 | |||||||||||||
| 178 | 13,34166 | |||||||||||||
| 179 | 13,37909 | |||||||||||||
| 180 | 13.41641 | |||||||||||||
| 181 | 13.45362 | |||||||||||||
| 182 | 13.49074 | |||||||||||||
| 183 | 13.52775 | |||||||||||||
| 184 | 13,56466 | |||||||||||||
| 185 | 13,60147 | |||||||||||||
| 186 | 13,63818 | |||||||||||||
| 187 | 13,67479 | |||||||||||||
| 188 | 13,71131 | |||||||||||||
| 189 | 13,74773 | |||||||||||||
| 190 | 13. 78405 78405 | |||||||||||||
| 191 | 13.82027 | |||||||||||||
| 192 | 13.85641 | |||||||||||||
| 193 | 13.89244 | |||||||||||||
| 194 | 13. | |||||||||||||
| 195 | 13. | |||||||||||||
| 196 | 14 | |||||||||||||
| 14 | ||||||||||||||
| 197 | 14.03567 | 14.03567 | 14.03567 | |||||||||||
| 200 | 14.14214 | |||||||||||||
| 201 | 14.17745 | |||||||||||||
| 202 | 14.21267 | |||||||||||||
| 203 | 14.24781 | |||||||||||||
| 204 | 14,28286 | |||||||||||||
| 205 | 14,31782 | |||||||||||||
| 206 | 14,3527 | |||||||||||||
| 207 | 14,38749 | |||||||||||||
| 208 | 14,42221 | |||||||||||||
| 209 | 14,45683 | |||||||||||||
| 210 | 14.49138 | |||||||||||||
| 211 | 14.52584 | |||||||||||||
| 212 | 14.56022 | |||||||||||||
| 213 | 14. 59452 59452 | |||||||||||||
| 214 | 14,62874 | |||||||||||||
| 215 | 14,66288 | |||||||||||||
| 216 | 14,69694 | |||||||||||||
| 217 | 14,73092 | |||||||||||||
| 218 | 14,76482 | |||||||||||||
| 219 | 14,79865 | |||||||||||||
| 220 | 14.8324 | |||||||||||||
| 221 | 14.86607 | |||||||||||||
| 222 | 14.89966 | |||||||||||||
| 223 | 14. | |||||||||||||
| 224 | 14. | |||||||||||||
| 225 | 15 | |||||||||||||
| 226 | 15.0333 | |||||||||||||
| 15.0333 | ||||||||||||||
| 227 | ||||||||||||||
| 230 | 15.16575 | |||||||||||||
| 231 | 15.19868 | |||||||||||||
| 232 | 15.23155 | |||||||||||||
| 233 | 15.26434 | |||||||||||||
| 234 | 15,29706 | |||||||||||||
| 235 | 15,32971 | |||||||||||||
| 236 | 15,36229 | |||||||||||||
| 237 | 15,3948 | |||||||||||||
| 238 | 15,42725 | |||||||||||||
| 239 | 15,45962 | |||||||||||||
| 240 | 15,49193 | |||||||||||||
| 241 | 15. 52417 52417 | |||||||||||||
| 242 | 15.55635 | |||||||||||||
| 243 | 15.58846 | |||||||||||||
| 244 | 15,6205 | |||||||||||||
| 245 | 15,65248 | |||||||||||||
| 246 | 15,68439 | |||||||||||||
| 247 | 15,71623 | |||||||||||||
| 248 | 15,74802 | |||||||||||||
| 249 | 15,77973 | |||||||||||||
| 250 | 15.81139 | |||||||||||||
| 251 | 15.84298 | |||||||||||||
| 252 | 15.87451 | |||||||||||||
| 253 | 15. | |||||||||||||
| 254 | 15. | |||||||||||||
| 255 | 15. | |||||||||||||
| 256 | 16 | |||||||||||||
| 257 | 16.03122 | 257 | 16.03122 | 257 | 16.03122 9045 | |||||||||
| 260 | 16.12452 | |||||||||||||
| 261 | 16.15549 | |||||||||||||
| 262 | 16.18641 | |||||||||||||
| 263 | 16.21727 | |||||||||||||
| 264 | 16,24808 | |||||||||||||
| 265 | 16,27882 | |||||||||||||
| 266 | 16,30951 | |||||||||||||
| 267 | 16,34013 | |||||||||||||
| 268 | 16,37071 | |||||||||||||
| 269 | 16,40122 | |||||||||||||
| 270 | 16.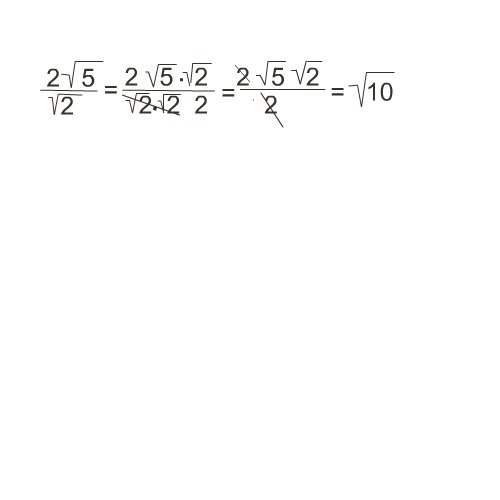 43168 43168 | |||||||||||||
| 271 | 16.46208 | |||||||||||||
| 272 | 16.49242 | |||||||||||||
| 273 | 16.52271 | |||||||||||||
| 274 | 16,55295 | |||||||||||||
| 275 | 16,58312 | |||||||||||||
| 276 | 16,61325 | |||||||||||||
| 277 | 16,64332 | |||||||||||||
| 278 | 16,67333 | |||||||||||||
| 279 | 16,70329 | |||||||||||||
| 280 | 16.7332 | |||||||||||||
| 281 | 16.76305 | |||||||||||||
| 282 | 16.79286 | |||||||||||||
| 283 | 16.8226 | |||||||||||||
| 284 | 16,8523 | |||||||||||||
| 285 | 16,88194 | |||||||||||||
| 286 | 16, | |||||||||||||
| 287 | 16, | |||||||||||||
| 288 | 16,97056 | |||||||||||||
| 289 | 17 | |||||||||||||
| 290 | 17.02939 | |||||||||||||
| 291 | 17.05872 | |||||||||||||
| 292 | 17.08801 | |||||||||||||
| 293 | 17. 11724 11724 | |||||||||||||
| 294 | 17,14643 | |||||||||||||
| 295 | 17,17556 | |||||||||||||
| 296 | 17,20465 | |||||||||||||
| 297 | 17,23369 | |||||||||||||
| 298 | 17,26268 | |||||||||||||
| 299 | 17,29162 | |||||||||||||
| 300 | 17.32051 | |||||||||||||
| 301 | 17.34935 | |||||||||||||
| 302 | 17.37815 | |||||||||||||
| 303 | 17.4069 | |||||||||||||
| 304 | 17,4356 | |||||||||||||
| 305 | 17,46425 | |||||||||||||
| 306 | 17,49286 | |||||||||||||
| 307 | 17,52142 | |||||||||||||
| 308 | 17,54993 | |||||||||||||
| 309 | 17,5784 | |||||||||||||
| 310 | 17.60682 | |||||||||||||
| 311 | 17.63519 | |||||||||||||
| 312 | 17.66352 | |||||||||||||
| 313 | 17.69181 | |||||||||||||
| 314 | 17,72005 | |||||||||||||
| 315 | 17,74824 | |||||||||||||
| 316 | 17,77639 | |||||||||||||
| 317 | 17,80449 | |||||||||||||
| 318 | 17,83255 | |||||||||||||
| 319 | 17,86057 | |||||||||||||
| 320 | 17. 88854 88854 | |||||||||||||
| 321 | 17. | |||||||||||||
| 322 | 17. | |||||||||||||
| 323 | 17.9722 | |||||||||||||
| 324 | 18 | |||||||||||||
| 325 | 18.02776 | |||||||||||||
| 326 | 18.05547 | |||||||||||||
| 327 | 18.08314 | 327 | 18.08314 | 327 | 18.08314 | |||||||||
| 330 | 18.1659 | |||||||||||||
| 331 | 18.19341 | |||||||||||||
| 332 | 18.22087 | |||||||||||||
| 333 | 18.24829 | |||||||||||||
| 334 | 18,27567 | |||||||||||||
| 335 | 18,30301 | |||||||||||||
| 336 | 18,3303 | |||||||||||||
| 337 | 18,35756 | |||||||||||||
| 338 | 18,38478 | |||||||||||||
| 339 | 18,41195 | |||||||||||||
| 340 | 18.43909 | |||||||||||||
| 341 | 18.46619 | |||||||||||||
| 342 | 18.49324 | |||||||||||||
| 343 | 18. 52 026 52 026 | |||||||||||||
| 344 | 18,54724 | |||||||||||||
| 345 | 18,57418 | |||||||||||||
| 346 | 18,60108 | |||||||||||||
| 347 | 18,62794 | |||||||||||||
| 348 | 18,65476 | |||||||||||||
| 349 | 18,68154 | |||||||||||||
| 350 | 18.70829 | |||||||||||||
| 351 | 18.73499 | |||||||||||||
| 352 | 18.76166 | |||||||||||||
| 353 | 18.+78829 | |||||||||||||
| 354 | 18,81489 | |||||||||||||
| 355 | 18,84144 | |||||||||||||
| 356 | 18,86796 | |||||||||||||
| 357 | 18,89444 | |||||||||||||
| 358 | 18, | |||||||||||||
| 359 | 18,9473 | |||||||||||||
| 360 | 18.97367 | |||||||||||||
| 361 | 19 | |||||||||||||
| 362 | 19.0263 | |||||||||||||
| 363 | 19.+05256 | |||||||||||||
| по ремонту 364 | 19,07878 | |||||||||||||
| 365 | 19,10497 | |||||||||||||
| 366 | 19,13113 | |||||||||||||
| 367 | 19,15724 | |||||||||||||
| 368 | 19,18333 | |||||||||||||
| 369 | 19,20937 | |||||||||||||
| 370 | 19. 23538 23538 | |||||||||||||
| 371 | 19.26136 | |||||||||||||
| 372 | 19.2873 | |||||||||||||
| 373 | 19.31321 | |||||||||||||
| 374 | 19,33908 | |||||||||||||
| 375 | 19,36492 | |||||||||||||
| 376 | 19,39072 | |||||||||||||
| 377 | 19,41649 | |||||||||||||
| 378 | 19,44222 | |||||||||||||
| 379 | 19,46792 | |||||||||||||
| 380 | 19.49359 | |||||||||||||
| 381 | 19.51922 | |||||||||||||
| 382 | 19.54482 | |||||||||||||
| 383 | 19.57039 | |||||||||||||
| 384 | 19,59592 | |||||||||||||
| 385 | 19,62142 | |||||||||||||
| 386 | 19,64688 | |||||||||||||
| 387 | 19,67232 | |||||||||||||
| 388 | 19,69772 | |||||||||||||
| 389 | 19,72308 | |||||||||||||
| 390 | 19.74842 | |||||||||||||
| 391 | 19.77372 | |||||||||||||
| 392 | 19. 79899 79899 | |||||||||||||
| 393 | 19.82423 | |||||||||||||
| 394 | 19,84943 | |||||||||||||
| 395 | 19,87461 | |||||||||||||
| 396 | 19,89975 | |||||||||||||
| 397 | 19, | |||||||||||||
| 398 | 19, | |||||||||||||
| 399 | 19,97498 | |||||||||||||
| 400 | 20 | |||||||||||||
| 401 | 20.02498 | |||||||||||||
| 402 | 20.04994 | |||||||||||||
| 403 | 20.07486 | |||||||||||||
| 404 | 20,09975 | |||||||||||||
| 405 | 20,12461 | |||||||||||||
| 406 | 20,14944 | |||||||||||||
| 407 | 20,17424 | |||||||||||||
| 408 | 20,19901 | |||||||||||||
| 409 | 20,22375 | |||||||||||||
| 410 | 20.24846 | |||||||||||||
| 411 | 20.27313 | |||||||||||||
| 412 | 20.29778 | |||||||||||||
| 413 | 20.3224 | |||||||||||||
| 414 | 20,34699 | |||||||||||||
| 415 | 20,37155 | |||||||||||||
| 416 | 20,39608 | |||||||||||||
| 417 | 20,42058 | |||||||||||||
| 418 | 20,44505 | |||||||||||||
| 419 | 20,46949 | |||||||||||||
| 420 | 20. 4939 4939 | |||||||||||||
| 421 | 20.51828 | |||||||||||||
| 422 | 20.54264 | |||||||||||||
| 423 | 20.56696 | |||||||||||||
| 424 | 20,59126 | |||||||||||||
| 425 | 20,61553 | |||||||||||||
| 426 | 20,63977 | |||||||||||||
| 427 | 20,66398 | |||||||||||||
| 428 | 20,68816 | |||||||||||||
| 429 | 20,71232 | |||||||||||||
| 430 | 20.73644 | |||||||||||||
| 431 | 20.76054 | |||||||||||||
| 432 | 20.78461 | |||||||||||||
| 433 | 20.80 865 | |||||||||||||
| 434 | 20,83267 | |||||||||||||
| 435 | 20,85665 | |||||||||||||
| 436 | 20,88061 | |||||||||||||
| 437 | 20, | |||||||||||||
| 438 | 20, | |||||||||||||
| 439 | 20, | |||||||||||||
| 440 | 20.97618 | |||||||||||||
| 441 | 21 | |||||||||||||
| 442 | 21. 0238 0238 | |||||||||||||
| 443 | 21.04757 | |||||||||||||
| 444 | 21,07131 | |||||||||||||
| 445 | 21,09502 | |||||||||||||
| 446 | 21,11871 | |||||||||||||
| 447 | 21,14237 | |||||||||||||
| 448 | 21,16601 | |||||||||||||
| 449 | 21,18962 | |||||||||||||
| 450 | 21.2132 | |||||||||||||
| 451 | 21.23676 | |||||||||||||
| 452 | 21.26029 | |||||||||||||
| 453 | 21.2 838 | |||||||||||||
| 454 | 21,30728 | |||||||||||||
| 455 | 21,33073 | |||||||||||||
| 456 | 21,35416 | |||||||||||||
| 457 | 21,37756 | |||||||||||||
| 458 | 21,40093 | |||||||||||||
| 459 | 21,42429 | |||||||||||||
| 460 | 21.44761 | |||||||||||||
| 461 | 21.47091 | |||||||||||||
| 462 | 21.49419 | |||||||||||||
| 463 | 21.51743 | |||||||||||||
| 464 | 21,54066 | |||||||||||||
| 465 | 21,56386 | |||||||||||||
| 466 | 21,58703 | |||||||||||||
| 467 | 21,61018 | |||||||||||||
| 468 | 21,63331 | |||||||||||||
| 469 | 21,65641 | |||||||||||||
| 470 | 21. 67948 67948 | |||||||||||||
| 471 | 21.70253 | |||||||||||||
| 472 | 21.72556 | |||||||||||||
| 473 | 21.74856 | |||||||||||||
| 474 | 21,77154 | |||||||||||||
| 475 | 21,79449 | |||||||||||||
| 476 | 21,81742 | |||||||||||||
| 477 | 21,84033 | |||||||||||||
| 478 | 21,86321 | |||||||||||||
| 479 | 21,88607 | |||||||||||||
| 480 | 21.9089 | |||||||||||||
| 481 | 21. | |||||||||||||
| 482 | 21.9545 | |||||||||||||
| 483 | 21.97726 | |||||||||||||
| 484 | 22 | |||||||||||||
| 485 | 22.02272 | |||||||||||||
| 486 | 22.04541 | |||||||||||||
| 487 | 22.06 | |||||||||||||
| 490 | 22.13594 | |||||||||||||
| 491 | 22.15852 | |||||||||||||
| 492 | 22.18107 | |||||||||||||
| 493 | 22. 2036 2036 | |||||||||||||
| 494 | 22,22611 | |||||||||||||
| 495 | 22,2486 | |||||||||||||
| 496 | 22,27106 | |||||||||||||
| 497 | 22,2935 | |||||||||||||
| 498 | 22,31591 | |||||||||||||
| 499 | 22,33831 | |||||||||||||
| 500 | 22.36068 | |||||||||||||
| 501 | 22.38303 | |||||||||||||
| 502 | 22.40536 | |||||||||||||
| 503 | 22.42766 | |||||||||||||
| 504 | 22,44994 | |||||||||||||
| 505 | 22,47221 | |||||||||||||
| 506 | 22,49444 | |||||||||||||
| 507 | 22,51666 | |||||||||||||
| 508 | 22,53886 | |||||||||||||
| 509 | 22,56103 | |||||||||||||
| 510 | 22.58318 | |||||||||||||
| 511 | 22.60531 | |||||||||||||
| 512 | 22.62742 | |||||||||||||
| 513 | 22.6495 | |||||||||||||
| 514 | 22,67157 | |||||||||||||
| 515 | 22,69361 | |||||||||||||
| 516 | 22,71563 | |||||||||||||
| 517 | 22,73763 | |||||||||||||
| 518 | 22,75961 | |||||||||||||
| 519 | 22,78157 | |||||||||||||
| 520 | 22. 80351 80351 | |||||||||||||
| 521 | 22.82542 | |||||||||||||
| 522 | 22.84732 | |||||||||||||
| 523 | 22.86919 | |||||||||||||
| 524 | 22.89105 | |||||||||||||
| 525 | 22. | |||||||||||||
| 526 | 22. | 526 | 22. | |||||||||||
| 527 | 527 | 527 | ||||||||||||
| 530 | 23.02173 | |||||||||||||
| 531 | 23.04344 | |||||||||||||
| 532 | 23.06513 | |||||||||||||
| 533 | 23.08 679 | |||||||||||||
| 534 | 23,10844 | |||||||||||||
| 535 | 23,13007 | |||||||||||||
| 536 | 23,15167 | |||||||||||||
| 537 | 23,17326 | |||||||||||||
| 538 | 23,19483 | |||||||||||||
| 539 | 23,21637 | |||||||||||||
| 540 | 23.2379 | |||||||||||||
| 541 | 23.25941 | |||||||||||||
| 542 | 23. 28089 28089 | |||||||||||||
| 543 | 23.30236 | |||||||||||||
| 544 | 23,32381 | |||||||||||||
| 545 | 23,34524 | |||||||||||||
| 546 | 23,36664 | |||||||||||||
| 547 | 23,38803 | |||||||||||||
| 548 | 23,4094 | |||||||||||||
| 549 | 23,43075 | |||||||||||||
| 550 | 23.45208 | |||||||||||||
| 551 | 23.47339 | |||||||||||||
| 552 | 23.49468 | |||||||||||||
| 553 | 23.51595 | |||||||||||||
| 554 | 23,5372 | |||||||||||||
| 555 | 23,55844 | |||||||||||||
| 556 | 23,57965 | |||||||||||||
| 557 | 23,60085 | |||||||||||||
| 558 | 23,62202 | |||||||||||||
| 559 | 23,64318 | |||||||||||||
| 560 | 23.66432 | |||||||||||||
| 561 | 23.68544 | |||||||||||||
| 562 | 23.70654 | |||||||||||||
| 563 | 23.72762 | |||||||||||||
| 564 | 23,74868 | |||||||||||||
| 565 | 23,76973 | |||||||||||||
| 566 | 23,79075 | |||||||||||||
| 567 | 23,81176 | |||||||||||||
| 568 | 23,83275 | |||||||||||||
| 569 | 23,85372 | |||||||||||||
| 570 | 23. 87467 87467 | |||||||||||||
| 571 | 23.89561 | |||||||||||||
| 572 | 23. | |||||||||||||
| 573 | 23. | |||||||||||||
| 574 | 23,9583 | |||||||||||||
| 575 | 23.97916 | |||||||||||||
| 576 | 24 | |||||||||||||
| 576 | 24 | |||||||||||||
| 576 | 24 | |||||||||||||
| 577 | 24,02082 | 24,02082 | 577 | 24,02082 | ||||||||||
| 580 | 24.08319 | |||||||||||||
| 581 | 24.10394 | |||||||||||||
| 582 | 24.12468 | |||||||||||||
| 583 | 24.14539 | |||||||||||||
| 584 | 24,16609 | |||||||||||||
| 585 | 24,18677 | |||||||||||||
| 586 | 24,20744 | |||||||||||||
| 587 | 24,22808 | |||||||||||||
| 588 | 24,24871 | |||||||||||||
| 589 | 24,26932 | |||||||||||||
| 590 | 24.28992 | |||||||||||||
| 591 | 24.31049 | |||||||||||||
| 592 | 24. 33105 33105 | |||||||||||||
| 593 | 24.35159 | |||||||||||||
| 594 | 24,37212 | |||||||||||||
| 595 | 24,39262 | |||||||||||||
| 596 | 24,41311 | |||||||||||||
| 597 | 24,43358 | |||||||||||||
| 598 | 24,45404 | |||||||||||||
| 599 | 24,47448 | |||||||||||||
| 600 | 24,4949 | |||||||||||||
| 601 | 24,5153 | |||||||||||||
| 602 | 24,53569 | |||||||||||||
| 603 | 24.55606 | |||||||||||||
| 604 | 24,57641 | |||||||||||||
| 605 | 24,59675 | |||||||||||||
| 606 | 24,61707 | |||||||||||||
| 607 | 24,63737 | |||||||||||||
| 608 | 24,65766 | |||||||||||||
| 609 | 24,67793 | |||||||||||||
| 610 | 24.69818 | |||||||||||||
| 611 | 24.71841 | |||||||||||||
| 612 | 24.73863 | |||||||||||||
| 613 | 24.+75884 | |||||||||||||
| 614 | 24,77902 | |||||||||||||
| 615 | 24,79919 | |||||||||||||
| 616 | 24,81935 | |||||||||||||
| 617 | 24,83948 | |||||||||||||
| 618 | 24,85961 | |||||||||||||
| 619 | 24,87971 | |||||||||||||
| 620 | 24,8998 | |||||||||||||
| 621 | 24, | |||||||||||||
| 622 | 24, | |||||||||||||
| 623 | 24. | |||||||||||||
| 624 | 24.97999 | |||||||||||||
| 625 | 25 | |||||||||||||
| 626 | 25,01999 | |||||||||||||
| 630 | 25.0998 | |||||||||||||
| 631 | 25.11971 | |||||||||||||
| 632 | 25.13961 | |||||||||||||
| 633 | 25.15949 | |||||||||||||
| 634 | 25,17936 | |||||||||||||
| 635 | 25,19921 | |||||||||||||
| 636 | 25,21904 | |||||||||||||
| 637 | 25,23886 | |||||||||||||
| 638 | 25,25866 | |||||||||||||
| 639 | 25,27845 | |||||||||||||
| 640 | 25.29822 | |||||||||||||
| 641 | 25.31798 | |||||||||||||
| 642 | 25.33772 | |||||||||||||
| 643 | 25.35744 | |||||||||||||
| 644 | 25,37716 | |||||||||||||
| 645 | 25,39685 | |||||||||||||
| 646 | 25,41653 | |||||||||||||
| 647 | 25,43619 | |||||||||||||
| 648 | 25,45584 | |||||||||||||
| 649 | 25,47548 | |||||||||||||
| 650 | 25. 4951 4951 | |||||||||||||
| 651 | 25.5147 | |||||||||||||
| 652 | 25.53429 | |||||||||||||
| 653 | 25.55386 | |||||||||||||
| 654 | 25,57342 | |||||||||||||
| 655 | 25,59297 | |||||||||||||
| 656 | 25,6125 | |||||||||||||
| 657 | 25,63201 | |||||||||||||
| 658 | 25,65151 | |||||||||||||
| 659 | 25,671 | |||||||||||||
| 660 | 25.69047 | |||||||||||||
| 661 | 25.70992 | |||||||||||||
| 662 | 25.72936 | |||||||||||||
| 663 | 25.74879 | |||||||||||||
| 664 | 25,7682 | |||||||||||||
| 665 | 25,78759 | |||||||||||||
| 666 | 25,80698 | |||||||||||||
| 667 | 25,82634 | |||||||||||||
| 668 | 25,8457 | |||||||||||||
| 669 | 25,86503 | |||||||||||||
| 670 | 25.88436 | |||||||||||||
| 671 | 25. | |||||||||||||
| 672 | 25. | |||||||||||||
| 673 | 25. | |||||||||||||
| 674 | 25. | |||||||||||||
| 675 | 25.98076 | |||||||||||||
| 676 | 26 | |||||||||||||
| 676 | 26 | |||||||||||||
| 677 | 677 | 26,0192 | 677 | 26,0192 | ||||||||||
| 680 | 26.07681 | |||||||||||||
| 681 | 26.09598 | |||||||||||||
| 682 | 26.11513 | |||||||||||||
| 683 | 26.13427 | |||||||||||||
| 684 | 26.15339 | |||||||||||||
| 685 | 26.1725 | |||||||||||||
| 686 | 26.1916 | |||||||||||||
| 26.210689 | 26.210689 | |||||||||||||
| 690 | 26.26785 | |||||||||||||
| 691 | 26.28688 | |||||||||||||
| 692 | 26.30589 | |||||||||||||
| 693 | 26.32489 | |||||||||||||
| 694 | 26,34388 | |||||||||||||
| 695 | 26,36285 | |||||||||||||
| 696 | 26,38181 | |||||||||||||
| 697 | 26,40076 | |||||||||||||
| 698 | 26,41969 | |||||||||||||
| 699 | 26,43861 | |||||||||||||
| 700 | 26. 45751 45751 | |||||||||||||
| 701 | 26.4764 | |||||||||||||
| 702 | 26.49528 | |||||||||||||
| 703 | 26.51415 | |||||||||||||
| 704 | 26,533 | |||||||||||||
| 705 | 26,55184 | |||||||||||||
| 706 | 26,57066 | |||||||||||||
| 707 | 26,58947 | |||||||||||||
| 708 | 26,60827 | |||||||||||||
| 709 | 26,62705 | |||||||||||||
| 710 | 26.64583 | |||||||||||||
| 711 | 26.66458 | |||||||||||||
| 712 | 26.68333 | |||||||||||||
| 713 | 26.70206 | |||||||||||||
| 714 | 26,72078 | |||||||||||||
| 715 | 26,73948 | |||||||||||||
| 716 | 26,75818 | |||||||||||||
| 717 | 26,77686 | |||||||||||||
| 718 | 26,79552 | |||||||||||||
| 719 | 26,81418 | |||||||||||||
| 720 | 26.83282 | |||||||||||||
| 721 | 26.85144 | |||||||||||||
| 722 | 26. 87006 87006 | |||||||||||||
| 723 | 26.88 866 | |||||||||||||
| 724 | 26, | |||||||||||||
| 725 | 26, | |||||||||||||
| 726 | 26, | |||||||||||||
| 727 | 26, | |||||||||||||
| 728 | 26,98148 | |||||||||||||
| 729 | 27 | |||||||||||||
| 730 | 27.01851 | |||||||||||||
| 731 | 27.03701 | |||||||||||||
| 732 | 27.0555 | |||||||||||||
| 733 | 27.07 397 | |||||||||||||
| 734 | 27,09243 | |||||||||||||
| 735 | 27,11088 | |||||||||||||
| 736 | 27,12932 | |||||||||||||
| 737 | 27,14774 | |||||||||||||
| 738 | 27,16616 | |||||||||||||
| 739 | 27,18455 | |||||||||||||
| 740 | 27.20294 | |||||||||||||
| 741 | 27.22132 | |||||||||||||
| 742 | 27.23968 | |||||||||||||
| 743 | 27.25803 | |||||||||||||
| 744 | 27,27636 | |||||||||||||
| 745 | 27,29469 | |||||||||||||
| 746 | 27,313 | |||||||||||||
| 747 | 27,3313 | |||||||||||||
| 748 | 27,34959 | |||||||||||||
| 749 | 27,36786 | |||||||||||||
| 750 | 27. 38613 38613 | |||||||||||||
| 751 | 27.40438 | |||||||||||||
| 752 | 27.42262 | |||||||||||||
| 753 | 27.44085 | |||||||||||||
| 754 с | 27,45906 | |||||||||||||
| 755 | 27,47726 | |||||||||||||
| 756 | 27,49545 | |||||||||||||
| 757 | 27,51363 | |||||||||||||
| 758 | 27,5318 | |||||||||||||
| 759 | 27,54995 | |||||||||||||
| 760 | 27,5681 | |||||||||||||
| 761 | 27,58623 | |||||||||||||
| 762 | 27.60435 | |||||||||||||
| 763 | 27.62245 | |||||||||||||
| 764 | 27,64055 | |||||||||||||
| 765 | 27,65863 | |||||||||||||
| 766 | 27,67671 | |||||||||||||
| 767 | 27,69476 | |||||||||||||
| 768 | 27,71281 | |||||||||||||
| 769 | 27,73085 | |||||||||||||
| 770 | 27.74887 | |||||||||||||
| 771 | 27.76689 | |||||||||||||
| 772 | 27.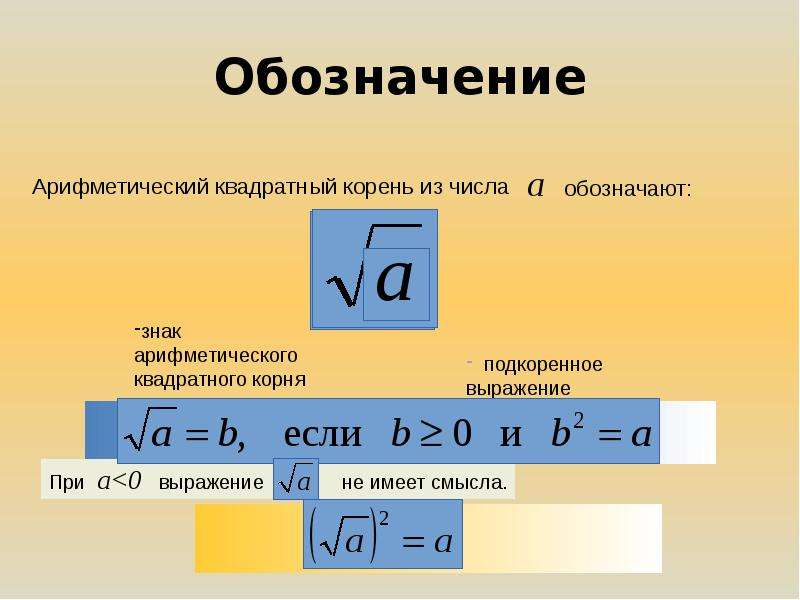 78489 78489 | |||||||||||||
| 773 | 27.80288 | |||||||||||||
| 774 | 27,82086 | |||||||||||||
| 775 | 27,83882 | |||||||||||||
| 776 | 27,85678 | |||||||||||||
| 777 | 27,87472 | |||||||||||||
| 778 | 27,89265 | |||||||||||||
| 779 | 27, | |||||||||||||
| 780 | 27. | |||||||||||||
| 781 | 27. | |||||||||||||
| 782 | 27. | |||||||||||||
| 783 | 27.98214 | |||||||||||||
| 784 | 28 | |||||||||||||
| 785 | 28.01785 | |||||||||||||
| 786 | 28.03569 | |||||||||||||
| 790 | 28.10694 | |||||||||||||
| 791 | 28.12472 | |||||||||||||
| 792 | 28.14249 | |||||||||||||
| 793 | 28.16026 | |||||||||||||
| 794 | 28,17801 | |||||||||||||
| 795 | 28,19574 | |||||||||||||
| 796 | 28,21347 | |||||||||||||
| 797 | 28,23119 | |||||||||||||
| 798 | 28,24889 | |||||||||||||
| 799 | 28,26659 | |||||||||||||
| 800 | 28. 28427 28427 | |||||||||||||
| 801 | 28.30194 | |||||||||||||
| 802 | 28.3196 | |||||||||||||
| 803 | 28.33725 | |||||||||||||
| 804 | 28,35489 | |||||||||||||
| 805 | 28,37252 | |||||||||||||
| 806 | 28,39014 | |||||||||||||
| 807 | 28,40775 | |||||||||||||
| 808 | 28,42534 | |||||||||||||
| 809 | 28,44293 | |||||||||||||
| 810 | 28.4605 | |||||||||||||
| 811 | 28.47806 | |||||||||||||
| 812 | 28.49561 | |||||||||||||
| 813 | 28.51315 | |||||||||||||
| 814 | 28,53069 | |||||||||||||
| 815 | 28,5482 | |||||||||||||
| 816 | 28,56571 | |||||||||||||
| 817 | 28,58321 | |||||||||||||
| 818 | 28,6007 | |||||||||||||
| 819 | 28,61818 | |||||||||||||
| 820 | 28.63564 | |||||||||||||
| 821 | 28.6531 | |||||||||||||
| 822 | 28. 67054 67054 | |||||||||||||
| 823 | 28.68798 | |||||||||||||
| 824 | 28,7054 | |||||||||||||
| 825 | 28,72281 | |||||||||||||
| 826 | 28,74022 | |||||||||||||
| 827 | 28,75761 | |||||||||||||
| 828 | 28,77499 | |||||||||||||
| 829 | 28,79236 | |||||||||||||
| 830 | 28.80972 | |||||||||||||
| 831 | 28.82707 | |||||||||||||
| 832 | 28.84441 | |||||||||||||
| 833 | 28.86174 | |||||||||||||
| 834 | 28,87906 | |||||||||||||
| 835 | 28,89637 | |||||||||||||
| 836 | 28, | |||||||||||||
| 837 | 28, | |||||||||||||
| 838 | 28, | |||||||||||||
| 839 | 28,9655 | |||||||||||||
| 840 | 28.98275 | |||||||||||||
| 841 | 29 | |||||||||||||
| 842 | 29.01724 | |||||||||||||
| 843 | 29.03446 | |||||||||||||
| 844 | 29,05168 | |||||||||||||
| 845 | 29,06888 | |||||||||||||
| 846 | 29,08608 | |||||||||||||
| 847 | 29,10326 | |||||||||||||
| 848 | 29,12044 | |||||||||||||
| 849 | 29,1376 | |||||||||||||
| 850 | 29. 15476 15476 | |||||||||||||
| 851 | 29.1719 | |||||||||||||
| 852 | 29.18904 | |||||||||||||
| 853 | 29.20616 | |||||||||||||
| 854 | 29,22328 | |||||||||||||
| 855 | 29,24038 | |||||||||||||
| 856 | 29,25748 | |||||||||||||
| 857 | 29,27456 | |||||||||||||
| 858 | 29,29164 | |||||||||||||
| 859 | 29,3087 | |||||||||||||
| 860 | 29.32576 | |||||||||||||
| 861 | 29.3428 | |||||||||||||
| 862 | 29.35984 | |||||||||||||
| 863 | 29.37686 | |||||||||||||
| 864 | 29,39388 | |||||||||||||
| 865 | 29,41088 | |||||||||||||
| 866 | 29,42788 | |||||||||||||
| 867 | 29,44486 | |||||||||||||
| 868 | 29,46184 | |||||||||||||
| 869 | 29,47881 | |||||||||||||
| 870 | 29.49576 | |||||||||||||
| 871 | 29.51271 | |||||||||||||
| 872 | 29. 52965 52965 | |||||||||||||
| 873 | 29.54657 | |||||||||||||
| 874 | 29,56349 | |||||||||||||
| 875 | 29,5804 | |||||||||||||
| 876 | 29,5973 | |||||||||||||
| 877 | 29,61419 | |||||||||||||
| 878 | 29,63106 | |||||||||||||
| 879 | 29,64793 | |||||||||||||
| 880 | 29.66479 | |||||||||||||
| 881 | 29.68164 | |||||||||||||
| 882 | 29.69848 | |||||||||||||
| 883 | 29.71 532 | |||||||||||||
| 884 | 29,73214 | |||||||||||||
| 885 | 29,74895 | |||||||||||||
| 886 | 29,76575 | |||||||||||||
| 887 | 29,78255 | |||||||||||||
| 888 | 29,79933 | |||||||||||||
| 889 | 29,8161 | |||||||||||||
| 890 | 29.83287 | |||||||||||||
| 891 | 29.84962 | |||||||||||||
| 892 | 29.86637 | |||||||||||||
| 893 | 29.+88311 | |||||||||||||
| 894 | 29,89983 | |||||||||||||
| 895 | 29, | |||||||||||||
| 896 | 29, | |||||||||||||
| 897 | 29, | |||||||||||||
| 898 | 29, | |||||||||||||
| 899 | 29,98333 | |||||||||||||
| 900 | 30 | |||||||||||||
| 901 | 30. 01666 01666 | |||||||||||||
| 902 | 30.03331 | |||||||||||||
| 903 | 30.04996 | |||||||||||||
| 904 | 30,06659 | |||||||||||||
| 905 | 30,08322 | |||||||||||||
| 906 | 30,09983 | |||||||||||||
| 907 | 30,11644 | |||||||||||||
| 908 | 30,13304 | |||||||||||||
| 909 | 30,14963 | |||||||||||||
| 910 | 30.16621 | |||||||||||||
| 911 | 30.18278 | |||||||||||||
| 912 | 30.19934 | |||||||||||||
| 913 | 30.21589 | |||||||||||||
| 914 | 30,23243 | |||||||||||||
| 915 | 30,24897 | |||||||||||||
| 916 | 30,26549 | |||||||||||||
| 917 | 30,28201 | |||||||||||||
| 918 | 30,29851 | |||||||||||||
| 919 | 30,31501 | |||||||||||||
| 920 | 30.3315 | |||||||||||||
| 921 | 30.34798 | |||||||||||||
| 922 | 30.36445 | |||||||||||||
| 923 | 30. 38092 38092 | |||||||||||||
| 924 | 30,39737 | |||||||||||||
| 925 | 30,41381 | |||||||||||||
| 926 | 30,43025 | |||||||||||||
| 927 | 30,44667 | |||||||||||||
| 928 | 30,46309 | |||||||||||||
| 929 | 30,4795 | |||||||||||||
| 930 | 30,4959 | |||||||||||||
| 931 | 30,51229 | |||||||||||||
| 932 | 30,52868 | |||||||||||||
| 933 | 30.54505 | |||||||||||||
| 934 | 30,56141 | |||||||||||||
| 935 | 30,57777 | |||||||||||||
| 936 | 30,59412 | |||||||||||||
| 937 | 30,61046 | |||||||||||||
| 938 | 30,62679 | |||||||||||||
| 939 | 30,64311 | |||||||||||||
| 940 | 30.65942 | |||||||||||||
| 941 | 30.67572 | |||||||||||||
| 942 | 30.69202 | |||||||||||||
| 943 | 30.70831 | |||||||||||||
| 944 | 30,72458 | |||||||||||||
| 945 | 30,74085 | |||||||||||||
| 946 | 30,75711 | |||||||||||||
| 947 | 30,77337 | |||||||||||||
| 948 | 30,78961 | |||||||||||||
| 949 | 30,80584 | |||||||||||||
| 950 | 30. 82207 82207 | |||||||||||||
| 951 | 30.83829 | |||||||||||||
| 952 | 30.8545 | |||||||||||||
| 953 | 30.8707 | |||||||||||||
| 954 | 30,88689 | |||||||||||||
| 955 | 30, | |||||||||||||
| 956 | 30, | |||||||||||||
| 957 | 30, | |||||||||||||
| 958 | 30, | |||||||||||||
| 959 | 30, | |||||||||||||
| 960 | 30.98387 | |||||||||||||
| 961 | 31 | |||||||||||||
| 962 | 31.01612 | |||||||||||||
| 963 | 31.03 224 | |||||||||||||
| 964 | 31,04835 | |||||||||||||
| 965 | 31,06445 | |||||||||||||
| 966 | 31,08054 | |||||||||||||
| 967 | 31,09662 | |||||||||||||
| 968 | 31,1127 | |||||||||||||
| 969 | 31,12876 | |||||||||||||
| 970 | 31.14482 | |||||||||||||
| 971 | 31.16087 | |||||||||||||
| 972 | 31. 17691 17691 | |||||||||||||
| 973 | 31.19295 | |||||||||||||
| 974 | 31.20897 | |||||||||||||
| 975 | 31.22499 | |||||||||||||
| 976 | 31.241 | |||||||||||||
| 977 | 976 | 31.241 | ||||||||||||
| 977 | 977 | |||||||||||||
| 980 | 31.30495 | |||||||||||||
| 981 | 31.32092 | |||||||||||||
| 982 | 31.33688 | |||||||||||||
| 983 | 31.35283 | |||||||||||||
| 984 | 31,36877 | |||||||||||||
| 985 | 31,38471 | |||||||||||||
| 986 | 31,40064 | |||||||||||||
| 987 | 31,41656 | |||||||||||||
| 988 | 31,43247 | |||||||||||||
| 989 | 31,44837 | |||||||||||||
| 990 | 31.46427 | |||||||||||||
| 991 | 31.48015 | |||||||||||||
| 992 | 31.49603 | |||||||||||||
| 993 | 31.5119 | |||||||||||||
| 994 | 31,52777 | |||||||||||||
| 995 | 31,54362 | |||||||||||||
| 996 | 31,55947 | |||||||||||||
| 997 | 31,57531 | |||||||||||||
| 998 | 31,59114 | |||||||||||||
| 999 | 31,60696 | |||||||||||||
| 1000 | 31. 62278 62278 |
Связанные
Часто используемые инструменты Miniwebtools:
Все минивеб-инструменты (отсортировано по названию):
PWA (прогрессивное веб-приложение) Инструменты (17) Финансовые калькуляторы (121) Здоровье и фитнес (31) Математика (161) Случайность (17) Спорт (8) Текстовые инструменты (30) Время и Дата (27) Инструменты для веб-мастеров (10) Хэш и контрольная сумма (8) Разное (108)Квадратный корень — Калькулятор капитана
Калькулятор квадратного корня
Обратите внимание: для работы этого калькулятора требуется JavaScript.Определение — Что такое квадратный корень?
Квадратный корень числа — это число, которое при умножении само на себя дает исходное число.
Например, квадратный корень из 9 равен 3, так как 3 x 3 = 9.
Квадратный корень из 25 равен 5, так как 5 x 5 = 25.
Квадратный корень из 49 равен 7, так как 7 x 7 = 49.
Квадратный корень может быть положительным или отрицательным (-3 x -3 равно 9, -5 x -5 = 25 и -7 x -7 = 49). Когда люди говорят «квадратный корень», они обычно имеют в виду положительный квадратный корень.
Когда люди говорят «квадратный корень», они обычно имеют в виду положительный квадратный корень.
Противоположность квадратному корню — это вычисление в квадрате (степень двойки).
Для чего используется квадратный корень?
С практической точки зрения, квадратный корень в геометрии можно использовать для определения длины стороны квадрата, когда площадь известна.
Формула— Как вычислить квадратный корень из числа
Не существует быстрой математической формулы для вычисления квадратного корня. Большинство калькуляторов используют метод очень быстрых проб и ошибок.
Метод 1 — Метод проб и ошибок
Метод проб и ошибок подходит для полных квадратов. Это может занять очень много времени для неидеальных квадратов, поскольку в них много десятичных знаков.
Чтобы найти квадратный корень методом проб и ошибок:
- Угадайте число, которое, по вашему мнению, может быть квадратным корнем.
- Умножьте это число на само себя
- Если результат слишком низкий, попробуйте другое большее число.
 Если результат слишком высокий, попробуйте другое меньшее число.
Если результат слишком высокий, попробуйте другое меньшее число. - Продолжайте, пока не найдете квадратный корень.
Пример. Методом проб и ошибок найти квадратный корень из 64:
- Попробуйте число — 5: 5 умножить на 5 = 25 (слишком мало)
- Попробуйте число, которое больше 6 — 10 — 10 умножить на 10 = 100 (слишком большое
- Попробуйте число от 6 до 10 — 8 — 8 умножить на 8 = 64 (ответ)
Метод 2 — Быстрый поиск корней из точных квадратных чисел
Этот метод позволяет быстрее найти корень из полного квадратного числа.Однако, если число не является точным корнем, этот метод не сработает.
Метод 3 — Быстрый поиск квадратного корня из любого числа
Этот метод позволяет найти квадратный корень из любого числа (включая неполные квадраты). Это занимает немного больше времени, чем метод 2.
Это занимает немного больше времени, чем метод 2.
Как ввести квадратный корень?
- Вы можете скопировать символ квадратного корня -> √ <- с этой страницы и вставить его в свой документ.
- На компьютере с Windows откройте карту символов, найдите символ квадратного корня и скопируйте его.Вставьте его там, где хотите символ.
- На компьютере Mac нажмите option + v для символа √.
Таблица чисел квадратного корня — полные квадраты
- √1 = 1, как 1 x 1 = 1
- √4 = 2, как 2 x 2 = 4
- √9 = 3, как 3 x 3 = 9
- √16 = 4, как 4 x 4 = 16
- √25 = 5, поскольку 5 x 5 = 25
- √36 = 6, поскольку 6 x 6 = 36
- √49 = 7, поскольку 7 x 7 = 49
- √64 = 8, как 8 x 8 = 64
- √81 = 9, поскольку 9 x 9 = 81
- √100 = 10, поскольку 10 x 10 = 100
- √121 = 11, поскольку 11 x 11 = 121
- √144 = 12, как 12 x 12 = 144
- √225 = 15, как 15 x 15 = 225
- √289 = 17, как 17 x 17 = 289
- √400 = 20, как 20 x 20 = 400
- √625 = 25, как 25 x 25 = 625
- √900 = 30, как 30 x 30 = 900
- √1089 = 33, как 33 x 33 = 1,089
- √2025 = 45, так как 45 x 45 = 2,025
- √ 2500 = 50, поскольку 50 x 50 = 2,500
- √3600 = 60, поскольку 60 x 60 = 3,600
- √5625 = 75, поскольку 75 x 75 = 5,625
- √10000 = 100, поскольку 100 x 100 = 10 000
Таблица чисел квадратного корня — несовершенные квадраты
Обратите внимание: для работы этой таблицы требуется JavaScript.
Источники и другие ресурсы
Как умножить квадратный корень
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно
искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Таким образом, если вы не уверены, что контент находится
на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как вы оцениваете значение квадратного корня?
Четкость квадрата
Прежде чем мы сможем понять, что такое квадратные корни, мы должны сначала вспомнить, что делает возведение в квадрат.2 равно 3 x 3, что дает нам 9.
Определение квадратного корня
Квадратный корень — это величина, обратная квадрату. Что такое обратное? Инверсии — это противоположности, поэтому, например, обратное сложение — это вычитание. Обратное к умножению — это деление. Они противоположны друг другу и имеют обратную связь.
Что такое идеальный квадрат?
Когда вы извлекаете квадратный корень из числа, вы можете получить десятичное число. Если вы можете получить в качестве ответа целое число, то исходное число, из которого вы нашли квадратный корень, является точным квадратным числом. Примеры списка идеальных квадратов включают числа 4, 9, 16, 25, 36 и 49. Щелкните здесь, чтобы получить более полный список идеальных квадратов, или воспользуйтесь этим калькулятором идеальных квадратов.
Примеры списка идеальных квадратов включают числа 4, 9, 16, 25, 36 и 49. Щелкните здесь, чтобы получить более полный список идеальных квадратов, или воспользуйтесь этим калькулятором идеальных квадратов.
Как найти квадратный корень без калькулятора
Давайте перейдем к рассмотрению некоторых примеров квадратного корня и узнаем, как находить ответы на квадратные корни. Сначала вам нужно помнить о шагах по нахождению квадратного корня, а именно:
- Оценка. Получите как можно более близкое к числу, которое вы пытаетесь извлечь квадратный корень, найдя два точных квадратных корня, которые дают близкое число.
- Разделить: разделите ваше число на один из квадратных корней, выбранных вами на предыдущем шаге.
- Среднее: Возьмите среднее значение шага 2 и корень.
- Повторите: Продолжайте повторять шаги 2 и 3, используя результаты, полученные на шаге 3, пока не получите число, достаточно точное для того, чтобы ответить на вопрос.

Проще говоря, чтобы оценить квадратные корни, которые не являются точными квадратами, без использования калькулятора, нам нужно хорошо знать точные квадратные числа.Сначала мы поместим число внутри знака квадратного корня в середине числовой строки, а затем найдем два ближайших идеальных квадратных числа слева и справа, чтобы сделать наилучшую оценку. Взгляните на некоторые из приведенных ниже примеров квадратных корней.
Корень квадратный из 5
Шаг 1: Оценка
Квадратные числа 2 и 3 равны 4 и 9 соответственно. Число 5 находится между этими двумя числами.
Шаг 2: Разделите
Разделите 5 на 2 или 3.В данном случае выберем 2. Получаем 2,5.
Шаг 3: Среднее значение
Среднее значение 2,5 и 2, что дает нам 2,25.
Шаг 4: повторить
Чтобы получить более точное число, продолжайте повторять шаги 2 и 3. В этом случае мы возьмем 5 и разделим его на 2,25, что равно 2,222. 2.
2.
Шаг 2: Разделите
Делим 20 на 5. Получаем 4.
Шаг 3: Среднее значение
Среднее значение 4 и 5, что дает нам 4,5.
Шаг 4: повторить
Чтобы получить более точное число, повторяйте шаги 2 и 3.
Вы должны получить окончательный ответ 4,47.
Корень квадратный из 0
В заключение, мы хотели выяснить, что такое квадратный корень из 0. Вы не можете извлечь квадратный корень из отрицательного числа, но 0 не является отрицательным числом.Квадратный корень из 0 на самом деле равен 0!
Если вы хотите попробовать найти больше квадратных корней, попробуйте эту забавную игру с множеством примеров.
Бесплатный калькулятор квадратного корня | Math Goodies
Работа с квадратными корнями — увлекательная тема для студентов-математиков, но она может быть сложной. Начинающие математики часто полагаются на предположения, например, ошибочно принимают квадрат 3 за 6 только потому, что 6 ощущается как тройка, посчитанная дважды. Но возведение в квадрат предполагает умножение, а не сложение. Когда мы возводим в квадрат 3 (или умножаем 3 на себя), мы получаем 9 — квадратный корень из 9 равен 3.
Но возведение в квадрат предполагает умножение, а не сложение. Когда мы возводим в квадрат 3 (или умножаем 3 на себя), мы получаем 9 — квадратный корень из 9 равен 3.
Квадратные корни не должны быть сложной задачей. На самом деле, легко запомнить таблицу идеальных квадратов и произвести впечатление на учителя. Но работа с несовершенными квадратами — или с числами, квадратные корни которых содержат дроби или десятичные дроби — не всегда бывает так просто. Здесь на помощь приходит наш бесплатный онлайн-калькулятор квадратного корня.
Как использовать наш бесплатный онлайн-калькулятор квадратного корня
Как и некоторые другие наши калькуляторы, этот бесплатный онлайн-калькулятор квадратного корня чрезвычайно прост в использовании.В калькуляторе всего четыре части:
- Числовое поле
- Кнопка расчета
- Кнопка очистки
- Поле квадратного корня
Чтобы найти квадратный корень с помощью нашего бесплатного онлайн-калькулятора квадратного корня:
- Щелкните ОЧИСТИТЬ, чтобы обновить калькулятор.

- Введите значение, квадратный корень которого вы хотите найти, в числовое поле.
- Щелкните ВЫЧИСЛИТЬ.
- Ваш ответ появится в поле квадратного корня.
- Щелкните ОЧИСТИТЬ, чтобы начать заново и найти другое значение.
Другие калькуляторы
Что такое квадратный корень?
Квадратный корень относится к любому числу, которое дает вам исходное число как произведение при умножении на само себя. Квадратные корни, обозначенные символом «√», принадлежат семейству показателей. Квадраты и корни — особые показатели. Любой квадрат x просто возводится в степень ½ или x1 / 2.
Пример
Например, когда вас спрашивают о квадратном корне из 16, вы ищите число, которое даст вам произведение 16 при умножении на само себя.Это число равно 4, потому что 4, умноженное на 4 — или возведенное в степень 2 (математически выражается как 42) — равно 16. 161/2 равно 4.
Работа с идеальными квадратами
Полные квадраты — это положительные числа, квадратные корни которых представляют собой целые числа. Ниже приведены наиболее распространенные способы найти квадратный корень из этих идеальных квадратов.
Ниже приведены наиболее распространенные способы найти квадратный корень из этих идеальных квадратов.
Повторное вычитание
Вычтите последовательные нечетные числа (1, 3, 5, 7 и т. Д.), Начиная с 1, из числа, квадратный корень которого вы пытаетесь найти, пока не дойдете до 0.
Например:
- 9 — 1 = 8
- 8–3 = 5
- 5 — 5 = 0
Вы выполнили 3 вычитания до 0. Корень квадратный из 9 равен 3.
Основная факторизация
Этот метод состоит из четырех этапов. Давайте пройдемся по каждому из них, чтобы найти квадратный корень из 144.
- Разбейте 144 на простые множители.
- Объедините похожие факторы.
- (2×2) x (2×2) x (3×3)
- Умножьте на один множитель из каждой пары.
- Квадратный корень из 144 равен 12.
Несовершенные квадраты: оценка и длинное деление
Повторное вычитание и разложение на простые множители действительно хорошо работают для полных квадратов, а иногда и для несовершенных квадратов.

 Помните, что стойкий краситель требует сухих волос, а безаммиачный наносится на чуть влажную шевелюру.
Помните, что стойкий краситель требует сухих волос, а безаммиачный наносится на чуть влажную шевелюру.




 Как мы знаем, 4 × 4 = 16 <20. Следовательно, делитель равен 4, а частное равно 4.
Как мы знаем, 4 × 4 = 16 <20. Следовательно, делитель равен 4, а частное равно 4. Итак, теперь ответ — 1216, а следующая цифра частного — 2.
Итак, теперь ответ — 1216, а следующая цифра частного — 2. Какой будет длина пола в комнате? Округлите ответ до ближайшей десятой.
Какой будет длина пола в комнате? Округлите ответ до ближайшей десятой.
 Если результат слишком высокий, попробуйте другое меньшее число.
Если результат слишком высокий, попробуйте другое меньшее число.
