Понятие квадратного корня из неотрицательного числа
здравствуйте тема сегодняшнего урока понятия квадратного корня давайте рассмотрим уравнение x квадрат равен 9 то есть нам нужно найти такое число квадрат которого равен 9 и сложно понять что это число 3 но также этому условию удовлетворяет число -3 таким образом вы заметили что мы сделали действие обратно и возведение в квадрат то есть по заданному чист квадрату мы нашли числа такой действенность назвать излечением корня квадратного корня что же такое квадратный корень квадратный корень из числа а это такое число b квадрат которого равен а то есть b квадрат равен а значит число b является квадратным корнем числа а по записи видно что а у нас равняется не которому квадрату но квадрат любого числа неотрицательных значит квадратный корень мы можем извлекать только из неотрицательных чисел то есть можно сказать что а больше равно 0 рассмотрим еще несколько примеров x квадрат равен 4 по аналогии с предыдущим мы можем понять что в данном случае x равен у нас плюс 2 либо минус 2 то есть данном случае уравнение имеет два решения или говорят два корня рассмотрим уравнение вида x квадрат равен нулю квадрат какого числа даёт 0 только числа ноль значит здесь у нас x равен 0 и рассмотрим такой 1 x квадрат равен минус 1 квадрат ни какого числа ним не может равняться ни отрицательному то есть данном случае корней у нас не будет или говорят x принадлежит пустому множество то есть вы видите что у нас квадратный корень может быть либо иметь два значения либо иметь одно значение либо не имеет значение вообще теперь ведем понятие арифметического квадратного корня зачастую в школе работая с квадратным корням мы будем понимать арифметический квадратный корень что же такое фонетически квадратный корень вот как мы только что решили что корень из 9 это чисто плюс минус 3 арифметическим квадратным корнем будет только его не отрицательная часть то есть только плюс 3 тогда пишет что корень из 9 равен 3 можно также записать корень из 4 равен двум корень из 0 0 но корень из отрицательного числа извлечь не можем таким образом мы поняли что арифметические квадратным корнем от химического дафна корни у нас удовлетворять следующим условий во первых выражение внутри корни так называемый подкоренное выражение должно быть больше равно 0 то есть а большим 0 само значение квадратного корня больше равно 0 по определению бы сказать что а технического ратной корея это не отрицательный квадратный корень и также мы знаем что уравнение вида x квадрат равно а зависимости от назначения а может иметь три разных решений если а больше 0 то x равняется плюс-минус корень и за если а равно нулю то x равняется нулю если а меньше нуля то x принадлежит пустого множества или говорят нет корней давайте рассмотрим несколько примеров попробуем извлечь асептические квадратный корень из числа 1 целая 24 25 переведём это в неправильную дробь получим 49 25 какое неотрицательное число возведенных квадрат даст нам 49 25 очевидно это 75 в некоторых случаях мы не можем точно извлечь квадрат квадратный корень например значение корень из 3 мы не можем записать в виде какого-то рационального числа тогда говорят что это число иррациональное за оставляет его в таком виде то есть корни страх это такое число квадрат которого равен 3 в частности к корню из 2 в квадрате дает 3 некоторых случаях мы можем использовать приближённое значение но это не всегда нам надо таким образом арифметический квадратный корень это такое неотрицательное число квадрат которого равен вот этому подкоренного выражения на этом данный видео урок окончен [музыка]
Что такое квадратный корень определение.
 Формулы корней Рациональные числа
Формулы корней Рациональные числаНеотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала .
Комплексные числа
Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:
Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если
, ,где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.
Обобщения
Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц , функций , операторов и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция .
Квадратный корень в информатике
Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).
Алгоритмы нахождения квадратного корня
Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.
Разложение в ряд Тейлора
при .Арифметическое извлечение квадратного корня
Для квадратов чисел верны следующие равенства:
То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так:
Выполнено 3 действия, квадратный корень числа 9 равен 3.
Недостатком такого способа является то, что если извлекаемый корень
не является целым числом, то можно узнать только его целую часть, но не
точнее. В то же время такой способ вполне доступен детям, решающим
простейшие математические задачи, требующие извлечения квадратного
корня.
В то же время такой способ вполне доступен детям, решающим
простейшие математические задачи, требующие извлечения квадратного
корня.
Грубая оценка
Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:
Если D нечётно, D = 2n + 1, тогда используем Если D чётно, D = 2n + 2, тогда используем
Два и шесть используются потому, что и
При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D это число двоичных цифр).
Геометрическое извлечение квадратного корня
Для ручного извлечения корня применяется запись, похожая на деление столбиком . Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234.567 можно представить, как 03 12 34 . 56 70. В отличие от деления снос производится такими группами по 2 цифры.
Наглядное описание алгоритма:
Площадь квадратного участка земли равна 81 дм². Найти его сторону. Предположим, что длина стороны квадрата равна х дециметрам. Тогда площадь участка равна х ² квадратным дециметрам. Так как по условию эта площадь равна 81 дм², то х ² = 81. Длина стороны квадрата — положительное число. Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Положительным числом, квадрат которого равен 81, является число 9. При решении задачи требовалось найти число х, квадрат которого равен 81, т. е. решить уравнение х ² = 81. Это уравнение имеет два корня: x 1 = 9 и x 2 = — 9, так как 9² = 81 и (- 9)² = 81. Оба числа 9 и — 9 называют квадратными корнями из числа 81.
Заметим, что один из квадратных корней х = 9 является положительным числом. Его называют арифметическим квадратным корнем из числа 81 и обозначают √81, таким образом √81 = 9.
Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а .
Например, числа 6 и — 6 являются квадратными корнями из числа 36. При этом число 6 является арифметическим квадратным корнем из 36, так как 6 — неотрицательное число и 6² = 36. Число — 6 не является арифметическим корнем.
Арифметический квадратный корень из числа а обозначается так: √а.
Знак называется знаком арифметического квадратного корня; а — называется подкоренным выражением. Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.
Выражение √а читается так: арифметический квадратный корень из числа а. Например, √36 = 6, √0 = 0, √0,49 = 0,7. В тех случаях, когда ясно, что речь идет об арифметическом корне, кратко говорят: «корень квадратный из а «.
Действие нахождения квадратного корня из числа называют извлечением квадратного корня. Это действие является обратным к возведению в квадрат.
Возводить в квадрат можно любые числа, но извлекать квадратные корни можно не из любого числа. Например, нельзя извлечь квадратный корень из числа — 4. Если бы такой корень существовал, то, обозначив его буквой х , мы получили бы неверное равенство х² = — 4, так как слева стоит неотрицательное число, а справа отрицательное.
Выражение √а имеет смысл только при а ≥ 0. Определение квадратного корня можно кратко записать так: √а ≥ 0, (√а )² = а . Равенство (√а )² = а справедливо при а ≥ 0. Таким образом, чтобы убедиться в том, что квадратный корень из неотрицательного числа а равен b , т. е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
е. в том, что √а =b , нужно проверить, что выполняются следующие два условия: b ≥ 0, b ² = а.
Квадратный корень из дроби
Так как и , то равенство верно. Итак, .
Теорема: Если а ≥ 0 и b > 0, то т. е. корень из дроби равен корню из числителя, деленному на корень из знаменателя. Требуется доказать, что: и .
Так как √а ≥0 и √b > 0, то .
По свойству возведения дроби в степень и определению квадратного корня теорема доказана. Рассмотрим несколько примеров.
Вычислить , по доказанной теореме .
Второй пример: Доказать, что , если а ≤ 0, b .
Еще примерчик: Вычислить .
.
Преобразование квадратных корней
Вынесение множителя из-под знака корня. Пусть дано выражение . Если а ≥ 0 и b ≥ 0, то по теореме о корне из произведения можно записать:
Такое преобразование называется вынесение множителя из под знака корня. Рассмотрим пример;
Рассмотрим пример;
Итак, при вынесении множителя из-под знака корня представляют подкоренное выражение в виде произведения, в котором один или несколько множителей являются квадратами неотрицательных чисел. Затем применяют теорему о корне из произведения и извлекают корень из каждого множителя. Рассмотрим пример: Упростить выражение А = √8 + √18 — 4√2 вынося в первых двух слагаемых множители из-под знака корня, получим:. Подчеркнем, что равенство справедливо только при а ≥ 0 и b ≥ 0. если же а
Факт 1.
\(\bullet\)
Возьмем некоторое неотрицательное число \(a\)
(то есть \(a\geqslant 0\)
). Тогда (арифметическим) квадратным корнем из числа \(a\)
называется такое неотрицательное число \(b\)
, при возведении которого в квадрат мы получим число \(a\)
: \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\]
Из определения следует, что \(a\geqslant 0, b\geqslant 0\)
. 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
. \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
). Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\)
. 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\)
.
2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Математика зародилась тогда, когда человек осознал себя и стал позиционироваться как автономная единица мира. Желание измерить, сравнить, посчитать то, что тебя окружает, — вот что лежало в основе одной из фундаментальных наук наших дней. Сначала это были частички элементарной математики, что позволили связать числа с их физическими выражениями, позже выводы стали излагаться лишь теоретически (в силу своей абстрактности), ну а через некоторое время, как выразился один ученый, «математика достигла потолка сложности, когда из нее исчезли все числа». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
С чего все начиналось
Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике. Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.
Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.
Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.
Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению. На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R 2 a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.
Наши дни
С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z 2 =y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.
В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным.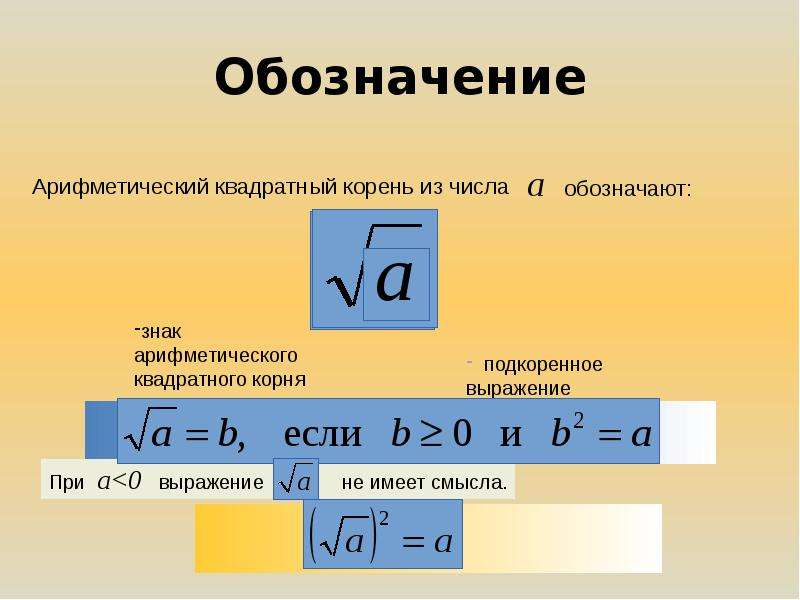 Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.
Свойства квадратного корня на поле R
Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.
Как найти корень числа?
Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:
1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю. Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Следующее нечетное число — это 11, остаток у нас следующий: 1
Для таких случаев существует разложение в ряд Тейлора:
√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , где n принимает значения от 0 до
+∞, а |y|≤1.
Графическое изображение функции z=√y
Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:
Кривая растет из начала координат и обязательно пересекает точку (1; 1).
Свойства функции z=√y на поле действительных чисел R
1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).
2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).
3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.
4. Функция z=√y ни четная, ни нечетная.
5. Функция z=√y не является периодической.
6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).
7. Точка пересечения графика функции z=√y также является и нулем этой функции.
8. Функция z=√y непрерывно растет.
9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.
Варианты изображения функции z=√y
В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y 1/2 . Такой вариант удобен, например, в возведении функции в степень: (√y) 4 =(y 1/2) 4 =y 2 . Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.
А в программировании заменой символа √ является комбинация букв sqrt.
Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Корень квадратный в комплексном поле С
По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3. Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6.
 Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ.
 Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n.
 Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
Напишите найденное n сверху справа, а квадрат n запишите снизу справа.- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа). Результат вычисления запишите под вычитаемым (квадратом числа n).
- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329.
 Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.
- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.

- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114). Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Понимание процесса
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе.
 Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8.
 То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8.
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Рекомендуем также
Функция Sqr
Возвращает значение типа Double, указывающее квадратный корень числа.
Синтаксис
Sqr (число)
ТребуемаяАргумент является значением double или любым допустимым значением числовое выражение больше нуля или равно.
Пример запроса
|
Выражение |
Результаты: |
|
SELECT UnitPrice, sqr(UnitPrice) AS SqrUnitPrice FROM ProductSales; |
Возвращает значения из столбца UnitPrice и их квадратного корня в столбце SqrUnitPrice. |
Пример VBA
Примечание: В примерах ниже показано, как использовать эту функцию в модуле Visual Basic для приложений (VBA). Чтобы получить дополнительные сведения о работе с VBA, выберите Справочник разработчика в раскрывающемся списке рядом с полем Поиск и введите одно или несколько слов в поле поиска.
В этом примере функция Sqr используется для вычисления квадратного корня числа.
Dim MySqr
MySqr = Sqr(4) ' Returns 2.
MySqr = Sqr(23) ' Returns 4.79583152331272.
MySqr = Sqr(0) ' Returns 0.
MySqr = Sqr(-4) ' Generates a run-time error.
Корень из числа: определения, примеры
Квадратный корень, арифметический квадратный корень
Чтобы понять определение корня из числа, и квадратного корня в частности, нужно иметь представление о степени с натуральным показателем. В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.
В этом пункте мы часто будем сталкиваться со второй степенью числа — квадратом числа.
Начнем с определения квадратного корня.
Определение
Квадратный корень из числа a — это число, квадрат которого равен a.
Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (52=5·5=25, (−0,3)2=(−0,3)·(−0,3)=0,09, (0,3)2=0,3·0,3=0,09 и 02=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 – это квадратный корень из нуля.
Следует отметить, что не для любого числа a существует действительное число, квадрат которого равен a. А именно, для любого отрицательного числа a не существует ни одного действительного числа b, квадрат которого равнялся бы a. В самом деле, равенство a=b2 невозможно для любого отрицательного a, так как b2 – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.
В самом деле, равенство a=b2 невозможно для любого отрицательного a, так как b2 – неотрицательное число при любом b. Таким образом, на множестве действительных чисел не существует квадратного корня из отрицательного числа. Иными словами, на множестве действительных чисел квадратный корень из отрицательного числа не определяется и не имеет смысла.
Отсюда вытекает логичный вопрос: «А для любого ли неотрицательного a существует квадратный корень из a»? Ответ – да. Обоснованием этого факта можно считать конструктивный способ, используемый для нахождения значения квадратного корня.
Тогда встает следующий логичный вопрос: «Каково число всех квадратных корней из данного неотрицательного числа a – один, два, три, или еще больше»? Вот ответ на него: если a равно нулю, то единственным квадратным корнем из нуля является нуль; если же a – некоторое положительное число, то количество квадратных корней из числа a равно двум, причем корни являются противоположными числами. Обоснуем это.
Обоснуем это.
Начнем со случая a=0. Сначала покажем, что нуль действительно является квадратным корнем из нуля. Это следует из очевидного равенства 02=0·0=0 и определения квадратного корня.
Теперь докажем, что 0 – единственный квадратный корень из нуля. Воспользуемся методом от противного. Предположим, что существует некоторое число b, отличное от нуля, которое является квадратным корнем из нуля. Тогда должно выполняться условие b2=0, что невозможно, так как при любом отличном от нуля b значение выражения b2 является положительным. Мы пришли к противоречию. Это доказывает, что 0 – единственный квадратный корень из нуля.
Переходим к случаям, когда a – положительное число. Выше мы сказали, что всегда существует квадратный корень из любого неотрицательного числа, пусть квадратным корнем из a является число b. Допустим, что существует число c, которое тоже является квадратным корнем из a. Тогда по определению квадратного корня справедливы равенства b2=a и c2=a, из них следует, что b2−c2=a−a=0, но так как b2−c2=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.
Тогда по определению квадратного корня справедливы равенства b2=a и c2=a, из них следует, что b2−c2=a−a=0, но так как b2−c2=(b−c)·(b+c), то (b−c)·(b+c)=0. Полученное равенство в силу свойств действий с действительными числами возможно лишь тогда, когда b−c=0 или b+c=0. Таким образом, числа b и c равны или противоположны.
Если же предположить, что существует число d, являющееся еще одним квадратным корнем из числа a, то рассуждениями, аналогичными уже приведенным, доказывается, что d равно числу b или числу c. Итак, число квадратных корней из положительного числа равно двум, причем квадратные корни являются противоположными числами.
Для удобства работы с квадратными корнями отрицательный корень «отделяется» от положительного. С этой целью вводится определение арифметического квадратного корня.
Определение
Арифметический квадратный корень из неотрицательного числа a – это неотрицательное число, квадрат которого равен a.
Для арифметического квадратного корня из числа a принято обозначение . Знак называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.
Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня – подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например, в записи число 151 – это подкоренное число, а в записи выражение a является подкоренным выражением.
При чтении слово «арифметический» часто опускается, например, запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о положительном квадратном корне из числа.
В свете введенного обозначения из определения арифметического квадратного корня следует, что и для любого неотрицательного числа a.
Квадратные корни из положительного числа a с помощью знака арифметического квадратного корня записываются как и . Например, квадратные корни из числа 13 есть и . Арифметический квадратный корень из нуля равен нулю, то есть, . Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишены смысла выражения и .
На базе определения квадратного корня доказываются свойства квадратных корней, которые часто применяются на практике.
Нахождение квадратных корней заслуживает детального изучения, этой теме посвящена отдельная статья извлечение квадратных корней.
В заключение этого пункта заметим, что квадратные корни из числа a являются решениями квадратного уравнения вида x2=a относительно переменной x.
К началу страницы
что это такое, как рассчитать, упражнения
THE квадратный корень это математическая операция, которая подходит для всех уровней обучения. Это частный случай радиация, в которой индекс радикала равен 2, то есть является обратной операцией степеней экспонентаравно 2. Когда положительное число имеет точный квадратный корень, мы говорим, что это число один идеальный квадрат.
Это частный случай радиация, в которой индекс радикала равен 2, то есть является обратной операцией степеней экспонентаравно 2. Когда положительное число имеет точный квадратный корень, мы говорим, что это число один идеальный квадрат.
Тоже читай:Свойства, содержащие комплексные числа
Определение и номенклатура элементов укоренениябыть Ва также B два вещественные числа а также нет а натуральное число ненулевое значение, поэтому:
В = укоренение
нет = индекс
√ = радикальный
В квадратные корни, как уже говорилось, являются частным случаем радиация. При написании квадратного корня необязательно указывать индекс равен двум.
Для других типов корней обязательно разместить индекс, то есть для п = 3, п = 4, n = 5…, необходимо в индексе радикала явно указать значение нет.
Тоже читай: Радикальное сокращение с той же скоростью
Не останавливайся сейчас… После рекламы есть еще кое-что;)
Как вычислить квадратный корень?Чтобы вычислить квадратный корень из настоящий номер, просто следуйте определению укоренения:
THE определение говорит нам, что квадратный корень действительного числа В это число B тогда и только тогда, когда число B в квадрате равно числу , то есть, мы должны представить себе число, которое квадратный, результат в числе внутри радикальный.
Примеры:
√36 = 6, поскольку 62 = 36
√ 121 = 11, потому что 112 = 121
Числа, имеющие квадратный корень, называются идеальные квадраты. Итак, из приведенных выше примеров числа 36 и 121 являются квадратами. Когда число не является идеальным квадратом, необходимо выполнить расчет неточных корней.
Итак, из приведенных выше примеров числа 36 и 121 являются квадратами. Когда число не является идеальным квадратом, необходимо выполнить расчет неточных корней.
1. Осознайте, исходя из определения квадратный корень, что бы ни мы ищем число, которое при поднятии до квадратный, приводит к числу в пределах радикальный. С учетом потенцирующие свойства, мы знаем, что число в квадрате всегда положительно. Это приводит нас к выводу, что невозможно извлечь квадратный корень из отрицательного числа в наборе вещественные числа.
Пример:
√ — 36 = ?
Из приведенного выше примера мы должны представить себе число, которое в квадрате дает -36. В наборе вещественные числа, это не невозможно.
2. Если корень является относительно большим числом, что сделало бы невозможным мысленный расчет, просто выполните разложение на простые числа и по возможности сгруппируйте их по степеням степени два.
Пример:
Давайте определим значение квадратного корня из 441.
√441
Чтобы определить корень числа 441, проведем разложение на простые числа:
441 = 32. 72
Таким образом,
√441 = √32. 72
Теперь, применив свойства излучения, мы должны:
√441 = 3. 7 = 21
Число 21 в квадрате равно 441.
Интеллектуальная карта: квадратный корень* Чтобы скачать интеллектуальную карту в формате PDF, кликните сюда!
Геометрическая интерпретация квадратного корняПредставьте себе земельный участок площадью 144 м2.
Чтобы определить длину стороны этого ландшафта квадратной формы, мы должны вспомнить, как рассчитать его площадь.
квадрат = 12
A представляет значение площади, а l — значение стороны.
Так как площадь стоит 144 м2, Мы должны:
144 = 12
Посмотрите на уравнение выше. Обратите внимание, что нам нужно найти число, которое в квадрате равно 144, то есть у нас есть определение квадратного корня! Потом:
Обратите внимание, что нам нужно найти число, которое в квадрате равно 144, то есть у нас есть определение квадратного корня! Потом:
√144 = 12
Число 144 в факторизованной форме:
144 = 22. 22. 32
Итак, нам нужно:
√144 = √22. 22. 32
Наконец,
√144 = 2. 2. 3 = 12
Таким образом, размер наземной стороны составляет 12 м.
решенные упражнения1. Составьте список идеальных квадратов от 1 до 100.
Идеальные квадраты от 1 до 100: 1, 4, 9, 16, 25, 36, 49, 64, 81 и 100
2. Найдите квадратный корень из числа 1024.
√1024
Чтобы определить корень 1024, сделаем разложение на простые числа:
1024 = 22. 22. 22. 22. 22
Потом,
Учитывая второе равенство с уже примененными свойствами рутирования.
* Ментальная карта Луиса Пауло Сильвы
Окончил математику
Робсон Луис
Учитель математики
Извлечение корня квадратного из числа. Что такое квадратный корень
До появления калькуляторов студенты и преподаватели вычисляли квадратные корни вручную. Существует несколько способов вычисления квадратного корня числа вручную. Некоторые из них предлагают только приблизительное решение, другие дают точный ответ.
Шаги
Разложение на простые множители
Разложите подкоренное число на множители, которые являются квадратными числами. В зависимости от подкоренного числа, вы получите приблизительный или точный ответ. Квадратные числа – числа, из которых можно извлечь целый квадратный корень. Множители – числа, которые при перемножении дают исходное число. Например, множителями числа 8 являются 2 и 4, так как 2 х 4 = 8, числа 25, 36, 49 являются квадратными числами, так как √25 = 5, √36 = 6, √49 = 7. Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
Квадратные множители – это множители, которые являются квадратными числами. Сначала попытайтесь разложить подкоренное число на квадратные множители.
- Например, вычислите квадратный корень из 400 (вручную). Сначала попытайтесь разложить 400 на квадратные множители. 400 кратно 100, то есть делится на 25 – это квадратное число. Разделив 400 на 25, вы получите 16. Число 16 также является квадратным числом. Таким образом, 400 можно разложить на квадратные множители 25 и 16, то есть 25 х 16 = 400.
- Записать это можно следующим образом: √400 = √(25 х 16).
Квадратные корень из произведения некоторых членов равен произведению квадратных корней из каждого члена, то есть √(а х b) = √a x √b. Воспользуйтесь этим правилом и извлеките квадратный корень из каждого квадратного множителя и перемножьте полученные результаты, чтобы найти ответ.
- В нашем примере извлеките корень из 25 и из 16.
- √(25 х 16)
- √25 х √16
- 5 х 4 = 20
Если подкоренное число не раскладывается на два квадратных множителя (а так происходит в большинстве случаев), вы не сможете найти точный ответ в виде целого числа. Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
Но вы можете упростить задачу, разложив подкоренное число на квадратный множитель и обыкновенный множитель (число, из которого целый квадратный корень извлечь нельзя). Затем вы извлечете квадратный корень из квадратного множителя и будете извлекать корень из обыкновенного множителя.
- Например, вычислите квадратный корень из числа 147. Число 147 нельзя разложить на два квадратных множителя, но его можно разложить на следующие множители: 49 и 3. Решите задачу следующим образом:
- = √(49 х 3)
- = √49 х √3
- = 7√3
Если нужно, оцените значение корня. Теперь можно оценить значение корня (найти приблизительное значение), сравнив его со значениями корней квадратных чисел, находящихся ближе всего (с обеих сторон на числовой прямой) к подкоренному числу. Вы получите значение корня в виде десятичной дроби, которую необходимо умножить на число, стоящее за знаком корня.
- Вернемся к нашему примеру. Подкоренное число 3.
 Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.- Этот метод также работает с большими числами. Например, рассмотрим √35. Подкоренное число 35. Ближайшими к нему квадратными числами будут числа 25 (√25 = 5) и 36 (√36 = 6). Таким образом, значение √35 расположено между 5 и 6. Так как значение √35 намного ближе к 6, чем к 5 (потому что 35 всего на 1 меньше 36), то можно заявить, что √35 немного меньше 6. Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Еще один способ – разложите подкоренное число на простые множители . Простые множители – числа, которые делятся только на 1 и самих себя. Запишите простые множители в ряд и найдите пары одинаковых множителей. Такие множители можно вынести за знак корня.
Такие множители можно вынести за знак корня.
- Например, вычислите квадратный корень из 45. Раскладываем подкоренное число на простые множители: 45 = 9 х 5, а 9 = 3 х 3. Таким образом, √45 = √(3 х 3 х 5). 3 можно вынести за знак корня: √45 = 3√5. Теперь можно оценить √5.
- Рассмотрим другой пример: √88.
- = √(2 х 44)
- = √ (2 х 4 х 11)
- = √ (2 х 2 х 2 х 11). Вы получили три множителя 2; возьмите пару из них и вынесите за знак корня.
- = 2√(2 х 11) = 2√2 х √11. Теперь можно оценить √2 и √11 и найти приблизительный ответ.
Вычисление квадратного корня вручную
При помощи деления в столбик
Этот метод включает процесс, аналогичный делению в столбик, и дает точный ответ. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой.
 Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».- Для примера вычислим квадратный корень числа 780,14. Нарисуйте две линии (как показано на рисунке) и слева сверху напишите данное число в виде «7 80, 14». Это нормально, что первая слева цифра является непарной цифрой. Ответ (корень из данного числа) будете записывать справа сверху.
Для первой слева пары чисел (или одного числа) найдите наибольшее целое число n, квадрат которого меньше или равен рассматриваемой паре чисел (или одного числа). Другими словами, найдите квадратное число, которое расположено ближе всего к первой слева паре чисел (или одному числу), но меньше ее, и извлеките квадратный корень из этого квадратного числа; вы получите число n. Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
- В нашем случае, первым слева числом будет число 7. Далее, 4
Вычтите квадрат числа n, которое вы только что нашли, из первой слева пары чисел (или одного числа).
 Результат вычисления запишите под вычитаемым (квадратом числа n).
Результат вычисления запишите под вычитаемым (квадратом числа n).- В нашем примере вычтите 4 из 7 и получите 3.
Снесите вторую пару чисел и запишите ее около значения, полученного в предыдущем шаге. Затем удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере второй парой чисел является «80». Запишите «80» после 3. Затем, удвоенное число сверху справа дает 4. Запишите «4_×_=» снизу справа.
Заполните прочерки справа.
- В нашем случае, если вместо прочерков поставить число 8, то 48 х 8 = 384, что больше 380. Поэтому 8 — слишком большое число, а вот 7 подойдет. Напишите 7 вместо прочерков и получите: 47 х 7 = 329. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Вычтите полученное число из текущего числа слева. Запишите результат из предыдущего шага под текущим числом слева, найдите разницу и запишите ее под вычитаемым.

- В нашем примере, вычтите 329 из 380, что равно 51.
Повторите шаг 4. Если сносимой парой чисел является дробная часть исходного числа, то поставьте разделитель (запятую) целой и дробной частей в искомом квадратном корне сверху справа. Слева снесите вниз следующую пару чисел. Удвойте число сверху справа и запишите полученный результат снизу справа с добавлением «_×_=».
- В нашем примере следующей сносимой парой чисел будет дробная часть числа 780.14, поэтому поставьте разделитель целой и дробной частей в искомом квадратном корне сверху справа. Снесите 14 и запишите снизу слева. Удвоенным числом сверху справа (27) будет 54, поэтому напишите «54_×_=» снизу справа.
Повторите шаги 5 и 6. Найдите такое наибольшее число на место прочерков справа (вместо прочерков нужно подставить одно и тоже число), чтобы результат умножения был меньше или равен текущему числу слева.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114).
 Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
- В нашем примере 549 х 9 = 4941, что меньше текущего числа слева (5114).
Если для квадратного корня вам необходимо найти больше знаков после запятой, напишите пару нулей у текущего числа слева и повторяйте шаги 4, 5 и 6. Повторяйте шаги, до тех пор пока не получите нужную вам точность ответа (число знаков после запятой).
Понимание процесса
Рассмотрим первую пару цифр Sa числа S (Sa = 7 в нашем примере) и найдем ее квадратный корень. В этом случае первой цифрой A искомого значения квадратного корня будет такая цифра, квадрат которой меньше или равен S a (то есть ищем такое A, при котором выполняется неравенство A² ≤ Sa
- Допустим, что нужно разделить 88962 на 7; здесь первый шаг будет аналогичным: рассматриваем первую цифру делимого числа 88962 (8) и подбираем такое наибольшее число, которое при умножении на 7 дает значение меньшее или равное 8. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
Мысленно представьте квадрат, площадь которого вам нужно вычислить. Вы ищите L, то есть длину стороны квадрата, площадь которого равна S.
 A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.- Пусть (10A+B)² = L² = S = 100A² + 2×10A×B + B² . Запомните, что 10A+B — это такое число, у которого цифра B означает единицы, а цифра A — десятки. Например, если A=1 и B=2, то 10A+B равно числу 12.(10A+B)² — это площадь всего квадрата, 100A² — площадь большого внутреннего квадрата, B² — площадь малого внутреннего квадрата, 10A×B — площадь каждого из двух прямоугольников. Сложив площади описанных фигур, вы найдете площадь исходного квадрата.
Для усвоения данного метода представьте число, квадратный корень которого необходимо найти, как площадь квадрата S. В этом случае вы будете искать длину стороны L такого квадрата. Вычисляем такое значение L, при котором L² = S.
Задайте букву для каждой цифры в ответе. Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Задайте букву для каждой пары первых цифр. Обозначим через S a первую пару цифр в значении S, через S b — вторую пару цифр и так далее.
Уясните связь данного метода с делением в столбик. Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Как и в операции деления, где каждый раз нас интересует только одна следующая цифра делимого числа, при вычислении квадратного корня мы последовательно работаем с парой цифр (для получения одной следующей цифры в значении квадратного корня).
Факт 1.
\(\bullet\)
Возьмем некоторое неотрицательное число \(a\)
(то есть \(a\geqslant 0\)
). Тогда (арифметическим) квадратным корнем из числа \(a\)
называется такое неотрицательное число \(b\)
, при возведении которого в квадрат мы получим число \(a\)
: \[\sqrt a=b\quad \text{то же самое, что }\quad a=b^2\]
Из определения следует, что \(a\geqslant 0, b\geqslant 0\)
. 2=400\\
\hline \end{array}\]
2=400\\
\hline \end{array}\]
Факт 3.
Какие действия можно выполнять с квадратными корнями?
\(\bullet\) Сумма или разность квадратных корней НЕ РАВНА квадратному корню из суммы или разности, то есть \[\sqrt a\pm\sqrt b\ne \sqrt{a\pm b}\]
Таким образом, если вам нужно вычислить, например, \(\sqrt{25}+\sqrt{49}\)
, то первоначально вы должны найти значения \(\sqrt{25}\)
и \(\sqrt{49}\)
, а затем их сложить. Следовательно, \[\sqrt{25}+\sqrt{49}=5+7=12\] Если значения \(\sqrt a\)
или \(\sqrt b\)
при сложении \(\sqrt
a+\sqrt b\)
найти не удается, то такое выражение дальше не преобразуется и остается таким, как есть. Например, в сумме \(\sqrt
2+ \sqrt {49}\)
мы можем найти \(\sqrt{49}\)
– это \(7\)
, а вот \(\sqrt
2\)
никак преобразовать нельзя, поэтому \(\sqrt 2+\sqrt{49}=\sqrt
2+7\)
. Дальше это выражение, к сожалению, упростить никак нельзя \(\bullet\)
Произведение/частное квадратных корней равно квадратному корню из произведения/частного, то есть \[\sqrt a\cdot \sqrt b=\sqrt{ab}\quad \text{и}\quad
\sqrt a:\sqrt b=\sqrt{a:b}\]
(при условии, что обе части равенств имеют смысл )
Пример: \(\sqrt{32}\cdot \sqrt 2=\sqrt{32\cdot
2}=\sqrt{64}=8\)
;
\(\sqrt{768}:\sqrt3=\sqrt{768:3}=\sqrt{256}=16\)
;
\(\sqrt{(-25)\cdot (-64)}=\sqrt{25\cdot 64}=\sqrt{25}\cdot \sqrt{64}=
5\cdot 8=40\)
. \(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
\(\bullet\)
Пользуясь этими свойствами, удобно находить квадратные корни из больших чисел путем разложения их на множители.
Рассмотрим пример. Найдем \(\sqrt{44100}\)
. Так как \(44100:100=441\)
, то \(44100=100\cdot 441\)
. По признаку делимости число \(441\)
делится на \(9\)
(так как сумма его цифр равна 9 и делится на 9), следовательно, \(441:9=49\)
, то есть \(441=9\cdot 49\)
.
Таким образом, мы получили: \[\sqrt{44100}=\sqrt{9\cdot 49\cdot 100}=
\sqrt9\cdot \sqrt{49}\cdot \sqrt{100}=3\cdot 7\cdot 10=210\]
Рассмотрим еще один пример: \[\sqrt{\dfrac{32\cdot 294}{27}}=
\sqrt{\dfrac{16\cdot 2\cdot 3\cdot 49\cdot 2}{9\cdot 3}}= \sqrt{
\dfrac{16\cdot4\cdot49}{9}}=\dfrac{\sqrt{16}\cdot \sqrt4 \cdot
\sqrt{49}}{\sqrt9}=\dfrac{4\cdot 2\cdot 7}3=\dfrac{56}3\]
\(\bullet\)
Покажем, как вносить числа под знак квадратного корня на примере выражения \(5\sqrt2\)
(сокращенная запись от выражения \(5\cdot
\sqrt2\)
). Так как \(5=\sqrt{25}\)
, то \
Заметим также, что, например,
1) \(\sqrt2+3\sqrt2=4\sqrt2\)
,
2) \(5\sqrt3-\sqrt3=4\sqrt3\)
3) \(\sqrt a+\sqrt a=2\sqrt a\)
. 2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
2\)
, поэтому \(\sqrt{16}=4\)
. А вот извлечь корень из числа \(3\)
, то есть найти \(\sqrt3\)
, нельзя, потому что нет такого числа, которое в квадрате даст \(3\)
.
Такие числа (или выражения с такими числами) являются иррациональными. Например, числа \(\sqrt3, \ 1+\sqrt2, \ \sqrt{15}\)
и т.п. являются иррациональными.
Также иррациональными являются числа \(\pi\)
(число “пи”, приблизительно равное \(3,14\)
), \(e\)
(это число называют числом Эйлера, приблизительно оно равно \(2,7\)
) и т.д.
\(\bullet\)
Обращаем ваше внимание на то, что любое число будет либо рациональным, либо иррациональным. А вместе все рациональные и все иррациональные числа образуют множество, называющееся множеством действительных (вещественных) чисел. Обозначается это множество буквой \(\mathbb{R}\)
.
Значит, все числа, которые на данный момент мы знаем, называются вещественными числами.
Факт 5.
\(\bullet\)
Модуль вещественного числа \(a\)
– это неотрицательное число \(|a|\)
, равное расстоянию от точки \(a\)
до \(0\)
на вещественной прямой. 2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
2\\
&2>2,25 \end{aligned}\]
Видим, что мы получили неверное неравенство. Следовательно, наше предположение было неверным и \(\sqrt 2-1Заметим, что прибавление некоторого числа к обеим частям неравенства не влияет на его знак. Умножение/деление обеих частей неравенства на положительное число также не влияет на его знак, а умножение/деление на отрицательное число меняет знак неравенства на противоположный!
Возводить обе части уравнения/неравенства в квадрат можно ТОЛЬКО ТОГДА, когда обе части неотрицательные. Например, в неравенстве из предыдущего примера возводить обе части в квадрат можно, в неравенстве \(-3
\(\bullet\)
Следует запомнить, что \[\begin{aligned}
&\sqrt 2\approx 1,4\\
&\sqrt 3\approx 1,7 \end{aligned}\]
Знание приблизительного значения данных чисел поможет вам при сравнении чисел!
\(\bullet\)
Для того, чтобы извлечь корень (если он извлекается) из какого-то большого числа, которого нет в таблице квадратов, нужно сначала определить, между какими “сотнями” оно находится, затем – между какими “десятками”, а потом уже определить последнюю цифру этого числа. 2=168\cdot 168=28224\)
.
2=168\cdot 168=28224\)
.
Следовательно, \(\sqrt{28224}=168\)
. Вуаля!
Для того чтобы достойно решить ЕГЭ по математике, прежде всего необходимо изучить теоретический материал, который знакомит с многочисленными теоремами, формулами, алгоритмами и т. д. На первый взгляд может показаться, что это довольно просто. Однако найти источник, в котором теория для ЕГЭ по математике изложена легко и понятно для учащихся с любым уровнем подготовки, — на деле задача довольно сложная. Школьные учебники невозможно всегда держать под рукой. А найти основные формулы для ЕГЭ по математике бывает непросто даже в Интернете.
Почему так важно изучать теорию по математике не только для тех, кто сдает ЕГЭ?
- Потому что это расширяет кругозор
. Изучение теоретического материала по математике полезно для всех, кто желает получить ответы на широкий круг вопросов, связанных с познанием окружающего мира. Все в природе упорядоченно и имеет четкую логику. Именно это и отражается в науке, через которую возможно понять мир.

- Потому что это развивает интеллект . Изучая справочные материалы для ЕГЭ по математике, а также решая разнообразные задачи, человек учится логически мыслить и рассуждать, грамотно и четко формулировать мысли. У него вырабатывается способность анализировать, обобщать, делать выводы.
Предлагаем вам лично оценить все преимущества нашего подхода к систематизации и изложению учебных материалов.
Как извлечь корень из числа. В этой статье мы будем учиться извлекать квадратный корень из четырехзначных и пятизначных чисел.
Давайте, для примера, извлечем квадратный корень из числа 1936.
Следовательно, .
Последняя цифра в числе 1936 — цифра 6. На 6 заканчивается квадрат числа 4 и числа 6. Следовательно, 1936 может быть квадратом числа 44 или числа 46. Осталось проверить с помощью умножения.
Значит,
Извлечем квадратный корень из числа 15129.
Следовательно, .
Последняя цифра в числе 15129 — цифра 9. На 9 заканчивается квадрат числа 3 и числа 7. Следовательно, 15129 может быть квадратом числа 123 или числа 127. Проверим с помощью умножения.
Следовательно, 15129 может быть квадратом числа 123 или числа 127. Проверим с помощью умножения.
Значит,
Как извлечь корень — видеоА теперь предлагаю вам посмотреть видео Анны Денисовой — «Как извлечь корень «, автора сайта » Простая физика «, в котором она рассказывает, как извлекать квадратные и кубические корни без калькулятора.
В видео рассматривается несколько способов извлечения корней:
1. Самый простой способ извлечения квадратного корня.
2. Подбором, используя квадрат суммы.
3. Вавилонский способ.
4. Способ извлечения квадратного корня в столбик.
5. Быстрый способ извлечения кубического корня.
6. Способ извлечения кубического корня в столбик.
Извлечение корня – обратная операция возведению степени. То есть Извлекая корень из числа Х, получим число, которое в квадрате даст то самое число Х.
Извлечение корня довольно-таки несложная операция. Таблица квадратов сможет облегчить работу по извлечению. Потому что, наизусть помнить все квадраты и корни невозможно, а числа могут встретиться большие.
Потому что, наизусть помнить все квадраты и корни невозможно, а числа могут встретиться большие.
Извлечение корня из числа
Извлечение квадратного корня из числа – просто. Тем более что это можно делать не сразу, а постепенно. Например, возьмем выражение √256. Изначально, незнающему человеку сложно дать ответ сразу. Тогда будем делать по шагам. Сначала разделим на просто число 4, из которого вынесем за корень выделенный квадрат.
Изобразим: √(644), тогда это будет равносильно 2√64. А как известно, по таблице умножения 64=8 8. Ответ будет 2*8=16.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни. За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Извлечение комплексного корня
Корень квадратный не может вычисляться из отрицательных чисел, потому что любое число в квадрате – положительное число!
Комплексное число – число i, которое в квадрате равно -1. То есть i2=-1.
То есть i2=-1.
В математике существует число, которое получается при извлечении корня из числа -1.
То есть есть возможность вычислить корень из отрицательного числа, но это уже относится к высшей математике, не школьной.
Рассмотрим пример такого извлечения корня: √(-49)=7*√(-1)=7i.
Калькулятор корня онлайн
С помощью нашего калькулятора, Вы сможете посчитать извлечение числа из квадратного корня:
Преобразование выражений, содержащих операцию извлечения корня
Суть преобразования подкоренных выражений в разложении подкоренного числа на более простые, из которых можно извлечь корень. Такие как 4, 9, 25 и так далее.
Приведем пример, √625. Поделим подкоренное выражение на число 5. Получим √(1255), повторим операцию √(25 25), но мы знаем, что 25 это 52. А значит ответом будет 5*5=25.
Но бывают числа, у которых корень таким методом не вычислить и просто нужно знать ответ или иметь таблицу квадратов под рукой.
√289=√(17*17)=17
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Математика зародилась тогда, когда человек осознал себя и стал позиционироваться как автономная единица мира. Желание измерить, сравнить, посчитать то, что тебя окружает, — вот что лежало в основе одной из фундаментальных наук наших дней. Сначала это были частички элементарной математики, что позволили связать числа с их физическими выражениями, позже выводы стали излагаться лишь теоретически (в силу своей абстрактности), ну а через некоторое время, как выразился один ученый, «математика достигла потолка сложности, когда из нее исчезли все числа». Понятие «квадратный корень» появилось еще в то время, когда его можно было без проблем подкрепить эмпирическими данными, выходя за плоскость вычислений.
С чего все начиналось
Первое упоминание корня, который на данный момент обозначается как √, было зафиксировано в трудах вавилонских математиков, положивших начало современной арифметике. Конечно, на нынешнюю форму они походили мало — ученые тех лет сначала пользовались громоздкими табличками. Но во втором тысячелетии до н. э. ими была выведена приближенная формула вычислений, которая показывала, как извлечь квадратный корень. На фото ниже изображен камень, на котором вавилонские ученые высекли процесс вывода √2 , причем он оказался настолько верным, что расхождение в ответе нашли лишь в десятом знаке после запятой.
Помимо этого, корень применялся, если нужно было найти сторону треугольника, при условии, что две другие известны. Ну и при решении квадратных уравнений от извлечения корня никуда не деться.
Наравне с вавилонскими работами объект статьи изучался и в китайской работе «Математика в девяти книгах», а древние греки пришли к выводу, что любое число, из которого не извлекается корень без остатка, дает иррациональный результат.
Происхождение данного термина связывают с арабским представлением числа: древние ученые полагали, что квадрат произвольного числа произрастает из корня, подобно растению. На латыни это слово звучит как radix (можно проследить закономерность — все, что имеет под собой «корневую» смысловую нагрузку, созвучно, будь то редис или радикулит).
Ученые последующих поколений подхватили эту мысль, обозначая его как Rx. Например, в XV веке, дабы указать, что извлекается корень квадратный из произвольного числа a, писали R 2 a. Привычная современному взгляду «галочка» √ появилась лишь в XVII веке благодаря Рене Декарту.
Наши дни
С точки зрения математики, квадратный корень из числа y — это такое число z, квадрат которого равен y. Иными словами, z 2 =y равносильно √y=z. Однако данное определение актуально лишь для арифметического корня, так как оно подразумевает неотрицательное значение выражения. Иными словами, √y=z, где z больше либо равно 0.
В общем случае, что действует для определения алгебраического корня, значение выражения может быть как положительным, так и отрицательным. Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Таким образом, в силу того, что z 2 =y и (-z) 2 =y, имеем: √y=±z или √y=|z|.
Благодаря тому, что любовь к математике с развитием науки лишь возросла, существуют разнообразные проявления привязанности к ней, не выраженные в сухих вычислениях. Например, наравне с такими занятными явлениями, как день числа Пи, отмечаются и праздники корня квадратного. Отмечаются они девять раз в сто лет, и определяются по следующему принципу: числа, которые обозначают по порядку день и месяц, должна быть корнем квадратным из года. Так, в следующий раз предстоит отмечать сей праздник 4 апреля 2016 года.
Свойства квадратного корня на поле R
Практически все математические выражения имеют под собой геометрическую основу, не миновала эта участь и √y, который определяется как сторона квадрата с площадью y.
Как найти корень числа?
Алгоритмов вычисления существует несколько. Наиболее простым, но при этом достаточно громоздким, является обычный арифметический подсчет, который заключается в следующем:
1) из числа, корень которого нам нужен, по очереди вычитаются нечетные числа — до тех пор, пока остаток на выходе не получится меньше вычитаемого или вообще будет равен нулю. Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Количество ходов и станет в итоге искомым числом. Например, вычисление квадратного корня из 25:
Следующее нечетное число — это 11, остаток у нас следующий: 1
Для таких случаев существует разложение в ряд Тейлора:
√(1+y)=∑((-1) n (2n)!/(1-2n)(n!) 2 (4 n))y n , где n принимает значения от 0 до
+∞, а |y|≤1.
Графическое изображение функции z=√y
Рассмотрим элементарную функцию z=√y на поле вещественных чисел R, где y больше либо равен нулю. График ее выглядит следующим образом:
Кривая растет из начала координат и обязательно пересекает точку (1; 1).
Свойства функции z=√y на поле действительных чисел R
1. Область определения рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль включен).
2. Область значений рассматриваемой функции — промежуток от нуля до плюс бесконечности (ноль опять же включен).
3. Минимальное значение (0) функция принимает лишь в точке (0; 0). Максимальное значение отсутствует.
4. Функция z=√y ни четная, ни нечетная.
5. Функция z=√y не является периодической.
6. Точка пересечения графика функции z=√y с осями координат лишь одна: (0; 0).
7. Точка пересечения графика функции z=√y также является и нулем этой функции.
8. Функция z=√y непрерывно растет.
9. Функция z=√y принимает лишь положительные значения, следовательно, график ее занимает первый координатный угол.
Варианты изображения функции z=√y
В математике для облегчения вычислений сложных выражений порой используют степенную форму написания корня квадратного: √y=y 1/2 . Такой вариант удобен, например, в возведении функции в степень: (√y) 4 =(y 1/2) 4 =y 2 . Этот метод является удачным представлением и при дифференцировании с интегрированием, так как благодаря ему корень квадратный представляется обычной степенной функцией.
А в программировании заменой символа √ является комбинация букв sqrt.
Стоит отметить, что в данной области квадратный корень очень востребован, так как входит в состав большинства геометрических формул, необходимых для вычислений. Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Сам алгоритм подсчета достаточно сложен и строится на рекурсии (функции, что вызывает сама себя).
Корень квадратный в комплексном поле С
По большому счету именно предмет данной статьи стимулировал открытие поля комплексных чисел C, так как математикам не давал покоя вопрос получения корня четной степени из отрицательного числа. Так появилась мнимая единица i, которая характеризуется очень интересным свойством: ее квадратом есть -1. Благодаря этому квадратные уравнения и при отрицательном дискриминанте получили решение. В С для корня квадратного актуальны те же свойства, что и в R, единственное, сняты ограничения с подкоренного выражения.
Квадратные корни. Арифметический квадратный корень
Цель урока: Дать понятие о корне из числа, научить находить =а по определению.
Ход урока
I. Актуализация знаний.
Что называется степенью с натуральным показателем? Основанием степени? Показателем степени?
- A*a*a=?
- X*x*a*a=?
- (x-a)*(x-a)=?
Вычислите
(-2); 3; 0,7; 2; (-1); (-1)
Что значит вычесть из числа a число b? (Это значит – найти такое число х=а-b, что х+b=а)
Что значит число a разделить на число b? (Это значит – найти такое число х=а*b, что х*b=а)
II. Вводная беседа.
Вводная беседа.
1. Сколько арифметических действий вы знаете?
(Сложение, вычитание, умножение, деление, возведение в степень. 5 действий.)
2. Назовите обратные им действия. (Сложение и вычитание имеют по одному обратному действию, которые называются “вычитание” и “деление”. Пятое действие – возведение в степень имеет два обратных действия: а) нахождение основания б) нахождение показателя
Определение Нахождение основания называется извлечением корня. Второе действие - логарифмирование. Его будем изучать в 11 классе.
Займемся 1-м действием. Так, наряду с задачей вычисления площади квадрата, сторона которого известна, с давних времен встречалась обратная задача:
Какую длину должна иметь сторона квадрата, чтобы его площадь равнялась b?
III. Введение определения
Решим задачу:
Площадь квадратного листа равна 49 м2. Чему равна длина стороны квадрата?
Решение: Пусть сторона листа – х м. Площадь S=x2
м2. Так как 72=49 и (–7)2=49, т.е. числа
7 и –7 называются квадратными корнями.
Площадь S=x2
м2. Так как 72=49 и (–7)2=49, т.е. числа
7 и –7 называются квадратными корнями.
Определение: Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
=b
b
b=a
При a, не имеет смысла.
Арифметический квадратный корень обозначается значком - радикал, корень.
Примеры =2, т.к. 20, 2=4
=9, т.к. 90, 9=81
-4, т.к. –4<0
4, т.к. 4-16
Из истории. Ещё 4000 лет назад вавилонские ученые составили наряду с таблицами умножения и таблицами обратных величин ( при помощи которых деление чисел сводилось к умножению) таблицы квадратов чисел и квадратных корней чисел. При этом они умели находить приблизительное значение квадратного корня из любого целого числа.
IV. Закрепление определения квадратного корня
№287. (устно).
Докажите, что:
а) число 5 есть арифметический квадратный корень из 25 (т.к. 50, 5=25)
б) число 0.3 есть арифметический квадратный корень из 0.09 (т.к. 0.30, 0.3=0.09)
в) число –7 не является арифметическим квадратным корнем из 49 ( т.к. –7<0)
г) число 0,6 не является арифметическим квадратным корнем из 3,6. (0,60, но о,623,6)
№289 (устно)
а)=
б) =
в) =
д) =
к)=
л)=
м) =
Вычислите:
в)+=
е) –7 + 5,4 =
з) + =
V. Закрепление нахождения значения корня.
№291.
Найдите значение выражения. (Один ученик решает у доски. Класс выполняет работу самостоятельно.)
б) при х=7; 23; 1,83.
Ответы:
Х=7; ===4
Х=23; ===8
Х=1,83; ===0,7
В) х+ при х=0; 0,1; 0,36.
Ответы:
Х=0 0+=0+0=0
Х=0,01 0,01+=0,01+0,1=0,11
Х=0,36 0,36+=0,36+0,6=0,96
№298. Найдите значение переменной х,
при котором:
Найдите значение переменной х,
при котором:
| б) =0,5 По определению Х=0,52 х=0,25 |
в) 2*=0 =0:2 =0 по определению х=02 х=0 |
е) 3-2=0 3=2 = х=()2 х= |
VI. Работа по таблицам квадратов.
Пользование таблицей. (Форзац учебника)
№295 (а,б). (устно)
а)=12 =17 =14 =16
б) =15 =13 =18 =19
VII. О знаке радикала
Прочитать по учебнику стр. 214. “В Эпоху возрождения”.
VIII. Вводим операцию ()2=а, при а0.
Из определения арифметического корня следует, при любом а, при котором выражение имеет смысл, верно равенство ()2=а
Вычислите
()2=а
()2=7
===3
===4
===5
Самостоятельная работа обучающего типа. (Приложение 1)
(Приложение 1)
IX. Три уровня сложности по возрастающей – на выбор учащегося.
1 вариант
х 25 0,36 0,0001 -16 2+ 256
2 вариант
а 3 9 -7 36 -13 -11 2 в 6 16 11 64 -12 11
3 вариант
а 4 0 5 10 12 в 0 -6 -12 24 9 2 -6
X. Итог урока
Итог урока
XI. Домашнее задание.
Самый быстрый словарь в мире | Vocabulary.com
квадратный корень число, которое при умножении само на себя равно заданному числу
квадратный ярд единица площади, равная одному ярду на один квадратный ярд
квадратный фут единица площади, равная одному футу на один квадратный фут
квадратный узел двойной узел, состоящий из двух полупетлей и используемый для соединения концов двух шнуров
корень сквои высокая трава из восточной части Северной Америки и Азии, имеющая синие ягодообразные плоды и толстый узловатый подвой, ранее использовавшаяся в медицинских целях
скворут высокая трава из восточной части Северной Америки и Азии, имеющая синие ягодообразные плоды и толстый узловатый подвой, ранее использовавшаяся в медицинских целях
квадратная скобка из двух знаков препинания ([ или ]), используемая для заключения текстового материала
квадратный стрелок откровенный и честный человек
квадратная широкая и прочная
с квадратным носком
квадратный носок с квадратным носком
квадратная гайка гайка квадратной формы
квадратный метр центар равен 1/100 ар
прямоугольное вооружение с прямыми парусами в качестве основных
квадратный в форме квадрата
прямохвостые с квадратным хвостом
квадратных метра, центар равен 1/100 ар
пугало чучело в виде человека для отпугивания птиц от семян
squirearchy дворяне, владеющие землей (рассматриваемые как класс)
scammonyroot тропический американский стелющийся или вьющийся травянистый многолетник с огромным крахмалистым корнем; иногда считается источником сладкого картофеля
Отрицательный квадратный корень: определение и обзор — видео и расшифровка урока
Что такое отрицательный квадратный корень?
Как было показано ранее, отрицательный квадратный корень является одним из двух квадратных корней из положительного числа. 2 = 121
2 = 121
А как насчет квадратного корня из отрицательного числа? Например, чему равен квадратный корень из -9? Мы можем попробовать 3, но 3 х 3 = 9.Мы можем попробовать -3, но (-3) x (-3) = 9. Эта дилемма связана с тем, что квадратный корень любого действительного числа x не может быть отрицательным. Следовательно, квадратного корня из отрицательного числа не существует, по крайней мере, в системе действительных чисел.
Следует помнить, что действительных чисел включают в себя все рациональные числа (например, целые числа 0 и 7, целое число -5 и дробь 2/3), а также иррациональные числа (например, число пи и квадратный корень из 3).
Однако математики преодолели эту проблему квадратных корней из отрицательных чисел, создав воображаемую единицу.2 + 4 = 0
Если мы найдем x , мы получим x = ± квадратный корень из -4. Каковы же возможные значения x ?
2 x 2 не равно -4, а (-2) x (-2) не равно -4.
Это говорит нам о том, что график этого квадратного уравнения не имеет решений, являющихся действительными числами. Другими словами, он не пересекает ось x .
Другими словами, он не пересекает ось x .
Однако мы можем дать ему воображаемое решение. Мы можем использовать свойство произведения квадратных корней и переписать квадратный корень из -4, как показано на рисунке 4.2 + 4 = 0, хотя это и мнимые решения.
Операции с мнимыми числами
Теперь давайте рассмотрим операции с мнимыми числами и начнем с простого примера:
- Упростим квадратный корень из -18 плюс квадратный корень из -50.
Решение этой проблемы показано на рис. 5. Сначала нам нужно упростить каждый член. Например, мы можем переписать квадратный корень из 18, используя три множителя: квадратный корень из -1, квадратный корень из 9 и квадратный корень из 2.(4 n +4) = 1
Мы можем использовать этот шаблон для упрощения любой степени i , если эта степень является положительным целым числом. Мнимая единица в степени 4 или любой кратной 4 равна 1. Для любых степеней i , имеющих показатель степени 5 или выше, разделите показатель степени на 4. 43.3 = — i
43.3 = — i
Итоги урока
Давайте повторим. Каждое положительное число имеет два квадратных корня: положительный квадратный корень и отрицательный квадратный корень. Однако в системе действительных чисел не существует квадратных корней из отрицательных чисел. Мнимая единица позволяет нам записывать квадратный корень из отрицательных чисел и выполнять операции с квадратными корнями из отрицательных чисел при следующих условиях:
- Воображаемая единица i равна квадратному корню из -1.2 равно -1.
- Мы можем выделить мнимую единицу из квадратного корня из отрицательного числа; однако мы не можем использовать свойство произведения квадратных корней для объединения двух членов, которые оба являются квадратным корнем из отрицательного числа.
| Телефон : | 780-427-5318 | |
| (Composer d’abord le 310-0000 pour obtenir une ligne sans frais) | ||
| Телекопьер: | 780-427-1179 | |
| Курьерский адрес: | cshelpdesk@gov. ab.ca ab.ca | |
Определение квадратного корня
Мы знаем, что $$$2\cdot2=4$$$ Следовательно, мы знаем, что число $$2$$, умноженное само на себя, равно $$4$$.
В этом разделе мы научимся находить число, которое при умножении само на себя дает конкретное число.
Квадратный корень из любого числа $$x$$ — это число, которое при умножении само на себя равно $$x$$.Он выражается как $$\sqrt{x}$$.
$$\sqrt{25}=5$$, поскольку $$5\cdot5=25$$. В этом случае говорят, что $$5$$ — это квадратный корень из $$25$$.
Или также $$\sqrt{9}=3$$, поскольку $$3\cdot3=9$$. $$3$$ — это квадратный корень из $$9$$.
А теперь посмотрим, что произойдет с $$-5$$.
Если мы умножим его само на себя, мы получим: $$(-5)\cdot(-5)=25$$, так как при умножении двух отрицательных чисел всегда получается положительное число, то есть: $$(-) \cdot(-)=+$$.
Таким образом, $$-5$$ также является квадратным корнем из $$25$$, так как умножение его само на себя дает $$25$$.
Таким образом, если мы вычислим квадратный корень из любого числа $$x$$, мы получим два решения: положительное решение и отрицательное решение. Они называются положительным корнем и отрицательным корнем соответственно. Таким образом, в общем случае мы можем написать:
$$\sqrt{x}=\left\{\begin{массив}{c} \mbox{положительный корень} =a \\ \mbox{отрицательный корень} =-a \end{массив} \right. \mbox{итак, удовлетворено, что }$$
$$ а\cdot a=x,(-a)\cdot(-a)=x$$
Давайте вычислим квадратный корень из $$36$$.
Поскольку мы знаем, что $$6\cdot6=36$$, мы уже можем сказать, каковы квадратные корни такого числа.
Положительный квадратный корень из $$36$$ равен $$6$$, поскольку $$6\cdot6=36$$.
Отрицательный квадратный корень из $$36$$ равен $$-6$$, поскольку $$(-6)\cdot(-6)=36$$.
Обычно пишут только положительный корень, и подразумевается, что это же число в его отрицательной форме также является корнем. С этого момента мы будем записывать только положительный корень числа, чтобы получить решение квадратного корня.
С этого момента мы будем записывать только положительный корень числа, чтобы получить решение квадратного корня.
До сих пор мы вычисляли квадратные корни, результатом которых были целые числа. Когда это происходит, говорят, что число, корень которого мы вычисляем, является полным квадратом. Другими словами, если корень числа $$x$$ — целое число, говорят, что $$x$$ — полный квадрат.
$$25$$ — полный квадрат, поскольку $$\sqrt{25}=5$$, а $$5$$ — целое число.
А также $$16$$ — идеальный квадрат, потому что $$\sqrt{16}=4$$, потому что $$4$$ — это число, удовлетворяющее условию $$4\cdot4=16$$.
Когда мы вычисляем квадратные корни из чисел, которые не являются полными квадратами, результатом становится не целое, а иррациональное число. Это означает, что это число невозможно записать как частное двух целых чисел.
В заключение, квадратный корень из целого числа всегда будет целым или иррациональным числом.
$$\sqrt{2}=1,414213562\ldots$$ — иррациональное число с бесконечным числом десятичных знаков.
Квадратный корень также можно вычислить, используя нецелые числа.Единственным необходимым условием для вычисления корня числа является его положительность.
Квадратный корень из отрицательного числа не существует, поскольку, используя правило умножения, при умножении двух положительных результатов результат положительный, а при умножении двух отрицательных — также положительный.
Таким образом, число, умноженное само на себя (произведение двух чисел с одинаковым знаком), не может дать отрицательный результат.
Короче говоря, для любого положительного числа, целого или нет, можно вычислить квадратный корень.
$$\sqrt{17,2}=4,1473$$, так как если вычислить $4,1473\cdot4,1473=17,2$$
Это корни наиболее часто встречающихся целых чисел, которые являются полными квадратами.
$$\sqrt{4}=2 \ \ \ \ $$ $$\sqrt{36}=6 \ \ \ \ $$ $$\sqrt{100}=10$$
$$\sqrt{9}=3 \ \ \ \ $$ $$\sqrt{49}=7 \ \ \ \ $$ $$\sqrt{121}=11$$
$$\sqrt{16}=4 \ \ \ $$ $$\sqrt{64}=8 \ \ \ $$ $$\sqrt{144}=12$$
$$\sqrt{25}=5 \ \ \ $$ $$\sqrt{81}=9 \ \ \ $$ $$\sqrt{169}=13$$
Имеет ли квадратный корень два значения?
Это часть серии статей о распространенных заблуждениях.
2} = \pm xx2=±x
Почему некоторые люди говорят, что это правда: Это именно то, чему меня учили в школе: когда вы извлекаете квадратный корень, ответ всегда «плюс-минус» какое-то значение.
Почему некоторые люди говорят, что это неверно: Когда вы возводите x,x,x в квадрат, оно становится положительным независимо от того, что было раньше; затем, когда вы извлекаете квадратный корень, он все еще положителен. Следовательно, ответ будет просто ∣x∣|x|∣x∣, а не ±x\pm x±x.
Укажите правильный ответ:\color{#20A900}{\text{Укажите правильный ответ:}}Укажите правильный ответ:Утверждение неверно \color{#D61F06}{\textbf{false}}false.
Объяснение:
В своей стандартной области неотрицательных действительных чисел x\sqrt{x}x определяется как «неотрицательное действительное число, которое при возведении в квадрат равно x.
x.x». Например, 25=5\sqrt{25} = 525=5 , а не ±5\pm 5±5. x\sqrt{x}x определяется таким образом, что это функция.
Функция представляет собой отношение или карту между набором входных значений (домен) и набором выходных значений (диапазон), которое обладает тем свойством, что каждый принятый вход соответствует ровно одному выходу.Парабола 2×2 не прошла бы тест вертикальной линии и не была бы функцией.
Расширение домена на все действительные числа и диапазона на комплексные числа:
Поведение функции извлечения квадратного корня при распространении на область всех действительных чисел (положительные действительные числа, отрицательные действительные числа и 0) точно отражает аргумент, сделанный выше. Квадратный корень из отрицательного числа является комплексным числом. Но даже с расширенным доменом x\sqrt{x}x определяется аналогичным образом, так что это все еще функция.2}}{|x|} + 1,∣x∣x2+1,
, где xxx — ненулевое действительное число.
См. также
идеальных квадратов и квадратных корней [Видео и практика]
Здравствуйте, в этом видео мы рассмотрим, как упростить квадратных корня и найти идеальных квадрата .
Символ в математике, который мы используем для представления квадратных корней, называется радикалом и выглядит следующим образом: \(\sqrt{}\).{1}\), но 1 не пишем, потому что это данность, в квадратных корнях есть что-то подобное. В изогнутом плече радикала есть заданная 2, которую мы обычно не пишем, когда ищем квадратный корень, \(\sqrt[2]{}\). Это число называется , индекс , и он определяет, какой корень подкоренного числа мы пытаемся найти. Например, это: \(\sqrt{20}\) запрашивает квадратный корень или второй корень из 20, а это: \(\sqrt[3]{125}\), которое мы читаем как « кубический корень из ста двадцати пяти», просит нас найти третий корень из 125.
Я хочу, чтобы вы попрактиковались в этом сами. Приостановите видео и пометьте разные части этого выражения: \(\sqrt[4]{200}\).
Думаешь, у тебя получилось? Корневой символ — радикал. Индекс равен 4, потому что это число на согнутой руке радикала. А подкоренное число — это число под подкоренным символом, поэтому в данном случае 200.
\(\sqrt{}\) — подкоренное число
4 — индекс
200 — подкоренное числоОтличная работа!
Теперь давайте поговорим о том, как мы находим квадратный корень из числа.Для этого мы спрашиваем себя: «Какое число, умноженное само на себя, даст нам подкоренное число?» Например, чему равен квадратный корень из 25: \(\sqrt{25}\)? Множители 25 равны \(5\умножить на 5\), что означает, что квадратный корень из 25 равен 5. Это также то, что мы называем идеальным квадратом. Совершенный квадрат — это когда мы упрощаем квадратный корень и под радикалом ничего не остается.
Чему равны квадратные корни из 36, 81 и 144? Поставьте видео на паузу и попробуйте сами.
Когда вы закончите, мы просмотрим их вместе.
\(\sqrt{36}=6, \text{ потому что}\text{ }6\times 6=36\)
\(\sqrt{81}=9, \text{ потому что}\text{ }9\times 9=81\)
\(\sqrt{144}=12, \text{ потому что}\text{ }12\times 12=144\)Мы получаем эти красивые числа, потому что мы извлекают квадратные корни из полных квадратов. Но что, если нам не дан идеальный квадрат? Что ж, тогда нам придется упрощать квадратный корень.
Упрощение квадратных корней
При упрощении квадратного корня мы вытащим все правильные квадраты из-под корня, а все, что останется от множителей подкоренного, останется под корнем.Давайте посмотрим на пример.
Упростите квадратный корень из 40: \(\sqrt{40}\).
Мы начнем с нахождения множителей 40, которые равны \({2}\times {2}\times {2}\times{5}\).
Так как \(2\times{2}\) образует идеальный квадрат, мы можем поставить 2 на передний план, и под радикалом останется \(2\times{5}\).
Больше нет полных квадратов, поэтому мы просто перемножаем эти числа, чтобы получить новое подкоренное число.
Следовательно, квадратный корень из 40 равен 2 квадратным корням из 10: \(\sqrt{40}\) = \(2\sqrt{10}\).
Теперь я хочу, чтобы вы попробовали один. Упростите квадратный корень из 96: 96. Приостановите видео здесь и упростите. Когда вы закончите, мы посмотрим на это вместе.
Думаешь, у тебя получилось? Сначала нам нужно найти множители числа 96.
\(96 = 2 \times {2}\times {2}\times {2} \times {2}\times{ 3}\)
It легко увидеть идеальные квадраты, когда множители записаны в такой форме. Мы можем вытащить два набора из 2 из нашего подкоренного числа, что оставит нам \(2\times{2}=4\) перед нашим новым радикалом.У нас все еще есть 2 и 3 из нашего списка множителей, поэтому мы перемножаем эти числа вместе, чтобы получить 6, и это наш новый подкоренной член. Поэтому самая упрощенная форма:
\(\sqrt{96}= 4\sqrt{6}\)
Надеюсь, это видео о квадратных корнях и полных квадратах было полезным.
Символ квадратного корняСпасибо за просмотр и удачной учебы!
— Как обсудить
Символ квадратного корня
Что означает символ квадратного корня?
Квадратный корень числа — это значение, умноженное само на себя, дает число.Пример: 4 × 4 = 16, поэтому квадратный корень из 16 равен 4. Символ — это любой положительный квадратный корень.
Как выглядит символ квадратного корня в этом контексте?
Каждое неотрицательное действительное число x имеет единственный неотрицательный квадратный корень, называемый кардинальным квадратным корнем, называемым x, где символ называется корневым знаком. Например, квадратный корень больше 9 равен 3, что называется √9 = 3, потому что 32 = 3 ⋅ 3 = 9, а 3 неотрицательны.
Можно также спросить, всегда ли квадратные корни положительны?
Каждое число, действительное или комплексное, имеет два квадратных корня, отрицающих друг друга.Знак корня при использовании с действительным числом указывает на большой или положительный квадратный корень.
Если это так, чтобы ответить на квалификационный вопрос, больший квадратный корень из положительного числа по определению всегда положителен.
В этом контексте, что такое квадратный корень и квадратный корень?
Квадратный корень. Квадратный корень противоположен квадрату. Вы можете думать об этом как о квадратном корне или числе, которое его возводит в квадрат.
Как находится квадратный корень?
Нахождение квадратного корня числа — это операция, обратная возведению этого числа в квадрат.Помните, что квадрат числа — это число, умноженное само на себя. Совершенные квадраты — это квадраты целых чисел. Квадратный корень из числа n, записанного ниже, — это число, которое дает n при умножении на себя.
Что означают 3 кубика?
Простой способ записать 3 кубика — это 33. Это означает, что трижды трижды умножаются сами на себя. Самый простой способ сделать это вычисление — сначала умножить (3×3), а затем умножить свой ответ на то же число, с которого вы начали с 3 x 3 x 3 = 9 x 3 = 27.
Как написать в квадрате?
Чтобы вставить символ a в Android, введите a и удерживайте 2. Пользователи Windows могут ввести альтернативный код в a в Блокноте. Вы можете использовать функцию экспоненты в Wordpad.
Что значит быть квадратным?
В математике квадрат — это результат умножения числа самого на себя. Глагол в квадрате используется для обозначения этой операции. Квадратура соответствует степени 2 и обозначается, например, головой 2, квадрат 3 можно записать как 32, что является числом 9.
Что такое квадратный корень на калькуляторе?
Графический калькулятор TI84 Plus Texas Instruments Чтобы найти квадратный корень числа, нажмите [2ND] (дополнительная функциональная клавиша), затем [√] (клавиша квадратного корня для вычисления квадратного корня числа), затем число, которое вы хотите найти квадратный корень, затем нажмите клавишу [ENTER].
Чему равен квадратный корень из 16?
Введите дату своего рождения, чтобы продолжить:
Поскольку число 7 простое, оно не имеет квадратных множителей и квадратный корень не может быть упрощен.
.Поскольку это иррациональное число, оно не может быть точно представлено через pq для целого числа p, q. Однако мы можем найти хорошие рациональные приближения для 7,
Что такое значок квадратного корня на iPhone?
OptionV используется для создания символа квадратного корня.
Можете ли вы получить отрицательный квадратный корень?
Поскольку квадратные корни не являются квадратными корнями, отрицательные числа не могут иметь квадратных корней. Получение квадратного корня из отрицательного числа не невозможно, просто его нет в последовательности чисел, с которой вы начали (последовательность положительных и отрицательных чисел с нулем).
Каково значение квадратного корня?
Квадратный корень числа — это значение, умноженное само на себя, дает число. Пример: 4 × 4 = 16, поэтому квадратный корень из 16 равен 4. Обратите внимание, что (-4) × (-4) тоже = 16, поэтому −4 также является квадратным корнем из 16. Символ может быть любым. означает положительный квадратный корень.
Чему равен квадрат 36?
Чему равна площадь 36-го квадрата = x².
Что такое упрощенный квадратный корень из 121?
Квадратный корень числа — это ответ на число, умноженное само на себя.Таким образом, квадратный корень из 121 равен 11, потому что 11×11 = 121.
.Чему равен квадрат 12?
Наш квадратный калькулятор назван удачно: это просто онлайн-инструмент для вычисления квадрата числа. Квадрат определяется как произведение любого числа, умноженного само на себя (x2). Например, квадрат 12 144 (произведение 12 на 12).
Чему равен квадрат 32?
Параграф 32 имеет радикальную форму 4√2. Это пример того, как найти квадратный корень из неполного квадрата без
.Чему равен квадратный корень из мнимого?
Мнимое число один (соответствует 1 для действительных чисел) равно √ (−1) (квадратный корень из отрицательной единицы).В математике мы используем i (для мнимого), а в электронике используют j (потому что я имею в виду, что он уже запущен, а следующая буква после i — j).

 Проверка на калькуляторе дает нам ответ 5,92 — мы были правы.
Проверка на калькуляторе дает нам ответ 5,92 — мы были правы. Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Сначала проведите вертикальную линию, делящую лист на две половины, а затем справа и немного ниже верхнего края листа к вертикальной линии пририсуйте горизонтальную линию. Теперь разделите подкоренное число на пары чисел, начиная с дробной части после запятой. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70». Напишите найденное n сверху справа, а квадрат n запишите снизу справа.
Напишите найденное n сверху справа, а квадрат n запишите снизу справа. Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
Запишите 7 сверху справа — это вторая цифра в искомом квадратном корне числа 780,14.
 Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее.
Обозначим через A первую цифру в значении L (искомый квадратный корень). B будет второй цифрой, C — третьей и так далее. То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
То есть ищем такое число d, при котором верно неравенство: 7×d ≤ 8
 Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу.
Ближайшими к нему квадратными числами будут числа 1 (√1 = 1) и 4 (√4 = 2). Таким образом, значение √3 расположено между 1 и 2. Та как значение √3, вероятно, ближе к 2, чем к 1, то наша оценка: √3 = 1,7. Умножаем это значение на число у знака корня: 7 х 1,7 = 11,9. Если вы сделаете расчеты на калькуляторе, то получите 12,13, что довольно близко к нашему ответу. Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70».
Так, число 79520789182,47897 записывается как «7 95 20 78 91 82, 47 89 70». Результат вычисления запишите под вычитаемым (квадратом числа n).
Результат вычисления запишите под вычитаемым (квадратом числа n).
 Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173.
Напишите 9 сверху справа и вычтите результат умножения из текущего числа слева: 5114 — 4941 = 173. A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.
A, B, C — цифры в числе L. Записать можно иначе: 10А + B = L (для двузначного числа) или 100А + 10В + С = L (для трехзначного числа) и так далее.

 2} = \pm xx2=±x
2} = \pm xx2=±x x.x». Например, 25=5\sqrt{25} = 525=5 , а не ±5\pm 5±5. x\sqrt{x}x определяется таким образом, что это функция.
x.x». Например, 25=5\sqrt{25} = 525=5 , а не ±5\pm 5±5. x\sqrt{x}x определяется таким образом, что это функция.

 Когда вы закончите, мы просмотрим их вместе.
Когда вы закончите, мы просмотрим их вместе.
 Спасибо за просмотр и удачной учебы!
Спасибо за просмотр и удачной учебы! Если это так, чтобы ответить на квалификационный вопрос, больший квадратный корень из положительного числа по определению всегда положителен.
Если это так, чтобы ответить на квалификационный вопрос, больший квадратный корень из положительного числа по определению всегда положителен.
 Поскольку это иррациональное число, оно не может быть точно представлено через pq для целого числа p, q. Однако мы можем найти хорошие рациональные приближения для 7,
Поскольку это иррациональное число, оно не может быть точно представлено через pq для целого числа p, q. Однако мы можем найти хорошие рациональные приближения для 7,
