Квадратный корень — это… Что такое Квадратный корень?

Квадра́тный ко́рень из (корень 2-й степени) — это решение уравнения вида . Наиболее часто под и подразумеваются числа, но в некоторых приложениях они могут быть и другими математическими объектами, например матрицами и операторами.

Применение операции корня к числам

Квадратный корень из числа  — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной .^[1][2] Часто под этим понятием подразумевают более узкое — т. н. арифметический квадратный корень — неотрицательное число.

Рациональные числа

Корень из рационального числа является рациональным числом, только если и (после сокращения общих множителей) являются квадратами натуральных чисел.

Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: , где зависит от

[3]^[4]. Верно и обратное: любая периодическая цепная дробь является квадратичной иррациональностью.

Действительные числа

При натуральных уравнение не всегда разрешимо в рациональных числах, что и привело к появлению новых числовых полей. Древнейшее из таких расширений — поле вещественных (действительных) чисел.

Теорема. Для любого положительного числа a существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку.^[5]

Неотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала .^[6]

Комплексные числа

Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если

,

то (см. Формула Муавра)

,

где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.

Квадратный корень как элементарная функция

Вещественный анализ

График функции

Квадратным корнем называют также функцию вещественной переменной , которая каждому ставит в соответствие арифметическое значение корня.^[7] Эта функция является частным случаем степенной функции с . Эта функция является гладкой при , в нуле же она непрерывна справа, но не дифференцируема.

Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в начале координат.

Обобщения

Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц^[8], функций^[9], операторов^[10] и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.

В алгебре применяется следующее формальное определение: Пусть  — группоид и . Элемент называется квадратным корнем из если .

Квадратный корень в элементарной геометрии

Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того. ^[11]

Квадратный корень в информатике

Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).

Алгоритмы нахождения квадратного корня

Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.

Разложение в ряд Тейлора

при .

Арифметическое извлечение квадратного корня

Для квадратов чисел верны следующие равенства:

и так далее.

То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так:

Выполнено 3 действия, квадратный корень числа 9 равен 3.

Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.

Грубая оценка

Многие алгоритмы вычисления квадратных корней из положительного действительного числа

S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:

Если D нечётно, D = 2n + 1, тогда используем

Если D чётно, D = 2n + 2, тогда используем

Два и шесть используются потому, что и

При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D это число двоичных цифр).

Геометрическое извлечение квадратного корня

В частности, если , а , то ^[12]

Итерационный аналитический алгоритм

Основная статья: Итерационная формула Герона

тогда

Столбиком

Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. Такой способ может быть освоен даже школьником. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.

Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234.567 можно представить, как 03 12 34 . 56 70. В отличие от деления снос производится такими группами по 2 цифры.

1. Записать число (в примере — 69696) на листке.
2. Найти , квадрат которого меньше или равен группе старших разрядов числа (старшая группа — самая левая не равная нулю), а квадрат больше группы старших разрядов числа. Записать найденное справа от N (это очередная цифра искомого корня). (На первом шаге примера , а ).
3. Записать квадрат под старшей группой разрядов. Провести вычитание из старшей группы разрядов выписанного квадрата числа и записать результат вычитания под ними.
4. Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число равное уже найденным цифрам результата (мы их выписываем справа от N) умноженное на 20. Назовём это число . (На первом шаге примера это число просто есть , на втором ).
5. Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа справа от результата вычитания. Назовем число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число , на втором ). Если сносится первая группа после десятичной точки числа , то нужно поставить точку справа от уже найденных цифр искомого корня.
6. Теперь нужно найти такое , что меньше или равно , но больше, чем . Записать найденное справа от N, как очередную цифру искомого корня. Вполне возможно, что окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как , но ) Если число найденных цифр уже удовлетворяет искомой точности прекращаем процесс вычисления.
7. Записать число под . Провести вычитание столбиком числа из и записать результат вычитания под ними. Перейти к шагу 4.

Наглядное описание алгоритма:

См. также

Примечания

1. ↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
2. ↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число ()… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
3. ↑ Теорема Лиувилля о приближении алгебраических чисел
4. ↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
5. ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
6. ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
7. ↑ Фихтенгольц, гл. 2, § 1
8. ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В.,
   Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
9. ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
10. ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
11. ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
12. ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148

Ссылки

Квадратный корень — это… Что такое Квадратный корень?

Квадра́тный ко́рень из (корень 2-й степени) — это решение уравнения вида . Наиболее часто под и подразумеваются числа, но в некоторых приложениях они могут быть и другими математическими объектами, например матрицами и операторами.

Применение операции корня к числам

Квадратный корень из числа  — это такое число, квадрат которого (результат умножения на себя) равен , то есть решение уравнения относительно переменной .^[1][2] Часто под этим понятием подразумевают более узкое — т. н. арифметический квадратный корень — неотрицательное число.

Рациональные числа

Корень из рационального числа является рациональным числом, только если и (после сокращения общих множителей) являются квадратами натуральных чисел.

Непрерывная дробь корня из рационального числа всегда является периодической (возможно с предпериодом) что позволяет с одной стороны легко вычислять хорошие рациональные приближения к ним с помощью линейных рекуррент, а с другой стороны ограничивает точность приближения: , где зависит от ^[3][4]. Верно и обратное: любая периодическая цепная дробь является квадратичной иррациональностью.

Действительные числа

При натуральных уравнение не всегда разрешимо в рациональных числах, что и привело к появлению новых числовых полей. Древнейшее из таких расширений — поле вещественных (действительных) чисел.

Теорема. Для любого положительного числа a существует ровно два вещественных корня, которые равны по модулю и противоположны по знаку.^[5]

Неотрицательный квадратный корень из положительного числа называется арифметическим квадратным корнем и обозначается с использованием знака радикала .^[6]

Комплексные числа

Над полем комплексных чисел решений всегда два, отличающихся только знаком (за исключением квадратного корня из нуля). Корень из комплексного числа часто обозначают как , однако использовать это обозначение нужно осторожно. Распространённая ошибка:

Для извлечения квадратного корня из комплексного числа удобно использовать экспоненциальную форму записи комплексного числа: если

,

то (см. Формула Муавра)

,

где корень из модуля понимается в смысле арифметического значения, а k может принимать значения k=0 и k=1, таким образом в итоге в ответе получаются два различных результата.

Квадратный корень как элементарная функция

Вещественный анализ

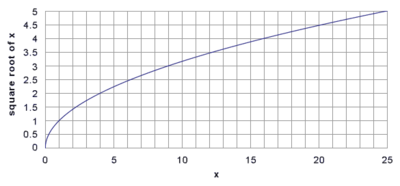График функции

Квадратным корнем называют также функцию вещественной переменной , которая каждому ставит в соответствие арифметическое значение корня.^[7] Эта функция является частным случаем степенной функции с . Эта функция является гладкой при , в нуле же она непрерывна справа, но не дифференцируема.

Как функция комплексного переменного корень — двузначная функция, листы которой соединяются в начале координат.

Обобщения

Квадратные корни вводятся как решения уравнений вида и для других объектов: матриц^[8], функций^[9], операторов^[10] и т. п. В качестве операции при этом могут использоваться достаточно произвольные мультипликативные операции, например, суперпозиция.

В алгебре применяется следующее формальное определение: Пусть  — группоид и . Элемент называется квадратным корнем из если .

Квадратный корень в элементарной геометрии

Квадратные корни тесно связаны с элементарной геометрией: если дан отрезок длины 1, то с помощью циркуля и линейки можно построить те и только те отрезки, длина которых записывается выражениями, содержащими целые числа, знаки четырёх действий арифметики, квадратные корни и ничего сверх того. ^[11]

Квадратный корень в информатике

Во многих языках программирования функционального уровня (а также языках разметки типа LaTeX) функция квадратного корня обозначается как sqrt (от англ. square root «квадратный корень»).

Алгоритмы нахождения квадратного корня

Нахождение или вычисление квадратного корня заданного числа называется извлечением (квадратного) корня.

Разложение в ряд Тейлора

при .

Арифметическое извлечение квадратного корня

Для квадратов чисел верны следующие равенства:

и так далее.

То есть, узнать целую часть квадратного корня числа можно, вычитая из него все нечётные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или равен нулю, и посчитав количество выполненных действий. Например, так:

Выполнено 3 действия, квадратный корень числа 9 равен 3.

Недостатком такого способа является то, что если извлекаемый корень не является целым числом, то можно узнать только его целую часть, но не точнее. В то же время такой способ вполне доступен детям, решающим простейшие математические задачи, требующие извлечения квадратного корня.

Грубая оценка

Многие алгоритмы вычисления квадратных корней из положительного действительного числа S требуют некоторого начального значения. Если начальное значение слишком далеко от настоящего значения корня, вычисления замедляются. Поэтому полезно иметь грубую оценку, которая может быть очень неточна, но легко вычисляется. Если S ≥ 1, пусть D будет числом цифр S слева от десятичной запятой. Если S < 1, пусть D будет числом нулей, идущих подряд, справа от десятичной запятой, взятое со знаком минус. Тогда грубая оценка выглядит так:

Если D нечётно, D = 2n + 1, тогда используем

Если D чётно, D = 2n + 2, тогда используем

Два и шесть используются потому, что и

При работе в двоичной системе (как внутри компьютеров), следует использовать другую оценку (здесь D это число двоичных цифр).

Геометрическое извлечение квадратного корня

В частности, если , а , то ^[12]

Итерационный аналитический алгоритм

Основная статья: Итерационная формула Герона

тогда

Столбиком

Этот способ позволяет найти приближённое значение корня из любого действительного числа с любой наперёд заданной точностью. Такой способ может быть освоен даже школьником. К недостаткам способа можно отнести увеличивающуюся сложность вычисления с увеличением количества найденных цифр.

Для ручного извлечения корня применяется запись, похожая на деление столбиком. Выписывается число, корень которого ищем. Справа от него будем постепенно получать цифры искомого корня. Пусть извлекается корень из числа с конечным числом знаков после запятой. Для начала мысленно или метками разобьём число N на группы по две цифры слева и справа от десятичной точки. При необходимости, группы дополняются нулями — целая часть дополняется слева, дробная справа. Так 31234.567 можно представить, как 03 12 34 . 56 70. В отличие от деления снос производится такими группами по 2 цифры.

1. Записать число (в примере — 69696) на листке.
2. Найти , квадрат которого меньше или равен группе старших разрядов числа (старшая группа — самая левая не равная нулю), а квадрат больше группы старших разрядов числа. Записать найденное справа от N (это очередная цифра искомого корня). (На первом шаге примера , а ).
3. Записать квадрат под старшей группой разрядов. Провести вычитание из старшей группы разрядов выписанного квадрата числа и записать результат вычитания под ними.
4. Слева от этого результата вычитания провести вертикальную черту и слева от черты записать число равное уже найденным цифрам результата (мы их выписываем справа от N) умноженное на 20. Назовём это число . (На первом шаге примера это число просто есть , на втором ).
5. Произвести снос следующей группы цифр, то есть дописать следующие две цифры числа справа от результата вычитания. Назовем число, полученное соединением результата вычитания и очередной группы из двух цифр. (На первом шаге примера это число , на втором ). Если сносится первая группа после десятичной точки числа , то нужно поставить точку справа от уже найденных цифр искомого корня.
6. Теперь нужно найти такое , что меньше или равно , но больше, чем . Записать найденное справа от N, как очередную цифру искомого корня. Вполне возможно, что окажется равным нулю. Это ничего не меняет — записываем 0 справа от уже найденных цифр корня. (На первом шаге примера это число 6, так как , но ) Если число найденных цифр уже удовлетворяет искомой точности прекращаем процесс вычисления.
7. Записать число под . Провести вычитание столбиком числа из и записать результат вычитания под ними. Перейти к шагу 4.

Наглядное описание алгоритма:

См. также

Примечания

1. ↑ «Корнем n-й степени из числа x называется число, n-я степень которого совпадает с x. При n = 2 и n = 3 корни называются соответственно квадратным и кубическим.» — определение из статьи «Алгебра» энциклопедии «Кругосвет»
2. ↑ «Извлечь корень n-й степени из числа а — это значит найти такое число (или числа) x, которое при возведении в n-ю степень даст данное число ()… Корень 2-й степени называется квадратным» — определение из статьи «Извлечение корня» «Большой советской энциклопедии» третьего издания.
3. ↑ Теорема Лиувилля о приближении алгебраических чисел
4. ↑ См. А. Я. Хинчин, Цепные дроби, М. ГИФМЛ, 1960, §§ 4, 10.
5. ↑ Фихтенгольц, Григорий Михайлович. Курс дифференциального и интегрального исчисления Том. 1. Введение, § 4 // Мат. анализ на EqWorld
6. ↑ Г.Корн, Т.Корн. Справочник по математике (для научных работников и инженеров). М., 1974 г., п. 1.2.1
7. ↑ Фихтенгольц, гл. 2, § 1
8. ↑ См., например: Гантмахер Ф. Р., Теория матриц, М.: Гос. изд-во технико-теоретической литературы, 1953, или: Воеводин В., Воеводин В., Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ, Спб.: БХВ-Петербург, 2006.
9. ↑ См., например: Ершов Л. В., Райхмист Р. Б., Построение графиков функций, М.: Просвещение, 1984, или: Каплан И. А., Практические занятия по высшей математике, Харьков: Изд-во ХГУ, 1966.
10. ↑ См., например: Хатсон В., Пим Дж., Приложения функционального анализа и теории операторов, М.: Мир, 1983, или: Халмош П., Гильбертово пространство в задачах, М.: Мир, 1970.
11. ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. (ГЛАВА III Геометрические построения. Алгебра числовых полей)
12. ↑ Р. Курант Г. Роббинс Что такое математика? МЦНМО, 2000. Стр. 148

Ссылки

Квадратный корень из степени

Прежде чем преступать к изучению новой темы, давайте вспомним определение модуля числа.

Итак, модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А (а).

Также модулем положительного числа называется само это число.

Модуль числа нуль равен нулю.

А модулем отрицательного числа называется противоположное ему число.

Задание: найти значение выражения , при  и при .

Легко заметить, что в первом примере в ответе тоже получается . Обратите внимание, в каждом из рассмотренных примеров, корень из квадрата числа равен модулю этого числа.

Теорема: При любом значении х верно равенство:

                         

Следовательно, При любом  значение выражения  совпадает со значением выражения .

Равенство  является тождеством.

Это тождество применяется при извлечении квадратного корня из степени с чётным показателем. Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .

Например: преобразуем выражения:

Задание 2: найдите значение выражения.

Итоги:

При любом значении икс верно равенство: .

Это равенство является тождеством и применяется при извлечении квадратного корня из степени с чётным показателем.

Чтобы извлечь корень из степени с чётным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством: .

Обсуждение:Квадратный корень — Википедия

Материал из Википедии — свободной энциклопедии

Корень уравнения и корень квадратный[править код]

Корень уравнения и корень квадратный почему называются одинаково? Кто назвал арифметические корни — корнями? И почему? —Nashev 08:07, 7 апреля 2013 (UTC)

Есть способ вычисления квадратного корня, основанный на свойствах нечетных чисел: Корень из 49 = 1 + 3 + 5 + 7 + 9 + 11 + 13 (7 сложений) Способ похож на метод столбиком, но есть различия. —Sergei Frolov 09:42, 12 января 2016 (UTC)

Что за ересь тут написана?[править код]

С каких это пор знак радикала стал означать т.н. алгебраический корень?

Ересь пропагандирует богопротивная Математическая энциклопедия, том 4, стр. 802:

Радикал — математический знак {\displaystyle {\sqrt {}}}, к-рым обозначают извлечение корня, т. е. решение двучленного алгебраич. уравнения вида xn−a=0{\displaystyle x^{n}-a=0}. Под символом a{\displaystyle {\sqrt {a}}} подразумевается один из корней этого уравнения.

Об арифметическом корне см. Арифметический корень. Ещё вопросы есть? LGB (обс.) 10:16, 8 сентября 2019 (UTC)

В отрывке из энциклопедии написано, что обозначается один из корней, а не все корни. Запись 9=±3{\displaystyle {\sqrt {9}}=\pm 3} можно считать безграмотной. Взгляните хотя бы на англ вариант статьи. По-моему выносить крайне редкое обозначение, которое неудобно из-за его неоднозначности (a{\displaystyle {\sqrt {a}}} — получается множество, а вовсе не число) как основное — крайне странно. И статья вроде как не называется «алгебраический корень», а называется просто квадратный корень.