| 1 | Вычислить | 2+2 | |
| 2 | Вычислить | 2^3 | |
| 3 | Вычислить | 4^2 | |
| 4 | Разложить на простые множители | 73 | |
| 5 | Вычислить | 6/2(1+2) | |
| 6 | Найти объем | сфера (5) | |
| 7 | Найти площадь | окружность (5) | |
| 8 | Вычислить | корень четвертой степени -625 | |
| 9 | Вычислить | -5^2 | |
| 10 | Вычислить | 2^4 | |
| 11 | Найти площадь поверхности | сфера (5) | |
| 12 | Вычислить | -3^2 | |
| 13 | Вычислить | 2^5 | |
| 14 | Вычислить | 6÷2(1+2) | |
| 15 | Вычислить | 3^2 | |
| 16 | Преобразовать в десятичную форму | 1/4 | |
| 17 | Вычислить | (-3)^3 | |
| 18 | Вычислить | -2^2 | |
| 19 | Вычислить | 2^2 | |
| 20 | Вычислить | 6^2 | |
| 21 | Вычислить | квадратный корень 3* квадратный корень 12 | |
| 22 | Вычислить | (-4)^2 | |
| 23 | Вычислить | -7^2 | |
| 24 | Преобразовать в десятичную форму | 3/4 | |
| 25 | Преобразовать в десятичную форму | 7/8 | |
| 26 | Вычислить | квадратный корень 28+ квадратный корень 63 | |
| 27 | Преобразовать в десятичную форму | 2/3 | |
| 28 | Найти площадь | окружность (7) | |
| 29 | Найти площадь | окружность (2) | |
| 30 | Вычислить | ||
| 31 | Разложить на простые множители | 6 | |
| 32 | Преобразовать в обыкновенную дробь | 0.75 | |
| 33 | Вычислить | — корень четвертой степени 625 | |
| 34 | Найти площадь | окружность (4) | |
| 35 | Преобразовать в десятичную форму | 3/8 | |
| 36 | Вычислить | 4^3 | |
| 37 | Разложить на простые множители | 8 | |
| 38 | Вычислить | 5^3 | |
| 39 | Преобразовать в десятичную форму | 3/8 | |
| 40 | Найти площадь | окружность (6) | |
| 41 | Преобразовать в десятичную форму | 3/4 | |
| 42 | Вычислить | (-4)^3 | |
| 43 | Вычислить | 3^3 | |
| 44 | Разложить на простые множители | 4 | |
| 45 | Найти объем | сфера (4) | |
| 46 | Перевести в процентное соотношение | 1/8 | |
| 47 | Найти площадь | окружность (3) | |
| 48 | Преобразовать в десятичную форму | 2/5 | |
| 49 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 50 | Вычислить | 5^2 | |
| 51 | Вычислить | (-2)^4 | |
| 52 | Разложить на простые множители | 2 | |
| 53 | Вычислить | корень четвертой степени 256 | |
| 54 | Вычислить | квадратный корень 81 | |
| 55 | Преобразовать в десятичную форму | 1/2 | |
| 56 | Вычислить | -4^2 | |
| 57 | Вычислить | -9^2 | |
| 58 | Вычислить | (-5)^2 | |
| 59 | Вычислить | (-8)^2 | |
| 60 | Разложить на простые множители | 741 | |
| 61 | Разложить на простые множители | 9 | |
| 62 | Найти объем | сфера (3) | |
| 63 | Вычислить | 3 квадратный корень 8*3 квадратный корень 10 | |
| 64 | Найти площадь | окружность (10) | |
| 65 | Найти площадь | окружность (8) | |
| 66 | Вычислить | -8^2 | |
| 67 | Вычислить | (-5)^3 | |
| 68 | Вычислить | (-2)^3 | |
| 69 | Вычислить | 10^6 | |
| 70 | Вычислить | 10^2 | |
| 71 | Вычислить | -6^2 | |
| 72 | Преобразовать в десятичную форму | 1/5 | |
| 73 | Преобразовать в десятичную форму | 4/5 | |
| 74 | Преобразовать в десятичную форму | 10% | |
| 75 | Найти площадь поверхности | сфера (6) | |
| 76 | Перевести в процентное соотношение | 3/5 | |
| 77 | Вычислить | (-2)^2 | |
| 78 | Разложить на простые множители | 12 | |
| 79 | Разложить на простые множители | 1162 | |
| 80 | Вычислить | 6^3 | |
| 81 | Вычислить | -3^4 | |
| 82 | Вычислить | 2^2 | |
| 83 | Вычислить | (-6)^2 | |
| 84 | Вычислить | (-7)^2 | |
| 85 | Найти площадь | окружность (1) | |
| 86 | Преобразовать в десятичную форму | 2/5 | |
| 87 | Вычислить | квадратный корень 2+ квадратный корень 2 | |
| 88 | Вычислить | 2^1 | |
| 89 | Вычислить | 2^6 | |
| 90 | Разложить на простые множители | what is the prime factoriztion of 40 use exponents to show any repeated prime factors | what is the prime factoriztion of use exponents to show any repeated prime factors |
| 91 | Вычислить | -2^3 | |
| 92 | Вычислить | 3^5 | |
| 93 | Вычислить | (-9)^2 | |
| 94 | Вычислить | 4^1 | |
| 95 | Вычислить | квадратный корень 100 | |
| 96 | Преобразовать в десятичную форму | 25% | |
| 97 | Найти длину окружности | окружность (5) | |
| 98 | Найти площадь поверхности | сфера (6) | |
| 99 | Найти объем | сфера (2) | |
| 100 | Найти объем | сфера (6) | |
www.mathway.com
2 в степени 2 в степени корень из 2 равно ?
2 во 2-ой степени равно 4.
2 во 2 степени 4^ означает степень Вопрос задан неясно, возможны два варианта толкования: а) (2^2)^koren(2), б) 2^(2^koren(2)). Ответы: а) 7.102993301… б) 6.342906794…
Это будет по идее трансцендентное число, потому что 2 в степени корень из двух — трансцендентное число.
touch.otvet.mail.ru
что значит число в степени 1/2 и -1/2?
в степени 1/2 это корень от числа, а -1/2 корень от перевернутого числа. например 3 в степени 1/2 это корень квадратный из 3, а в степени -1/2 это корень квадратный из 1/3
Дробный показатель означает корень, степень которого равен знаменателю, а числительпоказывает в какой степени взято число, которое записывается под знаком корня. Число в степени 1/2 = корню квадратному из этого числа. А вот такой пример: а в степени 3/5=корню пятой степени из а в третьей степени. Отрицательный показатель говорит а том, что вся эта степень переносится в знаменатель, но уже с положительным показателем. Например «а» в степени (-2)=1/а в квадрате. Число в степени (-1/2)= 1/число в степени 1/2= 1/корень квадратный из числа.
Это 0,5, проще пол литра.
1.1.5 Корень степени n > 1 и его свойства
Видеоурок 1: Степени и корни
Видеоурок 2: Свойства корня степени n > 1
Лекция: Корень степени n > 1 и его свойства
 Корень
Корень
Предположим, Вы имеете уравнение вида:
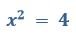
Решением данного уравнения будет х1 = 2 и х2 = (-2). В качестве ответа подходят оба решения, поскольку числа с равными модулями при возведении в четную степень дают одинаковый результат.
Это был простой пример, однако, что мы можем сделать в том случае, если, например,
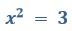
Давайте попробуем построить график функции y=x2. Её графиком является парабола:

На графике необходимо найти точки, которым соответствует значение у = 3. Данными точками является:

Это означает, что данное значение нельзя назвать целым числом, но можно представить в виде корня квадратного.
Любой корень — это иррациональное число. К иррациональным числам относятся корни, непериодические бесконечные дроби.
Квадратный корень — это неотрицательное число «а», подкоренное выражение которого равно данному числу «а» в квадрате.

Например,

То есть в результате мы получим только положительное значение. Однако в качестве решения квадратного уравнения вида

Решением будет х1 = 4, х2 = (-4).
 Свойства квадратного корня
Свойства квадратного корня
1. Какое бы значение не принимала величина x, данное выражение верно в любом случае:
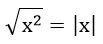
2. Сравнение чисел, содержащих квадратный корень. Чтобы сравнить данные числа, необходимо и одно, и второе число внести под знак корня. То число будет больше, чье подкоренное выражение больше.

Вносим число 2 под знак корня

А теперь давайте внесем число 4 под знак корня. В результате этого получим

И только теперь два полученных выражения можно сравнить:

3. Вынесение множителя из под корня.
Если подкоренное выражение может разложиться на два множителя, один из которых можно вынести из под знака корня, то необходимо пользоваться данным правилом.
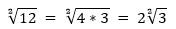
4. Существует свойство, обратное данному — внесение множителя под корень. Этим свойством мы заведомо воспользовались во втором свойстве:

 Корень степени n > 1
Корень степени n > 1
Под корнем n-ой степени некоторого числа «a» понимают число, которое при возведении в степень «n» даст число «а».
Иными словами можно сказать, что это решение следующего уравнения:

Например,
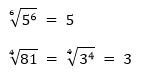
Если под корнем некоторой степени стоит степень, то для вынесения данного числа из под знака корня следует показатель степени разделить на степень корня.

cknow.ru