Формула корней квадратного уравнения
Мы с вами уже знаем, что Квадратным уравнением называется уравнение вида , где – переменная, , и – некоторые числа, причем .
В алгебре, геометрии, физике и др. науках очень часто решение задачи сводится к нахождению корней квадратных уравнений. Поэтому очень важно научиться решать квадратные уравнения.
Решить уравнение:
Мы с вами решили это уравнение методом выделения полного квадрата, т.е. применили формулу квадрата разности.
Решить уравнение:
Мы
снова нашли корни уравнения методом выделения полного
квадрата. Но этот метод частенько приводит к громоздким преобразованиям.
Поэтому древние математики вывели формулу корней квадратного уравнения,
которую можно применять при решении любого квадратного уравнения.
Можно получить эти формулы, решая квадратное уравнение в общем виде методом выделения полного квадрата.
Итак, рассмотрим квадратное уравнение общего вида , где .
Мы с вами определили, что знак дроби, записанной в правой части уравнения зависит от знака дискриминанта. Поэтому при решении этого уравнения возможны три случая.
Первый случай:
Вывод: уравнение , при , имеет два различных корня. Которые находят по формулам:
Обычно эти формулы объединяют в одну, записывая её следующим образом:
Второй случай:
Вывод: уравнение , при ,имеет единственный корень. Который вычисляется по формуле:
Третий случай:
Вывод:
уравнение , при ,не имеет корней.Таким образом: в зависимости от значения дискриминанта квадратное уравнение , может иметь:
1. Два различных корня: . При .
Два различных корня: . При .
2. Один корень: . При .
3. Не имеет корней. При .
Запишем алгоритм решения квадратных уравнений.
Задание: решить уравнения.
Обратите внимание, второй коэффициент в начальном уравнении чётный. Есть формула корней квадратного уравнения с чётным вторым коэффициентом. С помощью неё удобнее вычислять корни. Давайте выведем её.
Давайте найдём корни последнего уравнения по новой формуле.
Итоги:
Выражение называется дискриминантом квадратного уравнения.
При решении квадратного уравнения возможны три случая в зависимости от знака дискриминанта:
1) Если , то уравнение имеет два различных корня, которые вычисляются по формуле: .
2)
Если ,
то уравнение имеет единственный корень, который вычисляется по формуле .
3) Если , то уравнение не имеет корней.
Формула корней квадратного уравнения — презентация онлайн
Формула корнейквадратного уравнения.
Презентация Ликизюк М.И.
Цели и задачи урока
• Выработать умение применять квадратные
уравнения для решения алгебраических и
геометрических задач; продолжить формирование
практических и теоретических умений и навыков по
теме “Квадратные уравнения”;
• Способствовать умению анализировать условие
задач, развитию умения рассуждать, развитию
познавательного интереса, умению видеть связь
между математикой и окружающей жизнью;
• Воспитывать внимательность и культуру
мышления, самостоятельность и взаимопомощь.
План урока
1.Организационный момент.
Постановка целей и задач урока.
2. Фонетическая зарядка.
3. Устный опрос. Устный счет.
4. Изучение нового материала.
5.
 Закрепление. Решение примеров.
Закрепление. Решение примеров.6. Физ.минутка.
7. Обобщение.
8.Итог урока
9.Домашняя работа.
Говори правильно на уроке.
Коэффициент
Корень
Дискриминант
Переменная
Устный опрос
• 1.Дайте определение квадратного
уравнения, приведите примеры.
• 2.Назовите коэффициенты а , в , с в
уравнениях: 3×2-5x+2=0; -5×2+3x-7=0,
• x2+2x=0; 4×2-5=0
• 3. Дайте определение приведённого
квадратного уравнения , приведите
примеры.
• 4.Назовите приведённое квадратное
коэффициент и свободный член равны 2(3)
Устный счет
370+230=
:50=
∙30=
+340=
+14=
7,2:1000=
0,6∙100000=
1200:10000=
0,125∙1000000=
75:100000=
Определение квадратного
уравнения.
Опр. 1. Квадратным уравнением
называется уравнение вида ах2 + bх + с = 0,
где х –переменная, а, b и с — некоторые
числа, причем а 0.
Числа а, b и с — коэффициенты
квадратного уравнения.
 Число а называют
Число а называютпервым коэффициентом, b – вторым
коэффициентом и с – свободным членом.
С
Дискриминант квадратного
уравнения
Опр. 2. Дискриминантом квадратного
уравнения ах2 + bх + с = 0 называется
выражение b2 – 4ac.
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D 0
D 0
D 0
Если D 0
В этом случае уравнение ах2 + bх + с = 0
имеет два действительных корня:
b D
x1
2a
b D
и x2
.
2a
Памятка
Задачи
Решить уравнение 2х² — 5х +2=0
Решить уравнение 2х² — 3х +5=0
Решить уравнение х² -2х +1=0
Решить уравнение 2×2- 5x + 2 = 0
Здесь a = 2, b = -5, c = 2.
Имеем D = b2- 4ac = (-5)2- 4 2 2 = 9.
Так как D > 0, то уравнение имеет два корня.
Найдем их по формуле
5 3
1
x1
2 2
2
и
5 3
x2
2,
2 2
то есть x1 = 2 и x2 = 0,5 — корни заданного уравнения.
К задачам
Решить уравнение 2×2- 3x + 5 = 0
Здесь a = 2, b = -3, c = 5.

Найдем дискриминант D = b2- 4ac=
= (-3)2- 4·2·5 = -31, т.к. D
уравнение
не имеет действительных корней.
К задачам
Решить уравнение x2- 2x + 1 = 0
Здесь a = 1, b = -2, c = 1.
Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0
x
;
2a
2
x
1 .
2 1
Получили один корень х = 1.
К задачам
№1. Решите
уравнения:
а) х2+7х-44=0;
б) 9у2+6у+1=0;
в) –2t2+8t+2=0;
г) а+3а2= -11.
д) х2-10х-39=0;
е) 4у2-4у+1=0;
ж) –3t2-12t+6=0;
3) 4а2+5= а.
№2. а)При каких
значениях х равны
значения многочленов:
(1-3х)(х+1) и (х-1)(х+1)?
Б)При каких
значениях х равны
значения многочленов:
(2-х)(2х+1) и (х-2)(х+2)?
Ответы
№1.
А)х=-11, х=4
Б)y=-1/3
В)t=2±√5
Г)нет решения
Д)х=-3, х=13
Е)у=1/2
Ж)t=-2±√6
З)нет решения
№2
А)х=1/2, х=-1
Б)х=2, х=-1С
Итог урока.
• 1.Что вы узнали нового на уроке?
• 2.
 Чему равен D?
Чему равен D?• 3.Сколько корней имеет
уравнение , если
• D>0
• D
• D=0?
Найди «лишнее»
3х 8 х 11 0;
2
у 2 х 7 х 3;
2
2 х 9 0;
2
Свойства и способы поиска корней квадратного уравнения
Мир устроен так, что решение большого количества задач сводится к нахождению корней квадратного уравнения. Корни уравнений имеют важное значение для описания различных закономерностей. Это было известно еще землемерам древнего Вавилона. Астрономы и инженеры тоже были вынуждены решать такие задачи. Еще в VI веке нашей эры индийский ученый Ариабхата разработал основы нахождения корней квадратного уравнения. Формулы приобрели законченный вид в XIX веке.
Общие понятия
Предлагаем ознакомиться с основными закономерностями квадратичных равенств. В общем виде равенство может быть записано так:
ax2 + bx + c = 0,
Число корней квадратного уравнения может быть равно одному или двум. Быстрый анализ можно провести, используя понятие дискриминант:
D = b2 — 4ac
В зависимости от вычисленного значения получаем:
- При D > 0 существуют два различных корня.
 Формула в общем виде для определения корней квадратного уравнения выглядит как (-b± √D) / (2a).
Формула в общем виде для определения корней квадратного уравнения выглядит как (-b± √D) / (2a). - D = 0, в этом случае корень один и соответствует значению x = -b / (2a)
- D < 0, для отрицательного значения дискриминанта решения уравнения не существует.
Замечание: если дискриминант отрицательный, уравнение не имеет корней только в области вещественных чисел. Если алгебру расширить до понятия комплексных корней, то уравнение имеет решение.
Приведем цепочку действий, подтверждающую формулу нахождения корней.
Из общего вида уравнения, следует:
ax2 + bx = -c
Правую и левую части умножаем на 4a и добавляем b2, получаем
4a2x2 + 4abx + b2 = -4ac+b2
Преобразуем левую часть в виде квадрата многочлена (2ax + b)2. Извлекаем квадратный корень из обеих частей уравнения 2ax + b= -b ± √(-4ac + b2), переносим коэффициент b в правую часть, получим:
2ax = -b ± √(-4ac + b2)
Отсюда следует:
x = (-b ± √(b2 — 4ac))
Что и требовалось показать.
Частный случай
В некоторых случаях решение задачи может упроститься. Так, при четном коэффициенте b получим более простую формулу.
Обозначим k = 1/2b, тогда формула общего вида корней квадратного уравнения принимает вид:
x = (-k ± √(k2 — ac)) / a
При D = 0, получаем x = -k / a
Другим частным случаем будет решение уравнения при a = 1.
Для вида x2 + bx + c = 0 корни будут x = -k ± √(k2 — c) при дискриминанте больше 0. Для случая когда D = 0, корень будет определяться простой формулой: x = -k.
Использование графиков
Любой человек, даже не подозревая этого, постоянно сталкивается с физическими, химическими, биологическими и даже социальными явлениями, которые хорошо описываются квадратичной функцией.
Замечание: кривая, построенная на основании квадратичной функции, получила название параболы.
Приведем несколько примеров.
- При расчете траектории полета снаряда используют свойство движения по параболе тела, выпущенного под углом к горизонту.

- Свойство параболы равномерно распределять нагрузку широко используется в архитектуре.
Понимая всю важность параболической функции, разберемся, как с помощью графика исследовать ее свойства, используя понятия «дискриминант» и «корни квадратного уравнения».
В зависимости от величины коэффициентов a и b, существует всего шесть вариантов положения кривой:
- Дискриминант положительный, a и b имеют разные знаки. Ветви параболы смотрят вверх, у квадратичного уравнения два решения.
- Дискриминант и коэффициент b равны нулю, коэффициент a больше нуля. График расположен в положительной зоне, уравнение имеет 1 корень.
- Дискриминант и все коэффициенты имеют положительные значения. У квадратичного уравнения нет решения.
- Дискриминант и коэффициент а — отрицательные, b — больше нуля. Ветви графика направлены вниз, у уравнения два корня.
- Дискриминант и коэффициент b равны нулю, коэффициент a — отрицательный. Парабола смотрит вниз, у уравнения один корень.

- Значения дискриминанта и всех коэффициентов — отрицательные. Решений нет, значения функции полностью в отрицательной зоне.
Замечание: вариант a = 0 не рассматривается, так как в этом случае парабола вырождается в прямую.
Все сказанное хорошо иллюстрирует рисунок, представленный ниже.
Примеры решения задач
Условие: используя общие свойства, составьте квадратное уравнение, корни которого равны между собой.
Решение:
по условию задачи x1 = x2, или -b + √(b2 — 4ac) / (2a) = -b + √(b2 — 4ac) / (2a). Упрощаем запись:
-b + √(b2 — 4ac) / (2a) — (-b — √(b2 — 4ac) / (2a)) = 0, раскрываем скобки и приводим подобные члены. Уравнение принимает вид 2√(b2 — 4ac) = 0. Это утверждение верно, когда b2 — 4ac = 0, отсюда b2 = 4ac, тогда значение b = 2√(ac) подставляем в уравнение
ax2 + 2√(ac)x + c = 0, в приведенном виде получаем x2 + 2√(c / a)x + c = 0.
Ответ:
при a не равном 0 и любом c существует только одно решение, если b = 2√(c / a).
Квадратные уравнения при всей своей простоте имеют большое значение в инженерных расчетах. Практически любой физический процесс можно описать с некоторым приближением, используя степенные функции порядка n. Квадратное уравнение будет первым таким приближением.
Дискриминант – объяснение, формула и связь между корнями и дискриминантом
Квадратичный означает переменную, которая умножается сама на себя. Операция по существу включает возведение в квадрат. Общее квадратное уравнение –
ax2 + bx + c = 0
С помощью этой формулы можно найти корни квадратного уравнения. Этот корень относится к значению, представленному «x».
Что такое Дискриминантная квадратичная функция?
Квадратная формула: квадратичная формула.Он представлен как b²-4ac, а дискриминант может быть нулевым, положительным или отрицательным. Он указывает, будет ли решение отсутствовать, будет одно решение или два решения.
Он указывает, будет ли решение отсутствовать, будет одно решение или два решения.
Формула дискриминантной алгебры имеет следующие характеристики: —
Когда дискриминант равен нулю, это показывает, что существуют повторяющиеся действительные решения квадратного уравнения;
Для отрицательного дискриминанта ни одно из решений не является действительным числом;
Для положительного дискриминанта существуют два различных решения квадратного уравнения в виде действительных чисел.
Следующее квадратное уравнение покажет ряд решений, которые покажут учащимся, как найти дискриминант.
Например, данное квадратное уравнение имеет вид –
6×2 + 10x – 1 = 0
Из приведенного выше уравнения видно, что:
a = 6,
b = 10,
c = — 1
Применение чисел в дискриминанте –
b2 − 4ac
= 102 – 4 (6) (-1)
= 100 + 24
= 124
Учитывая, что дискриминант положительный, , есть два решения квадратного уравнения.
Связь между корнями и дискриминантом
Связь между дискриминантом и корнями можно понять из следующих случаев: , корни квадратного уравнения вещественные и неравные.
Здесь
a, b, c = действительные числа
a ≠ 0
дискриминант = ноль
Тогда корни квадратного уравнения действительны и равны.
Здесь
a, b, c = действительные числа
a ≠ 0
дискриминант = минус
Тогда корни квадратного уравнения не действительны и не равны. В этом случае корни составляют мнимые
Здесь
a, b, c = действительные числа
a ≠ 0
Дискриминант = положительный и полный квадрат
Тогда корни квадратного уравнения неравны, реальный и рациональный.
Что следует помнить при использовании квадратичной формулы
Абсолютно необходимо, чтобы уравнение было составлено правильно, иначе решение не может быть получено
Убедитесь, что 2a и квадратный корень из всего (b2 − 4ac) помещается в знаменатель
Обратите внимание на отрицательное значение b2.
 Поскольку оно не может быть отрицательным, обязательно измените его на положительное. Квадрат положительного или отрицательного всегда будет положительным
Поскольку оно не может быть отрицательным, обязательно измените его на положительное. Квадрат положительного или отрицательного всегда будет положительнымСохраняйте +/-. Обратите внимание на два решения
При использовании калькулятора число должно быть округлено до определенного числа знаков после запятой
Для подробного понимания дискриминанта вы можете воспользоваться онлайн-курсами или материалами в формате PDF Веданту .
Дискриминант квадратного уравнения
Дискриминант квадратного уравненияЧасть 3
Сегодня я хотел бы продолжить наш разговор о дискриминанте квадратного уравнения.Вы можете просмотреть части 1 и 2 этого обсуждения здесь:
Дискриминант квадратного уравнения. Часть 1
Дискриминант квадратного уравнения. Часть 2
Напомним, что дискриминант квадратного уравнения ax 2 + bx + c = 0 есть величина Δ03 Δ = б 2 – 4 ак То есть дискриминант — это просто выражение, стоящее под квадратным корнем в квадратной формуле. На прошлой неделе я попросил вас решить следующую задачу: Пример: Найдите дискриминант x 2 Обязательно попробуйте решить эту проблему самостоятельно, прежде чем читать следующее решение. Решение: В этом вопросе a = 1, b = 8 и c = 7. Таким образом, дискриминант равен Δ = b 2 – 4 ac = 8 2 – 4(1)(7) = 64 – 28 = 36 . Поскольку дискриминант положителен, отсюда следует, что два корня квадратного уравнения являются различными действительными числами. Более того, поскольку 36 — полный квадрат (6 2 = 36), его корни на самом деле рациональны. График функции y = x 2 + 8 x + 7 представляет собой направленную вверх параболу, пересекающую ось x в двух точках. Примечания: (1) В этом примере мы можем легко найти два корня уравнения, разложив на множители: x 2 + 8 x + 7 = 0 Таким образом, два корня равны –1 и –7. (2) Мы знаем, что парабола направлена вверх, потому что a = 1 > 0, (3) Также очень легко найти точку пересечения и параболы. Мы просто подставляем 0 вместо x в уравнение. Таким образом, мы получаем y = 7. Отсюда следует, что точка пересечения y параболы есть точка (0,7). До сих пор мы рассматривали случаи, когда дискриминант равен 0 и положителен.

( x + 1) ( x + 7) = 0
x + 1 = 0 или x + 7 = 0
x = –1 или x = –7 
Если дискриминант квадратного уравнения x 2 + bx + c = 0 отрицательный, то в квадратной формуле мы получаем отрицательное число под квадратным корнем. Квадратный корень из отрицательного числа является мнимым числом. Таким образом, мы получаем два сложных решения.
графически, если дискриминант отрицательный, график функции Y = AX 2 + BX + C — это парабола, которая не пересекается x -ось.
Примером служит желтая парабола на изображении выше.
Пример: Найдите дискриминант x 2 + 4 x + 8 = 0 . Затем опишите природу корней уравнения и опишите график функции y = x 2 + 4 x + 8 .
Завтра я опубликую решение этой задачи, а потом обсужу, что произойдет, если определитель будет отрицательным.Не стесняйтесь публиковать свои собственные решения в комментариях.
Если вам понравилась эта статья, поделитесь ею со своими друзьями на Facebook:
комментариев
комментариев
Видео-вопрос: Использование знака дискриминанта для определения числа комплексных корней квадратного уравнения
Стенограмма видео
Сколько невещественных корней будет у квадратного уравнения, если его дискриминант отрицательный?
Прежде чем мы сможем ответить на этот вопрос, давайте начнем с определения некоторых ключевых терминов.Квадратное уравнение имеет вид 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю. В этом примере мы будем думать исключительно о значениях 𝑎, 𝑏 и 𝑐, которые являются действительными числами. Но для любого квадратного уравнения 𝑎 не может быть равно нулю. Корнями этого квадратного уравнения являются решения или значения 𝑥, которые удовлетворяют 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю. И затем вопрос спрашивает нас, сколько невещественных корней будет у него, если дискриминант отрицателен.
Корнями этого квадратного уравнения являются решения или значения 𝑥, которые удовлетворяют 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю. И затем вопрос спрашивает нас, сколько невещественных корней будет у него, если дискриминант отрицателен.
Итак, что мы подразумеваем под дискриминантом? Что ж, чтобы ответить на это, вспомним квадратную формулу.Это говорит нам о том, что решения уравнения 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю: 𝑥 равно отрицательному 𝑏 плюс или минус квадратный корень из 𝑏 в квадрате минус четыре 𝑎𝑐 по всем двум 𝑎. Дискриминант — это выражение внутри квадратного корня. Мы используем Δ для его представления, и это 𝑏 в квадрате минус четыре 𝑎𝑐.
Отсюда следует, что если дискриминант, если 𝑏 в квадрате минус четыре 𝑎𝑐, положителен, когда мы извлекаем квадратный корень, мы получаем действительное решение. И, в частности, если дискриминант положителен, квадратный корень является ненулевым действительным числом.Это означает, что когда у нас есть положительный дискриминант, у квадратного уравнения есть два действительных решения. Другими словами, есть два действительных корня. Однако, если дискриминант равен нулю, мы берем квадратный корень из нуля, который равен нулю. Это означает, что наши решения 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю просто отрицательные 𝑏 более двух 𝑎. Итак, это на самом деле одно решение. Итак, когда дискриминант равен нулю, мы получаем один действительный корень.
Другими словами, есть два действительных корня. Однако, если дискриминант равен нулю, мы берем квадратный корень из нуля, который равен нулю. Это означает, что наши решения 𝑎𝑥 в квадрате плюс 𝑏𝑥 плюс 𝑐 равно нулю просто отрицательные 𝑏 более двух 𝑎. Итак, это на самом деле одно решение. Итак, когда дискриминант равен нулю, мы получаем один действительный корень.
А если дискриминант отрицательный, как в этом вопросе? Что ж, если оно отрицательное, мы извлекаем квадратный корень из отрицательного числа, что дает нам мнимое решение.Это означает, что на самом деле нет никаких реальных корней. Вместо этого мы получаем комплексные корни. Но сколько комплексных корней мы получим? Что ж, давайте предположим, что когда мы берем квадратный корень из 𝑏 в квадрате минус четыре 𝑎𝑐, мы получаем некоторое значение 𝑑, умноженное на 𝑖, где 𝑑 — константа, действительная константа, а 𝑖 — мнимое число, являющееся решением уравнения 𝑖 квадрат равен минус единице.
В этом случае решения нашего квадратного уравнения: 𝑥 равно отрицательному 𝑏 плюс или минус 𝑑𝑖 по двум 𝑎. Мы можем разделить это на два разных решения 𝑥 sub one и 𝑥 sub two.Это не настоящие, а сложные решения квадратного уравнения. Они отрицательны 𝑏 плюс 𝑑𝑖 больше двух 𝑎 и минус 𝑏 минус 𝑑𝑖 больше двух 𝑎 соответственно. Мы видим, что есть два комплексных решения квадратного уравнения, хотя дискриминант отрицательный.
Мы можем разделить это на два разных решения 𝑥 sub one и 𝑥 sub two.Это не настоящие, а сложные решения квадратного уравнения. Они отрицательны 𝑏 плюс 𝑑𝑖 больше двух 𝑎 и минус 𝑏 минус 𝑑𝑖 больше двух 𝑎 соответственно. Мы видим, что есть два комплексных решения квадратного уравнения, хотя дискриминант отрицательный.
Итак, ответ — два. Квадратное уравнение будет иметь два невещественных корня, если его дискриминант отрицателен.
Квадратичная формула — ChiliMath
Существует несколько методов решения квадратных уравнений.2+бх+с=0}
где a, b и c — действительные числа, но a не равно нулю a \ne 0; а x — неизвестная переменная, мы просто берем значения a, b и c, подставляем их в квадратичную формулу, а затем упрощаем, чтобы найти ответы. Ответы квадратных уравнений называются решениями, нулями или корнями.
Но прежде чем мы сможем применить квадратную формулу, мы должны убедиться, что квадратное уравнение имеет стандартную форму. Квадратное уравнение выражается в стандартной форме , если все переменные и коэффициенты находятся в одной части уравнения, а противоположная через символ равенства равна нулю.2+бх+с=0. Слово «квадратик» произошло от латинского слова « quadratus », что означает «квадрат». В алгебре слово в квадрате обозначает умножение числа или переменной на себя. Обратите внимание, что старший показатель степени переменной x в квадратном уравнении равен 2 (x возведен во 2-ю степень).
Квадратное уравнение выражается в стандартной форме , если все переменные и коэффициенты находятся в одной части уравнения, а противоположная через символ равенства равна нулю.2+бх+с=0. Слово «квадратик» произошло от латинского слова « quadratus », что означает «квадрат». В алгебре слово в квадрате обозначает умножение числа или переменной на себя. Обратите внимание, что старший показатель степени переменной x в квадратном уравнении равен 2 (x возведен во 2-ю степень).
Заметьте также, что в приведенной выше квадратичной формуле есть символ плюс или минус \color{red}\large{ \pm}, который подразумевает, что мы собираемся рассмотреть два случая при поиске решений.2} — 4ac}} } \над {2a}}}
Дискриминант квадратичной формулы дает очень полезную информацию о характере решений. Фактически, он может определить количество и тип решений квадратного уравнения.
Кроме того, при работе с дискриминантом нам все равно, насколько велико или мало число. 2} — 17x + 10.2} — 4\влево( 4\вправо)\влево( 1\вправо)
2} — 17x + 10.2} — 4\влево( 4\вправо)\влево( 1\вправо)
= 16 — 16
= 0
Поскольку дискриминант равен 0, квадратное уравнение имеет \color{red}1 действительное решение.
Проверим, действительно ли квадратное уравнение имеет один действительный корень.
Подставьте значения a, b и c в квадратичную формулу, затем упростите.
Решение: \Large{1 \over 2}. Да, существует только 90 131 одно 90 133 действительное числовое решение, предсказанное дискриминантом.2} — 4\влево( 1\вправо)\влево( 13\вправо)}
\большой{ = 16 — 52}
\большой{ = — 36}
Поскольку дискриминант отрицателен, квадратное уравнение будет иметь два комплексных решения .
Теперь решим уравнение по формуле.
Замените, затем упростите.
Комплексные решения 2 + 3i и 2 — 3i.
Поскольку решения представляют собой комплексные числа, график параболы , а не пересекает или касается оси x.
 Формула в общем виде для определения корней квадратного уравнения выглядит как (-b± √D) / (2a).
Формула в общем виде для определения корней квадратного уравнения выглядит как (-b± √D) / (2a).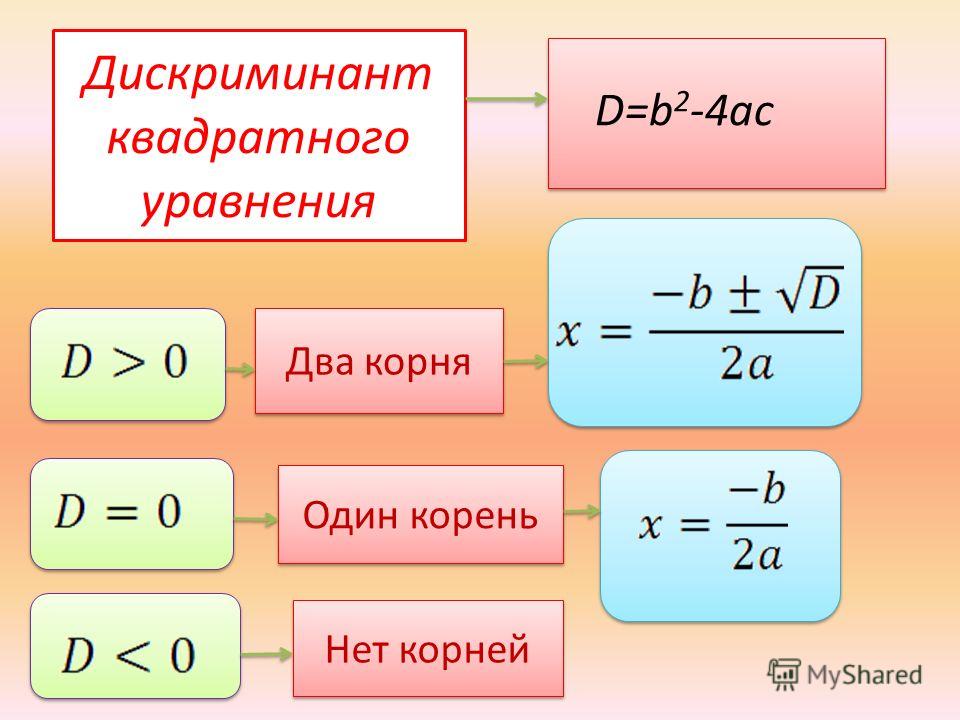

 Поскольку оно не может быть отрицательным, обязательно измените его на положительное. Квадрат положительного или отрицательного всегда будет положительным
Поскольку оно не может быть отрицательным, обязательно измените его на положительное. Квадрат положительного или отрицательного всегда будет положительным