Упаковка кругов в круге — Википедия

Материал из Википедии — свободной энциклопедии

Упаковка кругов в круге — это двумерная задача упаковки, целью которой является упаковка единичных кругов в как можно меньший круг.

^[1]

Эта задача упаковки была поставлена и исследовалась в 60-х годах 20-го века. Кравиц в 1967 опубликовал упаковки до 19 кругов без анализа оптимальности решений^[2]. Годом позже Грэм доказал, что найденные решения с числом кругов до 7 оптимальны^[3], а Пёрл (Pirl), независимо от него, что оптимальны упаковки до 10 кругов^[4]. Лишь в 1994 Мелиссеном (Melissen) была доказана оптимальность решения с 11 кругами^[5]. Фодор (Fodor) показал между 1999 и 2003 годами, что решения с 12^[6], 13^[7] и 19^[8]кругами оптимальны.

Грэм (Graham) и др. около 1998 предложили два алгоритма и нашли с помощью них упаковки до 65 кругов^[9]. Последний обзор задачи и приближённых решений до 2989 кругов (июнь 2014) дал Экард Спехт (Eckard Specht)

[10].

Минимальные решения (в случае существования нескольких минимальных решений показан только один вариант):

• S. Kravitz. Packing cylinders into cylindrical containers // Math. Mag. — 1967. — Т. 40. — С. 65-71.
• F. Fodor. The Densest Packing of 12 Congruent Circles in a Circle // Beiträge zur Algebra und Geometrie, Contributions to Algebra and Geometry. — 2000. — Т. 41. — С. 401–409.
• F. Fodor. The Densest Packing of 13 Congruent Circles in a Circle // Beiträge zur Algebra und Geometrie, Contributions to Algebra and Geometry. — 2003. — Т. 44. — С. 431–440.
• F. Fodor. The Densest Packing of 19 Congruent Circles in a Circle // Geom. Dedicata. — 1999. — Т. 74. — С. 139–145.
• R.L. Graham. Sets of points with given minimum separation (Solution to Problem El921) // Amer. Math. Monthly. — 1968. — Т. 75. — С. 192-193.
• R.L. Graham, B.D. Lubachevsky, K.J. Nurmela, P.R.J. Ostergard.
  Dense packings of congruent circles in a circle. // Discrete Math. — 1998. — С. 181:139–154.
• U. Pirl. Der Mindestabstand von n in der Einheitskreisscheibe gelegenen Punkten // Mathematische Nachrichten. — 1969. — Т. 40. — С. 111-124.
• H. Melissen. Densest packing of eleven congruent circles in a circle // Geometriae Dedicata. — 1994. — Т. 50. — С. 15-25.

Упаковка кругов — Википедия

Статья описывает упаковку кругов на поверхностях. Для связанной статьи об упаковке кругов с заданным графом пересечений, см. статью «Теорема об упаковке кругов».

Наиболее эффективный способ упаковать круги различных размеров не очевиден

В геометрии упаковка кругов — это изучение размещения кругов (одного размера или разных размеров) на заданной поверхности таким образом, что они не пересекаются и круги касаются друг друга. Соответствующая плотность упаковки

η размещения — это доля занятой кругами поверхности. Можно обобщить упаковки кругов на более высокие размерности — она называется упаковкой шаров, которая, обычно, работает с одинаковыми сферами.

В то время как окружности имеют относительно низкую максимальную плотность упаковки 0.9069 на евклидовой плоскости, эта плотность не минимальна. «Худшая» фигура упаковки плоскости не известна, хотя сглаженный восьмиугольник имеет плотность упаковки около 0.902414, что является наименьшей максимальной плотностью упаковки, известной для центрально-симметричных выпуклых фигур^[1]. Плотность упаковки вогнутых фигур, таких как звёздчатые многоугольники, может быть произвольно малой.

Ветвь математики, известная как «упаковка кругов», занимается геометрией и комбинаторикой упаковок кругов произвольного размера и из неё подымаются дискретные аналоги конформных отображений, римановых поверхностей и им подобные.

Одинаковые круги в шестиугольной упаковке, самая плотная упаковка. Шестиугольная упаковка естественного расположения одинаковых кругов с переходом на нерегулярное расположение неравных кругов.

Для двумерного евклидова пространства Жозеф Луи Лагранж доказал в 1773, что решётчатая упаковка кругов высшей плотности — это шестиугольная упаковка^[2], в которой центры кругов располагаются на шестиугольной решётке (расположенные зигзагом ряды, подобные сотам), а каждый круг окружён шестью другими окружностями. Плотность такой упаковки равна

ηh=π23≈0.9069.{\displaystyle \eta _{h}={\frac {\pi }{2{\sqrt {3}}}}\approx 0.9069.}

Аксель Туэ привёл первое доказательство, что эта упаковка оптимальна в 1890, показав,что шестиугольная решётка является самой плотной из всех возможных упаковок кругов, как регулярных, так и нерегулярных. Однако это доказательство считалось не вполне полным. Первое полноценное доказательство приписывается Ласло Фейеш Тоту (1940)

[2].

С другой стороны, были обнаружены жёсткие упаковки кругов низкой плотности.

Однородные упаковки[править | править код]

Существует 11 упаковок кругов на основе 11 однородных мозаик плоскости^[3]. В этих упаковках любая окружность может быть отображена на любую другую окружность путём отражения или вращения. Шестиугольные промежутки могут быть заполнены одним кругом, а двенадцатиугольные промежутки могут быть заполнены 7 кругами, образуя 3-однородные упаковки. Усечённая тришестиугольная мозаика^[en] с обоими типами промежутков могут быть заполнена как 4-однородная упаковка. Плосконосая тришестиугольная мозаика имеет две зеркальные формы.

Связанная задача — определение расположения с минимальной энергией одинаково расположенных точек, которые должны лежать на заданной поверхности. Задача Томсона

[en] рассматривает распределение электрических зарядов с наименьшей энергией на поверхности сферы. Задача Таммеса^[en] является обобщением этой задачи и максимизирует минимальное расстояние между кругами на сфере.

Упаковка кругов в простых ограниченных фигурах является общим типом задач занимательной математики. Влияние стен контейнера важно, и шестиугольная упаковка в общем случае не является оптимальной для малого числа кругов.

Компактная упаковка бинарных кругов с наиболее близкими размерами кругов

[4]. Упаковка также является самой плотной упаковкой кругов с этим отношением размеров (отношение 0.6375559772 с отношением упаковки (плотности) 0.910683)^[5]

Существует также ряд задач, которые разрешают размеры кругов быть неоднородными. Одним из таких расширений является задача нахождения максимально возможной плотности системы с двумя размерами кругов (бинарная система). Только девять определённых отношений радиусов позволяют компактную упаковку, в которой, если две окружности касаются, они вместе касаются также ещё двух кругов (если соединить отрезками центры касающихся окружностей, они триангулируют поверхность)^[4]. Для семи таких отношений радиусов известны компактные упаковки, на которых достигается максимальное возможное отношение упаковки (выше, чем для кругов одного диаметра) для смеси кругов данного отношения радиусов. Высшая плотность упаковки — 0.911627478 для отношения радиусов 0.545151042•

[5]^[6].

Также известно, что если отношение радиусов выше 0.742, бинарная смесь не может быть упакована лучше, чем круги одного размера^[5]. Верхние границы, которые могут быть достигнуты такой бинарной упаковкой для меньших отношений радиусов, также получены^[7].

Квадратурная амплитудная модуляция основана на упаковке кругов в круги фазовоамплитудного пространства. Модем передаёт данные как серии точек на 2-мерной фазовоамплитудной плоскости. Расстояния между точками определяет восприимчивость шума при передаче, в то время как диаметр внешней окружности определяет требуемую мощность передатчика. Производительность максимальна, когда сигнальное созвездие кодовых точек находится в центрах плотной упаковки окружностей. На практике часто применяется прямоугольная упаковка для упрощения декодирования.

Упаковка окружностей стала существенным средством в искусстве оригами, так как каждая часть в фигуре оригами требует круг на листе бумаге

[8]. Роберт Лэнг использовал математику упаковки кругов для разработки компьютерных программ, предназначенных для разработки сложных фигур оригами.

1. ↑ Weisstein, Eric W. Smoothed Octagon (англ.) на сайте Wolfram MathWorld.
2. ↑ ^{1 2} Chang, Hai-Chau & Wang, Lih-Chung (2010), «A Simple Proof of Thue’s Theorem on Circle Packing», arΧiv:1009.4322 [math.MG] 
3. ↑ Williams, 1979, с. 35-39.
4. ↑ ^{1 2} Kennedy, 2006, с. 255–267.
5. ↑ ^{1 2 3} Heppes, 2003, с. 241–262.
6. ↑ Kennedy.
7. ↑ de Laat, de Oliveira Filho, Vallentin.
8. ↑ Лекции по современному оригами «Robert Lang on TED.»

Круг (значения) — Википедия

Материал из Википедии — свободной энциклопедии

Перейти к навигации Перейти к поиску

Круг:

• Круг — геометрическая фигура.
• Круг — в переносном значении — цикл.
• Круг — окружение какого-либо лица, сообщество, кружок по интересам.

• Круг, Арнольд (1848—1904) — немецкий пианист и композитор.
• Круг, Вильгельм Траугот (1770—1842) — немецкий философ.
• Круг, Дидерих (1821—1880) — немецкий композитор.
• Круг, Иоганн Леопольд (1770—1843) — экономист, иностранный член и член-корреспондент Петербургской академии наук [1].
• Круг, Ирина Викторовна (род. 1976) — российская певица.
• Круг, Карл Адольфович (1873—1952) — советский электротехник, член-корреспондент АН СССР.
• Круг, Леопольд (1833—1898) — немецкий биолог, этнограф и дипломат.
• Круг, Манфред (1937—2016) — немецкий певец и актёр.
• Круг, Михаил Владимирович ( наст. фамилия: Воробьёв; 1962—2002) — российский певец, автор песен.
• Круг, Тори (род. 1991) — профессиональный американский хоккеист.
• Круг, Филипп Иванович (урождённый Иоганн Филипп Круг, нем. Johann Philipp Krug; 1764—1844) — российский археолог, нумизмат и историк.
• Круг, Хельмут (род. 1956) — футбольный арбитр из Германии.
• Круг фон Нидда, Фридрих Альберт Франц (Krug von Nidda; 1776—1843) — немецкий поэт-романтик.

• «Круг» — советский зенитно-ракетный комплекс.
• «Круг» — московская рок-группа 1980-х гг.
• «Круг» — украинский женский волейбольный клуб из Черкасс.
• Казачий круг — народное собрание у казаков.

Скрытая категория:

Квинтовый круг — Википедия

Материал из Википедии — свободной энциклопедии

Квинтовый круг (или кварто-квинтовый круг) — геометрическое представление хроматической звуковой системы в виде последовательности кварт и/или квинт. В квинтовый круг входят 12 разных высот (высотных классов), при этом предполагается, что квинты/кварты темперированы — именно темперация обеспечивает замкнутость круга. Квинтовый круг традиционно используется в учении о гармонии для визуализации родства мажорно-минорных тональностей.

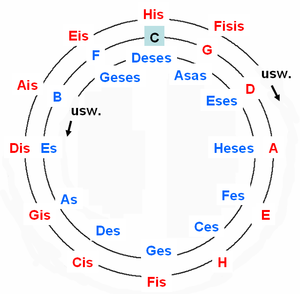Пример 1. Квинтовая спираль (схематическое представление)

Квинтовый круг — не природный феномен (как, например, обертоновый ряд), а схематическая конструкция, замкнутость которой обеспечивается только с учётом энгармонизма темперированных звуковых систем (в Примере 2 показан как Ges/Fis), в многоголосной музыке начиная с XVIII века, как правило,— равномерно темперированной системы. В строях (Пифагоровом, чистом) с использованием чистых квинт/кварт круг не замыкается (см. Пример 1; см. также Комма, Волчья квинта). Теоретическую схему, представляющую такие строи, именуют «квинтовой спиралью».

Квинтовый круг и родство тональностей[править | править код]

Квинтовый круг в мажорно-минорной тональности

В последовательности располагаются мажорные тональности в паре со своими параллельными минорными. При движении по часовой стрелке по квинтовому кругу от до-мажора, тоника каждой последующей тональности (G-D-A-E-H-F♯ мажор, e-h-f♯-c♯-g♯-d♯ минор) отстоит от предыдущей (вверх) на чистую квинту, а в записи при ключе добавляется один диез (в последовательности фа-до-соль-ре-ля-ми-си). При движении против часовой стрелки (F-B-E♭-A♭-D♭-G♭ мажор, d-g-c-f-b-e♭ минор), интервал (восходящий) составляет чистую кварту, а в записи добавляются бемоли (в обратном порядке — си-ми-ля-ре-соль-до-фа).

Так как октава состоит из 12 полутонов, кварта — из 5, а квинта — из 7, то 12 кварт или 12 квинт составляют несколько октав и следовательно тринадцатые тональности, если считать в любую сторону по квинтовому кругу, совпадают с до мажором. Так как 12 взаимно просто с 5 и 7, то все тональности можно получить, рассмотрев любые 12 подряд идущих в кругу. Из этого также следует, что тональности в конце концов совпадут, если двигаться в противоположные стороны (например, Ges = Fis). Поэтому обычно используют не более 5 шагов в каждом направлении, оставляя тональности с большим количеством знаков альтерации (D♭-b, G♭/F♯-e♭/d♯, C#-a#, C♭-a♭ и тональности с двойными диезами и бемолями) только в теории или в качестве упражнений.

Квинтовый круг (в оригинальной терминологии — «колесо») из рукописи «Мусикийской грамматики» Н. Дилецкого (1679)

Исторический очерк и рецепция в музыке[править | править код]

Впервые кварто-квинтовый круг был описан в книге «Идея грамматики мусикийской» (редакция 1679 года). Автор труда — теоретик и композитор Н. П. Дилецкий.

И. С. Бах показал художественную равнозначность всех тональностей в сборнике прелюдий и фуг под названием «Хорошо темперированный клавир». Во всех тональностях кварто-квинтового круга написаны 24 прелюдии Ф. Шопена и Д. Д. Шостаковича, 12 фуг цикла «Ludus tonalis» П. Хиндемита, а также многие другие музыкальные произведения.

• Квинтовый круг // Музыкальная энциклопедия. — М.: Советская энциклопедия, 1974. — Т. 2. — С. 765. — 960 с.