ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА. — МегаЛекции

П О Н Я Т И Е

 

Каждый предмет или явление обладает некими свойствами (признаками).

 

Получается, что составить понятие об объекте означает, прежде всего, умение отличить его от других сходных с ним объектов.

Можно сказать, что понятие – это мысленное содержание слова.

 

Понятие – это форма мысли, отображающая предметы в их наиболее общих и существенных признаках*.

 

Понятие – это форма мысли, а не форма слова, так как слово лишь метка, которой мы помечаем ту или иную мысль.

Слова могут быть различны, но при этом обозначать одно и то же понятие. По-русски – «карандаш», по-английски – «pencil», по-немецки – bleistift. Одна и та же мысль в разных языках имеет разное словесное выражение.

 

ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ. КРУГИ ЭЙЛЕРА.

 

По содержанию между понятиями могут быть два основных вида отношений:

сравнимость и несравнимость.

 

Понятия, имеющие в своих содержаниях общие признаки, называются СРАВНИМЫМИ («адвокат» и «депутат»; «студент» и «спортсмен»).

В противном случае, понятия считаются НЕСРАВНИМЫМИ («крокодил» и «блокнот»; «человек» и «пароход»).

Если кроме общих признаков понятия имеют и общие элементы объёма, то они называются СОВМЕСТИМЫМИ.

 

Существует шесть видов отношений между сравнимыми понятиями. Отношения между объёмами понятий удобно обозначать с помощью кругов Эйлера (круговые схемы, где каждый круг обозначает объём понятия).

ВИД ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ	ИЗОБРАЖЕНИЕ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА
РАВНОЗНАЧНОСТЬ (ТОЖДЕСТВЕННОСТЬ)   Объёмы понятий полностью совпадают. Т.е. это понятия, которые различаются по содержанию, но в них мыслятся одни и те же элементы объёма.	1) А – Аристотель В – основатель логики   2) А – квадрат В – равносторонний прямоугольник
ПОДЧИНЕНИЕ (СУБОРДИНАЦИЯ)   Объём одного понятия полностью входит в объём другого, но не исчерпывает его.	1) А – человек В – студент   2) А – животное В – слон
ПЕРЕСЕЧЕНИЕ (ПЕРЕКРЕЩИВАНИЕ)   Объёмы двух понятий частично совпадают. То есть понятия содержат общие элементы, но и включают элементы, принадлежащие только одному из них.	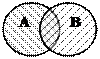1) А – юрист В – депутат   2) А – студент В – спортсмен
СОПОДЧИНЕНИЕ (КООРДИНАЦИЯ)   Понятия, не имеющие общих элементов, полностью входят в объём третьего, более широкого понятия.	1) А – животное В – кот; С – собака; D – мышь   2) А – драгоценный металл В – золото; С – серебро; D – платина
ПРОТИВОПОЛОЖНОСТЬ (КОНТРАРНОСТЬ)   Понятия А и В не просто включены в объём третьего понятия, а как бы находятся на его противоположных полюсах. То есть, понятие А имеет в своём содержании такой признак, которых в понятии В заменён на противополжный.	1) А – белый кот; В – рыжий кот (коты бывают и чёрными и серыми)   2) А – горячий чай; холодный чай (чай может быть и тёплым)   Т.е. понятия А и В не исчерпывают всего объёма понятия, в которое они входят.
ПРОТИВОРЕЧИЕ (КОНТРАДИКТОРНОСТЬ)   Отношение между понятиями, одно из которых выражает наличие каких-либо признаков, а другое – их отсутствие, то есть просто отрицает эти признаки, не заменяя их никакими другими.	1) А – высокий дом В – невысокий дом   2) А – выигрышный билет В – невыигрышный билет   Т.е. понятия А и не-А исчерпывают весь объём понятия, в которое они входят, так как между ними нельзя поставить никакое дополнительное понятие.

Упражнение: Определите вид отношений по объёму приведённых ниже понятий. Изобразите их с помощью кругов Эйлера.

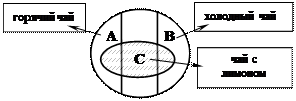1)А – горячий чай; В – холодный чай; С – чай с лимоном

Горячий чай (В) и холодный чай (С) – находятся

в отношении противоположности.

Чай с лимоном (С) может быть как горячим,

так и холодным, но может быть и, например, тёплым.

2) А – деревянный; В– каменный; С – строение; D– дом.

 

Всякое ли строение (С) – дом (D)? – Нет.

Всякий ли дом (D) – строение (С)? – Да.

 

Что-то деревянное (А) обязательно ли дом (D) или строение (С) – Нет.

Но можно найти деревянное строение (например, будка),

также можно найти деревянный дом.

 

Что-то каменное (В) не обязательно дом (D) или строение (С).

Но может быть и каменное строение, и каменный дом.

 

3) А – российский город; В – столица России;

С – Москва; D – город на Волге; Е – Углич.

 

Столица России (В) и Москва (С) – один и тот же город.

Углич (Е) является городом на Волге (D).

При этом, Москва, Углич, как и любой город на Волге,

являются российскими городами (А)

 

 

---

Рекомендуемые страницы:

Воспользуйтесь поиском по сайту:

megalektsii.ru

круги Эйлера — публикации с ключевым словом — Издательство «Креативная экономика»

Научные публикации (статьи и монографии) с ключевым словом круги Эйлера, выпущенные в Издательстве Креативная экономика (найдено: 1 за 2018 год).

1. Савалей В.В., Ивасенко А.Н.

Формально-логический подход к соотношению понятий рисков и неопределённостей // Креативная экономика. (№ 11 / 2018).  
В данной статье исследуется разнообразие точек зрения на проблему соотношения понятий рисков и неопределённостей при помощи формально-логического подхода. Для изучения точек зрения на проблему соотношения понятий была представлена следующая градация в виде групп: отождествление понятий, разделение понятий, взаимное дополнение понятий. Использование формально-логического подхода позволяет представить взаимодействие понятий, как логическое выражение, результатом которого является одна из точек зрения исследователей. Для наглядности были использованы такие операторы как конъюнкция, строгая дизъюнкция и импликация. Каждая из точек зрения имеет те или иные аргументы, но авторы данной статьи придерживаются мнения, что понятия рисков и неопределённостей взаимно дополняют друг друга, то есть находятся в отношении импликации. При использовании иных соотношений этих понятий могут возникнуть сложности при идентификации, оценке и учете рисков и неопределённостей. На основании изученных точек зрения, авторами был предложен алгоритм идентификации соотношения понятий рисков и неопределённостей, который может использоваться в исследовательских целях.

Савалей В.В., Ивасенко А.Н. Формально-логический подход к соотношению понятий рисков и неопределённостей // Креативная экономика. – 2018. – Том 12. – № 11. – с. 1825-1832. – doi: 10.18334/ce.12.11.39526.

---

---

Продолжить поиск в библиотеке по запросу «круги Эйлера»?

creativeconomy.ru

Использование кругов Эйлера на уроках истории при изучении Древней Греции в 5-м профильном гимназическом классе

Цель данной статьи – с наибольшей эффективностью рассмотреть и определить сложные для объяснения ученикам античные понятия, которые встречаются в программе пятого класса средней школы, и проследить отношения между этими понятиями. Для достижения поставленной цели требуется решить следующие задачи:

1. Кратко охарактеризовать теорию круговых схем Леонарда Эйлера;
2. Выделить примеры сложных античных понятий, встречающихся в программе по истории для пятого класса средней школы при изучении Древней Греции;
3. Представить их отношения с помощью кругов Эйлера для наиболее эффективного их усвоения и понимания учениками пятого класса средней школы.

Прежде чем перейти к решению поставленных задач, следует заметить, что данная статья предполагает, что учитель предоставляет учащимся углубленное изучение предмета в профильном гимназическом классе. Именно углубленное изучение предмета должны упростить применяемые педагогом круги Эйлера.

Все понятия находятся в определенных отношениях друг к другу. Далекие друг от друга по своему содержанию понятия, не имеющие общих признаков, называются “несравнимыми”, (например “монархия” и “меч”). Те понятия, которые имеют общие признаки, называются “сравнимыми”.

Сравнимые понятия делятся по объему на “совместимые” (объемы этих понятий совпадают полностью или частично) и “несовместимые” (объемы которых не совпадают ни в одном элементе).

Представим возможные сравнимые понятия в виде двух схем и проиллюстрируем их с помощью кругов Эйлера. Данные схемы будет служить определителем для отношения античных понятий.

Схема 1

В первом случае с помощью кругов Эйлера продемонстрированы тождественные понятии: “Геродот” и “автор Истории Греко-персидских войн в девяти книгах”. Эти понятия тождественны, поскольку только Геродот автор Истории Греко-персидских войн в девяти книгах и никто другой.

Второй случай представляет собой перекрещивающиеся понятия: “Аристократ” и “гражданин Афин”. Они перекрещивающиеся потому что не все аристократы граждане Афин. Есть ведь и аристократы Коринфа, Фив и других полисов. При этом несомненно, что некоторая часть от всех аристократов в Древней Греции была афинянами. Эта часть и показана пересечением кругов Эйлера. В то же время данные круги показывают, что не все граждане Афин были аристократами.

Третий случай представляет собой подчиняющие понятия. Так, несомненно, что в Древней Греции существовали разные виды воинов: гоплиты, пельтасты, всадники и др. В данном случае показано, что гоплит – это один из видов воинов в Древней Греции.

Схема 2

При соподчинении – объемы двух или нескольких понятий исключают друг друга, но принадлежат некоторому, более общему родовому понятию. Так по реформе Солона, граждане Афин был разделены на разряды по имущественному признаку. Феты и зевгиты исключают друг друга, но принадлежат более общему родовому понятию – “граждане Афин”.

Что касается противоположности, то при нем понятия являются видами одного и того же рода, но при этом одно из них не только отрицает признаки другого, но и заменяет их другими. Так понятие “демократия” отрицает признаки понятия “олигархии” и заменяет их своими признаками (например, отсутствие имущественного ценза при участи в политической жизни полиса и др.).

Наш опыт преподавания истории Древней Греции для учащихся пятого класса показывает, что учащимся данной возрастной группы сложно усвоить развернутое определение понятие “полис”.

Для начала определим данное понятие.

В учебниках истории для пятого класса понятие “полис” определяется как “город-государство” или даже “небольшое самостоятельное государство”. Ученики задают вопросы: “Что такое город-государство?”, “Как в город может входить сельская округа?” И они правы т.к. согласно правилам логики – в город не может входить сельская округа, но она может входить в полис. Учитывая специфику профильного гимназического образования, нам следует подробнее остановиться на термине “полис”.

Разберем определение классического греческого полиса.

В классическую эпоху (V-IV вв. до н.э.) слово “полис” было многозначно. В классическом греческом языке оно имело три основных значения: “город”, “государство” и “коллектив граждан”. Причем сами греки, поставили бы в этом триединстве на первое место не “город” (в принципе они допускали, что полис может и не быть городом) и не “государство”, а “коллектив граждан”, т.к. в каждом “полисе” они видели, в первую очередь, составляющих его живых людей, без которых это слово перестало бы иметь для них всякий смысл.

Приведем несколько фрагментов из источников, где ясно отражен данный взгляд на “полис”. Геродот, повествуя о споре между афинянином Фемистоклом и коринфянином Адимантом на военном совете греков перед Саламинским сражением (480 г. до н.э.), когда Афины были уже взяты персами, сообщает о Фемистокле, который заявил, что у его сограждан есть и город и земля, большие чем у коринфян, пока имеется у них снаряженными 200 кораблей, и нет такого эллинского народа, который мог бы отразить их нападение. Еще более красноречивым выглядит сообщение Фукидида, где афинский полководец и политический деятель Никий говорит что “государство (в греческом оригинале “полис” ) это люди, а не стены и не корабли без людей”.

Западные классицисты придерживаются подобного же взгляда на определение понятия “полис”, что и отечественные. Таким образом, мировое ученое сообщество сходится в своем определении понятия “полис”.

Для наиболее эффективного объяснения столь многозначного понятия для учащихся пятого класса можно прибегнуть к кругам Эйлера. Это позволяет также сопоставить античное понятие “полис” с современным понятием “город”, выделить общее и различие. Таким образом, учащиеся смогут полноценно понять многозначный термин “полис” и сравнить его с современным понятием “город”.

Многозначное понятие “полис” будет выглядеть с помощью кругов Эйлера следующим образом:

Во время объяснения материала следует подчеркнуть, что на схеме центральное место занимает именно “коллектив граждан”. Подобная “рожица” очень хорошо запоминается и воспроизводится учащимися. Этому есть несколько причин:

1. Визуальное восприятие облегчает процесс запоминания;
2. Эту схему, учащиеся переносят в тетрадь, тогда включается механическая память, что еще более эффективно отражается на процессе запоминания;
3. Для современных учащихся пятого класса интернет не кажется чем-то неизвестным. В личных сообщениях с помощью интернета или SMS сообщениях, с помощью мобильного телефона присутствует знак – смайл, с которым вышеприведенная схема, несомненно, будет ассоциироваться. Таким образом, ассоциативное мышление учащихся также будет задействовано.

Надеемся, что данная технология использования кругов Эйлера на уроках истории поможет учителям истории, как она помогает автору данной статьи и его ученикам.

urok.1sept.ru

КОМБИНАТОРИКА. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА.

КОМБИНАТОРИКА. РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ КРУГОВ ЭЙЛЕРА.

Щербакова А.Ю. 1

---

1

Коренец Е.И. 1

---

1

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

         

Именно математика дает

надежнейшие правила:

кто им следует – тому не опасен

обман чувств.

Л. Эйлер

Введение

Во все времена представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.

Комбинаторика – раздел математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из данных объектов. Особая примета комбинаторных задач – это вопрос, который можно сформулировать таким образом, что он начинался бы словами:

Термин «комбинаторика» происходит от латинского слова «combina», что в переводе на русский означает – «сочетать», «соединять».

Выбор объектов и расположением их в том или ином порядке приходится заниматься чуть ли не во всех областях человеческой деятельности, например конструктору, разрабатывающему новую модель механизма, учёному-агроному, планирующему распределение сельскохозяйственных культур на нескольких полях, химику, изучающему строение органических молекул, имеющих данный атомный состав.

Гипотеза работы: Решение комбинаторных задач с помощью кругов Эйлера развивает творческие способности, помогает при решении олимпиадных задач, имеет практическое применение.

Основополагающий вопрос: А все ли я знаю о комбинаторике?

Проблемный вопрос: Может ли помочь комбинаторика в реальной жизни?

Цель работы: изучить решение логических задач путем построения кругов (диаграмм)Эйлера.

Задачи:

• Познакомиться с историей возникновения науки комбинаторики;

• Находить возможные комбинации для решения комбинаторных задач

• Уметь составлять и решать задачи с помощью кругов Эйлера;

• Поработать с ресурсами Internet;

• Применять полученные знания в дальнейшем обучении;

• Расширить и углубить представление о практическом значении математики в жизни;

• Уметь работать с научно-познавательной литературой, анализировать, делать выводы.

Объект исследования : логические задачи.

Методы:отбор источников информации, изучение материала и анализ его.

Актуальность выбранной темы заключается в необходимости решения комбинаторных задач на уроках математики, применении их в жизни, т.к. они имеют социальную значимость, помогают разобраться в новых веяниях жизни. Основа хорошего понимания комбинаторики – умение считать, думать, рассуждать, находить удачные решения задач.

История комбинаторики

Комбинаторика занимается различного вида соединениями, которые можно образовать из элементов конечного множества. Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен»(Vвек до н.э.). По мнению её авторов, все в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Большой интерес математиков вызывали магические квадраты.(см.Приложение 1) Некоторые элементы комбинаторики были известны в Индии еще во II в. до н. э. Индийцы умели вычислять числа, которые сейчас называют «сочетания».Античные греки рассматривали комбинаторные задачи. Хрисипп (IIIв. до н. э.) и Гиппарх(II в.до н.э.) подсчитывали сколько следствий можно получить из 10 аксиом. У Хрисиппа получилось более миллиона. Во все века математики исследовали задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями. Позднее Д.Кардано провел исследование азартной игры в кости . (Азартными называют те игры, в которых выигрыш зависит не только от умения игрока, но и от случайности). Было замечено, что при многократном бросании однородного кубика (все шесть граней которого отмечены соответственно числами 1, 2, 3, 4, 5, 6) число очков от 1 до 6 выпадают в среднем одинаково часто, иными словами, выражаясь языком математики, выпадение определённого числа очков имеет вероятность, равную 1/6. Аналогично вероятность появления на верхней грани кости чётного числа очков равна 3/6, так как из шести равновозможных случаев чётное число появляется только в трёх. Математически заинтересовались азартной игрой П.Ферма и Б.Паскаль. Помимо азартных игр, комбинаторные методы использовались в криптографии — как для разработки шифров, так и их взломов. Комбинаторика и треугольник Паскаля. Паскаль много занимался биномиальными коэффициентами и открыл их способ вычисления. Число сочетаний можно вычислять не через факториал, а с помощью арифметического треугольника. Строится треугольник: его бедра и вершина состоят из единиц, а в основании каждый элемент строки получается суммированием двух стоящих непосредственно над ним элементов.(см.Приложение 2) Паскаль также как и Лейбниц считается основоположником современной комбинаторики .(см.Приложение 3) А вот сам термин комбинаторика придумал Лейбниц. В 1666г. он опубликовал книгу «Рассуждения о комбинаторном искусстве ». Его ученик — Якоб Бернулли (см.Приложение 4) — основатель теории вероятности, изложил много интересного о комбинаторике. Дал научное обоснование теории сочетаний и перестановок. Изучением размещений занимался Я. Бернулли во второй части своей книги «Искусство предугадывания» в 1713 г., в которой указал формулы для числа размещений из n элементов по k, выводились выражения для степенных сумм .

Позднее обнаружили тесную связь между комбинаторными и аналитическими задачами Абрахам де Муавр Джеймс Стирлинг. Они нашли формулы для нахождения факториала. Окончательно комбинаторику, как раздел математики, оформил в своих трудах Эйлер. Кроме перестановок и сочетаний Эйлер изучал разбиение, а также сочетания и размещения с условиями.

Современным отцом комбинаторики считается Пал Эрдёш. (см.Приложение 5) Он ввел вероятностный анализ. Внимание к комбинаторике повысился во второй половине XX века, с появлением компьютеров.

Многие специалисты в области математики и физики считают, что именно комбинаторная задача может стать толчком в развитии всех технических наук. Некоторые из них всерьез утверждают, что комбинаторика является подспорьем для всех современных наук, особенно космонавтики.

Области применения комбинаторики:

• учебные заведения ( составление расписаний)

• сфера общественного питания (составление меню)

• лингвистика (рассмотрение вариантов комбинаций букв)

• география (раскраска карт)

• спортивные соревнования (расчёт количества игр между участниками)

• производство (распределение нескольких видов работ между рабочими)

• агротехника (размещение посевов на нескольких полях)

• азартные игры (подсчёт частоты выигрышей)

• химия (анализ возможных связей между химическими элементами)

• экономика (анализ вариантов купли-продажи акций)

• криптография (разработка методов шифрования)

• доставка почты (рассмотрение вариантов пересылки)

• биология (расшифровка кода ДНК)

• военное дело (расположение подразделений)

• астрология (анализ расположения планет и созвездий

Теория конфигураций и теория перечисления

Наиболее разработанным разделом комбинаторики является теория конфигураций. Она рассматривает задачи выбора и расположения элементов некоторого множества, в соответствии с заданными правилами. Элементарными комбинаторными конфигурациями являются сочетания, размещения, перестановки. Для подсчёта числа этих конфигураций используются правила суммы и произведения.

Правило суммы:

Если элемент A можно выбрать m способами, а элемент B можно выбрать k способами, то выбор элемента A или B можно осуществить m + k способами.

Правило суммы можно перефразировать на теоретико-множественном языке. Обозначим через | A | число элементов множества A, через A B — объединение множеств A и B, через AxB — декартово произведение множеств A и B. Тогда для непересекающихся множеств A и B выполняется равенство:

| A B | = | A | + | B |.

Обобщением правила суммы является правило произведения.

Правило произведения:

Если элемент A можно выбрать m способами, а после каждого выбора элемента A элемент B можно выбрать k способами, тогда, упорядоченную пару элементов (A, B) можно выбрать m*k способами.

Правило произведения можно распространить на выбор последовательности (x₁, x₂, …, xn) произвольной конечной длиныn. На теоретико-множественном языке правило произведения формулируется так:

| Aх B | = | A | | B |.

Правило размещения.

Назовём множество, содержащееn элементов, n-множеством.

Последовательность (x₁, x₂, …, x_k ) длины k без повторяющихся элементов из элементов данного n-множества назовём k-размещением.

Обозначим символом число размещений из n по k элементов (от фран. «arrangement» — размещение). Используя правило произведения, вычислим число . Пусть произвольное размещение длины k имеет вид: (x₁, x₂, …, x_k ).

Элемент x₁ можно выбрать n способами. После каждого выбора x₁ элемент x₂ можно выбрать (n — 1) способами. После каждого выбора элементов x₁ и x₂ элемент x₃ можно выбрать (n — 2) способами, и т.д. После каждого выбора элементов x₁, x₂, …, x_k-1 элемент x_k можно выбрать (n -(k — 1)) = (n — k + 1) способами. Тогда, по правилу произведения, последовательность (x₁; x₂; , …, x_k ) можно выбрать числом способов, равным

n(n — 1)(n — 2) … (n — k + 1) = (1.1)

Произведение в левой части равенства (1.1) умножим и разделим на (n — k)!, получим:

. (1.2)

Если в форуме (1.2) k = n, то есть число Pn перестановок из n элементов

Pn = n! (от «permutation»- перестановка).

Правило сочетания.

k-подмножество данного n-множества называется k-сочетанием.

Обозначим через число k-сочетаний из данныхn элементов. Формулу для числа получим, рассуждая следующим образом. Если каждое сочетание упорядочить всеми возможными способами, то получим все k-последовательностей изn элементов, без повторений, то есть все k-размещения. Иными словами, Откуда: (1.3) или Предполагая, что n и k — целые положительные числа и 0!=1, сформулируем основные свойства сочетаний.

Основные свойства сочетаний.

1. Условились, что

Как выбрать формулу? (см.Приложение 6) Сводка формул для всех видов соединений. (см.Приложение 7)

Сочетания и размещения широко используются при вычислении классической вероятности случайных событий.

Пример. В корзине находятся 20 орехов, из которых 7 грецких. Наудачу выбирают 5 орехов. Найти вероятность того, что среди выбранных орехов содержатся 2 грецких.

Решение. Число исходов опыта . Случайное событие A — среди пяти выбранных орехов содержатся 2 грецких ореха. Число исходов, благоприятствующих событию A, равно: . Искомая вероятность .

Задачи.

1. Найти вероятность того, что случайно выбранное 5-значное (десятичное) число не содержит цифры 5.

2. Предприятие располагает 5 вакансиями для мужчин, 5 вакансиями для женщин и 4 вакансиями для работников любого пола. В отдел кадров предприятия обратилось 20 человек, среди которых 12 мужчин и 8 женщин. Сколькими способами предприятие может заполнить имеющиеся вакансии?

3. В классе 25 учеников, из которых 13 юношей и 12 девушек. Сколькими способами 25 учеников могут встать в шеренгу так, чтобы юноши после удаления из строя девушек, оказались построенными по росту; аналогично девушки после удаления из строя юношей оказались построенными по росту?

Круги Эйлера

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

На рисунке представлено множество – все возможные игрушки. Некоторые из игрушек являются конструкторами – они выделены в отдельный овал. Это часть большого множества «игрушки» и одновременно отдельное множество (ведь конструктором может быть и «Лего», и примитивные конструкторы из кубиков для малышей). Какая-то часть большого множества «игрушки» может быть заводными игрушками. Они не конструкторы, поэтому мы рисуем для них отдельный овал. Желтый овал «заводной автомобиль» относится одновременно к множеству «игрушки» и является частью меньшего множества «заводная игрушка». Поэтому и изображается внутри обоих овалов сразу.

Автор метода — ученый Леонард Эйлер (1707-1783) (см.Приложение 8) . Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Дело в том, что он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки. Метод Эйлера получил заслуженное признание и популярность. И после него немало ученых использовали его в своей работе, а также видоизменяли на свой лад. Например, чешский математик Бернард Больцано использовал тот же метод, но с прямоугольными схемами. Круги Эйлера имеют прикладное назначение. С их помощью на практике решаются задачи на объединение или пересечение множеств в математике, логике. Круги Эйлера можно разделить их на те, что описывают объединение каких-то понятий и описывают пересечение множеств по какому-то признаку. (см.Приложение9)

Пример пересечения — какую профессию выбрать? Нарисую схему в виде кругов Эйлера. Схема сразу расставит все по местам и поможет определиться с выбором. То, что окажется на пересечении всех трех кругов, и есть профессия, которая не только сможет прокормить, но и будет нравиться.

Чертеж, вроде этого, поможет определиться с выбором:

Рассмотрим несколько примеров задач, которые можно решить с помощью кругов Эйлера.

В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».

В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети интернет.

Запрос	Найдено страниц (в тысячах)
Крейсер | Линкор	7000
Крейсер	4800
Линкор	4500

Какое количество страниц (в тысячах) будет найдено по запросу Крейсер & Линкор?

Считается, что все вопросы выполняются практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.

Решение:

При помощи кругов Эйлера изобразим условия задачи. При этом цифры 1, 2 и 3 используем, чтобы обозначить полученные в итоге области.

Опираясь на условия задачи, составим уравнения:

1. Крейсер | Линкор: 1 + 2 + 3 = 7000

2. Крейсер: 1 + 2 = 4800

3. Линкор: 2 + 3 = 4500

Чтобы найти Крейсер & Линкор (обозначенный на чертеже как область 2), подставим уравнение (2) в уравнение (1) и выясним, что:

4800 + 3 = 7000, откуда получаем 3 = 2200.

Теперь этот результат мы можем подставить в уравнение (3) и выяснить, что:

2 + 2200 = 4500, откуда 2 = 2300.

Ответ: 2300 — количество страниц, найденных по запросу Крейсер & Линкор.

Вывод

Круги Эйлера помогают быстро и просто решить даже достаточно сложные или просто запутанные на первый взгляд задачи. Для этого необходимо запомнить порядок этапов :

1. Записать краткое условие.

2. Выполнить рисунок.

3. Записать данные в круги Эйлера.

4. Анализировать, рассуждать и записывать результаты в части круга.

5. Записать ответ.

Задачи:

1. Сколько существует натуральных чисел, меньших 1000, которые делятся на 3 , но не делятся на 2 и на 5?

2. Сколько существует различных десятизначных чисел, состоящих только из нулей и единиц, которые содержат не более трех единиц ?

3. Биатлонист проходит четыре огневые точки, на каждой он делает по 5 выстрелов. Сколько существует различных способов промахнуться не более 4?

4. По результатам одного социологического исследования, было установлено, что из 200 людей смотрящих телевизор, 110 человек смотрят спортивную передачу, 120 – комедии, 85 предпочитаю драмы, 50 смотрят драмы и спорт, 70 – комедии и спорт, 55 смотрят комедии и драмы и 30 человек смотрят все три вида передач. Сколько человек, смотрят спорт или комедии или драмы? сколько человек не смотрят ничего из вышеперечисленного?

5. Человек имеет 10 друзей и течение нескольких дней, приглашает некоторых из них в гости, так что компания, ни разу не повторяется. Сколько дней он может так делать?

6. Найти количество трехзначных чисел, которые делятся на 7, но не делятся на 2 и на 5.

7. На данный момент, в классе 20 учеников, получивших сначала учебного года, хотя одну двойку, 17 учеников, получивших не менее двух двоек, 8 учеников, получивших не менее трех двоек, три ученика получивших не менее 4 двоек, один ученик получивший 5 двоек, больше пяти двое нет ни у кого. Сколько всего двое в журнале?

Задача 1.

Решение:

Определение: множество А называется подмножество множества В, если каждый элемент множества А принадлежит множеству В.

Если в некоторой задаче считается что элементы принадлежат некоторым множествам, то это множество называется универсальным.

Например, в задаче № 1 универсальным множеством можно считать множество чисел, от 1 до 999.

A = количество элементов во множестве А

В = 333

Если число делится на 2 и 3, то число делится на 6

A В = 166

Если число делится на 3 и 5, то число делится на 15

В D = 66

При таком подсчете, мы дважды посчитали числа, которые входят во множество

АВD = 33

(В/А)/D = В — AВ — ВD + AВD = 333 – 166 – 66 + 33 = 134

Задача 2

Определение: Правило суммы.

Все множества способов подсчета можно разбить на пересекающиеся множества. Тогда общее количество способов вычисляется как сумма множеств.

С = = 1-0 единиц

С = = 10-1 единица

С = = 45

С = = 120

120+45+10+1=176

Задача 3.

С = = 1 способ – 0 промахов

C = = 20 способов – 1 промах

С = = 190 способов – 2 промаха

С = =1140 способов – 3 промаха

С = =4845 способов – 4 промаха

Всего 1 + 20 + 190 +1140 + 4845= 6196 способов

Задача 4.

Формула включений и исключений

А ВD = A + В +D — AВ — AD — ВD — AВD

а) А ВD = 110 + 120 + 85 – 70 -55 – 50 + 30 =170

б)200-170=30 человек ничего не смотрят

Задача 5.

Составим таблицу друзей

С = = 10 компаний из 1 человека

С = = 45 компаний из 2 человек

С = = 120 компаний из 3 человек

С = = 210 компаний из 4 человек

С = = 252 компании из 5 человек

С ==210 компаний из 6 человек

С = = 120 компаний из 7 человек

С = =45 компаний из 8 человек

С = =10 компаний из 9 человек

С = = 1 компания из 10 человек

Итого 10+45+120+210+252+210+120+45+10+1= 1023 способов

Задача 6.

Всего 900 трехзначных чисел.

A = 900:7=128 чисел

АВ =900:14=64 числа

АD = 900: 35=25 чисел

АВD =900:70=12 чисел

А = А — АВ — АD + АВD = 128 – 64 – 25 + 12 = 51 число

Задача 7.

Найдем количество учеников, получивших ровно четыре двойки.

1. 3 – 1= 2 ученика получили 4 двойки

Теперь узнаем количество учеников , получивших ровно три двойки, ровно две двойки и ровно одну двойку.

1. 8 – 2 — 1 = 5 учеников получили 3 двойки

2. 17 – 5 – 2 – 1 = 9 учеников получили 2 двойки

3. 20 – 9 – 5 – 2 – 1 = 3 ученика получили 1 двойку

4. 1×3 + 2×9 + 3×5 + 4×2 + 5×1 = 49 двоек в журнале

Вывод

Для решения данных логических задач, использовала круги Эйлера, что позволило успешно решить поставленные задачи. Этот способ показался мне удобным и надежным, так как он упрощает путь к решению задачи, делая его наглядным.

Заключение

В процессе изучения данной темы, я научилась грамотно оперировать такими понятиями как «множество», «объединение множеств», «пересечение множеств», «разность множеств» и использовать их при решении задач. В процессе решения задач я расширила свои знания по математике, познакомилась с ещё одним способом решения задач, который был мне мало знаком. Для решения задач с помощью кругов Эйлера можно воспользоваться алгоритмом, состоящим из нескольких этапов.

Применение кругов Эйлера позволяет легко решить задачи, которые обычным путем разрешимы составлением сложных уравнений. Моя гипотеза подтвердилась. Решения задач с громоздкими условиями и со многими данными просты и не требуют особых умозаключений. Применение кругов Эйлера придает задачам наглядность и простоту.

Практическая значимость заключается в расширении возможностей при решении логических задач. Пригодится для решения задач занимательного характера, позволит применять методы и правила для решения нетрадиционных задач. Приобретенные сведения и знания способствуют повышению интеллектуального развития, помогают развить умение наблюдать и анализировать.

Круги Эйлера – не просто занимательная и интересная штука, но и весьма полезный метод решения задач. Причем не только абстрактных задач на школьных уроках, но и вполне себе житейских проблем. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь. Сам Леонард Эйлер говорил: «круги подходят для того, чтобы облегчить наши размышления».

Список использованной литературы

1. Галеева Р. А. Тренируем мышление. Задачи на сообразительность / Р. А. Галеева, Г. С. Курбанов, И. В. Мельченко – Изд. 2 – е – Ростов н/Д: Феникс, 2006.

2. Игнатьев. Е.И. В царстве смекалки, или Арифметика для всех: Книга для семьи и школы. Опыт математической хрестоматии в 3 книгах/Худож. Н.Я. Бойко. – Ростов н/Д: Кн. Изд-во, 1995.

3. Рыбников К.А.Комбинаторный анализ. Очерки истории.-М.: Изд.мехмата МГУ1996.-124с.

4. История математики под редакцией Юшкевича А.П. М.: Наука Том 1.С древнейших времен до начала Нового времени.1970.

5. Нагибин Ф.Ф., Канин Е.С. Математическая шкатулка: Пособие для учащихся 4-8 кл. сред. Шк. – 5-е изд. – М.: Просвещение, 1988.

6. Увлекательные логические задачки, которые будут интересны детям и взрослым. http://logika.vobrazovanie.ru

Приложение

Приложение 1.

Приложение 2.

Приложение 3.

Приложение 4.

Якоб Бернулли.

Приложение 5.

Математика — это орудие, с помощью которого человек познает и покоряет себе окружающий мир.

Пал Эрдеш.

Приложение 6.

Приложение 7.

Приложение 8.

Приложение 9.

Просмотров работы: 3926

school-science.ru

Презентация к уроку по алгебре (5 класс) на тему: Круги Эйлера

Слайд 1

Автор: Макеенко Вадим, 5б кл . Руководитель: Венжик Т.Д. КРУГИ ЭЙЛЕРА

Слайд 2

ЛЕОНАРД ЭЙЛЕР ИДЕАЛЬНЫЙ МАТЕМАТИК XVIII ВЕКА, который ввел понятие объединения и пересечения множеств

Слайд 3

Эйлер писал, что «круги очень подходят для того, чтобы облегчить наши размышления». При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов и они получили название «круги Эйлера».

Слайд 4

Круги Эйлера Эйлеровы круги — принятый в логике способ моделирования, наглядного изображения отношений между объемами понятий с помощью кругов.

Слайд 5

Смысл логических связок становится более понятным, если проиллюстрировать их с помощью кругов Эйлера Круги Эйлера Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью . Школа 5-ые классы 9-ые классы 9 «А» класс Круги Эйлера – это тот метод, который наглядно демонстри-рует : лучше один раз увидеть, чем сто раз услышать. Его заслуга в том, что наглядность упрощает рассуждения и помогает быстрее и проще получить ответ . Метод Эйлера является незаменимым при решении некоторых задач .

Слайд 6

Задача 1. «Обитаемый остров» и «Стиляги» Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров » 11 человек смотрели фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»?

Слайд 7

Решение: Чертим два множества таким образом: 6 «Стиляги» «Обитаемый остров» 6 человек , которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров». 11 – 6 = 5 – человек, которые смотрели только «Стиляги». Получаем: «Стиляги» «Обитаемый остров» 9 5 6 Ответ: 5 человек смотрели только «Стиляги».

Слайд 8

Задача 2. «Гарри Поттер, Рон и Гермиона » На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон . Гермиона прочитала 7 книг , которых не читали ни Гарри Поттер, ни Рон , и две книги , которые читал Гарри Поттер . Всего Гарри Поттер прочитал 11 к ниг. Сколько книг прочитал только Рон ?

Слайд 9

Учитывая условия задачи, чертеж будет таков: Решение: 4 2 7 Гермиона Рон Гарри Поттер Так как Гарри Поттер всего прочитал 11 книг, из них 4 книги читал Рон и 2 книги – Гермиона , то 11 – 4 – 2 = 5 – книг прочитал только Гарри. Следовательно, 26 – 7 – 2 – 5 – 4 = 8 – книг прочитал только Рон . Ответ. 8 книг прочитал только Рон . 11 8

Слайд 10

ВЫВОД: Применение кругов Эйлера (диаграмм Эйлера-Венна) позволяет легко решить задачи, которые обычным путем разрешимы лишь при составлении системы трех уравнений с тремя неизвестными

Слайд 11

Источники информации: http:// f1.mylove.ru/0AkEJdLeQl.jpg http :// logika.vobrazovanie.ru/index.php?link=kr_e.html http:// inf.reshuege.ru/test?theme=256

nsportal.ru

Исследовательская работа «Занимательные круги Эйлера»

Управление образованием

Администрации города Юрги

IV учебно-исследовательская

конференция школьников

«Я познаю мир»

Секция: Математика — поиск решений

Занимательные круги Эйлера

Автор:

Галицкий Антон Игоревич

Класс: 6 «В»

МБОУ «СОШ № 14 г. Юрги»

Руководитель:

Гончарова Ирина Николаевна

Юрга 2017

Содержание:

1. Введение ………………………………………2

2. Основная часть

2.1. Биография Л. Эйлера………………………2-3

2.2. Научные достижения………………………3

2.2.1. “Круги Эйлера”……………………………3

2.2.2. Типы “кругов Эйлера”…………………..3

2.2.3. Практика: решение задач………………4-9

2.3. Интересные факты…………………………..10

2.4. Высказывания Л. Эйлера…………………10

3. Заключение………………………………………10

4. Список используемых………………………10

интернет-ресурсов.

1.Введение:

Цель изучения способа решения задач с помощью “кругов Эйлера” — показать необходимость их применения для упрощения вычислений.

Мои задачи:

-Познакомиться с великим математиком Л.Эйлером.

-Научиться решать задачи с помощью “кругов Эйлера”.

-Поделиться опытом решения задач с другими учениками.

2.Основная часть:

2.1.Биография Л.Эйлера

Леонард Эйлер, сын пастора, родился в 1707 году 15 апреля. Начальное образование мальчик получил дома. Отец вложил в мальчика всевозможные знания, надеясь на всестороннее воспитание сына. Способности к точным наукам проявились у ребенка с первых шагов их изучения. Все предметы давались Эйлеру легко.

Для талантливого ученика, швейцарский математик Бернулли устанавливает индивидуальный курс обучения и знакомит Эйлера с трудами математических гениев. Леонард Эйлер удостаивается первой ученой степени магистра искусств в возрасте шестнадцати лет. Эйлер поступает в Базельский университет на факультет медицины, при этом он не оставляет математику.

 С 1727 по 1740 год Эйлер, занявший пост руководителя кафедры математики, издает свои труды, посвященные геометрии, аналитической механике, арифметике. За издание работы о морских приливах и отливах ученый получает премию Академии наук Франции.

Эйлер одним из первых ученых получил приглашение на должность декана отделения математики.

Леонард Эйлер издаёт несколько трудов по математике. Математическому анализу ученый посвятил почти все свои математические труды.

Работая в Берлине, Эйлер не теряет связи с Россией. Он переписывается с Ломоносовым. В 1766 году он принимает приглашение императрицы и возвращается в Петербург в Академию наук.

Непрерывная работа, обучение студентов, написание трудов сказались на травмированном ранее глазе. Ученый стал терять зрение. Однако способности гения, его уникальная память помогали ему в его работе. Он диктовал свои статьи и соображения по геометрии и математике. Их число достигло 380 с 1769 по 1793 годы.

С момента становления ученого до его последних дней им было издано свыше 900 научных трудов. Труды Эйлера касались различных областей науки.

Научные исследования Леонард Эйлер продолжал до последних дней, будучи совсем слепым. Смерть наступила 18(29).09.1783г в результате инсульта.

2.2.Научные достижения

Леонардо Эйлер был не только математиком. Он также занимался математическим анализом, геометрией, теорией чисел. Создал важнейшие труды по механике, физике, астрономии и ряду прикладных наук. Во многих своих работах Эйлер развил идеи и методы, полное значение которых выяснилось лишь через сто и более лет после его смерти.

2.2.1. Круги Эйлера

“Круги Эйлера” –это особые чертежи, при помощи, которых наглядно представляют отношения между множествами.

2.2.2.Типы кругов Эйлера

Примеры наглядно представлены на слайдах.

2.2.3.Практика: решение задач

Задачи (как решать):

Лёгкий уровень

В классе 26 учеников. 18 учеников любят яблоки, а 16 учеников любят груши. Сколько учеников любят и яблоки, и груши?

Решение:

18+16-26=8 (уч.) любят и яблоки, и груши.

Ответ: 8 уч.

Средний уровень

На прилавке в магазине лежали 35 булочек. 17 из них были с повидлом, 25 были посыпаны маком, но были также булочки с повидлом и маком. Сколько было таких булочек? Также вычислите сколько было булочек только с повидлом и только с маком.

Решение:

1. 17+25-35=7(бул.) с повидлом и маком.

2. 35-17=18(бул.) с маком.

3. 35-25=10(бул.) с повидлом.

Ответ:7 бул., 18 бул.,10 бул.

Сложный уровень

В классе 26 учеников. 15 из них смотрели фильм про Супермена, а фильм про Бэтмена смотрели на 3 ученика больше, чем фильм про Супермена. А 4 ученика вообще не посмотрели эти фильмы. Сколько человек посмотрело и фильм про Супермена, и фильм про Бэтмена?

Решение:

1. 26-4=22(уч.) смотрели фильмы.

2. 15+3=18(уч) посмотрели фильм про Бэтмена.

3. 15+18-22=11(уч.) посмотрели фильм и про Бэтмена, и про Супермена. Ответ: 11 уч.

Задачи (самостоятельное решение):

Лёгкий уровень

В классе 20 учеников . 18 учеников любят красный цвет, а 19 учеников любят зелёный цвет. Сколько ребят любят и красный цвет, и зелёный цвет?

Решение:

18+19-20=17(уч.) любят красный, и зелёный цвет.

Ответ: 17 уч.

Средний уровень

1 “А” класс, в котором 23 ученика очень любят смотреть мультики. 15 детей любят смотреть мультик “Маша и Медведь”, а 18 детей любят смотреть мультик “Ми-ми-мишки”. Но есть и те кому нравится смотреть и первый, и второй мультик. Сколько таких детей? Также нужно вычислить сколько детей любят смотреть только мультик “Маша и Медведь”, и только мультик “Ми-ми-мишки”.

Решение:

1. 15+18-23=10(дет.) любят и мультик “Маша и Медведь”, и мультик “Ми-ми-мишки”.

2. 23-15=8(дет.) любят только мультик “Ми-ми-мишки”.

3. 23-18=5(дет.) любят только мультик “Маша и Медведь”

Ответ: 10 дет., 8 дет., 5 дет.

Сложный уровень

В доме живут 100 человек. На газету “Вестник” подписаны 65 чел., а на газету “Правда” подписаны на 18 человек больше, чем на газету “Вестник”. Но 10 человек не подписаны не на какую газету. Сколько человек подписано и на газету “Вестник”, и на газету “Правда”?

Решение:

1. 100-10=90(чел.) подписаны на какую-нибудь газету.

2. 65+18=83(чел.) подписано на “Правду”.

3. 65+83-100=58(чел.) подписано и на “Вестник”, и на “Правду”.

Ответ:58 чел.

Работы учеников

Итоги : статистика представлена на слайде.

2.4. Интересные факты о Л.Эйлере

Маркиз Кондорсе сообщает: однажды два студента, выполняя независимо сложные астрономические вычисления, получили немного различающиеся результаты в 50-м знаке, и обратились к Эйлеру за помощью. Эйлер проделал те же вычисления в уме и указал правильный результат.

Рассказывают, что Эйлер не любил театра, и если попадал туда, поддавшись уговорам жены, то чтобы не скучать, выполнял в уме сложные вычисления подобрав их объём так, чтобы хватило как раз до конца представления.

2.5. Высказывания Л. Эйлера.

Именно математика даёт надёжнейшие правила: тому кто им следует — тому не опасен обман чувств.

Все, что мы теперь достоверно знаем из физики, было прежде облечено в догадки, и если б никогда не допускались догадки, даже ошибочные, то мы бы не добыли ни одной истины.

3.Заключение:

Ценность задач, решаемых с помощью “кругов Эйлера” состоит в том, что бы решение задач с громоздкими условиями и со многими данными стали простыми и не вызывали особых умозаключений в науке математике.

В процессе моей работы я познакомился с выдающимся математиком Л. Эйлером, научился и применил на практике свои новые знания по решению задач с помощью “кругов Эйлера”. Также я поделился своим опытом с другими учениками. Задачи ребятам были понятны, способы решения с помощью “кругов Эйлера” оказались практичными и удобными.

4.Список используемых интернет — ресурсов.

http://2mir-istorii.ru — Мировая история.

https://yandex.ru/images/search?text=леонард%20эйлер%20 – Яндекс картинки.

http://citaty.info/man/leonard-eiler — Высказывания известных людей.

https://www.tutoronline.ru/blog/krugi-jejlera — “Круги Эйлера”.

 

 

infourok.ru