Радиус земли. Как впервые измерили радиус земли.

Радиус земли. Как впервые измерили радиус земли.

Древние египтяне заметили, что во время летнего солнцестояния солнце освещает дно глубоких колодцев в сиене (ныне Асуан), а в Александрии — нет. У Эратосфена Киренского (276 год до н. э. -194 год до н. э. ) появилась гениальная идея — использовать этот факт для измерения окружности и радиуса земли. В день летнего солнцестояния в Александрии он использовал скафис — чашу с длинной иглой, при помощи которого можно было определить под каким углом солнце находится на небе.

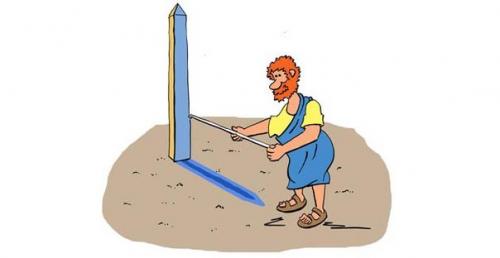Итак, после измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть сиена отстоит от александрии на 1/50 окружности земли. Расстояние между городами считалось равным 5, 000 стадиям, следовательно окружность земли равнялась 250, 000 стадиям, а радиус тогда 39, 790 стадиев.

Неизвестно каким стадием пользовался Эратосфен. Лишь в том случае, если греческим (178 метров), то его радиус земли равнялся 7, 082 км, если египетским, то 6, 287 км. Современные измерения дают для усреднённого радиуса земли величину 6, 371 км. В любом случае, точность для тех времён потрясающая.

Радиус земли в м. Какой радиус Земли?

Полярный радиус Земли — малая полуось эллипсоида Красовского, равная 6 356 863 м.

Экваториальный радиус Земли — большая полуось эллипсоида Красовского, равная 6 378 245 м.

Средний радиус Земли — 6 371 302 м.

История измерения радиуса Земли

Эраторсфен. Еще древние египтяне заметили, что во время летнего солнцестояния Солнце освещает дно глубоких колодцев в Сиене (ныне Асуан), а в Александрии — нет. У Эратосфена Киренского (276 год до н. э.—194 год до н. э.) появилась гениальная идея — использовать этот факт для измерения окружности и радиуса Земли. В день летнего солнцестояния в Александрии он использовал скафис — чашу с длинной иглой, при помощи которого можно было определить под каким углом Солнце находится на небе.
Итак, после измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть Сиена отстоит от Александрии на 1/50 окружности Земли. Расстояние между городами считалось равным 5 тыс. стадиев, следовательно окружность Земли равнялась 250 тыс. стадиев, а радиус тогда 39,8 тыс. стадиев.
Неизвестно каким стадием пользовался Эратосфен. Если греческим (178 метров), то его радиус Земли получался 7,08 тыс. км, если египетским, то 6,3 тыс. км. Современные измерения дают для усреднённого радиуса Земли величину 6,371 км. В любом случае, точность для тех времён потрясающая.

Радиус Марса. Размеры Марса

определяются не одной числовой характеристикой. Ученые обозначают его размер несколькими параметрами. Первый параметр – радиус. Его величина составляет 3 389,5 километров. Второй – окружность, которая численно равна 21 344 километра. Далее следует объем – 6,083·1010 км³. Последним параметром является масса Марса, которая равна 3,33022·1023 кг.

Для сравнения, диаметрсоставляет 53% от диаметра Земли. На первый взгляд это немного, но его величина сравнима с общей площадью суши на. Объем Марса составляет 15% от объема Земли, а масса – 11%. Из приведенных данных видно, что Марс небольшая планета, он в 2 раза меньше Земли и по величине – 7 планета в.

Сравнение размеров Земли, Марса и Луны

Несмотря на свой небольшой размер и отсутствие на нем жизни, у Марса много интересных особенностей. Самая высокая гора Солнечной системы –– находится на Красной планете. Марсианская– самая глубокая. Сотни тысяч кратеров покрывают поверхность Красной планеты. Северный полярный бассейн – крупнейшая из известных равнин, а равнина Эллада, размер которой 2100 км – глубочайшая на планете и третья по величине в Солнечной системе.

Экстремальные топографические особенности Красной планеты дополняют не менее экстремальные погодные условия. Марс – холодная планета. Средняя температура поверхности составляет 470С ниже нуля. Летом в районе экватора температура днем может подняться до +200С, а ночью упасть до -900С. Такие перепады температуры в 1100С вызывают сильнейшие ураганы, достигающие скорости торнадо. Они поднимают с поверхности Марса пыль, и тогда начинается пыльная буря. Астрономы наблюдали на Марсе бури, которые охватывали всю планету всего за несколько дней.

По мнению ученых, Марс в начале развития Солнечной системы был гораздо больших размеров. Размеры планеты уменьшились в результате внешнего воздействия, например столкновения с каким-то космическим телом, которое вызвало образование Северного полярного бассейна. Куски поверхности, разрушенной взрывом, преодолев гравитационное поле Марса, были выброшены в комическое пространство.

Итак, не только размеры Марса могут представлять интерес. О Красной планете можно узнать еще много интересного, все зависит от нашего с вами желания. Много интересного можно узнать и о других планетах –и

Как Эратосфен измерил радиус земли. Греческий астроном Эратосфен первым вычислил радиус Земли: любопытные факты

Точность измерения Эратосфена для тех времён была просто удивительная

Эратосфен Киренский (276 год до н.э. — 194 год до н.э.) — греческий математик, астроном, географ и поэт.

19 июня 240 года до н.э. Эратосфен использовал скафис (чашу с длинной иглой), с помощью которой можно было определить под каким углом Солнце находится на небе. Это был день летнего солнцестояния в Александрии.

Неудовлетворенный познаниями, приобретёнными в Александрии, Эратосфен отправился в Афины, где так тесно сблизился со школой Платона, что обыкновенно называл себя платоником.

Результатом изучения наук в этих обоих центрах древнегреческого просвещения была очень разносторонняя, почти энциклопедическая эрудиция Эратосфена; он писал, кроме сочинений по математике, астрономии, геодезии, географии и хронологии, ещё трактаты «о добре и зле», о комедии и др.

Царь Птолемей III Эвергет тотчас же после смерти Каллимаха вызвал Эратосфена из Афин и поручил ему заведование великой Александрийской библиотекой. Эрастофен — автор многих трудов по математике, астрономии, геодезии, географии. Один из интересных фактов жизни Эратосфена – вычисление радиуса Земли. 

Древние египтяне заметили, что во время летнего солнцестояния Солнце освещает дно глубоких колодцев в Сиене (ныне Асуан), а в Александрии — нет. Эратосфен использовал этот факт для измерения окружности и радиуса Земли.

После измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Поэтому Сиена отстает от Александрии на 1/50 окружности Земли. Расстояние между городами равнялось 5,000 стадиям, следовательно окружность Земли равнялась 250,000 стадий, а радиус тогда был 39,790 стадий.

Неизвестно какими стадиями пользовался Эратосфен. Если греческими (178 метров), то его радиус земли — 7,082 км, а если египетскими — 6,287 км.

Современные измерения дают для средний радиус Земли — 6,371 км.

В любом случае, точность измерения для тех времён просто удивительная!

Эратосфен прожил удивительную, насыщенную и долгую жизнь. На протяжении нескольких десятилетий оставался бессменным архивариусом Александрийской библиотеки. Он до последнего боготворил и больше всего на свете любил книги, источник знаний и ярчайших открытий. В старости, отстраненный от должности, ослепший и немощный, довел себя до крайней нищеты и уморил себя голодом в 194 г. до н.э.

Как сообщал портал «Знай.uа», астрономы открыли систему, в которой находятся сразу три землеподобные планеты. Более того, ученые обнаружили систему с двумя суперземлями.

Астрономам уже известно около 500 землеподобных планет. Проблема в том, что большинство из них либо слишком горячие, либо, наоборот, холодные, поэтому ученые продолжают поиск планет, похожих на Землю. 

Как измерили радиус земли сообщение 7 класс. Как древний грек измерил радиус Земли (3 фото)

Древние греки, наблюдая за лунными затмениями, обнаружили, что Земля отбрасывает круглую тень на Луну. Таким образом они поняли, что наша планета круглая. В те же времена египтяне провели такое наблюдение, которое заключалось в том, что во время летнего солнцестояния, Солнце освещает дно даже самых глубоких колодцев.

В те времена (240 лет до нашей эры) жил известный греческий математик, астроном, географ и поэт — Эратосфен Киренский. Он получал свое образование в Александрии, но неудовлетворенный тем образованием, отправился в Афины, где учился в платоновской школе, и впоследствии стал называть себя платоником.
После получения образования, имея почти энциклопедические познания, Эратосфен начал свою научную деятельность, впоследствии став известным, благодаря своим работам. Так, в один прекрасный момент, царь Птолемей III пригласил Эратосфена из Афин в Александрию заведовать великой Александрийской библиотекой.

Одно из самых величайших открытий Эратосфена — вычисление радиуса Земли. Посчитал он радиус благодаря колодцам и знанию о том, что Земля круглая. Во время солнцестояния в Александрии Эратосфен замерил при помощи чаши с длинной иглой под каким углом находится Солнце по отношению к Земле в Сиене. После измерения угол оказался 7 градусов 12 минут, то есть 1/50 окружности. Стало быть Сиена отстоит от Александрии на 1/50 окружности Земли, то есть — в 5000 стадиях, следовательно окружность Земли равнялась 250000 стадиям, а радиус тогда 39790 стадиев.
Согласно подсчетам Эратосфен получил значение 6287 км, которое отличается от истинного значения всего на менее чем на 100 км.

Видео Опровержение вычислений радиуса Земли Эратосфеном

Диаметр Земли и другие космические параметры

Каждый из нас изучал в школе много предметов: физику, химию, биологию, математику и другие. В этот список зачастую включалась и астрономия. Это интересная наука, рассказывающая нам про разные космические величины (расстояние от нашей планеты до Солнца, диаметр Земли, массу луны и иные), вселенские явления (черные дыры, звездопады, затмения и т. д.).

Согласитесь, что все это – очень важная и познавательная информация о том, что нас окружает. Но если кто-нибудь спросит нас о том, каков диаметр планеты Земля, мы вряд ли сможем правильно ответить. К сожалению, все, что мы учили в школе, имеет свойство постепенно забываться, если знания не поддерживать. Эта статья поможет возобновить некоторую «космическую» информацию.

Диаметр Земли

Считается, что этот показатель нашей планеты начал изучаться еще до Нашей эры. Знаменитый античный ученый-астроном Эратосфен, используя расстояние между городами и угол падения солнечных лучей, смог вычислить длину окружности нашей планеты, а потом – радиус и диаметр Земли. Так, средний показатель данной величины составляет примерно 12 756 километров. Согласитесь, что это достаточно много. Слово «средний» здесь употребляется, потому что Земля не имеет форму шара (но это и не эллипс, о котором в свое время так много говорили).

Это своеобразная вытянутая к полюсам форма, которую в настоящее время имеют обыкновение называть геоидом. Из-за такой «деформации» диаметр Земли по экватору отличается от соответствующего показателя по нулевому меридиану (вторая величина немного больше).

Другие важные параметры голубой планеты

Земля имеет очень большую и богатую историю, большую часть которой она хранит в себе и о которой, к сожалению, нам вряд ли доведется узнать. Нашей планете уже более четырех с половиной миллиардов лет. За это время она претерпела большое количество изменений. Земля является частью Солнечной системы и вращается по орбите вокруг ее центра – нашего светила. Расстояние до него от третьей планеты – примерно сто пятьдесят миллионов километров. Земля имеет всего один естественный спутник – всем известную Луну, которая оказывает значительное влияние на приливы на голубой планете. Длина экватора составляет примерно 40 076 километров, что почти на 44 километра больше длины меридиана (именно поэтому в зависимости от места измерения и меняется диаметр Земли).

Живая планета

Действительно, Земля в настоящее время является единственным изученным (местными учеными) местом во Вселенной, где есть живые организмы, которые появились здесь почти четыре миллиарда лет назад. Они обитают как на суше, так и в воде. А вода на нашей планете занимает более семидесяти процентов. Кроме наличия организмов, Земля также имеет свою жизнь. Она проявляется в движении тектонических плит: происходят извержения вулканов, сильные и слабые землетрясения. Это подтверждает тот факт, что наша Земля не останавливается в своем развитии и теперь. Никто не знает о том, какие еще сюрпризы подготовил нам дом людей – живая голубая планета.

Радиус Луны. Как в древней Греции астрономы рассчитывали расстояние до Луны

Расстояние от Земли до Луны

Луна стала первым небесным телом, до которого удалось рассчитать расстояние от Земли. Считается, что первыми это сделали астрономы в Древней Греции.

Измерить расстояние до Луны пытались с незапамятных времен – первым это попытался сделать Аристарх Самосский. Он оценил угол между Луной и Солнцем в 87 градусов, поэтому вышло, что Луна ближе Солнца в 20 раз (косинус угла равного 87 градуса равен 1/20). Ошибка измерений угла привела к 20-кратной ошибке, сегодня известно, что это отношение на самом деле равно 1 к 400 (угол равен примерно 89.8 градусов). Большая ошибка была вызвана трудностью оценок точного углового расстояния между Солнцем и Луной с помощью примитивных астрономических инструментов Древнего мира. Регулярные солнечные затмения к этому времени уже позволили древнегреческим астрономам сделать вывод о том, что угловые диаметры Луны и Солнца примерно одинаковы. В связи с этим Аристарх сделал вывод, что Луна меньше Солнца в 20 раз (на самом деле примерно в 400 раз).

Для вычисления размеров Солнца и Луны относительно Земли Аристарх использовал другой метод. Речь идет о наблюдениях лунных затмений. К этому времени древние астрономы уже догадались о причинах этих явлений: Луна затмевается тенью Земли.

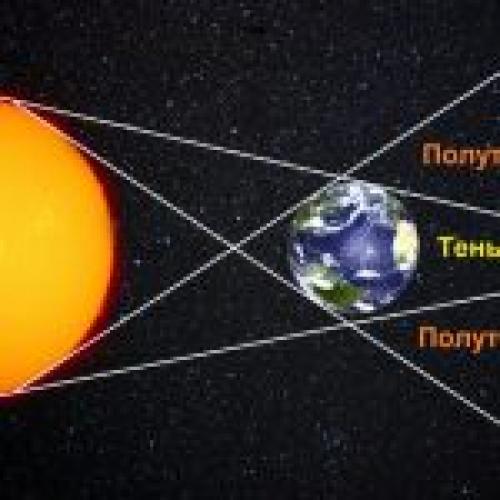
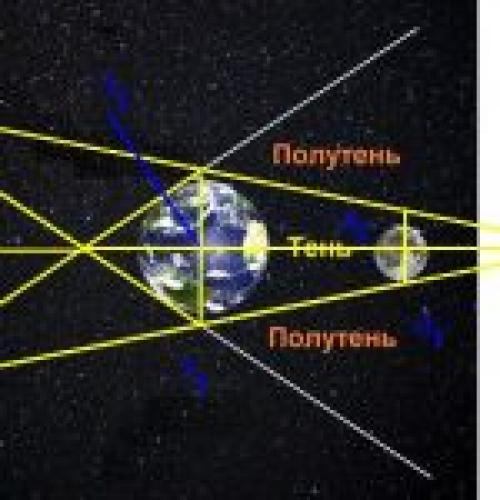
На схеме выше хорошо видно, что разность расстояний с Земли до Солнца и до Луны пропорциональна разнице между радиусами Земли и Солнца и радиусами Земли и её тени на расстояние Луны. Во времена Аристарха уже удалось оценить, что радиус Луны равен примерно 15 угловым минутам, а радиус земной тени составляет 40 угловых минут. То есть размер Луны получался примерно в 3 раза меньше размера Земли. Отсюда зная угловой радиус Луны можно было легко оценить, что Луна находится от Земли примерно в 40 диаметрах Земли. Древние греки могли лишь приблизительно оценить размеры Земли. Так Эратосфен Киренский (276 – 195 годы до нашей эры) на основе различий в максимальной высоте Солнца над горизонтом в Асуане и Александрии во время летнего солнцестояния определил, что радиус Земли близок к 6287 км (современное значение 6371 км). Если подставить это значение в оценку Аристарха насчет расстояния до Луны, то оно будет соответствовать примерно 502 тысяч км (современное значение среднего расстояния от Земли до Луны составляет 384 тысяч км).

Радиус Солнца. Размеры Солнца: масса, диаметр, радиус

Солнце — это колоссальный раскалённый шар, в центре которого происходит освобождение энергии из водорода. Водород трансформируется в гелий, а излучаемая энергия выделяется в космическое пространство. Люди в древности не зря обожествляли светило. Именно его энергия обеспечивает существование жизни на Земле .

Размеры Солнца

Диаметр

Солнце (Гелиос) — это ближайшая к нашей планете звезда. Она относится к категории «Жёлтых карликов». Подобно другим светилам, Гелиос не имеет прочной поверхности. Его первичным слоем принято считать фотосферу, излучающую энергию. А потому диаметр Солнца — ни что иное, как диаметр его фотосферы.

Измерить масштабы светила можно простым доступным способом. Для эксперимента необходимо тёмное помещение, куда солнечный луч проникает через маленькое отверстие . Плотную белую бумагу достаточно поставить напротив луча, и на поверхности листа появится крошечное изображение Солнца. Чем дальше будет бумага от отверстия, тем больше будет пятно. На расстоянии 107 см его диаметр составит 1 см. При удалении на 214 см возрастёт до 2 см. То есть диаметр настоящего светила в 107 раз меньше расстояния до Земли и составляет 1400000 км.

Учёные смогли определить точный диаметр Солнца в километрах, базируясь на эффекте под названием «Чётки Бейли». Чётками называют красные точки по окружности солнечного диска, которые становятся видимыми во время затмения. С их помощью астрономы точно выделили положение светила и смогли измерить его размеры.

Анализ исторических данных, дополненный регулярным современным мониторингом, показал, что диаметр Солнца подвержен изменениям. Так, в XVII веке светило было на 2 тыс.километров шире нынешнего. Астрономы установили, что звезда расширяется и сжимается в течение 160 минут. За этот же период меняется количество выбрасываемой энергии.

Радиус

Измерения длительности солнечных затмений и наблюдения за перемещением Меркурия и Венеры на фоне солнечного диска позволили учёным вычислить примерный радиус звезды. Он равен 695990 км.

Приборы на борту космических станций дали возможность уточнить расчёты. Исследования проводились методами гелиосейсмологии. При этом рассматривалось движение так называемых f-волн на поверхности Солнца. Этот способ вычислений дал несколько иной результат — на 300 км меньше (695700 км). Выявленная погрешность может иметь серьёзные последствия для изучения Солнца, его состава и активности.

Радиус будет иметь одинаковое значение во всех направлениях, поскольку Гелиос имеет правильную шарообразную форму.

Сравнение размеров небесных тел

Величину солнечного радиуса в астрономии применяют в качестве меры измерения габаритов других космических объектов:

• Полярная Звезда имеет 30 солнечных радиусов. Следовательно, она в 30 раз превышает параметры Солнца.
• Наша планета выглядит небольшой точкой на фоне главной звезды. Она в 109 раз уступает светилу по размеру.
• Зато крупнейшая планета Солнечной системы – Юпитер всего в 9,7 раза меньше Солнца.

Во Вселенной можно обнаружить звезды – гиганты, превосходящие во много раз наше светило . Крупнейшая звезда VY Canis Majoris, по мнению учёных, имеет 2100 диаметров Гелиоса.

Масса Солнца, её измерение и сравнение

Солнце — крупнейшее небесное тело в нашей звёздной системе (99,86% общей массы). На формирование массы солнца потребовалось почти 5 миллиардов лет.

Для измерения массы небесных тел разработаны три научных метода:

1. Гравиметрический. В этом способе применяют параметры измерений силы тяжести, которая характеризует поверхность измеряемого тела.
2. Третий закон Кеплера. Практикуется в том случае, если планета обладает, как минимум, одним спутником. Вычисления проводятся с учётом расстояния между планетой и её спутником, а также периода его обращения по орбите. Таким образом выясняется соотношение масс планеты и звезды.
3. Анализ заметных воздействий , вызываемых движением одних небесных тел относительно движения других.

В первую очередь с помощью геодезического метода выяснили массу нашей планеты. Она, по оценкам, составила 6*1024кг. Затем на основании Третьего закона Кеплера вычислили массу Луны – 73477*1022 кг. И в завершение узнали, чему равна масса Солнца — 19891*1030кг.

Солнечная масса стала абстрактной метрической единицей . Астрономы употребляют её для описания различных космических объектов. Самая гигантская известная звезда, Eta Carinae, оценивается в 150 масс Гелиоса.

Учёные составили прогноз солнечной активности на будущее. Опираясь на наблюдения за другими звёздами, они пришли к выводу, что звезда постепенно израсходует энергию фотосферы. Её размеры небывало расширятся. Ближайшие планеты — Меркурий и Венера будут поглощены. Возможно, что та же участь постигнет и Землю. Солнце преобразуется в Красного гиганта. Вслед за периодом роста последует катастрофическое сжатие. Светило сожмётся примерно до нынешних параметров Земли и будет именоваться Белым карликом .

форма, история, каким может быть, цифры

Начнём с определения, что такое радиус и для чего он нужен. Ну здесь всё довольно просто. Радиусом называют отрезок, который соединяет центр окружности с лежащей на ней точкой. То есть это длина данного отрезка. К тому же, он равный половине диаметра.
Таким образом, радиус Земли это длина от её центра до некой точки. Но тут прослеживается интересный момент.

Размеры земли

Каким может быть радиус Земли

На данный момент различают:

• экваториальный радиус-представляет собой линию от центра до точки экватора. Собственно, он имеет длину 6378,1 км.
• полярный соединяет центральную точку с географическим полюсом.

А как известно, различают Северный и Южный полюса. По данным учёных, он равен 6356,8 км. Как видно, его длина меньше предыдущего. Очевидно, что это связано с формой Земли. Как известно, наша планета не идеально округлая по форме, а немного приплюснута у полюсов. Поэтому на экваторе наблюдается выпуклость, которая и приводит к увеличению дистанции от одной точки до другой. Как раз этим и объясняется различие между рассматриваемыми дистанциями.

Линия экватора

Однако учёные определили средний радиус Земли. И он составляет 6371 км.
В итоге, отвечая на вопрос: чему равен радиус Земли, можно руководствоваться средним значением. Либо будет правильнее уточнить, что существует две разные длины этой характеристики планеты.
Также важно подметить, что радиус Земли рассчитывается, главным образом, в километрах.

История измерения

Безусловно, своей планетой люди интересовались ещё в древности. Помимо того, что они наблюдали за всем, что происходит вокруг неё, также проводились исследования и изучение Земли.

Ученые

Интересно, что в древние египтяне обратили внимание, что в дни летнего солнцестояния солнечные лучи проникали на дно колодцев в Сиене (старый город Египта). Однако в это же самое время, например, в Александрии такое не наблюдали. Этот факт использовал Эратосфен Киренский для определения угла, под которым Солнце находилось относительно Земли. Таким образом он установил, что данный угол равен 7 градусов 12 минут, или 1/50 часть окружности. На основании полученного результата, учёный сделал вывод, что Сиена находится от Александрии на это значение. Так как географическое расстояние было 5 тысяч стадиев, значит земная окружность составляла 250 тысяч стадиев. Но до сих пор непонятно, какие стадии применял Эратосфен. Потому как греческое значение подразумевает 178 метров, а например, египетское — 172,5 метров. Несмотря на это, его определение близко к современным подсчётам. Что разумеется, очень потрясает.

Полторы тысяч лет назад, все знали что Земля была центром вселенной. Пятьсот лет назад, все знали что Земля плоская, а пятнадцать минут назад, ты знал что люди были единственными на этой планете. Представь что ты будешь «знать» завтра.

Люди в черном (Men in Black)

Форма и радиус Земли

Интересно, что уже в древности были версии о неидеальной форме планеты.
Конечно, другие учёные также пытались измерить радиус Земли. К примеру, Жан Рише наблюдал за Марсом из Кайенны. Он заметил уменьшение периода движения секундного маятника в отличие от парижского наблюдения. Собственно, это является подтверждением уменьшения силы тяготения на экваторе. Что, в свою очередь, показывало на то, что земная форма не идеальная окружность.
Также многие другие пытались разобраться с тем, как выглядит наша планета. Потому что от этого напрямую зависит радиус и диаметр Земли. Стоит отметить, одно из самых важных градусных измерений. Его провёл В. Я. Струве. В основе работы лежит измерение дуги от Дуная до Финляндии. Причём она проходила по западной стороне России. Как выяснили учёные, длина дуги была более 2800 км. Кроме того, её охват составил свыше 25 градусов, а это 1/14 часть всей планетной окружности.

Василий Яковлевич Струве (1793-1864)

Бесспорно, за всё время люди прилагали массу усилий и попыток определить все характеристики Земли. Сегодня мы знаем больше, чем когда-либо. Более того, мы определили, что радиус Земли в среднем составляет 6371 км. Помимо этого современная наука выяснила диаметр, радиус орбиты, расстояние от Земли до других небесных тел и многое другое. К нашей радости, мы мало-помалу разгадываем вселенские задачи и секреты.

Планета Земля

КАК ДРЕВНИЕ ГРЕКИ РАССЧИТАЛИ РАЗМЕРЫ ЗЕМЛИ, ЛУНЫ, СОЛНЦА И РАССТОЯНИЯ ДО НИХ.: sorokovs — LiveJournal

То, что Земля не плоская, люди знали давно. Древние мореплаватели наблюдали, как постепенно меняется картина звездного неба: становятся видны новые созвездия, а другие, напротив, заходят за горизонт. Уплывающие вдаль корабли «уходят под воду», последними скрываются из вида верхушки их мачт. Кто первый высказал идею о шарообразности Земли, неизвестно. Скорее всего — пифагорейцы, считавшие шар совершеннейшей из фигур. Полтора века спустя Аристотель приводит несколько доказательств того, что Земля — шар. Главное из них: во время лунного затмения на поверхности Луны отчетливо видна тень от Земли, и эта тень круглая! С тех пор постоянно предпринимались попытки измерить радиус земного шара. Два простых способа изложены в упражнениях 1 и 2. Измерения, правда, получались неточными. Аристотель, например, ошибся более чем в полтора раза. Считается, что первым, кому удалось сделать это с высокой точностью, был греческий математик Эратосфен Киренский (276–194 до н. э.). Его имя теперь всем известно благодаря решету Эратосфена — способу находить простые числа (рис. 1). Рис. 1 Если вычеркнуть из натурального ряда единицу, затем вычеркивать все четные числа, кроме первого (самого числа 2), затем все числа, кратные трем, кроме первого из них (числа 3), и т. д., то в результате останутся одни простые числа. Среди современников Эратосфен был знаменит как крупнейший ученый-энциклопедист, занимавшийся не только математикой, но и географией, картографией и астрономией. Он долгое время возглавлял Александрийскую библиотеку — центр мировой науки того времени. Работая над составлением первого атласа Земли (речь, конечно, шла об известной к тому времени ее части), он задумал провести точное измерение земного шара. Идея была такова. В Александрии все знали, что на юге, в городе Сиена (современный Асуан), один день в году, в полдень, Солнце достигает зенита. Исчезает тень от вертикального шеста, на несколько минут освещается дно колодца. Происходит это в день летнего солнцестояния, 22 июня — день наивысшего положения Солнца на небе. Эратосфен направляет своих помощников1 в Сиену, и те устанавливают, что ровно в полдень (по солнечным часам) Солнце находится точно в зените. Одновременно (как написано в первоисточнике: «в тот же час»), т. е. в полдень по солнечным часам, Эратосфен измеряет длину тени от вертикального шеста в Александрии. Получился треугольник ABC (АС — шест, АВ — тень, рис. 2). Рис. 2 Итак, солнечный луч в Сиене (N) перпендикулярен поверхности Земли, а значит, проходит через ее центр — точку Z. Параллельный ему луч в Александрии (А) составляет угол γ = ACB с вертикалью. Пользуясь равенством накрест лежащих углов при параллельных, заключаем, что AZN = γ. Если обозначить через l длину окружности, а через х длину ее дуги AN, то получаем пропорцию . Угол γ в треугольнике АВС Эратосфен измерил, получилось 7,2°. Величина х — не что иное, как длина пути от Александрии до Сиены, примерно 800 км. Ее Эратосфен аккуратно вычисляет, исходя из среднего времени движения верблюжьих караванов, регулярно ходивших между двумя городами, а также используя данные бематистов — людей специальной профессии, измерявших расстояния шагами. Теперь осталось решить пропорцию , получив длину окружности (т. е. длину земного меридиана) l = 40000 км. Тогда радиус Земли R равен l/(2π), это примерно 6400 км. То, что длина земного меридиана выражается столь круглым числом в 40000 км, не удивительно, если вспомнить, что единица длины в 1 метр и была введена (во Франции в конце XVIII века) как одна сорокамиллионная часть окружности Земли (по определению!). Эратосфен, конечно, использовал другую единицу измерения — стадий (около 200 м). Стадиев было несколько: египетский, греческий, вавилонский, и каким из них пользовался Эратосфен — неизвестно. Поэтому трудно судить наверняка о точности его измерения. Кроме того, неизбежная ошибка возникала в силу географического положения двух городов. Эратосфен рассуждал так: если города находятся на одном меридиане (т. е. Александрия расположена в точности к северу от Сиены), то полдень в них наступает одновременно. Поэтому, сделав измерения во время наивысшего положения Солнца в каждом городе, мы должны получить правильный результат. Но на самом деле Александрия и Сиена — далеко не на одном меридиане. Сейчас в этом легко убедиться, взглянув на карту, но у Эратосфена такой возможности не было, он как раз и работал над составлением первых карт. Поэтому его метод (абсолютно верный!) привел к ошибке в определении радиуса Земли. Тем не менее, многие исследователи уверены, что точность измерения Эратосфена была высока и что он ошибся менее чем на 2%. Улучшить этот результат человечество смогло только через 2 тысячи лет, в середине XIX века. Над этим трудилась группа ученых во Франции и экспедиция В. Я. Струве в России. Даже в эпоху великих географических открытий, в XVI веке, люди не смогли достичь результата Эратосфена и пользовались неверным значением длины земной окружности в 37000 км. Ни Колумб, ни Магеллан не знали, каковы истинные размеры Земли и какие расстояния им придется преодолевать. Они-то считали, что длина экватора на 3 тысячи км меньше, чем на самом деле. Знали бы — может, и не поплыли бы. В чем причина столь высокой точности метода Эратосфена (конечно, если он пользовался нужным стадием)? До него измерения были локальными, на расстояниях, обозримых человеческим глазом, т. е. не более 100 км. Таковы, например, способы в упражнениях 1 и 2. При этом неизбежны ошибки из-за рельефа местности, атмосферных явлений и т. д. Чтобы добиться большей точности, нужно проводить измерения глобально, на расстояниях, сравнимых с радиусом Земли. Расстояние в 800 км между Александрией и Сиеной оказалось вполне достаточным. Как измерили Луну и Солнце. Три шага Аристарха Памятник Аристарху Самосскому в Салониках Греческий остров Самос в Эгейском море — теперь глухая провинция. Сорок километров в длину, восемь — в ширину. На этом крохотном острове в разное время родились три величайших гения — математик Пифагор, философ Эпикур и астроном Аристарх. Про жизнь Аристарха Самосского известно мало. Даты жизни приблизительны: родился около 310 до н.э., умер около 230 до н.э. Как он выглядел, мы не знаем, ни одного изображения не сохранилось (современный памятник Аристарху в греческом городе Салоники — лишь фантазия скульптора) . Много лет провел в Александрии, где работал в библиотеке и в обсерватории. Главное его достижение — книга «О величинах и расстояниях Солнца и Луны», — по единодушному мнению историков, является настоящим научным подвигом. В ней он вычисляет радиус Солнца, радиус Луны и расстояния от Земли до Луны и до Солнца. Сделал он это в одиночку, пользуясь очень простой геометрией и всем известными результатами наблюдений за Солнцем и Луной. На этом Аристарх не останавливается, он делает несколько важнейших выводов о строении Вселенной, которые намного опередили свое время. Не случайно его назвали впоследствии «Коперником античности». Вычисление Аристарха можно условно разбить на три шага. Каждый шаг сводится к простой геометрической задаче. Первые два шага совсем элементарны, третий — чуть посложнее. В геометрических построениях мы будем обозначать через Z, S и L центры Земли, Солнца и Луны соответственно, а через R, Rs и Rl — их радиусы. Все небесные тела будем считать шарами, а их орбиты — окружностями, как и считал сам Аристарх (хотя, как мы теперь знаем, это не совсем так). Мы начинаем с первого шага, и для этого немного понаблюдаем за Луной. Шаг 1. Во сколько раз Солнце дальше, чем Луна? Как известно, Луна светит отраженным солнечным светом. Если взять шар и посветить на него со стороны большим прожектором, то в любом положении освещенной окажется ровно половина поверхности шара. Граница освещенной полусферы — окружность, лежащая в плоскости, перпендикулярной лучам света. Таким образом, Солнце всегда освещает ровно половину поверхности Луны. Видимая нам форма Луны зависит от того, как расположена эта освещенная половина. При новолунии, когда Луна вовсе не видна на небе, Солнце освещает ее обратную сторону. Затем освещенная полусфера постепенно поворачивается в сторону Земли. Мы начинаем видеть тонкий серп, затем — месяц («растущая Луна»), далее — полукруг (эта фаза Луны называется «квадратурой»). Затем день ото дня (вернее, ночь от ночи) полукруг дорастает до полной Луны. Потом начинается обратный процесс: освещенная полусфера от нас отворачивается. Луна «стареет», постепенно превращаясь в месяц, повернутый к нам левой стороной, подобно букве «С», и, наконец, в ночь новолуния исчезает. Период от одного новолуния до другого длится примерно четыре недели. За это время Луна совершает полный оборот вокруг Земли. От новолуния до половины Луны проходит четверть периода, отсюда и название «квадратура». Рис. 3 Замечательная догадка Аристарха состояла в том, что при квадратуре солнечные лучи, освещающие половину Луны, перпендикулярны прямой, соединяющей Луну с Землей. Таким образом, в треугольнике ZLS угол при вершине L — прямой (рис. 3). Если теперь измерить угол LZS, обозначим его через α, то получим, что = cos α. Для простоты мы считаем, что наблюдатель находится в центре Земли. Это несильно повлияет на результат, поскольку расстояния от Земли до Луны и до Солнца значительно превосходят радиус Земли. Итак, измерив угол α между лучами ZL и ZS во время квадратуры, Аристарх вычисляет отношение расстояний до Луны и до Солнца. Как одновременно застать Солнце и Луну на небосводе? Это можно сделать ранним утром. Сложность возникает по другому, неожиданному, поводу. Во времена Аристарха не было косинусов. Первые понятия тригонометрии появятся позже, в работах Аполлония и Архимеда. Но Аристарх знал, что такое подобные треугольники, и этого было достаточно. Начертив маленький прямоугольный треугольник Z’L’S’ с тем же острым углом α = L’Z’S’ и измерив его стороны, находим, что , и это отношение примерно равно 1/400. Получается, что Солнце в 400 раз дальше от Земли, чем Луна. Эту константу — отношение расстояний от Земли до Солнца и от Земли до Луны — мы будем обозначать буквой κ. Итак, мы нашли, что κ = 400. Шаг 2. Во сколько раз Солнце больше Луны? Для того чтобы найти отношение радиусов Солнца и Луны, Аристарх привлекает солнечные затмения (рис. 4). Они происходят, когда Луна загораживает Солнце. При частичном, или, как говорят астрономы, частном, затмении Луна лишь проходит по диску Солнца, не закрывая его полностью. Порой такое затмение даже нельзя разглядеть невооруженным глазом, Солнце светит как в обычный день. Лишь сквозь сильное затемнение, например, закопченное стекло, видно, как часть солнечного диска закрыта черным кругом. Гораздо реже происходит полное затмение, когда Луна на несколько минут полностью закрывает солнечный диск. Рис. 4 В это время становится темно, на небе появляются звезды. Затмения наводили ужас на древних людей, считались предвестниками трагедий. Солнечное затмение наблюдается по-разному в разных частях Земли. Во время полного затмения на поверхности Земли возникает тень от Луны — круг, диаметр которого не превосходит 270 км. Лишь в тех районах земного шара, по которым проходит эта тень, можно наблюдать полное затмение. Поэтому в одном и том же месте полное затмение происходит крайне редко — в среднем раз в 200–300 лет. Аристарху повезло — он смог наблюдать полное солнечное затмение собственными глазами. На безоблачном небе Солнце постепенно начало тускнеть и уменьшаться в размерах, установились сумерки. На несколько мгновений Солнце исчезло. Потом проглянул первый луч света, солнечный диск стал расти, и вскоре Солнце засветило в полную силу. Почему затмение длится столь короткое время? Аристарх отвечает: причина в том, что Луна имеет те же видимые размеры на небе, что и Солнце. Что это значит? Проведем плоскость через центры Земли, Солнца и Луны. Получившееся сечение изображено на рисунке 5a. Угол между касательными, проведенными из точки Z к окружности Луны, называется угловым размером Луны, или ее угловым диаметром. Так же определяется угловой размер Солнца. Если угловые диаметры Солнца и Луны совпадают, то они имеют одинаковые видимые размеры на небе, а при затмении Луна действительно полностью загораживает Солнце (рис. 5б), но лишь на мгновение, когда совпадут лучи ZLи ZS. На фотографии полного солнечного затмения (см. рис. 4) ясно видно равенство размеров. Рис. 5 Вывод Аристарха оказался поразительно точен! В реальности средние угловые диаметры Солнца и Луны отличаются всего на 1,5%. Мы вынуждены говорить о средних диаметрах, поскольку они меняются в течение года, так как планеты движутся не по окружностям, а по эллипсам. Соединив центр Земли Z с центрами Солнца S и Луны L, а также с точками касания Р и Q, получим два прямоугольных треугольникаZSP и ZLQ (см. рис. 5a). Они подобны, поскольку у них есть пара равных острых углов β/2. Следовательно, . Таким образом, отношение радиусов Солнца и Луны равно отношению расстояний от их центров до центра Земли. Итак, Rs/Rl = κ = 400. Несмотря на то, что их видимые размеры равны, Солнце оказалось больше Луны в 400 раз! Равенство угловых размеров Луны и Солнца — счастливое совпадение. Оно не вытекает из законов механики. У многих планет Солнечной системы есть спутники: у Марса их два, у Юпитера — четыре (и еще несколько десятков мелких), и все они имеют разные угловые размеры, не совпадающие с солнечным. Теперь мы приступаем к решающему и самому сложному шагу. Шаг 3. Вычисление размеров Солнца и Луны и расстояний до них Итак, нам известно отношение размеров Солнца и Луны и отношение их расстояний до Земли. Эта информация относительна: она восстанавливает картину окружающего мира лишь с точностью до подобия. Можно удалить Луну и Солнце от Земли в 10 раз, увеличив во столько же раз их размеры, и видимая с Земли картина останется такой же. Чтобы найти реальные размеры небесных тел, надо соотнести их с каким-то известным размером. Но из всех астрономических величин Аристарху пока известен только радиус2земного шара R = 6400 км. Поможет ли это? Хоть в каком-то из видимых явлений, происходящих на небе, появляется радиус Земли? Не случайно говорят «небо и земля», имея в виду две несовместные вещи. И всё же такое явление есть. Это — лунное затмение. С его помощью, применив довольно хитроумное геометрическое построение, Аристарх вычисляет отношение радиуса Солнца к радиусу Земли, и цепь замыкается: теперь мы одновременно находим радиус Луны, радиус Солнца, а заодно и расстояния от Луны и от Солнца до Земли. ПОДРОБНОСТИ ВЫЧИСЛЕНИЙ ЗДЕСЬ Сравнивая окружности тени Земли на Луне во время лунного затмения, Аристарх нашёл число t = 8/3- отношение радиуса тени Земли к радиусу Луны.  Кроме того он уже вычислил κ = 400 (отношение радиуса Солнца к радиусу Луны, которое почти равно отношению расстояния Солнце-Земля к расстоянию Луна-Земля). После довольно нетривиальных геометрических построений Аристарх находит, что  отношение диаметров Солнца и Земли равно , а Луны и Земли равно . Подставляя известные нам величины κ = 400 и t = 8/3, получаем, что Луна примерно в 3,66 раза меньше Земли, а Солнце в 109 раз больше Земли. Так как радиус Земли R нам известен, находим радиус Луны Rl= R/3,66 и радиус Солнца Rs= 109R. Теперь расстояния от Земли до Луны и до Солнца вычисляются в один шаг, это может быть сделано с помощью углового диаметра. Угловой диаметр β Солнца и Луны составляет примерно полградуса (если быть совсем точным, 0,53°). Как древние астрономы его измеряли, об этом речь впереди. Опустив касательную ZQ на окружность Луны, получаем прямоугольный треугольник ZLQ с острым углом β/2 (рис. 10). Рис. 10 Из него находим , что примерно равно 215Rl, или 62R. Аналогично, расстояние до Солнца равно 215Rs = 23 455R. Всё. Размеры Солнца и Луны и расстояния до них найдены. О пользе ошибок На самом деле всё было несколько сложнее. Геометрия только формировалась, и многие привычные для нас еще с восьмого класса школы вещи были в то время совсем не очевидны. Аристарху потребовалось написать целую книгу, чтобы изложить то, что мы изложили на трех страницах. И с экспериментальными измерениями тоже всё было непросто. Во-первых, Аристарх ошибся с измерением диаметра земной тени во время лунного затмения, получив отношение t = 2 вместо . Кроме того, он, вроде бы, исходил из неверного значения угла β — углового диаметра Солнца, считая его равным 2°. Но эта версия спорная: Архимед в своем трактате «Псаммит» пишет, что, напротив, Аристарх пользовался почти правильным значением в 0,5°. Однако самая ужасная ошибка произошла на первом шаге, при вычислении параметра κ — отношения расстояний от Земли до Солнца и до Луны. Вместо κ = 400 у Аристарха получилось κ = 19. Как можно было ошибиться более чем в 20 раз? Обратимся еще раз к шагу 1, рисунок 3. Для того чтобы найти отношение κ = ZS/ZL, Аристарх измерил угол α = SZL, и тогда κ = 1/cos α. Например, если угол α был бы равен 60°, то мы получили бы κ = 2, и Солнце было бы вдвое дальше от Земли, чем Луна. Но результат измерения оказался неожиданным: угол α получался почти прямым. Это означало, что катет ZS во много раз превосходит ZL. У Аристарха получилось α = 87°, и тогда cos α =1/19  (напомним, что все вычисления у нас — приближенные). Истинное значение угла , и cos α =1/400. Так погрешность измерения менее чем в 3° привела к ошибке в 20 раз! Завершив вычисления, Аристарх приходит к выводу, что радиус Солнца равен 6,5 радиусов Земли (вместо 109). Ошибки были неизбежны, учитывая несовершенные измерительные приборы того времени. Важнее то, что метод оказался правильным. Вскоре (по историческим меркам, т. е. примерно через 100 лет) выдающийся астроном античности Гиппарх (190 – ок. 120 до н.э.) устранит все неточности и, следуя методу Аристарха, вычислит правильные размеры Солнца и Луны. Возможно, ошибка Аристарха оказалась в конце концов даже полезной. До него господствовало мнение, что Солнце и Луна либо вовсе имеют одинаковые размеры (как и кажется земному наблюдателю), либо отличаются несильно. Даже отличие в 19 раз удивило современников. Поэтому не исключено, что, найди Аристарх правильное отношение κ = 400, в это никто бы не поверил, а может быть, и сам ученый отказался бы от своего метода, сочтя результат несуразным. .. За 17 веков до Коперника он понял, что в центре мира находится не Земля, а Солнце. Так впервые появилась гелиоцентрическая модель и понятие Солнечной системы. Что в центре? Господствовавшее в Древнем Мире представление об устройстве Вселенной, знакомое нам по урокам истории, заключалось в том, что в центре мира — неподвижная Земля, вокруг нее по круговым орбитам вращаются 7 планет, включая Луну и Солнце (которое тоже считалось планетой). Завершается всё небесной сферой с прикрепленными к ней звездами. Сфера вращается вокруг Земли, делая полный оборот за 24 часа. Со временем в эту модель многократно вносились исправления. Так, стали считать, что небесная сфера неподвижна, а Земля вращается вокруг своей оси. Затем стали исправлять траектории движения планет: круги заменили циклоидами, т. е. линиями, которые описывают точки окружности при ее движении по другой окружности (об этих замечательных линиях можно прочитать в книгах Г. Н. Бермана «Циклоида», А. И. Маркушевича «Замечательные кривые», а также в «Кванте»: статья С. Верова «Тайны циклоиды» №8, 1975, и статья С. Г. Гиндикина «Звездный век циклоиды», №6, 1985). Циклоиды лучше согласовывались с результатами наблюдений, в частности, объясняли «попятные» движения планет. Это — геоцентрическая система мира, в центре которой — Земля («гея»). Во II веке она приняла окончательный вид в книге «Альмагест» Клавдия Птолемея (87–165), выдающегося греческого астронома, однофамильца египетских царей. Со временем некоторые циклоиды усложнялись, добавлялись всё новые промежуточные окружности. Но в целом система Птолемея господствовала около полутора тысячелетий, до XVI века, до открытий Коперника и Кеплера. Поначалу геоцентрической модели придерживался и Аристарх. Однако, вычислив, что радиус Солнца в 6,5 раз больше радиуса Земли, он задал простой вопрос: почему такое большое Солнце должно вращаться вокруг такой маленькой Земли? Ведь если радиус Солнца больше в 6,5 раз, то его объем больше почти в 275 раз! Значит, в центре мира должно находиться Солнце. Вокруг него вращаются 6 планет, включая Землю.3 А седьмая планета, Луна, вращается вокруг Земли. Так появиласьгелиоцентрическая система мира («гелиос» — Солнце). Уже сам Аристарх отмечал, что такая модель лучше объясняет видимое движение планет по круговым орбитам, лучше согласуется с результатами наблюдений. Но ее не приняли ни ученые, ни официальные власти. Аристарх был обвинен в безбожии и подвергся преследованиям. Из всех астрономов античности только Селевк стал сторонником новой модели. Больше ее не принял никто, по крайней мере, у историков нет твердых сведений на этот счет. Даже Архимед и Гиппарх, почитавшие Аристарха и развившие многие его идеи, не решились поставить Солнце в центр мира. Почему? Почему мир не принял гелиоцентрической системы? Как же получилось, что в течение 17 веков ученые не принимали простой и логичной системы мира, предложенной Аристархом? И это несмотря на то, что официально признанная геоцентрическая система Птолемея часто давала сбои, не согласуясь с результатами наблюдений за планетами и за звездами. Приходилось добавлять всё новые окружности (так называемые вложенные циклы) для «правильного» описания движения планет. Самого Птолемея трудности не пугали, он писал: «К чему удивляться сложному движению небесных тел, если их сущность нам неизвестна?» Однако уже к XIII веку этих окружностей накопилось 75! Модель стала столь громоздкой, что начали раздаваться осторожные возражения: неужели мир в самом деле устроен так сложно? Широко известен случай с Альфонсом X (1226–1284), королем Кастилии и Леона, государства, занимавшего часть современной Испании. Он, покровитель наук и искусств, собравший при своем дворе пятьдесят лучших астрономов мира, на одной из научных бесед обмолвился, что «если бы при сотворении мира Господь оказал мне честь и спросил моего совета, многое было бы устроено проще». Подобная дерзость не прощалась даже королям: Альфонс был низложен и отправлен в монастырь.4 Но сомнения остались. Часть из них можно было бы разрешить, поставив Солнце в центр Вселенной и приняв систему Аристарха. Его труды были хорошо известны. Однако еще много веков никто из ученых не решался на такой шаг. Причины были не только в страхе перед властями и официальной церковью, которая считала теорию Птолемея единственно верной. И не только в инертности человеческого мышления: не так-то просто признать, что наша Земля — не центр мира, а лишь рядовая планета. Все-таки для настоящего ученого ни страх, ни стереотипы — не препятствия на пути к истине. Гелиоцентрическая система отвергалась по вполне научным, можно даже сказать, геометрическим причинам. Если допустить, что Земля вращается вокруг Солнца, то ее траектория — окружность с радиусом, равным расстоянию от Земли до Солнца. Как мы знаем, это расстояние равно 23 455 радиусов Земли, т. е. более 150 миллионов километров. Значит, Земля в течение полугода перемещается на 300 миллионов километров. Гигантская величина! Но картина звездного неба для земного наблюдателя при этом остается такой же. Земля то приближается, то удаляется от звезд на 300 миллионов километров, но ни видимые расстояния между звездами (например, форма созвездий), ни их яркость не меняются. Это означает, что расстояния до звезд должны быть еще в несколько тысяч раз больше, т. е. небесная сфера должна иметь совершенно невообразимые размеры! Это, между прочим, осознавал и сам Аристарх, который писал в своей книге: «Объем сферы неподвижных звезд во столько раз больше объема сферы с радиусом Земля-Солнце, во сколько раз объем последней больше объема земного шара», т. е. по Аристарху выходило, что расстояние до звезд равно (23 455)2R, это более 3,5 триллионов километров. В реальности расстояние от Солнца до ближайшей звезды еще примерно в 11 раз больше. (В модели, которую мы представили в самом начале, когда расстояние от Земли до Солнца равно 10 м, расстояние до ближайшей звезды равно … 2700 километров!) Вместо компактного и уютного мира, в центре которого находится Земля и который помещается внутри относительно небольшой небесной сферы, Аристарх нарисовал бездну. И эта бездна испугала всех.

Как впервые измерили окружность Земли » Детская энциклопедия (первое издание)

Представления древних народов о Земле Как уточнялись знания о форме и величине Земли

Более точное определение размеров земного шара сделал древнегреческий ученый Эратосфен Киренский, живший за 200 лет до н. э.

Слева — определение высоты Солнца скафисом. В центре — схема направления солнечных лучей: в Сиене они падают вертикально, в Александрии — под углом в 7° 12′. Справа — направление луча солнца в Сиене в момент летнего солнцестояния.

Совершая путешествия из г. Александрии на юг, в г. Сиену (теперь Асуан), люди замечали, что там летом, в тот день, когда солнце бывает всего выше на небе (день летнего солнцестояния — 22 июня), в полдень оно освещает дно глубоких колодцев, т. е. бывает как раз над головой, в зените. Предметы в этот момент не дают тени. В Александрии же и в этот день солнце в полдень не доходит до зенита, не освещает дна колодцев, предметы дают тень.

Скафис — прибор для определения высоты Солнца над горизонтом.

Эратосфен измерил, насколько полуденное солнце в Александрии отклонено от зенита, и получил величину, равную 7°12′, что составляет 1/50 окружности. Это ему удалось сделать с помощью прибора, называемого скафисом. Скафис представлял собой чашу в форме полушария. В центре ее отвесно укреплялась игла. Тень от иглы падала на внутреннюю поверхность скафиса. Для измерения отклонения солнца от зенита (в градусах) на внутренней поверхности скафиса проводились окружности, помеченные цифрами. Если, например, тень доходила до окружности, помеченной цифрой 50, солнце стояло на 50° ниже зенита. Построив чертеж, Эратосфен совершенно правильно заключил, что Александрия отстоит от Сиены на 1/50 окружности Земли. Чтобы узнать окружность Земли, оставалось измерить расстояние между Александрией и Сиеной и умножить его на 50. Это расстояние было известно по времени, которое тратили караваны верблюдов на переход между городами. В единицах мер того времени оно равнялось 5000 стадий. Если 1/50 окружности Земли равняется 5000 стадии, то вся окружность Земли равна 5000 X 50 = = 250 000 стадий. В переводе на наши меры это расстояние приблизительно равно 39 500 км.

Зная длину окружности, можно вычислить и величину радиуса Земли.

Известно, что радиус всякой окружности в 6,283 раза меньше ее длины. Поэтому средний радиус Земли, по Эратосфену, оказался равным круглым числом 6290 км, а диаметр — 12 580 км.

Так Эратосфен нашел приблизительно размеры Земли, близкие к тем, которые определены точными приборами в наше время.

Эратосфен — Греческий математик, астроном, географ и поэт. Ученик Каллимаха, с 235 г. до н. э. — глава Александрийской библиотеки.

Скафис представляет собой чашу в форме полушария, в центре которой укрепляется игла. При ярком свете солнца тень от иглы падала на внутреннюю поверхность скафиса, на которой были нанесены окружности с цифрами, которые соответствовали значениям угла наклона солнца.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Представления древних народов о Земле Как уточнялись знания о форме и величине Земли

.

А вы знаете кто определил первым радиус Земли?

 Эратосфен — молодец, при помощи элементарных математических вычислений 2251 лет назад определил радиус Земли с ошибкой от определенного на сегодняшний день 5%. Это очень точный результат для того времени и тех возможностей.

 Солнце при своем годичном движении среди звёзд по эклиптике достигает максимального склонения в точке летнего солнцестояния, находящейся в созвездии Тельца, и вступает в знак Рака. В этот момент наступает астрономическое лето.
Интересно, что 21 июня Солнце в пунктах с широтой φ = 23°27′ в полдень находится в зените. В следующие дни склонение Солнца уменьшается, и оно будет проходить через зенит только южнее. Таким образом, параллель с φ = 23°27′ определяет северную границу мест, где Солнце хотя бы раз в году бывает в зените. Эта граница называется северным тропиком или тропиком Рака. Южная граница или тропик Козерога проходит по параллели φ = — 23°27′. Если Вы посмотрите на географическую карту, то увидите, что египетский город Асуан, где с нашей помощью построена гигантская асуанская плотина на реке Нил, расположен почти на Северном тропике. В древности этот город назывался Сиена. С измерением высоты Солнца в Сиене и Александрии, проведённого великим древнегреческим астрономом Эратосфеном, связано не только первое доказательство шарообразности Земли, но и первое прямое измерение длины земного меридиана.
Греческий астроном Эратосфен жил в III в. до нашей эры в городе Александрии. Он был очень разносторонне образованном человеком, его увлекали подчас очень далёкие друг от друга области науки, его даже в шутку на спортивный манер называли «пятиборцем», он, словно спортсмен, принимающий участие в пяти разных видах соревнований, всегда готов был ринуться в любую новую область знаний. В математике достаточно вспомнить знаменитое «решето Эратосфена», позволяющее определять простые числа.
Эратосфен знал, что в полдень в день летнего солнцестояния Солнце над Сиеной бывает настолько высоко, что его отражение видно на дне даже очень глубокого колодца. Отсюда Эратосфен сделал вывод, что Солнце в этот день в Сиене находится в зените и его высота равна точно 90°. Кроме того, Сиена лежит строго на юге от Александрии, т.е. эти города расположены на одном меридиане. Но в Александрии Солнце в этот день не в зените, что, как считал Эратосфен, указывает на шарообразность Земли – вывод, который в те времена противоречил общепризнанной точке зрения. Исходя из шарообразности Земли, он решил путём точных измерений определить длину земного меридиана. Для своих измерений в Александрии он воспользовался скафисом – чашеобразными солнечными часами со штырьком и делениями внутри них (более сложная разновидность гномона). Установленные вертикально, эти солнечные часы по тени от штырька дают возможность измерить высоту Солнца над горизонтом. И вот в полдень, в день летнего солнцестояния, когда в Сиене все предметы перестали отбрасывать тени, Эратосфен измерил его высоту на городской площади Александрии.
Солнце в Александрии, по измерениям Эратосфена, отстояло от зенита на 1/50 часть окружности. Следовательно, разность широт Александрии и Сиены равно этой величине, что в градусной мере составляет 7°12′. Так как наблюдения проводились в плодороднейшей долине Нила, где искусные шагатели-бематисты неоднократно проводили тщательные межевание земель, а бесчисленные караваны двигались друг другу навстречу, то расстояние между Александрией и Сиеной было известно в эпоху Эратосфена довольно точно по сравнению с другими местами. Это расстояние было равно 5000 греческих стадиев, следовательно, длина окружности земного меридиана была в 50 раз больше и равнялась 250 000 стадиям. При длине стадии в 158,5 м это соответствовало 39 600 км, всего на 400 км меньше современного точного значения.  Зная длину окружности Земного меридиана легко вычислить радиус. Это конечно же принимая фигуру Земли за сферу, а не эллипсоид.

P.S.  А Ватикан только в 1992 году признал, что Земля круглая и вращается вокруг своей оси:-)

Как измерить окружность Земли?: apxiv — LiveJournal

Меня периодически посещает ощущение что многие простые вещи специально излагаются так, чтобы читатель ничего не понимал и тупо заучивал, либо прочувствовал свою ничтожность перед изощренностью науки. Это всецело относится к известному по школьным учебникам феерическому способу Эратосфена измерения окружности земного шара. Может быть он на самом деле вычислял таким извращенским способом, но зачем этот бред тиражировать со школы?

О том, как можно запудрить мозги в простом вопросе, посмотрим на примере вычисления длины окружности Земли в морских милях, который является частным случаем измерения широты местности и длины пройденного пути по меридиану.

Если современному человеку дать задачу вычислить длину окружности Земли в морских милях, он в подавляющем большинстве случаев заглянет в интернет/справочники и решит примерно так: длину окружности Земли например по парижскому меридиану 40.000 км с помощью калькулятора разделит на современную морскую милю 1,852 км и получит 21.598,3 морских миль, что будет близко к действительности.

Теперь покажу как вычислить длину окружности Земли в уме и абсолютно точно. Для этого надо знать только одно: «Морская миля — единица измерения расстояния, применяемая в мореплавании и авиации. Первоначально морская миля определялась как длина дуги большого круга на поверхности земного шара размером в одну угловую минуту.» via

В одном угловом градусе 60 минут, в окружности — 360 градусов, то есть в окружности 360х60=21.600 угловых минут, что в данном случае соответствует длине окружности земного шара в 21.600 морских миль. И это — абсолютно точно, поскольку длина окружности земного шара по меридиану является эталоном, а угловая минута-миля — производная единица. Поскольку Земля — не идеальный сфероид, а слегка кривоватый, то мили на разных меридианах будут немного отличаться друг от друга, но это совершенно неважно для навигации, ибо угловая минута — она и в Африке угловая минута.

Широту местности с точностью до градусов вполне можно измерить даже примитивными приспособлениями вроде транспортира с отвесом, который не сильно отличается от реально применявшегося моряками квадранта и по существу то же самое что и астролябия:

Для более точных измерений углов впоследствии был изобретен секстант (мор. арго — секстан):

Современные люди слабо представляют себе что такое аналоговые вычислительные машины и как ими пользоваться. Для того, чтобы вычислить расстояние между двумя точками в меридиональном направлении, надо всего лишь измерить широты точек, а разность широт выраженная в угловых минутах и будет расстоянием между ними в морских милях. Все просто, удобно и практически применимо.

Если уж так сильно хочется выяснить сколько в морской миле стадий, саженей, аршинов или там египетских локтей, надо аккуратно на коленках промерить ими расстояние между точками с известным расстоянием в морских милях-угловых минутах. Но зачем? Как это практически применимо?

Эратосфен будто бы измерял углы с точностью до угловых секунд и разница широт Александрии составила у него 7° 6,7′, то есть 7х60=420+6,7=426,7 морских миль (угловых минут). Кажется, что еще надо? Но ему почему-то требуются дни пути верблюдов и стадии. Возникает ощущение чего-то надуманного — фейка или розыгрыша.

Метод Эратосфена согласно В. А. Бронштейн, Клавдий Птолемей, Гл.12. Работы Птолемея в области географии:

«Как известно, метод Эратосфена заключался в определении дуги меридиана между Александрией и Сиеной в день летнего солнцестояния. В этот день, по рассказам лиц, посещавших Сиену, Солнце в полдень освещало дно самых глубоких колодцев и, значит, проходило через зенит. Следовательно, широта Сиены равнялась углу наклона эклиптики к экватору, который Эратосфен определил в 23°51’20». В тот же день и час в Александрии тень от вертикального столбика гномона закрывала 1/50 часть окружности, центром которой служил кончик гномона. Это значит, что Солнце отстояло в полдень от зенита на 1/50 часть окружности, или на 7° 12′. Приняв расстояние между Александрией и Сиеной равным 5000 стадиев, Эратосфен нашел, что окружность земного шара равна 250 000 стадиев. Вопрос о точной длине стадия, принятого Эратосфеном, долгое время служил предметом дискуссий, поскольку существовали стадии длиной от 148 до 210 м <60>. Большинство исследователей принимали длину стадия 157,5 м («египетский» стадий). Тогда окружность Земли равна, по Эратосфену, 250 000-0,1575 = 39 375 км, что очень близко к действительному значению 40 008 км. Если же Эратосфен пользовался греческим («олимпийским») стадием длиной 185,2 м, то получалась окружность Земли уже 46 300 км.

По современным измерениям <97> широта Музея в Александрии 31°11,7′ широта Асуана (Сиены) 24° 5,0′, разница широт 7° 6,7′, чему соответствует расстояние между этими городами 788 км. Деля это расстояние на 5000, получим длину стадия, использованного Эратосфеном, 157,6 м. Значит ли это, что он использовал египетский стадий?

Этот вопрос сложнее, чем может показаться. Уже одно то, что Эратосфен привел явно округленное число — 5000 стадиев (а, скажем, не 5150 или 4890) не внушает к нему доверия. А если оценка Эратосфена была завышена хотя бы на 15%, получим, что он использовал египетский стадий в 185 м. Решить этот вопрос пока нельзя.» via

Теперь обратим внимание на следующие обстоятельства:

— Асуан (Сиена) и Александрия не находятся на одном меридиане, разница по долготе составляет 3°, то есть около 300 километров.

— Эратосфен не измерил расстояние, а принял исходя из дней пути верблюдов, которые ходили явно не по прямой линии.

— Совершенно неясно каким прибором Эратосфен измерял углы с точностью до секунд

— Непонятно какой стадий использован Эратосфеном для измерения расстояний и т.п.

Но при этом он будто бы получил достаточно точный резуль

Когда узнали, что Земля круглая ?

Как плоская истёртая монета,
На трёх китах покоилась планета.
И жгли учёных-умников в кострах —
Тех, что твердили: «Дело не в китах».
Н.Олев

Выйдя на улицу и оглядевшись вокруг, любой может убедиться: Земля плоская. Есть, конечно, возвышенности и впадины, горы и овраги. Но в целом ясно видно: плоская, по краям покатая. Древние с этим давно разобрались. Они видели, как караван скрывается за горизонтом. Поднимаясь на гору, наблюдатели замечали, что горизонт расширяется. Отсюда следовал неизбежный вывод: поверхность Земли представляет собой полусферу. У Фалеса [VI-V века до н.э.] Земля плавает, как кусок дерева, в бескрайнем океане.

Когда же эти представления изменились? В XIX веке утвердился ложный тезис, тиражирующийся до сих пор, что люди считали Землю плоской до великих географических открытий.

 

Так,  в пособии для учителей «Уроки по окружающему миру» 2007 года говорится: «Долгое время древние люди считали Землю плоской, лежащей на трёх китах или трёх слонах и прикрытой куполом неба… Над учёными, выдвинувшими гипотезу о шарообразной форме Земли, смеялись, их преследовала церковь. Первым в эту гипотезу поверил мореплаватель Христофор Колумб… Учитель может рассказать детям о том, что первым, кто своими глазами увидел, что Земля не плоская, был космонавт Юрий Гагарин».

На самом деле, уже в III веке до н.э. древнегреческий учёный Эратосфен Киренский (ок. 276-194 до н.э.) не только твёрдо знал, что Земля — шар, но и сумел измерить радиус Земли, получив величину 6311 км — с ошибкой не более 1 процента!

Около 250 года до нашей эры греческий ученый Эратосфен впервые довольно точно измерил земной шар. Эратосфен жил в Египте в городе Александрия. Он догадался сравнить высоту Солнца (или его угловое расстояние от точки над головой, зенита, которое так и называется  — зенитное расстояние) в один и тот же момент времени в двух городах — Александрии (на севере Египта) и Сиене (ныне Асуан, на юге Египта). Эратосфену было известно, что в день летнего солнцестояния (22 июня) Солнце в полдень освещает дно глубоких колодцев. Следовательно, в это время Солнце находится в зените. Но в Александрии в этот момент Солнце не бывает в зените, а отстоит от него на 7,2°.

 

 

Такой результат Эратосфен получил, изменяя зенитное расстояние Солнца с помощью своего несложного угломерного инструмента — скафиса. Это просто вертикальный шест — гномон, укрепленный на дне чаши (полусферы). Скафис устанавливают так, чтобы гномон принимал строго вертикальное положение (направлен в зенит) Освещенный солнцем шест отбрасывает тень на разделенную на градусы внутреннюю поверхность скафиса.

 

 

Так вот в полдень 22 июня в Сиене гномон тень не отбрасывает (Солнце в зените, его зенитное расстояние равно 0°), а в Александрии тень от гномона, как видно по шкале скафиса, отмечала деление 7,2°. Во времена Эратосфена расстояние от Александрии до Сиена считали равным 5000 греческих стадий (примерно 800 км). Зная все это, Эратосфен сопоставил дугу в 7,2° со всей окружностью в 360° градусов, а расстояние 5000 стадий — со всей окружностью земного шара (обозначим ее буквой X) в километрах. Тогда из пропорции получилось, что Х = 250 000 стадий, или примерно 40 000 км (представьте себе, это так и есть!).

Если вам известно, что длина окружности равна 2πR, где R — радиус окружности (а π ~ 3,14), зная длину окружности земного шара, легко найти его радиус (R):

Замечательно, что Эратосфену удалось очень точно измерить Землю (ведь и сегодня считают, что средний радиус Земли 6371 км!).

 

 

А ещё за сто лет до него Аристотель (384-322 до н.э.) привёл три классических доказательства шарообразности Земли.

Во-первых, при лунных затмениях край тени, отбрасываемой Землёй на Луну, всегда является дугой окружности, а единственное тело, способно давать такую тень при любом положении и направлении источника света, есть шар.

Во-вторых, корабли, удаляясь в море от наблюдателя, не постепенно теряются из виду за счёт далёкого расстояния, а почти мгновенно как бы «тонут», исчезая за линией горизонта.

И, в-третьих, некоторые звёзды можно увидеть только из определённых частей Земли, а для других наблюдателей они не видны никогда.

Но и Аристотель не был первооткрывателем шарообразности Земли, а только лишь привёл неопровержимые доказательства факта, о котором было известно ещё Пифагору Самосскому (ок. 560-480 до н.э.). Сам же Пифагор, возможно, опирался на свидетельства не учёного, а простого моряка Скилака Кариандского, который в 515 году до н.э. сделал описание своих плаваний по Средиземноморью.

 

 

А как же церковь?

Было решение об осуждении гелиоцентрической системы, утверждённое в 1616 году папой Павлом V. А вот преследования сторонников шарообразности Земли в христианских церквях не было. О том, что «раньше» церковь представляла Землю стоящей на китах или слонах, придумали в XIX веке.

Кстати, ВОТ ТУТ МОЖНО почитать за что действительно сожгли Джордано Бруно.

 

И всё-таки церковь отметилась в вопросе о форме Земли.

Из 265 человек, которые 20 сентября 1519 года отправились в кругосветное путешествие под водительством Магеллана, только 18 матросов 6 сентября 1522 года вернулись на последнем из кораблей, больные и истощённые. Вместо почестей команде досталось публичное покаяние за один потерянный день в результате движения по часовым поясам вокруг Земли в западном направлении. Так католическая церковь наказала героическую команду за ошибку в праздновании церковных дат.

Этот парадокс кругосветных путешествий долгое время не осознавался в обществе. В романе Жюля Верна «Вокруг света за 80 дней» Филеас Фогг в силу незнания едва не лишился всего состояния. В «Науке и жизни» 80-ых описываются конфликты команд, вернувшихся из «кругосветки», с бухгалтерией, не желающей оплачивать лишний день командировки.

Заблуждения и примитивные представления живучи не только в церкви.

 

 

 

Стоит наверное еще отметить один момент, дело в том, что фигура Земли отличается от шара.

Об этом ученые стали догадываться еще в XVIII веке, но какова в действительности Земля — сжата она у полюсов или у экватора — выяснить было трудно. Чтобы разобраться в этом, Французской академии наук пришлось снарядить две экспедиции. В 1735 году одна из них отправилась проводить астрономические и геодезические работы в Перу и занималась этим в экваториальном районе Земли около 10 лет, а другая, лапландская, трудилась в 1736–1737 годах вблизи Северного полярного круга. В результате выяснилось, что длина дуги одного градуса меридиана неодинакова у полюсов Земли и у ее экватора. Градус меридиана оказался у экватора длиннее, чем в высоких широтах (111,9 км и 110,6 км). Так может быть лишь в том случае, если Земля сжата у полюсов и представляет собой не шар, а тело, близкое по форме к сфероиду. У сфероида полярный радиус меньше экваториального (у земного сфероида полярный радиус короче экваториального почти на 21 км).

Полезно знать, что великий Исаак Ньютон (1643–1727) предвосхитил результаты экспедиций: он сделал правильный вывод о том, что Земля сжата, потому наша планета вращается вокруг оси. Вообще, чем быстрее вращается планета, тем больше должно быть ее сжатие. Поэтому, например, сжатие Юпитера больше, чем Земли (Юпитер успевает сделать оборот вокруг оси по отношению к звездам за 9 ч 50 мин, а Земля только за 23 ч 56 мин).

 

 

И еще. Истинная фигура Земли очень сложна и отличается не только от шара, но и от сфероида вращения. Правда, в данном случае речь идет о разнице не в километры, а …метры! Подобным тщательным уточнением фигуры Земли ученые занимаются по сей день, используя для этой цели специально проводимые наблюдения с искусственных спутников Земли. Так что вполне возможно, что в решении задачи, за которую давным-давно взялся Эратосфен, когда-нибудь и вам придется принять участие. Это очень нужное людям дело.

Какой же лучше всего запомнить вам фигуру нашей планеты? Думаю, что пока достаточно, если вы будете представлять Землю в виде шара с надетым на него «дополнительным поясом», своего рода «нашлепкой» на область экватора. Такое искажение фигуры Земли, превращающее ее из шара в сфероид, имеет немалые последствия. В частности, из-за притяжения Луной «дополнительного пояса» земная ось примерно за 26 000 лет описывает в пространстве конус. Это движение земной оси называется прецессионным. В результате роль Полярной звезды, которая сейчас принадлежит α Малой Медведицы, поочередно играют некоторые другие звезды (ею в будущем станет, например, α Лиры — Вега). Кроме того, из-за такого (прецессионного) движения земной оси знаки Зодиака все больше и больше не совпадают с соответствующими созвездиями. Другими словами, через 2000 лет после эпохи Птолемея «знак Рака», например, уже не совпадает с «созвездием Рака» и т. д. Впрочем, современные астрологи стараются не обращать на это внимания…

 

 

А откуда же взялось это дурацкое представление о плоской Земле на трёх слонах/китах? 

Нприме Фалес считал, что Земля плавает в воде, как кусок дерева. Анаксимандр представлял Землю в виде цилиндра (при этом указывал, что его диаметр ровно втрое больше высоты), на верхнем торце которого живут люди. Анаксимен считал, что Солнце и Луна такие же плоские, как и Земля, но поправил Анаксимандра, указав, что Земля хотя и плоская, но в плане не круглая, а прямоугольная, и не плавает в воде, а поддерживается сжатым воздухом. Гекатей на основе представлений Анаксимандра составил географическую карту. Анаксагор и Эмпедокл на это основоположникам ничего не возражали, считая такие представления не противоречащими физическим законам. Левкипп, считая Землю плоской, а атомы — падающими перпендикулярно этой плоскости в одном направлении, не мог понять, как же тогда атомы могут соединяться друг с другом, образуя тела — и говорил, что нет, атомы в своём падении должны хоть как-то, хоть чуть-чуть отклоняться. Демокрит в защиту плоской Земли приводил следующий довод: если бы Земля была шаром, то солнце, заходя и восходя, пересекалось бы горизонтом по дуге окружности, а не по прямой линии, как на самом деле. Эпикур решил мучившую Левкиппа проблему падения атомов на плоскую Землю, приписав атомам свободу воли, в силу которой они по своему хотению отклоняются и соединяются.

Очевидно, эти древнегреческие учёные-атеисты-материалисты опирались на мифологические представления, изложенные поэтическим языком у Гомера и Гесиода в 7-8 веках до н.э. Аналогичные мифы о плоской Земле были у индусов, шумеров, египтян, скандинавов. Но лезть ещё дальше туда мне не хочется — я пишу совсем о другом. Как курьёз можно отметить книгу «Христианская топография» Косьмы Индикоплова, написанную между 535 и 547 годами, в которой автор представляет Землю в виде плоского прямоугольника, накрытого выпуклой крышей неба — этакий ларец-сундук. Эта книга была сразу же раскритикована современником Косьмы Иоанном Грамматиком (ок. 490-570), который тогда приводил в качестве обоснования шарообразности Земли те же цитаты из Библии, что и я. Официальная же Церковь в этот спор о форме Земли не вмешивалась, её намного больше волновали еретические взгляды спорящих — Косьма был несторианином, а Иоанн тритеистом и монофиситом. Василий Великий неодобрительно относился к подобным спорам, считая сам их предмет не относящимся к вопросам веры.

Если же заняться поисками слонов/китов, то в первую очередь можно обратиться к популярному в своё время произведению славянской народно-духовной литературы — «Голубиной книге», где есть стих: «На семи китах земля основана». Народное предание о Голубиной книге восходит к «книге за семью печатями» в 5-й главе Откровения Иоанна Богослова, а стих про китов заимствован из апокрифа «Беседа трёх святителей». Выдающийся собиратель славянского фольклора А.Н.Афанасьев писал: «Между нашим простонародьем существует предание, что мир стоит на спине колоссального кита, и когда чудовище это, подавляемое тяжестью земного круга, поводит хвостом, – то бывает землетрясение. Иные утверждают, что исстари подпорою земли служили четыре кита, что один из них умер, и смерть его была причиною всемирного потопа и других переворотов во вселенной; когда же умрут и остальные три, в то время наступит кончина мира. Землетрясение бывает оттого, что киты, отлежав бока, повертываются на другую сторону. Рассказывают еще, что в начале было семь китов; но когда земля отяжелела от грехов человеческих, то четыре ушли в пучину эфиопскую, а во дни Ноя и все туда уходит. И поэтому случился всеобщий потоп». Некоторые лингвисты подозревают, что на самом деле морские животные тут ни при чём, а речь идёт о закреплении Земли по её четырём краям, поскольку в древнеславянском языке корень «кит» означал «край». В таком случае мы опять возвращаемся к Косьме Индикоплову, чья курьёзная книга о прямоугольной Земле была весьма популярна на Руси у простого народа.

 

 

«Общества плоской Земли»

Ну и, чтобы под конец повеселить утомлённого читателя, укажу на такой уже не курьёз, а полный маразм, как существование в наше просвещённое время «Общества плоской Земли». Впрочем, «Общество плоской Земли» существовало с 1956 года по начало XXI века и насчитывало в свои лучшие времена до 3 000 членов. Фотографии Земли из космоса они считали подделками, прочие факты – заговором властей и учёных.

У истоков Общества плоской Земли стоял английский изобретатель Сэмюэл Роуботэм (1816-1884), который в 19-м веке доказывал плоскую форму Земли. Его последователи основали Вселенское зететическое общество. В США идеи Роуботэма были восприняты Джоном Александром Доуи, основавшим в 1895 году Христианскую католическую апостольскую церковь. В 1906 году главой церкви стал заместитель Доуи Уилбур Гленн Волива, который отстаивал и пропагандировал плоскую форму Земли до своей смерти в 1942 году. В 1956 году Сэмюэл Шентон возродил Всемирное зететическое общество под названием Международное общество плоской Земли. На посту президента общества в 1971 году его сменил Чарльз Джонсон. За три десятилетия президентства Джонсона число сторонников общества значительно увеличилось: от нескольких членов до приблизительно 3000 человек из разных стран. Общество распространяло информационные бюллетени, листовки и тому подобную литературу, в которой отстаивалась модель плоской Земли. В лице своих руководителей общество утверждало, что высадка человека на Луну была мистификацией, снятой в Голливуде по сценарию Артура Кларка либо Стенли Кубрика. Чарльз Джонсон умер в 2001 году, и в настоящий момент дальнейшее существование Международного общества плоской Земли находится под вопросом. По заявлениям сторонников общества, все правительства Земли заключили мировой заговор с целью обмануть людей. Когда Сэмюэлю Шентону показали фотографии Земли с орбиты и спросили, что он о них думает, тот ответил: «Легко заметить, как фотографии такого сорта могут одурачить несведущего человека».

 

[источники]

источники

http://gazeta.aif.ru/_/online/kids/104/de24_01

http://ourplanetearth.ru/kak-uznali-formu-zemli

http://proza.ru/2009/09/23/952

seapeace.ru/seafarers/captains/274.html

 

Кстати, а вот знаете ли вы, Когда впервые сфотографировали Землю из космоса ?, а вот например кое-кто пытался выяснить Как возникает любовь ?. А вот для вас Волшебные ЧЕТЫРЕ ЧЕТВЕРКИ Оригинал статьи находится на сайте ИнфоГлаз.рф Ссылка на статью, с которой сделана эта копия — http://infoglaz.ru/?p=42342