Вес тела. Видеоурок. Физика 7 Класс

На тело, находящееся на опоре или подвесе, действует сила упругости, которая уравновешивает силу тяжести. Но в таком случае тело также должно действовать на опору или подвес силой упругости. На этом уроке мы подробнее познакомимся с этой силой, которая называется весом тела.

Тема: Взаимодействие тел

Урок: Вес тела

Прежде всего, вспомним, что такое сила тяжести. Это сила, с которой все тела притягиваются к Земле. Сила тяжести описывает взаимодействие тела с Земным шаром.

Поставим один груз на неподвижную опору, а другой поместим на подвес. Оба груза неподвижны. Значит, сила тяжести, действующая на них, уравновешена силой упругости, возникающей в опоре и подвесе.

 

Рис. 1. Тело на опоре и тело на подвесе

Но поскольку в природе существует только взаимодействие тел, то с такой же по величине силой, направленной в противоположную сторону, тела действуют на опору и подвес.

Сила, с которой тело действует на опору или растягивает подвес, называется весом тела.

Сила тяжести и вес тела – это величины, которые, как и скорость, имеют направление. Как вы помните, такие величины называются векторными. Их удобно представлять на рисунках в виде стрелок. Кроме того, у силы есть еще одна характеристика – точка приложения. Стрелка, изображающая силу, начинается в точке приложения силы.

Изобразим на одном рисунке силу тяжести тела, а на другом его вес.

Прежде всего, сила тяжести приложена к самому телу. Точка приложения силы тяжести называется центром тяжести тела. Направлена сила тяжести вертикально вниз.

Вес тела приложен не к телу, а к опоре. Его точка приложения расположена на опоре в точке соприкосновения с телом. А каково направление веса?

Вспомним, что вес тела направлен противоположно силе упругости опоры. Если тело неподвижно, то сила упругости опоры компенсирует силу тяжести, то есть направлена вертикально вверх. Следовательно, если тело неподвижно (или движется равномерно и прямолинейно), то вес тела также направлен вертикально вниз и численно равен силе тяжести.

Наконец, обозначим силу тяжести буквой 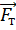 , а вес буквой .

 

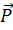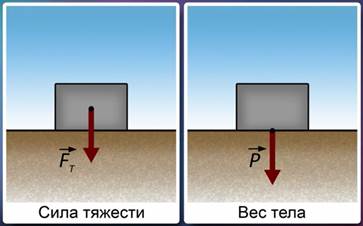
Рис. 2. Изображение векторов силы тяжести и веса тела

Еще раз обратите внимание: сила тяжести действует на тело, а вес – на опору или подвес.

На следующих уроках мы познакомимся с тем, как вычислить численное значение силы тяжести и веса тела.

Тела, находящиеся на опоре или подвесе, деформируют опору и подвес. Эта деформация не видна невооруженным глазом, но она существует. Ведь без деформации не появилась бы сила упругости, которая препятствует движению тела к центру Земли. Точно так же под действием опоры и подвеса деформируется тело (опора сжимает нижнюю часть тела, а подвес, наоборот, растягивает его верхнюю часть). Эта деформация тела и вызывает появление в теле силы упругости, которую мы и называем весом.

  

Список литературы

1. Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.

2. Перышкин А.В. Сборник задач по физике, 7 – 9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.

3. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7 – 9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

2. Единая коллекция Цифровых Образовательных Ресурсов (Источник).

 

Домашнее задание

Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7 – 9 классов №№ 333, 347, 354, 355.

interneturok.ru

Вес и невесомость

Существует различие между силой тяжести mg→ и весом тела. Понятие веса широко используется в повседневной жизни.

Определение 1

Вес тела – это сила, с которой притягивается тело Землей и действует на опору или подвес, причем неподвижно и относительно опоры или подвеса.

На рисунке 1.11.1 изображено неподвижное тело.

Определение 2

Система отсчета, связанная с Землей, называется

инерциальной.

Тело подвергается воздействию силы тяжести F→=mg→, направленной вертикально вниз, и силы упругости F→у=N→, действующей на него.

Реакция опоры

Определение 3

Силу N→ называют силой нормального давления или силой реакции опоры.

Действующие на тело силы всегда уравновешивают друг друга по формуле Fт→=-F→y=-N→. По третьему закону Ньютона имеем, что тело, подвергающееся воздействию силы P→ на опору, равняется по модулю силе реакции опоры направленной в противоположную сторону, тогда P→=-N→.

Из определения видно, что P→ называют весом тела. По соотношениям P→=Fт→=mg→ он равняется силе тяжести. Причем силы приложены к разным телам.

Рисунок 1.11.1. Вес тела и сила тяжести.  mg→ – сила тяжести, N→ – сила реакции опоры, P→

– сила давления тела на опору (вес тела). mg→=-N→=P→.

Когда тело находится в неподвижном подвешенном состоянии на пружине, тогда роль силы реакции опоры относят к упругой силе пружины. При ее растяжении определяется вес тела и сила его притяжения Землей. Для этого применяют рычажные весы, сравнивая вес данного тела с весом гирь на равноплечем рычаге. Когда они находятся в равновесии, можно достичь равенства массы тела суммарной массой гирь. Значение ускорения свободного падения от этого не зависит.

Пример 1

Если поднять в гору на 1 км пружинные весы, то их показания изменятся на 0,0003

zaochnik.com

Вес тела — урок. Физика, 7 класс.

Из-за притяжения Земли все тела имеют вес.

Сила, с которой тело давит на опору или растягивает подвес, называют весом.

Вес тела обозначают \(P\) и измеряют в ньютонах (\(H\)).  

 

Вес неподвижного тела равен P=mg.

Формула определения веса неподвижного тела точно такая же, как и формула силы тяжести (см. предыдущую тему «Сила. Сила тяжести»). Однако вес тела и сила тяжести — не одно и то же.

Например, сила тяжести свободно падающего трёхкилограммового кирпича приблизительно составляет \(30\) \(H\), (\(F = mg\)), а его вес \(P\) в момент падения равен \(0\) \(H\) (так как кирпич находится в состоянии невесомости).

 

Если помещённое на опору или подвешенное тело неподвижно по отношению к Земле или находится в равномерном движении вверх или вниз, тогда вес тела не меняется.

 

Вес меняется, когда тело перемещается вверх или вниз с ускорением.

Во время поездки в лифте, если мы двигаемся с ускорением вверх, наш вес увеличивается, хотя сила тяжести остаётся неизменной.

Состояние невесомости — это состояние, когда тело не давит на опору и не растягивает подвес. Такое происходит, когда тело свободно падает под воздействием только силы гравитации.

Почему в космическом корабле есть состояние невесомости?

Потому что космический корабль, обращаясь вокруг Земли, находится в свободном падении (он всё время как бы падает на Землю, но пролетает мимо). Это происходит, когда космический корабль достигает 1-й космической скорости — (7,9 км/с).

 

Если скорость космического корабля была бы меньше, он упал бы на Землю, а если корабль достиг бы 2-й космической скорости — (11,2 км/с), он стал бы искусственным спутником Солнца.

 

Если скорость космического корабля достигнет 3-й космической скорости — (16,7 км/с), тогда корабль направится из Солнечной системы к другим звёздам.

 

К сожалению, до ближайшей звёздной системы Альфа Центавра нужно лететь \(18000\) лет, так как она находится на расстоянии \(4\) световых лет.

 

Интересно, что для того, чтобы достичь Луны, ракета должна развить скорость, равную \(0,992\) от второй космической скорости.

 

www.yaklass.ru

когда возникает вес тела?точка приложения

Вес тела — сила, с которой тело действует на опору или подвес.

Вес тела возникает если есть сила тяжести

В статье мы рассмотрим понятие одной из основных сил механики и закона, с ней связанного. Итак, сила, возникающая в результате деформации тела и на­правленная в сторону, противоположную перемещению частиц тела при деформации, называется силой упругости.

на опору или подвес

touch.otvet.mail.ru

Каган И.Е. «Вес тела» (IX класс)

Цель урока: изучить вес тела в различных условиях.

Приборы и принадлежности: динамометры демонстрационный и Бакушинского, связка прямоугольных брусков, наклонная плоскость, прямолинейная планка (в качестве подставки), деревянный куб массой 200 г, деревянная полированная доска длиной 1,5 м, метровая линейка, два набора грузов с шестью грузиками в каждом, жестяная банка с водой, штатив с муфтой, шар для демонстрации невесомости, диск с подшипниками на оси, укрепленный на массивной подставке, стакан с водой, прозрачный скотч.

I. Методическое обоснование темы

Тема «Вес тела» является одной из важных и серьезных тем механики, имеет много нюансов, требующих внимания и размышления. Некоторые осложнения связаны с целым рядом расхождений в формулировках и определениях веса тела, а также в описаниях функции весов (особенно рычажных), имеющих место во многих учебниках и пособиях по физике и механике.

Для формирования логического мышления и способности рассуждать учащимся в принципе полезно знать о множестве таких разночтений, но сразу это сделать довольно трудно. Однако для того, чтобы опыты на таком уроке были понятны учащимся, а результаты разбора разных случаев логически доступны, они должны быть предварительно подготовлены по трем вопросам.

1. Что такое вес тела (т.е. нужно определить предмет обсуждения)?

2. Как изобразить вес тела?

3. Что измеряют весы?

1. Прохождение темы имеет смысл начинать с формулировки «веса тела», тем более, что учащиеся с ней сталкиваются уже в VII классе, изучая курс механики либо по учебнику А.В.Перышкина, Н.А.Родиной, либо по учебнику Л.А.Исаченковой, Ю.Д.Лещинского.

Необходимо отметить, что понятие «вес тела» неодинаково формулируется в различных учебниках и пособиях разных лет. Одна из самых популярных и, вероятно, точных формулировок выглядит так: «Вес – это сила, с которой тело действует на опору или подвес под действием притяжения к Земле (или силы тяжести)».

В целом ряде учебников по физике дается чуть-чуть другая формулировка веса: «Вес тела – это сила, с которой тело действует на горизонтальную (!) опору или подвес и т.д.».

А где взять «идеально горизонтальную» опору? Значит, на других, не горизонтальных, опорах вес будет уже другим? Более или менее приближенным? А, может, покоящееся тело сохраняет вес неизменным на любой опоре? И как быть с весом тела, движущегося равномерно прямолинейно?

В некоторых изданиях можно прочесть и другие формулировки веса.

В учебнике «Физика, 9» (авт. Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь, 2000) в § 32 (с. 129) в определении «силы веса» горизонтальная опора не упоминается, но на с. 131 «сила веса» численно приравнивается к нормальной силе реакции, что подтверждается рис. 133 на с. 131. Значит, величина веса зависит от угла наклона плоскости? Каким же будет вес покоящегося тела на вертикальной плоскости? Тем более, что на рис. 133 показана и сила трения.

В учебнике П.Г.Саенко «Физика, 9» (1992), § 25, с. 83 в определении веса «горизонтальная» опора не указывается, но на с. 84 автор все-таки к ней возвращается и, таким образом, себе противоречит.

То же самое можно прочитать в учебнике Ю.А.Селезнева «Основы элементарной физики» (1966, с. 46), где на одной и той же этой странице напечатаны два разных суждения.

Целый ряд авторов, переиздавая свои издания, сами себе противоречат. В одних своих работах они формулируют понятие веса покоящегося тела для любой опоры, в других – для горизонтальной опоры. Таковы учебники физики для 6-7 кл. А.В.Перышкина, Н.А.Родиной, «Методика преподавания физики в 6-7 кл.» под редакцией В.П.Орехова, А.В.Усовой, «Пособие по физике для поступающих в вузы» М.С.Цедрика, Ф.Г.Китуновича, А.С.Микулича, А.М.Качинского, задачники Н.Е.Савченко.

В некоторых изданиях встречаются и другие формулировки веса.

1. В учебнике Б.Б.Буховцева, Ю.Л.Климонтовича, Г.Я.Мякишева «Физика, механика» (1971, § 49) на с. 102 читаем: «…вес тела определяется всей совокупностью действующих на тело сил, а не только силой тяготения (так, вес тела в жидкости или воздухе меньше, чем в вакууме из-за появления выталкивающей силы)». Что же это такое – вес в воздухе, жидкости, вакууме?

2. «Курс физики» (Б.М.Яворский, А.А.Детлаф, Л.Б.Милковская, Г.П.Сергеев, 1965, т. 1), § 6.1, с. 98: «Сила Р,называемая весом тела или силой тяжести, вызывает падение незакрепленного тела к земле».

3. «Повторим физику» (Л.Б.Милковская, 72), § 3.5, с. 73: «Так как тела падают на землю под действием силы тяжести, т.е. своего веса, то P = m∙g».

4. «Законы природы» (Р.Е.Пайернс, 1962), гл. 1, с. 23: «Тот факт, что сила тяготения, действующая на тело, т.е. вес тела, точно пропорциональна его массе или инерции, пока является для нас неожиданным совпадением».

5. «Большой энциклопедический словарь. Физика» (гл. ред. А.М.Прохоров, 1999), с. 70, определяет, что «…вес – это численная величина силы тяжести, действующей на тело, находящееся вблизи земной поверхности».

6. «Физика. Ответы на вопросы для абитуриентов и учащихся 11 кл.» (2000), гл. 2, с. 27 (коллектив авторов), определяет, что «весом тела называют силу нормального давления, действующую на подставку со стороны тела».

7. И даже такие авторы, как Л.Д.Ландау, А.И.Китайгородский в книге «Физика для всех» (1974), с. 9, пишут, что «Вес – это сила, с которой тело притягивается к земле. Эту силу можно измерить пружинными весами».

1. Изображение веса на рисунках

Исходя из имеющихся формулировок веса и третьего закона Ньютона, учащиеся должны понять, что весу тела по модулю равна сила реакции опоры N, и какой она будет, таким будет по величине и вес тела (рис. 1) (m∙g = F_{тяжести}).

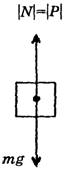
Рис. 1

Учащиеся должны изображать вес тела как силу, приложенную к опоре. Здесь мы имеет несколько вариантов.

а) Если покоящееся тело – материальная точка, а горизонтальная опора – нет (рис. 2).

Рис. 2

б) Если покоящееся тело и горизонтальная опора – не материальные точки (рис. 3). Элементарные силы реакции действуют на всю опору (рис. 3, а), мы учитываем действие результирующей силы реакции опоры. Следует заметить, что сила реакции опоры N может смещаться, если к телу, например, приложить дополнительную силу F по горизонтали (рис. 3, б).

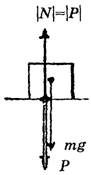
Рис. 3

      

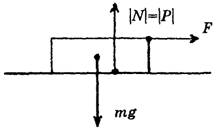
а                                                  б

Рис. 3

в) Если покоящееся тело и горизонтальная опора – материальные точки (рис. 4). M·g – сила тяжести самой опоры, Р –- вес покоящегося на опоре тела, N_о6 – общая сила реакции нижней опоры. Иногда такие случаи нужно учитывать в задачах.

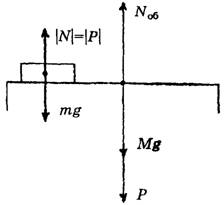
Рис. 4

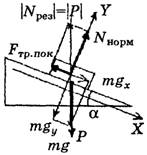
г) Если покоящееся тело – материальная точка, а наклонная опора – не материальная точка (рис. 5, а или 5, б).

           

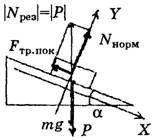
а                                                   б

Рис. 5

У покоящегося тела на любой опоре вес сохраняется (в инерциональной системе) и численно равен силе тяжести, т.е. |P| = |m∙g| = |N_pез|. Результирующая сила реакции N является векторной суммой силы нормальной реакции N_норм и силы трения покоя F_{тр. пок}.Вес тела Рприложен к опоре.

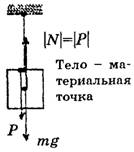
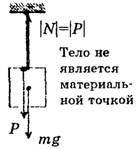
д) Покоящееся тело висит на вертикальном подвесе (рис. 6, а и 6, б).

              

а                                            б

Рис. 6

Составляющие F₁и F₂,образующие при векторном сложении результирующую силу реакции N,численно равную весу Р,сами по себе могут быть по величине больше веса (или одна из них или обе одновременно).

Это бывает на тросах, растянутых под большим углом (рис. 7), или на кронштейнах (рис. 8, а, 8, б).

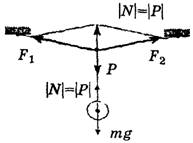
Рис. 7

                     

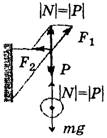
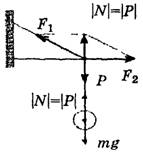
а                                                 б

Рис. 8

 

---

2. Что измеряют весы?

Многие скажут – «смотря какой конструкции это будут весы».

Обратимся к словарям.

Толковые словари С.И.Ожегова (с. 62) и Д.Н.Ушакова (т. 1, с. 262) утверждают, что весы – это прибор для измерения веса. При этом на с. 64 в первом словаре и т. 1, с. 273 во втором глагол «взвесить» означает – определить вес.

Энциклопедический словарь (1953), т. 1, с. 296, Физический энциклопедический словарь (1960), т. 1, с. 220, Малая Советская Энциклопедия (1958), т. 2, с. 343 (все под редакцией Б.А.Введенского) и Большая Советская Энциклопедия, под редакцией А.М.Прохорова (1971), т. 4, с. 568 указывают, что весы – это прибор для определения массы тела.

Все издания утверждают, что пружинные весы измеряют вес. В то же время многие издания утверждают, что рычажные (равноплечие) весы измеряют массу. Только в учебнике Б.М.Яворского, А.А.Пинского «Основы физики», т. 1, и Г.С.Ландсберга «Элементарный учебник физики», т. 1, указывается, что рычажные весы измеряют вес. Чему должен верить читатель?

Действительно, с пружинными весами все ясно. В их «весовой» функции даже невозможно усомниться.

А на рычажных весах вроде бы очень удобно измерять массу тела. Ведь при балансе чашек (в случае равенства весов тел) мы тут же можем судить о равенстве масс исследуемого тела и уравновешенных гирь.

Кроме того, рычажные весы имеют еще одно неоспоримое удобство. Равновесие чашек с грузами не нарушается, если их перевести на полюс, экватор, с Земли на Луну и т.д. (вес тела при этом меняется, а масса нет!).

Думается, равновесие рычажных весов здесь не нарушается не столько из-за постоянства масс тел, сколько из-за одинаковой кратности изменения весов тел на обеих чашках.

И почему ни одни весы ничего не показывают в состоянии полной невесомости (ведь масса тела остается неизменной и сила тяжести также!)?

Да потому, что в состоянии полной невесомости вес тела равен нулю, вот весы и фиксируют нулевой вес!

А как быть тогда, когда мы на рычажных весах взвешиваем пуховое тело или хлопок (вату)? Ведь это объемное тело, испытывающее ощутимое действие выталкивающей силы воздуха, которая в большинстве случаев незначительная и на гири, стоящие на второй чашке весов, почти не действует. При балансе чашек можно еще говорить о равенстве весов тел на чашках, но именно масса пухового тела при балансе чашек будет обязательно большей, чем совокупная масса гирь. И здесь уже рычажные весы не могут дать точный ответ о массе пухового тела!

А если в состоянии полной невесомости пытаться определить массу тела, то неизбежно нужно будет создать какое-то силовое взаимодействие этого тела с другим телом. Иначе говоря, весы все-таки в принципе созданы для определения силы, и «лишить» их своей весовой функции практически невозможно. Поэтому останавливаемся на точке зрения, что весы любой конструкции измеряют вес, но иногда позволяют оценить и массу. Разговоры о том, что весы градуируются в граммах, килограммах, тоннах и каратах, сути весовой функции весов не меняют.

В интересах доказательства назначения весов для определения массы предлагают даже ввести термин «массометр» («Толковый словарь школьника по физике», 1999, авторы К.К.Гомоюнов, М.Ф.Кесаманлы, Т.Г.Кесаманлы, с 39). Думается, что это не получится. Ведь с древних времен человека интересовала масса как мера тяжести (т.е. проблема веса) гораздо в большей степени, чем масса инертная.

И ссылки на то, что в седьмом классе мы учим детей определять массу на весах, ничего не меняют. Мы видим, какое сложное понятие – «вес тела», и не усложняем жизнь маленьким учащимся. А научить их практически пользоваться весами нужно еще с малых лет.

II. Ход урока

Такое множество формулировок и точек зрения запутывает и дезинформирует учащихся. Тем более, что противоречат друг другу, а иногда и самим себе довольно авторитетные авторы учебных и методических изданий.

К данному уроку учащиеся были подведены проблемно. Они ознакомились с разными формулировками веса, способами изображения веса и различными точками зрения на назначение весов как измерительного прибора (особенно рычажных равноплечих).

Исходя из такой преамбулы, можно более конкретно нацелить урок: на самых простых и доступных опытах убедиться в неизменности веса тела в инерциальных системах и его «изменчивости» в системах неинерциальных, т.е. когда тело будет иметь ускорение.

Предполагается определить вес покоящегося тела на разных опорах, выяснить, меняется ли вес при погружении тела в жидкость, и пронаблюдать, каким будет вес при наличии у тела ускорения.

Дополнительно к вышеперечисленному оборудованию были специально изготовлены два небольших приспособления. Из двух фанерок была сбита наклонная плоскость с приступочкой В внизу (рис. 9, а) и сделана связка из трех деревянных брусков (рис. 9, б).

           

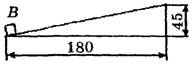
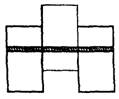
а                                                   б

Рис. 9

Средний брусок был несколько поднят, чтобы он не мог касаться опоры при вертикальном положении всей связки.

Первая часть урока. Вес покоящегося тела на различных плоскостях

а) Повторяем формулировку «веса» тела (без слова «горизонтальна»).

б) Устанавливаем стрелку демонстрационного динамометра (пружинных весов) на нуль, на верхнюю подставку динамометра помещаем горизонтальную планку, на которую кладем отдельно связку брусков и наклонную плоскость (как совокупность тел). Связка на планке лежит (рис. 10). Фиксируем показание весов.

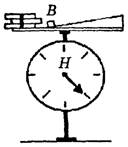
Рис. 10

в) Связку брусков кладем на наклонную плоскость (бруски покоятся) (рис. 11). Снова фиксируем показание весов и убеждаемся в его неизменности.

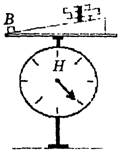
Рис. 11

г) Ничего не меняется в показании весов, если бруски стопорить о приступку В (рис. 12). Приступка В играет роль второй наклонной плоскости, заменяющей силу трения покоя. Как видим, на наклонной плоскости покоящееся тело весит столько же, сколько и на горизонтальной опоре. И это потому, что вес тела численно равен по величине не нормальной реакции тела на наклонной плоскости, а общей реакции, включающей и силу трения покоя и численно равной силе тяжести |m∙g|.

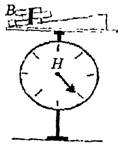
Рис. 12

д) А чему равен вес покоящегося тела на вертикальной плоскости? Если верить некоторым изданиям (например, учебнику «Физика, 9» (2000), авторы Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь, с. 131, рис. 133), утверждающим, что величина веса определяется величиной силы нормальной реакции тела на наклонной плоскости, то на вертикальной плоскости у тела вообще веса не будет, так как при этом N_норм = 0.

В таком случае наглядно и убедительно используется связка трех брусков. Средний брусок не касается опоры, когда связка стоит (рис. 13).

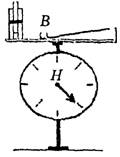
Рис. 13

Весы показывают совершенно одинаковый вес, стоит связка на двух брусках или на одном, будучи перевернутой (рис. 14). И не имеет абсолютно никакого значения, стоит связка брусков или лежит. Но когда связка лежит, давят на опору все три бруска, а если связка стоит? Весы подтверждают, что на опору все равно давят те же три бруска! Те бруски, которые не касаются опоры в каждом случае, весят или давят на нее благодаря силе трения покоя между вертикальными соприкасающимися стенками брусков.

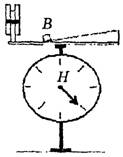
Рис. 14

Если бы тело, прижатое к вертикальной стенке и покоящееся на ней, не весило, уже давно был бы придуман способ укладки вещевого мешка или другой паковки, которые бы при одинаковом количестве упакованных предметов весили меньше. Но этот фокус не получается! Как бы ни был упакован вещевой мешок или чемодан, все предметы в нем будут весомы. И ни одни весы в мире не покажут уменьшения веса покоящегося тела на наклонной плоскости из-за увеличения угла наклонной плоскости.

Учащимся задаем итоговый вопрос: «Играет ли роль для определения веса покоящегося тела угол наклонной плоскости?» И получаем ответ: «Нет, не играет».

Учащимся было продемонстрировано уменьшение веса тела на наклонной плоскости, когда тело движется вниз практически без трения.

Был поставлен следующий эксперимент.

На рычаге длиной 1 м на одном конце была установлена почти вертикально доска высотой 1,5 м с подвешенным на нити кубом массой 200 г, а на другом – две коробки с грузиками по 1 Н (12 грузиков) (рис. 15).

Рис. 15

Все уравновешивается и балансирует.

Нить пережигается, куб начинает падать, и в это время противоположное плечо рычага с грузиками опускается, что свидетельствует об уменьшении веса тела на наклонной плоскости. Но в это время тело на ней не покоилось, а летело вниз практически без трения.

На первую часть урока уходит 14 минут.

Вторая часть урока. «Вес тела в жидкости или газе»

Во многих изданиях, особенно выпущенных в прежние годы, мы часто сталкиваемся с терминологией «вес тела в воде», «вес тела в воздухе» и др. Например, в «Сборнике вопросов и задач» различных лет (авторы П.А.Знаменский и др.) на с. 52 в задачах № 397 и № 400 – «вес в керосине», «вес в воздухе» – в № 403, «истинный вес хлопка в кипе» – с. 53, № 409.

Был поставлен следующий эксперимент. Взвешиваем на крюке демонстрационного динамометра деревянный куб (рис. 16) и начинаем подводить под него банку с водой. По мере погружения куба в воду стрелка динамометра показывает уменьшение нагрузки на динамометр, создавая иллюзию уменьшения веса. Когда куб начинает плавать в воде, стрелка динамометра устанавливается на нуле. Так что – плавающее тело вообще не имеет веса?

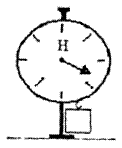
Рис. 16

Снова взвешиваем куб на крюке, снимаем его и взвешиваем банку с водой без куба. Затем в подвешенную на крюк банку с водой кладем плавать куб. И что же? Весы показывают суммарный вес банки с водой и куба.

Это значит, что тело в воде или другой жидкости сохраняет свой вес, т.е. понятия «вес в воде», «вес в воздухе» или «вес в вакууме» и т.д. не имеют смысла.

Есть одно понятие – вес тела, неизменный в инерциальных системах.

Уменьшение показаний динамометра при погружении тела в жидкость связано с появлением еще одной опоры – жидкости, которая «берет на себя» часть веса. То есть вес тела распределяется на две опоры точно так же, как вес рычага, лежащего на двух опорах. В случае плавающего тела жидкость «берет на себя» весь вес тела, вследствие чего динамометр, к которому привязана нить с таким телом, ничего и не показывает.

С помощью учащихся делаем вывод о постоянстве веса тела в инерциальных системах на любой опоре. Выясняем, что вес тела сохраняется у пассажира в равномерно движущемся лифте и у парашютиста, спускающегося равномерно на парашюте.

На эту часть урока уходит еще 12 минут.

Третья часть урока. Вес тела в пеинерциальных системах или вес тела, имеющего ускорение (пока по вертикали)

Начинаем с демонстрации подвешенных грузиков на динамометре Бакушинского (рис. 17).

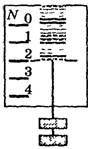
Рис. 17

Показываем динамометр с двумя грузиками в состоянии покоя или равномерного прямолинейного движения по вертикали в любую сторону. Динамометр показывает вес, равный 2H = m∙g,т.е. вес тела численно равен силе тяжести. Начинаем поднимать динамометр с грузиками вверх с ускорением. И пока сохраняется ускорение при подъеме, учащиеся ясно видят увеличение растяжения пружины (рис. 18). Объясняем, что увеличение веса – это перегрузка. Напоминаем, что она ощущается в самом начале подъема лифта и в конце его спуска при торможении.

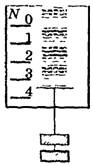
Рис. 18

До этого учащиеся уже решали задачи на расчет силы реакции при подъеме тела вверх с ускорением и знают, что она равна: 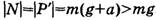, где Р’ – искусственный вес тела в данных условиях.

Приводим пример взвешивания с «походом», когда тело швыряют на весы и последние показывают «завышенный» вес. Выясняем, почему нас не устраивает, когда тело швыряют на весы (ведь не только из-за невежливости!), обращаем внимание учащихся на наличие торможения тела. Далее выясняем, чего мы ждем. Учащиеся отвечают, что мы ждем, когда весы уравновесятся и покажут в состоянии покоя вес тела, равный его силе тяжести.

Объясняем, что перегрузка не означает только увеличение воздействия на опору, а предполагает увеличение веса всего, что находится в такой системе. Увеличивается вес всех частей тела человека. Тяжелеет голова, руки, ноги, туловище, сердце, веки глаз, кровь и т.д. Нетренированный человек выдерживает троекратную перегрузку нормально. Особенно большие перегрузки бывают на тренировках космонавтов на больших скоростях (до 11-12 Р₀)и при выходе самолета из состояния пикирования. Поясняем всю тяжесть и опасность таких ситуаций.

Показываем уменьшение веса при спуске тела с ускорением вниз (рис. 19). Получаем «недогрузку» или частичную невесомость, которая ощущается в начале спуска лифта (пока есть ускорение вниз) или в конце его подъема с торможением. В этом случае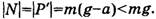

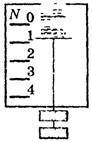
Рис. 19.

Поясняем, что именно тогда, когда ускорение исчезает, сила реакции N будет компенсировать силу тяжести. Только тогда |N| = m∙g = |P₀|,т.е. весу тела в состоянии покоя или равномерного прямолинейного движения.

Выясняем с учащимися, что с увеличением ускорения а по вертикали вниз «недогрузка» тела увеличивается, и при ускорении, равном g,вес становится равным нулю, т.е. наступает полная невесомость.

Обязательно обращаем внимание учащихся на то, что полная невесомость бывает только тогда, когда на тело действует одна-единственная сила – сила тяжести и тело находится в свободном падении.

Очень важно отметить, что если не учитывать сопротивление воздуха, полная невесомость имеет место при любых бросках.

Учащимся демонстрируется шар с подсветкой, которая зажигается внутри шара только в состоянии невесомости в любом броске. Шар можно бросать вертикально вверх, под углом к горизонту, горизонтально, ронять или подталкивать отвесно вниз. Шар светится только в полете, а учащиеся подтверждают, что при этом на тело действует только сила тяжести.

Подробно изучить явление полной невесомости на этом уроке невозможно. Эта тема достойна отдельного урока, который проводится после темы «Вес тела».

На эту часть урока уходит 10 минут.

Четвертая часть урока. Перегрузка при наличии ускорения тела по горизонтали

Был поставлен вопрос – каков вес тела при горизонтальном разгоне? Рассуждения проводятся на примере сосуда с водой.

В состоянии инерции (т.е. покоя или равномерного прямолинейного движения) на жидкость действуют сила тяжести m∙g и сила нормальной реакции N₀компенсирующие друг друга.

Для того, чтобы сообщить жидкости горизонтальное ускорение а,на нее необходимо подействовать горизонтальной силой т∙а (рис. 20).

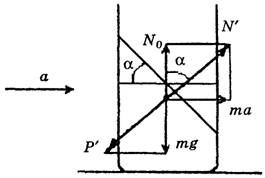
Рис. 20

При этом возникает результирующая сила реакции N’,по модулю большая, чем N₀(как гипотенуза прямоугольного треугольника). Так как искусственный вес Р’ жидкости по третьему закону Ньютона численно равен силе реакции N’,то и он возрастает, вследствие чего и возникает перегрузка.

Рассчитаем угол α.

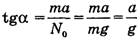
и не зависит от массы.

Тогда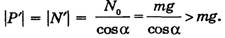

Следует обратить внимание учащихся на то, что на рис. 20 точка приложения веса Р’ не должна совпадать с центром масс жидкости.

Опыт с водой или другой не очень вязкой жидкостью очень нагляден из-за наклона свободной поверхности жидкости на угол α и ее «наплыва» на заднюю стенку (рис. 20).

Объясняем учащимся причину появления этого угла наклона. На угол α от вертикали отклоняется линия ответа, по которой направлен вес Р’. Плоскость свободной поверхности жидкости всегда перпендикулярна линии отвеса.

Как и углы с взаимно перпендикулярными сторонами, угол наклона жидкости также равен α. Если ускорение а постоянно, постоянным будет и угол α. При торможении ускорение тела отрицательное и жидкость «наплывает» на переднюю стенку (угол α отрицательный, a tg α – функция нечетная).

Практически бывает трудно сохранить долго ускорение по горизонтали постоянным. Тогда меняется угол наклона плоскости свободной поверхности жидкости и жидкость начинает плескаться. А если жидкость равномерно вращать? Ведь тогда центростремительное ускорение жидкости а будет постоянным и угол наклона α будет также постоянным. Учащимся демонстрируется установка с гироскопическим колесом (рис. 21). На краю колеса с помощью прозрачного скотча укрепляется стакан с водой. Колесо раскручивается вокруг своей оси и благодаря подшипникам на оси и большой инертности долго сохраняет скорость вращения практически постоянной.

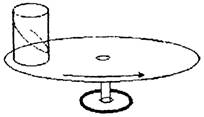
Рис. 21

При большой скорости вращения колеса учащиеся хорошо видят большой угол α наклона плоскости свободной поверхности воды к горизонту.

Постепенно скорость вращение колеса убывает и уменьшается угол a наклона воды.

На эту часть урока уходит 6 минут.

Итак, третья и четвертая части урока были посвящены изучению веса тела, имеющего ускорение. Учащиеся выяснили, что при наличии ускорения вес тела может быть различным – от больших перегрузок до полной невесомости.

Учащимся уместно задать «провокационный» вопрос: «Почему у покоящегося тела на экваторе вес меньший, чем на полюсе?» И находятся ребята, которые подмечают, что на экваторе тело имеет линейную скорость, как следствие этого у него есть центростремительное ускорение, и вес на экваторе должен отличаться от веса на полюсе.

III. Итоги урока

Учащиеся получили полное экспериментальное подтверждение, что:

1) в инерциальных системах отсчета тело, покоящееся или движущееся равномерно прямолинейно, неизменно сохраняет свой вес на любой опоре независимо от того, каков угол наклона опоры, а также жидкая это опора или твердая;

2) в неинерциальных системах отсчета вес тела может изменяться в зависимости от ускорения тела.

Урок вызвал живой интерес у учащихся класса. Они приняли активное участие в обсуждении опытов и их результатов.

На уроке пришлось обратить внимание учащихся на то, что на с. 131 учебника «Физики-9» (авторы Л.А.Исаченкова, И.И.Жолнеревич, И.Н.Медведь) приведен неверный рис. 133. Он был опровергнут экспериментами, проведенными на уроке. Там же имеются ошибки в описании невесомости тела в самолете.

alsak.ru

ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ВЕСА ТЕЛА ОТ УГЛА НАКЛОННОЙ ПЛОСКОСТИ.

ОПРЕДЕЛЕНИЕ ЗАВИСИМОСТИ ВЕСА ТЕЛА ОТ УГЛА НАКЛОННОЙ ПЛОСКОСТИ.

Нестеренко А.В. 1

---

1МБОУ Сладко-Балковская СОШ№13, 9 класс

Нестеренко В.В. 1

---

1МБОУ Сладко-Балковская СОШ №13

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

Определение веса тела во многих учебниках и источниках дается только причина возникновения и точка приложения силы, нигде не указано его конкретное направление и учащимся тяжело понять, куда все-таки направлен вес тела и как его определять. Когда тело находится на горизонтальной опоре, его вес равен силе реакции опоры по III закону Ньютона, а когда тело находится на наклонной плоскости, чему он равен: тоже силе реакции опоры, или нет? Куда направлен вес тела к центру Земли, или в сторону противоположную силе реакции опоры.

Отдельные интернет источники дают обоснования, что вес тела на наклонной плоскости зависит от силы трения http://www.alsak.ru/item/l-r-ix-3.html, и не зависит от угла наклона плоскости.

В перечнях лабораторных работ отсутствует экспериментальное определение веса тела на наклонной плоскости, и его зависимость от угла наклона наклонной плоскости.

Современное оборудование позволяет провести исследование зависимости веса тела от угла наклонной плоскости. При помощи электронных датчиков, подключаемых к устройству измерения и обработки данных (УИДОД) LabQuest мы сможем ответить на вопросы: «Как направлен вес тела на наклонной плоскости и чему он равен», «Зависит ли вес тела от силы трения?»

Формулировки определений веса тела.

Учебник физики 7 класс автор Л.Э. Генденштейн, А.Б. Кайдалов

«Весом тела называют силу, с которой тело давит на опору или растягивает подвес вследствие притяжения тела Землей».

Учебник физики 10 класс автор Л.Э. Генденштейн, Ю.И. Дик:

«Вес покоящегося тела равен действующей на это тело силе тяжести».

Учебник физики 10 класса автор Тихомирова С.А.

«Сила, с которой тело действует на подвес или опору вследствие притяжения к Земле, называется весом тела».

«Если тело и опора неподвижны или движутся равномерно и прямолинейно, то вес тела по модулю равен действующей на него силе тяжести».

«Если тело вместе с опорой движется с ускорением , направленным так же, как ускорение свободного падения, то его вес меньше действующей на тело силы тяжести».

«Если тело вместе с опорой движется с ускорением , направленным противоположно ускорению свободного падения, то его вес больше действующей на тело силы тяжести».

Учебник физики 10 класса А.А. Пинский, О.Ф. Кабардин

«Силу , равную , но приложенную к опоре, называют весом тела. Из рисунка видно, что сила на любой широте φ, отличной от 0º и 90º, не направлена к центру Земли.

…Поэтому на различных широтах сила , а значит, и вес тела P имеют различные значения. Заметим, что разница невелика, она меньше или равна (на экваторе) 0,34%»

Учебник физики 10 класс Г.Я. Мякишев

«Сила, с которой тело вследствие его притяжения Землей действует на опору или растягивает подвес, называются весом тела.»

«Вес обладает особенностями, существенно отличающими его от силы тяжести.

Во-первых, вес тела определяется всей совокупностью действующих на тело сил, а не только силой тяжести (так, вес тела в жидкости или в воздухе меньше, чем в вакууме, из-за появления выталкивающей силы. Во- вторых, вес тела, существенно зависит от ускорения, с которым движется опора (подвес)».

Из источника http://www.alsak.ru/item/l-r-ix-3.html Каган И.Е. «Вес тела» 9 класс получен вывод:

«1) в инерциальных системах отсчета тело, покоящееся или движущееся равномерно прямолинейно, неизменно сохраняет свой вес на любой опоре независимо от того, каков угол наклона опоры, а также жидкая это опора или твердая;

2) в неинерциальных системах отсчета вес тела может изменяться в зависимости от ускорения тела.»

Определение зависимости веса тела от угла наклонной плоскости.

Цель работы: экспериментально определить зависимость веса тела от наклонной плоскости, и зависимости от силы трения.

Оборудование: компьютер с программным обеспечением MS Office, Logger Pro 3.8.3, устройство измерения и обработки данных (УИДОД) LabQuest, цифровые датчики измерения силы с диапазоном ±10Н ±50 Н, и с диапазоном — 200 + 850Н, штативы, 2 кг гиря, нить, скотч, отвес, транспортир.

Теоретические обоснования.

Датчик силы позволяет измерить меру взаимодействия в Ньютонах, следовательно, если расположить его под различными углами и поместив сверху на него груз, то мы измерим именно вес тела. Для точности измерения, при каждом изменении угла датчик силы нужно обнулять, чтобы не внести погрешности веса самого чувствительного элемента.

Также можно измерить вес тела в движении под различными углами, если равномерно тянуть груз. Датчики фиксируют значения в течение определенного момента времени с интервалом 0,02 секунды. По построенному графику можно выделить средние значения силы. Обработку можно проводить как на УИДОДе, так и на компьютере передав значения в программу Logger Pro 3.8.3

Предположим, что вес тела на наклонной плоскости по III закону Ньютона равен по модулю силе реакции опоры, а направлен в противоположную сторону. Тогда исходя из проекций сил

Сила трения направлена вдоль наклонной плоскости и повлиять на вес тела не может. Сила реакции опоры на горизонтальной опоре равна силе тяжести.

Проведение эксперимента.

1. Выставляем датчик силы с диапазоном — 200 + 850Н в качестве наклонной плоскости на штативах. С помощью скотча закрепляем транспортир с отвесом и выставляем датчик под углом 0, обнуляем датчик.

1. Измеряем вес тела на горизонтальном датчике и сравниваем его со вторым датчиком на подвесе с диапазоном ±50 Н. Сила тяжести снятая с первого датчика с максимальным диапазоном 50Н показала 20Н, а сила тяжести снятая с горизонтального датчика показала 22 Н. Следовательно погрешность измерений уже составляет 2Н

1. Построим теоретический график зависимости веса тела от угла наклонной плоскости в Excel по формуле , приняв силу тяжести равной 20 Н, так как погрешность измерения этого датчика меньше из-за меньшего диапазона измерения в 50 Н.

1. Из анализа графика, видно, что для проведения эксперимента нужно брать углы больше 30º, так как при меньших углах изменение веса тела меньше погрешности измерения. Например, при 20º вес тела равен ≈ 19Н, то есть изменение веса тела составило 1Н при погрешности 2Н.

2. Устанавливаем угол наклона плоскости 30º, уравновешиваем гирю 2 кг вторым датчиком, заранее обнулив данные. Измеряем вес тела и силу натяжения. Записываем полученные данные в УИДОД. Равномерно тянем груз вверх и регистрируем данные.

1. Повторяем опыт при углах 45º и 60º , также перед измерениями обнулив датчики.

2. Анализируем полученные данные в УИДОД или передаем их в компьютер, в программу Logger Pro 3.8.3, либо в Excel, находим средние значения и заносим в таблицу.

	Вес тела, Н			Сила тяги, Н
градусы	в покое	в движении	в покое		в движении
30	18	16	14		12
45	14	12	14		16
60	9	8	17		19

1. Вес тела практически не отличается от того, что тело движется или находится в движении. Незначительное уменьшение веса во время движения можно объяснить вибрационными процессами, которые действуют в вертикальной плоскости, вызывая колебания чувствительного элемента. Также этим уменьшением можно пренебречь, так как ΔР = 2Н и погрешность измерения тоже равна 2Н.

2. Нанесем полученное значение веса тела на теоретический график зависимости

1. Анализируя график видно, что измеренные данные попадают в данную зависимость с учетом погрешности.

Заключение.

На основе экспериментальных данных можно сделать следующие выводы:

1. Вес тела уменьшается с увеличением угла наклонной плоскости, и направлен в противоположную сторону силе реакции опоры, определяется формулой

2. Вес тела не зависит от силы трения между наклонной плоскостью и телом.

Список использованных источников и литературы.

1. Физика 7 класс: учебник / Л.Э. Генденштейн, А.Б. Кайдалов под редакцией В.А. Орлова, И.И. Ройзена, 3-е изд., испр. – М. :Мнемозина, 2012, – 255 с.

2. Физика 10 класс: Ч. 1: учебник / Л.Э. Генденштейн, Ю.И. Дик; под ред. В.А. Орлова. – М.: Мнемозина, 2014. – 304 с.

3. Физика 10 класс: учебник /С.А. Тихомирова, Б.М. Яворский. – 3-е изд., испр– М.: Мнемозина, 2012. – 304 с.

4. Физика 10 класс: учебник /(О.Ф. Кабардин, В.А. Орлов, Э.Е. Эвенчик и др.) под ред. А.А. Пинского, О.Ф. Кабардина; Рос. Акад. Наук, Рос. Акад. Образования, изд-во «Просвещение». – 13-е изд. – М.: Просвещение, 2011. – 431 с.

5. Физика. Механика. 10 класс: учебник /М.М. Балашов, А.И. Гомонова, А.Б. Долицкий и др4 под ред. Г.Я. Мякишева. – 12-е изд., стереотип. – М. : Дрофа, 2010. – 495 с.

Просмотров работы: 2328

school-science.ru

Сила тяжести, трения, реакции опоры, упругости, Архимеда, сопротивления, вес. Направление, точка приложения, природа возникновения

Тестирование онлайн

Что надо знать о силе

Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом

Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!

Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.

Сила тяжести

На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.

Сила трения

Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

Сила реакции опоры

Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».

Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.

Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как

Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

Сила упругости

Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.

Закон Гука

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра

При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.

Подробнее о свойствах твердых тел здесь.

Вес тела

Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!

Формулы определения веса нет. Обозначается эта силы буквой .

Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.

Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила

Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!

Перегрузка — отношение веса к силе тяжести

Сила Архимеда

Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:

В воздухе силой Архимеда пренебрегаем.

Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.

Электрические силы

Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.

Схематичное обозначение действующих на тело сил

Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.

Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.

Главное запомнить

1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы

Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила

А сейчас сравним закон гравитации и силу тяжести

Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.

Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.

При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.

fizmat.by