«Площадь Наполеона» пасьянс без регистрации: играть бесплатно
Приглашаем сыграть в «Площадь Наполеона» — пасьянс редкой простоты и изящного расклада, одинаково интересный новичкам и опытным любителям пасьянсов. Эта старинная игра солитер на две колоды с заданием разложить все карты одной масти по основаниям и хитрыми правилами сортировки. Узнайте их и сыграйте в своё удовольствие!
На весь экран
Готовы играть в «Площадь Наполеона» онлайн: бесплатная версия без регистрации и скачивания доступна на русском языке прямо сейчас!
Описание пасьянса «Площадь Наполеона»
Пасьянс начинается с раздачи карт: 12 стопок (по 4 карты в каждой) образуют три стороны квадрата Наполеона, их можно собирать в группы, переносом между ячейками и сортировкой по убыванию масти. Например: пиковый валет принимает только десятку пик, затем 9, 8, 7.
Основанием служит 8 нижних ячеек — это поле Наполеона. Разложите на них все карты в восходящем порядке (от туза до короля каждой масти).
Остаток колоды образует запас с выдачей по 1 карте. Щёлкните по нему, если не видите ходов для сортировки, но не усердствуйте слишком: пересдач в игре нет.
Пробелы заполняют любые карты, резерв и фонды всегда активны — оттуда можно брать по одной верхней карте и возвращать в игру.
Как играть
Перенесите все карты каждой масти в центр игры, начиная с тузов до королей.
Стратегия
При раскладе пасьянса «Площадь Наполеона» важно освободить побольше резервных ячеек. Свободное место для манёвров поможет в рабочей сортировке и минимизирует вероятность блокировки резервных карт. Поэтому старайтесь запомнить позицию тузов при раздаче карт и стройте игру таким образом, чтобы скорее извлечь их на фонды. Задействуйте максимум возможностей сортировки на игровом поле без привлечения резерва, не перелистывайте карты
Особенности онлайн игры «Площадь Наполеона»
- карточный пасьянс на 2 полных колоды;
- играть бесплатно и без регистрации, во весь экран;
- интерфейс на русском;
- простой перезапуск текущего расклада, бесплатные подсказки, возврат хода.
Подсказка на случай, если ищете похожие игры: способ играть в «Площадь Наполеона» напоминает пасьянсы «Свободная ячейка» и «40 воров», а сложность сравнима с «Алжирским терпением».
Трактовка названия пасьянса «Площадь Наполеона» (Le Carré Napoléon) или «Поле Наполеона» вызывает много домыслов. Игру называют не только любимым пасьянсом Наполеона, но даже приписывают Бонапарту авторство — дескать, стратегия сортировки колод по масти помогала «размять мозг» в перерывах между сражениями. Вероятней другое: расклад пасьянса подобен особому построению войск пехоты во времена наполеоновских сражений. В любом случае, это лучший пасьянс для разминки мозга, убедитесь сами!
ollgames.ru
играть в бесплатный пасьянс без регистрации


Карточная игра пасьянс «Площадь Наполеона» приурочена имени Бонапарта не зря. Это один из самых стратегических и увлекательных пасьянсов на две колоды. Родство правил с игрой «Жозефина» уже явная отсылка к императору. Как и начальный макет расклада пасьянса квадратом символизирует «Формулу Наполеона», вменяющую каждому руководителю уравновешивать мужество и волю с интеллектом и умением планировать.
Играть в «Площадь Наполеона» во весь экран
Готовы играть в пасьянс «Площадь Наполеона» — бесплатно и без регистрации игрока (как гость). Онлайн версия доступна во весь экран и легко масштабируется под любые мониторы. Желаем приятной игры в пасьянс, пускай карточная стратегия поможет открыть в себе наполеоновский талант.
Как разложить пасьянс «Площадь Наполеона»
- Ваша цель — отсортировать карты по рангу и масти на восемь фондов, начиная с Тузов до Королей.
- Переместите карты на другие стопки таблиц в порядке убывания масти.
- Только одна карта может быть перемещена за раз.
- Резерв выдаётся по одной, без пересдачи.
- Пустующая стопка занимается без ограничений.
Стратегия выигрыша в пасьянс «Площадь Наполеона» (Napoleon’s Square) сходна с используемой в игре «Свободная ячейка». Только место временного хранения нужно высвобождать, разбирая одну из двенадцати доступных стопок. Заполняя пустые табличные места, сначала высвобождайте Тузов и стройте последовательности, освобождая больше карт к сортировке.
pasyansklassica.ru
Теорема Наполеона / math5school.ru
Известно, что Наполеон Бонапарт (1769–1821) увлекался математикой, больше всего – геометрией. В частности, известен его способ деления окружности на четыре равные части с помощью только циркуля. Будучи политическим деятелем, Наполеон всегда высоко ставил роль науки и учёных в строительстве государственности. Так о математике он говорил:
Процветание и совершенство математики тесно связаны с благосостоянием государства.
Как-то Наполеон, который тогда еще не был правителем Франции, спорил с известными математиками Лагранжем и Лапласом. Во время одной из дискуссий Лаплас прервал Наполеона словами:
Меньше всего мы желаем, чтоб вы, генерал, учили нас геометрии!
Интересно, что в дальнейшем Лаплас стал главным военным министром Наполеона.
Теорема Наполеона
Теорема, о которой пойдёт речь впервые была опубликована английским математиком Уильямом Резерфордом (1798–1871) в 1825 году, спустя 4 года после смерти Наполеона. Хотя Наполеон и занимался геометрией достаточно серьёзно и небезуспешно, как для непрофессионального математика, многие специалисты сомневаются в том, что он является автором теоремы, названной его именем. А теперь к сути.
Если на сторонах треугольника построить правильные треугольники, то получим конфигурацию из четырех треугольников, которую называют треугольниками Наполеона. Окружности, описанные вокруг построенных правильных треугольников, называют окружностями Торричелли.
Именно Наполеону Бонапарту – императору Франции и великому полководцу – история приписывает изучение этой конфигурации, формулировку и доказательство утверждения, известного как теорема Наполеона:
Если на сторонах произвольного треугольника извне его построены равносторонние треугольники, то их центры являются вершинами равностороннего треугольника.
В различных источниках приводятся разные доказательства теоремы Наполеона. Чаще всего можно встретить доказательства, основанные на свойствах поворота или использующие комплексные числа. С одним из элементарных доказательств, основанном на применении теоремы косинусов, можно познакомиться на сайте «Математика, которая мне нравится». Мы докажем теорему Наполеона, используя свойства окружности.
Пусть на сторонах треугольника АВС построены равносторонние треугольники АВС1, А1ВС и АВ1С; ω1, ω2 и ω3 – окружности, описаны вокруг этих треугольников (соответственно). Докажем, что ω1, ω2 и ω3 пересекаются в одной точке – точке Торричелли.
Обозначим точку пересечения окружностей, описанных вокруг треугольников А1ВС и АВ1С, как М. Тогда
∠АМС = 180° – 60° = ∠ВМС.
Отсюда
∠АМВ = 360° – 2 · 120° = 120°,
и точка М лежит на окружности, описанной вокруг АВС
Тогда
∠О1 + ∠АМВ = 180°,
∠О1 = 180° – ∠АМВ = 60°.
Аналогично: ∠О2 = ∠О3 = 60°, и треугольник О1О2О3 – правильный. Теорема Наполеона доказана.
Мы строили правильные треугольники извне заданного треугольника на его сторонах. Их ещё называют внешними треугольниками Наполеона для заданного треугольника. По аналогии, если правильные треугольники строят на сторонах треугольника внутрь его, то их называют внутренними треугольниками Наполеона для заданного треугольника. Треугольник с вершинами в центрах внутренних треугольников Наполеона также является правильным.
Теорема Петра-Дугласа-Неймана
Теорема Наполеона обобщается на случай произвольных треугольников теоремой Петра-Дугласа-Неймана:
Если подобные треугольники любой формы построены на сторонах треугольника внешним образом так, что каждый повёрнут относительно предыдущего, и три соответствующие точки этих треугольников соединены, то итоговый треугольник будет подобен этим внешним треугольникам.
Первая теорема Тебо
Аналогом теоремы Наполеона для параллелограммов является утверждение называемое первой теоремой Тебо:
Центры квадратов, построенных на сторонах параллелограмма, лежат в вершинах квадрата.
Теорема ван Обеля
Следует, пожалуй, упомянуть ещё один математический факт, опубликованный фламандским математиком ван Обелем (Henricus Hubertus van Aubel) в 1878 году, из которого теорема Тебо следует естественным образом:
Если на сторонах произвольного несамопересекающегося четырёхугольника построить квадраты внешним образом и соединить центры противоположных, то полученные отрезки будут равны и перпендикулярны.
Источники: Г.В. Апостолова. Геометрия 8 (Киев, «Генеза», 2008), Википедия.
<<< Назад
Смотрите так же:
Треугольники
Четырёхугольники
Окружность
math4school.ru
Проект « Задача Наполеона»
ВВЕДЕНИЕ.
Как-то попался мне на глаза журнал «Квант» №6 1972г., и 
в нём я прочитал интересную статью «Задача Наполеона».
Малоизвестным фактом для многих учеников
является то, что французский император Наполеон
Бонапарт был любителем математики и внес
определенный вклад в ее развитие.3
Напомню, что Наполеон I Бонапарт (годы жизни 1769-1821) родился в городке Аяччо на острове Корсика в дворянской семье.
В декабре 1778 года Наполеон был принят в колледж в Отёне, главным образом с целью обучения французскому языку. Особых успехов Наполеон добился в математике. Благодаря победе в конкурсе «Ожерелье королевы», он был принят в Королевскую кадетскую школу в Париже. Там он изучал следующие предметы: гидростатика, дифференциальное исчисление, вычисление интегралов, а также государственное право.
Окончив военную школу, он стал быстро делать карьеру и в 1796 году уже был командующим французской армией в Италии.
В 1802 году он был первым консулом Французской республики, а спустя два года, императором Франции.
Блестящий полководец, великий государственный деятель, он значительно расширил территорию империи, поставил в зависимость от Франции большинство стран Западной и Центральной Европы. Провел множество военных кампаний, самые яркие из которых – Бородинское сражение и битва при Ватерлоо.
Обладая аналитическим умом, он добился определенных успехов в области математики. Своими знаниями он поражал многих великих метематиков того времени. За заслуги в математике он был избран академиком Французской академии наук и стал магистром математики.1
Занимаясь математикой, Наполеон доказал теорему, которая теперь называется – теорема Наполеона: если на сторонах любого треугольника ABC построить равносторонние треугольники, то их центры М, N, K являются вершинами равностороннего треугольника.
Ещё он предложил простой способ построения квадрата одной линейкой с двумя засечками. Это решение стало существенным шагом к доказательству возможности при помощи только циркуля или только линейки с двумя засечками делать любые построения, выполнимые циркулем и линейкой без засечек.
Данная тема не включена в школьную программу и очень мало изучена, да и литературы не так много. Поэтому я решил дать общую характеристику этому вопросу.
Целью данной работы я ставлю изучение теоремы Наполеона и рассмотрение нескольких геометрических задач, составленных им. Также доказать теорему Тебо с помощью теоремы Наполеона.
Задачи:
изучить имеющуюся литературу по данной теме;
доказать теорему Наполеона с использованием геометрических преобразований ;
решить задачу Наполеона о равных треугольниках при искомой точке;
решить задачу Наполеона о квадрате, вписанном в окружность;
доказать теорему Тебо, с помощью теоремы Наполеона;
рассмотреть любимую головоломку Наполеона «Танграм».
ТЕОРЕМА НАПОЛЕОНА.
Теорема Наполеона звучит так: «Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников — тоже равносторонний».
План исследования задачи:
Построить произвольный треугольник;
На стороне AB построить равносторонний треугольник;
Построить центр M равностороннего треугольника;
На стороне BC построить равносторонний треугольник;
Построить центр N равностороннего треугольника;
На стороне AC построить равносторонний треугольник;
Построить центр K равностороннего треугольника;
Соединить центры M, N, K;
Сравнить отрезки MN, NK, MK;
-
Вывод.
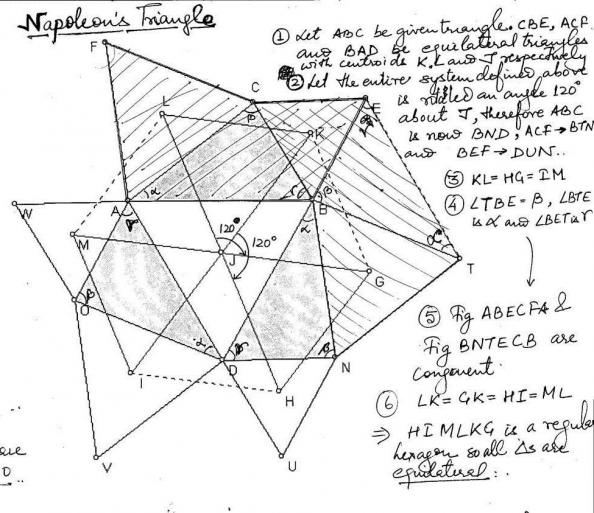
Доказательство:
Пусть М, N, К — центры равносторонних треугольников. Выполним дополнительное построение: соединим точки М, N, К с ближайшими (к каждой из них) двумя вершинами треугольника АВС и между собой (рис.1)
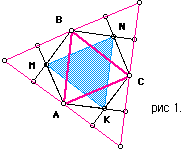
По свойствам равностороннего (правильного) треугольника АМ=МВ, ВN=NС, СК= КА; угол АМВ равен углу ВNС равен углу СКА равен 120°, а их сумма равна 360°. Выделим шестиугольник АМВNСК, а внешние к нему невыпуклые четырёхугольники отбросим. Получим фигуру, изображённую на рис.2
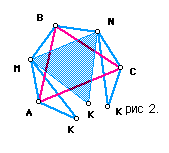
Отсекая теперь от этого шестиугольника треугольники МАК и NСК, перемещая их в плоскости в положение, которое указано на рис.3, получаем четырёхугольник МDNK.
Отрезок МN делит его на два равных (по трем сторонам) треугольника. Углы DNK и DМК равны 120° каждый. Поэтому углы NМК и МNК равны 60° каждый. Следовательно, треугольник МNК равносторонний, что и требовалось доказать.2; 9; 10
ЗАДАЧА О РАВНЫХ ТРЕУГОЛЬНИКАХ ПРИ ИСКОМОЙ ТОЧКЕ.
Одной из составленных Наполеоном Бонапартом геометрических задач является задача о равных треугольниках при искомой точке.
Звучит она так: в треугольнике ABC найти точку F, такую, что сумма расстояний от F до вершин A, B и C будет минимальна.
Решение данной задачи имеет единственное ограничение: наибольший угол треугольника должен быть меньше 120 °.
Решение:
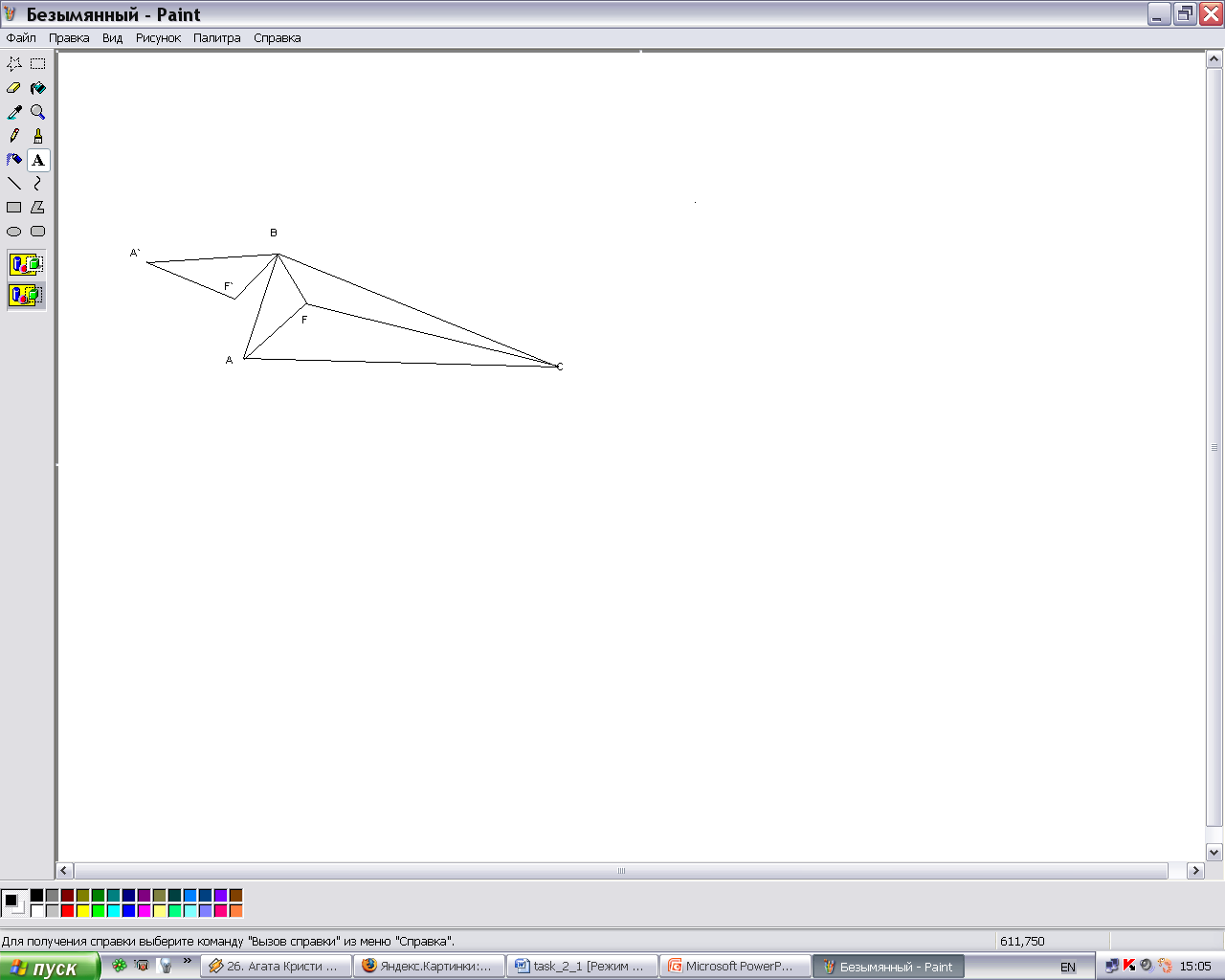
В этом случае AF = A’F’ и BF = B’F’ по построению, BF = F’F, потому что треугольник BFF’ равносторонний, значит сумма расстояний от F до A, B, C равна длине ломаной A’F’FC.
Эта сумма станет минимальной, если F примет такое положение, что ломаная станет прямой. Для этого нужно, чтобы участок AF’F стал прямым, т. е. чтобы Ð A’F’B и, следовательно, Ð AFB равнялся 120°.
Необходимо еще, чтобы участок F’FC стал прямым, т. е. Ð BFC равнялся 120°. Третий угол при точке F автоматически станет равным 120°. Итак, доказано, что все три угла при искомой точке F равны 120°.
ЗАДАЧА О КВАДРАТЕ, ВПИСАННОМ В ОКРУЖНОСТЬ.
По преданию Наполеон Бонапарт предложил итальянскому математику Маскерони эту задачу. Известно также, что во время беседы с Лагранжем и Лапласом (знаменитыми французскими математиками), Наполеон поразил их. Он объяснил им некоторые из предложенных Маскерони решений следующей его задачи.
Условие задачи Наполеона: необходимо найти вершины квадрата, вписанного в окружность с отмеченным центром
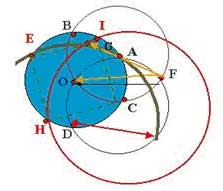
Решение, предложенное американским математиком Ф. Чини:
1.Выбрать на окружности произвольную точку А. Провести через нее окружность того же радиуса, что и первая.
2. Затем из точки пересечения второй окружности с первой (точки E — первая вершина) провести третью окружность, пересекающую первую окружность (в точке D).
3. Провести из этой точки D первую дугу (DA), пересекающую первую исходную окружность в точке E (вторая вершина квадрата).
4. Из точки F — как из центра пересечения второй и третьей окружности (внешней по отношению к первой) провести дугу радиусом FO в точке G. 5.Оставшиеся две вершины квадрата H, I, вписанного в исходную окружность, получите, проведя дугу радиуса CG с центром в точке C.11
5. ТЕОРЕМА ТЕБО.
Эта теорема является частным случаем теоремы Ван-Обеля и аналогична теореме Наполеона. Я попробую её доказать.
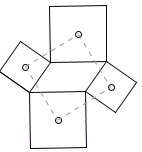
Теорема Тебо 1. Докажите, что центры квадратов, построенных на сторонах параллелограмма вне его, являются вершинами квадрата.7, 8
Решение:
Пусть K, L, M, N — центры квадратов, построенных соответственно
на сторонах AB BC, CD, DA параллелограмма ABCD; O — центр па-
раллелограмма. Применив теорему для треугольников ABK, BCL, CAO,
построенных на сторонах треугольника ABC, получаем, что треугольник
KOL — равнобедренный прямоугольный с прямым углом O. Аналогично,
треугольники LOM, MON, NOK — равнобедренные прямоугольные с пря-
мым углом O.
Другое решение можно получить, заметив, что KAN и KBL —
равные треугольники, получающиеся друг из друга поворотом на 90◦.
5. ГОЛОВОЛОМКА НАПОЛЕОНА.
Рассмотрим одну из головоломок — «Танграм».
Попытка — не пытка. Попробуйте и вы решить загадку Наполеона. Если даже попытка окажется безрезультатной — не огорчайтесь! В ваших руках окажется головоломка, которая всегда скрасит ваш досуг.
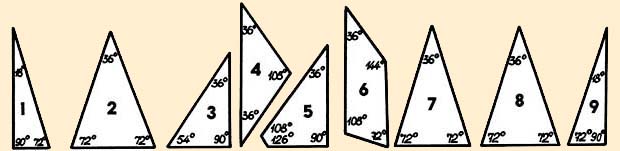
Деталей, напомним, девять: семь треугольников и два четырехугольника. Проще всего вырезать их из листа фанеры или пластика толщиной 3…6 мм. Подойдет прямоугольный кусок размером 94 х 40 или 141 х 60 мм. Поточнее разметьте его, как показано на рисунке. По линиям разметки лобзиком аккуратно выпилите заготовки. Края подровняйте плоским напильником и мелкой наждачной бумагой. Каждую деталь промаркируйте цифрами от 1 до 9. Головоломка готова. Из готовых деталей не составит труда построить по нашим рисункам квадрат и звезду, не говоря уж о прямоугольнике. Но прежде чем браться за решение головоломки, обратите внимание на одну особенность углов в деталях треугольной и четырехугольной формы: 18°, 36°, 90°, 108°, 126°, 144°. Заметили — они кратны цифре 18? Почему? Может, именно в этой кратности скрыта подсказка?5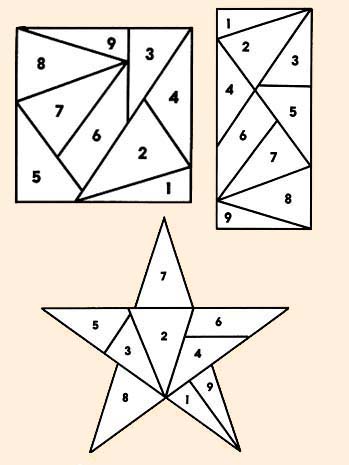

Очевидцы рассказывают, что среди прочих математических, шахматных и тактических задач по военному искусству император Наполеон любил задавать своим офицерам и эту головоломку: какие плоские геометрические фигуры можно построить из девяти предложенных в россыпь деталей?
Это игра-головоломка, направленная на воссоздание из геометрических фигур образных изображений. Наборы фигур представляют собой части разрезанной фигуры: квадрата, прямоугольника и т.п. Суть игры заключается в том, чтобы на плоскости из семи частей квадрата создавать самые разнообразные фигуры, более сложные. Головоломка используются для улучшения зрительной памяти.
Простую с виду задачу решить удавалось не каждому. Маршал Даву, говорят, сумел собрать из предложенных деталей квадрат, а Мюрат — и квадрат, и прямоугольник. Позже нашелся полковник, построивший звезду. Но никто до сих пор не сумел построить из этих деталей треугольник, ромб или трапецию… Да и есть ли решение вообще?
Танграм был любимой игрой Наполеона, который, лишившись трона, в изгнании проводил долгие часы за этой забавой, упражняя свое терпение и находчивость.
ЗАКЛЮЧЕНИЕ.
Проведенная работа позволила мне познакомиться с достижениями Наполеона Бонапарта в области геометрии. Книг об императоре очень много, в которых рассказывается о его семье, привычках, таланте полководца, но ни слова как о математике. Моё исследование даст возможность многим узнать Наполеона Бонапарта с другой стороны.
Мною изучена Теорема Наполеона и ее доказательство, рассмотрены геометрические задачи, доказана Теорема Тебо и головоломка Наполеона.
Данные знания позволят мне расширить мои возможности при решении различных геометрических задач, пополнят мой багаж малоизвестными фактами из геометрии.
Я предлагаю ученикам старших классов решить некоторые задачи, внешне не имеющих никакой связи с теоремой Наполеона. Можно решать задачи любыми методами, а можно получить решения данных задач как следствия из этого сильного факта. Я пока не могу решить все эти задачи, так как учусь ещё в 7 классе, но то, что попробую решить их в классах 9 – 11, – это точно.
1. На боковых сторонах трапеции ABCD построены треугольники ABE
и CDF так, что AE || CF и BE || DF. Докажите, что если E лежит на
стороне CD, то F лежит на стороне AB.
2. (З. Насыров) (задачник ”Кванта” 1992 г.) Круг поделили xордой AB
на два круговых сегмента и один из ниx повернули вокруг точки A на неко-
торый угол. Пусть при этом повороте точка B перешла в точку D. Докажи-
те, что отрезки, соединяющие середины дуг сегментов с серединой отрезка
BD, перпендикулярны друг другу.
3. (А. Заславский) (Геометрическая олимпиада им. И. Ф. Шарыгина)
На описанной окружности треугольника ABC взяты точки A1, B1, C1 так,
что AA1, BB1 и CC1 пересекаются в одной точке. При отражении A1, B1,
C1 относительно сторон BC, CA, AB соответственно получаются точки A2,
B2, C2. Докажите, что треугольники A1B1C1 и A2B2C2 подобны.6
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ:
Ришелье. Оливер Кромвель. Наполеон I. Князь Бисмарк: Биогр. Р 57 очерки. — М.: Республика, 1994.-320 с.: ил.
Энциклопедический словарь юного математика, 2-е изд., исп.и доп./Сост. Э-68 А.П. Савин. — М.: Педагогика, 1989.-352 с.: ил., стр 298.
Заславский А.А., Протасов В.Ю., Шарыгин Д.И. — Геометрические олимпиады им. И.Ф. Шарыгина — М.: МЦНМО, 2007 г.- 152 с.
Задача Наполеона. Квант, № 6, 1972, Березин В.Н.
http://napaleon.ru/napoleon
Е. Андреева «Головоломка Наполеона» http://jtdigest.narod.ru/dig2_02/napol.htm
Н.Н.Никитин, Г.Г.Маслова. Сборник задач по геометрии. Задача № 31. http://oldskola1.narod.ru/NiktinZ/d05.htm
Теорема Тебо 1. http://ru.wikipedia.org/wiki/%D2%E5%EE%F0%E5%EC%E0_%D2%E5%E1%EE
Анимация теоремы Наполеона
http://files.school-collection.edu.ru/dlrstore/02b7798e-607d-88ff-f603-9526ec4cf0bb/napoleon.html
10. Задача/Теорема Наполеона
http://webgrossmeister.dreamwidth.org/5035.html
11. Задача о квадрате, вписанном в окружность.
http://uchinfo.com.ua/zadachi/zadachi3.htm
Приложение:
Обложка и статья «Задача Наполеона» из журнала «Квант» №6 1972 г.


infourok.ru
Теорема Наполеона
Процветание и совершенство математики тесно связаны с благосостоянием государства.
В настоящей статье рассматривается доказательство одной из наиболее красивых теорем планиметрии, авторство которой приписывается великому полководцу и государственному деятелю Наполеону Бонапарту (1769 – 1821). Мало кто знает, что Наполеон – император Франции был очень даже неплохим математиком своего времени. С учетом того, что военной специализацией Наполеона была артиллерия, в этом ничего удивительного нет. Кроме того, за заслуги в математике в 1797 году он был избран членом Национального института наук и искусств по классу физики и математики.
В различных литературных источниках можно найти разные доказательства теоремы Наполеона. Однако приведенное ниже доказательство является наиболее простым и доступным для школьников.
Уместно напомнить, что к настоящему времени известная всем теорема Пифагора имеет более 400 различных доказательств.
Теорема. Если на каждой стороне произвольного треугольника построить по равностороннему треугольнику, то треугольник с вершинами в центрах равносторонних треугольников – тоже равносторонний.
Доказательство. Пусть стороны произвольного треугольника равны , , и .
Треугольники , и являются равносторонними с центрами в точках , и , соответственно.
Рассмотрим . Так как и равносторонние треугольники, то и . Кроме того, здесь и , т.е. .
Применяя теорему косинусов, можно записать
. (1)
Так как (теорема косинусов) и (площадь ), то и . В таком случае
.
Отсюда и из формулы (1) следует, что
или
. (2)
Поскольку в формулу (2) переменные входят симметрично, то повторив приведенные выше рассуждения относительно и , получим формулу (2). Следовательно, треугольник равносторонний. Теорема доказана.
Примечание. В доказанной теореме рассмотрен случай, когда построенные на сторонах равносторонные треугольники являются внешними. Однако данная теорема является истинной и в том случае, когда равносторонные треугольники будут внутренними. Только в таком случае формула (2) принимает вид
.
В заключение отметим, что Наполеону также приписывается авторство следующих геометрических задач на построение:
1. Используя только циркуль (без линейки), необходимо
а) разделить данный отрезок пополам;
б) найти центр данной окружности;
в) разделить окружность с отмеченным центром на четыре равные дуги.
2. Найти в треугольнике такую точку , чтобы сумма расстояний от до вершин была бы минимальной.
Рекомендуемая литература
1. Перельман Я.И. Занимательная геометрия. М.: Римис, 2016. – 320 с.
2. Березин В.Н. Задача Наполеона. – Журнал «Квант», № 6, 1972. – с. 29.
3. Коксетер Г.С., Грейтцер С.Л. Новые встречи с геометрией. М.: Наука, 1978. – 224 с.
Остались вопросы?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Урок-лекция «Некоторые геометрические увлечения Наполеона»
УРОК-ЛЕКЦИЯ
Тема занятия:
«Некоторые геометрические увлечения Наполеона»
Диамбекова Алла Лазаровна
педагог МКОУ ДОД ДДТ Дигорского района РСО-Алания.
Цель занятия – изучение некоторых геометрических увлечений Наполеона.
Задачи – а) рассмотреть три доказательства теоремы Наполеона;
б) ознакомиться с любимыми геометрическими головоломками императора;
ХОД ЗАНЯТИЯ
Математика как основа всех наук во все времена привлекала пытливые неординарные умы. Юрист Пьер Ферма (1601-1665) известен как самый загадочный математик среди слуг «царицы наук». Священник Иван Первушин (1827-1900) справился с вычислением простого числа Мерсенна с показателем 61 и нашёл делители для чисел Ферма с индексом 12 и 23, что являлось в теории чисел того времени очень большим достижением. Император Франции Наполеон Бонапарт (1769-1821) не упускал возможности позаниматься геометрией. Этот список можно продолжить, но я хочу остановиться на Наполеоне I.
Из истории всем известно, что император Франции был блестящим полководцем и великим государственным деятелем. Книг о Наполеоне — более двухсот тысяч! Историки знают, во что одевался Наполеон, что было у него на ногах, сколько стоили его носовые платки, что он любил есть и во сколько завтракал, каким был распорядок его дня. Академик Фредерик Массон на рубеже XX века выпустил 13-томное исследование «Наполеон и его семья», посвященное практически всем сторонам жизни Наполеона. Но в них мало написано о математических способностях великого императора.[2]
Бонапарт-математик – это скрытая от многих страница истории. В декабре 1778 года Наполеон был принят в колледж в Отёне, главным образом с целью обучения французскому языку. Особых успехов Наполеон добился в математике. Благодаря победе в конкурсе «Ожерелье королевы», он был принят в Королевскую кадетскую школу в Париже. Обладая аналитическим умом, он добился определенных успехов в области математики. Своими знаниями он поражал многих великих математиков того времени. За заслуги в математике он был избран академиком Французской академии наук и стал магистром математики. [6]
У императора было увлечение – составление геометрических задач. Некоторые его задачи отличаются простотой постановки и допускают изящные решения.[1]
Он находил время заниматься геометрией для собственного удовольствия, чувствовал в ней красоту и объект, достойный приложения остроумия и изобретательности. Одно из свидетельств тому – несколько составленных им задач на построение, вычисление неизвестной величины, доказательство утверждений евклидовой геометрии, а также геометрические игры-головоломки.
Теорема Наполеона.
На сторонах произвольного треугольника АВС внешним образом построены как на основаниях равносторонние треугольники (рис. 1). Доказать, что центры этих треугольников также являются вершинами равностороннего треугольника.
рис.1
Доказательство 1:
Задача имеет довольно изящное решение.
Пусть M, N, K – центры равносторонних треугольников. Выполним дополнительное построение: соединим точки M, N, K с ближайшими (к каждой из них) двумя вершинами треугольника АВС и между собой.
Т.к. M, N, K – центры равносторонних треугольников, то АМ = МВ, BN = NC, CK = KA;
< AMB = < BNC = < CKA = 120o, а их сумма равна 360о.
Выделим шестиугольник AMBNCK, а внешние к нему невыпуклые четырехугольники отбросим. Получим фигуру, изображенную на рис. 2.
 рис 2.
рис 2.  рис.3
рис.3
Отрезая теперь от упомянутого шестиугольника треугольники МАК и NCK, перемещая их в плоскости в положение, которое указано на рис. 3, получаем четырехугольник MDNK.
Отрезок MN делит его на два равных (по трем сторонам) треугольника. Углы DNK и DMK равны 120 каждый. Поэтому углы NMK и MNK равны 60
каждый. Поэтому углы NMK и MNK равны 60 каждый.
каждый.
Следовательно, треугольник MNK – равносторонний, что и требовалось доказать. [3]
Доказательство 2:
Лемма. Окружности, описанные около треугольников ABX, BCY и CAZ, пересекаются в одной точке. (рис. 4)
Доказательство леммы. Пусть P — точка пересечения окружностей, описанных около треугольников BCY и CAZ.
а). Предположим, что точка P лежит внутри треугольника ABC. Тогда из свойства вписанного четырехугольника вытекает, что углы BPC и CPA (рис. 5) равны 120 . Следовательно, угол APB=120
. Следовательно, угол APB=120 и точка P лежит также на окружности, описанной около
и точка P лежит также на окружности, описанной около  ABX.
ABX.
.  Рис. 4
Рис. 4
Доказательство теоремы.
Обозначим через M, N и K (рис.5) центры равносторонних треугольников ABX, BCY и CAZ соответственно. Прямая, соединяющая центры пересекающихся окружностей, перпендикулярна их общей хорде. Отсюда следует, что MN перпендикулярнa BP, NK перпендикулярнa CP и MK перпендикулярнa AP. В доказательстве леммы мы установили, что углы APB, BPC и CPA равны 120 . Так как сумма углов любого четырёхугольника равна 360
. Так как сумма углов любого четырёхугольника равна 360 , то каждый из углов MNK, NKM и KMN равен 60
, то каждый из углов MNK, NKM и KMN равен 60 , т.е. треугольник MNK- равносторонний, что и требовалось доказать. [2]
, т.е. треугольник MNK- равносторонний, что и требовалось доказать. [2]
 рис. 5
рис. 5
б). Пусть теперь Р лежит на самом треугольнике.(рис. 6) Очевидно, тогда Р совпадает с вершиной С и в данном треугольнике угол ВСА=120 , и это обеспечивает принадлежность точки Р окружности, описанной около
, и это обеспечивает принадлежность точки Р окружности, описанной около  АВХ. Т.е. лемма верна.
АВХ. Т.е. лемма верна.
Для доказательства теоремы в этом случае достаточно увидеть, что угол КМС из  МСО равен 60
МСО равен 60 Аналогично, угол СNВ равен 60
Аналогично, угол СNВ равен 60 В итоге получаем равносторонний
В итоге получаем равносторонний  MNK. Теорема доказана.
MNK. Теорема доказана.
в). Если в данном треугольнике один из углов больше 120 , то точка Р «выскочит» за треугольник. (рис. 7) В этом случае рассмотрим угол АРВ как сумму углов АРС и ВРС. Угол АРС – вписанный и опирается на дугу АС, на которую опирается также вписанный угол АZС в 60
, то точка Р «выскочит» за треугольник. (рис. 7) В этом случае рассмотрим угол АРВ как сумму углов АРС и ВРС. Угол АРС – вписанный и опирается на дугу АС, на которую опирается также вписанный угол АZС в 60 . Поэтому угол АРС равен 60
. Поэтому угол АРС равен 60 . Аналогично и угол ВРС. Значит, угол АРВ равен 120
. Аналогично и угол ВРС. Значит, угол АРВ равен 120 , и снова лемма доказана.
, и снова лемма доказана.
Докажем теорему для этого случая. В прямоугольном  угол
угол  равен 30
равен 30 и он вертикален с углом MD
и он вертикален с углом MD прямоугольного треугольника MD
прямоугольного треугольника MD Следовательно, угол KMN равен 60
Следовательно, угол KMN равен 60 . Аналогично и угол MNK. В итоге получаем равносторонний
. Аналогично и угол MNK. В итоге получаем равносторонний  MNK. Теорема доказана.
MNK. Теорема доказана.
Доказательство 3. Определим расстояние между центрами K и N из четырёхугольника NK , где
, где  и
и  — середины сторон BC и AC треугольника AВC. В этом четырёхугольнике (рис. 8)
— середины сторон BC и AC треугольника AВC. В этом четырёхугольнике (рис. 8)
 Рис. 8
Рис. 8
N ,
,  . Величины интересующих нас углов приведены на рисунке 9.
. Величины интересующих нас углов приведены на рисунке 9.
Рис. 9
Рассмотрим векторное равенство  +
+
Преобразуем его, возведя обе части в квадрат и применив свойства векторов:
KN2 = K 2 +
2 +  2 +
2 +  2 + 2 K
2 + 2 K
 + 2 K
+ 2 K + 2
+ 2  =
=  .
.
Поэтому  .
.
Но  .
.
Следовательно,  .
.
Симметрия полученной формулы относительно a, b и c указывает на то, что KN=NM=MK,т.е. треугольник правильный. Что и требовалось доказать.
Если исходный ∆АВС — равносторонний треугольник, то все внутренние центроиды стягиваются в точку, а треугольник, вершины которого являются внешними центроидами, вместе с исходным ∆АВС образуют фигуру, известную как «Звезда Давида».
Звезда Давида — эмблема в форме шестиконечной звезды (гексаграммы), в которой два равносторонних треугольника наложены друг на друга: верхний — концом вверх, нижний — концом вниз, образуя структуру из шести равносторонних треугольников, присоединенных к сторонам шестиугольника.
Звезда Давида изображена на флаге Государства Израиль и является одним из основных его символов. Согласно легенде, этот символ был изображён на щитах воинов царя Давида. [5]
Очевидцы рассказывают, что Наполеон любил задавать своим офицерам такую головоломку: какие плоские геометрические фигуры можно построить из девяти (рис.10) предложенных в россыпь деталей? Простую с виду задачу решить удавалось не каждому. Маршал Даву, говорят, сумел собрать из предложенных деталей квадрат, а Мюрат — и квадрат, и прямоугольник, а позже нашелся полковник, построивший звезду (рис.11). Но никто до сих пор не сумел построить из этих деталей треугольник, ромб или трапецию… Да и есть ли решение вообще? [6]
Я смог дать на этот вопрос положительный ответ, построив новые фигуры, приведённые на рисунке 14 в приложениях.
рис.10
 Рис.11
Рис.11
Обращаем внимание на одну особенность углов в деталях треугольной и четырехугольной формы: 18 , 36
, 36 , 54
, 54 , 72
, 72 , 90
, 90 , 108
, 108 , 126
, 126 , 144о — они кратны цифре 18? Почему? Может, именно в этой кратности скрыта подсказка?
, 144о — они кратны цифре 18? Почему? Может, именно в этой кратности скрыта подсказка?
Библиографический список
Березин В.Н. Задача Наполеона // Квант. — 1972. -№6,с.29.
Михайлов И.И. Задача Наполеона. – gavrilova. 21415s02.edusite/ru.
Савин А.П. Задача Наполеона//Энциклопедический словарь юного математика.- М:, Педагогика, 1985.-298с.
Тюганова Т. Задача Наполеона. – nsportal.ru.
Школьный проект «Геометрия глазами Наполеона Бонапарта». – junst-klin.ucoz.ru.
infourok.ru
Дневники Леди и теорема Наполеона.: vedaveta — LiveJournal
Продолжение, начало — Звезды Наполеона и эпохи Струве. Часть 1.В математике существует Теорема Наполеона. Эту теорему часто приписывается Наполеону Бонапарту (1769—1821),
Теорема, о которой пойдёт речь впервые была опубликована английским математиком Уильямом Резерфордом (1798–1871) в 1825 году, спустя 4 года после смерти Наполеона. Книга в которой была опубликована эта теорема называлась «The Ladies’ Diary». Зачем некой Леди знать тригонометрию?
Теорема Наполеона гласит:
Если на сторонах треугольника построить правильные треугольники, то получим конфигурацию из четырех треугольников, которую называют треугольниками Наполеона.
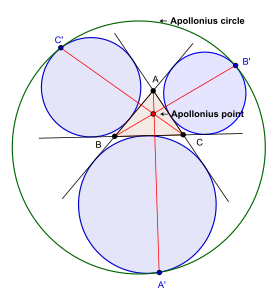
Окружности, описанные вокруг построенных правильных треугольников, называют окружностями Торричелли, также эту окружность называют McCay-Kreise (в переводе с английского «круг с моей края стороны») или Окружностями Аполло́ния.
Эту окружность, якобы, описал Аполлоний Пергский (др.-греч. Ἀπολλώνιος ὁ Περγαῖος, 262 до н. э. — 190 до н. э.) — древнегреческий математик, один из трёх (наряду с Евклидом и Архимедом) великих геометров античности, живших в III веке до н. э.
Окружность Аполония связана с биполярными координатами в ортогонольной эллиптической системе координат. Окружность — это место ( Geometrischer Ort) точек плоскости, отношение расстояний от которых до двух заданных точек есть величина постоянная, не равная единице.

Книга The Ladies’ Diary не являлась Дневником Леди, изучающей геометрию или математику!
The Ladies’ Diary — это астрономический альманах описывающий хронологию, праздничные торжества и затмения посвящённые OUR LADY — Богородицы или Παναγία.
The Diarian miscellany, consisting of all the useful and entertaining parts, both mathematical and poetical, extracted from the Ladies’ diary.




Помимо астрономического альманаха OUR LADY — Богородицы или Παναγία публиковали Gentleman’s diary, or Royal almanack, в этом альманахе повествовалось о хронологии Господских, или Herrenfest, или Деспотических приздников- Δεσποτικές εορτές или Велики празници
Историки-астрологи под эти праздники и даты сочиняли древнюю хронологию королей-кайзеров -императоров.
The ladies and gentlemens diary, or, Royal almanack : for … 1777 … : containing, besides the calendar, a great variety of aenigmas, rebusses, mathematical solutions, &c. &c.текст
Примечетельно что в альманахах Ladies’ diary и Gentleman’s diary разбирают проблему с треугольниками задолго до Резерфорда и до Наполеона Полистайте любой из этих альманахов они написаны вполне понятном современном английском языке



Книгу математика William Rutherford с доказательством теоремы Наполеона я не нашла, но зато обнаружила Вильяма Резерфорда литератора-историка писавшего произведения о древней истории A view of ancient history; including the progress of literature and the fine arts by Rutherford, William, D.D., master of Uxbridge Academy Publication date 1809 .
В предидущей статье в комментариях о Наполеоне / Апполоне дополнили: На сайте Urbane приводилась информация, что официальным девизом Наполеона Бонапарта Первого был «Nous Apoleon Bona Parte» — «Мы, Аполеон, на стороне добра». «Nous Apoleon Bona Parte» скорее «новый апполон правильной стороны»
Аполоний Пергский Apollonii Pergaei это имя- метод = A po Lunе per Gaei
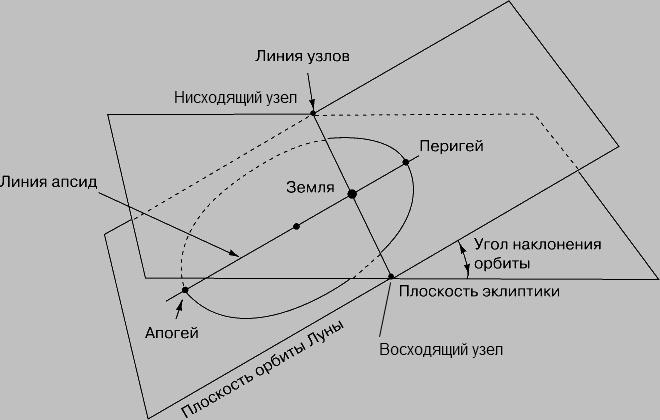
Луна и Гея земля являются гидом guide «проводник» итал. guida, от guidare «вести», из готск. witan «наблюдать,замечать ВЕДАТЬ» при описании положения светил по отношению друг к другу, при их движении по эллиптической орбите.


Аполуний= апо-луна, наиболее удалённая позиция (солнца) к луне; иногда в литературе пишут апо-селений или апо-цинтия (Periselenio/Pericintio/Perilunio Aposelenio/Apocintio/Apolunio)
С точки зрения орбитального движения светил Солнце находится в Апо-Лунии при полнолунии (противостояние или опозиция луны и солнца).
Для планет в противостоянии или опозиции к солнцу применяют термин синод — соединение; оно бывает верхним и нижним, но ранее термин синод употреблялся при расчёте Пасхи.
По полнолуниям в григорианском календаре расчитывают пасхалии. Пасха празднуется в первое воскресенье после первого весеннего полнолуния = после весеннего синода или апо-позиции Солнца и Луны.
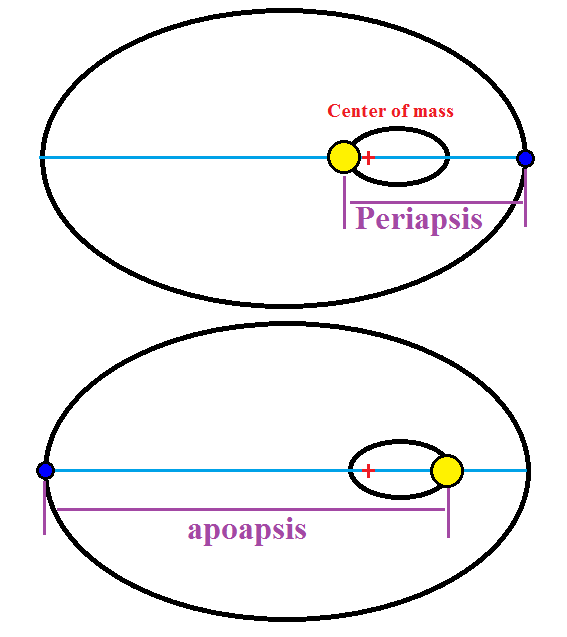
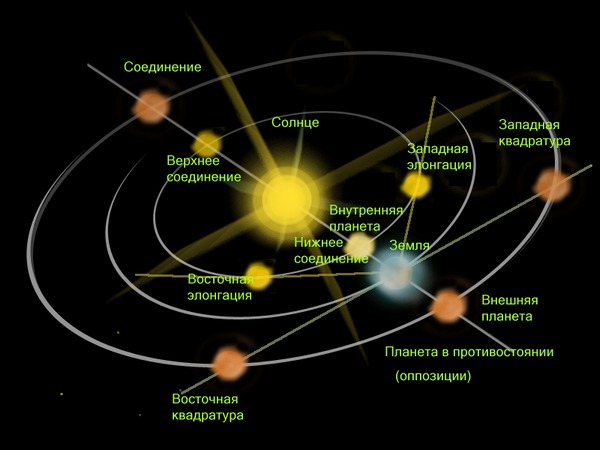
Термин Bona Parte применительно к Аполунию связан с методом расчета Пасхалии в григорианском календаре, в григорианских пасхалиях.
Эпакта -Bona Parte, возраст Луны в днях на начало года (ἐπάκτη, лат. epactae, ἐπακτὰἱ ἡμέραἱ — добавочные дни).
ἐπάκτη из πάκτωση — дань, плата за прокат, оброк, рента, договор об аренде.
bonum ī n. [bonus] однокоренное с duonus (дань) ad bonus = addonus= adonus
добро, благо
польза, выгода, преимущество
дарование
pl. имущество, состояние, достояние
Так как разница между продолжительностью солнечного и лунного годов составляет 11 дней то лунный год уПАКовывают отдолженными/арендованными днями. Это метод упаковки πάκτον + -ώνω pactum < paciscor < pax — миротворного круга.
Наполеон — это французский дефект выговора имени Новый Аполлинарий, такое имя новорожденному могли дать если он родился в полнолуние
В отношении Наполеони «кайзера -императора французов» сомневаюсь, что он был реальной исторической личностью
Нашла парочку книг о Наполеоне:
1. Napoléon et les femmes l’amour by Frédéric Masson Publication date 1717.
Наполеон еще не родился! В книге в тексте с датами всё в порядке, но в американском издании стоит 1717 год. Похоже, что американцы жили в ином хронологическом периоде
2. Citizen Bonaparte by Erckmann-Chatrian
Эркма́н-Шатриа́н (фр. Erckmann-Chatrian) —- литературное имя двух французских писателей, работавших совместно Эмиль Эркма́н (20.V.1822, г. Фальсбур, департамент Мозель, —- 14.III.1899, г. Люневиль, Мёрт и Мозель) и Шарль Луи Гратьен Александр Шатриа́н (18.XII.1826, Ле-Гран-Сольда, деп. Мёрт, — 3.IX.1890, Вильмомбль, департамент Сена).
Citizen Bonaparte (Гражданин Бонапарт) — это произведение от этих авторов; на русский язык его перевели под названием
История крестьянина. Роман в 4-х частях пер. Марка Вовчка.
А на французком книга называлась История пейзана Histoire d’un paysan (1867) —
peasant (non-noble person – простолюдин, земляк )
English: peasant
French: paysan
Spanish: paisano
Old French païsan From païs (“countryside”) From Latin pācem, accusative singular of pāx.
В отношении Ориона и эпох Струве выложу пару сканов из одной очень интересной книги:


Василий Яковлевич Строев Стру́ве (п)русский астроном и один из основоположников звёздной астрономии, основатель династии …. А Гершель другой астроном и другой основатель династии.
Когда разберусь, что это за эпохи с разницей /ошибкой в подсчётах в 50 лет, то выложу продолжение .
vedaveta.livejournal.com
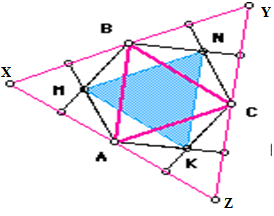
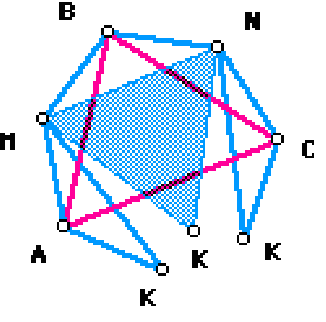 рис 2.
рис 2. 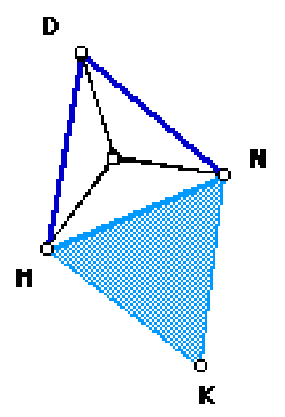 рис.3
рис.3 каждый. Поэтому углы NMK и MNK равны 60
каждый. Поэтому углы NMK и MNK равны 60 ABX.
ABX.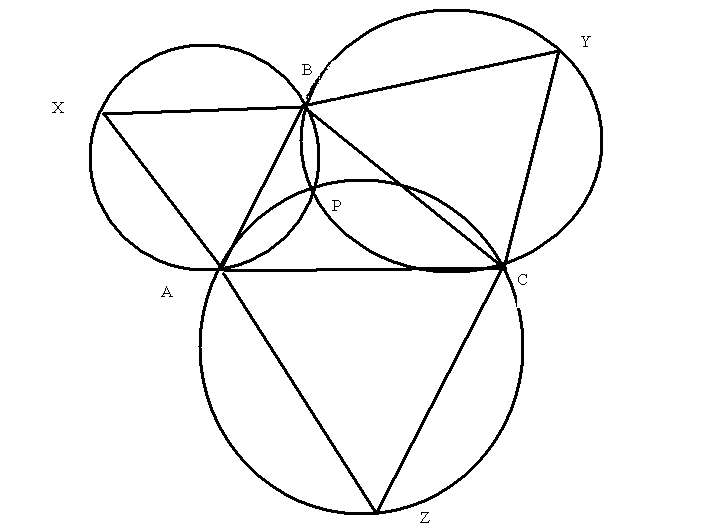 Рис. 4
Рис. 4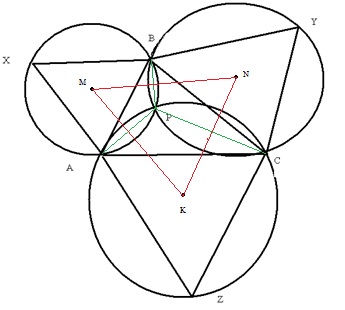 рис. 5
рис. 5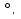 Аналогично, угол СNВ равен 60
Аналогично, угол СNВ равен 60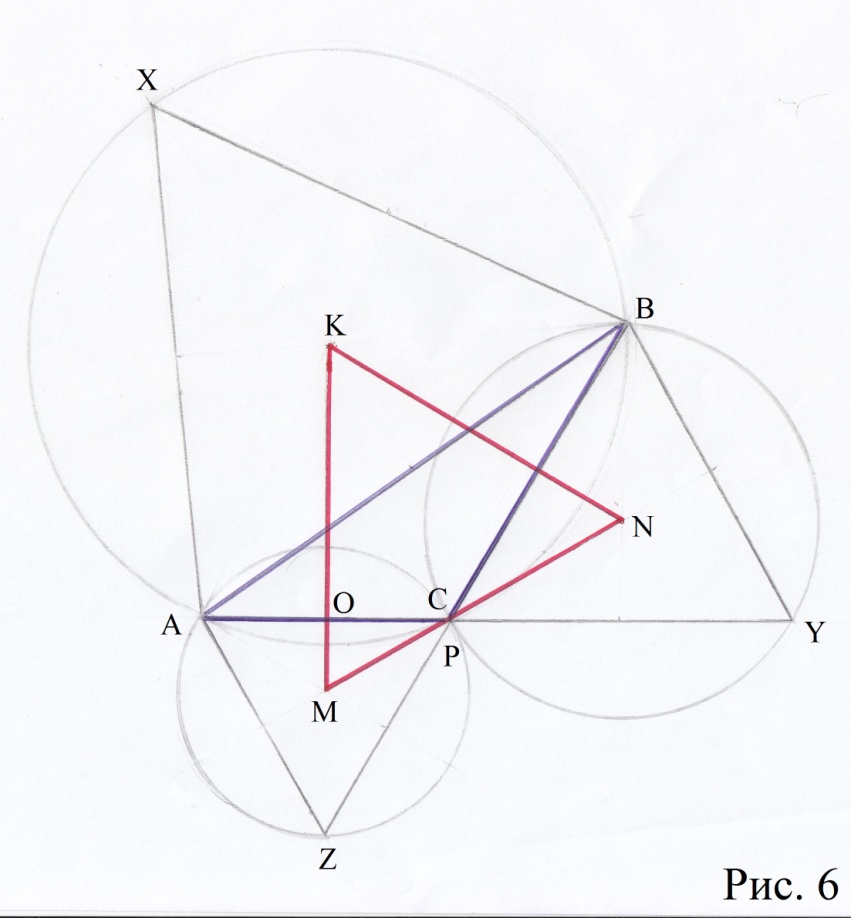
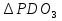 угол
угол 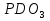 равен 30
равен 30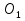 прямоугольного треугольника MD
прямоугольного треугольника MD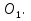 Следовательно, угол KMN равен 60
Следовательно, угол KMN равен 60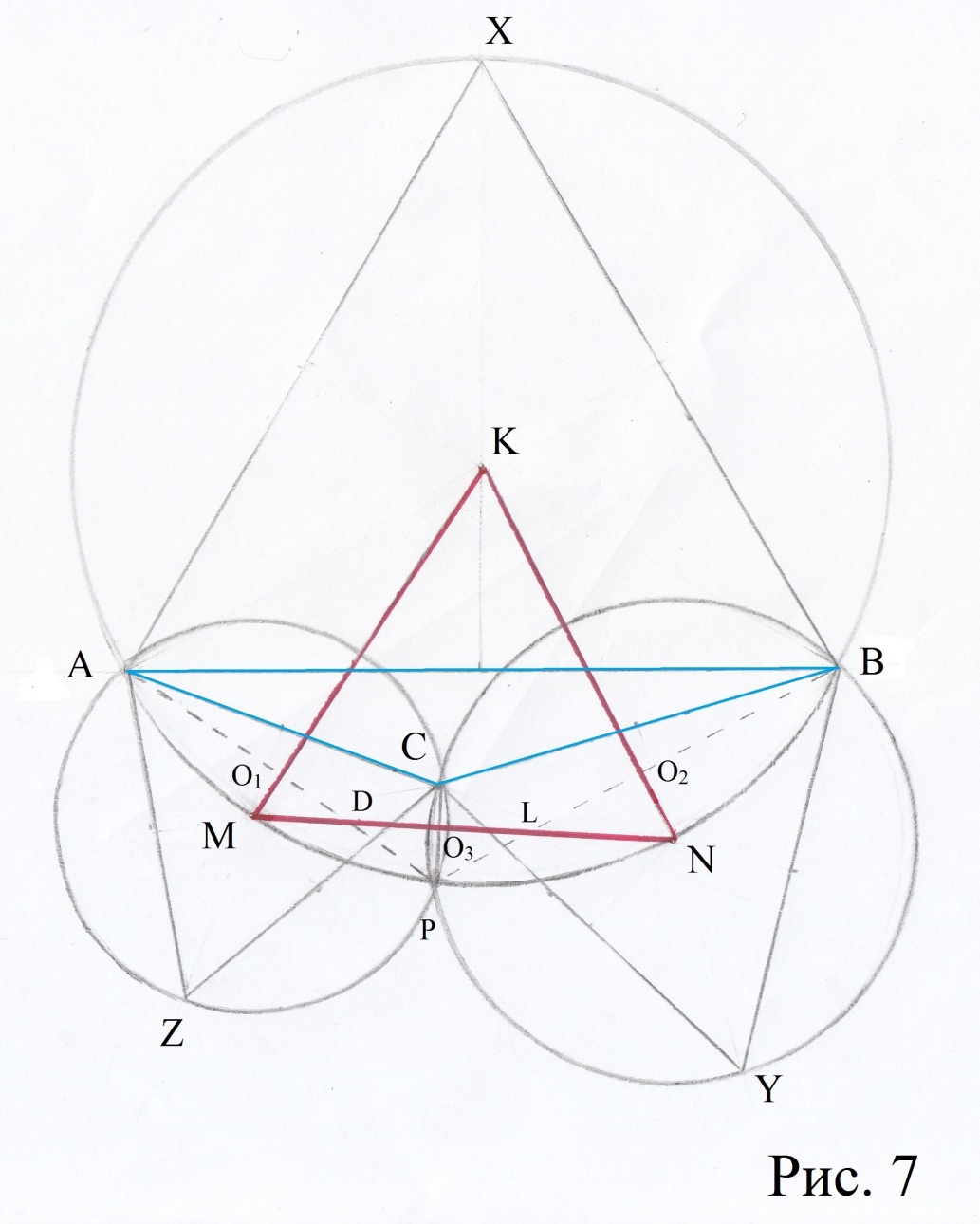
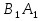 , где
, где 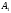 и
и 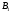 — середины сторон BC и AC треугольника AВC. В этом четырёхугольнике (рис. 8)
— середины сторон BC и AC треугольника AВC. В этом четырёхугольнике (рис. 8)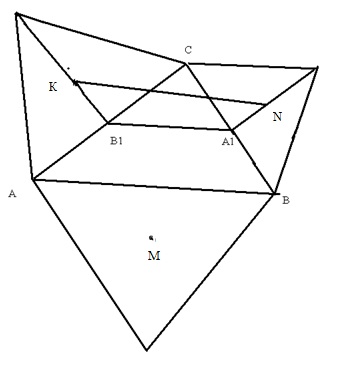 Рис. 8
Рис. 8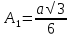 ,
, 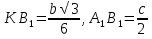 . Величины интересующих нас углов приведены на рисунке 9.
. Величины интересующих нас углов приведены на рисунке 9.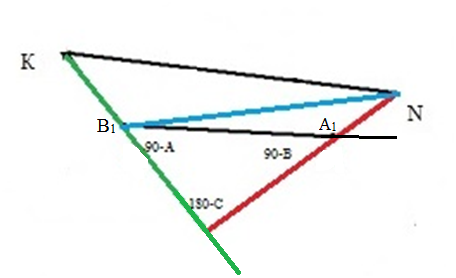
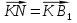 +
+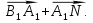
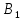 2 +
2 + 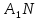 2 + 2 K
2 + 2 K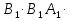
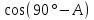 + 2 K
+ 2 K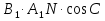 + 2
+ 2 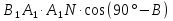 =
= 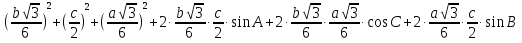 .
.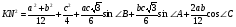 .
. .
. .
.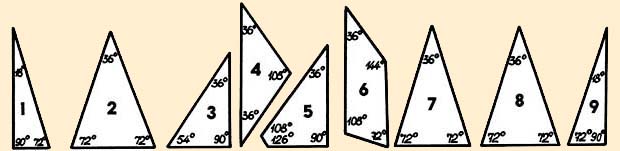
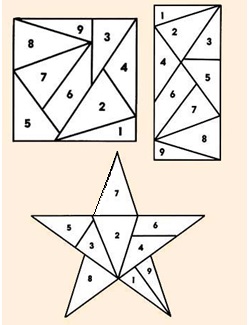 Рис.11
Рис.11