Функция корень n — степени из x, свойства и график
Функция корень n — степени из x, свойства и график
Вопросы занятия:
· рассмотреть свойства функции корень n-ой степени из x;
· рассмотреть график функции корень n-ой степени из x;
· рассмотреть примеры на построение и нахождение свойств функций этого вида.
Материал урока
Прежде чем перейти к изучению нового материала, давайте повторим основные понятия, с которыми мы познакомились на предыдущих уроках.
Корнем n-ой степени из неотрицательного числа a называют такое неотрицательное число, при возведении которого в степень n получается число а.
Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.
Обозначают:
Число а – это подкоренное число, число n – показатель корня.
Обобщая эти понятия, можно сказать, что из любого неотрицательного числа можно извлечь корень любой степени (второй, третьей, четвертой и так далее), а из отрицательного числа можно извлечь только корень нечётной степени.
То есть на [0; +∞) каждому числу x можно поставить в соответствие единственное число корень n-ой степени из x при любом значении n.
Другими словами, на множестве [0; +∞) можно говорить о функции:
Давайте попробуем найти свойства этой функции и построить её график.
Основные свойства:
Областью определения будет являться промежуток [0; +∞).
Поскольку корнем n-ой степени из неотрицательного числа является неотрицательное число, то областью значений функции будет промежуток [0; +∞).
Поскольку область определения функции не является симметричным множеством, то функция не является ни чётной, ни нечётной.
Операцию извлечения корня мы вводили как операцию обратную возведению в соответствующую степень.
Тогда можно сказать, что:
Зная это, нетрудно построить график функции.
Используя построенный график, мы можем записать оставшиеся свойства функции.
Функция возрастает на промежутке [0; +∞).
Функция не ограничена сверху, но ограничена снизу, например, прямой y = -0,5.
Наименьшим значением функции будет 0, наибольшего значения функция не имеет.
Функция непрерывна на всей области определения.
Функция выпукла вверх на всей области определения.
При изучении темы дифференцирование функций, мы говорили, что если функция дифференцируема в каждой точке некоторого промежутка, то она непрерывна на данном промежутке. Из курса базовой школы мы знаем:
Тогда:
Эта производная существует в любой точке промежутка [0; +∞) за исключением точки 0.
Таким образом, функция имеет производную в любой точке промежутка (0; +∞), то есть функция дифференцируема на промежутке (0; +∞).
Рассмотрим несколько примеров.
Пример.
Пример.
Мы с вами говорили о функции y равно корень n-ой степени из x только для неотрицательных значений аргумента.
Но если эн нечётное число, то выражение корень n-ой степени из x имеет смысл и для отрицательных x. Значит, можно говорить о функции:
Теперь давайте запишем свойства этой функции.
Областью определения будет промежуток (– ∞; + ∞)
.Областью значений будет промежуток (– ∞; + ∞).
Поскольку область определения является симметричным множеством, то можно исследовать данную функцию на чётность:
Получаем, что функция при нечётном n будет нечётной.
Давайте построим график функции.
Воспользуемся свойством нечётности функции и добавим к этой ветви ветвь, симметричную ей относительно начала координат.
По графику легко записать оставшиеся свойства функции.
Функция возрастает на всей области определения.
Функция не ограничена ни сверху ни снизу.
Функция не имеет ни наименьшего, ни наибольшего значений.
Функция непрерывна на всей области определения.
Функция выпукла вниз на промежутке (– ∞; 0) и выпукла вверх на промежутке (0; + ∞).
Рассмотрим несколько примеров.
Пример.
Пример.
Пример.
Дети и учеба — Информационный портал
С практической точки зрения наибольший интерес представляет использование производной для нахождения наибольшего и наименьшего значения функции. С чем это связано? Максимизация прибыли, минимизация издержек, определение оптимальной загрузки оборудования. .. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
.. Другими словами, во многих сферах жизни приходится решать задачи оптимизации каких-либо параметров. А это и есть задачи на нахождение наибольшего и наименьшего значения функции.
Следует отметить, что наибольшее и наименьшее значение функции обычно ищется на некотором интервале X , который является или всей областью определения функции или частью области определения. Сам интервал X может быть отрезком , открытым интервалом , бесконечным промежутком .
В этой статье мы будем говорить о нахождении наибольшего и наименьшего значений явно заданной функции одной переменной y=f(x) .
Навигация по странице.
Наибольшее и наименьшее значение функции — определения, иллюстрации.
Кратко остановимся на основных определениях.
Наибольшим значением функции , что для любого справедливо неравенство .
Наименьшим значением функции y=f(x) на промежутке X называют такое значение , что для любого справедливо неравенство .
Эти определения интуитивно понятны: наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение на рассматриваемом интервале при абсциссе .
Стационарные точки – это значения аргумента, при которых производная функции обращается в ноль.
Для чего нам стационарные точки при нахождении наибольшего и наименьшего значений? Ответ на этот вопрос дает теорема Ферма. Из этой теоремы следует, что если дифференцируемая функция имеет экстремум (локальный минимум или локальный максимум) в некоторой точке, то эта точка является стационарной. Таким образом, функция часто принимает свое наибольшее (наименьшее) значение на промежутке X в одной из стационарных точек из этого промежутка.
Также часто наибольшее и наименьшее значение функция может принимать в точках, в которых не существует первая производная этой функции, а сама функция определена.
Сразу ответим на один из самых распространенных вопросов по этой теме:»Всегда ли можно определить наибольшее (наименьшее) значение функции»? Нет, не всегда. Иногда границы промежутка X
совпадают с границами области определения функции или интервал X
бесконечен. А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
А некоторые функции на бесконечности и на границах области определения могут принимать как бесконечно большие так и бесконечно малые значения. В этих случаях ничего нельзя сказать о наибольшем и наименьшем значении функции.
Для наглядности дадим графическую иллюстрацию. Посмотрите на рисунки – и многое прояснится.
На отрезке
На первом рисунке функция принимает наибольшее (max y ) и наименьшее (min y ) значения в стационарных точках, находящихся внутри отрезка [-6;6] .
Рассмотрим случай, изображенный на втором рисунке. Изменим отрезок на . В этом примере наименьшее значение функции достигается в стационарной точке, а наибольшее — в точке с абсциссой, соответствующей правой границе интервала.
На рисунке №3 граничные точки отрезка [-3;2] являются абсциссами точек, соответствующих наибольшему и наименьшему значению функции.
На открытом интервале
На четвертом рисунке функция принимает наибольшее (max y
) и наименьшее (min y
) значения в стационарных точках, находящихся внутри открытого интервала (-6;6)
.
На интервале , о наибольшем значении никаких выводов сделать нельзя.
На бесконечности
В примере, представленном на седьмом рисунке, функция принимает наибольшее значение (max y ) в стационарной точке с абсциссой x=1 , а наименьшее значение (min y ) достигается на правой границе интервала. На минус бесконечности значения функции асимптотически приближаются к y=3 .
На интервале функция не достигает ни наименьшего, ни наибольшего значения. При стремлении к x=2 справа значения функции стремятся к минус бесконечности (прямая x=2 является вертикальной асимптотой), а при стремлении абсциссы к плюс бесконечности, значения функции асимптотически приближаются к y=3 . Графическая иллюстрация этого примера приведена на рисунке №8.
Алгоритм нахождения наибольшего и наименьшего значения непрерывной функции на отрезке .
Запишем алгоритм, позволяющий находить наибольшее и наименьшее значение функции на отрезке.
- Находим область определения функции и проверяем, содержится ли в ней весь отрезок
.

- Находим все точки, в которых не существует первая производная и которые содержатся в отрезке (обычно такие точки встечаются у функций с аргументом под знаком модуля и у степенных функций с дробно-рациональным показателем). Если таких точек нет, то переходим к следующему пункту.
- Определяем все стационарные точки, попадающие в отрезок . Для этого, приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни. Если стационарных точек нет или ни одна из них не попадает в отрезок, то переходим к следующему пункту.
- Вычисляем значения функции в отобранных стационарных точках (если такие имеются), в точках, в которых не существует первая производная (если такие имеются), а также при x=a и x=b .
- Из полученных значений функции выбираем наибольшее и наименьшее — они и будут искомыми наибольшим и наименьшим значениями функции соответственно.
Разберем алгоритм при решении примера на нахождение наибольшего и наименьшего значения функции на отрезке.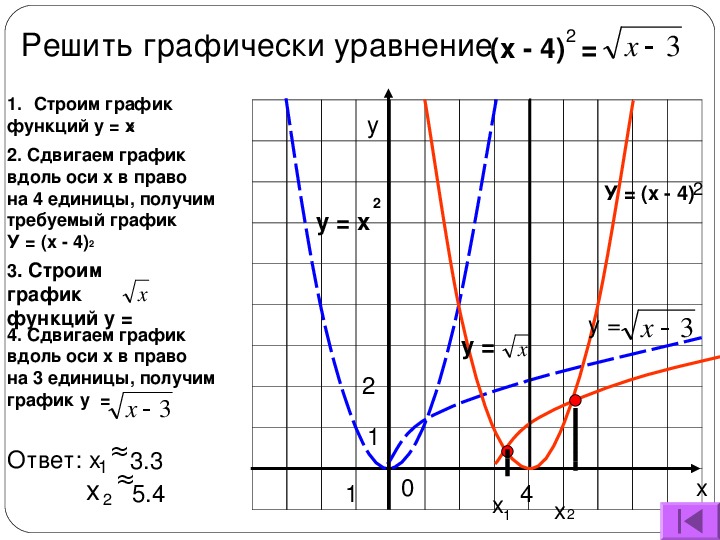
Пример.
Найти наибольшее и наименьшее значение функции
- на отрезке ;
- на отрезке [-4;-1] .
Решение.
Областью определения функции является все множество действительных чисел, за исключением нуля, то есть . Оба отрезка попадают в область определения.
Находим производную функции по :
Очевидно, производная функции существует во всех точках отрезков и [-4;-1] .
Стационарные точки определим из уравнения . Единственным действительным корнем является x=2 . Эта стационарная точка попадает в первый отрезок .
Для первого случая вычисляем значения функции на концах отрезка и в стационарной точке, то есть при x=1
, x=2
и x=4
:
Следовательно, наибольшее значение функции достигается при x=1 , а наименьшее значение – при x=2 .
Для второго случая вычисляем значения функции лишь на концах отрезка [-4;-1]
(так как он не содержит ни одной стационарной точки):
Решение.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Продифференцируем функцию:
Очевидно, производная существует на всей области определения функции.
Найдем стационарные точки. Производная обращается в ноль при . Эта стационарная точка попадает в интервалы (-3;1] и (-3;2) .
А теперь можно сопоставить полученные в каждом пункте результаты с графиком функции. Синими пунктирными линиями обозначены асимптоты.
На этом можно закончить с нахождением наибольшего и наименьшего значения функции. Алгоритмы, разобранные в этой статье, позволяют получить результаты при минимуме действий. Однако бывает полезно сначала определить промежутки возрастания и убывания функции и только после этого делать выводы о наибольшем и наименьшем значении функции на каком-либо интервале. Это дает более ясную картину и строгое обоснование результатов.
На практике довольно часто приходится использовать производную для того, чтобы вычислить самое большое и самое маленькое значение функции. Мы выполняем это действие тогда, когда выясняем, как минимизировать издержки, увеличить прибыль, рассчитать оптимальную нагрузку на производство и др., то есть в тех случаях, когда нужно определить оптимальное значение какого-либо параметра. Чтобы решить такие задачи верно, надо хорошо понимать, что такое наибольшее и наименьшее значение функции.
Обычно мы определяем эти значения в рамках некоторого интервала x , который может в свою очередь соответствовать всей области определения функции или ее части. Это может быть как отрезок [ a ; b ] , так и открытый интервал (a ; b) , (a ; b ] , [ a ; b) , бесконечный интервал (a ; b) , (a ; b ] , [ a ; b) либо бесконечный промежуток — ∞ ; a , (- ∞ ; a ] , [ a ; + ∞) , (- ∞ ; + ∞) .
В этом материале мы расскажем, как вычисляется наибольшее и наименьшее значение явно заданной функции с одной переменной y=f(x) y = f (x) .
Основные определения
Начнем, как всегда, с формулировки основных определений.
Определение 1
Наибольшее значение функции y = f (x) на некотором промежутке x – это значение m a x y = f (x 0) x ∈ X , которое при любом значении x x ∈ X , x ≠ x 0 делает справедливым неравенство f (x) ≤ f (x 0) .
Определение 2
Наименьшее значение функции y = f (x) на некотором промежутке x – это значение m i n x ∈ X y = f (x 0) , которое при любом значении x ∈ X , x ≠ x 0 делает справедливым неравенство f(X f (x) ≥ f (x 0) .
Данные определения являются достаточно очевидными. Еще проще можно сказать так: наибольшее значение функции – это ее самое большое значение на известном интервале при абсциссе x 0 , а наименьшее – это самое маленькое принимаемое значение на том же интервале при x 0 .
Определение 3
Стационарными точками называются такие значения аргумента функции, при которых ее производная обращается в 0 .
Зачем нам нужно знать, что такое стационарные точки? Для ответа на этот вопрос надо вспомнить теорему Ферма. Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Из нее следует, что стационарная точка – это такая точка, в которой находится экстремум дифференцируемой функции (т.е. ее локальный минимум или максимум). Следовательно, функция будет принимать наименьшее или наибольшее значение на некотором промежутке именно в одной из стационарных точек.
Еще функция может принимать наибольшее или наименьшее значение в тех точках, в которых сама функция является определенной, а ее первой производной не существует.
Первый вопрос, который возникает при изучении этой темы: во всех ли случаях мы может определить наибольшее или наименьшее значение функции на заданном отрезке? Нет, мы не можем этого сделать тогда, когда границы заданного промежутка будут совпадать с границами области определения, или если мы имеем дело с бесконечным интервалом. Бывает и так, что функция в заданном отрезке или на бесконечности будет принимать бесконечно малые или бесконечно большие значения. В этих случаях определить наибольшее и/или наименьшее значение не представляется возможным.
Более понятными эти моменты станут после изображения на графиках:
Первый рисунок показывает нам функцию, которая принимает наибольшее и наименьшее значения (m a x y и m i n y) в стационарных точках, расположенных на отрезке [ — 6 ; 6 ] .
Разберем подробно случай, указанный на втором графике. Изменим значение отрезка на [ 1 ; 6 ] и получим, что наибольшее значение функции будет достигаться в точке с абсциссой в правой границе интервала, а наименьшее – в стационарной точке.
На третьем рисунке абсциссы точек представляют собой граничные точки отрезка [ — 3 ; 2 ] . Они соответствуют наибольшему и наименьшему значению заданной функции.
Теперь посмотрим на четвертый рисунок. В нем функция принимает m a x y (наибольшее значение) и m i n y (наименьшее значение) в стационарных точках на открытом интервале (- 6 ; 6) .
Если мы возьмем интервал [ 1 ; 6) , то можно сказать, что наименьшее значение функции на нем будет достигнуто в стационарной точке. Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .
Наибольшее значение нам будет неизвестно. Функция могла бы принять наибольшее значение при x , равном 6 , если бы x = 6 принадлежала интервалу. Именно этот случай нарисован на графике 5 .
На графике 6 наименьшее значение данная функция приобретает в правой границе интервала (- 3 ; 2 ] , а о наибольшем значении мы не можем сделать определенных выводов.
На рисунке 7 мы видим, что функция будет иметь m a x y в стационарной точке, имеющей абсциссу, равную 1 . Наименьшего значения функция достигнет на границе интервала с правой стороны. На минус бесконечности значения функции будут асимптотически приближаться к y = 3 .
Если мы возьмем интервал x ∈ 2 ; + ∞ , то увидим, что заданная функция не будет принимать на нем ни наименьшего, ни наибольшего значения. Если x стремится к 2 , то значения функции будут стремиться к минус бесконечности, поскольку прямая x = 2 – это вертикальная асимптота. Если же абсцисса стремится к плюс бесконечности, то значения функции будут асимптотически приближаться к y = 3 . Именно этот случай изображен на рисунке 8 .
Именно этот случай изображен на рисунке 8 .
В этом пункте мы приведем последовательность действий, которую нужно выполнить для нахождения наибольшего или наименьшего значения функции на некотором отрезке.
- Для начала найдем область определения функции. Проверим, входит ли в нее заданный в условии отрезок.
- Теперь вычислим точки, содержащиеся в данном отрезке, в которых не существует первой производной. Чаще всего их можно встретить у функций, аргумент которых записан под знаком модуля, или у степенных функций, показатель которых является дробно рациональным числом.
- Далее выясним, какие стационарные точки попадут в заданный отрезок. Для этого надо вычислить производную функции, потом приравнять ее к 0 и решить получившееся в итоге уравнение, после чего выбрать подходящие корни. Если у нас не получится ни одной стационарной точки или они не будут попадать в заданный отрезок, то мы переходим к следующему шагу.
- Определим, какие значения будет принимать функция в заданных стационарных точках (если они есть), или в тех точках, в которых не существует первой производной (если они есть), либо же вычисляем значения для x = a и x = b .

- 5. У нас получился ряд значений функции, из которых теперь нужно выбрать самое больше и самое маленькое. Это и будут наибольшее и наименьшее значения функции, которые нам нужно найти.
Посмотрим, как правильно применить этот алгоритм при решении задач.
Пример 1
Условие: задана функция y = x 3 + 4 x 2 . Определите ее наибольшее и наименьшее значение на отрезках [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Решение:
Начнем с нахождения области определения данной функции. В этом случае ей будет множество всех действительных чисел, кроме 0 . Иными словами, D (y) : x ∈ (- ∞ ; 0) ∪ 0 ; + ∞ . Оба отрезка, заданных в условии, будут находиться внутри области определения.
Теперь вычисляем производную функции согласно правилу дифференцирования дроби:
y » = x 3 + 4 x 2 » = x 3 + 4 » · x 2 — x 3 + 4 · x 2 » x 4 = = 3 x 2 · x 2 — (x 3 — 4) · 2 x x 4 = x 3 — 8 x 3
Мы узнали, что производная функции будет существовать во всех точках отрезков [ 1 ; 4 ] и [ — 4 ; — 1 ] .
Теперь нам надо определить стационарные точки функции. Сделаем это с помощью уравнения x 3 — 8 x 3 = 0 . У него есть только один действительный корень, равный 2 . Он будет стационарной точкой функции и попадет в первый отрезок [ 1 ; 4 ] .
Вычислим значения функции на концах первого отрезка и в данной точке, т.е. для x = 1 , x = 2 и x = 4:
y (1) = 1 3 + 4 1 2 = 5 y (2) = 2 3 + 4 2 2 = 3 y (4) = 4 3 + 4 4 2 = 4 1 4
Мы получили, что наибольшее значение функции m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 будет достигнуто при x = 1 , а наименьшее m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 – при x = 2 .
Второй отрезок не включает в себя ни одной стационарной точки, поэтому нам надо вычислить значения функции только на концах заданного отрезка:
y (- 1) = (- 1) 3 + 4 (- 1) 2 = 3
Значит, m a x y x ∈ [ — 4 ; — 1 ] = y (- 1) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y (- 4) = — 3 3 4 .
Ответ: Для отрезка [ 1 ; 4 ] — m a x y x ∈ [ 1 ; 4 ] = y (2) = 3 , m i n y x ∈ [ 1 ; 4 ] = y (2) = 3 , для отрезка [ — 4 ; — 1 ] — m a x y x ∈ [ — 4 ; — 1 ] = y (- 1) = 3 , m i n y x ∈ [ — 4 ; — 1 ] = y (- 4) = — 3 3 4 .
См. на рисунке:
Перед тем как изучить данный способ, советуем вам повторить, как правильно вычислять односторонний предел и предел на бесконечности, а также узнать основные методы их нахождения. Чтобы найти наибольшее и/или наименьшее значение функции на открытом или бесконечном интервале, выполняем последовательно следующие действия.
- Для начала нужно проверить, будет ли заданный интервал являться подмножеством области определения данной функции.
- Определим все точки, которые содержатся в нужном интервале и в которых не существует первой производной. Обычно они бывают у функций, где аргумент заключен в знаке модуля, и у степенных функций с дробно рациональным показателем. Если же эти точки отсутствуют, то можно переходить к следующему шагу.
- Теперь определим, какие стационарные точки попадут в заданный промежуток. Сначала приравняем производную к 0 , решим уравнение и подберем подходящие корни. Если у нас нет ни одной стационарной точки или они не попадают в заданный интервал, то сразу переходим к дальнейшим действиям.
 Их определяет вид интервала.
Их определяет вид интервала.
- Если интервал имеет вид [ a ; b) , то нам надо вычислить значение функции в точке x = a и односторонний предел lim x → b — 0 f (x) .
- Если интервал имеет вид (a ; b ] , то нам надо вычислить значение функции в точке x = b и односторонний предел lim x → a + 0 f (x) .
- Если интервал имеет вид (a ; b) , то нам надо вычислить односторонние пределы lim x → b — 0 f (x) , lim x → a + 0 f (x) .
- Если интервал имеет вид [ a ; + ∞) , то надо вычислить значение в точке x = a и предел на плюс бесконечности lim x → + ∞ f (x) .
- Если интервал выглядит как (- ∞ ; b ] , вычисляем значение в точке x = b и предел на минус бесконечности lim x → — ∞ f (x) .
- Если — ∞ ; b , то считаем односторонний предел lim x → b — 0 f (x) и предел на минус бесконечности lim x → — ∞ f (x)
- Если же — ∞ ; + ∞ , то считаем пределы на минус и плюс бесконечности lim x → + ∞ f (x) , lim x → — ∞ f (x) .
- В конце нужно сделать вывод на основе полученных значений функции и пределов.
 Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Условие: дана функция y = 3 e 1 x 2 + x — 6 — 4 . Вычислите ее наибольшее и наименьшее значение в интервалах — ∞ ; — 4 , — ∞ ; — 3 , (- 3 ; 1 ] , (- 3 ; 2) , [ 1 ; 2) , 2 ; + ∞ , [ 4 ; + ∞) .
Решение
Первым делом находим область определения функции. В знаменателе дроби стоит квадратный трехчлен, который не должен обращаться в 0:
x 2 + x — 6 = 0 D = 1 2 — 4 · 1 · (- 6) = 25 x 1 = — 1 — 5 2 = — 3 x 2 = — 1 + 5 2 = 2 ⇒ D (y) : x ∈ (- ∞ ; — 3) ∪ (- 3 ; 2) ∪ (2 ; + ∞)
Мы получили область определения функции, к которой принадлежат все указанные в условии интервалы.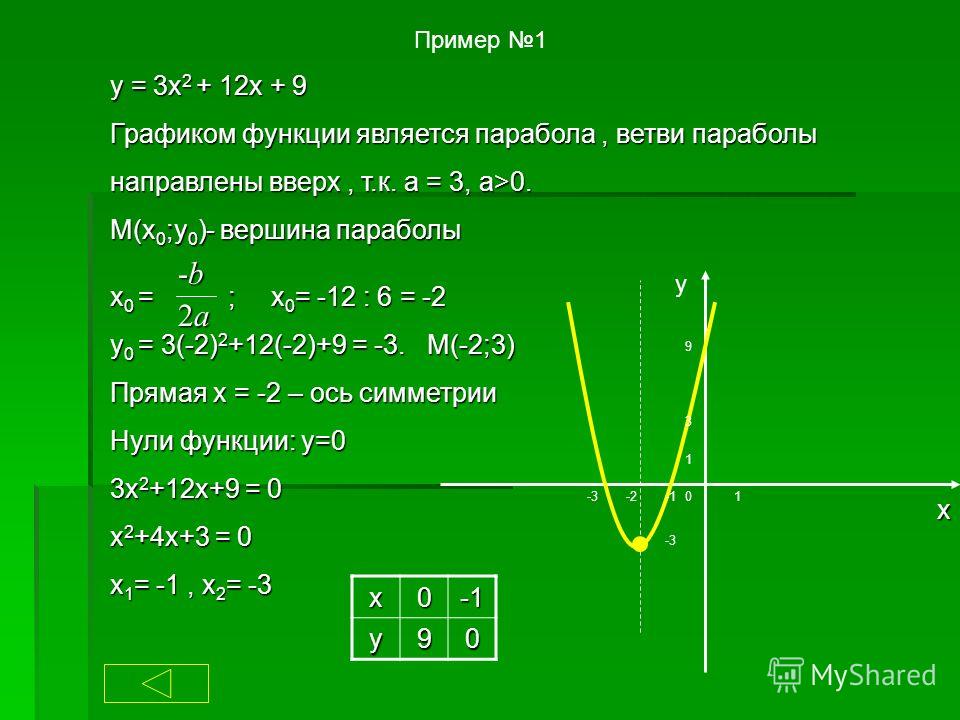
Теперь выполним дифференцирование функции и получим:
y » = 3 e 1 x 2 + x — 6 — 4 » = 3 · e 1 x 2 + x — 6 » = 3 · e 1 x 2 + x — 6 · 1 x 2 + x — 6 » = = 3 · e 1 x 2 + x — 6 · 1 » · x 2 + x — 6 — 1 · x 2 + x — 6 » (x 2 + x — 6) 2 = — 3 · (2 x + 1) · e 1 x 2 + x — 6 x 2 + x — 6 2
Следовательно, производные функции существуют на всей области ее определения.
Перейдем к нахождению стационарных точек. Производная функции обращается в 0 при x = — 1 2 . Это стационарная точка, которая находится в интервалах (- 3 ; 1 ] и (- 3 ; 2) .
Вычислим значение функции при x = — 4 для промежутка (- ∞ ; — 4 ] , а также предел на минус бесконечности:
y (- 4) = 3 e 1 (- 4) 2 + (- 4) — 6 — 4 = 3 e 1 6 — 4 ≈ — 0 . 456 lim x → — ∞ 3 e 1 x 2 + x — 6 = 3 e 0 — 4 = — 1
Поскольку 3 e 1 6 — 4 > — 1 , значит, m a x y x ∈ (- ∞ ; — 4 ] = y (- 4) = 3 e 1 6 — 4 . Это не дает нам возможности однозначно определить наименьшее значение функции. Мы можем только сделать вывод, что внизу есть ограничение — 1 , поскольку именно к этому значению функция приближается асимптотически на минус бесконечности.
Особенностью второго интервала является то, что в нем нет ни одной стационарной точки и ни одной строгой границы. Следовательно, ни наибольшего, ни наименьшего значения функции мы вычислить не сможем. Определив предел на минус бесконечности и при стремлении аргумента к — 3 с левой стороны, мы получим только интервал значений:
lim x → — 3 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 — 0 3 e 1 (x + 3) (x — 3) — 4 = 3 e 1 (- 3 — 0 + 3) (- 3 — 0 — 2) — 4 = = 3 e 1 (+ 0) — 4 = 3 e + ∞ — 4 = + ∞ lim x → — ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Значит, значения функции будут расположены в интервале — 1 ; + ∞
Чтобы найти наибольшее значение функции в третьем промежутке, определим ее значение в стационарной точке x = — 1 2 , если x = 1 . Также нам надо будет знать односторонний предел для того случая, когда аргумент стремится к — 3 с правой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e 4 25 — 4 ≈ — 1 . 444 y (1) = 3 e 1 1 2 + 1 — 6 — 4 ≈ — 1 . 644 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 — 3 + 0 + 3 (- 3 + 0 — 2) — 4 = = 3 e 1 (- 0) — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
У нас получилось, что наибольшее значение функция примет в стационарной точке m a x y x ∈ (3 ; 1 ] = y — 1 2 = 3 e — 4 25 — 4 .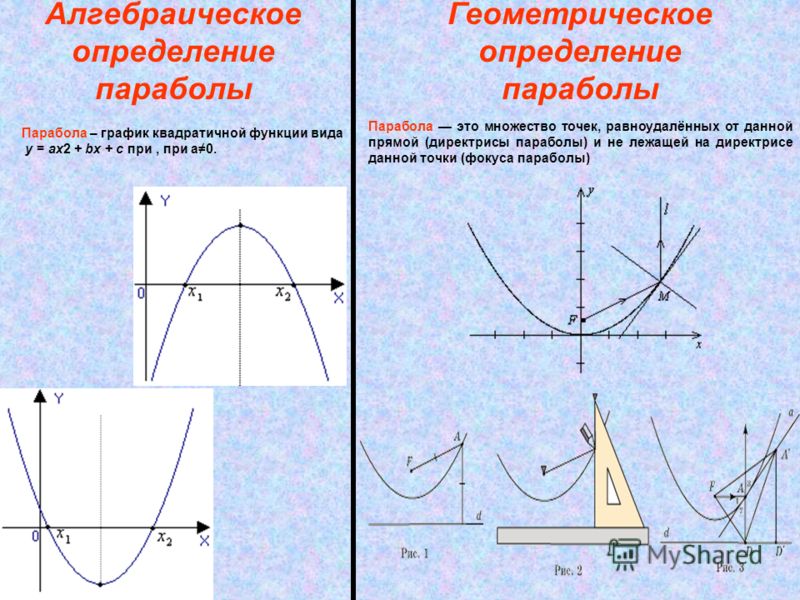 Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .
Что касается наименьшего значения, то его мы не можем определить. Все, что нам известно, – это наличие ограничения снизу до — 4 .
Для интервала (- 3 ; 2) возьмем результаты предыдущего вычисления и еще раз подсчитаем, чему равен односторонний предел при стремлении к 2 с левой стороны:
y — 1 2 = 3 e 1 — 1 2 2 + — 1 2 — 6 — 4 = 3 e — 4 25 — 4 ≈ — 1 . 444 lim x → — 3 + 0 3 e 1 x 2 + x — 6 — 4 = — 4 lim x → 2 — 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 (2 — 0 + 3) (2 — 0 — 2) — 4 = = 3 e 1 — 0 — 4 = 3 e — ∞ — 4 = 3 · 0 — 4 = — 4
Значит, m a x y x ∈ (- 3 ; 2) = y — 1 2 = 3 e — 4 25 — 4 , а наименьшее значение определить невозможно, и значения функции ограничены снизу числом — 4 .
Исходя из того, что у нас получилось в двух предыдущих вычислениях, мы можем утверждать, что на интервале [ 1 ; 2) наибольшее значение функция примет при x = 1 , а найти наименьшее невозможно.
На промежутке (2 ; + ∞) функция не достигнет ни наибольшего, ни наименьшего значения, т. е. она будет принимать значения из промежутка — 1 ; + ∞ .
е. она будет принимать значения из промежутка — 1 ; + ∞ .
lim x → 2 + 0 3 e 1 x 2 + x — 6 — 4 = lim x → — 3 + 0 3 e 1 (x + 3) (x — 2) — 4 = 3 e 1 (2 + 0 + 3) (2 + 0 — 2) — 4 = = 3 e 1 (+ 0) — 4 = 3 e + ∞ — 4 = + ∞ lim x → + ∞ 3 e 1 x 2 + x — 6 — 4 = 3 e 0 — 4 = — 1
Вычислив, чему будет равно значение функции при x = 4 , выясним, что m a x y x ∈ [ 4 ; + ∞) = y (4) = 3 e 1 14 — 4 , и заданная функция на плюс бесконечности будет асимптотически приближаться к прямой y = — 1 .
Сопоставим то, что у нас получилось в каждом вычислении, с графиком заданной функции. На рисунке асимптоты показаны пунктиром.
Это все, что мы хотели рассказать о нахождении наибольшего и наименьшего значения функции. Те последовательности действий, которые мы привели, помогут сделать необходимые вычисления максимально быстро и просто. Но помните, что зачастую бывает полезно сначала выяснить, на каких промежутках функция будет убывать, а на каких возрастать, после чего можно делать дальнейшие выводы. Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Так можно более точно определить наибольшее и наименьшее значение функции и обосновать полученные результаты.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Иногда в задачах B15 попадаются «плохие» функции, для которых сложно найти производную. Раньше такое было лишь на пробниках, но сейчас эти задачи настолько распространены, что уже не могут быть игнорированы при подготовке к настоящему ЕГЭ.
В этом случае работают другие приемы, один из которых — монотонность .
Функция f (x ) называется монотонно возрастающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:
x 1 x 1 ) x 2 ).
Функция f (x ) называется монотонно убывающей на отрезке , если для любых точек x 1 и x 2 этого отрезка выполняется следующее:
x 1 x 1 ) > f (x 2 ).
Другими словами, для возрастающей функции чем больше x
, тем больше f
(x
). Для убывающей функции все наоборот: чем больше x
, тем меньше f
(x
).
Например, логарифм монотонно возрастает, если основание a > 1, и монотонно убывает, если 0 0.
f (x ) = log a x (a > 0; a ≠ 1; x > 0)
Арифметический квадратный (и не только квадратный) корень монотонно возрастает на всей области определения:
Показательная функция ведет себя аналогично логарифму: растет при a > 1 и убывает при 0 0:
f (x ) = a x (a > 0)
Наконец, степени с отрицательным показателем. Можно записывать их как дробь. Имеют точку разрыва, в которой монотонность нарушается.
Все эти функции никогда не встречаются в чистом виде. В них добавляют многочлены, дроби и прочий бред, из-за которого становится тяжело считать производную. Что при этом происходит — сейчас разберем.
Координаты вершины параболы
Чаще всего аргумент функции заменяется на квадратный трехчлен вида y = ax 2 + bx + c . Его график — стандартная парабола, в которой нас интересуют:
- Ветви параболы — могут уходить вверх (при a > 0) или вниз (a
- Вершина параболы — точка экстремума квадратичной функции, в которой эта функция принимает свое наименьшее (для a > 0) или наибольшее (a
Наибольший интерес представляет именно вершина параболы , абсцисса которой рассчитывается по формуле:
Итак, мы нашли точку экстремума квадратичной функции. Но если исходная функция монотонна, для нее точка x
0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Но если исходная функция монотонна, для нее точка x
0 тоже будет точкой экстремума. Таким образом, сформулируем ключевое правило:
Точки экстремума квадратного трехчлена и сложной функции, в которую он входит, совпадают. Поэтому можно искать x 0 для квадратного трехчлена, а на функцию — забить.
Из приведенных рассуждений остается непонятным, какую именно точку мы получаем: максимума или минимума. Однако задачи специально составляются так, что это не имеет значения. Судите сами:
- Отрезок в условии задачи отсутствует. Следовательно, вычислять f (a ) и f (b ) не требуется. Остается рассмотреть лишь точки экстремума;
- Но таких точек всего одна — это вершина параболы x 0 , координаты которой вычисляются буквально устно и без всяких производных.
Таким образом, решение задачи резко упрощается и сводится всего к двум шагам:
- Выписать уравнение параболы y = ax 2 + bx + c и найти ее вершину по формуле: x 0 = −b /2a ;
- Найти значение исходной функции в этой точке: f
(x
0).
 Если никаких дополнительных условий нет, это и будет ответом.
Если никаких дополнительных условий нет, это и будет ответом.
На первый взгляд, этот алгоритм и его обоснование могут показаться сложными. Я намеренно не выкладываю «голую» схему решения, поскольку бездумное применение таких правил чревато ошибками.
Рассмотрим настоящие задачи из пробного ЕГЭ по математике — именно там данный прием встречается чаще всего. Заодно убедимся, что таким образом многие задачи B15 становятся почти устными.
Под корнем стоит квадратичная функция y = x 2 + 6x + 13. График этой функции − парабола ветвями вверх, поскольку коэффициент a = 1 > 0.
Вершина параболы:
x 0 = −b /(2a ) = −6/(2 · 1) = −6/2 = −3
Поскольку ветви параболы направлены вверх, в точке x 0 = −3 функция y = x 2 + 6x + 13 принимает наименьшее значение.
Корень монотонно возрастает, значит x 0 — точка минимума всей функции. Имеем:
Задача. Найдите наименьшее значение функции:
y = log 2 (x 2 + 2x + 9)
Под логарифмом снова квадратичная функция: y
= x
2 + 2x
+ 9. График — парабола ветвями вверх, т.к. a
= 1 > 0.
График — парабола ветвями вверх, т.к. a
= 1 > 0.
Вершина параболы:
x 0 = −b /(2a ) = −2/(2 · 1) = −2/2 = −1
Итак, в точке x 0 = −1 квадратичная функция принимает наименьшее значение. Но функция y = log 2 x — монотонная, поэтому:
y min = y (−1) = log 2 ((−1) 2 + 2 · (−1) + 9) = … = log 2 8 = 3
В показателе стоит квадратичная функция y = 1 − 4x − x 2 . Перепишем ее в нормальном виде: y = −x 2 − 4x + 1.
Очевидно, что график этой функции — парабола, ветви вниз (a = −1
x 0 = −b /(2a ) = −(−4)/(2 · (−1)) = 4/(−2) = −2
Исходная функция — показательная, она монотонна, поэтому наибольшее значение будет в найденной точке x 0 = −2:
Внимательный читатель наверняка заметит, что мы не выписывали область допустимых значений корня и логарифма. Но этого и не требовалось: внутри стоят функции, значения которых всегда положительны.
Следствия из области определения функции
Иногда для решения задачи B15 недостаточно просто найти вершину параболы. Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Искомое значение может лежать на конце отрезка , а вовсе не в точке экстремума. Если в задаче вообще не указан отрезок, смотрим на область допустимых значений исходной функции. А именно:
Обратите внимание еще раз: ноль вполне может быть под корнем, но в логарифме или знаменателе дроби — никогда. Посмотрим, как это работает на конкретных примерах:
Задача. Найдите наибольшее значение функции:
Под корнем снова квадратичная функция: y = 3 − 2x − x 2 . Ее график — парабола, но ветви вниз, поскольку a = −1
Выписываем область допустимых значений (ОДЗ):
3 − 2x − x 2 ≥ 0 ⇒ x 2 + 2x − 3 ≤ 0 ⇒ (x + 3)(x − 1) ≤ 0 ⇒ x ∈ [−3; 1]
Теперь найдем вершину параболы:
x 0 = −b /(2a ) = −(−2)/(2 · (−1)) = 2/(−2) = −1
Точка x 0 = −1 принадлежит отрезку ОДЗ — и это хорошо. Теперь считаем значение функции в точке x 0 , а также на концах ОДЗ:
y (−3) = y (1) = 0
Итак, получили числа 2 и 0. Нас просят найти наибольшее — это число 2.
Нас просят найти наибольшее — это число 2.
Задача. Найдите наименьшее значение функции:
y = log 0,5 (6x − x 2 − 5)
Внутри логарифма стоит квадратичная функция y = 6x − x 2 − 5. Это парабола ветвями вниз, но в логарифме не может быть отрицательных чисел, поэтому выписываем ОДЗ:
6x − x 2 − 5 > 0 ⇒ x 2 − 6x + 5
Обратите внимание: неравенство строгое, поэтому концы не принадлежат ОДЗ. Этим логарифм отличается от корня, где концы отрезка нас вполне устраивают.
Ищем вершину параболы:
x 0 = −b /(2a ) = −6/(2 · (−1)) = −6/(−2) = 3
Вершина параболы подходит по ОДЗ: x 0 = 3 ∈ (1; 5). Но поскольку концы отрезка нас не интересуют, считаем значение функции только в точке x 0:
y min = y (3) = log 0,5 (6 · 3 − 3 2 − 5) = log 0,5 (18 − 9 − 5) = log 0,5 4 = −2
Понятие наибольшего и наименьшего значений функции.
Понятие набольшего и наименьшего значений тесно связано с понятием критической точки функции.
Определение 1
$x_0$ называется критической точкой функции $f(x)$, если:
1) $x_0$ — внутренняя точка области определения;
2) $f»\left(x_0\right)=0$ или не существует.
Введем теперь определения наибольшего и наименьшего значения функции.
Определение 2
Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наибольшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство
Определение 3
Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наименьшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство
Теорема Вейерштрасса о непрерывной на отрезке функции
Введем для начала понятие непрерывной на отрезке функции:
Определение 4
Функция $f\left(x\right)$ называется непрерывной на отрезке $$, если она непрерывна в каждой точке интервала $(a,b)$, а также непрерывна справа в точке $x=a$ и слева в точке $x=b$.
Сформулируем теорему о непрерывной на отрезке функции.
Теорема 1
Теорема Вейерштрасса
Непрерывная на отрезке $$ функция $f\left(x\right)$ достигает на этом отрезке своего наибольшего и наименьшего значения, то есть существуют точки $\alpha ,\beta \in $ такие, что для всех $x\in $ выполняется неравенство $f(\alpha)\le f(x)\le f(\beta)$.
Геометрическая интерпретация теоремы изображена на рисунке 1.
Здесь функция $f(x)$ достигает своего наименьшего значения в точке $x=\alpha $ достигает своего наибольшего значения в точке $x=\beta $.
Схема нахождения наибольшего и наименьшего значений функции $f(x)$ на отрезке $$
1) Найти производную $f»(x)$;
2) Найти точки, в которых производная $f»\left(x\right)=0$;
3) Найти точки, в которых производная $f»(x)$ не существует;
4) Выбрать из полученных в пунктах 2 и 3 точек те, которые принадлежат отрезку $$;
5) Вычислить значение функции в точках, полученных в пункте 4, а также на концах отрезка $$;
6) Выбрать из полученных значений наибольшее и наименьшее значение. 2}=0\] \ \
2}=0\] \ \
3) $f»(x)$ не существует в точке $x=1$
4) $3\notin \left[-2,2\right],\ -1\in \left[-2,2\right],\ 1\in \left[-2,2\right]$, однако 1 не принадлежит области определения;
5) Значения:
\ \ \
6) Наибольшее из найденных значений — $1$, наименьшее из найденных значений — $-8\frac{1}{3}$. Таким образом, получим: \end{enumerate}
Ответ: $max=1,\ min==-8\frac{1}{3}$.
В задании B14 из ЕГЭ по математике требуется найти наименьшее или наибольшее значение функции одной переменной. Это достаточно тривиальная задача из математического анализа, и именно по этой причине научиться решать её в норме может и должен каждый выпускник средней школы. Разберём несколько примеров, которые школьники решали на диагностической работе по математике, прошедшей в Москве 7 декабря 2011 года.
В зависимости от промежутка, на котором требуется найти максимальное или минимальное значение функции, для решения этой задачи используется один из следующих стандартных алгоритмов.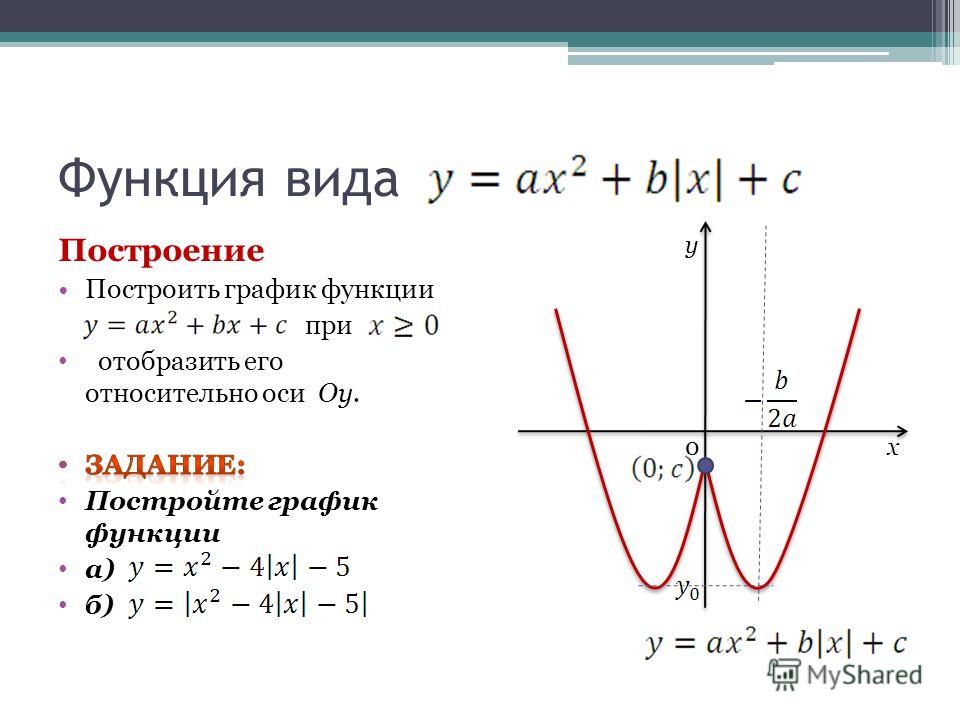
I. Алгоритм нахождения наибольшего или наименьшего значения функции на отрезке:
- Найти производную функции.
- Выбрать из точек, подозрительных на экстремум, те, которые принадлежат данному отрезку и области определения функции.
- Вычислить значения функции (не производной!) в этих точках.
- Среди полученных значений выбрать наибольшее или наименьшее, оно и будет искомым.
Пример 1. Найдите наименьшее значение функции
y = x 3 – 18x 2 + 81x + 23 на отрезке .
Решение: действуем по алгоритму нахождения наименьшего значения функции на отрезке:
- Область определения функции не ограничена: D(y) = R.
- Производная функции равна: y’ = 3x 2 – 36x + 81. Область определения производной функции также не ограничена: D(y’) = R.
- Нули производной: y’ = 3x 2 – 36x + 81 = 0, значит x 2 – 12x + 27 = 0, откуда x = 3 и x = 9, в наш промежуток входит только x = 9 (одна точка, подозрительная на экстремум).

- Находим значение функции в точке, подозрительной на экстремум и на краях промежутка. Для удобства вычислений представим функцию в виде: y = x 3 – 18x 2 + 81x + 23 = x (x -9) 2 +23:
- y (8) = 8 · (8-9) 2 +23 = 31;
- y (9) = 9 · (9-9) 2 +23 = 23;
- y (13) = 13 · (13-9) 2 +23 = 231.
Итак, из полученных значений наименьшим является 23. Ответ: 23.
II. Алгоритм нахождения наибольшего или наименьшего значения функции:
- Найти область определения функции.
- Найти производную функции.
- Определить точки, подозрительные на экстремум (те точки, в которых производная функции обращается в ноль, и точки, в которых не существует двухсторонней конечной производной).
- Отметить эти точки и область определения функции на числовой прямой и определить знаки производной (не функции!) на получившихся промежутках.
- Определить значения функции (не производной!) в точках минимума (те точки, в которых знак производной меняется с минуса на плюс), наименьшее из этих значений будет наименьшим значением функции.
 Если точек минимума нет, то у функции нет наименьшего значения.
Если точек минимума нет, то у функции нет наименьшего значения. - Определить значения функции (не производной!) в точках максимума (те точки, в которых знак производной меняется с плюса на минус), наибольшее из этих значений будет наибольшим значением функции. Если точек максимума нет, то у функции нет наибольшего значения.
Пример 2. Найдите наибольшее значение функции.
Преобразование выражений, содержащих квадратные корни (2)
Тема: Преобразование выражений, содержащих квадратные корни
Лекция.
— Вспомним основные понятия, связанные с квадратным корнем.
Теорема 1. Если , то .
Теорема 2. Если , то .
Теорема 3. При любом значении х верно равенство .
.
Теорема 4. , при .
— Рассмотрим простейшие примеры на применение свойств квадратного корня.
Пример
1. Найти значение выражения .
Найти значение выражения .
Для нахождения значения выражения, воспользуемся теоремой о корне из произведения:
Пример 2. Вычислить значение выражения .
— При вычислении значения выражения необходимо: во-первых, определить, можно ли применить теорему о корне из произведения, то есть можно ли извлечь корень из каждого множителя, если нет, то, во-вторых, следует подкоренное выражение представить в виде произведения множителей, каждый из которых является квадратом целого числа и применить теорему о корне из произведения.
Пример 3. Найти значение выражения
— По теореме о корне из дроби имеем
Пример 4. Найти значение выражения .
Применим тождество .
Получим: =4.
Пример 5. Найти значение выражения
Применим тождество
Получим:
Пример 6. Упростить выражение
Представим
степень в виде и воспользуемся тождеством ,
получим:.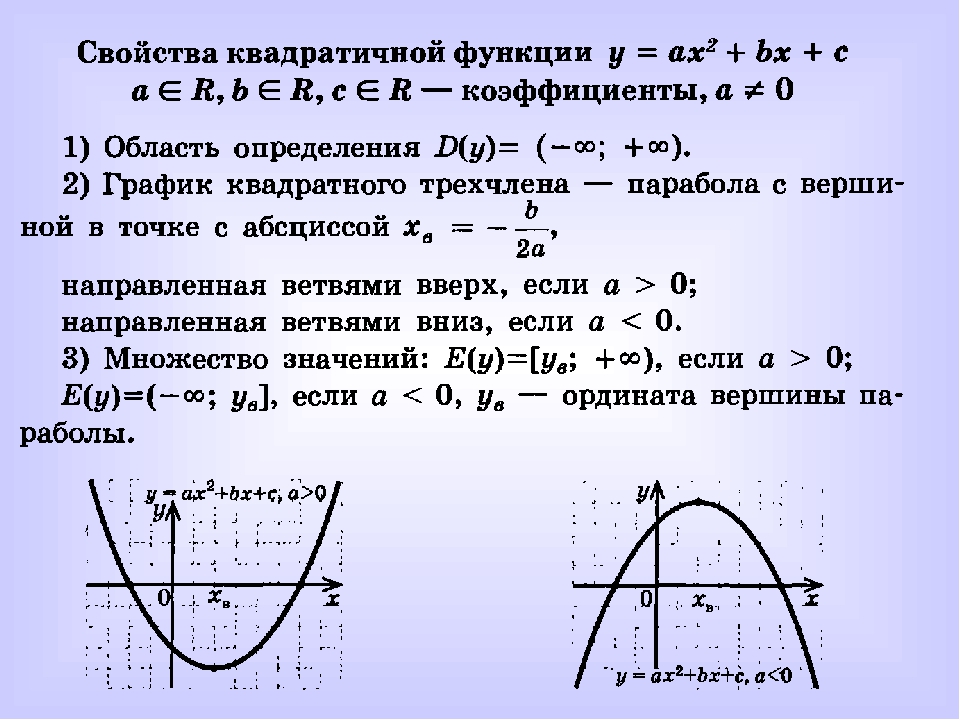
Так как при любом m, то . Итак, .
Также можно воспользоваться равенством .
.
Говоря простым языком, если под корнем степень с четным показателем, то при извлечении квадратного корня из этой степени, получаем степень с показателем в 2 раза меньшим.
Пример 7. Вычислить
Решение.
1 способ: Возведем в квадрат каждое число, из полученного уменьшаемого вычтем вычитаемое.
2 способ: Воспользуемся формулой сокращенного умножения
Пример 8. Вычислить , не используя таблицу квадратов чисел и микрокалькулятор.
Решение.
Разложим подкоренное число на простые множители:
Значит, . Получаем, что
Получаем, что
Вынесение множителя за знак корня
Для того чтобы вынести множитель из под знака корня, необходимо, выражение, стоящее под знаком корня, разложить на множители так, чтобы корень извлекался хотя бы из одного множителя.
Пример 9.
а) ;
b) ;
c)
Внесение множителя под знак корня
Для того чтобы внести множитель под знак квадратичного корня, надо возвести в квадрат этот множитель и внести его под корень.
Пример 10. а) ;
b) ;
c) .
Пример 11. Расположите числа в порядке возрастания :
— Чтобы расположить числа в порядке возрастания, сначала в каждом из чисел внесем множитель под знак корня:
— Расположим
в порядке возрастания полученные числа,
т.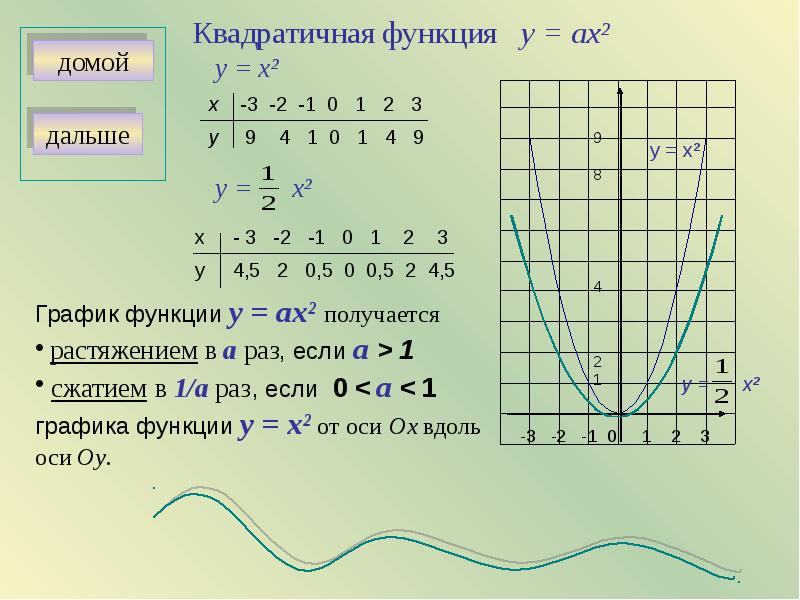 е. больше то число, у которого подкоренное
выражение больше:
е. больше то число, у которого подкоренное
выражение больше:
Следовательно
Пример 12. Упростить выражение .
Решение.
Воспользуемся тождеством .
Раскроем знак модуля, т.е. воспользуемся тем, что . Значит,
. Но тогда .
Пример 13. Упростить выражение .
Приведем к наименьшему общему знаменателю дроби, применим формулы сокращенного умножения:
Пример 14. Упростить выражение .
Решение:
Воспользуемся свойством умножения корней, т.е. подкоренные выражения внесем под один корень, далее воспользуемся формулой разности квадратов:
.
Длина дуги пространственной кривой
Длину дуги получают интегрированием дифференциала дуги от первой точки к конечной. Сложность вычислений заключается в том, что кривая, как правило, заданная двумя или и тремя уравнениями изменения координат по осям, а интегрирование нужно свести к одной координате.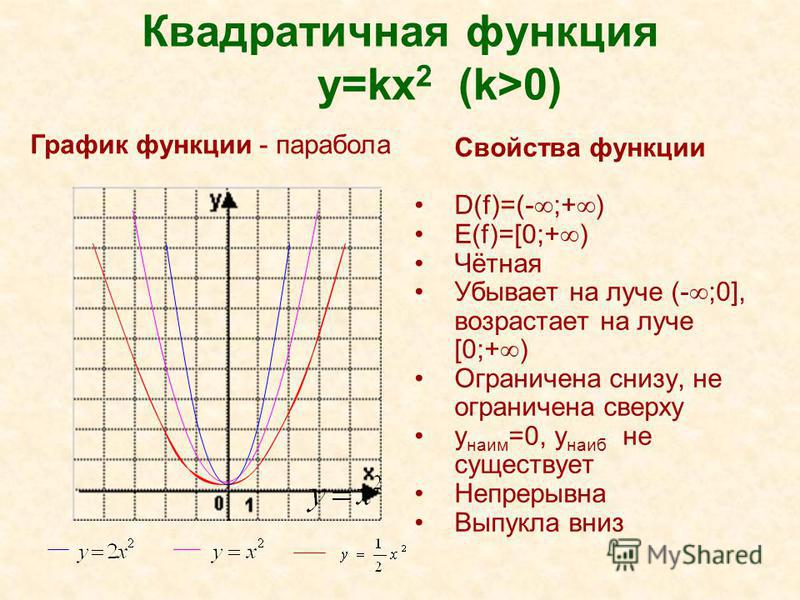 Для этого нужно найти дифференциал дуги.
Для этого нужно найти дифференциал дуги.
Формулы дифференциалу дуги для пространственных и плоских кривых, заданных явно и параметрически хорошо расписаны.
Их здесь повторять не будем, а лишь выделим цветом в формулах.
Когда известен дифференциал дуги, интеграл вычисляют всеми возможными способами:
непосредственное интегрирование, замена переменных, интегрирования частями.
Часть методов дальше применим для решения заданий.
Пример 1 Найти длину дуги пространственной кривой:
x=3t, y=3t2, z=2t3, от точки O(0,0,0) к точке A(3,3,2).
Решение: Найдем производные по переменной t от заданных функций x=x(t), y=y(t) и z=z(t):
x’=3, y’=6t, z’=6t2.
Производные нам нужны для нахождения дифференциала дуги ds заданной кривой:
Эта формула справедлива для всех пространственных кривых, заданных параметрически.
Следующим шагом определим пределы интегрирования.
Чтобы их найти нужно в уравнение пространственной кривой
подставить две точки О, А.
Складываем уравнение на определение пределов изменения параметра t:
При решении установили, что параметр должен принадлежать интервалу 0≤t≤1.
Вычислим длину дуги заданной кривой, при 0≤t≤1:
Интеграл найти не трудно, поскольку под корнем легко выделить квадрат, а дальше уже имеем дело с квадратичной функцией, которую легко интегрировать.
Дальше рассмотрим более сложные задания в которых вычисление производных и дифференциала дуги усложняется.
Пример 2 Найти длину дуги пространственной кривой (a>0) :
(x-y)2=a(x+y), x2-y2=9/8-z2, от точки O(0,0,0) к точке A(x0,y0,z0).
Решение: В подобных примерах целесообразно сделать замену переменных:
Тогда заданное уравнение (x-y)2=a(x+y) приобретет вид:
Отсюда
Подобные превращения выполняем для второго уравнения кривой
x2-y2=9/8-z2, или (x-y)(x+y)=9/8-z2:
отсюда
(1).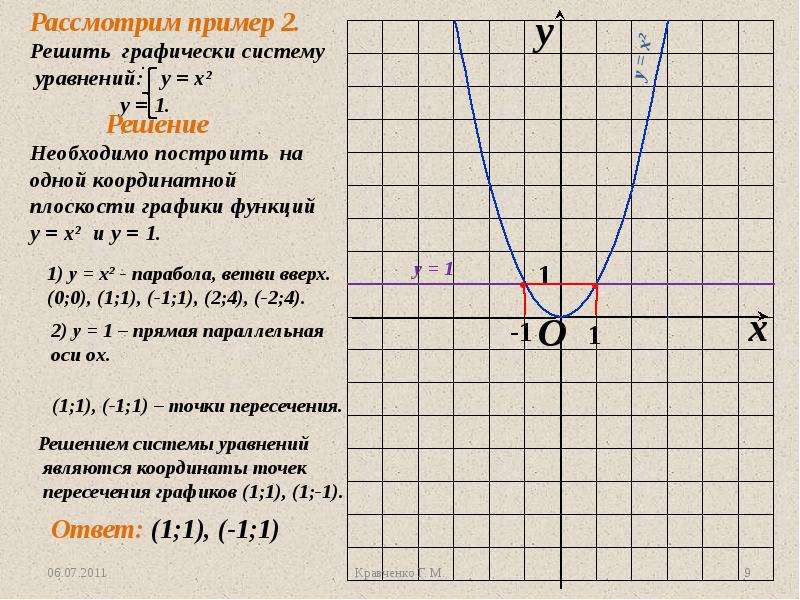
Имеем , получим:
(2).
Найдем производные по переменной z от функций u=u(z) и v=v(z):
после упрощений получим такие конечные значения
Запишем как изменяется z от точки O(0,0,0) к точке A(x0, y0, z0):
0≤z≤z0.
Следующим шагом найдем дифференциал дуги ds по формуле:
Под корнем выделили полный квадрат, поэтому дифференциал упростился.
Через интеграл вычисляем длину дуги кривой:
Найти интеграл в этом случае тоже не складывает больших трудностей.
Пример 3 Найти длину дуги пространственной кривой (a>0) :
от точки O(0,0,0) к точке A(x0, y0, z0).
Решение: Превратим заданные функции так, чтобы они выражались через переменную y:
отсюда получим
Для вычисления обратной функции к двум сторонам зависимости применили синус преобразование.
Дальше найденное значение обратной функции x(y) и подставляем во второе уравнение пространственной кривой
то есть
Окончательно получим
Значение функций в точке A(x0, y0, z0):
Найдем производные по переменной y функций x=x(y), z=z(y):
За свойством логарифма превратим логарифм дроби в разницу логарифмов
Такой прием поможет при вычислении производной составленной функции
Запишем пределы интегрирования y, когда точка проходит значение от O(0,0,0) к A(x0, y0, z0):
0≤y≤y0.
Дифференциал дуги ds кривой вычислим по формуле:
Длину дуги пространственной кривой найдем по формуле:
В интеграле сделали замену переменных и интегрировали частями.
Пример 4 Вычислить длину дуги пространственной кривой (a>0, c>0) :
x2+y2=cz, y/x=tg (z/c), от точки O(0,0,0) к точке A(x0, y0, z0).
Решение: Перейдем к полярной системе координат с помощью формул перехода:
Превращаем первое уравнение кривой
дальше второе
Из формул видим насколько проще стали уравнения кривой.
Запишем все три пространственные координаты через параметр угла φ:
здесь переменная пробегает значение 0≤φ≤z0/c, поскольку φ=z/c.
Запишем производные по переменной φ для функций x=x(φ), y=y(φ) но z=z(φ):
Вычислим дифференциал дуги ds кривой по формуле:
Не забывайте в подобных заданиях выделять полный квадрат под корнем.
Без этого Вы не сможете найти интеграла.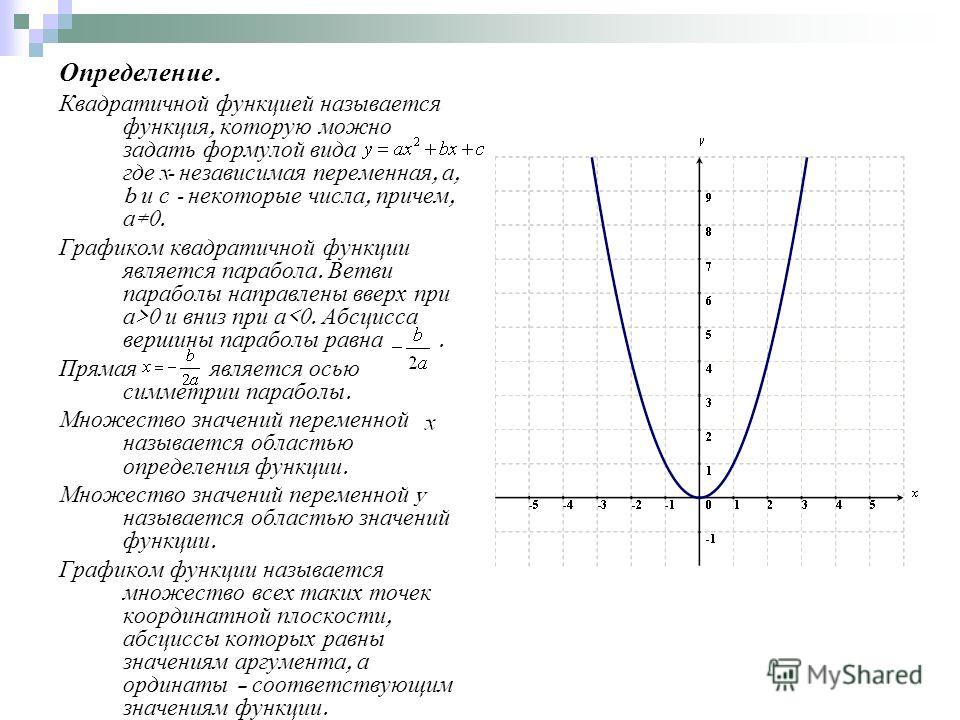
Через интеграл найдем длину дуги пространственной кривой:
Из приведенных примеров можно сделать вывод, что сложность вычисления криволинейных интегралов имеет место лишь в выборе системы координат, нахождении производных и дифференциалов дуг.
Найти интеграл в большинстве случаев достаточно легко, сложные задания, как правило, преподаватели Вам не дадут вычислять.
Определение квадратичной функции в алгебре.
Примеры квадратичной функции в следующих темах:
Что такое квадратичная функция?
- A квадратичная функция имеет общий вид:
- Квадратичное уравнение является частным случаем квадратичной функции с функцией , установленной равной нулю:
- Все квадратичные функции и увеличиваются, и уменьшаются.
- Наклон квадратичной функции , в отличие от наклона линейной функции , постоянно меняется.

- Квадратичная Функции могут быть выражены во многих различных формах.
Части параболы
- График квадратичной функции является параболой, и его части предоставляют ценную информацию о функции .
- График квадратичной функции представляет собой U-образную кривую, называемую параболой.
- В графиках квадратичных функций знак коэффициента $ a $ влияет на то, открывается ли график вверх или вниз.
- Таких точек не может быть больше одной, для графика квадратичной функции .
- Напомним, что если квадратичная функция установлена равной нулю, то результатом будет квадратное уравнение .
Графическая интерпретация квадратичных решений
- Корни квадратичной функции можно найти алгебраически или графически.
 2 — х — 2 руб.
2 — х — 2 руб.
- Корни квадратичной функции можно найти алгебраически или графически.
Дискриминант
- Дискриминант квадратичной функции — это функция ее коэффициентов, которая раскрывает информацию о ее корнях.
- Поскольку сложение и вычитание положительного числа приведет к разным значениям, положительный дискриминант дает два различных решения и два различных корня квадратичной функции .
- Поскольку добавление нуля и вычитание нуля в квадратном уравнении приводят к тому же результату, существует только один отличный корень у квадратичной функции .2 — х — 2.
Финансовые приложения квадратичных функций
- Для задач, связанных с квадратиками в финансах, полезно изобразить уравнение в виде графика.
- Из них легко найти критические значения функции путем осмотра.
- Метод построения графика функции для определения общих свойств может быть использован для решения финансовых проблем.
 2 + k $.2 + bx + c $.
2 + k $.2 + bx + c $. - Этот квадратный не является идеальным квадратом.
- Найдите нули квадратичной функции , заполнив квадрат
Стандартная форма и заполнение квадрата
- В алгебре параболы часто встречаются как графики квадратичных функций , например:
- Завершение квадрата может использоваться для решения любого квадратного уравнения .
- Это может быть применено к любому квадратному уравнению .
- График с квадратным уравнением .
- График этого квадратного уравнения представляет собой параболу с пересечением по оси x в точках -1 и -5.
Другие уравнения в квадратичной форме
- Многие уравнения без членов с нечетной степенью могут быть сокращены до квадратичных и решены теми же методами, что и квадратичные .
- Если подстановка может быть сделана так, что многочлен более высокого порядка принимает форму квадратичного , можно применить любой метод решения квадратного уравнения .

- Например, если уравнение четвертой степени является биквадратичным, то есть не включает членов нечетной степени, существует быстрый способ найти нули функции четвертой степени, преобразовав ее в квадратичную форму .
- Рассмотрим квадратичную функцию без членов с нечетной степенью, которая имеет вид:
- Используйте квадратную формулу , чтобы решить любое уравнение в форме квадратной формы
Решите квадратные уравнения, используя свойство квадратного корня — элементарная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Решите квадратные уравнения формы, используя свойство квадратного корня
- Решите квадратные уравнения вида, используя свойство квадратного корня
Прежде чем начать, пройдите тест на готовность.
- Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок).
- Упростить:.
Если вы пропустили эту проблему, просмотрите (рисунок). Коэффициент - :.
Если вы пропустили эту проблему, просмотрите (рисунок).
Квадратные уравнения — это уравнения вида, где. Они отличаются от линейных уравнений тем, что включают член с переменной во второй степени. Мы используем другие методы для решения квадратных уравнений, чем линейные, потому что простое сложение, вычитание, умножение и деление членов не выделят переменную.
Мы видели, что некоторые квадратные уравнения могут быть решены путем факторизации. В этой главе мы будем использовать три других метода для решения квадратных уравнений.
Решите квадратные уравнения вида
ax 2 = k Используя свойство квадратного корня Мы уже решили некоторые квадратные уравнения факторизацией. Давайте рассмотрим, как мы использовали факторинг для решения квадратного уравнения.
Мы можем легко использовать факторизацию, чтобы найти решения подобных уравнений, таких как и, потому что 16 и 25 являются точными квадратами.Но что происходит, когда у нас есть такое уравнение? Поскольку 7 не является полным квадратом, мы не можем решить уравнение факторизацией.
Все эти уравнения имеют форму.
Мы определили квадратный корень из числа следующим образом:
Это приводит к свойству квадратного корня.
Свойство квадратного корня
Если, и, то.
Обратите внимание, что свойство квадратного корня дает два решения уравнения вида: главный квадратный корень из и его противоположность.Мы также можем записать решение как.
Теперь мы снова решим уравнение, на этот раз используя свойство квадратного корня.
Что происходит, если константа не является точным квадратом? Давайте воспользуемся свойством квадратного корня, чтобы решить уравнение.
Решить:.
Решение
Решить:.
Решить:.
Как решить квадратное уравнение формы, используя свойство квадратного корняРешить:.
Решить:.
Решить:.
Решите квадратное уравнение, используя свойство квадратного корня.
- Выделите квадратичный член и сделайте его коэффициент равным единице.
- Использовать свойство квадратного корня.
- Упростите радикал.
- Проверьте решения.
Чтобы использовать свойство квадратного корня, коэффициент члена переменной должен быть равен 1. В следующем примере мы должны разделить обе части уравнения на 5, прежде чем использовать свойство квадратного корня.
Решить:.
Решить:.
Решить:.
Свойство квадратного корня начинается со слов «Если и». Что будет если? Так будет в следующем примере.
Решить:.
Решение
Решить:.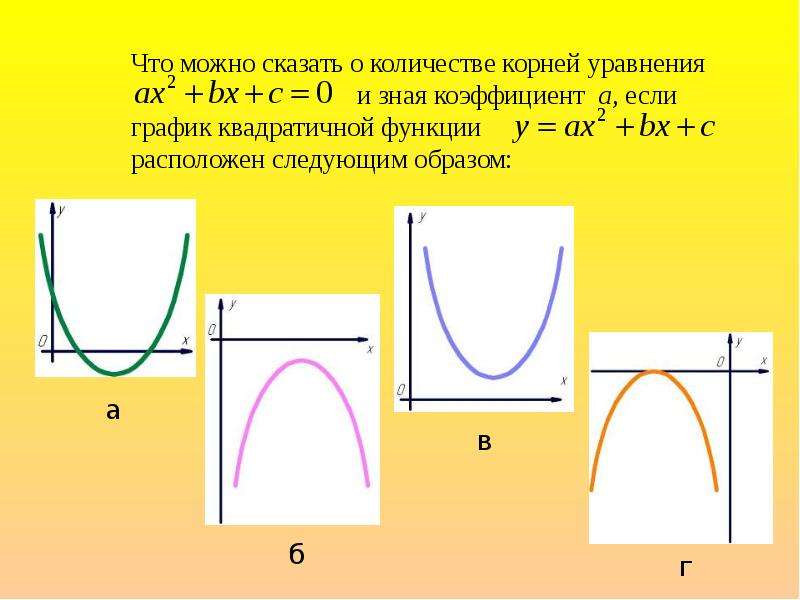
Решить:.
Помните, мы сначала изолируем квадратичный член, а затем делаем коэффициент равным единице.
Решить:.
Решить:.
Решить:.
Решения некоторых уравнений могут содержать дроби внутри радикалов. Когда это происходит, мы должны рационализировать знаменатель.
Решить:.
Решение
Решить:.
Решить:.
Решите квадратные уравнения вида
a ( x — h ) 2 = k Использование свойства квадратного корняМы можем использовать свойство квадратного корня для решения такого же уравнения.Мы будем рассматривать весь двучлен, как квадратичный член.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Решить:.
Помните, когда мы извлекаем квадратный корень из дроби, мы можем извлекать квадратный корень из числителя и знаменателя отдельно.
Решить:
Решение
Решить:
Решить:
Мы начнем решение следующего примера с выделения бинома.
Решить:.
Решение
Решить:.
Решить:.
Решить:.
Решение
Решить:.
Решить:.
Кажется, что левые части уравнений в следующих двух примерах не имеют формы. Но они представляют собой идеальные квадратные трехчлены, поэтому мы будем множить их в нужную нам форму.
Решить:.
Решение
Левая часть уравнения представляет собой трехчлен полного квадрата. Мы учтем это в первую очередь.
Решить:.
Решить:.
Решить:.
Решение
Мы снова замечаем, что левая часть уравнения представляет собой трехчлен в виде полного квадрата. Мы учтем это в первую очередь.
Решить:.
Решить:.
Ключевые понятия
- Свойство квадратного корня
Если, и, то.
Практика ведет к совершенству
Решите квадратные уравнения вида Используя свойство квадратного корня
В следующих упражнениях решите следующие квадратные уравнения.
Решите квадратные уравнения вида , используя свойство квадратного корня
В следующих упражнениях решите следующие квадратные уравнения.
Смешанная практика
В следующих упражнениях решите, используя свойство квадратного корня.
Повседневная математика
У Паолы достаточно мульчи, чтобы покрыть 48 квадратных футов.Она хочет использовать его, чтобы сделать три квадратных огорода равных размеров. Решите уравнение, чтобы найти длину каждой стороны сада.
Кэти составляет чертежи дома, который она проектирует. Она хочет, чтобы в гостиной было четыре квадратных окна одинакового размера, общей площадью 64 квадратных фута. Решите уравнение, чтобы найти длину сторон окон.
Письменные упражнения
Объясните, почему уравнение не имеет решения.
Объясните, почему уравнение имеет два решения.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Если бы большинство ваших чеков было:
… уверенно: Поздравляю! Вы достигли целей в этом разделе. Поразмышляйте над своими учебными навыками, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы убедиться в своей способности делать эти вещи? Быть конкретным.
… с некоторой помощью: Эту проблему нужно решать быстро, потому что темы, которые вы не осваиваете, становятся ухабами на вашем пути к успеху.В математике каждая тема основывается на предыдущей работе. Прежде чем двигаться дальше, важно убедиться, что у вас есть прочный фундамент. К кому обратиться за помощью? Ваши одноклассники и инструктор — хорошие ресурсы. Есть ли в кампусе место, где доступны репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет, я не понимаю! Это предупреждающий знак, игнорировать его нельзя. Вам следует немедленно обратиться за помощью, иначе вы быстро не справитесь. Как можно скорее обратитесь к своему инструктору, чтобы обсудить вашу ситуацию.Вместе вы сможете составить план оказания вам необходимой помощи.
функций
функцийКвадратичные функции
| Функции — квадратичные функции — Содержание |
Квадратичная функция имеет вид y равно a раз x в квадрате, плюс b умножить на x, плюс c. Это известно как квадратное уравнение. В первом члене x переменная берется в степень двух, используя степенную функцию, затем умноженный а затем добавлен ко второму члену, согласно оператору приоритет.Буквы а, б и c используются здесь как числовые константы. Квадратное уравнение имеет два решения для x называемые корнями, которые можно найти, решив уравнение или вставив числовые константы в общую формулу корней квадратного уравнения. Генерал квадратная формула : отрицательное b, плюс или минус квадратный корень величины b в квадрате минус 4, умноженное на a раз c, все разделено в 2 раза a. Решая конкретное уравнение с помощью используя эту формулу, получим два корня.Эти корня уравнения , где переменная y равно нулю. Если есть отрицательный число в квадратном корне при использовании общего квадратного уравнения решение требует комплексных чисел. Картография квадратное уравнение на декартовой плоскости приводит к в определенном типе изогнутых линий. Эти особые изогнутые линии являются геометрическими. конические сечения, называемые параболами. Область определения квадратичной функции — это множество всех действительных чисел и диапазона квадратичных функция зависит от конкретного уравнения.
| Функции — квадратичные функции — Примеры |
Квадратичная форма функции:
г = топор + bx + c
y равно a умножить на x в квадрате, плюс b умножить на x, плюс cРазложение квадратичной функции на ее корни:
Если y = x + 5x + 6
то же уравнение y = (х + 3) х (х + 2),
, то корни уравнения равны -2 и -3,
, поскольку они приводят к тому, что y быть нулевым.Используя квадратное уравнение, чтобы найти корни:
Если y = x + 2x — 3,
корни находятся по формуле -2 плюс или минус квадратный корень из сумма 2 в квадрате минус 4 умножить на -3, все деленное на 2.
Это равно -2 плюс или минус квадратный корень из 16 на два, что равно -2 плюс-минус 4 всего над 2,(-2 + 4) / 2 = 1,
(-2-4) / 2 = -3, а затем корни уравнения равны 1 и -3.
Обратите внимание, что y = (х — 1) х (х + 3)
совпадает с исходным уравнением y = х + 2х — 3.
Интерактивный разговор
Главы книги по математике
Определение квадратичной функции в алгебре.
Примеры квадратичной функции в следующих темах:
Что такое квадратичная функция?
- A квадратичная функция имеет общий вид:
- Квадратичное уравнение является частным случаем квадратичной функции с функцией , установленной равной нулю:
- Все квадратичные функции и увеличиваются, и уменьшаются.
- Наклон квадратичной функции , в отличие от наклона линейной функции , постоянно меняется.
- Квадратичная Функции могут быть выражены во многих различных формах.
Части параболы
- График квадратичной функции является параболой, и его части предоставляют ценную информацию о функции .
- График квадратичной функции представляет собой U-образную кривую, называемую параболой.
- В графиках квадратичных функций знак коэффициента $ a $ влияет на то, открывается ли график вверх или вниз.
- Таких точек не может быть больше одной, для графика квадратичной функции .
- Напомним, что если квадратичная функция установлена равной нулю, то результатом будет квадратное уравнение .
Графическая интерпретация квадратичных решений
- Корни квадратичной функции можно найти алгебраически или графически.2 — х — 2 руб.
Дискриминант
- Дискриминант квадратичной функции — это функция ее коэффициентов, которая раскрывает информацию о ее корнях.
- Поскольку сложение и вычитание положительного числа приведет к разным значениям, положительный дискриминант дает два различных решения и два различных корня квадратичной функции .
- Поскольку добавление нуля и вычитание нуля в квадратном уравнении приводят к тому же результату, существует только один отличный корень у квадратичной функции .2 — х — 2.
Финансовые приложения квадратичных функций
- Для задач, связанных с квадратиками в финансах, полезно изобразить уравнение в виде графика.
- Из них легко найти критические значения функции путем осмотра.
- Метод построения графика функции для определения общих свойств может быть использован для решения финансовых проблем. 2 + k $.2 + bx + c $.
- Этот квадратный не является идеальным квадратом.
- Найдите нули квадратичной функции , заполнив квадрат
Стандартная форма и заполнение квадрата
- В алгебре параболы часто встречаются как графики квадратичных функций , например:
- Завершение квадрата может использоваться для решения любого квадратного уравнения .
- Это может быть применено к любому квадратному уравнению .
- График с квадратным уравнением .
- График этого квадратного уравнения представляет собой параболу с пересечением по оси x в точках -1 и -5.
Другие уравнения в квадратичной форме
- Многие уравнения без членов с нечетной степенью могут быть сокращены до квадратичных и решены теми же методами, что и квадратичные .
- Если подстановка может быть сделана так, что многочлен более высокого порядка принимает форму квадратичного , можно применить любой метод решения квадратного уравнения .
- Например, если уравнение четвертой степени является биквадратичным, то есть не включает членов нечетной степени, существует быстрый способ найти нули функции четвертой степени, преобразовав ее в квадратичную форму .
- Рассмотрим квадратичную функцию без членов с нечетной степенью, которая имеет вид:
- Используйте квадратную формулу , чтобы решить любое уравнение в форме квадратной формы
Квадраты: многочлены второй степени
10
Решение квадратного уравнения с разложением на множители
Двойной корень
Квадратичное неравенство
Сумма и произведение корней
КВАДРАТИКА — ДРУГОЕ НАЗВАНИЕ многочлена 2-й степени.2 — самый высокий показатель степени.
1. Какой вид имеет полиномиальная функция 2-й степени?
y = ax 2 + bx + c
2. Какой вид имеет квадратное уравнение?
ось 2 + bx + c = 0
3. Что мы подразумеваем под корнем квадратичного?
Решение квадратного уравнения.
4. Сколько корней всегда у квадратичной?
Два, действительные или сложные.
5. График квадратичной всегда имеет форму, называемую -?
Парабола.
6. Каковы три метода решения квадратного уравнения,
6. То есть нахождения корней?
1. Факторинг. 2. Завершение квадрата.
3.Квадратичная формула.
Начнем с метода факторинга. В следующей теме мы представим как Завершение квадрата, так и формулу квадратного уравнения.
7. Если произведение множителей равно 0 — если ab = 0 — то что вы можете
7. сделать вывод о факторах a , b ?
Либо a = 0, либо b = 0.
Пример 1. Решение по факторингу.
f ( x ) = x 2 −2 x −3. Найдите корни f ( x ) и нарисуйте график y = f ( x ).
Решение . x 2 −2 x −3 = ( x + 1) ( x — 3).
Следовательно, корни — это −1 и 3. (См. Урок 37 по алгебре.) Это точки пересечения графа x .
Перехват y — постоянный член −3.
В каждом полиноме перехват y является постоянным членом, потому что постоянный член — это значение y , когда x = 0.
Пример 2. Двойной корень
f ( x ) = x 2 −10 x + 25. Найдите корни
f ( x ) и нарисуйте график y = f ( х ).
Решение . x 2 −10 x + 25 =
( x — 5) ( x — 5) = ( x — 5) 2 . Два корня равны, их 5, 5. 5 называется двойным корнем. (См. Урок 37 по алгебре, вопрос 4.)
При двойном корне график не пересекает ось x . Это просто трогает.
Двойной корень возникает, когда квадратичный является трехчленом полного квадрата: x 2 ± 2 ax + a 2 ; то есть, когда квадратичная величина является квадратом бинома: ( x ± a ) 2 .
Пример 3. Сколько действительных корней, т.е. корней, которые являются действительными числами, имеет квадратичный элемент каждого графа?
Ответ . График а) имеет два действительных корня. Он имеет два перехватчика x .
График б) не имеет реальных корней. Он не имеет перехватов x . Оба корня сложные.
График c) имеет два действительных корня. Но они двойной корень.
Пример 4.Квадратичное неравенство.
Решите это неравенство:
x 2 -4 x -5
Для этого осмотрите график
y = x 2 — 4 x — 5.
Решение . Для каких значений x эта квадратичная будет отрицательной? То есть где график под осью x ?
График отрицательный между корнями, которые равны -1 и 5.Решение неравенства равно −1 x. Мы также можем заметить, что квадратичная функция будет иметь положительные значения — график будет выше оси x — слева и справа от корней:
x x> 5.
В то время как квадратичный будет иметь значение 0 в корнях.
Мы рассмотрели три возможности:
Эта квадратичная величина равна 0 в двух корнях.
Это на меньше, чем 0 между двумя корнями.
Это на больше 0 слева и справа от двух корней.
Эти три возможности, которые верны для любого действительного числа, имеют причудливое название Закона трихотомии. Любое число должно быть либо равно, меньше или больше 0.
Закон трихотомии также принимает следующую форму:
Для любых действительных чисел a, b , либо a = b , a b, либо a > b .
Однако мы должны знать, какая из этих возможностей верна. Для любых двух чисел мы должны знать их относительный порядок. Это заложено в значении «числа».
Задача 1. Нарисуйте график y = x 2 — 2 x −8. То есть покажите перехват x и y .
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
x 2 −2 x — 8 = ( x + 2) ( x — 4). Следовательно, корни равны −2, 4. Пересечение y является постоянным членом −8.
Задача 2. Нарисуйте график
.y = x 2 + 4 x + 4.
x 2 + 4 x + 4 = ( x + 2) 2 .В −2 есть двойной корень. Перехват y — постоянный член, 4.
Задача 3.
а) Чтобы решить это квадратное неравенство —
x 2 + 2 x — 3> 0
—проверьте график
y = x 2 + 2 x — 3.
Квадратичное значение будет положительным — выше оси x — для значений x слева и справа от корня.Решение:
x x> 1.
б) Решите это квадратное неравенство:
x 2 + 2 x — 3
−3 х
Квадратичный будет отрицательным между корнями.
Проблема 4. Квадратичная имеет следующие корни. Запишите каждую квадратичную как произведение линейных множителей.
а) 3, 4 ( x — 3) ( x — 4)
б) −3, −4 ( x + 3) ( x + 4)
c) — r , s ( x + r ) ( x — s )
г) 3+, 3 — ( x — 3 -) ( x −3 +)
Сумма и произведение корней
Теорема. В квадратичной системе со старшим коэффициентом 1:
Сумма корней равна отрицательному коэффициенту x ;
произведение корней — постоянный член.
То есть, если
x 2 + bx + c = 0,
и корни r и s , затем
| r + s | = | — б , |
| RS | = | с . |
Ибо, если корни равны r и s , то квадратичный равен
| ( x — r ) ( x — s ) | = | x 2 — rx — sx + rs |
| = | x 2 — ( r + s ) x + rs . | |
Коэффициент x равен — ( r + s ), что является отрицательным значением суммы корней. Постоянный член рупий , который является их произведением.
Пример 5. Построить квадратичную с корнями 2 и 3.
Решение . Сумма корней равна 5, их произведение равно 6, следовательно, квадратичный равен x 2 -5 x + 6.
Сумма корней равна отрицательному коэффициенту x . Произведение корней — постоянный член.
Пример 6. Построить квадратичную с корнями 2 +, 2 -.
Решение . Сумма корней равна 4. Их произведение — разность двух квадратов: 2 2 — () 2 = 4 — 3 = 1.
Следовательно, квадратичный равен x 2 -4 x + 1.
Пример 7. Построить квадратичный, корни которого равны 2 + 3 i , 2 — 3 i , где i — комплексная единица.
Решение . Сумма корней равна 4. Произведение снова является разностью двух квадратов: 4–9 i 2 = 4 + 9 = 13.
Квадратичная с этими корнями равна
x 2 -4 x + 13.
Задача 5. Построить квадратичную с корнями −3, 4.
Сумма корней равна 1. Их произведение равно −12. Следовательно, квадратичный равен x 2 — x — 12.
Задача 6. Построить квадратичную с корнями 3 +, 3 -.
Сумма корней равна 6. Их произведение равно 9 — 3 = 6.
Следовательно, квадратичное равенство x 2 — 6 x + 6.
Задача 7. Построить квадрат, корни которого равны 2 + i , 2 — i .
Сумма корней равна 4. Их произведение равно 4 — ( i ) 2 = 4 + 5 = 9.
Следовательно, квадратичное равен x 2 — 4 x + 9.
*
В более общем смысле, для любого коэффициента x 2 , то есть, если квадратичный равен
топор 2 + bx + c ,
и корни r и s , затем
| r + s | = | – | b a | , |
| RS | = | c a | . | |
Когда a = 1, мы имеем теорему выше.
Следующая тема: Завершение квадрата
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.
Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Эл. Почта: [email protected]
Python Math: Найдите корни квадратичной функции
Python Math: Упражнение 30 с решением
Напишите программу на Python, чтобы найти корни квадратичной функции.2) + b * x + c «) a = float (input («a:»)) b = float (input («b:»)) c = float (input («c:»)) г = Ь ** 2 — 4 * а * с если r> 0: num_roots = 2 x1 = (((-b) + sqrt (r)) / (2 * a)) x2 = (((-b) — sqrt (r)) / (2 * a)) print («Есть 2 корня:% f и% f»% (x1, x2)) elif r == 0: num_roots = 1 х = (-b) / 2 * а print («Есть один корень:», x) еще: num_roots = 0 print («Нет корней, дискриминант
Пример вывода:
Квадратичная функция: (a * x ^ 2) + b * x + c а: 5 а: 20 с: 10 Есть 2 корня: -0.585786 и -3,414214
Схема:
Визуализировать выполнение кода Python:
Следующий инструмент визуализирует, что делает компьютер, шаг за шагом, когда он выполняет указанную программу:
Редактор кода Python:
Есть другой способ решить эту проблему? Разместите свой код (и комментарии) через Disqus.
Предыдущая: Напишите программу на Python для расчета индекса охлаждения ветром.
Далее: Напишите программу на Python для преобразования двоичного числа в десятичное.
Python: советы дня
Перемещает указанное количество элементов в конец списка
Пример:
def tips_offset (lst, смещение): return lst [смещение:] + lst [: смещение] print (tips_offset ([1, 2, 3, 4, 5, 6, 7, 8], 3)) print (tips_offset ([1, 2, 3, 4, 5, 6, 7, 8], -3))
Выход:
[4, 5, 6, 7, 8, 1, 2, 3] [6, 7, 8, 1, 2, 3, 4, 5]
Математических изображений | Полиномиальные функции (2): квадратичные функции
Две точки с разными значениями x определяют линейную функцию (полином степени меньше или равного 1)
Производная линейной функции — постоянная функция.
Три точки, не лежащие на одной прямой, определяют квадратичную функцию, параболу.
Квадратичная функция — это полиномиальная функция степени 2. Они имеют выражение (стандартная форма):
График квадратичной функции — это парабола.
Некоторые параболы разрезают ось абсцисс в двух точках. Мы называем эти точки корнями (или нулями) многочлена.
Эти корни можно получить, решив квадратное уравнение
Решения квадратного уравнения даются:
Дискриминант определяется как:
Если дискриминант больше 0, квадратное уравнение имеет два корня: x 1 , x 2 .Тогда мы можем напишите квадратичную функцию в факторизованной форме:
Некоторые параболы разрезают (или касаются) оси x только в одной точке.
В этом случае дискриминант равен нулю и решение квадратного уравнения:
Тогда мы говорим, что этот корень — двойной корень. В этом случае квадратичная функция в факторизованной форме имеет вид:
Некоторые параболы не пересекают ось абсцисс. В этом случае дискриминант меньше 0 и квадратное уравнение не имеет реальное решение.
Когда a — положительное число, парабола открывается вверх, но если a — отрицательное число, парабола открывается вниз. Здесь мы можем увидеть один пример с двумя настоящими корнями, один только с одним корнем, а другой без настоящих корней:
Каждая парабола имеет максимум или минимум (максимум, если а — отрицательное число, и минимум, если а — положительное число). Эта точка называется вершиной. Вертикальная линия через вершину — это ось симметрии параболы.Уравнение оси:
Вершиной параболы является точка с координатами:
Параболы представляют собой конические сечения:
Квадратичные функции с действительными или комплексными коэффициентами всегда имеют два корня (действительный или комплексный) (основная теорема алгебры):
РЕКОМЕНДАЦИИ
Майкл Спивак, «Исчисление», третье издание, Publish-or-Perish, Inc.
Том М. Апостол, «Исчисление», второе издание, John Willey and Sons, Inc.
Гельфанд И. Глаголева, Е.Е.Шноль, « Функции и графы », Dover Publications, Mineola, N.Y.
БОЛЬШЕ ССЫЛКИ
Степень с натуральными показателями — простые и важные функции. Их обратные функции — это степени с рациональными показателями (радикал или корень n-й степени)
Мы можем рассматривать полиномиальную функцию, проходящую через серию точек плоскости. Это проблема интерполяции, которая здесь решается с помощью интерполяционного полинома Лагранжа.
Производная линейной функции — постоянная функция.
Производная квадратичной функции — это линейная функция, то есть прямая линия.
В качестве введения в кусочно-линейные функции мы изучаем линейные функции, ограниченные открытым интервалом: их графики подобны отрезкам.
Кусочная функция — это функция, которая определяется несколькими подфункциями. Если каждый кусок является постоянной функцией, то кусочная функция называется кусочно-постоянной функцией или ступенчатой функцией.
Непрерывная кусочно-линейная функция определяется несколькими отрезками или лучами, соединенными без скачков между ними.
Производная кубической функции — это квадратичная функция, парабола.
Рациональные функции можно записать как отношение двух многочленов. Линейные рациональные функции — самые простые из таких функций.
Когда знаменатель рациональной функции имеет степень 2, функция может иметь две, одну или ни одной действительные особенности.
Многочлены Лагранжа — это многочлены, проходящие через n заданных точек. Мы используем полиномы Лагранжа, чтобы исследовать общую полиномиальную функцию и ее производную.
Если производная от F (x) равна f (x), то мы говорим, что неопределенный интеграл от f (x) по x равен F (x). Мы также говорим, что F — первообразная или примитивная функция от f.
Интегральное понятие ассоциируется с понятием площади. Мы начали рассматривать область, ограниченную графиком функции и осью абсцисс между двумя вертикальными линиями.
Монотонные функции на отрезке интегрируемы. В этих случаях мы можем ограничить ошибку, которую мы допускаем при приближении интеграла с помощью прямоугольников.
Если мы рассматриваем нижний предел интегрирования a как фиксированный и если мы можем вычислить интеграл для различных значений верхнего предела интегрирования b, то мы можем определить новую функцию: неопределенный интеграл от f.
Подсчитать площадь под прямой несложно. Это первый пример интеграции, который позволяет нам понять идею и ввести несколько основных понятий: интегральное как область, пределы интеграции, положительные и отрицательные области.
Вычислить площадь под параболой сложнее, чем вычислить площадь под линейной функцией. Мы покажем, как аппроксимировать эту область с помощью прямоугольников и что интегральная функция многочлена степени 2 является многочленом степени 3.
Мы можем увидеть некоторые основные понятия об интегрировании, применяемые к общей полиномиальной функции. Интегральные функции от полиномиальных функций — это полиномиальные функции с одной степенью выше, чем исходная функция.
Фундаментальная теорема исчисления говорит нам, что каждая непрерывная функция имеет первообразную, и показывает, как построить ее с помощью интеграла.
Вторая основная теорема исчисления — мощный инструмент для вычисления определенного интеграла (если мы знаем первообразную функции).
Увеличивая степень, полином Тейлора все больше и больше приближает экспоненциальную функцию.
Увеличивая степень, полином Тейлора все больше и больше приближает функцию синуса.
Функция не определена для значений меньше -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Функция имеет особенность в -1. Многочлены Тейлора относительно начала координат приближают функцию от -1 до 1.
Эта функция имеет две действительные особенности в точках -1 и 1.Многочлены Тейлора аппроксимируют функцию в интервале с центром в центре ряда. Его радиус — это расстояние до ближайшей особенности.
Это непрерывная функция, не имеющая реальных особенностей. Однако ряд Тейлора приближает функцию только в интервале. Чтобы понять это поведение, мы должны рассмотреть сложную функцию.
Комплексные степенные функции с натуральным показателем имеют в начале координат нуль (или корень) кратности n.
Многочлен степени 2 имеет два нуля или корня.На этом изображении вы видите овалы Кассини и лемнискату.
Комплексный полином степени 3 имеет три корня или ноль.
Каждый комплексный многочлен степени n имеет n нулей или корней.
.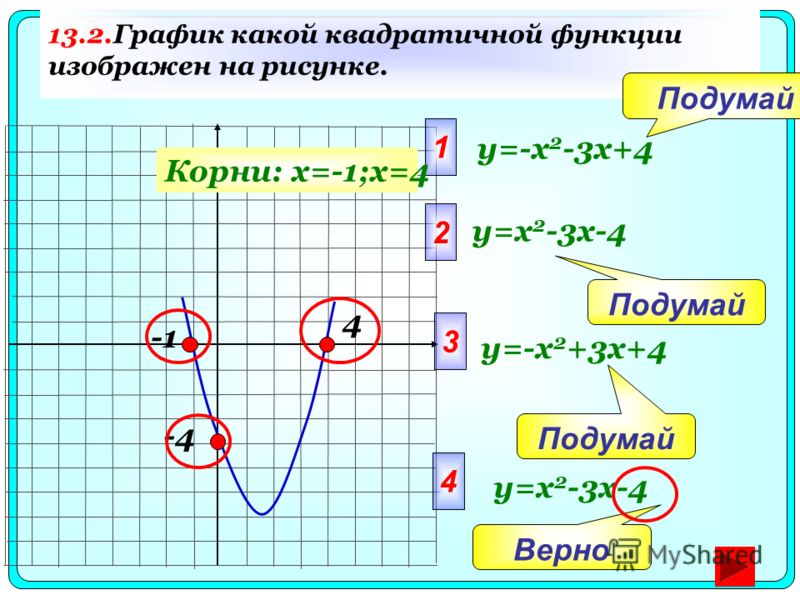

 Их определяет вид интервала.
Их определяет вид интервала.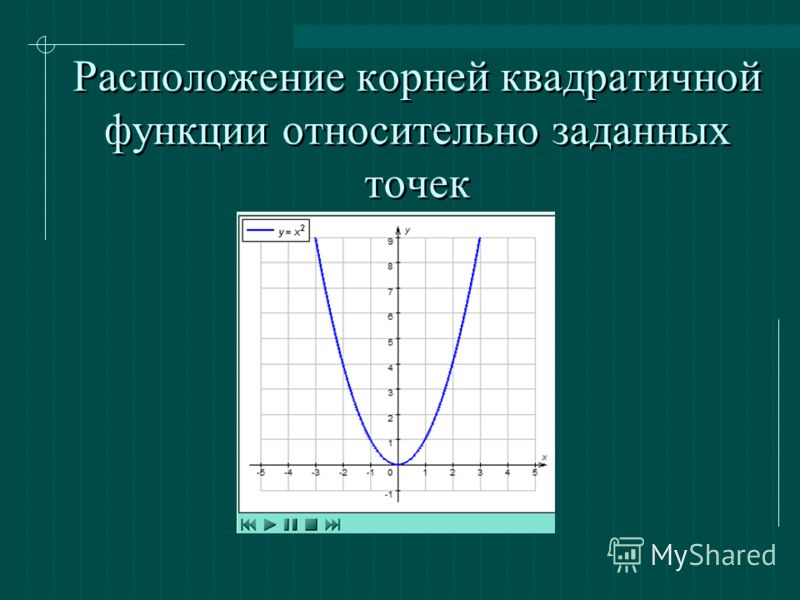 Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.
Здесь возможно множество вариантов. Так, если односторонний предел равен минус бесконечности или плюс бесконечности, то сразу понятно, что о наименьшем и наибольшем значении функции сказать ничего нельзя. Ниже мы разберем один типичный пример. Подробные описания помогут вам понять, что к чему. При необходимости можно вернуться к рисункам 4 — 8 в первой части материала.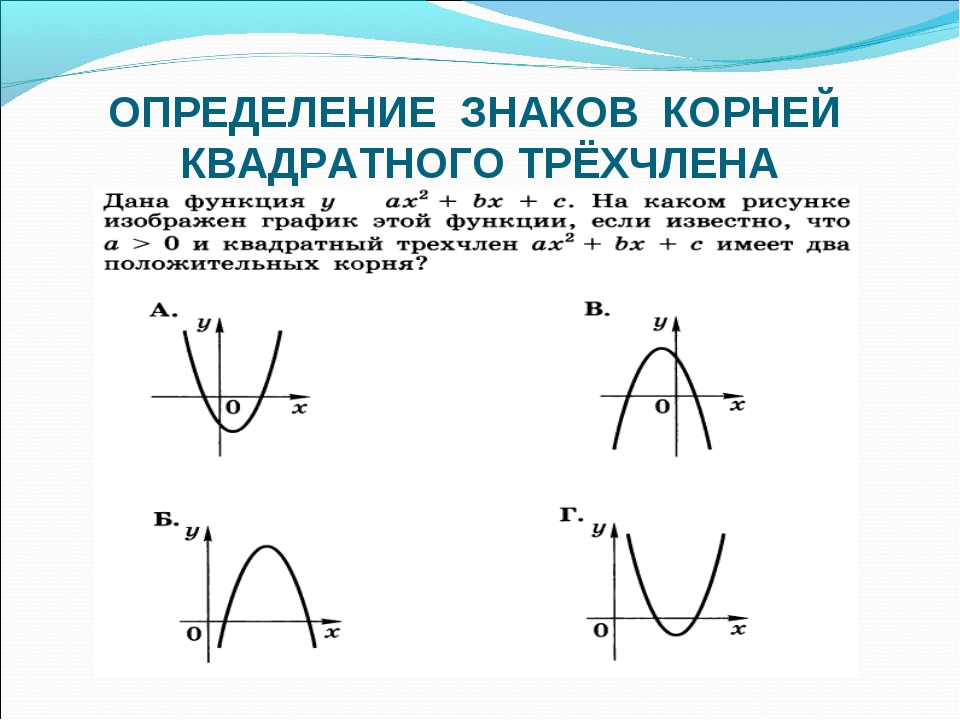 Если никаких дополнительных условий нет, это и будет ответом.
Если никаких дополнительных условий нет, это и будет ответом.
 Если точек минимума нет, то у функции нет наименьшего значения.
Если точек минимума нет, то у функции нет наименьшего значения.
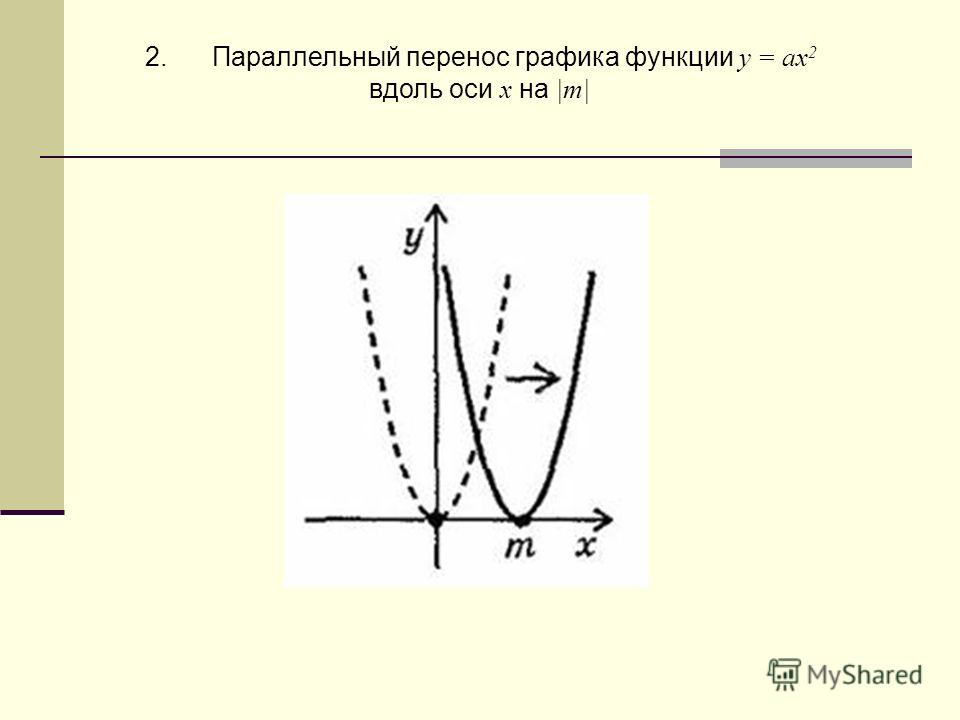 2 — х — 2
2 — х — 2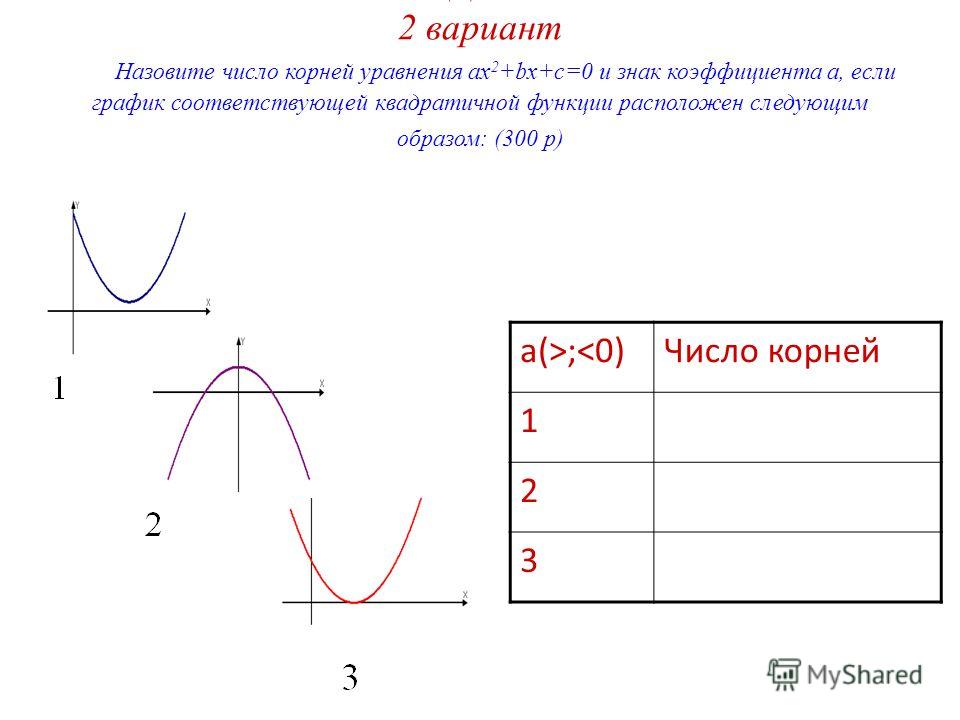 2 + k $.2 + bx + c $.
2 + k $.2 + bx + c $.