2.6 Силы в природе

До сих пор использовалось общее понятие силы, и не рассматривался вопрос о том, какие бывают силы и что они собой представляют. Несмотря на многообразие сил, встречающихся в природе, все их можно свести к четырем видам фундаментальных сил: 1) гравитационные; 2) электромагнитные; 3) ядерные; 4) слабые.

Гравитационные силы возникают между любыми телами. Их действие надо учитывать лишь в мире больших тел.

Электромагнитные силы действуют на заряды как неподвижные, так и движущиеся. Поскольку вещество построено из атомов, которые, в свою очередь состоят из электронов и протонов, то большинство сил, с которыми мы встречаемся в жизни — это электромагнитные силы. Ими являются, например, силы упругости, возникающие при деформации тел, силы трения.

Ядерные и слабые

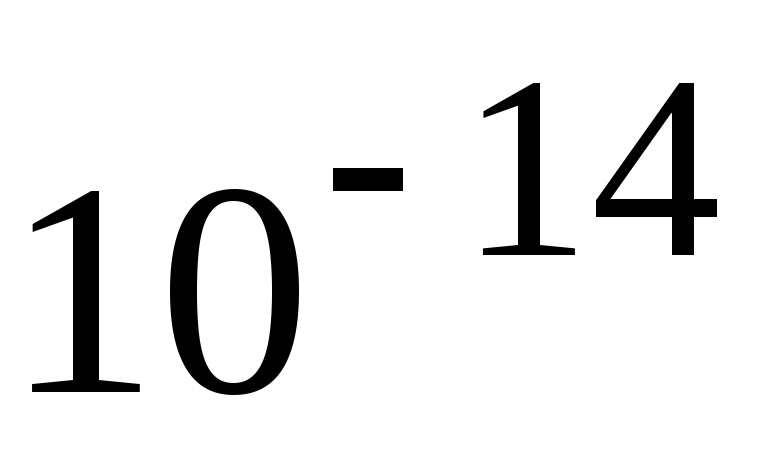силы проявляют себя на расстояниях, не превышающих м, поэтому эти силы заметны лишь в микромире. Вся классическая физика, а вместе с ней и понятие силы, неприменимы к элементарным частицам. Характеризовать точным образом взаимодействие этих частиц с помощью сил нельзя. Единственно возможным здесь становится энергетическое описание. Тем не менее, и в атомной физике часто говорят о силах. В этом случае терминсила становится синонимом слова взаимодействие.

Таким образом, в современной науке слово сила употребляется в двух смыслах: во-первых, в смысле механической силы – точной количественной меры взаимодействия; во-вторых, сила означает наличие взаимодействия определенного типа, точной количественной мерой которого может быть только энергия.

В механике рассматриваются три типа сил: гравитационные, упругие и силы трения. Кратко остановимся на них.

1. Гравитационные силы. Все тела в природе притягиваются друг к другу. Эти силы получили название гравитационных. Ньютон установил закон, названный законом всемирного тяготения: силы, с которыми притягиваются материальные точки, пропорциональны произведению их масс, обратно пропорциональны квадрату расстояния между ними и направлены вдоль прямой, соединяющих их, т.е.

, (2.16)

где М и т – массы тел; r – расстояние между телами;   гравитационная постоянная. Знак «» указывает на то, что это сила притяжения.

Из формулы (2.16) следует, что при т = М = 1 кг и r = 1 м,  = F, т.е. гравитационная постоянная равна модулю силы притяжения материальных точек единичной массы, находящихся на единичном расстоянии друг от друга. Впервые опытное доказательство закона всемирного тяготения проведено Кавендишем. Он сумел определить величину гравитационной постоянной:

. Очень малая величина указывает на то, что сила гравитационного взаимодействия значительна только в случае тел с большими массами.

2. Силы упругости. При упругих деформациях возникают силы упругости. Согласно закону Гука, модуль упругой силы пропорционален величине деформациих, т.е.

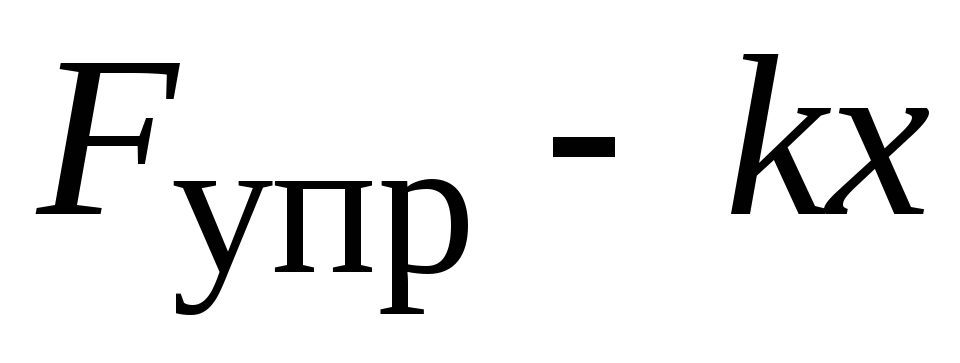, (2.17)

где k  коэффициент упругости. Знак «» определяет тот факт, что направление силы и деформации противоположны.

3. Силы трения. При перемещении соприкасающихся тел или их частей относительно друг друга возникают силы трения. Различают внутреннее (вязкое) и внешнее (сухое) трение.

Вязким трением называют трение между твердым телом и жидкой или газообразной средой, а также между слоями такой среды.

Внешним трением называют явление возникновения в месте контакта соприкасающихся твердых тел сил, препятствующих их взаимному перемещению. Если соприкасающиеся тела неподвижны, то между ними возникает сила при попытке сдвинуть одно тело относительно другого. Она называется силой трения покоя. Сила трения покоя не является однозначно определенной величиной. Она меняется от нуля до максимального значения силы, приложенной параллельно плоскости соприкосновения, при которой тело начинает двигаться (рис. 2.3).

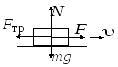
Рис. 2.3

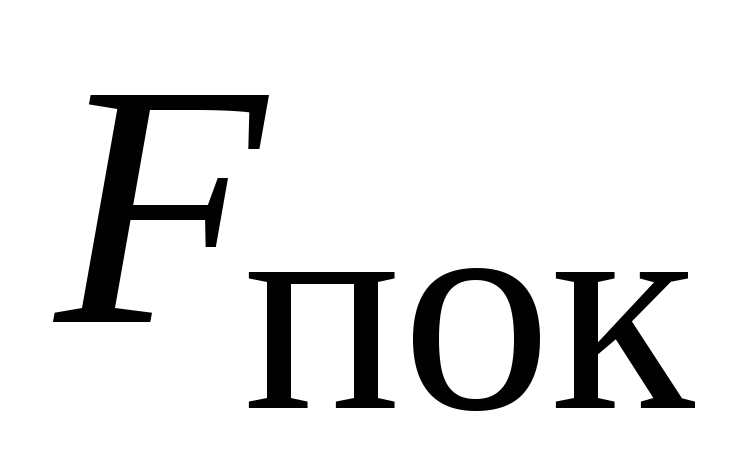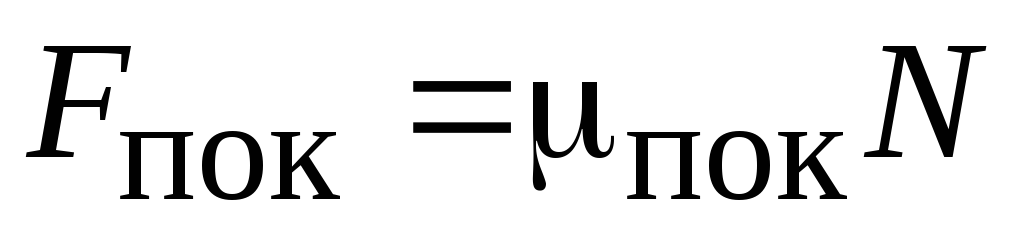Обычно силой трения покоя и называют эту максимальную силу трения. Модуль силы трения покоя пропорционален модулю силы нормального давления, который по третьему закону Ньютона равен модулю силы реакции опорыN, т.е. , где коэффициент трения покоя.

При движении тела по поверхности другого тела возникает сила трения скольжения. Установлено, что модуль силы трения скольжения так же пропорционален модулю силы нормального давленияN

, (2.19)

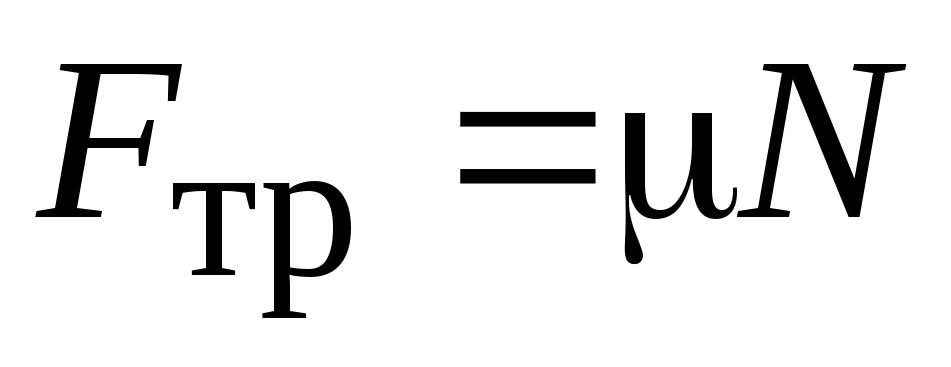
где   коэффициент трения скольжения. Установлено, что 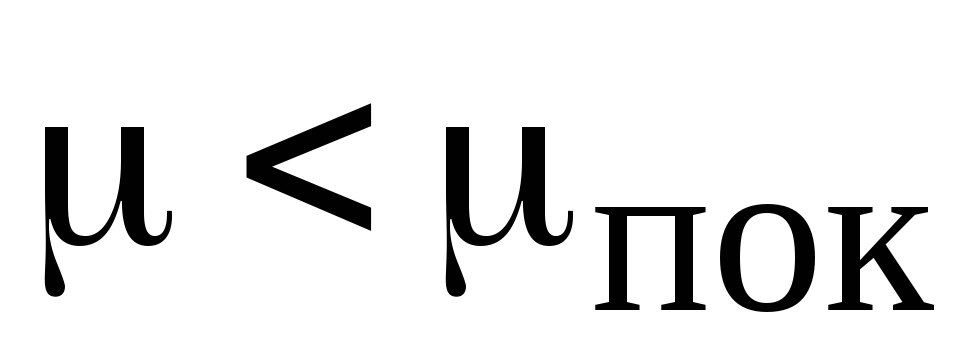, однако при решении многих задач их считают равными.

При решении задач учитывают следующие виды сил:

1. Сила тяжести 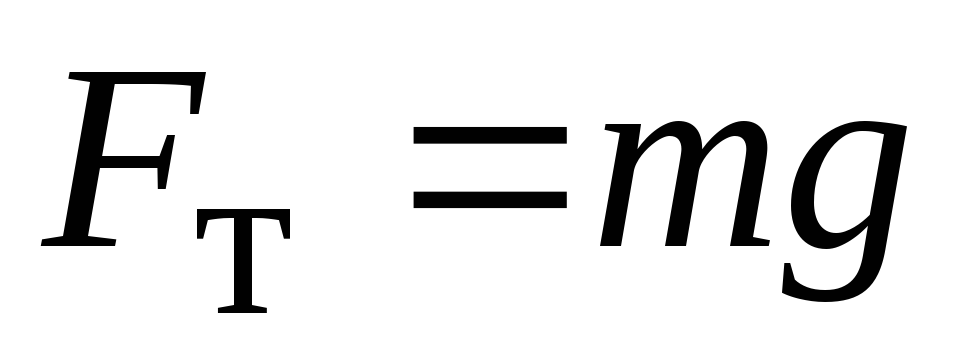 сила, с которой гравитационное поле Земли действует на тело (приложена эта сила к центру масс тела).

.

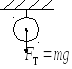
2. Вес тела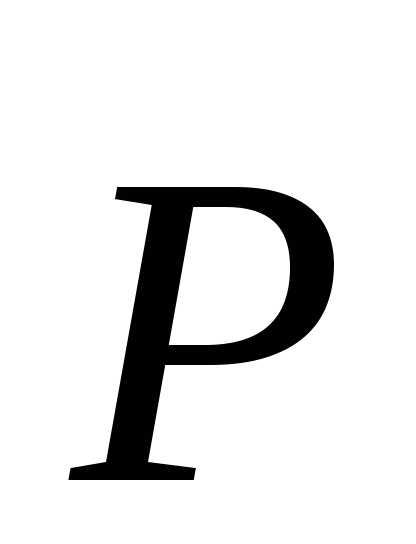

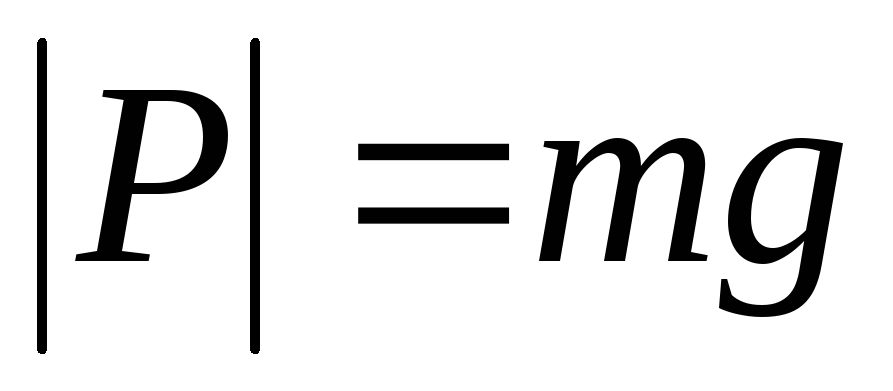 сила, с которой тело действует на горизонтальную опору или нить, удерживающую его от свободного падения (сила упругости по своей природе). Приложена сила к опоре (нити). В инерциальной системе отсчета .

3. Сила реакции опоры  сила, с которой поверхность опоры действует на тело (сила упругости по своей природе). Сила приложена к телу со стороны опоры и перпендикулярна поверхности соприкосновения.

4. Сила натяжения нити

 сила, с которой нить действует на тело, подвешенное к нити. Сила приложена к телу и направлена вверх по нити.

5. Сила трения .

Природа сил

Все известные взаимодействия и соответственно силы в природе сводятся к следующим четырем типам: гравитационное, электромагнитное, сильное, слабое.

Гравитационное взаимодействие свойственное всем телам во Вселенной, проявляется в виде взаимного притяжения всех тел в природе, независимо от среды в которой они находятся, в микромире элементарных частиц при обычных энергиях роли не играет. Ярким примером является притяжение Землей. Это взаимодействие подчиняется

закону всемирного тяготения: сила взаимодействия между двумя материальными точками массами m₁ и m₂ прямо пропорциональная произведению этих масс и обратно пропорциональная квадрату расстояния между ними. Математически этот закон имеет вид:

(3.7)

где G = 6,67 10^-11 Н м²/кг² — гравитационная постоянная, которая определяет силу притяжения между двумя одинаковыми телами с массами m₁ = m₂ = 1 кг на расстоянии r = 1 м.

Электромагнитное взаимодействие – взаимодействие между неподвижными и подвижными электрическими зарядами. Этим взаимодействием в частности обусловлены силы межмолекулярного и межатомного взаимодействия.

Взаимодействие между двумя точечными неподвижными зарядами

q₁ и q₂ подчиняется закону Кулона:

,

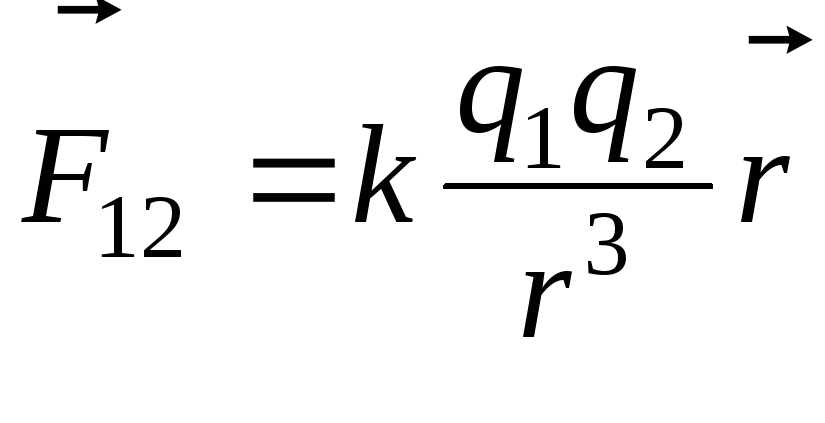где k = 9 10⁹ Н м²/Кл² – коэффициент пропорциональности.

Если заряд движется в магнитном поле, то на него действует сила Лоренца:

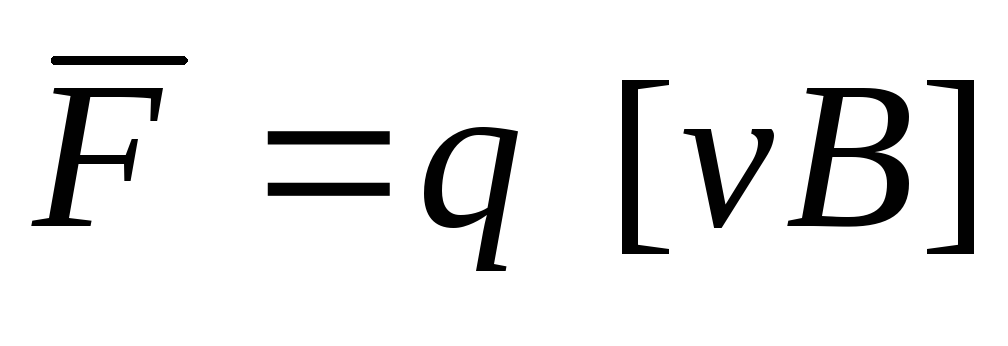
v – скорость заряда, В – вектор магнитной индукции.

Cильное взаимодействие обеспечивает связь нуклонов в ядре атома. Слабое отвечает за большинство распадов элементарных частиц, а также за процессы взаимодействия нейтрино с веществом.

В классической механике мы имеем дело с гравитационными и электромагнитными силами, которые приводят к появлению сил притяжения, сил упругости, сил трения и других.

Сила тяжести характеризует взаимодействие тела с Землей.

Вблизи Земли все тела падают приблизительно с одинаковым ускорением g    9,8  м/с², которое называется ускорением свободного падения. Отсюда следует, что вблизи Земли на каждое тело действует сила тяжести, которая направлена к центру Земли и равна произведению массы тела на ускорение свободного падения.

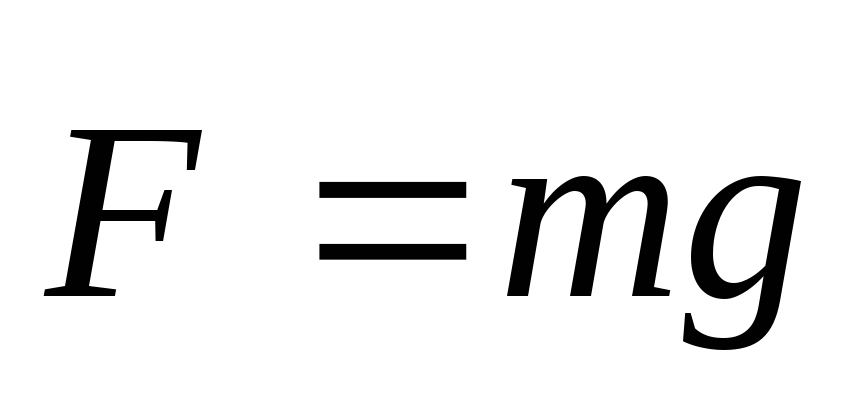
вблизи поверхности Земле поле однородно (g=const). Сравнивая 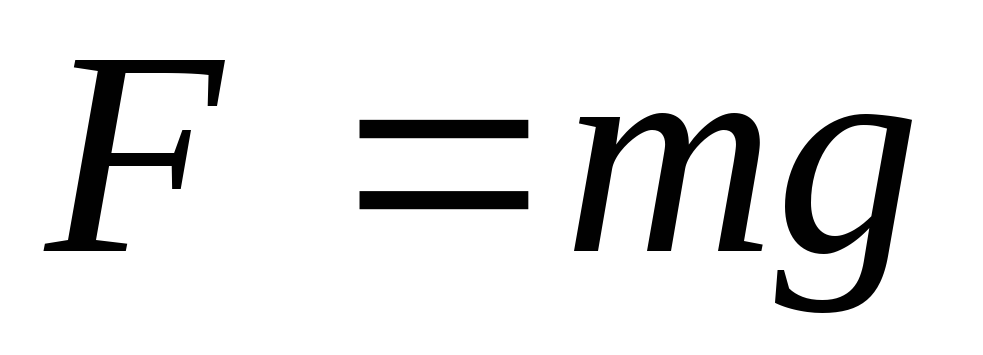с, получим, что.

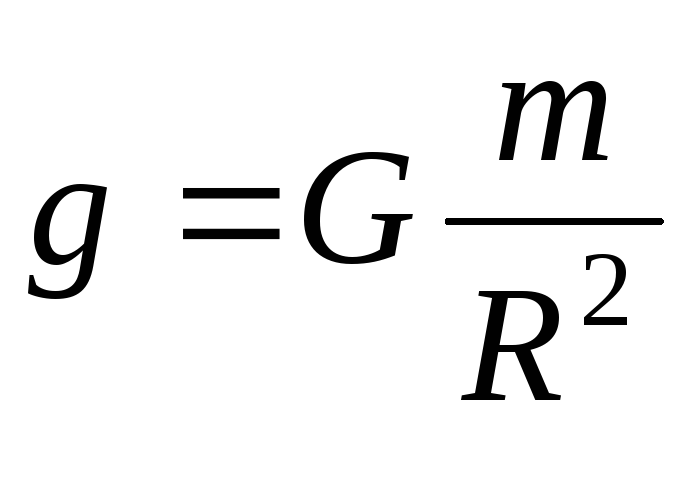Сила реакции опоры – сила , с которой опора действует на тело. Она приложена к телу и перпендикулярна поверхности соприкосновения. Если тело лежит на горизонтальной поверхности, то сила реакции опоры численно равна силе тяжести. Рассмотрим 2 случая.

1. Рассмотрим рис.

Пусть тело покоится, тогда на него действует две силы. Согласно 2 закону Ньютона

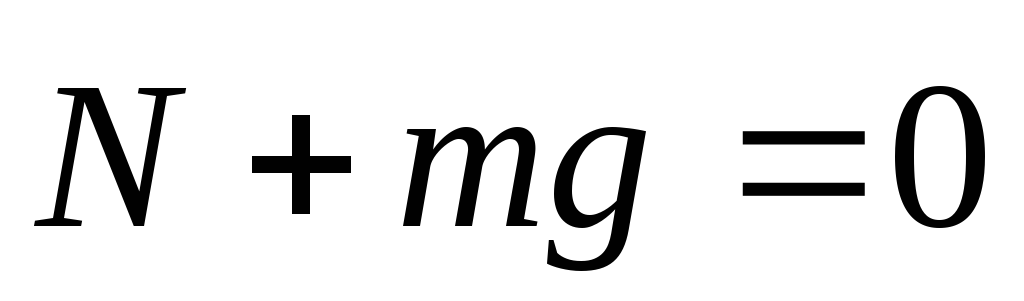
Найдем проекции этих сил на ось у и получим, что

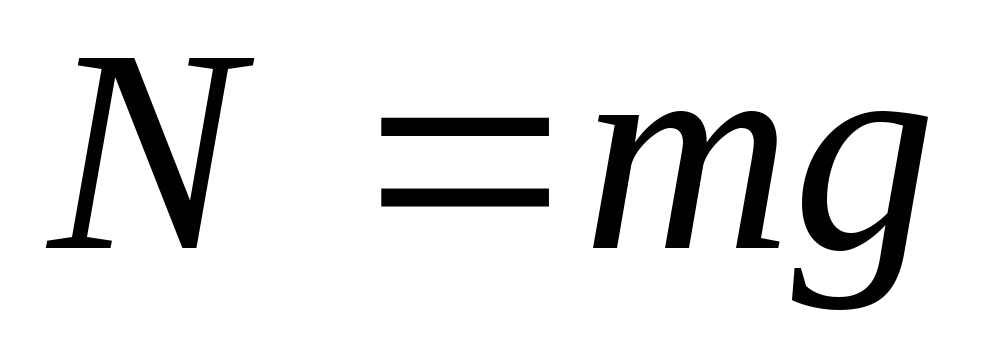
2. Пусть теперь тело находится на наклонной плоскости, составляющей угол с горизонтом (см. рис.).

Рассмотрим случай, когда тело будет покоиться, тогда на тело будут действовать две силы, уравнение движения выглядит аналогично первому случаю. Записав 2 закон Ньютона в проекции на ось у, получим, что сила реакции опоры численно равна проекции силы тяжести на перпендикуляр к этой поверхности

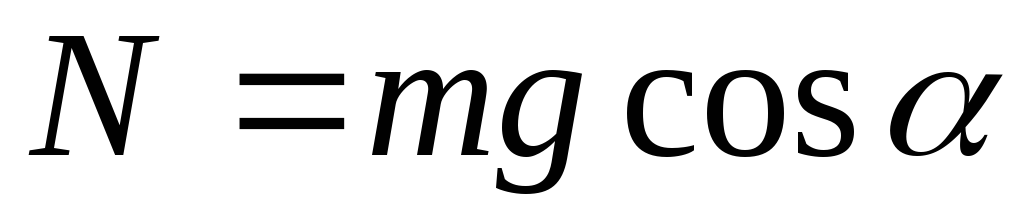
Вес тела – сила, с которой действует тело на опору или подвес. Вес тела равен по модулю силе реакции опоры и направлен противоположно

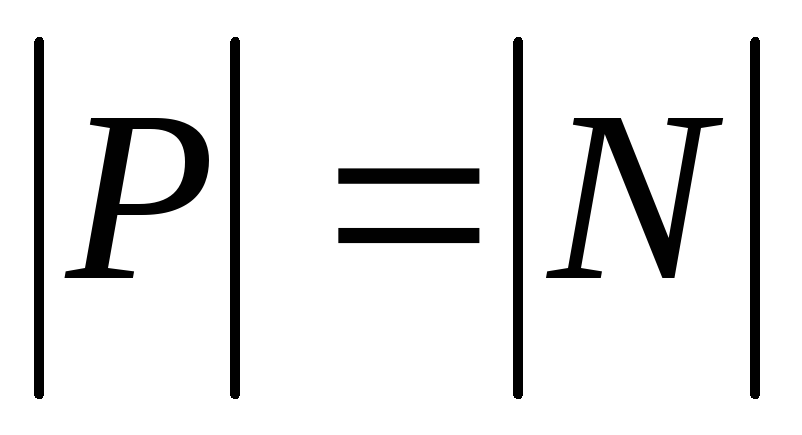
Часто путают силу тяжести и вес. Это обусловлено тем, что в случае неподвижной опоры эти силы совпадают по величине и по направлению Однако надо помнить, что эти силы приложены к разным телам: сила тяжести приложена к самому телу, вес приложен к подвесу или опоре. Кроме того, сила тяжести всегда равна mg, независимо от того покоится тело или движется, сила веса зависит от ускорения, с которым движутся опора и тело, причем она может быть как больше, так и меньше mg, в частности, в состоянии невесомости она обращается в нуль.

Сила упругости. Под действием внешних сил может происходить изменение формы тела – деформация. Если после прекращения действия силы форма тела возобновляется, деформация называется упругой. Для упругой деформации справедлив закон Гука:

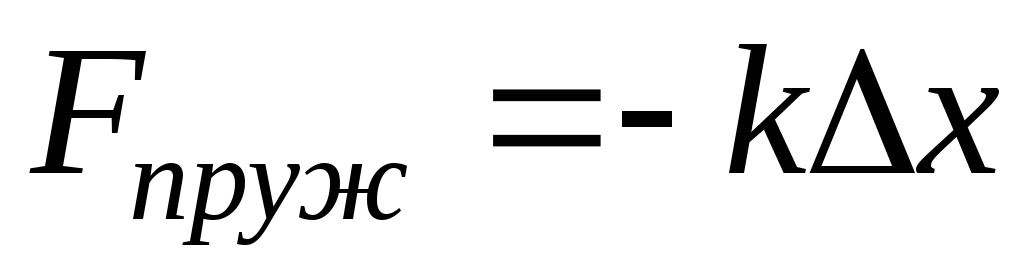
x — удлинение тела вдоль оси х, k  — коэффициент пропорциональности, который называют коэффициентом упругости.

При непосредственном соприкосновении тел помимо сил упругости могут возникать силы и другого типа, так называемые силы трения.

Силы трения.

Силы трения бывают двух видов:

1. Сила трения покоя.

2. Сила трения, обусловленная движением тел.

Сила трения покоя – сила, с которой действует поверхность на покоящееся на ней тело в направлении, противоположном приложенной к телу силе (см. рис) и равная ей по модулю

Силы трения 2 типа появляются при перемещении соприкасающихся тел или частей друг относительно друга. Трение, возникающее при относительном перемещении двух соприкасающихся тел, называют внешним. Трение между частями одного и того же сплошного тела (жидкость или газ), носит название внутреннего.

Сила трения скольжения действует на тело в процессе его перемещения по поверхности другого тела и равна произведению коэффициента трения  между этими телами на силу реакции опоры N и направлена в сторону, противоположную относительной скорости движения этого тела

F = N

Силы трения играют очень большую роль в природе. В нашей повседневной жизни трение нередко оказывается полезным. Например, затруднения которые испытывают пешеходы и транспорт во время гололедицы, когда трение между покрытием дороги и подошвами пешеходов или колесами транспорта значительно уменьшается. Не будь сил трения, мебель пришлось бы прикреплять к полу, как на судне во время качки, ибо она при малейшей негоризонтальности пола сползла бы в направлении покатости.

Закон сохранения импульса

Замкнутой (изолированной) системой тел называют такую систему, тела которой не взаимодействуют с внешними телами или если равнодействующая внешних сил равна нулю.

Если на систему материальных точек не действуют внешние силы, то есть система изолирована (замкнутая), из (3.12) выплывает, что

,

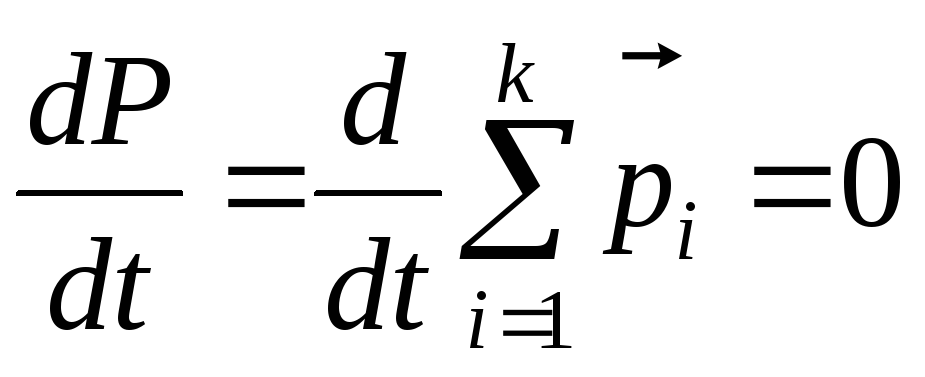или

(3.13)

Мы получили фундаментальный закон классической физики — закон сохранения импульса: в изолированной (замкнутой) системе суммарный импульс остается величиной постоянной. Для того, чтобы выполнялся закон сохранения импульса достаточно, чтобы система была замкнута.

Закон сохранения импульса является фундаментальным законом природы не знающим исключений.

В нерелятивистском случае можно ввести понятие центра масс (центра инерции) системы материальных точек, под которым понимают воображаемую точку, радиус-вектор которой , выражается через радиусы векторы материальных точек по формуле:

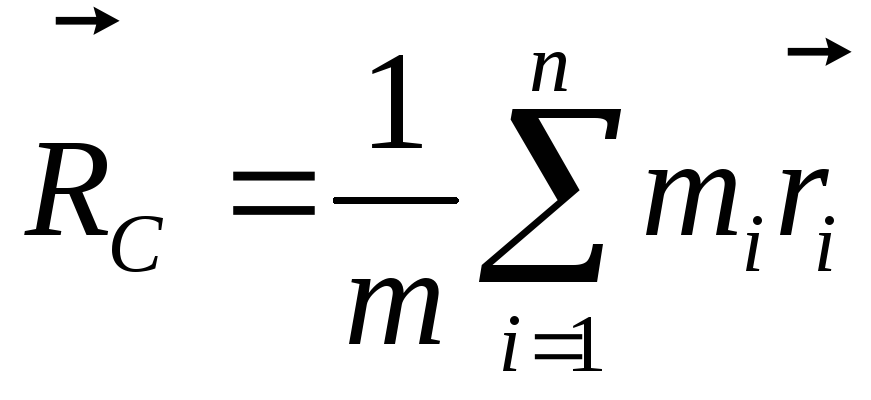(3.14)

Найдем скорость центра масс в данной системе отсчета, взяв производную по времени от соотношения (3.14)

. (3.14)

Импульс системы равняется произведению массы системы на скорость ее центра инерции.

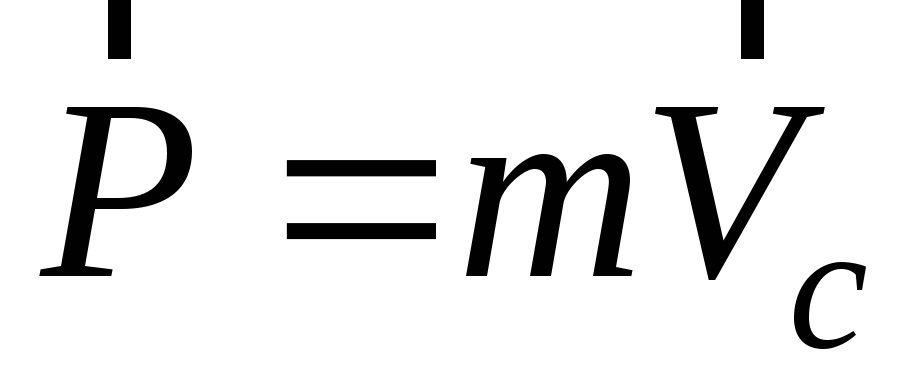. (3.15)

Понятие центра масс позволяет придать уравнению 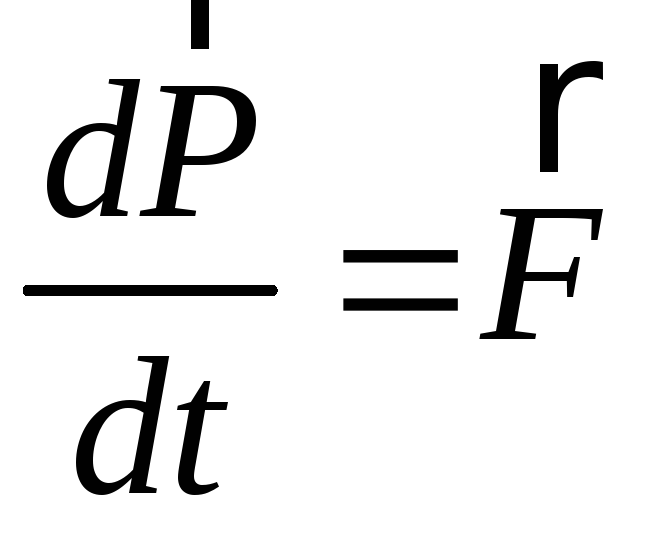другую форму, которая часто оказывается более удобной. Для этого достаточно учесть, что масса системы есть величина постоянная. Тогда

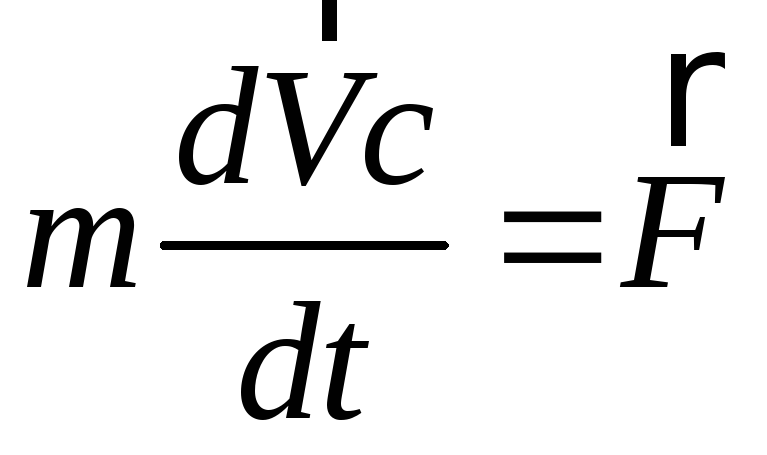(3.16)

где – сумма всех внешних сил, которые действуют на систему. Уравнение (3.16) – уравнение движенияцентра инерции системы. Теорема о движении центра масс гласит: центр масс движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на систему.

Если система замкнута, то 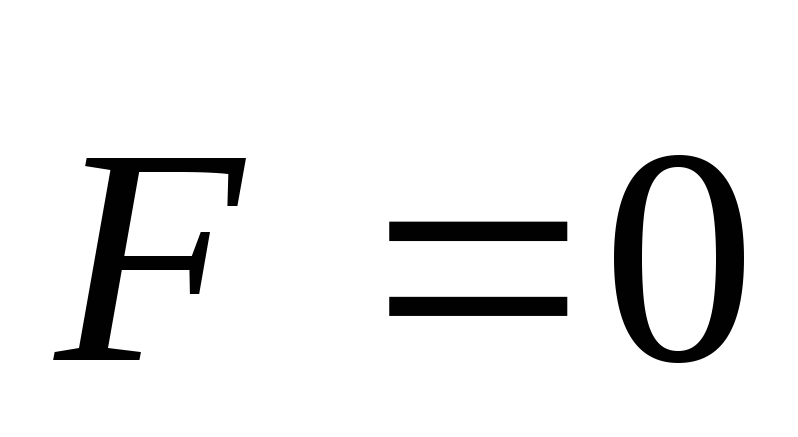. В этом случае уравнение (3.16) переходит в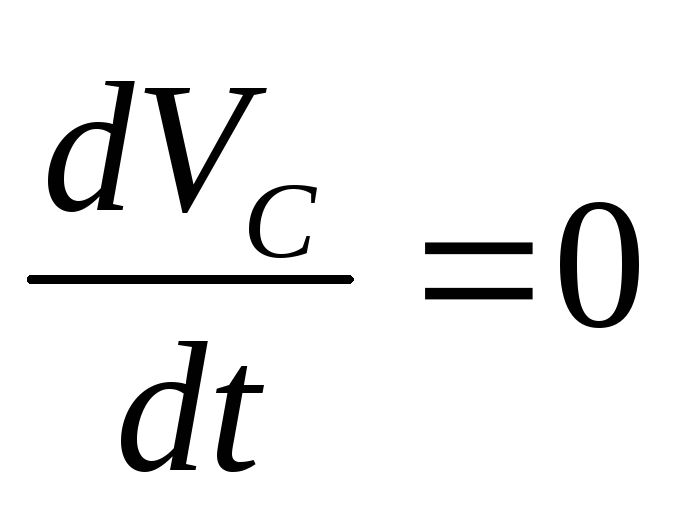, из которого следуетV=const. Центр масс замкнутой системы движется прямолинейно и равномерно.

Глава 6 виды сил в природе

6.1. Гравитационные силы. Закон всемирного тяготения

В природе существуют различные силы, которые характеризуют взаимодействие тел. Рассмотрим те силы, которые встречаются в механике.

Гравитационные силы

Вероятно, самой первой силой, существование которой осознал человек, являлась сила притяжения, действующая на тела со стороны Земли. И потребовались многие века для того, чтобы люди поняли, что сила тяготения действует между любыми телами. Первым этот факт понял английский физик Ньютон. Анализируя законы, которым подчиняется движение планет (законы Кеплера), он пришел к выводу, что наблюдаемые законы движения планет вокруг Солнца могут выполняться только в том случае, если между ними действует сила притяжения, прямо пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними. Понимая, что планеты и Солнце ничем, кроме размеров и масс, не отличаются от других тел, Ньютон сформулировал закон всемирного тяготения.

Любые два тела притягиваются друг к другу. Сила притяжения между точечными телами направлена по прямой, их соединяющей, прямо пропорциональна массам обоих тел и обратно пропорциональна квадрату расстояния между ними:

Под точечными телами в данном случае понимают тела, размеры которых во много раз меньше расстояния между ними.

Силы всемирного тяготения называют гравитационными силами. Коэффициент пропорциональности G называют гравитационной постоянной. Его значение было определено экспериментально: G = 6,7·10^-11 Н·м²/кг².

Сила тяготения, действующая вблизи поверхности Земли, направлена к ее центру и вычисляется по формуле

F = m·g.(6.2)

где g — ускорение свободного падения.

Роль силы тяготения в живой природе очень значительна так как от ее величины во многом зависят размеры, формы и пропорции живых существ.

6.2. Силы упругости. Закон Гука.

Силы, действующие на тело, не только создают его ускорение, но и меняют его форму — создают деформацию.

Например, если один конец пружины закрепить, а на другой конец подействовать силой F (потянуть рукой), то длина пружины увеличится на некоторую величину (х), после чего изменение длины прекратится, рис. 6.1.

Рис. 6.1. Возникновение силы упругости

Прекращение растяжения пружины объясняется тем, что при деформации пружины появляется сила, действующая в противоположную сторону и компенсирующая силу F.

Сила, возникающая при деформации тела и направленная в сторону, противоположную смещению частиц тела, называется силой упругости (F_у).

Сила упругости действует со стороны деформированного тела на тело, с которым оно соприкасается (в данном случае — со стороны пружины на руку).

Растяжение или сжатие под действием приложенной силы испытывает не только пружина, но и все твердые тела. Английский ученый Роберт Гук экспериментально установил следующий закон.

Сила упругости (F ), возникающая при малой (по сравнению с размерами тела) деформации, прямо пропорциональна величине деформации (х) и направлена в сторону, противоположную смещению частиц тела:

F_у = — k·x. (6.3)

Коэффициент пропорциональности k называется жесткостью тела (зависит от размеров, формы и материала). В СИ жесткость выражается в ньютонах на метр (Н/м).

При сжатии динамометра, растяжении эспандера, прыжках на батуте возникает сила упругости. В некоторых случаях, например, при прыжке с трамплина (рис. 6.2), очень важен процесс восстановления формы деформированного тела. Так, при прыжках в воду используют упругий трамплин, который, распрямляясь, сообщает телу спортсмена дополнительную скорость и он прыгает выше (сила упругости деформированного трамплина совершает положительную работу).

Рис. 6.2. Прыжок в воду с использованием трамплина

Виды сил вокруг нас

В окружающем нас мире бесчисленное множество тел, которые взаимодействуют друг с другом. Но, несмотря на это многообразие сил, несколько их видов принято выделять особо.

Силой упругости называют силу, которая возникает в теле при изменении его формы или размеров. Это происходит, если тело сжимают, растягивают, изгибают или скручивают. Например, сила упругости возникла в пружине в результате её сжатия и действует на кирпич.

Сила упругости всегда направлена противоположно той силе, которая вызвала изменение формы или размеров тела. В нашем примере упавший кирпич сжал пружину, то есть подействовал на неё с силой, направленной вниз. В результате в пружине возникла сила упругости, направленная в противоположную сторону, то есть вверх. Мы можем это утверждать, наблюдая отскок кирпича.

Силой тяготения называют силу, с которой все тела в мире притягиваются друг к другу (см. § 2-а). Разновидностью силы тяготения является сила тяжести – сила, с которой тело, находящееся вблизи какой-либо планеты, притягивается к ней. Например, на ракету, стоящую на Марсе, тоже действует сила тяжести.

Сила тяжести всегда направлена к центру планеты. На рисунке показано, что Земля притягивает мальчика и мяч с силами, направленными вниз, то есть к центру планеты. Как видите, направление «вниз» различно для различных мест на планете. Это будет справедливо и для других планет и космических тел. Более подробно силу тяжести мы изучим в § 3-г.

Силой трения называют силу, препятствующую проскальзыванию одного тела по поверхности другого. Рассмотрим рисунок. Резкое торможение автомобиля всегда сопровождается «визгом тормозов». Этот звук возникает из-за проскальзывания шин по асфальту. При этом шины сильно стираются, так как между колёсами и дорогой действует сила трения, препятствующая проскальзыванию.

Сила трения всегда направлена противоположно направлению (возможного) проскальзывания рассматриваемого тела по поверхности другого. Например, при резком торможении автомобиля его колёса проскальзывают вперёд, значит, действующая на них сила трения о дорогу направлена в противоположную сторону, то есть назад.

Сила трения возникает не только при скольжении одного тела по поверхности другого. Существует также сила трения покоя. Например, отталкиваясь ботинком от дороги, мы не наблюдаем его проскальзывания. При этом возникает сила трения покоя, благодаря которой мы движемся вперёд. В отсутствие этой силы мы бы не смогли сделать и шага, как, например, на льду.

Силой Архимеда (или выталкивающей силой) называют силу, с которой жидкость или газ действуют на погруженное в них тело – выталкивают его. На рисунке показано, что вода действует на пузырьки выдыхаемого рыбой воздуха – выталкивает их на поверхность. Вода также действует на рыбу и камни – она уменьшает их вес (силу, с которой камни давят на дно).

Архимедова сила обычно направлена вверх, противоположно силе тяжести. Более подробно она будет изучена в § 3-е.

Сила — Википедия

Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений. Деформация может возникать как в самом теле, так и в фиксирующих его объектах — например, пружинах.

Воздействие всегда осуществляется посредством полей, создаваемых телами и воспринимаемых рассматриваемым телом. Различные взаимодействия сводятся к четырём фундаментальным; согласно Стандартной модели физики элементарных частиц, эти фундаментальные взаимодействия (слабое, электромагнитное, сильное и, возможно, гравитационное) реализуются путём обмена калибровочными бозонами^[1].

Для обозначения силы обычно используется символ F — от лат. fortis (сильный).

Важнейший физический закон, в который входит сила, — второй закон Ньютона. Он гласит, что в инерциальных системах отсчёта ускорение материальной точки по направлению совпадает с приложенной силой, а по модулю пропорционально модулю силы и обратно пропорционально массе материальной точки.

Слово «сила» в русском языке является многозначным и нередко используется (само или в сочетаниях, в науке и обиходных ситуациях) в смыслах, отличных от физического определения термина.

Характеристики силы[править | править код]

Сила является векторной величиной. Она характеризуется модулем, направлением и точкой приложения. Также используют понятие линия действия силы, означающее проходящую через точку приложения силы прямую, вдоль которой направлена сила.

Зависимость силы от расстояния между телами может иметь различный вид, однако, как правило, при больших расстояниях сила стремится к нулю — поэтому отдалением рассматриваемого тела от других тел с хорошей точностью обеспечивается ситуация «отсутствия внешних сил»^[2]. Исключения возможны в некоторых задачах космологии, касающихся тёмной энергии^[3].

Кроме разделения по типу фундаментальных взаимодействий, существуют иные классификации сил, в том числе: внешние—внутренние (то есть действующие на материальные точки (тела) данной механической системы со стороны материальных точек (тел) не принадлежащих этой системе и силы взаимодействия между материальными точками (телами) данной системы^[4]), потенциальные и нет (потенциально ли поле изучаемых сил), упругие—диссипативные, сосредоточенные—распределённые (приложены в одной или многих точках), постоянные или переменные во времени.

При переходе из одной инерциальной системы отсчёта в другую преобразование сил осуществляется так же, как и полей соответствующей природы (например, электромагнитных, если сила электромагнитная). В пределе малых скоростей можно считать силу инвариантом.

Системой сил называется совокупность сил, действующих на рассматриваемое тело или на точки механической системы. Две системы сил называют эквивалентными, если их действие по отдельности на одно и то же твердое тело или материальную точку одинаково при прочих равных условиях^[4].

Уравновешенной системой сил (или системой сил, эквивалентной нулю) называется система сил, действие которой на твердое тело или материальную точку не приводит к изменению их кинематического состояния^[4].

Размерность силы[править | править код]

Размерность силы в Международной системе величин (англ. International System of Quantities, ISQ), на которой базируется Международная система единиц (СИ), и в системе величин LMT, используемой в качестве основы для системы единиц СГС, — LMT⁻². Единицей измерения в СИ является ньютон (русское обозначение: Н; международное: N), в системе СГС — дина (русское обозначение: дин, международное: dyn).

Равнодействующая системы сил[править | править код]

Если к не закреплённому телу приложено несколько сил, то каждая из них сообщает телу такое ускорение, какое она сообщила бы в отсутствие действия других сил. Это утверждение, основанное на опытных фактах, носит название принципа независимости действия сил (принципа суперпозиции). Поэтому при расчёте ускорения тела все действующие на него силы заменяют одной силой, называемой равнодействующей, а именно геометрической суммой всех действующих сил. В частном случае равенства равнодействующей сил нулю ускорение тела также будет нулевым. На этом основано измерение величины исследуемой силы, когда она компенсируется силой, величина которой известна.

Измерение сил[править | править код]

Для измерения сил используются два метода: статический и динамический^[5].

• Статический метод заключается в уравновешивании измеряемой силы другой силой, значение которой известно. Например, в качестве уравновешивающей силы может выступать сила упругости, возникающая в градуированной пружине, деформированной исследуемой силой. На использовании статического метода основаны приборы, называемые динамометрами.
• Динамический метод основан на использовании уравнения второго закона Ньютона ma→=F→{\displaystyle m{\vec {a}}={\vec {F}}}. Уравнение позволяет найти силу F→{\displaystyle {\vec {F}}}, действующую на тело, если известны масса тела m{\displaystyle m} и ускорение a→{\displaystyle {\vec {a}}} его поступательного движения относительно инерциальной системы отсчёта.

В древнем мире[править | править код]

Человечество вначале стало воспринимать понятие силы через непосредственный опыт передвижения тяжёлых предметов. «Сила», «мощность», «работа» при этом были синонимами (как и в современном языке за пределами естествознания). Перенос личных ощущений на объекты природы привёл к антропоморфизму: все предметы, которые могут воздействовать на другие (реки, камни, деревья) должны быть живыми, в живых существах должна содержаться та же сила, которую человек чувствовал в себе.

С развитием цивилизации сила была обожествлена, причём как египетский, так и месопотамский боги силы символизировали не только жестокость и мощь, но и наведение порядка во вселенной^[6]. Всемогущий Бог Библии также несёт в своих именах и эпитетах ассоциации с силой^[7].

В античности[править | править код]

Когда греческие учёные стали задумываться о природе движения, понятие силы возникло как часть учения Гераклита о статике как балансе противоположностей^[8]. Эмпедокл и Анаксагор пытались объяснить причину движения и пришли к понятиям, близким к понятию силы^[8]. У Анаксагора «ум» движет внешней по отношению к нему материей^[9]. У Эмпедокла движение вызывается борьбой двух начал, «любви» (филии) и «вражды» (фобии)^[9], которые Платон рассматривал как притяжение и отталкивание^[10]. При этом взаимодействие, по Платону, объяснялось в терминах четырёх элементов (огня, воды, земли и воздуха): близкие вещи притягиваются, земля к земле, вода к воде, огонь к огню^[11]. В древнегреческой науке каждый элемент также имел своё место в природе, которое старался занять. Таким образом, сила тяжести, например, объяснялась двумя способами: притяжением подобных вещей и стремлением элементов занять своё место^[12]. В отличие от Платона, Аристотель последовательно занимал вторую позицию, что отложило концепцию общей силы тяготения, которая бы объясняла движение земных и небесных тел, до времён Ньютона^[12].

Для обозначения понятия силы Платон использовал термин «динамис» («возможность» движения). Термин употреблялся в расширенном смысле, близком к современному понятию мощности: химические реакции, тепло и свет все также представляли собой динамисы^[13].

Аристотель рассматривал две разные силы: присущую самому телу («природу», физис) и силу, с которой одно тело тянет или толкает другое (при этом тела должны быть в контакте)^[14]. Именно это понятие о силе и легло в основу аристотелевой механики, хотя дуализм и препятствовал количественному определению силы взаимодействия двух тел (так как вес был природной силой, не связанной с взаимодействием, и потому не мог использоваться в качестве стандарта)^[15]. В случае природного движения (падения тяжёлого или подъёма лёгкого тела) Аристотель предложил формулу для скорости в виде отношения плотностей движущегося тела A и среды, сквозь которую происходит движение, B: v=A/B^[16] (очевидная проблема для случая равных плотностей была отмечена уже в VI веке^[17]).

Изучением сил в процессе конструирования простых механизмов занимался в III в. до н. э. Архимед^[18]. Архимед рассматривал силы в статике и чисто геометрически, и потому его вклад в развитие понятия силы незначителен^[19].

Вклад в развитие понятие силы внесли стоики. Согласно их учению, силы неразрывно связывали два тела через дальнодействующую «симпатию» или (у Посидония) через всеобщее напряжение, пронизывающее всё пространство. Стоики пришли к этим выводам путём наблюдения за приливами, где взаимодействие Луны, Солнца и воды в океане было трудно объяснить с позиции Аристотелева близкодействия (сам Аристотель считал, что Солнце, садясь в океан, вызывает ветры, приводящие к приливам)^[20].

В доклассической механике[править | править код]

Бэкон и Оккам вернули в науку идею о дальнодействии.

Бэкон называл дальнодействующие силы species (обычно этот специфичный для Бэкона термин не переводится) и рассматривал их распространение в среде как цепочку близких взаимодействий. Такие силы, по Бэкону, имели вполне телесный характер, ближайшим эквивалентом в современной физике является волна^[21].

Оккам первым отказался от аристотелевского описания взаимодействия как непосредственного контакта и декларировал возможность движителя воздействовать на движимое на расстоянии, приведя в качестве одного из примеров магниты^[22].

Ревизии подвергалась и аристотелевская формула v=A/B. Уже в VI веке Иоанн Филопон рассматривал в качестве правой части разность A-B, что кроме проблемной ситуации с одинаковыми плотностями позволило также описать движение в вакууме^[23]. В XIV веке Брадвардин предложил формулу v=log(A/B)^[24].

У Кеплера[править | править код]

Взгляды Кеплера на силу претерпели быстрое изменение. Ещё в 1600 году Кеплер рассматривает силы как свойство, подобное душе, которое руководит движением небесных тел. Однако уже к 1605 году Кеплер пришёл к выводу, что притяжение — это не действие, а реакция, силы притяжения относятся к материальному миру и подлежат математическому изучению. В 1607 году Кеплер пришёл к выводу, что приливы вызываются воздействием силы притяжения Луны на океаны^[25]. По мнению М. Дженнера, Кеплер пришёл к идее единой теории тяготения, охватывающей как падение тел, так и движение Луны, до Ньютона^[26].

В классической механике[править | править код]

С зарождением классической механики Бекманом и Декартом был сформулирован закон сохранения количества движения. После осознания этого факта, который похоронил аристотелевскую связь силы и скорости, у исследователей оставалось два выхода: определить силу как причину изменения скорости или отбросить понятие силы как таковое. Сам Декарт вначале применял понятие силы, чтобы объяснить ускоренное падение тела на землю, но со временем в попытке геометризации физики пришёл к выводу, что понятие силы является искусственным, и в 1629 году описывал процесс свободного падения без упоминания «силы»^[27]. С другой стороны, Галилей недвусмысленно рассматривал силу как причину увеличения скорости свободного падения^[28].

У Ньютона[править | править код]

В трудах Ньютона понятие силы было тесно связано с тяготением, поскольку интерпретация кеплеровских результатов в области движения планет в то время занимала все умы^[29]. Впервые понятие силы (лат. vis) встречается у Ньютона в «Началах» в двух контекстах: «присущей силы» (лат. vis insita), ньютоновской силы инерции и «приложенной силы» (лат. vis impressa), отвечающей за изменение движения тела. Ньютон также отдельно выделял центростремительную силу (к которой относил тяготение) с несколькими разновидностями: абсолютную силу (подобную современному полю тяготения), ускоряющую силу (эффект тяготения на единицу массы, современное ускорение) и движущую (произведение массы на ускорение)^[30]. Ньютон не даёт общего определения силы. Как отмечает М. Дженнер, второй закон Ньютона не является определением силы у самого автора закона (который явно различал определения и законы), сила у Ньютона является пресуществующим понятием, интуитивно эквивалентным силе мускулов^[31].

Современность[править | править код]

Конец XX века охарактеризовался спорами о том, необходимо ли в науке понятие силы и существуют ли силы в принципе — или это только термин, введённый для удобства^[32].

Бигелоу с соавторами в 1988 году аргументировали, что силы по сути определяют причинно-следственные отношения и потому не могут быть отброшены^[33]. М. Джеммер на это возразил, что в Стандартной модели и других физических теориях сила трактуется лишь как обмен моментом импульса, понятие силы потому сводится к более простому «взаимодействию» между частицами. Это взаимодействие описывается в терминах обмена дополнительными частицами (фотонами, глюонами, бозонами и, возможно, гравитонами)^[32]. Джеммер приводит следующее упрощённое пояснение: два конькобежца скользят по льду плечо к плечу, у обоих в руках находится по мячу. Быстрый и одновременный обмен мячами приведёт к отталкивающему взаимодействию^[34].

Стиннер отмечает, что эйнштейновский принцип эквивалентности сил гравитации и инерции по сути уничтожает понятие силы, в общей теории относительности внешние силы (F из уравнения F=ma) отсутствуют^[35].

Ньютон задался целью описать движение объектов, используя понятия инерции и силы. Сделав это, он попутно установил, что всякое механическое движение подчиняется общим законам сохранения. В 1687 г. Ньютон опубликовал свой знаменитый труд «Математические начала натуральной философии», в котором изложил три основополагающих закона классической механики (законы Ньютона)^[36][37].

Первый закон Ньютона[править | править код]

Первый закон Ньютона утверждает, что существуют системы отсчёта, в которых тела сохраняют состояние покоя или равномерного прямолинейного движения при отсутствии действий на них со стороны других тел или при взаимной компенсации этих воздействий^[37]. Такие системы отсчёта называются инерциальными. Ньютон предположил, что каждый массивный (подразумевается: «обладающий массой», а не «громоздкий») объект имеет определённый запас инерции, характеризующий «естественное состояние» движения этого объекта. Эта идея отрицает взгляд Аристотеля, который рассматривал только покой «естественным состоянием» объекта. Первый закон Ньютона противоречит аристотелевской физике, одним из положений которой является утверждение о том, что тело может двигаться с постоянной скоростью лишь под действием силы. Тот факт, что в механике Ньютона в инерциальных системах отсчёта покой неотличим от равномерного прямолинейного движения, является обоснованием принципа относительности Галилея. Среди совокупности тел принципиально невозможно определить, какие из них находятся «в движении», а какие «покоятся». Говорить о движении можно лишь относительно конкретной системы отсчёта. Законы механики выполняются одинаково во всех инерциальных системах, другими словами, все они механически эквивалентны. Последнее следует из так называемых преобразований Галилея^[38].

Второй закон Ньютона[править | править код]

Второй закон Ньютона имеет вид:

ma→=F→.{\displaystyle m{\vec {a}}={\vec {F}}.}

где m{\displaystyle m} — масса материальной точки, a→{\displaystyle {\vec {a}}} − её ускорение, F→{\displaystyle {\vec {F}}} — равнодействующая приложенных сил. Считается, что это «вторая самая известная формула в физике», хотя сам Ньютон никогда явным образом не записывал свой второй закон в этом виде. Впервые данную форму закона можно встретить в трудах К. Маклорена и Л. Эйлера.

Поскольку в любой инерциальной системе отсчёта ускорение тела одинаково и не меняется при переходе от одной системы к другой, сила тоже инвариантна по отношению к такому переходу.

Во всех явлениях природы сила, независимо от своего происхождения, проявляется только в механическом смысле, то есть как причина нарушения равномерного и прямолинейного движения тела в инерциальной системе координат. Обратная ситуация, а именно установление факта такого движения, свидетельствует не об отсутствии действующих на тело сил, а лишь о том, что действия этих сил взаимно уравновешиваются. Иначе: их векторная сумма есть вектор с модулем, равным нулю.

Второй закон Ньютона не играет роль определения силы, но позволяет находить её величину. Например, знание массы планеты и её центростремительного ускорения при движении по орбите позволяет вычислить величину силы гравитационного притяжения, действующей на эту планету со стороны Солнца.

Третий закон Ньютона[править | править код]

Для любых двух тел (назовём их тело 1 и тело 2) третий закон Ньютона утверждает, что сила действия тела 1 на тело 2 сопровождается появлением равной по модулю, но противоположной по направлению силы, действующей на тело 1 со стороны тела 2^[39]. Математически закон записывается так:

F→1,2=−F→2,1.{\displaystyle {\vec {F}}_{1,2}=-{\vec {F}}_{2,1}.}

Этот закон означает, что силы всегда возникают парами «действие-противодействие»^[37]. Если тело 1 и тело 2 находятся в одной системе, то суммарная сила в системе, обусловленная взаимодействием этих тел, равна нулю:

F→1,2+F→2,1=0.{\displaystyle {\vec {F}}_{1,2}+{\vec {F}}_{\mathrm {2,1} }=0.}

Это означает, что в замкнутой системе не существует несбалансированных внутренних сил. Это приводит к тому, что центр масс замкнутой системы (то есть такой, на которую не действуют внешние силы) не может двигаться с ускорением. Отдельные части системы могут ускоряться, но лишь таким образом, что система в целом остаётся в состоянии покоя или равномерного прямолинейного движения. Однако, в случае, если внешние силы подействуют на систему, её центр масс начнёт двигаться с ускорением, пропорциональным внешней результирующей силе и обратно пропорциональным массе системы^[1].

Кроме того, так как силы взаимодействия всегда направлены вдоль прямой, соединяющей взаимодействующие точки, равен нулю и суммарный момент этих сил (относительно любой точки):

(r→1−r→0)×F→1,2+(r→2−r→0)×F→2,1=(r→1−r→2)×F→1,2=0{\displaystyle ({\vec {r}}_{1}-{\vec {r}}_{0})\times {\vec {F}}_{1,2}+({\vec {r}}_{2}-{\vec {r}}_{0})\times {\vec {F}}_{\mathrm {2,1} }=({\vec {r}}_{1}-{\vec {r}}_{2})\times {\vec {F}}_{1,2}=0}

Все силы в природе основаны на четырёх типах фундаментальных взаимодействий. Максимальная скорость распространения всех видов взаимодействия равна скорости света в вакууме. Электромагнитные силы действуют между электрически заряженными телами, гравитационные — между массивными объектами. Сильное и слабое проявляются только на очень малых расстояниях, они ответственны за возникновение взаимодействия между субатомными частицами, включая нуклоны, из которых состоят атомные ядра.

Интенсивность сильного и слабого взаимодействия измеряется в единицах энергии (электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется существующей с античности традицией объяснять любые явления в окружаемом мире действием специфических для каждого явления «сил».

Понятие силы не может быть применено по отношению к явлениям субатомного мира. Это понятие из арсенала классической физики, ассоциирующейся (пусть даже только подсознательно) с ньютоновскими представлениями о силах, действующих на расстоянии. В субатомной физике таких сил уже нет: их заменяют взаимодействия между частицами, происходящие через посредство полей, то есть каких-то других частиц. Поэтому физики высоких энергий избегают употреблять слово сила, заменяя его словом взаимодействие^[40].

Взаимодействие каждого типа обусловлено обменом соответствующими «переносчиками»: электромагнитное — виртуальными фотонами, слабое — векторными бозонами, сильное — глюонами (а на больших расстояниях — мезонами). В отношении гравитационного взаимодействия имеются теоретические предположения (например, в теории струн или М-теории), что с ним также может быть связан свой переносчик-бозон, называемый гравитоном, но его существование пока не доказано. Эксперименты по физике высоких энергий, проведённые в 70−80-х годах XX в., подтвердили идею о том, что слабое и электромагнитное взаимодействия являются проявлениями более глобального электрослабого взаимодействия^[41]. В настоящее время делаются попытки объединения всех четырёх фундаментальных взаимодействий в одно (так называемая теория великого объединения).

Всё многообразие проявляющих себя в природе сил в принципе может быть сведено к этим четырём фундаментальным взаимодействиям. Например, трение − это проявление электромагнитных сил, действующих между атомами двух соприкасающихся поверхностей, и принципа запрета Паули^[42], который не позволяет атомам проникать в область друг друга. Сила, возникающая при деформации пружины, описываемая законом Гука, также является результатом действия электромагнитных сил между частицами и принципа запрета Паули, заставляющих атомы кристаллической решётки вещества удерживаться около положения равновесия^[1].

Однако на практике оказывается не только нецелесообразной, но и просто невозможной по условиям задачи подобная детализация рассмотрения вопроса о действии сил.

Гравитация[править | править код]

Гравитация (сила тяготения) — универсальное взаимодействие между любыми видами материи. В рамках классической механики описывается законом всемирного тяготения, сформулированным Ньютоном в уже упомянутом труде «Математические начала натуральной философии». Ньютон получил величину ускорения, с которым Луна движется вокруг Земли, положив при расчёте, что сила тяготения убывает обратно пропорционально квадрату расстояния от тяготеющего тела. Кроме этого, им же было установлено, что ускорение, обусловленное притяжением одного тела другим, пропорционально произведению масс этих тел^[43]. На основании этих двух выводов был сформулирован закон тяготения: любые материальные частицы притягиваются по направлению друг к другу с силой F{\displaystyle F}, прямо пропорциональной произведению масс (m1{\displaystyle m_{1}} и m2{\displaystyle m_{2}}) и обратно пропорциональной квадрату расстояния r{\displaystyle r} между ними:

F=Gm1m2R2.{\displaystyle F=G{\frac {m_{1}m_{2}}{R^{2}}}.}

Здесь G{\displaystyle G} − гравитационная постоянная^[44], значение которой впервые получил в своих опытах Генри Кавендиш. Используя данный закон, можно получить формулы для расчёта силы тяготения тел произвольной формы. Теория тяготения Ньютона хорошо описывает движение планет Солнечной системы и многих других небесных тел. Однако, в её основе лежит концепция дальнодействия, противоречащая теории относительности. Поэтому классическая теория тяготения неприменима для описания движения тел, перемещающихся со скоростью, близкой к скорости света, гравитационных полей чрезвычайно массивных объектов (например, чёрных дыр), а также переменных полей тяготения, создаваемых движущимися телами, на больших расстояниях от них^[45].

Более общей теорией гравитации является общая теория относительности Альберта Эйнштейна. В ней гравитация не характеризуется инвариантной силой, не зависящей от системы отсчёта. Вместо этого свободное движение тел в гравитационном поле, воспринимаемое наблюдателем как движение по искривлённым траекториям в трёхмерном пространстве-времени с переменной скоростью, рассматривается как движение по инерции по геодезической линии в искривлённом четырёхмерном пространстве-времени, в котором время в разных точках течёт по-разному. Причем эта линия в некотором смысле «наиболее прямая» — она такова, что пространственно-временной промежуток (собственное время) между двумя пространственно-временными положениями данного тела максимален. Искривление пространства зависит от массы тел, а также от всех видов энергии, присутствующих в системе^[1].

Электромагнитное взаимодействие[править | править код]

Электростатическое поле (поле неподвижных зарядов)

Развитие физики после Ньютона добавило к трём основным (длина, масса, время) величинам электрический заряд с размерностью «кулон» (C). Однако, исходя из требований практики, в качестве основной единицы измерения стали использовать не единицу заряда, а единицу силы электрического тока. Так, в системе СИ основной единицей является ампер, а единица заряда — кулон — производная от него.

Поскольку заряд как таковой не существует независимо от несущего его тела, электрическое взаимодействие тел проявляется в виде рассматриваемой в механике силы, служащей причиной ускорения. Применительно к электростатическому взаимодействию двух точечных зарядов с величинами q1{\displaystyle q_{1}} и q2{\displaystyle q_{2}}, располагающихся в вакууме, используется закон Кулона. В форме, соответствующей системе СИ, он имеет вид:

F→12=14πε0⋅q1⋅q2r122r→12r12,{\displaystyle {\vec {F}}_{12}={\frac {1}{4\pi \varepsilon _{0}}}\cdot {\frac {q_{1}\cdot q_{2}}{r_{12}^{2}}}{\frac {{\vec {r}}_{12}}{r_{12}}},}

где F→12{\displaystyle {\vec {F}}_{12}} — сила, с которой заряд 1 действует на заряд 2, r→12{\displaystyle {\vec {r}}_{12}} — вектор, направленный от заряда 1 к заряду 2 и по модулю равный расстоянию между зарядами, а ε0{\displaystyle \varepsilon _{0}} — электрическая постоянная, равная ≈ 8,854187817•10⁻¹²Ф/м. При помещении зарядов в однородную и изотропную среду сила взаимодействия уменьшается в ε раз, где ε — диэлектрическая проницаемость среды.

Сила направлена вдоль линии, соединяющей точечные заряды. Графически электростатическое поле принято изображать в виде картины силовых линий, представляющих собой воображаемые траектории, по которым перемещалась бы лишённая массы заряженная частица. Эти линии начинаются на одном и заканчиваются на другом заряде.

Магнитостатическое поле (поле постоянных токов)

Существование магнитного поля признавалось ещё в средние века китайцами, использовавшими «любящий камень» — магнит в качестве прообраза магнитного компаса. Графически магнитное поле принято изображать в виде замкнутых силовых линий, густота которых (так же, как и в случае электростатического поля) определяет его интенсивность. Исторически наглядным способом визуализации магнитного поля были железные опилки, насыпаемые, например, на лист бумаги, положенный на магнит.

Эрстед установил, что текущий по проводнику ток вызывает отклонение магнитной стрелки.

Фарадей пришёл к выводу, что вокруг проводника с током создаётся магнитное поле.

Ампер высказал гипотезу, признанную в физике в качестве модели процесса возникновения магнитного поля, которая предполагает существование в материалах микроскопических замкнутых токов, обеспечивающих совместно эффект естественного или наведённого магнетизма.

Ещё, Ампером было установлено, что в находящейся в вакууме системе отсчёта, по отношению к которой заряд находится в движении, то есть ведёт себя как электрический ток, возникает магнитное поле, интенсивность которого определяется вектором магнитной индукции B→{\displaystyle {\vec {B}}}, лежащим в плоскости, расположенной перпендикулярно по отношению к направлению движения заряда.

Тот же Ампер впервые измерил силу взаимодействия двух параллельных проводников с текущими по ним токами. Один из проводников создавал вокруг себя магнитное поле, второй реагировал на это поле сближением или удалением с поддающейся измерению силой, зная которую и величину силы тока можно было определить модуль вектора магнитной индукции.

Силовое взаимодействие между электрическими зарядами, не находящимися в движении относительно друг друга, описывается законом Кулона. Однако заряды, находящиеся в таком движении, порождают и магнитные поля, посредством которых созданные движением зарядов токи в общем случае приходят в состояние силового взаимодействия.

Принципиальным отличием силы, возникающей при относительном движении зарядов, от случая их стационарного размещения, является различие в геометрии этих сил. Для случая электростатики сила взаимодействия двух зарядов направлена по линии, их соединяющей. Поэтому геометрия задачи двумерна и рассмотрение ведётся в плоскости, проходящей через эту линию.

В случае токов сила, характеризующая магнитное поле, создаваемое током, расположена в плоскости, перпендикулярной току. Поэтому картина явления становится трёхмерной. Магнитное поле, создаваемое бесконечно малым по длине элементом первого тока, взаимодействуя с таким же элементом второго тока, в общем случае создаёт силу, действующую на него. При этом для обоих токов эта картина полностью симметрична в том смысле, что нумерация токов произвольна.

Закон взаимодействия токов используется для эталонирования постоянного электрического тока.

Сильное взаимодействие[править | править код]

Сильное взаимодействие — фундаментальное короткодействующее взаимодействие между адронами и кварками. В атомном ядре сильное взаимодействие удерживает вместе положительно заряженные (испытывающие электростатическое отталкивание) протоны, происходит это посредством обмена пи-мезонами между нуклонами (протонами и нейтронами). Пи-мезоны живут очень мало, времени жизни им хватает лишь на то, чтобы обеспечить ядерные силы в радиусе ядра, потому ядерные силы называют короткодействующими. Увеличение количества нейтронов «разбавляет» ядро, уменьшая электростатические силы и увеличивая ядерные, но при большом количестве нейтронов они сами, будучи фермионами, начинают испытывать отталкивание вследствие принципа Паули. Также при слишком сильном сближении нуклонов начинается обмен W-бозонами, вызывающий отталкивание, благодаря этому атомные ядра не «схлопываются».

Внутри самих адронов сильное взаимодействие удерживает вместе кв

Силы в природе — Класс!ная физика

Силы в природе

«Физика — 10 класс»

В главе 2 мы ввели понятие силы как количественной меры действия одного тела на другое.
В этой главе мы рассмотрим, какие силы рассматриваются в механике, чем определяются их значения.

Много ли видов сил существует в природе?
Перечислите известные вам силы.
Какую природу они имеют — гравитационную или электромагнитную?

На первый взгляд кажется, что мы взялись за непосильную и неразрешимую задачу: тел на Земле и вне её бесконечное множество.
Они взаимодействуют по-разному.

Так, например, камень падает на Землю; электровоз тянет поезд; нога футболиста ударяет по мячу; потёртая о мех эбонитовая палочка притягивает лёгкие бумажки, магнит притягивает железные опилки; проводник с током поворачивает стрелку компаса; взаимодействуют Луна и Земля, а вместе они взаимодействуют с Солнцем; взаимодействуют звёзды и звёздные системы, луч света отражается от зеркала и т. д.
Подобным примерам нет конца.

Похоже, что в природе существует бесконечное множество взаимодействий (сил)?
Оказывается, нет!

Четыре типа сил.

В безграничных просторах Вселенной, на нашей планете, в любом веществе, в живых организмах, в атомах, в атомных ядрах и в мире элементарных частиц мы встречаемся с проявлением всего лишь четырёх типов сил: гравитационных, электромагнитных, сильных (ядерных) и слабых.

Гравитационные силы, или силы всемирного тяготения, действуют между всеми телами, имеющими массу, — все тела притягиваются друг к другу.

Но это притяжение существенно обычно лишь тогда, когда хотя бы одно из взаимодействующих тел так же велико, как Земля или Луна.
Иначе эти силы столь малы, что ими можно пренебречь.

Электромагнитные силы действуют между частицами, имеющими электрические заряды.

Сфера их действия особенно обширна и разнообразна.

В атомах, молекулах, твёрдых, жидких и газообразных телах, живых организмах именно электромагнитные силы являются главными.
Такие, казалось бы, чисто механические силы, как силы трения и упругости, имеют электромагнитную природу.
Велика их роль в атомах.

Ядерные силы действуют между частицами в атомных ядрах и определяют свойства ядер.

Область действия ядерных сил очень ограничена.

Они заметны только внутри атомных ядер (т. е. на расстояниях порядка 10^-15 м).
Уже на расстояниях между частицами порядка 10^-13 м (в тысячу раз меньших размеров атома — 10^-10 м) они не проявляются совсем.

Слабые взаимодействия вызывают взаимные превращения элементарных частиц, определяют радиоактивный распад ядер, реакции термоядерного синтеза.

Они проявляются на ещё меньших расстояниях, порядка 10^-17 м.

Ядерные силы — самые мощные в природе.

Если интенсивность ядерных сил принять за единицу, то интенсивность электромагнитных сил составит 10^-2, гравитационных — 10-40, слабых взаимодействий — 10^-16.

Сильные (ядерные) и слабые взаимодействия проявляются на таких малых расстояниях, когда законы механики Ньютона, а с ними вместе и понятие механической силы теряют смысл.

Интенсивность сильного и слабого взаимодействий измеряется в единицах энергии (в электрон-вольтах), а не единицах силы, и потому применение к ним термина «сила» объясняется многовековой традицией все явления в окружающем мире объяснять действием характерных для каждого явления «сил».

В механике мы будем рассматривать только гравитационные и электромагнитные взаимодействия.

Силы в механике.

В механике обычно имеют дело с тремя видами сил — силами тяготения, силами упругости и силами трения.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Динамика — Физика, учебник для 10 класса — Класс!ная физика

Основное утверждение механики — Сила — Инертность тела. Масса. Единица массы — Первый закон Ньютона — Второй закон Ньютона — Принцип суперпозиции сил — Примеры решения задач по теме «Второй закон Ньютона» — Третий закон Ньютона — Геоцентрическая система отсчёта — Принцип относительности Галилея. Инвариантные и относительные величины — Силы в природе — Сила тяжести и сила всемирного тяготения — Сила тяжести на других планетах — Примеры решения задач по теме «Закон всемирного тяготения» — Первая космическая скорость — Примеры решения задач по теме «Первая космическая скорость» — Вес. Невесомость — Деформация и силы упругости. Закон Гука — Примеры решения задач по теме «Силы упругости. Закон Гука» — Силы трения — Примеры решения задач по теме «Силы трения» — Примеры решения задач по теме «Силы трения» (продолжение) —

1.2.5. Классификация сил. Гравитационные силы.

Упругие силы и силы трения

В современной физике рассматриваются четыре вида фундаментальных взаимодействий.

1) Гравитационное, обусловленное всемирным тяготением.

2) Электромагнитное, обусловленное взаимодействием электрических и магнитных полей.

3) Сильное или ядерное, обеспечивающее взаимосвязь нуклонов в ядре.

4) Слабое, ответственное за взаимодействие элементарных частиц.

Силы трения и упругости по своей природе являются электромагнитными, поскольку их физическая природа связана с молекулярным взаимодействием.

Гравитационные силы. Закон всемирного тяготения

Всякое тело изменяет свойства окружающего его пространства – создает в нем гравитационное поле. Это поле проявляет себя в том, что помещенное в него другое тело оказывается под действием силы, действующей на него со стороны другого тела. Таким образом, все тела в природе взаимодействуют между собой.

Закон взаимодействия тел в природе установлен Ньютоном для тел, принимаемых за материальные точки. Согласно этому закону, сила, с которой две материальные точки притягиваются друг к другу, прямо пропорциональна произведению масс этих точек 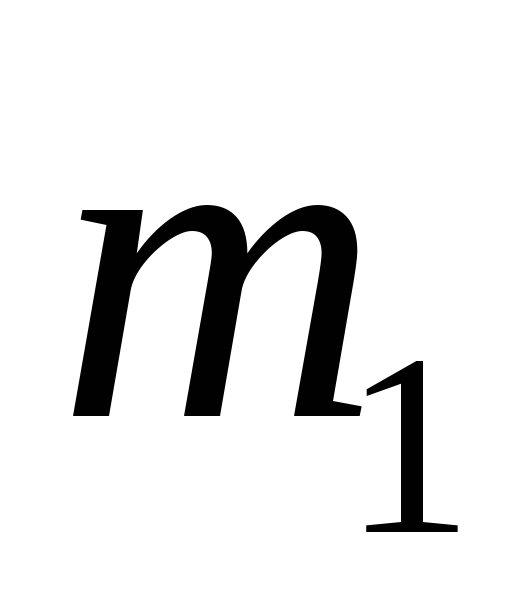и 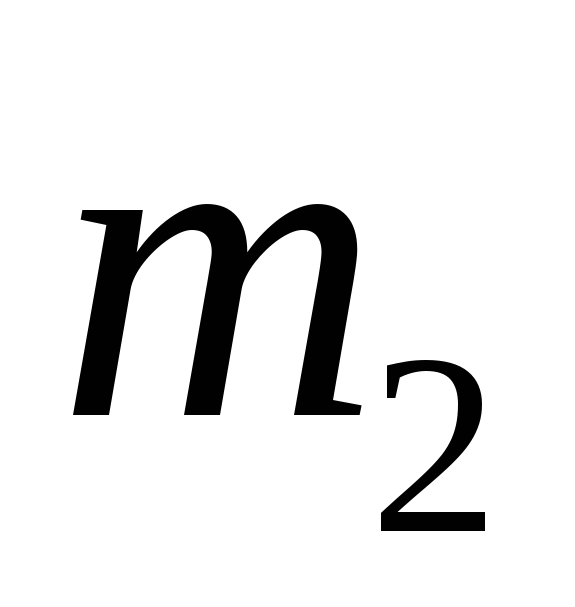и обратно пропорциональна квадрату расстояния между ними:

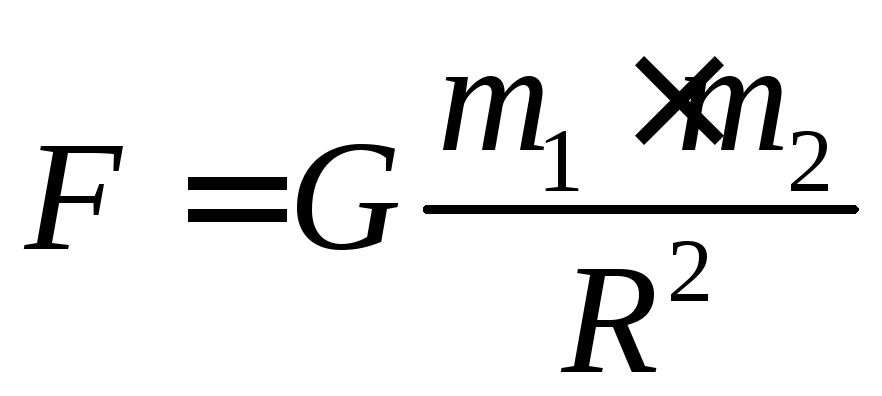, (11)

где 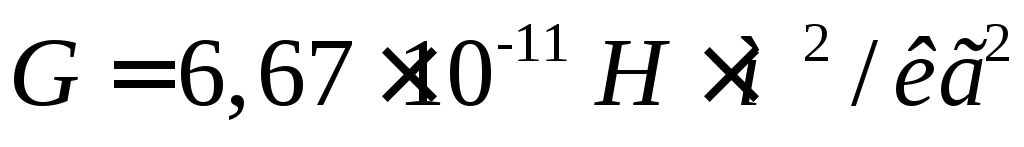— коэффициент пропорциональности, называемый гравитационной постоянной.

На любое тело вблизи поверхности Земли действует сила тяготения 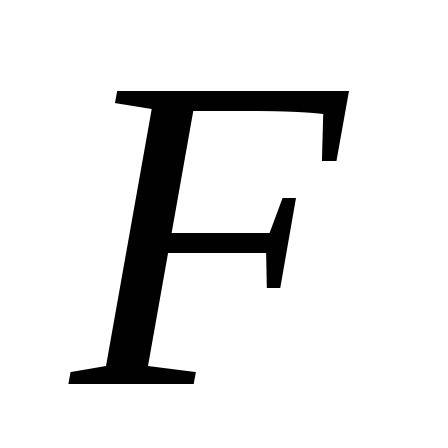, под влиянием которой, согласно 2-му закону Ньютона, тело начинает двигаться с ускорением, получившим название ускорения свободного падения 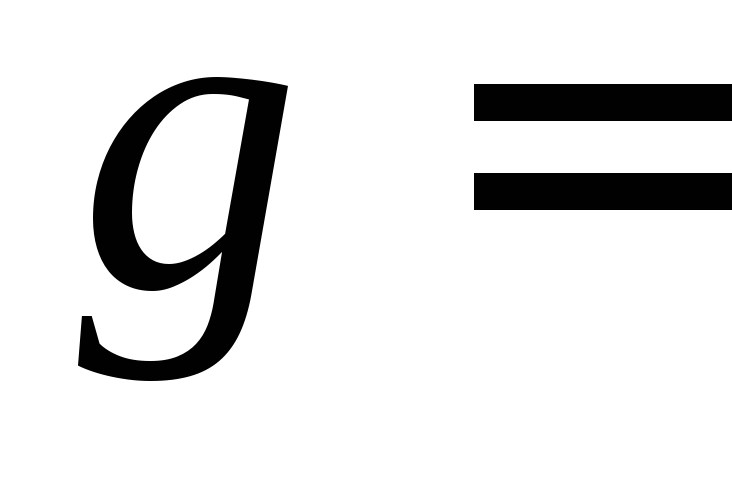9,8 м/с². Действительно, , ,тогда

, (12)

9,8 М/с2.

На тело, находящееся на поверхности Земли, действуют сила сила тяготения 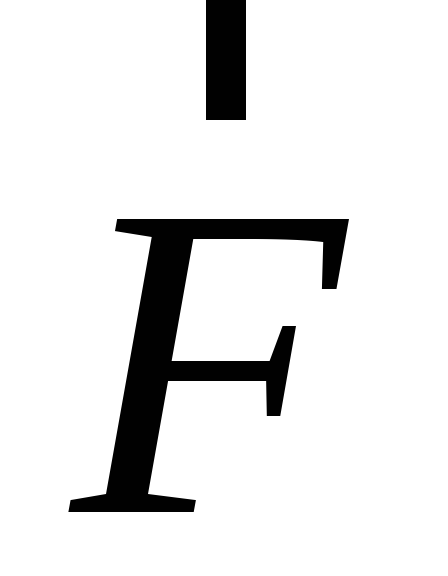и сила реакции земной поверхности 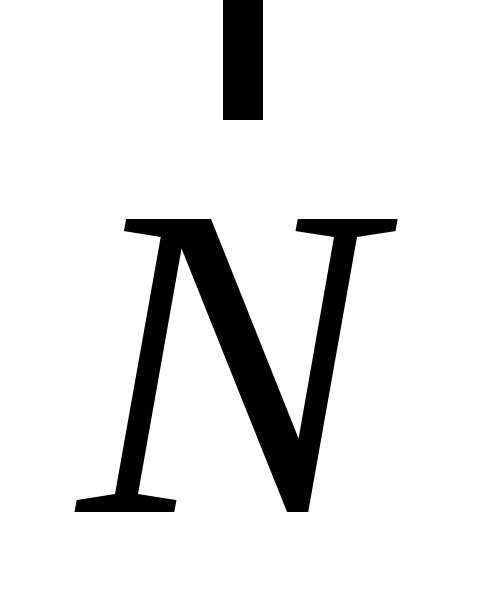; направление силы 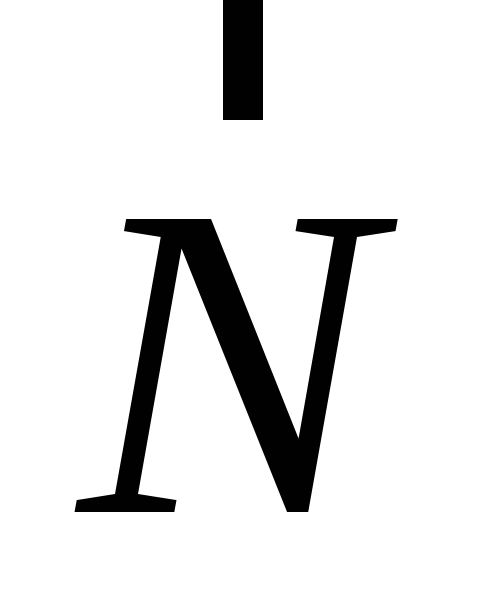определяется не только силой тяготения, но и вращением Земли (рис. 9). Равнодействующая этих двух сил — центростремительная сила — обеспечивает движение тела по окружности при суточном вращении Земли (вокруг оси ОО). Центростремительная сила равна 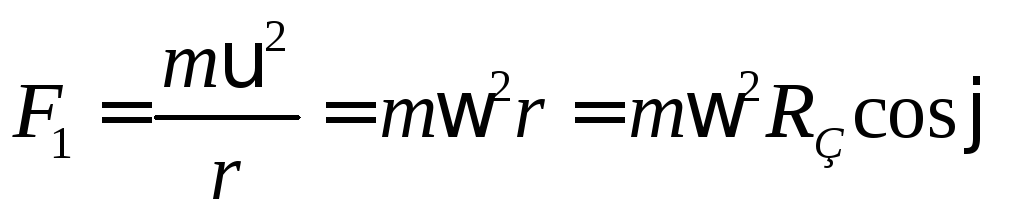, где 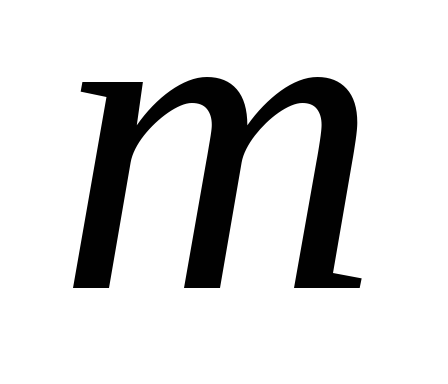– масса тела, 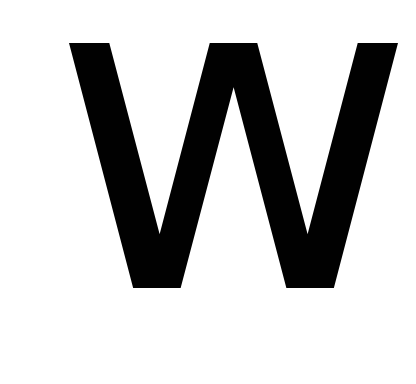— угловая скорость вращения Земли, 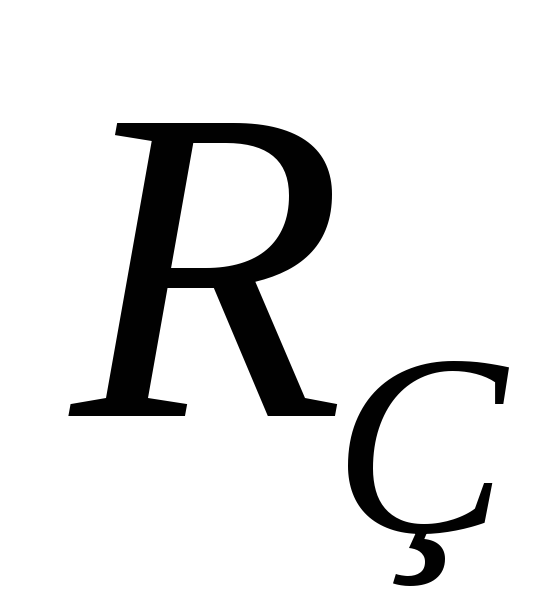— радиус Земли, — широта местности.

Сила тяжести , действующая на тело вследствие его притяжения к Земле, равна по модулю силе реакции опоры 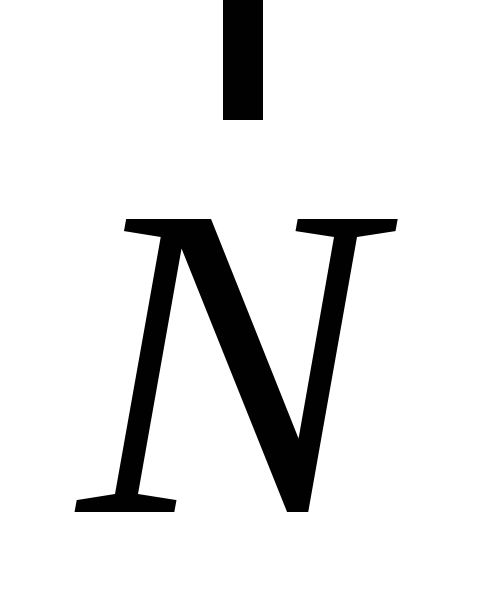и равна : .

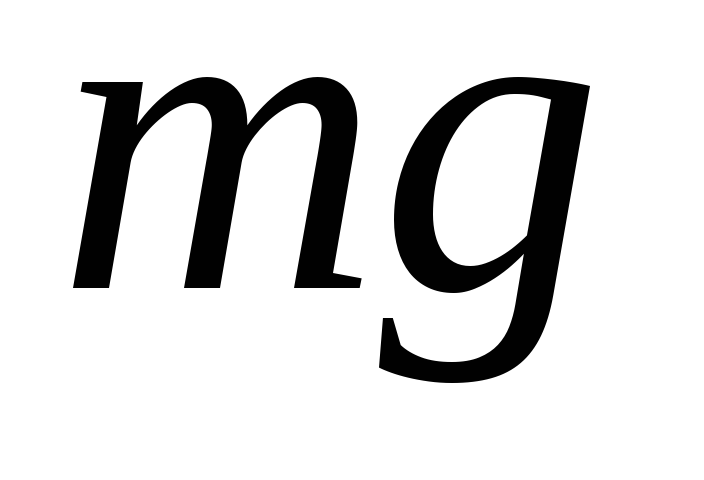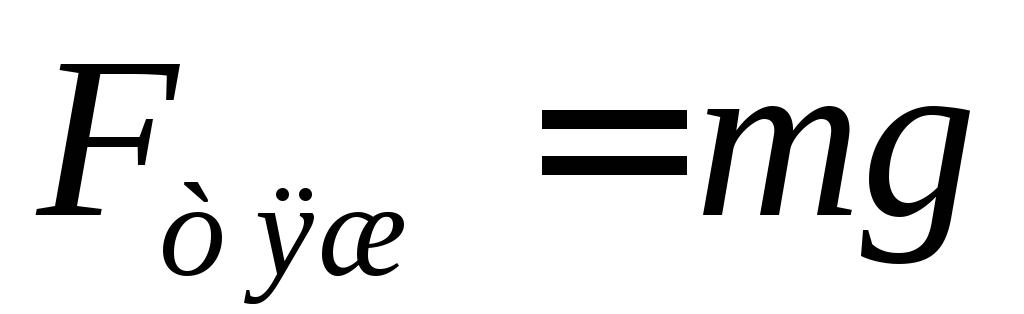Сила тяготения и сила тяжести по направлению совпадают только на полюсах и на экваторе, в других же точках на поверхности Земли между ними есть угол, зависящий от широты местности (рис.9). Это связано с тем, что все тела на Земле вместе с ней совершают вращательное движение по окружности, но каждое тело имеет свой радиус вращения .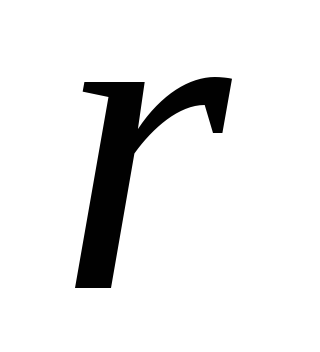

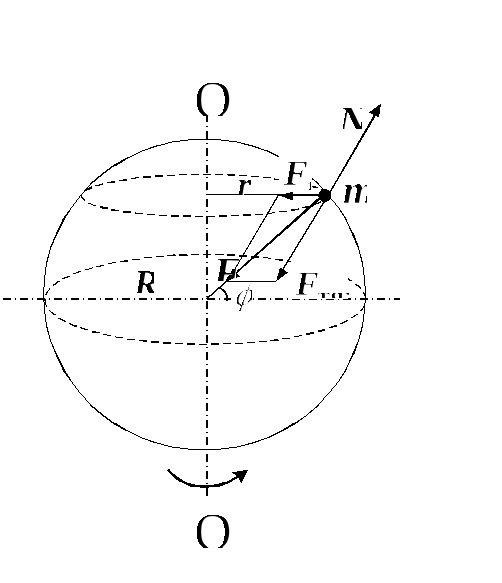
Рис. 9. Сила тяготения 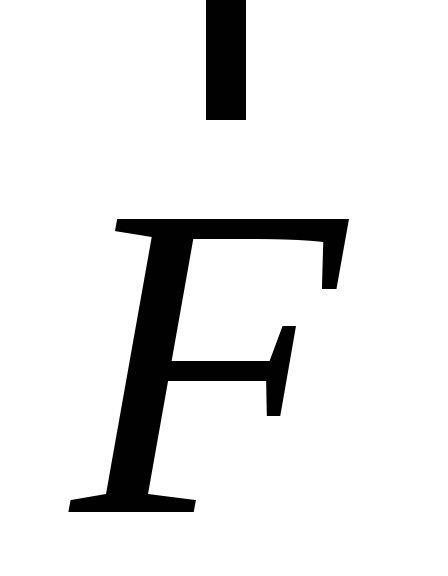и сила тяжести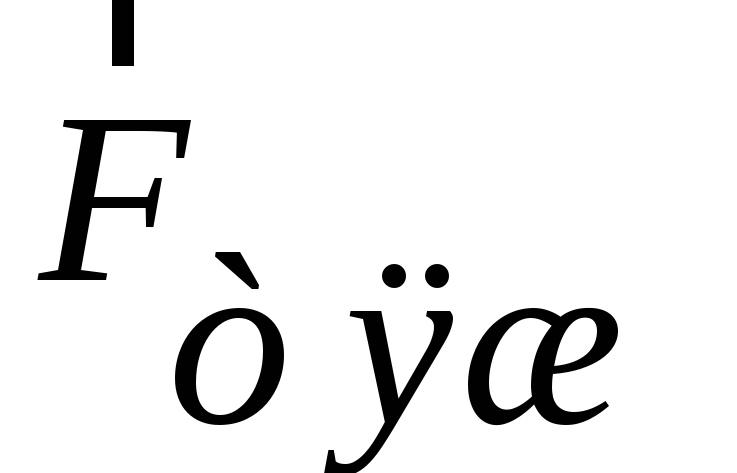

Так как угловая скорость 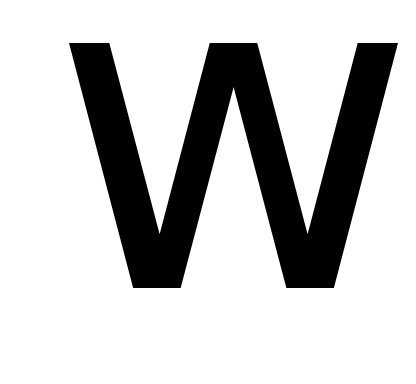вращения Земли очень мала, силой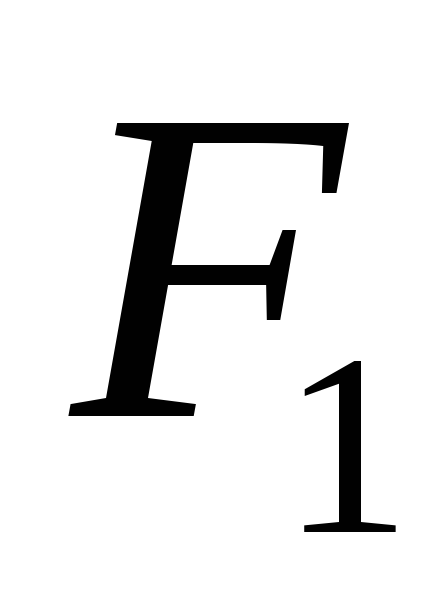можно пренебречь и.

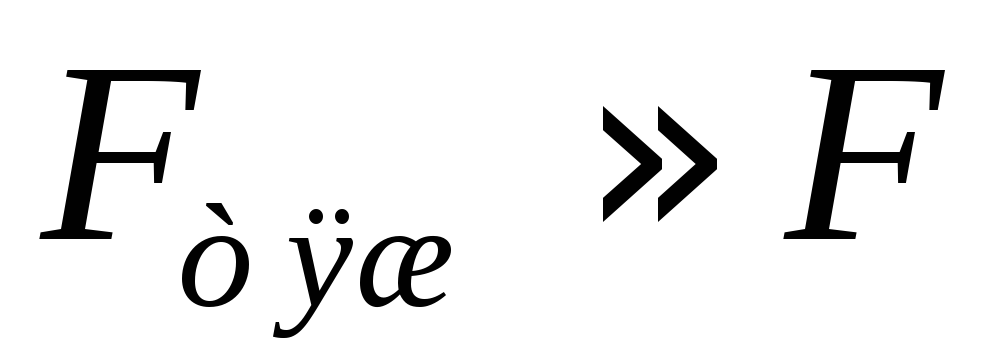Упругие силы

Упругие силы возникают в теле, испытывающем воздействие других тел или полей, и связаны с деформацией тела. Если после прекращения действия сил тело принимает первоначальные размеры и форму, деформация называется упругой. Упругие деформации наблюдаются в том случае, когда сила, вызывающая деформацию, не превосходит некоторого, определенного для каждого конкретного тела, значения (предела упругости).

По экспериментальному закону Гука, силы, возникающие при упругой деформации, прямо пропорциональны величине этой деформации и направлены в сторону, противоположную деформации:

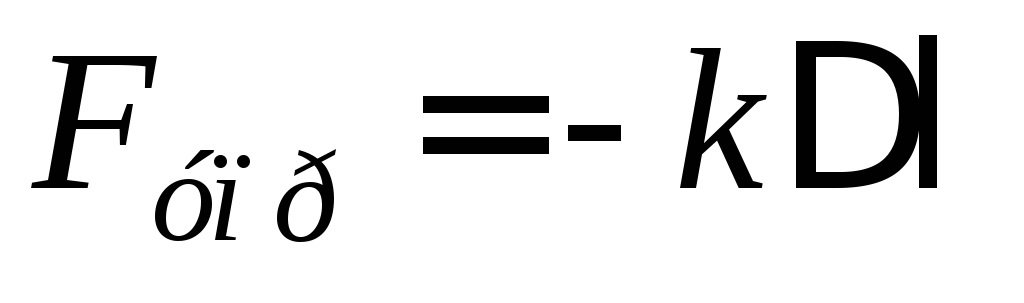, (13)

где 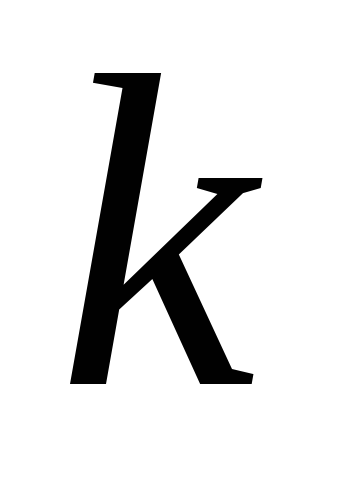– коэффициент жесткости (для пружины просто жесткость), измеряется в ньютонах на метр (Н/м), – деформация, – сила упругости (рис.10).

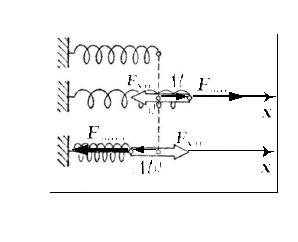
Рис. 10. Силы упругости

При растяжении или одностороннем сжатии однородные стержни ведут себя подобно пружине. Сила упругости распределена по всему деформированному телу.