10 способов решения уравнений 8-9 классы
10 способов решения уравнений
Содержание.
I. История развития квадратных уравнений ……………………….2
1. Квадратные уравнения в Древнем Вавилоне………………………..2
2. Как составлял и решал Диофант квадратные уравнения……………2
3. Квадратные уравнения в Индии………………………………………3
4. Квадратные уравнения у ал- Хорезми ………………………………4
5. Квадратные уравнения в Европе XIII — XVII вв……………………….5
6. О теореме Виета ………………………………………………………6
II. Способы решения квадратных уравнений ……………………….7
Способ…………………………………………………………………7
Способ…………………………………………………………………7
Способ…………………………………………………………………7
Способ………………………………………………………………….9
Способ………………………………………………………………….9
Способ……………………………………………………………….

Способ…………………………………………………………………12
Способ…………………………………………………………………13
Способ…………………………………………………………………15
Способ…………………………………………………………………16
III. Заключение……………………………………………………………..18
Литература……………………………………………………………….19
История развития квадратных уравнений.
1. Квадратные уравнения в Древнем Вавилоне.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X2 + X = ¾; X2 — X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
2. Как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение — 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 — х. Разность между ними 2х.
Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х, другое же меньше, т.е. 10 — х. Разность между ними 2х.
Отсюда уравнение:
(10 + х)(10 — х) = 96
или же:
100 — х2 = 96
х2 — 4 = 0 (1)Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у(20 — у) = 96,
у2 — 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
3. Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах2 + bх = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а, могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).
Соответствующее задаче 13 уравнение:
(x/8)2 + 12 = x
Бхаскара пишет под видом:
х2 — 64х = -768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 322, получая затем:
х2 — 64х + 322 = -768 + 1024,
(х — 32)2 = 256,
х — 32 = ± 16,
х1

4. Квадратные уравнения у ал — Хорезми.
В алгебраическом трактате ал — Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах2 + с = bх.
2) «Квадраты равны числу», т.е. ах2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах2 + с = bх.
5) «Квадраты и корни равны числу», т.е. ах2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах2.
Для ал — Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида
Автор излагает способы решения указанных уравнений, пользуясь приемами ал — джабр и ал — мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида
ал — Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал — Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Приведем пример:
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень»
(подразумевается корень уравнения х2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал — Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
5. Квадратные уравнения в Европе XIII — XVII вв.
Формулы решения квадратных уравнений по образцу ал — Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI — XVII вв.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:
х2 + bx = с,
при всевозможных комбинациях знаков коэффициентов b, с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
6. О теореме Виета.
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D, умноженное на A — A2, равно BD, то A равно В и равно D».
Чтобы понять Виета, следует вспомнить, что А, как и всякая гласная буква, означало у него неизвестное (наше х), гласные же В,D — коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
(а + b)х — х2 = ab,
т.е.
х2 — (а + b)х + аb = 0,
то
х1 = а, х2 = b.
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и по этому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
Итак: Квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ: Разложение левой части уравнения на множители.
Решим уравнение х2 + 10х — 24 = 0. Разложим левую часть на множители:
х2 + 10х — 24 = х2 + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х — 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = — 12. Это означает, что число 2 и — 12 являются корнями уравнения х2 + 10х — 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х2 + 6х — 7 = 0. Выделим в левой части полный квадрат.
Для этого запишем выражение х2 + 6х в следующем виде:
х2 + 6х = х2 + 2• х • 3.
В полученном выражении первое слагаемое — квадрат числа х, а второе — удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как
х2 + 2• х • 3 + 32 = (х + 3)2.
Преобразуем теперь левую часть уравнения
х2 + 6х — 7 = 0,
прибавляя к ней и вычитая 32. Имеем:
х2 + 6х — 7 = х2 + 2• х • 3 + 32 — 32 — 7 = (х + 3)2 — 9 — 7 = (х + 3)2 — 16.
Таким образом, данное уравнение можно записать так:
(х + 3)2 — 16 =0, (х + 3)2 = 16.
Следовательно, х + 3 — 4 = 0, х1 = 1, или х + 3 = -4, х2 = -7.
3. СПОСОБ: Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах2 + bх + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а2х2 + 4аbх + 4ас = 0,
((2ах)2 + 2ах • b + b2) — b2 + 4ac = 0,
(2ax + b)2 = b2 — 4ac,
2ax + b = ± √ b2 — 4ac,
2ax = — b ± √ b2 — 4ac,
• Примеры.
а) Решим уравнение: 4х2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b2 — 4ac = 72 — 4 • 4 • 3 = 49 — 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b2 — 4ac >0 , уравнение ах2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х2 — 4х + 1 = 0,
а = 4, b = — 4, с = 1, D = b2 — 4ac = (-4)2 — 4 • 4 • 1= 16 — 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 — 4ac = 0, то уравнение
ах2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b2 — 4ac = 32 — 4 • 2 • 4 = 9 — 32 = — 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b2 — 4ac < 0, уравнение
ах2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х2 + px + c = 0. (1)
(1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
x1 + x2 = — p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.
Например,
x2 – 3x + 2 = 0; x1 = 2 и x2 = 1, так как q = 2 > 0 и p = — 3 < 0;
x2 + 8x + 7 = 0; x1 = — 7 и x2 = — 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Например,
x2 + 4x – 5 = 0; x1 = — 5 и x2 = 1, так как q= — 5 < 0 и p = 4 > 0;
x2 – 8x – 9 = 0; x1 = 9 и x2 = — 1, так как q = — 9 < 0 и p = — 8 < 0.
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах2 + bх + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2х2 + аbх + ас = 0.
Пусть ах = у, откуда х = у/а; тогда приходим к уравнению
у2 + by + ас = 0,
равносильно данному. Его корни у1 и у2 найдем с помощью теоремы Виета.
Окончательно получаем х1 = у1/а и х1 = у2/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
• Пример.
Решим уравнение 2х2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета
у1 = 5 х1 = 5/2 x1 = 2,5
у2 = 6 x2 = 6/2 x2 = 3.
Ответ: 2,5; 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1 = 1,
х2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + b/a • x + c/a = 0.
Согласно теореме Виета
x1 + x2 = — b/a,
x1x2 = 1• c/a.
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x1 + x2 = — а + b/a= -1 – c/a,
x1x2 = — 1• ( — c/a),
т.е. х1 = -1 и х2 = c/a, что м требовалось доказать.
• Примеры.
Решим уравнение 345х2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х1 = 1, х2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х1 = 1, х2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k – четное число, то формулу корней
• Пример.
Решим уравнение 3х2 — 14х + 16 = 0.
Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;
D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;
Ответ: 2; 8/3
В. Приведенное уравнение
х2 + рх + q= 0
совпадает с уравнением общего вида, в котором а = 1, b = р и с = q. Поэтому для приведенного квадратного уравнения формула корней
Поэтому для приведенного квадратного уравнения формула корней
принимает вид:
Формулу (3) особенно удобно использовать, когда р — четное число.
•Пример. Решим уравнение х2 – 14х – 15 = 0.
Решение. Имеем: х1,2 =7±
Ответ: х1 = 15; х2 = -1.
7. СПОСОБ: Графическое решение квадратного уравнения.
Если в уравнении
х2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х2 = — px — q.
Построим графики зависимости у = х2 и у = — px — q.
График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —
прямая (рис. 1). Возможны следующие случаи:
1). Возможны следующие случаи:
— прямая и парабола могут пересекаться в двух точках,
абсциссы точек пересечения являются корнями квад- ратного уравнения;
— прямая и парабола могут касаться ( только одна общая точка), т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
• Примеры.
1) Решим графически уравнение х2 — 3х — 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х2 = 3х + 4.
Построим параболу у = х2 и прямую у = 3х + 4. Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13). Прямая и парабола пересекаются в двух точках
А и В с абсциссами х1 = — 1 и х2 = 4. Ответ: х1 = — 1;
х2 = 4.
2) Решим графически уравнение (рис. 3) х2 — 2х + 1 = 0.
Решение. Запишем уравнение в виде х2 = 2х — 1.
Построим параболу у = х2 и прямую у = 2х — 1.
Прямую у = 2х — 1 построим по двум точкам М (0; — 1)
и N(1/2; 0). Прямая и парабола пересекаются в точке А с
абсциссой х = 1. Ответ: х = 1.
3) Решим графически уравнение х2 — 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х2 = 5х — 5. Построим параболу у = х2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х2 — 2х + 5 = 0 корней не имеет.
Уравнение х2 — 2х + 5 = 0 корней не имеет.
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и
линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 — корни уравнения ах2 + bх + с = 0, и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Тогда по теореме о секущих имеем OB • OD = OA • OC, откуда OC = OB • OD/ OA= х1х2/ 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд AC и BD, поэтому
Итак:
1) построим точки (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a), окружность пересекает ось Ох в двух точках (рис. 6,а) В(х1; 0) и D(х2; 0), где х1 и х2 — корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис. 6,б) в точке В(х1; 0), где х1 — корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
• Пример.
Решим уравнение х2 — 2х — 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х1 = — 1; х2 = 3.
9. СПОСОБ: Решение квадратных уравнений с помощью
номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений,
помещенный на с. 83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
83 (см. Брадис В.М. Четырехзначные математические таблицы. — М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z2 + pz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-
там определить корни уравнения.
Криволинейная шкала номограммы построена
по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из
подобия треугольников САН и CDF получим
пропорцию
откуда после подстановок и упрощений вытекает уравнение
z2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
• Примеры.
1) Для уравнения z2 — 9z + 8 = 0 номограмма дает корни z1 = 8,0 и z2 = 1,0 (рис. 12).
12).
2) Решим с помощью номограммы уравнение
2z2 — 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2,
получим уравнение
z2 — 4,5z + 1 = 0.
Номограмма дает корни z1 = 4 и z2 = 0,5.
3) Для уравнения
z2 — 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t,
получим уравнение
t2 — 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t1 = 0,6 и t2 = 4,4, откуда z1 = 5t1 = 3,0 и z2 = 5t2 = 22,0.
10. СПОСОБ: Геометрический способ решения квадратных
уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал — Хорезми.
• Примеры.
1) Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом : «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата , сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4• 2,5х = 10х ) и четырех пристроенных квадратов (6,25• 4 = 25), т. е. S = х2 + 10х + 25. Заменяя
е. S = х2 + 10х + 25. Заменяя
х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у2 + 6у — 16 = 0.
Решение представлено на рис. 16, где
у2 + 6у = 16, или у2 + 6у + 9 = 16 + 9.
Решение. Выражения у2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у2 + 6у — 16 + 9 — 9 = 0 — одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у1 = 2, у2 = — 8 (рис. 16).
16).
3) Решить геометрически уравнение у2 — 6у — 16 = 0.
Преобразуя уравнение, получаем
у2 — 6у = 16.
На рис. 17 находим «изображения» выражения у2 — 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3. Значит, если к выражению у2 — 6у прибавить 9, то получим площадь квадрата со стороной у — 3. Заменяя выражение у2 — 6у равным ему числом 16,
получаем: (у — 3)2 = 16 + 9, т.е. у — 3 = ± √25, или у — 3 = ± 5, где у1 = 8 и у2 = — 2.
Заключение
Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.
Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.
Здесь я остановилась на вопросе решения квадратных уравнений, а что,
если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ.
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.
Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.
Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.
Литература:
1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. — М., Просвещение, 1981.
2. Брадис В.М. Четырехзначные математические таблицы для средней школы.
Изд. 57-е. — М., Просвещение, 1990. С. 83.
3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. — М., высшая школа, 1969.
4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. — М., Просвещение, 1972.
Пособие для учителя. — М., Просвещение, 1972.
5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. — М., Квант, № 4/72. С. 34.
6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. — 4-е, дополн. — М., Высшая школа, 1973.
7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. — М., Просвещение, 1970.
» Решение задач с помощью квадратных уравнений» алгебра 9 класс
Дата_____________________
Урок 48. Решение задач с помощью квадратных уравнений
Цели и задачи урока:
выработать умение применять квадратные уравнения для решения алгебраических и геометрических задач; продолжить формирование практических и теоретических умений и навыков по теме “Квадратные уравнения”;
способствовать умению анализировать условие задач, развитию умения рассуждать, развитию познавательного интереса, умению видеть связь между математикой и окружающей жизнью;
воспитывать внимательность и культуру мышления, самостоятельность и взаимопомощь.

Ход урока.
1.Организационный момент. Постановка целей и задач урока.
2.Устная работа.
1). Назовите коэффициенты квадратного уравнения:
а) 2х2-х+3=0; б) 4х+3х2-1=0; в) -7х+х2-0,5=0; г) 0,7-0,5х-х2=0;
д) х2+18+3х=0; е) 5х2=7х+24; ж) 12х=х2— 4; з) 6х2+7х=0;
и) х2+5=0; к) 7,2х2=4; л) 2х2=0; м) х(5-х)=0.
2). Укажите среди данных уравнений приведенные квадратные уравнения.
Проверка домашнего задания
Задача. Произведение двух последовательных натуральных чисел равно 552, а их сумма равна 47. Найдите эти числа. Найдите арифметический способ решения.
Решение. (Один из учащихся воспроизводит решение задачи на доске, объясняет) Разделим сумму чисел на два. 47 :2 = 23,5. Поставим точку с этой координатой на числовую прямую. 23 23,5 24 Это число заключено между целыми натуральными числами 23 и 24. Их сумма равна 47. Проверим, действительно ли произведение их равно 552, 23 * 24 =552. Ответ: 23 и 24.
Их сумма равна 47. Проверим, действительно ли произведение их равно 552, 23 * 24 =552. Ответ: 23 и 24.
3. Контроль усвоения материала (письменный опрос с последующей взаимопроверкой).
Вариант 1.
1).Напишите формулу корней квадратного уравнения ах2+вх+с=0.
2).Заполните таблицу:
а
в
с
в2-4ас
х1
х2
х1+х2
х1*х2
х2-6х+9=0
2
7
9
4х2=-7х
Вариант 2.
1). Напишите формулу корней квадратного уравнения ах2+2кх+с=0
2) Заполните таблицу:
а
в
с
в2-4ас
х1
х2
х1+х2
х1*х2
5х2-4х=0
3
0
-27
-2х2=-5-3х
Творческая работа.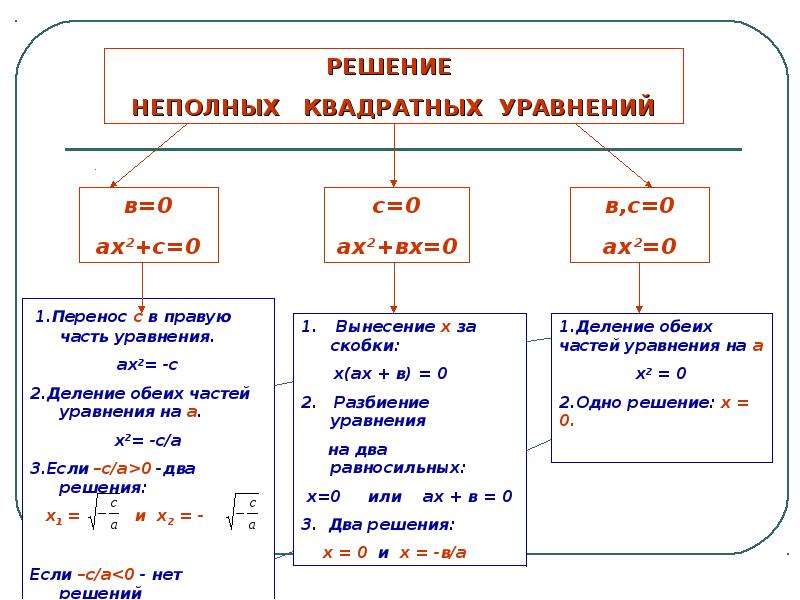
Составьте квадратное уравнение, используя следующие данные:
А) На гербе города Саратова изображена рыба. Посчитайте количество букв в названии и прибавьте к этому числу 1. Полученное число будет первым коэффициентом.
Ответ: Стерлядь, 8+1=9, а=9.
Б) В дате образования поселка Духовницкое сложите цифры и к сумме прибавьте 7. Полученное число будет вторым коэффициентом.
Ответ: 1778 г., 1+7+7+8=23, 23+7, в=30.
В) Наше село стоит на великой русской реке. Посчитайте количество букв в названии и возведите это число в квадрат. Полученное число будет третьим коэффициентом.
Ответ: Волга, 5, 52=25, с=25.
Г) Все коэффициенты положительные числа. Составьте квадратное уравнение, решите его, найдите сумму и произведение корней этого уравнения. Ответ: 9у2+30у+25=0; D=0, у1,2= -15/9; у1 +у2 = -15/9 + (-15/9)= -30/9= — 10/3; у*у = -15/9 * (-15/9)=225/81 =25/9.
4. Изучение нового материала (основные понятия).
Изучение нового материала (основные понятия).
(При рассмотрении решения задач опираюсь на знания учащихся, задаю наводящие вопросы, подвожу учащихся к самостоятельному решению).
Многие задачи алгебры, геометрии, физики, техники приводят к необходимости решения квадратных уравнений.
Мы с вами должны научиться проводить анализ задачи, вводить неизвестные величины, находить зависимость между данными задачи и неизвестными величинами.
Составим схему решения задач
Анализ условия
Выделение главных ситуаций
Введение неизвестных величин
Установление зависимости между данными задачи и неизвестными величинами
Составление уравнения
Решение уравнения
Запись ответа
Если в уравнении дискриминант положителен, решениями задачи могут быть оба корня уравнения. Иногда бывает, что по смыслу задачи ей удовлетворяет лишь один из корней квадратного уравнения.
Задача1. Произведение двух натуральных чисел равно 84. Одно из чисел на 5 больше другого. Найти эти числа.
Анализируем условие задачи, составляем и решаем уравнение.
Пусть меньшее из данных чисел равно х, тогда большее число равно х+5. По условию произведение этих чисел равно 84. Составим уравнение х(х+5)=84. Получили квадратное уравнение х2+5х-84=0. Решим это уравнение. D=52-4*1*(-84)=25+336=361=192, х1=(-5+19):2=7; х2=(-5-19):2=-12. Второй корень по смыслу задачи не подходит, т.к. даны натуральные числа. Значит меньшее число равно 7, а большее число равно 7+5=12.
Ответ: 7 и 12.
Рассмотрим задачу с геометрическим содержанием, для решения которой, применяется формула площади треугольника.
Задача 2. Найдите катеты прямоугольного треугольника, если известно, что один из них на 7 см больше другого, а площадь этого треугольника равна 30 см2.
Решение. Площадь прямоугольного треугольника равна половине произведения катетов. Длины катетов неизвестны. Площадь равна 30 см2.
Пусть х см-длина одного катета, (х+7) см-длина второго катета . Используя формулу площади треугольника составим уравнение: х(х+7)/2=30 . Решим уравнение: х2+7х=60 , х2+7х-60=0, D=289, х1=-12; х2=5. Так как длина отрезка величина положительная, то только х=5 удовлетворяет условию задачи. Найдем длину второго катета: 5+7=12 см. Ответ: 5см и 12 см.
Задача3. Мяч брошен вертикально вверх с начальной скоростью 40 м/с. Через сколько секунд оно окажется на высоте 60 м?
Решение. Из курса физики известно, что если не учитывать сопротивление воздуха, то высота h(м), на которой брошенный вертикально вверх мяч окажется через t(c), может быть найдена по формуле h=V0 t-gt2/2, где Vo(м/с)-начальная скорость, g-ускорение свободного падения, приближенно равное 10 м/с2. Подставив значения h и V в формулу, получим 60=40t-5t2. Получили квадратное уравнение, решим его. 5t2-40t+60=0, t2-8t+12=0, D=16, t1=2; t2=6. Рассмотрим график зависимости h от t, где h=40t-5t2. Из графика видно, что мяч, брошенный вертикально вверх, в течении первых 4с поднимается вверх до высоты 80 м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды: через 2 с и через 6 с после бросания. Условию задачи удовлетворяют оба найденных корня.
Подставив значения h и V в формулу, получим 60=40t-5t2. Получили квадратное уравнение, решим его. 5t2-40t+60=0, t2-8t+12=0, D=16, t1=2; t2=6. Рассмотрим график зависимости h от t, где h=40t-5t2. Из графика видно, что мяч, брошенный вертикально вверх, в течении первых 4с поднимается вверх до высоты 80 м, а затем начинает падать. На высоте 60 м от земли оно оказывается дважды: через 2 с и через 6 с после бросания. Условию задачи удовлетворяют оба найденных корня.
Ответ: на высоте 60 м тело окажется через 2 с и через 6 с.
Рассмотрим старинную задачу, которая решается с помощью теоремы Пифагора, но полученное при решении уравнение после упрощения оказывается линейным.
Задача 4. (Задача Бхаскары, Индия, XIIв.)
Цветок лотоса возвышался над тихим озером на полфута. Когда порыв ветра отклонил цветок от прежнего места на 2 фута, цветок скрылся под водой. Определите глубину озера.
Определите глубину озера.
Решение. Пусть отрезки АВ и АС изображают лотос в двух положениях. Если АD = х – глубина озера, то ВD = 1/2, АС = х+1/2.
Составим уравнение х2 + 22 = (х + 1/2)2,
Решим уравнение х2 + 22 = х2 +2*1/2х + (1/2)2, х2 + 4 — х2 –х -1/4 =0, х=3 >¾. Ответ: глубина озера 3 3/4 фута.
5. Закрепление материала.
№559. (Один учащийся у доски самостоятельно решает, потом комментирует решение задачи, остальные решают на месте, проверяют решение)
Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.
Решение.
Второе число Произведение чисел
х
х + 6
187
Составим уравнение х(х+6)=187. Решим его: х2+6х-187=0. D=784, х=11, х=-17. Второй корень по смыслу задачи не подходит, т. к. даны натуральные числа. Значит меньшее число равно 11. Второе число равно 11+6=17. Ответ: 11 и 17.
к. даны натуральные числа. Значит меньшее число равно 11. Второе число равно 11+6=17. Ответ: 11 и 17.
№563. (Самостоятельная работа, с последующей проверкой)
Найдите катеты прямоугольного треугольника, если известно, что их сумма равна 23 см, а площадь данного треугольника равна 60 см2. Решение. (х(23-х)):2=60. D=49, х1=8, х2=15. Ответ: 8 и 15.
6. Итоги урока. Мы рассмотрели задачи, которые решаются с помощью квадратного уравнения, учились видеть связь между математикой и окружающей жизнью, использовали в решении знания геометрии и физики.
7. Домашнее задание. П.23, № 560, 564,569(старинная задача). Дополнительные задания: № 576, 557.
Индивидуальное задание: Брат и сестра собирали малину. Когда сестра собрала 2/3 своего двухлитрового бидона, трехлитровый бидон брата был почти полон. Ребята поменялись бидонами и через некоторое время одновременно закончили сбор ягод. Во сколько раз брат работал быстрее сестры?
Решение.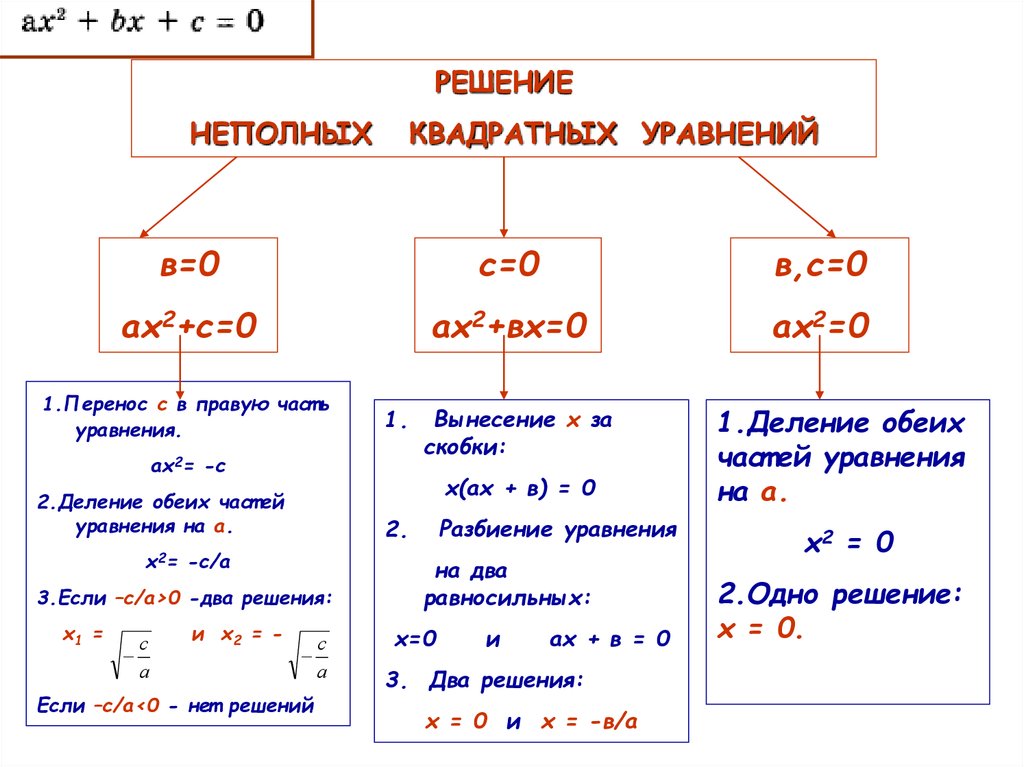 Сначала сестра собрала 2/3 * 2 = 4/3л малины. Пусть брат собрал в k раз больше (k>1), то есть 4/3k л. Потом сестра собрала 3 – 4/3k, а брат в k раз больше: 3k – 4/3k2, что составило 2 – 4/3 = 2/3 л. Составим уравнение
Сначала сестра собрала 2/3 * 2 = 4/3л малины. Пусть брат собрал в k раз больше (k>1), то есть 4/3k л. Потом сестра собрала 3 – 4/3k, а брат в k раз больше: 3k – 4/3k2, что составило 2 – 4/3 = 2/3 л. Составим уравнение
3k – 4/3k2 = 2/3,
Откуда k = 2 (k = ¼ не удовлетворяет условию k >1). То есть брат работает быстрее сестры в 2 раза. Ответ: в 2 раза.
Результативность урока: материал к уроку подбирался с учетом лекций А.В. Шевкина “Текстовые задачи в школьном курсе математики”, использовались его рекомендации. Урок прошел с хорошей результативностью. При изучении нового материала учащиеся практически самостоятельно решали предложенные задачи. Наблюдался хороший темп урока. Задачи, связанные с окружающей жизнью разнообразили стандартные задачи из учебника.
Биквадратные уравнения. Уравнения приводимые к квадратным
Вопросы занятия:
· повторить алгоритм решения уравнений, приводимых к квадратным;
· вспомнить, какие уравнения называются
биквадратными.
Материал урока
Мы уже с вами вспоминали, какие уравнения называются квадратными и как решать квадратные уравнения с помощью дискриминанта или теоремы Виета.
Также рассматривают так называемые биквадратные уравнения. Частичка би означает два, то есть биквадратное уравнение можно понимать, как квадратное в квадратном.
Звучит не очень понятно, но на самом деле – все просто.
Определение.
Биквадратным называется уравнение вида:
Обратите внимание, здесь переменная или выражение с переменной появляются только в четвертой и второй степени, это особенность таких уравнений.
Рассмотрим пример.
Пример.
Биквадратное уравнение введением новой переменной приводится к квадратному уравнению.
Решая
это уравнение, находим корни квадратного уравнения. Возвращаясь к замене, мы
получим в зависимости от корней квадратного уравнения или ни одного, или одно
или два квадратных уравнений. Решения этих уравнений и будут решениями
исходного биквадратного уравнения.
Решения этих уравнений и будут решениями
исходного биквадратного уравнения.
Теперь давайте вспомним, что:
Рассмотрим пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Пример.
Пример.
Рассмотрим ещё один пример.
Пример.
Итак, давайте теперь сформулируем алгоритм решения уравнений, сводящихся к квадратным в целом и решения биквадратных уравнений в частности.
Итоги урока.
Сегодня на уроке, мы рассмотрели алгоритм решения уравнений, приводимые к квадратным, вспомнили какие уравнения называются биквадратными. Рассмотрели несколько примеров.
Задание №9 ОГЭ по математике с решением
В девятом задании модуля алгебра ОГЭ по математике нам предлагают решить уравнения. Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными.
Это могут быть как линейные уравнения, которые решаются переносом всех известных членов в одну сторону, а неизвестных (x) в другую, так и квадратные уравнения, которые в свою очередь могут быть полными и неполными.
Судя по материалам ОГЭ и практике проведения экзамена, наиболее вероятным заданием может быть решение линейного или квадратного уравнения. Тем не менее мы рассмотрим задания по всей этой тематике. Сложность заданий как всегда возрастает от задания к заданию.
Ответом в задании №9 является целое число или конечная десятичная дробь.
Теория к заданию №9
Ниже я привел теорию по решениям линейных и квадратных уравнений:
Схема решения, правила и алгоритм действий при решении линейного уравнения:
Схема решения, правила и порядок действий при решении квадратного уравнения:
В трех типовых вариантах я разобрал данные случаи — в первом варианте вы найдете подробные указания по решению линейных уравнений, во втором разобран пример решения неполного квадратного уравнения, а в третьем — решение полного квадратного уравнения с вычислением дискриминанта.
Разбор типовых вариантов задания №9 ОГЭ по математике
Первый вариант задания (линейные уравнения)
Найдите корень уравнения:
10 ( x — 9 ) = 7
Решение:
Данное уравнение представляет собой обыкновенное уравнение первой степени и решается переносом всех известных частей в правую часть, оставив x слева.
Для начала следует раскрыть скобки: 10x — 90 = 7
Затем переносим 90 в правую часть (не забываем поменять знак):
10x = 7 + 90
10x = 97
Затем делим обе части на 10:
x = 9,7
Ответ: 9,7
Второй вариант задания (неполные квадратные уравнения)
Решите уравнение:
3 x² + 12 x = 0
Решение:
Это неполное квадратное уравнение, в котором не обязательно вычислять дискриминант, а достаточно вынести x за скобку:
x ( 3 x + 12 ) = 0
Произведение множителей тогда равно нулю, когда один из множителей равен нолю:
x = 0
или
3 x + 12 = 0
3 x = -12
x = -4
Так как в ответе просят указать наименьший корень, то это -4.
Ответ: -4
Третий вариант задания (квадратные уравнения)
Решите уравнение:
8 x² — 10x + 2 = 0
Решение:
Уравнение является полным квадратным уравнением, поэтому классическим вариантом решения является вычисление дискриминанта. Но в данном случае можно заметить, что все множители кратны двум, поэтому можно все уравнение разделить на 2 для удобства вычисления:
4 x² — 5x + 1 = 0
Далее вычисляем дискриминант:
D = b² — 4ac
D = 5² — 4 •4•1 = 9
Вычисляем корни:
x = (- b — √D) / 2a = (5 — 3 )/ 2 •4 = 0,25
x = (- b + √D) / 2a = (5 + 3 )/ 2 •4 = 1
Так как нам нужно выбрать меньший из корней по условию, то выбираем 0,25
Ответ: 0,25
Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)
Решите уравнение:
7х — 9 = 40
Решение:
В данной задаче нам предстоит решить линейное уравнение. Подход к решению таких уравнений достаточно простой — всё, что известно переносим в правую часть, всё, что неизвестно — оставляем в левой.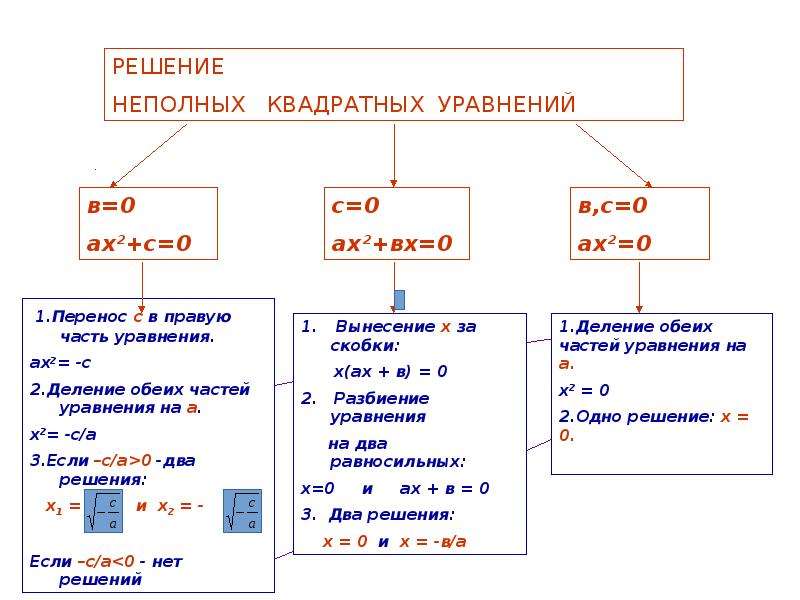 Далее выполняем необходимое арифметическое действие.
Далее выполняем необходимое арифметическое действие.
Решение:
7х — 9 = 40
Переносим 9 в правую часть (не забываем про смену знака):
7х = 40 + 9, что эквивалентно
7х = 49
х в нашем случае — это неизвестный множитель, следовательно, чтобы его найти, делим произведение на известный множитель:
х = 49/7, откуда
х = 7
Ответ: 7
Пятый вариант задания (рациональные уравнения)
Найдите корень уравнения:
Решение:
Прежде всего, исключим корень, который не входит в ОДЗ:
x+6≠0 → х≠–6
Далее решаем уравнение.
Представляем число 2 в уравнении справа в виде дроби 2/1. Уравнение получает вид пропорции:
Применим правило пропорции. Перемножим между собой крайние ее члены и средние:
1·1=(х+6)·2
Выполним умножение в левой части уравнения и раскроем скобки справа:
1=2х+12
Поменяем местами левую и правую части уравнения, чтобы оно приняло привычный вид:
2х+12=1
Переносим 12 из левой части в правую:
2х=1–12
2х=–11
Находим корень:
х=–11/2=–5,5
ОДЗ это значение не исключает, поэтому оно является искомым результатом.
Ответ: –5,5
Шестой вариант задания(рациональные уравнения)
Найдите корень уравнения:
Решение:
Обе части уравнения приводим к единому знаменателю 12:
Т.к. знаменатели в левой и правой частях уравнения одинаковы, не равны нулю и не содержат переменных, то их можно сократить (т.е. ими можно пренебречь). Тогда получаем:
11х=44
х=44:11
х=4
Ответ: 4
Неполные квадратные уравнения | Алгебра
Как решать неполные квадратные уравнения? Решение и количество корней зависят от вида уравнения.
Неполные квадратные уравнения бывают трёх видов.
Повторим теорию и рассмотрим примеры решения неполных квадратных уравнений каждого вида.
I. Неполные квадратные уравнения, к которых коэффициент c=0, то есть уравнение имеет вид ax²+bx=0.
Такие уравнения решаются разложением левой части уравнения на множители.
Общий множитель x выносим за скобки:
Это уравнение — типа «произведение равно нулю«. Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Второе уравнение — линейное. Решаем его:
Таким образом, неполное квадратное уравнение вида ax²+bx=0 имеет 2 корня,один из которых равен нулю, а второй — -b/a.
Примеры.
Общий множитель x выносим за скобки:
Это уравнение типа «произведение равно нулю». Произведение равно нулю, если хотя бы один из множителей равен нулю. Приравниваем к нулю каждый из множителей:
Ответ: 0; -18.
Общий множитель 5x выносим за скобки:
Приравниваем к нулю каждый множитель:
Ответ: 0; 3.
II. Неполные квадратные уравнения, к которых коэффициент b=0, то есть уравнение имеет вид ax²+c=0 (или ax²-c=0).
Неполное квадратное уравнение такого вида либо имеет два корня, которые отличаются только знаками (являются противоположными числами), либо не имеет корней.
1. Если знаки a и c — разные, уравнение имеет два корня.
В курсе алгебры 7 класса такие уравнения решают разложением левой части на множители по формуле разности квадратов (поскольку квадратные корни начинают учить только в курсе 8 класса, коэффициенты a и c в 7 классе обычно являются квадратами некоторых рациональных чисел):
Уравнение типа «произведение равно нулю». Приравниваем к нулю каждый из множителей:
Раскладываем левую часть уравнения по формуле разности квадратов:
Это уравнение — типа «произведение равно нулю». приравниваем к нулю каждый множитель:
Ответ: 7; -7.
Ответ: 2,25; -2,25.
2. Если знаки a и c — одинаковые, уравнение не имеет корней.
Корней нет, так как сумма положительных чисел не может равняться нулю.
Ответ: нет корней.
Корней нет, так как сумма отрицательных чисел не может равняться нулю.
Ответ: нет корней.
В курсе алгебры 8 класса, после изучения квадратных корней, эти уравнения обычно решают приводя к виду x²=d:
Примеры.
Ответ:±2.
Чтобы избавиться от иррациональности в знаменателе, умножаем и числитель, и знаменатель на √11:
Ответ:
Корней нет, так как квадратный корень не может равняться отрицательному числу.
Ответ: нет корней.
Нет корней, так как квадратный корень не может быть равным отрицательному числу.
Ответ: нет корней.
III. Неполные уравнения, в которых коэффициенты b=0 и c=0, то есть уравнение имеет вид ax²=0.
Уравнение такого рода имеет единственный корень x=0
В некоторых учебниках считается, что уравнение имеет два одинаковых корня, каждый из которых равен нулю:
Примеры.
Ответ: 0.
Ответ: 0.
Ответ: 0.
В следующий раз рассмотрим примеры решения полных квадратных уравнений.
Квадратные уравнения и уравнения, приводящиеся к квадратным. Мини-курс. 9 видео уроков. — Math
Квадратные уравнения. Какое квадратное уравнение называется полным? Формула дискриминанта и корней полного квадратного уравнения. Уравнения с дробями. Как избавиться от всех знаменателей сразу. Алгебра 8 класс. Примеры с решением и объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
#116 Урок 2.
 Неполные квадратные уравнения. Решение через дискриминант. Алгебра 8 класс.Математика.
Неполные квадратные уравнения. Решение через дискриминант. Алгебра 8 класс.Математика.Квадратные уравнения. Какое квадратное уравнение называется полным? Какое квадратное уравнение называется неполным? Формула дискриминанта и корней полного квадратного уравнения. Как решать неполное квадратное уравнение через дискриминант. Алгебра 8 класс. Примеры с решением и объяснением.
#117 Урок 3. Квадратные уравнения. Текстовые задачи. Алгебра 8 класс.
Решение текстовых задач составлением квадратного уравнения. Алгебра 8 класс. Примеры с решением.
- Пример 1: Найдите три последовательных целых числа, если удвоенный квадрат первого из них на 26 больше произведения второго и третьего чисел.
- Пример 2: Найдите четыре последовательных четных числа, если утроенное произведение второго и третьего чисел на 344 больше произведения первого и четвертого.

- Пример 3: Найдите стороны прямоугольника, если их разность равна 23 дм, а диагональ 37 дм.
- Пример 4: Сколько сторон имеет многоугольник, если в нем можно провести 77 диагоналей.
Задачи с объяснением. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
#118 Урок 4 Квадратные уравнения. Параметры. При каком значении параметра уравнение имеет 1 корень.Квадратные уравнения. Параметры. Алгебра 8 класс. Что такое параметр? Понятие параметра в математике. Определение параметра: Если в уравнение или неравенство наряду с неизвестной величиной входят неизвестные, но фиксированные числа, обозначаемые буквами, то они называются параметрами. Пример: 10х2 +4х+b=0; х — переменная; b — параметр; В уравнениях (неравенствах) коэффициенты при неизвестных или свободные члены заданные не конкретными числовыми значениями, а обозначенные буквами называются параметрами. Примеры с решением и объяснением.
Примеры с решением и объяснением.
- Пример 1: При каком значении а, число 1/3 является корнем уравнения…?
- Пример 2: При каком значении b имеет единственный корень уравнение? Условие единственности корня. Видеоуроки по математике. Устранение пробелов в знаниях. Подготовка к ЗНО ( ВНО ) по математике. Подготовка к ЕГЭ, ДПА ( ГИА ), ОГЭ по математике.
#119 Урок 5. Параметры. Решение квадратных уравнений с параметрами. Алгебра 8 класс. Математика.
Параметры. Решение квадратных уравнений с параметрами. Алгебра 8 класс. Квадратные уравнения. Примеры с решением и объяснением.
- Пример 1: Решить квадратное уравнение с параметром, если коэффициент при х2 фиксированное число.
- Пример 2: Решить квадратное уравнение с параметром, если коэффициент при х2 записано с использованием параметра.
youtube.com/embed/_G0_KXBP6Ss» frameborder=»0″ allowfullscreen=»allowfullscreen»/>
#120 Урок 6. Квадратные уравнения с модулем. Алгебра 8 класс. Решить уравнение. Модуль. Математика.Решение квадратных уравнений с модулем. Алгебра 8 класс. Примеры с решением.
- Пример 1: Решить квадратное уравнение с модулем, раскрыв модуль по определению.
- Пример 2: Решить квадратное уравнение с модулем, раскрыв модуль, используя свойства модуля.
Квадратные уравнения с модулем 8 класс; квадратное уравнение под модулем; квадратные уравнения с модулем примеры; решение квадратных уравнений с модулем 8 класс; квадратные уравнения с модулем примеры решения; решение квадратных уравнений содержащих модуль; как раскрыть модуль квадратного уравнения. Как решать квадратное уравнение с модулем. Как раскрыть модуль, используя его определение. Определение модуля. Свойства модуля. Решить квадратное уравнение. Решить через дискриминант. Сделать проверку. Посторонние корни. Как убрать посторонние корни. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика. Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.
Посторонние корни. Как убрать посторонние корни. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика. Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.
#121 Урок 7. Решение квадратных уравнений с использованием свойств функций. Алгебра 8 класс.
Квадратные уравнения. Использование свойств функций для решения квадратных уравнений. Оценка левой и правой частей уравнения. Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Примеры с решением.
- Пример 1: Решить иррациональное уравнение, приводящееся к квадратному, используя свойства функций.
- Пример 2: Решить уравнение, преобразовав условие по формулам сокращенного умножения и оценив левую и правую части уравнения.

- Пример 3: Решить уравнение с корнем и модулем.
#122 Урок 8. Решение квадратных уравнений с учетом ОДЗ. Область определения. Алгебра 8 класс.
Область определения функции, 4 случая: многочлен, дробь, квадратный корень и квадратные корень в знаменателе. ОДЗ дроби. ОДЗ корня. ОДЗ уравнения. Область определения квадратного корня. Область определения квадратного дроби. Область определения квадратного корня в знаменателе. Что такое область определения. Область определения теория. Область определения, табличка. Примеры с решением. Алгебра 8 класс. Решить квадратное уравнение с учетом ОДЗ. ОДЗ квадратного уравнения; как найти одз в квадратном уравнении; одз корня квадратного уравнения; 2 квадратных уравнения; решение квадратных уравнений; произведение квадратных уравнений; 3 квадратных уравнения. Математика. Образование. Подготовка к егэ, егэ математика, видео уроки, подготовка к зно, вно математика.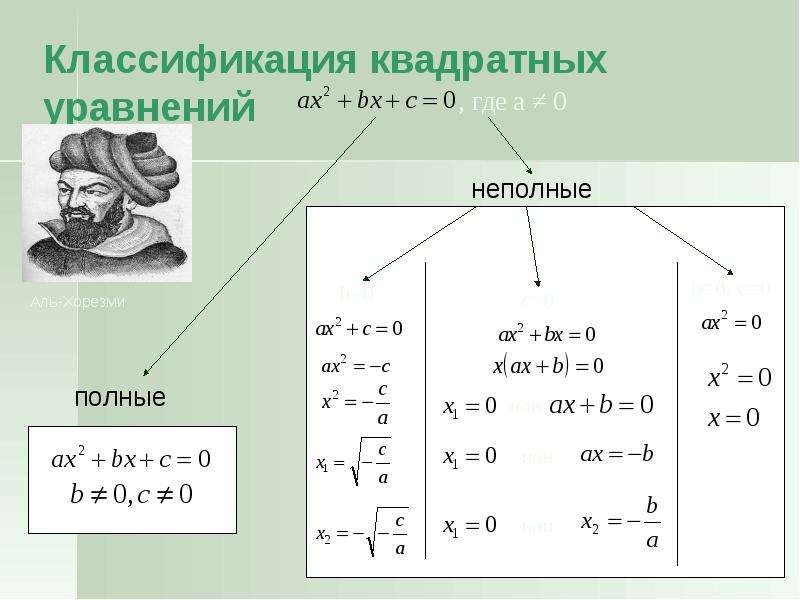 Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.
Видео уроки алгебра, алгебра видеоуроки, онлайн урок, математика видео уроки, онлайн урок, инфо урок, огэ, огэ математика. Дистанционное обучение.
#62 Урок 9. Решение квадратных и кубических уравнений разложением на множители.
Как решить квадратное или кубическое уравнение, разложив его на множители?
Общий алгоритм:
- Разложить на множители (вынести общий множитель за скобки, посмотреть формулы, посмотреть способ группировки).
- Приравнять каждый множитель к нулю.
- Решить полученные уравнения.
Формулы сокращенного умножения. Разность квадратов, разность кубов, квадрат разности.Примеры с решением. Решение кубических уравнений. Уравнение четвертой степени. Как решить уравнение?
- Пример 1: Решить кубическое уравнение разложением на множители.
- Пример 2: Решить кубическое уравнение, используя формулы сокращенного умножения.

- Пример 3: Решить кубическое уравнение, используя способ группировки.
- Пример 4: Решить уравнение 4-й степени разложением на множители.
Полезные материалы:
Арифметический квадратный корень. Мини-курс. Уроки 1-5.
Мини-курс. Рациональные дроби. Алгебра 7-8 класс.
Решение текстовых задач с помощью квадратных уравнений алгоритм и примеры
Алгоритм решения текстовых задач с помощью квадратных уравнений
Шаг 1. Проанализировать условие задачи, обозначить одно из неизвестных буквой (переменной). Если это удобно, обозначить все неизвестные разными буквами и выбрать «основную» переменную.
Шаг 2. Выразить другие неизвестные через основную переменную.
Шаг 3. Записать уравнение.
Шаг 4. Решить полученное уравнение.
Шаг 5. 2 $$
2 $$
$$ t = \frac{23 \pm 37}{12} = \left[ \begin{array}{cc} t_1 = — \frac{7}{6} \lt 0 \\ t_2 = 5 \end{array} \right. $$
Выбираем положительный корень t = 5.
Первая труба наполняет бассейн за 5 часов.
Вторая труба – на 2 часа дольше, т.е. за 7 часов.
Ответ: 5 ч и 7 ч
Пример 8*. Катер проплыл по течению 90 км за некоторое время. За то же время он бы проплыл против течения 70 км. Какое расстояние за это же время проплывёт плот?
Пусть v – собственная скорость катера, u — скорость течения (и плота), s — искомое расстояние, которое проплывёт плот.
Заполним таблицу:
Скорость, км/ч
Расстояние, км
Катер по течению
Катер против течения
По условию все три времени равны:
$$ \frac{90}{v+u} = \frac{70}{v-u} = \frac{s}{u} $$
Из первого уравнения:
$$ 90(v-u) = 70(v+u) \Rightarrow 90v-90u = 70v+70u \Rightarrow 20v = 160u \Rightarrow v = 8u $$
Скорость катера в 8 раз больше скорости течения. {2} — 6а & = 0 \\
3а(3а — 2) & = 0 \\
3а & = 0 \\
а & = 0 \\
\текст{или} & \\
3а — 2&=0\
а & = \ гидроразрыва {2} {3} \\
\следовательно, a = 0 & \text{ или } a = \frac{2}{3}
\конец{выравнивание*}
{2} — 6а & = 0 \\
3а(3а — 2) & = 0 \\
3а & = 0 \\
а & = 0 \\
\текст{или} & \\
3а — 2&=0\
а & = \ гидроразрыва {2} {3} \\
\следовательно, a = 0 & \text{ или } a = \frac{2}{3}
\конец{выравнивание*}
Страница не найдена | ZNNHS
Страница не найдена | ЗННХС | Официальный сайт Этот веб-сайт соответствует Руководству по обеспечению доступности веб-контента (WCAG 2.0) в качестве стандарта доступности для всех связанных с ним веб-разработок и услуг. WCAG 2.0 также является международным стандартом ISO 40500. Это подтверждает, что он является стабильным техническим стандартом, на который можно ссылаться. WCAG 2.0 содержит 12 руководств, организованных по 4 принципам: Воспринимаемый, Удобный, Понимаемый и Надежный (сокращенно POUR). Для каждого руководства есть проверяемые критерии успеха. Соответствие этим критериям измеряется тремя уровнями: A, AA или AAA. Руководство по пониманию и внедрению рекомендаций по обеспечению доступности веб-контента 2.0 доступен по адресу: https://www.w3.org/TR/UNDERSTANDING-WCAG20/ Специальные возможности Комбинация клавиш быстрого доступа Комбинация клавиш, используемая для каждого браузера. Chrome для Linux нажмите (Alt+Shift+shortcut_key)
Chrome для Windows нажмите (Alt+shortcut_key)
Для Firefox нажмите (Alt+Shift+shortcut_key)
Для Internet Explorer нажмите (Alt+Shift+shortcut_key), затем нажмите (ввод)
В Mac OS нажмите (Ctrl+Opt+shortcut_key) Заявление о специальных возможностях (комбинация + 0): страница заявления, на которой будут показаны доступные ключи специальных возможностей.Домашняя страница (комбинация + H): ключ доступа для перенаправления на домашнюю страницу.
Основной контент (комбинация + R): ярлык для просмотра раздела контента текущей страницы.
Часто задаваемые вопросы (комбинация + Q): Ярлык для страницы часто задаваемых вопросов.
Для каждого руководства есть проверяемые критерии успеха. Соответствие этим критериям измеряется тремя уровнями: A, AA или AAA. Руководство по пониманию и внедрению рекомендаций по обеспечению доступности веб-контента 2.0 доступен по адресу: https://www.w3.org/TR/UNDERSTANDING-WCAG20/ Специальные возможности Комбинация клавиш быстрого доступа Комбинация клавиш, используемая для каждого браузера. Chrome для Linux нажмите (Alt+Shift+shortcut_key)
Chrome для Windows нажмите (Alt+shortcut_key)
Для Firefox нажмите (Alt+Shift+shortcut_key)
Для Internet Explorer нажмите (Alt+Shift+shortcut_key), затем нажмите (ввод)
В Mac OS нажмите (Ctrl+Opt+shortcut_key) Заявление о специальных возможностях (комбинация + 0): страница заявления, на которой будут показаны доступные ключи специальных возможностей.Домашняя страница (комбинация + H): ключ доступа для перенаправления на домашнюю страницу.
Основной контент (комбинация + R): ярлык для просмотра раздела контента текущей страницы.
Часто задаваемые вопросы (комбинация + Q): Ярлык для страницы часто задаваемых вопросов. Контакт (комбинация + C): ярлык для контактной страницы или формы запросов.
Обратная связь (комбинация + K): ярлык для страницы обратной связи.
Карта сайта (комбинация + M): Ярлык для раздела карты сайта (футера агентства) на странице.
Поиск (Комбинация + S): Ярлык для страницы поиска. Нажмите клавишу esc или нажмите кнопку закрытия, чтобы закрыть это диалоговое окно.×
Контакт (комбинация + C): ярлык для контактной страницы или формы запросов.
Обратная связь (комбинация + K): ярлык для страницы обратной связи.
Карта сайта (комбинация + M): Ярлык для раздела карты сайта (футера агентства) на странице.
Поиск (Комбинация + S): Ярлык для страницы поиска. Нажмите клавишу esc или нажмите кнопку закрытия, чтобы закрыть это диалоговое окно.×
Возможно, запрошенная вами страница была перемещена в новое место или удалена с сайта.
Вернитесь на ДОМАШНЮЮ СТРАНИЦУ или найдите то, что вы ищете, в поле поиска ниже.
ОСНОВНОЙ ПОМЕЩЕНИЕ: Улица Генерала Луна, Эстака, город Диполог 7100 | (065)212-3604 © Городское отделение Диполог, 2019. 2}+bx+c\).Для всех других методов факторинга, таких как: 2}+bx+c\).Для всех других методов факторинга, таких как:
Пожалуйста, посетите Математическая алгебра для 9 класса – Методы факторизации. Предполагаемые знанияУчащиеся должны быть знакомы с основными алгебраическими методами, включая расширение специальных биномиальных произведений и простую арифметику. Также потребуется знание методов факторизации.2}+bx+c=0\) может иметь до двух действительных решений. Когда мы «решаем» квадратное уравнение, мы ищем значения \(x\), которые делают уравнение верным. Из основ арифметики мы знаем, что если произведение двух чисел равно нулю, то хотя бы одно из чисел должно быть равно нулю.
|
Каждая квадратичная форма выглядит уникально, что позволяет легче решать различные задачи в одной форме, чем в другой. Мы раскроем особенности каждой формы и способы переключения между формами.
Вернуться к оглавлению
Почему существуют формы квадратных уравнений?
Каждая форма квадратного уравнения имеет определенные преимущества. Признание преимуществ каждой отдельной формы может облегчить понимание и решение различных ситуаций.2+bx+c
Признание преимуществ каждой отдельной формы может облегчить понимание и решение различных ситуаций.2+bx+c
Преимущества стандартной формы включают быстрое определение конечного поведения функции и определение значений a, b и c.
Конечное поведение функции определяется старшим коэффициентом и степенью функции. Степень квадратного уравнения всегда равна двум. Старший коэффициент квадратного уравнения всегда представляет собой член а, если он записан в стандартной форме.
Если значение a положительное, парабола раскрывается, то есть функция поднимается влево и поднимается вправо.2+2х+1
Уведомление : отрицательное значение, степень 2, парабола открывается «вниз»
Одним из способов решения квадратного уравнения является использование квадратной формулы . Для этого мы должны определить значения a, b и c. Чтобы узнать больше об этом, прочитайте нашу подробную обзорную статью о квадратичной формуле.
О чем говорит
факторизованная форма квадратичного числа ?Теперь давайте рассмотрим, почему факторизованная форма полезна.Чтобы получить факторизованную форму, мы делаем именно то, на что это похоже: мы факторизуем уравнение из стандартной формы.
| Факторизованная форма квадратного уравнения : y=a(x-r_1)(x-r_2) |
В факторизованной форме квадратного уравнения мы также можем определить конечное поведение, используя значение а. Хотя степень не так легко определить, мы знаем, что есть только два фактора, делающих степень второй. Конечное поведение следует тем же правилам, которые описаны выше.
Дополнительным преимуществом факторизованной формы является идентификация нулей или пересечений x функции. Значение r_1 и значение r_2 оба являются нулями (также называемыми «решениями») квадратичной функции.
у= — (х + 2)(х — 3)
Нули: x = -2 \text{ и } x= 3
Следует отметить, что не все квадратичные уравнения имеют «действительные» нули (некоторые квадратичные уравнения требуют в качестве нулей мнимых чисел), поэтому факторизованная форма не всегда применима. 2+7х-9
2+7х-9
… имеет стандартную форму и говорит нам, что a=3, b=7 и c=-9.
Что такое факторизованная форма квадратного числа?| Факторизованная форма квадратного уравнения: y=a(x-r_1)(x-r_2) |
В факторизованная форма , мы являются r_1 и r_2. Нашими переменными остаются x и y, а a — коэффициент.
В уравнении в факторизованной форме:
у=3(х+8)(х-6)
…две точки пересечения по оси x равны -8 и 6, а значение a равно 3.2+16
…который находится в форме вершины, вершина (2,16) и значение a равно -2.
Преобразование между формами квадратных уравнений
Часто нам нужно много разной информации о квадратных уравнениях. Может быть полезно увидеть одно и то же квадратное уравнение в нескольких формах. Точно так же, как хамелеон может менять цвет в различных ситуациях, мы можем изменять формы квадратичных уравнений в соответствии со своими потребностями.
Меняй формы квадратика как хамелеон!
Способность быстро и точно переключаться между формами позволяет нам хорошо понимать квадратное уравнение и легко находить необходимую информацию.2+5х-24. Давайте вспомним, как выглядит Factored Form:
.| Факторизованная форма квадратного уравнения : y=a(x-r_1)(x-r_2) |
сумма 5. Мы можем перечислить множители -24 и их суммы:
| факторы | сумма факторов | |
|---|---|---|
| -24 и 1 | -24 + 1 = -23 | |
| -1 и 24 | -1 + 24 = 23 | |
| -12 и 2 | -12 + 2 = -10 | |
| -2 и 12 | -2 и 12 | -2 + 12 = 10 |
| -6 и 4 | -6 + 4 = -2 | |
| -4 и 6 | -4 + 6 = 2 | |
| -8 и 3 | -8 + 3 = -5 | |
| -3 и 8 | -3 + 8 = 5 |
Два значения, которые умножаются на -24 и имеют в сумме 5, это -3 и 8. 2+5х-24
2+5х-24
у=(х-3)(х+8)
Для определения нулей приравняем уравнение к нулю . Затем мы можем решить, установив каждый фактор равным нулю:
(х-3)(х+8)=0
Следовательно, нули функции равны 3 и -8. Окончательная факторизованная форма уравнения:
у=(х-3)(х+8)
Чтобы узнать больше об этом подходе, прочитайте нашу статью о решении квадратных уравнений с помощью факторизации.
Вернуться к оглавлению
Преобразовать стандартную форму в вершинную форму
Вместо нулей у нас могут спросить вершину квадратного уравнения.2+6x-5
…которое задано в стандартной форме, и определить вершину уравнения. Для этого мы преобразуем это в вершинную форму.
Чтобы преобразовать в вершинную форму, мы должны выполнить процесс, называемый «завершением квадрата». По сути, мы создаем трехчлен, который мы можем разложить на идеальный квадрат.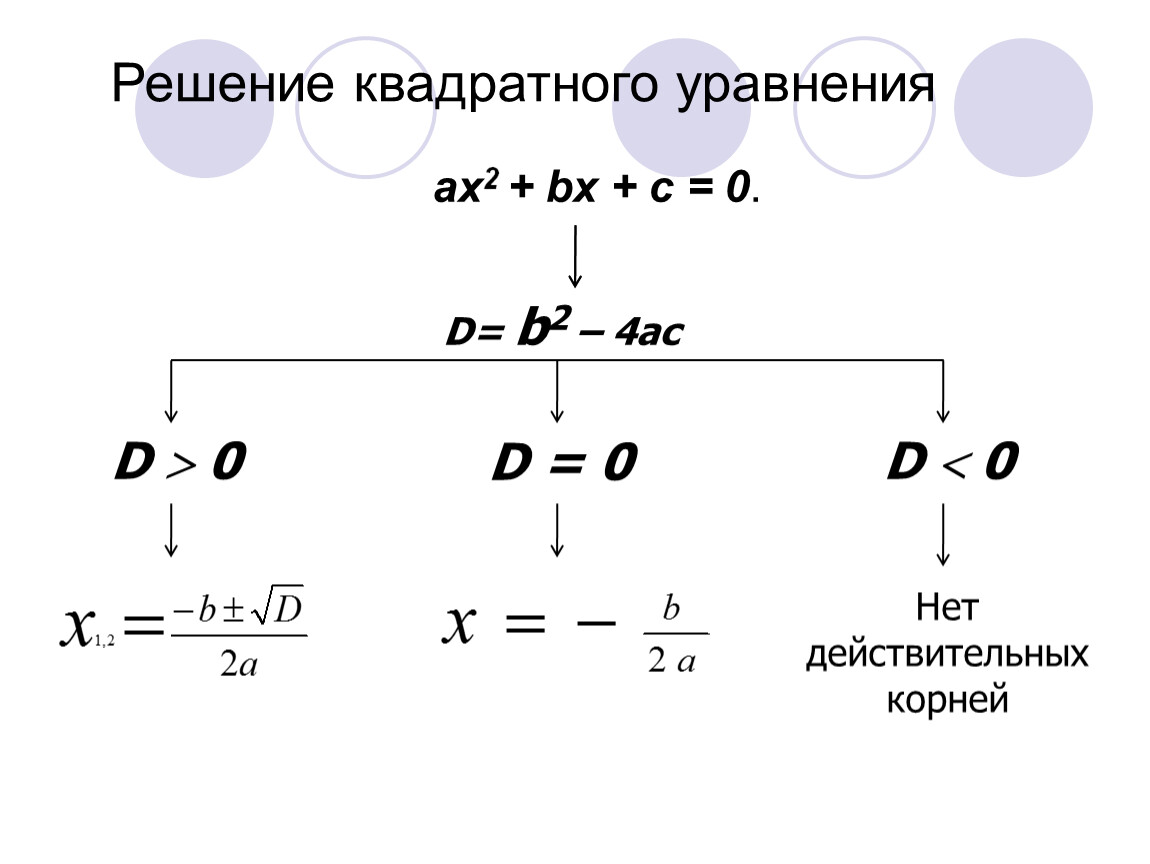 2.2-14
2.2-14
Преобразование из квадратичной формы в стандартную форму довольно распространено, поэтому вы также можете посмотреть это полезное видео для другого примера.
Вернуться к оглавлению
Преобразование факторизованной формы в стандартную форму
Чтобы преобразовать уравнение из факторизованной формы в стандартную форму, нужно просто перемножить коэффициенты. Например, изменим квадратное уравнение:
у=(3х-2)(-х+7)
…в стандартную форму.2+28х+88.
Вернуться к оглавлению
Свободная практика с формами квадратичных чисел
Чтобы получить ответы на некоторые бесплатные практические вопросы по формам квадратичных уравнений, ознакомьтесь с практическим курсом Альберта по алгебре 1! Все вопросы Альберта включают объяснения решений и способы избежать распространенных ошибок.
Кроме того, лицензированные преподаватели Альберта могут назначить учащимся этот короткий тематический тест по алгебре 1, посвященный вершинам, корням и различным формам квадратичных уравнений.
Наконец, ознакомьтесь с другими нашими подробными обзорными руководствами по алгебре 1, чтобы узнать больше о квадратичных вычислениях.
Возраст и числа — Алгебра среднего уровня
Квадратичные текстовые задачи — это третий тип текстовых задач, охватываемых MATQ 1099, причем первый представляет собой линейные уравнения с одной переменной, а второй — линейные уравнения с двумя или более переменными. Квадратные уравнения можно использовать в тех же типах текстовых задач, с которыми вы сталкивались ранее, за исключением того, что при работе с заданными данными вы в конечном итоге построите квадратное уравнение.Чтобы найти решение, вам потребуется либо факторизовать квадратное уравнение, либо использовать подстановку.
Сумма двух чисел равна 18, а произведение этих двух чисел равно 56. Что это за числа?
Во-первых, мы знаем две вещи:
Замена во втором уравнении дает:
Умножение дает:
Что переставляется на:
Во-вторых, разложите это квадратичное число, чтобы получить наше решение:
Следовательно:
Разность квадратов двух последовательных четных целых чисел равна 68. Что это за числа?
Что это за числа?
Переменные, используемые для двух последовательных целых чисел (четных или нечетных), это и . Уравнение, используемое для решения этой задачи, таково. Упрощение дает:
Это означает, что два целых числа равны 16 и 18.
Произведение возрастов Салли и Джоуи теперь на 175 больше, чем произведение их возрастов пятью годами ранее. Если Салли на 20 лет старше Джоуи, каков их нынешний возраст?
Уравнения:
Замена S дает нам:
Это означает, что Джоуи 10 лет, а Салли 30 лет.
Для вопросов с 1 по 12 напишите и решите уравнение, описывающее взаимосвязь.
- Сумма двух чисел равна 22, а произведение этих двух чисел равно 120. Что это за числа?
- Разность двух чисел равна 4, а произведение этих двух чисел равно 140. Что это за числа?
- Разность двух чисел равна 8, а сумма квадратов этих двух чисел равна 320. Что это за числа?
- Сумма квадратов двух последовательных четных целых чисел равна 244.
 Что это за числа?
Что это за числа? - Разница квадратов двух последовательных четных целых чисел равна 60. Что это за числа?
- Сумма квадратов двух последовательных четных целых чисел равна 452. Что это за числа?
- Найдите три последовательных четных числа, произведение первых двух на 38 больше, чем произведение третьего числа.
- Найдите три последовательных нечетных числа, произведение первых двух которых на 52 больше, чем произведение третьего числа.
- Произведение возрастов Алана и Терри на 80 больше, чем произведение их возрастов 4 года назад.Если Алан на 4 года старше Терри, каков их текущий возраст?
- Произведение возрастов Кэлли и Кэти на 130 меньше, чем произведение их возрастов через 5 лет. Если Кэлли на 3 года старше Кэти, каков их текущий возраст?
- Произведение возраста Джеймса и Сьюзен через 5 лет на 230 больше, чем произведение их возраста сегодня. Каков их возраст, если Джеймс на год старше Сьюзен?
- Произведение возрастов (в днях) двух новорожденных младенцев Симрана и Джесси через два дня будет на 48 больше, чем произведение их сегодняшних возрастов.
 Сколько лет малышам, если Джесси на 2 дня старше Симрана?
Сколько лет малышам, если Джесси на 2 дня старше Симрана?
Вопросы
Для вопросов с 13 по 20 напишите и решите уравнение, описывающее взаимосвязь.
- Поезд проехал 240 км с определенной скоростью. При замене двигателя на усовершенствованную модель скорость увеличилась на 20 км/ч, а время в пути на рейс сократилось на 1 час. Какова была скорость каждого двигателя?
- Мистер Джонс регулярно навещает свою бабушку, которая живет в 100 км от него.Недавно открылась новая автострада, и, хотя длина автострады составляет 120 км, он может ехать в среднем на 20 км/ч быстрее и тратит на поездку на 30 минут меньше времени. Какова скорость мистера Джонса как на старом маршруте, так и на автостраде?
- Если бы велосипедист ехал на 5 км/ч быстрее, ему потребовалось бы на 1,5 часа меньше времени, чтобы проехать 150 км. Найдите скорость велосипедиста.
- Если бы транзитный автобус двигался на 15 км в час быстрее, ему потребовалось бы на 1 час меньше, чтобы проехать 180 км.
 Какова была средняя скорость этого автобуса?
Какова была средняя скорость этого автобуса? - Велосипедист едет в хижину в 72 км вверх по долине и возвращается через 9 часов.Его скорость возвращения на 12 км/ч больше, чем его скорость движения. Найдите его скорость как на пути, так и на обратном пути.
- Велосипедист проехал 120 км и вернулся через 7 часов. На обратном пути скорость увеличилась на 10 км/ч. Найдите скорость этого велосипедиста, движущегося в обе стороны.
- Расстояние между двумя автовокзалами 240 км. Если скорость автобуса увеличить на 36 км/ч, то поездка займет на 1,5 часа меньше. Какова обычная скорость автобуса?
- Пилот пролетел с постоянной скоростью 600 км.Вернувшись на следующий день, летчик летел против встречного ветра со скоростью 50 км/ч, чтобы вернуться в исходную точку. Если самолет находился в воздухе всего 7 часов, какова была средняя скорость этого самолета?
Найдите длину и ширину прямоугольника, длина которого на 5 см больше ширины, а площадь равна 50 см 2 .
Во-первых, площадь этого прямоугольника определяется как , что означает, что для этого прямоугольника , или .
Умножение этого дает нам:
Что переставляется на:
Во-вторых, мы факторизуем этот квадрат, чтобы получить наше решение:
Отклоняем решение.
Это означает, что .
Если длину каждой стороны квадрата увеличить на 6, площадь умножится на 16. Найдите длину одной стороны исходного квадрата.
Необходимо учитывать две площади: площадь меньшего квадрата, равная , и площадь большего квадрата, равная .
Связь между этими двумя:
Упрощение дает:
Поскольку это задача, требующая разложения на множители, проще всего использовать квадратное уравнение:
Подстановка этих значений в yields или (reject).
Ник и Хлоя хотят окружить свою свадебную фотографию 60 на 80 см рогожей одинаковой ширины.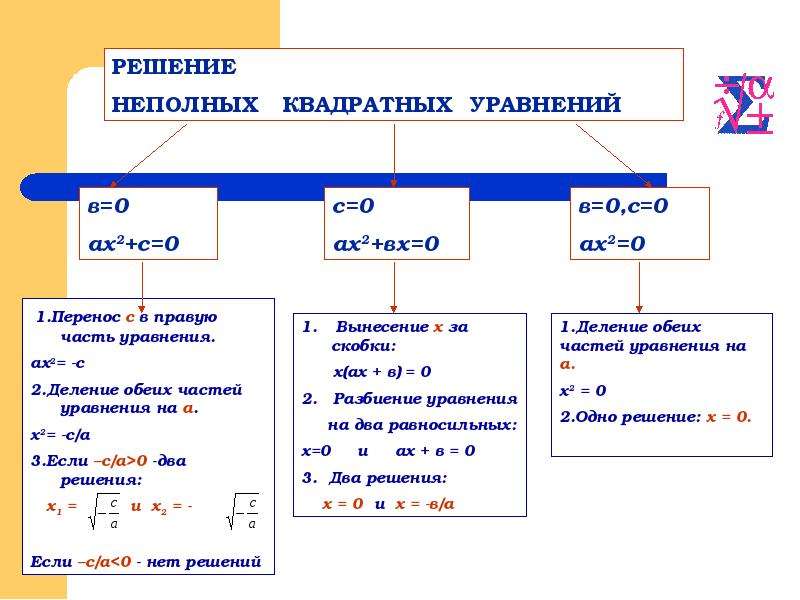 Полученное фото и паспарту накрыть 1 м 2 листом дорогого архивного стекла. Найдите ширину коврика.
Полученное фото и паспарту накрыть 1 м 2 листом дорогого архивного стекла. Найдите ширину коврика.
Во-первых, площадь этого прямоугольника определяется как , что означает, что для этого прямоугольника:
или в см:
Умножение этого дает нам:
Что переставляется на:
Что сокращается до:
Во-вторых, мы факторизуем этот квадрат, чтобы получить наше решение.
Легче всего использовать квадратное уравнение, чтобы найти наши решения.
Подстановка значений в yields:
Вопросы
Для вопросов с 21 по 28 напишите и решите уравнение, описывающее взаимосвязь.
- Найдите длину и ширину прямоугольника, длина которого на 4 см больше ширины, а площадь равна 60 см 2 .
- Найдите длину и ширину прямоугольника, ширина которого на 10 см меньше длины, а площадь равна 200 см 2 .

- Большой прямоугольный сад в парке шириной 120 м и длиной 150 м. Призван подрядчик, чтобы добавить кирпичную дорожку вокруг этого сада. Если площадь дорожки 2800 м 2 , то какой ширины дорожка?
- Парковый бассейн шириной 10 м и длиной 25 м. Покрытие для бассейна покупается для покрытия бассейна, перекрывая все 4 стороны на одинаковую ширину. Если площадь покрытия за пределами бассейна составляет 74 м 2 , насколько широка площадь перекрытия?
- В ландшафтном плане прямоугольная клумба запроектирована так, чтобы ее длина была на 4 м больше ширины.Если для растений на грядке необходимо 60 м 2 , то какими должны быть размеры прямоугольной грядки?
- Если сторона квадрата увеличивается на 5 единиц, площадь увеличивается на 4 квадратных единицы. Найдите длину сторон исходного квадрата.
- Участок прямоугольной формы имеет длину на 20 м больше ширины и площадь 2400 м 2 . Найдите размеры участка.
- Длина комнаты на 8 м больше ее ширины.
 Если и длину, и ширину увеличить на 2 м, площадь увеличится на 60 м 2 .Найдите размеры комнаты.
Если и длину, и ширину увеличить на 2 м, площадь увеличится на 60 м 2 .Найдите размеры комнаты.
Объяснение урока: Применение квадратных уравнений
В этом объяснении мы научимся решать текстовые задачи, формируя и решая квадратные уравнения.
Время от времени нам будет даваться задача составить и решить квадратные уравнения на основе по реальному сценарию. Довольно часто это будут проблемы, связанные с площадью и поиск неизвестных длин или любого другого поля, в котором появляются квадратные уравнения.
Стандартный подход к этим вопросам заключается в извлечении ключевой информации
из вопроса и используйте это, чтобы составить уравнение, которое затем можно решить
используя стандартные методы. Чтобы продемонстрировать это, мы рассмотрим ряд
примеры, внимательно рассматривая каждый из шагов, необходимых для достижения решения.
Пример 1. Нахождение периметра прямоугольника по его площади и разнице между Его размеры
Чему равен периметр прямоугольника, длина которого на 7 см больше, чем его ширина и площадь которого 78 см 2 ?
Ответ
Для начала может быть полезно нарисовать схему, представляющую сценарий описано.Мы знаем, что длина на 7 см больше, чем ширину, поэтому назовем ширину 𝑥, в сантиметры, и длина 𝑥+7. Это дает нам следующий прямоугольник.
Мы знаем, что площадь прямоугольника вычисляется путем умножения его длины по его ширине. Здесь длина равна 𝑥+7, а ширина равна 𝑥. Поскольку площадь равна 78, мы можем использовать это, чтобы сформировать следующее уравнение: 𝑥(𝑥+7)=78.
Если мы затем воспользуемся распределительным свойством, чтобы раскрыть скобки, мы получим 𝑥+7𝑥=78.
Вычитание 78 с обеих сторон дает нам
𝑥+7𝑥−78=0.
На данный момент у нас есть квадратное уравнение в форме, которую можно решить. Мы можем проверить, можно ли уравнение разложить на множители, или мы можем решить, заполнив квадрат или по формуле квадрата. Если принять во внимание фактор пар 78, у нас есть 1 782 393 266,13.
Нам нужны два числа, которые умножаются на -78 и складываются на 7; используя пары факторов, мы видим, что это −6 и 13.
Таким образом, коэффициенты уравнения выглядят следующим образом: (𝑥−6)(𝑥+13)=0.
Затем наши решения для 𝑥 рассчитываются путем определения точки, в которых каждый из двух множителей равен нулю. Это, 𝑥=6 и 𝑥=−13.
Учитывая, что 𝑥 — это длина, она не может быть отрицательной, поэтому наше решение должно быть 𝑥=6.
Наконец, нам нужно определить периметр прямоугольника, т. е.
сумма длин сторон. Мы знаем, что ширина
6 см
и длина
6+7=13см,
поэтому периметр определяется как
6+6+13+13=38. cm
cm
В нашем предыдущем примере мы заметили ключевое различие между решением квадратичных уравнения в математическом смысле и в контексте реального мира. Мы видели, что лежащий в основе квадратичный имеет два решения; однако, поскольку 𝑥 была длина, она должна быть положительной, что означает, что одно из решений недействительно. Всегда полезно проверить ответы, найденные в конце этих типов. проблем, чтобы убедиться, что они имеют смысл в контексте их реального мира сценарий.
Мы увидим аналогичный сценарий в нашем следующем вопросе, связанном с поиском положительное число, удовлетворяющее определенному свойству.
Пример 2. Составление и решение квадратных уравнений
Определите положительное число, квадрат которого вдвое больше его значения на 15.
Ответ
Первое, что нам нужно сделать, это перевести формулировку задачи на
уравнение. Пусть 𝑥 будет числом, которое мы пытаемся найти. Первая часть информации, которую мы получаем, это то, что 𝑥
положительный; то есть 𝑥>0. Во-вторых, нам говорят квадрат числа,
𝑥, вдвое превышает его значение,
2𝑥, на 15. Это означает, что разница
между 𝑥 и 2𝑥 равно 15. Следовательно,
𝑥−2𝑥=15.
Во-вторых, нам говорят квадрат числа,
𝑥, вдвое превышает его значение,
2𝑥, на 15. Это означает, что разница
между 𝑥 и 2𝑥 равно 15. Следовательно,
𝑥−2𝑥=15.
Вычитая 15 из обеих частей уравнения, мы получаем следующее квадратичный в стандартной форме: 𝑥−2𝑥−15=0.
Теперь мы можем решить это уравнение, чтобы найти значение 𝑥. Обратите внимание, что 15 произведение 3 и 5. Кроме того, мы можем заметить, что 3−5=−2.Следовательно, мы можно разложить уравнение следующим образом: (𝑥−5)(𝑥+3)=0.
Таким образом, либо 𝑥−5=0, либо 𝑥+3=0. Решая каждое уравнение, получаем 𝑥=5 и 𝑥=−3. Однако нам сказали, что мы ищем положительное число; следовательно, решение равно 5.
В нашем следующем примере мы решим другую задачу, связанную с длинами в прямоугольник, на этот раз с помощью квадратичной формулы.
Пример 3. Использование квадратных уравнений для решения задач
Стороны прямоугольного треугольника равны длинам
𝑛 см,
3(𝑛+1) см,
и (3𝑛+4) см. Найдите длину его наименьшей стороны.
Найдите длину его наименьшей стороны.
Подсказка : Сначала решите, какая сторона является гипотенузой.
Ответ
Так как это задача на длины прямоугольного треугольника, это хорошая идея зарисовать информацию, которую мы получили. Для этого нам сначала нужно определите длину гипотенузы. Заметим, что одна из сторон имеет длину 𝑛 см, поэтому 𝑛 должен быть положительным. Мы тоже обратите внимание, что 3(𝑛+1)=3𝑛+3 меньше, чем другая длина, 3𝑛+4, значит, это гипотенуза.Это дает нам следующий.
Самая короткая сторона имеет длину 𝑛, поэтому нам нужно определить значение 𝑛. Мы можем сделать это, применив теорему Пифагора к прямоугольному треугольнику; мы получили (3𝑛+4)=𝑛+(3(𝑛+1)).
Распределение показателей в скобках дает нам 9𝑛+24𝑛+16=𝑛+9(𝑛+1)9𝑛+24𝑛+16=𝑛+9𝑛+18𝑛+9.
Затем мы можем собрать одинаковые члены и переставить их, чтобы сформировать квадратное уравнение:
9𝑛+24𝑛+16=10𝑛+18𝑛+90=10𝑛+18𝑛+9−9𝑛−24𝑛−160=𝑛−6𝑛−7.
Мы можем решить эту задачу, найдя пару чисел, произведение которых −7 и сумма которых равна −6. Мы видим, что это −7 и 1, поэтому мы имеем 0=(𝑛+1)(𝑛−7).
Чтобы произведение было равно нулю, один из множителей должен быть равен нулю. Следовательно, либо 𝑛=−1, либо 𝑛=7. Поскольку 𝑛 — длина стороны, она должна быть положительный, поэтому 𝑛=7.
Наконец, самая короткая сторона треугольника имеет длину 𝑛 см, так что самая короткая сторона имеет длину 7 см.
Прежде чем мы продолжим, стоит отметить, что все уникальные проблемы, которые мы
Имейте с квадратичными также возникают при применении их к реальным сценариям. Например, мы не всегда можем факторизовать квадратичные числа, и иногда нам нужно будет
применить квадратичную формулу, чтобы найти корни, которые мы можем затем округлить до
соответствующую степень точности. Другая возможность заключается в том, что может быть
0,1 или 2 решения в зависимости от знака дискриминанта и есть
все еще реальные ограничения на возможные значения переменных.
Давайте рассмотрим пример задачи, в которой встречаются обе эти ситуации. Представьте, что вход в туннель моделируется параболой с уравнением ℎ(𝑥)=−2𝑥+3𝑥+4, где ℎ(𝑥) — высота туннеля в метров и 𝑥 — горизонтальное смещение в метров от известная точка, как показано.
Мы хотим использовать это, чтобы найти максимальную ширину входа в туннель. Мы можем во-первых, обратите внимание, что параболы открываются наружу, поэтому максимальная ширина приходится на самая нижняя часть туннеля, когда ℎ(𝑥)=0.Следовательно, мы можем найти значения 𝑥 этих точек, решив уравнение −2𝑥+3𝑥+4=0.
Мы не можем решить это с помощью факторизации, поэтому воспользуемся квадратичной формулой, которая утверждает, что решения квадратичного 𝑎𝑥+𝑏𝑥+𝑐=0 являются 𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎.
В этом квадрате имеем 𝑎=−2, 𝑏=3 и 𝑐=4. Подставляя эти значения и упрощая, имеем 𝑥=−3±√3−4(−2)(4)2(−2)=−3±√41−4.
Поскольку выражение для корней далее не упрощается,
мы будем давать корни до двух знаков после запятой.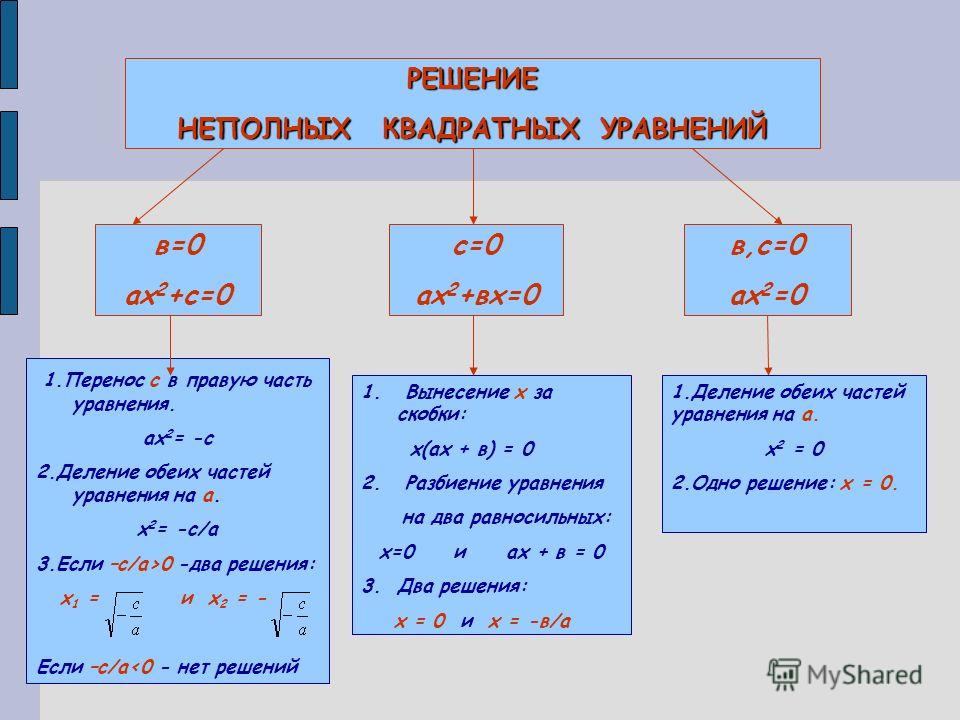 У нас есть
𝑥≈2,35 и 𝑥≈−0,85. Тогда максимальная ширина равна
разница между этими значениями, которую мы находим, используя точные значения
корней. С точностью до двух знаков после запятой это
3,20 м.
У нас есть
𝑥≈2,35 и 𝑥≈−0,85. Тогда максимальная ширина равна
разница между этими значениями, которую мы находим, используя точные значения
корней. С точностью до двух знаков после запятой это
3,20 м.
В наших последних трех примерах мы будем решать различные задачи по геометрии и теории чисел путем составления и решения квадратных уравнений.
Пример 4. Использование квадратных уравнений для решения задач
На рисунке показана прямоугольная призма, площадь развертки которой равна 580.Найдите значение 𝑥.
Ответ
Сначала заметим, что площадь сетки этой прямоугольной призмы будет
столько же, сколько площадь его поверхности. Другими словами, сумма площадей
граней прямоугольной призмы составляет 580 квадратных единиц. Нам нужно начать с
найти выражение для этой суммы. Для этого заметим, что имеется 6
грани и противоположные грани имеют одинаковую площадь. Наконец, мы знаем, что каждый
лицо является либо прямоугольником, либо квадратом, поэтому площадь каждого лица равна длине
раз ширина. Это позволяет нам найти площадь каждой грани следующим образом.
Это позволяет нам найти площадь каждой грани следующим образом.
Длина лицевой стороны равна 𝑥, а ширина равна 3, поэтому его площадь 3𝑥. Длина верхней грани 𝑥 а его ширина равна 2𝑥, поэтому его площадь равна 𝑥×2𝑥=2𝑥. Длина стороны лица равны 2𝑥, а их ширина равна 3, поэтому их площадь равна 2𝑥×3=6𝑥.
Поскольку каждой грани по две, площадь поверхности равна сумме двух умноженных на каждое выражение, дающее площадь поверхности=2×3𝑥+2×2𝑥+2×6𝑥=6𝑥+4𝑥+12𝑥=4𝑥+18𝑥.
Нам говорят, что это равно 580, что дает нам уравнение 4𝑥+18𝑥=580.
Вычитаем 580 с обеих сторон, чтобы получить 4𝑥+18𝑥−580=0.
Затем мы могли бы попытаться решить это с помощью факторизации; тем не менее, продукт
4×580 имеет много пар множителей, поэтому проще применить квадратичную формулу. Напомним, квадратичная формула утверждает, что решения квадратичного уравнения
𝑎𝑥+𝑏𝑥+𝑐=0 являются
𝑥=−𝑏±√𝑏−4𝑎𝑐2𝑎.
В этом квадрате имеем 𝑎=4, 𝑏=18 и 𝑐=−580.Подстановка этих значений и упрощение дает нам 𝑥=−18±√18−4(4)(−580)2(4)=−18±988.
Вычисляя каждый корень отдельно, получаем, что 𝑥=10 или 𝑥=−292. Поскольку 𝑥 представляет собой длину, она должна быть положительной; следовательно, 𝑥=10.
Пример 5. Составление и решение квадратных уравнений
Найдите положительное число, которое на 66 меньше своего квадрата более чем в два раза.
Ответ
Если мы назовем положительное число, которое пытаемся найти 𝑥, то нам скажут что 𝑥 на 66 меньше, чем удвоенный его квадрат.Дважды квадрат 𝑥 равно 2𝑥, а поскольку 𝑥 на 66 меньше чем это, мы можем добавить 66 к 𝑥, чтобы создать эквивалентное выражение, поэтому мы имеем 2𝑥=𝑥+66.
Мы можем решить это квадратное уравнение для 𝑥, сначала переставив уравнение, чтобы получить 2𝑥−𝑥−66=0.
Далее нам нужно найти два числа, которые при умножении дают
2×(-66)=-132 и прибавить, чтобы получить -1. Рассматривая пары факторов
132, мы видим, что это −12 и 11.Мы используем их, чтобы переписать
уравнение как
2𝑥−12𝑥+11𝑥−66=0,
Рассматривая пары факторов
132, мы видим, что это −12 и 11.Мы используем их, чтобы переписать
уравнение как
2𝑥−12𝑥+11𝑥−66=0,
Теперь вычтем общий множитель 2𝑥 из первых двух членов и общий коэффициент 11 в последних двух терминах, чтобы получить 2𝑥(𝑥−6)+11(𝑥−6)=0.
Наконец, мы убираем общий множитель (𝑥−6), давая нам (𝑥−6)(2𝑥+11)=0.
Чтобы произведение двух чисел было равно нулю, один из множителей должен быть нуль. Следовательно, либо 𝑥−6=0, либо 2𝑥+11=0. Решая каждое уравнение, получаем 𝑥=6 или 𝑥=-112.Поскольку нам говорят, что 𝑥 положителен, мы имеем 𝑥=6.
Следовательно, положительное число, которое на 66 меньше, чем удвоенный его квадрат, равно 6.
В нашем последнем примере мы построим и решим квадратное уравнение из геометрическая задача на приравнивание площадей трапеции и Прямоугольник.
Пример 6. Использование квадратных уравнений для решения задач
На рисунке показаны трапеция и прямоугольник.
- Напишите выражение для площади прямоугольника.
- Напишите выражение для площади трапеции.
- Если площадь трапеции и прямоугольника одинакова, найдите значение 𝑥 используя подходящее уравнение.
Ответ
Часть 1
Напомним, что площадь прямоугольника равна произведению ширины на длину. в диаграмме прямоугольник имеет длину 𝑥−9 и ширина 2𝑥+1. Следовательно, его площадь есть произведение выражений: (2𝑥+1)(𝑥−9).
Часть 2
Напомним, что площадь трапеции равна половине суммы параллели
стороны (или стороны основания), умноженные на высоту перпендикуляра.Мы видим в
картина, что параллельные стороны имеют длину 𝑥 и
𝑥+6, поэтому их сумма равна 𝑥+𝑥+6=2𝑥+6. Мы также можем отметить, что
перпендикулярная высота равна 𝑥−7. Значит, площадь этой трапеции равна
половина произведения этих выражений, которое дается выражением
12(𝑥−7)(2𝑥+6)=(𝑥−7)(𝑥+3).
Часть 3
Если площадь трапеции и прямоугольника равны, то выражения для их площади должны быть равны; приравнивая эти выражения, имеем (𝑥−7)(𝑥+3)=(2𝑥+1)(𝑥−9).
Распределив скобки в левой части уравнения, мы имеем (𝑥−7)(𝑥+3)=𝑥−4𝑥−21.
Распределяя скобки в правой части уравнения, у нас есть (2𝑥+1)(𝑥−9)=2𝑥−17𝑥−9.
Приравнивание разложений каждого выражения для площадей дает нам 𝑥−4𝑥−21=2𝑥−17𝑥−9.
Затем мы можем преобразовать это в квадратное уравнение в стандартной форме как следует: 0=2𝑥−17𝑥−9−𝑥+4𝑥+210=𝑥−13𝑥+12.
Далее, мы можем решить это уравнение, используя факторинг, заметив, что (−12)×(−1)=12 и -1+(-12)=-13; это дает 0=(𝑥−12)(𝑥−1).
Затем мы можем приравнять каждый множитель к нулю, чтобы увидеть, что 𝑥=12 и 𝑥=1 являются решениями уравнения.
У нас может возникнуть соблазн заключить, что оба эти значения являются решениями
так как они оба положительны; однако мы видим, что прямоугольник имеет
длина 𝑥−9. Это означает, что 𝑥 не может быть
меньше 9; в противном случае эта длина была бы отрицательной.
Это означает, что 𝑥 не может быть
меньше 9; в противном случае эта длина была бы отрицательной.
Следовательно, значение 𝑥 равно 12.
Давайте закончим повторением некоторых важных моментов этого объяснения.
Ключевые моменты
- В некоторых задачах нам может понадобиться извлечь информацию из вопроса и использовать это, чтобы составить квадратное уравнение.
- Часто бывает необходимо упростить квадратное уравнение до стандартной формы чтобы его можно было решить.
- Мы можем использовать любой из стандартных методов решения квадратного уравнения, включая разложение на множители, завершение квадрата, разложение на множители по группам и использование квадратичного формула.
- Мы должны сверять любые решения с контекстом проблемы; иногда, только одно решение будет подходящим в данном контексте.
Квадратные уравнения — SAT Math
Объяснение: Корни уравнения — это точки, в которых функция равна нулю. Мы можем положить каждую функцию равной нулю и определить, какие функции имеют один корень, а какие нет.
Мы можем положить каждую функцию равной нулю и определить, какие функции имеют один корень, а какие нет.
Еще одна информация поможет.Если квадратичная функция имеет один корень, то она должна быть полным квадратом. Это связано с тем, что квадратичная функция, являющаяся полным квадратом, может быть записана в виде (x – a) 2 . Если мы установим (x – a) 2 = 0, чтобы найти корень, мы увидим, что a — единственное значение, которое решает уравнение, и, следовательно, a — единственный корень. Кроме того, квадратное уравнение является полным квадратом, если его можно записать в виде a 2 x 2 + 2abx + b 2 = (ax + b) 2 .
Рассмотрим выбор f(x) = 4x 2 – 4x+1. Чтобы найти корни, мы установили f(x) = 0,
.4x 2 – 4x+1 = 0
Мы замечаем, что 4x 2 — 4x + 1 является полным квадратом, поскольку мы можем записать его как (2x – 1) 2 . Таким образом, это уравнение имеет только один корень и не может быть ответом.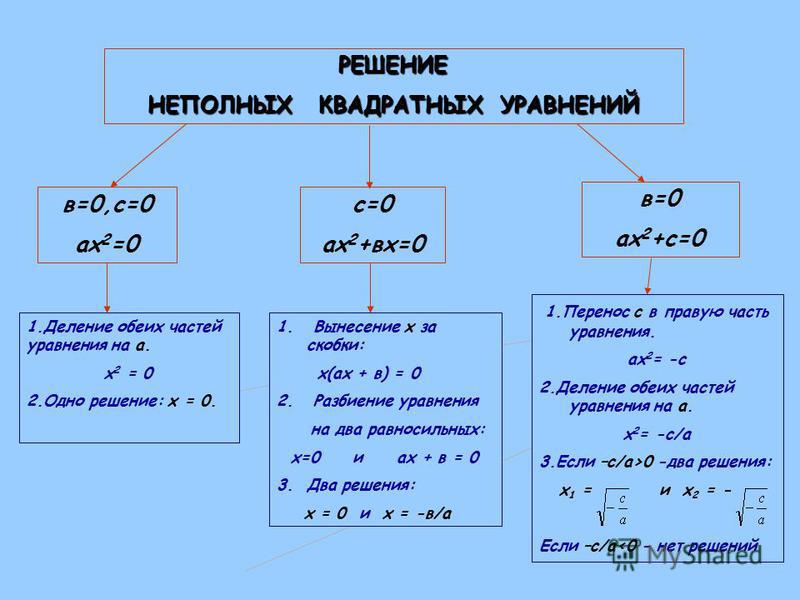
Если мы посмотрим на f(x) = x 2 –2x + 1, мы увидим, что x 2 – 2x + 1 также является полным квадратом, потому что его можно записать как (x – 1) 2 .Эта функция также имеет один корень.
Далее мы исследуем f(x) = (1/4)x 2 + x + 1. Положим f(x) = (1/4)x 2 + x + 1 = 0,
(1/4)х 2 + х + 1 = 0
Мы можем умножить обе части на четыре, чтобы избавиться от дроби.
x 2 + 4x + 4 = 0
(х + 2) 2 = 0
Эта функция также является полным квадратом и имеет единственный корень.
Теперь рассмотрим выбор f(x) = (–1/9)x 2 + 6x – 81.
f(x) = (–1/9)x 2 + 6x – 81 = 0
Умножьте обе части на -9.
x 2 – 54x + 729 = 0
(х – 27) 2 = 0,
Наконец, давайте посмотрим на f(x) = 9x 2 – 6x + 4. Это НЕ МОЖЕТ быть записано в виде полного квадрата, потому что оно не имеет формы a 2 x 2 + 2abx + b 2 = (ах + б) 2 .





 2}-4x=x(x-4)\)
2}-4x=x(x-4)\)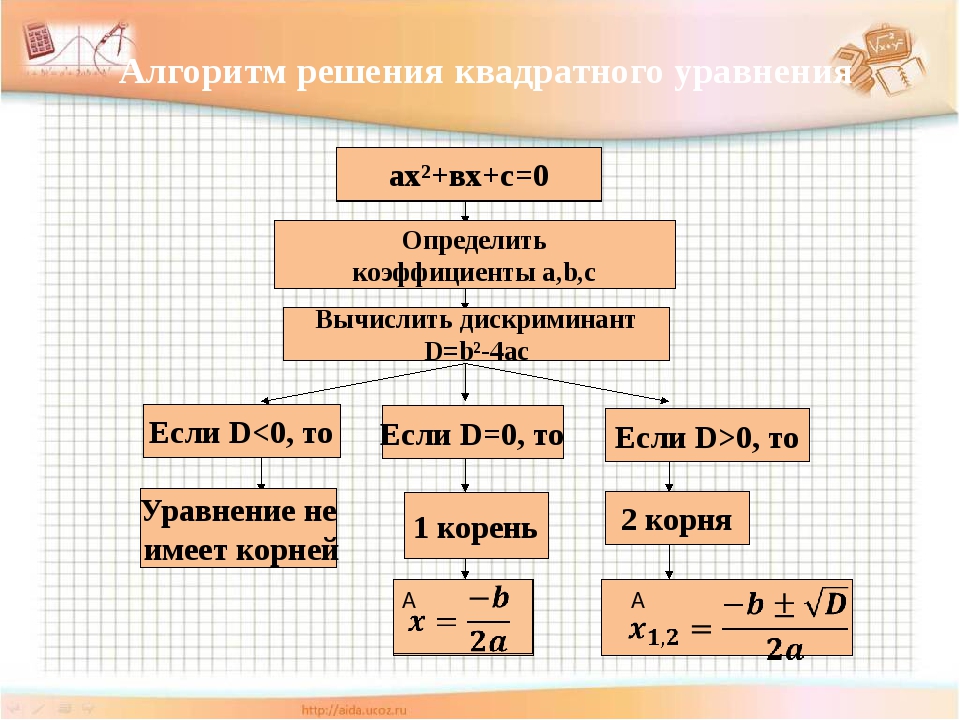
 2}+x-3=0\).2}-4(10(2)}}{2(1)}\)
2}+x-3=0\).2}-4(10(2)}}{2(1)}\) 2}-5x+6=0\) (используйте квадратичную формулу)
2}-5x+6=0\) (используйте квадратичную формулу)
 Что это за числа?
Что это за числа? Сколько лет малышам, если Джесси на 2 дня старше Симрана?
Сколько лет малышам, если Джесси на 2 дня старше Симрана? Какова была средняя скорость этого автобуса?
Какова была средняя скорость этого автобуса?
 Если и длину, и ширину увеличить на 2 м, площадь увеличится на 60 м 2 .Найдите размеры комнаты.
Если и длину, и ширину увеличить на 2 м, площадь увеличится на 60 м 2 .Найдите размеры комнаты.