Квадратные уравнения примеры и решения: Решение квадратных уравнений, примеры, тесты. Особые случаи. Разложение квадратного трехчлена на множители. Теорема Виета прямая, обратная — Детская игровая комната «Волшебный лес»

Posted on 20.01.197424.01.2022 by alexxlab

Содержание

Примеры решения квадратных и биквадратных уравнений

Пример 4. Решить квадратное уравнение x² + 12x + 36 = 0.

Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 12, c = 36.

Так как b = 12 — четное число, то вычислим дискриминант D₁ :

D₁ = (b/2)² — ac = 6² — 1*36 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = (-6)/1 = -6.

Это уравнение можно решить и без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:
x² + 12x + 36 = 0 (x+6)² = 0 x = -6.

Ответ: -6.

Пример 5. Решить квадратное уравнение 4x² -28x + 49 = 0.

Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 4, b = -28, c = 49.

Так как b = -28 — четное число, то вычислим дискриминант D₁ :

D₁ = (b/2)² — ac = (-14)² — 4*49 = 196-196 = 0, следовательно, уравнение имеет единственный корень x = (-b/2)/a = 14/4 = 7/2.

Это уравнение также можно решить без вычисления дискриминанта, преобразовав квадратный трехчлен по формуле сокращенного умножения:

4x² -28x + 49 = 0 (2x-7)² = 0 2x = 7 x = 7/2.

Ответ: 7/2.

Пример 6. Решить уравнение .

Решение.
Приведем к общему знаменателю левую часть уравнения:

Умножив обе части уравнения на -4, получим x² + 3x = 0. Это неполное квадратное уравнение решим способом разложения на множители:
x² + 3x = 0 x(x+3) = 0

x = 0, x = 0,
x — 3 = 0 x = 3.

Ответ: 0, 3.

Пример 7. Решить уравнение .

Решение.
Приведем к общему знаменателю левую часть и правую части уравнения:

Получим 6x² + 3x = 20x-10 6x² + 3x — 20x + 10 = 0 6x² — 17x + 10 = 0.

Вычислим дискриминант квадратного трехчлена: a = 6, b = -17, c = 10,

D = b² — 4ac = (-17)² — 4*6*10 = 289 — 240 = 49 > 0, следовательно, уравнение имеет два действительных корня.

Ответ: 5/6, 2.

Пример 8. Решить уравнение .

Решение.
Вычислим дискриминант квадратного трехчлена. У нас a = 1, b = 2√2, c = 1.

Так как b = 2√2, то есть b делится на 2 (b/2 = √2), вычислим дискриминант D₁:

D₁ = (b/2)² — ac = (√2)² — 1*1 = 1 > 0. Cледовательно, уравнение имеет два действительных корня.

Ответ: -√2-1, -√2+1.

Пример 9. Решить уравнение .

Решение.
Умножим левую и правую части уравнения на 6:

Вычислим дискриминант полученного квадратного трехчлена. У нас a = 3, b = -6, c = 2.

Так как b = -6, то есть b делится на 2 (b/2=3), вычислим дискриминант D

D₁ = (b/2)² — ac = 3² — 3*2 = 3 > 0. Cледовательно, уравнение имеет два действительных корня.

Ответ: (3-√3)/3, (3+√3)/3.

Пример 10. Решить уравнение x⁴ — 17x² + 16 = 0.

Решение.
Исходное уравнение является биквадратным. Сделав замену переменной t = x² => x⁴ = t², перейдем к эквивалентному исходному квадратному уравнению:

x⁴ — 17x² + 16 = 0 => t² — 17t + 16 = 0.

Вычислим дискриминант квадратного трехчлена: a = 1, b = -17, c = 16,

D = b² — 4ac = (-17)² — 4*1*16 = 289-64 = 225 > 0, следовательно, уравнение имеет два действительных корня.

По найденным значениям t, решая уравнения x² = t, найдем корни исходного биквадратного уравнения:

Таким образом, исходное уравнение имеет 4 действительных корня.

Ответ: ±1, ±4.

Пример 11. Решить уравнение 9x⁴ + 32x² — 16 = 0.

9x⁴ + 32x² — 16 = 0 => 9t² + 32t — 16 = 0

Вычислим дискриминант квадратного трехчлена. У нас a = 9, b = 32, c = -16.

Так как b = 32, то есть b делится на 2 (b/2=16), вычислим дискриминант D₁:

D₁ = (b/2)² — ac = 16² — 9*(-16) = 400 >0. Cледовательно, уравнение имеет два действительных корня.

По найденным значениям t, решая уравнения x² = t, найдем корни исходного биквадратного уравнения:

Первое уравнение x

2 = -4 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x= ±2/3.

Ответ: ±2/3.

Пример 12. Решить уравнение x⁴ + 3x² — 10 = 0.

x⁴ + 3x² — 10 = 0 => t² + 3t — 10 = 0

Вычислим дискриминант полученного квадратного трехчлена: a = 1, b = 3, c = -10,

D = b² — 4ac = 3² — 4*1*(-10) = 9+40 = 49 > 0, следовательно, уравнение имеет два действительных корня.

По найденным значениям t, решая уравнения x² = t, найдем корни исходного биквадратного уравнения:

Первое уравнение x² = -5 корней не имеет, а второе, а значит, и исходное, имеет два действительных корня x = ±√2.

Ответ: ±√2.

Квадратные уравнения, примеры решений

Теория по квадратным уравнениям

ОПРЕДЕЛЕНИЕ Квадратным уравнением называется уравнение вида , где .

Возможны такие случаи:

, тогда имеем квадратное уравнение вида и .

, тогда имеем квадратное уравнение вида , если ; если – корней нет.

, тогда имеем квадратное уравнение вида .

, тогда имеем полное квадратное уравнение , которое решается или с помощью дискриминанта:

Или по теореме Виета:

Примеры

ПРИМЕР 1

Задание

Решить следующие неполные квадратные уравнения

Решение

1) В уравнении вынесем за скобки .

Произведение равно нулю, если один из сомножителей равен нулю, следовательно:

или

2) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :

3) В уравнении перенесем свободный член вправо и раздели его на коэффициент при :

У данного квадратного уравнения нет корней.

4) уравнение равносильно уравнению , которое имеет два совпадающих корня .

Ответ

Корней нет

ПРИМЕР 2

Задание

Решить квадратное уравнение

Решение

Подсчитаем для заданного уравнения, чему равен дискриминант:

Так как , то уравнение имеет два совпадающих корня:

Ответ

ПРИМЕР 3

Задание

Решить уравнение

Решение

Вычислим дискриминант для исходного уравнения, получим:

Так как , данное уравнение решений не имеет.

Ответ

Корней нет.

ПРИМЕР 4

Задание

Решить квадратное уравнение

Решение

Дискриминант заданного уравнения, равен

Следовательно, уравнение имеет два различных корня

Ответ

ПРИМЕР 5

Задание

Решить уравнение, используя теорему Виета:

Решение

Пусть и – корни квадратного уравнения, по следствию из теоремы Виета

Проанализируем полученные равенства. Произведение корней отрицательно, следовательно, корни имеют разные знаки. Разложим –12 на множители, учитывая, что они должны быть числами разного знака. Возможны такие варианты: –12 и 1; 12 и –1; –6 и 2; 6 и –2; –4 и 3; 4 и –3. Так как сумма корней равна 1, то корнями будут числа и .

Ответ

Квадратные уравнения с параметрами

Тема занятия «КВАДРАТНЫЕ УРАВНЕНИЯ С ПАРАМЕТРАМИ»

Цели занятия:

Образовательная: углубить ранее полученные знания об уравнениях с параметрами, закрепить навыки решения уравнений;

Воспитательная: воспитывать навыки учебного труда, умение работать в группах;

Развивающая: развивать логическое мышление, формировать потребность к приобретению знаний.

Опрос:

Вспомним условия расположения корней уравнения,при условии , что оба корня положительные, отрицательные, разных знаков.

Рассмотрим примеры решения квадратных уравнений с параметрами.

ПРИМЕР 1.

Решить уравнение

Решение:

1.Если , то мы имеем линейное уравнение:

2.Если найдём дискриминант D квадратного уравнения :

а)Если , то

б)Если т. е. то

в)Если то действительных корней нет .

Ответ: если

если

решений нет, если

ПРИМЕР 2.

Решить уравнение

Решение:

Уравнение равносильно системе:

Решим уравнение

1.Если т.е. имеем :

Условие выполнено, т.к.

Выясним, при каких значениях Для этого решим уравнения :

Понятно, что при всех отрицательных значениях параметра равенство в первом уравнении невозможно, при возведя в квадрат обе части равенства , мы получим что невозможно.

Второе из рассматриваемых уравнений невозможно при положительных значениях ,а при имеем , как и в первом случае , неверное равенство

Таким образом , если

2.Если то

Т.е. в данном случае уравнение не имеет решений.

3.Если то дискриминант квадратного уравнения отрицательный и, таким образом, нет действительных корней.

Ответ: если

решений нет, если

ПРИМЕР 3.

Определить количество корней уравнения в зависимости от :

Решение:

Обозначим Тогда исходное уравнение имеет вид

или .

Количество корней зависит от знака D₁.

D₁=

1.Если то данное уравнение не имеет корней.

2.При уравнение имеет единственный корень: Итак,

Это уравнение не имеет корней.

3.Если то корни уравнения

Итак ,необходимо выяснить , сколько корней имеет совокупность уравнений:

В первом уравнении дискриминант отсюда следует, что оно не имеет решений при любых значениях параметра

Во втором уравнении

1)Если т.е. то данное уравнение имеет один корень.

2)Если т.е.

Уравнение не имеет действительных корней.

3)Если т.е. уравнение имеет два корня .

Ответ: Два корня , если

один корень, если

действительных корней нет, если

ПРИМЕР 4.

При каких значениях параметра уравнение

имеет единственное решение?

Решение:

Данное уравнение равносильно системе :

Найдём дискриминант квадратного уравнения :

Если , уравнение имеет один корень что удовлетворяет условию

При получим:

Уравнение имеет одно решение , если т. е. при

Ответ: Уравнение имеет один корень, если

ПРИМЕР 5.

При каких значениях параметра уравнение имеет

два разных действительных корня?

Решение:

Данное биквадратное уравнение сводится к совокупности уравнений:

Уравнение имеет два разных корня, если

Ответ: уравнение имеет два разных корня , если

ПРИМЕР 6.

При каких значениях параметра уравнение

имеет единственное решение ?

Решение:

Данное уравнение равносильно системе :

система будет иметь одно решение ,если

т.е. при

Ответ: уравнение имеет единственное решение при

ПРИМЕР 7.

Сколько решений имеет уравнение в зависимости от значения параметра ?

Решение:

Данное уравнение равносильно системе :

При или уравнение имеет два решения, в других случаях – три.

Ответ: два решения , если

три решения, если

ПРИМЕР 8.

При каких значениях параметра уравнение

имеет единственное решение ?

Решение:

Данное уравнение равносильно системе :

Решив квадратное уравнение , имеем :

Система имеет единственное решение, если т.е. или, когда

Ответ: уравнение имеет единственное решение, если

ПРИМЕР 9.

При каких значениях параметра уравнение

имеет единственное решение?

Решение:

1.Если то мы получим линейное уравнение

При

При решений нет .

2.При дискриминант D должен равняться нулю, т.е.

Случай уже рассмотрен .

Ответ:уравнение имеет единственное решение при

ПРИМЕР 10.

При каких значениях параметра сумма корней уравнения

равна 2?

Решение:

Чтобы уравнение имело корни ,

По теореме Виета,

Таким образом, имеем систему:

Ответ: при

ПРИМЕР 11.

При каких значениях параметра уравнение

имеет два разных положительных корня ?

Решение:

Для того, чтобы квадратное уравнение имело два разных действительных корня, необходимо, чтобы дискриминант

По теореме Виета:

Таким образом, имеем систему неравенств :

Ответ: уравнение имеет два разных положительных корня,

если .

ПРИМЕР 12.

При каких значениях параметра один корень уравнения

меньше, чем -2 , три других- больше -1 ?

Решение:

В условии задачи идёт речь о четырёх корнях , т.е. Пусть тогда

данное уравнение примет вид

Чтобы данное уравнение имело четыре действительных корня , которые удовлетворяют условию задачи , необходимо, чтобы корни уравнения относительно t удовлетворяли условиям:

Итак имеем систему неравенств :

где

Ответ: при

ПРИМЕР 13.

При каких значениях параметра уравнение имеет

единственный корень ? Найти его.

Решение:

а) тогда

б) тогда

Ответ: при

ПРИМЕР 14.

Определить количество целых значений параметра из промежутка ,

при которых квадратное уравнение имеет два разных корня.

Решение:

Для того , чтобы квадратное уравнение имело два разных корня, необходимо, чтобы

Ответ: 4.

ПРИМЕР 15.

При каком наименьшем целом значении уравнение

имеет четыре решения ?

Решение :

Построим в одной системе координат графики функций и

Видим, что при эти графики имеют четыре точки пересечения.

Ответ:

ПРИМЕР 16.

Найдите количество целых значений , при которых сумма корней уравнения принадлежит промежутку .

Решение:

Сумма корней уравнения равна

Итак ,

Целые числа, которые удовлетворяют условию 11, 12,13, 14,15.

Ответ: пять.

ПРИМЕР 17.

Найдите количество целых значений , при которых произведение корней уравнения принадлежит промежутку .

Решение:

Произведение корней уравнения равно

Итак,

Целые числа , которые удовлетворяют условию это 23, 24, 25.

Ответ:три.

ПРИМЕР 18.

При каком наименьшем натуральном значении параметра корни уравнения являются рациональными числами?

Решение:

Для того ,чтобы корни уравнения были рациональными числами, необходимо, чтобы выражение было полным квадратом ,т. е.

будет полным квадратом при наименьшем натуральном значении

Ответ: при

ПРИМЕР 19.

При каком значении параметра квадратное уравнение

имеет корни, равные по абсолютной величине и противоположные по значению ?

Решение:

разделим на

Ответ: при

ПРИМЕР 20.

При каком наибольшем целом значении параметра корни уравнения

находятся по разные стороны промежутка ?

Решение:

Запишем левую часть уравнения как функцию

Нарисуем график этой функции ( схематично).

Мы видим, что корни уравнения находятся по разные стороны промежутка

, если выполняются условия:

Ответ:

ПРИМЕР 21.

При каком значении параметра сумма квадратов корней уравнения

равна 12?

Решение:

По теореме Виета: По условию: тогда

Т.е.

Ответ:

ПРИМЕР 22.

При каком значении параметра произведение корней уравнения

будет наибольшим?

Решение:

По теореме Виета произведение корней этого уравнения равняется :

Сумма двух положительных чисел принимает наименьшее значение, если одно из слагаемых равно нулю. Итак ,

Ответ:

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ.

1.Решить уравнение:

Ответы:

1) если

корней нет, если если если

2) если

при корней нет при

3) если корней нет, если

2.При каких значениях параметра уравнение

имеет единственное решение ?

Ответ: ни при каких.

3.При каких значениях параметра уравнение

имеет два разных действительных корня?

Ответ: при

4.При каких значениях параметра уравнение

имеет единственное решение ?

Ответ: при

5.Сколько решений имеет уравнение в зависимости от параметра ?

Ответ: два корня, если

три корня, если

6.При каких значениях параметра уравнение

имеет единственное решение?

Ответ: при

7.При каком значении параметра произведение корней уравнения

равно 8?

Ответ: при

8.При каких значениях параметра уравнение имеет

два разных отрицательных корня ?

Ответ: при

9. При каких значениях параметра уравнение имеет

два разных действительных отрицательных корня?

Ответ: при

10.При каких значениях параметра уравнение имеет корни разных знаков ?

Ответ: при

11.При каких значениях параметра уравнение имеет

корни такие, что и ?

Ответ: при

12.Найти все значения , при которых один из корней уравнения

меньше чем 1, а второй – больше 1.

Ответ:

13.Найти все значения , при которых корни уравнения

больше, чем 1.

Ответ:

Квадратные уравнения — Kid-mama

Из этой статьи вы узнаете:

1Квадратные уравнения — это уравнения вида ax² + bx + c = 0

где x — переменная, a, b, c — некоторые числа, причем a ≠ 0 .

2Коэффициенты квадратного уравнения

Числа a, b, c называют коэффициентами уравнения, причем каждое из них имеет свое название:

Число а называют первым (или старшим) коэффициентом. Число b — вторым коэффициентом, а число c — свободным членом.

Пример 1:

квадратное уравнение – 3x²+ 4x + 7 = 0 имеет следующие коэффициенты :

a = –3, b = 4, c = 7.

Пример 2:

квадратное уравнение 6x²– 4x – 7 = 0 имеет следующие коэффициенты :

a = 6, b = –4, c = –7.

3Неполные квадратные уравнения и их решение

Если в квадратном уравнении хотя бы один из коэффициентов b и c равен нулю, то такое уравнение называется неполным.

Существует три вида неполных квадратных уравнений:

ax² = 0 ( в случае, когда b = 0, с = 0)
ax² + bx = 0 ( в случае, когда b ≠ 0, с = 0)
ax² + c = 0 ( в случае, когда b = 0, с ≠ 0)

Неполные квадратные уравнения легко решаются, рассмотрим решение каждого вида:

Поскольку a ≠ 0, то данное уравнение имеет всего один корень x = 0.

Например, квадратное уравнение –19 x² = 0 имеет один корень : x = 0.

Для решения такого уравнения выносят x за скобки и получают уравнение вида

x (ax + b) = 0

Это уравнение имеет всегда два корня (так как в левой части у нас два множителя x и (ax + b), а если хотя бы один из множителей равен нулю, то и все произведение равно нулю) .

x₁ = 0, а x₂можно найти, решив простое линейное уравнение в скобках :

ax + b = 0

ax = –b

x₂ = –b/a

Например, решим квадратное уравнение 5x² + 2x = 0

x(5x + 2)= 0 Сразу напишем, что x₁ = 0. Далее найдем x₂.

Для этого решим уравнение 5x + 2 = 0

5x = –2

x = –2/5

Ответ: x₁ = 0, x₂ = –2/5

Это уравнение также нужно преобразовать:

ax² =–c

x² = –c/a

Так как с ≠ 0, то возможны два случая: –c/a < 0, и –c/a > 0.

В первом случае уравнение x² = –c/a корней не имеет, так как квадрат числа всегда положительный. Во втором случае, то есть когда –c/a > 0, уравнение имеет два корня:

Пример 1:

2x² + 8 = 0

2x² = -8

x² = –8/2

x² = –4 Корней нет.

Пример 2:

3x² – 15 = 0

3x² = 15

x² = 15/3

x² = 5

4Приведённое квадратное уравнение

Если в квадратном уравнении коэффициент a = 1, то такое уравнение называют приведённым. Приведенные уравнения также могут быть неполными.

Примеры приведённых уравнений:

Любое неприведённое квадратное уравнение можно преобразовать в приведённое, разделив обе части уравнения на коэффициент a, (поскольку в левой части уравнения сумма, то на а делим каждое слагаемое):

Пример 1:

Преобразуем неприведённое квадратное уравнение 2x² – 6x + 8 = 0 в приведённое, для этого делим левую и правую часть уравнения на 2, получаем приведённое уравнение:

x²– 3x + 4 = 0

Пример 2:

–4x² + 12x = 0 Делим обе части уравнения на -4, и получаем приведённое уравнение:

x² – 3x = 0

5Решение квадратного уравнения ax² + bx + c = 0

Для того, чтобы решить квадратное уравнение, нужно сначала найти его дискриминант (D) по формуле:

При этом возможны три случая:

__________________________________________________

Если D < 0, то уравнение корней не имеет.
Если D = 0, то уравнение имеет один корень :

Если D > 0, то уравнение имеет два корня:

————————————————————————————————————-

6Формула корней квадратного уравнения выглядит так:

Эта формула подходит и для второго случая, когда D = 0, так как

Алгоритм решения квадратного уравнения

Найти дискриминант D
Если D < 0, написать, что корней нет
Если D ≥ 0 , найти корни по формуле корней квадратного уравнения.

_________________________________________________________________

Пример 1:

Для данного уравнения a = 3, b = -2, с = -16

Дискриминант уравнения:

Дискриминант больше нуля, находим корни:

Пример 2 :

Для данного уравнения a = -0,5 b = 2 c = -2

Дискриминант уравнения:

Уравнение имеет один корень. Найдем его:

Пример 3 :

Для данного уравнения a = 1 b = -6 c = 11

Дискриминант уравнения:

Дискриминант D<0, корней нет

Ответ: корней нет.

Урок 3. квадратные уравнения, неравенства и их системы — Алгебра и начала математического анализа — 10 класс

Алгебра и начала математического анализа, 10 класс

Урок №3. Квадратные уравнения, неравенства и их системы.

Перечень вопросов, рассматриваемых в теме:

систематизация знаний учащихся о решении квадратных уравнений и неравенств;
установление зависимости количества и расположения корней квадратного уравнения от его коэффициентов и значения дискриминанта;
способы решения квадратных уравнений и неравенств с параметрами.

Глоссарий по теме:

Параметр — (от греч. parametron — отмеривающий) в математике, величина, числовые значения которой позволяют выделить определенный элемент из множества элементов того же рода.

Основная литература:

Колягин Ю. М., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. 10 класс. Базовый и углублённый уровни. — М.: Просвещение, 2017.

Ткачева М. В., Федорова Н. Е. Алгебра и начала математического анализа. Тематические тесты. 10 класс. Базовый и профильный уровни. 2016.

Шабунин М. И., Ткачева М. В., Фёдорова Н.Е. и др. Алгебра и начала математического анализа. Дидактические материалы. 10 класс. Профильный уровень. 2016.

Теоретический материал для самостоятельного изучения

В курсе средней школы будут рассматриваться показательные, логарифмические, тригонометрические уравнения и неравенства. Чтобы облегчить дальнейшее изучение специальных уравнений, нужно уметь решать квадратные уравнения и неравенства, устанавливать и объяснять зависимость вида решения от его коэффициентов и дискриминанта, представлять геометрическую интерпретацию задач.

Квадратные уравнения.

На уроке будем рассматривать различные способы решения квадратных уравнений.

Как определить, сколько корней имеет уравнение, подскажет дискриминант.

Дискриминант – это число, которое находим по формуле

Если D <0 корней нет, если D = 0 один корень, если D> 0 два корня.

Если дискриминант D> 0 , корни можно найти по формуле:

Если D = 0 , то

Рассмотрите пример. Решить уравнение

Шаг 1. Выпишем коэффициенты a, b, c.

Шаг 2. Найдем дискриминант. D=16.

Шаг 3. Запишем формулу корней и подставим значения. Вычислим значения корней:

Заметим:

1.Перед решением квадратного уравнения привести его к стандартному виду.

2. Избавьтесь от минуса перед . Для этого надо умножить всё уравнение на -1.

3. Если в уравнении есть дробные коэффициенты, умножьте уравнение на общий знаменатель.

4. Проверяйте корни по теореме Виета. Это просто, когда a=1.

Рассмотрите другие формулы:

, где второй коэффициент b=2k – четное число.

Приведенное квадратное уравнение , старший коэффициент равен a= 1, проще решать по теореме Виета.

Уравнение (х-3) (х+5) =0 является квадратным. Для его решения воспользуйтесь свойством: произведение равно 0, когда один из множителей равен 0.

Осталось вспомнить, как решаются неполные квадратные уравнения. Неполные — значит один или два коэффициента равны нулю.

Для решения систем уравнений применяются все методы решения: подстановки, сложения, графический.

Рассмотрим несколько примеров:

Пример 1.

Если из одного из уравнений можно выразить х или у, применяем метод подстановки. Выразите х из первого уравнения и подставьте во второе. Решите и найдите корни.

Пример 2.

Применяем метод сложения. Выполнив сложение, получаем уравнение , далее x= ±5. Находим у= ±2. Составляем возможные пары чисел.

Записываем ответ: (5; 2), (5; -2), (-5; 2), (- 5; -2).

Пример 3. Иногда проще ввести новые переменные. 2+ bx + c больше или меньше нуля.

Шаг 1. Запишем соответствующее неравенству квадратное уравнение и найдем его корни. Отметим корни на оси OХ и схематично покажем расположение ветвей параболы «вверх» или «вниз».

Шаг 2. Расставим на оси знаки, соответствующие знаку квадратичной функции: там, где парабола выше оси, ставим +, а там, где ниже –.

Шаг 3. Выписываем интервалы, соответствующие знаку неравенства. Если неравенство нестрогое, корни входят в интервал, если строгое не входят.

Вспомните возможные случаи расположения корней на оси и ветвей параболы в зависимости от коэффициента а и дискриминанта.

Метод интервалов упрощает схему решения. По-прежнему находим корни квадратного трехчлена, расставляем на числовой прямой. Определяем знаки на интервалах + или – по схеме:

если а>0 + — +, если а <0 — + -. Или путём подстановки произвольного значения квадратный трехчлен.

Рассмотрим несколько примеров:

D=0 все точки параболы выше оси и только одна х=2 на оси ОХ -нет решений.

D<0 коэффициент а=2>0 ветви вверх. Парабола выше оси, все значения положительны, значит х- любое число. Неравенство не имеет решений.

Далее рассмотрим схему решения системы неравенств.

Алгоритм решения системы неравенств.

1.Решить первое неравенство системы, изобразить его графически на оси x.

2.Решить второе неравенство системы, изобразить его графически на оси x.

3.Выбрать в ответ те участки, в которых решение первого и второго неравенств пересекаются. Записать ответ.

Часть 3

Теперь, когда мы разобрали решение квадратных уравнений и неравенств переходим к решению самых сложных заданий с параметрами. Если в уравнении или неравенстве некоторые коэффициенты заданы не числовыми значениями, а обозначены буквами, то они называются параметрами, а само уравнение или неравенство параметрическим.

Первый шаг в решении — найти особое значение параметра.

Второй шаг – определить допустимые значения.

Если в задаче требуется определить знаки корней квадратного уравнения, то, как правило, удобнее использовать теорему Виета.

Но прежде, чем применять теорему Виета, обязательно нужно проверить, что уравнение имеет корни! Для этого вычисляем дискриминант.

Рассмотрите примеры решения неравенства с параметром.

Графический метод решения обладает несомненным преимуществом – можно представить решение наглядно.

Для любого свойства, сформулированного на алгебраическом языке, нужно уметь давать геометрическую интерпретацию и, наоборот, по поведению графика параболы дать общую оценку коэффициентов квадратного трехчлена и его корней.

Например, если старший коэффициент квадратного трехчлена меньше 0, то ветви параболы направлены вниз. Если дискриминант больше 0, то трехчлен имеет различные действительные корни и парабола пересекает ось абсцисс в двух точках и т.д.

Мы рассмотрели лишь некоторые примеры, иллюстрирующие применение графического метода к решению квадратных уравнений и неравенств. Более подробно с методами решения квадратных уравнений, неравенств, их систем вы можете, поработав с интерактивными моделями.

Задания тренировочного модуля с разбором.

Пример 1.

При каких значениях параметра, а квадратное уравнение

имеет только один корень?

Находим дискриминант D=25-4∙2∙5a=25-40a. Уравнение имеет один корень, если D=0, т.е. 25-40a=0, а=5/8.

Пример 2.

Определите, на каком интервале значения квадратного трехчлена отрицательны?

Решаем неравенство: . Находим дискриминант квадратного трехчлена D= 1-4∙2∙ (-1) =1+8=9. Находим корни . Расставляем точки на числовой прямой.

Старший коэффициент а=2 ветви параболы вверх. Знаки чередуются + — +. Записываем ответ: — 0,5< х <1.

Сложные квадратные уравнения примеры с решением. Квадратные уравнения

Уравнение вида

Выражение D = b 2 — 4 ac называют дискриминантом квадратного уравнения. Если D = 0, то уравнение имеет один действительный корень; если D > 0, то уравнение имеет два действительных корня.
В случае, когда D = 0 , иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Используя обозначение D = b 2 — 4 ac , можно переписать формулу (2) в виде

Если b = 2 k , то формула (2) принимает вид:

где k = b / 2 .
Последняя формула особенно удобна в тех случаях, когда b / 2 — целое число, т.е. коэффициент b — четное число.
Пример 1: Решить уравнение 2 x 2 — 5 x + 2 = 0 . Здесь a = 2, b = -5, c = 2 . Имеем D = b 2 — 4 ac = (-5) 2- 4*2*2 = 9 . Так как D > 0 , то уравнение имеет два корня. Найдем их по формуле (2)

Итак x 1 =(5 + 3) / 4 = 2, x 2 =(5 — 3) / 4 = 1 / 2 ,
то есть x 1 = 2 и x 2 = 1 / 2 — корни заданного уравнения.
Пример 2: Решить уравнение 2 x 2 — 3 x + 5 = 0 . Здесь a = 2, b = -3, c = 5 . Находим дискриминант D = b 2 — 4 ac = (-3) 2- 4*2*5 = -31 . Так как D 0 , то уравнение не имеет действительных корней.

Неполные квадратные уравнения. Если в квадратном уравнении ax 2 + bx + c =0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным . Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Пример 1: решить уравнение 2 x 2 — 5 x = 0 .
Имеем x (2 x — 5) = 0 . Значит либо x = 0 , либо 2 x — 5 = 0 , то есть x = 2.5 . Итак, уравнение имеет два корня: 0 и 2.5
Пример 2: решить уравнение 3 x 2 — 27 = 0 .
Имеем 3 x 2 = 27 . Следовательно корни данного уравнения — 3 и -3 .

Теорема Виета. Если приведенное квадратное уравнение x 2 + px + q =0 имеет действительные корни, то их сумма равна — p , а произведение равно q , то есть

x 1 + x 2 = -p ,
x 1 x 2 = q

(сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену).

», то есть уравнения первой степени. В этом уроке мы разберем, что называют квадратным уравнением и как его решать.

Что называют квадратным уравнением

Важно!

Степень уравнения определяют по наибольшей степени, в которой стоит неизвестное.

Если максимальная степень, в которой стоит неизвестное — «2 », значит, перед вами квадратное уравнение.

Примеры квадратных уравнений

5x 2 − 14x + 17 = 0
−x 2 + x + = 0
x 2 + 0,25x = 0
x 2 − 8 = 0

Важно! Общий вид квадратного уравнения выглядит так:

A x 2 + b x + c = 0

«a », «b » и «c » — заданные числа.

«a » — первый или старший коэффициент;
«b » — второй коэффициент;
«c » — свободный член.

Чтобы найти «a », «b » и «c » нужно сравнить свое уравнение с общим видом квадратного уравнения «ax 2 + bx + c = 0 ».

Давайте потренируемся определять коэффициенты «a », «b » и «c » в квадратных уравнениях.

5x 2 − 14x + 17 = 0 −7x 2 − 13x + 8 = 0 −x 2 + x + = 0 x 2 + 0,25x = 0

Уравнение	Коэффициенты

a = −7 b = −13 с = 8


x 2 − 8 = 0

Как решать квадратные уравнения

В отличии от линейных уравнений для решения квадратных уравнений используется специальная формула для нахождения корней .

Запомните!

Чтобы решить квадратное уравнение нужно:

привести квадратное уравнение к общему виду «ax 2 + bx + c = 0 ». То есть в правой части должен остаться только «0 »;
использовать формулу для корней:

Давайте на примере разберем, как применять формулу для нахождения корней квадратного уравнения. Решим квадратное уравнение.

X 2 − 3x − 4 = 0

Уравнение « x 2 − 3x − 4 = 0 » уже приведено к общему виду «ax 2 + bx + c = 0 » и не требует дополнительных упрощений. Для его решения нам достаточно применить формулу нахождения корней квадратного уравнения .

Определим коэффициенты «a », «b » и «c » для этого уравнения.

x 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =

С её помощью решается любое квадратное уравнение.

В формуле «x 1;2 = » часто заменяют подкоренное выражение
«b 2 − 4ac » на букву «D » и называют дискриминантом . Более подробно понятие дискриминанта рассматривается в уроке «Что такое дискриминант ».

Рассмотрим другой пример квадратного уравнения.

x 2 + 9 + x = 7x

В данном виде определить коэффициенты «a », «b » и «c » довольно сложно. Давайте вначале приведем уравнение к общему виду «ax 2 + bx + c = 0 ».

X 2 + 9 + x = 7x
x 2 + 9 + x − 7x = 0
x 2 + 9 − 6x = 0
x 2 − 6x + 9 = 0

Теперь можно использовать формулу для корней.

X 1;2 =
x 1;2 =
x 1;2 =
x 1;2 =
x =

x = 3
Ответ: x = 3

Бывают случаи, когда в квадратных уравнениях нет корней. Такая ситуация возникает, когда в формуле под корнем оказывается отрицательное число.

Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:

Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.

Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:

Квадратное уравнение – это уравнение вида:

где коэффициенты a, b и с произвольные числа, при чём a≠0.

В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:

1. Имеют два корня.

2. *Имеют только один корень.

3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней

Как вычисляются корни? Просто!

Вычисляем дискриминант. Под этим «страшным» словом лежит вполне простая формула:

Формулы корней имеют следующий вид:

*Эти формулы нужно знать наизусть.

Можно сразу записывать и решать:

Пример:

1. Если D > 0, то уравнение имеет два корня.

2. Если D = 0, то уравнение имеет один корень.

3. Если D

Давайте рассмотрим уравнение:

По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…

Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:

х 1 = 3 х 2 = 3

Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.

Теперь следующий пример:

Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.

Вот и весь процесс решения.

Квадратичная функция.

Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).

Это функция вида:

где х и у — переменные

a, b, с – заданные числа, при чём a ≠ 0

Графиком является парабола:

То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.

Рассмотрим примеры:

Пример 1: Решить 2x 2 +8 x –192=0

а=2 b=8 c= –192

D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Ответ: х 1 = 8 х 2 = –12

*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.

Пример 2: Решить x 2 –22 x+121 = 0

а=1 b=–22 c=121

D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Получили, что х 1 = 11 и х 2 = 11

В ответе допустимо записать х = 11.

Ответ: х = 11

Пример 3: Решить x 2 –8x+72 = 0

а=1 b= –8 c=72

D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224

Дискриминант отрицательный, решения в действительных числах нет.

Ответ: решения нет

Дискриминант отрицательный. Решение есть!

Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.

Понятие комплексного числа.

Немного теории.

Комплексным числом z называется число вида

z = a + bi

где a и b – действительные числа, i – так называемая мнимая единица.

a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.

Мнимая единица равна корню из минус единицы:

Теперь рассмотрим уравнение:

Получили два сопряжённых корня.

Неполное квадратное уравнение.

Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.

Случай 1. Коэффициент b = 0.

Уравнение приобретает вид:

Преобразуем:

Пример:

4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2

Случай 2. Коэффициент с = 0.

Уравнение приобретает вид:

Преобразуем, раскладываем на множители:

*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.

Пример:

9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0

x 1 = 0 x 2 = 5

Случай 3. Коэффициенты b = 0 и c = 0.

Здесь понятно, что решением уравнения всегда будет х = 0.

Полезные свойства и закономерности коэффициентов.

Есть свойства, которые позволяют решить уравнения с большими коэффициентами.

а x 2 + bx + c =0 выполняется равенство

a + b + с = 0, то

— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство

a + с = b , то

Данные свойства помогают решить определённого вида уравнения.

Пример 1: 5001 x 2 –4995 x – 6=0

Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит

Пример 2: 2501 x 2 +2507 x +6=0

Выполняется равенство a + с = b , значит

Закономерности коэффициентов.

1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.

Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.

х 1 = –6 х 2 = –1/6.

2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

х 1 = 15 х 2 = 1/15.

3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны

аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

х 1 = – 17 х 2 = 1/17.

4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны

аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.

Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.

х 1 = 10 х 2 = – 1/10

Теорема Виета.

Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.

45 = 1∙45 45 = 3∙15 45 = 5∙9.

В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.

Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.

СПОСОБ ПЕРЕБРОСКИ

При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а ± b+c ≠ 0, то используется прием переброски, например:

2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)

По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1

Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим

х 1 = 5 х 2 = 0,5.

Каково обоснование? Посмотрите что происходит.

Дискриминанты уравнений (1) и (2) равны:

Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:

У второго (изменённого) корни получаются в 2 раза больше.

Потому результат и делим на 2.

*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.

Ответ: х 1 = 5 х 2 = 0,5

Кв. ур-ие и ЕГЭ.

О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).

Что стоит отметить!

1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:

15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.

Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).

2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже. ..»)

Виды квадратных уравнений

Что такое квадратное уравнение? Как оно выглядит? В термине квадратное уравнение ключевым словом является «квадратное». Оно означает, что в уравнении обязательно должен присутствовать икс в квадрате. Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и просто число (свободный член). И не должно быть иксов в степени, больше двойки.

Говоря математическим языком, квадратное уравнение — это уравнение вида:

Здесь a, b и с – какие-то числа. b и c – совсем любые, а а – любое, кроме нуля. Например:

Здесь а =1; b = 3; c = -4

Здесь а =2; b = -0,5; c = 2,2

Здесь а =-3; b = 6; c = -18

Ну, вы поняли…

В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с коэффициентом а, икс в первой степени с коэффициентом b и свободный член с.

Такие квадратные уравнения называются полными.

А если b = 0, что у нас получится? У нас пропадёт икс в первой степени. От умножения на ноль такое случается.) Получается, например:

5х 2 -25 = 0,

2х 2 -6х=0,

-х 2 +4х=0

И т.п. А если уж оба коэффицента, b и c равны нулю, то всё ещё проще:

2х 2 =0,

-0,3х 2 =0

Такие уравнения, где чего-то не хватает, называются неполными квадратными уравнениями. Что вполне логично.) Прошу заметить, что икс в квадрате присутствует во всех уравнениях.

Кстати, почему а не может быть равно нулю? А вы подставьте вместо а нолик.) У нас исчезнет икс в квадрате! Уравнение станет линейным. И решается уже совсем иначе…

Вот и все главные виды квадратных уравнений. Полные и неполные.

Решение квадратных уравнений.

Решение полных квадратных уравнений.

Квадратные уравнения решаются просто. По формулам и чётким несложным правилам. На первом этапе надо заданное уравнение привести к стандартному виду, т.е. к виду:

Если уравнение вам дано уже в таком виде — первый этап делать не нужно.) Главное — правильно определить все коэффициенты, а , b и c .

Формула для нахождения корней квадратного уравнения выглядит так:

Выражение под знаком корня называется дискриминант . Но о нём — ниже. Как видим, для нахождения икса, мы используем только a, b и с . Т.е. коэффициенты из квадратного уравнения. Просто аккуратно подставляем значения a, b и с в эту формулу и считаем. Подставляем со своими знаками! Например, в уравнении:

а =1; b = 3; c = -4. Вот и записываем:

Пример практически решён:

Это ответ.

Всё очень просто. И что, думаете, ошибиться нельзя? Ну да, как же…

Самые распространённые ошибки – путаница со знаками значений a, b и с . Вернее, не с их знаками (где там путаться?), а с подстановкой отрицательных значений в формулу для вычисления корней. Здесь спасает подробная запись формулы с конкретными числами. Если есть проблемы с вычислениями, так и делайте !

Предположим, надо вот такой примерчик решить:

Здесь a = -6; b = -5; c = -1

Допустим, вы знаете, что ответы у вас редко с первого раза получаются.

Ну и не ленитесь. Написать лишнюю строчку займёт секунд 30. А количество ошибок резко сократится . Вот и пишем подробно, со всеми скобочками и знаками:

Это кажется невероятно трудным, так тщательно расписывать. Но это только кажется. Попробуйте. Ну, или выбирайте. Что лучше, быстро, или правильно? Кроме того, я вас обрадую. Через некоторое время отпадёт нужда так тщательно всё расписывать. Само будет правильно получаться. Особенно, если будете применять практические приёмы, что описаны чуть ниже. Этот злой пример с кучей минусов решится запросто и без ошибок!

Но, частенько, квадратные уравнения выглядят слегка иначе. Например, вот так:

Узнали?) Да! Это неполные квадратные уравнения .

Решение неполных квадратных уравнений.

Их тоже можно решать по общей формуле. Надо только правильно сообразить, чему здесь равняются a, b и с .

Сообразили? В первом примере a = 1; b = -4; а c ? Его вообще нет! Ну да, правильно. В математике это означает, что c = 0 ! Вот и всё. Подставляем в формулу ноль вместо c, и всё у нас получится. Аналогично и со вторым примером. Только ноль у нас здесь не с , а b !

Но неполные квадратные уравнения можно решать гораздо проще. Безо всяких формул. Рассмотрим первое неполное уравнение. Что там можно сделать в левой части? Можно икс вынести за скобки! Давайте вынесем.

И что из этого? А то, что произведение равняется нулю тогда, и только тогда, когда какой-нибудь из множителей равняется нулю! Не верите? Хорошо, придумайте тогда два ненулевых числа, которые при перемножении ноль дадут!
Не получается? То-то…
Следовательно, можно уверенно записать: х 1 = 0 , х 2 = 4 .

Всё. Это и будут корни нашего уравнения. Оба подходят. При подстановке любого из них в исходное уравнение, мы получим верное тождество 0 = 0. Как видите, решение куда проще, чем по общей формуле. Замечу, кстати, какой икс будет первым, а какой вторым — абсолютно безразлично. Удобно записывать по порядочку, х 1 — то, что меньше, а х 2 — то, что больше.

Второе уравнение тоже можно решить просто. Переносим 9 в правую часть. Получим:

Остаётся корень извлечь из 9, и всё. Получится:

Тоже два корня. х 1 = -3 , х 2 = 3 .

Так решаются все неполные квадратные уравнения. Либо с помощью вынесения икса за скобки, либо простым переносом числа вправо с последующим извлечением корня.
Спутать эти приёмы крайне сложно. Просто потому, что в первом случае вам придется корень из икса извлекать, что как-то непонятно, а во втором случае выносить за скобки нечего…

Дискриминант. Формула дискриминанта.

Волшебное слово дискриминант ! Редкий старшеклассник не слышал этого слова! Фраза «решаем через дискриминант» вселяет уверенность и обнадёживает. Потому что ждать подвохов от дискриминанта не приходится! Он прост и безотказен в обращении.) Напоминаю самую общую формулу для решения любых квадратных уравнений:

Выражение под знаком корня называется дискриминантом. Обычно дискриминант обозначается буквой D . Формула дискриминанта:

D = b 2 — 4ac

И чем же примечательно это выражение? Почему оно заслужило специальное название? В чём смысл дискриминанта? Ведь -b, или 2a в этой формуле специально никак не называют… Буквы и буквы.

Дело вот в чём. При решении квадратного уравнения по этой формуле, возможны всего три случая.

1. Дискриминант положительный. Это значит, из него можно извлечь корень. Хорошо корень извлекается, или плохо – вопрос другой. Важно, что извлекается в принципе. Тогда у вашего квадратного уравнения – два корня. Два различных решения.

2. Дискриминант равен нулю. Тогда у вас получится одно решение. Так как от прибавления-вычитания нуля в числителе ничего не меняется. Строго говоря, это не один корень, а два одинаковых . Но, в упрощённом варианте, принято говорить об одном решении.

3. Дискриминант отрицательный. Из отрицательного числа квадратный корень не извлекается. Ну и ладно. Это означает, что решений нет.

Честно говоря, при простом решении квадратных уравнений, понятие дискриминанта не особо-то и требуется. Подставляем в формулу значения коэффициентов, да считаем. Там всё само собой получается, и два корня, и один, и ни одного. Однако, при решении более сложных заданий, без знания смысла и формулы дискриминанта не обойтись. Особенно — в уравнениях с параметрами. Такие уравнения — высший пилотаж на ГИА и ЕГЭ!)

Итак, как решать квадратные уравнения через дискриминант вы вспомнили. Или научились, что тоже неплохо.) Умеете правильно определять a, b и с . Умеете внимательно подставлять их в формулу корней и внимательно считать результат. Вы поняли, что ключевое слово здесь – внимательно?

А теперь примите к сведению практические приёмы, которые резко снижают количество ошибок. Тех самых, что из-за невнимательности.… За которые потом бывает больно и обидно…

Приём первый . Не ленитесь перед решением квадратного уравнения привести его к стандартному виду. Что это означает?
Допустим, после всяких преобразований вы получили вот такое уравнение:

Не бросайтесь писать формулу корней! Почти наверняка, вы перепутаете коэффициенты a, b и с. Постройте пример правильно. Сначала икс в квадрате, потом без квадрата, потом свободный член. Вот так:

И опять не бросайтесь! Минус перед иксом в квадрате может здорово вас огорчить. Забыть его легко… Избавьтесь от минуса. Как? Да как учили в предыдущей теме! Надо умножить всё уравнение на -1. Получим:

А вот теперь можно смело записывать формулу для корней, считать дискриминант и дорешивать пример. Дорешайте самостоятельно. У вас должны получиться корни 2 и -1.

Приём второй. Проверяйте корни! По теореме Виета. Не пугайтесь, я всё объясню! Проверяем последнее уравнение. Т.е. то, по которому мы записывали формулу корней. Если (как в этом примере) коэффициент а = 1 , проверить корни легко. Достаточно их перемножить. Должен получиться свободный член, т.е. в нашем случае -2. Обратите внимание, не 2, а -2! Свободный член со своим знаком . Если не получилось – значит уже где-то накосячили. Ищите ошибку.

Если получилось — надо сложить корни. Последняя и окончательная проверка. Должен получиться коэффициент b с противоположным знаком. В нашем случае -1+2 = +1. А коэффициент b , который перед иксом, равен -1. Значит, всё верно!
Жаль, что это так просто только для примеров, где икс в квадрате чистый, с коэффициентом а = 1. Но хоть в таких уравнениях проверяйте! Всё меньше ошибок будет.

Приём третий .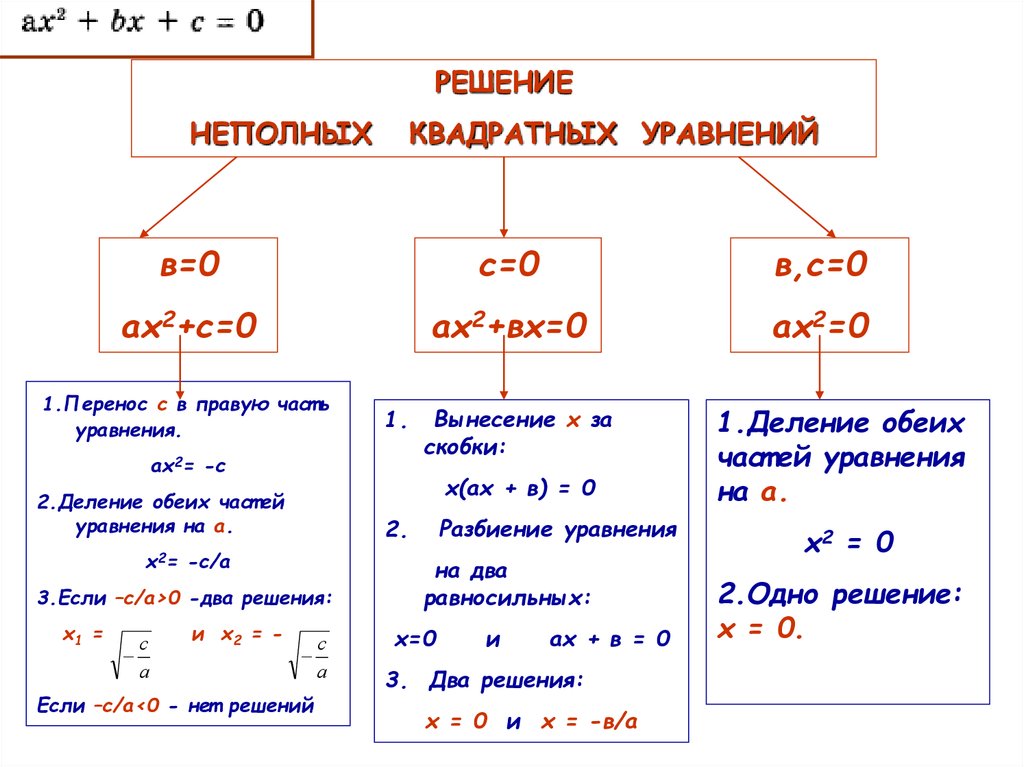 Если в вашем уравнении есть дробные коэффициенты, — избавьтесь от дробей! Домножьте уравнение на общий знаменатель, как описано в уроке «Как решать уравнения? Тождественные преобразования». При работе с дробями ошибки, почему-то так и лезут…

Кстати, я обещал злой пример с кучей минусов упростить. Пожалуйста! Вот он.

Чтобы не путаться в минусах, домножаем уравнение на -1. Получаем:

Вот и всё! Решать – одно удовольствие!

Итак, подытожим тему.

Практические советы:

1. Перед решением приводим квадратное уравнение к стандартному виду, выстраиваем его правильно .

2. Если перед иксом в квадрате стоит отрицательный коэффициент, ликвидируем его умножением всего уравнения на -1.

3. Если коэффициенты дробные – ликвидируем дроби умножением всего уравнения на соответствующий множитель.

4. Если икс в квадрате – чистый, коэффициент при нём равен единице, решение можно легко проверить по теореме Виета. Делайте это!

Теперь можно и порешать.)

Решить уравнения:

8х 2 — 6x + 1 = 0

х 2 + 3x + 8 = 0

х 2 — 4x + 4 = 0

(х+1) 2 + x + 1 = (x+1)(x+2)

Ответы (в беспорядке):

х 1 = 0
х 2 = 5

х 1,2 = 2

х 1 = 2
х 2 = -0,5

х — любое число

х 1 = -3
х 2 = 3

решений нет

х 1 = 0,25
х 2 = 0,5

Всё сходится? Отлично! Квадратные уравнения — не ваша головная боль. Первые три получились, а остальные — нет? Тогда проблема не в квадратных уравнениях. Проблема в тождественных преобразованиях уравнений. Прогуляйтесь по ссылке, это полезно.

Не совсем получается? Или совсем не получается? Тогда вам в помощь Раздел 555. Там все эти примеры разобраны по косточкам. Показаны главные ошибки в решении. Рассказывается, разумеется, и о применении тождественных преобразований в решении различных уравнений. Очень помогает!

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Эта тема поначалу может показаться сложной из-за множества не самых простых формул. Мало того что сами квадратные уравнения имеют длинные записи, еще и корни находятся через дискриминант. Всего получается три новые формулы. Не очень просто запомнить. Это удается только после частого решения таких уравнений. Тогда все формулы будут вспоминаться сами собой.

Общий вид квадратного уравнения

Здесь предложена их явная запись, когда самая большая степень записана первой, и дальше — по убыванию. Часто бывают ситуации, когда слагаемые стоят вразнобой. Тогда лучше переписать уравнение в порядке убывания степени у переменной.

Введем обозначения. Они представлены в таблице ниже.

Если принять эти обозначения, все квадратные уравнения сводятся к следующей записи.

Причем коэффициент а ≠ 0. Пусть эта формула будет обозначена номером один.

Когда уравнение задано, то непонятно, сколько корней будет в ответе. Потому что всегда возможен один из трех вариантов:

в решении будет два корня;
ответом будет одно число;
корней у уравнения не будет совсем.

И пока решение не доведено до конца, сложно понять, какой из вариантов выпадет в конкретном случае.

Виды записей квадратных уравнений

В задачах могут встречаться их разные записи. Не всегда они будут выглядеть как общая формула квадратного уравнения. Иногда в ней будет не хватать некоторых слагаемых. То что было записано выше — это полное уравнение. Если в нем убрать второе или третье слагаемое, то получится нечто другое. Эти записи тоже называются квадратными уравнениями, только неполными.

Причем исчезнуть могут только слагаемые у которых коэффициенты «в» и «с». Число «а» не может быть равно нулю ни при каких условиях. Потому что в этом случае формула превращается в линейное уравнение. Формулы для неполного вида уравнений будут такими:

Итак, видов всего два, кроме полных, есть еще и неполные квадратные уравнения. Пусть первая формула будет иметь номер два, а вторая — три.

Дискриминант и зависимость количества корней от его значения

Это число нужно знать для того, чтобы вычислить корни уравнения. Оно может быть посчитано всегда, какой бы ни была формула квадратного уравнения. Для того чтобы вычислить дискриминант, нужно воспользоваться равенством, записанным ниже, которое будет иметь номер четыре.

После подстановки в эту формулу значений коэффициентов, можно получить числа с разными знаками. Если ответ положительный, то ответом уравнения будут два различных корня. При отрицательном числе корни квадратного уравнения будут отсутствовать. В случае его равенства нулю ответ будет один.

Как решается квадратное уравнение полного вида?

По сути, рассмотрение этого вопроса уже началось. Потому что сначала нужно найти дискриминант. После того как выяснено, что имеются корни квадратного уравнения, и известно их число, нужно воспользоваться формулами для переменных. Если корней два, то нужно применить такую формулу.

Поскольку в ней стоит знак «±», то значений будет два. Выражение под знаком квадратного корня — это дискриминант. Поэтому формулу можно переписать по-другому.

Формула номер пять. Из этой же записи видно, что если дискриминант равен нулю, то оба корня примут одинаковые значения.

Если решение квадратных уравнений еще не отработано, то лучше до того, как применять формулы дискриминанта и переменной, записать значения всех коэффициентов. Позже этот момент не будет вызывать трудностей. Но в самом начале бывает путаница.

Как решается квадратное уравнение неполного вида?

Здесь все гораздо проще. Даже нет необходимости в дополнительных формулах. И не понадобятся те, что уже были записаны для дискриминанта и неизвестной.

Сначала рассмотрим неполное уравнение под номером два. В этом равенстве полагается вынести неизвестную величину за скобку и решить линейное уравнение, которое останется в скобках. В ответе будет два корня. Первый — обязательно равен нулю, потому что имеется множитель, состоящий из самой переменной. Второй получится при решении линейного уравнения.

Неполное уравнение под номером три решается переносом числа из левой части равенства в правую. Потом нужно разделить на коэффициент, стоящий перед неизвестной. Останется только извлечь квадратный корень и не забыть записать его два раза с противоположными знаками.

Далее записаны некоторые действия, помогащие научиться решать всевозможные виды равенств, которые превращаются в квадратные уравнения. Они будут способствовать тому, что ученик сможет избежать ошибок по невнимательности. Эти недочеты бывают причиной плохих оценок при изучении обширной темы «Квадратные уравнения (8 класс)». Впоследствии эти действия не нужно будет постоянно выполнять. Потому что появится устойчивый навык.

Сначала нужно записать уравнение в стандартном виде. То есть сначала слагаемое с самой большой степенью переменной, а потом — без степени и последним — просто число.

Если перед коэффициентом «а» появляется минус, то он может усложнить работу для начинающего изучать квадратные уравнения. От него лучше избавиться. Для этой цели все равенство нужно умножить на «-1». Это значит, что у всех слагаемых изменится знак на противоположный.

Таким же образом рекомендуется избавляться от дробей. Просто умножить уравнение на соответствующий множитель, чтобы знаменатели сократились.

Примеры

Требуется решить следующие квадратные уравнения:

х 2 − 7х = 0;

15 − 2х − х 2 = 0;

х 2 + 8 + 3х = 0;

12х + х 2 + 36 = 0;

(х+1) 2 + х + 1 = (х+1)(х+2).

Первое уравнение: х 2 − 7х = 0. Оно неполное, поэтому решается так, как было описано для формулы под номером два.

После вынесения за скобки получается: х (х — 7) = 0.

Первый корень принимает значение: х 1 = 0. Второй будет найден из линейного уравнения: х — 7 = 0. Легко заметить, что х 2 = 7.

Второе уравнение: 5х 2 + 30 = 0. Снова неполное. Только решается оно так, как описано для третьей формулы.

После перенесения 30 в правую часть равенства: 5х 2 = 30. Теперь нужно выполнить деление на 5. Получается: х 2 = 6. Ответами будут числа: х 1 = √6, х 2 = — √6.

Третье уравнение: 15 − 2х − х 2 = 0. Здесь и далее решение квадратных уравнений будет начинаться с их переписывания в стандартный вид: − х 2 − 2х + 15 = 0. Теперь пришло время воспользоваться вторым полезным советом и умножить все на минус единицу. Получается х 2 + 2х — 15 = 0. По четвертой формуле нужно вычислить дискриминант: Д = 2 2 — 4 * (- 15) = 4 + 60 = 64. Он представляет собой положительное число. Из того, что сказано выше, получается, что уравнение имеет два корня. Их нужно вычислить по пятой формуле. По ней получается, что х = (-2 ± √64) / 2 = (-2 ± 8) / 2. Тогда х 1 = 3, х 2 = — 5.

Четвертое уравнение х 2 + 8 + 3х = 0 преобразуется в такое: х 2 + 3х + 8 = 0. Его дискриминант равен такому значению: -23. Поскольку это число отрицательное, то ответом к этому заданию будет следующая запись: «Корней нет».

Пятое уравнение 12х + х 2 + 36 = 0 следует переписать так: х 2 + 12х + 36 = 0. После применения формулы для дискриминанта получается число ноль. Это означает, что у него будет один корень, а именно: х = -12/ (2 * 1) = -6.

Шестое уравнение (х+1) 2 + х + 1 = (х+1)(х+2) требует провести преобразования, которые заключаются в том, что нужно привести подобные слагаемые, до того раскрыв скобки. На месте первой окажется такое выражение: х 2 + 2х + 1. После равенства появится эта запись: х 2 + 3х + 2. После того как подобные слагаемые будут сосчитаны, уравнение примет вид: х 2 — х = 0. Оно превратилось в неполное. Подобное ему уже рассматривалось чуть выше. Корнями этого будут числа 0 и 1.

Алгебра. Квадратные уравнения. Часть I (практические задачи)

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Похоже, вы находитесь на устройстве с «узкой» шириной экрана ( т. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.2} + 3 = 0\) Решение

1. Решение квадратных уравнений методом факторинга

Общая форма квадратного уравнения

ах ² + бх + с = 0

, где x — переменная, а a , b и c — константы.

Примеры квадратных уравнений

(а) 5 х ² — 3 х — 1 = 0 является квадратное уравнение в квадратной форме где

`a = 5`, `b = -3`, `c = -1`

(б) 5 + 3 т — 4.9 t ² = 0 есть квадратное уравнение в квадратной форме.

Здесь `a = -4,9`, `b = 3`, `c = 5`
[Это уравнение возникло при нахождении времени, когда снаряд под действием силы тяжести попадает в земля. ]

(в) _{( х + 1) ² = 4 является квадратичным
уравнение, но не в квадратичной форме.}

Необходимо расширить и упростить до:

х ² + 2 х — 3 = 0

Резюме

В общем, квадратное уравнение:

должен содержать термин x ²
НЕ ДОЛЖЕН содержать термины со степенями выше x ² например. x ³ , x ⁴ и т.д.

Примеры неквадратичных уравнений

bx − 6 = 0 НЕ является квадратным уравнением, потому что в нем нет члена x ².
x ³ − x ² − 5 = 0 НЕ является квадратным уравнением, поскольку существует член x ³ (не допускается в квадратных уравнениях).

Решения квадратного уравнения Уравнение

Решение уравнения состоит из всех чисел (корней), которые делают уравнение истинным .

Все квадратные уравнения имеют 2 решения (т.е. 2 корня). Они могут быть:

реальный и отличный
действительный и равный
мнимый (сложный)

Пример 1

Квадратное уравнение x ² − 7 x + 10 = 0 имеет корни из

`x = 2` и `x = 5`. (Ниже мы покажем, как найти эти корни.)

Это можно увидеть, подставив в уравнение:

Когда х = 2,

x ² − 7 x + 10

= (2) ² − 7(2) + 10
= 4 — 14 + 10
= 0

(аналогично это можно показать для x = 5).В этом примере корни действительные и различные .

Пример 2

Квадратное уравнение x ² − 6 x + 9 = 0 имеет двойных корней из x = 3 (оба корня одинаковы)

Это можно увидеть, подставив x = 3 в уравнение:

x ² − 6 x + 9

= (3) ² — 6(3) + 9
= 9 — 18 + 9
= 0

Пример 3

Квадратное уравнение

х ² + 9 = 0

имеет мнимых корней из

`x=sqrt(-9)` или `-sqrt(-9)`

Узнайте больше о мнимых числах.

Решение квадратного уравнения с помощью факторинга

Пока мы будем иметь дело только с квадратными уравнениями, которые можно факторизовать (разложить на множители).

Если вам нужно напоминание о том, как учитывать фактор, вернитесь к разделу:

Факторинг трехчленов.

Используя тот факт, что произведение равно нулю, если любой из его множителей равен нулю, мы выполняем следующие шаги:

(i) Перенесите все члены влево и упростите, оставив ноль на правая сторона.

(ii) Факторизация квадратного выражения

(iii) Установить каждый коэффициент равным нулю

(iv) Решить полученные линейные уравнения

(v) Проверить решения в исходном уравнении

Пример 4

Решите x ² — 2 x — 15 = 0

Ответить

х ² — 2 х — 15 = 0

Факторинг дает:

( х — 5)( х + 3) = 0

Теперь, если одно из условий ( x — 5) или ( x + 3) равно 0, произведение равно нулю. Итак, делаем вывод:

( х — 5) = 0, поэтому
х = 5

или

( х + 3) = 0, поэтому
х = — 3

Следовательно, корни равны x = 5 и x = − 3.

Мы правы?

Проверяем корни в исходном уравнении по замена.

Когда х = 5:

х ² − 2 х − 15

= (5) ² − 10 − 15
= 25 — 10 — 15
= 0

(Аналогично, когда мы подставляем `x = -3`, мы также получаем `0`.2 = 16`

`у= +-4`

Шаг 5: Подставьте любое значение (мы будем использовать `+4`) в скобках `u`, что даст нам те же корни квадратного уравнения, которые мы нашли выше:

`x=(1-u)=1-4 = -3,` или

`х=(1+и)=1+4 = 5`

Подробнее об этом подходе см. 2+ 6x + 1 = 0`

Ответить

9 х ² + 6 х + 1 = 0

Факторинг дает:

(3 х + 1)(3 х + 1) = 0

Итак, мы заключаем:

(3 х + 1) = 0,

поэтому

`х=-1/3`

Мы говорим, что существует двойной корень из `x = -1/3`.2 = 0`

`у= 0`

Шаг 5: Подставьте `u=0` в скобки `u`, получив тот же (повторяющийся) корень квадратного уравнения, который мы нашли выше:

`x=-1/3-0 = -1/3` или `x=-1/3+0 = -1/3`

Пример 6 (включая дроби)

Решить

`2-1/х=3/(х+2)`

Ответить

`2-1/х=3/(х+2)`

Умножить на `x(x+2)`, чтобы удалить знаменатели (основания) дробей:

`2x(x+2)-(x(x+2))/x=(3(x)(x+2))/(x+2)`

Отмена дает:

`2x(x+2)-(x+2)=3x`

Раскрытие скобок:

`2x^2+4x-x-2=3x`

`2x^2-2=0`

`х^2-1=0`

Факторинг дает:

`(х+1)(х-1)=0`

Итак, `x = -1` или `x = 1`.

ПРОВЕРКА: Подстановка `x = -1` как в левую, так и в правую части вопроса дает:

`»LHS»=2-1/x=2-1/-1=3`

`»RHS»=3/(x+2)=3/(-1+2)=3=»LHS» `

Аналогично, для `x = +1`,

LHS `= 2 — 1 = 1`
RHS `= 3/3 = 1 =` LHS

Упражнения

Определите, являются ли приведенные ниже уравнения квадратными. Если так, определить a , b , и в.

а.2−12x + 2 = 0`

Итак, да, это квадратное уравнение с

`a = 9`, `b = -12`, `c = 2`

Найти x :

2 х ² − 7 х + 6 = 3

Ответить

2 х ² − 7 х + 6 = 3

2 х ² − 7 х + 3 = 0
(2 х — 1)( х — 3) = 0

Так

`x=1/2` или `x=3`. 2 = 49/16 — 24/16 = 25/16`
`u= +-5/4`

Шаг 5: Подставьте любое значение (мы будем использовать `+5/4`) в скобки `u`, что даст нам те же корни квадратного уравнения, которые мы нашли выше:

`x=7/4-5/4 = 1/2` или `x=7/4+5/4 = 3`

РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙ

РЕШЕНИЕ КВАДРАТИЧНЫХ УРАВНЕНИЙ

Примечание:

Квадратное уравнение — это полиномиальное уравнение второй степени.
U-образный график квадратичного уравнения называется параболой.
Квадратное уравнение имеет два решения. Либо два различных реальных решения, одно двойное действительное решение или два мнимых решения.
Существует несколько методов решения квадратного уравнения:
1. Факторинг
2. Завершение квадрата
3. Квадратичная формула
4. Графики
Все методы начинаются с установки уравнения равным нулю.

Найдите x в следующем уравнении.

Пример 1:

Уравнение уже обнулено.

Метод 1: Факторинг

Способ 2: Заполнение квадрата

Разделите обе части уравнения на 2.

Добавьте к обеим частям уравнения.

Добавьте к обеим частям уравнения:

Фактор левой части и упрощение правой части:

Возьмите квадратный корень из обеих частей уравнения:

Добавьте к обеим частям уравнения:

Метод 3: квадратичная формула

Квадратичная формула

В уравнении a есть коэффициент члена, b — коэффициент члена x , а c — константа.Замените 2 на на , -1 на b , и -1 для c в квадратичной формуле и упрощать.

Метод 4: График

График y = левая часть уравнения или и график y = правая часть уравнения или y =0.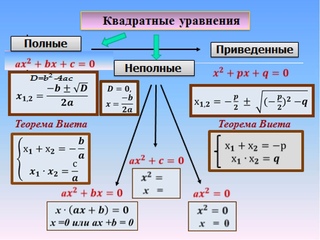 График y =0 не более того чем ось х. Итак, вы будете искать, где график пересекает ось x. Другой способ сказать это состоит в том, что x-перехваты являются решениями этого уравнения.

Вы можете видеть на графике, что есть два x-перехвата, один в 1 и один в .

Ответы 1 и Эти ответы могут или не могут быть решениями исходных уравнений. Вы должны убедиться, что эти ответы являются решениями.

Проверьте эти ответы в исходном уравнении.

Проверьте решение x =1, подставив 1 в исходное уравнение вместо x. Если левая часть уравнения равна правой части уравнение после замены, вы нашли правильный ответ.

Левая сторона:
Правая сторона:

Так как левая часть исходного уравнения равна правой части исходное уравнение после того, как мы подставим значение 1 вместо x, тогда x = 1 — это решение.
Проверьте решение, подставив в исходное уравнение для х. Если левая часть уравнения равна правая часть уравнения после подстановки, вы нашли правильный ответ.
Левая сторона:
Правая сторона:
Так как левая часть исходного уравнения равна правой части исходное уравнение после того, как мы подставим значение вместо x, тогда это решение.
Решения уравнения 1 и

Если вы хотите работать с другим примером, нажмите «Пример».

Если вы хотите проверить себя, решив некоторые задачи, подобные этой например, нажмите Проблема

Если вы хотите вернуться к содержанию уравнения, нажмите Содержание.
[Алгебра] [Тригонометрия] [Геометрия] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра]

Домашняя страница S.O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.

Автор:Нэнси Маркус

Copyright 1999-2022 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователь онлайн за последний час
Решение квадратных уравнений с помощью факторинга
Чтобы решить квадратное уравнение, используя факторинг :
1 .Преобразуйте уравнение, используя стандартную форму, в которой одна сторона равна нулю.
2 . Фактор ненулевая сторона.
3 . Установите каждый множитель равным нулю (помните: произведение множителей равно нулю тогда и только тогда, когда один или несколько множителей равны нулю).
4 . Решите каждое полученное уравнение.
Пример 1:
Решите уравнение, Икс 2 − 3 Икс − 10 знак равно 0
Фактор левой стороны: ( Икс − 5 ) ( Икс + 2 ) знак равно 0
Установите каждый фактор равным нулю: Икс − 5 знак равно 0 или Икс + 2 знак равно 0
Решите каждое уравнение: Икс знак равно 5 или Икс знак равно − 2
Набор решений { 5 , − 2 } .
Пример 2:
Решите уравнение, 2 Икс 2 + 5 Икс знак равно 12
Установите правую сторону на ноль: 2 Икс 2 + 5 Икс − 12 знак равно 0
Фактор левой стороны: ( 2 Икс − 3 ) ( Икс + 4 ) знак равно 0
Установите каждый фактор равным нулю: 2 Икс − 3 знак равно 0 или Икс + 4 знак равно 0
Решите каждое уравнение: Икс знак равно 3 2 или Икс знак равно − 4
Набор решений { 3 2 , − 4 } .
Решение квадратных уравнений — GMAT Math
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права. Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \ достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем а ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:

Решение квадратных уравнений с помощью квадратичной формулы — алгебра среднего уровня
Цели обучения
К концу этого раздела вы сможете:
Решение квадратных уравнений с помощью квадратной формулы
Использование дискриминанта для предсказания количества и типа решений квадратного уравнения
Определите наиболее подходящий метод решения квадратного уравнения
Прежде чем начать, пройдите этот тест на готовность.
Оценка, когда и
Если вы пропустили эту проблему, просмотрите (рисунок).
Упрощение:
Если вы пропустили эту проблему, просмотрите (рисунок).
Упрощение:
Если вы пропустили эту проблему, просмотрите (рисунок).
Решение квадратных уравнений с помощью квадратной формулы
Когда мы решали квадратные уравнения в последнем разделе, дополняя квадрат, мы каждый раз делали одни и те же шаги. К концу набора упражнений вы, возможно, задавались вопросом: «А нет ли более простого способа сделать это?» Ответ «да».Математики ищут закономерности, когда делают что-то снова и снова, чтобы облегчить себе работу. В этом разделе мы выведем и используем формулу для нахождения решения квадратного уравнения.
Мы уже видели, как решить формулу для конкретной переменной «вообще», так что мы проделаем алгебраические шаги только один раз, а затем используем новую формулу, чтобы найти значение конкретной переменной. Теперь мы пройдем этапы заполнения квадрата, используя общую форму квадратного уравнения, чтобы решить квадратное уравнение для x.
Начнем со стандартной формы квадратного уравнения и решим его для x , заполнив квадрат.
Квадратичная формула
Решения квадратного уравнения вида ах ² + bx + с = 0, где находятся по формуле:
Чтобы использовать квадратичную формулу, мы подставляем значения a , b и c из стандартной формы в выражение в правой части формулы.Тогда упростим выражение. Результатом является пара решений квадратного уравнения.
Обратите внимание, что формула представляет собой уравнение. Убедитесь, что вы используете обе части уравнения.
Как решить квадратное уравнение с помощью квадратичной формулы
Решите с помощью квадратичной формулы:
Решите с помощью квадратичной формулы: .
Решите с помощью квадратичной формулы: .
Решите квадратное уравнение, используя квадратную формулу.
Запишите квадратное уравнение в стандартной форме: x ² + b x + c = 0. Определите значения a , b и c 90.
Напишите квадратную формулу. Затем замените значения на , на и на .
Упростить.
Проверьте решения.
Если вы произносите формулу, когда пишете ее в каждой задаче, вы быстро ее запомните! И помните, квадратичная формула — это УРАВНЕНИЕ.Убедитесь, что вы начали с « x =».
Решите с помощью квадратичной формулы:
Решите с помощью квадратичной формулы: .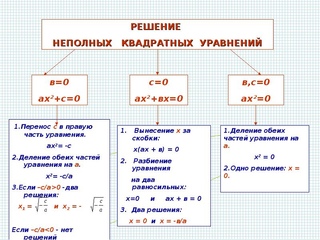
Решите с помощью квадратичной формулы: .
Когда мы решали квадратные уравнения, используя свойство квадратного корня, мы иногда получали ответы, содержащие радикалы. Это может произойти и при использовании квадратичной формулы. Если мы получаем радикал в качестве решения, окончательный ответ должен иметь радикал в его упрощенной форме.
Решите с помощью квадратичной формулы:
Решите с помощью квадратичной формулы: .
Решите с помощью квадратичной формулы: .
Когда мы подставляем на , b и c в квадратную формулу, а подкоренное число отрицательное, квадратное уравнение будет иметь мнимые или комплексные решения. Мы увидим это в следующем примере.
Решите с помощью квадратичной формулы:
Решите с помощью квадратичной формулы: .
Решите с помощью квадратичной формулы: .
Помните, что для использования квадратичной формулы уравнение должно быть записано в стандартной форме: x ² + bx + c = 0. Иногда нам нужно будет выполнить некоторые алгебраические вычисления, чтобы привести уравнение к стандартной форме. форме, прежде чем мы сможем использовать квадратную формулу.
Решите с помощью квадратичной формулы:
Наш первый шаг — привести уравнение к стандартной форме.
Решите с помощью квадратичной формулы:
Решите с помощью квадратичной формулы:
Когда мы решали линейные уравнения, если в уравнении было слишком много дробей, мы очищали дроби, умножая обе части уравнения на ЖК-дисплее. Это дало нам эквивалентное уравнение — без дробей — для решения. Мы можем использовать ту же стратегию с квадратными уравнениями.
Решите с помощью квадратичной формулы:
Наш первый шаг — очистить дроби.
Решите с помощью квадратичной формулы: .
Решите с помощью квадратичной формулы: .
Подумайте об уравнении ( x − 3) ² = 0. Из свойства нулевого произведения мы знаем, что это уравнение имеет только одно решение,
х = 3.
В следующем примере мы увидим, как использование квадратичной формулы для решения уравнения, стандартная форма которого представляет собой точный квадратный трехчлен, равный 0, дает только одно решение.Обратите внимание, что после упрощения подкоренной дроби оно становится равным 0, что приводит только к одному решению.
Решите с помощью квадратичной формулы:
Знаете ли вы, что 4 x ² − 20 x + 25 является совершенным квадратным трехчленом. Это эквивалентно (2 x − 5) ² ? Если вы решите
4 x ² − 20 x + 25 = 0, разложив на множители и затем используя свойство квадратного корня, вы получите тот же результат?
Решите с помощью квадратичной формулы:
Решите с помощью квадратичной формулы:
Использование дискриминанта для прогнозирования количества и типа решений квадратного уравнения
Когда мы решали квадратные уравнения в предыдущих примерах, иногда мы получали два действительных решения, одно действительное решение, а иногда два комплексных решения. Есть ли способ предсказать количество и тип решений квадратного уравнения без фактического решения уравнения?
Да, выражение под радикалом квадратной формулы позволяет нам легко определить количество и тип решений. Это выражение называется дискриминантом.
Дискриминант
Давайте посмотрим на дискриминант уравнений в некоторых примерах, а также на количество и тип решений этих квадратных уравнений.
Использование дискриминанта, b ² − 4 ac , для определения количества и типа решений квадратного уравнения
Для квадратного уравнения вида ах ² + bx + с = 0,
Если b ² − 4 ac > 0, уравнение имеет 2 действительных решения.
если b ² − 4 ac = 0, уравнение имеет 1 действительное решение.
если b ² − 4 ac < 0, уравнение имеет 2 комплексных решения.
Определите количество решений каждого квадратного уравнения.
ⓐⓑⓒ
Чтобы определить количество решений каждого квадратного уравнения, посмотрим на его дискриминант.
ⓐ
Поскольку дискриминант положительный, у уравнения есть 2 действительных решения.
ⓑ
Поскольку дискриминант отрицателен, уравнение имеет два комплексных решения.
ⓒ
Поскольку дискриминант равен 0, уравнение имеет 1 действительное решение.
Определите количество и тип решений каждого квадратного уравнения.
ⓐⓑⓒ
ⓐ 2 комплексных раствора; ⓑ 2 реальных решения; ⓒ 1 реальный раствор
Определите количество и тип решений каждого квадратного уравнения.
ⓐⓑⓒ
ⓐ 2 реальных решения; ⓑ 2 комплексных решения; ⓒ 1 реальный раствор
Определите наиболее подходящий метод для решения квадратного уравнения
Мы суммируем четыре метода, которые мы использовали для решения квадратных уравнений ниже.
Методы решения квадратных уравнений
Факторинг
Свойство квадратного корня
Завершение квадрата
Квадратичная формула
Учитывая, что у нас есть четыре метода решения квадратного уравнения, как решить, какой из них использовать? Факторинг часто является самым быстрым методом, поэтому мы пробуем его в первую очередь. Если уравнение или мы используем свойство квадратного корня. Для любого другого уравнения, вероятно, лучше всего использовать квадратную формулу.Помните, что вы можете решить любое квадратное уравнение, используя квадратную формулу, но это не всегда самый простой метод.
Как насчет метода завершения квадрата? Большинство людей считают этот метод громоздким и предпочитают его не использовать. Нам нужно было включить его в список методов, потому что мы завершили квадрат в целом, чтобы вывести квадратную формулу. Вы также будете использовать процесс заполнения квадрата в других областях алгебры.
Определите наиболее подходящий метод решения квадратного уравнения.
Сначала попробуйте Факторинг . Если квадратичные факторы легко, этот метод очень быстро.
Далее попробуйте свойство квадратного корня . Если уравнение соответствует форме или его можно легко решить с помощью свойства Square Root.
Используйте квадратичную формулу . Любое другое квадратное уравнение лучше всего решать с помощью квадратной формулы.
В следующем примере эта стратегия используется, чтобы решить, как решать каждое квадратное уравнение.
Определите наиболее подходящий метод для решения каждого квадратного уравнения.
ⓐⓑⓒ
ⓐ
Поскольку уравнение находится в наиболее подходящем методе, это использовать свойство квадратного корня.
ⓑ
Мы понимаем, что левая часть уравнения представляет собой точный квадратный трехчлен, поэтому наиболее подходящим методом будет факторинг.
ⓒ
Хотя нашей первой мыслью может быть попытка факторинга, размышления обо всех возможностях метода проб и ошибок приводят нас к выбору квадратичной формулы как наиболее подходящего метода.
Определите наиболее подходящий метод для решения каждого квадратного уравнения.
ⓐⓑⓒ
ⓐ факторинг; ⓑ Свойство квадратного корня; ⓒ Квадратичная формула
Определите наиболее подходящий метод для решения каждого квадратного уравнения.
ⓐⓑⓒ
ⓐ Квадратичная формула;
ⓑ Факторинг или свойство квадратного корня ⓒ Свойство квадратного корня
Ключевые понятия
Квадратичная формула
Решения квадратного уравнения вида x ² + bx + c = 0 находятся по формуле:
Как решить квадратное уравнение с помощью квадратной формулы.
Запишите квадратное уравнение в стандартной форме: x ² + b x + c = 0. Определите значения a , b , c .
Напишите квадратную формулу. Затем подставьте значения на , на b , на .
Упростить.
Проверьте решения.
Использование дискриминанта, b ² − 4 ac , для определения количества и типа решений квадратного уравнения
Для квадратичного уравнения формы AX ² + BX + C = 0,
Если B ² — 4 AC > 0, уравнение имеет 2 реальных решения.
если b ² − 4 ac = 0, уравнение имеет 1 действительное решение.
если b ² − 4 ac < 0, уравнение имеет 2 комплексных решения.
методов решения квадратных уравнений:
Факторинг
Свойство квадратного корня
Завершение квадрата
Квадратичная формула
Как определить наиболее подходящий метод решения квадратного уравнения.
Сначала попробуйте факторинг. Если квадратичные факторы легко, этот метод очень быстро.
Далее попробуйте свойство квадратного корня . Если уравнение соответствует форме x ² = k или a ( x − h ) ² = k , его можно легко решить с помощью свойства Square.
Используйте квадратичную формулу . Любое другое квадратное уравнение лучше всего решать с помощью квадратной формулы.
Практика делает совершенным
Решение квадратных уравнений с помощью квадратичной формулы
В следующих упражнениях решите с помощью квадратичной формулы.
Использование дискриминанта для предсказания числа действительных решений квадратного уравнения
В следующих упражнениях определите количество действительных решений для каждого квадратного уравнения.
Определение наиболее подходящего метода решения квадратного уравнения
В следующих упражнениях определите наиболее подходящий метод (факторинг, вычисление квадратного корня или квадратную формулу) для решения каждого квадратного уравнения. Не решить.
Письменные упражнения
Решить уравнение
ⓐ заполнив квадрат
ⓑ с использованием квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
Решить уравнение
ⓐ заполнив квадрат
ⓑ с использованием квадратичной формулы
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство выполнения целей этого раздела.
ⓑ Что этот контрольный список говорит вам о вашем мастерстве в этом разделе? Какие шаги вы предпримете для улучшения?
Глоссарий
дискриминант
В квадратной формуле величина b ² − 4 ac называется дискриминантом.
Примеры квадратных уравнений, решение квадратных уравнений
Квадратное уравнение — это полиномиальное уравнение степени 2 , что означает, что &nbsp2 равно наибольшая степень в уравнении.
Уравнение также устанавливается равным нулю.
Уравнение вида:
топор ² + Ьх + с = 0,
, где a ≠ 0.
Графики квадратных уравнений
На графике квадратные уравнения представляют собой параболу/кривую с максимальной или минимальной точкой поворота. где-то.
Если a положительны в квадратном уравнении, кривая будет иметь минимальный поворот точка.
Например, кривая x ² выглядит так:
Если a отрицательное значение, кривая будет иметь максимальную точку поворота.
Например, кривая -x ² выглядит так:
Примеры решения квадратных уравнений
Цель решения примеров квадратных уравнений, состоит в том, чтобы выяснить, где уравнение равно 0 , таким образом найдя корни/нули.
То есть значения, при которых кривая уравнения касается оси x .
Подход можно сформулировать так: решить, найти корни, найти нули, но при решении они означают одно и то же. квадратика.
Квадратное уравнение может иметь &nbsp2 решения/корни, &nbsp1 решение или не иметь реальные решения, показанные ниже.

При решении примеров квадратных уравнений часто уравнения могут быть довольно аккуратными, и поэтому их можно решается относительно быстро методом факторизации квадратичных чисел в виде:

( x + a )( x + b )
На странице Удаление кронштейнов представлены дополнительные объяснение для тех, кто не знаком с подходом.
Примеры
(1.1)
x ² + 3 х − 4 = 0
=> ( x − 1 )( x + 4 ) = 0
По свойству нулевого фактора,
, если a × b = 0 , &nbspтогда либо a , либо b должен быть 0 , или оба.
Итак:
( х − 1 )( х + 4 ) = 0 ,
, то либо ( x − 1 ) = 0 или ( x + 4 ) = 0
=> ( x − 1 ) = 0 , х = 1
=> ( x + 4 ) = 0 , х = — 4
Решения/корни x ² + 3 x − 4 = 0 есть x = — 4 , x
1 .
(1.2)
x ² + 4 х + 4 = 0
=> ( x + 2 ) ( x
8 + 2 ) = 0 => x = — 4 = — 4 = — 4 = — 4 = — 4 = — 4 = — 4 = — 4 = — 4 = — 4 = — 4
Ситуация с двумя одинаковыми решениями означает, что существует только одно решение, 1 точка где кривая касается оси x .
(1.3)
Иногда при решении квадратичных уравнений уравнение изначально может быть не равно нулю.
В этом случае. Любые числа справа от знака равенства необходимо переместить влево, а когда они есть, природа меняется.
Либо от положительного к отрицательному, либо от отрицательного к положительному.
а) x ² + 3 x = — 2
x ² + 3 х + 2 = 0

=> ( x + 8) ( x 8 + 1 ) = 0 , x = — 2 x = — 1
б) x ² = 6 x − 8 8
х ² − 6 х + 8 = 0
=> ( x — 2 ) ( 2 ) ( x — 4 ) = 0 , x = 2 7 x = 4
Два других основных метода решения квадратичных уравнений:
Использование квадратичной формулы или Заполнение квадрата .
Домой
›
Квадратные уравнения
› Примеры решения квадратных уравнений

Вернуться к НАЧАЛУ страницы .