Квадратный корень из 5 — это… Что такое Квадратный корень из 5?

Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.^[1]

Его приблизительное значение с 59 цифрами после запятой является:

Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.^[2]

Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:

Вавилонский метод

Вычисление корня из 5, начиная с r₀ = 2, где r_n+1 = (r_n + 5/r_n) / 2:

Золотое сечение

√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.

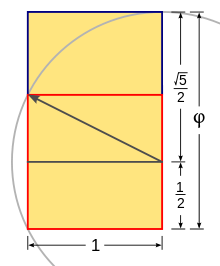
Золотое сечение φ — среднее арифметическое 1 и корня из 5.^[3]

() алгебраически можно выразить так:

Числа Фибоначчи могут быть выражены через корень из 5 так:

Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:^[4]

Алгебра

Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.

Число 6 представляется в данном кольце двумя способами:

Поле  — абелево расширение рациональных чисел.

Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:

Тождества Рамануджана

Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.^[5][6]

Например, случай непрерывных дробей Роджерса-Рамануджана:

См. также

Примечания

1. ↑ Dauben, Joseph W. (June 1983) Scientific American Georg Cantor and the origins of transfinite set theory. Volume 248; Page 122.
2. ↑ R. Nemiroff and J. Bonnell: The first 1 million digits of the square root of 5
3. ↑ Browne, Malcolm W. (July 30, 1985) New York Times Puzzling Crystals Plunge Scientists into Uncertainty. Section: C; Page 1. (Note — this is a widely cited article).
4. ↑ Richard K. Guy: «The Strong Law of Small Numbers». American Mathematical Monthly, vol. 95, 1988, pp. 675—712
5. ↑ Ramanathan, K. G. (1984), ««On the Rogers-Ramanujan continued fraction»», Indian Academy of Sciences. Proceedings. Mathematical Sciences Т. 93 (2): 67-77, MR813071, ISSN 0253-4142, DOI 10.1007/BF02840651 
6. ↑ Eric W. Weisstein, «Ramanujan Continued Fractions», <http://mathworld.wolfram.com/RamanujanContinuedFractions.html>  at MathWorld

Ссылки

Квадратный корень из 3 — это… Что такое Квадратный корень из 3?

Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.

Его приблизительным значением с 69 цифрами после запятой является:

Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).

Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.

Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].

Геометрия

Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.

Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен

Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.

является длиной диагонали куба со стороной 1.

Использование в других областях

Энергетика

При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения

См. также

Ссылки

Быстрый обратный квадратный корень — это… Что такое Быстрый обратный квадратный корень?

Вычисление освещения и отражения (показано на примере шутера от первого лица OpenArena) использует в коде быстрый инверсный квадратный корень для вычисления углов падения и отражения.

Быстрый обратный квадратный корень (иногда называемый Быстрый InvSqrt() или по шестнадцатеричной константе 0x5f3759df) — это метод вычисления обратного квадратного корня для 32-битных чисел с плавающей запятой. Алгоритм был, вероятно, разработан в Silicon Graphics в 1990-х, а реализация появилась в 1999 году в исходном коде компьютерной игры Quake III Arena, но данный метод не появлялся на общедоступных форумах, таких как Usenet, до 2002—2003–х годов. Алгоритм генерирует достаточно точные результаты, используя уникальное первое приближение метода Ньютона. В то время основным преимуществом алгоритма был отказ от дорогих вычислительных операций с плавающей запятой в пользу целочисленных операций. Обратные квадратные корни используются для расчета углов падения и отражения для освещения и затенения в компьютерной графике.

Алгоритм принимает 32-битное беззнаковое число с плавающей запятой (unsigned float) в качестве исходных данных, сохраняет 1/2 числа для дальнейшего использования, после чего преобразует биты, представляющее оригинальное число с плавающей запятой в целое. Далее производится логическое смещение вправо на один бит и результат вычитается из «магической» константы 0x5f3759df. Это первое приближение обратного квадратного корня исходного числа. После производится обратное преобразование результата в число с плавающей запятой и вычисляется одна итерация метода Ньютона для получения более точного приближения. Алгоритм позволяет вычислять приблизительное значение обратного квадратного корня в среднем в 4 раза быстрее, чем деление чисел с плавающей запятой.

Алгоритм изначально приписывался Джону Кармаку, но изучение вопроса показало, что код имел более глубокие корни как в аппаратной, так и в программной сферах компьютерной графики. Исправления и изменения производились как Silicon Graphics так и 3dfx Interactive, при этом как самое раннее использование известна реализация Гэри Таролли для SGI Indigo. Неизвестно, как выводилась эта константа изначально, однако расследование проливает свет на возможные методы.

С выходом в свет в 1998 году набора инструкций 3DNow! в процессорах фирмы AMD появилась ассемблерная инструкция PFRSQRT для быстрого приближенного вычисления инверсного квадратного корня.

Мотивация

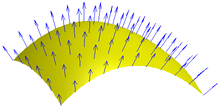Поверхность нормалей широко используются в расчетах освещения и затенения, требующих расчета норм для векторов. Здесь показано поле векторов нормали к поверхности.

Инверсный квадратный корень числа с плавающей запятой используется для вычисления нормализованного вектора. Так как программа с 3D графикой использует эти нормализованные векторы для определения освещения и отражения, миллионы этих вычислений должны выполняться за секунду. До того как было создано специальное аппаратное обеспечение для обработки трансформаций и освещения, программное обеспечение вычислений могло быть медленным. В частности, в начале 1990-х, когда код был разработан, большинство вычислений с плавающей запятой отставало по производительности от операций с целыми числами.

Чтобы нормализовать вектор, его длина определяется путем вычисления его нормы: квадратный корень суммы квадратов компонент вектора. Когда каждый компонент вектора делится на его длину, новый вектор, называемый единичным направлен в том же направлении.

 — это евклидова норма вектора, аналог Евклидовой дистанции между двумя точками в пространстве.

 — это нормализованный единичный вектор. Вычисленное обозначим как ,

, определяет соотношение единичного вектора и обратного квадратного корня от .

Quake III Arena использует алгоритм быстрого обратного квадратного корня для ускорения обработки графики вычислительными блоками, но с тех пор алгоритм уже был реализован в некоторых специализированных аппаратных вершинных шейдерах, используя специальные программируемые матрицы (FPGA).

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.

Быстрый обратный квадратный корень — это… Что такое Быстрый обратный квадратный корень?

Вычисление освещения и отражения (показано на примере шутера от первого лица OpenArena) использует в коде быстрый инверсный квадратный корень для вычисления углов падения и отражения.

Быстрый обратный квадратный корень (иногда называемый Быстрый InvSqrt() или по шестнадцатеричной константе

0x5f3759df) — это метод вычисления обратного квадратного корня для 32-битных чисел с плавающей запятой. Алгоритм был, вероятно, разработан в Silicon Graphics в 1990-х, а реализация появилась в 1999 году в исходном коде компьютерной игры Quake III Arena, но данный метод не появлялся на общедоступных форумах, таких как Usenet, до 2002—2003–х годов. Алгоритм генерирует достаточно точные результаты, используя уникальное первое приближение метода Ньютона. В то время основным преимуществом алгоритма был отказ от дорогих вычислительных операций с плавающей запятой в пользу целочисленных операций. Обратные квадратные корни используются для расчета углов падения и отражения для освещения и затенения в компьютерной графике.

Алгоритм принимает 32-битное беззнаковое число с плавающей запятой (unsigned float) в качестве исходных данных, сохраняет 1/2 числа для дальнейшего использования, после чего преобразует биты, представляющее оригинальное число с плавающей запятой в целое. Далее производится логическое смещение вправо на один бит и результат вычитается из «магической» константы 0x5f3759df. Это первое приближение обратного квадратного корня исходного числа. После производится обратное преобразование результата в число с плавающей запятой и вычисляется одна итерация метода Ньютона для получения более точного приближения. Алгоритм позволяет вычислять приблизительное значение обратного квадратного корня в среднем в 4 раза быстрее, чем деление чисел с плавающей запятой.

Алгоритм изначально приписывался Джону Кармаку, но изучение вопроса показало, что код имел более глубокие корни как в аппаратной, так и в программной сферах компьютерной графики. Исправления и изменения производились как Silicon Graphics так и 3dfx Interactive, при этом как самое раннее использование известна реализация Гэри Таролли для SGI Indigo. Неизвестно, как выводилась эта константа изначально, однако расследование проливает свет на возможные методы.

С выходом в свет в 1998 году набора инструкций 3DNow! в процессорах фирмы AMD появилась ассемблерная инструкция PFRSQRT для быстрого приближенного вычисления инверсного квадратного корня.

Мотивация

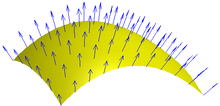Поверхность нормалей широко используются в расчетах освещения и затенения, требующих расчета норм для векторов. Здесь показано поле векторов нормали к поверхности.

Инверсный квадратный корень числа с плавающей запятой используется для вычисления нормализованного вектора. Так как программа с 3D графикой использует эти нормализованные векторы для определения освещения и отражения, миллионы этих вычислений должны выполняться за секунду. До того как было создано специальное аппаратное обеспечение для обработки трансформаций и освещения, программное обеспечение вычислений могло быть медленным. В частности, в начале 1990-х, когда код был разработан, большинство вычислений с плавающей запятой отставало по производительности от операций с целыми числами.

Чтобы нормализовать вектор, его длина определяется путем вычисления его нормы: квадратный корень суммы квадратов компонент вектора. Когда каждый компонент вектора делится на его длину, новый вектор, называемый единичным направлен в том же направлении.

 — это евклидова норма вектора, аналог Евклидовой дистанции между двумя точками в пространстве.

 — это нормализованный единичный вектор. Вычисленное обозначим как ,

, определяет соотношение единичного вектора и обратного квадратного корня от .

Quake III Arena использует алгоритм быстрого обратного квадратного корня для ускорения обработки графики вычислительными блоками, но с тех пор алгоритм уже был реализован в некоторых специализированных аппаратных вершинных шейдерах, используя специальные программируемые матрицы (FPGA).

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.