Определение квадратный корень общее значение и понятие. Что это такое квадратный корень

Прежде чем полностью перейти к анализу смысла, мы должны установить, что этимологическое происхождение математического термина «квадратный корень» встречается на латыни, а точнее в объединении двух слов: основание и квадрат, которое можно перевести как «из четыре. «

В области математики корнем называется определенное значение, которое необходимо умножить на себя (либо на одну, либо на несколько возможностей), чтобы получить определенное число. Когда делается ссылка на квадратный корень из числа, идентифицируется число, которое при умножении на один раз приводит к получению первого числа .

Чтобы привести конкретный случай в качестве примера: квадратный корень из 16 равен 4, так как 4 на 4 равняется 16 . Другими словами, мы можем сказать, что, если мы умножим 4 на себя (4 × 4), мы получим число 16, что равносильно тому, чтобы сказать, что 4 в квадрате приводит к 16.

Квадратный корень из 9, с другой стороны, равен 3 . Объяснение операции идентично предыдущему примеру: 3 × 3 = 9, то есть 3 в квадрате или 3, умноженные на себя, позволяют нам получить число 9. Вопрос «какое число умножено на себя, приводит к 9 ? » ( « Какое число для возведения во вторую степень приводит к 9? » Или « Что такое квадратный корень из 9? » ) Дает нам ответ № 3.

Среди наиболее значимых свойств, которые определяют квадратный корень, мы должны заявить, что мы находим тот факт, что он превращает рациональные числа в алгебраические.

Также нельзя не учитывать тот факт, что квадратный корень может быть выполнен по-другому, исходя из «объектов», которые он использует для разработки. Таким образом, например, это может быть сделано с комплексными числами, с кватернионными числами (расширение действительных чисел) или даже с матрицами.

Вопрос о так называемых квадратных корнях был проанализирован во время пифагорейской фазы, после обнаружения, что квадратный корень из двух не был рациональным (потому что не было никакого коэффициента, чтобы выразить это). Расширив определение квадратного корня, математики начали предлагать существование мнимых чисел и комплексных чисел .

Однако, есть гораздо более старые документы, которые показывают нам, как наши предки также использовали вышеупомянутые математические операции, которые теперь занимают нас. В этом смысле необходимо подчеркнуть, что египтяне прибегали к тем же самым, и, таким образом, это можно проверить в известном папирусе Ахмеса, датированном 1650 годом до нашей эры, который был реализован во времена правления Апофиса I.

Копией документа девятнадцатого века до нашей эры является этот цитируемый папирус, также известный как Papiro Rhind, который состоит из ряда задач математического типа, где в дополнение к вышеупомянутым корням есть вычисления площадей, дробей, тригонометрии, правил трех, уравнения линейного типа, прогрессии и четные распределения пропорционального класса.

Символ, который используется для обозначения корня, был создан Кристофом Рудольфом в 1525 году из буквы r, хотя с расширением его удара, чтобы стилизовать его. {2n+1}} \right) \\ \end{align}\]

Мы будем использовать эти свойства на всю катушку в третьей части урока. А пока начнём с более простых вещей.

1. Корни из точных степеней

При работе с корнями многие ученики допускают одну и ту же ошибку. Они пытаются подменить чёткие правила алгебры интуитивными размышлениями. И на первый взгляд всё выглядит хорошо. Взгляните на примеры:

Во всех трёх случаях мы видим, что под корнем стоят точные квадраты. Их можно переписать так:

Может показаться, что для упрощения выражения достаточно убрать степень и знак корня. На практике это не так:

Из третьей строки видно, что просто убрать степень и корень с отрицательного основания нельзя, ведь корень не может быть отрицательным! Вторая строка объясняет нам, что именно происходит: квадрат делает число под корнем положительным, а дальше мы извлекаем этот самый корень и вновь получаем положительное число. В итоге строки 1 и 2 ведут к извлечению корня из одного и того же числа — 64.

Вывод?

1.1. Корень из точного квадрата

А вывод такой: корень из квадрата не меняет положительные числа, а отрицательные меняет на противоположные. Это в точности совпадает с определением модуля:

Для удобства дальнейших размышлений предлагаю взять на вооружение вот такое определение модуля:

Это определение чрезвычайно полезно для решения сложных задач с параметрами. Об этом как-нибудь в следующий раз. А пока давайте потренируемся:

Опыт моих учеников: поначалу довольно непривычно выписывать эти множители (1, 0 и −1), но затем человек привыкает и пишет всё на автомате. А затем и вовсе перестаёт писать — всё происходит в его голове, но навык добавления множителей остаётся (и очень пригодится, когда мы считаем коэффициенты многочленов).

Потренируйтесь самостоятельно:

Задание. Найдите значение выражения:

[Показать ответы]

Отдельное внимания заслуживают двойные корни, вложенные друг в друга:

Для них замена корня модулем тоже работает, но возникает вопрос: как корректно раскрыть модуль? Придётся сравнивать корни:

Откуда такое смелое утверждение во второй строке? Существует два способа доказать неравенство в красных скобках:

• 1.
  Использовать свойства корней;
• 2.Составить цепочку неравенств.

Я приведу оба:

Сравнение корней — отдельная серьёзная тема. Ей посвящён целый урок. Поэтому давайте просто решим второе задание:

Задание. Вычислите значение выражения:

[показать ответ]

1.2. Корень из чётной степени

Идём дальше. Вновь запишем нашу волшебную формулу:

Капитан очевидность как бы намекает: эта формула верна не только для квадратов, но и для всех чётных степеней:

Другими словами, корень из любой чётной степени понижает эту степень ровно в два раза, но взамен навешивает на неё модуль! Рассмотрим примеры:

Обратите внимание на последнюю строку: изначально под корнем стоит довольно громоздкое число. Вычислять его напролом — возводить в квадрат, а затем извлекать корень — безумие. Но формула понижения степени редуцирует задачу до устной — отличная экономия времени на экзамене.:)

Попробуйте сами:

Задание 2. Найдите значение выражения:

[Показать ответы]

Вывод: если видите корень из степени, то смело понижайте степень вдвое, убирайте корень, но взамен ставьте модуль. Всегда. Обязательно. Ок? Переходим ко второй части урока.

2. Корни из произведения и частного

Перед тем как давать какие-либо новый формулы, напомню важный факт. Корень из суммы не равен сумме корней:

Иначе мы бы получили вот такие бредовые выкладки:

Вроде бы, капитаноочевидно, но многие даже в старших классах допускают такие ошибки.

А теперь разберём ещё два свойства корней.

2.1. Умножение и деление корней

Корни можно умножать и делить. Правила просты:

Примеры:

Попробуйте сами:

Задание 3. Найдите значение выражения:

[показать ответы]

Как видите, с помощью формул мы разбиваем сложный корень на несколько простых.

Мы знаем, то все формулы работают как слева-направо, так и справа-налево, поэтому корни можно «склеивать». При этом новый корень может легко вычисляться, хотя исходные части — не вычисляются вообще. Например:

Попробуйте повторить этот трюк:

Задание 4. Найдите значение выражения:

[показать ответы]

2.

2. Проблемы с областью определения

Но есть одна тонкость. Взгляните, например, на формулу произведения корней:

Напомню: знак радикала обозначает арифметический квадратный корень, который извлекается только из неотрицательных чисел и сам является числом неотрицательным.

С левой стороны от знака равенства стоит один корень, а справа — целых два. Поэтому области определения левой и правой части этого равенства различны:

В чём конкретно состоит различие?

В первой строке мы видим произведение, поэтому неравенство (1) верно всякий раз, когда знаки множителей совпадают. В частности, оба множителя могут быть отрицательными, но их произведение всё равно будет положительным.

Вторая строка — система из двух неравенств, и здесь отрицательные числа нас уже не устроят. Вывод:

Красным я выделил ситуацию, которая допустима для корня из произведения, но становится недопустимой для произведения корней.

Поскольку любое равенство определено лишь тогда, когда определена и левая, и правая его части, дополним исходные правила специальными требованиями:

И вот в таком виде их уже можно использовать — везде и всегда!

Может показаться, что эти ограничения несущественны. Или искусственны. Чуть выше мы никак их не учитывали и всё прекрасно посчитали. Поэтому вопрос: когда ограничения области определения становятся существенным?

Ответ: когда под корнями стоят не конкретные числа, а переменные. К примеру, пусть даны числа:

Очевидно, что произведение двух отрицательных чисел будет положительным. И хотя корень из произведения будет определён, извлекать корни из отдельных множителей нельзя:

Значит, нужно сделать так, чтобы множители под корнем стали положительными. И тут нам на помощь приходит старое доброе число −1:

Добавление минусов к каждому из двух множителей нисколько не повлияло на произведение, но привело к возникновению двух новых множителей, каждый из которых уже точно положителен:

Помните об этом преобразовании, когда сталкиваетесь с произведением отрицательных выражений под знаком корня. Источником такой отрицательности могут быть условия задачи, либо следствия из области определения (такое часто встречается в логарифмических уравнениях и неравенствах, которые изучаются в 10—11 классах).

Ну а мы немного потренируемся и пойдём к третьей части урока — работе с переменными.

Задание 5. Найдите значение выражения:

[показать ответы]

Переходим к самому весёлому.:)

3. Работа с переменными

Если не считать определения, то мы знаем о корнях две вещи. Во-первых, корни понижают степени, но добавляют модули:

Во-вторых, корни можно умножать и делить. Но не всегда:

До сих пор мы тренировались лишь на конкретных числах. И многие могут удивляться: зачем все эти рассуждения про модули и ограничения?

Сейчас мы заменим числа буквами — и задача резко усложнится. Или не усложнится — если вы внимательно изучите то, что написано дальше.:)

3.1. Раскрытие модуля через свойства степеней

Начнём с простого. Мы уже знаем, как избавляться от точной степени:

Попробуем применить эту формулу к двум различным выражениям:

В первой строке мы без труда раскрыли модуль, поскольку знаем, что число под модулем отрицательно. Затем посчитали — получили ответ.

Но как раскрыть модуль во второй строке? Ведь правила раскрытия будут меняться в зависимости от того, какое значение принимает переменная. И если никаких дополнительных ограничений на переменную нет, то модуль так и останется нераскрытым. Взгляните:

Замените выражение тождественно равным, не содержащим знака корня:

Из приведённых примеров видно:

• В строках (2) и (4) мы можем раскрыть модуль, ничего не зная о переменной;
• В строках (1) и (3) раскрыть модуль не удалось.

Почему? Чётные степени в строках (2) и (4) при любом значении переменной будут положительным числом или нулём. Поэтому модуль однозначно раскрывается со знаком «плюс».

Нечётная степень в строках (1) и (3) таким свойством не обладает: она может оказаться как положительным числом, так и отрицательным. Поэтому модуль раскрыть нельзя.

Попробуйте сами:

Задание. Замените выражение тождественно равным, не содержащим знака корня:

[показать ответ]

Чётные степени всегда неотрицательны, нечётные степени могут принимать любой знак:

Тем не менее, модуль нечётной степени тоже можно раскрыть. Если в задаче есть дополнительные условия.

3.2. Учёт дополнительных ограничений

Зачастую в самом условии задачи содержатся ограничения на переменную, которые помогают однозначно раскрыть модуль. Пример:

Упростите выражение:

Работаем по тем правилам, которые изучали выше:

Обратите внимание: в строке (2) чётные степени под корнем дают три неотрицательных числа, поэтому корень можно разбить на три изолированных множителя — область определения при этом не поменяется; затем в строке (3) мы видим чётную степень под модулем и раскрываем его.

Ещё раз запишем результат и дополним его исходными условиями:

В первом случае выражение под модулем положительно или ноль, поэтому модуль однозначно раскрывается со знаком «плюс». Во втором — отрицательно или ноль, поэтому модуль раскрывается со знаком «минус»:

Возможно, у вас возникает вопрос: почему мы пишем множитель 1 или −1, но не рассматриваем отдельно множитель 0? В этом фишка модуля:

Таким образом, в нуле модуль можно раскрывать любым удобным способом.

Попробуйте самостоятельно:

Задание. Упростите выражение:

[показать ответ]

Это были весьма примитивные выражения, сводящиеся к раскрытию модуля. На них мы отработали важный новый навык. Теперь воспользуемся этим навыком для решения более интересных задач.

3.3. Упрощение выражений

Последний и самый интересный раздел этого урока.

Откуда берутся дополнительные ограничения на переменные? Существует ровно два источника таких ограничений:

• 1.Условие задачи. Например, если переменная — это длина отрезка на чертеже, то можно без ущерба для здоровья полагать, что она неотрицательна (а если всё-таки отрицательна, то у вас неправильный чертёж).
• 2.Неявные следствия из исходного выражения / уравнения / неравенства. Тут всё намного интереснее: анализ следствий из исходного условия — увлекательный процесс, доступный лишь хорошо подготовленным ученикам.

Начнём с первого пункта — ограничений, явно указанных в условии задачи. Примеры:

Упростите выражение:

С первым выражением всё просто:

Со вторым уже интереснее. Заметим, что в первом числителе стоит формула сокращённого умножения, а дробь под корнем гарантированно имеет неотрицательный числитель и знаменатель:

Вспомним исходные ограничения:

И раскроем модули:

Как видите, нам удалось избавиться не только от модулей, но и от дробей.:)

Обратите внимание

Материал, представленный дальше, относится скорее к следующему уроку — «Внесение и вынесение множителей из-под знака корня». Его изучение прямо сейчас не является обязательным, но может оказаться весьма полезным для сильных учеников.

Наконец, разберёмся с неявными ограничениями. Ещё раз запишем самую первую формулу:

Пусть известно, что подмодульное выражение неотрицательно. Тогда модуль можно убрать:

С отрицательными величинами тоже можно провернуть такой трюк:

Но любое равенство работает как слева-направо, так и справа-налево. Следовательно, если нам известен знак переменной, мы можем внести её под знак корня:

Это замечание позволит упрощать выражения, которые неподготовленному ученику покажутся неприступными.

Остаётся лишь один вопрос: где взять знак переменной? Ответ: ограничения на переменную часто скрыты в области определения. Например:

Упростите выражения:

Решение:

В первой строке мы видим корень, поэтому выпишем область определения. Это даст нам ограничения на переменную и поможет внести её под знак корня:

То же самое со вторым выражением:

В итоге мы получили выражение, тождественно равное нулю. Однако помните: это равенство сохраняется только для отрицательных значений переменной! Для положительных значений исходное выражение вообще не определено.

Операция, которую мы только что провернули, как раз и называется внесением переменной под знак радикала.

В заключение хотел бы рассмотреть типичную ситуацию для сложных алгебраических задач, когда под корнем стоят, на первый взгляд, противоположные числа.

Упростите выражение:

Заметим, что самый первый корень накладывает жёсткие ограничения на переменную:

Под остальными корнями стоят неотрицательные выражения, поэтому дальше всё просто:

Наличие неявного ограничения позволило нам раскрыть модуль даже у нечётной степени. Обратите внимание на этот переход:

Как мы помним из краткой вводной, минусы можно выносить (и вносить) из основания нечётной степени. Это можно сделать как после раскрытия модуля, так и в самом начале — прямо под корнем:

Красным я отметил одинаковые выражения, стоящие под корнем и в основании степени. Именно такая форма записи (а не игра с минусами) является предпочтительной, например, в логарифмических уравнениях и неравенствах.

Но это тема совсем другого урока. А на сегодня хватит.:)

Смотрите также:

1. Умножение корней n-й степени
2. Корень степени N
3. Следствия из теоремы Виета
4. Задача B3 — работа с графиками
5. C2: расстояние между двумя прямыми
6. Задача B2 на проценты: вычисление полной стоимости покупки

Квадратные корниS-KUZ ‹ Сергей Кузнецов — репетитор по математике

Что такое квадратный корень?

Это понятие очень простое. Естественное, я бы сказал. Математики на каждое действие стараются найти противодействие. Есть сложение — есть и вычитание. Есть умножение — есть и деление. Есть возведение в квадрат… Значит есть и извлечение квадратного корня! Вот и всё. Это действие (извлечение квадратного корня) в математике обозначается вот таким значком:

Сам значок называется красивым словом «радикал«.

Как извлечь корень? Это лучше рассмотреть на примерах.

Как извлечь (или посчитать — это всё едино) корень квадратный из 4? Нужно просто сообразить: какое число в квадрате даст нам 4? Да конечно же 2! Значит:

Сколько будет квадратный корень из 9? А какое число в квадрате даст нам 9? 3 в квадрате даст нам 9! Т.е:

А вот сколько будет квадратный корень из нуля? Не вопрос! Какое число в квадрате ноль даёт? Да сам же ноль и даёт! Значит:

Уловили, что такое квадратный корень? Тогда считаем примеры:

Ответы (в беспорядке): 6; 1; 4; 9; 5.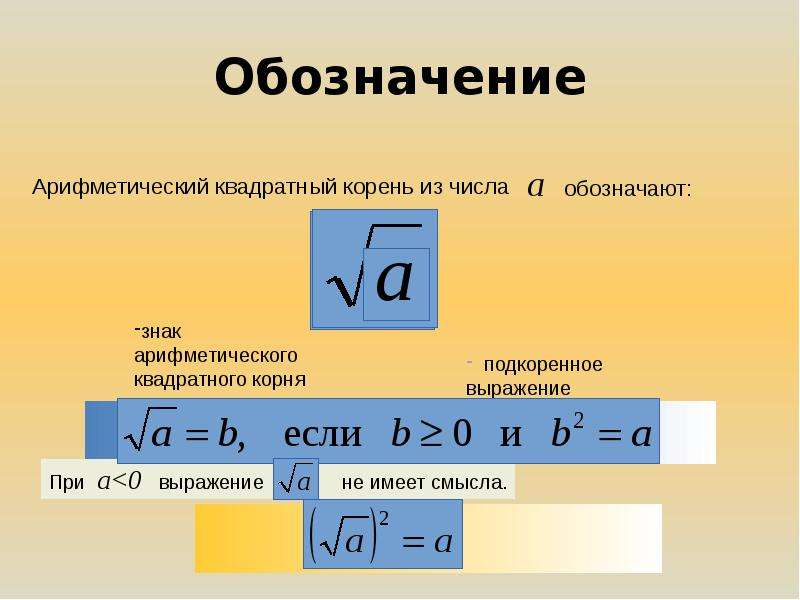

Решили? Действительно, уж куда проще-то?!

Но… Что делает человек, когда видит какое-нибудь задание с корнями?

Тосковать начинает человек… Не верит он в простоту и лёгкость корней. Хотя, вроде, и знает, что такое квадратный корень…

Всё потому, что человек проигнорировал несколько важных пунктиков при изучении корней. Потом эти пунктики жестоко мстят на контрольных и экзаменах…

Пунктик первый. Корни надо узнавать в лицо!

Сколько будет корень квадратный из 49? Семь? Верно! А как вы узнали, что семь? Возвели семёрку в квадрат и получили 49? Правильно! Обратите внимание, чтобы извлечь корень из 49 нам пришлось проделать обратную операцию — возвести 7 в квадрат! И убедиться, что мы не промахнулись. А могли и промахнуться…

В этом и есть сложность извлечения корней.

Возвести в квадрат можно любое число без особых проблем. Умножить число само на себя столбиком — да и все дела. А вот для извлечения корня такой простой и безотказной технологии нет. Приходится подбирать ответ и проверять его на попадание возведением в квадрат.

Этот сложный творческий процесс — подбор ответа — сильно упрощается, если вы помните квадраты популярных чисел. Как таблицу умножения. Если, скажем, надо умножить 4 на 6 — вы же не складываете четверку 6 раз? Сразу выплывает ответ 24. Хотя, не у всех он выплывает, да…

Для свободной и успешной работы с корнями достаточно знать квадраты чисел от 1 до 20. Причём тудаи обратно. Т.е. вы должны легко называть как, скажем, 11 в квадрате, так и корень квадратный из 121. Чтобы добиться такого запоминания, есть два пути. Первый — выучить таблицу квадратов. Это здорово поможет решать примеры. Второй — решать побольше примеров. Это здорово поможет запомнить таблицу квадратов.

И никаких калькуляторов! Только для проверки. Иначе на экзамене будете тормозить нещадно…

Итак, что такое квадратный корень и как извлекать корни — думаю, понятно. Теперь выясним ИЗ ЧЕГО можно их извлекать.

 

Пунктик второй. Корень, я тебя не знаю!

Из каких чисел можно извлекать квадратные корни? Да почти из любых. Проще понять, из чего нельзяих извлекать.

Попробуем вычислить вот такой корень:

Для этого нужно подобрать число, которое в квадрате даст нам -4. Подбираем.

Что, не подбирается? 2² даёт +4. (-2)² даёт опять +4! Вот-вот… Нет таких чисел, которые при возведении в квадрат дадут нам отрицательное число! Хотя я такие числа знаю. Но вам не скажу). Поступите в институт — сами узнаете.

Такая же история будет с любым отрицательным числом. Отсюда вывод:

Выражение, в котором под знаком квадратного корня стоит отрицательное число — не имеет смысла! Это запретная операция. Такая же запретная, как и деление на ноль. Запомните этот факт железно!Или, другими словами:

Квадратные корни из отрицательных чисел извлечь нельзя!

Зато из всех остальных — можно. Например, вполне можно вычислить

или

На первый взгляд это очень сложно. Подбирать дроби, да в квадрат возводить… Не волнуйтесь. Когда разберёмся со свойствами корней, такие примеры будут сводиться к всё той же таблице квадратов. Жизнь станет проще!

Ну ладно дроби. Но нам ведь ещё попадаются выражения типа:

или

и т.д…

Ничего страшного. Всё то же самое. Корень квадратный из двух — это число, которое при возведении в квадрат даст нам двойку. Только число это совсем неровное… Вот оно:

Что интересно, эта дробь не кончается никогда… Такие числа называются иррациональными. В квадратных корнях это — самое обычное дело. Кстати, именно поэтому выражения с корнями называютиррациональными. Понятно, что писать всё время такую бесконечную дробь неудобно. Поэтому вместо бесконечной дроби так и оставляют:

Если при решении примера у вас получилось что-то неизвлекаемое, типа:

то так и оставляем. Это и будет ответ.

Нужно чётко понимать, что под значками

, , ……

и так далее, скрываются просто числа! Неровные, лохматые, иррациональные, но числа!

Конечно, если корень из числа извлекается ровно, вы обязаны это сделать. Ответ задания в виде, например

никто не оценит… Надо корень посчитать и написать

х = 4.

А вот

вполне себе полноценный ответ.

И, конечно, надо знать на память приблизительные значения:

Это знание здорово помогает оценить ситуацию в сложных заданиях.

Идём дальше.

 

Пунктик третий. Самый хитрый.

Основную путаницу в работу с корнями вносит как раз этот пунктик. Именно он придаёт неуверенность в собственных силах… Разберёмся с этим пунктиком как следует!

Для начала опять извлечём квадратный корень их четырёх. Что, уже достал я вас с этим корнем?) Ничего, сейчас интересно будет!

Какое число даст в квадрате 4? Ну два, два — слышу недовольные ответы…

Верно. Два. Но ведь и минус два даст в квадрате 4… А между тем, ответ

правильный, а ответ

грубейшая ошибка. Вот так.

Так в чём же дело?

Действительно, (-2)² = 4. И под определение корня квадратного из четырёх минус два вполне подходит… Это тоже корень квадратный из четырёх.

Но! В школьном курсе математики принято считать за квадратные корни

только неотрицательные числа! Т.е ноль и все положительные. Даже термин специальный придуман: арифметический квадратный корень из числа а — это неотрицательное число, квадрат которого равен а. Отрицательные результаты при извлечении арифметического квадратного корня попросту отбрасываются. В школе все квадратные корни — арифметические. Хотя особо об этом не упоминается.

Ну ладно, это понятно. Это даже и лучше — не возиться с отрицательными результатами… Это ещё не путаница.

Путаница начинается при решении квадратных уравнений. Например, надо решить вот такое уравнение.

Уравнение простое, пишем ответ (как учили):

Такой ответ (совершенно правильный, кстати) — это просто сокращённая запись двух ответов:

и

Стоп-стоп! Чуть выше я написал, что квадратный корень — число всегда неотрицательное! А здесь один из ответов — отрицательный! Непорядок. Это первая ( но не последняя) проблемка, которая вызывает недоверие к корням… Решим эту проблемку. Запишем ответы (чисто для понимания!) вот так:

Скобки сути ответа не меняют. Просто я отделил скобками знаки от корня. Теперь наглядно видно, что сам корень (в скобках) — число всё равно неотрицательное! А знаки — это результат решения уравнения. Ведь при решении любого уравнения мы должны записать все иксы, которые при подстановке в исходное уравнение дадут верный результат. В наше уравнение подходит корень из пяти (положительный!) как с плюсом, так и с минусом.

Если вы

просто извлекаете квадратный корень из чего-либо, вы всегда получаете один неотрицательный результат. Например:

Потому, что это —

арифметический квадратный корень.

Но если вы решаете какое-нибудь квадратное уравнение, типа:

то

всегда получается два ответа (с плюсом и минусом):

Потому, что это — решение уравнения.

Надеюсь, что такое квадратный корень со своими пунктиками вы уяснили. Теперь осталось узнать, что можно делать с корнями, каковы их свойства. И какие там пунктики и подводные кор… извините, камни!)

 

Формулы корней. Свойства квадратных корней.

 

В предыдущем уроке мы разобрались, что такое квадратный корень. Пришла пора разобраться, какие существуют формулы для корней, каковы свойства корней, и что со всем этим можно делать.

Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…

Начнём с самой простой. Вот она:

Напоминаю: а и b — неотрицательные числа! Иначе формула смысла не имеет…

Это свойство корней, как видите простое, короткое и безобидное. Но с помощью этой формулы корней можно делать массу полезных вещей! Разберём на примерах все эти полезные вещи.

Полезная вещь первая. Эта формула позволяет нам умножать корни.

 

Как умножать корни?

Да очень просто. Прямо по формуле. Например:

Казалось бы, умножили, и что? Много ли радости?! Согласен, немного… А вот как вам такой пример?

Из множителей корни ровно не извлекаются. А из результата — отлично! Уже лучше, правда? На всякий случай сообщу, что множителей может быть сколько угодно. Формула умножения корней всё равно работает. Например:

Так, с умножением всё ясно, зачем нужно это свойство корней — тоже понятно.

Полезная вещь вторая. Внесение числа под знак корня.

 

Как внести число под корень?

Предположим, что у нас есть вот такое выражение:

Можно ли спрятать двойку внутрь корня? Легко! Если из двойки сделать корень, сработает формула умножения корней. А как из двойки корень сделать? Да тоже не вопрос! Двойка — это корень квадратный из четырёх!

Вот и пишем:

Корень, между прочим, можно сделать из любого неотрицательного числа! Это будет корень квадратный из квадрата этого числа. 3 — корень из 9. 8 — корень из 64. 11 — корень из 121. Ну, и так далее.

Конечно, расписывать так подробно нужды нет. Разве что, для начала… Достаточно сообразить, что любое неотрицательное число, умноженное на корень, можно внести под корень. Но — не забывайте! — под корнем это число станет квадратом самого себя. Это действие — внесение числа под корень — можно ещё назвать умножением числа на корень. В общем виде можно записать:

Процедура простая, как видите. А зачем она нужна?

Как и любое преобразование, эта процедура расширяет наши возможности. Возможности превратить жестокое и неудобное выражение в мягкое и пушистое). Вот вам простенький пример:

Как видите, свойство корней, позволяющее вносить множитель под знак корня, вполне годится для упрощения.

Кроме того, внесение множителя под корень позволяет легко и просто сравнивать значения различных корней. Безо всякого их вычисления и калькулятора! Третья полезная вещь.

 

Как сравнивать корни?

Это умение очень важно в солидных заданиях, при раскрытии модулей и прочих крутых вещах.

Сравните вот эти выражения. Какое из них больше? Без калькулятора! С калькулятором каждый… э-э-э… короче, каждый справится!)

Так сразу и не скажешь… А если внести числа под знак корня?

и

Запомним (вдруг, не знали?): если число под знаком корня больше, то и сам корень — больше! Отсюда сразу правильный ответ, безо всяких сложных вычислений и расчётов:

и, следовательно:

Здорово, да? Но и это ещё не всё! Вспомним, что все формулы работают как слева направо, так и справа налево. Мы пока формулу умножения корней слева направо употребляли. Давайте запустим это свойство корней наоборот, справа налево. Вот так:

И какая разница? Разве это что-то даёт!? Конечно! Сейчас сами увидите.

Предположим, нам нужно извлечь (без калькулятора!) корень квадратный из числа 6561. Кое-кто на этом этапе и падёт в неравной борьбе с задачей… Но мы упорные, мы не сдаёмся! Полезная вещь четвёртая.

 

Как извлекать корни из больших чисел?

Вспоминаем формулу извлечения корней из произведения. Ту, что я чуть выше написал. Но где у нас произведение!? У нас огромное число 6561 и всё… Да, произведения здесь нет. Но если нам надо — мы егосделаем! Разложим это число на множители. Имеем право.

Для начала сообразим, на что делится это число ровно? Что, не знаете!? Признаки делимости забыли!? Зря.На 3 и на 9 делится это число. Потому, что сумма цифр (6+5+6+1=18) делится на эти числа. Это один из признаков делимости. На три нам делить ни к чему (сейчас поймёте, почему), а вот на 9 поделим. Хотя бы и уголком. Получим 729. Вот мы и нашли два множителя! Первый — девятка (это мы сами выбрали), а второй — 729 (такой уж получился). Уже можно записать:

Улавливаете идею? С числом 729 поступим аналогично. Оно тоже делится на 3 и 9. На 3 опять не делим, делим на 9. Получаем 81. А это число мы знаем! Записываем:

Всё получилось легко и элегантно! Корень пришлось по кусочкам извлекать, ну и ладно. Так можно поступать с любыми большими числами. Раскладывать их на множители, и — вперёд!

Кстати, а почему на 3 делить не надо было, догадались? Да потому, что корень из трёх ровно не извлекается! Имеет смысл раскладывать на такие множители, чтобы хотя бы из одного корень хорошо извлекался. Это 4, 9, 16 ну, и так далее. Делите своё громадное число на эти числа поочерёдно, глядишь, и повезёт!

Но не обязательно. Может и не повезти. Скажем, число 432 при разложении на множители и использовании формулы корней для произведения даст такой результат:

Ну и ладно. Всё равно мы упростили выражение. В математике принято оставлять под корнем самое маленькое число из возможных. В процессе решения все зависит от примера (может и без упрощения всё посокращается), а вот в ответе надо дать результат, который уже дальнейшему упрощению не поддаётся.

Кстати, знаете, что мы с вами сейчас с корнем из 432 сделали?

Мы вынесли множители из-под знака корня! Вот так называется эта операция. А то попадётся задание — «вынести множитель из-под знака корня» а мужики-то и не знают…) Вот вам ещё одно применение свойства корней. Полезная вещь пятая.

 

Как вынести множитель из-под корня?

Легко. Разложить подкоренное выражение на множители и извлечь корни, которые извлекаются. Смотрим:

Ничего сверхъестественного. Важно правильно выбрать множители. Здесь мы разложили 72 как 36·2. И всё получилось удачно. А могли разложить иначе: 72 = 6·12. И что!? Ни из 6, ни из 12 корень не извлекается… Что делать?!

Ничего страшного. Или поискать другие варианты разложения, или продолжать раскладывать всё до упора! Вот так:

Как видим, всё получилось. Это, кстати, не самый быстрый, но самый надёжный способ. Раскладывать число на самые маленькие множители, а затем собирать в кучки одинаковые. Способ успешно применяется и при перемножении неудобных корней. Например, надо вычислить:

Перемножать всё — сумасшедшее число получится! И как потом из него корень извлекать?! Опять на множители раскладывать? Не, лишняя работа нам ни к чему. Сразу раскладываем на множители и собираем одинаковые по кучкам:

Вот и всё. Конечно, раскладывать до упора не обязательно. Всё определяется вашими личными способностями. Довели пример до состояния, когда вам всё ясно, значит, можно уже считать. Главное — не ошибаться. Не человек для математики, а математика для человека!)

Применим знания к практике? Начнём с простенького:

1. Вычислить:

 

2. Вычислить (без калькулятора!):

 

3. Вычислить:

 

Слегка усложним:

 

4. Вычислить:

 

Чуть ближе к ГИА:

 

5. Выполнить действия:

 

Ну и, самое крутое, прямо как в ГИА:

 

6. Укажите наибольшее из следующих чисел:

 

Ответы для заданий 1 — 4, в беспорядке: 2; 1; 9, 96.

Ответы на задания 5 — 6 здесь не дам). В этих примерах главное не ответ, а принцип решения. Если знаете как делать подобные задания, ответ сам получится. Если не знаете, ответ особого смысла не имеет).

Подведём итоги.

Обратите внимание. Всего одно свойство корней, одна небольшая формула умножения корней — и какие разнообразные возможности для практического применения!

Формула умножения корней позволяет:
— умножать корни,
— вносить число под корень,
— сравнивать корни,
— извлекать корни из больших чисел,
— выносить множитель из-под корня.

И все эти возможности вытекают из одной небольшого свойства корней. Мощное свойство, но… одно. Это — как табурет на одной ножке…) Сидеть можно, но с изрядными усилиями.

В нашем арсенале есть ещё два свойства корней. Одно — простое, второе — не очень. Но разобраться с ними можно и нужно. Оба этих свойства — в следующем уроке. Там же — примеры для тренировки. Там же описана одна тупая, но очень популярная ошибка в корнях, после которой люди бьют себя по голове и страшно ругаются…

 

Как делить корни?

 

Продолжаем развлечение? В предыдущих уроках мы осознали, что такое квадратный корень. И разобрались как умножать корни. Формулу умножения корней мы разобрали по винтикам. Очень уж она полезная в решении примеров! Осталось ещё две. Переходим к следующей формуле. Это будет деление корней.

Формула столь же проста, как и умножение. Вот она:

Напоминаю: здесь а — неотрицательное число (больше или равно нулю), b — положительное (больше нуля)! Иначе формула смысла не имеет… Об этих тонкостях мы ниже поговорим.

У формулы деления корней возможности не так обширны, как у умножения. Что можно делать прямо по формуле? Очевидно, делить корни.

 

Элементарно. Вот вам примерчик:

В этом примере деление корней помогло нам получить хороший ответ. Бывают более хитрые преобразования. Например:

Здесь мы превратили двойку в корень квадратный из четырёх. Исключительно для того, чтобы формулуделения корней в дело употребить. Как видите, ничего здесь сложного нет.

Рассмотрим формулу деления корней в обратном направлении. Справа налево. Вот так:

Какие возможности раскрывает нам такая запись? Ничего нового, думаете? Ошибаетесь! Забавно, но простая запись формулы в другом направлении частенько высвечивает дополнительные возможности!

В нашем случае такая формулировка деления корней здорово помогает извлекать корни из дробей! Например, пусть нам надо извлечь квадратный корень из дроби 25/144. Спокойно пишем себе:

Вот и все дела! От работы с дробью целиком, мы переходим к работе отдельно с числителем, отдельно со знаменателем. Что гораздо проще. А если дробь десятичная? Не вопрос! Если сразу корень не можете извлечь — переводите десятичную дробь в обыкновенную, и — вперёд! По формуле деления корней. Например:

Бывает ещё круче, когда корень из смешанного числа надо извлечь! Как поступаем? Правильно! Переводим смешанное число в неправильную дробь — и по знакомой формуле деления корней! К примеру, вот так:

Что, забыли, как переводить дроби? Срочно прокрутите страницу выше и вспоминайте. А то ни дробь преобразовать, ни сократить её… И зачем вам тогда квадратные корни?

Надеюсь, что деление корней проблем не составляет. Простая и безобидная формула, простое употребление. Теперь в нашем арсенале уже две формулы. Умножение и деление корней. Табурет на двух ножках. Сидеть можно, но… некомфортно.)

Займёмся последним свойством квадратных корней. Здесь уже будут некоторые тонкости и подводные камни. Это свойство кратко называют корень из квадрата. Или корень в квадрате. Или корень из степени. Корень в степени. Всяко называют. Но суть одна. Это возведение в степень подкоренного выражения или самого корня.

Можно ли корень возвести в квадрат? А почему нет? Умножить корень сам на себя — да все дела! И не только в квадрат можно. В любую степень. А извлечь корень из квадрата? Да тоже не проблема! Мы же умеем корень из произведения извлекать. Так что можно извлечь корень не только из квадрата, но и из любой степени.

Но именно эти действия вызывают массу проблем… С этим надо разобраться основательно. Что мы сейчас и сделаем. Начнём с безобидного действия. С корня в квадрате.

 

Как возвести корень в квадрат?

Так как посчитать корень в квадрате? Очень просто. Прямо по смыслу корня. Что такое корень квадратный из двух, например? Это число, которое при возведении в квадрат должно дать двойку. Так вот, если мы число, которое при возведении в квадрат должно дать двойку, возведём-таки в этот самый квадрат? Что получим? Двойку, конечно! Т.е. подкоренное выражение. Или, в общем виде:

Вот и всё! Никаких подводных камней, всё строго по формуле! Возведение в квадрат корня квадратного из любого выражения даст нам это самое выражение. Понятно, что а — число неотрицательное. Иначе формула смысла не имеет.

А если корень не в квадрате, а в другой степени? Не вопрос! Если, конечно, знаете действия со степенями… По правилам этих действий сами приведём исходное выражение к корням в квадрате и всё посчитаем. Например, вот так (расписываю подробно):

Как видим, корень исчезает, Степень результата в два раза меньше исходной степени.

Если степень нечётная — разложим исходное выражение на множители, и все дела:

Так поступаем с любой степенью корня из любого выражения, и всё у нас посчитается, упростится и получится. Корень в квадрате — штука бесхитростная. Разберёмся теперь с корнем из квадрата.

 

Как извлечь корень из квадрата?

Пусть у нас есть хорошее число 2. Возведём его в квадрат.

2² = 4

Кто бы спорил? А теперь давайте обратно, извлечём из результата квадратный корень:

Опять всё чудесно, правда? С чего начали, к тому и вернулись! Стало быть, можно записать:

Оно и естественно, правда? Возведение в квадрат компенсируется обратной операцией — извлечением квадратного корня. В общем виде формула выглядит вот так:

Стоп! Внимание! Во всех учебниках, справочниках и пособиях рядом с такой формулой всегда пишут:»где а — больше, либо равно нулю». В этих словах, которые многие просто пропускают, и кроются главные сложности корней. Потому, что в примерах а частенько бывает отрицательным! Пока и мы будем считать, что а — неотрицательное. Для простоты. 

Продолжаем. Корень из квадрата извлекается просто. А если у нас подкоренное выражение не в квадрате, а в другой степени? Допустим, в четвёртой? Да нет проблем. Приведём нашу степень к квадрату. Вот так:

2⁴=(2²)²

Для таких преобразований надо опять-таки знать действия со степенями, но тут уж ничего не поделаешь…

Теперь по формуле корня из квадрата:

Вот и всё. Корень из любой чётной степени даст в результате подкоренное выражение в степени, в два раза меньше исходной. Корень из 3¹⁰ ? Легко! Это будет 3⁵. Корень из 5¹⁸ ? Запросто! Это будет 5⁹. Ну, и так далее.

А если степень нечётная? Подумаешь! Раскладываем подкоренное выражение на множители — и вперёд! Используем вынесение множителя из-под корня. Например:

 

 

Всё просто. Но до сего момента мы работали только с неотрицательными числами и выражениями. Как только в игру вступают отрицательные величины, простота куда-то пропадает начисто… Вернём эту простоту и ясное понимание.

Вот тут и будет мрачный заяц. Для лучшего запоминания.) Концентрируем внимание и собираем весь интеллект в кулак!)

Итак, откуда в корнях могут появиться отрицательные числа и выражения?

Пунктик первый. Отрицательные значения даны прямо в задании. Вспоминаем пример корня из квадрата двойки:

Здесь всё понятно и просто.

А теперь попробуем вычислить:

Берём, и просто считаем, безо всяких формул:

(-2)

² = 4

Извлекаем корень из четырёх и получаем 2. Так как арифметический квадратный корень (а в школе мы работаем только с такими!) —

всегда число неотрицательное! То есть:

А если бы мы использовали формулу:

получили бы не два, а

минус два! Что является ошибкой.

Не работает эта формула для отрицательных значений.

Для того, чтобы формула корня из квадрата работала для

всех значений а, она записывается вот так:

Это и есть последнее, третье свойство корней. Корень из квадрата. Третья ножка для табурета.)

Здесь появляется страшный значок для старшеклассников. Модуль. Если вы пока не сильны в раскрытии модулей, не волнуйтесь. Здесь он означает лишь то, что при любом знаке а, результат извлечения корня из квадрата будет всегда неотрицательный. Формула стала полноценной. Модуль просто отсекает минусы:

Пунктик второй. Отрицательные значения спрятаны в буквах и дополнительных условиях. Например, требуется упростить выражение:

где х<0.

Казалось бы, ответ прост. Получится просто х. Но зачем тогда дополнительная информация?! Приходится соображать. Если х<0, это отрицательное число. Минус два, или минус тридцать, там… Но корень квадратный отрицательным быть не может! Это будет точно х, но он должен быть с плюсом! Где взять плюс? А мы его сделаем! Если перед заведомо отрицательным числом, поставить минус, это число станет, число станет… положительным! И верное решение выглядит так.

Собственно, это и есть главная трудность в работе с корнями. В отличие от более простых разделов математики, здесь правильный ответ частенько не вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.)

И как справляться со всем разнообразием заданий с корнями? А есть ещё иррациональные уравнения и неравенства, где эти пунктики играют главную роль…

Спокойно! Вникайте и запоминайте.

 

Главный практический совет по работе с квадратными корнями.

В любом задании с квадратными корнями

лично контролируйте знаки подкоренного выражения и результата извлечения корня.

Прикидывайте, и оценивайте ситуацию, исходя из внешнего вида примера и

всех дополнительных условий задания. Если под знаком корня — минус, дальше можно не решать. Выражение не имеет смысла. Что нам делать нечего, бессмысленные выражения решать?!

Если под корнем всё нормально, плюс, а в результате извлечения получается заведомый минус — сделайте из него плюс! Этого требуют правила действий с квадратными корнями.

Ну вот, основные тонкости корней мы разобрали. Теперь об одной ошибке, рассказать про которую я обещал в предыдущем уроке. Эта ошибка ничего общего с тонкостями не имеет! Это абсолютно тупой косяк, о котором и говорить-то неловко. Но надо. Слишком часто он встречается…

Обратите внимание! Все свойства корней связаны с умножением-делением. И ни одного — со сложением-вычитанием! На сложение-вычитание корней — не существует специальных формул!

Однако народ складывает… И не самый трудный народ… Поэтому громко напоминаю:

или:

Хотя одинаковые корни можно, конечно, складывать-вычитать. Как приводить подобные с буквами. Например:

или:

Но эти действия к специфическим свойствам корней не имеют никакого отношения.

 

 

А теперь попрактикуемся в корнях. От примитивных заданий до продвинутых. Все ответы даны в беспорядке.

 

Вычислить:

Ответы: 1, 9, 2.

 

Примитив? Тогда решаем дальше.

Упростить:

Ответы: 3а⁴ b, -4а⁴ b⁵ , 3а.

 

Получилось? Неплохо. А как вам эти примерчики?

 

Вычислить (все буквы — неотрицательные):

Ответы (в беспорядке): выражение не имеет смысла; 5; 4; 1; -3; 0,5

 

Всё нормально!? Отлично. Корни — не ваша проблема.

Материал позаимствован с замечательного сайта: http://egesdam.ru/page260.php . Спасибо автору за понятное изложение материала!

Нахождение квадратного корня. Квантовый ум [Грань между физикой и психологией]

Нахождение квадратного корня

Теперь давайте пойдем в противоположном направлении и исследуем получение квадратного корня чисел. Если 4 в квадрате – это 16 (поскольку 4 х 4 = 16), то каков квадратный корень числа 16? Иными словами, какое число при умножении само на себя дает 16? Ответ, разумеется, 4; 4 – это квадратный корень числа 16. Квадратный корень числа подобен его семени, его сущности, которая его создает. Сущность числа 16 – это 4; сущность числа 9 – это 3 и так далее.

С психологической точки зрения, квадратный корень области вашей жизни, в которой вы бываете очень спонтанным, простодушным и полным энергии, можно было бы символизировать ребенком. Иными словами, фантастическое переживание, символизируемое ребенком, представляет собой квадратный корень области жизни, являющейся очень спонтанной. Мы могли бы сказать, что элементы наших сновидений, фантазий и телесных переживаний – это квадратные корни целых областей нашей жизни, которые мы обычно маргинализируем либо еще не развили.

Если возведение в квадрат – это психологическая операция, которая может быть сознательно управляемый либо автономным процессом, происходящим с нами в повседневной жизни, то извлечение квадратного корня чего-либо представляет собой нахождение его источника. При нахождении квадратного корня мы можем по своей воле возвращаться к источнику переживания в повседневной жизни либо позволять этому случаться автономно, просто засыпая.

Получение квадратного корня вещей – это полезная психологическая практика. Подумайте об области, которая развертывалась из сновидения в предыдущем упражнении на возведение в квадрат, но теперь двигайтесь в обратном направлении. Замечайте, каким образом сновидение представляет собой квадратный корень этой области.

Или попробуйте думать о другой области своей жизни, о которой вам хотелось бы знать больше. В течение минуты по-настоящему чувствуйте эту область своей жизни или думайте о ней и описывайте ее. Теперь, вместо того чтобы дожидаться сновидения об этой области, догадайтесь о ее квадратном корне, ее сущности. Не дожидайтесь, когда вы ляжете спасть, чтобы увидеть сон. Найдите квадратный корень этой области сейчас. Найдите символ, который при возведении в квадрат дал бы начало этой области. Найдите ее корень, ее ключ.

Данный текст является ознакомительным фрагментом.

Продолжение на ЛитРес

Как вычислить квадратный корень вручную / Бери и делай

Если число умножить на само себя, то результат этого действия будет называться квадратом этого числа. Например, 3 × 3, или 3², равняется 9, где число 9 является квадратом числа 3. Обратное действие, когда надо узнать, какое число, возведенное в квадрат, даст число 9, называется извлечением квадратного корня. Хоть это кажется сложным и несколько утомительным, зная алгоритмы решения, вы легко справитесь с подобной задачей.

«Бери и Делай» предлагает познакомиться с несколькими способами извлечения квадратного корня, которые могут пригодиться не только в школе, но и в реальной жизни.

Что полезно знать об извлечении квадратного корня

Извлечение арифметического квадратного корня похоже на действие, обратное возведению числа во вторую степень, или в квадрат. Но это не совсем так. К примеру, если неотрицательное число (a) и равное ему по модулю отрицательное число (—a) возвести в квадрат, то в результате получится одно и то же неотрицательное число. При попытке совершить обратное действие мы не сможем восстановить знак числа и определить, возводилось ли в квадрат отрицательное или неотрицательное число, мы будем знать лишь модуль числа. Поэтому из определения квадратного корня для любого действительного числа справедливо равенство:

√a² = |a|

То, что находится под знаком корня, называется подкоренным числом, или выражением. В примере выше справа от знака равенства находится модуль числа a. Далее мы отталкиваемся от того, что извлечь квадратный корень можно только из положительного числа. При этом если a ≥ 0, то (√a)² = a.

Важно: Могут быть ситуации, в которых важна двузначность корня. Тогда перед его знаком ставится знак ± (плюс-минус), например так делается в формуле решения квадратного уравнения.

Квадратный корень нуля и единицы

Существует несколько простых правил, которые легко запомнить:

Как извлечь корень из чисел, квадраты которых известны

Для некоторых чисел квадраты известны, поэтому их можно всегда посмотреть в соответствующей таблице, а какие-то (наиболее используемые в том или ином случае) даже выучить наизусть. Например, зная таблицу умножения, вы без проблем извлечете квадратный корень из любого числа до 100, если этот корень извлекается нацело или без остатка (как на картинке выше).

При этом такой квадрат называется полным, или точным. Например, если число 2 возвести в квадрат, то получится число 4, которое является полным, или точным, квадратом числа 2. Соответственно, большую трудность представляет вычисление квадратного корня из числа, которое не является полным квадратом. Также есть числа, из которых невозможно извлечь корень, например √2, можно лишь обнаружить приближенное значение. При работе с квадратными корнями, которые извлекаются нацело и кажутся достаточно простыми, тоже могут возникнуть сложности.

Пример № 1: Необходимо вычислить √0,09.

Число 0,09 является десятичной дробью. Но мы можем забыть об этом и представить ее в виде целого числа 9. Далее мы вспоминаем, что число 9 получается, если взять число 3 в квадрате. Тогда √9 = 3. Далее вспоминаем правило умножения десятичных дробей: количество знаков после запятой в результате умножения десятичных дробей будет равняться сумме количества знаков после запятой каждой дроби. Тогда при вычислении √0,09 (где после запятой два знака) нам нужно найти такую десятичную дробь, у которой будет только один знак после запятой. Получается, что ответ — это 0,3. Проверим, умножив 0,3 на само себя, и получим в результате 0,09. Значит, √0,09 = 0,3.

Пример № 2: На картинке выше записаны два примера. Как вы думаете, в результате получается одно и то же число или два разных?

В первом примере под одним корнем одно число, под другим — другое. Мы не можем их сложить между собой, а затем вычислить корень (складывать или вычитать можно только одинаковые квадратные корни, при этом работа ведется только с множителями, которые стоят слева от корня, а само подкоренное выражение не изменяется). Необходимо вычислить корень для каждого конкретного числа, а затем сложить результаты. В этом случае мы имеем дело с полными квадратами, поэтому легко вычислить, что √144 = 12, а √25 = 5. Теперь складываем полученные числа и получаем результат первого примера: 12 + 5 = 17.

Во втором примере под одним корнем находится выражение. Чтобы вычислить квадратный корень, сначала надо упростить выражение, выполнив действие сложения под корнем: 144 + 25 = 169. Теперь из числа 169 мы извлекаем квадратный корень и получаем 13.

Таким образом, в результате решения каждого примера получаются разные числа.

Вычисление квадратного корня через разложение на простые множители

Согласно правилу, чтобы умножить один квадратный корень на другой, нужно перемножить их подкоренные выражения, а результат записать под общим знаком корня (при условии что подкоренные выражения или числа больше или равны нулю). Получается, чтобы вычислить квадратный корень из числа, мы можем разложить подкоренное число на простые множители, а затем произведение представить в виде степени с нужным показателем и извлечь корень.

На картинке выше число 3 136 мы разложили на простые множители. Таким образом, корень из этого числа будет равен корню, под которым будет выражение 2² × 2² × 2² × 7². Зная, что по свойству квадратного корня (√a)² = a, мы можем упростить выражение до 2 × 2 × 2 × 7 = 56. Таким образом, квадратный корень из 3 136 равняется 56.

Главный минус этого способа в том, что число не всегда можно разложить до конца и это занимает много времени.

Метод вычета нечетного числа

Этот метод основан на том, что квадрат натурального числа n можно представить в виде суммы первых n нечетных чисел, например:

1² = 1
2² = 1 + 3 = 4
3² = 1 + 3 + 5 = 9
4² = 1 + 3 + 5 + 7 = 16

Тогда при вычислении квадратного корня из числа можно вычитать нечетные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или не окажется равен нулю. После этого нужно посчитать количество операций — это число и будет целой частью числа извлекаемого квадратного корня.

Пример: Необходимо вычислить √16.

Сначала вычтем из числа нечетные числа по порядку:

16 — 1 = 15
15 — 3 = 12
12 — 5 = 7
7 — 7 = 0

Мы получили ноль, что означает, что корень извлекается нацело. Теперь посчитаем количество действий. Выполнено 4 действия, значит, √16 = 4.

Основным минусом данного способа является то, что он удобен только в случае с небольшими числами.

Вычисление квадратного корня уголком или столбиком

Этот способ позволяет извлечь квадратный корень из любого числа с высокой точностью, но может показаться достаточно сложным, если в ответе число состоит из большого количества цифр. Ниже один из вариантов его записи на бумаге.

На картинке выше изображены следующие элементы:

• Знак корня указывает, что производится вычисление квадратного корня.
• Показатель степени, который будет равен 2, если вам нужно найти квадратный корень, и в таком случае его необязательно обозначать цифрой.
• Подкоренное число, или выражение, из которого извлекается квадратный корень.
• Результат — место, где записывается конечный результат всей операции.
• Вспомогательные линии — строки, где выполняются математические действия, приводящие к окончательному решению задачи.
• Остаток — сумма, которая может остаться после завершения вычислений, если корень извлекается не нацело.

Выше в качестве примера показано извлечение квадратного корня из числа 81. Чтобы лучше объяснить весь процесс, возьмем в качестве примера натуральное число 50 419 и попытаемся найти его квадратный корень.

1. Разделите цифры подкоренного числа на пары, двигаясь справа налево. В этом конкретном примере число состоит из 5 цифр, а значит, и самая левая из них, пятерка, остается без пары.

2. Найдите число, которое при умножении на само на себя даст результат, максимально приближенный к первой цифре подкоренного числа (но не больше ее). Запишите это число в строку результата справа. Затем вычтите полученный результат из первой цифры подкоренного числа и запишите ответ.

3. Перенесите следующие 2 цифры подкоренного числа (в данном случае это цифры 0 и 4), записав их рядом с остатком от вычитания. В данном случаем мы получим число 104.

Теперь найденное число, записанное в строке результата справа вверху (2), умножаем на 2, получаем число 4 и записываем его в строке ниже.

4. Теперь справа от полученного числа 4 нужно записать выражение. Для этого найдите такое целое число, чтобы после того, как вы его подставите в правое выражение 4_ × _, результат был равным или максимально приближенным к числу остатка (104), но не превышал его.

В данном случае лучше всего подойдет двойка, потому что тогда мы получим 42 × 2 = 84, то есть число, которое меньше 104. Если взять тройку, то 43 × 3 = 129, а это число уже больше, чем 104. Теперь нужно вычесть полученный результат (84) из 104 и записать остаток под новой горизонтальной чертой.

5. Снесите оставшиеся цифры подкоренного числа. Запишите найденное вами на прошлом шаге число (2) в строку результата, в результате чего теперь там будет число 22.

Как и раньше, число из строки результата умножаете на 2, получаете в данном случае 44 и записываете во вспомогательной строке.

6. Снова найдите такое целое число, чтобы после добавления его в выражение 44_ × _ у вас в результате получилось число, равное или максимально приближенное к числу 2 019 (но не большее). В нашем примере лучше всего подойдет четверка, так как 444 × 4 = 1 776. Число 1 776 меньше числа 2 019 (если бы мы взяли 5 и подставили ее в выражение, то получили бы в результате число 2 225, которое больше, чем 2 019). Запишите подобранное вами число (4) в строку результата.

Теперь полученный результат (1 776) необходимо вычесть из числа 2 019 и записать остаток (243) под новой горизонтальной чертой. Наличие остатка говорит о то, что мы еще не вычислили точный квадратный корень. Как продолжить вычисления, если в подкоренном числе закончились цифры для переноса? Это означает, что квадратным корнем является не целое число, а десятичная дробь. Для продолжения расчетов к остатку переносим два нуля и повторяем действия так, как делали выше.

Умножаем 224 на 2, результат записываем на вспомогательной линии. Подбираем число к выражению 448_×_, чтобы результат был равным или максимально приближенным к числу 24 300. В этом нам поможет пятерка, благодаря которой получаем число 22 425. Пятерку записываем в поле результата после запятой. Снова получаем остаток, снова переносим два нуля и продолжаем расчет.

Выше не картинке представлены дальнейшие действия, но нет окончательного ответа. Таким образом можно продолжать вычислять точный корень, пока в остатке не появится ноль. Но нужно понимать, что не всегда корень можно извлечь.

На первый взгляд кажется, что данный метод сложный и долгий, но многое зависит от конкретного числа и, соответственно, его корня. Например, попробуйте указанным выше способом вычислить корень из числа 2 116. На это уйдет меньше минуты и займет всего пару действий.

Внимание: в октябре 2021 года мы исправили фактические неточности в этой статье.

Арифметический квадратный корень

Если а больше или равно 0 и n – натуральное число, которое больше 1, то будет существовать только лишь одно, неотрицательно число х, при котором выполняется равенство . Именно это число х и называется арифметическим квадратным корнем n-ой степени из неотрицательного числа а. Число а называют подкоренным числом, а n – показателем корня . Если n = 2, то показатель корня обычно опускают и называют такое выражение арифметическим квадратным корнем. Стоит отметить, что довольно-таки часто вместо слова «корень» употребляют слово «радикал».

А теперь давайте рассмотрим, как можно извлечь квадратный корень из натурального числа.

Например, нам необходимо извлечь корень из натурального числа к, причем нам точно, известно, что корень извлекается. Чтобы сделать это довольно удобным способом, следует воспользоваться следующими правилами:

1. Разбить число к на грани (начинать с последней цифры и справа налево) и включить в каждую грань по две рядом стоящие цифры. При этом стоит обратить внимание, что если к состоит из четного числа цифр, то в первой левой грани будет 2 цифры, если же число цифр в к нечетное, то в первой левой грани будет 1 цифра. Количество наших граней показывает количество цифр результата. На первый взгляд все просто и понятно.
2. Далее нам необходимо подобрать наибольшую цифру, но такую, чтобы ее квадрат не превосходил числа, которое находится в первой грани. Эта цифра и будет первой цифрой результата.
3. Полученную первую цифру результата возводим в квадрат и вычитаем полученное из первой грани число, а затем припишем к найденной разности справа вторую грань. У нас выйдет какое-то число А. Удваиваем часть результата, которую имеем и получаем число а. Теперь следует подобрать такую наибольшую цифру х, чтобы произведение числа ах на х не было больше числа А. Цифра х – вторая цифра результата.
4. Следующий шаг практически повторяет весь третий пункт. Продолжать находить следует до тех пор, пока не используется последняя грань.

Свойства квадратного (арифметического) корня

Почему квадратный корень из числа Пи — иррациональное число?

Вас когда-нибудь спрашивали, что такое квадратный корень из числа пи? Отказ от ответственности: быстрый ответ заключается в том, что точного ответа нет! Поскольку все квадратные корни иррациональных чисел являются иррациональными числами, квадратный корень из числа пи также является иррациональным числом. Однако это не означает, что мы не можем приблизить ответ. Точно так же, как мы приближаем значение пи к 3,14, мы можем приблизить квадратный корень из пи к 1,77.

Определение квадратных корней

Умножение числа само по себе называется возведением в квадрат или нахождением квадрата числа.Например, 9 в квадрате равно 81, потому что 9 х 9 = 81. Квадратный корень — это обратная операция возведения в квадрат. Вместо того, чтобы умножать число само на себя, он находит число, равное исходному числу при умножении на себя. Например, квадратный корень из 9 равен 3, потому что 3 x 3 = 9.

Квадрат 9 равен 81.

Квадратный корень из 9 равен 3.

Квадратные корни часто встречаются при решении квадратичных функций или выполнении вычислений для определенных теорем, таких как теорема Пифагора.Оно выражается с помощью символа или аббревиатуры sqrt, но также может быть выражено с помощью экспонент. Квадратный корень из числа — это то же самое, что возведение этого числа в степень 1/2. Другими словами:

Что такое иррациональные числа?

Иррациональные числа — это числа, которые не могут быть выражены в виде дроби a/b, где числитель и знаменатель a и b ненулевые целые числа. Другими словами, иррациональные числа никогда не могут быть представлены в десятичной форме без бесконечного числа цифр.

Примером этого являются цифры числа пи. Пи — одно из самых известных иррациональных чисел. Другие иррациональные числа включают золотое сечение фи или число Эйлера E (основание натуральных логарифмов).

Расширение наших математических горизонтов

Запрос на нахождение квадратного корня из числа Пи часто считается бессмысленным вопросом. Но известные математики расширили наше понимание математики, задавая трансцендентные вопросы, подобные этим.

Это заставляет нас думать не только о числах, но и о целых числах или десятичных дробях, которые мы обычно используем, когда работаем с многоугольниками или коэффициентами в алгебраических выражениях.

Если вас интересуют такие вопросы, которые выходят за рамки алгебраических чисел, просто посмотрите, что такое гаусс или числа Гаусса, или почему у нас вообще есть категория для комплексных и мнимых чисел. А пока просто скажите, что квадратный корень из числа пи — это иррациональное число, приблизительно равное 1,77.

Помощь с домашним заданием по математике

Нахождение квадратного корня из числа

Что такое квадратный корень?

Чтобы объяснить квадратные корни, давайте сделаем шаг назад и вспомним, что значит возвести число в квадрат.Возвести в квадрат — значит возвести число во вторую степень. Квадратные корни противоположны этому и на самом деле являются обратной операцией возведения в квадрат. Извлечь квадратный корень — значит найти два одинаковых множителя числа.

Как найти квадратный корень из числа

Для чисел, которые являются идеальными квадратами, вы можете найти целые числа в качестве ответов. Однако для чисел, которые не являются идеальными квадратами, вам придется использовать метод, включающий оценку (или вы можете использовать таблицу квадратных и квадратных корней).

Нахождение квадратного корня из чисел с полным квадратом

Давайте сначала рассмотрим этот вопрос здесь:

корень 64

Чему равен квадратный корень из 64? Если у вас есть калькулятор, вы всегда можете просто ввести его и получить ответ. Но знаете ли вы, как найти квадратный корень из числа без калькулятора?

Теперь, если вы помните свои совершенные числа в квадрате, корень из 64 равен восьми. Восемь раз восемь дает вам 64. Но допустим, вы не можете свободно вспоминать совершенные числа.Как бы мы сделали это с нуля?

Сначала вам нужно будет найти все простые множители числа 64. Итак, давайте сделаем это:

простые множители корня 64

Представьте, что теперь вопрос принимает вид 2x2x2x2x2x2 — здесь 2 умножается на 6. Итак, мы только что определили, что 64 — это просто квадратный корень из шести двоек, перемноженных вместе.

радикальный знак

Прежде чем мы двинемся дальше, мы должны помнить, что знак радикала на самом деле означает «квадратный корень». Символ квадратного корня действительно должен быть написан здесь с маленькой двойкой:

. квадратный корень

Поскольку это квадратный корень, вы можете выбрать пару одинаковых чисел для работы и вывести их из-под корня.В этом случае мы возьмем 2 из первой пары двоек, еще 2 из второй пары и еще 2 из последней пары. Это должно выглядеть примерно так:

вынимая пары

Теперь, если вы умножите двойки друг на друга, что вы получите? Вы обнаружите, что получили 8, что в точности совпадает с тем, что вы запомнили бы, если бы знали свои идеальные квадраты. Однако это правильный способ найти квадратный корень из числа без запоминания.

Нахождение квадратного корня из чисел, не являющихся полными квадратами

Основной метод нахождения квадратного корня из числа, не являющегося полным квадратом, заключается в следующем:

1. Оценка: выберите число, которое при возведении в квадрат близко, но меньше, чем квадратный корень из числа, которое вы пытаетесь найти.

2. Разделить: разделите число, для которого вы нашли квадратный корень, на число, которое вы выбрали на шаге 1

3. Среднее: возьмите среднее число, полученное на шаге 2, и квадратный корень

.

4. Повтор: Повторяйте шаги 2 и 3, пока число не будет достаточно точным для вас

Теперь вы научились извлекать квадратный корень из чисел, которые одновременно являются и не являются квадратами. Продолжайте наши уроки, чтобы узнать, как работать с различными примерами радикальных чисел.

Шлюз

Veuillez réessayer данс quelques мгновения. Si le problème сохраняется, veuillez communiquer avec le service de soutien method de Alberta Education (доступно на английском языке).

Телефон :		780-427-5318
		(Composer d’abord le 310-0000 pour obtenir une ligne sans frais)
Телекопьер:		780-427-1179
Курьерский адрес:		cshelpdesk@gov. ab.ca

Квадраты и квадратные корни – различия и примеры

Что такое квадрат числа?

В математике квадрат числа — это результат умножения числа самого на себя. Слово «квадрат» обычно эквивалентно возведению числа в степень 2 и обозначается надстрочным индексом 2.

Например, квадрат 4 записывается как 4 ² , что дает 16 в качестве ответа.В этом случае 16 — площадь номера 4.

ниже представляет собой список квадратов первых двенадцати цифр:

1 х 1 = 1 7 х 7 = 49
2 x 2 = 4 8 x 8 = 64
3 x 3 = 9 9 x 9 = 160145 4 x 4 = 16 10 x 10 = 100 11 x 11 = 121
6 x 6 = 36 12 x 12 = 144

Возведение в квадрат отрицательных чисел

Возведение в квадрат отрицательного числа является положительным числом.Например, -3 x -3 станет 9, однако 3 x 3 = -9, потому что -3 отличается от 3.

Что такое квадратный корень из числа?

Квадратный корень — это операция, обратная возведению числа в квадрат. Другими словами, квадратный корень — это операция, которая отменяет показатель степени 2. Квадратный корень из числа x таков, что число y является квадратом x, упрощенно записывается как y ²  = x.

Например, 5 и – 5 являются квадратными корнями из 25, потому что:

5 x 5 = 25 и -5 x -5 = 25.

Квадратный корень из числа x обозначается знаком корня √x или x ^1/2 . Например, квадратный корень из 16 представлен как √16 = 4. Число, для которого вычисляется квадратный корень, называется подкоренным числом. В этом выражении √16 = 4 число 16 является подкоренным числом.

Свойства

• Совершенно квадратное число имеет совершенный квадратный корень.
• Четное совершенное число имеет четный квадратный корень.
• Нечетное совершенное число имеет нечетный квадратный корень.
• Квадратный корень из отрицательного числа не определен.
• Только числа, заканчивающиеся четным числом нулей, имеют квадратный корень.

Нахождение квадратного корня из чисел

• Повторное вычитание :
  Этот метод включает успешное и многократное вычитание из числа нечетных чисел, таких как 1, 3, 5 и 7, до тех пор, пока не будет достигнут ноль. Квадрат числа равен количеству или частоте вычитания числа.Предположим, нам нужно вычислить квадрат совершенного числа, такого как 16, количество выполненных вычитаний равно 4, поэтому квадратный корень из 16 равен 4. факторизуется последовательными делениями. Простые множители группируются в пары, и вычисляется произведение каждого числа. Таким образом, произведение равно квадратному корню из числа. Чтобы найти квадрат совершенного числа, такого как: 144, выполните следующее:

1. 144 = 2 × 2 × 2 × 2 × 3 × 3.
2. Соедините простые множители.
3. Выбор одного числа из каждой пары.
4. 2 × 2 × 3 = 12.
5. Таким образом, √144 = 12.

• Метод деления:
  Метод деления является подходящим методом вычисления квадрата большого числа.
  
  Ниже приведены необходимые шаги:

1. Над каждой парой цифр, начиная с правой стороны, ставится черта.
2. Разделить левое число на число, квадрат которого меньше или эквивалентен числам под левым концом.
3. Возьмите это число как делитель и частное. Точно так же возьмите самое левое число в качестве делимого.
4. Разделите, чтобы получить результат.
5. Потяните следующее число с помощью полосы справа от остатка.
6. Умножьте делитель на 2.
7. Справа от этого нового делителя найдите подходящее делимое. Этот процесс повторяется до тех пор, пока мы не получим ноль в качестве остатка. Следовательно, квадрат числа равен частному.

Для чего в реальном мире используются квадратные корни и возведение в квадрат?

В математике возведение в квадрат действительно легко понять. Квадрат число означает умножение его само на себя. Возведение в квадрат написано математическим символы, поставив 2 над числом, которое вы возводите в квадрат, чтобы показать, что умножается в 2 раза.

Квадратный корень сложнее понять. Когда вы вычисляете квадратный корень из числа, которое вы хотите найти исходное число, которое был возведен в квадрат. Таким образом, квадратный корень из 9 равен 3. Квадраты и квадратные корни приходите парами. В этом примере 3 в квадрате равно 9, а квадратный корень из 9 равно 3.

Квадраты всегда легко вычислить, но найти квадратный корень сложно. сложный.Квадратные корни сложны, потому что квадратный корень числа часто представляет собой длинное десятичное число. Квадратный корень из 4 (2 x 2), 9 (3 x 3) или 256 (16 x 16) легко найти. Но что насчет квадратный корень из 5? Квадратный корень из 5 равен 2,236! Проверь это для себя, возведя в квадрат 2,236. Представьте, какой сложный квадрат корень очень большого числа становится! Существуют разные методы для вычисление квадратных корней, но обычно вы будете использовать таблицу или калькулятор когда вам нужно найти квадратный корень.

Если квадратные корни такие сложные, почему вам важно узнать о них? Одна из причин заключается в том, что квадратные корни используются во всех случаях. время учеными, инженерами и даже людьми, работающими на заводах. Прежде чем узнать больше о квадратных корнях, вам нужно узнать о нормальное распределение.

Нормальное распределение

Нормальное распределение — это способ рассмотрения разнообразия в группе подобных вещей. Давайте посмотрим на пример. Подумайте обо всех учениках в вашем классе.Несмотря на то, что все примерно одного возраста, школьники имеют разную высоту. Кто-то самый высокий, кто-то самый низкий а остальные в классе примерно такого же роста.

Если записать рост всех в классе, а затем поставить высоты в порядке от самой низкой до самой высокой, вы можете сосчитать, сколько студенты каждого роста. Ваш список может получиться примерно таким:

4 фута в высоту — 1 (самый низкий)

4 фута 1 дюйм — 2

4 фута 2 дюйма — 3

4 фута 3 дюйма — 5

4 фута 4 дюйма — 8

4 фута 5 дюймов — 7

4 фута 6 дюймов — 4

4 фута 7 дюймов — 2

4 фута 8 дюймов — 1 (самый высокий)

Вы можете видеть, что большинство высот составляет от 4 футов 3 дюймов. и 4 фута 5 дюймов, некоторые короче и лишь некоторые выше.В математике и статистике это называется нормальным распределением. и образец графика нормального распределения показан ниже.

Нормальное распределение показывает, сколько в просматриваемой группе at, называемые совокупностью, имеют каждое значение. В этом примере население это ученики в вашем классе, а то, что измеряется, является ростом. Хотя этот график не совсем соответствует цифрам, которые мы составили Например, он показывает, как выглядит типичное нормальное распределение.

Пример нормального распределения

При нормальном распределении на каждом конце графика есть значения это указывает на то, что лишь немногие представители населения имеют это значение, и они называются хвостами нормального распределения.За этом примере самые короткие члены класса учитываются на слева, а самые высокие считаются справа. Все остальные считаются в середине графика.

Квадраты, квадратный корень и нормальное распределение

В реальном мире людям интересно узнать, какие значения являются «нормальными» и какие значения выходят за пределы нормы, те значения, которые находятся в хвостах распределения. Учащиеся не могут контролировать рост они растут, так что вы не хотите называть самых низких и самых высоких детей в вашем классе ненормальные! Рост студента был просто простым примером посмотреть и понять.

Но многие фабрики используют нормальное распределение, чтобы убедиться, что продукция, которую они производят, качественная. Бизнес люди на заводе вырабатывают нормальное распределение продукта и не продавайте какие-либо предметы, которые измеряются в хвостах распределения. Есть много других применений нормального распределения; заводы это всего лишь один простой пример.

Какое отношение нормальное распределение имеет к квадратам и квадратам корни? Множество! Уравнения для нахождения хвостов нормального распределения используйте квадраты и квадратные корни!

Как работают квадратные числа и квадратные корни?

Решая математические задачи, вы можете встретить термин «квадрат», например, 6 ² (шесть в квадрате) или квадратный корень из 16. В данном случае мы не говорим о формах. Если вам интересно, как работают квадратные числа и квадратные корни, вот некоторые вещи, которые вы должны знать.

Image By Marques

Возведение чисел в квадрат

Вы поймете, что вам нужно возвести число в квадрат, когда увидите цифру 2 в надстрочном индексе. Например,

При работе с квадратными числами вы можете услышать такие термины, как «возведение в квадрат» или «экспонента». Чтобы возвести любое число в квадрат, нужно просто умножить это число само на себя. В этом примере мы можем найти ответ, записав задачу:

Следует отметить, что ответ будет неотрицательным, даже если вы начнете с отрицательного числа.Например:

Но что произойдет, если базовое число равно 0? Поскольку 0 x 0 = 0, то:

Квадратные корни

Квадратные корни включают операцию, обратную возведению в квадрат. Поэтому нужно определить, какое число нужно умножить само на себя, чтобы получилось число под корнем. Вы узнаете, что вам нужно найти квадратный корень, когда увидите радикал, например:

Иногда у вас будут идеальные квадраты.Это числа с квадратным корнем, который является целым числом. Однако в большинстве случаев вы будете получать десятичные числа. Некоторые из чисел, которые являются полными квадратами, включают:

Нахождение квадратных корней: Факторизация простых чисел

Один из способов найти квадратный корень числа состоит в том, чтобы использовать факторизацию простых чисел. Это делается путем разложения больших чисел на более мелкие совершенные корни, если это возможно. Например:

Работая над поиском правильных квадратов, попробуйте разделить это число на более мелкие числа, например, на 2 или 3.Продолжайте делить число, пока не сможете извлечь несколько полных квадратных корней.

Если число не является идеальным, вы должны просто привести решение к простейшей форме. Один из примеров:

Поскольку квадратный корень из 3 будет включать десятичные числа (1,73205080757), вы можете оставить число под радикалом. Ваше окончательное решение будет таким:

Поиск квадратных корней: Калькуляторы

Если у вас есть научный калькулятор, вы можете быстро найти квадратный корень из любого числа.Для этого сначала найдите подкоренной ключ. После нажатия этой клавиши добавьте число, для которого вы хотите найти квадратный корень. Поскольку число может включать несколько знаков после запятой, планируйте округление числа до ближайших сотых или тысячных.

Важно уметь находить квадраты и квадратные корни, особенно при изучении нормального распределения. Выберите вычисление квадратного корня вручную или с помощью калькулятора в зависимости от того, насколько точным вы хотите получить ответ.

• Джейми окончил Университет имени Бригама Янга в Айдахо по специальности «Английский язык».Она провела несколько лет, обучая и репетиторству студентов в начальной, средней школе и колледже. В настоящее время она работает составителем контрактов и разработчиком учебных программ для курсов онлайн-обучения. В свободное время она любит бегать и проводить время со своими мальчиками!

  Посмотреть все сообщения

Безопасность | Стеклянная дверь

Пожалуйста, подождите, пока мы проверим, что вы реальный человек. Ваш контент появится в ближайшее время. Если вы продолжаете видеть это сообщение, отправьте электронное письмо чтобы сообщить нам, что у вас возникли проблемы.

Veuillez терпеливейший кулон Que Nous vérifions Que Vous êtes une personne réelle. Votre contenu s’affichera bientôt. Si vous continuez à voir ce сообщение, связаться с нами по адресу Pour nous faire part du problème.

Bitte warten Sie, während wir überprüfen, dass Sie wirklich ein Mensch sind. Ихр Inhalt wird в Kürze angezeigt. Wenn Sie weiterhin diese Meldung erhalten, Информировать Sie uns darüber bitte по электронной почте и .

Даже Гедульд а.у.б. terwijl мы verifiëren u een человек согнуты. Uw содержание wordt бинненкорт вергегевен. Als u dit bericht blijft zien, stuur dan een электронная почта naar om ons te informeren по поводу ваших проблем.

Espera mientras verificamos Que eres una persona real. Tu contenido se sostrará кратко. Si continúas recibiendo este mensaje, информация о проблемах enviando электронная коррекция .

Espera mientras verificamos Que eres una persona real. Tu contenido aparecerá en краткийSi continúas viendo este mensaje, envía un correo electronico a пункт informarnos Que Tienes Problemas.

Aguarde enquanto confirmamos que você é uma pessoa de verdade. Сеу контеудо será exibido em breve. Caso continue recebendo esta mensagem, envie um e-mail para Para Nos Informar Sobre O Problema.

Attendi mentre verificiamo che sei una persona reale. Il tuo contenuto verra кратко визуализировать. Se continui a visualizzare questo message, invia удалить все сообщения по электронной почте indirizzo для информирования о проблеме.

Пожалуйста, включите Cookies и перезагрузите страницу.

Этот процесс выполняется автоматически.