Кубический корень — Википедия
Материал из Википедии — свободной энциклопедии
 График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}
График функции y=x3{\displaystyle y={\sqrt[{3}]{x}}}Куби́ческий ко́рень из a, обозначающийся как a3{\displaystyle {\sqrt[{3}]{a}}} или как a1/3 — это число x,{\displaystyle x,} куб которого равен a.{\displaystyle a.} Другими словами, это решение уравнения x3=a{\displaystyle x^{3}=a} (обычно подразумеваются вещественные решения).
Кубический корень — нечётная функция. В отличие от квадратного корня, кубический корень может быть извлечён и из отрицательных чисел (так, чтобы получился действительный результат):
- −x3=−x3{\displaystyle {\sqrt[{3}]{-x}}=-{\sqrt[{3}]{x}}}
Кубический корень из комплексного числа (из любого числа) c{\displaystyle c} имеет ровно три значения (частный случай свойства корня n-ой степени):
- c3=|c|3(cosϕ+2kπ3+isinϕ+2kπ3),k=0,1,2,ϕ=argc.{\displaystyle {\sqrt[{3}]{c}}={\sqrt[{3}]{\left|c\right|}}\left(\cos {\frac {\phi +2k\pi }{3}}+i\sin {\frac {\phi +2k\pi }{3}}\right),\quad k=0,1,2,\quad \phi =\arg {c}.}
Здесь под |c|3{\displaystyle {\sqrt[{3}]{\left|c\right|}}} понимается арифметический корень из положительного числа |c|.{\displaystyle \left|c\right|.}
В частности
- 13={1cos2π3+isin2π3=−12+i32cos2π3−isin2π3=−12−i32{\displaystyle {\sqrt[{3}]{1}}={\begin{cases}1\\\cos {\frac {2\pi }{3}}+i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {2\pi }{3}}-i\sin {\frac {2\pi }{3}}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}
- −13={−1cosπ3+isinπ3=12+i32cosπ3−isinπ3=12−i32{\displaystyle {\sqrt[{3}]{-1}}={\begin{cases}-1\\\cos {\frac {\pi }{3}}+i\sin {\frac {\pi }{3}}={\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\cos {\frac {\pi }{3}}-i\sin {\frac {\pi }{3}}={\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{cases}}}
Два комплексных значения кубического корня получаются из вещественных по формуле:
- x32,3=x3(−12±i32).{\displaystyle {\sqrt[{3}]{x}}_{2,3}={\sqrt[{3}]{x}}\left(-{\frac {1}{2}}\pm i{\frac {\sqrt {3}}{2}}\right).}
Эти значения необходимо знать для решения кубических уравнений по формуле Кардано.
Показательная форма[править | править код]
Корень из комплексных чисел можно определить так:
- x1/3=exp(13lnx){\displaystyle x^{1/3}=\exp({\tfrac {1}{3}}\ln {x})}
Где ln — главная ветвь натурального логарифма.
Если представить x{\displaystyle x} как
- x=rexp(iθ){\displaystyle x=r\exp(i\theta )}
то формула кубического числа такова:
- x3=r3exp(13iθ).{\displaystyle {\sqrt[{3}]{x}}={\sqrt[{3}]{r}}\exp({\tfrac {1}{3}}i\theta ).}
Это геометрически означает, что в полярных координатах мы берем кубический корень радиуса и делим полярный угол на три, для того, чтобы определить кубический корень. Значит, если x{\displaystyle x} комплексное, то −83{\displaystyle {\sqrt[{3}]{-8}}} будет обозначать не −2{\displaystyle -2}, а будет 1+i3.{\displaystyle 1+i{\sqrt {3}}.}
Кубический корень не может быть извлечён с помощью циркуля и линейки. Именно поэтому неразрешимы сводимые к извлечению кубического корня классические задачи: удвоение куба, трисекция угла, а также построение правильного семиугольника.
При постоянной плотности вещества размеры двух подобных тел относятся друг к другу как кубические корни их масс. Так, если один арбуз весит вдвое больше, чем другой, то его диаметр (а также окружность) будет всего лишь чуть больше, чем на четверть (на 26 %) больше, чем у первого; и на глаз будет казаться, что разница в весе не столь существенна. Поэтому при отсутствии весов (продажа на глазок) обычно более выгодно покупать бо́льший плод.
Столбиком[править | править код]
Перед началом необходимо разделить число на тройки (целую часть — справа налево, дробную — слева направо). Когда Вы достигли десятичной запятой, в конце результата необходимо поставить десятичную запятую.
Алгоритм таков:
- Найдите число, куб которого меньше первой группы цифр, но при её увеличении на 1 она становится больше. Выпишите найденное число справа от данного числа. Под ним запишите число 3.
- Запишите куб найденного числа под первой группой цифр и произведите вычитание. Результат после вычитания запишите под вычитаемым. Далее снесите следующую группу цифр.
- Далее найденный промежуточный ответ заменим буквой a{\displaystyle a}. Вычислите по формуле 300×a2×x+30×a×x2+x3{\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} такое число x{\displaystyle x}, что его результат меньше нижнего числа, но при увеличении на 1 становится больше. Запишите найденное x{\displaystyle x} справа от ответа. Если достигнута необходимая точность, прекратите вычисления.
- Запишите под нижним числом результат вычисления по формуле 300×a2×x+30×a×x2+x3{\displaystyle 300\times a^{2}\times x+30\times a\times x^{2}+x^{3}} и произведите вычитание. Перейдите к пункту 3.
- Корн Г., Корн Т. 1.3-3. Представление суммы, произведения и частного. Степени и корни // Справочник по математике. — 4-е издание. — М.: Наука, 1978. — С. 32—33.
Обсуждение:Корень (математика) — Википедия
Материал из Википедии — свободной энциклопедии
Алгебраический корень и арифметический корень[править код]
- — для неотрицательного аргумента:
| a=b{\displaystyle {\color {red}{\sqrt {\color {black}a}}}=b} | где a≥0,b∈(−∞;+∞){\displaystyle a\geq 0,b\in (-\infty ;+\infty )} |
- — для отрицательного аргумента:
| a=i|a|=b{\displaystyle {\color {red}{\sqrt {\color {black}a}}}=i{\color {red}{\sqrt {\color {black}|a|}}}=b} | где a≥0,b∈C{\displaystyle a\geq 0,b\in \mathbb {C} } |
- — для комплексного аргумента (формула Муавра):
| a=||a||ei(ϕ+2πk)/2=b{\displaystyle {\color {red}{\sqrt {\color {black}a}}}=\left|{\color {red}{\sqrt {\color {black}|a|}}}\right|e^{i(\phi +2\pi k)/2}=b} | где a,b∈C,ϕ∈(−π2;π2),k=0,1{\displaystyle a,b\in \mathbb {C} ,\phi \in \left(-{\frac {\pi }{2}};{\frac {\pi }{2}}\right),k=0,1} |
__________ Спойлер __________ Обычно формула Муавра записывается с использованием алгебраического и арифметического корней:
|
- Например:
| 16=±4{\displaystyle {\color {red}{\sqrt {\color {black}16}}}=\pm 4} | Поскольку (±4)2=16{\displaystyle (\pm 4)^{2}=16} |
| −9=±3i{\displaystyle {\color {red}{\sqrt {\color {black}-9}}}=\pm 3i} | Поскольку (±3i)2=−9{\displaystyle (\pm 3i)^{2}=-9} |
- — для неотрицательного аргумента:
| a=b{\displaystyle {\color {blue}{\sqrt {\color {black}a}}}=b} | где a,b≥0{\displaystyle a,b\geq 0} |
- — для отрицательного или комплексного аргумента арифметический корень не определен (т.е. не существует).
- Например:
- Связь между арифметическим и алгебраическим корнями.
- — Для неотрицательного аргумента:
| a=|a|=b{\displaystyle {\color {blue}{\sqrt {\color {black}a}}}=\left|{\color {red}{\sqrt {\color {black}a}}}\right|=b} | где a,b≥0{\displaystyle a,b\geq 0} |
| a=±a=c{\displaystyle {\color {red}{\sqrt {\color {black}a}}}=\pm {\color {blue}{\sqrt {\color {black}a}}}=c} | где a≥0,c∈(−∞;+∞){\displaystyle a\geq 0,c\in (-\infty ;+\infty )} |
- — для отрицательного или комплексного аргумента связь между арифметическим и алгебраическим корнями установить невозможно (невозможно выразить один корень через другой). >> Kron7 15:33, 24 мая 2013 (UTC)
Если не придираться к строгости определений, то с написанным согласен. Исключение — последняя фраза: «связь невозможно установить» просто потому, что отрицательные и комплексные числа не входят в область определения арифметического корня. Кстати, хорошо оформлено, не хотите перенести в статью Арифметический корень? Она скоро будет переименована просто в Корень (математика) (см. её СО) и дополнена как раз в духе вами написанного, нынешняя преамбула и Свойства станут разделом об арифметическом корне, комплексную часть надо расширить. LGB 16:22, 24 мая 2013 (UTC)
- Касательно «связь невозможно установить» — разумеется, что причиной этому разные области определения корней.
- На счет переименования. Я считаю, что нужно ЛИБО создать одну статью (как вы и сказали Корень (математика)), но при этом разделу «Арифметический корень» уделить должное (большое) внимание, поскольку он используется не реже алгебраический корень, ЛИБО создать 2 статьи для обоих корней (точнее создать одну для алг. корня и отредактировать уже существующую ариф. корня). Я считаю, что оба понятия заслуживают независимой статьи, но также хотелось бы видеть их в одной статье, где четко будет указана разница между ними. Т.е. тут я не могу остановиться на конкретном решении. Как решите — так и будет. Но оба термина должны в полной мере быть описаны так или иначе.
- Возможно стоит добавить раздел для особых обобщений корня на случай таких экзотических объектов как
- ———
- ———
- …
- Вот тогда, мне кажется, можно будет номенировать статью Корень (математика) на избранную
- На счет переноса инф из раздела «Алгебраический корень и арифметический корень» в статью арифметический корень. Весьма неудобно, что две разные функции алг и ариф корни обозначаются одинаково — знаком радикала. По этому я в данном разделе и разукрасил их в разные цвета. К примеру, формула Муавра (та, что в спойлере), где используются одновременно оба корня просто вводит в заблуждение (это как, когда при решении задачи по радиоактивному распаду для обозначения постоянной распада и длины волны излучения использовать одно и то же обозначение — λ, что вызовет кучу путаниц).
- Если мы будем в одной статье описывать оба корня, то возможно стоить их так же искусственно раскрасить (возможно не в красный, а то он слишком выделяется, но все же). Это особенно актуально при выражении одного корня через другой. Если так, то я могу уже добавлять эту инфу.
- Но, из всего мною написанного, я не уверен в следующей записи:
- Если алгебраический квадратный корень имеет всегда 2 значения (2-значная ф-ция) и мы возьмем по модулю его, то получим два одинаковых значения, но не одно. Например,
- Ведь корень x{\displaystyle x} кратности n{\displaystyle n} (т.е. x1,n¯{\displaystyle x_{\overline {1,\;n}}}, где x1=x2=…=xn{\displaystyle x_{1}=x_{2}=\ldots =x_{n}}) и однозначный корень x{\displaystyle x}, где x=x1=x2=…=xn{\displaystyle x=x_{1}=x_{2}=\ldots =x_{n}} — разные вещи. >> Kron7 11:44, 28 мая 2013 (UTC)
- На избранную для корня я не претендую. Вносить туда подробный материал для кватернионов, матриц и прочего вряд ли стоит, лучше выделить его в отдельные статьи, как в англ-вики. Там всё не просто, скажем, для кватернионов квадратный корень похож на комплексный случай, но есть исключение — корень из отрицательного вещ. числа имеет бесконечно много значений (трёхмерная сфера в пространстве чисто мнимых кватернионов). Для матриц ещё сложнее.
- Неплохо бы обозначать корни разными цветами, думаю, ОРИСС’ом это не сочтут, дело оформительское. Но смешивать в одной формуле корни разного цвета, вы правы, вряд ли стоит. LGB 17:41, 28 мая 2013 (UTC)
- «Но смешивать в одной формуле корни разного цвета, вы правы, вряд ли стоит.» — нет, я как раз сделал ударение, что раскраска разных корней в разные цвета особо поможет в формулах, где одновременно используются оба корня. Как пример — формула Муавра a=|a|ei(ϕ+2πk)/2{\displaystyle {\color {red}{\sqrt {\color {black}a}}}={\color {blue}{\sqrt {\color {black}|a|}}}e^{i(\phi +2\pi k)/2}}.
- Что скажете по поводу
- Ведь корень x{\displaystyle x} кратности n{\displaystyle n} (т.е. x1,n¯{\displaystyle x_{\overline {1,\;n}}}, где x1=x2=…=xn{\displaystyle x_{1}=x_{2}=\ldots =x_{n}}) и однозначный корень x{\displaystyle x}, где x=x1=x2=…=xn{\displaystyle x=x_{1}=x_{2}=\ldots =x_{n}} — разные вещи. >> Kron7 11:44, 28 мая 2013 (UTC)
- ? >> Kron7 08:50, 29 мая 2013 (UTC)
- Моё мнение: ни в формуле Муавра, ни в других местах лучше не смешивать корни разного смысла. Собственно, вы же сами это показали на примере неприятностей с формулой 4=|4|=|±2|.{\displaystyle ~{\color {blue}{\sqrt {\color {black}4}}}=\left|{\color {red}{\sqrt {\color {black}4}}}\right|=|\pm 2|.} Потому что слева число, а справа — числовое множество. А в формуле Муавра есть простой выход — вместо корня справа использовать r{\displaystyle r}, тем более что далее идёт парное к нему φ.{\displaystyle \varphi .} LGB 11:47, 29 мая 2013 (UTC)
- На счет формулы Муавра, я не совсем вас понял. r{\displaystyle r} — это модуль комплексного числа. Какое он имеет отношение к корню, который из него извлекается? Ну вот я заменил |a| на r:
| a=|a|ei(ϕ+2πk)/2{\displaystyle {\color {red}{\sqrt {\color {black}a}}}={\color {blue}{\sqrt {\color {black}|a|}}}e^{i(\phi +2\pi k)/2}} | a=rei(ϕ+2πk)/2{\displaystyle {\color {red}{\sqrt {\color {black}a}}}={\color {blue}{\sqrt {\color {black}r}}}e^{i(\phi +2\pi k)/2}} |
- Ничего не изменилось. Корень как был, так и остался. Замена позволила лишь спрятать модуль. Я не думаю, что у нас получится убрать этот арифметический корень из правой части. Да и не нужно. Он там по определению должен быть. А то, что разных цветов корни в одной формуле, то это не наша проблема. Так была выведена данная формула. Все претензии к Абрахам де Муавру.
- Связь между разными корнями нужно показать. Только вот эту:
- >> Kron7 13:25, 29 мая 2013 (UTC)
Я, как обещал, создал статью Корень (математика), Арифметический корень теперь перенаправлен туда. Будем дополнять уже эту статью. Вы не будете возражать, если я весь данный раздел обсуждения перенесу на её СО? Мне кажется, там он более уместен, нежели в статье Комплексное число. LGB 13:33, 29 мая 2013 (UTC)
- Вот я его и перенес. >> Kron7 14:35, 29 мая 2013 (UTC)
- Прекрасно. Я неаккуратно выразился насчёт формулы Муавра, имелось в виду ввести в качестве модуля результата новую переменную, скажем, ρ{\displaystyle \rho }, и отдельно указать, что ρ=rn{\displaystyle ~\rho =\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}. Тогда смешения корней разного смысла в одной формуле не будет. Хотя не думаю, что читателю это сильно поможет, особенно если вы введёте расцветку. А вторая формула: a=±a{\displaystyle ~{\color {red}{\sqrt {\color {black}a}}}=\pm {\color {blue}{\sqrt {\color {black}a}}}}, уже изложена в тексте словесно, надо ли повторяться? LGB 15:56, 29 мая 2013 (UTC)
- Я так и понял, просто если мы сделаем замену ρ=rn{\displaystyle ~\rho ={\color {blue}{\sqrt[{\color {black}n}]{\color {black}r}}}}, то придется затем описать, что такое ρ{\displaystyle ~\rho } и снова получим арифметический корень.
- На счет связи a=±a{\displaystyle ~{\color {red}{\sqrt {\color {black}a}}}=\pm {\color {blue}{\sqrt {\color {black}a}}}}, то это только для кв. корней, а для корней n-й степени связь будет слишком сложная (много случаев и писанины) и нет смысла этим заниматься. >> Kron7 08:32, 30 мая 2013 (UTC)
- Прекрасно. Я неаккуратно выразился насчёт формулы Муавра, имелось в виду ввести в качестве модуля результата новую переменную, скажем, ρ{\displaystyle \rho }, и отдельно указать, что ρ=rn{\displaystyle ~\rho =\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}. Тогда смешения корней разного смысла в одной формуле не будет. Хотя не думаю, что читателю это сильно поможет, особенно если вы введёте расцветку. А вторая формула: a=±a{\displaystyle ~{\color {red}{\sqrt {\color {black}a}}}=\pm {\color {blue}{\sqrt {\color {black}a}}}}, уже изложена в тексте словесно, надо ли повторяться? LGB 15:56, 29 мая 2013 (UTC)
Замечания по тексту, часть 1[править код]
- Какая разница между следующими двумя определениями:
Корень n-й степени из числа a{\displaystyle a} определяется как такое число b{\displaystyle b}, что bn=a.{\displaystyle ~b^{n}=a.}
- и
Корень n-й степени из числа a{\displaystyle a} есть решение x{\displaystyle x} уравнения xn=a{\displaystyle ~x^{n}=a}
Kron7 14:48, 29 мая 2013 (UTC)
- Хочу сразу сделать одно общее замечание: статья предназначена в первую очередь для школьника, поэтому стиль и уровень должны быть по возможности школьными. Потом я введу несколько разделов для более продвинутых читателей (функция корня и её анализ, обобщения и др.), но текущий материал пока школьный. Поэтому прошу убрать из формул все кванторы, а часть текста лучше и понятнее изложить словами (скажем, факт нечётности). Теперь о двух (собственно, трёх) определениях — конечно же, они равносильны и даже почти одинаковы, но вторая формулировка более алгоритмична в том смысле, что подсказывает читателю, как находить корень. Третья формулировка связывает извлечение корня с корнем многочлена специального вида, что тоже полезно. LGB 16:05, 29 мая 2013 (UTC)
- Ок. Кванторы убрал (если для школьника — согласен). Что касается четности, в школе рассказывают как математически указать, что данное число — четное. Но я изменил на текст. >> Kron7 08:32, 30 мая 2013 (UTC)
- Хочу сразу сделать одно общее замечание: статья предназначена в первую очередь для школьника, поэтому стиль и уровень должны быть по возможности школьными. Потом я введу несколько разделов для более продвинутых читателей (функция корня и её анализ, обобщения и др.), но текущий материал пока школьный. Поэтому прошу убрать из формул все кванторы, а часть текста лучше и понятнее изложить словами (скажем, факт нечётности). Теперь о двух (собственно, трёх) определениях — конечно же, они равносильны и даже почти одинаковы, но вторая формулировка более алгоритмична в том смысле, что подсказывает читателю, как находить корень. Третья формулировка связывает извлечение корня с корнем многочлена специального вида, что тоже полезно. LGB 16:05, 29 мая 2013 (UTC)
- Думаю, стоит переформулировать:
Обозначение: b=an,{\displaystyle b={\sqrt[{n}]{a}},} символ (знак корня) в правой части называется радикалом n-й степени. Число a{\displaystyle a} чаще всего вещественное или комплексное. Число n — натуральное число, называемое степенью корня; как правило, оно больше или равно 2.
- Радикал n-й степени? Ведь такого нет. Есть просто радикал — вот символ радикала: a{\displaystyle {\sqrt {\color {white}a}}} Kron7 14:48, 29 мая 2013 (UTC)
- Вы правы, про степень радикала надо убрать. LGB 16:05, 29 мая 2013 (UTC)
* Вот такого обозначения вообще не существует a2{\displaystyle {\sqrt[{2}]{\color {white}a}}}. Kron7 14:48, 29 мая 2013 (UTC)
- Вплоть до пояснения, что показатель 2 можно опускать, такая запись допустима, поскольку определению записи в тексте статьи она не противоречит. LGB 16:05, 29 мая 2013 (UTC)
- На сколько я знаю, двойка для кв корня не просто опускается для красоты, но и просто символьно не может там находиться, поскольку символа a2{\displaystyle {\sqrt[{2}]{\color {white}a}}} не существует, так же как и a1{\displaystyle {\sqrt[{1}]{\color {white}a}}}. Аналогично тому, как в уравнениях хим. реакций указывать коэф. 1, где не просто не принято его ставить из-за красоты, но и просто такая запись недопустима. Т.е. запись 2×2+1x=0{\displaystyle 2x^{2}+1x=0} — вполне адекватная (да, принято не писать коэффициент 1, но если и указать его, то ошибкой это не будет — просто некорректная запись), а вот запись 2h3+1O2=2h3O{\displaystyle 2H_{2}+1O_{2}=2H_{2}O} — неправильная (единицу нельзя там ставить — такие правила оформления), также записи a2{\displaystyle {\sqrt[{2}]{a}}} и a1{\displaystyle {\sqrt[{1}]{a}}} нельзя использовать, поскольку символов a2{\displaystyle {\sqrt[{2}]{\color {white}a}}} и a1{\displaystyle {\sqrt[{1}]{\color {white}a}}} нет.
- Единственный способ использовать символ a2{\displaystyle {\sqrt[{2}]{\color {white}a}}} — это добавить термин «формально». Также как и с неопределенностями (0/0,…), но не думаю, что это стоить делать. Сейчас этот момент в статье красиво описан и без данного символа. >> Kron7 08:32, 30 мая 2013 (UTC)
- Вплоть до пояснения, что показатель 2 можно опускать, такая запись допустима, поскольку определению записи в тексте статьи она не противоречит. LGB 16:05, 29 мая 2013 (UTC)
- Свойства корней из вещественных чисел
| Старый текст | Существование и единственность Существование и единственность корня n-й степени из вещественного числа a{\displaystyle a} зависит от чётности степени n и от знака числа a.{\displaystyle a.}
| ||
| Новый текст | Свойства
|
Квадратный корень из 5 — это… Что такое Квадратный корень из 5?
Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.[1]
Его приблизительное значение с 59 цифрами после запятой является:
Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.[2]
Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:
Вавилонский метод
Вычисление корня из 5, начиная с r0 = 2, где rn+1 = (rn + 5/rn) / 2:
Золотое сечение
√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.Золотое сечение φ — среднее арифметическое 1 и корня из 5.[3]
() алгебраически можно выразить так:
Числа Фибоначчи могут быть выражены через корень из 5 так:
Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:[4]
Алгебра
Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Число 6 представляется в данном кольце двумя способами:
Поле — абелево расширение рациональных чисел.
Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:
Тождества Рамануджана
Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.[5][6]
Например, случай непрерывных дробей Роджерса-Рамануджана:
См. также
Примечания
- ↑ Dauben, Joseph W. (June 1983) Scientific American Georg Cantor and the origins of transfinite set theory. Volume 248; Page 122.
- ↑ R. Nemiroff and J. Bonnell: The first 1 million digits of the square root of 5
- ↑ Browne, Malcolm W. (July 30, 1985) New York Times Puzzling Crystals Plunge Scientists into Uncertainty. Section: C; Page 1. (Note — this is a widely cited article).
- ↑ Richard K. Guy: «The Strong Law of Small Numbers». American Mathematical Monthly, vol. 95, 1988, pp. 675—712
- ↑ Ramanathan, K. G. (1984), ««On the Rogers-Ramanujan continued fraction»», Indian Academy of Sciences. Proceedings. Mathematical Sciences Т. 93 (2): 67-77, MR813071, ISSN 0253-4142, DOI 10.1007/BF02840651
- ↑ Eric W. Weisstein, «Ramanujan Continued Fractions», <http://mathworld.wolfram.com/RamanujanContinuedFractions.html> at MathWorld
Ссылки
Квадратный корень из 2 — это… Что такое Квадратный корень из 2?
 Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
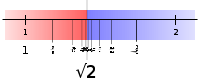 Квадратный корень из 2.
Квадратный корень из 2.Хорошим и часто используемым приближением к является дробь . Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.
История
 Вавилонская глиняная табличка с примечаниями.
Вавилонская глиняная табличка с примечаниями.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного корня из двух. В результате алгоритма получается приблизительное значение в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:
- 3/2 = 1.5
- 17/12 = 1.416…
- 577/408 = 1.414215…
- 665857/470832 = 1.4142135623746…
В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Шигеру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
Свойства квадратного корня из двух
Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора,образующего угол 45° с координатными осями:
Одно из интересных свойств √2 состоит в следующем:
- .Потому что
Это является результатом свойства серебряного сечения.
Другое интересное свойство √2:
Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:
- и
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
Квадратный корень из двух может быть также использован для приближения π:
С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:
- .
Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух является пропорцией формата бумаги ISO 216. Соотношение сторон таково, что при разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции.
См. также
Квадратный корень из 5 — это… Что такое Квадратный корень из 5?
Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число. [1]
Его приблизительное значение с 59 цифрами после запятой является:
Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.[2]
Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:
Вавилонский метод
Вычисление корня из 5, начиная с r0 = 2, где rn+1 = (rn + 5/rn) / 2:
Золотое сечение
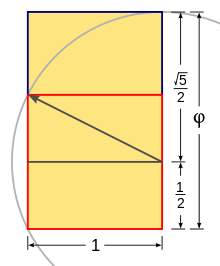 √5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.
√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.() алгебраически можно выразить так:
Числа Фибоначчи могут быть выражены через корень из 5 так:
Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:[4]
Алгебра
Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Число 6 представляется в данном кольце двумя способами:
Поле — абелево расширение рациональных чисел.
Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:
Тождества Рамануджана
Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями.[5][6]
Например, случай непрерывных дробей Роджерса-Рамануджана:
См. также
Примечания
- ↑ Dauben, Joseph W. (June 1983) Scientific American Georg Cantor and the origins of transfinite set theory. Volume 248; Page 122.
- ↑ R. Nemiroff and J. Bonnell: The first 1 million digits of the square root of 5
- ↑ Browne, Malcolm W. (July 30, 1985) New York Times Puzzling Crystals Plunge Scientists into Uncertainty. Section: C; Page 1. (Note — this is a widely cited article).
- ↑ Richard K. Guy: «The Strong Law of Small Numbers». American Mathematical Monthly, vol. 95, 1988, pp. 675—712
- ↑ Ramanathan, K. G. (1984), ««On the Rogers-Ramanujan continued fraction»», Indian Academy of Sciences. Proceedings. Mathematical Sciences Т. 93 (2): 67-77, MR813071, ISSN 0253-4142, DOI 10.1007/BF02840651
- ↑ Eric W. Weisstein, «Ramanujan Continued Fractions», <http://mathworld.wolfram.com/RamanujanContinuedFractions.html> at MathWorld
Ссылки
Целочисленный квадратный корень — Википедия
Целочисленный квадратный корень (isqrt) натурального числа n — это положительное число m, которое равно наибольшему целому числу, меньшему либо равному квадратному корню из n,
- isqrt(n)=⌊n⌋.{\displaystyle {\mbox{isqrt}}(n)=\lfloor {\sqrt {n}}\rfloor .}
Например, isqrt(27)=5{\displaystyle {\mbox{isqrt}}(27)=5} поскольку 52=25<27{\displaystyle 5^{2}=25<27} и 62=36>27{\displaystyle 6^{2}=36>27}.
Одним из путей вычисления n{\displaystyle {\sqrt {n}}} и isqrt(n){\displaystyle {\mbox{isqrt}}(n)} — использование метода Ньютона для поиска решения уравнения x2−n=0{\displaystyle x^{2}-n=0}, используя итеративную формулу[1][2]
- xk+1=12(xk+nxk),k≥0,x0>0.{\displaystyle {x}_{k+1}={\frac {1}{2}}\left(x_{k}+{\frac {n}{x_{k}}}\right),\quad k\geq 0,\quad x_{0}>0.}
Последовательность {xk}{\displaystyle \{x_{k}\}} сходится квадратично к n{\displaystyle {\sqrt {n}}} при k→∞{\displaystyle k\to \infty }[3]. Можно доказать, что если x0=n{\displaystyle x_{0}=n} выбрано в качестве начального значения, можно останавливаться, как только
- |xk+1−xk|<1{\displaystyle |x_{k+1}-x_{k}|<1},
чтобы обеспечить, что ⌊xk+1⌋=⌊n⌋.{\displaystyle \lfloor x_{k+1}\rfloor =\lfloor {\sqrt {n}}\rfloor .}
Использование только целочисленного деления[править | править код]
Для вычисления ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor } для очень больших целых чисел n можно использовать частное деления с остатком при обеих операциях деления. Преимуществом является использование только целых чисел для каждого промежуточного значения, что освобождает от использования представления чисел в виде чисел с плавающей запятой. Это эквивалентно использованию итеративной формулы
- xk+1=⌊12(xk+⌊nxk⌋)⌋,k≥0,x0>0,x0∈Z.{\displaystyle {x}_{k+1}=\left\lfloor {\frac {1}{2}}\left(x_{k}+\left\lfloor {\frac {n}{x_{k}}}\right\rfloor \right)\right\rfloor ,\quad k\geq 0,\quad x_{0}>0,\quad x_{0}\in \mathbb {Z} .}
Основываясь на факте, что
- ⌊12(xk+⌊nxk⌋)⌋=⌊12(xk+nxk)⌋,{\displaystyle \left\lfloor {\frac {1}{2}}\left(x_{k}+\left\lfloor {\frac {n}{x_{k}}}\right\rfloor \right)\right\rfloor =\left\lfloor {\frac {1}{2}}\left(x_{k}+{\frac {n}{x_{k}}}\right)\right\rfloor ,}
можно показать, что последовательность достигает ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor } за конечное число итераций [4].
Однако ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor } не обязательно будет неподвижной точкой итеративной формулы, приведённой выше. Можно показать, что ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor } будет неподвижной точкой тогда и только тогда, когда n+1{\displaystyle n+1} не является полным квадратом. Если n+1{\displaystyle n+1} является полным квадратом, последовательность не сходится, а переходит в цикл длины два, поочерёдно меняя ⌊n⌋{\displaystyle \lfloor {\sqrt {n}}\rfloor } и ⌊n⌋+1{\displaystyle \lfloor {\sqrt {n}}\rfloor +1}. Для прекращения работы достаточно проверить, что либо последовательность сходится (повторение предыдущего значения), либо что следующее значение ровно на единицу больше текущего, в последнем случае новое значение отбрасывается.
Используя битовые операции[править | править код]
Если * означает умножение, << означает сдвиг влево, а >> — логический сдвиг вправо, рекурсивный алгоритм поиска целочисленного квадратного корня из любого натурального числа следующий:
function integerSqrt(n):
if n < 0:
error "integerSqrt работает только с неотрицательным входом"
else if n < 2:
return n
else:
smallCandidate = integerSqrt(n >> 2) << 1
largeCandidate = smallCandidate + 1
if largeCandidate*largeCandidate > n:
return smallCandidate
else:
return largeCandidate
Или итерации вместо рекурсии:
function integerSqrt(n):
if n < 0:
error "integerSqrt работает только с неотрицательным входом"
# Находим наибольший сдвиг.
shift = 2
nShifted = n >> shift
while nShifted ≠ 0 and nShifted ≠ n:
shift = shift + 2
nShifted = n >> shift
shift = shift - 2
# Находим цифры результата.
result = 0
while shift ≥ 0:
result = result << 1
candidateResult = result + 1
if candidateResult*candidateResult ≤ n >> shift:
result = candidateResult
shift = shift - 2
return result
Хотя n{\displaystyle {\sqrt {n}}} является иррациональным числом для большинства значений n{\displaystyle n}, последовательность {xk}{\displaystyle \{x_{k}\}} содержит только рациональные члены, если x0{\displaystyle x_{0}} рационально. Таким образом, используя этот метод, нет необходимости выходить за пределы поля рациональных чисел, чтобы вычислить isqrt(n){\displaystyle {\mbox{isqrt}}(n)}, что имеет некоторое теоретическое преимущество.
Можно показать, что c=1{\displaystyle c=1} является наибольшим числом для критерия остановки
- |xk+1−xk|<c {\displaystyle |x_{k+1}-x_{k}|<c\ },
который обеспечивает, что ⌊xk+1⌋=⌊n⌋{\displaystyle \lfloor x_{k+1}\rfloor =\lfloor {\sqrt {n}}\rfloor } в вышеприведённом алгоритме.
В приложениях, использующих отличные от рациональных чисел форматы (например, плавающую запятую), константу остановки следует выбрать меньшей единицы, чтобы избежать ошибок округления.
Мнимая единица — Википедия

Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляться также в обобщённом смысле не только для комплексных чисел[⇨].
В математике, физике мнимая единица обозначается как латинская i{\displaystyle i} или j{\displaystyle j}. Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения.
Причиной введения мнимой единицы является то, что не каждое полиномиальное уравнение f(x)=0{\displaystyle f(x)=0} с вещественными коэффициентами имеет решения в поле вещественных чисел. Так, уравнение x2+1=0{\displaystyle x^{2}+1=0} не имеет вещественных корней. Однако оказывается, что любое полиномиальное уравнение с комплексными коэффициентами имеет комплексное решение — «Основная теорема алгебры».
Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения: нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Утверждение, что мнимая единица — это «квадратный корень из −1», не совсем точно: ведь «−1» имеет два квадратных корня, один из которых можно обозначить как «i», а другой как «−i». Какой именно корень принять за мнимую единицу — неважно: все равенства сохранят силу при одновременной замене всех «i» на «−i» и «−i» на «i». Однако из-за этой двусмысленности, чтобы избежать ошибочных выкладок, не следует применять обозначение для i{\displaystyle i} через радикал (как −1{\displaystyle {\sqrt {-1}}}).
Мнимая единица — это число, квадрат которого равен −1. Т.е. i{\displaystyle i} — это одно из решений уравнения
- x2+1=0,{\displaystyle x^{2}+1=0,} или x2=−1.{\displaystyle x^{2}=-1.}
И тогда его вторым решением будет −i{\displaystyle -i}, что проверяется подстановкой.
Степени i{\displaystyle i} повторяются в цикле:
- …{\displaystyle \ldots }
- i−3=i{\displaystyle i^{-3}=i}
- i−2=−1{\displaystyle i^{-2}=-1}
- i−1=−i{\displaystyle i^{-1}=-i}
- i0=1{\displaystyle i^{0}=1}
- i1=i{\displaystyle i^{1}=i}
- i2=−1{\displaystyle i^{2}=-1}
- i3=−i{\displaystyle i^{3}=-i}
- i4=1{\displaystyle i^{4}=1}
- …{\displaystyle \ldots }
Что может быть записано для любой степени в виде:
- i4n=1{\displaystyle i^{4n}=1}
- i4n+1=i{\displaystyle i^{4n+1}=i}
- i4n+2=−1{\displaystyle i^{4n+2}=-1}
- i4n+3=−i.{\displaystyle i^{4n+3}=-i.}
где n — любое целое число.
Отсюда: in=inmod4{\displaystyle i^{n}=i^{n{\bmod {4}}}} где mod 4 — это остаток от деления на 4.
Из тождества Эйлера следует, что число ii{\displaystyle i^{i}} является вещественным:
- ii=e(iπ/2)i=ei2π/2=e−π/2=0,20787957635…{\displaystyle i^{i}={e^{(i\pi /2)i}}=e^{i^{2}\pi /2}=e^{-\pi /2}=0{,}20787957635\ldots }.
Точнее, в комплексном анализе возведение в степень: xy=exp(y⋅Lnx){\displaystyle x^{y}=\exp(y\cdot \operatorname {Ln} x)} является многозначной функцией, поэтому
- ii=e−π(1+4n)2{\displaystyle i^{i}=e^{-{\frac {\pi (1+4n)}{2}}}}, где n∈Z{\displaystyle n\in \mathbb {Z} }.
Также верно, что (−i)(−i)=ii{\displaystyle (-i)^{(-i)}=i^{i}}.
Факториал мнимой единицы i можно определить как значение гамма-функции от аргумента 1 + i:
- i!=Γ(1+i)≈0.4980−0.1549i.{\displaystyle i!=\Gamma (1+i)\approx 0.4980-0.1549i.}
Также
- |i!|=πsinh(π)≈0.521564….{\displaystyle |i!|={\sqrt {\pi \over \sinh(\pi )}}\approx 0.521564….}[1]
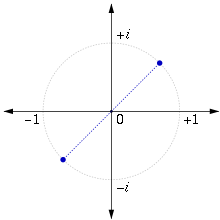 Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)
Корни квадратные из мнимой единицы
Корни кубические из мнимой единицы (вершины треугольника)В поле комплексных чисел корень n-й степени имеет n решений. На комплексной плоскости корни из мнимой единицы находятся в вершинах правильного n-угольника, вписанного в окружность с единичным радиусом.
- uk=cosπ2+2πkn+i sinπ2+2πkn,k=0,1,…,n−1{\displaystyle u_{k}=\cos {\frac {{\frac {\pi }{2}}+2\pi k}{n}}+i\ \sin {\frac {{\frac {\pi }{2}}+2\pi k}{n}},\quad k=0,1,…,n-1}
В частности, i={1+i2; −1−i2}{\displaystyle {\sqrt {i}}=\left\{{\frac {1+i}{\sqrt {2}}};\ {\frac {-1-i}{\sqrt {2}}}\right\}} и i3={−i; i+32; i−32}{\displaystyle {\sqrt[{3}]{i}}=\left\{-i;\ {\frac {i+{\sqrt {3}}}{2}};\ {\frac {i-{\sqrt {3}}}{2}}\right\}}
Также корни из мнимой единицы могут быть представлены в показательном виде:
- uk=e(π2+2πk)in,k=0,1,…,n−1{\displaystyle u_{k}=e^{\frac {({\frac {\pi }{2}}+2\pi k)i}{n}},\quad k=0,1,…,n-1}
В конструкции удвоения по Кэли — Диксону или в рамках алгебры по Клиффорду «мнимых единиц расширения» может быть несколько. Но в этом случае могут возникать делители нуля и иные свойства, отличные от свойств комплексного «i». Например, в теле кватернионов три антикоммутативных мнимых единицы, а также имеется бесконечно много решений уравнения x2=−1{\displaystyle x^{2}=-1}.
К вопросу об интерпретации и названии[править | править код]
 | Гаусс утверждал также, что если бы величины 1, −1 и √−1 назывались соответственно не положительной, отрицательной и мнимой единицей, а прямой, обратной и побочной, то у людей не создавалось бы впечатления, что с этими числами связана какая-то мрачная тайна. По словам Гаусса, геометрическое представление дает истинную метафизику мнимых чисел в новом свете. Именно Гаусс ввел термин «комплексные числа» (в противоположность «мнимым числам» Декарта) и использовал для обозначения √−1 символ i. Морис Клайн, «Математика. Утрата определённости». Глава VII. Нелогичное развитие: серьёзные трудности на пороге XIX в. |  |
Обычное обозначение i{\displaystyle i}, но в электро- и радиотехнике мнимую единицу принято обозначать j{\displaystyle j}, чтобы не путать с обозначением мгновенной силы тока: i=i(t){\displaystyle i=i(t)}.
В языке программирования Python мнимая единица записывается как 1j.
В языке программирования Wolfram Language мнимая единица записывается как I.