Наибольшее и наименьшее значение функции на отрезке. Решение задач
Отыскание максимумов и минимумов — одна из самых распространенных задач при исследованиях функций.
Непрерывная на отрезке функция принимает свое наибольшее или наименьшее значение, либо в критических точках (в точках, в которых производная обращается в нуль или не существует), принадлежащих исследуемому промежутке, или на его концах .
На практике нахождения максимумов и минимумов похоже на отыскания локального экстремума, только добавляются края промежутка. Возможны случаи, когда максимумы и минимумы функций находятся в точках локального экстремума, а возможные — на краях отрезка.
Рассмотрим ряд примеров, чтобы ознакомить Вас с методикой исследования.
————————————
Примеры.
Определить наибольшее и наименьшее значение фунции на промежутке.
Сборник В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах».
1. (4.55.б)
Функция определена на всем множестве действительных чисел
Найдем производную функции
Приравняем ее к нулю и определим критические точки
Проверим знак производной слева и справа от найденной точки
Производная при переходе через точку меняет знак с положительного на отрицательный , следовательно она является точкой локального максимума.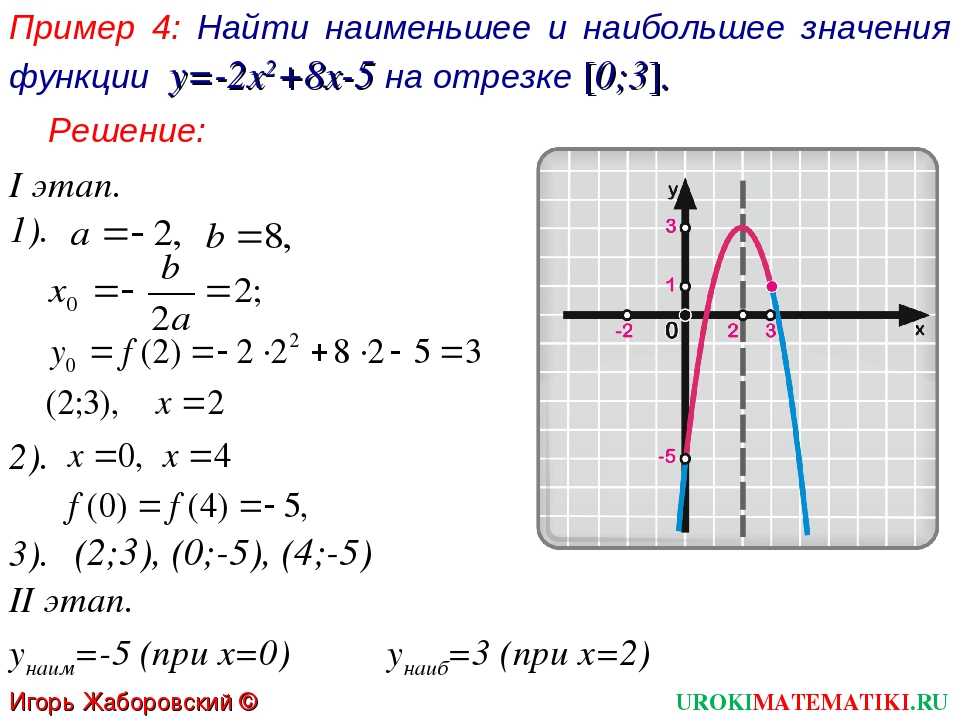
Найдем значение функции в точке
и на краях отрезка
Таким образом функция достигает максимума в точке локального экстремума и минимума на одном из краев отрезка .
2. (4.55.д)
На заданном промежутке функция определена; вычислим ее производную
Приравнивая нуля найдем критическую точку
Заданная точка принадлежит отрезку. Найдем значения функции во всех точках
Функция приобретает максимум и минимум в точках
3. (4.55.є)
Функция определена для всех значений аргумента .
Найдем производную
Из выражения видно, что производная отлична от нуля на промежутке определения, однако в точке она не существует.
Вычислим значение функции
Наибольшее значение функция принимает в точке , а наименьшее значение в критической точке .
————————————
Приведем решения задач из сборника Дубовика В. П., Юрика И.И. «Высшая математика».
П., Юрика И.И. «Высшая математика».
4. (5.770)
Функция определена везде, потому приступим сразу к вычислению производной
Приравняем ее к нулю и находим критические точки
Найдем значения функции во всех подозрительных на экстремум точках
Из полученного набора значений следует, что функция принимает максимум и минимум на краях отрезка
5. (5.771)
На заданном интервале функция определена, проводим дифференцировку
Приравняв к нулю производную получим
Другую критическую точку найдем из условия, что производная не существует
Одна совпадает с началом отрезка. Вычислим значение функции на краях отрезка и в критических точках
Таким образом функция принимает максимальное значение в критической точке, а минимальное на конце отрезка
Из приведенных решений можно сделать выводы, что главным в исчислении является знание функций и умение дифференцировать. Все остальное сводится к отысканию значений функций в точках и анализа результатов. Изучайте свойства элементарных функций, правила нахождения производных, это Вам пригодится при решении примеров.
Все остальное сводится к отысканию значений функций в точках и анализа результатов. Изучайте свойства элементарных функций, правила нахождения производных, это Вам пригодится при решении примеров.
———————————————-
Посмотреть материалы:
Наиболшее и наименьшее значений непререрывной функции на промежутке
Вопросы занятия:
· рассмотреть применение производных для отыскания наибольшего и наименьшего значений функции на промежутке.
Материал урока.
Пусть у нас есть график некоторой функции f(x) на промежутке [a; b]. По графику легко найти наибольшее и наименьшее значения функции на промежутке. Иногда наибольшее и наименьшее значения можно отыскать и без построения графика.
Например,
А
как же быть в других случаях, когда наличие наибольшего и наименьшего значения
функции на промежутке не так очевидно? Можно, конечно, каждый раз строить
график функции и с помощью него находить игрек наибольшее и наименьшее. Но это
не очень удобно и долго.
Но это
не очень удобно и долго.
Для того, чтобы избежать построения графика функции воспользуемся следующими утверждениями.
1. Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего, и своего наименьшего значений.
Справедливость данного утверждения мы не будем доказывать.
2. Наибольшего и наименьшего значений непрерывная функция может достигать как на концах отрезка, так и внутри него.
Это утверждение можно проиллюстрировать графиками функций.
Видно, что на первом графике наибольшее и наименьшее значения достигаются во внутренних точках. На втором графике наибольшее значение достигается в конце промежутка, а наименьшее значение достигается во внутренней точке.
3. Если наибольшее или наименьшее значение достигается внутри отрезка, то только в стационарной или критической точке.
Для
доказательства данного утверждения достаточно вспомнить, что в данном случае
идёт речь об экстремумах функции, а экстремум достигается только в стационарной
или критической точке.
Давайте сформулируем алгоритм нахождения наименьшего и наибольшего значений непрерывной функции игрек равно f(x) на отрезке [a; b].
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё один пример.
Пример.
Как находить наибольшее и наименьшее значение функции на отрезке мы разобрались. А что же делать, если надо найти эти значения на незамкнутом интервале? Там же невозможно найти значения на концах промежутка. Можно конечно построить график функции, но тогда мы получим приближенные значения и опять же это долго.
Для решения таких задач удобно пользоваться следующей теоремой.
Теорема.
Пусть функция y = f(x)
а) если x = x0 − точка максимума, то yнаиб = f(x0);
б) если x
= x0
− точка минимума, то yнаим
= f(x0).
Давайте геометрически проиллюстрируем эту теорему.
Рассмотрим несколько примеров.
Пример.
Рассмотрим ещё один пример.
Пример.
Наибольшее и наименьшее значение функции. Алгебра
Дата публикации:
.Что будем изучать:
1. Нахождение наибольшего и наименьшего значения по графику функции.
2. Нахождение наибольшего и наименьшего значения с помощью производной.
3. Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y=f(x) на отрезке [a;b].
4. Наибольшее и наименьшее значение функции на незамкнутом интервале.
5. Примеры.
Нахождение наибольшего и наименьшего значения по графику функции
Ребята, мы с вами находили наибольшее и наименьшее значения функции и раньше. Мы смотрели на график функции и делали вывод, где функция достигает наибольшего значения, а где — наименьшего.
Давайте повторим:
По графику нашей функции видно, что наибольшее значение достигается в точке x= 1, оно равно 2. Наименьшее значение достигается в точке x= -1, и оно равно -2. Данным способом довольно просто находить наибольшие и наименьшие значения, но не всегда существует возможность построить график функции.
Нахождение наибольшего и наименьшего значения с помощью производной
Ребята, а как вы думаете, как с помощью производной можно найти наибольшее и наименьшее значение?
Ответ можно найти в теме экстремумы функции. Там мы с вами находили точки максимума и минимума, не правда ли термины похожи. Однако, путать наибольшее и наименьшее значение с максимум и минимум функции нельзя, это разные понятия.Итак, давайте введем правила:
а) Если функция непрерывна на отрезке, то она достигает своего наибольшего и наименьшего значения на этом отрезке.
б) Наибольшего и наименьшего значения функция может достигать как на концах отрезках, так и внутри него. Давайте рассмотрим этот пункт подробнее.
Давайте рассмотрим этот пункт подробнее.
На рисунке а функция достигает своего наибольшего и наименьшего значения на концах отрезках [a;b].
На рисунке б функция достигает своего наибольшего и наименьшего значения внутри отрезка [a;b].
На рисунке в точка минимума находится внутри отрезка, а точка максимума — на конце отрезка, в точке b.
Алгоритм поиска наибольшего и наименьшего значения непрерывной функции y= f(x) на отрезке [a;b]
- Найти производную f'(x).
- Найти стационарные и критические точки внутри отрезка [a;b].
- Вычислить значение функции в стационарных и критических точках, а так же в f(a) и f(b). Выбрать наименьшее и наибольшее значения, это и будут точки наименьшего и наибольшего значения функции.
Наибольшее и наименьшее значение функции на незамкнутом интервале
Ребята, а как же искать наибольшее и наименьшее значение функции на незамкнутом интервале? Для этого воспользуемся важной теоремой, которая доказывается в курсе высшей математики. 3}{3}$ + 2x2 + 4x — 5 на отрезке
3}{3}$ + 2x2 + 4x — 5 на отрезке
а) [-9;-1], б) [-3;3], в) [3;9].
Решение: Найдем производную: y’= x2 + 4x + 4.
Производная существует на всей области определения, тогда нам надо найти стационарные точке.
Дальнейшие расчеты проведем для требуемых отрезков.
а) Найдем значения функции на концах отрезка и в стационарной точки.
Тогда yнаим.= -122, при x= -9; yнаиб.= y = -7$\frac{1}{3}$, при x= -1.
б) Найдем значения функции на концах отрезка и в стационарной точке. Наибольшее и наименьшее значение достигается на концах отрезка.
Тогда yнаим.= -8, при x= -3, yнаиб.= 34, при x= 3.
в) Стационарная точка не попадает на наш отрезок, найдем значения на концах отрезка.
Тогда yнаим.= 34, при x= 3, yнаиб.= 436, при x= 9.
Пример
Найти наибольшее и наименьшее значение функции y= x2 — 3x + 5 + |1-x| на отрезке [0;4].
Решение: Раскроем модуль и преобразуем нашу функцию:
y= x2 — 3x + 5 + 1 — x, при x ≤ 1. 2 + 3}$= $\frac{3√3}{6}$= $\frac{√3}{2}$.
2 + 3}$= $\frac{3√3}{6}$= $\frac{√3}{2}$.
Ответ: y наиб.= $\frac{√3}{2}$.
Задачи для самостоятельного решения
а) Найти наибольшее и наименьшее значение функции y= x4 — 3x3 + 2x2 — 9x + 1
на отрезке а) [-3;1], б) [2;5], в) [-4;7].
б) Найти наибольшее и наименьшее значение функции y= x2 — 6x + 8 + |x — 2| на отрезке [-1;5].
в) Найти наибольшее и наименьшее значение функции y= $-2x-\frac{1}{2x}$ на луче (0;+∞).
Как найти наибольшее значение функции y. Наибольшее и наименьшее значение функции
Пусть функция $z=f(x,y)$ определена и непрерывна в некоторой ограниченной замкнутой области $D$. Пусть в этой области заданная функция имеет конечные частные производные первого порядка (за исключением, быть может, конечного количества точек). Чтобы найти наибольшее и наименьшее значения функции двух переменных в данной замкнутой области требуется выполнить три шага простого алгоритма.
Алгоритм поиска наибольшего и наименьшего значений функции $z=f(x,y)$ в замкнутой области $D$.
 2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.
2-4x$ в замкнутой области, ограниченной линиями $x=3$, $y=0$ и $y=x+1$.Будем следовать указанному выше , но для начала разберёмся с чертежом заданной области, которую обозначим буквой $D$. Нам заданы уравнения трёх прямых, кои эту область ограничивают. Прямая $x=3$ проходит через точку $(3;0)$ параллельно оси ординат (оси Oy). Прямая $y=0$ — это уравнение оси абсцисс (оси Ox). Ну, а для построения прямой $y=x+1$ найдём две точки, через которые и проведём данную прямую. Можно, конечно, подставить вместо $x$ парочку произвольных значений. Например, подставляя $x=10$, получим: $y=x+1=10+1=11$. Мы нашли точку $(10;11)$, лежащую на прямой $y=x+1$. Однако лучше отыщем те точки, в которых прямая $y=x+1$ пересекается с линиями $x=3$ и $y=0$. Почему это лучше? Потому, что мы одним выстрелом уложим пару зайцев: получим две точки для построения прямой $y=x+1$ и заодно выясним, в каких точках эта прямая пересекает иные линии, ограничивающие заданную область. Прямая $y=x+1$ пересекает прямую $x=3$ в точке $(3;4)$, а прямую $y=0$ — в точке $(-1;0)$.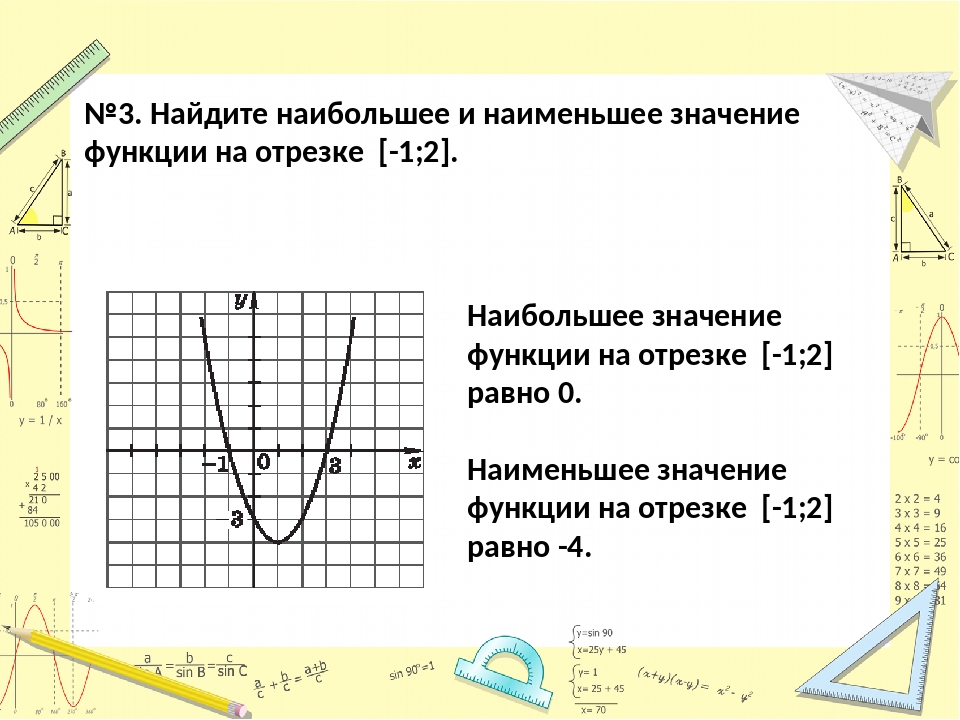
Как были получены точки $(3;4)$ и $(-1;0)$? показать\скрыть
Начнём с точки пересечения прямых $y=x+1$ и $x=3$. Координаты искомой точки принадлежат и первой, и второй прямой, поэтому для нахождения неизвестных координат нужно решить систему уравнений:
$$ \left \{ \begin{aligned} & y=x+1;\\ & x=3. \end{aligned} \right. $$
Решение такой системы тривиально: подставляя $x=3$ в первое уравнение будем иметь: $y=3+1=4$. Точка $(3;4)$ и есть искомая точка пересечения прямых $y=x+1$ и $x=3$.
Теперь отыщем точку пересечения прямых $y=x+1$ и $y=0$. Вновь составим и решим систему уравнений:
$$ \left \{ \begin{aligned} & y=x+1;\\ & y=0. \end{aligned} \right. $$
Подставляя $y=0$ в первое уравнение, получим: $0=x+1$, $x=-1$. Точка $(-1;0)$ и есть искомая точка пересечения прямых $y=x+1$ и $y=0$ (оси абсцисс).
Всё готово для построения чертежа, который будет иметь такой вид:
Вопрос примечания кажется очевидным, ведь всё видно по рисунку. Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.
Однако стоит помнить, что рисунок не может служить доказательством. Рисунок — лишь иллюстрация для наглядности.
Наша область была задана с помощью уравнений прямых, которые её ограничивают. Очевидно, что эти прямые определяют треугольник, не так ли? Или не совсем очевидно? А может, нам задана иная область, ограниченная теми же прямыми:
Конечно, в условии сказано, что область замкнута, поэтому показанный рисунок неверен. Но чтобы избегать подобных двусмысленностей, области лучше задавать неравенствами. Нас интересует часть плоскости, расположенная под прямой $y=x+1$? Ок, значит, $y ≤ x+1$. Наша область должна располагаться над прямой $y=0$? Отлично, значит $y ≥ 0$. Кстати, два последних неравенства легко объединяются в одно: $0 ≤ y ≤ x+1$.
$$ \left \{ \begin{aligned} & 0 ≤ y ≤ x+1;\\ & x ≤ 3. \end{aligned} \right. $$
Эти неравенства и задают область $D$, причём задают её однозначно, не допуская никаких двусмысленностей. Но как это поможет нам в том вопросе, что указан в начале примечания? Ещё как поможет:) Нам нужно проверить, принадлежит ли точка $M_1(1;1)$ области $D$. 2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
2-12\cdot(-3)+16\cdot 4=125.
\end{aligned}
На следует выбрать наибольшее и наименьшее значения из тех, что мы получили на первом и втором шагах. Но в данном случае выбор невелик:) Имеем:
$$ z_{min}=-75; \; z_{max}=125. $$
Ответ : $z_{min}=-75; \; z_{max}=125$.
Процесс поиска наименьшего и наибольшего значения функции на отрезке напоминает увлекательный облёт объекта (графика функции) на вертолёте с обстрелом из дальнобойной пушки определённых точек и выбором из этих точек совсем особенных точек для контрольных выстрелов. Точки выбираются определённым образом и по определённым правилам. По каким правилам? Об этом мы далее и поговорим.
Если функция y = f (x )
непрерывна на отрезке [a , b ]
,
то она достигает на этом отрезке наименьшего и наибольшего значений . Это
может произойти либо в точках экстремума , либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции ,
непрерывной на отрезке [a , b ]
, нужно
вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее
и наибольшее.
Пусть, например, требуется определить наибольшее значение функции f (x ) на отрезке [a , b ] . Для этого следует найти все её критические точки, лежащие на [a , b ] .
Критической точкой называется точка, в которой функция определена , а её производная либо равна нулю, либо не существует. Затем следует вычислить значения функции в критических точках. И, наконец, следует сравнить между собой по величине значения функции в критических точках и на концах отрезка (f (a ) и f (b ) ). Наибольшее из этих чисел и будет наибольшим значением функции на отрезке [a , b ] .
Аналогично решаются и задачи на нахождение наименьших значений функции .
Ищем наименьшее и наибольшее значения функции вместе
Пример 1. Найти наименьшее и наибольшее значения функции на отрезке [-1, 2] .
Решение. Находим производную данной функции . Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
Приравняем производную нулю ()
и получим две критические точки: и
. Для нахождения
наименьшего и наибольшего значений функции на заданном отрезке достаточно вычислить её значения на
концах отрезка и в точке ,
так как точка не
принадлежит отрезку [-1, 2]
. Эти значения функции — следующие: ,
,
. Из этого следует, что наименьшее значение функции (на графике ниже обозначено красным), равное -7, достигается на правом конце отрезка — в точке
, а наибольшее (тоже
красное на графике), равно 9,
— в критической точке .
Если функция непрерывна в некотором промежутке и этот промежуток не является отрезком (а является, например, интервалом; разница между интервалом и отрезком: граничные точки интервала не входят в интервал, а граничные точки отрезка входят в отрезок), то среди значений функции может и не быть наименьшего и наибольшего. Так, например, функция, изображённая на рисунке ниже, непрерывна на ]-∞, +∞[ и не имеет наибольшего значения.
Однако для любого промежутка (закрытого, открытого или бесконечного) справедливо
следующее свойство непрерывных функций.
Пример 4. Найти наименьшее и наибольшее значения функции на отрезке [-1, 3] .
Решение. Находим производную данной функции как производную частного:
.
Приравниваем производную нулю, что даёт нам одну критическую точку: . Она принадлежит отрезку [-1, 3] . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Сравниваем эти значения. Вывод: , равного -5/13, в точке и наибольшего значения , равного 1, в точке .
Продолжаем искать наименьшее и наибольшее значения функции вместе
Есть преподаватели, которые по теме нахождения наименьшего и наибольшего значений функции
не дают студентам для решения примеры сложнее только что рассмотренных, то есть таких, в которых функция —
многочлен либо дробь, числитель и знаменатель которой — многочлены. Но мы не ограничимся такими примерами,
поскольку среди преподавателей бывают любители заставить студентов думать по полной (таблице производных). Поэтому в ход пойдут логарифм и тригонометрическая функция.
Поэтому в ход пойдут логарифм и тригонометрическая функция.
Пример 6. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции как производную произведения :
Приравниваем производную нулю, что даёт одну критическую точку: . Она принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Результат всех действий: функция достигает наименьшего значения , равного 0, в точке и в точке и наибольшего значения , равного e ² , в точке .
Пример 7. Найти наименьшее и наибольшее значения функции на отрезке .
Решение. Находим производную данной функции:
Приравниваем производную нулю:
Единственная критическая точку принадлежит отрезку . Для нахождения наименьшего и наибольшего значений функции на заданном отрезке находим её значения на концах отрезка и в найденной критической точке:
Вывод: функция достигает наименьшего значения , равного ,
в точке и наибольшего
значения , равного , в точке
.
В прикладных экстремальных задачах нахождение наименьшего (наибольшего) значений функции, как правило, сводится к нахождению минимума (максимума). Но больший практический интерес имеют не сами минимумы или максимумы, а те значения аргумента, при которых они достигаются. При решении прикладных задач возникает дополнительная трудность — составление функций, описывающих рассматриваемое явление или процесс.
Пример 8. Резервуар ёмкостью 4 , имеющий форму параллелепипеда с квадратным основанием и открытый сверху, нужно вылудить оловом. Каковы должны быть размеры резервуара, чтобы на его покрытие ушло наименьшее количество материала?
Решение. Пусть x — сторона основания, h — высота резервуара, S — площадь его поверхности без крышки, V — его объём. Площадь поверхности резервуара выражается формулой , т.е. является функцией двух переменных . Чтобы выразить S как функцию одной переменной, воспользуемся тем, что , откуда . Подставив найденное выражение h в формулу для S :
Исследуем эту функцию на экстремум. Она определена и дифференцируема всюду в
]0, +∞[
, причём
Она определена и дифференцируема всюду в
]0, +∞[
, причём
.
Приравниваем производную нулю () и находим критическую точку . Кроме того, при производная не существует, но это значение не входит в область определения и поэтому не может быть точкой экстремума. Итак, — единственная критическая точка. Проверим её на наличие экстремума, используя второй достаточный признак. Найдём вторую производную . При вторая производная больше нуля (). Значит, при функция достигает минимума . Поскольку этот минимум — единственный экстремум данной функции, он и является её наименьшим значением . Итак, сторона основания резервуара должна быть равна 2 м, а его высота .
Пример 9. Из пункта A , находящегося на линии железной дороги, в пункт С , отстоящий от неё на расстоянии l , должны переправляться грузы. Стоимость провоза весовой единицы на единицу расстояния по железной дороге равна , а по шоссе она равна . К какой точке М линии железной дороги следует провести шоссе, чтобы транспортировка груза из А в С была наиболее экономичной (участок АВ железной дороги предполагается прямолинейным)?
Наибольшее (наименьшее) значение функции – это самое большое (маленькое) принимаемое значение ординаты на рассматриваемом интервале.
Чтобы найти наибольшее или наименьшее значение функции необходимо:
- Проверить, какие стационарные точки входят в заданный отрезок.
- Вычислить значение функции на концах отрезка и в стационарных точках из п.3
- Выбрать из полученных результатов наибольшее или наименьшее значение.
Чтобы найти точки максимума или минимума необходимо:
- Найти производную функции $f»(х)$
- Найти стационарные точки, решив уравнение $f»(х)=0$
- Разложить производную функции на множители.
- Начертить координатную прямую, расставить на ней стационарные точки и определить знаки производной в полученных интервалах, пользуясь записью п.3.
- Найти точки максимума или минимума по правилу: если в точке производная меняет знак с плюса на минус, то это будет точка максимума (если с минуса на плюс, то это будет точка минимума). На практике удобно использовать изображение стрелок на промежутках: на промежутке, где производная положительна, стрелка рисуется вверх и наоборот.
 2}$
2}$4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции
$f(g(x))′=f′(g(x))∙g′(x)$
$f′(x)=cos′(5x)∙(5x)′= — sin(5x)∙5= -5sin(5x)$
Найдите точку минимума функции $y=2x-ln(x+11)+4$
1. Найдем ОДЗ функции: $х+11>0; х>-11$
2. Найдем производную функции $y»=2-{1}/{x+11}={2x+22-1}/{x+11}={2x+21}/{x+11}$
3. Найдем стационарные точки, приравняв производную к нулю
${2x+21}/{x+11}=0$
Дробь равна нулю если числитель равен нулю, а знаменатель не равен нулю
$2x+21=0; x≠-11$
4. Начертим координатную прямую, расставим на ней стационарные точки и определим знаки производной в полученных интервалах. Для этого подставим в производную любое число из крайней правой области, например, нуль.
$y»(0)={2∙0+21}/{0+11}={21}/{11}>0$
5. В точке минимума производная меняет знак с минуса на плюс, следовательно, точка $-10,5$ — это точка минимума.
Ответ: $-10,5$
Найдите наибольшее значение функции $y=6x^5-90x^3-5$ на отрезке $[-5;1]$
1.
 2=0 ; х-3=0; х+3=0$
2=0 ; х-3=0; х+3=0$$х=0;х=3;х=-3$
3. Выберем стационарные точки, которые принадлежат заданному отрезку $[-5;1]$
Нам подходят стационарные точки $х=0$ и $х=-3$
4. Вычислим значение функции на концах отрезка и в стационарных точках из п.3
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word . Если же задана функция f(x,y) , следовательно, необходимо найти экстремум функции двух переменных . Также можно найти интервалы возрастания и убывания функции .
Правила ввода функций :
Необходимое условие экстремума функции одной переменной
Уравнение f» 0 (x *) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x * первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x с, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f 0 (x) дважды дифференцируемая по x , принадлежащему множеству D . Если в точке x * выполняется условие:
Если в точке x * выполняется условие:F» 0 (x *) = 0
f»» 0 (x *) > 0То точка x * является точкой локального (глобального) минимума функции.
Если в точке x * выполняется условие:
F» 0 (x *) = 0
f»» 0 (x *)То точка x * — локальный (глобальный) максимум.
Пример №1 . Найти наибольшее и наименьшее значения функции: на отрезке .
Решение.
Критическая точка одна x 1 = 2 (f’(x)=0). Эта точка принадлежит отрезку . (Точка x=0 не является критической, так как 0∉).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 / 2 , f(3)=3 8 / 81
Ответ: f min = 5 / 2 при x=2; f max =9 при x=1Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π / 3 +2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x= π / 3 +2πk, k∈Z – точки минимума функции; , значит x=- π / 3 +2πk, k∈Z – точки максимума функции.
Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x 0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.СХОЖИЕ СТАТЬИ
Полезное
Реклама
Новое
Максимальные и минимальные значения — подход к исчислению
10
Поворотные точки графика
МЫ ГОВОРИМ, ЧТО ФУНКЦИЯ f ( x ) имеет относительное максимальное значение x = a ,
, если f ( a ) на больше , чем любое предшествующее или последующее значение.
Мы называем это «относительным» максимумом, потому что другие значения функции на самом деле могут быть больше.
Мы говорим, что функция f ( x ) имеет относительное минимальное значение в x = b ,
, если f ( b ) на меньше , чем любое значение, непосредственно предшествующее или последующее.Опять же, другие значения функции могут быть меньше. С таким пониманием мы откажемся от термина «относительный».
Значение функции, значение y , максимальное или минимальное, называется экстремальным значением.
Теперь, что характеризует график при экстремальном значении?
Касательная к кривой горизонтальна . Мы видим это в точках A и B . Наклон каждой касательной — производная при оценке как a или b — равен 0.
f ‘ ( x ) = 0.
Более того, в точках непосредственно от слева от максимума — в точке C — наклон касательной положительный: f ‘ ( x )> 0.
 В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )Другими словами, максимум f ‘ ( x ) меняет знак с + на -.
Как минимум f ‘ ( x ) меняет знак с — на +. Мы видим, что в точках E и F .
Также можно заметить, что максимум на A график вогнут вниз.(Тема 14 Precalculus.) Хотя как минимум, на B , он вогнутый вверх.
Значение x , при котором функция имеет максимум или минимум, называется критическим значением. На рисунке —
— критические значения: x = a и x = b .
Критические значения определяют точки поворота, в которых касательная параллельна оси x .Критические значения — если таковые имеются — будут решений от до f ‘ ( x ) = 0.
Пример 1. Пусть f ( x ) = x 2 — 6 x + 5.

Есть ли критические значения — какие-то поворотные моменты? Если да, то определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума?
Решение . f ‘ ( x ) = 2 x — 6 = 0 подразумевает x = 3. (Урок 9 алгебры)
x = 3 — единственное критическое значение. Это x — точка поворота. Чтобы определить y -coordinate, оцените f при этом критическом значении — оцените f (3):
f ( x ) = x 2 — 6 x + 5 f (3) = 3 2 — 6 · 3 + 5 = −4. Крайнее значение — 4. Чтобы увидеть, является ли он максимумом или минимумом, в этом случае мы можем просто посмотреть на график.

f ( x ) — парабола, и мы видим, что точка поворота минимальна.
Найдя значение x , где производная равна 0, мы обнаружили, что вершина параболы находится в точке (3, −4).
Но мы не всегда сможем посмотреть на график.Алгебраическим условием минимума является то, что f ‘ ( x ) меняет знак с — на +. Мы видим это в точках E , B , F выше. Величина наклона увеличивается.
Теперь сказать, что наклон увеличивается, значит сказать, что при критическом значении вторая производная (Урок 9), которая представляет собой скорость изменения наклона, равна положительному значению .
Опять же, вот f ( x ):
f ( x ) = x 2 — 6 x + 5. f ‘ ( x ) = 2 x — 6. 
f » ( x ) = 2. f » оценивается при критическом значении 3 — f » (3) = 2 — положительно. Это алгебраически говорит нам, что критическое значение 3 определяет минимум.
Достаточные условия
Теперь мы можем сформулировать эти достаточные условия для экстремальных значений функции при критическом значении a :
Функция имеет минимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = положительное число.Функция имеет максимальное значение x = a , если f ‘ ( a ) = 0
и f’ ‘ ( a ) = отрицательное число.В случае максимума наклон тангенса равен , при уменьшении — он изменяется от положительного к отрицательному. Мы видим, что в точках C , A , D .

Пример 2. Пусть f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3.
Есть ли крайние значения? Во-первых, существуют ли какие-либо критические значения — решения для f ‘ ( x ) = 0 — и определяют ли они максимум или минимум? И каковы координаты на графике этого максимума или минимума? Где поворотные моменты?
Раствор . f ‘ ( x ) = 6 x 2 — 18 x + 12 = 6 ( x 2 — 3 x + 2) = 6 ( x -1) ( x -2) = 0 означает:
x = 1 или x = 2.
(Урок алгебры 37.)
Это критические значения.
 Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.f ‘ ( x ) = 6 x 2 — 18 x + 12. f » ( x ) = 12 х — 18. f » (1) = 12-18 = −6. Вторая производная отрицательна. Таким образом, функция имеет максимум x = 1.
Чтобы найти y -coördinate — экстремальное значение — на этом максимуме мы оцениваем f (1):
f ( x ) = 2 x 3 — 9 x 2 + 12 x -3 f (1) = 2–9 + 12–3 = 2. 
Максимум приходится на точку (1, 2).
Далее, определяет ли x = 2 максимум или минимум?
f ‘ ( x ) = 12 x — 18. f » (2) = 24–18 = 6. Вторая производная положительна.Следовательно, функция имеет минимум x = 2.
Чтобы найти y -coördinate — экстремальное значение — при этом минимуме, мы оцениваем f (2):
f ( x ) = 2 x 3 — 9 x 2 + 12 x — 3. f (2) = 16–36 + 24–3 = 1. 
Минимум находится в точке (2, 1).
Вот собственно график f ( x ):
Решения для f » ( x ) = 0 указывают точку перегиба в этих решениях, а не максимум или минимум. Пример: y = x 3 . y » = 6 x = 0 подразумевает x = 0. Но x = 0 — это точка перегиба на графике y = x 3 , а не максимум или минимум .
Другой пример: y = sin x . Решение y » = 0 — это произведение числа π, которое является точками перегиба.
Задача 1. Найти координаты вершины параболы,
y = x 2 — 8 x + 1.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!y ‘ = 2 x — 8 = 0.

Это подразумевает x = 4. Это x -координата вершины. Чтобы найти y -coordinate, оцените y как x = 4:
.y = 4 2 — 8 · 4 + 1 = −15.
Вершина находится в точке (4, −15).
Задача 2. Проверьте каждую функцию на наличие максимумов и минимумов.
a) y = x 3 — 3 x 2 + 2.
y ‘ = 3 x 2 — 6 x = 3 x ( x -2) = 0 означает
x = 0 или x = 2.
y ‘ ( x ) = 6 x — 6.
у » (0) = −6.
Вторая производная отрицательна. Это означает, что максимальное значение равно x = 0. Это максимальное значение составляет
.y (0) = 2.
Далее,
y ‘ (2) = 12 — 6 = 6.

Вторая производная положительна. Это означает, что существует минимум x = 2.Это минимальное значение —
.y (2) = 2 3 — 3 · 2 2 + 2 = 8-12 + 2 = −2.
б) y = −2 x 3 — 3 x 2 + 12 x + 10.
При x = 1 максимум y = 17.
При x = −2 минимум y = −10.
c) y = 2 x 3 + 3 x 2 + 12 x — 4.
Поскольку f ‘ ( x ) = 0 не имеет реальных решений, нет никаких экстремальных значений.
d) y = 3 x 4 — 4 x 3 — 12 x 2 + 2.
При x = 0 максимальное значение y = 2.
При x = −1 минимум y = −3.
При x = 2 минимум y = −30.

Следующий урок: Применение максимальных и минимальных значений
Содержание | Дом
Сделайте пожертвование, чтобы TheMathPage оставалась в сети.
Даже 1 доллар поможет.Авторские права © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: themathpage @ яндекс.com
Максимум функции
Максимум функции Лори Пирман
EMT 725
Задача: найти максимум f (x) = (1-x) (1 + x) (1 + x).Один из подходов к этой проблеме — построить график функции на графическом калькуляторе. или компьютерный инструмент построения графиков, чтобы получить оценку максимума. Я использовал Algebra Xpresser для построения графика f (x).
Это часть полученного мной графика (показывает интервал от 0 до 1):Из этого графика я могу оценить, что максимальное значение составляет около 1.18. Это максимум происходит, когда x составляет около 0,33.
 Можно продолжать увеличивать «верхнюю часть»
холма »на рисунке, чтобы получить более точные оценки.
Можно продолжать увеличивать «верхнюю часть»
холма »на рисунке, чтобы получить более точные оценки.
Исчисление можно использовать для более точного определения максимума f ‘(x).
Теперь нам нужно установить f ‘(x) = 0, чтобы получить критические значения.
f ‘(x) = (3x-1) (x + 1) = 0Возможен относительный максимум (или минимум), когда x = 1/3 или x = -1.
Теперь мы можем использовать тест первой или второй производной, чтобы определить, где мы иметь относительный максимум.
Примечание: -1 не входит в наш интервал от 0 до 1, но я все равно это проверю.
f » (x) = — 6x-2
Я буду использовать второй производный тест.
f » (-1) — положительное значение. Отсюда следует, что при x = -1 график f (x) вогнута вверх.
Таким образом, f (-1) — относительный минимум.
f » (1/3) — отрицательное значение. Отсюда следует, что при x = 1/3 график вогнутая вниз.
f (1/3) — относительный максимум.В интервале от 0 до 1 есть максимум, который равен f (1/3) = 1.
 185185
185185
Теперь давайте воспользуемся таблицей, чтобы оценить максимум f (x) в интервал от 0 до 1.
По моему графику Algebra Xpresser я мог сказать, что в интервале [0,1], максимум имел место где-то между x = 0,2 и x = 0,5. Ниже представлен разворот таблица листов со значениями x с шагом 0,01, которые находятся в этом интервале.Если мне нужно еще лучшее приближение, я могу посмотреть на меньший интервал, например [0,32,0,34].
(Я могу сказать из предыдущей таблицы, что этот интервал содержит максимум.) Теперь, когда я сузил интервал, содержащий максимум, легче смотреть на даже меньшие приращения,
таким образом получая более точное приближение к максимальному значению. (Видеть под таблицей.)Из этой таблицы видно, что максимум происходит примерно при х = 0,333.
Можно продолжить этот процесс «приближения» по максимуму значение, используя меньшие интервалы и меньшие приращения для каждой новой таблицы. Чем больше раз это будет сделано, тем точнее будет максимальное значение.
 3> или = f (x)
3> или = f (x)
1.185185> or = f (x) с равенством тогда и только тогда, когда (2-2x) = (1 + x).
Максимальное значение f (x) составляет около 1,185, и это происходит, когда x = 1/3.Вернуться к странице 725 EMT Лори
Определить минимальное или максимальное значение квадратичной функции
Пример 6: Определение максимального дохода
Цена единицы товара влияет на его спрос и предложение. То есть, если цена за единицу повышается, спрос на товар обычно снижается.Например, у местной газеты сейчас 84 000 подписчиков при ежеквартальной оплате 30 долларов. Исследование рынка показало, что, если владельцы поднимут цену до 32 долларов, они потеряют 5000 подписчиков. Если предположить, что подписка линейно связана с ценой, какую цену должна взимать газета за ежеквартальную подписку, чтобы максимизировать свой доход?
Решение
Доход — это сумма денег, которую приносит компания. В этом случае доход можно найти, умножив цену за подписку на количество подписчиков или количество.
 Мы можем ввести переменные: p для цены за подписку и Q для количества, что даст нам уравнение [latex] \ text {Revenue} = pQ. [/ Latex]
Мы можем ввести переменные: p для цены за подписку и Q для количества, что даст нам уравнение [latex] \ text {Revenue} = pQ. [/ Latex]Поскольку количество подписчиков меняется в зависимости от цены, нам нужно найти взаимосвязь между переменными. Мы знаем, что в настоящее время [latex] p = 30 [/ latex] и [latex] Q = 84 000. [/ Latex] Мы также знаем, что если цена вырастет до 32 долларов, газета потеряет 5000 подписчиков, что дает вторую пару значений , [латекс] p = 32 [/ латекс] и [латекс] Q = 79 000.[/ latex] Из этого мы можем найти линейное уравнение, связывающее две величины. Уклон
[латекс] \ begin {case} m = \ frac {79 000 — 84 000} {32 — 30} \ hfill \\ \ text {} = \ frac {-5 000} {2} \ hfill \\ \ text {} = -2,500 \ hfill \ end {case} [/ latex]
Это говорит нам о том, что газета потеряет 2500 подписчиков на каждый доллар, на который они поднимут цену. Затем мы можем найти перехват y .
[латекс] \ begin {case} \ text {} Q = -2500p + b \ hfill & \ text {Заменить в точке} Q = 84 000 \ text {и} p = 30 \ hfill \\ 84 000 = -2500 \ left (30 \ right) + b \ hfill & \ text {Решить для} b \ hfill \\ \ text {} b = 159 000 \ hfill & \ hfill \ end {case} [/ latex]
Это дает нам линейное уравнение [latex] Q = -2,500p + 159,000 [/ latex], связывающее стоимость и количество подписчиков.
 {2} + 159 000p \ hfill \ end {case} [/ latex]
{2} + 159 000p \ hfill \ end {case} [/ latex]Теперь у нас есть квадратичная функция дохода как функции платы за подписку. Чтобы найти цену, которая максимизирует доход газеты, мы можем найти вершину.
[латекс] \ begin {case} h = — \ frac {159 000} {2 \ left (-2,500 \ right)} \ hfill \\ \ text {} = 31,8 \ hfill \ end {cases} [/ latex]
Модель говорит нам, что максимальный доход будет достигнут, если газета будет взимать 31,80 доллара за подписку. Чтобы определить максимальный доход, мы оцениваем функцию дохода.{2} +159 000 \ влево (31,8 \ вправо) \ hfill \\ \ text {} = 2,528 100 \ hfill \ end {case} [/ latex]
Используйте график для определения абсолютного максимума и абсолютного минимума
Существует разница между нахождением наивысшей и самой низкой точек на графике в области вокруг открытого интервала (локально) и нахождением наивысшей и самой низкой точек на графике для всего домена. Координаты [latex] y \ text {-} [/ latex] (выходные данные) в наивысшей и самой низкой точках называются абсолютным максимумом и абсолютным минимумом соответственно.
 {3} [/ latex] — одна из таких функций.
{3} [/ latex] — одна из таких функций.Общее примечание: абсолютные максимумы и минимумы
Абсолютный максимум [латекс] f [/ латекс] при [латексе] x = c [/ latex] равен [латексу] f \ left (c \ right) [/ latex], где [латекс] f \ left ( c \ right) \ ge f \ left (x \ right) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].
Абсолютный минимум [латекс] f [/ латекс] при [латексе] x = d [/ latex] равен [латексу] f \ left (d \ right) [/ latex], где [латекс] f \ left ( d \ right) \ le f \ left (x \ right) [/ latex] для всех [latex] x [/ latex] в домене [latex] f [/ latex].
Пример 10: Поиск абсолютных максимумов и минимумов из графика
Для функции [латекс] f [/ латекс], показанной на рисунке 11, найдите все абсолютные максимумы и минимумы.
Рисунок 11
Решение
Посмотрите на график [латекс] f [/ латекс]. График достигает абсолютного максимума в двух местах: [latex] x = -2 [/ latex] и [latex] x = 2 [/ latex], потому что в этих местах график достигает своей наивысшей точки в области определения функции.
 .Абсолютный максимум — это координата y при [латекс] x = -2 [/ латекс] и [латекс] x = 2 [/ латекс], то есть [латекс] 16 [/ латекс].
.Абсолютный максимум — это координата y при [латекс] x = -2 [/ латекс] и [латекс] x = 2 [/ латекс], то есть [латекс] 16 [/ латекс].График достигает абсолютного минимума при [latex] x = 3 [/ latex], потому что это самая низкая точка области определения графика функции. Абсолютный минимум — координата y при [latex] x = 3 [/ latex], которая равна [latex] -10 [/ latex].
Нахождение максимумов и минимумов с использованием производных
Где функция в верхней или нижней точке? Исчисление может помочь!
Максимум — это высокая точка, а минимум — это низкая точка:
В плавно меняющейся функции максимум или минимум всегда там, где функция выравнивает (за исключением седловой точки ).
Где он расплющивается? Где наклон равен нулю .
Где нулевой наклон? Производная говорит нам!
Давайте сразу рассмотрим пример:
Пример: в воздух подброшен мяч.
 Его высота в любой момент времени t определяется выражением:
Его высота в любой момент времени t определяется выражением:ч = 3 + 14т — 5т 2
Какая у него максимальная высота?
Используя производные, мы можем найти наклон этой функции:
h = 0 + 14-5 (2т)
= 14-10т(См. Ниже этот пример, чтобы узнать, как мы нашли эту производную.)
Теперь найдите, когда наклон равен нулю :
14–10 т = 0
10 т = 14
t = 14/10 = 1,4
Наклон равен нулю при t = 1,4 секунды
А высота на тот момент:
h = 3 + 14 × 1,4 — 5 × 1,4 2
ч = 3 + 19,6 — 9,8 = 12,8
А так:
Максимальная высота 12.8 м (при t = 1,4 с)
Краткое руководство по производным инструментам
Производная определяет наклон функции.
В предыдущем примере мы взяли это:
ч = 3 + 14т — 5т 2
и придумал эту производную:
h = 0 + 14-5 (2т)
= 14-10т, который сообщает нам наклон функции в любое время t
Мы использовали эти производные правила:
- Наклон значения константы (например, 3) равен 0
- Наклон линии , такой как 2x, равен 2, поэтому 14t имеет наклон 14
- Квадрат Функция, такая как t 2 , имеет наклон 2t, поэтому 5t 2 имеет наклон 5 (2t)
- А потом сложили: 0 + 14 — 5 (2t)
Как узнать, что это максимум (или минимум)?
Мы видели это на графике! Но иначе.
 .. деривативы снова приходят на помощь.
.. деривативы снова приходят на помощь.Возьмем производную от наклона (вторая производная исходной функции):
Производная от 14 до 10t равна −10
Это означает, что наклон постоянно уменьшается (-10): при движении слева направо наклон сначала положительный (функция возрастает), проходит через ноль (плоская точка), а затем наклон становится отрицательным (функция падает). :
Уклон, который становится меньше (и идет через 0), означает максимум.Это называется тестом второй производной
На графике выше я показал наклон до и после, но на практике мы проводим тест в точке, где наклон равен нулю :
Тест второй производной
Когда наклон функции равен нулю при x , а вторая производная при x равна:
- меньше 0, это локальный максимум
- больше 0, это местный минимум
- равно 0, тогда тест не пройден (хотя могут быть и другие способы выяснить)
«Вторая производная: меньше 0 — максимум, больше 0 — минимум»
Пример: найти максимумы и минимумы для:
y = 5x 3 + 2x 2 — 3x
Производная (наклон):
y = 15x 2 + 4x — 3
Квадратичный с нулями в:
Могут ли они быть максимальными или минимальными? (Не смотрите пока на график!)
Вторая производная равна y » = 30x + 4
При x = −3/5:
у » = 30 (−3/5) + 4 = −14
меньше 0, поэтому −3/5 — это локальный максимум
При x = +1/3:
г ‘= 30 (+1/3) + 4 = +14
больше 0, поэтому +1/3 — это локальный минимум
(Теперь вы можете посмотреть на график.
 )
)слов
Высшая точка называется максимумом (множественное число максимумов ).
Нижняя точка называется минимумом (множественное число: минимум ).
Общее слово для максимума или минимума — экстремум (множественное число экстремум ).
Мы говорим локальный максимум (или минимум), когда могут быть более высокие (или более низкие) точки в другом месте, но не поблизости.
Еще один пример
Пример: найти максимумы и минимумы для:
y = x 3 — 6x 2 + 12x — 5
Производная:
y = 3x 2 — 12x + 12
Которая квадратична только с одним нулем при x = 2
Это максимум или минимум?
Вторая производная равна y » = 6x — 12
При x = 2:
у » = 6 (2) — 12 = 0
это 0, поэтому тест не пройден
И вот почему:
Это седловина .
 .. наклон действительно становится нулевым, но он не является ни максимальным, ни минимальным.
.. наклон действительно становится нулевым, но он не является ни максимальным, ни минимальным.Должен быть дифференцируемым
И еще важный технический момент:
Функция должна быть дифференцируемой (производная должна существовать в каждой точке своего домена).
Пример: Как насчет функции f (x) = | x | (абсолютная величина) ?
| x | выглядит так: При x = 0 происходит очень резкое изменение!
Фактически, он не дифференцируется там (как показано на дифференцируемой странице).
Итак, мы не можем использовать этот метод для функции абсолютного значения.
Функция также должна быть непрерывной, но любая дифференцируемая функция также является непрерывной, поэтому об этом не нужно беспокоиться.
Наибольшая целочисленная функция и график
Краткий обзор
- Функция наибольшего целого числа также известна как функция пола.

- Он записывается как $$ f (x) = \ lfloor x \ rfloor $$.
- Значение $$ \ lfloor x \ rfloor $$ — это наибольшее целое число, которое на меньше или , равное $$ x $$.
Определение
Наибольшая целочисленная функция определяется как
$$ \ lfloor x \ rfloor = \ mbox {наибольшее целое число} $$ меньше или равно $$ x $$.
В математических обозначениях мы бы записали это как
$$ \ lfloor x \ rfloor = \ max \ {m \ in \ mathbb {Z} | m \ leq x \} $$
Запись «$$ m \ in \ mathbb {Z} $$» означает «$$ m $$ — целое число».
Примеры
Пример 1 — Основные вычисления
Оцените следующее.

- $$ \ lfloor 2.7 \ rfloor $$
- $$ \ lfloor -1,4 \ rfloor $$
- $$ \ lfloor 8 \ rfloor $$
Если мы рассмотрим числовую строку с целыми числами и 2,7, нанесенными на нее, мы увидим
Наибольшее целое число, которое на меньше 2.7 равно 2. Итак, $$ \ lfloor 2.7 \ rfloor = 2 $$.
Если мы рассмотрим числовую строку с целыми числами и нанесенными на нее -1,3, мы увидим
Поскольку наибольшее целое число, которое на меньше -1,3, равно -2, $$ \ lfloor -1,3 \ rfloor = -2 $$.
Поскольку $$ \ lfloor x \ rfloor = $$ наибольшее целое число, которое меньше или равно $$ x $$, мы знаем, что $$ \ lfloor 8 \ rfloor = 8 $$.

Построение графика наибольшей целочисленной функции
Чтобы понять поведение этой функции в терминах графика, давайте построим таблицу значений.
ТАБЛИЦА$$ \ begin {array} {| c | c |} \ hline x & \ lfloor x \ rfloor \\ \ hline -1.5 & -2 \\ -1,25 & -2 \\ -1 & -1 \\ -0,75 & -1 \\ -0,5 & -1 \\ -0,25 и -1 \\ 0 & 0 \\ 0,25 & 0 \\ 0,5 & 0 \\ 0,75 & 0 \\ 1 и 1 \\ 1,25 и 1 \\ 1.5 и 1 \\ \ hline \ end {массив} $$
Таблица показывает нам, что функция увеличивается до следующего наибольшего целого числа каждый раз, когда значение x становится целым числом.
Отвечать Это приводит к следующему графику.
Это приводит к следующему графику.Пример 2
Нарисуйте график $$ y = \ left \ lfloor \ frac 1 2x \ right \ rfloor $$.
РешениеМы знаем, как должен выглядеть базовый график, поэтому нам просто нужно понять, как фактор $$ \ frac 1 2 $$ повлияет на вещи. Мы можем сделать это двумя способами: мы можем составить таблицу значений или можем интерпретировать это как преобразование.
ТАБЛИЦА
$$ \ begin {align *} \ begin {array} {| c | c | c |} \ hline x & \ frac 1 2 x & \ left \ lfloor \ frac 1 2 x \ right \ rfloor \\ [6pt] \ hline -2 и -1.5 & -2 \\ [6pt] -1,5 и -0,75 и -1 \\ [6pt] -1 & -0,5 & -1 \\ [6pt] -0,5 и -0,25 и -1 \\ [6pt] 0 & 0 & 0 \\ [6pt] 0,5 и 0,25 и 0 \\ [6pt] 1 & 0,5 & 0 \\ [6pt] 1,5 и 0,75 и 0 \\ [6pt] 2 и 1 и 1 \\ [6pt] \ hline \ end {массив} \ end {выровнять *} $$
Мы замечаем из таблицы, что значения функции переходят к следующему значению, когда $$ x $$ четно.

ПРЕОБРАЗОВАНИЕ
Мы можем интерпретировать $$ y = \ left \ lfloor \ frac 1 2 x \ right \ rfloor $$ как горизонтальный участок, который удваивает длину каждой части.
Отвечать:Решение уравнений
Существует формула, которая может помочь нам при работе с уравнениями, включающими функцию пола.
$$ \ lfloor x \ rfloor = m \ qquad \ mbox {тогда и только тогда, когда} \ quad m \ leq x
(помните, $$ m $$ — целое число!)
Так, например, $$ \ lfloor x \ rfloor = 8 $$ тогда и только тогда, когда $$ 8 \ leq x
Пример 3
Решите уравнение $$ \ lfloor 2x + 5 \ rfloor = 9 $$.
Шаг 1
Перепишем уравнение, используя неравенство.
$$ 9 \ leq 2x + 5 Шаг 2
Решите неравенство.
$$ \ begin {align *} 9 & \ leq 2x + 5 Отвечать:
В интервальной записи уравнение верно для $$ x \ в [2, 2.5) $$.
Пример 4
Решите уравнение $$ \ lfloor 1.25 + \ lfloor x \ rfloor \ rfloor = 12 $$.
Шаг 1Замените $$ \ lfloor x \ rfloor $$ на $$ u $$. Это называется «заменой переменной», и это облегчает работу с уравнением.
$$ \ begin {align *} \ lfloor 1.
Шаг 2 25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
\ lfloor 1,25 + u \ rfloor & = 12
\ end {выровнять *}
$$
25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
\ lfloor 1,25 + u \ rfloor & = 12
\ end {выровнять *}
$$Заменить уравнение одним из неравенств, где $$ m = 12 $$
$$ 12 \ leq 1.25 + u Шаг 3Решите неравенство.
$$ \ begin {align *} 12 & \ leq 1.25 + u
Поскольку $$ \ lfloor x \ rfloor $$ является целым числом, единственный способ удовлетворить приведенные выше неравенства — $$ \ lfloor x \ rfloor = 11 $$.
Шаг 4Определите значение $$ x $$.
Опять же, используя неравенства, мы знаем
$$ 11 \ leq x Отвечать:
$$ 11 \ leq x
Продолжить практические задачиОшибка: Нажмите «Не робот», затем повторите попытку.
 2f (x) = x2 и g (x) = x + 2g (x) = x + 2g (x) = x + 2.2 — (х + 2) |} {2}.
min (x2, x + 2) = 2×2 + (x + 2) −∣x2− (x + 2) ∣. График выглядит так:
2f (x) = x2 и g (x) = x + 2g (x) = x + 2g (x) = x + 2.2 — (х + 2) |} {2}.
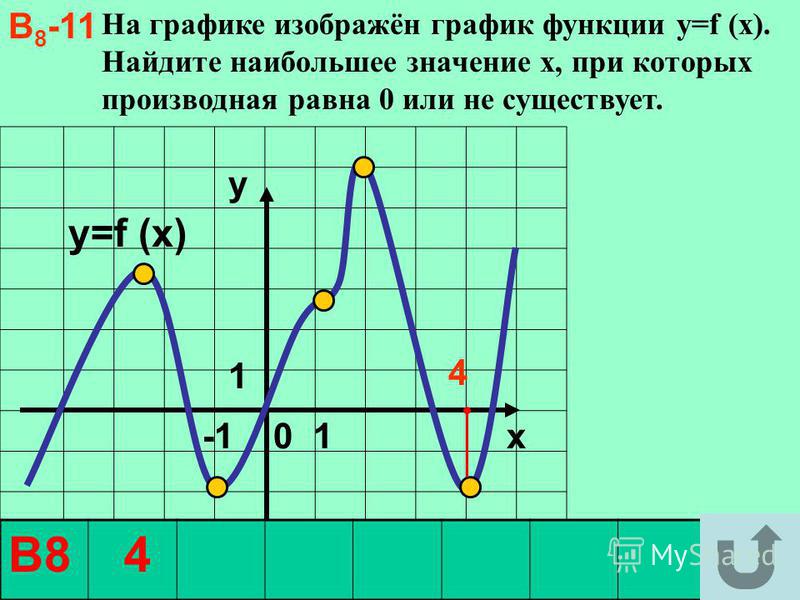
min (x2, x + 2) = 2×2 + (x + 2) −∣x2− (x + 2) ∣. График выглядит так: - Как видите, он принимает форму f (x) f (x) f (x) (параболы), когда f (x) f (x) f (x ) меньше, а g (x) g (x) g (x) (линейная часть), когда g (x) g (x) g (x) меньше.
- Эту аккуратную формулу можно объяснить, разделив дробь для выражения вверх: min (f (x), g (x)) = f (x) + g (x) −∣f (x) −g ( х) ∣2 = f (x) + g (x) 2 − ∣f (x) −g (x) ∣2 \ begin {выровнено} \ мин (е (х), \ г (х)) & = \ гидроразрыва {f (x) + g (x) — | f (x) — g (x) |} {2} \\ & = \ гидроразрыв {f (x) + g (x)} {2} — \ frac {| f (x) — g (x) |} {2} \ end {выровнен} min (f (x), g (x)) = 2f (x) + g (x) −f (x) −g (x) ∣ = 2f (x) + g (x) −2∣ f (x) −g (x) ∣
- Здесь первое слагаемое f (x) + g (x) 2 \ frac {f (x) + g (x)} {2} 2f (x) + g (x) — среднее значение двух функций; графически это находится посередине между двумя функциями.Второй член ∣f (x) −g (x) ∣2 \ frac {| f (x) — g (x) |} {2} 2∣f (x) −g (x) ∣ равен половине абсолютного значения между двумя функциями; графически это половина расстояния между двумя функциями.

 2}$
2}$ 2=0 ; х-3=0; х+3=0$
2=0 ; х-3=0; х+3=0$ Если в точке x * выполняется условие:
Если в точке x * выполняется условие:

 В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )
В то время как в точках непосредственно к справа — в точке D — наклон отрицательный: f ‘ ( x )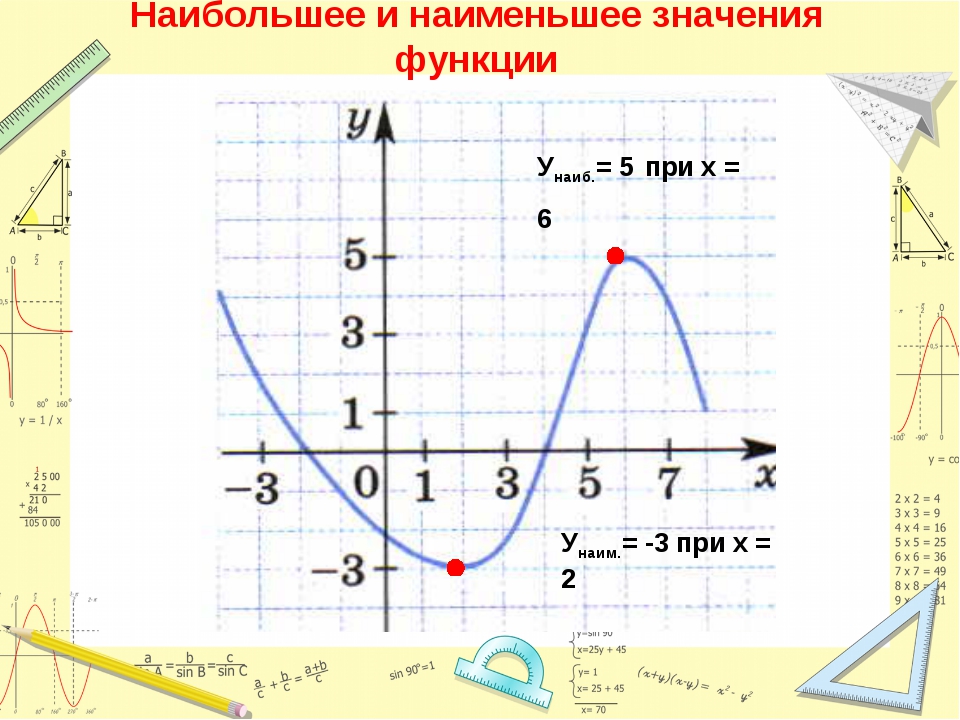



 Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.
Каждый определяет максимум или минимум? Чтобы ответить, мы должны оценить вторую производную для каждого значения.



 Можно продолжать увеличивать «верхнюю часть»
холма »на рисунке, чтобы получить более точные оценки.
Можно продолжать увеличивать «верхнюю часть»
холма »на рисунке, чтобы получить более точные оценки.  185185
185185  3> или = f (x)
3> или = f (x)  Мы можем ввести переменные: p для цены за подписку и Q для количества, что даст нам уравнение [latex] \ text {Revenue} = pQ. [/ Latex]
Мы можем ввести переменные: p для цены за подписку и Q для количества, что даст нам уравнение [latex] \ text {Revenue} = pQ. [/ Latex] {2} + 159 000p \ hfill \ end {case} [/ latex]
{2} + 159 000p \ hfill \ end {case} [/ latex] {3} [/ latex] — одна из таких функций.
{3} [/ latex] — одна из таких функций. .Абсолютный максимум — это координата y при [латекс] x = -2 [/ латекс] и [латекс] x = 2 [/ латекс], то есть [латекс] 16 [/ латекс].
.Абсолютный максимум — это координата y при [латекс] x = -2 [/ латекс] и [латекс] x = 2 [/ латекс], то есть [латекс] 16 [/ латекс]. Его высота в любой момент времени t определяется выражением:
Его высота в любой момент времени t определяется выражением: .. деривативы снова приходят на помощь.
.. деривативы снова приходят на помощь. )
) .. наклон действительно становится нулевым, но он не является ни максимальным, ни минимальным.
.. наклон действительно становится нулевым, но он не является ни максимальным, ни минимальным.


 Это приводит к следующему графику.
Это приводит к следующему графику.

 25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
\ lfloor 1,25 + u \ rfloor & = 12
\ end {выровнять *}
$$
25 + \ lfloor x \ rfloor \ rfloor & = 12 \\ [6pt]
\ lfloor 1,25 + u \ rfloor & = 12
\ end {выровнять *}
$$ 2f (x) = x2 и g (x) = x + 2g (x) = x + 2g (x) = x + 2.2 — (х + 2) |} {2}.
min (x2, x + 2) = 2×2 + (x + 2) −∣x2− (x + 2) ∣. График выглядит так:
2f (x) = x2 и g (x) = x + 2g (x) = x + 2g (x) = x + 2.2 — (х + 2) |} {2}.
min (x2, x + 2) = 2×2 + (x + 2) −∣x2− (x + 2) ∣. График выглядит так: