Как вычислить квадратный корень числа в Excel —
Микрофост Эксель это чрезвычайно мощный инструмент, который можно использовать для решения сложных расчетов. Однако многие случайные пользователи используют Excel только для базовых потребностей в табулировании, не используя его для выполнения даже самых простых математических операций. Но есть ситуации, когда вы вынуждены делать вычисления в Excel, чтобы ускорить процесс. Один из наиболее распространенных расчетов, которые пользователи Excel должны сделать, это выяснение квадратного корня числа.
Имея это в виду, мы создали статью с пятью различными методами, которые помогут вам вычислить квадратный корень из числа в Excel. Все они приведут к одному и тому же результату, но некоторые из них легче, чем другие. Приведенные ниже методы упорядочены по сложности, поэтому попробуйте придерживаться первых трех методов, если вы не заядлый пользователь Excel.
Давай начнем!
Метод 1: Расчет квадратного корня с использованием функции SQRTИспользование функции SQRT — один из самых простых способов узнать квадратный корень числа.
Синтаксис для этого метода есть:
SQRT (число)
Заметка: число является заполнителем для фактического номера или для ссылки на ячейку, которая содержит номер.
пример
Для простоты, скажем, мы хотим узнать квадратный корень из числа 9 (расположен на A2). Чтобы сделать это с помощью функции SQRT, все, что нам нужно сделать, это вставить следующую формулу в ячейку результата (БИ 2): ‘= SQRT (А2)».
Использование функции SQRTЗамечания: Имейте в виду, что мы могли бы также использовать номер напрямую, вместо ссылки на ячейку — = SQRT (9)
Тем не менее, есть одна небольшая проблема в использовании функции SQRT напрямую — если вы попытаетесь передать отрицательное число, он покажет #NUM! ошибка вместо фактического результата.
Избежать #NUM! При ошибках при использовании функции SQRT рекомендуется использовать функцию ABS вместе с функцией SQRT. Функция ABS конвертирует число в абсолютное число. В нашем случае он преобразует отрицательные числа в положительные числа. Вот пример:
Пример с использованием функции ABSМетод 2: Расчет квадратного корня с использованием функции PowerИспользование функции POWER — это еще один способ вычисления квадратного корня числа в Excel. Тем не менее, он работает немного по-другому по сравнению с функцией SQRT. Используя функцию POWER, мы можем найти квадратный корень определенного числа, увеличив число до N-й степени.
Вот синтаксис для метода:
МОЩНОСТЬ (число, мощность)
Замечания: число является заполнителем для фактического номера или ссылки на ячейку, в то время как мощность это показатель, чтобы поднять число до этой степени.
Учитывая тот факт, что мы хотим найти квадратный корень числа, мы можем использовать атрибут power как «1/2». В этом случае формула становится МОЩНОСТЬ (число 1/2).
примерДля простоты давайте снова предположим, что нам нужно найти квадратный корень числа ячейки A2 (в нашем случае это 9). Чтобы сделать это, мы можем использовать аргумент власти как 1/2 в полученной ячейке (B2).
Пример использования функции Power для поиска квадратного корняМетод 3: Использование оператора экспоненты, чтобы найти квадратный корень числаМногие опытные пользователи Excel считают этот метод самым простым способом найти квадратный корень числа. Мы решили поставить его на 3-е место, так как это не так часто. Это подразумевает использование оператора экспоненты, чтобы получить нам результат.
Оператор экспоненты позволит нам поднять число до любой степени. Подобно методу 2, мы можем использовать (1/2) в качестве показателя степени, чтобы получить число квадратного корня в результирующей ячейке. (1/2) в ячейке результата даст нам число квадратного корня.
(1/2) в ячейке результата даст нам число квадратного корня.
Этот метод немного продвинут, поэтому, если вы не знакомы со сценариями VBA, попробуйте придерживаться первых трех методов. Четвертый способ найти квадратный корень числа — использовать коды VBA.
Для решения этого конкретного сценария есть два разных кода, которые вы можете использовать для возврата квадратного корня из числа. Продолжайте читать ниже для кодов, а также инструкции о том, как обеспечить их соблюдение.
Всякий раз, когда вы запустите этот код VBA, он проверит значение выбранной ячейки. Если это значение является числом, оно непосредственно вычислит квадратный корень этого числа и покажет его в окне сообщения.
Но имейте в виду, что этот код будет работать только до тех пор, пока вы не выберете более одной ячейки
Код:
Sub getSquareRoot () Dim Rng As Range Dim sqr As Long Если Application.Как вставить и запустить код VBA в Excel(1/2) MsgBox "Квадратный Корень" кв " является " sqr, vbOKOnly, "Квадратное корневое значение" еще MsgBox "Пожалуйста, введите номер.", VbOKOnly, "Ошибка" End If End Sub
Если вы решите использовать код VBA, вы можете выбрать один из двух приведенных выше вариантов — выбрать тот, который имеет больше смысла для всего, что вы пытаетесь сделать.
Но чтобы использовать этот код, вам нужно знать, как его вставить и запустить. Вот краткое руководство по всему на случай, если вам понадобится дальнейшее руководство:
- Откройте таблицу, к которой вы хотите применить код VBA, и нажмите Alt + F11 открыть Visual Basic Editor (VBE).
- Как только вы находитесь внутри Visual Basic Editor, щелкните правой кнопкой мыши таблицу, на которую вы нацеливаетесь, и выберите Вставить> Модуль (используя контекстное меню).
Вставка кода VBA - После того, как код был вставлен.
 Нажмите Ctrl + S сохранить изменения. Затем выберите местоположение для вашего измененного документа Excel и нажмите Сохранить кнопка.
Нажмите Ctrl + S сохранить изменения. Затем выберите местоположение для вашего измененного документа Excel и нажмите Сохранить кнопка.
Сохранение измененного документа Excel - Если вам будет предложено не сохранить проект VB как книгу без макросов, нажмите нет по подсказке.
Выбор типа файла с поддержкой макросов - Под Сохранить как тип, установите тип файла Книга с поддержкой макросов Excel.
Задание типа файла в качестве книги Excel с поддержкой макросов - После сохранения кода нажмите Alt + Q, чтобы закрыть редактор VBA и вернуться к своей книге.
- Теперь, чтобы открыть ранее созданный код VBA, нажмите Alt + F8 открыть макрос Диалог. Как только вы попадете туда, выберите макрос, который вы хотите запустить, и нажмите Бежать кнопка.
Выполнение кода VBA, который мы ранее создали - Через некоторое время вы увидите результат вашего кода VBA.

Результат кода VBA 1
Это самый продвинутый метод из множества, но у этой стратегии есть огромное преимущество — она позволяет конвертировать несколько чисел в их квадратные корни.
Создание мощного запроса, способного сделать это, немного трудоемко, но сэкономит вам много времени, если у вас много чисел, которые нужно преобразовать в квадратные корни.
Другое большое преимущество этого мощного запроса состоит в том, что вы получите динамический метод — это означает, что каждый раз, когда вы вводите новое значение в таблицу, он автоматически возвращает квадратный корень из этого числа.
Если вы решили создать мощный запрос, способный сделать это, следуйте инструкциям ниже:
- Сначала выберите любую ячейку в таблице и перейдите на ленту вверху, чтобы выбрать Данные> Получить Преобразовать данные, затем нажмите на Из таблицы.

Выбрав любую ячейку, перейдите к данным и нажмите «Из таблицы / диапазона» (в разделе «Получить»). Преобразовать данные) - Как только вы нажмете на это, Excel откроет мощный редактор запросов, который включает вашу таблицу. Нажмите Хорошо чтобы подтвердить создание вашей таблицы.
Создание таблицы из ваших чисел - В редакторе Power Query перейдите на ленту вверху и нажмите на Добавить столбец Вкладка. Затем нажмите на Пользовательский столбец.
Перейти к Добавить столбец и нажмите на Пользовательский столбец - Это откроет новое окно Custom Column. Как только вы попадете туда, введите Квадратный корень под Имя новой колонки. Затем перейдите вниз и вставьте следующую формулу в поле формулы столбца «Пользовательский»:
= Number.Sqrt ([Числа])
Квадратная формула для Power Query - Нажмите Хорошо подтвердить создание этого нового пользовательского столбца.
 Вы заметите, что таблица только что получила дополнительный столбец с квадратными корнями чисел, которые у нее были ранее.
Вы заметите, что таблица только что получила дополнительный столбец с квадратными корнями чисел, которые у нее были ранее.
Конечный результат запроса POWER квадратного корня
Квадратный корень из 3;2;5 — Квадратный Корень
Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3.
Его приблизительным значением с 69 цифрами после запятой является:
Округленное значение 1.732 является правильным с точностью до 0,01 %. Приблизительной правильной дробью является (1,7321 42857…).
Квадратный корень из 3 является иррациональным числом. Также известен как Феодоровская постоянная, названная в честь Феодора Киренского.
Может быть выражен в виде непрерывной дроби [1; 1, 2, 1, 2, 1, 2, …].
Геометрия
Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.Если равносторонний треугольник со сторонами длиной 1 делится на две равные половины, пересечением внутреннего угла для составления прямого угла с одной стороной, то получившийся прямоугольный треугольник имеет гипотенузу со стороной 1 и катеты длиной 1/2 и Поэтому тангенс 60° равен
Так же, это расстояние между параллельными сторонами правильного шестиугольника со сторонами 1.
является длиной диагонали куба со стороной 1.
Использование в других областях
Энергетика
При трехфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в больше модуля фазного напряжения
Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:
- 1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…
Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).
Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1. Квадратный корень из 2.Хорошим и часто используемым приближением к является дробь . Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.
Несмотря на то, что числитель и знаменатель дроби лишь двузначные
целые, оно отличается от реального значения меньше, чем на 1/10000.
История
Вавилонская глиняная табличка с примечаниями.Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:
Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:
Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.
Алгоритмы вычисления
Существует множество алгоритмов для вычисления значения квадратного
корня из двух. В результате алгоритма получается приблизительное
значение в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней. Он состоит в следующем:
Самый популярный алгоритм для этого, который используется во многих
компьютерах и калькуляторах, это вавилонский метод вычисления квадратных
корней. Он состоит в следующем:
Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:
- 3/2 = 1.5
- 17/12 = 1.416…
- 577/408 = 1.414215…
- 665857/470832 = 1.4142135623746…
В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.
Свойства квадратного корня из двух
Половина √2 приблизительно равна 0. 70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:
Одно из интересных свойств √2 состоит в следующем:
- .Потому что
Это является результатом свойства серебряного сечения.
Другое интересное свойство √2:
Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:
- и
Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.
Квадратный корень из двух может быть также использован для приближения :
С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.
Доказательство иррациональности
Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:
- .
Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда
Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.
Непрерывная дробь
Квадратный корень из двух может быть представлен в виде непрерывной дроби:
Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:
Квадрат последней приведенной дроби равен (округлённо) 2,000000177.
Размер бумаги
Квадратный корень из двух является пропорцией формата бумаги ISO 216. Соотношение сторон таково, что при разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции.
Квадратный корень из числа 5 — положительное действительное число, которое при умножении само на себя даёт число 5. Это иррациональное и алгебраическое число.[1]
Его приблизительное значение с 59 цифрами после запятой является:
Округлённое значение 2.236 является правильным с точностью до 0,01 %. Компьютерная вычисленная точность составляет не менее 1 000 000 знаков.[2]
Может быть выражено в виде непрерывной дроби [2; 4, 4, 4, 4, 4, 4, …], последовательно это дроби:
Вавилонский метод
Вычисление корня из 5, начиная с r0 = 2, где rn+1 = (rn + 5/rn) / 2:
Золотое сечение
√5/2 — диагональ половины квадрата, представляет собой геометрическое представление о золотом сечении.
Золотое сечение φ — среднее арифметическое 1 и корня из 5.[3]
() алгебраически можно выразить так:
Числа Фибоначчи могут быть выражены через корень из 5 так:
Отношение √5 к φ и наоборот дают интересные зависимости непрерывных дробей с числами Фибоначчи и числами Люка:[4]
Алгебра
Кольцо содержит числа вида , где a и b целые числа и мнимое число . Это кольцо является примером области целостности, не являющейся факториальным кольцом.
Число 6 представляется в данном кольце двумя способами:
Поле — абелево расширение рациональных чисел.
Теорема Кронекера — Вебера утверждает, что корень из 5 можно выразить линейной комбинацией корней из единицы:
Тождества Рамануджана
Корень из 5 появляется во множестве тождеств Рамануджана с непрерывными дробями. [5][6]
[5][6]
Например, случай непрерывных дробей Роджерса-Рамануджана:
Арифметический квадратный корень
Если а больше или равно 0 и n – натуральное число, которое больше 1, то будет существовать только лишь одно, неотрицательно число х, при котором выполняется равенство . Именно это число х и называется арифметическим квадратным корнем n-ой степени из неотрицательного числа а. Число а называют подкоренным числом, а n – показателем корня . Если n = 2, то показатель корня обычно опускают и называют такое выражение арифметическим квадратным корнем. Стоит отметить, что довольно-таки часто вместо слова «корень» употребляют слово «радикал».
А теперь давайте рассмотрим, как можно извлечь квадратный корень из натурального числа.
Например, нам необходимо извлечь корень из натурального числа к, причем нам точно, известно, что корень извлекается. Чтобы сделать это довольно удобным способом, следует воспользоваться следующими правилами:
- Разбить число к на грани (начинать с последней цифры и справа налево) и включить в каждую грань по две рядом стоящие цифры.
 При этом стоит обратить внимание, что если к состоит из четного числа цифр, то в первой левой грани будет 2 цифры, если же число цифр в к нечетное, то в первой левой грани будет 1 цифра. Количество наших граней показывает количество цифр результата. На первый взгляд все просто и понятно.
При этом стоит обратить внимание, что если к состоит из четного числа цифр, то в первой левой грани будет 2 цифры, если же число цифр в к нечетное, то в первой левой грани будет 1 цифра. Количество наших граней показывает количество цифр результата. На первый взгляд все просто и понятно. - Далее нам необходимо подобрать наибольшую цифру, но такую, чтобы ее квадрат не превосходил числа, которое находится в первой грани. Эта цифра и будет первой цифрой результата.
- Полученную первую цифру результата возводим в квадрат и вычитаем полученное из первой грани число, а затем припишем к найденной разности справа вторую грань. У нас выйдет какое-то число А. Удваиваем часть результата, которую имеем и получаем число а. Теперь следует подобрать такую наибольшую цифру х, чтобы произведение числа ах на х не было больше числа А. Цифра х – вторая цифра результата.
- Следующий шаг практически повторяет весь третий пункт. Продолжать находить следует до тех пор, пока не используется последняя грань.
 (1/2)
(1/2)Вычислить квадратный корень без калькулятора
Вы здесь: Главная → Статьи → Алгоритм извлечения квадратного корняБольшинство людей в современном мире считают, что, поскольку калькуляторы могут находить квадратные корни, детям не нужно учиться находить квадратные корни, используя какой-либо метод карандаша и бумаги. Однако изучение, по крайней мере, метода «угадай и проверь» для нахождения квадратного корня на самом деле поможет студентам ПОНИМАТЬ и запомнить саму концепцию квадратного корня!
Итак, даже если в вашем учебнике по математике тема нахождения квадратного корня без калькулятора может полностью отсутствовать, подумайте о том, чтобы позволить студентам изучить и практиковать хотя бы метод «угадать и проверить».Поскольку на самом деле он имеет дело с КОНЦЕПЦИЕЙ квадратного корня, я бы счел его необходимым для обучения студентов.
В зависимости от ситуации и учащихся, метод «угадай и проверь» можно выполнить либо с помощью простого калькулятора, не имеющего кнопки квадратного корня, либо с помощью вычислений с использованием бумаги и карандаша.

Нахождение квадратного корня методом угадывания и проверки
Чтобы найти десятичное приближение, скажем, к √2, сначала сделайте первоначальное предположение, затем возведите его в квадрат и, в зависимости от того, насколько близко вы подошли, улучшите свое предположение.Поскольку этот метод включает возведение в квадрат предположения (умножение самого числа на само число), он использует фактическое определение квадратного корня , и поэтому может быть очень полезным при обучении концепции квадратного корня.
Пример: что такое квадратный корень из 20?
Вы можете начать с того, что заметите, что, поскольку √16 = 4 и √25 = 5, то √20 должно быть между 4 и 5.
Тогда угадайте √20; скажем, например, что это 4.5. Возведите это в квадрат, посмотрите, будет ли результат больше или меньше 20, и улучшите свое предположение на основе этого.Повторяйте этот процесс, пока не получите желаемую точность (количество десятичных знаков).
 Это так просто и может стать отличным экспериментом для студентов!
Это так просто и может стать отличным экспериментом для студентов!Пример: найти √6 до 4 знаков после запятой
Поскольку 2 2 = 4 и 3 2 = 9, мы знаем, что √6 находится между 2 и 3. Давайте предположим (или оценим), что оно равно 2,5. В квадрате получаем 2,5 2 = 6,25. Это слишком много, поэтому мы немного уменьшаем нашу оценку. Давайте попробуем 2.4 дальше. Чтобы найти квадратный корень из 6 до четырех десятичных знаков, нам нужно повторять этот процесс, пока у нас не будет пяти десятичных знаков, а затем мы округлим результат.
Оценка Площадь оценки Высокая / низкая 2,4 5,76 Слишком низкая 2,45 6,0025 Слишком высокая, но очень близкая 2,449 5,997601 Слишком мало 2.  4495
44956,00005025 Слишком много, поэтому квадратный корень из 6 должен быть между 2.449 и 2.4495. 2.4493 5.99 9 Слишком низко 2.4494 5.99956036 Слишком мало, поэтому квадратный корень из 6 должен находиться между 2,4494 и 2,4495 2,44945 5.9998053025oo поэтому квадратный корень из 6 должен находиться в диапазоне от 2,44945 до 2,4495. Этого достаточно итераций, поскольку теперь мы знаем, что √6 будет округлено до 2,4495 (а не до 2,4494).
Нахождение квадратных корней с помощью алгоритма
Существует также алгоритм вычисления квадратного корня, напоминающий алгоритм деления в столбик, и его изучали в школах за несколько дней до появления калькуляторов. См. Пример ниже, чтобы узнать это. Хотя изучение этого алгоритма может быть необязательным в современном мире с калькуляторами, разработка некоторых примеров может использоваться в качестве упражнения в основных операциях для учащихся средней школы, а изучение логики, лежащей в основе этого, может быть хорошим упражнением для мышления для учащихся средней школы.

Пример: Найдите √645 с точностью до одного десятичного знака.
Сначала сгруппируйте числа под корнем попарно справа налево, оставляя одна или две цифры слева (в данном случае 6). Для каждой пары чисел вы получите одну цифру квадратного корня.
Для начала найдите номер чей квадрат меньше или равен первой паре или первому числу, и напишите это над линией квадратного корня (2):Затем продолжайте так:
2 √ 6 .45 — 4 (4 _) 2 45 2 √ 6 .  45
45— 4 (45) 2 4511 Возвести 2 в квадрат и получить 4, напишите, что под 6 и вычтите.Сбейте следующую пару цифр. Затем удвойте число над квадратным корнем символьная строка (выделена) и запишите его в скобках, поставив рядом с ним пустую строку, как показано. Дальше подумайте, какое однозначное число может что-то перейдите на пустую строку так, чтобы сорок что-то умножить на что-то быть меньше или равно 245.
45 х 5 = 225
46 x 6 = 276, поэтому 5 работает.2 5
√ 6 ,45 .  00
00-4 (45) 2 45 -2 25 20 00 2 5
√ 6 .45 . 00 -4 (45) 2 45 -2 25 (50_) 20 00 2 5
.  3
3√ 6 ,45 . 00 -4 (45) 2 45 -2 25 (503) 20 00 Напишите 5 в начале строки.Вычислите 5 x 45, напишите, что ниже 245, вычтите, введите следующую пару цифр (в данном случае десятичные цифры 00). Затем удвойте число над линией (25) и напишите удвоенное число (50) в скобках с пустой строкой рядом с ним как указано: Подумайте, что однозначное число может пойти что-то на пустом линия так что пятьсот- что-то раз что-то будет меньше или равно 2000.  503 х 3 = 1509
503 х 3 = 1509
504 x 4 = 2016, поэтому 3 работает.2 5
. 3 √ 6 ,45 . 00 ,00 -4 (45) 2 45 -2 25 (503) 20 00 — 15 09 4
91 00 2 5
.  3
3√ 6 ,45 . 00 ,00 -4 (45) 2 45 -2 25 (503) 20 00 — 15 09 (506_) 4
91 00 2 5
.  3
39 √ 6 ,45 . 00 ,00 -4 (45) 2 45 -2 25 (503) 20 00 — 15 09 (506_) 4 91 00 Вычислите 3 x 503, напишите, что ниже 2000, вычесть, сбейте следующие цифры. 
Затем удвойте «число» 253, которое находится над линией (без учета десятичной точки), и в скобках напишите удвоенное число 506 с пустой строкой рядом как указано: 5068 х 8 = 40544
5069 x 9 = 45621, что меньше 49100, поэтому 9 работает.Таким образом, до одного десятичного знака, √ 645 = 25.4
Комментарии посетителей
Я смутно помню, как изучал алгоритм извлечения квадратного корня в K-12, но, честно говоря, я не вижу в этом алгоритме никакой ценности, кроме любопытства. И я не из «реформаторской» толпы. Я полностью верю, что студентам не дадут калькулятор для использования до продвинутой алгебры или предварительного исчисления, а затем только научный калькулятор (не график). Вы действительно верите, что ученик уровня K-7 поймет, как / почему работает этот алгоритм?Я был рад узнать, что вы рекомендовали метод «оценки и проверки».
 Это то, что я также порекомендовал своей дочери, которая сейчас изучает квадратные корни в программе своей домашней школы. Метод «оценки и проверки» — хорошее упражнение в вычислении, умножении, а также запоминании полных квадратов.
Это то, что я также порекомендовал своей дочери, которая сейчас изучает квадратные корни в программе своей домашней школы. Метод «оценки и проверки» — хорошее упражнение в вычислении, умножении, а также запоминании полных квадратов.Другой метод, более подходящий для студентов класса алгебры, — это упрощение радикала с помощью принятого метода. Затем найдите оставшийся квадратный корень с помощью метода оценки. Например, чтобы найти SQRT (1400), упростите до SQRT (100) * SQRT (14), что равно 10 * SQRT (14).Затем найдите SQRT (14) методом оценки. Для квадратных корней из полных квадратов даже оценка не требуется.
Можно даже превратить задачу нахождения квадратного корня в упражнение по компьютерному программированию, попросив студентов написать программу на javascript или другом языке, чтобы использовать систематический числовой метод оценки этого квадратного корня с помощью метода проверки и предположения. Или, на уровне исчисления, студент может написать программу, которая использует полином Тейлора для вычисления квадратного корня.

Михаил Саковски
Инструктор математики
Привет,Обратил внимание на несколько комментариев, связанных с использованием алгоритма для поиска квадратный корень из числа. В некоторых комментариях говорилось, что находить результат с помощью бумаги и ручки против калькулятора — это архаично. Что Может быть и так. Однако, когда я был на первом курсе в старшей школе (начало 70-х) Герр Куиннелл упомянул — когда класс подходил к концу — некоторые из того, что можно делать с математикой, в том числе находить квадратные корни.Итак, я спросил его, как это было сделано. Он показал мне метод алгоритма на борту.
Я не могу говорить о ценности знания того, как это используется в других профессии. В электронике нахождение квадратного корня является неотъемлемой частью часть дизайна. У нас есть части, называемые резисторами. Они помогают в ограничении тока в схемах. Эти детали имеют номинальную мощность. Номинал резистора измеряется в «омах». В математическом смысле это можно найти, разделив вольт по амперам.
 10 вольт разделить на 0,001 ампера — это сопротивление 10 000 Ом.
В качестве примера квадратного корня, если я знаю, что резистор на 10000 Ом имеет
мощность 0,25 Вт
Я могу рассчитать максимальное напряжение наихудшего случая, которое может появиться на нем,
прежде, чем может произойти повреждение. Это можно найти, взяв сопротивление
значение — умножение
рейтинг мощности — и нахождение квадратного корня. Корень квадратный из 2500 равен 50.
Эта часть выдерживала 50 вольт.
10 вольт разделить на 0,001 ампера — это сопротивление 10 000 Ом.
В качестве примера квадратного корня, если я знаю, что резистор на 10000 Ом имеет
мощность 0,25 Вт
Я могу рассчитать максимальное напряжение наихудшего случая, которое может появиться на нем,
прежде, чем может произойти повреждение. Это можно найти, взяв сопротивление
значение — умножение
рейтинг мощности — и нахождение квадратного корня. Корень квадратный из 2500 равен 50.
Эта часть выдерживала 50 вольт.Моя точка зрения — я мог рассчитать результат «искусственными средствами».Так как кто-то нашел время, чтобы показать мне, как вычислить квадратный корень на доске, Мне не нужно было искать калькулятор. К тому времени я бы нашел калькулятор я уже придумал ответ. Найдите время, чтобы показать студентам то, как делается квадратный корень, имеет значение. Они не могут на самом деле поставить это можно использовать позже в жизни — но некоторые просто могут.
Гарт Цена, CET
Я просто писал еще один комментарий, и каким-то образом компьютер отправил его до того, как я закончил. Я, должно быть, нажал не ту клавишу. Итак, позвольте мне закончить, сказав, что дети впервые в мире и исследуют его. Вычисление квадратного корня от руки было бы для них увлекательным занятием и отличным способом узнать о других темах математики. Да, кстати, у меня вообще не было никаких уроков по квадратным корням до старшей школы, а потом мы не научились их вычислять. Нас учили множить число под корень и извлекать точные квадраты, оставляя не- идеальные квадраты под корень.ПОТОМУ ЧТО ДАЖЕ УЧИТЕЛЬ НЕ ЗНАЛ, КАК СДЕЛАТЬ ПРАВИЛЬНО. До свидания с Богом
Я, должно быть, нажал не ту клавишу. Итак, позвольте мне закончить, сказав, что дети впервые в мире и исследуют его. Вычисление квадратного корня от руки было бы для них увлекательным занятием и отличным способом узнать о других темах математики. Да, кстати, у меня вообще не было никаких уроков по квадратным корням до старшей школы, а потом мы не научились их вычислять. Нас учили множить число под корень и извлекать точные квадраты, оставляя не- идеальные квадраты под корень.ПОТОМУ ЧТО ДАЖЕ УЧИТЕЛЬ НЕ ЗНАЛ, КАК СДЕЛАТЬ ПРАВИЛЬНО. До свидания с БогомРоберт Монро
это один из лучших сайтов, которые я посетил для правильного решения проблемы. Вы можете называть меня аркаиком, но когда я ходил в школу, они учили деление в столбик, чтобы находить квадратный корень из числа.
В БОЛЬШИНСТВЕ ЭТО УЧИТ ДУМАТЬ. Использование калькулятора — это чистая лень. Я чувствую, что наши дети думают, что получение основ в школе (РАННЕЕ) — это архаично.Вот почему, когда вы заходите в магазин и выставляете счет 16,75, и вы передаете кассиру двадцатидолларовую купюру, однодолларовую купюру и 75 центов, они понятия не имеют, какой должна быть сдача, если кассовый аппарат не сообщает им, сколько чтобы дать тебе. Это приводит к ленивому мышлению ИЛИ НЕМЫШЛЕНИЮ ВООБЩЕ.
Это приводит к ленивому мышлению ИЛИ НЕМЫШЛЕНИЮ ВООБЩЕ.
Спасибо за ваше время.Раш Керлин
Я искал в Интернете давно забытую процедуру поиска квадратного корня вручную и наткнулся на вашу веб-страницу. и хотел сказать, что многие (или вся) критика стандартного алгоритма называет его «архаичным», «тупиковым» методом и т. д.в пользу вавилонского метода не может быть оправдано. Дело в том, что использование бумаги и карандаша для деления длинных чисел или нахождения квадратных корней является архаичным и представляет собой тупиковый процесс в 21 веке, независимо от того, какую рутину мы используем, поскольку мы больше не делаем этого из практических соображений. расчеты. Итак, вопрос в том, чему мы должны научить, чтобы познакомить студентов с фундаментальными техниками? Вавилонский метод — это численный метод, в отличие от другого метода, и имеет смысл обучить стандартной программе, которая работает сначала для любых чисел, а затем для других приближенных численных методов, вместо того, чтобы использовать численные методы типа предиктора-корректора, утверждающие, что они имеют применение где-то еще. Если мы пойдем с методами типа предиктор-корректор, необходимо также провести анализ ошибок, что не требуется для стандартного метода, поскольку в стандартной подпрограмме правильные цифры добавляются одну за другой на каждом шаге (в отличие от вавилонского метода, где содержание цифр может изменяться при каждом усреднении).
Если мы пойдем с методами типа предиктор-корректор, необходимо также провести анализ ошибок, что не требуется для стандартного метода, поскольку в стандартной подпрограмме правильные цифры добавляются одну за другой на каждом шаге (в отличие от вавилонского метода, где содержание цифр может изменяться при каждом усреднении).С наилучшими пожеланиями,
Карл I. Иаков
Профессор, Школа инженерии полимеров, текстиля и волокон
Профессор, Школа машиностроения им. Г. В. Вудраффа
Технологический институт Джорджии
Вы ответили на вопрос «Поиск квадратного корня с помощью алгоритма».Я заметил, что ответ был оспорен несколькими людьми по нескольким причинам. Я хотел бы отметить, что предложенное решение является старейшим методом вычисления квадратного корня в западном мире. Меня описал Леонардо Пикано, также известный как Фибоначчи, в его книге Liber Abaci, глава 14. Первое издание было «написано» в 1202 году, а второе издание было «написано» в 1228 году. Я говорю «написано», потому что это было буквально написано от руки, как и все копии. Работа Иоганна Гутенберга над печатным станком началась только в 1436 году.
Я говорю «написано», потому что это было буквально написано от руки, как и все копии. Работа Иоганна Гутенберга над печатным станком началась только в 1436 году.
Леонардо научился этому методу во время своих арабских путешествий по Средиземному морю, а арабы научились этому у индуистской нации вокруг современной Индии. Метод в примере, который вы показываете, включает в себя некоторую современную интерпретацию, облегчающую чтение. Леонардо также показал геометрическую взаимосвязь, которая связана с тем, что мы сегодня понимаем под «аккордами». Это очень простое решение вопроса без использования калькулятора.Дэвид Т. Кэрротт, доктор философии
Я прочитал ваше предложение по вычислению квадратного корня без калькулятора.Я преподаю математику для учителей начальной школы и развивающие математические курсы (алгебра) для взрослых. Я считаю, что следует сосредоточиться на понимании числа, а не на упражнении по заученному алгоритму. Я предлагаю вам попросить ученика определить пару полных квадратов, между которыми находится число.
 Например, при нахождении sqrt 645 он попадает между sqrt 625, который равен 25, и sqrt 676, который равен 26. Таким образом, sqrt 645 должен быть между 25 и 26. Где он находится между? Всего 50 номеров от 676 до 625.645 — это 20 чисел больше 625, поэтому 20/50 = 0,4.
Таким образом, sqrt 645 очень близко к 25,4
Например, при нахождении sqrt 645 он попадает между sqrt 625, который равен 25, и sqrt 676, который равен 26. Таким образом, sqrt 645 должен быть между 25 и 26. Где он находится между? Всего 50 номеров от 676 до 625.645 — это 20 чисел больше 625, поэтому 20/50 = 0,4.
Таким образом, sqrt 645 очень близко к 25,4
Этот метод предоставляет учащимся процесс, который улучшает их понимание чисел, не ожидая, что они запомнят алгоритм, и дает ответ с точностью до десятых.Андреа С. Леви, ред.
В настоящее время я учусь в MCC. Я изучаю курс для учителей начальной математики. Мы должны составить план урока, чтобы научить младших школьников пользоваться теоремой Пифагора.Мне нужно научиться разбирать теорию Пифагора для элементарного ребенка. Я застрял в квадратной корневой части.
Прочтите мой ответ на этот вопрос.
Метод, который вы показываете в статье, архаичен. Есть НАМНОГО более эффективный алгоритм. (Это алгоритм, который фактически используется негласно внутри калькулятора, когда вы нажимаете кнопку извлечения квадратного корня. )
)1. Оцените квадратный корень как минимум с 1 цифрой.
2. Разделите эту оценку на число, квадратный корень которого вы хотите найти.
3. Найдите среднее значение частного и делителя. Результатом становится новая оценка.Прелесть этого метода в том, что точность оценки растет очень быстро. Каждый цикл по существу удваивает количество правильных цифр. От 1-значной начальной точки вы можете получить 4-значный результат за два цикла. Если вы уже знаете квадратный корень из нескольких цифр, например sqrt (2) = 1,414, один цикл деления и среднего даст вам удвоение цифр (в данном случае восемь).
Этот метод не только позволяет вручную находить квадратные корни, но и может использоваться, если у вас есть только дешевый четырехфункциональный калькулятор. Если ученики могут получить квадратный корень вручную, они не найдут квадратного корня таким загадочным. Также этот метод является хорошим первым примером последовательного решения проблемы.
Дэвид Чендлер
Другой способ называется Вавилонский метод угадать и разделить, и он действительно быстрее.
 Это также то же самое, что и при применении метода Ньютона.См., Например, поиск квадратного корня из 20 с использованием 10 в качестве начального предположения:
Это также то же самое, что и при применении метода Ньютона.См., Например, поиск квадратного корня из 20 с использованием 10 в качестве начального предположения:Угадать Разделить Найти среднее значение 10 20/10 = 2 среднее 10 и 2, чтобы дать новое предположение 6 6 20/6 = 3,333 среднее значение 3,333 и 6 дает 4,6666 4,666 20 / 4,666 = 4,1414 среднее значение 4.666,4,1414 = 4,4048 4,4048 20 / 4,4048 = 4,5454 среднее значение = 4,4700 4,4700 20 / 4,4700 = 4,4742 среднее значение = 4,4721 4,4721 20 / 4,4721 20 / 4,4 4,47217 среднее значение = 4,47214 Это уже с 4 десятичными знаками 4,47214 20 / 4,47214 = 4,472132 среднее значение = 4,472135 4.  472135
47213520 / 4,472135 = 4,472137 среднее значение = 4,472136
Плакат утверждает, что метод статьи «архаичен» и что «вавилонский метод» более эффективен. На первый взгляд может показаться, что это так, потому что в примере с плакатом вычисляется квадратный корень из двузначного целого числа 20 вместо 645 в примере статьи.Однако я фактически разработал пример статьи (квадратный корень из 645), используя оба метода, и обнаружил, что вавилонский метод требует 9 «циклов деления и среднего», чтобы прийти к ответу.Кроме того, вавилонский метод требует от ученика выполнения пятизначного деления в столбик — немалый подвиг для ученика начальной или средней школы. С другой стороны, метод, описанный в статье, требует от студента выполнить только одну задачу из четырех шагов и длинного деления, решив не более полдюжины или около того задач умножения из четырех цифр на 1 цифру.
Следовательно, разумно сделать вывод, что вавилонский метод больше подходит для решения с помощью калькулятора или решения с помощью компьютера, в то время как метод статьи больше подходит для решения с помощью карандаша и бумаги.

Поскольку предметом статьи было то, как научить ученика начальной или средней школы легко находить квадратные корни карандашным методом, «архаичный» метод статьи кажется наиболее подходящим.
Алексей
В ответ на сообщение Алекса: как вам понадобилось 9 циклов, чтобы произвести 25,4 цикла с использованием вавилонского метода на 645? Это займет 1,5 шага, если вы используете свое предположение как 25
1) 645/25 = 25,8
(25 + 25,8) / 2 = 25,42) 645/25.4 ≈ 25,39
Вавилонский метод очень эффективен, если уже известно много полных квадратов для приближения к исходному значению. Я считаю, что студенты не могут понять причины, лежащие в основе алгоритма в этом посте, в то время как метод деления и среднего кажется более интуитивным, если они раньше работали со средними значениями.
Даниил
Я сомневаюсь в том, чтобы обучать методу деления в столбик для извлечения квадратных корней. Вавилонский метод легче запомнить и понять, и он дает столько же практики в базовой арифметике. Что еще более важно, он имеет четкую связь с такими темами, как метод Ньютона и рекурсивные последовательности, которые будут встречаться в исчислении и за его пределами. Метод длинного деления несколько быстрее для ручного расчета, но он не приводит к другим важным темам — это тупик.
Что еще более важно, он имеет четкую связь с такими темами, как метод Ньютона и рекурсивные последовательности, которые будут встречаться в исчислении и за его пределами. Метод длинного деления несколько быстрее для ручного расчета, но он не приводит к другим важным темам — это тупик.Дэвид
Я учился на старых компьютерных схемах и бинарных аппаратных алгоритмах. Метод, используемый для вычисления корня из 645, является методом, используемым в высокопроизводительных двоичных вычислениях, поскольку он требует только сдвига, вычитания и сравнения, которые являются командами одного цикла / этапа или перенаправлены на сопроцессор.Преобразуйте число в двоичное, разделите его на 2 битовые группы и используйте описанную выше процедуру. Умножение и деление требует от 10 до сотен циклов / стадий и уничтожает преформ и конвейеры. Квадратный корень вычисляется быстрее, чем деление, поскольку деление выполняется через 1 бит за цикл / этап, а квадратный корень проходит через 2 бита за цикл.
Брэд
что такое квадратный корень из -1?Тамара Ярдли
-1 не может иметь квадратный корень (по крайней мере, не действительный), потому что любые два числа с одинаковым «знаком» (+/- положительный или отрицательный) при умножении будут равны положительному числу.Попробуйте: +2 × +2 = 4 и -2 × -2 = 4.
Так как квадратный корень из числа должен равняться этому числу при умножении на себя. Когда вы умножаете это число на себя и задаете его как полное уравнение (n * n = x), два множителя (n и n) либо положительны, либо отрицательны, так как это одно и то же число. Следовательно, их продукт будет положительным. Никакое действительное число, умноженное само на себя, не будет равно отрицательному числу, поэтому -1 не может иметь действительный квадратный корень.
Блейк
Квадратный корень из -1 не является действительным числом.Обозначается буквой i и называется мнимой единицей. Из i и его кратных мы получаем чисто мнимые числа, такие как 2i, 5.
 6i, -12i и так далее. Это приводит к совершенно новой системе счисления комплексных чисел, в которой числа имеют действительную и мнимую части (например, 5 + 3i или -20 — 40i). И с помощью этой системы счисления можно сделать много увлекательной математики!
6i, -12i и так далее. Это приводит к совершенно новой системе счисления комплексных чисел, в которой числа имеют действительную и мнимую части (например, 5 + 3i или -20 — 40i). И с помощью этой системы счисления можно сделать много увлекательной математики!
Я пытался найти в сети старый способ вычисления квадратного корня путем деления в столбик. ДА, я нашел это.Прочтите ответы и не соглашусь со многими плакатами.Найти квадрат 645 легко, если вы знаете 252 и 262, но я никогда не запоминал квадраты чисел от 1 до 30 или около того, я запоминал только до 12X12 (старая имперская система)
Угадать, что в квадрате 645 будет около 25, — это здорово, но если вы угадаете, что это 2, то перед вами стоит большая проблема.
Я вижу, что «другие» плакаты находят более легкие и быстрые способы … вот в чем проблема сегодня. Будем искать легкий путь без понимания.С вашим методом это может сделать любой, у кого есть навыки деления в столбик и простого умножения.
 Самое простое решение — купить калькулятор и избегать всех умственных способностей. ржу не могу
Самое простое решение — купить калькулятор и избегать всех умственных способностей. ржу не могукорень квадратный из 645 мммм 20
645/20 = 32,25 в среднем 52,25 = 26,25
645 / 26,25 = 24,57, среднее значение 50,82 = 25,41Метод усреднения, кажется, работает, но он не учит большому делению … вроде как выше / ниже в The Price is Right.
Я предполагаю, что квадрат 645 равен 25.41 …. ничего себе, это работает с первого раза, чему я научился, ничего.
Используя метод усреднения, каков квадратный корень из 9331671 …. моя первая предполагаемая оценка — 10, получайте удовольствие!
9331671/10 = 933167,1 + 10 = 9331681,1 / 2 = 466588,55
9331671 / 466588,55 = 19,999785 + 466588,55 = 466607,57 / 2 = 233303,285
9331671 / 233303,285 = 39,99802 + 233303,285 = 233343,27 / 2 = 116671,235
…
…
…
…
…
Ах да, это дети из 3 или 4 класса, которые занимаются длинной математикой с 8-значными числами. .. так много для усреднения. И какова степень значимости, поскольку мы работаем с одним десятичным знаком или 3 … не нужно «усреднять» слишком рано, иначе мы можем потерять значащие цифры. Если мы работаем с миллиардами, то слишком быстрое снижение цифр может иметь ОГРОМНУЮ разницу.
.. так много для усреднения. И какова степень значимости, поскольку мы работаем с одним десятичным знаком или 3 … не нужно «усреднять» слишком рано, иначе мы можем потерять значащие цифры. Если мы работаем с миллиардами, то слишком быстрое снижение цифр может иметь ОГРОМНУЮ разницу.Адриан
Я непрофессионал, который зашел на сайт через поиск в Google на тему «как вычислить квадратный корень». Я прочитал презентацию, затем посмотрел ответы. Я должен сказать, что был встревожен комментарием Андреа С.Леви, редактор Д., где она предположила, что запоминание алгоритма менее желательно, чем понимание числа.В настоящее время я работаю техническим писателем в фирме, которая занимается разработкой программного обеспечения для кредитных союзов. Понимание всех алгоритмов, используемых в финансовом мире, крайне важно для нас, чтобы делать то, что мы делаем. Фактически, один из расчетов, который мы используем для определения амортизации потребительского кредита с комиссией за определенный период времени, поразительно похож на представление квадратного корня.
 Расчет должен быть написан инженером-программистом для машины, чтобы в конечном итоге он оставался в сознании человека.Если инженер не знает алгоритма, последствия будут нести тысячи потребителей. Я полагаю, что запоминание — это просто еще один инструмент в коробке. Используйте его, когда это уместно.
Расчет должен быть написан инженером-программистом для машины, чтобы в конечном итоге он оставался в сознании человека.Если инженер не знает алгоритма, последствия будут нести тысячи потребителей. Я полагаю, что запоминание — это просто еще один инструмент в коробке. Используйте его, когда это уместно.С уважением,
Майкл Келли
Ньюбери-Парк, Калифорния.
Последний комментатор на странице (Адриан) сказал, что она никогда не учила квадраты от 1 до 30. Это напоминает трюк, который я недавно изучил для нахождения квадратов, близких к 50. Начните с квадрата 50, 2500, добавьте в 100 раз больше расстояние между 50 и числом, а затем сложите квадрат расстояния 50 и числа.Например, 43 2 = 2500 — 700 + 49 = 1849. Это происходит от простого тождества FOIL (50 + x) 2 = 2500 — 100x + x 2 . В этом тождестве x — это расстояние между 50 и числом. Если число 43 (как в моем примере), x равно -7. Если число 54, то x равно 4. Таким образом, если вы запомните свои квадраты от 1 до 25, вы получите квадраты от 26 до 75 «бесплатно».
Если идея запоминания квадратов от 1 до 25 кажется сложной, это не так. Несколько недель назад, не зная этого трюка, я знал сразу около 13 человек, а еще несколько разбросаны тут и там.Я составил таблицу в Excel, перечислив числа от 1 до 25 рядом с их квадратами, распечатал ее и повесил на стену своего кабинета. Квадраты, которые я не запомнил в этих первых 25, теперь я могу получить за несколько секунд (например, для квадрата 23 я все еще считаю от 20 квадратов: 400, 441, 484, * 529 *). Даже не зная их всех, я могу найти квадраты от 1 до 75 менее чем за 10 секунд (мыслительный процесс для нахождения 73 в квадрате навскидку: «73 больше 23, чем 50. Что снова возведено в квадрат 23?» 400, 441, 484, 529! 2500 + 2300 + 529 = 5329.Сделанный!»)
Дэвид Леви
См. Также
Другой пример использования алгоритма извлечения квадратного корня
Объяснение того, почему работает этот алгоритм извлечения квадратного корня.
Бесплатные рабочие листы для вычисления квадратного корня, включая генератор рабочих листов
Геометрический вид алгоритма извлечения квадратного корня
Квадратный корень методом деления и среднего
Объяснение и пример старинного алгоритма приближения квадратных корней.
Алгоритмы извлечения квадратного корня
Формулы для рекуррентного отношения и итерации Ньютона, которые можно использовать для аппроксимации квадратных корней. Для математически мыслящих.Кромка квадратная
Новый способ получения квадратного корня из специальной группы чисел более простым способом.Квадратный корень числа
Прежде чем понять, что такое квадратный корень из числа, важно понять значение корня из числа.
Корень числа равен размеру числа. Например, вот как найти корень из 16.Во-первых, нам нужно разложить множитель 16. Различные способы множителя 16 показаны ниже.
16 = 1 × 16
16 = 2 × 8
16 = 4 × 4
Корень из 16 равен 4, потому что 4 является равным множителю для 16. Мы называем 4 квадратным корнем из 16, и мы напишите √16 = 4.
4 называется квадратным корнем, потому что мы должны возвести 4 в квадрат или возвести 4 в степень 2, чтобы получить 16.

Другие примеры, показывающие, как найти квадратный корень из числа.
Найдите квадратный корень из 4. Вы можете разложить 4 на множители двумя разными способами.4 = 1 × 4
4 = 2 × 2
Равный множитель равен 2, поэтому 2 является квадратным корнем из 4, и мы пишем √4 = 2.
Найдите квадратный корень из 64.
64 = 1 × 64
64 = 2 × 32
64 = 4 × 16
68 = 8 × 8
Равный множитель равен 8, поэтому квадрат 64 равен 8, и мы пишем √64 = 8.
Может ли квадратный корень числа быть отрицательным?
Да, конечно! Если умножить положительное число само на себя, получится положительный результат. Если вы умножите отрицательное число само на себя, вы также получите положительный результат.
Например, поскольку -8 × -8 = 64, -8 также является квадратным корнем из 64. Однако, если не указано иное, знак квадратного корня (√) относится к положительному корню числа, также называемому главным квадратом.
 корень.
корень.Может ли квадратный корень числа быть действительным числом?
Для чисел выше квадратный корень был равен целому числу.не всегда можно получить квадратный корень как целое число.
Иногда при нахождении квадратного корня вы можете получить действительное число.
Например, с помощью калькулятора квадратного корня ниже найдите квадратный корень из 5.
Результат включает множество чисел после десятичной точки.
Готовы к серьезным испытаниям? Как и в случае с делением в столбик, научитесь вычислять квадратный корень без калькулятора для любого числа, не являющегося точным квадратом. Я обещаю, вы не будете слишком сильно потеть!
Учителя! Вам нужна готовая таблица с квадратными корнями, к которой учащиеся могут быстро обращаться при решении своих основных математических задач? Получите таблицу квадратных корней.
Моделирование квадратов и поиск квадратного корня числа
Результаты обучения
- Найдите квадратный корень из полного квадрата
- Объясните, почему квадратный корень отрицательного числа не является действительным числом
Упростите выражения с помощью квадратного корня
Чтобы начать этот раздел, нам нужно повторить некоторые важные термины и обозначения.
 {2} [/ latex], что мы читаем вслух как «n в квадрате».{2} = 9 [/ latex]
{2} [/ latex], что мы читаем вслух как «n в квадрате».{2} = 9 [/ latex]
Число [латекс] 9 [/ latex] называется полным квадратом, потому что это квадрат целого числа.Выполнение упражнения по манипуляции математикой Квадратные числа помогут вам лучше понять идеальные квадратные числа.
На диаграмме показаны квадраты счетных чисел от [латекс] 1 [/ латекс] до [латекс] 15 [/ латекс]. Вы можете обратиться к нему, чтобы определить идеальные квадраты.Идеальные квадраты
Полный квадрат — это квадрат целого числа.{2} & = \ left (-8 \ right) \ left (-8 \ right) \\ & = 64 \ hfill \ end {array} [/ latex]
Когда мы умножаем два отрицательных числа, произведение всегда будет положительным . Итак, квадрат отрицательного числа всегда положителен.
На диаграмме показаны квадраты отрицательных целых чисел от [латекс] -1 [/ латекс] до [латекс] -15 [/ латекс].
Вы заметили, что эти квадраты такие же, как квадраты положительных чисел?Квадратные корни
Иногда нам нужно посмотреть на соотношение между числами и их квадратами в обратном порядке.
 {2} = 100 [/ latex] также, поэтому [latex] -10 [/ latex] также является квадратным корнем из [latex] 100 [/ latex]. Следовательно, и [латекс] 10 [/ латекс], и [латекс] -10 [/ латекс] являются квадратными корнями из [латекса] 100 [/ латекса].
{2} = 100 [/ latex] также, поэтому [latex] -10 [/ latex] также является квадратным корнем из [latex] 100 [/ latex]. Следовательно, и [латекс] 10 [/ латекс], и [латекс] -10 [/ латекс] являются квадратными корнями из [латекса] 100 [/ латекса].
Итак, каждое положительное число имеет два квадратных корня: один положительный и один отрицательный.
Что, если нам нужен только положительный квадратный корень из положительного числа? Знак корня , [латекс] \ sqrt {\ phantom {0}} [/ latex], означает положительный квадратный корень. Положительный квадратный корень также называется главным квадратным корнем.{2} = 121 \ hfill & & & 11 \ hfill \ end {array} [/ latex]В следующем видео показано еще несколько примеров того, как можно упростить извлечение квадратного корня из полного квадрата.
Каждое положительное число имеет два квадратных корня, а знак корня указывает на положительный. Пишем [латекс] \ sqrt {100} = 10 [/ латекс]. Если мы хотим найти отрицательный квадратный корень из числа, мы помещаем минус перед знаком корня. Например, [латекс] — \ sqrt {100} = — 10 [/ латекс].
пример
Упростить. Ⓐ [латекс] — \ sqrt {9} [/ latex] ⓑ [латекс] — \ sqrt {144.} [/ Латекс]
Показать решениеРешение
ⓐ [латекс] — \ sqrt {9} [/ латекс] Негатив перед радикальным знаком. [латекс] -3 [/ латекс] ⓑ [латекс] — \ sqrt {144} [/ латекс] Негатив перед радикальным знаком.{2} = — 25? [/ Latex]
Ни одно из чисел, с которыми мы до сих пор имели дело, не имеет квадрата [латекс] -25 [/ latex]. Почему? Любое положительное число в квадрате является положительным, и любое отрицательное число в квадрате также положительно. В следующей главе мы увидим, что все числа, с которыми мы работаем, называются действительными числами. Итак, мы говорим, что не существует действительного числа, равного [latex] \ sqrt {-25} [/ latex]. Если нас просят найти квадратный корень из любого отрицательного числа, мы говорим, что решение не является действительным числом.пример
Упростите: ⓐ [латекс] \ sqrt {-169} [/ latex] ⓑ [латекс] — \ sqrt {121} [/ latex].
Показать решениеРешение
ⓐ Не существует действительного числа с квадратом [латекс] -169 [/ латекс]. Следовательно, [латекс] \ sqrt {-169} [/ latex] не является действительным числом.
ⓑ Отрицательный знак стоит перед знаком корня, поэтому мы находим противоположность квадратного корня из [латекс] 121 [/ латекс].[латекс] — \ sqrt {121} [/ латекс] Негатив перед радикалом. [латекс] -11 [/ латекс] Калькулятор корня
Калькулятор квадратного корня
Калькулятор кубического корня
Калькулятор общего корня
Калькулятор связанных показателей | Научный калькулятор | Калькулятор журналаВ математике, общий корень или корень n th числа a — это другое число b , которое при умножении на себя n раз дает a .В формате уравнения:
n √a = b
б н = аОценка корня
Некоторые общие корни включают квадратный корень, где n = 2, и кубический корень, где n = 3. Вычисление квадратных корней и n th корней является довольно трудоемким. Это требует оценки, проб и ошибок. Существуют более точные и эффективные способы вычисления квадратных корней, но ниже приведен метод, не требующий глубокого понимания более сложных математических концепций.Для расчета √a:
- Оценить число b
- Разделите a на b . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение b и c и использовать результат как новое предположение
- Повторите шаг два
EX: Найти √27 до 3 десятичных знаков Предположение: 5.125
27 ÷ 5.125 = 5,268
(5,125 + 5,268) / 2 = 5,197
27 ÷ 5,197 = 5,195
(5,195 + 5,197) / 2 = 5,196
27 ÷ 5,196 = 5,196Оценка n
th КореньВычисление корней n th может быть выполнено с использованием аналогичного метода с изменениями для работы с n . Вычисление квадратного корня полностью вручную утомительно. Оценить более высокие корни n th , даже если использовать калькулятор для промежуточных шагов, значительно утомительнее.Для тех, кто разбирается в рядах, см. Здесь более математический алгоритм для вычисления корней n th . Для более простого, но менее эффективного метода перейдите к следующим шагам и примеру. Для расчета n √a:
- Оценить число b
- Разделите a на b n-1 . Если возвращаемое число c является точным до желаемого десятичного разряда, остановитесь.
- Среднее значение: [b × (n-1) + c] / n
- Повторите шаг два
EX: Найти 8 √15 до 3 знаков после запятой Угадай: 1.432
15 ÷ 1,4327 = 1,405
(1,432 × 7 + 1,405) / 8 = 1,388
15 ÷ 1,388 7 = 1,403
(1,403 × 7 + 1,388) / 8 = 1,402Тогда должно быть ясно, что дальнейшие вычисления приведут к округлению до 1,403, в результате чего 1,403 будет окончательной оценкой с точностью до 3 знаков после запятой.
Корень (числа) — определение математического слова
Корень (числа) — определение математического слова — Открытый справочник по математикеКорень числа x — это другое число, которое при умножении на себя заданное количество раз дает x.
Например, третий корень (также называемый кубическим корнем) из 64 равен 4, потому что если вы умножите три четверки вместе, вы получите 64:
4 × 4 × 4 = 64
Это было бы записано как Вышеупомянутое будет означать «третий корень 64 — 4» или «кубический корень 64 — 4» .- Второй корень обычно называют «квадратным корнем».
- Третий корень числа обычно называют «кубическим корнем»,
- После этого они называются корнем n, например корень 5, корень 7 и т. Д.
Иногда бывает два корня
Для каждого корня четной степени (например, 2-го, 4-го, 6-го….) есть два корня. Это потому, что умножение двух положительных или двух отрицательных чисел дает положительный результат. Например, рассмотрим квадратный корень из 9.
Какое число, умноженное на само себя, даст 9?
Очевидно 3 будут работать:3 × 3 = 9
Но так будет -3:-3 × -3 = 9
Когда таких корней два, если не указано иное, мы имеем в виду положительный. Строго говоря, когда мы пишем √ 4, мы имеем в виду положительный корень, +2.Это называется «главный корень».
Корни отрицательных чисел
У отрицательных чисел нет реальных корней четного порядка. Например, квадратного корня из -9 не существует, потому что -3 × -3 = + 9, а также +3 × +3 = + 9. Это относится ко всем корням четного порядка, 2-му (квадратному) корню, 4-му корню, 6-му корню и так далее.
Однако — это корня нечетного порядка отрицательных чисел. Например, –3 — это кубический корень из –27. Это потому что –3 × –3 × –3 = –27.Первые два члена при умножении дают +9, затем следующее умножение дает
+9 × –3 = –27. Это относится ко всем корням нечетного порядка, таким как 3-й (кубический) корень, 5-й корень, 7-й корень и т. Д.Мнимые числа
Выше сказано, что действительного квадратного корня из отрицательного числа не существует. Обратите внимание на слово «настоящий». Это говорит о том, что нет настоящий номер это квадратный корень отрицательного числа.
Однако в математике и инженерии нам часто нужно найти квадратный корень из отрицательного числа.Чтобы решить эту проблему, мы вводим понятие «мнимого» числа. Он включает в себя символ i , который обозначает квадратный корень из отрицательного числа. Или, другими словами, i 2 = –1
На практике мы можем использовать его для выражения квадратного корня из любого отрицательного числа. Например Это означает, что квадратный корень из –25 — это квадратный корень из +25, умноженный на квадратный корень из отрицательной единицы.
Подробнее о мнимых числах см. Мнимые числа.
Символы
Radicand
То, что вы находите корень.Радикальный символ
Символ √ , означающий «корень из». Длина турника важна. См. Примечание ниже.градусов
Сколько раз подкоренное выражение умножается само на себя. 2 означает квадратный корень, 3 означает кубический корень. После этого они называются корнем 4-й, 5-й и так далее. Если он отсутствует, предполагается, что это 2 — квадратный корень.Другой способ записи
Корни также можно записать в экспоненциальной форме. В общем Так, например, кубический корень x будет записан Что будет произноситься как «х в степени одной трети».
Другие экспоненты и основные темы
(C) Открытый справочник по математике, 2011 г.
Все права защищены.Как вычислить квадратный корень
Понимание того, как вычислять математические задачи вручную, является важным навыком. Одна математическая концепция, которая иногда используется в бизнес-анализе, — извлечение квадратного корня. Вычисление квадратного корня вручную позволяет понять, как работает формула.
В этой статье мы описываем, как используются квадратные корни, и объясняем три способа их вычисления вручную.
Связано: 10 лучших навыков и методов обучения
Использование квадратного корня
Квадратные корни используются для нахождения хвостов при нормальном распределении, которое представляет собой график, показывающий, где будет находиться большинство чисел в наборе данных. . Они особенно полезны для определения ключевых показателей эффективности (KPI), понимания того, насколько хорошо люди справятся с тестом и насколько вероятен результат.
Нормальное распределение основано на стандартных отклонениях или блоках оценок от среднего всех оценок.Хвосты нормального распределения обычно представляют собой наивысшие и самые низкие 5% оценок, при этом большинство оценок попадают в одно стандартное отклонение по обе стороны от среднего.
Связано: Важность когнитивных способностей в вашей карьере
Как вычислить квадратные корни вручную
Есть несколько способов вычислить квадратный корень. Решение квадратного корня — это умноженное на само число число, равное числу под символом квадратного корня, которое выглядит как √.Почти все калькуляторы имеют функцию извлечения квадратного корня, которую вы можете использовать. Вот несколько способов, которыми вы можете вычислить это вручную:
- Факторинг по квадратам
- Факторинг в длинной форме
- Метод длинного деления
Факторинг по квадратам
Разложение на множители квадратного корня означает, что вы находите самые близкие числа которые умножаются вместе. Самые простые квадратные корни — это те, которые делятся непосредственно на квадраты, например √100, но более сложные включают несколько квадратных корней, например √225.Вот шаги, чтобы найти квадратный корень с помощью факторизации:
- Найдите множители . Факторы — это числа, которые вы умножаете, чтобы найти итог под символом квадратного корня. Для √100 множители будут √ (10 x 10). Коэффициент √225 будет равен √ (25 x 9).
- Разделите множители на их собственные квадратные корни . Поскольку оба множителя √100 равны 10, квадратный корень из 100 равен 10. Для √225 вы должны разделить множители под их собственными знаками квадратного корня, так что формула будет √25 x √9.
- Найдите отдельные квадраты . Затем вы найдете квадраты каждого из отдельных факторов. √25 = 5 и √9 = 3. Оставшаяся формула будет иметь вид 5 x 3.
- Завершите решение уравнения . Теперь, когда вы знаете, что такое упрощенные квадраты, вы обнаружите, что 5 x 3 = 15. Итак, √225 = 15.
Фактор в длинной форме
Иногда вы не знаете, какие множители квадратного корня квадраты. Вы можете разбить квадратный корень на каждый отдельный фактор, а затем решить его.Например, чтобы получить коэффициент длинного формата √225, выполните следующие действия:
- Найдите множители. Самый очевидный множитель 225 — пять, поэтому вы должны начать с √225 = √ (5 x 45). Вы бы упростили еще больше, найдя множители 45: √ (5 x 5 x 9). Последний коэффициент, который вы можете упростить, — это 9, поэтому ваш окончательный коэффициент длинной формы будет выглядеть как √ (5 x 5 x 3 x 3).
- Извлеките повторяющиеся факторы. Когда вы видите одно и то же число дважды в качестве множителя, вы перечисляете его один раз за пределами символа квадратного корня.В данном случае у нас есть две пятерки и две тройки, поэтому уравнение будет иметь вид 5 x 3.
- Решите оставшееся уравнение. Последний шаг — завершить решение уравнения. В этом случае 5 x 3 = 15.
Метод длинного деления
Бывают случаи, когда вы можете не сразу распознать множители. Метод длинного деления позволяет найти квадратный корень без оценки. Для этого метода мы найдем √361. Вот шаги к методу длинного деления:
- Разделите основание квадратного корня на пары .Начиная справа, сгруппируйте числа в пары. В нашем примере 361 будет 3 61.
- Найдите наибольший квадрат, который делится на первое число или пару . Это даст вам первое число в вашем ответе. Первое число слева — 3. Наибольший квадрат, входящий в него, равен единице, потому что 1 x 1 = 1, а 2 x 2 = 4.
- Вычтите квадрат из первого числа или пары. Вычитание квадрата из первого числа даст вам остаток, который будет включен в следующий шаг.В этом примере 3 — 1 = 2.
- Перейдите к следующей паре. Следующее число, с которым вы будете работать, будет комбинацией вычтенного квадрата и следующей пары. В этом случае они составили бы трехзначное число. Когда вы опускаете 61 вниз, число, которое вы будете использовать для нахождения следующей цифры в квадратном корне, будет 261.
- Умножьте первую цифру квадрата на два. Это будет первая цифра в множителе для нахождения второй цифры квадратного корня.В этом примере первая цифра квадратного корня — единица. 1 x 2 = 2.
- Составьте следующее уравнение для множителей . Уравнение для следующего шага основано на цифре из шага пять и числе из шага четыре. Первым множителем будет двузначное число, где первая цифра — это число из пятого шага. Уравнение будет выглядеть как 2_ x _.
- Найдите число, заполняющее пробелы. Это число будет следующей цифрой в решении для √361. Число, которое заполнит пробелы, будет таким же, и это будет самая высокая цифра, где множители меньше или равны числу на четвертом шаге.В этом примере номер цели 261. Мы начнем с 9, поэтому уравнение будет иметь вид 29 x 9 = 261.
- Поместите число рядом с первой цифрой. В этом примере квадрат равен 19.
Как вручную найти квадратный корень
Как вручную найти квадратный кореньКак найти квадратный корень вручную
Вот почти забытое искусство: с появлением электронных калькуляторы, скорее всего, доживут до XXI века только на бумаге и в воспоминаниях стариков.
Из какого числа вы хотите найти квадратный корень? Вот один из них, который мы будем использовать:
46656
Сначала разделите число, которое нужно извлекать из квадратного корня, на пары цифр, начиная с десятичной точки. То есть никакая пара цифр не должна пересекаться десятичная точка. (Например, разделите 1225 на «12 25», а не на «1 22 5»; 6.5536 на «6,55 36», а не на «6,5 53 6».)
Затем вы можете поместить несколько линий на каждую пару цифр и полосу на слева, что-то вроде длинного деления.
+ --- ---- ---- | 4 66 56Найдите наибольшее число, квадрат которого меньше или равен ведущему пара цифр. В этом случае первая пара цифр — 4; самое большое число квадрат которого меньше или равен 4 равен 2.
Поместите это число слева, и над первой парой цифр.
2 + --- ---- ---- 2 | 4 66 56Теперь возведите это число в квадрат и вычтите из пары первых цифр.
2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 0Выдвинуть левую скобу; умножьте последнюю (и единственную) цифру левой число на 2, поместите его слева от разницы, которую вы только что вычислили, и оставьте рядом с ним пустой десятичный знак.
2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0Затем опустите следующую пару цифр и поместите ее вправо разницы.
2 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 4_ | 0 66Найдите наибольшее число для этого пустого десятичного разряда, чтобы число, умноженное на уже существующее число плюс десятичный разряд, будет меньше чем текущая разница. Например, если 1 * 41 равно ≤ 66, то 2 * 42 ≤ 66 и т. Д. В данном случае это 1. Поместите это число в оставленное вами поле, и в следующем десятичном разряде в строке результатов вверху.
2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66Теперь вычтите продукт, который вы только что нашли.
2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 25Теперь повторите, как прежде: возьмите число в левом столбце (здесь 41) и удвойте его последнюю цифру (что даст вам 42). Скопируйте это ниже в левый столбец и оставьте рядом с ним пустое место. (Двойная последняя цифра с переносом: для Например, если у вас было не 41, а 49, что составляет 40 + 9, вы должны скопировать 40 + 18 что равно 58.) Также опустите следующую пару цифр справа.
2 1 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 42_ 25 56Теперь найдите самую большую цифру (назовите ее #) такую, что 42 # * # ≤ 2556. Здесь получается, что 426 * 6 = 2556 точно.
2 1 6 + --- ---- ---- 2 | 4 66 56 | -4 + ---- 41 | 0 66 | - 41 + -------- 426 | 25 56 | - 25 56 + ------------- 0Когда разница равна нулю, у вас есть точный квадратный корень, и вы Выполнено.В противном случае вы можете продолжать находить больше десятичных знаков до тех пор, пока как ты хочешь.
Вот еще один пример с меньшим количеством аннотаций.
7. 2 8 0 1 ... + ---------------------- 7 | 53. 00 00 00 00 00 | 49 + ---------------------- 142 | 4 00 | 2 84 + ---------------------- 1448 | 1 16 00 | 1 15 84 + ---------------------- 14560 | 16 00 | 0 + ---------------------- 145601 | 16 00 00 | 14 56 01 + ---------------------- | 1 43 99 00 ...Джон Керл
john dot r dot kerl at lmco точка com
Июль 1998 г.
 (1/2)
MsgBox "Квадратный Корень" кв " является " sqr, vbOKOnly, "Квадратное корневое значение"
еще
MsgBox "Пожалуйста, введите номер.", VbOKOnly, "Ошибка"
End If
End Sub
(1/2)
MsgBox "Квадратный Корень" кв " является " sqr, vbOKOnly, "Квадратное корневое значение"
еще
MsgBox "Пожалуйста, введите номер.", VbOKOnly, "Ошибка"
End If
End Sub Нажмите Ctrl + S сохранить изменения. Затем выберите местоположение для вашего измененного документа Excel и нажмите Сохранить кнопка.
Нажмите Ctrl + S сохранить изменения. Затем выберите местоположение для вашего измененного документа Excel и нажмите Сохранить кнопка.

 Вы заметите, что таблица только что получила дополнительный столбец с квадратными корнями чисел, которые у нее были ранее.
Вы заметите, что таблица только что получила дополнительный столбец с квадратными корнями чисел, которые у нее были ранее. При этом стоит обратить внимание, что если к состоит из четного числа цифр, то в первой левой грани будет 2 цифры, если же число цифр в к нечетное, то в первой левой грани будет 1 цифра. Количество наших граней показывает количество цифр результата. На первый взгляд все просто и понятно.
При этом стоит обратить внимание, что если к состоит из четного числа цифр, то в первой левой грани будет 2 цифры, если же число цифр в к нечетное, то в первой левой грани будет 1 цифра. Количество наших граней показывает количество цифр результата. На первый взгляд все просто и понятно. (1/2)
(1/2)
 Это так просто и может стать отличным экспериментом для студентов!
Это так просто и может стать отличным экспериментом для студентов! 4495
4495
 45
45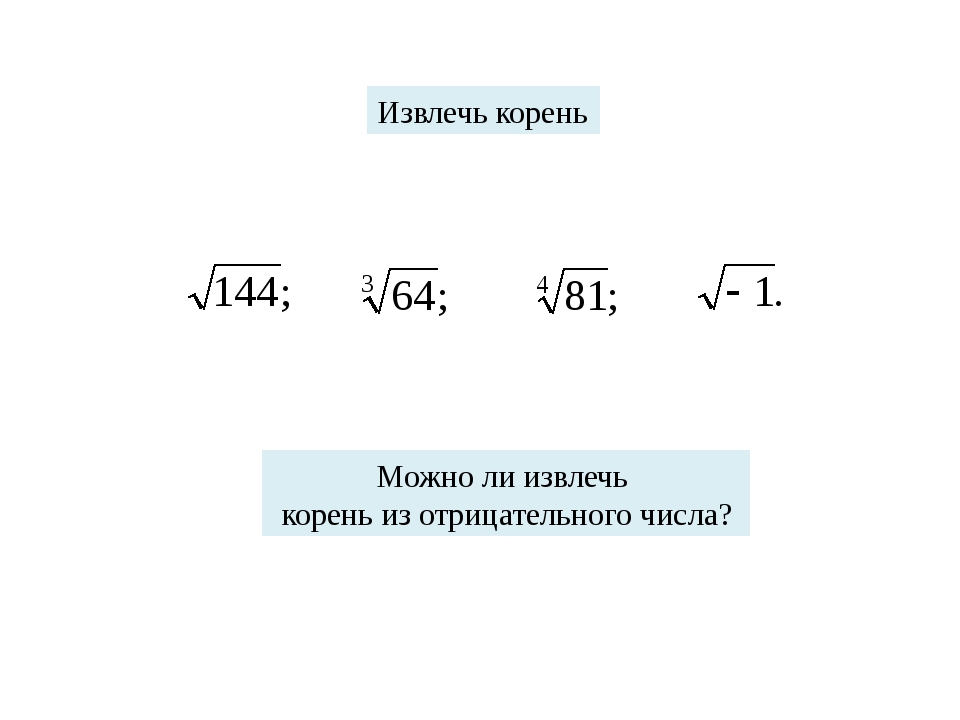 00
00 3
3 503 х 3 = 1509
503 х 3 = 1509  3
3 3
3
 Это то, что я также порекомендовал своей дочери, которая сейчас изучает квадратные корни в программе своей домашней школы. Метод «оценки и проверки» — хорошее упражнение в вычислении, умножении, а также запоминании полных квадратов.
Это то, что я также порекомендовал своей дочери, которая сейчас изучает квадратные корни в программе своей домашней школы. Метод «оценки и проверки» — хорошее упражнение в вычислении, умножении, а также запоминании полных квадратов.
 10 вольт разделить на 0,001 ампера — это сопротивление 10 000 Ом.
В качестве примера квадратного корня, если я знаю, что резистор на 10000 Ом имеет
мощность 0,25 Вт
Я могу рассчитать максимальное напряжение наихудшего случая, которое может появиться на нем,
прежде, чем может произойти повреждение. Это можно найти, взяв сопротивление
значение — умножение
рейтинг мощности — и нахождение квадратного корня. Корень квадратный из 2500 равен 50.
Эта часть выдерживала 50 вольт.
10 вольт разделить на 0,001 ампера — это сопротивление 10 000 Ом.
В качестве примера квадратного корня, если я знаю, что резистор на 10000 Ом имеет
мощность 0,25 Вт
Я могу рассчитать максимальное напряжение наихудшего случая, которое может появиться на нем,
прежде, чем может произойти повреждение. Это можно найти, взяв сопротивление
значение — умножение
рейтинг мощности — и нахождение квадратного корня. Корень квадратный из 2500 равен 50.
Эта часть выдерживала 50 вольт. Я, должно быть, нажал не ту клавишу. Итак, позвольте мне закончить, сказав, что дети впервые в мире и исследуют его. Вычисление квадратного корня от руки было бы для них увлекательным занятием и отличным способом узнать о других темах математики. Да, кстати, у меня вообще не было никаких уроков по квадратным корням до старшей школы, а потом мы не научились их вычислять. Нас учили множить число под корень и извлекать точные квадраты, оставляя не- идеальные квадраты под корень.ПОТОМУ ЧТО ДАЖЕ УЧИТЕЛЬ НЕ ЗНАЛ, КАК СДЕЛАТЬ ПРАВИЛЬНО. До свидания с Богом
Я, должно быть, нажал не ту клавишу. Итак, позвольте мне закончить, сказав, что дети впервые в мире и исследуют его. Вычисление квадратного корня от руки было бы для них увлекательным занятием и отличным способом узнать о других темах математики. Да, кстати, у меня вообще не было никаких уроков по квадратным корням до старшей школы, а потом мы не научились их вычислять. Нас учили множить число под корень и извлекать точные квадраты, оставляя не- идеальные квадраты под корень.ПОТОМУ ЧТО ДАЖЕ УЧИТЕЛЬ НЕ ЗНАЛ, КАК СДЕЛАТЬ ПРАВИЛЬНО. До свидания с Богом Это приводит к ленивому мышлению ИЛИ НЕМЫШЛЕНИЮ ВООБЩЕ.
Это приводит к ленивому мышлению ИЛИ НЕМЫШЛЕНИЮ ВООБЩЕ.  Если мы пойдем с методами типа предиктор-корректор, необходимо также провести анализ ошибок, что не требуется для стандартного метода, поскольку в стандартной подпрограмме правильные цифры добавляются одну за другой на каждом шаге (в отличие от вавилонского метода, где содержание цифр может изменяться при каждом усреднении).
Если мы пойдем с методами типа предиктор-корректор, необходимо также провести анализ ошибок, что не требуется для стандартного метода, поскольку в стандартной подпрограмме правильные цифры добавляются одну за другой на каждом шаге (в отличие от вавилонского метода, где содержание цифр может изменяться при каждом усреднении). Я говорю «написано», потому что это было буквально написано от руки, как и все копии. Работа Иоганна Гутенберга над печатным станком началась только в 1436 году.
Я говорю «написано», потому что это было буквально написано от руки, как и все копии. Работа Иоганна Гутенберга над печатным станком началась только в 1436 году. Например, при нахождении sqrt 645 он попадает между sqrt 625, который равен 25, и sqrt 676, который равен 26. Таким образом, sqrt 645 должен быть между 25 и 26. Где он находится между? Всего 50 номеров от 676 до 625.645 — это 20 чисел больше 625, поэтому 20/50 = 0,4.
Таким образом, sqrt 645 очень близко к 25,4
Например, при нахождении sqrt 645 он попадает между sqrt 625, который равен 25, и sqrt 676, который равен 26. Таким образом, sqrt 645 должен быть между 25 и 26. Где он находится между? Всего 50 номеров от 676 до 625.645 — это 20 чисел больше 625, поэтому 20/50 = 0,4.
Таким образом, sqrt 645 очень близко к 25,4  )
) Это также то же самое, что и при применении метода Ньютона.См., Например, поиск квадратного корня из 20 с использованием 10 в качестве начального предположения:
Это также то же самое, что и при применении метода Ньютона.См., Например, поиск квадратного корня из 20 с использованием 10 в качестве начального предположения: 472135
472135
 Что еще более важно, он имеет четкую связь с такими темами, как метод Ньютона и рекурсивные последовательности, которые будут встречаться в исчислении и за его пределами. Метод длинного деления несколько быстрее для ручного расчета, но он не приводит к другим важным темам — это тупик.
Что еще более важно, он имеет четкую связь с такими темами, как метод Ньютона и рекурсивные последовательности, которые будут встречаться в исчислении и за его пределами. Метод длинного деления несколько быстрее для ручного расчета, но он не приводит к другим важным темам — это тупик.
 6i, -12i и так далее. Это приводит к совершенно новой системе счисления комплексных чисел, в которой числа имеют действительную и мнимую части (например, 5 + 3i или -20 — 40i). И с помощью этой системы счисления можно сделать много увлекательной математики!
6i, -12i и так далее. Это приводит к совершенно новой системе счисления комплексных чисел, в которой числа имеют действительную и мнимую части (например, 5 + 3i или -20 — 40i). И с помощью этой системы счисления можно сделать много увлекательной математики!  Самое простое решение — купить калькулятор и избегать всех умственных способностей. ржу не могу
Самое простое решение — купить калькулятор и избегать всех умственных способностей. ржу не могу .. так много для усреднения. И какова степень значимости, поскольку мы работаем с одним десятичным знаком или 3 … не нужно «усреднять» слишком рано, иначе мы можем потерять значащие цифры. Если мы работаем с миллиардами, то слишком быстрое снижение цифр может иметь ОГРОМНУЮ разницу.
.. так много для усреднения. И какова степень значимости, поскольку мы работаем с одним десятичным знаком или 3 … не нужно «усреднять» слишком рано, иначе мы можем потерять значащие цифры. Если мы работаем с миллиардами, то слишком быстрое снижение цифр может иметь ОГРОМНУЮ разницу. Расчет должен быть написан инженером-программистом для машины, чтобы в конечном итоге он оставался в сознании человека.Если инженер не знает алгоритма, последствия будут нести тысячи потребителей. Я полагаю, что запоминание — это просто еще один инструмент в коробке. Используйте его, когда это уместно.
Расчет должен быть написан инженером-программистом для машины, чтобы в конечном итоге он оставался в сознании человека.Если инженер не знает алгоритма, последствия будут нести тысячи потребителей. Я полагаю, что запоминание — это просто еще один инструмент в коробке. Используйте его, когда это уместно.


 корень.
корень. {2} [/ latex], что мы читаем вслух как «n в квадрате».{2} = 9 [/ latex]
{2} [/ latex], что мы читаем вслух как «n в квадрате».{2} = 9 [/ latex]  {2} = 100 [/ latex] также, поэтому [latex] -10 [/ latex] также является квадратным корнем из [latex] 100 [/ latex]. Следовательно, и [латекс] 10 [/ латекс], и [латекс] -10 [/ латекс] являются квадратными корнями из [латекса] 100 [/ латекса].
{2} = 100 [/ latex] также, поэтому [latex] -10 [/ latex] также является квадратным корнем из [latex] 100 [/ latex]. Следовательно, и [латекс] 10 [/ латекс], и [латекс] -10 [/ латекс] являются квадратными корнями из [латекса] 100 [/ латекса].