Пирамида и усеченная пирамида
Как можно построить пирамиду? На плоскости р построим какой-либо многоугольник, например пятиугольник ABCDE. Вне плоскости р возьмем точку S. Соединив точку S отрезками со всеми точками многоугольника, получим пирамиду SABCDE (рис.).
Точка S называется вершиной, а многоугольник ABCDE — основанием этой пирамиды. Таким образом, пирамида с вершиной S и основанием ABCDE — это объединение всех отрезков [SM], где М ∈ ABCDE.
Треугольники SAB, SBC, SCD, SDE, SEA называются боковыми гранями пирамиды, общие стороны боковых граней SA, SB, SC, SD, SE — боковыми ребрами.
Пирамиды называются треугольными, четырехугольными, п-угольными в зависимости от числа сторон основания. На рис. даны изображения треугольной, четырехугольной и шестиугольной пирамид.
Плоскость, проходящая через вершину пирамиды и диагональ основания, называется диагональной, а полученное сечение —
Отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания, называется высотой пирамиды (концами этого отрезка являются вершина пирамиды и основание перпендикуляра).
Пирамида называется правильной, если основание пирамиды—правильный многоугольник и вершина пирамиды проектируется в его центр.
Все боковые грани правильной пирамиды — конгруэнтные равнобедренные треугольники. У правильной пирамиды все боковые ребра конгруэнтны.
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды. Все апофемы правильной пирамиды конгруэнтны.
Если обозначить сторону основания через а, а апофему через h, то площадь одной боковой грани пирамиды равна 1/2 ah .
Сумма площадей всех боковых граней пирамиды называется
площадью боковой поверхности пирамиды и обозначается через Sбок.Так как боковая поверхность правильной пирамиды состоит из n конгруэнтных граней, то
Sбок. = 1/2 ahn = Ph/2,
где Р — периметр основания пирамиды. Следовательно,
Sбок. = Ph/2
т. е. площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.
Площадь полной поверхности пирамиды вычисляется по формуле
S = Socн. + Sбок..
Объем пирамиды равен одной трети произведения площади ее основания Socн. на высоту Н:
V = 1/3 Socн. Н.
Вывод этой и некоторых других формул будет дан в одной из последующих глав.
Построим теперь пирамиду другим способом. Пусть дан многогранный угол, например, пятигранный, с вершиной S (рис.).
Проведем плоскость р так, чтобы она пересекала все ребра данного многогранного угла в разных точках А, В, С, D, Е (рис.). Тогда пирамиду SABCDE можно рассматривать как пересечение многогранного угла и полупространства с границей р, в котором лежит вершина S.
Очевидно, что число всех граней пирамиды может быть произвольным, но не меньшим четырех. При пересечении трехгранного угла плоскостью получается треугольная пирамида, у которой четыре грани. Любую треугольную пирамиду иногда называют тетраэдром, что означает четырехгранник.
Усеченную пирамиду можно получить, если пирамиду пересечь плоскостью, параллельной плоскости основания.
На рис. дано изображение четырехугольной усеченной пирамиды.
Усеченные пирамиды также называются треугольными, четырехугольными, n-угольными в зависимости от числа сторон основания. Из построения усеченной пирамиды следует, что она имеет два основания: верхнее и нижнее. Основания усеченной пирамиды — два многоугольника, стороны которых попарно параллельны. Боковые грани усеченной пирамиды — трапеции.
Высотой усеченной пирамиды называется отрезок перпендикуляра, проведенного из любой точки верхнего основания к плоскости нижнего.
Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и плоскостью сечения, параллельной основанию. Высота боковой грани правильной усеченной пирамиды (трапеции) называется апофемой.
Можно доказать, что у правильной усеченной пирамиды боковые ребра конгруэнтны, все боковые грани конгруэнтны, все апофемы конгруэнтны.
Если в правильной усеченной n-угольной пирамиде через а и bn обозначить длины сторон верхнего и нижнего оснований, а через h — длину апофемы, то площадь каждой боковой грани пирамиды равна
1/2( а + bn ) h
Сумма площадей всех боковых граней пирамиды называется площадью ее боковой поверхности и обозначается Sбок. . Очевидно, что для правильной усеченной n-угольной пирамиды
Sбок. = n • 1/2( а + bn ) h .
Так как па = Р и nbn= Р1 — периметры оснований усеченной пирамиды, то
Sбок. = 1/2 (Р + Р1) h ,
т. е. площадь боковой поверхности правильной усеченной пирамиды равна половине произведения суммы периметров ее оснований на апофему.
Сечение, параллельное основанию пирамиды
Теорема. Если пирамиду пересечь плоскостью, параллельной основанию, то:
1) боковые ребра и высота разделятся на пропорциональные части;
2) в сечении получится многоугольник, подобный основанию;
3) площади сечения и основания относятся, как квадраты их расстояний от вершины.
Теорему достаточно доказать для треугольной пирамиды.
Так как параллельные плоскости пересекаются третьей плоскостью по параллельным прямым, то (АВ) || (А1В1), (BС) ||( В1C1), (AС) || (A1С1) (рис.).
Параллельные прямые рассекают стороны угла на пропорциональные части, и поэтому
$$ \frac{\left|{SA}\right|}{\left|{SA_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|}=\frac{\left|{SC}\right|}{\left|{SC_1}\right|} $$Следовательно, ΔSAB ~ ΔSA1B1 и
$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|} $$ΔSBC ~ ΔSB1C1 и
$$ \frac{\left|{BC}\right|}{\left|{B_{1}C_1}\right|}=\frac{\left|{SB}\right|}{\left|{SB_1}\right|}=\frac{\left|{SC}\right|}{\left|{SC_1}\right|} $$Соответственные углы треугольников ABC и A1B1C1 конгруэнтны, как углы с параллельными и одинаково направленными сторонами. Поэтому
ΔABC ~ ΔA1B1C1
Площади подобных треугольников относятся, как квадраты соответствующих сторон:
$$ \frac{S_{ABC}}{S_{A_1 B_1 C_1}}=\frac{\left|{AB}\right|^2}{\left|{A_{1}B_1}\right|^2} $$но
$$ \frac{\left|{AB}\right|}{\left|{A_{1}B_1}\right|}=\frac{\left|{SH}\right|}{\left|{SH_1}\right|} $$Следовательно,
$$ \frac{S_{ABC}}{S_{A_1 B_1 C_1}}=\frac{\left|{SH}\right|^2}{\left|{SH_1}\right|^2} $$Теорема. Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.
Пусть (черт. 84) В и В1— площади оснований двух пирамид, H — высота каждой из них, b и b1 — площади сечений плоскостями, параллельными основаниям и удалёнными от вершин на одно и то же расстояние h.
Согласно предыдущей теореме мы будем иметь:
$$ \frac{b}{B}=\frac{h^2}{H^2}\: и \: \frac{b_1}{B_1}=\frac{h^2}{H^2} $$откуда
$$ \frac{b}{B}=\frac{b_1}{B_1}\: или \: \frac{b}{b_1}=\frac{B}{B_1} $$
Следствие. Если В = В1, то и b = b1 , т. е. если у двух пирамид с равными высотами основания равновелики, то равновелики и сечения, равноотстоящие от вершины.
razdupli.ru
Усечённые пирамиды — геометрические тела
Готовый набор «Волшебные грани»
Для сборки многогранников мы можем вам предложить уже готовые развёртки — вырезанные и подогнутые.
Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.
Кроме того, в самом выпуске вы найдете информацию о строении многогранников.

Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника, собранного из этих деталей:
Сборка правильной четырехугольной пирамиды:
Вращение готового многогранника (усечённой четырехугольной пирамиды), собранного из этих деталей:
Сборка пирамиды со звёздчатым основанием:
Вращение готового многогранника, собранного из этих деталей:
Сборка би-пирамиды с основанием в форме пятиконечной звезды:
Вращение готового многогранника, собранного из этих деталей:
mnogogranniki.ru
Усечённая пирамида — это… Что такое Усечённая пирамида?
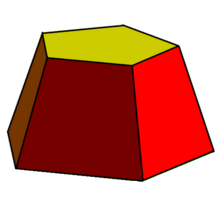 Усеченная пирамида
Усеченная пирамидаУсечё́нная пирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию.
Произвольная усечённая пирамида
Формулы для усечённой пирамиды
Объём пирамиды , где — площади оснований, — высота усечённой пирамиды.
Площадь боковой поверхности равна сумме площадей боковых граней усечённой пирамиды.
Правильная усечённая пирамида
Определение
Правильная усечённая пирамида — многогранник, образованный правильной пирамидой и её сечением, параллельным основанию.
Формулы
- (Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы)
- , где — площади оснований, а — двугранный угол при основании пирамиды.
См. также
 | В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 15 мая 2011. |
dic.academic.ru
Пирамида. Усеченная пирамида
Пирамидой называется многогранник, одна из граней которого многоугольник (основание), а все остальные грани – треугольники с общей вершиной (боковые грани) (рис. 15). Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис. 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.

Рис. 15
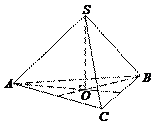
Рис. 16
Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
Теоремы
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.
2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Для вычисления объема произвольной пирамиды верна формула:

где V – объем;
Sосн – площадь основания;
H – высота пирамиды.
Для правильной пирамиды верны формулы:
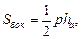
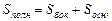

где p – периметр основания;
hа – апофема;
H – высота;
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности;
Sосн – площадь основания;
V – объем правильной пирамиды.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением
называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
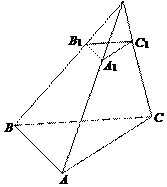
Рис. 17
Для усеченной пирамиды справедливы формулы:

 (4)
(4)
где S1, S2 – площади верхнего и нижнего оснований;
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности;
H – высота;
V – объем усеченной пирамиды.
Для правильной усеченной пирамиды верна формула:
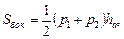
где p1 , p2 – периметры оснований;
hа – апофема правильной усеченной пирамиды.
Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Решение. Сделаем рисунок (рис. 18).
 |
Рис. 18
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: 
 т.е.
т.е.  Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс
Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс  необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части:
необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части:  и
и 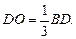 Из
Из 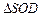
 Из
Из  находим:
находим: 
Ответ: 
Пример 2. Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны  см и
см и  см, а высота 4 см.
см, а высота 4 см.
Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований  и
и  Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Подставив все данные в формулу, вычислим объем усеченной пирамиды:

Ответ: 112 см3.
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).
 |
Рис. 19
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из 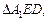 где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований.
где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. 

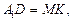 так как
так как  (см. рис. 20) и
(см. рис. 20) и 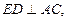
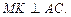 С другой стороны ОК – радиус вписанной в
С другой стороны ОК – радиус вписанной в  окружности и
окружности и 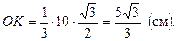 ОМ – радиус вписанной в
ОМ – радиус вписанной в  окружности:
окружности:

 MK = DE.
MK = DE.
По теореме Пифагора из 

Площадь боковой грани: 
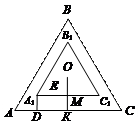
Рис. 20
Ответ: 
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j. Найти площадь полной поверхности пирамиды.
Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей 
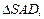

 и площади трапеции ABCD.
и площади трапеции ABCD.
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:


Рис. 21
Аналогично 
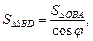
 и значит
и значит  Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.

Рис. 22
Так как в трапецию можно вписать окружность, то 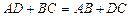 или
или 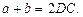 Из
Из  по теореме Пифагора имеем
по теореме Пифагора имеем

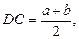
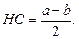
Тогда 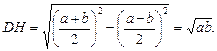
Площадь трапеции: 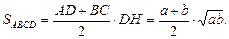
Значит,
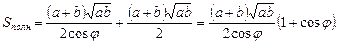
Ответ: 
Пример 5.Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.
Решение. Сделаем рисунок (рис. 23).

Рис. 23
Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( 
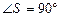 ), два других – равные треугольники
), два других – равные треугольники  Рассмотрим
Рассмотрим 


 – по условию. Вычислим его площадь:
– по условию. Вычислим его площадь: 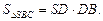 Так как
Так как  равнобедренный, то
равнобедренный, то  а так как
а так как  то
то  и следовательно в
и следовательно в 


Тогда 
Рассмотрим 
 SE найдем из
SE найдем из 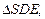
 По теореме Пифагора имеем
По теореме Пифагора имеем  Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 24).
Найдем DE. Для этого рассмотрим равносторонний треугольник основания (рис. 24). 

 В
В  отрезок DE является средней линией, значит,
отрезок DE является средней линией, значит,  Находим SE:
Находим SE:
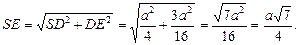

Рис. 24
Теперь 
Площадь боковой поверхности пирамиды равна:

Ответ: 
Похожие статьи:
poznayka.org
Задачи на усеченную пирамиду
Многогранник, у которого одна из граней – многоугольник, а все остальные грани – треугольники с общей вершиной, называется пирамидой.
Эти треугольники, из которых составлена пирамида, называют боковыми гранями, а оставшийся многоугольник – основанием пирамиды.
В основании пирамиды лежит геометрическая фигура – n-угольник. В таком случае пирамиду называют еще n-угольной.
Треугольную пирамиду, все ребра которой равны, называют тетраэдром.
Ребра пирамиды, которые не принадлежат основанию, называются боковыми, а их общая точка – это вершина пирамиды. Другие ребра пирамиды обычно называют сторонами основания.
Пирамиду называют правильной, если у нее в основании лежит правильный многоугольник, а все боковые ребра равны между собой.
Расстояние от вершины пирамиды до плоскости основания называется высотой пирамиды. Можно сказать, что высота пирамиды есть отрезок, перпендикулярный основанию, концы которого находятся в вершине пирамиды и на плоскости основания.
Для любой пирамиды имеют место следующие формулы:
1) Sполн = S бок + Sосн, где
Sполн – площадь полной поверхности пирамиды;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней пирамиды;
S осн – площадь основания пирамиды.
2) V = 1/3 Sосн · Н, где
V – объем пирамиды;
Н – высота пирамиды.
Для правильной пирамиды имеет место:
Sбок = 1/2 Pосн h, где
Pосн – периметр основания пирамиды;
h – длина апофемы, то есть длина высоты боковой грани, опущенной из вершины пирамиды.
Часть пирамиды, заключенная между двумя плоскостями – плоскостью основания и секущей плоскостью, проведенной параллельно основанию, называют усеченной пирамидой.
Основание пирамиды и сечение пирамиды параллельной плоскостью называются основаниями усеченной пирамиды. Остальные грани называют боковыми. Расстояние между плоскостями оснований называют высотой усеченной пирамиды. Ребра, которые не принадлежат основаниям, называются боковыми.
Кроме того, основания усеченной пирамиды подобные n-угольники. Если основания усеченной пирамиды – правильные многоугольники, а все боковые ребра равны между собой, то такая усеченная пирамида называется правильной.
Для произвольной усеченной пирамиды имеют место следующие формулы:
1) Sполн = Sбок + S1 + S2, где
Sполн – площадь полной поверхности;
Sбок – площадь боковой поверхности, т.е. сумма площадей всех боковых граней усеченной пирамиды, которые представляют собой трапеции;
S1, S2 – площади оснований;
2) V = 1/3( S1 + S2 + √(S1 · S2 ))H, где
V – объем усеченной пирамиды;
H – высота усеченной пирамиды.
Для правильной усеченной пирамиды также имеем:
Sбок = 1/2(P1 + P2) · h, где
P1 , P2 – периметры оснований;
h – апофема (высота боковой грани, представляющей собой трапецию).
Рассмотрим несколько задач на усеченную пирамиду.
Задача 1.
В треугольной усеченной пирамиде с высотой, равной 10, стороны одного из оснований равны 27, 29 и 52. Определите объем усеченной пирамиды, если периметр другого основания равен 72.
Решение.
Рассмотрим усеченную пирамиду АВСА1В1С1, изображенную на рисунке1. 
1. Объем усеченной пирамиды может быть найден по формуле
V = 1/3H · (S1 + S2 + √(S1 · S2)), где S1 – площадь одного из оснований, можно найти по формуле Герона
S = √(p(p – a)(p – b)(p – c)),
т.к. в задаче даны длины трех сторон треугольника.
Имеем: p1 = (27 + 29 + 52)/2 = 54.
S1 = √(54(54 – 27)(54 – 29)(54 – 52)) = √(54 · 27 · 25 · 2) = 270.
2. Пирамида усеченная, а значит, в основаниях лежат подобные многоугольники. В нашем случае треугольник АВС подобен треугольнику А1В1С1. Кроме того, коэффициент подобия можно найти как отношение периметров рассматриваемых треугольников, а отношение их площадей будет равно квадрату коэффициента подобия. Таким образом, имеем:
S1/S2 = (P1)2/(P2)2 = 1082/722 = 9/4. Отсюда S2 = 4S1/9 = 4 · 270/9 = 120.
Итак, V = 1/3 · 10(270 + 120 + √(270 · 120)) = 1900.
Ответ: 1900.
Задача 2.
В треугольной усеченной пирамиде через сторону верхнего основания проведена плоскость параллельно противоположному боковому ребру. В каком отношении разделился объем усеченной пирамиды, если соответственные стороны оснований относятся как 1 : 2?
Решение.
Рассмотрим АВСА1В1С1 – усеченную пирамиду, изображенную на рис. 2.
Так как в основаниях стороны относятся как 1 : 2, то площади оснований относятся как 1 : 4 (треугольник АВС подобен треугольнику А1В1С1).
Тогда объем усеченной пирамиды равен:
V = 1/3h · (S1 + S2 + √(S1 · S2)) = 1/3h · (4S2 + S2 + 2S2) = 7/3 · h · S2, где S2 – площадь верхнего основания, h – высота.
Но объем призмы АDEA1B1C1 составляет V1 = S2 · h и, значит,
V2 = V – V1 = 7/3 · h · S2 — h · S2 = 4/3 · h · S2.
Итак, V2 : V1 = 3 : 4.
Ответ: 3 : 4.
Задача 3.
Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 и 1, а высота равна 3. Через точку пересечения диагоналей пирамиды параллельно основаниям пирамиды проведена плоскость, делящая пирамиду на две части. Найти объем каждой из них.
Решение.
Рассмотрим усеченную пирамиду АВСDА1В1С1D1, изображенную на рис. 3.
Обозначим О1О2 = х, тогда ОО₂ = О1О – О1О2 = 3 – х.
Рассмотрим треугольник В1О2D1 и треугольник ВО2D:
угол В1О2D1 равен углу ВО2D как вертикальные;
угол ВDO2 равен углу D1B1O2 и угол O2ВD равен углу B1D1O2 как накрест лежащие при B1D1 || BD и секущих B₁D и BD₁ соответственно.
Следовательно, треугольник В1О2D1 подобен треугольнику ВО2D и имеет место отношение сторон:
В1D1/ВD = О1О2/ОО2 или 1/2 = х/(х – 3), откуда х = 1.
Рассмотрим треугольник В1D1В и треугольник LО2B: угол В – общий, а так же имеется пара односторонних углов при B1D1 || LM, значит, треугольник В1D1В подобен треугольнику LО2B, откуда В1D : LO2 = OO1 : OO2 = 3 : 2, т.е.
LO2 = 2/3 · B1D1, LN = 4/3 · B1D1.
Тогда SKLMN = 16/9 · SA1B1C1D1 = 16/9.
Итак, V1 = 1/3 · 2(4 + 16/9 + 8/3) = 152/27.
V2 = 1/3 · 1 · (16/9 + 1 + 4/3) = 37/27.
Ответ: 152/27; 37/27.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Усеченная пирамида
Материал урока.
На прошлых уроках мы работали с пирамидами. Давайте вспомним, какой многогранник называется пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.
Многогранник, составленный из -угольника  и
и  треугольников, называется пирамидой.
треугольников, называется пирамидой.

Пирамида называется правильной, если ее основание – правильный многоугольник.
Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.
Пусть нам дана пирамида PA1A2…An. Проведем секущую плоскость β, параллельную плоскости основания пирамиды и пусть эта плоскость пересекает боковые ребра в точках B1,B2,…, Bn.

Плоскость β разбивает пирамиду на две фигуры: пирамиду PB1B2…Bn и многогранник. Многогранник, гранями которого являются n-угольники A1A2…An и B1B2…Bn, расположенные в параллельных плоскостях и n четырехугольников A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называется усеченной пирамидой.
Вокруг нас много примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной пирамиды.клавиши клавиатуры и другие предметы.
N-угольники A1A2…An и B1B2…Bn называются соответственно верхним и нижним основанием. Четырехугольники A1A2B2B1, A2A3B3B2,…, AnA1B1Bn называются боковыми гранями.
Отрезки A1B1,…, AnBn называются боковыми рёбрами усеченной пирамиды.
Усеченную пирамиду обозначают так A1A2…AnB1B2…Bn. Возьмем на верхнем основании произвольную точку C и из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр называется высотой усеченной пирамиды.

Теперь давайте докажем, что боковые грани усеченной пирамиды – это трапеции.
Для доказательства рассмотрим грань A1A2B2B1. Понятно, что для других боковых граней доказательство будет проводится аналогично.

Поскольку секущая плоскость проводилась параллельно плоскости основания, то можно записать, что A1A2 параллельно B1B2. Очевидно, что две другие стороны четырехугольника A1A2B2B1 не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно, что все остальные боковые грани тоже будут трапециями.
Как и в случае с пирамидой, усеченная пирамида тоже может быть правильной.
Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

Основаниями усеченной пирамиды являются правильные многоугольники, а боковые грани – равнобедренные трапеции.
Высоты этих трапеций называются апофемами.

Объединение боковых граней называется боковой поверхностью усеченной пирамиды, а объединение всех граней называется полной поверхностью усеченной пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.

А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.

Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной усеченной пирамиды.
Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.
Доказательство.

Запишем формулу для нахождения площади боковой поверхности усеченной пирамиды.

Поскольку усеченная пирамида правильная, значит, ее гранями будут равнобедренные трапеции.

Площадь равнобедренной трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани есть ничто иное как апофема усеченной пирамиды.

Подставим все в исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем стороны по основаниям. Тогда получим, что площадь боковой поверхности будет равна произведению полусуммы периметров оснований усеченной пирамиды на апофему.

Что и требовалось доказать.
Решим несколько задач.
Задача. Стороны
оснований правильной усеченной четырехугольной пирамиды  равны
равны  и
и  . Высота пирамиды
равна
. Высота пирамиды
равна  . Найти площадь
боковой поверхности.
. Найти площадь
боковой поверхности.
Решение.




Ответ. 120 см2
Решим еще одну задачу.
Задача. Пирамида пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.
Решение.


Что и требовалось доказать.
Решим еще одну задачу.
Задача. Правильная
треугольная пирамида  с высотой
с высотой  и стороной основания
равной
и стороной основания
равной  рассечена плоскостью
рассечена плоскостью
 , проходящей через
середину
, проходящей через
середину  высоты
высоты  параллельно
основанию
параллельно
основанию  . Найти площадь
боковой поверхности полученной усеченной пирамиды.
. Найти площадь
боковой поверхности полученной усеченной пирамиды.
Решение.

 Ответ.
135
Ответ.
135 см2.
см2.
Подведем итоги урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной усеченной пирамиды. Решили несколько задач.
videouroki.net
Энергетическая конструкция человека. Усеченная пирамида с навершием.
Переключение навигации- О нас
- О проекте
- Обратная связь
- Ваше мнение
- Предложить материал
- Журнал изменений
- О нас
- О проекте
- Обратная связь
- Ваше мнение
- Журнал изменений
- Предложить материал
- Войти
- Регистрация
- Рус
- Eng
- Были:
- Ригден Джаппо,
- Ахура Мазда,
- Осирис,
- Архангел Гавриил,
- Джабраил,
- Агапит Печерский,
- Кетцалькоатль
- Ожидаем:
- Имам Махди,
- Утешитель,
- Святой Дух,
- Майтрейя,
- Калки Аватар,
- Машиах,
- Гэсэр-хан
- Главная
- О нас
- О проекте
- Обратная связь
- Ваше мнение
- Предложить материал
- Журнал изменений
- Исконные Знания
- Беседы с И.М. Даниловым
- Книги
- Истина на всех одна
- Иллюзия и Путь
- Жизнь
- Сознание и Личность. От заведомо мёртвого к вечно живому
- Пророчества
- Религии
- Христианство
- Ислам
- Буддизм
- Индуизм
- Иудаизм
- Зороастризм
- Символика и мифология
- Символика и Мифология
- Астрономия
- Мир Пирамид
rgdn.info