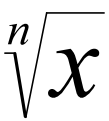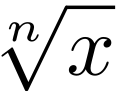Квадратный корень из 2 — Википедия

1,4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 3501384623 0912297024 9248360558 5073721264 4121497099 9358314132 2266592750 5592755799 9505011527 8206057147 0109559971 6059702745 3459686201 4728517418 6408891986 0955232923 0484308714 3214508397 6260362799 5251407989 6872533965 4633180882 9640620615 2583523950 5474575028 7759961729 8355752203 3753185701 1354374603 4084988471 6038689997 0699004815 0305440277 9031645424 7823068492 9369186215 8057846311 1596668713 0130156185 6898723723 5288509264 8612494977 1542183342 0428568606 0146824720 7714358548 7415565706 9677653720 2264854470 1585880162 0758474922 6572260020 8558446652 1458398893 9443709265 9180031138 8246468157 0826301005 9485870400 3186480342 1948972782 9064104507 2636881313 7398552561 1732204024 5091227700 2269411275 7362728049 5738108967 5040183698 6836845072 5799364729 0607629969 4138047565 4823728997 1803268024 7442062926 9124859052 1810044598 4215059112 0249441341 7285314781 0580360337 1077309182 8693147101 7111168391 6581726889 4197587165 8215212822 9518488472

---

Значение √2 с первой тысячей разрядов десятичной дроби^[1]. Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.

Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: 2.{\displaystyle {\sqrt {2}}.}

Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).

Квадратный корень из 2.

Хорошим и часто используемым приближением к 2{\displaystyle {\sqrt {2}}} является дробь 9970{\displaystyle {\tfrac {99}{70}}}. Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.

Вавилонская глиняная табличка с максимально точным указанием длины диагонали единичного квадрата четырёхзначным шестидесятеричным числом.

Вавилонская глиняная табличка (ок. 1800–1600 до н. э.) даёт наиболее точное приближённое значение 2{\displaystyle {\sqrt {2}}} при записи в четырёх шестидесятеричных цифрах, что после округления составляет 6 точных десятичных цифр:

1+2460+51602+10603=1.41421(296).{\displaystyle 1+{\frac {24}{60}}+{\frac {51}{60^{2}}}+{\frac {10}{60^{3}}}=1.41421(296).}

Другое раннее приближение этого числа в древнеиндийском математическом тексте, называемом «Шульба-сутры» (ок. 800—200 до н. э.) даётся следующим образом:

1+13+13⋅4−13⋅4⋅34=577408≈1.414215686.{\displaystyle 1+{\frac {1}{3}}+{\frac {1}{3\cdot 4}}-{\frac {1}{3\cdot 4\cdot 34}}={\frac {577}{408}}\approx 1.414215686.}

Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта, которого за это открытие, по разным вариантам легенды, пифагорейцы не то убили, не то изгнали, поставив ему в вину разрушение главной пифагорейской доктрины о том, что «всё есть [натуральное] число». Поэтому квадратный корень из 2 иногда называют постоянной Пифагора, так как именно пифагорейцы доказали его иррациональность, тем самым открыв существование иррациональных чисел^{[источник не указан 2300 дней]}.

Существует множество алгоритмов для приближения значения квадратного корня из двух обыкновенными или десятичными дробями. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:

an+1=an+2an2=an2+1an.{\displaystyle a_{n+1}={\frac {a_{n}+{\frac {2}{a_{n}}}}{2}}={\frac {a_{n}}{2}}+{\frac {1}{a_{n}}}.}

Чем больше повторений в алгоритме (то есть, чем больше n{\displaystyle n}), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Несколько первых приближений, начиная с a0=1{\displaystyle a_{0}=1}:

• 32=1,5{\displaystyle {\frac {3}{2}}={\color {Green}1}{,}5}
• 1712=1,416…{\displaystyle {\frac {17}{12}}={\color {Green}1{,}41}6\ldots }
• 577408=1,414215…{\displaystyle {\frac {577}{408}}={\color {Green}1{,}41421}5\ldots }
• 665857470832=1,4142135623746…{\displaystyle {\frac {665857}{470832}}={\color {Green}1{,}41421356237}46\ldots }

В 1997 году Ясумаса Канада вычислил значение 2{\displaystyle {\sqrt {2}}} до 137 438 953 444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Сигэру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор с частотой 3,6 ГГц и 16 ГБ ОЗУ.

Для запоминания значения корня из двойки с восемью знаками после запятой (1,41421356) можно воспользоваться следующим текстом (число букв в каждом слове соответствует десятичной цифре): «И плод у меня, но у них много корней».

Половина 2{\displaystyle {\sqrt {2}}} приблизительно равна 0,70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора, образующего угол 45° с координатными осями:

22=12=12=cos⁡45∘=sin⁡45∘.{\displaystyle {\frac {\sqrt {2}}{2}}={\sqrt {\frac {1}{2}}}={\frac {1}{\sqrt {2}}}=\cos 45^{\circ }=\sin 45^{\circ }.}

Одно из интересных свойств 2{\displaystyle {\sqrt {2}}} состоит в следующем:

 12−1=2+1{\displaystyle \ {1 \over {{\sqrt {2}}-1}}={\sqrt {2}}+1}. Потому что (2+1)(2−1)=2−1=1.{\displaystyle ({\sqrt {2}}+1)({\sqrt {2}}-1)=2-1=1.}

Это является результатом свойства серебряного сечения.

Другое интересное свойство 2{\displaystyle {\sqrt {2}}}:

2+2+2+⋯=2.{\displaystyle {\sqrt {2+{\sqrt {2+{\sqrt {2+\cdots }}}}}}=2.}

Квадратный корень из двух может быть выражен в мнимых единицах i, используя только квадратные корни и арифметические операции:

i+iii{\displaystyle {\frac {{\sqrt {i}}+i{\sqrt {i}}}{i}}} и −i−i−i−i.{\displaystyle {\frac {{\sqrt {-i}}-i{\sqrt {-i}}}{-i}}.}

Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.

222 ⋅⋅⋅=2{\displaystyle {\sqrt {2}}^{{\sqrt {2}}^{{\sqrt {2}}^{\ \cdot ^{\cdot ^{\cdot }}}}}=2}

Квадратный корень из двух может быть также использован для приближения π{\displaystyle \pi }:

2m2−2+2+⋯+2→π{\displaystyle 2^{m}{\sqrt {2-{\sqrt {2+{\sqrt {2+\cdots +{\sqrt {2}}}}}}}}\to \pi \quad }при m→∞.{\displaystyle m\to \infty .}

С точки зрения высшей алгебры, 2{\displaystyle {\sqrt {2}}} является корнем многочлена x2−2{\displaystyle x^{2}-2} и поэтому является целым алгебраическим числом^[2]. Множество чисел вида a+b2{\displaystyle a+b{\sqrt {2}}}, где a,b{\displaystyle a,b} — рациональные числа, образует алгебраическое поле. Оно обозначается Q[2]{\displaystyle \mathbb {Q} [{\sqrt {2}}]} и является подполем поля вещественных чисел.

Применим доказательство от противного: допустим, 2{\displaystyle {\sqrt {2}}} рационален, то есть представляется в виде дроби mn{\displaystyle {\frac {m}{n}}}, где m{\displaystyle m} — целое число, а n{\displaystyle n} — натуральное.

Возведём предполагаемое равенство в квадрат:

2=mn⇒2=m2n2⇒m2=2n2{\displaystyle {\sqrt {2}}={\frac {m}{n}}\Rightarrow 2={\frac {m^{2}}{n^{2}}}\Rightarrow m^{2}=2n^{2}}.

Так как разложение m2{\displaystyle m^{2}} на простые множители содержит 2{\displaystyle 2} в чётной степени, а 2n2{\displaystyle 2n^{2}} — в нечётной, равенство m2=2n2{\displaystyle m^{2}=2n^{2}} невозможно. Значит, исходное предположение было неверным, и 2{\displaystyle {\sqrt {2}}} — иррациональное число.

Квадратный корень из двух может быть представлен в виде непрерывной дроби:

 2=1+12+12+12+12+⋱.{\displaystyle \ {\sqrt {2}}=1+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+{\cfrac {1}{2+\ddots }}}}}}}}.}

Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь mn{\displaystyle {\frac {m}{n}}}, то последующая имеет вид m+2nm+n{\displaystyle {\frac {m+2n}{m+n}}}. Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:

32; 75; 1712; 4129; 9970; 239169; 577408; 1393985; 33632378…{\displaystyle {\frac {3}{2}};\ {\frac {7}{5}};\ {\frac {17}{12}};\ {\frac {41}{29}};\ {\frac {99}{70}};\ {\frac {239}{169}};\ {\frac {577}{408}};\ {\frac {1393}{985}};\ {\frac {3363}{2378}}\dots }

Квадрат последней приведенной дроби равен (округлённо) 2,000000177.

Квадратный корень из двух используется в соотношении сторон листа бумаги формата ISO 216. Соотношение сторон равно 1:2{\displaystyle 1:{\sqrt {2}}}. При разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции. Это позволяет нумеровать форматы бумаги одним числом по убыванию площади листа (числу разрезов): А0, А1, А2, А3, А4,…

• Клауди Альсина. Секта чисел. Теорема Пифагора. — М.: Де Агостини, 2014. — 152 с. — (Мир математики: в 45 томах, том 5). — ISBN 978-5-9774-0633-8.

Арифметический квадратный корень

Вспомним, что такое арифметический квадратный корень.

Уравнение  имеет два решения:  и .

Это числа, квадрат которых равен .

А как решить уравнение ?

Если мы нарисуем график функции , то увидим, что и у этого уравнения есть два решения, одно из которых положительно, а другое отрицательно.

Но эти решения не являются целыми числами. Более того, они не являются рациональными. Для того чтобы записать эти решения, мы вводим специальный символ квадратного корня.

Арифметический квадратный корень из числа  — это такое неотрицательное число, квадрат которого равен .

Запомните это определение.

Арифметический квадратный корень обозначается .

Согласно определению,

Приведем несколько примеров.

Еще раз повторим определение: Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a

Это значит, что (это наши первые два примера). Очевидно,

А с третьим примером интереснее: поскольку по определению.

Обратите внимание:

1) В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при

2) Выражение всегда неотрицательно, т. е. Например,

Свойства арифметического квадратного корня:

Запомним: выражения и не равны друг другу.Легко проверить.

, верно? Как вы думаете, чему в общем случае равен

На этот вопрос мы ответим немного позже. А сейчас решим несколько задач из вариантов Профильного ЕГЭ по математике.

1. Найдите значение выражения

Обратите внимание: не равен

Ответ: 6.

2. Найдите значение выражения

Применили формулу разности квадратов:

Ответ: 33.

3. Вычислите:

Применили формулу квадрата суммы.

4. Найдите значение выражения при

Ответ: 5

Иногда — например, при решении неравенств — надо сравнить два выражения, содержащих знак корня.

5. Что больше: или ?

Никаких приближенных вычислений!

Напомним еще раз, что , так что «убирать» корни мы не можем.

, значит,

График функции 

Построим график функции Возьмем несколько значений аргумента x, причем таких, что квадратный корень из них является целым числом.

	0	1	4	9	16	25
	0	1	2	3	4	5

Область определения функции:

Область значений функции:

Вот как выглядит график функции

Нарисуем в одной системе координат графики функций и при

Что же мы видим? При графики функций и симметричны относительно прямой

То, что для функции является областью определения, для функции — область значений (при неотрицательных x).

Такие функции называют взаимно-обратными. 

Корень из квадрата: 

Если вы внимательно читаете эту статью, то помните, что один вопрос остался без ответа. Чему равен ?

Здесь a — некоторое число или выражение. По определению арифметического квадратного корня, — это такое неотрицательное число, квадрат которого равен Оно равно a при и равно -a при Узнаете определение модуля? Запомним:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

Квадратный корень, формула, калькулятор | Формулы с примерами

Квадратный корень 8 класс

Формула, определение
Квадратный корень из числа a — в алгебре является число (b),
квадрат которого равен a ( a ? 0 ).

Калькулятор квадратного корня онлайн, возвести в квадрат онлайн

Правило Числа 6 и -6 это квадратные корни из 36, поскольку 6² = 36 и (-6)² = 36.

Пример 4² = (-4)² = 16;

9² = (-9)² = 81;

21² = (-21)² = 441.

Арифметический квадратный корень, формула

Формула, определение
Арифметическим квадратным корнем

из числа a — называется неотрицательное число ( c ), квадрат которого равен a; обозначается как ?a:

Пример ?9 = 3, так как 3² = 9 и 3 > 0;

?49 = 7, так как 7² = 49 и 7 > 0;

?36 ? -6, так как -6

Правило
! Квадратный корень и арифметический квадратный корень это
разные понятия.

! Запись ?a читают: «квадратный корень из a». Слово «арифметический»
при чтении опускают.

! Знак « ? » всегда означает «арифметический квадратный корень
из числа».

Пример (?1,2)² = 1,2;

(?455)² = 455;

(?583)² = 583.

Формулы по алфавиту:

© 2020 Все права защищены
При использовании материалов данного сайта обязательно указывать ссылку на источник

Квадратный корень из 2 — это… Что такое Квадратный корень из 2?

Квадратный корень из 2 равен длине гипотенузы в прямоугольном треугольнике с длиной катетов 1.

Квадратный корень из числа 2 — положительное вещественное число, которое при умножении само на себя даёт число 2. Обозначение: Приведём значение корня из 2 с 65 знаками после запятой:

1,414 213 562 373 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99…

Геометрически корень из 2 можно представить как длину диагонали квадрата со стороной 1 (это следует из теоремы Пифагора). Вероятно, это было первое известное в истории математики иррациональное число (то есть число, которое нельзя точно представить в виде дроби).

Квадратный корень из 2.

Хорошим и часто используемым приближением к является дробь . Несмотря на то, что числитель и знаменатель дроби лишь двузначные целые, оно отличается от реального значения меньше, чем на 1/10000.

История

Вавилонская глиняная табличка с примечаниями.

Вавилонская глиняная табличка (ок. 1800—1600 до н. э.) даёт приближённое значение в четырёх шестидесятеричных цифрах, что составляет 8 десятичных цифр:

Другое раннее приближение этого числа в древнеиндийском математическом тексте, Шульба-сутры (ок. 800—200 до н. э.) даётся следующим образом:

Пифагорейцы обнаружили, что диагональ квадрата несоизмерима с его стороной, или на современном языке, что квадратный корень из двух является иррациональным. Мало что известно с определённостью о времени и обстоятельствах этого выдающегося открытия, но традиционно его авторство приписывается Гиппасу из Метапонта.

Алгоритмы вычисления

Существует множество алгоритмов для вычисления значения квадратного корня из двух. В результате алгоритма получается приблизительное значение в виде обыкновенной или десятичной дроби. Самый популярный алгоритм для этого, который используется во многих компьютерах и калькуляторах, это вавилонский метод вычисления квадратных корней. Он состоит в следующем:

Чем больше повторений в алгоритме (то есть, чем больше «n»), тем лучше приближение квадратного корня из двух. Каждое повторение приблизительно удваивает количество правильных цифр. Приведём несколько первых приближений:

• 3/2 = 1.5
• 17/12 = 1.416…
• 577/408 = 1.414215…
• 665857/470832 = 1.4142135623746…

В 1997 году Ясумаса Канада вычислил значение √2 до 137,438,953,444 десятичных знаков после запятой. В феврале 2007 года рекорд был побит: Шигеру Кондо вычислил 200 миллиардов десятичных знаков после запятой в течение 13 дней и 14 часов, используя процессор 3.6 GHz с 16 ГБ ОЗУ. Среди математических констант только было вычислено более точно.

Свойства квадратного корня из двух

Половина √2 приблизительно равна 0.70710 67811 86548; эта величина даёт в геометрии и тригонометрии координаты единичного вектора,образующего угол 45° с координатными осями:

Одно из интересных свойств √2 состоит в следующем:

.Потому что

Это является результатом свойства серебряного сечения.

Другое интересное свойство √2:

Квадратный корень из двух может быть выражен в мнимых единицах i используя только квадратные корни и арифметические операции:

и

Квадратный корень из 2 является единственным числом, отличным от 1, чья бесконечная тетрация равна его квадрату.

Квадратный корень из двух может быть также использован для приближения π:

С точки зрения высшей алгебры, является корнем многочлена и поэтому является целым алгебраическим числом. Множество чисел вида , где — рациональные числа, образует алгебраическое поле. Оно обозначается и является подполем поля вещественных чисел.

Доказательство иррациональности

Применим доказательство от противного: допустим, рационален, то есть представляется в виде несократимой дроби , где и — целые числа. Возведём предполагаемое равенство в квадрат:

.

Отсюда следует, что чётно, значит, чётно и . Пусть , где целое. Тогда

Следовательно, чётно, значит, чётно и . Мы получили, что и чётны, что противоречит несократимости дроби . Значит, исходное предположение было неверным, и — иррациональное число.

Непрерывная дробь

Квадратный корень из двух может быть представлен в виде непрерывной дроби:

Подходящие дроби данной непрерывной дроби дают приближённые значения, быстро сходящиеся к точному квадратному корню из двух. Способ их вычисления прост: если обозначить предыдущую подходящую дробь , то последующая имеет вид . Скорость сходимости здесь меньше, чем у метода Ньютона, но вычисления гораздо проще. Выпишем несколько первых приближений:

Квадрат последней приведенной дроби равен (округлённо) 2,000000177.

Размер бумаги

Квадратный корень из двух является пропорцией формата бумаги ISO 216. Соотношение сторон таково, что при разрезании листа пополам параллельно его короткой стороне получатся два листа той же пропорции.

См. также

Знак корня — Википедия

Материал из Википедии — свободной энциклопедии

Знак корня
√∛
	√: square root ∛: cube root
Юникод	√: U+221A ∛: U+221B
HTML-код	√‎:  или  ∛‎:  или
UTF-16	√‎: 0x221A ∛‎: 0x221B
	√: %E2%88%9A ∛: %E2%88%9B
Мнемоника	√: √

Знак корня (знак радикала) (√) в математике — условное обозначение {\displaystyle {\sqrt {\quad }}} для корней, по умолчанию квадратных. В общем случае (для корней n-й степени) показатель степени ставится над «птичкой»: знак 3{\displaystyle {\sqrt[{3\,}]{\quad }}} используется для кубических корней, 4{\displaystyle {\sqrt[{4\,}]{\quad }}} — для корней 4-й степени и т. п.; для квадратного корня также можно использовать «полное» обозначение 2{\displaystyle {\sqrt[{2\,}]{\quad }}}.

Знак корня происходит из строчной латинской буквы r (начальной в лат. radix — корень), сросшейся с надстрочной чертой: ранее надчёркивание выражения использовалось вместо нынешнего заключения его в скобки. Так что a+b{\displaystyle {\sqrt {a+b}}} есть всего лишь видоизменённый способ записи выражения  ra+b¯{\displaystyle \ r{\overline {a+b}}}.

Впервые такое обозначение использовал немецкий математик Кристоф Рудольф в 1525 году. Им также были изобретены символы и для корней третьей и четвёртой степеней соответственно^[1].

• 

  американский вариант

• 

  немецкий вариант

• 

  русский вариант ^[2]

• 

В некоторых типографских традициях (например, в германской) принято верхнюю черту знака корня снабжать справа небольшой обращённой вниз засечкой. В Американской типографике (в частности, системе T_EΧ) этой детали нет.

Длина и высота знака корня должны быть такими, чтобы полностью покрывать подкоренное выражение. При соседстве в одной строке нескольких подкоренных выражений разной (но близкой) высоты часто бывает принято все знаки корня подстраивать под самое высокое из них.

Знак корня используют только для выражений, помещающихся в пределах строки, а для более длинных вместо abcde…n{\displaystyle {\sqrt[{n\,}]{abcde\dots }}} применяют эквивалентную запись (abcde…)1/n{\displaystyle (abcde\dots )^{1/n}}. Впрочем, в некоторых руководствах по набору и вёрстке упоминается разрыв подкоренного выражения на несколько строк; при этом знак корня ставится над первой, а над продолжением подкоренного выражения ставится черта; в месте разрыва строк и знак корня, и черта над продолжением снабжаются стрелками, обращёнными наружу.

• Florian Cajori: A History of Mathematical Notations (Two Volume in One), Cosimo, 2011 (Nachdruck). ISBN 1-61640-571-6.

Плюс (+) Минус (−) Знак умножения (· или ×) Знак деления (: или /) Обелюс (÷) Знак корня (√) Факториал (!) Знак интеграла (∫) Набла (∇) Знак равенства (=, ≈, ≡ и др.) Знаки неравенства (≠, >, < и др.) Пропорциональность (∝) Скобки (( ), [ ], ⌈ ⌉, ⌊ ⌋, { }, ⟨ ⟩) Вертикальная черта (|) Косая черта, слеш (/) Обратная косая черта, бэкслеш (\) Знак бесконечности (∞) Знак градуса (°) Штрих (′, ″, ‴, ⁗) Звёздочка (*) Процент (%) Промилле (‰) Тильда (~) Карет (^) Циркумфлекс (ˆ) Плюс-минус (±) Знак минус-плюс (∓) Десятичный разделитель (, или .) Символ конца доказательства (∎)

Квадратный корень из 3 — Википедия

Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ{\displaystyle e^{\pi }} и π
Система счисления	Оценка числа √3
Десятичная	1,7320508075688772935…
Двоичная	1,1011101101100111101…
Шестнадцатеричная	1,BB67AE8584CAA73B…
Шестидесятеричная	1; 43 55 22 58 27 57 56 …
Рациональные приближения	5/3; 7/4; 19/11; 26/15[1]; 71/41; 97/56; 265/153[1]; 362/209; 989/571; 1351/780[1] (перечислено в порядке увеличения точности)
Непрерывная дробь	1+11+12+11+12+11+⋱{\displaystyle 1+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {1}{1+\ddots }}}}}}}}}}}

1,7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756 7562614141 5406703029 9699450949 9895247881 1655512094 3736485280 9323190230 5582067974 8201010846 7492326501 5312343266 9033228866 5067225466 8921837971 2270471316 6036786158 8019049986 5373798593 8946765034 7506576050 7566183481 2960610094 7602187190 3250831458 2952395983 2997789824 5082887144 6383291734 7224163984 5878553976 6795806381 8353666110 8431737808 9437831610 2088305524 9016700235 2071114428 8695990956 3657970871 6849807289 9493296484 2830207864 0860398873 8697537582 3173178313 9599298300 7838702877 0539133695 6331210370 7264019249 1067682311 9928837564 1141422016 7427521023 7299427083 1059898459 4759876642 8889779614 7837958390 2288548529 0357603385 2808064381 9723446610 5968972287 2865264153 8226646984 2002119548 4155278441 1812865345 0703519165 0016689294 4154808460 7127714399 9762926834 6295774383 6189511012 7148638746 9765459824 5178855097 5379013880 6649619119 6222295711 0555242923 7231921977 3826256163 1468842032 8537166829 3864961191 7049738836 3954959381

---

Первые 1000 знаков значения √3^[2].

Квадратный корень из числа 3 — положительное действительное число, которое при умножении само на себя даёт число 3. Обозначение: 3.{\displaystyle {\sqrt {3}}.}

Содержание

• 1 Значение
• 2 Применение
  • 2.1 Геометрия и тригонометрия
  • 2.2 Электроэнергетика
• 3 См. также
• 4 Литература
• 5 Примечания
• 6 Ссылки

Квадратный корень из 3 является иррациональным числом, то есть не может быть точно представлен никакой дробью. С точностью до 0,01 % значение 3≈1,732.{\displaystyle {\sqrt {3}}\approx 1{,}732.} Хорошее приближение даёт также обыкновенная дробь 9756≈1.73214.{\displaystyle {\tfrac {97}{56}}\approx 1{.}73214.}

Может быть также выражен:

• непрерывной дробью [1; 1, 2, 1, 2, 1, 2, …];
• бесконечным вложенным радикалом:

3=−1+212+12+12+….{\displaystyle {\sqrt {3}}=-1+2{\sqrt {{\frac {1}{2}}+{\sqrt {{\frac {1}{2}}+{\sqrt {{\frac {1}{2}}+…}}}}}}.}

Геометрия и тригонометрия[править | править код]

Квадратный корень из 3 равен длине между параллельными сторонами правильного шестиугольника со сторонами 1.

Если длина стороны равностороннего треугольника равна 1, то каждая высота этого треугольника равна 3/2.{\displaystyle {\sqrt {3}}/2.}

3{\displaystyle {\sqrt {3}}} равен также:

• тангенсу 60°;
• расстоянию между параллельными сторонами правильного шестиугольника со сторонами 1;
• длине диагонали куба со стороной 1;
• длине стороны равностороннего треугольника, у которого радиус описанной окружности равен 1.

Электроэнергетика[править | править код]

При трёхфазной системе токов модуль напряжения между двумя фазами (линейное напряжение) в 3{\displaystyle {\sqrt {3}}} больше модуля фазного напряжения.

• Квадратный корень из 2
• Квадратный корень из 5

• Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
• Щетников А. И. К вопросу о рациональных приближениях 3{\displaystyle {\sqrt {3}}} у Архимеда: новая реконструкция.. — Труды вторых Колмогоровских чтений. — Ярославль: Изд. ЯГПУ, 2004. — С. 136—144. — 382 с.

1. ↑ ^{1 2 3} Эти приближения были известны Архимеду
2. ↑ The square root of three

• Proof that square root of 3 is irrational (англ.)
• Weisstein, Eric W. Theodorus’ Constant (англ.) на сайте Wolfram MathWorld.

Иррациональные числа
Постоянная Апери (ζ(3)) Константа Эрдёша — Борвейна (E) Постоянные Фейгенбаума Мечта софомора Константа простых чисел (ρ) Пластическое число (ρ) Логарифм двойки (ln 2) Корень 12-й степени из 2 (12√2) Квадратный корень из 2 (√2) Квадратный корень из 3 (√3) Квадратный корень из 5 (√5) Золотое сечение (φ) Сверхзолотое сечение (ψ) Серебряное сечение (δS) e Пи Постоянная Гельфонда (eπ) Постоянная Гельфонда — Шнайдера (2√2)
Шизофренические Трансцендентные Тригонометрические