Линейное уравнение с двумя переменными и его график, примеры

График линейного уравнения с двумя переменными

В линейном уравнении с двумя переменными ax+by=c , a и b называют коэффициентами при переменных, c — свободным членом.

Если хотя бы один из коэффициентов при переменных не равен нулю, графиком линейного уравнения с двумя переменными является прямая.

Действительно:

$$ ax+by = c \iff y = — \frac{a}{b} x+ \frac{c}{b} $$

Если сравним полученное уравнение $с y = kx+ \tilde b$ (см. §38 данного справочника), получаем:

$$ k = -\frac{a}{b} , \tilde b = \frac{c}{b}$$

Графиком $y = kx+ \tilde b$ является прямая, угловой коэффициент k определяет угол наклона, слагаемое $\tilde b$ – точку пересечения прямой с осью Y (см. §39 данного справочника).

Точки пересечения с осями координат:

${\left\{ \begin{array}{c} x = 0 \\ y = \frac{c}{b}\end{array} \right.}, {\left\{ \begin{array}{c} x = \frac{c}{a} \\ y = 0\end{array} \right.}$

Внимание!

График линейной функции ax+by=c с ненулевыми коэффициентами очень удобно чертить по двум точкам пересечения с осями координат: точка на оси X ( $\frac{c}{a}$;0) и точка на оси Y (0; $\frac{c}{b}$)

Равенство нулю коэффициентов при переменных:

$a = 0,b \neq 0$

$a \neq 0, b = 0$

$0x+2y = 4 \Rightarrow y = 2$

График – прямая, параллельная оси Х.

$3x+0y = 3 \Rightarrow x = 1$

График – прямая, параллельная оси У.

0x+0y = 0

x, $y \in \Bbb R$ — любое действительное число.

График – вся координатная плоскость

0x+0y = 5

Решений нет.

График – пустое множество.

Взаимное расположение графиков двух уравнений

$$ a_1 x+b_1 y = c_1 и a_2 x+b_2 y = c_2 $$

$ \frac{a_1}{a_2} \neq \frac{b_1}{b_2} $

$ \frac{a_1}{a_2} = \frac{b_1}{b_2} \neq \frac{c_1}{c_2} $

$ \frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2} $

Прямые пересекаются

Прямые параллельны

Прямые совпадают

Примеры

Пример 1. Постройте график линейного уравнения по двум точкам пересечения с осями.

Пример 2. Постройте в одной координатной плоскости графики, найдите точку пересечения:

а) x+2y = 4 и x-2y = 4

Точка пересечения (4;0)

б) x+y = 4 и x-y = -1

Точка пересечения (1,5;2,5)

Линейное уравнение с двумя переменными и его график (конспект+ презентация)

Цели урока:

выработать у обучающихся умение строить графики линейного уравнения с двумя переменными, решать задачи, используя при составлении математической модели две переменные;

развивать познавательные навыки обучающихся, критическое и творческое мышление; воспитание познавательного интереса к математике, настойчивости, целеустремленности в учебе.

Задачи:

ввести понятие линейного уравнения как математическую модель реальной ситуации;

научить по виду определять линейное уравнение и его коэффициенты;

научить по заданному значению х находить соответствующее значение у, и наоборот;

ввести алгоритм построения графика линейного уравнения и научить применять его на практике;

научить составлять линейное уравнение, как математическую модель задачи.

На уроке кроме ИКТ технологий используются проблемное обучение, элементы развивающего обучения, технология группового взаимодействия.

Тип урока: урок формирования умений и навыков.

I. Организационный этап. Слайд 1.

Проверка готовности учащихся к уроку, сообщение темы урока, целей и задач.

II. Устная работа.

1. Слайд 2. Из предложенных уравнений выбрать линейное уравнение с двумя переменными:

А) 3х – у = 14

Б) 5у + х² = 16

В) 7ху – 5у = 12

Г) 5х + 2у = 16

Ответ: а, г.

Дополнительный вопрос: Какое уравнение с двумя переменными называется линейным?

Слайд 3.

Ответ: ах + ву + с = 0.

Слайд 4. Отработка понятия линейного уравнения на примерах (устная работа).

Слайд 5-6. Назвать коэффициенты линейного уравнения.

2. Слайд 7. Выбрать точку, которая принадлежит графику уравнения 2х + 5у = 12

А(-1; -2), В(2; 1), С(4; -4), D(11; -2).

Ответ: D(11; -2).

Дополнительный вопрос: Что является графиком уравнения с двумя переменными? Слайд 8.

Ответ: прямая.

3. Слайд 9. Найдите абсциссу точки М(х; -2), принадлежащей графику уравнения 12х – 9у = 30.

Ответ: х = 1.

Дополнительный вопрос: Что называется решением уравнения с двумя переменными? Слайд 10.

Ответ: решением уравнения с двумя переменными называется пара значений переменных, обращающая это уравнение в верное равенство.

4. Слайд 11.

1. На каком рисунке у графика линейной функции положительный угловой коэффициент
2. На каком рисунке у графика линейной функции отрицательный угловой коэффициент
3. График какой функции мы не изучали?

5. Слайд 12. Назовите числовой промежуток, соответствующий геометрической модели:

А). (-6 ; 8) Б). (-6 ; 8] В).[- 6; 8) Г).[-6 ;8]

X

-6 8

III. Постановка цели урока.

Сегодня на уроке мы будем закреплять умение строить графики линейного уравнения с двумя переменными, решать задачи, используя при составлении математической модели две переменные (необходимость составления линейного уравнения для решения задачи с двумя неизвестными).

Постарайтесь быть настойчивыми и целеустремленными при выполнении заданий.

IV. Закрепление. Слайд 13.

Задача. Из городов А и В, расстояние между которыми 500 км, навстречу друг другу вышли два поезда, каждый со своей постоянной скоростью. Известно, что первый поезд вышел на 2 ч раньше второго. Через 3ч после выхода второго поезда они встретились. Чему равны скорости поездов? Составить математическую модель к задаче и найти два решения.

Слайд 14. (Составление математической модели к задаче). Демонстрация составления математической модели.

— Что является решением линейного уравнения с двумя переменными?

Учитель ставит вопрос: сколько решений имеет линейное уравнение с двумя переменными? Ответ: бесконечно много.

Учитель : как можно найти решения линейного уравнения с двумя переменными? Ответ: подобрать.

Учитель: как легче подобрать решения уравнения?

Ответ: подобрать одну переменную, например х, и из уравнения найти другую — у.

Слайд 15.

— Проверьте являются ли пары следующих значений решением уравнения.

Задача.

Слайд 16.

Два тракториста вспахали вместе 678 га. Первый тракторист работал 8 дней, а второй 11 дней. Сколько гектаров вспахивал за день каждый тракторист? Составьте линейное уравнения с двумя переменными к задаче и найдите 2 решения.

Слайд 17-18.

— Что называют графиком уравнения с двумя переменными? Рассмотреть различные случаи.

Слад 19. Алгоритм построения графика линейной функции.

Слайд 20. (устно) Рассмотреть пример построения графика линейного уравнения с двумя переменными.

V. Работа по учебнику.

Слайд 21. Построить график уравнения:

стр. 269

I вариант № 1206 (б)

II вариант № 1206 (в)

VI. Самостоятельная работа. Слайд 22.

Вариант 1.

1. Какие из пар чисел (1;1), (6;5), (9;11) являются решением уравнения 5х – 4у — 1 =0?

2. Постройте график функции 2х + у = 4.

Вариант 2.

1. Какие из пар чисел (1;1), (1;2), (3;7) являются решением уравнения 7х – 3у — 1 =0?

2. Постройте график функции 5х + у – 4 = 0.

(С последующей проверкой, проверка Слайд 23-25)

VII. Закрепление. Слайд 26.

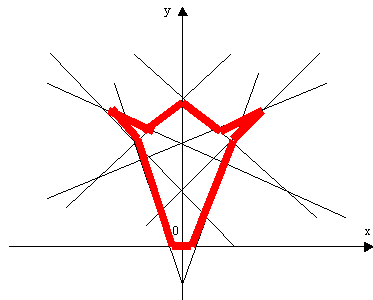
Постройте правильно. (Задание для всех учащихся класса). Построить с помощью линий цветок, о котором идёт речь:

Известно около 120 видов этих цветов, распространенных, главным образом в Средней, Восточной и Южной Азии и Южной Европе.

Ботаники считают, что эта культура возникла в Турции в ХII столетии Мировую славу растение обрело вдали от своей родины, в Голландии, по праву названной Страной этих цветов.

На различных художественно-оформленных изделиях (и ювелирных) часто встречаются мотивы этих цветов.

Вот легенда об этом цветке.

В золотистом бутоне желтого цветка было заключено счастье. До этого счастья никто не мог добраться, ибо не было такой силы, которая смогла бы открыть его бутон.

Но однажды по лугу шла женщина с ребенком. Мальчик вырвался из рук матери, со звонким смехом подбежал к цветку, и золотистый бутон раскрылся. Беззаботный детский смех совершил то, чего не смогла сделать никакая сила. С тех пор и повелось дарить эти цветы только тем, кто испытывает счастье.

Необходимо построить графики функций и выделить ту ее часть, для точек которой выполняется соответствующее неравенство:

у = х + 6,

4 < х < 6;

у = -х + 6,

-6 < х <-4;

у = — 1/3 х + 10,

-6 < х < -3;

у = 1/3 х +10,

3 < х < 6;

у = -х + 14,

0 < х < 3;

у = х + 14,

-3 < х < 0;

у = 5х – 10,

2 < х < 4;

у = — 5х – 10,

-4 < х < -2;

у = 0,

-2 < х < 2.

У нас получился рисунок – ТЮЛЬПАН. Слайд 27.

VIII. Рефлексия. Слайд 28.

Оцените свои знания, полученные на уроке.

IX. Домашнеее задание. Слайд 29.

П.43, №1206 (г-е), 1208 (г-е), 1214

Открытый урок по алгебре в 7 классе по теме «Линейное уравнение с двумя переменными и его график»

Открытый урок в 7 классе по теме:

«Линейное уравнение и его график»

Тип урока: урок формирования умений и навыков (усвоения нового материала)

Цели урока:

• Обучающая: выработать (содействовать, научить) у учеников умение строить график линейного уравнения с двумя переменными; развивать математический кругозора, мышление, речь, память, внимание.

• Развивающая: развивать творческую сторону мыслительной деятельности; создавать условия для проявления познавательной деятельности учащихся; умение работать в группе.

• Воспитывающая: воспитание познавательного интереса к математике, настойчивости, целеустремленности в учебе, ответственности за свою работу.

• Способствовать формированию компетенций: учебно-познавательной и рефлексивной; формированию объективной самооценки; интереса к изучаемому предмету

Задачи урока через планируемые результаты.

   ЛИЧНОСТНЫЕ. Формировать у обучающихся положительное отношение к школе и учебной деятельности, интерес к изучаемому материалу. Формировать объективную самооценку и взаимооценку. Воспитывать уважительное отношение к одноклассникам.

   ПРЕДМЕТНЫЕ. Обобщить и систематизировать знания обучающихся о линейном уравнении с двумя переменными.

  МЕТАПРЕДМЕТНЫЕ.

Регулятивные. Обучающиеся учатся принимать и сохранять учебную задачу, соответствующую этапу обучения; понимать выделенные учителем ориентиры действия в учебном материале; адекватно воспринимать оценку одноклассниками своей работы.

Коммуникативные. Обучающиеся учатся договариваться, приходить к общему решению, использовать в общении правила вежливости. Обучающиеся получат возможность научиться формулировать собственное мнение, строить понятные для окружающих высказывания, задавать вопросы, адекватно использовать средства устного общения для решения учебных задач.

Познавательные. Обучающиеся учатся осуществлять поиск нужной информации в учебном пособии; понимать знаки, символы, уметь их применять; понимать заданный вопрос, в соответствии с ним строить ответ в устной форме.

Этапы урока:

1.Организационный этап.

Организационный этап.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3. Актуализация опорных знаний

2. Мотивация учебной деятельности.

3. Проверка домашнего задания.

Организационный этап.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3. Актуализация опорных знаний

4. Актуализация опорных знаний.

5. Первичное усвоение новых знаний.

6. Первичное закрепление знаний, умений и навыков.

7. Информация о домашнем задании, инструктаж по его выполнению.

8. Рефлексия (подведение итогов урока)

9. Дополнительное (творческое задание) для тех, кто быстрее всех закончит работу

в классе (можно на дом).

Ход урока.

1. Организационный этап (отсутствующих отметить, записать в тетрадь число…)

2. Мотивация учебной деятельности (Слайд 1 (cм. презентацию)

Чем больше я знаю, 
Тем больше умею.
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно хнычет и скучает. (Роман Сеф).

(Роман Семенович Сеф (Роальд Семенович Фаермарк; 1931-2009)-детский поэт, писатель, драматург, переводяик)-википендия.

• Как вы понимаете эти слова? Как мы можем отнести их к сегодняшнему уроку?

• Да, сегодня вам самим предстоит открыть новые знания.

• Прежде, чем совершать открытие, нам предстоит проверить себя, готовы ли мы, а именно всё ли было усвоено на предыдущих уроках, имеются ли слабые места?

• Перед вами лежат листы контроля знаний (листы самооценки). С их помощью будем оценивать каждый этап сегодняшнего урока. Давайте оформим быстренько эти листы: ФИ, класс …

Карта самооценки Ф.И. уч-ся _______________________ дата __________

3. Проверка домашнего задания

Дом.задание

№ задания

№ 1046 (абвг) –

4 балла

№ 1047 (аб)

2 балла

№ 1049 (аб)

2 балла

№ 1050

1 балл

№ 1051 (абвг) –

4 балла

Итого

всего баллов

Баллы

Мах – 13 баллов

Возьмите лист контроля и оцените свою работу на этом этапе урока

мах балл — 13 баллов

3. Актуализация опорных знаний. Устная работа.

1. Какую тему мы с вами изучаем?

(Линейное уравнение с двумя переменными)

2. Какие из ниже приведенных уравнений являются линейными? (Слайд 2) Почему? Обоснуйте. Дайте определение линейного уравнения с двумя переменными? …(Линейным уравнением с двумя переменными называется уравнение вида ах +ву+с = 0, где х и у – переменные, а коэффициенты а,в,с – любые числа.)

3. Вместо точек поставьте числа так, чтобы полученная пара чисел являлась решением данного уравнения (Слайд 3)

Что называется решением линейного уравнения с двумя

переменными?….(Решением уравнения с двумя переменными называется

пара значений переменных, обращающая это уравнение в верное числовое

равенство)

4. Выберите точку, которая принадлежит графику уравнения (Слайд 4)

1. А сколько решений имеет линейное уравнение с двумя переменными?

2. Можно ли найти все решения линейного уравнения с двумя переменными? Нет, их бесконечное множество.

5. А теперь еще вспомним построение точек на координатной плоскости

(Слайд 5) Запишите буквы, которым соответствуют данные координаты. Получится слово, которое я адресую каждому, кто справится с этим заданием (молодец!)

Возьмите лист контроля и оцените свою работу на этом этапе урока

мах балл — 5 баллов

6. Как можно найти решения линейного уравнения с двумя переменными? Ответ: подобрать. А как легче подобрать решения уравнения? (выразить одну переменную через другую)

III Поиграем Учитель – ученик!!! Самостоятельная работа (Слайд 6)

2 ученика выполняют на карточке задания у доски, а остальные в тетрадях на месте. Кто справиться с заданием быстрее, тот и будет учителем (проверять у доски решение своих одноклассников.) При проверке можно обменяться тетрадями и проверять у соседа.

Возьмите лист контроля и оцените свою работу на этом этапе урока

мах балл —7 баллов

IV Работа в группах (3-4 группы получают задание на карточках и строят на А2 графики уравнений) (Слайд 7)

Готовые решения вывешивают на доску, прикрепляют магнитом и защищают!

• Где возникли затруднения?

• Почему? (Потому, что мы не умеем строить такие графики?)

• А если мы не умеем строить такие графики, то какую поставим перед собой цель? (Научиться строить график линейного уравнения с двумя переменными)

• Тогда какова же тема нашего урока? (График линейного уравнения с двумя переменными) (Слайд 8)

• А кто все — таки построил график в задании 4? – молодцы и чуть позже я задам вопрос как этого можно добиться?

Возьмите лист контроля и оцените свою работу на этом этапе урока

мах балл — 8 баллов

V Постановка проблемы

• Как вы думаете, как мы будем строить график линейного уравнения с двумя переменными? (задание № 4 в групповой работе) Выслушать детей и если возможно, то сформулировать алгоритм построения…

• Алгоритм построения графика линейного уравнения с двумя переменными, где а ≠ 0 и в ≠ 0: (Слайд 9 – 10)

1. Выразим у через х (получим линейную функцию…)

2. Придадим переменной х два конкретных значения и найдем соответствующие значения у

3. Построим на координатной плоскости найденные в п.2 две точки

4. Проведем через эти точки прямую – она и будет графиком линейного уравнения с двумя переменными.

VI Первичное закрепление

Из учебника № 1057 (а,б,г) ( три ученика выполняют у доски)

Возьмите лист контроля и оцените свою работу на этом этапе урока

мах балл — 6 баллов

VII Самостоятельная работа с проверкой (Слайд 11 – 14)

(обмен тетрадями)

Возьмите лист контроля и оцените свою работу на этом этапе урока

мах балл — 3 балла

РЕФЛЕКСИЯ:

Возьмите лист контроля и оцените свою работу на этом уроке

мах балл — 42 балла

38-42 – «5», 29 – 37 – «4», 18 – 28 – «3» , меньше 18 баллов – «2»

• Нарисуйте смайлик : у меня все отлично, у меня все хорошо, возникли трудности (Слайд 15)

Домашнее задание (Слайд 16)

Дополнительное задание (построение цветка) (Слайд 17 – 19)

1. Организационный этап.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3. Актуализация опорных знаний.

План-конспект урока (алгебра, 7 класс) по теме: «Линейное уравнение с двумя переменными и его график»7-й класс .

№	Этап урока	Название используемых ЭОР (с указанием  порядкового номера из Таблицы 2)	Деятельность учителя (с указанием действий с ЭОР, например, демонстрация)	Деятельность ученика	Время (в мин.)
1	Организационный момент		Проверяет  готовность к уроку, сообщает тему, цель, ход урока.	Слушают и делают записи в тетрадях	2
2	Актуализация знаний	Модуль 1, задания  1,2,3 «Решение линейных уравнений» П1	Организует опрос с использованием ЭОР, комментирует ответы учащихся, корректируя их. Демонстрация ЭОР. 1.Дайте определение уравнения с одной переменной. 2.Дайте определение корня уравнения. 3.Задание модуля (сцена 1). 4.Что значит решить уравнение? 5.Задание модуля (сцены 2,3).  6.Какие уравнения  называются равносильными? 7.Сформулируйте свойства уравнений.	Формулируют основные понятия: определение линейного уравнения, решение линейного уравнения, равносильные уравнения.	5
3	Объяснение нового материала	Модуль 2, сцены 6, 7, 8 «Линейное уравнение с двумя переменными и его график. И1»	Демонстрация ЭОР. Предлагает демонстрацию нового материала, контролирует ход выполнения работы. Дает задание: составить алгоритм построения графика линейного уравнения с двумя переменными.	1.Знакомятся с предложенной информацией. 2.Рисуют в тетради таблицу зависимости графика от коэффициентов а,в,с. 3. Записывают в тетрадях пример построения графика уравнения. 4.Составляют алгоритм построения графика линейного уравнения.	10
4	Организация деятельности учащихся по применению знаний в разнообразных ситуациях.		Дает задание по учебнику: №1009(а), 1012(а, в, д), №1014. Организует самостоятельную  работу учащихся по вариантам.	Знакомятся с заданием и задают вопросы по его условию. №1009:Выполняют задания, комментируя и обосновывая ответ, ссылаясь на определение. №1012:Выполняют в тетрадях. Работают в парах. Взаимопроверка. № 1014: Обосновывают, опираясь на свойства уравнений.	11
5	Контроль и самоконтроль.	Модуль 3. «Линейное уравнение с двумя переменными и его график. К1» Сцены 1-5	Комментирует задания, оказывает помощь по необходимости. Оценивает выполнение заданий (отмечает в оценочном листе).	Выполняют задания. Работают в парах. Вводят ответы в задания модуля, контролируют выполнение заданий и анализируют ошибки.	10
6	Домашнее задание.		Записывает на доске: №1009(б, в),  № 1111, комментирует его. Предлагает выполнить дома творческие задания: 1.При каком значении параметра a график уравнения а) (а-2)x+(2а-6)y+8=0 параллелен оси абсцисс, б) (3а-1)x+ (а-1)y-6=0 параллелен оси ординат	Записывают домашнее задание	2
7	Итог урока		Задает вопросы. Анализирует ответы учащихся, оценивает их деятельность 1.Что является графиком линейного уравнения с двумя переменными? 2. При каком условии график линейного уравнения с двумя переменными параллелен оси: а)абсцисс;  б) ординат? Приведите примеры. 3. При каких условиях графиком линейного уравнения с двумя переменными будет координатная плоскость? Приведите примеры	Отвечая на вопросы учителя, делают обобщение изученного материала.	4
8	Рефлексия				1

График линейного уравнения с двумя переменными

Урок алгебры в 7 классе по теме «График линейного уравнения с двумя переменными»

Данный урок полезен тем учителям, которые применяют активные методы обучения на уроке. Данный урок предполагает наличие у учащихся минимальных навыков групповой работы. А также умение учителя использовать на уроке презентацию.

Тип урока: урок формирования умений и навыков.

Цели урока:

— выработать у учеников умение строить графики линейного уравнения с двумя переменными;

— развивать познавательные навыки учащихся, критическое и творческое мышление; умение работать в группе;

— воспитание познавательного интереса к математике, настойчивости, целеустремленности в учебе, коллективизма и ответственности за свою работу.

Структуру урока и виды деятельности учителя и учащихся можно посмотреть в таблице

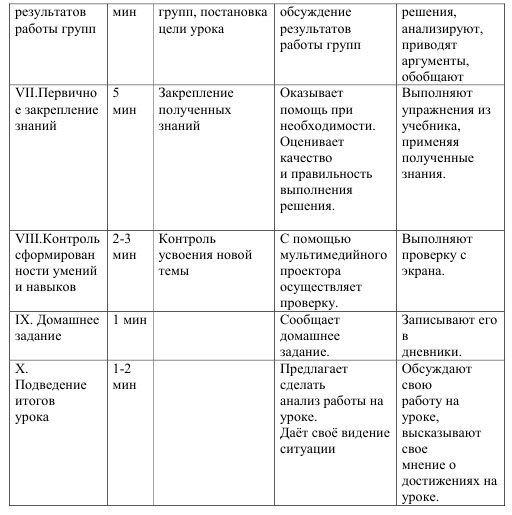
ХОД УРОКА

1. Организационный этап.

Сегодня на уроке нам потребуются карандаши и линейки. Проверьте свою готовность к уроку. Откройте тетради и запишите дату сегодняшнего урока.

2. Мотивация

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время. У нас всего 40 мин, но мне бы очень хотелось, чтобы они не тянулись, а пролетели. Не оказались прожитыми впустую, а были затрачены с пользой.

3.  Проверка домашнего задания

Какую тему мы с вами изучаем?  (Линейное уравнение с двумя переменными)

А что называется линейным уравнением с двумя переменными?  (Дают определение)

А) Давайте проверим ваше домашнее задание – как вы научились различать линейные и нелинейные уравнения с двумя переменными (фронтальная проверка)

Б) Ваше второе домашнее задание связано с выражением одной переменной уравнения через другую. Давайте проверим, как вы связали линейное уравнение и его преобразование к новому виду?

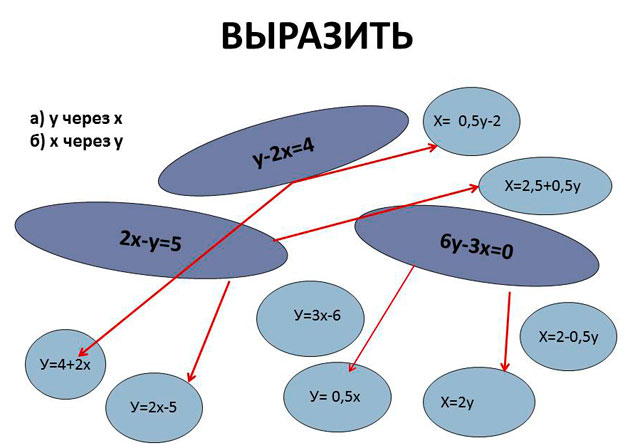
А какими правилами вы пользовались для того, чтобы выразить переменные? (Рассказывают правила решения уравнений)

А зачем нам нужно выражать одну переменную через другую? (Чтобы найти решения уравнения)

Что называется решением линейного уравнения с двумя переменными? (Дают определение)

Можем ли мы найти все решения  уравнения? (Нет, так как их бесконечное количество)

4. Усвоение новых знаний

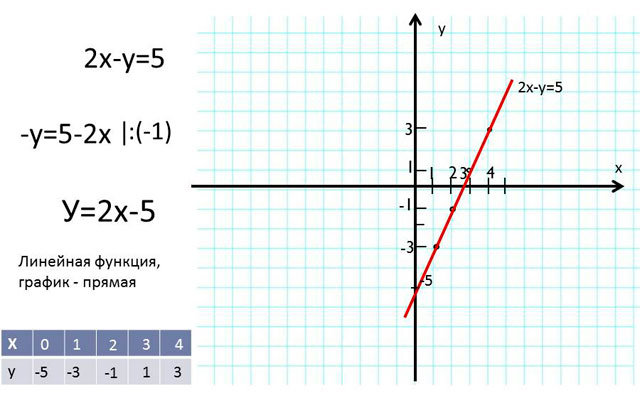
Давайте запишем уравнение 2х-у=5 и найдём несколько его решений.

(Слайд презентации открывается постепенно, по мере решения проблемы)

Выразим у через х.

Начнём искать решения уравнения.  (Найти одну пару)

Любую пару чисел х и у мы можем изобразить наглядно – как?  (Отметить точку в системе координат)

Давайте все решения, которые будем находить отмечать в системе координат.

Приложите линейку к построенным точкам. Обратите внимание, что все эти точки лежат на одной прямой. Почему все решения линейного уравнения с одной переменной лежат на одной прямой? (Потому, что у=2х-5 – линейная функция, а её графиком является прямая)

Какой же вывод мы можем сделать из этого факта?

(1 — линейное уравнение имеет график, 2 – График линейного уравнения – прямая)

Надо ли искать так много решений, как искали мы, для того, чтобы построить график? (Нет, достаточно двух решений)

5. Работа в группах

Сейчас я предлагаю вам поработать в группах и попробовать построить графики уравнений вместе с товарищами. (Карточки с заданиями и листы для оформления решения, маркеры раздаются перед уроком. – Для графиков и Задания для групп.)

(Учащиеся работают в группах. Затем готовые решения вывешиваются на доску.)

6.  Анализ результатов работы групп

Посмотрите внимательно, ребята, на полученные графики. Вы согласны с решениями других групп?  (Учащиеся исправляют ошибки в решениях других групп. Защищают свои решения)

Замечаете ли вы различия в полученных графиках? Какие?

(Одни прямые проходят через начало координат, а другие – нет)

С чем это связано? Почему у нас получилось два вида прямых? Чем же отличаются уравнения, соответствующие этим графикам?

(с≠0 и с=0)

Действительно, при с=0 мы переходим от уравнения к прямой пропорциональности, график которой проходит через начало координат. Значит, мы выявили графики двух видов.

А шторкой ниже закрыты ещё другие случаи зависимости графика от коэффициентов уравнения, которые мы рассмотрим на следующем уроке.

7. Первичное закрепление знаний

А сейчас каждый из вас пусть самостоятельно выполнит задание № 1048а на странице 193.

8. Контроль сформированности умений и навыков

Проверьте правильность выполнения. (правильное решение можно показать на доске»

У кого правильно? Какие возникли трудности?

9. . Домашнее задание

 Запишите домашнее задание. Повторить правила. Обязательно выполнить № 1049аб. Дополнительное задание — № 1152. Выполняя это задание,  помните, что координаты любой точки графика уравнения соответствуют его решению.

10. Подведение итогов урока. Оцените свою работу на уроке по данным критериям.  Помните, что если сомневаетесь в правильности своей оценки, – воздержитесь, получите оценку на следующем уроке.

Но я могу сказать, что мне понравилась работа (перечислить учащихся, активно работавших на уроке)

Спасибо за работу. Надеюсь, что время, потраченное нами,  не прошло зря.

Анализ урока.

Данный урок показал, что участие детей в освоении нового материала может быть активным. Это достигается работой в группе, подобранной так, чтобы в неё входили ученики с различной мотивацией и уровнем подготовки. Тогда в процессе активного освоения знаний происходит обучение детей не только учителем, но и другими учащимися. На данном уроке ученики рассуждали, делали выводы, аргументировали и критиковали. Такое взаимообучение бывает намного эффективнее традиционного обучения. Переход на ФГОС нового поколения и требует освоения учителем таких активных методов работы с учащимися, а также применения ИКТ с целью оптимизации времени урока.

Урок алгебры 7 класс. Линейное уравнение с двумя переменными и его график.

Урок алгебры 7 класс.

Тема урока. Линейное уравнение с двумя переменными и его график.

1 модуль. Урок-установка к теме: «Системы линейных уравнений с двумя переменными».

Цели урока:

1. Образовательная. Формирование понятий: линейное уравнение с двумя переменными, решение линейного уравнения с двумя переменными, график линейного уравнения с двумя переменными, система линейных уравнений с двумя переменными; формирование умений строить графики линейных уравнений с двумя переменными. Ознакомление учащихся со способами решения систем линейных уравнений с двумя переменными, с составлением системы линейных уравнений с двумя переменными по условию задачи.

2. Развивающая. Развитие мышления учащихся через умение выделять главное, развитие сознательного восприятия учебного материала, внимания и памяти.

3. Воспитательная. Содействие воспитанию культуры письменной и устной математической речи, графической культуры; формирование умения работать в парах, умения оценивать друг друга и давать себе самооценку.

Цель. Ход урока.

1. Мотивация

Системы уравнений, как и отдельные уравнения используются для решения сложных и необходимых задач. Ранее мы отмечали, что довольно часто математической моделью реальной ситуации служит линейное уравнение с одной переменной или уравнение, которое после преобразований сводится к линейному.

1,2 слайд. Исаак Ньютон сказал: «Чтобы решить вопрос, относящийся к числам или к отвлеченным отношениям величин, нужно лишь перевести задачу с родного языка на алгебраический».

Сегодня нам предстоит сделать первые шаги в данном направлении.

Но для этого нам нужно вспомнить материал предыдущих тем.

2. Актуализация опорных знаний.

Как называется функция у=-2х+7?

Как определить, принадлежат ли точки А(-4;15), В(4,1) графику функции?

Что является графиком функции?

Сколько точек необходимо?

Построим график функции у=-х+2.

Без построения определите, будут ли пересекаться прямые? Как они могут располагаться?

Что называется уравнением? Что значит — решить уравнение? Решить уравнение 9х-7=6х+14. Сколько решений может иметь такое уравнение? ——

3. Знакомство с установкой и осознание нового материала.

Урок 1. Уравнение с двумя переменными. График линейного уравнения с двумя переменными.

Слайд 3-5.

Слайд 3. Работа с установкой. Что является решением линейного уравнения с двумя переменными? Найти решение уравнения х-3у=10. Как это удобнее сделать? Х=3у+10 Слайд 4

Проверим, какие из пар чисел (6;-4) , (2;1) являются решениями следующих уравнений х+у=2, х-у=10 . Слайд 5

График уравнения х+у=2 у нас уже есть, построим график х-у=10, определим координаты точки пересечения.

Урок 2. Системы линейных уравнений с двумя переменными. Графический способ решения. Способ подстановки.

Слайд 6-8

Как определить количество решений системы уравнений?

Определим алгоритм решения системы линейных уравнений с двумя переменными. Какую систему мы уже решили?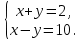

Слайд 9

Работа с установкой. В чем заключается способ подстановки?

Слайд 10

Решим систему способом подстановки.

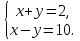
Слайд 11

Урок 3. Системы линейных уравнений с двумя переменными. Способ сложения. Решение задач составлением системы уравнений.

Работа с установкой. В чем заключается способ сложения?

Слайд 12

Решим систему способом сложения.

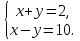
Урок 4,5. Многие задачи, в частности те, в которых нужно найти значение двух величин, удобно решать при помощи систем уравнений.

Слайд 13,14

4. Рефлексия. Осмысление результатов работы.

— Что нового узнали?

— Чему научились?

-Что показалось самым трудным?

Сегодня мы решили одну систему линейных уравнений с двумя переменными тремя способами. Следует обратить внимание на равноправие трёх способов решения систем. Преимуществом геометрического языка является его наглядность, зато алгебраический язык позволяет сводить задачу к точным вычислениям. На следующем уроке мы продолжим работать над темой и рассмотрим подробнее тему: «Уравнение с двумя переменными. График линейного уравнения с двумя переменными».

2 модуль.

Ход урока.

1. Закрепление и осознание знаний.

Самостоятельная работа с учебником. Работа в парах. Стр.217 отвечаем на вопросы по вариантам. Фронтальная работа. Стр.218 устные упражнения.

Решение упражнений у доски.

1. Определяем какая из пар является решением уравнения.

2. Выражаем одну переменную через другую.

3. Определяем принадлежность точки графику.

4. Строим график линейного уравнения с двумя переменными.

2. Подведение итогов урока.

На 22 грн купили несколько тетрадей по 5 грн и ручек по 3 грн. Сколько купили тетрадей и ручек? Решая задачу, количество тетрадей обозначь за х, а ручек за у. Составить уравнение по условию задачи. Назовите пару чисел, являющуюся решением этого уравнения.

3 модуль.

1. Закрепление знаний.

Решение упражнений у доски.

1. Построение в одной плоскости графиков двух уравнений. №1035

2. Составление уравнения, график которого пересекает оси координат в заданных точках. №1043

3. Самостоятельная работа с взаимопроверкой (обратная сторона доски).

А. Выразить переменную у через х. Пользуясь полученной формулой нати 2 решения. Х+у=12; у-х=10.

Б. Построить график уравнения, определив точки пересечения графика с координатными осями. 3Х+5у=15; 4у+3х=12.

В. Сколько решений имеет уравнение

(х-1)²+(у+2)²=0; (х+1)²+(у-2)²=0;

Каждое задание 4 балла.

2. Подведение итогов урока. Выставление оценок.

Конспект урока алгебры в 7 классе по теме «График линейного уравнения с двумя переменными»

Конспект урока алгебры в 7 классе по теме «График линейного уравнения с двумя переменными»

Автор: Николаева Евгения Николаевна, учитель математики «МБОУ СОШ № 20» г. Шахты, РО

УМК: алгебра 7 класс, под редакцией С.А. Теляковского

Тип урока: урок формирования умений и навыков.

Характеристика класса, в котором урок был проведён. В классе 50% учащихся с высокой мотивацией к обучению — 10 учеников, 6 – со средним уровнем и 4 ученика – с низкой мотивацией.

Цели урока:

— выработать у учеников умение строить графики линейного уравнения с двумя переменными;

— развивать познавательные навыки учащихся, критическое и творческое мышление; умение работать в группе;

— воспитание познавательного интереса к математике, настойчивости, целеустремленности в учебе, коллективизма и ответственности за свою работу.

Структуру урока и виды деятельности учителя и учащихся можно посмотреть в таблице

ХОД УРОКА

1. Организационный этап.

Сегодня на уроке нам потребуются карандаши и линейки. Проверьте свою готовность к уроку. Откройте тетради и запишите дату сегодняшнего урока.

2. Мотивация

Я хочу загадать вам загадку:

Что самое быстрое, но и самое медленное.

Самое большое, но и самое маленькое.

Самое продолжительное, но и самое краткое.

Самое дорогое, но и дёшево ценимое нами?

Это ребята – время. У нас всего 40 мин, но мне бы очень хотелось, чтобы они не тянулись, а пролетели. Не оказались прожитыми впустую, а были затрачены с пользой.

3.  Проверка домашнего задания

Какую тему мы с вами изучаем?  (Линейное уравнение с двумя переменными)

А что называется линейным уравнением с двумя переменными?  (Дают определение)

А) Давайте проверим ваше домашнее задание – как вы научились различать линейные и нелинейные уравнения с двумя переменными (фронтальная проверка)

Б) Ваше второе домашнее задание связано с выражением одной переменной уравнения через другую. Давайте проверим, как вы связали линейное уравнение и его преобразование к новому виду?

А какими правилами вы пользовались для того, чтобы выразить переменные? (Рассказывают правила решения уравнений)

А зачем нам нужно выражать одну переменную через другую? (Чтобы найти решения уравнения)

Что называется решением линейного уравнения с двумя переменными? (Дают определение)

Можем ли мы найти все решения  уравнения? (Нет, так как их бесконечное количество)

4. Усвоение новых знаний

Давайте запишем уравнение 2х-у=5 и найдём несколько его решений.

(Слайд презентации открывается постепенно, по мере решения проблемы)

Выразим у через х.

Начнём искать решения уравнения.  (Найти одну пару)

Любую пару чисел х и у мы можем изобразить наглядно – как?  (Отметить точку в системе координат)

Давайте все решения, которые будем находить отмечать в системе координат.

Приложите линейку к построенным точкам. Обратите внимание, что все эти точки лежат на одной прямой. Почему все решения линейного уравнения с одной переменной лежат на одной прямой? (Потому, что у=2х-5 – линейная функция, а её графиком является прямая)

Какой же вывод мы можем сделать из этого факта?

(1 — линейное уравнение имеет график, 2 – График линейного уравнения – прямая)

Надо ли искать так много решений, как искали мы, для того, чтобы построить график? (Нет, достаточно двух решений)

5. Работа в группах

Сейчас я предлагаю вам поработать в группах и попробовать построить графики уравнений вместе с товарищами. (Карточки с заданиями и листы для оформления решения, маркеры раздаются перед уроком. – Для графиков и Задания для групп.)

(Учащиеся работают в группах. Затем готовые решения вывешиваются на доску.)

6.  Анализ результатов работы групп

Посмотрите внимательно, ребята, на полученные графики. Вы согласны с решениями других групп?  (Учащиеся исправляют ошибки в решениях других групп. Защищают свои решения)

Замечаете ли вы различия в полученных графиках? Какие?

(Одни прямые проходят через начало координат, а другие – нет)

С чем это связано? Почему у нас получилось два вида прямых? Чем же отличаются уравнения, соответствующие этим графикам?

(с≠0 и с=0)

Действительно, при с=0 мы переходим от уравнения к прямой пропорциональности, график которой проходит через начало координат. Значит, мы выявили графики двух видов.

А шторкой ниже закрыты ещё другие случаи зависимости графика от коэффициентов уравнения, которые мы рассмотрим на следующем уроке.

7. Первичное закрепление знаний

А сейчас каждый из вас пусть самостоятельно выполнит задание № 1048а на странице 193.

8. Контроль сформированности умений и навыков

Проверьте правильность выполнения

У кого правильно? Какие возникли трудности?

9. . Домашнее задание

 Запишите домашнее задание. Повторить правила. Обязательно выполнить № 1049аб. Дополнительное задание — № 1152. Выполняя это задание, помните, что координаты любой точки графика уравнения соответствуют его решению.

10. Подведение итогов урока. Оцените свою работу на уроке по данным критериям.  Помните, что если сомневаетесь в правильности своей оценки, – воздержитесь, получите оценку на следующем уроке.