Раздел I. Механика Кинематика материальной точки. Основные понятия и уравнения кинематики
Кинематика изучает механическое
движение тел без рассмотрения причин,
вызывающих это движение. Большинство
задач на кинематику связано с
равнопеременным прямолинейным движением.
Равномерное прямолинейное движение
можно рассматривать как частный случай
равнопеременного движения при выполнении
условия 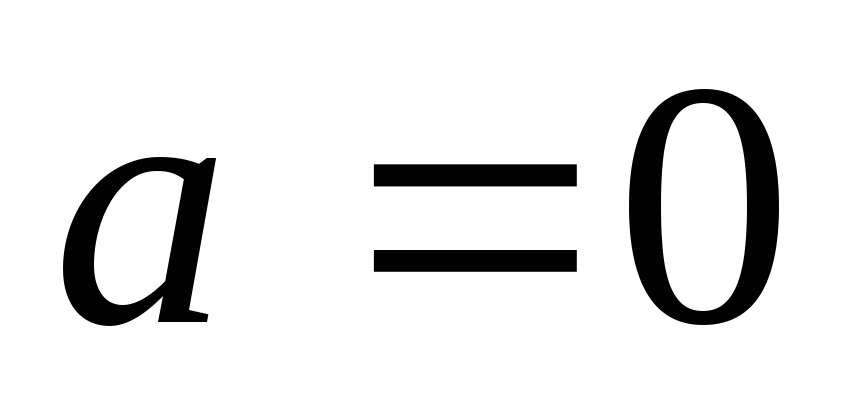 .
.
Простейшим видом криволинейного движения является равномерное движение точки по окружности. Более сложным является криволинейное движение тел, брошенных горизонтально или под углом к горизонту. Такое движение можно рассматривать как результат двух одновременных прямолинейных движений по осям, одна из которых параллельна, а вторая перпендикулярна поверхности Земли.
Материальная точка – это тело, формой и размерами которого можно пренебречь при решении данной задачи.
Система отсчета – это система координат, снабженная часами и связанная с совокупностью тел (материальных точек), относительно которой рассматривается движение других тел (материальных точек).
Множество точек пространства, через которые прошла материальная точка при движении относительно выбранной системы отсчета, называется траекторией материальной точки.
Путь – это расстояние S, пройденное точкой вдоль траектории в направлении движения за рассматриваемый промежуток времени.
Перемещение – это вектор 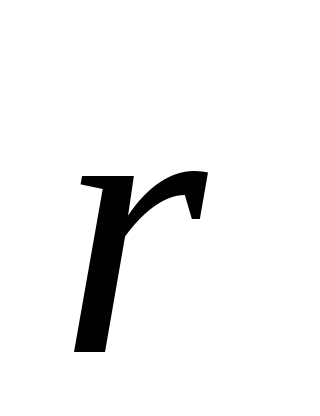 ,
соединяющий положения движущейся точки
в начале и в конце некоторого промежутка
времени. Вектор перемещения направлен
вдоль хорды траектории точки.
,
соединяющий положения движущейся точки
в начале и в конце некоторого промежутка
времени. Вектор перемещения направлен
вдоль хорды траектории точки.
Уравнение движения вдоль координатной оси:
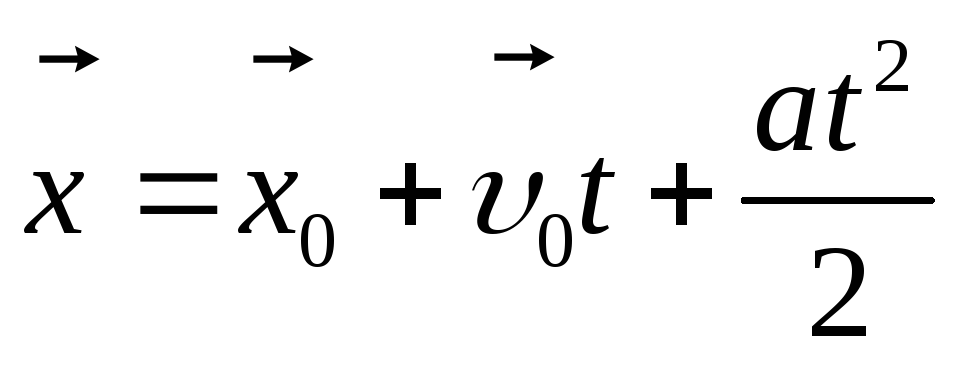 .
.
Скорость точки  –
векторная физическая величина,
характеризующая направление и быстроту
движения точки.
–
векторная физическая величина,
характеризующая направление и быстроту
движения точки.
Средняя скорость 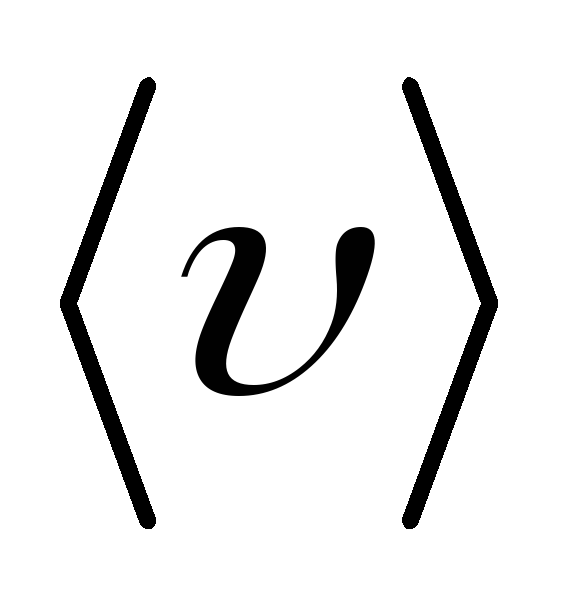 – это векторная величина, равная
отношению приращения радиуса-вектора
точки Δrв промежутке
времени отtдоt+Δtк продолжительности этого промежутка
Δt:
– это векторная величина, равная
отношению приращения радиуса-вектора
точки Δrв промежутке
времени отtдоt+Δtк продолжительности этого промежутка
Δt:
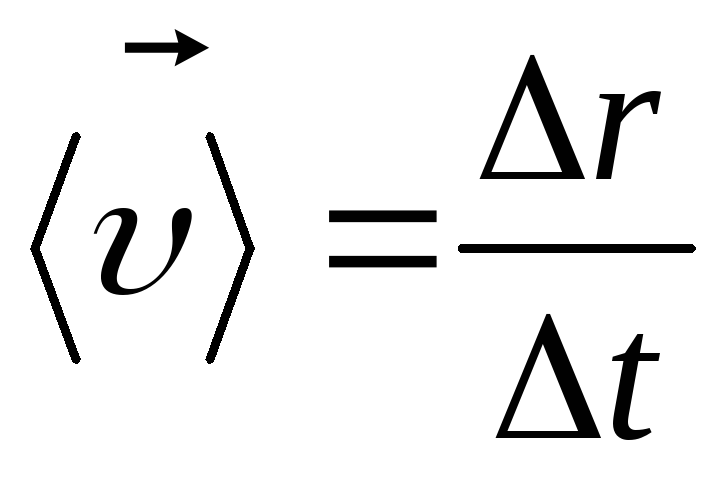
Мгновенная скорость: 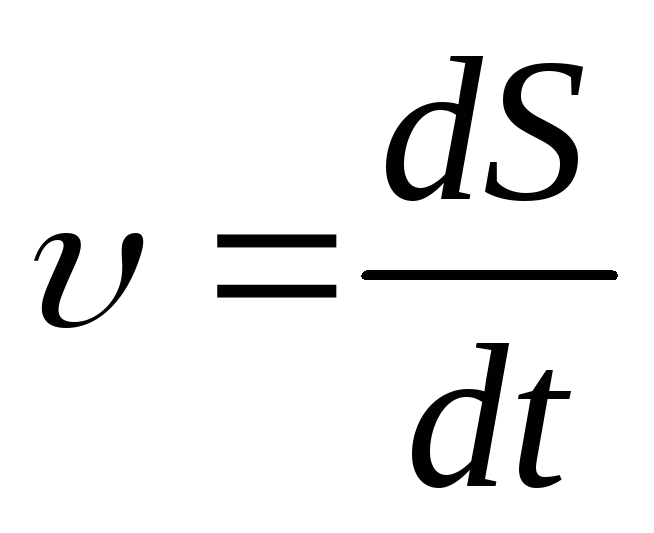 .
.
Это скорость в данный момент времени или данной точки траектории.
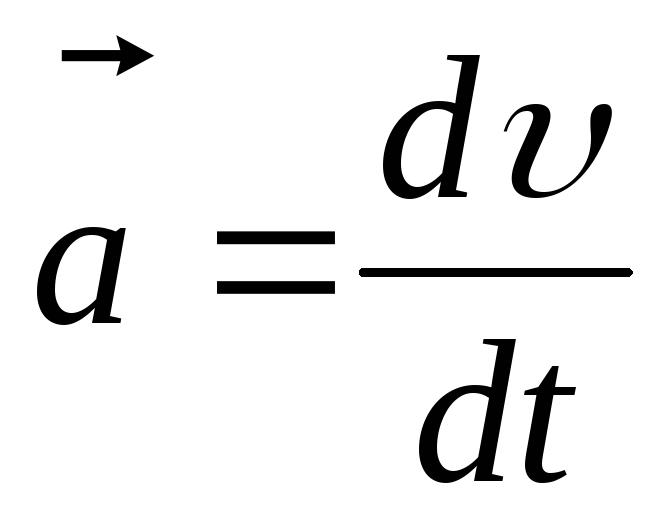 .
.
В случае равнопеременного движения зависимости пути и скорости от времени имеют следующий вид:
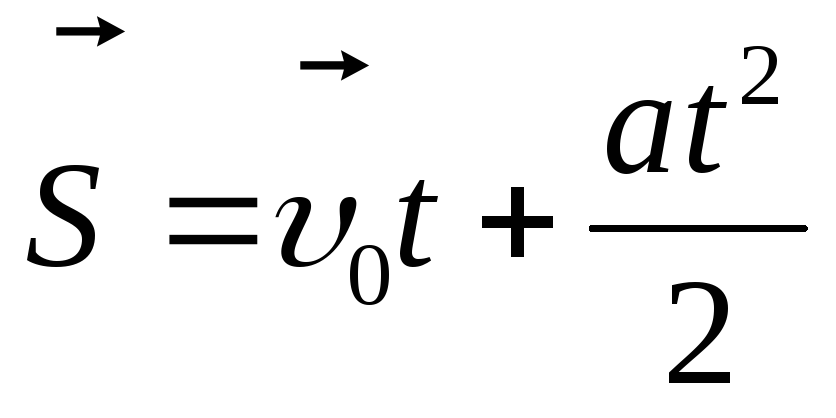 ,
,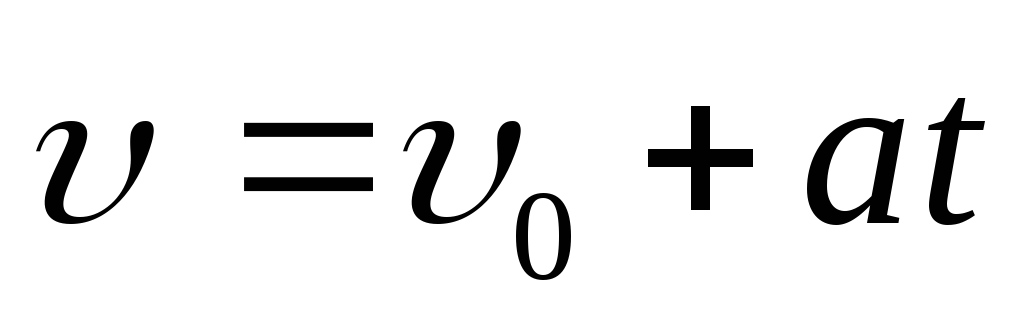 ,
,
где 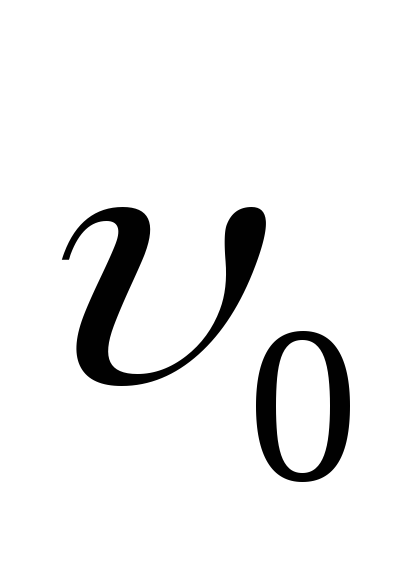 –
начальная скорость движения тела.
–
начальная скорость движения тела.
При движении тела в одной системе координат относительно другой скорость тела будет определяться векторным сложением скоростей тела и систем:


 – вектор скорости движения тела в
неподвижной системе отсчета,
– вектор скорости движения тела в
неподвижной системе отсчета,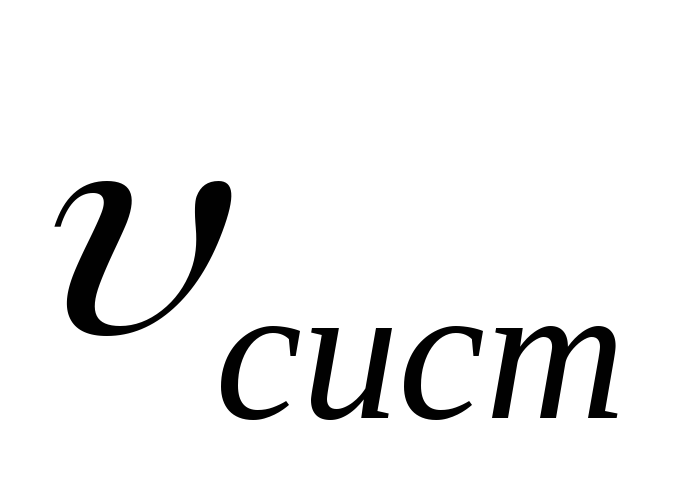 – вектор скорости движущейся системы
отсчета,
– вектор скорости движущейся системы
отсчета,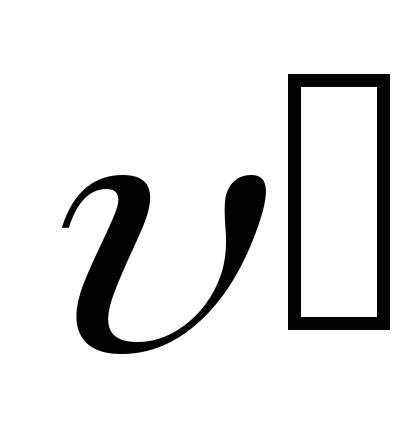 – вектор скорости тела в движущейся
системе отсчета.
– вектор скорости тела в движущейся
системе отсчета.
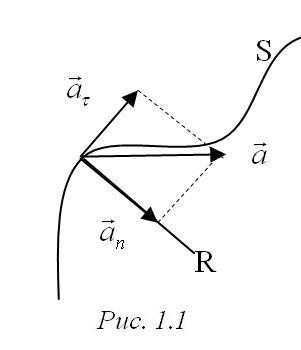
При ускоренном криволинейном движении
вектор ускорения  будет лежать в плоскости криволинейной
траектории. В этом случае вектор
будет лежать в плоскости криволинейной
траектории. В этом случае вектор удобно разложить на две составляющие
вдоль двух основных направлений –
касательной к траектории
удобно разложить на две составляющие
вдоль двух основных направлений –
касательной к траектории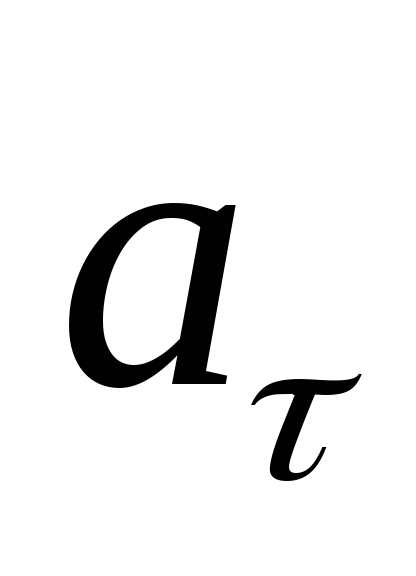
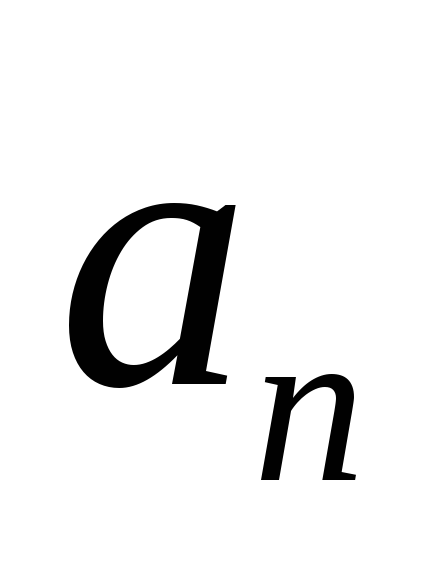 (см. рис.1.1). Тогда
(см. рис.1.1). Тогда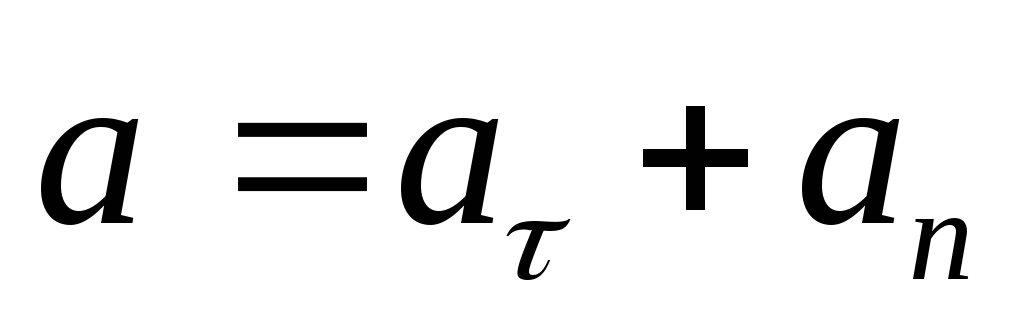 ,
, где 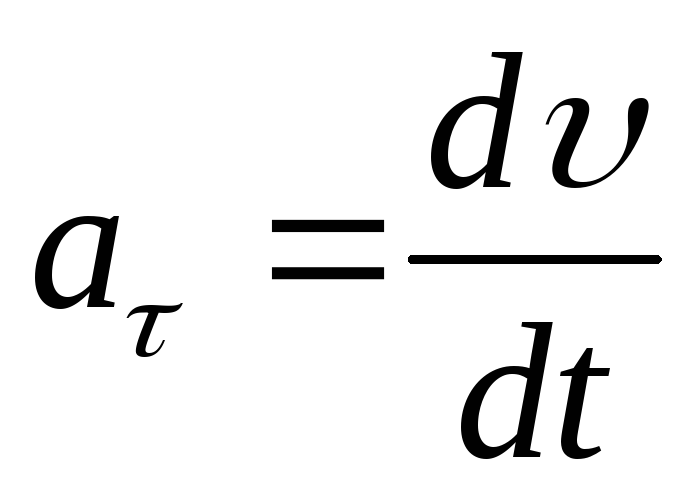 – тангенциальное ускорение,
– тангенциальное ускорение,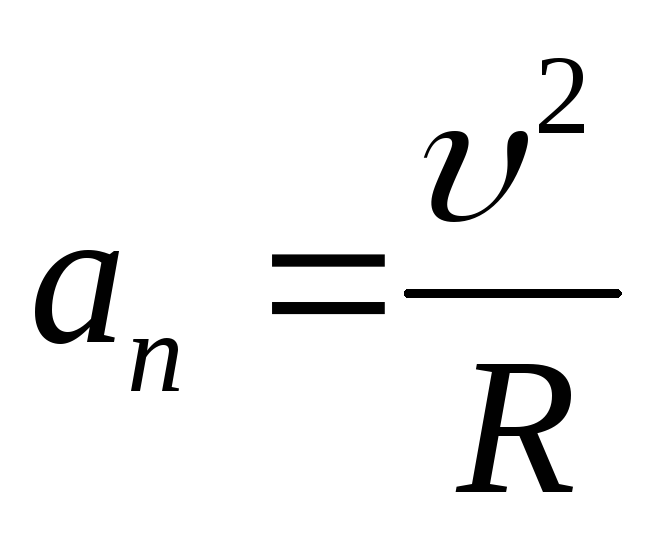 – нормальное ускорение,R– радиус кривизны траектории.
– нормальное ускорение,R– радиус кривизны траектории.
При вращательном равномерном движении значения угловой скорости ω и ускорения ε будут зависеть от углового перемещения φ:
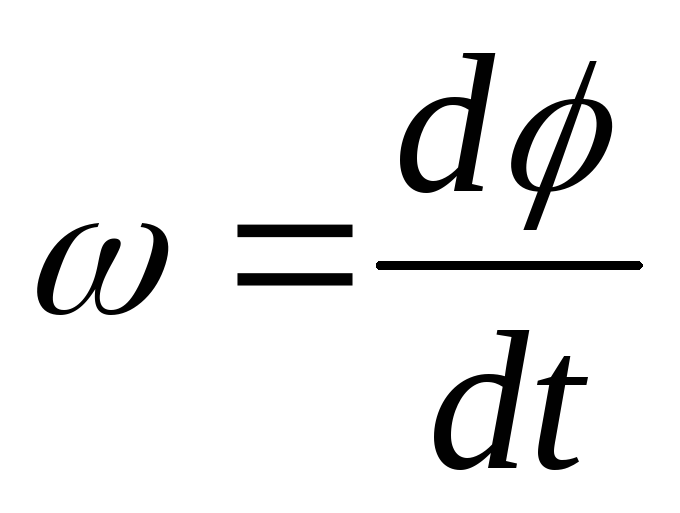 ,.
,.
Средняя угловая скорость 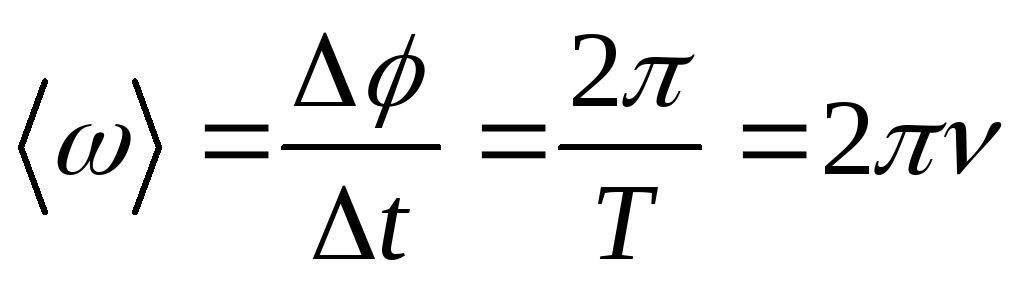
где Т – период вращения, ν – частота
вращения (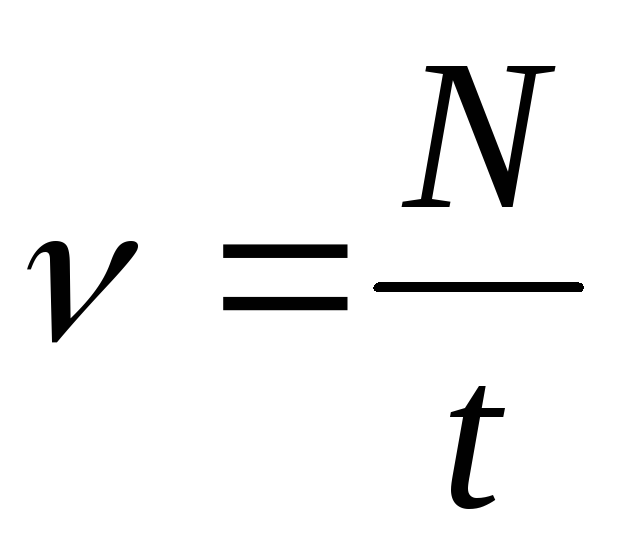 ,
гдеN– число оборотов
за времяt).
,
гдеN– число оборотов
за времяt).
Уравнения углового перемещения и угловой скорости для равнопеременного вращательного движения будут иметь вид:
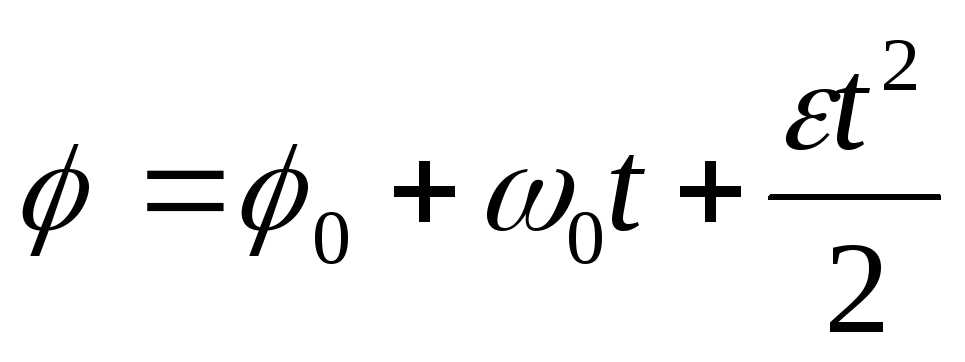 ,
,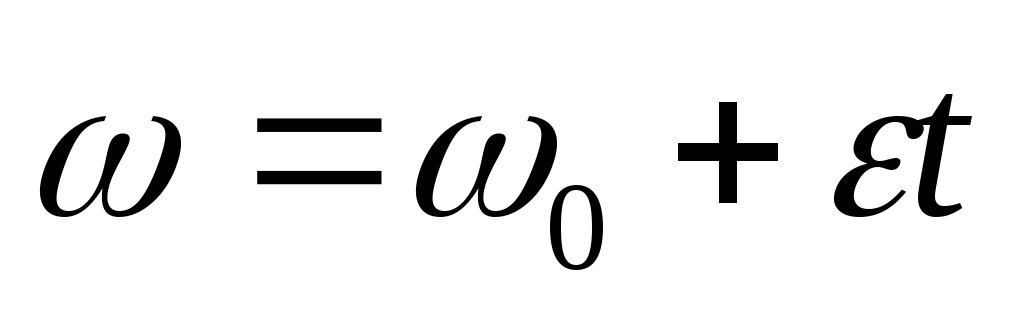 ,
,
где φ0и ω0– начальные угловые перемещение и скорость, соответственно.
Между линейными и угловыми величинами существует следующая связь:
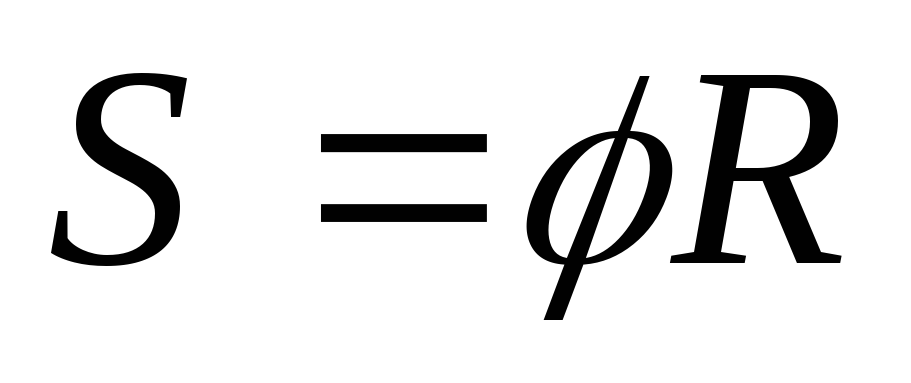 ,
,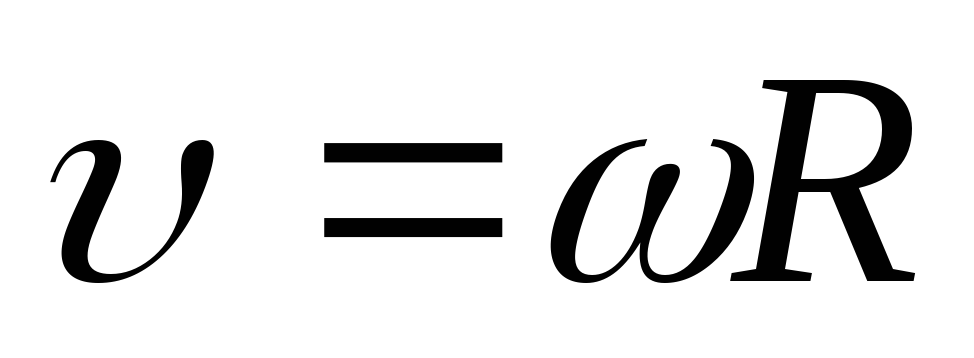
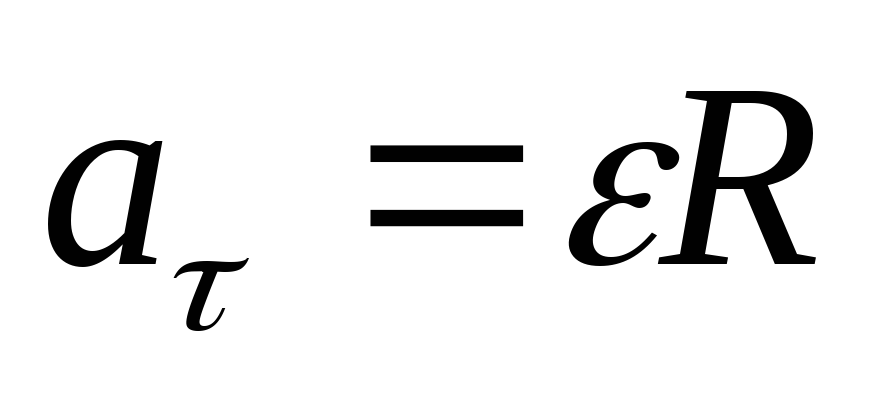 ,
,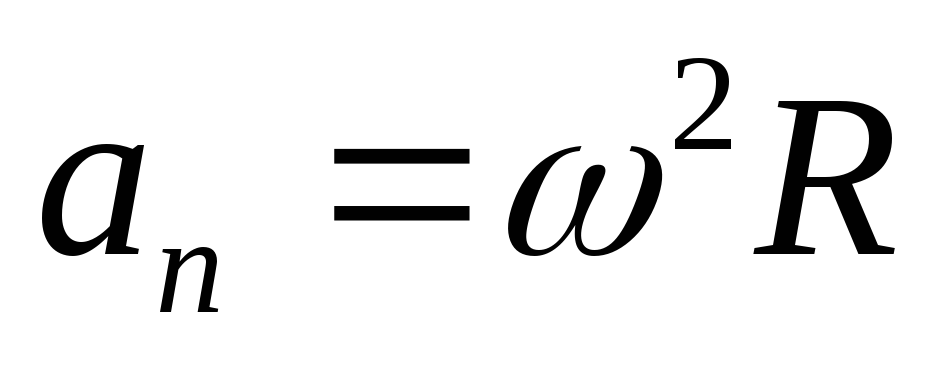 ,
,где R– расстояние от оси вращения.
studfile.net
Раздел 1. Физические основы механики Основные формулы Кинематика поступательного движения
1. Скорость при прямолинейном движении в общем случае
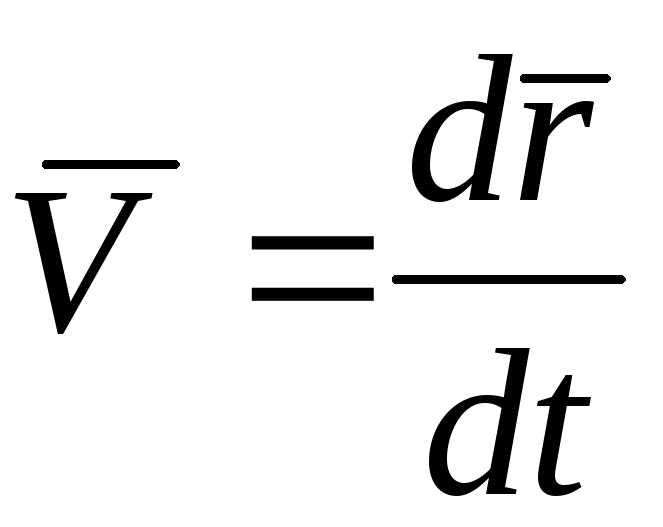 =
Vx
=
Vx 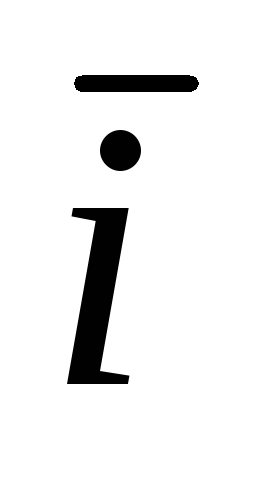 + Vy
+ Vy 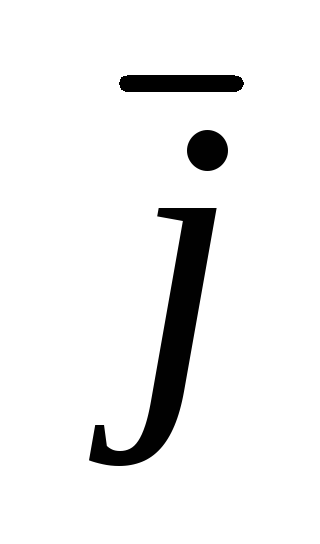 + Vz
+ Vz 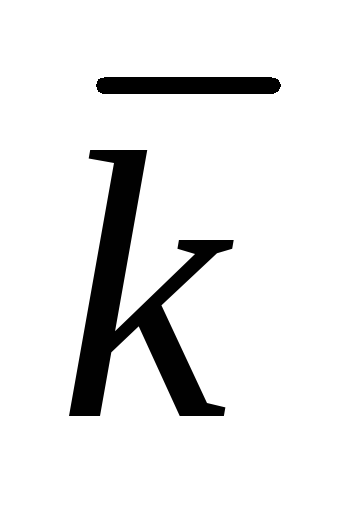 ,
,
V 2 = Vx2+ Vy2+ Vz2.
2. Ускорение
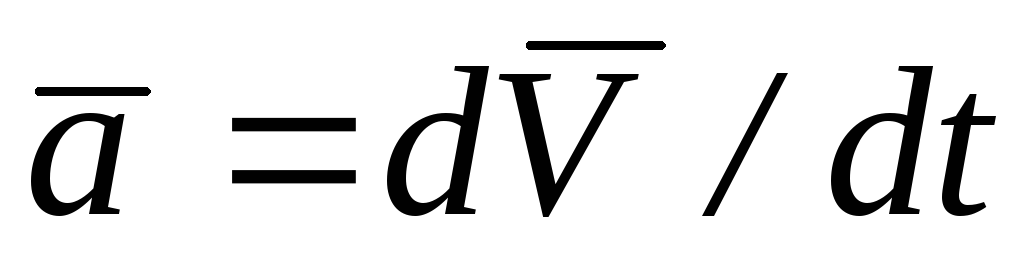 =
ax
=
ax 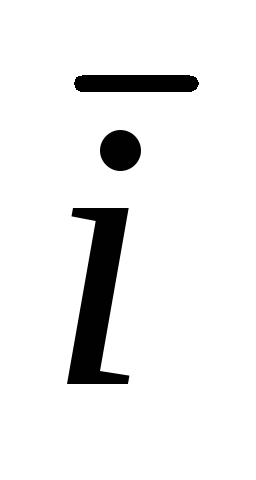 + ay
+ ay 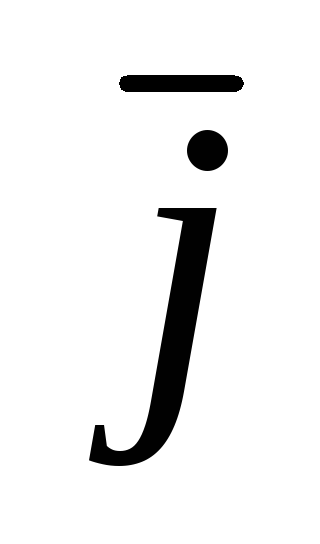 + az
+ az 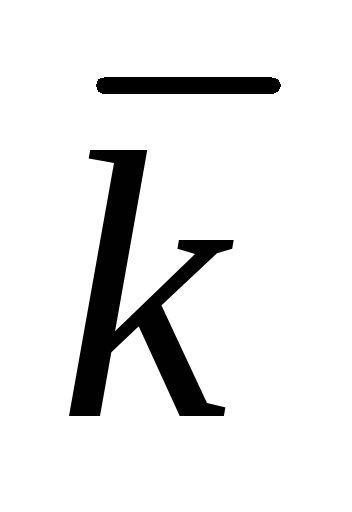 ,
,
a 2 = ax2+ ay2+ az2
3. Уравнения кинематики равноускоренного поступательного движения:
V=V0+at,
S=V0
где V – скорость тела в момент времени t; V0 – начальная скорость; a – ускорение движения тела; S – путь, пройденный за время t; t – время движения тела.
4. Полное ускорение при криволинейном движении
a2=a2+an2,
где aτ = dV/dt– тангенциальное ускорение;an = V2/R– нормальное ускорение.
Кинематика вращательного движения
5. Угловая скорость при вращательном движении в общем случае
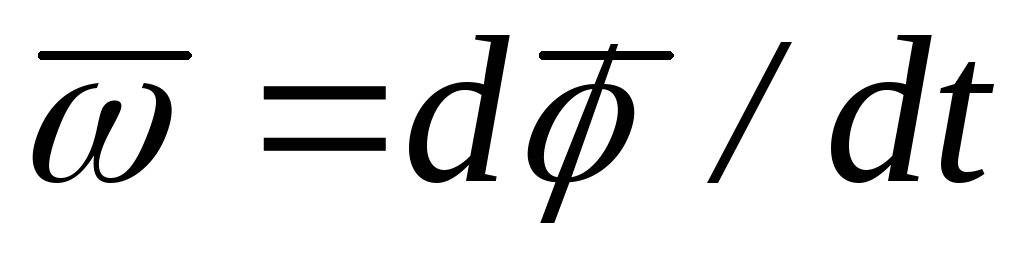 .
.
6. Угловое ускорение
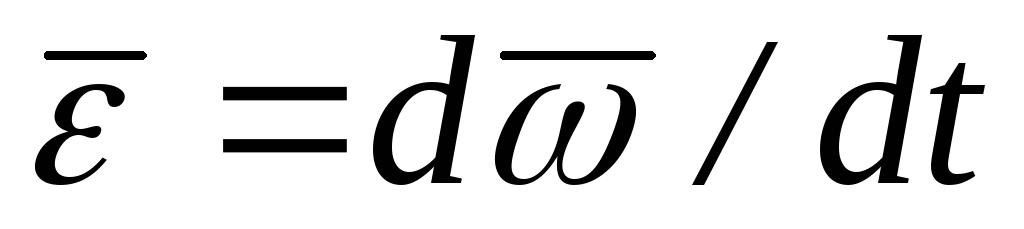 .
.
7. Уравнения кинематики равноускоренного вращательного движения:
ω = ω0+t, = ω0t+t2/2,
где ω –угловая скорость в момент времениt;ω0– начальная угловая скорость;– угловое ускорение, с которым вращается тело;t– время вращения тела; – угол поворота за времяt.
8. Угловая скорость при равномерном вращательном движении
ω = /t = 2π/T = 2π ν,
где T– период обращения;ν– частота обращения, т. е. число оборотов в единицу времени.
9. Формулы, связывающие угловые и линейные величины при рассмотрении движения вращающегося тела:
S = R, V = ω R,
а = R, an = ω 2 R = V2/R,
где R– радиус траектории, по которой движется тело;a– тангенциальное ускорение;an– нормальное или центростремительное ускорение.
Динамика поступательного движения
10. Основной закон динамики поступательного движения
 dt=d(m
dt=d(m ).
).
11. Второй закон Ньютона
 =
=  /m,
/m,
где  – ускорение тела;
– ускорение тела; – сила, действующая на тело; m–
масса тела.
– сила, действующая на тело; m–
масса тела.
12. Закон Гука
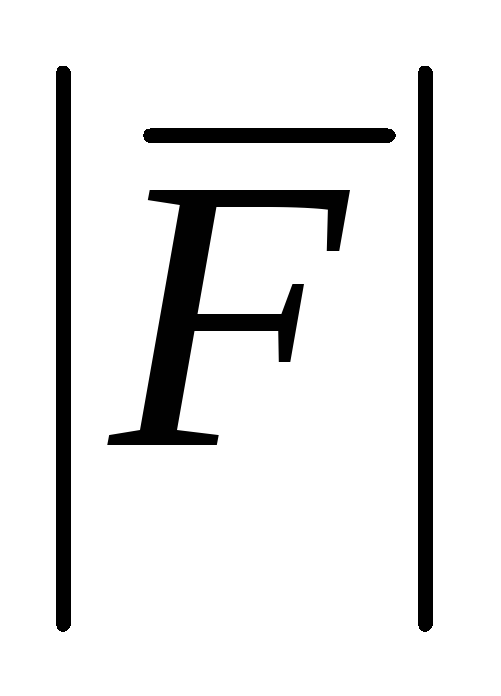 = – kx,
= – kx,
где k– коэффициент упругости;х– величина деформации.
13. Сила трения
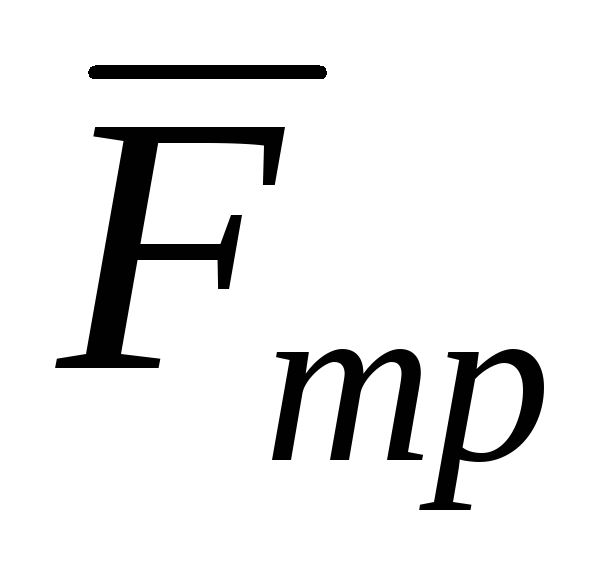 =
=  ,
,
где – коэффициент трения;N– сила нормального давления, прижимающая тело к плоскости при скольжении.
14. Гравитационная сила
F=Gm1m2/r2,
где F– сила гравитационного притяжения между двумя точечными массамиm1иm2;r– расстояние между ними;G– гравитационная постоянная.
15. Закон сохранения импульса
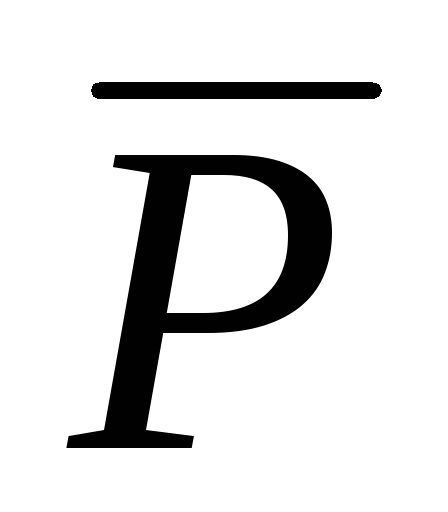 = m1
= m1 1+m2
1+m2 2+ …. +mi
2+ …. +mi i=const.
i=const.
16. Скорость движения тел после неупругого, центрального удара
 = (m1
= (m1 1+m2
1+m2 2)/(m1+m2),
2)/(m1+m2),
где m1–
масса первого тела;m2–
масса второго тела; 1– скорость первого тела до удара;
1– скорость первого тела до удара; 2– скорость второго тела до удара.
2– скорость второго тела до удара.
17. Скорости первого и второго тел после упругого соударения:
 1=[(m1–m2)
1=[(m1–m2)  1 + 2m2
1 + 2m2 2]
/(m1+m2),
2]
/(m1+m2),
 2=[(m2–m1)
2=[(m2–m1)  2 + 2m1
2 + 2m1 1]
/(m1+m2),
1]
/(m1+m2),
18. Механическая работа
A=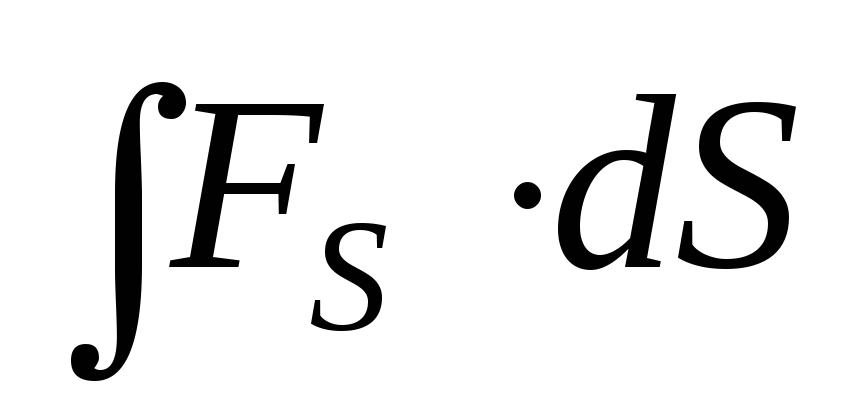 ,
,
где FS– проекция силы на направление пути;S– величина участка пути.
В частном случае постоянной силы, действующей под неизменным углом к перемещению, имеем
A=FScos ,
где F– модуль вектора силы;S– модуль вектора перемещения;– угол между векторами силы и перемещения.
19. Мощность
N=dA/dt.
При постоянной мощности
N = A/t = F V cos α,
где А– работа, произведенная какой-либо силой;t– время, за которое произведена эта работа.
20. Кинетическая энергия
Wк= mV2/2,
где m– масса движущегося тела;V– скорость, с которой это тело движется.
21. Потенциальная энергия тела в поле силы тяжести (вблизи поверхности Земли)
Wп = mgh,
где m– масса тела;g– ускорение свободного падения;h– высота тела над поверхностью Земли.
22. Закон сохранения механической энергии
Wк+Wп=const.
23. Давление в жидкости и газе
P = Fдав/S,
где Fдав– cила давления;S– площадь поверхности.
24. Закон Архимеда
Fa = жgVпогр,
где ж– плотность жидкости;g– уcкорение свободного падения;Vпогр– объем жидкости, вытесненной погруженной частью тела.
studfile.net
Формулы МКТ / Блог
Молекулярная физика: основные формулы для решения задач
Основы молекулярно-кинетической теории
- v=\frac{N}{N_A}
- M=\frac{m}{v}=m_{0}N_{A}
- n=\frac{N}{V}
- NA = 6.02214129 × 1023 Моль-1 – постоянная Авогадро
Основное уравнение МКТ
Основное уравнение МКТ идеального газа:
- p=\frac{2}{3}n \overline{ E_K}
Уравнение Клайперона-Менделеева (уравнение состояния идеального газа)
- \frac{p_1V_1}{T_1}=\frac{p_2V_2}{T_2}=const
Уравнение состояния идеального газа:
- pV=vRT=\frac{m}{M}RT
- R = kNA – универсальная газовая постоянная.
Изотермический закон (закон Бойля-Мариотта)
- pV =const при Т = const.
- p_1V_1=p_2V_2=const
Изохорный закон (закон Шарля)
- \frac{p}{T}=const при V=const
- \frac{p_1}{T_1}=\frac{p_2}{T_2}=const
Изобарный закон (закон Гей-Люссака)
- \frac{V}{T}=const при p=const
- \frac{V_1}{T_1}=\frac{V_2}{T_2}=const
Закон Дальтона
- p =p_1 + p_2 + p_3 + … = (n_1 + n_2 + n_3 + …)kT
Средняя квадратичная скорость движения молекул газа:
- \overline {v}=\sqrt{\frac{3kT}{m_0}}=\sqrt{\frac{3RT}{M}}
- R = 8.3144621 м2 кг с-2 К-1 Моль-1 – универсальная газовая постоянная.
Средняя кинетическая энергия поступательного движения молекул:
- \overline{E_K}=\frac{3}{2}kT
Средняя кинетическая энергия молекул газа
- \overline{E_K}=\frac{3pV}{2N}=\frac{3pMV}{2mN_A}
Давление идеального газа на стенки сосуда
- p=nkT
- k = 1.3806488 × 10-23 м2 кг с-2 К-1 – постоянная Больцмана.
Абсолютная температура
Плотность
Смотри так же:
bingoschool.ru
Кинематические уравнения движения
Кинематические уравнения движения используются, чтобы описать перемещение объекта в пространстве. Так как при поступательном движении все точки объекта движутся одинаково, то его удобно представлять материальной точкой: она имеет определенную массу, однако её размерами можно пренебречь. Чтобы количественно описать движение точки, нужно ввести временную и пространственные координаты. При поступательном движении удобней всего пользоваться декартовой системой координат.
Положение такой точки в пространстве описывается радиус-вектором:
Можно спроектировать его на оси координат, тогда получим систему скалярных уравнений. Эти уравнения и называют кинематическими уравнениями движения:
Характеристики кинематического уравнения движения
Длина пути точки, пройденного ею с начального момента до момента t, обозначается и является скалярной величиной. Если движение прямолинейное, то вектор перемещения , соединяющий начальное и конечное положение точки, совпадает с путем точки, . Если же движение криволинейное, обычно находят с помощью геометрических построений.
Длина пути, пройденная точкой за конечное время t, может быть найдена с помощью формулы:
Здесь v – функция изменения скорости точки во времени, — начальная скорость, а – ускорение, t – время.
Если движение равномерное, то есть скорость остается неизменной, пройденный путь можно найти проще:
Скорость – величина векторная; она характеризует не только быстроту движения точки, но и направление этого движения. Она направлена так же, как и вектор перемещения. Средняя скорость может быть рассчитана:
Если интервал времени , вектор перемещения стремится к тому, чтобы совпадать с путем перемещения, и тогда может быть вычислена мгновенная скорость:
Ускорение точки (в векторном или скалярном виде) мы узнаем, взяв производную от скорости по времени:
Если движение криволинейно, ускорение можно разложить на две составляющие: тангенциальное ускорение и центростремительное ускорение :
где R – это радиус кривизны рассматриваемой траектории. Модуль ускорения, включающего обе компоненты, при криволинейном движении:
Если движение имеет прямолинейный характер, ускорение имеет только тангенциальную составляющую.
Примеры решения задач
ru.solverbook.com
Основные понятия кинематики и уравнения
Что представляют собой основные понятия кинематики? Что это вообще за наука и изучением чего она занимается? Сегодня мы поговорим о том, что представляет собой кинематика, какие основные понятия кинематики имеют место в задачах и что они означают. Дополнительно поговорим о величинах, с которыми наиболее часто приходится иметь дело.
Кинематика. Основные понятия и определения

Для начала поговорим о том, что она собой представляет. Одним из наиболее изучаемых разделов физики в школьном курсе является механика. За ней в неопределенном порядке следует молекулярная физика, электричество, оптика и некоторые другие разделы, такие как, например, ядерная и атомная физика. Но давайте подробнее разберемся с механикой. Этот раздел физики занимается изучением механического движения тел. В нем устанавливаются некоторые закономерности и изучаются его способы.
Кинематика как часть механики
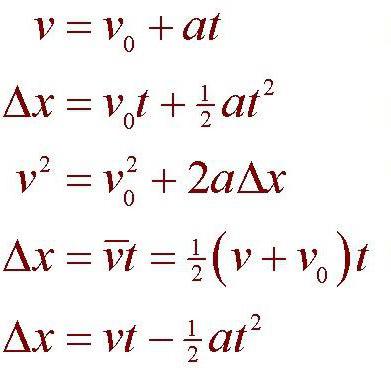
Последняя подразделяется на три части: кинематика, динамика и статика. Эти три поднауки, если их так можно назвать, имеют некоторые особенности. Например, статика изучает правила равновесия механических систем. Сразу же в голову приходит ассоциация с чашами весов. Динамика изучает закономерности движения тел, но при этом обращает внимание на силы, действующие на них. А вот кинематика занимается тем же самым, только в учет силы не принимаются. Следовательно, не учитывается в задачах и масса тех самых тел.
Основные понятия кинематики. Механическое движение

Субъектом в этой науке является материальная точка. Под ней понимается тело, размерами которого, по сравнению с определенной механической системой, можно пренебречь. Это так называемое идеализированное тело, сродни идеальному газу, который рассматривают в разделе молекулярной физики. Вообще, понятие материальной точки, как в механике в общем, так и в кинематике в частности, играет достаточно важную роль. Наиболее часто рассматривается так называемое поступательное движение.
Что это значит и каким оно может быть?
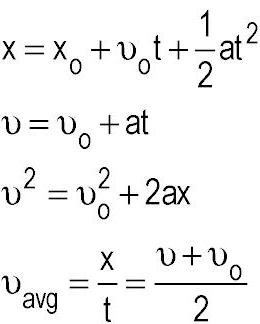
Обычно движения подразделяют на вращательное и поступательное. Основные понятия кинематики поступательного движения связаны в основном с применяемыми в формулах величинами. О них мы поговорим позднее, а пока что вернемся к типу движения. Понятно, что если речь идет о вращательном, то тело крутится. Соответственно, поступательным движением будет называться перемещение тела в плоскости или линейно.
Теоретическая база для решения задач

Кинематика, основные понятия и формулы которой рассматриваем сейчас, имеет огромное количество задач. Это достигается за счет обычной комбинаторики. Один из методов разнообразия здесь – изменение неизвестных условий. Одну и ту же задачу можно представить в разном свете, просто меняя цель ее решения. Требуется найти расстояние, скорость, время, ускорение. Как видите, вариантов целое море. Если же сюда подключить условия свободного падения, простор становится просто невообразимым.
Величины и формулы
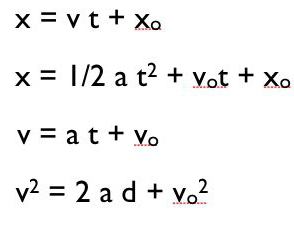
Прежде всего сделаем одну оговорку. Как известно, величины могут иметь двоякую природу. С одной стороны, определенной величине может соответствовать то или иное численное значение. Но с другой, она может иметь и направление распространения. Например, волна. В оптике мы сталкиваемся с таким понятием, как длина волны. Но ведь если есть когерентный источник света (тот же самый лазер), то мы имеем дело в пучком плоскополяризованных волн. Таким образом, волне будет соответствовать не только численное значение, обозначающее ее длину, но и заданное направление распространения.
Классический пример
Подобные случаи являются аналогией в механике. Допустим, перед нами катится тележка. По характеру движения мы можем определить векторные характеристики ее скорости и ускорения. Сделать это при поступательном движении (например, по ровному полу) будет чуточку сложнее, поэтому мы рассмотрим два случая: когда тележка закатывается наверх и когда она скатывается вниз.
Итак, представим себе, что тележка едет вверх по небольшому уклону. В таком случае она будет замедляться, если на нее не действуют внешние силы. Но в обратной ситуации, а именно, когда тележка скатывается сверху вниз, она будет ускоряться. Скорость в двух случаях направлена туда, куда движется объект. Это нужно взять за правило. А вот ускорение может изменять вектор. При замедлении оно направлено в противоположную для вектора скорости сторону. Этим объясняется замедление. Аналогичную логическую цепочку можно применить и для второй ситуации.
Остальные величины
Только что мы поговорили о том, что в кинематике оперируют не только скалярными величинами, но и векторными. Теперь сделаем еще один шаг вперед. Кроме скорости и ускорения при решении задач применяются такие характеристики, как расстояние и время. Кстати, скорость подразделяется на начальную и мгновенную. Первая из них является частным случаем второй. Мгновенная скорость — эта та скорость, которую можно найти в любой момент времени. А с начальной, наверное, все и так понятно.
Задача
Немалая часть теории была изучена нами ранее в предыдущих пунктах. Теперь осталось только привести основные формулы. Но мы сделаем еще лучше: не просто рассмотрим формулы, но и применим их при решении задачи, чтобы окончательно закрепить полученные знания. В кинематике используется целый набор формул, комбинируя которые, можно добиться всего, чего нужно для решения. Приведем задачу с двумя условиями, чтобы разобраться в этом полностью.
Велосипедист тормозит после пересечения финишной черты. Для полной остановки ему потребовалось пять секунд. Узнайте, с каким ускорением он тормозил, а также какой тормозной путь успел пройти. Тормозной путь считать линейным, конечную скорость принять равной нулю. В момент пересечения финишной черты скорость была равна 4 метрам в секунду.
На самом деле, задача достаточно интересная и не такая простая, как может показаться на первый взгляд. Если мы попробуем взять формулу расстояния в кинематике (S = Vot +(-) (at^2/2)), то ничего у нас не выйдет, поскольку мы будем иметь уравнение с двумя переменными. Как же поступить в таком случае? Мы можем пойти двумя путями: сначала вычислить ускорение, подставив данные в формулу V = Vo – at или же выразить оттуда ускорение и подставить его в формулу расстояния. Давайте используем первый способ.
Итак, конечная скорость равна нулю. Начальная – 4 метра в секунду. Путем переноса соответствующих величин в левые и правые части уравнения добиваемся выражения ускорения. Вот оно: a = Vo/t. Таким образом, оно будет равно 0,8 метров на секунду в квадрате и будет нести тормозящий характер.
Переходим к формуле расстояния. В нее просто подставляем данные. Получим ответ: тормозной путь равен 10 метрам.
fb.ru