Линейные дифференциальные уравнения первого порядка
Определение. Линейным уравнением первого порядка
называется уравнение, линейное
относительно искомой функции и ее
производной. Общий вид линейного д.у.1: 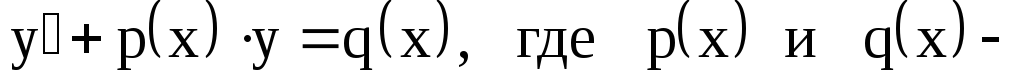 непрерывные функции или постоянные.
Если
непрерывные функции или постоянные.
Если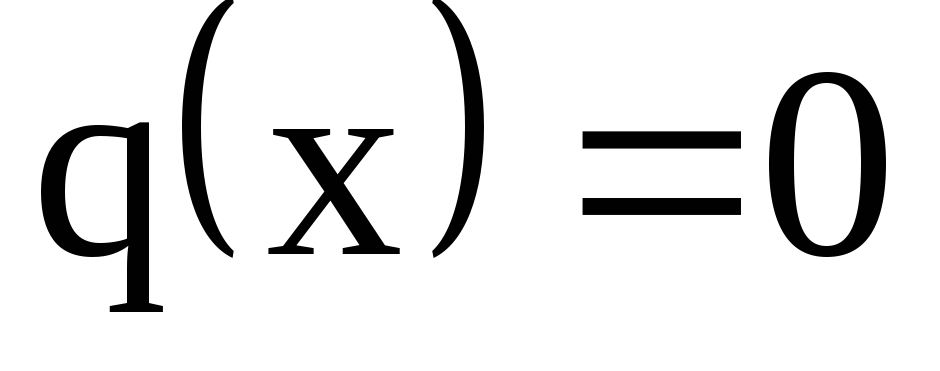 ,
то уравнение
,
то уравнение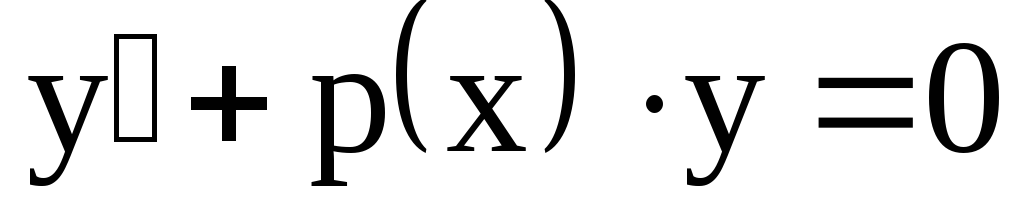 решается как дифференциальное уравнение
с разделяющимися переменными.
решается как дифференциальное уравнение
с разделяющимися переменными.
Рассмотрим уравнения:
1) 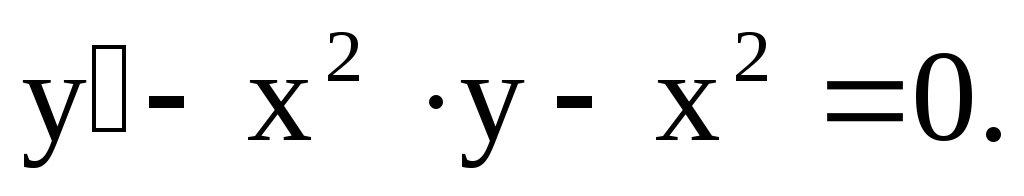 Это уравнение является линейным по
определению
Это уравнение является линейным по
определению
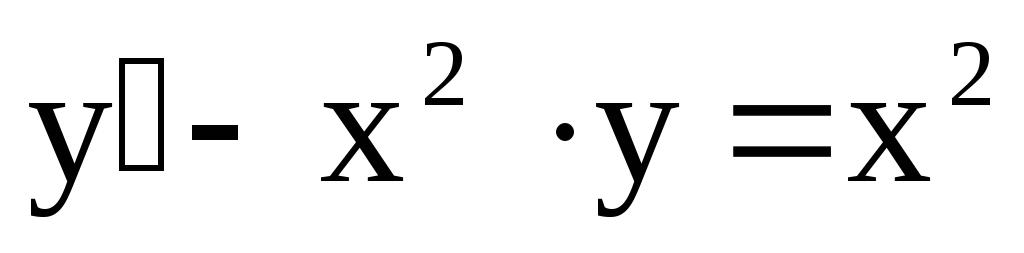

2)  Это
уравнение не является линейным, т. к.
функцияy в уравнении имеет не первую степень,
а выше
Это
уравнение не является линейным, т. к.
функцияy в уравнении имеет не первую степень,
а выше
3) 
Уравнение является
линейным по определению. Но проще
рассматривать его как однородное д.у.1: 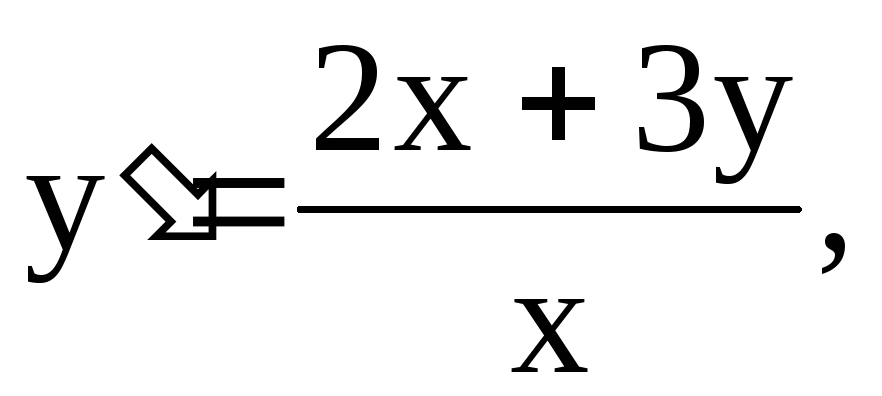 где
где – однородная функция нулевого измерения.
– однородная функция нулевого измерения.
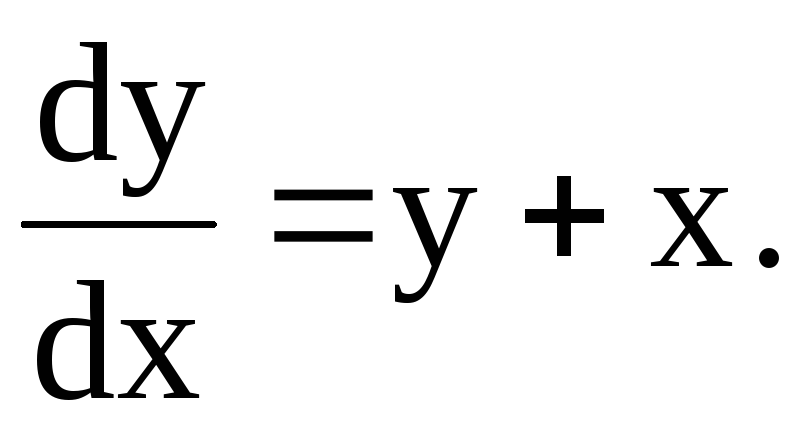 Запишем уравнение в виде
Запишем уравнение в виде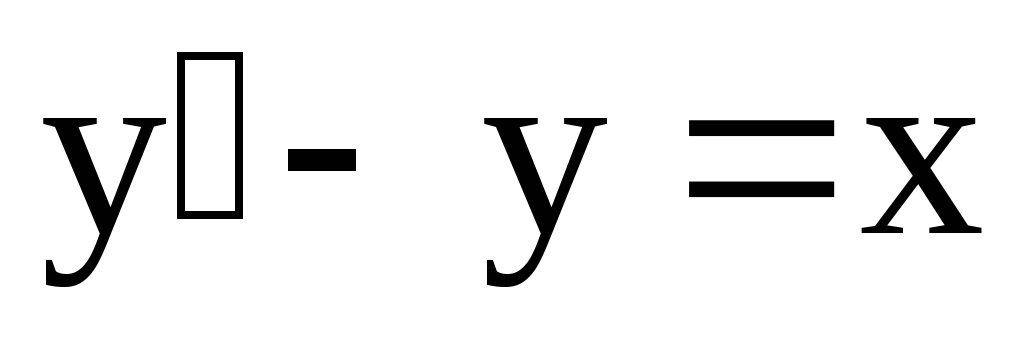 .
Это линейное д.у.1.
.
Это линейное д.у.1.Решение линейного дифференциального уравнения первого порядка
Общее решение
ищется в виде 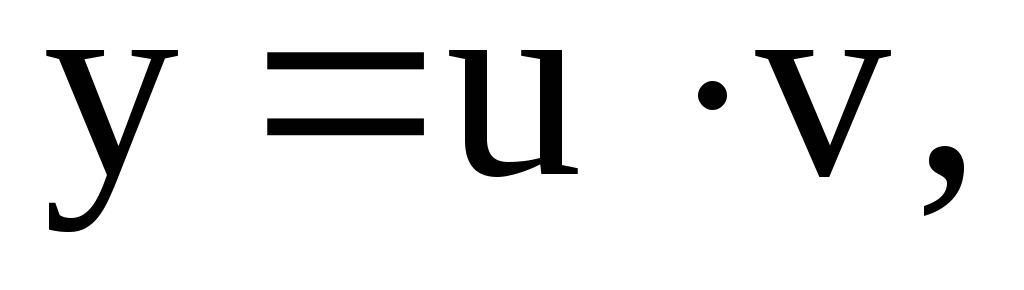 где
где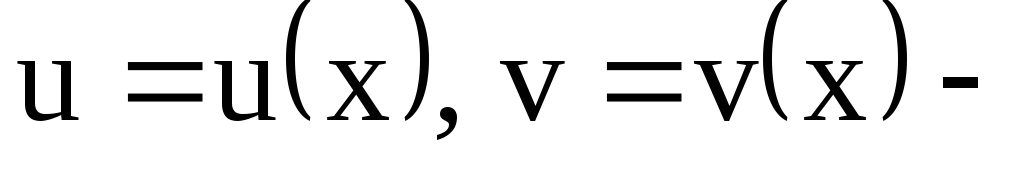 некоторые функции.
некоторые функции.
Покажем на
примере, что любую функцию 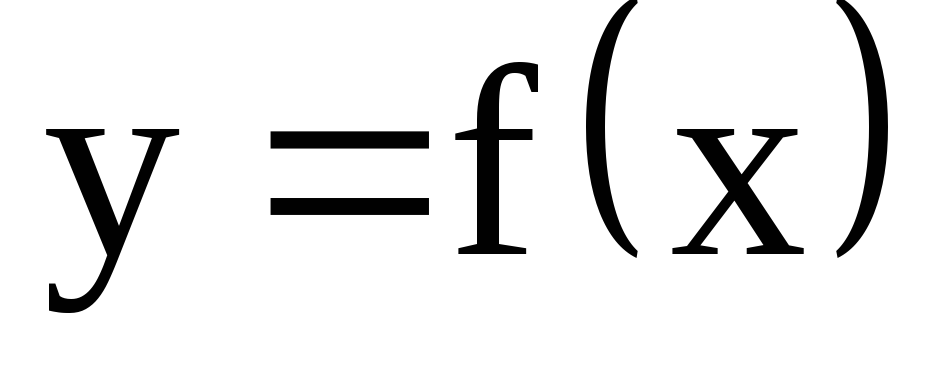 можно представить в виде произведения
двух функций, одна из которых выбирается
произвольно, а вторая зависит от этого
выбора.
можно представить в виде произведения
двух функций, одна из которых выбирается
произвольно, а вторая зависит от этого
выбора.
Пусть 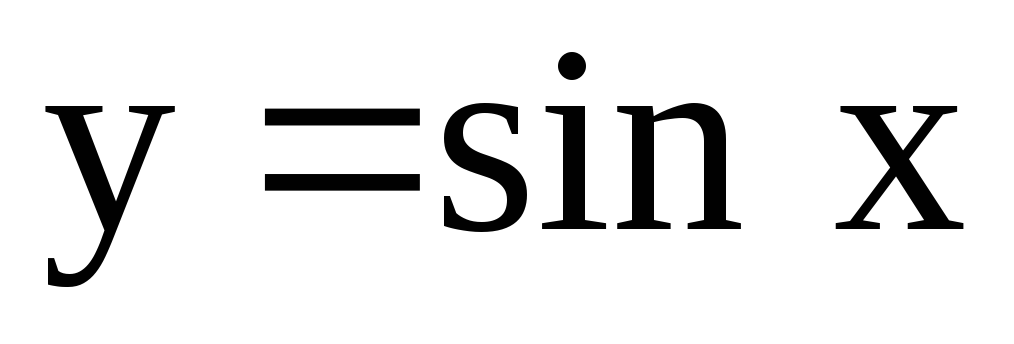 .
Можно
.
Можно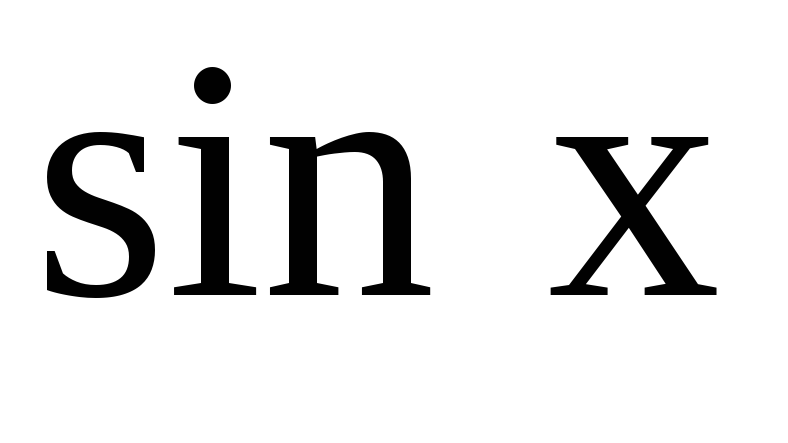
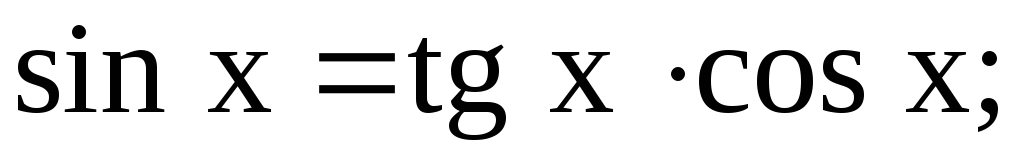
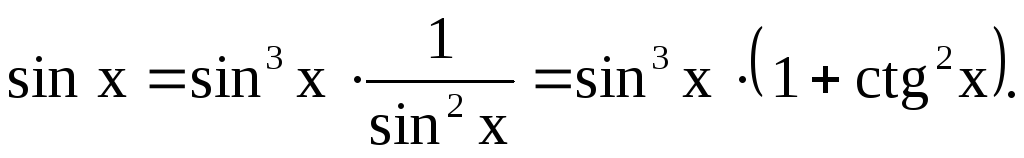
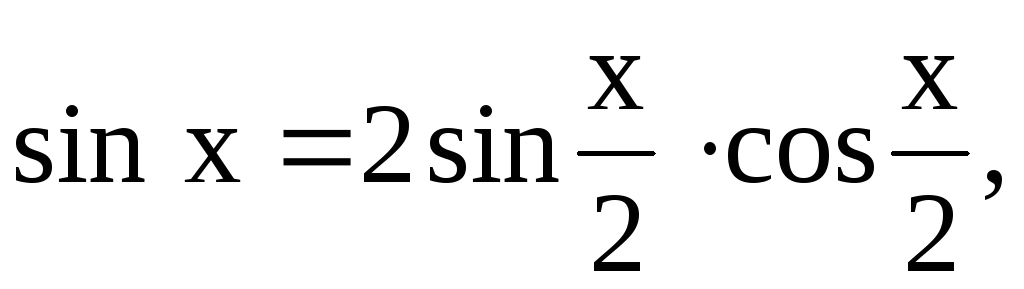 где первый множитель
выбирается произвольно.
где первый множитель
выбирается произвольно.
Указанная подстановка 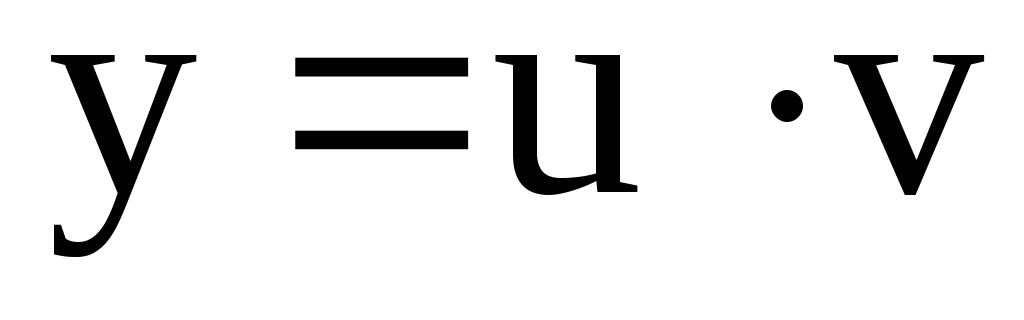 приводит линейное д.у.1 к решению двух
д.у. с разделяющимися переменными.
Покажем это в общем виде. В линейное
уравнение
приводит линейное д.у.1 к решению двух
д.у. с разделяющимися переменными.
Покажем это в общем виде. В линейное
уравнение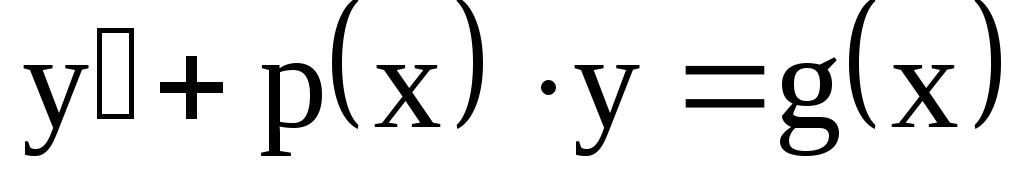 подставимПолучим
подставимПолучим
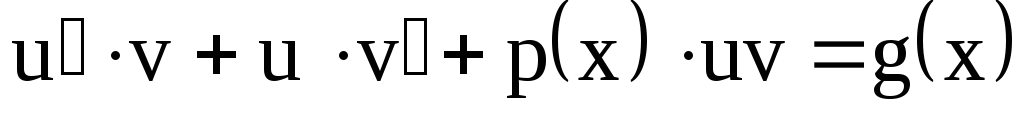
или
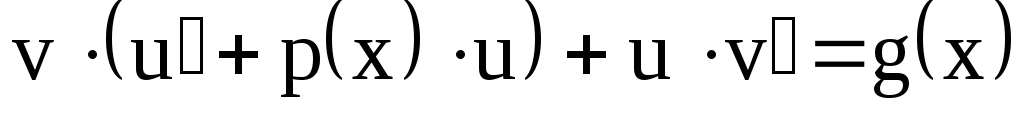
Выберем функцию u такой, чтобы
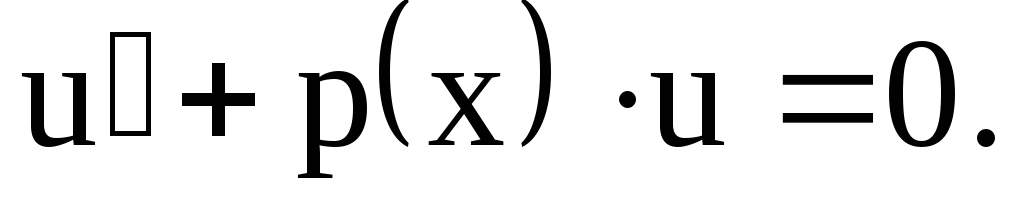 (5)
(5)
Уравнение (5) – дифференциальное уравнение с разделяющимися переменными:
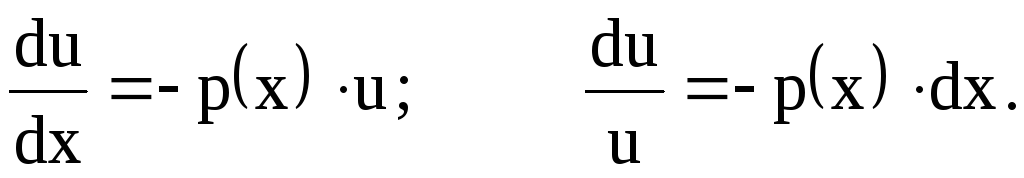 Интегрируя, найдем
функцию
Интегрируя, найдем
функцию 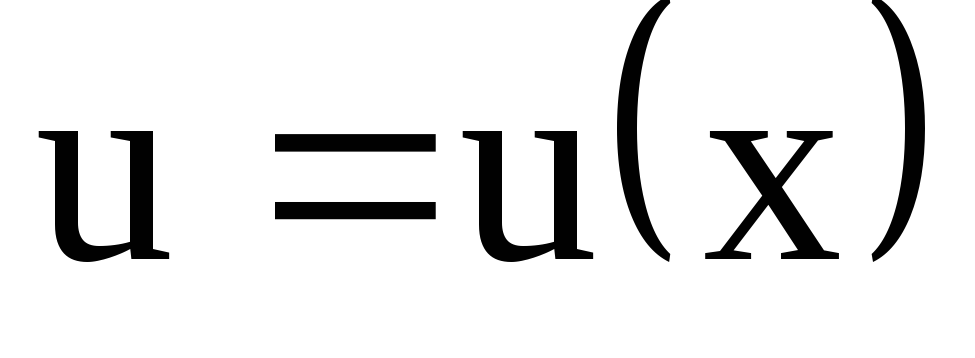 без
без
учета произвольной
постоянной. Подставим найденную функцию 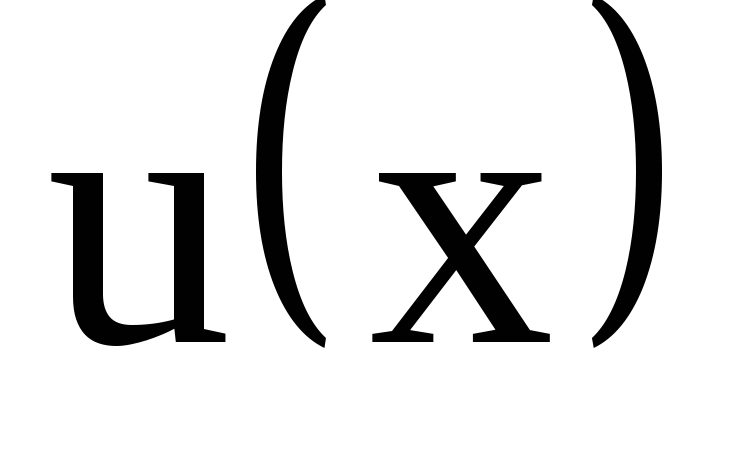 в уравнение (4) и получим
в уравнение (4) и получим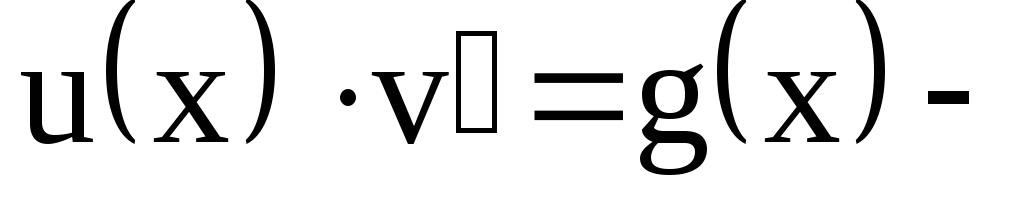
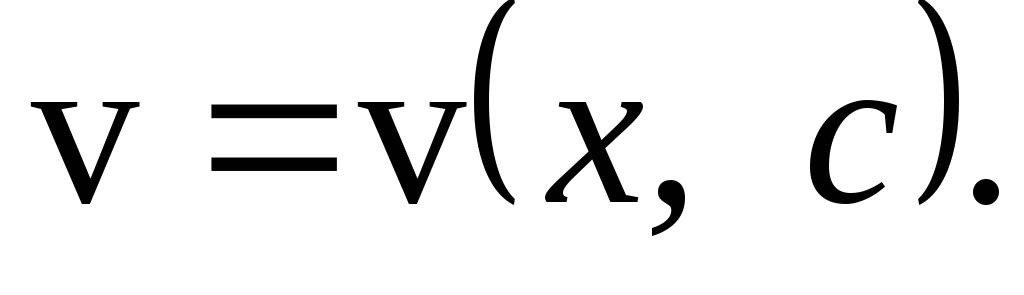 Тогда
Тогда 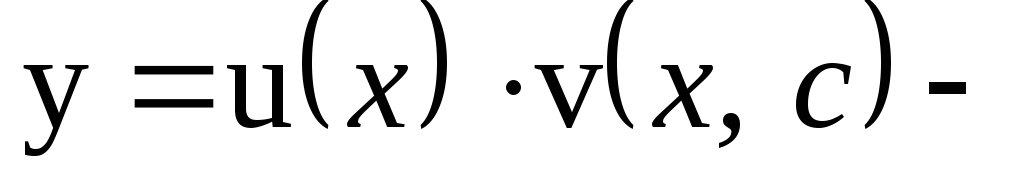 общее решение линейного д. у. 1.
общее решение линейного д. у. 1.
Пример 1. Найти общее решение уравнения 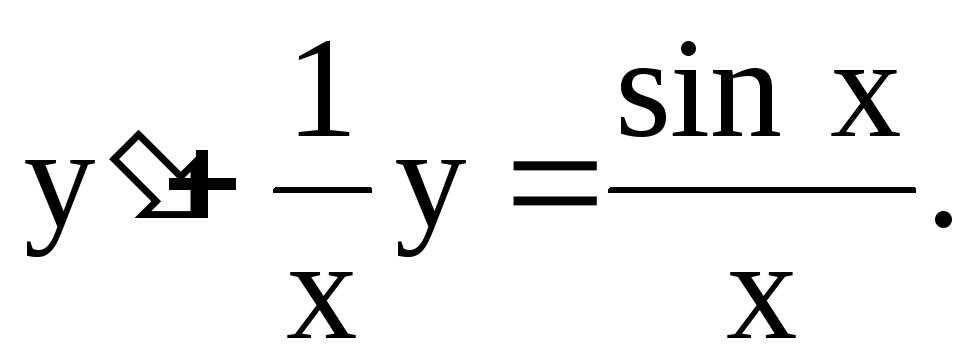
Решаем подстановкой
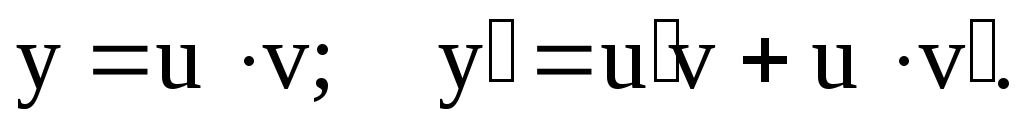
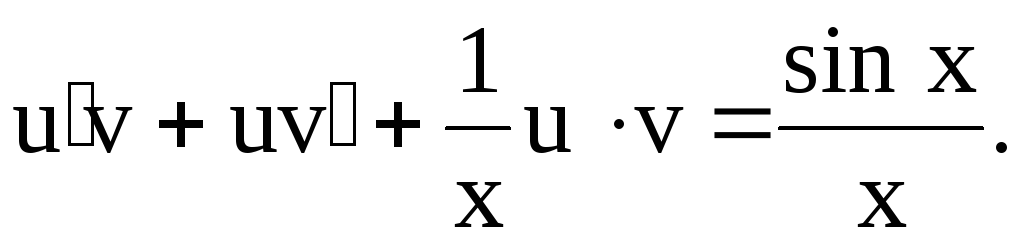
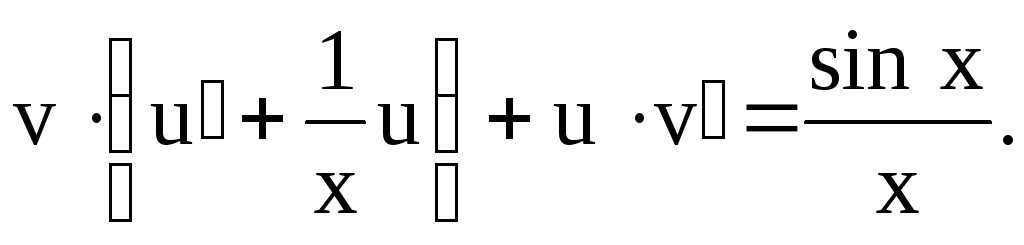 (6)
(6)


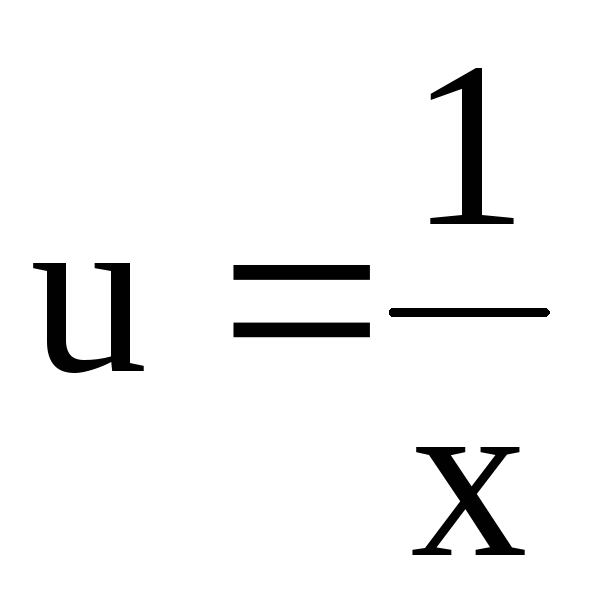 подставим в (6).
подставим в (6).
Общее решение: 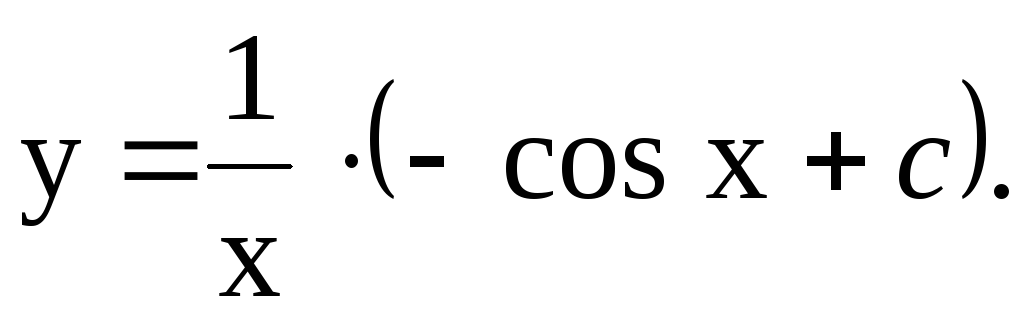
Пример 2. Найти частное решение дифференциального уравнения
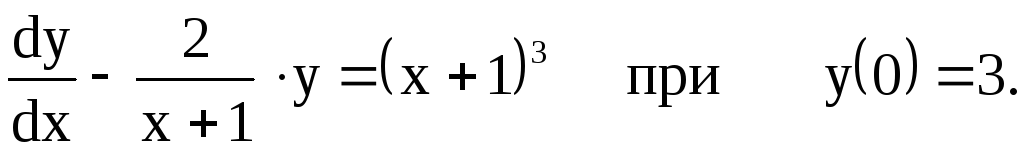
Подстановка: 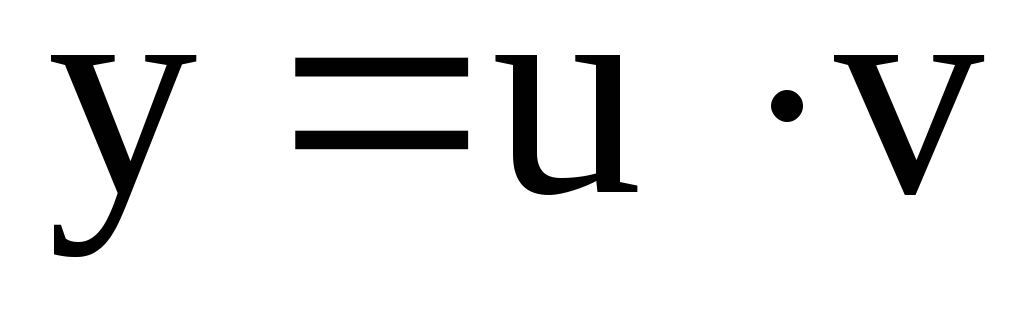 .
.
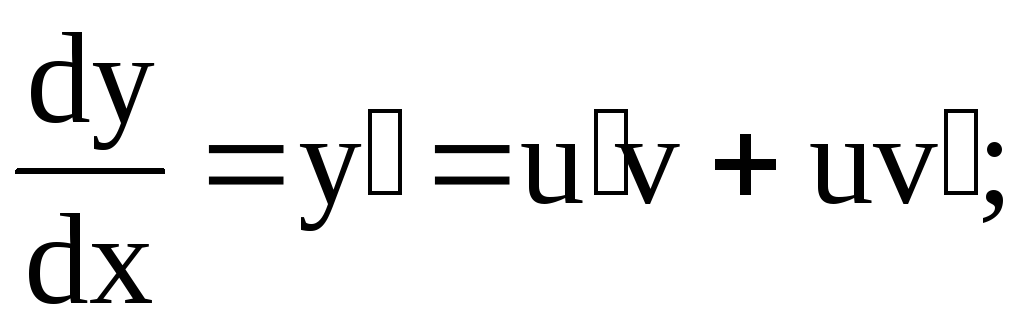
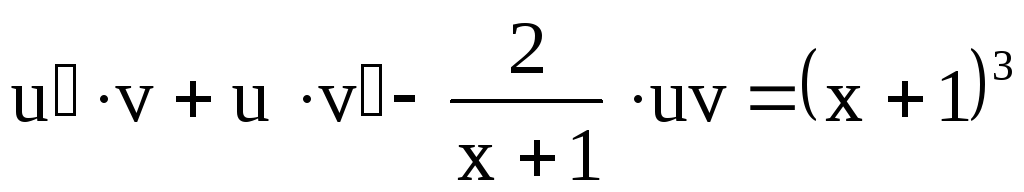
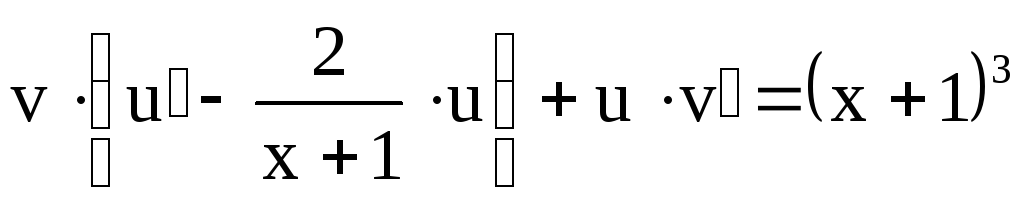 (7)
(7)
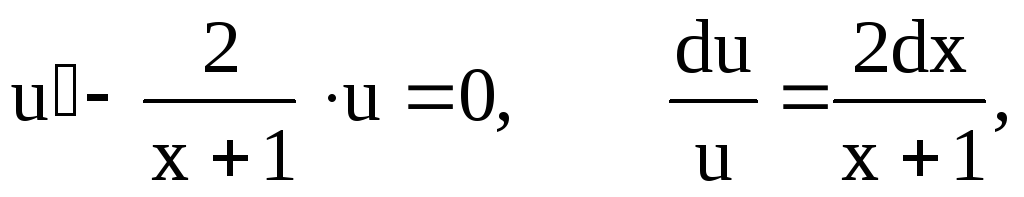

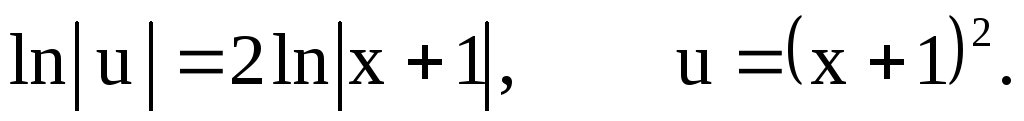
Подставим найденную
функцию u
в уравнение (7): 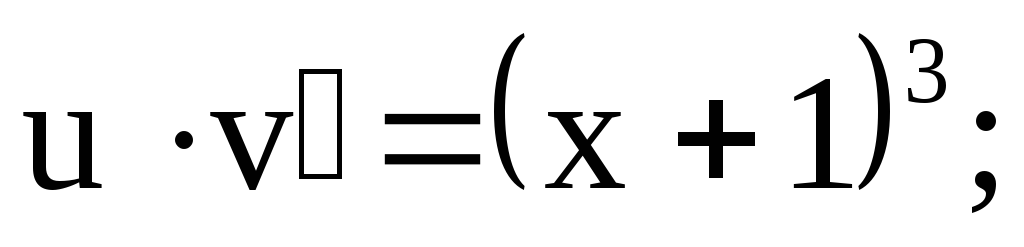
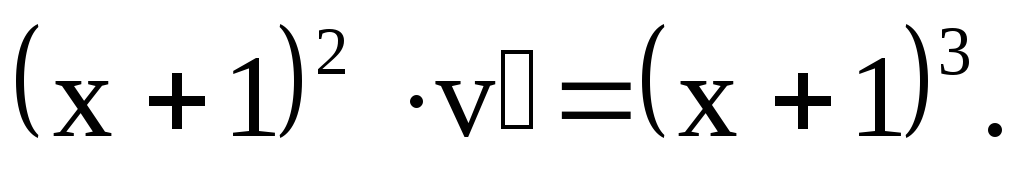
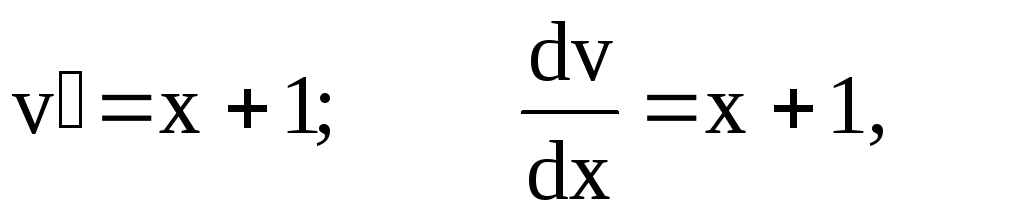
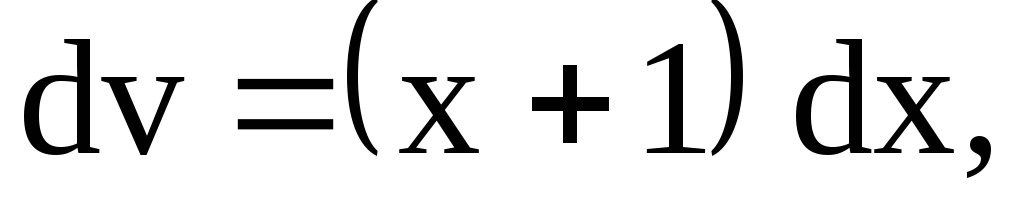
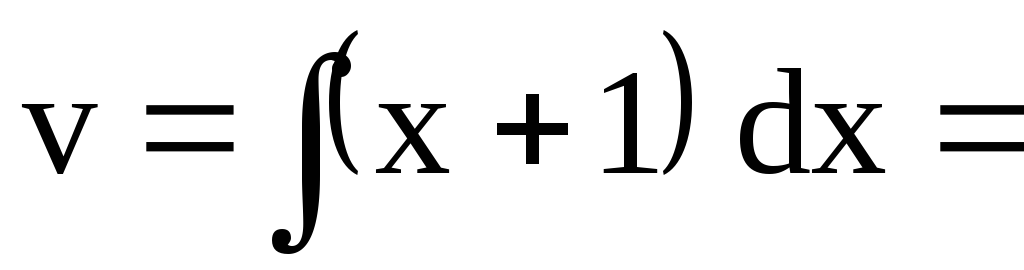

Таким образом, общее решение данного уравнения будет иметь вид
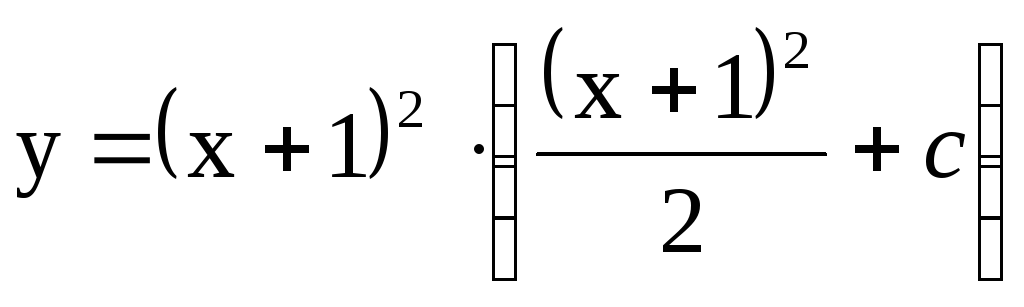
или 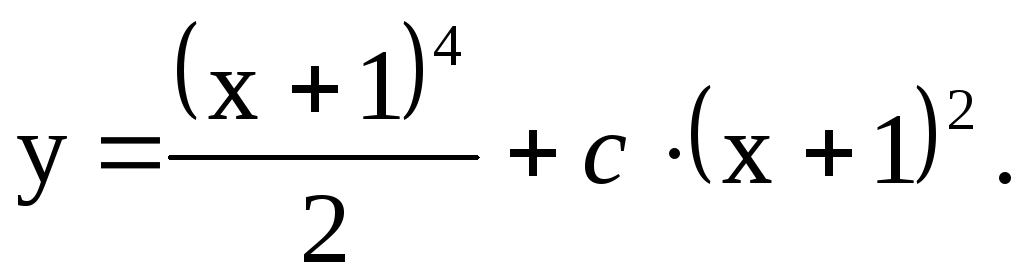
Найдем частное
решение дифференциального решения,
удовлетворяющее начальному условию 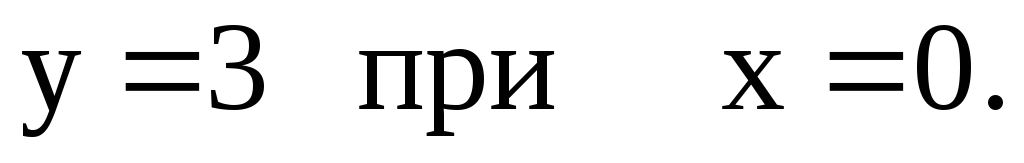
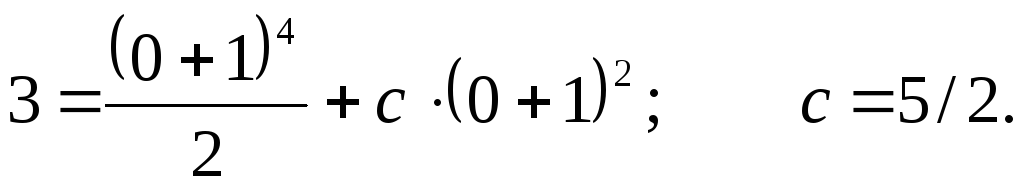
Следовательно, искомое частное решение такое:
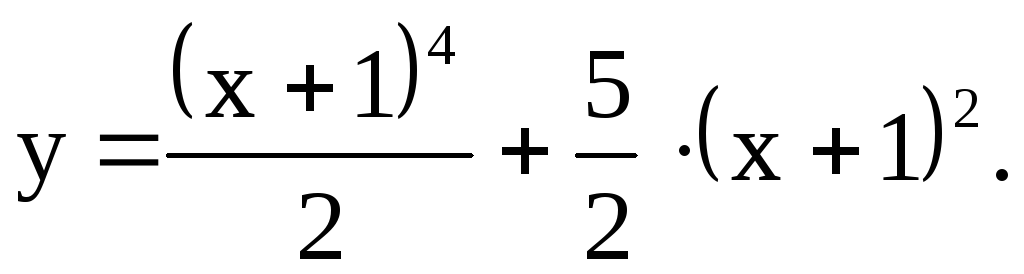
Уравнения, приводящиеся к линейным (уравнения Бернулли)
Уравнение вида 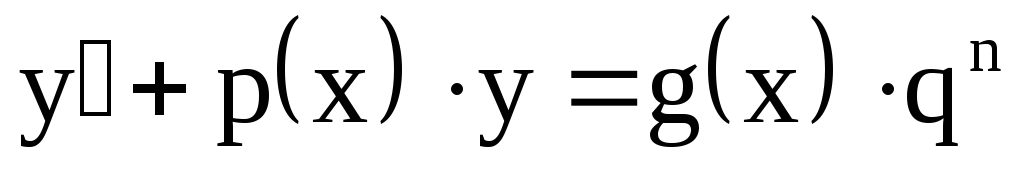 называется уравнением Бернулли. Здесь n
– действительное число, причем при n
= 0 получим линейное уравнение; при
называется уравнением Бернулли. Здесь n
– действительное число, причем при n
= 0 получим линейное уравнение; при 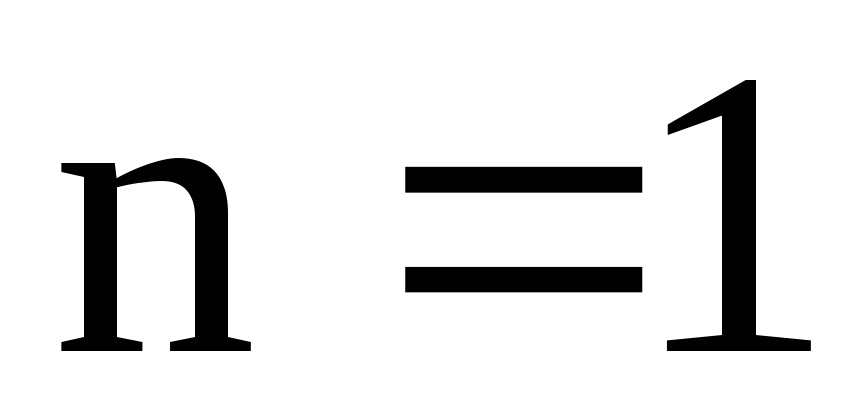 получим уравнение с разделяющимися
переменными. При
получим уравнение с разделяющимися
переменными. При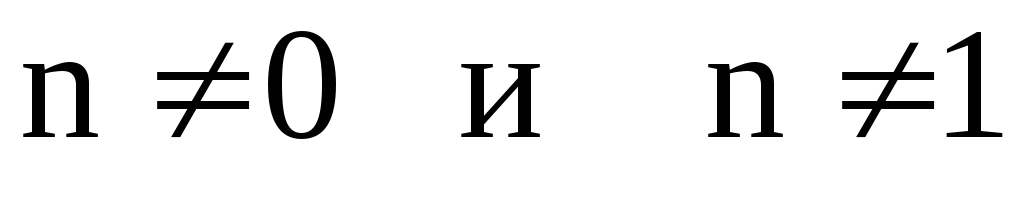 уравнение Бернулли приводится к
линейному, поэтому решается подстановкой
уравнение Бернулли приводится к
линейному, поэтому решается подстановкой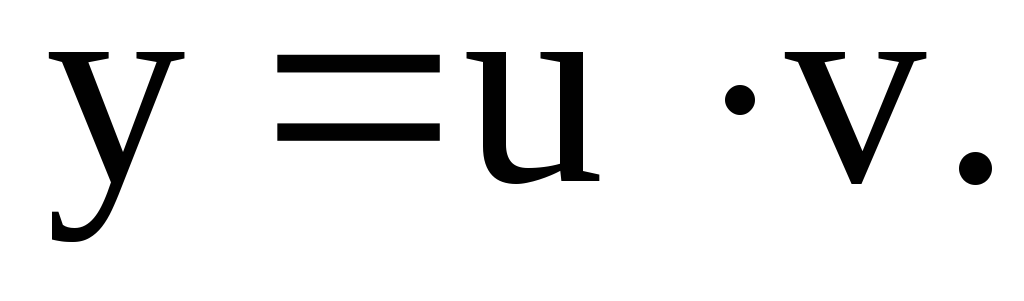
Пример. Найти общее решение уравнения

Разделив левую и правую части уравнения на х, представим его в виде
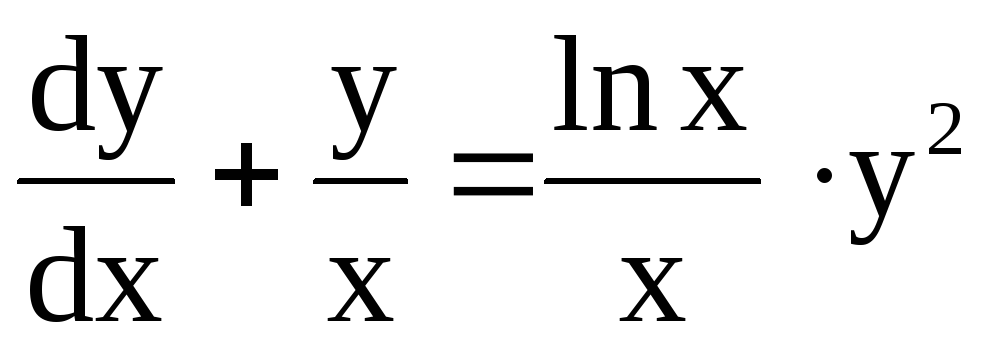 .
Можно утверждать, что это уравнение
имеет общий вид
.
Можно утверждать, что это уравнение
имеет общий вид
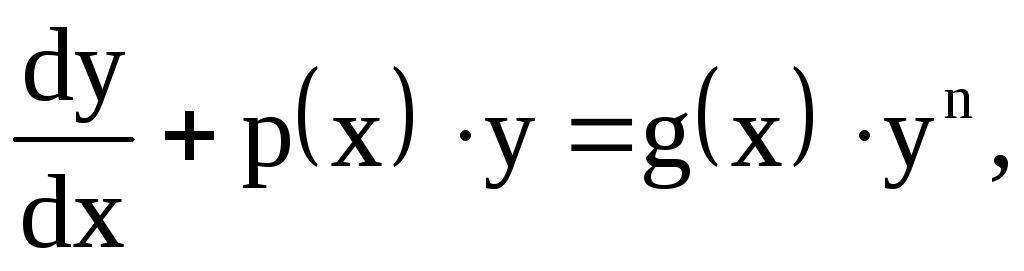
т. е. является
уравнением Бернулли. Решаем его
подстановкой 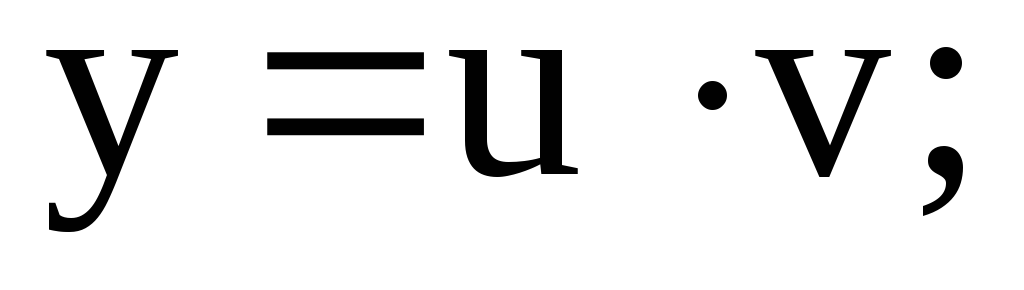
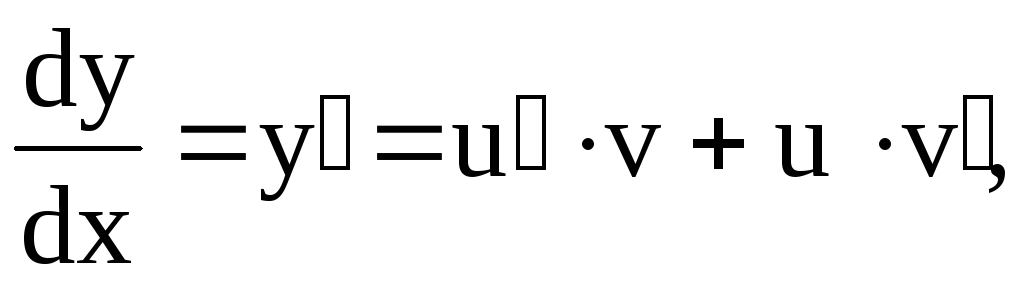
где  – вспомогательные функции.
– вспомогательные функции.
Подставим  в исходное уравнение:
в исходное уравнение:
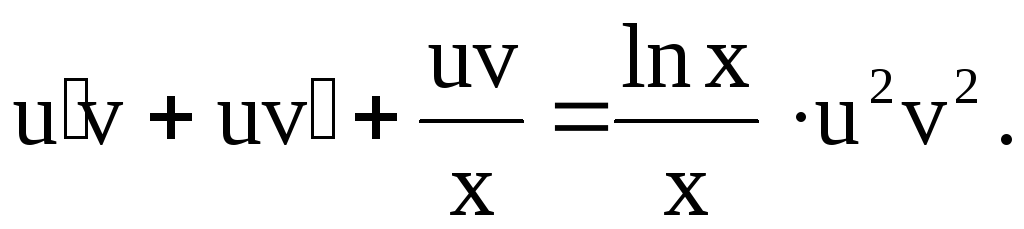
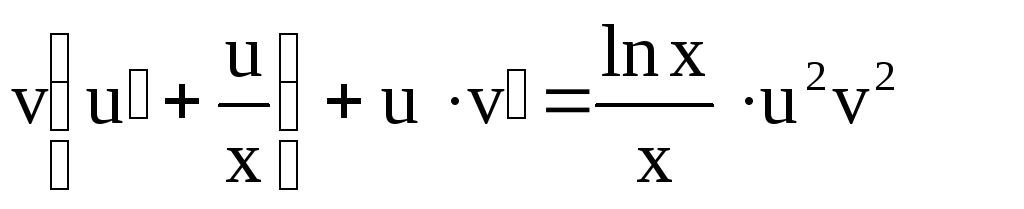 (8)
(8)

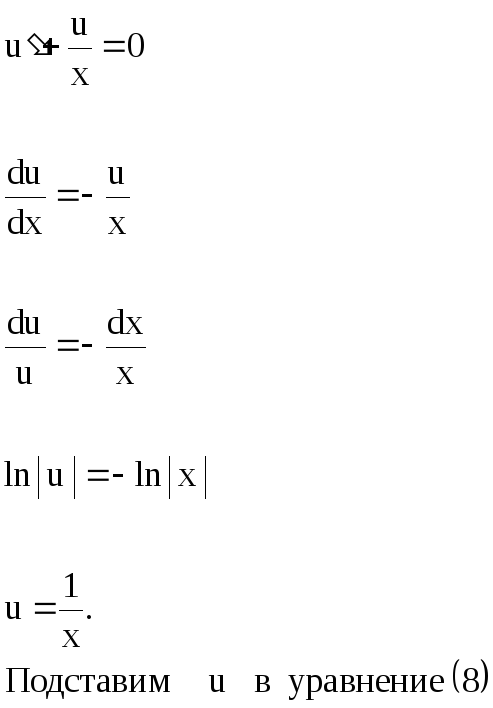
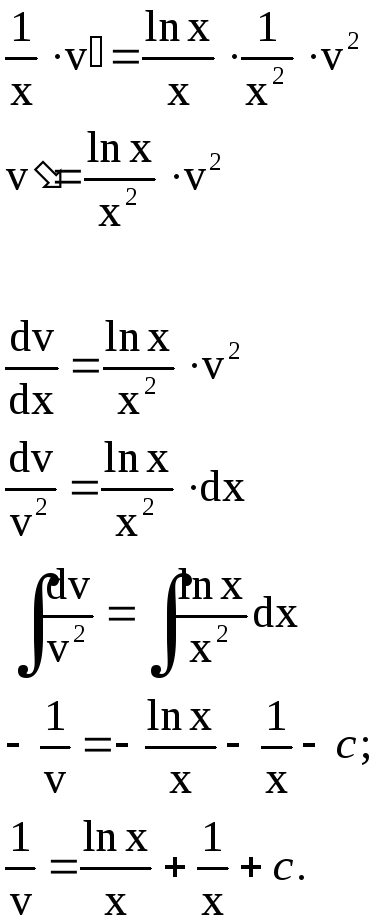
Для получения общего интеграла найдем
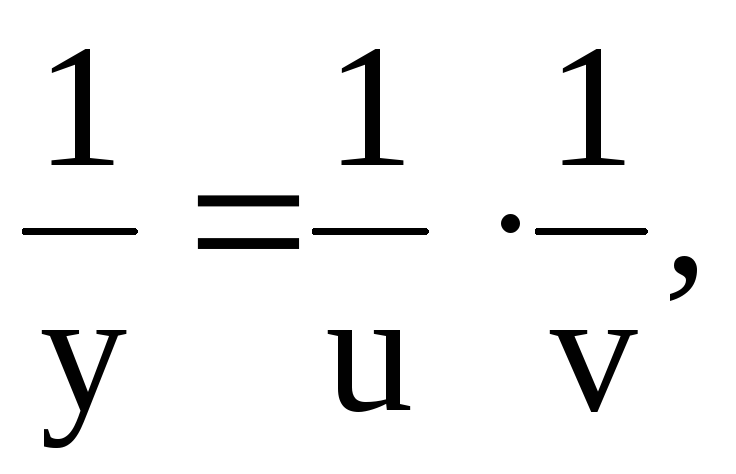
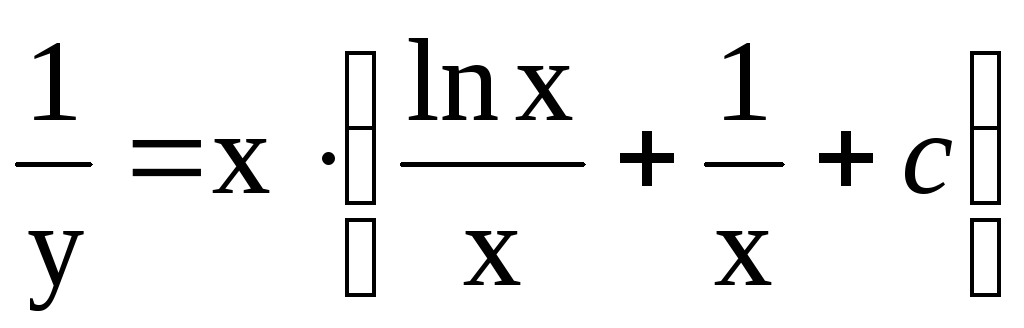
или
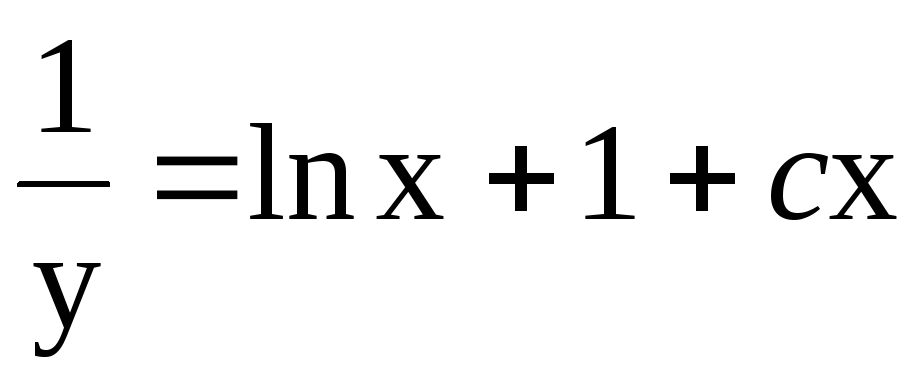 .
.
Замечание. Неопределенный интеграл 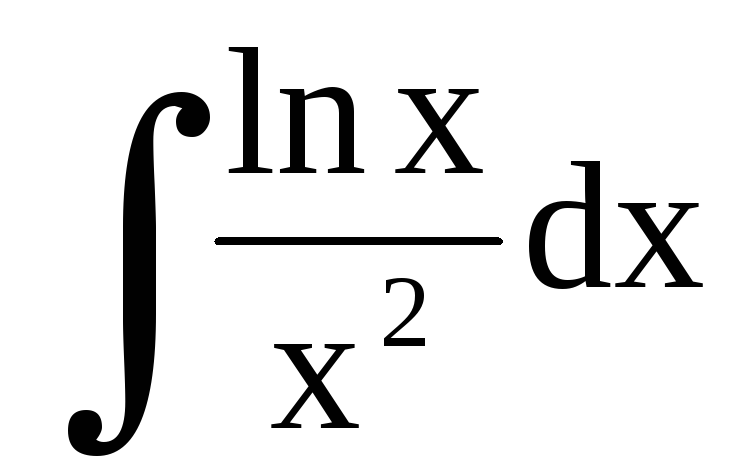 найден с применением
найден с применением
формулы интегрирования по частям:
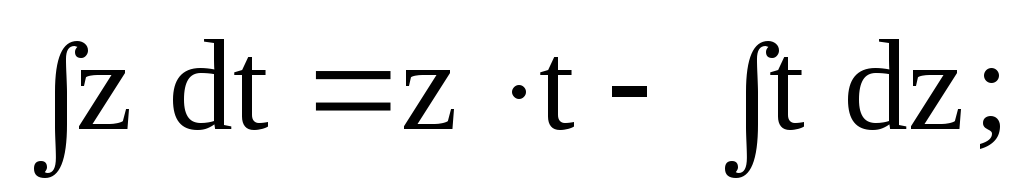
Производим подстановку
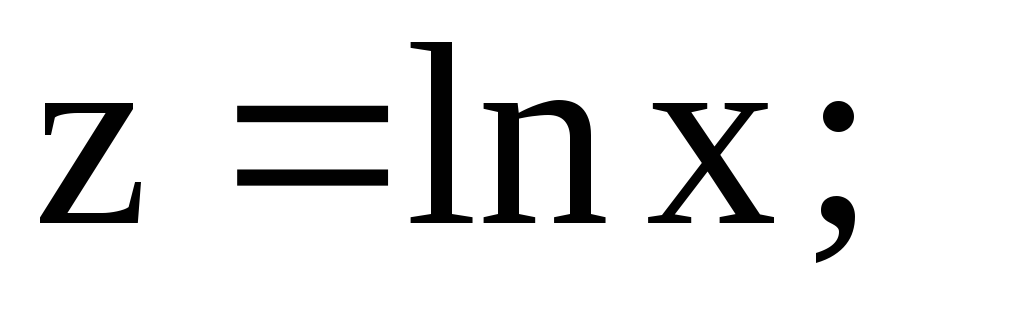
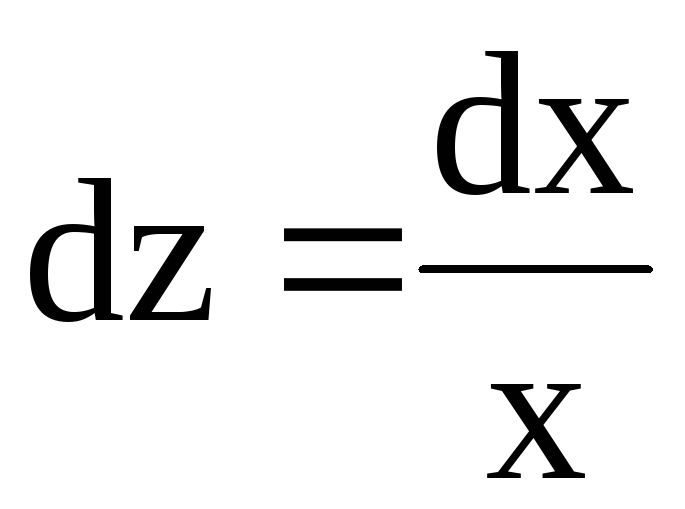 ;
;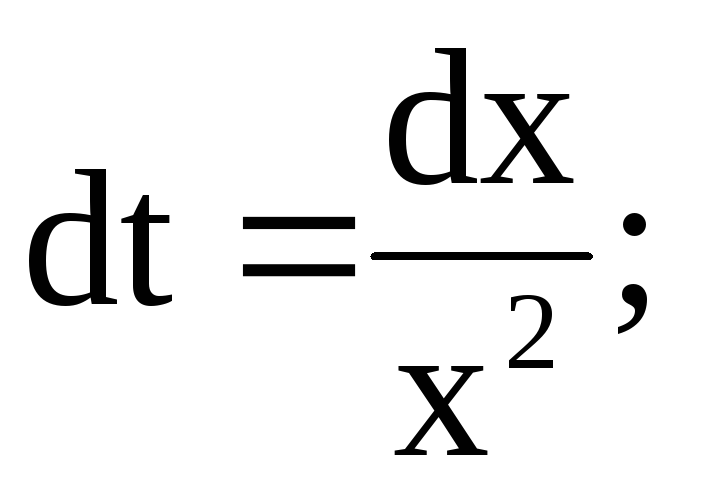
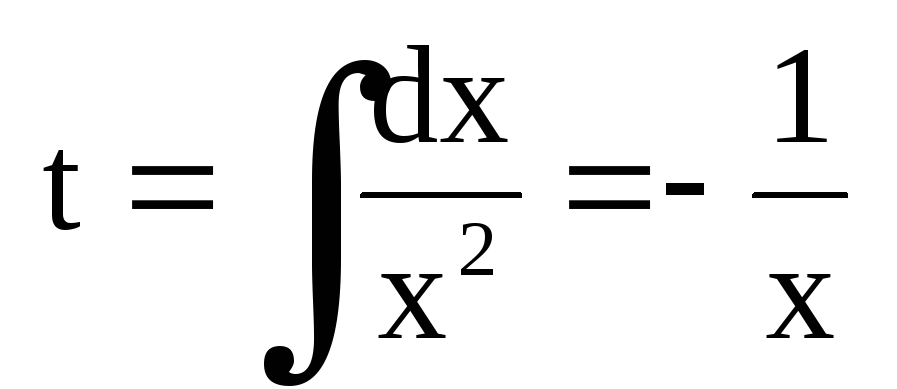 .
.
Тогда 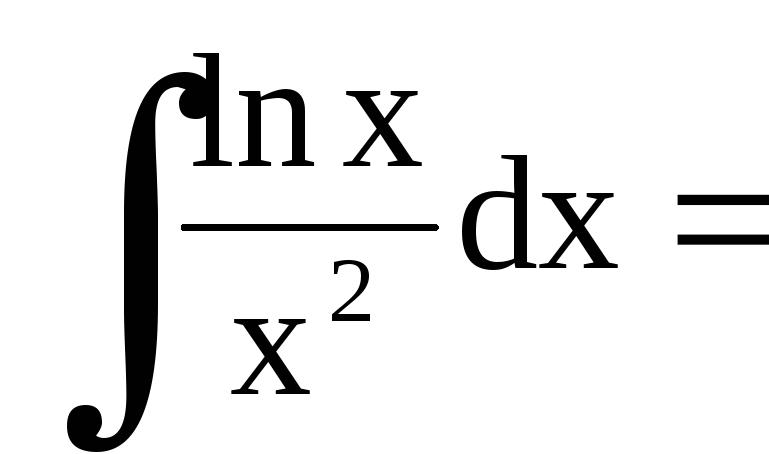
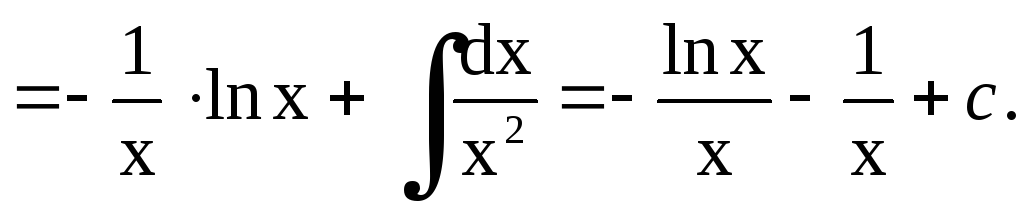
studfile.net
Линейные дифференциальные уравнения 1 порядка
Линейные
дифференциальные уравнения это вида 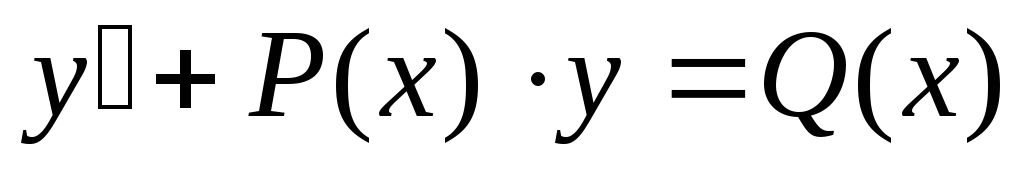 ,
гдеP(x),
Q(x)
– непрерывные функции.
,
гдеP(x),
Q(x)
– непрерывные функции.
 и
и  входят в уравнение линейно, т.е не
перемножаются между собой.
входят в уравнение линейно, т.е не
перемножаются между собой.
С делаем
замену:
делаем
замену: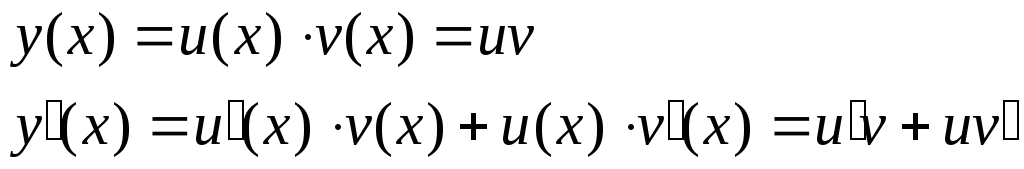
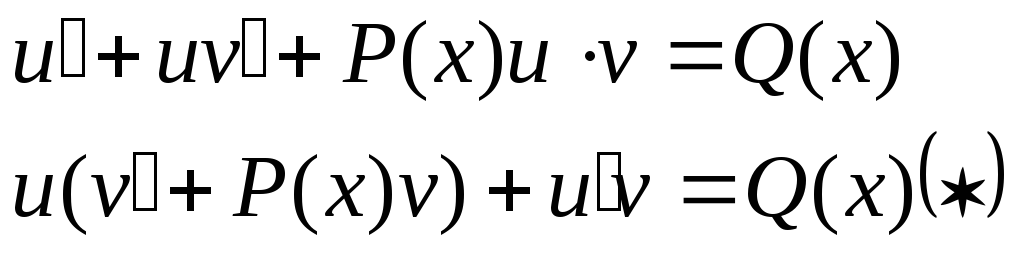

Приравняем скобку к 0
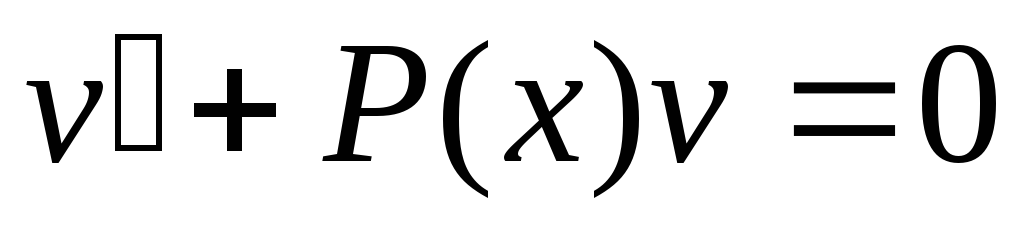 подставим
подставим 
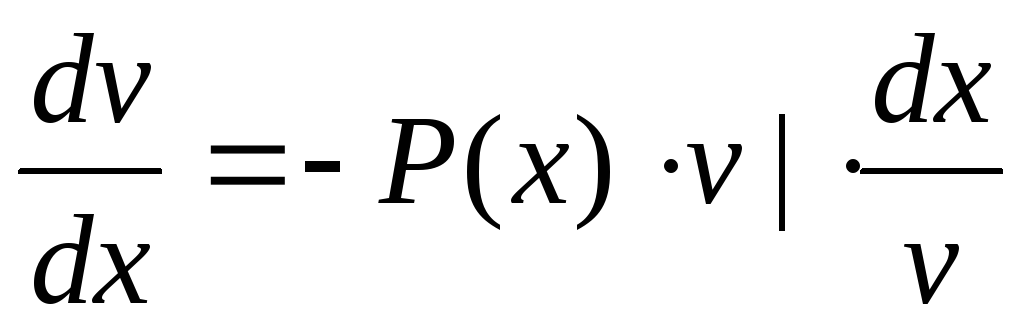 — дифференциальное
уравнение с разделяющимися переменными.
— дифференциальное
уравнение с разделяющимися переменными.
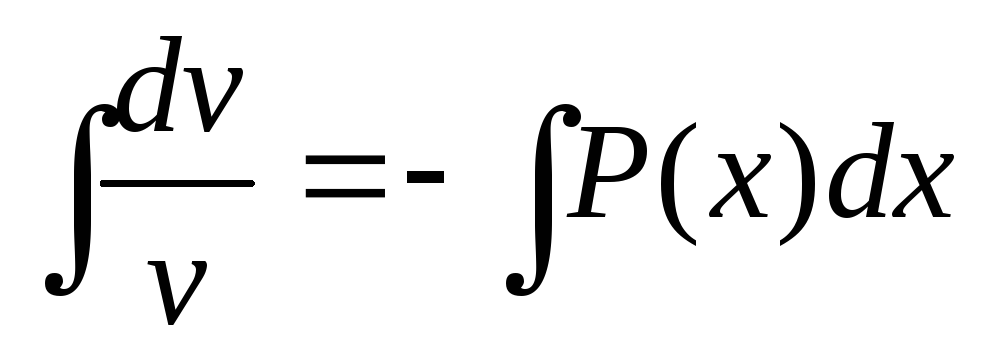
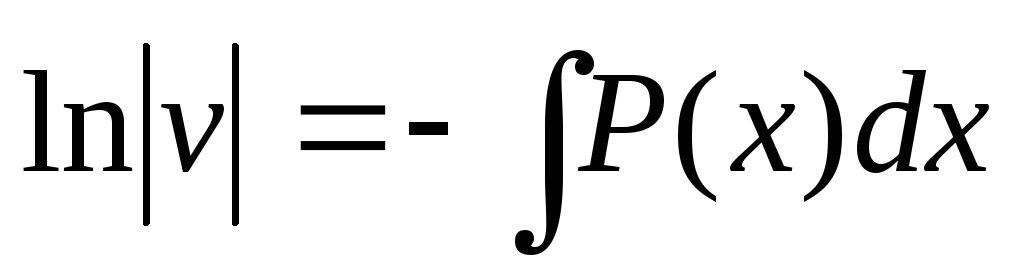 константу
интегрирования не прибавляем, т.к
достаточно одного частного решения.
константу
интегрирования не прибавляем, т.к
достаточно одного частного решения.
Выразим явно 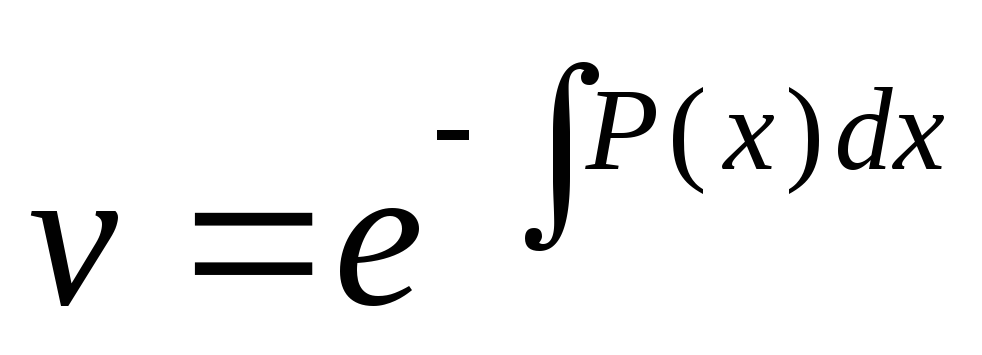
Подставим  в
(*)
в
(*) 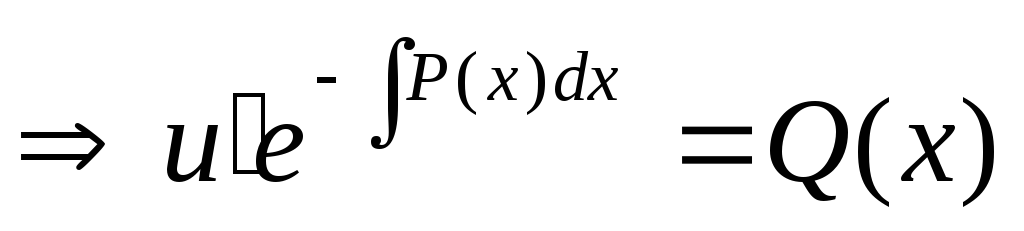
Выразим 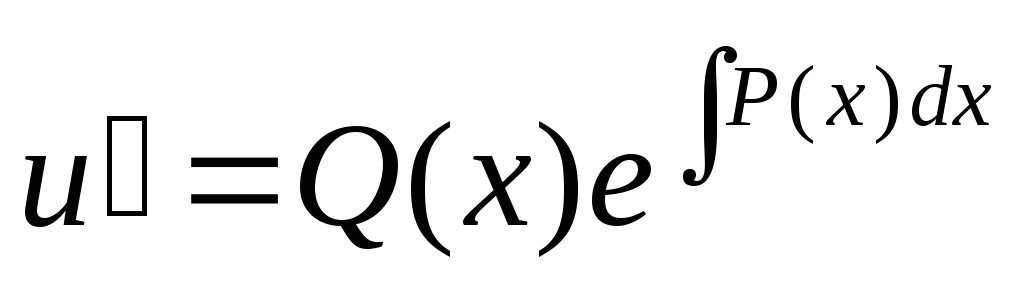
Т.к 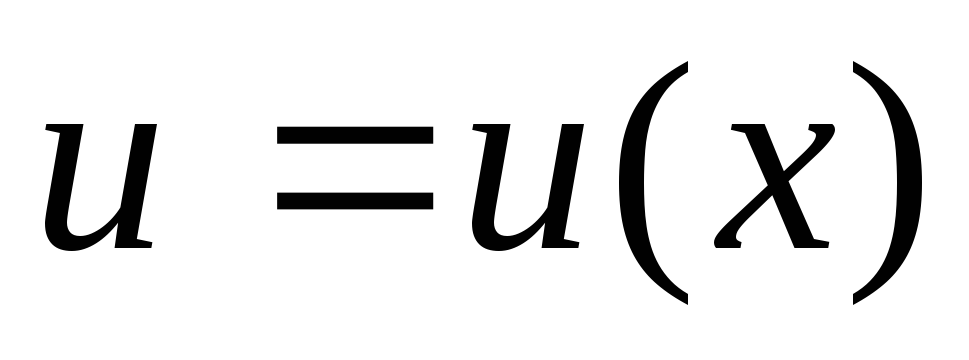 ,
то проинтегрируем обе части последнего
уравнения по х
,
то проинтегрируем обе части последнего
уравнения по х
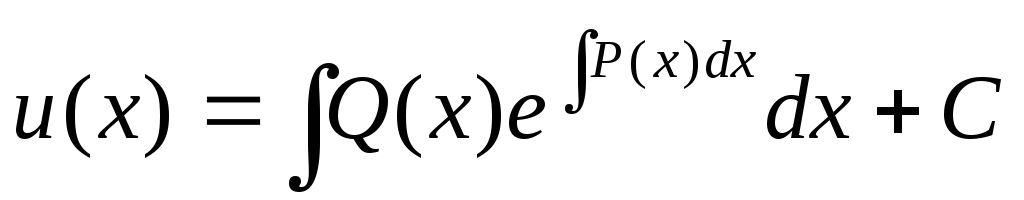
Общее решение линейного уравнения:
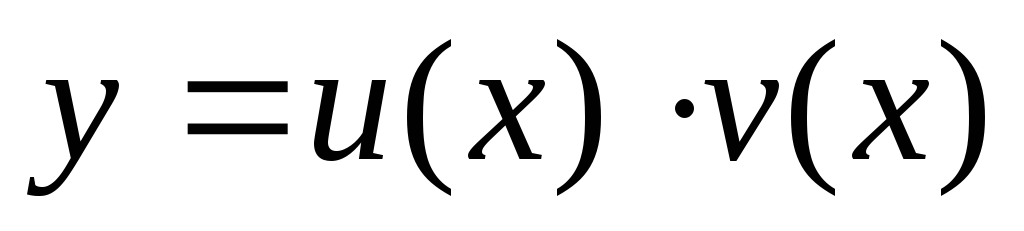 — всегда получается
в явном виде.
— всегда получается
в явном виде.
Пример:
1)
2 )
)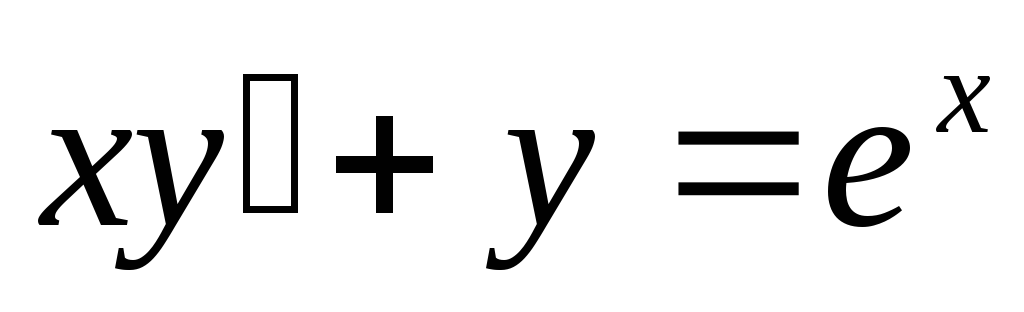 y(1)=2
y(1)=2
Уравнения Бернулли
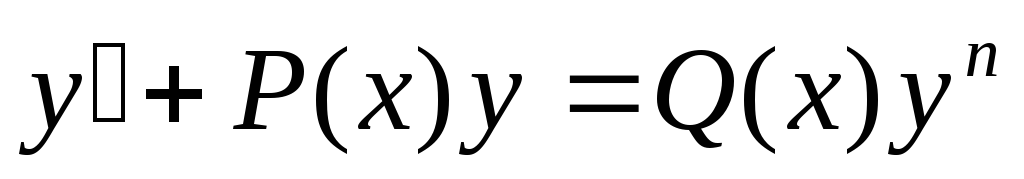
 ,
где
,
где 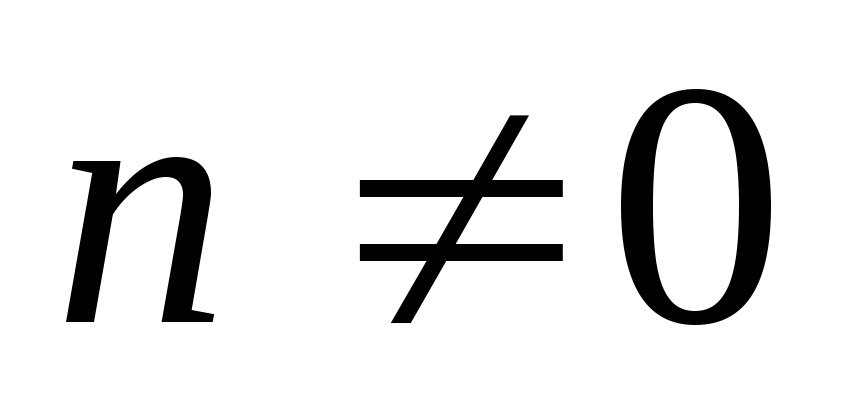 ;1
;1
Решаются такие уравнения так же как и линейные
Замена 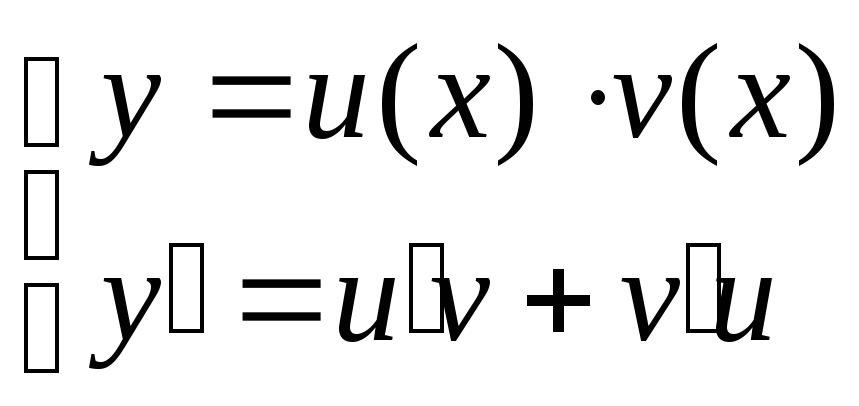
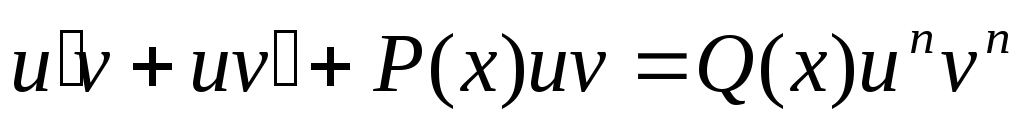

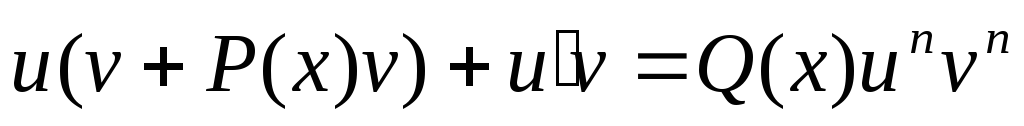

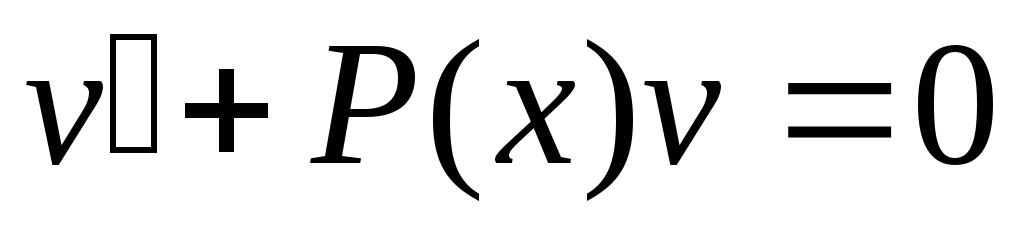
Явно 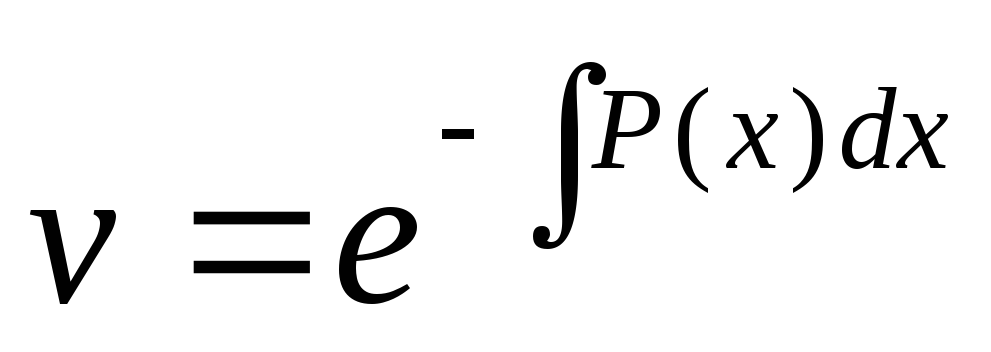

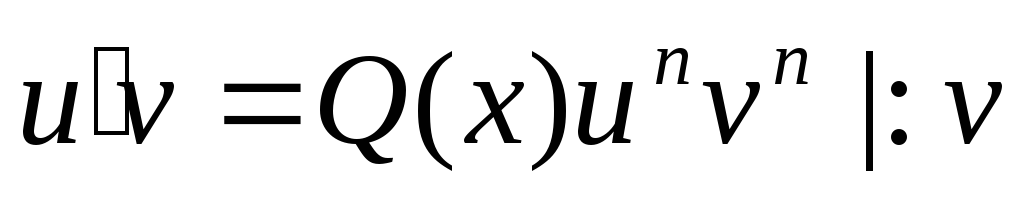
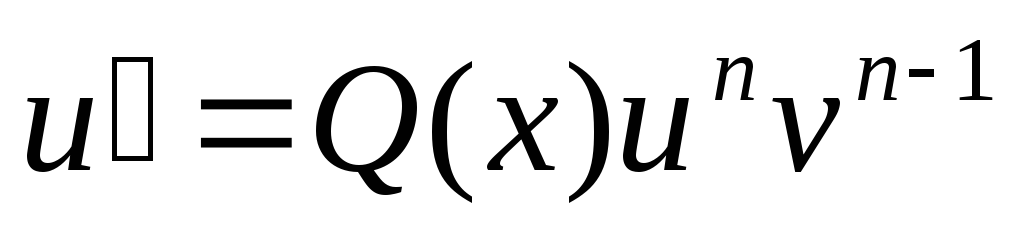 —
дифференциальное уравнение с разделяющимися
переменными.
—
дифференциальное уравнение с разделяющимися
переменными.
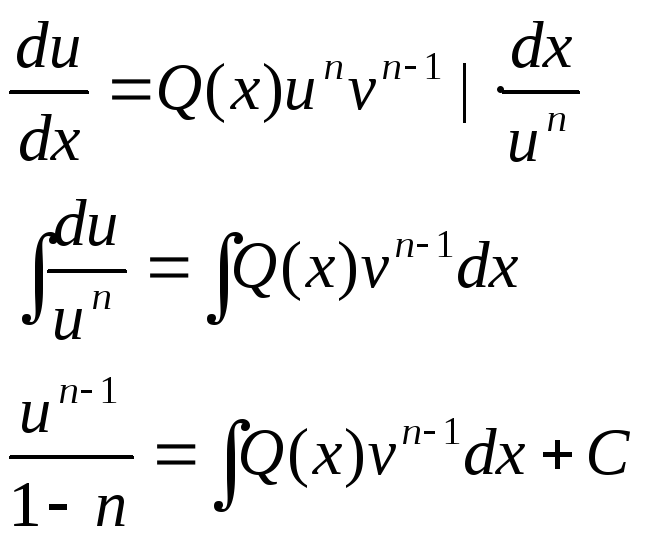
выразим явно u
и найдём общее решение 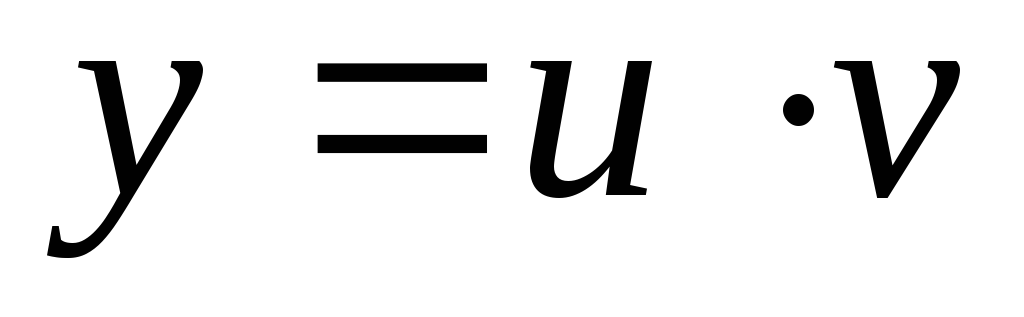
Примеры:
1)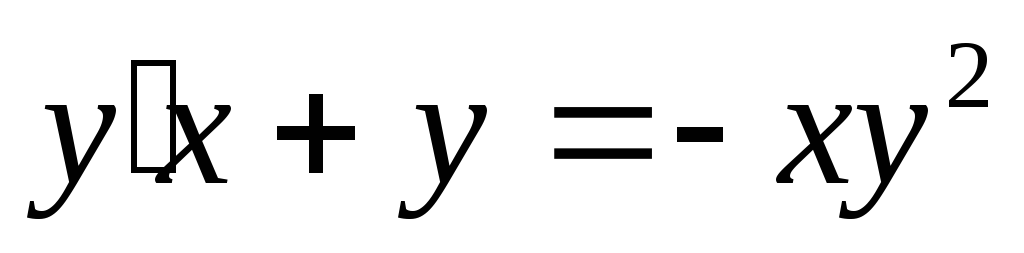
Дифференциальные уравнения высших порядков
Определение: Дифференциальное уравнение порядка n называется уравнение вида:

уравнение вида: 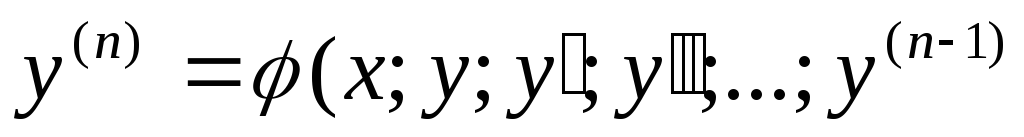
 – называется уравнением
разрешенным относительно старшей
производной. Для такого уравнения справедлива теорема
Коши.
– называется уравнением
разрешенным относительно старшей
производной. Для такого уравнения справедлива теорема
Коши.
Теорема Коши.
Если функция  в
(*) непрерывна вместе с частными
производными:
в
(*) непрерывна вместе с частными
производными:
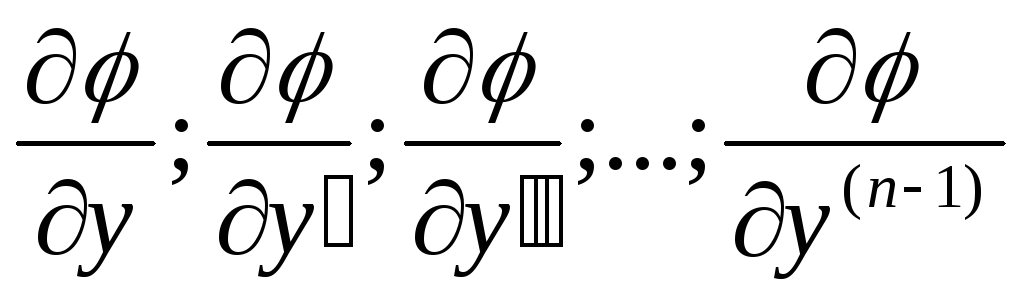 в области содержащей
значения
в области содержащей
значения
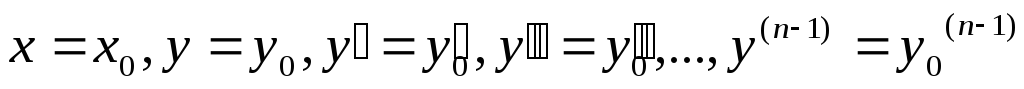 ,
то существует единственное решение
дифференциального уравнения
,
то существует единственное решение
дифференциального уравнения  удовлетворяющее начальным условиям:
удовлетворяющее начальным условиям:
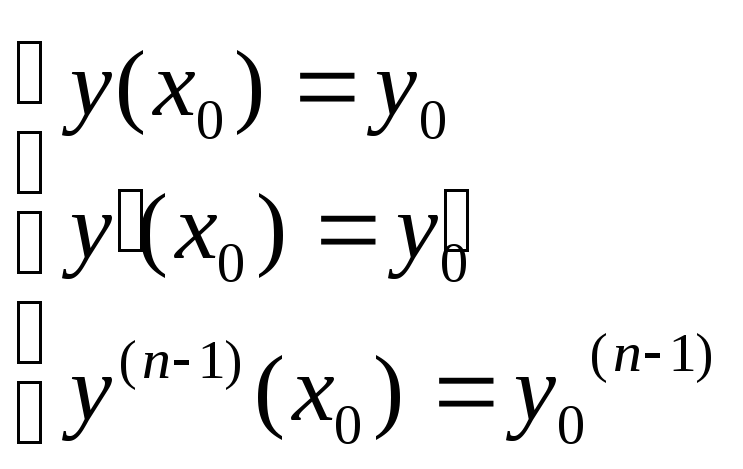
Замечание: для
дифференциальных уравнений 2 порядка 
начальные условия имеют вид:
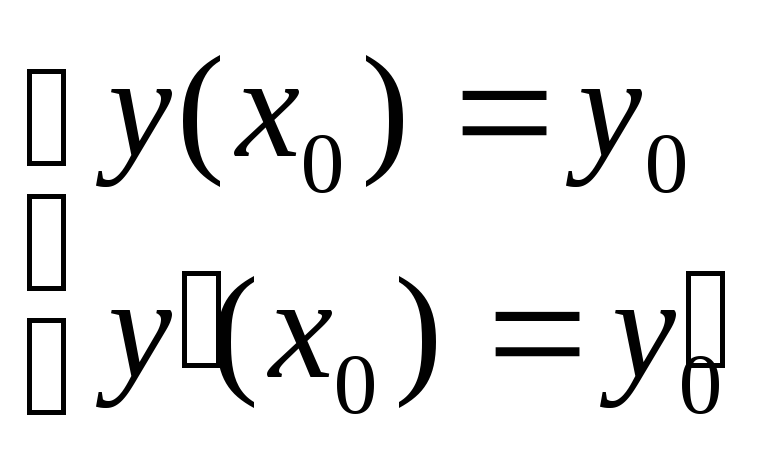
Решить дифференциальное уравнение порядка n означает:
1)Найти общее решение (общий интеграл)
2)Найти частное решение (частный интеграл), удовлетворяющее заданным условиям.
Определение: Общим решением дифференциального уравнения 2 порядка
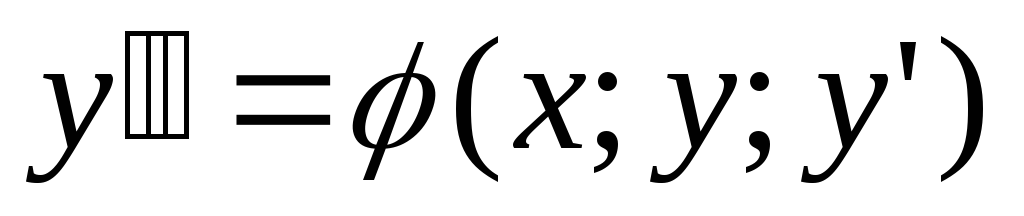 является функция
является функция 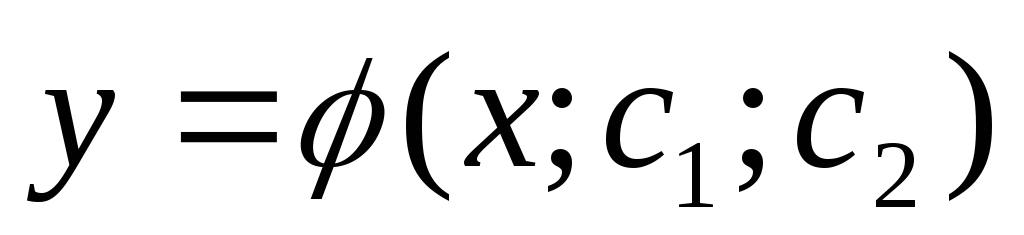 ,
такая что:
,
такая что:
1) при любых значениях с1 и с2 эта функция – решение.
2) каковы бы ни были начальные условия на области, в которой выполняется теорема Коши всегда можно подобрать значения с1 и с2 удовлетворяющие начальным условиям.
Определение: Частным решением дифференциального уравнения 2 порядка является решение, при конкретных значениях с1 и с2.
Замечание: общее
решение дифференциального уравнения
2 порядка может быть получено в неявном
виде: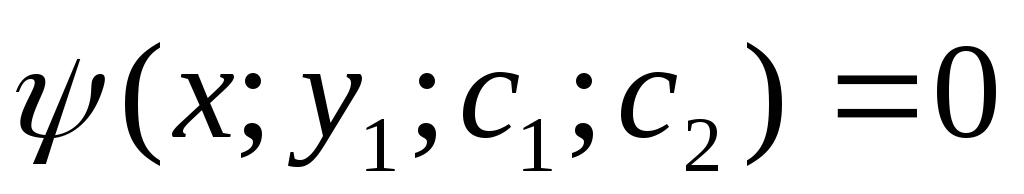
Дифференциальные уравнения 2 порядка, допускающие понижение порядка
1 )
Уравнения вида:
)
Уравнения вида: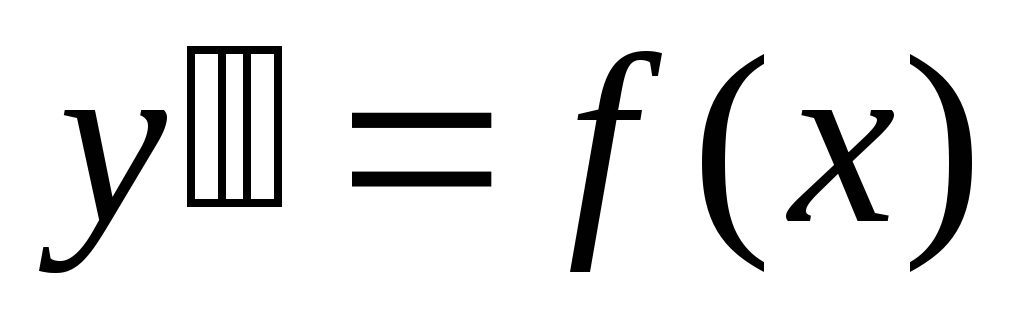
уравнение решается двукратным интегрированием по переменной х.
Проинтегрируем 1 раз по х.
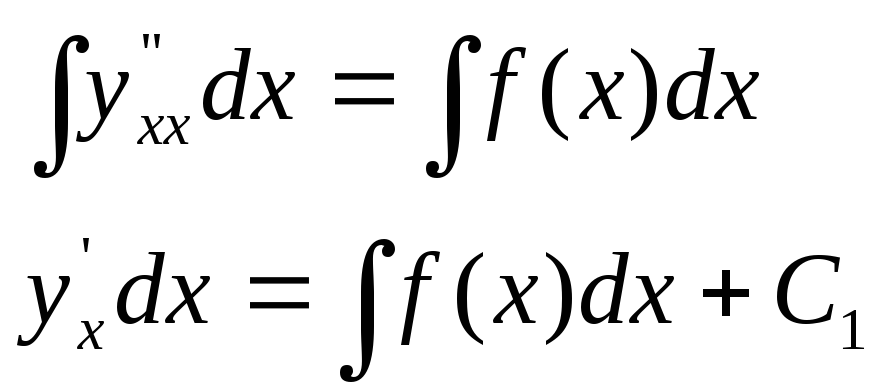
Проинтегрируем 2 раз по х
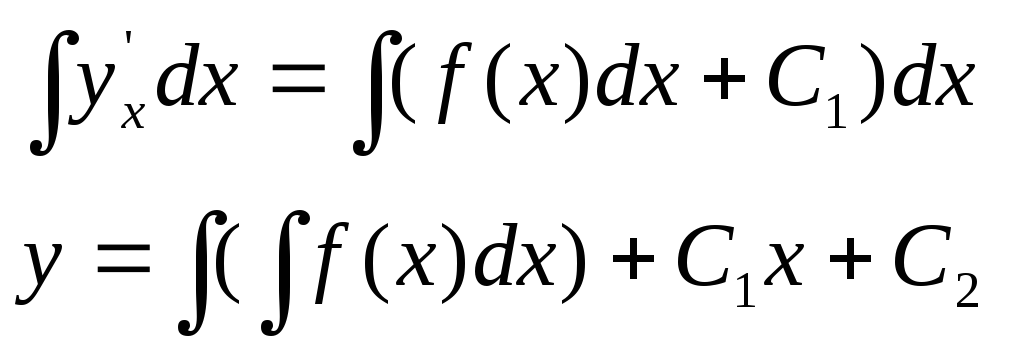
общее решение.
Замечание: для
дифференциального уравнения порядка
n: 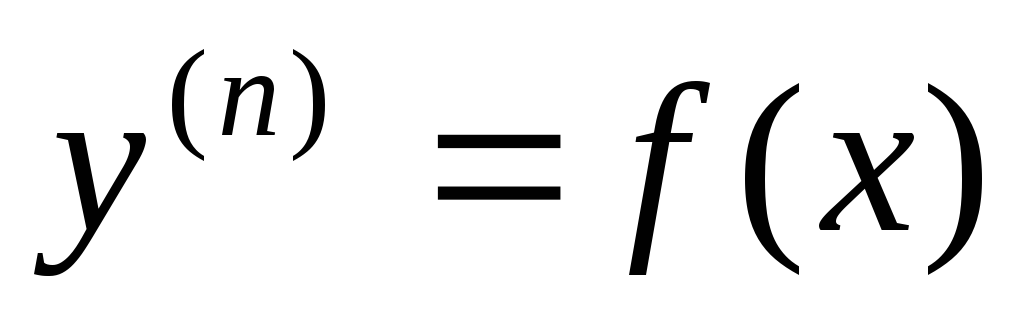 —
интегрировать нужноn
раз.
—
интегрировать нужноn
раз.
Примеры:
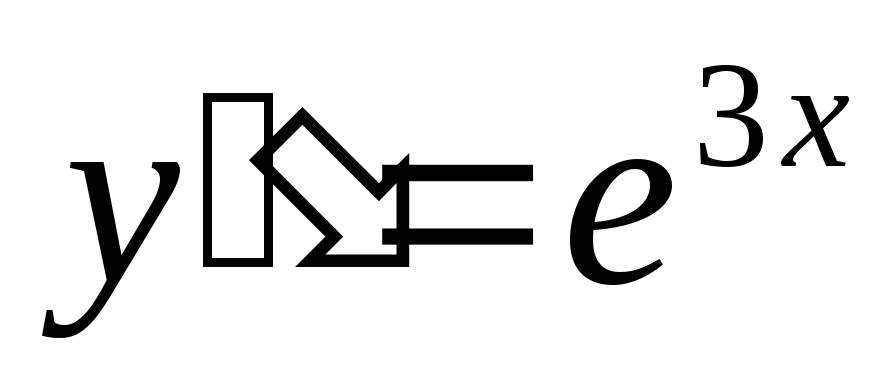
2) Дифференциальные уравнения не содержащие явно y.
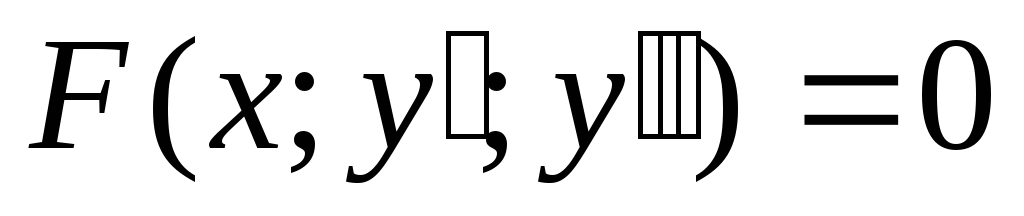
 — нет явно y
— нет явно y
Замена 
Подставим замену в дифференциальное уравнение, получим
получим дифференциальное уравнение 1 порядка.
Найдём решение этого уравнения:
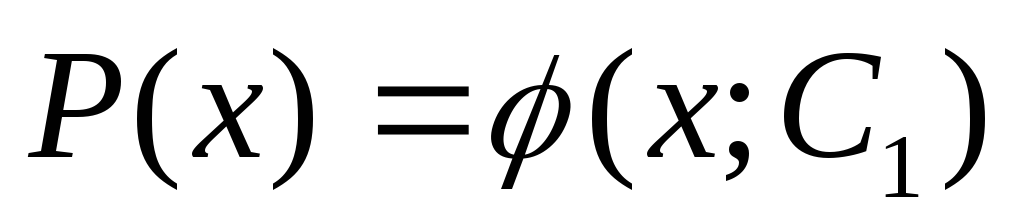
сделаем обратную
замену 
п роинтегрируем
обе части по х
роинтегрируем
обе части по х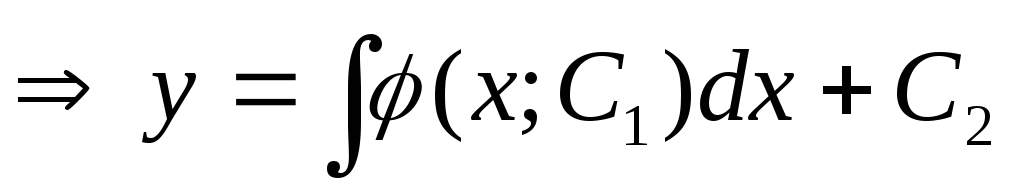 —
общее решение
—
общее решение
Пример:
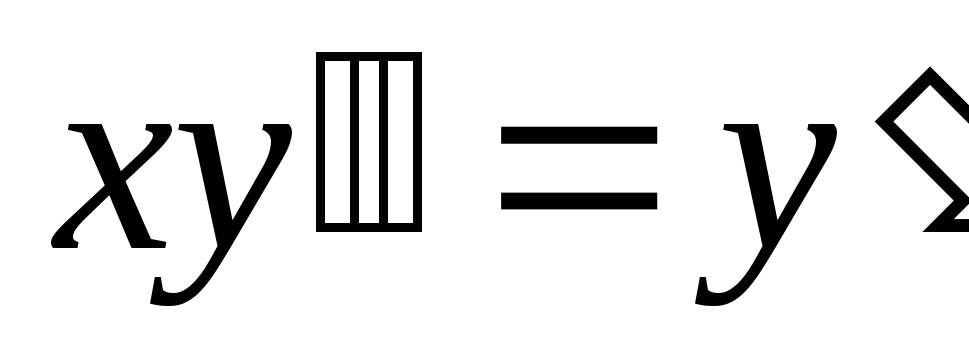
3) Дифференциальные уравнения 2 порядка не содержащие явно х.
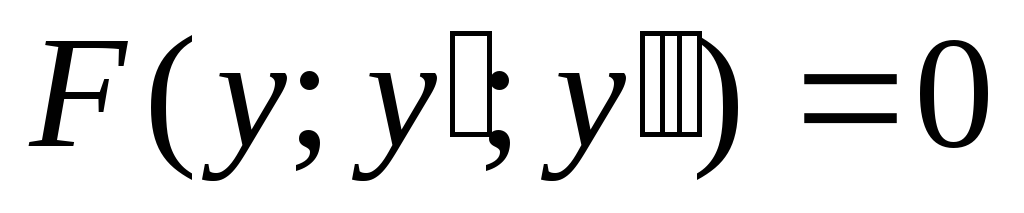 —
нет явно х.
—
нет явно х.
З амена:
у-новая переменная
амена:
у-новая переменная
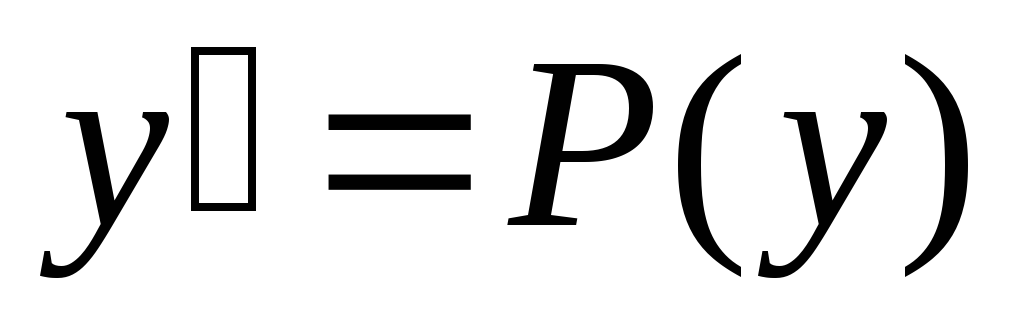 —
новая функция
—
новая функция
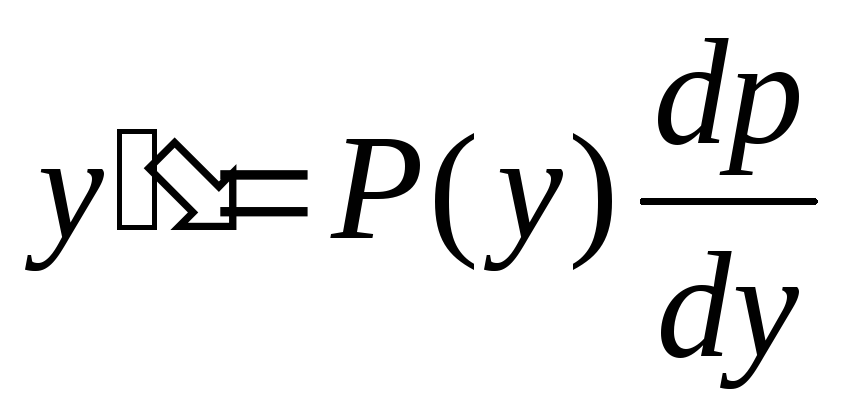 —
её производная
—
её производная
Подставим замену в исходное уравнение
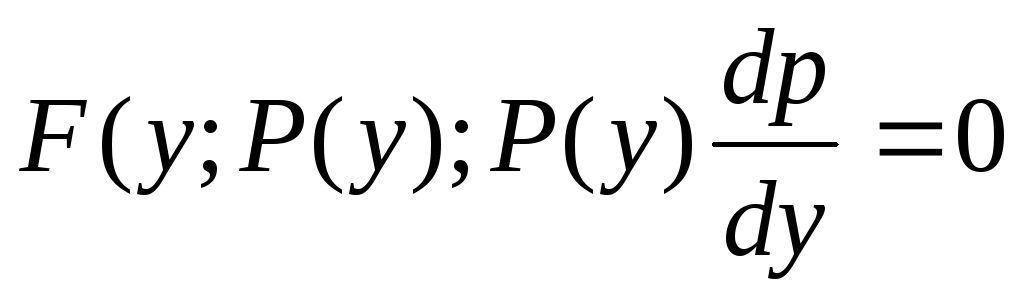
получим дифференциальное уравнение 1 порядка:
 —
его решение
—
его решение
Сделаем обратную замену —
 —
дифференциальное уравнение с разделяющимися
переменными. Разделим переменные:
—
дифференциальное уравнение с разделяющимися
переменными. Разделим переменные:
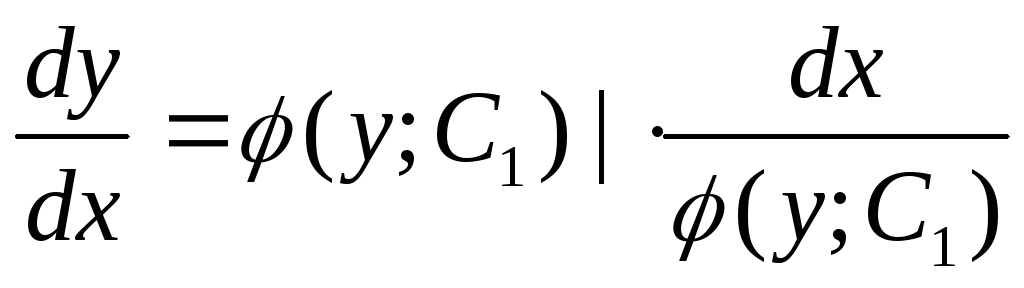
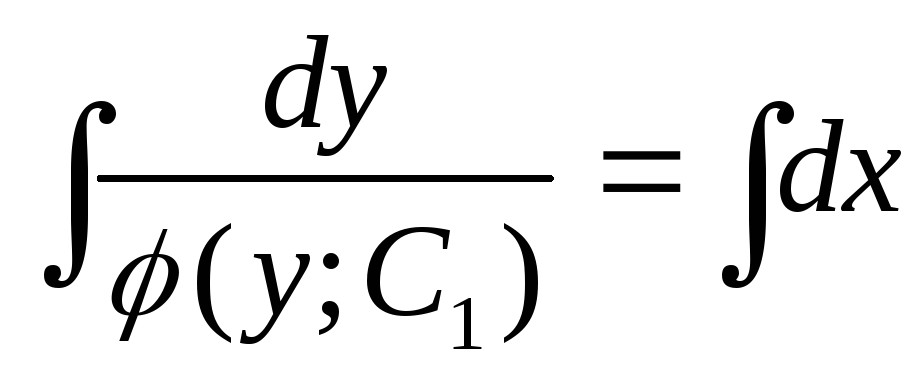 ;
; 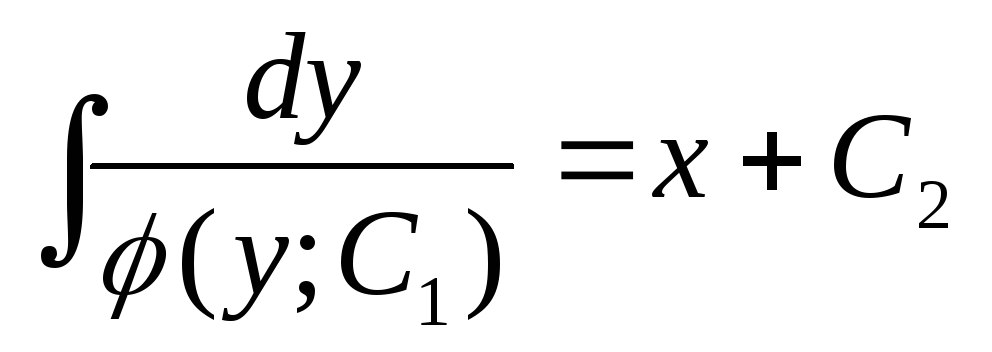 —
общее решение (вид неявный)
—
общее решение (вид неявный)
Примеры:
1.
2. 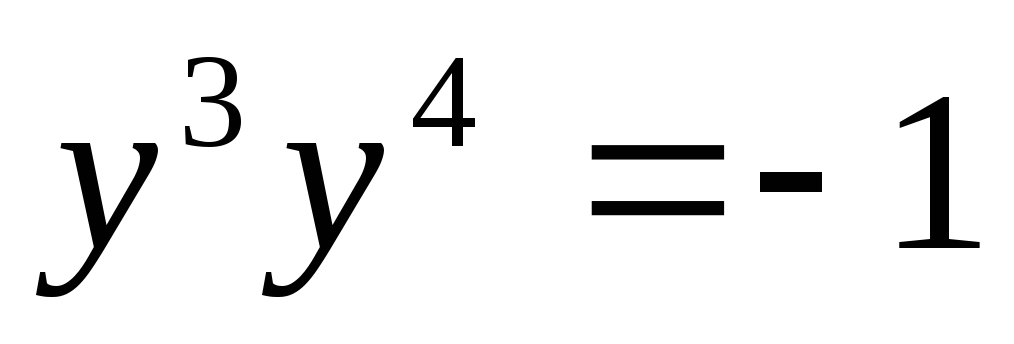
studfile.net
4.10 Линейное однородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
Определение. Линейным однородным дифференциальным уравнением высшего (n-го) порядка с постоянными коэффициентами называется уравнение вида
 ,
,
где коэффициенты 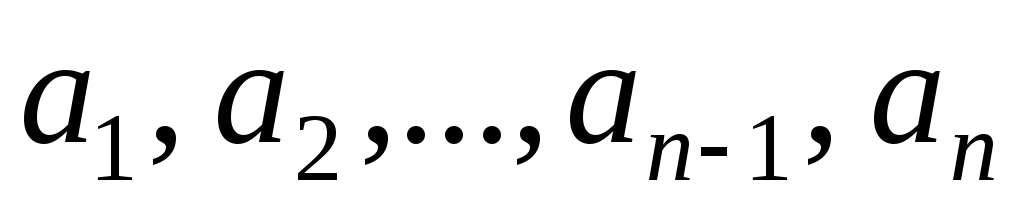 –
заданные действительные числа.
–
заданные действительные числа.
Метод
решения. Согласно теореме 4.3 общим решением 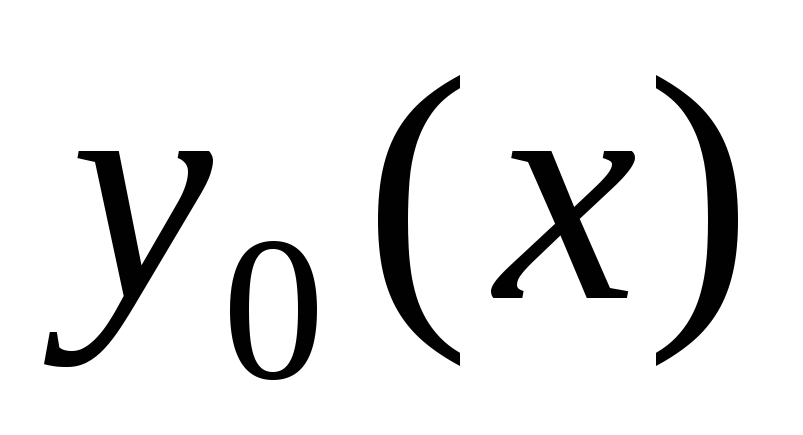 на отрезке
на отрезке 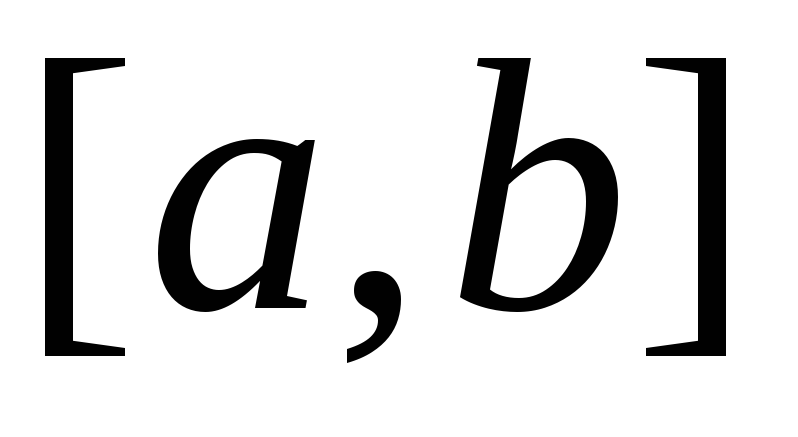 линейного однородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами является линейная
комбинация
линейного однородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами является линейная
комбинация
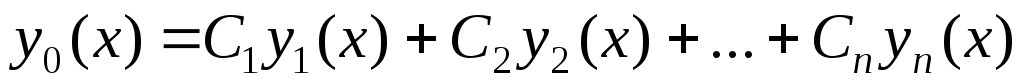
– линейно независимых
на том же отрезке частных решений этого
уравнения 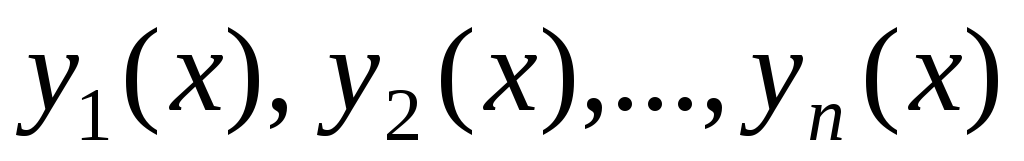 .
.
Для их нахождения составляется и решается характеристическое уравнение
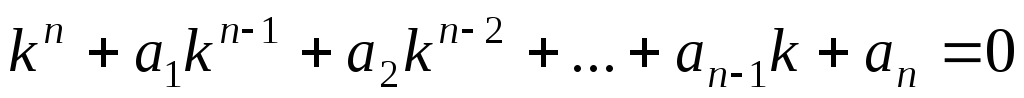 ,
,
получаемое заменой
в исходном дифференциальном уравнении
производных 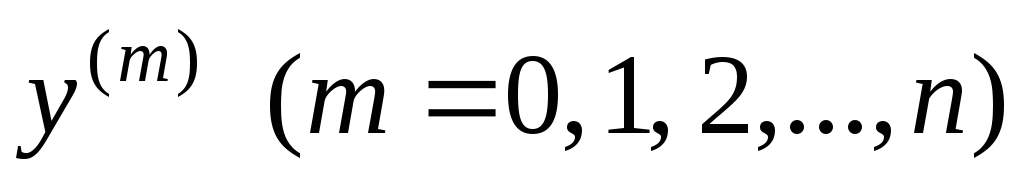 искомой функции степенями
искомой функции степенями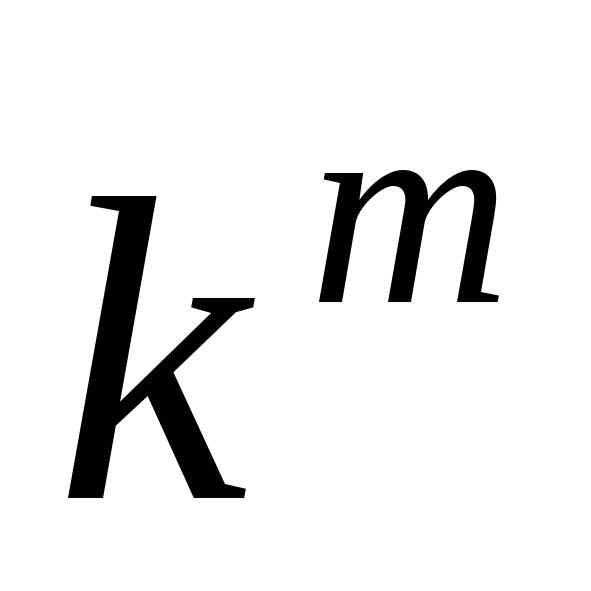 ,
причем сама функция
,
причем сама функция заменяется единицей. Характеристическое
уравнение – это алгебраическое уравнение
степениn.
заменяется единицей. Характеристическое
уравнение – это алгебраическое уравнение
степениn.
Каждому из n корней характеристического уравнения соответствует одно из n линейно независимых частных решений линейного однородного дифференциального уравнения, причем:
– каждому действительному простому корню k соответствует частное решение вида
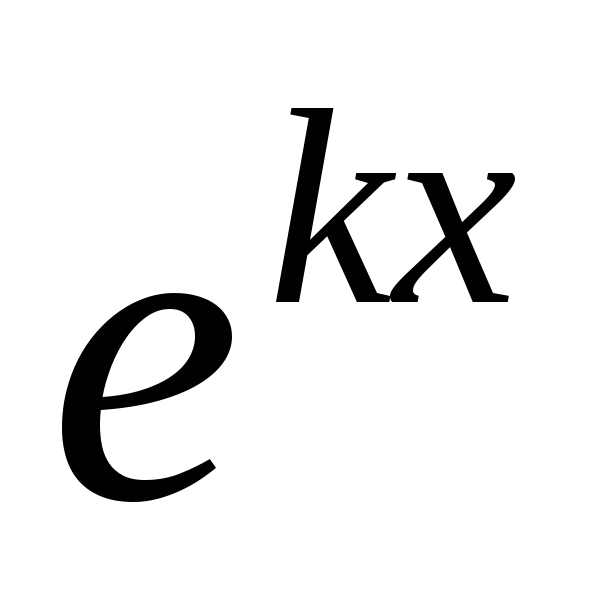 ;
;
– каждому
действительному корню k кратности  соответствуют
соответствуют частных решений вида
частных решений вида
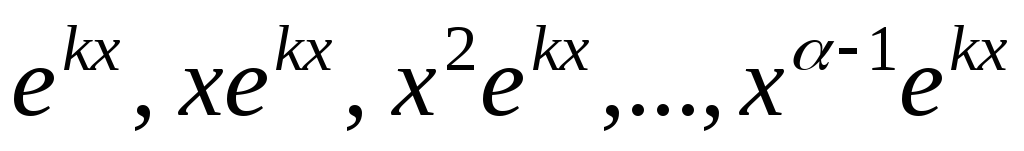 ;
;
–
каждой паре комплексных сопряженных
простых корней 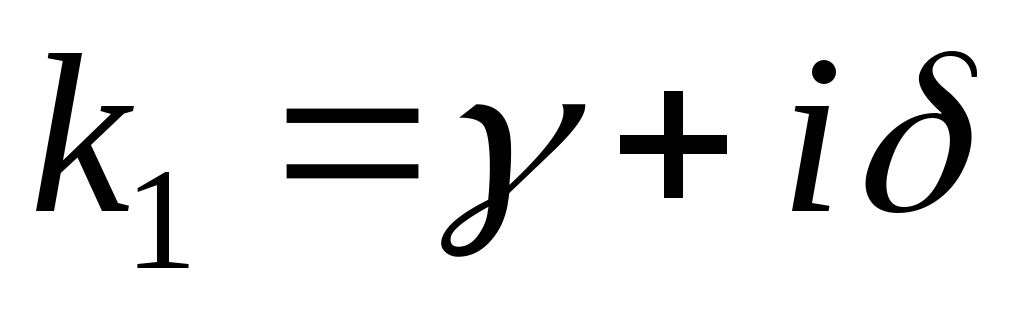 и
и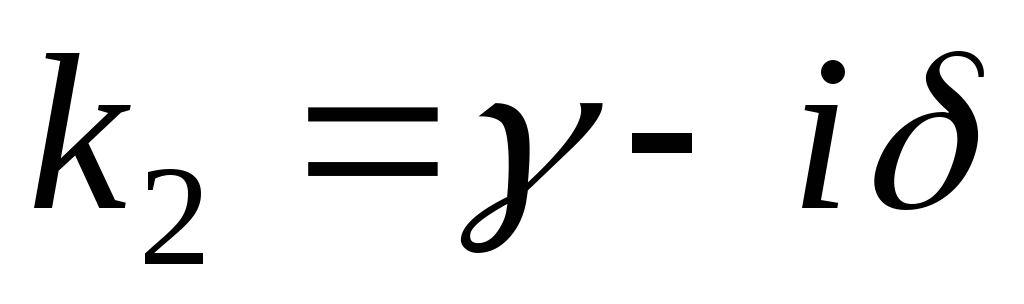 соответствует два частных решения вида
соответствует два частных решения вида
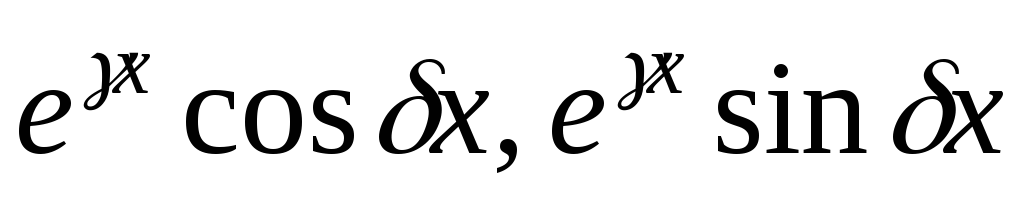 ;
;
–
каждой паре комплексных сопряженных
корней 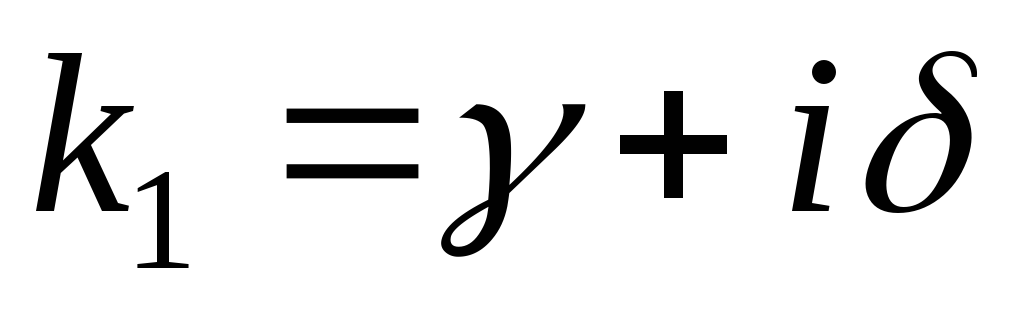 и
и кратности
кратности соответствуют 2
соответствуют 2 частных решений вида
частных решений вида
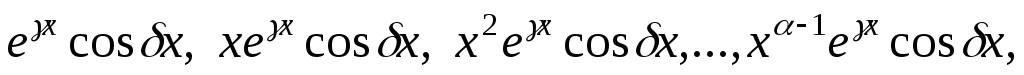
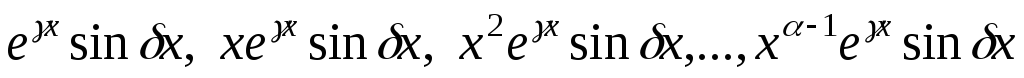 .
.
Составляя линейную комбинацию из найденных частных решений, получаем общее решение линейного однородного уравнения с постоянными коэффициентами.
Примеры
1) Найти общее решение однородного дифференциального уравнения .
Характеристическое уравнение и его решения:
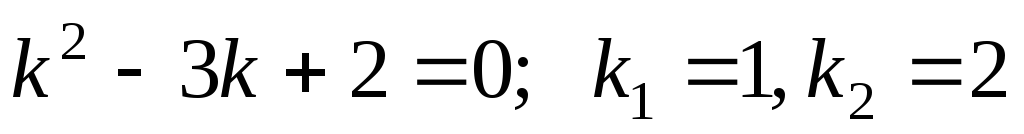 –два действительных
простых корня.
–два действительных
простых корня.
Частные решения однородного дифференциального уравнения:
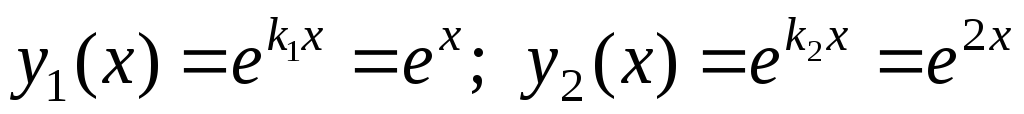 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
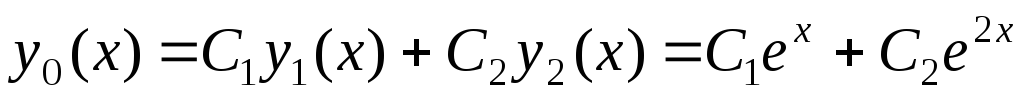 .
.
2) Найти общее решение однородного дифференциального уравнения
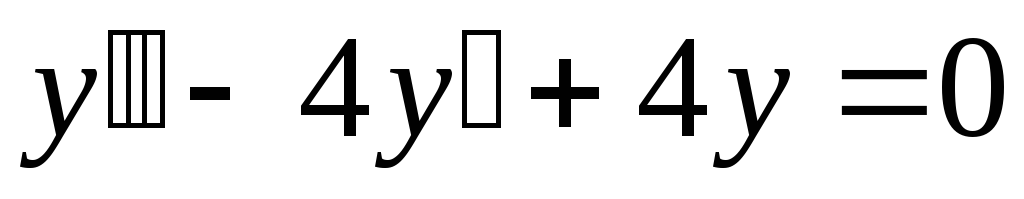 .
.
Характеристическое уравнение и его решения:
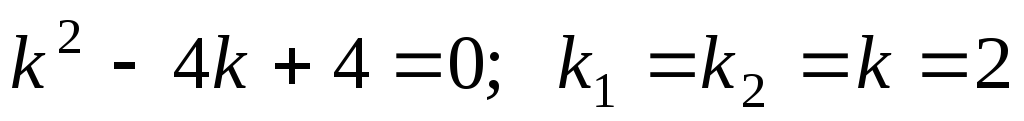 –двукратный
действительный корень.
–двукратный
действительный корень.
Частные решения однородного дифференциального уравнения:
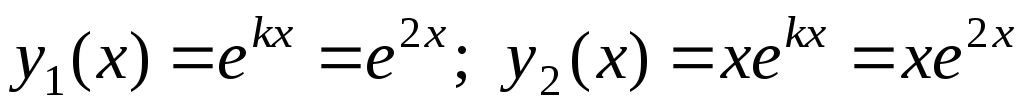 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
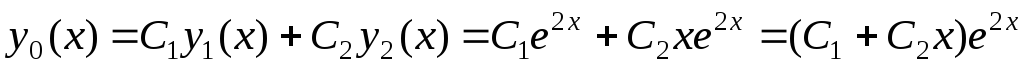 .
.
3) Найти общее решение однородного дифференциального уравнения
 .
.
Характеристическое уравнение и его решения:
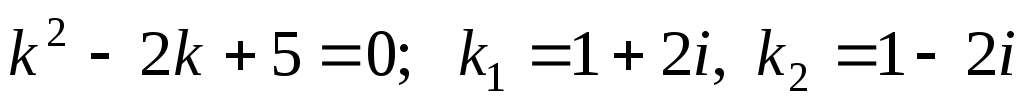 –пара комплексно
сопряженных простых корней
–пара комплексно
сопряженных простых корней 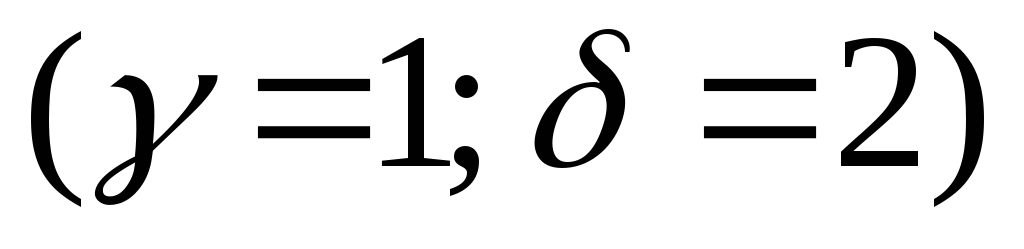 .
.
Частные решения однородного дифференциального уравнения:
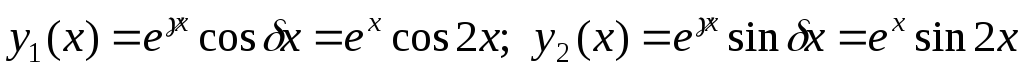 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
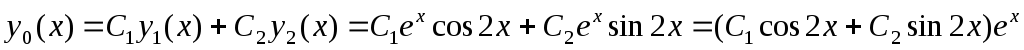 .
.
4) Найти общее решение однородного дифференциального уравнения
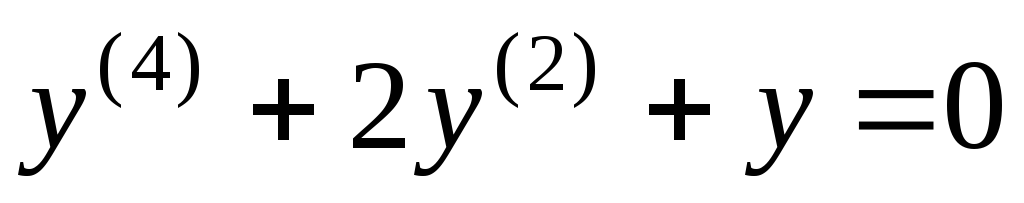 .
.
Характеристическое уравнение и его решения:
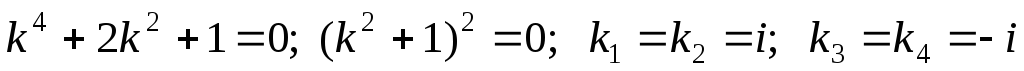 –двукратные
комплексно
сопряженные корни
–двукратные
комплексно
сопряженные корни 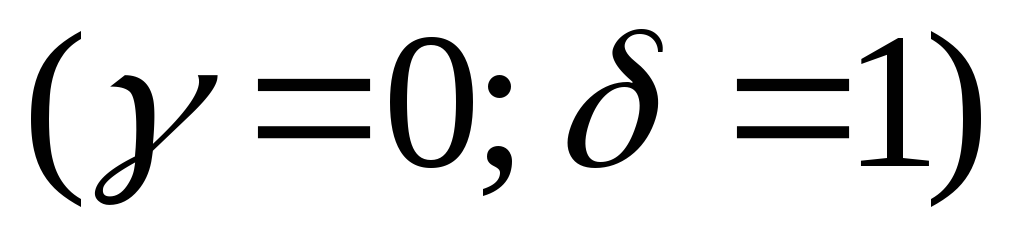 .
.
Частные решения однородного дифференциального уравнения:
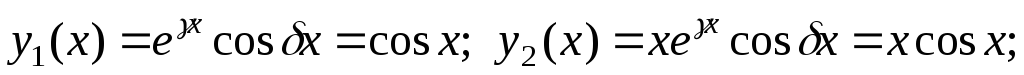
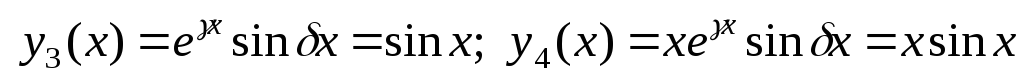 .
.
Общее решение исходного однородного дифференциального уравнения является линейной комбинацией полученных частных решений:

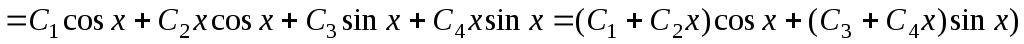 .
.
4.11 Линейное неоднородное дифференциальное уравнение высшего порядка с постоянными коэффициентами
Определение. Линейным неоднородным дифференциальным уравнением высшего (n-го) порядка с постоянными коэффициентами называется уравнение вида
 ,
,
где коэффициенты 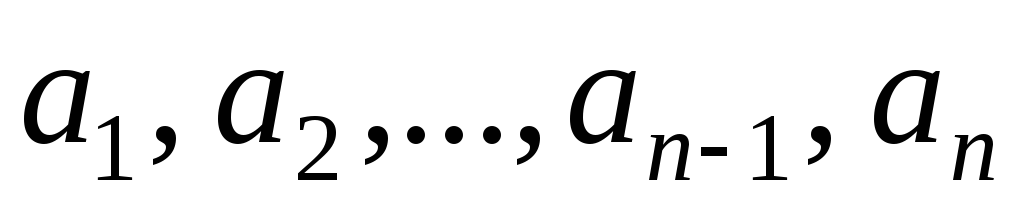 –
заданные действительные числа, а
–
заданные действительные числа, а –
заданная функция.
–
заданная функция.
Метод решения. Согласно теореме 4.4 общим решением 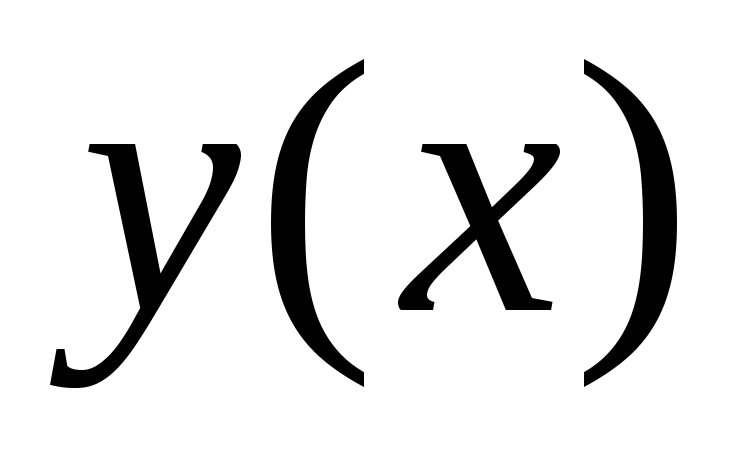 на отрезке
на отрезке 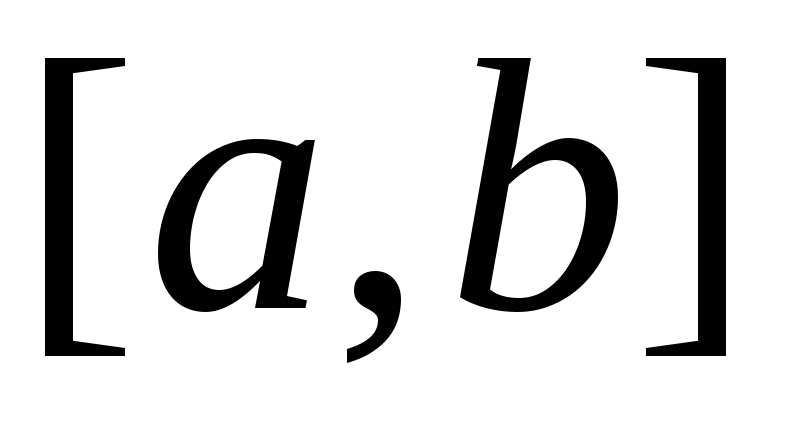 линейного неоднородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами и непрерывной правой
частью
линейного неоднородного дифференциального
уравнения высшего порядка с постоянными
коэффициентами и непрерывной правой
частью 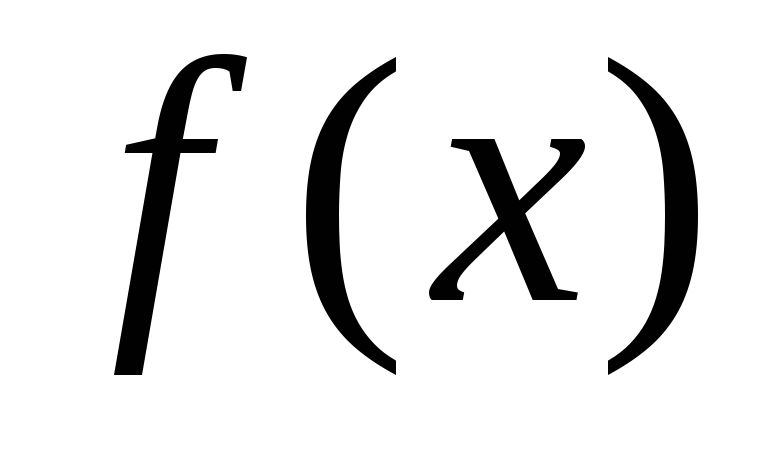 является сумма общего решения
является сумма общего решения

соответствующего однородного уравнения
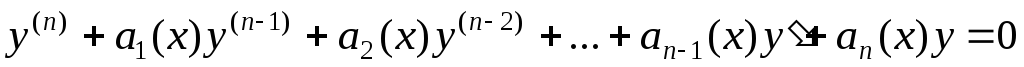
и какого-нибудь
частного решения 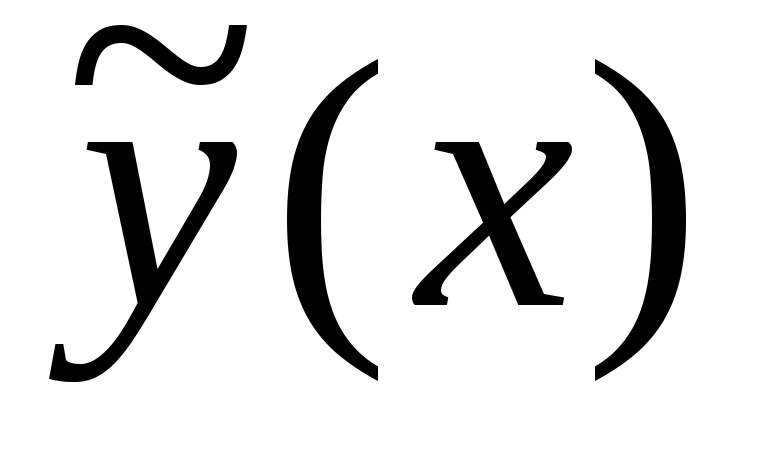 неоднородного уравнения:
неоднородного уравнения:
 .
.
Общее решение
однородного уравнения находить уже
умеем, поэтому остается рассмотреть
вопрос о нахождении частного решения  неоднородного уравнения.
неоднородного уравнения.
Если правая часть
неоднородного уравнения, т.е. функция 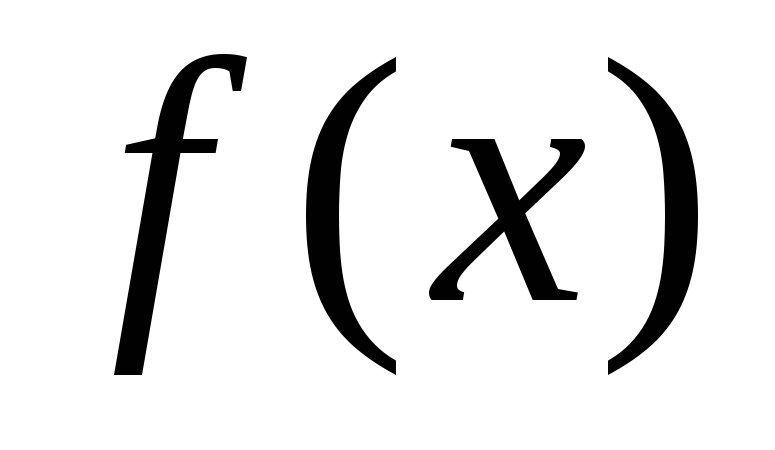 –
многочлен, либо показательная функция,
либо тригонометрические функции
–
многочлен, либо показательная функция,
либо тригонометрические функции  или
или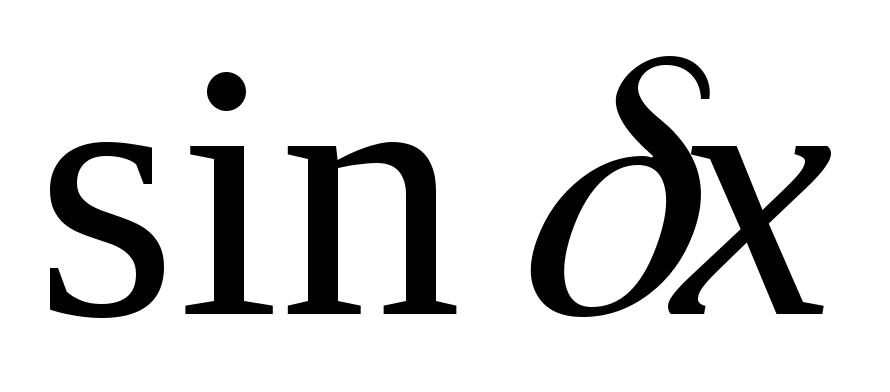 ,
либо линейная комбинация перечисленных
функций, то частное решение
,
либо линейная комбинация перечисленных
функций, то частное решение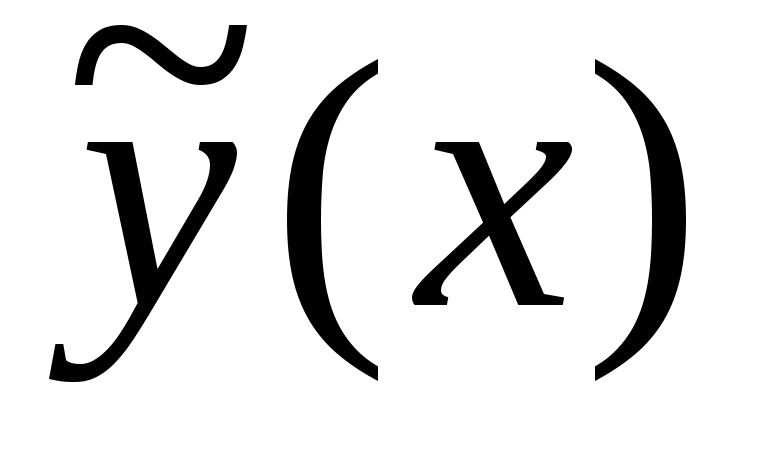 неоднородного уравнения может быть
найдено методом неопределенных
коэффициентов.
неоднородного уравнения может быть
найдено методом неопределенных
коэффициентов.
Если же правая
часть неоднородного уравнения есть
произвольная непрерывная функция, то
частное решение 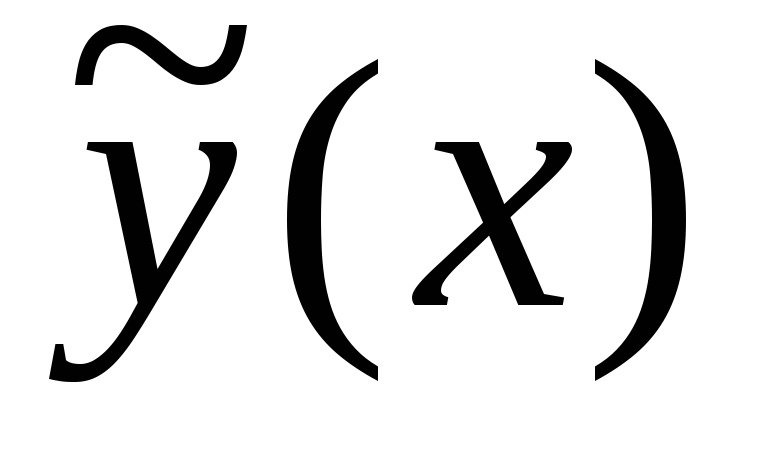 неоднородного уравнения может быть
найдено методом вариации произвольных
постоянных.
неоднородного уравнения может быть
найдено методом вариации произвольных
постоянных.
Рассмотрим оба
перечисленных метода нахождения частного
решения 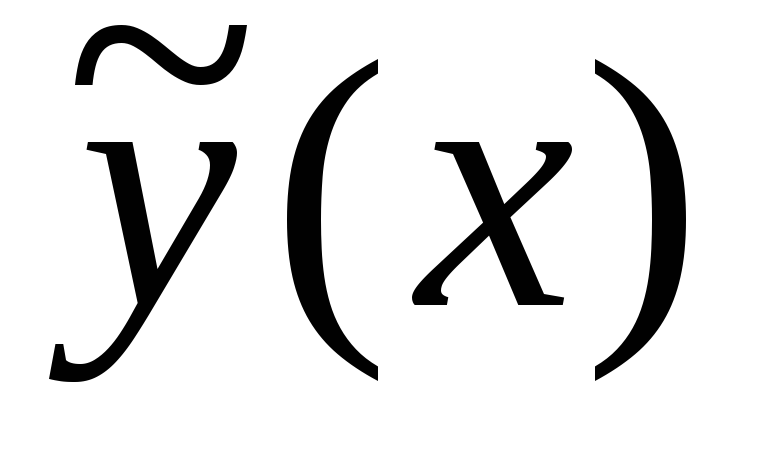 неоднородного уравнения.
неоднородного уравнения.
Метод неопределенных коэффициентов
Пусть правая часть неоднородного дифференциального уравнения с постоянными коэффициентами имеет вид
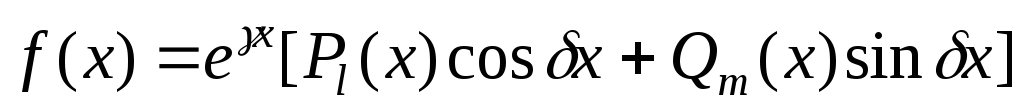 ,
,
где
и – действительные постоянные,
– действительные постоянные,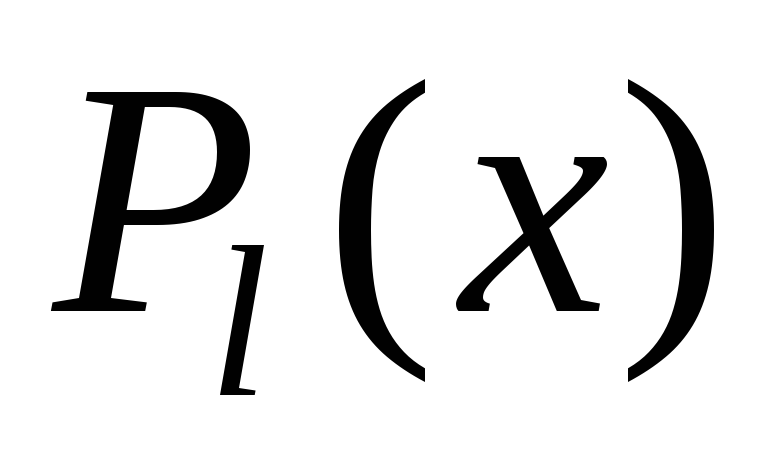 и
и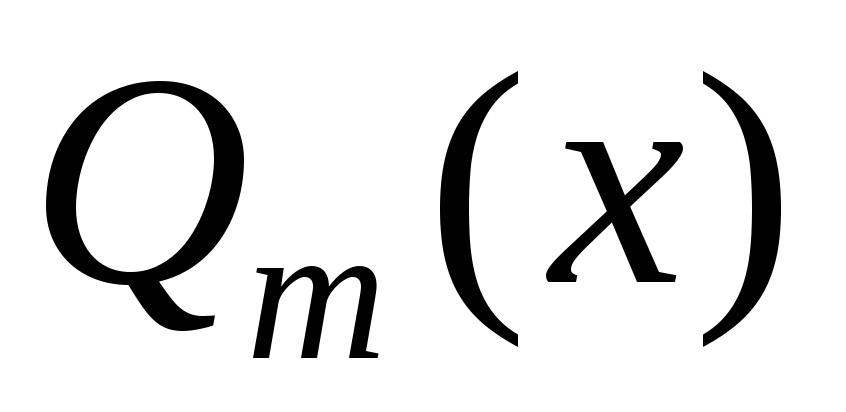 –
многочлены от x соответственно l-й
и m-й
степени.
–
многочлены от x соответственно l-й
и m-й
степени.
Тогда частное решение неоднородного уравнения ищем в виде
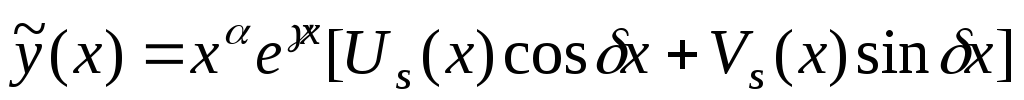 .
.
Здесь  равно показателю кратности корня
равно показателю кратности корня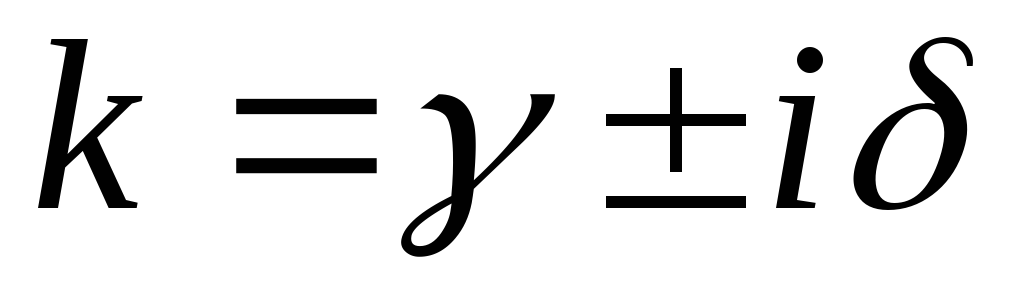 в характеристическом уравнении
в характеристическом уравнении
 .
.
Если характеристическое
уравнение такого корня не имеет, то
следует положить 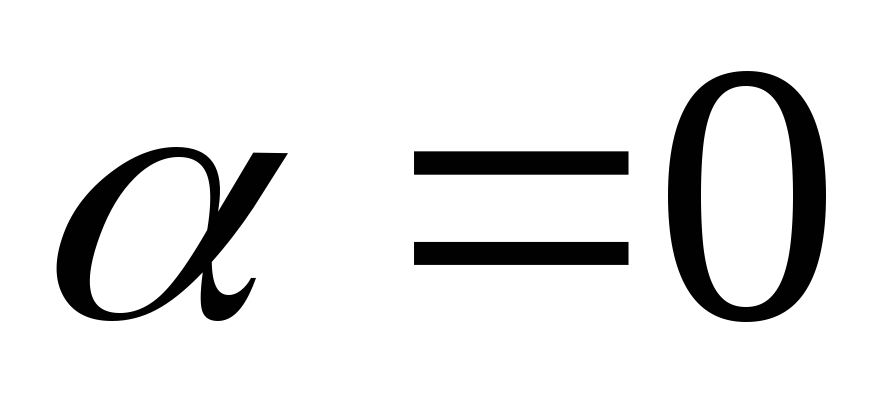 .
.
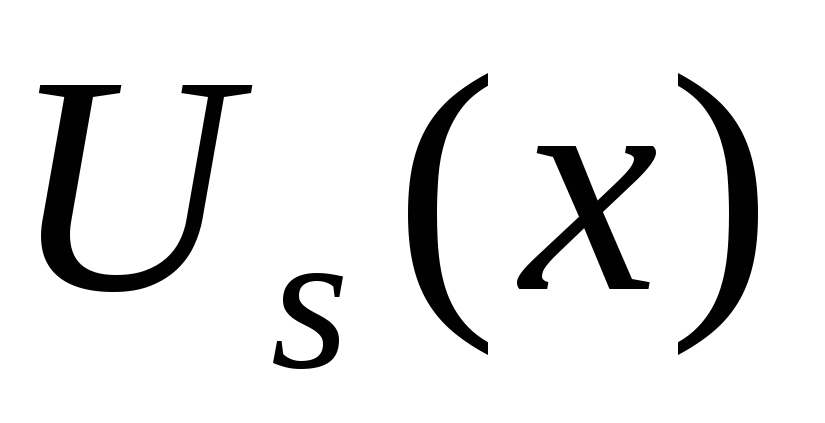 и
и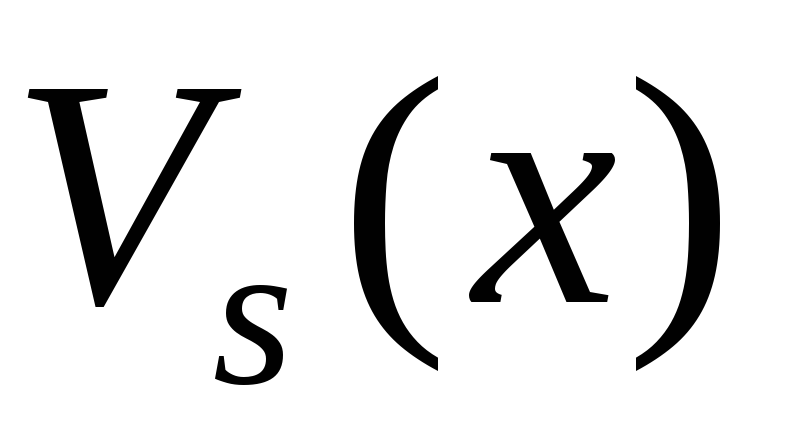 –полные (т.е. содержащие все степени x от 0 до s)
многочлены от x степени s с неопределенными коэффициентами,
причем s равно наибольшему из чисел l и m:
–полные (т.е. содержащие все степени x от 0 до s)
многочлены от x степени s с неопределенными коэффициентами,
причем s равно наибольшему из чисел l и m:
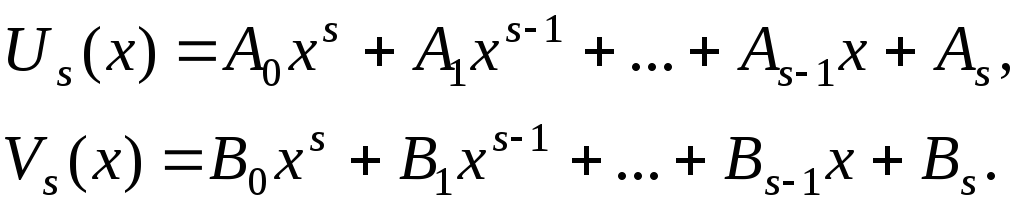
Если в выражение
функции 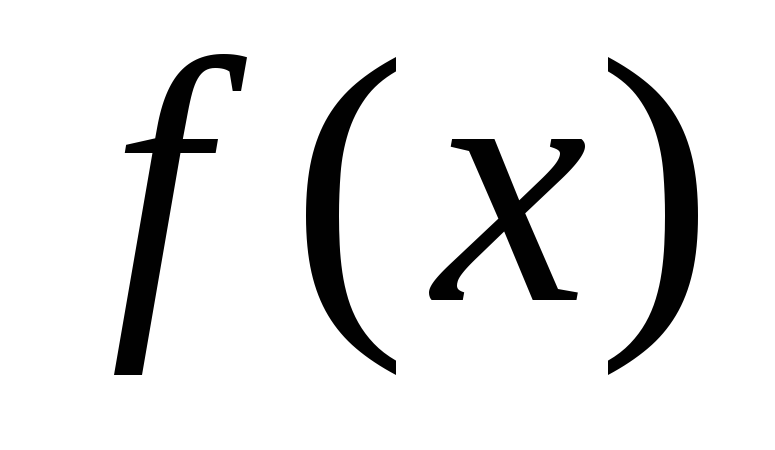 входит хотя бы одна из функций
входит хотя бы одна из функций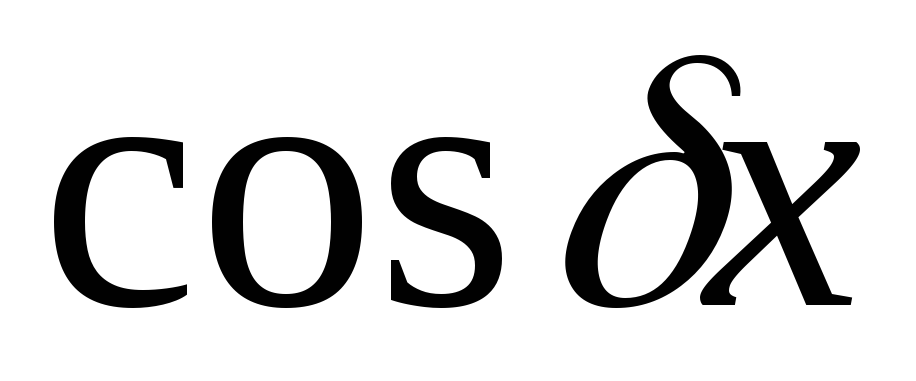 или
или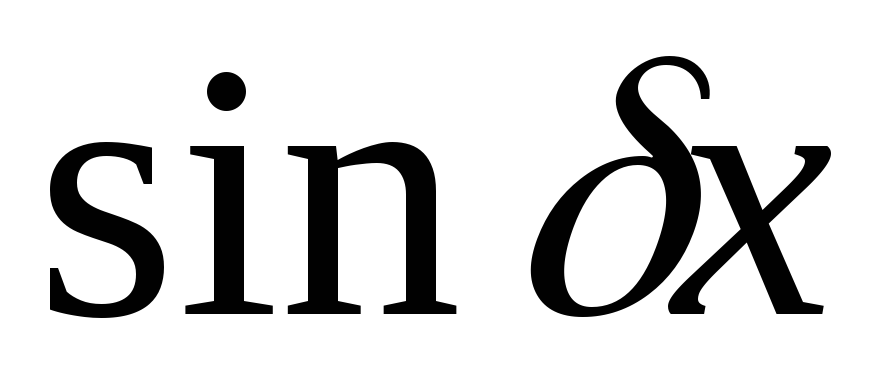 ,
то в решение
,
то в решение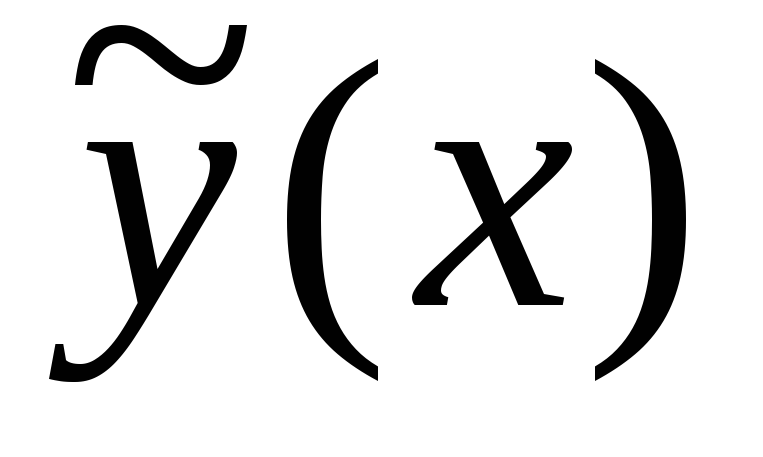 надо всегда вводитьобе эти функции.
надо всегда вводитьобе эти функции.
Неопределенные
коэффициенты 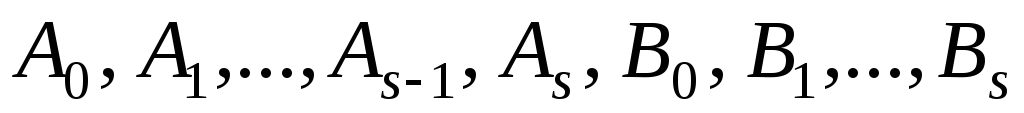 находятсяиз
системы линейных алгебраических
уравнений, получаемых отождествлением
коэффициентов подобных членов в правой
и левой частях исходного линейного
неоднородного дифференциального
уравнения после подстановки в него
находятсяиз
системы линейных алгебраических
уравнений, получаемых отождествлением
коэффициентов подобных членов в правой
и левой частях исходного линейного
неоднородного дифференциального
уравнения после подстановки в него 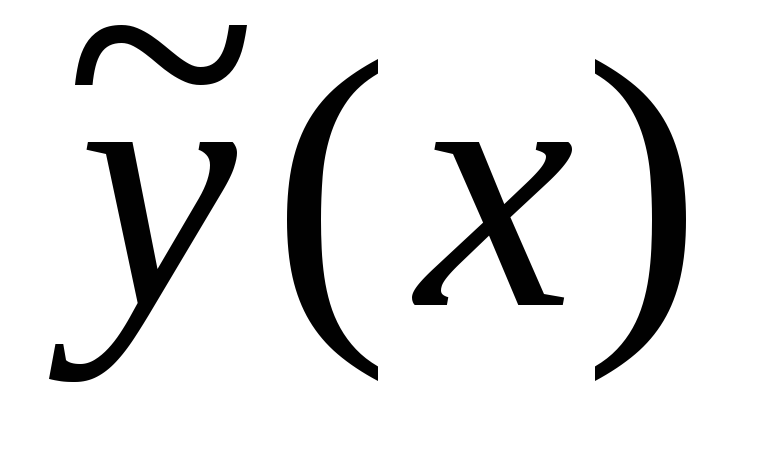 вместоy,
вместоy,  вместо
вместо ,
, вместо
вместо и т.д.
и т.д.
Если правая часть исходного дифференциального уравнения есть сумма нескольких функций рассматриваемой структуры:
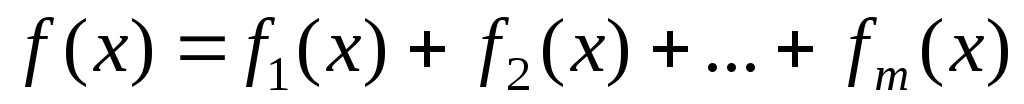 ,
,
и 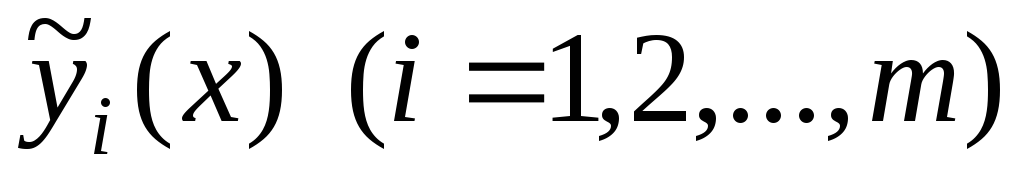 –
соответствующие решения уравнений
–
соответствующие решения уравнений
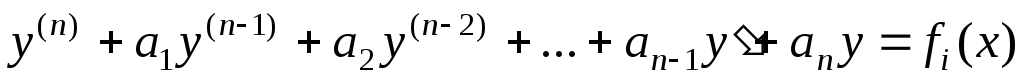 ,
,
то сумма
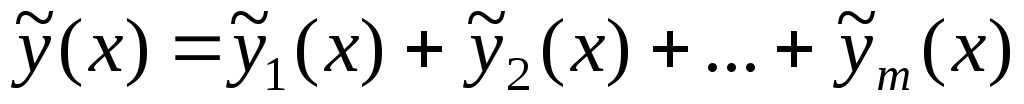 ,
,
как легко установить, является частным решением исходного уравнения (принцип наложения решений).
Пример. Найти общее решение неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами
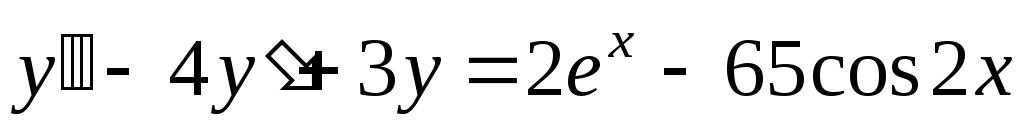 .
.
Решение данного неоднородного уравнения производится в три этапа.
1) Сначала находим общее решение соответствующего однородного уравнения:
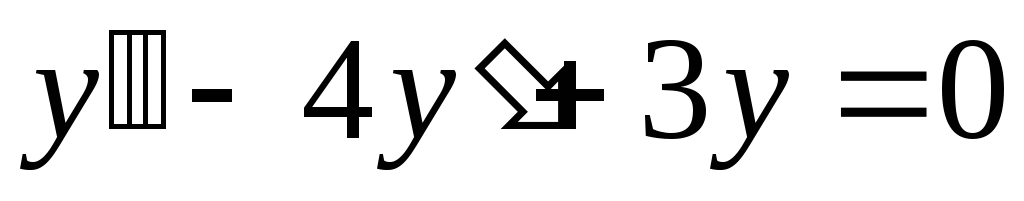
Для этого составляем и решаем характеристическое уравнение:
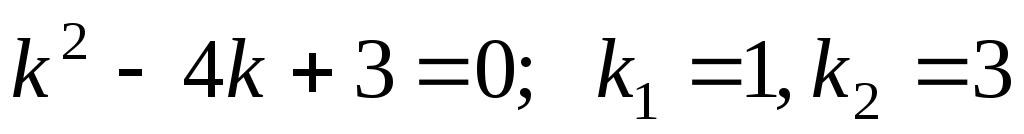 –
два действительных
простых корня.
–
два действительных
простых корня.
Частные решения однородного дифференциального уравнения:
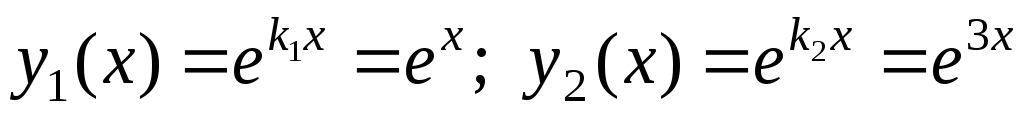 .
.
Общее решение соответствующего однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
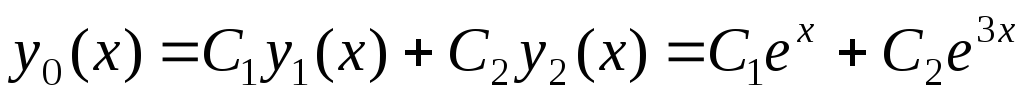 .
.
2) Далее ищем частное решение исходного неоднородного уравнения в виде
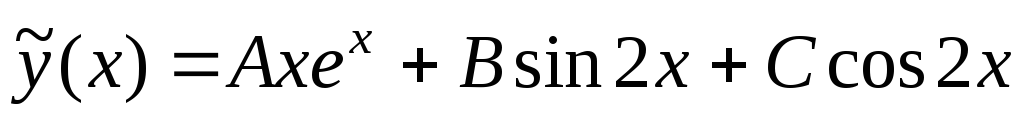 ,
,
так как
характеристическое уравнение имеет
корень 
 ,
а также согласно принципу наложения
решений для правых частей
,
а также согласно принципу наложения
решений для правых частей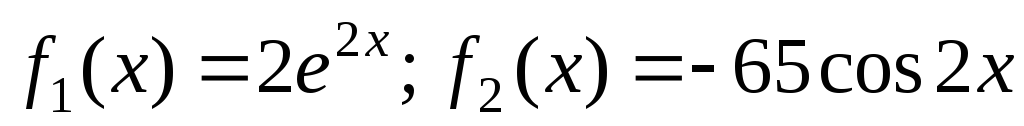 .
.
Для определения
коэффициентов  находим производные
находим производные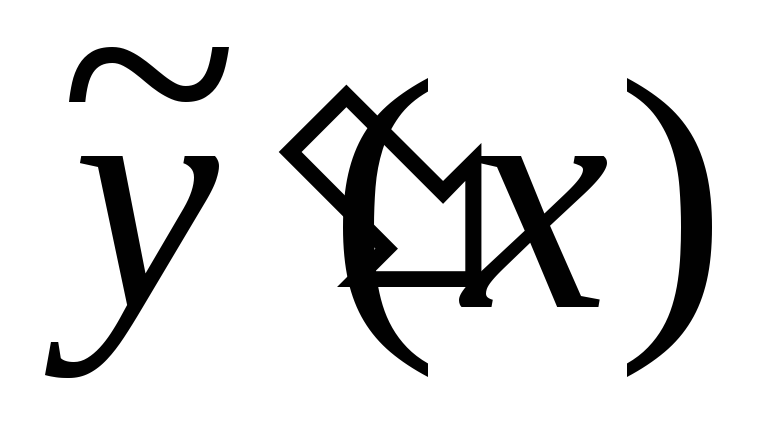 и
и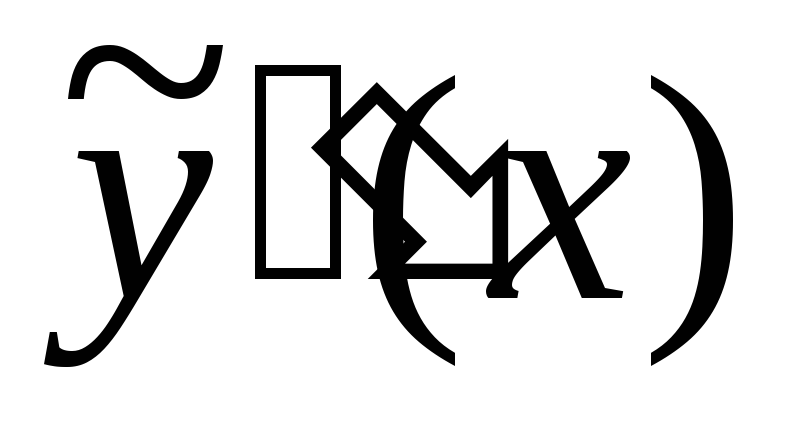 :
:
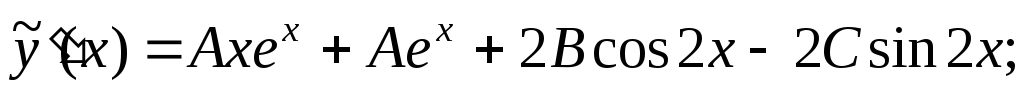
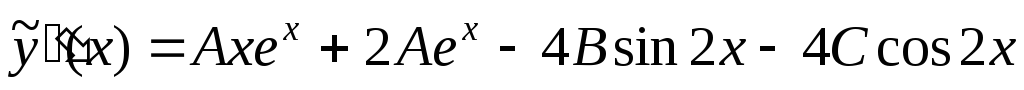
и подставляем их в исходное неоднородное уравнение:
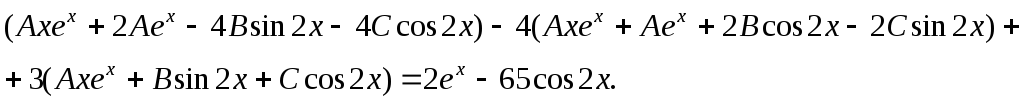 Раскроем
скобки и приведем подобные в левой части
равенства:
Раскроем
скобки и приведем подобные в левой части
равенства:
 .
.
Приравнивая
коэффициенты у подобных членов из обеих
частей равенства, получим систему
уравнений для определения коэффициентов 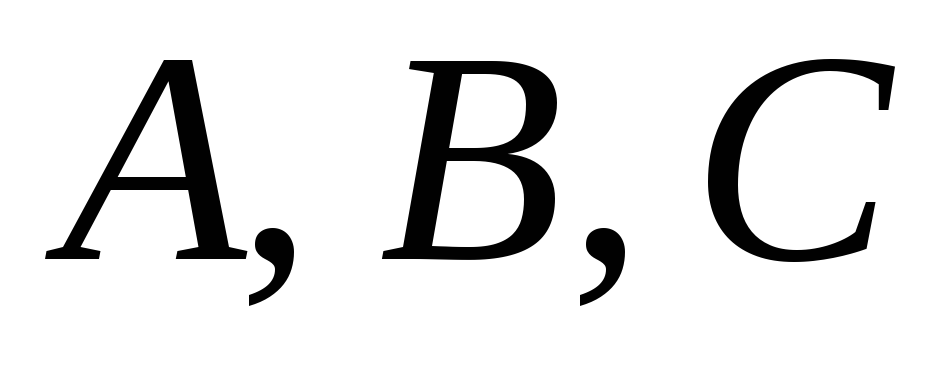 и найдем их значения:
и найдем их значения:
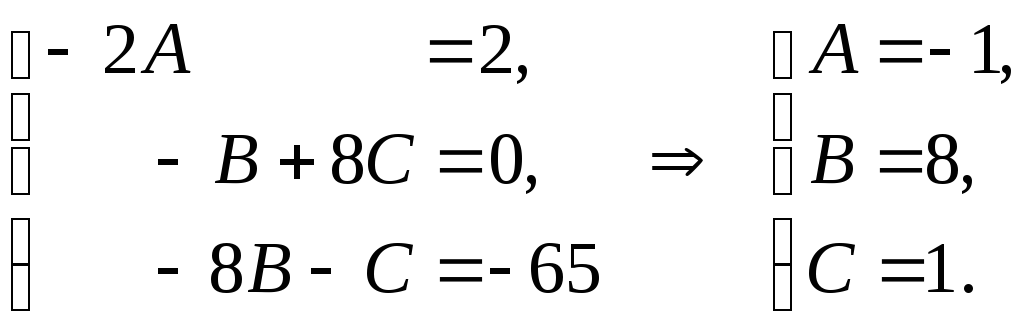
Таким образом, частное решение неоднородного уравнения имеет вид:
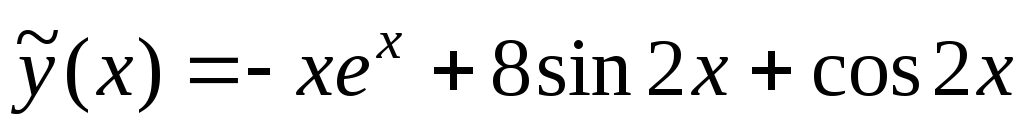 .
.
3) Общее решение исходного неоднородного дифференциального уравнения найдем как сумму общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения:
.
Метод вариации произвольных постоянных (метод Лагранжа)
Частное решение линейного неоднородного дифференциального уравнения
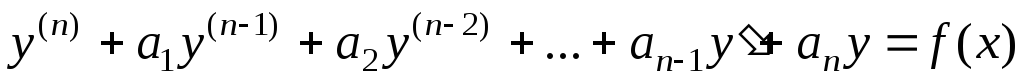
можно найти методом вариации произвольных постоянных, если известно общее решение
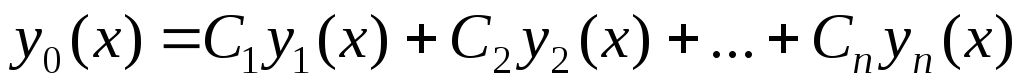
соответствующего однородного уравнения
.
Именно, будем искать частное решение неоднородного уравнения в виде
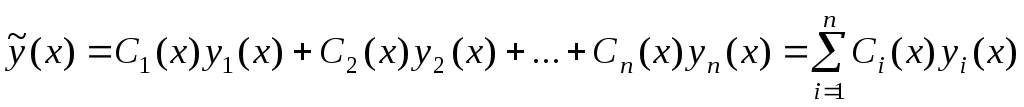 ,
,
где  –
неизвестные функции, для определения
которых
нужно
составить n уравнений.
–
неизвестные функции, для определения
которых
нужно
составить n уравнений.
Найдем  :
:
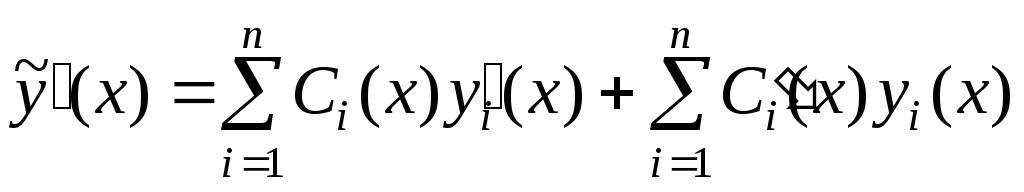 .
.
Положив
 ,
,
получим первое из n искомых уравнений.
Найдем  :
:
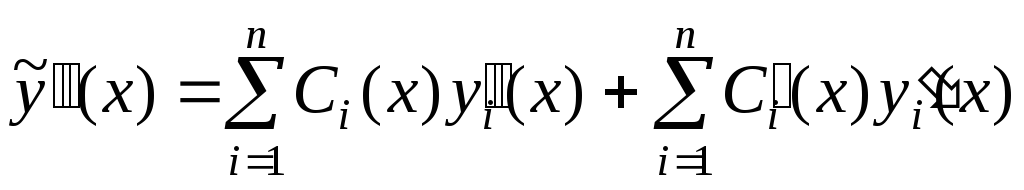 .
.
Положив
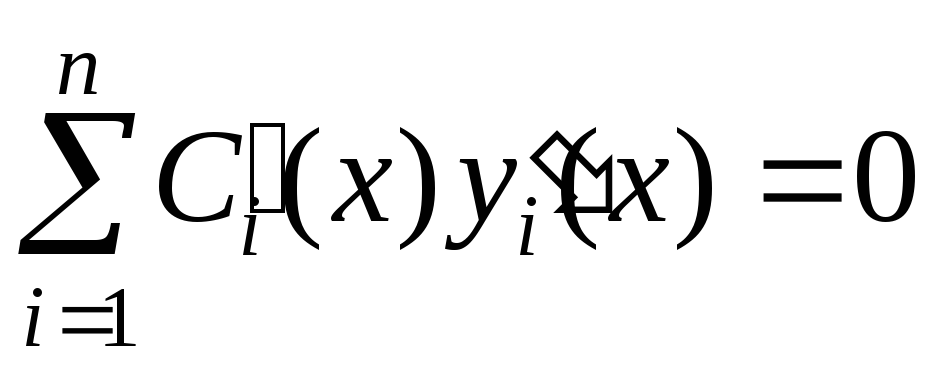 ,
,
получим второе из n искомых уравнений.
Продолжая аналогичным
образом, найдем  :
:
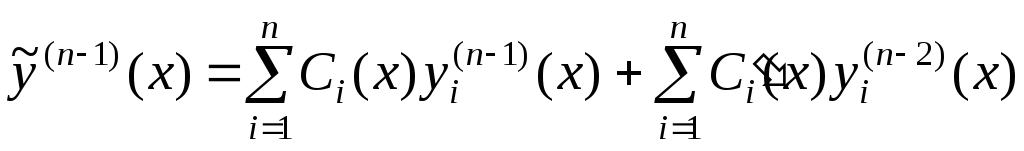 .
.
Положив
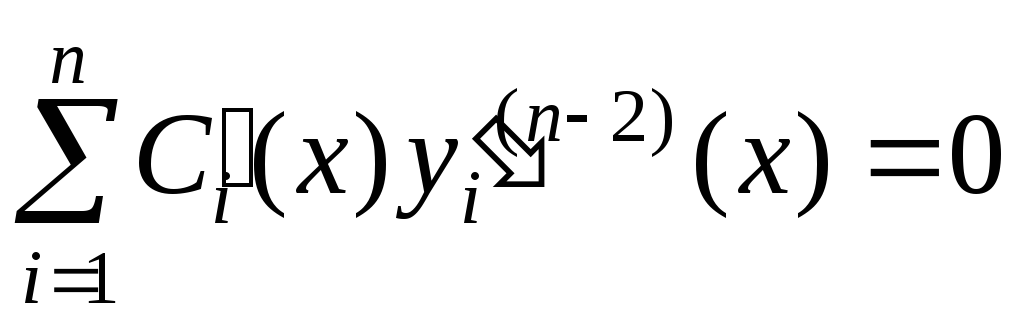 ,
,
получим 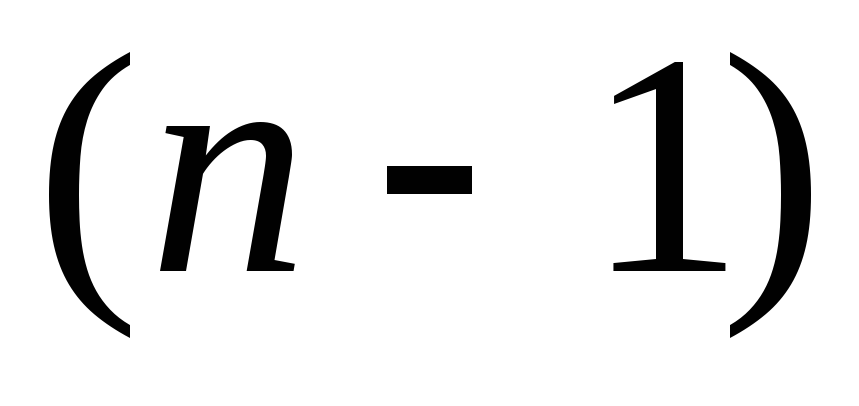 -е
изn искомых уравнений.
-е
изn искомых уравнений.
Найдем 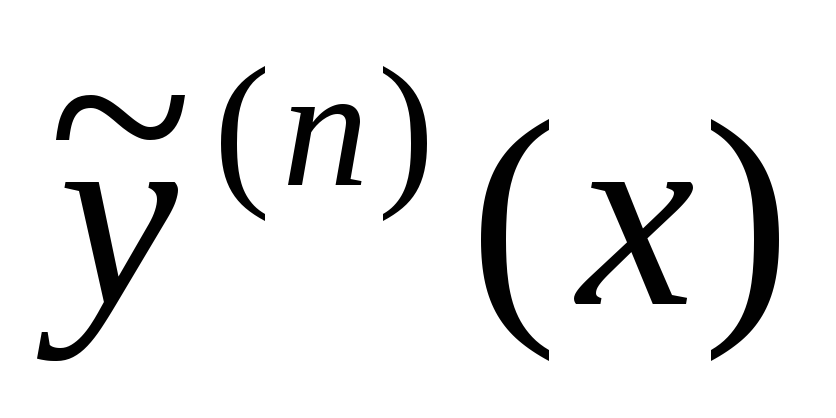 :
:
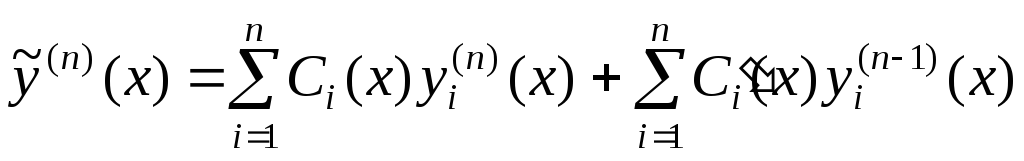
и, подставив в
исходное неоднородное уравнение 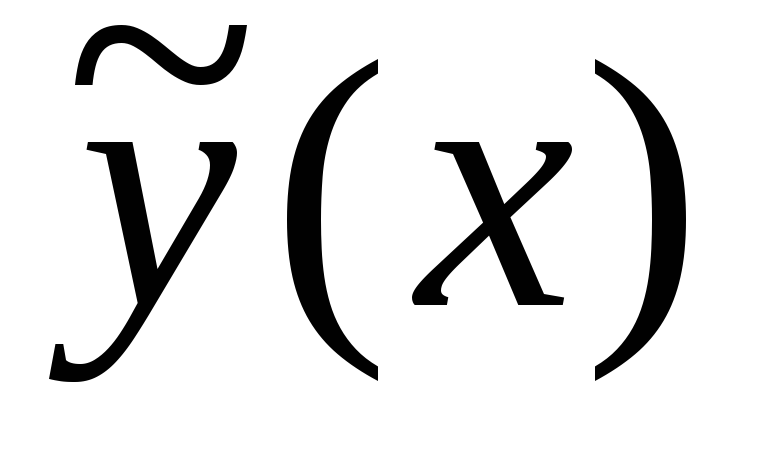 вместоy,
вместоy,  вместо
вместо  ,
, вместо
вместо ,…,
,…, вместо
вместо ,
получим последнееn-е
из n искомых
уравнений для определения n неизвестных
функций
,
получим последнееn-е
из n искомых
уравнений для определения n неизвестных
функций 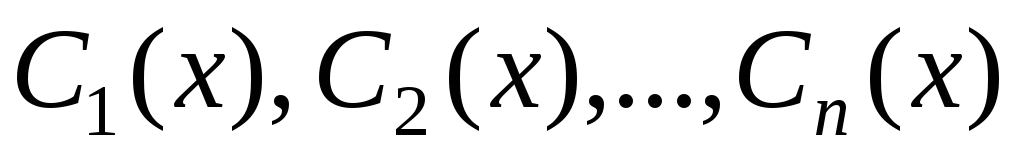 :
:
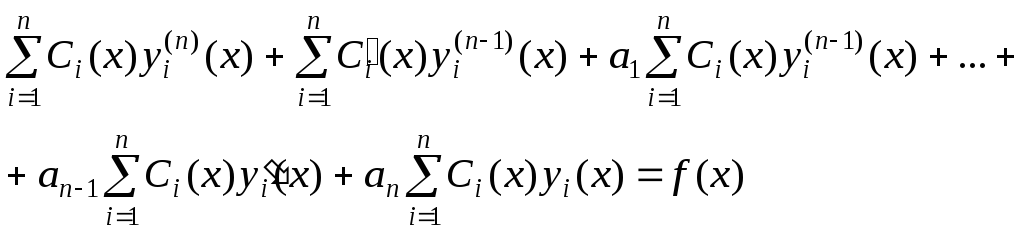
или
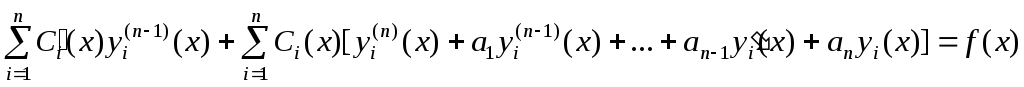 ,
,
или
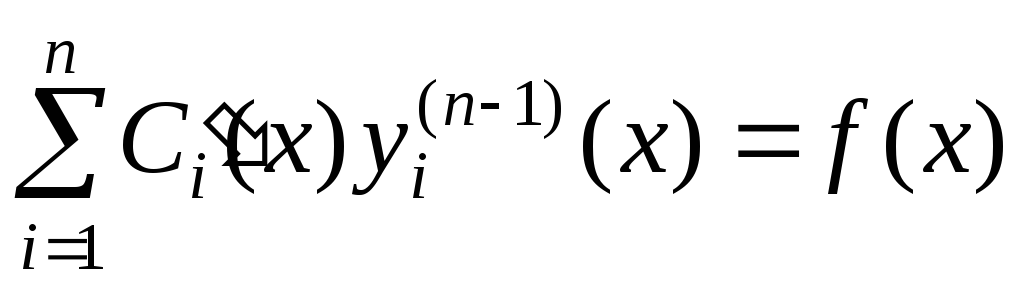 ,
,
так как 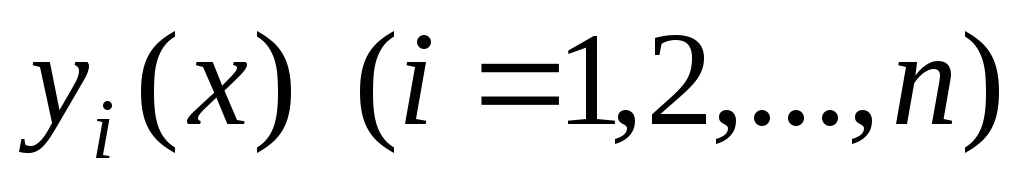 –
решения однородного уравнения
–
решения однородного уравнения
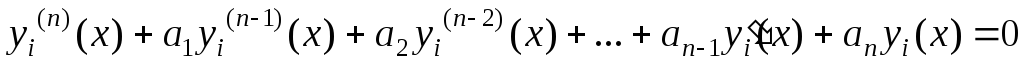 .
.
Таким образом,
получили систему из n линейных
неоднородных алгебраических уравнений
для определения производных от n неизвестных функций 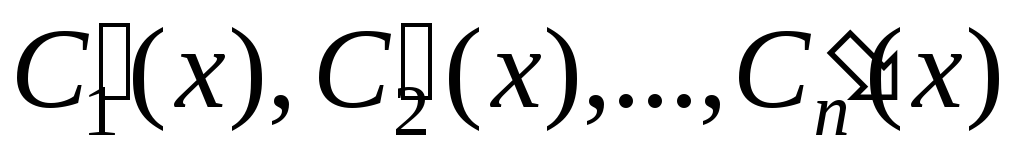 :
:
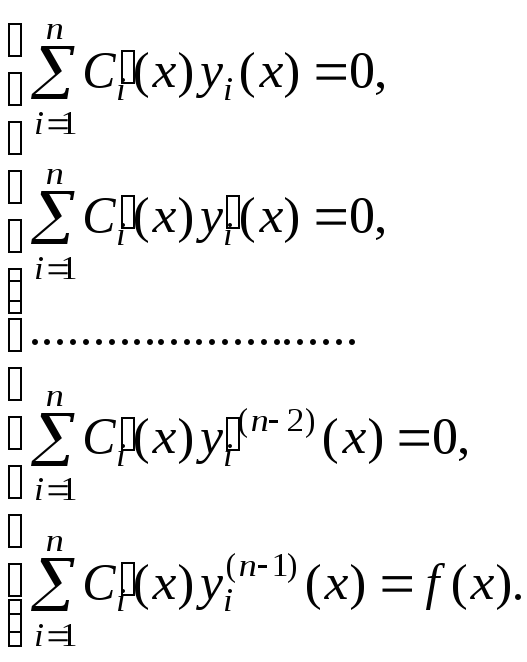
Примем без
доказательства, что определитель системы
отличен от нуля. Тогда система имеет
единственное решение 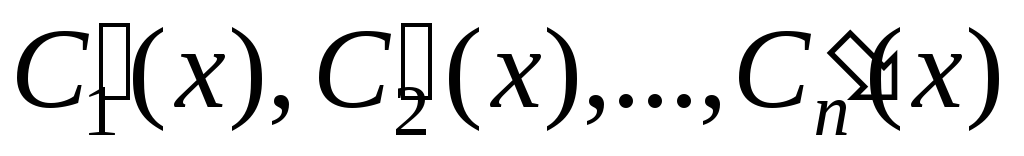 .
Определив все
.
Определив все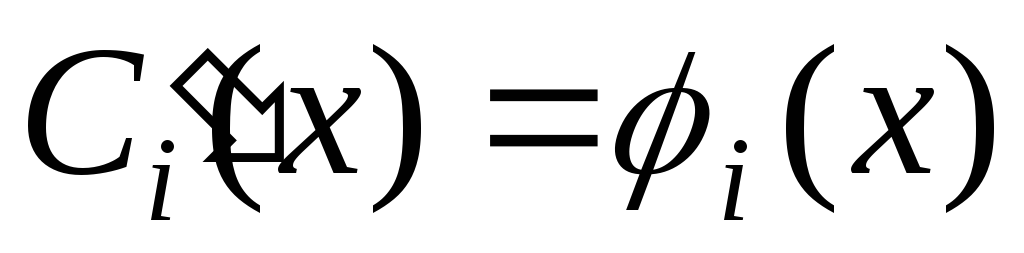 ,
после интегрирования получаем
,
после интегрирования получаем
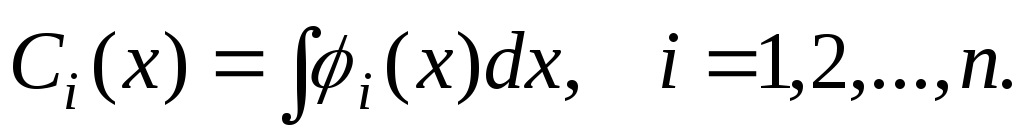 ,
,
Следовательно, частное решение исходного линейного неоднородного дифференциального уравнения имеет вид
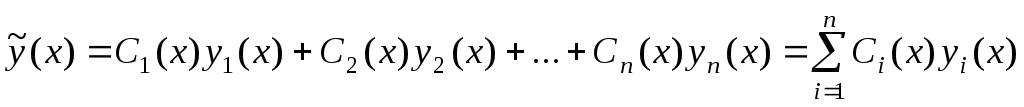 ,
,
где функции 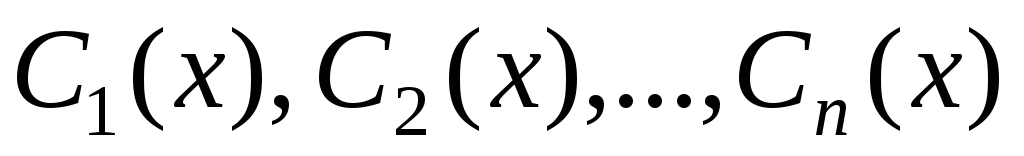 определяются полученными равенствами,
а
определяются полученными равенствами,
а –
известные линейно независимые частные
решения соответствующего однородного
уравнения.
–
известные линейно независимые частные
решения соответствующего однородного
уравнения.
Пример. Найти частное решение неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами
 .
.
1) Сначала находим общее решение соответствующего однородного уравнения
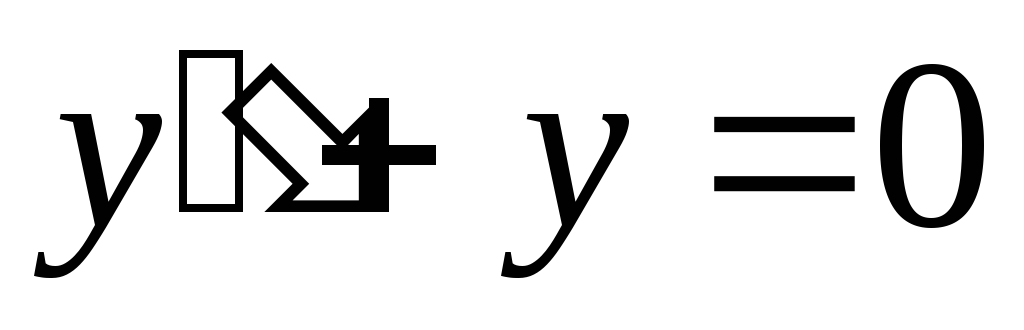 .
.
Для этого составляем и решаем характеристическое уравнение:
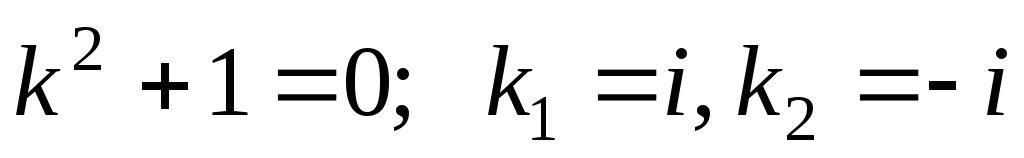 –
пара комплексно
сопряженных простых корней
–
пара комплексно
сопряженных простых корней 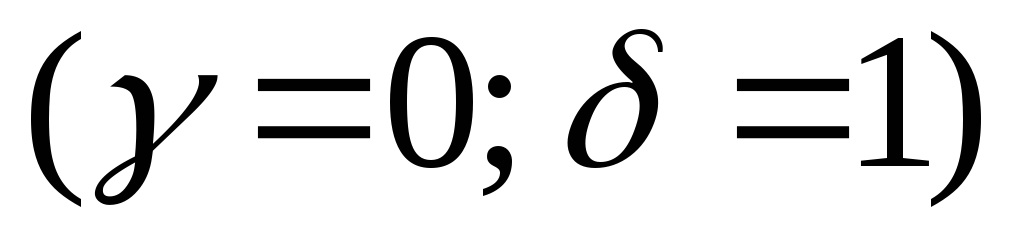 .
.
Частные решения соответствующего однородного дифференциального уравнения:
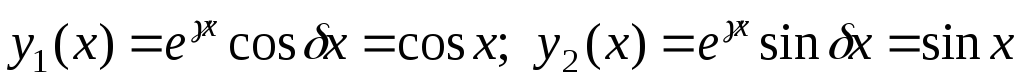 .
.
Общее решение соответствующего однородного дифференциального уравнения является линейной комбинацией полученных частных решений:
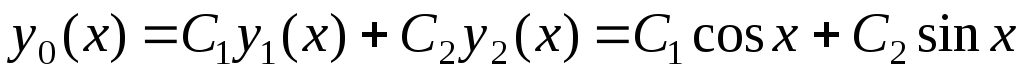 .
.
2) Далее ищем частное решение исходного неоднородного дифференциального уравнения в виде
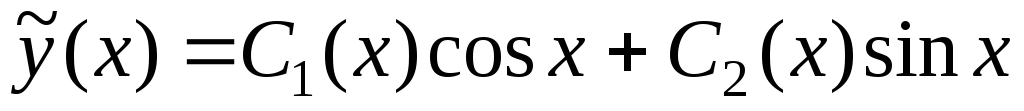 .
.
Составляем и
решаем систему неоднородных алгебраических
уравнений для определения 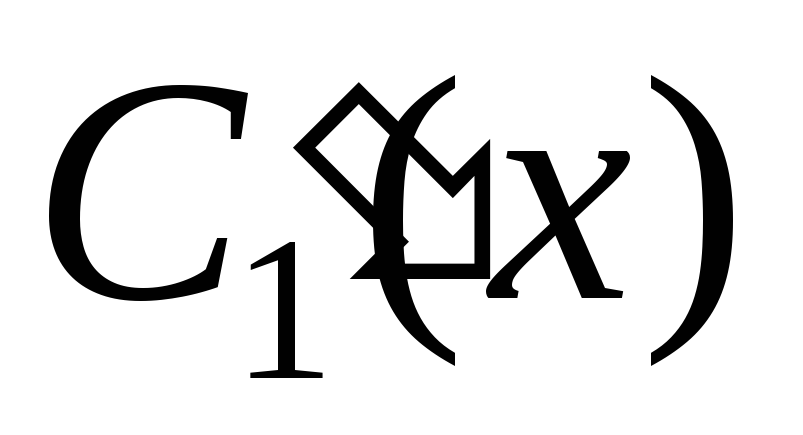 и
и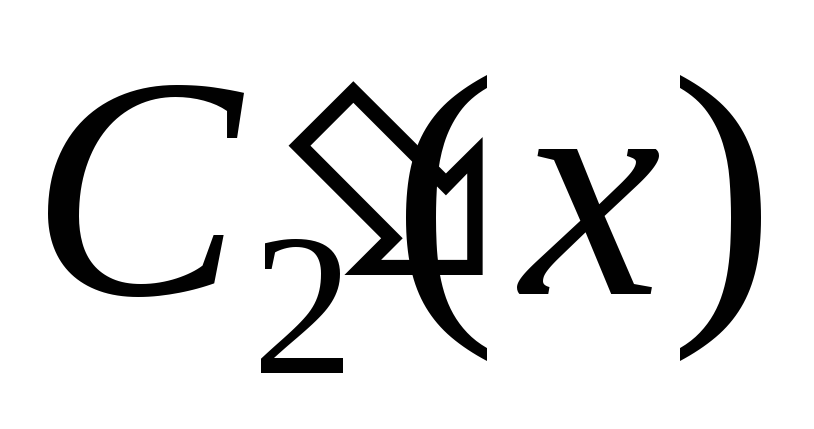 :
:
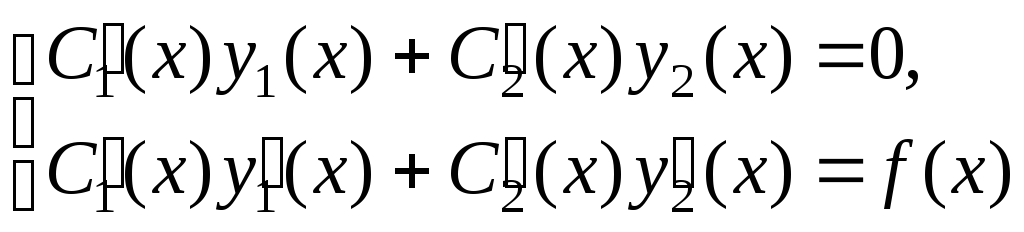
или
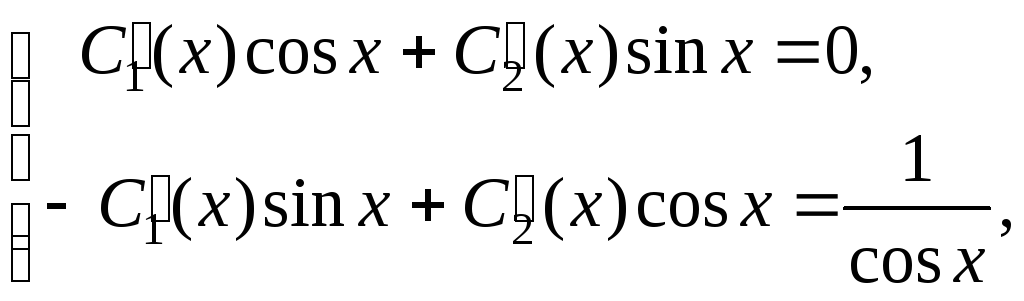
откуда находим

Таким образом, частное решение исходного неоднородного дифференциального уравнения высшего порядка с постоянными коэффициентами имеет вид
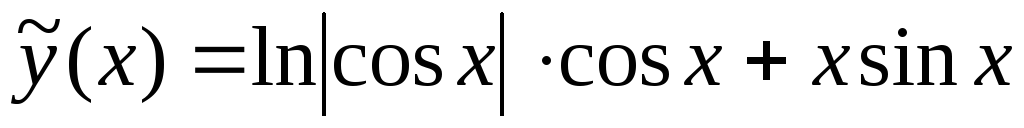 .
.
studfile.net
Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Метод решения
Рассмотрим линейное однородное дифференциальное уравнение с постоянными коэффициентами:
(1) .
Его решение можно получить следуя общему методу понижения порядка.
Однако проще сразу получить фундаментальную систему n линейно независимых решений и на ее основе составить общее решение. При этом вся процедура решения сводится к следующим шагам.
Ищем решение уравнения (1) в виде . Получаем характеристическое уравнение:
(2) .
Оно имеет n корней. Решаем уравнение (2) и находим его корни . Тогда характеристическое уравнение (2) можно представить в следующем виде:
(3) .
Каждому корню соответствует одно из линейно независимых решений фундаментальной системы решений уравнения (1). Тогда общее решение исходного уравнения (1) имеет вид:
(4) .
Действительные корни
Рассмотрим действительные корни. Пусть корень однократный. То есть множитель входит в характеристическое уравнение (3) только один раз. Тогда этому корню соответствует решение
.
Пусть – кратный корень кратности p. То есть
. В этом случае множитель входит в характеристическое уравнение (3) ⇑ p раз:
.
Этим кратным (равным) корням соответствуют p линейно независимых решений исходного уравнения (1):
; ; ; …; .
Комплексные корни
Рассмотрим комплексные корни характеристического уравнения (3) ⇑. Выразим комплексный корень через действительную и мнимую части:
.
Поскольку коэффициенты исходного уравнения (1) ⇑ действительные, то кроме корня имеется комплексно сопряженный корень
.
Пусть комплексный корень однократный. Тогда паре корней соответствуют два линейно-независимых решения уравнения (1) ⇑:
; .
Пусть – кратный комплексный корень кратности p. Тогда комплексно сопряженное значение также является корнем характеристического уравнения кратности p и множитель входит в разложение на множители (3) ⇑ p раз:
.
Этим 2p корням соответствуют 2p линейно независимых решений:
; ; ; … ;
; ; ; … .
После того как фундаментальная система линейно независимых решений найдена, по формуле (4) ⇑ получаем общее решение уравнения (1) ⇑.
Примеры решений задач
Пример 1
Решить уравнение:
.
Решение
Ищем решение в виде . Составляем характеристическое уравнение:
.
Преобразуем его:
;
;
.
Рассмотрим корни этого уравнения. Мы получили четыре комплексных корня кратности 2:
; .
Им соответствуют четыре линейно-независимых решения исходного уравнения:
; ; ; .
Также мы имеем три действительных корня кратности 3:
.
Им соответствуют три линейно-независимых решения:
; ; .
Общее решение исходного уравнения имеет вид:
.
Ответ
.
Пример 2
Решить уравнение
Решение
Ищем решение в виде . Составляем характеристическое уравнение:
.
Решаем квадратное уравнение.
.
Мы получили два комплексных корня:
.
Им соответствуют два линейно-независимых решения:
.
Общее решение уравнения:
.
Ответ
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
7.ЛИНЕЙНЫЕ НЕОДНОРОДНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ
Линейным неоднородным дифференциальным уравнением (ЛНДУ) n-го порядка с постоянными коэффициентами называется уравнение вида
y(n) + a1y(n-1) +….. + an-1y′ + any = f(x), | (7.1) |
где a1, a2,a3 ….,an-1,an – действительные числа; y = f(x) – данная функция.
Рассмотрим ЛНДУ второго порядка |
|
y′′+ a1 y′+ a2 y = f (x) | (7.2) |
и соответствующее ему однородное уравнение (ЛОДУ) |
|
y′′+ a1 y′+ a2 y = 0. | (7.3) |
Пусть y1 и y2 – фундаментальная система решений уравнения (7.3), тогда
есть общее решение уравнения (7.3).
Теорема (о структуре общего решения ЛНДУ).
Общее решение неоднородного уравнения (7.2) равно сумме общего решения соответствующего однородного (7.3) и частного решения неоднородного уравнения (7.2):
yон = yоо + yчн .
Доказательство. Так как yоо- общее решение уравнения (7.3), то по определению решения эта функция обращает уравнение (7.3) в верное равенство. Так как учн- частное решение уравнения (7.2), то функция учн
также обращает это уравнение в тождество. | Имеем два тождества: | |||
| ′′ | ′ |
|
|
| уоо | + a1 yоо + a2 yоо ≡ 0 | ||
|
|
|
| — найдем их сумму: |
( yчн)′′+ a1( yчн)′+ a2 yчн ≡ f (x) | ||||
′′ | ′′ | ′ | ′ |
|
( yоо + yчн) + a1( yоо + yчн) + a2 ( yоо + yчн) ≡ f (x) или | ||||
( yоо + yчн)′′+ a1( yоо + yчн)′+ a2 ( yоо + yчн) ≡ f (x). | ||||
Следовательно, | yон = yоо + yчн является общим решением | |||
уравнения (7.2). | # |
|
|
|
7.1. Нахождение частного решения ЛНДУ со специальной правой частью
В том случае, когда правая часть дифференциальных уравнений (7.1) и (7.2) в общем случае имеет вид
f (x) = eαx [Pm (x) cos βx +Qn (x)sin βx],
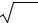
где Pm(x) и | Qn(x) — многочлены переменной x степеней m и n;α, β — | |||
действительные | числа, | используется | метод | неопределенных |
коэффициентов (или метод подбора). |
|
| ||
Частное решение yчн | дифференциального уравнения (7.2) зависит в | |||
каждом конкретном случае от вида функции f(x) и от выражения α ±iβ
(где | i = −1 ), | которое | сравнивается | с | корнями характеристического | |
уравнения, составленного для соответствующего ЛОДУ (7.3). |
| |||||
Возможны случаи: |
|
|
| r | ||
1. | Если | α ±iβ | является | корнем кратности | ||
| характеристического уравнения |
|
|
| ||
|
|
| k 2 + a k + a | = 0 | (*) | |
|
|
| 1 | 2 |
|
|
(r – означает сколько раз α ±iβ совпадет с корнями характеристического уравнения). Тогда частное решение находится в виде
|
|
|
| y | = xreαx [M | l | (x)cos βx + N | (x)sin βx], | |||||||
|
|
|
| чн |
|
|
|
|
|
|
|
| l |
| |
где | Ml (x) и Nl (x) — | многочлены со | своими неопределенными | ||||||||||||
коэффициентами, при этом l = max{m, n}. |
|
| |||||||||||||
Например, если |
|
|
|
|
|
|
|
|
|
|
| ||||
l = 0, | то |
|
| M0 (x) = Ax0 = A |
| — многочлен нулевой степени, | |||||||||
l =1, | то |
|
| M1(x) = Ax + B |
|
| — |
|
| многочлен первой степени, | |||||
l = 2, | то |
|
| M 2 (x) = Ax2 + Bx +C — | многочлен второй степени, | ||||||||||
l = 3, | то |
|
| M3 (x) = Ax3 + Bx2 +Cx + D — | многочлен 3-й степени, | ||||||||||
l, то | M | l | (x) = A xl + A xl −1 +… + A | — многочлен степени l. | |||||||||||
|
|
| 0 |
| 1 |
|
|
|
|
| l |
|
|
| |
2. | Если | α ±iβ | не |
| является | корнем характеристического | |||||||||
уравнения |
| (*), то | r = 0 | и |
| x0 =1, | тогда частное решение yчн имеет | ||||||||
вид |
|
|
| y | = eαx [M | l | (x)cos βx + N | (x)sin βx]. | |||||||
|
|
|
| чн |
|
|
|
|
|
|
| l |
|
| |
Пример 1. Найти общее решение уравнения
y′′−6 y′+9 y = 5e3x
Решение. Находим общее решение соответствующего ЛОДУ:
y′′−6 y′+9 y = 0 .
Его характеристическое уравнение k 2 −6k +9 = 0 имеет корни k1 = k2 = 3. Общее решение однородного уравнения при равных корнях характеристического уравнения имеет вид
yоо = C1e3x +C2 xe3x = e3x (C1 +C2 x) .
Правая часть неоднородного уравнения имеет вид f (x) = 5e3x.
α = 3, β = 0 α ±iβ = 3 — является кратным корнем кратности r = 2
характеристического уравнения, l = max{0,0} = 0 , поэтому
yчн = x2e3x [M0 (x)cos0x + N0 (x)sin 0x] = Ax2e3x.
Дважды дифференцируем yчн:
( yчн)′ = 2Axe3x +3Ax2e3x
( yчн)′′ = 2Ae3x + 6Axe3x + 6Axe3x +9Ax2e3x =
=2Ae3x +12Axe3x +9Ax2e3x
иподставляем полученные выражения в данное уравнение:
2Ae3x +12Axe3x | +9Ax2e3x −12Axe3x −18Ax2e3x +9x2e3x = 5e3x. | ||||||||||||||||||||
В результате получим |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
|
|
|
| 2Ae3x | = 5e3x 2A = 5 A = 2,5. | ||||||||||||||||
Тогда y | = 2,5x2e3x. А общее решение неоднородного уравнения | ||||||||||||||||||||
чн |
|
|
|
|
|
|
|
|
|
|
| = e3x |
|
|
| x) + 2,5x2e3x. | |||||
y | он | = y |
| + y |
| (C +C | 2 | ||||||||||||||
|
|
|
|
| оо |
| чн |
|
| 1 |
|
|
|
|
|
| |||||
Ответ: y = e3x (C +C | 2 | x) + 2,5x2e3x. ■ |
|
|
|
|
|
|
| ||||||||||||
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Пример 2. Решить задачу Коши для уравнения |
| ′ | |||||||||||||||||||
y | ′′ | + y | ′ | − 2 y = cos x −3sin x , |
|
|
|
|
| ||||||||||||
|
|
| если y(0) =1, y (0) = 2. | ||||||||||||||||||
Решение. Находим общее решение соответствующего ЛОДУ | |||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| y′′+ y′− 2 y = 0. |
|
|
|
| |||||
Его характеристическое уравнение: | k 2 + k − 2 = 0, | ||||||||||||||||||||
|
|
|
|
|
| k = −1 ±3; |
| k =1;k | 2 | = −2. | |||||||||||
|
|
|
|
|
|
| 1,2 |
|
|
| 2 |
|
| 1 |
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Общее решение ЛОДУ | при различных корнях характеристического | ||||||||||||||||||||
уравнения имеет вид |
| = C ek1x + C |
| ek2 x = C e x |
|
|
| e−2x . | |||||||||||||
|
|
| y | оо | 2 |
| + C | 2 | |||||||||||||
|
|
|
|
|
|
| 1 |
|
|
|
|
| 1 |
|
|
| |||||
Правая часть данного уравнения: | f (x) = cos x −3sin x. | ||||||||||||||||||||
α = 0, β =1 α ±iβ = ±i | — не являются корнями характеристического | ||||||||||||||||||||
уравнения r = 0, |
| l = max{0,0} = 0 . |
|
|
|
|
|
|
| ||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yчн = x r eαx | [M l (x) cos βx + Nl (x) sin βx] = A cos x + B sin x. | ||||||||||||||||||||
Дифференцируя, получим |
|
|
|
|
|
|
|
|
|
|
| ||||||||||
′ |
|
|
|
|
|
|
|
|
|
|
|
|
| , | ′′ | = −A cos x − B sin x . | |||||
yчн = −Asin x + B cos x | yчн | ||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
| ′ | ′′ |
|
|
|
|
|
|
| |
Подставим значения yчн , yчн , y | чн в данное уравнение, будем иметь | ||||||||||||||||||||
− Acos x − Bsin x − Asin x + B cos x −
− 2A cos x − 2B sin x ≡ cos x − 3sin x .
Приравнивая коэффициенты при сosx | и sinx в левой и правой частях, | |
получим систему |
|
|
−3A + B =1 |
| A = 0, |
| B =1. | |
− A −3D = −3 |
| |
Тогда | y | чн | = sin x, а |
| y | он | = y | оо | + y | чн | = C e x +C | 2 | e−2x +sin x — | ||||||||
|
|
|
|
|
|
|
|
|
| 1 |
|
|
|
| |||||||
общее решение данного уравнения. |
|
|
|
|
|
|
|
|
|
|
|
| |||||||||
Найдем | ′ | = C1e | x | − 2C2e | −2x | + cos x. |
|
|
|
|
|
|
|
|
| ||||||
yон |
|
|
|
|
|
|
|
| y =1, y′ = 2 : | ||||||||||||
Используя начальные условия, найдем С1 и С2 | при | x=0, | |||||||||||||||||||
|
| 1 = C | +C |
|
|
|
| C | +C |
| =1 |
| C |
| =1, | ||||||
|
|
| 1 |
| 2 |
|
|
| 1 |
| 2 |
| 1 |
|
|
| |||||
| 2 | = C2 − 2C2 +1 |
| C1 − 2C2 =1 |
| C2 = 0. | |||||||||||||||
Подставляя значения С1 и С2 в общее решение, получим частное
решение yчаст. = ex + sin x . Ответ: yчаст. = ex + sin x . ■
7.2. Принцип наложения (суперпозиции)
Этот метод основан на следующей теореме:
Теорема. Если правая часть f (x) ЛНДУ (7.1) представляет сумму двух функций, т.е. f (x) = f1(x) + f2 (x) , то частное решение такого ДУ можно получить как сумму частных решений аналогичных уравнений с правыми частями соответственно f1(x) и f2 (x) , т.е.
yчн = y1чн(x) + y2чн(x) .
Доказательство. Рассмотрим два уравнения:
y′′+ a1 y′+ a2 y = f1(x) и y′′+ a1 y′+ a2 y = f2 (x) .
Пусть y1чн(x) и y2чн(x) являются частными решениями этих уравнений соответственно, тогда имеем два тождества:
( y1чн)′′+ a1( y1чн)′+ a2 y1чн ≡ f1(x) — найдем их сумму:
( y2чн)′′+ a1( y2чн)′+ a2 y2чн ≡ f2 (x)
[( y1чн)′′+( y2чн)′′] + a1[( y1чн)′+( y2чн)′] +
+ a2 ( y1чн + y2чн) ≡ f1(x) + f2 (x)
или ( y1чн + y2чн)′′+ a1( y1чн + y2чн)′+ a2 ( y1чн + y2чн) ≡ f1(x) + f2 (x).
Следовательно, yчн = y1чн + y2чн является решением уравнения
y′′+ a1 y′+ a2 y = f1(x) + f2 (x) . #
Пример. Найти общее решение уравнения
y′′+ y′ = x + e2x .
Решение. Так как правая часть уравнения
f (x) = x + e2x = f (x) + f | 2 | (x) , | то | по | теореме общее решение | ||||||||||||||||
|
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
данного уравнения будет иметь вид |
|
|
|
|
|
|
|
|
| ||||||||||||
|
|
|
|
| yон = yоо + yчн1 + yчн2 . |
|
|
| |||||||||||||
Найдем | yоо. Для этого рассмотрим уравнение y′′+ y′ = 0, его | ||||||||||||||||||||
характеристическое уравнение |
| k 2 + k = 0 имеет корни k1=0; k2= -1. | |||||||||||||||||||
Тогда | y | оо | = C ek1x | +C | 2 | ek2 x | = C e0x +C | 2 | e−x | = C +C | 2 | e−x | |||||||||
|
|
| 1 |
|
|
|
|
|
|
|
| 1 |
|
| 1 |
| |||||
Найдем у1чн. |
|
|
|
|
|
|
|
|
|
| y′′+ y′ = x |
|
|
|
| ||||||
Для этого рассмотрим уравнение |
|
|
|
| |||||||||||||||||
Правая часть |
| f1(x) = x α1 = 0; β1 = 0;l =1. |
|
|
| ||||||||||||||||
Так как | α1 ±iβ1 = 0 ± 0i = 0 — является простым корнем |
|
| ||||||||||||||||||
характеристического уравнения r =1, тогда |
|
|
|
|
|
| |||||||||||||||
|
| y |
| = xr eα1x | [M | l | (x) cos β x + N | l | (x) sin β x] = |
| |||||||||||
|
| 1чн |
|
|
|
|
|
|
|
|
|
| 1 |
|
| 1 |
|
| |||
| = x[(Ax + B)cos0x + (Cx + D)sin 0x] = x( Ax + B). | ||||||||||||||||||||
Подставим y1чн = Ax2 + Bx , ( y1чн)′ = 2Ax + B , | ( y1чн)′′ = 2A в | ||||||||||||||||||||
рассматриваемое уравнение | y′′+ y′ = x : |
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
| 2A + 2Ax + B = x , |
|
|
|
|
| ||||||||||
используя условие равенства многочленов, получим |
|
|
| ||||||||||||||||||
|
|
|
|
| 2A =1 |
|
| 1 |
|
|
|
|
| ||||||||
|
|
|
|
|
| A = 2 , |
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
| 2A + B = 0 |
| B =1. |
|
|
| ||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| 1 x2 |
|
|
| ||||
Таким образом, получим |
| y |
|
|
| = | − x. |
|
|
|
|
|
| ||||||||
Найдем у2чн . |
|
|
|
|
| 1чн |
| 2 |
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
| y′′+ y′ = e2x |
|
|
| ||||||||
Для этого рассмотрим уравнение |
|
|
| ||||||||||||||||||
Правая часть | f2 (x) = e2x . Для | f2 (x) :α2 = 2; β2 = 0; l = 0 . | |||||||||||||||||||
α2 ± β2i = 2 ± 0i = 2 — |
| не |
|
|
| является | корнем | характеристического | |||||||||||||
уравнения r = 0, поэтому
y2чн = xr eα2 x [Ml (x) cos β2 x + Nl (x) sin β2 x]= = x0e2x [Acos 0x + B sin 0x]= Ae2x ;
studfile.net
Линейные дифференциальные уравнения высших порядков
Уравнение вида: 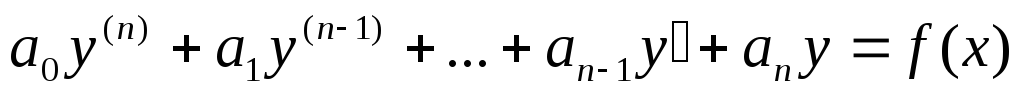 называется
линейным дифференциальным уравнением
высшего порядка, гдеa0,а1,…аn-функции
переменной х или константы, причём
a0,а1,…аn и f(x)
считаются непрерывными.
называется
линейным дифференциальным уравнением
высшего порядка, гдеa0,а1,…аn-функции
переменной х или константы, причём
a0,а1,…аn и f(x)
считаются непрерывными.
Если a0=1(если  то
на него можно разделить)
то
на него можно разделить) уравнение примет вид:
уравнение примет вид:
Если 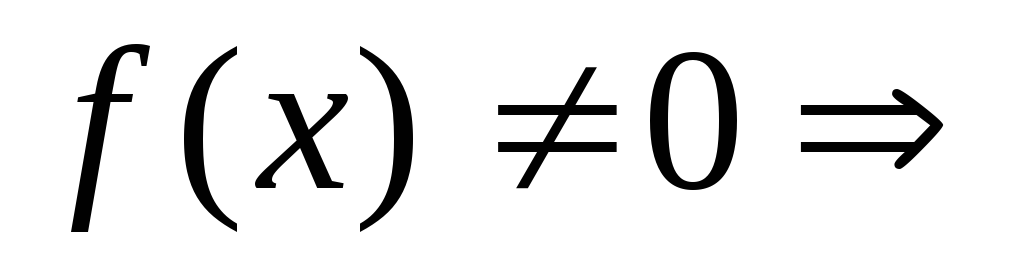 уравнение
неоднородное.
уравнение
неоднородное.
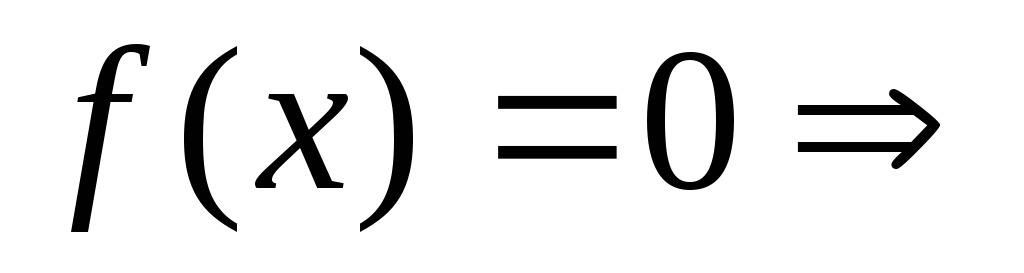 уравнение однородное.
уравнение однородное.
Линейные однородные дифференциальные уравнения порядка n
Уравнение вида: 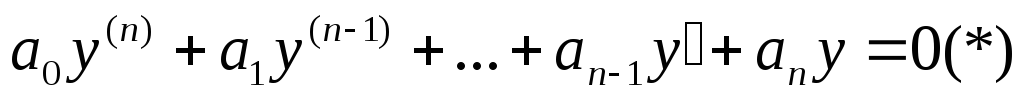 называются
линейными однородными дифференциальными
уравнениями порядкаn.
называются
линейными однородными дифференциальными
уравнениями порядкаn.
Для этих уравнений справедливы следующие теоремы:
Теорема 1: Если 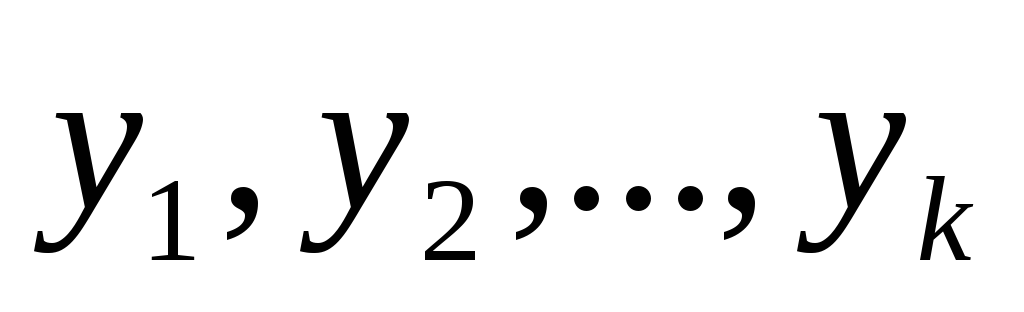 —
решение
—
решение , то сумма
, то сумма 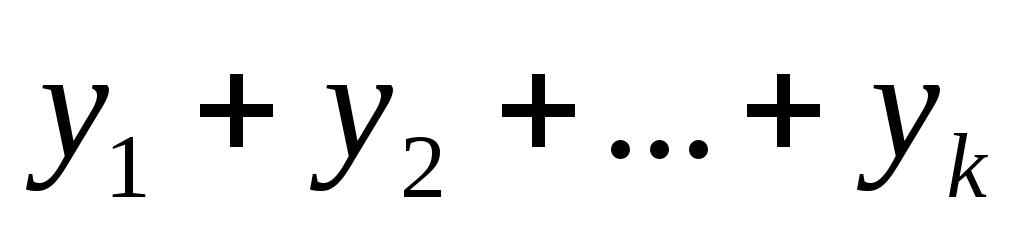 —
тоже решение
—
тоже решение
Доказательство:
подставим сумму в 
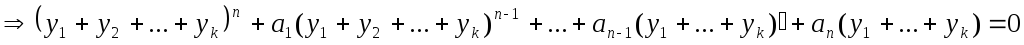
Т.к производная любого порядка от суммы равна суме производных, то можно перегруппироватся , раскрыв скобки:
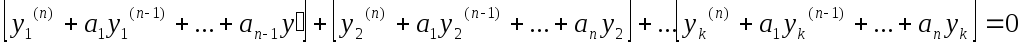
т.к y1 и y2 – решение.
0=0(верно) сумма
тоже решение.
сумма
тоже решение.
теорема доказана.
Теорема 2: Если
y0-решение  ,
то
,
то 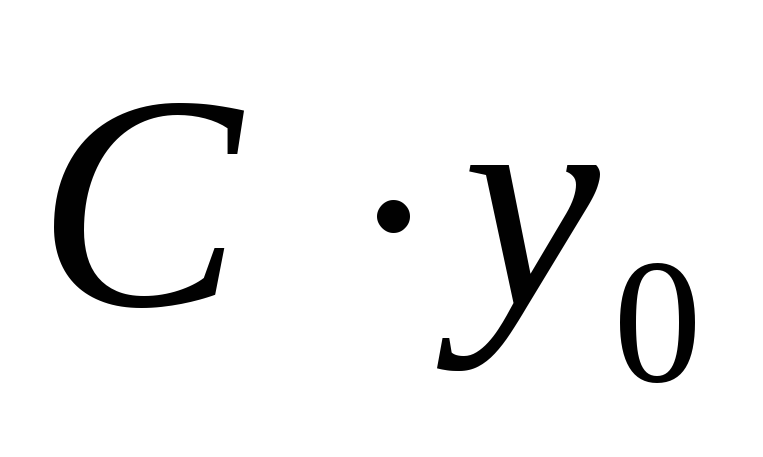 — тоже решение
— тоже решение .
.
Доказательство:
Подставим 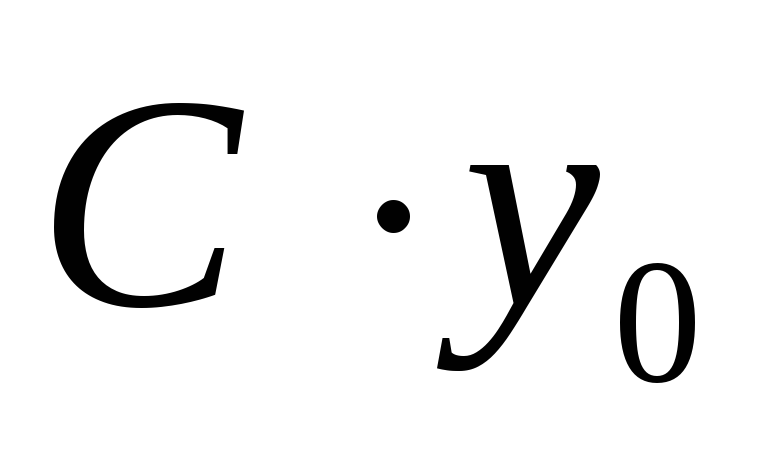 в
уравнение
в
уравнение
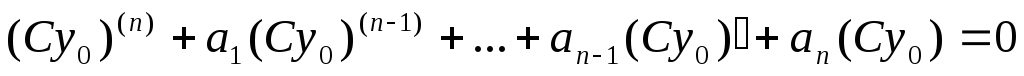
т.к С выносится за знак производной, то
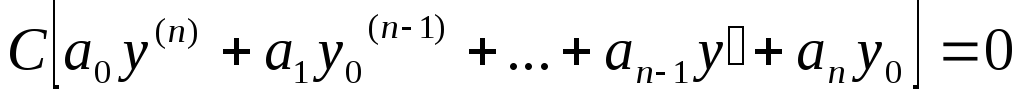

т.к 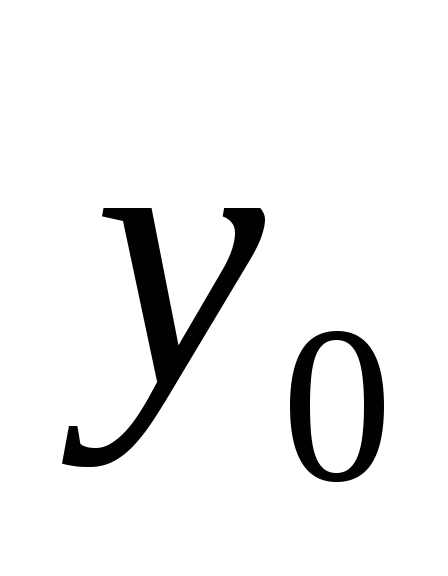 решение,
0=0(верно)
решение,
0=0(верно) Сy0-тоже
решение.
Сy0-тоже
решение.
теорема доказана.
Следствие из Т1
и Т2: если  —
решения (*)
—
решения (*) линейеая комбинация
линейеая комбинация -тоже
решение (*).
-тоже
решение (*).
Линейно независимые и линейно зависимые системы функций. Определитель Вронского и его свойства
Определение: Система функций 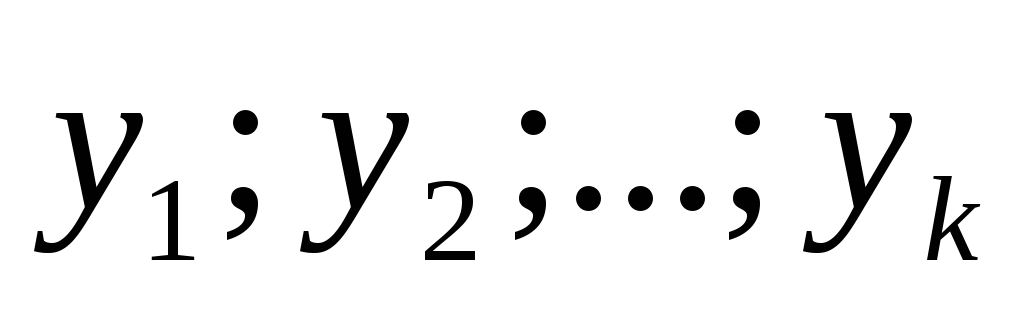 —
называется линейно независимой , если
линейная комбинация
—
называется линейно независимой , если
линейная комбинация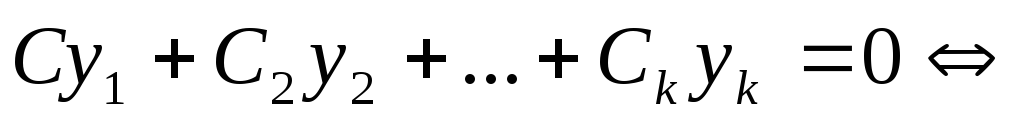 коэффициенты
коэффициенты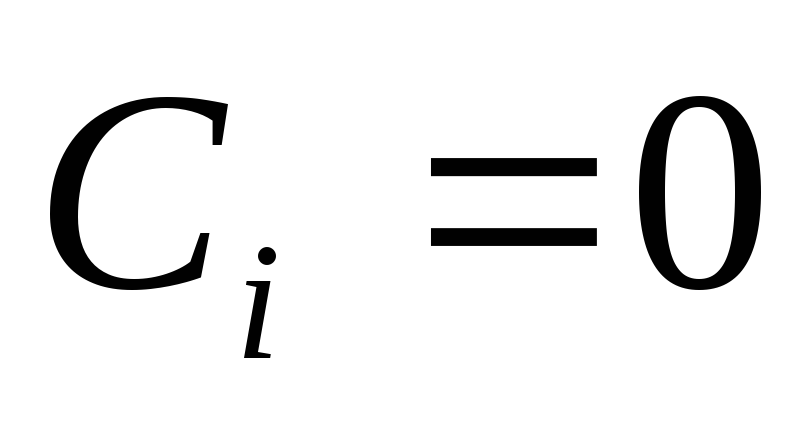 .
.
Определение: Систему
функций 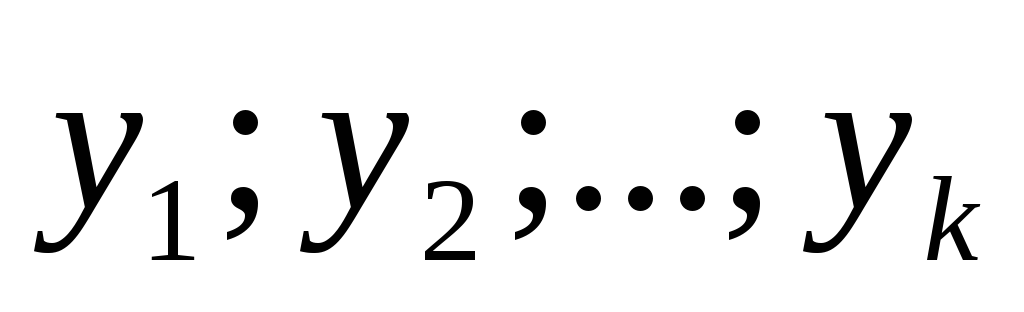 —
называют линейно зависимой, если
—
называют линейно зависимой, если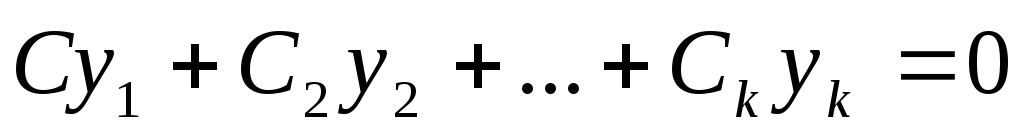 и
есть коэффициенты
и
есть коэффициенты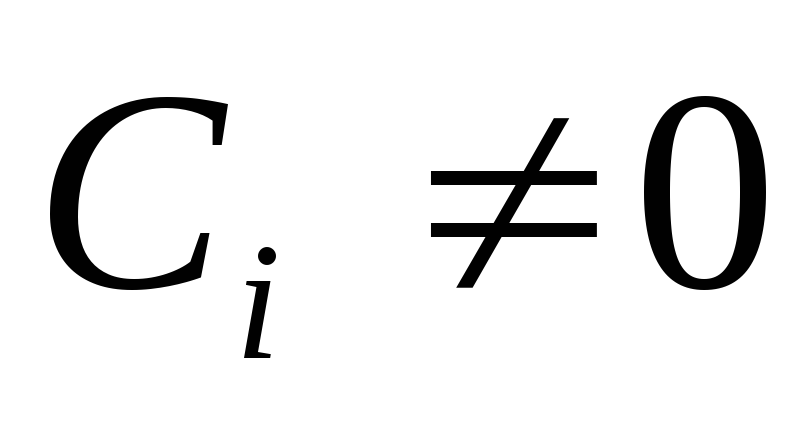 .
.
В озьмём
систему двух линейно зависимых функций
озьмём
систему двух линейно зависимых функций т.к
т.к или
или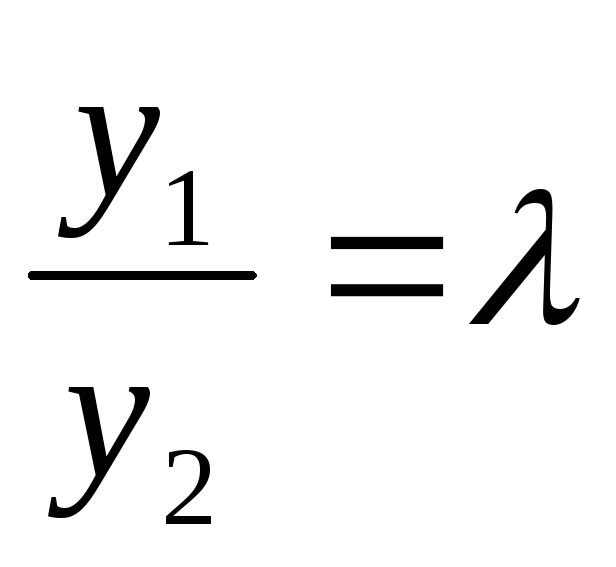 —
условие линейной независимости двух
функций.
—
условие линейной независимости двух
функций.
Примеры:
1)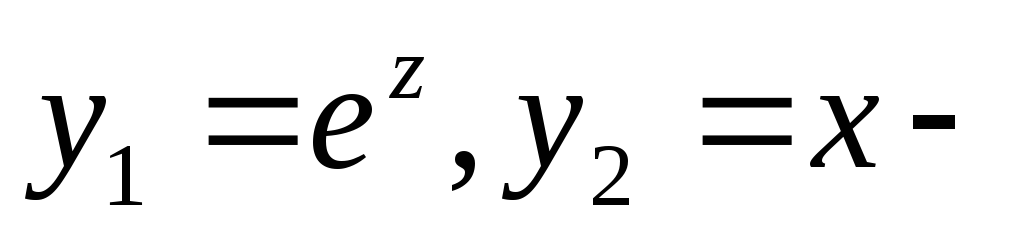 линейно независимы
линейно независимы
2)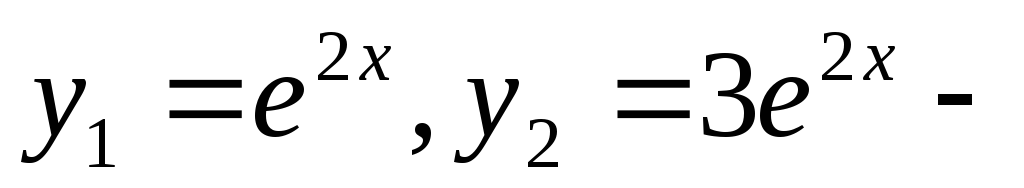 линейно зависимы
линейно зависимы
3)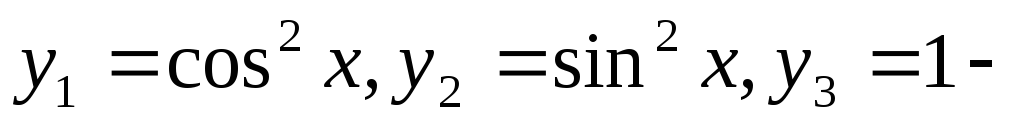 линейно зависимы
линейно зависимы
Определение: Дана система
функций  —
функций переменной х.
—
функций переменной х.
Определитель 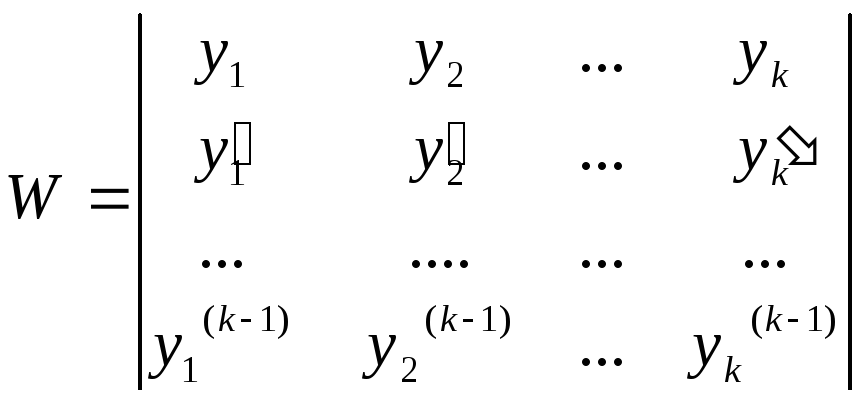 -определитель
Вронского для системы функций
-определитель
Вронского для системы функций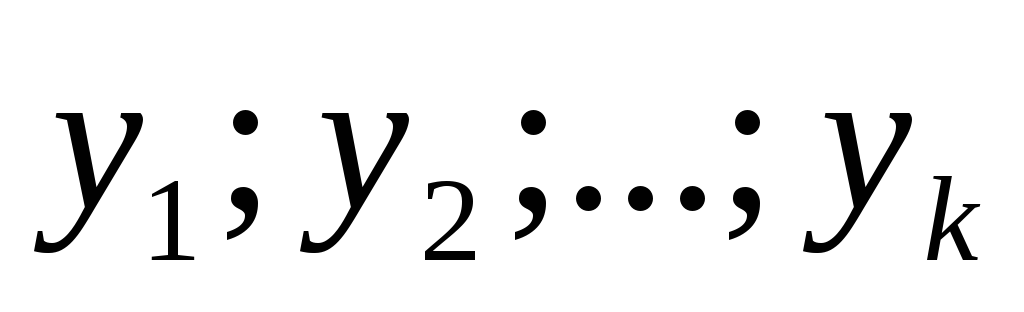 .
.
Для системы двух функций определитель Вронского выглядит следующим образом:
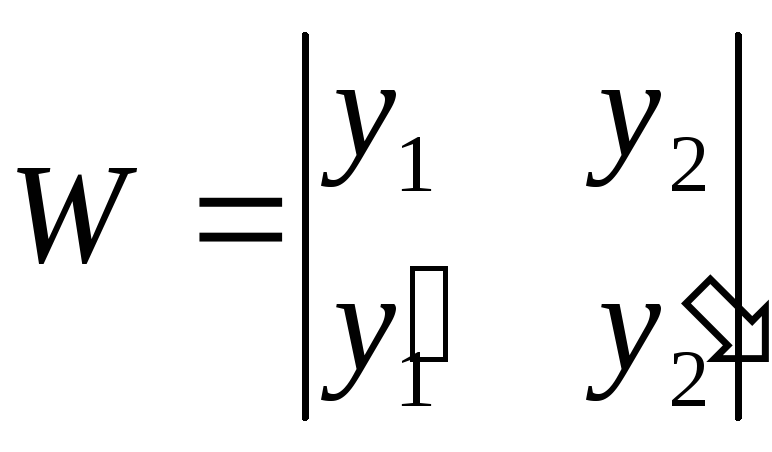
Свойства определителя Вронского:
Если
 —
линейно зависимы на [a;b]
—
линейно зависимы на [a;b] на
этом отрезке.
на
этом отрезке.Если
 — линейно независимые, решения
дифференциального уравнения
— линейно независимые, решения
дифференциального уравнения при
любых значениях х в области, где
определены функции а1…аn
при
любых значениях х в области, где
определены функции а1…аn
Теорема: Об общем решении линейного однородного дифференциального уравнения 2 порядка.
Если y1 и y2 – линейно независимые решения линейного однородного дифференциального уравнения 2 порядка, то
 общее
решение имеет вид:
общее
решение имеет вид:
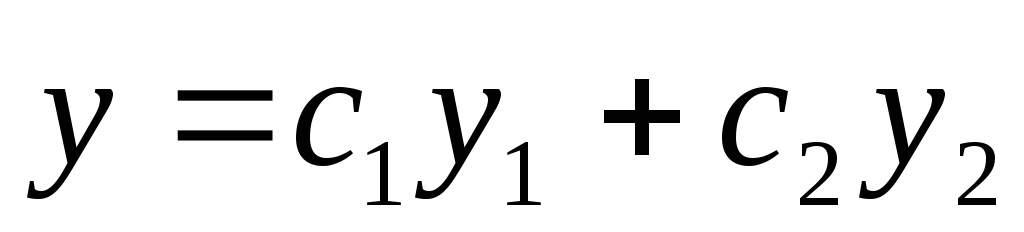
Доказательство: 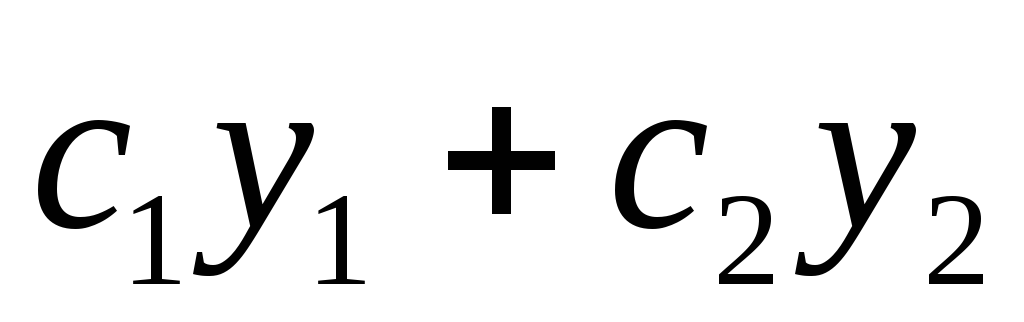 —
решение по следствию из Т1 и Т2.
—
решение по следствию из Т1 и Т2.
Если даны начальные
условия то 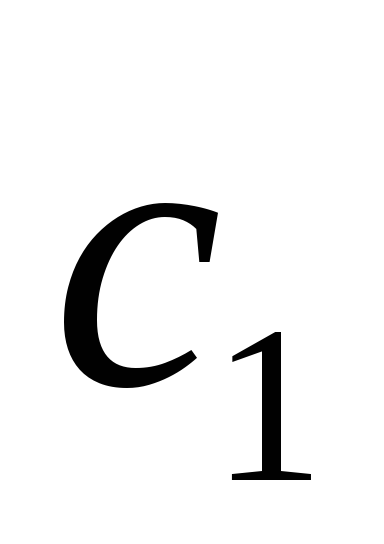 и
и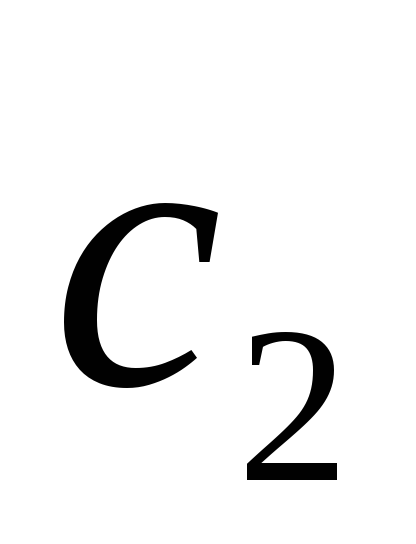 должны находится однозначно.
должны находится однозначно.
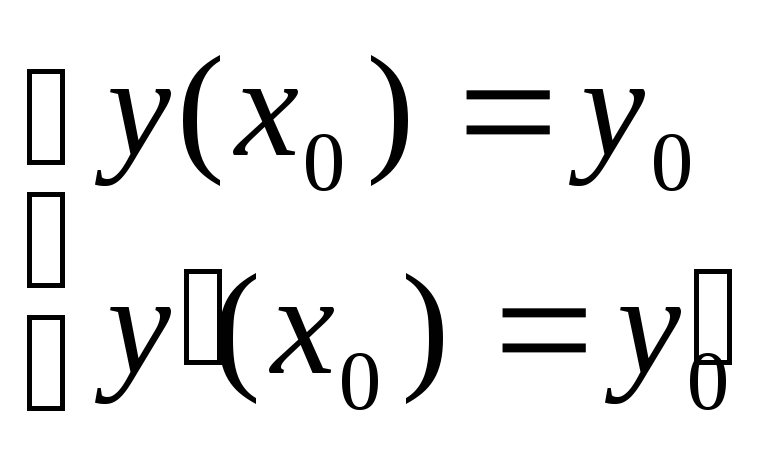 —
начальные условия.
—
начальные условия.
Составим систему
для нахождения 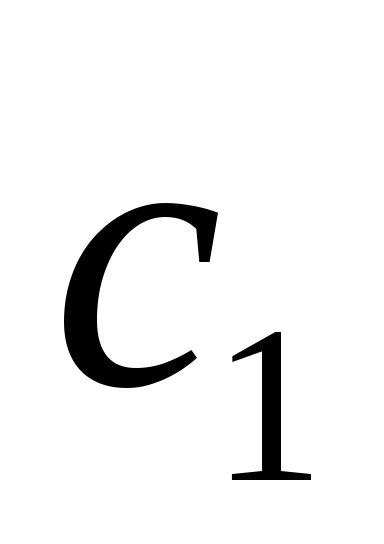 и
и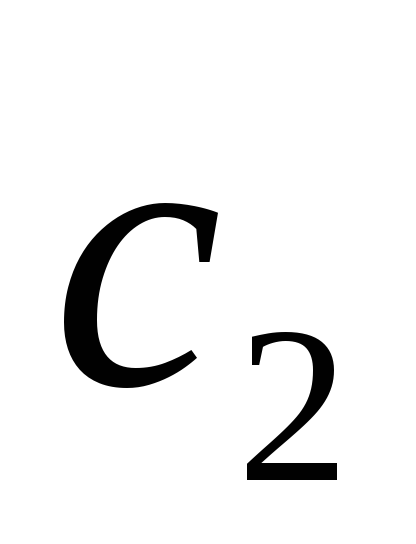 .
Для этого подставим начальные условия
в общее решение.
.
Для этого подставим начальные условия
в общее решение.
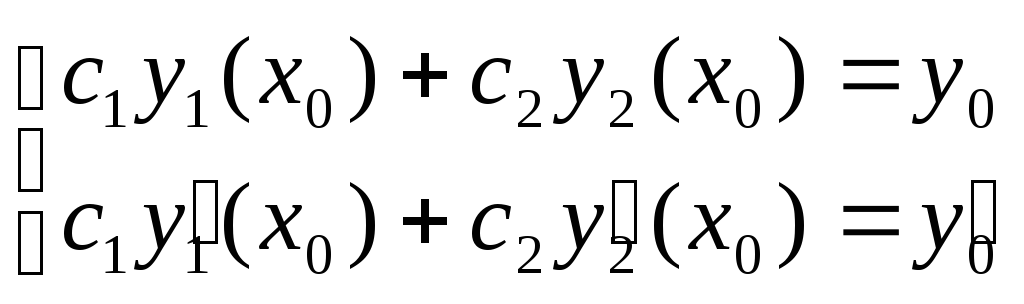
определитель этой
системы: 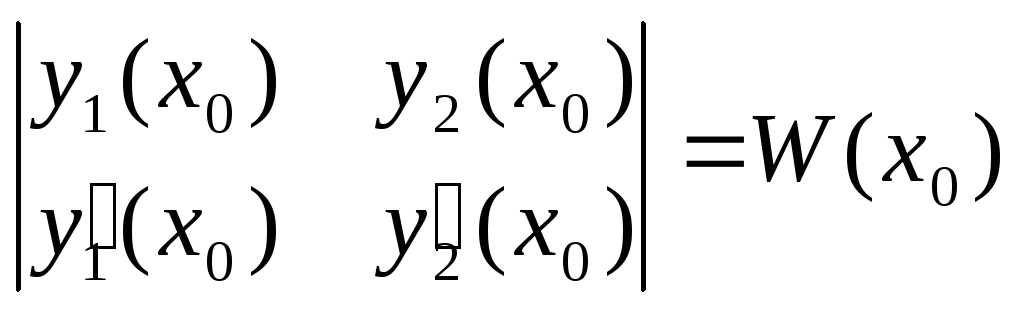 —
определитель Вронского, вычисленный в
точке х0
—
определитель Вронского, вычисленный в
точке х0
т.к 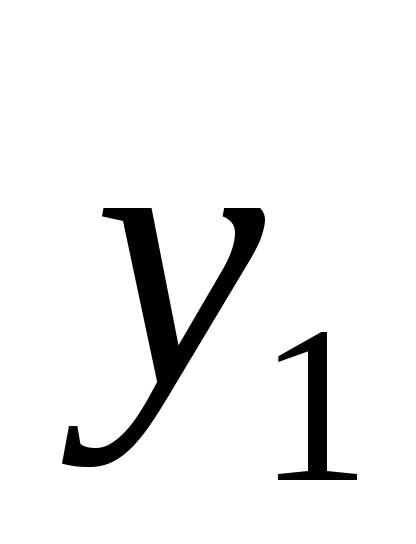 и
и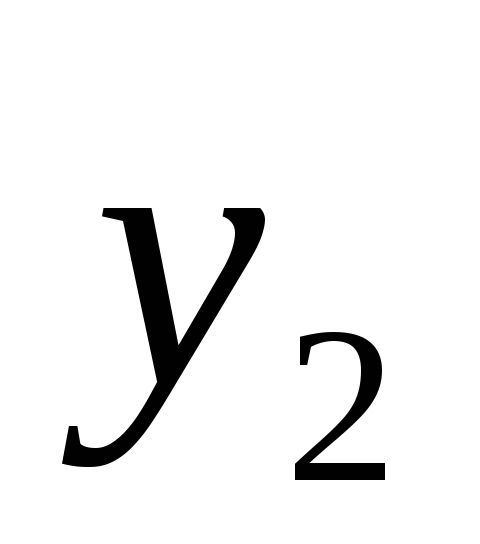 линейно
независимы
линейно
независимы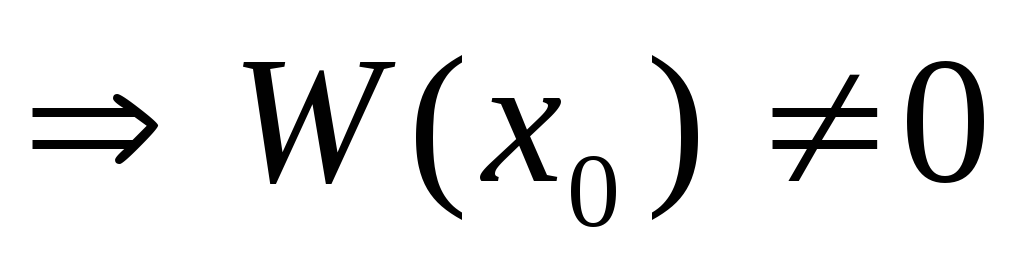 (по
20)
(по
20)
т.к определитель
системы не равен 0, то система имеет
единственное решение и 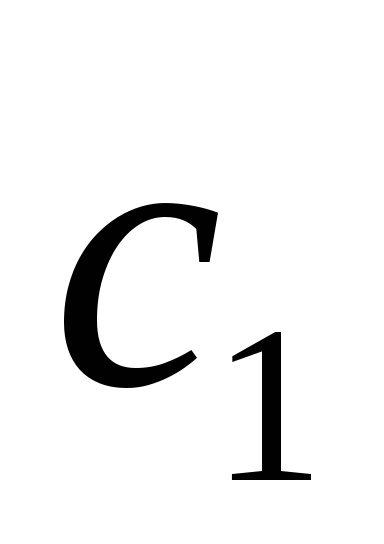 и
и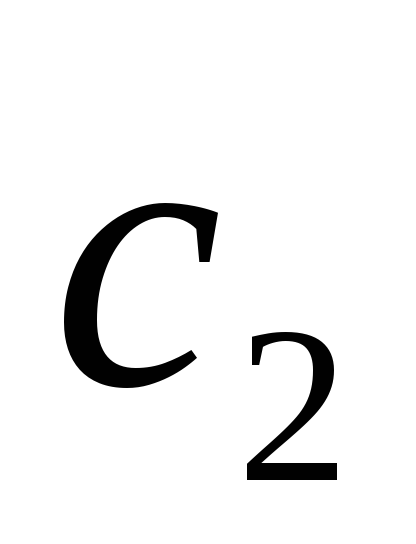 находятся из системы однозначно.
находятся из системы однозначно.
Общее решение линейного однородного дифференциального уравнения порядка n
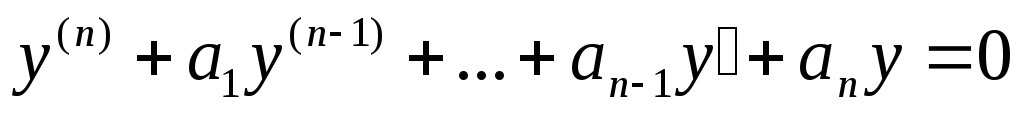 (*)
(*)
Можно показать
что уравнение имеет n
линейно независимых решений 
Определение: n
линейно независимых решений  линейного однородного дифференциального
уравнения порядкаn
называется фундаментальной
системой решения.
линейного однородного дифференциального
уравнения порядкаn
называется фундаментальной
системой решения.
 О
О бщее
решение линейного однородного
дифференциального уравнения порядкаn
, т.е (*) – линейная комбинация фундаментальной
системы решений:
бщее
решение линейного однородного
дифференциального уравнения порядкаn
, т.е (*) – линейная комбинация фундаментальной
системы решений:
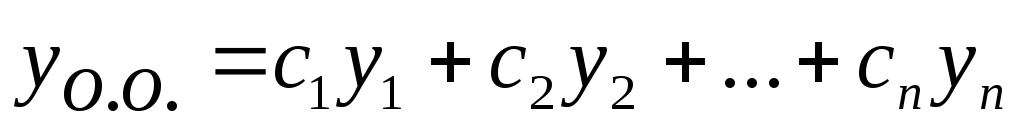 ,
где
,
где  —
фундаментальная система решения.
—
фундаментальная система решения.
Линейные однородные дифференциальные уравнения 2 порядка с постоянными коэффициентами
Э то
уравнения вида:
то
уравнения вида: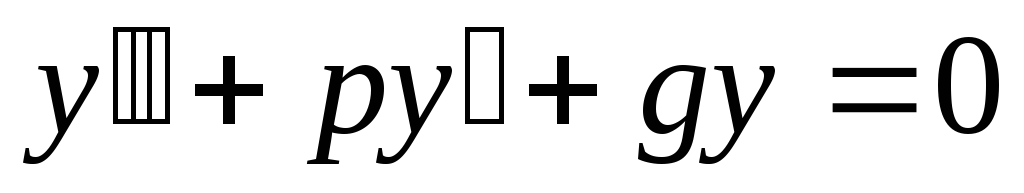 , гдеp
и g
– числа(*)
, гдеp
и g
– числа(*)
Определение: Уравнение 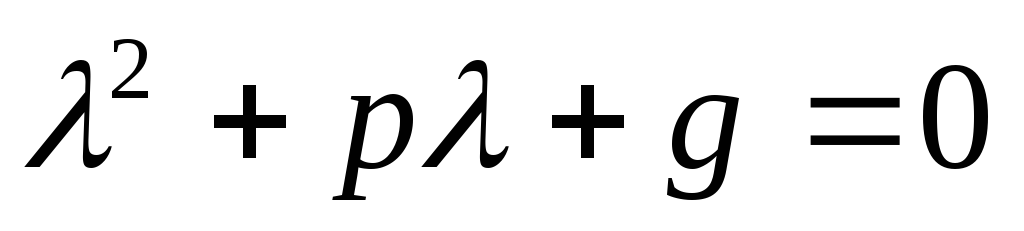 —
называетсяхарактеристическим
уравнением дифференциального
уравнения (*) – обычное квадратное
уравнение, решение которого зависит от
D,
возможны следующие случаи:
—
называетсяхарактеристическим
уравнением дифференциального
уравнения (*) – обычное квадратное
уравнение, решение которого зависит от
D,
возможны следующие случаи:
1)D>0 — два действительных различных решения.
— два действительных различных решения.
2)D=0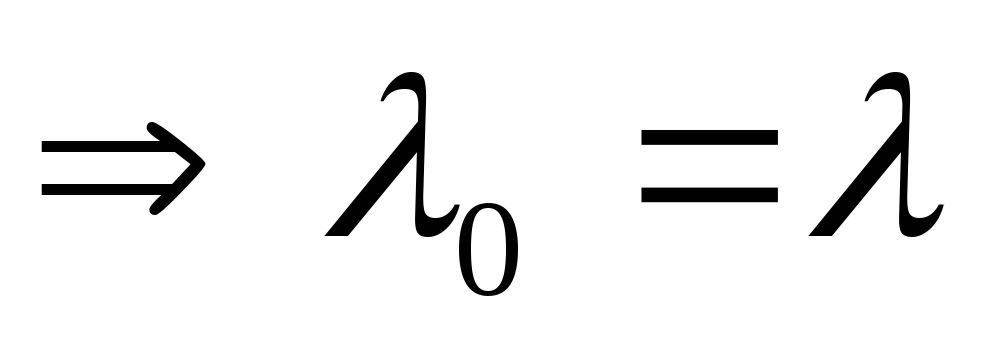 — один действительный корень кратности
2.
— один действительный корень кратности
2.
3)D<0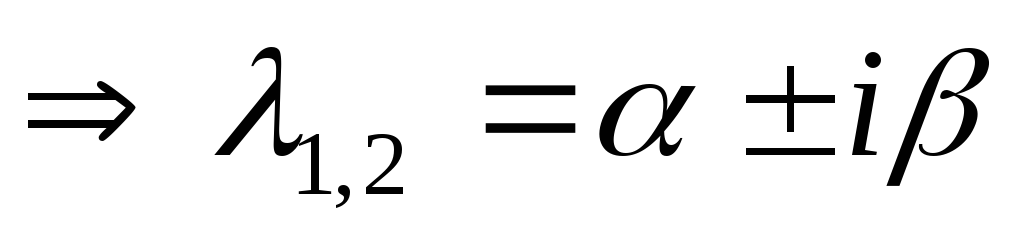 —
два комплексно сопряжённых корня.
—
два комплексно сопряжённых корня.
Для каждого из
этих случаев укажем фундаментальную
систему решений, составленную из 2
функций 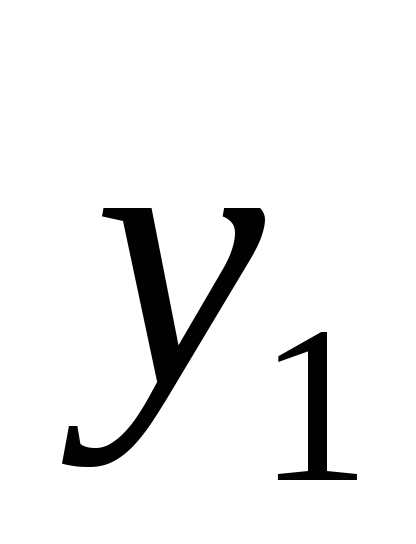 и
и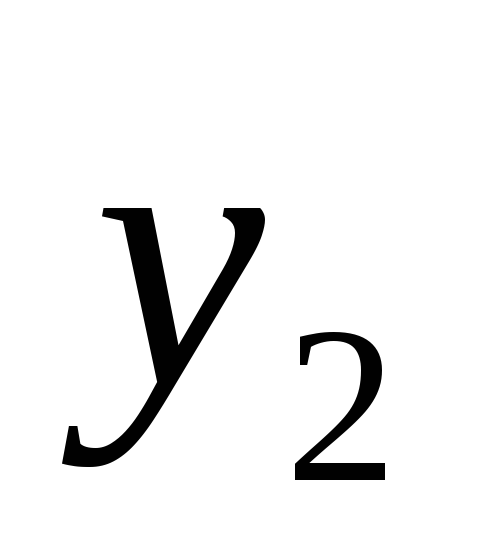 .
.
Будем показывать что:
1) 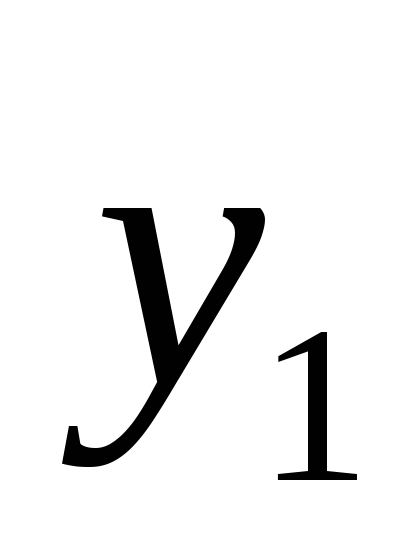 и
и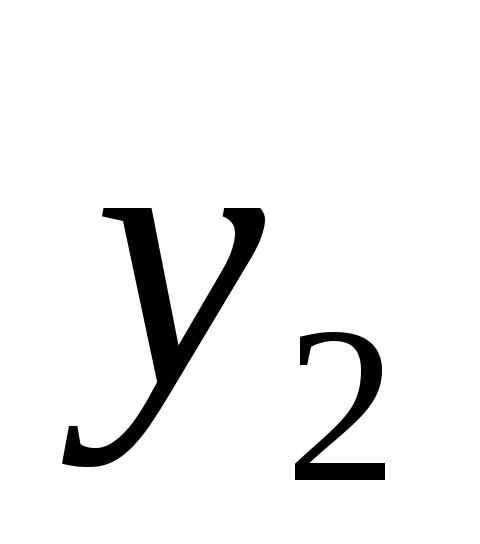 —
ЛНЗ
—
ЛНЗ
2)  и
и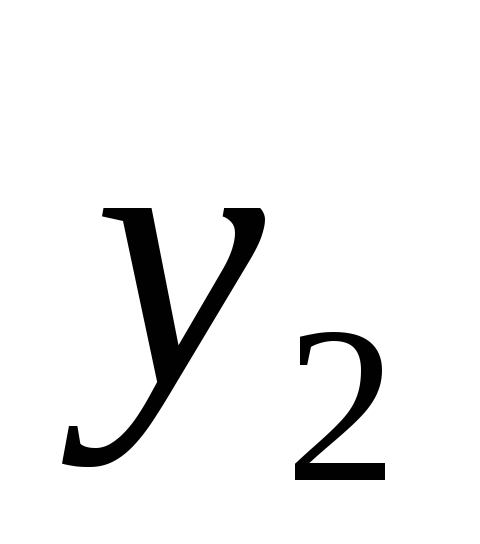 —
решение (*)
—
решение (*)
Рассмотрим 1
случай D>0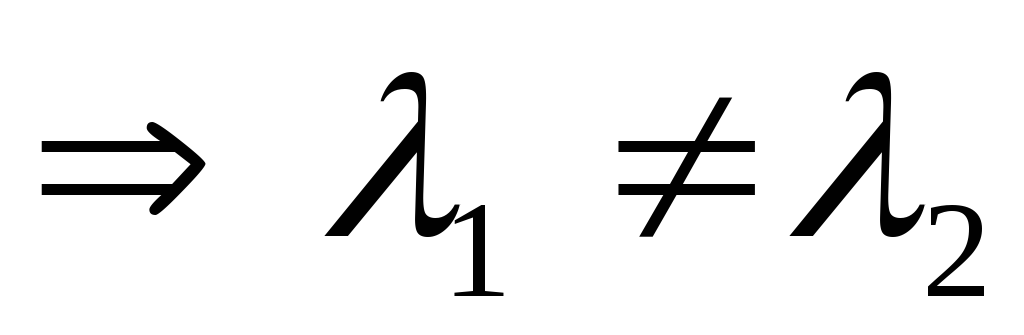 — 2 действительных различных корня.
— 2 действительных различных корня.
Х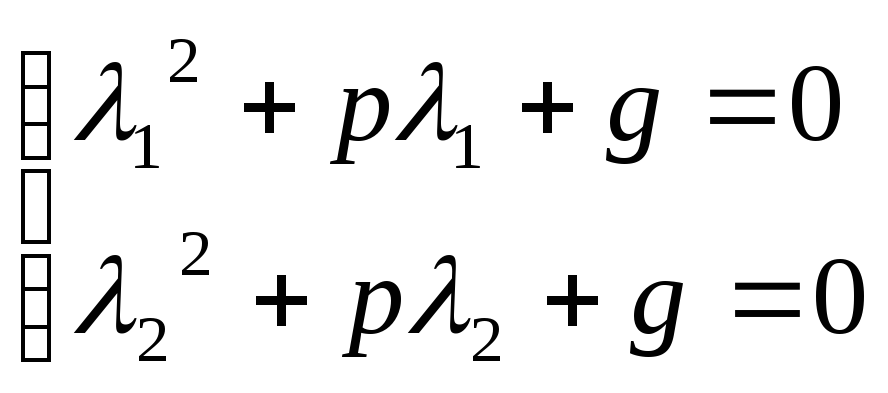 арактеристическое
уравнение:
арактеристическое
уравнение: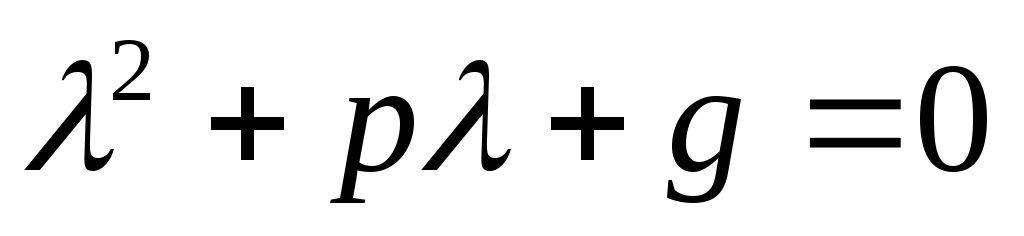
В качестве ФСР
возьмём: 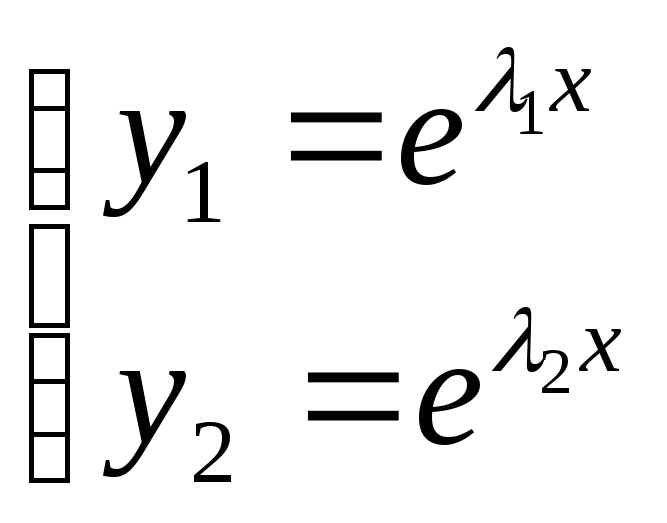
а) покажем ЛНЗ 
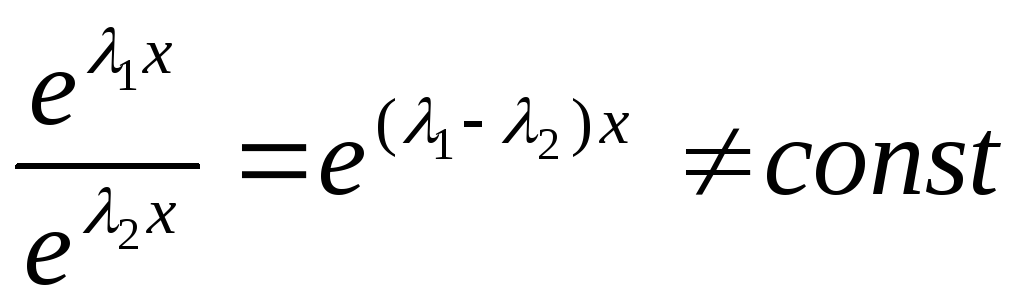
б) покажем, что  — решение
(*), подставим
— решение
(*), подставим 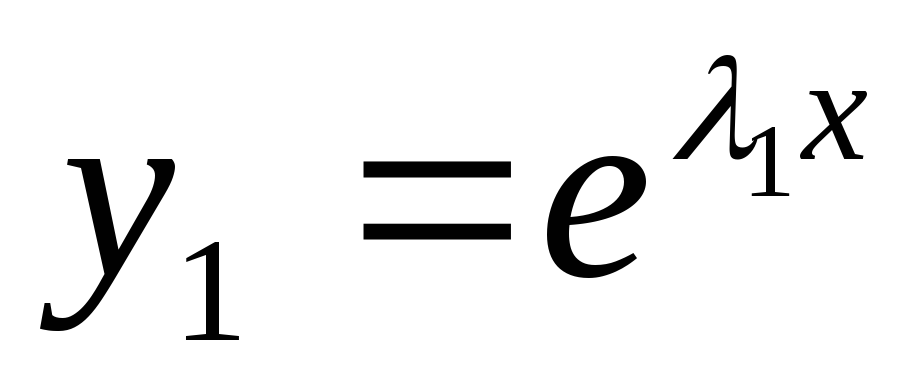
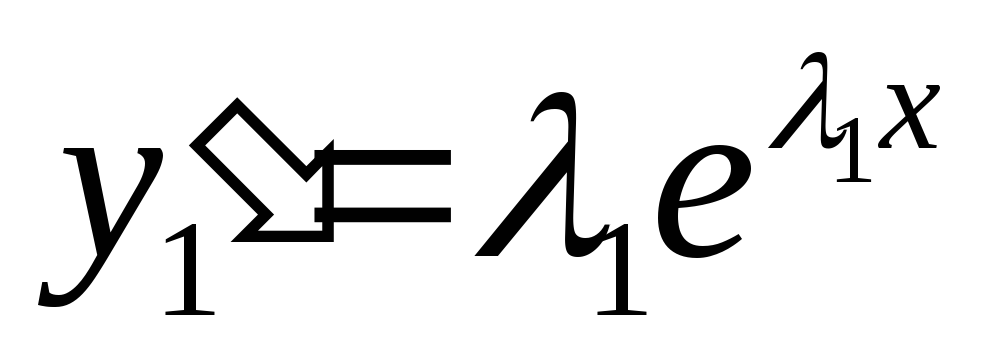
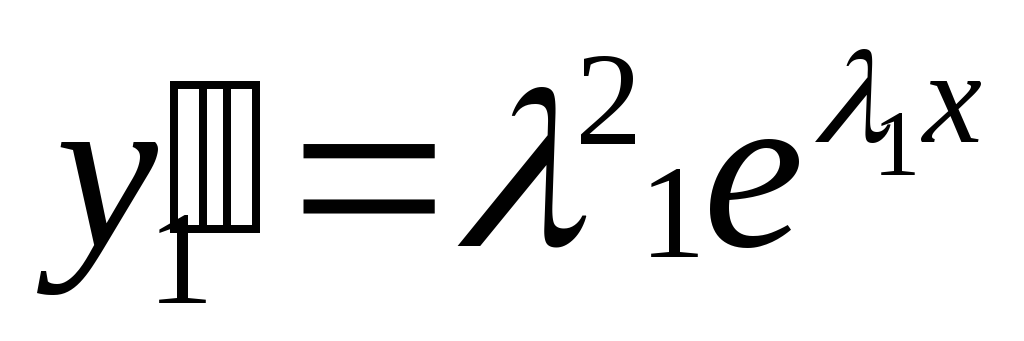
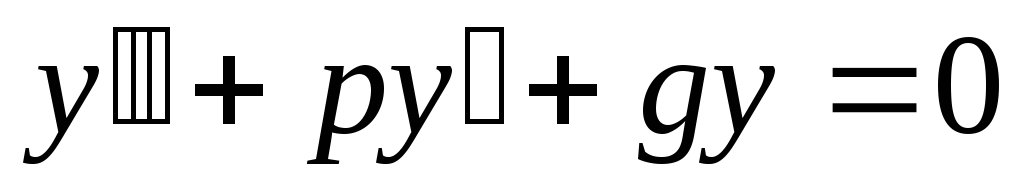
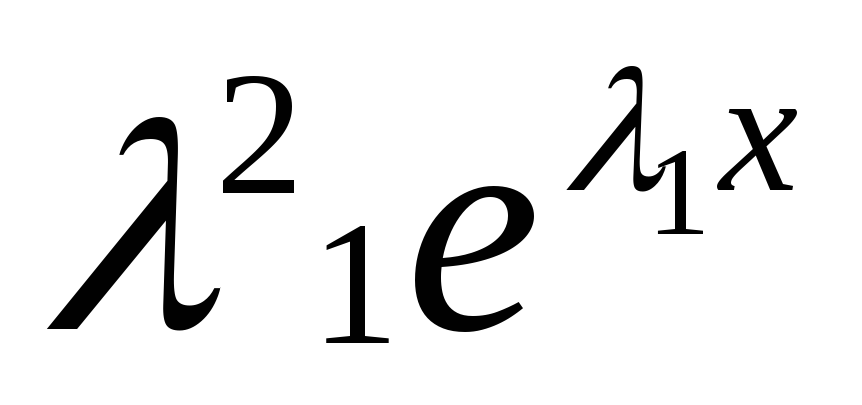 +p
+p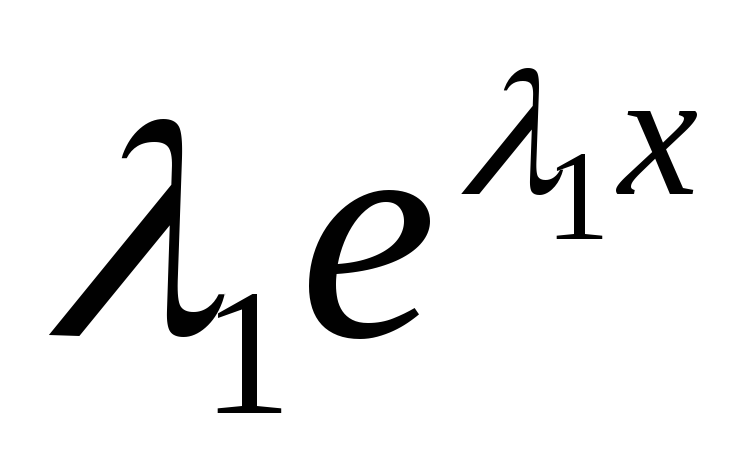 +g
+g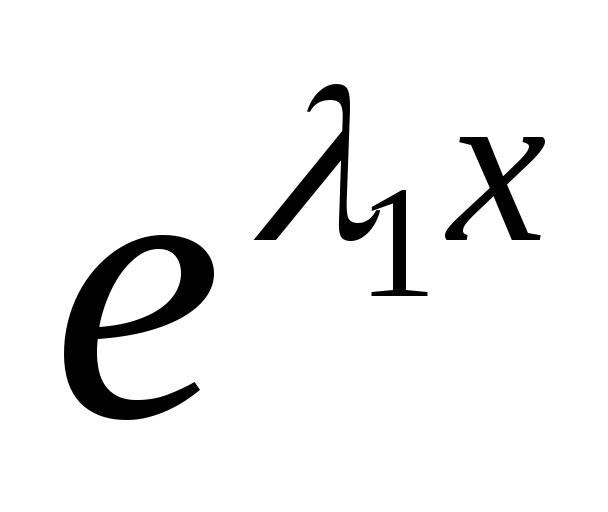 =0
=0
 верное
равенство
верное
равенство
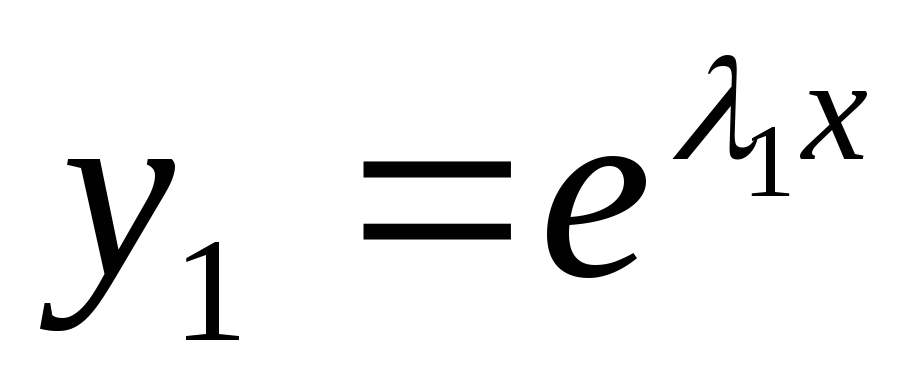 решение
(*)
решение
(*)
аналогично показывается для y2.
В ывод:
ывод: 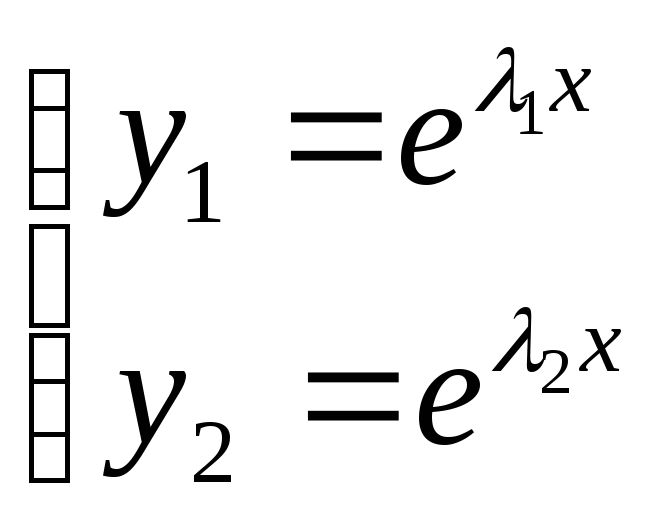 —
ФСР (*)
—
ФСР (*) общее
решение
общее
решение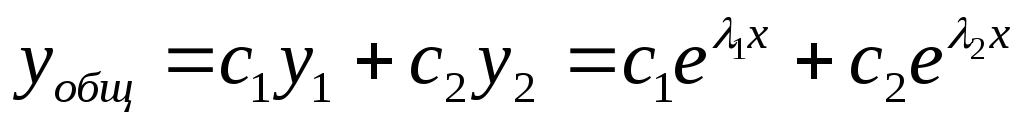
Рассмотрим
2случай: D=0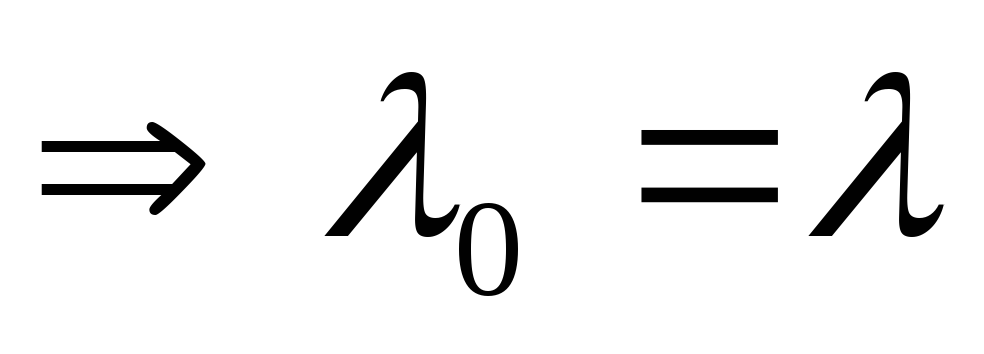 — 1 действительный корень кратности 2.
— 1 действительный корень кратности 2.

В качестве ФСР
возьмём: 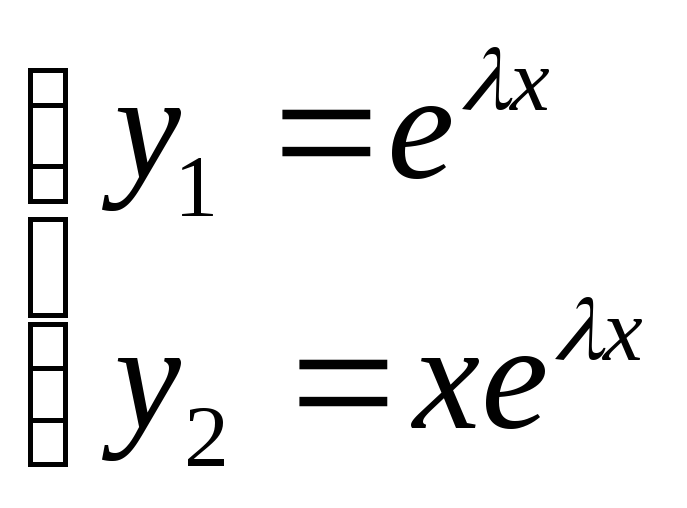
ЛНЗ: ЛНЗ есть.
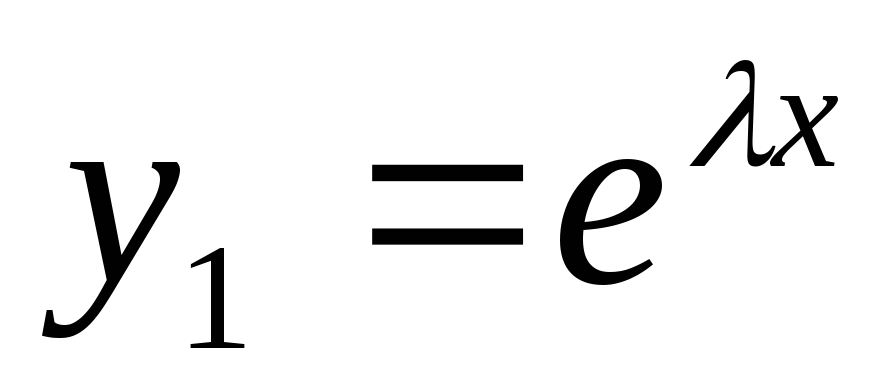 -решение уравнения
(см. 1 случай). Покажем что
-решение уравнения
(см. 1 случай). Покажем что 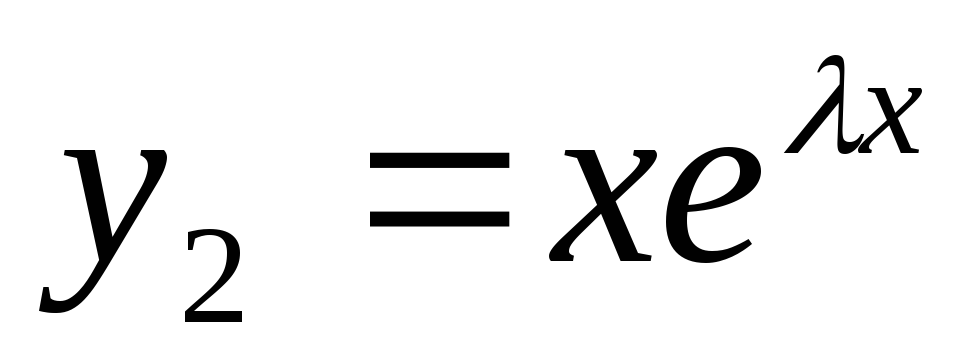 —
решение.
—
решение.
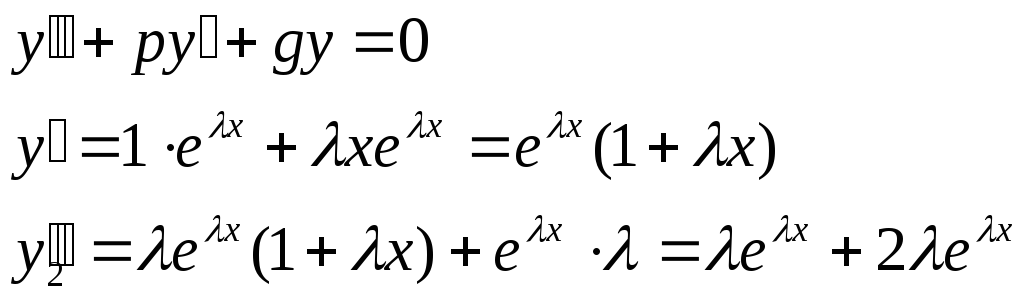
подставим в ДУ

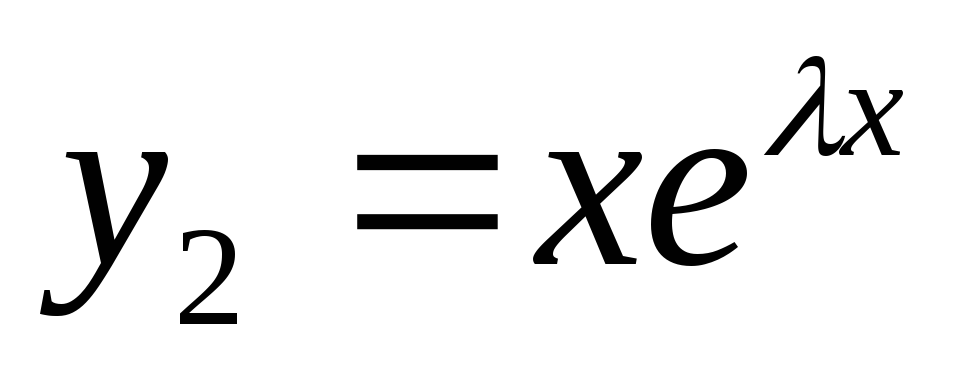 -решение.
-решение.
Вывод: ФСР 
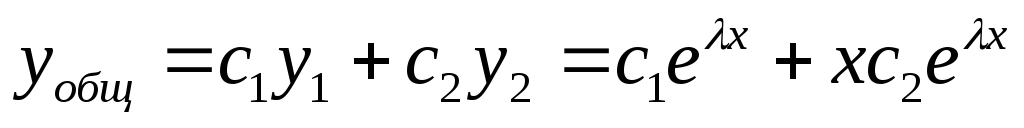

Пример:
3 случай: D<0 —
2 комплексно сопряжённых корня.
—
2 комплексно сопряжённых корня.

подставим 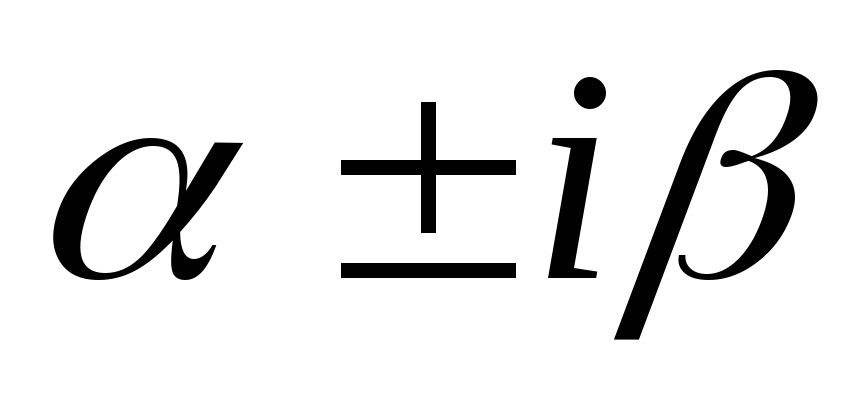 в характ. уравнение
в характ. уравнение
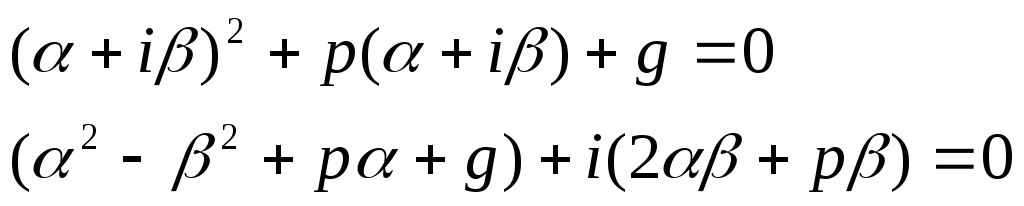
к омплексное
число равно 0, когда действительная и
мнимая часть равны 0.
омплексное
число равно 0, когда действительная и
мнимая часть равны 0.
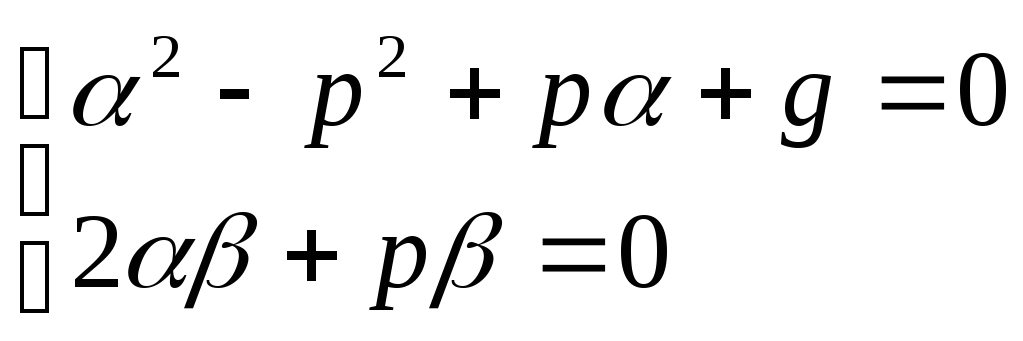 — будем использовать.
— будем использовать.
Покажем, что 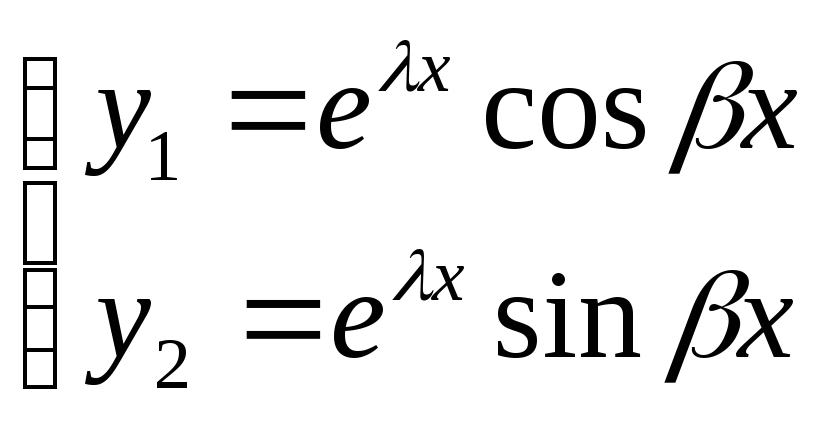 —
образуют ФСР.
—
образуют ФСР.
А)ЛНЗ: 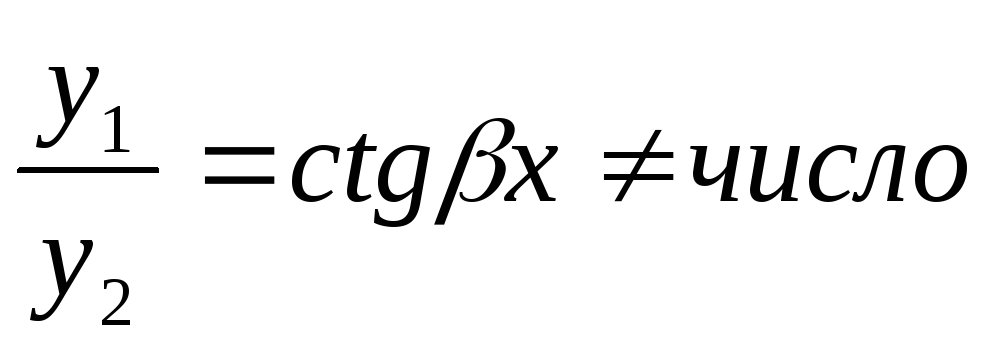
Б)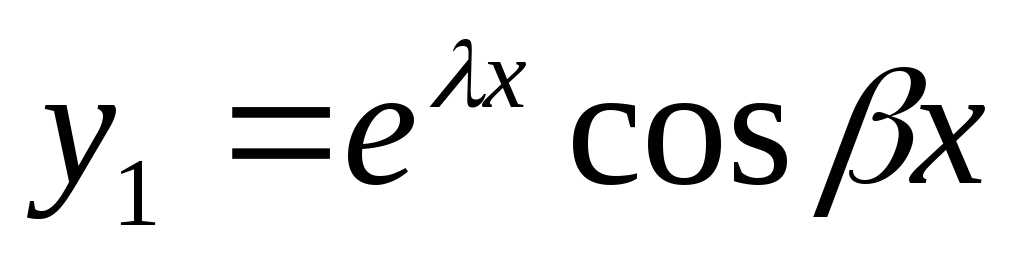 -решение ДУ
-решение ДУ
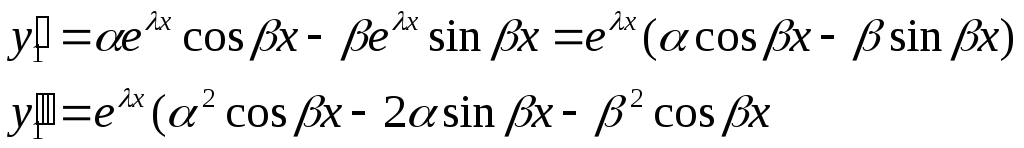
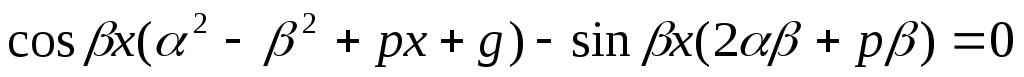
верное равенство —
решение ДУ.
—
решение ДУ.
Аналогично
показывается, что  тоже
решение.
тоже
решение.
В ывод:ФСР:
ывод:ФСР: 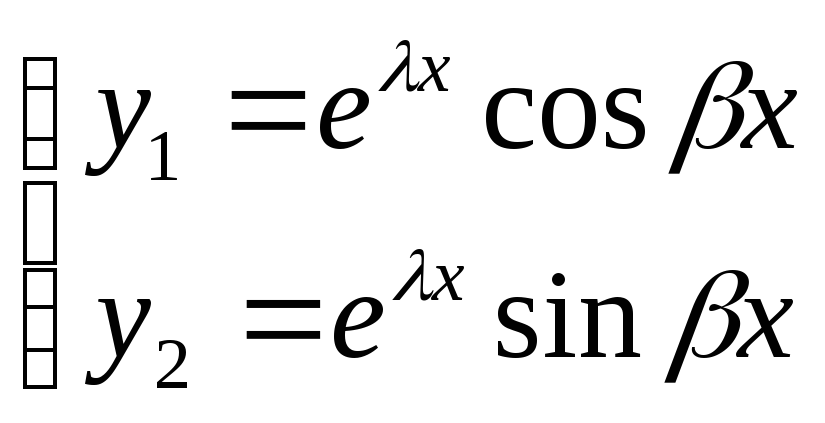
Общее решение: 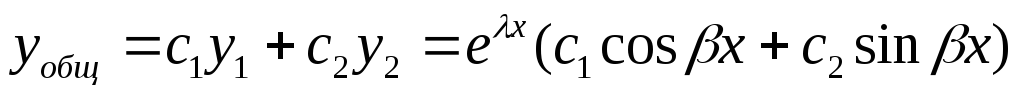
Пример:
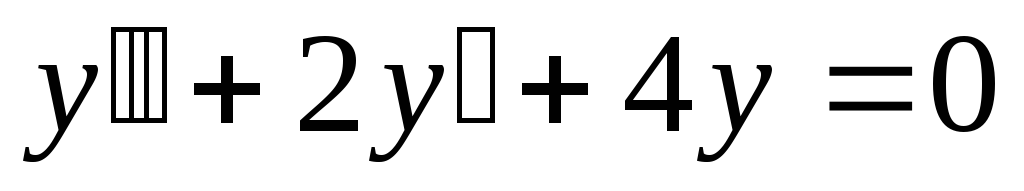
Если заданы н.у.
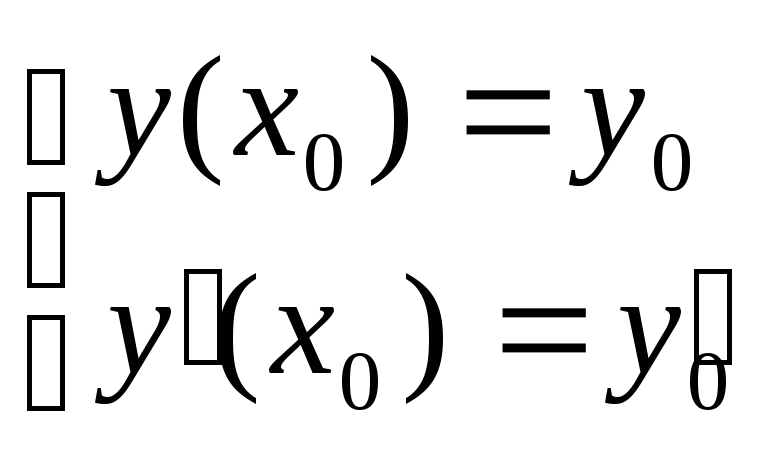 —
то сначала находят общее решение
—
то сначала находят общее решение 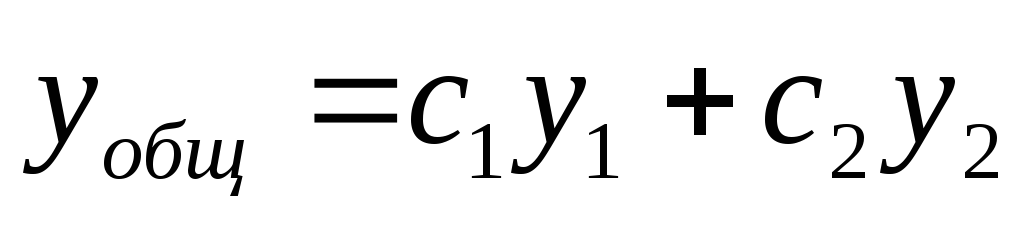 ,
его производную:
,
его производную: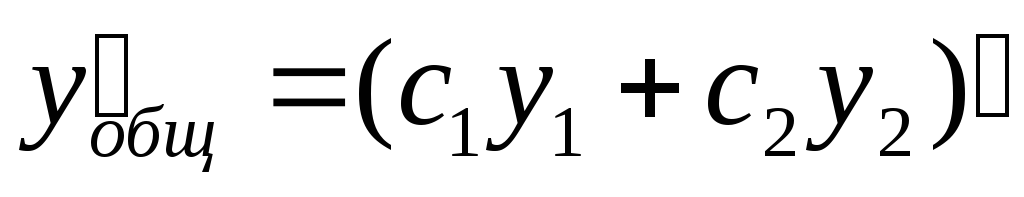 ,
а потом в эту систему подставляют н.у и
находят
,
а потом в эту систему подставляют н.у и
находят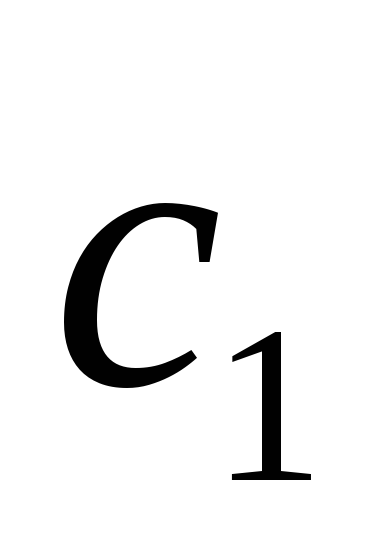 и
и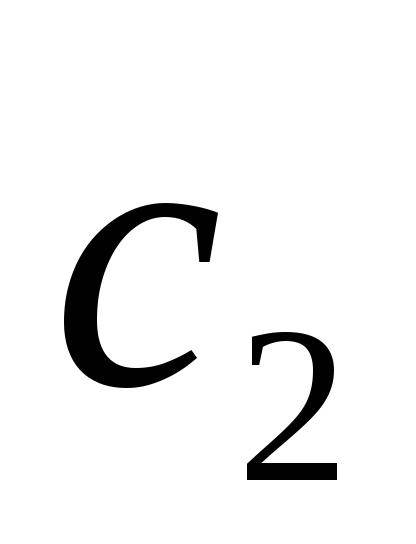 .
.
Пример:
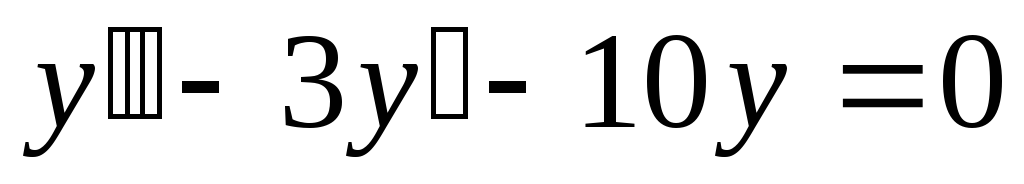 Н.у:
Н.у: 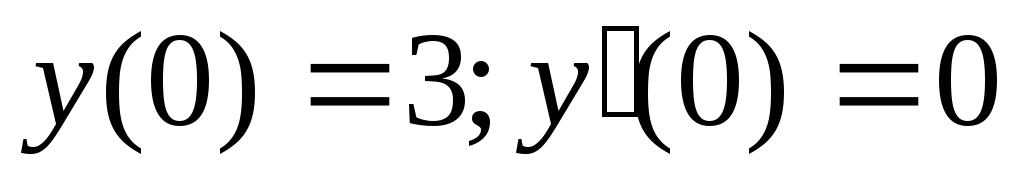
studfile.net
Дифференциальные уравнения n-го порядка
16
Дифференциальные уравнения n-ого порядка.
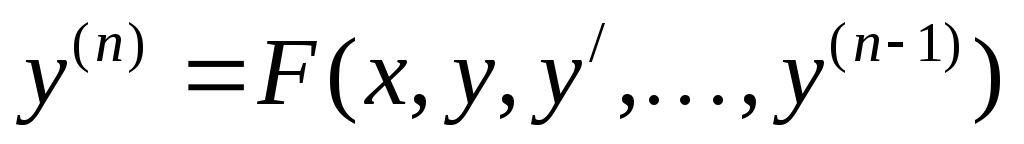 (1)
(1)
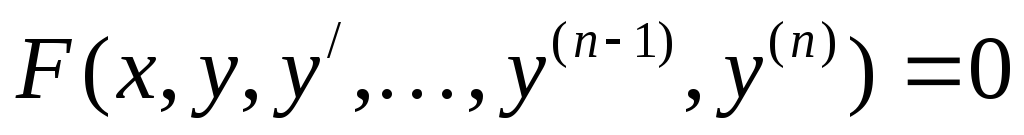 (2)
(2)
Если уравнение разрешимо относительно старшей производной то имеет вид (1). Так же уравнение n-го порядка можно представить в виде системы из n уравнений первого порядка.
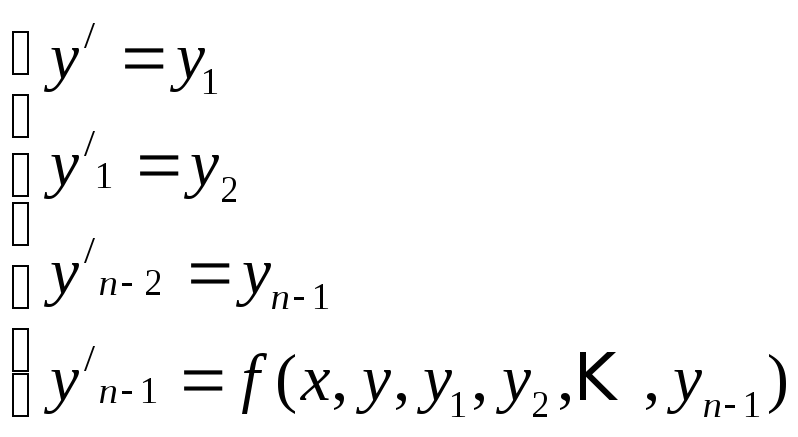 (3)
(3)
Для уравнения n-ого порядка выполнены условия теоремы о существовании и единственности для системы так как (1)~(2)~(3).
Простейшие случаи понижения порядка.
Уравнение не содержат искомой функции и ее производной до порядка k-1 включительно, то есть
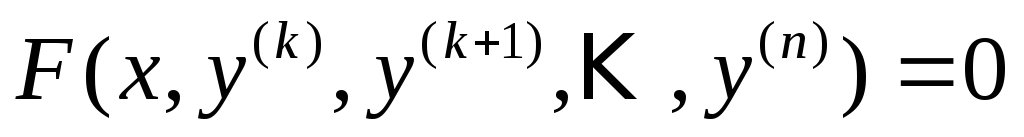 .
(4)
.
(4)
В
этом случае порядок может быть понижен
до 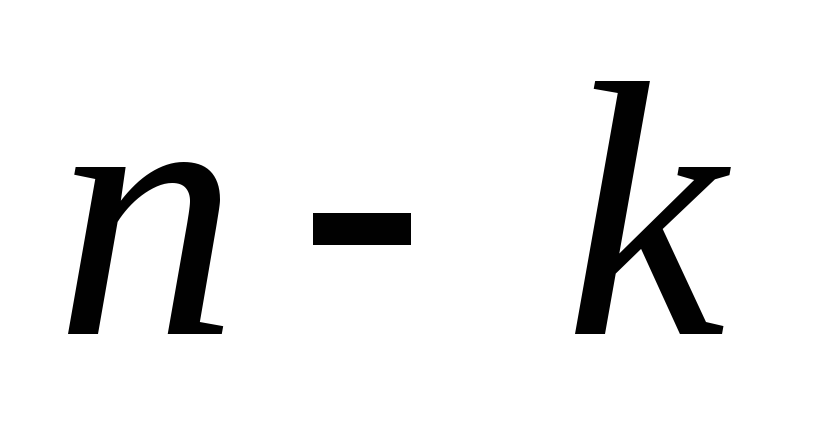 заменой
заменой 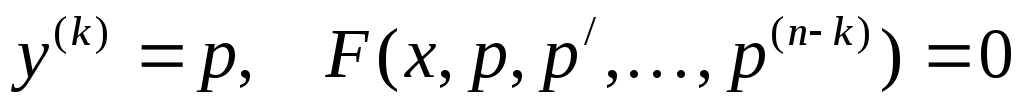 .
Если из этого уравнения выразить
.
Если из этого уравнения выразить 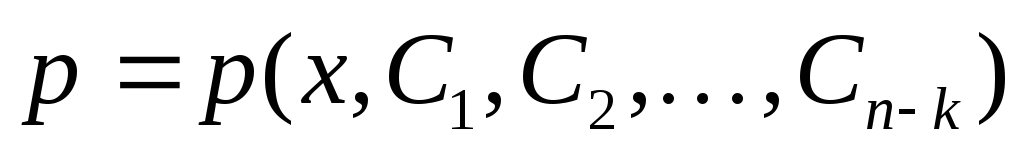 тогда решение y
можно определить k-кратным
интегрируемым функции p.
тогда решение y
можно определить k-кратным
интегрируемым функции p.
Пример. 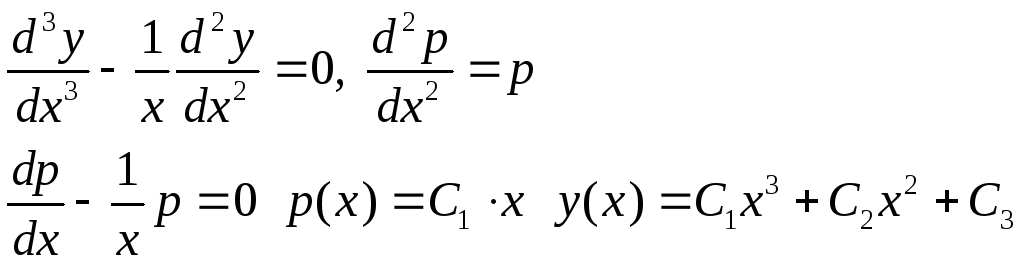 .
.
Уравнение, не содержащие неизвестного переменного
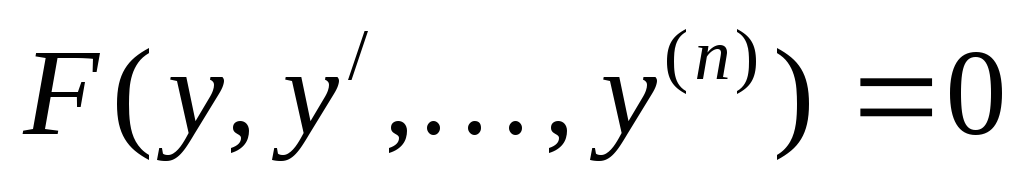 (5)
(5)
В
этом случае порядок можно понизить на
единицу подстановкой 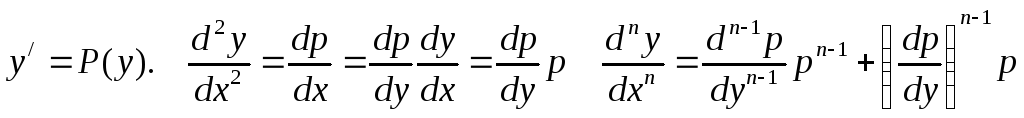 .
.
Пример. 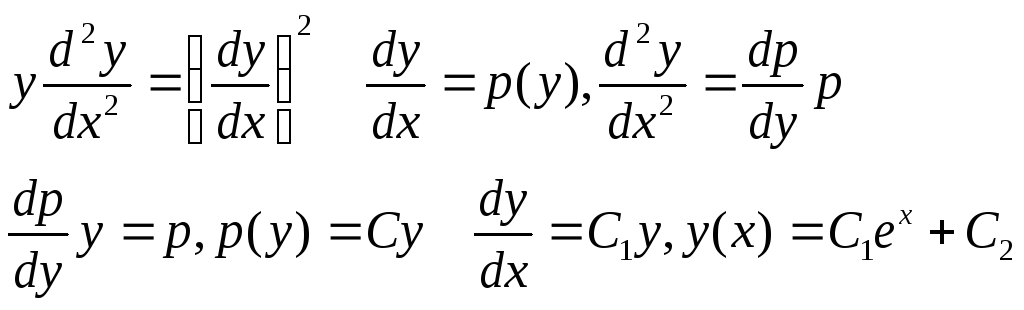 .
.
Левая часть уравнения
 (6)
(6)
есть
производная некоторого дифференциального
выражения (n-1)-го
порядка. 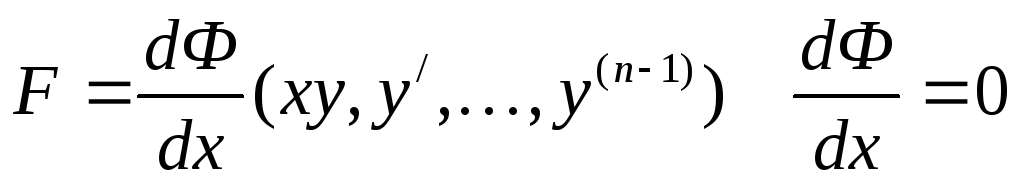 .
Если
.
Если 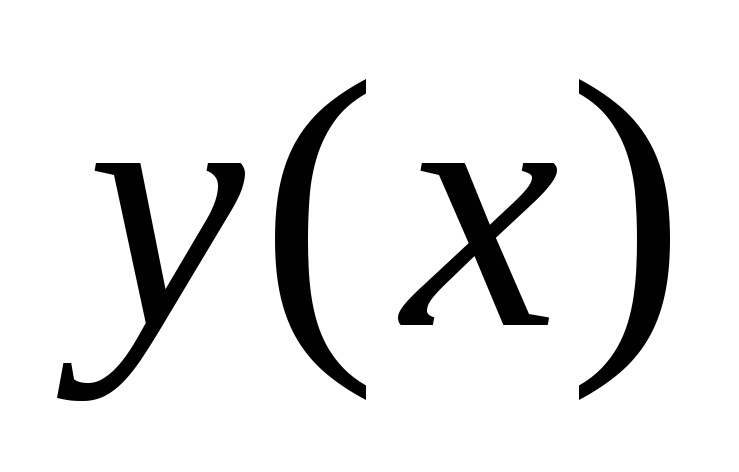 —
решение последнего уравнения,
следовательно, существует
—
решение последнего уравнения,
следовательно, существует  .
Мы получили первый интеграл уравнения
(6) и понизили на единицу степень решаемого
уравнения.
.
Мы получили первый интеграл уравнения
(6) и понизили на единицу степень решаемого
уравнения.
Замечание. Иногда левая
часть (6) становится производной
дифференциального уравнения (n-1)-го
порядка только при умножении на 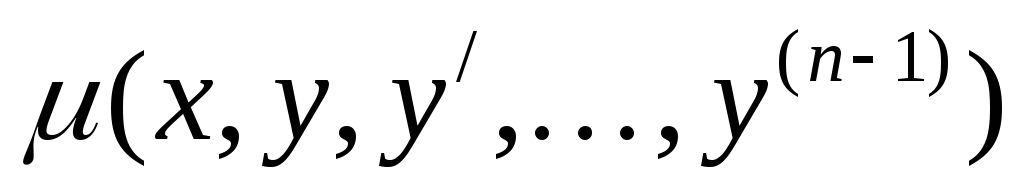 поэтому здесь могут появиться лишнее
решения (обращающие
поэтому здесь могут появиться лишнее
решения (обращающие  в ноль) или мы можем потерять решение,
если
в ноль) или мы можем потерять решение,
если  разрывная функция.
разрывная функция.
Пример. 
Уравнение
 (7)
(7)
однородно
относительно  и его производных.
и его производных.
 .
.
Или  ,
где показатель
,
где показатель  определяется
из условий однородности.
определяется
из условий однородности.
Порядок
этого уравнения может быть понижен на
единицу заменой:  .
.
Если
подставить эти соотношения в (7) и учесть
однородность функции F , то в итоге
в получим: 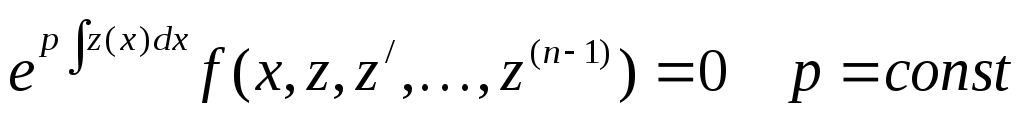 .
.
Пример. 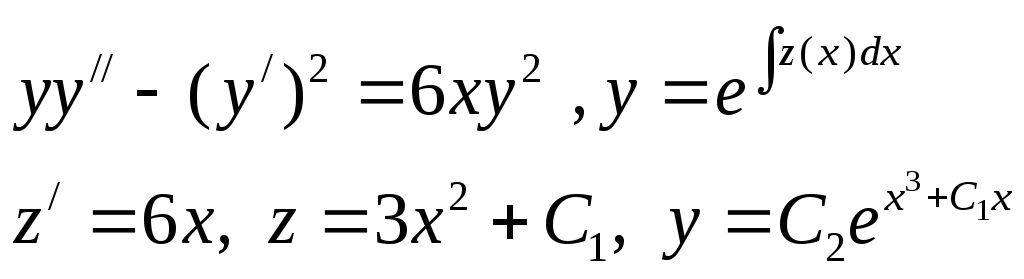 .
.
Дифференциальные уравнения второго порядка,
допускающие понижение порядка.
Пусть дано уравнение
 . (8)
. (8)
Подстановка  .
.
Если
уравнение (8) можно разрешить относительно
старшей производной, то уравнение 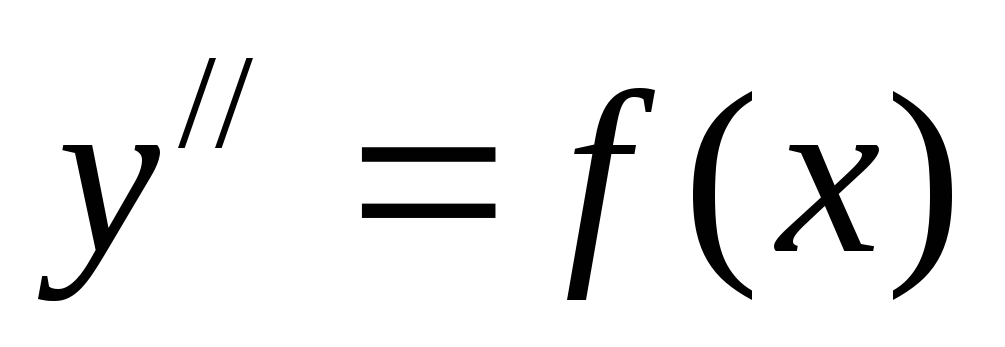 два раза интегрируется по переменной x.
два раза интегрируется по переменной x.
Можно
ввести параметр и заменить уравнение
(8) его параметрическим представлением: 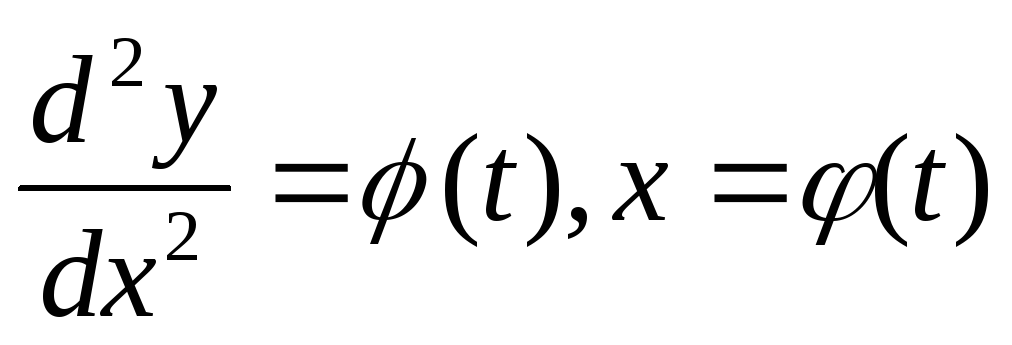 .
Воспользовавшись соотношением для
дифференциалов:
.
Воспользовавшись соотношением для
дифференциалов: 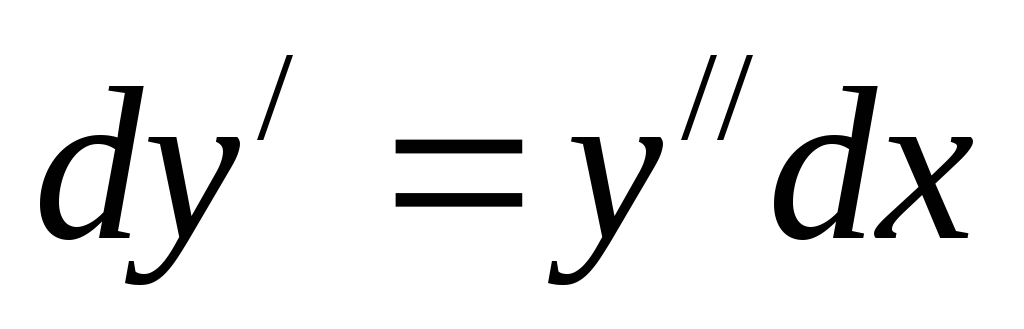 , получаем:
, получаем:  и
и 
II . 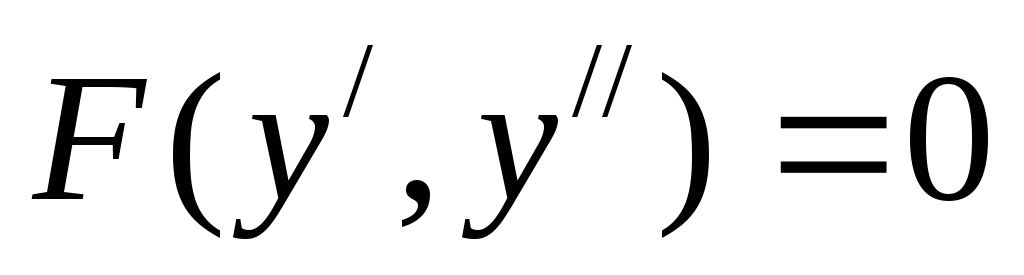 (9)
(9)
Воспользуемся параметрическим представлением:
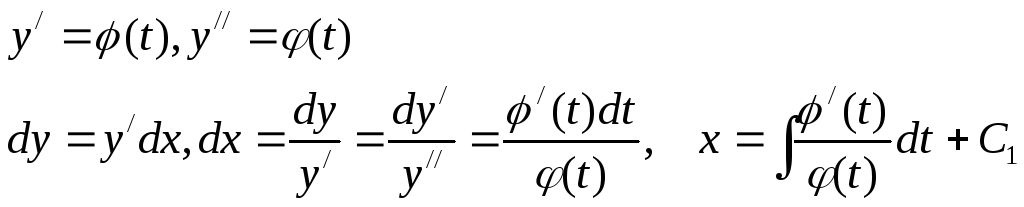
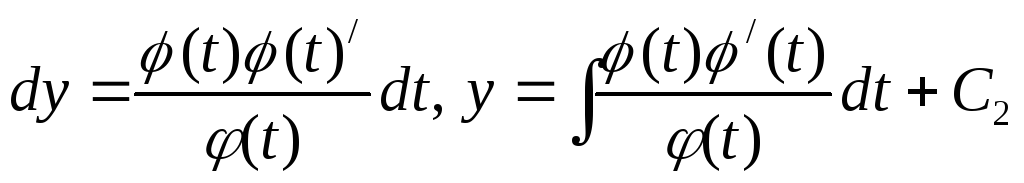
III. 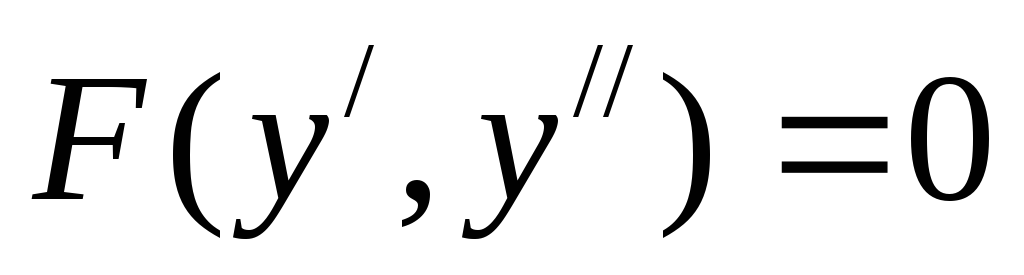 .
(10)
.
(10)
Понизить
порядок можно заменой: 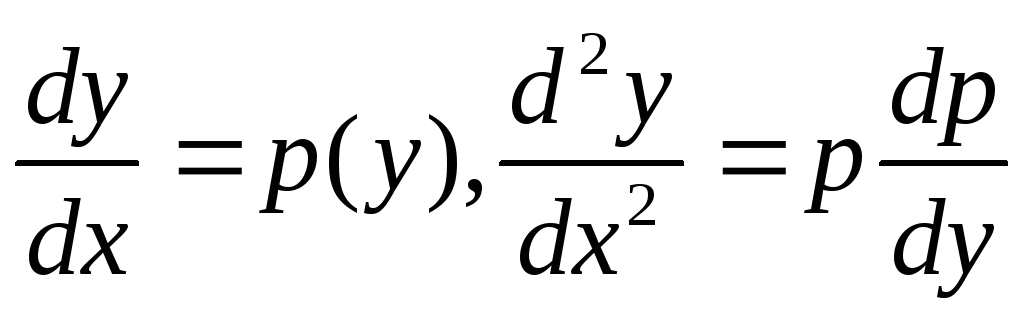 .
.
Если уравнение (10) разрешимо относительно
старшей производной 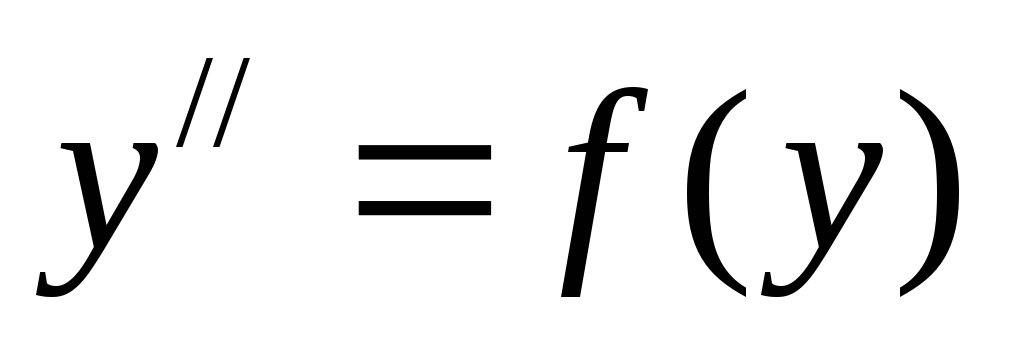 ,
то помножим правую и левую часть на
,
то помножим правую и левую часть на 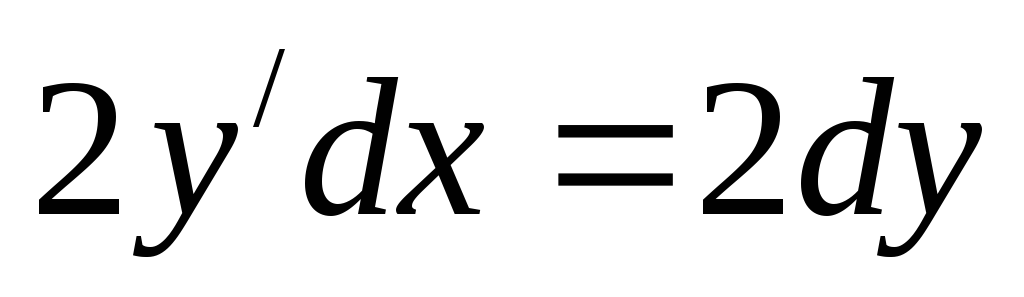 .
Получим:
.
Получим: 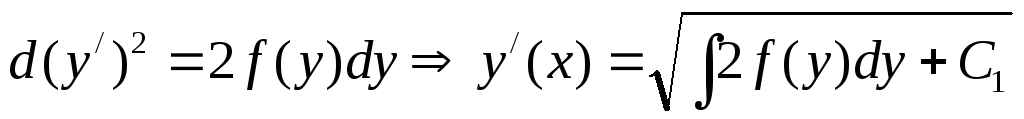 .Это уравнение с разделяющимися
переменными:
.Это уравнение с разделяющимися
переменными: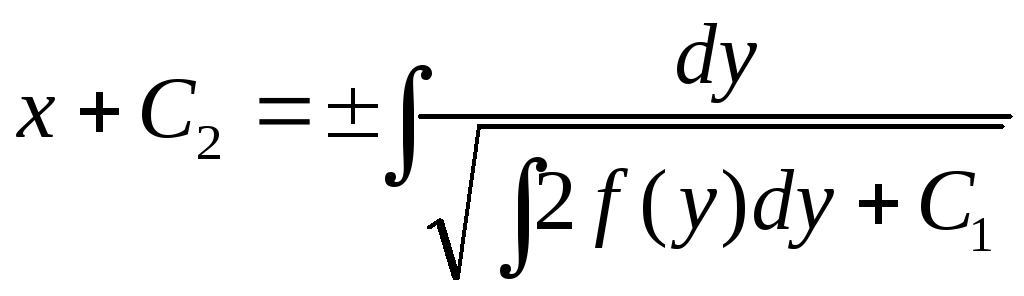 .
.
Можно уравнение (10) заменить его
параметрическим представлением: 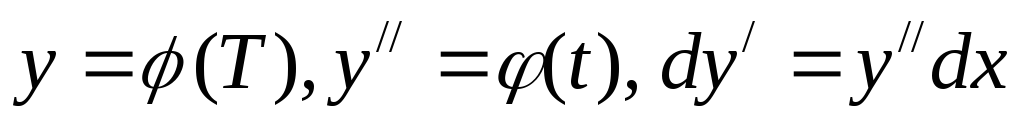 .
Воспользуемся свойствами дифференциала:
.
Воспользуемся свойствами дифференциала: 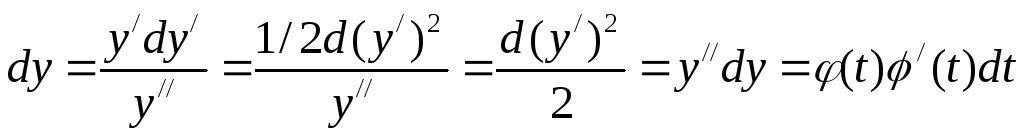
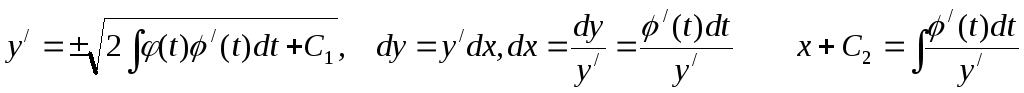 .
.
Пример. 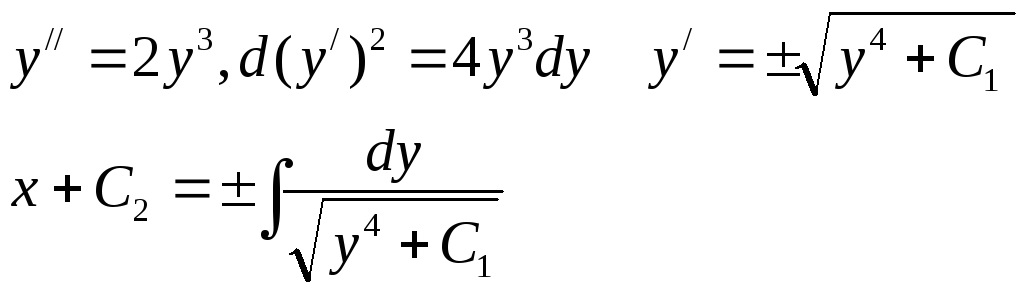 .
.
Линейные дифференциальные уравнения n-ого порядка.
Определение. Линейными
дифференциальными уравнениями n-го
порядка называются уравнения вида: 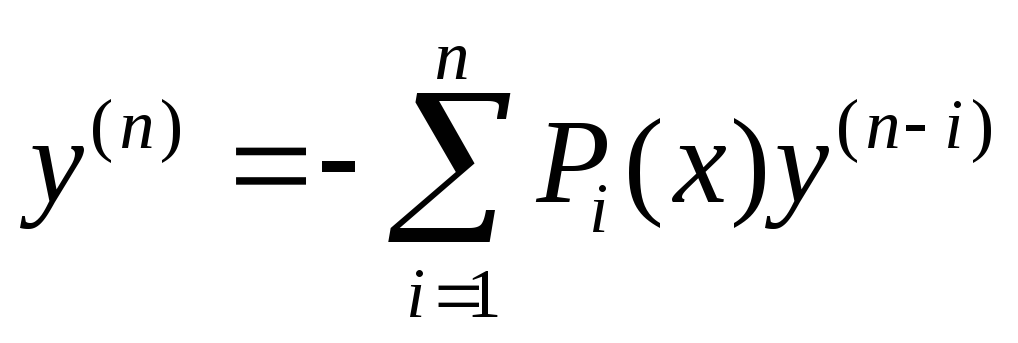 . (1)
. (1)
Если коэффициенты 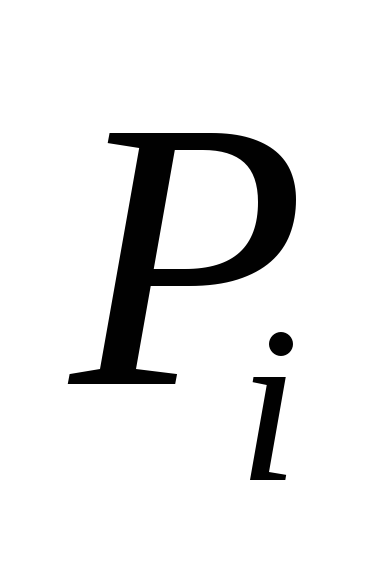 непрерывны на
непрерывны на  ,
то в окрестности любых начальных значений
вида:
,
то в окрестности любых начальных значений
вида: 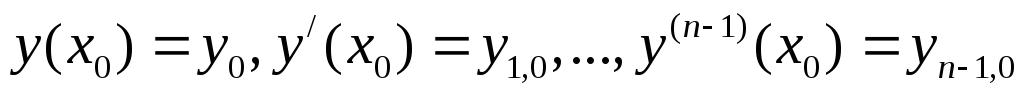 ,
где
,
где 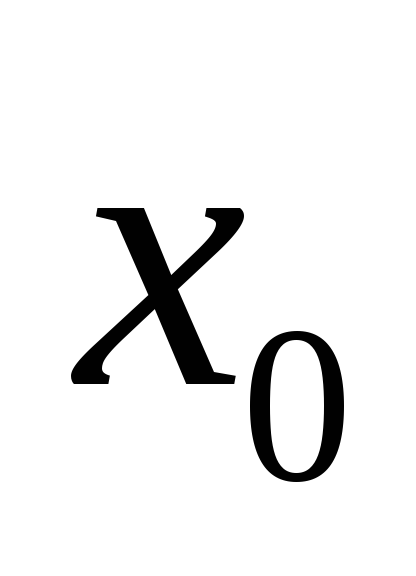 принадлежит интервалу, то в окрестности
этих начальных значений удовлетворяются
условия теоремы о существовании и
единственности. Линейность и
однородность уравнения (1) сохраняется
при любом преобразовании
принадлежит интервалу, то в окрестности
этих начальных значений удовлетворяются
условия теоремы о существовании и
единственности. Линейность и
однородность уравнения (1) сохраняется
при любом преобразовании  ,
где
,
где  — произвольная n раз
дифференцируемая функция. Причем
— произвольная n раз
дифференцируемая функция. Причем 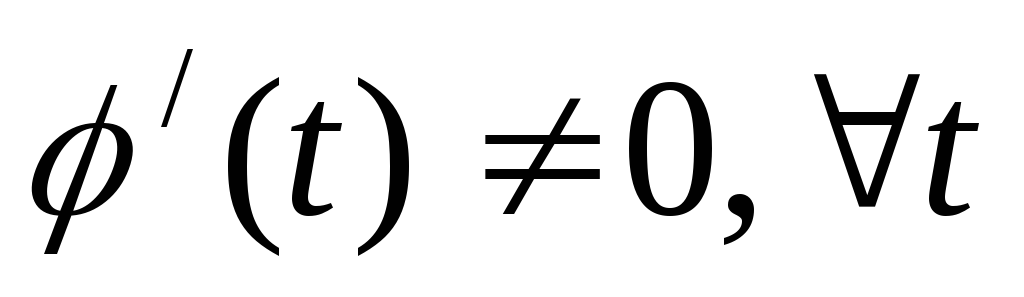 .
Линейность и однородность сохраняется
при линейном и однородном преобразовании
неизвестной функции
.
Линейность и однородность сохраняется
при линейном и однородном преобразовании
неизвестной функции 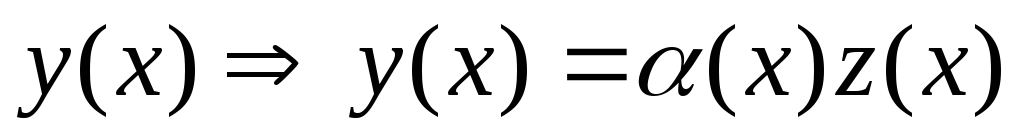 .
.
Введем линейный дифференциальный
оператор: 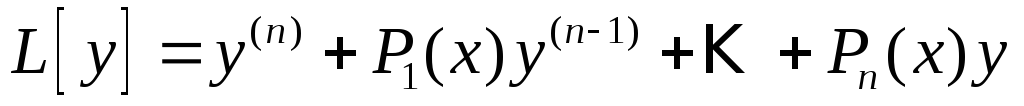 ,
тогда (1) можно записать так:
,
тогда (1) можно записать так: 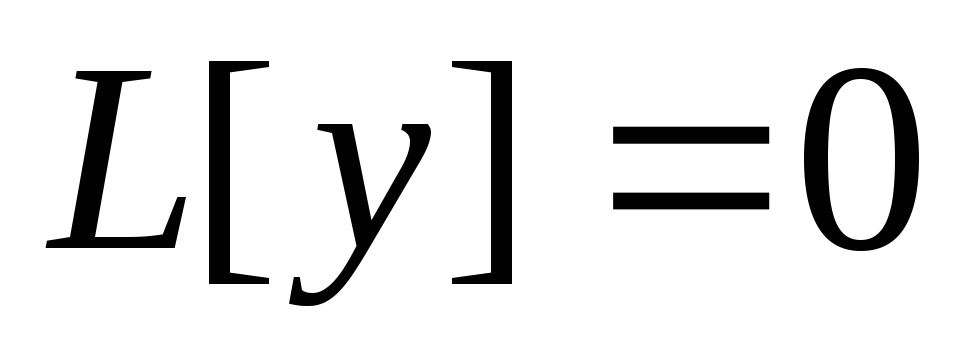 .
Определитель Вронского для
.
Определитель Вронского для 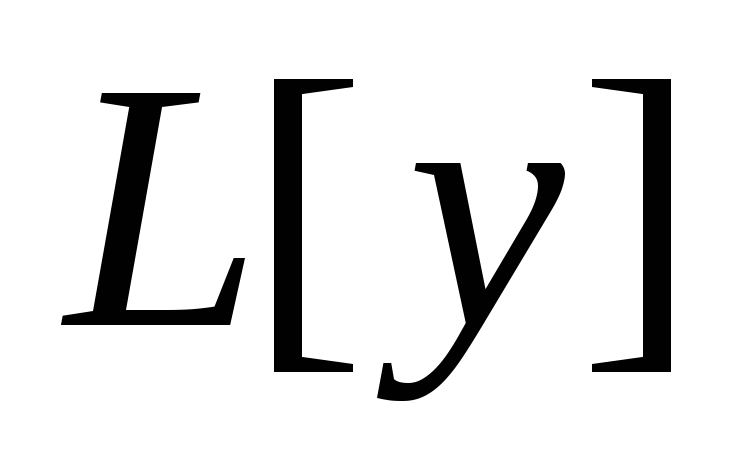 будет иметь вид:
будет иметь вид:
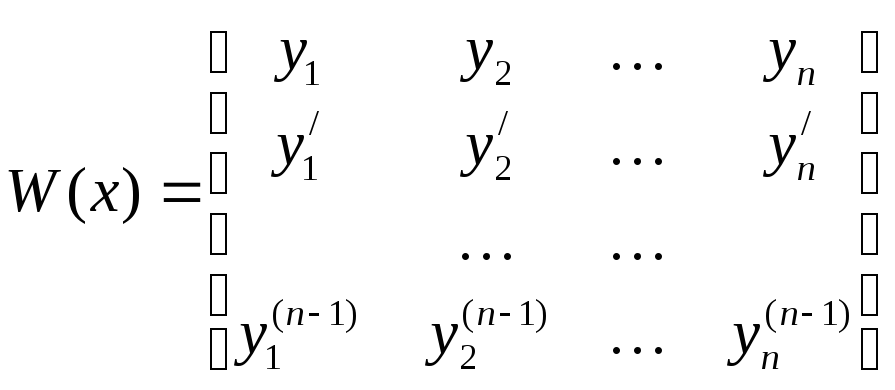 ,
где
,
где 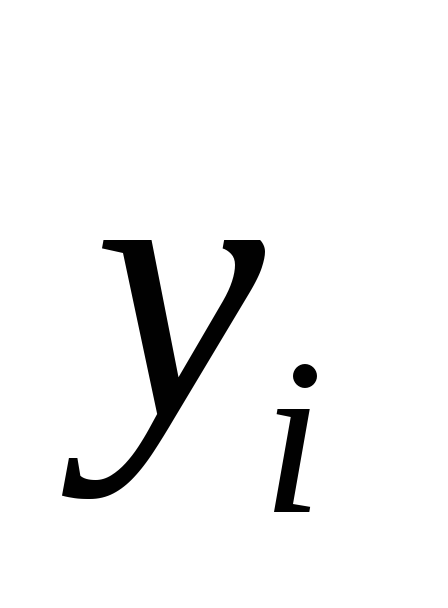 —
линейно независимые решения уравнения
(1).
—
линейно независимые решения уравнения
(1).
Теорема 1. Если линейно независимые
функции 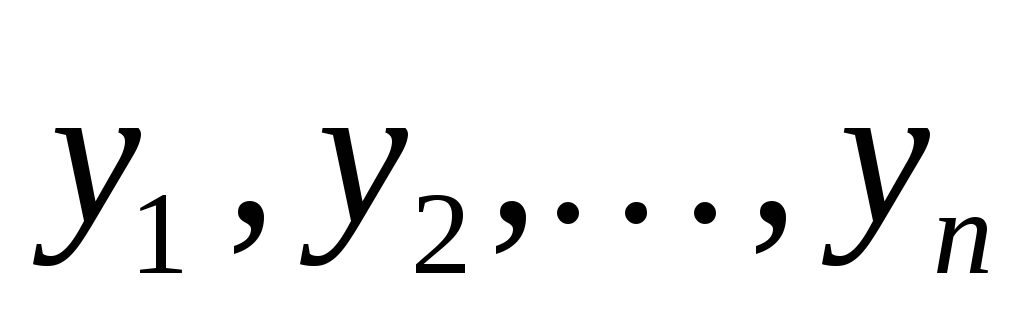 — это решение линейного однородного
уравнения (1) с непрерывными на
— это решение линейного однородного
уравнения (1) с непрерывными на 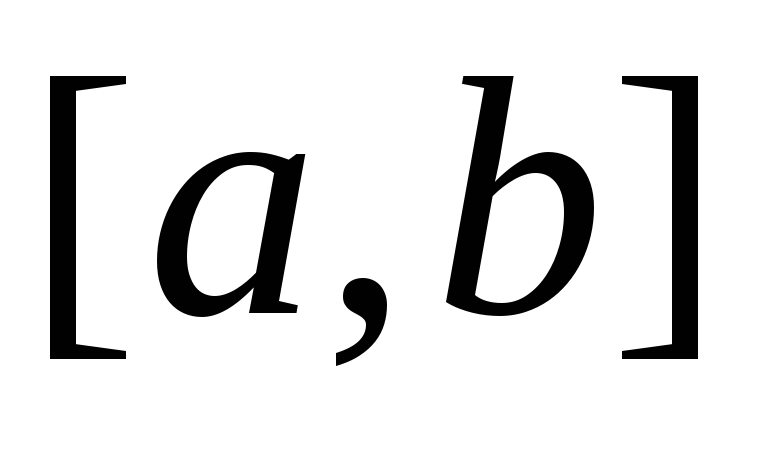 коэффициентами
коэффициентами 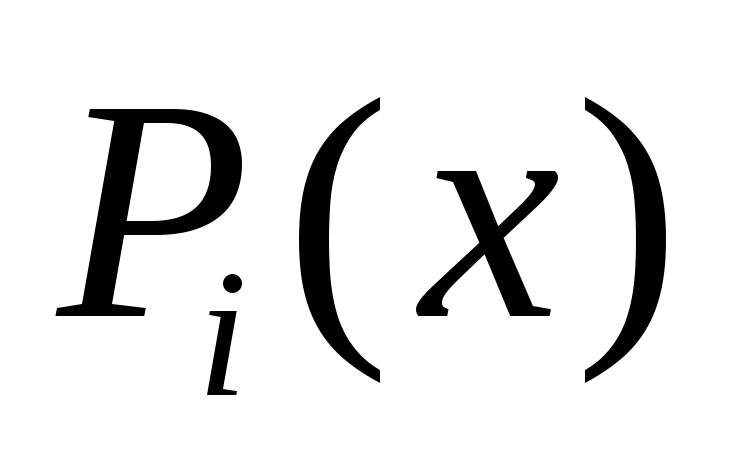 ,
то определитель Вронского
,
то определитель Вронского  не
обращается в ноль ни в одной точке
отрезка
не
обращается в ноль ни в одной точке
отрезка 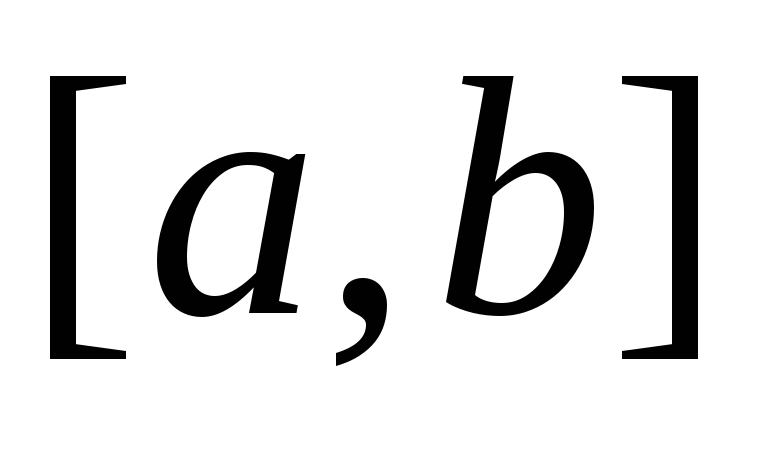 .
.
( доказывается аналогично случаю системы линейных дифференциальных уравнений)
Теорема 2. Общим решением линейного
однородного уравнения (1) с непрерывными
на 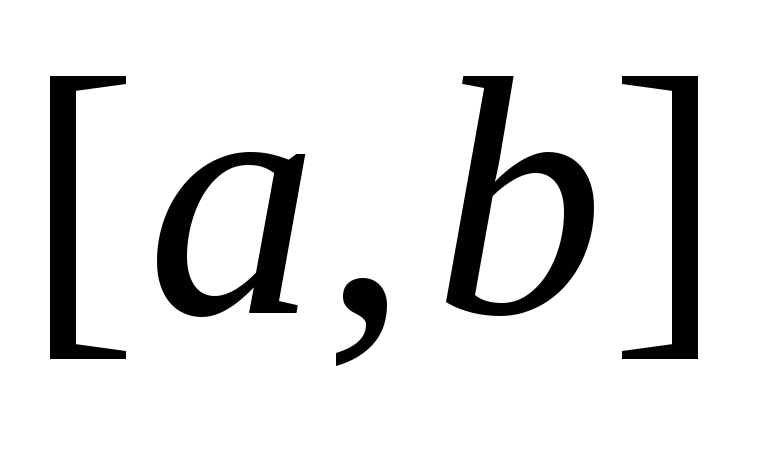 коэффициентами
коэффициентами 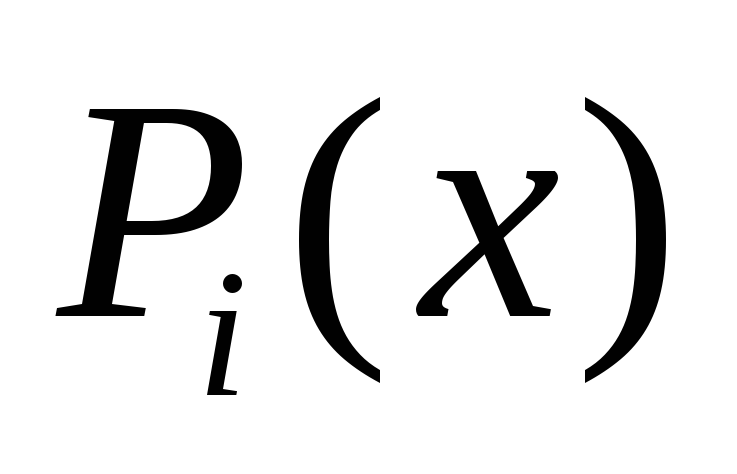 будет линейная комбинация решений
будет линейная комбинация решений 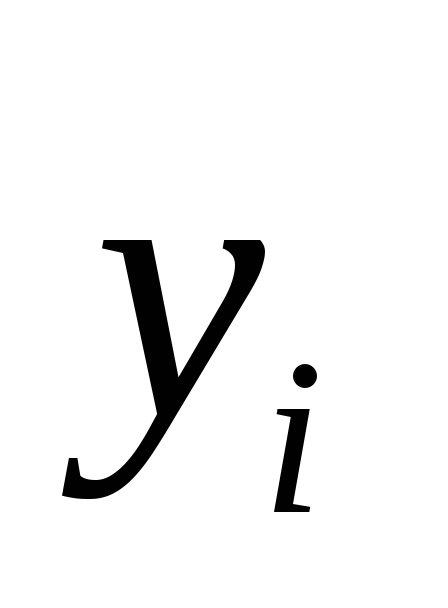 ,
то есть
,
то есть 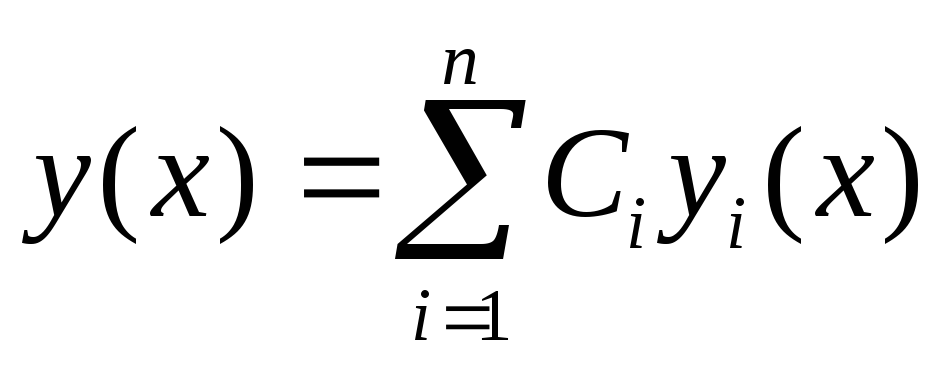 (2), где
(2), где 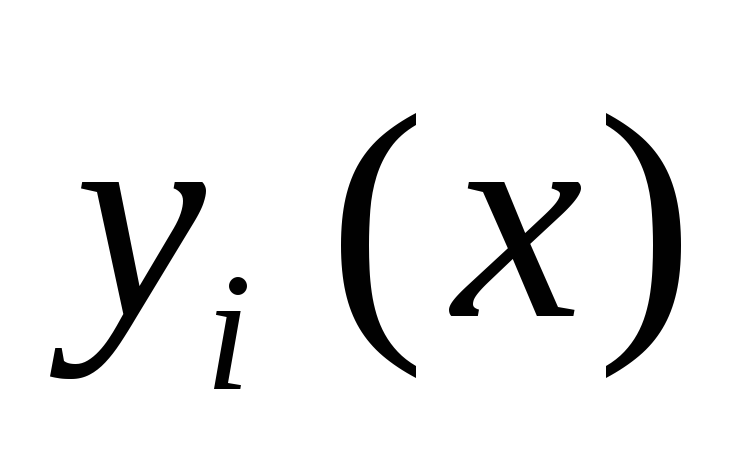 линейно
независимые на отрезке
линейно
независимые на отрезке 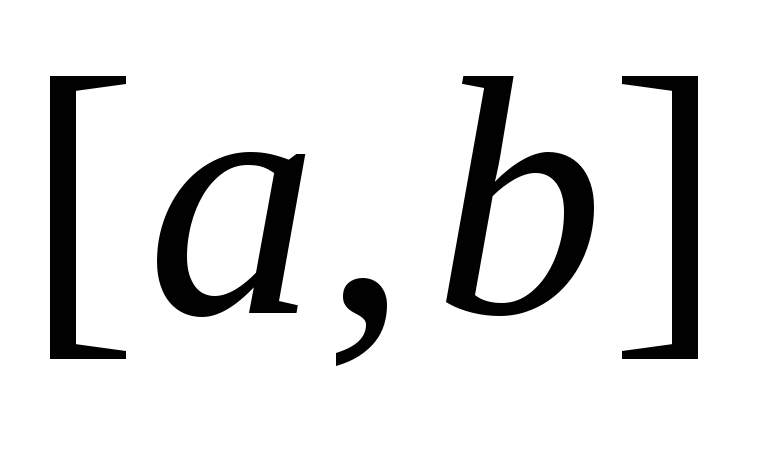 частные решения (1).
частные решения (1).
( доказывается аналогично случаю системы линейных дифференциальных уравнений)
Следствие. Максимальное число линейно независимых решений (1) равно его порядку.
Зная одно нетривиальное частное
решение уравнения (1) — 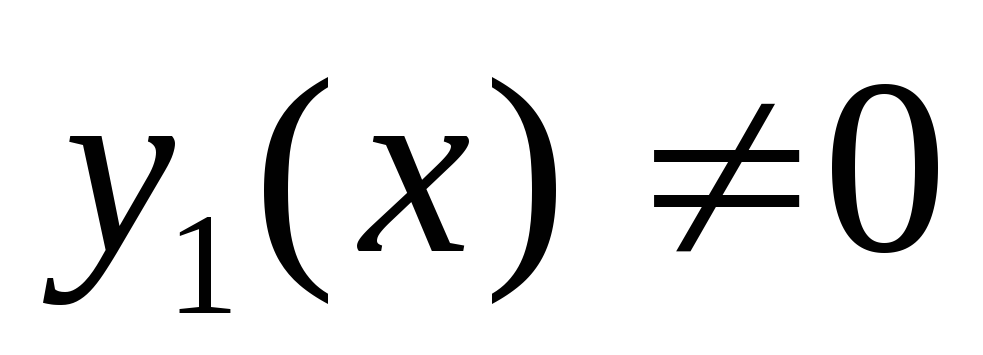 ,
можно сделать подстановку
,
можно сделать подстановку  и понизить порядок уравнения, сохранив
его линейность и неоднородность.
Обычно эту подстановку разбивают на
две
и понизить порядок уравнения, сохранив
его линейность и неоднородность.
Обычно эту подстановку разбивают на
две 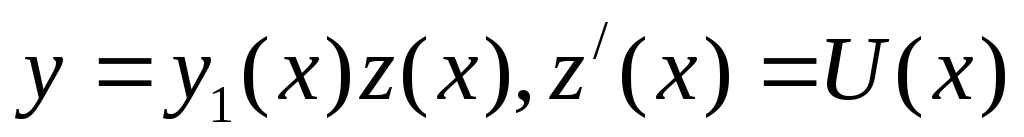 .
Поскольку это линейно однородное
представление, то оно сохраняет линейность
и однородность (1), а значит (1) должно
быть приведено к виду
.
Поскольку это линейно однородное
представление, то оно сохраняет линейность
и однородность (1), а значит (1) должно
быть приведено к виду 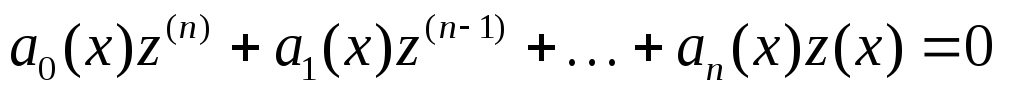 .
Решению
.
Решению 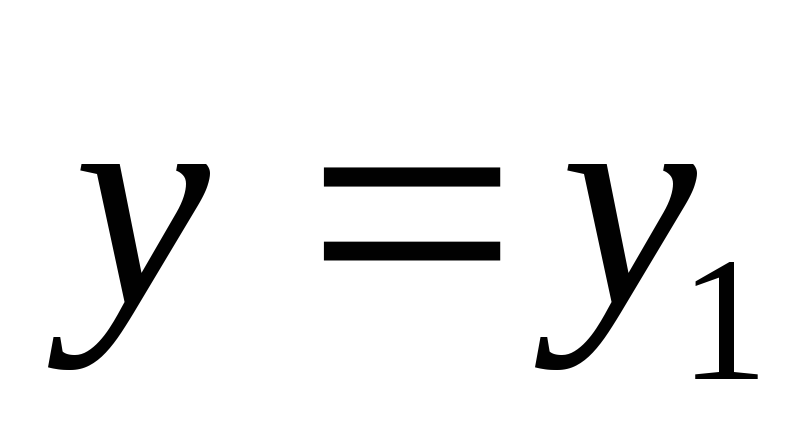 в силу
в силу 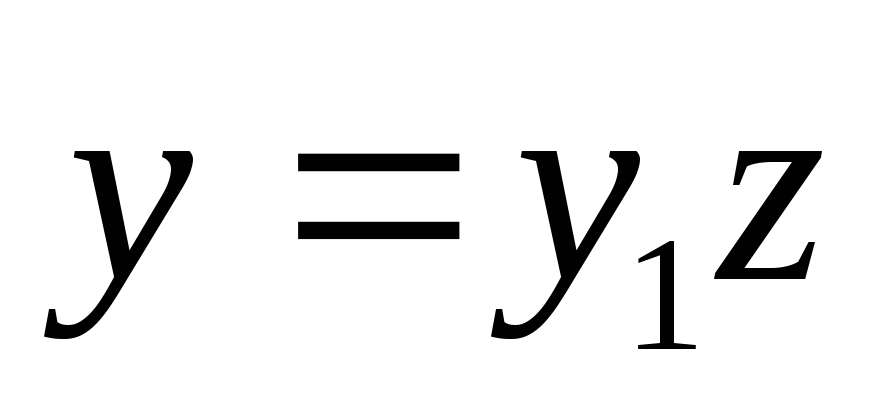 соответствует решение
соответствует решение 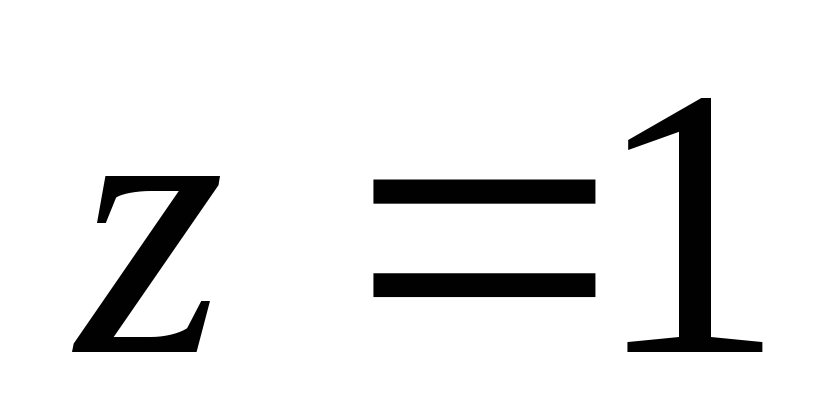 ,
и, следовательно,
,
и, следовательно, 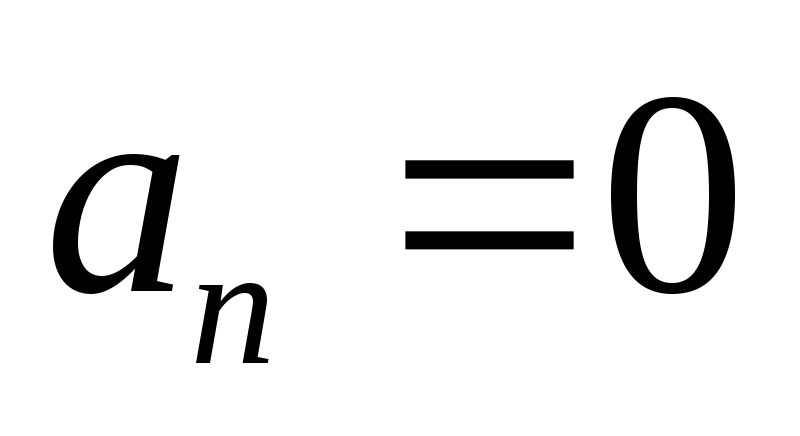 .
Сделав замену
.
Сделав замену  ,
получим уравнение с порядком
,
получим уравнение с порядком 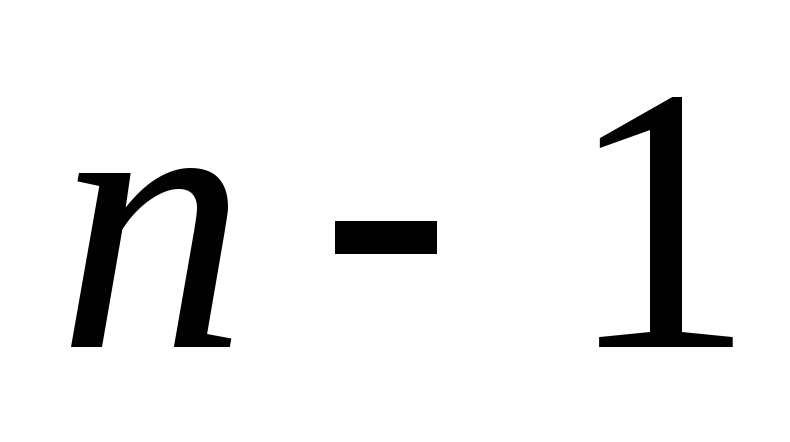 .
.
Лемма. 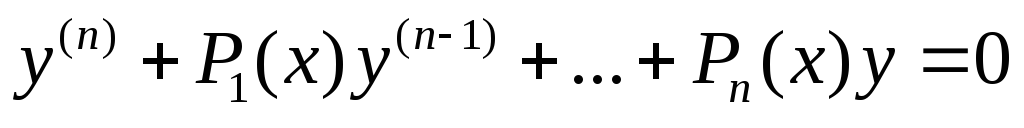 (3)
(3)
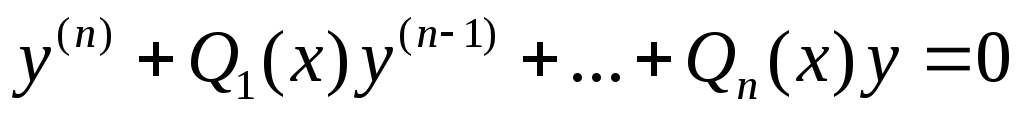 (4)
(4)
Два уравнения вида (3) и (4), где Qiи Pi – непрерывные на [a,b] функции, имеющие общую фундаментальную систему решений, совпадают, т.е. Qi(x)=Pi(x), i=1,2,…n, x[a,b]
На основании леммы можно сделать вывод, что фундаментальная система решений y1 y2 …yn полностью определяет линейное однородное уравнение (3).
Найдем вид уравнения (3), имеющего фундаментальную систему решений y1 y2 …yn. Любой решение y(x) уравнения (3) линейно зависит от фундаментальной системы решений, а это значит, что W[y1 y2 …yn y]=0. Разложим определитель Вронского W[y1 y2 …yn y] по последнему столбцу.
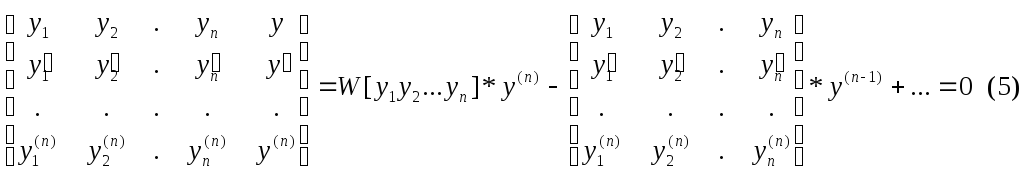
Уравнение (5) является искомым линейным дифференциальным уравнением, имеющим данную систему фундаментальных решений. Мы можем (5) разделить на W[y1 y2 …yn], т.к. он не равен нулю x[a,b]. Тогда:
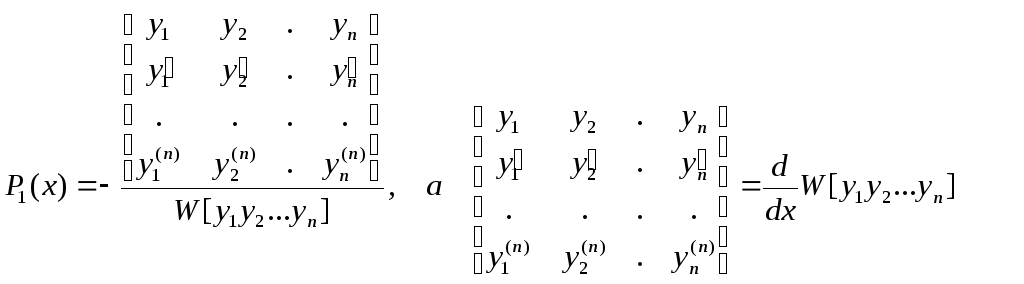 (*)
(*)
По правилу дифференцирования определителя, производная от определителя равна сумме по i=1,2…n определителей, i-ая строка каждого из которых равна производной от i –ой строки исходного определителя. В этой сумме все определители, кроме последнего, равны нулю (т.к. у них по две одинаковые строки), а последний равен (*). Таким образом, получим:
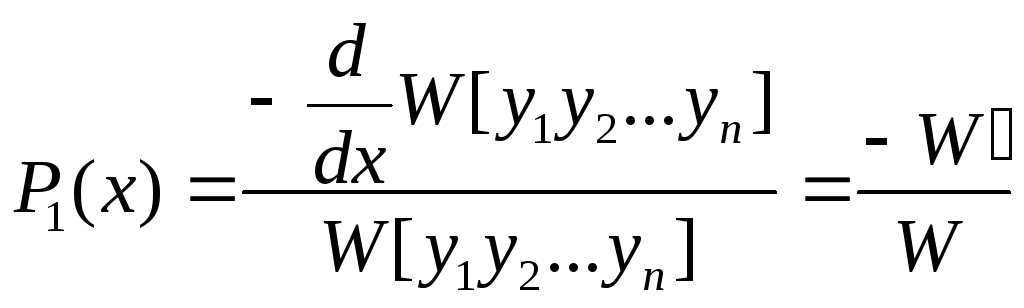 ,
тогда:
,
тогда: 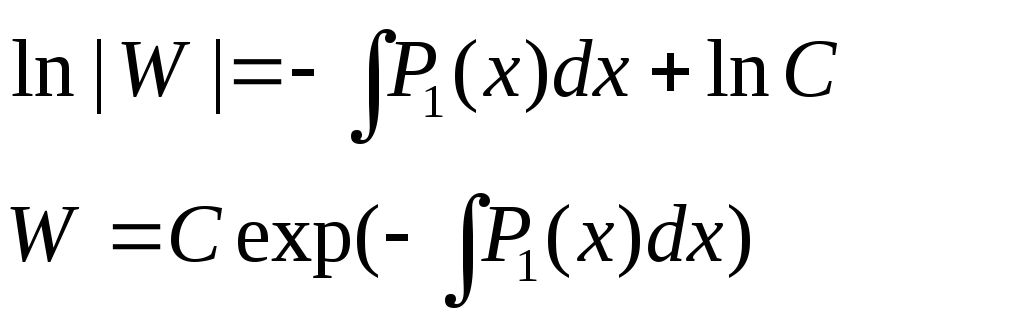 (6)
(6)
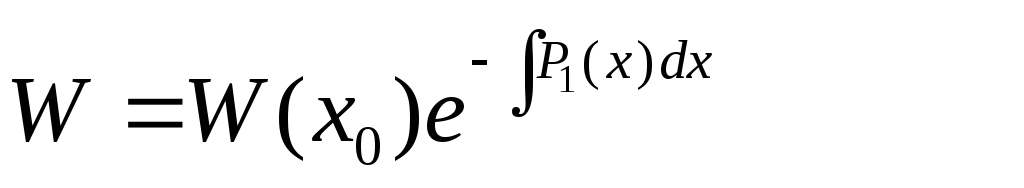 (7)
(7)
Определение. Формулы (6) и (7) называются формулами Остроградского-Лиувиля.
Используем (7) для интегрирования линейного однородного уравнения второго порядка. И пусть нам известно одно из решений y1 уравнения (8).
 (8)
(8)
Согласно (7) любое решение (8) должно удовлетворять следующему соотношению:
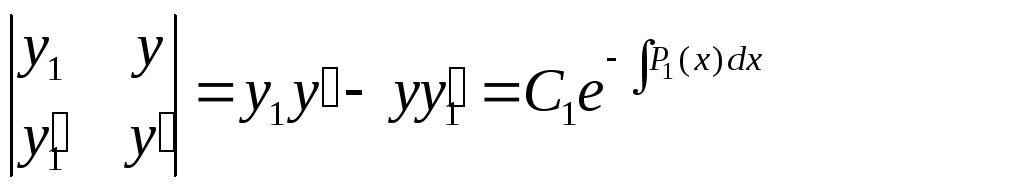 (9)
(9)
Воспользуемся методом интегрирующего множителя.
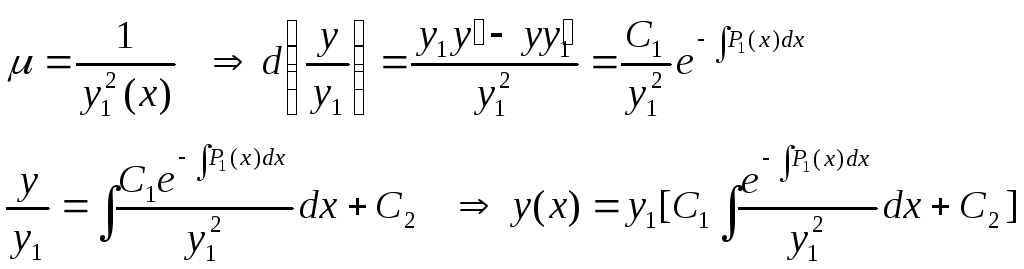

Линейные однородные уравнения с
постоянными коэффициентами.
Если в линейном однородном уравнении все коэффициенты постоянны,
a0y(n)+a1y(n-1)+….+any=0, (1)
L[y]=0, (2)
то частные решения (1) могут быть определены в виде: y=ekx, где k — постоянная.
a0knekx+a1kn-1ekx+….+an k0ekx=0 a0kn+a1kn-1+….+an=0 (3)
Определение. (3) — характеристическое уравнение.
Вид решения (1) определяется корнями характеристического уравнения (3).
1). Все корни вещественные и различные, тогда:
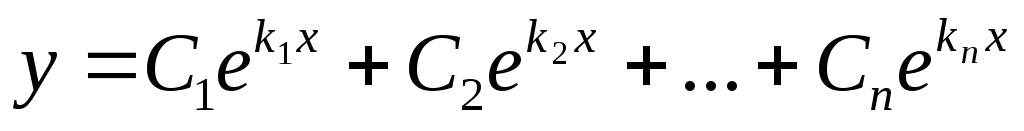
2). Если все коэффициенты вещественные, то корни могут быть комплексно-сопряженные.
k1=+i k2=-i
Тогда решения имеют вид:
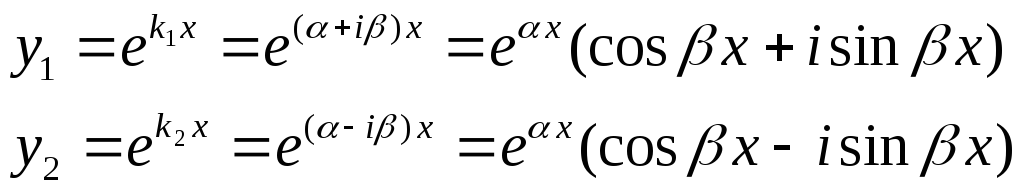
Согласно теореме: если оператор с вещественными коэффициентами имеет комплексно-сопряженные решения, то их действительная и мнимая части также являются решениями. Тогда:
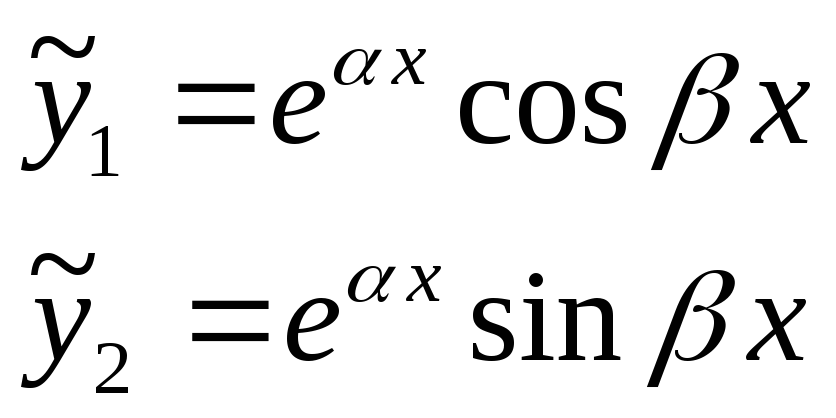

Пример.
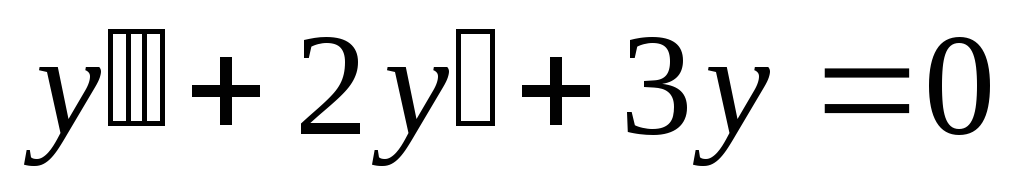 Решение
представим в виде
Решение
представим в виде 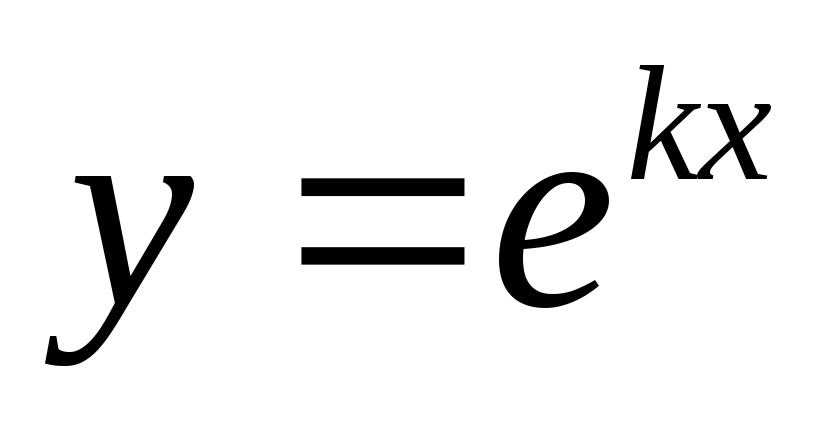 ,
тогда характеристическое уравнение
имеет вид:
,
тогда характеристическое уравнение
имеет вид:
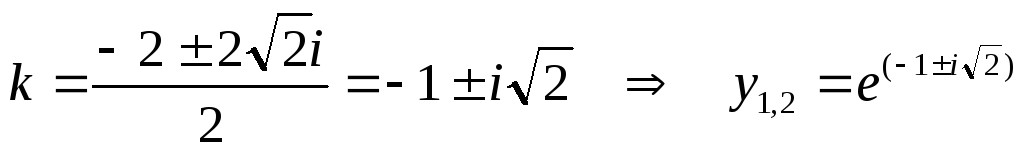 ,
получим два решения:
,
получим два решения:
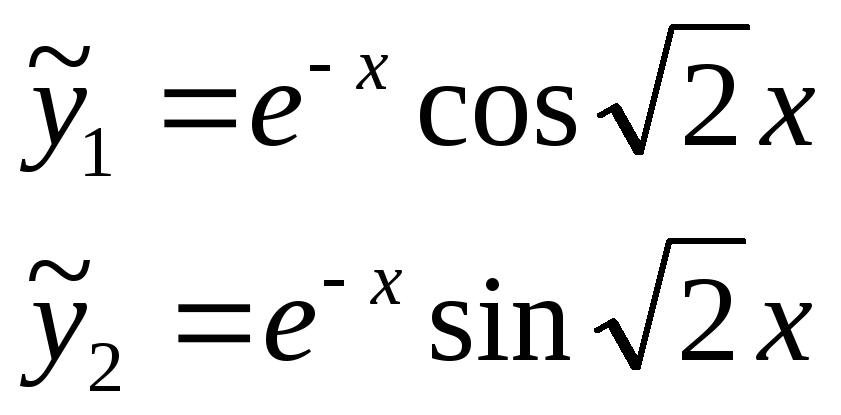
 тогда
искомая функция:
тогда
искомая функция: 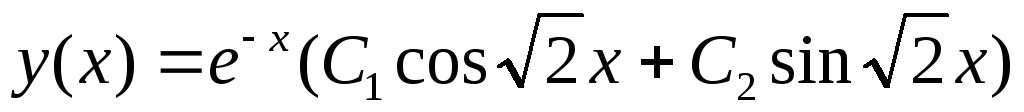
3).
Имеются кратные корни: ki с кратностью i. В этом случае число различных решений 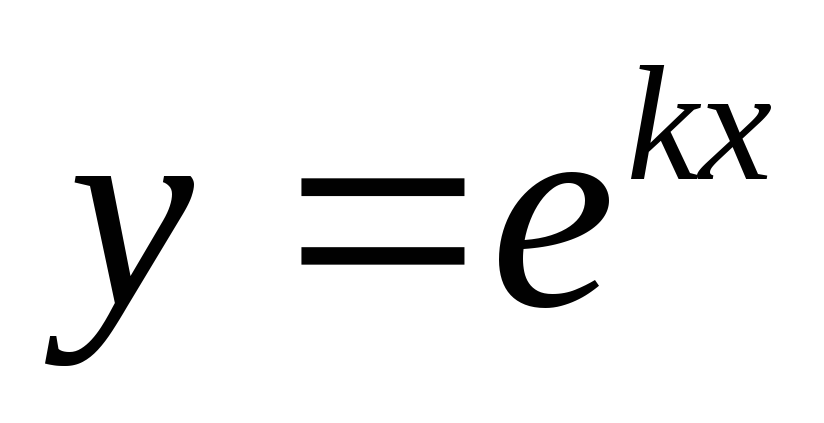 будет
меньше n,
следовательно, нужно искать недостающие
линейно-независимые решения в другом
виде. Например:
будет
меньше n,
следовательно, нужно искать недостающие
линейно-независимые решения в другом
виде. Например:
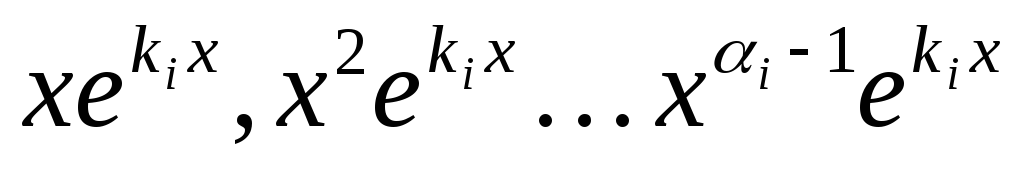
Доказательство:
Допустим,
ki=0,
если подставить его в (3), то получим, что 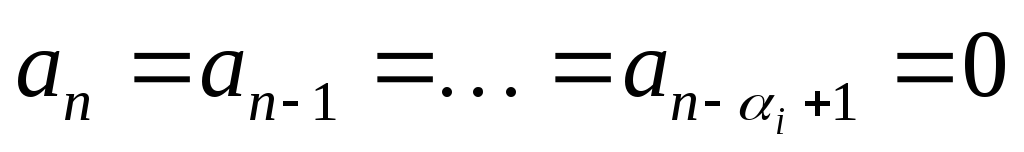 ,
тогда:
,
тогда:
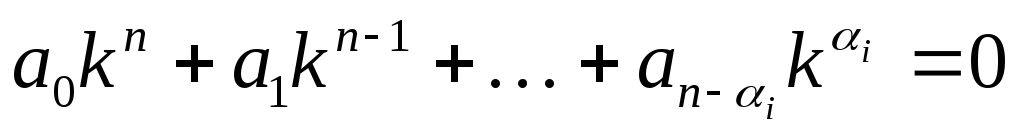 (4)
(4)
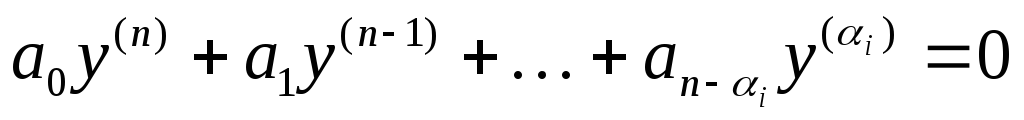 (5)
(5)
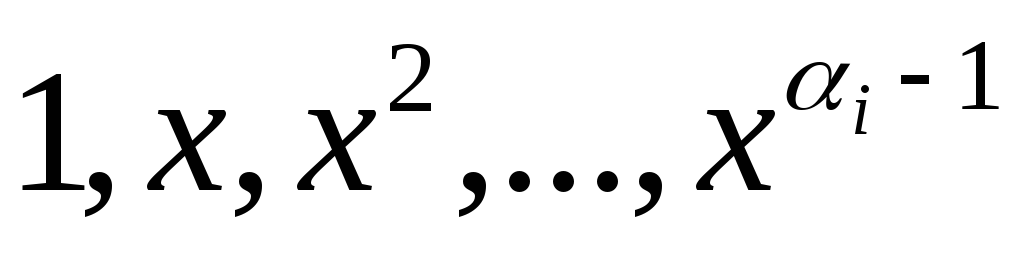 —
частные решения (3).
—
частные решения (3).
Пусть
ki0,
сделаем замену 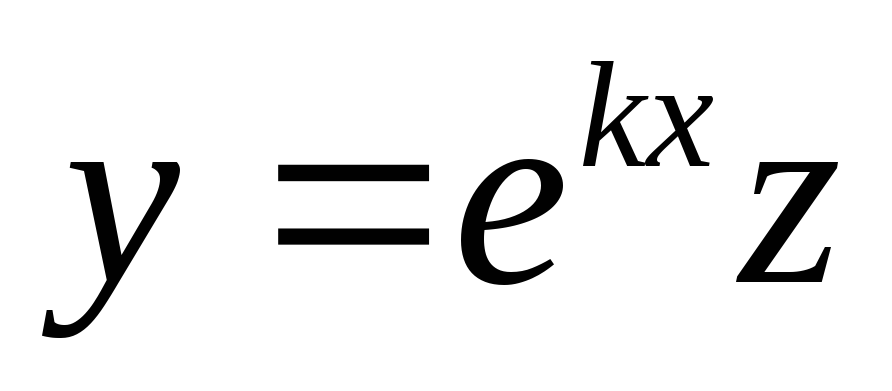 (6)
(6)
Подставим (6) в (1), получим относительно z линейное однородное уравнение n-го порядка с постоянными коэффициентами (7).
 (7)
(7)
Корни (3) отличаются от корней характеристического уравнения (7) на слагаемое ki.
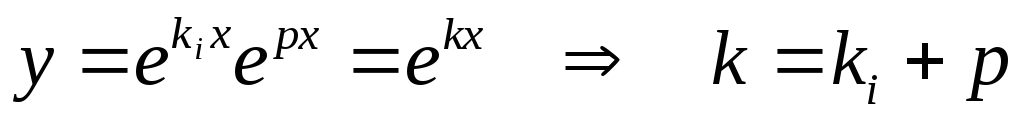
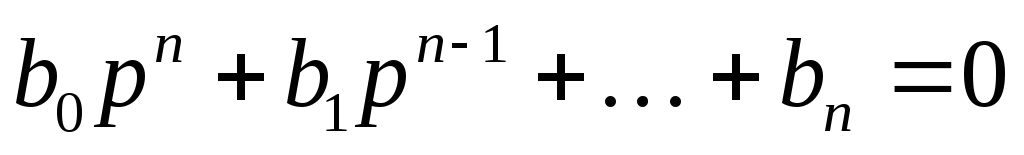
 (8)
(8)
Если
k=ki , то тогда этому k
соответствует решение уравнения (7) с
корнем p=0
, т.е. соответствуют решения вида z=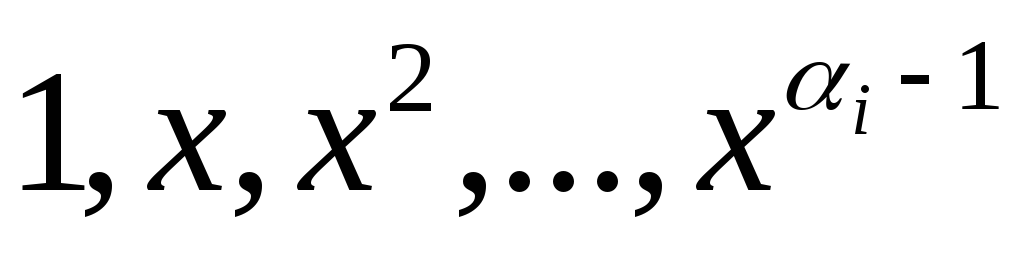 ,
тогда y=
,
тогда y=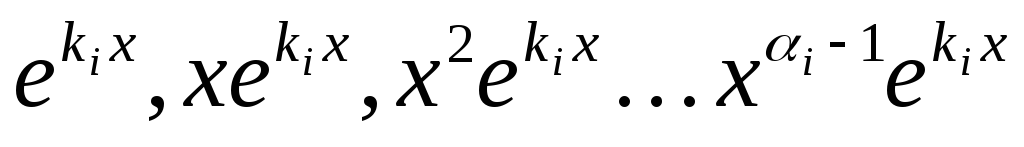 —
решение уравнения (1). А общее решение
имеет вид:
—
решение уравнения (1). А общее решение
имеет вид:
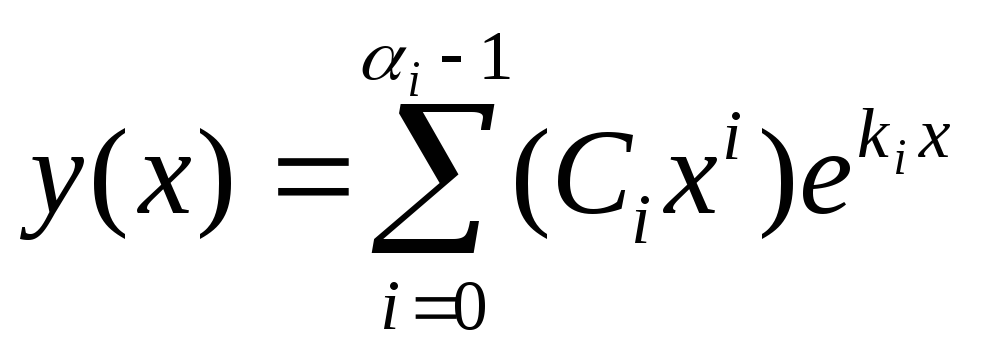 решение
для ki
решение
для ki
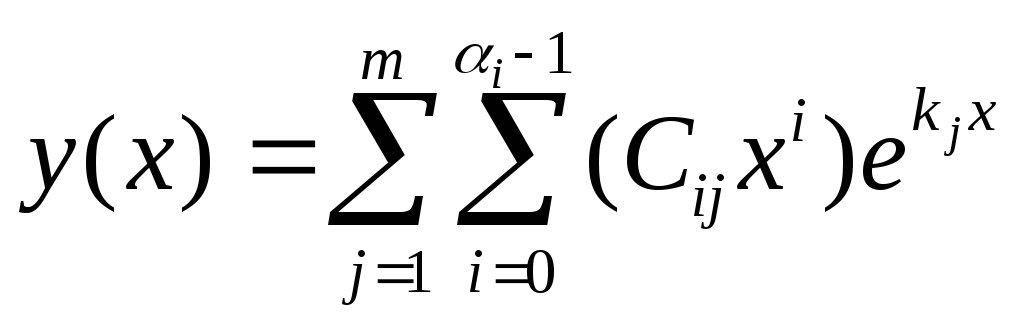
Уравнение Эйлера.
Определение. Уравнение вида:
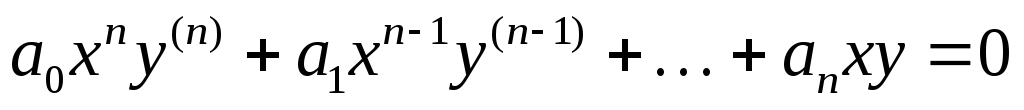 ,
(1)
,
(1)
ai-постоянные коэффициенты, называется уравнением Эйлера.
Уравнение Эйлера заменой x=et сводится к линейному однородному уравнению с постоянными коэффициентами.
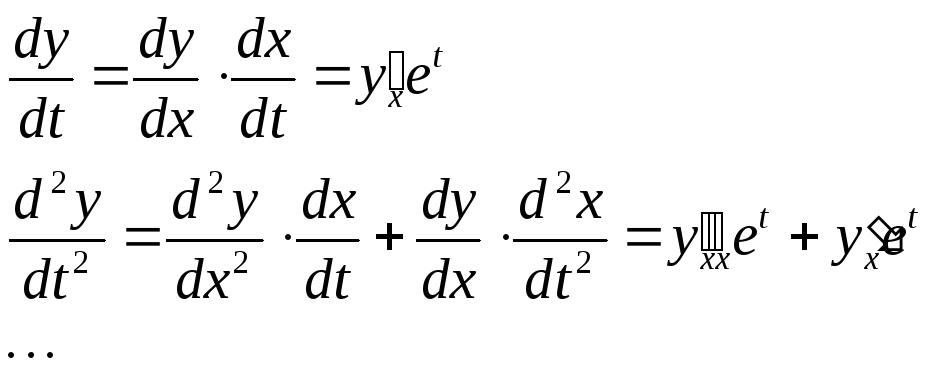
Можно
искать решения в виде y=xk,
тогда они имеют вид: 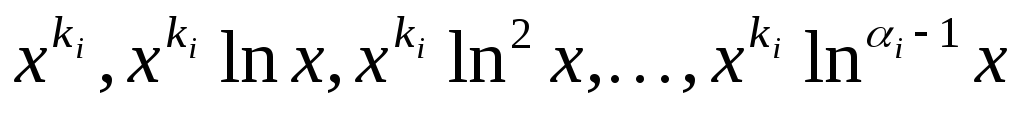
Линейные неоднородные уравнения.
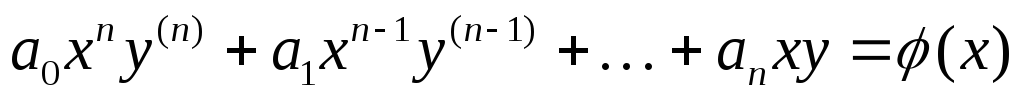 (1)
(1)
Если a0(x)0, то разделив на этот коэффициент уравнение (1), получим:
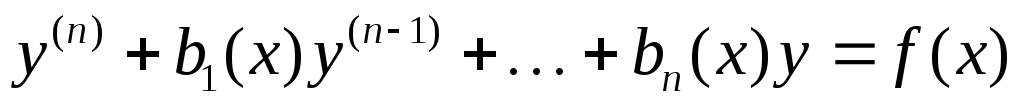 .
(2)
.
(2)
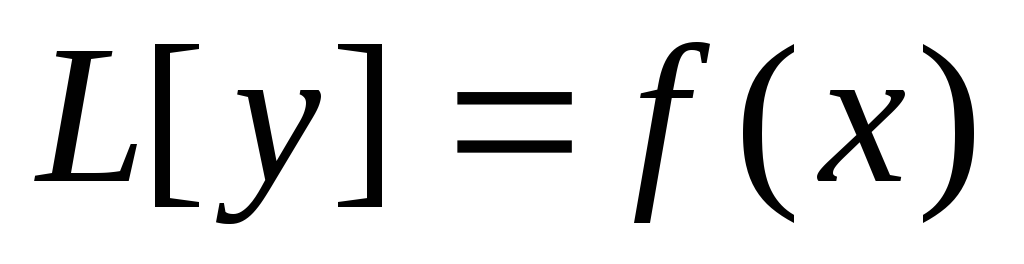 .
.
Если
на [a,b]
bi и f
непрерывны, то (2) имеет единственное
решение, удовлетворяющее соответствующим
начальным условиям 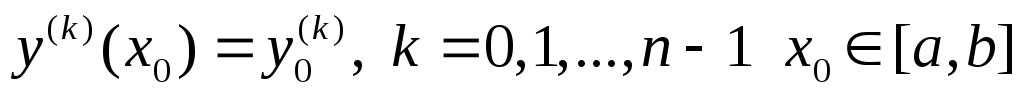 .
Если в явном виде выразить старшие
производные из (2), то получим уравнение,
правая часть которого удовлетворяет
теореме о существовании и единственности.
Так как оператор L
линейный, значит, для (2) выполняется:
.
Если в явном виде выразить старшие
производные из (2), то получим уравнение,
правая часть которого удовлетворяет
теореме о существовании и единственности.
Так как оператор L
линейный, значит, для (2) выполняется:
1). 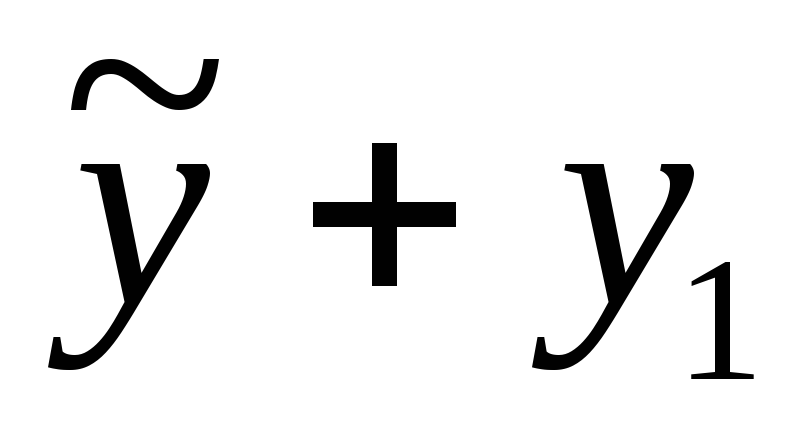 — решение (2), если
— решение (2), если 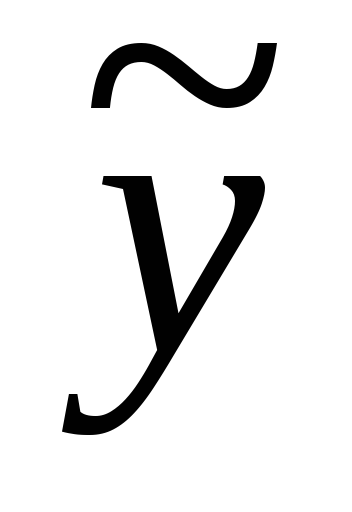 — решение неоднородного уравнения (2), а
— решение неоднородного уравнения (2), а  —
решение соответствующего однородного
уравнения.
—
решение соответствующего однородного
уравнения.
2).
Если  —
решения
—
решения 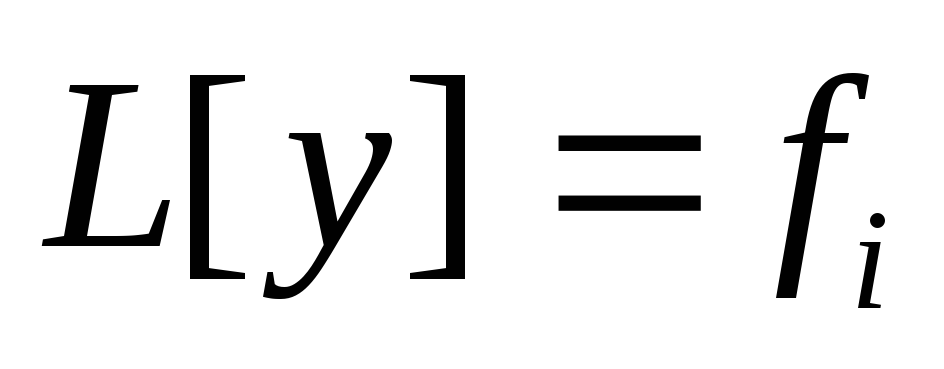 ,
то
,
то 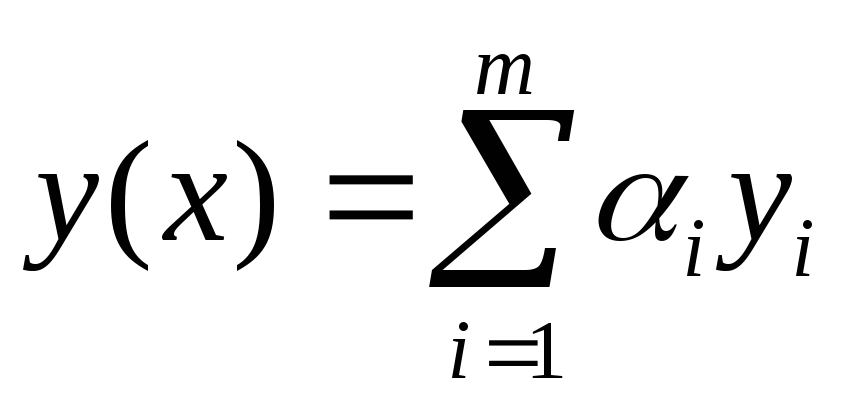 решение
уравнения
решение
уравнения 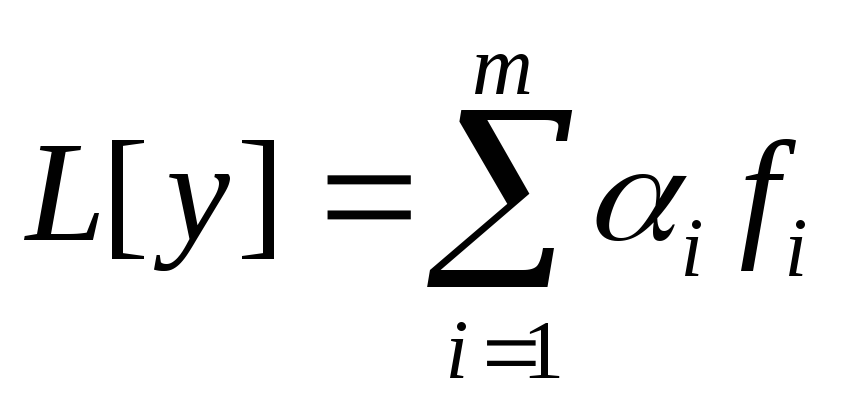 .
.
Свойство
2 – принцип суперпозиции, он справедлив
при
,
если ряд  — сходится и допускает m-кратное
почленное дифференцирование.
— сходится и допускает m-кратное
почленное дифференцирование.
3)
Пусть дано операторное уравнение 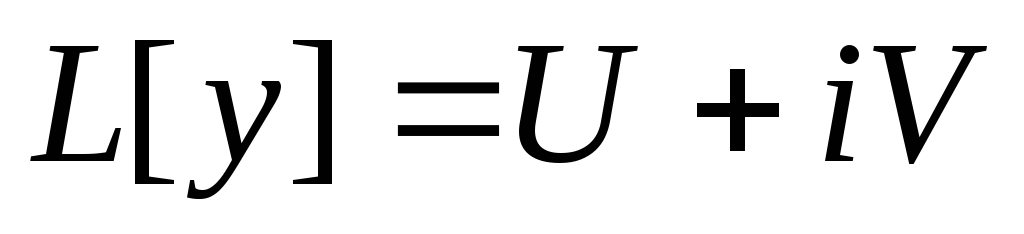 ,
где L
– это оператор с коэффициентами
,
где L
– это оператор с коэффициентами  ,
все
,
все  — вещественные. Функции U
и V
тоже вещественные. Тогда, если это
уравнение имеет решение
— вещественные. Функции U
и V
тоже вещественные. Тогда, если это
уравнение имеет решение  ,
то решением этого же уравнения будут и
мнимая и вещественная части y:
,
то решением этого же уравнения будут и
мнимая и вещественная части y:  и
и  .
При чем каждый из них соответствует
решению
.
При чем каждый из них соответствует
решению 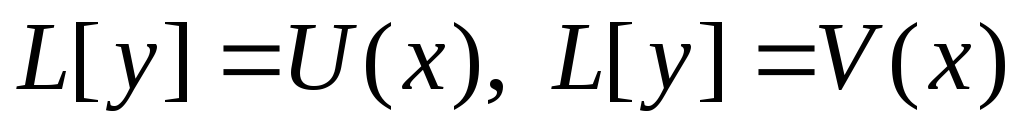 .
.
Теорема.
Общее решение неоднородного уравнения n-порядка 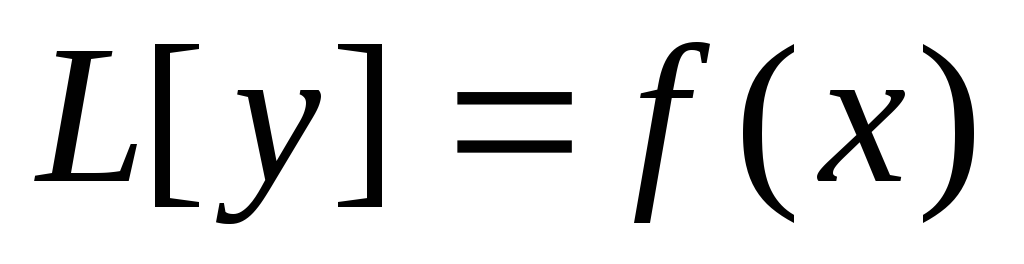 на
отрезке [a,b]
при условии, что все коэффициенты
на
отрезке [a,b]
при условии, что все коэффициенты 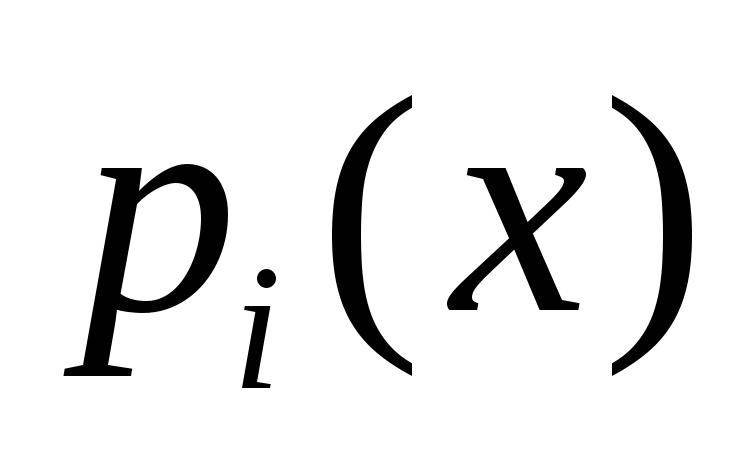 и
правая часть
и
правая часть 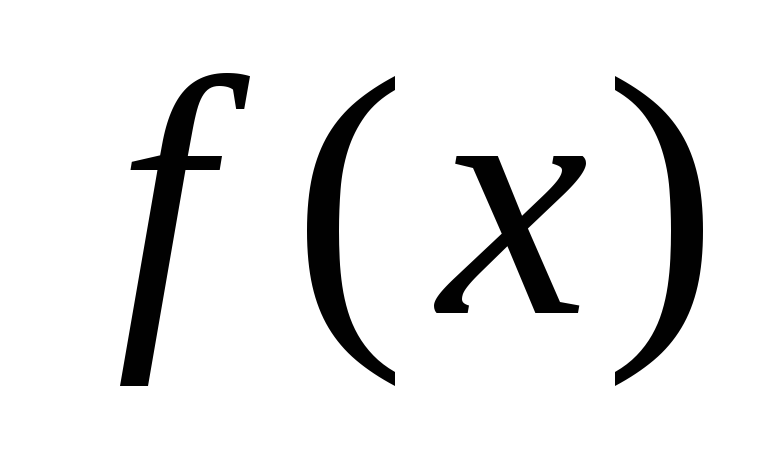 —
непрерывные функции, можно представить
в виде суммы общего решения, соответствующей
однородной системы
—
непрерывные функции, можно представить
в виде суммы общего решения, соответствующей
однородной системы 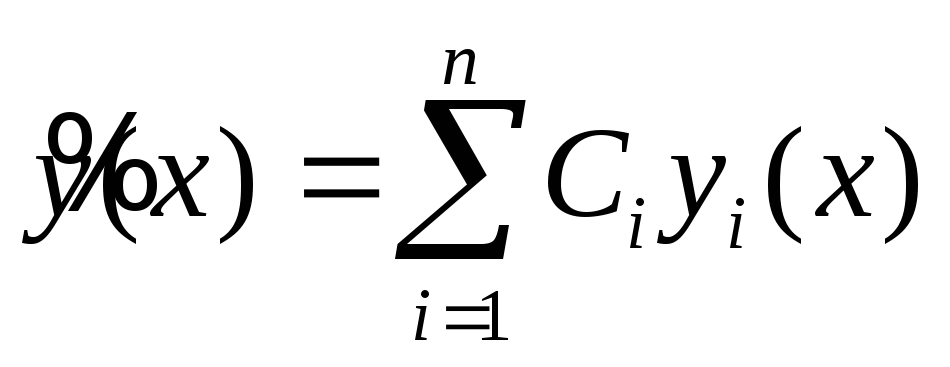 и
частного решения неоднородной —
и
частного решения неоднородной —  .
.
Т.е.
решение 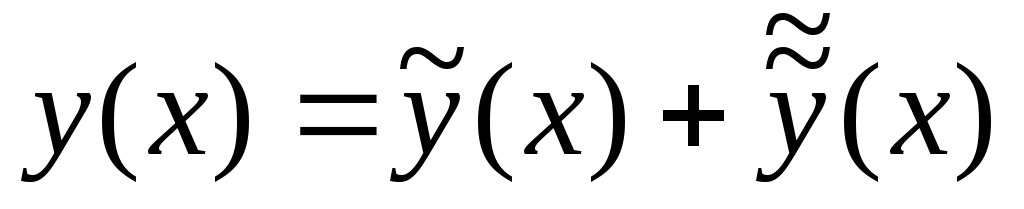 .
.
Если невозможно в явном виде подобрать частные решения неоднородной системы, то можно воспользоваться методом вариации постоянной. Решение будем искать в виде:
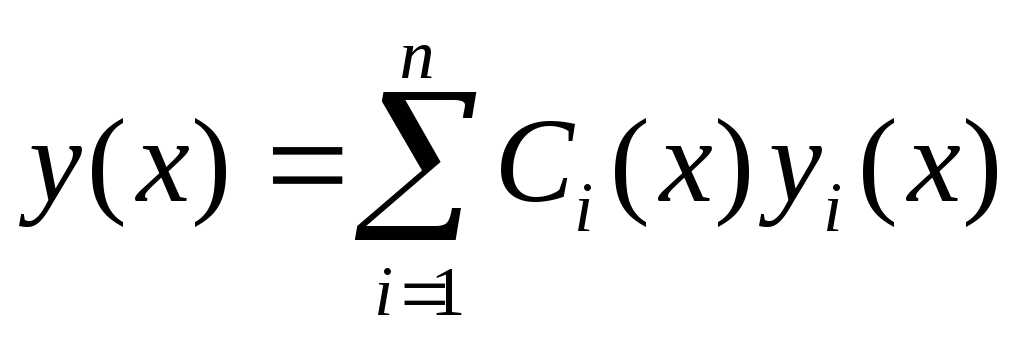 (3)
(3)
где 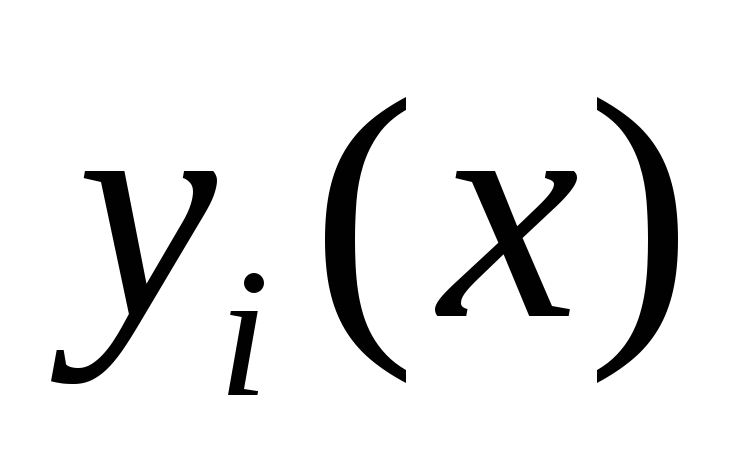 решения
однородной системы,
решения
однородной системы, 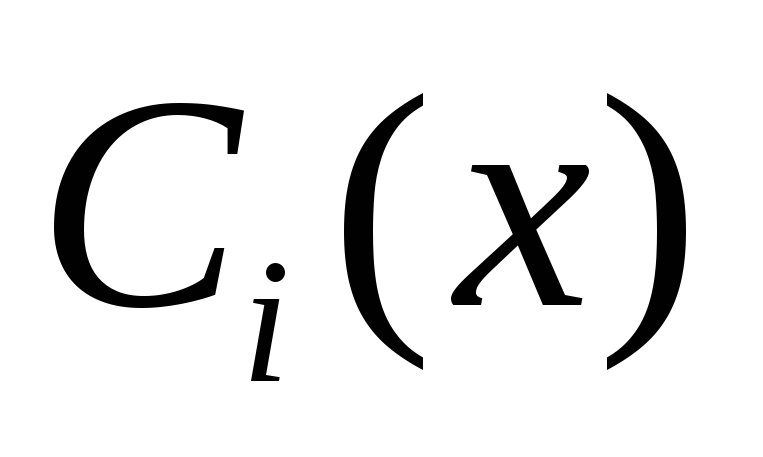 —
неизвестные функции.
—
неизвестные функции.
Всего
неизвестных функций 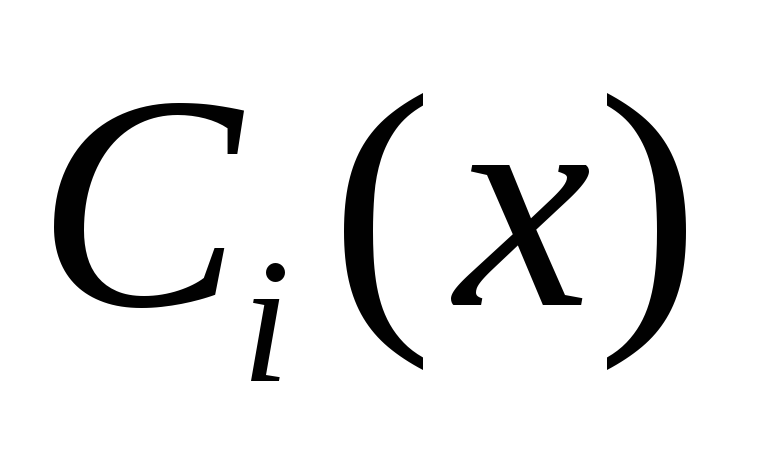 —
n.
Они должны удовлетворять исходному
уравнению (2).
—
n.
Они должны удовлетворять исходному
уравнению (2).
Подставив
в уравнение (2) выражение y(x),
мы получим условия для определения
только одной неизвестной функции. Чтобы
определить остальные (n-1)-ну
функции, необходимо еще (n-1)-но
дополнительное условие, их можно выбрать
произвольно. Выберем их так, чтобы
решение (2) — y(x)
имело вид такой же, как если бы 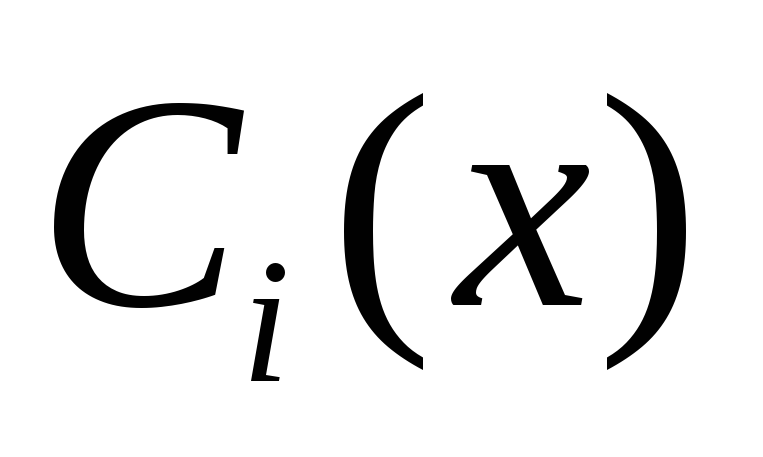 были
константами.
были
константами.
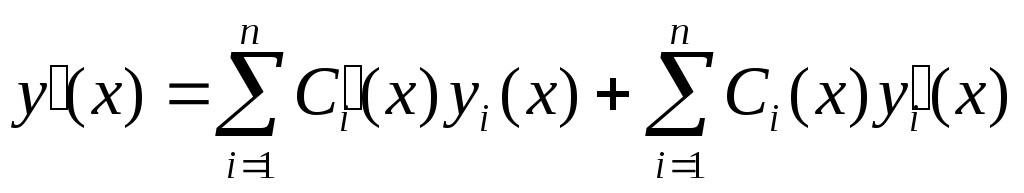 ,
,
т.к. 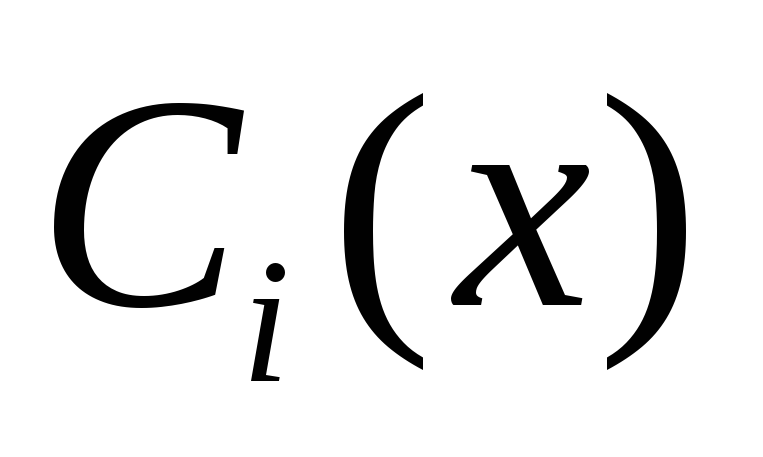 ведут себя как константы, то
ведут себя как константы, то 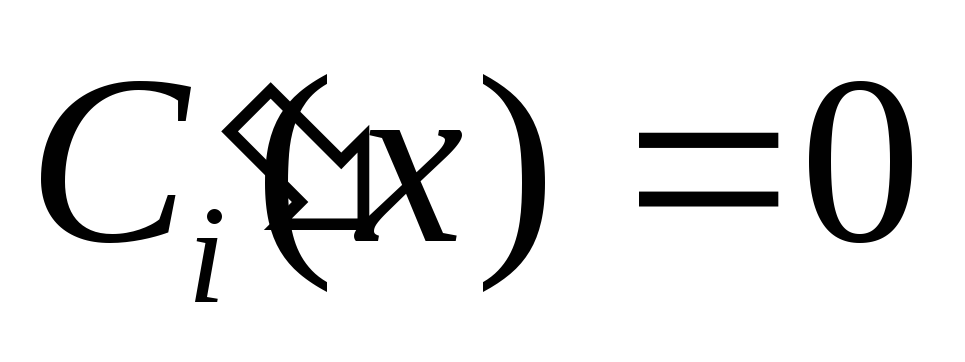 ,
значит, и
,
значит, и 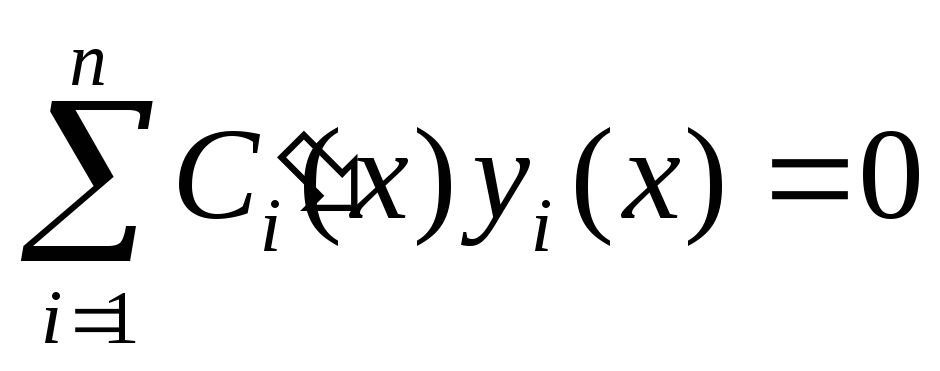 .
.
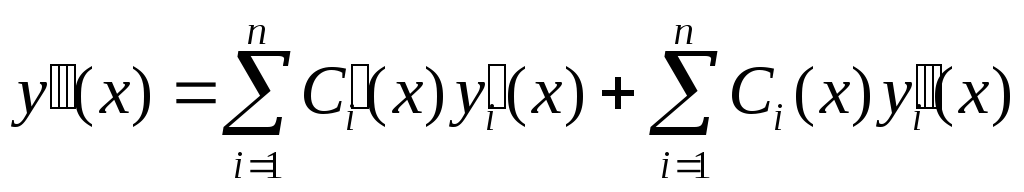
…
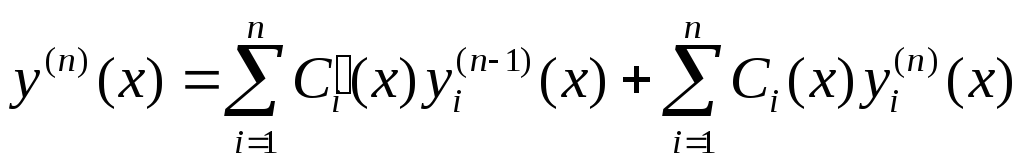
Т.о.
мы получим (n-1)-но
условие дополнительно к уравнению (1).
Если подставить выражение для производных
в уравнение (1) и учесть все полученные
условия и то, что yi – решение соответствующей однородной
системы, то мы получим последнее условие
для  .
.
Перейдем к системе:
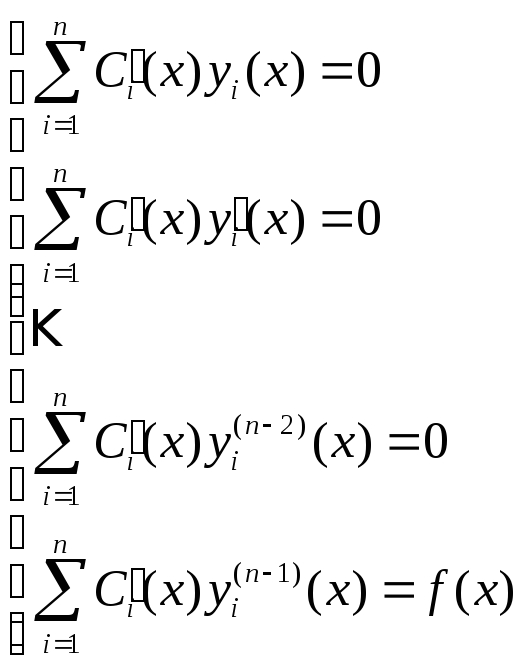 (3)
(3)
Определитель системы (3) – это (W) определитель Вронского, а т.к. yi – это решения однородной системы, то W0 на [a,b].
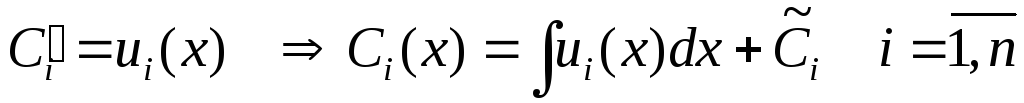 (4)
(4)
Пример. Неоднородное уравнение
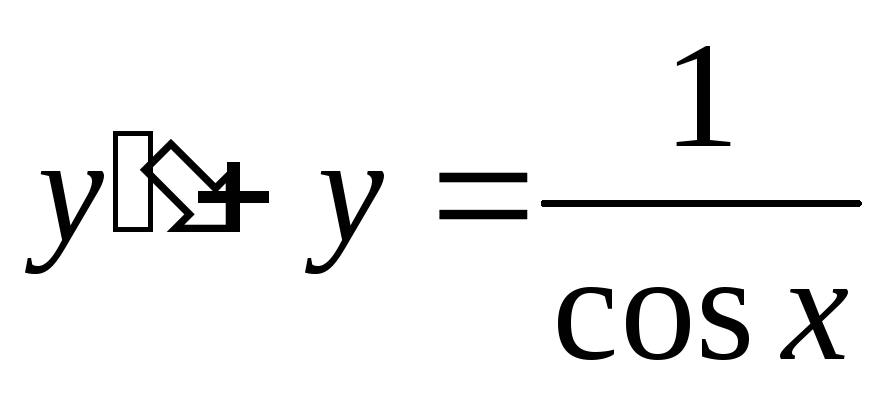 ,
соответствующее ему однородное уравнение
,
соответствующее ему однородное уравнение 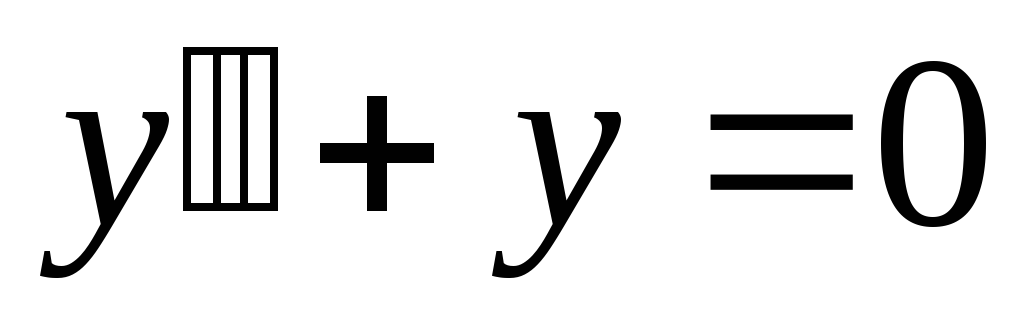
Решение ищем в виде y=ekx. Характеристическое уравнение k2+1=0, т.е. k1,2=i
y=eix=cos x +i sin x,
общее решение — 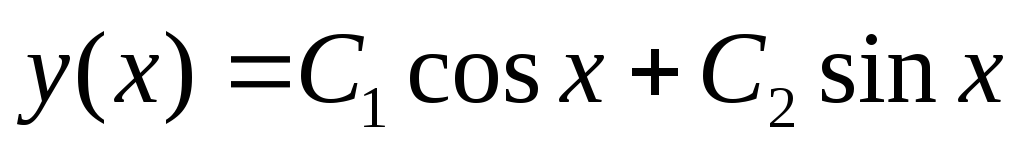
Воспользуемся методом вариации постоянной:
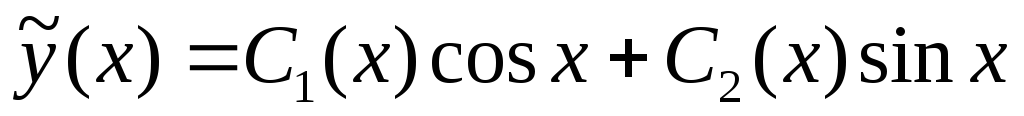
Условия
для  :
:
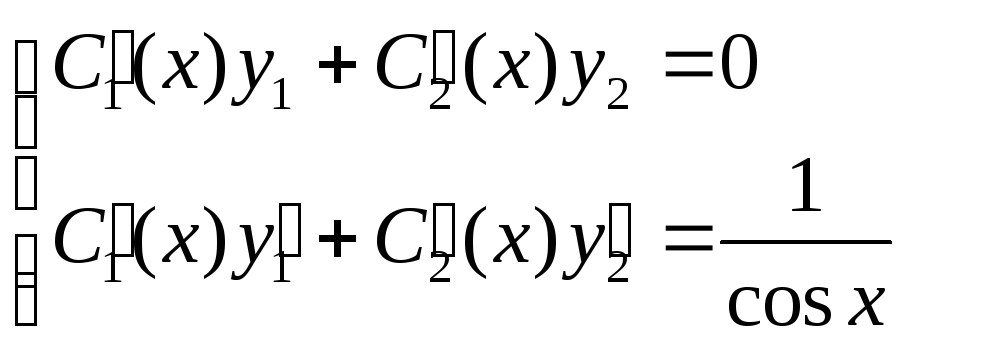 ,
что эквивалентно записи:
,
что эквивалентно записи: 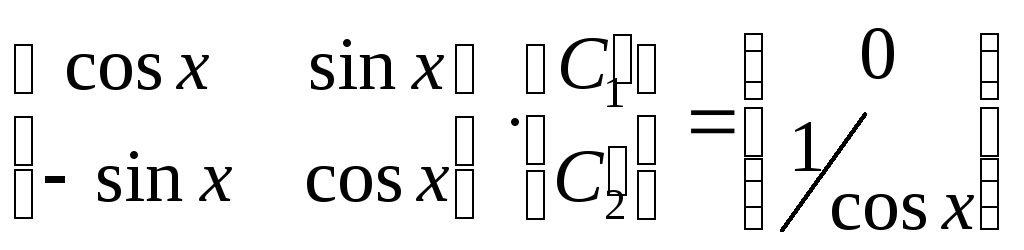
Отсюда:
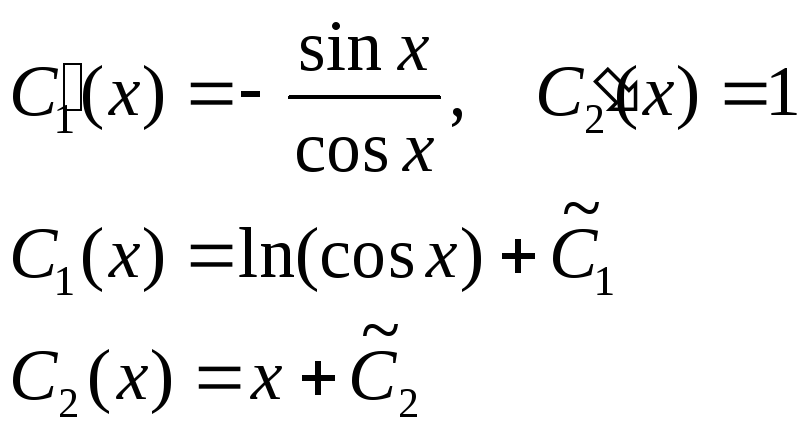
studfile.net
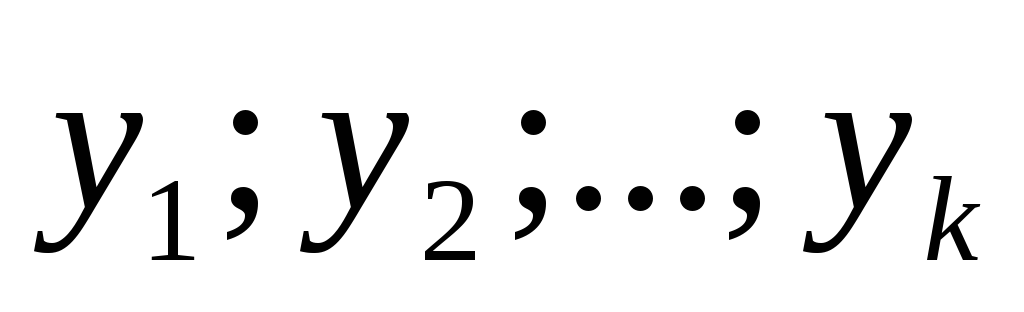 —
линейно зависимы на [a;b]
—
линейно зависимы на [a;b]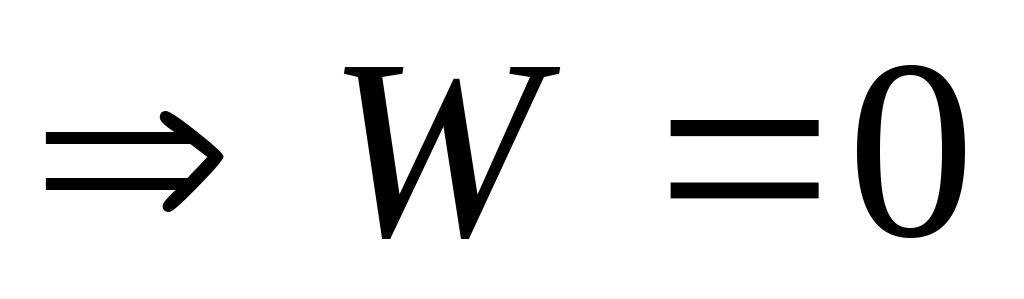 на
этом отрезке.
на
этом отрезке.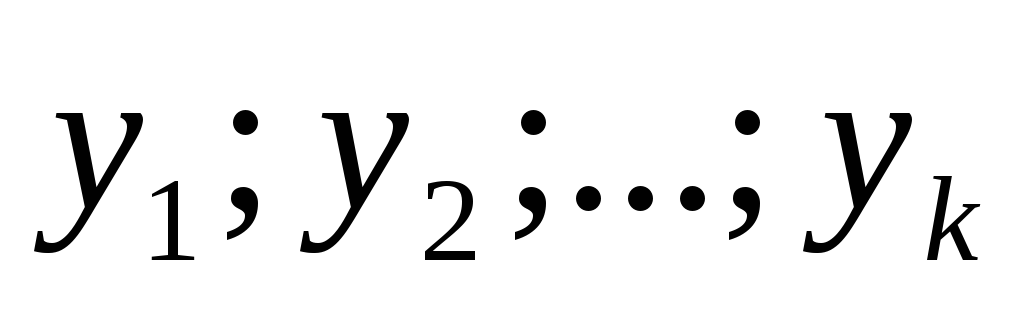 — линейно независимые, решения
дифференциального уравнения
— линейно независимые, решения
дифференциального уравнения при
любых значениях х в области, где
определены функции а1…аn
при
любых значениях х в области, где
определены функции а1…аn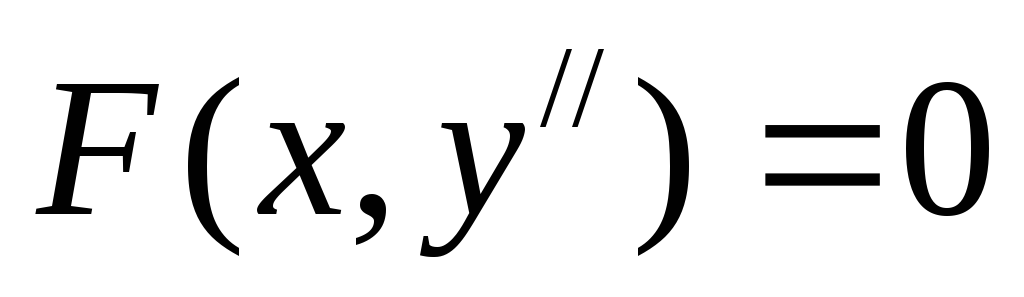 . (8)
. (8)