Линейные и квадратные уравнения
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). \[f(x)=g(x) \qquad \qquad (1)\]Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой \(x\).
Замечание
Заметим, что \(x\) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида \((1)\) будем называть множество значений переменной \(x\), при которых определены (то есть не теряют смысла) функции \(f(x)\) и \(g(x)\).
Пример
Уравнение \(\dfrac {10}{x-1}=5\) определено при всех значениях переменной \(x\), кроме \(x=1\), потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль.
Определение
Корнем уравнения называется то числовое значение \(x\), при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число \(x=3\), потому как тогда уравнение принимает вид \(\dfrac{10}{3-1}=5\) или, что то же самое, \(5=5\), что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение \(\dfrac 1x=0\) ни при каких значениях \(x\) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. У нашей дроби числитель \(1\ne 0\).
2) Фраза “решить уравнение” означает найти все корни данного уравнения или доказать, что корней нет.
Определение
Два уравнения равносильны (или эквивалентны), если они имеют одинаковые решения. 3=64\) является \(x=4\).
3=64\) является \(x=4\).
Линейные уравнения
Линейные уравнения – уравнения, которые можно представить в виде \(ax+b=0\), где \(a\) и \(b\) – какие-либо числа.
Проще говоря, это такие уравнения, в которых переменные (обычно иксы) в первой степени. При этом не должно быть переменных в знаменателях дробей.
|
Например: |
\(2x+7=0\) |
Здесь \(a=2, b=7\) |
||
|
\(5=0\) |
А тут \(a=0, b=5\) (пояснение: данное уравнение может быть представлено в виде \(0\cdot x+5=0\)) |
|||
|
\(-7(5-3y)=91\) |
Здесь \(a\) и \(b\) изначально не определены, но преобразовав уравнение, мы сможем их найти. |
|||
|
\(\frac{x+2}{3}\)\(+x=1-\)\(\frac{3}{4}\)\(x\) |
Тоже самое, \(a\) и \(b\) пока что неизвестны. |
Решение линейных уравнений
При решении линейных уравнений, мы стремимся найти корень, то есть такое значение для переменной, которое превратит уравнение в правильное равенство.
В простых уравнениях корень очевиден сразу или легко находиться подбором. Например, понятно, что корнем уравнения \(x+3=5\) будет число \(2\), ведь именно двойка при подстановке ее вместо икса даст \(5=5\) – верное равенство.
Однако в более сложных случаях ответ сразу не виден. И тогда на помощь приходят равносильные преобразования.
Чтобы найти корень уравнения нужно
равносильными преобразования привести данное нам уравнение к виду\(x=[число]\)
Это число и будет корнем.
То есть, мы преобразовываем уравнение, делая его с каждым шагом все проще, до тех пор, пока не сведем к совсем примитивному уравнению «икс = число», где корень – очевиден. Наиболее часто применяемыми при решении линейных уравнений являются следующие преобразования:
1. Прибавление или вычитание из обеих частей уравнения одинакового числа или выражения.
Например
\(6x-5=1\) \(|+5\)
\(6x-5+5=1+5\)
\(6x=6\)
Обратите внимание, что тот же результат мы могли бы получить быстрее – просто записав пятерку с другой стороны уравнения и поменяв при этом ее знак. Собственно, именно так и делается школьный «перенос через равно со сменой знака на противоположный».
2. Умножение или деление обеих частей уравнения на одинаковое число или выражение.
Например: разделим уравнение \(-2x=8\) на минус два
\(-2x=8\) \(|:(-2)\)
\(x=-4\)
Обычно данный шаг выполняется в самом конце, когда уравнение уже приведено к виду \(ax=b\), и мы делим на \(a\), чтобы убрать его слева.
3. Использование свойств и законов математики: раскрытие скобок, приведение подобных слагаемых, сокращение дробей и т.д.
Например: раскроем скобки в уравнении \(2(3+x)=4(3x-2)-5\)
\(6+2x=12x-8-5\)
Чаще всего при решении линейного уравнения приходиться делать несколько разных преобразований.
Пример. Решить линейное уравнение \(6(4-x)+x=3-2x\)
Решение:
|
\(6(4-x)+x=3-2x\) |
Раскрываем скобки |
|
|
\(24-6x+x=3-2x\) |
Приводим подобные слагаемые |
|
|
\(24-5x=3-2x\) |
Прибавляем \(2x\) слева и справа |
|
|
\(24-5x+2x=3\) |
Вычитаем \(24\) из обеих частей уравнения |
|
|
\(-5x+2x=3-24\) |
Опять приводим подобные слагаемые |
|
|
\(-3x=-21\) |
Теперь делим уравнение на \(-3\), тем самым убирая коэффициент перед иксом в левой части. |
|
|
\(x=7\) |
Ответ: \(7\)
Ответ найден. Однако давайте его проверим. Если семерка действительно корень, то при подстановке ее вместо икса в первоначальное уравнение должно получиться верное равенство — одинаковые числа слева и справа. Пробуем.
Проверка:
\(6(4-7)+7=3-2\cdot7\)
\(6\cdot(-3)+7=3-14\)
\(-18+7=-11\)
\(-11=-11\)
Сошлось. Значит, семерка и в самом деле является корнем исходного линейного уравнения.
Не ленитесь проверять подстановкой найденные вами ответы, особенно если вы решаете уравнение на контрольной или экзамене.
Остается вопрос – а как определить, что делать с уравнением на очередном шаге? Как именно его преобразовывать? Делить на что-то? Или вычитать? И что конкретно вычитать? На что делить?
Ответ прост:
Ваша цель – привести уравнение к виду \(x=[число]\), то есть, слева икс без коэффициентов и чисел, а справа – только число без переменных.
 Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.
Поэтому смотрите, что вам мешает и делайте действие, обратное тому, что делает мешающий компонент.Чтобы лучше это понять, разберем по шагам решение линейного уравнения \(x+3=13-4x\).
Давайте подумаем: чем данное уравнение отличается от \(x=[число]\)? Что нам мешает? Что не так?
Ну, во-первых, мешает тройка, так как слева должен быть только одинокий икс, без чисел. А что «делает» тройка? Прибавляется к иксу. Значит, чтобы ее убрать — вычтем такую же тройку. Но если мы вычитаем тройку слева, то должны вычесть ее и справа, чтобы равенство не было нарушено.
\(x+3=13-4x\) \(|-3\)
\(x+3-3=13-4x-3\)
\(x=10-4x\)
Хорошо. Теперь что мешает? \(4x\) справа, ведь там должны быть только числа. \(4x\) вычитается — убираем прибавлением.
\(x=10-4x\) \(|+4x\)
\(x+4x=10-4x+4x\)
Теперь приводим подобные слагаемые слева и справа.
\(5x=10\)
Уже почти готово. Осталось убрать пятерку слева. Что она «делает»? Умножается на икс. Поэтому убираем ее делением.
\(5x=10\) \(|:5\)
\(\frac{5x}{5}\)\(=\)\(\frac{10}{5}\)
\(x=2\)
Решение завершено, корень уравнения – двойка. Можете проверить подстановкой.
Заметим, что чаще всего корень в линейных уравнениях только один. Однако могут встретиться два особых случая.
Особый случай 1 – в линейном уравнении нет корней.
Пример. Решить уравнение \(3x-1=2(x+3)+x\)
Решение:
|
\(3x-1=2(x+3)+x\) |
Раскроем скобки |
|
|
\(3x-1=2x+6+x\) |
Приведем подобные слагаемые |
|
|
\(3x-1=3x+6\) |
Перенесем члены с переменной влево, а просто числа — вправо, меняя при этом знаки |
|
|
\(3x-3x=6+1\) |
Опять приведем подобные слагаемые |
|
|
\(0=7\) |
Ну и при каком иксе ноль станет равен \(7\)? Ни при каком, тут икс вообще никак не влияет и не может «исправить» неверность получившегося равенства. |
Ответ: нет корней.
На самом деле, то, что мы придем к такому результату было видно раньше, еще когда мы получили \(3x-1=3x+6\). Вдумайтесь: как могут быть равны \(3x\) из которых вычли \(1\), и \(3x\) к которым прибавили \(6\)? Очевидно, что никак, ведь с одним и тем же выражением сделали разные действия! Понятно, что результаты будут отличаться.
Особый случай 2 – в линейном уравнении бесконечное количество корней.
Пример. Решить линейное уравнение \(8(x+2)-4=12x-4(x-3)\)Решение:
|
\(8(x+2)-4=12x-4(x-3)\) |
Начинаем преобразовывать – раскрываем скобки |
|||
|
\(8x+16-4=12x-4x+12\) |
Приводим подобные слагаемые |
|||
|
\(8x+12=8x+12\) |
Переносом через равно собираем иксы справа, а числа слева |
|||
|
\(8x-8x=12-12\) |
И вновь приводим подобные |
|||
|
\(0=0\) |
Очевидно, что тут “подойдет” любое значение для икса, ведь он никак не влияет на полученное уравнение. |
Опять приводим подобные. |
||
|
\(2x=10\) |
Вот так. Оказывается, исходное уравнение – вполне себе линейное, а иксы в квадрате не более чем ширма, чтоб нас запутать. 🙂 Дорешиваем, деля уравнение на \(2\), и получаем ответ. |
Ответ: \(x=5\)
Пример. Решить линейное уравнение \(\frac{x+2}{2}\) \(-\) \(\frac{1}{3}\) \(=\) \(\frac{9+7x}{6}\)
Решение:
|
\(\frac{x+2}{2}\) \(-\) \(\frac{1}{3}\) \(=\) \(\frac{9+7x}{6}\) |
Уравнение не похоже на линейное, дроби какие-то. |
|
|
\(6\cdot\)\((\frac{x+2}{2}\) \(-\) \(\frac{1}{3})\) \(=\) \(\frac{9+7x}{6}\)\(\cdot 6\) |
Раскрываем скобку слева |
|
|
\(6\cdot\)\(\frac{x+2}{2}\) \(-\) \(6\cdot\)\(\frac{1}{3}\) \(=\) \(\frac{9+7x}{6}\)\(\cdot 6\) |
Теперь сокращаем знаменатели |
|
|
\(3(x+2)-2=9+7x\) |
Вот теперь похоже на обычное линейное! Дорешиваем его. Раскрываем скобки |
|
|
\(3x+6-2=9+7x\) |
Переносом через равно собираем иксы справа, а числа слева |
|
|
\(3x-7x=9-6+2\) |
Приводим подобные слагаемые |
|
|
\(-4x=5\) |
Ну и поделив на \(-4\) правую и левую часть, получаем ответ |
Ответ: \(x=-1,25\)
Смотрите также:
Линейная функция
Решение уравнений умножением
Неизвестная величина может быть связана с известной величиной не только знаком + или -, но может быть разделена на какую-нибудь величину, как в этом уравнении: $\frac{x}{a} = b$.
Здесь решение не может быть найдено, как в предыдущих примерах, переносом члена уравнения. Но если оба члена уравнения умножить на a, уравнение примет вид
$x = ab.$
То есть, знаменатель дроби в левой части сокращается. Это может быть доказано свойствами дробей.
Так, $x = \frac{ax}{a} = \frac{3x}{3} = \frac{(a + b)x}{a + b} = \frac{dx + 5x}{d + 5}$. Для каждого из этих примеров, x умножается и делится на одну и ту же величину, и такое действие не изменяет значения величин. Поэтому,
Когда неизвестная величина разделена на известную величину, уравнение решается путем умножения каждой стороны на эту известную величину.
Те же самые переносы должны быть сделаны в этом случае, как и в предыдущих примерах. Однако надо помнить, что умножать необходимо каждый член уравнения.
Пример 1. Решите уравнение $\frac{x}{c} + a = b + d$
Умножаем обе стороны на $c$
Произведение будет $x + ac = bc + cd$
И $x = bc + cd — ac$.
Пример 1. Решите уравнение $\frac{x}{a+b} + d = h$
Умножаем на $a + b$ $x + ad + bd = ah + bh$.
И $x = ag + bh — ad — bd.$
Когда неизвестное значение находится в знаменателе дроби, уравнение решается похожим способом, то есть умножением уравнения на знаменатель.
Пример 3. Решите уравнение $\frac{6}{10-x} + 7 = 8$
Умножая на $10 — x$ $6 + 70 — 7x = 80 — 8x$
Тогда $x = 4$.
Хотя это и не обязательно, но часто очень удобно избавиться от знаменателя дроби, состоящего только из известных величин. Это можно сделать, похожим способом, когда избавляются от знаменателя, включающего в себя неизвестную величину.
Возьмем для примера $\frac{x}{a} = \frac{d}{b} + \frac{h}{c}$
Умножаем на a $x = \frac{ad}{b} + \frac{ah}{c}$
Умножаем на b $bx = ad + \frac{abh}{c}$
Умножаем на c $bcx = acd + abh$.
Или, мы можем умножить на произведение всех знаменателей сразу.
В этом же самом уравнении $\frac{x}{a} = \frac{d}{b} + \frac{h}{c}$
Умножаем члены на abc $\frac{abcx}{a} = \frac{abcd}{b} + \frac{abch}{c}$
В уравнении можно избавиться от дробей, умножая каждую сторону уравнения на все знаменатели.
При избавлении от дробей в уравнении необходимо соблюдать правильность написания знаков и коэффициентов каждой дроби в процессе раскрытия скобок
Уравнение $\frac{a — d}{x} = c — \frac{3b — 2hm — 6n}{r}$ является
равным этому уравнению $ar — dr = crx -3bx + 2hmx + 6nx$.
Урок 2. Линейные уравнения с одной переменной и дробными свободными членами
Уравнение, у которого коэффициенты всех или некоторых членов – дробные числа, можно заменить равносильным уравнением с целыми коэффициентами (для этого обе две части уравнения надо умножить на наименьшее общее кратное знаменателей дробных коэффициентов).
Уравнение
После умножения обоих его частей на 14 получим
(5х – 4) × 7= (16х + 1) × 2; 35х – 28
= 32х + 2.
Легко убедиться в том, что первое и последнее уравнения имеют один корень х = 10.
Общая схема решения уравнений первой степени.
Пусть необходимо решить уравнение:
Умножим все члены на наименьшее общее кратное знаменателей, которое равно 12. После сокращения получим: 4(х – 4) + 6(х + 1) – 12
= 30(х – 3) + 24х – 2(11х + 43). Чтобы выделить члены, в которых находятся неизвестные и свободные члены, раскроем скобки: 4х – 16 + 6х + 6 –12
= 30х – 90 + 24х – 22х – 86. Сгруппируем в одной части члены, которые содержат неизвестные, а в другой – свободные члены: 4х + 6х – 30х – 24х + 22х
= –90 – 86 + 16 – 6 + 12.
 Приведём подобные члены: Поделим обе части на –22. Получим: Как видим, корень можно найти по такой схеме: – привести уравнение к целому виду; – раскрыть скобки; – сгруппировать члены, которые содержат неизвестные,
в одной части уравнения, а свободные
члены – в другой; – свести подобные члены; – решить уравнение вида ах = b,
которое получили после приведения подобных членов.
Приведём подобные члены: Поделим обе части на –22. Получим: Как видим, корень можно найти по такой схеме: – привести уравнение к целому виду; – раскрыть скобки; – сгруппировать члены, которые содержат неизвестные,
в одной части уравнения, а свободные
члены – в другой; – свести подобные члены; – решить уравнение вида ах = b,
которое получили после приведения подобных членов.Однако эта схема не обязательна для любого уравнения. Во-первых, при решении многих простых уравнений приходится начинать не с первого, а со второго, третьего и может пятого этапу. Во-вторых, некоторые промежуточные этапы могут оказаться ненужными. В-третьих, иногда бывает выгодно для простоты решения нарушить порядок, указанной схемы.
Задания к уроку 2
Другие уроки:
4.7 Решение уравнений с дробями — Предварительная алгебра 2e
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли дробь решением уравнения
- Решите уравнения с дробями, используя свойства сложения, вычитания и деления равенства
- Решите уравнения, используя свойство умножения равенства
- Переведите предложения в уравнения и решите
Будьте готовы 4. 17
17
Прежде чем начать, пройдите этот тест на готовность. Если вы пропустили проблему, вернитесь к указанному разделу и просмотрите материал.
Вычислить x+4x+4, когда x=−3x=−3
Если вы пропустили эту проблему, просмотрите пример 3.23.
Будьте готовы 4.18
Решите: 2y−3=9,2y−3=9.
Если вы пропустили эту проблему, просмотрите пример 3.61.
Будьте готовы 4.19
Решить: y−3=−9y−3=−9
Если вы пропустили эту проблему, просмотрите пример 4.28.
Определить, является ли дробь решением уравнения
Как мы видели в разделе «Решение уравнений со свойствами равенства на вычитание и сложение» и «Решение уравнений с использованием целых чисел»; Свойство деления равенства, решение уравнения — это значение, которое дает истинное утверждение при замене переменной в уравнении. В этих разделах мы нашли целые числа и целые решения уравнений. Теперь, когда мы поработали с дробями, мы готовы найти решения уравнений в виде дробей.
Шаги, которые мы предпринимаем, чтобы определить, является ли число решением уравнения, одинаковы, независимо от того, является ли решение целым числом, целым числом или дробью.
How To
Определить, является ли число решением уравнения.
- Шаг 1. Подставьте число вместо переменной в уравнении.
- Шаг 2. Упростите выражения в обеих частях уравнения.
- Шаг 3. Определить, верно ли полученное уравнение. Если это правда, число является решением.Если это не так, число не является решением.
Пример 4.95
Определите, является ли каждое из следующих решений решением x−310=12.x−310=12.
- ⓐx=1x=1
- ⓑх=45х=45
- ⓒx=−45x=−45
Решение
Поскольку x=1x=1 не дает истинного уравнения, 11 не является решением уравнения.
Поскольку x=45x=45 дает истинное уравнение, 4545 является решением уравнения x−310=12.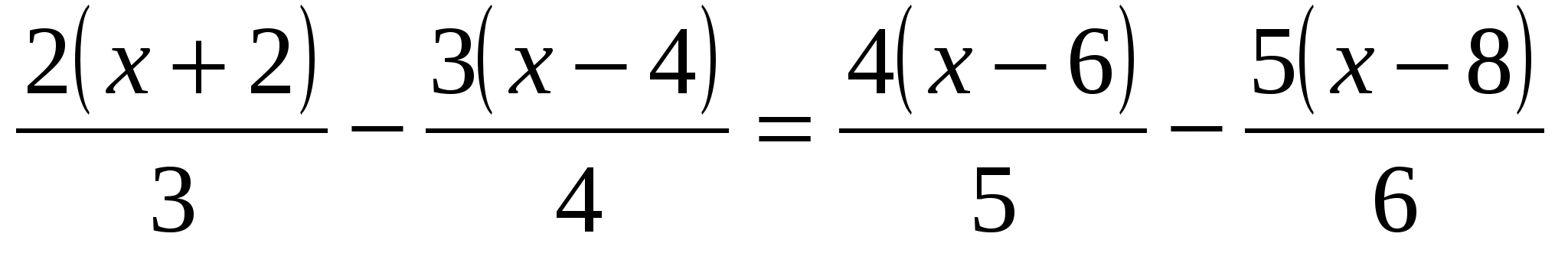 x−310=12.
x−310=12.
Поскольку x=−45x=−45 не дает истинного уравнения, −45−45 не является решением уравнения.
Попробуйте 4.189
Определите, является ли каждое число решением данного уравнения.
х-23=16х-23=16:
- ⓐx=1x=1
- ⓑх=56х=56
- ⓒx=-56x=-56
Попробуйте 4.190
Определите, является ли каждое число решением данного уравнения.
г-14=38г-14=38:
- ⓐy=1y=1
- ⓑу=-58у=-58
- ⓒy=58y=58
Решите уравнения с дробями, используя свойства сложения, вычитания и деления равенства
В Решать уравнения со свойствами вычитания и сложения равенства и Решать уравнения, используя целые числа; Свойство деления равенства, мы решали уравнения, используя свойства равенства сложения, вычитания и деления.Мы будем использовать эти же свойства для решения уравнений с дробями.
Свойства равенства сложения, вычитания и деления
Для любых чисел a,b,a,b и c,c,
Таблица 4.3
Другими словами, когда вы прибавляете или вычитаете одну и ту же величину из обеих частей уравнения или делите обе части на одну и ту же величину, вы все равно получаете равенство.
Пример 4.96
Решите: у+916=516.у+916=516.
Решение
Поскольку y=−14y=−14 делает y+916=516y+916=516 верным утверждением, мы знаем, что нашли решение этого уравнения.
Попробуйте 4.191
Решите: у+1112=512.у+1112=512.
Попробуйте 4.192
Решите: у+815=415.у+815=415.
Мы использовали свойство равенства вычитания в примере 4. 96. Теперь воспользуемся дополнительным свойством равенства.
96. Теперь воспользуемся дополнительным свойством равенства.
Пример 4.97
Решите: a−59=−89.a−59=−89.
Решение
Поскольку a=-13a=-13 делает уравнение верным, мы знаем, что a=-13a=-13 является решением уравнения.
Попробуйте 4.193
Решите: a−35=−85.a−35=−85.
Попробуйте 4.194
Решите: n−37=−97.п-37=-97.
Может показаться, что в следующем примере нет дроби, но давайте посмотрим, что произойдет, когда мы решим его.
Пример 4.98
Решение
| 10q=4410q=44 | ||
| Разделите обе части на 10, чтобы отменить умножение. | 10q10=441010q10=4410 | |
| Упрощение. | q=225q=225 | |
| Чек: | ||
Подставьте q=225q=225 в исходное уравнение. | 10(225)=?4410(225)=?44 | |
| Упрощение. | 102(225)=?44102(225)=?44 | |
| Умножить. | 44=44✓44=44✓ | |
Решением уравнения была дробь 225,225. Оставляем как неправильную дробь.
Попробуйте 4.195
Решите: 12u=-76.12u=-76.
Решение уравнений с дробями с использованием свойства умножения равенства
Рассмотрим уравнение x4=3.х4=3. Мы хотим знать, какое число, деленное на 44, дает 3,3. Итак, чтобы «отменить» деление, нам нужно будет умножить на 4,4. Свойство умножения на равенство позволит нам сделать это. Это свойство говорит о том, что если мы начнем с двух равных величин и умножим их на одно и то же число, результаты будут равны.
Свойство равенства умножения
Для любых чисел a,b,a,b и c,c,
еслиa=b,thenac=bc. ifa=b,thenac=bc.
ifa=b,thenac=bc.Если вы умножите обе части уравнения на одно и то же число, вы все равно получите равенство.
Давайте воспользуемся свойством умножения равенства, чтобы решить уравнение x7=−9.x7=−9.
Попробуйте 4.197
Решите: f5=−25.f5=−25.
Попробуйте 4.198
Решите: h9=-27.h9=-27.
Пример 4.100
Решите: p−8=−40.p−8=−40.
Решение
Здесь pp делится на −8,−8. Мы должны умножить на −8−8, чтобы выделить pp.
Попробуйте 4.199
Решите: c−7=−35.c−7=−35.
Попробуйте 4.200
Решите: x−11=−12.x−11=−12.
Решение уравнений с коэффициентом −1−1
Посмотрите на уравнение −y=15.−y=15. Похоже, что yy уже изолирован? Но перед y,y стоит знак минус, поэтому он не изолирован.
Существует три различных способа выделения переменной в уравнении этого типа. Мы покажем все три способа в примере 4. 101.
101.
Попробуйте 4.202
Решите: −c=−23.−c=−23.
Решение уравнений с дробным коэффициентом
Когда у нас есть уравнение с коэффициентом дроби, мы можем использовать свойство равенства умножения, чтобы сделать коэффициент равным 1.1.
Например, в уравнении:
Коэффициент xx равен 34,34. Чтобы найти x,x, нам нужно, чтобы его коэффициент был равен 1,1. Поскольку произведение числа и его обратного числа равно 1,1, наша стратегия здесь будет состоять в том, чтобы изолировать xx путем умножения на обратное число 34,34. Мы сделаем это в примере 4.102.
Пример 4.102
Решение
Обратите внимание, что в уравнении 34x=24,34x=24 мы могли бы разделить обе части на 3434, чтобы получить xx отдельно.Деление — это то же самое, что и умножение на обратное, поэтому мы получим тот же результат. Но большинство людей согласны с тем, что умножать на обратное проще.
Пример 4.103
Решите: −38w=72.−38w=72.
Решение
Коэффициент представляет собой отрицательную дробь. Помните, что число и его обратная величина имеют один и тот же знак, поэтому обратная величина коэффициента также должна быть отрицательной.
Попробуйте 4.205
Решите: −47a=52.−47а=52.
Попробуйте 4.206
Решите: −79w=84.−79w=84.
Перевести предложения в уравнения и решить
Теперь мы рассмотрели все четыре свойства равенства — вычитание, сложение, деление и умножение. Мы перечислим их все вместе здесь для удобства.
| Свойство равенства вычитания: Для любых действительных чисел a, b, a, b и c, c, , если a=b,a=b, то a−c=b−ca−c =б-в. | Дополнительное свойство равенства: Для любых действительных чисел a, b, a, b и c, c, , если a=b,a=b, то a+c=b+c.  а+с=б+с. а+с=б+с. |
| Свойство равенства деления: Для любых чисел a, b, a, b и c, c, где c≠0c≠0 если a=b,a=b, то ac=bcac=bc | Свойство равенства умножения: Для любых действительных чисел a, b, a, b и cc Если a=b,a=b, то ac=bcac=bc |
Когда вы складываете, вычитаете, умножаете или делите одну и ту же величину из обеих частей уравнения, вы все равно получаете равенство.
В следующих нескольких примерах мы будем переводить предложения в уравнения, а затем решать уравнения.Может быть полезно просмотреть таблицу перевода в разделе Вычислить, упростить и перевести выражения.
Пример 4.104
Переведите и решите: nn разделить на 66 равно −24,−24.
Попробуйте 4.207
Переведите и решите: nn разделить на 77 равно -21,-21.
Попробуйте 4. 208
208
Переведите и решите: nn разделить на 88 равно −56,−56.
Пример 4.105
Переведите и решите: Частное qq и −5−5 равно 70.70.
Попробуйте 4.209
Переведите и решите: Частное qq и −8−8 равно 72,72.
Попробуйте 4.210
Переведите и решите: Частное pp и −9−9 равно 81,81.
Пример 4.106
Переведите и решите: Две трети ff равны 18,18.
Попробуйте 4.211
Переведите и решите: Две пятых от ff равно 16,16.
Попробуйте 4.212
Переведите и решите: Три четверти ff равно 21,21.
Пример 4.107
Переведите и решите: Частное мм и 5656 равно 34,34.
Решение
| Частное мм и 5656 равно 3434. | ||
| Перевести. | m56=34m56=34 | |
Умножьте обе стороны на 5656, чтобы получить мм. | 56(m56)=56(34)56(m56)=56(34) | |
| Упрощение. | m=5·36·4m=5·36·4 | |
| Удалить общие множители и умножить. | м=58м=58 | |
| Проверить: | ||
| Является ли частное 5858 и 5656 равным 3434? | 5856=?345856=?34 | |
| Переписать как деление. | 58÷56=?3458÷56=?34 | |
| Умножьте первую дробь на обратную вторую. | 58·65=?3458·65=?34 | |
| Упростить. | 34=34✓34=34✓ | |
Наше решение проверяет.
Попробуйте 4.213
Переведи и реши. Частное nn и 2323 равно 512,512.
Попробуйте 4.214
Переведи и реши Частное cc и 3838 равно 49,49.
Пример 4.108
Переведи и реши: Сумма трех восьмых и xx равна трем с половиной.
Решение
Мы записываем ответ как смешанное число, потому что в исходной задаче использовалось смешанное число.
Проверить:
Является ли сумма трех восьмых и 318318 равной трем с половиной?
| 38+318=?31238+318=?312 | |
| Доп. | 348=?312348=?312 |
| Упрощение. | 312=312✓312=312✓ |
Проверка решения.
Попробуйте 4.215
Переведите и решите: Сумма пяти восьмых и xx равна одной четвертой.
Попробуйте 4.216
Переведите и решите: Разница между одной и тремя четвертыми и xx составляет пять шестых.
Раздел 4.7 Упражнения
Практика ведет к совершенству
Определите, является ли дробь решением уравнения
В следующих упражнениях определите, является ли каждое число решением данного уравнения.
498.х-25=110х-25=110:
- ⓐx=1x=1
- ⓑх=12х=12
- ⓒx=−12x=−12

г-13=512г-13=512:
- ⓐy=1y=1
- ⓑу=34у=34
- ⓒу=-34у=-34
ч+34=25ч+34=25:
- ⓐ ч=1ч=1
- ⓑ В=720В=720
- ⓒ ч=-720ч=-720
к+25=56к+25=56:
- ⓐk=1k=1
- ⓑк=1330к=1330
- ⓒk=-1330k=-1330
Решите уравнения с дробями, используя свойства сложения, вычитания и деления равенства
В следующих упражнениях решите.
508.х-(-320)=-1120х-(-320)=-1120
509.z-(-512)=-712z-(-512)=-712
512.с+(-12)=-89с+(-12)=-89
513.к+(-13)=-45к+(-13)=-45
Решите уравнения с дробями, используя свойство равенства умножения
В следующих упражнениях решите.
536.−611u=−24−611u=−24
537.−512В=−15−512В=−15
Смешанная практика
В следующих упражнениях решите.
Превратите предложения в уравнения и решите
В следующих упражнениях переведите в алгебраическое уравнение и решите.
550.nn разделить на восемь равно −16,−16.
551.nn разделить на шесть равно −24,−24.
552.мм разделить на −9−9 равно −7,−7.
553.мм разделить на −7−7 равно −8,−8.
554.Частное ff и −3−3 равно −18,−18.
555.Частное ff и −4−4 равно −20,−20.
556.Частное gg и двенадцать равно 8,8.
557.Частное gg и девять равно 14,14.
558.Три четверти qq равно 12,12.
559.Две пятых qq равны 20,20.
560.Семь десятых pp равны −63,−63.
561.Четыре девятых pp равны −28,−28.
562.мм разделить на 44 равно минус 6,6.
563.Частное чч и 22 равно 43,43.
564.Три четверти zz — это 15,15.
565.Частное аа и 2323 равно 34,34.
566. Сумма пяти шестых и xx равна 12,12.
Сумма трех четвертых и xx равна 18,18.
568.Разница между yy и одной четвертой составляет −18,−18.
569.Разница yy и одной трети составляет −16,−16.
Математика на каждый день
570.Покупки Тереза купила пару туфель на распродаже за 48 долларов 48 долларов. Цена продажи составила 2323 от обычной цены. Найдите обычную цену обуви, решив уравнение 23p=4823p=48
. 571.Игровой домик Стол в детском игровом домике размером 3535 от взрослого стола. Стол для игрового домика имеет высоту 1818 дюймов. Найдите высоту стола для взрослых, решив уравнение 35h=18,35h=18.
Письменные упражнения
572.Пример 4.100 описывает три метода решения уравнения −y=15.−y=15. Какой метод вы предпочитаете? Почему?
573. Ричард считает, что решение уравнения 34x=2434x=24 равно 16,16. Объясните, почему Ричард ошибается.
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
ⓑ В целом, после просмотра контрольного списка, как вы думаете, хорошо ли вы подготовились к следующей главе? Почему или почему нет?
Решение многошаговых линейных уравнений | Пурпурная математика
Пурпурная математика
На предыдущих двух страницах мы рассмотрели решение одношаговых линейных уравнений; то есть уравнения, требующие одного сложения или вычитания или требующие одного умножения или деления.Однако для решения большинства линейных уравнений требуется более одного шага. Какие шаги следует использовать и в каком порядке?
Для многошаговых линейных уравнений мы будем использовать те же шаги, что и раньше; единственная разница в том, что мы не закончим после одного шага. Нам все равно придется сделать как минимум еще один шаг. В каком порядке следует выполнять эти действия? Что ж, это будет варьироваться в зависимости от уравнения, но есть некоторые общие рекомендации, которые могут оказаться полезными.
Нам все равно придется сделать как минимум еще один шаг. В каком порядке следует выполнять эти действия? Что ж, это будет варьироваться в зависимости от уравнения, но есть некоторые общие рекомендации, которые могут оказаться полезными.
MathHelp.com
Переменная находится в левой части (LHS) уравнения.В настоящее время оно умножается на семь, а затем к нему прибавляется двойка. Мне нужно отменить «умножить на семь» и «плюс два».
Нет правила о том, какую операцию «отменить» я должен выполнить в первую очередь. Однако, если я сначала разделю на 7, я обязательно создам дроби. Лично я предпочитаю избегать дробей, если это возможно, поэтому я почти всегда делаю плюс/минус перед каждым разом/делением. Возможно, мне все равно придется иметь дело с дробями, но, по крайней мере, я могу отложить их ближе к концу моей работы.
Однако, если я сначала разделю на 7, я обязательно создам дроби. Лично я предпочитаю избегать дробей, если это возможно, поэтому я почти всегда делаю плюс/минус перед каждым разом/делением. Возможно, мне все равно придется иметь дело с дробями, но, по крайней мере, я могу отложить их ближе к концу моей работы.
Начиная с «плюс два», я вычитаю два из каждой части уравнения. Только тогда я разделю на семь. Моя работа выглядит так:
7x + 2 = -54
-2 -2
————
7x = -56
—
7 7
х = -8
Выполнив сначала плюс/минус, я избежал дробей.Как видите, в ответе нет дробей, поэтому я сделал себе одолжение, выполнив деление в последнюю очередь. Мое решение:
По моему опыту форматирование домашней работы и демонстрация работы в том виде, в котором я сделал это выше, вполне приемлемо для всех. Однако (предупреждение!), неплохо было бы также четко переписать свой окончательный ответ в конце каждого упражнения, как показано (выделено фиолетовым цветом) выше. Не ожидайте, что ваш оценщик потратит время на то, чтобы копаться в вашей работе и пытаться выяснить, что вы, вероятно, имели в виду в своем ответе.Отформатируйте свою работу так, чтобы смысл был понятен.
Однако (предупреждение!), неплохо было бы также четко переписать свой окончательный ответ в конце каждого упражнения, как показано (выделено фиолетовым цветом) выше. Не ожидайте, что ваш оценщик потратит время на то, чтобы копаться в вашей работе и пытаться выяснить, что вы, вероятно, имели в виду в своем ответе.Отформатируйте свою работу так, чтобы смысл был понятен.
В этом уравнении переменная (в левой части) умножается на минус пять, а затем из нее вычитается семь. В надежде (как всегда!) избежать дробей, я сначала добавлю семь к любой части уравнения. Только тогда я разделю на минус пять. Моя работа выглядит так:
-5x — 7 = 108
+7 +7
————-
-5x = 115
— —
-5 -5
х = -23
Я аккуратно показал свою работу.Теперь четко перепишу свое решение в конце работы:
Переменная (в левой части уравнения) умножается на три, а затем из нее вычитается девять. Я позабочусь сначала о девятке, а потом о троих:
Я позабочусь сначала о девятке, а потом о троих:
3x — 9 = 33
+9 +9
————
3x = 42
— —
3 3
х = 14
В этом случае, опять же, в моем решении нет дробей:
В этом уравнении в левой части есть два члена, которые содержат переменные.Итак, мой первый шаг — объединить эти «подобные термины» слева. Тогда я могу решить:
Итак, теперь мое уравнение:
Хотя поначалу оно могло показаться более сложным, на самом деле это уравнение, состоящее из одного шага. Я решу делением на двенадцать:
12х = 72
— —
12 12
х = 6
Мой ответ:
В этом уравнении у меня есть члены с переменными по обе стороны уравнения. Чтобы решить, мне нужно получить все эти переменные члены на одной стороне уравнения.
Чтобы решить, мне нужно получить все эти переменные члены на одной стороне уравнения.
Нет правила, говорящего, какой из двух членов я должен переместить, 4 x или 6 x . Однако по опыту я узнал, что, чтобы избежать отрицательных коэффициентов для моих переменных, я должен переместить член x с меньшим коэффициентом. Это означает, что в данном случае я вычту 4 x из левой части в правую:
4x — 6 = 6x
-4x -4x
————-
-6 = 2x
Теперь у меня есть одношаговое уравнение, которое я решу делением на два:
Мое решение:
В приведенном выше упражнении переменная (в моей работе) оказалась в правой части уравнения.Это совершенно нормально. Переменная не «требуется» оказаться в левой части уравнения; мы просто привыкли видеть его там. Таким образом, результат «–3 = 90 741 x 90 235» вполне приемлем и означает то же самое, что и « x = –3».
Таким образом, результат «–3 = 90 741 x 90 235» вполне приемлем и означает то же самое, что и « x = –3».
Однако (внимание!), я слышал, что некоторые преподаватели настаивают на том, чтобы переменная располагалась в левой части уравнения в окончательном ответе . (Нет, я не выдумываю.) Так что, несмотря на то, что «–3 = x » вполне допустимо в работе, эти инструкторы сочтут это «неправильным», если вы оставите ответ таким образом.Если у вас есть какие-либо сомнения относительно настроек форматирования вашего преподавателя, спросите сейчас.
Решить 8
x – 1 = 23 – 4 x
В этом уравнении у меня есть переменные по обе стороны уравнения, а также случайные числа по обе стороны. Мне нужно получить переменные термины с одной стороны и свободные числа с другой стороны. Поскольку я хотел бы избежать отрицательных коэффициентов для моих переменных, я буду перемещать меньшее из двух условий; а именно -4 x , который в настоящее время находится справа. Чтобы получить свободные числа на стороне, противоположной переменным терминам, я буду перемещать -1, которая в настоящее время находится слева. Для выполнения этих шагов не существует определенного «правильного» порядка; поскольку они оба связаны с добавлением, люди обычно делают их вместе за один шаг. Сначала я сделаю переменные члены, а затем свободные числа:
Поскольку я хотел бы избежать отрицательных коэффициентов для моих переменных, я буду перемещать меньшее из двух условий; а именно -4 x , который в настоящее время находится справа. Чтобы получить свободные числа на стороне, противоположной переменным терминам, я буду перемещать -1, которая в настоящее время находится слева. Для выполнения этих шагов не существует определенного «правильного» порядка; поскольку они оба связаны с добавлением, люди обычно делают их вместе за один шаг. Сначала я сделаю переменные члены, а затем свободные числа:
8х — 1 = 23 — 4х
+4x +4x
——————
12х — 1 = 23
+1 +1
————
12х = 24
На данный момент у меня есть одношаговое уравнение, для решения которого требуется одно деление:
12х = 24
— —
12 12
х = 2
Тогда мой ответ:
Если бы в приведенном выше примере я сделал первые два шага за один раз, это выглядело бы так:
8х — 1 = 23 — 4х
+4x +1 +1 +4x
——————
12х = 24
— —
12 12
х = 2
Возможно, когда вы только начинаете, лучше делать каждый шаг отдельно. Но как только вы освоитесь с процессом (и надежно получите правильные значения), не стесняйтесь начинать комбинировать некоторые шаги.
Но как только вы освоитесь с процессом (и надежно получите правильные значения), не стесняйтесь начинать комбинировать некоторые шаги.
Решить 5 + 4
x – 7 = 4 x – 2 – x
Это уравнение запутано во всех смыслах! Прежде чем я смогу решить, мне нужно объединить одинаковые члены с обеих сторон уравнения:
5 + 4 x – 7 = 4 x – 2 – x
(5 – 7) + 4 х = (4 х – 1 х ) – 2
–2 + 4 х = 3 х – 2
Теперь, когда я упростил каждую часть уравнения, я могу заняться решением.
-2 + 4х = 3х — 2
-3x -3x
——————
-2 + 1x = -2
+2 +2
——————
1x = 0
Я добавил (обычно не указанную) 1 к переменному члену в правой части исходного уравнения, чтобы помочь мне следить за тем, что я делаю; это не «необходимо».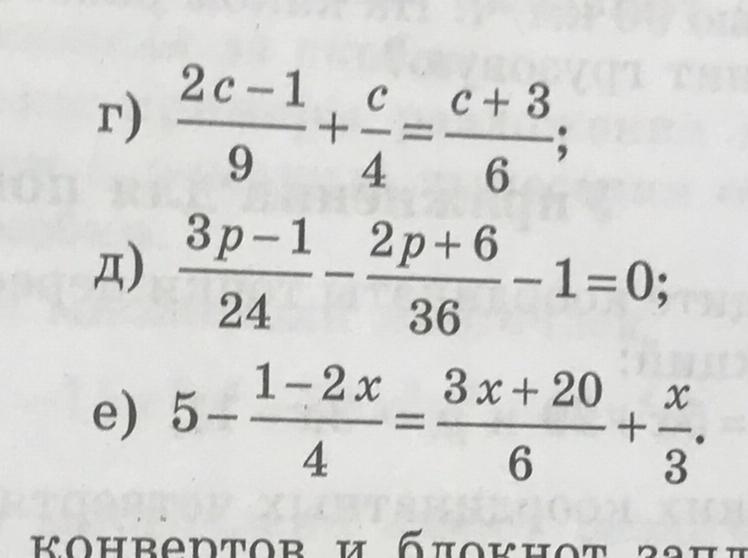 И это не ожидается в окончательном ответе, который правильно указан как:
И это не ожидается в окончательном ответе, который правильно указан как:
Для x совершенно нормально иметь нулевое значение.Ноль является допустимым решением. Не говорите, что это уравнение «не имеет решения»; у него действительно есть решение, и это решение равно x = 0,
.Решить 0,2
x + 0,9 = 0,3 – 0,1 x
Это уравнение решается так же, как и все другие линейные уравнения, которые я решал. Просто выглядит на хуже из-за десятичных знаков.Но это легко исправить!
Каким бы ни было наибольшее количество знаков после запятой в любом из коэффициентов, я могу умножить с обеих сторон на «1», за которым следует это количество нулей. В этом случае все десятичные дроби имеют один десятичный разряд, поэтому я умножу на 10:
10(0,2 х + 0,9) = 10(0,3 – 0,1 х )
10(0,2 х ) + 10(0,9) = 10(0,3) – 10(0,1 х )
2 х + 9 = 3 – 1 х
Теперь я могу решить как обычно:
2x + 9 = 3 — 1x
+1x +1x
——————
3x + 9 = 3
-9 -9
————
3x = -6
— —
3 3
х = -2
То, что в исходном уравнении были десятичные разряды, не означает, что я застрял с ними. Отложите этот трюк на потом; это пригодится.
Отложите этот трюк на потом; это пригодится.
Между прочим, если бы коэффициент с наибольшим количеством знаков после запятой имел два знака после запятой , то я бы умножил обе части уравнения на 100; для трех знаков после запятой я бы умножил на 1000; и так далее.
Решить
Ик! Фракции! Но, как и с десятичными знаками в предыдущем упражнении, мне не нужно зацикливаться на дробях.В этом случае я буду умножать, чтобы «очистить» знаменатели, что даст мне более красивое уравнение для решения.
Чтобы упростить вычисления для уравнений с дробями, я сначала умножу обе части на общий знаменатель различных дробей. У этого уравнения общий знаменатель равен 12, поэтому я умножу все на 12 (или, при умножении на дробь, умножу на
12/1): Теперь с этим уравнением работать намного удобнее. Я продолжу свое решение, вычитая меньшие 2 x с обеих сторон:
Я продолжу свое решение, вычитая меньшие 2 x с обеих сторон:
3x + 12 = 2x + 6
-2x -2x
——————
1x + 12 = 6
-12 -12
——————
1x = -6
Я уберу 1 из переменной, когда напишу свой окончательный ответ:
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении многоэтапного линейного уравнения.Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустить виджет и продолжить урок.)
(Нажав «Нажмите, чтобы просмотреть шаги» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления.)
URL-адрес: https://www. purplemath.com/modules/solvelin3.htm
purplemath.com/modules/solvelin3.htm
| Начальная алгебра Урок 14. Решение линейных уравнений
Цели обучения
Введение
Учебник
Практические задачи
Нужна дополнительная помощь по этим темам?
|
Решение линейных уравнений: часть II
Алгебра позволяет нам решать целые классы приложений, используя буквальные уравнения. Формула, которая суммирует целые классы задач или формул. Формулы часто имеют более одной переменной и описывают или моделируют конкретную реальную проблему. Например, известная формула D=rt описывает пройденное расстояние в терминах средней скорости и времени; зная любые две из этих величин, мы можем определить третью.Используя алгебру, мы можем решить уравнение для любой из переменных и вывести еще две формулы.
Например, известная формула D=rt описывает пройденное расстояние в терминах средней скорости и времени; зная любые две из этих величин, мы можем определить третью.Используя алгебру, мы можем решить уравнение для любой из переменных и вывести еще две формулы.
Если мы разделим обе части на r , то получим формулу t=Dr. Используйте эту формулу, чтобы найти время, учитывая расстояние и скорость.
Если обе части разделить на t , то получим формулу r=Dt. Используйте эту формулу, чтобы найти скорость, учитывая пройденное расстояние и время, необходимое для преодоления этого расстояния. Используя методы, изученные до этого момента, мы теперь имеем три эквивалентные формулы, связывающие расстояние, среднюю скорость и время:
Когда задано буквальное уравнение, часто необходимо решить для одной из переменных через другие.Используйте свойства равенства, чтобы изолировать указанную переменную.
Пример 9: Решите для a : P=2a+b.
Решение: Цель состоит в том, чтобы изолировать переменную a .
Пример 10: Решите для y : z=x+y2.
Решение: Цель состоит в том, чтобы изолировать переменную y .
Попробуйте! Решите для b : 2a−3b=c.
Тематические упражнения
Часть A: Поиск решений
Является ли данное значение решением линейного уравнения?
1.2(3x+5)−6=3x−8; х=−4
2. -х+17-8х=9-х; х=-1
3. 4(3x−7)−3(x+2)=−1; х=13
4. −5−2(x−5)=−(x+3); х=-8
5. 7−2(12x−6)=x−1; х=10
6. 3x−23(9x−2)=0; х=49
Часть B: Решение линейных уравнений
Решить.
7. 4x−7=7x+5
8. −5x+3=−8x−9
9. 3х-5=2х-17
3х-5=2х-17
10.−2y−52=3y+13
11. −4x+2=7x−20
12. 4x−3=6x−15
13. 9x−25=12x−25
14. 12г+15=-6г+23
15. 1,2x−0,7=3x+4,7
16. 2,1х+6,1=-1,3х+4,4
17. 2,02x+4,8=14,782−1,2x
18. −3,6x+5,5+8,2x=6,5+4,6x
19. 12x−23=x+15
20. 13x−12=−14x−13
21.−110 лет + 25 = 15 лет + 310
22. х-203=52х+56
23. 23г+12=58г+3724
24. 13+43х=107х+13-221х
25. 89-1118х=76-12х
26. 13−9x=49+12x
27. 12x−5+9x=44
28. 10−6x−13=12
29. −2+4x+9=7x+8−2x
30. 20x−5+12x=6−x+7
31. 3а+5-а=2а+7
32. −7b+3=2−5b+1−2b
33.7x−2+3x=4+2x−2
34. −3x+8−4x+2=10
−3x+8−4x+2=10
35. 6х+2-3х=-2х-13
36. 3x−0,75+0,21x=1,24x+7,13
37. -х-2+4х=5+3х-7
38. −2y−5=8y−6−10y
39. 110x−13=130−115x−715
40. 58−43x+13=−39x−14+13x
Часть C. Решение линейных уравнений с использованием скобок
Решить.
41.−5(2y−3)+2=12
42. 3(5x+4)+5x=−8
43. 4−2(x−5)=−2
44. 10−5(3x+1)=5(x−4)
45. 9−(x+7)=2(x−1)
46. −5(2x−1)+3=−12
47. 3x−2(x+1)=x+5
48. 5x−3(2x−1)=2(x−3)
49. −6(x−1)−3x=3(x+8)
50. −35(5x+10)=12(4x−12)
51. 3.1(2x−3)+0.5=22.2
52.4.22−3.13(x−1)=5.2(2x+1)−11.38
53. 6(x−2)−(7x−12)=14
54. −9(x−3)−3x=−3(4x+9)
−9(x−3)−3x=−3(4x+9)
55. 3−2(x+4)=−3(4x−5)
56. 12−2(2x+1)=4(x−1)
57. 3(x+5)−2(2x+3)=7x+9
58. 3(2x−1)−4(3x−2)=−5x+10
59. −3(2a−3)+2=3(a+7)
60. −2(5x−3)−1=5(−2x+1)
61. 12(2x+1)−14(8x+2)=3(x−4)
62.−23(6x−3)−12=32(4x+1)
63. 12(3x−1)+13(2x−5)=0
64. 13(х-2)+15=19(3х+3)
65. −2(2x−7)−(x+3)=6(x−1)
66. 10(3x+5)−5(4x+2)=2(5x+20)
67. 2(x−3)−6(2x+1)=−5(2x−4)
68. 5(х-2)-(4х-1)=-2(3-х)
69. 6(3x−2)−(12x−1)+4=0
70. −3(4x−2)−(9x+3)−6x=0
Часть D: Буквенные уравнения
Найдите указанную переменную.
71. Найдите w : A=l⋅w.
72. Найдите и : F=ma.
73. Решите для w : P=2l+2w.
74. Найдите r : C=2πr.
75. Решите для b : P=a+b+c.
76. Решите для C : F=95C+32.
77. Решите для ч : A=12bh.
78.Решите для t : I=Prt.
79. Найдите y : ax+by=c.
80. Решите для ч : S=2πr2+2πrh.
81. Найдите x : z=2x+y5.
82. Решите для c : a=3b−2c3.
83. Решите для b : y=mx+b.
84. Решите для м : y=mx+b.
85. Найдите y : 3x−2y=6.
86. Найдите y : −5x+2y=12.
87. Найдите y : x3−y5=1.
88. Найдите y : 34x−15y=12.
Переведите следующие предложения в линейные уравнения и затем решите.
89. Сумма 3 х и 5 равна сумме 2 х и 7.
90. Сумма −5 x и 6 равна разности 4 x и 2.
91. Разность 5 х и 25 равна разнице 3 х и 51.
92. Сумма 12х и 34 равна 23х.
93. Число n , деленное на 5, равно сумме удвоенного числа и 3.
94. Отрицательное десятикратное число n равно сумме трехкратного числа и 13.
Часть E: Темы форума
95.Каково происхождение слова алгебра ?
96. Что считается основным делом алгебры?
97. Почему решение уравнений является такой важной темой алгебры?
98. Разместите несколько реальных линейных формул, не представленных в этом разделе.
99. Исследуйте и обсудите вклад Диофанта Александрийского.
100. Создайте свою собственную идентичность или противоречие и поделитесь на доске обсуждений.Предложите решение и объясните, как вы его нашли.
Создайте свою собственную идентичность или противоречие и поделитесь на доске обсуждений.Предложите решение и объясните, как вы его нашли.
Как решать одношаговые уравнения с дробями
Шаги для решения
Когда дело доходит до решения одношаговых уравнений, количество шагов, которое мы делаем, соответствует числу, которое следует из названия — один! Одношаговые уравнения — это уравнения, которые включают сложение, вычитание, умножение или деление обеих частей уравнения на одно и то же число, переменную или член, чтобы выделить и найти переменную.
Мы видим, что для решения одношаговых уравнений мы просто складываем, вычитаем, умножаем или делим одно и то же число с обеих сторон, чтобы найти неизвестную переменную. Поэтому, чтобы решить одношаговые уравнения с дробями, нам просто нужно знать, как складывать, вычитать, умножать и делить дроби, поэтому давайте быстро освежим в памяти правила этих операций над дробями.
Чтобы сложить или вычесть дроби, находим общий знаменатель, складываем или вычитаем числители, а затем упрощаем результат.Мы можем использовать следующее правило для сложения или вычитания дробей.
Удивительно, но умножать и делить дроби проще, чем складывать и вычитать дроби, особенно умножать дроби. Чтобы умножить дроби, мы просто умножаем числители, умножаем знаменатели, а затем упрощаем результат.
Довольно просто, не так ли? Наконец, чтобы разделить дроби, мы просто превращаем это в задачу умножения, умножая числитель на обратную величину знаменателя, где , обратная дроби, получается путем замены числителя и знаменателя местами.
Хорошо, теперь, когда мы освежили в памяти выполнение арифметических операций с дробями, мы можем решать одношаговые уравнения с дробями за один шаг. То есть изолируйте переменную в одной части уравнения, добавляя, вычитая, умножая или разделяя дробь из обеих частей уравнения. Чтобы определить, какую операцию использовать, мы просто используем операцию, противоположную той, которая используется в исходном уравнении.Следующая таблица иллюстрирует эту концепцию.
То есть изолируйте переменную в одной части уравнения, добавляя, вычитая, умножая или разделяя дробь из обеих частей уравнения. Чтобы определить, какую операцию использовать, мы просто используем операцию, противоположную той, которая используется в исходном уравнении.Следующая таблица иллюстрирует эту концепцию.
Одновременные уравнения с дробями — Math Central
Алика,
Я переписал ваш вопрос сюда:
Первое, что я сделал бы, это преобразовал бы любые смешанные дроби в неправильные дроби, а затем умножил бы одно из уравнений на некоторый коэффициент так, чтобы один из членов был отрицательным значением соответствующего члена в другом уравнении. В этом случае я бы умножил первое уравнение на -1/4, чтобы оно имело член — x /12, который является отрицательным членом x /12 во втором уравнении:
Теперь я могу устранить члены x , сложив вместе соответствующие стороны уравнения. Я добавляю две левые стороны и две правые стороны:
Я добавляю две левые стороны и две правые стороны:
Когда я переделаю это, условия x отменяются.
Теперь я могу найти и . Затем я могу использовать значение y , чтобы найти х , используя любое из исходных уравнений.
Надеюсь, это поможет,
Стивен Ла Рок.
Привет Алика,
Это система, которую вы хотите решить путем исключения:
Работать с уравнениями, содержащими дроби, может быть сложно, так почему бы нам не изменить их, чтобы избавиться от дробей?
Из предыдущего математического опыта вы должны знать, что можно выполнять любые операции с обеими частями уравнения и при этом сохранять равенство.Например, я могу умножить обе части уравнения 5 = 5 на 2, чтобы получить 10 = 10.
Давайте воспользуемся этим свойством, чтобы упростить первое уравнение в вашей системе:
Чтобы исключить дроби, нам нужно умножить обе части уравнения на наименьшее общее кратное знаменателей (3, 6 и 3) — в данном случае 6.
Распределяя 6 и упрощая, получаем:
Как видите, с этим уравнением работать намного проще, чем с исходным.
Выполните ту же процедуру для второго уравнения, только начните с преобразования смешанного числа в неправильную дробь:
Умножение на наименьшее общее кратное знаменателей, 12
Теперь система уравнений была преобразована во что-то похожее на это:
2х — у = -4
х — 3г = 18
Вы сможете решить ее отсюда.Просто примените метод исключения к новой системе, и вы получите ответ.
Примечание. Когда вы проверяете свой ответ на этот тип вопроса, используйте исходную систему, чтобы убедиться, что при исключении дробей не было допущено математических ошибок.
Эшли
Решение линейных уравнений с простыми алгебраическими дробями (10) – AlamandaMaths
[полная ширина background_color = «» background_image = «» background_parallax = «нет» enable_mobile = «нет» parallax_speed = «0. 3″ background_repeat=”без повтора” background_position=”слева вверху” video_url=”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0.5 ″ video_mute=”да” video_loop=”да” исчезает=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сотня_процентов = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor =»» класс =»» id = »»][fusion_text]
3″ background_repeat=”без повтора” background_position=”слева вверху” video_url=”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0.5 ″ video_mute=”да” video_loop=”да” исчезает=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сотня_процентов = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor =»» класс =»» id = »»][fusion_text]
Решение линейных уравнений с использованием простых алгебраических дробей (VCMNA340)
[/fusion_text][fusion_text] LO: Для решения линейных уравнений с простыми алгебраическими дробями.
Знать:
- Что такое линейное уравнение.
- Что означает знак «=».
- Для сложения дробей с разными знаменателями.
- Собрать похожие термины.
- Для выполнения 4 операций с алгебраическими выражениями.

Понять:
- Что линейные уравнения должны быть уравновешены с обеих сторон, и процесс решения линейных уравнений заключается в поиске пропущенного значения, которое уравновешивает обе части уравнения.
Сделать:
- Я могу решать простые линейные уравнения с простыми алгебраическими дробями.
[/fusion_text][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0,3″ background_repeat=”no-repeat” background_position=”left top” video_url= ”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0.5″ video_mute=”yes” video_loop=”yes” fade=”no” border_size =”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сто_процентов=”нет” equal_height_columns=”нет” hide_on_mobile=”нет” menu_anchor=” ” class=”” id=””][title size=”1″ content_align=”left” style_type=”none” sep_color=”” margin_top=”” margin_bottom=”” class=”” id=””] Решение Линейные уравнения с алгебраическими дробями слева вверху» border_position = «а ll” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0. 1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”none” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_half ][one_half last=”да” spacing=”да” center_content=”нет” hide_on_mobile=”нет” background_color=”” background_image=”” background_repeat=”не повторять” background_position=”слева вверху” border_position=”все” border_size =”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0.1 ″ class=»» id=»»][fusion_text]
1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”none” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_half ][one_half last=”да” spacing=”да” center_content=”нет” hide_on_mobile=”нет” background_color=”” background_image=”” background_repeat=”не повторять” background_position=”слева вверху” border_position=”все” border_size =”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0.1 ″ class=»» id=»»][fusion_text]
Решение линейных уравнений с алгебраическими дробями очень похоже на решение линейных уравнений.
В самом простом сценарии (алгебраические выражения с одинаковым знаменателем) вам просто нужно сложить алгебраические выражения, как если бы вы складывали дроби с одинаковым знаменателем.

[/fusion_text][/one_half][one_half last=”no” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”no-repeat” background_position=”left top” border_position=”all” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0.1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”none” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_half ][one_half last=”да” spacing=”да” center_content=”нет” hide_on_mobile=”нет” background_color=”” background_image=”” background_repeat=”не повторять” background_position=”слева вверху” border_position=”все” border_size =”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0. 1 ″ class=»» id=»»][fusion_text]
1 ″ class=»» id=»»][fusion_text]
Решение линейных уравнений с алгебраическими дробями очень похоже на решение линейных уравнений.
В более сложных сценариях (алгебраические выражения с другим знаменателем) вы должны выполнить те же действия, что и при сложении дробей с разными знаменателями.
Сначала вам нужно найти
общий знаменатель между двумя знаменателями, а затем преобразовать оба выражения так, чтобы они имели одинаковый знаменатель.Потом решишь уравнение. [/fusion_text][/one_half][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0,3″ background_repeat=”no-repeat” background_position=”left top ” video_url=”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0.5″ video_mute=”yes” video_loop=”yes” fade=” no” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сотня_процентов=”no” equal_height_columns=”no” hide_on_mobile=”no” menu_anchor=”” class=”” id=””][title size=”1″ content_align=”left” style_type=”none” sep_color=”” margin_top=”” margin_bottom=”” class=”” id=”” ] Метод блок-схемы/Метод возврата [/title][one_full last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”no-repeat” background_position = «слева вверху» border_position = «все» борд er_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0. 1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”center” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_full ][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0,3″ background_repeat=”no-repeat” background_position=”left top” video_url=»» video_aspect_ratio=” 16:9″ video_webm=»» video_mp4=»» video_ogv=»» video_preview_image=»» overlay_color=»» overlay_opacity=»0.5″ video_mute=”да” video_loop=”да” fade=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сто_процент = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor = «» класс = «» id = »» [размер заголовка = «1» content_align = «левый» style_type = «нет» sep_color = «» margin_top =”” margin_bottom=”” class=”” id=””] Модель/метод баланса [/title][one_full last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color= ”” background_image=”” background_repeat=”не повторять” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type =”” animation_direction=”” animation_speed=”0.
1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”center” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_full ][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0,3″ background_repeat=”no-repeat” background_position=”left top” video_url=»» video_aspect_ratio=” 16:9″ video_webm=»» video_mp4=»» video_ogv=»» video_preview_image=»» overlay_color=»» overlay_opacity=»0.5″ video_mute=”да” video_loop=”да” fade=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сто_процент = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor = «» класс = «» id = »» [размер заголовка = «1» content_align = «левый» style_type = «нет» sep_color = «» margin_top =”” margin_bottom=”” class=”” id=””] Модель/метод баланса [/title][one_full last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color= ”” background_image=”” background_repeat=”не повторять” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type =”” animation_direction=”” animation_speed=”0. 1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”center” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_full ][button link=”#” color=”default” size=”” type=”” shape=”” target=”_self” title=”” gradient_colors=”|” градиент_hover_colors=»|» акцент_цвет=”” акцент_hover_color=”” bevel_color=”” border_width=”1px” icon=”” icon_position=”слева” icon_divider=”нет” модальный=”” animation_type=”0″ animation_direction=”слева” animation_speed=”1″ выравнивание=”” класс=”” id=””]Виртуальные манипуляции[/button][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0.3″ background_repeat=”без повтора” background_position=”слева вверху” video_url=”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0.
1″ class=”” id=””][imageframe lightbox=”no” lightbox_image=”” style_type=”none” hover_type=”none” bordercolor=”” bordersize=”0px” borderradius=”0″ stylecolor=”” align=”center” link=”” linktarget=”_self” animation_type=”0″ animation_direction=”down” animation_speed=”0.1″ hide_on_mobile=”no” class=”” id=””] [/imageframe][/one_full ][button link=”#” color=”default” size=”” type=”” shape=”” target=”_self” title=”” gradient_colors=”|” градиент_hover_colors=»|» акцент_цвет=”” акцент_hover_color=”” bevel_color=”” border_width=”1px” icon=”” icon_position=”слева” icon_divider=”нет” модальный=”” animation_type=”0″ animation_direction=”слева” animation_speed=”1″ выравнивание=”” класс=”” id=””]Виртуальные манипуляции[/button][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0.3″ background_repeat=”без повтора” background_position=”слева вверху” video_url=”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0. 5 ″ video_mute=”да” video_loop=”да” исчезает=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сотня_процентов = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor = «» class = «» id = «»][ размер заголовка = «1» content_align = «left» style_type = «none» sep_color = «» margin_top = ”” margin_bottom=”” class=”” id=””] шагов для решения линейных уравнений с алгебраическими дробями [/title][one_full last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no ” background_color=”” background_image=”” background_repeat=”без повтора” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom= ”” animation_type=”” animation_direction=”” анимация _скорость = «0.1 ″ class=»» id=»»][fusion_text]
5 ″ video_mute=”да” video_loop=”да” исчезает=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сотня_процентов = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor = «» class = «» id = «»][ размер заголовка = «1» content_align = «left» style_type = «none» sep_color = «» margin_top = ”” margin_bottom=”” class=”” id=””] шагов для решения линейных уравнений с алгебраическими дробями [/title][one_full last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no ” background_color=”” background_image=”” background_repeat=”без повтора” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom= ”” animation_type=”” animation_direction=”” анимация _скорость = «0.1 ″ class=»» id=»»][fusion_text]
Определите ЖК всех членов уравнения.
Умножьте каждый член на ЖКИ и упростите.

Решите полученное уравнение.
[/fusion_text][/one_full][/fullwidth][fullwidth background_color=”” background_image=”” background_parallax=”none” enable_mobile=”no” parallax_speed=”0,3″ background_repeat=”no-repeat” background_position=”left top” video_url=”” video_aspect_ratio=”16:9″ video_webm=”” video_mp4=”” video_ogv=”” video_preview_image=”” overlay_color=”” overlay_opacity=”0.5″ video_mute=”да” video_loop=”да” fade=”нет” border_size=”0px” border_color=”” border_style=”” padding_top=”20″ padding_bottom=”20″ padding_left=”0″ padding_right=”0″ сто_процент = «нет» equal_height_columns = «нет» hide_on_mobile = «нет» menu_anchor = «» класс = «» id = »» [размер заголовка = «1» content_align = «левый» style_type = «нет» sep_color = «» margin_top =”” margin_bottom=”” class=”” id=””] Линейные уравнения с алгебраическими дробями Видео [/title][one_half last=”no” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”без повтора” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=” ” анимация_тип=”” анимация_направление=”” анимация_скорость=”0. 1″ class=»» id=»»][youtube id=»https://www.youtube.com/watch?v=sLbiWpoL88Q» width=»600″ height=»350″ autoplay=»no» api_params=» ” class=””][/youtube][/one_half][one_half last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”no-repeat ” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0.1″ class=”” id=””][youtube id=”https://www.youtube.com/watch?v=10TJfOy3H-w” width=”600″ height=”350″ autoplay=”no” api_params =”” class=””][/youtube][/one_half][one_half last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”no -повторить” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=” 0.
1″ class=»» id=»»][youtube id=»https://www.youtube.com/watch?v=sLbiWpoL88Q» width=»600″ height=»350″ autoplay=»no» api_params=» ” class=””][/youtube][/one_half][one_half last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”no-repeat ” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=”0.1″ class=”” id=””][youtube id=”https://www.youtube.com/watch?v=10TJfOy3H-w” width=”600″ height=”350″ autoplay=”no” api_params =”” class=””][/youtube][/one_half][one_half last=”yes” spacing=”yes” center_content=”no” hide_on_mobile=”no” background_color=”” background_image=”” background_repeat=”no -повторить” background_position=”слева вверху” border_position=”все” border_size=”0px” border_color=”” border_style=”” padding=”” margin_top=”” margin_bottom=”” animation_type=”” animation_direction=”” animation_speed=” 0. 1″ class=»» id=»»][youtube id=»https://www.youtube.com/watch?v=k7poJsKLAI0″ width=»600″ height=»350″ autoplay=»no» api_params=» ” class=””][/youtube][/one_half][button link=”#” color=”default” size=”” type=”” shape=”” target=”_self” title=”” gradient_colors=” |” градиент_hover_colors=»|» акцент_цвет=”” акцент_hover_color=”” bevel_color=”” border_width=”1px” icon=”” icon_position=”слева” icon_divider=”нет” модальный=”” animation_type=”0″ animation_direction=”слева” animation_speed=”1″ Alignment=»» class=»» id=»»]Следующий урок[/button][/fullwidth]
1″ class=»» id=»»][youtube id=»https://www.youtube.com/watch?v=k7poJsKLAI0″ width=»600″ height=»350″ autoplay=»no» api_params=» ” class=””][/youtube][/one_half][button link=”#” color=”default” size=”” type=”” shape=”” target=”_self” title=”” gradient_colors=” |” градиент_hover_colors=»|» акцент_цвет=”” акцент_hover_color=”” bevel_color=”” border_width=”1px” icon=”” icon_position=”слева” icon_divider=”нет” модальный=”” animation_type=”0″ animation_direction=”слева” animation_speed=”1″ Alignment=»» class=»» id=»»]Следующий урок[/button][/fullwidth]



 Поэтому ответ – в этом линейном уравнении нет корней.
Поэтому ответ – в этом линейном уравнении нет корней.
 {2}+8x-6x=-6+16\)
{2}+8x-6x=-6+16\)
 .. Однако давайте избавимся от знаменателей, умножив обе части уравнения на общий знаменатель всех дробей – шестерку
.. Однако давайте избавимся от знаменателей, умножив обе части уравнения на общий знаменатель всех дробей – шестерку
 В Учебник
13. Свойство умножения равенства 90 970, которое мы рассмотрели с помощью
свойство умножения равенства, а также положить эти две идеи
вместе.
В этом уроке мы будем решать линейные уравнения, используя
комбинация
упрощения и различных свойств равенства.
В Учебник
13. Свойство умножения равенства 90 970, которое мы рассмотрели с помощью
свойство умножения равенства, а также положить эти две идеи
вместе.
В этом уроке мы будем решать линейные уравнения, используя
комбинация
упрощения и различных свойств равенства.
 10 под. 10
10 под. 10  3 под. 3
3 под. 3  2 подп. 2
2 подп. 2  20 добавить 20
20 добавить 20  Также обратите внимание, что мы получили утверждение FALSE , где -1 не равно 12. Это не означает, что x = 12 или x = -1.
Также обратите внимание, что мы получили утверждение FALSE , где -1 не равно 12. Это не означает, что x = 12 или x = -1. Всякий раз, когда это происходит, ваш ответ
ВСЕ РЕАЛЬНЫЕ ЦИФРЫ.
Всякий раз, когда это происходит, ваш ответ
ВСЕ РЕАЛЬНЫЕ ЦИФРЫ.  По ссылке вы найдете ответ
а также любые шаги, которые привели к поиску этого ответа.
По ссылке вы найдете ответ
а также любые шаги, которые привели к поиску этого ответа.
