Решение систем линейных уравнений методом обратной матрицы онлайн
Одним из популярных методов решения систем линейных алгебраических уравнений (СЛАУ) является метод обратной матрицы. Рассмотрим этот метод подробнее на примере решения СЛАУ, состоящей из двух уравнений с двумя неизвестными.
a11xa12yb1a21xa22yb2
Введем обозначения: A — матрица СЛАУ, которая имеет вид:
Aa11a12a21a22
X — вектор столбец неизвестных, которые нам нужно найти:
Xxy
B — вектор столбец свободных коэффициентов:
Bb1b2
В результате, исходную СЛАУ можно записать в матричной форме:
AXB
Решим это матричное уравнение, для чего домножим его обе части слева на матрицу A
A1AXA1B
Здесь,
A-1
— это матрица, обратная к матрице
A. Такая матрица существует для любой квадратной невырожденной матрицы (т.е. такой, определитель которой не равен нулю).
Такая матрица существует для любой квадратной невырожденной матрицы (т.е. такой, определитель которой не равен нулю).
Эти условия показывают границы применимости метода обратной матрицы для решения СЛАУ. Во-первых: матрица СЛАУ A должна быть квадратной. Это означает, что количество уравнений должно быть равно количеству неизвестных. Во-вторых: определитель матрицы A должен быть отличен от нуля:
A0
Кроме того, обратная матрица обладает ещё одним замечательным свойством: её произведение на исходную матрицу коммутативно и равно единичной матрице:
A1AAA1E
Возвращаясь к решению нашего матричного уравнения, получаем:
EXXA1B
Таким образом, для того, чтобы решить СЛАУ методом обратной матрицы, сначала нам нужно убедиться, что обратная матрица существует, затем найти её и умножить на вектор
B.
Наш онлайн калькулятор предназначен для решения СЛАУ методом обратной матрицы. Калькулятор выдаёт пошаговое решение с описанием действий на русском языке. Уравнения СЛАУ вводятся в калькулятор в естественном виде. В качестве коэффициентов уравнения можно вводить не только числа и дроби, но и параметры — в этом случае калькулятор выдаст решение в общем виде.
Решить систему уравнений через матрицу онлайн. Обратная матрица
Этот способ, другими словами метод обратной матрицы, называют так, так как решение сводится к обычному матричному уравнению, для решения которого нужно найти обратную матрицу.
Матричный метод решения СЛАУ с определителем, который больше или меньше нуля состоит в следующем:
Предположим, есть СЛУ (система линейных уравнений) с n неизвестными (над произвольным полем):
Значит, её легко перевести в матричную форму:
AX=B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A −1 — обратную матрицу к матрице A: A −1 (AX)=A −1 B.
Т.к. A −1 A=E , значит, X=A −1 B . Правая часть уравнения дает столбец решений начальной системы. Условием применимости матричного метода есть невырожденность матрицы A . Необходимым и достаточным условием этого есть неравенство нулю определителя матрицы A :
detA≠0.
Для однородной системы линейных уравнений , т.е. если вектор B=0 , выполняется обратное правило: у системы AX=0 есть нетривиальное (т. е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
е. не равное нулю) решение лишь когда detA=0 . Эта связь между решениями однородных и неоднородных систем линейных уравнений называется альтернатива Фредгольма.
Т.о., решение СЛАУ матричным методом производится по формуле . Либо, решение СЛАУ находят при помощи обратной матрицы
Известно, что у квадратной матрицы А порядка n на n есть обратная матрица A −1 только в том случае, если ее определитель ненулевой. Таким образом, систему n линейных алгебраических уравнений с n неизвестными решаем матричным методом только в случае, если определитель основной матрицы системы не равен нулю.
Не взирая на то, что есть ограничения возможности применения такого метода и существуют сложности вычислений при больших значениях коэффициентов и систем высокого порядка, метод можно легко реализовать на ЭВМ.
Пример решения неоднородной СЛАУ.
Для начала проверим, не равен ли нулю определитель матрицы коэффициентов у неизвестных СЛАУ.
Теперь находим союзную матрицу , транспонируем её и подставляем в формулу для определения обратной матрицы.
Подставляем переменные в формулу:
Теперь находим неизвестные, перемножая обратную матрицу и столбик свободных членов.
Итак, x=2; y=1; z=4.
При переходе от обычного вида СЛАУ к матричной форме будьте внимательными с порядком неизвестных переменных в уравнениях системы. Например :
НЕЛЬЗЯ записать как:
Необходимо, для начала, упорядочить неизвестные переменные в кадом уравнении системы и только после этого переходить к матричной записи:
Кроме того, нужно быть внимательными с обозначением неизвестных переменных, вместо x 1 , x 2 , …, x n могут оказаться другие буквы. К примеру :
в матричной форме записываем так:
Матричным методом лучше решать системы линейных уравнений, в которых количество уравнений совпадает с числом неизвестных переменных и определитель основной матрицы системы не равен нулю.
Метод обратной матрицы – эточастный случай матричного уравнения
Решить систему с матричным методом
Решение : Запишем систему в матричной форме.Решение системы найдем по формуле (см.последнюю формулу)
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решаетсяметодом исключение неизвестных (методом Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре.
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).
Таким образом:
– матрица миноров соответствующих элементов матрицы .
– матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Повторюсь, выполненные шаги мы подробно разбирали на уроке
Теперь записываем обратную матрицу:
Ни в коем случае не вносимв матрицу, это серьезно затруднит дальнейшие вычисления . Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
Осталось провести матричное умножение. Умножать матрицы можно научиться на урокеДействия с матрицами . Кстати, там разобран точно такой же пример.
Обратите внимание, что деление на 60 выполняется в последнюю очередь .
Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.
Ответ :
Пример 12
Решить систему с помощью обратной матрицы.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса) . Доступно объяснить алгоритм не так-то просто, но я старался!.
Желаю успехов!
Ответы:
Пример 3:
Пример 6:
Пример 8: , . Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).
Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).
Примеры 10, 12:
Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если Вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
На практике так подробно, конечно, не расписывают, а пишут короче:
Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »
Записываю результат во вторую строку: »
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!
Вернемся к нашей системе . Она уже почти решена.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:
И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число:
Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения . Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :
Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :
Результат записываем во вторую строку:
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Результат записываем в третью строку:
На практике эти действия обычно выполняются устно и записываются в один шаг:
Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :
А мысленный ход самих расчётов я уже рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
«Игрек» и «зет» известны, дело за малым:
Ответ:
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх:
Да тут подарок получился:
Ответ: .
Пример 4
Решить систему линейных уравнений методом Гаусса
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:
Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:
Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:
Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка.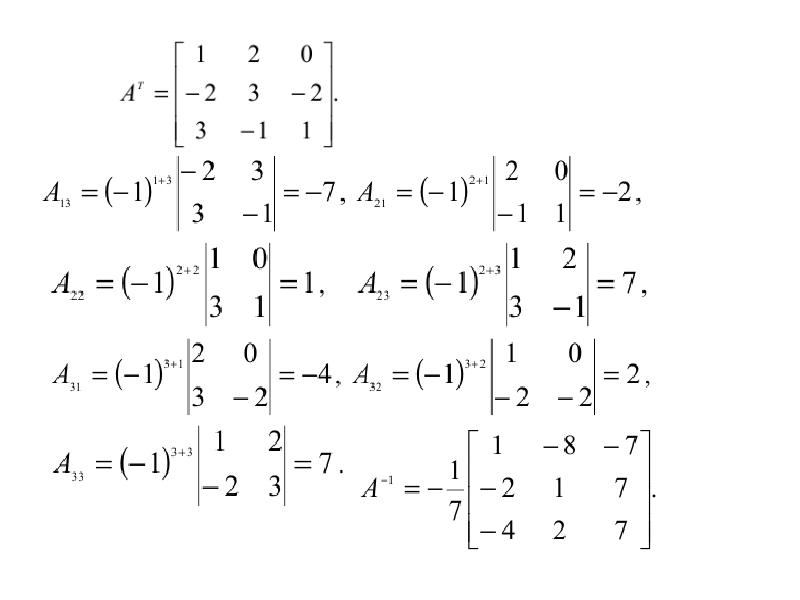 Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример 2: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.
Обратный ход:
Ответ: .
Пример 4: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы
(3) К третьей строке прибавили вторую, умноженную на –1.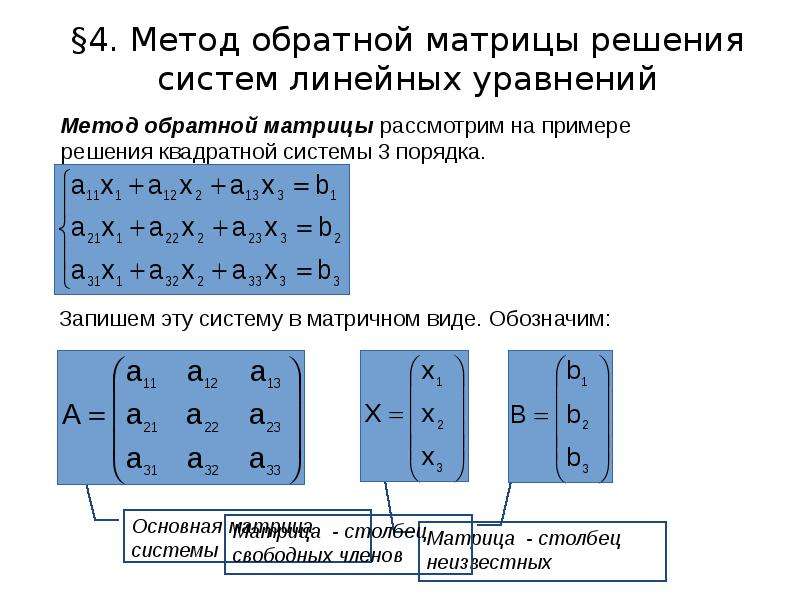
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена .
(5) К третьей строке прибавили вторую, умноженную на 6.
(6) Вторую строку умножили на –1, третью строку разделили на -83. .Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, ; .Если свободные члены
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».
×
Предупреждение
Очистить все ячейки?
Закрыть Очистить
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Матричный метод решения систем линейных уравнений
Рассмотрим следующую систему линейных уравнений:
Учитывая определение обратной матрицы, имеем A −1 A =E , где E — единичная матрица. Следовательно (4) можно записать так:
Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b .
Примеры решения системы линейных уравнений матричным методом
Пример 1. Решить следующую систему линейных уравнений матричным методом:
Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:
Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:
Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:
Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :
Матричный вид записи системы линейных уравнений: Ax=b , где
Вычислим все алгебраические дополнения матрицы A :
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| , |
| . |
Обратная матрица вычисляется из следующего выражения.
Уравнения вообще, линейные алгебраические уравнения и их системы, а также методы их решения занимают в математике, как теоретической, так и прикладной, особое место.
Это связано с тем обстоятельством, что подавляющее большинство физических, экономических, технических и даже педагогических задач могут быть описаны и решены с помощью разнообразных уравнений и их систем. В последнее время особую популярность среди исследователей, ученых и практиков приобрело математическое моделирование практически во всех предметных областях, что объясняется очевидными его преимуществами перед другими известными и апробированными методами исследования объектов различной природы, в частности, так называемых, сложных систем. Существует великое многообразие различных определений математической модели, данных учеными в разные времена, но на наш взгляд, самое удачное, это следующее утверждение. Математическая модель – это идея, выраженная уравнением. Таким образом, умение составлять и решать уравнения и их системы – неотъемлемая характеристика современного специалиста.
Для решения систем линейных алгебраических уравнений наиболее часто используются методы: Крамера, Жордана-Гаусса и матричный метод.
Матричный метод решения — метод решения с помощью обратной матрицы систем линейных алгебраических уравнений с ненулевым определителем.
Если выписать коэффициенты при неизвестных величинах xi в матрицу A, неизвестные величины собрать в вектор столбец X, а свободные члены в вектор столбец B, то систему линейных алгебраических уравнений можно записать в виде следующего матричного уравнения A · X = B, которое имеет единственное решение только тогда, когда определитель матрицы A не будет равен нулю. При этом решение системы уравнений можно найти следующим способом X = A -1 · B , где A -1 — обратная матрица.
Матричный метод решения состоит в следующем.
Пусть дана система линейных уравнений с n неизвестными:
Её можно переписать в матричной форме: AX = B , где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:
Умножим это матричное уравнение слева на A -1 — матрицу, обратную к матрице A : A -1 (AX ) = A -1 B
Так как A -1 A = E , получаем X = A -1 B . Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A . Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A : detA ≠ 0.
Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A . Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A : detA ≠ 0.
Для однородной системы линейных уравнений, то есть когда вектор B = 0 , действительно обратное правило: система AX = 0 имеет нетривиальное (то есть не нулевое) решение только если detA = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.
Пример решения неоднородной системы линейных алгебраических уравнений .
Убедимся в том, что определитель матрицы, составленный из коэффициентов при неизвестных системы линейных алгебраических уравнений не равен нулю.
Следующим шагом будет вычисление алгебраических дополнений для элементов матрицы, состоящей из коэффициентов при неизвестных. Они понадобятся для нахождения обратной матрицы.
Они понадобятся для нахождения обратной матрицы.
Конспект лекций по дисциплине математика.
Занятие №5 (Лисичкин В.Т., Соловейчик И.Л. Математика)
Раздел 1. Линейная алгебраТема 1.2. Системы линейных уравнений
Основные понятия и определения: общий вид системы линейных алгебраических уравнений (СЛАУ) с 3-мя неизвестными. Совместные определенные, совместные неопределенные, несовместные СЛАУ. Решение СЛАУ методом обратной матрицы.
Система линейных алгебраических уравнений (сокращенно СЛАУ) из m уравнений с n неизвестными имеет вид
(6)
Числа являются коэффициентами при искомых неизвестных в уравнениях системы. Первый индекс чисел показывает, в каком уравнении это число находится, а второй − при каком по номеру неизвестном. Числа стоят в правых частях системы.
Набор чисел называется решением системы (6), если при подстановке этих чисел вместо неизвестных в каждое уравнение (6) получается верное числовое равенство.
Система может иметь решения, а может не иметь. Если система имеет решения, то она может иметь только одно решение (т.е. только один набор ), а может иметь более одного решения. В зависимости от описанной ситуации системы делятся на совместные и несовместные, определенные и неопределенные.
Совместная система – имеет хотя бы одно решение. Совместные системы могут быть определенными и неопределенными. Определенная система – имеет единственное решение. Неопределенная – имеет более одного решения. Специфика систем линейных уравнений вида (6) такова, что если эта система имеет более одного решения, то она имеет бесконечное число решений.
По системе (6) можно формально построить следующие матрицы (которые имеют свои названия):
– матрица коэффициентов, – столбец неизвестных, – столбец правых частей, – расширенная матрица системы. Матрица коэффициентов А называется также основной матрицей системы (6).
Матрица коэффициентов А называется также основной матрицей системы (6).
С помощью этих матриц система (6) может быть записана в компактной матричной форме:
(7) .
В этом легко убедиться, расписав поэлементно произведение матриц в (7) − получим в точности систему (6). Поэтому задача решения системы (6) эквивалентна поиску неизвестной матрицы-столбца , удовлетворяющей матричному уравнению (7).
Случай, когда число уравнений совпадает с числом неизвестных (
m = n )В этом важном частном случае система (6) принимает вид :
(8)
Для поиска решения снова представим эту систему в матричной форме (см. (7)):
(8а) ,
где матрица коэффициентов, столбец неизвестных и правых частей имеют вид
, , .
Обозначим через Δ определитель матрицы коэффициентов А: . Этот определитель называется главным определителем системы (8). Допустим, что матрица А не вырождена, т.е. . В этом случае, как указывалось выше, существует обратная матрица . Умножив слева (порядок при умножении матриц важен!) обе части матричного уравнения (8а) на , последовательно получим : . Можно показать, что полученное таким образом решение является единственным. Таким образом, справедлива следующая
Этот определитель называется главным определителем системы (8). Допустим, что матрица А не вырождена, т.е. . В этом случае, как указывалось выше, существует обратная матрица . Умножив слева (порядок при умножении матриц важен!) обе части матричного уравнения (8а) на , последовательно получим : . Можно показать, что полученное таким образом решение является единственным. Таким образом, справедлива следующая
Теорема. Система (8) имеет единственное решение (т.е. является определенной системой) тогда и только тогда, когда определитель матрицы коэффициентов . В этом случае решение (8) может быть получено по формуле
(8б) .
Отыскание решения системы по формуле (8б) носит название матричного метода решения систем. Он предполагает вычисление обратной матрицы для матрицы коэффициентов.
Пример. Решить матричным методом систему .
Решение. Матрица коэффициентов, столбец неизвестных и правых частей для этой системы имеют вид , , . Для матрицы А такого вида ранее (в параграфе «Обратная матрица») была построена обратная к ней . Поэтому по формуле (8б) последовательно получаем
==. Отсюда получаем следующее решение системы : , и .
Пример. Решить матричным методом систему .
Решение. Матрица коэффициентов, столбец неизвестных и правых частей для этой системы имеют вид , , . Построим обратную матрицу по формуле (5а), которая была выведена для матриц именно второго порядка. В нашем случае , . Тогда по формуле (8б) получаем: ==, а потому , .
Примеры решения систем линейных алгебраических уравнений матричным методом.
Рассмотрим матричный метод на примерах..
Пример.
Решите СЛАУ матричным методом.
Решение.
Первое уравнение системы не содержит неизвестной переменной x2, второе – x1, третье – x3. То есть, коэффициенты перед этими неизвестными переменными равны нулю. Перепишем систему уравнений как . От такого вида проще перейти к матричной форме записи СЛАУ . Убедимся в том, что эта система уравнений может быть решена с помощью обратной матрицы. Другими словами, покажем что :
То есть, коэффициенты перед этими неизвестными переменными равны нулю. Перепишем систему уравнений как . От такого вида проще перейти к матричной форме записи СЛАУ . Убедимся в том, что эта система уравнений может быть решена с помощью обратной матрицы. Другими словами, покажем что :
Построим обратную матрицу с помощью матрицы из алгебраических дополнений:
тогда,
Осталось найти решение СЛАУ:
Рекомендуем выполнить проверку.
Ответ:
.
При переходе от обычного вида системы линейных алгебраических уравнений к ее матричной форме следует быть внимательным с порядком следования неизвестных переменных в уравнениях системы. К примеру, СЛАУ НЕЛЬЗЯ записать как . Нужно сначала упорядочить все неизвестные переменные во всех уравнениях системы, а потом переходить к матричной записи:
или
Также будьте внимательны с обозначением неизвестных переменных, вместо
x1, x2, …, xn могут быть любые другие буквы. Например, СЛАУ в матричной форме запишется как .
Например, СЛАУ в матричной форме запишется как .
Пример.
Найдите решение системы линейных алгебраических уравнений с помощью обратной матрицы.
Решение.
Упорядочив неизвестные переменные в уравнениях системы, запишем ее в матичной форме . Вычислим определитель основной матрицы:
Он отличен от нуля, поэтому решение системы уравнений может быть найдено с помощью обратной матрицы как . Найдем обратную матрицу по формуле :
Получим искомое решение:
Ответ:
x = 0, y = -2, z = 3.
Пример.
Найдите решение системы линейных алгебраических уравнений матричным методом.
Решение.
Определитель основной матрицы системы равен нулю
поэтому, мы не можем применить матричный метод.
Пример:
Решить систему линейных уравнений матричным методом
:
Решение:
Обозначим: А = — матрица коэффициентов при неизвестных,
Х = — матрица неизвестных, В = — матрица свободных членов.
Прежде всего, найдем матрицу А-1, обратную матрице А.
Определитель основной матрицы системы:
.
Алгебраические дополнения всех элементов:
Отсюда
Тогда
Х = = ,
и, следовательно х1=2; х2=3; х3=-2.
Пример
Решить систему линейных алгебраических уравнений.
Решение.
1) Запишем систему трех линейных уравнений в матричной форме
Найдем обратную матрицу. Напомним, что
где — определитель матрицы , а — транспонированная матрица алгебраических дополнений элементов определителя матрицы.
Вычислим определитель матрицы
Матрица алгебраических дополнений состоит из элементов , которые вычисляются через миноры по правилу
Миноры — это определители на порядок меньшие от определителя , которые образуются вычеркиванием в нем -й строки и — го столбца. На первый взгляд звучит слишком запутано, но при вычислениях все станет понятно и просто.
На первый взгляд звучит слишком запутано, но при вычислениях все станет понятно и просто.
Найдем алгебраические дополнения к определителю
Запишем найденную матрицу алгебраических дополнений
и протранспонируем ее
Находим обратную матрицу
С помощью обратной матрицы находим решение системы линейных уравнений
Домашнее задание
Л4, стр. 81-85, № 68; 70 (Лисичкин В.Т., Соловейчик И.Л.)
№68. Решить матричным методом систему
.
№70. Решить матричным методом систему
Занятие №6 (Лисичкин В.Т., Соловейчик И.Л. Математика)
Раздел 1. Линейная алгебраТема 1.2. Системы линейных уравнений
Применение формул Крамера к решению СЛАУ.
Решение систем линейных уравнений методом Крамера
Метод Крамера состоит в том, что мы последовательно находим главный определитель матрицы коэффициентов A системы (8) и n вспомогательных определителей i (i =1, 2, …, n), которые получаются из определителя заменой i-го столбца столбцом правых частей.
Правило Крамера формулируется следующим образом.
1. Если главный определитель , то система (8) имеет единственное решение, которое может быть вычислено по следующим формулам Крамера:
x 1 = 1 / , x 2 = 2 / , … , x n= n / .
2. Если главный определитель , а хотя бы один из определителей 1, 2 , … , n не равен нулю, то система (8) не имеет решений (т.е. несовместна).
3. Если = 1= 2 = … = n = 0, то система (8) является неопределенной, причем имеет бесконечно много решений.
Пример. Решить систему методом Крамера.
Решение. Заметим, что раньше эта система уже была решена матричным методом. Матрица коэффициентов и столбец правых частей для этой системы имеют вид , . Находим главный определитель : . Он не равен нулю, поэтому система имеет единственное решение, которое найдем по формулам Крамера: x=1/,
y =2 /, z=3 / . Определители 1, 2 и 3 получаются из главного определителя заменой соответствующего столбца на столбец правых частей: , , . Тогда по формулам Крамера : x=1, y =0, z=1.
Определители 1, 2 и 3 получаются из главного определителя заменой соответствующего столбца на столбец правых частей: , , . Тогда по формулам Крамера : x=1, y =0, z=1.
Пример 1. Решить методом Крамера систему .
Решение. Эта система тоже была выше решена матричным методом. Матрица коэффициентов и столбец правых частей для этой системы имеют вид , . Главный определитель системы . Определители , . По формулам Крамера x=1/,
y =2 /, а потому , .
Пример 2. Решить систему линейных алгебраических уравнений.
Решение.
Для этого выпишем систему линейных уравнений в виде
Найдем определитель основной части
Для вычисления вспомогательных определителей ставим столбец свободных членов на место первой строки для и на место второй для . В результате получим
В результате получим
Подставим найденные значения в формулы Крамера
и найдем неизвестные
Из рассмотренного примера видим что вычисление при двух уравнениях с двумя неизвестными достаточно простые.
Пример 3. Найти решение системы уравнений:
D = = 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;
D1 = = (28 – 48) – (42 – 32) = -20 – 10 = -30.
x1 = = 1;
D2 = = 5(28 – 48) – (16 – 56) = -100 + 40 = -60.
x2 = = 2;
D3 = = 5( 32 – 42) + (16 – 56) = -50 – 40 = -90.
x3 = = 3.
Пример 4.
Решить систему уравнений методом Крамера
Решение:
Составим и вычислим сначала главный определитель этой системы:
Так как , то система имеет единственное решение, которое можно найти по правилу Крамера:
где получаются из определителя путем замены 1-го, 2-го или 3-го столбца, соответственно, на столбец свободных членов.
Таким образом:
Итак, — единственное решение.
Пример 5
Решение.
Запишем систему трех алгебраических уравнений в удобном для решения виде
Найдем детерминант системы по правилу треугольников
Для вычисления дополнительных определителей подставляем столбец свободных членов на место первого, второго и третьего столбцов. В результате получим
Вычисляем неизвестные за формулами Крамера
Для данного примера нахождения решения также не слишком сложно, хотя по сравнению с системой двух уравнений вычислений заметно прибавилось.
Пример 6. Решить систему уравнений методом Крамера
Решение:
Составим главный определитель этой системы:
Используя свойства определителя, создадим в первом столбце нули. Для этого
Для этого
Вторую и третью строку оставим без изменеий,
Умножим вторую строку на -2 и добавим к первой
Умножим вторую строку на -1 и добавим к четвертой
После этих преобразований значение определителя не изменится, но он наберет следующий вид
Теперь, воспользовавшись определением определителя и разложив его по элементам четвертого столбца, получим:
Итак, главный определитель системы уравнений отличен от нуля. По правилу Крамера такая система имеет единственное решение. Найдем его. Для этого создадим и вычислим еще четыре определители:
По правилу Крамера имеем решение:
Итак, — единственное решение.
Пример 7
Решение.
Записываем систему уравнений четвертого порядка в виде
Находим главный определитель системы. При вычислении детерминантов четвертого порядка их необходимо раскладывать за строками или столбцами у каторых больше всего нулей. Поскольку в данном случае нулей главный определитель не имеет то разложим его за первой строкой
При вычислении детерминантов четвертого порядка их необходимо раскладывать за строками или столбцами у каторых больше всего нулей. Поскольку в данном случае нулей главный определитель не имеет то разложим его за первой строкой
и найдем соответствующие определители третьего порядка
Подставим найденные значения в определитель
По такой же схеме вычисляем вспомогательные определители, напомню лишь, что они образуются заменой столбца в главном определителе на столбец свободных членов (обозначен черным цветом).
Подставив в формулы Крамера, после вычислений будем иметь
Домашнее задание
Л4, стр. 81-89, № 77; 80 (Лисичкин В.Т., Соловейчик И.Л.)
№77. Решить по формулам Крамера систему уравнений
.
№80. Решить по формулам Крамера систему уравнений
Решить по формулам Крамера систему уравнений
Занятие №7 (Лисичкин В.Т., Соловейчик И.Л. Математика)
Раздел 1. Линейная алгебраТема 1.2. Системы линейных уравнений
Решение СЛАУ методом Гаусса.
Решение систем линейных уравнений методом Гаусса
Элементарными преобразованиями строк матрицы называются следующие :
перестановка местами каких-либо двух строк матрицы;
умножение какой-либо строки матрицы на любое (не равное нулю) число;
прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, предварительно умноженных на одно и то же число.
Метод Гаусса состоит в приведении системы к равносильной системе ступенчатого вида (так называемы прямой ход метода Гаусса) и решении полученной системы (обратных ход метода Гаусса).
Пример 1. Решить методом Гаусса систему .
Решение. Прямой ход метода Гаусса заключается в приведении этой системы с помощью ее элементарных преобразований к ступенчатому виду.
Расширенная матрица системы имеет вид .
Приведем сначала к ступенчатой матрице, используя элементарные преобразования строк.
.
Получили ступенчатую матрицу. Суть преобразований отмечена под матрицами. Например, (2) − (1) означает: из элементов второй строки вычтем элементы первой; (3) − 2∙(1) : из элементов третьей строки вычтем элементы первой, умноженные на 2. Таким образом, прямой ход метода Гаусса приводит к следующей системе ступенчатого вида: .
. Совершим обратный ход метода Гаусса − решим эту систему. Из последнего уравнения получаем z = −2. Подставляя это значение z во второе уравнение системы, получим − y − 2 = −4, откуда y = 2. Подставляя z = −2 и y = 2 в первое уравнение, получаем x + 6 − 4 = 5, откуда x = 3. Таким образом, решение исходной системы: x = 3, y = 2, z = −2.
Подставляя z = −2 и y = 2 в первое уравнение, получаем x + 6 − 4 = 5, откуда x = 3. Таким образом, решение исходной системы: x = 3, y = 2, z = −2.
Пример 2. Решить методом Гаусса систему .
Рассмотрим расширенную матрицу системы и приведем ее к ступенчатому виду. Иногда для наглядности последний столбец расширенной матрицы (это добавленный к основной матрице столбец правых частей системы) отделяют вертикальной чертой. Прямой ход метода Гаусса:
~ .
По последней матрице запишем систему линейных уравнений и проведем обратный ход:
.
Пример 3.
Решить системы линейных уравнений методом Гаусса:
Решение.
Преобразуем расширенную матрицу системы
~~
Таким образом, получаем систему линейных уравнений
Ответ: (1, 2, 3)
Пример 4. Методом Гаусса решить систему уравнений:
Методом Гаусса решить систему уравнений:
х1 + 2х2 – х3 = 7
2х1 – 3х2 + х3 = 3
4х1 + х2 – х3 = 16.
Решение. Преобразуем расширенную матрицу системы
1 2 -1 7 1 2 -1 7 1 2 -1 7
2 -3 1 3 ~ 0 -7 3 -11 ~ 0 -7 3 -11 .
4 1 -1 16 0 -7 3 -12 0 0 0 -1
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = -1, следовательно, данная система несовместна, то есть не имеет решений.
Пример 5.
Решить системы линейных уравнений методом Гаусса:
Решение.
Преобразуем расширенную матрицу системы
~~
Итак, уравнение, соответствующее третьей строке последней матрицы, противоречиво – оно привелось к неверному равенству 0 = -17, следовательно, данная система несовместна, то есть не имеет решений.
Пример 6.
Решить системы линейных уравнений методом Гаусса:
Решение.
Преобразуем расширенную матрицу системы
~~~
~~~.
Таким образом, получаем систему линейных уравнений
Ответ: (1, -1, 2, 0)
Домашнее задание
Л3, стр. 103-108 (Пехлецкий И.Д.)
Л4, стр. 89-91, № 85; 89 (Лисичкин В.Т., Соловейчик И.Л.)
№85. Решить методом Гаусса систему .
№89. Решить методом Гаусса систему
Решить методом крамера онлайн с подробным решением. Линейные уравнения. Решение систем линейных уравнений. Метод Крамера. Системы линейных алгебраических уравнений
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
Габриэль Крамер — швейцарский математик, ученик и друг Иоганна Бернулли, один из создателей линейной алгебры. Крамер рассмотрел систему произвольного количества линейных уравнений с квадратной матрицей. Решение системы
он представил в виде столбца дробей с общим знаменателем — определителем матрицы. Метод Крамера основан на
использовании определителей в решении систем линейных уравнений, что позволяет существенно ускорить процесс
решения. Данный метод может быть применен в решении системы стольких линейных уравнений, сколько в каждом
уравнении неизвестных. Главное, чтобы определитель системы не был равен «0», тогда метод Крамера может быть
использован в решении, если «0» — данный метод использовать нельзя. Также данный метод может быть применен
для решения систем линейных уравнений с единственным решением.
Крамер рассмотрел систему произвольного количества линейных уравнений с квадратной матрицей. Решение системы
он представил в виде столбца дробей с общим знаменателем — определителем матрицы. Метод Крамера основан на
использовании определителей в решении систем линейных уравнений, что позволяет существенно ускорить процесс
решения. Данный метод может быть применен в решении системы стольких линейных уравнений, сколько в каждом
уравнении неизвестных. Главное, чтобы определитель системы не был равен «0», тогда метод Крамера может быть
использован в решении, если «0» — данный метод использовать нельзя. Также данный метод может быть применен
для решения систем линейных уравнений с единственным решением.
Теорема Крамера. Если определитель системы отличен от нуля, то система линейных уравнений имеет одно
единственное решение, причём неизвестное равно отношению определителей. В знаменателе — определитель
системы, а в числителе — определитель, полученный из определителя системы путём замены коэффициентов при
этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого
порядка.
Эта теорема имеет место для системы линейных уравнений любого
порядка.
Допустим, дано СЛАУ такого вида:
\[\left\{\begin{matrix} 3x_1 + 2x_2 =1\\ x_1 + 4x_2 = -3 \end{matrix}\right.\]
Согласно теореме Крамера получаем:
Ответ: \
Где можно решить уравнение методом Крамера онлайн решателем?
Решить уравнение вы можете на нашем сайте https://сайт. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Пусть система линейных уравнений содержит столько уравнений, каково количество независимых переменных, т.е. имеет вид
Такие системы линейных уравнений называются квадратными. Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
Определитель, составленный из коэффициентов при независимых переменных системы (1.5), называется главным определителем системы. Мы будем обозначать его греческой буквой D. Таким образом,
. (1.6)
Если в главном определителе произвольный (j -ый) столбец, заменить столбцом свободных членов системы (1.5), то можно получить еще n вспомогательных определителей:
(j = 1, 2, …, n ). (1.7)
Правило Крамера решения квадратных систем линейных уравнений заключается в следующем. Если главный определитель D системы (1.5) отличен от нуля, то система имеет и притом единственное решение, которое можно найти по формулам:
(1.8)
Пример 1.5. Методом Крамера решить систему уравнений
.
Вычислим главный определитель системы:
Так как D¹0, то система имеет единственное решение, которое можно найти по формулам (1.8):
Таким образом,
Действия над матрицами
1. Умножение матрицы на число. Операция умножения матрицы на число определяется следующим образом.
Операция умножения матрицы на число определяется следующим образом.
2. Для того чтобы умножить матрицу на число, нужно все ее элементы умножить на это число. То есть
. (1.9)
Пример 1.6. .
Сложение матриц.Данная операция вводится только для матриц одного и того же порядка.
Для того чтобы сложить две матрицы, необходимо к элементам одной матрицы прибавить соответствующие элементы другой матрицы:
(1.10)
Операция сложения матриц обладает свойствами ассоциативности и коммутативности.
Пример 1.7. .
Умножение матриц.Если число столбцов матрицы А совпадает с числом строк матрицы В , то для таких матриц вводится операция умножения:
2
Таким образом, при умножении матрицы А размерности m ´n на матрицу В размерности n ´k мы получаем матрицу С размерности m ´k . При этом элементы матрицы С вычисляются по следующим формулам:
Задача 1. 8. Найти, если это возможно, произведение матриц AB и BA :
8. Найти, если это возможно, произведение матриц AB и BA :
Решение. 1) Для того чтобы найти произведение AB , необходимо строки матрицы A умножить на столбцы матрицы B :
2) Произведение BA не существует, т. к. количество столбцов матрицы B не совпадает с количеством строк матрицы A .
Обратная матрица. Решение систем линейных уравнений матричным способом
Матрица A — 1 называется обратной к квадратной матрице А , если выполнено равенство:
где через I обозначается единичная матрица того же порядка, что и матрица А :
.
Для того чтобы квадратная матрица имела обратную необходимо и достаточно, чтобы ее определитель был отличен от нуля. Обратную матрицу находят по формуле:
, (1.13)
где A ij — алгебраические дополнения к элементам a ij матрицы А (заметим, что алгебраические дополнения к строкам матрицы А располагаются в обратной матрице в виде соответствующих столбцов).
Пример 1.9. Найти обратную матрицу A — 1 к матрице
.
Обратную матрицу найдем по формуле (1.13), которая для случая n = 3 имеет вид:
.
Найдем det A = | A | = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 — 3 × 3 × 3 — 1 × 5 × 4 — 2 × 2 × 8 = 24 + 30 + 24 — 27 — 20 — 32 = — 1. Так как определитель исходной матрицы отличен от нуля, то обратная матрица существует.
1) Найдем алгебраические дополнения A ij :
Для удобства нахождения обратной матрицы, алгебраические дополнения к строкам исходной матрицы мы расположили в соответствующие столбцы.
Из полученных алгебраических дополнений составим новую матрицу и разделим ее на определитель det A . Таким образом, мы получим обратную матрицу:
Квадратные системы линейных уравнений с отличным от нуля главным определителем можно решать с помощью обратной матрицы. Для этого систему (1.5) записывают в матричном виде:
где
Умножая обе части равенства (1. 14) слева на A — 1 , мы получим решение системы:
14) слева на A — 1 , мы получим решение системы:
, откуда
Таким образом, для того чтобы найти решение квадратной системы, нужно найти обратную матрицу к основной матрице системы и умножить ее справа на матрицу-столбец свободных членов.
Задача 1.10. Решить систему линейных уравнений
с помощью обратной матрицы.
Решение. Запишем систему в матричном виде: ,
где — основная матрица системы, — столбец неизвестных и — столбец свободных членов. Так как главный определитель системы , то основная матрица системы А имеет обратную матрицу А -1 . Для нахождения обратной матрицы А -1 , вычислим алгебраические дополнения ко всем элементам матрицы А :
Из полученных чисел составим матрицу (причем алгебраические дополнения к строкам матрицы А запишем в соответствующие столбцы) и разделим ее на определитель D. Таким образом, мы нашли обратную матрицу:
Решение системы находим по формуле (1. 15):
15):
Таким образом,
Решение систем линейных уравнений методом обыкновенных жордановых исключений
Пусть дана произвольная (не обязательно квадратная) система линейных уравнений:
(1.16)
Требуется найти решение системы, т.е. такой набор переменных , который удовлетворяет всем равенствам системы (1.16). В общем случае система (1.16) может иметь не только одно решение, но и бесчисленное множество решений. Она может так же вообще не иметь решений.
При решении подобных задач используется хорошо известный из школьного курса метод исключения неизвестных, который еще называется методом обыкновенных жордановых исключений. Суть данного метода заключается в том, что в одном из уравнений системы (1.16) одна из переменных выражается через другие переменные. Затем эта переменная подставляется в другие уравнения системы. В результате получается система, содержащая на одно уравнение и на одну переменную меньше, чем исходная система. Уравнение, из которого выражалась переменная, запоминается.
Этот процесс повторяется до тех пор, пока в системе не останется одно последнее уравнение. В процессе исключения неизвестных некоторые уравнения могут превратиться в верные тождества, например . Такие уравнения из системы исключаются, так как они выполняются при любых значениях переменных и, следовательно, не оказывают влияния на решение системы. Если в процессе исключения неизвестных хотя бы одно уравнение становится равенством, которое не может выполняться ни при каких значениях переменных (например ), то мы делаем вывод, что система не имеет решения.
Если в ходе решения противоречивых уравнений не возникло, то из последнего уравнения находится одна из оставшихся в нем переменных. Если в последнем уравнении осталась только одна переменная, то она выражается числом. Если в последнем уравнении остаются еще и другие переменные, то они считаются параметрами, и выраженная через них переменная будет функцией этих параметров. Затем совершается так называемый «обратный ход». Найденную переменную подставляют в последнее запомненное уравнение и находят вторую переменную. Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
Затем две найденные переменные подставляют в предпоследнее запомненное уравнение и находят третью переменную, и так далее, вплоть до первого запомненного уравнения.
В результате мы получаем решение системы. Данное решение будет являться единственным, если найденные переменные будут числами. Если же первая найденная переменная, а затем и все остальные будут зависеть от параметров, то система будет иметь бесчисленное множество решений (каждому набору параметров соответствует новое решение). Формулы, позволяющие найти решение системы в зависимости от того или иного набора параметров, называются общим решением системы.
Пример 1.11.
x
После запоминания первого уравнения и приведения подобных членов во втором и третьем уравнении мы приходим к системе:
Выразим y из второго уравнения и подставим его в первое уравнение:
Запомним второе уравнение, а из первого найдем z :
Совершая обратный ход, последовательно найдем y и z . Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
Для этого сначала подставим в последнее запомненное уравнение , откуда найдем y :
.
Затем подставим и в первое запомненное уравнение , откуда найдем x :
Задача 1.12. Решить систему линейных уравнений методом исключения неизвестных:
. (1.17)
Решение. Выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение
В данной системе первое и второе уравнения противоречат друг другу. Действительно, выражая y , получим, что 14 = 17. Данное равенство не выполняется, ни при каких значениях переменных x , y , и z . Следовательно, система (1.17) несовместна, т.е. не имеет решения.
Читателям предлагаем самостоятельно проверить, что главный определитель исходной системы (1.17) равен нулю.
Рассмотрим систему, отличающуюся от системы (1.17) всего лишь одним свободным членом.
Задача 1.13. Решить систему линейных уравнений методом исключения неизвестных:
. (1.18)
(1.18)
Решение. Как и прежде, выразим из первого уравнения переменную x и подставим ее во второе и третье уравнения:
.
Запомним первое уравнение и приведем подобные члены во втором и третьем уравнении. Мы приходим к системе:
Выражая y из первого уравнения и подставляя его во второе уравнение , мы получим тождество 14 = 14, которое не влияет на решение системы, и, следовательно, его можно из системы исключить.
В последнем запомненном равенстве переменную z будем считать параметром. Полагаем . Тогда
Подставим y и z в первое запомненное равенство и найдем x :
.
Таким образом, система (1.18) имеет бесчисленное множество решений, причем любое решение можно найти по формулам (1.19), выбирая произвольное значение параметра t :
(1.19)
Так решениями системы, например, являются следующие наборы переменных (1; 2; 0), (2; 26; 14) и т. д. Формулы (1.19) выражают общее (любое) решение системы (1. 18).
18).
В том случае, когда исходная система (1.16) имеет достаточно большое количество уравнений и неизвестных, указанный метод обыкновенных жордановых исключений представляется громоздким. Однако это не так. Достаточно вывести алгоритм пересчета коэффициентов системы при одном шаге в общем виде и оформить решение задачи в виде специальных жордановых таблиц.
Пусть дана система линейных форм (уравнений):
, (1.20)
где x j — независимые (искомые) переменные, a ij — постоянные коэффициенты
(i = 1, 2,…, m ; j = 1, 2,…, n ). Правые части системы y i (i = 1, 2,…, m ) могут быть как переменными (зависимыми), так и константами. Требуется найти решений данной системы методом исключения неизвестных.
Рассмотрим следующую операцию, называемую в дальнейшем «одним шагом обыкновенных жордановых исключений». Из произвольного (r -го) равенства выразим произвольную переменную (x s ) и подставим во все остальные равенства. Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Разумеется, это возможно только в том случае, когда a rs ¹ 0. Коэффициент a rs называется разрешающим (иногда направляющим или главным) элементом.
Мы получим следующую систему:
. (1.21)
Из s -го равенства системы (1.21) мы впоследствии найдем переменную x s (после того, как будут найдены остальные переменные). S -я строка запоминается и в дальнейшем из системы исключается. Оставшаяся система будет содержать на одно уравнение и на одну независимую переменную меньше, чем исходная система.
Вычислим коэффициенты полученной системы (1.21) через коэффициенты исходной системы (1.20). Начнем с r -го уравнения, которое после выражения переменной x s через остальные переменные будет выглядеть следующим образом:
Таким образом, новые коэффициенты r -го уравнения вычисляются по следующим формулам:
(1.23)
Вычислим теперь новые коэффициенты b ij (i ¹ r ) произвольного уравнения. Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
Для этого подставим выраженную в (1.22) переменную x s в i -е уравнение системы (1.20):
После приведения подобных членов, получим:
(1.24)
Из равенства (1.24) получим формулы, по которым вычисляются остальные коэффициенты системы (1.21) (за исключением r -го уравнения):
(1.25)
Преобразование систем линейных уравнений методом обыкновенных жордановых исключений оформляется в виде таблиц (матриц). Эти таблицы получили название «жордановых».
Так, задаче (1.20) ставится в соответствие следующая жорданова таблица:
Таблица 1.1
| x 1 | x 2 | … | x j | … | x s | … | x n | |
| y 1 = | a 11 | a 12 | a 1j | a 1s | a 1n | |||
…………………………………………………………………. . . | ||||||||
| y i = | a i 1 | a i 2 | a ij | a is | a in | |||
| ………………………………………………………………….. | ||||||||
| y r = | a r 1 | a r 2 | a rj | a rs | a rn | |||
| …………………………………………………………………. | ||||||||
| y n = | a m 1 | a m 2 | a mj | a ms | a mn |
Жорданова таблица 1.1 содержит левый заглавный столбец, в который записывают правые части системы (1.20) и верхнюю заглавную строку, в которую записывают независимые переменные.
Остальные элементы таблицы образуют основную матрицу коэффициентов системы (1.20). Если умножить матрицу А на матрицу , состоящую из элементов верхней заглавной строки, то получится матрица , состоящая из элементов левого заглавного столбца. То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
То есть, по существу, жорданова таблица это матричная форма записи системы линейных уравнений: . Системе (1.21) при этом соответствует следующая жорданова таблица:
Таблица 1.2
| x 1 | x 2 | … | x j | … | y r | … | x n | |
| y 1 = | b 11 | b 12 | b 1 j | b 1 s | b 1 n | |||
| ………………………………………………………………….. | ||||||||
| y i = | b i 1 | b i 2 | b ij | b is | b in | |||
| ………………………………………………………………….. | ||||||||
| x s = | b r 1 | b r 2 | b rj | b rs | b rn | |||
…………………………………………………………………. | ||||||||
| y n = | b m 1 | b m 2 | b mj | b ms | b mn |
Разрешающий элемент a rs мы будем выделять жирным шрифтом. Напомним, что для осуществления одного шага жордановых исключений разрешающий элемент должен быть отличен от нуля. Строку таблицы, содержащую разрешающий элемент, называют разрешающей строкой. Столбец, содержащий разрешающий элемент, называют разрешающим столбцом. При переходе от данной таблицы к следующей таблице одна переменная (x s ) из верней заглавной строки таблицы перемещается в левый заглавный столбец и, наоборот, один из свободных членов системы (y r ) из левого заглавного столбца таблицы перемещается в верхнюю заглавную строку.
Опишем алгоритм пересчета коэффициентов при переходе от жордановой таблицы (1.1) к таблице (1.2), вытекающий из формул (1.23) и (1.25).
1. Разрешающий элемент заменяется обратным числом:
2. Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
Остальные элементы разрешающей строки делятся на разрешающий элемент и изменяют знак на противоположный:
3. Остальные элементы разрешающего столбца делятся на разрешающий элемент:
4. Элементы, не попавшие в разрешающую строку и разрешающий столбец, пересчитываются по формулам:
Последняя формула легко запоминается, если заметить, что элементы, составляющие дробь , находятся на пересечении i -ой и r -ой строк и j -го и s -го столбцов (разрешающей строки, разрешающего столбца и той строки и столбца, на пересечении которых находится пересчитываемый элемент). Точнее, при запоминании формулы можно использовать следующую диаграмму:
-21-26-13-37Совершая первый шаг жордановых исключений, в качестве разрешающего элемента можно выбрать любой элемент таблицы 1.3, расположенный в столбцах x 1 ,…, x 5 (все указанные элементы не равны нулю). Не следует только выбирать разрешающий элемент в последнем столбце, т. к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
к. требуется находить независимые переменные x 1 ,…, x 5 . Выбираем, например, коэффициент 1 при переменной x 3 в третьей строке таблицы 1.3 (разрешающий элемент показан жирным шрифтом). При переходе к таблице 1.4 переменная x 3 из верхней заглавной строки меняется местами с константой 0 левого заглавного столбца (третья строка). При этом переменная x 3 выражается через остальные переменные.
Строку x 3 (табл.1.4) можно, предварительно запомнив, исключить из таблицы 1.4. Из таблицы 1.4 исключается так же третий столбец с нулем в верхней заглавной строке. Дело в том, что независимо от коэффициентов данного столбца b i 3 все соответствующие ему слагаемые каждого уравнения 0·b i 3 системы будут равны нулю. Поэтому указанные коэффициенты можно не вычислять. Исключив одну переменную x 3 и запомнив одно из уравнений, мы приходим к системе, соответствующей таблице 1.4 (с вычеркнутой строкой x 3). Выбирая в таблице 1. 4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
4 в качестве разрешающего элемента b 14 = -5, переходим к таблице 1.5. В таблице 1.5 запоминаем первую строку и исключаем ее из таблицы вместе с четвертым столбцом (с нулем наверху).
Таблица 1.5 Таблица 1.6
Из последней таблицы 1.7 находим: x 1 = — 3 + 2x 5 .
Последовательно подставляя уже найденные переменные в запомненные строки, находим остальные переменные:
Таким образом, система имеет бесчисленное множество решений. Переменной x 5 , можно придавать произвольные значения. Данная переменная выступает в роли параметра x 5 = t. Мы доказали совместность системы и нашли ее общее решение:
x 1 = — 3 + 2t
x 2 = — 1 — 3t
x 3 = — 2 + 4t . (1.27)
x 4 = 4 + 5t
x 5 = t
Придавая параметру t различные значения, мы получим бесчисленное множество решений исходной системы. Так, например, решением системы является следующий набор переменных (- 3; — 1; — 2; 4; 0).
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами.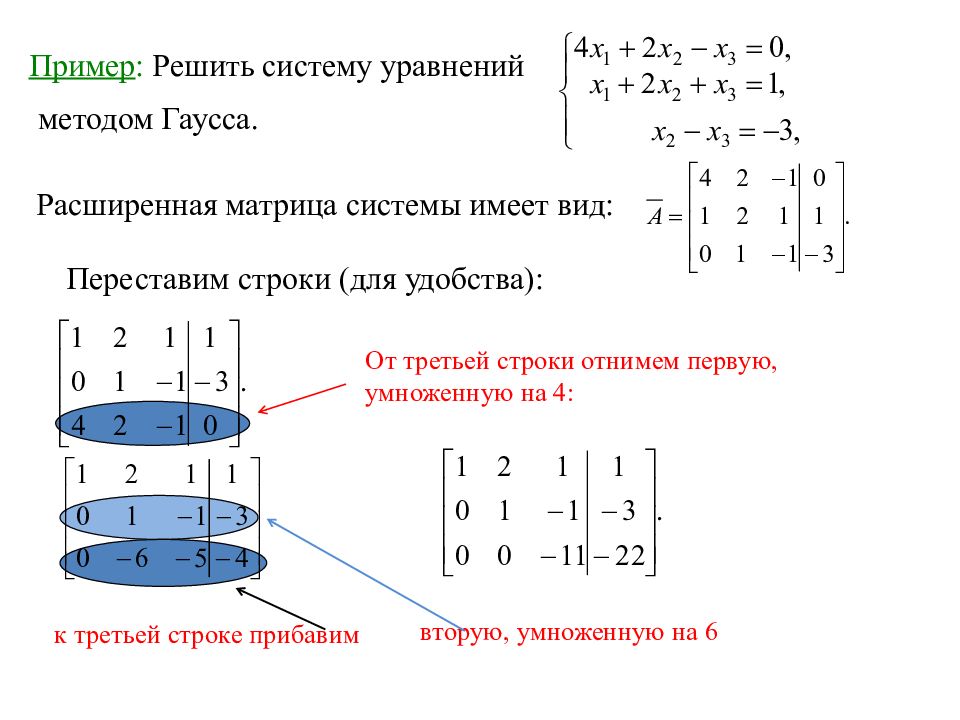 Эта теорема имеет место для системы линейных уравнений любого порядка.
Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
—
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют
какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих
переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное.
На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов.
То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества
экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко
ходить не надо.
За примерами далеко
ходить не надо.
Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Решение систем линейных уравнений с помощью матриц. Матричный метод онлайн. Решение систем матриц
Для решения произвольной системы линейных уравнений нужно уметь решать системы, в которых число уравнений равно числу неизвестных, — так называемые системы крамеровского типа :
a 11 x 1 + a 12 x 2 +… + a 1n x n = b 1 ,
a 21 x 1 + a 22 x 2 +… + a 2n x n = b 2 , (5.3)
… … … … … …
a n1 x 1 + a n1 x 2 +… + a nn x n = b n .
Системы (5.3) решаются
одним из следующих способов: 1) методом
Гаусса, или методом исключения неизвестных;
2) по формулам Крамера;
3) матричным
методом.
Пример 2.12 . Исследовать систему уравнений и решить ее, если она совместна:
5x 1 — x 2 + 2x 3 + x 4 = 7,
2x 1 + x 2 + 4x 3 — 2x 4 = 1,
x 1 — 3x 2 — 6x 3 + 5x 4 = 0.
Решение. Выписываем расширенную матрицу системы:
.
Вычислим ранг основной матрицы системы. Очевидно, что, например, минор второго порядка в левом верхнем углу = 7 0; содержащие его миноры третьего порядка равны нулю:
Следовательно, ранг основной матрицы системы равен 2, т.е. r(A) = 2. Для вычисления ранга расширенной матрицы A рассмотрим окаймляющий минор
значит, ранг расширенной матрицы r(A) = 3. Поскольку r(A) r(A), то система несовместна.
Тема 2. СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ.
Основные понятия.
Определение 1 . Системой m линейных уравнений с n неизвестными называется система вида:
где и — числа.
Определение 2 . Решением системы (I) называется такой набор неизвестных , при котором каждое уравнение этой системы обращается в тождество.
Определение 3 . Система (I) называется совместной , если она имеет хотя бы одно решение и несовместной , если она не имеет решений. Совместная система называется определенной , если она имеет единственное решение, и неопределенной в противном случае.
Определение 4 . Уравнение вида
называется нулевым , а уравнение вида
называется несовместным . Очевидно, что система уравнений, содержащая несовместное уравнение, является несовместной.
Определение 5 . Две системы линейных уравнений называются равносильными , если каждое решение одной системы служит решением другой и, наоборот, всякое решение второй системы является решением первой.
Матричная запись системы линейных уравнений.
Рассмотрим систему (I) (см. §1).
Обозначим:
Матрица коэффициентов при неизвестных
Матрица – столбец свободных членов
Матрица – столбец неизвестных
.
Определение 1. Матрица называется основной матрицей системы (I), а матрица — расширенной матрицей системы (I).
По определению равенства матриц системе (I) соответствует матричное равенство:
.
Правую часть этого равенства по определению произведения матриц (см. определение 3 § 5 главы 1 ) можно разложить на множители:
, т.е.
Равенство (2) называется матричной записью системы (I) .
Решение системы линейных уравнений методом Крамера.
Пусть в системе (I) (см. §1) m=n , т.е. число уравнений равно числу неизвестных, и основная матрица системы невырожденная, т.е. . Тогда система (I) из §1 имеет единственное решение
где Δ = det A называется главным определителем системы (I), Δ i получается из определителя Δ заменой i -го столбца на столбец из свободных членов системы (I).
Пример.Решить систему методом Крамера:
.
По формулам (3) .
Вычисляем определители системы:
,
,
.
Чтобы получить определитель , мы заменили в определителе первый столбец на столбец из свободных членов; заменяя в определителе 2-ой столбец на столбец из свободных членов, получаем ; аналогичным образом, заменяя в определителе 3-ий столбец на столбец из свободных членов, получаем . Решение системы:
Решение систем линейных уравнений с помощью обратной матрицы.
Пусть в системе(I) (см. §1) m=n и основная матрица системы невырожденная . Запишем систему (I) в матричном виде (см. §2 ):
т.к. матрица A невырожденная, то она имеет обратную матрицу (см. теорему 1 §6 главы 1 ). Умножим обе части равенства (2) на матрицу , тогда
По определению обратной матрицы . Из равенства (3) имеем
Решить систему с помощью обратной матрицы
.
Обозначим
В примере (§ 3)мы вычислили определитель , следовательно, матрица A имеет обратную матрицу . Тогда в силу (4) , т.е.
Тогда в силу (4) , т.е.
. (5)
Найдем матрицу (см. §6 главы 1 )
, , ,
, , ,
,
.
Метод Гаусса.
Пусть задана система линейных уравнений:
. (I)
Требуется найти все решения системы (I) или убедиться в том, что система несовместна.
Определение 1. Назовем элементарным преобразованием системы (I) любое из трёх действий:
1) вычёркивание нулевого уравнения;
2) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на число l;
3) перемена местами слагаемых в уравнениях системы так, чтобы неизвестные с одинаковыми номерами во всех уравнениях занимали одинаковые места, т.е. если, например, в 1-ом уравнении мы поменяли 2-ое и 3-е слагаемые, тогда то же самое необходимо сделать во всех уравнениях системы.
Метод Гаусса состоит в том, что система (I) с помощью элементарных преобразований приводится к равносильной системе, решение которой находится непосредственно или устанавливается её неразрешимость.
Как было описано в §2 система (I) однозначно определяется своей расширенной матрицей и любое элементарное преобразование системы (I) соответствует элементарному преобразованию расширенной матрицы:
.
Преобразование 1) соответствует вычёркиванию нулевой строки в матрице , преобразование 2) равносильно прибавлению к соответствующей строке матрицы другой её строки, умноженной на число l, преобразование 3) эквивалентно перестановке столбцов в матрице .
Легко видеть, что, наоборот, каждому элементарному преобразованию матрицы соответствует элементарное преобразование системы (I). В силу сказанного, вместо операций с системой (I) мы будем работать с расширенной матрицей этой системы.
В матрице 1-ый столбец состоит из коэффициентов при х 1 , 2-ой столбец — из коэффициентов при х 2 и т.д. В случае перестановки столбцов следует учитывать, что это условие нарушается. Например, если мы поменяем 1-ый и 2-ой столбцы местами, то теперь в 1-ом столбце будут коэффициенты при х 2 , а во 2-ом столбце — коэффициенты при х 1 .
Будем решать систему (I) методом Гаусса.
1. Вычеркнем в матрице все нулевые строки, если такие имеются (т.е. вычеркнем в системе (I) все нулевые уравнения).
2. Проверим, есть ли среди строк матрицы строка, в которой все элементы, кроме последнего, равны нулю (назовём такую строку несовместной). Очевидно, что такой строке соответствует несовместное уравнение в системе (I) , следовательно, система (I) решений не имеет и на этом процесс заканчивается.
3. Пусть матрица не содержит несовместных строк (система (I) не содержит несовместных уравнений). Если a 11 =0 , то находим в 1-ой строке какой-нибудь элемент (кроме последнего) отличный от нуля и переставляем столбцы так, чтобы в 1-ой строке на 1-ом месте не было нуля. Будем теперь считать, что (т.е. поменяем местами соответствующие слагаемые в уравнениях системы (I)).
4. Умножим 1-ую строку на и сложим результат со 2-ой строкой, затем умножим 1-ую строку на и сложим результат с 3-ей строкой и т.д. Очевидно, что этот процесс эквивалентен исключению неизвестного x 1 из всех уравнений системы (I), кроме 1-ого. В новой матрице получаем нули в 1-ом столбце под элементом a 11 :
.
5. Вычеркнем в матрице все нулевые строки, если они есть, проверим, нет ли несовместной строки (если она имеется, то система несовместна и на этом решение заканчивается). Проверим, будет ли a 22 / =0 , если да, то находим во 2-ой строке элемент, отличный от нуля и переставляем столбцы так, чтобы . Далее умножаем элементы 2-ой строки на и складываем с соответствующими элементами 3-ей строки, затем — элементы 2-ой строки на и складываем с соответствующими элементами 4-ой строки и т.д., пока не получим нули под a 22 /
.
Произведенные действия эквивалентны исключению неизвестного х 2 из всех уравнений системы (I), кроме 1-ого и 2-ого. Так как число строк конечно, поэтому через конечное число шагов мы получим, что либо система несовместна, либо мы придём к ступенчатой матрице (см. определение 2 §7 главы 1 ) :
,
Выпишем систему уравнений, соответствующую матрице . Эта система равносильна системе (I)
.
Из последнего уравнения выражаем ; подставляем в предыдущее уравнение, находим и т.д., пока не получим .
Замечание 1. Таким образом, при решении системы (I) методом Гаусса мы приходим к одному из следующих случаев.
1. Система (I) несовместна.
2. Система (I) имеет единственное решение, если в матрице число строк равно числу неизвестных ().
3. Система (I) имеет бесчисленное множество решений, если число строк в матрице меньше числа неизвестных ().
Отсюда имеет место следующая теорема.
Теорема. Система линейных уравнений либо несовместна, либо имеет единственное решение, либо – бесконечное множество решений.
Примеры. Решить систему уравнений методом Гаусса или доказать ее несовместность:
б) ;
а) Перепишем заданную систему в виде:
.
Мы поменяли местами 1-ое и 2-ое уравнение исходной системы, чтобы упростить вычисления (вместо дробей мы с помощью такой перестановки будем оперировать только целыми числами).
Составляем расширенную матрицу:
.
Нулевых строк нет; несовместных строк нет, ; исключим 1-ое неизвестное из всех уравнений системы, кроме 1-го. Для этого умножим элементы 1-ой строки матрицы на «-2» и сложим с соответствующими элементами 2-ой строки, что равносильно умножению 1-го уравнения на «-2» и сложению со 2-ым уравнением. Затем умножим элементы 1-ой строки на «-3» и сложим с соответствующими элементами третьей строки, т.е. умножим 2-ое уравнение заданной системы на «-3» и сложим с 3-им уравнением. Получим
.
Матрице соответствует система уравнений). — (см. определение 3§7 главы 1).
Метод обратной матрицы – эточастный случай матричного уравнения
Решить систему с матричным методом
Решение : Запишем систему в матричной форме.Решение системы найдем по формуле (см.последнюю формулу)
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если, то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решаетсяметодом исключение неизвестных (методом Гаусса).
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
Порядок расчета миноров совершенно не важен, здесь я их вычислил слева направо по строкам. Можно было рассчитать миноры по столбцам (это даже удобнее).
Таким образом:
– матрица миноров соответствующих элементов матрицы .
– матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Повторюсь, выполненные шаги мы подробно разбирали на уроке Как найти обратную матрицу?
Теперь записываем обратную матрицу:
Ни в коем случае не вносимв матрицу, это серьезно затруднит дальнейшие вычисления . Деление нужно было бы выполнить, если бы все числа матрицы делились на 60 без остатка. А вот внести минус в матрицу в данном случае очень даже нужно, это, наоборот – упростит дальнейшие вычисления.
Осталось провести матричное умножение. Умножать матрицы можно научиться на урокеДействия с матрицами . Кстати, там разобран точно такой же пример.
Обратите внимание, что деление на 60 выполняется в последнюю очередь .
Иногда может и не разделиться нацело, т.е. могут получиться «плохие» дроби. Что в таких случаях делать, я уже рассказал, когда мы разбирали правило Крамера.
Ответ :
Пример 12
Решить систему с помощью обратной матрицы.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Наиболее универсальным способом решения системы является метод исключения неизвестных (метод Гаусса) . Доступно объяснить алгоритм не так-то просто, но я старался!.
Желаю успехов!
Ответы:
Пример 3:
Пример 6:
Пример 8: , . Вы можете посмотреть или скачать образец решения данного примера (ссылка ниже).
Примеры 10, 12:
Продолжаем рассматривать системы линейных уравнений. Этот урок является третьим по теме. Если Вы смутно представляете, что такое система линейных уравнений вообще, чувствуете себя чайником, то рекомендую начать с азов на странице Далее полезно изучить урок .
Метод Гаусса – это просто! Почему? Известный немецкий математик Иоганн Карл Фридрих Гаусс еще при жизни получил признание величайшего математика всех времен, гения и даже прозвище «короля математики». А всё гениальное, как известно – просто! Кстати, на деньги попадают не только лохи, но еще и гении – портрет Гаусса красовался на купюре в 10 дойчмарок (до введения евро), и до сих пор Гаусс загадочно улыбается немцам с обычных почтовых марок.
Метод Гаусса прост тем, что для его освоения ДОСТАТОЧНО ЗНАНИЙ ПЯТИКЛАССНИКА.Необходимо уметь складывать и умножать! Не случайно метод последовательного исключения неизвестных преподаватели часто рассматривают на школьных математических факультативах. Парадокс, но у студентов метод Гаусса вызывает наибольшие сложности. Ничего удивительного – всё дело в методике, и я постараюсь в доступной форме рассказать об алгоритме метода.
Сначала немного систематизируем знания о системах линейных уравнений. Система линейных уравнений может:
1) Иметь единственное решение.
2) Иметь бесконечно много решений.
3) Не иметь решений (быть несовместной ).
Метод Гаусса – наиболее мощный и универсальный инструмент для нахождения решениялюбой системы линейных уравнений. Как мы помним, правило Крамера и матричный метод непригодны в тех случаях, когда система имеет бесконечно много решений или несовместна. А метод последовательного исключения неизвестных в любом случае приведет нас к ответу! На данном уроке мы опять рассмотрим метод Гаусса для случая №1 (единственное решение системы), под ситуации пунктов №№2-3 отведена статья. Замечу, что сам алгоритм метода во всех трёх случаях работает одинаково.
Вернемся к простейшей системе с урока Как решить систему линейных уравнений?
и решим ее методом Гаусса.
На первом этапе нужно записать расширенную матрицу системы :
. По какому принципу записаны коэффициенты, думаю, всем видно. Вертикальная черта внутри матрицы не несёт никакого математического смысла – это просто отчеркивание для удобства оформления.
Справка: рекомендую запомнить термины линейной алгебры. Матрица системы – это матрица, составленная только из коэффициентов при неизвестных, в данном примере матрица системы: . Расширенная матрица системы – это та же матрица системы плюс столбец свободных членов, в данном случае: . Любую из матриц можно для краткости называть просто матрицей.
После того, как расширенная матрица система записана, с ней необходимо выполнить некоторые действия, которые также называются элементарными преобразованиями .
Существуют следующие элементарные преобразования:
1) Строки матрицы можно переставлять местами. Например, в рассматриваемой матрице можно безболезненно переставить первую и вторую строки:
2) Если в матрице есть (или появились) пропорциональные (как частный случай – одинаковые) строки, то следует удалить из матрицы все эти строки кроме одной. Рассмотрим, например матрицу . В данной матрице последние три строки пропорциональны, поэтому достаточно оставить только одну из них: .
3) Если в матрице в ходе преобразований появилась нулевая строка, то ее также следуетудалить . Рисовать не буду, понятно, нулевая строка – это строка, в которой одни нули .
4) Строку матрицы можно умножить (разделить) на любое число, отличное от нуля . Рассмотрим, например, матрицу . Здесь целесообразно первую строку разделить на –3, а вторую строку – умножить на 2: . Данное действие очень полезно, поскольку упрощает дальнейшие преобразования матрицы.
5) Это преобразование вызывает наибольшие затруднения, но на самом деле ничего сложного тоже нет. К строке матрицы можно прибавить другую строку, умноженную на число , отличное от нуля. Рассмотрим нашу матрицу из практического примера: . Сначала я распишу преобразование очень подробно. Умножаем первую строку на –2: , и ко второй строке прибавляем первую строку умноженную на –2 : . Теперь первую строку можно разделить «обратно» на –2: . Как видите, строка, которую ПРИБАВЛЯЛИ – не изменилась . Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ .
На практике так подробно, конечно, не расписывают, а пишут короче:
Еще раз: ко второй строке прибавили первую строку, умноженную на –2 . Умножают строку обычно устно или на черновике, при этом мысленный ход расчётов примерно такой:
«Переписываю матрицу и переписываю первую строку: »
«Сначала первый столбец. Внизу мне нужно получить ноль. Поэтому единицу вверху умножаю на –2: , и ко второй строке прибавляю первую: 2 + (–2) = 0. Записываю результат во вторую строку: »
«Теперь второй столбец. Вверху –1 умножаю на –2: . Ко второй строке прибавляю первую: 1 + 2 = 3. Записываю результат во вторую строку: »
«И третий столбец. Вверху –5 умножаю на –2: . Ко второй строке прибавляю первую: –7 + 10 = 3. Записываю результат во вторую строку: »
Пожалуйста, тщательно осмыслите этот пример и разберитесь в последовательном алгоритме вычислений, если вы это поняли, то метод Гаусса практически «в кармане». Но, конечно, над этим преобразованием мы еще поработаем.
Элементарные преобразования не меняют решение системы уравнений
! ВНИМАНИЕ: рассмотренные манипуляции нельзя использовать , если Вам предложено задание, где матрицы даны «сами по себе». Например, при «классических» действиях с матрицами что-то переставлять внутри матриц ни в коем случае нельзя!
Вернемся к нашей системе . Она уже почти решена.
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду :
(1) Ко второй строке прибавили первую строку, умноженную на –2. Кстати, почему первую строку умножаем именно на –2? Для того чтобы внизу получить ноль, а значит, избавиться от одной переменной во второй строке.
(2) Делим вторую строку на 3.
Цель элементарных преобразований – привести матрицу к ступенчатому виду: . В оформлении задания прямо так и отчеркивают простым карандашом «лестницу», а также обводят кружочками числа, которые располагаются на «ступеньках». Сам термин «ступенчатый вид» не вполне теоретический, в научной и учебной литературе он часто называется трапециевидный вид или треугольный вид .
В результате элементарных преобразований получена эквивалентная исходной система уравнений:
Теперь систему нужно «раскрутить» в обратном направлении – снизу вверх, этот процесс называется обратным ходом метода Гаусса .
В нижнем уравнении у нас уже готовый результат: .
Рассмотрим первое уравнение системы и подставим в него уже известное значение «игрек»:
Рассмотрим наиболее распространенную ситуацию, когда методом Гаусса требуется решить систему трёх линейных уравнений с тремя неизвестными.
Пример 1
Решить методом Гаусса систему уравнений:
Запишем расширенную матрицу системы:
Сейчас я сразу нарисую результат, к которому мы придём в ходе решения:
И повторюсь, наша цель – с помощью элементарных преобразований привести матрицу к ступенчатому виду. С чего начать действия?
Сначала смотрим на левое верхнее число:
Почти всегда здесь должна находиться единица . Вообще говоря, устроит и –1 (а иногда и другие числа), но как-то так традиционно сложилось, что туда обычно помещают единицу. Как организовать единицу? Смотрим на первый столбец – готовая единица у нас есть! Преобразование первое: меняем местами первую и третью строки:
Теперь первая строка у нас останется неизменной до конца решения . Уже легче.
Единица в левом верхнем углу организована. Теперь нужно получить нули вот на этих местах:
Нули получаем как раз с помощью «трудного» преобразования. Сначала разбираемся со второй строкой (2, –1, 3, 13). Что нужно сделать, чтобы на первой позиции получить ноль? Нужно ко второй строке прибавить первую строку, умноженную на –2 . Мысленно или на черновике умножаем первую строку на –2: (–2, –4, 2, –18). И последовательно проводим (опять же мысленно или на черновике) сложение, ко второй строке прибавляем первую строку, уже умноженную на –2 :
Результат записываем во вторую строку:
Аналогично разбираемся с третьей строкой (3, 2, –5, –1). Чтобы получить на первой позиции ноль, нужно к третьей строке прибавить первую строку, умноженную на –3 . Мысленно или на черновике умножаем первую строку на –3: (–3, –6, 3, –27). И к третьей строке прибавляем первую строку, умноженную на –3 :
Результат записываем в третью строку:
На практике эти действия обычно выполняются устно и записываются в один шаг:
Не нужно считать всё сразу и одновременно . Порядок вычислений и «вписывания» результатов последователен и обычно такой: сначала переписываем первую строку, и пыхтим себе потихонечку – ПОСЛЕДОВАТЕЛЬНО иВНИМАТЕЛЬНО :
А мысленный ход самих расчётов я уже рассмотрел выше.
В данном примере это сделать легко, вторую строку делим на –5 (поскольку там все числа делятся на 5 без остатка). Заодно делим третью строку на –2, ведь чем меньше числа, тем проще решение:
На заключительном этапе элементарных преобразований нужно получить еще один ноль здесь:
Для этого к третьей строке прибавляем вторую строку, умноженную на –2 :
Попробуйте разобрать это действие самостоятельно – мысленно умножьте вторую строку на –2 и проведите сложение.
Последнее выполненное действие – причёска результата, делим третью строку на 3.
В результате элементарных преобразований получена эквивалентная исходной система линейных уравнений:
Круто.
Теперь в действие вступает обратный ход метода Гаусса. Уравнения «раскручиваются» снизу вверх.
В третьем уравнении у нас уже готовый результат:
Смотрим на второе уравнение: . Значение «зет» уже известно, таким образом:
И, наконец, первое уравнение: . «Игрек» и «зет» известны, дело за малым:
Ответ:
Как уже неоднократно отмечалось, для любой системы уравнений можно и нужно сделать проверку найденного решения, благо, это несложно и быстро.
Пример 2
Это пример для самостоятельного решения, образец чистового оформления и ответ в конце урока.
Следует отметить, что ваш ход решения может не совпасть с моим ходом решения, и это – особенность метода Гаусса . Но вот ответы обязательно должны получиться одинаковыми!
Пример 3
Решить систему линейных уравнений методом Гаусса
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1 . То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде , и, соответственно, , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх:
Да тут подарок получился:
Ответ: .
Пример 4
Решить систему линейных уравнений методом Гаусса
Это пример для самостоятельного решения, он несколько сложнее. Ничего страшного, если кто-нибудь запутается. Полное решение и образец оформления в конце урока. Ваше решение может отличаться от моего решения.
В последней части рассмотрим некоторые особенности алгоритма Гаусса.
Первая особенность состоит в том, что иногда в уравнениях системы отсутствуют некоторые переменные, например:
Как правильно записать расширенную матрицу системы? Об этом моменте я уже рассказывал на уроке Правило Крамера. Матричный метод . В расширенной матрице системы на месте отсутствующих переменных ставим нули:
Кстати, это довольно легкий пример, поскольку в первом столбце уже есть один ноль, и предстоит выполнить меньше элементарных преобразований.
Вторая особенность состоит вот в чём. Во всех рассмотренных примерах на «ступеньки» мы помещали либо –1, либо +1. Могут ли там быть другие числа? В ряде случаев могут. Рассмотрим систему: .
Здесь на левой верхней «ступеньке» у нас двойка. Но замечаем тот факт, что все числа в первом столбце делятся на 2 без остатка – и другая двойка и шестерка. И двойка слева вверху нас устроит! На первом шаге нужно выполнить следующие преобразования: ко второй строке прибавить первую строку, умноженную на –1; к третьей строке прибавить первую строку, умноженную на –3. Таким образом, мы получим нужные нули в первом столбце.
Или еще такой условный пример: . Здесь тройка на второй «ступеньке» тоже нас устраивает, поскольку 12 (место, где нам нужно получить ноль) делится на 3 без остатка. Необходимо провести следующее преобразование: к третьей строке прибавить вторую строку, умноженную на –4, в результате чего и будет получен нужный нам ноль.
Метод Гаусса универсален, но есть одно своеобразие. Уверенно научиться решать системы другими методами (методом Крамера, матричным методом) можно буквально с первого раза – там очень жесткий алгоритм. Но вот чтобы уверенно себя чувствовать в методе Гаусса, следует «набить руку», и прорешать хотя бы 5-10 десять систем. Поэтому поначалу возможны путаница, ошибки в вычислениях, и в этом нет ничего необычного или трагического.
Дождливая осенняя погода за окном…. Поэтому для всех желающих более сложный пример для самостоятельного решения:
Пример 5
Решить методом Гаусса систему 4-х линейных уравнений с четырьмя неизвестными.
Такое задание на практике встречается не так уж и редко. Думаю, даже чайнику, который обстоятельно изучил эту страницу, интуитивно понятен алгоритм решения такой системы. Принципиально всё так же – просто действий больше.
Случаи, когда система не имеет решений (несовместна) или имеет бесконечно много решений, рассмотрены на уроке Несовместные системы и системы с общим решением . Там же можно закрепить рассмотренный алгоритм метода Гаусса.
Желаю успехов!
Решения и ответы:
Пример 2: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.
Выполненные элементарные преобразования:
(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –1. Внимание! Здесь может возникнуть соблазн из третьей строки вычесть первую, крайне не рекомендую вычитать – сильно повышается риск ошибки. Только складываем!
(2) У второй строки сменили знак (умножили на –1). Вторую и третью строки поменяли местами. Обратите внимание , что на «ступеньках» нас устраивает не только единица, но еще и –1, что даже удобнее.
(3) К третьей строке прибавили вторую строку, умноженную на 5.
(4) У второй строки сменили знак (умножили на –1). Третью строку разделили на 14.
Обратный ход:
Ответ: .
Пример 4: Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
Выполненные преобразования:
(1) К первой строке прибавили вторую. Таким образом, организована нужная единица на левой верхней «ступеньке».
(2) Ко второй строке прибавили первую строку, умноженную на 7. К третьей строке прибавили первую строку, умноженную на 6.
Со второй «ступенькой» всё хуже , «кандидаты» на неё – числа 17 и 23, а нам нужна либо единичка, либо –1. Преобразования (3) и (4) будут направлены на получение нужной единицы
(3) К третьей строке прибавили вторую, умноженную на –1.
(4) Ко второй строке прибавили третью, умноженную на –3.
Нужная вещь на второй ступеньке получена .
(5) К третьей строке прибавили вторую, умноженную на 6.
(6) Вторую строку умножили на –1, третью строку разделили на -83. .Очевидно, что плоскость однозначно определяется тремя различными точками, не лежащими на одной прямой. Поэтому достаточно популярны трёхбуквенные обозначения плоскостей – по принадлежащим им точкам, например, ; .Если свободные члены
Решение системы по формулам крамера. Правило Крамера. Метод обратной матрицы
Методы Крамера и Гаусса – одни из самых популярных методов решения СЛАУ . К тому же, в ряде случаев целесообразно использовать именно конкретные методы. Сессия близка, и сейчас самое время повторить или освоить их с нуля. Сегодня разбираемся с решением методом Крамера. Ведь решение системы линейных уравнений методом Крамера — весьма полезный навык.
Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений – система уравнений вида:
Набор значений x , при котором уравнения системы обращаются в тождества, называется решением системы, a и b – вещественные коэффициенты. Простенькую систему, состоящую из двух уравнений с двумя неизвестными, можно решить в уме либо выразив одну переменную через другую. Но переменных (иксов) в СЛАУ может быть гораздо больше двух, и здесь простыми школьными манипуляциями не обойтись. Что же делать? Например, решать СЛАУ методом Крамера!
Итак, пусть система состоит из n уравнений с n неизвестными.
Такую систему можно переписать в матричном виде
Здесь A – основная матрица системы, X и B , соответственно, матрицы-столбцы неизвестных переменных и свободных членов.
Решение СЛАУ методом Крамера
Если определитель главной матрицы не равен нулю (матрица невырожденная), систему можно решать по методу Крамера.
Согласно методу Крамера, решение находится по формулам:
Здесь дельта – определитель главной матрицы, а дельта x n-ное – определитель, полученный из определителя главной матрицы путем заменой n-ного столбца на столбец свободных членов.
В этом и заключается вся суть метода Крамера. Подставляя найденные по вышеприведенным формулам значения x в искомую систему, убеждаемся в правильности (или наоборот) нашего решения. Чтобы Вы быстрее уловили суть, приведем ниже пример подробного решения СЛАУ методом Крамера:
Даже если у Вас не получится с первого раза, не расстраивайтесь! Немного практики, и Вы начнете щелкать СЛАУ как орешки. Более того, сейчас совершенно необязательно корпеть над тетрадью, решая громоздкие выкладки и исписывая стержень. Можно легко решить СЛАУ методом Крамера в режиме онлайн, лишь подставив в готовую форму коэффициенты. Испробовать онлайн калькулятор решения методом Крамера можно, к примеру, на этом сайте .
А если система оказалась упорной и не сдается, Вы всегда можете обратиться за помощью к нашим авторам, например, чтобы . Будь в системе хоть 100 неизвестных, мы обязательно решим ее верно и точно в срок!
Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).
Определители
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
;
.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
Согласно теореме Крамера имеем:
Итак, решение системы (2):
онлайн-калькулятором , решающим методом Крамера.
Три случая при решении систем линейных уравнений
Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:
Первый случай: система линейных уравнений имеет единственное решение
(система совместна и определённа)
Второй случай: система линейных уравнений имеет бесчисленное множество решений
(система совместна и неопределённа)
** ,
т.е. коэффициенты при неизвестных и свободные члены пропорциональны.
Третий случай: система линейных уравнений решений не имеет
(система несовместна)
Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .
Примеры решения систем линейных уравнений методом Крамера
Пусть дана система
.
На основании теоремы Крамера
………….
,
где
—
определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:
Пример 2.
.
Следовательно, система является определённой. Для нахождения её решения вычисляем определители
По формулам Крамера находим:
Итак, (1; 0; -1) – единственное решение системы.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.
Пример 3. Решить систему линейных уравнений методом Крамера:
.
Решение. Находим определитель системы:
Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных
По формулам Крамера находим:
Итак, решение системы — (2; -1; 1).
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
К началу страницы
Продолжаем решать системы методом Крамера вместе
Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.
Пример 6. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных
Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.
Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.
В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных — буквы. За примерами далеко ходить не надо.
Следующий пример — на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.
Пример 8. Решить систему линейных уравнений методом Крамера:
Решение. Находим определитель системы:
Находим определители при неизвестных
Для того чтобы освоить данный параграф Вы должны уметь раскрывать определители «два на два» и «три на три». Если с определителями плохо, пожалуйста, изучите урок Как вычислить определитель?
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицы
Метод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
В ходе решения расчет миноров лучше расписать подробно, хотя, при определенном опыте их можно приноровиться считать с ошибками устно.
В первой части мы рассмотрели немного теоретического материала, метод подстановки, а также метод почленного сложения уравнений системы. Всем, кто зашел на сайт через эту страницу рекомендую ознакомиться с первой частью. Возможно, некоторым посетителям покажется материал слишком простым, но по ходу решения систем линейных уравнений я сделал ряд очень важных замечаний и выводов, касающихся решения математических задач в целом.
А сейчас мы разберём правило Крамера, а также решение системы линейных уравнений с помощью обратной матрицы (матричный метод). Все материалы изложены просто, подробно и понятно, практически все читатели смогут научиться решать системы вышеуказанными способами.
Сначала мы подробно рассмотрим правило Крамера для системы двух линейных уравнений с двумя неизвестными. Зачем? – Ведь простейшую систему можно решить школьным методом, методом почленного сложения!
Дело в том, что пусть иногда, но встречается такое задание – решить систему двух линейных уравнений с двумя неизвестными по формулам Крамера. Во-вторых, более простой пример поможет понять, как использовать правило Крамера для более сложного случая – системы трех уравнений с тремя неизвестными.
Кроме того, существуют системы линейных уравнений с двумя переменными, которые целесообразно решать именно по правилу Крамера!
Рассмотрим систему уравнений
На первом шаге вычислим определитель , его называют главным определителем системы .
метод Гаусса .
Если , то система имеет единственное решение, и для нахождения корней мы должны вычислить еще два определителя:
и
На практике вышеуказанные определители также могут обозначаться латинской буквой .
Корни уравнения находим по формулам:
,
Пример 7
Решить систему линейных уравнений
Решение : Мы видим, что коэффициенты уравнения достаточно велики, в правой части присутствуют десятичные дроби с запятой. Запятая – довольно редкий гость в практических заданиях по математике, эту систему я взял из эконометрической задачи.
Как решить такую систему? Можно попытаться выразить одну переменную через другую, но в этом случае наверняка получатся страшные навороченные дроби, с которыми крайне неудобно работать, да и оформление решения будет выглядеть просто ужасно. Можно умножить второе уравнение на 6 и провести почленное вычитание, но и здесь возникнут те же самые дроби.
Что делать? В подобных случаях и приходят на помощь формулы Крамера.
;
;
Ответ : ,
Оба корня обладают бесконечными хвостами, и найдены приближенно, что вполне приемлемо (и даже обыденно) для задач эконометрики.
Комментарии здесь не нужны, поскольку задание решается по готовым формулам, однако, есть один нюанс. Когда используете данный метод, обязательным фрагментом оформления задания является следующий фрагмент: «, значит, система имеет единственное решение» . В противном случае рецензент может Вас наказать за неуважение к теореме Крамера.
Совсем не лишней будет проверка, которую удобно провести на калькуляторе: подставляем приближенные значения в левую часть каждого уравнения системы. В результате с небольшой погрешностью должны получиться числа, которые находятся в правых частях.
Пример 8
Ответ представить в обыкновенных неправильных дробях. Сделать проверку.
Это пример для самостоятельного решения (пример чистового оформления и ответ в конце урока).
Переходим к рассмотрению правила Крамера для системы трех уравнений с тремя неизвестными:
Находим главный определитель системы:
Если , то система имеет бесконечно много решений или несовместна (не имеет решений). В этом случае правило Крамера не поможет, нужно использовать метод Гаусса .
Если , то система имеет единственное решение и для нахождения корней мы должны вычислить еще три определителя:
, ,
И, наконец, ответ рассчитывается по формулам:
Как видите, случай «три на три» принципиально ничем не отличается от случая «два на два», столбец свободных членов последовательно «прогуливается» слева направо по столбцам главного определителя.
Пример 9
Решить систему по формулам Крамера.
Решение : Решим систему по формулам Крамера.
, значит, система имеет единственное решение.
Ответ : .
Собственно, здесь опять комментировать особо нечего, ввиду того, что решение проходит по готовым формулам. Но есть пара замечаний.
Бывает так, что в результате вычислений получаются «плохие» несократимые дроби, например: .
Я рекомендую следующий алгоритм «лечения». Если под рукой нет компьютера, поступаем так:
1) Возможно, допущена ошибка в вычислениях. Как только Вы столкнулись с «плохой» дробью, сразу необходимо проверить, правильно ли переписано условие . Если условие переписано без ошибок, то нужно пересчитать определители, используя разложение по другой строке (столбцу).
2) Если в результате проверки ошибок не выявлено, то вероятнее всего, допущена опечатка в условии задания. В этом случае спокойно и ВНИМАТЕЛЬНО прорешиваем задание до конца, а затем обязательно делаем проверку и оформляем ее на чистовике после решения. Конечно, проверка дробного ответа – занятие неприятное, но зато будет обезоруживающий аргумент для преподавателя, который ну очень любит ставить минус за всякую бяку вроде . Как управляться с дробями, подробно расписано в ответе для Примера 8.
Если под рукой есть компьютер, то для проверки используйте автоматизированную программу, которую можно бесплатно скачать в самом начале урока. Кстати, выгоднее всего сразу воспользоваться программой (еще до начала решения), Вы сразу будете видеть промежуточный шаг, на котором допустили ошибку! Этот же калькулятор автоматически рассчитывает решение системы матричным методом.
Замечание второе. Время от времени встречаются системы в уравнениях которых отсутствуют некоторые переменные, например:
Здесь в первом уравнении отсутствует переменная , во втором – переменная . В таких случаях очень важно правильно и ВНИМАТЕЛЬНО записать главный определитель:
– на месте отсутствующих переменных ставятся нули.
Кстати определители с нулями рационально раскрывать по той строке (столбцу), в которой находится ноль, так как вычислений получается заметно меньше.
Пример 10
Решить систему по формулам Крамера.
Это пример для самостоятельного решения (образец чистового оформления и ответ в конце урока).
Для случая системы 4 уравнений с 4 неизвестными формулы Крамера записываются по аналогичным принципам. Живой пример можно посмотреть на уроке Свойства определителя. Понижение порядка определителя – пять определителей 4-го порядка вполне решабельны. Хотя задача уже весьма напоминает ботинок профессора на груди у студента-счастливчика.
Решение системы с помощью обратной матрицыМетод обратной матрицы – это, по существу, частный случай матричного уравнения (см. Пример №3 указанного урока).
Для изучения данного параграфа необходимо уметь раскрывать определители, находить обратную матрицу и выполнять матричное умножение. Соответствующие ссылки будут даны по ходу объяснений.
Пример 11
Решить систему с матричным методом
Решение : Запишем систему в матричной форме:
, где
Пожалуйста, посмотрите на систему уравнений и на матрицы. По какому принципу записываем элементы в матрицы, думаю, всем понятно. Единственный комментарий: если бы в уравнениях отсутствовали некоторые переменные, то на соответствующих местах в матрице нужно было бы поставить нули.
Обратную матрицу найдем по формуле:
, где – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы .
Сначала разбираемся с определителем:
Здесь определитель раскрыт по первой строке.
Внимание! Если , то обратной матрицы не существует, и решить систему матричным методом невозможно. В этом случае система решается методом исключения неизвестных (методом Гаусса) .
Теперь нужно вычислить 9 миноров и записать их в матрицу миноров
Справка: Полезно знать смысл двойных подстрочных индексов в линейной алгебре. Первая цифра – это номер строки, в которой находится данный элемент. Вторая цифра – это номер столбца, в котором находится данный элемент:
То есть, двойной подстрочный индекс указывает, что элемент находится в первой строке, третьем столбце, а, например, элемент находится в 3 строке, 2 столбце
I.4. Решение систем линейных алгебраических уравнений методом обратной матрицы
(схема 17)
Матрица, имеющая отличный от нуля определитель, называется невырожденной; имеющая равный нулю определитель – вырожденной.
Матрица A-1 называется обратной для заданной квадратной матрицы , если при умножении матрицы на обратную ей как справа, так и слева, получается единичная матрица, то есть
A-1∙A=A∙A-1=E. (1.7)
Заметим, что в данном случае произведение матриц A и A-1 коммутативно.
Теорема 1.2. Необходимым и достаточным условием существования обратной матрицы для заданной квадратной матрицы, является отличие от нуля определителя заданной матрицы
Если главная матрица системы оказалась при проверке вырожденной, то для нее не существует обратной, и рассматриваемый метод применить нельзя.
Для невырожденной матрицы можно найти обратную ей матрицу A-1 по следующему алгоритму.
1. Транспонируем матрицу A в матрицу AT .
2. Вычисляем алгебраические дополнения элементов матрицы AT и записываем их в матрицу .
3. Составим обратную матрицу A-1 по формуле:
. (1.8)4. Сделаем проверку правильности найденной матрицы А-1 согласно формуле (1.7). Заметим, что данная проверка может быть включена в итоговую проверку самого решения системы.
Система (1.5) линейных алгебраических уравнений может быть представлена в виде матричного уравнения: A∙X=B, где A – главная матрица системы, – столбец неизвестных, – столбец свободных членов. Умножим это уравнение слева на обратную матрицу A-1, получим: A-1∙A∙X=A-1∙B. Так как по определению обратной матрицы A-1∙A=E, то уравнение принимает вид
E∙X=A-1∙B или X=A-1∙B . (1.9)
Таким образом, чтобы решить систему линейных алгебраических уравнений нужно столбец свободных членов умножить слева на матрицу, обратную для главной матрицы системы. После этого следует сделать проверку полученного решения.
Пример 1.6. Решить систему методом обратной матрицы
Решение. Вычислим главный определитель системы
.Следовательно, матрица невырожденная и обратная к ней матрица существует.
Найдём алгебраические дополнения всех элементов главной матрицы :
Запишем алгебраические дополнения в матрицу
. Воспользуемся формулами (1.8) и (1.9) для нахождения решения системы . Отсюда x=2, y=0, z=1Решить систему линейных уравнений методом обратной матрицы онлайн
Одним из известных методов решения систем линейных алгебраических уравнений (СЛАУ) является метод обратной матрицы . Предположим, у нас есть СЛАУ двух уравнений с двумя неизвестными.
a11xa12yb1a21xa22yb2
Введем обозначения: А — матрица СЛАУ вида:
Аа11а12а21а22
Икс — вектор-столбец неизвестных, которые необходимо найти:
ХХХ
Б — векторный столбец свободных коэффициентов:
Bb1b2
Итак, исходную СЛАУ можно переписать в матричных обозначениях:
АХБ
Чтобы решить это матричное уравнение, умножьте обе его части слева на Матрица -1 :
A1AXA1B
Здесь, А -1 — матрица, обратная матрице А.Такая матрица существует для любой квадратной невырожденной матрицы (т.е. ее определитель не равен нулю).
Приведенные выше условия показывают границы применимости метода обратной матрицы для решения СЛАУ. Прежде всего: матрица СЛАУ А должен быть квадратным. Это означает, что количество уравнений должно быть равно количеству переменных. На втором месте: определитель матрицы А не должен быть равен нулю:
А0
Кроме того, обратная матрица обладает замечательным свойством: ее произведение на исходную матрицу коммутативно и равно единичной матрице:
А1ААА1Е
Возвращаясь к решению нашего матричного уравнения, получаем:
EXXA1B
Итак, чтобы решить СЛАУ методом обратной матрицы, в первую очередь нужно проверить, существует ли обратная матрица, а затем найти ее и умножить на вектор Б.
Цель нашего онлайн-калькулятора состоит в том, чтобы решить СЛАУ методом обратной матрицы . Калькулятор находит пошаговое решение. Уравнения СЛАУ вводятся в натуральном виде. Коэффициентом уравнения могут быть не только числа и дроби, но и параметры. В последнем случае калькулятор выдает решение в общепринятой форме.
Калькулятор системы линейных уравнений
Этот калькулятор решит систему линейных уравнений любого типа с показанными шагами, используя метод исключения Гаусса-Жордана, метод обратной матрицы или правило Крамера.
Связанный калькулятор: Калькулятор системы уравнений
Система уравнений:5x-2y=1, x+3y=7
Через запятую, например, x+2y=5,3x+5y=14.
Оставьте пустым для автоматического определения или укажите переменные, такие как x,y (через запятую).
Метод:Исключение Гаусса-Джордана Метод обратной матрицыПравило Крамера
Если калькулятор что-то не рассчитал, или вы обнаружили ошибку, или у вас есть предложение/отзыв, пожалуйста, напишите его в комментариях ниже.
Ваш ввод
Решить $$$\begin{case} 5 x — 2 y = 1 \\ x + 3 y = 7 \end{cases}$$$ для $$$x$$$, $ $$y$$$ методом исключения Гаусса-Жордана.
Решение
Запишите расширенную матрицу: $$$\left[\begin{array}{cc|c}5 & -2 & 1\\1 & 3 & 7\end{array}\right]$ $$.
Выполните исключение Гаусса-Жордана (шаги см. в калькуляторе исключения Гаусса-Жордана): $$$\left[\begin{array}{cc|c}5 & -2 & 1\\0 & \frac{17 {5} & \frac{34}{5}\end{массив}\right]$$$.
Обратная замена:
$$$y = \frac{\frac{34}{5}}{\frac{17}{5}} = 2$$$
$$$x = \frac{ 1 — \влево(-2\вправо) \влево(2\вправо)}{5} = 1$$$
Ответить
$$$x = 1$$$, $$$y = 2$$$A
Калькулятор обратной матрицы — eMathHelp
Калькулятор найдет обратную (если она существует) квадратную матрицу, используя метод исключения Гаусса или метод сопряжения, с показанными шагами.{-1}$$$ методом исключения Гаусса-Джордана.
Решение
Чтобы найти обратную матрицу, дополните ее единичной матрицей и выполните операции со строками, пытаясь сделать единичную матрицу слева. Тогда справа будет обратная матрица.
Итак, дополним матрицу единичной матрицей:
$$$\left[\begin{array}{cc|cc}2 & 1 & 1 & 0\\1 & 3 & 0 & 1\end{array }\right]$$$
Разделить строку $$$1$$$ на $$$2$$$: $$$R_{1} = \frac{R_{1}}{2}$$$.
$$$\left[\begin{array}{cc|cc}1 & \frac{1}{2} & \frac{1}{2} & 0\\1 & 3 & 0 & 1\end {array}\right]$$$
Вычесть строку $$$1$$$ из строки $$$2$$$: $$$R_{2} = R_{2} — R_{1}$$$.
$$$\left[\begin{array}{cc|cc}1 & \frac{1}{2} & \frac{1}{2} & 0\\0 & \frac{5}{2} } & — \frac{1}{2} & 1\end{array}\right]$$$
Умножить строку $$$2$$$ на $$$\frac{2}{5}$$$: $$$R_{2} = \frac{2 R_{2}}{5}$$$.
$$$\left[\begin{array}{cc|cc}1 & \frac{1}{2} & \frac{1}{2} & 0\\0 & 1 & — \frac{1 }{5} & \frac{2}{5}\end{array}\right]$$$
Вычесть строку $$$2$$$, умноженную на $$$\frac{1}{2}$$$ из строки $$$1$$$: $$$R_{1} = R_{1} — \frac{R_{2}}{2}$$$.
$$$\left[\begin{array}{cc|cc}1 & 0 & \frac{3}{5} & — \frac{1}{5}\\0 & 1 & — \frac{ 1}{5} & \frac{2}{5}\end{array}\right]$$$
Готово. Слева — единичная матрица. Справа — обратная матрица.
Ответить
Обратная матрица: $$$\left[\begin{array}{cc}\frac{3}{5} & — \frac{1}{5}\\- \frac{1}{5} & \frac{2}{5}\end{массив}\right] = \left[\begin{массив}{cc}0,6 и -0.2\\-0,2 и 0,4\конец{массив}\справа].$$$A
Метод обратной матрицы — Бесплатная помощь по математике
Система решения линейных уравнений: (урок 5 из 5)
Метод обратной матрицы
Предположим, вам дано уравнение с одной переменной, например, $4x = 10$. потом вы найдете значение $x$, которое решает это уравнение, умножив уравнение, обратное 4: $\color{blue}{\frac14} \cdot 4x = \color{blue}{\frac14} \cdot 10$, поэтому решение будет $x = 2.5$.
Иногда мы можем сделать что-то очень похожее на решение систем линейных уравнения; в этом случае мы будем использовать обратную матрицу коэффициентов. Но сначала мы должны проверить, что эта инверсия существует! Условия существования матрицы, обратной матрице коэффициентов, такие же, как при использовании Правило Крамера, то есть
1. В системе должно быть одинаковое количество уравнения как переменные, то есть матрица коэффициентов системы должна быть квадратный.
2. Определитель матрица коэффициентов должна быть отличной от нуля. Причина, конечно, в том, что обратная матрицы существует именно тогда, когда ее определитель отличен от нуля.
3. Чтобы использовать этот метод, следуйте шаги продемонстрированы на следующей системе:
$$ \begin{выровнено} -х + 3у + г &= 1 \\ 2х + 5у &= 3\\ 3x + у — 2z &= -2 \end{выровнено} $$Шаг 1: Перепишите систему, используя умножение матриц:
$$ \left ( {\ begin {массив} {* {20} {c}} — 1\\ 2\\ 3 \end{массив}\begin{массив}{*{20}{c}} 3\\ 5\\ 1 \end{массив}\begin{массив}{*{20}{c}} 1\\ 0\\ — 2 \end{массив}} \right)\left( {\begin{массив}{*{20}{c}} Икс\\ у\\ г \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} 1\\ 3\\ — 2 \end{массив}} \right) $$и записав матрицу коэффициентов как A, мы имеем
$$ А \ влево ( {\ begin {массив} {* {20} {c}} Икс\\ у\\ г \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} 1\\ 3\\ — 2 \end{массив}} \right) $$Шаг 2: Найдите обратную матрицу коэффициентов A.{ — 1}}\left( {\begin{массив}{*{20}{c}} 1\\ 3\\ {- 2} \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} { — \фракция{{10}}{9}}\\ {\ гидроразрыва {4} {9}} \\ { — \фракция{{13}}{9}} \end{массив}\begin{массив}{*{20}{c}} {\ гидроразрыва {7} {9}} \\ { — \фракция{1}{9}}\\ {\ гидроразрыва {{10}} {9}} \end{массив}\begin{массив}{*{20}{c}} { — \фракция{5}{9}}\\ {\ гидроразрыва {2} {9}} \\ { — \фракция{{11}}{9}} \end{массив}} \right)\left( {\begin{массив}{*{20}{c}} 1\\ 3\\ {- 2} \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} {21}\\ {- 3}\\ {39} \end{массив}} \right) $$
и так решение
$$ \left ( {\ begin {массив} {* {20} {c}} Икс\\ у\\ г \end{массив}} \right) = \left( {\begin{массив}{*{20}{c}} {21}\\ {- 3}\\ {39} \end{массив}} \right) $$Система линейных уравнений и обращение матриц
Система линейных уравнений и обращение матрицЭтот учебный объект JavaScript E-labs предназначен для решения систем линейных уравнений до трех уравнений с тремя неизвестными.Это также позволяет нам найти обратную матрицу.Другие учебные объекты JavaScript для принятия решений из этой серии относятся к разным областям применения в разделе МЕНЮ на этой странице.
При вводе данных для перехода от ячейки к ячейке в матрице данных используйте клавишу Tab , а не клавиши со стрелками или клавиши ввода.Инструкции и приложения:
- Неизвестные имена переменных: X1, X2, X3,..и X10, в зависимости от того, есть ли у вас одно уравнение, два уравнения или три уравнения с одной неизвестной, двумя неизвестными или тремя неизвестными переменными соответственно.
- Начиная с левого верхнего угла, замените столько нулей в матрице данных коэффициентами неизвестных переменных в уравнениях вместе с их правыми значениями, сколько необходимо. Матрица коэффициентов должна представлять собой квадратную матрицу, расположенную в верхнем левом углу матрицы данных, поэтому не оставляйте пустых строк между ними.
- JavaScript основан на операциях строки Gauss-Jordan (GJ). Требование для операций GJ состоит в том, что первый элемент в матрице коэффициентов должен быть ненулевым. Поэтому сначала введите коэффициент всех уравнений, имеющих ненулевой коэффициент X1; затем введите все остальные уравнения. То есть любое уравнение с нулевыми коэффициентами для X1 должно стоять в конце таблицы ввода данных.
Численный пример 1. Рассмотрим следующую систему уравнений:
Х2 + Х3 = 5
3Х1 + Х3 = 6
-Х1 + Х2 = 1Матрица коэффициентов переменных:
0 1 1
3 0 1
-1 1 0Первая запись первого столбца равна нулю, хотя в нем всегда есть хотя бы один ненулевой элемент.Следовательно, мы должны перестроить систему уравнений таким образом, чтобы любое уравнение с нулевым коэффициентом X1 оказалось среди последнего набора уравнений. То есть, рассматривая эквивалентную систему уравнений:
3Х1 + Х3 = 6
-Х1 + Х2 = 1
Х2 + Х3 = 5Решите эту эквивалентную систему уравнений, введя ее коэффициент и значения RHS в таблицу ввода данных, затем нажмите кнопку «Рассчитать». Выходом является решение: X1 = 1, X2 = 2 и X3 = 3, что можно проверить подстановками.
- Нахождение обратной матрицы с помощью системы уравнений: Чтобы найти обратную квадратную матрицу размера n, решите n систем уравнений с единичным вектором в правой части. Следующий числовой пример иллюстрирует этот процесс:
Численный пример 2. Предположим, мы хотим найти обратную (A -1 ) следующую матрицу (если она существует) A:
В общем, чтобы найти A -1 , столбец за столбцом, решите n систем уравнений, имеющих матрицу коэффициентов A, но с n различными векторами идентичности в качестве их RHS-значений.
Для этого числового примера мы должны решить следующие две системы уравнений:
2Х1 + Х1 = 1
Х1 — Х2 = 0и
2Х1 + Х1 = 0
Х1 — Х2 = 1Обратите внимание, что коэффициенты переменных X1 и X2 являются матрицей A в обеих системах уравнений, однако RHS являются двумя единичными векторами в n = 2-мерном пространстве.
Решения первой и второй систем уравнений в соответствии с приведенной выше инструкцией дают первый и второй столбцы матрицы A -1 .
Чтобы найти первый столбец A -1 , решите:
2Х1 + Х1 = 1
Х1 — Х2 = 0Это дает X1 = 1/3, X2 = 1/3. Чтобы найти второй столбец A -1 , решите:
2Х1 + Х1 = 0
Х1 — Х2 = 1Это дает X1 = 1/3, X2 = -2/3. Следовательно, A -1 p равно
1/3 1/3 А -1 = 1/3 -2/3 - Примечание: Матрица, имеющая обратную, называется невырожденной или обратимой.Матрица называется вырожденной, если она не имеет обратной. Например, следующая матрица является сингулярной:
1 6 4
2 4 -1
-1 2 5Поэтому при применении описанной выше процедуры обращения матрицы, если матрица вырожденная, то по крайней мере из систем уравнений не имеет решения.
- Для редактирования ваших данных, включая добавление/изменение/удаление, вам не нужно нажимать на кнопку «очистить», а заново вводить свои данные заново.Вы можете просто добавить, изменить число на другое в той же ячейке или удалить число из ячейки, установив его значение равным нулю. После редактирования нажмите кнопку «Рассчитать».
Это полезно, например. найти обратную матрицу A 10×10 , где мы должны изменить только значения RHS.
Для расширенного редактирования или использования JavaScript для нового набора данных используйте кнопку «Очистить».
Для получения технических подробностей вернитесь к:
тем по линейной алгебре.Пожалуйста, отправьте свои комментарии по адресу:
Профессор Хоссейн Аршам
МЕНЮ
Заявление об авторских правах. Добросовестное использование материалов, представленных на этом веб-сайте, в соответствии с Руководством по добросовестному использованию образовательных мультимедиа от 1996 г. разрешено только в некоммерческих целях и в учебных целях.
Этот сайт может быть переведен и/или зеркально отображен в неизменном виде (включая эти уведомления) на любом сервере с общедоступным доступом. Все файлы доступны по адресу http://home.ubalt.edu/ntsbarsh/Business-stat для зеркалирования.Пожалуйста, пришлите мне по электронной почте ваши комментарии, предложения и проблемы. Спасибо.
Вернуться к:Домашняя страница доктора Аршама
ЕОФ: 1994-2015 гг.
Использование обратной матрицы для решения системы линейных уравнений
Матрицы
Матрица представляет собой прямоугольный массив чисел, заключенных в скобки.Чтобы решить систему уравнений с использованием матриц, нам нужно создать три разных вида матриц.
Первая матрица, которую мы будем использовать, называется матрицей коэффициентов , которая представляет собой просто коэффициенты или числа перед каждой переменной в системе уравнений. Мы должны быть уверены, что наша система уравнений выстроена так, что каждая переменная находится в одном столбце.
Если мы посмотрим на пример системы линейных уравнений, то в первом уравнении коэффициенты равны 1 перед x и 2 перед y .Во втором уравнении у нас есть 3 перед x и 5 перед y . Поскольку у нас есть два x и 2 y , у нас будет матрица 2×2, то есть две строки и два столбца. Мы назовем эту матрицу A .
Строки представляют различные уравнения, а столбцы представляют различные переменные. Первая строка — коэффициенты первого уравнения, вторая строка — коэффициенты второго уравнения.Первый столбец — это коэффициенты x , а второй столбец — коэффициенты y .
Вторая нужная нам матрица называется матрицей переменных . Матрица переменных всегда будет состоять из одного столбца с переменными в каждой строке. В этом случае, поскольку у нас есть две переменные, у нас будет матрица 2×1, где у нас есть две строки и один столбец. Мы назовем эту матрицу X , используя заглавную букву, чтобы различать строчные буквы x в задаче.
Если мы вернемся к исходной системе уравнений, то увидим, что мы использовали коэффициенты и переменные. Остается только то, чему равны уравнения. Третья матрица называется константной матрицей , которая содержит константы системы уравнений. Мы назовем эту матрицу B . Опять же, это матрица 2×1, потому что она состоит из двух строк и одного столбца.
Первое уравнение было равно 5, поэтому это число стоит в первой строке.Второе уравнение было равно 14, так что это число идет во второй строке.
После того, как вы превратили систему уравнений в матрицы, как нам решить систему, чтобы найти ответ?
Использование обратных матриц для решения систем уравнений
Теперь, когда мы знаем, какие матрицы нам нужны, мы можем сложить их вместе, чтобы создать матричное уравнение. Матричное уравнение содержит матрицу коэффициентов, переменную матрицу и постоянную матрицу и может быть решено. Существенно, что мы знаем, что если мы умножим матрицу A на матрицу X , она будет равна матрице B .
Чтобы решить матричное уравнение, подумайте об уравнении A ( X ) = B . Если бы мы хотели найти X , нам нужно было бы разделить B на A . Однако при работе с матрицами мы не можем делить. Вместо этого мы умножим на величину, обратную A . Мы показываем, что умножаем на обратное, используя отрицательную единицу в качестве показателя степени.
Нахождение обратной матрицы 2×2
Чтобы найти обратную матрицу 2×2, мы сначала поменяем местами значения a и d , затем мы сделаем b и c отрицательными, наконец, мы умножим на определитель. Определитель матрицы равен единице, превышающей различные числа и и до .
Для матрицы A , a = 1, b = 2, c = 3 и d = 5. Таким образом, мы подставляем эти значения в обратную формулу.
Теперь упростим. Сначала упростим определитель. Один раз пять будет пять, а два раза три будет шесть. Пять минус шесть минус один. Единица, деленная на отрицательную единицу, равна отрицательной единице.
Затем мы умножаем все элементы матрицы на отрицательную единицу, что дает нам обратную A .
Умножение матриц
Теперь, когда у нас есть обратная матрица, нам нужно умножить обратную матрицу на постоянную матрицу. Обратная матрица представляет собой матрицу 2×2, а постоянная матрица представляет собой матрицу 2×1. Для умножения матриц количество столбцов в первой матрице должно совпадать с количеством строк во второй матрице. Результирующая матрица будет иметь то же количество строк, что и первая матрица, и то же количество столбцов, что и вторая матрица.
Красным обведено количество столбцов в первой матрице и количество строк во второй матрице, и они должны совпадать.
Чтобы умножить матрицы, мы умножаем строки на столбцы.
В этом случае мы собираемся умножить первую строку A в обратном порядке на первый столбец B , а затем добавить элементы.
Возьмем минус пять раз по пять и прибавим это к двум раза по четырнадцать и получим 3.
Затем мы берем вторую строку A в обратном порядке и умножаем ее на первый столбец B , а затем добавляем элементы.
Мы умножаем три раза на пять и прибавляем к минусу один раз четырнадцать, что дает нам 1.
Поскольку первая строка нашей матрицы переменных была x , а вторая строка была y , наши решения этой системы уравнений равны x = 3 и y = 1.Мы обнаружили, что каждый взрослый билет стоит 3 доллара, а каждый детский билет стоит 1 доллар.
Резюме урока
Чтобы решить систему уравнений , где у нас есть два или более уравнений, содержащих две или более переменных, используя обратные матрицы, мы можем выполнить следующие шаги.
- Создайте матрицу коэффициентов , A , которая содержит коэффициенты переменных из системы уравнений.
- Создайте матрицу переменных , X , содержащую переменные из системы уравнений.
- Создайте матрицу констант , B , содержащую константы из системы уравнений.
- Напишите матричное уравнение, AX = B .
- Найдите обратную матрицу A , переставив элементы a и d , поменяв знаки элементов b и c и затем умножив на определитель , который равен единице на разность ad и г. до н.э. г.
- Умножить A обратное умножение на B постоянную матрицу.
7.7 Решение систем с инверсиями — Алгебра колледжа с соответствующей поддержкой
Цели обучения
В этом разделе вы:
- Найдите обратную матрицу.
- Решите систему линейных уравнений, используя обратную матрицу.
Основные навыки
Цели обучения
- Оценить определитель матрицы 2×2 (IA 4.6.1)
- Вычисление определителя матрицы 3×3 (IA 4.6.2)
Задача 1: Оценить определитель матрицы 2×2 (IA 4.6.1)
Если матрица имеет одинаковое количество строк и столбцов, мы называем ее квадратной матрицей. Каждая квадратная матрица имеет связанное с ней действительное число, называемое ее определителем.
Определитель
Определитель любой квадратной матрицы abcdabcd , где a, b, c и d — действительные числа, равен abcd=ad-bcabcd=ad-bc
Чтобы получить действительное числовое значение определителя, мы вычитаем произведения диагоналей, как показано на рисунке.
Пример 1
Найдите определитель матрицы 2×2 4-23-14-23-1
Решение
| Напишите определитель | |
| Вычесть произведения диагоналей | 4(-1)-3(-2)4(-1)-3(-2) |
| Упрощение | -4+62-4+62 |
Практика ведет к совершенству
Найдите определитель матрицы 2×2.
Задача 2: вычислить определитель матрицы 3×3 (IA 4.6.2)
Чтобы вычислить определитель матрицы 3×3, мы должны уметь вычислять минор элемента определителя.
Второстепенный элемент записи — это определитель 2×2, найденный удалением строки и столбца в определителе 3×3, содержащем запись.
Например, чтобы найти второстепенную запись a 1 , мы удаляем строку и столбец, которые ее содержат. Итак, мы исключаем первую строку и первый столбец.Затем запишем оставшийся определитель 2×2.
Чтобы найти минор записи b 2 , мы удаляем строку и столбец, которые его содержат. Итак, мы исключаем вторую строку и второй столбец. Затем запишем оставшийся определитель 2×2.
Пример 2
Для определителя |4−2310−3−2−42|,|4−2310−3−2−42| найдите и оцените минор числа ⓐ a1a1 ⓑ b3b3
Решение
ⓐ
ⓑ
| Удалите строку и столбец, содержащие b3.б3. | |
| Запишите оставшийся определитель 2×22×2. | |
| Оценить. | |
| Упрощение. |
Попробуйте #1
Для следующего определителя найдите и оцените минор числа c2
4-2310-3-2-424-2310-3-2-42
| Удалите строку и столбец, содержащие c2c2. | ____________________________________________ |
| Запишите оставшийся определитель 2×22×2. | ____________________________________________ |
| Оценивайте и упрощайте. | ____________________________________________ |
Стратегия вычисления определителя матрицы 3×3
Чтобы вычислить определитель 3×3, мы можем разложить по младшим, используя любую строку или столбец. Выбор строки или столбца, отличного от первой строки, иногда облегчает работу.
Когда мы расширяем любую строку или столбец, мы должны быть осторожны со знаком членов в расширении.Чтобы определить знак терминов, мы используем следующую схему шаблона знаков.
+-+-+-+-++-+-+-+-+
Расширение по младшим по первой строке для вычисления определителя 3×3.
Чтобы вычислить определитель 3×3 путем расширения по младшим по первой строке, мы используем следующий шаблон:
ПРИМЕЧАНИЕ. Мы можем вычислить определитель матрицы, разложив миноры по любой строке или столбцу. Если строка или столбец содержат нулевую запись, расширение по этой строке или столбцу приводит к меньшему количеству вычислений.
Пример 3
Вычислите определитель матрицы 3×3, разложив ее по минорам по первой строке.
2-3-1320-1-1-22-3-1320-1-1-2
Практика делает совершенным
3.Вычислите определитель матрицы 3×3, разложив его по младшим по первой строке. -5-1-440-32-26-5-1-440-32-26
Нэнси планирует инвестировать 10 500 долларов в две разные облигации, чтобы распределить свой риск. Первая облигация имеет годовой доход 10%, а вторая облигация имеет годовой доход 6%.Сколько Нэнси должна инвестировать в каждую облигацию, чтобы получить доход в размере 8,5% от двух облигаций? Каков наилучший метод решения этой проблемы?
Есть несколько способов решить эту проблему. Как мы видели в предыдущих разделах, системы уравнений и матриц полезны при решении реальных проблем, связанных с финансами. После изучения этого раздела у нас будут инструменты для решения проблемы связи с использованием обратной матрицы.
Нахождение обратной матрицы
Мы знаем, что мультипликативная обратная величина действительного числа aa равна a−1,a−1, и aa−1=a−1a=(1a)a=1.аа-1=а-1а=(1а)а=1. Например, 2−1=122−1=12 и (12)2=1.(12)2=1. Мультипликативная обратная матрица аналогична по своей концепции, за исключением того, что произведение матрицы AA и ее обратной матрицы A-1A-1 равно единичной матрице. Единичная матрица представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах. Мы идентифицируем матрицы идентичности по InIn, где nn представляет размерность матрицы. Упражнение 7.2 и следующие уравнения.
I3=[100010001]I3=[100010001]Единичная матрица действует как 1 в матричной алгебре.Например, AI=IA=A.AI=IA=A.
Матрица, имеющая мультипликативную обратную, обладает свойствами
АА-1=ИА-1А=ИАА-1=ИА-1А=ЯМатрица, имеющая мультипликативную обратную, называется обратимой матрицей. Только квадратная матрица может иметь мультипликативную обратную, поскольку обратимость AA-1=A-1A=I, AA-1=A-1A=I является требованием. Не все квадратные матрицы имеют обратную, но если AA обратима, то A−1A−1 уникальна. Мы рассмотрим два метода нахождения обратной матрицы 2 × 22 × 2 и третий метод, который можно использовать как для матриц 2 × 22 × 2, так и для матриц 3 × 33 × 3.
Тождественная матрица и мультипликативная обратная
Единичная матрица In,In представляет собой квадратную матрицу, содержащую единицы по главной диагонали и нули во всех остальных местах.
I2=[1001]I3=[100010001] 2×2 3×3I2=[1001]I3=[100010001] 2×2 3×3Если AA представляет собой n×nn×n матрица, а BB — это n×nn×n матрица такая, что AB=BA=In,AB=BA=In, тогда B=A−1,B=A−1, мультипликативная обратная матрица A.A.
Пример 1
Демонстрация того, что матрица идентичности действует как 1
Для заданной матрицы A покажите, что AI=IA=A.АИ=ИА=А.
Решение
Используйте умножение матриц, чтобы показать, что произведение AA и тождества равно произведению тождества и A.
AI=[34−25][1001]=[3⋅1+4⋅03⋅0+4⋅1−2⋅1+5⋅0−2⋅0+5⋅1]=[34−25]AI= [34−25][1001]=[3⋅1+4⋅03⋅0+4⋅1−2⋅1+5⋅0−2⋅0+5⋅1]=[34−25] IA=[1001 ][34−25]=[1⋅3+0⋅(−2)1⋅4+0⋅50⋅3+1⋅(−2)0⋅4+1⋅5]=[34−25]IA= [1001][34−25]=[1⋅3+0⋅(−2)1⋅4+0⋅50⋅3+1⋅(−2)0⋅4+1⋅5]=[34−25]Как
Имея две матрицы, покажите, что одна из них мультипликативно обратна другой.
- Даны матрица AA порядка n×nn×n и матрица BB порядка n×nn×n, умноженные на AB.AB.
- Если AB=I,AB=I, то найти произведение BA.BA. Если BA=I, BA=I, то B=A-1B=A-1 и A=B-1.A=B-1.
Пример 2
Демонстрация того, что матрица
A является мультипликативной обратной матрицей BПокажите, что данные матрицы мультипликативно обратны друг другу.
A=[15−2−9],B=[−9−521]A=[15−2−9],B=[−9−521]Решение
Умножить ABAB и BA.БА. Если оба произведения равны единице, то две матрицы являются обратными друг другу.
AB=[15−2−9]·[−9−521]=[1(−9)+5(2)1(−5)+5(1)−2(−9)−9(2)− 2(−5)−9(1)]=[1001]AB=[15−2−9]·[−9−521]=[1(−9)+5(2)1(−5)+5 (1)−2(−9)−9(2)−2(−5)−9(1)]=[1001] BA=[−9−521]·[15−2−9]=[−9 (1)−5(−2)−9(5)−5(−9)2(1)+1(−2)2(−5)+1(−9)]=[1001]BA=[− 9−521]·[15−2−9]=[−9(1)−5(−2)−9(5)−5(−9)2(1)+1(−2)2(−5 )+1(−9)]=[1001]AA и BB обратны друг другу.
Попробуйте #2
Покажите, что следующие две матрицы являются обратными друг другу.
А=[14-1-3],В=[-3-411]А=[14-1-3],В=[-3-411]Нахождение мультипликативного обратного с помощью умножения матриц
Теперь мы можем определить, являются ли две матрицы обратными, но как нам найти обратную заданную матрицу? Поскольку мы знаем, что произведение матрицы и ее обратной является единичной матрицей, мы можем найти обратную матрицу, составив уравнение, используя матричное умножение.
Пример 3
Нахождение мультипликативного обратного с помощью умножения матриц
Используйте умножение матриц, чтобы найти обратную заданную матрицу.
А=[1−22−3]А=[1−22−3]Решение
Для этого метода мы умножаем AA на матрицу, содержащую неизвестные константы, и приравниваем ее к единице.
[1−22−3] [abcd]=[1001][1−22−3] [abcd]=[1001]Найдите произведение двух матриц слева от знака равенства.
[1-22-3] [abcd]=[1a-2c1b-2d2a-3c2b-3d][1-22-3] [abcd]=[1a-2c1b-2d2a-3c2b-3d]Затем настройте система уравнений с записью в строке 1, столбце 1 новой матрицы, равной первой записи тождества, 1.Установите запись в строке 2, столбце 1 новой матрицы, равной соответствующей записи идентификатора, которая равна 0.
1a-2c=1 R12a-3c=0 R21a-2c=1 R12a-3c=0 R2Используя операции со строками, умножьте и сложите следующим образом: (−2)R1+R2→R2.(−2)R1+R2→R2. Сложите уравнения и решите для c.c.
1a−2c=10+1c=−2c=−21a−2c=10+1c=−2c=−2Обратная подстановка для решения а.о.
a−2(−2)=1a+4=1a=−3a−2(−2)=1a+4=1a=−3Запишите другую систему уравнений, задающую запись в строке 1, столбце 2 новой матрицы равно соответствующей записи идентификатора, 0.Установите запись в строке 2, столбце 2, равной соответствующей записи идентификатора.
1b-2d=0R12b-3d=1R21b-2d=0R12b-3d=1R2Используя операции со строками, умножьте и сложите следующим образом: (-2)R1+R2=R2.(-2)R1+R2=R2. Сложите два уравнения и решите для d.d.
1b−2d=00+1d=1d=11b−2d=00+1d=1d=1Еще раз подставим обратно и найдем b.b.
b−2(1)=0b−2=0b=2b−2(1)=0b−2=0b=2 A−1=[−32−21]A−1=[−32−21]Нахождение мультипликативного обратного путем увеличения с помощью тождества
Другой способ найти мультипликативное обратное — это увеличить с помощью тождества.Когда матрица AA преобразуется в I,I, расширенная матрица II преобразуется в A-1.A-1.
Например, учитывая
дополнить AA идентификатором
Выполнение операций над строками с целью превращения AA в личность.
- Поменяйте местами ряд 1 и ряд 2.
- Умножьте строку 2 на −2−2 и прибавьте к строке 1. [1121|-2110][1121|-2110]
- Умножить строку 1 на −2−2 и прибавить к строке 2. [110−1|−215−2][110−1|−215−2]
- Добавить строку 2 к строке 1.[100−1|3−15−2][100−1|3−15−2]
- Умножить строку 2 на -1,-1. [1001|3-1-52][1001|3-1-52]
Мы нашли матрицу A−1.A−1.
A−1=[3−1−52]A−1=[3−1−52]Нахождение мультипликативной обратной матрицы 2×2 с использованием формулы
Когда нам нужно найти мультипликативную обратную матрицу 2× Матрица 22 × 2, мы можем использовать специальную формулу вместо умножения матриц или увеличения на единицу.
Если AA представляет собой матрицу 2×22×2, например
мультипликативная обратная AA задается формулой
A-1=1ad-bc[d-b-ca]A-1=1ad-bc[d-b-ca], где ad-bc≠0.объявление-BC≠0. Если ad-bc=0,ad-bc=0, то AA не имеет обратного.
Пример 4
Использование формулы для нахождения мультипликативной обратной матрицы
AИспользуйте формулу, чтобы найти мультипликативное значение, обратное числу
. А=[1−22−3]А=[1−22−3]Решение
Используя формулу, мы имеем
A−1=1(1)(−3)−(−2)(2)[−32−21]=1−3+4[−32−21]=[−32−21]A−1=1 (1)(−3)−(−2)(2)[−32−21]=1−3+4[−32−21]=[−32−21]Анализ
Мы можем проверить, что наша формула работает, используя один из других методов для вычисления обратного значения.Давайте дополним AA личностью.
[1-22-3|1001][1-22-3|1001]Выполнение операций над строками с целью превращения AA в личность.
- Умножьте строку 1 на -2-2 и прибавьте к строке 2. [1-201|10-21][1-201|10-21]
- Умножить строку 1 на 2 и прибавить к строке 1. [1001|−32−21][1001|−32−21]
Итак, мы проверили исходное решение.
А-1=[-32-21]А-1=[-32-21]Попробуйте #3
Используйте формулу, чтобы найти обратную матрицу A.А. Подтвердите свой ответ, дополнив его единичной матрицей.
Пример 5
Нахождение обратной матрицы, если она существует
Найдите обратную матрицу, если она существует.
Решение
Воспользуемся методом пополнения тождеством.
- Поменяйте местами ряд 1 и ряд 2.
- Умножьте строку 1 на −3 и прибавьте к строке 2. [1200|10−31][1200|10−31]
- Больше мы ничего сделать не можем. Нули в строке 2 означают, что эта матрица не имеет обратной.
Нахождение мультипликативной обратной матрицы 3×3
К сожалению, у нас нет формулы, аналогичной формуле для матрицы 2×22×2, для нахождения обратной матрицы 3×33×3. Вместо этого мы дополним исходную матрицу единичной матрицей и используем операции со строками, чтобы получить обратную.
Учитывая 3×33×3 матрица
А=[231331241]А=[231331241]дополнить AA идентификационной матрицей
А|Я=[231331241 | 100010001]A|I=[231331241 | 100010001]Для начала напишем расширенную матрицу с единицей справа и AA слева. Выполняя элементарные операции над строками так, чтобы единичная матрица оказалась слева, мы получим обратную матрицу справа. Мы найдем обратную этой матрице в следующем примере.
Как
Для заданной матрицы 3×33×3 найдите обратную
- Запишите исходную матрицу, дополненную единичной матрицей справа.
- Используйте элементарные операции со строками, чтобы идентификатор отображался слева.
- То, что получается справа, является обратной исходной матрицей.
- Используйте умножение матриц, чтобы показать, что AA-1=IAA-1=I и A-1A=IA.A-1A=I.
Пример 6
Нахождение обратной матрицы 3 × 3
Для заданной матрицы A,A размером 3×33×3 найдите обратную.
А=[231331241]А=[231331241]Решение
Дополните AA единичной матрицей, а затем начните операции со строками, пока единичная матрица не заменит A.A. Матрица справа будет обратной матрице A.A.
[231331241|100010001]→Развязка R2 и R1[331231241|010100001][231331241|100010001]→Развязка R2 и R1[331231241|010100001] −R2+R1=R1→[100231241|−110100001]−R2+R1=R1→[100231241|−110100001] −R2+R3=R3→[100231010|−110100−101]−R2+R3=R3→[100231010 |−110100−101] R3↔ R2→[100010231|−110−101100]R3↔ R2→[100010231|−110−101100] −2R1+R3=R3→[100010031|−110−1013−20]−2R1+ R3=R3→[100010031|−110−1013−20] −3R2+R3=R3→[100010001|−110−1016−2−3]−3R2+R3=R3→[100010001|−110−1016−2− 3]Таким образом,
А-1=В=[-110-1016-2-3]А-1=В=[-110-1016-2-3]Анализ
Чтобы доказать, что B=A-1,B=A-1, давайте перемножим две матрицы вместе, чтобы увидеть, равно ли произведение тождеству, если AA-1=IAA-1=I и A-1A=I.А-1А=I.
AA−1=[231331241] [−110−1016−2−3]=[2(−1)+3(−1)+1(6)2(1)+3(0)+1(−2 )2(0)+3(1)+1(−3)3(−1)+3(−1)+1(6)3(1)+3(0)+1(−2)3(0 )+3(1)+1(−3)2(−1)+4(−1)+1(6)2(1)+4(0)+1(−2)2(0)+4( 1)+1(−3)]=[100010001]AA−1=[231331241] [−110−1016−2−3]=[2(−1)+3(−1)+1(6)2( 1)+3(0)+1(-2)2(0)+3(1)+1(-3)3(-1)+3(-1)+1(6)3(1)+3 (0)+1(-2)3(0)+3(1)+1(-3)2(-1)+4(-1)+1(6)2(1)+4(0)+ 1(−2)2(0)+4(1)+1(−3)]=[100010001] A−1A=[−110−1016−2−3] [231331241]=[−1(2)+ 1(3)+0(2)−1(3)+1(3)+0(4)−1(1)+1(1)+0(1)−1(2)+0(3)+ 1(2)−1(3)+0(3)+1(4)−1(1)+0(1)+1(1)6(2)+−2(3)+−3(2) 6(3)+−2(3)+−3(4)6(1)+−2(1)+−3(1)]=[100010001]A−1A=[−110−1016−2−3 ] [231331241]=[−1(2)+1(3)+0(2)−1(3)+1(3)+0(4)−1(1)+1(1)+0(1 )−1(2)+0(3)+1(2)−1(3)+0(3)+1(4)−1(1)+0(1)+1(1)6(2) +−2(3)+−3(2)6(3)+−2(3)+−3(4)6(1)+−2(1)+−3(1)]=[100010001]Попробуйте #4
Найдите обратную матрицу 3×33×3.
А=[2-1711-111-703-2]А=[2-1711-111-703-2]Решение системы линейных уравнений с использованием обратной матрицы
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: XX — матрица, представляющая переменные системы, и BB — это матрица, представляющая константы. Используя умножение матриц, мы можем определить систему уравнений с тем же количеством уравнений в качестве переменных, что и
.Чтобы решить систему линейных уравнений с помощью обратной матрицы, пусть AA будет матрицей коэффициентов, пусть XX будет переменной матрицей, а пусть BB будет постоянной матрицей.Таким образом, мы хотим решить систему AX=B.AX=B. Например, посмотрите на следующую систему уравнений.
a1x+b1y=c1a2x+b2y=c2a1x+b1y=c1a2x+b2y=c2Из этой системы матрица коэффициентов равна
Переменная матрица
А постоянная матрица
Тогда AX=BAX=B выглядит как
. [a1b1a2b2] [xy]=[c1c2][a1b1a2b2] [xy]=[c1c2]Вспомните ранее в этом разделе обсуждение умножения действительного числа на его обратное, (2−1)2=(12)2=1 .(2−1)2=(12)2=1. Чтобы решить одно линейное уравнение ax=bax=b относительно x,x, мы должны просто умножить обе части уравнения на мультипликативную обратную (обратную) а.а. Таким образом,
ax=b (1a)ax=(1a)b(a−1 )ax=(a−1)b[(a−1)a]x=(a−1)b 1x=(a−1 )b x=(a−1)b ax=b (1a)ax=(1a)b(a−1 )ax=(a−1)b[(a−1)a]x=(a−1) b 1x=(a−1)b x=(a−1)bЕдинственная разница между решением линейного уравнения и системы уравнений, записанной в матричной форме, заключается в том, что найти обратную матрицу сложнее, и матрица умножение — более длительный процесс.Однако цель та же — изолировать переменную.
Мы подробно рассмотрим эту идею, но будет полезно начать с системы 2×22×2, а затем перейти к системе 3×33×3.
Решение системы уравнений с использованием обратной матрицы
Для данной системы уравнений запишите матрицу коэффициентов A,A, переменную матрицу X,X и постоянную матрицу B.B. Тогда
Умножьте обе части на значение, обратное AA, чтобы получить решение.
(A-1)AX=(A-1)B[(A-1)A]X=(A-1)BIX=(A-1)BX=(A-1)B(A-1)AX= (A−1)B[(A−1)A]X=(A−1)BIX=(A−1)BX=(A−1)BВопросы и ответы
Если матрица коэффициентов не имеет обратной, значит ли это, что система не имеет решения?
Нет, если матрица коэффициентов необратима, система может быть несовместной и не иметь решения или быть зависимой и иметь бесконечно много решений.
Пример 7
Решение системы 2 × 2 с использованием обратной матрицы
Решите данную систему уравнений, используя обратную матрицу.
3x+8y=54x+11y=73x+8y=54x+11y=7Решение
Запишите систему в терминах матрицы коэффициентов, матрицы переменных и матрицы констант.
A=[38411],X=[xy],B=[57]A=[38411],X=[xy],B=[57]Затем
[38411] [xy]=[57][38411] [xy]=[57]Сначала нам нужно вычислить A−1.A−1. Используя формулу для вычисления обратной матрицы 2 на 2, мы имеем:
A−1=1ad−bc[d−b−ca] =13(11)−8(4)[11−8−43] =11[11−8−43]A−1=1ad−bc[d− b−ca] =13(11)−8(4)[11−8−43] =11[11−8−43]Итак,
A−1=[11−8−43]A−1=[11−8−43]Теперь мы готовы решать.Умножьте обе части уравнения на A−1.A−1.
(A−1)AX=(A−1)B[11−8−43] [38411] [xy]=[11−8−43] [57][1001] [xy]=[11(5)+ (−8)7−4(5)+3(7)][xy]=[−11](A−1)AX=(A−1)B[11−8−43] [38411] [xy] =[11−8−43] [57][1001] [xy]=[11(5)+(−8)7−4(5)+3(7)][xy]=[−11]решение (−1,1).(−1,1).
Вопросы и ответы
Можем ли мы найти XX, найдя произведение BA-1?BA-1?
Нет, напомним, что умножение матриц не является коммутативным, поэтому A−1B≠BA−1.А-1В≠ВА-1. Рассмотрим наши действия по решению матричного уравнения.
(A-1)AX=(A-1)B[(A-1)A]X=(A-1)BIX=(A-1)BX=(A-1)B(A-1) AX=(A−1)B[(A−1)A]X=(A−1)BIX=(A−1)BX=(A−1)BОбратите внимание, что на первом шаге мы умножили обе части уравнение на A−1,A−1, но A−1A−1 находился слева от AA с левой стороны и слева от BB с правой стороны. Поскольку умножение матриц не является коммутативным, порядок имеет значение.
Пример 8
Решение системы 3 × 3 с использованием обратной матрицы
Решите следующую систему, используя обратную матрицу.
5x+15y+56z=35-4x-11y-41z=-26-x-3y-11z=-75x+15y+56z=35-4x-11y-41z=-26-x-3y-11z=-7Решение
Напишите уравнение AX=B.AX=B.
[51556−4−11−41−1−3−11] [xyz]=[35−26−7][51556−4−11−41−1−3−11] [xyz]=[35−26− 7]Во-первых, мы найдем обратное AA путем увеличения тождества.
[51556-4-11-41-1-3-11|100010001][51556-4-11-41-1-3-11|100010001]Умножить строку 1 на 15,15.
[13565-4-11-41-1-3-11|1500010001][13565-4-11-41-1-3-11|1500010001]Умножить строку 1 на 4 и прибавить к строке 2.
[1356501195-1-3-11|15004510001][1356501195-1-3-11|15004510001]Добавить строку 1 к строке 3.
[13565011950015|150045101501][13565011950015|150045101501]Умножить строку 2 на -3 и прибавить к строке 1.
[10−15011950015|−115−3045101501][10−15011950015|−115−3045101501]Умножить строку 3 на 5.
[10−1501195001|−115−304510105][10−1501195001|−115−304510105]Умножить строку 3 на 1515 и прибавить к строке 1.
[10001195001|−2−314510105][10001195001|−2−314510105]Умножить строку 3 на -195−195 и прибавить к строке 2.
[100010001|−2−31−31−19105][100010001|−2−31−31−19105]Итак,
A-1=[-2-31-31-19105]A-1=[-2-31-31-19105]Умножьте обе части уравнения на A-1.A-1. Мы хотим, чтобы A-1AX=A-1B:A-1AX=A-1B:
[−2−31−31−19105] [51556−4−11−41−1−3−11] [xyz]=[−2−31−31−19105] [35−26−7][−2− 31−31−19105] [51556−4−11−41−1−3−11] [xyz]=[−2−31−31−19105] [35−26−7]Таким образом,
A−1B=[−70+78−7−105−26+13335+0−35]=[120]A−1B=[−70+78−7−105−26+13335+0−35]=[ 120]Решение (1,2,0).(1,2,0).
Попробуйте #5
Решите систему, используя обратную матрицу коэффициентов.
2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2 2x−17y+11z=0 −x+11y−7z=8 3y−2z=−2Как
Дана система уравнений. Решите с помощью калькулятора обратные матрицы.
- Сохраните матрицу коэффициентов и матрицу констант как матричные переменные [A][A] и [B].[Б].
- Введите умножение в калькулятор, вызывая каждую переменную матрицы по мере необходимости.
- Если матрица коэффициентов обратима, калькулятор представит матрицу решения; если матрица коэффициентов необратима, калькулятор выдаст сообщение об ошибке.
Пример 9
Использование калькулятора для решения системы уравнений с обратными матрицами
Решите систему уравнений с обратными матрицами с помощью калькулятора
2x+3y+z=323x+3y+z=-272x+4y+z=-22x+3y+z=323x+3y+z=-272x+4y+z=-2Решение
На странице матрицы калькулятора введите матрицу коэффициентов в качестве матричной переменной [A],[A] и введите матрицу констант в качестве матричной переменной [B].[Б].
[A]=[231331241], [B]=[32−27−2][A]=[231331241], [B]=[32−27−2]На главном экране калькулятора введите умножение для решения X, X, вызывая каждую переменную матрицы по мере необходимости.
Оценить выражение.
[−59−34252][−59−34252]7.7 Упражнения по секциям
Вербальные
1.В предыдущем разделе мы показали, что умножение матриц некоммутативно, то есть в большинстве случаев AB≠BAAB≠BA.Можете ли вы объяснить, почему умножение матриц является коммутативным для обратных матриц, то есть A−1A=AA−1?A−1A=AA−1?
2.Любая ли матрица 2×22×2 имеет обратную? Объясните, почему да или почему нет. Объясните, какое условие необходимо для существования обратного.
3.Можете ли вы объяснить, может ли матрица 2×22×2 с целым рядом нулей иметь обратную?
4.Может ли матрица с целым столбцом нулей иметь обратную? Объясните, почему да или почему нет.
5.Может ли матрица с нулями по диагонали иметь обратную? Если да, то найдите пример. Если нет, то докажите, почему. Для простоты предположим матрицу 2×22×2.
Алгебраический
В следующих упражнениях покажите, что матрица AA является обратной матрицей B.B.
6.А=[10-11],В=[1011]А=[10-11],В=[1011]
7.А=[1234],В=[-2132-12]А=[1234],В=[-2132-12]
8.А=[4570],В=[01715-435]А=[4570],В=[01715-435]
9.А=[-2123-1],В=[-2-1-6-4]А=[-2123-1],В=[-2-1-6-4]
10.А=[10101-1011],В=12[21-10110-11]А=[10101-1011],В=12[21-10110-11]
11.A=[123402169],B=14[60-217-3-5-1224]A=[123402169],B=14[60-217-3-5-1224]
12.A=[3821115612],B=136[−684−67−261−1−225]A=[3821115612],B=136[−684−67−261−1−225]
Для следующих упражнений найдите мультипликативную обратную каждую матрицу, если она существует.
16.[−4−3−58][−4−3−58]
19.[0,51,51-0,5][0,51,51-0,5]
20.[106−217302][106−217302]
21.[01-3410105][01-3410105]
22.[12-1-341-2-4-5][12-1-341-2-4-5]
23.[19−32564−27][19−32564−27]
24.[1-23-48-12142][1-23-48-12142]
25.[121212131415161718][121212131415161718]
В следующих упражнениях решите систему, используя обратную матрицу 2×22×2.
27.5x−6y=−614x+3y=−25x−6y=−614x+3y=−2
28.8х+4у=-1003х-4у=18х+4у=-1003х-4у=1
29.3x−2y=6−x+5y=−23x−2y=6−x+5y=−2
30.5x−4y=−54x+y=2,35x−4y=−54x+y=2,3
31.−3x−4y=912x+4y=−6−3x−4y=912x+4y=−6
32.−2x+3y=310−x+5y=12−2x+3y=310−x+5y=12
33.85x−45y=25−85x+15y=71085x−45y=25−85x+15y=710
34.12x+15y=-1412x-35y=-9412x+15y=-1412x-35y=-94
В следующих упражнениях решите систему, используя обратную систему 3×33×3. матрица.
35.3x-2y+5z=215x+4y=37x-2y-5z=53x-2y+5z=215x+4y=37x-2y-5z=5
36.4x+4y+4z=402x-3y+4z=-12-x+3y+4z=94x+4y+4z=402x-3y+4z=-12-x+3y+4z=9
37.6x−5y−z=31−x+2y+z=−63x+3y+2z=136x−5y−z=31−x+2y+z=−63x+3y+2z=13
38.6x−5y+2z=−42x+5y−z=122x+5y+z=126x−5y+2z=−42x+5y−z=122x+5y+z=12
39.4x-2y+3z=-122x+2y-9z=336y-4z=14x-2y+3z=-122x+2y-9z=336y-4z=1
40.110x-15y+4z=-41215x-20y+25z=-101310x+4y-310z=23110x-15y+4z=-41215x-20y+25z=-101310x+4y-310z=23
41.12x−15y+15z=31100−34x−14y+12z=740−45x−12y+32z=1412x−15y+15z=31100−34x−14y+12z=740−45x−12y+32z=14
42.0,1x+0,2y+0,3z=-1,40,1x-0,2y+0,3z=0,60,4y+0,9z=-20,1x+0,2y+0,3z=-1,40,1x-0,2y+0,3z =0,60,4г+0,9г=-2
Технология
В следующих упражнениях используйте калькулятор для решения системы уравнений с обратными матрицами.
43.2х-у=-3-х+2у=2,32х-у=-3-х+2у=2,3
44.−12x−32y=−432052x+115y=314−12x−32y=−432052x+115y=314
45.12,3x-2y-2,5z=236,9x+7y-7,5z=-78y-5z=-1012,3x-2y-2,5z=236,9x+7y-7,5z=-78y-5z=-10
46. 0,5x-3y+6z=-0,80,7x-2y=-0,060,5x+4y+5z=00,5x-3y+6z=-0,80,7x-2y=-0,060,5x+4y+5z=0
Расширения
Для следующих упражнений найдите обратную заданную матрицу.
47.[1010010101100011][1010010101100011]
48.[−1025000202−101−301][−1025000202−101−301]
49.[1-230010214-23-5011][1-230010214-23-5011]
50.[1202302100003010200100120][1202302100003010200100120]
51.[100000010000001000000100000010111111][100000010000001000000100000010111111]
Реальные приложения
Для следующих упражнений напишите систему уравнений, описывающую ситуацию. Затем решите систему, используя обратную матрицу.
52.На баскетбольный матч продано 2400 билетов. Если цены на 1 и 2 этаж были разными, а общая сумма денег составила 64 000 долларов, сколько стоил каждый билет?
53.Если в предыдущем упражнении вам сказали, что на второй этаж продано на 400 билетов больше, чем на первый, сколько стоил каждый билет?
54.Привод еды собрал 2 по-разному типа законсервированных товаров, зеленых фасолей и фасолей почки. Общее количество собранных банок составило 350, а общий вес всей пожертвованной еды составил 348 фунтов 12 унций. Если банки с зеленой фасолью весят на 2 унции меньше, чем банки с фасолью, сколько из каждой банки было пожертвовано?
55.Учеников попросили принести в класс свои любимые фрукты.95% фруктов состояли из бананов, яблок и апельсинов. Если апельсины были в два раза популярнее бананов, а яблоки на 5% менее популярны, чем бананы, каков процент каждого фрукта в отдельности?
56.Женское общество провело распродажу выпечки, чтобы собрать деньги, и продавало пирожные и печенье с шоколадной крошкой. Они оценили пирожные в 1 доллар, а печенье с шоколадной крошкой — в 0,75 доллара. Они собрали 700 долларов и продали 850 предметов. Сколько пирожных и сколько печенья было продано?
57.Магазину одежды необходимо заказать новый инвентарь.В продаже есть три разных типа шляп: соломенные шляпы, шапочки и ковбойские шляпы. Соломенная шляпа стоит 13,99 долларов, шапочка — 7,99 долларов, а ковбойская шляпа — 14,49 долларов. Если в прошлом квартале было продано 100 головных уборов, выручка от продаж составила 1119 долларов, а количество проданных шапок было на 10 больше, чем ковбойских шляп, сколько каждой из них должен заказать магазин одежды взамен уже проданных?
58.Анна, Эшли и Андреа вместе весят 370 фунтов. Если Андреа весит на 20 фунтов больше, чем Эшли, а Анна весит 1.В 5 раз больше Эшли, сколько весит каждая девочка?
59.Трое соседей по комнате поделились пакетом из 12 плиток мороженого, но никто не помнит, кто сколько съел. Если Том съел в два раза больше плитки мороженого, чем Джо, а Альберт съел на три плитки меньше, чем Том, сколько плиток мороженого съел каждый сосед по комнате?
60.Фермер построил курятник из проволочной сетки, дерева и фанеры. Проволочная сетка стоила 2 доллара за квадратный фут, дерево — 10 долларов за квадратный фут, а фанера — 5 долларов за квадратный фут.Фермер потратил в общей сложности 51 доллар, а общее количество использованных материалов составило 14 футов 2,14 фута 2. Он использовал проволочную сетку на 3 фута 23 фута больше, чем фанеру. Сколько каждого материала использовал фермер?
61.У Джея на заднем дворе растут лимонные, апельсиновые и гранатовые деревья. Апельсин весит 8 унций, лимон 5 унций, а гранат 11 унций. Джей собрал 142 фрукта общим весом 70 фунтов 10 унций. Он собрал в 15,5 раз больше апельсинов, чем гранатов. Сколько плодов каждого сорвал Джей?
.