Линейные уравнения с одной переменной

1. Презентацию подготовила учитель ГОУ СОШ № 1961 города Москвы Чистякова Людмила Константиновна

2. Решение линейных уравнений с одной переменной

3. Определение

Линейным уравнением с одной переменной
называется уравнение вида aх + b = с,
где а, в, с – числа, х – переменная.
Например:
3х + 8 = 0,
14 – 2х =9;
– 4х = 10.
• Решить уравнение – это значит найти
все его корни или доказать, что корней
нет.
• Корнем уравнения с одной переменной
называется значение переменной, при
котором уравнение обращается в верное
равенство.
• При решении уравнений с одной переменной
используются следующие свойства:
• Если в уравнении перенести слагаемое из
одной части в другую, изменив его знак, то
получится уравнение, равносильное данному;
• Если обе части уравнения умножить или
разделить на одно и то же число, то получится
уравнение, равносильное данному.

6. Алгоритм решения уравнения

1. Раскрыть скобки.
2. Перенести слагаемые, содержащие
переменную, в одну часть уравнения, а
числа без переменной – в другую часть.
3. Упростить, привести подобные
слагаемые.
4. Найти корень уравнения.
5. Сделать проверку.

7. Раскрытие скобок

Если перед скобками стоит знак « +», то
скобки можно опустить, сохранив знак
каждого слагаемого, заключенного в
скобки.
Пример.
(25 –3х) + (–2х + 6) = 25 – 3х – 2х + 6 =
= 31 – 5х.

8. Раскрытие скобок

Если перед скобками стоит знак « -», то скобки
можно опустить, изменив знак каждого
слагаемого, заключенного в скобки.
( 6х – 3) – ( 14 – 2х) = 6х – 3 –14 + 2х =
= 8х – 17;
12 + ( х – 3) – (– 3х + 1) = 12 + х – 3 +3х –
– 1 = 8 + 4х.

9. Распределительное свойство умножения

а(в + с) =ав +ас
а(в – с) = ав – ас
Примеры:
6 ( 3 – 2х) = 18 – 12х;
– 5 ( а + 3) = – 5а –15.

10. Примеры решения уравнений

4(х + 5) = 12;
4х + 20 = 12;
4х =12 – 20;
4х = — 8;
х = — 8 : 4;
х = — 2.

11. Пример 2

5х = 2х + 6;
5х – 2х = 6;
3х =6;
х = 6 : 3;
х = 2.

12. Пример 3

3 (х + 6) + 4 = 8 – ( 5х + 2)
3х + 18 + 4 = 8 – 5х – 2
3х + 5х = — 18 – 4 + 8 — 2
8х = — 16
х = — 16 : 8
х=-2

13. Задания для самостоятельного решения

• Решить уравнение
1). 2х + 5 = 2 (- х + 1) + 11
2). 6у – 3(у – 1) = 4 + 5у
3). 4 ( х – 1) – 3 = — (х + 7) + 8
4). – 2(5 у – 9) + 2 = 15 + 7(- х + 2)
5). 12 + 4(х – 3) – 2х = (5 – 3х) + 9

14. Ответы

1) 2
2) — 0,5
3) 1,6
4) — 3
5) 2,8

15. СПАСИБО ЗА ВНИМАНИЕ

Линейные неравенства с одной переменной

Как решать линейные неравенства с одной переменной вида ax+b>cx+d?

Для этого используем всего два правила.

1) Слагаемые можно переносить из одной части неравенства в другую с противоположным знаком.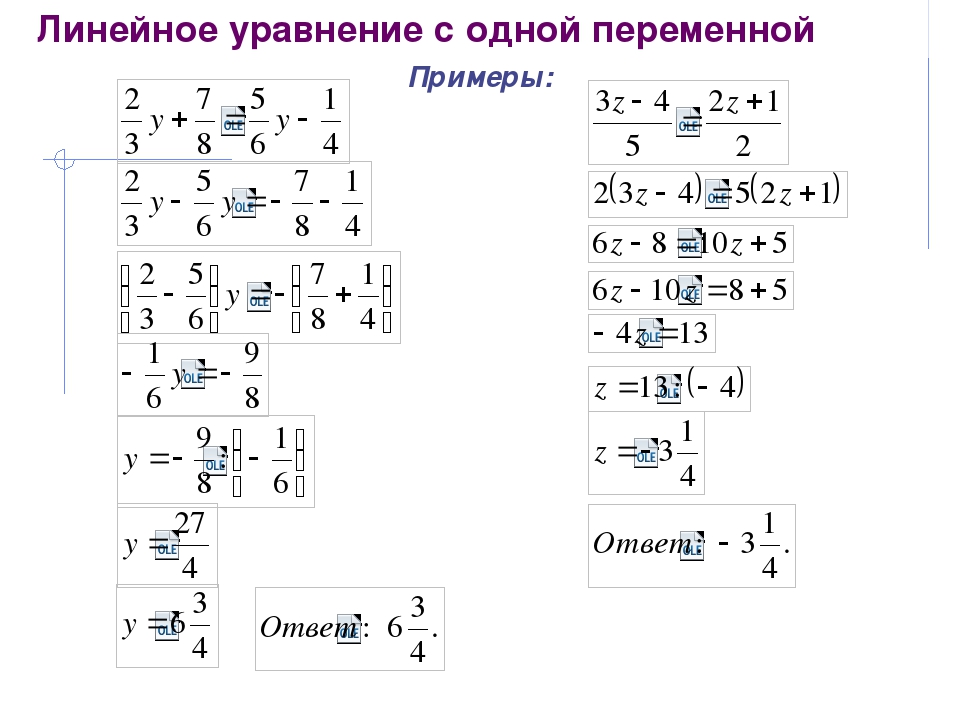 Знак неравенства при этом не меняется.

2) Обе части неравенства можно разделить на число, стоящее перед иксом (или другой переменной). При делении на положительное число знак неравенства не меняется. При делении на отрицательное число знак неравенства изменяется на противоположный.

В общем виде решение линейного неравенства с одной переменной

   

можно изобразить так:

1) Неизвестные переносим в одну сторону, известные — в другую с противоположными знаками:

   

   

2) Если число перед иксом не равно нулю (a-c≠0), обе части неравенства делим на a-c.

Если a-c>0, знак неравенства не изменяется:

   

   

Если a-c<0, знак неравенства изменяется на противоположный:

   

   

Если a-c=0, то это — частный случай. Частные случаи решения линейных неравенств рассмотрим отдельно.

Примеры.

   

Это — линейное неравенство. Переносим неизвестные в одну сторону, известные — в другую с противоположными знаками:

   

   

Обе части неравенства делим на число, стоящее перед иксом.

Так как -2<0, знак неравенства изменяется на противоположный:

   

   

   

Так как неравенство строгое, 10 на числовой прямой отмечаем выколотой точкой. Штриховка от 10 влево, на минус бесконечность. 

Так как неравенство строгое и точка выколотая, 10 записываем в ответ с круглой скобкой.

Ответ:

   

   

Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположными знаками:

   

   

Обе части неравенства делим на число, стоящее перед иксом. Так как 10>0, знак неравенства при этом не изменяется:

   

   

   

Так как неравенство нестрогое, -2,3 на числовой прямой отмечаем закрашенной точкой. Штриховка от -2,3 идёт вправо, на плюс бесконечность.

Так как неравенство строгое и точка закрашенная, -2,3 в ответ записываем с квадратной скобкой.

Ответ:

   

   

Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположным знаком.

   

   

Обе части неравенства делим на число, стоящее перед иксом. Поскольку 3>0, знак неравенства при этом не изменяется:

   

   

Так как неравенство строгое, x=2/3 на числовой прямой изображаем выколотой точкой.

Так как неравенство строгое и точка выколотая, в ответ 2/3 записываем с круглой скобкой.

Ответ:

   

   

Это — линейное неравенство. Неизвестные — в одну сторону, известные — в другую с противоположными знаками:

   

   

Обе части неравенства делим на число, стоящее перед иксом. Так как -4 — отрицательное число, знак неравенства при этом изменяется на противоположный:

   

   

   

Поскольку неравенство нестрогое, -2,25 на числовой прямой отмечаем закрашенной точкой. 

Так как неравенство нестрогое и точка закрашенная, -2,25 включаем в ответ, то есть записываем с квадратной скобкой.

Ответ:

   

 

Решать линейные неравенства с одной переменной в алгебре приходится не только в виде отдельных примеров, но также при нахождении области определения функций, области допустимых значений выражений, решении уравнений и более сложных неравенств. Вот почему важно вовремя понять эту тему и научиться применять её.

Линейное уравнение с одной переменной [7 класс]

Линейные уравнения — одна из самых простых тем в математике, которую проходят в 7 классе. Хотя бы раз с линейными уравнениями сталкивался каждый, не существует никаких трудностей в их решении, и подчиняются такие уравнения всего паре базовых правил.

Для того, чтобы разобраться в теме, необходимо в первую очередь вспомнить, какие же уравнения называют линейными.

Простые уравнения с одной переменной

Как гласит определение, линейным уравнением с одной переменной называют равенство, состоящее из букв и чисел и содержащее только одну переменную. Так, примерами могут служить:

• х – 4 = 8;
• х + 5 = 13;
• х : 3 = 3;
• 6х = 12.

Для того, чтобы решить уравнение, нужно просто найти его корень — иными словами, установить, при каком числовом значении переменной приведенное равенство будет правильным. Существуют и ситуации, когда равенство не может быть правильным ни при каких обстоятельствах — в таких случаях говорят, что корней у уравнения нет. И это также считается решением.

Согласно каким правилам решают линейные уравнения?

Существуют два правила, или свойства, которые делают работу с линейными уравнениями более простой и быстрой.

• Первое свойство гласит, что часть уравнения, или слагаемое, допустимо перенести на другую сторону уравнения, при этом изменив знак. Равенство в этом случае останется верным. Например, уравнение х – 6 = 12 можно записать следующим образом: х = 12 + 6. В ответе получится число 18, и простая проверка покажет, что решение совершенно правильное, поскольку 18 – 6 = 12.
• Второе свойство гласит, что можно взять некоторое число, не равное нулю, и разделить или умножить на него две части уравнения. В таком случае, при соблюдении всех условий, равенство останется верным. Например, это можно продемонстрировать в уравнении 3х = 9. Выражение записывается следующим образом: 3х : 3 = 9 : 3. Таким образом, 3х : 3 = 3, и в данном выражении х = 3.

Простейшие линейные уравнения, приведенные в примерах, вряд ли могут вызвать какие-то затруднения. Но в задачниках встречаются и более сложные, многосоставные выражения с одной переменной — и для их решения свойства окажутся очень полезными, поскольку помогут сэкономить время и силы.

Как правило, найти корни уравнения невозможно, если в буквенно-числовой записи присутствует число 0. Например, уравнение вида 0 * х = 5 верного решения не имеет, поскольку любое число при умножении или делении на ноль может давать только ноль. В таком случае пишут, что корней у уравнения нет.

Линейные уравнения с двумя переменными.

7-й класс

Цели урока:

• Образовательные:
  • повторить тему: «Уравнения. Линейные уравнения. Равносильные уравнения и их свойства»;
  • обеспечить усвоение учащимися понятия  линейных уравнений с двумя переменными и их решением.
• Развивающие
  :
  • формировать интеллектуальные способности:
  • умение сравнивать, строить аналоги, выделять  главное;
  • умение обобщать и систематизировать пройденный материал;
  • развивать логическое мышление, память, воображение, математическую речь;
  • развивать активную познавательную деятельность. 
• Воспитательные:
  • воспитывать самостоятельность, активность, заинтересованность  учащихся  на всех этапах урока;
  • формировать такие качества характера, как усидчивость, настойчивость, целеустремлённость.  

Задачи, которые должен решать учитель, на уроке:

• учить выделять главную мысль в тексте;
• учить задавать вопросы учителю, самому себе или ученикам;
• учить использовать приобретённые знания для решения нестандартных задач;
• учить умению математически правильно высказать  свою мысль.

Задачи, которые должны  решать ученики на данном уроке: 

• знать определение линейного уравнения с двумя переменными;
• уметь составлять простые линейные уравнения;
• уметь правильно находить значения переменных а, в  и с; 
• уметь выделять среди уравнений линейные уравнения с двумя переменными; 
• ответить на вопрос: что является решением линейного уравнения с двумя переменными?
• как узнать: является ли пара чисел решением уравнения?   
• уметь выразить одну переменную через другую.

Тип урока: урок  усвоения нового материала.

ХОД УРОКА

I. Организационный момент

II. Повторение пройденного материала

1)  На доске записи: 2х,  2х + 5 , 2х + 5 = 17.

2) Вопросы к классу:

– Дайте определение этим выражениям. (Ожидаемые ответы: произведение, одночлен,  сумма, многочлен, уравнение.)
– Что называется уравнением?
– Уравнение нужно…? (Решать)
– Что значит «решить уравнение»?
– Что является корнем уравнения?
– Какие уравнения являются равносильными?
– Какие свойства равносильности уравнений вы знаете?

III. Актуализация знаний учащихся

3) Задание всему классу:

– Преобразуйте выражения:(двое работают у доски). 

а) 2(х + 8) + 4(2х – 4) =                 б) 4(х – 2) + 2(3у + 4) =

После преобразования получили: а) 10х;    б) 4х + 6у:

– С помощью их составьте уравнения (ученики предлагают – учитель записывает уравнения на доске): 10х = 30;      4х + 6у = 28.

Вопросы:

– Как называется первое уравнение?
– Почему линейное?
– Сравните  второе уравнение с первым. Попробуйте сформулировать определение второго уравнения (Ожидаемый ответ: уравнение с двумя переменными; акцентируется внимание учащихся на  вид уравнения – линейное).

IV. Изучение нового материала

1) Объявляется тема урока. Запись темы в тетрадях. Самостоятельное  формулирование   учащимися определения уравнения с двумя переменными, линейного уравнения с двумя переменными (по аналогии с определением линейного уравнения с одной переменной), примеры уравнений с двумя переменными. Обсуждение проходит в форме фронтальной  беседы, диалога – рассуждения.

2) Задание  классу:

а) Напишите по два линейных уравнения с двумя переменными (учитель и ученики прослушивают ответы нескольких учеников; по выбору учителя один из них записывает свои уравнения на доске).  

б) Совместно с учениками определяются задачи  и вопросы, на которые они должны получить ответ на данном уроке.  Каждый ученик получает карточки с этими вопросами.

в) Работа с учащимися по решению этих вопросов и задач:

– Определите, какие из этих уравнений являются линейными  уравнениями с двумя переменными а) 6х² = 36; б) 2х – 5у = 9:  в) 7х + 3у³; г) 1/2х + 1/3у = 6 и т.д. Проблема может возникнуть с уравнением  х : 5 – у : 4 = 3 (знак деления нужно записать в виде дроби). Какие свойства равносильности уравнений нужно применить? (Ответы учащихся) Определите значения коэффициентов  а, в и с.

– Линейные уравнения с двумя переменными, как и все уравнения нужно решать. Что же является решением линейных уравнений с двумя переменными? (Дети дают определение).

Пример: Найдите решения уравнения: а) х – у = 12, ответы запишем в виде (х; у) или  х = …;  у = ….   Сколько решений имеет уравнение?

Примеры:  Найдите решения следующих уравнений  а) 2х + у = 7; б) 5х – у = 4.  Как вы нашли решения этих уравнений? (Подбирали).

– Как узнать, является ли пара чисел решением линейного уравнения с двумя переменными?

3) Работа с учебником.

– Найти в учебнике те места, где выделена главная мысль темы данного урока

а) Устное выполнение заданий: №1092,  №1094.

б) Решение примеров №1096 (для слабых учащихся),  №1097 (для сильных).

в) Повторить свойства равносильности уравнений.

Задание: применяя свойства равносильности уравнений, выразите переменную У через переменную Х в уравнении 5х + 2у = 12 («минута» на самостоятельное решение, затем общий обзор решения на доске  с последующим объяснением).

г) Выполнение примера  № 1099 (один из учащихся выполняет  задание у доски).

Историческая справка

1. Ребята,  уравнения, с которыми мы сегодня познакомились на уроке, называются  Диофантовыми  линейными уравнениями с двумя переменными, по имени древнегреческого учёного и математика Диофанта, жившего около 3,5 тысяч лет тому назад. Древние математики сначала составляли задачи, а затем трудились над их решением. Таким образом, было составлено множество задач, с которыми мы и знакомимся, и учимся их решать.

2. А также эти уравнения называются неопределёнными уравнениями. Над решением таких уравнений трудились многие математики. Одним из них является Пьер Ферма – французский математик. Он занимался теорией решения неопределённых уравнений.

V. Итог урока

1)  Обобщение пройденного материала на уроке. Ответы  на все вопросы, поставленные перед учениками в начале урока:

– Какие уравнения называются линейными с двумя переменными?
– Что называется решением линейного уравнения с двумя переменными?
– Как записывается это решение?
– Какие уравнения называются равносильными?
– Назовите свойства равносильности уравнений?
– Какие задачи мы на уроке решали, на какие вопросы отвечали?

2) Выполнение самостоятельной работы.

Для слабых:

– Найдите значения переменных а, в и с  в  уравнении  –1,1х + 3,6у = – 34?
– Найдите хотя бы одно решение уравнения х – у = 35?
– Являются ли пара чисел (3; 2) решением данного линейного уравнения с двумя переменными  2х – у = 4?

Для сильных:

– Составьте  линейное  уравнение с двумя переменными  к задаче Диофанта: Во дворе дома ходят  фазаны и кролики. Количество всех ног оказалось равным 26.
– Выразите переменную   у   через  х   в уравнении  3х – 5у = 8.

VI. Сообщение домашнего задания

Просмотр всех заданий по учебнику, беглый анализ каждого задания, выбор задания. 

• Для  слабых учащихся:  № 1093, № 1095б).
• Для  сильных: 1) №1101,  №1104 (а).  2)  решить задачу Диофанта, найти все натуральные  решения этого уравнения.  

Дополнительно, по желанию учащихся – №1105.

Вместо заключения: Я работаю учителем математики более 40 лет. И хочу заметить, что открытый урок – не всегда бывает самым лучшим уроком. Очень часто случается так, что иногда обычные уроки приносят учителю больше радости и удовлетворения. И тогда  с сожалением думаешь, что никто не увидел этого  урока – творения учителя и учащихся.

Урок – это единый организм,  единое целое, именно на уроке  приобретается  личностный и нравственный опыт  воспитания, как учащихся, так и учителя.  45 минут урока –   это так много и так мало. Много – потому что за это время можно с учениками «заглянуть» в глубину веков и, «вернувшись»  оттуда, узнать очень много нового, интересного, и ещё  успеть изучить новый материал.

До каждого ученика нужно довести понимание того, что именно математика является базисом интеллектуального развития человека. А основой для этого является развитие логического  мышления. Поэтому перед  каждом уроком ставлю себе и ученикам цель: научить учащихся успешно работать с определениями, умело отличать неизвестное от  известного, доказанное от недоказанного, анализировать, сравнивать, классифицировать, ставить перед собой вопросы и научиться  умело их решать. Пользоваться аналогиями, но если не сможешь выбраться самостоятельно, то рядом с тобой не только учитель, но главный твой  помощник – книга. 

Конечно, открытый урок является некоторым итогом творческой работы учителя. И учителя, присутствовавшие на данном уроке, должны обратить внимание на главное: систему работы, новизны, идею. Здесь, я думаю, особо важного значения не имеет  какую  методику преподавания  применяет учитель на уроке: старую, современную или новые инновационные технологии, главное, чтобы её применение  была  уместна и эффективна для учителя и учащихся.

Я очень рада, что в моей жизни есть школа, дети, уроки и такие добрые коллеги. Спасибо вам всем!

линейных уравнений с одной переменной

Линейное уравнение с одной переменной — это основное уравнение, используемое для представления и решения неизвестной величины. Его легко изобразить графически, и это всегда прямая линия. Линейное уравнение — это простой способ представить математическое утверждение. Любая переменная или символ могут использоваться для представления неизвестных величин, но обычно переменная «x» используется для представления неизвестной величины в линейном уравнении с одной переменной. Решение линейного уравнения включает в себя набор простых методов.Переменные изолируются на одной стороне уравнения, а константы изолируются на другой стороне уравнения, чтобы получить окончательное значение неизвестной величины.

Что такое линейное уравнение с одной переменной?

Прежде чем узнать о линейном уравнении с одной переменной, давайте быстро пройдемся по смыслу линейных уравнений. Линейное уравнение — это тип уравнения, в котором степень каждой переменной в уравнении точно равна единице. Линейные уравнения с одной переменной — это такие уравнения, в которых присутствует только одна переменная и существует только одно решение уравнения.Когда он нарисован на графике, он выглядит как прямая линия либо по горизонтали, либо по вертикали.

Линейное уравнение с одной переменной имеет вид ax+b=0, где a и b — любые два целых числа, а x — неизвестная переменная, имеющая только одно решение. Давайте поймем это на примере: «4, добавленное к определенному числу, дает 10». Найдите это число. Как мы можем представить эту проблему более простым способом? Мы можем сказать, x + 4 = 10, найти x. Мы присвоили этому номеру переменную; это называется уравнением.Это помогает нам писать такие большие задачи короче. В этом уравнении есть одна переменная, которая равна х, а наивысшая степень х равна единице. Уравнения такого типа известны как линейных уравнений с одной переменной , потому что степень переменной x равна единице.

Решение линейного уравнения с одной переменной

Общая форма линейного уравнения с одной переменной: Ax + B = 0. Здесь A — коэффициент при x, x — переменная, а B — постоянный член.Коэффициент и постоянный член должны быть разделены, чтобы найти окончательное решение этого линейного уравнения.

Теперь давайте посмотрим, как решить линейное уравнение с одной переменной. Уравнение похоже на весы с одинаковыми весами с обеих сторон.

Если мы прибавим или вычтем одно и то же число из обеих частей уравнения, оно останется в силе. Точно так же, если мы умножим или разделим одно и то же число на обе части уравнения, оно останется верным. Рассмотрим уравнение 3x-2=4.Выполним математические операции над левой и правой сторонами так, чтобы баланс не нарушился. Давайте добавим 2 с обеих сторон, чтобы уменьшить LHS до 3x. Это не нарушит баланс. Новое левое число равно 3x-2+2=3x, а новое правое число равно 4+2=6. Теперь давайте разделим обе части на 3, чтобы уменьшить LHS до x. Таким образом, у нас есть 3x/3=6/3. Следовательно, мы имеем х = 2,

.

Описанные выше действия по решению линейных уравнений с одной переменной можно обобщить в пунктах, перечисленных ниже.

• Шаг 1: Сохраняйте переменный член с одной стороны и константы с другой стороны уравнения, добавляя или вычитая обе части уравнения.
• Шаг 2: Упростите постоянные члены.
• Шаг 3: Изолируйте переменную с одной стороны, умножив или разделив ее на обе части уравнения.
• Шаг 4: Упростите и напишите ответ.

Линейное уравнение с одной переменной и нелинейные уравнения

Помимо линейных уравнений с одной переменной, у нас есть другие нелинейные уравнения, которые имеют многочисленные приложения в геометрии, тригонометрии и исчислении.Линейные уравнения с одной переменной являются одностепенными уравнениями и представляются линией на координатной плоскости. С другой стороны, нелинейное уравнение представляет собой кривую или нелинейное представление на оси координат. Нелинейное уравнение имеет более высокую степень. Несколько примеров нелинейных уравнений представляют собой уравнения кривых, таких как окружность, парабола, эллипс, гипербола.

Некоторыми примерами линейных уравнений являются x = 5, 3x + 7 = 9, 4x + 2y = 11. И некоторые примеры нелинейных уравнений представляют собой уравнение окружности — x ² + y ² = 25, уравнение эллипса — х ² /9 + у ² /16= 1, уравнение гиперболы — х ² /16 — у ² / 25 =1.

Важные примечания

Следующие пункты помогут нам четко обобщить понятия, используемые в линейных уравнениях с одной переменной.

1. Степень переменной в линейных уравнениях должна быть точно равна единице.
2. График линейного уравнения с одной переменной представляет собой прямую линию, горизонтальную или вертикальную.
3. На решение линейного уравнения с одной переменной не влияет добавление, вычитание, умножение или деление любого числа в обеих частях уравнения.

Линейное уравнение с одной переменной См. также

Проверьте статьи, приведенные ниже, связанные с концепцией линейных уравнений с одной переменной.

Часто задаваемые вопросы о линейном уравнении с одной переменной

Что такое линейное уравнение с одной переменной с примером?

Линейное уравнение с одной переменной имеет вид ax + b = 0. Линейное уравнение с одной переменной — это уравнения, в которых высшая степень каждого члена равна единице, существует одно возможное решение уравнения и присутствует только одна переменная в этом.Пример линейного уравнения с одной переменной: 3y+2=0.

Какова степень переменной в линейном уравнении с одной переменной?

Степень переменной в линейном уравнении с одной переменной равна 1. Ссылаясь на пример, 3a + 4 = 11, степень переменной ‘a’ равна 1.

Может ли линейное уравнение иметь более одной переменной?

Да, линейные уравнения могут иметь более одной переменной. Мы называем такие уравнения линейными уравнениями с двумя переменными или линейными уравнениями с тремя переменными.Линейные уравнения с двумя переменными имеют вид ax + by + c = 0, а линейное уравнение с тремя переменными имеет вид ax + by + cz + d = 0. Здесь x, y, z — переменные, a , b и c — коэффициенты, а d — константа. Эти линейные уравнения широко используются в линейном программировании для поиска оптимальных решений.

Как решать линейные уравнения с одной переменной?

Шаги для решения линейных уравнений с одной переменной перечислены ниже:

• Сохраняйте переменный член с одной стороны и константы с другой стороны уравнения, добавляя или вычитая обе части уравнения.
• Упростите постоянные условия.
• Изолируйте переменную с одной стороны, умножив или разделив один и тот же член на обе части уравнения.
• Упрости и напиши ответ.

Как решить линейное уравнение с одной переменной с переменными с обеих сторон?

Чтобы решить линейное уравнение с одной переменной с переменными с обеих сторон, мы сначала подводим все члены с переменными с одной стороны и константами с другой стороны уравнения.Затем мы упрощаем уравнение, изолируем переменную и записываем окончательный ответ уравнения. Давайте посмотрим на простое уравнение, чтобы понять это: 4x + 1 = 2x + 7 ⇒ 4x — 2x = 7 — 1 ⇒ 2x = 6 ⇒ x = 6/2 ⇒ x = 3.

Какие этапы решения линейных уравнений с одной переменной?

Наиболее общее правило для решения линейных уравнений состоит в том, что мы можем складывать, вычитать, умножать или делить одно и то же слагаемое на обе части уравнения, чтобы мы могли найти значение присутствующей в нем переменной.Шаги для решения линейных уравнений с одной переменной приведены ниже:

• Изолируйте переменный член с одной стороны, добавляя или вычитая один и тот же член с обеих сторон уравнения.
• Умножьте или разделите обе части на коэффициент переменной, чтобы мы могли иметь только переменную в одной части уравнения.
• Упростите и получите ответ в виде «x=c».

Какова общая форма линейного уравнения с одной переменной?

Общая форма линейных уравнений с одной переменной: Ax + B = 0, где x — переменная, A — коэффициент при x, а b — постоянный член.

Решение линейных уравнений с одной переменной

---

8 класс. Решение линейных уравнений с одной переменной

Рейтинг: 

http://map.mathshell.org/materials/download.php?fileid=1286

Общие базовые стандарты

Стандарты содержания

8.EE.7 Решение линейных уравнений с одной переменной.

8.EE.7a Приведите примеры линейных уравнений с одной переменной с одним решением, бесконечным числом решений или отсутствием решений.Покажите, какая из этих возможностей имеет место, последовательно преобразовывая данное уравнение в более простые формы, пока не получится эквивалентное уравнение вида x = a, a = a или a = b (где a и b — разные числа).

8.EE.7b Решите линейные уравнения с коэффициентами рациональных чисел, включая уравнения, решения которых требуют расширения выражений с использованием свойства дистрибутивности и сбора подобных членов.

Стандарты математической практики

МП.1 – Разбираться в проблемах и настойчиво решать их.

MP.3 – Придумывать жизнеспособные аргументы и критиковать рассуждения других

MP.7 — Найдите и используйте структуру

.

Описание урока

На этом уроке под названием «Решение линейных уравнений с одной переменной» с сайта map.mathshell.org учащиеся начинают с выполнения предварительного задания, в ходе которого учащиеся начинают изучать, что означает истинность уравнения. Учащихся просят критически оценить работу двух учащихся для этой оценки.Урок переходит к обсуждению того, как узнать, что уравнение истинно, и определению значений, чтобы сделать уравнение верным. Учащиеся совместно определяют, всегда ли, иногда или никогда не будет истинным уравнение, представляющее три возможных решения линейного уравнения (одно решение, отсутствие решения, бесконечное множество решений). Урок также включает в себя задание по сопоставлению карточек, где учащиеся сопоставляют разные уравнения с другими уравнениями с тем же решением. Уроки содержат огромное количество информации для наводящих вопросов, способствующих рассуждению и развитию концептуального понимания.

Предостережения

Некоторые из предостережений этого урока включают отсутствие поддержки для изучающих английский язык. Также отсутствует поддержка культурного разнообразия. Уроку не хватает дополнительной поддержки для учащихся, работающих как выше, так и ниже уровня класса. Есть образцы решений, но нет критерия для предоставления объективных оценок. Отсутствует применение к реальным сценариям и возможность продвигать передачу. Также должен быть добавлен какой-то способ настроить это для более мультикультурных студентов.

Обоснование выбора

Урок представляет собой насыщенный урок, в котором учащиеся работают на уровне строгости CCSS. Учащиеся активно участвуют в этой деятельности, используя практические манипуляции для сопоставления разных карточек и используя несколько представлений концепции. Существует взвешенный подход к работе с понятиями и процедурами.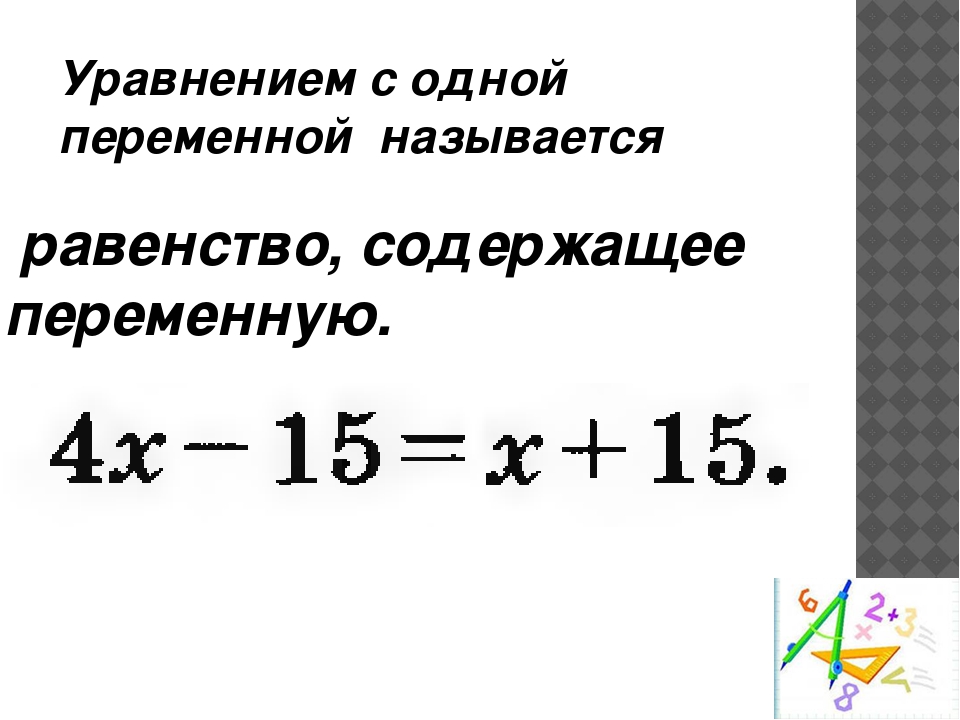 Студенты должны сообщать о своем понимании в нескольких форматах, обосновывать свои рассуждения и критиковать рассуждения других.Самый ценный ресурс урока — это вопросы, заданные учителям, которые способствуют рассуждению учащихся. Эти стратегии задавания вопросов, а также потенциальные области непонимания полезны для учителей, помогая им предвидеть и исправлять непонимание учащихся.

Решение алгебраического линейного уравнения с одной переменной Рон Куртус

SfC Главная > Арифметика > Алгебра >

Рона Куртуса (пересмотрено 18 января 2022 г.)

Линейное уравнение с одной переменной состоит из чисел или констант, умноженных на переменную.Стандартная форма такого уравнения: ax + b = 0 , где a и b — константы, а x — переменная. Часто уравнение имеет более сложную форму. Решение уравнения находится путем обработки обеих частей уравнения, чтобы привести его к форме, аналогичной x = −b/a .

Возможные вопросы:

• Как вы работаете над уравнением?
• Как решить для x ?
• Что произойдет, если уравнение будет иметь более сложную форму?

Этот урок ответит на эти вопросы.

---

---

Правила решения

Когда у вас есть линейное уравнение с одной переменной, ваша цель состоит в том, чтобы манипулировать выражениями так, чтобы в итоге вы получили переменную x слева от знака равенства, а константы — справа. То есть решение уравнения.

Например, решение уравнения 4a = 3 − x равно x = 3 − 4a .

Основное правило

Основное правило, используемое при решении уравнений в алгебре:

То, что вы делаете слева от знака равенства, вы должны делать справа.

Если вы добавляете термин слева, вы должны добавить тот же термин справа. Если вы умножаете термин в левой части, вы должны умножить тот же термин в правой части.

Примеры

В уравнении 4a = 3 − x вы хотите получить x слева, а остальные элементы справа. Вы выполняете следующие операции:

Добавьте x к обеим частям уравнения.

4а + х = 3 − х + х

4а + х = 3

Вычтите 4a из обеих частей уравнения.

4а — 4а + х = 3 — 4а

x = 3 − 4a , что является решением уравнения.

Решение путем объединения одинаковых членов

Вы можете решить уравнение типа 2x + 3 = −4x − 7 , сначала получив все члены x в левой части и все постоянные члены в правой части. Далее вы комбинируете похожие термины. Затем вы делите на кратное x , чтобы получить решение.

Пример

Рассмотрим уравнение:

2x + 3 = −4x − 7

Добавьте 4x с обеих сторон.

2х + 4х + 3 = -4х + 4х — 7

Объедините похожие термины.

6x + 3 = −7

Вычесть 3 с обеих сторон.

6x + 3 − 3 = −7 − 3

Объедините похожие термины.

6x = −10

Разделите обе части на 6 .

6x/6 = −10/6

Упростите дробь.

х = -5/3 или х = -1 2/3

Примечание : рекомендуется действовать шаг за шагом, вместо того, чтобы пытаться делать несколько дел одновременно или делать что-то в уме.

Другой пример

Рассмотрим уравнение:

2x/3 + 3 − x = 2(x + 2) − 5

Умножьте, чтобы избавиться от скобок.

2x/3 + 3 − x = 2x + 4 − 5

2x/3 + 3 − x = 2x − 1

Избавьтесь от дроби, умножив обе ее части на 3.

3(2x/3 + 3 — x) = 3(2x — 1)

Умножьте, чтобы избавиться от скобок.

2х + 9 — 3х = 6х — 3

Объедините похожие термины.

9 — х = 6х — 3

Вычесть 9 с обеих сторон.

−x = 6x − 12

Вычесть 6x с обеих сторон.

−7x = −12

Разделить на −7 .

х = 12/7 или х = 1 5/7

Переменная в дроби

Существуют уравнения, в которых член размером x является частью знаменателя уравнения. В таком случае вы должны умножить обе части уравнения на член x , чтобы оно не содержало переменных дробей.Точно так же вы хотите удалить любые дроби в уравнении, но умножить на знаменатель уравнения.

Пример

Рассмотрим уравнение:

2x/(x + 1) = 7/12

Умножьте обе части на (x + 1) .

2x(x + 1)/(x + 1) = 7(x + 1)/12

Упростите дробь (x + 1)/(x + 1) = 1 .

2x = 7(x + 1)/12

Умножьте обе стороны на 12 .

24x = 7(x + 1)

Умножьте с дистрибутивным законом или умножьте, чтобы избавиться от круглых скобок.

24x = 7x + 7

Вычесть 7x с обеих сторон.

24x — 7x = 7x — 7x + 7

Объедините похожие термины.

17x = 7

Разделите на 17 , чтобы получить решение уравнения.

х = 7/17

Другой пример

Рассмотрим уравнение:

1/(5x − 3) = 3/x

Умножьте обе части на (5x − 3) .

1 = 3(5x — 3)/x

Умножить обе стороны на x .

х = 3(5х — 3)

Обратите внимание, , что иногда эти два шага объединяются и называются «перекрестным умножением» уравнения.Одна проблема заключается в том, что сокращение может привести к ошибкам. Кроме того, лучше знать, что вы делаете и почему для лучшего понимания.

Умножение с дистрибутивным законом (убрать скобки).

х = 15х — 9

Вычесть 15x с обеих сторон.

−14 х = −9

Разделите обе стороны на −14 x .

х = 9/14

Резюме

Линейное уравнение с одной переменной состоит из чисел или констант, умноженных на переменную.Стандартная форма такого уравнения: ax + b = 0 , где a и b — константы, а x — переменная. Часто уравнение имеет более сложную форму.

Решение уравнения находится путем обработки уравнения, чтобы привести его к форме, аналогичной x = −b/a . Другими словами, вам нужны только x в левой части уравнения, а остальные элементы в правой части уравнения. Правило таково: что делаешь с левой стороны, то делаешь и с правой.

---

Шаг за шагом

---

Ресурсы и ссылки

Полномочия Рона Куртуса

Веб-сайты

Ресурсы по алгебре

Книги

(Примечание: Школа чемпионов может получать комиссионные от покупки книг)

Лучшие книги по алгебре

---

Поделиться этой страницей

Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:

---

Студенты и исследователи

Веб-адрес этой страницы:
www.школа-для-чемпионов.com/алгебра/
linear_equation_one_variable.htm

Разместите его в качестве ссылки на своем веб-сайте или в качестве ссылки в своем отчете, документе или диссертации.

Copyright © Ограничения

---

Где ты сейчас?

Школа Чемпионов

Темы по алгебре

Решение алгебраического линейного уравнения с одной переменной

---

Линейные уравнения с одной переменной

Общая форма линейного уравнения: jx + k = 0.В этом уравнении j и k — целые числа, и решение x может быть только 1. Например, 8x + 7 = 10 — это уравнение, которое является линейным и содержит только одну переменную. Единственным типом решения этого уравнения является x = ⅜ . В случае линейного уравнения с двумя переменными будет два решения, так как оно имеет две переменные. Список формул для линейных уравнений сокращает время, затрачиваемое на поиск этих формул. Список очень помогает учащимся убедиться, что они не пропустят ни одной формулы во время подготовки к экзаменам на доске или конкурсным экзаменам.

На рабочем листе мы приступаем к работе над линейными уравнениями с одним определением переменной, реальными примерами линейных уравнений с одной переменной, формулами, решениями, текстовыми задачами и рабочим листом.

Что такое линейное уравнение с одной переменной?

Когда в уравнении есть переменная одного из максимумов одного порядка, то оно называется линейным уравнением с одной переменной. Линейное уравнение обычно записывается как jx + k = 0. В этом уравнении j и k — два целых числа, и решение для x может быть только одно.Например, 5x + 6 = 10 — это линейное уравнение, в котором есть только одна переменная. Единственное решение, которое вы получите для этого уравнения, это x = ⅘. Вот еще несколько примеров этих уравнений: 13x — 92 = 139, 27x — 9 = 81.

Различные типы линейных уравнений

Существует три основных типа линейных уравнений. Они следующие:

• линейные уравнения с одной переменной

• линейные уравнения с двумя переменными

• линейные уравнения с тремя переменными.

Формула линейного уравнения

Стандартная форма линейного уравнения обычно выражается в следующей форме: jx + k =0. В этом уравнении j и k — два целых числа, решение для x может быть только одно, а значение j и k никогда не может быть равно нулю.

Процесс решения линейных уравнений с переменной

Когда вы решаете уравнение, имеющее только одно решение, выполните следующие действия:

• Сначала найдите НОК.Если есть какие-либо фракции, то вы должны очистить их.

• Следующий шаг включает в себя упрощение обеих частей уравнения, как это происходит.

• Далее вы должны изолировать переменную с одной стороны.

• Наконец, вам нужно проверить результат, который вы получили.

Решение уравнений с одной переменной: TEAS || ЗарегистрированоNursing.org

Основные термины и терминология, относящиеся к решению уравнений с одной переменной

• Алгебра: раздел математики, в котором есть хотя бы одно неизвестное число или переменная.
• Переменная: неизвестное число в алгебраическом уравнении
• Обратные математические вычисления: Противоположные вычисления
• Обратный математический расчет для сложения: вычитание
• Обратный математический расчет для вычитания: сложение
• Обратное математическое вычисление для умножения: Деление
• Обратное математическое вычисление деления: умножение

Алгебраические уравнения

Обозначение алгебраических выражений:

1 – степень (показатель степени)
2 – коэффициент
3 – член
4 – оператор
5 – постоянный член
x y c – переменные/константы

Проще говоря, алгебра — это раздел математики, в котором есть хотя бы одно неизвестное число или переменная.

Переменная в алгебре — это неизвестное число в алгебраическом уравнении. Переменные обозначаются любой буквой, но x — это наиболее часто используемая буква переменной, которая используется в алгебре с одной неизвестной переменной, а любые другие буквы используются, когда в алгебраическом уравнении имеется более одного неизвестного числа или переменной, например показано на картинке выше. Наиболее часто используемая буква для второй переменной — y, однако, как указано выше, можно использовать любую букву.

В этом разделе вы узнаете, как решать алгебраические уравнения только с одним неизвестным числом или переменной в алгебраическом уравнении, поэтому в этом разделе мы будем использовать только x в качестве неизвестного числа или переменной в алгебраическом уравнении, хотя любая буква может быть используется, как указано выше.

Решение алгебраических уравнений

Процедура решения алгебраических уравнений следующая:

1. Поместите все неизвестные переменные (x) слева от знака равенства (=)
2. Поместите все константы или известные числа справа от знака равенства (=)
3. Выполнить обратные математические вычисления для всех неизвестных или x до тех пор, пока только 1 x или x не окажется слева от знака равенства (=)

Обратные математические вычисления — это противоположные вычисления.

Например:

• Обратным математическим вычислением для сложения является вычитание.
• Обратным математическим вычислением для вычитания является сложение.
• Обратным математическим вычислением для умножения является деление.
• Обратным математическим вычислением для деления является умножение.

Обратные математические вычисления важны и необходимы в алгебре, но они также полезны для проверки ваших ответов на вычисления сложения, вычитания, умножения и деления.

Вот несколько примеров того, как вычисления сложения могут быть проверены и подтверждены с помощью обратного математического вычисления вычитания:

Дополнительный расчет:

24 + 56 = 80

Обратное вычисление вычитания:

80 – 24 = 56

80 – 56 = 24

Дополнительный расчет:

2 + 560 = 562

Обратное вычисление вычитания:

562 – 2 = 560

562 — 560 = 2

Вот несколько примеров того, как вычисления вычитания могут быть проверены и подтверждены с помощью обратного математического вычисления сложения:

Расчет вычитания:

35 – 27 = 8

Обратный расчет сложения:

8 + 27 = 35

Расчет вычитания:

55 – 20 = 35

Обратный расчет сложения:

35 + 25 = 55

Вот несколько примеров того, как вычисления умножения могут быть проверены и проверены с помощью обратного математического вычисления деления:

Расчет умножения:

35 х 50 = 1750

Обратное вычисление деления:

1750 ÷ 50 = 35

1750 ÷ 35 = 50

Расчет умножения:

2. 7 х 8,4 = 22,68

Обратное вычисление деления:

22,68 ÷ 2,7 = 8,4

22,68 ÷ 8,4 = 2,7

Вот несколько примеров того, как вычисления деления могут быть проверены и подтверждены с помощью обратного математического вычисления умножения:

Расчет деления:

722 ÷ 4 = 180,5

Обратное вычисление умножения:

180,5 х 4 = 722

Расчет деления:

82.6 ÷ 4 = 20,65

Обратное вычисление умножения:

20,65 х 4 = 82,6

Настройка и решение алгебраических уравнений

Вот несколько примеров составления алгебраических уравнений с x в левой части и константами в правой части алгебраического уравнения:

Пример 1. Настройка и систематизация алгебраических уравнений

11 х + 2 = 46

• Настройка с x слева и константами справа от знака =:

11 х + 2 = 46

Пример 2. Настройка и систематизация алгебраических уравнений

х + 30 = 110

• Настройка с x слева и константами справа от знака =:

х + 30 = 110

Пример 3. Настройка и систематизация алгебраических уравнений

14 — 3 = 3 х + 2

• Настройка с x слева и константами справа от знака =:

3 х + 2 = 14 — 3

Пример 4. Настройка и систематизация алгебраических уравнений

46 -2 = 11 х

• Настройка с x слева и константами справа от знака =:

11 х = 46 — 2

Пример 5. Настройка и систематизация алгебраических уравнений

33.3 х + 7 = 276

• Настройка с x слева и константами справа от знака =:

33,3 х + 7 = 276

Теперь, когда уравнения составлены, как указано выше, пришло время решить уравнение и узнать точное значение неизвестного x. Процедура для этого показана ниже для каждого из пяти приведенных выше уравнений.

Пример 1. Решение алгебраического уравнения

1. 11 х + 2 = 46
2. 11 х = 46 – 2
3. 11 х = 44
4. х = 44 ÷ 11
5. х = 4

Ответ: 4

Пример 2. Решение алгебраического уравнения

• х + 30 = 110
• х = 110 – 30
• х = 80

Ответ: 80

Пример 3. Решение алгебраического уравнения

• 3 х + 2 = 14 — 3
• 3 х = 14 – 3 – 2
• 3 х = 9
• х = 9 ÷ 3
• х = 3

Ответ: 3

Пример 4. Решение алгебраического уравнения

• 11 х = 46 — 2
• 11 х = 44
• х = 44 ÷ 11
• х = 4

Ответ: 4

Пример 5. Решение алгебраического уравнения

• 33.3 х + 7 = 276
• 33,3 х = 276 -7
• 33,3 х = 269
• х = 269 ÷ 33,3
• x = 8,08 округлить до сотых

Ответ: 8. 08

Вот несколько примеров выполнения обратных или противоположных вычислений для неизвестных (x) в алгебраическом уравнении:

Пример 1

Алгебраическое уравнение: 2 х + 7 = 19

Решение уравнения с обратными вычислениями:

Выполнить обратный расчет.Вычтите 7 из обеих сторон знака равенства (=)

• 2 х + 7 — 7 = 19 – 7
• 2 х = 12
• Разделите обе части знака равенства (=) на 2.

Ответ: х = 6

Чтобы проверить этот ответ, подставьте 6 вместо каждого x в исходном алгебраическом уравнении, как показано ниже:

• 2 (6) + 7 = 19
• 12 + 7 = 19
• 19 = 19

Если числа (19) одинаковы по обе стороны от знака равенства, вычисление x как 6 верно.Когда числа разные для каждой стороны знака равенства, расчет неправильный и неправильный.

Пример 2

Алгебраическое уравнение: 2 x — 7 = 19

Решение уравнения с обратными вычислениями:

Выполнить обратный расчет. Добавьте 7 к обеим сторонам знака равенства (=)

• 2 х — 7 + 7 = 19 + 7
• 2 х = 26
• Разделите обе части знака равенства (=) на 2.

Ответ: х = 13

Чтобы проверить этот ответ, подставьте 13 вместо каждого x в исходном алгебраическом уравнении, как показано ниже:

• 2 х — 7 = 19
• 2 (13) — 7 = 19
• 26 — 7 = 19
• 19 = 19

Если числа (19) одинаковы по обе стороны от знака равенства, вычисление x как 13 верно.Когда числа разные для каждой стороны знака равенства, расчет неправильный и неправильный.

Упрощенные алгебраические уравнения

В дополнение к решению алгебраических уравнений, как вы узнали выше, вы также можете увидеть другие типы алгебраических вычислений на вашем TEAS. Например, вы можете получить упрощенные алгебраические расчеты и решение для x с помощью словесной задачи.

Вас могут спросить, каково решение или ответ для алгебраических вычислений, таких как приведенные ниже.

Пример 1

Каков ответ на 2 х + 6 х – 2, когда х равно 4?

• 2 (4) + 6 (4) – 2
• 8 + 24 – 2 = 30

Ответ: 30

Пример 2

Каков ответ на 3 х + 2 х + 2, когда х равно 8?

• 3 (8) + 2 (8) + 2
• 24 + 16 + 2 = 42

Ответ: 42

Пример 3

Какой ответ на 3 ² х + 2 х + 2, когда х равно 5?

• 9 (5) + 2 (5) + 2
• 45 + 10 + 2 = 57

Ответ: 57

Пример 4

Каков ответ на 2 ² х — 2 х / 2, когда х равно 8?

• 4 (8) – 2 (8) / 2
• 32 -16 ÷ 2
• 16 ÷ 2 = 8

Ответ: 8

Алгебраические задачи со словами

У вас могут быть проблемы со словами на экзамене TEAS, которые нужно решить и вычислить с помощью алгебры.

Простой способ определить, нужно ли решать текстовую задачу и вычислять ее с помощью алгебры, — это задать вопрос: «Есть ли неизвестные в этой текстовой задаче?» Если ответ на этот вопрос положительный, то эту задачу со словами нужно решить и рассчитать с помощью алгебры. Если ответ на этот вопрос отрицательный, то эту задачу со словами НЕ нужно решать и вычислять с помощью алгебры.

Ниже приведены некоторые алгебраические задачи со словами:

Алгебраическая задача #1:

Сколько вам нужно положить на свой сберегательный счет, чтобы утроить свои деньги на этом счете, если в текущий момент у вас есть 657 долларов.

Ответ: Вам нужно будет положить на свой сберегательный счет 1971 доллар.

Алгебраическая задача № 2:

Что на 5 больше, чем на 2 дюжины?

• х = 2 (12) + 5
• х = 24 + 5
• х = 29

Ответ: 29 на 5 больше, чем на 2 дюжины. В одной дюжине 12.

Алгебраическая задача № 3:

Что такое 2/7 (одна седьмая) веса предмета, если 3/7 (три седьмых) составляют 68 фунтов? (Этот расчет представляет собой двухэтапный расчет.Во-первых, вы должны вычислить, что составляет 1/7, а затем вы должны вычислить, что составляет 2/7 веса объекта.

Как узнать, что такое 1/7:

• 3/7 : 68 = 2/7 : х
• 3/7 х = 68 х 2/7
• 3 х = 68
• x = 19,43 округлить до сотых
• 1/7 веса составляет 19,43 фунта, когда 3/7 веса составляет 68 фунтов
• Следующим шагом является определение 2/7 веса, когда 1/7 равно 19,43.
• х = 2 (19,43)
• х = 38.86

Ответ: 38,86 фунтов в 2/7 от общего веса, когда общий вес на 3/7 от общего веса составляет 68 фунтов.

СВЯЗАННЫЕ ЧАЙНЫЕ НОМЕРА И СОДЕРЖАНИЕ АЛГЕБРЫ :

Ален Берк RN, MSN является признанным на национальном уровне преподавателем медсестер. Она начала свою трудовую деятельность учителем начальной школы в Нью-Йорке, а затем поступила в муниципальный колледж Квинсборо, чтобы получить степень младшего специалиста по сестринскому делу. Она работала дипломированной медсестрой в отделении интенсивной терапии местной больницы, и в это время она решила стать преподавателем медсестер. Она получила степень бакалавра наук в области сестринского дела в колледже Эксельсиор, входящем в состав Университета штата Нью-Йорк, и сразу после окончания учебы поступила в аспирантуру Университета Адельфи на Лонг-Айленде, штат Нью-Йорк. Она получила диплом с отличием в Адельфи, получив двойную степень магистра в области сестринского образования и управления сестринским делом, и сразу же начала работу над докторской диссертацией по сестринскому делу в том же университете. Она является автором сотен курсов для медицинских работников, включая медсестер, она работает консультантом по медсестрам в медицинских учреждениях и частных корпорациях, она также является утвержденным поставщиком непрерывного образования для медсестер и других дисциплин, а также является членом Американской ассоциации медсестер. Целевая группа ассоциации по компетентности и обучению членов медсестер.

Последние сообщения Alene Burke, RN, MSN (см. все)

Linear Equations

Линейные предложения с одной переменной могут быть уравнениями или неравенствами. Их объединяет то, что переменная имеет показатель степени 1, который понимается и поэтому никогда не записывается (за исключением учебных целей). Их также можно изобразить на графике в виде прямой линии.

Уравнение — это утверждение, в котором говорится, что два математических выражения равны. Линейное уравнение с одной переменной — это уравнение с показателем степени 1 в переменной.Они также известны как уравнений первой степени , потому что наивысший показатель степени переменной равен 1. Все линейные уравнения в итоге могут быть записаны в виде x + b = c , где a , b и c — действительные числа, а a ≠ 0. Предполагается, что вы знакомы со свойствами сложения и умножения уравнений.

• Собственное свойство уравнений: , если A , B , и C , и C — это реальные числа и A = B , затем A + C = г + гр.

• Свойство умножения уравнений: Если a , b и c являются действительными числами и a = b , то ac =

  bc .

Цель решения линейных уравнений состоит в том, чтобы изолировать переменную по обе стороны уравнения, используя свойство сложения уравнений, а затем использовать свойство умножения уравнений, чтобы изменить коэффициент переменной на 1.

Пример 1

Решите для х : 6(2 х – 5) = 4(8 х + 7).

Чтобы изолировать x с обеих сторон уравнения, вы можете либо добавить -12 x к обеим сторонам, либо добавить -32 x к обеим сторонам.

Умножьте каждую сторону на (или разделите каждую сторону на 20).

Решение . На это указывает размещение решения внутри фигурных скобок, чтобы сформировать набор.Этот набор называется набором решений уравнения. Вы можете проверить это решение, заменив x на в исходном уравнении. Набор решений такой.

Пример 2

Решить для x : .

Это уравнение будет проще решать, если сначала очистить дробные значения. Для этого найдите наименьший общий знаменатель (НОД) для всех знаменателей в уравнении и умножьте обе части уравнения на это значение, используя распределительное свойство.

Не забывайте, что –2 распределяется между и , и x , и 4. Упростите обе части, объединив одинаковые термины.

Вы можете проверить это сами. Набор решений такой.

Как составить уравнения и неравенства с одной переменной

Создание уравнений и неравенств с одной переменной

Как мы только что видели, мы можем создавать уравнения и неравенства с одной переменной, используя информацию, представленную в задаче.Шаги для этого следующие:

1. Идентифицировать неизвестное и представить его с помощью переменной.
2. Составьте уравнение или неравенство, используя эту переменную.
3. Решите уравнение или неравенство, чтобы найти ответ на задачу.

Вероятно, самым сложным шагом является Шаг 2, где мы устанавливаем уравнение или неравенство. Чем больше мы работаем над созданием уравнений и неравенств с одной переменной, тем больше знакомимся с процессом, поэтому давайте рассмотрим еще пару примеров.

Другие примеры

Предположим, что Ларри строит прямоугольное цементное основание, на котором будет установлена ​​статуя в парке. Он знает, что площадь основания должна быть 15 квадратных футов, а ширина должна быть на 2 фута меньше длины. Чего он не знает, так это того, какими должны быть размеры основания. Давайте разберемся с этим!

Во-первых, мы признаем, что мы ищем длину и ширину основания. Мы также знаем, что ширина на 2 фута короче длины, поэтому, если мы допустим длину x , то ширина будет x — 2.

Теперь нам просто нужно составить уравнение для x , используя информацию из задачи. Площадь прямоугольника находится путем умножения длины на ширину. Следовательно, площадь прямоугольного основания равна:

• Площадь = (длина)(ширина) = х ( х — 2) = х 2 — 2 х

Нам также известно, что площадь должна быть 15 квадратных футов, поэтому мы приравняем это значение к формуле, которую мы только что нашли, чтобы получить наше уравнение с одной переменной.

Отлично! Теперь нам просто нужно решить уравнение для x . Это квадратное уравнение, поэтому давайте используем факторинг для его решения.

Получаем, что х = 5, значит длина основания будет 5 футов. Ширина на два фута короче, поэтому ширина составляет 3 фута, а размеры основания составляют 5 футов на 3 фута.

Еще один быстрый пример! Предположим, что Чак отвечает за благотворительный розыгрыш.Его бюджет составляет 100 долларов, и он уже потратил 40 долларов на расходные материалы. Ему нужно купить несколько брелоков в качестве призов за дверь, и каждый брелок стоит 5 долларов. Сколько брелков он может купить, не выходя за рамки своего бюджета?

Хммм… ну, неизвестно, сколько брелков может купить Чак, поэтому пусть это будет x . Мы знаем, что бюджет составляет 100 долларов, поэтому его общая потраченная сумма должна быть меньше или равна этой сумме. Он уже потратил 40 долларов, а поскольку каждый брелок стоит 5 долларов, общая сумма, которую он потратил бы на брелки, составляет 5 x .Следовательно, общая потраченная сумма будет суммой этих двух сумм, или 5 x + 40, поэтому мы имеем следующее неравенство.

Все, что нам нужно сделать, это решить это неравенство для x , чтобы найти, сколько брелоков он может купить.

Получаем, что x ≤ 12, так что Чак может купить до 12 брелков и при этом уложиться в бюджет.

Краткий обзор урока

Уравнение с одной переменной — это уравнение, содержащее ровно одну переменную.