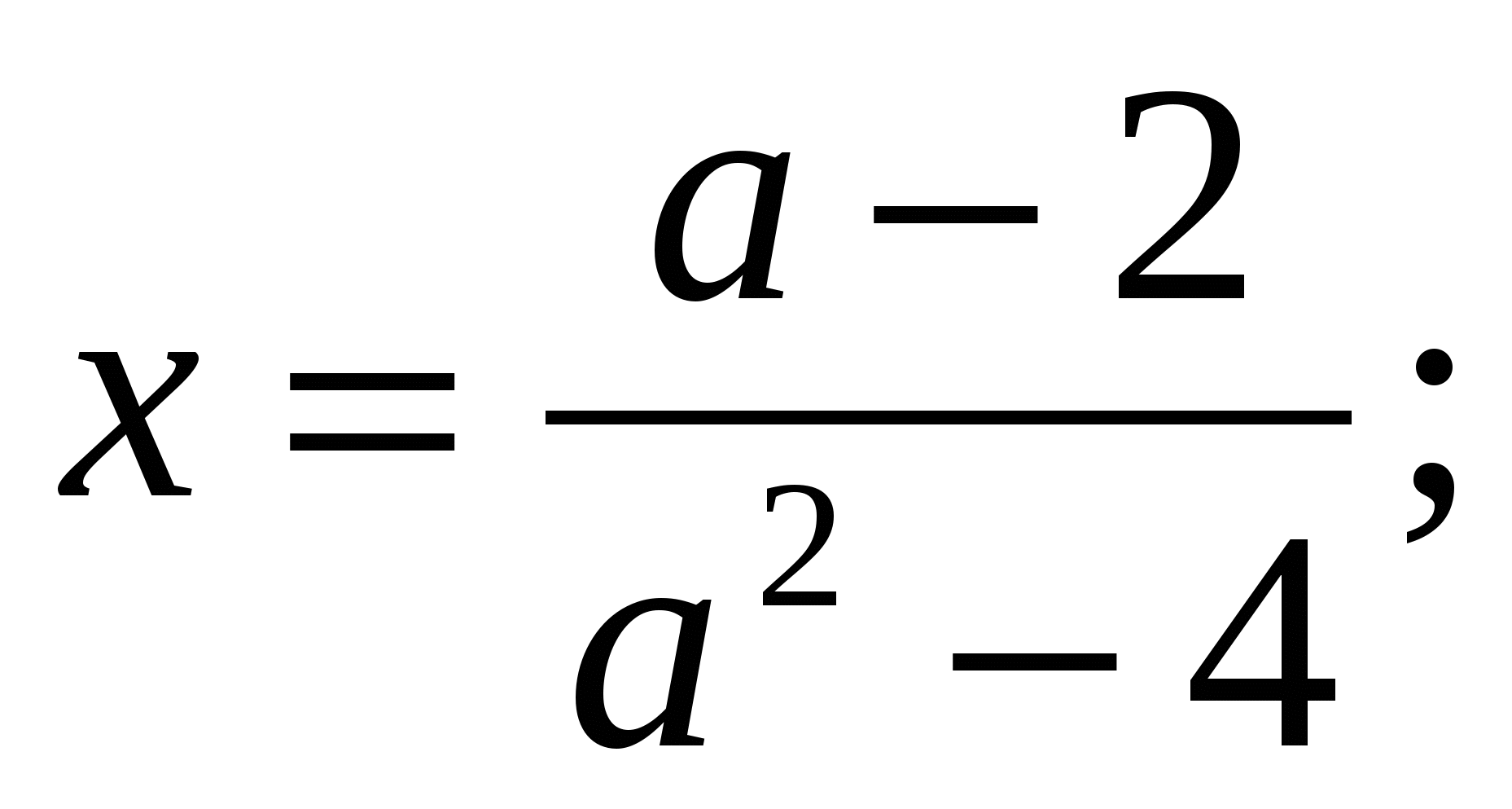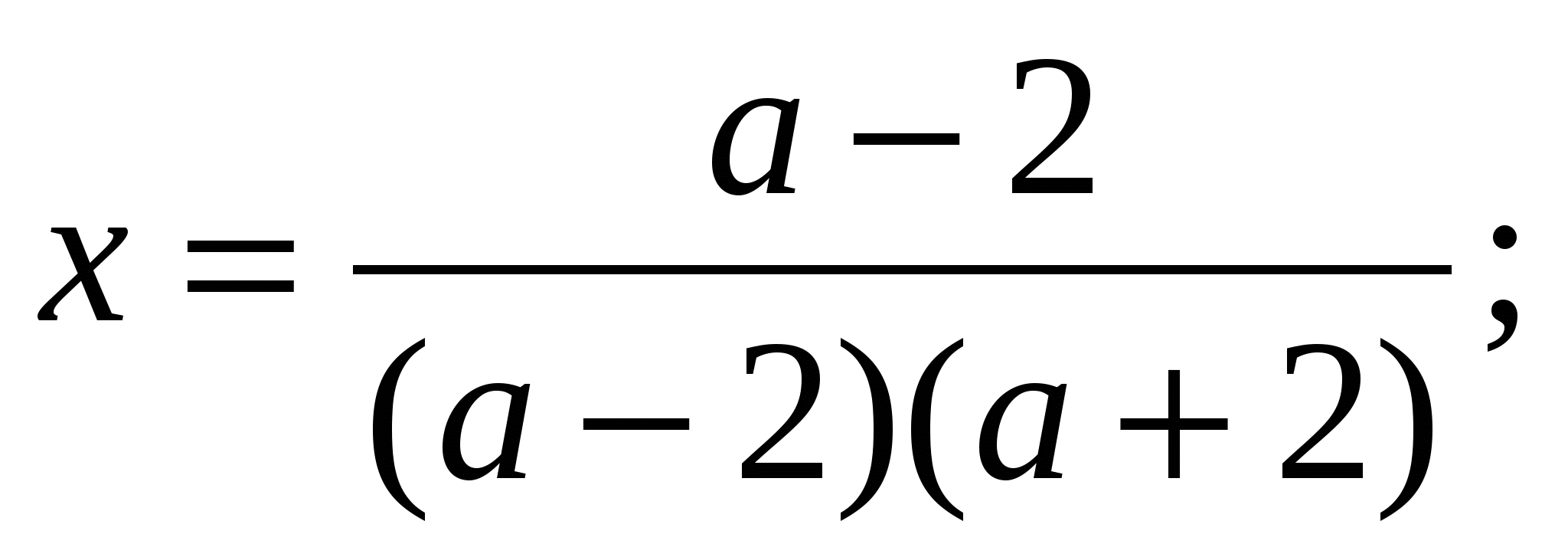Решение линейных уравнений и неравенств с параметрами в 10 классе.

Урок в 10 классе

«Решение линейных уравнений и неравенств с параметрами».

Выполнила: Галстян Г.С.

Учитель математики МОУ «СОШ №11»

Воскресенск, 2017

Конспект урока в 10 классе

Тема урока: «Решение линейных уравнений и неравенств с параметрами».

Цель: — повторить, закрепить и привести в систему знания и умения решать линейные уравнения и неравенства с параметрами, полученные в 9 классе;

-развивать логическое мышление, математическую речь, интерес к изучению математики;

— воспитывать аккуратность. Взаимопонимание. (слайд 2)

Форма работы: фронтальная беседа, работа в парах.

Метод работы: — методы организации учебно-познавательной деятельности: наглядные, практические, исследовательские;

— методы стимулирования и мотивации учебно-познавательной деятельности: учебная дискуссия, эмоциональное воздействие;

-методы контроля: письменный, самопроверка.

Оборудование: проектор, карточки.

Литература: Учебник 10-11 класса «Алгебра и начала анализа 10-11» Мордкович А.Г. – изд. Мнемозина, 2012г, задачник 10-11 класса «Алгебра и начала анализа 10-11» Мордкович А.Г. – изд. Мнемозина, 2012г.

Ход урока.

I.Организационный момент.

II.Актуализация знаний.

У. Обычно в уравнении или неравенстве буквами обозначаются переменные.

У. Что значит решить уравнение или неравенство?

ОТВ. Решить уравнение или неравенство означает найти множество значений неизвестных, удовлетворяющих этому уравнению или неравенству.

У. Иногда уравнения и неравенства, кроме букв, обозначающих неизвестные, содержат другие буквы, называемые параметрами.

Определение. Переменная, значение которой на протяжении некоторого контекста остается фиксированным, называется параметром, по отношению к этому контексту. (слайд3)

Когда предлагают решить уравнение или неравенство с параметрами, тем самым указывают, что переменные, названные параметрами, должны рассматриваться как произвольные, но фиксированные коэффициенты.

Предавая параметрам разные числовые значения, получаем различные уравнения или неравенства, например, в линейном уравнении ax+b=0 или неравенстве ax+b≥0,

x- переменная, a и b- параметры.

При решении уравнений или неравенств надо сначала найти множество допустимых значений параметров, а затем разбить это множество на части, в каждом из которых ответ выражается функцией через параметры.

Определение. Множество значений параметра, при каждом из которых или существуют в области действительных чисел, называют областью допустимых значений параметра. (слайд 4)

Пример 1. Данное уравнение имеет смысл при

Пример 2.×x≤2a – имеет смысл при

a ≥3.

Определение. Число называют допустимым значением переменной x, если f и g действительны при каждом допустимом значении параметра.

Определение. Областью определения неравенства (уравнения) множества всех допустимых значений x, при которых уравнение (неравенство) имеет смысл.

В примере 1. x , в примере 2. x.(слайд 5)

Вспомним решение линейных уравнений и неравенств с параметрами a и b.

№1.ax=b, x.

1. Если a – единственный корень.

2. Если a=0, b=0, то 0x=0, — уравнение имеет множество корней.

3. Если a=0, b0x=b – уравнение корней не имеет.

№2. axb, x.

1.Если aнеравенство имеет множество решений. Если , то неравенство решений не имеет.

2. Если , то.

3. .

III. Закрепление теоретических навыков.

Решают у доски по карточкам.

№1. Решить уравнение относительно x.

3(2a – x) = ax+1.

Решение:

1. a =-3, уравнение корней не имеет;

2. то .

Ответ: а) а= -3, уравнение корней не имеет; б) , то .

№2. Решить неравенство относительно x.

3(2a – x) ax+1.

Решение:

1. а;

2. а

3. а.

Для самостоятельного решения с последующей проверкой ответов.

1. ах – 3=х+2. Ответ: а=1, нет корней; а.

2. ах – 3 х +2. Ответ: а=1, нет решений; а1, х ; а1, х.(слайд 6)

IV.Исследовательская деятельность. (работа в парах)

Решите уравнение и неравенство с параметром задачник № 60.1; № 60,3; № 60.4(б).

№60.1 При каких значениях параметра m уравнение mx – x + 1= :

а) имеет ровно один корень;

б) не имеет корней;

в) имеет более одного корня?

Решение:

mx – x + 1= ;

mx – x = – 1;

x (m – 1) = – 1;

а) m1, x=;

б) таких m нет;

в) m = 1, 0x = 0, х- любое число.

Ответ: а) m1, x=; б) таких m нет; в) m = 1, 0x = 0, х- любое число.

№60.3 Решение уравнение (относительно х):

а) ; б)

Решение:

а) ;

;

(а – 2) (а + 2) х = ;

1. а = 2, а — 2; 0х = 0, х – любое число.

2. а = — 2, а = 2, а — 2, 0х = — 4, решений нет.

3. а — 2, а 2, х = .

Ответ: а = 2, а — 2; 0х = 0, х – любое число; а = — 2, а = 2, а — 2, 0х = — 4, решений нет; а — 2, а 2, х = .

б) ;

Решение:

;

;

;

1. а = — 1, а 0, 0х = 0, х – любое число;

2. а 0, а — 1, х =, х = а;

3. а =0, корней нет.

Ответ: а = — 1, а 0, 0х = 0, х – любое число; а 0, а — 1, х = а; а =0, корней нет.

№60.4 (а) Решите неравенство (относительно х):

а) mx – x + 1.

Решение:

(mx – x)– 1;

(m – 1) x – 1;

1. m = 1, 0x 0, х – любое число;

2. m 1, m , x m +1;

3. m 1, m 1, x m + 1.

Ответ: m = 1, 0x ≥ 0, х – любое число; m ≠ 1, m >1, x ≥ m +1; m ≠ 1, m < 1, x ≤ m + 1.

V. Итог.

Сегодня на уроке мы повторили решение линейных уравнений и неравенств с параметрами. На следующем уроке мы будем рассматривать решение квадратных уравнений и неравенств с параметрами.

VI. Домашнее задание. (слайд 7)

1. Повторить решение квадратных уравнений и неравенств;

2. Учебник с.383 параграф 60 (до примера 2) – прочитать;

3. Задачник №60.2; № 60.4(б) решить.

infourok.ru

Презентация к уроку по алгебре (10 класс) по теме: Решение систем линейных уравнений с параметрами

Слайд 1

Презентация: «Решение систем линейных уравнений с параметрами» Учитель математики МБОУ СОШ № 16 г. Красногорска Павлова Наталья Ивановна

Слайд 2

Задачи с параметрами представляют для учащихся наибольшую сложность. Это самые трудные задания части С Единого государственного экзамена. Универсальных указаний по решению задач с параметрами дать нельзя, приходится рассматривать различные случаи – в зависимости от значений параметров и методы решения задач различны. Но знание некоторых правил и алгоритмов решения необходимо.

Слайд 3

Решить систему уравнений – это значит найти такие значения переменных, которые обращают каждое уравнение системы в верное равенство. Параметр (от греч. parametron отмеривающий) – показатель, величина, значение которой остается постоянным в пределах рассматриваемой задачи.

Слайд 4

Что значит решить уравнение с параметром? Это значит показать, каким образом для любого значения параметра можно найти соответствующие значения корней, если они существуют, или установить, что при этом значении параметра корней нет.

Слайд 5

Пусть задана система уравнений: Каждое уравнение на плоскости представляет собой некоторую прямую. Для двух прямых на плоскости возможны три случая: 1. Прямые пересекаются. Тогда система уравнений имеет единственное решение. 2. Прямые параллельны. Тогда система не имеет решений. 3. Прямые совпадают. Тогда система имеет бесконечное множество решений. a 1 x +b 1 y = c 1 a 2 x +b 2 y = c 2 , где а 1 , а 2 , в 1 , в 2 , с 1 , с 2 – отличные от нуля числа

Слайд 6

Для системы линейных уравнений справедливо: 1. Если , то система имеет бесконечное множество решений. 2. Если , то система не имеет решений. 3. Если , то система имеет единственное решение. Основные методы решения линейной системы : — метод подстановки ; — метод исключения неизвестного ; — метод определителей .

Слайд 7

Пример 1. При каких a и b система уравнений имеет бесконечное множество решений? 5x + ay = 2, 15x + 6y = 3b. Решение: Система имеет бесконечное множество решений, если выполняется равенство: Ответ: a = 2, b = 2 .

Слайд 8

Пример 2. При каком а система уравнений имеет решение, не имеет решений, имеет бесконечное множество решений? x — 5y = 7, ax – y = -3 . Решение: 1. Если , то есть , то система имеет единственное решение. 2. Если , то есть , то система не имеет решений.

Слайд 9

3. Если , то система имеет бесконечное множество решений. Но такого a нет. Ответ: 1) при — единственное решение ; 2) при — не имеет решений ; 3) бесконечное множество решений не принимает ни при каком a .

Слайд 10

Пример 3. При каких значениях параметра а система двух уравнений имеет бесконечное множество решений? Решение: Система имеет бесконечное множество решений, если выполняются соотношения:

Слайд 11

Ответ: a = 1 .

Слайд 12

Пример 4. При каком значении m система уравнений имеет бесконечное множество решений? Не имеет решений? Решение: Система имеет бесконечное множество решений, либо не имеет решений, если коэффициенты при x и y пропорциональны, т.е.

Слайд 13

Если m =3, то — решений нет ; если m =-3 , то — бесконечное множество решений. Ответ: 1) при m =-3 – бесконечное множество решений ; 2) при m =3 – решений нет.

Слайд 14

Метод подстановки. Применяя данный метод, надо учитывать, что каждый из коэффициентов при неизвестных может обращаться в нуль. Поэтому необходимо рассмотреть случай обращения в нуль коэффициента при этом неизвестном. Пример 5. Для всех значений параметра a решить систему: (1) (2)

Слайд 15

Решение : Пусть , тогда = x=5, y=-1 . Пусть , тогда из (1) имеем: Подставляя вместо x во второе уравнение, получим систему, равносильную данной.

Слайд 18

Метод исключения. Пример 6. Для каждого значения a решить систему: Решение: — решений нет.

Слайд 19

2). Пусть a ≠ 0, тогда, умножая второе уравнение исходной системы на -a , получим: Заменяя второе уравнение системы (2) суммой ее первого и второго уравнений, получим систему, равносильную исходной:

Слайд 20

Из (2): , подставляя это значение в первое уравнение системы (2), получим Ответ: 1) при a= 0, решений нет; 2) при a≠0 ,

Слайд 21

Пример 7. Найти все значения параметра a , для каждого из которых числа x и y удовлетворяющие системе уравнений удовлетворяют также неравенству x>y . Решение: Сложим уравнения системы, получим подставим в (1) уравнение.

Слайд 22

Т.к. по условию x>y , то Ответ: при a

Слайд 23

Пример 8. Определить a , при котором система уравнений не имеет решений. Решение: Умножим обе части уравнения (1) на (a+6) , а (2) на 4. Получим: Сложив эти уравнения, получим:

Слайд 24

Умножим обе части уравнения (1) на (-2), а (2) на a: Сложив эти уравнения, получим: Рассмотрим систему, составленную из (*) и (**):

Слайд 25

При a≠{-4;-2} система имеет решение: при а=-2 система выполняется при любых x и y, следовательно, из исходной системы При a=-4 левые части уравнения системы равны 0, правые не равны 0, след., система не имеет решения. Ответ: a=-4 .

Слайд 26

Решение линейной системы при помощи определителей. Пусть дана линейная система: Тогда решение системы примет вид:

Слайд 27

Если определитель системы △≠ 0 , то система определена, т.е имеет единственное решение. Если △=0 и =0, то система не определена, т.е имеет бесконечное множество решений. Если △=0 и ≠0, то система противоречива и решений не имеет.

Слайд 28

Пример 9. Найти все значения a , при которых система имеет единственное решение. Решение: Система имеет единственное решение, если △≠0, т.е, Ответ: при a≠6 .

Слайд 29

Пример 10. Найти все a , для которых система не имеет решения. Решение: Т.к. Значит, система не имеет решения, если Ответ: при a=

Слайд 30

Пример 11. Найти все a , при которых система имеет бесконечное множество решений. Решение: система имеет бесконечное множество решений, если Ответ: при a=30 .

Слайд 31

Литература: П.Ф. Севрюков , А.Н. Смоляков Школа решения задач с параметрами: учебно-методическое пособие. М.: Илекса ; Народное образование; Ставрополь; Сервисшкола , 2011. Субханкулова С.А. Задачи с параметрами. М.:Илекса,2012. Скорнкова Л.А. Математика 10-11 классы: задачи с параметрами. Волгоград: Учитель, 2010. Кочагин В.В. ГИА 2012. Математика: Сборник заданий: 9 класс/ В.В. Кочагин , М.Н. Кочагина . – М.:Эксмо , 2011.

nsportal.ru

Разработка урока «Уравнения с параметрами». 10 класс

Общеобразовательная школа

І-ІІІ ступеней №2 отдела образования администрации города Кировское,

учитель математики

Бондаренко В.Л.

10 класс. Алгебра

Тема урока: Решение уравнений с параметрами в программе Advanced Grapher.

Цель урока:

Обучающая — организовать работу учащихся по закреплению знаний, умений и навыков решения уравнений с параметрами. Показать на примере применение программы Advanced Grapher с использованием метода самостоятельной практической деятельности.

Развивающая — обеспечить получение новых знаний и развитие в учащихся навыков, способствующих применению полученных знаний и умений для решения более сложных уравнений с параметрами.

Воспитательная — формирование информационной культуры, умения и навыков самостоятельного овладения знаниями.

Оборудование:

1. компьютеры с установленной операционной системой Advanced Grapher компьютер учителя -1 шт, компьютер ученика -12 шт;

2. проектор, экран;

3. учебник Нелин Е.П., Алгебра и начало анализа, профильный уровень, 10 класс. – Харьков: Издательство «Гимназия», 2010.

Тип урока: урок усовершенствования знаний и умений учащихся по теме «Решение уравнений с параметрами».

Ход урока

І.Организационный момент.

Сообщение темы, целей и задач урока.

ІІ.Объяснение учителя.

Определение:

Уравнение (неравенство) с параметрами – математическое уравнение (неравенство), внешний вид и решение которого зависит от значения одного или нескольких параметров, обозначенных буквами (а, в , с и т.д.).

Решить уравнение с параметром означает:

1. Найти все системы значений параметров, при которых данное уравнение имеет решение.

2. Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.

Задачи, связанные с решением уравнений с параметрами, часто встречаются на олимпиадах разных уровней, на различных конкурсах. Актуальность данной темы определяется необходимостью уметь решать такие уравнения с параметрами при сдаче Единого Государственного экзамена и на вступительных экзаменах в высшие учебные заведения.

Задачи с параметрами играют важную роль в формировании логического мышления и математической культуры у школьников, но их решение вызывает значительные затруднения. Это связано с тем, что каждое уравнение с параметрами представляет собой целый класс обычных уравнений, для каждого из которых должно быть получено решение. 

Значительный вклад в изучение вопроса методики решения уравнений с параметрами сделали такие ученые как Горнштейн П.И., Полонский В.Б., М.С., Цыпкин А.Г., Пинский А.И., Новоселов С.И., Никонов Е.Ю., Ткачук В.В., Локоть В.В., Мордкович А.Г и др.

Универсального метода решения задач с параметрами не существует.

Часто пользуются аналитическим (с использованием формул, свойств функций) и графическими методами.

Рассмотрим несколько примеров решения таких задач.

ІІІ. Решение упражнений.

Задание №1. Решить уравнение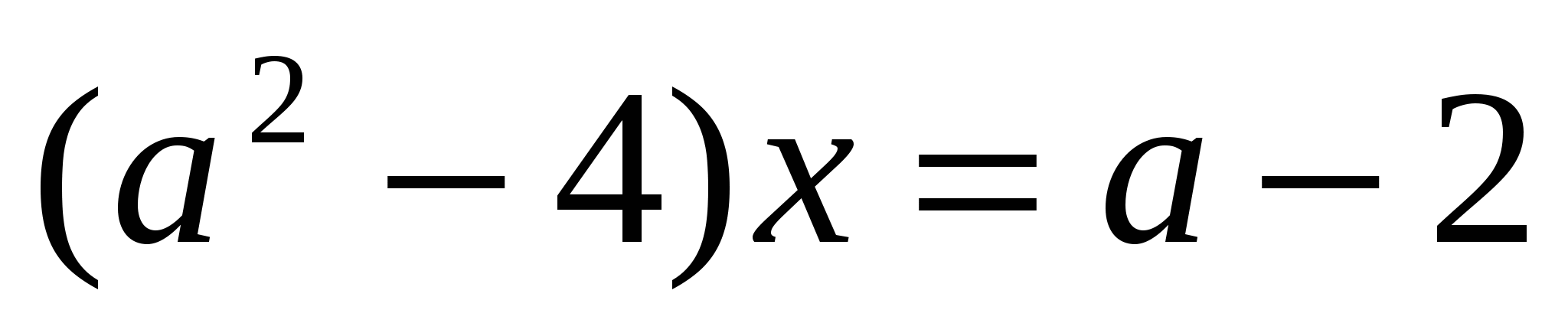

Решение:

При решении данного уравнения необходимо рассмотреть случаи, когда 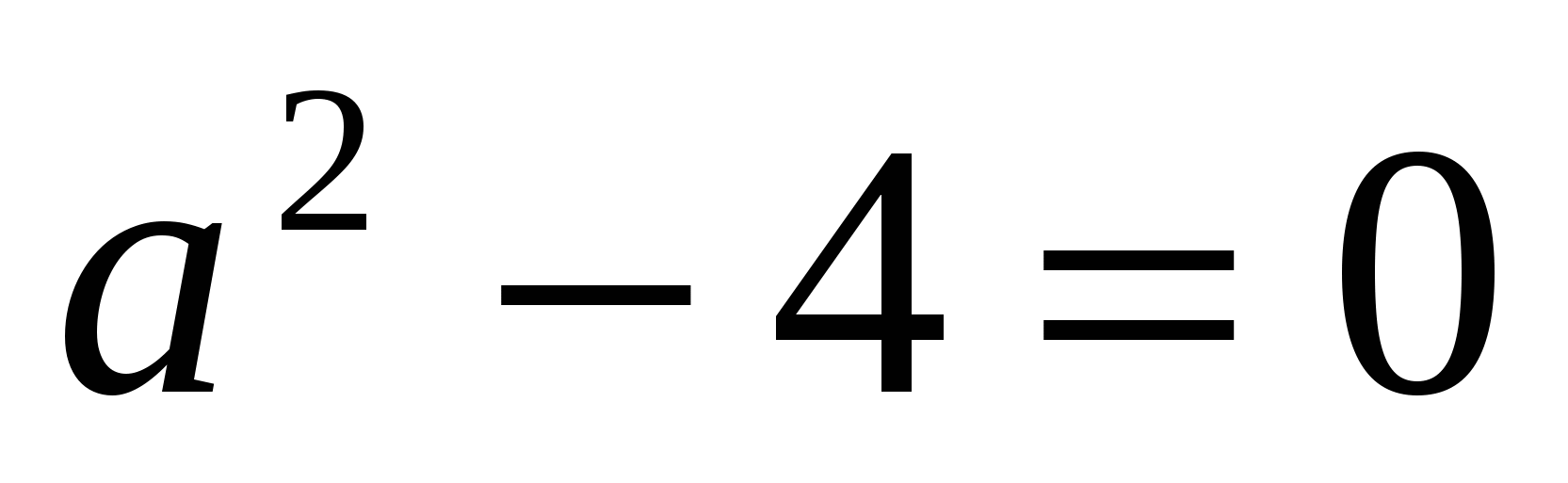(это происходит, когда а = 2, или а = -2) и случай, когда .

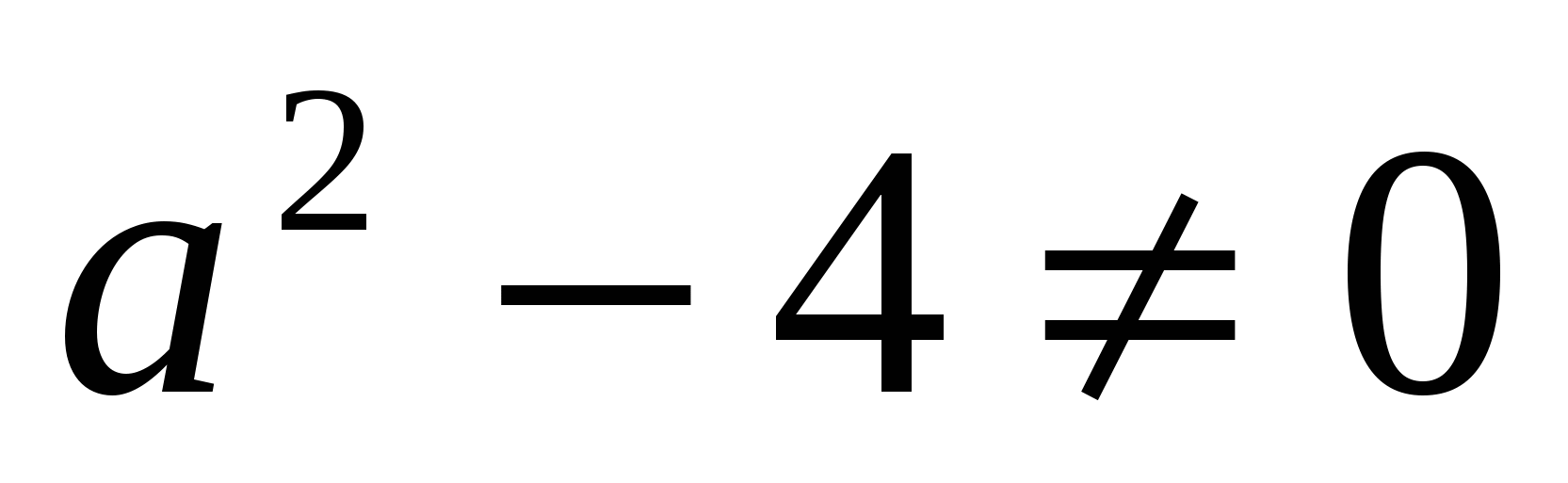Значит:

1. Если а = 2, уравнение имеет вид 0 · х = 0, тогда х – любое число.

2. Если а = — 2, уравнение имеет вид 0 · х = — 4, тогда уравнение не имеет решений.

3. Если а2, а-2, тогда уравнение имеет вид

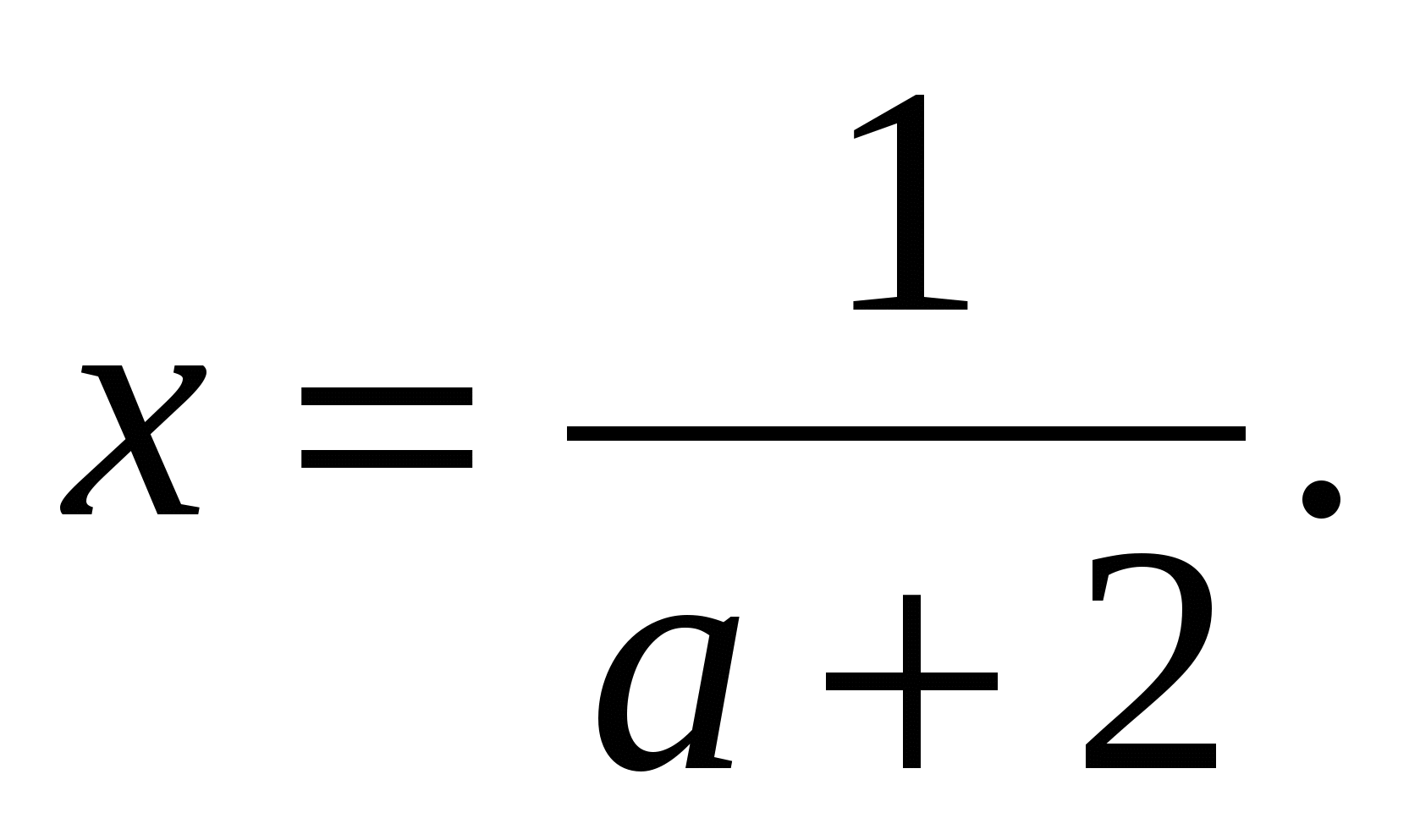
Ответ: если а = 2, то х – любое число; если а = — 2, то уравнение не имеет решений; если а2, а-2, то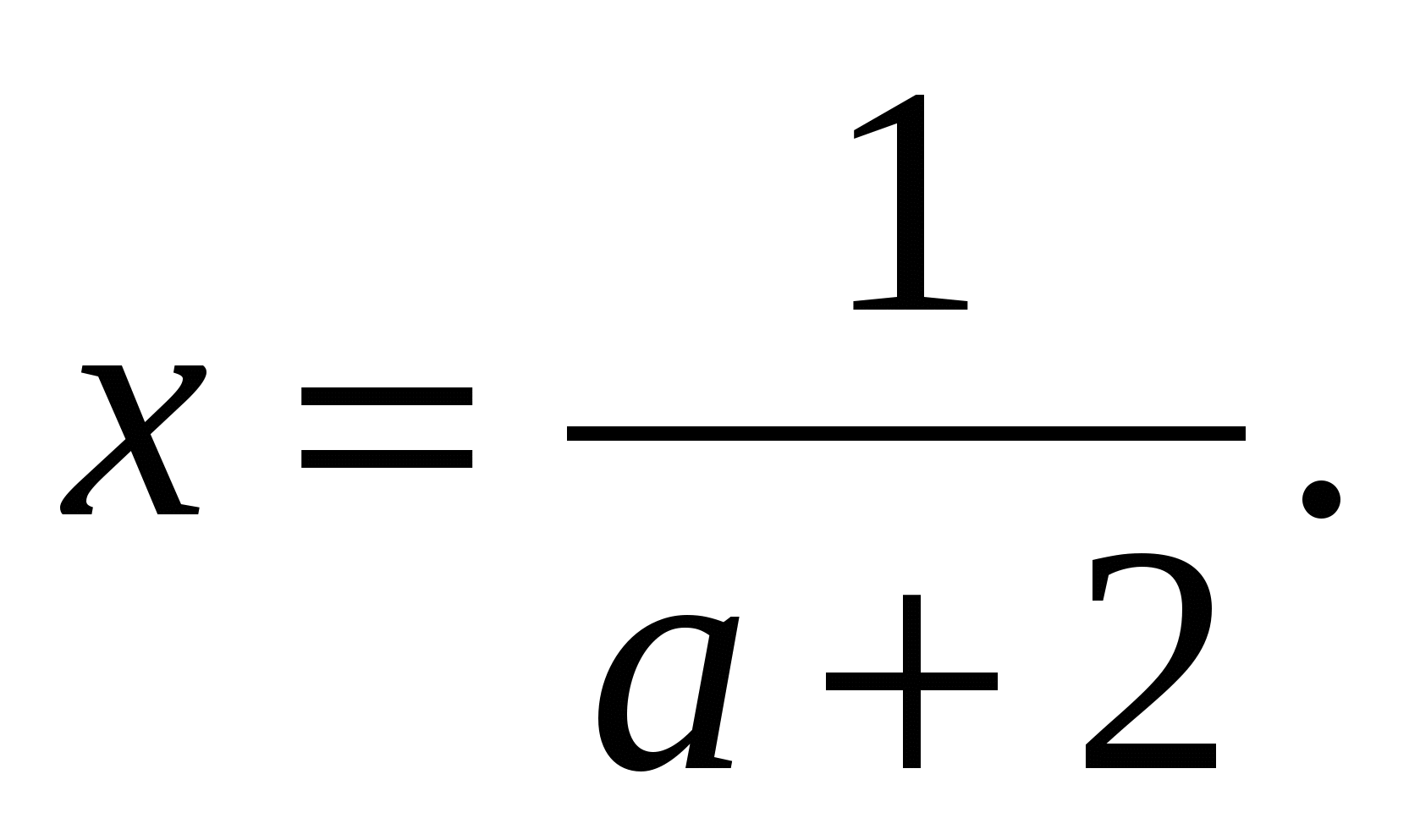

Задание №2.

1. Пользуясь собственным опытом, выполните решение предложенной ниже турнирной задачи.

Задача. «Количество решений». Найдите все значения параметра 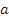, при которых уравнение 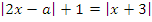имеет один корень.

Решение:

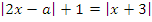, ОДЗ: хR, аR.

Решим уравнение графическим способом. Для этого рассмотрим функции

у = |x + 3| — 1 и у = |2х — а|. Построим графики функций в одной системе координат.

Алгоритм построение графика у = |x + 3| — 1.

1 шаг: у = х + 3 – графиком является прямая, сдвинутая вверх по оси ОУ на 3 единицы. Точки пересечения с ОХ (у = 0), х = — 3.

2 шаг: у = |x + 3| — часть прямой, которая расположена выше оси ОХ остается без изменения. Часть прямой, находящаяся ниже оси ОХ отображается симметрично этой оси вверх.

3 шаг: у = |x + 3| — 1 — полученный график опускаем вниз на 1 единицу.

Результат:

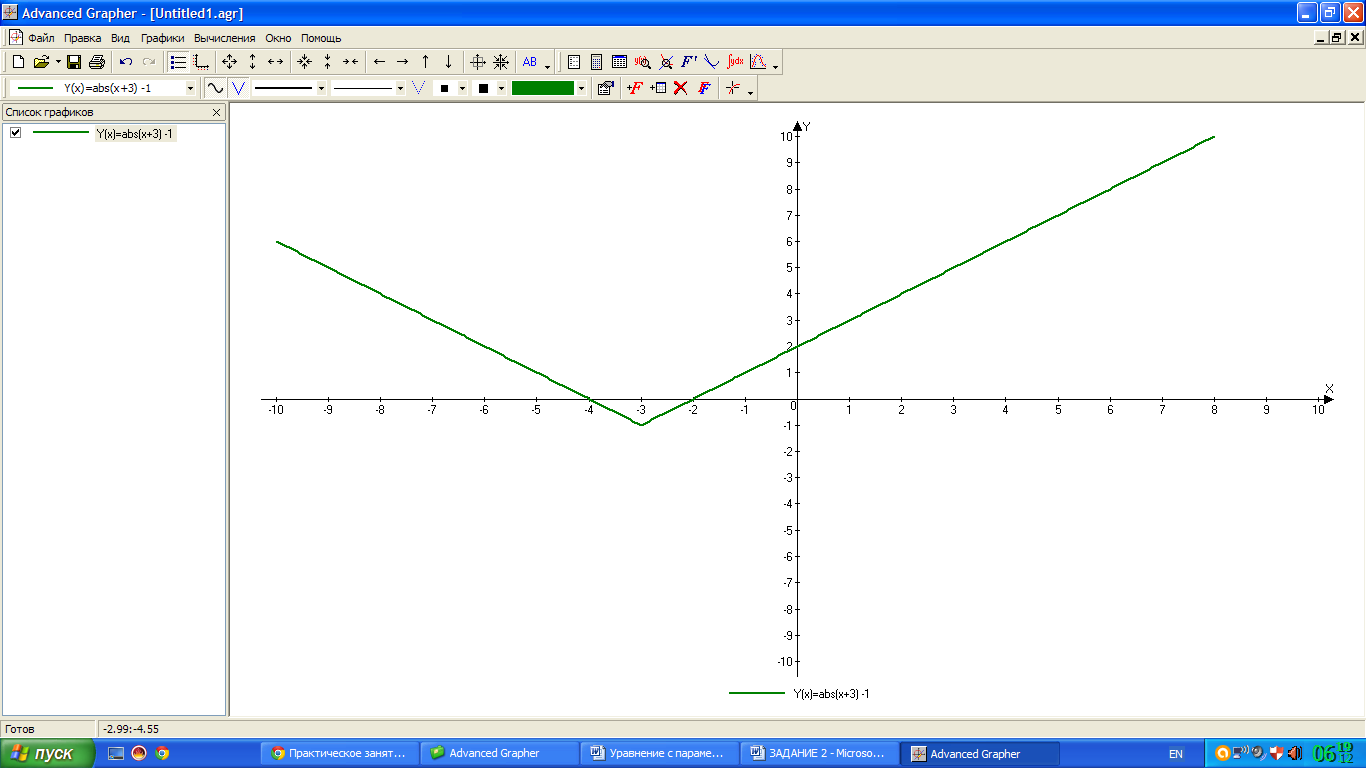
Точки пересечения с ОХ (у = 0) 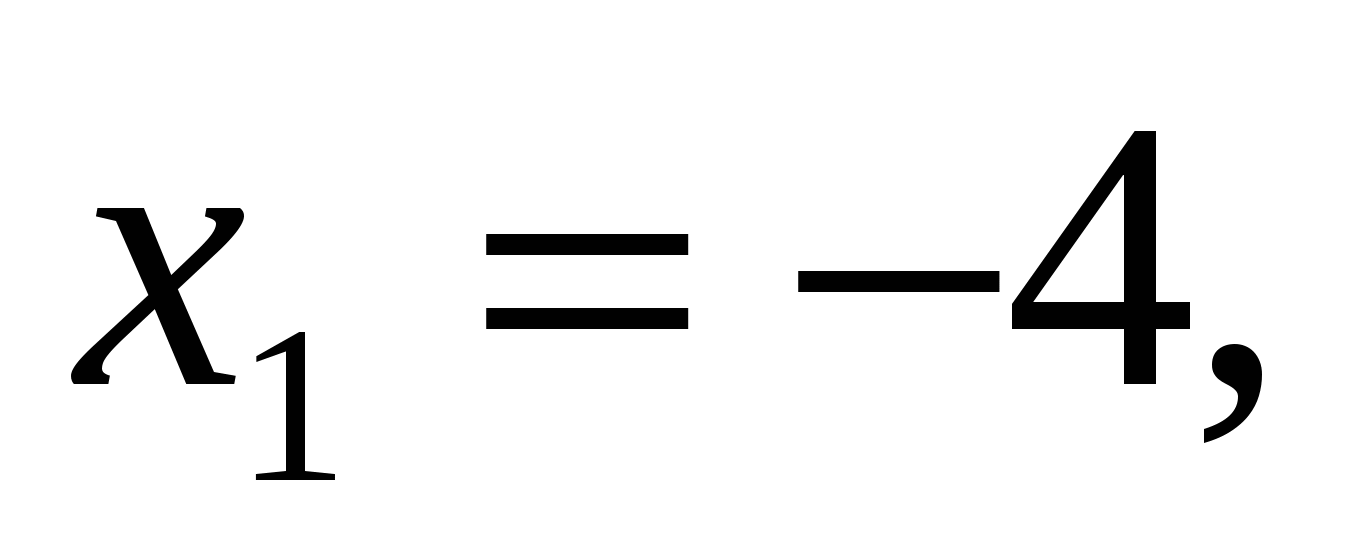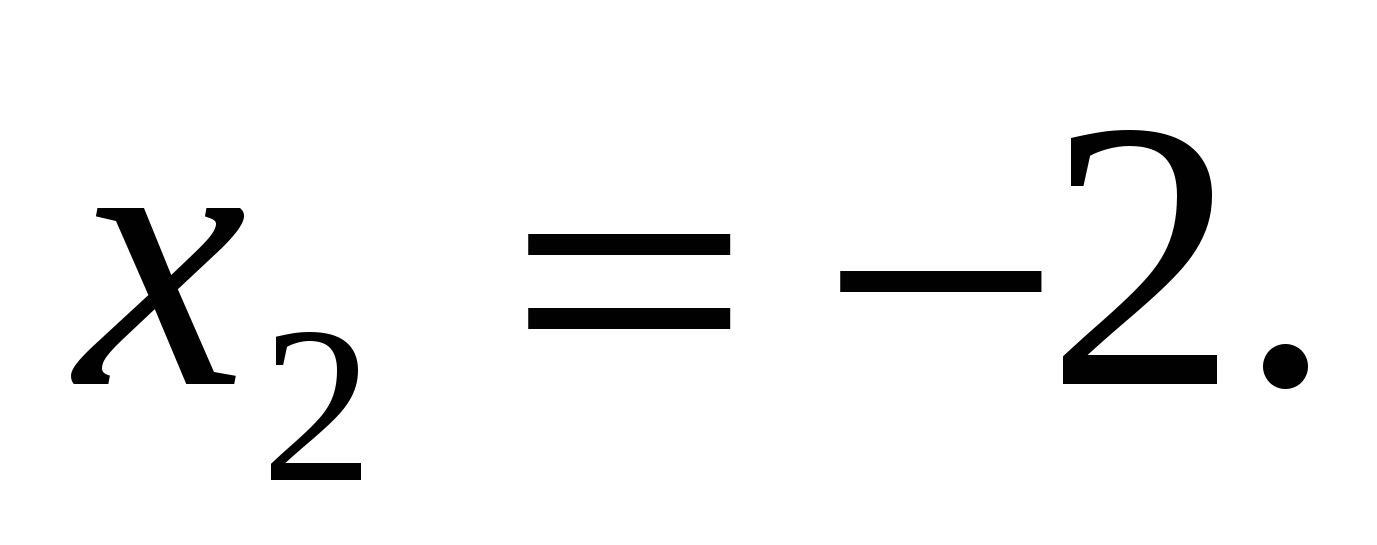Точки пересечения с ОУ (х = 0) у = 2.

Алгоритм построения графика у = |2х — а|.

1 шаг: у = 2х – графиком является прямая пропорциональность. График проходит через начало координат.

2 шаг: у = 2х – а. В зависимости от параметра а график сдвигается параллельным переносом вдоль оси ОУ вверх (если а<0) или вниз (если а>0).

3 шаг: у = |2х — а|. Часть графика, находящаяся выше оси ОХ остается без изменения, часть графика, находящаяся ниже оси ОХ отображается симметрично оси ОХ вверх.

Пример:

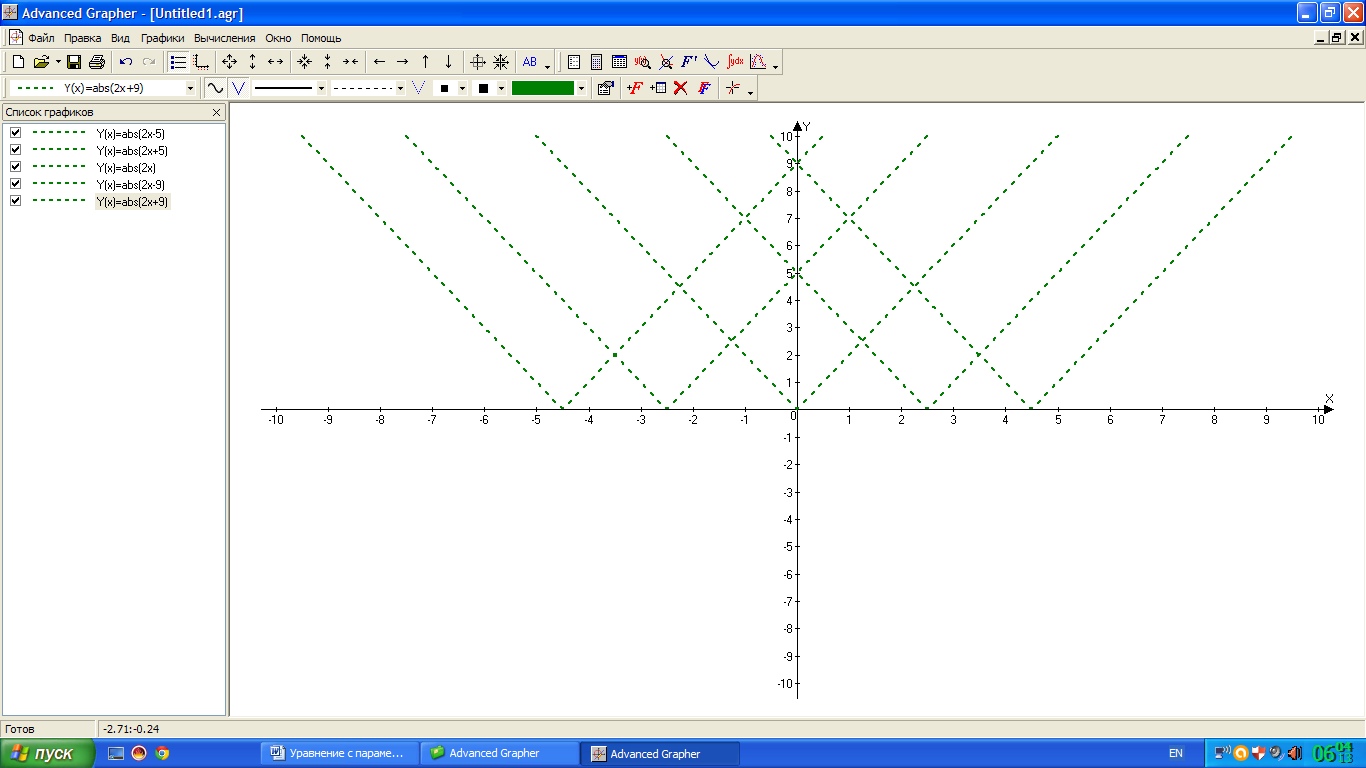
При построении графиков в одной системе координат видно, что они будут иметь одну общую точку (одно решение уравнения) при 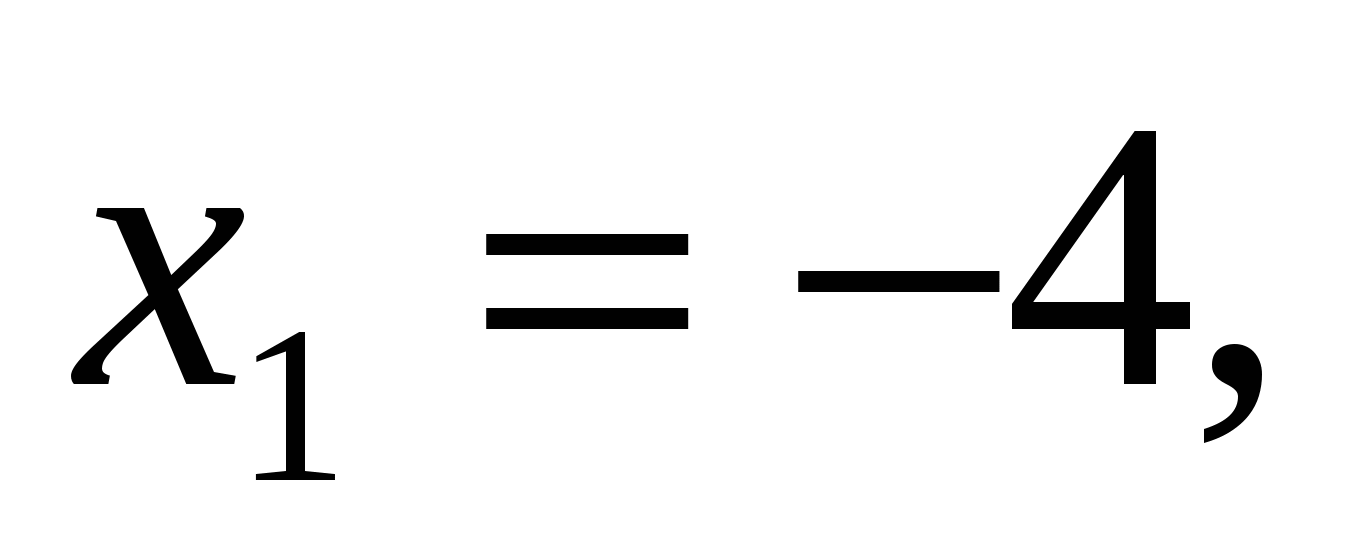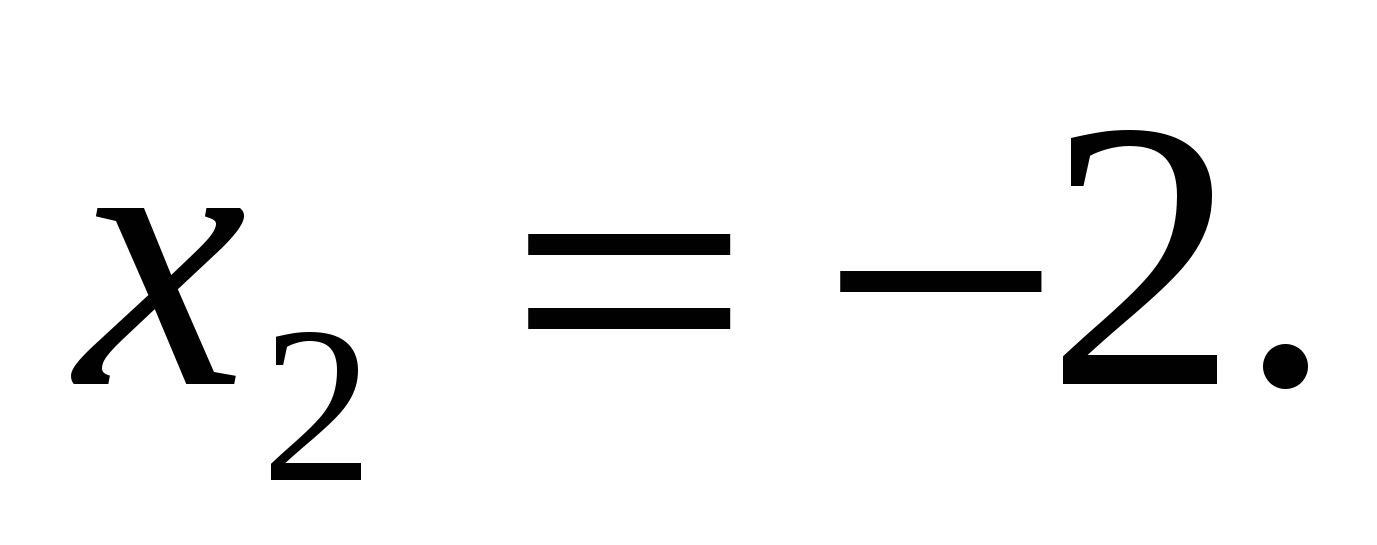Значит:

Если 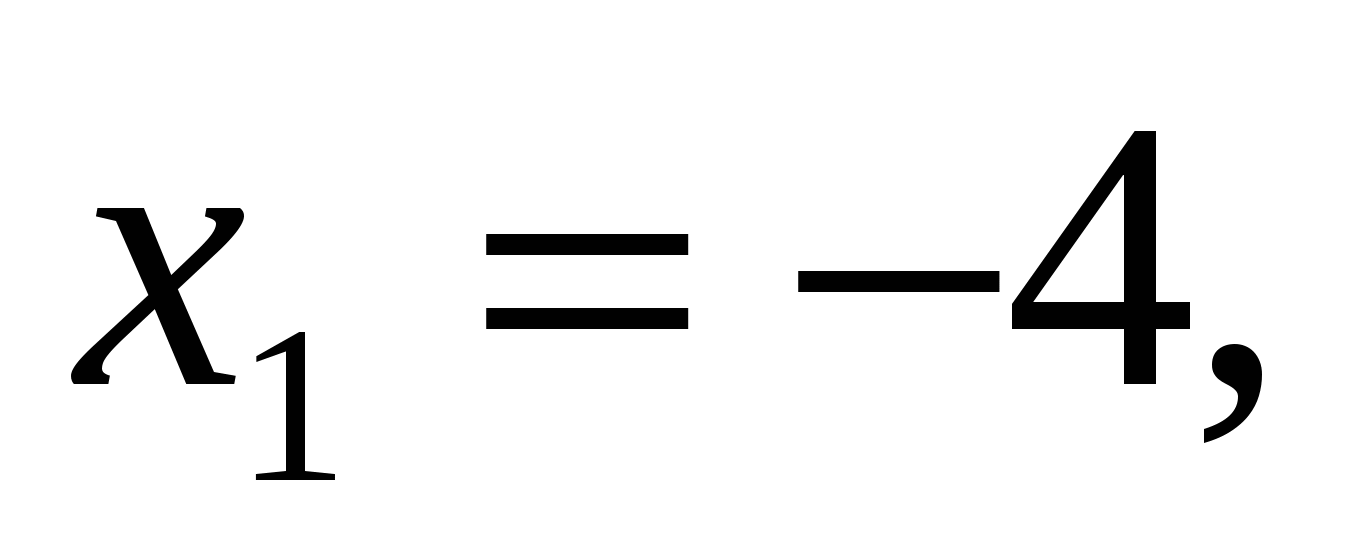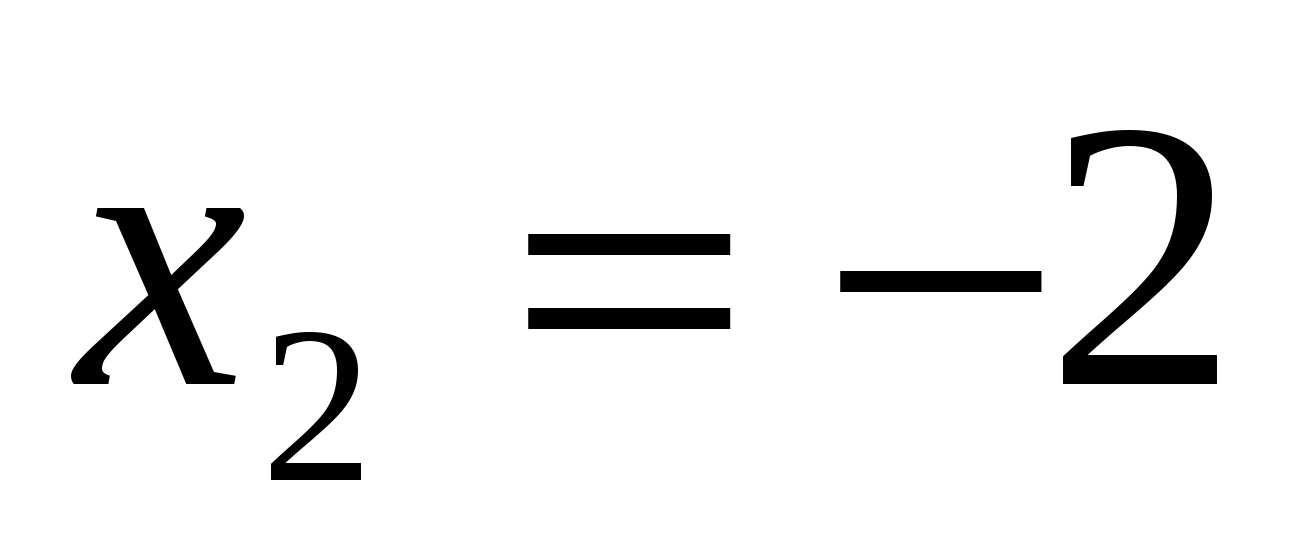, то уравнение имеет одно решение.

Если х( 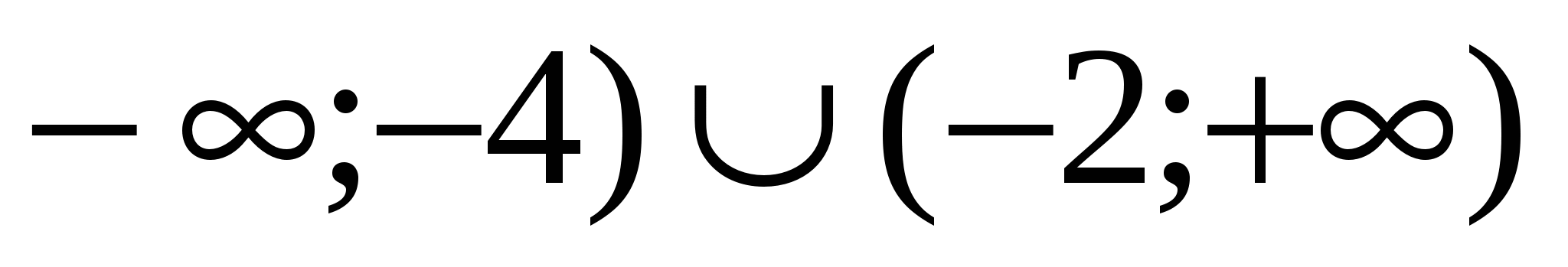— уравнение имеет 2 решения.

Если х(-4;-2) – уравнение не имеет решений.

Графически это выглядит так:

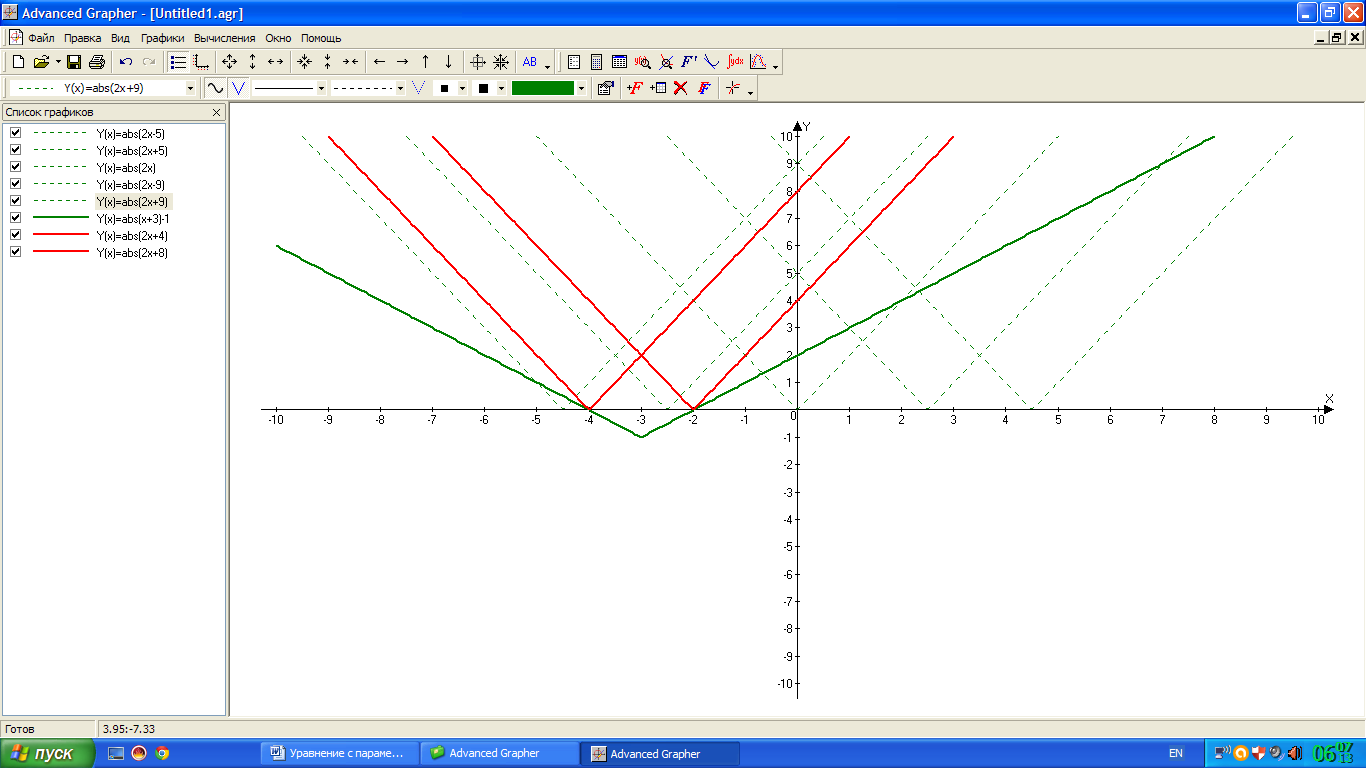
Найдем значение параметра а, при котором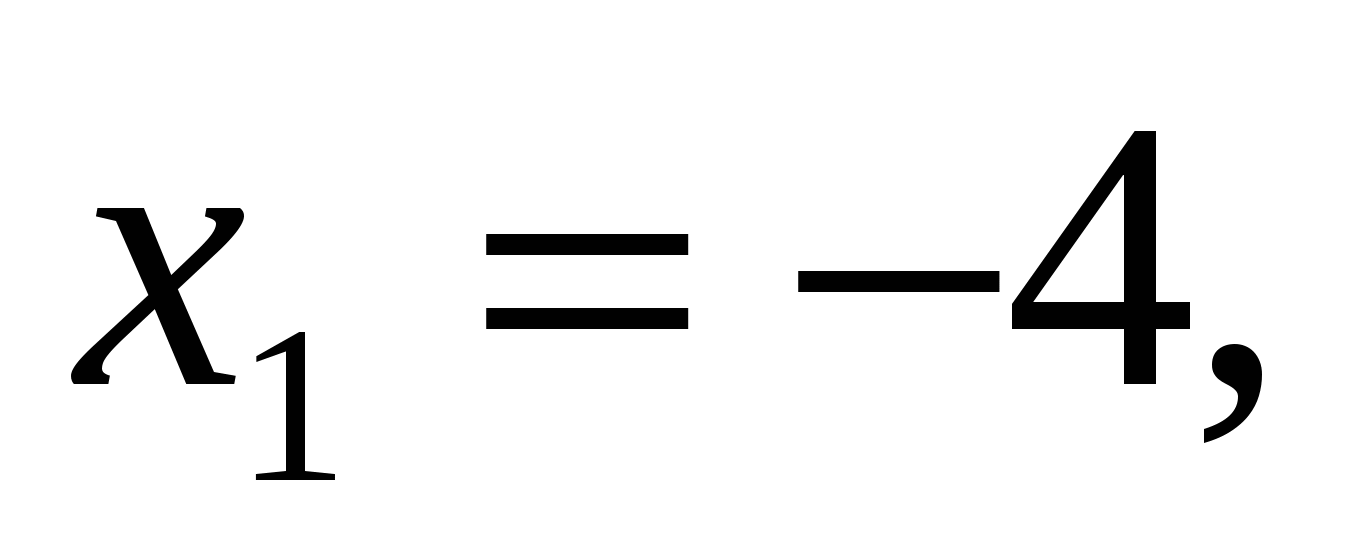

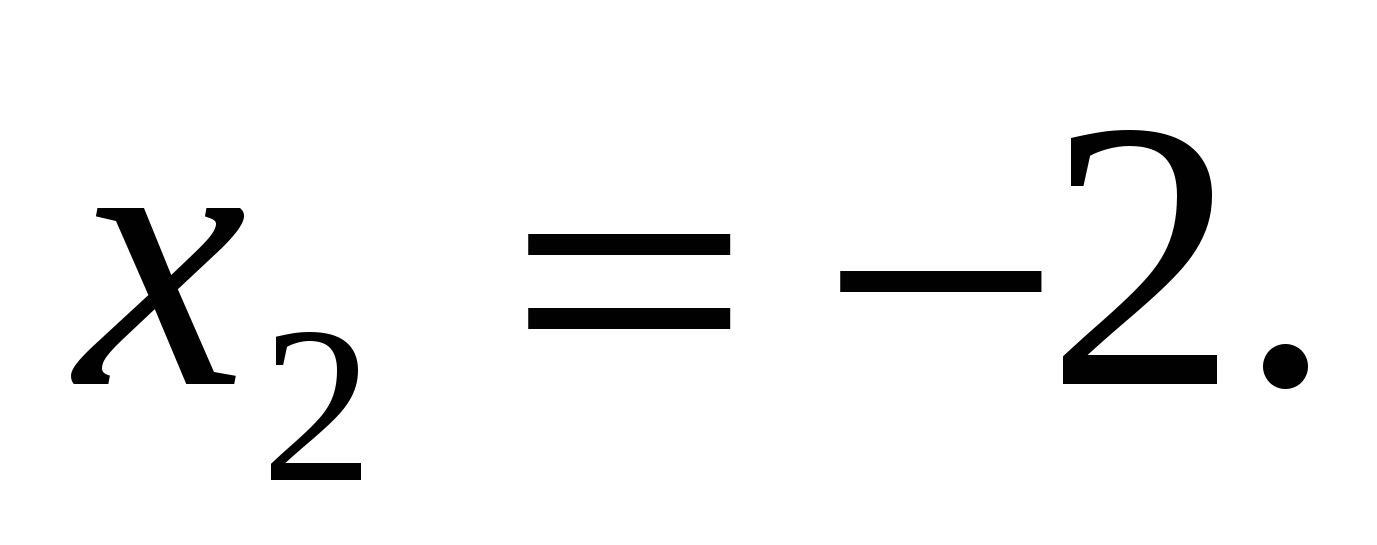
Если х = -2, то у = 0, имеем |-4-а| = 0, а = -4.

Если х = -4, то у = 0, имеем |-8-а| = 0, а = -8.

Ответ: уравнение имеет одно решение, если а= -4 или а= -8.

ІV. Домашнее задания

Используя программу Advanced Grapher, найдите все значения параметра а, при котором уравнение 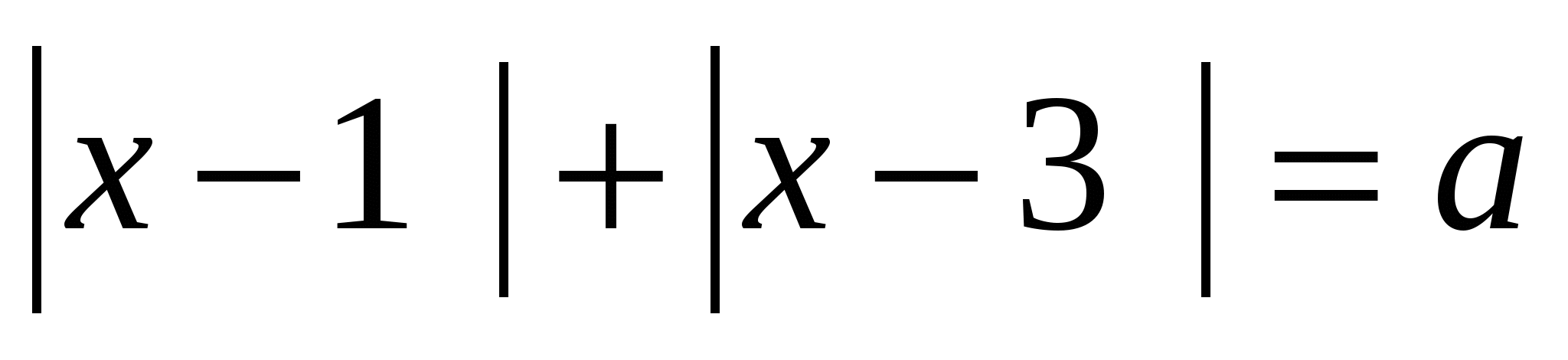имеет больше двух решений.

Решение:

В программе Advanced Grapher строим график функции у = |х-1| + |х-3|.

Получим:

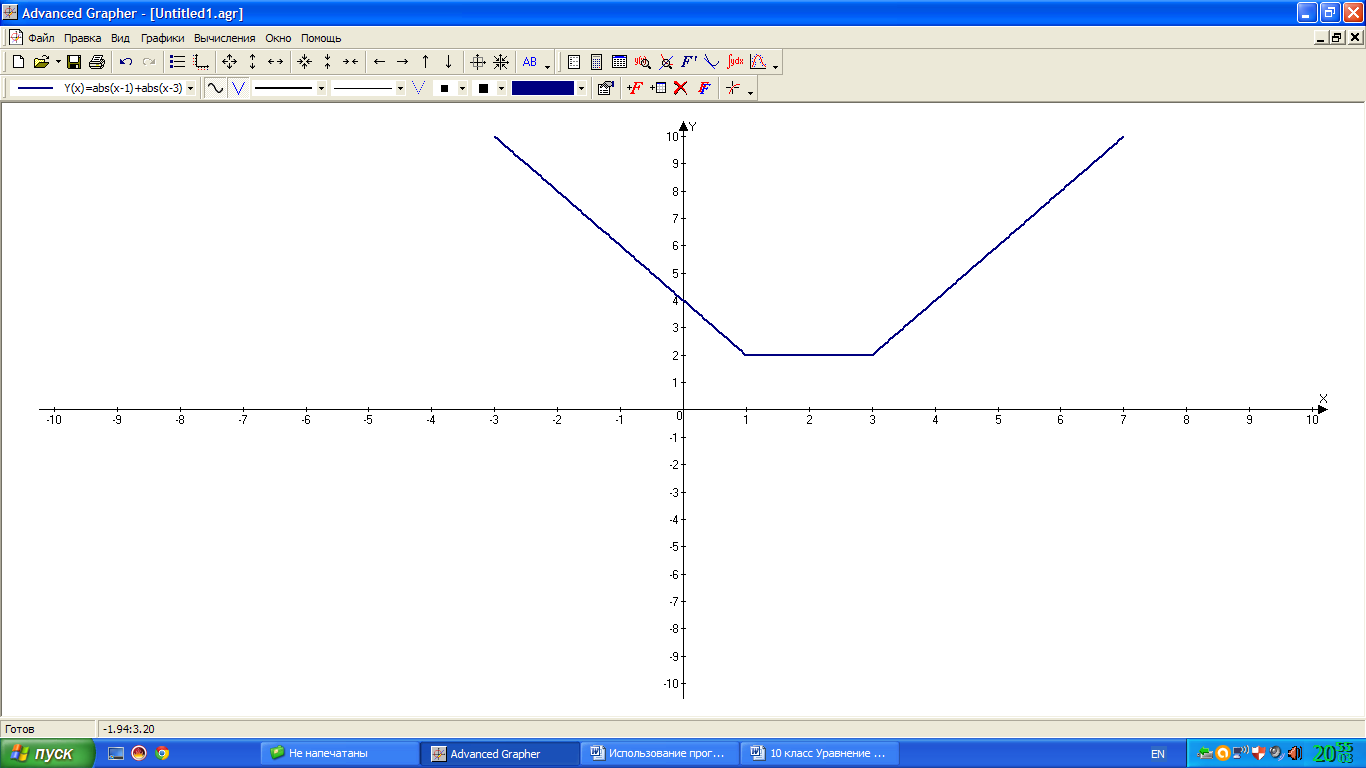
В этой же системе координат строим графики у = а, если а = 5; 2; -3. Это используем для того, чтобы показать, количество возможных решений:

-если а < 2, то уравнение не имеет решений;

-если а = 2, то уравнение имеет бесконечное множество решений;

-если а > 2, то уравнение имеет два решения.

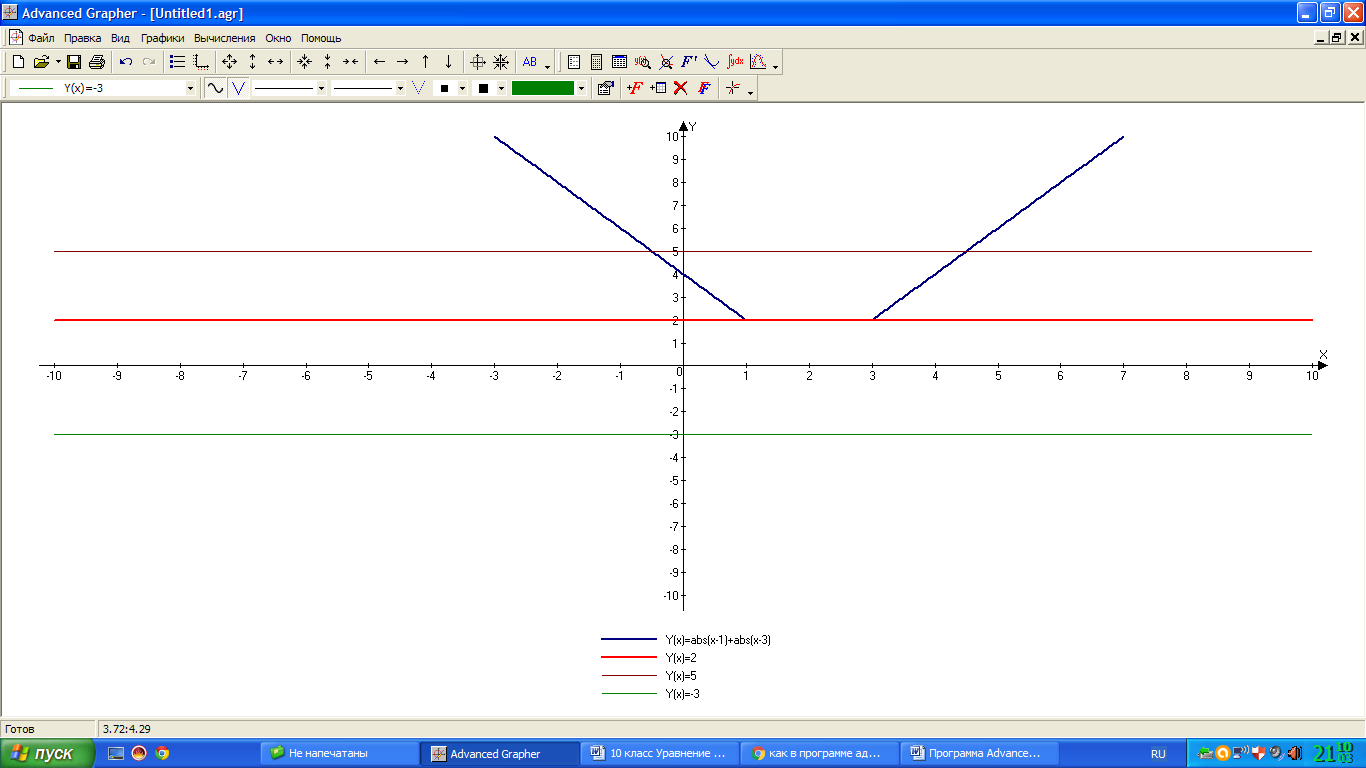
Ответ: а = 2.

infourok.ru

«Уравнения и параметры» — Математика

Исторические задачи.

Многие задачи, решаемые алгебраически, могут быть решены и без помощи уравнений. Люди умели это делать задолго до возникновения алгебры, потому что им это было нужно для жизни и работы. Не случайно задачи на сообразительность имеются в фольклоре, сказках и легендах разных народов. Вот несколько таких задач.

Задача Пифагора ( Пифагор , ок. 570 – ок. 500 г.до н.э.) .

Учителя спросили: «Скажи, о великий Пифагор, сколько у тебя учеников?» И он ответил: «Половина изучает математику, четверть – музыку, седьмая часть пребывает в молчании и, кроме того, есть еще три женщины». Узнайте число учеников Пифагора.

Одна из известных русских задач.

Летела стая гусей, а навстречу им летит один гусь и говорит: «Здравствуйте, сто гусей!» — «Нас не сто гусей, — отвечает вожак,- если бы нас было столько, сколько теперь, да еще столько, да полстолька, да четверть столько, да еще ты, гусь, с нами, так тогда нас было бы сто гусей» Сколько гусей было в стае?

Задача из «Арифметики» Магницкого.

«Послан человек из Москвы на Вологду, и велено ему в хождении своем совершати на всякий день по 40 верст; потом другий человек в другий день послан вслед его, и велено ему идти за день 45 верст, и ведательно есть, в коликий день постигнет второй первого?»

Задача Диофанта.

Найти три числа, чтобы большее превышало среднее на третью часть наименьшего, среднее было бы больше наименьшего на третью часть большего, наименьшее же на 10 превышало третью часть среднего.

Р е ш е н и и е.

Задача Пифагора. Пусть х- число учеников, тогда

х + х + х + 3 =х,

Ответ: 28 учеников.

Одна из известных русских задач. Пусть х – число гусей в стае, тогда

х + х + 0,5х + 0,25х + 1 = 100,

Ответ: 36 гусей. .

Задача из «Арифметики» Магницкого.

1 верста = 500 саженям = 1500 аршинам = 3500 футам = 1,0668 км.

Ответ: через 8 дней.

Задача Диофанта. Пусть 3х среднее, тогда третья часть будет х,

наименьшее – ( х + 10).

1 х + 10

3х – (х + 10) = — (3х + ——— ).

3 3

Ответ: среднее – 37,5; наименьшее – 22,5; наибольшее – 45.

multiurok.ru

ПРОГРАММА ЭЛЕКТИВНОГО КУРСА «РЕШЕНИЕ УРАВНЕНИЙ И НЕРАВЕНСТВ С ПАРАМЕТРАМИ» (10 КЛАСС)

Элективный курс

10 класс (1 час в неделю)

РЕШЕНИЕ УРАВНЕНИЙ

и

НЕРАВЕНСТВ С ПАРАМЕТРАМИ

Всего 34 часа

На выполнение практической части 4 часа

Содержание курса реализуется при использовании пособий:

В.В.Сильвестров, Уравнения и неравенства с параметрами, Чебоксары,2004г.

А.В.Мерлин, Н.И.Мерлина, Задачи по элементарной математике

Ж «Математика в школе»

Основная функция элективного курса направлена на повышение интереса к математике. Общеизвестно, что на вступительных экзаменах в ВУЗы ранее, а сейчас в связи с потребностью подготовки обучающихся к сдаче единых экзаменов, повсеместно, встречаются задачи с параметрами.

Понятие параметра является важным математическим понятием, которое систематически используется в школьном курсе математики и в смежных дисциплинах.

С понятием параметра (без употребления этого термина) обучающиеся в сущности уже встречались в курсе алгебры 7 класса, когда изучались линейные уравнения, при изучении линейной функции; в курсе алгебры 8 класса при изучении квадратных уравнений. Вообще, когда рассматриваются уравнения определенного вида, то при решении таких уравнений используются коэффициенты, выполняющие роль параметров.

Данный элективный курс предназначен для учащихся 10 класса, желающих углубить свои знания в области математики.

Значимость заданий с параметрами не ограничивается лишь их диагностической ценностью , так как способствует повышению качества знаний и умений обучающихся, интеллектуальному развитию, а также позволяет формировать у них представление об особенностях реальной исследовательской деятельности.

Элективный курс поможет учащимся обогатить свой опыт новыми приемами в классификации различных задач курса математики, в том числе и задачи повышенного уровня сложности, поможет учителю показать красоту и совершенство , сложность и изощренность математических методов в решении задач. Курс способствует организации интенсивной мыслительной деятельности учащихся.Он содержит материалы, которые помогут обучающимся самостоятельно и рационально организовать свою учебную работу. Это поможет избежать им лишних перегрузок, снять стресс и т.д.

К постановке задач с параметрами приводят, например, следующие исследовательские задачи:

• выявление условий разрешимости тех или иных математических задач;

• вывод общей вычислительной формулы и определение границ ее применимости;

• изучение условий сохранения и степени варьирования свойств математических объектов;

• установление границ влияния характеристик реального объекта на тот или иной с ним связанный, процесс, изучаемый с помощью метода математического моделирования и т. п.

Элективный курс построен в соответствии с дидактическими принципами (посильности, научности, доступности, преемственности, систематичности ,последовательности, сознательности, творческой активности).

В курсе систематизированы методы решения задач с параметрами, начиная с самых простых – линейных уравнений, включая более сложные, квадратные и т.д.

Подробно рассмотрены методы решения задач, связанных с расположением корней квадратного трехчлена относительно точки, луча, отрезка. Рассмотрены уравнения и неравенства с модулями, показательные и логарифмические уравнения, тригонометрические уравнения и неравенства, системы уравнений и неравенств. Для облегчения решения задач с параметрами наряду с обычными методами используется метод алгоритмизации.

Задачи данного курса не просты в решении, что позволяет повысить учебную мотивацию обучающихся и проверить свои способности к математике.

Цель курса: научить учащихся решать уравнения и неравенства с параметрами.

Задачи курса:

2. Познакомить обучающихся с понятием «параметр».

3. Сформировать умение решать линейные уравнения и неравенства.

4. Сформировать умение решать дробно-рациональные уравнения.

5. Сформировать умение решать квадратные уравнения и неравенства.

6. Рассмотреть различные способы их решения.

7. Развивать исследовательскую и познавательную деятельность обучающихся.

8. Вызвать интерес у обучающихся к изучаемой теме.

Методическая основа курса. Требования к уровню освоения содержания курса.

В технологии проведения занятий предусмотрены этапы изучения теории, решения практических задач, исследовательские работы, также обучающие самостоятельные работы, формой итогового контроля может стать контролирующая самостоятельная работа, запланирован ряд заданий для самопроверки обучающихся степени усвоения данного курса.

Ожидаемый результат:

В результате изучения данного курса обучающиеся должны уметь решать различные уравнения, неравенства четко записывать ответ, так как ответ составная часть решения уравнения и неравенства. В ответе должно быть указано для каждого значения параметра, сколько корней имеет это уравнение и какого вида.

Этот результат может быть достигнут благодаря использованию различных видов деятельности учащихся (решение практических задач, устные сообщения, работа с текстами, практическая работа, работа в группах).

Контроль знаний и умений учащихся будет осуществляться через тестовые работы, практические работы, итоговые работы.

Изучение элективного курса завершается итоговой тестовой работой.

Кол-во часов

Виды деятельности

Тип урока

1.

Уравнения, содержащие параметры.

1

метод «погружения» работа с учебниками 7,8-го классов; аналитическая работа.

2.

Решение линейных уравнений, содержащих параметры.

4

исследовательская работа; работа в группах; составление справочника; аналитическая работа; обучающая самостоятельная работа.

3.

Решение линейных неравенств, содержащих параметры.

4

беседа учителя; работа в группах при практической работе; составление справочника; аналитическая работа.

4.

Решение простейших рациональных уравнений и неравенств.

4

— беседа учителя; аналитическая работа; составление справочника.

5.

Квадратные уравнения. Теорема Виета.

5

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

6.

Системы линейных уравнений

2

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

7.

Системы уравнений и неравенств второго порядка

2

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

8.

Уравнения и неравенства с модулями

2

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

9.

Иррациональные уравнения и неравенства

2

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

10.

Показательные и логарифмические уравнения и неравенства

3

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

11.

Тригонометрические уравнения и неравенства

3

— изучение теории; составление справочника; аналитическая работа; работа в группах; обучающая самостоятельная работа.

12.

Тестовая работа

2

Итоговая работа

infourok.ru

Линейное уравнение с параметром

Вопросы занятия:

·  рассмотреть линейные уравнения с параметрами;

·  сформулировать алгоритм решения линейных уравнений с параметрами.

Материал урока

Определение.

Уравнения, содержащие помимо неизвестных, ещё и буквенные величины называются уравнениями с параметрами.

Линейные уравнения, записанные в общем виде, рассматривают как уравнение с параметрами.

Например,

Как правило, для любого уравнения особым значением параметра является то, про котором коэффициент при переменной обращается в ноль.

Рассмотрим пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Решим ещё одно уравнение.

Пример.

Рассмотрим ещё одно уравнение.

Пример.

Решим ещё один пример.

Пример.

Теперь давайте попробуем сформулировать алгоритм решения линейных уравнений с параметром.

Итоги урока

Сегодня на уроке мы рассмотрели линейные уравнения с параметрами, сформулировали алгоритм решения таких уравнений.

videouroki.net

Линейные уравнения с параметрами и уравнения, приводимые к линейным

I введение

Тема “Решение и исследование уравнений с параметрами” присутствует в материалах Единого государственного экзамена. Не все выпускники справляются с задачей, которую в школе “не проходили”. Данная тема является одной из самых трудных в курсе алгебры. Задачи с параметрами рассматривают в школьном курсе пока крайне редко, бессистемно, поэтому при решении таких задач у учеников обычно возникают затруднения. Совершенно очевидно, что к “встрече” с такими задачами надо специально готовиться.

Данные задачи играют значительную роль в формировании логического мышления и математической культуры школьников, позволяют проверить первоначальные навыки исследовательской деятельности. Учащиеся, владеющие методами решения задач с параметрами, успешно справляются с другими задачами.

Известны различные типы уравнений и неравенств с параметрами: дробно-рациональные, иррациональные, тригонометрические, показательные, логарифмические, степенные. Чаще всего они сводятся к следующим четырём основным видам:

1. линейные уравнения с параметром,
2. линейные неравенства с параметром,
3. квадратичные уравнения с параметром,
4. квадратичные неравенства с параметром.

Рассмотрим уравнение

Пусть, тогда уравнение примет вид

Решим его:

 

Пусть , тогда уравнение примет вид , решением которого является любое действительное значение .

Пусть , тогда уравнение примет вид . Решив его, получим, что . В этом случае уравнение не имеет решения.

Следовательно, сам факт существования решения зависит от значения параметра .

Определение. Исследовать и решить уравнение с параметром это значит :

— найти все системы значений параметров, при которых данное уравнение имеет решение;

— найти все решения для каждой найденной системы значений параметров, т.е. для неизвестного и параметра должны быть указаны свои области допустимых значений.

II  Простейшие линейные уравнения с параметром

1.

Ответ:

при корней нет,

при

2.

Ответ:

при корней нет,

при

3.

Ответ:

при корней нет,

при .

4.

Ответ:

при корней нет,

при .

5.

Ответ:

при

при

6.

Ответ:

при

при

7.

Ответ:

при

при

8.

Ответ:

при

при

9.

Ответ:

если , то корней нет

если ,

если

10.

1)

2.

3.

Ответ:

при , корней нет

если ,

при

Таким образом, при решении линейных уравнений с параметром сначала его нужно привести к виду, удобному для исследования (стандартный канонический вид линейного уравнения с параметром), выполнив ряд преобразований, потом следует определить контрольные значения параметра, т.е. те значения, при которых коэффициент при обращается в ноль. Эти значения разбивают множество значений параметра на несколько множеств, которые необходимо исследовать.

III Линейные уравнения с параметром, имеющие стандартный канонический вид

– стандартный канонический вид линейного уравнения с параметром

Примеры:

1)

Ответ:

если

если

2)

Ответ:

при

при

при

3)

Ответ:

при

при

при

IV. Уравнения, приводимые к линейным уравнениям с параметром

Схема решения уравнений, приводимых к линейным :

1. Указать и исключить все значения параметра и переменной, при которых уравнение теряет смысл
2. Умножить обе части уравнения на общий знаменатель, не равный нулю
3. Привести уравнение-следствие к виду и решить его
4. Исключить значения параметра, когда найденный корень принимает значения, при которых уравнение теряет смысл
5. Записать ответ

1.Примеры решений уравнений, содержащих параметр в знаменателе:

1)

Умножим уравнение на :

Ответ:

при

при

при

2)

Умножим уравнение на :

Ответ:

при

при

при

2. Примеры решений уравнений, содержащих и параметр и переменную в знаменателе

Умножим уравнение на :

Исключим те a, при которых :

Ответ:

при

при

при

urok.1sept.ru