Градус (геометрия) — Википедия
У этого термина существуют и другие значения, см. Градус.Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
 Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.
Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году
Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления[2][3].
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
- 1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)
- 1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…
- 1∘=400360{\displaystyle 1^{\circ }={\frac {400}{360}}} градов=1,(1) градов=1,11111111111… градов
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей[5]; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).
Минуты и секунды в других системах измерения:
- 1′=2π360∘⋅60′=1′p′≈1′3437,747′{\displaystyle 1’={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60′}}={\frac {1′}{p’}}\approx {\frac {1′}{3437{,}747′}}}[4]≈2,90888208⋅10−4 rad{\displaystyle \approx 2{,}90888208\cdot 10^{-4}~{\text{rad}}} (1 минута в радианах)
- 1″=2π360∘⋅60′⋅60″=1″p″≈1″206264,8″{\displaystyle 1»={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60’\cdot 60»}}={\frac {1»}{p»}}\approx {\frac {1»}{206264{,}8»}}}[4]≈4,848136811⋅10−6 rad{\displaystyle \approx 4{,}848136811\cdot 10^{-6}~{\text{rad}}} (1 секунда в радианах).
Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.
Угловая секунда[править | править код]
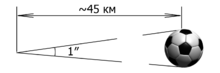
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[6]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[7].
Использование[править | править код]
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s). Соотношение между этими величинами определяется формулой 1s=15″.[8]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[6][9], что является простой транслитерацией с англ. arcsecond.
Дольные единицы[править | править код]
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[7]. Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[10], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
| Единица | Величина | Обозначение | Аббревиатура | Радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin, ′^{\displaystyle {\hat {‘}}}, MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10−6 секунды | μas | 4,8481368 prad |
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.[источник не указан 2737 дней]
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)[11][12].
- ↑ Weisstein, Eric W. Degree (англ.). Wolfram MathWorld. Дата обращения 26 ноября 2017.
- ↑ James Hopwood Jeans. The Growth of Physical Science. — 1947. — С. 7.
- ↑ Murnaghan, Francis D. Analytic geometry. — New York: Prentice-Hall, inc., 1946. — P. 2.
- ↑ 1 2 3 Переводные множители — <57,295779513>, <3437,747>, <206264,8> — см. Радиан#Связь радиана с другими единицами.
- ↑ Боголюбов, 1983, с. 393—394.
- ↑ 1 2 Англо-русско-английский астрономический словарь (неопр.). Astronet. Дата обращения 23 декабря 2007.
- ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Справочник. Некоторые внесистемные единицы (неопр.). ASTROLAB. Дата обращения 23 декабря 2007.
- ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003.
- ↑ Гурьянов С. Почему звезды называются именно так? (неопр.). проект «Астрогалактика» (29 октября 2005 года). Дата обращения 26 декабря 2007.
- ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
ru.wikipedia.org
Меры углов
Для измерения углов используются градусы или радианы.
\(1\) градус (обозначается \(1^\circ \)) представляет собой \( \dfrac{1}{360}\) полного оборота. Развернутый угол равен \(180^\circ \), прямой угол равен \(90^\circ \).
Радианной мерой угла называется отношение длины дуги, для которой данный угол является центральным, к радиусу окружности. Угол равен \(1\) радиану (обозначается \(1 \text{ рад }\)), если дуга, на которую он опирается, равна радиусу окружности.
\(1\) градус содержит \(60\) угловых минут: \(1^\circ = 60’\).
\(1\) угловая минута, в свою очередь, содержит \(60\) угловых секунд: \(1′ = 60»\)
Значение \(1\) радиана в градусах
\(1 \text{ рад } = \dfrac{180^\circ}{\pi}\ \approx 57^\circ 17’45»\)
Значение \(1\) градуса в радианах
\(1^\circ = \dfrac{\pi}{180} \text{ рад } \approx 0.017453 \text{ рад }\)
Значение \(1\) угловой минуты в радианах
\(1′ = \dfrac{\pi}{\left( {180 \cdot 60} \right)} \text{ рад } \approx 0.000291 \text{ рад }\)
Значение \(1\) угловой секунды в радианах
\(1» = \dfrac{\pi}{\left( {180 \cdot 3600} \right)} \text{ рад } \approx 0.000005 \text{ рад }\)
Переход от градусной меры к радианной
\(x = \dfrac{\pi\alpha}{{180^\circ}}\),
где \(x\) − величина угла в радианах, \(\alpha\) − величина угла в градусах.
Переход от радианной меры к градусной
\(\alpha = \dfrac{ 180^\circ x}{\pi}\),
где \(\alpha\) − величина угла в градусах, \(x\) − величина угла в радианах.
Радианная мера стандартных углов
| Угол в градусах | \(\alpha\) | \(0^\circ\) | \(30^\circ\) | \(45^\circ\) | \(60^\circ\) | \(90^\circ\) | \(180^\circ\) | \(270^\circ\) | \(360^\circ\) |
|---|---|---|---|---|---|---|---|---|---|
| Угол в радианах | \(x \text{ рад }\) | 0 | \(\dfrac{\pi}{6}\) | \(\dfrac{\pi}{4}\) | \(\dfrac{\pi}{3}\) | \(\dfrac{\pi}{2}\) | \(\pi\) | \(\dfrac{3\pi}{2}\) | \(2\pi\) |
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
calcsbox.com
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Рассмотрим тригонометрические круги, изображенные на рисунке 1 и рисунке 2.

Рис.1

Рис.2
На тригонометрическом круге, изображенном на рисунке 1, центральные углы измерены в градусах, а на тригонометрическом круге, изображенном на рисунке 2, те же центральные углы измерены в радианах.
Углом в 1 градус называют угол, составляющий  полного угла. Углом в k° называют угол в k раз больший угла в 1° .
полного угла. Углом в k° называют угол в k раз больший угла в 1° .
Углом в 1 радиан называют центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной 1 . Углом в k радиан называют центральный угол тригонометрического круга в k раз больший угла в 1 радиан.
Следствие 1. Углом в k радиан является центральный угол тригонометрического круга, которому соответствует дуга окружности тригонометрического круга длиной k .
Следствие 2. Полный угол является углом в 2π радиан.
Для того, чтобы найти формулы, связывающие градусную и радианную меры угла, рассмотрим рисунки 3 и 4
 |  |
| Рис.3 | Рис.4 |
 |
| Рис.3 |
 |
| Рис.4 |
На этих рисунках изображены прямые углы, причем на рисунке 3 прямой угол измерен в градусах и равен 90° , а на рисунке 4 прямой угол измерен в радианах и равен  радиан. Следовательно,
радиан. Следовательно,

Таким образом, формулы, связывающие градусную и радианную меры угла, имеют вид


Поскольку  , то
, то


По этой причине углы, составляющие целое число радиан, изображаются на тригонометрическом круге так, как это показано на рисунке 5.

Рис.5
Замечание. Тригонометрическая формула sin α означает, что рассматривается синус угла в α радиан, а тригонометрическая формула sin α° означает, что рассматривается синус угла в α градусов. По такому же правилу определяются значения косинуса, тангенса и котангенса.
Пример. Найти наименьшее из чисел:

Решение. Поскольку


то наименьшим числом является число cos 3 .

На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.
www.resolventa.ru
Радианная мера угла
Прежде, чем приступить к рассмотрению новой темы, давайте
вспомним, что градусом называют величину
центрального угла, которому соответствует  часть
окружности. Градусная мера угла – это положительное число, которое
показывает, сколько раз градус и его части укладываются в измеряемом угле.
часть
окружности. Градусная мера угла – это положительное число, которое
показывает, сколько раз градус и его части укладываются в измеряемом угле.
А углы можно измерять только в градусах? Сегодня на уроке мы рассмотрим ещё одну единицу измерения углов.
Давайте
изобразим окружность с центром в точке  и
радиусом
и
радиусом  .
Затем проведём вертикальную прямую, которая касается окружности в точке
.
Затем проведём вертикальную прямую, которая касается окружности в точке  .
Эту прямую мы будем считать числовой осью с началом отсчёта в точке
.
Эту прямую мы будем считать числовой осью с началом отсчёта в точке  .
Положительным направлением на прямой будем считать направление вверх. За
единичный отрезок на числовой оси возьмём радиус окружности.
.
Положительным направлением на прямой будем считать направление вверх. За
единичный отрезок на числовой оси возьмём радиус окружности.
Отметим
на прямой несколько точек:  и
и
 ,
,
 и
и
 ,
,
 и
и
 ,
,
 и
и
 ,
,
 и
и
 .
.

Теперь
представим нашу прямую в виде нерастяжимой нити, которая закреплена на
окружности в точке  .
Будем наматывать нить на окружность. При этом точки на числовой прямой с
координатами
.
Будем наматывать нить на окружность. При этом точки на числовой прямой с
координатами 
 ,
,
 ,
,
 перейдут
соответственно в точки окружности
перейдут
соответственно в точки окружности  ,
,
 ,
,

 .
При этом длина дуги
.
При этом длина дуги  равна
равна
 ,
длина дуги
,
длина дуги  равна
равна
 ,
длина дуги
,
длина дуги  равна
равна
 ,
длина дуги
,
длина дуги  равна
равна
 .
.
Получается, что каждой точке прямой ставится в соответствие некоторая точка окружности.
Так,
точке прямой с координатой  ставится
в соответствие точка
ставится
в соответствие точка  .
А значит, угол
.
А значит, угол  можем
считать единичным? Да, и его мерой мы будем измерять другие углы. Например,
угол
можем
считать единичным? Да, и его мерой мы будем измерять другие углы. Например,
угол 
 ,
а угол
,
а угол  равным
равным
 .
.А где используют такой способ измерения углов? Такой способ измерения углов широко используется в математике и физике. Говорят, что углы измеряются в радианной мере.
Единичный
угол  называют
углом в один радиан. Записывают так:
называют
углом в один радиан. Записывают так:  рад.
рад.
И
напомним, что длина дуги  равна
радиусу нашей окружности.
равна
радиусу нашей окружности.
Сейчас
давайте рассмотрим окружность радиуса  .
И отметим на ней дугу
.
И отметим на ней дугу  ,
равную длине радиуса окружности, и угол
,
равную длине радиуса окружности, и угол  .
.

И такой угол называется углом в один радиан? Верно.
Запомните! Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в один радиан.
Интересно,
а скольким градусам равен угол в один радиан? Давайте найдём градусную меру
угла в один радиан. Мы знаем из курса геометрии, что дуге длиной  ,
то есть полуокружности, соответствует центральный угол, равный
,
то есть полуокружности, соответствует центральный угол, равный  .
Следовательно, дуге окружности длиной
.
Следовательно, дуге окружности длиной  соответствует
угол в
соответствует
угол в 
Выше
мы назвали такой угол углом в один радиан, а значит, можем записать, что  рад
рад
 .
.
 ,
тогда
,
тогда  рад
рад
 .
.
Если
угол содержит  рад,
то
рад,
то 
 .
Эту формулу называют формулой перехода от радианной меры к градусной.
.
Эту формулу называют формулой перехода от радианной меры к градусной.Давайте
с вами найдём градусную меру угла, равного  рад.
Для этого воспользуемся формулой перехода от радианной меры к градусной.
Подставим
рад.
Для этого воспользуемся формулой перехода от радианной меры к градусной.
Подставим  вместо
вместо
 :
:
 .
Сократим на
.
Сократим на  и
на
и
на  .
И в результате получим
.
И в результате получим  .
.
Можно
ли, наоборот, перейти от градусной меры к радианной? Конечно, можно, но такой
переход будет чуть сложнее. Так как угол в  равен
равен
 рад,
то
рад,
то  рад.
Тогда
рад.
Тогда  рад.
Такую формулу называют формулой перехода от градусной меры к радианной.
рад.
Такую формулу называют формулой перехода от градусной меры к радианной.
Найдём
радианную меру угла, равного  .
Воспользуемся формулой перехода от градусной меры к радианной. Подставим
.
Воспользуемся формулой перехода от градусной меры к радианной. Подставим  вместо
вместо
 :
:
 .
Сократим
.
Сократим  и
и
 на
на
 .
И в результате получим
.
И в результате получим  .
.
Обратите
внимание, что при обозначении меры угла в радианах слово «радиан» обычно не
пишут:  .
При этом обозначение градуса в записи меры угла пропускать нельзя.
.
При этом обозначение градуса в записи меры угла пропускать нельзя.
В следующей таблице представлены углы в градусной и радианной мере, с которыми мы будем встречаться чаще всего.

Отметим,
что радианная мера углов позволяет значительно упростить многие формулы в
математике, физике, механике. В частности, радианная мера угла удобна для
вычисления длины дуги окружности. Так, выше мы выяснили, что угол в  рад
стягивает дугу, длина которой равна радиусу
рад
стягивает дугу, длина которой равна радиусу  ,
а значит, угол в
,
а значит, угол в  рад
стягивает дугу длиной:
рад
стягивает дугу длиной:  .
Если
.
Если  ,
то эта формула принимает совсем простой вид:
,
то эта формула принимает совсем простой вид:  ,
то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
,
то есть длина дуги равна величине центрального угла, стягиваемого этой дугой.
Сейчас,
прежде чем приступить к выполнению заданий, мы докажем, что площадь кругового
сектора радиуса  ,
образованного углом в
,
образованного углом в  рад,
равна
рад,
равна  ,
где
,
где  .
.
Докажем
это. Известно, что площадь круга вычисляется по формуле:  .
Площадь полукруга, то есть кругового сектора в
.
Площадь полукруга, то есть кругового сектора в  рад:
рад:
 .
Тогда площадь сектора в
.
Тогда площадь сектора в  рад
в
рад
в  раз
меньше, то есть
раз
меньше, то есть  .
Следовательно, площадь сектора в
.
Следовательно, площадь сектора в  рад
равна
рад
равна  .
.
Ну а сейчас давайте выполним несколько заданий.
Первое задание.
Найдите градусную меру угла, выраженную в радианах: а)  ;
б)
;
б)  ; в)
; в)  ;
г)
;
г)  ;
д)
;
д)  .
.
Решение.

Второе задание.
Найдите радианную меру угла, выраженного в градусах: а)  ;
б)
;
б)  ;
в)
;
в)  ;
г)
;
г)  .
.
Решение.

Следующее задание.
Чему равен радиус окружности, если дуге длиной  см
соответствует центральный угол в
см
соответствует центральный угол в  рад?
рад?
Решение.

И ещё одно задание.
Дуге кругового сектора соответствует угол, равный  рад.
Чему равна площадь сектора, если радиус круга равен
рад.
Чему равна площадь сектора, если радиус круга равен  см?
см?
Решение.

Ну а сейчас немного истории.
Впервые радиан как единица измерения был использован английским математиком Роджером Котсом в 1713 году. Он считал, что радиан является наиболее естественной единицей измерения углов. Термин «радиан» впервые появился в печати в 1873 году в экзаменационных билетах Университета Квинса в Белфасте, составленных британским инженером и физиком Джеймсом Томсоном.
В 1960 году XI Генеральной конференцией по мерам и весам радиан был принят в качестве единицы измерения плоских углов в Международной системе единиц (СИ).
videouroki.net
Град (геометрия) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Гон.Град (гон), Градиан, метрическая минута, метрическая секунда — единицы измерения плоских углов.
Град (гон) (русское обозначение: град; международное: gon, g) — сотая часть прямого угла. Используется также наименование «метрический градус»[1]. В Российской Федерации град (гон) допущен к использованию в качестве внесистемной единицы без ограничения срока с областью применения «геодезия»[2].
Исторически плоские углы измеряли в градусах, минутах и секундах. Однако эта непозиционная система была неудобна для практических расчётов, поэтому в конце XVIII века во Франции при введении метрической системы мер в качестве основной единицы измерения плоских углов был предложен град (фр. grade — вариация слова gradus). Название гон (gon — от греч. γονία — угол) используется в Германии, Швеции и некоторых других странах северной Европы.
Соотношение града с другими единицами измерения углов описывается формулой:
Иногда для града (международного градуса) используется обозначение C. По аналогии с разбиением градуса на минуты и секунды град (международный градус) разбивают на метрические минуты (CC) и секунды (CCC) — в граде 100 метрических минут, в минуте — 100 секунд[1]. Метрическая минута также иногда называется сантиград.
В настоящее время грады практически не используются, хотя возможность их применения часто закладывается в микрокалькуляторах и различном математическом программном обеспечении.
Одна метрическая минута дуги земного меридиана имеет длину одного километра. Соответственно, если бы переход на грады вместо градусов состоялся, то километр вытеснил бы морскую милю (равную одной традиционной угловой минуте).
Шаговые двигатели обычно имеют 200 или 400 шагов на оборот, то есть, один шаг равен 2 или 1 град.
ru.wikipedia.org
Секунда (единица измерения углов) — это… Что такое Секунда (единица измерения углов)?
Градус, минута, секунда — общепринятые единицы измерения плоских углов и земного шара.
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом углу, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккады (вавилоняне) — соответственно делению года в вавилонском календаре на 360 дней.
Минуты и секунды
В измерении углов традиционно используется шестидесятеричная система счисления. По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).
- 1′ =
 ≈ 2,9088821×10-4 радиан.
≈ 2,9088821×10-4 радиан. - 1″ =
 ≈ 4,8481368×10-6 радиан.
≈ 4,8481368×10-6 радиан.
Угловая секунда
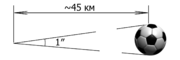
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[2].
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15″.[3]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[1][4], что является простой транслитерацией с англ. arcsecond.
Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[2]. Однако, согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[5], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т.п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.[6]
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP).[7][8]
Примечания
Литература
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
Урок Радианная мера угла
Урок 2
Радианная мера углов и дуг
Для чего же нужна числовая окружность? Почему она так важна для науки вообще и для нас в частности? Начнем рассматривать области ее практического применения.
К ак было сказано, числовая окружность используется, когда точка движется не прямолинейно, например, при изучении вращательного движения.
ак было сказано, числовая окружность используется, когда точка движется не прямолинейно, например, при изучении вращательного движения.
Движение точки по окружности можно представить двумя способами.
Во-первых, можно сказать, что точка В прошла по окружности путь t.
Во-вторых, можно сказать, что подвижный радиус ОВ образовал с неподвижным радиусом ОА угол t. Поскольку он получен поворотом радиуса ОВ, то он называется «угол поворота».
Результат будет один и тот же.
Кстати, подвижный радиус ОВ называется радиус–вектором точки В.
Таким образом, мы можем измерять движение точки по кругу с помощью угла, на который она повернулась. Т.е. для произвольного числа t мы построили угол t, определяемый двумя лучами – неподвижным и тем, который проходит через построенную точку.
При таком обобщении понятия угла постепенно отходят от его геометрического образа как части плоскости, лежащей между двумя лучами. Фактически слово «угол» становится для нас синонимом слова «число».
Теперь нужно выбрать меру измерения таких новых углов – углов поворота.
Понятие об измерении углов известно из геометрии. При измерении углов принимают некоторый определенный угол за единицу измерения и с ее помощью измеряют другие углы.
За единицу измерения можно принять любой угол:
на практике уже более трех тысяч лет за единицу измерения величины угла принята 1/360 часть полного оборота, которую называют градусом;
в технике за единицу измерения принимают полный оборот;
в мореплавании за единицу измерения углов принят румб, равный
1/32 части полного оборота;в артиллерии за единицу измерения углов принята 1/60 часть полного оборота, которую называют большим делением угломера (1/100 часть большого деления угломера называют малым делением угломера).
Для измерения новых углов – углов поворота – привычные нам градусы не подходят, потому, что градусами измеряют только углы, а здесь одной меркой должны измеряться и углы, и расстояния.
Выход нашли Ньютон и Лейбниц — они стали измерять эти углы этими расстояниями.
Вопрос: «Чем измеряется расстояние на числовой окружности?»,
другими словами,
«Чему равен единичный отрезок числовой окружности?».
Так появилась универсальная мера измерения и углов, и дуг — радиусная мера или, как ее чаще называют, радианная мера.
Для закрепления изученного
материала рассмотреть ОК–3.
Ответить на вопросы 3, 4.
Еще раз подчеркнуть универсальность радианной меры, с помощью которой можно измерять и углы, и расстояния (дуги).
3. Какая величина принимается за единицу измерения при градусном измерении углов?
4. Что такое радиан?
Ответить на вопрос 8.
Отсюда истекает сложность, заключающаяся в двойственном применении числа – рассмотреть примечание.
8. При каком условии длина дуги равна ее радианной мере?
Ответить на вопрос 7.
Дополнительный вопрос:
«А как построить угол, равный числу (–1)?»
7. Почему ошибочна запись = 180?

Помимо того, что радианная мера лучше приспособлена для изучения криволинейного (кругового) движения, она существенно упростила многие расчеты и формулы:
длина дуги окружности: 
 ;
;
площадь сектора: 
 .
.
Рассмотреть формулы перехода от градусной меры к радианной и наоборот.
Ответить на вопросы 5, 6.
5. По каким формулам переводят градусную меру угла в радианную и наоборот?
6. Выразите в радианах углы, равные 30, 45, 60, 90, 180, 270, 360.
Решать задачи № 9(пр) – № 14(пр)
При решении № 13(пр) напомнить ученикам о правиле именования дуг, принятое нами на прошлом уроке. 
9. Выразите в радианах:
1) 1; 4) 10; 7) 15; 10) 30;
2) 45; 5) 60; 8) 70; 11) 90;
3) 225; 6) 240; 9) 320; 12) 330.
10. Переведите из градусной меры в радианную:
1) 120; 3) 220; 5) 300; 7) 765;
2) 210; 4) 150; 6) 315; 8) 675.
11. Выразите в градусах:
1) ; 4) ; 7) ; 10) ;
2) ; 5) ; 8) 1,5; 11) 3;
3) 0,25; 6) ; 9) –; 12) .
12. Переведите из радианной меры в градусную:
1) ; 3) ; 5) ; 7) ;
2 ) ; 4) ; 6) ; 8) .
) ; 4) ; 6) ; 8) .
13. Окружность разделена на шесть равных частей. Выразить в градусах и радианах сумму дуг:
1)  ;
;
2)  .
.
14. Угол А трапеции ABCD (AD || BC) на 70 меньше угла В и на 10 больше угла D. Найдите радианную меру каждого из углов трапеции.
infourok.ru
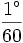 ≈ 2,9088821×10-4 радиан.
≈ 2,9088821×10-4 радиан.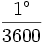 ≈ 4,8481368×10-6 радиан.
≈ 4,8481368×10-6 радиан.