Тренировочные задания по теме «Линейные уравнения»
Уровень 3. Линейные уравнения.
Вариант 1.
Решить уравнение.
Вариант 2. Решить уравнение.
Вариант 3. Решить уравнение.
Вариант 4. Решить уравнение.
Вариант5. Решить уравнение.
— 9 + a = — 36
a =
— 6 + x = — 54
x =
— 8 + y = — 56
y =
— 6 + y = — 18
y =
— 4 + x = — 20
x =
6 — b = — 72
b =
3 — y = — 36
y =
8 — x = — 96
x =
4 — x = — 28
x =
8 —
y =
52 = — 13 — x
x =
48 = — 12 — b
b =
75 = — 25 — a
a =
75 = — 15 — a
a =
39 = — 13 — d
d =
5 + y = — 9
y =
10 + a = — 53
a =
2 + b = — 15
b =
2 + b = — 13
b =
4 + a = — 9
a =
— 9 — t = 3
t =
— 48 — x = 6
x =
— 12 — x = 9x =
— 12 — x = 3
x =
— 18 — x = 6
x =
— 3 + z = 7
z =
— 17 + k = 4
k =
— 7 + n = 6
n =
— 11 + n = 6
n =
— 7 + y = 10
y =
— 9 — d = 12
d =
— 15 — y = 25
y =
— 14 — f = 32
f =
— 14 — f = — 24
f =
— 6 — m = — 14
m =
Вариант 7. Решить уравнение.
Вариант 8. Решить уравнение.
Вариант 9.
Решить уравнение.
Вариант 10.
Решить уравнение.
— 3 + b = — 12
b =
— 4 + b = — 32
b =
— 7 + x = — 63
x =
— 5 + x = — 45
x =
— 7 + a = — 49
a =
5 — m = — 35
m =
7 — m = — 84
m =
3 — y = — 15
y =
9 — y = — 72
y =
2 — b = — 18
b =
42 = — 14 — xx =
70 = — 14 — x
x =
72 = — 12 — b
b =
60 = — 15 — d
d =
56 = — 14 — x
x =
4 + a = — 18
a =
4 + a = — 22
a =
10 + a = — 41
a =
4 + a = — 11
a =
5 + y = — 7
y =
— 24 — y = 6
y =
— 24 — y = 4
y =
— 48 — x = 8
x =
— 18 — x = 12
x =
— 16 — t = 4
t =
— 13 + z = 8
z =
— 13 + z = 10
z =
— 17 + k = 12
k =
— 11 + y = 10
y =
— 3 + z = 5
z =
— 12 — q = — 15
q =
— 12 — q = 45
q =
— 15 — y = — 20
y =
— 6 — m = 16
m =
— 9 — d = — 15
d =
infourok.ru
задания по алгебре. Решение линейных уравнений
Линейные уравнения.Линейные уравнения — не самая сложная тема школьной математики. Но есть там свои фишки, которые могут озадачить даже подготовленного ученика. Разберёмся?)
Обычно линейное уравнение определяется, как уравнение вида:
ax + b = 0 где а и b – любые числа.
Типа:
2х + 7 = 0. Здесь а=2, b=7
0,1х — 2,3 = 0 Здесь а=0,1, b=-2,3
12х + 1/2 = 0 Здесь а=12, b=1/2
И так далее.
Ничего сложного, правда? Особенно, если не замечать слова: «где а и b – любые числа»… А если заметить, да неосторожно задуматься?) Ведь, если а=0,b=0 (любые же числа можно?), то получается забавное выражение:
0=0
Но и это ещё не всё! Если, скажем, а=0, а b=5, получается совсем уж что-то несусветное:
5=0
Что напрягает и подрывает доверие к математике, да…) Особенно на экзаменах. А ведь из этих странных выражений ещё и икс найти надо! Которого нету вообще. И, что удивительно, этот икс очень просто находится. Мы научимся это делать. В этом уроке.
Как узнать линейное уравнение по внешнему виду? Это, смотря какой внешний вид.) Фишка в том, что линейными уравнениями называются не только уравнения вида ax + b = 0, но и любые уравнения, которые преобразованиями и упрощениями сводятся к этому виду. А кто ж его знает, сводится оно, или нет?)
Чётко распознать линейное уравнение можно в некоторых случаях. Скажем, если перед нами уравнение, в которых есть только неизвестные в первой степени, да числа. Причём в уравнении нет дробей с делением на неизвестное, это важно! А деление на число, или дробь числовая – это пожалуйста! Например:
Это линейное уравнение. Здесь есть дроби, но нет иксов в квадрате, в кубе и т.д., и нет иксов в знаменателях, т.е. нет деления на икс. А вот уравнение
нельзя назвать линейным. Здесь иксы все в первой степени, но есть деление на выражение с иксом. После упрощений и преобразований может получиться и линейное уравнение, и квадратное, и всё, что угодно.
Получается, что узнать линейное уравнение в каком-нибудь замудрёном примере нельзя, пока его почти не решишь. Это огорчает. Но в заданиях, как правило, не спрашивают о виде уравнения, правда? В заданиях велят уравнения решать. Это радует.)
Решение линейных уравнений. Примеры.
Всё решение линейных уравнений состоит из тождественных преобразований уравнений. Кстати, эти преобразования (целых два!) лежат в основе решенийвсех уравнений математики. Другими словами, решение любого уравнения начинается с этих самых преобразований. В случае линейных уравнений, оно (решение) на этих преобразованиях и заканчивается полноценным ответом. Имеет смысл по ссылке сходить, правда?) Тем более, там тоже примеры решения линейных уравнений имеются.
Для начала рассмотрим самый простой пример. Безо всяких подводных камней. Пусть нам нужно решить вот такое уравнение.
х — 3 = 2 — 4х
Это линейное уравнение. Иксы все в первой степени, деления на икс нету. Но, собственно, нам без разницы, какое это уравнение. Нам его решать надо. Схема тут простая. Собрать всё, что с иксами в левой части равенства, всё, что без иксов (числа) — в правой.
Для этого нужно перенести -4х в левую часть, со сменой знака, разумеется, а -3 — в правую. Кстати, это и есть первое тождественное преобразование уравнений. Удивлены? Значит, по ссылке не ходили, а зря…) Получим:
х + 4х = 2 + 3
Приводим подобные, считаем:
5х = 5
Что нам не хватает для полного счастья? Да чтобы слева чистый икс был! Пятёрка мешает. Избавляемся от пятёрки с помощью второго тождественного преобразования уравнений. А именно — делим обе части уравнения на 5. Получаем готовый ответ:
х=1
Пример элементарный, разумеется. Это для разминки.) Не очень понятно, к чему я тут тождественные преобразования вспоминал? Ну ладно. Берём быка за рога.) Решим что-нибудь посолиднее.
Например, вот это уравнение:
С чего начнём? С иксами — влево, без иксов — вправо? Можно и так. Маленькими шажочками по длинной дороге. А можно сразу, универсальным и мощным способом. Если, конечно, в вашем арсенале имеются тождественные преобразования уравнений.
Задаю вам ключевой вопрос: что вам больше всего не нравится в этом уравнении?
95 человек из 100 ответят: дроби! Ответ правильный. Вот и давайте от них избавимся. Поэтому начинаем сразу со второго тождественного преобразования. На что нужно умножить дробь слева, чтобы знаменатель сократился напрочь? Верно, на 3. А справа? На 4. Но математика позволяет нам умножать обе части наодно и то же число. Как выкрутимся? А умножим обе части на 12! Т.е. на общий знаменатель. Тогда и тройка сократится, и четвёрка. Не забываем, что умножать надо каждую часть целиком. Вот как выглядит первый шаг:
Раскрываем скобки:
Обратите внимание! Числитель (х+2) я взял в скобки! Это потому, что при умножении дробей, числитель умножается весь, целиком! А теперь дроби и сократить можно:
Раскрываем оставшиеся скобки:
Не пример, а сплошное удовольствие!) Вот теперь вспоминаем заклинание из младших классов: с иксом – влево, без икса – вправо! И применяем это преобразование:
Приводим подобные:
И делим обе части на 25, т.е. снова применяем второе преобразование:
Вот и всё. Ответ: х=0,16
Берём на заметку: чтобы привести исходное замороченное уравнение к приятному виду, мы использовали два (всего два!) тождественных преобразования – перенос влево-вправо со сменой знака и умножение-деление уравнения на одно и то же число. Это универсальный способ! Работать таким образом мы будем слюбыми уравнениями! Совершенно любыми. Именно поэтому я про эти тождественные преобразования всё время занудно повторяю.)
Как видим, принцип решения линейных уравнений простой. Берём уравнение и упрощаем его с помощью тождественных преобразований до получения ответа. Основные проблемы здесь в вычислениях, а не в принципе решения.
Но… Встречаются в процессе решения самых элементарных линейных уравнений такие сюрпризы, что могут и в сильный ступор вогнать…) К счастью, таких сюрпризов может быть только два. Назовём их особыми случаями.
Особые случаи при решении линейных уравнений.
Сюрприз первый.
Предположим, попалось вам элементарнейшее уравнение, что-нибудь, типа:
2х+3=5х+5 — 3х — 2
Слегка скучая, переносим с иксом влево, без икса — вправо… Со сменой знака, всё чин-чинарём… Получаем:
2х-5х+3х=5-2-3
Считаем, и… опаньки!!! Получаем:
0=0
Само по себе это равенство не вызывает возражений. Нуль действительно равен нулю. Но икс-то пропал! А мы обязаны записать в ответе, чему равен икс.Иначе, решение не считается, да…) Тупик?
Спокойствие! В таких сомнительных случаях спасают самые общие правила. Как решать уравнения? Что значит решить уравнение? Это значит, найти все значения икса, которые, при подстановке в исходное уравнение, дадут нам верное равенство.
Но верное равенство у нас уже получилось! 0=0, куда уж вернее?! Остаётся сообразить, при каких иксах это получается. Какие значения икса можно подставлять в исходное уравнение, если эти иксы всё равно посокращаются в полный ноль? Ну же?)
Да!!! Иксы можно подставлять любые! Какие хотите. Хоть 5, хоть 0,05, хоть -220. Они всё равно сократятся. Если не верите — можете проверить.) Поподставляйте любые значения икса в исходное уравнение и посчитайте. Всё время будет получаться чистая правда: 0=0, 2=2, -7,1=-7,1 и так далее.
Вот вам и ответ: х — любое число.
Ответ можно записать разными математическими значками, суть не меняется. Это совершенно правильный и полноценный ответ.
Сюрприз второй.
Возьмём то же элементарнейшее линейное уравнение и изменим в нём всего одно число. Вот такое будем решать:
2х+1=5х+5 — 3х — 2
После тех же самых тождественных преобразований мы получим нечто интригующее:
0=2
Вот так. Решали линейное уравнение, получили странное равенство. Говоря математическим языком, мы получили неверное равенство. А говоря простым языком, неправда это. Бред. Но тем, не менее, этот бред — вполне веское основание для правильного решения уравнения.)
Опять соображаем, исходя из общих правил. Какие иксы, при подстановке в исходное уравнение, дадут нам верное равенство? Да никакие! Нет таких иксов. Чего ни подставляй, всё посократится, останется бред.)
Вот вам и ответ: решений нет.
Это тоже вполне полноценный ответ. В математике такие ответы частенько встречаются.
Вот так. Сейчас, надеюсь, пропажа иксов в процессе решения любого (не только линейного) уравнения вас нисколько не смутит. Дело уже знакомое.)
Теперь, когда мы разобрались со всеми подводными камнями в линейных уравнениях, имеет смысл их порешать.
А на ЕГЭ они будут? — слышу вопрос практичных людей. Отвечаю. В чистом виде — нет. Слишком элементарны. А вот в ГИА, или при решении задачек в ЕГЭ, вы с ними столкнётесь обязательно! Так что, меняем мышку на ручку и решаем.
Ответы даны в беспорядке: 2,5; нет решений; 51; 17.
Получилось?! Поздравляю! У вас хорошие шансы на экзаменах.)
Не сходятся ответы? М-да… Это не радует. Эта не та тема, без которой можно обойтись. Рекомендую посетить Раздел 555. Там очень подробно расписано, чтонадо делать, и как это делать, чтобы не запутаться в решении. На примере этих уравнений.
А как решать уравнения более хитрые, — это в следующей теме.
infourok.ru
Выборка заданий по математике. ОГЭ. 6 класс. Линейные уравнения. ФИПИ.РешуОГЭ.
Блок 12. Подборка заданий для учащихся 6 класс. Линейные уравнения. Источник ФИПИ, РешуОГЭ.
Тип 1.
1. Решите уравнение 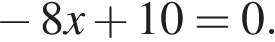
2. Решите уравнение 
3. Решите уравнение 10x + 1 = − 8.
4. Решите уравнение 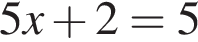
5. Решите уравнение 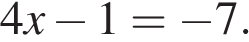
6. Решите уравнение 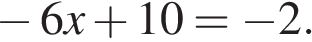
7. Решите уравнение 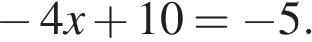
8. Решите уравнение 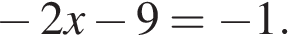
9. Решите уравнение 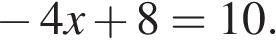
10. Решите уравнение 
11. Решите уравнение − 5x − 6 = 0.
12. Решите уравнение 5x − 8 = 0.
13. Решите уравнение 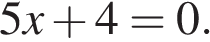
14. Решите уравнение 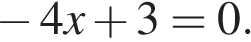
15. Решите уравнение 
16. Решите уравнение 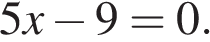
17. Решите уравнение 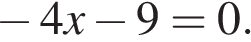
18. Решите уравнение 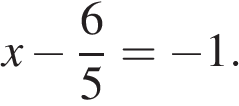
Тип 2.
1. Найдите корень уравнения 3x+3=5x
2. Найдите корень уравнения 6x+1=− 4x
3. Найдите корень уравнения x+3=− 9x
4. Найдите корень уравнения x−2=− 3x
5. Найдите корень уравнения − 2x−4=3x
6. Найдите корень уравнения − x−7=x
7. Найдите корень уравнения − 3x−9=2x
8. Найдите корень уравнения − 4x−9=6x
9. Найдите корень уравнения − 2x−7=− 4x
10. Найдите корень уравнения − 8x−3=− 6x
11. Решите уравнение 6x + 13 = x.
Тип 3.
1. При каком значении 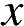 значения выражений
значения выражений  и
и 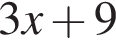 равны?
равны?
2. При каком значении x значения выражений 10x − 6 и 6x + 5 равны?
3. При каком значении x значения выражений 2x − 4 и 6x + 8 равны?
4. При каком значении x значения выражений 3x − 2 и 2x + 4 равны?
5. Решите уравнение 
6. Решите уравнение − 7 − 2x = − 6x + 10.
7. Решите уравнение 2 + 3x = − 7x − 5.
8. Решите уравнение − 1 −3x = 2x + 1.
9. Найдите корень уравнения 8+7x=9x+4
10. Найдите корень уравнения − 5+9x=10x+4
11. Найдите корень уравнения − 4+7x=8x+1
12. Найдите корень уравнения 9+8x=6x−2
13. Найдите корень уравнения − 1−3x=2x+1
14. Найдите корень уравнения − 4−6x=4x−3
15. Найдите корень уравнения 1−10x=5x+10
16. Найдите корень уравнения 7+8x=− 2x−5
17. Найдите корень уравнения − 5+2x=− 2x−3
Тип 4.
1. Решите уравнение 4(x − 6) = 5.
2. Решите уравнение 5(x + 4) = − 9.
3. Найдите корень уравнения 4(x−8)=− 5
4. Найдите корень уравнения 5(x+9)=− 8
5. Найдите корень уравнения 4(x−2)=− 1
6. Найдите корень уравнения 4(x+1)=9
7. Найдите корень уравнения 10(x+2)=− 7
Начало формыКонец формы
8.
Найдите корень уравнения 4(x+10)=− 1
9. Найдите корень уравнения 5(x−6)=2
10. Найдите корень уравнения 10(x−9)=7
11. Решите уравнение 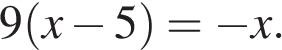
12. Решите уравнение 6(5 − x) = − 8x − 7.
13. Решите уравнение 9(x − 6) = 4x.
14. Решите уравнение 10(x + 4) = 9x.
15. Решите уравнение 4(x − 7) = 3x.
16. Решите уравнение 5(x − 7) = 9x.
17. Решите уравнение 3(x − 8) = 5x.
Тип 5.
1. Решите уравнение 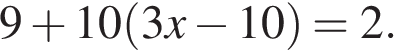
2. Решите уравнение 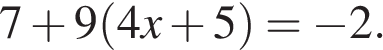
3. Решите уравнение 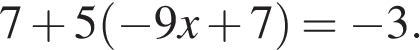
4. Решите уравнение 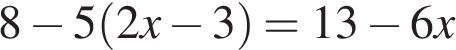 .
.
5. Решите уравнение 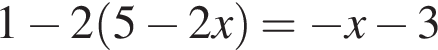 .
.
6. Решите уравнение 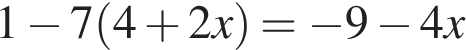 .
.
7. Решите уравнение −2(5 − 3x) = 7x + 3.
8. Решите уравнение 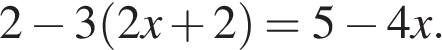
9. Решите уравнение 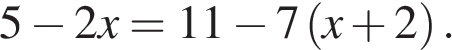
Тип 6.
1. Решите уравнение 
2. Решите уравнение 
3. Решите уравнение 
4. Решите уравнение x − 3 − 4(x + 1) = 5(4 − x) − 1.
5. Решите уравнение − 3x + 1 − 3(x + 3) = − 2(1 − x) + 2.
6. Решите уравнение − 2x + 5 + 4(x − 1) = − 4(− 4 − x) + 3.
7. Решите уравнение 2x − 4 − 3(x − 4) = − 2(− 3 − x) − 4.
8. Решите уравнение 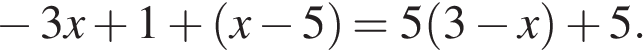
9. Решите уравнение 
10. Решите уравнение 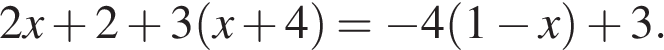
11. Решите уравнение 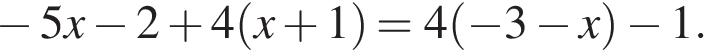
12. Решите уравнение 
13. Решите уравнение 
14. Решите уравнение 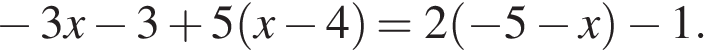
15. Решите уравнение 
infourok.ru