Диаметр окружности круга • как найти ⬅️ формула
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.
Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости.
Круг — часть плоскости, лежащая внутри окружности, а также сама окружность.
Если говорить проще, окружность — это замкнутая линия, как, например, обруч и велосипедное колесо. Круг — часть плоскости, ограниченная окружностью, как блинчик или вырезанный из картона кружок.
Диаметр — отрезок, который соединяет две точки окружности и проходит через ее центр.
Радиус — отрезок, который соединяет центр окружности и любую точку на ней.
Как узнать диаметр. Формулы
В данной теме нам предстоит узнать три формулы:
1. Общая формула.
Исходя из основных определений нам известно, что значение диаметра равно двум радиусам: D = 2 × R, где D — диаметр, R — радиус.
2. Если перед нами стоит задача найти диаметр по длине окружности
D = C : π, где C — длина окружности, π — это константа, которая равна отношению длины окружности к диаметру, она всегда равна 3,14.
Чтобы получить правильный ответ, можно поделить столбиком или использовать онлайн-калькулятор.
3. Если есть чертеж окружности
- Начертить внутри круга прямую горизонтальную линию. Ее месторасположение не играет значительной роли.
- Отметить точки пересечения прямой и окружности.
- Начертить при помощи циркуля две окружности одного радиуса (больше, чем радиус первоначальной окружности), первую — с центром в точке A, вторую — с центром в точке B.

- Провести прямую через две точки, в которых произошло пересечение. Отметить точки пересечения полученной прямой с окружностью. Диаметр равен этому отрезку.
- Теперь осталось измерить диаметр круга при помощи линейки. Получилось!
Эти простые формулы могут пригодиться не только на школьных уроках, но и если вы решите освоить профессию дизайнера интерьера, архитектора или модельера одежды.
Круг и линия. Строение и законы ума
Читайте также
Глава 15. Нелинейная линия
Глава 15. Нелинейная линия В 1877 году, когда планета Марс находилась необычно близко к Земле, всего на расстоянии 60 миллионов километров, итальянский астроном Джованни Скиапарелли объявил, что он открыл каналы — canali — на поверхности соседа Земли. Эти каналы представляли
Глава 2 Линия смерти и линия жизни
Глава 2 Линия смерти и линия жизни
1.
Вкусовая линия времени
Вкусовая линия времени Если вы не дегустатор, то большого значения на первом этапе работы с памятью вкусовая линия времени для вас не имеет. Но если есть желание наилучшим образом привести в порядок свою память, можно потратить тридцать минут на выставление вкусовой
Родословная. Мамина линия
Родословная. Мамина линия Моя бабушка стоит особого внимания. Фигура колоритная. Марина Харитоновна – яркий продукт советского времени. Ее мать Стюра была старшей в страшно нищей крестьянской семье. У нее было восемь братьев и сестер. Родители в период коллективизации
Родословная.
 Папина линия
Папина линияРодословная. Папина линия Отец мой тоже из простой семьи, ее корни на Украине. Он первый из своих родственников получил высшее образование. Его мать (не знаю ее профессии) была в немецком концлагере. Ее угоняли в Германию, каким-то образом оттуда она бежала. Развелась со
Линия грез
Линия грез …Все мы совершаем в жизни много ошибок, а потом мечтаем о том, как было бы здорово вернуть прошлое и все исправить. Я вам не обещаю «в детство плацкартный билет», но ошибки можно исправить, причем это будет похоже на возврат в прошлое… В. Зеланд …У каждого из
Обобщающая Линия Жизни
Обобщающая Линия Жизни
(До сих пор этот комментарий демонстрировался частично, это те части Процесса Сущностной Трансформации, с которыми вы уже внутренне довольно близко знакомы.
Шаг 10. Обобщающая Линия Жизни
Шаг 10. Обобщающая Линия Жизни После раскрытия всех частей в плане обладания их Сущностными Состояниями, достижения ими вашего сегодняшнего возраста и полного их переноса и присутствия в вашем теле, полезно создать Обобщающую Линию Жизни. Этот процесс помогает усилить
Шаг 10. Обобщающая линия жизни
Шаг 10. Обобщающая линия жизни Если вы работали более чем с одной частью и с двумя или более Сущностными Состояниями, внесите в список и учтите каждое Сущностное Состояние, когда вы будете рассматривать [Сущностное Состояние (или Состояния)] в следующем шаге упражнения. а)
Обобщающая линия жизни
Обобщающая линия жизни
16. Позвольте своему прошлому струиться позади вас и будущему перед вами в виде тропинки. 17. Со своими Сущностными Состояниями, струящимися сквозь вас, позвольте себе перенестись назад над вашим прошлым, до момента зачатия. 18. Опуститесь на линию
Позвольте своему прошлому струиться позади вас и будущему перед вами в виде тропинки. 17. Со своими Сущностными Состояниями, струящимися сквозь вас, позвольте себе перенестись назад над вашим прошлым, до момента зачатия. 18. Опуститесь на линию
Линия жизни
Линия жизни Есть еще одна техника, которая в клинической практике помогает осознать и исцелить болезненные воспоминания, — это написание автобиографии по годам. Для осуществления методики нужно изложить свою жизнь на бумаге. Начните с дедушек и бабушек, запишите все,
6.3.4.1. Линия самоотрицания
6.3.4.1. Линия самоотрицания Выше был подробно описан данный тип личности, а чуть ранее – неуверенная стратегия, которая им часто актуализируется. Начнем с подросткового возраста и рассмотрим динамику решения задач – формирования половой идентичности, принятия гендерных
6.
 3.4.3. Линия доминирования
3.4.3. Линия доминирования6.3.4.3. Линия доминирования Подростки такого типа в полном смысле стремятся к самоутверждению. Цель – защита собственной ценности путем экстериоризации внутреннего напряжения, экстериоризации конфликтов. В крайних своих вариантах самоутверждение обнаруживается в
Окружность, круг, секущая и сектор
Окружность и круг — геометрические фигуры, взаимосвязанные между собой. Окружность есть граничная ломаная линия (кривая) круга,
Определение. Окружность — замкнутая кривая, каждая точка которой равноудалена от точки, называемой центром окружности.
Для построения окружности выбирается произвольная точка О, принятая за центр окружности, и с помощью циркуля проводится замкнутая линия.
Если точку О центра окружности соединить с произвольными точками на окружности, то все полученные отрезки будут между собой равны, и называются такие отрезки радиусами, сокращенно обозначаются латинской маленькой или большой буквой «эр» (r или R). Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Радиусов в окружности можно провести столько же, сколько точек имеет длина окружности.
Отрезок, соединяющий две точки окружности и проходящий через ее центр, называется диаметром. Диаметр состоит из двух радиусов, лежащих на одной прямой. Диаметр обозначается латинской маленькой или большой буквой «дэ» (d или D).
Правило. Диаметр окружности равен двум ее радиусам.
d = 2r
D = 2R
Длина окружности обозначается латинской большой буквой «цэ» (C). Длина окружности пропорциональна ее диаметру. Формулы для расчета длины окружности по ее радиусу и диаметру:
C = ¶d
C = 2¶r
- Примеры
- Дано: d = 100 см.

- Длина окружности: C = 3,14 * 100 см = 314 см
- Дано: d = 25 мм.
- Длина окружности: С = 2 * 3,14 * 25 = 157 мм
Секущая окружности и дуга окружности
Всякая секущая (прямая линия) пересекает окружность в двух точках и делит ее на две дуги. Величина дуги окружности зависит от расстояния между центром и секущей и измеряется по замкнутой кривой от первой точки пересечения секущей с окружностью до второй.
Дуги окружности делятся секущей на большую и малую, если секущая не совпадает с диаметром, и на две равные дуги, если секущая проходит по диаметру окружности.
Если секущая проходит через центр окружности, то ее отрезок, расположенный между точками пересечения с окружностью, есть диаметр окружности, или самая большая хорда окружности.
Чем дальше секущая расположена от центра окружности, тем меньше градусная мера меньшей дуги окружности и больше — большей дуги окружности, а отрезок секущей, называемый хордой, уменьшается по мере удаления секущей от центра окружности.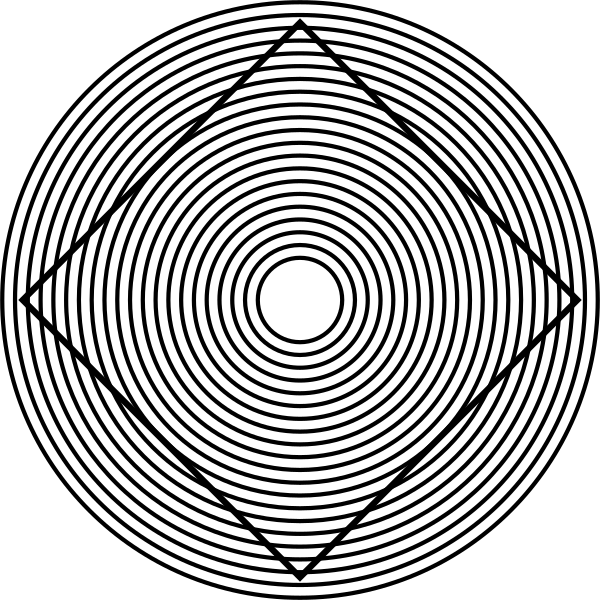
Определение. Кругом называется часть плоскости, лежащая внутри окружности.
Центр, радиус, диаметр окружности являются одновременно центром, радиусом и диаметром соответствующего круга.
Так как круг — это часть плоскости, то одним из его параметров является площадь.
Правило. Площадь круга (S) равна произведению квадрата радиуса ( r 2 ) на число ¶.
- Примеры
- Дано: r = 100 см
- Площадь круга:
- S = 3,14 * 100 см * 100 см = 31 400 см 2 ≈ 3м 2
- Дано: d = 50 мм
- Площадь круга:
- S = ¼ * 3,14 * 50 мм * 50 мм = 1 963 мм 2 ≈ 20 см 2
Если в круге провести два радиуса к разным точкам окружности, то образуется две части круга, которые называется секторами. Если в круге провести хорду, то часть плоскости между дугой и хордой называется сегментом окружности.
Определение. Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Сектор — это часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги. Сектор, образованный радиусами, расположенными под углом в 90° называется квадрантом.
Площадь сектора составляет только часть площади круга, и ее величина пропорциональна длине дуги m или зависит от величины центрального угла a, образованного двумя радиусами с вершиной в центре круга.
Формула для вычисления площади сектора:
где S — площадь сектора; m — длина дуги; r — радиус круга; а — угловая величина дуги (и градусах).
Изогнутый текст вокруг круга или другой фигуры
Для изгиба текста вокруг фигуры можно использовать текст WordArt с эффектом Transform (Преобразование). Если нужно, чтобы текст полностью окружал фигуру, потребуется немного больше усилий. Объект WordArt также можно вставить несколько раз, чтобы задать обтекание текста вокруг фигур с прямыми границами.
-
Перейдите в > WordArtи выберите нужный стиль WordArt.
Примечание: Значок WordArt находится в группе Текст и может отображаться по-разному в зависимости от используемой версии и размера экрана. Значок также может выглядеть так, как или .
-
Замените замещатель WordArt собственным текстом.
-
Выделите свой текст WordArt.
-
Перейдите в формат фигуры или Средства рисования, выберите Текстовые эффекты >Преобразовать и выберите нужный вид.

Примечание: В зависимости от размера экрана могут отображаться только значки стилей WordArt.
Дополнительные методы
Обтекать круг Чтобы создать текст, который полностью обкругит фигуру, выберите Круг в области По пути ,а затем перетащите любой из хронологий размера, чтобы получить нужный размер и фигуру.
Обтекать прямые края Чтобы обтекать текст вокруг фигуры с прямыми краями, например прямоугольника, вставьте объекты WordArt для каждого края. В этом примере объект WordArt вставлен четыре раза, по одному для каждой стороны фигуры.
Перемещение и копирование групп Чтобы переместить или скопировать несколько объектов WordArt в виде одной фигуры, см. группу и разгруппировку фигур, рисунков и других объектов.
группу и разгруппировку фигур, рисунков и других объектов.
Точный угол управления Угол наклона текста WordArt по отношению к фигуре можно точно настроить с помощью инструмента вращения.
Если вам требуется очень точное управление фигурами и текстом или вы создаете сложное сочетание фигур и текста, создайте текст вокруг фигуры с помощью стороннее графического редактора, а затем скопируйте его и Office документ.
См. также
Добавление фигур
Вставка объекта WordArt
Создание изогнутого или кругового текста WordArt
-
Перейдите в >WordArt.

-
Выберите нужный стиль WordArt.
-
Введите текст.
-
Выделите текст WordArt.
-
Перейдите в формат фигуры > текстовые эффекты > Transform (Преобразовать) и выберите нужный эффект.
Дополнительные методы
Обтекать круг Чтобы создать текст, который полностью обкругит фигуру, выберите Круг в области По пути ,а затем перетащите любой из хронологий размера, чтобы получить нужный размер и фигуру.
Обтекать прямые края Чтобы обтекать текст вокруг фигуры с прямыми краями, например прямоугольника, вставьте объекты WordArt для каждого края. В этом примере объект WordArt вставлен четыре раза, по одному для каждой стороны фигуры.
Перемещение и копирование групп Чтобы переместить или скопировать несколько объектов WordArt в виде одной фигуры, см. группу и разгруппировку фигур, рисунков и других объектов.
Точный угол управления Угол наклона текста WordArt по отношению к фигуре можно точно настроить с помощью инструмента вращения.
Если вам требуется очень точное управление фигурами и текстом или вы создаете сложное сочетание фигур и текста, создайте текст вокруг фигуры с помощью стороннее графического редактора, а затем скопируйте его и Office документ.
В Word в Интернете вы можете увидеть wordArt, который уже есть в вашем документе, но чтобы добавить другие, необходимо открыть или изменить документ в версии Word.
С помощью функций шрифта на вкладке Главная можно изменить цвет и размер шрифта, а также применить к тексту полужирное наличность, наличность или подчеркивается.
Не удается найти страницу | Autodesk Knowledge Network
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings. TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
TAGS}}
{{$item}}
{{l10n_strings.PRODUCTS}}
{{l10n_strings.DRAG_TEXT}}
{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings.LANGUAGE}} {{$select.selected.display}}{{article.content_lang.display}}
{{l10n_strings. AUTHOR}}
AUTHOR}}
{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$select.selected.display}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}ярлыки и маркировки по стирке, температуре, отжиму, глажке, отбеливанию и сушке
Неправильный уход за одеждой вызывает быстрый износ ткани и потерю привлекательного вида, поэтому перед стиркой, сушкой или отбеливанием какой-либо одежды нужно внимательно посмотреть на ее ярлык со значком. Там в виде условных обозначений указаны нюансы ухода за конкретной тканью.
Там в виде условных обозначений указаны нюансы ухода за конкретной тканью.
Стирка
Основным процессом ухода за большинством видов одежды является стирка. На ярлыке, пришитом с внутренней стороны вещи, вы увидите, какая именно стирка рекомендуется производителем, при какой температуре разрешено стирать вещь, можно ли ее отбеливать и отжимать.
Значок, по которому вы сможете понять, как стирать ту или иную вещь, напоминает по виду тазик с водой. Если на вашей этикетке изображен лишь такой «тазик», то вещь стирают в машинке на любой программе, то есть ее допустимо как замачивать, так и отжимать.
Другие варианты такого значка расшифровывают следующим образом:
- Подчеркнутый одной линией «тазик» обозначает необходимость использования щадящей стирки.
 Такую вещь нельзя стирать на программе с высоким количеством оборотов, а загружать машинку советуют лишь на 2/3 от допустимого объема белья.
Такую вещь нельзя стирать на программе с высоким количеством оборотов, а загружать машинку советуют лишь на 2/3 от допустимого объема белья. - Если под «тазиком» вы увидели две линии, такая вещь может стираться лишь на режиме «деликатная стирка». Объем белья в машинке советуют уменьшить до 1/3 максимально рекомендуемого. Если вы хотите постирать такую вещь руками, то следует прополоскать такую одежду в большом объеме воды, а отжимать очень аккуратно или не отжимать вообще.
- «Тазик» с погруженной в него рукой указывает на необходимость стирать такую вещь руками. Температура стирки при этом не должна быть выше +40 С. Кроме того, такую одежду не следует сильно тереть и отжимать. Как правило, такой значок вы увидите на одежде из гипюра, шифона, трикотажа, атласа и подобных деликатных материалов.
- Размещенное в кружке изображение стиральной машинки означает запрет на машинную стирку. Такое обозначение характерно для тканей, которые могут полинять, порваться или растянуться во время прокручивания в барабане.
 Также этот значок вы увидите на нарядах с пайетками, бисером, стразами и другим декором, способным оторваться при стирке в машинке.
Также этот значок вы увидите на нарядах с пайетками, бисером, стразами и другим декором, способным оторваться при стирке в машинке. - Перечеркнутый «тазик» подскажет вам, что данную вещь вообще стирать нельзя. Такой значок вы увидите на изделиях, которые относят в химчистку, поскольку даже бережная стирка руками может им повредить.
Температурный режим
Обращать внимание на обозначения температуры воды при стирке важно, чтобы вещь не села, не потеряла свой цвет и не стала бесформенной.
О допустимой температуре вы можете узнать по двум вариантам обозначений – внутри «тазика» с водой вы увидите либо число, либо точки в разном количестве:
- 30º или 1 точка – вещь стирают при температуре не выше +30ºС, отжим должен быть минимальным.

- 40º или 2 точки – для стирки такой вещи температура должна не превышать +40ºС.
- 50º или 3 точки – вещь можно стирать при температуре до +50ºС.
- 60º или 4 точки – для стирки такой вещи устанавливается температура +60ºС.
- 70ºили 5 точек – стирать такую вещь можно при +70ºС.
- 95º или 6 точек – такая вещь может стираться при температуре +95ºС.
Отжим
Неправильно выбранная интенсивность отжима способна стать причиной усадки или повреждения одежды.
Значок, который подскажет вам об особенностях отжима вещи, представляет собой квадрат с кругом внутри. Увидев такой знак, вы можете не переживать, что вещь постирается с высокой интенсивностью отжима. Кроме того, такое обозначение допускает применение машинной сушки.
Другие варианты круга внутри квадрата расшифровываются так:
- Если данный знак подчеркнут одной линией, для такой вещи и отжим, и сушка в машинке должны быть щадящими.
- Если под знаком вы увидите две линии, то такая одежда должна стираться на программе с отжимом с малым числом оборотов, а машинная сушка также должна быть деликатной.
- Если внутри круга в квадрате вы увидите точки, это подскажет вам режим машинной сушки для данной вещи. Как и на утюге, число точек указывает на интенсивность сушки, например, если точка одна, то режим должен быть щадящим, а если точек три, то сушка может быть быстрой и с применением высоких температур.
- Если круг внутри квадрата зарисован, то нагрев при машинной сушке недопустим (одежду можно обработать лишь холодным воздухом).
- Перечеркнутый квадрат с кругом означает запрет на отжимание во время стирки и сушку в стиральной машинке.

- Перечеркнутое изображение перекрученной одежды указывает на то, что такую вещь нельзя ни выкручивать, ни отжимать.
Машинная сушка
Рекомендации по сушке одежды после стирки представлены знаком квадрата. Если вы видите просто пустой квадратик, такую вещь сушить можно.
Другие варианты квадрата нужно расшифровывать так:
- Если пустой квадрат перечеркнут, такую вещь сушить нельзя.
- Если вверху квадрата изображен полукруг, одежду разрешено сушить вертикально – либо на плечиках, либо на бельевой веревке.
- Три вертикальные линии внутри квадрата подскажут вам, что вещь недопустимо отжимать, а следует повесить сушить еще мокрой.

- Одна горизонтальная полоска внутри квадрата указывает на необходимость сушки на горизонтальной поверхности, иначе ткань деформируется и растянется. Обычно такая сушка рекомендуется для трикотажа и шерсти.
- Две диагональные линии в верхнем левом углу квадрата обозначают запрет на сушку под прямыми лучами солнца. Одежду с таким значком на ярлыке следует сушить только в тени. Обычно это белая ткань, которая под солнечным светом становится желтоватой, а также яркая одежда, способная выгорать.
Отбеливание
Прежде чем воспользоваться отбеливателем, обязательно отыщите на этикетке треугольник:
- Если треугольник есть, отбеливание разрешено.

- Если такой треугольник будет перечеркнутым, то, соответственно, отбеливание запрещено.
- Также обратите внимание на буквы внутри – если в треугольнике вы видите «Cl», то можете воспользоваться для отбеливания средствами с хлором.
- Если зачеркнут треугольник с буквами «Cl», то отбеливание разрешено, но хлорсодержащие средства применять нельзя. Такое же значение у треугольника, внутри которого проходят две диагональные линии.
Без значков
Хотя на большинстве одежды производители отмечают особенности стирки значками, встречается также одежда, на ярлыках которой вы увидите надписи на английском. Расшифровать их можно так:
- Machine wash – вещь можно стирать в машинке
- Hand wash only – для такой вещи допустима только стирка руками
- Wash separately – окраска такой вещи нестойкая и может полинять на другую одежду, поэтому стирать ее придется изолированно
- Hot wash – для стирки используйте горячую воду
- Warm wash – такую вещь стирайте в теплой воде
- Cold wash – для стирки такой вещи вода не должна быть теплой
- No wash/Do not wash – такой надписью производитель предупреждает, что вещь стирать нельзя
Химическая чистка
Обозначения, связанные с особенностью химической обработки одежды, интересуют в основном сотрудников химчисток, поскольку указывают, какая именно чистка допустима для конкретной одежды.
- Самым важным для обычного обывателя значком, связанным с химчисткой, является перечеркнутый круг. Он подскажет, что такую вещь в салон химчистки везти не следует, так как химическая чистка ей противопоказана.
- Круглый значок без каких-либо букв обозначает, что для вещи используется сухая чистка. Зачастую такое обозначение вы найдете на шерстяной, кожаной, шелковой или замшевой одежде.
- Если внутри круга есть буква, она подсказывает, какими химическими средствами допустимо выполнять очистку ткани. Это могут быть буквы А, F, P или W. А черточка под кругом подскажет работнику химчистки, что обработка должна быть деликатной.
Глажка
Во время проглаживания ткань поддается воздействию высокой температуры, поэтому каждый производитель отмечает на ярлыке оптимальный температурный режим в зависимости от ткани. К примеру, льняную или хлопковую ткань можно гладить с сильным нагревом утюга, а применение пара лишь поможет разглаживанию складок. Если же вы перегреете утюг при глажке синтетики или шерсти, вещь будет испорчена.
К примеру, льняную или хлопковую ткань можно гладить с сильным нагревом утюга, а применение пара лишь поможет разглаживанию складок. Если же вы перегреете утюг при глажке синтетики или шерсти, вещь будет испорчена.
Режим глажки на ярлыке обозначается изображением утюга. Если вы увидели просто «утюг» без точек, то такую вещь можно как гладить с любым нагревом, так и обрабатывать паром. Другие изображения «утюга» расшифровывайте так:
- Одна точка внутри «утюга» разрешает нагревать утюг во время глажки максимум до 110ºС. Это бережная глажка, которую применяют преимущественно для синтетических материалов, например, вискозы или полиамида.
- Две точки внутри «утюга» разрешают нагрев до 150ºС. Этот температурный режим используют при глажке шелка, полиэстера, шерсти.
- Три точки внутри «утюга» разрешают нагреть утюг до самой высокой температуры (+200ºС).
 Такой режим обычно выбирают для обработки хлопковых и льняных изделий.
Такой режим обычно выбирают для обработки хлопковых и льняных изделий. - «Утюг» внутри круга обозначает температурный режим глажки до 140ºС.
- Перечеркнутый «утюг» запрещает гладить изделие. Это обозначение часто встречается на махровой ткани или нейлоне.
- Если перечеркнуты ножки «утюга», то при глажке нельзя применять увлажнение. Обычно такая рекомендация присутствует на ярлыке шелковой, атласной и сатиновой одежды, которую запрещено отпарывать.
Советы
Все описанные выше обозначения располагаются на ярлыке, представляющем собой тканевую бирку. На такой бирке также указывают фирму-производителя одежды, состав вещи и ее размер.
Отыскать ярлык можно с внутренней стороны одежды, рассмотрев внутренние швы изделия. На куртке такая бирка обычно находится с левой стороны на уровне талии. К брюкам и джинсам бирку пришивают либо сзади, либо сбоку по шву. На свитере, рубашке, футболке и другой легкой одежде ярлык можно найти либо на боковом шве, либо под воротником сзади.
На куртке такая бирка обычно находится с левой стороны на уровне талии. К брюкам и джинсам бирку пришивают либо сзади, либо сбоку по шву. На свитере, рубашке, футболке и другой легкой одежде ярлык можно найти либо на боковом шве, либо под воротником сзади.
Чтобы закрепить все прочитанное, посмотрите содержательное, веселое и легкое для восприятие видео от автора «Абалдеть Channel»:
Создание схемы линий Московского метро 3.0
Появилась задача — на новой схеме метро должна быть новая кольцевая ветка. Проектное название — Малое кольцо железной дороги (МКЖД).
Начинаем работу со студийного эскиза на 2025 год (слегка измененный вариант этой схемы, вероятно, знаком читателю как совместная схема московского метро и кольцевой железной дороги).
Дело в том, что примерно к 2025 году в Москве достроят Третий пересадочный контур (ТПК) — еще одну кольцевую ветку. МКЖД и ТПК допустимо назвать симметричными относительно первой кольцевой: МКЖД смещена относительно нее на север почти на столько же, на сколько на юг смещен ТПК.
Обе новые кольцевые при этом взаимодействуют друг с другом и линиями вокруг, пересекаются не один раз — короче, наука геометрия говорит нам о том, что концентрическими окружностями эти ветки нарисовать не получится и придется их обе ломать, оставляя просто замкнутыми кривыми. Решаем готовиться к будущему заранее и гнем МКЖД таким образом, каким она будет погнута когда-то.
С другой стороны, ТПК станет замкнутой кольцевой веткой через 10 лет, а до этого будет открываться небольшими участками по несколько станций (например, Каховская ветка — один из открытых уже участков). МКЖД же сразу открывается полностью и сразу называется кольцом. Сохранить привычный для всех вид московской схемы важнее. Ломаная ветка вокруг кольца по эстетике проигрывает просто двум кольцам.
МКЖД же сразу открывается полностью и сразу называется кольцом. Сохранить привычный для всех вид московской схемы важнее. Ломаная ветка вокруг кольца по эстетике проигрывает просто двум кольцам.
Вспоминаем, что в последней итерации схем у большинства из них существенно увеличился физический размер (исчез алфавитный указатель, сами форматы стали шире и выше, из-за чего где-то пришлось добавлять белые поля, чтобы схема не выглядела в вагоне слишком большой), поэтому если что-то будет не влезать, то в случае чего мы раздвинем ветки пошире. Быстро готовим эскиз и решаем рисовать МКЖД в виде круга.
Географически МКЖД распространяется далеко на север от центра Москвы.
В первом эскизе эта особенность учтена. Такой подход позволяет легко разместить большое количество станций между МКЖД и кольцевой линией наверху схемы, не создавая дыр между кольцами в нижней части.
Вариант со сдвинутыми кольцами смущает, но из-за географии и удобства размещения станций сперва начинаем разрабатывать именно его. Для начала проходим по схеме «широкой кистью», не вдаваясь в детали: кладем МКЖД и добавляем новые станции, обозначаем ключевые пересадки, выпрямляем синюю линию внутри кольца.
Для начала проходим по схеме «широкой кистью», не вдаваясь в детали: кладем МКЖД и добавляем новые станции, обозначаем ключевые пересадки, выпрямляем синюю линию внутри кольца.
Грубый эскиз необходим, чтобы оценить общую картину и увидеть наиболее проблемные места. Несмотря на то что МКЖД откроется только осенью 2016 года, в начале проектирования станции кольцевой железной дороги обозначаем как уже открытые — кегль шрифта у открытых станций больше, чем у закрытых, и если проектировать схему с закрытыми станциями, то при их открытии найти место для новых подписей будет сложно. А так просто выключим потом станции МКЖД.
После оценки эскиза выделяем три главные проблемы:
— верх Сокольнической линии изгибается у МКЖД и разрушает сетку построения схемы;
— очень тесно на западе, между голубой и фиолетовыми ветками;
— пока неясно, как развести «Александровский сад» и «Площадь Революции» (пересадка у «Площади» отвалилась от зеленой ветки, а если ее двигать левее, надписи налезают друг на друга).
Начинаем спасать запад. Чтобы найти место для станций между кольцевой линией и МКЖД, синюю и голубую ветки опускаем вниз. Станции разрядились, но голубая и синяя ветки находятся очень близко к кольцу. При таком соседстве станция «Хорошево» подписывает и МКЖД, и Филевскую ветку, а «Шелепиха» — еще и «Беговую».
Пытаясь решить эти проблемы, отодвигаем линии метро. Заодно ищем, как бы красиво погнуть голубую и синюю ветки внутри кольца.
Вроде бы все нормально — надписи стоят равномерно. Но важно помнить, что МКЖД только строится. Выключаем станции и получаем дыру между МКЖД и голубой веткой.
Перекомпоновываем надписи по-другому, не забывая о поиске оптимального положения желтой, синей и голубой веток внутри кольца.
Получается очередной вариант схемы.
Плохо, конечно, что центр масс перестал быть в центре кольцевой. А по-другому и не сделаешь, казалось тогда. Наверху, где «Петровско-Разумовская», вон сколько станций между кольцами, а внизу — «Серпуховская» и всего пара других. И, не меняя положения колец, продолжаем работу.
И, не меняя положения колец, продолжаем работу.
Верх Сокольнической линии долго извивается, принимая причудливые формы. Сначала он загибался у внутреннего края МКЖД, повторяя географию, но в существующей сетке схемы это смотрится очень странно.
Поэтому линию выпрямляем, закончив пересадкой на «Открытое шоссе».
Решение не походит — пересадку с «Черкизово» на «Черкизовскую» так не покажешь. Поэтому изгиб линии возвращаем, пытаясь сделать его «более лучше».
Но, когда выключаем «Ярославскую», «Белокаменную», «Открытое шоссе» и «Черкизово» на МКЖД, уменьшив шрифт и сделав серыми, снаружи кольца в этом месте появляется дыра, а внутри кольца — все так же плотно. Поэтому конец ветки вытаскиваем, инвертировав порядок станций.
Оказывается, пересадка «Черкизово» — «Черкизовская» будет располагаться не в «теплом» контуре, а проходить по улице. Обозначение уличной пересадки — два кружка с точками — длиннее обозначения «теплой» пересадки, поэтому приходится искать другие решения.
Наконец-то линия встает как надо.
В центре решаем избавиться от изгиба над звездой.
Если просто разгладить линию и попытаться развести «Александровский сад» и «Площадь Революции», то приходится использовать чит-коды — поворот руля и растягивание пересадки.
Получив по рукам за такое, дизайнер возвращает прежний вид пересадкам и начинает искать честные способы разместить звезду, «Александровский сад» и «Площадь Революции». И почти получается, только не хватает места звезде, а «Охотный Ряд» отрывается от линии.
Чтобы вернуть «Охотный Ряд» на место, придаем зеленой линии дополнительный изгиб.
Понимаем, что это был неважный способ решить проблему. От второго изгиба зеленой ветки отказываемся, сдвинув левее первый.
Зеленая линия тащит за собой пересадку «Тверская» — «Чеховская» — «Пушкинская», а также «Белорусскую» и немного меняет сетку схемы.
Это небольшое изменение сетки и еще несколько других, не замеченных во время борьбы со сложными местами, впоследствии приводят к незабываемой ночи перед сдачей схемы в печать. Но мы пока об этом не догадываемся.
Но мы пока об этом не догадываемся.
В разгар проектирования приходит пожелание от заказчика: поменять шрифт на Москоу Санс, чтобы схема была выполнена в едином стиле с транспортной навигацией. Москоу Санс отличается от Директа, использованного в схеме, пропорциями букв — слова, набранные им, получаются шире, — поэтому замена шрифта влечет за собой изменение схемы.
Например, чтобы «Пушкинская» на картинке внизу влезла между линиями, предлагаем подвинуть зеленую ветку влево. После надо немного опустить пересадку на «Белорусской» и решить, что сделать с «Беговой». Да, у нас еще «Кузнецкий Мост» не помещается. И «Трубная». А если сдвинуть вправо оранжевую ветку? И так по всей схеме.
Словом, поменять шрифт — задача далеко не на один день. И заказчик дает дополнительную неделю.
Процесс проектирования удачно представляется гифкой.
Поставив новый шрифт и решив основные проблемы, показываем схему арт-директору.
Арт-директор: Кольцо — узнаваемый символ московской схемы, и нужно эту красоту сохранить. Поэтому кольца должны быть выровнены относительно друг друга.
Поэтому кольца должны быть выровнены относительно друг друга.
К следующему утру готовим три схемы, чтобы оценить варианты и выбрать лучший.
Вариант с усеченным кольцом арт-директор сразу вычеркивает — символом Московского метро не может быть спущенное колесо. Смещенные кольца забракованы еще вчера. Выровненные кольца побеждают. Но с ними есть проблема: вверху, где «Петровско-Разумовская», пространство между кольцами забито станциями, а на противоположной стороне, где «Серпуховская», так пусто, что даже бегемотик помещается.
Заполняем пустоту, переместив «Нагатинскую» и «Нагорную» внутрь кольца. Считаем, что в качестве временного решения на несколько месяцев вполне норм, но помечаем себе как домашнее задание на будущее.
В ночь перед сдачей тиража в печать прилетает идея поправить сетку.
Становится понятно, что ночь будет долгой и незабываемой. Берем паузу, наливаем чай и перерисовываем схему. К утру схема расправляет плечи, набирает воздуха полной грудью и целиком преображается.
В прошлой версии бант прятался в реке.
В схеме 3.0 он повязан на ленту реки.
Пока готовим анонс, получаем известие об открытии трех станций: «Технопарк», «Румянцево» и «Саларьево». К открытию «Саларьева» нужно внести изменения в схему:
— «Нагатинскую» и «Нагорную» вынести за пределы МКЖД;
– МКЖД переименовать во Вторую кольцевую;
– добавить «Севастопольский проспект» на Вторую кольцевую.
Появляется еще немного времени на добавление станций, заодно успеваем провести небольшую работу над шероховатостями.
Пересадка «Полежаевская» — «Хорошево» отличалась от других длиной.
Физически она самая длинная — 850 метров. Но на схеме два вида пересадок на Вторую кольцевую: в «теплом» контуре и уличные. Градаций по длине нет. Это был компромисс из-за сжатых сроков разработки.
Хронологическое отступление
В первых вариантах схемы со смещенными кольцами было достаточно места для пяти станций с двумя пересадками.
Одно время мы думали, что пересадки длиной больше 300 метров показывать не нужно. И на пересечении Второй кольцевой с седьмой линией пересадок не стало. Жаться не надо, станции расставляем свободно, и получается красота.
Позже узнаём, что такие пересадки надо показать. Это означает появление связей «Хорошево» — «Полежаевская» и «Ходынка» — «Октябрьское Поле» вновь. И между ними нужно запихнуть «Новопесчаную».
Хоть пересадки и стоят под разными углами, но, кажется, все хорошо. Все пять станций стоят неплохо, на надписи голубой линии не давят. Однако при таком раскладе «Волоколамская» залезает на зеленую ветку — много чести для строящейся станции.
Но все разрешимо: разводим «Щукинскую» и «Спартак», чтобы поставить «Волоколамскую», а «Новопесчаную» ставим над «Хорошево».
Но после бессонной ночи с перерисовкой схемы станциям становится совсем тесно, особенно «Новопесчаной».
И вот, чтобы дать ей вздохнуть, приходится растягивать пересадку.
Назад в настоящее
Мы нашли способ укоротить злосчастную пересадку.
Также поправляем верх схемы. Расставляем как следует ребят в коммунальной квартире имени «Петровско-Разумовской» и поворачиваем наверх монорельс, чтобы в освободившемся месте разместить станции с обеих сторон Сокольнической линии.
Разобравшись с этим, переходим к перемещению станций. Поначалу кажется, что перемещение и добавление новой станции на схему, которая проектировалась с другими требованиями, откроет портал в ад. Сперва просто передвинули станции. Получилось не настолько ужасно, как казалось.
Чтобы разместить все станции, осторожно вытягиваем южные линии. Но немного — схема должна остаться в рамках формата. Осталось понять, как органично заполнить получившееся место.
От лишних надписей все же отказываемся.
Пока схема ждет печати, Вселенная посылает нам новые иконки.
Арт-директор предлагает заполнить пустоту внизу колец контурным логотипом метро.
Или подписью Москвы-реки?
Нет, пусть пока там будет контурный логотип.
Часть II
Из каких частей состоит круг?
Части круга
Окружность (или периметр) круга состоит из множества точек, находящихся на одинаковом расстоянии (равноудаленном) от центра круга.
Дуга является частью окружности круга. Если дуга больше половины окружности, то она называется большой дугой. Если она меньше половины окружности, ее называют малой дугой.
Диаметр 1nhxanhfkss.3.$blocks-article-row-2.1:$zk6cqp3-2=10.1.1.$3.$1″> делит круг точно пополам и проходит через центр.
Радиус составляет половину длины диаметра и соединяется с центром одним концом.
Хорда — это прямая линия внутри круга, которая касается окружности в 2 точках, но не касается центра окружности.
Касательная — это прямая линия вне круга, которая касается окружности только в одной точке.
1.1.$7″> Сегмент — это область, ограниченная хордой и дугой (похожа на дольку апельсина или грейпфрута).
Сектор — это область, ограниченная 2 радиусами (радиусами) и дугой (выглядит как кусок торта или пиццы).
Пересечение линии и окружности
В этом уроке речь пойдет о пересечении прямой и окружности .
Из-за его длины я разделю урок на три части. В первом речь пойдет о положении линии относительно окружности. Второй выведет небольшое выражение для получения длины хорды, пересекаемой окружностью на прямой.В последней части будут обсуждаться условия, при которых линия становится касательной к окружности.
Начнем.
Пересечение линии и окружности
Имея линию и окружность, линия может либо
- пересекают окружность в двух разных точках,
- коснуться круга только в одной точке или
- вообще не пересекают круг.

Перетащите ползунок в симуляции, чтобы изучить это.
Что будет определять, будет ли эта линия пересекать окружность в двух разных точках, касаться окружности в одной точке или не будет пересекать окружность ни в одной точке?
Есть два способа думать об этом.
Метод 1Пусть уравнение окружности будет x 2 + y 2 = a 2 , а уравнение прямой будет y = mx + c .
Во-первых, если мы попытаемся «решить» два уравнения с двумя неизвестными, я получу квадратное уравнение в x , которое выглядит так
(1 + m 2 )x 2 + 2cmx + c 2 – a 2 = 0
Что геометрически означают корни этого квадрата (скажем, x 1 и x 2 )?
Теперь, если вы помните, когда мы говорили об уравнениях в целом, x и y в уравнениях представляют соответственно x и y координаты всех точек на кривой. Следовательно, корни предыдущего уравнения будут представлять собой координаты x точек пересечения прямой и окружности.
Следовательно, корни предыдущего уравнения будут представлять собой координаты x точек пересечения прямой и окружности.
Фактически, решая любые два уравнения координатной геометрии, мы получаем x (или y ) координат точек пересечения двух кривых, представленных уравнениями.
На данный момент меня интересуют не сами корни, а их природа. Теперь вот ссылка — если мы получим два разных действительных корня, то прямая пересечет окружность в двух разных точках.Если мы получим два совпадающих корня, то прямая касается окружности только в одной точке (т.е. в двух совпадающих точках). Наконец, если мы не получим никаких действительных корней из сформированного уравнения, линия не будет касаться или пересекать окружность.
И как вы это определите? Природа корней квадратного уравнения связана с его дискриминантом. Итак, все, что нам нужно сделать, это найти дискриминант квадратного уравнения и проверить его знак. Положительный знак означает пересечение в двух различных точках, нуль означает касание, а отрицательный знак означает, что линия не пересекает окружность и не касается ее.
Вот цифра, обобщающая то, что я только что сказал.
Точно такой же метод можно было бы использовать для определения положения линии в случае других конических сечений, т. е. параболы, эллипса и гиперболы.
Но в случае с кругами геометрические свойства несколько упростят задачу. Вот как.
Метод 2Чтобы определить положение линии относительно окружности, все, что нам нужно сделать, это найти ее расстояние от центра окружности и сравнить его с ее радиусом.Тогда
- если расстояние меньше радиуса, линия должна пересекать окружность в двух различных точках.
- если расстояние равно радиусу, то линия будет касаться окружности.
- , если расстояние больше радиуса, линия будет лежать полностью за пределами круга.
Вот еще одна симуляция, в которой вы можете наблюдать вышеуказанные условия.
Надеюсь, это было проще понять, чем сложное квадратное уравнение.
Итоги урока
Чтобы определить положение линии относительно окружности, найдем ее расстояние от центра окружности. Пусть d будет этим расстоянием, а r будет радиусом окружности. Тогда
Пусть d будет этим расстоянием, а r будет радиусом окружности. Тогда
- если d < r , то линия пересекает круг в двух различных точках.
- если d = r , то линия касается окружности в одной точке.
- если d > r , то линия не пересекает/не касается окружности.
Я продолжу с несколькими связанными примерами в следующем уроке, прежде чем перейти ко второй части.
углов в круге – объяснение и примеры
Концепция углов необходима при изучении геометрии, особенно в кругах. Вы уже видели несколько теорем , связанных с окружностями , и все они включают в себя углы.
Эта статья посвящена исключительно углам окружности.
Вы также узнаете, как найти угол в окружности.Для определения углов и частей окружности вы можете обратиться к предыдущим статьям. Вы также узнаете, что влечет за собой внутренний угол и внешний угол круга.
Что такое угол окружности?
Каков угол окружности? Или, точнее, как можно образовать угол внутри фигуры, у которой нет краев?
Ответ состоит в том, что углы образуются внутри круга с радиусами, хордами и касательными. Давайте посмотрим на это ниже. Угол окружности — это угол, образованный между радиусами, хордами или касательными окружности.
Мы видели разные типы углов в разделе «Углы» , но в случае с кругом, в основном, есть четыре типа углов. Это центральный, вписанный, внутренний и внешний углы. Давайте рассмотрим каждый из них по отдельности ниже.
Центральный угол образован двумя радиусами, а его вершина лежит в центре окружности.
На приведенной выше диаграмме ∠ AOB = центральный угол
, где дуга AB — это дуга, на которую она опирается.
В окружности сумма центрального угла малого и большого сегментов равна 360 градусам.
С другой стороны, вписанный угол образован между двумя хордами, вершина которых лежит на окружности.
На приведенном выше рисунке ∠ AOB — это вписанный угол.
Как найти меру угла?
Как найти центральный угол:
Формула для нахождения центрального угла:
Центральный угол = (длина дуги x 360)/2πr
, где r — радиус окружности.
Как найти вписанный угол:
Формула для вписанного угла:
Вписанный угол = ½ дуги, проведенной между точками
Ранее мы изучали внутренние и внешние углы треугольников и многоугольников. Пришло время изучить их и для кругов.
Внутренний угол окружности
Внутренний угол окружности образован на пересечении двух линий, пересекающихся внутри окружности.
На диаграмме выше, если b и a являются дугами, пересекаемыми, то внутренний угол x равен половине суммы дуг.
x = ½ (b + a)
Внешний угол окружности
Внешний угол окружности — это угол, вершина которого находится вне окружности, а стороны угла являются секущими или касательными круг.
Величина внешнего угла равна половине разности величин образуемых дуг.
Формула для наружного угла дана
Внешний угол, ∠ 7 BoA = ½ (b — a)
Позвольте работать на нескольких примерах:
Пример 1
Найдите центральный угол отрезка, длина дуги которого равна 15.7 см, а радиус 6 см.
Решение
Центральный угол = (длина дуги x 360)/2πr
Центральный угол = (15,7 x 360)/2 x 3,14 x 6 угол 150 градусов.
Пример 2
На приведенной ниже диаграмме пересекаемые дуги составляют 60 градусов и 120 градусов соответственно.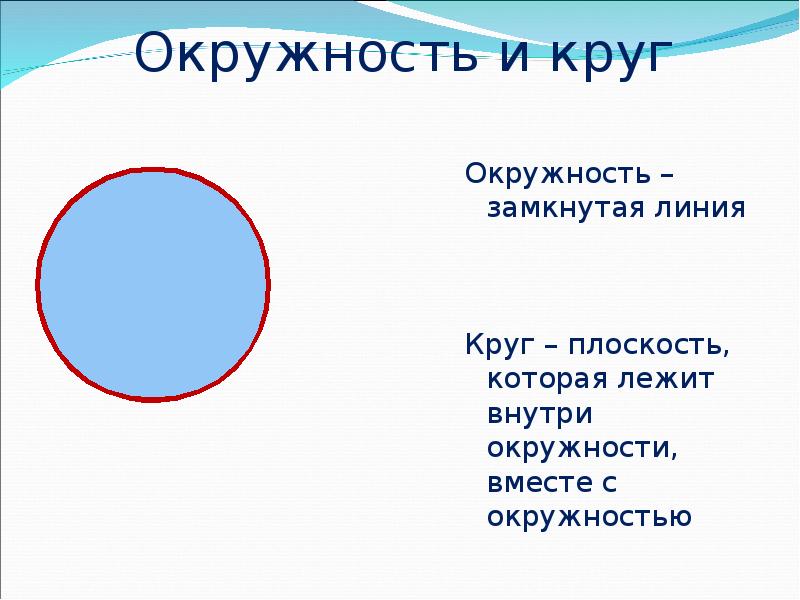 Найдите градусную меру внешнего угла x?
Найдите градусную меру внешнего угла x?
Решение
Внешний угол, х = ½ (b – a)
х = ½ (120º – 60º)
х = 30 0 8 30 градусов.
Пример 3
Найдите величину недостающего центрального угла в следующем круге.
Решение
Сумма центральных углов окружности = 360°
80° + 120° + x = 360°
Упростить.
200° + x = 360°
Вычесть по 200° с обеих сторон.
x = 160 º
Следовательно, недостающий центральный угол равен 160 градусам.
Пример 4
Какова мера ∠BOA и ∠AOE в круге, показанном ниже?
Решение
Так как BE — прямая (диаметр окружности), то
∠BOA + AOE = 180°
(x + 50) ° + (x + 180) ° =
2x + 60°= 180°
Вычтите 60° с обеих сторон.
2x = 120°
Разделив обе стороны на 2, мы получим
x = 60°
Теперь подставим.
(x + 50) ° = 60° + 50°
= 110°
(x + 10) ° = 60° + 10°
= 70°
Следовательно, мера ∠BOA и ∠AOE составляет 110° и 70° соответственно.
Пример 5
Найдите внутренний угол следующей окружности.
Решение
Дано измерение пересекаемых дуг как 150° и 100°.
Внутренний угол, x = ½ (150° + 100°)
= ½ x 250°
=125°
Таким образом, внутренний угол равен 125°.
Предыдущий урок | Главная страница | Следующий урокОкружности, дуги и сектора
Окружность
Окружность состоит из трех основных компонентов:
- Окружность, которая является внешним краем круга.
- Радиус, который проходит от любой точки окружности до центра окружности.

- Диаметр, соединяющий окружность через центр окружности.
Вычисление длины окружности
Между всеми окружностями существует взаимосвязь, так что длина окружности, деленная на диаметр, всегда имеет одно и то же отношение.
Это отношение называется Пи, 16-й буквой греческого алфавита, которая является иррациональным числом и имеет символ π.
переставляя это дает формулу
Очень часто π доводят до 2 знаков после запятой и используют значение 3.14
Пример
Найдите длину окружности диаметром 4 см.
Используйте кнопку «пи» на калькуляторе и дайте правильный ответ с точностью до двух знаков после запятой.
Так как диаметр круга в два раза больше его радиуса, d=2r
Пример
Найдите длину окружности, радиус которой 4 см.
Используйте кнопку «пи» на калькуляторе и дайте правильный ответ с точностью до двух знаков после запятой.
Площадь круга
Чтобы найти площадь круга, попробуйте подсчитать количество квадратов внутри него.
Это даст приблизительную площадь.
Можно также разрезать круг на сегменты и выложить их рядом друг с другом.
Здесь круг разделен на 8 равных частей.
Когда круг разрезается на все более мелкие части, получается прямоугольник.
Используя уравнение Площадь = длина x ширина,
Пример
Найдите площадь круга радиусом 4 см.
Используйте кнопку «пи» на калькуляторе и дайте правильный ответ с точностью до двух знаков после запятой.
Пример
Найдите площадь круга диаметром 4 см.
Используйте кнопку «пи» на калькуляторе и дайте правильный ответ с точностью до двух знаков после запятой.![]()
так
Дуги и сектора – Терминология
Дуга является частью кривой.
Это часть длины окружности.
Сектор – это часть окружности, заключенная между двумя радиусами.
Хорда – это линия, соединяющая две точки на кривой.
Хорда может быть диаметром
Уравнение дуг и секторов
так
Дуги
Пример
Какова длина дуги АВ?
Пример
Найдите радиус следующей окружности:
Секторы
Пример
Какова площадь сектора AOB?
Пример
Найдите радиус следующей окружности:
Пример
Какова длина дуги AB ?
Хорды, биссектрисы и касательные
Касательная касается окружности только в одной точке.
Пифагор в круге
Пример
Какое значение x ?
Уменьшите радиус!
По теореме Пифагора
Угол в полуокружности
Угол в полуокружности равен 90°
© Александр Форрест
Длина хорды, разделенная на равные сегменты
Калькулятор длины хорды
радиус (м, фут ..)
нет. отрезки
Длину — L — хорды при делении окружности на равное количество отрезков можно рассчитать по таблице ниже. Длина хорды — L — в таблице указана для «единичного круга» с радиусом = 1 .
Чтобы вычислить фактическую длину хорды, умножьте длину «единичного круга» — L — на радиус фактического круга.
Пример — Длина хорды
Окружность с радиусом 3 м разделена на 24 сегмента .Из таблицы ниже: длина — L — одной хорды в «единичной окружности» с 24 сегментами составляет 0,2611 единиц .
Длина хорды для окружности с радиусом 3 м может быть рассчитана как
0,2611 (3 м) = 0,7833 м
Суммарная длина всех хорд в окружности может быть рассчитана как
(0,7833 м) 24
= 6,2653 (3 м)
= 18.7959 м
Окружность круга может быть рассчитана как
C = 2 π R
= 2 π (3 м)
= 18,8496 м
9| Количество Сегменты — N — N — — N — | Центральный угол — θ — | длина одного аккорда — L — — L — — L — | ||||
|---|---|---|---|---|---|---|
| градусов | ||||||
| 2 | 180. 0000 0000 | 3,1416 | 2,0000 | 4,0000 | ||
| 4 | 90,0000 | 1,5708 | 1,4142 | 5,6569 | ||
| 6 | 60,0000 | 1,0472 | 1,0000 | 6,0000 | ||
| 8 | 45.0000 | 0.7854 | 0.7654 | 6.1229 | ||
| 10 | 10 | 36.0000 | 0.6283 | 0.6180 | 6,1803 | |
| 12 | +30,0000 | 0,5236 | 0,5176 | 6,2117 | ||
| 14 | 25,7143 | 0,4488 | 0,4450 | 6,2306 | ||
| 16 | 22,5000 | 0,3927 | 0.3902 | 6.2429 | ||
| 18 | 18 | 20.0000 | 0.3491 | 0.3473 | 6.2513 | |
| 20 | 18.0000 | 0,3142 | 0,3129 | 6,2574 | ||
| 22 | 16,3636 | 0,2856 | 0,2846 | 6,2619 | ||
| 24 | 15,0000 | 0,2618 | 0,2611 | 6,2653 | ||
| 26 | 13. 8462 8462 | 2 | 0.2417 | 0.2411 | 6.2679 | |
| 28 | 28 | 12.8571 | 0.2244 | 0.2239 | 6,2700 | |
| 30 | +12,0000 | 0,2094 | 0,2091 | 6,2717 | ||
| 32 | 11,2500 | 0,1963 | 0,1960 | 6,2731 | ||
| 34 | 10,5882 | 0,1848 | 0.1845 | 6.2742 | ||
| 36 | 10.0000 | 10.0000 | 0.1745 | 0.1743 | 6.2752 | |
| 9 | 9.4737 | +0,1653 | 0,1652 | 6,2760 | ||
| 40 | 9,0000 | 0,1571 | 0,1569 | 6,2767 | ||
| 42 | 8,5714 | 0,1496 | 0,1495 | 6,2773 | ||
| 44 | 8.1818 | 8.1818 | 0.1428 | 0.1427 | 6.2778 | |
| 46 | ||||||
| 46 | 7. 8261 8261 | 0.1366 | 0.1365 | 6,2783 | ||
| 48 | +7,5000 | 0,1309 | 0,1308 | 6,2787 | ||
| 50 | 7,2000 | 0,1257 | 0,1256 | 6,2791 | ||
| 52 | 6,9231 | 0,1208 | 0.1208 | 6.2794 | ||
| 54 | ||||||
| 54 | 6.6667 | 0.1164 | 0.1163 | 6.2796 | ||
| 56 | 6.4286 | +0,1122 | 0,1121 | 6,2799 | ||
| 58 | 6,2069 | 0,1083 | 0,1083 | 6,2801 | ||
| 60 | 6,0000 | 0,1047 | 0,1047 | 6,2803 | ||
| 62 | 5.8065 | 0.1013 | 0.1013 | 6.2805 | ||
| 64 | ||||||
| 64 | 5.6250 | 0.0982 | 0.0981 | 6,2807 | ||
| 66 | 5,4545 | 0,0952 | 0,0952 | 6,2808 | ||
| 68 | 5,2941 | 0,0924 | 0,0924 | 6,2810 | ||
| 70 | 5,1429 | 0,0898 | 0. 0897 0897 | 6.2811 | ||
| 72 | 72 | 50000666 | 5.0873 | 0.0872 | 6.2812 | |
| 74 | 4.8649 | 0,0849 | 0,0849 | 6,2813 | ||
| 76 | 4,7368 | 0,0827 | 0,0826 | 6,2814 | ||
| 78 | 4,6154 | 0,0806 | 0,0805 | 6,2815 | ||
| 80 | 4.5000 | 0.0785 | 0.0785 | 6.2816 | ||
| 82 | ||||||
| 82 | 43902 | 0.0766 | 0.0766 | 6.2816 | ||
| 84 | 4.2857 | 0,0748 | 0,0748 | 6,2817 | ||
| 86 | 4,1860 | 0,0731 | 0,0730 | 6,2818 | ||
| 88 | 4,0909 | 0,0714 | 0.0714 | 6.2819 | ||
| 40000 | 0.0698 | 0,0698 | 0,0698 | 6. 2819 2819 | ||
| 92 | 3.9130 | 0,0683 | 0,0683 | 6,2820 | ||
| 94 | 3,8298 | 0,0668 | 0,0668 | 6,2820 | ||
| 96 | 3,7500 | 0,0654 | 0,0654 | 6,2821 | ||
| 98 | 3.6735 | 0.0641 | 0.0641 | 6.2821 | ||
| 100 | 100 | 36000 | 0.0628 | 0.0628 | 6,2822 | |
| 102 | 3,5294 | 0,0616 | 0,0616 | 6,2822 | ||
| 104 | 3,4615 | 0,0604 | 0,0604 | 6,2822 | ||
| 106 | 3,3962 | 0,0593 | 0.0593 | 6.2823 | ||
| 108 | ||||||
| 108 | 33333 | 0,0582 | 0,0582 | 6.2823 | ||
| 110 | 3.2727 | 0,0571 | 0,0571 | 6,2823 | ||
| 112 | 3,2143 | 0,0561 | 0,0561 | 6,2824 | ||
| 114 | 3,1579 | 0,0551 | 0,0551 | 6,2824 | ||
| 116 | 3. 1034 1034 | 0.0542 | 0,0542 | 6.2824 | ||
| 9 | ||||||
| 118 | 3,0508 | 0,0532 | 0.0532 | +6,2824 | ||
| 120 | 3,0000 | 0,0524 | 0,0524 | 6,2825 | ||
| 122 | 2,9508 | 0,0515 | 0,0515 | 6,2825 | ||
| 124 | 2,9032 | 0,0507 | 0.0507 | 6.2825 | ||
| 126 | ||||||
| 126 | 28571 | 0,0499 | 0,0499 | 0,0499 | 6.2825 | |
| 128 | 2.8125 | 0,0491 | 0,0491 | 6,2826 | ||
| 130 | 2,7692 | 0,0483 | 0,0483 | 6,2826 | ||
| 132 | 2,7273 | 0,0476 | 0,0476 | 6,2826 | ||
| 134 | 2.6866 | 0.0469 | 0.0469 | 6.2826 | ||
| 136 | ||||||
| 136 | 26471 | 0. 0462 0462 | 0.0462 | 6,2826 | ||
| 138 | 2,6087 | 0,0455 | 0,0455 | 6,2826 | ||
| 140 | 2,5714 | 0,0449 | 0,0449 | 6,2827 | ||
| 142 | 2,5352 | 0,0442 | 0.0442 | 6.2827 | 6.2827 | |
| 144 | ||||||
| 144 | 2,5000 | 0,0436 | 0.0436 | 6.2827 | ||
| 146 | 2.4658 | 0,0430 | 0,0430 | 6,2827 | ||
| 148 | 2,4324 | 0,0425 | 0,0425 | 6,2827 | ||
| 150 | 2,4000 | 0,0419 | 0,0419 | 6,2827 | ||
| 152 | 2.3684 | 23684 | 0.0413 | 0.0413 | 6.2827 | |
| 154 | ||||||
| 154 | 23377 | 0.0408 | 0.0408 | 6,2827 | ||
| 156 | 2,3077 | 0,0403 | 0,0403 | 6,2828 | ||
| 158 | 2,2785 | 0,0398 | 0,0398 | 6,2828 | ||
| 160 | 2,2500 | 0,0393 | 0. 0393 0393 | 6.2828 | ||
| 162 | ||||||
| 162 | 22222 | 0,0388 | 0.0388 | 6.2828 | ||
| 164 | 2.1951 | 0,0383 | 0,0383 | 6,2828 | ||
| 166 | 2,1687 | 0,0379 | 0,0378 | 6,2828 | ||
| 168 | 2,1429 | 0,0374 | 0,0374 | 6,2828 | ||
| 170 | 2.1176 | 0.0370 | 0.0370 | 6.2828 | ||
| 172 | ||||||
| 172 | 2,0930 | 0,0365 | 0.0365 | 6.2828 | ||
| 174 | 2,0690 | 0,0361 | 0,0361 | 6,2828 | ||
| 176 | 2,0455 | 0,0357 | 0,0357 | 6,2829 | ||
| 178 | 2,0225 | 0,0353 | 0.0353 | 0.0353 | 6.2829 | |
| 180 | ||||||
| 180 | 2,0000 | 0,0349 | 0,0349 | 0. 0349 0349 | 6.2829 | |
| 182 | 1.9780 | 0,0345 | 0,0345 | 6,2829 | ||
| 184 | 1,9565 | 0,0341 | 0,0341 | 6,2829 | ||
| 186 | 1,9355 | 0,0338 | 0,0338 | 6,2829 | ||
| 188 | 1.9149 | 0.0334 | 0.0334 | 6.2829 | ||
| 190 | 190 | 1.8947 | 0.0331 | 0.0331 | 6,2829 | |
| 192 | 1,8750 | 0,0327 | 0,0327 | 6,2829 | ||
| 194 | 1,8557 | 0,0324 | 0,0324 | 6,2829 | ||
| 196 | 1,8367 | 0,0321 | 0.0321 | 0.0321 | 6.2829 | |
| 198 | ||||||
| 198 | 1.8182 | 0.0317 | 0,0317 | 6.2829 | ||
| 200 | 1.8000 | 0,0314 | 0,0314 | 6,2829 | ||
| 202 | 1,7822 | 0,0311 | 0,0311 | 6,2829 | ||
| 204 | 1,7647 | 0,0308 | 0,0308 | 6,2829 | ||
| 206 | 1. 7476 7476 | 0.0305 | 0.0305 | 6.2829 | ||
| 208 | 1,7308 | 0,0302 | 0.0302 | +6,2829 | ||
| 210 | 1,7143 | 0,0299 | 0,0299 | 6,2830 | ||
| 212 | 1,6981 | 0,0296 | 0,0296 | 6,2830 | ||
| 214 | 1,6822 | 0,0294 | 0.0294 | 6.2830 | ||
| 216 | ||||||
| 216 | 216 | 1.6667 | 0.0291 | 0,0291 | 6.2830 | |
| 218 | 1.6514 | 0,0288 | 0,0288 | 6,2830 | ||
| 220 | 1,6364 | 0,0286 | 0,0286 | 6,2830 | ||
| 222 | 1,6216 | 0,0283 | 0,0283 | 6,2830 | ||
| 224 | 1.6071 | 0.0280 | 0.0280 | 6.2830 | ||
| 226 | 226 | 1. 5929 5929 | 0.0278 | 0.0278 | 6,2830 | |
| 228 | 1,5789 | 0,0276 | 0,0276 | 6,2830 | ||
| 230 | 1,5652 | 0,0273 | 0,0273 | 6,2830 | ||
| 232 | 1,5517 | 0,0271 | 0.0271 | 6.2830 | ||
| 234 | ||||||
| 234 | 234 | 1,5385 | 0,0269 | 0,0269 | 6.2830 | |
| 236 | 1.5254 | 0,0266 | 0,0266 | 6,2830 | ||
| 238 | 1,5126 | 0,0264 | 0,0264 | 6,2830 | ||
| 240 | 1,5000 | 0,0262 | 0,0262 | 6,2830 | ||
| 242 | 1.4876 | 0.0260 | 0.0260 | 6.2830 | ||
| 244 | ||||||
| 244 | 1.4754 | 0.0258 | 0.0258 | 6,2830 | ||
| 246 | 1,4634 | 0,0255 | 0,0255 | 6,2830 | ||
| 248 | 1,4516 | 0,0253 | 0,0253 | 6,2830 | ||
| 250 | 1,4400 | 0,0251 | 0. 0251 0251 | 0.0251 | 6.2830 | |
| 252 | ||||||
| 252 | 1.4286 | 0,0249 | 0,0249 | 6.2830 | ||
| 254 | 1.4173 | 0,0247 | 0,0247 | 6,2830 | ||
| 256 | 1,4063 | 0,0245 | 0,0245 | 6,2830 | ||
| 258 | 1,3953 | 0,0244 | 0,0244 | 6,2830 | ||
| 260 | 1.3846 | 0.0242 | 0.0242 | 6.2830 | ||
| 262 | ||||||
| 262 | 1,3740 | 0,0240 | 0.0240 | 6,2830 | ||
| 264 | 1,3636 | 0,0238 | 0,0238 | 6,2830 | ||
| 266 | 1,3534 | 0,0236 | 0,0236 | 6,2830 | ||
| 268 | 1,3433 | 0,0234 | 0.0234 | 0.0234 | 6.2830 | |
| 270 | ||||||
| 270 | 1,3333 | 0,0233 | 0,0233 | 6. 2830 2830 | ||
| 272 | 1.3235 | 0,0231 | 0,0231 | 6,2830 | ||
| 274 | 1,3139 | 0,0229 | 0,0229 | 6,2830 | ||
| 276 | 1,3043 | 0,0228 | 0,0228 | 6,2830 | ||
| 278 | 1.2950 | 0.0226 | 0.0226 | 6.2831 | ||
| 280 | ||||||
| 280 | 1.2857 | 0.0224 | 0.0224 | 6,2831 | ||
| 282 | 1,2766 | 0,0223 | 0,0223 | 6,2831 | ||
| 284 | 1,2676 | 0,0221 | 0,0221 | 6,2831 | ||
| 286 | 1,2587 | 0,0220 | 0.0220 | 6.2831 | ||
| 288 | ||||||
| 288 | 288 | 1.2500 | 0,0218 | 0.0218 | 0.0218 | 6.2831 |
| 290 | 1.2414 | 0,0217 | 0,0217 | 6,2831 | ||
| 292 | 1,2329 | 0,0215 | 0,0215 | 6,2831 | ||
| 294 | 1,2245 | 0,0214 | 0,0214 | 6,2831 | ||
| 296 | 1. 2162 2162 | 0.0212 | 0.0212 | 6.2831 | ||
| 298 | 1.2081 | 0.0211 | 0.0211 | 6,2831 | ||
| в 300 | 1,2000 | 0,0209 | 0,0209 | 6,2831 | ||
| 302 | 1,1921 | 0,0208 | 0,0208 | 6,2831 | ||
| 304 | 1,1842 | 0,0207 | 0.0207 | 6.2831 | ||
| 306 | ||||||
| 306 | 1,1765 | 0.0205 | 0.0205 | 0.0205 | 6.2831 | |
| 308 | 1.+1688 | 0,0204 | 0,0204 | 6,2831 | ||
| 310 | 1,1613 | 0,0203 | 0,0203 | 6,2831 | ||
| 312 | 1,1538 | 0,0201 | 0,0201 | 6,2831 | ||
| 314 | 1.1465 | 0,0200 | 0.0200 | 6.2831 | ||
| 316 | ||||||
| 316 | 1. 1392 1392 | 0,0199 | 0.0199 | 6,2831 | ||
| 318 | 1,1321 | 0,0198 | 0,0198 | 6,2831 | ||
| 320 | 1,1250 | 0,0196 | 0,0196 | 6,2831 | ||
| 322 | 1,1180 | 0,0195 | 0.0195 | 6.2831 | ||
| 324 | 324 | 1.1111 | 0,0194 | 0.0194 | 0,0194 | 6.2831 |
| 326 | 1.1043 | 0,0193 | 0,0193 | 6,2831 | ||
| 328 | 1,0976 | 0,0192 | 0,0192 | 6,2831 | ||
| 330 | 1,0909 | 0,0190 | 0,0190 | 6,2831 | ||
| 332 | 1.0843 | 0.0189 | 0.0189 | 6.2831 | ||
| 334 | 1,0778 | 0.0188 | 0.0188 | 6,2831 | ||
| 336 | 1,0714 | 0,0187 | 0,0187 | 6,2831 | ||
| 338 | 1,0651 | 0,0186 | 0,0186 | 6,2831 | ||
| 340 | 1,0588 | 0,0185 | 0. 0185 0185 | 6.2831 | ||
| 342 | 342 | 1.0526 | 0,0184 | 0.0184 | 6.2831 | |
| 344 | 1.0465 | 0,0183 | 0,0183 | 6,2831 | ||
| 346 | 1,0405 | 0,0182 | 0,0182 | 6,2831 | ||
| 348 | 1,0345 | 0,0181 | 0,0181 | 6,2831 | ||
| 350 | 1.0286 | 0.0180 | 0.0180 | 6.2831 | ||
| 352 | ||||||
| 352 | 1.0227 | 0.0178 | 0.0178 | 6,2831 | ||
| 354 | 1,0169 | 0,0177 | 0,0177 | 6,2831 | ||
| 356 | 1,0112 | 0,0176 | 0,0176 | 6,2831 | ||
| 358 | 1,0056 | 0,0176 | 0.0176 | 6.2831 | ||
| 360 | 1.0000 | 0,0175 | 0. 0175 0175 | 0,0175 | 6.2831 | |
Иллюстративная математика
Задача
Мистер.Уоткинс попросил своих учеников провести линию симметрии окружности. с центром $O$, изображенным ниже:
Лиза нарисовала рисунок ниже. Лиза права?
Брэд нарисовал картинку ниже. Изображение Брэда правильное?
- Сколько осей симметрии у окружности? Объяснять.
- Объясните, почему каждая линия симметрии делит окружность пополам.
- Объясните, почему каждая линия симметрии окружности должна проходить через центр.
Комментарий IM
Окружность имеет бесконечное число симметрий. Это контрастирует с многоугольниками
такие как треугольники и четырехугольники, рассмотренные в 4.G Линии симметрии треугольников
и
4.G Линии симметрии четырехугольников. Круг в каком-то смысле является наиболее симметричной двухмерной фигурой, и отчасти поэтому он так знаком. Монеты, циферблаты, колеса, изображение полной луны в небе: все это примеры кругов, с которыми мы сталкиваемся регулярно.
Монеты, циферблаты, колеса, изображение полной луны в небе: все это примеры кругов, с которыми мы сталкиваемся регулярно.
Это учебная задача, которая дает учащимся возможность рассуждать о линиях симметрии и обнаружить, что круг имеет бесконечное количество линий симметрии. Несмотря на то, что понятие бесконечного числа линий довольно абстрактно, четвероклассники могут понимать бесконечность неформальным образом. Точно так же, как между любыми двумя дробями на числовой прямой всегда есть дробь, всегда есть другая линия, проходящая через центр круга «между» любыми двумя линиями, проходящими через центр круга.Итак, если вы определите определенное количество линий, вы можете утверждать, что всегда есть как минимум еще одна.
В старших классах учащиеся должны вернуться к этому заданию с двух точек зрения:
- Алгебраическая перспектива, использующая уравнение, определяющее круг, и
- Геометрическая перспектива с использованием определения отражений с точки зрения перпендикулярных линий.

Эта задача включает в себя экспериментальный рабочий лист GeoGebra с целью что инструкторы могли бы использовать его для более интерактивной демонстрации соответствующий содержательный материал.Файл следует считать черновиком версию, и отзывы о ней в разделе комментариев весьма поощряется как с точки зрения предложений по улучшению, так и с точки зрения идей по его эффективному использованию. Файл можно запустить через бесплатный онлайн приложение GeoGebra или запустите локально, если GeoGebra была установлена на компьютере.
найти длину части прямой y=4-2x, лежащей внутри окружности радиусом 3 с центром в начале координат
Окружность с центром в точке (h,k) и радиусом r равна (x-h) 2 +(y-k) 2 = r 2
круг радиусом 3 с центром в начале координат:
x 2 + y 2 = 9 {уравнение 1}
y = 4-2x {уравнение 2}
У нас есть круг и линия. Нам нужно найти точки
Нам нужно найти точки
и найдите расстояние между этими двумя точками.
Замените y на 4-2x в первом уравнении и найдите x.
х 2 + (4-2х) 2 = 9
x 2 + 16 — 16x + 4x 2 — 9 = 0
5x 2 — 16x + 7 = 0
Используя квадратное уравнение с a=5, b=-16, c=7
х = [16 ±√((-16) 2 -4(5)(7))]/2(5)
х = (16 ±√116)/10
х = (16 ± 10.77033)/10
х = 26,77033/10 = 2,677033
или
х = 5,22967/10 = 0,522967
У нас есть 2 значения x, где линия пересекает окружность.
Подставьте их в одно из исходных уравнений, чтобы найти соответствующий
значений у. Возьмем y = 4-2x
.
Для х = 2,677033
г = 4 — 2 (2,677033) = -1,354066
Точка пересечения (2.677033, -1.354066)
для х = 0. 522967
522967
у = 4 — 2 (0,522967) = 2,954066
Точка пересечения (0,522967, 2,954066)
Используя формулу расстояния
D из (X 1 , Y 1 ) по (x 2 , Y 2 ) = √ [(x 2 -x 1 ) 2 + (Y 2 — у 1 ) 2 ]
определить расстояние между двумя точками пересечения.
Это будет длина сегмента линии, который находится в пределах
круг.
d = √[(2,677033-0,522967) 2 +(-1,354066-2,954066) 2 ]
= √(4,64000033 + 18,56000133)
= √23.2000166
= 4,816638
Вы можете округлить до необходимого количества знаков после запятой
д ≅ 4,82
.



 Такую вещь нельзя стирать на программе с высоким количеством оборотов, а загружать машинку советуют лишь на 2/3 от допустимого объема белья.
Такую вещь нельзя стирать на программе с высоким количеством оборотов, а загружать машинку советуют лишь на 2/3 от допустимого объема белья. Также этот значок вы увидите на нарядах с пайетками, бисером, стразами и другим декором, способным оторваться при стирке в машинке.
Также этот значок вы увидите на нарядах с пайетками, бисером, стразами и другим декором, способным оторваться при стирке в машинке.


 Такой режим обычно выбирают для обработки хлопковых и льняных изделий.
Такой режим обычно выбирают для обработки хлопковых и льняных изделий.

