Логарифмические неравенства как решаются – Логарифмические уравнения, системы и неравенства — Математика — Теория, тесты, формулы и задачи — Детская игровая комната «Волшебный лес»

Posted on 01.04.202030.12.2019 by alexxlab

Содержание

Решение логарифмических неравенств с переменным основанием

Решение логарифмических неравенств с переменным основанием.

В этой статье мы поговорим о том, как решать логарифмические неравенства, которые содержат неизвестную величину в основании логарифма.

Как мы помним, при решении логарифмических неравенств, мы сравниваем основание логарифма с единицей. Если в основании логарифма стоит выражение, зависящее от неизвестного, то нам надо рассмотреть два случая: когда это выражение больше единицы, и когда оно принимает значение от нуля до единицы.

Но есть и более простой способ.

Рассмотрим решение логарифмического неравенства с переменным основанием в общем виде.

Пусть неравенство имеет вид

$log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Мы помним, что

Если основание логарифма больше единицы (p(x)>1), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется.

Если основание логарифма больше нуля и меньше единицы (0<p(x)<1), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный.

Чтобы не рассматривать эти два случае по отдельности, давайте запишем переход от логарифмов к выражениям, стоящим под знаком логарифма в таком виде:

$log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Знак первого множителя в этом произведении определяет знак второго множителя:

если p(x)>1, то f(x)>g(x) — знак неравенства сохраняется

если 0<p(x)<1, то f(x)<g(x) — знак неравенства меняется на противоположный.

Тогда, с учетом ОДЗ, исходное неравенство

$log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$ $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

будет равносильно системе:

$log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Последние четыре неравенства системы — ОДЗ исходного неравенства.

Решим, для примера, такое неравенство:

$log_{x^2+3x}{(x+3)}<1$

Представим правую часть неравенства в виде логарифма по основанию x^2+3x

Получим неравенство:

$log_{x^2+3x}{(x+3)}<log_{x^2+3x}{(x^2+3x)}$ $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Перейдем к равносильной системе неравенств:

$delim{lbrace}{matrix{4}{1}{{(x^2+3x-1)((x+3)-(x^2+3x))<0} {x+3>0} {x^2+3x>0}{x^2+3x<>1}}}{ }$ $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Решим каждое неравенство системы по отдельности, на своей координатной прямой.

Сначала преобразуем первое неравенство системы к виду

$( x^2+3x-1)({-{x}^2-2x+3})<0$ $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

и решим это неравенство методом интервалов.

Корни квадратного трехчлена в первых скобках:

$x_1={-3+sqrt{13}}/2$ , $x_1={-3-sqrt{13}}/2$

Корни квадратного трехчлена во вторых скобках:

x_1=1 , x_2=-3 .

Нанесем эти корни на координатную прямую и расставим знаки:

x_2=-3

Решение второго неравенства системы:

x>-3 $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Решение третьего неравенства: $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

Теперь совместим решение всех неравенств на одной координатной прямой:

Нас интересует промежуток, над которым проходит три стрелки.

Ответ: .

А теперь я предлагаю вам посмотреть ВИДЕОУРОК, в котором я объясняю решение логарифмического неравенства с переменным основанием и с модулем в выражении, стоящем под знаком логарифма:

$log_{(x^2-2x-3)}{{delim{$ $log_{p(x)}{f(x)}>log_{p(x)}{g(x)}$

И.В. Фельдман, репетитор по математике.

ege-ok.ru

14 . Логарифмические неравенства. Основные методы решения логарифмических неравенств

Логарифмическим неравенством называется такое неравенство, в котором неизвестная величина содержится или под знаком логарифма, или в его основании.

Особенностью решения логарифмических неравенств является учет ОДЗ входящих в него логарифмов. В отличие от логарифмических уравнений, условия, определяющие ОДЗ, целесообразно записывать вместе с решением в одной системе, так как в ходе решения некоторые условия на ОДЗ учитываются сразу. Необходимо внимательно следить за величиной основания логарифма, так как при положительном основании логарифма, которое меньше единицы, знак неравенства меняется на противоположный.

Типы неравенств и способы их решения

Всюду далее f(x), g(x), h(x) – некоторые выражения с переменной.

I тип: неравенство вида: 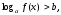(5) где a > 0.

1. Если 0 < a < 1, то неравенство (5) равносильно системе 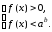(6)

2. Если a > 1, то неравенство (5) равносильно системе

Заметим, что в этом случае первое неравенство системы (6) можно не решать, так как во втором неравенстве 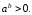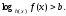(7)

Решение неравенства (7) сводится к решению совокупности двух систем:

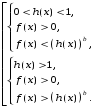
Неравенство f(x) > 0 во второй системе можно не решать, так как оно справедливо при выполнении двух других неравенств этой системы.

II тип: неравенство вида: 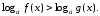(8)

1. Если 0 < a < 1, то неравенство (8) равносильно системе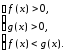(9)

Неравенство g(x) > 0 в системе (9) можно не решать, так как оно выполняется при условии выполнения двух других неравенств этой системы.

2. Если 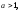то неравенство (8) равносильно системе (10)

Неравенство 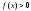в системе (10) можно не решать. 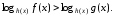(11)

Поскольку в основании содержится переменная величина, то в общем случае решение неравенства (11) зависит от величины основания по сравнению с числом 1. Поэтому решаем совокупность двух систем:

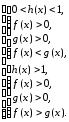
III тип: неравенство вида (12), где F – некоторое выражение относительно

Необходимо заменить 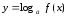и решить неравенство F(y) > 0. Полученные в качестве решения последнего неравенства промежутки записывают в виде неравенств относительно y, а затем возвращаются к старой переменной.

Аналогично решают неравенства I – III типов, в которых вместо знака

> использованы знаки , <, .

15. Основные методы решения тригонометрических уравнений

Простейшие тригонометрические уравнения

1. Уравнение 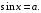(1). Если 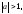то уравнение (1) решений не имеет, так как

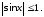
Если 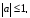то уравнение имеет решение, которое находят по формуле

(2)

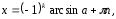
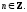
Частные случаи уравнения (1): уравнение 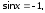решение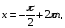

уравнение решение 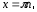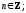уравнение 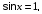решение

2. Уравнение

(3). Если

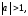то уравнение решений не имеет, так как

Если то уравнение (3) имеет решение, которое находят по формуле (4)

Частные случаи уравнения (3): уравнение 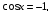решение

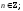
уравнение 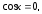решение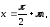 уравнение 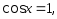решение

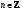
3. Уравнение (5). Решение уравнения (5) находят по формуле

(6). 4. Уравнение

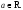(7)

Решение уравнения (7) находят по формуле (8)

Основной путь решения тригонометрических уравнений обычно состоит в приведении этого уравнения к алгебраическому уравнению относительно одной тригонометрической функции одного аргумента. При этом широко используются формулы тождественных преобразований тригонометрических функций.

Метод замены переменных – один из основных при решении тригонометрических уравнений и может применяться как сам по себе, так и в сочетании с другими методами на одном из этапов решения.

Метод разложения на множители заключается в переносе всех слагаемых в одну часть уравнения и разложении ее на множители. После этого уравнение распадается на совокупность нескольких более простых уравнений.

Уравнения вида 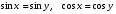и т.п. решаются на основании следующих равносильностей, вытекающих из определения тригонометрических функций и решений простейших тригонометрических уравнений (здесь ):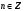

; ;

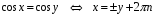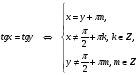
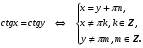
Уравнения вида , , сводятся к квадратному уравнению замено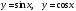й и соответственно.

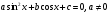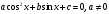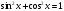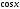Уравнения вида , с помощью формулы предварительно приводятся к квадратному уравнению относительно или 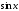соответственно.

Уравнение вида 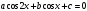после применения формулы и замены 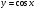сводится к квадратному уравнению.

Уравнение вида 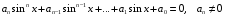заменой 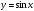сводится к алгебраическому уравнению -й степени. Аналогично решаются подобные уравнения вида, где вместо синуса записаны или .

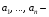Уравнение вида где , действительные числа, называется однородным уравнением -й степени относительно и .

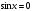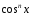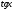Так как корни уравнений и не являются корнями этого уравнения, то делением на или его можно привести к алгебраическому уравнению относительно или .

Уравнение вида сводится к однородному уравнению с помощью формул , , .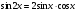

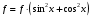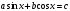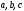Уравнение вида , где – действительные числа, причем 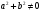, можно решить введением вспомогательного аргумента: .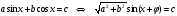

Другие способы решения уравнения :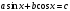

1) с помощью формул синуса и косинуса двойного угла это уравнение можно привести к однородному уравнению, которое затем сводится к квадратному относительно

2) возведением уравнения в квадрат, при этом имеет место равносильность

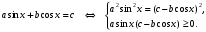
Уравнения вида 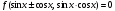, , 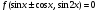где рациональная функция. Поскольку имеет место тождество 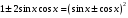, подстановкой (тогда 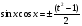, где «+» соответствует подстановке и «–» – подстановке 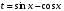) данное уравнение можно свести к рациональному уравнению относительно .

Метод понижения степени состоит в использовании формул понижения степени тригонометрических функций с помощью формул , , , .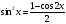

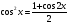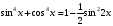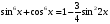Метод преобразования суммы тригонометрических функций в произведение. После применения формул преобразования суммы в произведение уравнение иногда удается либо разложить на множители, либо существенно упростить.

Метод преобразования произведения тригонометрических функций в сумму заключается в применении формул преобразования произведения тригонометрических функций в сумм. После их применения уравнение либо удается либо разложить на множители, либо существенно упростить.

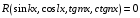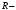Метод универсальной подстановки. Уравнения вида , где рациональная функция, 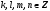, с помощью тригонометрических формул двойного и тройного аргумента, а также формул сложения можно привести к рациональному уравнению относительно 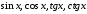. После этого с помощью формул универсальной тригонометрической подстановки

; ; ;

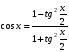исходное уравнение может быть сведено к рациональному уравнению относительно переменной .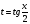

Метод подстановки , которая часто используется при решении уравнений, содержащих 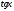и 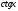. При этом другие тригонометрические функции выражаются через 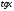по формулам

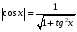, , где .

В результате исходное уравнение может быть сведено к рациональному относительно переменной .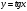

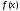Функциональные методы решения. Если уравнение не удается свести с помощью различных преобразований к уравнению того или иного стандартного вида, для которого известен определенный метод решения, может оказаться полезным использование таких свойств функций и , как ограниченность, монотонность, четность, периодичность и др.

studfile.net

Решение систем логарифмических и показательных неравенств с репетитором

До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.

Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.

1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства» и «Решение задач C3 ЕГЭ по математике с репетитором — показательные уравнения и неравенства».

2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.

3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».

Пересечением множеств называется множество, которому принадлежат только те элементы, которые есть у каждого из этих множеств.

Другими словами, если даны два множества 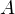и 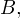то их пересечением будет являться множество следующего вида: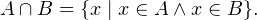 $A \cap B = \{x \mid x\in A \wedge x \in B\}.$

Изображение пересечения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. У Дианы в сумочке находится «множество», состоящее из {ручки, карандаша, линейки, тетрадки, расчески}. У Алисы в сумочке находится «множество», состоящее из {записной книжки, карандаша, зеркальца, тетрадки, котлеты по-киевски}. Пересечением этих двух «множеств» будет «множество», состоящее из {карандаша, тетрадки}, поскольку оба этих «элемента» есть и у Дианы, и у Алисы.

Объединением множеств называется множество, которое состоит из всех элементов исходных множеств.

Другими словами, если даны два множества 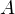и 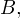то их объединением будет являться множество следующего вида: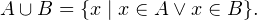 $A \cup B = \{ x \mid x\in A \vee x\in B\}.$

Изображение объединения множеств с помощью «кругов Эйлера»

Объяснение на пальцах. Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из {ручки, карандаша, линейки, тетрадки, расчески, записной книжки, зеркальца, котлеты по-киевски}, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может содержать в себе одинаковых элементов.

Перейдем непосредственно к примерам.

Пример 1. Решите систему неравенств:

$\begin{cases}4^x-6\cdot 2^x+8\geqslant 0, \\ \log_3\frac{2x^2+3x-5}{x+1}\leqslant 1.\end{cases}$

Решение задачи C3.

1. Решаем сперва первое неравенств. Используя замену 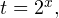t=2^x, переходим к неравенству:

$$t^2-6t+8\geqslant 0\Leftrightarrow \left[\begin{array}{l}t\leqslant 2, \\ t\geqslant 4.\end{array}\right.$

Переходим к обратной подстановке:

$\left[\begin{array}{l}2^x\leqslant 2^1, \\ 2^x\geqslant 2^2\end{array}\right.\Leftrightarrow\left[\begin{array}{l}x\leqslant 1, \\ x\geqslant 2.\end{array}\right.\Leftrightarrow$

$x\in(-\mathcal{1};1]\cup[2;+\mathcal{1}).$

2. Решаем теперь второе неравенство. Область его допустимых значений определяется неравенством:

$\frac{2x^2+3x-5}{x+1}>0\Leftrightarrow x\in(-2,5;-1)\cup(1;+\mathcal{1}).$

В области допустимых значений с учетом того, что основание логарифма 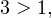3>1, переходим к равносильному неравенству:

$\frac{2x^2+3x-5}{x+1}\leqslant 3\Leftrightarrow \frac{x^2-4}{x+1}\leqslant 0\Leftrightarrow$

$x\in (-\mathcal{1};-2]\cup(-1;2].$

Исключая решения, не входящие в область допустимых значений, получаем промежуток $x\in (-2,5;-2]\cup(1;2].$

3. Ответом к системе неравенств будет пересечение полученных промежутков, то есть $x\in(-2,5;-2]\cup\{2\}.$

Графическое изображение решения системы неравенств задание C3

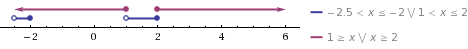
Полученные промежутки на числовой прямой. Решение — их пересечение

Пример 2. Решите систему неравенств:

$\begin{cases} 2^x+16\cdot 2^{-x}\geqslant 17, \\ 2\log_9(4x^2+1)\leqslant \log_3(3x^2+4x+1).\end{cases}$

Решение задачи C3.

1. Решаем сперва первое неравенство. Умножаем обе части на 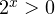2^x>0 и делаем замену 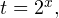t=2^x, в результате чего приходим к неравенству:

$t^2-17t+16\geqslant 0\Leftrightarrow \left[\begin{array}{l}t\leqslant 1, \\ t\geqslant 16.\end{array}\right.$

Переходим к обратной подстановке:

$\left[\begin{array}{l}2^x\leqslant 2^0, \\ 2^x\geqslant 2^4\end{array}\right.\Leftightarrow\left[\begin{array}{l}x\leqslant 0, \\ x\geqslant 4\end{array}\right.\Leftrightarrow$

$x\in(-\mathcal{1};0]\cup[4;+\mathcal{1}).$

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

$\begin{cases}4x^2+1>0, \\ 3x^2+4x+1>0\end{cases}\Leftrightarrow x\in(-\mathcal{1};-1)\cup\left(-\frac{1}{3};+\mathcal{1}\right).$

Воспользовавшись свойствами логарифмов, в области допустимых значений переходим к равносильному неравенству:

$\log_3(4x^2+1)\leqslant\log_3(3x^2+4x+1)\Leftrightarrow$

$4x^2+1\leqslant 3x^2+4x+1\Leftrightarrow x^2-4x\leqslant 0\Leftrightarrow x\in[0;4].$

Данный промежуток целиком входит в область допустимых значений данного неравенства.

3. Общее решение системы будет являться пересечением полученных промежутков, то есть $x=\{0,4\}.$

Графическое изображение полученных числовых промежутков задача C3

Графическое изображение полученных промежуток. Решение системы — их пересечение

Пример 3. Решите систему неравенств:

$\begin{cases}3^x<1+12\cdot 3^{-x}, \\ 2\operatorname{ln}\frac{1}{3x-2}+\operatorname{ln}(5-2x)\geqslant 0.\end{cases}$

Решение задачи C3.

1. Решаем сперва первое неравенство. Умножаем обе его части на 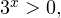3^x>0, после чего получаем неравенство:

$$3^{2x}-3^x-12<0.$

Используя подстановку 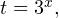t=3^x, переходим к следующему неравенству:

$t^2-t-12<0\Leftrightarrow -3<t<4.$

Переходим к обратной подстановке:

$-3<3^x<4^2\Leftrightarrow x\in(-\mathcal{1};\log_34).$

2. Решаем теперь второе неравенство. Определим сначала область допустимых значений этого неравенства:

$\begin{cases} \frac{1}{3x-2}>0, \\ 5-2x>0 \end{cases}\Leftrightarrow \begin{cases}x>\frac{2}{3}, \\ x<2,5\end{cases}\Leftrightarrow x\in\left(\frac{2}{3}; 2,5\right).$

В области допустимых значений переходим к равносильному неравенству:

$\operatorname{ln}\frac{5-2x}{(3x-2)^2}\geqslant 0\Leftrightarrow \frac{5-2x}{(3x-2)^2}\geqslant 1\Leftrightarrow$

$\frac{9x^2-10x-1}{(3x-2)^2}\leqslant 0\Leftrightarrow x\in\left[\frac{5-\sqrt{34}}{9};\frac{5+\sqrt{34}}{9}\right].$

Обращаем внимание, что

$\frac{5+\sqrt{34}}{9}<\frac{5+\sqrt{36}}{9}=\frac{11}{9}<2,5$

$\frac{5-\sqrt{34}}{9}=\frac{\sqrt{25}-\sqrt{34}}{9}<0<\frac{2}{3}.$

Тогда с учетом области допустимых значений получаем: $x\in\left(\frac{2}{3};\frac{5+\sqrt{34}}{9}\right].$

3. Находим общее решения неравенств. Сравнение полученных иррациональных значений узловых точек — задача в данном примере отнюдь не тривиальная. Сделать это можно следующим образом. Так как

$\frac{5+\sqrt{34}}{9}<\frac{5+\sqrt{39,0625}}{9}=\frac{5}{4},$

$\log_34 = \log_3\sqrt[4]{256}>\log_3\sqrt[4]{243}=\log_33^{\frac{5}{4}} = \frac{5}{4},$

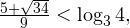то $\frac{5+\sqrt{34}}{9}<\log_34,$ и окончательный ответ к системе имеет вид: $x\in\left(\frac{2}{3};\frac{5+\sqrt{34}}{9}\right].$

Пример 4. Решите систему неравенств:

$\begin{cases}\log_{\log_x 3x}(4x-1)\geqslant 0, \\ 21^x-9\cdot 7^x-3^x+9\leqslant 0.\end{cases}$

Решение задачи С3.

1. Решим сперва второе неравенство:

$7^x\cdot 3^x-9\cdot 7^x-3^x+9\leqslant 0\Leftrightarrow$

$7^x\cdot (3^x-9)-(3^x-9)\leqslant 0\Leftrightarrow$

$(7^x-1)\cdot(3^x-9)\leqslant 0\Leftrightarrow x\in[0;2].$

2. Первое неравенство исходной системы представляет собой логарифмическое неравенство с переменным основанием. Удобный способ решения подобных неравенств описан в статье «Сложные логарифмические неравенства», в его основе лежит простая формула:

$\log_{k(x)}f(x)\lor \log_{k(x)}g(x)\Rightarrow$

$\Rightarrow (f(x)-g(x))\cdot (k(x)-1)\lor 0.$

Вместо знака 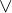$\lor$ может быть подставлен любой знак неравенства, главное, чтобы он был один и тот же в обоих случаях. Использование данной формулы существенно упрощает решение неравенства:

$\log_{\log_x 3x}(4x-1)\geqslant \log_{\log_x 3x} 1\Rightarrow$

$(4x-2)\cdot(\log_x 3x - 1)\geqslant 0\Leftrightarrow$

$\frac{4x-2}{\log_3 x}\geqslant 0\Leftrightarrow x\in\left(0;\frac{1}{2}\right]\cup(1;+\mathcal{1}).$

Определим теперь область допустимых значений данного неравенства. Она задается следующей системой:

$\begin{cases}4x-1>0, \\ \log_x 3x > 0, \\ \log_x 3x\ne 1, \\ x> 0, \\ x\ne 1\end{cases}\Leftrightarrow \begin{cases}x>\frac{1}{4}, \\ \log_x 3x >\log_x 1, \\ x\ne 1, \\ x>0, \\ x\ne 1\end{cases}\Leftrightarrow$

$\begin{cases}x>\frac{1}{4}, \\ (3x-1)(x-1)>0 \\ x>0, \\ x\ne 1\end{cases}\Leftrightarrow x\in\left(\frac{1}{4};\frac{1}{3}\right)\cup(1;+\mathcal{1}).$

Легко видеть, что одновременно этот промежуток будет являться и решением нашего неравенства.

3. Окончательным ответом исходной системы неравенств будет пересечение полученных промежутков, то есть $x\in\left(\frac{1}{4};\frac{1}{3}\right)\cup(1;2].$

Пример 5. Решите систему неравенств:

$\begin{cases}25^x-30\cdot 5^x+125\geqslant 0,\\ \log_x(x-1)\cdot \log_x(x+1)\leqslant 0.\end{cases}$

Решение задания C3.

1. Решаем сперва первое неравенство. Используем подстановку 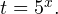t=5^x. Переходим к следующему квадратному неравенству:

$t^2-30t+125\geqslant 0\Leftrightarrow \left[\begin{array}{l}5^x\leqslant 5, \\ 5^x\geqslant 25\end{array}\right.\Leftrightarrow \left[\begin{array}{l}x\leqslant 1, \\ x\geqslant 2.\end{array}\right.$

2. Решаем теперь второе неравенство. Область его допустимых значений определяется системой:

$\begin{cases}x>0, \\ x\ne 1, \\ x-1>0, \\ x+1 > 0\end{cases}\Leftrightarrow x\in(1;+\mathcal{1}).$

Данное неравенство равносильно следующей смешанной системе:

$\left[\begin{array}{l}\begin{cases}\log_x(x-1)\leqslant 0, \\ \log_x(x+1)\geqslant 0,\end{cases} \\ \begin{cases}\log_x(x-1)\geqslant 0, \\ \log_x(x+1)\leqslant 0.\end{cases}\end{array}\right.$

В области допустимых значений, то есть при 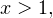x>1, используя равносильные преобразования переходим к следующей смешанной системе:

$\left[\begin{array}{l}\begin{cases} x-1\leqslant 1, \\ x+1\geqslant 1,\end{cases} \\ \begin{cases}x-1\geqslant 1, \\ x+1\leqslant 1.\end{cases}\end{array}\right.\Leftrightarrow\left[\begin{array}{l}\begin{cases} x\leqslant 2, \\ x\geqslant 0,\end{cases} \\ \begin{cases}x\geqslant 2, \\ x\leqslant 0.\end{cases}\end{array}\right.\Leftrightarrow x\in[0;2].$

С учетом области допустимых значений получаем: $x\in(1;2].$

3. Окончательным решением исходной системы является пересечение полученных промежутков, то есть 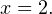x=2.

Изображение полученных промежутков на числовой прямой

Пример 6. Решите систему неравенств:

$\begin{cases}\frac{3\cdot 64^x+2^x-70}{64^x-2}\geqslant 3, \\ \log_3^2(x+3)-3\log_3(x+3)+2\leqslant 0.\end{cases}$

Решение задачи C3.

1. Решаем сперва первое неравенство. Равносильными преобразованиями приводим его к виду:

$\frac{2^x-64}{64^x-2}\geqslant 0\Leftrightarrow \frac{2^x-2^6}{2^{6x}-2^1}\geqslant 0$

$\Leftrightarrow \frac{x-6}{6x-1}\geqslant 0\Leftrightarrow x\in\left(-\mathcal{1};\frac{1}{6}\right)\cup[6;+\mathcal{1}).$

2. Решаем теперь второе неравенство. Область его допустимых значений определяется промежутком: 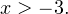x>-3. Используя замену переменной 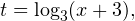$t=\log_3(x+3),$ переходим к следующему квадратичному неравенству:

$t^2-3t+2\leqslant 0\Leftrightarrow 1\leqslant t\leqslant 2\Leftrightarrow 1\leqslant \log_3(x+3)\leqslant 2\Leftrightarrow$

$3\leqslant x+3\leqslant 9\Leftrightarrow 0\leqslant x\leqslant 6.$

Этот ответ целиком принадлежит области допустимых значений неравенства.

3. Пересечением полученных в предыдущих пунктах промежутков получаем окончательный ответ к системе неравенств: 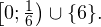$\left[0;\frac{1}{6}\right)\cup\{6\}.$

Сегодня мы с вами решали системы логарифмических и показательных неравенств. Задания подобного рода предлагались в пробных вариантах ЕГЭ по математике в течение всего ныне идущего учебного года. Однако, как репетитор по математике, имеющий опыт подготовки к ЕГЭ, могу сказать, что это вовсе не означает, что аналогичные задания будут в реальных вариантах ЕГЭ по математике в июне.

Позволю себе высказать одно предостережение, адресованное в первую очередь репетиторам и школьным учителям, занимающимся подготовкой старшеклассников к сдаче ЕГЭ по математике. Весьма опасно готовить школьников к экзамену строго по заданным темам, ведь в этом случае возникает риск полностью «завалить» его даже при незначительном изменении ранее заявленного формата заданий. Математическое образование должно быть полным. Уважаемые коллеги, пожалуйста, не уподобляйте роботам своих учеников так называемым «натаскиванием» на решение определенного типа задач. Ведь нет ничего хуже формализации мышления человека.

Всем удачи и творческих успехов!

Профессиональный репетитор по физике и математике
Сергей Валерьевич

Если пробовать, то есть два варианта: получится или не получится. Если не пробовать — всего один.
© Народная мудрость

yourtutor.info

55. Логарифмические неравенства | Решение задач по математике и другим

Логарифмическим неравенством называется такое неравенство, в котором неизвестная величина содержится или под знаком логарифма, или в его основании.

Типы неравенств и способы их решения

Всюду далее F(X), G(X), H(X) – некоторые выражения с переменной.

I тип: неравенство вида

(6.16)

Где A > 0.

1. Если 0 < A < 1, то неравенство (6.16) равносильно системе

(6.17)

2. Если A > 1, то неравенство (6.16) равносильно системе

Заметим, что в этом случае первое неравенство системы (6.17) можно не решать, так как во втором неравенстве

(6.18)

Решение неравенства (6.18) сводится к решению совокупности двух систем:

Неравенство F(X) > 0 во второй системе можно не решать, так как оно справедливо при выполнении двух других неравенств этой системы.

II тип: неравенство вида

(6.19)

1. Если 0 < A < 1, то неравенство (6.19) равносильно системе

(6.20)

Неравенство G(X) > 0 в системе (6.20) можно не решать, так как оно выполняется при условии выполнения двух других неравенств этой системы.

2. Если то неравенство (6.19) равносильно системе

(6.21)

Неравенство в системе (6.21) можно не решать.

(6.22)

Поскольку в основании содержится переменная величина, то в общем случае решение неравенства (6.22) зависит от величины основания по сравнению с числом 1. Поэтому решаем совокупность двух систем:

III тип: неравенство вида

(6.23)

Где F – некоторое выражение относительно

Необходимо заменить и решить неравенство F(Y) > 0. Полученные в качестве решения последнего неравенства промежутки записывают в виде неравенств относительно Y, а затем возвращаются к старой переменной.

Аналогично решают неравенства I – III типов, в которых вместо знака > использованы знаки ³, <, £.

Пример 1. Решить неравенство

Решение. Имеем неравенство I типа. Так как основание логарифма меньше числа 1, то решение неравенства сводится к решению системы

Используем далее метод интервалов (рис. 6.13).

Рис. 6.13

Получаем ответ:

Пример 2. Решить неравенство

Решение. Данное неравенство относится к I типу. Поэтому решаем совокупность двух систем

Первая система решений не имеет. Решаем вторую систему

Второе неравенство этой системы не решаем, так как оно справедливо, если выполняется последнее неравенство. Получаем:

Используем метод интервалов (рис. 6.14).

Рис. 6.14

Получаем ответ:

Пример 3. Решить неравенство

Решение. Это неравенство II типа, причем основание логарифма больше числа 1. Поэтому решаем систему

Получаем

Подводя итог, приходим к ответу:

Пример 4. Решить неравенство

Решение. Имеем неравенство III типа.

Заменяем и решаем кубическое неравенство

Разлагаем левую часть неравенства на множители:

Используем далее метод интервалов (рис. 6.15).

Рис. 6.15

Получили решение Записываем его в виде:

Возвращаемся к неизвестной X и с учетом ОДЗ заданного неравенства имеем:

Получаем ответ:

< Предыдущая		Следующая >

matica.org.ua

Решение логарифмических неравенств с переменным основанием

14 . Логарифмические неравенства. Основные методы решения логарифмических неравенств

15. Основные методы решения тригонометрических уравнений

Решение систем логарифмических и показательных неравенств с репетитором

55. Логарифмические неравенства | Решение задач по математике и другим

Добавить комментарий Отменить ответ