Логарифмические неравенства, примеры решений
Теория по логарифмическим неравенствам
Решение логарифмических неравенств основывается на свойстве монотонности логарифмической функции: функция монотонно возрастает, если , и монотонно убывает, если . При этом учитывается, что подлогарифмическое выражение может принимать только положительные значения. Таким образом, для неравенства вида
при потенцировании, для значений знак неравенства сохраняется; а для значений , меняется на противоположный.
В случае если переменная содержится и в основании, и в подлогарифмическом выражении, например , решение разбивается два случая, когда и, когда , то есть
Так же некоторые логарифмические неравенства можно решить методом замены переменной.
Примеры
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Логарифмические неравенства
1.Решить неравенство:
![Rendered by QuickLaTeX.com \[\log_{11} (3x-1)>1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-13981c0ff5c1a940b11692a11b829330_l3.png)
ОДЗ:
![Rendered by QuickLaTeX.com \[3x-1>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c7de607604ef9749a0c22f01df5cbfd2_l3.png)
![Rendered by QuickLaTeX.com \[x>\frac{1}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ae3eccdea2cddbff50b6dc230aae099c_l3.png)
![Rendered by QuickLaTeX.com \[\log_{11} (3x-1)> \log_{11} 11\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0e5ba02969cb2b68fd96675211ef6283_l3.png)
Так как основание логарифма больше 1, то знак неравенства сохраняем:
![Rendered by QuickLaTeX.com \[3x-1> 11\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-05c26fe1f2c333d8be67655d3276e9ee_l3.png)
![Rendered by QuickLaTeX.com \[3x> 12\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-45a4c460dee6e777ccfb9e560aa1866a_l3.png)
![Rendered by QuickLaTeX.com \[x> 4\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b62324bbee93ed84bfac50183b8b0138_l3.png)
Ответ: 
2.Решить неравенство:
![Rendered by QuickLaTeX.com \[\log_{\frac{1}{3}} (7x-1)>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab27147c670342ce32b60602a34cd26e_l3.png)
ОДЗ:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{7x-1>0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7a7a38049966e21cbe99d23712315c41_l3.png)
![Rendered by QuickLaTeX.com \[x>\frac{1}{7}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c082bfe3fc5726ecb48d847e1e681f11_l3.png)
Решение:
![Rendered by QuickLaTeX.com \[\log_{\frac{1}{3}} (7x-1)> \log_{\frac{1}{3}} 1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-83721e629a3c298eedd8e0270263e0be_l3.png)
Так как основание логарифма меньше 1, то знак неравенства меняем:
![Rendered by QuickLaTeX.com \[7x-1< 1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0fad7e90bc001c8adb0018a7d55f7a18_l3.png)
![Rendered by QuickLaTeX.com \[7x< 2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-460f4a1bbc3469adf5529f69ad71badc_l3.png)
![Rendered by QuickLaTeX.com \[x< \frac{2}{7}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-48b3f9c7eb576abe8f8a4ccd576562fa_l3.png)
Пересекаем решение и ОДЗ, имеем: 
3.Решить неравенство:
![Rendered by QuickLaTeX.com \[2\log_{\frac{1}{9}} \frac{2-3x}{x}\geqslant -1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-86fb84c1578c2ca1adce4a7206eb5eac_l3.png)
ОДЗ:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{2-3x}{x}>0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5a3292c430c5baa076caf182351edeec_l3.png)
Решим методом интервалов. Корень числителя –  , корень знаменателя
, корень знаменателя  – эта точка выколота всегда, корень числителя – тоже выколотая точка, так как знак строгий. Таким образом,
– эта точка выколота всегда, корень числителя – тоже выколотая точка, так как знак строгий. Таким образом, 
Решение:
![Rendered by QuickLaTeX.com \[-\log_3 \frac{2-3x}{x}\geqslant -\log_3 3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6529a14ae7fb4fb9d8e316c1d6cebe43_l3.png)
![Rendered by QuickLaTeX.com \[\log_3 \frac{2-3x}{x}\leqslant \log_3 3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-11a3b89b36d2ecb87fb03ecd02396eb3_l3.png)
Переходим к сравнению подлогарифмических выражений, знак сохраняем: основание больше 1:
![Rendered by QuickLaTeX.com \[\frac{2-3x}{x}\leqslant 3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0fd3ae977e4e7d96a2bc78a97fc4a470_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2-3x}{x}-3\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e7bef731aff5445b6ae7b563b6a05eb3_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2-3x}{x}-\frac{3x}{x}\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b6207eab8c4125b314cba627daaf5026_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2-6x}{x}\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b98b3b693fc73dc6163d5dcce5eea08b_l3.png)
Корень числителя –  , корень знаменателя
, корень знаменателя  – эта точка выколота всегда, корень числителя – точка закрашенная, она войдет в решение, так как знак неравенства не строгий. Таким образом,
– эта точка выколота всегда, корень числителя – точка закрашенная, она войдет в решение, так как знак неравенства не строгий. Таким образом, 
При наложении решения на ОДЗ получим:
Ответ:  .
.
4.Решить неравенство:
![Rendered by QuickLaTeX.com \[2\log_3 (-x) -\log_{\frac{1}{3}}(4+x)\leqslant \log_3 (x+1)^2+2\log_9 (10+x)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-181f91e8231eaba11b2fcfe2b3944e6a_l3.png)
ОДЗ:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{-x>0}\\{4+x>0}\\{10+x}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aa87804e84d7f30333eed7416e2dca00_l3.png)
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{x<0}\\{x>-4}\\{x>-10}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-64920b2f97357c59c719d04be960ee16_l3.png)
Решение этой системы – 
Решение:
![Rendered by QuickLaTeX.com \[\log_3 x^2 +\log_3 (4+x)\leqslant \log_3 (x+1)^2+\log_3 (10+x)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-522b1102904196e7afb67cd548851a12_l3.png)
![Rendered by QuickLaTeX.com \[x^2(4+x)\leqslant (x+1)^2 (10+x)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9290b13a267367c904534a481e57f273_l3.png)
![Rendered by QuickLaTeX.com \[4x^2+x^3\leqslant (x^2+2x+1)(10+x)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0447deee140f6219e7aa3d00ac7703a5_l3.png)
![Rendered by QuickLaTeX.com \[-8x^2-21x-10\leqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f91f8763f6e76ba9b8e202c0eb942844_l3.png)
![Rendered by QuickLaTeX.com \[8x^2+21x+10\geqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d6ad3d1878395e48bee6f3eeee65c35b_l3.png)
![Rendered by QuickLaTeX.com \[8x^2+21x+10\geqslant 0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d6ad3d1878395e48bee6f3eeee65c35b_l3.png)
Корни: 
![Rendered by QuickLaTeX.com \[x_{1,2}=\frac{-21 \pm 11}{16}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d30d8306c5b3ec0a7cdb849460155fa8_l3.png)
![Rendered by QuickLaTeX.com \[x_1=-2, x_2=-\frac{5}{8}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-77946f029b14486cf4810988ae19e2a3_l3.png)
Поскольку знак неравенства нестрогий, то точки входят в решение: на рисунке их нужно изобразить закрашенными. Решение неравенства: ![Rendered by QuickLaTeX.com x \in (-\infty; -2] \cup [-\frac{5}{8};+\infty)](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-997ed17e476186e4a8731f4d4b3d5aa1_l3.png) .
.
Накладывая решение на область допустимых значений, получаем:
Ответ: ![Rendered by QuickLaTeX.com x \in (-4; -2] \cup [-\frac{5}{8};0)](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-be2b329093f2cc6c71edee39cb063add_l3.png)
5.Решить неравенство:
![Rendered by QuickLaTeX.com \[2\log_2 x -\log_2 (2x-2)>1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-48db13a24b1b3ceb1b7820740c9038e2_l3.png)
ОДЗ:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{x>0}\\{2x-2>0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2b0a0801b1ae3c5c3b617aa5dfeef175_l3.png)
Решение этой системы – 
Решение:
![Rendered by QuickLaTeX.com \[\log_2 x^2 -\log_2 (2x-2)>\log_2 2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7923f7f7bb3e65904b4dbc51d0a1f13e_l3.png)
![Rendered by QuickLaTeX.com \[\log_2 \frac{x^2}{2x-2}>\log_2 2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b4875d42030d090c588d3a4214b8d609_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x^2}{2x-2}>2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1094548f0e4da9317897d3ce5d28d147_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x^2-2(2x-2)}{2x-2}>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6b67f45b5127dcc29cc37e49ef68d2bb_l3.png)
![Rendered by QuickLaTeX.com \[\frac{(x-2)^2}{2(x-1)}>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-825d65edec834cdb2f16d267d97f5371_l3.png)
Точка 1 является выколотой – это корень знаменателя, точка 2 – корень четной кратности, а мы помним, что в таких точках знак интервала не изменяется! Поэтому решение будет выглядеть так:
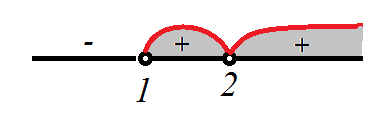
Решение неравенства
Решение неравенства:
![Rendered by QuickLaTeX.com \[x \in (1;2) \cup (2; +\infty)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-786192b2443b108f1c24f6e40a021fd2_l3.png)
Это полностью укладывается в ОДЗ, поэтому ответ таким и будет:
Ответ: 
6.Решить неравенство:
![Rendered by QuickLaTeX.com \[\log_x{\frac{6-5x}{4x+5}}>1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a5886dc7e64d2cd6250a7fa3c3372d97_l3.png)
ОДЗ:
![Rendered by QuickLaTeX.com \[\begin{Bmatrix}{\frac{6-5x}{4x+5}>0}\\{4x+5 \neq 0}\\{x\neq 1}\\ {x>0}\end{matrix}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-023a4e480b1161fdbca976973d393cb7_l3.png)
Допустимые значения  :
: 
Решение неравенства проведем методом рационализации:
![Rendered by QuickLaTeX.com \[\log_x{\frac{6-5x}{4x+5}}>\log_x x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-de4295daff8b1e6d698577a4f11366d2_l3.png)
![Rendered by QuickLaTeX.com \[(x-1)\left(\frac{6-5x}{4x+5}}- x\right)>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c81515008ca41cc50f07360e495400d8_l3.png)
![Rendered by QuickLaTeX.com \[(x-1)\left(\frac{6-5x-x(4x+5)}{4x+5}}\right)>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8e47e4261a2e50e4bfb16598768be981_l3.png)
Упрощаем:
![Rendered by QuickLaTeX.com \[(x-1)\left(\frac{-4x^2-10x+6}{4(x+\frac{5}{4})}\right)>0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e2526598fe5c5f64c9463dbd680c0771_l3.png)
![Rendered by QuickLaTeX.com \[(x-1)\left(\frac{2x^2+5x-3}{2(x+\frac{5}{4})}\right)<0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-659b03b22a81ccba6c1309449f73097f_l3.png)
Раскладываем на множители:
![Rendered by QuickLaTeX.com \[\frac{(x-1)(x+3)(x-\frac{1}{2})}{2(x+\frac{5}{4})}<0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dcf276f72494ed4e5a726c3abbcfb509_l3.png)
Отмечаем полученные точки на координатной прямой:
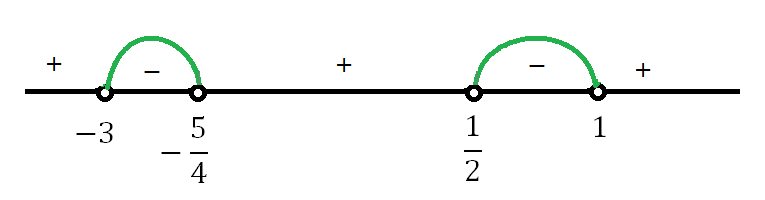
Решение неравенства
Наложив это решение на ОДЗ, имеем: 
Ответ: 
easy-physic.ru
Решение логарифмических неравенств. Видеоурок. Алгебра 11 Класс
В данном уроке мы рассмотрим решение более сложных логарифмических неравенств, покажем, каким образом оно сводится к решению простейших логарифмических неравенств.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»
Тема: Показательная и логарифмическая функция
Урок: Решение логарифмических неравенств
Ключом к решению логарифмических неравенств являются свойства логарифмической функции, т.е. функции вида  (
(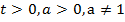 ). Здесь t – независимая переменная, а= конкретное число, у – зависимая переменная, функция.
). Здесь t – независимая переменная, а= конкретное число, у – зависимая переменная, функция.
Вспомним основные свойства логарифмической функции.
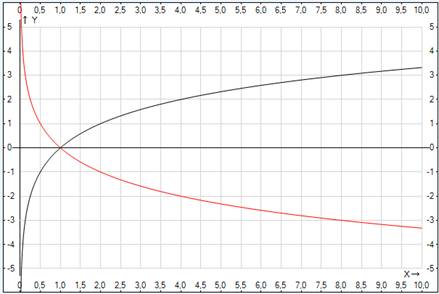
Рис. 1. График логарифмической функции при различных основаниях
Функция монотонна на всей своей области определения. При 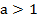 монотонно возрастает, т.е. большему значению аргумента соответствует большее значение функции,
монотонно возрастает, т.е. большему значению аргумента соответствует большее значение функции, 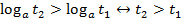 . При
. При 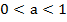 монотонно убывает, т.е. большему значению аргумента соответствует меньшее значение функции,,
монотонно убывает, т.е. большему значению аргумента соответствует меньшее значение функции,, 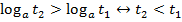 .
.
Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.
Рассмотрим решение логарифмического неравенства, когда основание логарифма 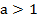 .
.
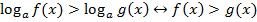
То есть знак неравенства сохраняется.
При этом необходимо не забыть про ОДЗ, т.к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:
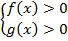
Решением исходного неравенства является эквивалентное неравенство 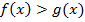 , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел получаем систему неравенств, которая соответствует исходному неравенству:
, поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел получаем систему неравенств, которая соответствует исходному неравенству:
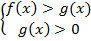
Пример 1 – решить неравенство:
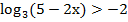
Согласно методике решения простейших логарифмичеких неравенств, первым действием необходимо уравнять основания логарифмов, в данном случае представить п
interneturok.ru
Урок 5. Логарифмические неравенства. Системы логарифмических неравенств. Теория.
На этом уроке мы рассмотрим метод решения логарифмических неравенств, основанный на свойствах логарифмической функции. Также мы поговорим о видах логарифмических неравенствах и систем логарифмических неравенств.
Данный урок поможет подготовиться к одному из типов задания С3.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 5. Логарифмические неравенства. Системы логарифмических неравенств
Теория
Конспект урока
На предыдущем уроке мы рассмотрели решение логарифмических уравнений и их систем. На этом уроке речь пойдет о логарифмических неравенствах и их системах.
Мы уже говорили о логарифмической функции и ее свойствах. Важным свойством, которым мы пользовались для решения логарифмических уравнений: монотонность.
Для  график логарифмической функции выглядит следующим образом:
график логарифмической функции выглядит следующим образом:
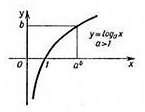
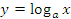 — возрастающая функция: чем больше
— возрастающая функция: чем больше  , тем больше
, тем больше 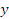 . Значит,
. Значит,  . В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ:
. В отличие от уравнений, здесь проверкой обойтись не удастся, поэтому необходимо учитывать ОДЗ:  .
.
Объединяя, получаем:  .
.
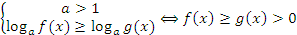
Для  график логарифмической функции выглядит следующим образом:
график логарифмической функции выглядит следующим образом:

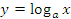 — убывающая функция: чем больше
— убывающая функция: чем больше  , тем меньше
, тем меньше 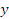
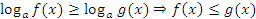 .
.ОДЗ:  .
.
Объединяя, получаем: 
 .
.
interneturok.ru
Решение логарифмических неравенств
 Решение логарифмических неравенств имеет много общего с решением показательных неравенств:
Решение логарифмических неравенств имеет много общего с решением показательных неравенств:
а) При переходе от логарифмов к выражениям, стоящим под знаком логарифма, мы также сравниваем основание логарифма с единицей;
б) Если мы решаем логарифмическое неравенство с помощью замены переменных, то нужно решать относительно замены до получения простейшего неравенства.
Однако, есть одно очень важное отличие: поскольку логарифмическая функция имеет ограниченную область определения, при переходе от логарифмов к выражениям, стоящим под знаком логарифма, необходимо учитывать область допустимых значений.
Если при решении логарифмического уравнения можно найти корни уравнения, а потом сделать проверку, то при решении логарифмического неравенства этот номер не проходит: при переходе от логарифмов к выражениям, стоящим под знаком логарифма необходимо записывать ОДЗ неравенства.
Итак. Простейшее логарифмическое неравенство имеет вид:

 , где V — один из знаков неравенства: <,>, ≤ или ≥.
, где V — один из знаков неравенства: <,>, ≤ или ≥.Если основание логарифма больше единицы (
 )
) , то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство
, то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства сохраняется, и неравенство


равносильно системе:


Если основание логарифма больше нуля и меньше единицы ( ), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство
), то при переходе от логарифмов к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный, и неравенство


равносильно системе:


Рассмотрим примеры решения логарифмических неравенств.
1. Решим неравенство:


Так как основание логарифмов в обеих частях неравенства меньше 1, при переходе к выражениям, стоящим под знаком логарифма, знак неравенства меняется на противоположный. Выражения, стоящие под знаком логарифма должны быть строго больше нуля. Перейдем к системе:


Обратите внимание: мы указываем, что больше нуля должно быть меньшее из выражений, которые стоят под знаком логарифма. В этом случает большее выражение автоматически будет больше нуля.
Решим систему неравенств:


Корни квадратного трехчлена:  ,
, 
Отсюда:

Ответ: 
2. Решим неравенство:


Мы видим, что в основании логарифмов стоят степени числа 2, поэтому мы можем привести логарифмы к одному основанию. Сделаем это, воспользовавшись свойствами логарифмов:


Перенесем логарифм с отрицательным коэффициентом из левой части неравенства в правую (так как умножать легче, чем делить).


Так как в неравенстве присутствуют логарифмы с одинаковым основанием и в первой степени, мы можем представить обе части неравенства в виде логарифма по основанию 2:


Теперь мы можем перейти от логарифмов к выражениям, стоящим под знаком логарифма. Основание больше 1, поэтому знак неравенства сохраняется. Не забываем про ОДЗ:


Отсюда:


Ответ: 
3. Решим неравенство:

В нашем неравенстве логарифм стоит в квадрате, поэтому это логарифмическое неравенство мы будем решать с помощью замены переменных.
Сначала приведем логарифмы к одному основанию:

Введем замену переменных:
 .
.
Получим квадратное неравенство:

Значит,  .
.
Запишем это двойное неравенство в виде системы:


Вот только теперь, когда мы получили систему простейших неравенств относительно  , мы можем вернуться к исходной переменной.
, мы можем вернуться к исходной переменной.



Перейдем к выражениям, стоящим под знаком логарифма:



Последнее неравенство системы — это ОДЗ неравенства. Заметим, что оно выполняется, если выполняется второе неравенство системы, поэтому нет необходимости его решать.
Решим систему.
Первое неравенство системы преобразуется к виду

 Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значениях
Дискриминант этого квадратного трехчлена отрицателен, старший коэффициент положителен, поэтому неравенство верно при любых действительных значениях  .
.
Второе неравенства преобразуется к виду 
 , отсюда
, отсюда ![{x}in{[0;1]} {x}in{[0;1]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_d2e667029942bb357ef33d4ffbb46ea9.png)
Ответ: ![{x}in{[0;1]} {x}in{[0;1]}](/800/600/https/ege-ok.ru/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_980.5_d2e667029942bb357ef33d4ffbb46ea9.png)

И.В. Фельдман, репетитор по математике.
ege-ok.ru
Логарифмические неравенства
\(\blacktriangleright\) На ОДЗ верны следующие формулы:
\[\large{\begin{array}{|lcl|} \hline \log_a1=0& \qquad & \log_aa=1\\ &&\\ \log_{a^n}{b^m}=\frac mn\log_{|a|}{|b|}&& a^{\log_bc}=c^{\log_ba}\\ &&\\ \log_a{bc}=\log_a{|b|}+\log_a{|c|}&& \log_a{\dfrac bc}=\log_a{|b|}-\log_a{|c|}\\ &&\\ \log_ab\cdot \log_bc=\log_ac & \Longleftrightarrow & \log_bc=\dfrac{\log_ac}{\log_ab}\\ &&\\ \log_ab\cdot \log_ba=1 & \Longleftrightarrow & \log_ab=\dfrac1{\log_ba}\\ &&\\ \hline \end{array}}\]
\(\blacktriangleright\) Стандартное логарифмическое неравенство \[{\Large{\log_a{h(x)}\geqslant \log_a{g(x)} \quad
(*)}}\] где \(a>0,\ a\ne 1\)
(на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
Логарифмическая функция \(f(x)=\log_ax\) является возрастающей, если число \(a>1\), и убывающей, если \(0<a<1\), и определена при всех положительных \(x\) (то есть ее область определения \(x\in (0;+\infty)\)).
На графике приведен пример возрастающей логарифмической функции \(f_1(x)=\log_2x\) и убывающей логарифмической функции \(f_2(x)=\log_{\,0,5}x\).
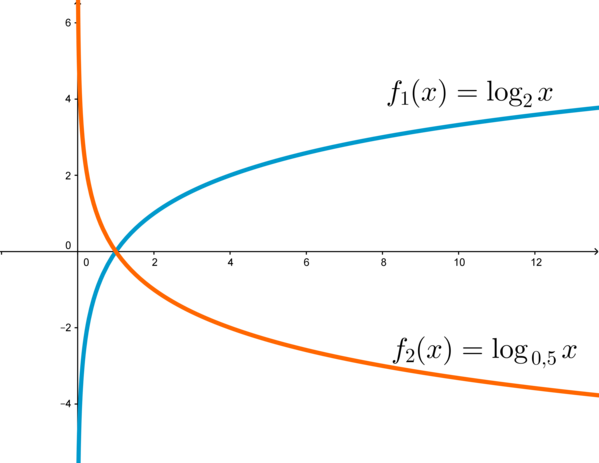
Напомним, что функция возрастает, если при увеличении \(x\) увеличивается и \(f(x)\). Функция убывает, если при увеличении \(x\) уменьшается \(f(x)\).
Таким образом, неравенство \((*)\) есть не что иное, как сравнение \(f(h)\) и \(f(g)\). Если функция \(f\) — возрастает, то неравенство \(f(h)\geqslant f(g)\) равносильно неравенству \(h\geqslant g\), а если убывает — то неравенству \(h\leqslant g\).
Поэтому для того, чтобы решить неравенство \((*)\), нужно сравнить основание \(a\) с единицей:
если \({\large{a>1}}\), то данное неравенство равносильно системе (не забываем про ОДЗ!) \[{\Large{\begin{cases} h(x)\geqslant g(x)\\ g(x)>0 \end{cases}}}\] Заметим, что условие \(h(x)>0\) учитывается автоматически в такой системе, т.к. если \(h\geqslant g\), а \(g>0\), то и \(h>0\).
если \({\large{0<a<1}}\), то данное неравенство равносильно системе \[{\Large{\begin{cases} h(x)\leqslant g(x)\\ h(x)>0 \end{cases}}}\]
Заметим, что условие \(g(x)>0\) учитывается автоматически в такой системе.
\(\blacktriangleright\) Напомним, что область значений логарифмической функции — все числа, т.е. \(\log_ax\in \mathbb{R}\) при всех возможных \(a\) и \(x\).
\(\blacktriangleright\) С помощью формулы \({\Large {b=\log_a{a^b}}}\) можно любое число \(b\) представить в виде логарифма по необходимому основанию \(a>0,\ a\ne 1\).
Пример 1. Решить неравенство \(\log_2 {(x^2+7)}>4\)
Представим по формуле \(4=\log_2{2^4}=\log_2{16}\), тогда неравенство примет вид \[\log_2{(x^2+7)}>\log_2 {16} \Leftrightarrow \begin{cases} x^2+7>16\\ x^2+7>0 \end{cases}\] (знак неравенства не сменится, т.к. основание логарифмов \(2>1\)).
Второе неравенство \(x^2+7>0\) (это и есть ОДЗ) выполнено при всех \(x\).
Первое неравенство системы равносильно \(x^2-9>0 \Leftrightarrow
(x-3)(x+3)>0 \Rightarrow x\in (-\infty;-3)\cup(3;+\infty)\).
Таким образом, после пересечения решений обоих неравенств системы решением исходного неравенства будут \(x\in
(-\infty;-3)\cup(3;+\infty)\).
\(\blacktriangleright\) Рассмотрим неравенства вида \[{\Large{\log_{h(x)}{f(x)}\geqslant \log_{h(x)}{g(x)}}}\] (на месте знака \(\geqslant\) может стоять любой из знаков \(\leqslant,\
>,\ <\))
То есть когда в основании логарифма находится не конкретное число, а функция, зависящая от \(x\).
Данное неравенство равносильно совокупности: \[{\Large{\left[\begin{gathered} \begin{aligned} &\begin{cases} h(x)>1\\ f(x)\geqslant g(x)\\ g(x)>0 \end{cases}\\[4pt] &\begin{cases} 0<h(x)<1\\ f(x)\leqslant g(x)\\ f(x)>0 \end{cases} \end{aligned} \end{gathered} \right.}}\]
Иногда удобно выписать ОДЗ отдельно. Тогда неравенство будет равносильно системе: \[{\Large{\begin{cases} f(x)>0 \quad (\textbf{ОДЗ})\\ g(x)>0 \quad (\textbf{ОДЗ})\\[3pt] \left[\begin{gathered} \begin{aligned} &\begin{cases} h(x)>1\\ f(x)\geqslant g(x) \end{cases}\\[3pt] &\begin{cases} 0<h(x)<1\\ f(x)\leqslant g(x) \end{cases} \end{aligned} \end{gathered} \right. \end{cases}}}\]
Пример 2. Решить неравенство \(\log_x{(3x-1)}>1\)
Данное неравенство равносильно:
\(\log_x{(3x-1)}>\log_xx \ \Leftrightarrow \ \left[ \begin{gathered} \begin{aligned} &\begin{cases} x>1\\ 3x-1> x\\ x>0 \end{cases}\\ &\begin{cases} 0<x<1\\ 3x-1< x\\ 3x-1>0 \end{cases} \end{aligned} \end{gathered} \right. \ \Leftrightarrow \ \left[ \begin{gathered} \begin{aligned} &x>1\\ &\dfrac13<x<\dfrac12 \end{aligned} \end{gathered} \right. \ \Leftrightarrow \quad x\in \left(\dfrac13;\dfrac12\right)\cup\Big(1;+\infty\Big)\)
Пример 3. Решить неравенство \(\log_{x^2}{(x+1)^2}\leq 1\)
Выпишем ОДЗ для аргумента логарифма: \((x+1)^2>0 \Rightarrow
x\ne -1\).
Для основания логарифма ОДЗ отдельно выписывать не имеет смысла, т.к. мы будем учитывать его в самом решении: рассматривать случаи, когда основание больше \(1\) и когда оно находится между \(0\) и \(1\).
Таким образом, на ОДЗ неравенство равносильно совокупности (учитывая, что \(1=\log_{x^2}{x^2}\)) \[\left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x^2>1\\
(x+1)^2\leqslant x^2
\end{cases}\\[2pt]
&\begin{cases}
0<x^2<1\\
(x+1)^2\geqslant x^2
\end{cases}
\end{aligned}
\end{gathered}
\right. \quad \Leftrightarrow \quad \left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x^2-1>0\\
(x+1)^2-x^2\leqslant 0
\end{cases}\\[2pt]
&\begin{cases}
x^2<1\\
x^2>0\\
(x+1)^2- x^2\geqslant 0
\end{cases}
\end{aligned}
\end{gathered}
\right.\quad \Leftrightarrow \quad \left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
(x-1)(x+1)>0\\
(x+1-x)(x+1+x)\leqslant 0
\end{cases}\\[2pt]
&\begin{cases}
(x-1)(x+1)<0\\
x\ne 0\\
(x+1-x)(x+1+x)\geqslant 0
\end{cases}
\end{aligned}
\end{gathered}
\right.\quad \Leftrightarrow \quad\]
\[\quad \Leftrightarrow \quad
\left[
\begin{gathered}
\begin{aligned}
&\begin{cases}
x\in (-\infty;-1)\cup(1;+\infty)\\
x\in (-\infty;-\dfrac12\big]
\end{cases}\\[2pt]
&\begin{cases}
x\in (-1;1)\\
x\ne 0\\
x\in\big[-\dfrac12;+\infty)
\end{cases}
\end{aligned}
\end{gathered}
\right. \quad \Leftrightarrow \quad x\in
\Big(-\infty;-1\Big)\cup\Big[-\dfrac12;0\Big)\cup\Big(0;1\Big)\]
Пересекая данный ответ с ОДЗ (\(x\ne -1\)), получим тот же ответ.
\(\blacktriangleright\) Таким образом, как правило, для того, чтобы система (совокупность) не выглядела слишком огромной, удобно записывать ОДЗ неравенства отдельно, а затем просто пересекать решение системы (совокупности) с этим ОДЗ. Что мы и сделали в примере \(3\).
shkolkovo.net
Логарифмические неравенства. Как решать логарифмические неравенства?
Если проще: это неравенства, в которых неизвестные (иксы) или выражения с ними находятся внутри логарифмов.
Примеры:
\(\log_3x≥\log_39\)
\(\log_3 {(x^2-3)}< \log_3{(2x)}\)
\(\log_{x+1}{(x^2+3x-7)}>2\)
\(\lg^2{(x+1)}+10≤11 \lg{(x+1)}\)
Как решать логарифмические неравенства:
Любое логарифмическое неравенство нужно стремиться привести к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\) (символ \(˅\) означает любой из знаков сравнения). Такой вид позволяет избавиться от логарифмов и их оснований, сделав переход к неравенству выражений под логарифмами, то есть к виду \(f(x) ˅ g(x)\).
Но при выполнении этого перехода есть одна очень важная тонкость:
\(-\) если основание логарифма — число и оно больше 1 — знак неравенства при переходе остается прежним,
\(-\) если основание — число большее 0, но меньшее 1 (лежит между нулем и единицей), то знак неравенства должен меняться на противоположный, т.е.
|
\(\log_2{(8-x)}<1\) Решение: |
\(\log\)\(_{0,5}\)\((2x-4)\)≥\(\log\)\(_{0,5}\)\({(x+1)}\) Решение: |
Очень важно! В любом неравенстве переход от вида \(\log_a{f(x)} ˅ \log_a{g(x)}\) к сравнению выражений под логарифмами можно делать только если:
\(-\) вы написали ОДЗ для исходного неравенства. Напоминаю ОДЗ для логарифма \(\log_ab\):
\(b>0\), \(a>0\), \(a≠1\).
\(-\) число в основании логарифмов слева и справа одинаково;
\(-\) логарифмы слева и справа — «чистые», то есть нет никаких коэффициентов, умножений, делений и т.д. – только одинокие логарифмы и слева, и справа;
Кстати, в конце (после решения) не забудьте пересечь решения неравенства с ОДЗ.
Например:
|
1) \(\log_3{(x^2-3)}>\log_3{(2x)}\) |
Не написали ОДЗ и не пересекли с ним решение. Неравенство решено неверно. |
|
2) \(\log_5{(x-7)}≤\log_3{4} \) |
Основания логарифмов разные, переход к \(x-7≤4\) невозможен. |
|
3) \(\log_6{(x-2)}-\log_6{x}<\log_6{(2x)}\) |
Логарифмы не «чистые», так как слева есть разность логарифмов. Переход к \((x-2)-x<2x\) невозможен. |
|
4) \(\log_2{(x^2-24)}≥-\log_2x\) |
Логарифмы не «чистые» т.к. справа есть минус перед логарифмом. Переход к \(x^2-24≥-x\) невозможен. |
Заметим, однако, что неравенства 3 и 4 можно легко решить, если воспользоваться свойствами логарифмов.
Пример. Решить неравенство: \(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\)
Решение:
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤-1\) |
Выпишем ОДЗ. |
|
ОДЗ: \(\frac{3x-2}{2x-3}\)\(>0\) |
ОДЗ представляет собой дробно-рациональное неравенство. Решим его с помощью метода интервалов. Вынесем в числителе за скобки \(3\), а в знаменателе \(2\), чтобы убрать коэффициенты перед иксами. |
|
\(\frac{3(x-\frac{2}{3})}{2(x-\frac{3}{2})}\) \(>0\) |
Теперь очевидно, что корни у нас – числа \(\frac{2}{3}\) и \(\frac{3}{2}\) |
|
|
Запишем ОДЗ в виде интервалов. |
|
\(x∈(-∞;\)\(\frac{2}{3}\)\()∪(\)\(\frac{3}{2}\)\(;∞)\) |
С ОДЗ закончили, переходим к решению. |
|
Решение: |
Воспользовавшись свойствами логарифмов
и свойствами степени, преобразуем правую часть: |
|
\(\log\)\(_{\frac{1}{3}}{\frac{3x-2}{2x-3}}\)\(≤\log\) \(_{\frac{1}{3}}\)\(3\) |
Мы привели неравенство к виду \(\log_a{f(x)} ˅ \log_a{g(x)}\). Теперь можно избавиться от логарифмов и оснований. Нужно только определиться, менять знак сравнения или нет. Основание \(\frac{1}{3}<1\), следовательно, знак меняем. |
|
\(\frac{3x-2}{2x-3}\)\(≥\) \(3\) |
Переносим \(3\) и приводим к общему знаменателю, пользуясь свойствами дробей. |
|
\(\frac{3x-2-3(2x-3)}{2x-3}\)\(≥\) \(0\) |
Раскрываем скобки, приводим подобные слагаемые. |
|
\(\frac{-3x+7}{2x-3}\)\(≥\) \(0\) |
Умножаем неравенство на \(-1\), не забыв при этом перевернуть знак сравнения. |
|
\(\frac{3x-7}{2x-3}\)\(≤\) \(0\) |
Далее выносим \(3\) из числителя и \(2\) из знаменателя. |
|
\(\frac{3(x-\frac{7}{3})}{2(x-\frac{3}{2})}\)\(≤\) \(0\) |
Построим числовую ось и отметим на ней точки \(\frac{7}{3}\) и \(\frac{3}{2}\). Обратите внимание, точка из знаменателя – выколота, несмотря на то, что неравенство нестрогое. Дело в том, что эта точка не будет решением, так как при подстановке в неравенство приведет нас к делению на ноль. |
|
|
Теперь на ту же числовую ось наносим ОДЗ и записываем в ответ тот промежуток, который попадает в ОДЗ. |
|
|
Записываем окончательный ответ. |
Пример. Решить неравенство: \(\log^2_3x-\log_3x-2>0\)
Решение:
|
\(\log^2_3x-\log_3x-2>0\) |
Выпишем ОДЗ. |
|
ОДЗ: \(x>0\) |
Приступим к решению. |
|
Решение: \(\log^2_3x-\log_3x-2>0\) |
Перед нами типичное квадратно-логарифмическое неравенство. Делаем замену. |
|
\(t=\log_3x\) |
Раскладываем левую часть неравенства на множители. |
|
\(D=1+8=9\) |
Решаем неравенство методом интервалов. |
|
|
Теперь нужно вернуться к исходной переменной – иксу. Для этого перейдем к совокупности, имеющей такое же решение, и сделаем обратную замену. |
|
\(\left[ \begin{gathered} t>2 \\ t<-1 \end{gathered} \right.\) \(\Leftrightarrow\) \(\left[ \begin{gathered} \log_3x>2 \\ \log_3x<-1 \end{gathered} \right.\) |
Преобразовываем \(2=\log_39\), \(-1=\log_3\frac{1}{3}\). |
|
\(\left[ \begin{gathered} \log_3x>\log_39 \\ \log_3x<\log_3\frac{1}{3} \end{gathered} \right.\) |
Делаем переход к сравнению аргументов. Основания у логарифмов больше \(1\), поэтому знак неравенств не меняется. |
|
\(\left[ \begin{gathered} x>9 \\ x<\frac{1}{3} \end{gathered} \right.\) |
Соединим решение неравенства и ОДЗ на одном рисунке. |
|
|
Запишем ответ. |
Смотрите также:
Показательные неравенства
cos-cos.ru