Все формулы площади параллелограмма

---

1. Формула площади параллелограмма через стороны и углы

 

 

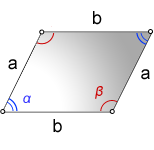
a, b — стороны параллелограмма

α, β — углы параллелограмма

 

Формула площади через стороны и углы параллелограмма, (S):

 

Калькулятор — вычислить, найти площадь параллелограмма:

a(сторона)=

b(сторона)=

α или β (угол в градусах)= ( sin α=sin β )

S=

 

2. Формула площади параллелограмма через сторону и высоту

 

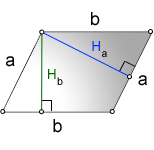
a, b — стороны параллелограмма

H_b — высота на сторону b

H_a — высота на сторону a

 

Формула площади через стороны и высоты параллелограмма, (S):

---

 

 

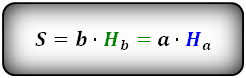
3. Формула площади параллелограмма через диагонали и угол между ними

 

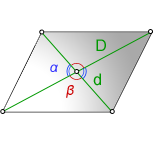
D — большая диагональ

d —меньшая диагональ

α, β — углы между диагоналями

 

Формула площади через диагонали параллелограмма и угол между ними , (S):

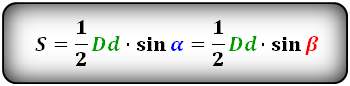
Калькулятор — вычислить, найти площадь параллелограмма:

D (большая диагональ)=

d (меньшая диагональ )=

α или β (угол в градусах)= ( sin α=sin β )

S=

---

---

 

Формулы для параллелограмма:

Как найти стороны параллелограмма

Как найти диагонали параллелограмма

Острый угол и тупой угол параллелограмма

Углы между диагоналями параллелограмма

Формула суммы квадратов диагоналей параллелограмма

Высота параллелограмма и угол пересечения высот

Свойства и длина биссектрисы параллелограмма

Периметр параллелограмма

Все формулы по геометрии

 

Площадь параллелограмма

Площадь параллелограмма, формулы и калькулятор для вычисления площади в режиме онлайн.

Для вычисления площади параллелограмма применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади в режиме онлайн.

Площадь параллелограмма – это численная характеристика, характеризующая размер плоскости, ограниченной геометрической фигурой, образованной четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

1

Площадь параллелограмма по основанию и высоте параллелограмма

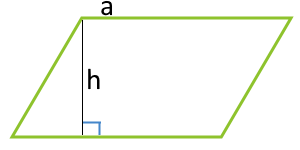
a — сторона

h — высота

… подготовка …

---

2

Площадь параллелограмма по стороне и высоте, опущенной на эту сторону

b — сторона

h_b — высота

… подготовка …

---

3

Площадь параллелограмма по двум сторонам и углу между ними

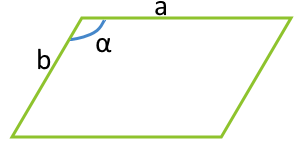
a — сторона

b — сторона

α° — угол между сторонами

… подготовка …

---

4

Площадь параллелограмма по двум диагоналям и углу между этими диагоналями

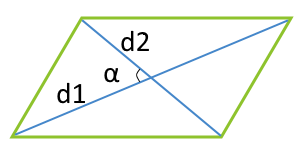
d₁ — диагональ

d₂ — диагональ

α° — угол между диагоналями

… подготовка …

---

5

Площадь параллелограмма по вписанной окружности и стороне

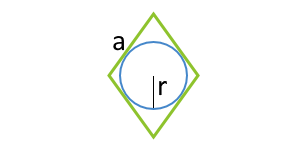
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

a — сторона

r — радиус вписанной окружности

… подготовка …

---

6

Площадь параллелограмма по вписанной окружности и углу между сторонами

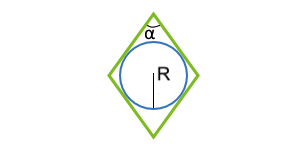
Данная формула применима только для параллелограммов, в которые можно вписать окружность. Таким параллелограммом может являться только ромб.

r — радиус вписанной окружности

α° — угол между сторонами

… подготовка …

---

Определения

Параллелограмм — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами), у которой противоположные стороны попарно параллельны и равны между собой.

Высота параллелограмма – это отрезок проведенный из вершины параллелограмма к противоположной стороне под углом в 90 градусов.

Некоторые свойства параллелограмма:

• Сумма углов параллелограмма равна 360 градусов
• Сумма углов, прилегающих к любой из сторон равна 180 градусов
• Противоположные стороны параллельны и имеют одинаковую длину
• Противолежащие углы равны

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км², м², см², мм² и т.д.

Площадь параллелограмма

Выберите каким способом считать площадь параллелограмма:

Размеры:

Результат:

Решение

Теория

Параллелограмм — это четырёхугольник у которого противоположные стороны параллельны.

У параллелограмма противоположные стороны и противоположные углы равны.

Высота параллелограмма — это перпендикуляр, опущенный из любой точки одной стороны параллелограмма на прямую, содержащую противоположную сторону.

Высотой параллелограмма также называют длину этого перпендикуляра. Расстояние между противоположными сторонами параллелограмма равно высоте параллелограмма.

Формулы площади параллелограмма

Площадь параллелограмма через сторону и высоту

aha

S = a \cdot h_a

• S — площадь параллелограмма
• a — сторона
• h — высота опущенная на сторону a

bhb

S = b \cdot h_b

• S — площадь параллелограмма
• a — сторона
• h — высота опущенная на сторону b

---

 

Площадь параллелограмма через стороны и углы

S = a \cdot b \cdot \sin \alpha

S = a \cdot b \cdot \sin \beta

• S — площадь параллелограмма
• a, b — противоположные стороны параллелограмма
• α, β — углы между диагоналями (в градусах)

---

 

Площадь параллелограмма через диагонали и угол между ними

S = \dfrac{1}{2} \cdot D \cdot d \cdot \sin \alpha

S = \dfrac{1}{2} \cdot D \cdot d \cdot \sin \beta

• S — площадь параллелограмма
• D — большая диагональ параллелограмма
• d — меньшая диагональ параллелограмма
• α, β — углы между диагоналями (в градусах)

Площадь параллелограмма | Треугольники

Площадь параллелограмма можно найти по стороне и проведённой к этой стороне высоте, по двум сторонам и углу, по диагоналям и углу между ними.

 I. Площадь параллелограмма по стороне и высоте

Площадь параллелограмма равна произведению стороны параллелограмма на высоту, проведённую к этой стороне.

Формула для нахождения площади параллелограмма через сторону и высоту:

   

Например,площадь параллелограмма ABCD через высоту можно найти по одной из формул:

   

или

 

   

 

II. Площадь параллелограмма по сторонам и углу

Площадь параллелограмма равна произведению его сторон на синус угла между ними.

Формула для нахождения площади параллелограмма через стороны и угол:

   

Например, площадь параллелограмма ABCD

   

По свойствам параллелограмма, противоположные углы параллелограмма равны:

   

   

Сумма углов параллелограмма, прилежащих к одной стороне, равна 180º, то есть,

   

   

А так как синус тупого угла равен синусу смежного ему угла, то

   

   

Таким образом, площадь параллелограмма можно найти как произведение его двух любых не смежных сторон на синус любого угла.

III. Площадь параллелограмма по диагоналям

Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.

Формула площади параллелограмма через диагонали:

   

Например, площадь параллелограмма ABCD

   

А так как

   

то в качестве угла между диагоналями можно брать любой угол — как острый, так и тупой (прямой — в ромбе и квадрате).

Площадь параллелограмма — формула, пример расчета, калькулятор

Параллелограмм – это четырехугольник, у которого стороны попарно параллельны.

В этой фигуре противоположные стороны и углы равны между собой. Диагонали параллелограмма пересекаются в одной точке и делятся ей пополам. Формулы площади параллелограмма позволяют найти значение через стороны, высоту и диагонали. Параллелограмм также может быть представлен в частных случаях. Ими считаются прямоугольник, квадрат и ромб.
Для начала рассмотрим пример расчета площади параллелограмма по высоте и стороне, к которой она опущена.

Этот случай считается классическим и не требует дополнительного разбирательства. Лучше рассмотрим формулу вычисления площади через две стороны и угол между ними. Этот же способ применяется в расчете площади треугольника по теореме косинусов и синусов. Если даны стороны и угол между ними, то площадь рассчитывается так: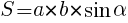

Допустим, дан параллелограмм со сторонами a = 4 см, b = 6 см. Угол между ними α = 30°. Найдем площадь: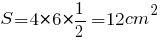

Площадь параллелограмма через диагонали

Формула площади параллелограмма через диагонали позволяет быстро найти значение.
Для вычислений понадобится величина угла, расположенного между диагоналями.

Рассмотрим пример расчета площади параллелограмма через диагонали. Пусть дан параллелограмм с диагоналями D = 7 см, d = 5 см. Угол, лежащий между ними α=30°. Подставим данные в формулу: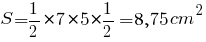

Пример расчета площади параллелограмма через диагональ дал нам прекрасный результат – 8,75.

Зная формулу площади параллелограмма через диагональ можно решать множество интересных задач. Давайте рассмотрим одну из них.

Как найти площадь параллелограмма — онлайн калькулятор

Чтобы найти площадь параллелограмма воспользуйтесь нашим удобным онлайн калькулятором:

Онлайн калькулятор

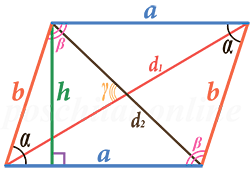
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.

Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):

• длину стороны a и длину высоты h
• длины сторон a и b, и угол α
• длины сторон a и b, и угол β
• длины сторон a и b, и длину любой из диагоналей (d₁ или d₂)
• длины диагоналей d₁ и d₂, и угол между ними γ

Подставьте значения в соответствующие поля и получите результат.

Зная длину стороны a и длину высоты h

Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?

Формула

S = a⋅h

Пример

Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:

S = 8 ⋅ 4 = 32 см²

Зная длины сторон a и b, и угол α

Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?

Формула

S = a⋅b⋅sinα

Пример

Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:

S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см²

Зная длины сторон a и b, и угол β

Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?

Формула

S = a⋅b⋅sin(180 — β)

Пример

Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:

S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см²

Зная длины сторон a и b, и длину диагонали (d₁ или d₂)

Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?

Формула

S = 2√p⋅(p-a)⋅(p-b)⋅(p-d), где p=(a+b+d)/2

Пример

Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:

p = (8 + 5 +11)/2 = 12

S = 2√12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅√12⋅4⋅7⋅1 = 2⋅√336 = 36.66 см²

Зная длины диагоналей d₁ и d₂, и угол между ними γ

Чему равна площадь параллелограмма S если известны длины диагоналей d₁ и d₂, и угол между ними γ?

Формула

S = ½⋅d₁⋅d₂⋅sinγ

Пример

Если диагональ параллелограмма d₁ = 11 см, диагональ d₂ = 7 см, а ∠γ = 45° то:

S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см²

См. также

Площадь параллелограмма | Мозган калькулятор онлайн

На данной странице калькулятор поможет рассчитать площадь параллелограмма онлайн. Для расчета задайте длину основания, высоту или длины диагоналей и угол между ними.

Параллелограмм — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Через основание и высоту

---

---

Формула для нахождения площади параллелограмма через основание и высоту:

a — длина основания; h — высота.

---

Через основания и угол между ними

---

---

Формула для нахождения площади параллелограмма через основания и угол между ними:

a, b — длина основания; α — угол между основаниями.

---

Через диагонали и угол между ними

---

---

Формула для нахождения площади параллелограмма через диаганали и угол между ними:

d1, d2 — диагонали; α — угол между диагоналями.