Логарифмические неравенства. Видеоурок. Алгебра 11 Класс

Тема: Метод интервалов

Урок: Логарифмические неравенства

Ключом к решению логарифмических неравенств являются свойства логарифмической функции, т. е. функции вида 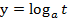 (). Здесь t – независимая переменная, а – конкретное число, у – зависимая переменная, функция.

Вспомним основные свойства логарифмической функции.

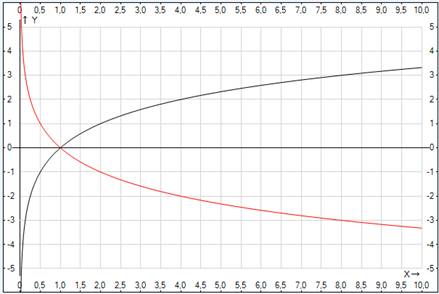
Рис. 1. График логарифмической функции при различных основаниях

1. Область определения: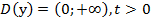

;

2. Область значений: ;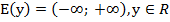

3. Функция монотонна на всей своей области определения. При 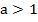 монотонно возрастает (когда аргумент возрастает от нуля до плюс бесконечности, функция возрастает от минус до плюс бесконечности, ). При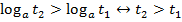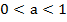

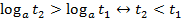 монотонно убывает (когда аргумент возрастает от нуля до плюс бесконечности, функция убывает от плюс до минус бесконечности, ).

Именно монотонность логарифмической функции позволяет решать простейшие логарифмические неравенства.

Рассмотрим решение логарифмического неравенства, когда основание логарифма .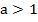

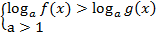
Неравенство необходимо решать, применяя эквивалентные, равносильные преобразования. Рассмотрим схему. Поскольку мы рассматриваем логарифмическую функцию с основанием, большим единицы, помним, что функция монотонно возрастает. Отсюда:

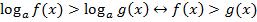
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:

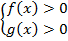
Решением исходного неравенства является эквивалентное неравенство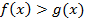

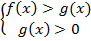
, поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:

Например:

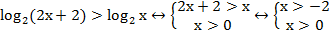
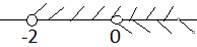
Рис. 2. Иллюстрация решения примера

Ответ: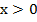

Рассмотрим решение логарифмического неравенства, когда основание логарифма .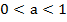

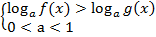
Поскольку мы рассматриваем логарифмическую функцию с основанием, лежащим в пределах от нуля до единицы, помним, что функция монотонно убывает. Отсюда:

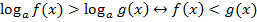
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:

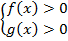
Решением исходного неравенства является эквивалентное неравенство 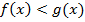, поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:

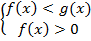
Например:

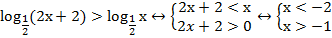
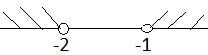
Рис. 3. Иллюстрация решения примера

Ответ: нет решений

 

Выполним обобщение. Мы рассматриваем простейшие логарифмические неравенства, т. е. неравенства вида:

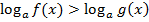
Все остальные более сложные логарифмические неравенства сводятся к простейшим.

Методика решения:

1. Уравнять основания логарифмов;

2. Сравнить подлогарифмические выражения:

— при 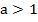 сохранить знак неравенства;

— при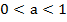

 изменить знак неравенства на противоположный;

3. Учесть ОДЗ;

 

Пример 1 – решить неравенство:

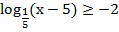
Уравняем основания логарифмов. Для этого число в правой части представим в виде логарифма с нужным основанием:

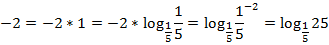
Итак, имеем неравенство:

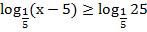
Основание логарифма меньше единицы, имеем эквивалентную систему:

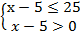
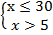
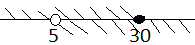
Рис. 4. Иллюстрация решения примера 1

Ответ: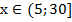

Пример 2 – решить неравенство:

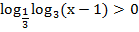
Уравняем основания:

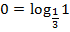
Имеем неравенство:

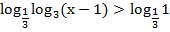
Основание логарифма меньше единицы, имеем эквивалентную систему:

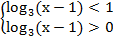
Имеем систему двух простейших логарифмических неравенств. Уравняем основания в каждом из них:

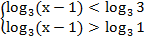
В обоих случаях основание логарифма больше единицы, запишем эквивалентные системы:

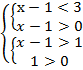
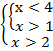
Рис. 5. Иллюстрация к решению примера 2

Ответ: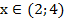

Итак, мы изучили простейшие логарифмические неравенства. На следующем уроке мы рассмотрим, каким образом более сложные неравенства сводятся к простейшим

 

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.

2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа. 

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

  

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Webmath.ru (Источник).

2. Tutoronline.ru (Источник).

 

Домашнее задание

1. Алгебра и начала анализа, 10–11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 516, 517, 525;

2. Решить неравенство:

а) ;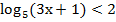

б) ;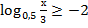

в) ;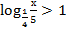

г) ;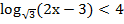

3. Решить неравенство:

а) ;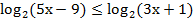

б) ;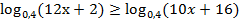

в) ;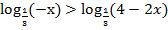

г)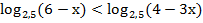

 

Логарифмические неравенства. Алгебра, 11 класс: уроки, тесты, задания.

1.	Определение логарифма (основание целое число) Сложность: лёгкое	4
2.	Определение логарифма (основание — дробь) Сложность: лёгкое	4
3.	Область определения логарифмической функции Сложность: лёгкое	3
4.	Сумма логарифмов (десятичный логарифм) Сложность: лёгкое	3
5.	Логарифмическое неравенство, сводимое к линейному (основание больше 1) Сложность: лёгкое	3
6.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
7.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
8.	Логарифмическое неравенство, сводимое к линейному (определение логарифма) Сложность: среднее	4
9.	Логарифмическое неравенство, сводимое к линейному (убывающая функция) Сложность: среднее	4
10.	Логарифмическое неравенство, сводимое к линейному (основание меньше 1) Сложность: среднее	6
11.	Метод введения новой переменной (квадратичная) Сложность: среднее	7
12.	Сумма логарифмов (основание меньше 1) Сложность: среднее	4
13.	Наибольшее значение логарифмического неравенства Сложность: среднее	10
14.	Логарифмическое неравенство, сводимое к квадратичному (возрастающая функция) Сложность: сложное	9
15.	Неизвестное основание Сложность: сложное	13

Урок по теме «Логарифмические неравенства «

Урок №1

Название предмета Алгебра и начала математического анализа.

Класс :11

УМК Алгебра и начала математического анализа. Мордкович А.Г.,2011г.

Уровень обучения базовый,

Тема урока: Логарифмические неравенства

Общее количество часов, отведенное на изучение темы 3

Цель урока:

-организовать деятельность учащихся по изучению новой темы;

-ввести понятие логарифмического неравенства; сформулировать и доказать теорему о равносильном переходе к системе неравенств; формировать умение решать логарифмические неравенства переходом к равносильной системе неравенств.

-формировать умение решать логарифмические неравенства методом подстановки и с помощью свойств логарифма.

Предметные умения:

1.Знание различных методов решения логарифмических неравенств:

-сведение неравенств к равносильной системе или совокупности систем;

-расщепление неравенств;

-метод интервалов;

-введение новой переменной;

-метод рационализации.

— устанавливать связь между целью деятельности и ее результатом.

Техническое обеспечение урока мультимедийный проектор

Содержание урока

I Организационный момент.

II Атуализация знаний.

Устная работа

1. Что называется логарифмом.

2. Перечислите свойства логарифмом.

3. Представить в виде логарифма с основанием 2 число. (Слайд 2)

а) 16; б) 64; в) ;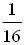

4. Вычислите.

а) log ₃ 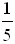+ log ₃ 45;

б) ;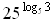

в) ;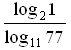

5. Вспомним основные свойства логарифмической функции.

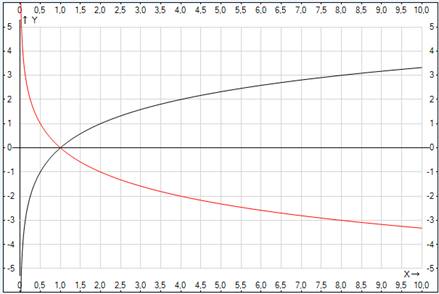
Рис. 1. График логарифмической функции при различных основаниях

1. Область определения: ;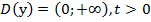

2. Область значений: ;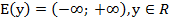

3. Функция монотонна на всей своей области определения. При 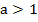 монотонно возрастает (когда аргумент возрастает от нуля до плюс бесконечности, функция возрастает от минус до плюс бесконечности, 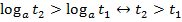). При  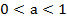монотонно убывает (когда аргумент возрастает от нуля до плюс бесконечности, функция убывает от плюс до минус бесконечности, ).

III. Объяснение нового материала

Определение:

Неравенства, которые содержат переменную под знаком логарифма или в его основании, называются логарифмическими.

Решение логарифмических неравенств основывается на свойстве монотонности логарифмической функции.

1. Неравенство 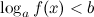в случае, если 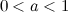сводится к равносильному неравенству 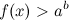. Если же 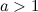— то к неравенству .

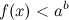Аналогично неравенство 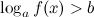равносильно неравенствам 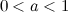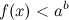для : ; для : .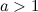

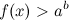Пример 1:

Задание. Решить неравенство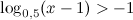

Решение. ОДЗ: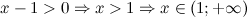

Учитывая выше написанное, получаем, что заданное логарифмическое неравенство равносильно неравенству:

  или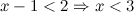  

В пересечении с ОДЗ получаем, что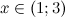

Ответ: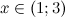

2. Рассмотрим решение логарифмического неравенства, когда основание логарифма .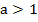

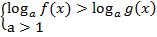
Неравенство необходимо решать, применяя эквивалентные, равносильные преобразования. Рассмотрим схему. Поскольку мы рассматриваем логарифмическую функцию с основанием, большим единицы, помним, что функция монотонно возрастает. Отсюда:

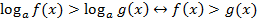
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:

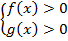
Решением исходного неравенства является эквивалентное неравенство 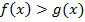, поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:

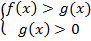
Например:

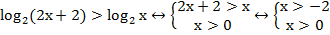
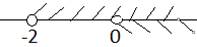
Рис. 2. Иллюстрация решения примера

Ответ: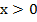 

3. Рассмотрим решение логарифмического неравенства, когда основание логарифма .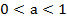

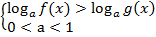
Поскольку мы рассматриваем логарифмическую функцию с основанием, лежащим в пределах от нуля до единицы, помним, что функция монотонно убывает. Отсюда:

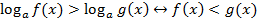
При этом необходимо не забыть про ОДЗ, т. к. под логарифмом могут стоять строго положительные выражения. ОДЗ представлено системой:

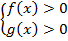
Решением исходного неравенства является эквивалентное неравенство , поэтому для соблюдения ОДЗ достаточно защитить меньшее из чисел. Получаем систему неравенств, которая соответствует исходному неравенству:

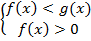
Например:

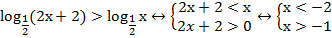
Рис. 3. Иллюстрация решения примера

Ответ: нет решений

IV. Закрепление.

№ 45.4.

а) log ₅ x > log ₅ (3x – 4) 
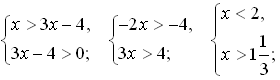  1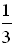 < x < 2.

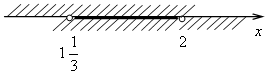
б) log _0,6 (2x – 1) < log _0,6 x 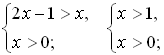  x > 1.

Ответ: а) 1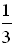 < x < 2; б) x > 1.

При решении этого упражнения особое внимание обращаем на транзитивность двух неравенств из ОДЗ:

Имеем: x > 3x – 4; 3x – 4 > 0  x > 0.

Получаем, неравенство x > 0 лишнее в этой системе, достаточно (1) и (2):

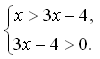
3. № 45.6, № 45.7 (а; б).

Эти упражнения представляют собой логарифмические неравенства, сводящиеся к решению квадратных неравенств.

Вспоминаем алгоритм решения квадратного неравенства:

1 шаг. Решаем соответственное квадратное уравнение ax² + bx +
+ c = 0.

2 шаг. Изображаем схематично расположение параболы относительно оси Oх в зависимости от знака коэффициента а и полученных решений уравнения.

3 шаг. Определяем графически абсциссы точек, удовлетворяющих неравенству, и записываем ответ.

Решение:

№ 45.6.

а) log ₃ (x² + 6) < log ₃ 5x 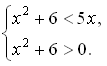

Второе неравенство системы верно для любого х.

Решаем отдельно первое неравенство.

x² + 6x < 5x;

x² – 5x + 6 < 0;

x² – 5x + 6 = 0;

х₁ = 2; х₂ = 3.

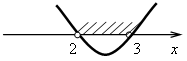
Значит, решением являются 2 < х < 3.

в) lg (x² – 8)  lg (2 – 9x) 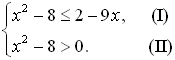

I) x² – 8  2 – 9x;

x² – 8 – 2 + 9x  0;

x² + 9x – 10  0;

x² + 9x – 10 = 0;

х₁ = –10; х₂ = 1.

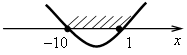
II) x² – 8 > 0;

x² – 8 = 0;

x² = 8;

x = ±2.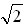

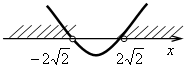
Решением системы неравенств является пересечение полученных промежутков.

Значит, –10  x < –2.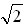

Ответ: а) 2 < x < 3; в) –10  x < –2.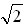

№ 45.7 (а).

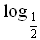(6 – x) 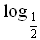 x² 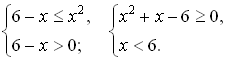

Решим первое неравенство системы.

x² + x – 6  0;

x² + x – 6 = 0;

х₁ = –3; х₂ = 2.

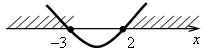
Решением системы неравенств является пересечение следующих промежутков:

Значит, x  –3 или 2  x < 6.

Ответ: а) x  –3; 2  x < 6.

VI. Итоги урока. Рефлексия

Вопросы учащимся:

– Неравенства какого вида называются логарифмическими?

–Каким образом осуществляется переход от логарифмического неравенства к алгебраическому?

– Какими условиями определяется ОДЗ логарифмического неравенства? Как используется транзитивность неравенств для упрощения получаемой системы неравенств?

Домашнее задание: № 45.3 (в; г), № 45.5, № 45.7 (в; г).

Решение логарифмических неравенств

Цели урока:

Дидактические:

• 1 уровень – научить решать простейшие логарифмические неравенства, применяя определение логарифма, свойства логарифмов;
• 2 уровень – решать логарифмические неравенства, выбирая самостоятельно способ решения;
• 3 уровень – уметь применять знания и умения в нестандартных ситуациях.

Развивающие: развивать память, внимание, логическое мышление, навыки сравнения, уметь обобщать и делать выводы

Воспитательные: воспитывать аккуратность, ответственность за выполняемое задание, взаимопомощь.

Методы обучения: словесный, наглядный, практический, частично-поисковый, самоуправления, контроля.

Формы организации познавательной деятельности учащихся: фронтальный, индивидуальный, работа в парах.

Оборудование: набор тестовых заданий, опорный конспект, чистые листы для решений.

Тип урока: изучение нового материала.

Ход урока

1. Организационный момент. Объявляются тема и цели урока, схема проведения урока: каждому ученику выдается оценочный лист, который ученик заполняет в течении урока; для каждой пары учеников – печатные материалы с заданиями, выполнять задания нужно в парах; чистые листы для решений; опорные листы: определение логарифма; график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств.

Все решения после самооценки сдаются учителю.

Оценочный лист учащегося

Учебный элемент 1	Учебный элемент 2	Учебный элемент 3	Учебный элемент 4	Учебный элемент 5
1. 2. 3. 4. 5.	1. 2. 3. 4.	1. 2. 3	1. 2.	1. 2.
итог	итог	итог	итог	итог
Общий итог:

2. Актуализация знаний.

Указания учителя. Вспомните определение логарифма, график логарифмической функции и ее свойства. Для этого прочитайте текст на с.88–90, 98–101 учебника “Алгебра и начала анализа 10–11” под редакцией Ш.А Алимова, Ю.М Колягина и др.

Ученикам раздаются листы, на которых записаны: определение логарифма; изображен график логарифмической функции, ее свойства; свойства логарифмов; алгоритм решения логарифмических неравенств, пример решения логарифмического неравенства, сводящегося к квадратному.

3. Изучение нового материала.

Решение логарифмических неравенств основано на монотонности логарифмической функции.

Алгоритм решения логарифмических неравенств:

А) Найти область определения неравенства (подлогарифмическое выражение больше нуля).
Б) Представить (если возможно) левую и правую части неравенства в виде логарифмов по одному и тому же основанию.
В) Определить, возрастающей или убывающей является логарифмическая функция: если t>1, то возрастающая; если 0<t>1, то убывающая.
Г) Перейти к более простому неравенству (подлогарифмических выражений), учитывая, что знак неравенства сохранится, если функция возрастает, и изменится, если она убывает.

Учебный элемент № 1.

Цель: закрепить решение простейших логарифмических неравенств

Форма организации познавательной деятельности учащихся: индивидуальная работа.

Задания для самостоятельной работы на 10 минут. Для каждого неравенства имеются несколько вариантов ответов, нужно выбрать верный и проверить по ключу.

КЛЮЧ: 13321, максимальное кол-во баллов – 6 б.

Указания учителя. Проверьте и оцените свою работу. Правильные ответы возьмите у учителя, проставьте количество набранных баллов себе в оценочный лист. Подписанные листы с решениями сдать учителю

Учебный элемент № 2.

Цель: закрепить решение логарифмических неравенств, применяя свойства логарифмов.

Указания учителя. Вспомните основные свойства логарифмов. Для этого прочитайте текст учебника на с.92, 103–104.

Задания для самостоятельной работы на 10 минут.

КЛЮЧ: 2113, максимальное кол-во баллов – 8 б.

Учебный элемент № 3.

Цель: изучить решение логарифмических неравенств методом сведения к квадратному.

Указания учителя: метод сведения неравенства к квадратному состоит в том, что нужно преобразовать неравенство к такому виду, чтобы некоторую логарифмическую функцию обозначить новой переменной, получив при этом квадратное неравенство относительно этой переменной.

Применим метод интервалов.

Указания учителя: Проверьте и оцените работу, правильные ответы возьмите у учителя. Поставьте количество баллов в оценочный лист.

Вы прошли первый уровень усвоения материала. Теперь вам придется самостоятельно выбрать метод решения логарифмических уравнений, используя все свои знания и возможности.

Учебный элемент № 4.

Цель: закрепить решение логарифмических неравенств, выбрав самостоятельно рациональный способ решения.

Задания для самостоятельной работы на 10 минут

Указания учителя. Проверьте и оцените свою работу, правильные ответы возьмите у учителя. Проставьте полученные баллы в оценочный лист.

Учебный элемент № 5.

Указания учителя. Молодцы! Вы освоили решение уравнений второго уровня сложности. Целью дальнейшей вашей работы является применение своих знаний и умений в более сложных и нестандартных ситуациях.

Задания для самостоятельного решения:

Указания учителя. Замечательно, если вы справились со всем заданием. Молодцы!

4. Итог урока. Проверьте и оцените свою работу. Подсчитайте количество баллов. Проставьте количество баллов в оценочный лист.

Оценка за весь урок зависит от числа набранных баллов по всем учебным элементам:

• если N ≥ 20, то вы получаете оценку “5”,
• при 16 ≤ N ≤ 19 – оценка “4”,
• при 8 ≤ N ≤ 15 – оценка “3”,
• при N < 8 выполнить работу над ошибками к следующему уроку (решения можно взять у учителя).

Оценочные лисы сдать учителю.

5. Домашнее задание: если вы набрали не более 15 б – выполните работу над ошибками (решения можно взять у учителя), если вы набрали более 15 б – выполните творческое задание по теме “Логарифмические неравенства”.

§5.2. Решение логарифмических неравенств. Алгебра и начала математического анализа, 10 класс: уроки, тесты, задания.

1.	Определение логарифма (основание целое число) Сложность: лёгкое	4
2.	Определение логарифма (основание — дробь) Сложность: лёгкое	4
3.	Область определения логарифмической функции Сложность: лёгкое	3
4.	Сумма логарифимов (десятичный логарифм) Сложность: лёгкое	3
5.	Логарифмическое неравенство, сводимое к линейному (основание больше 1) Сложность: лёгкое	3
6.	Логарифмическое неравенство (основание меньше 1) Сложность: лёгкое	1
7.	Разность логарифмов (убывающая функция) Сложность: лёгкое	3
8.	Логарифмическое неравенство, сводимое к линейному (определение логарифма) Сложность: среднее	4
9.	Логарифмическое неравенство, сводимое к линейному (убывающая функция) Сложность: среднее	4
10.	Логарифмическое неравенство, сводимое к линейному (основание меньше 1) Сложность: среднее	6
11.	Метод введения новой переменной (квадратичная) Сложность: среднее	7
12.	Сумма логарифмов (основание меньше 1) Сложность: среднее	4
13.	Наибольшее значение логарифмического неравенства Сложность: среднее	10
14.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
15.	Логарифмическое неравенство (квадратичное) Сложность: среднее	2
16.	Логарифмическое неравенство (определение логарифма) Сложность: среднее	4
17.	Логарифмическое неравенство (убывающая функция) Сложность: среднее	6
18.	Логарифмическое неравенство, сводимое к квадратичному (основание больше 1) Сложность: среднее	7
19.	Логарифмическое неравенство, сводимое к квадратичному (возрастающая функция) Сложность: сложное	9
20.	Неизвестное основание Сложность: сложное	13