Формулы логарифмов. Логарифмы примеры решения.

Сегодня мы поговорим о формулах логарифмов и дадим показательные примеры решения.

Ранее мы уже познакомились с понятием логарифма. А также рассмотрели основные свойства и примеры решения.

Формулы логарифмов сами по себе подразумевают шаблоны решения согласно основным свойствам логарифмов. Прежде применять формулы логарифмов для решения напомним для вас, сначала все свойства:

Теперь на основе этих формул(свойств), покажем примеры решения логарифмов.

Примеры решения логарифмов на основании формул.

Логарифм положительного числа b по основанию a (обозначается log_ab) — это показатель степени, в которую надо возвести a, чтобы получить b, при этом b > 0, a > 0, а 1.

Согласно определения log_ab = x, что равносильно a^x = b, поэтому log_aa^x = x.

Логарифмы, примеры:

log₂8 = 3, т.к. 2³ = 8

log₇49 = 2, т.к. 7² = 49

log₅1/5 = -1, т.к. 5^-1 = 1/5

Десятичный логарифм — это обычный логарифм, в основании которого находится 10. Обозначается как lg.

lg100 = 2

log₁₀100 = 2, т.к. 10² = 100

Натуральный логарифм — также обычный логарифм логарифм, но уже с основанием е (е = 2,71828… — иррациональное число). Обозначается как ln.

Формулы или свойства логарифмов желательно запомнить, потому что они понадобятся нам в дальнейшем при решении логарифмов, логарифмических уравнений и неравенств. Давайте еще раз отработаем каждую формулу на примерах.

• Основное логарифмическое тождество
  a ^log_ab = b

  Пример.

  8^2log₈3 = (8^2log₈3)²

  = 3² = 9

• Логарифм произведения равен сумме логарифмов
  log_a (bc) = log_ab + log_ac

  Пример.

  log₃8,1 + log₃10 = log₃ (8,1*10) = log₃81 = 4

• Логарифм частного равен разности логарифмов
  log_a (b/c) = log_ab — log_ac

  Пример.

  9 ^log₅50/9 ^log₅2 = 9 ^{log₅50- log₅2} = 9 ^log₅25 = 9 ² = 81

• Свойства степени логарифмируемого числа и основания логарифма

  Показатель степени логарифмируемого числа log_ab ^m = mlog_ab

  Показатель степени основания логарифма log_aⁿb =1/n*log_ab

  log_aⁿb ^m = m/n*log

  ab,

  если m = n, получим log_aⁿb ⁿ = log_ab

  Пример.

  log₄9 = log_2²3 ² = log₂3

• Переход к новому основанию
  log_ab = log_cb/log_ca,

  если c = b, получим log_bb = 1

  тогда log_ab = 1/log_ba

  Пример.

  log_0,83*log₃1,25 = log_0,83*log_0,81,25/log_0,83 = log_0,81,25 = log_4/55/4 = -1

Как видите, формулы логарифмов не так сложны как кажутся. Теперь рассмотрев примеры решения логарифмов мы можем переходить к логарифмическим уравнениям. Примеры решения логарифмических уравнений мы более подробно рассмотрим в статье: «Решение логарифмических уравнений. Как решать, на примерах». Не пропустите!

Если у вас остались вопросы по решению, пишите их в комментариях к статье.

Заметка: решили получить образование другого класса обучение за рубежом как вариант развития событий.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Простейшие логарифмические уравнения

18 сентября 2013

Сегодня мы научимся решать самые простые логарифмические уравнения, где не требуются предварительные преобразования и отбор корней. Но если научиться решать такие уравнения, дальше будет намного проще.

Простейшее логарифмическое уравнение — это уравнение вида log_af (x) = b, где a, b — числа (a > 0, a ≠ 1), f (x) — некоторая функция.

Отличительная особенность всех логарифмических уравнений — наличие переменной x под знаком логарифма. Если изначально в задаче дано именно такое уравнение, оно называется простейшим. Любые другие логарифмические уравнения сводятся к простейшим путем специальных преобразований (см. «Основные свойства логарифмов»). Однако при этом надо учитывать многочисленные тонкости: могут возникнуть лишние корни, поэтому сложные логарифмические уравнения будут рассмотрены отдельно.

Как решать такие уравнения? Достаточно заменить число, стоящее справа от знака равенства, логарифмом по тому же основанию, что и слева. Затем можно избавиться от знака логарифма. Получим:

log_af (x) = b ⇒ log_af (x) = log_aa^b ⇒ f (x) = a^b

Получили обычное уравнение. Его корни являются корнями исходного уравнения.

Вынесение степеней

Зачастую логарифмические уравнения, которые внешне выглядят сложно и угрожающе, решаются буквально в пару строчек без привлечения сложных формул. Сегодня мы рассмотрим именно такие задачи, где все, что от вас потребуется — аккуратно свести формулу к канонической форме и не растеряться при поиске области определения логарифмов.

Сегодня, как вы уже наверняка догадались из названия, мы будем решать логарифмические уравнения по формулам перехода к канонической форме. Основной «фишкой» данного видеоурока будет работа со степенями, а точнее, вынесение степени из основания и аргумента. Давайте рассмотрим правило:

Аналогичным образом можно вынести степень и из основания:

Как видим, если при вынесении степени из аргумента логарифма у нас просто появляется дополнительный множитель спереди, то при вынесении степени из основания — не просто множитель, а перевернутый множитель.

Это нужно помнить.

Наконец, самое интересное. Данные формулы можно объединить, тогда мы получим:

Разумеется, при выполнении данных переходов существуют определенные подводные камни, связанные с возможным расширением области определения или, наоборот, сужением области определения. Судите сами:

log₃x² = 2 ∙ log₃x

Если в первом случае в качестве x могло стоять любое число, отличное от 0, т. е. требование x ≠ 0, то во втором случае нас устроят лишь x, которые не только не равны, а строго больше 0, потому что область определения логарифма состоит в том, чтобы аргумент был строго больше 0. Поэтому напомню вам замечательную формулу из курса алгебры 8—9 класса:

То есть, мы должны записать нашу формулу следующим образом:

log₃x² = 2 ∙ log₃ |x|

Тогда никакого сужения области определения не произойдет.

Однако в сегодняшнем видеоуроке никаких квадратов не будет. Если вы посмотрите на наши задачи, то увидите только корни. Следовательно, применять данное правило мы не будем, однако его все равно необходимо держать в голове, чтобы в нужный момент, когда вы увидите квадратичную функцию в аргументе или основании логарифма, вы вспомните это правило и все преобразования выполните верно.

Итак, первое уравнение:

Для решения такой задачи предлагаю внимательно посмотреть на каждое из слагаемых, присутствующих в формуле.

Давайте перепишем первое слагаемое в виде степени с рациональным показателем:

Смотрим на второе слагаемое: log₃ (1 − x). Здесь делать ничего не нужно, здесь все уже преобразовании.

Наконец, 0, 5. Как я уже говорил в предыдущих уроках, при решении логарифмических уравнений и формул очень рекомендую переходить от десятичных дробей к обычным. Давайте так и сделаем:

0,5 = 5/10 = 1/2

Перепишем наше исходную формулу с учетом полученных слагаемых:

log₃ (1 − x) = 1

Теперь переходим к канонической форме:

log₃ (1 − x) = log₃ 3

Избавляемся от знака логарифма, приравнивая аргументы:

1 − x = 3

−x = 2

x = −2

Все, мы решили уравнение. Однако давайте все-таки подстрахуемся и найдем область определения. Для этого вернемся к исходной формуле и посмотрим:

1 − x > 0

−x > −1

x < 1

Наш корень x = −2 удовлетворяет это требование, следовательно, x = −2 является решением исходного уравнения. Вот теперь мы получили строгое четкое обоснование. Все, задача решена.

Переходим ко второй задаче:

Давайте разбираться с каждым слагаемым отдельно.

Выписываем первое:

Первое слагаемое мы преобразовали. Работаем со вторым слагаемым:

Наконец, последнее слагаемое, которое стоит справа от знака равенства:

Подставляем полученные выражения вместо слагаемых в полученной формуле:

log₃x = 1

Переходим к канонической форме:

log₃x = log₃ 3

Избавляемся от знака логарифма, приравнивая аргументы, и получаем:

x = 3

Опять же, давайте на всякий случай подстрахуемся, вернемся к исходному уравнению и посмотрим. В исходной формуле переменная x присутствует только в аргументе, следовательно,

x > 0

Во втором логарифме x стоит под корнем, но опять же в аргументе, следовательно, корень должен быть больше 0, т. е. подкоренное выражение должно быть больше 0. Смотрим на наш корень x = 3. Очевидно, что он удовлетворяет это требование. Следовательно, x = 3 является решением исходного логарифмического уравнения. Все, задача решена.

Ключевых моментов в сегодняшнем видеоуроке два:

1) не бойтесь преобразовывать логарифмы и, в частности, не бойтесь выносить степени за знак логарифма, при этом помните нашу основную формулу: при вынесении степени из аргумента она выносится просто без изменений как множитель, а при вынесении степени из основания эта степень переворачивается.

2) второй момент связан с само канонической формой. Переход к канонической форме мы выполняли в самом конце преобразования формулы логарифмического уравнения. Напомню следующую формулу:

a = log_bb^a

Разумеется, под выражением «любое число b», я подразумеваю такие числа, которые удовлетворяют требования, накладываемые на основание логарифма, т. е.

1 ≠ b > 0

Вот при таких b, а поскольку основание у нас уже известно, то это требование будет выполняться автоматически. Но при таких b — любых, которые удовлетворяют данное требование — данный переход может быть выполнен, и у нас получится каноническая форма, в которой можно избавиться от знака логарифма.

Расширение области определения и лишние корни

В процессе преобразования логарифмических уравнений может произойти неявное расширение области определения. Зачастую ученики этого даже не замечают, что приводит к ошибкам и неправильным ответам.

Начнем с простейших конструкций. Простейшим логарифмическим уравнением называется следующее:

log_af(x) = b

Обратите внимание: x присутствует лишь в одном аргументе одного логарифма. Как мы решаем такие уравнения? Используем каноническую форму. Для этого представляем число b = log_aa^b, и наше уравнение перепишется в следующем виде:

log_af(x) = log_aa^b

Данная запись называется канонической формой. Именно к ней следует сводить любое логарифмическое уравнение, которое вы встретите не только в сегодняшнем уроке, но и в любой самостоятельной и контрольной работе.

Как прийти к канонической форме, какие приемы использовать — это уже вопрос практики. Главное понимать: как только вы получите такую запись, можно считать, что задача решена. Потому что следующим шагом будет запись:

f(x) = a^b

Другими словами, мы избавляемся от знака логарифма и просто приравниваем аргументы.

К чему весь этот разговор? Дело в том, что каноническая форма применима не только к простейшим задачам, но и к любым другим. В частности и к тем, которые мы будем решать сегодня. Давайте посмотрим.

Первая задача:

В чем проблема данного уравнения? В том, что функция стоит сразу в двух логарифмах. Задачу можно свести к простейшей, просто вычтя один логарифм из другого. Но возникают проблемы с областью определения: могут появиться лишние корни. Поэтому давайте просто перенесем один из логарифмов вправо:

Вот такая запись уже гораздо больше похожа на каноническую форму. Но есть еще один нюанс: в канонической форме аргументы должны быть одинаковы. А у нас слева стоит логарифм по основанию 3, а справа — по основанию 1/3. Знаит, нужно привести эти основания к одному и тому же числу. Например, вспомним, что такое отрицательные степени:

1/3 = 3⁻¹

А затем воспользуемся вынесем показатель «−1» за пределы log в качестве множителя:

Обратите внимание: степень, которая стояла в основании, переворачивается и превращается в дробь. Мы получили почти каноническую запись, избавившись от разных оснований, но взамен получили множитель «−1» справа. Давайте внесем этот множитель в аргумент, превратив его в степень:

Разумеется, получив каноническую форму, мы смело зачеркиваем знак логарифма и приравниваем аргументы. При этом напомню, что при возведении в степень «−1» дробь просто переворачивается — получается пропорция.

Воспользуемся основным свойством пропорции и перемножим ее крест-накрест:

(x− 4) (2x− 1) = (x− 5) (3x− 4)

2x² − x− 8x + 4 = 3x² − 4x− 15x + 20

2x² − 9x + 4 = 3x² − 19x + 20

x² − 10x + 16 = 0

Перед нами приведенное квадратное уравнение, поэтому решаем его с помощью формул Виета:

(x − 8)(x − 2) = 0

x₁ = 8; x₂ = 2

Вот и все. Думаете, уравнение решено? Нет! За такое решение мы получим 0 баллов, потому что в исходном уравнении присутствуют сразу два логарифма с переменной x. Поэтому требуется учесть область определения.

И здесь начинается самое веселое. Большинство учеников путаются: в чем состоит область определения логарифма? Разумеется, все аргументы (у нас их два) должны быть больше нуля:

(x− 4)/(3x− 4) > 0

(x− 5)/(2x− 1) > 0

Каждое из этих неравенств нужно решить, отметить на прямой, пересечь — и только потом посмотреть, какие корни лежат на пересечении.

Скажу честно: такой прием имеет право на существование, он надежный, и вы получите правильный ответ, однако в нем слишком много лишних действий. Поэтому давайте еще раз пройдемся по нашему решению и посмотрим: где именно требуется применить область определения? Другими словами, нужно четно понимать, когда именно возникают лишние корни.

1. Изначально у нас было два логарифма. Потом мы перенесли один из них вправо, но на область определения это не повлияло.
2. Затем мы выносим степень из основания, но логарифмов все равно остается два, и в каждом из них присутствует переменная x.
3. Наконец, мы зачеркиваем знаки log и получаем классическое дробно-рациональное уравнение.

Именно на последнем шаге происходит расширение области определения! Как только мы перешли к дробно-рациональному уравнению, избавившись от знаков log, требования к переменной xрезко поменялись!

Следовательно, область определения можно считать не в самом начале решения, а только на упомянутом шаге — перед непосредственным приравниваем аргументов.

Здесь-то и кроется возможность для оптимизации. С одной стороны, от нас требуется, чтобы оба аргумента были больше нуля. С другой — далее мы приравниваем эти аргументы. Следовательно, если хотя бы один и них будет положителен, то и второй тоже окажется положительным!

Вот и получается, что требовать выполнение сразу двух неравенств — это излишество. Достаточно рассмотреть лишь одну из этих дробей. Какую именно? Та, которая проще. Например, давайте разберемся с правой дробью:

(x− 5)/(2x− 1) > 0

Это типичное дробно-рациональное неравенство, решаем его методом интервалов:

Как расставить знаки? Возьмем число, заведомо большее всех наших корней. Например 1 млрд. И подставляем его дробь. Получим положительное число, т.е. справа от корня x = 5 будет стоять знак «плюс».

Затем знаки чередуются, потому что корней четной кратности нигде нет. Нас интересуют интервалы, где функция положительна. Следовательно, x∈ (−∞; −1/2)∪(5; +∞).

Теперь вспоминаем про ответы: x = 8 и x = 2. Строго говоря, это еще не ответы, а лишь кандидаты на ответ. Какой из них принадлежит указанному множеству? Конечно, x = 8. А вот x = 2 нас не устраивает по области определения.

Итого ответом к первому логарифмическому уравнению будет x = 8. Вот теперь мы получили грамотное, обоснованное решение с учетом области определения.

Переходим ко второму уравнению:

log₅ (x − 9) = log_0,5 4 − log₅ (x − 5) + 3

Напоминаю, что если в уравнении присутствует десятичная дробь, то от нее следует избавиться. Другими словами, перепишем 0,5 в виде обычной дроби. Сразу замечаем, что логарифм, содержащий это основание, легко считается:

Это очень важны момент! Когда у нас и в основании, и в аргументе стоят степени, мы можем вынести показатели этих степеней по формуле:

Возвращаемся к нашему исходному логарифмическому уравнению и переписываем его:

log₅ (x− 9) = 1 − log₅ (x− 5)

Получили конструкцию, довольно близкую к канонической форме. Однако нас смущают слагаемые и знак «минус» справа от знака равенства. Давайте представим единицу как логарифм по основанию 5:

log₅ (x − 9) = log₅ 5¹ − log₅ (x − 5)

Вычтем логарифмы справа (при этом их аргументы делятся):

log₅(x − 9) = log₅ 5/(x− 5)

Прекрасно. Вот мы и получили каноническую форму! Зачеркиваем знаки logи приравниваем аргументы:

(x − 9)/1 = 5/(x − 5)

Это пропорция, которая легко решается умножением крест-накрест:

(x − 9)(x − 5) = 5¹

x² − 9x − 5x + 45 = 5

x² − 14x + 40 = 0

Очевидно, перед нами приведенное квадратное уравнение. Оно легко решается с помощью формул Виета:

(x − 10)(x − 4) = 0

x₁ = 10

x₂ = 4

Мы получили два корня. Но это не окончательные ответы, а лишь кандидаты, потому что логарифмическое уравнение требует еще и проверки области определения.

Напоминаю: не надо искать, когда каждый из аргументов будет больше нуля. Достаточно потребовать, чтобы один аргумент — либо x − 9, либо 5/(x − 5) — был больше нуля. Рассмотрим первый аргумент:

x − 9 > 0

x > 9

Очевидно, что этому требованию удовлетворяет лишь x = 10. Это и есть окончательный ответ. Все задача решена.

Еще раз ключевые мысли сегодняшнего урока:

1. Как только переменная x появляется в нескольких логарифмах, уравнение перестает быть элементарным, и для него придется считать область определения. Иначе можно запросто записать в ответ лишние корни.
2. Работу с самой областью определения можно существенно упростить, если выписывать неравенство не сразу, а ровно в тот момент, когда мы избавляемся от знаков log. Ведь когда аргументы приравниваются друг к другу, достаточно потребовать, чтобы больше нуля был лишь один из них.

Разумеется, мы сами выбираем, из какого аргумента составлять неравенство, поэтому логично выбирать самый простой. Например, во втором уравнении мы выбрали аргумент (x − 9) —линейную функцию, в противовес дробно-рациональному второму аргументу. Согласитесь, решать неравенство x − 9 > 0 значительно проще, чем 5/(x − 5) > 0. Хотя результат получается один и тот же.

Данное замечание существенно упрощает поиск ОДЗ, но будьте внимательны: использовать одно неравенство вместо двух можно только том случае, когда аргументы именно приравниваются друг к другу!

Конечно, кто-то сейчас спросит: а что, бывает по-другому? Да, бывает. Например, в самом шаге, когда мы перемножаем два аргумента, содержащие переменную, заложена опасность возникновения лишних корней.

Судите сами: сначала требуется, чтобы каждый из аргументов был больше нуля, но после перемножения достаточно, чтобы их произведение было больше нуля. В результате упускается случай, когда каждая из этих дробей отрицательна.

Поэтому если вы только начинаете разбираться со сложными логарифмическими уравнениями, ни в коем случае не перемножайте логарифмы, содержащие переменную x — уж слишком часто это приведет к возникновению лишних корней. Лучше сделайте один лишний шаг, перенесите одно слагаемое в другую сторону составьте каноническую форму.

Ну, а как поступать в том случае, если без перемножения таких логарифмов не обойтись, мы обсудим в следующем видеоуроке.:)

Еще раз о степенях в уравнении

Сегодня мы разберем довольно скользкую тему, касающуюся логарифмических уравнений, а точнее — вынесение степеней из аргументов и оснований логарифмов.

Я бы даже сказал, речь пойдет о вынесении четных степеней, потому что именно с четными степенями возникает большинство затруднений и при решении реальных логарифмических уравнений.

Начнем с канонической формы. Допустим, у нас есть уравнение вида log_af(x) = b. В этом случае мы переписываем число b по формуле b = log_aa^b. Получается следующее:

log_af(x) = log_aa^b

Затем мы приравниваем аргументы:

f(x) = a^b

Канонической формой называется предпоследняя формула. Именно к ней стараются свести любое логарифмическое уравнение, каким бы сложным и страшным оно не казалось на первый взгляд.

Вот давайте и попробуем. Начнем с первой задачи:

Предварительное замечание: как я уже говорил, все десятичные дроби в логарифмическом уравнении лучше перевести ее в обычные:

0,001 = 1/1000

0,5 = 5/10 = 1/2

Перепишем наше уравнение с учетом этого факта. Заметим, что и 1/1000, и 100 являются степенью десятки, а затем вынесем степени отовсюду, где они есть: из аргументов и даже из основания логарифмов:

И вот здесь у многих учеников возникает вопрос: «Откуда справа взялся модуль?» Действительно, почему бы не написать просто (х − 1)? Безусловно, сейчас мы напишем (х − 1), но право на такую запись нам дает учет области определения. Ведь в другом логарифме уже стоит (х − 1), и это выражение должно быть больше нуля.

Но когда мы выносим квадрат из основания логарифма, мы обязаны оставить в основании именно модуль. Поясню почему.

Дело в том, что с точки зрения математики вынесение степени равносильно извлечению корня. В частности, когда из выражения (x− 1)² выносится квадрат, мы по сути извлекаем корень второй степени. Но корень из квадрата — это не что иное как модуль. Именно модуль, потому что даже если выражение х − 1 будет отрицательным, при возведении в квадрат «минус» все равно сгорит. Дальнейшее извлечение корня даст нам положительное число — уже без всяких минусов.

В общем, чтобы не допускать обидных ошибок, запомните раз и навсегда:

Корень четной степени из любой функции, которая возведена в эту же степень, равен не самой функции, а ее модулю:

Возвращаемся к нашему логарифмическому уравнению. Говоря про модуль, я утверждал, что мы можем безболезненно снять его. Это правда. Сейчас объясню почему. Строго говоря, мы обязаны были рассмотреть два варианта:

1. x− 1 > 0 ⇒ |х − 1| = х − 1
2. x − 1 < 0 ⇒ |х − 1| = −х + 1

Каждый из этих вариантов нужно было бы решить. Но есть одна загвоздка: в исходной формуле уже присутствует функция (х − 1) без всякого модуля. И следуя области определения логарифмов, мы вправе сразу записать, что х − 1 > 0.

Это требование должно выполняться независимо от всяких модулей и других преобразований, которые мы выполняем в процессе решения. Следовательно, второй вариант рассматривать бессмысленно — он никогда не возникнет. Даже если при решении этой ветки неравенства мы получим какие-то числа, они все равно не войдут в окончательный ответ.

В общем, можно считать, что |х − 1| = х − 1. Тогда наше уравнение перепишется в следующем виде:

Теперь мы буквально в одном шаге от канонической формы логарифмического уравнения. Давайте представим единицу в следующем виде:

1 = log_{x − 1} (x− 1)¹

Кроме того, внесем множитель −4, стоящий справа, в аргумент:

log_{x − 1} 10⁻⁴ = log_{x − 1} (x− 1)

Перед нами каноническая форма логарифмического уравнения. Избавляемся от знака логарифма:

10⁻⁴ = x− 1

Но поскольку в основании стояла функция (а не простое число), дополнительно потребуем, чтобы эта функция была больше нуля и не равна единице. Получится система:

Поскольку требование х − 1 > 0 выполняется автоматически (ведь х − 1 = 10⁻⁴), одно из неравенств можно вычеркнуть из нашей системы. Второе условие также можно вычеркнуть, потому что х − 1 = 0,0001 < 1. Итого получаем:

х = 1 + 0,0001 = 1,0001

Это единственный корень, который автоматически удовлетворяет всем требованиям области определения логарифма (впрочем, все требования были отсеяны как заведомо выполненные в условиях нашей задачи).

Итак, второе уравнение:

3 log_3xx = 2 log_9xx²

Чем это уравнение принципиально отличается от предыдущего? Уже хотя бы тем, что основания логарифмов — 3х и 9х — не являются натуральными степенями друг друга. Следовательно, переход, который мы использовали в предыдущем решении, невозможен.

Давайте хотя бы избавимся от степеней. В нашем случае единственная степень стоит во втором аргументе:

3 log_3xx = 2 ∙ 2 log_9x|x|

Впрочем, знак модуля можно убрать, ведь переменная х стоит еще и в основании, т.е. х > 0 ⇒ |х| = х. Перепишем наше логарифмическое уравнение:

3 log_3xx = 4 log_9xx

Получили логарифмы, в которых одинаковые аргументы, но разные основания. Как поступить дальше? Вариантов тут множество, но мы рассмотрим лишь два из них, которые наиболее логичны, а самое главное — это быстрые и понятные приемы для большинства учеников.

Первый вариант мы уже рассматривали: в любой непонятной ситуации переводите логарифмы с переменным основанием к какому-нибудь постоянному основанию. Например, к двойке. Формула перехода проста:

Разумеется, в роли переменной с должно выступать нормальное число: 1 ≠ c > 0. Пусть в нашем случае с = 2. Теперь перед нами обычное дробно-рациональное уравнение. Собираем все элементы слева:

Очевидно, что множитель log₂x лучше вынести, поскольку он присутствует и в первой, и во второй дроби.

Дальше все просто. Произведение равно нулю, когда хотя бы один из множителей равен нулю:

log₂x = 0;

х = 1;

3 log₂ 9х = 4 log₂ 3x

Разбиваем каждый log на два слагаемых:

log₂ 9х = log₂ 9 + log₂x = 2 log₂ 3 + log₂ x;

log₂ 3x = log₂ 3 + log₂x

Перепишем обе части равенства с учетом этих фактов:

3 (2 log₂ 3 + log₂x) = 4 (log₂ 3 + log₂x)

6 log₂ 3 + 3 log₂x = 4 log₂ 3 + 4 log₂x

2 log₂ 3 = log₂x

Теперь осталось внести двойку под знак логарифма (она превратится в степень: 3² = 9):

log₂ 9 = log₂x

Перед нами классическая каноническая форма, избавляемся от знака логарифма и получаем:

х = 9

Как и предполагалось, этот корень оказался больше нуля. Осталось проверить область определения. Посмотрим на основания:

3х ≠ 1

9х ≠ 1

Но корень x = 9 удовлетворяет этим требованиям. Следовательно, он является окончательным решением.

Вывод из данного решения просто: не пугайтесь длинных выкладок! Просто в самом начале мы выбрали новое основание наугад — и это существенно усложнило процесс.

Но тогда возникает вопрос: какое же основание является оптимальным? Об этом я расскажу во втором способе.

Давайте вернемся к нашему исходному уравнению:

3 log_3xx = 2 log_9xx²

3 log_3xx = 2 ∙ 2 log_9x |x|

х > 0 ⇒ |х| = х

3 log_3xx = 4 log_9xx

Теперь немного подумаем: какое число или функция будет оптимальным основанием? Очевидно, что лучшим вариантом будет с = х — то, что уже стоит в аргументах. В этом случае формула log_ab = log_cb/log_ca примет вид:

Другими словами, выражение просто переворачивается. При этом аргумент и основание меняется местами.

Эта формула очень полезна и очень часто применяется при решении сложных логарифмических уравнений. Однако при использовании этой формулы возникает один очень серьезный подводный камень. Если вместо основания мы подставляем переменную х, то на нее накладываются ограничения, которых ранее не наблюдалось:

0 < х ≠ 1

Такого ограничения в исходном уравнении не было. Поэтому следует отдельно проверить случай, когда х = 1. Подставим это значение в наше уравнение:

3 log₃ 1 = 4 log₉ 1

0 = 0

Получаем верное числовое равенство. Следовательно, х = 1 является корнем. Точно такой же корень мы нашли в предыдущем методе в самом начале решения.

А вот теперь, когда мы отдельно рассмотрели этот частный случай, смело полагаем, что х ≠ 1. Тогда наше логарифмическое уравнение перепишется в следующем виде:

3 log_x 9x = 4 log_x 3x

Раскладываем оба логарифма по той же формуле, что и раньше. При этом заметим, что log_xx = 1:

3 (log_x 9 + log_xx) = 4 (log_x 3 + log_xx)

3 log_x 9 + 3 = 4 log_x 3 + 4

3 log_x 3² − 4 log_x 3 = 4 − 3

2 log_x 3 = 1

Вот мы и пришли к канонической форме:

log_x 9 = log_xx¹

x = 9

Получили второй корень. Он удовлетворяет требованию х ≠ 1. Следовательно, х = 9 наравне с х = 1 является окончательным ответом.

Как видим, объем выкладок немножко сократился. Но при решении реального логарифмического уравнения количество действий будет намного меньше еще и потому, что от вас не требуется столь подробно расписывать каждый шаг.

Ключевое правило сегодняшнего урока состоит в следующем: если в задаче присутствует четная степень, из которой извлекают корень такой же степени, то на выходе мы получи модуль. Однако этот модуль можно убрать, если обратить внимание на область определения логарифмов.

Но будьте внимательны: большинство учеников после этого урока считают, что им все понятно. Но при решении реальных задач они не могут воспроизвести всю логическую цепочку. В результате уравнение обрастает лишними корнями, а ответ получается неправильным.

Поэтому обязательно практикуйтесь: скачивайте задачи для самостоятельной работы, решайте их и сравнивайте с ответами. А у меня на сегодня все.:)

Смотрите также:

1. Логарифмические уравнения: несколько видеоуроков по теме
2. Квадратные уравнения относительно логарифма
3. Сводный тест по задачам B12 (1 вариант)
4. Геометрическая вероятность
5. Симметрия корней и оптимизация ответов в тригонометрии
6. Задача C1: еще одно показательное уравнение

Натуральный логарифм х 4 9. Логарифмы: примеры и решения

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a c = b: log a b = c ⇔ a c = b (a > 0, a ≠ 1, b > 0) &nbsp&nbsp&nbsp&nbsp&nbsp&nbsp

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество a log a b = b (a > 0, a ≠ 1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма log a a = 1 (a > 0, a ≠ 1) (3)
log a 1 = 0 (a > 0, a ≠ 1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.

Логарифм произведения и логарифм частного log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0) (5)

Log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.

Действительно, выражение log a (f (x) g (x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму log a f (x) + log a g (x) , мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма log a b p = p log a b (a > 0, a ≠ 1, b > 0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

Log a (f (x) 2 = 2 log a f (x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

Log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1) (9)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log 5 125 = 3. Мы использовали формулу перехода к новому основанию (8).

Таблица формул, связанных с логарифмами

a log a b = b (a > 0, a ≠ 1)

log a a = 1 (a > 0, a ≠ 1)

log a 1 = 0 (a > 0, a ≠ 1)

log a (b c) = log a b + log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b c = log a b − log a c (a > 0, a ≠ 1, b > 0, c > 0)

log a b p = p log a b (a > 0, a ≠ 1, b > 0)

log a b = log c b log c a (a > 0, a ≠ 1, b > 0, c > 0, c ≠ 1)

log a b = 1 log b a (a > 0, a ≠ 1, b > 0, b ≠ 1)

нередко берут цифру е = 2,718281828 . Логарифмы по данному основанию именуют натуральным . При проведении вычислений с натуральными логарифмами общепринято оперировать знаком l n , а не log ; при этом число 2,718281828 , определяющие основание, не указывают.

Другими словами формулировка будет иметь вид: натуральный логарифм числа х — это показатель степени , в которую нужно возвести число e , чтобы получить x .

Так, ln(7,389…) = 2, так как e 2 =7,389… . Натуральный логарифм самого числа e = 1, потому что e 1 =e , а натуральный логарифм единицы равен нулю, так как e 0 = 1.

Само число е определяет предел монотонной ограниченной последовательности

вычислено, что е = 2,7182818284… .

Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!

На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.

График натурального логарифма (функции y = ln x ) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:

Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a .

Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».

Если анализировать натуральный логарифм , как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:

e ln(a) =a (a>0)

ln(e a) =a

По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:

ln (xy ) = ln (x ) + ln (y )

ln (х/у)= lnx — lny

Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e , но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.

Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x . Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма выступает минус бесконечность ( -∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.

Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.

Логарифмом числа b по основанию а называется показатель степени, в который нужно возвести число а чтобы получить число b.

Если , то .

Логарифм — крайне важная математическая величина , поскольку логарифмическое исчисление позволяет не только решать показательные уравнения, но и оперировать с показателями, дифференцировать показательные и логарифмические функции, интегрировать их и приводить к более приемлемому виду, подлежащему расчету.

Вконтакте

Все свойства логарифмов связаны напрямую со свойствами показательных функций. Например, тот факт, что означает, что:

Следует заметить, что при решении конкретных задач, свойства логарифмов могут оказаться более важными и полезными, чем правила работы со степенями.

Приведем некоторые тождества:

Приведем основные алгебраические выражения:

;

.

Внимание! может существовать только при x>0, x≠1, y>0.

Постараемся разобраться с вопросом, что такое натуральные логарифмы. Отдельный интерес в математике представляют два вида — первый имеет в основании число «10», и носит название «десятичный логарифм». Второй называется натуральным. Основание натурального логарифма — число «е». Именно о нем мы и будем детально говорить в этой статье.

Обозначения:

• lg x — десятичный;
• ln x — натуральный.

Используя тождество можно увидеть, что ln e = 1, как и то, что lg 10=1.

График натурального логарифма

Построим график натурального логарифма стандартным классическим способом по точкам. При желании, проверить правильно ли мы строим функцию, можно при помощи исследования функции. Однако, есть смысл научится строить его «вручную», чтобы знать, как правильно посчитать логарифм.

Функция: y = ln x. Запишем таблицу точек, через которые пройдет график:

Поясним, почему мы выбрали именно такие значения аргумента х. Всё дело в тождестве: . Для натурального логарифма это тождество будет выглядеть таким образом:

Для удобства мы можем взять пять опорных точек:

;

;

.

;

.

Таким образом, подсчет натуральных логарифмов — довольно несложное занятие, более того, он упрощает подсчеты операций со степенями, превращая их в обычное умножение.

Построив по точкам график, получаем приблизительный график:

Область определения натурального логарифма (т.е. все допустимые значения аргумента Х) — все числа больше нуля.

Внимание! В область определения натурального логарифма входят только положительные числа! В область определения не входит х=0. Это невозможно исходя из условий существования логарифма .

Область значений (т.е. все допустимые значения функции y = ln x) — все числа в интервале .

Предел натурального log

Изучая график, возникает вопрос — как ведет себя функция при y

Очевидно, что график функции стремится пересечь ось у, но не сможет этого сделать, поскольку натуральный логарифм при х

Предел натурального log можно записать таким образом:

Формула замены основания логарифма

Иметь дело с натуральным логарифмом намного проще, чем с логарифмом, имеющим произвольное основание. Именно поэтому попробуем научиться приводить любой логарифм к натуральному, либо выражать его по произвольному основанию через натуральные логарифмы.

Начнем с логарифмического тождества:

Тогда любое число, либо переменную у можно представить в виде:

где х — любое число (положительное согласно свойствам логарифма).

Данное выражение можно прологарифмировать с обеих сторон. Произведем это при помощи произвольного основания z:

Воспользуемся свойством (только вместо «с» у нас выражение):

Отсюда получаем универсальную формулу:

.

В частности, если z=e, то тогда:

.

Нам удалось представить логарифм по произвольному основанию через отношение двух натуральных логарифмов.

Решаем задачи

Для того чтобы лучше ориентироваться в натуральных логарифмах, рассмотрим примеры нескольких задач.

Задача 1 . Необходимо решить уравнение ln x = 3.

Решение: Используя определение логарифма: если , то , получаем:

Задача 2 . Решите уравнение (5 + 3 * ln (x — 3)) = 3.

Решение: Используя определение логарифма: если , то , получаем:

.

Еще раз применим определение логарифма:

.

Таким образом:

.

Можно приближенно вычислить ответ, а можно оставить его и в таком виде.

Задача 3. Решите уравнение .

Решение: Произведем подстановку: t = ln x. Тогда уравнение примет следующий вид:

.

Перед нами квадратное уравнение. Найдем его дискриминант:

Первый корень уравнения:

.

Второй корень уравнения:

.

Вспоминая о том, что мы производили подстановку t = ln x, получаем:

В статистике и теории вероятности логарифмические величины встречаются очень часто. Это неудивительно, ведь число е — зачастую отражает темп роста экспоненциальных величин.

В информатике, программировании и теории вычислительных машин, логарифмы встречаются довольно часто, например для того чтобы сохранить в памяти N понадобится битов.

В теориях фракталов и размерностях логарифмы используются постоянно, поскольку размерности фракталов определяются только с их помощью.

В механике и физике нет такого раздела, где не использовались логарифмы. Барометрическое распределение, все принципы статистической термодинамики, уравнение Циолковского и прочее — процессы, которые математически можно описать только при помощи логарифмирования.

В химии логарифмирование используют в уравнениях Нернста, описаниях окислительно-восстановительных процессов.

Поразительно, но даже в музыке, с целью узнать количество частей октавы, используют логарифмы.

Натуральный логарифм Функция y=ln x ее свойства

Доказательство основного свойства натурального логарифма

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a b *a c = a b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log a b=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log 2 8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а b >0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10 х = 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, 10 2 =100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log 10 100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a c =b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3 4 =81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log 3 81 = 4). Для отрицательных степеней правила такие же: 2 -5 = 1/32 запишем в виде логарифма, получим log 2 (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log 2 (x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм 2 x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а logaB =B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log d (s 1 *s 2) = log d s 1 + log d s 2. При этом обязательным условием является: d, s 1 и s 2 > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log a s 1 = f 1 и log a s 2 = f 2 , тогда a f1 = s 1 , a f2 = s 2. Получаем, что s 1 *s 2 = a f1 *a f2 = a f1+f2 (свойства степеней), а далее по определению: log a (s 1 *s 2)= f 1 + f 2 = log a s1 + log a s 2, что и требовалось доказать.
3. Логарифм частного выглядит так: log a (s 1/ s 2) = log a s 1 — log a s 2.
4. Теорема в виде формулы приобретает следующий вид: log a q b n = n/q log a b.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log a b = t, получается a t =b. Если возвести обе части в степень m: a tn = b n ;

но так как a tn = (a q) nt/q = b n , следовательно log a q b n = (n*t)/t, тогда log a q b n = n/q log a b. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log 2 4 + log 2 128 = log 2 (4*128) = log 2 512. Ответ равен 9.
2. log 4 8 = log 2 2 2 3 = 3/2 log 2 2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log 2 (2x-1) = 4. Решение:
перепишем выражение, немного его упростив log 2 (2x-1) = 2 2 , по определению логарифма получим, что 2x-1 = 2 4 , следовательно 2x = 17; x = 8,5.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Это может быть, например, калькулятор из базового набора программ операционной системы Windows. Ссылка на его запуск упрятана довольно в главное меню ОС — раскройте его щелчком по кнопке «Пуск», затем откройте его раздел «Программы», перейдите в подраздел «Стандартные», а затем в секцию «Служебные» и, наконец, щелкните пункт «Калькулятор». Можно вместо мыши и перемещений по меню использовать клавиатуру и диалог запуска программ — нажмите сочетание клавиш WIN + R, наберите calc (это имя исполняемого файла калькулятора) и нажмите клавишу Enter.

Переключите интерфейс калькулятора в расширенный режим, позволяющий осуществлять . По умолчанию он открывается в «обычном» виде, а вам нужен «инженерный» или « » (в зависимости от версии используемой ОС). Раскройте в меню раздел «Вид» и выберите соответствующую строку.

Введите аргумент, натуральный которого нужно вычислить. Это можно сделать как с клавиатуры, так и щелкая мышкой соответствующие кнопки в интерфейсе калькулятора на экране.

Кликните кнопку с надписью ln — программа рассчитает логарифма по основанию e и покажет результат.

Воспользуйтесь каким-либо из -калькуляторов в качестве альтернативного вычисления значения натурального логарифма. Например, тем, который размещен по адресу http://calc.org.ua . Его интерфейс предельно прост — есть единственное поле ввода, куда вам надо впечатать значение числа, логарифм от которого надо вычислить. Среди кнопок найдите и щелкните ту, на которой написано ln. Скрипт этого калькулятора не требует отправки данных на сервер и ответа, поэтому результат вычисления вы получите практически мгновенно. Единственная особенность, которую следует учитывать — разделителем между дробной и целой частью вводимого числа здесь обязательно должна быть точка, а не .

Термин «логарифм » произошел от двух греческих слов, одно из которых обозначает «число», а другое — «отношение». Им обозначают математическую операцию вычисления переменной величины (показателя степени), в которую надо возвести постоянное значение (основание), чтобы получить число, указанное под знаком логарифм а. Если основание равно математической константе, называемое числом «e», то логарифм называют «натуральным».

Вам понадобится

• Доступ в интернет, Microsoft Office Excel или калькулятор.

Инструкция

Воспользуйтесь во множестве представленными в интернете -калькуляторами — это, пожалуй, и простой способ вычисления натурального а. Поиском соответствующего сервиса вам заниматься не придется, так как многие поисковые системы и сами имеют встроенные калькуляторы, вполне пригодные для работы с логарифм ами. Например, перейдите на главную страницу самого крупного сетевого поисковика — Google. Никаких кнопок для ввода значений и выбора функций здесь не потребуется, просто наберите в поле ввода запроса нужное математическое действие. Скажем, для вычисления логарифм а числа 457 по основанию «e» введите ln 457 — этого будет вполне достаточно, чтобы Google отобразил с точностью до восьми знаков после запятой (6,12468339) даже без нажатия кнопки отправки запроса на сервер.

Используйте соответствующую встроенную функцию, если необходимость вычисления значения натурального логарифм а возникает при работе с данными в популярном табличном редакторе Microsoft Office Excel. Эта функция здесь вызывается с использованием общепринятого обозначения такого логарифм а в верхнем регистре — LN. Выделите ячейку, в которой должен быть отображен результат вычисления, и введите знак равенства — так в этом табличном редакторе должны начинаться записи в ячейках, содержащих в подразделе «Стандартные» раздела «Все программы» главного меню. Переключите калькулятор в более функциональный режим, нажав сочетание клавиш Alt + 2. Затем введите значение, натуральный логарифм которого требуется вычислить, и кликните в интерфейсе программы кнопку, обозначенную символами ln. Приложение произведет вычисление и отобразит результат.

Видео по теме

Урок математики «Логарифмы и их свойства»

Цели и задачи урока:

• рассмотреть понятие логарифма числа и свойства логарифмов;
• дать понятие десятичного и натурального логарифма;
• овладеть знаниями и умениями использовать основное логарифмическое тождество, формулы перехода от одного основания к другому в процессе решения упражнений;
• развивать мышление учащихся при выполнении упражнений;
• продолжить формировать умение правильно воспринимать и активно запоминать новую информацию;
• научить учащихся определять логарифм числа и его свойства;
• вычислять значения несложных логарифмических выражений.

Тип урока: усвоение новых знаний.

Методическое обеспечение: проектор, презентация к уроку, учебники, индивидуальные карточки.

Ход занятия

1. Организационный момент

Перед началом урока преподаватель проводит проверку подготовленности кабинета к занятию.

Приветствие учащихся, определение отсутствующих, заполнение группового журнала. Сообщается тема и цель урока. (Слайд 2)

2. Актуализация знаний

В кратком вступительном слове преподаватель акцентирует внимание студентов о важной

роли логарифмов в курсе математики, а также в общетехнических и специальных дисциплинах, при этом подчеркивает значение десятичных и натуральных логарифмов.

3. Повторение ранее изученного материала

Экспресс-опрос

Преподаватель задает вопросы:

а) Что такое степень; что такое основание степени; что такое показатель степени.

б) Работа над основными свойствами степеней. Рассмотреть связь между показателями степеней в равенствах

в) Решить устно примеры:

4. Изучение нового материала

План

1. Логарифм числа. Основные свойства логарифмов.

2. Основное логарифмическое тождество.

2. Формула перехода одного основания логарифмов к другому.

3. Десятичный логарифм.

4. Натуральный логарифм.

Преподаватель излагает новый учебный материал

Логарифм числа

Понятие логарифма числа связано с решением показательных уравнений.

Остановимся на решении двух показательных уравнений. Решение уравнения не вызывает труда. Так как то данное уравнение примет вид Поэтому уравнение имеет единственное решение

А теперь попробуем решить уравнение По теореме о корне это уравнение также имеет единственное решение. Однако, в отличие от предыдущего уравнения, это уравнение является иррациональным числом. Докажем, что корень данного уравнения является числом рациональным, т.е. Тогда выполняется равенство или Но в любой натуральной степени будет числом четным, а в любой натуральной степени – число нечетное. Получаем противоречие, которое и доказывает, что корень уравнения – число иррациональное. Обдумывая, ситуацию с показательным уравнением математики ввели в рассмотрение новый символ – логарифм. С помощью этого символа корень уравнения записали так: (читается : логарифм числа по основанию

Остановимся теперь на понятии логарифма числа. Очень часто приходится решать задачу: известно, что необходимо найти показатель степени т.е. решить задачу, обратную возведению числа в степень. При нахождении этого показателя степени и возникает понятие логарифма числа по основанию

дается определение логарифма (Слайд 3)

Например

а) log ₃ 81 = 4, так как 3⁴ = 81;

б) log ₅ 125 = 3, так как 5³ = 125;

в) log _0,5 16 = -4, так как (0,5)^-4 = 16;

г) , так как ==

Введение основного логарифмического тождества (Слайд 4)

Обратите внимание на то, что является корнем уравнения , а поэтому =8

Таким образом и получается основное логарифмическое тождество

Это равенство является краткой символической записью определения логарифмов.

Решить примеры согласно тождеству: ;

=5; .

Подчеркнем, что и одна и таже математическая модель

Операцию нахождения логарифма числа называют ЛОГАРИФМИРОВАНИЕМ. (Слайд5) Эта операция является обратной по отношению к возведению в степень с соответствующим основанием. Сравните.

Основные свойства логарифмов (Слайд 6)

Эти свойства вытекают из определения логарифма и свойств показательной функции.

При любом a > 0 (a 1) и любых положительных x и y выполнены равенства:

• log_a 1 = 0.
• log_a a = 1.
• log_a xy = log_a x + log_a y.
• log_a = log_a x — log_a y.
• log_a x^p = p log_a x

для любого действительного p.

Решить примеры устно. Найти x

1. Ответ:
2. Ответ:
3. Ответ:
4. Ответ:
5. Ответ:

Десятичные и натуральные логарифмы (Слайд 7)

На практике рассматриваются логарифмы по различным основаниям, в частности по основанию 10.

Логарифмом положительного числа по основанию 10 называют десятичным логарифмом числа в и обозначается, т.е. вместо пишут .

Например, (Слайд № 6)

Натуральным логарифмом (обозначается In) называется логарифм по основанию e

Примеры вычисления десятичных логарифмов (Слайд 8)

1. так как
2. , так как
3. так как
4. так как
5. так как
6. так как

Формулы перехода от одного основания логарифм к другому (Слайд8)

На практике рассматривается логарифм по различным основаниям. Отсюда возникает необходимость формулы перехода от одного основания к логарифму по другому основанию. (Слайд № 6)

Решить пример типа:

Упростить выражения:

a)

б)

в)

Ответ. a) ; б); в)

5. Закрепление изученного материала

Решить устно.

Найти логарифм по основанию a числа представленного в виде степени с основанием a

Работа в парах.

Найдите число (484,485,486)

Решить устно.

Упростите выражения, пользуясь основным логарифмическим тождеством.

1) 2) 3) 4)

Выполнить упражнения. Заполнить пропуски (письменно). (Слайд 10)

6. Подведение итогов

1. Выставление и комментирование оценок на уроке

2. Домашнее задание: п37. Решить №481, 486, 487.

7. Рефлексия

Преподаватель задает учащимся вопросы:

• Какая тема была изучена на уроке?
• Достигнута ли цель урока?

Учащиеся призваны воспроизвести в памяти то, что усвоили, и проанализировать выводы, которые были сделаны в течение всего занятия.

• Что вам сегодня больше всего запомнилось на уроке, что понравилось?

Решение логарифмических уравнений — ChiliMath

Обычно существует два типа логарифмических уравнений. Внимательно изучите каждый случай, прежде чем приступить к рассмотрению приведенных ниже рабочих примеров.

Типы логарифмических уравнений

• Первый тип выглядит так.

Если у вас есть один логарифм на каждой стороне уравнения с одинаковым основанием, вы можете установить аргументы, равные друг другу, и решить. Аргументами здесь являются алгебраические выражения, представленные \ color {blue} M и \ color {red} N.

• Второй тип выглядит так.

Если у вас есть один логарифм на одной стороне уравнения, вы можете выразить его в виде экспоненциального уравнения и решить.

Давайте научимся решать логарифмические уравнения на нескольких примерах.

---

Примеры решения логарифмических уравнений

Пример 1: Решите логарифмическое уравнение.

Поскольку мы хотим преобразовать левую часть в одно логарифмическое уравнение, мы должны использовать правило произведения в обратном порядке, чтобы сжать его.Вот правило на всякий случай, если вы забыли.

• Распределить: \ left ({x + 2} \ right) \ left (3 \ right) = 3x + 6

• Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу.

• Затем решите линейное уравнение. Я знаю, что у тебя есть эта часть!

Просто большое предостережение. ВСЕГДА проверяйте решенные значения с помощью исходного логарифмического уравнения.

Помнить :

• Хорошо, иметь значения x, такие как положительные, 0 и отрицательные числа.
• Однако НЕ ДОПУСКАЕТСЯ иметь логарифм отрицательного числа или логарифм нуля, 0, при замене или вычислении в исходное уравнение логарифма.

⚠︎ ВНИМАНИЕ: логарифм отрицательного числа и логарифм нуля не определены.

{\ log _b} \ left ({{\ rm {negative \, \, number}}} \ right) = {\ rm {undefined}}

{\ log _b} \ left (0 \ right) = {\ rm {undefined}}

Теперь давайте проверим наш ответ, является ли x = 7 допустимым решением.Подставьте обратно в исходное логарифмическое уравнение и проверьте, соответствует ли оно истинному утверждению.

Да! Поскольку x = 7 проверок, у нас есть решение в \ color {blue} x = 7.

---

Пример 2: Решите логарифмическое уравнение.

Начните с сжатия логарифмических выражений слева в один логарифм с помощью правила произведения. Мы хотим иметь по одному логарифмическому выражению для каждой стороны уравнения. Будьте готовы решить квадратное уравнение, так как x будет иметь степень 2.2} — 2x

• Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу

• Решите квадратное уравнение, используя метод факторизации. Но вам нужно переместить все на одну сторону, заставив противоположную сторону равной 0.

• Установите каждый коэффициент равным нулю, затем решите относительно x.

x — 5 = 0 означает, что x = 5

x + 2 = 0 означает, что x = — 2

Итак, возможные решения: x = 5 и x = — 2.Не забывайте всегда подставлять возможные решения обратно в исходное логарифмическое уравнение.

Давайте проверим наши возможные ответы x = 5 и x = — 2, если они будут действительными решениями. Подставьте обратно в исходное логарифмическое уравнение и проверьте, соответствует ли оно истинному утверждению.

После проверки наших значений x мы обнаружили, что x = 5 определенно является решением. Однако x = -2 генерирует некоторые отрицательные числа внутри скобок (логарифм нуля и отрицательные числа не определены), что заставляет нас исключить x = -2 как часть нашего решения.

Следовательно, окончательное решение будет просто \ color {blue} x = 5. Мы не принимаем во внимание x = -2, потому что это постороннее решение.

---

Пример 3: Решите логарифмическое уравнение.

Это интересная проблема. Здесь мы имеем дело с различиями логарифмических выражений по обе стороны уравнения. Упростите или уплотните бревна с обеих сторон, используя правило Quotient Rule, которое выглядит следующим образом.

• Разница в журналах подсказывает нам использовать правило квотиента.Преобразуйте операцию вычитания снаружи в операцию деления внутри скобок. Сделайте это с обеими сторонами уравнений.

• Я думаю, что мы готовы установить каждый аргумент равным друг другу, так как мы можем уменьшить проблему до одного логарифмического выражения для каждой стороны уравнения.

• Отбросьте журналы, установите аргументы (внутри скобок) равными друг другу. Обратите внимание, что это рациональное уравнение. Один из способов решить эту проблему — получить Cross Product .

• Это выглядит так после получения перекрестного продукта.

• Упростите обе стороны с помощью свойства распределения. На этом этапе мы понимаем, что это всего лишь квадратное уравнение. Тогда ничего страшного. Сдвиньте все в одну сторону, и тогда одна часть уравнения станет равной нулю.

• Это легко факультативно. Теперь установите каждый коэффициент равным нулю и решите относительно x.

• Итак, это наши возможные ответы.

Я предоставлю вам проверить наши возможные ответы обратно в исходное логарифмическое уравнение. Вы должны убедиться, что \ color {blue} x = 8 — единственное решение, а x = -3 — нет, поскольку он генерирует сценарий, в котором мы пытаемся получить логарифм отрицательного числа. Фигово!

---

Пример 4: Решите логарифмическое уравнение.

Если вы видите «журнал» без явного или письменного основания, предполагается, что он имеет основание 10. Фактически, логарифм с основанием 10 известен как десятичный логарифм .

Нам нужно сжать обе части уравнения в одно логарифмическое выражение. С левой стороны мы видим различие журналов, что означает, что мы применяем правило Quotient Rule, в то время как с правой стороны требуется правило продукта, потому что они представляют собой сумму журналов.

Есть только одна вещь, на которую вы должны обратить внимание на левую сторону. Вы видите этот коэффициент \ Large {1 \ over 2} \ ,?

Что ж, мы должны представить это как экспоненту, используя правило мощности в обратном порядке.

• Выведите этот коэффициент \ large {1 \ over 2} как показатель степени (см. Крайний левый член)

• Упростите показатель степени (все еще относится к крайнему левому члену)

• Затем сократите бревна с обеих сторон уравнения. Используйте правило частного слева и правило продукта справа.

• Здесь я использовал разные цвета, чтобы показать, что, поскольку у нас одна и та же база (если явно не показано, предполагается, что это база 10), можно установить их равными друг другу.

• Удаление журналов и просто приравнивание аргументов внутри скобок.

• На этом этапе вы можете решить рациональное уравнение, выполнив перекрестное произведение. Переместите все члены в одну сторону уравнения, затем вычтите их.

• Установите каждый коэффициент равным нулю и решите относительно x.

Пора проверить свои потенциальные ответы. Когда вы проверите x = 0 обратно в исходное логарифмическое уравнение, вы получите выражение, которое включает в себя получение логарифма нуля, который не определен, что означает — нехорошо! Итак, мы должны игнорировать или отбросить \ color {red} x = 0 как решение.

Проверка \ Large {x = {3 \ over 4}} подтверждает, что действительно \ Large {\ color {blue} {x = {3 \ over 4}}} — единственное решение.

---

Пример 5: Решите логарифмическое уравнение.

Эта проблема связана с использованием символа \ ln вместо \ log для обозначения логарифма.

Думайте о \ ln как о особом логарифме с основанием e, где e \ приблизительно 2,71828.

• Используйте правило продукта с правой стороны

• Сначала запишите переменную, затем константу, чтобы быть готовым к использованию метода FOIL.

• Упростите два бинома, умножив их вместе.

• На этом этапе я просто закодировал выражение в круглых скобках цветом, чтобы показать, что мы готовы установить их равными друг другу.

• Ага! Здесь мы говорим, что содержимое в левой скобке равно содержимому в правой скобке.

Не забудьте символ \ pm.

• Далее, упрощая, мы должны получить следующие возможные ответы.

Проверьте, являются ли найденные выше возможные ответы возможными, подставив их обратно в исходные логарифмические уравнения.

Вы должны убедиться, что ЕДИНСТВЕННЫМ допустимым решением является \ large {\ color {blue} x = {1 \ over 2}}, что делает \ large {\ color {red} x = — {1 \ over 2}} лишним. отвечать.

---

Пример 6: Решите логарифмическое уравнение.

В этом уравнении есть только одно логарифмическое выражение. Мы рассматриваем это как второй случай, когда у нас

Мы преобразуем уравнение из логарифмической формы в экспоненциальную, а затем решим его.4} = 81.

Вы должны убедиться, что значение \ color {blue} x = 12 действительно является решением логарифмического уравнения.

---

Пример 7: Решите логарифмическое уравнение.

Соберите все логарифмические выражения на одной стороне уравнения (оставьте его слева) и переместите константу в правую часть. Используйте правило частного, чтобы выразить разницу журналов в виде дробей в скобках логарифма.

• Переместите все логарифмические выражения в левую часть уравнения, а константу — вправо.{\ color {красный} 1} = 5.

• Это рациональное уравнение из-за наличия переменных в числителе и знаменателе.

Я бы решил это уравнение, используя правило перекрестного произведения. Но сначала я должен выразить правую часть уравнения с явным знаменателем, равным 1. То есть 5 = ​​{\ large {{5 \ over 1}}}

• Выполните перекрестное умножение, а затем решите полученное линейное уравнение.

Когда вы проверяете x = 1 обратно в исходное уравнение, вы должны согласиться с тем, что \ large {\ color {blue} x = 1} является решением логарифмического уравнения.

---

Пример 8: Решите логарифмическое уравнение.

Эта проблема очень похожа на №7. Давайте соберем все логарифмические выражения слева, оставив константу справа. Поскольку у нас есть разница в журналах, мы будем использовать правило Quotient Rule.

• Переместите выражения журнала в левую часть, а константу оставьте вправо.

• Примените правило частного, так как они представляют собой разность журналов.

• Я использовал здесь разные цвета, чтобы показать, куда они уходят после перезаписи в экспоненциальной форме.

• Обратите внимание, что выражение внутри круглых скобок остается на своем текущем месте, а \ color {red} 5 становится показателем степени основания.

• Чтобы решить это рациональное уравнение, примените правило перекрестного произведения.

• Упростите правую часть с помощью свойства распределения. Похоже, мы имеем дело с квадратным уравнением.

• Переместите все в левую сторону и сделайте правую сторону равной нулю.

Выносим трехчлен за скобки. Установите каждый коэффициент равным нулю, затем решите относительно x.

• Когда вы решаете для x, вы должны получить эти значения x как потенциальные решения.

Убедитесь, что вы проверили возможные ответы из исходного логарифмического уравнения.

Согласитесь, что \ color {blue} x = -32 — единственное решение. Это делает \ color {red} x = 4 посторонним решением, так что не обращайте на него внимания.

---

Пример 9: Решите логарифмическое уравнение

Я надеюсь, что теперь вы получили основное представление о том, как подходить к этому типу проблемы. Здесь мы видим три логических выражения и константу. Давайте разделим логарифмические выражения и константу на противоположных сторонах уравнения.

• Давайте оставим лог-выражения слева, а константу — справа.

• Начните с сжатия выражений журнала с помощью правила продукта для обработки суммы журналов.

• Затем сожмите выражения журнала, используя правило Quotient Rule, чтобы учесть разницу в журналах.

• На этом этапе я использовал разные цвета, чтобы показать, что готов выразить логарифмическое уравнение в его экспоненциальной форме.

• Сохраните выражение внутри символа группировки ( синий ) в том же месте, сделав константу \ color {red} 1 с правой стороны как показатель степени основания 7.

• Решите это рациональное уравнение, используя перекрестное произведение. Выразите 7 как \ large {7 \ over 1}.

• Переместите все члены в левую часть уравнения. Выносим за скобки трехчлен. Затем установите каждый коэффициент равным нулю и решите относительно x.

• Это ваши потенциальные ответы. Всегда проверяйте свои ценности.

Очевидно, что когда мы подставляем x = -8 обратно в исходное уравнение, получается логарифм с отрицательным числом.Следовательно, вы исключаете \ color {red} x = -8 как часть вашего решения.

Таким образом, единственное решение — \ color {blue} x = 11.

---

Пример 10: Решите логарифмическое уравнение.

• Сохраните логарифмическое выражение слева и переместите все константы в правую сторону.

• Думаю, мы готовы преобразовать это логарифмическое уравнение в экспоненциальное уравнение.

• Выражение внутри круглых скобок остается в своем текущем положении, а константа 3 становится показателем степени логарифмической базы 3.3} = 27. Перед нами простое радикальное уравнение.

Отметьте этот отдельный урок, если вам нужно напомнить, как решать различные типы радикальных уравнений.

• Чтобы избавиться от радикального символа в левой части, возведите обе части уравнения в квадрат.

• После возведения в квадрат обеих сторон, похоже, у нас есть линейное уравнение. Просто решите это как обычно.

Верните свой потенциальный ответ в исходное уравнение.

После этого вы должны убедиться, что действительно \ color {blue} x = -104 — верное решение.

---

Практика с рабочими листами

---

Возможно, вас заинтересует:

Уплотняющие логарифмы

Расширяющиеся логарифмы

Объяснение логарифма

Правила логарифмирования

Решение экспоненциальных уравнений с использованием логарифмов

В нашем предыдущем уроке вы узнали, как решать экспоненциальные уравнения без логарифмов. На этот раз мы хотим решить экспоненциальное уравнение , требующее использования логарифмов . Почему? Причина в том, что мы не можем манипулировать экспоненциальным уравнением, чтобы иметь одинаковую или общую основу для обеих сторон уравнения. Если вы столкнулись с проблемой такого типа, выполните следующие действия:

---

Шаги для решения экспоненциальных уравнений с использованием логарифмов

1) Держите экспоненциальное выражение отдельно от одной стороны уравнения.

2) Найдите логарифмы обеих частей уравнения.{2x}} = 21.

Преимущество этого уравнения в том, что экспоненциальное выражение уже выделено в левой части. Теперь мы можем логарифмировать обе части уравнения. Не имеет значения, какое основание логарифма использовать. Окончательный ответ должен быть таким же. Наилучший выбор для базы логарифмической операции — 5, поскольку она является базой самого экспоненциального выражения. Однако мы также будем использовать в вычислениях общую основу 10 и естественную основу \ color {red} e (обозначенную \ color {blue} ln), чтобы показать, что в конечном итоге все они имеют одинаковые ответы. .{x — 5}}} \ right) = 12.

Как видите, экспоненциальное выражение слева не само по себе. Мы должны исключить число 2, которое умножает экспоненциальное выражение. Для этого разделите обе части на 2. В результате мы получим только экспоненциальное выражение слева и 6 справа после упрощения.

Пора взять бревно с обеих сторон. Поскольку экспоненциальное выражение имеет основание 3, это удобное основание для работы с журналом. Кроме того, мы также решим эту проблему, используя естественное основание e, чтобы сравнить, согласуются ли наши окончательные результаты.{x — 2}}}}}}} \ right) — 7 = 13.

Сначала это похоже на беспорядок. Однако, если вы знаете, с чего начать, решение этой проблемы становится простым. В первую очередь нам следует упростить выражение внутри скобок. Используйте правило деления экспоненты, скопировав общее основание числа е и вычтя верхнюю на нижнюю степень.

Теперь выделите экспоненциальное выражение, сложив обе части на 7, а затем разделив все уравнение на 2. х} + 3 = 53.

Обратите внимание, что экспоненциальное выражение возводится в x. Упростите это, применив Силу к Правилу Силы. Сделайте это, скопировав основание 10 и умножив его показатель на внешний показатель. После этого он должен выглядеть так.

Теперь мы можем выделить экспоненциальное выражение, вычтя обе части на 3, а затем умножив обе части на 2.

Возьмите логарифм обеих сторон с основанием 10. Если вы просто видите журнал \ color {red} без какой-либо конкретной основы, предполагается, что его основание равно 10.х снова.

Наконец, установите каждый коэффициент равным нулю и решите относительно x, как обычно, используя логарифмы.

---

Вам также может быть интересно:

Решение экспоненциальных уравнений без логарифмов

РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ

РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ

1. Чтобы решить логарифмическое уравнение, перепишите уравнение в экспоненциальной форме и решите относительно переменной.

Пример 1: Решите относительно x в уравнении Ln ( x ) = 8.

Решение:

Шаг 1: Пусть обе стороны будут степенями основания e. Уравнение Ln ( x ) = 8 можно переписать.

Шаг 2: К настоящему времени вы должны знать, что, когда основание экспоненты и основание логарифма одинаковы, в левой части можно записать x. Теперь уравнение можно записать .

Шаг 3: Точный ответ

и приблизительный ответ

Чек: Вы можете проверить свой ответ двумя способами.Вы можете построить график функции Ln ( x ) -8 и посмотреть, где она пересекает ось x. Если вы правы, график должен пересекать ось x в ответе, который вы получили алгебраически.
Вы также можете проверить свой ответ, подставив значение x в начальное уравнение и определите, равна ли левая часть правой. За Например, если Ln (2,980.95798704) = 8, вы правы. Это так, и вы правы.

Пример 2: Решите относительно x в уравнении 7 Log (3 x ) = 15.

Решение:

Шаг 1: Выделите логарифмический член перед преобразованием логарифмического уравнения в экспоненциальное уравнение. Разделите обе части исходного уравнения на 7:

Шаг 2: Преобразуйте логарифмическое уравнение в экспоненциальное уравнение: если основание не указано, это означает, что основание логарифма равно 10. Напомним также, что логарифмы являются показателями степени, поэтому показатель степени равен .Уравнение

теперь можно написать

Шаг 3: Разделите обе части приведенного выше уравнения на 3:

это точный ответ и приблизительный ответ.

Чек: Вы можете проверить свой ответ двумя способами: построив график функции

или подставив значение x в исходное уравнение. Если вы выберете построение графика, точка пересечения по оси x должна быть такой же, как и ответ, который вы полученный ( ).
Если вы выберете замену, значение левой части оригинала уравнение должно равняться значению правой части уравнения после того, как вы вычислили значение каждой стороны на основе вашего ответа на x.

Пример 3: Решите относительно x в уравнении

Решение:

Шаг 1: Обратите внимание, что первый член Ln ( x -3) действителен только тогда, когда x > 3; термин Ln ( x -2) действителен только тогда, когда x > 2; и термин Ln (2 x +24) действителен только тогда, когда x > -12.Если мы потребуем, чтобы x был любым действительным числом больше 3, все три члена будут действительными. Если все три члена верны, то уравнение верно.

Шаг 2: Упростим левую часть приведенного выше уравнения: по свойствам логарифмов мы знаем, что

Шаг 3: Теперь уравнение можно записать

Шаг 4: Пусть каждая сторона приведенного выше уравнения будет показателем степени основания e:

Шаг 5: Упростите приведенное выше уравнение:

Другой способ взглянуть на уравнение на шаге 3 — понять, что если Ln ( a ) = Ln ( b ), тогда a должно быть равно b. В случае этой проблемы, то

Шаг 6: Упростите левую часть приведенного выше уравнения:

Шаг 7: Вычтем 2x + 24 с каждой стороны:

Шаг 8: Разложите на множители левую часть приведенного выше уравнения:

Шаг 9: Если произведение двух множителей равно нулю, по крайней мере один из множителей должен быть равен нулю.Если . Если . x = 9 — наше единственное решение. Почему 9 — единственное решение? Мы определили наш домен как все действительные числа больше 3.

Чек: Вы можете проверить свой ответ, построив график функции

и определение того, равен ли отрезок оси x также 9. Если это так, вы правильно разобрались с проблемой.
Вы также можете проверить свой ответ, заменив 9 слева x и правые части исходного уравнения. Если после подстановки левый сторона уравнения имеет то же значение, что и правая часть уравнения, вы правильно решили проблему.

Если вы хотите просмотреть другой пример, щелкните «Пример».

Решите следующие задачи. Если вы хотите просмотреть ответ и решение, нажмите «Ответить».

Задача 1: Решите относительно x в уравнении

Ответ

Задача 2: Решите относительно x в уравнении

Ответ

Задача 3: Решите относительно x в уравнении

Ответ

Задача 4: Решите относительно x в уравнении

Ответ

Задача 5: Решите относительно x в уравнении

Ответ

Задача 6: Решите относительно x в уравнении

Ответ

[Назад к правилам логарифмов] [Назад к экспоненциальным функциям] [Алгебра] [Тригонометрия] [Сложный Переменные] S.Домашняя страница O.S MATHematics

Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S. O.S. Математика CyberBoard.

Автор: Нэнси Маркус

Авторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час

Примеры логарифмов и практические задачи

1. Домашняя страница
2. Математика
3. Рабочие листы по математике

Возьмем действительное число x, а b ^x представляет собой уникальное действительное число.Если мы напишем a = b ^x , тогда показатель x будет логарифмом a с логарифмической базой b, и мы можем записать a = b ^x как
журнал _b a = x
Запись x = log _b a называется записью логарифма .
Перед переходом к примеру посмотрите на этот логарифм , правила и калькулятор логарифмов.

Пример записи логарифма:
(i) 3 = log ₄ 64 эквивалентно 4 ³ = 64
(ii) 1/2 = log ₉ 3 эквивалентно √9 = 3

Примеры логарифмов
1. Измените приведенный ниже логарифм лагарифма ₂₅ 5 = 1/2 в экспоненциальную форму
журнал ₂₅ 5 = 25 ^1/2 = 5

2. Измените 1/8 = 8 ^-1 на логарифмическую.
Решение:
1/8 = 8 ^-1 = лог ₈ 8

3. Оцените значение журнала ₄ 8
Решение:
x = журнал ₄ 8
Тогда мы можем сказать
4 ^x = 8 = 2 ³ , извлечение квадратного корня из обеих сторон
2 ^x = 2 ^3/2
x = 3/2

4.Найдите значение x из журнала _x 100 = 2
раствор:
журнал _b 1000 = 3
Мы можем записать это как,
б ³ = 1000
b ³ = 10 ³
Итак, из приведенного выше уравнения
б = 10
5. Найдите значение для журнала ₅ 8 + ₅ (1/1000)
Решение:
журнал ₅ 8 + ₅ (1/1000) = журнал ₅ (8 x 1/1000)
= журнал ₅ (1/125)
= журнал ₅ (1/5) ³
= журнал ₅ (5) ^-3
= -3log ₅ (5)
= -3 х 1
= -3

6. Решить 2log ₅ 3 X log ₉ x + 1 = log ₅ 3
Решение:
Мы можем переписать приведенное выше уравнение в формате ниже
=> журнал ₅ 3 ² X журнал ₉ x = журнал ₅ 3 — 1
=> журнал ₅ 9 X журнал ₉ x = журнал ₅ 3 — журнал ₅ 5
=> журнал ₅ 9 X журнал ₉ x = журнал ₅ (3/5)
Используя изменение основного правила в левой части, мы получаем
=> журнал ₅ x = журнал ₅ (3/5)
Значение X = 3/5

Практические задачи логарифмирования:
1.Найдите логарифм для следующих уравнений
(i) журнал ₅ 125
(ii) журнал ₂ (2√2)
(iii) журнал _1/3 27

2. Найдите значение x в следующих уравнениях.
(i) журнал _x 0,001 = -2
(ii) √log ₂ x = 3
(iii) 2 журнала ₉ x = 1

3. Упростите следующее выражение до одного члена.
(i) журнал ₁₀ 2 + журнал ₁₀ 10
(ii) 3log ₃ 2 + 4-8 log ₃ 3
(iii) журнал ₁₀ 5 + журнал ₁₀ 20 — журнал ₁₀ 24 + журнал ₁₀ 25-4

4.Решите следующее уравнение логарифма
(i) 3log ₅ 2 = 2log ₅ x
(ii) xlog ₁₆ 8 = -1
(iii) журнал ₅ (10 + x) = журнал ₅ (3 + 4x)

Как решать логарифмические уравнения

Решение логарифмических уравнений

Правила или законы логарифмов:

Как вы знаете, логарифм — это математическая операция, обратная возведению в степень. Это выражается сокращением «журнал».Прежде чем приступить к решению логарифмических уравнений, есть несколько стратегий и «правил», с которыми мы должны сначала ознакомиться.

Прежде всего, чтобы решать логарифмические уравнения, как и в случае с многочленами, вы должны уметь строить графики логарифмических функций. Посмотрите наше видео о построении графиков логарифмических функций для обзора, если это необходимо. Кроме того, прежде чем мы перейдем к правилам логарифмирования, важно, чтобы вы также понимали одну из простейших стратегий логарифмирования — изменение базовой формулы.Опять же, посмотрите наше видео об изменении базовой формулы, если вам нужно напомнить. Теперь, когда вы все это освоили, давайте взглянем на некоторые из наиболее важных правил логарифмирования:

1) Правило логарифмического произведения

Обычно правило произведения логарифмов определяется следующим образом:

log⁡A + log⁡B = log⁡ (A × B) \ log A + \ log B = \ log (A \ times B) logA + logB = журнал (A × B)

То есть, при добавлении двух журналов из с одной и той же базой , вы можете переписать выражение как один журнал, умножив члены в логарифмическом выражении.

2) Правило логарифмического частного

Как правило, правило частного логарифмов определяется следующим образом:

log⁡A − log⁡B = log⁡ (AB) \ log A — \ log B = \ log (\ frac {A} {B}) logA − logB = log (BA)

То есть, при вычитании двух журналов из из одной и той же базы вы можете переписать выражение как один журнал, разделив члены в логарифмическом выражении. {B} = B \ times \ log Alog (A) B = B × logA

То есть, когда у члена в логарифмическом выражении есть показатель степени, вы можете уменьшить этот показатель и умножить его на журнал.{\ log_ {A} (B)} = BAlogA (B) = B

То есть поднятие логарифма числа по основанию равняется этому числу.

6) Правило идентификации журнала

В целом правило идентичности логарифмов определяется следующим образом:

log⁡AA = 1 \ log_ {A} A = 1 logA A = 1

То есть, если взять логарифм чего-то на основе того же самого, логарифмическое выражение будет просто равно 1.

7) Особые журналы

Хотя это не обязательно правила, есть пара журналов, которые вы должны знать наизусть, чтобы упростить задачу.Их:

журнал⁡1 = 0 \ журнал 1 = 0 журнал1 = 0 log⁡0 = undefined \ log 0 = undefined log0 = undefined

Оба этих случая всегда верны, независимо от основания. Кроме того, первый особый случай иногда называют правилом логарифмического нуля.

Все эти правила, вместе взятые, представляют собой чрезвычайно мощные инструменты, которые мы можем использовать для решения любой логарифмической задачи.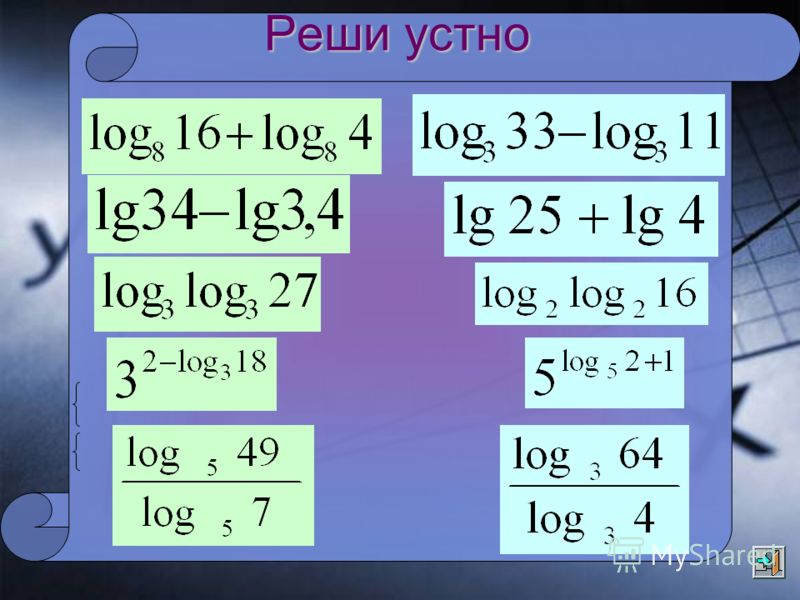 Чтобы посмотреть видеообзор этих концепций, посмотрите наши видеоролики о свойствах логарифмов и правиле частного для логарифмов.Теперь, когда мы рассмотрели основы, давайте приступим к решению проблем с журналом!

Как решать проблемы с журналом:

Как и все в математике, лучший способ научиться решать задачи журнала — это выполнять некоторые практические задачи! Мы будем использовать правила, которые мы только что обсудили, для решения некоторых примеров.

Пример 1:

Решите логарифмическое уравнение:

log⁡ (3 − x) + log⁡ (4−3x) −log⁡ (x) = log⁡7 \ log (3 — x) + \ log (4 — 3x) — \ log (x) = \ log 7log (3 − x) + журнал (4−3x) −log (x) = log7

Шаг 1. Используйте известные правила журнала

В любой проблеме, связанной с решением логарифмических уравнений, первым делом всегда старайтесь упростить, используя правила журнала.{2} — 20x + 12 = 03×2−20x + 12 = 0 (3x − 2) (x − 6) = 0 (3x — 2) (x — 6) = 0 (3x − 2) (x − 6) = 0 3x − 2 = 0 или x − 6 = 03x — 2 = 0 или x — 6 = 03x − 2 = 0 или x − 6 = 0 x = 23 или x = 6x = \ frac {2} {3} или x = 6x = 32 или x = 6

Шаг 3.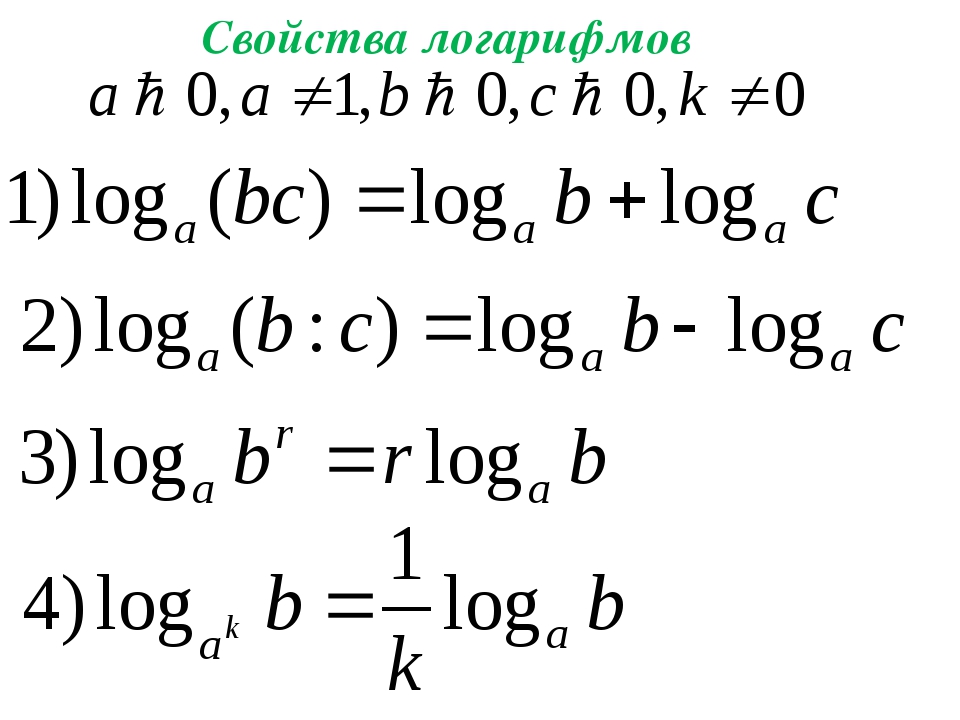 Проверьте решения

Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.

log⁡ (3−23) + log⁡ (4−3 (23)) — log⁡ (23) = log⁡7 \ log (3 — \ frac {2} {3}) + \ log (4 — 3 ( \ frac {2} {3})) — \ log (\ frac {2} {3}) = \ log 7log (3−32) + log (4−3 (32)) — log (32) = log7

Решение x = 23x = \ frac {2} {3} x = 32 является правильным.

log⁡ (3−6) + log⁡ (4−3 (6)) — log⁡ (6) = log⁡7 \ log (3-6) + \ log (4-3 (6)) — \ log ( 6) = \ log 7log (3−6) + log (4−3 (6)) — log (6) = log7

Решение x = 6x = 6x = 6 отклоняется, поскольку логарифм отрицательного числа не определен.

Пример 2:

Шаг 1. Используйте известные правила журнала

В этом случае мы будем использовать правила журнала мощности и частного. Мы делаем это, чтобы попытаться составить полиномиальное / алгебраическое уравнение, которое легче решить. Это показано ниже:

2log⁡3 (x + 4) −log⁡3 (−x) = 22 \ log_ {3} (x + 4) — \ log_ {3} (-x) = 22log3 (x + 4) −log3 ( −x) = 2 log⁡3 (x + 4) 2 − log⁡3 (−x) = 2 \ log_ {3} (x + 4) ^ {2} — \ log_ {3} (-x) = 2log3 (x + 4 ) 2 − log3 (−x) = 2 log⁡3 (x2 + 8x + 16 − x) = 2 \ log_ {3} (\ frac {x ^ {2} + 8x + 16} {- x}) = 2log3 (−xx2 + 8x + 16) = 2

Шаг 2. Упростите

Мы можем преобразовать в экспоненциальную форму, потому что на одной стороне есть журнал, а на другой — нет.{2} + 17x + 16 = 0x2 + 17x + 16 = 0 (х + 16) (х + 1) = 0 (х + 16) (х + 1) = 0 (х + 16) (х + 1) = 0 x = −16orx = −1x = -16 или x = -1x = −16orx = −1

Шаг 4. Проверьте решения

Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.

2log⁡3 ((- 16) +4) −log⁡3 (- (- 16)) = 22 \ log_ {3} ((-16) + 4) — \ log_ {3} (- (- 16)) = 22log3 ((−16) +4) −log3 (- (- 16)) = 2

Решение x = -16 отклоняется.

2log⁡3 ((- 1) +4) −log⁡3 (- (- 1)) = 22 \ log_ {3} ((-1) + 4) — \ log_ {3} (- (- 1)) = 22 log3 ((−1) +4) −log3 (- (- 1)) = 2

Решение x = -1 правильное.

Пример 3:

Шаг 1. Упростите

Умножьте обе части уравнения на 2, чтобы избавиться от дроби.

log⁡2x = 2 + 12log⁡2 (x − 3) \ log_ {2} x = 2 + \ frac {1} {2} \ log_ {2} (x — 3) log2 x = 2 + 21 log2 (Х − 3) 2log⁡2x = 4 + log⁡2 (x − 3) 2 \ log_ {2} x = 4 + \ log_ {2} (x — 3) 2log2 x = 4 + log2 (x − 3)

Шаг 2. Используйте известные правила журнала

В этом случае мы будем использовать силу правил журнала и частного журнала. Затем мы можем упростить, как в предыдущем примере, чтобы получить экспоненциальную форму.{2} — 16x + 48 = 0x2−16x + 48 = 0 (x − 4) (x − 12) = 0 (x — 4) (x — 12) = 0 (x − 4) (x − 12) = 0 х = 4 или х = 12 х = 4 или х = 12 х = 4 или х = 12

Шаг 4. Проверьте решения

Поскольку изначально у нас было логарифмическое уравнение, нам нужно проверить наши ответы, чтобы убедиться, что они верны.

log⁡24 = 2 + 12log⁡2 (4−3) \ log_ {2} 4 = 2 + \ frac {1} {2} \ log_ {2} (4–3) log2 4 = 2 + 21 log2 (4−3)

Решение x = 4 подтверждается.

log⁡212 = 2 + 12log⁡2 (12−3) \ log_ {2} 12 = 2 + \ frac {1} {2} \ log_ {2} (12–3) log2 12 = 2 + 21 log2 (12−3)

То же самое и x = 12.{-2} x = 10−2 неверно.

И это тоже все! Чтобы проверить свою работу с будущими практическими задачами, обязательно воспользуйтесь этим отличным калькулятором. Наконец, для видеообзора всего, что мы только что рассмотрели, посмотрите наше видео о том, как решать уравнения журнала.

College Algebra Урок 46: Логарифмические уравнения Цели обучения После изучения этого руководства вы сможете: Решите логарифмические уравнения. Введение В этом уроке я расскажу, как решать уравнения, которые имеют логарифмические выражения. В этих уравнениях вы заметите что переменная, которую мы ищем, находится внутри выражений журнала. Мы перепишем логарифмическое уравнение экспоненциально, используя определение журналы, чтобы помочь нам получить x вне журнала. Если вам нужен обзор определения функций журнала, смело переходите to Урок 43: Логарифмические функции . На старт, внимание, марш!!!!! Учебник Решение логарифмического уравнения вида Шаг 1. Запишите как одно бревно изолированное с одной стороны. Получите журнал с одной стороны все, что не входит в журнал, с другой сторона вашего уравнения, используя обратные операции. Также используйте свойства журналов, чтобы записать его так, чтобы журнал был только один. Если вам нужен обзор свойств журналов, см. Учебное пособие по 44: Логарифмические свойства . Шаг 2: Использование определение логарифмов записать в экспоненциальной форме. Напоминание о том, что определение логарифмов — это логарифмическая функция с базой b , где b > 0 и b 0, и определяется как если и только если. Если вам нужен обзор определения функций журнала, не стесняйтесь перейти к Урок 43: Логарифмический Функции . Теперь, когда переменная отсутствует в журнале, найдите переменную, используя обратные операции для завершения задачи. Пример 1 : Решите логарифмическое уравнение. Округлите ответ до двух десятичных знаков. Это уже сделано за нас в этой задаче. * Перепишите в экспоненциальной форме * Основание = 5 и экспонента = 3 * 5 в кубе 125 * Решить относительно x Пример 2 : Решите логарифмическое уравнение. Округлите ответ до двух десятичных знаков. * Воспользуйтесь продуктом правило записать как один журнал * один журнал изолирован * Перепишите в экспоненциальной форме * Основание = 10 и экспонента = 2 Помните, что когда в журнале нет базы, это означает, что это общий журнал, или журнал с основанием 10. Если вам нужен обзор общих журналы, не стесняйтесь переходить к Учебник 43: Логарифмические функции . * 10 в квадрате равно 100 * Решить относительно x * Коэффициент трехчлен * Установить 1-й коэффициент = 0 * Установите 2-й коэффициент = 0 Поскольку -25 создаст отрицательное число внутри оба журнала в этой проблеме, и мы НЕ МОЖЕМ взять журнал с отрицательным числом, нам придется выбросить x = -25 как одно из наши решения. Окончательный ответ: x = 4. Пример 3 : Решите логарифмическое уравнение. Округлите ответ до двух десятичных знаков. * Перепишите в экспоненциальной форме * Основание = 3 и экспонента = 2 * 3 в квадрате равно 9 * Решить относительно x * Умножьте обе стороны на ЖК-дисплей x + 2 Пример 4 : Решите логарифмическое уравнение. Округлите ответ до двух десятичных знаков. * Сумма, обратная сумме 3, является вспомогательной. 3 * одно бревно изолированное * Перепишите в экспоненциальной форме * Основание = e и показатель степени = 1 Помните, что когда у вас есть ln, это означает, что это натуральный журнал, или база журнала e .Если вам нужен обзор натурального журналы, не стесняйтесь переходить к Учебник 43: Логарифмические функции . * Квадрат с двух сторон для удаления корня * Решить относительно x * Воспользуйтесь калькулятором, чтобы найти e в квадрате Практические задачи Это практические задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти типы проблем. Math работает как и все в противном случае, если вы хотите добиться успеха в этом, вам нужно практиковать это. Даже лучшим спортсменам и музыкантам помогали на протяжении всего пути. практиковаться, практиковаться, практиковаться, чтобы стать лучше в своем виде спорта или инструменте. На самом деле не бывает слишком много практики. Чтобы получить от них максимальную отдачу, вы должны решить проблему на свой, а затем проверьте свой ответ, щелкнув ссылку для ответа / обсуждения для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа. Практические задачи 1a — 1d: Решите логарифмическое уравнение. Вокруг твоего ответ с двумя десятичными знаками. Нужна дополнительная помощь по этим темам? Последний раз редактировал Ким Сьюард 24 марта 2011 г. Авторские права на все содержимое (C) 2002 — 2011, WTAMU и Kim Seward. Все права защищены.

Логарифмическая функция: определение и примеры — стенограмма видео и урока

Логарифмы:

Логарифм — это показатель степени. Любое экспоненциальное выражение можно переписать в логарифмической форме. Например, если у нас 8 = 23, то основание равно 2, показатель степени равен 3, а результат равен 8. Это можно переписать в логарифмической форме как

3 = журнал2 8.

Обратите внимание, как были переставлены числа. Нижний индекс логарифма — это основание, число в левой части уравнения — это показатель степени, а число рядом с логарифмом — это результат (также называемый аргументом логарифма). Теперь попробуйте переписать некоторые из следующего в логарифмической форме:

упражнение:

Запишите каждое из следующих значений в логарифмической форме:

1,25 = 52

2. 64 = 43

3. 1 = 50

4.1/4 = 2-2

Ответы:

1,2 = log5 25

2. 3 = log4 64

3. 0 = log5 1

4.-2 = log2 1/4

Теперь мы также можем начать с выражения в логарифмической форме и переписать его в экспоненциальной форме. Например, выражение 3 = log5 125 можно переписать как 125 = 53.

Здесь 5 — основание, 3 — показатель степени и 125 — результат. Теперь попробуйте следующее:

Заданий:

Перепишите каждое из следующего в экспоненциальной форме:

1.4 = log2 16

2. 2 = log3 9

3. 1/2 = log9 3

4. 3/2 = log4 8

Ответы:

1. 24 = 16

2. 32 = 9

3. 91/2 = 3

4. 43/2 = 8

Теперь попробуйте решить несколько уравнений. Например, y = log2 8 можно переписать как 2y = 8.

Поскольку 8 = 23, получаем y = 3.

Как упоминалось в начале этого урока, y представляет собой показатель степени, а также логарифм. Следовательно, логарифм — это показатель степени.0 → у = 0,

3. y = log9 27 → 9y = 27 → (32) y = 33 → 32y = 33 → 2y = 3 → y = 3/2

4. y = log4 1/16 → 4y = 1/16 → 4y = 4-2 → y = -2

Графики логарифмических функций

Рассмотрим логарифмическую функцию y = log2 (x).

Мы можем проанализировать его график, изучив его связь с соответствующей экспоненциальной функцией y = 2x.

Обратите внимание, что

Так как 20 = 1

(1, 0) находится на графике y = log2 (x) \ \ [0 = log2 (1)]

и

(0, 1) \ \ находится на графике \ y = 2x

Так как \ 22 = 4

(4, 2) \ \ находится на графике \ y = log2 (x) \ \ [2 = \ log2 (4)]

и

(2, 4) \ находится на графике \ y = 2x

Так как \ 23 = 8

(8, 3) \ находится на графике \ y = log2 (x) \ \ [3 = log2 (8)]

и

(3, 8) \ \ находится на графике \ y = 2x

}]

В общем, это верно, (a, b) находится на графике y = 2x тогда и только тогда, когда (b, a) находится на графике y = log2 (x).