Функция журнала (Visual Basic для приложений)

• Статья
• 06/11/2021
• Чтение занимает 2 мин
• 1 contributor

Были ли сведения на этой странице полезными?

Да Нет

Хотите оставить дополнительный отзыв?

Отзывы будут отправляться в корпорацию Майкрософт.

Нажав кнопку «Отправить», вы разрешаете использовать свой отзыв для улучшения продуктов и служб Майкрософт. Политика конфиденциальности.

Отправить

В этой статье

Возвращает значение типа Double, указывающее натуральный логарифм от числа.

Синтаксис

Журнал(номер)

Необходимый аргумент номера — это двойное или любое допустимые числовая выражения больше нуля.

Примечания

Натуральный логарифм — это логарифм по основанию e. Константа e приблизительно 2.718282.

Вы можете вычислить логарифмы по основанию n для любого числа x, разделив натуральный логарифм x на натуральный логарифм n

, как показано ниже:

Журнал n(x) = Журнал(x)/ Журнал(n)

В следующем примере иллюстрируется настраиваемый элемент Function, вычисляющий логарифмы по основанию 10:

Static Function Log10(X)
    Log10 = Log(X) / Log(10#)
End Function

Пример

Функция Oct используется в данном примере для возврата натурального логарифма от числа.

Dim MyAngle, MyLog
' Define angle in radians.
MyAngle = 1.3
' Calculate inverse hyperbolic sine.
MyLog = Log(MyAngle + Sqr(MyAngle * MyAngle + 1))

См. также

Поддержка и обратная связь

Есть вопросы или отзывы, касающиеся Office VBA или этой статьи? Руководство по другим способам получения поддержки и отправки отзывов см. в статье Поддержка Office VBA и обратная связь.

Вычисление значения логарифмического выражения

В этой статье вы познакомитесь со всеми типами логарифмических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.

16 видео помогут вам понять как использовать свойства логарифмов при упрощении логарифмических выражений.

Вы можете попытаться решить каждый пример самостоятельно, и затем свериться с ответом. А можете сначала посмотреть видео с решением аналогичного задания.

Пример 1.  Найти значение выражения:

Посмотреть ответ:

показать

Ответ: 6

Видеорешение аналогичного задания:

 

Пример 2.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 30

Видеорешение аналогичного задания:

 

Пример 3.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 0,125

Видеорешение аналогичного задания:

 

Пример 4.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 1,5

Видеорешение аналогичного задания:

 

Пример 5.  Найти значение выражения: Посмотреть ответ:

показать

Ответ: 3

Видеорешение аналогичного задания:

 

Пример 6.   Найти значение выражения:

Посмотреть ответ:

показать

Ответ: 3

Видеорешение аналогичного задания:

 

Пример 7.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 0,75

Видеорешение аналогичного задания:

 

Пример 8.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 216

Видеорешение аналогичного задания:

 

Пример 9.  Найти значение выражения:
Посмотреть ответ:

показать

Ответ: 1

Видеорешение аналогичного задания:

 

Пример 10.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 0,75

Видеорешение аналогичного задания:

 

Пример 11. Найти значение выражения:Посмотреть ответ:

показать

Ответ: 1

Видеорешение аналогичного задания:

 

Пример 12.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 3

Видеорешение аналогичного задания:

 

Пример 13.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: -2

Видеорешение аналогичного задания:

 

Пример 14.  Найти значение выражения:Посмотреть ответ:

показать

Ответ: 0,5625

Видеорешение аналогичного задания:

 

Пример 15.

 Найти значение выражения:Посмотреть ответ:

показать

Ответ: -0,2

Видеорешение аналогичного задания:

 

Пример 16.  Найти значение выражения:

Посмотреть ответ:

показать

Ответ: 25

Видеорешение аналогичного задания:

 

 

И.В. Фельдман, репетитор по математике.

Вычисление логарифмов

Математика – это ключ и дверь ко всем наукам. 

Великий итальянский ученый  Галилео Галилей

К числу типовых задач, предлагаемых на вступительных испытаниях, являются  задачи, связанные с вычислением логарифмов. Для успешного решения таких задач необходимо знать свойства логарифмов и иметь навыки решения соответствующих задач.

В настоящей статье сначала приводятся основные понятия и свойства, используемые при решении таких задач, а затем рассматриваются примеры решения задач на вычисление логарифмов.

Основные понятия и свойства

Появлению логарифмов человечество обязано шотландскому математику Джону Неперу (1550 – 1617), который 1614 году опубликовал сочинение «Описание удивительной таблицы логарифмов».

Первоначально приведем основные свойства логарифмов, использование которых позволяет вычислять довольно-таки сложные логарифмы из заданий конкурсных испытаний по математике.

Основное логарифмическое тождество записывается в виде

,               (1)

где  ,    и  .

К числу наиболее известных свойств логарифмов относятся следующие равенства:

1. Если , ,  и  , то   ,  ,

,  .

2. Если , , ,  и  , то   .

3. Если  , ,  и  , то   .

4. Если   , ,  и  натуральное число,  то  

.

5. Если   , ,  и  натуральное число,  то  

6. Если   , ,    и   ,  то  .

7. Если   , ,    и   ,  то  .

Более сложные свойства логарифмов формулируются посредством следующих утверждений.

8.  Если  , , ,  и  , то  

.

9.  Если  , ,  и  , то  

.   

10.  Если  , , ,  и  , то  

.

    Доказательство последних двух свойств логарифмов приведено в учебном пособии автора «Математика для старшеклассников: дополнительные разделы школьной математики» (М.: Ленанд / URSS, 2014).  

    Если  , то логарифм    называется «десятичным» и обозначается . Если  , где  натуральная константа, введенная Леонардом Эйлером (1707 – 1783), то логарифм имеет название «натуральный» и он обозначается  .

    Отметим, что в настоящее время имеются различные таблицы десятичных и натуральных логарифмов, которые широко используются в инженерных расчетах.

Рассмотрим примеры задач на вычисление логарифмов, решение которых основано на применении приведенных выше свойств.

Примеры решения задач

Пример 1.   Вычислить  .

Решение.  Обозначим    и  .  Так как  

   и    ,  то

  и   .

Поскольку  ,  и  , то  .  

Ответ:  .

Пример 2.   Вычислить  .

Решение. Так как  , где   и , то

.

Ответ:  .

Пример 3. Вычислить  .

Решение. Используя формулу (1), получаем . В этой связи   .

Ответ:  .

Пример 4. Вычислить  .

Решение.  Так как      и   ,  то

.

Ответ:  .

Пример 5.   Вычислить  .

Решение. Поскольку  , то    или  .

Ответ:  .

Пример 6. Вычислить  .

Решение. Так как   и  ,  то

.

Ответ:  .

Пример 7. Вычислить  .

Решение. Так как   и  ,  то

.

Ответ:  .

Пример 8.  Вычислить  .

Решение. Используя свойства 2 и 4, можно записать

.

Ответ:   .

Пример 9.  Вычислить  . 

Решение.  Принимая во внимание свойство 8, здесь имеем

.

Поскольку  , то отсюда получаем  .

Ответ:  .

Пример 10.  Вычислить  .

Решение.  Здесь, используя свойства 1 и 2, получаем

.

Ответ:  .

Пример 11.  Вычислить  .

Решение.  Используя свойства 4 и 5, а также формулу (1), можно записать  

  и   

.

Поскольку  , то  .  В этой связи имеем

.

Ответ:  .

Пример 12.  Доказать, что   .

Доказательство. Обозначим . Если преобразовать    на основе двукратного применения свойства 8, то получим  .

Равенство доказано.

Пример 13. Вычислить  . 

Решение.  Используя свойство 3, получаем

.               (2)

Так как     ,    и   

,  то выражение (2) принимает вид

.

Ответ:  .

Пример 14.   Упростить  .

Решение.  Так как    и   , то  

  или  .

Тогда       .

Ответ:  .

Пример 15.  Вычислить  . 

Решение. Согласно свойству 10 имеем . Далее, из свойства 9 следует, что  .  В этой связи

.

Следовательно, окончательно получаем  .

Ответ:  .

Пример 16.  Вычислить    при условии, что

.

Решение.  Так как , то   или  . Преобразуем выражение на основе использования свойств 1 и 2, следующим образом:

 или   .

Так как  , то отсюда получаем   .

Ответ:  .

Пример 17.  Вычислить  , если    и  .

Решение.  Так как    и  

,  то  .

Ответ:  .

Пример 18.  Дано: и . Выразить посредством функции, зависящей от переменной  .

Решение.  Используя свойства 1 и 2, представим    и   посредством следующих формул:

,               (3)

.               (4)

Так как обе формулы содержат  , то для решения задачи необходимо выразить    из формулы (4) и полученное выражение подставить в формулу (3). Поскольку         

   или   ,   то

.

Ответ:  

Пример 19.  Доказать, что   .

Доказательство.  Обозначим  .  Преобразуем    следующим образом:  .  Так как  , то . Далее воспользуемся неравенством Коши  или  , которое выполняется для любых    и  .

В таком случае  .

Неравенство доказано.

Примечание. При доказательстве неравенства использовалось свойство логарифмической функции: если , то функции является возрастающей на всей области определения.

Пример 20.  Дано: , ,  ,  и . Вычислить  .

Решение.  Так как  , то согласно свойству 3 имеем

  или   .  

Так как  , ,    и  ,  то

,   ,  ,    и   .

Ответ:  .

Для более глубокого изучения методов решения задач на вычисление логарифмов целесообразно обратиться к учебным пособиям, приведенных в списке рекомендованной литературы.  

   

Рекомендуемая литература

1.  Кушнир А.И. Шедевры школьной математики (задачи и решения в двух книгах). – Киев: Астарта, книга 1, 1995. – 576 с.

2. Сборник задач по математике для поступающих во втузы / Под ред. М.И. Сканави. – М.: Мир и Образование, 2013. – 608 с.

3. Супрун В.П. Математика для старшеклассников: дополнительные разделы школьной программы. – М.: Ленанд / URSS, 2014. – 216 с.

Остались вопросы? 

Чтобы получить помощь репетитора – зарегистрируйтесь.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

вычисления логарифмов — Колпаков Александр Николаевич

Комплект простейших заданий уровня А на вычисление логарифмов, который репетитор по математике регулярно использует на своих занятиях с большинством учеников. Материал предназначен для учащихся 10-11 классов и преподавателей в помощь при подготовке к ЕГЭ, а также для текущей школьной работы, направленной на отработку вычислительных навыков.

Вычислите:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

18)

19)

20)

Напутствие репетитора по математике:
Вычисляя логарифмы, применяйте следующие формулы:
и
Для решения каждого задания представьте основание логарифма и число под его знаком в виде степени с одним и тем же основанием и вынесите полученные показатели из-под логарифма в его коэффициент.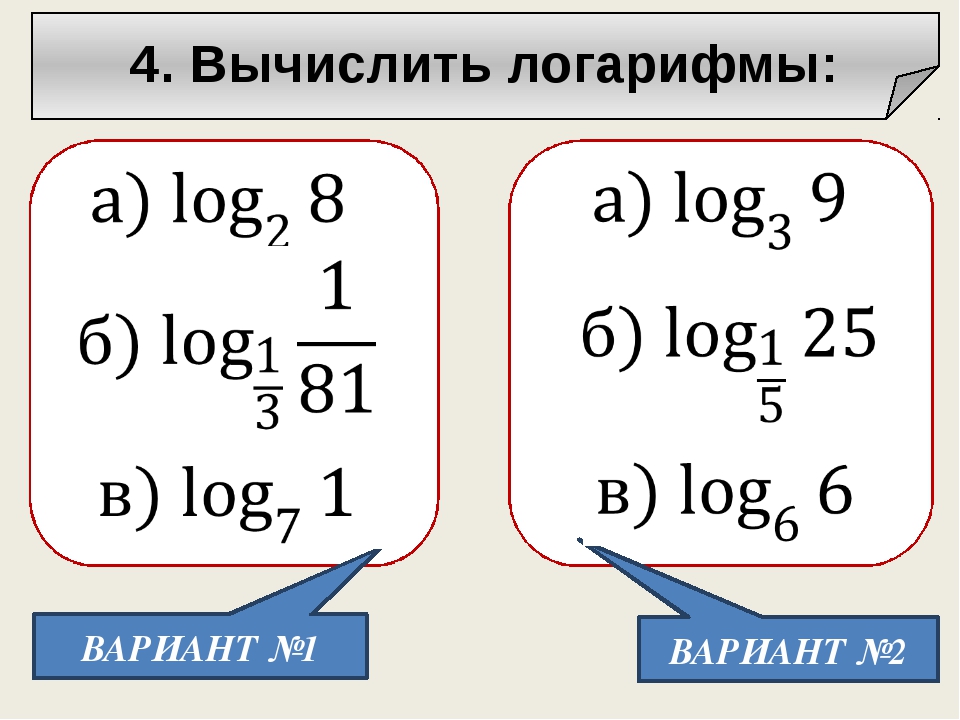 Логарифм с оставшимися равными числами будет равен единице.

Надо сказать, что в 80% задачниках по математике (школьных учебниках и пособиях по подготовке к ЕГЭ) крайне мало вычислительных упражнений на логарифмы, связанных со свойствами степеней. Если репетитор по математике использует стандартные пособия, то в его распоряжении оказывается обычно не более 5 — 6 примеров на логарифмы по каждому алгоритму их вычисления. Я уже давно не пользуюсь никакими задачниками и предлагаю ученикам свои материалы. В заданиях перемешиваю различные виды чисел: десятичные, обыкновенные, корни, дроби, степени с отрицательными показателями.

Вычислите логарифмы с использованием следующих формул:
и

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

Задачи на основное логарифмическое тождество:

1)

2)

3)

4)

5)

6)

7)

8)

9)

10)

11)

12)

13)

14)

15)

16)

17)

Задачи на формулу перехода к новому основанию

1)

2)

3)

4)

5)

6)

7)

8)

9)

Комментарий репетитора по математике относительно состава задач. Задания на логарифмы составлены по классическим законам методики и дидактики и имеют достаточное количеством однотипных упражнений. На первый взгляд может показаться, что все номера, взятые из одного раздела, как две капли воды похожи друг на друга. Отличие наблюдается только в числах. Но любой опытный репетитор по математике Вам скажет, что достаточно в одном из таких однотипных примеров поменять какое-нибудь целое число, например, на иррациональное или на дробное и перед ученик мгновенно растеряется. Поэтому я постарался обыграть все возможные числовые ситуации разнообразить номера десятичными и обыкновенными дробями, корнями разных степеней, комбинациями действий и коэффициентов, окружающих логарифмы.

В реальности я подаю задания ученику на отдельном листочке А4 с максимально плотным расположением примеров. Все на одном листе! Один из таких планов с представлен ниже:

Ученикам:
Задания можно использовать для самостоятельной подготовки к ЕГЭ по математике с целью научиться решать простейшие задачи на логарифмы из части В. Регулярно повторяйте с репетитором формулы, ибо без их уверенного запоминания Вам будет нелегко соориентироваться в вычислениях, в которых применяются сразу две или даже три формулы сразу.

Преподавателям:
Напишите свое мнение о качестве материалов. Понравилась ли Вам подборка упражнений? Насколько велика потребность в таких задачах у репетитора по математике? Помогли ли мои упражнения в практической работе? Пишите, комментируйте! Присылайте интересные логарифмические задания на вычисления, которые встретились Вам в тот или иной период подготовки к ЕГЭ.

Колпаков А.Н. Репетитор по математике — автор комплекта.

Понятие логарифма. Основное логарифмическое тождество

1.	Определение логарифма (основание — целое число)	1 вид — рецептивный	лёгкое	1 Б.	Вычисление логарифма по определению.
2.	Определение логарифма (основание — дробь)	1 вид — рецептивный	лёгкое	1 Б.	Вычисление логарифма по определению.
3.	Неизвестное под знаком логарифма	1 вид — рецептивный	среднее	2 Б.	Найти неизвестное число под знаком логарифма по основанию и показателю степени.
4.	Неизвестное основание логарифма (целое число)	1 вид — рецептивный	среднее	2 Б.	Вычисление неизвестного основания логарифма по определению (основание — целое число).
5.	Неизвестное основание логарифма (обыкновенная дробь)	1 вид — рецептивный	среднее	3 Б.	Вычисление неизвестного основания логарифма по определению логарифма (основание — обыкновенная дробь).
6.	Основное логарифмическое тождество (сложение)	2 вид — интерпретация	среднее	3 Б.	Применение основного логарифмического тождества.
7.	Основное логарифмическое тождество (вычитание)	2 вид — интерпретация	среднее	3 Б.	Применение основного логарифмического тождества.
8.	Основное логарифмическое тождество (произведение)	2 вид — интерпретация	среднее	3 Б.	Применение основного логарифмического тождества.
9.	Основное логарифмическое тождество (основание — дробь)	2 вид — интерпретация	среднее	4 Б.	Применение основного логарифмического тождества (основание — дробь).
10.	Область допустимых значений логарифма	2 вид — интерпретация	сложное	4 Б.	Определение области допустимых значений логарифма с применением разности квадратов.
11.	Определение логарифма (неизвестный показатель степени)	2 вид — интерпретация	сложное	4 Б.	Вычисление неизвестного показателя степени по определению логарифма. Под знаком логарифма — корень n-oй степени.
12.	Определение логарифма (неизвестное основание)	2 вид — интерпретация	сложное	6 Б.	Вычисление неизвестного основания по определению логарифма. Под знаком логарифма — корень n-oй степени.

Десятичный логарифм: как рассчитывается?

Степень отдельно взятого числа называется математическим термином, придуманным несколько столетий назад. В геометрии и алгебре встречается два варианта – десятичные и натуральные логарифмы. Они рассчитываются разными формулами, при этом уравнения, отличающиеся написанием, всегда равны друг другу. Это тождество характеризует свойства, которые относятся к полезному потенциалу функции.

Особенности и важные признаки

На данный момент различают десять известных математических качеств. Самыми распространенными и востребованными из них являются:

• Подкоренной log, разделенный на величину корня, всегда такой же, как и десятичный логарифм √.
• Произведение log всегда равно сумме производителя.
• Lg = величине степени, перемноженной на число, которое в нее возводится.
• Если от log делимого отнять делитель, получится lg частного.

Кроме того, есть уравнение, основанное на главном тождестве (считается ключевым), переход к обновленному основанию и несколько второстепенных формул.

Вычисление десятичного логарифма — довольно специфическая задача, поэтому к интегрированию свойств в решение необходимо подходить осторожно и регулярно проверять свои действия и последовательность. Нельзя забывать и о таблицах, с которыми нужно постоянно сверяться, и руководствоваться только найденными там данными.

Разновидности математического термина

Главные отличия математического числа «спрятаны» в основании (a). Если оно имеет показатель 10, то это десятичный log. В обратном случае «a» преобразуется в «у» и обладает трансцендентными и иррациональными признаками. Также стоит отметить, что натуральная величина рассчитывается специальным уравнением, где доказательством становится теория, изучаемая за пределами школьной программы старших классов.

Логарифмы десятичного типа получили широкое применение при вычислении сложных формул. Составлены целые таблицы, облегчающие расчеты и наглядно показывающие процесс решения задачи. При этом перед непосредственным переходом к делу нужно возвести log в стандартный вид. К тому же в каждом магазине школьных принадлежностей можно найти специальную линейку с нанесенной шкалой, помогающей решить уравнение любой сложности. Десятичный логарифм числа называется Бригговым, или цифрой Эйлера, в честь исследователя, который первым опубликовал величину и обнаружил противопоставление двух определений.

Два вида формулы

Все типы и разновидности задач на вычисление ответа, имеющие в условии термин log, обладают отдельным названием и строгим математическим устройством. Показательное уравнение является практически точной копией логарифмических расчетов, если смотреть со стороны правильности решения. Просто первый вариант включает в себя специализированное число, помогающее быстрее разобраться в условии, а второй заменяет log на обыкновенную степень. При этом вычисления с применением последней формулы должны включать в себя переменное значение.

Разница и терминология

Оба главных показателя обладают собственными особенностями, отличающими числа друг от друга:

• Десятичный логарифм. Важная деталь числа – обязательное наличие основания. Стандартный вариант величины равен 10. Маркируется последовательностью – log x или lg x.
• Натуральный. Если его основанием является знак «e», представляющий собой константу, идентичную строго рассчитанному уравнению, где n стремительно движется к бесконечности, то приблизительный размер числа в цифровом эквиваленте составляет 2.72. Официальная маркировка, принятая как в школьных, так и в более сложных профессиональных формулах, – ln x.
• Разные. Кроме основных логарифмов встречаются шестнадцатиричные и двоичные виды (основание 16 и 2 соответственно). Есть еще сложнейший вариант с базовым показателем 64, подпадающий под систематизированное управление адаптивного типа, с геометрической точностью производящее расчет итогового результата.

Терминология включает в себя следующие величины, входящие в алгебраическую задачу:

• значение;
• аргумент;
• основание.

Вычисление log числа

Есть три способа быстро и в устной форме сделать все необходимые расчеты по нахождению интересующего результата с обязательным правильным итогом решения. Изначально приближаем десятичный логарифм к своему порядку (научная запись числа в степени). Каждую положительную величину можно задать уравнением, где она будет равен мантиссе (цифра от 1 до 9), перемноженной на десятку в n-й степени. Такой вариант подсчета создан на основе двух математических фактов:

• произведение и сумма log всегда имеют одинаковый показатель;
• логарифм, взятый из числа от одного до десяти, не может превышать величину в 1 пункт.

1. Если ошибка в вычислении все-таки происходит, то она никогда не бывает меньше одного в сторону вычитания.
2. Точность повышается, если учесть, что lg с основанием три имеет итоговый результат – пять десятых от единицы. Поэтому любое математическое значение больше 3 автоматически добавляет к ответу один пункт.
3. Практически идеальная точность достигается, если под рукой есть специализированная таблица, которую можно легко применять в своих оценочных действиях. С ее помощью можно выяснить, чему равен десятичный логарифм до десятых процентов от оригинального числа.

История вещественного log

Шестнадцатый век остро испытывал потребности в более сложных исчислениях, чем было известно науке того времени. Особенно это касалось деления и умножения многозначных цифр с большой последовательностью, в том числе дробей. В конце второй половины эпохи сразу несколько умов пришли к выводу о сложении чисел с помощью таблицы, которая сопоставляла две прогрессии: арифметическую и геометрическую. При этом все базовые расчеты должны были упираться в последнюю величину. Таким же образом ученые интегрировали и вычитание.

Первое упоминание об lg состоялось в 1614 году. Это сделал любитель-математик по фамилии Непер. Стоит отметить, что, несмотря на огромную популяризацию полученных результатов, в формуле была сделана ошибка из-за незнаний некоторых определений, появившихся позже. Она начиналась с шестого знака показателя. Наиболее близки к пониманию логарифма были братья Бернулли, а дебютное узаконивание произошло в восемнадцатом столетии Эйлером. Он же и распространил функцию в область образования.

История комплексного log

Дебютные попытки интегрировать lg в широкие массы делали на заре 18-го века Бернулли и Лейбниц. Но целостных теоретических выкладок они так и не сумели составить. По этому поводу велась целая дискуссия, но точного определения числу не присваивали. Позже диалог возобновился, но уже между Эйлером и Даламбером. Последний был в принципе согласен со множеством фактов, предлагаемых основателем величины, но считал, что положительный и отрицательный показатели должны быть равны. В середине столетия формула была продемонстрирована в качестве окончательного варианта. Кроме того, Эйлером была опубликована производная десятичного логарифма и составлены первые графики. Потому что есть 10^®и 2L4 1、 Накопление ошибок, обусловленных вычислением числа контролируемых логарифмов в соответствии с первым method. In таким образом, значительно более высокая точность может быть достигнута при сохранении автоматизации расчетов, присущей 2-му способу. Это очень ценно, особенно если вы составляете большую таблицу.

Смотрите также:

Решение задач по математическому анализу

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

Как считать логарифмы в уме

В предыдущем посте рассматривались приближения для триггерных функций, которые достаточно просты для вычисления без калькулятора. Мне было интересно, смогу ли я придумать что-то подобное для логарифмов. Я начинаю с базы логов 10. Позже в посте я покажу, как найти логи в других базах из базы логов 10.

Пусть

х = м х 10 ^р .

, где 1 ≤ м ≤ 10. Затем

лог ₁₀ ( х ) = лог ₁₀ ( м ) + р

, поэтому без ограничения общности можно принять 1 ≤ x ≤ 10.

Но мы можем еще немного сузить наш диапазон. Если x  > 3, вычислите логарифм x ‘ =  x /10, а если x  < 0,3, то вычислите логарифм 10 x . Итак, мы будем считать

0,3 ≤ х ≤ 3.

Для x в этом диапазоне

log ₁₀ ( x ) ≈ ( x – 1)/( x + 1)

— очень хорошее приближение.Абсолютная ошибка менее 0,0327 на интервале [0,3, 3].

Примеры

log ₁₀ 0,6 ≈ (0,6 – 1)/(0,6 + 1) = -1/4 = -0,25. Точно: -0,2218

log ₁₀ 1776 = 3 + log ₁₀ 1,776 ≈ 3 + 0,776/2,776 = 3,2795. Точно: 3,2494

log ₁₀ 9000 = 4 + log ₁₀ 0,9 ≈ 4 – 0,1/1,9 = 3,9473. Точно: 3,9542

Прочие базы

Логарифмы по всем основаниям пропорциональны, поэтому вы можете конвертировать между логарифмом с основанием 10 и логарифмом с любым другим основанием путем умножения на константу пропорциональности.

log _b ( x ) = log ₁₀ ( x ) / log ₁₀ ( b ).

Итак, предположим, например, что вы хотите вычислить log ₂ 48. Поскольку 48 = 32 × 1,5, мы имеем

log ₂ 48 = log ₂ 32 + log ₂ 1,5 = 5 + log ₁₀ 1,5 / log ₁₀ 2

Мы можем аппроксимировать log ₁₀ 1,5 как 1/5 и log ₁₀ 2 как 1/3, чтобы получить

.

log ₂ 48 = 5 + 3/5 = 5.6.

Точное значение 5,585.

Если вы хотите использовать это для натуральных журналов, вы можете запомнить

1/log ₁₀ e = log _e 10 = 2,3.

Обновление : есть лучший способ работать с другими базами. Смотрите этот пост. В том же посте объясняется, почему аппроксимация особенно проста для журналов с основанием 10.

Больше точности

Абрамовиц и Стеган уточняют приближение t = ( x – 1)/( x + 1). Они используют интервал [1/√10, √10], а не [0,3, 3]. Этот несколько отличающийся интервал симметричен относительно 0 при преобразовании в t . Уравнение 4.1.41 прогоняет t через кубический многочлен и снижает абсолютную ошибку до менее чем 6 × 10 ^-4 . Уравнение 4.1.42 использует полином 9-й степени от t , чтобы уменьшить абсолютную ошибку ниже 10 ^-9 .

Следующий

Мой следующий пост покажет, как вычислить 10 ^x аналогичным образом.

Похожие сообщения

Объяснение логарифмов: все, что вам нужно знать

Что такое логарифмы: полное объяснение

Логарифм — это степень, в которую возводят определенное число, чтобы получить другое число.До изобретения калькуляторов и различных типов сложных компьютеров ученым и математикам было трудно вычислять очень большие числа. Логарифмы могут помочь им в этом. Ниже приводится несколько примеров.

Четыре в пятой степени записывается следующим образом:   45  = 1024.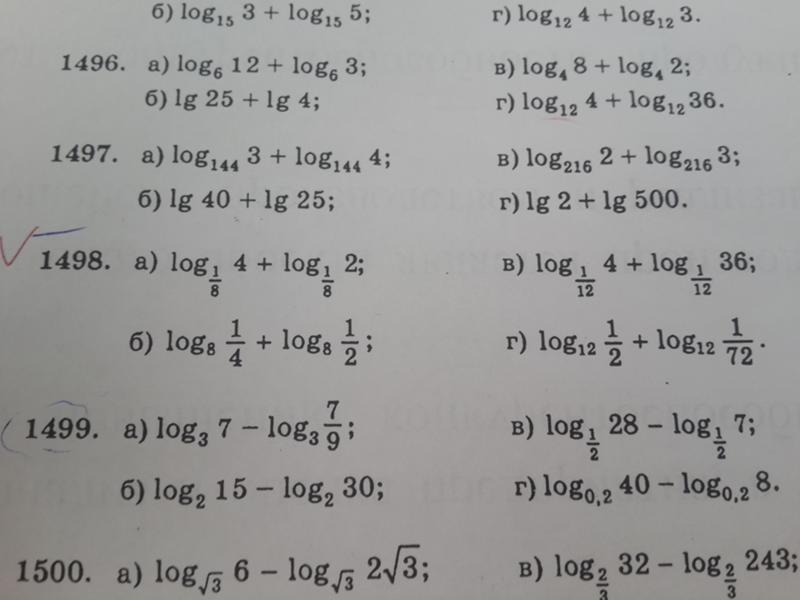

Это также можно записать следующим образом: 4 x 4 x 4 x 4 x 4 = 1024.

Другой способ объяснить это означает, что 4 в степени 5 означает, что 4 умножается на 5.

Тем, кто не разбирается в математике, иногда трудно понять, как логарифмы вписываются в реальный мир и связаны с ним. Однако логарифмы используются в науке и математике для решения множества сложных задач. В большинстве случаев числа, используемые в логарифмах, намного больше, чем числа, используемые в приведенных выше примерах.

Джону Нейпиру приписывают изобретение понимания того, как на самом деле работают логарифмы.

Логарифмы: точное определение

Точное определение логарифма — это степень или показатель степени для определенного числа, которое возводится для получения другого определенного числа.Логарифмы наиболее кратко описываются как кратчайший путь в математике. Например, умножение — это, по сути, кратчайший путь для сложения, а показатели степени — кратчайший путь для умножения. Логарифмы — это кратчайший путь к показателям степени.

В логарифмах есть закономерности, которые довольно легко понять. Например, логарифм 100 по основанию 10 равен 2. Логарифм 1000 по основанию 10 равен 3. Также важно понимать натуральные логарифмы, которые объясняют логарифмы как с точки зрения времени, так и с точки зрения роста.Логарифмы использовались в течение сотен лет, пока в конце 19 века механические машины не смогли вычислять большие числа, а в конце концов компьютеры взяли на себя эту задачу в 20 веке.

Умножение гелозии

Как работают логарифмы?

Логарифмы работают, предоставляя метод, который позволяет выполнять более сложные математические операции, такие как умножение, деление и вычисление корня, посредством сложения и вычитания. Все числа можно выразить в так называемой экспоненциальной форме, то есть 8 можно записать как 2, 25 как 5 и так далее.

Что делает логарифмы такими полезными, так это тот факт, что операции умножения и деления сводятся к простому сложению и вычитанию. Когда очень большие числа выражаются в виде логарифма, умножение превращается в сложение показателей степени. Логарифмы ускоряют и упрощают вычисления. Их использование может значительно сократить количество времени, необходимого для умножения больших чисел.

Ученые могут найти произведение двух разных чисел, x и y, найдя индивидуальный логарифм каждого числа, сложив логарифмы вместе, а затем сверившись с таблицей, чтобы найти точное число с вычисленным логарифмом.Это называется его антилогарифмом. Существуют также логарифмические законы или правила, которые помогают тем, кто использует логарифмы. Разные таблицы будут включать разные законы или правила, связанные с логарифмами. MathCentre включает в себя некоторые из самых основных правил, касающихся логарифмов.

Оригинальный рисунок шкалы Гюнтера из 1624 Уильяма Отреда

Как вы создаете логарифмы?

Создание логарифмов начинается с понимания основных формул, таких как следующие.

log2 16 = 4, потому что 24 = 2 × 2 × 2 × 2 = 16

Создание логарифмов основано на понимании того, что умножение или деление чисел в геометрической прогрессии связано со сложением или вычитанием соответствующих чисел.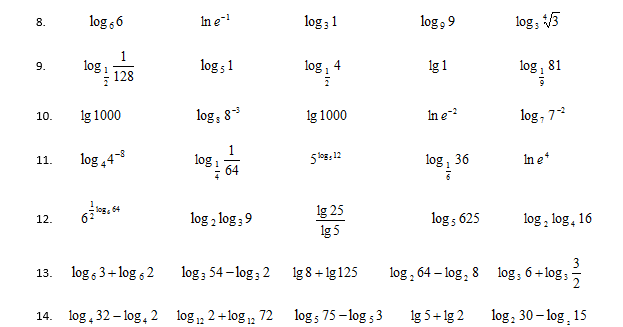 Мы можем лучше понять этот процесс как часть законов возведения в степень. Занесение этих чисел в таблицу облегчит сложные расчеты.

При создании логарифмов из данных необходимо выполнить несколько шагов.Процесс можно запустить, поместив входные значения в один столбец и выходные значения в другой столбец, чтобы выполнить логарифмическую регрессию. Есть также графики журналов, которые представляют логарифмы. Один тип графика может включать использование логарифмической шкалы на одной оси и линейной шкалы на другой.

Логарифмические функции можно понимать как в основном обратную функцию возведения в степень. Логарифмическая функция такова: f(x) = log b(x). Константа «b» является основанием логарифма. Другой способ понять эту концепцию — при построении графика как логарифмической функции, так и обратной функции, также отображается линия y = x.Обратная функция и ее логарифмическая функция симметричны.

Круги пропорции Утреда Круги пропорций Логарифмическая линейка Роберта Бисакера

Кто создал логарифмы?

Понятие логарифмов было известно в древней Вавилонии примерно в 1800 г. до н.э. Были обнаружены глиняные таблички, содержащие таблицы с последовательными степенями целых чисел. Однако шотландцу Джону Нейпиру приписывают звание изобретателя за то, что он понял, как на самом деле работают логарифмы.В 1594 году Нейпир начал работать над тригонометрическими таблицами и потратил двадцать лет на их уточнение. Его величайшая математическая работа Mirifici Logarithmorum Canonis Descriptio  (Описание чудесного канона логарифмов) была опубликована в 1614 году и посвящена логарифмам.

В конце 1614 года один из самых известных английских математиков того времени, Генри Бриггс (1561–1631), профессор геометрии в Грешем-колледже в Лондоне, получил копию « Descriptio » Нэпьера и к марту следующего года написал, что:
Нейпир, лорд Маркинстон, поставил мою голову и руки на работу с его новыми и замечательными логарифмами.Я надеюсь увидеть его этим летом, если будет угодно Богу; ибо я никогда не видел книги, которая понравилась бы мне больше и заставила бы меня больше удивиться.

Нейпир умер в 1617 году, а Генри Бриггс в 1624 году опубликовал таблицу логарифмов, рассчитанных до 14 знаков после запятой. Они были для чисел от 1 до 20 000, а также для чисел от 90 000 до 100 000. Адриан Влак, голландский издатель, создал таблицу, в которую были добавлены недостающие 70 000 значений.

Логарифмическая линейка Джеймса Ватта Логарифмическая линейка Сохо Фуллера Логарифмическая линейка Тахера (1887 г.) самым ясным и простым образом исходное представление о логарифмах.Важно отметить, что Нейпир смотрел на логарифмы не через призму алгебры, а через призму геометрии.

Многие ученые и математики на протяжении столетий смогли опираться на первоначальные работы Нейпира, Бриггса и Бюрги, расширить понимание области математики и создать различные инструменты, которые используются до сих пор. Сюда входят логарифмические шкалы Эдмунда Гюнтера, а также логарифмическая линейка Уильяма Отреда и круговая логарифмическая линейка.

Каковы применения логарифмов?

Есть много примеров и практических применений логарифмов. Одним из основных приложений является поиск решения задач возведения в степень. Таблица логарифмов, составленная Генри Бриггсом в 1617 году, может помочь людям выполнить шаги при решении логарифмических математических задач. Это было вскоре после изобретения Нейпира, но в этой таблице в качестве базы использовалось 10. Первая таблица Бриггса включала основные логарифмы всех целых чисел от 1 до 1000.

Логарифмическая линейка, представляющая собой пару разделенных шкал, используемых для вычислений, была приложением логарифмов.Логарифмическая линейка без помощи калькулятора может решить проблемы, используя числовые линии.

Несколько законов и теорий включали использование логарифмов. Примеры включают теорию вероятности и законы, касающиеся подбрасывания честной монеты. Соотношение орла и решки основано на законе повторного логарифма.

Примеры логарифмов в реальной жизни

В реальной практике есть несколько конкретных примеров логарифмов.

• Измерение землетрясений – Логарифмические функции являются частью шкалы Рихтера, которая используется для измерения силы землетрясений. Это конкретно связано с тем, сколько энергии высвобождается во время землетрясения. Сейсмографы обнаруживают движения в земле. Из-за логарифмической системы шкалы каждое увеличение силы землетрясения на целое число означает десятикратное увеличение амплитуды.
• Измерение звука в децибелах . Измерение в децибелах — еще один пример использования логарифмов. Согласно Physclips, децибел — это логарифмическая единица измерения уровня звука. Он также часто используется в электронике и в области связи.
• Измерение pH-балансов – Логарифмы в химии могут использоваться для измерения кислотности и щелочности различных веществ. Есть рабочие листы, которые показывают различные вещества и логарифмические формулы, которые используются для расчета рН.

Логарифмические правила – объяснение и примеры

Что такое логарифм? Зачем мы их изучаем? И каковы их правила и законы?

Начнем с того, что логарифм числа «b» можно определить как степень или степень, в которую нужно возвести другое число «a», чтобы получить результат, равный числу b.

Мы можем представить это утверждение символически как;

log _a  b = n.

Точно так же мы можем определить логарифм числа как обратную его степень. Например, log _a b = n можно экспоненциально представить как; а ^п = б.

Таким образом, мы можем заключить, что;

a ⁿ  = b ⇔ log _a  b = n.

Хотя логарифмы изучают в школах для упрощения вычислений с большими числами, они по-прежнему играют важную роль в нашей повседневной жизни.

Давайте рассмотрим некоторые из этих применений логарифмов:

• Мы используем логарифмы для измерения кислотности и щелочности химических растворов.
• Измерение интенсивности землетрясений производится по шкале Рихтера с использованием логарифмов.
• Уровень шума измеряется в дБ (децибелах) по логарифмической шкале.
• Экспоненциальные процессы, такие как распад отношения активных изотопов, рост бактерий, распространение эпидемии в популяции и охлаждение трупа, анализируются с использованием логарифмов.
• Для расчета периода выплаты кредита используется логарифм.
• В исчислении логарифм используется для различения сложных задач и определения площади под кривыми.

Как и у показателей степени, у логарифмов есть правила и законы, которые работают так же, как правила показателей степени. Важно отметить, что законы и правила логарифмов применимы к логарифмам любого основания. Однако во всех вычислениях должна использоваться одна и та же база.

Мы можем использовать законы и правила логарифмирования для выполнения следующих операций:

• Приведение логарифмических функций к экспоненциальной форме.
• Сложение
• Вычитание
• Умножение
• Деление
• Расширение и сжатие
• Решение логарифмических уравнений.

Законы логарифмов

Логарифмические выражения могут быть записаны по-разному, но в соответствии с определенными законами, называемыми законами логарифмов. Эти законы могут быть применены к любому основанию, но при расчете используется одно и то же основание.

Четыре основных закона логарифмов включают:

Закон правила произведения

Первый закон логарифмов утверждает, что сумма двух логарифмов равна произведению логарифмов.Первый закон представлен как;

⟹ Журнал + log b = log ab

Пример:

8 Log ₂ 5 + log ₂ 4 = log ₂ (5 × 4) = log ₂ 20
1. log ₁₀ 6 + log ₁₀ 3 = log ₁₀ (6 x 3) = log ₁₀ 18

• log x + log y = log (x * y) = log xy

0

000000000 log x = log (4x * x) = log 4x ²

Закон правила частного

Вычитание двух логарифмов A и B равно делению логарифмов.

⟹ лог A − лог B = лог (A/B)

Пример:

1. лог ₁₀ 6 – лог ₁₀ 3 = лог ₁₀ (6/3) = лог 20120 209021
2. Журнал ₂ 4x — Log ₂ x = log ₂ (4x / x) = log ₂ 4

4 2

Закон об уровне мощности

⟹ Журнал A ^N = N Журнал A

Пример:

1. Log ₁₀ 5 ³ = 3 log ₁₀ 5
2. 2 log x = log x ²
²
2 1 8 5 ln x ² = ln x ^{(2 * 5 )} = ln x ¹⁰

Изменение закона базового правила

⟹ log _b x = (log _A x) / (log _A b)

Пример 4:

• лог ₄ 16 = (лог 16) / (лог 4).

Правила логарифмов

Логарифмы — очень дисциплинированная область математики. Они всегда применяются в соответствии с определенными правилами и положениями.

При игре с логарифмами необходимо помнить следующие правила:

• Учитывая, что a ⁿ = b ⇔ log _a  b = n, логарифм числа b определен только для положительных действительных чисел.

⟹ a > 0 (a ≠ 1), a ⁿ  > 0.

• Логарифм положительного действительного числа может быть отрицательным, нулевым или положительным.

примеры

1. 3 ² = 9 ⇔ Log ₃ 9 = 2
8 5 ⁴ = 625 ⇔ log ₅ 625 = 4 8 7 ⁰ = 1 ⇔ Log ₇ 1 = 0
2. 2 ^-3 = ¹ = ^{8 ⇔ log ₂ ( 1 / ₈ ) = -3}
8 10 ^-2 = 0,01 ⇔ log ₁₀ 01 = -2
3. 2 ⁶ = 64 ⇔ log ₂ 64 = 6
4. 3 ^{— 4} = 1/3 ⁴ = 1/81 ⇔ Log ₃ 1/81 = -4
5. 10 ^-2 = 1/100 = 0. 01 ⇔ log ₁₀ 01 = -2
• Логарифмические значения данного числа различны для разных оснований.

примеры

1. LOG ₉ 81 ≠ LOG ₃ 81 1 8 LOG ₂ 16 ≠ LOG ₄ 16
• Логарифмы на базу 10 называются общими логарифми. Когда логарифм записывается без основания нижнего индекса, мы предполагаем, что основание равно 10.

Примеры

1. log 21 = log ₁₀
2. log 0.05 = log ₁₀ 05
• Логарифм по основанию «е» называется натуральным логарифмом. Константа e приблизительно равна 2,7183. Натуральные логарифмы выражаются как ln x, что равно log _e
• Логарифмическое значение отрицательного числа является мнимым.
• Логарифм 1 по любому конечному ненулевому основанию равен нулю.
  A ⁰ = 1 ⟹ LOG _A 1 = 0.
1 = 0. 0

Пример:

7 ⁰ = 1 ⇔ Журнал ₇ 1 = 0

• Логарифм любого положительного числа к тому же основанию равно 1.

а ¹ = а ⟹ log _а а = 1.

Примеры

1. Log ₁₀ 10 = 1
10 = 1 8 Log ₂ 2 = 1 ₂ 2 = 1 2 = 1 2 = 1
• Учитывая, что X = log _A M, то 10202020

  = A

Пример 1

Оцените следующее выражение.

log ₂ ​8 + log ₂ ​4

Решение

Применяя закон правила произведения, получаем;

log ₂ ​8 + log ₂ ​4 = log ₂ (8 x 4)

= log ₂ 32

Перепишите 32 в экспоненциальной форме, чтобы получить показатель степени.

32 = 2 ⁵

Поэтому 5 — это правильный ответ

пример 2

оценить журнал ₃ 162 — журнал ₃ 2

Решение

Это выражение вычитания; поэтому мы применяем закон частного правила.

log ₃

162 — log ₃ 2 = log ₃ (162/2)

= log ₃ 81

Написать аргумент в экспоненциальной форме

81 = 3 ⁴

Следовательно, ответ 4.

Пример 3

Разверните приведенное ниже логарифмическое выражение.

Log ₃ (27x ² Y ⁵ )

)

Решение

(27x ^{2 (27x 2 y 5 ) = log ₃ 27 + log ₃ x 2 + log ₃ y 5}

= log ₃ (9) + log ₃ (3) + 2log ₃ x + 5log ₃ y

Но журнал ₃ 9 = 3

Подставить, чтобы получить.

= 3 + log ₃ (3) + 2log ₃ x + 5log ₃ y

y

Пример 4

Рассчитать значение log _√2 64.

Решение

⟹ log _√2 64 = log _√2 (2) ⁶

⟹ log _√2 64 = 6Log _√2 (2)

⟹ log _√2 64 = 6Log _√2 (√2) ²

⟹ log _√2 64 = 6 * 2Log _√2 (√2)

⟹ log _√2 64 = 12 * 2 (1)

⟹ log _√2 64 = 12

Пример 5

Найдите x, если log _0.1 (0,0001) = x

Решение

⟹ log _0.1 (0,0001) = log _0,1 (0.1) ⁴

⟹ log _0.1 (0,0001) = 4Log _0,1 0,1

⟹ log _0.1 (0,0001) = 4 (1)

⟹ log _0,1 (0,0001) = 4

Следовательно, x = 4.

Пример 6

Найти значение x , 2log x = 4log3

Решение

2logx = 4log3

Разделите каждую сторону на 2.

⟹ log x = (4log3) / 2

⟹ log x = 2log3

⟹ log x = log31 2

⟹ log X = log9

x =

x = Пример 70002 Вычислить log ₂ (5x + 6) = 5

Решение

Переписать уравнение в экспоненциальной форме

2 ⁵ = 5x + 6

Упростить.

32 = 5x + 6

32 = 5x + 6

Вычтите обе стороны уравнения на 6

32 — 6 = 5x + 6 — 6

26 = 5x

x = 26/5

Пример 8

Решите log x + log (x−1) = log (3x + 12)

Решение

⇒ log [x (x — 1)] = log (3x + 12)

Чтобы получить, отбросьте логарифмы;

⇒ [x (x − 1)] = (3x + 12)

Применить распределительное свойство, чтобы убрать скобки.

⇒ x ² — x = 3x + 12

⇒ x ² — x — 3x — 12 = 0

⇒ x ² — 4x — 12 = 0

⇒ (x — 6) ( x+2) = 0

⇒x = − 2, x= 6

Поскольку аргумент логарифма не может быть отрицательным, то правильный ответ: x = 6.

Пример 9

– ln (2x) = ln 4x

Solution

ln [32/(2x)] = ln 4x

Отбросьте натуральные бревна.

[32/ (2x)] = 4x

32/ (2x) = 4x.

Крест умножить.

32 = (2x)4x

32 = 8x ²

Разделите обе стороны на 8, чтобы получить;

x ² = 4

x = – 2, 2

Поскольку мы не можем иметь логарифм отрицательного числа, то х = 2 остается правильным ответом.

Вопросы практики
1. оценить журнал ₄ 64 + log ₄ 16
₄ 16 8 Log ₃ 14-2Log ₃ 5 8 Оценить 2 журнала ₃ 5 + Log ₃ 40 — 3 log ₃ 10 8 Log ₂ 4 + Log ₂ 4 + Log ₂ 5 1 ₂ 5 8 Развернуть журнал ₃ (XY ³ / √z)
2. Конденсация следующее выражение 5 ln x + 13 ln (x ³ + 5) – 1/2 ln (x + 1)
3. Упростить log _a 28 – log _a 4 как единичный логарифм
4. Найти значение log ₅ 8 + ₅ (1/1000) 2 (1/1000) 1
5. Решить для x в логарифм 3Log ₅ 2 = 2Log ₅ x
6. Перезапись log12 + log 5 в виде одного logarithm

Math.у = х

Функция JavaScript Math.log() эквивалентна ln(x) по математике.

Параметры

Возвращаемое значение

Натуральный логарифм (по основанию e ) заданного числа. Если число отрицательное, возвращается NaN .

Если значение x равно 0, возвращаемое значение всегда -Бесконечность .

Если значение x отрицательное, возвращаемое значение всегда НаН .

Поскольку log() является статическим методом Math , вы всегда используете его как Math.log() , а не как метод объекта Math , который вы создан ( Math не является конструктором).

Если вам нужен натуральный логарифм 2 или 10, используйте константы Math.LN2 или Матем.LN10 . Если вам нужен логарифм по основанию 2 или 10, используйте Math.log2() или Math.log10() . Если вам нужен логарифм для другие базы, используйте Math. log(x) / Math.log(otherBase), как в примере ниже; ты можешь хотите предварительно рассчитать 1 / Math.log (otherBase).

Использование Math.log()

  Math.log(-1);
Матем.лог(0);
Math.log(1);
Math.log(10);
  

Использование Math.log() с другой базой

Следующая функция возвращает логарифм y по основанию х (т.е. logxy\log_x у):

  функция getBaseLog(x, y) {
  вернуть Math.log(y) / Math.log(x);
}
  

Если вы запустите getBaseLog(10, 1000) , он вернет 2.9999999999999996 из-за округления с плавающей запятой, что очень близко к фактическому ответу 3.

Таблицы BCD загружаются только в браузере

Логарифмы: ранняя история знакомой функции — Джон Нейпир знакомит с логарифмами избавление практиков от вычислительного бремени. В частности, шотландский математик Джон Нейпир был известен своими устройствами, помогающими в вычислениях.

Он изобрел хорошо известный математический артефакт — искусные нумерационные стержни, более причудливо известные как «кости Нейпира», которые предлагали механические средства для облегчения вычислений. (Для получения дополнительной информации о «костях Нейпира» см. статью «Джон Нейпир: его жизнь, его журналы и его кости» (2006 г.).) prosthaphaeresis, десятичных дробей и арифметика с символьным индексом, чтобы решить проблему сокращения вычислений.Он ценил то, что по большей части практикующие специалисты, выполнявшие трудоемкие вычисления, обычно выполняли их в контексте тригонометрии. Поэтому, помимо разработки логарифмического отношения, Нейпир поместил его в тригонометрический контекст, чтобы оно было еще более актуальным.

Рис. 1. Джон Нейпир (1550-1617)
(из архива истории математики MacTutor)

Нейпир впервые опубликовал свою работу о логарифмах в 1614 году под названием Mirifici logarithmorum canonis descriptio, , что буквально переводится как Описание чудесной таблицы логарифмов. В самом деле, само название, выбранное Нейпиром, раскрывает его большие амбиции в отношении этой техники — предоставление таблиц, основанных на соотношении, которое было бы не чем иным, как «чудодейством» для практиков. Помимо краткого обзора математических деталей, Нейпир дал своей концепции техническое выражение. Он придумал термин из двух древнегреческих терминов: logos, , означающий пропорцию, и arithmos, , означающий число; смешивая их, получается слово «логарифм».Нейпир использовал это слово, а также обозначения «естественные» и «искусственные» для чисел и их логарифмов соответственно в своем тексте.

Несмотря на очевидную связь с существующими методами протезирования и последовательностями, Нэпир обосновал свою концепцию логарифма в кинематической структуре. Мотивация этого подхода до сих пор не совсем понятна историками математики. Нейпир представил две частицы, движущиеся по двум параллельным линиям. Первая линия имела бесконечную длину, а вторая — фиксированную длину (см. рис. 2 и 3).Нейпир представил, что две частицы стартуют из одного и того же (горизонтального) положения в одно и то же время с одинаковой скоростью. Первую частицу он привел в равномерное движение по линии бесконечной длины так, чтобы она прошла равные расстояния за равные времена. Вторую частицу он привел в движение на конечном отрезке так, чтобы ее скорость была пропорциональна расстоянию, оставшемуся от частицы до фиксированной конечной точки отрезка.

Рисунок 2. Две параллельные линии Нейпира с движущимися частицами
(Изображение предоставлено Landmarks of Science Series, NewsBank-Readex)

Точнее, в любой момент еще не пройденное расстояние по второй (конечной) прямой равнялось синусу, а пройденное расстояние по первой (бесконечной) прямой было логарифмом синуса.Это привело к тому, что по мере уменьшения синусов логарифмы Непера увеличивались. При этом синусы уменьшались в геометрической пропорции, а логарифмы возрастали в арифметической пропорции. Мы можем резюмировать объяснение Нэпьера следующим образом ( Descriptio I, 1 (стр. 4); см. рис. 3): \[AC = \log_{nap}(\gamma\omega)\;\;{\rm where}\ ;\;\gamma\omega = {\rm Sin}\,\theta_{1}\]

\[AD = \log_{nap}(\delta\omega)\;\;{\rm где}\;\;\delta\omega = {\rm Sin}\,\theta_{2}\]

\[AE = \log_{nap}(\epsilon\omega)\;\;{\rm где}\;\;\epsilon\omega = {\rm Sin}\,\theta_{3}\]

и так далее, так что в более общем виде: \[x={\rm Sin}\,(\theta)\]

\[y={\log_{nap}}(x)\], где \( \log_{nap}\) используется, чтобы отличить конкретное понимание Нейпиром концепции логарифма от современного.

Рисунок 3. Соотношение между двумя линиями и логарифмами и синусами

Napier сгенерировал числовые записи для таблицы, воплощающей это отношение. Он упорядочил свою таблицу, делая приращения дуги \(\тета\) минуту за минутой, затем перечисляя синус каждой дуги минуты, а затем соответствующий логарифм. Однако с точки зрения того, как он на самом деле вычислял эти записи, он фактически работал бы противоположным образом, сначала генерируя логарифмы, а затем выбирая те, которые соответствуют синусу дуги, которые соответственно формировали аргумент. {\circ}\) в угловых минутах и ​​по симметрии предоставил значения для всего первого квадранта. Отрывок на рисунке 4 дает первую половину первой степени и, по симметрии, справа последнюю половину восемьдесят девятой степени.

Чтобы заполнить таблицы, Нейпир вычислил почти десять миллионов записей, из которых выбрал соответствующие значения. Сам Нейпир подсчитал, что вычисление такого количества записей заняло у него двадцать лет, что относит начало его усилий к 1594 году.

Рисунок 4. Первая страница таблиц Нейпира
(Изображение предоставлено Landmarks of Science Series, NewsBank-Readex)

Нейпир часто демонстрировал преимущества своего метода. Например, он решал задачу, связанную с вычислением средних пропорций, иногда называемых средним геометрическим. Он рассмотрел обычный способ, которым это должно быть вычислено, и указал, что его метод с использованием логарифмов не только находит ответ «раньше» (то есть быстрее!), но также использует только одно сложение и одно деление на два! Он заявил:

. Пусть даны крайние значения 1000000 и 500000 и ищется среднее пропорциональное: это обычно находится путем умножения данных крайних значений одно на другое и извлечения квадратного корня из произведения.Но мы находим это раньше таким образом; Мы складываем логарифм экстремумов 0 и 693147, сумма которых равна 693147, которую мы делим на 2, а частное 346573 будет логарифмом. среднего пропорционального желаемого. По которому среднее пропорциональное 707107, а его дуга 45 градусов находятся по-прежнему…. находят сложением одного и делением на два. (Книга I, 5 (стр. 25), в переводе Эдварда Райта)

Чтобы найти среднее пропорциональное традиционными методами, Нейпир заметил, что нужно вычислить произведение, а затем извлечь квадратный корень; то есть: \[\sqrt{1 000 000 \times 500 000} = \sqrt{500 000 000 000} \приблизительно 707106.78\] Этот метод включает умножение двух больших чисел и длительное извлечение квадратного корня. В качестве альтернативы Нейпир предложил (с вычислениями до 6 значащих цифр):

\[693147 \div 2 = 346573\;\;\;{\rm to}\;\;6\;\;{\rm значащее}\;\;{\rm цифры}\]

\[\Rightarrow {\rm mean}\;\;{\rm пропорциональна} = 707107,\;\;\;{\rm as}\;\;{\rm required,}\], что он справедливо считал гораздо проще вычислить.

Логарифмы

Введение

логарифма были изобретены Нейпиром. До того, как у нас появились калькуляторы, логарифмы упрощали вычисления, поскольку сводили умножение и деление к сложению и вычитанию. В наши дни логарифмы менее важны для этой цели.

Логарифмы

Логарифм записывается как log _a ( x ), где а — число, называемое основанием. Обычно логарифмы записываются по основанию 10 или иногда по основанию 2 для двоичных чисел, но это может быть любое число.Если логарифм по основанию e = 2,71828…, то мы называем его натуральным логарифмом, потому что это единственное основание логарифма, которое имеет скорость изменения, равную тому, что изменяется. Также пишутся натуральные логи, ln( u ). In происходит от латинского log naturalis.

Правила логарифмов

журнал _a (0) не определен(1)

log _a (1) = 0(2)

log _a ( u v ) = log _a ( u ) + log _a ( v ) (3)

log _a ( u/v ) = log _a ( u ) — log _a ( v )(4)

log _a ( u ) ⁿ = n log _a ( u )(5)

log _b ( u ) = log _a ( u )/log _a ( b ) — изменение основания(6)

Где b — старое основание, a — новое основание, u — аргумент логарифма.

log _a (1/ u ) = — log _a ( u ) из (2) и (4).(7)

С помощью этих правил мы можем манипулировать экспоненциальными функциями. Логи — это функции, обратные

.

Экспоненциальная функция

Мы видели, как преобразовать число в логарифмическое число, но что если нам дан логарифм числа и мы хотим узнать, каким было исходное число? Это достигается с помощью экспоненциальных функций. Показательная функция является обратной функцией логарифмической функции.

Что сказать, что A ^{Log _{5 A} ( U )} = U или Log _{5 A} (A ^U ) = U

Если у нас есть логарифм по основанию 10, обратная функция будет 10 ^u .

Для натуральных логарифмов обратной функцией является e ^u или exp( u ). В частности, log ₁₀ (10 ^u ) = u

и 10 ^{лог ₁₀ ( u )} = u (8)

ln( e ^u ) = u или e ^{ln( u )} = u (9)

Пример

Какое значение числа дает следующие логи по основанию 10:

i) 1, ii) 12, iii) -2, iv) 2. 6, в)-5,43

Ответы

1. бревно ₁₀ x = 1
   x = 10 ¹ = 10
2. log ₁₀ x = 12
   x = 10 ¹² = 1×10 ¹²
3. log ₁₀ x = -2
   x = 10 ^-2 = 0,02
4. log ₁₀ х = 2,6
   х = 10 ^2,6 = 501,187
5. log ₁₀ х = 12
   х = 10 ^-5.43 = 3,71535 х 10 ^-6

Логарифмические весы

Логарифмы используются для увеличения диапазона, в котором числа могут быть осмысленно видны. Логарифмы особенно полезны, когда данные простираются от очень маленьких до очень больших. Есть много примеров использования:

• Астрономия — величины звезд
• В химии шкала pH представляет собой логарифмическую шкалу, охватывающую 15 порядков магнитуды и измеряющую концентрацию ионов H в растворе. рН 0 составляет 10 000 000, деионизированная вода имеет рН 7, 1, а рН 14 составляет 1/10 000 000
• Акустика — интенсивность звука измеряется в децибелах (дБ). дБ= 10 log ₁₀ ( I/I ₀ ), где I — интенсивность звука, измеренная в Вт·м ^-2 , I _{0 1 -4} определяется как Вт м ^-2 .
• Сейсмология — по шкале Рихтера. Землетрясение силой 5 баллов в десять раз мощнее землетрясения силой 4 балла, которое в десять раз мощнее землетрясения силой 3 балла и так далее.
• Инженеры часто используют логарифмическую шкалу (дБм) для измерения выходной мощности фотонных устройств.
• Палермская шкала опасности технического воздействия — логарифмическая шкала, которая измеряет вероятность столкновения Земли с метеоритом такого размера. значение по шкале Палермо, равное -2, указывает на то, что обнаруженное событие потенциального воздействия всего на 1% более вероятно, чем случайное фоновое событие, происходящее в промежуточные годы, значение, равное нулю, указывает на то, что отдельное событие столь же опасно, как и фоновая опасность, и значение +2 указывает на событие, которое в 100 раз более вероятно, чем фоновое воздействие объекта, по крайней мере, такого же размера до даты рассматриваемого потенциального воздействия. ^[1]
• Жертвы войны ^[2] Логарифмическая шкала для измерения общего числа погибших в различных конфликтах. Одна смерть соответствует магнитуде 0. Террористическая кампания, в результате которой погибло 100 человек, соответствует магнитуде 2. Вторая мировая война унесла в общей сложности 62 000 000 жертв, что соответствует магнитуде 7,79. Соотношение числа погибших легко сравнить, например, во Вьетнамском конфликте США потеряли около 50 000 солдат, (магнитуда 4.69), в гражданской войне за независимость потери США составили 6824 человека (величина 3,83). Соотношение потерь, следовательно, 4,69-3,83 = 0,864, что составляет 10 ^0,864 ≅ 7,3 раза.

Лотерея жизни

Даже обсуждалось, что нам следует принять логарифмическую шкалу риска. Недостатком этого, однако, является то, что относительно немногие люди понимают логарифмы достаточно хорошо, чтобы не запутаться. Однако было предложено ^[3] , что люди уже понимают «риск» выигрыша различных призов в Национальной лотерее. Вероятность каждого большего приза увеличивается примерно логарифмически. Вероятность события сопоставляется с соответствующей вероятностью вытягивания такого количества шаров при ставке в 5 фунтов стерлингов. Это может быть особенно полезно для практикующих врачей, которым приходится сообщать о широком спектре рисков широкой публике. Логарифмический риск определяется выражением

.

10 — log ₁₀ (1/ P ( x )), где P ( x ) — вероятность возникновения события.В таблице 1 приведены шкалы вероятности выигрыша в лотерею, вероятность, вербальная шкала риска и логарифмическая шкала риска.

Используя эту шкалу, высоковероятное событие сравнимо с вытягиванием 3 одинаковых шаров или 9 по логарифмической шкале. Средневероятное событие сравнивается с шансом вытянуть 4 совпадающих шара или 8 по логарифмической шкале и так далее. Крайне маловероятное событие по сравнению с вытягиванием 6 шаров, которое сопряжено с «риском» 1 из 2 796 763. (помните, ставка 5 фунтов) или меньше 4 по логарифмической шкале. За один год, если вы участвуете в 2 розыгрышах в неделю, это 104 розыгрыша в год.Таким образом, шанс выиграть в течение одного года при ставке в 5 фунтов стерлингов равен 104/2796763 = 1 из 26892, или 5,57 по логарифмической шкале.

9 80

№ шаров	вероятность	словесных масштабов	в журнале
3	1 в 11	высокий	9
4	1: 206	Умеренный	8
4 + B	1 в 8878		7
5	1 в 11 098	очень низко	6
5 + B	1 в 466,127	минимальные	4-5
6	1 в 2 71240	1 в 2 71240	незначительный	<4
B = бонусный шар

Таблица 1.Риск выигрыша в национальной лотерее Великобритании.

Еще одно маловероятное событие — убийство. Трудно определить риск. Это зависит от многих факторов, таких как ваш возраст, социальный класс и т. д. В Великобритании в качестве риска быть убитым в год предлагается цифра 51 на 1 000 000, что соответствует вероятности 1 на 19 600. . (логарифмическая шкала 5,7)

Люди отдают предпочтение хорошим событиям, а не плохим (или плохим событиям, а не хорошим, если вы работаете в СМИ), что искажает их представления о риске.Я встречаю людей, которые играют в Национальную лотерею и верят, что у них есть хорошие шансы выиграть джекпот, но они не выходят, думая: «Ха-ха. Это может быть мой счастливый день! о том, что меня убили, поэтому я сомневаюсь в полезности этой логарифмической шкалы.

Каталожные номера

[1] «Количественная оценка риска потенциального воздействия на Землю» Чесли и др. (Икар 159, 423-432 (2002)).

[2] Брайан Хейс, «Статистика смертельных ссор», Am. Sci.90, 10–13 (янв.–Фев. 2002).

[3] Д.М. Кэмпбелл, «Язык риска и диалекты Важно выражать риск в относительном, а не в абсолютном выражении», BMJ. 1998 18 апреля; 316(7139): 1242.

Быстрое вычисление логарифмов без калькулятора

Логарифмы — одна из самых сложных математических тем на MCAT, потому что многие из нас не изучали их со школы и, вероятно, так и не научились считать логарифмы без калькулятора.

Это хорошая/плохая новость.Плохая новость заключается в том, что проблемы pH и интенсивности звука из общей химии и физики потребуют от вас работы с логарифмами без калькулятора. Хорошая новость заключается в том, что есть трюк, который упрощает вычисление логарифмов и поразит ваших друзей своими математическими способностями в уме.

Сначала краткий обзор того, что такое логарифмы и почему они важны для MCAT: десятичный логарифм или оператор «логарифм» (иногда называемый «логарифм ₁₀ ») наиболее полезен при описании чего-то, что измеряется на очень большом шкала.

Владение логарифмами было необходимо ученым и инженерам в 19-м и начале 20-го веков, потому что их можно было использовать для упрощения всех видов сложных вычислений. Современные компьютеры сделали эти навыки устаревшими, но десятичные логарифмы все еще используются в таких задачах, как расчеты pH, где основная шкала изменяется в соответствии со степенью 10.

В химии кислотность можно измерить по линейной шкале от [H+] = 0,00000000000001M до [H+] = 1M. Однако разница в 1 млн [H+] на самом деле не имеет значения.Мы видим реальные различия в кислотности между веществами, когда [Н+] одного в 100 или 1000 (и более!) раз больше, чем [Н+] другого.

Расчет pH позволяет нам измерять кислотность по логарифмической шкале от pH=14 до pH=0. Точно так же, как более разумно измерять расстояние между Токио и Лондоном в милях, а не в дюймах, более полезно описывать кислотность, используя pH, а не [H+].

Как именно это работает? Логарифмическая функция используется для решения уравнений, где переменная представляет собой показатель степени с основанием 10.Например, 10 ^X = 100. Логарифмический оператор позволяет найти X и записать эквивалентное выражение в виде log(100) = X. 10 ^X = 100 — экспоненциальная форма выражения, а log(100 ) = X — логарифмическая форма.

Легче всего определить логарифм степени 10, потому что решение равно степени степени. Продолжая приведенный выше пример, мы можем решить уравнение, переписав log(100) как log(10 ² ) = 2,

.

Конечно, на MCAT вам потребуется аппроксимировать журнал значений, которые не являются простыми степенями 10.Обратите внимание, что ключевое слово здесь приблизительно равно . Один из самых важных принципов овладения математикой MCAT — помнить, что вам не нужно вычислять точный ответ на каждую задачу, вам просто нужно подобраться достаточно близко к и выбрать правильный ответ из списка возможных вариантов.

Вспомним, что pH – это отрицательный логарифм [H+]. Мы можем аппроксимировать отрицательный логарифм количества, используя формулу

– log(m x 10 ^-n ) ≈ n – 0.м


, где m — число от 1 до 10, а n — целое число (целое число).

Несколько быстрых примеров с использованием аппроксимации:


-log (3 x 10 ^-5

0) ≈ 5 — 0,3 = 4.7
-Log (7.1 x 10 ^-9 ) ≈ 9 — 0.71 = 8.29
-Log (2,5 x 10 ² ) ≈ 2 – 0,25 = 1,75


Вот и все!


Давайте закончим парой проблем с pH:


В: Каков рН 4.2 x 10 ^-3 M HNO ₃ раствор?


а) 1.61
б) 2.38
в) 3.42
г) 4.20


A: Поскольку HNO ₃ является сильной кислотой, [H+] = 4,2 x 10 ^-3 M. pH раствора равен отрицательному логарифму концентрации. В этом случае pH = –log(4,2 x 10 ^-3 ). Используя приближение, мы можем решить –log(4,2 x 10 ^-3 ) ≈ 3 – 0,42 ≈ 2,5, что близко к ответу b).


Q: K _a кислоты, чей буфер имеет pH 3,62 в растворе, содержащем равные M кислоты и сопряженного основания, ближе всего к:


a) 1,02 x 10 ^-7
b) 3,62 x 10 ^-5
c) 2,40 x 10 ^-4
d) 7,23 x 10 ^-2

4
4

В этой задаче важно отметить, что когда кислота находится в растворе, содержащем равные количества кислоты и сопряженного основания, рН равен pK _a .

Следовательно, мы имеем pH = 3,62 = pK _a . Однако мы пытаемся найти K _a , а не pK _a (напомним также, что pK _a = –log(K _a ) ), и нам нужно будет использовать приближение, которое мы изучили ранее. но наоборот.


pH = n – 0,m ≈ –log(m x 10 ^-n )


Мы можем переписать значение pH 3,62 как 4 – 0,38, представив его в виде n – 0,m, показанном выше. Это дает нам

рН = 4 – 0.38 ≈ –log(m x 10 ^-n )


Теперь мы можем заменить m и n, чтобы аппроксимировать K _на в правой части.


pH = 4 – 0,38 ≈ –log(3,8 x 10 ^-4 )


Таким образом, приблизительное значение K _a равно 3,8 x 10 ^-4 M, что ближе всего к ответу c).

Мы надеемся, что эти инструкции по вычислению логарифмов без калькулятора помогут вам победить MCAT! Обязательно ознакомьтесь с остальными сериями советов и рекомендаций MCAT:


.