Ломаная геометрия: Ломаная — это… Что такое Ломаная? – Начальные геометрические понятия. Ломаная — урок. Математика, 5 класс. — Детская игровая комната «Волшебный лес»

Posted on 27.06.202021.03.2020 by alexxlab

Содержание

Многоугольники — урок. Геометрия, 8 класс.

Ломаной называется фигура, которая состоит из точек и соединяющих их отрезков.

Точки называются вершинами ломаной, а отрезки — звеньями ломаной.

Виды ломаных

Ломаная называется замкнутой, если у неё концы совпадают.

Если концы ломаной не совпадают, то она называется незамкнутой.

Ломаная называется простой, если она не имеет самопересечений. Обе ломаные выше являются простыми.

На следующем рисунке — ломаная с самопересечением.

Многоугольник

Многоугольник — это простая замкнутая ломаная линия и конечная часть

плоскости, которую она ограничивает.

Вершины ломаной линии называются вершинами многоугольника, а её звенья — сторонами многоугольника.

Отрезок, соединяющий две вершины, не лежащие на одной стороне, называется диагональю многоугольника.

\(A\), \(B\), \(C\), \(D\), \(E\) — вершины;
\(AB\), \(BC\), \(CD\), \(DE\), \(AE\) — стороны;
\(AC\), \(AD\), \(BE\), \(BD\), \(CE\) — диагонали.

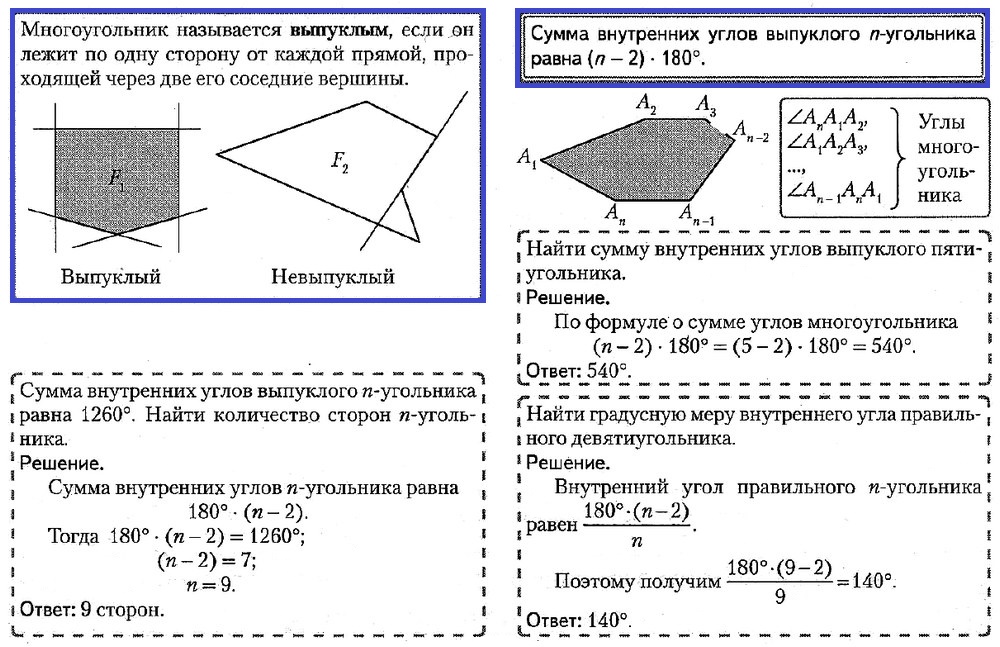
Многоугольник, у которого все углы меньше 180°, называется выпуклым многоугольником.

Пятиугольник \(ABCDE\) является выпуклым многоугольником.

Сумма углов выпуклого \(n\)-угольника

В общем случае многоугольник можно назвать \(n\)-угольником, это означает, что у данного многоугольника \(n\) сторон и \(n\) вершин.

Сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.

Любой выпуклый многоугольник можно разделить на треугольники. Количество треугольников на \(2\) меньше, чем количество сторон в многоугольнике.

Сумма внутренних углов любого треугольника равна 180°.

Поэтому сумма углов выпуклого \(n\)-угольника равна 180°⋅n−2.

Пример:

вычисли сумму внутренних углов выпуклого одиннадцатиугольника.

Можно нарисовать рисунок, но это не обязательно для решения задачи.
Используем формулу:
180°⋅n−2=180°⋅11−2=180°⋅9=1620°.

Конспект «Ломаная. Многоугольник + ЗАДАЧИ»

«Ломаная. Многоугольник
+ ключевые ЗАДАЧИ»

ОПРЕДЕЛЕНИЯ

Ломаная А₁А₂А₃…А_n — фигура, состоящая из точек А₁, А₂, А₃, …, А_n и отрезков А₁А₂, А₂А₃, …, А_n-1А_n, которые их соединяют. Точки А₁, А₂, А₃, …, А_n называют

вершинами ломаной, а отрезки А₁А₂, А₂А₃, …, А_n-1А_n — звеньями ломаной.

Простая лoманая — лoманая, не имеющая точек самопересечения.
Замкнутая лoманая — лoманая, концы которой соединяются.
Длина ломаной — сумма длин ее звеньев.

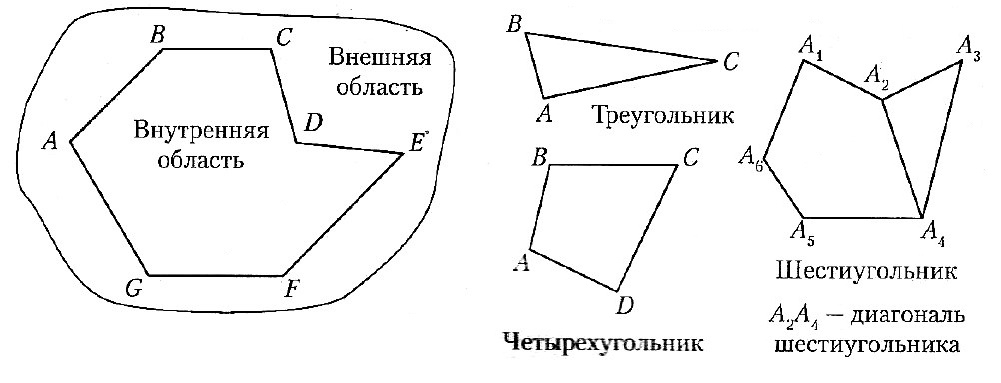
Многоугольник — простая замкнутая ломаная, соседние звенья которой не лежат на одной прямой; вершины ломаной называют вершинами многоугольника, а звенья ломаной — сторонами многоугольника. Многоугольник с n вершинами (n сторонами) называют n-угольником.

Диагональ многоугольника — отрезки, соединяющие несоседние вершины многоугольника.

Выпуклый многoугольник — многоугoльник, лежащий в одной полуплоскости относительно любой прямой, содержащей его сторону.
Угол выпуклого многоугольника при данной вершине — угол, образованный его сторонами, сходящимися в этой вершине.
Внешний угол выпуклого многоугольника при данной вершине — угол, смежный с внутренним углом многоугольника при этой вершине.

ПРИМЕРЫ РЕШЕНИЯ КЛЮЧЕВЫХ ЗАДАЧ

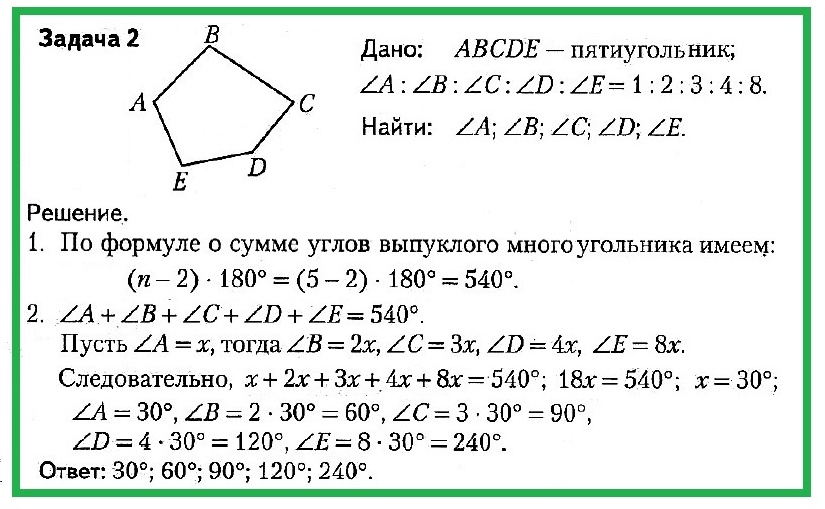
Задача № 1. Дано: ABCD — четырехугольник; ∠A = ∠B = ∠C; ∠D = 135.
Найти: ∠A, ∠B, ∠C.

Задача № 2. Дано: ABCDE — четырехугольник; ∠A : ∠B : ∠C : ∠D : ∠E = 1 : 2 : 3 : 4 : 8. Найти: ∠A, ∠B, ∠C, ∠D, ∠E.

Это конспект по теме «Ломаная. Многоугольник + ЗАДАЧИ». Выберите дальнейшие действия:

15. Ломаные | учебник для 7 класса «ГЕОМЕТРИЯ»

15. Ломаные

Фигура, образованная конечным набором отрезков, расположенных так, что конец первого является началом второго, конец второго — началом третьего и т. д., называется ломаной линией, или просто ломаной (рис. 15.1). Отрезки называются сторонами ломаной, а их концы — вершинами ломаной.

Длиной ломаной называется сумма длин её сторон.

Ломаная обозначается последовательным указанием её вершин. Например, ломаная ABCDE, ломаная А1А2. •• А

п.

Ломаная называется простой, если она не имеет точек самопересечения (рис. 15.2).

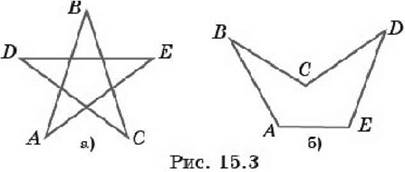
Ломаная называется замкнутой, если начало первого отрезка ломаной совпадает с концом последнего (рис. 15.3). Замкнутую ломаную, у которой точками самопересечения являются только начальная и конечная точки, также называют простой (рис. 15.3, б).

Вопросы

1. Что называется ломаной? Что называется: а) сторонами;

6) вершинами ломаной?

2. Как обозначается ломаная?

3. Что называется длиной ломаной?

4. Какая ломаная называется: а) простой; б) замкнутой?

Задачи

1. Простая ломаная имеет 10 вершин. Сколько у неё сторон?

2. Простая замкнутая ломаная имеет 20 сторон. Сколько у неё вершин?

3. Укажите, какие фигуры, изображённые на рисунке 15.4, являются простыми ломаными?

5. Сравните длины ломаных A\B\C\D\ и А2В2С2Р2 на рисунке 15.6, не измеряя их.

6. Изобразите замкнутую пятистороннюю ломаную, которая имеет: а) две точки самопересечения; б) три точки самопересечения;

в) пять точек самопересечения.

7. Сколько ломаных: а) длины 4; б) длины 5, проходящих по сторонам сетки, состоящей из единичных квадратов, соединяет точки А и В (рис. 15.7)?

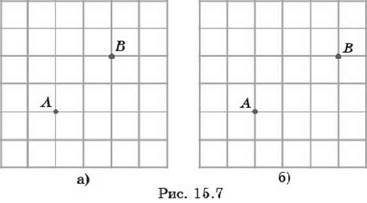
8. Сколько ломаных длины 6, проходящих по сторонам сетки, состоящей из единичных квадратов, соединяют точки А, В и С (рис. 15.8)?

9*. Изобразите: а) четырёхстороннюю ломаную; б) шестистороннюю ломаную, проходящую через все данные точки на рисунке 15.9.

План-конспект урока на тему: Ломаная линия. Длина ломаной линии.

Урок математики.

4 класс.

Тип урока: комбинированный

Цели урока:

-закрепление понятия «ломаная линия» и её компонентов;

-знакомство с алгоритмом нахождения длины ломаной.

Задачи:

Обучающие:

формировать у учащихся умение планировать деятельность, осуществлять контроль и самоконтроль;
совершенствовать вычислительные и измерительные навыки

Коррекционно-развивающие:

развивать логическое мышление, пространственное воображение, внимание, память;
корригировать уровень развития математической речи;
развивать икт компетенции.

Воспитательные:

активизировать познавательную активность,

повышать интерес к предмету.

Формировать УУД:

Познавательные:

– различать ломаные линии и их компоненты,

– ориентироваться в геометрических объектах (треугольник, прямоугольник, квадрат, многоугольник),

– осуществлять сравнение ломаных линий

Личностные:

-понимать значение границ собственного знания и «незнания»;

-осознавать причины своего успеха (неуспеха), связывая успехи с усилиями, трудолюбием.

Регулятивные:

-планировать своё действие в соответствии с поставленной задачей и условиями её реализации.

Коммуникативные:

-слушать и понимать речевые инструкции учителя;

-оформлять свои мысли в устной форме;

-договариваться с одноклассниками совместно с учителем о правилах поведения на уроке следовать им.

Оборудование:

— Математика. 4 класс: учебник для cпециальных (коррекционных) образовательных учреждений VIII вида/М.Н.Перова. — М.: «Просвещение». 2014

-раздаточный материал

-интерактивная доска

-компьютер

Структура урока

Деятельность учителя	Деятельность учащихся		ИКТ
1.Организационный момент
Вот звонок нам дал сигнал, Поработать час настал. Так что время не теряем И урок наш начинаем. -Улыбнитесь друг другу и садитесь. Руки? Ноги? Локти? Спина? Начинаем урок.		— На месте! — На месте! — У края! — Прямая!
2. Проверка домашнего задания
-Кто напомнит тему прошлого урока. -Ребята, а что такое ломаная линия? -Какое домашнее задание вы должны были выполнить к сегодняшнему уроку? -Проверяем, как вы справились с заданием. Внимание на экран: — Какие виды ломаных линий вы знаете? -В чём отличие замкнутой ломаной линии от незамкнутой? -Что мы знаем о замкнутой ломаной линии? -Показать на рисунке многоугольники. -Назвать части ломаной линии. -Обозначить буквами вершины любой ломаной линии. -Назвать вершины. -Посчитать звенья и назвать их.		Ломаная линия. Ломаная линия – это линия, которая состоит из отрезков, не лежащих на одной прямой. Нам было задано составить рисунок из ломаных линий на интерактивной доске. Замкнутые и незамкнутые ломаные линии. Концы замкнутой ломаной линии соединены (замкнуты), концы незамкнутой ломаной линии разъединены (разомкнуты). Замкнутая ломаная линия является границей многоугольника. Квадрат, прямоугольник, треугольник и многоугольник Отрезки или звенья, вершины.	Работа с интерактивной доской. 1 слайд «Ломаная линия» 2 слайд Составление рисунка. Показать их на рисунке.
2.2 Физкультминутка. А теперь, ребята, встали. Руки быстро вверх подняли. В стороны, вперёд, назад. Повернули вправо, влево, В стороны, вперёд, назад. Тихо сели, вновь за дело. Руки? Ноги? Локти? Спина?		— На месте! — На месте! — У края! — Прямая!	3 слайд Музыкальная физкультминутка.
3.Сообщене новой темы. Устный счёт.
Сегодня на уроке мы будем учиться определять длину ломаной линии.			4 слайд тема урока «Длина ломаной линии»
4.Устный счёт.
4.1Для вычисления длины ломаной нам понадобится верный помощник. А какой, вы узнаете, когда выполните задание. Внимание на экран: -В этом слове столько букв, сколько нечётных чисел в числовом ряду от 0 до 14. -Каждая буква имеет свой порядковый номер в алфавите. Например, под номером 13 зашифрована буква 13-я буква в алфавите. -Наш верный помощник? Проверьте, у всех на парте присутствует линейка.		7 букв Открывают буквы. Линейка.	5 слайд Числовой ряд 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
4.2 Физкультминутка для глаз			6 слайд Звёздное небо
5. Первичное закрепление и коррекция новых знаний.
5.1 Работа с раздаточным материалом. -Ребята, ваши глаза отдохнули? — А как вы думаете, какой геометрической фигурой является звезда? -А какая линия является границей многоугольника? -Исходя из этого, какой вывод можно сделать? -Сейчас я вам раздам вот такие красивые звёзды и красную блестящую нить. Вы расположите нить по контуру звезды. -Нить превратилась в границу многоугольника, приняв форму звезды, и является чем? -Затем вы расправите нить и прикладываете её к линейке. Таким образом, мы что узнаем? —Отложили в сторону раздаточный материал. Что остаётся? -Т.о., можно сделать вывод, что длину ломаной линии можно измерить с помощью чего? 5.2 Работа с учебником -Открываем тетради, записываем число, классная работа. -Открываем учебник на странице 108 , выполняем задание № 3 -Читаем задание. -Работаем только с линией 1 и линией 2. -Составляем алгоритм выполнения данного задания. -С чего начнём? -С помощью чего мы будем измерять длину ломаной? -Мы сможем измерить сразу всю ломаную при помощи линейки? -А как мы будем измерять длину ломаной? -Далее сложим длину всех звеньев ломаной и получим длину ломаной. -Чтобы сравнить длину ломаных, мы начертим отрезки. Алгоритм выполнения задания понятен -Из скольки звеньев состоит ломаная 1? -Какова длина первого звена? -Какова длина второго звена? -Какова длина всей ломаной? -Как узнали? Чертим отрезок, равный длине этой ломаной. Отрезки чертим друг под другом, отступ вниз 2 клетки, длину отрезка подписываем. -Из скольки звеньев состоит ломаная 2? -Какова длина первого звена? — Какова длина второго звена? -Какова длина третьего звена? -Какова длина всей ломаной? Чертим отрезок, равный длине этой ломаной. Сравните длины ломаных линий с помощью отрезков. Какой отрезок длиннее? Следовательно, какая ломаная линия длиннее?	Да Многоугольник Замкнутая ломаная линия Граница звезды – это замкнутая ломаная линия. Работа с раздаточным материалом. Замкнутой ломаной линией. Длину нити и длину замкнутой ломаной линии. Линейка. С помощью линейки. Работа с учебником. Найдём длину первой ломаной линии. Линейки. Нет По звеньям. из 2-х звеньев 2 см 2 см 4 см Сложили длину всех звеньев. из 3-х звеньев 1 см 2см 3 см 6см Номер 2 Номер 2		7 слайд Звезда 8 слайд Алгоритм выполнения задания.
5.3Физкультминутка. А теперь, выйдите все из-за парт, и при помощи рук попытайтесь смоделировать геометрические фигуры, которые появится на экране.			9 слайд Моделирование геометрических фигур.
6. Закрепление знаний в новых ситуациях. Формирование умений.
Задача Ёжику надо добраться до своего домика. Дорожка к домику состоит из двух тропинок. Длина первой тропинки 7 см, длина второй тропинки в 4 раза больше первой. Какова длина всей дорожки?	Решение у доски. Задача Условие Решение		10, 11.12 слайды Задача
7. Повторение пройденного материала (базисных, ведущих знаний).
Наш урок подошёл к концу. -Что нового вы узнали сегодня на уроке? -Как находят длину ломаной линии?	Научились находить длину ломаной линии. Сначала с помощью линейки находят длину каждого звена ломаной, а затем складывают длину всех звеньев ломаной.
8.Задание на дом.
-Открываем дневники, записываем домашнее задание. с.108 № 3 -Работаем с ломаными 3 и 4. Работа аналогичная классной работе, алгоритм выполнения задания тот же. -Вычисляете длину ломаных -Чертите отрезки -Сравниваете длину ломаных			11. Домашнее задание.
9. Подведение итогов урока.
-Оценки за урок -А сейчас по традиции, Кому было интересно на уроке, рисует в тетради солнышко, кому скучно – рисуют тучку. Урок окончен. Спасибо всем за работу.			12. Спасибо за работу.

Характеристика учащихся по возможностям обучения

По возможностям обучения учащихся класса на уроках математики можно разделить на три группы.

I группу составляют ученики, наиболее успешно овладевающие программным материалом. (Колпаков Миша, Зюзин Дима, Шугаров Гена) Они понимают объяснение учителя, запоминают изучаемый материл, но самостоятельно сделать элементарные выводы и обобщения не могут. Их отличает низкий уровень самостоятельности в выполнении всех видов работ, они нуждаются в помощи учителя, как активизирующей, так и организующей. Перенос знаний в новые условия не затруднён. Но при этом снижается темп работы, допускаются ошибки. Они владеют вычислительными и измерительными навыками, навыками табличного умножения и деления. У них наиболее развита математическая речь.

Ко II группе относятся ученики, которые с трудом усваивают программный материал, нуждаясь в разнообразных видах помощи (словесно-логической, наглядной и предметно-практической). (Мельникова Екатерина, Пигалов Денис, Дубинин Денис) У них нарушено звукопроизношение. Они посещают занятия с педагогом –логопедом. Отсутствует связная речь. Им трудно сформулировать ответ на вопрос. Они лучше справляются с письменными заданиями. Учащиеся с большим трудом запоминают математические правила потому, что не понимают их, за словами, которые они пытаются заучить, нет реальных представлений. Нуждаются в помощи учителя на всех этапах урока.

III группа (Столярова Вера) – низкий уровень мотивации к обучению в целом. Крайне замедленный темп работы. Она нуждаются в ведении дополнительных приемов обучения, постоянном контроле и подсказках во время выполнения работ. Сделать выводы с некоторой долей самостоятельности, использовать прошлый опыт ей недоступно. Требуется четкое неоднократное объяснение учителя при выполнении любого задания. Знания усваиваются чисто механически, быстро забываются.

Урок геометрии в 6-м классе по теме: «Ломаная. Ломаная на кубе»

Геометрия обладает особой выразительностью: можно, посмотрев на иллюстрации, уловить математический смысл текста.

Предмет геометрии составляют идеальные образы – геометрические фигуры. В архитектуре же эти идеальные образы получают материальное воплощение, а вместе с ним и новое звучание.

С точки зрения математики в архитектурных сооружениях всех времён царит единство числа и фигуры. Но истинный зодчий так соединяет геометрию “математическую” и геометрию “архитектурную”, что никогда не удаётся до конца раскрыть тайны очарования его творений.

Знаменитый зодчий ХХ века, француз Ле Корбюзье писал: “Архитектура – это способность нашего сознания закреплять в материальных формах чувство эпохи”.

Что означают эти слова?

Какова она – эта красота?

И каково оно – “чувство эпохи”?

Как они связаны с геометрией?

И дворцы Востока, и древнерусские храмы, и готические соборы – это часть каменной летописи мира. Но для нас это не просто страницы истории – это ещё и зримая геометрия Добра, Красоты, Совершенства. И геометрия несёт свою долю ответственности за наше совершенство, на каком бы уровне строгости мы её не изучали.

Мы с вами продолжаем идти маленькими шагами к Храму, который зовётся Геометрией.

ХОД УРОКА.

Рисунок 1.

Сравните первую и вторую геометрические фигуры. Что общего между ними вы заметили?

Рисунок 2.

Отметьте все фигуры, которые устроены так же, как фигуры на первом рисунке.

Разбейте их на группы.

Почему вы так распределили эти фигуры?

Как бы вы их назвали?

Итак, такие геометрические фигуры называются ломаными линиями или просто – ломаными.

Какие ломаные вошли в первую группу? А во вторую? А теперь изобразите отдельно все оставшиеся ломаные. Почему они не вошли в группы?

Все ломаные состоят из отрезков, которые называются звеньями ломаной.

Рисунок 3.

Это простые незамкнутые ломаные.

Рисунок 4.

Это простые замкнутые ломаные.

Рисунок 5.

Эти ломаные не являются простыми.

Крайние точки называются концами ломаной или началом и концом ломаной.

Посмотрим ещё раз внимательно на геометрические фигуры, изображённые на рис.4.

Можете ли вы выделить уже знакомые геометрические фигуры?

Ученик: Ромб, квадрат, шестиугольник, параллелограмм.

Учитель: “Посмотрите на них с точки зрения ломаной”.

Ученик: “Это простые замкнутые ломаные”

Учитель: “Как ещё можно назвать эти фигуры?”

Ученик: “Многоугольники”.

Учитель: “О каком понятии шла речь на уроке?”

Ученик: “О ломаной”.

Учитель: “Сформулируем тему сегодняшнего урока и его цель”.

На доске записывается тема урока, ребята пишут в тетрадях.

А сейчас наступает момент, когда наша работа с фигурами может стать особенно красивой. И красота эта возникнет благодаря неожиданным, оригинальным соединениям различных ломаных на чертеже.

Рисунок 6.

Присмотритесь внимательно к работам мастеров. Поучимся у них умению соединять геометрические фигуры так, чтобы получилась бы настоящая картина из фигур.

Чтобы легче было понять схемы, посмотрим на каждый шаг построения.

Рисунок 7.

Разобравшись в схеме, выполните построение у себя в тетрадях.

А теперь посмотрим на ломаную с другой стороны.

Изобразим куб у себя в тетрадях. (На доске – изображение куба.)

Рисунок 8.

Можно ли из точки А попасть в точку А₁, двигаясь по рёбрам куба и побывав при этом во всех вершинах куба ровно один раз? Покажите путь и назовите получившуюся ломаную.

Ответ: АDD₁C₁BB₁A₁

А теперь решим такую задачу.

Задача 1.

Мы имеем стеклянный куб. На его поверхности расположена ломаная с вершинами, совпадающими с некоторыми вершинами куба.

Изобразите, как выглядит данная ломаная спереди, сверху и слева.

Рисунок 9.

Как проходят звенья ломаной?

Ученик: “Звенья ломаной проходят по рёбрам куба”.

Задача 2.

В этой задаче звенья ломаной идут не только по рёбрам куба, но и по диагонали грани куба, а вершины, как и прежде, находятся в некоторых вершинах куба.

Изобразите вид спереди, вид сверху и вид слева этой ломаной.

Рисунок 10.

При работе с конструкциями из кубиков определять виды конструкции было легче, так как соседние кубики имели общую грань. Здесь задача посложнее. Чтобы представить себе виды ломаной, приходится мысленно отпечатывать ломаную на одну, другую, третью грани куба.

Итак, в центре всех наших размышлений, разговоров и действий всегда находится геометрическая фигура, какой бы она не была: плоской или пространственной.

Итог урока.