Лучи прямые отрезки: 1. Начальные геометрические понятия. Точки, прямые, лучи и отрезки — Детская игровая комната «Волшебный лес»

Posted on 24.04.197615.02.2022 by alexxlab

Содержание

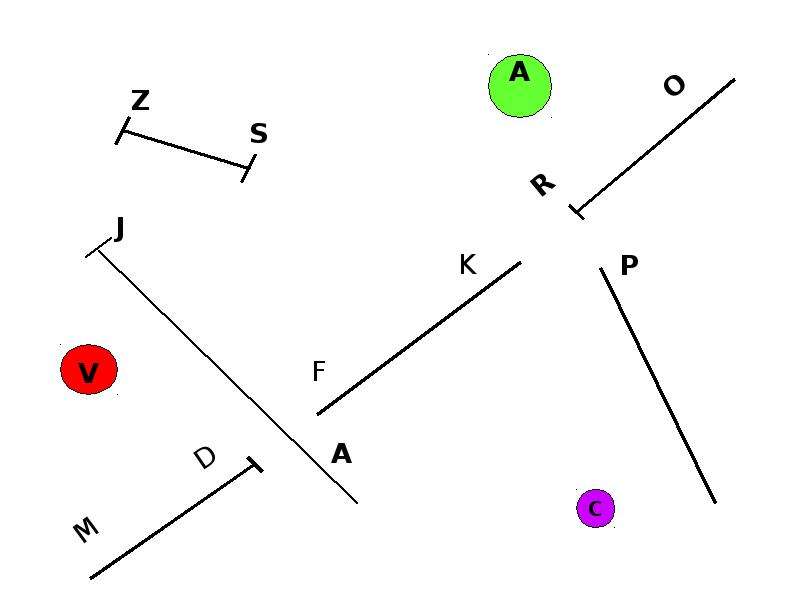
Что такое лучи отрезки прямые. лучи AB и AC совпадают

Посещая дополнительные занятия мы поняли, что не умеем оперировать понятиями точка, линия, угол, луч, отрезок, прямая, кривая, замкнутая линии и рисовать их, точнее рисовать можем, но идентифицировать не получается.

Дети должны различать линии, кривые, окружности. Это развивает у них графику и чувство правильности при занятиях рисованием, аппликацией. Важно знать, какие основные геометрические фигуры существую, что из себя представляют. Разложите карточки перед ребенком, попросите нарисовать точно так же как на картинке. Повторите несколько раз.

На занятиях нам выдали следующие материалы:

Небольшая сказка.

В стране Геометрии жила-была точка. Она была маленькой. Ее оставил карандаш, когда наступил на лист тетради, и никто ее не замечал. Так и жила она, пока не попала в гости к линиям. (На доске рисунок.)

Посмотрите, какие это были линии. (Прямые и кривые.)

Прямые линии похожи на натянутые веревочки, а веревочки, которые не натянули, — это кривые линии.

Сколько прямых линий? (2.)

Сколько кривых? (3.)

Прямая линия начала хвастаться: «Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»

Очень интересно стало точке посмотреть на нее. Сама-то точка малюсенькая. Вышла она да так увлеклась, что не заметила, как наступила на прямую линию. И вдруг исчезла прямая линия. На ее месте появился луч.

Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.

Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.

И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.

Вот так маленькая точка смогла изменить жизнь больших линий.

Так кто догадался кто вместе с котиком пришел к нам в гости?(прямая линия, луч, отрезок и точка)

Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.

Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)

О каких линиях вы узнали? (О прямой, луче, отрезке.)

Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)

(Берем две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)

Что узнали о луче? (У него есть начало, но нет конца.) (Педагог берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)

Что узнали об отрезке? (Унего есть и начало, и конец.) (Педагог отрезает другой конец нитки и показывает, что нитка не тянется. У нее есть и начало, и конец.)

Как начертить прямую линию? (Провести по линейке линию.)

Как начертить отрезок? (Поставить две точки и соединить их.)

И конечно прописи:

Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.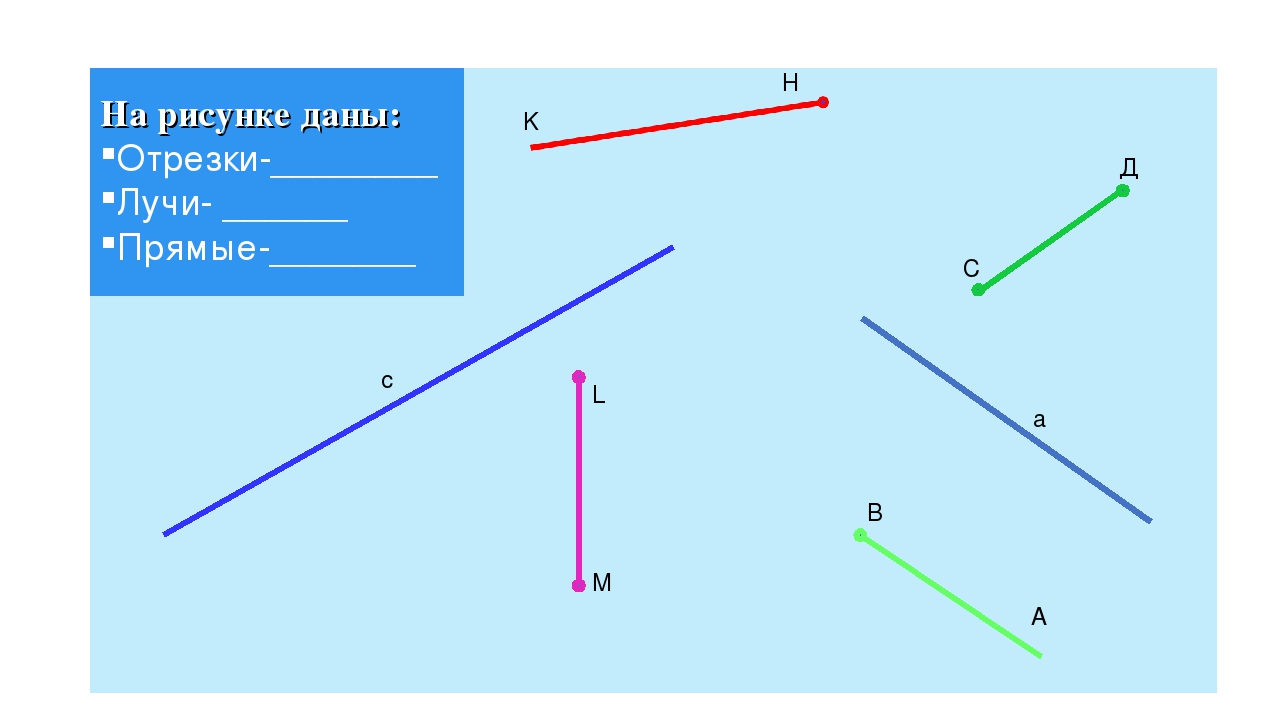

Точка в математике

Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.

На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.

Отрезок в математике

Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.

На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.

Прямая в математике

Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.

На рисунке изображены две прямые: CD и EF.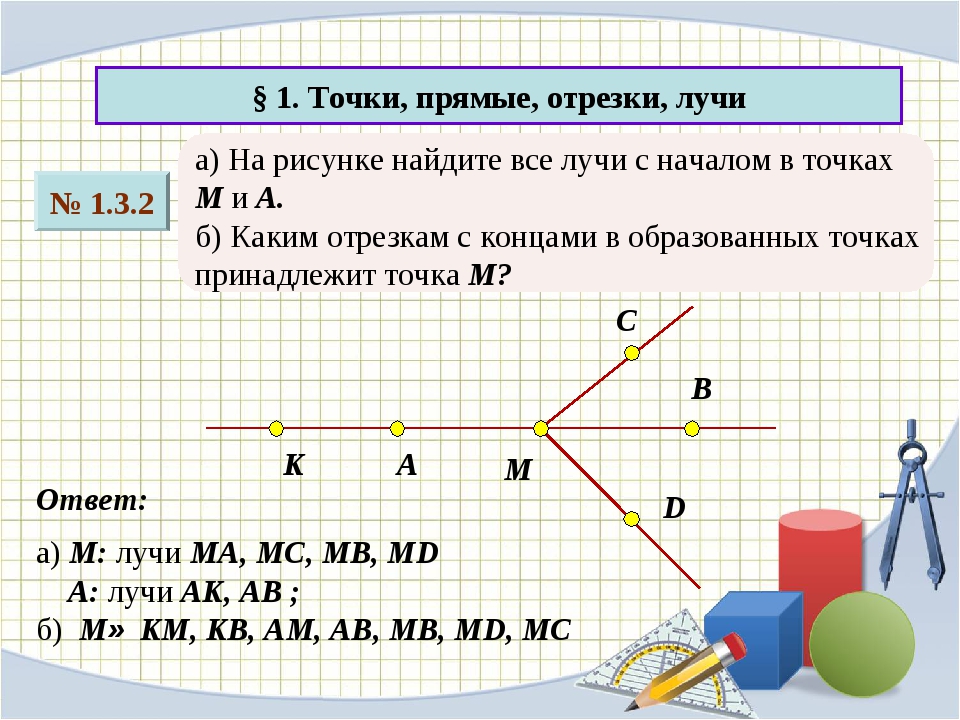

Луч в математике

Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.

На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.

Числовая прямая в математике

Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.

На рисунке изображена числовая прямая, а также луч OD и ED

Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».

Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.

К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия. Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.

Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.

На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы.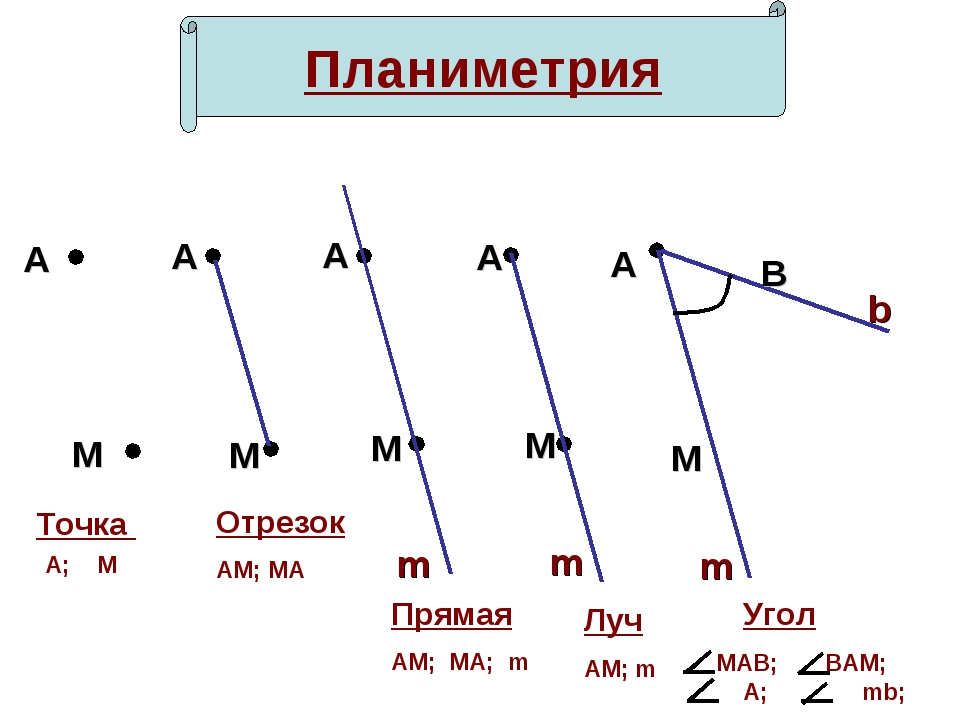 Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.

В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена. Символически записываем отрезок \(AB\).

Что такое точка в математике?

Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.

Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.

При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.

4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.

Конспект урока по математике

в 1 классе.

Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч.

Составила и провела

Бувайлова Елена Ивановна

Тема: Точка. Кривая линия. Прямая линия. Отрезок. Луч

Цель: в ходе выполнения практических заданий и наблюдений научить различать разные виды линий.

Планируемые результаты: учащиеся научатся различать и называть прямую линию, кривую, отрезок, луч, ломаную; пользоваться линейкой для черчения; соотносить реальные предметы и их элементы с изученными геометрическими линиями и фигурами; выполнять мыслительные операции анализа и синтеза и делать умозаключения; применять полученные ранее знания в измененных условиях; слушать собеседника и вести диалог; слушать учителя и выполнять его требования; оценивать себя, границы своего знания и незнания; работать в паре и оценивать товарища.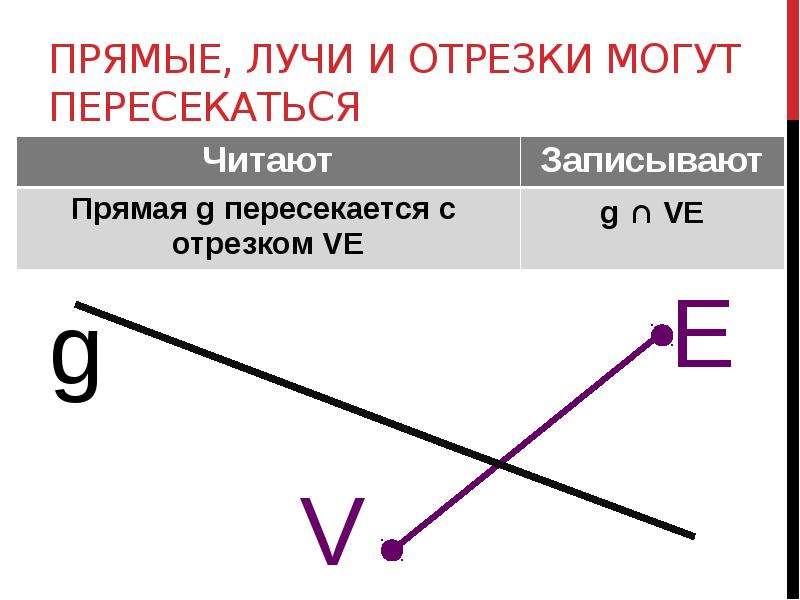

Ход урока

1.Организационный момент

Математика зовёт

Первоклашек на урок,

Числа нас ведут вперёд

Будем знать всё «на зубок»

2.Актуализация знаний

К нам сегодня на урок пришел в гости кот Тишка с незнакомыми друзьями, а какие это друзья вы назовете их чуть позже

а) Прямой и обратный счёт в пределах 10.

Индивидуальный опрос.

б) Задачи в стихах:

Тишка – кот такой глупышка,

Очень рыбу любит Тишка.

На рыбалке побывал,

Два пескарика поймал,

Щуки две и два ерша.

Жизнь у Тишки хороша!

Кто быстрее сосчитал,

Сколько рыбок кот поймал? (6)

На забор взлетел петух,

Повстречал ещё там двух.

Сколько стало петухов? (3)

По тропинке в лесок

Покатился колобок.

Встретил серого зайчишку,

Встретил волка, встретил мишку,

Да плутовку лису

Повстречал он в лесу

Отвечай поскорей

Сколько встретил колобок зверей. (4)

Игра «Молчанка»

(Учитель показывает пропуск, учащиеся соответствующую цифру на веере цыфр.)

4 — □ = 2 5 — □= 2

4 — □ = 3 5 — 1 = □

1 + 3 = □ □ — 3=1

□ -4=1 1 + □ = 2

3. Физкультминутка

4. Самоопределение к деятельности

Посмотрите, какие это были линии. (Прямые и кривые.)

Прямые линии похожи на натянутые веревочки, а веревочки,

которые не натянули, — это кривые линии.

Сколько прямых линий? (2.)

Сколько кривых? (3.)

Прямая линия начала хвастаться: « Я самая длинная! У меня нет ни начала, ни конца! Я бесконечная!»

Он тоже был очень длинный, но все-таки не такой, как прямая линия. У него появилось начало.

Испугалась точка: «Что же я наделала!» Хотела она убежать, да как назло наступила опять на луч.

И на месте луча появился отрезок. Он не хвастался, какой он большой, у него уже были и начало, и конец.

Вот так маленькая точка смогла изменить жизнь больших линий.

Так кто догадался кто вместе с котиком пришел к нам в гости?( прямая линия, луч, отрезок и точка )

Правильно вместе с котиком пришли прямая линия, луч, отрезок и точка к нам на урок.

Кто догадался, что мы будем делать на этом уроке? (Учиться распознавать и чертить прямую линию, луч, отрезок.)

5. Работа по теме урока

Практическая работа

О каких линиях вы узнали? (О прямой, луче, отрезке. )

Что узнали о прямой линии? (Она не имеет ни начала, ни конца. Она бесконечная.)

(Учитель берет две катушки ниток, натягивает их, изображая прямую линию, и разматывая то одну, то другую, демонстрирует, что прямую можно продолжать в оба конца до бесконечности.)

Что узнали о луче? (У него есть начало, но нет конца.) (Учитель берет ножницы, разрезает нитку. Показывает, что теперь линию можно продолжать только в один конец.)

Что узнали об отрезке? (Унего есть и начало, и конец.) (Учитель отрезает другой конец нитки и показывает, что нитка

не тянется. У нее есть и начало, и конец.)

6.Работа по учебнику

— Посмотрите на рисунок на с. 40 . Расскажите, чем прямая линия отличается от кривой. (Прямая линия натянута, кривая — нет.)

Что вы запомнили о прямой линии, луче, отрезке? (Ответы детей.)

Как начертить прямую линию? (Провести по линейке линию .)

Как начертить отрезок? (Поставить две точки и соединить их. )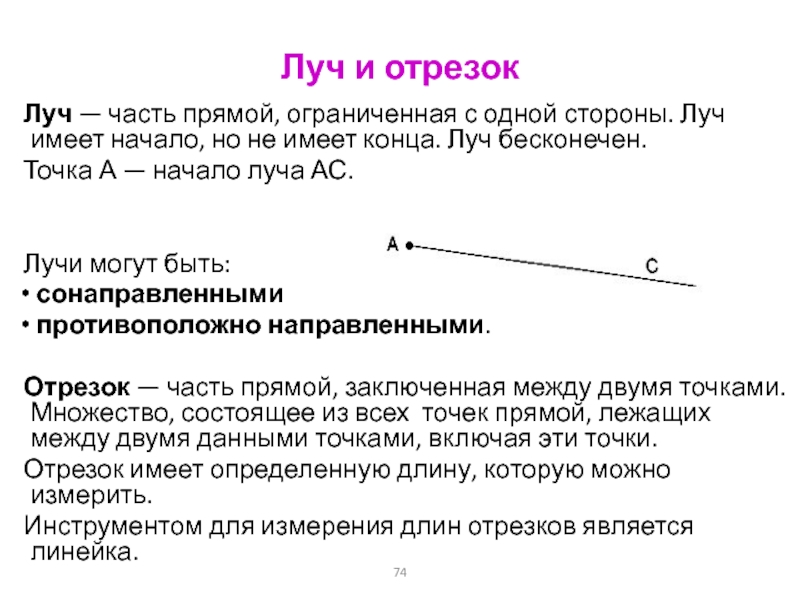

7.Физкультминутка

В понедельник я купался,

(Движения руками, выполняемые при плавании.)

А во вторник рисовал,

(Изобразить рисование.)

В среду долго умывался,

(Изобразить умывание.)

А в четверг в футбол играл.

(Бег на месте.)

В пятницу я бегал, прыгал,

(Прыжки на месте.)

Очень долго танцевал.

(Покружиться.)

А в субботу, воскресенье

(Хлопки в ладоши.)

Целый день я отдыхал.

(Сесть на корточки, руки под щеку.)

8.Закрепление изученного материала

Работа в тетради с печатной основой

Откройте тетрадь на с. 15. Рассмотрите линии. На какие группы их можно разделить? (Прямые — 2,3, 5 и кривые -1,4.)

Выполните следующее задание.

Сколько прямых можно провести через две точки? (Одну. )

Сколько кривых можно провести через две точки? (Много.)

Прочитайте следующее задание.

Раскрасьте рисунки самостоятельно.

9. Пальчиковая гимнастика

Работа в тетради

Тишка хочет научиться изображать прямую, отрезок, луч.

А теперь начертите в тетради прямую, отрезок, луч и кривую линию, по которым побежит кот Тишка.

Обсудить в парах начерченные линии.

10.Работа по учебнику

Прочитайте задание на полях на с. 40. Как узнать, какой отрезок самый длинный? (Посчитать, сколько клеточек составляет длина каждого отрезка.)

Посчитайте и скажите, какой отрезок самый длинный. (Синий.)

Какой отрезок самый короткий? (Красный.)

Рассмотрите рисунок на с. 41. Расскажите соседу по парте, какие линии вы видете.

(Работа в парах.)

Посмотрите на рисунки и записи, приведенные ниже.

Какие записи подходят к рисункам?

Объясните их смысл.

(4 + 1 = 5- к 4 цыплятам прибежал еще один.

Стало 5 цыплят. 5-2 = 3- плавали 5 утят, 2 утенка ушли.

Осталось 3утенка.

Записи 4- 1 = 3и 5- 1 = 4не подходят.)

урок понравился

Было трудно, но интересно

урок не понравился

Подведение итогов урока

Что нового вы узнали о линиях?

Где в жизни встречаются прямые линии? кривые линии?

А, что могут означать для кота: точка, прямая, кривая линия?

(Точка похожа на клубок –он может поиграть, покатать;

Луч – попускать «зайчиков»

Прямая линия на дорогу –где нужно соблюдать правила ПДД;

Кривая линия – на извилистую тропинку, где он может поиграть в догонялки со своими друзьями)

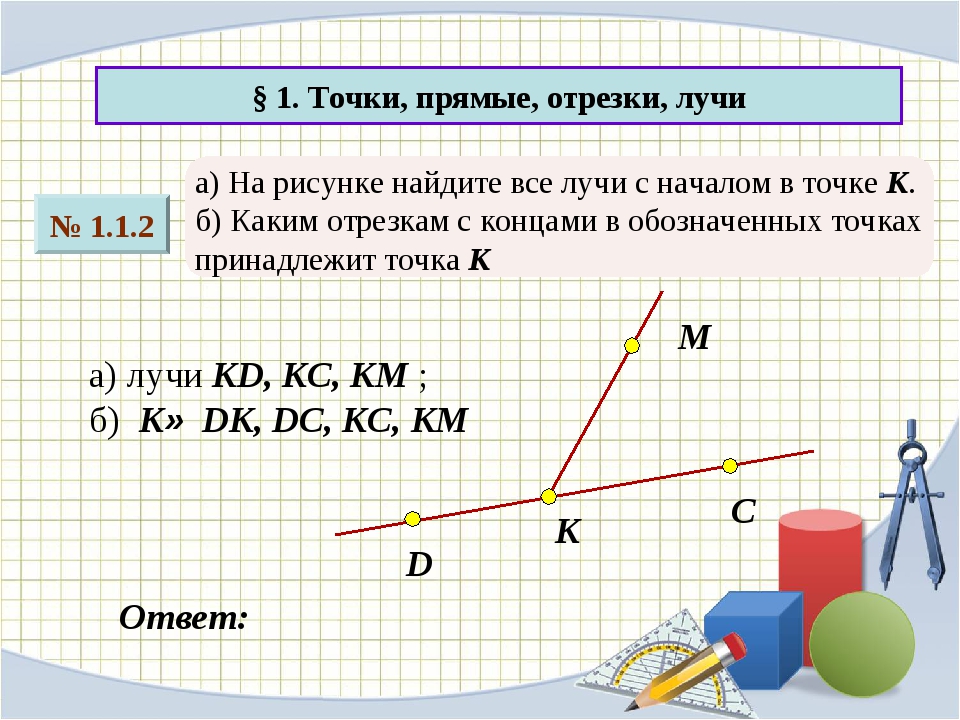
Точки, прямые, отрезки / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Начальные геометрические сведения
Точки, прямые, отрезки

Чтобы изобразить прямую на листе бумаги необходимы карандаш и линейка (Рис. 1). Причем, прямая не имеет начала и конца, то есть мы изображаем лишь часть прямой, но при этом можно дочертить прямую в одну из сторон, либо сразу в обе стороны.

Обозначать прямые принято малыми латинскими буквами ( и т.д.) (Рис.2, ), но бывают случаи, когда прямые обозначены большими латинскими буквами (АВ, CD, MN и т.д.) (Рис.2, б), точки же всегда обозначают большими латинскими буквами (А, В, С и т.д) (Рис.2. ).

Возможны два варианта расположения точек относительно прямой:

Точки лежат на данной прямой или говорят, что прямая проходит через эти точки, на Рис.2 такими точками являются А и В. Для краткости, при решении задач используют запись (читается — точка А принадлежит прямой или точка А лежит на прямой ), аналогично будет и для точки В ().
Точки не лежат на данной прямой или говорят, что прямая не проходит через эти точки, на Рис.2 такими точками являются С и D. Для краткости, при решении задач используют запись (читается — точка С не принадлежит прямой или точка С не лежит на прямой ), аналогично будет и для точки D ().

Важно знать, что через любые две точки можно провести прямую и притом только одну.

Если мы рассмотрим две прямые, то возможны два варианта расположения этих двух прямых друг относительно друга:

Прямые пересекаются, то есть имеют одну общую точку (Рис.3). Для записи пересекающихся прямых используют специальный символ — , т.е. (читают: прямая пересекает прямую b).

Прямые не пересекаются, то есть не имеют общих точек (Рис.4). Для записи не пересекающихся прямых используют специальный символ — , т.е. (читают: прямая m не пересекает прямую n).

На Рис.5, под пунктом ) красным цветом выделена часть прямой, ограниченная двумя точками. Такая часть прямой называется отрезком. Точки ограничивающие отрезок, называются его концами. На Рис. 5, под пунктом б) изображен отрезок с концами А и В. Такой отрезок можно обозначить АВ или ВА. Отрезок АВ содержит все точки прямой, лежащие между точками А и В, а так же и сами точки А и В.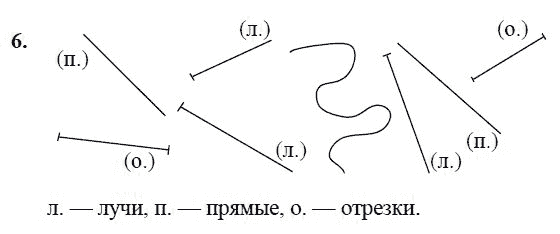

Смежные отрезки — это отрезки, не лежащие на одной прямой и имеющие один общий конец. На рисунке 6 отрезки АВ и АС смежные, точка А — общий конец.

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Провешивание прямой на местности

Луч

Угол

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 30, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 12, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 207, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 323, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 326, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 7, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1003, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1166, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Пользовательское соглашение

Урок математики в 1-м классе по теме «Прямая. Луч. Отрезок»

Цели:

Сформировать представление о понятиях «прямая», «луч», «отрезок».
Закрепить навыки письменных и устных вычислений.
Развивать внимание, память, логическое мышление.
Повторить состав числа 9

Ход урока.

1. Орг. момент.

Учитель: Создадим хорошее настроение. Улыбнитесь друг другу. Садитесь! Руки?

Дети: На месте!

У: Ноги?

Д: На месте!

У: Спина?

Д:Прямая!

2. Устный счет

1. Найдите закономерность, и вставь пропущенные числа.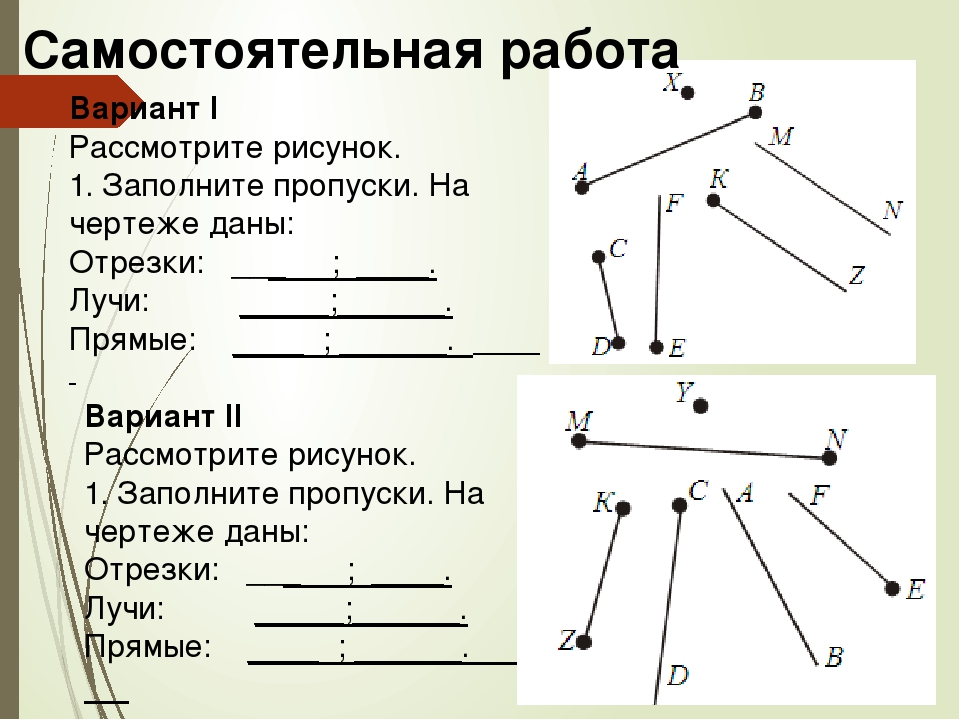 Запиши их в тетрадь:

3, 6,..,..,..,15,..,..,24,..,… .

2. Сегодня к вам на урок пришла мудрая змея. Посмотрите, какая она необычная

У: Прочитайте числа. В каком порядке они записаны?

Д: В порядке возрастания

У: Как получается следующее число?

Д: К числу прибавляют 2.

У: Назовите следующие числа.

Д: Это число 8, 10.

У: Какое число «Лишнее»?

Д: Лишнее число 10, оно двузначное, другие однозначные.

У: Назовите геометрические фигуры?

Д: Треугольник, круг, квадрат.

У: Какая фигура «Лишняя»?

Д: Круг. У него нет углов. Треугольник. Он другого цвета.

У: Какой арифметический знак записан?

Д: Знак «плюс»

У: Назовите по-другому.

Д: Знак сложения.

У: В какой части формулировки задачи используется знак вопроса?

Д: В вопросе.

У: Прочитайте слово.

Д: Осталось.

У: Составьте задачу, чтоб спрашивалось «Сколько осталось?».

А сейчас еще раз внимательно смотрим на змею (закрывается рисунок).

Запиши все, что вы запомнили, в том порядке, в каком записано на змее, начиная с головы.

Дети работают. Затем рисунок открывается дети проверяют

Поднимите руку те кто ошибся.

(работа в группах)

Рассмотрите изображенные фигуры. Распределите их на группы по каким-либо признакам.

Д: По форме, цвету, размеру, настроению

У: Какие равенства можно составить?

Дети называют равенства, а учитель записывает их на доске.

2+7+9
5+4+9
1+8+9
3+6+9

У: Что заметили?

Мы повторили состав числа 9.

У: Молодцы! А теперь расшифруйте слова (анаграммы):

МАЯПРЯ
РЕЗООТК
КИНИТ
ЧУЛ

Это слова «луч», «прямая», «отрезок», «нитки».

У: Все ли расшифрованные слова вам знакомы?

Д: Да.

У: Где вы встречались с ними?

Д: Нитки используем на уроках трудах, Отрезок-для составления схем.

У: Какое слово лишнее?

Д: Нитки. Они не относятся к уроку математики.

У: Все эти слова сегодня помогут нам сделать «открытие».

3. «Открытие» детьми нового

У: У меня в руках 2 катушки ниток. Я раздвигаю их в разные стороны.

Помогает ученик, пока позволяет классная комната

У: Что заметили?

Д: Это прямая линия, только в воздухе.

У: Можно ее продолжить в обоих направлениях?

Д: Да.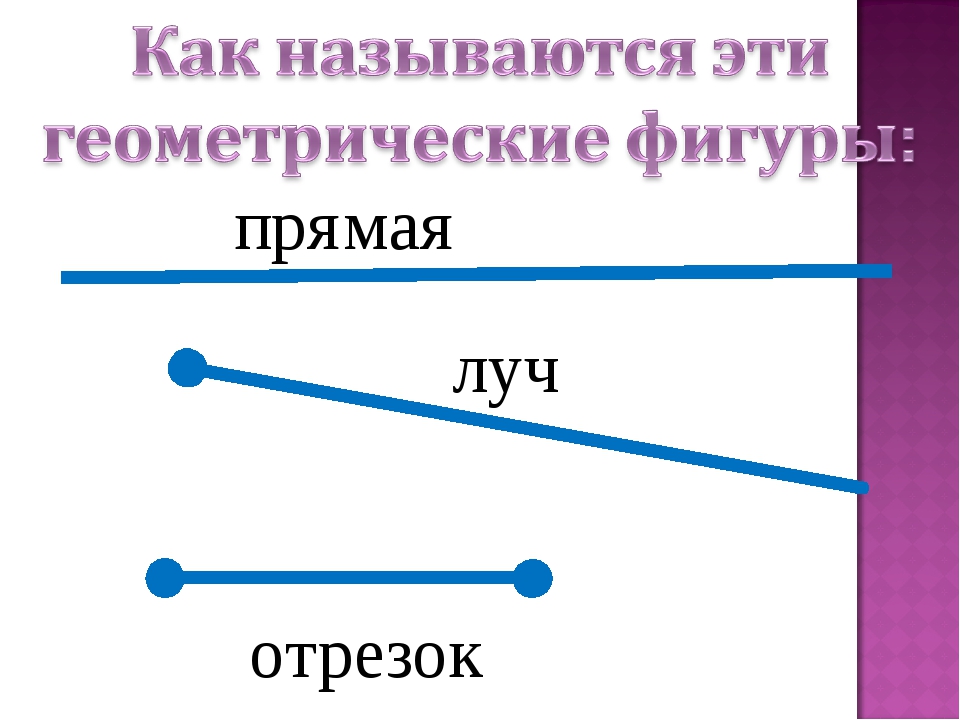 Ее можно продолжить в обоих направлениях без конца.

У: Согласна. Какая разница между этими приспособлением и прямой?

Д: Нитки на катушках могут закончиться, а прямая нет.

У: Можно ли изобразить прямую линию на доске?

Д: Да, можно.

Учитель чертить на доске, дети — в тетрадях

У: У людей есть имена, у животных – клички. Прямую линию можно обозначить одной или двумя буквами. Предложите имя прямой линии.

(Дети предлагают:h или АВ)

Теперь нашу прямую я разрежу ножницами. К месту разреза прикреплю желтый круг.

Что получилось? На что похоже?

Д: На солнечный луч.

У: Можно продолжить луч со стороны разреза?

Д: Нет. Мешает круг и нечего продолжать

У: А с другой стороны?

Д: Можно продолжить до бесконечности.

У.Сравните луч и прямую линию.

Д: Прямую можно продолжить в обе стороны, а луч только в одну. Луч имеет начало.

У: Правильно

Учитель чертит луч на доске, а дети в тетрадях.

Луч обозначается двумя прописными буквами. На первом месте всегда указывает начало луча (Дети предлагают название луча)

У луча я отрезаю ту часть, которую можно продолжить до бесконечности и прикрепляю еще один желтый круг.

Что получилось?

Д: Это отрезок. Линия, ограниченная с двух сторон.

У: Сравните луч и отрезок.

Д: У луча есть только начало, а у отрезка и начало и конец.

У: Можно отрезок изобразить на доске, в тетради?

Д: Да.

Учитель чертит на доске. Дети — в тетрадях

У: Отрезок обозначается двумя буквами, но порядок букв при чтении и записи не имеет значения.

(дети обозначают отрезок).

Что нового узнали для себя о прямой, луче, отрезке? (Ответы детей)

4. Первичное закрепление с проговариванием.

На доске

Найдите отрезок, луч, прямую. Покажите. Объясните свой выбор.

5. Физкультминутка

6. Обучающая самостоятельная работа с проверкой в классе.

1. Обведите с помощью линейки на чертеже прямые линии красным карандашом, лучи – синим, а отрезки – зеленым.

2. У: Сколько прямых проведено через точку А?

Д: Три.

У: Проведите еще две прямые, проходящие через точку А. (Дети сами проводят линии)

Сколько прямых можно провести через одну точку?

Д: Много.

У: Посмотри, как проведена прямая через А и В, а потом сам проведи прямые через точки С и Д. Сколько прямых можно провести через две точки?

Д: Одну.

У: Проведите отрезок АВ и отметь на нем точки С и Д. Сколько отрезков ты видишь на чертеже ?

Дети отмечают по – разному. Затем вместе находят на большом отрезке шесть маленьких отрезков: АВ, АС, АД, ВС, СД, ВД.

7. Закрепление.

Тетрадь – учебник №2 стр. 15 №31

8. Итог урока.

Рефлексия.

Какое открытие мы с вами сделали на уроке?

Что понравилось вам больше всего?

Создание и интерпретация линейных графиков и графиков сегментов

Линейные графики

Давайте посмотрим, как построить линейный график. Мы изучим два способа сделать это.

Метод 1: Таблица XY

Допустим, у нас есть уравнение y = 2 x + 1, которое следует общей формуле y = м x + b 0 90 0 9 м, где 90 90 м 90 0 0 а b — это пересечение y . Мы можем настроить таблицу, присваивая значения x , а затем вычисляя y .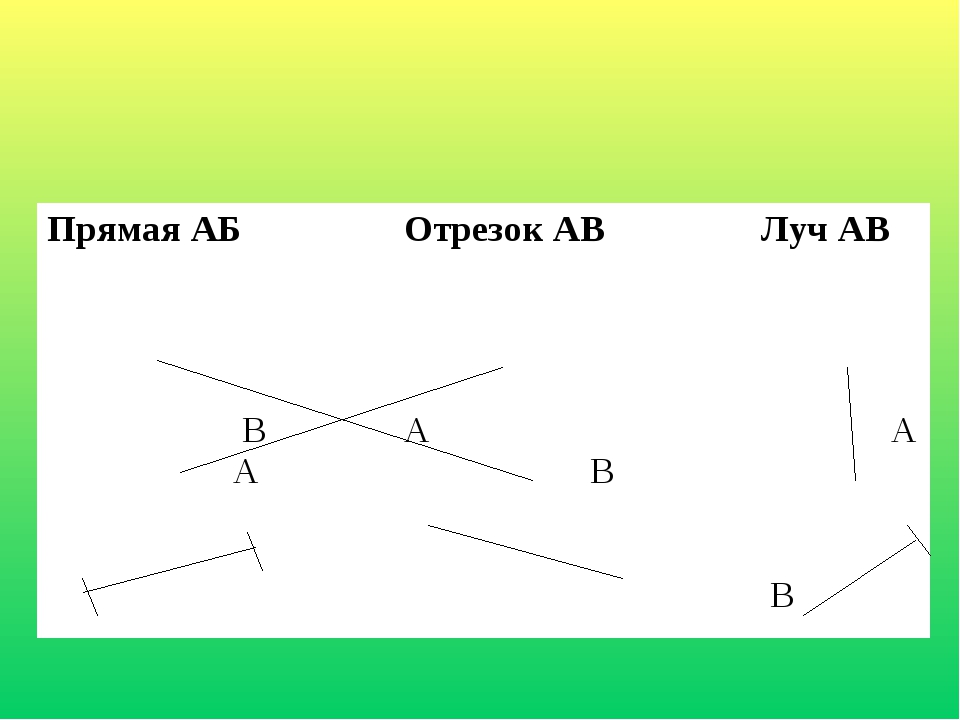

Таблица X-Y
Х	Д
-2	2(-2) + 1 = -3
-1	(2)(-1) + 1 = -1
0	(2)(0) + 1 = 1
1	(2)(1) + 1 = 3
2	(2)(2) + 1 = 5

Теперь мы можем нанести эти точки на сетку x-y и соединить точки прямой линией.

Нанесение точек и соединение их прямой линией

Эта линия продолжается в обоих направлениях вечно, но (поскольку это довольно далеко) мы обрезаем график и помещаем стрелки на каждый конец линии, показывая, что она продолжается вечно.

Метод 2: Y-пересечение и наклон

Давайте рассмотрим другой способ построения графика того же уравнения, y = 2 x + 1.

Y-пересечение

пересекает ось y .Чтобы построить эту точку, вы перемещаетесь на 1 единицу вверх от начала координат по оси y .

Y-пересечение — это константа в уравнении для линии

Теперь нам нужна еще одна точка для построения нашей линии.

Наклон

В нашем уравнении 2 перед x — это наклон линии. Наклон — это скорость, с которой линия увеличивается или уменьшается. Уклон обычно называют «подъемом над бегом».» Наклон — это всегда дробь, где вы двигаетесь вверх по числителю и в сторону по знаменателю. В нашем случае 2 на самом деле 2/1, то есть мы перемещаемся на 2 единицы вверх и на 1 единицу вправо. Мы также можем сказать, что наклон равен -2/-1, что означает, что мы сместимся на 2 единицы вниз и на 1 единицу влево. Если мы нанесем эти два местоположения, у нас будет две точки, и мы сможем провести нашу линию.

Построение двух точек с использованием наклона из уравнения

Графики линейных сегментов

График сегментов линий отличается от предыдущей линии, которую мы построили.Разница в том, что наша линия не будет уходить в бесконечность ни в одном направлении. Графики линейных сегментов имеют ограниченный домен , который представляет собой набор значений x . Давайте построим ту же линию, что и раньше, но ограничим домен. — значения меньше 0 включительно и больше 3.Незакрашенный кружок на линии означает, что значение не включено.

Линейный сегмент будет либо включать конечные точки, либо исключать их

Интерпретация линейных графиков

Линейные графики без смысла — это просто линейные графики. Мы можем придать линейным графикам смысл, если допустим, что оси x и y имеют единицы измерения. Чтобы определить значение наклона линии или сегмента линии, мы помещаем х -единиц на х -единиц и получаем скорость.Давайте посмотрим на несколько графиков и интерпретируем, что означают наклоны линий с точки зрения ставок.

Линейный график со смыслом, потому что он имеет единицы по обеим осям

Этот график показывает м по оси y , которая представляет положение в метрах. Единица измерения оси x равна s , то есть времени в секундах. Размещение единиц измерения по оси y по оси x дает нам м / с , то есть скорость. Скорость — это скорость, которая говорит нам, как быстро что-то движется и в каком направлении оно движется. Линейный график положения и времени, подобный этому, даст вам понять, что скорость объекта постоянна: это потому, что наклон (наша скорость) будет одинаковым для любых двух точек на линейном графике.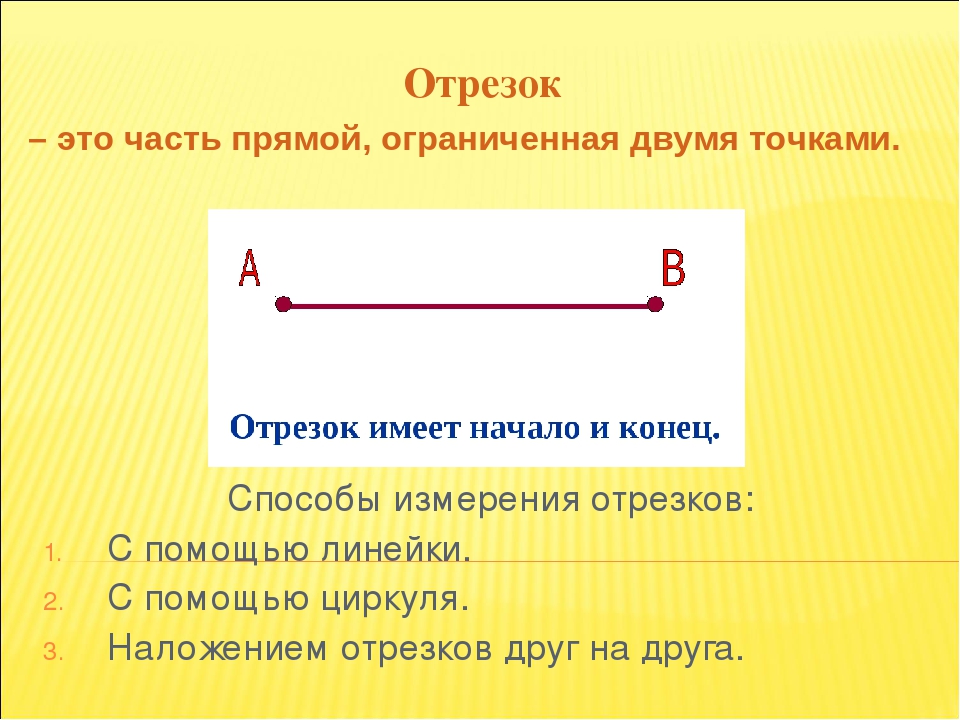

Следующий график, который мы рассмотрим, относится к температуре.

Температура по оси Y и длина по оси X

Размещение единицы измерения по оси и над единицей измерения по оси x дает Кельвин/метр.Это скорость изменения температуры по длине, и график зависимости температуры от длины может дать один из способов взглянуть на передачу тепла.

Резюме урока

Линии на графике дают скорость , которая является отношением одной вещи к другой. Интерпретация линейного графика просто включает в себя размещение единиц измерения по оси y над единицами измерения по оси x и определение того, что представляет наклон .

Чтобы построить линию на сетке, вы можете использовать один из двух способов:

Создайте таблицу со значениями x и y .Выбираются значения x , которые должны включать положительные и отрицательные значения. Эти значения подставляются в уравнение для расчета значений и . Затем эти точки наносятся на сетку и соединяются прямой линией.
Постройте точку пересечения y , которая является константой ( b ) в общем уравнении y = m x + b . Затем используйте значение м , которое представляет собой уклон, для построения двух других точек.Наклон всегда является частью того, как далеко нужно двигаться вверх и как далеко двигаться. Это также известно как «подъем против пробега».

Графики линейных сегментов не продолжаются вечно, но их домен ( x -значений) ограничен.

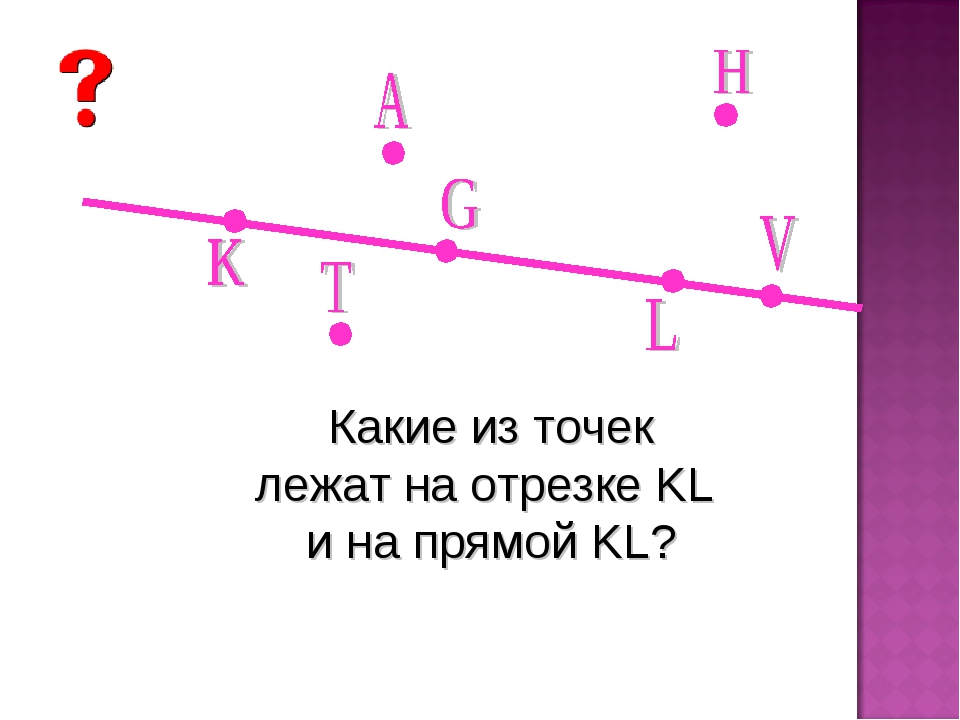
Урок: Прямые линии, отрезки и лучи

Урок: Прямые линии, отрезки и лучи | Нагва
Портал деактивирован.Обратитесь к администратору портала.
На этом уроке мы научимся определять точки, прямые, лучи, отрезки прямых и конечные точки.
План урока
Студенты смогут
определите, изображена ли на фигуре точка, отрезок, луч или линия,
назовите эти объекты, например, «линия А»,
нарисуйте отрезки, лучи и линии, проходящие через заданные точки,
определяют точки, лежащие на заданной прямой, отрезке или луче.
Видео урока
15:54
Nagwa — стартап в области образовательных технологий, цель которого — помочь учителям учить, а ученикам учиться.
Copyright © 2022 Nagwa
Все права защищены
Nagwa использует файлы cookie, чтобы обеспечить вам максимальное удобство на нашем веб-сайте. Узнайте больше о нашей Политике конфиденциальности.
Принимать
Решено: Начертить ряд соединенных прямых линий с помощью le… — Сообщество поддержки Adobe
AI CC 2017.1.0
Я ищу способ рисования ряда соединенных прямых отрезков, каждый из которых имеет азимут (направление по компасу) в градусах и длину. В некоторых случаях они образуют замкнутый неправильный многоугольник (правильный термин?). В остальных случаях закрытия нет.
Люди, знакомые с документами по недвижимости, поймут, что это чертежи юридических описаний собственности и границ СШ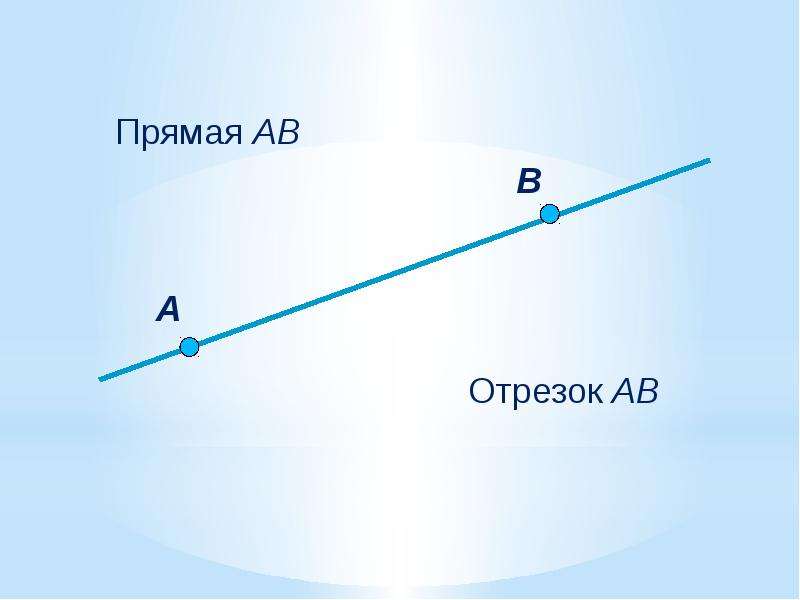А. Ага.
Я попробовал очевидный метод: несколько раз использовал инструмент Line Segment («/»). Для пеленга на юридическом языке «44 градуса юга 29 минут на восток» сначала я отбрасываю минуты. Юг равен 270°, поэтому я вычисляю (270 — 44) и ввожу результат как угол. Мой масштаб 1 мм = 100 футов, поэтому я ввожу «3,2 мм» в качестве длины. (Установка «общих» единиц измерения по умолчанию в миллиметры помогает в этом.)
Я все еще работаю над тем, как указать конечную точку сегмента ‘n’ в качестве начала сегмента ‘n+1’. Наблюдение за глазами происходит медленно и неточно.Я не понял, как указать инструменту «Сегмент линии» использовать последний определенный конец пути или текущую проданную метку в качестве начальной точки для следующего сегмента. (Есть способ? Предложения приветствуются!)
Есть ли лучший способ нарисовать серию соединенных прямых отрезков?
Есть ли способ отличить один сегмент от другого? ДЕЙСТВИТЕЛЬНО легко заблудиться, особенно когда последовательные сегменты очень похожи.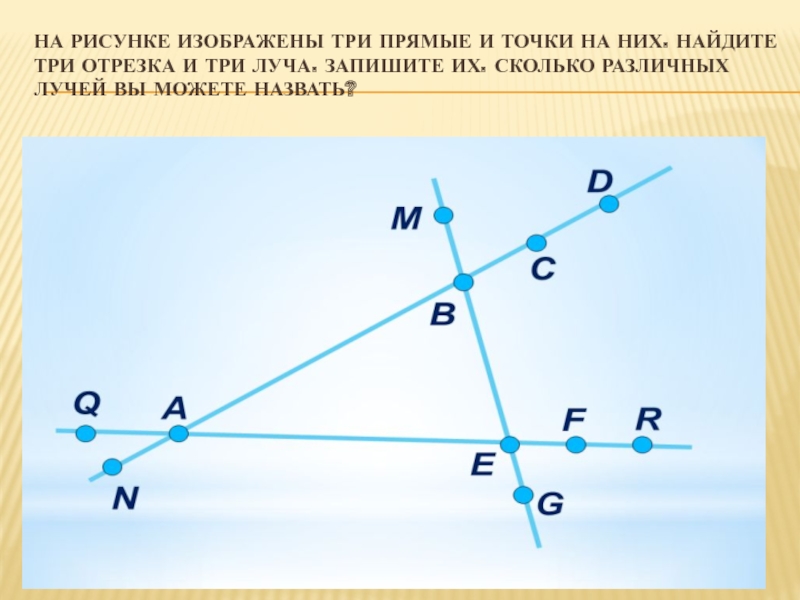 («Я только что нарисовал сегмент 10 или сегмент 11?») Начинать заново неинтересно.Видимый размер или наклонная длина? (Окно—>Информация показывает только размер по горизонтали и вертикали.) Плагин?
Двойной дополнительный балл, если это может быть достигнуто с помощью какой-либо формы сценария. Я могу взломать JS, чтобы сделать это, если кто-то поможет мне начать. (Мой опыт работы с JS связан исключительно с DW.)
У меня их немного, около 30, от 5 до 20 сегментов в каждой. Я хотел бы найти способ использовать ИИ для выполнения этой работы. Очевидно, если бы я делал это каждый день, я бы переключился на специализированное приложение для управления земельными ресурсами.
TIA
Генри
линий и углов — определения, свойства, типы, практические вопросы
Древние математики ввели понятие линий для представления прямых объектов, ширина и глубина которых пренебрежимо малы. Линии, рассматриваемые Евклидом как ширина за вычетом длины, составляют основу евклидовой геометрии.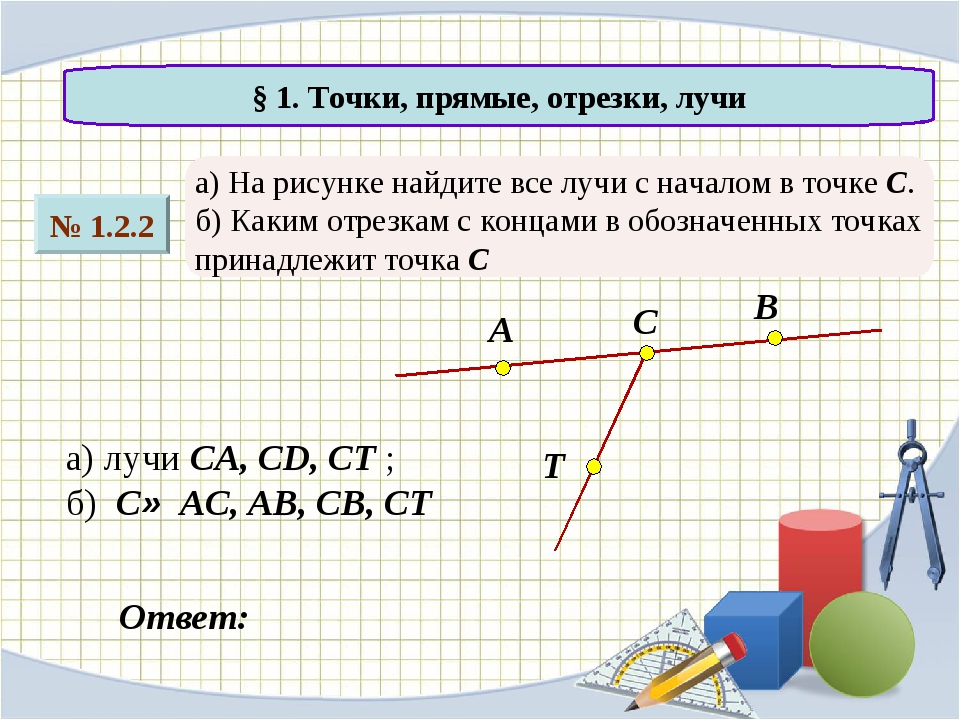
Когда два луча (часть прямой) пересекаются в одной плоскости, они образуют угол.Точка пересечения называется вершиной.
В этой статье мы рассмотрим основные свойства, определения и типы линий и углов, связанных с геометрией. Мы также рассмотрим несколько примеров, чтобы вы лучше поняли свойства линий и углов. Прежде чем мы двинемся дальше, взгляните на пятиэтапный план подготовки к GMAT, чтобы набрать 700+ на GMAT:

Определение строки
Линия не имеет конечных точек. Он имеет бесконечную длину.
Определение сегмента линии
Отрезок — это отрезок прямой, или, другими словами, можно сказать, что отрезок — это линия с двумя концами.
Например, , На диаграмме показана линия L, и один сегмент этой линии — AB.
На плоскости может быть много линий или отрезков.
И эти линии можно разделить на несколько типов в зависимости от относительного расположения одной строки относительно другой строки.
Типы линий
Пересекающиеся линии
Две прямые пересекаются, если они пересекаются в одной точке.
Например, L ₁ и L ₂ являются пересекающимися линиями на приведенной ниже диаграмме
.
Параллельные линии
Пара прямых параллельна, если они никогда не пересекаются.
Например, L ₁ , L ₂ и L ₃ являются параллельными линиями на приведенной ниже диаграмме.
Поперечная линия
Поперечная линия пересекает две или более линий в разных точках.
Например, линия L ₃ является поперечной линией на приведенной ниже диаграмме.
Далее мы рассмотрим углы и их свойства.
Набрав Q50-51 на GMAT, вы получите 700+ баллов GMAT. Начните свой путь к получению Q50-51 на GMAT с помощью онлайн-курса подготовки e-GMAT на основе искусственного интеллекта. Наш xPERT не только выбирает наиболее оптимизированный путь обучения, но и отслеживает ваши улучшения, гарантируя, что вы быстро и надежно достигнете целевого показателя Quant. Посмотрите это видео, чтобы узнать больше:

Угол – что это такое?
Угол образуется при пересечении двух прямых.Обозначим угол символом ∠.
Угол состоит из двух катетов и одной общей вершины, в которой сходятся две прямые.
Например, ∠AOD образуется при пересечении линий AB и CD.
Кроме того, между ветвями AO и OD образуется ∠AOD, поэтому мы включаем A, O и D в название угла.
Знаете ли вы, что положение точек катетов не имеет значения, если общей вершиной является средняя буква в имени угла
Измерение угла
Угол измеряется в градусах.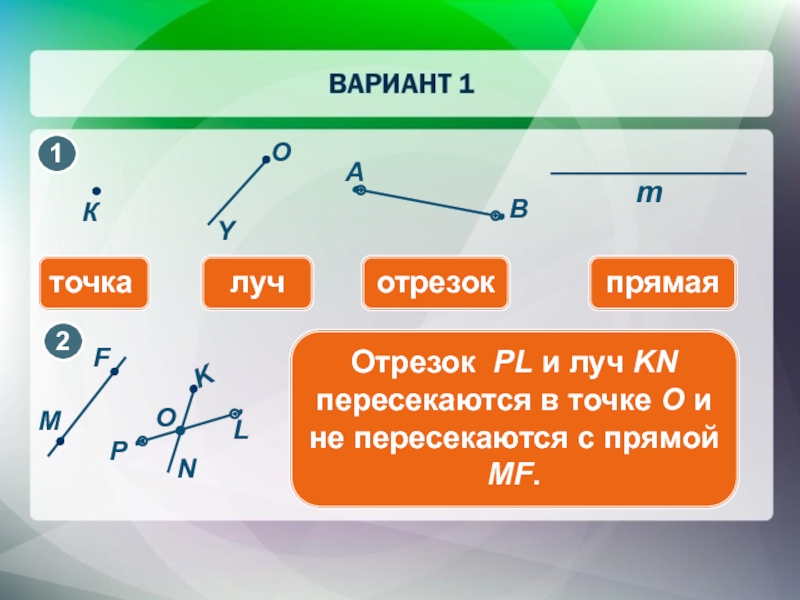
Угол может измеряться от нуля (0) градусов до 360 градусов. На основании измерения угла они делятся на четыре типа:
Острый угол
Прямой угол
Тупой угол
Рефлекторный угол
Острый угол
Когда измерение угла находится в диапазоне от 0 до 90 градусов.
Прямой угол
Когда измерение угла составляет ровно 90 градусов.
Если между двумя прямыми имеется прямой угол, то говорят, что эти две прямые перпендикулярны друг другу .
Тупой угол
При измерении угла между 90 и 180 градусами.
Прямая линия имеет угол 180 градусов.
Угол рефлекса
При измерении угла между 180 и 360 градусами.
Мы обсудили основные типы углов.
Теперь обсудим углы, образованные при пересечении двух прямых.
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. По состоянию на 4 октября 2021 года мы являемся самой популярной компанией по подготовке к GMAT на сайте gmatclub: по состоянию на 4 октября 2021 года мы получили более 2200 отзывов.
Углы, образованные между двумя пересекающимися прямыми
Вертикально противоположные углы
При пересечении двух прямых получается 4 угла.
И углы , которые противоположны друг другу в точке пересечения , известны как вертикально противоположные углы .
Вертикально противоположные углы всегда равны.
Теперь обсудим углы, образованные при пересечении двух прямых третьей прямой, т. е. поперечной линией.
Углы, образованные поперечной линией
Когда поперечная линия пересекает две прямые, образуются восемь углов, как показано на рисунке.
Теперь из этой диаграммы получается несколько специальных пар углов.
Например: если вы заметили , что (∠1, ∠3), (∠2, ∠4), (∠5, ∠7) и (∠6, ∠8) являются вертикально противоположными углами.
Аналогично получаем еще несколько видов углов. Давайте обсудим их.
Другие типы уголков
Внутренние и внешние углы
Внутренние углы — это углы, находящиеся внутри области между двумя линиями.
И внешние углы — это те, которые присутствуют внутри этой области.
Например:
∠2, ∠3, ∠5 и ∠8 — внутренние углы.
А, ∠1, ∠4, ∠6 и ∠7 — внешние углы.
Соответствующие углы
Два угла называются соответственными, если они лежат по одну сторону от поперечной линии так, что:
Один угол — внутренний,
Другой — внешний угол
Например:
(∠4, ∠8), (∠3, ∠7), (∠1, ∠5) и (∠2, ∠6) — 4 пары соответствующих углов
Альтернативные внутренние углы
Два внутренних угла, находящихся по разные стороны от поперечной линии, называются параллельными внутренними углами.
Например:
(∠2, ∠8) и (∠3, ∠5) — альтернативные внутренние углы.
Альтернативные внешние углы
Два внешних угла, находящихся по разные стороны от поперечной линии, называются альтернативными внешними углами.
Например:
(∠1, ∠7) и (∠4, ∠6) — альтернативные внешние углы.
Примечание: Если поперечная линия пересекает две параллельные прямые, то соответствующие углы, альтернативные внутренние углы и альтернативные внешние углы равны.
Итак, мы рассмотрели все типы углов.
Давайте теперь узнаем о некоторых свойствах углов.
Свойства углов
Сумма углов одной стороны прямой
Сумма всех углов по одну сторону прямой всегда равна 180 градусов.
Например, сумма ∠1, ∠2 и ∠3 составляет 180 градусов.
Сумма углов вокруг точки
Сумма всех углов вокруг точки всегда равна 360 градусам.
Например, сумма углов (∠1, ∠2 и ∠3) вокруг точки O составляет 360 градусов.
Если вам понравилась эта статья, вот еще несколько статей, которые могут вам понравиться:
Применение свойств линий и углов в вопросах
Линии и углы — Вопрос 1
На приведенной выше диаграмме линия CD параллельна линии EF. Если ∠AHD и ∠JIE равны 118° и 30° соответственно, то какова мера угла GIB?
30
32
34
40
62
Раствор
Шаг 1: Дано
линия CD параллельна линии EF.
∠AHD =118°
∠JIE = 30°
Шаг 2: найти
Этап 3: Подход и разработка
Нам нужно найти меру угла GIB.
Итак, при заданной информации мы знаем, что прямая CD параллельна прямой EF, а прямая AB им перпендикулярна.
Следовательно, ∠DHI = ∠FIB, так как оба угла являются соответствующими.
Мы можем найти ∠dhi или ∠fib как
∠AHD + ∠dhi = 180 °
118 ° + ∠fib = 180 °
∠fib = 62 °
Теперь, ∠fib = ∠fig + ∠GIB
Судя по диаграмме, ∠FIG = ∠JIE, так как это вертикально противоположные углы между EF и JG.
∠fib = ∠fig + ∠gib
62 ° = ∠jie + ∠gib
62 ° = 30 ° + ∠gib
∠gib = 32 ° 60256
Следовательно, правильный ответ вариант Б.
Линии и углы — Вопрос 2
На приведенной выше диаграмме угол DFE и угол BFC представлены X и Y соответственно. Если ∠AFC = 100° и ∠BFE = 45°, то каково значение Y-X?
20
25
30
35
40
Раствор
Шаг 1: Дано
∠DFE = X
∠BFC = Y
∠AFC = 100°
∠BFE = 45°
Шаг 2: найти
3
Этап 3: Подход и разработка
Чтобы найти Y-X, нам нужно сначала найти Y и X.
Мера угла Y:
Нам дано ∠AFC = 100° и
∠AFC + ∠BFC = 180°, так как сумма углов на одной стороне прямой равна 180°
100° + ∠BFC = 180°

Мера угла X:
Нам дано ∠BFE = 45° и
∠DFE + ∠BFE + ∠BFC = 180°, поскольку сумма углов на одной боковой прямой составляет 180°.
X + 45° +80°= 180°
Следовательно, Y – X = 80° – 55° = 25°.
Таким образом, правильный ответ — вариант Б.
Если вы планируете сдавать GMAT, мы можем предоставить вам доступ к качественному онлайн-контенту для подготовки. По состоянию на 4 октября 2021 года мы являемся самой популярной компанией по подготовке к GMAT на сайте gmatclub: по состоянию на 4 октября 2021 года мы получили более 2200 отзывов.
Узнайте больше о прямых линиях
В сегодняшней статье мы рассмотрим несколько прямых линий .Первое, что стоит на повестке дня, — определить, что именно представляют собой прямые линии, чтобы отличить их от изогнутых линий. Затем мы рассмотрим понятия лучей, отрезков прямых и открытых лучей.
Что такое линия?
Каждая линия состоит из точек, что является наименьшей графической единицей.
Ряд точек, выстроенных одна за другой, образует непрерывную полосу, которую мы будем называть «линией».
Когда точки всегда идут в одном направлении, они образуют прямую линию . Представьте, если бы мы могли видеть каждую из этих точек, образующих линию, это, вероятно, выглядело бы примерно так.
Когда точки, сохраняя порядок, постоянно меняют направление, они образуют изогнутую линию . Если бы мы могли видеть каждую точку кривой линии, она могла бы выглядеть примерно так.
Что такое луч?
Луч — это прямая бесконечная линия: она никогда не заканчивается. Визуально представить эти линии невозможно, поэтому мы рисуем лучи без точек на концах, понимая, что это означает, что линия на этом не останавливается, а продолжается до бесконечности.
Для наименования луча мы используем строчные буквы, например:
Однако мы также можем закрыть эти лучи, и тогда луч станет отрезком прямой. Каждый из концов этого сегмента представляет собой последнюю точку луча. Эти точки или концы написаны прописными буквами и названы в соответствии с двумя его концами:
.
Сегмент AB
Если мы ограничим этот луч только с одной стороны, получится открытый луч.