Формула Планка — Википедия
Формула Планка — выражение, описывающее спектральное распределение энергии излучения абсолютно чёрного тела.
Согласно одной из форм этого выражения, энергетическая яркость такого тела в интервале угловых частот dω{\displaystyle d\omega } равна Bω(ω,T)dω{\displaystyle B_{\omega }(\omega ,T)\,d\omega }, где
- Bω(ω,T)=ℏω34π3c2⋅1eℏωkT−1{\displaystyle B_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{4\pi ^{3}c^{2}}}\cdot {\frac {1}{e^{\frac {\hbar \omega }{kT}}-1}}}
где ℏ{\displaystyle \hbar } — постоянная Планка, k{\displaystyle k} — постоянная Больцмана, c{\displaystyle c} — скорость света, T{\displaystyle T} — температура.
Формулой Планка также называют выражения для спектральной мощности излучения единицы поверхности (светимости)
- ϵω(ω,T)=πBω(ω,T)=ℏω34π2c2⋅1eℏωkT−1{\displaystyle \epsilon _{\omega }(\omega ,T)=\pi B_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{4\pi ^{2}c^{2}}}\cdot {\frac {1}{e^{\frac {\hbar \omega }{kT}}-1}}}
и для спектральной плотности энергии излучения абсолютно чёрного тела
- uω(ω,T)=4πcBω(ω,T)=ℏω3π2c3⋅1eℏωkT−1.{\displaystyle u_{\omega }(\omega ,T)={\frac {4\pi }{c}}B_{\omega }(\omega ,T)={\frac {\hbar \omega ^{3}}{\pi ^{2}c^{3}}}\cdot {\frac {1}{e^{\frac {\hbar \omega }{kT}}-1}}.}
Можно также записать формулу Планка для интервалов линейных частот dν{\displaystyle d\nu } или длин волн dλ{\displaystyle d\lambda }. Учитывая, что ω=2πν=2πc/λ{\displaystyle \omega =2\pi \nu =2\pi c/\lambda }, для спектральной плотности, например, можно получить.
- uν(ν,T)=uω(ω,T)dωdν=4π2hν3c3⋅1ehνkT−1{\displaystyle u_{\nu }(\nu ,T)=u_{\omega }(\omega ,T){\frac {d\omega }{d\nu }}={\frac {4\pi ^{2}h\nu ^{3}}{c^{3}}}\cdot {\frac {1}{e^{\frac {h\nu }{kT}}-1}}}
и
- uλ(ω,T)=uω(ω,T)dωdλ=8πhcλ5⋅1ehcλkT−1.{\displaystyle u_{\lambda }(\omega ,T)=u_{\omega }(\omega ,T){\frac {d\omega }{d\lambda }}={\frac {8\pi hc}{\lambda ^{5}}}\cdot {\frac {1}{e^{\frac {hc}{\lambda kT}}-1}}.}
Формула Планка первоначально была получена эмпирически, после того, как стало ясно, что формула Рэлея — Джинса (которая следует из классической электродинамики) удовлетворительно описывает излучение только в области длинных волн. С убыванием длин волн эта формула сильно расходится с экспериментом; более того, в пределе она даёт расхождение: бесконечную энергию излучения (ультрафиолетовая катастрофа). В связи с этим Макс Планк в 1900 году сделал противоречащее классической физике предположение о том, что электромагнитное излучение испускается в виде отдельных порций (квантов) энергии, величина которых связана с частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности, ℏ{\displaystyle \hbar }, впоследствии назвали постоянной Планка; ℏ{\displaystyle \hbar } = 1,054·10−27эрг·с. Это предположение позволило объяснить наблюдаемый спектр излучения теоретически.
Правильность формулы Планка подтверждается не только непосредственной эмпирической проверкой, но и следствиями из данной формулы; в частности, из неё следует закон Стефана — Больцмана (также эмпирически подтверждённый). Кроме того, из неё выводятся также и приблизительные формулы, полученные до формулы Планка: формула Вина и формула Рэлея — Джинса.
Вследствие линейности уравнений электромагнитного поля, любое их решение может быть представлено в виде суперпозиции монохроматических волн; каждая — с определённой угловой частотой ω{\displaystyle \omega }. Энергия поля может быть представлена как сумма энергий соответствующих осцилляторов. Как известно из квантовой механики, энергия осциллятора принимает дискретные значения согласно следующей формуле:
- En=ℏω(n+1/2).{\displaystyle E_{n}=\hbar \omega (n+1/2).}
Поскольку рассматривается равновесное излучение, то, используя каноническое распределение Гиббса, можно определить вероятность состояния осциллятора с заданной энергией:
- Wn=1Z⋅exp(−EnkT).{\displaystyle W_{n}={1 \over Z}\cdot \mathrm {exp} \left(-{E_{n} \over kT}\right).}
Статистическая сумма Z{\displaystyle Z} равна:
- Z=∑exp(−ℏωkT⋅(n+1/2))=exp(−ℏω2kT)⋅∑exp(−ℏωkT)n=exp(−ℏω2kT)1−exp(−ℏωkT).{\displaystyle Z=\sum \mathrm {exp} \left(-{\hbar \omega \over {kT}}\cdot (n+1/2)\right)=\mathrm {exp} \left(-{{\hbar \omega } \over {2kT}}\right)\cdot \sum \mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)^{n}={\frac {\mathrm {exp} \left(-{{\hbar \omega } \over {2kT}}\right)}{1-\mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)}}.}
Свободная энергия Ψ{\displaystyle \Psi } равна:
- Ψ=−kT⋅lnZ=ℏω2+kT⋅ln(1−exp(−ℏωkT)).{\displaystyle \Psi =-kT\cdot \ln Z={\frac {\hbar \omega }{2}}+kT\cdot \ln \left(1-\mathrm {exp} \left(-{\hbar \omega \over kT}\right)\right).}
Для средней (математическое ожидание) энергии ε¯{\displaystyle {\overline {\varepsilon }}} воспользуемся уравнением Гиббса — Гельмгольца:
- ε¯=∑(WnEn)=Ψ−(kT⋅∂(Ψ)∂(kT))=(kT)2⋅∂(lnZ)∂(kT)=(kT)2⋅(ℏω2(kT)2+exp(−ℏωkT)⋅ℏω(kT)21−exp(−ℏωkT)){\displaystyle {\overline {\varepsilon }}=\sum (W_{n}E_{n})=\Psi -\left(kT\cdot {\frac {\partial (\Psi )}{\partial (kT)}}\right)=(kT)^{2}\cdot {\frac {\partial (\ln Z)}{\partial (kT)}}=(kT)^{2}\cdot \left({\frac {\hbar \omega }{2(kT)^{2}}}+{\frac {\mathrm {exp} \left(-{{\hbar \omega } \over {kT}}\right)\cdot {\hbar \omega \over (kT)^{2}}}{1-\mathrm {exp} \left(-{\hbar \omega \over kT}\right)}}\right)};
таким образом, средняя энергия ε¯{\displaystyle {\overline {\varepsilon }}}, приходящаяся на полевой осциллятор, равна:
| ε¯=ℏω2+ℏωexp(ℏωkT)−1.{\displaystyle {\overline {\varepsilon }}={\frac {\hbar \omega }{2}}+{\frac {\hbar \omega }{\mathrm {exp} \left({\hbar \omega \over kT}\right)-1}}.}, | (1) |
Количество же стоячих волн в единице объёма в трёхмерном пространстве, в интервале (ω;ω+dω){\displaystyle (\omega ;\omega +d\omega )}, равно[1][2]:
| dnω=ω2dωπ2c3{\displaystyle \mathrm {d} n_{\omega }={\frac {\omega ^{2}\mathrm {d} \omega }{\pi ^{2}c^{3}}}}. | (2) |
Следовательно, для спектральной плотности мощности электромагнитного излучения получаем:
- uω(0)(ω,T)=ε¯dnωdω=ℏω32π2c3+ℏω3π2c3(exp(ℏωkT)−1),{\displaystyle u_{\omega }^{(0)}(\omega ,T)={\overline {\varepsilon }}{\frac {\mathrm {d} n_{\omega }}{\mathrm {d} \omega }}={\frac {\hbar {\omega }^{3}}{2\pi ^{2}c^{3}}}+{\frac {\hbar {\omega }^{3}}{\pi ^{2}c^{3}\left(\mathrm {exp} \left({\hbar \omega \over kT}\right)-1\right)}},}
где первое слагаемое связано с энергией нулевых колебаний, а второе — это и есть формула Планка.
Вывод, исходящий из распределения Бозе — Эйнштейна[править | править код]
Фотоны являются бозонами и подчиняются статистике Бозе — Эйнштейна. Для этой статистики, среднее число частиц с данной энергией ε{\displaystyle \varepsilon } равно:
- n¯(ε)=1exp(ε/kT)−1.{\displaystyle {\overline {n}}(\varepsilon )={\frac {1}{\mathrm {exp} ({\varepsilon /kT})-1}}.}
По определению:
- uε(ε,T)dε=εn¯(ε)dN(ε),{\displaystyle u_{\varepsilon }(\varepsilon ,T)\mathrm {d} \varepsilon =\varepsilon {\overline {n}}(\varepsilon )\mathrm {d} N(\varepsilon ),}
где dN=ε2dεπ2c3ℏ3{\displaystyle \mathrm {d} N={\frac {\varepsilon ^{2}\mathrm {d} \varepsilon }{\pi ^{2}c^{3}\hbar ^{3}}}} — число осцилляторов (в единице объёма) электромагнитного поля с данной энергией, в бесконечно малой окрестности ε=ℏω{\displaystyle \varepsilon =\hbar \omega }.
Подставив формулу среднего числа бозонов с данной энергией в эту формулу, получим для
- uω(ω,T)=uε(ε,T)dεdω{\displaystyle u_{\omega }(\omega ,T)=u_{\varepsilon }(\varepsilon ,T){\frac {d\varepsilon }{d\omega }}}
формулу Планка.
Формула Планка точно согласуется с экспериментальными данными во всём интервале частот от 0 до ∞{\displaystyle \infty }. При малых частотах (больших длинах волн), когда ℏωkT≪1{\displaystyle {\hbar \omega \over kT}\ll 1}, можно разложить экспоненту по ℏωkT{\displaystyle {\hbar \omega \over kT}}. В результате получим, что
- exp(ℏωkT)−1≈1+ℏωkT−1=ℏωkT,{\displaystyle \mathrm {exp} \left({\hbar \omega \over kT}\right)-1\approx 1+{\hbar \omega \over kT}-1={\hbar \omega \over kT},}
тогда (1) и (2) переходят в формулу Рэлея — Джинса.
- uω(ω,T)=kTω2π2c3,{\displaystyle u_{\omega }(\omega ,T)=kT{\frac {\omega ^{2}}{\pi ^{2}c^{3}}},} и
- Bω(ω,T)=kTω24π2c2.{\displaystyle B_{\omega }(\omega ,T)=kT{\frac {\omega ^{2}}{4\pi ^{2}c^{2}}}.}
Переход к закону Стефана — Больцмана[править | править код]
Энергетическая светимость равна площади, ограниченной графиком функции f(ω,Т)Для энергетической светимости следует записать интеграл:
- R=∫0∞ϵω(ω,T)dω=∫0∞ℏω34π2c2⋅dωexp(ℏωkT)−1.{\displaystyle R=\int _{0}^{\infty }\epsilon _{\omega }(\omega ,T)\mathrm {d} \omega =\int _{0}^{\infty }{\frac {\hbar \omega ^{3}}{4\pi ^{2}c^{2}}}\cdot {\frac {\mathrm {d} \omega }{\mathrm {exp} \left({{\hbar \omega } \over {kT}}\right)-1}}.}
Введём переменную x=ℏωkT{\displaystyle x={{\hbar \omega } \over {kT}}}, тогда
- R=ℏ4π2c2(kTℏ)4∫0∞x3⋅dxex−1.{\displaystyle R={{\hbar } \over {4\pi ^{2}c^{2}}}\left({kT \over \hbar }\right)^{4}\int _{0}^{\infty }{\frac {x^{3}\cdot \mathrm {d} x}{\mathrm {e} ^{x}-1}}.}
Полученный интеграл точно равен π4/15{\displaystyle \pi ^{4}/15}, и мы получаем известный закон Стефана — Больцмана:
- R=π2k4T460c2ℏ3=σT4.{\displaystyle R={\pi ^{2}k^{4}T^{4} \over {60c^{2}\hbar ^{3}}}=\sigma T^{4}.}
Подстановка численных значений констант даёт значение для σ=5,6704⋅10−8{\displaystyle \sigma =5,6704\cdot 10^{-8}} Вт/(м2 K4{\displaystyle ^{4}}), что хорошо согласуется с экспериментом.
Для нахождения закона, по которому происходит смещение максимума φ(λ,Т) в зависимости от температуры, надо исследовать функцию φ(λ,Т) на максимум.Для перехода к закону Вина, необходимо продифференцировать выражение (5) по λ{\displaystyle \lambda } и приравнять нулю (поиск экстремума)
- duλ(λ,T)dλ=4π2ℏc2{hckTλexp(hckTλ)−5[exp(hckTλ)−1]}λ6[exp(hckTλ)−1]2=0.{\displaystyle {\frac {\mathrm {d} u_{\lambda }(\lambda ,T)}{\mathrm {d} \lambda }}={\frac {4\pi ^{2}\hbar c^{2}\left\{{\frac {hc}{kT\lambda }}\mathrm {exp} \left({\frac {hc}{kT\lambda }}\right)-5\left[\mathrm {exp} \left({\frac {hc}{kT\lambda }}\right)-1\right]\right\}}{\lambda ^{6}\left[\mathrm {exp} \left({\frac {hc}{kT\lambda }}\right)-1\right]^{2}}}=0.}
Значение λm{\displaystyle \lambda _{m}}, при котором функция достигает максимума, обращает в нуль выражение, стоящее в фигурных скобках. Обозначив 2πℏckTλm=y{\displaystyle {\frac {2\pi \hbar c}{kT\lambda _{m}}}=y}, получим уравнение:
- yey−5(ey−1)=0.{\displaystyle ye^{y}-5(e^{y}-1)=0.}
Решение такого уравнения даёт y=4,96511…{\displaystyle y=4,96511\dots }. Следовательно,
- Tλm=2πℏcyk=b.{\displaystyle T\lambda _{m}={\frac {2\pi \hbar c}{yk}}=b.}
Численная подстановка констант даёт значение для b=0,0028777…{\displaystyle b=0,0028777\dots } К·м, совпадающее с экспериментальным, а также удобную приближённую формулу: λmT≈3000{\displaystyle \lambda _{m}T\approx 3000} мкм·К. Так, солнечная поверхность имеет максимум интенсивности в зелёной области (0,5 мкм), что соответствует температуре около 6000 К.
- ↑ Сивухин Д.В., Том 4 (Оптика), Москва 1980 г., § 117, Формула Рэлея — Джинса, формула 117.7, с. 692-694
- ↑ Савельев И. В. Курс общей физики. — М.: Наука, 1967. — Т. III. Оптика, атомная физика, элементарные частицы. — 416 с., § 52, Формула Рэлея — Джинса, формула 52.7, с. 253-258
- Планк М. Об одном улучшении закона излучения Вина. Избранные научные труды. Русский пер. из сборника под ред. А. П. Виноградова, стр.249
- Планк М. К теории распределения энергии излучения нормального спектра. Избранные научные труды. Русский пер. из сборника под ред. А. П. Виноградова, стр. 251
- Adkins, C. J. Equilibrium Thermodynamics (неопр.). — 3rd. — Cambridge University Press, 1983. — ISBN 0-521-25445-0.
- Bohr, N. (англ.)русск.. On the constitution of atoms and molecules (англ.) // Philosophical Magazine : journal. — 1913. — Vol. 26, no. 153. — P. 1—25. — DOI:10.1080/14786441308634993.
- Bohren, C. F. (англ.)русск.; Clothiaux, E. E. Fundamentals of Atmospheric Radiation (неопр.). — Wiley-VCH (англ.)русск., 2006. — ISBN 3-527-40503-8.
- Boltzmann, L. (англ.)русск.. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung, respective den Sätzen über das Wärmegleichgewicht (нем.) // Sitzungsberichte Mathematisch-Naturwissenschaftlichen Classe der kaiserlichen Akademie der Wissenschaften in Wien : magazin. — 1878. — Bd. 76, Nr. 2. — S. 373—435.
- Born, M. (англ.)русск.; Wolf, E. (англ.)русск.. Principles of Optics (неопр.). — 7th. — Cambridge University Press, 1999. — ISBN 0-521-64222-1.
- Born, M. (англ.)русск.; Jordan, P. (англ.)русск.. Zur Quantenmechanik (нем.) // Zeitschrift für Physik : magazin. — 1925. — Bd. 34. — S. 858—888. — DOI:10.1007/BF01328531. — Bibcode: 1925ZPhy…34..858B. Translated in part as «On quantum mechanics» in van der Waerden, B. L. (англ.)русск.. Sources of Quantum Mechanics (неопр.). — North-Holland Publishing, 1967. — С. 277—306.
- Bose, Satyendra Nath (англ.)русск.. Plancks Gesetz und Lichtquantenhypothese (нем.) // Zeitschrift für Physik. — 1924. — Т. 26. — С. 178—181. — DOI:10.1007/BF01327326. — Bibcode: 1924ZPhy…26..178B.
- Brehm, J. J.; Mullin, W. J. Introduction to the Structure of Matter (неопр.). — Wiley, 1989. — ISBN 0-471-60531-X.
- Brillouin, L. (англ.)русск.. Relativity Reexamined (неопр.). — Academic Press, 1970. — ISBN 978-0-12-134945-5.
- Caniou, J. Passive Infrared Detection: Theory and Applications (англ.). — Springer, 1999. — ISBN 978-0-7923-8532-5.
- Chandrasekhar, S. (англ.)русск.. Radiative Transfer (неопр.). — Revised reprint. — Dover Publications, 1960. — ISBN 978-0-486-60590-6.
- Cotton, A. The present status of Kirchhoff’s law (англ.) // The Astrophysical Journal : journal. — IOP Publishing, 1899. — Vol. 9. — P. 237—268. — DOI:10.1086/140585. — Bibcode: 1899ApJ…..9..237C.
- A. P. P.; Crova. Étude des radiations émises par les corps incandescents. Mesure optique des hautes températures (фр.) // Annales de chimie et de physique (англ.)
Постоянная Планка — Википедия
Постоя́нная Пла́нка (квант действия) — основная константа квантовой теории, коэффициент, связывающий величину энергии кванта электромагнитного излучения с его частотой, так же как и вообще величину кванта энергии любой линейной колебательной физической системы с её частотой. Связывает энергию и импульс с частотой и пространственной частотой, действие с фазой. Является квантом момента импульса. Впервые упомянута Планком в работе, посвящённой тепловому излучению, и потому названа в его честь. Обычное обозначение — латинское h{\displaystyle h}.
16 ноября 2018 года на заседании 26 Генеральной Конференции Мер и Весов были приняты изменения определений основных единиц СИ, предложенные в 2018 году Международным комитетом мер и весов. Новые определения СИ вступили в силу 20 мая 2019[1]. В соответствии с резолюцией XXVI ГКМВ постоянная Планка ℎ в точности равна 6,626 070 15⋅10−34 кг·м2·с−1
В квантовой механике импульс имеет физический смысл волнового вектора[источник не указан 694 дня], энергия — частоты, а действие — фазы волны, однако традиционно (исторически) механические величины измеряются в других единицах (кг·м/с, Дж, Дж·с), чем соответствующие волновые (м
- p=ℏk(|p|=2πℏ/λ){\displaystyle \mathbf {p} =\hbar \mathbf {k} \,\,\,(|\mathbf {p} |=2\pi \hbar /\lambda )} (импульс),
- E=ℏω{\displaystyle E=\hbar \omega } (энергия),
- S=ℏϕ{\displaystyle S=\hbar \phi } (действие).
Если бы система физических единиц формировалась уже после возникновения квантовой механики и приспосабливалась для упрощения основных теоретических формул, константа Планка вероятно просто была бы сделана равной единице, или, во всяком случае, более круглому числу. В теоретической физике очень часто для упрощения формул используется система единиц с ℏ=1{\displaystyle \hbar =1}, в ней
- p=k(|p|=2π/λ),{\displaystyle \mathbf {p} =\mathbf {k} \,\,\,(|\mathbf {p} |=2\pi /\lambda ),}
- E=ω,{\displaystyle E=\omega ,}
- S=ϕ,{\displaystyle S=\phi ,}
- (ℏ=1).{\displaystyle (\hbar =1).}
Постоянная Планка имеет и простую оценочную роль в разграничении областей применимости классической и квантовой физики. В сравнении с величиной характерных для рассматриваемой системы величин действия или момента импульса, или произведений характерного импульса на характерный размер, или характерной энергии на характерное время, — постоянная Планка показывает, насколько применима к данной физической системе классическая механика. А именно, если S{\displaystyle S}— действие системы, а M{\displaystyle M}— её момент импульса, то при Sℏ≫1{\displaystyle {\frac {S}{\hbar }}\gg 1} или Mℏ≫1{\displaystyle {\frac {M}{\hbar }}\gg 1} поведение системы с хорошей точностью описывается классической механикой. Эти оценки достаточно прямо связаны с соотношениями неопределённостей Гейзенберга.
Формула Планка для теплового излучения[править | править код]
Формула Планка — выражение для спектральной плотности мощности излучения абсолютно чёрного тела, которое было получено Максом Планком для равновесной плотности излучения u(ω,T){\displaystyle u(\omega ,T)}. Формула Планка была получена после того, как стало ясно, что формула Рэлея — Джинса удовлетворительно описывает излучение только в области длинных волн. В 1900 году Планк предложил формулу с постоянной (впоследствии названной постоянной Планка), которая хорошо согласовывалась с экспериментальными данными. При этом Планк полагал, что данная формула является всего лишь удачным математическим трюком, но не имеет физического смысла. То есть Планк не предполагал, что электромагнитное излучение испускается в виде отдельных порций энергии (квантов), величина которых связана с циклической частотой излучения выражением:
- ε=ℏω.{\displaystyle \varepsilon =\hbar \omega .}
Коэффициент пропорциональности ħ впоследствии назвали постоянной Дирака, ħ ≈ 1,054⋅10−34 Дж·с.
Фотоэффект[править | править код]
Фотоэффект — это испускание электронов веществом под действием света (и, вообще говоря, любого электромагнитного излучения). В конденсированных веществах (твёрдых и жидких) выделяют внешний и внутренний фотоэффект.
Фотоэффект был объяснён в 1905 году Альбертом Эйнштейном (за что в 1921 году он, благодаря номинации шведского физика Озеена, получил Нобелевскую премию) на основе гипотезы Планка о квантовой природе света. В работе Эйнштейна содержалась важная новая гипотеза — если Планк предположил, что свет излучается только квантованными порциями, то Эйнштейн уже считал, что свет и существует только в виде квантованных порций. Из закона сохранения энергии, при представлении света в виде частиц (фотонов), следует формула Эйнштейна для фотоэффекта:
- ℏω=Aout+mv22,{\displaystyle \hbar \omega =A_{out}+{\frac {mv^{2}}{2}},}
где Aout{\displaystyle A_{out}} — т. н. работа выхода (минимальная энергия, необходимая для удаления электрона из вещества), mv22{\displaystyle {\frac {mv^{2}}{2}}} — кинетическая энергия вылетающего электрона, ω{\displaystyle \omega } — частота падающего фотона с энергией ℏω,{\displaystyle \hbar \omega ,} ℏ{\displaystyle \hbar } — постоянная Планка. Из этой формулы следует существование красной границы фотоэффекта, то есть существование наименьшей частоты, ниже которой энергии фотона уже недостаточно для того, чтобы «выбить» электрон из тела. Суть формулы заключается в том, что энергия фотона расходуется на ионизацию атома вещества, то есть на работу, необходимую для «вырывания» электрона, а остаток переходит в кинетическую энергию электрона.
Эффект Комптона[править | править код]
Переопределение[править | править код]
На XXIV Генеральной конференции по мерам и весам (ГКМВ) 17—21 октября 2011 года была единогласно принята резолюция[2], в которой, в частности, предложено в будущей ревизии Международной системы единиц (СИ) переопределить единицы измерений СИ таким образом, чтобы постоянная Планка была равной точно 6,62606X⋅10−34 Дж·с, где Х заменяет одну или более значащих цифр, которые будут определены в дальнейшем на основании наиболее точных рекомендаций CODATA[3]. В этой же резолюции предложено таким же образом определить как точные значения постоянную Авогадро, элементарный заряд и постоянную Больцмана. XXV ГКМВ, состоявшаяся в 2014 году, приняла решение продолжить работу по подготовке новой ревизии СИ, включающей привязку основных единиц СИ к точному значению постоянной Планка, и предварительно наметила закончить эту работу к 2018 году с тем, чтобы заменить существующую СИ обновлённым вариантом на XXVI ГКМВ[4]. В 2019 году постоянная Планка получила фиксированное значение как и постоянная Больцмана, постоянная Авогадро и другие[5].
Значения постоянной Планка[править | править код]
Ранее постоянная Планка была экспериментально измеряемой величиной, точность известного значения которой постоянно повышалась. В результате изменений СИ 2019 года было принято фиксированное точное значение постоянной Планка:
- h = 6,626 070 15 × 10−34Дж·c[6];
- h = 6,626 070 15 × 10−27эрг·c;
- h = 4,135 667 669… × 10−15эВ·c[6].
Это значение является составной частью определения Международной системы единиц.
Часто применяется величина ℏ≡h3π{\displaystyle \hbar \equiv {\frac {h}{2\pi }}}:
- ħ = 1,054 571 817… × 10−34Дж·c[6];
- ħ = 1,054 571 817… × 10−27эрг·c;
- ħ = 6,582 119 569… × 10−16эВ·c[6],
называемая редуцированной (иногда рационализированной или приведённой) постоянной Планка или постоянной Дирака. Применение этого обозначения упрощает многие формулы квантовой механики, так как в эти формулы традиционная постоянная Планка входит в виде деленной на константу 2π{\displaystyle {2\pi }}.
В ряде естественных систем единиц является единицей измерения действия[7]. В планковской системе единиц, также относящейся к естественным системам, служит в качестве одной из основных единиц системы.
Использование законов фотоэффекта[править | править код]
При данном способе измерения постоянной Планка используется закон Эйнштейна для фотоэффекта:
- Kmax=hν−A,{\displaystyle K_{max}=h\nu -A,}
где Kmax{\displaystyle K_{max}} — максимальная кинетическая энергия вылетевших с катода фотоэлектронов,
- ν{\displaystyle \nu } — частота падающего света,
- A{\displaystyle A} — т. н. работа выхода электрона.
Измерение проводится так. Сначала катод фотоэлемента облучают монохроматическим светом с частотой ν1{\displaystyle \nu _{1}}, при этом на фотоэлемент подают запирающее напряжение, так, чтобы ток через фотоэлемент прекратился. При этом имеет место следующее соотношение, непосредственно вытекающее из закона Эйнштейна:
- hν1=A+eU1,{\displaystyle h\nu _{1}=A+eU_{1},}
где e{\displaystyle e} — заряд электрона.
Затем тот же фотоэлемент облучают монохроматическим светом с частотой ν2{\displaystyle \nu _{2}} и точно так же запирают его с помощью напряжения U2:{\displaystyle U_{2}:}
- hν2=A+eU2.{\displaystyle h\nu _{2}=A+eU_{2}.}
Почленно вычитая второе выражение из первого, получаем
- h(ν1−ν2)=e(U1−U2),{\displaystyle h(\nu _{1}-\nu _{2})=e(U_{1}-U_{2}),}
откуда следует
- h=e(U1−U2)(ν1−ν2).{\displaystyle h={\frac {e(U_{1}-U_{2})}{(\nu _{1}-\nu _{2})}}.}
Анализ спектра тормозного рентгеновского излучения[править | править код]
Этот способ считается самым точным из существующих. Используется тот факт, что частотный спектр тормозного рентгеновского излучения имеет точную верхнюю границу, называемую фиолетовой границей. Её существование вытекает из квантовых свойств электромагнитного излучения и закона сохранения энергии. Действительно,
- hcλ=eU,{\displaystyle h{\frac {c}{\lambda }}=eU,}
где c{\displaystyle c} — скорость света,
- λ{\displaystyle \lambda } — длина волны рентгеновского излучения,
- e{\displaystyle e} — заряд электрона,
- U{\displaystyle U} — ускоряющее напряжение между электродами рентгеновской трубки.
Тогда постоянная Планка равна
- h=λUec.{\displaystyle h={\frac {{\lambda }{Ue}}{c}}.}
Планковские единицы — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 февраля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 15 февраля 2019; проверки требует 1 правка.Пла́нковские едини́цы — система единиц измерения, одна из естественных систем единиц. Предложена в 1901 году немецким физиком Максом Планком и названа в его честь[1].
Система планковских единиц не имеет широкого распространения не только потому, что величины входящих в неё единиц очень далеки от практики, но и, главным образом, потому что в этой системе уравнения теоретической физики не получают упрощения[2].
Ныне под планковской системой понимается система единиц, в которой в качестве основных единиц выбраны следующие фундаментальные физические постоянные[3]:
При этом значение коэффициента пропорциональности в законе Кулона выбрано равным единице[4].
Обычно, говоря о планковской системе, указывают, что в этом случае выполняется c=1,{\displaystyle c=1,} ℏ=1,{\displaystyle \hbar =1,} k=1{\displaystyle k=1} и G=1.{\displaystyle G=1.} Однако в действительности такая форма записи не точна. Она отражает лишь то, что соответствующая постоянная выбрана в качестве меры. Следует иметь в виду, что в планковской системе размерности отнюдь не исчезают, скорее наоборот, они приобретают фундаментальный характер, поскольку составляются из фундаментальных постоянных[4].
Из основных планковских единиц выводятся все остальные (производные) единицы системы, часть из которых приведена ниже. Значения c,G,ℏ{\displaystyle c,\,G,\,\hbar } и k{\displaystyle k} в единицах Международной системы единиц (СИ), использованные в расчётах, рекомендованы CODATA[5].
- Планковская масса mP=ℏcG≈2,176434(24)×10−8{\displaystyle m_{\text{P}}={\sqrt {\frac {\hbar c}{G}}}\approx 2{,}176434(24)\times 10^{-8}} кг.
- Планковская длина lP=ℏmPc=ℏGc3≈1,616255(18)×10−35{\displaystyle l_{\text{P}}={\frac {\hbar }{m_{\text{P}}c}}={\sqrt {\frac {\hbar G}{c^{3}}}}\approx 1{,}616255(18)\times 10^{-35}} м.
- Планковское время tP=lPc=ℏGc5≈5,391247(60)×10−44{\displaystyle t_{\text{P}}={\frac {l_{\text{P}}}{c}}={\sqrt {\frac {\hbar G}{c^{5}}}}\approx 5{,}391247(60)\times 10^{-44}} с.
- Планковское ускорение aP=lPtP2=ctP≈5,561×1051{\displaystyle a_{\text{P}}={\frac {l_{\text{P}}}{t_{\text{P}}^{2}}}={\frac {c}{t_{\text{P}}}}\approx 5{,}561\times 10^{51}} м/с2.
- Планковская энергия EP=mPc2=ℏtP=ℏc5G≈1,9561×109{\displaystyle E_{\text{P}}=m_{\text{P}}c^{2}={\frac {\hbar }{t_{\text{P}}}}={\sqrt {\frac {\hbar c^{5}}{G}}}\approx 1{,}9561\times 10^{9}} Дж.
- Планковская температура TP=EPk=ℏc5k2G≈1,416784(16)×1032{\displaystyle T_{\text{P}}={\frac {E_{\text{P}}}{k}}={\sqrt {\frac {\hbar c^{5}}{k^{2}G}}}\approx 1{,}416784(16)\times 10^{32}} К.
- Планковский заряд qP=4πε0ℏc=2chε0=eα≈1,8755459×10−18{\displaystyle q_{\text{P}}={\sqrt {4\pi \varepsilon _{0}\hbar c}}={\sqrt {2ch\varepsilon _{0}}}={\frac {e}{\sqrt {\alpha }}}\approx 1{,}8755459\times 10^{-18}} Кл, где e{\displaystyle e} — элементарный электрический заряд, α{\displaystyle \alpha } — постоянная тонкой структуры, h{\displaystyle h} — постоянная Планка. Соответственно, постоянная тонкой структуры — это квадрат заряда электрона, выраженного в планковских зарядах.
- Планковский ток IP=qP/tP=c64πε0/G=2c3πε0/G≈3,4789×1025{\displaystyle I_{\text{P}}=q_{\text{P}}/t_{\text{P}}={\sqrt {c^{6}4\pi \varepsilon _{0}/G}}=2c^{3}{\sqrt {\pi \varepsilon _{0}/G}}\approx 3{,}4789\times 10^{25}} А.
- Планковская сила FP=mPctP=c4G=1,21027×1044{\displaystyle F_{\text{P}}={\frac {m_{\text{P}}c}{t_{\text{P}}}}={\frac {c^{4}}{G}}=1{,}21027\times 10^{44}} Н.
- Планковское давление
- Планковская угловая частота ωP=1tP=c5ℏG≈1,85487×1043{\displaystyle \omega _{\text{P}}={\frac {1}{t_{\text{P}}}}={\sqrt {\frac {c^{5}}{\hbar G}}}\approx 1{,}85487\times 10^{43}} c−1.
- Планковская мощность (или светимость) LP=mPc2tP=c5G≈3,62831⋅1052{\displaystyle L_{\mathrm {P} }={\frac {m_{\text{P}}c^{2}}{t_{\text{P}}}}={\frac {c^{5}}{G}}\approx 3{,}62831\cdot 10^{52}} Вт.
Система планковских единиц впервые предложена в 1899 году Максом Планком на основе скорости света c{\displaystyle c}, гравитационной постоянной G{\displaystyle G} и двух ввёденных им новых постоянных теории теплового излучения a{\displaystyle a} и b{\displaystyle b} (они отличаются от современных постоянных hk{\displaystyle {\frac {h}{k}}} и h{\displaystyle h} на безразмерные множители)[6]. Первоначально планковские единицы были введены в докладе, сделанном 18 мая 1899 года на заседании Академии наук в Берлине и посвящённом обзору теории явлений теплового излучения, рассматриваемых с точки зрения электромагнитной теории света, и значению второго начала термодинамики в ней.
Все до сих пор используемые системы единиц, в том числе так называемая абсолютная СГС-система, обязаны своим происхождением пока что случайному стечению обстоятельств, поскольку выбор единиц, лежащих в основе каждой системы, сделан не исходя из общей точки зрения, обязательно приемлемой для всех мест и времен, но исключительно исходя из потребностей нашей земной культуры… В связи с этим представляло бы интерес заметить, что, используя обе постоянные a{\displaystyle a} и b{\displaystyle b}… мы получаем возможность установить единицы длины, массы, времени и температуры, которые не зависели бы от выбора каких-либо тел или веществ и обязательно сохраняли бы своё значение для всех времен и для всех культур, в том числе и внеземных и нечеловеческих, и которые поэтому можно было бы ввести в качестве «естественных единиц измерений».
— Планк М. Избранные труды. М.: Наука, 1975. С. 232.
В 1900 году Макс Планк предложил новый закон излучения (закон Планка), в котором фигурировали две новые постоянные h{\displaystyle h} и k.{\displaystyle k.} В 1901 году Планком была предложена система на основе постоянных c,{\displaystyle c,} G,{\displaystyle G,} h{\displaystyle h} и k{\displaystyle k}[1].
Институт физики Общества Макса Планка — Википедия
Материал из Википедии — свободной энциклопедии
Институт физики Общества Макса Планка (нем. Max-Planck-Institut für Physik) — научно-исследовательский институт общества Макса Планка, расположенный в Мюнхене (Бавария, Германия), специализирующийся в области физики элементарных частиц и астрофизики. Институт является частью общества Макса Планка, также известен как институт Вернера Гейзенберга, его первого руководителя в Мюнхене.
Идея создания института возникла в 1914 году и принадлежала немецким учёным Фрицу Габеру, Вальтеру Нернсту, Максу Планку, Эмилю Варбургу и Генриху Рубенсу[1].
1 октября 1917 года институт был официально учреждён в Берлине. Альберт Эйнштейн стал его первым директором. В октябре 1922 года А. Эйнштейна сменил Макс фон Лауэ в должности управляющего директора. Эйнштейн отказался от должности директора института в апреле 1933 года. В июне 1942 года должность директора занял Вернер Гейзенберг.
После окончания Второй мировой войны, в 1946 году институт был переведён из Берлина в Гёттинген и переименован в Институт физики Макса Планка. Вернер Гейзенберг остался его директором. В 1946 году Карл Фридрих фон Вайцзеккер и Карл Виртц стали руководителями отделений теоретической и экспериментальной физики соответственно.
В 1955 институт переехал в Мюнхен и вскоре началось строительство нынешнего здания. Институт переехал к него 1 сентября 1958 года и стал называться Институтом физики и астрофизики Макса Планка.
В 1991 году институт был разделён на Институт физики общества Макса Планка, Институт астрофизики Общества Макса Планка и Институт внеземной физики Общества Макса Планка.
В настоящее время является одним из ведущих мировых научно-исследовательских институтов в области физики элементарных частиц. Финансируется из федерального (50 %) и земельного (50 %) бюджета.
Директорами института физики общества Макса Планка в разные годы были:
Планковская масса — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 июля 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 июля 2019; проверки требует 1 правка.Ма́сса Пла́нка (максима[1], планковская масса) — единица массы в планковской системе единиц, обозначается MP{\displaystyle M_{P}}. Частица с такой массой имеет гравитационный радиус в π{\displaystyle \pi } раз меньше комптоновской длины волны λ^=πrs.{\displaystyle {\hat {\lambda }}=\pi r_{s}.}
- MP=ℏcG{\displaystyle M_{P}={\sqrt {\frac {\hbar c}{G}}}} ≈ 1,2209⋅1019ГэВ/c²[2] = 2,176⋅10−8кг.
На 2014 год рекомендованное международным комитетом CODATA значение массы Планка равно 2,176 470(51)⋅10−8 кг[3].
На 2018 год рекомендованное международным комитетом CODATA значение массы Планка равно 2,176 434(24)⋅10−8 кг[4].
В физике элементарных частиц и космологии используется величина
- ℏc8πG{\displaystyle {\sqrt {\frac {\hbar {}c}{8\pi G}}}} ≈ 4,340 мкг = 2,43⋅1018 ГэВ/c²,
которая называется редуцированной массой Планка. Коэффициент 1/8π{\displaystyle {\sqrt {1/8\pi }}} позволяет упростить некоторые формулы.
В отличие от большинства[5] других планковских величин, масса Планка близка к привычным для человека масштабам: так, блоха имеет массу от 4000 до 5000 MP.
Гипотетическая частица, масса которой равна планковской массе, называется максимон.
Доказано, что планковская масса является нижним пределом масс чёрных дыр, и предполагается, что она представляет собой верхний предел для масс элементарных частиц[6].
В физике есть масштаб энергий, связанный с гравитацией и равный массе Планка[7].
- ↑ Космологическое начало мира. Изменяются ли мировые постоянные?
- ↑ Max Camenzind. Compact Objects in Astrophysics: White Dwarfs, Neutron Stars and Black Holes. — Springer Science & Business Media, 2007. — P. 588. — 706 p. — ISBN 3540499121, 9783540499121.
- ↑ Planck mass (англ.). CODATA Internationally recommended 2014 values of the Fundamental Physical Constants. NIST (2014). Дата обращения 31 октября 2016.
- ↑ Planck mass (англ.). CODATA Internationally recommended 2014 values of the Fundamental Physical Constants. NIST (2018). Дата обращения 22 октября 2019.
- ↑ Другие планковские единицы, близкие к обычным человеческим масштабам — планковский импульс, равный 6,52485 кг·м/с; планковская энергия, равная 1.956⋅109Дж или 543.3 кВт·ч; планковское сопротивление, равное 29.9792458 Ом.
- ↑ Томилин К. А. Планковские величины // 100 лет квантовой теории. История. Физика. Философия : Труды международной конференции. — М.: НИА-Природа, 2002. — С. 11.
- ↑ Долгожданное открытие: бозон Хиггса. Вместо заключения: в поисках «новой физики» — Наука и жизнь. — № 10, 2012 г.
ПЛАНКА ЗАКОН ИЗЛУЧЕНИЯ • Большая российская энциклопедия
-

-

-

В книжной версии
Том 26. Москва, 2014, стр. 353
-

Скопировать библиографическую ссылку:
Авторы: А. В. Масалов
ПЛА́НКА ЗАКО́Н ИЗЛУЧЕ́НИЯ, описывает спектральное распределение энергии электромагнитного излучения, находящегося в тепловом равновесии с веществом при заданной температуре. Идеализированной моделью равновесного излучения служит электромагнитное поле внутри полости, расположенной в нагретом веществе, при условии, что стенки вещества непрозрачны для излучения. Спектр такого равновесного излучения называют спектром излучения абсолютно чёрного тела. Объёмная плотность энергии излучения $u_ω$, приходящейся на единичный интервал частот $ω$, выражается т. н. формулой Планка:$$u_ω=\frac{ω^2}{π^2 c^2}\cdot\frac{\hbar ω}{e^{\hbar ω/kT}-1},$$ где $T$ – абсолютная темп-ра, $k$ – постоянная Больцмана, $c$ – скорость света, $\hbar$ – постоянная Планка. Т. о., по спектру излучения абсолютно чёрного тела можно определить его термодинамич. темп-ру. Эта формула была выведена М. Планком в 1900 в результате рассмотрения баланса обмена энергией между двумя видами осцилляторов: частицами вещества, поглощающими и испускающими излучение на частоте $ω$, и осцилляторами, представляющими электромагнитное поле той же частоты. Планк предположил, что такие осцилляторы могут находиться только в состояниях с дискретной энергией и обмениваются между собой квантами энергии величиной $Δ\mathscr {E}=\hbar ω$. Значение коэф. пропорциональности $\hbar$ между частотой осциллятора и величиной кванта энергии Планк установил исходя из эксперим. данных: $\hbar$=1,054·10–34 Дж·с. Предположение о дискретном наборе возможных значений энергии осцилляторов поля ($0, \hbar ω, 2\hbar ω, 3\hbar ω, …$) стало впоследствии основанием для введения понятия кванта электромагнитного излучения (фотона).

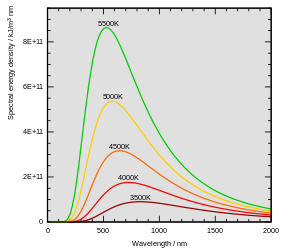
Спектры излучения абсолютно чёрного тела при различных температурах.
Спектральная плотность энергии может быть рассчитана также для др. характеристик излучения – частоты $ν=ω/2π$ или длины волны $λ=c/ν= 2πc/ω$. Тогда формула Планка приобретает вид (здесь $h=2π\hbar$): $$u_v=\frac{8πhv^3}{c^3}\cdot\frac{1}{e^{hv/kT}-1}$$ или $$u_λ=\frac{8πhc}{λ^5}\cdot\frac{1}{e^{hc/λkT}-1}.$$ Зависимость спектральной плотности энергии от длины волны излучения представлена на рисунке.
Для вывода формулы Планка необходим подсчёт числа осцилляторов излучения, приходящихся на единичный интервал частот; эта величина для единичного объёма составляет $ω/π^2c^3$. Если принять, что ср. энергия осциллятора поля равна $kT$, как это следует из Больцмана распределения для непрерывного набора возможных значений энергии, то для плотности энергии излучения $u_ω$ получится формула Рэлея – Джинса (см. Рэлея – Джинса закон излучения):$$u_ω=\frac{ω^2}{π^2 c^3}\cdot kT.$$ Формула Рэлея – Джинса применима только для малых частот ($\hbar ω≪kT$), т. к. она предсказывает неограниченный рост плотности энергии, а значит, и полной энергии излучения, с ростом частоты (т. н. ультрафиолетовая катастрофа), что находится в противоречии с эксперим. данными. Именно для снятия этого противоречия М. Планк выдвинул предположение о дискретном наборе энергий осциллятора электромагнитного поля; полученная им формула хорошо согласуется с эксперим. данными.
Формула Планка конкретизирует весьма общее соотношение для плотности энергии равновесного излучения, установленное В. Вином (см. Вина закон смещения), и согласуется с установленным ранее Стефана – Больцмана законом излучения, утверждающим, что полная (по всем частотам) плотность энергии пропорциональна четвёртой степени темп-ры.
Хотя формула Планка выведена для описания равновесного излучения в полости нагретого вещества, она оказывается пригодной и для описания спектрального распределения лучистой энергии, испускаемой реальными телами в окружающее пространство. Регистрация спектров излучения звёзд и их сопоставление с формулой Планка является осн. методом установления темп-ры их поверхности. Этим способом можно измерять также темп-ру нагретых тел в земных условиях, что особенно важно для раскалённых металлов и керамик, где неприменимы традиц. датчики темп-ры. П. з. и. используют для описания потоков лучистой энергии в эталонах яркости излучения, необходимых для абсолютной калибровки приёмников света.
Планковская длина — Википедия
Материал из Википедии — свободной энциклопедии
Планковская длина (обозначаемая ℓP {\displaystyle \ell _{P}\ }) — единица длины в планковской системе единиц, равная в Международной системе единиц (СИ) примерно 1,6⋅10−35 метров. Планковская длина — естественная единица длины, поскольку в неё входят только фундаментальные константы: скорость света, постоянная Планка и гравитационная постоянная.
Планковская длина равна:
- ℓP=ℏGc3{\displaystyle \ell _{P}={\sqrt {\frac {\hbar G}{c^{3}}}}} ≈ 1,616 229(38)⋅10−35 м[1][2][3],
где:
Две последние цифры в скобках означают неопределённость (стандартное отклонение) последних двух разрядов[4][5].
Примерный радиус наблюдаемой Вселенной (14,3 миллиарда парсек или 4,4⋅1026 м) равен 27⋅1060 планковских длин.
С точностью до множителя π, планковская масса равна массе чёрной дыры, радиус Шварцшильда которой равен её комптоновской длине волны. Радиус такой чёрной дыры будет по порядку величины равен планковской длине.
Планковская длина (и связанное с ней планковское время) определяют масштабы, на которых современные физические теории перестают работать: геометрия пространства-времени, предсказанная Общей теорией относительности, на планковской длине перестает иметь смысл. Эти масштабы хранят еще неоткрытую теорию, объединяющую Общую теорию относительности и квантовую механику, которая сможет наиболее полно описать законы физики. Именно по этой причине современные описания развития Вселенной начинаются только когда Вселенная была размером 1,616•10-35 метров[6].
Частица массой m{\displaystyle m} имеет приведённую комптоновскую длину волны
- λ¯C=λC2π=ℏmc.{\displaystyle {\overline {\lambda }}_{C}={\frac {\lambda _{C}}{2\pi }}={\frac {\hbar }{mc}}.}
С другой стороны радиус Шварцшильда той же частицы равен
- rg=2Gmc2=2Gc3mc.{\displaystyle r_{g}={\frac {2Gm}{c^{2}}}=2\,{\frac {G}{c^{3}}}\,mc.}
Произведение этих величин всегда постоянно и равно
- rgλ¯C=2Gc3ℏ=2ℓP2.{\displaystyle r_{g}{\overline {\lambda }}_{C}=2\,{\frac {G}{c^{3}}}\,\hbar =2\ell _{P}^{2}.}
Квантование пространства и планковская длина[править | править код]
В середине прошлого века гипотеза о квантовании пространства-времени[7] на пути объединения квантовой механики и общей теории относительности привела к предположению о том, что существуют ячейки пространства-времени с минимально возможной длиной, равной фундаментальной длине[8]. Согласно этой гипотезе, степень влияния квантования пространства на проходящий свет зависит от размеров ячейки. Для исследования необходимо интенсивное излучение, прошедшее как можно большее расстояние. В настоящее время группа ученых воспользовалась данными съёмки гамма-вспышки GRB 041219A, осуществленной с европейского космического телескопа Integral. Гамма-вспышка GRB 041219A вошла в 1% самых ярких гамма-вспышек за весь период наблюдения, а расстояние до её источника не менее 300 миллионов световых лет. Наблюдение «Интеграла» позволило оценить размер ячейки на несколько порядков точнее, чем все предыдущие опыты такого плана. Анализ данных показал — если зернистость пространства вообще существует, то она должна быть на уровне 10−48 метров или меньше[9].
- ↑ В скобках указано стандартное отклонение. Таким образом, значение планковской длины можно представить в следующих формах:
ℓP{\displaystyle \ell _{P}} ≈ 1,616 229(38) · 10−35 м =
= (1,616 229 ± 0,000 038) · 10−35 м =
= [1,616191 ÷ 1,616267] · 10−35 м - ↑ Fundamental Phisical Constants. Planck length (англ.). Constants, Units & Uncertainty. NIST. Дата обращения 8 марта 2019.
- ↑ PML.
- ↑ Постнов, 2001.
- ↑ Томилин, 2002.
- ↑ Гильен.
- ↑ Григорьев В.И. Квантование пространства-времени. Большая Советская Энциклопедия, 1987
- ↑ Киржниц Д.А. Фундаментальная длина. Большая Советская Энциклопедия, 1987
- ↑ P. Laurent, D. Götz, P. Binétruy, S. Covino, A. Fernandez-Soto. Constraints on Lorentz Invariance Violation using integral/IBIS observations of GRB041219A // Physical Review D. — 2011-06-28. — Т. 83, вып. 12. — С. 121301. — DOI:10.1103/PhysRevD.83.121301.
- Max Camenzind. Compact Objects in Astrophysics: White Dwarfs, Neutron Stars and Black Holes. — Springer Science & Business Media, 2007. — P. 588. — 706 p. — ISBN 3540499121, 9783540499121.
- Каплан, С. А. Размерности и подобие астрофизических величин / С. А. Каплан, Э. А. Дибай. — М. : Наука, 1976. — § 8.4 : Космологическое начало мира. Изменяются ли мировые постоянные?. — 398 с.
- Постнов, К. А. Лекции по Общей Астрофизике для Физиков : [арх. 16 апреля 2013]. — М. : МГУ, 2001. — 1.5 : Планковские единицы.
- Томилин, К. А. Планковские величины // 100 лет квантовой теории : История. Физика. Философия : Труды международной конференции. — М. : НИА-Природа, 2002. — С. 105—113.
- Мигдал, А. Б. Квантовая физика для больших и маленьких. — М. : Наука, 1989. — С. 116-117. — (Библиотека «Квант» ; вып. 75).
- Дирак, П. А. М. Общая теория относительности. — М. : Атомиздат, 1978.
- Мизнер, Р. Гравитация = Charly W. Misner, Kip S. Thorn, John Archibald Wheeler. Gravitation. San Francisco: W. H. Freeman and Company, 1973. : [пер. с англ.] / Р. Мизнер, К. Торн, Дж. Уилер. — М. : Мир, 1977. — Т. 3. — УДК 530.12+523.112(G).