Как найти Масштаб в Математике?
Понятие масштаба
Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.
Масштаб — это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.
Другими словами, масштабом называют отношение длины отрезка на карте к длине соответствующего отрезка на местности.
- Например, одна тысячная (1:1000) означает, что все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Масштаб бывает трех видов:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м — это величина масштаба;
- линейный, зная величину масштаба, можно определить расстояния.
Определение масштаба на карте
На математике в 6 классе обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.
Нужно потратить очень много сил, чтобы изобразить дом в натуральную величину, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.
Масштаб — это отношение размера изображения к размеру изображаемого объекта.
Масштаб карты — это отношение длины отрезка на карте к его действительной длине на местности.
На карте Российской Федерации указан масштаб (1 : 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на местности этот отрезок составит 15 км.
Численные масштабы карт и соответствующие им масштабы на местности:
Масштаб 1 : 100 000
- 1 мм на карте — 100 м (0,1 км) на местности
- 1 см на карте — 1000 м (1 км) на местности
- 10 см на карте — 10000 м (10 км) на местности
Масштаб 1 : 10000
- 1 мм на карте — 10 м (0,01 км) на местности
- 1 см на карте — 100 м (0,1 км) на местности
- 10 см на карте — 1000 м (1 км) на местности
Масштаб 1 : 5000
- 1 мм на карте — 5 м (0,005 км) на местности
- 1 см на карте — 50 м (0,05 км) на местности
- 10 см на карте — 500 м (0,5 км) на местности
Масштаб 1 : 2000
- 1 мм на карте — 2 м (0,002 км) на местности
- 1 см на карте — 20 м (0,02 км) на местности
- 10 см на карте — 200 м (0,2 км) на местности
Масштаб 1 : 1000
- 1 мм на карте — 100 см (1 м) на местности
- 1 см на карте — 1000 см (10 м) на местности
- 10 см на карте — 100 м на местности
Масштаб 1 : 500
- 1 мм на карте — 50 см (0,5 метра) на местности
- 1 см на карте — 5 м на местности
- 10 см на карте — 50 м на местности
Масштаб 1 : 200
- 1 мм на карте — 0,2 м (20 см) на местности
- 1 см на карте — 2 м (200 см) на местности
- 10 см на карте — 20 м (0,2 км) на местности
Масштаб 1 : 100
- 1 мм на карте — 0,1 м (10 см) на местности
- 1 см на карте — 1 м (100 см) на местности
- 10 см на карте — 10м (0,01 км) на местности
Решение задач на масштаб
Для закрепления темы решим несколько математических задач на масштаб за 6 класс.
Как решаем:
8 см — это 1 часть
8 * 10 000 = 80 000 (см) — это 10 000 частей
80 000 см = 800 м
Ответ: 800 м
Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1:5000000.
Как решаем:
400 км = 400 000 м = 40 000 000 см
40000000 : 5000000 = 40 : 5 = 8
Ответ: 8 см
Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить в виде отрезка длиной в 14 см?
Как решаем:
700 км = 700 000 м = 70 000 000 см
70 000 000 : 14 = 5 000 000
Ответ: уменьшить в 5 000 000 раз.
Еще больше практики — в детской школе Skysmart. Ученики занимаются на интерактивной платформе, в комфортном темпе и с поддержкой внимательных учителей.
Чтобы ребенок занимался математикой в удовольствие и чувствовал себя увереннее в школе, запишите его на бесплатный вводный урок. Познакомим с форматом и вдохновим на учебу!
Урок математики 6 класс тема «масштаб» цели
ПЕРЕПЕЛИЦА НАТАЛЬЯ ВАСИЛЬЕВНА
Учитель математики и информатики
Муниципальное бюджетное общеобразовательное учреждение Богородицкая средняя общеобразовательная школа № 20
2012-2014 учебный год
Урок математики 6 класс
Тема: «Масштаб»
Цели:
1.Организовать деятельность учащихся для закрепления понятия
«масштаб», решение задач с помощью пропорции. Рассмотреть связь
математики с географией и различными областями жизни.
2. Способствовать развитию памяти, вычислительных навыков,
логического мышления, общеучебных навыков, математически
грамотной речи, умения сравнивать
и обобщать.
3. Помогать учащимся воспитывать трудолюбие, умение общаться,
аккуратность.
Типы урока:
Совершенствование знаний, умений, навыков при решении задач с
использованием масштаба.
Методы обучения:
Наглядный, практический, словесный.
Формы:
Общеклассная, групповая, парная, дифференцированная.
Ход урока.
Организационный момент отсутствующие.
Добрый день, друзья!
Я рада встречи с вами!
Хотела объявить тему урока, но все буквы рассыпались, помогите собрать:
«ТАБШМАС» (масштаб)
Наш урок – «Путешествие по карте»
Цели урока: (Формулируют учащиеся).
Закрепить понятие масштаба карты, научиться решать задачи с
помощью пропорции при заданном масштабе, установить связь
математики с другими предметами.
Актуализация опорных знаний.
Чтобы не ошибиться при решении задач вы должны быстро и без ошибочно выполнить действия, вычислять.
На столе лежат задания для быстрого счёта. Учащиеся работают максимум две минуты. Затем выполняют самопроверку, сопоставляя свои решения с
решениями на доске.( на обратной стороне доски).
Оценивают по критериям:
9-10 заданий – «5»
8 заданий – «4»
6 -7 заданий – «3»
Чтобы отправляться в путешествие по карте нужно иметь некоторые
специальные знания, например, масштаб.
Где вы встречались с понятием «масштаб»? (на уроках географии виды и обозначения и по таблице.)
Что такое масштаб?
(Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.)
Масштаб (немецкий tab-мера, stab-палка)
При решении задач не забывайте о правильном её оформлении.
Задача:
На карте – 10см.
Местность — ?см.
Масштаб – 1:500000
Решение:
Пусть Х см – длина отрезка на местности, тогда составим
уравнение:
10 : Х = 1 : 500000
Тогда, Х = 10 500000 = 5000000
5000000 см = 50 км
Ответ: 50 км длина отрезка на местности.
3. Обучающий этап.
1. Работа с картой (устно)
Рассмотрим 3 карты Москвы. (Атлас 6 класса, страница 25)
Попробуйте объяснить сходство и различие карт.
(Сходство в том, что карты одной и той же территории, различие: сделана в
разных масштабах.)
Вывод: с уменьшением масштаба карты – увеличивается площадь
изображенной территории (1:1000000 уменьшается)
2.Следующая карта, которую мы рассмотрим
– это карта России (стр.
Каждому ряду предлагается задание. У работающих у доски есть прверяющие
с соответствующего ряда.
1 ряд.
Найти расстояние от Ставрополя до Краснодара. Используйте все данные
карты.
На карте – 1,2 см
На местности — ? см
Масштаб – 1: 20000000
Решение:
Пусть Х см длина отрезка на местности, тогда составим уравнение:
1,2 : Х = 1 : 20000000
Х = 1,2 20000000
Х = 24000000
24000000 см = 240 км
Ответ: 240 км расстояние от Ставрополя до Краснодара.
2 ряд. Работают не открывая атласа.
Известно, что расстояние от Ставрополя до Москвы 1240 км. Изобразите
отрезок-расстояние, примените масштаб 1: 20000000. Сравните с отрезком на
карте.
На карте -? см
На местности – 1240 км = 124000000 см
Масштаб -1:20000000
Пусть Х см длина на карте, тогда составим уравнение:
Х : 124000000 = 1:20000000
Х = 124000000:20000000
Х = 6,2
6,2 см
Ответ: 6,2 см длина отрезка на местности.
3 ряд
Получают карты, на которых нет масштаба.
Отрезку на карте, длина которого 3,6 см соответствует расстоянию на
местности 720 км. Каково расстояние между г. Ставрополем и г. Ростовом,
если на карте расстояние между ними 1,6 см.
На карте 3,6см 1,6см
На местности 720 км = 72000000 см ? см
Масштаб ?
. Решение:
1.Найдём масштаб карты
3,6 36 1
72000000 720000000 20000000
2.Пусть Х см длина отрезка на местности, тогда составим уравнение:
1,6 1
Х 20000000
Х = 32000000
32000000 см = 320 км
Ответ: 320 км расстояние между
Ставрополем и Ростовом.
4.Физкульминутка
Ребята мы с вами активно работали, немного отдохнём.
Буратино потянулся
Раз нагнулся, два нагнулся
Руки в сторону развёл
Ключик видно не нашёл,
Чтобы ключик нам достать
На носочки надо встать
5.Незря мы занялись разминкой.Поднимите руку те, кто увлекается спортом.
Какое большое событие нас ожидает? (Зимние Олимпийские игры).
Где они будут проходить?(Италия, Турин).Давайте вычислим длину пути
Олимпийского огня, если бы он двигался по кратчайшему пути.
На карте – 21см
На местности — ? см
Масштаб – 1:6000000
Решение:
1
Х 6000000
Х = 21 6000000
Х = 126000000
126000000 см = 1260 км
Ответ: 1260 км длина пути следования
олимпийского огня.
6.Итог урока.
Подведём итог урока: достигли ли мы цели урока ? Да мы научились решать
задачи с использованием масштаба и пропорции. Показали хорошие знания.
Выставляю отметки.
Домашнее задание потребует развития ваших творческих способностей,
А также помощи ваших родителей.
Составить план вашего дома в масштабе 1:100 (подсказкой вам послужит
№ 808).
7. Дополнительное задание (при наличии времени)
1.Бактерия имеет длину 0,04 мм. Художники её изобразили в масштабе 1000:1
Какова длина бактерии на рисунке?
0,04 1000 = 40 мм = 4 см.
Ответ: 4см длина бактерии на рисунке.
2.Карта автомобильных дорог для чего? (Знать километраж, количество бензина
на определённый участок пути.
Масштаб и его применение | Обучонок
В представленной исследовательской работе по математике на тему «Масштаб и его применение» я постараюсь выяснить при каком масштабе будет удобно располагать объекты на листе А4.
Работа над исследовательским проектом о масштабе поможет закрепить мне полученные знания по математике.
В моем исследовательском проекте по математике «Масштаб и его применение» мне необходимо будет уточнить и сопоставить математические расчёты с полученными данными.
В ходе исследовательской работы по математике о масштабе и его применении я надеюсь, что масштабы которые я задам, позволят расположить мне объекты на альбомном листе А4.
Также, в практической части своей работы я рассмотрю и математически решу интересные задачи на расстояние и масштаб.
Оглавление
Введение
Основная часть
1. Определение масштаба.
2. Решение интересных задач на масштаб.
Выводы
Приложения.
Введение
На уроках математики в 6 классе мы проходили эту интересную тему, из которой узнали, как, используя масштаб, можно найти расстояние на местности, зная длину отрезка на карте, соответствующего этому расстоянию на местности, и наоборот.
Рисуя на бумаге изображение предметов, мы чаще всего вынуждены изменять их настоящие размеры: большие предметы приходится изображать в уменьшенном виде, а маленькие – увеличивать.
Участки земной поверхности изображают на бумаге в уменьшенном виде. Примером такого изображения служит любая карта, план. А маленькие детали изображают на чертежах в увеличенном виде.
Но чертеж, карта или план должны давать представление о настоящих размерах предметов. Поэтому на чертежах и картах делают специальную запись, показывающую отношение длины отрезка на карте или чертеже к его настоящей длине.
Тема моего исследовательского проекта по математике «Масштаб и его применение».
Цель проекта: выяснить при каком масштабе будет удобно располагать объекты на листе А4.
Задачи проекта:
- закрепить школьные знания по математике;
- уточнить, сопоставимы ли математические расчёты с полученными данными.
Гипотеза: выкройки наиболее эффективно чертить 1:10, планировку квартиры 1:100; паспорт дома 1:1000; карту города 1:10000; карту района 1:100000.
Ожидаемый результат: заданные мною масштабы, позволят расположить объекты на альбомном листе.
Оборудование:
При математических расчётах: линейка, карандаш, циркуль, калькулятор, карта.
На практике: лист А 4, линейка, карандаш.
Определение масштаба
Масштаб – это дробь, где в числителе единица, а в знаменателе то число, которое показывает во сколько раз уменьшено расстояние на плане местности, чем на местности.
Например: 1:1000 (одна тысячная) значит, все расстояния на местности уменьшены в тысячу раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Масштаб бывает:
- численный, выражается в числах 1:1000;
- именованный, выражается словами, то есть см переводим в м: в 1см 10м, 10м – это величина масштаба;
- линейный, зная величину масштаба, мы можем определить расстояния.
Посмотрим на карту. Вверху указан масштаб (1 : 500 000). Говорят, что карта сделана в масштабе одна пятисоттысячная. Это значит, что 1 см на карте соответствует 500 000 см на местности. Значит, отрезок на карте в 1 см соответствует отрезку на местности в 5 км.
А если я возьму на карте отрезок длиной в 3 см, то на местности это будет отрезок длиной в 15 км.
Я скачал с интернета карту Кабардино-Балкарской Республики. Карта республики с масштабом 1:10000, то есть в 1 см 100 метров, а масштаб окрестностей 1:100000 в 1 см 1 километр. Я сразу нашёл по ней мое родное село.
Итак, масштаб (нем. Maßstab, букв. «мерная палка»: Maß «мера», Stab «палка») — в общем, отношение двух линейных размеров.
Во многих областях практического применения масштабом называют отношение размера изображения к размеру изображаемого объекта.
Понятие масштаба наиболее распространено в геодезии, картографии и проектировании — отношение натуральной величины объекта к величине его изображения.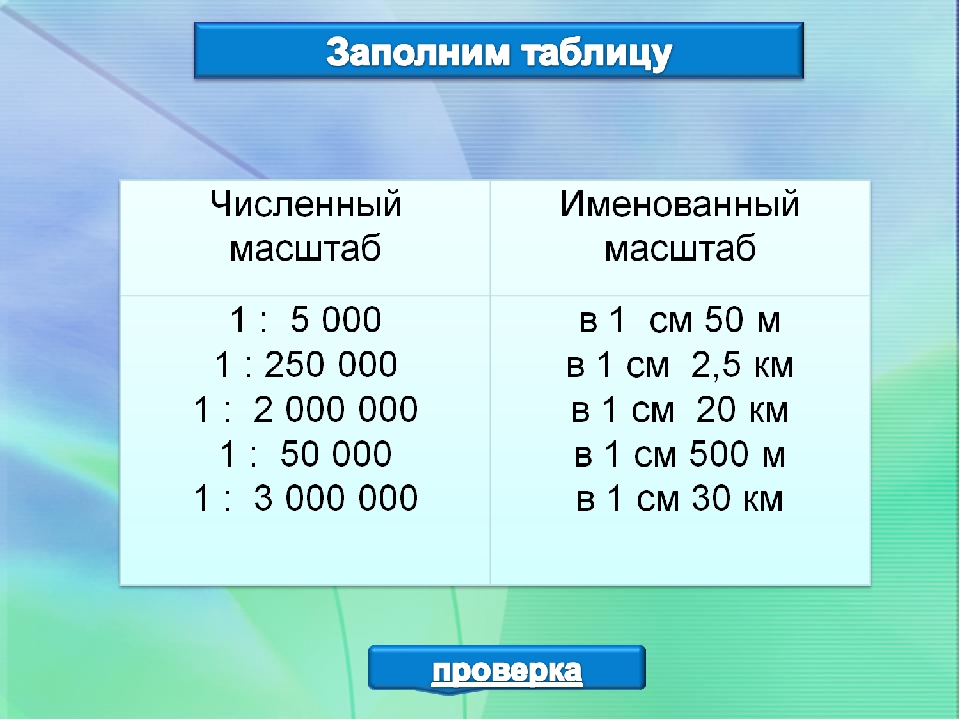
Человек не в состоянии изобразить большие объекты, например дом, в натуральную величину, и поэтому при изображении большого объекта в рисунке, чертеже, макете и так далее, человек уменьшает величину объекта в несколько раз: в два, пять, десять, сто, тысяча и так далее раз. Число показывающее, во сколько раз уменьшен изображенный объект, есть масштаб.
Масштаб применяется и при изображении микромира. Человек не может изобразить живую клетку, которую рассматривает в микроскоп, в натуральную величину и поэтому увеличивает величину ее изображения в несколько раз.
Число, показывающее во сколько раз, произведено увеличение или уменьшение реального явления при его изображении, определено как масштаб.
Некоторые фотографы измеряют масштаб как отношение размеров объекта к размерам его изображения на бумаге, экране или ином носителе.
Правильная методика определения масштаба зависит от контекста, в котором используется изображение.
Выводы
Сравнил свои предположения, выдвинутые в моей гипотезе с надписями на выкройках, картах и технических планах дома и квартиры.
Оказалось, что кое-где я ошибся в 10 и даже в 100 раз.
Итак, я предположил, что:
- выкройки наиболее эффективно чертить 1:10;
- планировку квартиры 1:100;
- паспорт дома 1:1000;
- карту города 1:10000;
- карту района 1:100000.
На самом деле, план квартиры обычно берут в масштабе 1:200; масштабы карт оказались точно такими же, как и в оригинале, но располагаются они аж на 6 альбомных листах!
Так что в который раз, я убеждаюсь, что прежде чем предполагать, нужно несколько раз пересчитать.
Таким образом, мы сформировали понятие масштаба, карты, чертежа, отрабатывали решение задач на вычисление длины отрезка на местности и на карте.
Решение задач на масштаб
Задача 1. Расстояние между двумя городами равно 400 км. Найдите длину отрезка, соединяющего эти города на карте, выполненной в масштабе 1:5000000.
Решение:
400км = 400000м = 40000000см
40000000 : 5000000 = 40 : 5 = 8 (см)
Задача 2.
Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км от центра до центра. По автотрассе протяженность маршрута 700 км.
Во сколько раз надо уменьшить это расстояние, чтобы его можно было изобразить на слайде в виде отрезка длиной в 14 см?
Решение:
700км = 700000м = 70000000см
70000000см : 14см = 5000000(раз)
Задача 3. По физической карте России определите реальное расстояние между Москвой и Санкт-Петербургом.
М1 : 20000000, если на карте расстояние равно 3 см.
Решение:
| на карте | на местности |
|---|---|
| 1см | 20000000см = 200км |
| 3см | Х км |
Х = 3 ∙ 200 = 600 (км)
Задача 4. На карте с масштабом 1/50000 расстояние равно 5 см. Найдите расстояние на местности.
Решение:
5 см ∙ 50000 = 250000 см = 2500 м = 2,5 км
Алгоритм нахождения расстояния на местности
Если масштаб задан дробью с числителем 1, то: |
Задача 5. На карте с масштабом 1 : 150000 расстояние между деревней и станцией равно 2,8 см. Найти расстояние между ними на местности.
Решение:
2,8 см ∙ 150000 = 420000 см = 4200 м = 4,2 км.
Выводы
Цель моей исследовательской работы по математике «Масштаб и его применение» достигнута, так как в ходе проекта я выяснил масштаб, в котором будет удобно располагать объекты на листе А4.
Также, в процессе исследовательского проекта по математике о применении масштаба я закрепил знания, полученные на уроках математики, а также подтвердил свою гипотезу. Все-таки выкройки наиболее эффективно чертить в масштабе 1:10, планировку квартиры 1:100; паспорт дома 1:1000; карту города 1:10000, а карту района в масштабе 1:100000.
В итоге работы я получил, что заданные мною масштабы позволяют расположить объекты на альбомном листе.
Если страница Вам понравилась, поделитесь в социальных сетях:
Масштаб. Практическое применение. Решение задач.
Практическое применение. Решение задач.
Просмотр содержимого документа
«Масштаб. Практическое применение. Решение задач.»
Масштаб
6 класс
Автор учебника: Никольский С. М. Учитель: Петрова И. Н.
При составлении планов и географических карт участки земной поверхности изображают на бумаге в уменьшенном виде. Важно, чтобы при этом полученный рисунок давал представление о реальных размерах изображенной на нем местности. Для этого на карте (плане) делают специальную запись, показывающую, во сколько раз длина отрезка на рисунке меньше длины соответствующего отрезка на местности.
Отношение длины отрезка на плане к его настоящей длине называется МАСШТАБОМ.
Масштаб, выраженный отношением чисел, называют численным масштабом.
Для географических карт численный масштаб выражают дробью, числитель которой равен 1, а знаменатель – числу, показывающему, во сколько раз любое расстояние на карте меньше соответствующего расстояния на местности.
Задача №1.
Масштаб на карте 1 : 20 000. Расстояние между двумя селами на карте 25 см. Каково расстояние между этими селами на местности?
На карте – 25 см
На местности – ?
Масштаб – 1 : 20 000
Решение:
Так как масштаб 1 : 20 000, это означает, что
25 см x 20 000 = 500 000 см = 5 км – расстояние на местности в 20 000 раз больше, чем на карте.
Ответ: 5 км
Задача №2.
Расстояние между двумя городами 200 км. Каково расстояние между этими городами на карте, масштаб которой 1 : 5 000 000?
На карте – ?
На местности – 200 км
Масштаб – 1 : 5 000 000
Решение:
Так как масштаб 1 : 5 000 000, это означает, что
200 км : 5 000 000 = 20 000 000 см : 5 000 000 = 4 см – расстояние на карте в 5 000 000 раз меньше, чем на местности.
Ответ: 4 см
Задача №3.
Расстояние между городами А и В равно 45 км. Расстояние между городами А и В на карте равно 15 см. Определите масштаб карты.
На карте – 15 см
На местности – 45 км
Масштаб – 1 : ?
Решение:
Ответ: 1 : 300 000
масштаб
6.1.4. Масштаб.
Отношение длины отрезка на карте к длине соответствующего расстояния на местности называют масштабом карты.
В соответствии со своим масштабом карты так и называют: пятитысячная, десятитысячная и т.д.
Пятитысячная карта, т. е. карта с масштабом 1:5000 означает, что 1 см на карте соответствует 5000 см на местности. Но мы не меряем расстояния на местности в сантиметрах. Переводим 5000 см в метры. Так как 1 м = 100 см, то 5000 см=50 м.
Следовательно, 50 м на местности изображены на пятитысячной карте отрезком, равным 1 см. Что же можно изобразить на пятитысячной карте? Например, наш сквер, имеющий прямоугольную форму с размерами 600 м х 200 м (длина сквера 600 метров, а ширина 200 метров). На карте с масштабом 1:5000 сквер будет изображен прямоугольником длиной 12 см (600:50=12) и шириной 4 см (200:50=4).
На десятитысячной карте, т.е. карте с масштабом 1:10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.
Как «читать» эту карту? Найдем расстояние между интересующими нас объектами в сантиметрах и умножим на 10000 (см), а затем переведем в метры.
На двадцатипятитысячных, пятидесятитысячных картах изображают небольшие населенные пункты.
На стотысячных, двухсоттысячных картах можно изображать крупные города.
Одному сантиметру стотысячной карты соответствуют 100 000 см на местности. Переведем в метры: 100 000 см = 1000 м, а затем в километры: 1000 м=1 км.
Итак, 100 000 см=1 км. Сделаем вывод: чтобы перевести число сантиметров в километры, нужно разделить это число на 100 000 (или просто «убрать» пять нулей). Теперь нам проще будет представить масштабирование 1:100 000. На 1 см на карте приходится 1 км на местности. Если расстояние от вашего города до дачного поселка составляет 10км (по прямой!), то на стотысячной карте это расстояние представляет собой отрезок длиной 10см.
На двухсоттысячной карте (М=1:200 000) в 1 см изображается фактическое расстояние, равное 2 км (200 000 см=2 км).
На трехсоттысячной карте с масштабом 1:300 000 под каждым сантиметром подразумевают фактическое расстояние в 3 км (300 000 см=3 км).
На пятитысячной карте 1 см соответствует 5 км на местности.
На миллионной карте 1 см соответствует 10 км на местности. На таких картах изображают области, края.
А на каких картах можно изобразить страны? Обычно карты стран, Республик имеют масштаб 1:8 000 000 или 1: 10 000 000.
Большая карта Мира, которую вы изучаете в школе, имеет масштаб 1: 25 000 000.
Чтобы напечатать эту карту в атласе нужно ее уменьшить. И тогда масштаб карты Мира в атласе может составить 1: 60 000 000 или 1:75 000 000, если атлас будет поменьше.
Задача 1. Пользуясь картой масштабом 1:12 250 000, найдите расстояние (по прямой) между Астаной и Таразом на местности.
Решение.
На карте 1 см соответствует 12 250 000 см или (делим число сантиметров на 100 000 — переносим запятую на 5 цифр влево) 122, 5 км.
Измерим линейкой расстояние между Астаной и Таразом на карте. Получилось 7,5 см. Нужно узнать, сколько километров соответствует отрезку на карте в 7,5 см. Итак:
1 см ———-122,5 км
7,5 см——- х км. Можно составить пропорцию, а можно рассуждать так: в 1 см — 122,5 км, тогда в 7,5 см — в 7,5 раз больше. Следовательно, 122,5·7,5=918,75. Округлим до целых: 918,75≈919.
Ответ: от Астаны до Тараза (по прямой) 919 км.
Задача 2. Найти масштаб карты, если расстояние от Астаны до Атырау (по прямой) на местности составляет 1500 км.
Решение.
Измеряем линейкой расстояние от Астаны до Атырау.
Получилось 7,5 см. По условию можно записать:
7,5 см ———- 1500 км. Найти масштаб карты — означает узнать, сколько километров (а потом, обязательно, — сантиметров на местности) соответствуют отрезку в 1 см на карте. Запишем:
1 см ———— х км. Можно составить пропорцию: 7,5:1=1500:х, из которой найти ее крайний член х. А можно рассуждать так: 1500 км изображены отрезком в 7,5 см, значит, отрезок в 1 см будет соответствовать расстоянию в 7,5 раз меньшему, и нужно число 1500 разделить на 7,5.
х=1500:7,5;
х=15000:75;
х=200. Мы нашли, сколько км на местности приходится на 1 см на карте. Выразим 200 км в сантиметрах (для этого нам просто нужно приписать к числу 200 справа 5 нулей).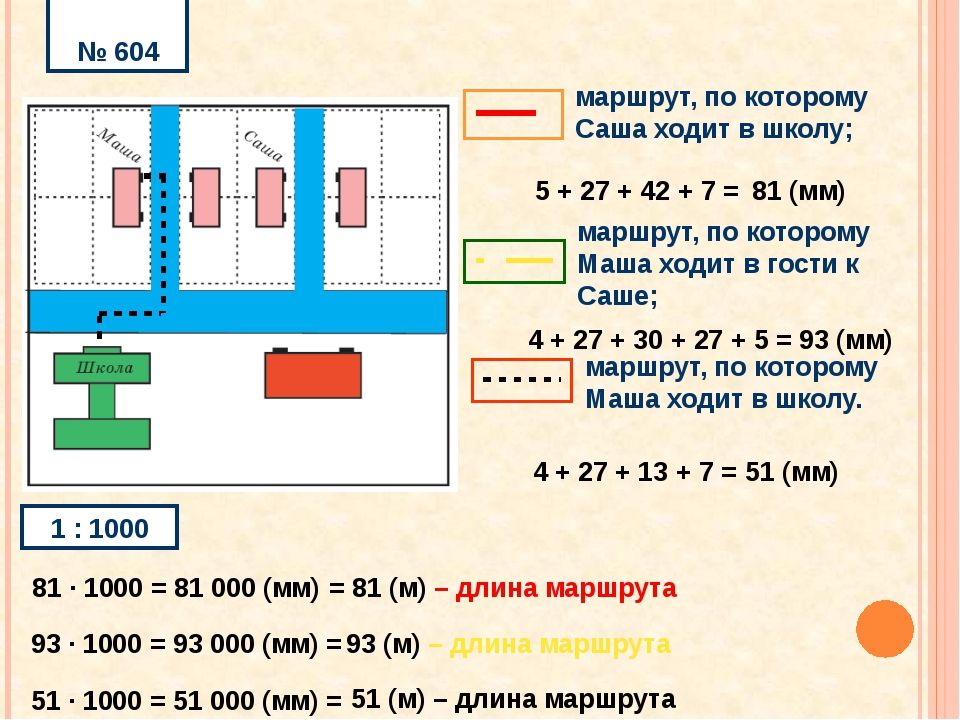
200 км=20 000 000 см. Масштаб карты 1:20 000 000.
Ответ: М=1:20 000 000.
Смотрите видео: «Масштаб».
Презентация «Масштаб» — математика, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
Масштабурок математики в 6 классе. Учитель математикишколы№13г. Самарканд. Ислямова З. М.
Номер слайда 2
Номер слайда 3
девиз урока.
Масштаб — это ваш друг и брат Знайте это, вы, друзья,Шар земной, страну и город. Не увидеть без меня.
Номер слайда 4
Школа 13 город Самарканд
Номер слайда 5
Масштаб (нем.
Maßstab) в переводе с немецкого – «мерная палка»
Номер слайда 6
Масштаб – это отношение длиныотрезка на карте или планек его действительнойдлине на местности
Номер слайда 7
Номер слайда 8
1 мм1дм1 км•10•10•10001 м•10:1000:10:10:101 см.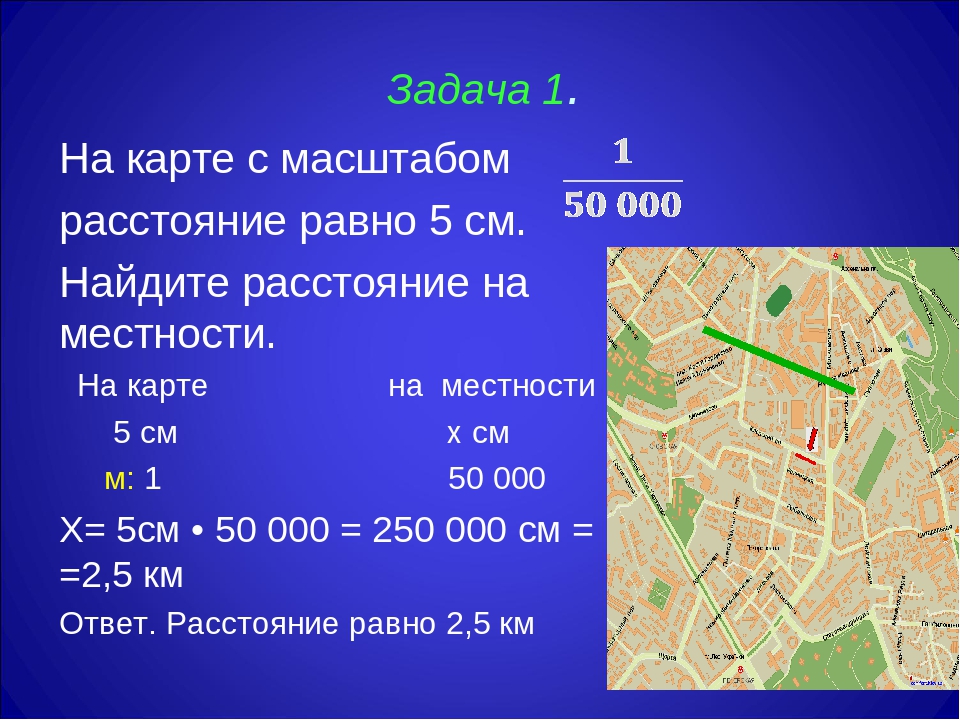
М е р ы д л и н ы
Номер слайда 9
Переведите численный масштаб в именованный и наоборот. Численный: а) 1:1 000;в 1 см – 10 мб)1:75 000 000.в 1 см – 750 км. Именованный: а)в 1см – 50км; 1:5 000 000б)в 1см – 200м1:20 000 Какой из масштабов крупнее? а)1:25 ;б) 1:300; в)1:50 000. Помни: 1км=100 000см, 1м=100см 1:25
Номер слайда 10
Что называют отношением двух чисел (величин)?Что показывает отношение двух чисел? Найдите отношение:1см к 40м1см к 50км1см к 23см1:231:40001:5 000 000 Помни: 1км=100 000см, 1м=100см Что означают эти отношения?
Номер слайда 11
Вычислите площадь квартиры, если сторона одной клетки плана равна 1 см.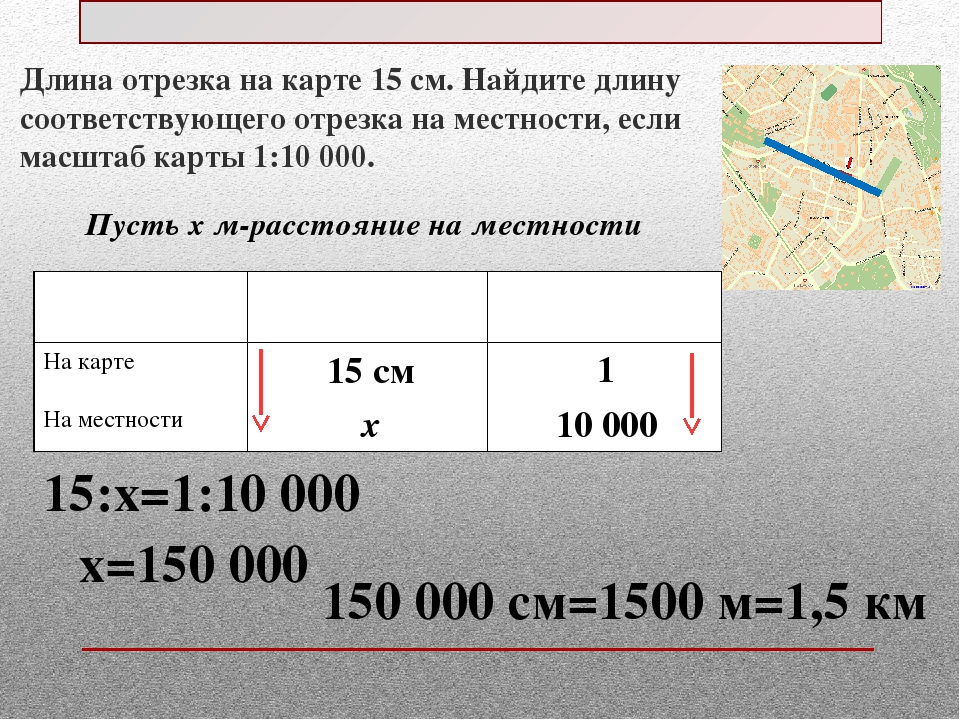
Ответ дайте в м².
Номер слайда 12
Решениена планена местности1см100см
Номер слайда 13
Применение масштаба В геодезии, картографии и проектировании.
В моделизме. В программировании. В кинотехнике. В фотографии. В математике.
Номер слайда 14
Применение масштаба в геодезии, картографии и проектировании.
Номер слайда 15
Модель пожарной машины в уменьшенном масштабе.
Модель атома в высоком масштабе увеличения
Номер слайда 16
Номер слайда 17
Архитекторы — специалисты, которые создают здания и их комплексы, образующие среду для жизни людей: жилищные, спортивные, театральные, парковые сооружения, улицы, города.
Номер слайда 18
Номер слайда 19
Самарканд – 2022
Номер слайда 20
Номер слайда 21
Архитектор должен уметь хорошо ориентироваться в пространстве, представить в уме будущее сооружение, создать его образ.
Архитекторы должны уметь проектировать и конструировать. В этом вы обычно тренируетесь, когда собираете из деталей конструктора какое-либо сооружение.
Номер слайда 22
Город нашей мечты1. Многоэтажные дома2. Школа3. Больница4. Супермаркет5. Банк
Номер слайда 23
Банк.
Жилой дом. Ресторан. Школа. Супермаркет. Больница
Номер слайда 24
Площадь нашего города. Длина 84 см. Ширина 60 см. Площадь 84х60=5040 кв.см. Масштаб 1:10000 Длина 840000см= 8,4км. Ширина 600000см=6км. Площадь 50.4 кв.км
Номер слайда 25
Об умном человеке говорят: “масштабно мыслит”.
Будем этому учиться!
Номер слайда 26
Домашнее задание
Номер слайда 27
великан и мальчик-с-пальчик решили жить в одном доме.
Каким он должен быть, чтобы им обоим было в нем удобно? Придумайте дом:
Номер слайда 28
Было интересно…Было трудно…Я понял(а), что…Теперь я могу…У меня получилось…. Мне захотелось…Моё пожелание учителям…Рефлексия
Как найти масштаб в математике
Масштабом называют отношение двух линейных размеров. Его использование позволяет создавать чертежи, карты, модели реальных объектов.
Благодаря масштабированию можно показать в уменьшенном виде большой объект и, наоборот, в увеличенном – маленький.Вам понадобитсяПри решении математических задач по теме «Масштаб» можно столкнуться с различными практическими ситуациями, в которых необходимо его применение. Например, как узнать масштаб карты? Возьмите любой атлас и откройте его на одной из страниц. В ее нижней части обычно находится линейка, на которой показано, сколько километров на местности соответствует одному сантиметру на карте. Например, масштаб 1:7 500 000 говорит о том, что один сантиметр карты равен 75 километрам на местности. Масштаб 1: 35 000 000 – это 350 километров на местности. Масштаб 1:200 000 – в одном сантиметре два километра.
Легко увидеть, что масштаб указывается в сантиметрах. Чтобы перевести сантиметры в привычные километры, необходимо отсчитать с правой стороны пять знаков. Например, в масштабе 1:10 000 000 отсчитайте пять знаков справа, получится 1: 100,00000. То есть в 1 см 100 км. Зная этот принцип, вы всегда сможете быстро определить соответствие значений карты реальному расстоянию на местности.
При выполнении чертежных работ реальные размеры объекта уменьшаются или увеличиваются в некоторое количество раз. Существуют определенные стандарты, которых следует придерживаться. Например, при изготовлении моделей кораблей, танков, самолетов, автомобилей и т.д. обычно используются масштабы 1:24, 1:32, 1:48, 1:72, 1:144. Нетрудно догадаться, что модели меньше реальных прототипов в указанное число раз. Если вы, например, будете собирать или изготавливать модели в масштабе 1:72 (самый распространенный вариант), то они будут отличаться в размерах так же, как и реальные объекты.
Иногда с масштабированием сталкиваются при увеличении какого-либо рисунка. Чтобы точно увеличить изображение, сначала расчертите его на клетки, выбрав для них определенный размер – например, 1 сантиметр. Далее лист бумаги расчертите на клетки, увеличенные в нужном масштабе. Так, если рисунок надо увеличить в два раза, следует использовать клетки со стороной 2 см. Расчертив лист, вы сможете по клеткам легко перенести на него контуры исходного рисунка.
Как найти Масштаб в Математике?
Понятие масштаба
Чтобы понять, что такое масштаб в математике нужно вспомнить тему отношений чисел и пропорций.
Масштаб — это дробь, где в числителе единица, а в знаменателе то число, показывает во сколько раз уменьшено расстояние на плане местности, чем на самой местности.
Другими словами, масштабом называют отношение отрезка на карте к длине соответствующего отрезка на местности.
- Например, одна тысячная (1: 1000) означает, что все расстояния на местности уменьшены в раз. Чем больше число в знаменателе дроби, тем больше уменьшение и тем больше охват территории.
Масштаб бывает трех видов:
- численный, выражается в числах 1: 1000;
- именованный, выражается словами, то есть см переводим в м : в 1см 10м, 10м — это величина масштаба;
- линейный, зная область масштаба, можно определить расстояния.
Определение масштаба на карте
На математике в 6 обязательно будут задания, как найти масштаб карты. Разберемся в этом вопросе.
Нужно потратить очень много сил, чтобы изобразить дом в натуральном представлении, поэтому и придумали такой инструмент, как масштаб. Ведь намного проще описать большой объект в рисунке, чертеже или макете.
Масштаб — это отношение размера изображения к размеру изображаемого объекта.
Масштаб — это длина карты длины отрезка на карте его действительной длине на местности.
На карте Российской Федерации указан масштаб (1: 500 000). Читается это так: карта сделана в масштабе одна пятисот тысячная. Такой масштаб значит, что в 1 см на карте помещается 500 000 см реального расстояния. То есть отрезок на изображении в 1 см соответствует отрезку на местности в 5 км. А если взять отрезок в 3 см, то на этой местности отрезок составит 15 км.
Численные масштабы карт и соответствующие им масштабы на местности:
Масштаб 1: 100 000
- 1 мм на карте — 100 м (0,1 км) на местности
- 1 см на карте — 1000 м (1 км) на местности
- 10 см на карте — 10000 м (10 км) на местности
Масштаб 1: 10000
- 1 мм на карте — 10 м (0,01 км) на местности
- 1 см на карте — 100 м (0,1 км) на местности
- 10 см на карте — 1000 м (1 км) на местности
Масштаб 1: 5000
- 1 мм на карте — 5 м (0,005 км) на местности
- 1 см на карте — 50 м (0,05 км) на местности
- 10 см на карте — 500 м (0,5 км) на местности
Масштаб 1: 2000
- 1 мм на карте — 2 м (0,002 км) на местности
- 1 см на карте — 20 м (0,02 км) на местности
- 10 см на карте — 200 м (0,2 км) на местности
Масштаб 1: 1000
- 1 мм на карте — 100 см (1 м) на местности
- 1 см на карте — 1000 см (10 м) на местности
- 10 см на карте — 100 м на местности
Масштаб 1: 500
- 1 мм на карте — 50 см (0,5 метра) на местности
- 1 см на карте — 5 м на местности
- 10 см на карте — 50 м на местности
Масштаб 1: 200
- 1 мм на карте — 0,2 м (20 см) на местности
- 1 см на карте — 2 м (200 см) на местности
- 10 см на карте — 20 м (0,2 км) на местности
Масштаб 1: 100
- 1 мм на карте — 0,1 м (10 см) на местности
- 1 см на карте — 1 м (100 см) на местности
- 10 см на карте — 10м (0,01 км) на местности
Решение задач на масштаб
Для закрепления темы решим несколько математических задач на масштаб за 6 класс.
Пример 1. Длина отрезка на карте равна 8 см. Найдите нужный отрезка на местности, если карты равенство 1: 10 000.
Как решаем:
8 см — это 1 часть
8 * 10 000 = 80 000 (см) — это 10 000 частей
80 000 см = 800 м
Ответ: 800 м
Пример 2. Расстояние между двумя городами 400 км. Найти длину отрезка, который соединяет эти города на карте, выполненный в масштабе 1: 5000000.
Как решаем:
400 км = 400 000 м = 40 000 000 см
40000000: 5000000 = 40: 5 = 8
Ответ: 8 см
Пример 3. Расстояние от Москвы до Санкт-Петербурга по прямой составляет примерно 635 км. По автотрассе протяженность маршрута 700 км. Во сколько раз надо было уменьшить это, чтобы его можно было изобразить в виде отрезка длиной в 14 см?
Как решаем:
700 км = 700 000 м = 70 000 000 см
70 000 000: 14 = 5 000 000
Ответ: уменьшить в 5 000 000 раз.
Еще больше практики — в детской школе Skysmart. Ученики занимаются на интерактивной платформе, в комфортном темпе и с помощью внимательных учителей.
ребенок занимался математикой в удовольствие и чувствовал себя увереннее в школе, запишите его на бесплатный вводный урок. Познакомим с форматом и вдохновим на учебу!
Разработка урока по математике в 6 классе на тему «Масштаб»
Библиографическое описание:
Бородина, М.Ю. Разработка урока по математике в 6 классе на тему «Масштаб» / М. Ю. Бородина. — Текст: непосредственный // Молодой ученый. — 2019. — № 9 (247). — С. 185-186. — URL: https://moluch.ru/archive/247/56829/ (дата обращения: 01.02.2021).
Взаимодействие с другими людьми В статье предлагается разработка урока математики 6 класса по учебнику Н. Я. Виленкин, В. И. Жохов, А.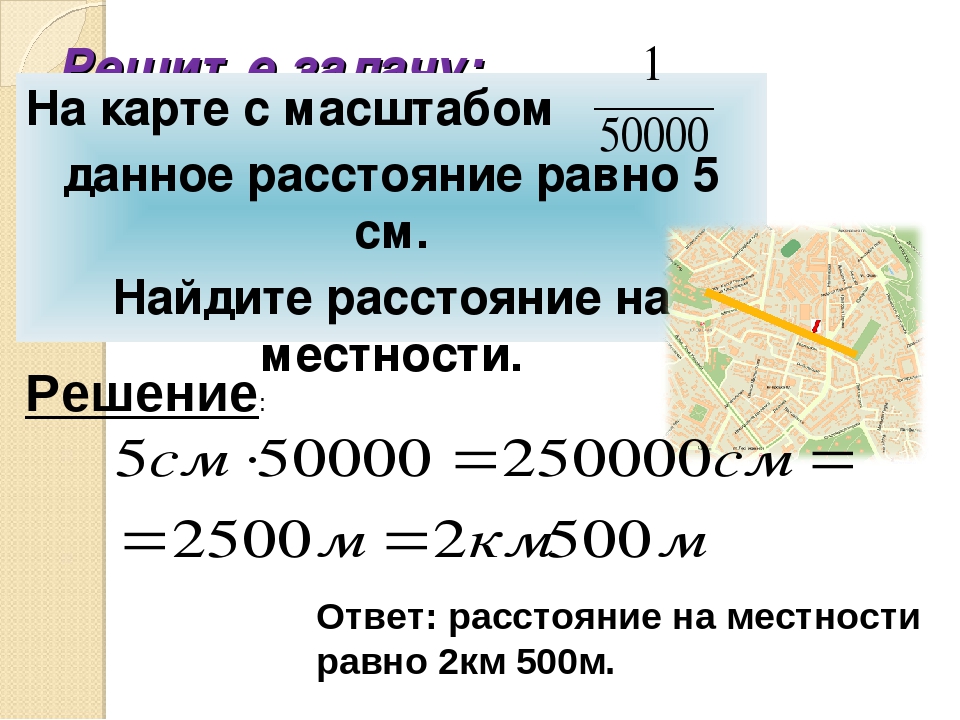
С. Предлагается разработка урока в виде лабораторно-практической работы, используя карты с разным масштабом, где после обучающийся должен сделать вывод.
Ключевые слова: масштаб, карта.
Тип урока: изучение нового материала.
Цель: Ввести понятие «масштаб», рассмотреть масштаб.
Задачи :
— образовательные:
- повышение мотивации к изучению предметов математики и географии;
- вести понятие масштаб, виды масштаба;
- работать с географическими картами.
— развивающие:
- дополнительно умение анализировать, сравнивать и делать выводы.
— воспитательные:
- воспитание интереса у обучающихся к школьным предметам;
- воспитанию любви к родному краю.
Ход урока
Любой географический объект, участок земной поверхности можно изобразить на бумаге в уменьшенном виде.На уроках географии вы уже познакомились с понятием масштаб и научились определять расстояние на карте и на местности. Работая с картами разного масштаба, вы должны сделать вывод на расстоянии на местности. Но сначала повторим материал прошлого урока.
- Что называется отношением?
- Что показывает отношение?
- Найдите отношение величин: 12 см и 48 см; 3 см и 12 м.
- Повторить измерения: Выразите в сантиметрах: 1 дм = ___ см, 1 м = ___ см, 1 км = _____________ см.
Изучение нового материала
«Масштаб (от немецкого — мера и Stab — палка) — отношение длины отрезка на карте, плане, аэро- или космическом снимке к его действующей длине на местности.
Как вы уже знаете географические карты, разные масштабы, например:
1: 500–1 см на карте соответствует 500 см или 5 м на местности;
1: 100–1 см на карте равенство 100 см или 1 м на местности;
1: 1000–1 см на карте равенство 1000 см или 10 м на местности.
Прочитайте: 1: 10000; 1: 25000; 1: 2 000 000.
Масштабы имеют три вида: увеличение, уменьшение и уменьшение в натуральную.
Начертите в тетрадях квадрат со стороны 100 см в масштабе 1:20 (сторона 5 см).
Где используется масштаб? (глобус, учебник географии, карты, различные схемы, уроки трудового обучения).
Также рассматрибы:
«Словесный» — это «вид масштаба, словесное указание того, какое расстояние на местности соответствует 1 см на карте, плане, снимке».Например, в 1 см — 1 м. Начертите в этом масштабе (в 1 см — 1 м.) Прямоугольник со стороны 4 и 2 м.
«Численный» — например, 1: 10000000 см. где нужно в правой части перевести сантиметры в метры или в километры, например 1 см — 10 км.
«Линейный» масштаб — вспомогательная мерная линейка, наносимая на карты для облегчения измерения размеров.
Решение задач:
1. Длина отрезка на местности 250 км.
Найдите нужный отрезка на карте, если масштаб карты 1: 1000000.
Решение: 250 км = 25000000 см; 25000000: 1000000 = 25 см.
2. Масштаб плана 1: 500. Какому расстоянию на местности соответствует участок длины: 1) 20 см, 2) 3 см, 3) 7 см
Решение: т. к. в 1 см — 500 см, 10 · 500 = 5000 см = 50 м;
3 · 500 = 1500 см = 15 м; 7 · 500 = 3500 см = 35 м.
Лабораторно — практическая работа
Важнейшим документом в истории человечества является географическая карта, где изображаются любые территории, объекты.
Сейчас вы проведете лабораторно — практическую работу по картам нашей Кемеровской области. В конце работы запишите вывод о том, как нанести масштаб на расстояние на расстояние на местности.
У вас на столах есть несколько карт Кемеровской области — нашей Родины.
- Найдите на карте столицу Кузбасса, и наш город шахтеров.
- Найдите расстояние (используя линейку) между этими городами. Какое расстояние у вас получилось? Каким масштабом вы пользовались?
- Какие еще города есть в нашей области?
- Выберите два города и по картам найдите расстояние между ними на местности.Рассмотрите еще по три примера и сделайте вывод.
Какое расстояние у вас получилось? Каким масштабом вы пользовались?Итог урока:
— Что показывает масштаб?
— Назовите основные виды масштаба.
— Где можно применить масштаб?
— Каким видом масштаба мы пользуемся чаще всего?
Домашнее задание : № 840, 841, 846 (а).
Литература:
- Математика. 6 класс: учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. — 30-е изд., Стер. — М .: Мнемозина, 2015.
- Учебник «География», М.: Вентана-Граф, 2014 А. А. Летягин 6 класс
- Математика 6 класс С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. –М .: Просвещение 2016.
- Физические и контурные карты кемеровской области.
Основные термины (генерируются автоматически) : масштаб, местность, вид масштаба, какое расстояние, вывод, нового изучения материала, Кемеровская область, практическая работа.
Презентация «Масштаб» — математика, презентации
библиотека
материалов
Содержание слайдов
Номер слайда 1
Проверка домашней работы.Стр.8№ 12, 17 (в), 18 (в), 19 (ж, з)
Номер слайда 2
№ 12
Номер слайда 3
№ 12
Номер слайда 4
№ 17 (в)
Номер слайда 5
№ 18 (в)
Номер слайда 6
№ 19 (ж, з)
Номер слайда 7
Математический диктант «Неудачники жалуются.
Чемпионы тренируются «12.09.2019
Номер слайда 8
1 вариант 2 вариант 1.Величина или число? А) 71 кг / 68 г а) 12км / 3мин б) 17 м / 19 с б) 8км / 10с 2. Найти отношение: 5 к 7 к 3. Упростить отношение: 17кг: 510г 19км: 570м 4. Перевести 24 км / ч в м / мин 36 км / ч в м / мин
Номер слайда 9
Разгадайте ребус.
Масштаб
Номер слайда 10
Масштаб12.09.2019 «Неудачники жалуются. Чемпионы тренируются»
Номер слайда 11
Цели урока: 1.
Дать определение понятия масштаб.2. Определить область применения масштаба.3. Научиться решать задачи по теме.
Номер слайда 12
Что такое масштаб? Каким он бывает?
Номер слайда 13
1) Отношением называется.
… 2) Отношение показывает во сколько раз …. или …. Ответ: масса слона больше массы мыши в 20 000 раз. Масса мыши 200 грамм, а масса слона 4 тонны. Чья масса больше и во сколько раз? 4 т = 4 000 кг = 4 000 000г4 000 000: 50 = 20 000
Номер слайда 14
Масштаб.Модель клетки 2000: 1 Масштаб — длина отрезка на плане его настоящей длине.
Номер слайда 15
На карте 5см.
На местности 5 м = 500 см. Например: Составим отношение: Или 1: 100
Номер слайда 16
Если размеры на карте меньше, чем размеры в действительности, то масштаб записывают так: М 1: 100 Такой масштаб называется численным.М 1: 500 М 1: 2500
Номер слайда 17
Численный масштаб.
Именованный масштаб. Линейный масштаб
Номер слайда 18
Масштаб 1: 100показывает, что размеры уменьшены в 100 раз.Масштаб 1: 500 Масштаб 1: 1000 Масштаб 1: 500 000 Масштаб 1: 2500000
Номер слайда 19
Масштаб: 1: 100 000 показывает, что?
Номер слайда 20
Масштаб: 1: 12 000 000 показывает, что?
Номер слайда 21
Масштаб: 1: 11 000 000 показывает, что?
Номер слайда 22
Масштаб: 1: 15 000 000 показывает, что?
Номер слайда 23
Масштаб: 1: 14 500 000 показывает, что?
Номер слайда 24
М 5: 1 М 500: 1 М 100 000 000: 1 Если размеры на рисунке больше, чем размеры в действительности, то масштаб записывают так:
Номер слайда 25
Паук М 5: 1показывает, что размерыувеличены в 5 раз.
Номер слайда 26
Паук М 3: 1показывает, что?
Номер слайда 27
Инфузория туфелька М 160: 1показывает, что?
Номер слайда 28
М 100 000 000: 1 Молекула метанапоказывает, что?
Номер слайда 29
8 смлагерь туристовозеро Глубокоелес8см · 5000 = 1: 5 000 Определите расстояние от стоянки туристов до леса.
400 мстанция Озерноеболото. М 1: 5 0008см · 5000 = 40 000 см8см · 5000 = 40 000 см = 400 м
Номер слайда 30
М 1: 100024 см15 см · 1000 = 150 м · 1000 = 240 м6 см * 1000 = 60 м6 см.Вася. Витя. Петя. Коля. Найдите расстояние от дома Коли до домов его друзей. Стр. 10 №25
Номер слайда 31
Стр.
10 № 25
Номер слайда 32
1: 1001: 500? Ответьте на вопросы: Какой из масштабов карта более подробная? Во сколько раз на местности больше, чем на плане, если местность изображена в масштабе 1: 100? ; 1: 500? 123
Номер слайда 33
Какая была цель урока? Справились?
Номер слайда 34
На дом: п.
1.2, стр.8№ 24, 26 Успехов вам !!!
Номер слайда 35
Автор: Ермолаева Ирина Алексеевнаучитель информатики и математики МОУ «Павловская сош» с.Павловск. Алтайский край
Номер слайда 36
Для создания шаблона использовались источники: http: // lake.
k12.fl.us/cms/cwp/view.asp?A=3&Q=427619 Автор: Ермолаева Ирина Алексеевна учитель информатики МОУ «Павловская сош»
Урок математики 6 класс тема «масштаб» цели
ПЕРЕПЕЛИЦА НАТАЛЬЯ ВАСИЛЬЕВНА
Учитель математики и информатики
Муниципальное бюджетное общеобразовательное учреждение Богородицкая средняя общеобразовательная школа № 20
2012-2014 учебный год
Урок математики 6 класс
Тема: «Масштаб»
Цели:
1.Организовать деятельность учащихся для закрепления понятия
«Масштаб», решение задач с помощью пропорции. Рассмотреть связь
математики с географией и различными областями жизни.
2. Способствовать развитию памяти, вычислительных навыков,
логического мышления, общеучебных навыки, математически
грамотной речи, умения сравнивать
и обобщать.
3. Помогать учащимся воспитывать трудолюбие, умение общаться,
аккуратность.
Типы урока:
Совершенствование знаний, умений, навыки при решении задач с
Использование масштаба.
Методы обучения:
Наглядный, практический, словесный.
Формы:
Общеклассная, групповая, парная, дифференцированная.
Ход урока.
Организационный момент отсутствующие.
Добрый день, друзья!
Я рада встречи с вами!
Хотела объявить тему урока, но все буквы рассыпались, помогите собрать:
« ТАБШМАС» (масштаб)
Наш урок — «Путешествие по карте»
Цели урока: (Формулируют учащиеся).
Закрепить понятие масштаба карты, научиться решать задачи с
с помощью пропорции при заданном масштабе, установить связь
математики с другими предметами.
Актуализация опорных знаний.
Чтобы не ошибиться при решении задач вы должны быстро и без ошибочно выполнить действия, вычислять.
На столе лежат задания для быстрого счёта. Учащиеся работают максимум две минуты. Затем выполнить самопроверку, сопоставляя свои решения с
решения на доске. (на обратной стороне доски).
Оценивают по критериям:
9-10 заданий — «5»
8 заданий — «4»
6-7 заданий — «3»
Чтобы отправляться в путешествие по карта нужно иметь некоторые
специальные знания, например, масштаб.
Где вы встречались с понятием «масштаб»? (на уроках географии виды и обозначения и по таблице)
Что такое масштаб?
(Отношение длины отрезка на карте к длине соответствующий отрезка на местности масштабом карты.)
Масштаб (немецкий таб-мера, stab-палка)
При решении задач не забывайте о
правильном её оформлении.
Задача:
На карте — 10см.
Местность -? См.
Масштаб — 1: 500000
Решение:
Пусть Х см — длина отрезка на местности, тогда составим
уравнение:
10: Х = 1: 500000
Тогда, Х = 10 500000 = 5000000
5000000 см = 50 км
Ответ: 50 км длина отрезка на местности.
3. Обучающий этап.
1. Работа с картой (устно)
Рассмотрим 3 карты Москвы. (Атлас 6 класса, страница 25)
Попробуйте объяснить сходство и различие карт.
(Сходство в том, что карты одной и той же территории, различие: сделана в
разных масштабах.)
Вывод: с уменьшением масштаба карты — увеличенная площадь
изображенной территории (1: 1000000 уменьшается)
2.
Следующая карта, которую мы рассмотрим
— это карта России (стр.17).
Каждому ряду предлагается предложение. У используемые у доски есть прверяющие
с соответствующим рядом.
1 ряд.
Найти расстояние от Ставрополя до Краснодара. Используйте все данные
карты.
На карте — 1,2 см
На местности -? см
Масштаб — 1: 20000000
Решение:
Пусть Х см длина отрезка на местности, тогда составим уравнение:
1,2: Х = 1: 20000000
Х = 1,2 20000000
Х = 24000000
24000000 см = 240 км
Ответ: 240 км расстояние от Ставрополя до Краснодара.
2 ряд. Работают не открывая атласа.
Известно, что расстояние от Ставрополя до Москвы 1240 км. Изобразите
отрезок-расстояние, примените масштаб 1: 20000000. Другим с отрезком на
карта.
На карте -? см
На местности — 1240 км = 124000000 см
Масштаб -1: 20000000
Решение:
Пусть Х см длина на карте, тогда составим уравнение:
Х: 124000000 = 1: 20000000
Х = 124000000: 20000000
Х = 6,2
6,2 см
Ответ: 6,2 см длина отрезка на местности.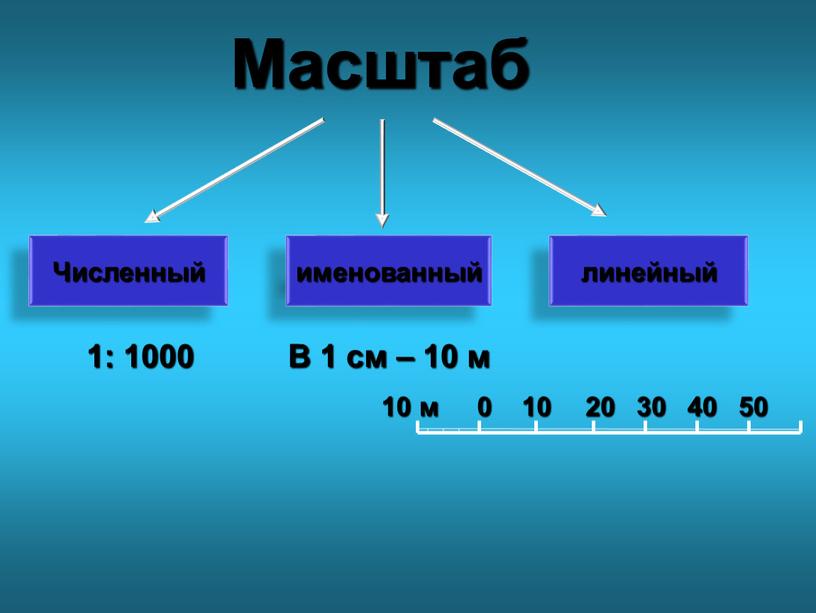
3 ряда
Получают карты, на которых нет масштаба.
Отрезку на карте, длина которого 3,6 см расстояний на
местности 720 км. Каково расстояние между г. Ставрополем и г. Ростовом,
если на карте расстояние между ними 1,6 см.
На карте 3,6см 1,6см
На местности 720 км = 72000000 см? см
Масштаб?
. Решение:
1.Найдём масштаб карты
3,6 36 1
72000000 720000000 20000000
2.Пусть Х см длина отрезка на местности, тогда составим уравнение:
1,6 1
Х 20000000
Х = 32000000
32000000 см = 320 км
Ответ: 320 км расстояние между Ставрополем и Ростовом.
4.Физкульминутка
Ребята мы с вами активно работали, немного отдохнём.
Буратино потянулся
Раз нагнулся, два нагнулся
Руки в сторону развёл
Ключик видно не нашёл,
Чтобы ключик нам достать
На носочки надо встать
5.
Незря мы занялись
разминкой.Поднимите руку те, кто
увлекается спортом.
Какое большое событие нас ожидает? (Зимние Олимпийские игры).
Где они будут проходить? (Италия, Турин) .Давайте вычислим длину пути
Олимпийского огня, если бы он двигался по кратчайшему пути.
На карте — 21см
На местности -? см
Масштаб — 1: 6000000
Решение:
1
Х 6000000
Х = 21 6000000
Х = 126000000
126000000 см = 1260 км
Ответ: 1260 км длина пути следования олимпийского огня.
6.Итог урока.
Подведём итог урока: достигли ли мы цели урока? Да мы научились решать
возможности с использованием масштаба и пропорции. Показали хорошие знания.
Выставляю отметки.
Домашнее задание потребует развития ваших творческих способностей,
А также помощи ваших родителей.
Составить план вашего дома в масштабе 1: 100 (подсказкой вам послужит
№ 808).
7. Дополнительное задание ( при наличии времени)
1 .Бактерия имеет длину 0,04 мм. Художники её изобразили в масштабе 1000: 1
Какова длина бактерии на рисунке?
0,04 1000 = 40 мм = 4 см.
Ответ: 4см длина бактерии на рисунке.
2.Карта автомобильных дорог для чего? (Знать километраж, количество бензина
на определенный участок пути.
Тест по математике Масштаб (6 класс)
Сложность: знаток. Последний раз тест пройден 50 минут назад.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем математики — более 33 лет.
Вопрос 1 из 10
Как правильно записать масштаб карты, если один сантиметр на карте соответствует двум сантиметрам на миллион местности?
- Правильный ответ
- Неправильный ответ
- Вы и еще 92% ответили правильно
- 92% ответили правильно на этот вопрос
В вопросе ошибка?
Следующий вопрос ОтветитьВопрос 2 из 10
Расстояние, равное 60 м, изображено на участке отрезком, длиной 4 см.
Определите масштаб плана.- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 56% участников
- 44% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 3 из 10
На одном чертеже деталь изображена в масштабе 1: 5, а на другом — та же деталь в масштабе изображение 5: 1. На каком чертеже детали получилось увеличенным в 5 раз по сравнению с действительным размерами детали?
- Правильный ответ
- Неправильный ответ
- Вы и еще 79% ответили правильно
- 79% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 4 из 10
Квадрат с длиной стороны 24 см изображён на чертеже в масштабе 1: 8.
Какова длина стороны квадрата на чертеже?- Правильный ответ
- Неправильный ответ
- Вы и еще 77% ответили правильно
- 77% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 5 из 10
Длина тела жука 8 мм. Этот жук изображён в книге в масштабе 4: 1. Какова длина тела жука на рисунке в книге?
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 55% участников
- 45% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 6 из 10
Расстояние между двумя посёлками изображено на участке длиной 3 см.
Масштаб плана 1: 5000. Каково расстояние между посёлками в действительности?- Правильный ответ
- Неправильный ответ
- Вы и еще 57% ответили правильно
- 57% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 7 из 10
Высота вазы 0,4 м. Какую высоту будет иметь ее изображение на рисунке, сделанном в масштабе 1: 2?
- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 52% участников
- 48% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 8 из 10
Равносторонний треугольник с длиной стороны 36 см, изображён на чертеже в масштабе 1: 4.
Какова длина, стороны треугольника на чертеже?- Правильный ответ
- Неправильный ответ
- Вы и еще 76% ответили правильно
- 76% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 9 из 10
Высота стакана 10 см. Какую высоту будет иметь стакан, если его изобразить на рисунке в масштабе 1: 2?
- Правильный ответ
- Неправильный ответ
- Вы и еще 74% ответили правильно
- 74% ответили правильно на этот вопрос
В вопросе ошибка?
ОтветитьВопрос 10 из 10
Расстояние, равное 100 м, изображено на отрезком длиной 2 см.
Определите масштаб плана- Правильный ответ
- Неправильный ответ
- Вы ответили лучше 53% участников
- 47% ответили правильно на этот вопрос
В вопросе ошибка?
Ответить
Определите масштаб плана.
Какова длина стороны квадрата на чертеже?
Масштаб плана 1: 5000. Каково расстояние между посёлками в действительности?
Какова длина, стороны треугольника на чертеже?
Определите масштаб планаДоска почёта
Чтобы попасть сюда — пройдите тест.
ТОП-3 тестакоторые проходят вместе с этимТест «Масштаб» (6 класс) рассчитан на учеников средней школы.Ответы к заданиям уже даны, поэтому с помощью теста можно быстро оценить себя и более качественно подготовиться к занятию по теме. Вопросы проверяют умение расшифровывать масштабы и преобразовывать их.
Тест по математике «Масштаб» целесообразно использовать в процессе подготовки к тематической контрольной работе, итоговой проверке.
Рейтинг теста
Средняя оценка: 3.7. Всего получено оценок: 306.
А какую оценку вы? Чтобы узнать — пройдите тест.
Решения | Самостоятельная 9. Масштаб — Математика, 6 класс
1. Выберите верное утверждение.
Вариант 1.Если карты 1: 2000, то реальные значения по сравнению с масштабом отрезка на карте будут:
Верный ответ: б) увеличены в 2000 раз.
Вариант 2. Если масштаб карты 1: 40 000, то расстояния на карте по сравнению с реальными расстояниями будут:
Верный ответ: в) увеличены в 40 000 раз.
2.
Вариант 1. Определите масштаб карты, если 3 см на карте соответствуют 90 000 см на местности.
3
= 1x; \ dfrac {3} {} = \ dfrac {1} {x};3 = x1; x =
⋅1: 3 = 30000.x = \ cdot 1: 3 = 30000.x =⋅1: 3 = 30000. Ответ: 1: 30000.1: 30000.1: 30000.
Вариант 2. Определите масштаб карты, если 5 см на карте соответствуют 150 000 см на местности.
5150000 = 1x; \ dfrac {5} {150000} = \ dfrac {1} {x}; 1500005 = x1;
x = 150000⋅1: 5 = 30000.x = 150000 \ cdot 1: 5 = 30000. x = 150000⋅1: 5 = 30000.
Ответ: 1: 30000.1: 30000.1: 30000.
3.
Вариант 1. Найдите расстояние между двумя городами на местности, если масштаб карты равен 1: 1 000 000. а расстояние между ними на карте равно 6,3 см. Ответ запишите в километрах.
6.3x = 11000000; \ dfrac {6.3} {x} = \ dfrac {1} {1000000}; x6.3 = 10000001;
x = 6.31000000: 1 = 6300000x = 6.3 \ cdot 1000000: 1 = 6300000x = 6.3⋅1000000: 1 = 6300000 см = 63 км.
Ответ: 63 км.
Вариант 2. Расстояние между двумя городами 360 км. Каким будет это расстояние на карте, масштаб равенства 1: 4 000 000? Ответ запишите в сантиметрах.
360 км = 36 000 000 см;
x36000000 = 14000000; \ dfrac {x} {36000000} = \ dfrac {1} {4000000}; 36000000x = 40000001;
x = 36000000⋅1: 4000000 = 9x = 36000000 \ cdot 1: 4000000 = 9x = 36000000⋅1: 4000000 = 9 см.
Ответ: 9 см.
4. На рисунке дан план земельного участка прямоугольной формы. Сделайте необходимые измерения и вычислите площадь этого участка.
Вариант 1
aaa — длина;
5a = 12000; \ dfrac {5} {a} = \ dfrac {1} {2000}; a5 = 20001;
a = 5⋅2000: 1 = 10000a = 5 \ cdot 2000: 1 = 10000a = 5⋅2000: 1 = 10000 (см) = 100 (м) — длина;
bbb — ширина;
2b = 12000; \ dfrac {2} {b} = \ dfrac {1} {2000}; b2 = 20001;
b = 2⋅2000: 1 = 4000b = 2 \ cdot 2000: 1 = 4000b = 2⋅2000: 1 = 4000 (см) = 40 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
40⋅100 = 400040 \ cdot 100 = 400040⋅100 = 4000 (м 2 ) — площадь.
Ответ: 4000 м 2 .
Вариант 2
aaa — длина;
6a = 14000; \ dfrac {6} {a} = \ dfrac {1} {4000}; a6 = 40001;
a = 6⋅40000: 1 = 24000a = 6 \ cdot 40000: 1 = 24000a = 6⋅40000: 1 = 24000 (см) = 240 (м) — длина;
bbb — ширина;
2b = 14000; \ dfrac {2} {b} = \ dfrac {1} {4000}; b2 = 40001;
b = 2⋅4000: 1 = 8000b = 2 \ cdot 4000: 1 = 8000b = 2⋅4000: 1 = 8000 (см) = 80 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
240⋅80 = 19200240 \ cdot 80 = 19200240⋅80 = 19200 м 2 — площадь.
Ответ: 19 200 м 2 .
5.
Вариант 1. Длина детали на чертеже, масштаб которого 1: 4, равна 4 см. Какова будет длина этой детали на чертеже в масштабе 5: 1?
1) 4x = 14; \ dfrac {4} {x} = \ dfrac {1} {4}; x4 = 41;
x = 4⋅4: 1 = 16x = 4 \ cdot 4: 1 = 16x = 4⋅4: 1 = 16 (см) — длина детали в реальности;
2) x16 = 51; \ dfrac {x} {16} = \ dfrac {5} {1}; 16x = 15;
x = 16⋅5⋅1 = 80x = 16 \ cdot 5 \ cdot 1 = 80x = 16⋅5⋅1 = 80 (см) — длина детали на чертеже.
Ответ: 80 см.
Вариант 2. Длина детали на чертеже, масштаб которого 4: 1, равна 4 см.Какова будет длина этой детали на чертеже в масштабе 1: 3?
1) 60x = 41; \ dfrac {60} {x} = \ dfrac {4} {1}; x60 = 14;
x = 60⋅1: 4 = 15x = 60 \ cdot 1: 4 = 15x = 60⋅1: 4 = 15 (см) — длина детали в действительности;
2) x15 = 13; \ dfrac {x} {15} = \ dfrac {1} {3}; 15x = 31;
x = 15⋅: 3 = 5x = 15 \ cdot: 3 = 5x = 15⋅: 3 = 5 (см) — длина детали на чертеже.
Ответ: 5 см.
6.1.4. Масштаб.
Отношение длины отрезка на карте длине расстояния на местности масштабом карты.
В соответствии со своим масштабом карты так и называют: пятитысячная, десятитысячная и т.д.
Пятитысячная карта , т. е. карта с масштабом 1: 5000 означает, что 1 см на карте соответствует 5000 см на местности. Но мы не меряем расстояния на местности в сантиметрах.Переводим 5000 см в метры. Так как 1 м = 100 см , то 5000 см = 50 м . Следовательно, 50 м на местности изображены на пятитысячной карте отрезком, равным 1 см. Что же можно изобразить на пятитысячной карте? Например, наш сквер, имеющий прямоугольную форму с размерами 600 м х 200 м (длина сквера 600 метров , а ширина 200 метров ). На карте с масштабом 1: 5000 сквер будет изображен прямоугольником длиной 12 см ( 600: 50 = 12 ) и шириной 4 см ( 200: 50 = 4 ).
На десятитысячной карте, т.е. карта с масштабом 1: 10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.
Как «читать» эту карту? Найдем расстояние между интересующими нас объектами в сантиметрах и умножим на 10000 (см) , переведем в метры.
На двадцатипятитысячных, пятидесятитысячных картах изображают небольшие населенные области.
На стотысячных, двухсоттысячных картах можно изображать крупных города.
Одному сантиметру стотысячной карты соответствуют 100 000 см на местности. Переведем в метры: 100 000 см = 1000 м, а затем в километры: 1000 м = 1 км.
Итак, 100 000 см = 1 км . Сделаем вывод: , чтобы перевести число сантиметров в километры, нужно разделить это число на 100 000 (или просто «убрать» пять нулей). Теперь нам проще будет представить масштабирование 1: 100 000. На 1 см на карте приходится 1 км на местности. Если расстояние от вашего города до дачного поселка составляет 10км (по прямой!), То на стотысячной карте это расстояние представляет собой отрезок длиной 10см .
На двухсоттысячной карта (М = 1: 200 000) в 1 см изображается фактическое расстояние, равное 2 км (200 000 см = 2 км).
На трехсоттысячной карте с масштабом 1: 300 000 под каждым сантиметром подразумевают фактическое расстояние в 3 км (300 000 см = 3 км).
На пятитысячной карте 1 см соответствует 5 км на местности.
На миллионной карте 1 см соответствует 10 км на местности. На таких картах изображают области, края.
А на каких картах можно изобразить страны? Обычно карты стран, Республик имеют масштаб 1: 8 000 000 или 1: 10 000 000.
Большая карта Мира, которую вы изучаете в школе, имеет масштаб 1: 25 000 000.
Чтобы напечатать эту карту в атласе нужно ее уменьшить. И тогда масштаб карты Мира в атласе может составить 1: 60 000 000 или 1:75 000 000, если атлас будет поменьше.
ча 1. Пользуясь Задачей масштабом 1:12 250 000 , найдите расстояние (по прямому) между Астаной и Таразом на местности.
Решение.
На карте 1 см соответствует 12 250 000 см или (делим число сантиметров на 100 000 — переносим запятую на 5 цифр влево) 122, 5 км.
Измерим линейкой расстояние между Астаной и Таразом на карте. Получилось 7,5 см. Нужно узнать, сколько километров соответствует отрезку на карте в 7,5 см. Итак:
1 см ———- 122,5 км
7,5 см ——- х км. Можно составить пропорцию, а можно рассуждать так: в 1 см — 122,5 км, тогда в 7,5 см — в 7,5 раз больше. Следовательно, 122,5 · 7,5 = 918,75. Округлим до целых: 918,75≈919.
Ответ: от Астаны до Тараза (по прямой) 919 км.
Задача 2. Найти масштаб карты, если расстояние от Астаны до Атырау (по прямой) на местности составляет 1500 км.
Решение.
Измеряем линейкой расстояние от Астаны до Атырау.Получилось 7,5 см . По условию можно записать:
7,5 см ———- 1500 км. Найти масштаб карты — означает узнать, сколько километров (а потом, обязательно, — сантиметров на местности) соответствуют отрезку в 1 см на карте. Запишем:
1 см ———— х км. Можно составить пропорцию: 7,5: 1 = 1500: х , из чего найти ее крайний член х . А можно рассуждать так: 1500 км изображены отрезком в 7,5 см , значит, отрезок в 1 см будет соответствовать расстоянию в 7,5 раз меньшему, и нужно число 1500 разделить на 7, 5 .
х = 1500 : 7,5;
х = 15000 : 75;
х = 200. Мы нашли, сколько км на местности приходится на 1 см на карте. Выразим 200 км в сантиметрах (для этого нам просто нужно приписать к числу 200 справа 5 нулей).
200 км = 20000000 см. Масштаб карты 1:20 000 000.
Ответ: М = 1: 20 000 000.
Смотрите видео: «Масштаб».
.
3 = x1; x =
⋅1: 3 = 30000.x = \ cdot 1: 3 = 30000.x =⋅1: 3 = 30000. Ответ: 1: 30000.1: 30000.1: 30000.
Вариант 2. Определите масштаб карты, если 5 см на карте соответствуют 150 000 см на местности.
5150000 = 1x; \ dfrac {5} {150000} = \ dfrac {1} {x}; 1500005 = x1;
x = 150000⋅1: 5 = 30000.x = 150000 \ cdot 1: 5 = 30000. x = 150000⋅1: 5 = 30000.
Ответ: 1: 30000.1: 30000.1: 30000.
3.
Вариант 1. Найдите расстояние между двумя городами на местности, если масштаб карты равен 1: 1 000 000. а расстояние между ними на карте равно 6,3 см. Ответ запишите в километрах.
6.3x = 11000000; \ dfrac {6.3} {x} = \ dfrac {1} {1000000}; x6.3 = 10000001;
x = 6.31000000: 1 = 6300000x = 6.3 \ cdot 1000000: 1 = 6300000x = 6.3⋅1000000: 1 = 6300000 см = 63 км.
Ответ: 63 км.
Вариант 2. Расстояние между двумя городами 360 км. Каким будет это расстояние на карте, масштаб равенства 1: 4 000 000? Ответ запишите в сантиметрах.
360 км = 36 000 000 см;
x36000000 = 14000000; \ dfrac {x} {36000000} = \ dfrac {1} {4000000}; 36000000x = 40000001;
x = 36000000⋅1: 4000000 = 9x = 36000000 \ cdot 1: 4000000 = 9x = 36000000⋅1: 4000000 = 9 см.
Ответ: 9 см.
4. На рисунке дан план земельного участка прямоугольной формы. Сделайте необходимые измерения и вычислите площадь этого участка.
Вариант 1
aaa — длина;
5a = 12000; \ dfrac {5} {a} = \ dfrac {1} {2000}; a5 = 20001;
a = 5⋅2000: 1 = 10000a = 5 \ cdot 2000: 1 = 10000a = 5⋅2000: 1 = 10000 (см) = 100 (м) — длина;
bbb — ширина;
2b = 12000; \ dfrac {2} {b} = \ dfrac {1} {2000}; b2 = 20001;
b = 2⋅2000: 1 = 4000b = 2 \ cdot 2000: 1 = 4000b = 2⋅2000: 1 = 4000 (см) = 40 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
40⋅100 = 400040 \ cdot 100 = 400040⋅100 = 4000 (м 2 ) — площадь.
Ответ: 4000 м 2 .
Вариант 2
aaa — длина;
6a = 14000; \ dfrac {6} {a} = \ dfrac {1} {4000}; a6 = 40001;
a = 6⋅40000: 1 = 24000a = 6 \ cdot 40000: 1 = 24000a = 6⋅40000: 1 = 24000 (см) = 240 (м) — длина;
bbb — ширина;
2b = 14000; \ dfrac {2} {b} = \ dfrac {1} {4000}; b2 = 40001;
b = 2⋅4000: 1 = 8000b = 2 \ cdot 4000: 1 = 8000b = 2⋅4000: 1 = 8000 (см) = 80 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
240⋅80 = 19200240 \ cdot 80 = 19200240⋅80 = 19200 м 2 — площадь.
Ответ: 19 200 м 2 .
5.
Вариант 1. Длина детали на чертеже, масштаб которого 1: 4, равна 4 см. Какова будет длина этой детали на чертеже в масштабе 5: 1?
1) 4x = 14; \ dfrac {4} {x} = \ dfrac {1} {4}; x4 = 41;
x = 4⋅4: 1 = 16x = 4 \ cdot 4: 1 = 16x = 4⋅4: 1 = 16 (см) — длина детали в реальности;
2) x16 = 51; \ dfrac {x} {16} = \ dfrac {5} {1}; 16x = 15;
x = 16⋅5⋅1 = 80x = 16 \ cdot 5 \ cdot 1 = 80x = 16⋅5⋅1 = 80 (см) — длина детали на чертеже.
Ответ: 80 см.
Вариант 2. Длина детали на чертеже, масштаб которого 4: 1, равна 4 см.Какова будет длина этой детали на чертеже в масштабе 1: 3?
1) 60x = 41; \ dfrac {60} {x} = \ dfrac {4} {1}; x60 = 14;
x = 60⋅1: 4 = 15x = 60 \ cdot 1: 4 = 15x = 60⋅1: 4 = 15 (см) — длина детали в действительности;
2) x15 = 13; \ dfrac {x} {15} = \ dfrac {1} {3}; 15x = 31;
x = 15⋅: 3 = 5x = 15 \ cdot: 3 = 5x = 15⋅: 3 = 5 (см) — длина детали на чертеже.
Ответ: 5 см.
6.1.4. Масштаб.
Отношение длины отрезка на карте длине расстояния на местности масштабом карты.
В соответствии со своим масштабом карты так и называют: пятитысячная, десятитысячная и т.д.
Пятитысячная карта , т. е. карта с масштабом 1: 5000 означает, что 1 см на карте соответствует 5000 см на местности. Но мы не меряем расстояния на местности в сантиметрах.Переводим 5000 см в метры. Так как 1 м = 100 см , то 5000 см = 50 м . Следовательно, 50 м на местности изображены на пятитысячной карте отрезком, равным 1 см. Что же можно изобразить на пятитысячной карте? Например, наш сквер, имеющий прямоугольную форму с размерами 600 м х 200 м (длина сквера 600 метров , а ширина 200 метров ). На карте с масштабом 1: 5000 сквер будет изображен прямоугольником длиной 12 см ( 600: 50 = 12 ) и шириной 4 см ( 200: 50 = 4 ).
На десятитысячной карте, т.е. карта с масштабом 1: 10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.
Как «читать» эту карту? Найдем расстояние между интересующими нас объектами в сантиметрах и умножим на 10000 (см) , переведем в метры.
На двадцатипятитысячных, пятидесятитысячных картах изображают небольшие населенные области.
На стотысячных, двухсоттысячных картах можно изображать крупных города.
Одному сантиметру стотысячной карты соответствуют 100 000 см на местности. Переведем в метры: 100 000 см = 1000 м, а затем в километры: 1000 м = 1 км.
Итак, 100 000 см = 1 км . Сделаем вывод: , чтобы перевести число сантиметров в километры, нужно разделить это число на 100 000 (или просто «убрать» пять нулей). Теперь нам проще будет представить масштабирование 1: 100 000. На 1 см на карте приходится 1 км на местности. Если расстояние от вашего города до дачного поселка составляет 10км (по прямой!), То на стотысячной карте это расстояние представляет собой отрезок длиной 10см .
На двухсоттысячной карта (М = 1: 200 000) в 1 см изображается фактическое расстояние, равное 2 км (200 000 см = 2 км).
На трехсоттысячной карте с масштабом 1: 300 000 под каждым сантиметром подразумевают фактическое расстояние в 3 км (300 000 см = 3 км).
На пятитысячной карте 1 см соответствует 5 км на местности.
На миллионной карте 1 см соответствует 10 км на местности. На таких картах изображают области, края.
А на каких картах можно изобразить страны? Обычно карты стран, Республик имеют масштаб 1: 8 000 000 или 1: 10 000 000.
Большая карта Мира, которую вы изучаете в школе, имеет масштаб 1: 25 000 000.
Чтобы напечатать эту карту в атласе нужно ее уменьшить. И тогда масштаб карты Мира в атласе может составить 1: 60 000 000 или 1:75 000 000, если атлас будет поменьше.
ча 1. Пользуясь Задачей масштабом 1:12 250 000 , найдите расстояние (по прямому) между Астаной и Таразом на местности.
Решение.
На карте 1 см соответствует 12 250 000 см или (делим число сантиметров на 100 000 — переносим запятую на 5 цифр влево) 122, 5 км.
Измерим линейкой расстояние между Астаной и Таразом на карте. Получилось 7,5 см. Нужно узнать, сколько километров соответствует отрезку на карте в 7,5 см. Итак:
1 см ———- 122,5 км
7,5 см ——- х км. Можно составить пропорцию, а можно рассуждать так: в 1 см — 122,5 км, тогда в 7,5 см — в 7,5 раз больше. Следовательно, 122,5 · 7,5 = 918,75. Округлим до целых: 918,75≈919.
Ответ: от Астаны до Тараза (по прямой) 919 км.
Задача 2. Найти масштаб карты, если расстояние от Астаны до Атырау (по прямой) на местности составляет 1500 км.
Решение.
Измеряем линейкой расстояние от Астаны до Атырау.Получилось 7,5 см . По условию можно записать:
7,5 см ———- 1500 км. Найти масштаб карты — означает узнать, сколько километров (а потом, обязательно, — сантиметров на местности) соответствуют отрезку в 1 см на карте. Запишем:
1 см ———— х км. Можно составить пропорцию: 7,5: 1 = 1500: х , из чего найти ее крайний член х . А можно рассуждать так: 1500 км изображены отрезком в 7,5 см , значит, отрезок в 1 см будет соответствовать расстоянию в 7,5 раз меньшему, и нужно число 1500 разделить на 7, 5 .
х = 1500 : 7,5;
х = 15000 : 75;
х = 200. Мы нашли, сколько км на местности приходится на 1 см на карте. Выразим 200 км в сантиметрах (для этого нам просто нужно приписать к числу 200 справа 5 нулей).
200 км = 20000000 см. Масштаб карты 1:20 000 000.
Ответ: М = 1: 20 000 000.
Смотрите видео: «Масштаб».
.
\ cdot 1: 3 = 30000.x =⋅1: 3 = 30000. Ответ: 1: 30000.1: 30000.1: 30000.
Вариант 2. Определите масштаб карты, если 5 см на карте соответствуют 150 000 см на местности.
5150000 = 1x; \ dfrac {5} {150000} = \ dfrac {1} {x}; 1500005 = x1;
x = 150000⋅1: 5 = 30000.x = 150000 \ cdot 1: 5 = 30000. x = 150000⋅1: 5 = 30000.
Ответ: 1: 30000.1: 30000.1: 30000.
3.
Вариант 1. Найдите расстояние между двумя городами на местности, если масштаб карты равен 1: 1 000 000. а расстояние между ними на карте равно 6,3 см. Ответ запишите в километрах.
6.3x = 11000000; \ dfrac {6.3} {x} = \ dfrac {1} {1000000}; x6.3 = 10000001;
x = 6.31000000: 1 = 6300000x = 6.3 \ cdot 1000000: 1 = 6300000x = 6.3⋅1000000: 1 = 6300000 см = 63 км.
Ответ: 63 км.
Вариант 2. Расстояние между двумя городами 360 км. Каким будет это расстояние на карте, масштаб равенства 1: 4 000 000? Ответ запишите в сантиметрах.
360 км = 36 000 000 см;
x36000000 = 14000000; \ dfrac {x} {36000000} = \ dfrac {1} {4000000}; 36000000x = 40000001;
x = 36000000⋅1: 4000000 = 9x = 36000000 \ cdot 1: 4000000 = 9x = 36000000⋅1: 4000000 = 9 см.
Ответ: 9 см.
4. На рисунке дан план земельного участка прямоугольной формы. Сделайте необходимые измерения и вычислите площадь этого участка.
Вариант 1
aaa — длина;
5a = 12000; \ dfrac {5} {a} = \ dfrac {1} {2000}; a5 = 20001;
a = 5⋅2000: 1 = 10000a = 5 \ cdot 2000: 1 = 10000a = 5⋅2000: 1 = 10000 (см) = 100 (м) — длина;
bbb — ширина;
2b = 12000; \ dfrac {2} {b} = \ dfrac {1} {2000}; b2 = 20001;
b = 2⋅2000: 1 = 4000b = 2 \ cdot 2000: 1 = 4000b = 2⋅2000: 1 = 4000 (см) = 40 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
40⋅100 = 400040 \ cdot 100 = 400040⋅100 = 4000 (м 2 ) — площадь.
Ответ: 4000 м 2 .
Вариант 2
aaa — длина;
6a = 14000; \ dfrac {6} {a} = \ dfrac {1} {4000}; a6 = 40001;
a = 6⋅40000: 1 = 24000a = 6 \ cdot 40000: 1 = 24000a = 6⋅40000: 1 = 24000 (см) = 240 (м) — длина;
bbb — ширина;
2b = 14000; \ dfrac {2} {b} = \ dfrac {1} {4000}; b2 = 40001;
b = 2⋅4000: 1 = 8000b = 2 \ cdot 4000: 1 = 8000b = 2⋅4000: 1 = 8000 (см) = 80 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
240⋅80 = 19200240 \ cdot 80 = 19200240⋅80 = 19200 м 2 — площадь.
Ответ: 19 200 м 2 .
5.
Вариант 1. Длина детали на чертеже, масштаб которого 1: 4, равна 4 см. Какова будет длина этой детали на чертеже в масштабе 5: 1?
1) 4x = 14; \ dfrac {4} {x} = \ dfrac {1} {4}; x4 = 41;
x = 4⋅4: 1 = 16x = 4 \ cdot 4: 1 = 16x = 4⋅4: 1 = 16 (см) — длина детали в реальности;
2) x16 = 51; \ dfrac {x} {16} = \ dfrac {5} {1}; 16x = 15;
x = 16⋅5⋅1 = 80x = 16 \ cdot 5 \ cdot 1 = 80x = 16⋅5⋅1 = 80 (см) — длина детали на чертеже.
Ответ: 80 см.
Вариант 2. Длина детали на чертеже, масштаб которого 4: 1, равна 4 см.Какова будет длина этой детали на чертеже в масштабе 1: 3?
1) 60x = 41; \ dfrac {60} {x} = \ dfrac {4} {1}; x60 = 14;
x = 60⋅1: 4 = 15x = 60 \ cdot 1: 4 = 15x = 60⋅1: 4 = 15 (см) — длина детали в действительности;
2) x15 = 13; \ dfrac {x} {15} = \ dfrac {1} {3}; 15x = 31;
x = 15⋅: 3 = 5x = 15 \ cdot: 3 = 5x = 15⋅: 3 = 5 (см) — длина детали на чертеже.
Ответ: 5 см.
6.1.4. Масштаб.
Отношение длины отрезка на карте длине расстояния на местности масштабом карты.
В соответствии со своим масштабом карты так и называют: пятитысячная, десятитысячная и т.д.
Пятитысячная карта , т. е. карта с масштабом 1: 5000 означает, что 1 см на карте соответствует 5000 см на местности. Но мы не меряем расстояния на местности в сантиметрах.Переводим 5000 см в метры. Так как 1 м = 100 см , то 5000 см = 50 м . Следовательно, 50 м на местности изображены на пятитысячной карте отрезком, равным 1 см. Что же можно изобразить на пятитысячной карте? Например, наш сквер, имеющий прямоугольную форму с размерами 600 м х 200 м (длина сквера 600 метров , а ширина 200 метров ). На карте с масштабом 1: 5000 сквер будет изображен прямоугольником длиной 12 см ( 600: 50 = 12 ) и шириной 4 см ( 200: 50 = 4 ).
На десятитысячной карте, т.е. карта с масштабом 1: 10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.
Как «читать» эту карту? Найдем расстояние между интересующими нас объектами в сантиметрах и умножим на 10000 (см) , переведем в метры.
На двадцатипятитысячных, пятидесятитысячных картах изображают небольшие населенные области.
На стотысячных, двухсоттысячных картах можно изображать крупных города.
Одному сантиметру стотысячной карты соответствуют 100 000 см на местности. Переведем в метры: 100 000 см = 1000 м, а затем в километры: 1000 м = 1 км.
Итак, 100 000 см = 1 км . Сделаем вывод: , чтобы перевести число сантиметров в километры, нужно разделить это число на 100 000 (или просто «убрать» пять нулей). Теперь нам проще будет представить масштабирование 1: 100 000. На 1 см на карте приходится 1 км на местности. Если расстояние от вашего города до дачного поселка составляет 10км (по прямой!), То на стотысячной карте это расстояние представляет собой отрезок длиной 10см .
На двухсоттысячной карта (М = 1: 200 000) в 1 см изображается фактическое расстояние, равное 2 км (200 000 см = 2 км).
На трехсоттысячной карте с масштабом 1: 300 000 под каждым сантиметром подразумевают фактическое расстояние в 3 км (300 000 см = 3 км).
На пятитысячной карте 1 см соответствует 5 км на местности.
На миллионной карте 1 см соответствует 10 км на местности. На таких картах изображают области, края.
А на каких картах можно изобразить страны? Обычно карты стран, Республик имеют масштаб 1: 8 000 000 или 1: 10 000 000.
Большая карта Мира, которую вы изучаете в школе, имеет масштаб 1: 25 000 000.
Чтобы напечатать эту карту в атласе нужно ее уменьшить. И тогда масштаб карты Мира в атласе может составить 1: 60 000 000 или 1:75 000 000, если атлас будет поменьше.
ча 1. Пользуясь Задачей масштабом 1:12 250 000 , найдите расстояние (по прямому) между Астаной и Таразом на местности.
Решение.
На карте 1 см соответствует 12 250 000 см или (делим число сантиметров на 100 000 — переносим запятую на 5 цифр влево) 122, 5 км.
Измерим линейкой расстояние между Астаной и Таразом на карте. Получилось 7,5 см. Нужно узнать, сколько километров соответствует отрезку на карте в 7,5 см. Итак:
1 см ———- 122,5 км
7,5 см ——- х км. Можно составить пропорцию, а можно рассуждать так: в 1 см — 122,5 км, тогда в 7,5 см — в 7,5 раз больше. Следовательно, 122,5 · 7,5 = 918,75. Округлим до целых: 918,75≈919.
Ответ: от Астаны до Тараза (по прямой) 919 км.
Задача 2. Найти масштаб карты, если расстояние от Астаны до Атырау (по прямой) на местности составляет 1500 км.
Решение.
Измеряем линейкой расстояние от Астаны до Атырау.Получилось 7,5 см . По условию можно записать:
7,5 см ———- 1500 км. Найти масштаб карты — означает узнать, сколько километров (а потом, обязательно, — сантиметров на местности) соответствуют отрезку в 1 см на карте. Запишем:
1 см ———— х км. Можно составить пропорцию: 7,5: 1 = 1500: х , из чего найти ее крайний член х . А можно рассуждать так: 1500 км изображены отрезком в 7,5 см , значит, отрезок в 1 см будет соответствовать расстоянию в 7,5 раз меньшему, и нужно число 1500 разделить на 7, 5 .
х = 1500 : 7,5;
х = 15000 : 75;
х = 200. Мы нашли, сколько км на местности приходится на 1 см на карте. Выразим 200 км в сантиметрах (для этого нам просто нужно приписать к числу 200 справа 5 нулей).
200 км = 20000000 см. Масштаб карты 1:20 000 000.
Ответ: М = 1: 20 000 000.
Смотрите видео: «Масштаб».
.
Ответ: 1: 30000.1: 30000.1: 30000.
Вариант 2. Определите масштаб карты, если 5 см на карте соответствуют 150 000 см на местности.
5150000 = 1x; \ dfrac {5} {150000} = \ dfrac {1} {x}; 1500005 = x1;
x = 150000⋅1: 5 = 30000.x = 150000 \ cdot 1: 5 = 30000. x = 150000⋅1: 5 = 30000.
Ответ: 1: 30000.1: 30000.1: 30000.
3.
Вариант 1. Найдите расстояние между двумя городами на местности, если масштаб карты равен 1: 1 000 000. а расстояние между ними на карте равно 6,3 см. Ответ запишите в километрах.
6.3x = 11000000; \ dfrac {6.3} {x} = \ dfrac {1} {1000000}; x6.3 = 10000001;
x = 6.31000000: 1 = 6300000x = 6.3 \ cdot 1000000: 1 = 6300000x = 6.3⋅1000000: 1 = 6300000 см = 63 км.
Ответ: 63 км.
Вариант 2. Расстояние между двумя городами 360 км. Каким будет это расстояние на карте, масштаб равенства 1: 4 000 000? Ответ запишите в сантиметрах.
360 км = 36 000 000 см;
x36000000 = 14000000; \ dfrac {x} {36000000} = \ dfrac {1} {4000000}; 36000000x = 40000001;
x = 36000000⋅1: 4000000 = 9x = 36000000 \ cdot 1: 4000000 = 9x = 36000000⋅1: 4000000 = 9 см.
Ответ: 9 см.
4. На рисунке дан план земельного участка прямоугольной формы. Сделайте необходимые измерения и вычислите площадь этого участка.
Вариант 1
aaa — длина;
5a = 12000; \ dfrac {5} {a} = \ dfrac {1} {2000}; a5 = 20001;
a = 5⋅2000: 1 = 10000a = 5 \ cdot 2000: 1 = 10000a = 5⋅2000: 1 = 10000 (см) = 100 (м) — длина;
bbb — ширина;
2b = 12000; \ dfrac {2} {b} = \ dfrac {1} {2000}; b2 = 20001;
b = 2⋅2000: 1 = 4000b = 2 \ cdot 2000: 1 = 4000b = 2⋅2000: 1 = 4000 (см) = 40 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
40⋅100 = 400040 \ cdot 100 = 400040⋅100 = 4000 (м 2 ) — площадь.
Ответ: 4000 м 2 .
Вариант 2
aaa — длина;
6a = 14000; \ dfrac {6} {a} = \ dfrac {1} {4000}; a6 = 40001;
a = 6⋅40000: 1 = 24000a = 6 \ cdot 40000: 1 = 24000a = 6⋅40000: 1 = 24000 (см) = 240 (м) — длина;
bbb — ширина;
2b = 14000; \ dfrac {2} {b} = \ dfrac {1} {4000}; b2 = 40001;
b = 2⋅4000: 1 = 8000b = 2 \ cdot 4000: 1 = 8000b = 2⋅4000: 1 = 8000 (см) = 80 (м) — ширина;
S = a⋅b; S = a \ cdot b; S = a⋅b;
240⋅80 = 19200240 \ cdot 80 = 19200240⋅80 = 19200 м 2 — площадь.
Ответ: 19 200 м 2 .
5.
Вариант 1.
Длина детали на чертеже, масштаб которого 1: 4, равна 4 см. Какова будет длина этой детали на чертеже в масштабе 5: 1?
1) 4x = 14; \ dfrac {4} {x} = \ dfrac {1} {4}; x4 = 41;
x = 4⋅4: 1 = 16x = 4 \ cdot 4: 1 = 16x = 4⋅4: 1 = 16 (см) — длина детали в реальности;
2) x16 = 51; \ dfrac {x} {16} = \ dfrac {5} {1}; 16x = 15;
x = 16⋅5⋅1 = 80x = 16 \ cdot 5 \ cdot 1 = 80x = 16⋅5⋅1 = 80 (см) — длина детали на чертеже.
Ответ: 80 см.
Вариант 2. Длина детали на чертеже, масштаб которого 4: 1, равна 4 см.Какова будет длина этой детали на чертеже в масштабе 1: 3?
1) 60x = 41; \ dfrac {60} {x} = \ dfrac {4} {1}; x60 = 14;
x = 60⋅1: 4 = 15x = 60 \ cdot 1: 4 = 15x = 60⋅1: 4 = 15 (см) — длина детали в действительности;
2) x15 = 13; \ dfrac {x} {15} = \ dfrac {1} {3}; 15x = 31;
x = 15⋅: 3 = 5x = 15 \ cdot: 3 = 5x = 15⋅: 3 = 5 (см) — длина детали на чертеже.
Ответ: 5 см.
6.1.4. Масштаб.
Отношение длины отрезка на карте длине расстояния на местности масштабом карты.
В соответствии со своим масштабом карты так и называют: пятитысячная, десятитысячная и т.д.
Пятитысячная карта , т. е. карта с масштабом 1: 5000 означает, что 1 см на карте соответствует 5000 см на местности. Но мы не меряем расстояния на местности в сантиметрах.Переводим 5000 см в метры. Так как 1 м = 100 см , то 5000 см = 50 м . Следовательно, 50 м на местности изображены на пятитысячной карте отрезком, равным 1 см. Что же можно изобразить на пятитысячной карте? Например, наш сквер, имеющий прямоугольную форму с размерами 600 м х 200 м (длина сквера 600 метров , а ширина 200 метров ).
На карте с масштабом 1: 5000 сквер будет изображен прямоугольником длиной 12 см ( 600: 50 = 12 ) и шириной 4 см ( 200: 50 = 4 ).
На десятитысячной карте, т.е. карта с масштабом 1: 10000 можно изобразить лесопарк. 1 см на этой карте означает 10000 см или 100 м на местности.
Как «читать» эту карту? Найдем расстояние между интересующими нас объектами в сантиметрах и умножим на 10000 (см) , переведем в метры.
На двадцатипятитысячных, пятидесятитысячных картах изображают небольшие населенные области.
На стотысячных, двухсоттысячных картах можно изображать крупных города.
Одному сантиметру стотысячной карты соответствуют 100 000 см на местности.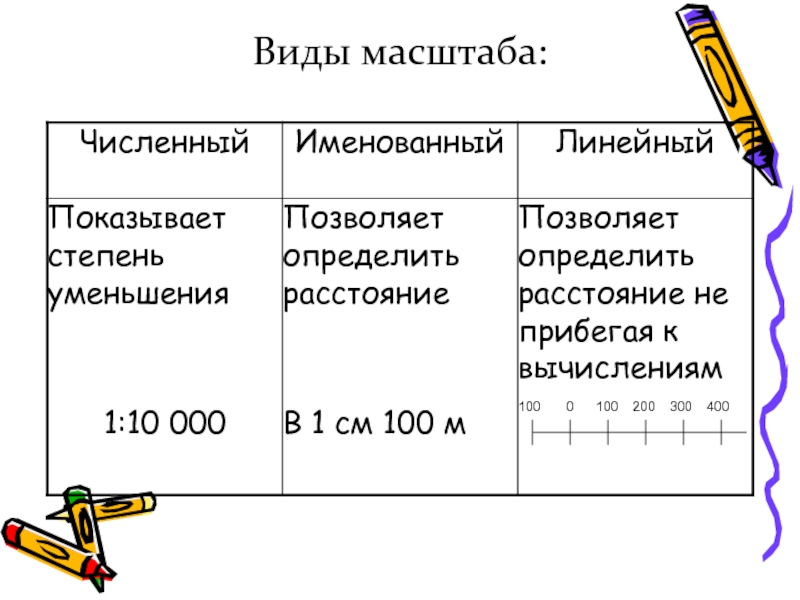
Переведем в метры: 100 000 см = 1000 м, а затем в километры: 1000 м = 1 км.
Итак, 100 000 см = 1 км . Сделаем вывод: , чтобы перевести число сантиметров в километры, нужно разделить это число на 100 000 (или просто «убрать» пять нулей). Теперь нам проще будет представить масштабирование 1: 100 000. На 1 см на карте приходится 1 км на местности. Если расстояние от вашего города до дачного поселка составляет 10км (по прямой!), То на стотысячной карте это расстояние представляет собой отрезок длиной 10см .
На двухсоттысячной карта (М = 1: 200 000) в 1 см изображается фактическое расстояние, равное 2 км (200 000 см = 2 км).
На трехсоттысячной карте с масштабом 1: 300 000 под каждым сантиметром подразумевают фактическое расстояние в 3 км (300 000 см = 3 км).
На пятитысячной карте 1 см соответствует 5 км на местности.
На миллионной карте 1 см соответствует 10 км на местности. На таких картах изображают области, края.
А на каких картах можно изобразить страны? Обычно карты стран, Республик имеют масштаб 1: 8 000 000 или 1: 10 000 000.
Большая карта Мира, которую вы изучаете в школе, имеет масштаб 1: 25 000 000.
Чтобы напечатать эту карту в атласе нужно ее уменьшить. И тогда масштаб карты Мира в атласе может составить 1: 60 000 000 или 1:75 000 000, если атлас будет поменьше.
ча 1. Пользуясь Задачей масштабом 1:12 250 000 , найдите расстояние (по прямому) между Астаной и Таразом на местности.
Решение.
На карте 1 см соответствует 12 250 000 см или (делим число сантиметров на 100 000 — переносим запятую на 5 цифр влево) 122, 5 км.
Измерим линейкой расстояние между Астаной и Таразом на карте. Получилось 7,5 см. Нужно узнать, сколько километров соответствует отрезку на карте в 7,5 см. Итак:
1 см ———- 122,5 км
7,5 см ——- х км. Можно составить пропорцию, а можно рассуждать так: в 1 см — 122,5 км, тогда в 7,5 см — в 7,5 раз больше. Следовательно, 122,5 · 7,5 = 918,75. Округлим до целых: 918,75≈919.
Ответ: от Астаны до Тараза (по прямой) 919 км.
Задача 2. Найти масштаб карты, если расстояние от Астаны до Атырау (по прямой) на местности составляет 1500 км.
Решение.
Измеряем линейкой расстояние от Астаны до Атырау.Получилось 7,5 см . По условию можно записать:
7,5 см ———- 1500 км. Найти масштаб карты — означает узнать, сколько километров (а потом, обязательно, — сантиметров на местности) соответствуют отрезку в 1 см на карте.
Запишем:
1 см ———— х км. Можно составить пропорцию: 7,5: 1 = 1500: х , из чего найти ее крайний член х . А можно рассуждать так: 1500 км изображены отрезком в 7,5 см , значит, отрезок в 1 см будет соответствовать расстоянию в 7,5 раз меньшему, и нужно число 1500 разделить на 7, 5 .
х = 1500 : 7,5;
х = 15000 : 75;
х = 200. Мы нашли, сколько км на местности приходится на 1 см на карте. Выразим 200 км в сантиметрах (для этого нам просто нужно приписать к числу 200 справа 5 нулей).
200 км = 20000000 см. Масштаб карты 1:20 000 000.
Ответ: М = 1: 20 000 000.
Смотрите видео: «Масштаб».
.