Закон Архимеда: вытеснение жидкости погруженным телом
Закон Архимеда — один из первых физических законов, изучаемых учениками средней школы. Хотя бы примерно этот закон помнит любой взрослый человек, как бы далек он ни был от физики. Но иногда полезно вернуться к точным определениям и формулировкам — и разобраться в деталях этого закона, которые могли позабыться.
О чем говорит закон Архимеда?
Существует легенда, что свой знаменитый закон древнегреческий ученый открыл, принимая ванну. Погрузившись в емкость, наполненную водой до краев, Архимед обратил внимание, что вода при этом выплеснулась наружу — и испытал озарение, мгновенно сформулировав суть открытия.
Скорее всего, в реальности дело обстояло иначе, и открытию предшествовали долгие наблюдения. Но это не столь важно, потому что в любом случае Архимеду удалось открыть следующую закономерность:
- погружаясь в любую жидкость, тела и объекты испытывают на себе сразу несколько разнонаправленных, но направленных перпендикулярно по отношению к их поверхности сил;
- итоговый вектор этих сил направлен вверх, поэтому любой объект или тело, оказавшись в жидкости в состоянии покоя, испытывает на себе выталкивание;
- при этом сила выталкивания в точности равна коэффициенту, который получится, если умножить на ускорение свободного падения произведение объема предмета и плотности жидкости.
Итак, Архимед установил, что тело, погружённое в жидкость, вытесняет такой объём жидкости, который равен объёму самого тела. Если в жидкость погружается только часть тела, то оно вытеснит жидкость, объём которой будет равен объёму только той части, которая погружается.
Та же самая закономерность действует и для газов — только здесь объем тела необходимо соотносить с плотностью газа.
Можно сформулировать физический закон и немного проще — сила, которая выталкивает из жидкости или газа некий предмет, в точности равна весу жидкости или газа, вытесненных этим предметом при погружении.
Закон записывается в виде следующей формулы:
Какое значение имеет закон Архимеда?
Закономерность, открытая древнегреческим ученым, проста и совершенно очевидна. Но при этом ее значение для повседневной жизни невозможно переоценить.
Именно благодаря познаниям о выталкивании тел жидкостями и газами мы можем строить речные и морские суда, а также дирижабли и воздушные шары для воздухоплавания. Тяжелые металлические корабли не тонут благодаря тому, что их конструкция учитывает закон Архимеда и многочисленные следствия из него — они построены так, что могут удерживаться на поверхности воды, а не идут ко дну. По аналогичному принципу действуют воздухоплавательные средства — они используют выталкивающие способности воздуха, в процессе полета становясь как бы легче него.
Похожие статьи
Закон Архимеда • Джеймс Трефил, энциклопедия «Двести законов мироздания»
«Эврика!» («Нашел!») — именно этот возглас, согласно легенде, издал древнегреческий ученый и философ Архимед, открыв принцип вытеснения. Легенда гласит, что сиракузский царь Герон II попросил мыслителя определить, из чистого ли золота сделана его корона, не причиняя вреда самому царскому венцу. Взвесить корону Архимеду труда не составило, но этого было мало — нужно было определить объем короны, чтобы рассчитать плотность металла, из которого она отлита, и определить, чистое ли это золото.
Дальше, согласно легенде, Архимед, озабоченный мыслями о том, как определить объем короны, погрузился в ванну — и вдруг заметил, что уровень воды в ванне поднялся. И тут ученый осознал, что объем его тела вытеснил равный ему объем воды, следовательно, и корона, если ее опустить в заполненный до краев таз, вытеснит из него объем воды, равный ее объему. Решение задачи было найдено и, согласно самой расхожей версии легенды, ученый побежал докладывать о своей победе в царский дворец, даже не потрудившись одеться.
Однако, что правда — то правда: именно Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Давление, которое ранее действовало на вытесненную жидкость, теперь будет действовать на твердое тело, вытеснившее ее. И, если действующая вертикально вверх выталкивающая сила окажется больше силы тяжести, тянущей тело вертикально вниз, тело будет всплывать; в противном случае оно пойдет ко дну (утонет). Говоря современным языком, тело плавает, если его средняя плотность меньше плотности жидкости, в которую оно погружено.
Закон Архимеда можно истолковать с точки зрения молекулярно-кинетической теории. В покоящейся жидкости давление производится посредством ударов движущихся молекул. Когда некий объем жидкости вымещается твердым телом, направленный вверх импульс ударов молекул будет приходиться не на вытесненные телом молекулы жидкости, а на само тело, чем и объясняется давление, оказываемое на него снизу и выталкивающее его в направлении поверхности жидкости. Если же тело погружено в жидкость полностью, выталкивающая сила будет по-прежнему действовать на него, поскольку давление нарастает с увеличением глубины, и нижняя часть тела подвергается большему давлению, чем верхняя, откуда и возникает выталкивающая сила. Таково объяснение выталкивающей силы на молекулярном уровне.
Такая картина выталкивания объясняет, почему судно, сделанное из стали, которая значительно плотнее воды, остается на плаву. Дело в том, что объем вытесненной судном воды равен объему погруженной в воду стали плюс объему воздуха, содержащегося внутри корпуса судна ниже ватерлинии. Если усреднить плотность оболочки корпуса и воздуха внутри нее, получится, что плотность судна (как физического тела) меньше плотности воды, поэтому выталкивающая сила, действующая на него в результате направленных вверх импульсов удара молекул воды, оказывается выше гравитационной силы притяжения Земли, тянущей судно ко дну, — и корабль плывет.
elementy.ru
Конспект «Закон Архимеда» — УчительPRO
Закон Архимеда. Плавание тел
Сумму сил гидростатического давления, действующих на тело, покоящееся внутри жидкости, называют силой Архимеда.
Закон Архимеда. На погружённое в жидкость (или газ) тело действует выталкивающая и направленная вертикально вверх сила, равная по модулю весу вытесненной этим телом жидкости (или газа).
FА = pж • g • Vж = mж • g = Pж
где: FА — Архимедова сила, pж — плотность жидкости, g — ускорение свободного падения, Vж — объем жидкости, mж — масса жидкости, Pж — вес жидкости.

Плавание — это способность тела удерживаться на поверхности жидкости или на определённом уровне внутри жидкости. На любое тело, находящееся в жидкости, действуют две силы, направленные в противоположные стороны:
Тело тонет, если рт > рж ; тело всплывает, если рт < рж .
Условие плавания тела на поверхности жидкости: для плавания тела на поверхности жидкости необходимо, чтобы сила тяжести уравновешивалась выталкивающей силой: Fв = М • g
Условие плавания тела на поверхности жидкости можно представить в виде рт • Vт = рж • Vж .

Конспект урока «Архимедова сила».
Следующая тема: «Сообщающиеся сосуды. Шлюзы».
uchitel.pro
17. Закон Архимеда
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:

где  — плотностьжидкости (газа),
— плотностьжидкости (газа), 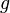
 — объём погружённого тела (или часть
объёма тела, находящаяся ниже поверхности).
Если тело плаваетна поверхности или равномерно движется
вверх или вниз, то выталкивающая сила
(называемая также архимедовой силой)
равна по модулю (и противоположна по
направлению) силе тяжести, действовавшей
на вытесненный телом объём жидкости
(газа), и приложена кцентру
тяжестиэтого объёма.
— объём погружённого тела (или часть
объёма тела, находящаяся ниже поверхности).
Если тело плаваетна поверхности или равномерно движется
вверх или вниз, то выталкивающая сила
(называемая также архимедовой силой)
равна по модулю (и противоположна по
направлению) силе тяжести, действовавшей
на вытесненный телом объём жидкости
(газа), и приложена кцентру
тяжестиэтого объёма.  Тело плавает, если
сила Архимеда уравновешивает силу
тяжести тела.
Тело плавает, если
сила Архимеда уравновешивает силу
тяжести тела.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давленийна примере прямоугольного тела.


где PA, PB — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
18. Равновесие тела в покоящейся жидкости
Для однородного тела плавающего на поверхности справедливо соотношение
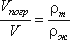 где: V —
объем плавающего тела; ρm —
плотность тела.
где: V —
объем плавающего тела; ρm —
плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется остойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O’-O», представляющей ось симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O’-O». Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным — в противном случае.
 Рис. 2.5. Поперечный
профиль судна
Рис. 2.5. Поперечный
профиль судна
Теперь рассмотрим условия равновесия судна:
1)если h > 0, то судно возвращается в первоначальное положение; 2)если h = 0, то это случай безразличного равновесия; 3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.
Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.
studfile.net
Закон Архимеда — Википедия. Что такое Закон Архимеда
Зако́н Архиме́да — один из законов статики жидкостей (гидростатики) и газов (аэростатики): на тело, погружённое в жидкость или газ, действует выталкивающая или подъёмная сила, равная весу объёма жидкости или газа, вытесненного частью тела, погружённой в жидкость или газ. Закон открыт Архимедом в III веке до н. э. Выталкивающая сила также называется архимедовой или гидростатической подъёмной силой[1][2].
В соответствии с законом Архимеда для выталкивающей силы выполняется[3]:
- FA=ρgV,{\displaystyle F_{A}=\rho gV,}
где:
Дополнения
Выталкивающая или подъёмная сила по направлению противоположна силе тяжести, прикладывается к центру тяжести объёма, вытесняемого телом из жидкости или газа.
Если тело плавает (см. плавание тел) или равномерно движется вверх или вниз, то выталкивающая или подъёмная сила по модулю равна силе тяжести, действующей на вытесненный телом объём жидкости или газа.
 Плавание тела. Сила Архимеда (FA{\displaystyle F_{A}}) уравновешивает вес тела (Fp{\displaystyle F_{p}}):
Плавание тела. Сила Архимеда (FA{\displaystyle F_{A}}) уравновешивает вес тела (Fp{\displaystyle F_{p}}): FA=Fp;{\displaystyle F_{A}=F_{p};}
ρж g Vж = ρт g Vт
Например, воздушный шарик объёмом V{\displaystyle V}, наполненный гелием, летит вверх из-за того, что плотность гелия (ρH{\displaystyle \rho _{H}}) меньше плотности воздуха (ρO{\displaystyle \rho _{O}}):
FA>Fp;{\displaystyle F_{A}>F_{p};}
ρOgV>ρHgV.{\displaystyle \rho _{O}gV>\rho _{H}gV.}
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела, погруженного в жидкость или газ. В силу симметрии прямоугольного тела, силы давления, действующие на боковые грани тела, уравновешиваются. Давление (PA{\displaystyle P_{A}}) и сила давления (FA{\displaystyle F_{A}}), действующие на верхнюю грань тела, равны:
- PA=ρghA;{\displaystyle P_{A}=\rho gh_{A};}
- FA=ρghAS,{\displaystyle F_{A}=\rho gh_{A}S,}
где:
Давление (PB{\displaystyle P_{B}}) и сила давления (FB{\displaystyle F_{B}}), действующие на нижнюю грань тела, равны:
- PB=ρghB;{\displaystyle P_{B}=\rho gh_{B};}
- FB=ρghBS,{\displaystyle F_{B}=\rho gh_{B}S,}
где:
- PB{\displaystyle P_{B}} — давление, оказываемое жидкостью или газом на нижнюю грань тела, Па;
- FB{\displaystyle F_{B}} — сила давления, действующая на нижнюю грань тела и направленная вверх, Н;
- hB{\displaystyle h_{B}} — расстояние между поверхностью жидкости или газа и нижней гранью тела, м.
Сила давления жидкости или газа на тело определяется разностью сил FB{\displaystyle F_{B}} и FA{\displaystyle F_{A}}:
- FB−FA=ρghBS−ρghAS=ρg(hB−hA)S=ρghS=ρgV,{\displaystyle F_{B}-F_{A}=\rho gh_{B}S-\rho gh_{A}S=\rho g\left(h_{B}-h_{A}\right)S=\rho ghS=\rho gV,}
где:
- h=hB−hA{\displaystyle h=h_{B}-h_{A}} — расстояние между верхней и нижней гранями тела (в случае частичного погружения высота части тела, погружённой в жидкость или газ), м;
- V{\displaystyle V} — объём тела, погружённого в жидкость или газ (в случае частичного погружения объём части тела, погружённой в жидкость или газ), м3.
Разница давлений:
- PB−PA=ρghB−ρghA=ρgh.{\displaystyle P_{B}-P_{A}=\rho gh_{B}-\rho gh_{A}=\rho gh.}
В отсутствие гравитационного поля, то есть, в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, к полю центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление p{\displaystyle p} на глубине h{\displaystyle h}, оказываемое жидкостью плотностью ρ{\displaystyle \rho } на тело, есть p=ρgh{\displaystyle p=\rho gh}. Пусть плотность жидкости (ρ{\displaystyle \rho }) и напряжённость гравитационного поля (g{\displaystyle g}) — постоянные величины, а h{\displaystyle h} — параметр. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат Oxyz{\displaystyle Oxyz}, причём выберем направление оси z совпадающим с направлением вектора g→{\displaystyle {\vec {g}}}. Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку dS{\displaystyle dS}. На неё будет действовать сила давления жидкости направленная внутрь тела, dF→A=−pdS→{\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}}. Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
- F→A=−∫SpdS→=−∫SρghdS→=−ρg∫ShdS→=∗−ρg∫Vgrad(h)dV=∗∗−ρg∫Ve→zdV=−ρge→z∫VdV=(ρgV)(−e→z).{\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z}).}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
- ∗h(x,y,z)=z;{\displaystyle {}^{*}h(x,y,z)=z;}
- ∗∗grad(h)=∇h=e→z.{\displaystyle ^{**}grad(h)=\nabla h={\vec {e}}_{z}.}
Получаем, что модуль силы Архимеда равен ρgV{\displaystyle \rho gV}, и направлена сила Архимеда в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Условие плавания тел
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести FT{\displaystyle F_{T}} и силы Архимеда FA{\displaystyle F_{A}}, которые действуют на это тело. Возможны следующие три случая:
- FT>FA{\displaystyle F_{T}>F_{A}} — тело тонет;
- FT=FA{\displaystyle F_{T}=F_{A}} — тело плавает в жидкости или газе;
- FT<FA{\displaystyle F_{T}<F_{A}} — тело всплывает до тех пор, пока не начнёт плавать.
Другая формулировка (где ρt{\displaystyle \rho _{t}} — плотность тела, ρs{\displaystyle \rho _{s}} — плотность среды, в которую тело погружено):
- ρt>ρs{\displaystyle \rho _{t}>\rho _{s}} — тело тонет;
- ρt=ρs{\displaystyle \rho _{t}=\rho _{s}} — тело плавает в жидкости или газе;
- ρt<ρs{\displaystyle \rho _{t}<\rho _{s}} — тело всплывает до тех пор, пока не начнёт плавать.
См. также
Видеоурок: закон АрхимедаПримечания
Ссылки
wiki.sc
Эврика! Закон Архимеда
Архимед – греческий механик, физик, математик, инженер. Родился в Сиракузах (Сицилия). Его отец Фидий был астрономом и математиком. Отец занимался воспитанием и образованием сына. От него Архимед унаследовал способности к математике, астрономии и механике. Архимед обучался в Александрии (Египет), которая в то время была культурным и научным центром. Там он познакомился с Эратосфеном – греческим математиком, астрономом, географом и поэтом, который стал наставником Архимеда и покровительствовал ему долгое время.
 Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
Архимед сочетал в себе таланты инженера-изобретателя и ученого-теоретика. Он стал основателем теоретической механики и гидростатики, разработал методы нахождения площадей поверхностей и объемов различных фигур и тел.
По легенде, Архимеду принадлежит множество удивительных технических изобретений, которые завоевали ему славу среди современников. Предполагают, что Архимед с помощью зеркал и отражения солнечных лучей смог поджечь римский флот, который осадил Александрию. Этот случай является наглядным примером отличного владения оптикой.
Архимеду также приписывают изобретение катапульты, военной метательной машины, конструирование планетария, в котором планеты двигались. Учёный создал винт для подъёма воды (Архимедов винт), который до сих пор используется и представляет собой водоподъемную машину, вал с винтовой поверхностью, находящийся в наклонной трубе, погруженной в воду. Во время вращения винтовая поверхность вала перемещает воду по трубе на разные высоты.
 Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Архимед написал много научных трудов: «О спиралях», «О коноидах и сфероидах», «О шаре и цилиндре», «О рычагах», «О плавающих телах». А в трактате «О песчинках» он подсчитал количество песчинок в объёме земного шара.
Свой знаменитый закон Архимед открыл при интересных обстоятельствах. Царь Гиреон II, которому служил Архимед, хотел узнать, не подмешивали ли ювелиры серебро к золоту, когда изготавливали корону. Для этого необходимо определить не только массу, но объём короны, чтобы рассчитать плотность металла. Определить объём изделия неправильной формы – непростая задача, над которой Архимед долго размышлял.
 Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Решение пришло Архимеду в голову, когда он погрузился в ванну: уровень воды в ванне поднялся после того, как тело учёного было опущено в воду. То есть объем его тела вытеснил равный ему объем воды. С криком «Эврика!» Архимед побежал во дворец, даже не потрудившись одеться. Он опустил корону в воду и определил объем вытесненной жидкости. Задача была решена!
Таким образом, Архимед открыл принцип плавучести. Если твердое тело погрузить в жидкость, оно вытеснит объем жидкости, равный объему погруженной в жидкость части тела. Тело может плавать в воде, если его средняя плотность меньше плотности жидкости, в которую его поместили.
Закон Архимеда гласит: на всякое тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вверх и равная весу вытесненной им жидкости или газа.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
blog.tutoronline.ru
Закон Архимеда — это… Что такое Закон Архимеда?
Зако́н Архиме́да — один из главных законов гидростатики и статики газов.
Формулировка и пояснения
Закон Архимеда формулируется следующим образом[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:
где — плотность жидкости (газа), — ускорение свободного падения, а — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
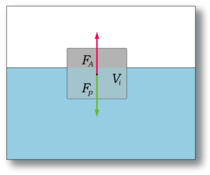 Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.
Тело плавает, если сила Архимеда уравновешивает силу тяжести тела.Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
где PA, PB — давления в точках A и B, ρ — плотность жидкости, h — разница уровней между точками A и B, S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
В теоретической физике также применяют закон Архимеда в интегральной форме:
- ,
где — площадь поверхности, — давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствие гравитационного поля, то есть в состоянии невесомости, закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции, поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами.
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) — на этом основано центрифугирование. Пример для поля немеханической природы: проводящее тело вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине есть . При этом считаем давление жидкости и напряжённость гравитационного поля постоянными величинами, а — параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат , причём выберем направление оси z совпадающим с направлением вектора . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку . На неё будет действовать сила давления жидкости направленная внутрь тела, . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса.
Получаем, что модуль силы Архимеда равен , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Условие плавания тел
Поведение тела, находящегося в жидкости или газе, зависит от соотношения между модулями силы тяжести и силы Архимеда , которые действуют на это тело. Возможны следующие три случая:
- — тело тонет;
- — тело плавает в жидкости или газе;
- — тело всплывает до тех пор, пока не начнет плавать.
Другая формулировка (где — плотность тела, — плотность среды, в которую оно погружено):
- — тело тонет;
- — тело плавает в жидкости или газе;
- — тело всплывает до тех пор, пока не начнет плавать.
См. также
Примечания
- ↑ Всё написанное ниже, если не оговорено иное, относится к однородному полю силы тяжести (например, вблизи поверхности планеты).
Ссылки
dic.academic.ru